СПРАВКА
Источник публикации
М., 2019
Примечание к документу
Название документа
"Методическое пособие по проектированию железобетонных пространственных конструкций покрытий и перекрытий"
"Методическое пособие по проектированию железобетонных пространственных конструкций покрытий и перекрытий"
Содержание
ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ
"ФЕДЕРАЛЬНЫЙ ЦЕНТР НОРМИРОВАНИЯ, СТАНДАРТИЗАЦИИ
И ТЕХНИЧЕСКОЙ ОЦЕНКИ СООТВЕТСТВИЯ В СТРОИТЕЛЬСТВЕ"
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО ПРОЕКТИРОВАНИЮ ЖЕЛЕЗОБЕТОННЫХ ПРОСТРАНСТВЕННЫХ
КОНСТРУКЦИЙ ПОКРЫТИЙ И ПЕРЕКРЫТИЙ
Настоящее методическое пособие (далее - пособие) содержит разъяснение особенностей методик расчета и правил конструирования пространственных железобетонных конструкций зданий и сооружений, а также примеры расчета некоторых видов таких конструкций.
Пособие обеспечивает развитие положений СП 387.1325800.2018 "Железобетонные пространственные конструкции покрытий и перекрытий. Правила проектирования", СП 63.13330.2018 "СНиП 52-01-2003 "Бетонные и железобетонные конструкции. Основные положения", СП 70.13330.2012 "СНиП 3.03.01-87 Несущие и ограждающие конструкции", для обеспечения рационального проектирования пространственных покрытий и перекрытий зданий различного назначения, повышения надежности и долговечности, снижения материалоемкости и стоимости пространственных железобетонных конструкций.
Современный подход к расчету железобетонных оболочек и складок базируется преимущественно на применении численных методов с использованием программных комплексов и компьютерной техники. Применение таких методов целесообразно в случаях расчетов конструкций со сложными геометрической формой и характером граничных условий, при необходимости учета произвольной нагрузки, в том числе усилий предварительного обжатия оболочки, неравномерных снеговых и ветровых нагрузок.
Приведенные в пособии примеры расчета оболочек и складок основаны на применении ручных методов расчета, достоверность которых обоснована результатами экспериментальных исследований и опытом проектирования. Такие методы могут с успехом использоваться при обосновании технических решений и для проверки результатов компьютерных расчетов при рабочем проектировании.
Пособие предназначено для применения специалистами, чья деятельность связана с проектированием пространственных железобетонных конструкций, специалистами государственных и иных органов экспертизы и согласования, преподавателями и студентами строительных учебных заведений.
Пособие разработано авторским коллективом АО "НИЦ "Строительство" - НИИЖБ им. А.А. Гвоздева (руководитель работы - канд. техн. наук Б.С. Соколов - разделы 1 - 6; кандидаты техн. наук И.Г. Овчинникова - разделы 2, 5.3, 5.6, В.А. Титаев - раздел 5.7, инж. Д.В. Пасхин - разделы 5.4, 6).
Рекомендации настоящего пособия распространяются на проектирование железобетонных оболочек, складок и других тонкостенных пространственных конструкций покрытий и перекрытий зданий и сооружений различного функционального назначения, изготовляемых из тяжелого и мелкозернистого бетонов, и эксплуатируемых в климатических условиях Российской Федерации (при систематическом воздействии температур не выше 50 °C и не ниже минус 70 °C), в среде с неагрессивной степенью воздействия при статическом действии нагрузки.
В настоящем методическом пособии использованы ссылки на следующие нормативные документы:
ГОСТ 8239-89 Двутавры стальные горячекатаные. Сортамент
ГОСТ 10922-2012 Арматурные и закладные изделия, их сварные, вязаные и механические соединения для железобетонных конструкций. Общие технические условия
ГОСТ 13015-2012 Изделия бетонные и железобетонные для строительства. Общие технические требования. Правила приемки, маркировки, транспортирования и хранения
ГОСТ 13840-68 Канаты стальные арматурные 1x7. Технические условия
ГОСТ 14098-2014 Соединения сварные арматуры и закладных изделий железобетонных конструкций. Типы, конструкции и размеры
ГОСТ 25820-2014 Бетоны легкие. Технические условия
ГОСТ 27751-2014 Надежность строительных конструкций и оснований. Основные положения
ГОСТ 27772-2015 Прокат для строительных стальных конструкций. Общие технические условия
ГОСТ 34028-2016 Прокат арматурный для железобетонных конструкций. Технические условия
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду ГОСТ Р 53772-2010, а не ГОСТ 53772-2010. |
ГОСТ 53772-2010 Канаты стальные арматурные семипроволочные стабилизированные. Технические условия
СП 14.13330.2018 "СНиП II-7-81*. Строительство в сейсмических районах" (с изменением N 1)
СП 16.13330.2017 "СНиП II-23-81* Стальные конструкции" (с изменениями N 1, N 2)
СП 20.13330.2016 "СНиП 2.01.07-85* Нагрузки и воздействия" (с изменениями N 1, N 2)
СП 21.13330.2012 "СНиП 2.01.09-91 Здания и сооружения на подрабатываемых территориях и просадочных грунтах" (с изменением N 1)
СП 22.13330.2016 "СНиП 2.02.01-83* Основания зданий и сооружений" (с изменениями N 1, N 2, N 3)
СП 25.13330.2012 "СНиП 2.02.04-88 Основания и фундаменты на вечномерзлых грунтах" (с изменениями N 1, N 2, N 3, N 4)
СП 28.13330.2017 "СНиП 2.03.11-85 Защита строительных конструкций от коррозии" (с изменениями N 1, N 2)
СП 48.13330.2019 "СНиП 12-01-2004 Организация строительства"
СП 63.13330.2018 "СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения" (с изменением N 1)
СП 70.13330.2012 "СНиП 3.03.01-87 Несущие и ограждающие конструкции" (с изменениями N 1, N 3)
СП 96.13330.2016 "СНиП 2.03.03-85 Армоцементные конструкции"
СП 112.13330.2011 "СНиП 21-01-97* Пожарная безопасность зданий и сооружений"
СП 131.13330.2018 "СНиП 23-01-99* Строительная климатология"
СП 304.1325800.2017 Конструкции большепролетных зданий и сооружений. Правила эксплуатации
СП 387.1325800.2018 Железобетонные пространственные конструкции покрытий и перекрытий. Правила проектирования (с изменением N 1)
Примечание - При пользовании настоящим пособием целесообразно проверить действие ссылочных документов в информационной системе общего пользования - на официальном сайте федерального органа исполнительной власти в сфере стандартизации в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего свода правил в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде стандартов.
В настоящем Пособии применены термины по СП 63.13330, СП 387.1325800 и ГОСТ 27751, а также следующие термины с соответствующими определениями:
3.1 вспарушенная панель: Пространственный элемент перекрытия с плоской верхней поверхностью, плоским контуром и переменной толщиной, увеличивающейся к контуру.
3.2 метод моделирования: Экспериментальный метод исследования строительных конструкций на моделях, в результате которого устанавливают основные параметры строительных объектов, их несущую способность и воспринимаемые ими воздействия.
3.3 панель-оболочка: Пространственный элемент покрытия длиной, соответствующей размеру пролета между опорами.
4.1.1 Железобетонные пространственные конструкции должны быть обеспечены с требуемой надежностью от возникновения предельных состояний всех видов расчетом, выбором показателей качества материалов, назначением размеров и конструированием согласно СП 387.1325800. При этом должны быть выполнены технологические требования при изготовлении конструкций и соблюдены требования по эксплуатации зданий и сооружений, по экологии, устанавливаемые соответствующими нормативными документами (НД).
4.1.2 Применение железобетонных пространственных конструкций в средах с агрессивным воздействием допускается при выполнении требований, установленных СП 28.13330 и СП 387.1325800.
При проектировании пространственных конструкций в особых условиях (в районах с расчетной сейсмичностью 7 баллов и более, на просадочных грунтах и подрабатываемых территориях, на вечномерзлых грунтах) следует учитывать соответственно СП 14.13330, СП 21.13330, СП 22.13330 и СП 25.13330.
4.1.3 Конструктивные решения пространственных конструкций покрытий и перекрытий зданий и сооружений следует выбирать исходя из технико-экономической целесообразности их применения в конкретных условиях строительства с учетом архитектурных, технологических и производственных требований, максимального снижения их материало-, трудо-, энергоемкости и стоимости.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
4.1.5 Элементы сборных и сборно-монолитных пространственных конструкций рекомендуется проектировать с учетом условий механизации их изготовления на заводах или полигонах, а железобетонные монолитные пространственные конструкции - с учетом механизированного выполнения опалубочных, арматурных и бетонных работ в соответствии с СП 48.13330 и СП 70.13330.
Сборные и сборно-монолитные пространственные конструкции рекомендуется проектировать из унифицированных плоских, цилиндрических или иных панелей, преимущественно ребристых, монтируемых с применением укрупнительной сборки или из крупноразмерных элементов, изготовленных вблизи места возведения конструкции.
Панели-оболочки и панели-складки следует проектировать с учетом особенностей их транспортирования и складирования.
Применение укрупненных тонкостенных элементов покрытий и перекрытий длиной более 24 м или шириной (высотой) более 3,2 м, а также массой более 15 т должно быть обосновано с учетом их транспортирования и монтажа.
4.1.6 Железобетонные покрытия пространственного типа следует проектировать с учетом комплекса требований по гидро- и теплоизоляции, по водоотводу, по устройству различных проходок через покрытие, фонарных и других проемов и отверстий.
Сборные пространственные конструкции рекомендуется проектировать повышенной готовности - утепленными, с гидроизоляцией и т.п.
4.1.7 При проектировании большепролетных конструкций следует предусматривать мониторинг технического состояния при эксплуатации. Осуществление эксплуатации большепролетных пространственных железобетонных конструкций покрытий и перекрытий должно выполняться в соответствии с требованиями СП 304.1325800.
4.2.1 Расчеты железобетонных пространственных конструкций следует выполнять по предельным состояниям первой и второй групп.
Расчеты по предельным состояниям первой группы включают расчет по прочности, с учетом в необходимых случаях деформированного состояния конструкции перед разрушением, расчет по устойчивости формы (общей и локальной); в необходимых случаях - расчет по устойчивости положения (опрокидывание, скольжение, всплывание).
Расчеты по предельным состояниям второй группы включают расчеты по образованию трещин, раскрытию трещин и деформациям.
Расчеты выполняют в соответствии с СП 63.13330 и СП 387.1325800.
Расчет стальных деталей и элементов, входящих в состав пространственного покрытия, выполняют по СП 16.13330.
4.2.2 В расчетах пространственных конструкций покрытий и перекрытий по предельным состояниям следует рассматривать различные расчетные ситуации в соответствии с ГОСТ 27751 для всех воздействий на конструкции или их элементы на стадиях изготовления, транспортирования, возведения и эксплуатации, а также в аварийных ситуациях. Расчетные модели должны соответствовать принятым конструктивным решениям пространственных конструкций и воздействиям для каждой рассматриваемой стадии (ГОСТ 27751).
4.2.3 Расчеты железобетонных пространственных конструкций следует проводить с учетом наличия трещин и неупругих деформаций в бетоне и арматуре.
Усилия и деформации от различных воздействий в конструкциях и в образуемых ими системах зданий и сооружений следует определять методами строительной механики с учетом физической и геометрической нелинейности работы конструкций.
Усилия и деформации допускается определять в предположении упругой работы железобетонных элементов с последующей корректировкой результатов расчета для учета влияния физической нелинейности их работы.
4.2.4 При проектировании железобетонных пространственных конструкций их надежность обеспечивают применением в расчетах расчетных значений нагрузок и воздействий, расчетных значений характеристик материалов, определяемых с помощью соответствующих частных коэффициентов надежности по нормативным значениям этих характеристик, и учетом уровня ответственности зданий и сооружений (ГОСТ 27751).
Для большепролетных сооружений с пролетом более 120 м коэффициент надежности по ответственности следует принимать не менее 1,2.
Нормативные значения нагрузок и воздействий, подразделение нагрузок на постоянные и временные (длительные и кратковременные), значения коэффициентов надежности по нагрузке и коэффициентов сочетаний следует принимать согласно СП 20.13330.
При расчете пространственных покрытий пролетом более 100 м или с очертанием поверхности, не предусмотренным СП 20.13330, распределение нагрузок от действия снега и ветра по поверхности покрытия допускается определять по экспериментальным данным на основе результатов исследования моделей сооружений в аэродинамических трубах.
4.2.5 Усилия и деформации в пространственных конструкциях следует определять в зависимости от особенностей конструкции согласно СП 387.1325800.
4.2.6 Диафрагмы и бортовые элементы оболочек, складок, многогранников и сводов-оболочек из условия их совместной работы с полем конструкции следует включать в расчет с учетом их жесткости и схемы нагружения.
4.2.7 Отверстия в плитах ребристых оболочек, размеры которых больше расстояний между ребрами сборных элементов, а для гладких оболочек - размерами более 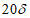 , должны учитываться при расчете конструкции.
, должны учитываться при расчете конструкции.
4.2.8 Предварительно напряженные элементы пространственных конструкций следует рассчитывать с учетом СП 63.13330.
4.2.9 При расчете по прочности железобетонных элементов на действие сжимающей продольной силы следует учитывать случайный эксцентриситет ea, принимаемый по СП 63.13330.
4.2.10 Расчет по устойчивости формы тонкостенных пространственных конструкций следует проводить с учетом начальных несовершенств и деформаций ползучести бетона при длительном действии нагрузки.
Максимальные значения начального несовершенства (отклонений от проектных геометрических размеров при изготовлении и монтаже, а также неоднородности бетона по толщине тонкостенной конструкции) следует определять опытным путем или задавать по аналогии с конструкциями подобного типа, для которых установлены их возможные значения. При отсутствии опытных данных учет начальных несовершенств рекомендуется выполнять в запас величины критической нагрузки умножением модуля деформаций бетона на коэффициент 0,75.
Деформации ползучести бетона при длительном действии нагрузки учитываются в соответствии с требованиями СП 63.13330.
Расчеты по устойчивости формы конструкции и по устойчивости положения следует проводить согласно требованиям НД на отдельные виды конструкций. В отсутствие таких требований минимальный коэффициент запаса по устойчивости формы следует принимать равным 3; минимальный коэффициент запаса на опрокидывание равным 1,5 при наиболее неблагоприятных значениях коэффициентов надежности по нагрузке.
4.2.11 Для тонкостенных элементов пространственных конструкций следует производить проверку местной устойчивости и прочности в соответствии с СП 387.1325800.
4.2.12 При выборе расчетной схемы сборно-монолитных пространственных конструкций следует учитывать податливость стыков и особенности передачи усилий через них. При передаче усилий через закладные детали и приваренные к ним стержни или пластины податливость стыка допускается учитывать исходя из значения 0,5 - 1 мм на каждое такое соединение. При передаче сжимающих усилий через стыки, омоноличенные мелкозернистым бетоном, податливость стыка допускается учитывать снижением значения начального модуля упругости мелкозернистого бетона и введением в расчет пониженной местной или усредненной жесткости с учетом отношения ширины стыков к расстоянию между ними.
4.2.13 Прогибы элементов в железобетонных пространственных конструкциях не должны превышать предельно допустимых значений, приведенных в СП 20.13330, при этом прогиб покрытий в виде сводов, оболочек двоякой кривизны или в виде многогранников пролетом 18 - 60 м должен быть не более 1/400 пролета, а пролетом более 60 м - 1/500 пролета.
4.2.14 При расчете элементов сборных пространственных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от массы элементов следует принимать с коэффициентом динамичности, равным 1,60 - при транспортировании, 1,40 - при подъеме и монтаже. Допускается принимать более низкие, обоснованные в установленном порядке, значения коэффициента динамичности, но не ниже 1,25.
4.2.15 Устойчивость пространственных конструкций покрытий и перекрытий зданий и сооружений против прогрессирующего обрушения при локальных аварийных воздействиях следует обеспечивать избыточной несущей способностью "ключевых" элементов, конструктивными мерами и применением материалов, обеспечивающих развитие в конструктивных элементах и их соединениях пластических деформаций.
Расчет на прогрессирующее обрушение следует выполнять на действие нормативных нагрузок, с применением нормативных значений прочностных характеристик арматуры и бетона и с учетом физической, геометрической и конструктивной нелинейностей.
4.2.16 Большепролетные пространственные конструкции зданий и сооружений следует рассчитывать на усилия от изменения температуры, а в случае необходимости - и от усадки бетона, возникающие в конструкциях вследствие заделки их в основание и взаимодействия наружных и внутренних конструкций с разными температурными и усадочными деформациями.
Расчетные значения температур принимаются для различных климатических районов Российской Федерации по СП 131.13330, а значения расчетных приведенных температур - в соответствии с СП 20.13330.
Расчет проводят на неблагоприятные сочетания летних (июльских) и зимних (январских) приведенных температур, которые могут быть как в период строительства, так и в период эксплуатации зданий.
Расчет усилий и деформаций пространственных конструкций на изменение температуры допускается выполнять в упругой стадии, при этом следует учитывать податливость стыковых соединений (для сборных конструкций) и основания.
Изгибную и продольную жесткости стыков для сборных конструкций следует определять по СП 63.13330 - как для армированных бетонных сечений, с учетом трещин, пластических свойств и ползучести бетона.
4.2.17 Железобетонные пространственные покрытия и перекрытия должны соответствовать требованиям пожарной безопасности, приведенным в СП 112.13330.
При проектировании пространственных конструкций зданий и сооружений, относящихся к повышенному уровню ответственности, отказы которых после пожара могут привести к тяжелым экономическим и экологическим последствиям, а также конструкций, восстановление которых потребует больших материальных затрат, следует обеспечивать их огнесохранность.
4.2.18 Для повышения пределов огнестойкости или обеспечения огнесохранности пространственных конструкций следует применять огнезащитные покрытия.
4.3.1 Для железобетонных тонкостенных пространственных конструкций следует применять бетоны и арматуру, предусмотренные СП 63.13330.
4.3.2 Для несущих тонкостенных пространственных конструкций рекомендуется применять тяжелые, в том числе мелкозернистые, бетоны классов по прочности на сжатие от B20 до B60 или легкие бетоны по прочности на сжатие не ниже B12,5 (ГОСТ 25820).
Легкие бетоны классов по прочности на сжатие B7,5 и B10 (ГОСТ 25820) допускается применять в совмещенных пространственных конструкциях покрытий.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду ГОСТ Р 53772, а не ГОСТ 53772. |
4.3.3 В качестве предварительно напряженной арматуры растянутых бортовых элементов большепролетных пространственных конструкций рекомендуется использовать канатную проволочную арматуру по ГОСТ 53772, ГОСТ 13840 или пучки из таких канатов, защищенные от коррозии до замоноличивания цинкованием или иными способами, допускаемыми СП 28.13330.
4.3.4 Класс по прочности на сжатие тяжелого мелкозернистого бетона, применяемого для омоноличивания несущих стыков, должен быть не ниже проектного класса по прочности на сжатие бетона стыкуемых элементов.
При омоноличивании конструктивных стыков класс по прочности на сжатие тяжелого бетона или бетона на пористых заполнителях должен быть не ниже B10.
4.4.1 При проектировании железобетонных пространственных конструкций покрытий и перекрытий следует выполнять конструктивные требования, предусмотренные СП 63.13330.
4.4.2 Монолитные пространственные конструкции следует проектировать гладкими или ребристыми.
Толщину плиты  и шаг ребер прямоугольного или трапециевидного сечения следует определять расчетом поля оболочки или плит складки на прочность, устойчивость или локальную несущую способность и назначать с учетом конструктивных и технологических требований.
и шаг ребер прямоугольного или трапециевидного сечения следует определять расчетом поля оболочки или плит складки на прочность, устойчивость или локальную несущую способность и назначать с учетом конструктивных и технологических требований.
4.4.3 Для возможности применения многократно оборачиваемой (подвижной и переносной) опалубки рекомендуется применять тонкостенные конструкции:
- с линейчатыми поверхностями (цилиндрические, гиперболические оболочки, коноиды, призматические складки);
- с поверхностями переноса положительной гауссовой кривизны (параболические и круговые оболочки).
4.4.4 Стрелу подъема монолитных оболочек следует принимать от 1/10 до 1/5 пролета. Угол наклона касательной к поверхности монолитных покрытий с горизонтом для их бетонирования на односторонней опалубке следует принимать не более 35°, для бетонирования более крутых поверхностей следует использовать двухстороннюю опалубку или торкретирование.
4.4.5 В качестве бортовых элементов оболочек, складок, многогранников рекомендуется использовать балки, рамы или арки преимущественно с прямоугольной или квадратной формой поперечного сечения высотой не менее 1/80 пролета, или фермы.
4.4.6 Переход от плиты к бортовым элементам и ребрам следует выполнять плавным, в виде вута шириной до 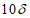 . Если устройство вута недостаточно для восприятия краевых изгибающих моментов, следует предусматривать утолщения плиты от
. Если устройство вута недостаточно для восприятия краевых изгибающих моментов, следует предусматривать утолщения плиты от 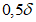 до
до  . При необходимости в плите следует предусматривать плавное утолщение от центра к бортовым элементам.
. При необходимости в плите следует предусматривать плавное утолщение от центра к бортовым элементам.
4.4.7 Армирование монолитных пространственных конструкций рекомендуется проектировать с применением готовых сварных сеток и каркасов.
У растянутой грани изгибаемых плит следует предусматривать не менее одной арматурной сетки. Сжатые плиты, толщина которых определяется условием обеспечения местной несущей способности или устойчивости, и растянутые плиты рекомендуется армировать по расчету двумя сетками, располагаемыми симметрично относительно срединной поверхности с обеспечением минимально допустимого значения защитного слоя бетона.
В случае, если в плите конструкции арматура по расчету не требуется, то следует предусматривать конструктивное армирование плиты одной сеткой из арматурных стержней диаметром 3 - 4 мм с шагом не более 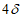 и не более 200 мм.
и не более 200 мм.
4.4.8 Участки плиты оболочек и складок, в которых главные растягивающие напряжения  превышают значение расчетного сопротивления бетона осевому растяжению Rbt, следует армировать исходя из условия полного восприятия арматурой растягивающих усилий. При этом допускать
превышают значение расчетного сопротивления бетона осевому растяжению Rbt, следует армировать исходя из условия полного восприятия арматурой растягивающих усилий. При этом допускать 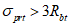 не рекомендуется - в этом случае толщину соответствующих участков конструкции следует увеличивать.
не рекомендуется - в этом случае толщину соответствующих участков конструкции следует увеличивать.
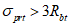 не рекомендуется - в этом случае толщину соответствующих участков конструкции следует увеличивать.
не рекомендуется - в этом случае толщину соответствующих участков конструкции следует увеличивать.4.4.9 Для восприятия растягивающих усилий в контурных элементах, диафрагмах и затяжках большепролетных покрытий рекомендуется предусматривать предварительно напрягаемую арматуру, располагаемую в каналах или пазах с последующим замоноличиванием бетоном или в трубчатых каналообразователях без сцепления с бетоном с последующим их заполнением противокоррозионными составами.
4.4.10 В бортовых элементах балочных оболочек и складок до 80% рабочей растянутой арматуры допускается размещать у растянутой грани. В тонкостенных элементах пространственных конструкций растянутую арматуру рекомендуется располагать равномерно вдоль растянутой зоны сечения оболочки, складки или многогранника.
4.4.11 Сборно-монолитные конструкции покрытий и перекрытий следует проектировать с использованием в качестве несущей опалубки железобетонных или армоцементных (по СП 96.13330) тонкостенных элементов, обеспечивающих создание готовой поверхности потолка. Несущую опалубку пространственных конструкций следует рассчитывать на усилия от собственного веса, от веса уложенного монолитного бетона и монтажных нагрузок. Поверхность несущей опалубки, соприкасающаяся с монолитным бетоном, и выпуски арматуры должны обеспечивать совместную работу опалубки и монолитного бетона.
4.4.12 При проектировании сборно-монолитных конструкций рекомендуется предусматривать сборные диафрагмы, бортовые элементы или ребра. Сборные диафрагмы и бортовые элементы следует изготовлять железобетонными - в том числе с несущей арматурой, и металлическими.
Для обеспечения передачи контактных усилий между монолитным бетоном и сборными элементами в них рекомендуется предусматривать шпонки, упоры, выпуски арматуры и закладные детали (по 4.4.18 - 4.4.20).
4.4.13 Для снижения размеров поперечного сечения сборных элементов при проектировании рекомендуется предусматривать на время монтажа временные затяжки, опоры и другие подкрепляющие устройства. Выбирать бетон и арматуру рекомендуется с учетом условий изготовления, предусмотренных проектом производства работ (ППР) по СП 70.13330.
4.4.14 Сборные пространственные конструкции рекомендуется проектировать из тонкостенных панельных, блочных (арочных) и других сборных элементов, которые после установки на место соединяются путем омоноличивания стыков и сварки закладных деталей.
Форма и размеры элементов сборных конструкций должны удовлетворять требованиям расчета и назначаться с учетом технологии их изготовления, транспортирования и монтажа - в том числе монтажа блоками с применением укрупнительной сборки монтажных элементов на строительной площадке (СП 70.13330).
При проектировании сборных пространственных конструкций и их элементов допускаемые отклонения от их номинальных размеров следует назначать согласно ГОСТ 13015.
4.4.15 Очертание срединной поверхности сборных оболочек покрытий следует принимать с учетом удобства расчленения конструкции покрытия или перекрытия на минимальное число типов панелей и других элементов при максимальной их повторяемости.
Размеры поперечных сечений сборных элементов, как правило, должны быть не менее: по толщине плиты 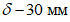 ; по высоте сечения основных ребер панелей h - 1/20 их длины; по ширине сечения ребер панелей b - 40 мм.
; по высоте сечения основных ребер панелей h - 1/20 их длины; по ширине сечения ребер панелей b - 40 мм.
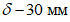 ; по высоте сечения основных ребер панелей h - 1/20 их длины; по ширине сечения ребер панелей b - 40 мм.
; по высоте сечения основных ребер панелей h - 1/20 их длины; по ширине сечения ребер панелей b - 40 мм.4.4.16 В местах действия краевых моментов и максимальных главных растягивающих напряжений допускается утолщение плиты, в том числе с помощью слоя монолитного бетона, укладываемого по сборным плитам. При этом должны быть предусмотрены необходимое дополнительное армирование монолитного слоя (например, в углах оболочек положительной гауссовой кривизны) и конструктивные и технологические мероприятия для обеспечения сцепления монолитного слоя со сборными панелями. Толщину плиты сборных элементов допускается принимать переменной - плавно изменяющейся между ребрами или ступенчатой, постоянной в пределах пролета.
В случае, когда арматуры, установленной в сборных элементах, недостаточно, следует предусматривать дополнительное армирование в виде предварительно напряженных поясов и отдельных элементов или стержней, укладываемых в процессе возведения конструкции. Предварительное напряжение такой арматуры следует осуществлять натяжением на бетон и последующим обетонированием. Стержни или сетки дополнительного армирования допускается укладывать в стыках между панелями и другими элементами (например, для обеспечения неразрезности в местах сопряжения соседних оболочек).
4.4.17 Сосредоточенные нагрузки рекомендуется прикладывать к ребрам жесткости, диафрагмам и бортовым балкам оболочек и складок.
4.4.18 Стыки сборных пространственных конструкций должны быть рассчитаны и сконструированы из условия надежной передачи от одного элемента к другому усилий, возникающих в соединении при монтаже (в стыках укрупненных элементов и при навесной сборке без лесов) и в процессе эксплуатации.
Расчет стыков конструкций по прочности следует выполнять в зависимости от вида передаваемых через них усилий. Расчетные стыки оболочек, складок и многогранников рекомендуется конструировать со шпонками - для обеспечения передачи касательных, сжимающих или растягивающих усилий. При значении напряжения сцепления бетона замоноличивания с бетоном сборных элементов 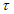 , не превышающем значение 0,25Rbt, в сжатых стыках допускается учитывать сопротивление трению.
, не превышающем значение 0,25Rbt, в сжатых стыках допускается учитывать сопротивление трению.
К конструктивным стыкам требование расчета по прочности не предъявляется.
4.4.19 Соединение арматуры в стыках следует осуществлять сваркой стержней с закладными деталями или между собой, а также путем перепуска концов стержней и сеток согласно ГОСТ 14098 и ГОСТ 10922. Для уменьшения длины перепуска арматурных стержней допускается их стыкование с помощью перепуска петель диаметром (или размером стороны) не менее 10d с заделкой в шов каждой петли на длину не менее 15d (d - диаметр стыкуемых стержней). При расположении петель в вертикальной плоскости внутри петель по их периметру должны быть заложены продольные по стыку стержни (рисунок 4.4.1, г, д). При расположении петель в горизонтальной плоскости к ним следует приваривать продольные стержни. Расчетные стыки на период монтажа допускается проектировать без омоноличивания, предусматривая передачу возникающих в них усилий через соединительные металлические детали (рисунок 4.4.1, ж).
Металлические детали стыков должны быть защищены от коррозии согласно СП 28.13330.
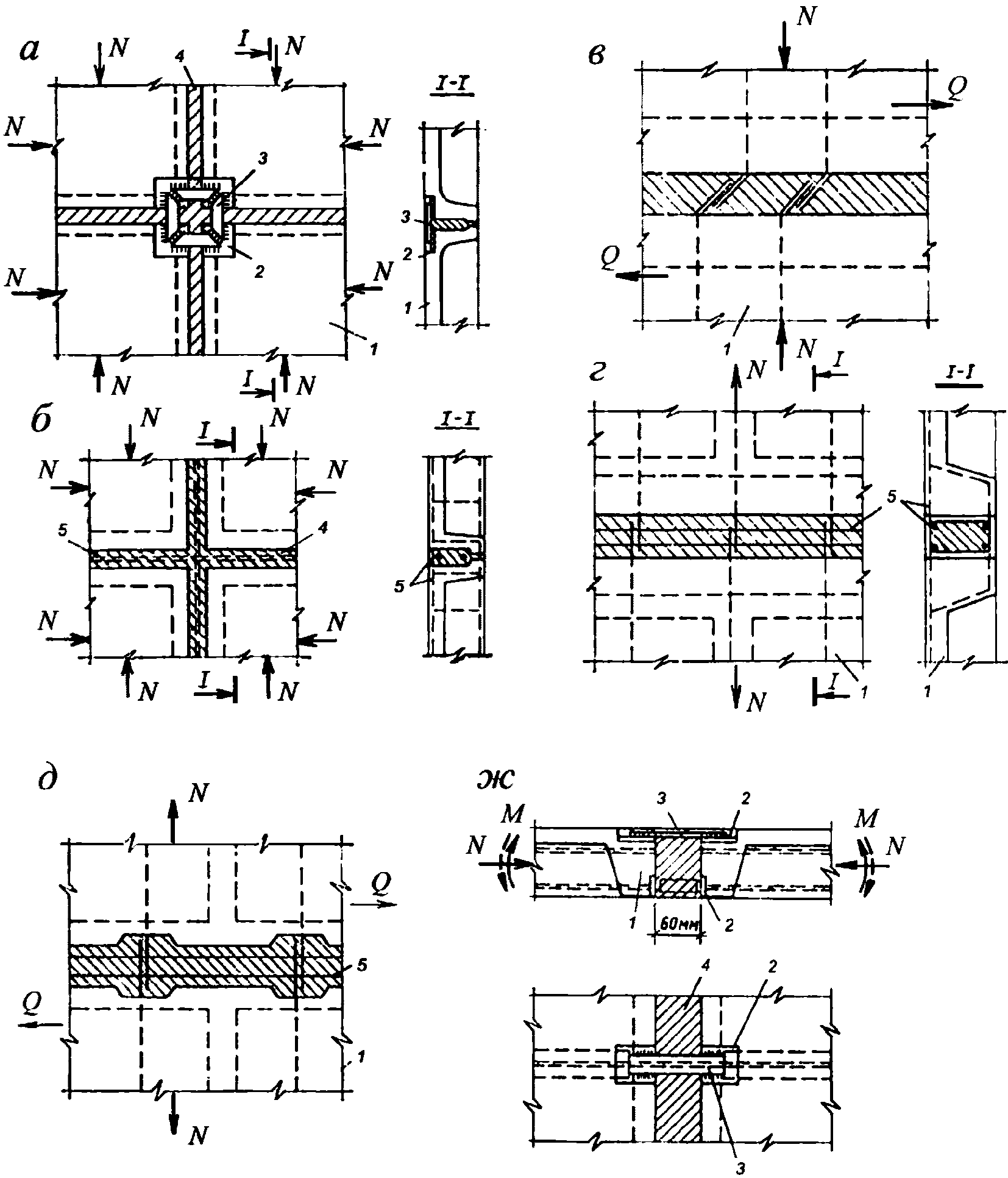
а - сжатый стык панелей со сварными накладками; б - то же,
с перепуском арматуры; в - то же, с отгибами при наличии
сдвигающих усилий; г - растянутый стык; д - то же,
при наличии сдвигающих усилий; е - стык со сварной
накладкой и шпонками, работающий на сдвиг; ж - то же,
испытывающий сжатие с изгибом; и - стык панелей висячей
оболочки на ванте; к - стык панелей и диафрагмы смежных
оболочек и схема шпонки стыка; 1 - панель; 2 - закладная
деталь; 3 - соединительная накладка; 4 - бетон
замоноличивания; 5 - продольная арматура стыка; 6 - ванта
в трубке с защитной смазкой; 7 - диафрагма с выпусками
арматуры; 8 - сварной шов; 9 - шпонки
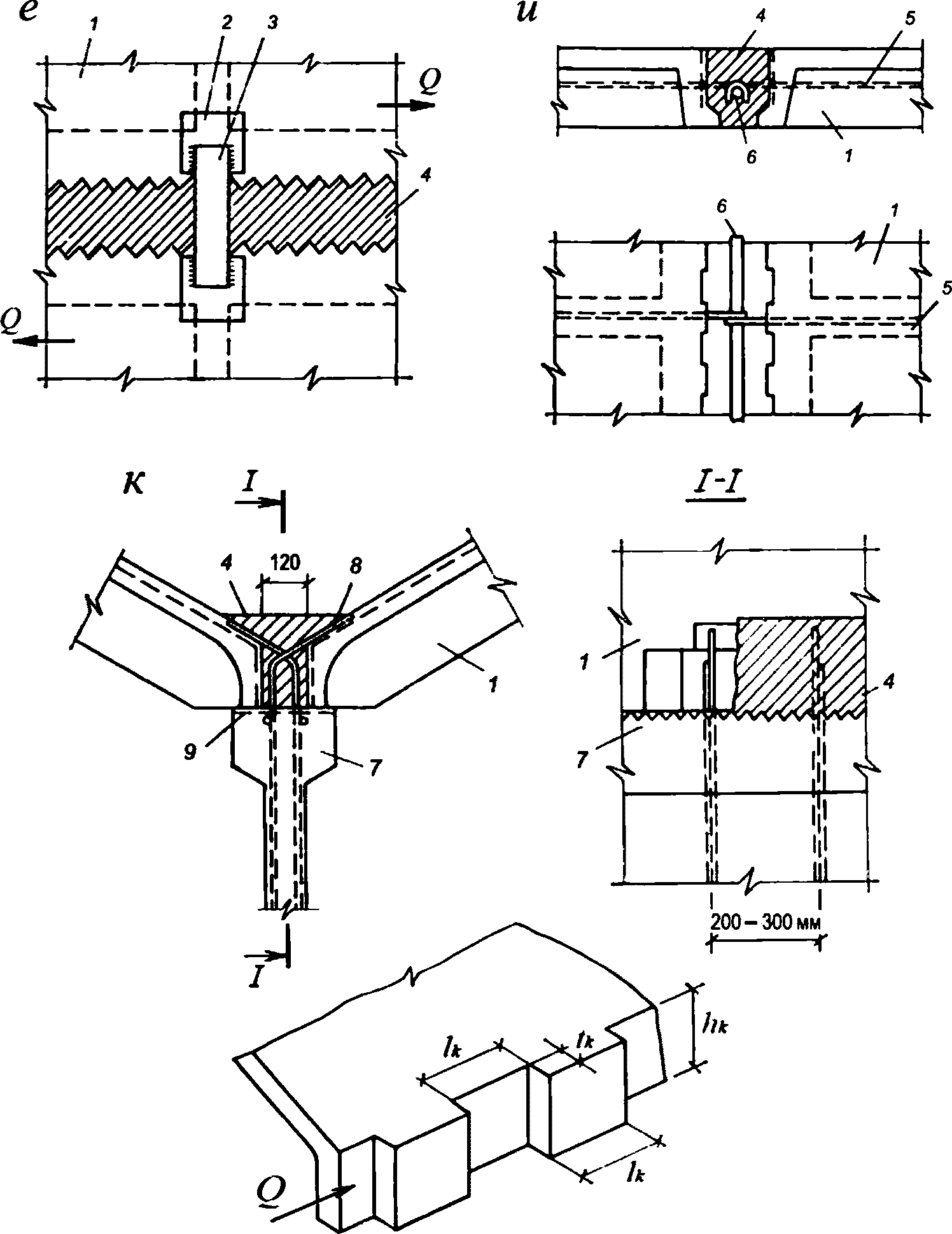
4.4.20 В стыках железобетонных элементов со стальными диафрагмами и бортовыми элементами вместо шпонок в металлической конструкции следует предусматривать жесткие упоры (рисунок 4.4.2) или стержневые анкеры. Жесткие упоры следует предусматривать также в стыках с железобетонными диафрагмами - в случае, если шпонок недостаточно для восприятия сдвигающих усилий.
Соединение арматуры в стыках следует осуществлять сваркой стержней с закладными деталями или между собой, а также перепуском концов стержней и сеток согласно ГОСТ 14098 и ГОСТ 10922.
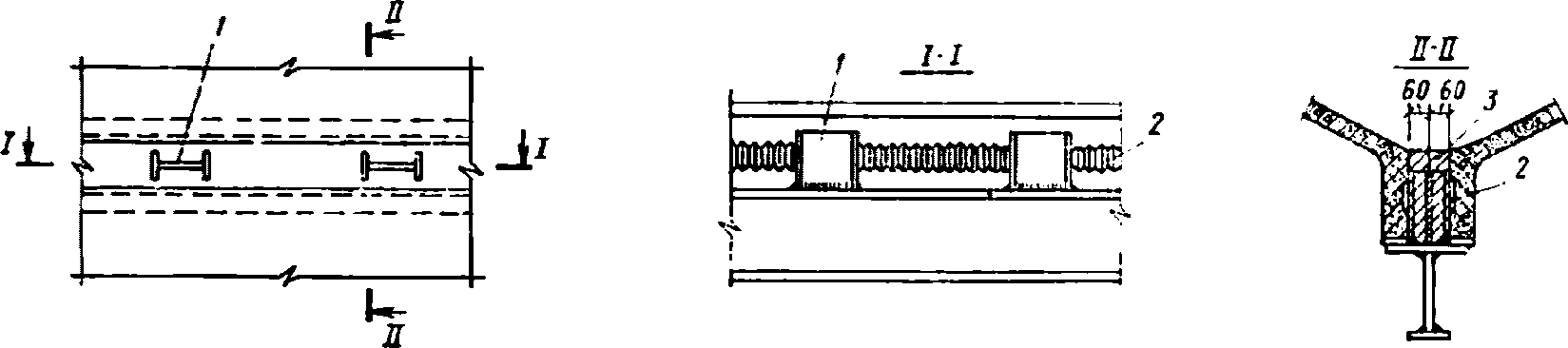
1 - стальной упор; 2 - шпонки; 3 - бетон замоноличивания
и металлических элементов
4.4.21 Размер ширины стыков следует назначать с учетом допусков для размеров собираемых элементов и принимать равным не менее 40 мм и, как правило, не более 150 мм.
Прочность бетона сборных элементов при местном сжатии в стыке должна быть обеспечена.
Ширина раскрытия трещин на уровне арматуры должна быть не более допустимой по СП 63.13330.
4.4.22 Для сокращения размеров и числа закладных деталей и стержней, проектируемых в стыке, и для упрощения работ по стыкованию арматуры допускается основную арматуру в элементах и в стыках покрытий сосредоточивать на отдельных участках в зоне ребер, пересекаемых стыком, а при отсутствии ребер - на участках протяженностью в 5 - 10 толщин плиты при расстоянии между участками в 10 - 20 толщин плиты.
4.4.23 В стыках элементов, работающих на растяжение или изгиб, все растягивающие усилия должны быть восприняты арматурой (как правило, продолжением основной арматуры ребер стыкуемых элементов).
В стыках, воспринимающих касательные усилия сдвига с помощью шпонок, размеры выступов и углублений, образуемых в бетоне сборных элементов и в бетоне замоноличивания, должны удовлетворять расчету шпонок на смятие Q1 и Q2 по формулам:
Q1 <= Rblktknk; (4.4.1)
где Rb, Rbt - расчетные сопротивления бетона сборных элементов или бетона омоноличивания соответственно при осевом сжатии и растяжении;
lk, hk, tk, nk - длина, высота, глубина и учитываемое число шпонок (рисунок 4.4.1, и).
Если через стык передаются местные сдвигающие усилия, то шпонки учитывают только в зоне действия этих усилий, при этом две крайних шпонки не учитывают.
Гибкие выпуски арматуры и соединения закладных деталей, расположенные перпендикулярно к оси стыка, как правило, не учитываются в расчете на усилия сдвига. Их устанавливают для восприятия возможных растягивающих усилий, перпендикулярных к оси шва, и по конструктивным соображениям. Если такое армирование может полностью воспринимать эти растягивающие усилия, то в формуле (4.4.2) вместо 2Rbt допускается принимать 3Rbt.
Если шпоночный шов обжат усилием N, перпендикулярным к плоскости шва, то высоту шпонки допускается определять по формуле
 (4.4.3)
(4.4.3)и принимать уменьшенной против высоты, определенной по формуле (4.4.2), но не более чем в два раза.
4.4.24 Отверстия и проемы различной формы в тонкостенных пространственных конструкциях допускается устраивать в пределах расстояния между диафрагмами или ребрами жесткости. Световые проемы могут также устраиваться с перепадом поверхностей покрытия или путем раздвижки оболочек, складок или сводов.
Отверстия в плите оболочек и складок рекомендуется проектировать круглыми, овальными или многоугольными с округлением углов радиусом  .
.
Отверстия со сторонами размером (или диаметром) не более 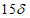 следует выполнять с установкой конструктивной арматуры, окаймляющей отверстие, диаметром не менее 8 мм при
следует выполнять с установкой конструктивной арматуры, окаймляющей отверстие, диаметром не менее 8 мм при 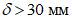 (рисунок 4.4.3).
(рисунок 4.4.3).
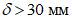 (рисунок 4.4.3).
(рисунок 4.4.3).В зоне отверстий размером более 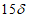 края плиты должны выполняться с утолщением и армированием, устанавливаемыми расчетами. Утолщение следует принимать высотой не менее
края плиты должны выполняться с утолщением и армированием, устанавливаемыми расчетами. Утолщение следует принимать высотой не менее  , шириной не менее
, шириной не менее  и площадью сечений бетона и арматуры не менее площади сечения бетона и арматуры в поперечном сечении вырезанной части плиты. Утолщения вокруг отверстий, устраиваемых в растянутых полках, должны содержать количество арматуры, достаточное для восприятия усилия, приходящегося на вырезанную часть полки.
и площадью сечений бетона и арматуры не менее площади сечения бетона и арматуры в поперечном сечении вырезанной части плиты. Утолщения вокруг отверстий, устраиваемых в растянутых полках, должны содержать количество арматуры, достаточное для восприятия усилия, приходящегося на вырезанную часть полки.
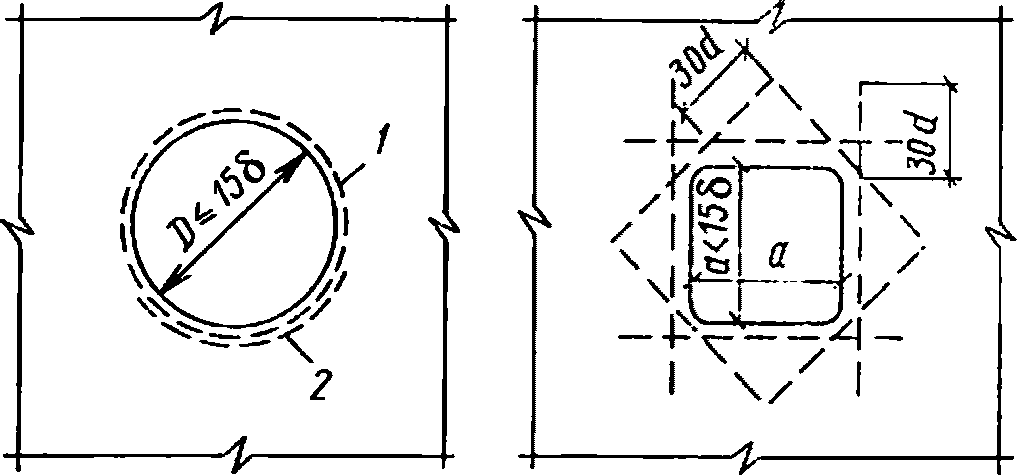
1 - арматура; 2 - стык арматуры с перепуском на 30d
или равнопрочный сварной стык
4.4.25 В пространственных покрытиях и перекрытиях следует предусматривать их разрезку постоянными и временными температурно-усадочными швами, расстояние между которыми назначают в зависимости от климатических условий, конструктивных особенностей сооружения, последовательности производства работ и т.п.
Температурно-усадочные деформации пространственных конструкций должны компенсироваться за счет гибких или качающихся колонн, а также шарнирно подвижных или упруго-деформируемых (например, полимерных прокладок) опорных устройств. При больших (100 м и более) пролетах, как правило, применяют свободно податливые опоры при условии неподвижного закрепления покрытия не менее чем в двух точках по сторонам контура или в углах.
В многопролетных покрытиях деформационные швы устраивают между парными бортовыми элементами.
В складчатых и волнистых сводчатых покрытиях деформационные швы, с целью повышения их водонепроницаемости, рекомендуется проектировать на гребне у складки или волны свода.
Деформационные швы покрытия должны совпадать со швами, перерезающими стены, если специально не предусмотрены мероприятия для независимого деформирования стен и покрытия.
В распорных покрытиях пролетом более 40 м, опирающихся жестко или шарнирно непосредственно на фундаменты, температурно-усадочные деформации следует учитывать как при расчете, так и при конструировании.
Покрытия с круглой или с полигональной формой в плане (оболочки вращения, складчатые купола и т.п.) диаметром более 40 м, в которых не могут быть предусмотрены деформационные швы, должны опираться по контуру на гибкие колонны или подвижные опоры в радиальном направлении, допускающие компенсацию температурных и усадочных деформаций.
5.1.1 Купола проектируют в виде пологих или подъемистых тонкостенных оболочек. Элементами куполов служат, как правило, осесимметричная (в т.ч. сферическая) оболочка вращения и растянутое усилием распора купола опорное кольцо [1].
При проектировании куполов следует учитывать требования раздела 4.
Подъем (высоту) куполов рекомендуется принимать не менее 1/10 диаметра опорного контура оболочки.
Толщину стенок гладких куполов рекомендуется принимать равной от 1/800 до 1/600 радиуса кривизны оболочки в вершине.
В ребристых куполах оболочка подкрепляется ортогональной сетью меридиональных и кольцевых ребер. Толщина оболочки и размеры сечения ребер должны быть не менее предусмотренных разделом 4.
Высоту ребер сборных куполов-оболочек определяют из условий изготовления, транспортирования и монтажа элементов.
Опорное кольцо может лежать на сплошном, образованном стенами, основании или на отдельных колоннах.
5.1.2 Армирование гладких оболочек при толщине до 70 мм рекомендуется выполнять конструктивно, одиночной сеткой из стержней диаметром 4 - 6 мм, с шагом 150 - 200 мм. При большей толщине рекомендуется устанавливать две сетки.
В зоне примыкания оболочки к кольцу толщину оболочки увеличивают и устанавливают дополнительную сетку со стержнями диаметром 6 - 8 мм меридионального направления. Число стержней рассчитывают по максимальному меридиональному изгибающему моменту.
В местах действия на купол сосредоточенных нагрузок, а также около отверстий и проемов предусматривают дополнительную конструктивную или расчетную арматуру.
Опорное кольцо рекомендуется выполнять предварительно напряженным. Выбор значения усилия обжатия и конструирование опорного кольца следует выполнять из условия обеспечения трещиностойкости кольца и допустимой ширины раскрытия трещин согласно СП 63.13330.
5.1.3 Купола следует рассчитывать по предельным состояниям двух групп по 4.2, при этом усилия в элементах куполов допускается определять методами теории упругости, изложенными в 10.6 - 10.10 СП 387.1325800.2018.

а - схема купола; б - схема усилий; 1 - ось вращения;
2 - параллель; 3 - меридиан; 4 - краевая параллель
Расчет купола с осесимметричной оболочкой с вертикальной осью вращения допускается выполнять по безмоментной теории с последующим наложением усилий краевого эффекта. Условия применимости безмоментной теории:
- плавные изменения толщины стенок купола и радиуса кривизны меридиана;
- равномерные симметричные нагрузки, действующие на оболочку;
- свободные радиальные и угловые перемещения краев оболочки в направлении меридиональных усилий по касательной к меридиану.
В остальных случаях напряженно-деформированное состояние купола следует определять с учетом действия изгибающих моментов.
Расчет по прочности сечений, жесткости и трещиностойкости железобетонных элементов купола выполняют по СП 63.13330.
5.1.4 Формулы для определения мембранных усилий в сферических замкнутой и незамкнутой (с центральным отверстием) оболочке по безмоментной теории на отдельные виды нагрузок, принятые в расчете, приведены в таблице 5.1.1.
Таблица 5.1.1
по безмоментной теории
Схема нагружения | N1 | N2 | Nk | Примечание | ||
Сферическая замкнутая оболочка | ||||||
Нагрузка от собственного веса g, кПа: а) толщина оболочки постоянная |  | 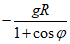 |  |  | 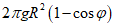 | При 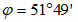 N2 = 0 |
б) толщина оболочки меняется по ф:  | 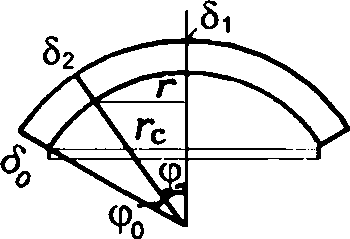 |  |  |  |  | Вес единицы площади оболочки: в пяте - g0, в ключе - g1 |
Равномерно распределенная нагрузка на горизонтальной проекции p, кПа |  |  | 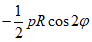 | 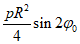 |  | При 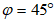 N2 = 0 |
Сферическая незамкнутая оболочка | ||||||
Нагрузка от собственного веса g, кПа (толщина оболочки постоянная) |  | 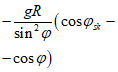 | 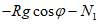 | 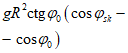 | 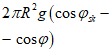 | Усилие в фонарном кольце Nsk = 0 |
Равномерно распределенная нагрузка на горизонтальной проекции p, кПа | 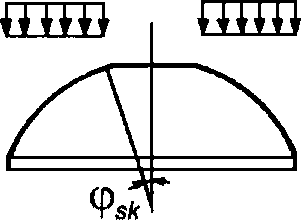 | 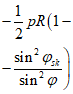 |  |  |  | Nsk = 0 |
Вертикальная распред. линейная нагрузка на фонарном кольце Pk, кН/м |  | 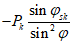 | 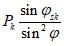 | 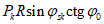 |  | |
В таблице 5.1.1 приняты обозначения:
N1 - усилия в оболочке по направлению меридиана на единицу длины кольцевого сечения 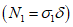 ;
;
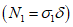 ;
;N2 - кольцевое усилие на единицу длины меридиана  ;
;
 ;
;Nsk - усилие в фонарном кольце;
Nk - усилие в опорном кольце;
R - радиус кривизны сферической оболочки;
g - нагрузка от собственного веса оболочки толщиной 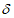 ;
;
p - равномерно распределенная нагрузка по горизонтальной проекции;
Pk - вертикальная распределенная линейная нагрузка на фонарном кольце.
5.1.5 При расчете оболочек с использованием конечно-элементных программ распределение односторонней снеговой нагрузки следует принимать в соответствии с Б.11 СП 20.13330.2016.
При одностороннем нагружении купола нагрузкой q ее распределение по поверхности z допускается определять (СП 387.1325800) по формуле
где q - нагрузка на единицу площади горизонтальной поверхности, равная снеговой по СП 20.13330;
Нормальные усилия N1, N2 и сдвигающие усилия Q определяют по формулам:
 (5.1.3)
(5.1.3)Формулы (5.1.2) - (5.1.4) получены из условия равенства эпюр полного объема односторонней снеговой нагрузки при ее распределении по формуле (5.1.1) и по В.1.4 СП 20.13330.2016.
5.1.6 Краевые изгибающие моменты M и распор купола H вблизи кольца определяют методом сил из решения системы канонических уравнений, выражающих совместность угловых и линейных перемещений купола и опорного кольца по линии их контакта.
Уравнения метода сил для случая жесткого сопряжения оболочки купола и опорного кольца имеют следующий вид:
Значения коэффициентов:
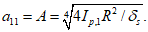 (5.1.6)
(5.1.6)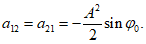 (5.1.7)
(5.1.7) (5.1.8)
(5.1.8)Значение свободных членов при нагрузке по поверхности:
 (5.1.9)
(5.1.9) (5.1.10)
(5.1.10)Значения свободных членов при нагрузке по проекции (снеговая нагрузка):
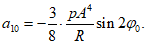 (5.1.11)
(5.1.11)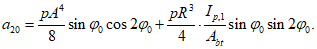 (5.1.12)
(5.1.12)Усилия вдоль меридиана  и
и  :
:
где:  ;
;  ;
;  . Отсчет s - длины дуги по меридиану - ведется от места примыкания оболочки купола к нижнему опорному кольцу.
. Отсчет s - длины дуги по меридиану - ведется от места примыкания оболочки купола к нижнему опорному кольцу.
 ;
;  ;
;  . Отсчет s - длины дуги по меридиану - ведется от места примыкания оболочки купола к нижнему опорному кольцу.
. Отсчет s - длины дуги по меридиану - ведется от места примыкания оболочки купола к нижнему опорному кольцу.Кольцевые усилия с учетом нагрузки в основной системе T2 определяют по формуле
 (5.1.15)
(5.1.15)Пример 1
Задание: для покрытия над зданием запроектировать сборный железобетонный сферический купол диаметром 90 м с фонарным отверстием диаметром 12 м. Здание расположено в III ветровом и III снеговом районах. Купол установлен на высоте 20 м от поверхности земли в открытой местности.
Расчет купола методами теории упругости
Подъем купола по требованиям технологии и из условия отсутствия растягивающих напряжений по всей его поверхности в кольцевом направлении выбираем равным 12,5 м. Отношение стрелы подъема f к диаметру d составляет 1/7,2.
При заданной стреле подъема радиус сферы (рисунок 5.1.1, а) определяют по формуле
R = (d2 + 4f2)/8f = (902 + 4·12,52)/(8·12,5) = 87,25 м.
С целью уточнения размеров сборных элементов оболочки задаемся размерами фонарного и опорного колец, а также размерами стыка между элементами оболочки. Для установки элементов оболочки в местах сопряжения их с фонарным и опорным кольцами в последних предусматриваются кольцевые выступы (рисунок 5.1.2, г).
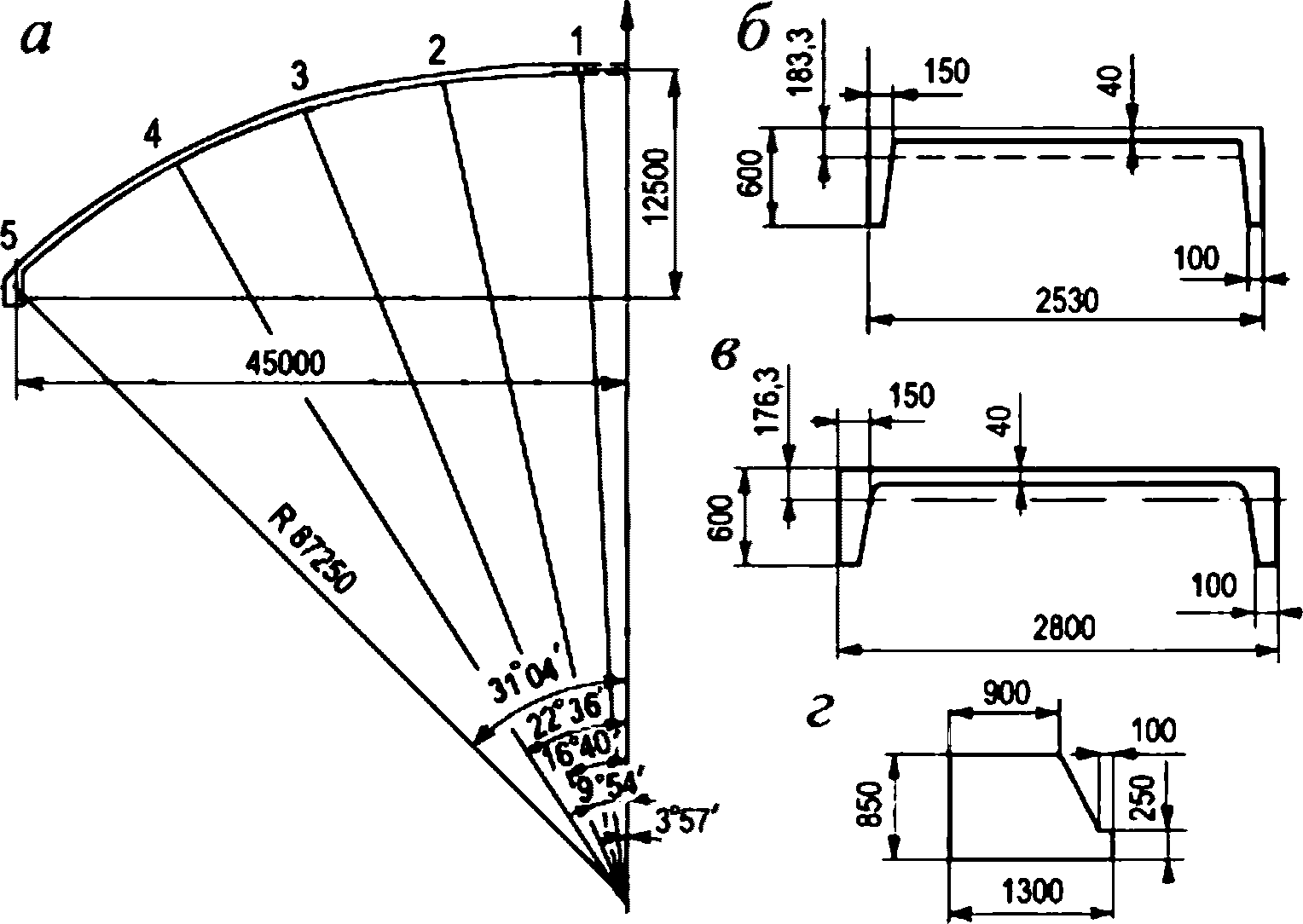
а - схема и геометрические размеры; б - расчетное сечение
оболочки купола у нижнего опорного кольца; в - то же, у низа
верхней панели; г - то же, нижнего опорного кольца
Нижнюю часть купола расчленяем на 112 панелей, верхнюю - на 56 (рисунок 5.1.3). Нижнее опорное кольцо запроектировано из сборных блоков и армируется предварительно напряженной арматурой, напрягаемой электротермическим способом из стали А600 по ГОСТ 34028, которую укладывают по наружной грани опорного кольца с последующим омоноличиванием преднапряженной арматуры. При таком способе членения элементов оболочки размеры сечений сборных элементов определяются условиями транспортирования, складирования и монтажа элементов до омоноличивания стыков. Элементы оболочек выполняем с кривизной в одном направлении. Размеры панелей показаны на рисунке 5.1.4.
Для восприятия сдвигающих усилий по всем граням элементов оболочки купола предусматриваются шпонки (рисунок 5.1.4, е) и дополнительные стальные закладные элементы, соединяемые накладками с целью обеспечения непрерывности кольцевой арматуры. Размеры продольных ребер принимаем из условий монтажа равными 100 x 600 мм (рисунок 5.1.4, д). Толщину собственно оболочки принимаем равной 40 мм, класс бетона B40 (Rb = 17,0 МПа, Rbt = 1,15 МПа, Eb = 36000 МПа, 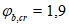 ).
).
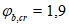 ).
).
а - план; б - разрез I-I; 1 - колонна, 2 - нижнее опорное
кольцо; 3 - плита П1; 4 - плита П2; 5 - светоаэрационный
фонарь; 6 - верхнее опорное кольцо

а, б - плита П2 (продольный разрез и план); в, г - плита П1;
д - плиты П1 и П2 (поперечный разрез); е - деталь устройства
шпонок по бортам плит П1 и П2; 1 - строповочные петли;
2 - арматурная сетка; 3 - сварные каркасы
В соответствии с СП 20.13330 полное расчетное значение равномерной снеговой нагрузки на горизонтальную проекцию покрытия определяется по формуле

где Sg - вес снегового покрова на 1 м2 горизонтальной поверхности земли, который для III снегового района равен 1,5 кПа;
коэффициент 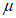 (Б.11 СП 20.13330.2016) равен 1,0 при
(Б.11 СП 20.13330.2016) равен 1,0 при 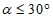 ,
,  при
при 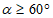 ; промежуточные значения определяются линейной интерполяцией; в данном случае максимальный угол 31°04' близок к 30°, поэтому по всей поверхности принят
; промежуточные значения определяются линейной интерполяцией; в данном случае максимальный угол 31°04' близок к 30°, поэтому по всей поверхности принят  ;
;
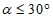 ,
, 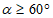 ; промежуточные значения определяются линейной интерполяцией; в данном случае максимальный угол 31°04' близок к 30°, поэтому по всей поверхности принят
; промежуточные значения определяются линейной интерполяцией; в данном случае максимальный угол 31°04' близок к 30°, поэтому по всей поверхности принят термический коэффициент ct = 1;
коэффициент ветрового сноса по формуле (10.3) СП 20.13330.2016;
ce = 0,85 + 0,00375(d - 60) = 0,85 + 0,00375(90 - 60) = 0,9625.
Нормативные и расчетные нагрузки на купол приведены в таблице 5.1.2.
Наименование нагрузки | Нормативная, кПа | Расчетная, кПа | |
Собственный вес купола | 3,70 | 1,1 | 4,07 |
Пароизоляция | 0,05 | 1,3 | 0,07 |
Утеплитель из минераловатных плит | 0,15 | 1,3 | 0,20 |
Гидроизоляционный ковер | 0,15 | 1,3 | 0,20 |
Итого постоянная по поверхности | 4,06 | - | 4,54 |
Снеговая нагрузка S по проекции | 1,44 | 1,4 | 2,02 |
Расчетная погонная нагрузка на фонарное кольцо 18,6 кН/м складывается из нагрузок собственного веса кольца 7,5 кН/м, фонаря 5,0 кН/м, снеговой нагрузки на фонаре 6,1 кН/м.
Координаты сечений купола приведены в таблице 5.1.3.
ИС МЕГАНОРМ: примечание. Сноска дана в соответствии с официальным текстом документа. |
Номер точки | Значения координат точек | ||
x, м | y, м | ||
1 | 6,0 | 12,25 | 3°57' |
2 | 15,0 | 11,75 | 9°54' |
3 | 25,0 | 8,85 | 16°40' |
4 | 33,5 | 5,85 | 22°36' |
5 | 45,0 | 0 | 31°04' |
Соответствующий точке угол в меридиональном сечении оболочки, отсчитываемый от оси вращения (рисунок 5.1.2, а). | |||
По формулам, приведенным в таблице 5.1.1, определены мембранные усилия, которые приведены в таблице 5.1.4. Усилия приведены раздельно для нагрузки от собственного веса (поверхностная нагрузка интенсивностью g = 4,54 кПа), от снеговой нагрузки (по горизонтальной проекции при S = 1,8 кПа) и погонной нагрузки по фонарному кольцу Pk = 18,6 кН.
Таблица 5.1.4
и по горизонтальной проекции, кН/м
Номер точки | Меридиональные усилия | Кольцевые усилия | ||||||
Нагрузка по поверхности, 4,54 кПа | Нагрузка по проекции, 1,8 кПа | Нагрузка по фонар. кольцу, 18,6 кН/м | Суммарное усилие, кН/м | Нагрузка по поверхности, 4,54 кПа | Нагрузка по проекции, 1,8 кПа | Нагрузка по фонар. кольцу, 18,6 кН/м | Суммарное усилие, кН/м | |
1 | 0 | 0 | -270,01 | -270,01 | -395,17 | -175,41 | +270,01 | -300,57 |
2 | -167,72 | -73,98 | -43,35 | -285,03 | -222,51 | -97,06 | +43,35 | -276,22 |
3 | -190,87 | -83,04 | -15,58 | -289,48 | -188,61 | -78,71 | +15,58 | -251,74 |
4 | -199,59 | -85,29 | -8,68 | -293,56 | -166,10 | -64,93 | +8,68 | -222,35 |
5 | -209,83 | -86,55 | -4,81 | -301,19 | -129,47 | -42,76 | +4,81 | -167,42 |
Значения нормальных N1, N2 и сдвигающих S усилий при одностороннем нагружении купола снеговой нагрузкой, определяемой по формулам (5.1.2) - (5.1.4), приведены в таблицах 5.1.5 - 5.1.7.
Таблица 5.1.5
снеговой нагрузки, кН/м
Номер точки | ||||||||
0° | 15° | 30° | 45° | 60° | 75° | 90° | ||
1 | 3°57' | -53,23 | -53,71 | -54,16 | -54,54 | -54,81 | -55,05 | -55,10 |
2 | 9°54' | -53,23 | -54,39 | -55,35 | -56,41 | -57,15 | -57,59 | -57,77 |
3 | 16°40' | -53,23 | -55,13 | -56,95 | -58,55 | -59,71 | -60,45 | -60,78 |
4 | 22°36' | -53,23 | -55,86 | -58,00 | -60,23 | -61,85 | -62,80 | -63,18 |
5 | 31°04' | -53,23 | -56,50 | -59,60 | -62,33 | -64,29 | -65,57 | -66,11 |
Таблица 5.1.6
Кольцевые усилия N2 от односторонней снеговой нагрузки, кН/м
Номер точки | ||||||||
0° | 15° | 30° | 45° | 60° | 75° | 90° | ||
1 | 3°57' | -53,23 | -54,60 | -56,00 | -57,04 | -58,43 | -58,43 | -58,67 |
2 | 9°54' | -53,23 | -56,77 | -60,04 | -62,92 | -64,94 | -66,42 | -66,94 |
3 | 16°40' | -53,23 | -59,17 | -64,71 | -69,50 | -73,12 | -75,47 | -76,26 |
4 | 22°36' | -53,23 | -61,21 | -68,66 | -75,05 | -79,94 | -83,02 | -84,10 |
5 | 31°4' | -53,23 | -63,88 | -74,40 | -82,93 | -89,63 | -93,67 | -95,28 |
Таблица 5.1.7
Номер точки | ||||||||
0° | 15° | 30° | 45° | 60° | 75° | 90° | ||
1 | 3°57' | 1,80 | -1,72 | -1,55 | -1,26 | -0,90 | -0,46 | 0,00 |
2 | 9°54' | 3,36 | -3,24 | -2,90 | -2,37 | -1,68 | -0,86 | 0,00 |
3 | 16°40' | -7,27 | -7,03 | -6,30 | -5,13 | -3,62 | -1,87 | 0,00 |
4 | 22°36' | -10,63 | -10,28 | -9,21 | -7,52 | -5,67 | -2,75 | 0,00 |
5 | 31°4' | -16,89 | -16,32 | -14,63 | -11,94 | -8,43 | -4,37 | 0,00 |
Расчет ветровых нагрузок следует выполнять в соответствии с СП 20.13330. Аэродинамические коэффициенты принимаются по пункту В.1.4 СП 20.13330.2016.
Расчеты показали, что при параметрах h1/l = 20/90 = 0,222 и f/l = 12,5/90 = 0,139 направление давления ветра соответствует отсосу по всей поверхности купола: коэффициенты ce в точках A, B и C равны соответственно -0,8; -0,6 и -0,2.
При нормативном значении ветрового давления w0 = 0,38 кПа, коэффициенте kz = 1,3 (при расчетной высоте h = h1 + 0,7f = 28,75 м для местности типа A) и коэффициенте надежности по нагрузке 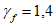 расчетные значения средней составляющей ветровой нагрузки не превышают -0,55 кПа. Значения меридиональных и кольцевых (превалирующих) усилий от действия таких ветровых нагрузок по сравнению с усилиями от других нагрузок весьма малы и противоположны по знаку, что позволяет отказаться от учета ветровых нагрузок в расчете рассматриваемой конструкции купола.
расчетные значения средней составляющей ветровой нагрузки не превышают -0,55 кПа. Значения меридиональных и кольцевых (превалирующих) усилий от действия таких ветровых нагрузок по сравнению с усилиями от других нагрузок весьма малы и противоположны по знаку, что позволяет отказаться от учета ветровых нагрузок в расчете рассматриваемой конструкции купола.
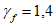 расчетные значения средней составляющей ветровой нагрузки не превышают -0,55 кПа. Значения меридиональных и кольцевых (превалирующих) усилий от действия таких ветровых нагрузок по сравнению с усилиями от других нагрузок весьма малы и противоположны по знаку, что позволяет отказаться от учета ветровых нагрузок в расчете рассматриваемой конструкции купола.
расчетные значения средней составляющей ветровой нагрузки не превышают -0,55 кПа. Значения меридиональных и кольцевых (превалирующих) усилий от действия таких ветровых нагрузок по сравнению с усилиями от других нагрузок весьма малы и противоположны по знаку, что позволяет отказаться от учета ветровых нагрузок в расчете рассматриваемой конструкции купола.Расчет прогиба купола
Расчет прогиба купола w определяем приближенно по безмоментной теории расчета применительно к оболочкам положительной кривизны, свободно опертым по контуру как для гладкой оболочки приведенной толщины 


где q - полное нормативное значение нагрузки по таблице 5.1.2;

Относительный прогиб  что значительно меньше допустимого нормативного значения прогиба 1/500l.
что значительно меньше допустимого нормативного значения прогиба 1/500l.
 что значительно меньше допустимого нормативного значения прогиба 1/500l.
что значительно меньше допустимого нормативного значения прогиба 1/500l.Расчет опорного кольца
Расчетное усилие растяжения в опорном кольце Nk может быть определено по формулам таблицы 5.1.1 или через суммарные меридиональные усилия N1 в точке 5 по формуле

Принимаем класс бетона кольца B35 (Rbt,ser = 1,95 МПа, Eb = 34500 МПа,  ).
).
 ).
).Принимаем армирование кольца из 16 групп по пять предварительно напрягаемых канатов К7-15,7-1860 по ГОСТ Р 53772 с Rs = 1435 МПа (Asp = 120,0 см2) и 13 стержней ненапряженной арматуры  с Rs = 435 МПа (As = 40,84 см2). Устанавливаем группы напрягаемых канатов в два ряда (рисунок 5.1.5). Ненапряженной арматурой А500 армируем сборные кольца. Ненапряженная арматура в стыках сваривается из условий равнопрочности. Таким образом, арматура может воспринять усилие 120,0·1435 + 40,84·435 = 19000 кН > Nk.
с Rs = 435 МПа (As = 40,84 см2). Устанавливаем группы напрягаемых канатов в два ряда (рисунок 5.1.5). Ненапряженной арматурой А500 армируем сборные кольца. Ненапряженная арматура в стыках сваривается из условий равнопрочности. Таким образом, арматура может воспринять усилие 120,0·1435 + 40,84·435 = 19000 кН > Nk.
 с Rs = 435 МПа (As = 40,84 см2). Устанавливаем группы напрягаемых канатов в два ряда (рисунок 5.1.5). Ненапряженной арматурой А500 армируем сборные кольца. Ненапряженная арматура в стыках сваривается из условий равнопрочности. Таким образом, арматура может воспринять усилие 120,0·1435 + 40,84·435 = 19000 кН > Nk.
с Rs = 435 МПа (As = 40,84 см2). Устанавливаем группы напрягаемых канатов в два ряда (рисунок 5.1.5). Ненапряженной арматурой А500 армируем сборные кольца. Ненапряженная арматура в стыках сваривается из условий равнопрочности. Таким образом, арматура может воспринять усилие 120,0·1435 + 40,84·435 = 19000 кН > Nk.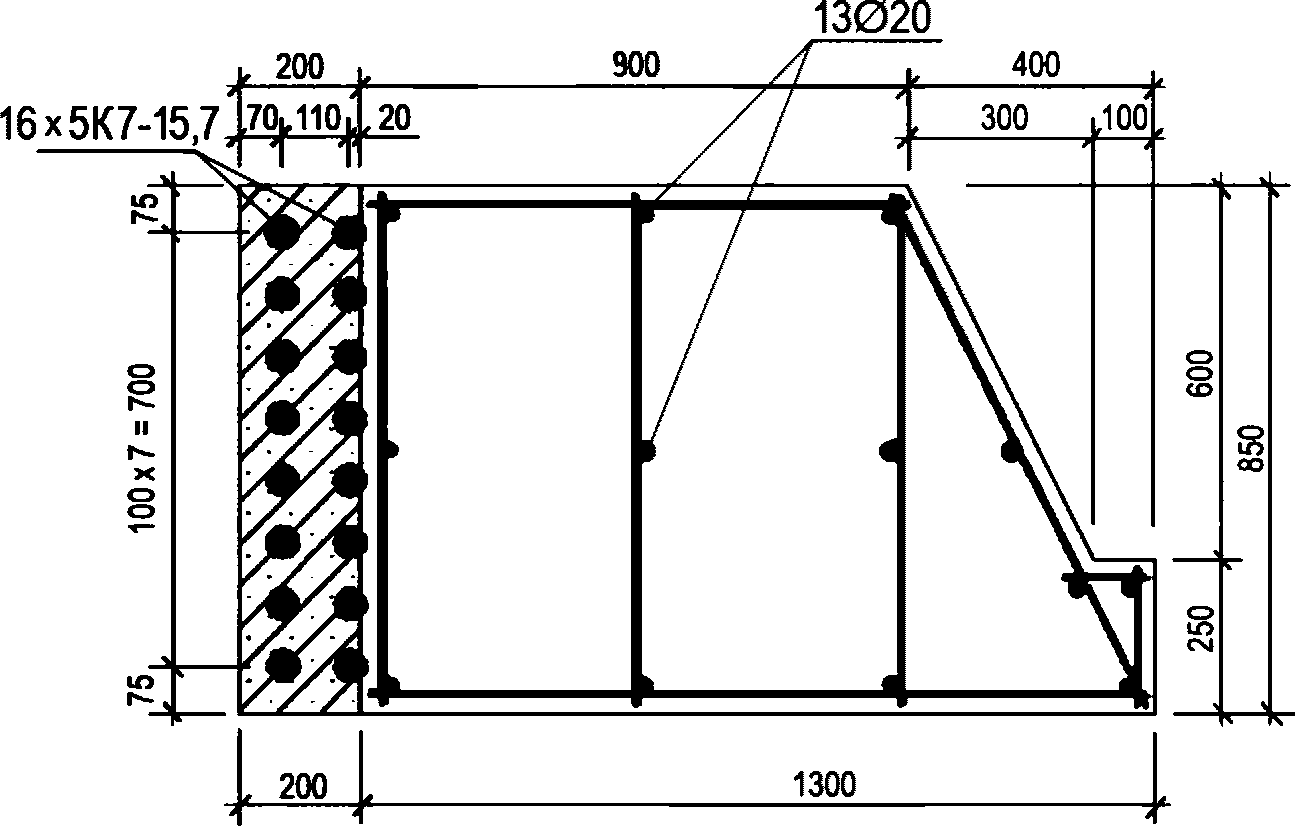
опорного кольца купола
Площадь сечения опорного кольца без учета набетонки равна:
Ak = 0,85·0,9 + 0,3·0,6/2 + 0,25·0,4 = 0,955 м2.
Натяжение арматуры на бетон производится механическим способом с созданием в ней напряжений 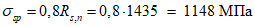 .
.
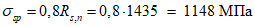 .
.Передаточная прочность бетона Rbp = 24,5 МПа.
Определяем потери предварительного напряжения арматуры (по СП 63.13330). Считаем, что длина сборного элемента составляет 1/28 длины опорного кольца,  .
.
 .
.Первые потери:
- от деформации анкеров натяжных устройств
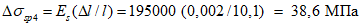 ;
;- от трения арматуры о поверхность бетона
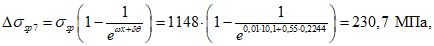
где  для бетонной поверхности;
для бетонной поверхности; 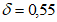 для стержней периодического профиля;
для стержней периодического профиля;
 для бетонной поверхности;
для бетонной поверхности; 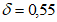 для стержней периодического профиля;
для стержней периодического профиля;
Суммарные первые потери 38,6 + 230,7 = 269,3 МПа.
Вторые потери:
- от релаксации напряжений в арматуре

- от усадки бетона

- от ползучести бетона

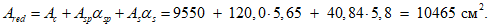
С учетом первых потерь:




- от упругого обжатия бетона неодновременно натягиваемой арматуры при n = 8
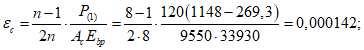
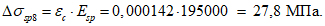
Суммарные потери

Напряжение в арматуре за вычетом всех потерь составляет

Усилие обжатия контура составляет
P = 658·120,0·10-1 - (39 + 120,9)40,84·10-1 = 7243 кН.
Площадь кольца с учетом набетонки, закрывающей напрягаемую арматуру, составляет
Abt = 9550 + 20·85 = 11250 см2.
Усилие, воспринимаемое сечением кольца при образовании трещин, составляет

Здесь 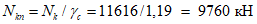 - нормативное значение усилия растяжения в опорном кольце;
- нормативное значение усилия растяжения в опорном кольце;
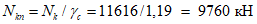 - нормативное значение усилия растяжения в опорном кольце;
- нормативное значение усилия растяжения в опорном кольце;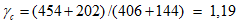 - среднее значение коэффициента надежности по нагрузке (отношение полных расчетных и нормативных нагрузок, таблица 5.1.2).
- среднее значение коэффициента надежности по нагрузке (отношение полных расчетных и нормативных нагрузок, таблица 5.1.2).Ширину раскрытия нормальных трещин в опорном кольце находим по СП 63.13330:
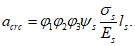
Здесь 

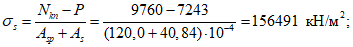
ls - базовое расстояние между смежными нормальными трещинами;
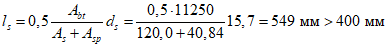 - принимаем ls = 400 мм.
- принимаем ls = 400 мм.Тогда 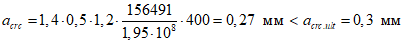 - меньше предельно допустимой ширины раскрытия трещин при продолжительном действии нагрузки.
- меньше предельно допустимой ширины раскрытия трещин при продолжительном действии нагрузки.
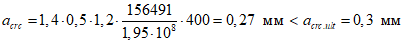 - меньше предельно допустимой ширины раскрытия трещин при продолжительном действии нагрузки.
- меньше предельно допустимой ширины раскрытия трещин при продолжительном действии нагрузки.Проверка устойчивости купола
Критическую нагрузку qcr определяем согласно СП 387.1325800 как для гладкой оболочки с приведенной (фиктивной) толщиной 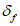 . Приведенную толщину оболочки и фиктивный модуль деформаций бетона Ef определяем в уширенной части верхней панели (рисунок 5.1.2, в), так как в этой зоне купола наименьшее значение критической нагрузки.
. Приведенную толщину оболочки и фиктивный модуль деформаций бетона Ef определяем в уширенной части верхней панели (рисунок 5.1.2, в), так как в этой зоне купола наименьшее значение критической нагрузки.
Площадь поперечного сечения панели Ap = 280·4 + 2·12,5·56 = 2520 см2.
Статический момент относительно наружной грани сечения
Sp = 280·4·2 + 2·10·56(4 + 56/2) + 2(5·56)/2·(4 + 56/3) = 44427 см3.
Расстояние от центра тяжести z = 44427/2520 = 17,63 см.
Момент инерции поперечного сечения
Ip = 280·43/12 + 280·4(17,63 - 2)2 + 2·10·563/12 + 2·10·56(56/2 + 4 - 17,63)2 + 2·5·563/36 + 5·56(4 + 56/3 - 17,63)2 = 854961 см4.

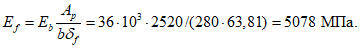
Модуль деформаций при длительном действии нагрузки
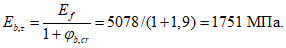
Критическая нагрузка
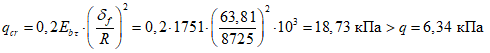 (без учета нагрузки от фонаря, которая незначительна), устойчивость купола обеспечена.
(без учета нагрузки от фонаря, которая незначительна), устойчивость купола обеспечена.Определение усилий краевого изгиба по приближенной моментной теории в месте сопряжения оболочки и опорного кольца
Опорное кольцо препятствует свободному перемещению краев оболочки, что приводит к возникновению в этих местах нормальных сил и изгибающих моментов. Оболочка соединяется с кольцом жестко.
Определяем геометрические характеристики панели оболочки в месте примыкания ее к опорному кольцу с учетом меридиональных ребер (рисунок 5.1.2, б).
Площадь сечения панели Ap = 253·4 + 2·12,5·56 = 2412 см2.
Статический момент относительно наружной грани
Sp = 253·4·2 + 2·10·56(4 + 56/2) + 2(5·56)/2·(4 + 56/3) = 44211 см3.
Расстояние до центра тяжести z = 44211/2412 = 18,33 см.
Момент инерции панели
Ip = 253·43/12 + 253·4(18,33 - 2)2 + 2·10·563/12 + 2·10·56(56/2 + 4 - 18,33)2 + 2·5·563/36 + 5·56(4 + 56/3 - 18,33)2 = 827157 см4.
Момент инерции на единицу длины Ip1 = 827157/253 = 3269 см3.
Приведенная толщина оболочки с учетом кольцевых ребер
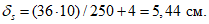
Ip1/Abt = 0,003269/1,125 = 0,0029.
Коэффициенты системы уравнений (5.1.5) по 5.1.6:

a12 = a21 = -(6,542/2)·0,51604 = -11,04 м2.
a22 = (6,543/2 + 0,0029·87,252)·0,516042 = 43,12 м3.
Значение свободных членов при нагрузке по поверхности:
a10 = -[(4,54·6,544)/(2·87,25)]·0,51604 = -24,56;
a20 = (4,54·6,544/4)[0,85657 - 1/(1 + 0,85657)]·0,51604 + 4,54·87,253·0,0029·(1 - 0,85657)0,85657 - 5738,4·0,0029·87,25·0,51604 = 665,77.
Значения свободных членов при нагрузке по проекции (снеговая нагрузка):
a10 = -(3/8)·(2,02·6,544/87,25)·0,88404 = -14,04;
a20 = (2,02·6,544/8)·0,51604·0,46742 + 0,0029·(2,02·87,253/4)·0,88404·0,51604 = 555,17.
Значения краевых усилий при нагрузке от собственного веса покрытия с предварительным напряжением арматуры опорного кольца определяется из уравнений (5.1.5):

При нагрузке снегом плюс постоянная нагрузка с предварительным напряжением опорного кольца
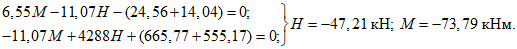
2R/A2 = (2·87,25)/6,542 = 4,08;

Значения величин изгибающих моментов и кольцевых усилий вдоль меридиана в зависимости от значений  приведены в таблице 5.1.8.
приведены в таблице 5.1.8.
0 | 1 | 0 | 73,79 | -348,99 |
0,2 | 0,8024 | 0,1627 | 45,29 | -231,05 |
0,4 | 0,6174 | 0,2610 | 23,23 | -136,89 |
0,6 | 0,4530 | 0,3093 | 6,97 | -64,98 |
1,0 | 0,1988 | 0,3096 | -11,81 | 23,83 |
1,4 | 0,0419 | 0,2430 | -17,69 | 58,53 |
1,8 | -0,0376 | 0,1610 | -16,55 | 61,7 |
2,2 | -0,0652 | 0,0896 | -12,48 | 49,73 |
2,6 | -0,0636 | 0,0383 | -7,97 | 33,73 |
3,0 | -0,0493 | 0,0070 | -4,24 | 19,31 |
Приведенные в таблице 5.1.8 усилия от влияния краевого эффекта суммируют с усилиями от нагрузки в основной системе (суммарными мембранными усилиями по таблице 5.1.4) и на эти усилия проверяют прочность и трещиностойкость железобетонных ребер плит в приконтурной зоне в соответствии с СП 63.13330.
Эпюры усилий в куполе от влияния краевого эффекта и предварительного напряжения приведены на рисунке 5.1.6.
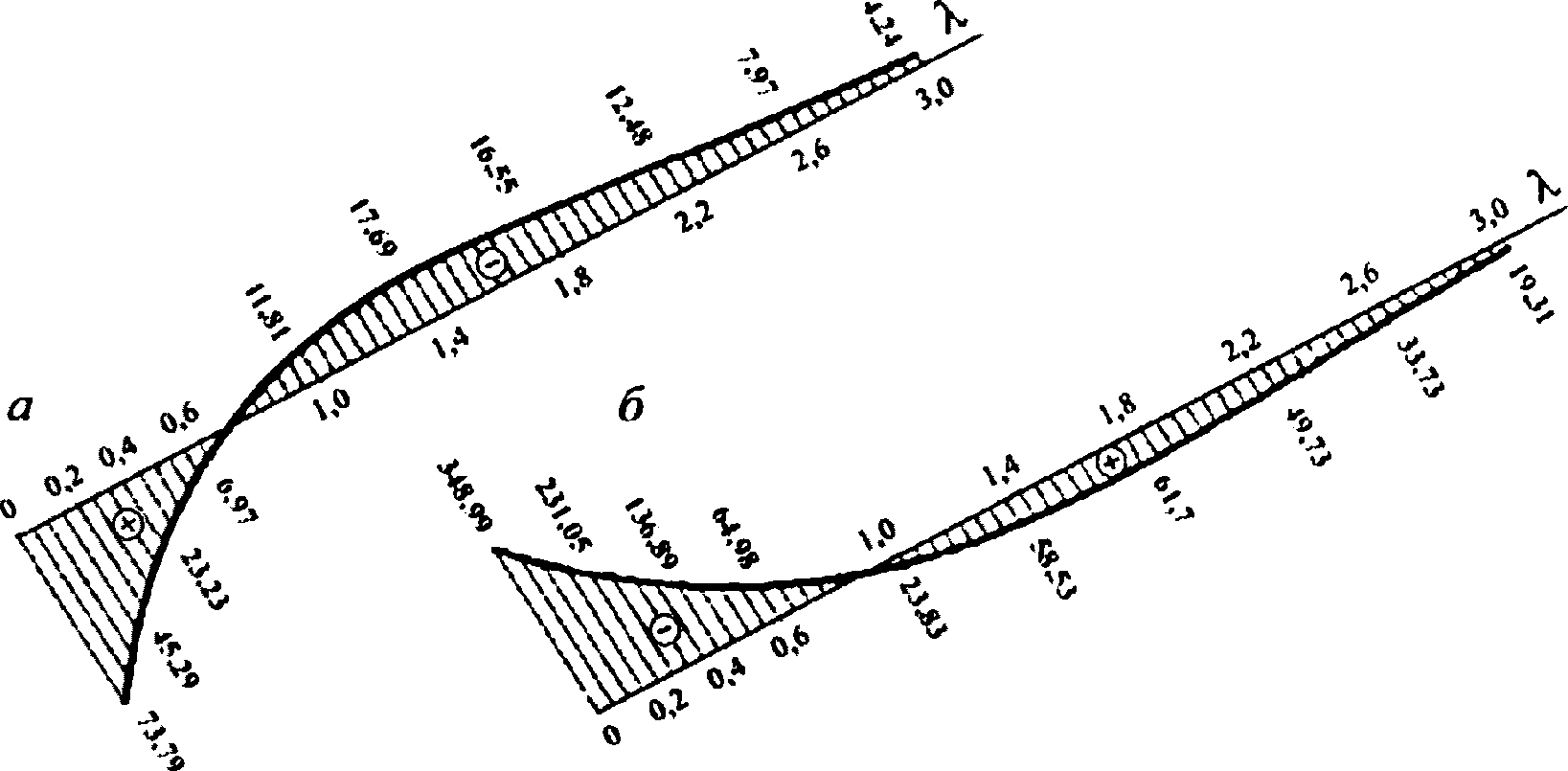
а - эпюра изгибающих моментов; б - эпюра кольцевых усилий
краевого эффекта и предварительного напряжения
при жестком сопряжении купола с опорным кольцом
5.1.7 Расчет куполов по несущей способности выполняют кинематическим способом метода предельного равновесия (пункты 10.11 - 10.15 СП 387.1325800.2018).
Схема разрушения купола принимается в виде системы сквозных меридиональных трещин, начинающихся у растянутого контура и соединенных по концам раскрывающимися вниз кольцевыми пластическими шарнирами (рисунок 5.1.7). Эта схема - наиболее вероятная форма обращения купола в пространственный механизм в случае, когда напряжения во всей арматуре контурного кольца достигают расчетного сопротивления на растяжение.
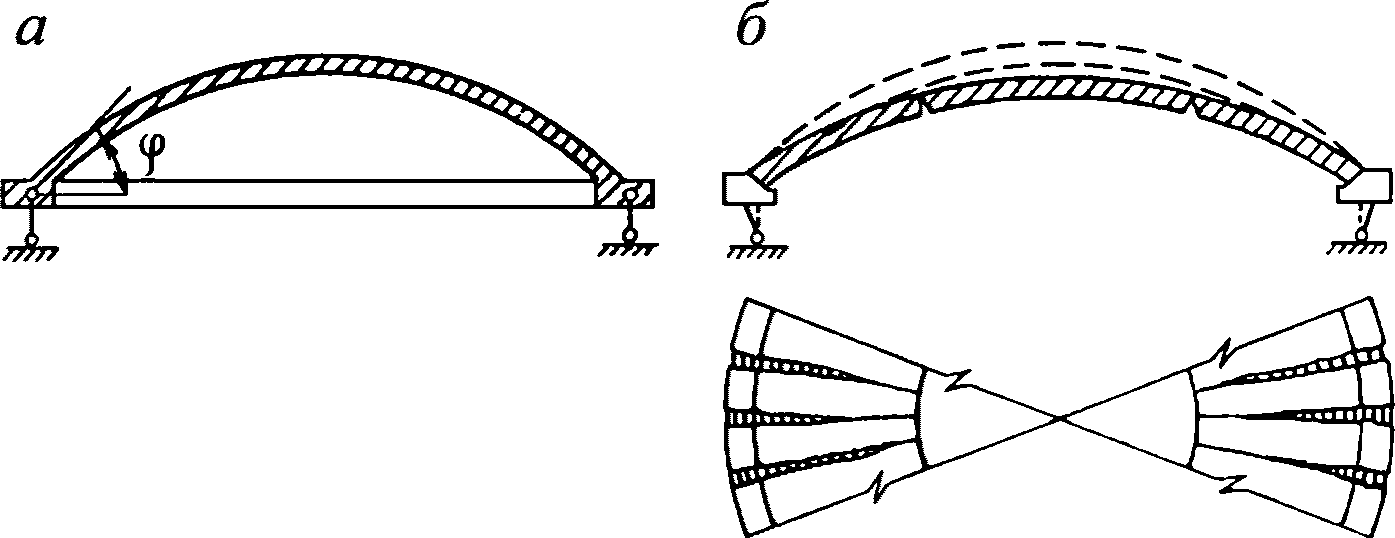
а - поперечное сечение; б - схема разрушения
5.1.8 Расчет несущей способности купола допускается выполнять приближенным способом по "балочной" схеме [2]. Для свободно опертых по контуру сферических оболочек вращения с меридионально-кольцевой схемой разрушения расчет производится из условия равновесия рассматриваемой части оболочки (рисунок 5.1.8). При этом работой внутренних сил в кольцевом пластическом шарнире можно пренебречь.
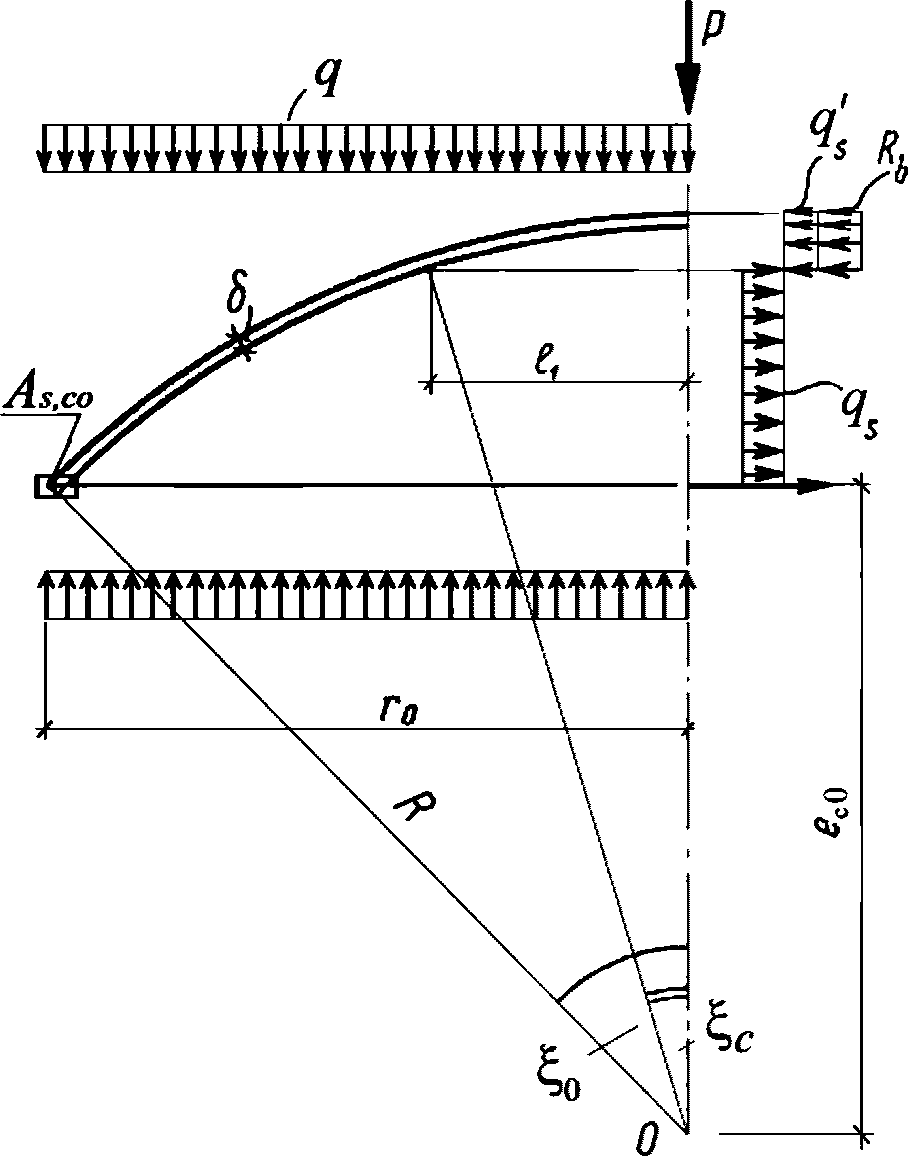
Из условия равенства нулю суммы проекций усилий на горизонтальную ось угловую координату 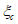 , ограничивающую сжатую зону бетона, определяют по формуле
, ограничивающую сжатую зону бетона, определяют по формуле
где B = Rbh0 + qs + q's;
As,co - площадь сечения всех кольцевых стержней опорного кольца;
R - радиус кривизны срединной поверхности купола;
Rb - призменная прочность бетона;
qs, q's - погонные усилия, воспринимаемые кольцевой арматурой купола соответственно в растянутой и сжатой зонах рассматриваемого сечения купола;
h0 - рабочая высота сечения поля оболочки.
Из равенства моментов внешних и внутренних сил после интегрирования:
 (5.1.18)
(5.1.18)ec0 - расстояние от центра тяжести рабочей арматуры кольца до центра окружности 0;
M - момент внешних сил относительно оси, проходящей через центр окружности 0.
Зная выражение для M, из формулы (5.1.17) можно найти величину суммарной внешней нагрузки P (рисунок 5.1.7) по формуле
где k - коэффициент, зависящий от вида опирания и характера внешней нагрузки (0 <= k <= 1);
r0 - радиус основания купола.
Формулы для определения k для характерных случаев опирания и различных видов нагружения приведены в таблице 5.1.9.
Вид нагрузки | Вид опирания | ||||
на три точки | на четыре точки | на пять точек | на шесть точек | по всему контуру | |
Равномерно распределенная по всей поверхности |  | 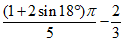 | См. на три точки | ||
Кольцевая, распределенная по радиусу x |  | 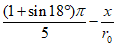 | То же | ||
Сосредоточенная в вершине оболочки | 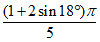 | " | 1 | ||
Собственная масса оболочки | 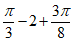 | 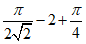 | 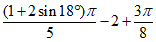 | " | |
Задание: рассчитать несущую способность монолитного железобетонного купола по "балочной" схеме с диаметром опорного кольца 2r0 = 36 м. Стрела подъема купола f = 6 м, толщина  . Класс бетона B35 (Rb = 19,5 МПа). Кольцевая арматура нижней и верхней сеток и меридиональная арматура нижней сетки
. Класс бетона B35 (Rb = 19,5 МПа). Кольцевая арматура нижней и верхней сеток и меридиональная арматура нижней сетки 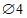 Вр500 (Rs = 415 МПа, Rsc = 360 МПа) с шагом 200 мм (As,cb = As,cu = As,ml = 0,628 см2/м), меридиональная арматура верхней сетки
Вр500 (Rs = 415 МПа, Rsc = 360 МПа) с шагом 200 мм (As,cb = As,cu = As,ml = 0,628 см2/м), меридиональная арматура верхней сетки  Вр500 с шагом 200 мм (As,mu = 0,353 см2/м). Опорное кольцо армировано
Вр500 с шагом 200 мм (As,mu = 0,353 см2/м). Опорное кольцо армировано 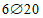 А500 (R's = 435 МПа, As,co = 18,85 см2). Армирование As,ml и As,mu вдоль меридиана постоянно. Опорное кольцо опирается на несущие конструкции по всему периметру. Осесимметричная нагрузка интенсивностью q равномерно распределена по горизонтальной проекции купола.
А500 (R's = 435 МПа, As,co = 18,85 см2). Армирование As,ml и As,mu вдоль меридиана постоянно. Опорное кольцо опирается на несущие конструкции по всему периметру. Осесимметричная нагрузка интенсивностью q равномерно распределена по горизонтальной проекции купола.
 . Класс бетона B35 (Rb = 19,5 МПа). Кольцевая арматура нижней и верхней сеток и меридиональная арматура нижней сетки
. Класс бетона B35 (Rb = 19,5 МПа). Кольцевая арматура нижней и верхней сеток и меридиональная арматура нижней сетки Радиус кривизны купола


Предельные погонные усилия в кольцевой арматуре купола
qs = (As,cb + As,cu)Rs = 2·0,628·415·10-1 = 52,124 кН/м;
q's = 0,628·360·10-1 = 22,608 кН/м;
h0 = 70 - 20 = 50 мм;
B = Rbh0 + qs + q's = 19,5·5·10 + 52,124 + 22,608 = 1049,7 кН/м.
Угловая координата границы сжатой зоны бетона  по формуле (5.1.16)
по формуле (5.1.16)
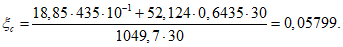
Из формул (5.1.17) и (5.1.18) получаем

Преобразуем это уравнение относительно M с учетом 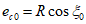
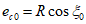
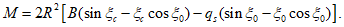
M = 2·302[1049,7·(0,05796 - 0,05799·0,8) -
- 52,124·(0,6 - 0,6435·0,8)] = 13863,5 кНм.
Из формулы (5.1.19) и таблицы 5.1.9 при равномерно распределенной нагрузке и опирании по всему контуру (k = 1/3)
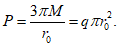
Несущая способность купола
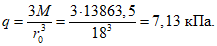
5.1.9 Предельная стадия работы тонкостенных куполов характеризуется влиянием изменения их геометрии под нагрузкой на несущую способность конструкции [2, 3]. В основе расчета несущей способности купола с учетом деформированного состояния лежит меридионально-кольцевая схема разрушения, представленная на рисунке 5.1.7.
Расстояние l1 до кольцевого пластического шарнира (рисунок 5.1.8) определяем по формуле
где  ;
; 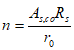 ;
; 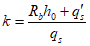 .
.
 ;
; 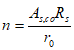 ;
; 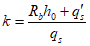 .
.Здесь As,co - площадь сечения кольцевых стержней опорного кольца;
Rs - расчетное сопротивление арматурных стержней опорного кольца;
h0 - рабочая высота сечения поля оболочки;
qs, q's - погонные усилия, воспринимаемые кольцевой арматурой купола, соответственно в растянутой и сжатой зонах рассматриваемого сечения купола.
В начальной стадии деформирования несущую способность оболочки определяют по формуле
где  <*>
<*>
 <*>
<*>
m - погонное значение предельного изгибающего момента в кольцевом пластическом шарнире
здесь As,mb - площадь сечения меридиональной арматуры нижней сетки на единицу длины кольцевого направления;
x - высота сжатой зоны сечения, определяемая с соблюдением условия 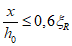 , где
, где  - граничное значение относительной высоты сжатой зоны по СП 63.13330.
- граничное значение относительной высоты сжатой зоны по СП 63.13330.
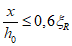 , где
, где При подстановке в (5.1.21) и в выражение для M <*> значениям w <*> = 0 получим предельную нагрузку для оболочки без учета деформированного состояния.
В предельном состоянии критическому значению прогиба соответствует значение:
Подставив (5.1.23) в (5.1.21), получим предельное значение нагрузки, отвечающее несущей способности оболочки с учетом деформированного состояния:
где 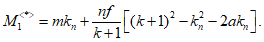 <*>
<*>
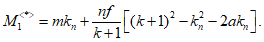 <*>
<*>Пример 3
Рассмотрим расчет несущей способности оболочки из примера 2 с учетом деформированного состояния.
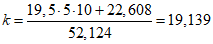 (q's и qs см. пример 2);
(q's и qs см. пример 2);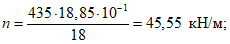
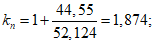
a = k + 1 - kn = 19,139 + 1 - 1,874 = 18,265;

k <*> = 182[1 + 1,874/20,139 + 1,8742/20,1392] = 356,955.
Граничная высота сжатой зоны бетона
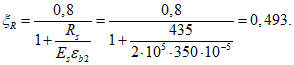

Предельный погонный изгибающий момент в кольцевом пластическом шарнире по формуле (5.1.22)
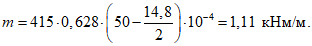
Определяем предельное значение нагрузки, отвечающее несущей способности оболочки с учетом деформированного состояния по формуле (5.1.24):
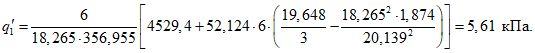
Несущая способность оболочки без учета деформированного состояния при w <*> = 0 по формуле (5.1.21) составит:

--------------------------------
Полученное значение несущей способности близко (с разницей в 3%) к найденному в примере 2, составляющему 7,13 кПа.
Поскольку значение несущей способности купола с учетом его деформированного состояния существенно ниже (на 19%), при проектировании следует ориентироваться на величину предельной нагрузки q'1 = 5,61 кПа.
5.2.1 Пологими считаются такие выпуклые оболочки на прямоугольном плане, у которых стрелы подъема на контуре не превышают 1/10 длины соответствующей стороны контура.
В качестве срединной поверхности пологих оболочек рекомендуется использовать поверхность переноса или вращения. Образующими для всех поверхностей рекомендуется принимать круговые кривые или близкие к круговым.
5.2.2 Гладкие и ребристые пологие оболочки следует конструировать в соответствии с разделом 4.
Толщина  и армирование средней зоны гладких оболочек, где действуют только сжимающие усилия, предварительно назначают конструктивно и проверяют расчетом на устойчивость.
и армирование средней зоны гладких оболочек, где действуют только сжимающие усилия, предварительно назначают конструктивно и проверяют расчетом на устойчивость.
В ребристых сборных оболочках толщину поля панелей средней зоны назначают с учетом технологических возможностей производства и проверяют расчетом на заданное значение расчетной нагрузки.
5.2.3 Толщину поля в приконтурных и угловых зонах оболочки рекомендуется увеличивать для размещения дополнительной арматуры и восприятия усилий, более высоких по сравнению с действующими в центральной зоне.
Толщину оболочки в угловой зоне назначают по расчету при соблюдении условия для главных растягивающих и главных сжимающих напряжений  ,
, 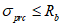 и с учетом обеспечения возможности размещения необходимого числа арматуры.
и с учетом обеспечения возможности размещения необходимого числа арматуры.
 ,
, 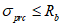 и с учетом обеспечения возможности размещения необходимого числа арматуры.
и с учетом обеспечения возможности размещения необходимого числа арматуры.Увеличение толщины сборной оболочки в угловых зонах рекомендуется выполнять с помощью набетонки монолитного железобетона, укладываемого поверх сборных плит. В пределах набетонки располагают дополнительную косую рабочую арматуру, устанавливаемую по расчету.
5.2.4 В приконтурных участках оболочки в зоне действия изгибающих моментов следует укладывать дополнительную арматуру. Если эта арматура воспринимает положительные моменты, то она располагается в нижней зоне плиты. Основную сетку при этом располагают в верхней зоне. Для восприятия растягивающих усилий, действующих параллельно контуру, у нижней грани оболочки на приопорных участках укладывают рабочую или конструктивную арматуру.
Для восприятия главных растягивающих напряжений, действующих в угловых зонах, к основной арматуре рекомендуется добавлять косую, перпендикулярную к диагонали плана. В оболочках пролетом более 40 м эту арматуру рекомендуется выполнять предварительно напряженной. Вблизи углов оболочки эту арматуру рекомендуется заменять обычной.
Арматуру для восприятия главных растягивающих напряжений принимают в виде отдельных стержней или сеток и располагают у верхней и нижней поверхностей плит оболочки.
В сборных оболочках плиты рекомендуется армировать сварными сетками и каркасами. В местах сопряжения полки с ребром рекомендуется устраивать вуты.
5.2.5 Оболочки по контуру следует опирать на диафрагмы, выполняемые в виде арок, ферм или балок, а также криволинейных брусьев, уложенных на стены или ряд колонн.
Контурные балки рекомендуется применять в отдельно стоящих оболочках при часто расположенных по периметру здания колоннах, а в многоволновых оболочках - по наружным рядам колонн.
Для пролетов 18 и 24 м контурные элементы принимают железобетонными, при больших пролетах рекомендуется применять раскосные стальные фермы или сталежелезобетонные криволинейные контурные брусья.
5.2.6 Усилия и деформации в отдельно стоящих оболочках рекомендуется определять расчетом методом конечных элементов с учетом конструктивных особенностей оболочек (наличие ребер, отверстий, переломов поверхности) и фактической жесткости бортовых диафрагм.
Предварительные расчеты пологих оболочек допускается выполнять по безмоментной теории с учетом краевого эффекта (11.10 - 11.12 СП 387.1325800.2018) или по моментной теории.
Безмоментную линейную теорию с учетом изгибающих моментов, возникающих в приопорных зонах, допускается применять для предварительных расчетов шарнирно-опертых гладких оболочек со стрелой подъема 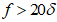 при равномерно распределенной нагрузке.
при равномерно распределенной нагрузке.
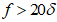 при равномерно распределенной нагрузке.
при равномерно распределенной нагрузке.5.2.7 Усилия при равномерно распределенной нагрузке при расчете отдельно стоящих квадратных в плане оболочек со сторонами l по моментной теории рекомендуется определять по формулам:
- нормальные силы N1 в направлении оси x и N2 в направлении оси y по линии y = 0
- сдвигающие усилия S по граням оболочки
- изгибающие моменты M в направлении оси x по линии y = 0
- поперечные силы Q, действующие по граням оболочки
- главные усилия Npr,1 и Npr,2, действующие в оболочке соответственно в направлении ее диагонали и нормально к ней
В формулах (5.2.1) - (5.2.5)  ,
,  , kM, kQ, kpr,1(2) - коэффициенты, принимаемые по таблицам 5.2.1 - 5.2.6 в зависимости от относительной координаты точки x/l (0 <= x/l <= 0,5) и значений параметра
, kM, kQ, kpr,1(2) - коэффициенты, принимаемые по таблицам 5.2.1 - 5.2.6 в зависимости от относительной координаты точки x/l (0 <= x/l <= 0,5) и значений параметра 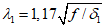 или
или 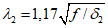 , равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции);
, равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции); 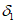 - толщина оболочки, приведенная по площади;
- толщина оболочки, приведенная по площади;  - толщина оболочки, приведенная по моменту инерции.
- толщина оболочки, приведенная по моменту инерции.
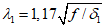 или
или 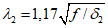 , равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции);
, равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции);  - толщина оболочки, приведенная по моменту инерции.
- толщина оболочки, приведенная по моменту инерции.x/l | Коэффициент 100 | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,05 | 0,1865 | 0,114 | 0,0587 | 0,0358 | 0,0238 | 0,0146 | 0,088 |
0,1 | 0,3655 | 0,2245 | 0,1153 | 0,0698 | 0,0468 | 0,0287 | 0,0176 |
0,15 | 0,5321 | 0,327 | 0,1684 | 0,1016 | 0,0685 | 0,0419 | 0,0256 |
0,2 | 0,6811 | 0,4199 | 0,2161 | 0,1308 | 0,0879 | 0,0539 | 0,0327 |
0,3 | 0,9149 | 0,5666 | 0,2921 | 0,1768 | 0,1188 | 0,0733 | 0,0442 |
0,4 | 1,0559 | 0,6563 | 0,3385 | 0,205 | 0,1379 | 0,0848 | 0,0512 |
0,5 | 1,1023 | 0,6864 | 0,354 | 0,2144 | 0,1441 | 0,0884 | 0,0535 |
x/l | Коэффициент 100 | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,02 | 0,3094 | 0,2577 | 0,1905 | 0,1494 | 0,122 | 0,0941 | 0,0698 |
0,05 | 0,7324 | 0,5963 | 0,4177 | 0,3059 | 0,2339 | 0,1618 | 0,1043 |
0,07 | 0,9715 | 0,7733 | 0,5158 | 0,3607 | 0,2608 | 0,168 | 0,1008 |
0,1 | 1,2517 | 0,9587 | 0,5839 | 0,3801 | 0,259 | 0,156 | 0,091 |
0,15 | 1,5174 | 1,0899 | 0,587 | 0,3474 | 0,2258 | 0,1352 | 0,0818 |
0,2 | 1,5819 | 1,0559 | 0,5229 | 0,3032 | 0,1985 | 0,1229 | 0,0743 |
0,3 | 1,4122 | 0,9057 | 0,4164 | 0,2506 | 0,1684 | 0,1039 | 0,0628 |
0,4 | 1,2 | 0,7271 | 0,3695 | 0,2236 | 0,1498 | 0,0924 | 0,0551 |
0,5 | 1,1023 | 0,6864 | 0,354 | 0,2144 | 0,1441 | 0,0884 | 0,0535 |
x/l | Коэффициент 100kS для определения сдвигающих усилий S при значениях | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 2,7015 | 1,917 | 1,0608 | 0,7112 | 0,5008 | 0,3439 | 0,225 |
0,05 | 2,6043 | 1,8166 | 0,9706 | 0,6272 | 0,4239 | 0,2749 | 0,1671 |
0,1 | 2,3519 | 1,6014 | 0,7859 | 0,4827 | 0,3103 | 0,1927 | 0,1154 |
0,15 | 2,0156 | 1,3295 | 0,6033 | 0,3576 | 0,2334 | 0,1441 | 0,0862 |
0,2 | 1,6509 | 1,0608 | 0,4594 | 0,271 | 0,1843 | 0,1114 | 0,0676 |
0,3 | 0,9843 | 0,6082 | 0,2597 | 0,1574 | 0,1171 | 0,065 | 0,0393 |
0,4 | 0,465 | 0,2732 | 0,1204 | 0,0734 | 0,0588 | 0,0301 | 0,0181 |
0,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
x/l | Коэффициент 100 kM для определения изгибающих моментов M1 при значениях | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,01 | 0,0514 | 0,0402 | 0,0275 | 0,0204 | 0,0159 | 0,0116 | 0,0082 |
0,02 | 0,0936 | 0,0715 | 0,0464 | 0,0326 | 0,0241 | 0,0162 | 0,01 |
0,03 | 0,1276 | 0,0979 | 0,0584 | 0,0388 | 0,0269 | 0,163 | 0,0088 |
0,04 | 0,1543 | 0,1118 | 0,0646 | 0,0403 | 0,0261 | 0,0141 | 0,0063 |
0,05 | 0,1743 | 0,1225 | 0,0667 | 0,0388 | 0,0232 | 0,0109 | 0,0038 |
0,07 | 0,1978 | 0,1307 | 0,0617 | 0,0305 | 0,015 | 0,0049 | 0,0006 |
0,08 | 0,202 | 0,13 | 0,057 | 0,024 | 0,01 | 0,0026 | -0,0001 |
0,09 | 0,203 | 0,125 | 0,049 | 0,019 | 0,007 | 0,001 | -0,0004 |
0,1 | 0,2016 | 0,1196 | 0,0438 | 0,0155 | 0,0047 | 0,0001 | -0,0004 |
0,12 | 0,1902 | 0,1038 | 0,0306 | 0,0076 | 0,0009 | -0,0007 | -0,0003 |
0,15 | 0,1611 | 0,0763 | 0,0146 | 0,0009 | -0,0012 | -0,0006 | 0 |
0,18 | 0,1271 | 0,0466 | 0,0041 | -0,0016 | -0,0008 | 0 | 0 |
0,2 | 0,1028 | 0,0351 | 0,0003 | -0,0009 | -0,0008 | 0 | 0 |
0,25 | 0,052 | 0,009 | -0,0003 | -0,0011 | -0,0001 | 0 | 0 |
0,3 | 0,0163 | 0 | -0,0002 | -0,0001 | 0 | 0 | 0 |
0,35 | -0,0031 | 0 | -0,0002 | 0 | 0 | 0 | 0 |
0,4 | -0,0998 | -0,0001 | 0 | 0 | 0 | 0 | 0 |
0,5 | -0,0178 | -0,0001 | 0 | 0 | 0 | 0 | 0 |
x/l | Коэффициент kQ для определения поперечных сил Q при значениях | ||||
4 | 5 | 7 | 9 | 11 | |
0 | 0 | 0 | 0 | 0 | 0 |
0,02 | 0,0328 | 0,0296 | 0,0256 | 0,0224 | 0,0204 |
0,04 | 0,0456 | 0,04 | 0,032 | 0,0268 | 0,0224 |
0,05 | 0,0512 | 0,044 | 0,0344 | 0,028 | 0,0232 |
0,07 | 0,0576 | 0,048 | 0,036 | 0,0284 | 0,0228 |
0,1 | 0,0628 | 0,0504 | 0,036 | 0,0272 | 0,0216 |
0,15 | 0,0636 | 0,0504 | 0,0336 | 0,0252 | 0,0208 |
0,2 | 0,0616 | 0,0484 | 0,032 | 0,0248 | 0,0204 |
0,25 | 0,0596 | 0,0464 | 0,0316 | 0,0248 | 0,0204 |
0,3 | 0,0584 | 0,0448 | 0,032 | 0,0252 | 0,0208 |
0,4 | 0,0564 | 0,0448 | 0,0316 | 0,0248 | 0,0204 |
0,5 | 0,056 | 0,0456 | 0,0316 | 0,0248 | 0,0208 |
x/l | y/l | Коэффициент 100kpr,1(2) для определения главных усилий Npr,1(2) при значениях | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | ||
Усилие в направлении диагонали | ||||||||
0 | 0,5 | 2,7015 | 1,917 | 1,0608 | 0,7112 | 0,5008 | 0,3439 | 0,225 |
0,1 | 0,4 | 2,4215 | 1,7104 | 0,9677 | 0,6069 | 0,4097 | 0,2492 | 0,1471 |
0,2 | 0,3 | 2,0819 | 1,3664 | 0,6799 | 0,3978 | 0,2623 | 0,1618 | 0,0981 |
0,3 | 0,2 | 1,6037 | 0,988 | 0,4799 | 0,2886 | 0,1941 | 0,1197 | 0,0756 |
0,5 | 0 | 1,1023 | 0,6864 | 0,354 | 0,2144 | 0,1441 | 0,0884 | 0,0535 |
Усилие перпендикулярно диагонали | ||||||||
0 | 0,5 | -2,7015 | -1,917 | -1,0608 | -0,7112 | -0,5008 | -0,3439 | -0,225 |
0,1 | 0,4 | -1,3087 | -0,7643 | -0,3008 | -0,1428 | -0,0873 | -0,0547 | -0,0362 |
0,2 | 0,3 | 0,1373 | 0,1704 | 0,0912 | 0,0424 | 0,0238 | 0,0173 | 0,009 |
0,3 | 0,2 | 0,8172 | 0,4997 | 0,2296 | 0,1374 | 0,0926 | 0,0571 | 0,0314 |
0,5 | 0 | 1,1023 | 0,6864 | 0,354 | 0,2143 | 0,144 | 0,0884 | 0,0534 |
В случае действия кососимметричной нагрузки (нагрузки одной величины, но разного знака на симметричных половинах плана оболочки) в формулах (5.2.1) - (5.2.3) коэффициенты 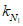 ,
, 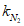 , kS, kM заменяются соответственно коэффициентами
, kS, kM заменяются соответственно коэффициентами 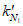 ,
, 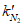 ,
, 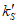 ,
,  , принимаемыми по таблицам 5.2.7 - 5.2.10 в зависимости от относительной координаты точки x/l (0 <= x/l <= 0,5) и значений параметра
, принимаемыми по таблицам 5.2.7 - 5.2.10 в зависимости от относительной координаты точки x/l (0 <= x/l <= 0,5) и значений параметра 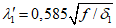 или
или  , равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции).
, равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции).
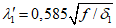 или
или  , равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции).
, равных 4, 5, 7, 9, 11, 14 и 18 (промежуточные значения принимаются по линейной интерполяции).x/l | Коэффициент | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,01 | 0,004 | 0,0022 | 0,0013 | 0,0009 | 0,0004 | 0,0004 | 0 |
0,02 | 0,0075 | 0,0049 | 0,0026 | 0,0013 | 0,0009 | 0,0004 | 0,0004 |
0,025 | 0,0093 | 0,0062 | 0,0031 | 0,0018 | 0,0013 | 0,0009 | 0,0004 |
0,035 | 0,0128 | 0,0084 | 0,0044 | 0,0026 | 0,0018 | 0,0009 | 0,0009 |
0,05 | 0,0186 | 0,0119 | 0,0062 | 0,0035 | 0,0026 | 0,0013 | 0,0009 |
0,07 | 0,0252 | 0,0164 | 0,0084 | 0,0049 | 0,0035 | 0,0022 | 0,0013 |
0,1 | 0,0349 | 0,0225 | 0,0115 | 0,0071 | 0,0049 | 0,0031 | 0,0018 |
0,15 | 0,0482 | 0,0309 | 0,0159 | 0,0097 | 0,0062 | 0,004 | 0,0022 |
0,2 | 0,0566 | 0,0362 | 0,0186 | 0,011 | 0,0075 | 0,0044 | 0,0026 |
0,25 | 0,0597 | 0,038 | 0,0194 | 0,0119 | 0,008 | 0,0049 | 0,0031 |
x/l | Коэффициент | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,01 | 0,0917 | 0,0734 | 0,0522 | 0,0402 | 0,0323 | 0,0247 | 0,0181 |
0,02 | 0,1786 | 0,1414 | 0,0977 | 0,0725 | 0,0557 | 0,0398 | 0,0265 |
0,025 | 0,2188 | 0,1719 | 0,1162 | 0,084 | 0,0627 | 0,0433 | 0,0278 |
0,035 | 0,2926 | 0,225 | 0,145 | 0,0999 | 0,0716 | 0,046 | 0,0278 |
0,05 | 0,3832 | 0,2846 | 0,1688 | 0,1096 | 0,0743 | 0,0447 | 0,026 |
0,07 | 0,4667 | 0,3297 | 0,1803 | 0,1083 | 0,0703 | 0,0442 | 0,0256 |
0,1 | 0,5149 | 0,3474 | 0,1737 | 0,1012 | 0,0667 | 0,0415 | 0,0252 |
0,15 | 0,5282 | 0,339 | 0,1618 | 0,0981 | 0,065 | 0,0402 | 0,0243 |
0,2 | 0,5021 | 0,3116 | 0,1587 | 0,0964 | 0,0641 | 0,0398 | 0,0239 |
0,25 | 0,4888 | 0,3072 | 0,1578 | 0,0959 | 0,0636 | 0,0393 | 0,0239 |
x/l | Коэффициент  | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,005 | 0,0129 | 0,01 | 0,0069 | 0,0051 | 0,004 | 0,03 | 0,022 |
0,01 | 0,0234 | 0,0179 | 0,0116 | 0,0082 | 0,0061 | 0,0041 | 0,0026 |
0,015 | 0,0319 | 0,0245 | 0,0146 | 0,0097 | 0,0068 | 0,0041 | 0,0022 |
0,02 | 0,0385 | 0,028 | 0,0162 | 0,01 | 0,0065 | 0,0036 | 0,0016 |
0,025 | 0,0437 | 0,0306 | 0,0167 | 0,0097 | 0,0058 | 0,0028 | 0,001 |
0,035 | 0,0495 | 0,0327 | 0,0154 | 0,0076 | 0,0038 | 0,0012 | 0,0002 |
0,05 | 0,0503 | 0,0299 | 0,01 | 0,0039 | 0,0012 | 0 | -0,0001 |
0,06 | 0,0479 | 0,026 | 0,0077 | 0,0019 | 0,0002 | -0,0002 | -0,0001 |
0,07 | 0,0429 | 0,0214 | 0,0049 | 0,0006 | -0,0002 | -0,0002 | 0 |
0,09 | 0,0319 | 0,0117 | 0,001 | -0,0004 | -0,0002 | 0 | 0 |
0,1 | 0,0262 | 0,0088 | 0,0001 | -0,0002 | -0,0002 | 0 | 0 |
0,15 | 0,0044 | 0 | 0 | 0 | 0 | 0 | 0 |
0,2 | -0,0017 | 0 | 0 | 0 | 0 | 0 | 0 |
0,25 | -0,0035 | 0 | 0 | 0 | 0 | 0 | 0 |
x/l | y/l | Коэффициент | ||||||
4 | 5 | 7 | 9 | 11 | 14 | 18 | ||
По граням y = +/- l/2 | ||||||||
0 | - | 0,6736 | 0,4778 | 0,2829 | 0,1887 | 0,1357 | 0,0906 | 0,0588 |
0,02 | - | 0,6577 | 0,4623 | 0,2678 | 0,1742 | 0,122 | 0,0777 | 0,0482 |
0,05 | - | 0,5856 | 0,3987 | 0,2135 | 0,13 | 0,0862 | 0,0525 | 0,0314 |
0,1 | - | 0,4111 | 0,2639 | 0,1291 | 0,0765 | 0,0508 | 0,0314 | 0,019 |
0,15 | - | 0,2449 | 0,1512 | 0,0751 | 0,0455 | 0,0305 | 0,019 | 0,0114 |
0,2 | - | 0,1154 | 0,0676 | 0,0354 | 0,0217 | 0,0146 | 0,088 | 0,0053 |
0,25 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
По граням x = 0 и x = l | ||||||||
- | 0,5 | 0,6736 | 0,4778 | 0,2829 | 0,1887 | 0,1357 | 0,0906 | 0,0588 |
- | 0,45 | 0,6184 | 0,3956 | 0,2152 | 0,1313 | 0,0871 | 0,053 | 0,0318 |
- | 0,4 | 0,4318 | 0,2749 | 0,1361 | 0,0809 | 0,0539 | 0,0332 | 0,0203 |
- | 0,3 | 0,2002 | 0,126 | 0,0645 | 0,0389 | 0,0261 | 0,0159 | 0,0097 |
- | 0,2 | 0,0968 | 0,0623 | 0,0318 | 0,019 | 0,0128 | 0,008 | 0,0049 |
- | 0,1 | 0,0402 | 0,0256 | 0,0133 | 0,008 | 0,0053 | 0,0031 | 0,0022 |
5.2.8 Расчет прогиба w отдельно стоящих квадратных в плане оболочек при действии равномерно распределенной нагрузки выполняется приближенно по безмоментной теории расчета применительно к оболочкам положительной кривизны, свободно опертым по контуру
где q - нормативное значение нагрузки;
R - радиус кривизны оболочки;
Задание: Запроектировать пологую сборную железобетонную оболочку покрытия здания на квадратном плане со сторонами размером l = 42 м (рисунок 5.2.1). Здание расположено в III снеговом районе. Сферическая поверхность оболочки имеет радиус R = 53,5 м. Оболочка собирается из ребристых цилиндрических плит номинальными размерами в плане 3 x 6 м. Монтаж оболочки ведется с помощью монтажных секций с размерами 3 x 18 м, собираемых из трех плит 3 x 6 м.

Определяем общие геометрические параметры оболочки:
- подъем оболочки f = fc + fk,
где 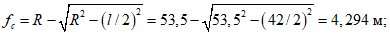
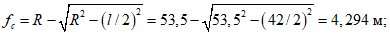
- радиус контура оболочки Rk = R - fc = 53,5 - 4,294 = 49,206 м;
- подъем оболочки на контуре f1 = f2 = fk
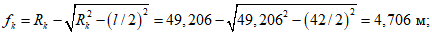
- общий подъем оболочки f = fc + fk = 4,294 + 4,706 = 9 м;
- толщину собственно оболочки (полки плиты) принимаем 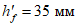 .
.
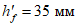 .
.Принимаем бетон класса B30 (Rb = 17,0 МПа, Rbt = 1,15 МПа, Eb = 32500 МПа).
Определяем геометрические характеристики плиты (рисунок 5.2.2):
площадь сечения плиты 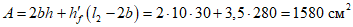 ;
;
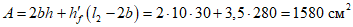 ;
;статический момент инерции относительно верхней грани полки (ось y0)
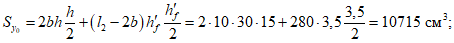
положение центра тяжести сечения 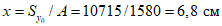 ;
;
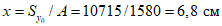 ;
;момент инерции относительно оси yc:
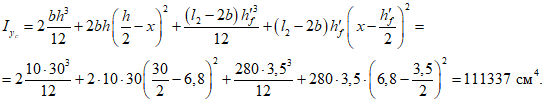
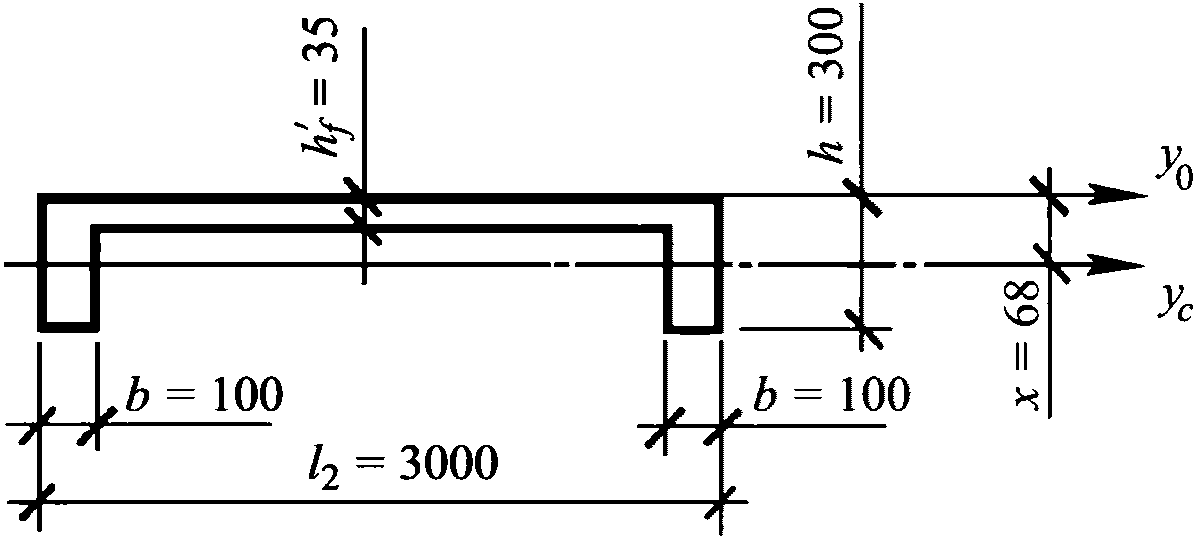
Определяем приведенную фиктивную толщину оболочки:
- по площади  (1 см учитывает бетон шва замоноличивания);
(1 см учитывает бетон шва замоноличивания);
 (1 см учитывает бетон шва замоноличивания);
(1 см учитывает бетон шва замоноличивания);- по моменту инерции
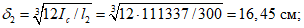
- по радиусу инерции
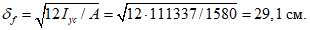
В соответствии с СП 20.13330 полное расчетное значение равномерной снеговой нагрузки на горизонтальную проекцию покрытия определяется по формуле

где Sg - вес снегового покрова на 1 м2 горизонтальной поверхности земли, который для III снегового района равен 1,5 кПа;
коэффициент  (по Б.11 СП 20.13330.2016 для купольных покрытий) равен 1,0 при
(по Б.11 СП 20.13330.2016 для купольных покрытий) равен 1,0 при  , угол наклона оболочки покрытия в поперечном направлении при пролете оболочки 42 м и радиусе кривизны R = 53,5 м:
, угол наклона оболочки покрытия в поперечном направлении при пролете оболочки 42 м и радиусе кривизны R = 53,5 м:  , поэтому по всей поверхности принят
, поэтому по всей поверхности принят 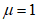 ;
;
 , угол наклона оболочки покрытия в поперечном направлении при пролете оболочки 42 м и радиусе кривизны R = 53,5 м:
, угол наклона оболочки покрытия в поперечном направлении при пролете оболочки 42 м и радиусе кривизны R = 53,5 м:  , поэтому по всей поверхности принят
, поэтому по всей поверхности принят термический коэффициент ct = 1;
коэффициент ветрового сноса по (10.3) СП 20.13330 ce = 0,85.
Сбор нагрузок на оболочку приведен в таблице 5.2.11.
Таблица 5.2.11
Вид нагрузки | Нормативная нагрузка, кПа | Расчетная нагрузка, кПа | |
Собственный вес плит оболочки со швами замоноличивания ( 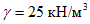 ; ;  ) ) | 1,575 | 1,1 | 1,73 |
Вес утеплителя (  ; ; 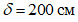 ) ) | 0,92 | 1,3 | 1,2 |
Вес цементной стяжки ( 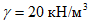 ; ;  ) ) | 0,6 | 1,3 | 0,78 |
Вес гидроизоляционного ковра и пароизоляции | 0,21 | 1,3 | 0,27 |
Итого | 4,58 | - | 5,77 |
Симметричная расчетная нагрузка составляет q = 5,77 кПа.
Проверка оболочки на устойчивость
Критическую нагрузку qcr определяем согласно СП 387.1325800 как для гладкой оболочки с приведенной (фиктивной) толщиной  . Фиктивный модуль упругости при расстоянии между ребрами плит b = 3,0 м:
. Фиктивный модуль упругости при расстоянии между ребрами плит b = 3,0 м: 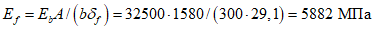 .
.
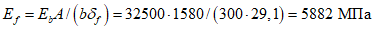 .
.Модуль деформации бетона при продолжительном действии нагрузки принят при средней относительной влажности воздуха 40% - 75%
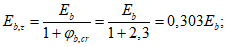
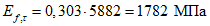 .
.Интенсивность допустимой критической нагрузки qcr не должна превышать интенсивности полной расчетной нагрузки q:
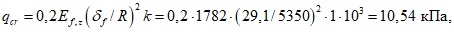
где k = 1 для сферической поверхности.
Устойчивость оболочки обеспечена, так как qcr = 10,54 кПа > q = 5,11 кПа.
Расчет оболочки на равномерно распределенную симметричную нагрузку
Определяем значения параметров  и
и  :
:
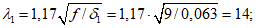

Проверяем принятую толщину полки плиты оболочки (в центре). Определяем нормальные усилия на 1 м длины
Nxx = Nyy = -ql2/(8f) = -5,77·422/(8·9) = -141,4 кН/м.
Напряжения в полке плиты  - принятая толщина полки
- принятая толщина полки 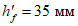 достаточна.
достаточна.
 - принятая толщина полки
- принятая толщина полки 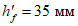 достаточна.
достаточна.Определяем наибольшие значения нормальных сил N1 и N2, действующих в поле оболочки (рисунок 5.2.3):
- в направлении оси x по линии y = 0 по (5.2.1):

x/l = 0, | N1 = -1615,6·0 = 0; |
x/l = 0,05, | N1 = -1615,6·0,0146 = -23,6 кН/м; |
x/l = 0,1, | N1 = -1615,6·0,0287 = -46,4 кН/м; |
x/l = 0,15, | N1 = -1615,6·0,0419 = -67,7 кН/м; |
x/l = 0,2, | N1 = -1615,6·0,0539 = -87,1 кН/м; |
x/l = 0,3, | N1 = -1615,6·0,0733 = -118,4 кН/м; |
x/l = 0,4, | N1 = -1615,6·0,0848 = -137,0 кН/м; |
x/l = 0,5 | N1 = -1615,6·0,0884 = -142,8 кН/м; |
- в направлении оси y по линии y = 0 по (5.2.1):

x/l = 0, | N2 = 0; |
x/l = 0,02, | N2 = -1615,6·0,0941 = -152,0 кН/м; |
x/l = 0,05, | N2 = -1615,6·0,1618 = -261,4 кН/м; |
x/l = 0,07, | N2 = -1615,6·0,168 = -271,4 кН/м; |
x/l = 0,1, | N2 = -1615,6·0,156 = -252,0 кН/м; |
x/l = 0,15, | N2 = -1615,6·0,1352 = -218,4 кН/м; |
x/l = 0,2, | N2 = -1615,6·0,1229 = -198,6 кН/м; |
x/l = 0,3, | N2 = -1615,6·0,1039 = -167,9 кН/м; |
x/l = 0,4, | N2 = -1615,6·0,0924 = -149,3 кН/м; |
x/l = 0,5, | N2 = -1615,6·0,0884 = -142,8 кН/м. |
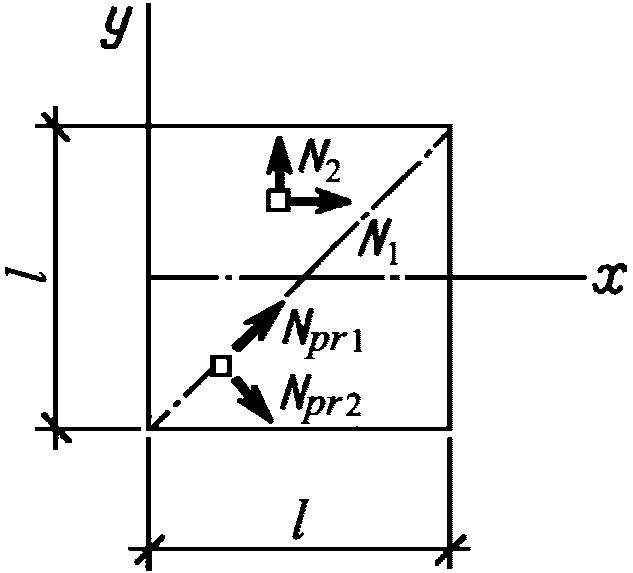
нормальных и главных усилий в оболочке
Наибольшие напряжения, действующие в поле оболочки, составляют
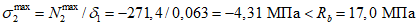 - прочность сечения оболочки обеспечена.
- прочность сечения оболочки обеспечена.Определяем сдвигающие усилия S по граням оболочки по (5.2.2):
S = 161560ks кН/м,
где коэффициент ks определяем по таблице 5.2.3 при 

x/l = 0, | S = 1615,6·0,3439 = 556 кН/м; |
x/l = 0,05, | S = 1615,6·0,2749 = 444 кН/м; |
x/l = 0,1, | S = 1615,6·0,1927 = 311 кН/м; |
x/l = 0,15, | S = 1615,6·0,1441 = 233 кН/м; |
x/l = 0,2, | S = 1615,6·0,1114 = 180 кН/м; |
x/l = 0,3, | S = 1615,6·0,065 = 105 кН/м; |
x/l = 0,4, | S = 1615,6·0,0301 = 49 кН/м; |
x/l = 0,5, | S = 1615,6·0 = 0. |
При равномерно распределенной нагрузке значительные моменты возникают только на приопорных участках оболочки. Определяем наибольшие изгибающие моменты, действующие в направлении оси x при y = 0 по (5.2.3):
M1 = 5,77·422kM = 10178kM,
где коэффициент kM находим по таблице 5.2.4.
Для  максимальное значение M1 - при x/l = 0,05.
максимальное значение M1 - при x/l = 0,05.
 максимальное значение M1 - при x/l = 0,05.
максимальное значение M1 - при x/l = 0,05.По интерполяции:

Определяем поперечные силы Q, действующие по граням оболочки по (5.2.4):
Q = 5,77·42·kQ = 242,3kQ кН/м,
где коэффициент kQ находим по таблице 5.2.5 при 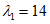 (так как в таблице нет значений kQ при
(так как в таблице нет значений kQ при  , принимаем в запас значения коэффициента kQ при
, принимаем в запас значения коэффициента kQ при 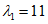 ):
):
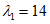 (так как в таблице нет значений kQ при
(так как в таблице нет значений kQ при  , принимаем в запас значения коэффициента kQ при
, принимаем в запас значения коэффициента kQ при x/l = 0, | Q = 242,3·0 = 0; |
x/l = 0,02, | Q = 242,3·0,0204 = 4,9 кН/м; |
x/l = 0,04, | Q = 242,3·0,0224 = 5,4 кН/м; |
x/l = 0,05, | Q = 242,3·0,0232 = 5,6 кН/м; |
x/l = 0,07, | Q = 242,3·0,0228 = 5,5 кН/м; |
x/l = 0,1, | Q = 242,3·0,0216 = 5,2 кН/м; |
x/l = 0,15, | Q = 242,3·0,0208 = 5,0 кН/м; |
x/l = 0,2, | Q = 242,3·0,0204 = 4,9 кН/м; |
x/l = 0,25, | Q = 242,3·0,0204 = 4,9 кН/м; |
x/l = 0,3, | Q = 242,3·0,0208 = 5,0 кН/м; |
x/l = 0,4, | Q = 242,3·0,0204 = 4,9 кН/м; |
x/l = 0,5, | Q = 242,3·0,0208 = 5,0 кН/м. |
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 5.2.4 отсутствует. |
Определяем главные усилия Npr,1 и Npr,2 (рисунок 5.2.4) по (5.2.5):
Npr,1(2) = -161560kpr,1(2),
где kpr,1(2) находим по таблице 5.2.7 при 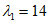 :
:
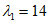 :
:- в направлении диагонали:
x/l = 0, | y/l = 0,5, | Npr,1 = -1615,6·0,3439 = -556 кН/м; |
x/l = 0,1, | y/l = 0,4, | Npr,1 = -1615,6·0,2492 = -403 кН/м; |
x/l = 0,2, | y/l = 0,3, | Npr,1 = -1615,6·0,1618 = -261 кН/м; |
x/l = 0,3, | y/l = 0,2, | Npr,1 = -1615,6·0,1197 = -193 кН/м; |
x/l = 0,5, | y/l = 0, | Npr,1 = -1615,6·0,0884 = -143,0 кН/м; |
- перпендикулярно к диагонали:
x/l = 0, | y/l = 0,5, | Npr,2 = -1615,6·(-0,3439) = 556 кН/м; |
x/l = 0,1, | y/l = 0,4, | Npr,2 = -1615,6·(-0,0547) = 88 кН/м; |
x/l = 0,2, | y/l = 0,3, | Npr,2 = -1615,6·0,0173 = -28 кН/м; |
x/l = 0,3, | y/l = 0,2, | Npr,2 = -1615,6·0,0571 = -92 кН/м; |
x/l = 0,5, | y/l = 0, | Npr,2 = -1615,6·0,0884 = -143,0 кН/м. |
Эпюры усилий приведены на рисунке 5.2.5.

ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |
Расчет оболочки при неравномерном распределении снега на покрытии
Равномерно распределенная нагрузка от покрытия без учета снеговой нагрузки составляет q1 = 3,98 кПа.
В соответствии с Б.11 СП 20.13330.2016 при неравномерном распределении снега на покрытии по варианту 2 коэффициент 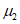 при z <= r1 = R sin 30° = 53,5·0,5 = 26,75 м вычисляется по формуле
при z <= r1 = R sin 30° = 53,5·0,5 = 26,75 м вычисляется по формуле 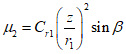 , где
, где 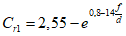 . Здесь f = fc = 4,294 м; d = l = 42 м; тогда Cr1 = 2,018.
. Здесь f = fc = 4,294 м; d = l = 42 м; тогда Cr1 = 2,018.
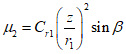 , где
, где 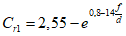 . Здесь f = fc = 4,294 м; d = l = 42 м; тогда Cr1 = 2,018.
. Здесь f = fc = 4,294 м; d = l = 42 м; тогда Cr1 = 2,018.В проектных расчетах, выполняемых с применением программных комплексов, следует использовать эпюру распределения коэффициента 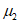 по СП 20.13330.
по СП 20.13330.
Для предварительных расчетов с использованием зависимостей моментной теории допустимо упрощение, заключающееся в приведении эпюры распределения к равномерной из равенства объемов эпюр и нагруженных площадей.
Для геометрических параметров данной оболочки объем эпюры распределения коэффициента 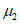 по СП 20.13330 на нагруженной снегом половине площади составляет 483 м2. Тогда расчетная равномерно распределенная снеговая нагрузка на половине площади оболочки составляет 1,79·483/(42·21) = 0,98 кПа.
по СП 20.13330 на нагруженной снегом половине площади составляет 483 м2. Тогда расчетная равномерно распределенная снеговая нагрузка на половине площади оболочки составляет 1,79·483/(42·21) = 0,98 кПа.
Представляем снеговую нагрузку в виде симметричной q5 = 0,98/2 = 0,49 кПа и кососимметричной q4 = +/- 0,49 кПа составляющих (рисунок 5.2.6, а).

а - симметричное и кососимметричное распределения снеговой
нагрузки; б - полная нагрузка на покрытие (план)
Симметричная нагрузка, включающая вес снега q5 и вес покрытия q1, составит
q6 = q1 + q5 = 3,98 + 0,49 = 4,47 кПа.
Полная нагрузка на левой и правой сторонах покрытия, как показано на рисунке 5.2.6, б, составляет соответственно
q2 = q6 + q4 = 4,47 + 0,49 = 4,96 кПа;
q3 = q6 - q4 = 4,47 - 0,49 = 3,98 кПа.
Находим коэффициенты 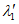 и
и  для кососимметричной нагрузки:
для кососимметричной нагрузки:
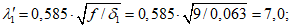
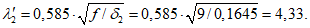
Для симметричной нагрузки 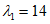 и
и 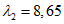 .
.
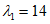 и
и 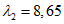 .
.Определяем наибольшие значения изгибающих моментов, действующих в направлении оси x при y = 0 по (5.2.3), коэффициент kM находим по таблице 5.2.4 при 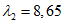 , а
, а  - по таблице 5.2.10 при
- по таблице 5.2.10 при 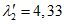 .
.
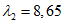 , а
, а 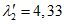 .
.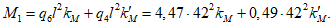
Наибольшие значения изгибающих моментов получаются при x/l = 0,05 и составляют 

Определяем наибольшие значения нормальных сил N1, действующих в направлении оси x по линии y = 0 по (5.2.1). Коэффициенты 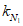 находим по таблице 5.2.1 при
находим по таблице 5.2.1 при  , а
, а  - по таблице 5.2.7 при
- по таблице 5.2.7 при 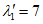
 , а
, а 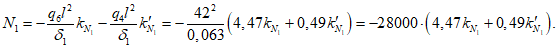
Наибольшие значения N1 получаются при x/l = 0,5.
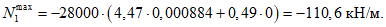
Определяем нормальные силы N2 в направлении оси y по линии y = 0 по (5.2.1). Коэффициенты 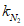 находим по таблице 5.2.2 при
находим по таблице 5.2.2 при 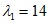 ,
, 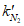 - по таблице 5.2.8 при
- по таблице 5.2.8 при 
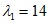 ,
, 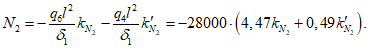
Наибольшие значения N2 получаются при x/l = 0,07.

Наибольшие напряжения, действующие в поле оболочки при несимметричной нагрузке, составляют  , что меньше, чем при симметричной нагрузке (4,31 МПа).
, что меньше, чем при симметричной нагрузке (4,31 МПа).
 , что меньше, чем при симметричной нагрузке (4,31 МПа).
, что меньше, чем при симметричной нагрузке (4,31 МПа).Сдвигающие усилия по граням оболочки определяем по (5.2.2), коэффициенты kS - по таблице 5.2.3 при  , а
, а 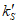 - по таблице 5.2.9 при
- по таблице 5.2.9 при 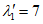
 , а
, а 
По граням y = +/- l/2:
x/l = 0, | S = 280·(4,47·0,3439 + 0,49·0,2829) = 469,2 кН/м; |
x/l = 0,05, | S = 280·(4,47·0,2749 + 0,49·0,2135) = 373,4 кН/м; |
x/l = 0,1, | S = 280·(4,47·0,1927 + 0,49·0,1291) = 258,9 кН/м; |
x/l = 0,15, | S = 280·(4,47·0,1441 + 0,49·0,0751) = 190,7 кН/м; |
x/l = 0,2, | S = 280·(4,47·0,1114 + 0,49·0,0354) = 144,3 кН/м; |
x/l = 0,3, | S = 280·(4,47·0,065 - 0,49·0,0354) = 76,5 кН/м; |
x/l = 0,4, | S = 280·(4,47·0,0301 - 0,49·0,1291) = 20,0 кН/м; |
x/l = 0,5, | S = 280·(4,47·0 - 0,49·0,2829) = -38,8 кН/м. |
По граням x = 0, x = l:
u/l = 0,5, | S = 280·(4,47·0,3439 + 0,49·0,2829) = 469,2 кН/м; |
u/l = 0,45, | S = 280·(4,47·0,2749 + 0,49·0,2152) = 373,6 кН/м; |
u/l = 0,4, | S = 280·(4,47·0,1927 + 0,49·0,1361) = 259,9 кН/м; |
u/l = 0,3, | S = 280·(4,47·0,1114 + 0,49·0,0645) = 148,3 кН/м; |
u/l = 0,2, | S = 280·(4,47·0,065 + 0,49·0,0318) = 85,7 кН/м; |
u/l = 0,1, | S = 280·(4,47·0,0301 + 0,49·0,0133) = 39,5 кН/м; |
u/l = 0, | S = 0. |
Полученные сдвиговые усилия при односторонней снеговой нагрузке ниже значений усилий, полученных от равномерно распределенной симметричной нагрузки. Поэтому расчет прочности в дальнейшем производим по усилиям, полученным от симметричной нагрузки.
Эпюры сдвигающих усилий приведены на рисунке 5.2.7.
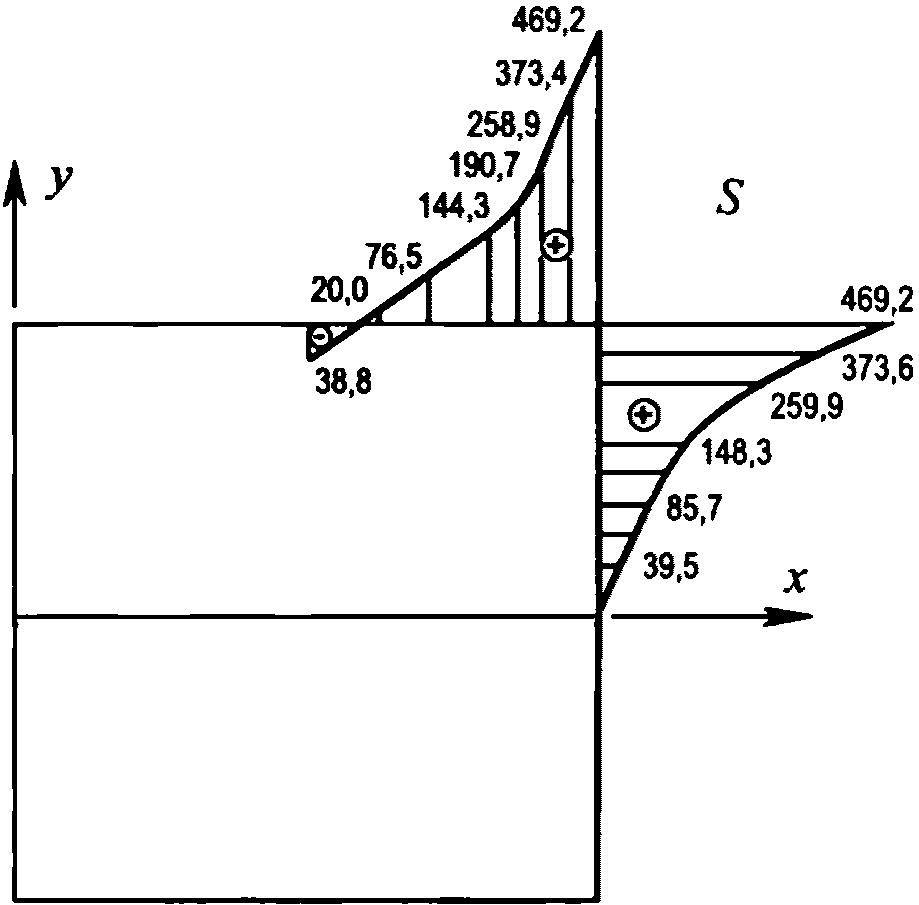
неравномерной снеговой нагрузки
Расчет приконтурной зоны оболочки
Для восприятия главных растягивающих усилий Npr,2 в углах пологой оболочки необходимо установить дополнительную арматуру, а для восприятия усилий Npr,1 - выполнить набетонку.
Для армированной набетонки принимаем арматуру класса A500 (Rs = 435 МПа) и бетон класса B25 (Rb = 14,5 МПа). Эпюру главных растягивающих сил Npr,2 разбиваем на участки длиной 0,1 диагонали оболочки, на границах которых определяем значения усилий по диагонали (рисунок 5.2.8).
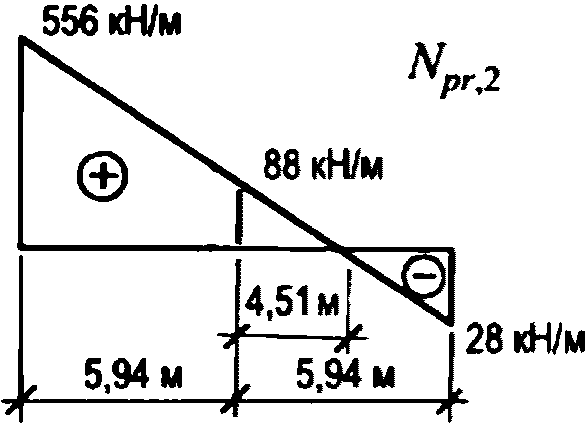
На первом участке со средним усилием Npr,2 = (556 + 88)/2 = 322 кН/м требуемое количество арматуры As = Npr,2/Rs = 32200/4350 = 7,4 см2/м.
На втором участке со средним усилием Npr,2 = 88/2 = 44 кН/м требуемое количество арматуры As = 4400/4350 = 1,01 см2/м.
Принимаем на первом участке стержневую арматуру  A500 с шагом 0,15 м, а на втором участке -
A500 с шагом 0,15 м, а на втором участке -  A500 с шагом 0,3 м. Дополнительно все поле набетонки армируем сеткой из арматуры класса B500
A500 с шагом 0,3 м. Дополнительно все поле набетонки армируем сеткой из арматуры класса B500 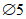 с шагом 200 x 200 мм.
с шагом 200 x 200 мм.
Определяем толщину набетонки по усилиям Npr,1 (рисунок 5.2.9).

Толщину набетонки определяем из условия Nc <= RbAb, где Ab = hb - площадь сжатой зоны бетона. Принимаем b = 1 пог. м. Тогда толщина набетонки h = Nc/Rb. На первом участке h1 = 5560/1450 = 3,8 см; на втором участке h2 = 4030/1450 = 2,8 см. Учитывая, что толщина полки плиты 35 мм, на других участках набетонку не делают.
Расчет прогиба оболочки
Расчет прогиба выполняем по формуле (5.2.6)
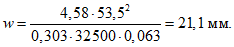
w/l = 21,1/42000 ~= 1/2000, что значительно меньше максимально допустимого по СП 387.1325800 значения прогиба, равного (1/400)l.
Расчет плиты
В сборных элементах оболочки - плитах (рисунок 5.2.10) наибольшие усилия возникают в монтажной стадии, когда плита работает на нагрузку собственного веса.
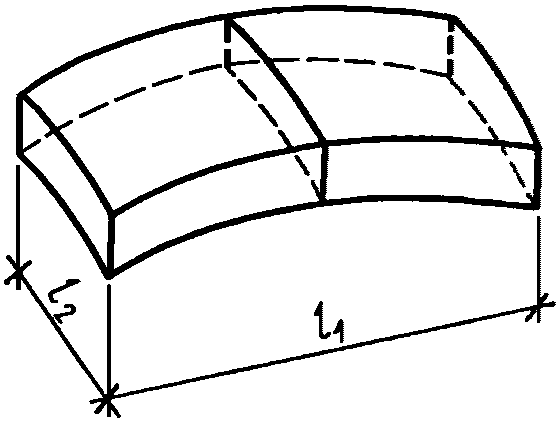
Нормативная нагрузка от собственного веса плиты без учета швов замоноличивания
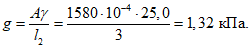
С учетом коэффициента динамичности при монтаже, равного 1,4, нагрузка на 1 м2 плиты
g = 1,32·1,4 = 1,84 кПа.
На два ребра приходится нагрузка
q = gl2 = 1,84·3 = 5,53 кН/м.
Определяем момент в ребрах:
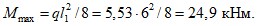
Расчетное сечение плиты приведено на рисунке 5.2.11. В расчете учтены свесы полки суммарной шириной, равной 12 толщинам полки. Расчет выполняется по СП 63.13330.
Здесь b = 20 см (на два ребра), h0 = h - a = 30 - 4 = 26 см, Rb = 17 МПа; Rbt,ser = 1,75 МПа.
Проверяем условие
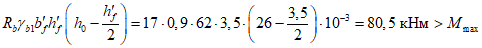 - сжатая зона сечения располагается в полке.
- сжатая зона сечения располагается в полке.При расчете без учета верхней арматуры (в запас):
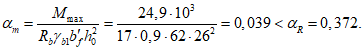
Принимаем арматуру в ребрах класса A500 с Rs = 435 МПа (на два ребра):
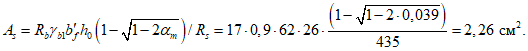
Принимаем в каждом ребре 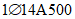 с площадью 1,54 см2.
с площадью 1,54 см2.
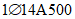 с площадью 1,54 см2.
с площадью 1,54 см2.5.2.9 Несущая способность поля плиты сборной оболочки определяется методом предельного равновесия, при этом схема разрушения поля плиты принимается аналогичной конвертной схеме разрушения плоских плит, опертых по контуру (рисунок 5.2.12). В отличие от последних, части сечения по линиям излома вдоль криволинейных сторон плиты также криволинейные.
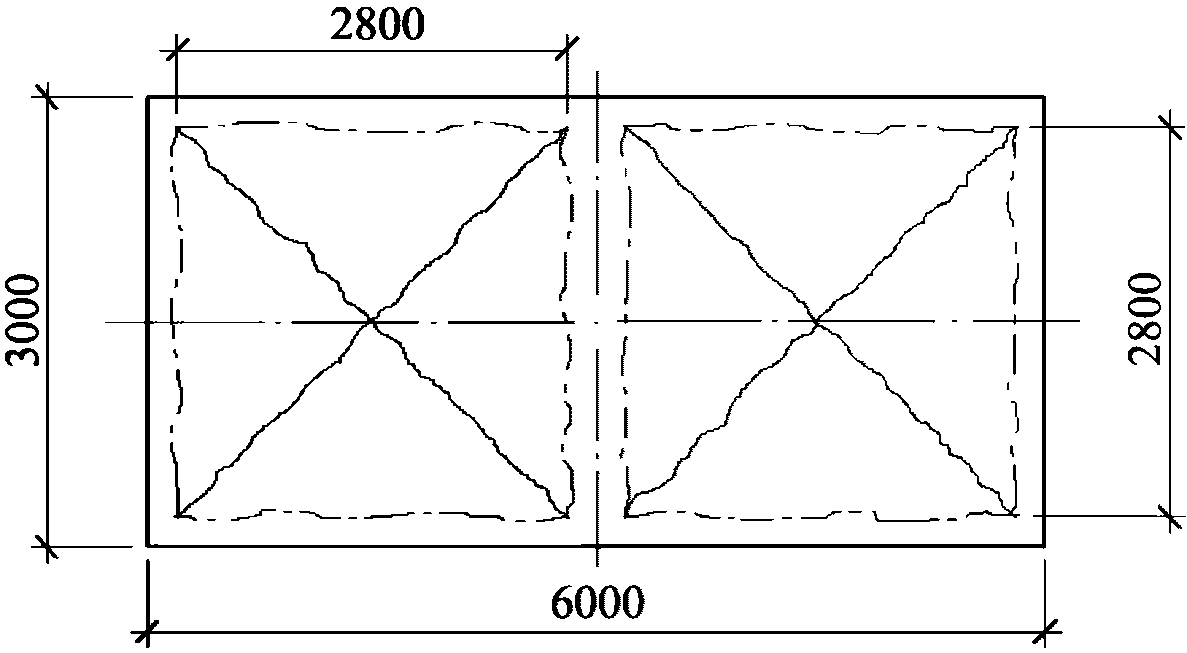
В криволинейных сечениях длину x участков сжатия согласно СП 387.1325800 рекомендуется находить из условия равновесия по формуле
где fs - площадь арматуры на единицу длины сечения полки;
r - радиус кривизны панели;
Предельный момент 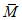 в криволинейном сечении определяют по формуле
в криволинейном сечении определяют по формуле
где
Значение предельной нагрузки q на единицу площади проекции полки при принятом армировании определяют по формуле
где 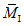 ,
, 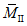 ,
, 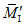 ,
,  ,
, 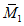 ,
, 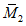 - предельные моменты в сечениях; индексы I и II относятся к опорным сечениям, 1 и 2 - к пролетным;
- предельные моменты в сечениях; индексы I и II относятся к опорным сечениям, 1 и 2 - к пролетным;
ls1, ls2 - пролеты полки (расстояние между внутренними гранями ребер).
Задание: определить несущую способность поля панелей оболочки из примера 4. Армирование поля панелей арматурой 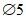 мм класса B500 в виде сварной сетки с шагом арматуры 150 мм в обоих направлениях (fs = 1,307 см2/м; Rs = 435 МПа; Rsc = 415 МПа).
мм класса B500 в виде сварной сетки с шагом арматуры 150 мм в обоих направлениях (fs = 1,307 см2/м; Rs = 435 МПа; Rsc = 415 МПа).
Размеры сторон зоны разрушения принимаются равными шагу ребер за вычетом их ширины: ls1 = ls2 = 2,8 м (рисунок 5.2.12).
Определяем значение угла 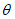 :
:

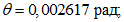

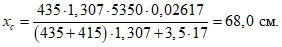

В связи со значительной пологостью оболочки расстояние z между центрами тяжести арматуры и сжатой зоны бетона в криволинейной линии излома оказалось меньше значения  для поля плиты: z = 0,92 см < h0 = 1,75 см. В этом случае не учитываем криволинейность линии излома и принимаем
для поля плиты: z = 0,92 см < h0 = 1,75 см. В этом случае не учитываем криволинейность линии излома и принимаем 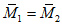 ;
;  ;
; 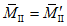 .
.
 для поля плиты: z = 0,92 см < h0 = 1,75 см. В этом случае не учитываем криволинейность линии излома и принимаем
для поля плиты: z = 0,92 см < h0 = 1,75 см. В этом случае не учитываем криволинейность линии излома и принимаем 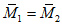 ;
;  ;
; 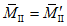 .
.Определяем значения x по прямолинейным линиям излома

Изгибающие моменты на единицу длины линии излома:


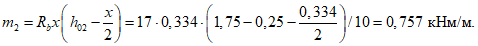
В нашем случае формула (5.2.10) приобретает вид

Собственный вес плиты толщиной 35 мм составляет
g = 0,035·25·1,1 = 0,963 кПа.
Расчетная нагрузка на 1 м2 плиты без учета массы ребер (таблица 5.2.11)
q* = 5,77 - 1,73 + 0,963 = 5,003 кПа < 5,28 кПа, следовательно, принятое армирование поля плиты удовлетворяет условием прочности.
Пример 6
Задание: определить несущую способность поля цилиндрической плиты с учетом изгибающего момента 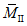 в криволинейной линии излома опорного сечения. Радиус кривизны цилиндрической поверхности r = 23 м, как в плитах типовых цилиндрических оболочек размерами 18 x 24 м и 18 x 30 м. Прочие геометрические и физические характеристики - по примеру 5.
в криволинейной линии излома опорного сечения. Радиус кривизны цилиндрической поверхности r = 23 м, как в плитах типовых цилиндрических оболочек размерами 18 x 24 м и 18 x 30 м. Прочие геометрические и физические характеристики - по примеру 5.
Размеры сторон зоны разрушения (рисунок 5.2.12) принимаются равными расстоянию между внутренними гранями ребер, т.е. ls1 = ls2 = 2,8 м.
Определяем значение угла 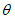 :
:

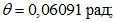

В криволинейных сечениях длину xc участков сжатия находим по формуле (5.2.7)

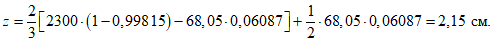


Изгибающие моменты на единицу длины линии излома:
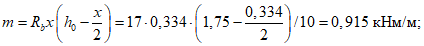
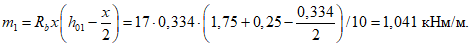
Изгибающие моменты на длине линии излома:


Определяем q по формуле (5.2.10), преобразованной для данного случая:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
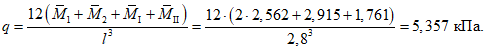
По сравнению с расчетом плиты-оболочки как плоской плиты ее несущая способность увеличилась на 7,1%. Такой расчет рекомендуется выполнять для расчета несущей способности поля плит, расположенных в приконтурной зоне. Армирование поля плит вне приконтурной зоны может быть уменьшено учетом сжимающих усилий, действующих вдоль криволинейной образующей панелей, в соответствии с СП 387.1325800.
5.2.10 Расчет опорного контура выполняется на действие краевых нагрузок от оболочки (сдвигающих сил S и поперечных сил Q) и от массы контура. Значения Q и S принимаются в предположении, что оболочка шарнирно закреплена на "идеальном" (абсолютно жестком в плоскости и гибком из плоскости) контуре. Упругая податливость контура вдоль оси в расчете не учитывается. Контурный пояс рассчитывается как многократно статически неопределимая криволинейная многопролетная балка. Силы Q и S считаются приложенными в центре тяжести пояса.
Пример 7
Задание: запроектировать опорный контур оболочки по примеру 4. Контурный ригель сборно-монолитный, сечением 600 x 400 мм в сборной части, армированный стальными профилями в сборной части и стержневой арматурой в монолитной части. Ригель опирается на колонны с шагом 6 м.
Распределение усилий получено при расчете оболочки на равномерно распределенную симметричную нагрузку (рисунок 5.2.5). На рисунке 5.2.13 показаны геометрическая схема контура и эпюры S и Q как исходные данные для расчета контура.

а - геометрическая схема контура; б - схема разбивки контура
на участки; в - эпюры усилий S и Q на контуре оболочки;
г - схема действия усилий S и Q
Определяем нагрузки на опорный контур (контурный ригель). Для этого контур разбиваем на равные участки 1 ... 12 (рисунок 5.2.13, а, б), на границах которых находим сосредоточенные силы S и Q, направленные по горизонтали и вертикали.
Определяем сосредоточенные сдвигающие силы S в точках 1 ... 12 (рисунок 5.2.13, в):
S1 = 556·1 м = 556 кН;
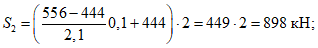
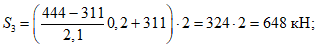
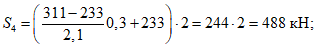


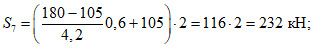
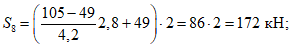
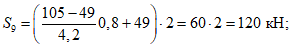
S10 = 49·3·2/4,2 = 70 кН;
S11 = 49·1·2/4,2 = 23 кН; S12 = 0.
Вычисляем сосредоточенные поперечные силы Q в точках 1 ... 12:
Q1 = 0; Q2...4 = 5,6·2 = 11,2 кН; Q5...11 = 5,0·2 = 10,0 кН; Q12 = 5,0·1 = 5,0 кН.
Радиус контура Rk = 49,206 м, стрела подъема оболочки fk = 4,706 м (пример 4).
Определяем вертикальные и горизонтальные составляющие сил Q и S (рисунок 5.2.13, г):

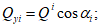
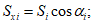
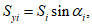
где 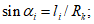
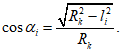
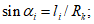
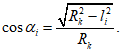
Высоты подъема точек 1 ... 12 на контуре:
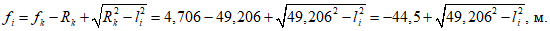
Результирующие вертикальные и горизонтальные силы, действующие на контур:
Pxi = Qxi + Sxi и Pyi = Qyi + Syi.
Результаты расчета приведены в таблице 5.2.12.
Номер точки | Значения параметров | ||||||||||
fki, мм | Qi, кН | Qxi, кН | Qyi, кН | Si, кН | Sxi, кН | Syi, кН | Pxi, кН | Pyi, кН | |||
1 | 0,4268 | 0,9044 | 0 | 0 | 0 | 0 | -556 | -503 | 237 | -503 | 237 |
2 | 0,3860 | 0,9224 | 0,89 | 11,2 | 4,3 | 10,1 | -898 | -828 | 347 | -824 | 357 |
3 | 0,3450 | 0,9384 | 1676 | 11,2 | 3,9 | 10,5 | -648 | -608 | 224 | -604 | 234 |
4 | 0,3048 | 0,9524 | 2364 | 11,2 | 3,4 | 10,7 | -488 | -465 | 149 | -462 | 160 |
5 | 0,2642 | 0,9645 | 2958 | 10,0 | 2,6 | 9,6 | -380 | -367 | 100 | -364 | 110 |
6 | 0,2235 | 0,9747 | 3461 | 10,0 | 2,2 | 9,7 | -302 | -294 | 67 | -292 | 77 |
7 | 0,1829 | 0,9831 | 3876 | 10,0 | 1,8 | 9,8 | -232 | -228 | 42 | -226 | 52 |
8 | 0,1423 | 0,9898 | 4206 | 10,0 | 1,4 | 9,9 | -172 | -170 | 24 | -169 | 34 |
9 | 0,1016 | 0,9948 | 4451 | 10,0 | 1,0 | 9,9 | -120 | -119 | 12 | -118 | 22 |
10 | 0,061 | 0,9981 | 4614 | 10,0 | 0,6 | 10,0 | -70 | -70 | 4 | -69 | 14 |
11 | 0,0203 | 0,9998 | 4696 | 10,0 | 0,2 | 10,0 | -23 | -23 | 0,5 | -23 | 10 |
12 | 0 | 1 | 4706 | 5,0 | 0 | 5,0 | 0 | 0 | 0 | 0 | 5 |
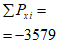 |  | ||||||||||
Определяем нормальные усилия в контурном ригеле в сечениях 1 ... 12:
 или
или 
N12 = 0; | N6 = 605 + 292 = 897 кН; |
N11 = 23 кН; | N5 = 897 + 364 = 1261 кН; |
N10 = 23 + 69 = 92 кН; | N4 = 1261 + 462 = 1723 кН; |
N9 = 92 + 118 = 210 кН; | N3 = 1723 + 604 = 2327 кН; |
N8 = 210 + 169 = 379 кН; | N2 = 2327 + 824 = 3151 кН; |
N7 = 379 + 226 = 605 кН; | N1 = 3151 + 503 = 3654 кН. |
Наибольшее растягивающее усилие в центре ригеля N = 3654 кН.
Вес ригеля сечением 600 x 400 мм: 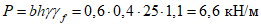 .
.
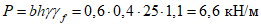 .
.При монтаже оболочки нагрузка на ригель от веса монтажной секции пролетом 18 м с весом плит 1,73 кН/м2 составляет q1 = 1,73·18/2 = 15,6 кН/м.
С учетом веса ригеля нагрузка на ригель составляет q2 = 15,6 + 6,6 = 22,2 кН/м.
Максимальное значение распределенных поперечных сил, действующих в контуре оболочки, Qmax = 5,6 кН/м. От этой нагрузки, прибавляя вес ригеля, определяем изгибающий момент в ригеле как в неразрезной балке (рисунок 5.2.14):
q3 = Qmax + P = 5,6 + 6,6 = 12,2 кН/м; Mmax = q3l2/12 = 12,2·62/12 = 36,6 кНм.
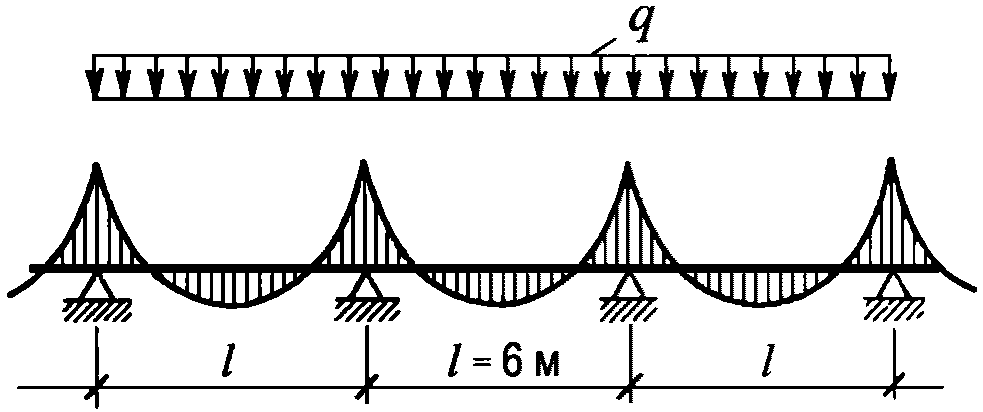
Расчетные комбинации усилий в ригеле:
- эксплуатационная N11 = 3654 кН; M1 = 36,6 кНм;
- монтажная N12 = 0; M2 = M = 22,2·62/12 = 66,6 кНм.
Расчет контурного ригеля на монтажную нагрузку
Схема армирования ригеля приведена на рисунке 5.2.15.

сталежелезобетонного ригеля
Геометрические характеристики двутавра N 36 по ГОСТ 8239: A1 = 61,9 см2; Ix = 13380 см4; Wx = 743 см3; Ry = 310 МПа (сталь класса С345 по ГОСТ 27772).
Ригель рассчитываем как изгибаемый металлический элемент:
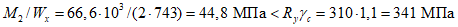 - прочность ригеля в сечении на изгибающий момент в стадии монтажа обеспечена.
- прочность ригеля в сечении на изгибающий момент в стадии монтажа обеспечена.Расчет контурного ригеля в стадии эксплуатации
Растягивающая сила N11 = 3654 кН воспринимается арматурой и прокатными двутаврами (рисунок 5.2.15). Принимаем арматуру 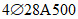 с A2 = 24,63 см2 и Rs = 435 МПа.
с A2 = 24,63 см2 и Rs = 435 МПа.
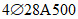 с A2 = 24,63 см2 и Rs = 435 МПа.
с A2 = 24,63 см2 и Rs = 435 МПа.Определяем доли усилия, воспринимаемые отдельно двумя двутаврами сборного элемента и арматурой монолитной части пропорционально предельным усилиям растяжения в них:
N1 = 2A1Ry = 2·61,9·310/10 = 3838 кН; N2 = A2Rs = 24,63·435/10 = 1071 кН.
Соответственно доля усилия, воспринимаемая стальными двутаврами - 78,2%, доля усилия, воспринимаемая арматурой - 21,8%.
Усилия, возникшие в двутаврах и в арматуре

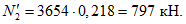
Проверяем прочность сечений прокатных элементов и стержневой арматуры:


Расчет стыка контурного ригеля
Проводим расчет по равнопрочности сечений. Усилие, которое может воспринять полка двутавра N 36: Nf = AfRy = 17,835·310/10 = 552,9 кН. Усилие, которое может воспринять стенка двутавра (рисунок 5.2.16): Nw = AwRy = 25,155·310/10 = 779,8 кН.
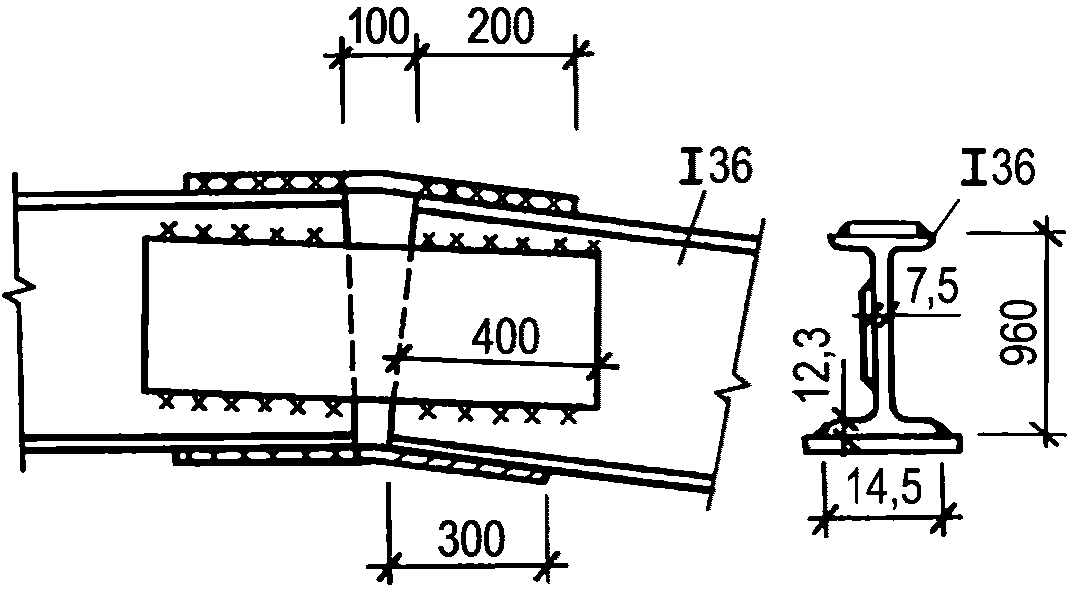
Накладки принимаем из стали С245 с Ry = 235 МПа. Площадь верхней накладки A1 = 12,0·1,6 = 19,2 см2, нижней накладки A2 = 25,0·1,6 = 40 см2, накладки на стенку двутавра A3 = 30,0·1,2 = 36 см2.
Усилие, которое могут воспринять накладки N = (19,2 + 40 + 36) 235/10 = 2237 кН. Ввиду того, что ригель состоит из двух двутавров, 2N = 4474 кН > Nmax = 3654 кН - прочность стыка по сечению накладок обеспечена.
Пример 8
Задание: подобрать сечения элементов монтажной секции пролетом 18 м из трех плит 3 x 6 м (рисунок 5.2.17). Нагрузка от собственного веса плиты q1 = 1,6 кПа. Монтажная нагрузка p = 0,7 кПа.
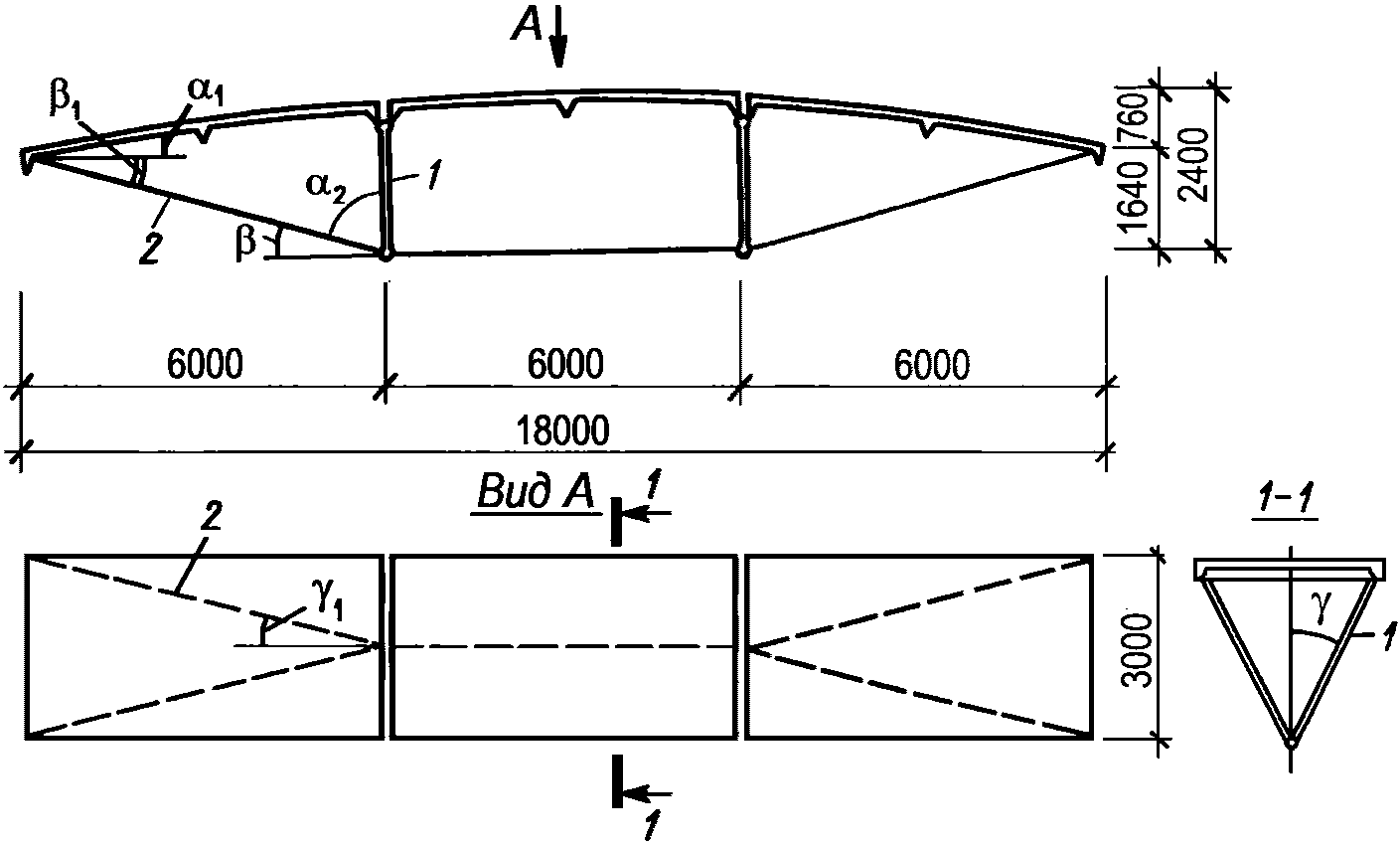
1 - стойка шпренгеля; 2 - опорный подкос
из трех плит 3 x 6 м
Монтажную секцию рассчитываем как шпренгельную ферму.
Геометрические параметры фермы:
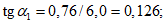
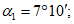

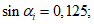
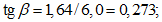
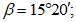
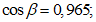

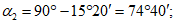


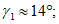
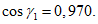
Нагрузка собственного веса плиты с учетом коэффициента динамичности, равного 1,4, составляет q2 = 1,6·1,4 = 2,24 кПа. Нагрузка собственного веса плиты с учетом монтажной нагрузки, равной p = 0,7 кПа, составляет 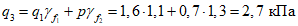 , что больше q2 = 2,24 кПа, где
, что больше q2 = 2,24 кПа, где  и
и  - коэффициенты надежности по нагрузке.
- коэффициенты надежности по нагрузке.
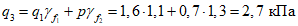 , что больше q2 = 2,24 кПа, где
, что больше q2 = 2,24 кПа, где Равномерно распределенная погонная нагрузка на секцию q = 2,7·3 = 8,1 кН/м.
Усилие в нижнем поясе шпренгеля H = ql2/(8f) = 8,1·18,02/(8·2,5) = 131,22 кН.
Усилие в наклонном элементе нижнего пояса (опорный подкос):

Усилие в стойке 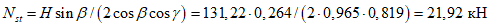 .
.
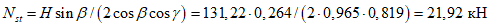 .
.Определяем сечения элементов шпренгеля.
Сечение нижнего пояса 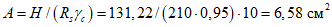 , где Rs = 210 МПа для арматуры класса A240;
, где Rs = 210 МПа для арматуры класса A240; 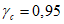 - коэффициент условий работы. Принимаем нижний пояс из арматуры
- коэффициент условий работы. Принимаем нижний пояс из арматуры 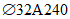 площадью сечения 8,04 см2.
площадью сечения 8,04 см2.
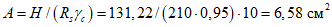 , где Rs = 210 МПа для арматуры класса A240;
, где Rs = 210 МПа для арматуры класса A240; 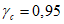 - коэффициент условий работы. Принимаем нижний пояс из арматуры
- коэффициент условий работы. Принимаем нижний пояс из арматуры 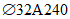 площадью сечения 8,04 см2.
площадью сечения 8,04 см2.Сечение опорного подкоса 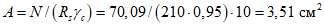 . Принимаем опорный подкос из арматуры
. Принимаем опорный подкос из арматуры 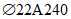 с площадью сечения 3,8 см2.
с площадью сечения 3,8 см2.
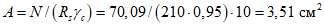 . Принимаем опорный подкос из арматуры
. Принимаем опорный подкос из арматуры 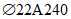 с площадью сечения 3,8 см2.
с площадью сечения 3,8 см2.Определяем сечение стойки.
Требуемая площадь сечения стойки при расчете на осевое сжатие 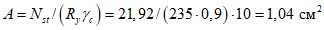 , где Ry = 235 МПа для труб из стали С245.
, где Ry = 235 МПа для труб из стали С245.
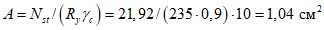 , где Ry = 235 МПа для труб из стали С245.
, где Ry = 235 МПа для труб из стали С245.Требуемая площадь сечения стойки при расчете на устойчивость:  .
.
 .
.При длине стойки lef = 2200 мм и гибкости 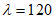 требуемый радиус инерции
требуемый радиус инерции 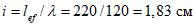 .
.
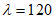 требуемый радиус инерции
требуемый радиус инерции 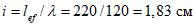 .
.Принимаем трубу  с радиусом инерции i = 1,95 см и площадью сечения A = 8,64 см2. Тогда гибкость
с радиусом инерции i = 1,95 см и площадью сечения A = 8,64 см2. Тогда гибкость 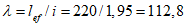 . По СП 16.13330 определяем коэффициент
. По СП 16.13330 определяем коэффициент 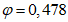 при
при 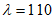 и Ry = 235 МПа.
и Ry = 235 МПа.
 с радиусом инерции i = 1,95 см и площадью сечения A = 8,64 см2. Тогда гибкость
с радиусом инерции i = 1,95 см и площадью сечения A = 8,64 см2. Тогда гибкость 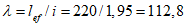 . По СП 16.13330 определяем коэффициент
. По СП 16.13330 определяем коэффициент 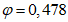 при
при 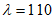 и Ry = 235 МПа.
и Ry = 235 МПа.Напряжение в сечении 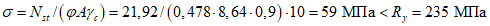 .
.
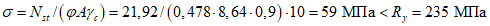 .
.В результате расчета шпренгельной фермы как статически неопределимой системы построены эпюры усилий M, Q и N, приведенные на рисунке 5.2.18.
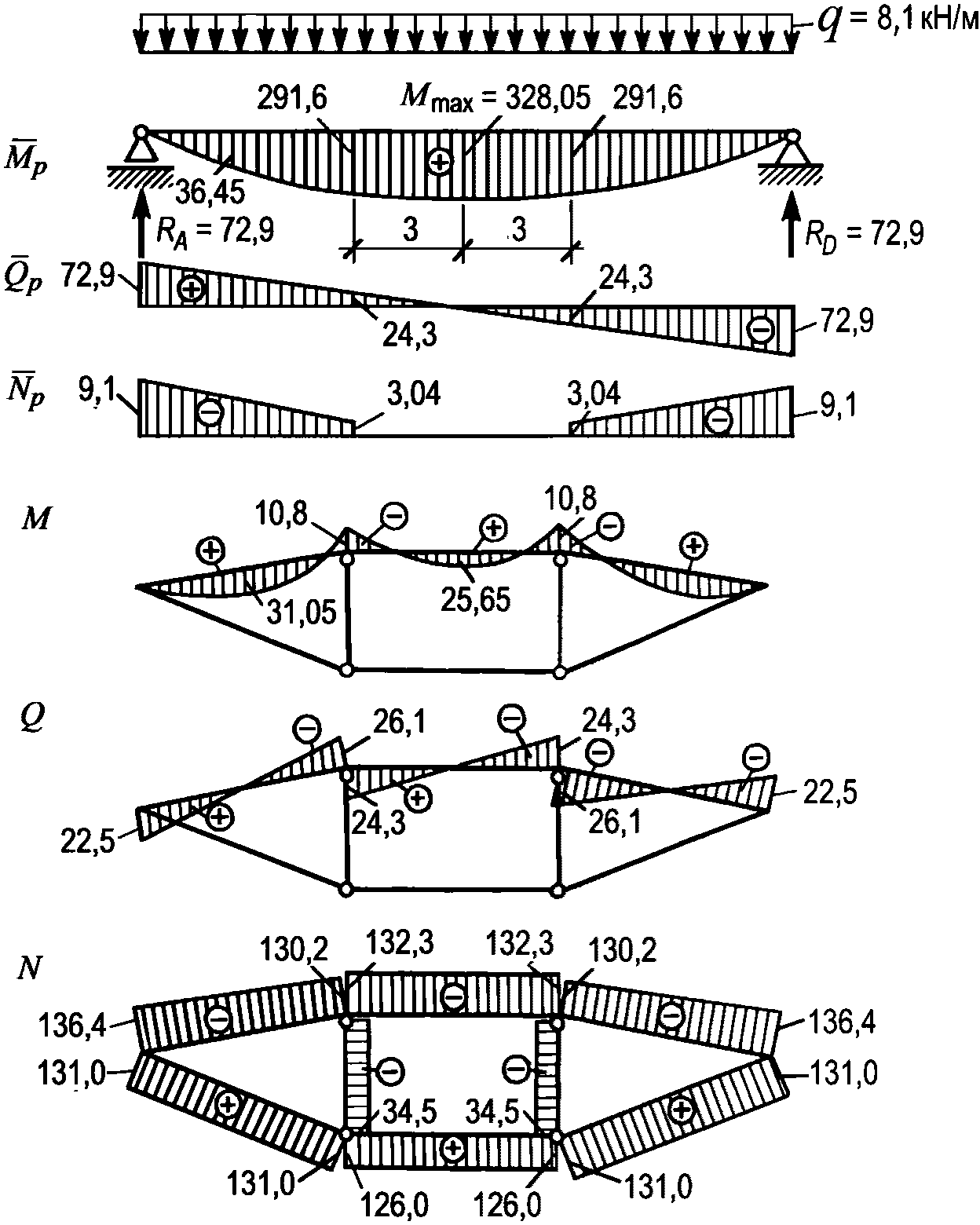
шпренгельной фермы на полную расчетную нагрузку
Из сравнения полученных усилий с усилиями, воспринимаемыми элементами шпренгельной фермы, можно делать вывод, что шпренгельная ферма с принятыми сечениями элементов удовлетворяет требованиям по прочности и жесткости.
5.3.1 Цилиндрическими оболочками (рисунок 5.3.1) называют тонкостенные конструкции, состоящие из следующих основных элементов:
- тонкой плиты, очерченной по цилиндрической поверхности (собственно оболочки);
- бортовых элементов, окаймляющих оболочку вдоль крайних образующих;
- поперечных диафрагм по криволинейным краям, опирающихся на колонны или стены.

1 - бортовой элемент; 2 - цилиндрические панели;
3 - затяжки торцевой диафрагмы
К длинным цилиндрическим оболочкам относятся цилиндрические оболочки с отношением расстояния между осями опорных диафрагм (пролет оболочки) l1 к расстоянию между бортовыми элементами l2 (длина волны) l1/l2 >= 1 [4].
5.3.2 Высоту оболочки h, включая высоту сечения бортовой балки, рекомендуется назначать равной (1/6 - 1/8)l1, а стрелу подъема f - равной (1/6 - 1/8)l2.
Продольные края оболочки в пролете могут быть свободными или опираться на колонны или стены.
Поперечное сечение оболочек рекомендуется принимать кругового очертания, как наиболее простое в производстве работ.
5.3.3 Сборные и сборно-монолитные цилиндрические оболочки выполняют ребристыми, монолитные, как правило, - гладкими.
Ребристые монолитные оболочки рекомендуется применять в тех случаях, когда вследствие наличия сосредоточенных нагрузок, особенностей очертания оболочки, условий ее опирания, больших пролетов или других причин для гладкой оболочки требуется большая толщина и устройство массивных бортовых элементов.
Во избежание местной потери устойчивости монолитной оболочки между поперечными ребрами расстояние между ними рекомендуется назначать не больше, чем  , где r - радиус кривизны оболочки, tcur,pl - толщина оболочки.
, где r - радиус кривизны оболочки, tcur,pl - толщина оболочки.
 , где r - радиус кривизны оболочки, tcur,pl - толщина оболочки.
, где r - радиус кривизны оболочки, tcur,pl - толщина оболочки.5.3.4 Бортовые элементы для оболочек со свободно висящими краями рекомендуется принимать в виде балок, расположенных ниже края оболочки. Размеры сечений бортовых элементов определяют по расчету и с учетом конструктивных требований. Рекомендуемые размеры сечения бортового элемента: высота d = (0,3 ... 0,5)h, ширина (2 ... 4)tcur,pl. Высоту сечения бортовых элементов рекомендуется принимать равной 1/20 - 1/30 пролета l1.
Многоволновые оболочки следует проектировать монолитно связанными между собой и с общими бортовыми элементами - крайними и промежуточными. Промежуточные бортовые элементы, соединяющие отдельные волны многоволновых оболочек, проектируют аналогично крайним бортовым элементам.
5.3.5 Средние и торцевые диафрагмы цилиндрических оболочек устраивают обычно в виде арок с затяжкой (рисунок 5.3.1) - как наиболее экономичных по расходу материалов.
При небольшом пролете волны оболочки и небольшой стреле подъема f диафрагмы проектируют в виде балок переменной высоты. Для облегчения диафрагмы и пропуска коммуникаций в стенке балок устраивают отверстия.
Допускается проектировать диафрагмы других видов, например, при опирании на стену - в виде криволинейного бруса.
5.3.6 При наличии скалывающих напряжений на опорах более 0,8Rbt рекомендуется, не утолщая всей оболочки или складки, предусматривать местные утолщения у опор, которые при определении усилий не учитываются.
5.3.7 Элементы сборных оболочек допускается проектировать из разных материалов: бортовые балки и диафрагмы - из бетонов высоких марок с применением предварительного напряжения; элементы оболочек - из легких или ячеистых бетонов для обеспечения, кроме несущих и ограждающих функций, функции теплоизоляции.
5.3.8 Продольную рабочую арматуру рекомендуется располагать в основном в нижней части бортовых элементов, оставшуюся часть - по высоте сечения бортовых элементов или в их верхней зоне. Кроме основной арматуры в бортовых элементах устанавливается поперечная и монтажная арматура. Арматуру бортовых элементов оболочек и арматуру затяжек диафрагм рекомендуется выполнять предварительно напряженной.
В неразрезных многопролетных оболочках кроме основной растянутой арматуры в пролете следует устанавливать арматуру в верхней части оболочки для восприятия растягивающих напряжений над опорами (диафрагмами), располагая ее в средней зоне растянутой части дуги.
Не менее 50% растянутой арматуры над опорой следует продлевать на длину 1,2b0 в каждую сторону от диафрагмы (b0 - расстояние от опоры до сечения с нулевыми моментами).
5.3.9 В сжатой зоне оболочки, а также на участках, где главные растягивающие напряжения меньше Rbt, следует устанавливать конструктивную продольную арматуру с шагом 150 - 250 мм, площадью сечения не менее 0,2% сечения бетона.
Сечение арматуры, необходимое для обеспечения прочности оболочки при действии поперечных изгибающих моментов, следует определять как для плит. По длине волны арматура, воспринимающая поперечные моменты, устанавливается соответственно эпюре моментов в растянутой зоне. В местах примыкания плит к бортовым элементам и диафрагмам следует устанавливать двойные сетки из арматуры диаметром 5 - 8 мм с шагом стержней не более 20 см.
В ребристых оболочках ребра, воспринимающие поперечные моменты, следует армировать двойной арматурой с поперечными стержнями, а плита армируется конструктивно - одиночной сеткой.
5.3.10 На участках, где  , требуемое сечение арматуры следует определять по растягивающим напряжениям, действующим под углом 45° к образующей. Значение этих напряжений определяется по формуле
, требуемое сечение арматуры следует определять по растягивающим напряжениям, действующим под углом 45° к образующей. Значение этих напряжений определяется по формуле
 , требуемое сечение арматуры следует определять по растягивающим напряжениям, действующим под углом 45° к образующей. Значение этих напряжений определяется по формуле
, требуемое сечение арматуры следует определять по растягивающим напряжениям, действующим под углом 45° к образующей. Значение этих напряжений определяется по формуле (5.3.1)
(5.3.1)где 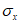 и
и  - соответственно нормальные и сдвигающие напряжения, действующие в рассматриваемой точке.
- соответственно нормальные и сдвигающие напряжения, действующие в рассматриваемой точке.
В местах, где арматурной сетки недостаточно для восприятия главных растягивающих усилий, следует устанавливать дополнительные арматурные стержни под углом 45° к образующей или усиливать арматурную сетку дополнительными стержнями.
Сечение арматуры на единицу длины должно удовлетворять условию
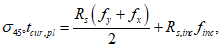 (5.3.2)
(5.3.2)где fy, fx, finc - сечения арматуры продольного направления, арматуры поперечного направления и косой (установленной под углом 45° к образующей) арматуры соответственно на единицу длины плиты;
Rs,inc - расчетное сопротивление косой арматуры плиты.
Принятые сечения арматуры продольного и поперечного направления не должны различаться более чем на 20%.
Стержни косой арматуры и арматуры поперечного направления, воспринимающие главные растягивающие усилия, должны быть заанкерены в бортовом элементе. Выше нейтральной оси арматурные стержни должны быть заведены не менее чем на 20 диаметров за сечение, где главные растягивающие напряжения могут быть восприняты основной сеткой.
5.3.11 Конструкцию стыка между элементами в сборных оболочках и складках следует принимать в зависимости от характера и значений передающихся через стык усилий.
В средней части оболочек и складок, в нормальных сечениях которой действуют в основном сжимающие усилия, стыки допускается выполнять путем омоноличивания шпоночных швов бетоном.
Стыки бортовых элементов, в нормальных сечениях которых действуют значительные растягивающие усилия, рекомендуется выполнять предварительно напряженными, с использованием напрягаемой арматуры в качестве расчетного армирования. Арматуру размещают в специально оставленных в бортовых элементах каналах и закрепляют по торцам оболочки. Для обеспечения совместной работы предварительно напряженной арматуры с бетоном каналы заполняются цементным тестом под давлением.
Стыки в продольных сечениях оболочек, в которых помимо сдвигающих и незначительных нормальных сил действуют изгибающие моменты и перерезывающие силы, выполняют сваркой выпусков арматуры ребер соединяемых элементов или сваркой с помощью накладок закладных деталей элементов и последующим омоноличиванием бетоном.
Стыки смежных элементов угловых зон оболочек, где действуют значительные по значению главные растягивающие усилия, выполняют сваркой выпусков арматуры элементов или сваркой с помощью накладок закладных деталей элементов, или путем установки в заранее предусмотренные в элементах углубления сварных каркасов в соответствии с СП 387.1325800.
5.3.12 В общем случае определение усилий в длинных цилиндрических и складчатых оболочках рекомендуется производить с учетом деформации поперечного контура в соответствии с полумоментной теорией. При этом изгибающие моменты M1, действующие на площадках поперечного сечения оболочки, соответствующие им поперечные силы Q1, а также крутящие моменты T и T1 ввиду их незначительности принимают равными нулю (рисунок 5.3.2). Силы N, действующие нормально к площадкам продольного сечения, а также возникающие на тех же площадках поперечные силы Q учитывают в расчете, но не учитывают при подборе сечений. Размеры сечений определяют по нормальным усилиям N1, действующим на площадках поперечного сечения, скалывающим усилиям S и изгибающим моментам M, действующим на площадках продольного сечения оболочки или складки.
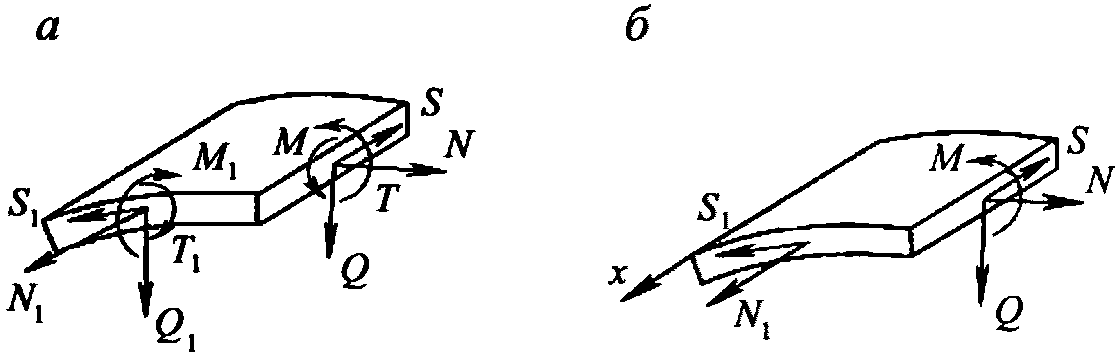
а - полная схема усилий; б - усилия, учитываемые при расчете
цилиндрических оболочках
5.3.13 В частных случаях (например, для оболочек, опертых по углам, при действии равномерно распределенной нагрузки и значении отношения l1/l2 >= 1, при повышенной жесткости поперечных ребер и др.), когда взаимное влияние поперечных изгибающих моментов и продольных нормальных усилий отсутствует или незначительно, выполняют расчет оболочки как балки криволинейного поперечного сечения (рисунок 5.3.3).
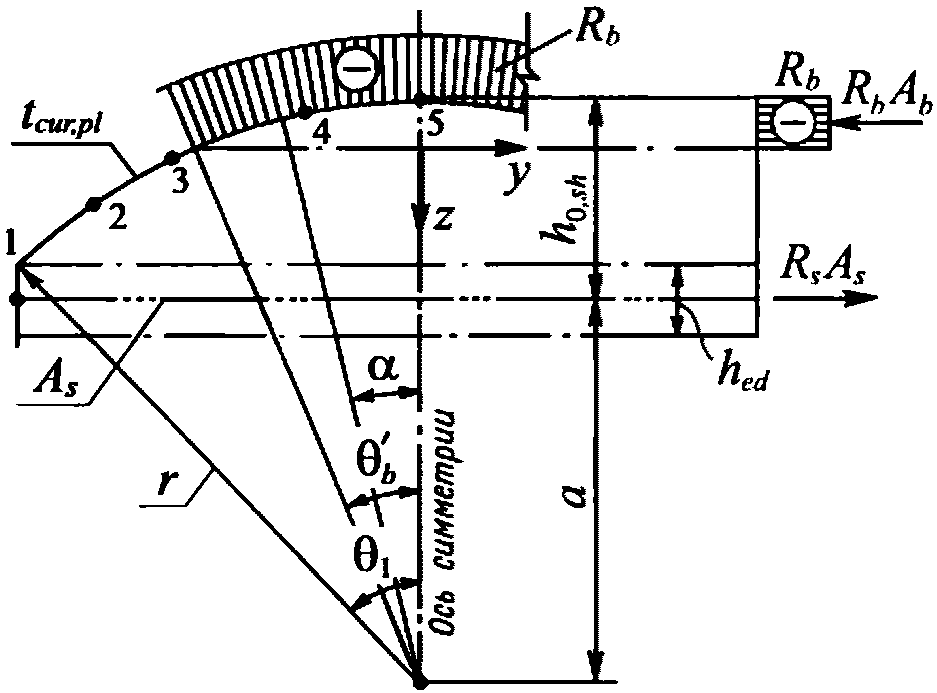
нормальном к продольной оси изгибаемой цилиндрической
оболочки, при расчете по прочности
При очертании криволинейной части сечения оболочки по дуге окружности момент внутренних сил относительно центра дуги поперечного сечения оболочки
Условие равновесия продольных сил в сечении
В формулах (5.3.3) и (5.3.4):
a - расстояние от центра дуги поперечного сечения оболочки до центра рабочей продольной арматуры;
ИС МЕГАНОРМ: примечание. Обозначение дано в соответствии с официальным текстом документа. |
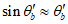 определяется по формуле
определяется по формулеh0,sh = r - a - расстояние от центра рабочей продольной арматуры до осевой линии дуги поперечного сечения оболочки.
Полная площадь сечения растянутой арматуры, размещаемой в одной бортовой балке, вычисляется по формуле
В промежуточной бортовой балке площадь арматуры As должна быть удвоена.
5.3.14 В многоволновых покрытиях, опертых по углам, крайние полуволны допускается рассчитывать по упрощенной схеме - как полуволны одноволновой оболочки. Средние волны многоволновых оболочек и складок допускается рассчитывать как оболочки, у которых продольные края закреплены от смещений в горизонтальной плоскости и поворота в плоскости поперечного сечения.
5.3.15 Расчет оболочки после назначения ее геометрических размеров выполняют в следующей последовательности:
- предварительно определяют требуемое сечение продольной арматуры бортовых элементов по формуле
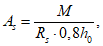 (5.3.7)
(5.3.7)где M - изгибающий момент от внешних нагрузок в расчетном поперечном сечении оболочки;
h0 - рабочая высота сечения оболочки, равная полной высоте за вычетом расстояния от нижней грани бортового элемента до равнодействующей усилий в растянутой арматуре;
- проводят расчет оболочки в упругой постановке с учетом арматуры бортовых элементов;
- по полученным из этого расчета усилиям подбирают арматуру поперечного направления плиты по СП 63.13330;
- на основе расчета на предыдущем этапе по СП 63.13330 находят положение равнодействующей усилий в сжатой зоне сечения, расстояния от нее до центра тяжести растянутого бетона zb и арматуры zs и значение момента внешних сил Mcrc, соответствующего появлению трещин;
- проводят расчет оболочки с учетом трещин и по СП 63.13330 определяют перемещения оболочки и ширину раскрытия трещин в бортовых элементах;
Во избежание хрупкого разрушения оболочек в углах от скалывания значение скалывающих напряжений должно быть не более 2,5Rbt. На участках, где напряжения скалывания больше указанного значения, необходимо выполнять местное утолщение плиты. При этом выполнять перерасчет конструкции в целом не требуется.
5.3.17 Расчет по прочности, жесткости и трещиностойкости длинных цилиндрических оболочек следует проводить с учетом образования трещин в бортовых элементах и в плите, и трещин вдоль образующих в плите или трещин в поперечных ребрах (в том числе образовавшихся на стадии монтажа конструкции) в соответствии с СП 63.13330. Допускается не учитывать при расчете косые трещины в углах оболочки.
Расчет по образованию трещин в нормальных сечениях и вдоль образующих следует проводить с учетом неупругих деформаций бетона в растянутой зоне.
Усилия для расчета длинных цилиндрических и складчатых оболочек по образованию и раскрытию трещин, по жесткости и прочности следует определять по 5.3.12 с учетом деформаций поперечного контура как для упругой системы.
5.3.18 Расчет по прочности, жесткости и раскрытию трещин оболочки с трещинами в продольных сечениях допускается выполнять на действие только изгибающих моментов по СП 63.13330.
Расчет оболочки по прочности следует проводить с учетом перераспределения усилий между их продольными сечениями. Образование трех продольных пластических шарниров приводит к значительному увеличению деформаций и раскрытию трещин.
Задание: для покрытия здания с сеткой колонн 12 x 30 м запроектировать сборную железобетонную цилиндрическую оболочку. Здание расположено в III снеговом районе.
Конструкция оболочки включает в себя бортовые элементы, окаймляющие оболочку вдоль крайних образующих. Бортовые элементы изготавливаются отдельно длиной на пролет, т.е. 30 м, в виде сборных преднапряженных балок. Криволинейная часть оболочки состоит из сборных железобетонных ребристых панелей цилиндрической формы с размерами в плане 3 x 12 м.
Панели смежных волн опираются на общий для них бортовой элемент, где замоноличиваются, образуя жесткий узел. Шаг бортовых элементов принят равным шагу колонн, т.е. 12 м. Таким образом, оболочка представляет собой однопролетную многоволновую конструкцию. Поперечное сечение балки принято переменной высоты - на опорах 800 мм, а в середине пролета - 1400 мм, при этом верхнему поясу придано сегментное очертание, в результате чего оболочка имеет небольшую вторую кривизну в продольном направлении.
Торцевая диафрагма оболочки имеет пролет 12 м и принята в виде арки, верхним поясом которой служит ребро торцевой панели. Затяжка этой арки изготавливается отдельно в виде железобетонного предварительно напряженного бруса.
Конструкция оболочки показана на рисунках 5.3.1 и 5.3.4.

а - сечение оболочки посередине пролета;
б - поперечное сечение бортовой балки посередине пролета
цилиндрической оболочки
Элементы оболочки выполняются из тяжелого бетона класса B35 (Rb = 19,5 МПа, Rbt = 1,3 МПа, Eb = 34,5·103 МПа).
Нагрузки на оболочку, принятые в расчете, приведены в таблице 5.3.1.
Вид нагрузки | Нормативное значение нагрузки, кПа | Коэффициент надежности по нагрузке | Расчетное значение нагрузки, кПа |
Собственная масса оболочки, приведенная к горизонтальной проекции | 2,5 | 1,1 | 2,75 |
Теплоизоляция, пароизоляция, гидроизоляционный ковер | 1,3 | 1,3 | 1,69 |
Снег (III район), Sg = 1,5 кПа | 1,28 <*> | 1,4 | 1,8 |
ИТОГО | 5,08 | 6,24 | |
<*> Коэффициент ce, учитывающий снос снега покрытия, принят равным 0,85. Снеговая нагрузка принята равномерно распределенной | |||
Определяем геометрические характеристики оболочки.
Назначаем высоту поперечного сечения оболочки hsh посередине пролета, включая сечение бортовой балки, равной 3100 мм, что соответствует примерно l1/10, а стрелу подъема fcur,pl криволинейной части оболочки - равной 1500 мм, т.е. около 1/8 ширины оболочки (пролета l2).
Криволинейную часть внешней поверхности оболочки принимаем очерченной по дуге круга радиусом

Значение l2 принимаем в соответствии с конструкцией узла соединения плиты оболочки с бортовым элементом (рисунок 5.3.4, б).
Исходя из радиуса r', находим центральный угол 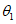 для половины дуги криволинейной части оболочки:
для половины дуги криволинейной части оболочки:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
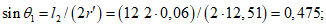
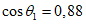 , чему соответствует угол
, чему соответствует угол 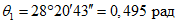 .
.Радиус срединной поверхности r = 12,51 - 0,02 = 12,49 м.
Площадь поперечного сечения криволинейной плиты:
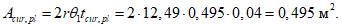
Площадь бортовой балки в сечении посередине пролета (до замоноличивания стыковой полости оболочки):
Aed = 0,08·1,4 + 0,22(0,1 + 0,05 + 0,35) = 0,222 м2.
Общая площадь поперечного сечения оболочки посередине пролета с учетом площади сечения замоноличенной стыковой полости 0,3·0,2 = 0,06 м2.
Ash = 0,495 + 0,222 + 0,06 = 0,777 м2.
Определяем момент инерции поперечного сечения оболочки. Первоначально находим положение центра тяжести сечения:
криволинейной плиты: y'cur,pl = f/3 = 1,48/3 = 0,493 м;
бортовой балки в сечении посередине пролета (до замоноличивания стыковой полости оболочки):
y'ed = [0,08·1,4·0,7 + 0,22(0,1·0,05 + 0,05·0,575 + 0,35·1,225)]/0,222 = 0,812 м;
yed = 1,4 - 0,812 = 0,588 м.
Для всего поперечного сечения оболочки посередине пролета с учетом замоноличенной стыковой полости:
y'sh = [0,495·0,493 + 0,222(0,812 + 0,2 + 1,5) + 0,2·0,3(0,1 + 1,5)]/0,777 = 1,16 м;
ysh = 3,1 - 1,16 = 1,94 м.
Момент инерции сечения криволинейной плиты:

Момент инерции бортовой балки в сечении посередине пролета до замоноличивания стыковой полости приводим без вычислений: Ied = 0,0493 м4. В результате момент инерции всего поперечного сечения оболочки посередине пролета с учетом замоноличенной стыковой полости составит:
Ish = 0,0965 + 0,0493 + 0,3·0,23/12 + 0,495·0,6572 + 0,222·1,3422 + 0,3·0,2·0,432 = 0,77 м4.
Расчет оболочки в продольном направлении
Расчет по прочности на действие изгибающих моментов и подбор продольной арматуры бортовых балок
В качестве напрягаемой арматуры для армирования бортовой балки принимаем арматурные канаты  мм класса К1400 с Rs = 1215 МПа. Максимальный изгибающий момент в середине пролета от расчетной нагрузки на оболочку шириной 12 м Fd = 6,24·12 = 74,88 кН/м составляет
мм класса К1400 с Rs = 1215 МПа. Максимальный изгибающий момент в середине пролета от расчетной нагрузки на оболочку шириной 12 м Fd = 6,24·12 = 74,88 кН/м составляет
Md = 74,88·29,62/8 = 8200 кНм.
Оболочку на прочность в продольном направлении рассчитываем по предельным состояниям как простую балку.
Половина центрального угла, охватывающего участок сжатой зоны дуги поперечного сечения оболочки, по формуле (5.3.5)
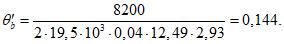
Полная площадь сечения растянутой арматуры, размещаемой в одной промежуточной бортовой балке, по формуле (5.3.6)
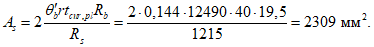
Принимаем 20 арматурных канатов  мм класса К1400 с площадью напрягаемой арматуры Asp = 2830 мм2. Другие расчеты и конструирование балки выполняются по аналогии с плоскими балками и здесь не приводятся.
мм класса К1400 с площадью напрягаемой арматуры Asp = 2830 мм2. Другие расчеты и конструирование балки выполняются по аналогии с плоскими балками и здесь не приводятся.
Расчет по прочности на действие поперечных сил и подбор арматуры криволинейной плиты
На поперечные силы оболочку рассчитываем как обычную упругую систему, в этом случае представляющую собой простую балку. Такой расчет для крайних четвертей оболочки вполне приемлем. В средней зоне оболочки, где поперечные силы имеют минимальные значения, а изгибающие моменты - максимальные, криволинейная часть оболочки работает на сжатие в продольном направлении, и лимитирующим здесь является устойчивость плиты. Однако, учитывая, что сборные оболочки снабжены продольными и поперечными ребрами, устойчивость криволинейной плиты, как правило, обеспечивается.
Главные растягивающие напряжения определяются, исходя из плоского напряженного состояния. Нормальные напряжения, действующие в обоих направлениях, определяют по формуле
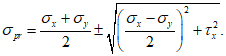 (5.3.8)
(5.3.8)Имея в виду, что нормальные напряжения в поперечном направлении относительно малы, их можно не учитывать, приняв 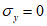 :
:
Каждая панель шириной 3 м рассчитывается на среднее значение ординаты балочной эпюры поперечной силы, т.е. в сечениях на расстояниях от опоры x1 = 1,3 м; x2 = 4,3 м; x3 = 7,3 м.
Рассчитаем две панели: первую от опоры (торцевую) и вторую (рядовую).
Расчет криволинейной плиты торцевой панели
Геометрические характеристики поперечного сечения оболочки в сечении на расстоянии x1 = 1,3 м от опоры:
- бортовая балка: hed = 1,1 м, Aed = 0,242 м2, z'ed = 0,56 м, Ied = 0,032 м4;
- полное сечение оболочки: Ash = 0,737 м2, z'sh = 0,996 м, Ish = 0,5247 м4;
- изгибающий момент в сечении:
Mx = 0,5Fdx(l1 - x) = 0,5·74,88·1,3·(29,6 - 1,3) = 137,74 кН·м;
- поперечная сила в сечении: Qx = Fd(0,5l1 - x) = 74,88·(0,5·29,6 - 1,3) = 1010,9 кН.
На участках, где 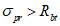 , сечение арматуры определяется исходя из растягивающих напряжений, действующих под углом 45° к образующей.
, сечение арматуры определяется исходя из растягивающих напряжений, действующих под углом 45° к образующей.
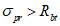 , сечение арматуры определяется исходя из растягивающих напряжений, действующих под углом 45° к образующей.
, сечение арматуры определяется исходя из растягивающих напряжений, действующих под углом 45° к образующей.Главные растягивающие напряжения, действующие в плите оболочки, определяем по формуле (5.3.9),
где 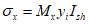 ;
;
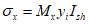 ;
;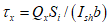 ;
;yi - ордината точки рассматриваемого сечения дуги (криволинейной плиты оболочки);
Si - статический момент дуги, находящейся выше рассматриваемого сечения, площадь Ai = 2raitcur,pl, стрела 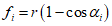 :
:
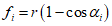 :
: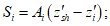
b - ширина элемента: b = 2tcur,pl;
zi = fi/3 - расстояние до центра тяжести i-й дуги.
Результаты расчета главных растягивающих напряжений приведены в таблице 5.3.2.
Обозначение параметра | Значение параметра для точки поперечного сечения (рисунок 5.3.7) | ||||
1 | 2 | 3 | 4 | 5 | |
28°20'43" | 21°15' | 14°10' | 7°5' | 0 | |
(рад) | (0,4947) | (0,371) | (0,2474) | (0,1237) | (0) |
0,475 | 0,362 | 0,245 | 0,1235 | 0 | |
0,88 | 0,931 | 0,97 | 0,993 | 1 | |
Ai, м2 | 0,495 | 0,37 | 0,25 | 0,124 | 0 |
fi, м | 1,48 | 0,86 | 0,37 | 0,087 | 0 |
zi, м | 0,49 | 0,29 | 0,12 | 0,03 | 0 |
Si, м3 | 0,25 | 0,26 | 0,22 | 0,12 | 0 |
6,03 | 6,27 | 5,3 | 2,9 | 0 | |
yi, м | 0,484 | 0,156 | 0,636 | 0,926 | 0,996 |
0,64 | -0,21 | -0,83 | -1,21 | -13,2 | |
6,7 | 6,06 | 4,53 | 1,93 | 0 | |
Из результатов расчета видно, что во всех точках сечения криволинейной плиты торцевой панели оболочки главные растягивающие напряжения превышают Rbt = 1,3 МПа и, следовательно, для подбора арматуры необходимо вычислить N45.
Усилие N45, действующее в точках сечения криволинейной плиты под углом 45° к образующей, определяем по формуле
где 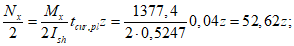
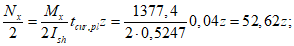
здесь z - расстояние от точек дуги до центра тяжести сечения оболочки;
Qx - поперечная сила в рассматриваемом сечении оболочки от нагрузки, приходящейся на половину единичной плоскости оболочки.
Подставив все значения величин в (5.3.11), получаем:

где 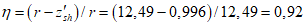 .
.
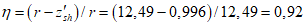 .
.Расчет криволинейной плиты второй от торца панели
Расчет второй от торца панели (сечение на расстоянии x2 = 4,3 м от опоры) выполняется аналогично. В этом случае:
hed = 1,3 м; | Aed = 0,258 м2; | z'ed = 0,663 м; |
Ied = 0,0508 м4; | Ash = 0,753 м2; | z'sh = 1,053 м; |
Ish = 0,618 м4; | Mx = 4073,1 кНм; | Qx = 786,2 кН; |
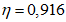 ; ; | Nx/2 = 131,82z; |  . . |
Результаты расчета усилий N45 по формуле (5.3.10) приведены в таблице 5.3.3 (значение функций углов - в таблице 5.3.2).
Панель | Номер точки | Значение параметра | |||
z, м | 0,5Nx, кН/м | N45, кН/м | |||
Торцевая (первая от опоры) | 1 | -0,484 | 238,95 | 25,47 | 264,42 |
2 | 0,156 | 248,6 | -8,12 | 240,4 | |
3 | 0,636 | 209,1 | -33,47 | 175,63 | |
4 | 0,926 | 116,6 | -48,73 | 67,87 | |
5 | 0,996 | 0 | -52,41 | -52,41 | |
Рядовая (вторая от опоры) | 1 | -0,427 | 173,49 | 56,29 | 229,78 |
2 | 0,213 | 175,94 | -28,29 | 147,65 | |
3 | 0,693 | 145,9 | -91,35 | 54,55 | |
4 | 0,983 | 80,9 | -129,58 | -48,68 | |
5 | 1,053 | 0 | -138,8 | -138,8 | |
Исходя из опыта применения длинных цилиндрических оболочек и результатов исследований, на арматуру можно передать не полное усилие N45, а лишь 70% вычисленного выше. Остальная часть усилий воспринимается бетоном. Таким образом, в точках 1, 2, 3 дуги оболочки второй от опоры панели усилие Ns, воспринимаемое арматурой, соответственно составляет 160,84; 103,4; 38,2 кН/м. Эпюра этих усилий дана на рисунке 5.3.5, а.
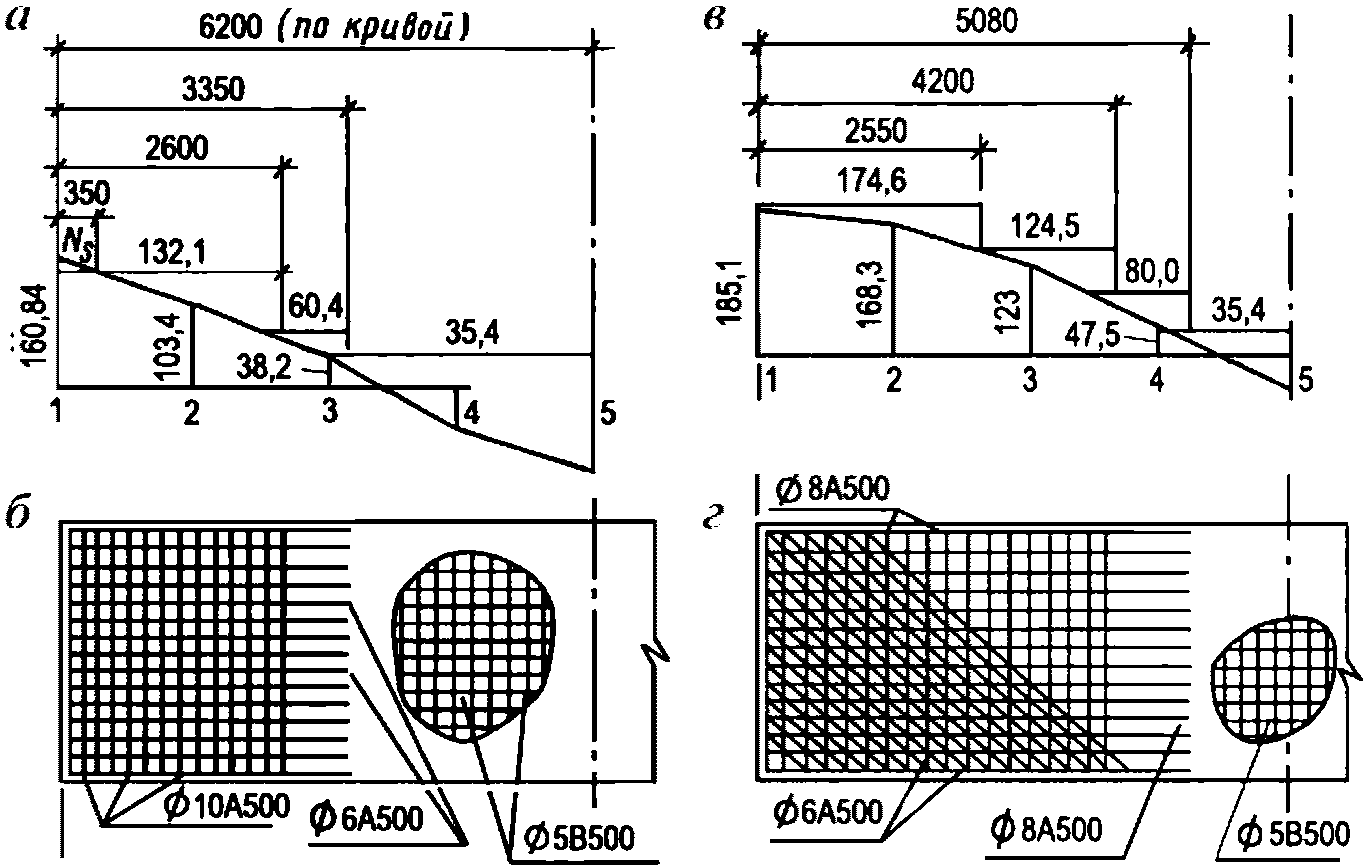
а, б - эпюра материалов и схема армирования второй от торца
панели; в, г - то же, торцевой панели
Вторую от торца панель армируем основной сеткой, укладываемой по всей площади криволинейной плиты, и дополнительными сетками на крайних участках в зонах, прилегающих к бортовым балкам.
Продольную арматуру в сжатой зоне оболочки (в точках 4 и 5 сечения криволинейной плиты) устанавливаем конструктивно, причем площадь сечения этой арматуры должна быть не менее 0,2% сечения бетона. Следовательно, As = 0,002·1000·40 = 80 мм2/м.
Основную сетку, укладываемую по всей площади второй панели, выполняем из стержней  с шагом 200 мм в обоих направлениях. Несущая способность этой сетки на единицу длины составляет
с шагом 200 мм в обоих направлениях. Несущая способность этой сетки на единицу длины составляет
 с шагом 200 мм в обоих направлениях. Несущая способность этой сетки на единицу длины составляет
с шагом 200 мм в обоих направлениях. Несущая способность этой сетки на единицу длины составляетNs = 0,5(As + Asw)Rs = 0,5(98,2 + 98,2)415 = 4075,3 Н/м ~= 40,8 кН/м.
На крайних участках плиты (точки 1, 2, 3) устанавливаем дополнительные сетки из стержней 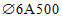 (поперечная арматура оболочки) и
(поперечная арматура оболочки) и  (продольная арматура оболочки) с шагом 200 мм в каждом направлении (рисунок 5.3.5, б). Длину стержней
(продольная арматура оболочки) с шагом 200 мм в каждом направлении (рисунок 5.3.5, б). Длину стержней 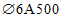 в сетке назначаем такой, чтобы они перешли за точку, где они не требуются по расчету (точка на расстоянии 40 мм от точки 3 по дуге влево), на длину анкеровки, равную 250 мм. Таким образом, округленно длину этих стержней принимаем (от точки 1) 3350 мм. Несущая способность арматуры на этом участке Ns = 0,5·41·435 + 40800 = 71,5 кН/м.
в сетке назначаем такой, чтобы они перешли за точку, где они не требуются по расчету (точка на расстоянии 40 мм от точки 3 по дуге влево), на длину анкеровки, равную 250 мм. Таким образом, округленно длину этих стержней принимаем (от точки 1) 3350 мм. Несущая способность арматуры на этом участке Ns = 0,5·41·435 + 40800 = 71,5 кН/м.
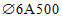 (поперечная арматура оболочки) и
(поперечная арматура оболочки) и  (продольная арматура оболочки) с шагом 200 мм в каждом направлении (рисунок 5.3.5, б). Длину стержней
(продольная арматура оболочки) с шагом 200 мм в каждом направлении (рисунок 5.3.5, б). Длину стержней 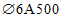 в сетке назначаем такой, чтобы они перешли за точку, где они не требуются по расчету (точка на расстоянии 40 мм от точки 3 по дуге влево), на длину анкеровки, равную 250 мм. Таким образом, округленно длину этих стержней принимаем (от точки 1) 3350 мм. Несущая способность арматуры на этом участке Ns = 0,5·41·435 + 40800 = 71,5 кН/м.
в сетке назначаем такой, чтобы они перешли за точку, где они не требуются по расчету (точка на расстоянии 40 мм от точки 3 по дуге влево), на длину анкеровки, равную 250 мм. Таким образом, округленно длину этих стержней принимаем (от точки 1) 3350 мм. Несущая способность арматуры на этом участке Ns = 0,5·41·435 + 40800 = 71,5 кН/м.Этой несущей способности на эпюре Ns соответствует точка на расстоянии 780 мм влево от точки 3. От этой точки до края панели на длине 2,3 м устанавливаем стержни  с шагом 200 мм по дуге и добавляем один шаг за точку пересечения эпюр (2500 мм по дуге).
с шагом 200 мм по дуге и добавляем один шаг за точку пересечения эпюр (2500 мм по дуге).
 с шагом 200 мм по дуге и добавляем один шаг за точку пересечения эпюр (2500 мм по дуге).
с шагом 200 мм по дуге и добавляем один шаг за точку пересечения эпюр (2500 мм по дуге).Несущая способность арматуры основной и дополнительной сеток на этом участке криволинейной плиты Ns = 0,5·393·435 + 71470 = 156950 Н/м = 156,95 кН/м.
Неперекрытая часть эпюры Ns (крайняя полоса криволинейной плиты шириной 350 мм) может быть воспринята арматурными каркасами ребер панели - увеличивать арматуру плиты здесь не обязательно. Эпюра материалов этой плиты приведена на рисунке 5.3.5, а, а схема армирования - на рисунке 5.3.5, б.
Для торцевой панели сохраняем тот же принцип армирования (основная и дополнительная сетки) и, кроме того, укладываем в угловых зонах косую арматуру (рисунок 5.3.5, в, г). Значения усилий Ns, передаваемых на арматуру в точках 1, 2, 3, 4 дуги оболочки торцевой панели, соответственно составляют 185,1; 168,3; 123; 47,5 кН/м. Эпюра этих усилий показана на рисунке 5.3.5, в. В точке 5 арматура ставится конструктивно, как и в рядовой панели.
Основную сетку принимаем 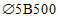 с шагом 200 мм в обоих направлениях. Несущая способность арматуры сетки подсчитана ранее и составляет Ns = 40,8 кН/м.
с шагом 200 мм в обоих направлениях. Несущая способность арматуры сетки подсчитана ранее и составляет Ns = 40,8 кН/м.
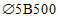 с шагом 200 мм в обоих направлениях. Несущая способность арматуры сетки подсчитана ранее и составляет Ns = 40,8 кН/м.
с шагом 200 мм в обоих направлениях. Несущая способность арматуры сетки подсчитана ранее и составляет Ns = 40,8 кН/м.От точки пересечения вычисленного значения эпюры материалов Ns с эпюрой усилий N45 (140 мм вправо от точки 4) укладываем дополнительную поперечную арматуру оболочки -  на 1 м и заводим стержни этой арматуры за указанную точку на длину анкеровки lan = 280 мм. Полная длина этих стержней по дуге составит 1,55·3 + 0,14 + 0,28 = 5,08 м. Несущая способность арматуры: Ns = 40800 + 0,5·251·435 = 95,4 кН/м.
на 1 м и заводим стержни этой арматуры за указанную точку на длину анкеровки lan = 280 мм. Полная длина этих стержней по дуге составит 1,55·3 + 0,14 + 0,28 = 5,08 м. Несущая способность арматуры: Ns = 40800 + 0,5·251·435 = 95,4 кН/м.
 на 1 м и заводим стержни этой арматуры за указанную точку на длину анкеровки lan = 280 мм. Полная длина этих стержней по дуге составит 1,55·3 + 0,14 + 0,28 = 5,08 м. Несущая способность арматуры: Ns = 40800 + 0,5·251·435 = 95,4 кН/м.
на 1 м и заводим стержни этой арматуры за указанную точку на длину анкеровки lan = 280 мм. Полная длина этих стержней по дуге составит 1,55·3 + 0,14 + 0,28 = 5,08 м. Несущая способность арматуры: Ns = 40800 + 0,5·251·435 = 95,4 кН/м.В точке пересечения этого значения Ns с эпюрой усилий (0,97 м влево от точки 4) добавляем продольную арматуру оболочки -  с прибавлением одного шага для перекрытия эпюры. В результате общая несущая способность основной и дополнительной сеток Ns = 40800 + 251·435 = 150 кН/м.
с прибавлением одного шага для перекрытия эпюры. В результате общая несущая способность основной и дополнительной сеток Ns = 40800 + 251·435 = 150 кН/м.
 с прибавлением одного шага для перекрытия эпюры. В результате общая несущая способность основной и дополнительной сеток Ns = 40800 + 251·435 = 150 кН/м.
с прибавлением одного шага для перекрытия эпюры. В результате общая несущая способность основной и дополнительной сеток Ns = 40800 + 251·435 = 150 кН/м.Оставшуюся часть эпюры Ns перекрываем добавлением косой арматуры. Принимаем эту арматуру из  с шагом 200 мм и устанавливаем ее в угловой зоне, начиная с точки пересечения эпюры усилий с полученным значением Ns (0,5 м влево от точки 3). Несущая способность всей арматуры, установленной в угловой зоне криволинейной плиты, Ns = 149985 + 141·435 = 211,32 кН/м, что больше максимального усилия Ns, действующего в торцевой панели оболочки, и, следовательно, прочность плиты оболочки обеспечена.
с шагом 200 мм и устанавливаем ее в угловой зоне, начиная с точки пересечения эпюры усилий с полученным значением Ns (0,5 м влево от точки 3). Несущая способность всей арматуры, установленной в угловой зоне криволинейной плиты, Ns = 149985 + 141·435 = 211,32 кН/м, что больше максимального усилия Ns, действующего в торцевой панели оболочки, и, следовательно, прочность плиты оболочки обеспечена.
 с шагом 200 мм и устанавливаем ее в угловой зоне, начиная с точки пересечения эпюры усилий с полученным значением Ns (0,5 м влево от точки 3). Несущая способность всей арматуры, установленной в угловой зоне криволинейной плиты, Ns = 149985 + 141·435 = 211,32 кН/м, что больше максимального усилия Ns, действующего в торцевой панели оболочки, и, следовательно, прочность плиты оболочки обеспечена.
с шагом 200 мм и устанавливаем ее в угловой зоне, начиная с точки пересечения эпюры усилий с полученным значением Ns (0,5 м влево от точки 3). Несущая способность всей арматуры, установленной в угловой зоне криволинейной плиты, Ns = 149985 + 141·435 = 211,32 кН/м, что больше максимального усилия Ns, действующего в торцевой панели оболочки, и, следовательно, прочность плиты оболочки обеспечена.Расчет бортовых балок по образованию трещин, нормальных к продольной оси оболочки
Для расчета трещиностойкости оболочки в стадии эксплуатации необходимо учесть напряжения, возникающие в бортовой балке на всех этапах ее работы, в том числе на всех этапах монтажа.
Для этого рассмотрим порядок монтажа оболочки:
- на несущие колонны цеха устанавливают бортовые элементы оболочки, работающие как балки пролетом 30 м;
- под каждую балку в точках на расстоянии 11,8 м от обеих колонн для уменьшения монтажных усилий подводят две временные промежуточные опоры в виде стоек (без вывески собственной массы балки);
- по балкам укладывают криволинейные 12-метровые панели, после чего производится замоноличивание швов оболочки; на этом этапе балка еще работает по трехпролетной схеме, причем криволинейные панели в работе не участвуют, а представляют собой нагрузку на балку;
- после набора необходимой прочности бетоном замоноличивания швов временные промежуточные опоры убирают - оболочка включается в работу полным сечением.
Расчет оболочки по образованию трещин выполняем для упругой стадии работы конструкции от действия постоянных и временных (длительных и кратковременных) нормативных нагрузок.
Для бетона B35 для предельных состояний второй группы Rb,ser = 25,5 МПа, Rbt,ser = 1,95 МПа.
Предварительное напряжение арматуры 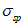 для арматуры класса К1400 принимают не более 0,8Rsn.
для арматуры класса К1400 принимают не более 0,8Rsn.
Принимаем  .
.
 .
.Принимаем передаточную прочность бетона Rbp = 22,5 МПа < 0,65·35 = 22,75 МПа.
Рассчитаем потери предварительного напряжения арматуры по СП 63.13330.
Первые потери:
- от релаксации напряжений арматуры при механическом способе натяжения:

- потери от температурного перепада 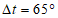 :
:
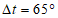 :
: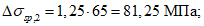
- потери от деформаций стальной формы: 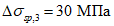 ;
;
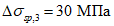 ;
;- потери от деформаций анкеров:
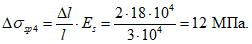
Суммарные первые потери:

Вторые потери:
- потери от усадки бетона:
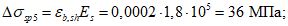
- потери напряжений в рассматриваемой напрягаемой арматуре от ползучести бетона определяют по формуле
где  - коэффициент ползучести бетона;
- коэффициент ползучести бетона;
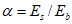 ;
;P(1) - усилие предварительного обжатия с учетом первых потерь, определяемое по формуле
здесь  - сумма первых потерь напряжения;
- сумма первых потерь напряжения;
e0p1 - эксцентриситет усилия P(1) относительно центра тяжести приведенного сечения элемента;
ys,red - расстояние между центрами тяжести рассматриваемой напрягаемой арматуры и приведенного поперечного сечения элемента;
ИС МЕГАНОРМ: примечание. Обозначение дано в соответствии с официальным текстом документа. |
M - изгибающий момент от собственного веса элемента, действующий в стадии обжатия в рассматриваемом сечении;
Ared и Ired - площадь приведенного сечения и ее момент инерции относительно центра тяжести приведенного сечения.
В нашем примере приведенное сечение включает в себя площадь сечения бетона и площадь сечения продольной напрягаемой арматуры с коэффициентом приведения арматуры к бетону  .
.
 .
.Геометрические характеристики приведенного сечения:
площадь приведенного сечения:
Ared = 222000 + 2830·5,2174 = 236765 мм2;
статический момент приведенного сечения бетона относительно растянутой грани:
Sred = 80·1400·700 + 220(100·50 + 50·575 + 350·1225) + 14765(1400 - 170) = 198,311·106 мм3;
расстояние от центра тяжести приведенного сечения до растянутой в стадии эксплуатации грани:
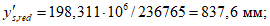
ys,red = 1400 - 837,6 = 562,4 мм;
момент инерции приведенного сечения относительно его центра тяжести:
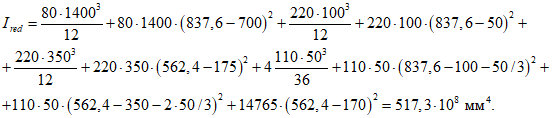
Усилие предварительного обжатия P(1) за вычетом первых потерь (5.3.14):
P(1) = 2830·(1050 - 191,5) = 2429,5·103 кН.
e0p1 = 562,4 - 170 = 392,4 мм.
Напряжения в бетоне 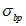 на уровне центра тяжести напрягаемой арматуры определяем по формуле (5.3.13), где от собственной массы бетона балки, равной 5 кН/м:
на уровне центра тяжести напрягаемой арматуры определяем по формуле (5.3.13), где от собственной массы бетона балки, равной 5 кН/м:
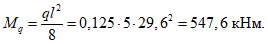
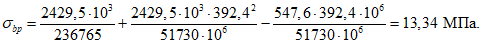
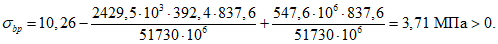

Отношение 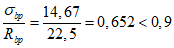 , требование СП 63.13330 удовлетворяется.
, требование СП 63.13330 удовлетворяется.
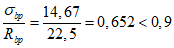 , требование СП 63.13330 удовлетворяется.
, требование СП 63.13330 удовлетворяется.Определяем значение 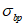 в приопорном сечении при минимальном значении Mq.
в приопорном сечении при минимальном значении Mq.
Принимаем конструктивно утолщение стенки балки с 80 до 120 мм на длине 1 м от края балки. Высота балки в этом сечении 840 мм.
Определяем основные характеристики сечения:
Ared = 80·840 + 110000 + 14,765 = 191965 мм2;
Sred = 97297 мм3; Ired = 142,476·108 мм4;
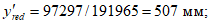
y = 840 - 507 = 333 мм.
Момент от массы бетона на краю зоны утолщения (на 1 м от края балки) Mq = 740 кНм.
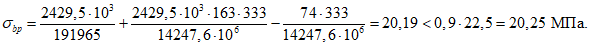
Требование СП 63.13330 удовлетворяется.
Определяем потери от ползучести бетона в среднем сечении по длине балки по формуле (5.3.12)
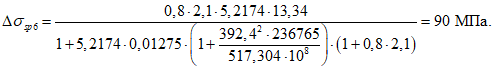
Напряжения  с учетом всех потерь равны:
с учетом всех потерь равны:
Определяем усилие обжатия P с учетом всех потерь:
P = 732,5·2830 = 2073 кН.
Без приведения расчетов на рисунке 5.3.6 показаны эпюры изгибающих моментов и оболочки, построенные по приведенным ниже значениям воздействий:
а) от собственной массы балки (gn = 5 кН/м): Mn = 5·29,62/8 = 548 кНм (рисунок 5.3.6, а);
б) от предварительного натяжения арматуры силой P:
на опоре: Msup = Pesup = 2073·(0,332 - 0,17) = 336 кНм;
в пролете: Mmax = Pemax = 2073·(0,5624 - 0,17) = 813 кНм (рисунок 5.3.6, б);
в) от массы криволинейных панелей: gn = 24,3 кНм (рисунок 5.3.6, в);
г) суммарная эпюра от собственной массы балки, от предварительного натяжения арматуры и от массы криволинейных панелей - при работе балки по трехпролетной схеме (рисунок 5.3.6, г);
д) от реакций временных опор величиной 239 кН, передаваемых на оболочку в момент снятия временных промежуточных стоек (рисунок 5.3.6, д);
е) от массы теплоизоляции, кровли и снега: gn + sn = (1,3 + 1,26)·12 = 30,72 кН/м (рисунок 5.3.6, е).
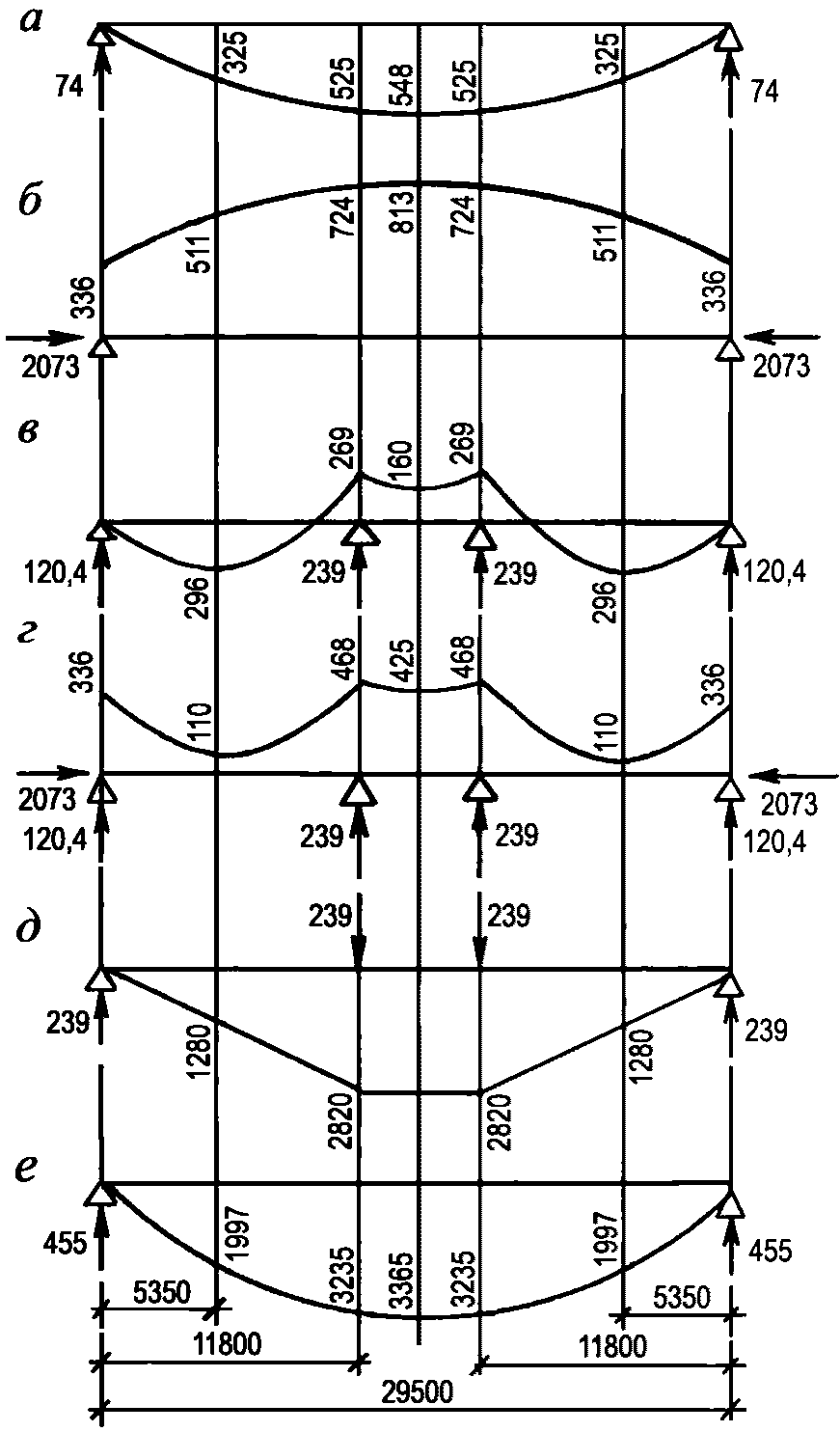
а - от собственного веса балки; б - от предварительного
напряжения; в - от массы незамоноличенных панелей;
г - суммарная по эпюрам а - в; д - при освобождении
промежуточных опор; е - от массы утеплителя,
рулонного ковра и снега
нагрузок, действующих в бортовой балке до замоноличивания
(эпюры а - г) и в замоноличенной оболочке (эпюры д, е)
Для определения трещиностойкости оболочки вычисляем значения напряжений в предварительно напряженном бортовом элементе, возникающих в нем до замоноличивания, от действия изгибающего момента Mn = 548 - 813 - 160 = -425 кНм и продольной силы Nn = 2073 кН (рисунок 5.3.6, а, б, в). Для этого нам нужны параметры приведенного сечения посередине пролета. Приводим их без вычислений:
Aed,red = 236765 мм2; Ied,red = 51,73·109 мм4;  ; yed,red = 562,4 мм.
; yed,red = 562,4 мм.
 ; yed,red = 562,4 мм.
; yed,red = 562,4 мм.Напряжения в бетоне балки до замоноличивания вычисляем по формуле
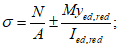
в крайнем верхнем волокне

в крайнем нижнем волокне
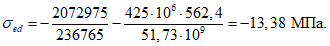
Определяем также значения напряжений в элементах оболочки после замоноличивания и снятия временных опор на действие изгибающего момента Mn = 2820 + 3365 = 6185 кНм (рисунок 5.3.6, д, е). Значения параметров приведенного сечения оболочки посередине пролета приводим без вычислений:
Ash,red = 788700 мм2; Ish,red = 816,5·109 мм4; 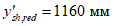 ; ysh,red = 1940 мм.
; ysh,red = 1940 мм.
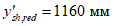 ; ysh,red = 1940 мм.
; ysh,red = 1940 мм.Напряжения:
в крайнем сжатом волокне бетона оболочки

на уровне верхнего волокна бетона балки
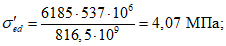
в крайнем растянутом волокне бетона оболочки

Эпюры напряжений в сечении оболочки по этапам нагружения, в т.ч. результирующая, приведены на рисунке 5.3.7. Как видно из результирующей эпюры (рисунок 5.3.7, в), трещиностойкость оболочки обеспечена, т.к. нижнее краевое напряжение в зоне размещения напрягаемой арматуры 1,55 МПа < Rbt,ser = 1,95 МПа.

а - до замоноличивания; б - после замоноличивания;
в - суммарная
оболочки посередине пролета
Трещиностойкость других сечений оболочки проверяется аналогичным образом.
Расчет по деформациям
При расчете оболочки по деформациям в соответствии с СП 63.13330 учитываем действие постоянных, длительных и кратковременных нагрузок, а также обратный выгиб бортового элемента от действия предварительного обжатия и вследствие усадки и ползучести бетона. При этом принимаем во внимание установленный выше порядок монтажа оболочки. Расчет выполняем на нормативные нагрузки.
Для определения кривизны оси оболочки от действия кратковременной части временной нагрузки (равной 0,5 снеговой) вычисляем изгибающий момент от этой нагрузки (СП 20.13330)
Ms = 0,5·1,28·12·29,62/8 = 841,1 кНм

Определяем момент внешних сил Mg. К моменту от массы криволинейных панелей, представленному на рисунке 5.3.6, в, добавляем момент от массы балки в рассматриваемой трехпролетной схеме. Тогда в среднем сечении момент от массы оболочки составит 160·29,3/24,3 = 192,92 кНм.
Вместе с изгибающими моментами по схемам д и г на рисунке 5.3.6 суммарный внешний момент составляет
Mg = 2820 + 3365 - 193 = 5992 кНм.
Изгибающий момент от длительных нагрузок, прикладываемых к оболочке после замоноличивания и снятия временных опор, составляет
Mi = 5992 - 1076,36 = 4915,64 кНм.
Значение кривизны оси оболочки от действия этого момента:

где 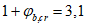 .
.
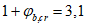 .
.Для определения обратной кривизны, обусловленной выгибом бортового элемента под действием предварительного обжатия, возникающего до замоноличивания оболочки, рассматриваем нагрузки, изображенные на схемах а и б рисунка 5.3.6. Усилие предварительного натяжения принято здесь с коэффициентом точности натяжения 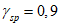 .
.
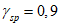 .
.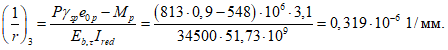
Для определения кривизны, обусловленной выгибом балки вследствие усадки и ползучести бетона от усилия предварительного обжатия, вычисляем соответствующие относительные деформации бетона на уровне центра тяжести растянутой продольной арматуры  и крайнего сжатого волокна
и крайнего сжатого волокна 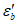 . Эти напряжения были вычислены ранее и равны соответственно 13,34 МПа и 3,71 МПа. Потери от усадки и ползучести в первом случае составляют:
. Эти напряжения были вычислены ранее и равны соответственно 13,34 МПа и 3,71 МПа. Потери от усадки и ползучести в первом случае составляют:
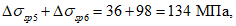
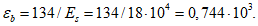
На уровне крайнего сжатого волокна:
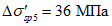 , а
, а 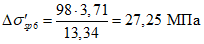 .
.
Следовательно, относительная деформация бетона на уровне крайнего сжатого волокна:

Кривизну балки вследствие усадки и ползучести от предварительного обжатия находим, учитывая, что усадка и ползучесть бетона на момент монтажа проявляются еще не полностью. Условно принимаем их в размере 50%. Тогда

Полное значение кривизны

Стрелку прогиба однопролетной оболочки от равномерно распределенной нагрузки определяем по известной формуле
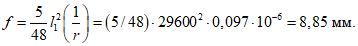
Таким образом, значение наибольшего прогиба составляет 1/3340 пролета, что свидетельствует о достаточной жесткости конструкции.
5.3.19 Для расчета в поперечном направлении оболочки, нагруженной равномерно распределенной поверхностной нагрузкой, необходимо рассматривать условия равновесия полоски единичной ширины, вырезанной в любом сечении x по длине оболочки. Такая полоска представляет собой криволинейную плиту. Эту плиту можно рассчитать как круговую бесшарнирную арку пролетом, равным ширине оболочки. На рисунке 5.3.8 показаны внешние и внутренние усилия, воздействующие на вырезанную из оболочки элементарную полоску. Внешняя нагрузка F, приходящаяся на вырезанную полоску, уравновешивается приращением поперечной силы или, что то же, приращением сдвигающих усилий 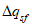 . Зная закон изменения сдвигающих усилий по сечению оболочки, из условия их равновесия можно определять поперечные изгибающие моменты и соответствующие им поперечные и нормальные усилия, действующие в сечении вырезанной полоски.
. Зная закон изменения сдвигающих усилий по сечению оболочки, из условия их равновесия можно определять поперечные изгибающие моменты и соответствующие им поперечные и нормальные усилия, действующие в сечении вырезанной полоски.
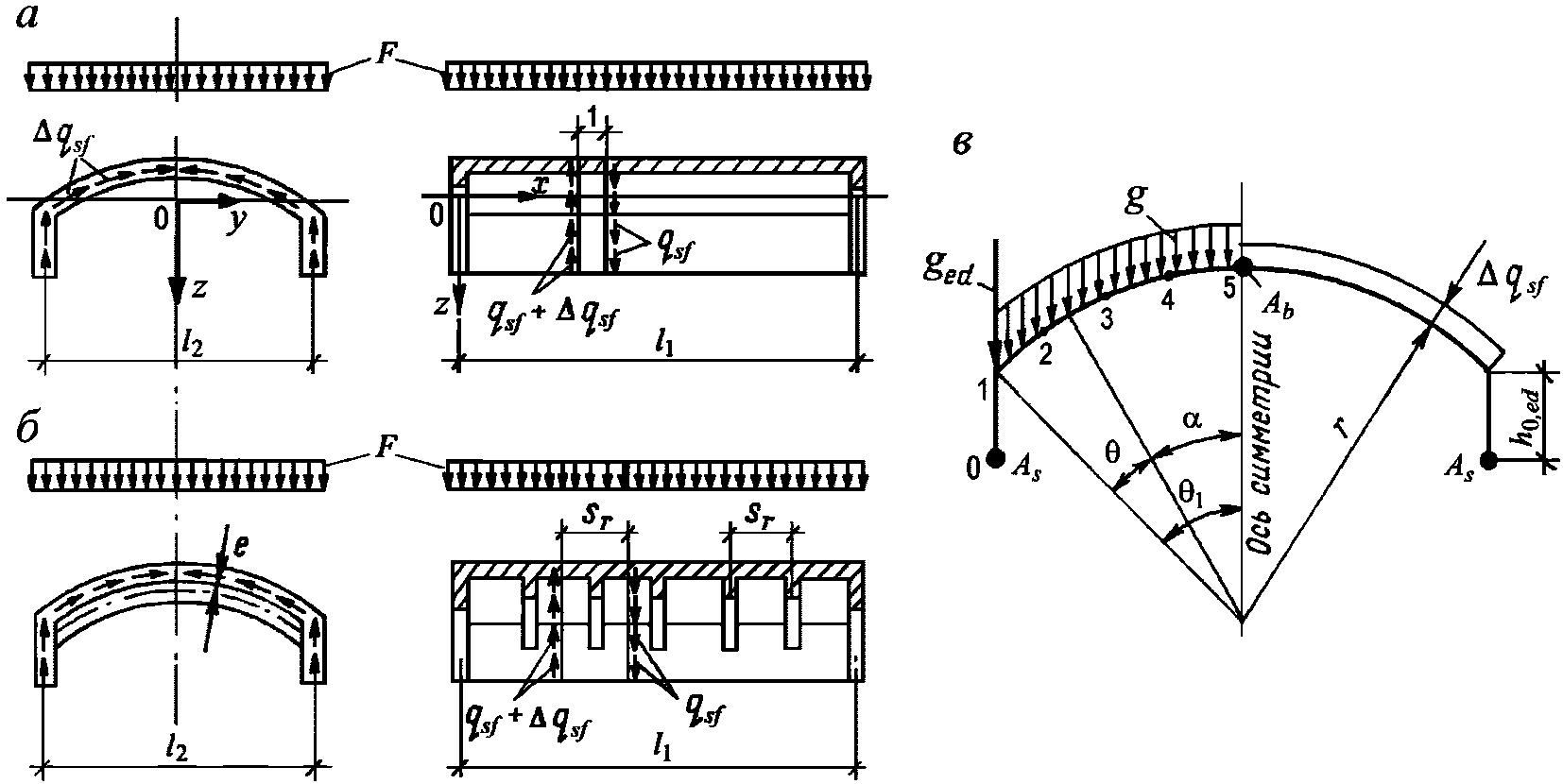
а - в гладких; б - в ребристых; в - схема нагрузки (слева)
и эпюра сдвигающих усилий (справа) в сечении, нормальном
к продольной оси оболочки
в одноволновых длинных цилиндрических оболочках
Сдвигающие усилия и их приращения, действующие на элементарную полоску оболочки, можно представить в виде эпюры постоянной напряженности по всему сечению оболочки (рисунок 5.2.8, в). Такое допущение базируется на условии, что сжатая зона оболочки относительно мала, а именно 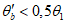 . Такая предпосылка позволяет условно представить сечение оболочки в виде двух стержней - продольного жесткого сжатого стрингера и продольного растянутого одиночного стержня. В стрингере условно концентрируют всю площадь сжатой зоны бетона. Его располагают в центре тяжести этой зоны (или условно в шелыге). В растянутом стержне условно сосредоточивают сечение всей рабочей арматуры нижней зоны бортового элемента. Размещают этот стержень в центре тяжести площади сечения рабочей арматуры в каждом бортовом элементе. При этом допущении значение интенсивности сдвигающих усилий gsf можно определить как частное от деления поперечной силы Qx в данном сечении на расстояние между центрами тяжести арматуры и сжатого бетона. Таким же образом получим и интенсивность приращения сдвигающих усилий - делением приращения поперечной силы на плечо пары внутренних сил в сечении
. Такая предпосылка позволяет условно представить сечение оболочки в виде двух стержней - продольного жесткого сжатого стрингера и продольного растянутого одиночного стержня. В стрингере условно концентрируют всю площадь сжатой зоны бетона. Его располагают в центре тяжести этой зоны (или условно в шелыге). В растянутом стержне условно сосредоточивают сечение всей рабочей арматуры нижней зоны бортового элемента. Размещают этот стержень в центре тяжести площади сечения рабочей арматуры в каждом бортовом элементе. При этом допущении значение интенсивности сдвигающих усилий gsf можно определить как частное от деления поперечной силы Qx в данном сечении на расстояние между центрами тяжести арматуры и сжатого бетона. Таким же образом получим и интенсивность приращения сдвигающих усилий - делением приращения поперечной силы на плечо пары внутренних сил в сечении
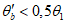 . Такая предпосылка позволяет условно представить сечение оболочки в виде двух стержней - продольного жесткого сжатого стрингера и продольного растянутого одиночного стержня. В стрингере условно концентрируют всю площадь сжатой зоны бетона. Его располагают в центре тяжести этой зоны (или условно в шелыге). В растянутом стержне условно сосредоточивают сечение всей рабочей арматуры нижней зоны бортового элемента. Размещают этот стержень в центре тяжести площади сечения рабочей арматуры в каждом бортовом элементе. При этом допущении значение интенсивности сдвигающих усилий gsf можно определить как частное от деления поперечной силы Qx в данном сечении на расстояние между центрами тяжести арматуры и сжатого бетона. Таким же образом получим и интенсивность приращения сдвигающих усилий - делением приращения поперечной силы на плечо пары внутренних сил в сечении
. Такая предпосылка позволяет условно представить сечение оболочки в виде двух стержней - продольного жесткого сжатого стрингера и продольного растянутого одиночного стержня. В стрингере условно концентрируют всю площадь сжатой зоны бетона. Его располагают в центре тяжести этой зоны (или условно в шелыге). В растянутом стержне условно сосредоточивают сечение всей рабочей арматуры нижней зоны бортового элемента. Размещают этот стержень в центре тяжести площади сечения рабочей арматуры в каждом бортовом элементе. При этом допущении значение интенсивности сдвигающих усилий gsf можно определить как частное от деления поперечной силы Qx в данном сечении на расстояние между центрами тяжести арматуры и сжатого бетона. Таким же образом получим и интенсивность приращения сдвигающих усилий - делением приращения поперечной силы на плечо пары внутренних сил в сечениигде g - постоянная нагрузка, равномерно распределенная по криволинейной поверхности;
s - временная нагрузка, равномерно распределенная по горизонтальной проекции;
ged - постоянная нагрузка от массы бортовых элементов (рисунок 5.3.9, б).
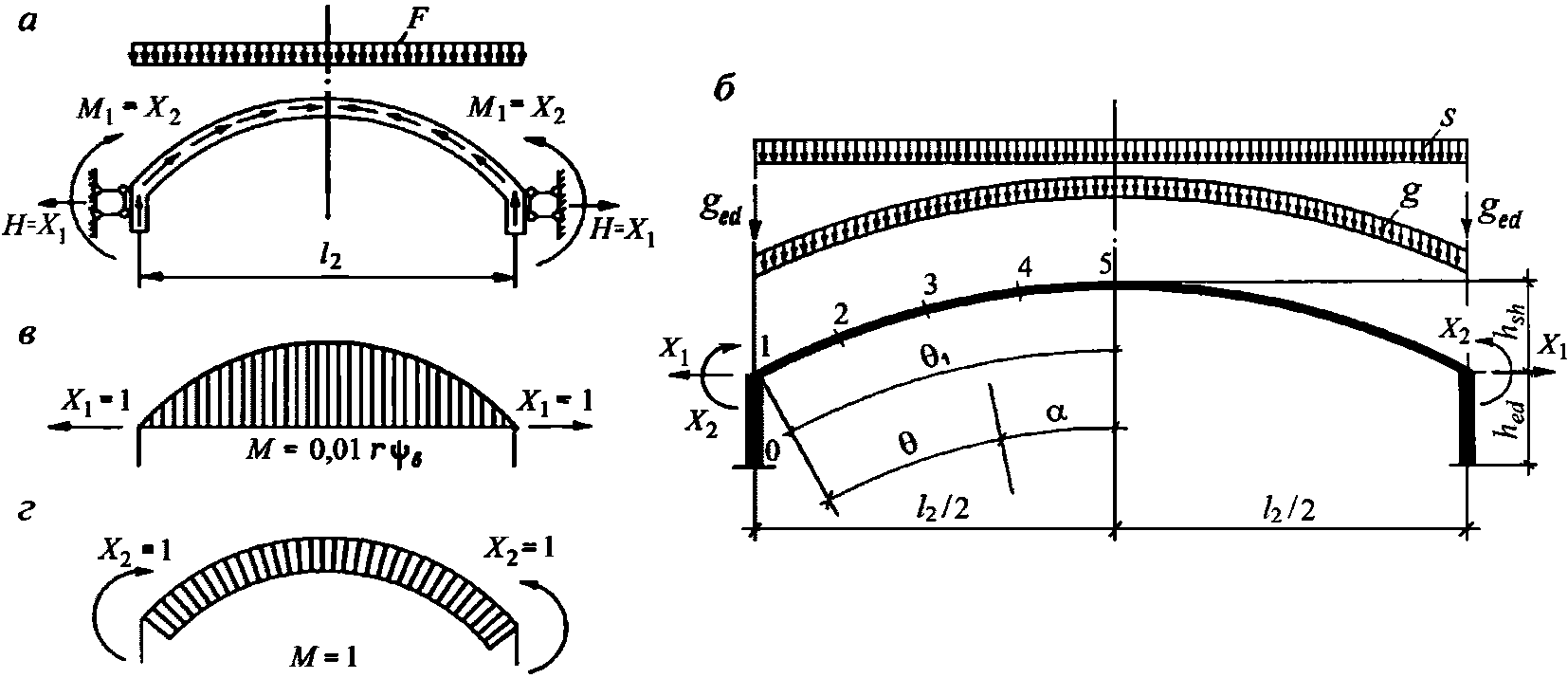
а - расчетные граничные условия; б - схема приложения
нагрузок; в - эпюра моментов от X1 = 1;
г - эпюра моментов от X2 = 1
в средней волне длинной цилиндрической оболочки
Бортовые элементы (балки) средних волн оболочки условно считаем не смещающимися в горизонтальном направлении и не поворачивающимися вокруг горизонтальной оси. Тогда расчетная схема арки, представляющей собой полоску единичной ширины, соответствует приведенной на рисунке 5.3.9, а, а усилия определяют расчетом дважды статически неопределимой системы.
Неизвестные X1 и X2 (рисунок 5.3.9) получаем из решения системы канонических уравнений метода сил (5.3.16).
где
Значения коэффициентов Ci для ряда значений половины центрального угла  криволинейных плит в поперечных сечениях волны оболочки приведены в таблице 5.3.4.
криволинейных плит в поперечных сечениях волны оболочки приведены в таблице 5.3.4.
Коэффициенты Ci | Значения коэффициента для угла | ||||
25° | 26° | 27° | 28° | 29° | |
C1 | 20,335 | 24,667 | 29,698 | 35,506 | 42,175 |
C2 | 70,921 | 82,240 | 95,476 | 109,810 | 125,620 |
C3 | 1,311 | 1,655 | 2,072 | 2,572 | 3,167 |
C4 | 9,071 | 9,772 | 10,494 | 11,237 | 12,000 |
C5 | 2,717 | 3,051 | 3,411 | 3,798 | 4,212 |
C6 | 0,150 | 0,175 | 0,204 | 0,236 | 0,271 |
C7 | 11,351 | 13,761 | 16,556 | 19,780 | 23,480 |
C8 | 10,370 | 12,946 | 15,500 | 18,426 | 21,756 |
C9 | 1,345 | 1,510 | 1,686 | 1,876 | 2,079 |
C10 | 1,270 | 1,518 | 1,676 | 1,845 | 2,023 |
Окончание таблицы 5.3.4
Коэффициенты Ci | Значения коэффициента для угла | |||||
30° | 32° | 34° | 36° | 38° | 40° | |
C1 | 49,794 | 68,262 | 91,720 | 121,070 | 157,280 | 201,400 |
C2 | 143,000 | 182,790 | 229,820 | 284,710 | 348,070 | 420,450 |
C3 | 3,874 | 5,680 | 8,131 | 11,399 | 15,678 | 21,203 |
C4 | 12,782 | 14,401 | 16,087 | 17,833 | 19,633 | 21,479 |
C5 | 4,755 | 5,628 | 0,723 | 7,946 | 9,303 | 10,799 |
C6 | 0,310 | 0,401 | 0,511 | 0,641 | 0,794 | 0,974 |
C7 | 27,701 | 37,914 | 50,859 | 67,011 | 86,890 | 111,040 |
C8 | 25,527 | 34,541 | 45,767 | 59,516 | 76,102 | 95,832 |
C9 | 2,395 | 2,769 | 3,301 | 3,893 | 4,547 | 5,264 |
C10 | 2,106 | 2,617 | 3,063 | 3,548 | 4,070 | 4,527 |
Поперечные изгибающие моменты определяются из суммы моментов всех сил, взятых с одной стороны, относительно сечения с угловой координатой 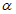 по следующим формулам:
по следующим формулам:
для отдельно стоящей одноволновой оболочки:
для средней волны многоволновой оболочки:
В формуле (5.3.18) первый член в квадратных скобках, умноженный на (0,1r)2, представляет собой изгибающий момент от приращения сдвигающих сил 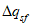 , а второй - от внешней нагрузки; N - продольное усилие на единицу длины оболочки; e - расстояние между серединой сечения плиты оболочки и центром тяжести таврового сечения ребристой оболочки.
, а второй - от внешней нагрузки; N - продольное усилие на единицу длины оболочки; e - расстояние между серединой сечения плиты оболочки и центром тяжести таврового сечения ребристой оболочки.
Эксцентриситет e приложения продольной силы в гладких оболочках равен нулю. Если же под плитой оболочки расположены ребра, то перед последним членом уравнений ставится знак "минус". Положительному значению моментов соответствует растяжение в волокнах нижней поверхности плиты оболочки, а положительному значению продольных усилий - растяжение. В формуле (5.3.19) значение M принимается по формуле (5.3.18), но без последнего члена.
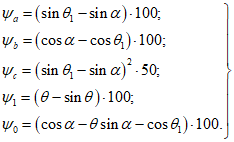 (5.3.20)
(5.3.20)Значения коэффициентов  для ряда значений углов
для ряда значений углов 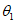 и
и 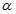 (в пяти точках поперечного сечения, отмеченных на рисунке 5.3.9, б) приведены в таблице 5.3.5.
(в пяти точках поперечного сечения, отмеченных на рисунке 5.3.9, б) приведены в таблице 5.3.5.
Номер точки | Коэффициенты | ||||||||
25° (0,436) | 26° (0,454) | 27° (0,471) | 28° (0,489) | 29° (0,506) | 30° (0,524) | 32° (0,559) | 34° (0,593) | ||
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 10,118 | 10,456 | 10,787 | 11,110 | 11,425 | 11,732 | 12,318 | 12,868 | |
3 | 20,618 | 21,342 | 22,055 | 22,755 | 23,443 | 24,118 | 25,428 | 26,682 | |
4 | 31,375 | 32,516 | 33,645 | 34,760 | 35,861 | 36,947 | 39,075 | 41,138 | |
5 | 42,262 | 43,837 | 45,399 | 46,947 | 48,481 | 50,000 | 52,992 | 55,919 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 4,062 | 4,385 | 4,718 | 5,063 | 5,419 | 5,785 | 6,550 | 7,355 | |
3 | 6,659 | 7,758 | 8,136 | 8,735 | 9,353 | 9,990 | 11,321 | 12,727 | |
4 | 8,775 | 9,478 | 10,206 | 10,960 | 11,738 | 12,542 | 14,222 | 15,998 | |
5 | 9,369 | 10,120 | 10,900 | 11,705 | 12,538 | 13,397 | 15,195 | 17,097 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,5118 | 0,5467 | 0,5818 | 0,6172 | 0,6527 | 0,6881 | 0,7587 | 0,8279 | |
3 | 2,1255 | 2,7774 | 2,4320 | 2,5890 | 2,7479 | 2,9084 | 3,2330 | 3,5597 | |
4 | 4,9220 | 5,2867 | 5,6600 | 6,0413 | 6,4301 | 6,8255 | 7,6341 | 8,4618 | |
5 | 8,9303 | 9,6085 | 10,305 | 11,020 | 11,752 | 12,500 | 14,041 | 15,635 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,0216 | 0,0243 | 0,0272 | 0,0304 | 0,0337 | 0,0373 | 0,0453 | 0,0543 | |
3 | 0,1726 | 0,1943 | 0,2174 | 0,2424 | 0,2693 | 0,2980 | 0,3615 | 0,4334 | |
4 | 0,5810 | 0,6532 | 0,7312 | 0,8151 | 0,9052 | 1,0016 | 1,2142 | 1,4548 | |
5 | 1,3714 | 1,5414 | 1,7248 | 1,9221 | 2,1336 | 2,3599 | 2,8586 | 3,4219 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,5559 | 0,5978 | 0,6409 | 0,6850 | 0,7301 | 0,7761 | 0,8706 | 0,9680 | |
3 | 2,2768 | 2,4536 | 2,6359 | 2,8235 | 3,0163 | 3,2142 | 3,6241 | 4,0519 | |
4 | 5,2122 | 5,6250 | 6,0521 | 6,4931 | 6,9479 | 7,4162 | 8,3923 | 9,4194 | |
5 | 9,3690 | 10,1206 | 10,899 | 11,705 | 12,538 | 13,397 | 15,195 | 17,046 | |
 | 0,0937 | 0,1012 | 0,1090 | 0,1171 | 0,1254 | 0,1340 | 0,1520 | 0,1710 | |
Продольная сила в плите у пересечения с бортовым элементом (точка 1 на рисунке 5.3.9, б) вычисляется по формуле
Продольная сила в других точках плиты далее по дуге определяется по формуле
Задание: для длинной цилиндрической оболочки, рассматриваемой в примере 9, рассчитать внутренние усилия, действующие в поперечном направлении.
На поперечную полоску оболочки шириной 1 м действуют следующие расчетные нагрузки: постоянная, равномерно распределенная по криволинейной поверхности g = 3,5 кН/м; временная (снег), равномерно распределенная по горизонтальной проекции s = 1,8 кН/м; постоянная от массы бортовых элементов ged = 4 кН. Схема приложения нагрузок - на рисунке 5.3.9, б.
Расчет оболочки в поперечном направлении выполняем в соответствии с 5.3.19.
Приращения сдвигающих усилий для полоски посередине пролета оболочки, где высота сечения бортового элемента (с учетом замоноличенной стыковой полости) hed = 1,6 м, находим по формуле (5.3.15)
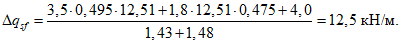
Коэффициенты при неизвестных системы (5.3.16) определим по формулам (5.3.17):


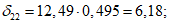
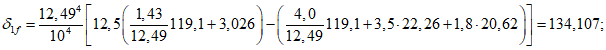
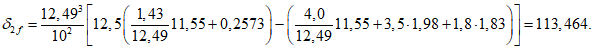
Найденные значения коэффициентов подставляем в канонические уравнения (5.3.16):
7,8X1 + 6,26X2 = -134,107;
6,26X1 + 6,18X2 = -113,464.
В результате решения этих уравнений получаем X1 = 13,142 кНм; X2 = -5,047 кНм.
Для вычисления значений продольных сил и изгибающих моментов в точках дуги поперечного сечения оболочки определяем некоторые, необходимые для подстановки в формулы (5.3.19), (5.3.21) и (5.3.22), геометрические характеристики сечения посередине пролета. Значения характеристик для точек 1 ... 5 поперечного сечения - в таблице 5.3.6.
Обозначение параметра | Значение параметра для точки поперечного сечения | ||||
1 | 2 | 3 | 4 | 5 | |
0 | 7°5' | 14°10' | 21°15' | 28°20'43" | |
(рад.) | (0) | (0,1237) | (0,2475) | (0,371) | (0,4947) |
0 | 0,1235 | 0,245 | 0,362 | 0,475 | |
1 | 0,993 | 0,97 | 0,931 | 0,88 | |
28°20' | 21°15' | 14°10' | 7°5' | 0 | |
(рад.) | (0,4947) | (0,371) | (0,2474) | (0,1237) | (0) |
0,475 | 0,362 | 0,245 | 0,1235 | 0 | |
0,88 | 0,931 | 0,97 | 0,993 | 1 | |
0 | 11,3 | 23 | 35,15 | 47,5 | |
0 | 5,1 | 9 | 11,3 | 12 | |
0 | 0,64 | 2,65 | 6,18 | 11,28 | |
0 | 0,03 | 0,25 | 0,9 | 2 | |
0 | 0,69 | 2,94 | 6,72 | 12 | |
zcur.pl, м | 0 | 0,64 | 1,12 | 1,41 | 1,48 |
Значения продольной силы для точки 1 находим по формуле (5.3.21):
N1 = (4,0 - 12,5·1,43)·0,475 - 13,142·0,88 = -18,156 кН,
а для остальных точек дуги - по формуле (5.3.22):
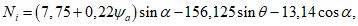
например:
N2 = (7,75 + 0,22·11,3)·0,362 - 156,125·0,1237 - 13,142·0,931 = -27,84 кН.
Изгибающий момент для точки 1 вычисляем по (5.3.19), при этом первое и второе слагаемые формулы в точке 1 обращаются в ноль:
Mmt,i = X2 - N1e = -5,047 + 18,156·0,032 = -4,47 кНм.
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Эксцентриситет продольной силы при вычислении Mmt,I принят e = 32 мм.
Для вычисления изгибающих моментов Mmt,i в остальных точках дуги необходимо сначала определить значения моментов в этих точках по формуле (5.3.18) как для одноволновой оболочки, но без последнего члена формулы:
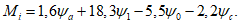
Например:
M2 = 1,733·11,3 + 19,5·0,03 - 5,46·0,69 - 2,8·0,64 + 27,84·0,032 = 15,5 кНм.
Mmt,2 = 15,5 - 13,142·0,01·12,49·5,1 - 5,047 = 2,08 кНм.
Опуская арифметические выкладки, приводим на рисунке 5.3.10, б эпюры N, кН/м, и M, кНм/м, вычисленные для всех точек поперечного сечения оболочки.
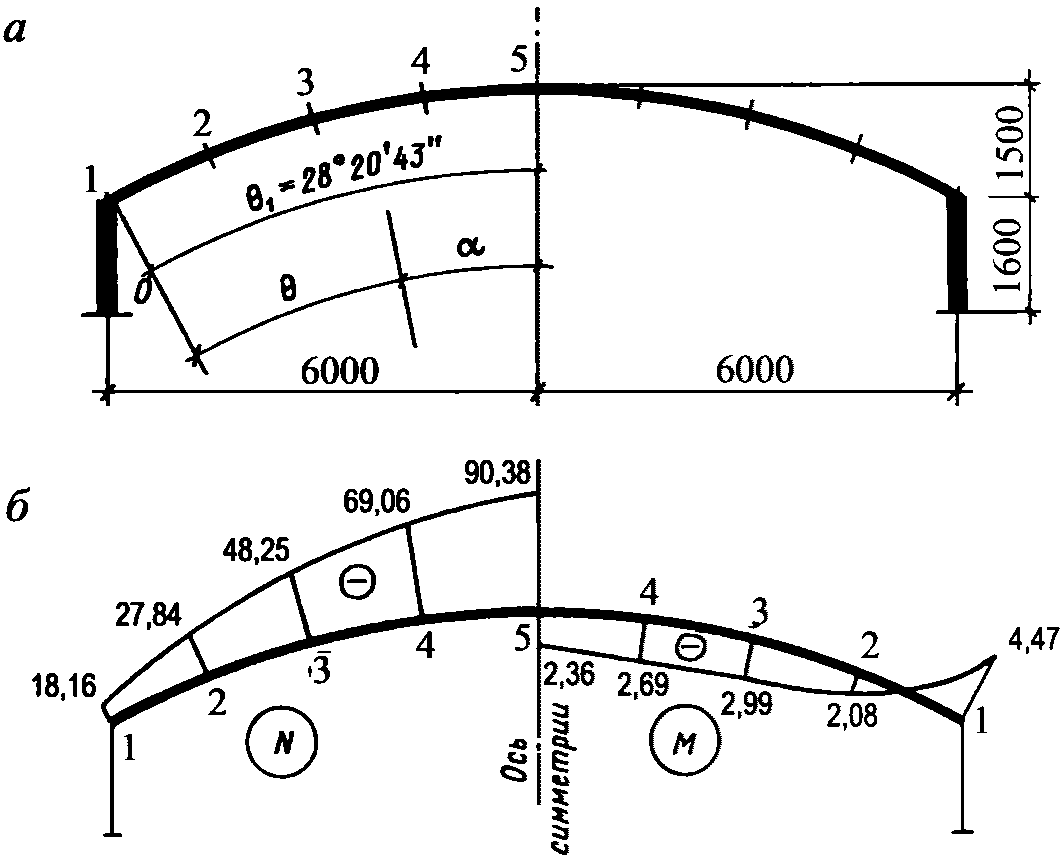
а - расчетная геометрия; б - эпюры нормальных сил (кН)
и изгибающих моментов (кНм) на 1 м длины оболочки
на поперечные изгибающие моменты
В приведенном примере расчета оболочка ребристая - поперечные ребра с шагом 3 м, поэтому вычисленные значения поперечных изгибающих моментов и продольных сил умножают на 3 м и полученное усилие передают на основную арматуру ребер, рассчитывая тавровое сечение ребристой плиты.
5.3.20 Диафрагмы рассчитывают как плоские стержневые или балочные конструкции на действие нагрузки от собственного веса и опорного давления, передаваемого в виде сдвигающих сил, касательных к срединной поверхности оболочки или складки, обратных по направлению и равных по значению сдвигающим усилиям в оболочке на контуре - по линии ее сопряжения с диафрагмой (рисунок 5.3.11).
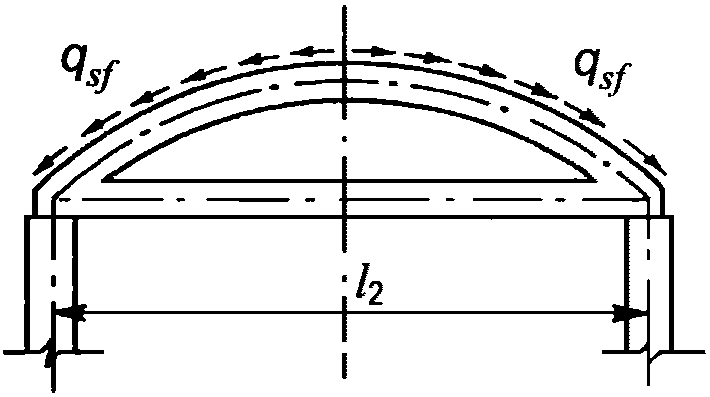
на торцевую диафрагму
Значения сдвигающих сил определяют из расчета оболочек и складок как упругих систем.
Сумма проекций сдвигающих сил на вертикальную ось должна уравновешиваться балочной опорной реакцией оболочки.
Для вычисления сдвигающих сил необходимо найти значение статического момента отсеченной части сечения криволинейной плиты с центральным углом 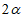 (рисунок 5.3.10, а), которое может быть определено по формуле
(рисунок 5.3.10, а), которое может быть определено по формуле
 (5.3.23)
(5.3.23)Значение сдвигающих сил qsf в любой точке срединной поверхности криволинейной плиты, очерченной по дуге окружности, с осью симметрии и вертикальными бортовыми элементами, расположенными ниже края криволинейной плиты, можно вычислять по формуле (5.3.11), принимая для Q значение нагрузки, приходящейся на половину длины оболочки и диафрагмы, т.е. опорную реакцию торцевой диафрагмы.
Сумма проекций сдвигающих сил на вертикальную ось определяется по формуле
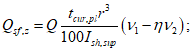 (5.3.24)
(5.3.24)здесь 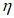 - коэффициент, определяющий положение центра тяжести сечения плиты оболочки:
- коэффициент, определяющий положение центра тяжести сечения плиты оболочки: 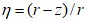 ;
;
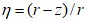 ;
;z - расстояние от точки на срединной поверхности в шелыге криволинейной плиты до центра тяжести ее сечения.
Внешнюю нагрузку на торцевую арочную диафрагму в виде сдвигающих сил, действующих в торцевом опорном сечении оболочки, целесообразно определять в точках 1 ... 5, показанных на рисунке 5.3.9, б.
Усилия 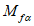 ,
, 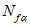 и
и 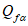 от сдвигающих сил, действующих на арку, определим для сечений в пяти точках с угловой координатой
от сдвигающих сил, действующих на арку, определим для сечений в пяти точках с угловой координатой 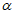 (точки 1' ... 5'), показанных на рисунке 5.3.12, в. Для вычисления усилий воспользуемся следующими формулами:
(точки 1' ... 5'), показанных на рисунке 5.3.12, в. Для вычисления усилий воспользуемся следующими формулами:
где  ;
;
 ;
;Q - опорная реакция торцевой диафрагмы (половина опорной реакции оболочки).

а - геометрическая и расчетная схемы арки; б - сечение арки;
в - ординаты точек на оси арки; г - эпюры усилий в основной
системе арки от H = 1; д - то же, от внешней нагрузки
(сдвигающих сил); е - суммарные эпюры
Значения коэффициентов 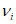 , подсчитанные для углов
, подсчитанные для углов 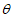 в пяти точках дуги (рисунок 5.3.9, б), приведены в таблице 5.3.7.
в пяти точках дуги (рисунок 5.3.9, б), приведены в таблице 5.3.7.
Коэффициент | Номер точки | Значение коэффициента для угла | |||||||
25° | 26° | 27° | 28° | 29° | 30° | 32° | 34° | ||
1 | 5,331 | 5,978 | 6,673 | 7,417 | 8,212 | 9,059 | 10,911 | 12,982 | |
2 | 5,331 | 5,978 | 6,673 | 7,417 | 8,212 | 9,059 | 10,911 | 12,982 | |
3 | 5,331 | 5,978 | 6,673 | 7,417 | 8,212 | 9,059 | 10,911 | 12,982 | |
4 | 5,331 | 5,978 | 6,673 | 7,417 | 8,212 | 9,059 | 10,911 | 12,982 | |
5 | 5,331 | 5,978 | 6,673 | 7,417 | 8,212 | 9,059 | 10,911 | 12,982 | |
1 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,31 | 11,256 | 13,446 | |
2 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,31 | 11,256 | 13,446 | |
3 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,31 | 11,256 | 13,446 | |
4 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,31 | 11,256 | 13,446 | |
5 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,31 | 11,256 | 13,446 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 10,118 | 10,456 | 10,787 | 11,11 | 11,425 | 11,732 | 12,318 | 12,868 | |
3 | 20,618 | 21,342 | 22,055 | 22,755 | 23,443 | 24,118 | 25,428 | 26,682 | |
4 | 31,375 | 32,517 | 33,645 | 34,76 | 35,861 | 36,947 | 39,075 | 41,138 | |
5 | 42,262 | 43,837 | 45,399 | 46,947 | 48,481 | 50,0 | 52,992 | 55,919 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,017 | 0,020 | 0,023 | 0,027 | 0,031 | 0,035 | 0,045 | 0,057 | |
3 | 0,129 | 0,150 | 0,174 | 0,201 | 0,23 | 0,263 | 0,339 | 0,429 | |
4 | 0,402 | 0,470 | 0,545 | 0,629 | 0,721 | 0,824 | 1,061 | 1,343 | |
5 | 0,878 | 1,024 | 1,188 | 1,370 | 1,572 | 1,795 | 2,309 | 2,923 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,018 | 0,021 | 0,024 | 0,028 | 0,032 | 0,037 | 0,047 | 0,06 | |
3 | 0,132 | 0,154 | 0,179 | 0,207 | 0,238 | 0,273 | 0,353 | 0,45 | |
4 | 0,412 | 0,481 | 0,56 | 0,647 | 0,744 | 0,852 | 1,101 | 1,402 | |
5 | 0,897 | 1,048 | 1,218 | 1,407 | 1,618 | 1,851 | 2,391 | 3,04 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 8,107 | 8,749 | 9,414 | 10,100 | 10,807 | 11,536 | 13,054 | 14,652 | |
3 | 13,869 | 14,965 | 16,099 | 17,269 | 18,475 | 19,717 | 22,304 | 25,024 | |
4 | 17,147 | 18,486 | 19,868 | 21,291 | 22,756 | 24,260 | 27,383 | 30,652 | |
5 | 17,861 | 19,217 | 20,611 | 22,040 | 23,504 | 25,000 | 28,081 | 31,270 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 8,312 | 8,988 | 9,691 | 10,421 | 11,176 | 11,958 | 13,599 | 15,346 | |
3 | 14,147 | 15,290 | 16,476 | 17,704 | 18,975 | 20,289 | 23,041 | 25,960 | |
4 | 17,437 | 18,924 | 20,259 | 21,742 | 23,273 | 24,850 | 28,142 | 31,611 | |
5 | 18,142 | 19,544 | 20,989 | 22,475 | 24,000 | 25,565 | 28,802 | 32,174 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,463 | 0,519 | 0,580 | 0,645 | 0,715 | 0,790 | 0,953 | 1,136 | |
3 | 1,683 | 1,889 | 2,111 | 2,348 | 2,602 | 2,873 | 3,468 | 4,135 | |
4 | 3,398 | 3,812 | 4,258 | 4,736 | 5,247 | 5,792 | 6,986 | 8,325 | |
5 | 5,331 | 5,978 | 6,672 | 7,417 | 8,211 | 9,058 | 10,910 | 12,981 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2 | 0,475 | 0,534 | 0,599 | 0,688 | 0,742 | 0,821 | 0,996 | 1,195 | |
3 | 1,723 | 1,938 | 2,169 | 2,418 | 2,686 | 2,972 | 3,604 | 4,319 | |
4 | 3,469 | 3,899 | 4,363 | 4,862 | 5,396 | 5,968 | 7,229 | 8,652 | |
5 | 5,433 | 6,102 | 6,823 | 7,596 | 8,425 | 9,310 | 11,256 | 13,446 | |
При расчете диафрагм следует учитывать эксцентричное приложение сдвигающих сил по отношению к оси элементов конструкции.
Пример 11
Задание: для длинной цилиндрической оболочки, рассматриваемой в примерах 9 и 10, рассчитать изгибающие моменты и поперечные силы для проектирования торцевой диафрагмы.
Параметры опорного сечения оболочки, примыкающего к торцевой диафрагме: площадь сечения бортовой балки Aed = 0,3·1,0 = 0,3 м2; площадь сечения криволинейной плиты Acur,pl = 0,495 м2; общая площадь опорного сечения оболочки Ash = 0,795 м2; момент инерции сечения оболочки Ish,sup = 0,541 м4; расстояние от центра тяжести сечения оболочки до оси сечения криволинейной плиты в шелыге z = 1,07 м;  .
.
 .
.Поскольку в нашем конструктивном решении оболочка примыкает к торцевой арке поверху (рисунок 5.3.12, б), сдвигающие силы передаются от плиты оболочки на ось арки с эксцентриситетом e = 180 мм. Кроме того, опорный узел арки выполнен так, что затяжка присоединяется к арке с эксцентриситетом 250 мм (рисунок 5.3.12, а). Эти эксцентриситеты учитываются расчетом.
Определяем значения усилий:
Q = 6,24·12,0·0,5·29,6·0,5 = 554,1 кН;

Подставив в формулу (5.3.25) известные значения, получаем:
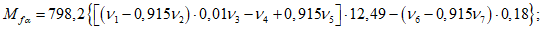

ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Результаты расчета 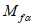 и
и 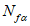 приведены в таблице 5.3.8. Эпюры этих усилий даны на рисунке 5.3.12, д. После определения нагрузок и эпюр от них можно приступить к расчету арки.
приведены в таблице 5.3.8. Эпюры этих усилий даны на рисунке 5.3.12, д. После определения нагрузок и эпюр от них можно приступить к расчету арки.
Номер точки в сечении | Значение параметра | |||||||||
1' | 798,2 | 7,7 | 7,88 | 0 | 0 | 0 | 0 | 0 | 0 | -189 |
2' | 798,2 | 7,7 | 7,88 | 11,3 | 0,0282 | 0,0286 | 10,34 | 10,67 | 449 | 321 |
3' | 798,2 | 7,7 | 7,88 | 23,0 | 0,221 | 0,228 | 17,68 | 18,15 | 848 | 759 |
4' | 798,2 | 7,7 | 7,88 | 35,1 | 0,660 | 0,679 | 21,79 | 22,30 | 1125 | 1062 |
5' | 798,2 | 7,7 | 7,88 | 47,5 | 1,440 | 1,48 | 22,54 | 23,0 | 1249 | 1197 |
Двухшарнирная арка - одиножды статически неопределимая система. Раскрытие статической неопределимости выполняем методом сил. В качестве лишней неизвестной используем усилие в затяжке, т.е. распор. Искомое усилие получаем из формулы
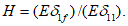
Усилия в основной системе от единичного распора H = 1 вычисляются элементарно и показаны на рисунке 5.3.12, г.
Опуская перемножение эпюр по методу Верещагина, приводим окончательный результат вычисления перемещений. При этом сечение арки принято по рисунку 5.3.12, б. Площадь поперечного сечения и момент инерции арки соответственно Aa = 0,095 м2, Ia = 0,00145 м4.
Сечение затяжки Atd = 0,2·0,2 = 0,04 м2.

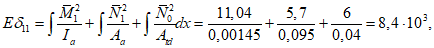
откуда H = 4,82·106/8,4·103 = 573,8 кН.
Суммарные эпюры изгибающих моментов, кНм, и продольных сил, кН, показаны на рисунке 5.3.12, е.
5.4.1 Панель-оболочка КЖС (крупноразмерная, железобетонная, сводчатая) представляет собой короткий цилиндрический пологий предварительно напряженный свод-оболочку с двумя ребрами-диафрагмами сегментного очертания (рисунки 5.4.1, 5.4.2), в нижней утолщенной части которых располагается предварительно напряженная арматура. Номинальные размеры панелей в плане рекомендуется принимать равными 3 x 12; 3 x 18 и 3 x 24 м.

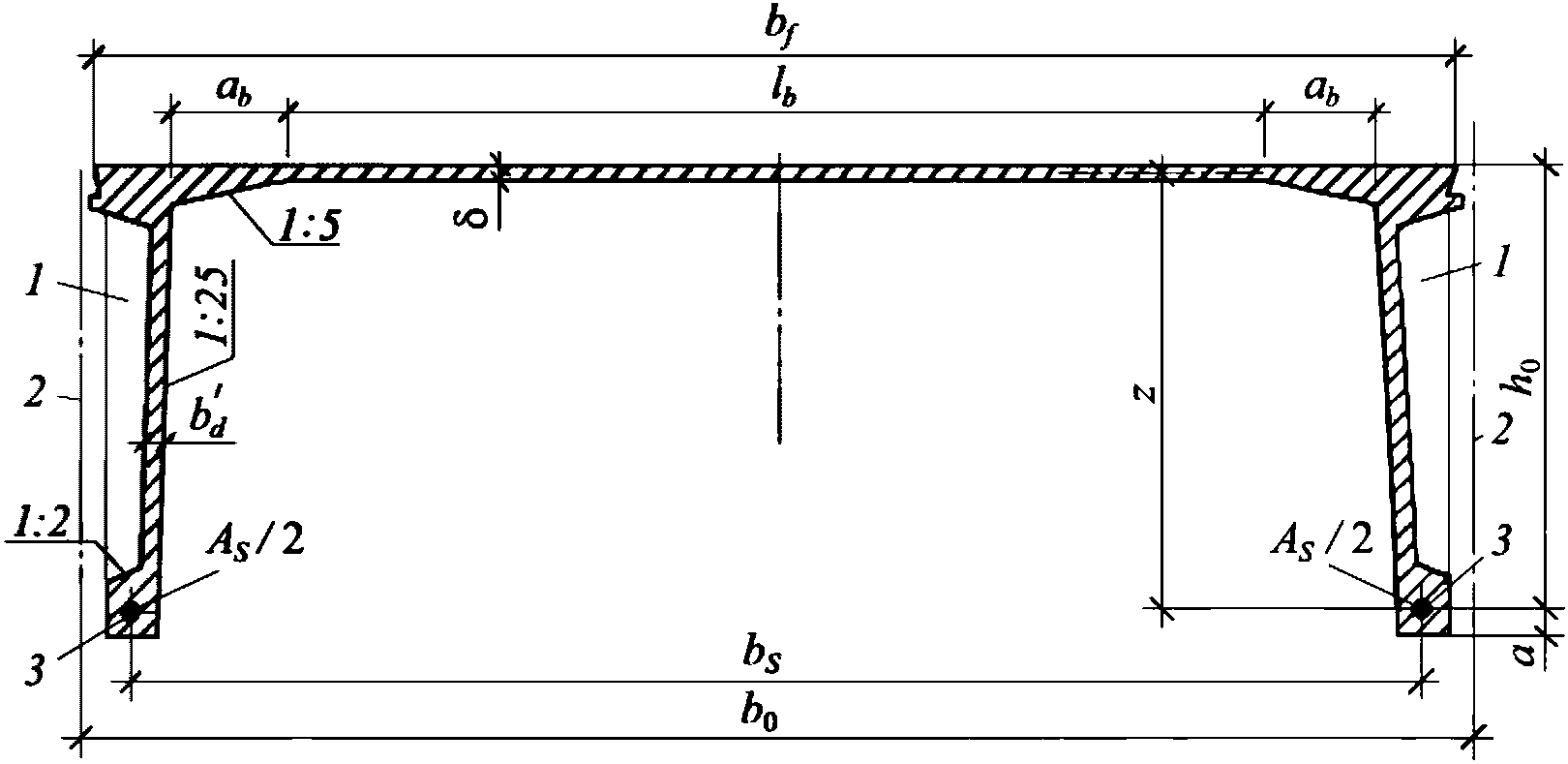
1 - вертикальное ребро жесткости; 2 - разбивочная ось;
3 - напрягаемая рабочая арматура
Высоту поперечного сечения панели в середине пролета hc принимают равной 1/20 - 1/15l0 в зависимости от значения нагрузки и размера пролета. Очертание верхней поверхности оболочки рекомендуется принимать по квадратной параболе.
5.4.2 Панели-оболочки КЖС предназначаются для покрытий зданий с пролетами 12, 18, 24 м и с другими пролетами. Панели-оболочки КЖС применяют в покрытиях однопролетных и многопролетных зданий с фонарями и без фонарей, бескрановых, а также в зданиях, оборудованных подвесным транспортом грузоподъемностью до 5 т.
Панели КЖС опирают на продольные несущие стены, продольные железобетонные балки прямоугольного сечения высотой 500 - 600 мм - при шаге колонн 6 м, предварительно напряженные железобетонные двутавровые балки с высотой сечения 1000 - 1200 мм или фермы раскосно-шпренгельного типа с предварительно напряженной арматурой при шаге колонн 12 м.
5.4.3 Панели КЖС рекомендуется проектировать из бетонов классов B25 - B40 по прочности на сжатие в зависимости от размеров пролета и нагрузок. В тех случаях, когда это технически и экономически целесообразно, панели-оболочки КЖС рекомендуется проектировать из бетонов тех же классов на пористых заполнителях. Рекомендуется проектировать комплексные панели-оболочки повышенной заводской готовности с плитным утеплителем (без стяжки) и кровлей, приклеенными на заводе-изготовителе.
Минимальную толщину поля оболочки следует принимать не менее 30 мм; диафрагмы рекомендуется проектировать облегченной кессонированной конструкции с вертикальными ребрами жесткости и с минимальной толщиной стенки, равной 40 мм. Толщину стенки в первом от опоры кессоне диафрагмы принимают не менее 50 мм. Сопряжение оболочки с диафрагмами выполняют с применением пологих вутов с уклоном i = 1:5 (рисунок 5.4.2).

а - продольный разрез; б - план опорной части;
1 - 5 - номера характерных точек продольного сечения
по оси панели; 6 - ось напрягаемой арматуры диафрагмы;
7 - ось оболочки
5.4.4 Основную напрягаемую рабочую арматуру панели рекомендуется проектировать из двух предварительно напряженных элементов, расположенных в нижней утолщенной зоне диафрагм, и принимать из одного или двух вплотную расположенных стержней в каждом ребре (диафрагме).
По концам напрягаемых элементов рабочей арматуры предусматривают прикрепленные к ним стальные анкерные детали (рисунок 5.4.3), обеспечивающие надежное заанкеривание рабочей арматуры в бетоне опорного узла панели.
Армирование оболочки выполняют сварной арматурной сеткой. Коэффициент армирования средней части пролета между точками 4 - 5 (рисунок 5.4.4) должен быть не менее: 0,3% - для арматуры поперечного направления; 0,2% - продольного.
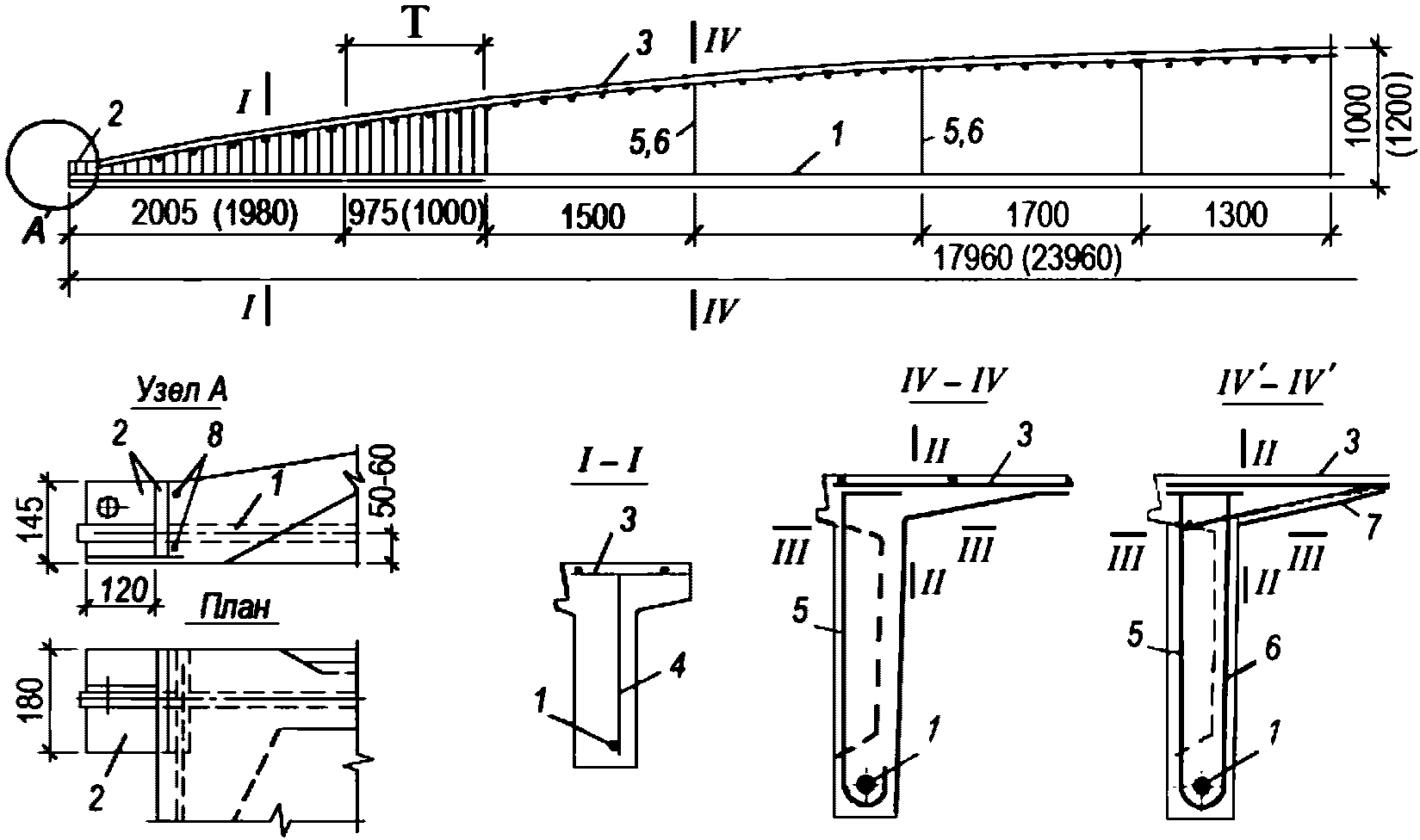
1 - напрягаемая арматура диафрагмы; 2 - анкер;
3 - арматурная сетка оболочки; 4 - поперечная арматура
диафрагмы (на участке T устанавливается только при наличии
подвесного транспорта); 5 - подвеска наружная; 6 - подвеска
внутренняя; 7 - сетка в вуте; 8 - торцевая арматура
(сечение IV' - IV' при наличии подвесных кранов
и для сегментных сводов)
размером 3 x 18 (24) м
Диафрагмы, как правило, армируют сварными каркасами только в опорных зонах (на участках длиной 0,1l0 или более - в зависимости от результатов расчета), а также стержнями-подвесками, расположенными в вертикальных ребрах диафрагм.
5.4.5 Для устройства светоаэрационных или зенитных фонарей панели следует проектировать с проемами (рисунок 5.4.5) размерами 2,5 x 6 м - для панелей размерами 3 x 18 м и 2,5 x 9 м - для панелей 3 x 24 м.
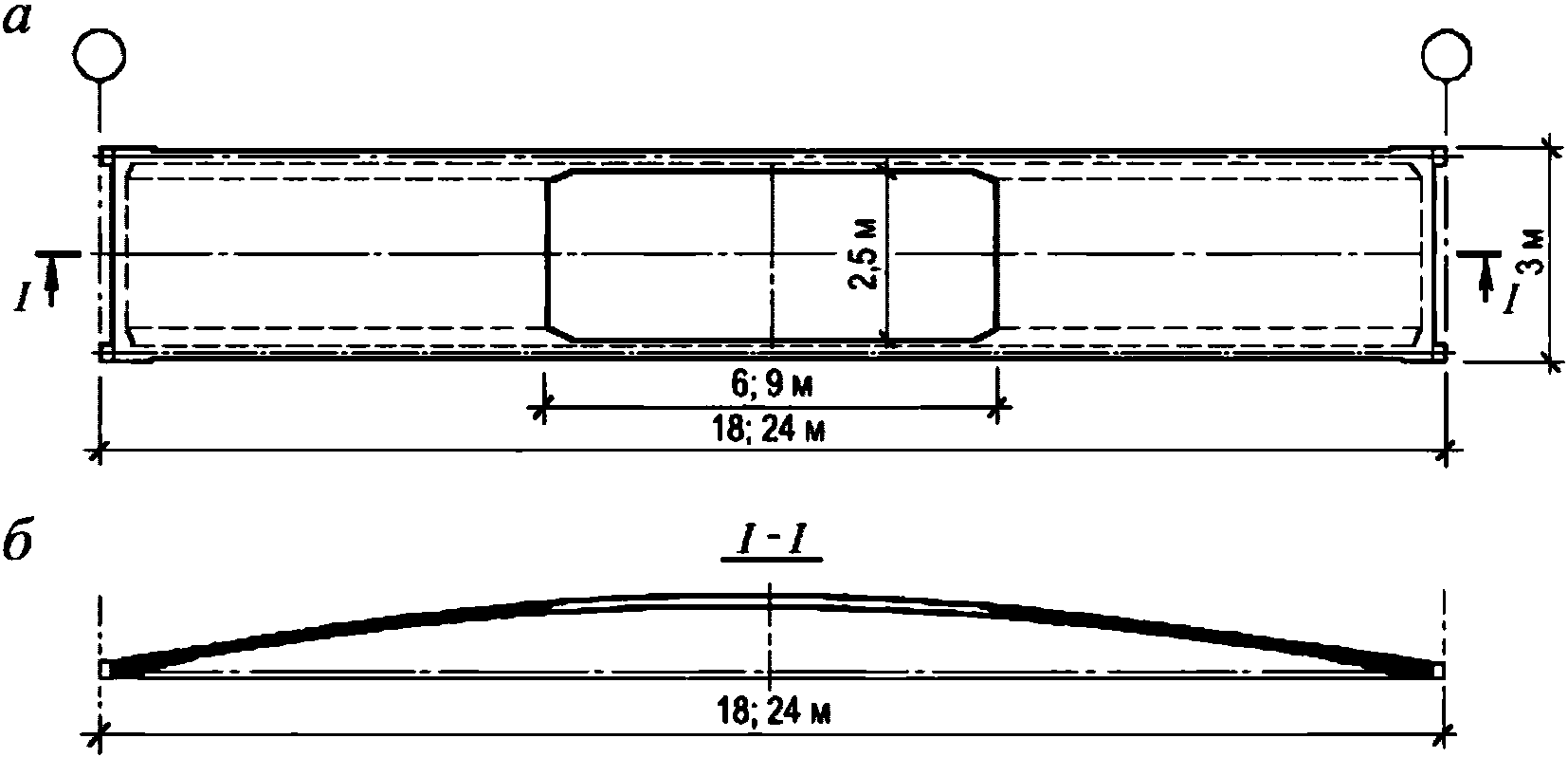
а - план; б - продольный разрез по оси панели
для светоаэрационного или зенитного фонаря
По периметру фонарного проема в оболочке предусматривают плавное утолщение до 70 - 80 мм; сжатую зону диафрагм в пределах проема рекомендуется соответственно усиливать. Армирование вокруг проема оболочки и сжатой зоны диафрагм принимают по расчету.
5.4.6 Для обеспечения совместной работы панелей КЖС с каркасом здания должно быть предусмотрено их крепление сваркой во всех четырех углах панели к продольным несущим конструкциям покрытия. Крепление рекомендуется осуществлять с применением листовых шарниров, обеспечивающих возможность поворота сечения панели в вертикальной плоскости. Жесткое крепление панелей, создающее их защемление на опорах, не допускается.
Строповку панели при ее подъеме следует осуществлять только за отверстия в угловых анкерных деталях (поз. 2 на рисунке 5.4.4).
На всех стадиях производства, складирования, транспортирования и монтажа панель-оболочка должна опираться только на угловые анкерные детали.
5.4.7 Усилия и деформации в панели-оболочке КЖС рекомендуется определять расчетом методом конечных элементов с учетом геометрической и физической нелинейностей.
Допускается расчет по несущей способности и устойчивости пологой цилиндрической панели-оболочки КЖС, у которых отношение l0/b0 >= 4, выполнять по методике расчетных предельных состояний как цилиндрического свода, работающего совместно с деформирующимися диафрагмами, в соответствии с 5.4.8 - 5.4.11.
5.4.8 Требуемые для обеспечения общей несущей способности панели-оболочки КЖС площади сечения As рабочей арматуры диафрагм и толщину оболочки  (рисунок 5.4.3, а) определяют из условий:
(рисунок 5.4.3, а) определяют из условий:
где M - изгибающий момент в рассматриваемом сечении панели;
z0 - стрела подъема оболочки (т.е. расстояние по вертикали от оси оболочки до оси рабочей арматуры диафрагмы в середине пролета);
Rs - расчетное сопротивление рабочей арматуры диафрагм;
bf - ширина панели поверху;
0,75 - для панелей шириной 3 м;
0,9 - для доборных панелей шириной 2 м;
1,0 - для доборных панелей шириной 1,5 м;
Толщину оболочки  на участке, примыкающем к опоре, определяют с учетом усилий, действующих в опорной зоне.
на участке, примыкающем к опоре, определяют с учетом усилий, действующих в опорной зоне.
5.4.9 Принятую из условия обеспечения несущей способности по формуле (5.4.2) толщину оболочки следует проверять из условия обеспечения устойчивости оболочки на условные критические напряжения сжатия по формуле
где lb - расчетный пролет оболочки, равный расстоянию в свету между вутами (рисунок 5.4.2);
M0,n - изгибающий момент от расчетных нагрузок в середине пролета панели при коэффициенте надежности по нагрузке  ;
;
y0 - расстояние от центра тяжести приведенного сечения панели в середине пролета до оси оболочки;
I0,red - момент инерции приведенного поперечного сечения панели в середине ее пролета.
5.4.10 Площадь сечения стержней торцевой рабочей арматуры (поз. 8 на рисунке 5.4.4) при опирании панели на продольные несущие конструкции следует определять по большему из значений усилий Ne, вычисленных по формулам:
где g - расчетная нагрузка от веса панели, кН/м2;
2 - сопротивление отрыву при съеме панели с формы, кН/м2;
l - расчетный пролет панели (рисунок 5.4.3, а);
bs - расстояние между осями рабочей арматуры диафрагм (рисунок 5.4.2);
bsup - ширина панели на опоре.
Для торцевой арматуры рекомендуется применять сталь класса не ниже A400.
5.4.11 Расчет диафрагм панели-оболочки КЖС на поперечную силу производят с учетом разгружающего действия вертикальных составляющих сил сжатия в оболочке. Часть поперечной силы Qd, воспринимаемой диафрагмами, определяют по формуле
при этом должно выполняться условие
где Q0 - полное значение поперечной силы в рассматриваемом сечении панели x, отсчитываемом от рабочей поверхности анкера рабочей арматуры диафрагмы (рисунок 5.4.3, а);
h0 - рабочая высота сечения.
При соблюдении условия (5.4.7) на участках диафрагм длиной 0,1l, примыкающих к опорам, во всех случаях следует устанавливать конструктивную поперечную арматуру из проволоки класса B500 диаметром не менее 5 мм с шагом 100 мм, а при наличии на участках диафрагм сосредоточенных нагрузок от подвесного транспорта - не менее 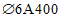 с шагом 100 мм. Кроме того, при назначении шага поперечных стержней следует соблюдать требования СП 63.13330. Также следует устанавливать стержни-подвески в вертикальных ребрах жесткости диафрагм (рисунок 5.4.4), располагаемые с шагом 1,5 - 1,6 м. При наличии подвесного транспорта стержни-подвески выполняют двойными.
с шагом 100 мм. Кроме того, при назначении шага поперечных стержней следует соблюдать требования СП 63.13330. Также следует устанавливать стержни-подвески в вертикальных ребрах жесткости диафрагм (рисунок 5.4.4), располагаемые с шагом 1,5 - 1,6 м. При наличии подвесного транспорта стержни-подвески выполняют двойными.
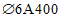 с шагом 100 мм. Кроме того, при назначении шага поперечных стержней следует соблюдать требования СП 63.13330. Также следует устанавливать стержни-подвески в вертикальных ребрах жесткости диафрагм (рисунок 5.4.4), располагаемые с шагом 1,5 - 1,6 м. При наличии подвесного транспорта стержни-подвески выполняют двойными.
с шагом 100 мм. Кроме того, при назначении шага поперечных стержней следует соблюдать требования СП 63.13330. Также следует устанавливать стержни-подвески в вертикальных ребрах жесткости диафрагм (рисунок 5.4.4), располагаемые с шагом 1,5 - 1,6 м. При наличии подвесного транспорта стержни-подвески выполняют двойными.Если условие (5.4.7) не соблюдается, поперечную арматуру следует устанавливать по расчету, при этом требуемую площадь сечения поперечной арматуры в диафрагмах вычисляют по формуле
где fx - площадь сечения одного поперечного (вертикального) стержня каркаса диафрагмы;
|Qd| - абсолютное значение части поперечной силы, воспринимаемой обеими диафрагмами панели, определяемое по формуле (5.4.6);
z - плечо внутренней пары сил (расстояние по вертикали от оси напрягаемой арматуры до срединной поверхности поля оболочки) в рассматриваемом сечении;
u - шаг поперечных стержней каркаса диафрагмы.
В знаменателе формулы (5.4.8) знак плюс для левой половины панели принимается в тех случаях, когда значение Qd положительно, и минус - когда значение Qd отрицательно.
5.4.12 Площадь рабочей поверхности анкера рабочей арматуры каждой диафрагмы следует проверять исходя из условия
где M1 - изгибающий момент на всю ширину панели в сечении, расположенном на расстоянии 1,5 м от рабочей поверхности анкера;
z1 - расстояние по вертикали от оси рабочей арматуры диафрагмы до оси оболочки в этом же сечении.
При нагрузках от подвесных кранов изгибающий момент M1 и значение z1 следует вычислять в сечении под грузом, ближайшим к опоре.
5.4.13 Прогиб w0sh в середине пролета предварительно напряженной панели-оболочки КЖС при кратковременном действии равномерно распределенной нагрузки следует определять по формуле
 (5.4.10)
(5.4.10)где qn - нормативное значение равномерно распределенной на полосе оболочки единичной ширины нагрузки;
Eb1 = 0,85Eb;
I0,red - момент инерции приведенного поперечного сечения панели КЖС в середине пролета.
Значение прогиба w0l панели в середине пролета с учетом длительного действия нагрузки и предварительного напряжения определяют по формуле
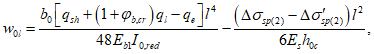 (5.4.11)
(5.4.11)где gsh - кратковременно действующая часть нагрузки;
ql - длительно действующая часть нагрузки;
qe - эквивалентная по моменту в середине пролета равномерно распределенная нагрузка от сил предварительного напряжения, определяемая по формуле
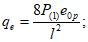 (5.4.12)
(5.4.12)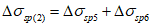 - сумма потерь предварительного напряжения рабочей арматуры от усадки и ползучести бетона согласно СП 63.13330;
- сумма потерь предварительного напряжения рабочей арматуры от усадки и ползучести бетона согласно СП 63.13330;Es - модуль упругости рабочей арматуры диафрагм;
h0c - рабочая высота поперечного сечения панели в середине пролета;
P(1) - равнодействующая усилий в напрягаемой арматуре до обжатия бетона, определяемая при коэффициенте точности натяжения 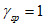 ;
;
e0p - расстояние от оси напрягаемой арматуры до центра тяжести приведенного сечения панели в середине пролета.
5.4.14 Расчет по образованию трещин в диафрагмах панелей КЖС рекомендуется выполнять согласно СП 63.13330 с учетом:
- разгружающего действия веса панели при 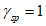 во всех случаях при определении потерь предварительного напряжения в арматуре;
во всех случаях при определении потерь предварительного напряжения в арматуре;
- неупругих деформаций бетона - значение момента сопротивления Wpl приведенного сечения панели для растянутой грани допускается определять по формуле
Wpl = 1,3W, (5.4.13)
где W - момент сопротивления для растянутой грани сечения, определяемый в соответствии с правилами сопротивления упругих материалов по формуле
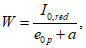 (5.4.14)
(5.4.14)где a - расстояние от нижней грани ребра до оси напрягаемой арматуры (рисунок 5.4.2).
5.4.15 Оболочку панели-оболочки КЖС рекомендуется рассчитывать на изгиб в направлении ее образующей как короткую цилиндрическую оболочку между диафрагмами. При этом необходимо учитывать изменения геометрической схемы конструкции вследствие роста прогибов, появления и развития трещин в диафрагмах и уменьшения кривизны оболочки в процессе ее нагружения.
Расчет производят из условия, чтобы значение нагрузки qb, передающейся на диафрагмы за счет изгиба оболочки, не превышало значения предельной нагрузки по несущей способности оболочки на изгиб, определенной методом предельного равновесия.
Расчет несущей способности оболочки на изгиб следует производить при:
- нагрузке, равномерно распределенной по всей поверхности оболочки;
- снеговой нагрузке, расположенной на половине пролета с учетом коэффициента снегоотложения 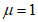 , а на участках нижних покрытий при перепаде высот - с учетом коэффициента
, а на участках нижних покрытий при перепаде высот - с учетом коэффициента 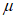 , определяемого согласно СП 20.13330;
, определяемого согласно СП 20.13330;
- нагружении диафрагм сосредоточенными нагрузками от симметрично расположенных подвесных кранов;
- нагружении сосредоточенными нагрузками от стоек каркаса фонаря и т.п.
Для каждого случая следует проводить расчет на возможные неблагоприятные сочетания нагрузок с коэффициентами сочетаний, принимаемыми по СП 20.13330.
При этом учитывают, что при нагрузке, приложенной к полю оболочки, изгибающая нагрузка положительна (направлена вниз), при нагрузке, приложенной к диафрагмам, - отрицательна (направлена вверх), а снеговая нагрузка, приложенная на одной половине пролета, создает на ней положительную изгибающую нагрузку, на другой - отрицательную. Силы предварительного напряжения рабочей арматуры диафрагм создают положительную изгибающую нагрузку на оболочку.
5.4.16 При равномерном нагружении (рисунок 5.4.6) максимальное значение расчетной изгибающей нагрузки qb,max рассчитывают по формуле
где qM - расчетная равномерно распределенная нагрузка, приложенная непосредственно к оболочке с учетом ее веса (без учета веса диафрагм);
w0,max - расчетный прогиб панели в середине пролета, определяемый по формуле (5.4.16);
q - эквивалентная по моменту в середине пролета расчетная равномерно распределенная нагрузка с учетом веса панели;
qN - вертикальная нагрузка, эквивалентная по нормальной силе, возникающей в оболочке от предварительного напряжения панели, определяемая по формуле (5.4.20);
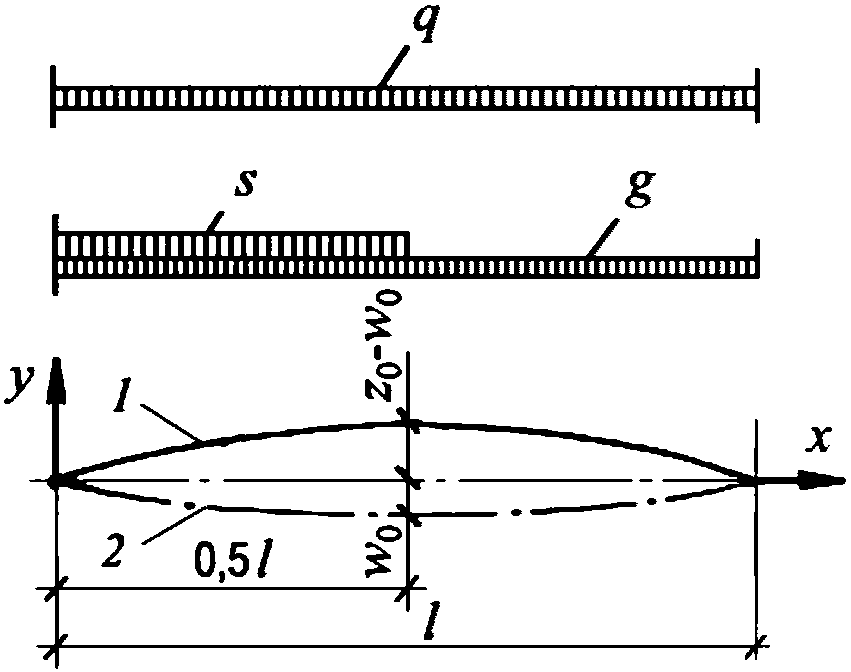
1 - ось оболочки; 2 - ось рабочей арматуры диафрагмы
Величины, входящие в формулу (5.4.15), определяют по формулам:
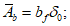

где 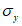 - предел текучести арматуры диафрагм;
- предел текучести арматуры диафрагм;
wy - прогиб панели, соответствующий началу текучести арматуры диафрагм;
wp - выгиб панели от сил предварительного напряжения;
Es - модуль упругости рабочей арматуры диафрагм;
P - равнодействующая усилий в напрягаемой арматуре с учетом всех потерь предварительного напряжения;
здесь A0,red - площадь приведенного сечения панели в середине ее пролета.
При определении изгибающей нагрузки qb,max значения 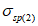 и P, входящие в формулы (5.4.17), (5.4.18) и (5.4.20), вычисляют при
и P, входящие в формулы (5.4.17), (5.4.18) и (5.4.20), вычисляют при 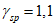 .
.
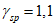 .
.5.4.17 Минимальное значение изгибающей нагрузки qb,min при равномерном нагружении панели определяют по формуле
где w0,min - расчетный прогиб панели в середине пролета при нагрузке, равной q, определяемый по формуле
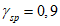 .
.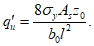 (5.4.24)
(5.4.24)5.4.18 При нагружении панели-оболочки постоянной равномерно распределенной нагрузкой g в сочетании с нагрузкой от снега s, расположенной на левой половине пролета (рисунок 5.4.6), изгибающие нагрузки соответственно для левой qb,l и правой qb,r половин пролета определяют по формулам:
где qM,l и qM,r - равномерно распределенные нагрузки, приложенные непосредственно к оболочке соответственно на левой и правой половинах пролета с учетом собственного веса оболочки;
здесь w0,max, w0,min - вычисляют по формулам (5.4.16) и (5.4.23), заменяя q на qc, определяемую по формуле
В формуле (5.4.25) параметры w0,max и qN вычисляют при 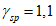 ; в формуле (5.4.26) параметры w0,min и qN вычисляют при
; в формуле (5.4.26) параметры w0,min и qN вычисляют при  .
.
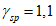 ; в формуле (5.4.26) параметры w0,min и qN вычисляют при
; в формуле (5.4.26) параметры w0,min и qN вычисляют при  .
.При расчете несущей способности оболочки на изгиб методом предельного равновесия схему разрушения оболочек принимают в виде, приведенном на рисунке 5.4.7.
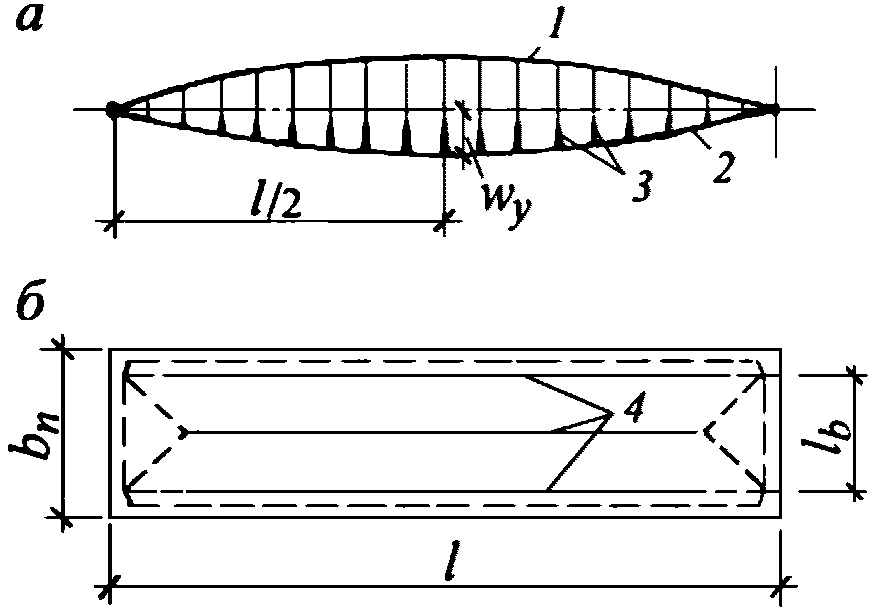
а - вид на диафрагму; б - план; 1 - оболочка; 2 - рабочая
арматура диафрагм; 3 - трещины в диафрагме;
4 - пластические шарниры в оболочке
При армировании одной сварной сеткой с рабочими стержнями, расположенными вдоль образующей оболочки (поперек панели), и при схеме излома с образованием трех пластических шарниров (по оси панели и по линиям сопряжения оболочки с вутами диафрагм) значение предельной нагрузки qu, кН/м2, определяют по формуле
где Rs - расчетное сопротивление рабочей арматуры оболочки, МПа;
As - площадь сечения рабочей арматуры, м2, на 1 м оболочки;
lb - расстояние в свету между вутами диафрагм, м;
Абсолютные значения расчетных изгибающих нагрузок, найденные по формулам (5.4.15), (5.4.22), (5.4.25) и (5.4.26), не должны превышать предельной изгибающей нагрузки, определенной по формуле (5.4.29).
5.4.19 Прочность сопряжения оболочки с диафрагмами следует проверять расчетом на изгиб сечений II - II и III - III (рисунок 5.4.4) при действии на оболочку расчетных изгибающих нагрузок. При этом принимается, что изгибающие моменты в вертикальном II - II (у начала вута) и горизонтальном сечениях III - III (по диафрагме) одинаковы. Значения расчетных изгибающих моментов M2 и M3 для этих сечений определяют по формуле
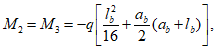 (5.4.30)
(5.4.30)где q - расчетная изгибающая нагрузка для рассматриваемой схемы нагружения;
ab и lb - см. рисунок 5.4.2.
5.4.20 Прогиб w0l панели в середине пролета с учетом длительного действия нагрузки и предварительного напряжения определяют по формуле
где qsh - кратковременно действующая часть нагрузки;
ql - длительно действующая часть нагрузки;
qe - эквивалентная по моменту в середине пролета равномерно распределенная нагрузка от сил предварительного напряжения, определяемая по формуле
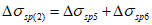 - сумма потерь предварительного напряжения рабочей арматуры от усадки и ползучести бетона согласно СП 63.13330;
- сумма потерь предварительного напряжения рабочей арматуры от усадки и ползучести бетона согласно СП 63.13330;Es - модуль упругости рабочей арматуры диафрагм;
h0c - рабочая высота поперечного сечения панели в середине пролета;
P(1) - равнодействующая усилий в напрягаемой арматуре до обжатия бетона, определяемая при коэффициенте точности натяжения 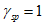 ;
;
e0p - расстояние от оси напрягаемой арматуры до центра тяжести приведенного сечения панели в середине пролета;
B - ширина панели.
Пример 12
Задание: для покрытия многопролетного здания с пролетами 24 м запроектировать панель-оболочку размерами 3 x 24 м. Здание расположено в III снеговом районе.
Материал панели-оболочки - легкий бетон класса B30 на плотном мелком заполнителе марки по средней плотности D1750. Удельный вес бетона g = 1,75·9,81 = 17,2 кН/м3; Rb = 17 МПа; Rbt,ser = 1,75 МПа; Rbt = 1,15 МПа; Eb = 19000 МПа.
Напрягаемая арматура изготовлена из термически упрочненной свариваемой арматурной стали периодического профиля класса А600 с нормативным значением сопротивления растяжению Rs,ser = 600 МПа и расчетным сопротивлением Rs = 520 МПа; Es = 200000 МПа. Плита оболочки армируется холоднодеформированной арматурой периодического профиля класса В500 с Rs = 415 МПа.
Для армирования диафрагм используется арматура класса А500 с Rs = 435 МПа и Rsw = 300 МПа.
Коэффициент приведения площади арматуры к площади бетона:
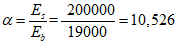 .
.Конструктивные размеры панели-оболочки приведены на рисунках 5.4.8 и 5.4.9.

а - план; б - вид сбоку; 1 - вертикальное
ребро жесткости; 2 - разбивочная ось

1 - напрягаемая арматура; 2 - вертикальное ребро жесткости
(к примеру расчета)
Номинальные размеры панели b0 x l0 = 3 x 24 м.
Высота сечения в середине пролета hc = l0/20 = 24000/20 = 1200 мм; то же, по оси опоры hk = 250 мм > 0,01 l0 = 0,01·24000 = 240 мм для увязки с размерами анкера из уголка 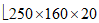 .
.
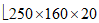 .
.Длина нижнего горизонтального участка у опор x6-5 ~= 1,5 hk = 380 мм (рисунок 5.4.10). Угол наклона нижней поверхности оболочки у опоры 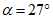
 .
.
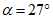
 .
.
I - стержни торцевой арматуры; II - анкер рабочей
продольной арматуры; 1 ... 6 номера характерных точек
продольного сечения посередине панели; 3 - ось оболочки
между диафрагмами
Расчетный пролет панели l = l0 - 300 = 24000 - 300 = 23700 мм.
Очертание верхней поверхности оболочки по параболе 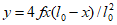 .
.
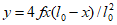 .
.Подъем оболочки f = hc - hk = 1200 - 250 = 950 мм. Ширина нижнего пояса двух диафрагм 2bf = 2·100 = 200 мм; высота утолщения hf = 100 мм. Ширина панели 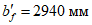 .
.
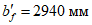 .
.Размеры вутов полки и утолщения верхнего пояса диафрагм даны на рисунке 5.4.9. Толщина крайних от опор панелей стенок диафрагм b1 = 100 мм; то же, остальных панелей, b = 40 мм. Вертикальные ребра жесткости размерами сечения 2 x 80 x 80 мм расположены через 1,5 м. Плечо внутренней пары сил в середине пролета панели z0 = 1200 - 30/2 - 50 = 1135 мм.
Наибольшей высоте стенок диафрагм параболического очертания между поясами в середине пролета h' = 1200 - (133 + 125) = 942 мм соответствует максимальное значение неравномерной нагрузки gmax. Эту нагрузку целесообразно заменить равномерно распределенной, эквивалентной по изгибающему моменту в середине пролета панели. Для вычисления M половина стенки диафрагмы разделена на треугольник F1 = h' l/4 и параболический сегмент F2 = h' l/12 (рисунок 5.4.11).

диафрагмы параболического очертания: нагрузка от площади
F1 - треугольника; F2 - параболического сегмента
Изгибающий момент в середине пролета от фактической нагрузки M' = 5gmax l2/48. Эквивалентная по изгибающему моменту нагрузка q' = 8M'/l2 = 0,833gmax. В этом случае с учетом веса стенки и ребер жесткости q' = 1,3 кН/м или 1,3/3 = 0,37 кН/м2.
Равномерно распределенные нагрузки для средней части пролета панели КЖС приведены в таблице 5.4.1.
Наименование нагрузки | Нормативная нагрузка, кПа | Коэффициент надежности по нагрузке | Расчетная нагрузка, кПа |
Постоянная от веса: | |||
- кровли | 1,11 | 1,3 | 1,44 |
- полки панели | 0,52 | 1,1 | 0,57 |
- вута полки 0,045·0,22·17,2/3 | 0,06 | 1,1 | 0,07 |
- нижнего пояса 0,2·0,1·17,2/3 | 0,11 | 1,1 | 0,12 |
- верхнего пояса 0,11·0,08·2·17,2/3 | 0,10 | 1,1 | 0,11 |
- стенок диафрагм | 0,37 | 1,1 | 0,41 |
ИТОГО | gser = 2,27 | g = 2,72 | |
Временная (снеговая, III район), Sg = 1,5 кПа | sser = 1,28 <*> | 1,4 | s = 1,8 |
ВСЕГО | (g + s)ser = 3,55 | g + s = 4,52 | |
<*> Коэффициент ce, учитывающий снос снега с покрытия, принят равным 0,85. Снеговая нагрузка принята равномерно распределенной | |||
Нагрузка веса местного утолщения оболочки у опор панели (рисунок 5.4.10):
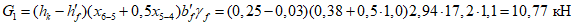 .
.Эта нагрузка не заменяется эквивалентной равномерно распределенной, а учитывается для определения усилий при статическом расчете панели. Центр тяжести дополнительной нагрузки расположен на расстоянии 0,6 м от опор.
Поперечная сила и изгибающий момент с учетом местного утолщения оболочки у опор:
Qmax = (g + s)b0 l/2 + G1 = 4,52·3·23,7/2 + 10,77 = 171,5 кН;
Mmax = (g + s)b0 l2/8 = 4,52·3·23,72/8 = 952 кНм.
Расчет оболочки КЖС по общей несущей способности и устойчивости
Требуемая площадь сечения рабочей предварительно напряженной арматуры А600 в нижнем поясе диафрагм по формуле (5.4.1):
As = 952·103/(1135·520) = 1613 мм2.
Принимаем  А600 с As = 1608 мм2.
А600 с As = 1608 мм2.
Требуемая толщина средней части свода оболочки находится из условия прочности по формуле (5.4.2):
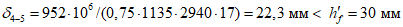 , назначенной по конструктивным соображениям.
, назначенной по конструктивным соображениям.Геометрические характеристики сечения в середине пролета КЖС, необходимые для проверки оболочки по устойчивости, приводим без расчета:
Ared = 258512 мм2; Sred = 200544040 мм3.
Расстояние от нижней грани до центра тяжести сечения y = Sred/Ared = 776 мм;
h - y = 1200 - 776 = 424 мм;
эксцентриситет усилия предварительного обжатия e0p = 776 - 50 = 726 мм;
расстояние от центра тяжести сечения до оси сжатой полки y0 = z0 - e0p = 1135 - 726 = 409 мм.
Момент инерции приведенного сечения Ired = 50788·106 мм4.
Изгибающий момент от нагрузки с коэффициентом надежности  :
:
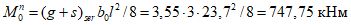 .
.Проверка толщины оболочки на условное критическое напряжение сжатия по формуле (5.4.3):
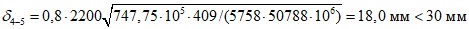 ,
,где в качестве модуля деформаций бетона принят  - модуль деформаций бетона при продолжительном действии нагрузки по СП 63.13330;
- модуль деформаций бетона при продолжительном действии нагрузки по СП 63.13330;
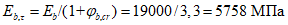 ;
;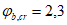 для бетона B30 при нормальной относительной влажности воздуха.
для бетона B30 при нормальной относительной влажности воздуха.Назначенная толщина оболочки  удовлетворяет условиям прочности и устойчивости.
удовлетворяет условиям прочности и устойчивости.
 удовлетворяет условиям прочности и устойчивости.
удовлетворяет условиям прочности и устойчивости.Геометрическое построение верхней поверхности оболочки КЖС и ее переменной толщины на приопорных участках панели (рисунок 5.4.10) выполняется с использованием уравнения верхней поверхности оболочки
y = 4fx(l - x)l2 = 4·950x(23600 - x)/236002 = 68228x(23600 - x)·10-10.
Уравнение переменной толщины оболочки приводится формулой для h6-4:
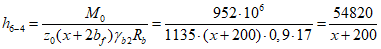 .
.Однако нижняя поверхность оболочки на некотором расстоянии от опоры имеет конструктивные изломы; горизонтальный участок длиной x6-5 = 380 мм от опоры переходит в наклонный под углом 27°, пересекающийся с криволинейной нижней поверхностью. Ординаты, мм, точек всех поверхностей приведены в таблице 5.4.2.
x | 0 | 200 | 400 | 600 | 800 | 1000 | 1140 | 1200 | 1400 | 1600 | 1800 | 2000 |
y | 0 | 32 | 63 | 94 | 124 | 154 | 177 | 183 | 212 | 240 | 267 | 294 |
h6-4 | 240 | 137 | 91 | 68 | 55 | 46 | 41 | 39 | 34 | постоянная h = 30 | ||
y - h6-4 | -240 | -105 | -28 | 26 | 69 | 108 | 136 | 144 | 178 | 210 | 237 | 264 |
y' | -240 | -240 | -230 | -130 | -10 | 70 | 140 | - | - | - | - | - |
Отметки нижней поверхности оболочки определяются как разности (y - h6-4). Уравнение секущей плоскости y' = -240 + 0,5(x - 380) от x = 380 до x = 1140 мм - места пересечения (0,5 ~= tg27°). В месте пересечения плоскости с параболической поверхностью по ее образующей делают плавное закругление небольшого радиуса, с тем, чтобы избежать концентрации напряжений.
Площадь сечения стержней торцевой арматуры As1 определяют из наибольшего по величине усилия Ne по формулам (5.4.4) и (5.4.5), где g = 2,72 - 1,44 = 1,28 кН/м2 - нагрузка от собственного веса панели.
Ne = (1,216 + 2)·23,72·2,84/(64·1,135) = 70,62 кН;
Ne = 520·1608·2,84/(8·2,94) = 100,965 кН > 70,62 кН.
Требуемое количество арматуры класса А500 As = 100965/435 = 232 мм2. Принимаем  А500 с As = 308 мм2.
А500 с As = 308 мм2.
Изгибающий момент от расчетной нагрузки в сечении на расстоянии 1,5 м от рабочей поверхности анкера (точка 4 на рисунке 5.4.10) при (g + s) = 4,52 кН/м2:
M1 = 4,52·3(1,5 + 0,05)(23,7 - 1,55)/2 = 232,77 кНм.
Расстояние по вертикали от оси рабочей арматуры до оси оболочки в том же сечении:
z1 = 4·1,135(1,5 + 0,05)(23,7 + 1,55)/23,7 = 0,28 м.
Требуемую площадь рабочей поверхности анкера продольной арматуры каждой диафрагмы найдем по формуле (5.4.9):
A1 = 232770000/(2·280·17·1,0) = 24450 мм2.
При ширине полки 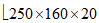 l1 = 250 мм требуется длина анкера l2 = 100 мм.
l1 = 250 мм требуется длина анкера l2 = 100 мм.
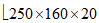 l1 = 250 мм требуется длина анкера l2 = 100 мм.
l1 = 250 мм требуется длина анкера l2 = 100 мм.Для расчета по прочности сечений, наклонных к продольной оси диафрагм; сечений оболочки между диафрагмами и для проверки панели КЖС по предельным состояниям второй группы необходимы характеристики предварительного напряжения арматуры и усилий обжатия бетона, определение которых выполняем по СП 63.13330.
Предварительно напряженная арматура  А600 с Asp = 1608 мм2, Rsp = 600 МПа.
А600 с Asp = 1608 мм2, Rsp = 600 МПа.
Способ натяжения арматуры - электротермический. Технология изготовления плиты с применением пропаривания.
Первые потери напряжений:
- потери от релаксации напряжений в арматуре при 

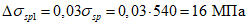 .
.- потери от деформации стальной формы и анкеров натяжных устройств при электротермическом способе натяжения арматуры не учитываются: 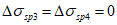 .
.
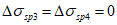 .
.Таким образом, сумма первых потерь 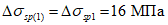 , а усилие обжатия с учетом первых потерь равно P(1) = 1608·(540 - 16) = 842592 Н.
, а усилие обжатия с учетом первых потерь равно P(1) = 1608·(540 - 16) = 842592 Н.
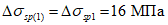 , а усилие обжатия с учетом первых потерь равно P(1) = 1608·(540 - 16) = 842592 Н.
, а усилие обжатия с учетом первых потерь равно P(1) = 1608·(540 - 16) = 842592 Н.В соответствии с вычисленными ранее значениями: ysp = e0p1 = 726 мм проверяем максимальное сжимающее напряжение бетона  от действия усилия P(1) по формуле
от действия усилия P(1) по формуле
Полагая изгибающий момент от собственного веса M равным нулю:
 .
.Передаточную прочность бетона принимаем равной Rbp = 0,7B = 0,7·30 = 21 МПа.
 .
.Вторые потери напряжений:
- потери от усадки:
 .
.- потери от ползучести определяем по формуле
где  - коэффициент ползучести бетона, равный 2,3;
- коэффициент ползучести бетона, равный 2,3;
Определяем напряжение бетона на уровне арматуры S при ys = ysp = 726 мм.
Для этого определяем момент в середине пролета от собственного веса плиты:
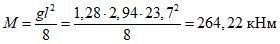 .
.Тогда по формулам (5.4.33) и (5.4.34):
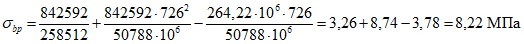 .
.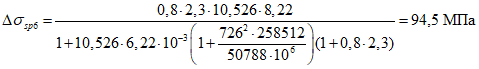 .
.Вторые потери равны:
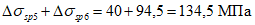 .
.Суммарное значение потерь напряжения:
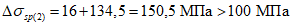 .
.Напряжение  с учетом всех потерь:
с учетом всех потерь:
 .
.Усилие обжатия с учетом всех потерь:
 .
.Расчет прочности сечений, наклонных к продольной оси панели, по поперечной силе
Расчет выполняем согласно СП 63.13330.
Ранее было получено, что поперечная сила на опоре составляет 171,5 кН или на каждую из диафрагм Q = 171,5/2 = 85,8 кН.
Опорным сечением считаем сечение диафрагмы за опорной балкой, т.е. на расстоянии 380 мм от торца панели (рисунок 5.4.10). Здесь h0 = 240 + 65 - 50 = 255 мм.
В соответствии с 5.4.11 на участках диафрагм длиной 0,85 - 0,1l, примыкающих к опорам (рисунок 5.4.4), необходимо устанавливать конструктивную поперечную арматуру. Принимаем для каркаса арматуру 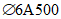 с шагом u = 100 мм.
с шагом u = 100 мм.
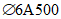 с шагом u = 100 мм.
с шагом u = 100 мм.Усилие в поперечной арматуре на единицу длины элемента
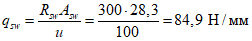 ,
,где Rsw = 300 МПа (для арматуры А500);
Asw = 28,3 мм2 - для 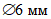 .
.
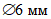 .
.Задаемся проекцией наклонного сечения c0 = 2h0 = 2·255 = 510 мм и найдем высоту сечения на расстоянии 380 + 510 = 890 мм от торца панели. Из рисунка 5.4.10 следует, что h = 155 + 240 = 395 мм.
Расчетное значение проекции наклонной трещины найдем по формуле
где  - угол наклона верхней поверхности плиты с конца наклонной трещины:
- угол наклона верхней поверхности плиты с конца наклонной трещины:
 .
.Определяем средние сжимающие напряжения в бетоне от воздействия продольных сил в долях от прочности бетона
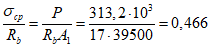 ,
,где A1 - площадь диафрагмы b x h = 100·395 = 39500 мм2;
P = 626,3/2 = 313,2 кН - усилие обжатия бетона на одну диафрагму.
Поскольку 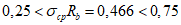 , принимаем
, принимаем 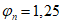 .
.
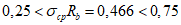 , принимаем
, принимаем 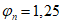 .
. .
.Принимаем невыгоднейшее значение c1 = c = 447 мм.
На расстоянии 380 + 447 = 827 мм полная и рабочая высоты поперечного сечения диафрагмы равны:
h = 827·0,174 + 240 = 384 мм; h0 = 384 - 50 = 334 мм.
Определим  для этого сечения, где A1 = 100·384 = 38400 мм2;
для этого сечения, где A1 = 100·384 = 38400 мм2;
 ;
; , принимаем
, принимаем  .
. .
.Qsw = 0,75qswc0 = 0,75·84,9·447 = 28463 Н.
Вычисляем значение Q1 на расстоянии l1 = 380 + 526 = 906 мм от торца панели:
Q1 = Q - (g + s)(b0/2)l1 = 85,8 - 4,52·1,5·0,827 = 80,2 кН.
Qb + Qsw = 53,8 + 28,5 = 82,3 > 80,2 кН - прочность наклонного сечения обеспечена.
Расчет поля оболочки на изгиб вдоль образующей
В расчете максимального значения изгибающей нагрузки принимаем  .
.
 .
.Вертикальная нагрузка, эквивалентная по нормальной силе, по формуле (5.4.20):
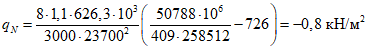 .
.Коэффициент неравномерности распределения сжимающих сил по формуле (5.4.21):
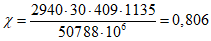 .
.Предельная по арматуре диафрагм равномерно распределенная нагрузка по формуле (5.4.19):
 .
.Выгиб панели от сил предварительного напряжения по формуле (5.4.18):
 .
.Прогиб панели в момент начала текучести арматуры диафрагм по формуле (5.4.17):
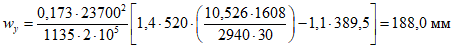 .
.w0,max = wy = 188,0 мм, поскольку q ~= qu.
Местная нагрузка на оболочку без учета веса диафрагм:
qm = 2,72 - 0,64 + 1,8 = 3,88 кН/м2.
Максимальное значение расчетной изгибающей нагрузки при равномерном нагружении панели по (5.4.15):
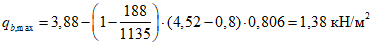 .
.В расчете минимальной величины изгибающей нагрузки принимаем 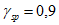 .
.
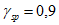 .
.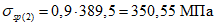 .
.P = 350,55·1698·10-3 = 563,68 кН.
По формуле (5.4.17):
 .
.С учетом  :
:
 :
:
wp = -57,1·0,9/1,1 = -46,7 мм.
По формуле (5.4.23):
 .
.Минимальная величина изгибающей нагрузки при равномерном нагружении панели по формуле (5.4.22):
 .
.При односторонней снеговой нагрузке по формуле (5.4.27):
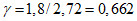 .
.По формуле (5.4.28):
qc = 2,72 + 0,5·1,8 = 3,62 кН/м2.
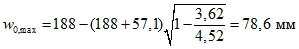 .
.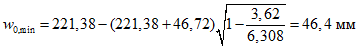 .
.Изгибающая нагрузка для левой половины пролета по формуле (5.4.25):
 .
.Изгибающая нагрузка для правой половины пролета по формуле (5.4.26):
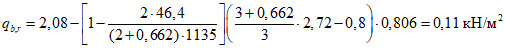 .
.Таким образом, наибольшая изгибающая нагрузка получилась при равномерном нагружении оболочки снегом qb,max = 1,38 кН/м2.
При расчете армирования полки плиты ее рассматривают как балочную плиту с пролетом между вутами (220 мм, рисунок 5.4.9) с учетом перераспределения усилий в предельном состоянии.
Расчетный момент M = 1,38·2,22/16 = 0,417 кНм.
При рабочей высоте оболочки h0 = h/2 = 30/2 = 15 мм;
расчетный коэффициент 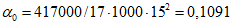 ;
;
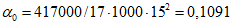 ;
;относительная высота сжатой зоны бетона  .
.
 .
.Требуемая площадь сечения арматуры  класса В500 с Rs = 435 МПа:
класса В500 с Rs = 435 МПа:
 класса В500 с Rs = 435 МПа:
класса В500 с Rs = 435 МПа:As = 0,116·15·1000·17/435 = 68 мм2.
Принимаем в поперечном направлении 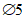 В500 с шагом 200 мм: As = 98 мм2/п. м. Процент армирования оболочки
В500 с шагом 200 мм: As = 98 мм2/п. м. Процент армирования оболочки 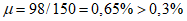 . В продольном направлении требуется только 0,2% или площадь сечения арматуры As = 0,2·15000/100 = 30 мм2. Принимаем
. В продольном направлении требуется только 0,2% или площадь сечения арматуры As = 0,2·15000/100 = 30 мм2. Принимаем 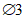 В500 с шагом 200 мм, т.е. As = 7,1·5 = 35,5 мм2/п. м.
В500 с шагом 200 мм, т.е. As = 7,1·5 = 35,5 мм2/п. м.
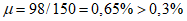 . В продольном направлении требуется только 0,2% или площадь сечения арматуры As = 0,2·15000/100 = 30 мм2. Принимаем
. В продольном направлении требуется только 0,2% или площадь сечения арматуры As = 0,2·15000/100 = 30 мм2. Принимаем Проверим прочность сопряжения оболочки с диафрагмами по (5.4.30). Размеры пролета полки панели и вута lb = 2,2 м и ab = 0,22 м (рисунок 5.4.9).
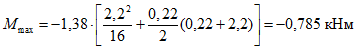 .
.Сечение вута оболочки в плоскости грани диафрагм (рисунок 5.4.2):
h = 75 мм; h0 = 75 - 15 = 60 мм; арматура 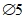 В500 с шагом 200 мм.
В500 с шагом 200 мм.
Высота сжатой зоны бетона при восприятии изгибающего момента отрицательного знака x = 435·98/(17·1000) = 2,508 мм.
Несущая способность сечения вута:
Madm = 17·2,508(60 - 2,508/2) = 2,5 кНм > 0,785 кНм.
Изгибающий момент другого знака может быть воспринят сечением без арматуры в растянутой зоне. Момент сопротивления бетонного сечения с учетом неупругих деформаций бетона по формуле Wpl = bh2/3,5 = 1000·752/3,5 = 1607143 мм3.
Несущая способность сечения вута без арматуры в растянутой зоне:
M = RbtWpl = 1,15·1607143 = 1,848 кНм > 0,785 кНм, т.е. дополнительной арматуры в вутах сечения полки не требуется.
Предельная нагрузка по схеме излома с образованием трех шарниров по формуле (5.4.29)
 ,
,что больше нагрузок, полученных по формулам (5.4.15), (5.4.22) и (5.4.25); это подтверждает, что несущая способность оболочки на изгиб обеспечена.
Проверка панели КЖС по предельным состояниям второй группы
Расчет по образованию трещин
Изгибающий момент в сечении КЖС посередине пролета от нормативной нагрузки с 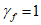 :
:
Mser = 3,55·3·23,72/8 = 747,7 кНм.
Момент сопротивления сечения относительно нижней грани сечения:
Wred = Ired/y = 50788·106/776 = 6,55·107 мм3.
То же, с учетом неупругих деформаций бетона:
Wpl = 1,3Wred = 1,3·6,55·107 = 8,52·107 мм3.
Для легкого бетона класса B30 с плотным мелким заполнителем Rb,ser = 22 МПа; Rbt,ser = 1,75 МПа; усилие предварительного напряжения арматуры с учетом всех потерь P = 626,32 кН.
Расстояние от центра тяжести приведенного сечения до точки ядра, наиболее удаленной от растянутой зоны:
r = Wred/Ared = 6,55·107/2,85·105 = 230 мм.
Изгибающий момент, воспринимаемый сечением, нормальным к продольной оси, при образовании трещин:
Mcr = Rbt,ser·Wpl + p(e0p + r) = 1,75·8,52·107 + 626,32·103 (726 + 230) = 747,9 кНм > Mser = 747,7 кНм, т.е. трещины не образуются.
Расчет по деформациям
Равнодействующая усилий в напрягаемой арматуре до обжатия бетона:
P(1) = 1608(540 - 16) = 842,59 кН.
Эквивалентная по моменту в середине пролета равномерно распределенная нагрузка от сил предварительного напряжения по формуле (5.4.32):

Прогиб панели в середине пролета с учетом длительного действия нагрузки и предварительного напряжения по формуле (5.4.31):
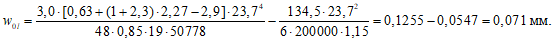
Допустимый прогиб составляет 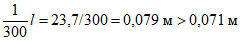 .
.
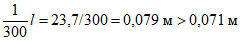 .
.Следовательно, прогиб конструкции удовлетворяет требованиям СП 20.13330.
5.5.1 Оболочки отрицательной гауссовой кривизны в форме гиперболического параболоида (гипара) на квадратном и прямоугольном планах применяют для покрытий производственных, общественных и складских зданий [5]. Размеры перекрываемого плана могут изменяться в пределах от 10 до 70 м и более.
В покрытиях могут применяться однолепестковые и многолепестковые гипары (рисунок 5.5.1).

а - однолепестковый; б - четырехлепестковый
Многолепестковые гипары образуются комбинацией однолепестковых гипаров.
При возникновении в гипарах усилий распора рекомендуется предусматривать устройство затяжек.
5.5.2 Гипары выполняют сборными и монолитными.
Монолитные оболочки, как правило, проектируют гладкими, без ребер.
В сборных оболочках разрезку на плиты осуществляют по направлению прямолинейных образующих и направляющих, а плиты по краям окаймляют ребрами. Геометрические размеры и армирование ребер назначают с учетом требований монтажа. Совпадение геометрии двух поверхностей - исходной и получаемой в результате сборки плит - достигается за счет переменной толщины монолитных швов.
Гипары, как правило, проектируют с контурными элементами, в качестве которых обычно используют бортовые балки и фермы. Оболочки по контуру допускается опирать на ряд стоек. По линиям сопряжения отдельных лепестков в оболочках располагают коньковые балки (рисунок 5.5.1, б).
При больших пролетах растянутые контурные элементы и коньковые балки рекомендуется выполнять с предварительным напряжением арматуры.
Сечения бортовых элементов рекомендуется назначать минимально возможными.
5.5.3 Армирование гипаров рекомендуется принимать, располагая стержни по прямолинейным образующим и направляющим поверхности. Для армирования плит рекомендуется применять сварные сетки из холоднодеформированной проволоки класса В500. Нижние углы однолепестковых и многолепестковых гипаров допускается армировать косыми стержнями криволинейного очертания, служащими для восприятия главных растягивающих усилий.
5.5.4 Стыки плит сборных гипаров должны обеспечивать восприятие сдвигающих и нормальных усилий. Стыки следует проектировать с учетом требований 4.4.
5.5.5 Расчет гипаров производят в соответствии с требованиями 4.2.
Усилия и перемещения допускается определять исходя из предположения упругой работы материала по моментной теории с учетом влияния жесткостей контурных элементов и коньковых балок.
Расчет четырехлепестковой оболочки рекомендуется выполнять в следующей последовательности:
- как оболочки по безмоментной теории;
- как шпренгельной системы, поскольку план конструкции - вытянутый прямоугольник;
- в стадии монтажа как балочной конструкции;
- расчет несущей способности методом предельного равновесия.
5.5.6 Несущую способность гладких гипаров на квадратном плане при действии равномерно распределенной нагрузки допускается определять по методу предельного равновесия.
Предельная нагрузка q на оболочку включает массу оболочки, контурных ребер и коньковых балок
q = p + g + ge, (5.5.1)
где p - интенсивность предельной внешней нагрузки;
g - равномерно распределенная нагрузка от веса оболочки;
ge - приведенная равномерно распределенная нагрузка от веса контурных ребер, формулы для ее определения приводятся ниже для каждого рассматриваемого случая.
В приведенных ниже формулах (5.5.4) - (5.5.23) используются безразмерные параметры
где l - сторона квадратного плана однолепестковой оболочки (по рисунку 5.5.1 l = a = b);
f - стрела подъема оболочки (по рисунку 5.5.1, а - f = f1 = f2);
hr, br - соответственно высота и ширина контурного ребра (рисунок 5.5.2, б);
Rb - расчетное значение сопротивления бетона осевому сжатию;
Rs,i, Rs,1 - расчетные значения сопротивления растяжению арматуры соответственно поля и углов;
Rs,r - то же, для арматуры ребра;
u x u - размер ячейки арматурной сетки (рисунок 5.5.2, а);
Ai, A1 - площадь сечения арматурного стержня соответственно сетки и угловой арматуры;
u1 - шаг угловой арматуры (рисунок 5.5.2, а);
Ar - площадь всей арматуры в ребре;
At - площадь сечения затяжки;
Rs,t - нормативное значение сопротивления растяжению металла затяжки;
h0r - расстояние от центра тяжести арматуры ребра до срединной поверхности оболочки (рисунок 5.5.2, б);
d - расстояние от угла оболочки до последнего стержня угловой арматуры (рисунок 5.5.2, а).
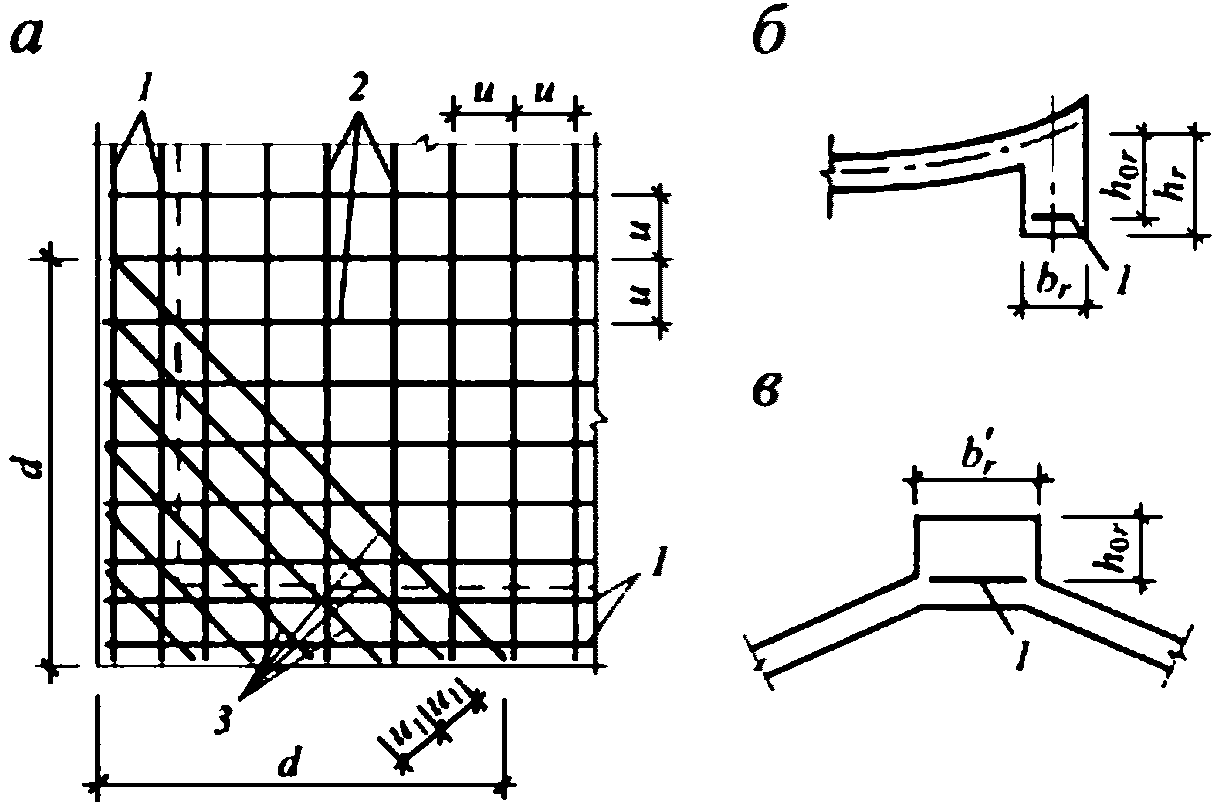
а - армирование нижнего угла; б - примыкание оболочки
к контурному ребру; в - то же, к коньковому ребру
в четырехлепестковом покрытии с горизонтальными
коньками; 1 - арматура ребра; 2 - арматура поля
оболочки; 3 - угловая арматура
5.5.7 При расчете опертых на нижние углы однолепестковых гипаров (рисунок 5.5.1, а), когда углы закреплены от горизонтальных смещений, предельную нагрузку q на оболочку следует определять по формуле
где коэффициент Ki принимается в зависимости от значения коэффициента  , определяемого по формуле
, определяемого по формуле
При 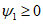 (рисунок 5.5.3, б, когда нейтральная ось линии излома не пересекает ребер)
(рисунок 5.5.3, б, когда нейтральная ось линии излома не пересекает ребер)
а при 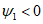 (рисунок 5.5.3, в, когда нейтральная ось проходит в пределах ребер)
(рисунок 5.5.3, в, когда нейтральная ось проходит в пределах ребер)
где  .
.
 .
.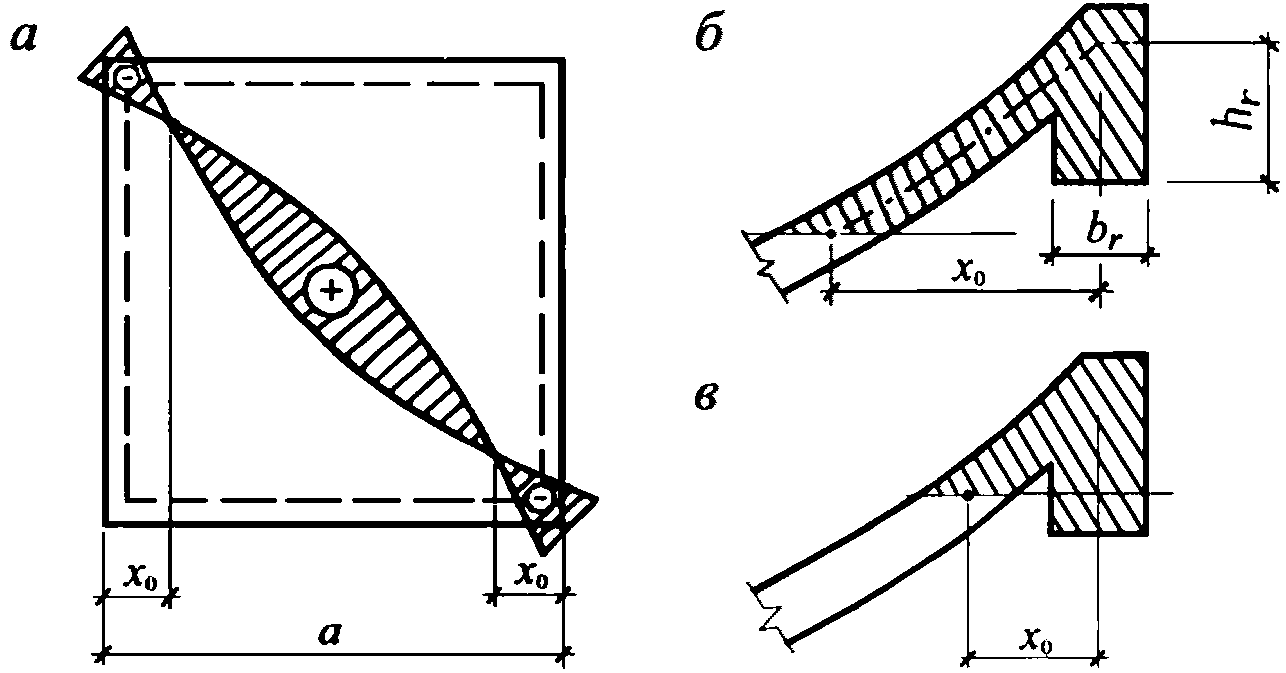
а - схема излома; б, в - схемы расположения нейтральной оси
Для оболочек без контурных ребер значение коэффициента Ki определяют по формуле (5.5.5) при 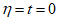 .
.
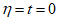 .
.Приведенную нагрузку ge от массы контурных ребер определяют по формуле
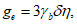 (5.5.7)
(5.5.7)где  - объемный вес бетона ребер.
- объемный вес бетона ребер.
Полное закрепление углов от горизонтальных смещений достигается установкой жесткой затяжки или контрфорсов.
Жесткость затяжки, при которой углы могут считаться несмещаемыми, рекомендуется определять по формуле (5.5.15).
5.5.8 При расчете опертых на нижние углы однолепестковых гипаров, когда углы не закреплены или частично закреплены от горизонтальных смещений, например, затяжками (рисунок 5.5.1, б), предельную нагрузку q находят по формуле
 (5.5.8)
(5.5.8)где
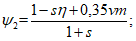 (5.5.10)
(5.5.10)- при  (нейтральная ось проходит вне контурных ребер)
(нейтральная ось проходит вне контурных ребер)
 (нейтральная ось проходит вне контурных ребер)
(нейтральная ось проходит вне контурных ребер)- при  (нейтральная ось пересекает ребра)
(нейтральная ось пересекает ребра)
 (нейтральная ось пересекает ребра)
(нейтральная ось пересекает ребра)здесь 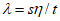 ;
;
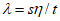 ;
;При расчете оболочки без окаймляющих ребер коэффициент Kj следует определять по формуле (5.5.11) при 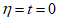 , а предельную нагрузку на оболочку без затяжки определять, принимая в формулах (5.5.9) - (5.5.13) v = 0.
, а предельную нагрузку на оболочку без затяжки определять, принимая в формулах (5.5.9) - (5.5.13) v = 0.
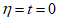 , а предельную нагрузку на оболочку без затяжки определять, принимая в формулах (5.5.9) - (5.5.13) v = 0.
, а предельную нагрузку на оболочку без затяжки определять, принимая в формулах (5.5.9) - (5.5.13) v = 0.Приведенную равномерно распределенную нагрузку ge от веса ребер определяют по формуле
Площадь сечения затяжки At, при которой обеспечивается несмещаемость нижних углов оболочки, находят из условия
где
В формулах (5.5.16) и (5.5.17) значение коэффициента Ki вычисляют в зависимости от значения 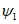 по формулам (5.5.5) или (5.5.6), а значение коэффициента Kj - в зависимости от значения
по формулам (5.5.5) или (5.5.6), а значение коэффициента Kj - в зависимости от значения 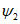 по формулам (5.5.11) или (5.5.12).
по формулам (5.5.11) или (5.5.12).
При выполнении условия (5.5.15) несущую способность оболочки определяют согласно 5.5.7.
5.5.9 При расчете четырехлепесткового покрытия с горизонтальными коньками (рисунок 5.5.1, б, покрытие опирается на треугольные фермы или на стены; коньковые балки расположены выше оболочки) предельную нагрузку q на оболочку определяют по формуле (5.5.3), где значение коэффициента Ki принимают в зависимости от значения  , определяемого по формуле
, определяемого по формуле
При  (нейтральная ось линии излома не пересекает коньковой балки) значение коэффициента Ki вычисляют по формуле
(нейтральная ось линии излома не пересекает коньковой балки) значение коэффициента Ki вычисляют по формуле
 (5.5.19)
(5.5.19)где
 (5.5.20)
(5.5.20)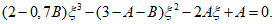 (5.5.21)
(5.5.21)При 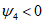 (нейтральная ось линии излома пересекает коньковую балку) значение коэффициента Ki вычисляют по формуле
(нейтральная ось линии излома пересекает коньковую балку) значение коэффициента Ki вычисляют по формуле
 ;
;где
Приведенную равномерно распределенную нагрузку ge от веса коньковых балок определяют по формуле (5.5.14).
Задание: запроектировать покрытие здания в виде сборной четырехлепестковой составной оболочки с горизонтальными коньками размерами в плане 6 x 18 м, с опиранием по углам и затяжками по контуру. Здание расположено в III снеговом районе.
Оболочка собирается из четырех панелей в форме гиперболического параболоида с размерами сторон lAB = 9,2 м, lAD = 3,6 м (рисунок 5.5.4). Стрелы подъема оболочки по сторонам контура f = 2 м. Плиты ребристые с высотой контурного ребра 350 мм и толщиной плиты 30 мм из тяжелого бетона класса B30 (Rb = 17 МПа, Rbt = 1,2 МПа, Eb = 32500 МПа). Ребра плит армированы горячекатаной арматурой класса А500 (Rs = 435 МПа, Rsc = 400 МПа), поле плит - армировано арматурой 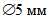 класса Вр500 (Rs = 415 МПа).
класса Вр500 (Rs = 415 МПа).
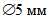 класса Вр500 (Rs = 415 МПа).
класса Вр500 (Rs = 415 МПа).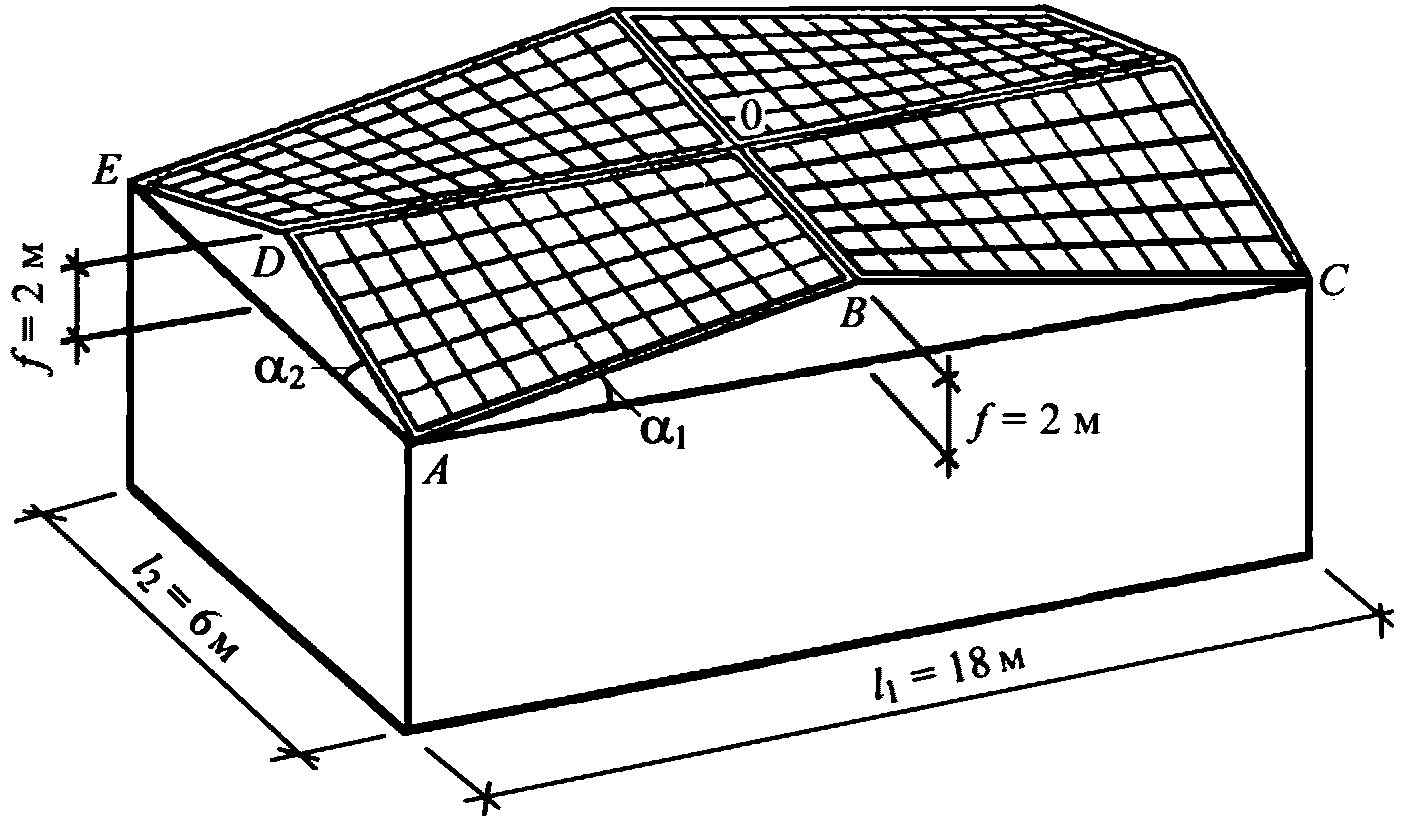
четырехлепестковой оболочки с горизонтальными коньками
В таблице 5.5.1 приведен сбор нагрузок для расчета оболочки в стадии эксплуатации.
Таблица 5.5.1
Вид нагрузки | Нормативная нагрузка, кПа | Расчетная нагрузка, кПа | |
Собственный вес оболочки g (при  и приведенной толщине и приведенной толщине 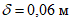 ) ) | 1,5 | 1,1 | 1,65 |
Вес утеплителя (  ; ; 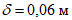 ) ) | 0,15 | 1,3 | 0,23 |
Вес цементной стяжки (  ; ;  ) ) | 0,3 | 1,3 | 0,39 |
Вес рубероидного ковра и пароизоляции | 0,25 | 1,3 | 0,33 |
Всего q0 | 2,205 | 2,60 | |
Снеговая s (III снеговой район) | 1,28 <*> | 1,80 | |
Итого q | 3,485 | - | 4,40 |
Расчет конструкции по безмоментной теории
Предполагается, что оболочка находится в состоянии чистого сдвига при отсутствии нормальных напряжений, параллельных бортовым элементам (рисунок 5.5.5).

в отдельной панели в виде гиперболического параболоида
Для скрученных параллелограммов с одной пониженной вершиной главные растягивающие и главные сжимающие напряжения равны касательным напряжениям, которые на единицу длины составляют:
 ,
,где 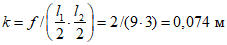 - средний коэффициент искривления.
- средний коэффициент искривления.
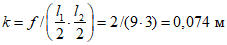 - средний коэффициент искривления.
- средний коэффициент искривления.Наибольшие напряжения в поле оболочки толщиной 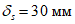 равны
равны
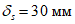 равны
равны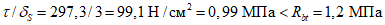 ;
;- толщина поля оболочки достаточная.
Наибольшие усилия в продольном и поперечном бортовых элементах:
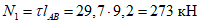 ;
;  .
.Проверяем бортовой элемент с высотой сечения h = 35 см на сжатие.
Площадь сечения бортового элемента (рисунок 5.5.6) 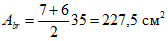 .
.
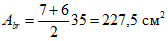 .
.
контурного ребра панели
Расчетная длина бортового элемента l0 = 0,8 lAB = 0,8·9,2 = 7,36 м (коэффициент 0,8 принят по 8.1.17 СП 63.13330.2018).
Принимаем 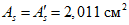
 .
.
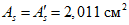
 .
.Определяем предельное значение продольной силы, которое способен воспринять бортовой элемент.
 ,
,где  - коэффициент, учитывающий длительность загружения, гибкость и характер армирования элемента, по таблице 8.1 СП 63.13330.2018 при l0/h = 7,36/0,35 = 21 и классе бетона B30. Следовательно, прочность конструкции обеспечена.
- коэффициент, учитывающий длительность загружения, гибкость и характер армирования элемента, по таблице 8.1 СП 63.13330.2018 при l0/h = 7,36/0,35 = 21 и классе бетона B30. Следовательно, прочность конструкции обеспечена.
Определяем усилия в затяжках AC и AE из условия равновесия сил в опорном узле (см. рисунки 5.5.4 и 5.5.7):
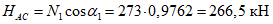 ;
; ,
,где 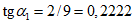 ;
; 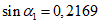 ;
; 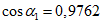 ;
;
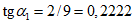 ;
; 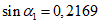 ;
; 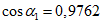 ;
; ;
; 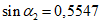 ;
; 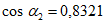 .
.
Определяем требуемую площадь сечения затяжек. Для затяжки AC
As,треб = HAC/Rs = 266500/43500 = 6,126 см2.
Принимаем затяжку из арматуры  А500 с As = 6,158 см2.
А500 с As = 6,158 см2.
Для затяжки AE
As,треб = HAE/Rs = 8895,0/43500 = 2,045 см2.
Принимаем затяжку из арматуры  А500 с As = 2,545 см2.
А500 с As = 2,545 см2.
Проверяем поперечное сечение сетки, установленной в полке плиты, на растяжение. Принимаем сетку из холоднотянутой проволоки класса В500 диаметром 5 мм с ячейками 200 x 200 мм (Rs = 415 МПа, площадь поперечного сечения одного стержня As = 0,196 см2).
Усилие, возникающее в одном стержне сетки от эксплуатационной нагрузки,
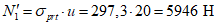 , где u = 20 см - шаг стержней в сетке.
, где u = 20 см - шаг стержней в сетке.Несущая способность одного стержня  В500 равна
В500 равна
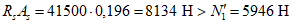 . Прочности арматуры достаточно.
. Прочности арматуры достаточно.Поверочный расчет оболочки как шпренгельной системы
Оболочку в виде гиперболических параболоидов с вытянутым планом в соответствии с результатами экспериментальных исследований для приближенного расчета можно представить как шпренгельную или арочную систему с пролетом, равным наибольшему пролету оболочки (рисунок 5.5.8). Верхний пояс такой системы - сама оболочка, при этом верхний пояс имеет переменное поперечное сечение с максимальной высотой на опоре и минимальной в середине пролета. Нижний пояс системы - затяжки, устанавливаемые по длинной стороне покрытия, соответственно наибольшая высота системы получается в середине верхнего пояса.
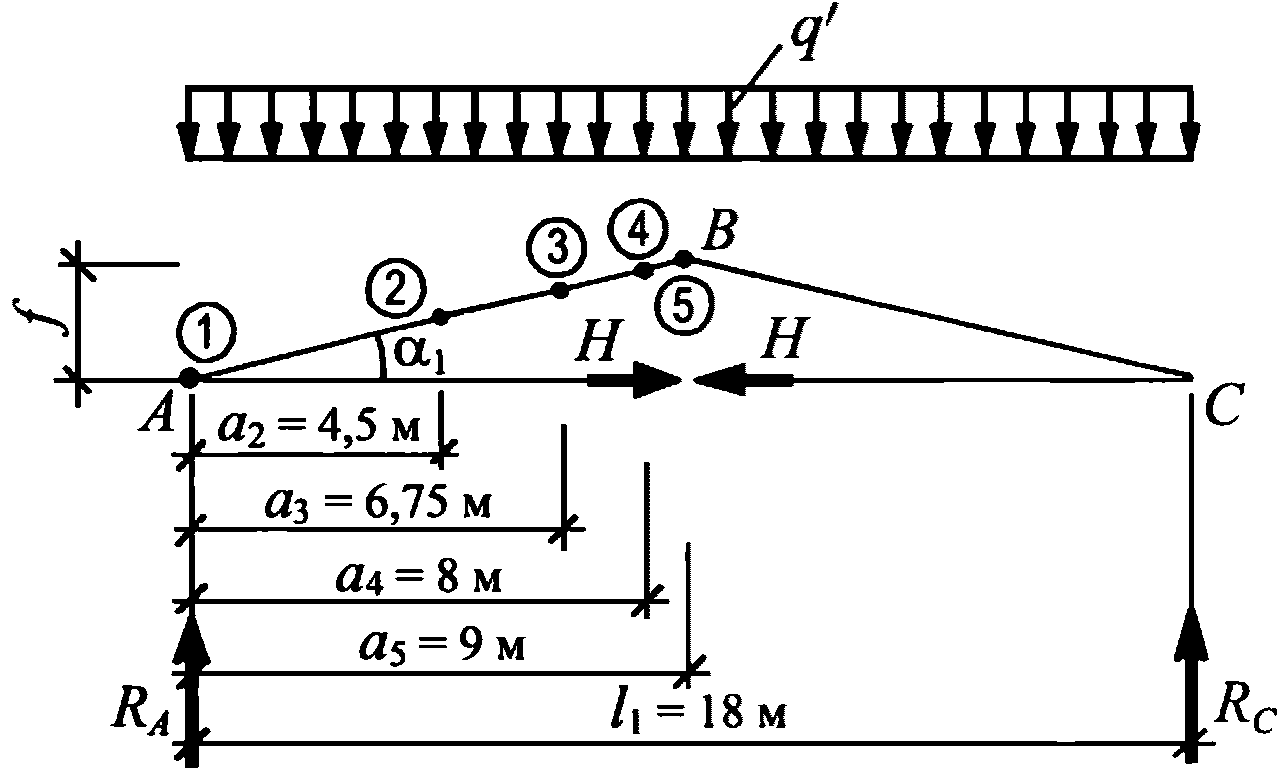
в виде шпренгельной системы
Определяем изгибающие моменты и нормальные силы в нескольких поперечных сечениях для выявления наиболее невыгодной комбинации, учитывая, что закон изменения изгибающих моментов по пролету не соответствует закону изменения высоты поперечного сечения, которая изменяется по прямолинейной зависимости вследствие линейчатости геометрической формы оболочки.
Опорные реакции RA и RC в шпренгельной системе от равномерно распределенной нагрузки: q' = ql2 = 4400·6 = 26400 Н/м = 2,64 кН/м:
RA = RC = q'l1/2 = 26,4·18/2 = 237,6 кН.
Максимальный изгибающий момент определяем в середине пролета:
 .
.Распор H = Mmax/f = 1069,2/2 = 534,6 кН.
Определяем нормальные силы N и изгибающие моменты M в сечениях 1 ... 5. При этом в вершину B условно вводим шарнир и рассматриваем конструкцию как балку пролетом l1/2 (рисунок 5.5.8):
 ;
;M1 = 0; M2 = 26,4(18·4,5/4 - 4,52/2) = 267,3 кНм;
M3 = 26,4(18·6,75/4 - 6,752/2) = 200,2 кНм;
M4 = 26,4(18·8/4 - 82/2) = 105,6 кНм; M5 = 0.
Для определения нормальных сил проектируем все силы на ось AB (см. рисунки 5.5.7 и 5.5.8):
 .
.N1 = 237,6·0,2169 + 534,6·0,9762 - 0 = 573,6 кН;
N2 = 237,6·0,2169 + 534,6·0,9762 - 26,4·4,5·0,2169 = 547,63 кН;
N3 = 237,6·0,2169 + 534,6·0,9762 - 26,4·6,75·0,2169 = 534,75 кН;
N4 = 273,6·0,2169 + 534,6·0,9762 - 26,4·8·0,2169 = 527,6 кН;
N5 = 273,6·0,2169 + 534,6·0,9762 - 26,4·9·0,2169 = 521,86 кН.
Эпюры нормальных сил и изгибающих моментов приведены на рисунке 5.5.9. Проверяем несущую способность конструкции в сечениях 2 и 5. В остальных сечениях несущая способность проверяется аналогично.

в шпренгельной системе
Геометрические размеры шпренгельной системы в сечении 2 приведены на рисунке 5.5.10.

шпренгельной системы в сечении 2
Расчет сечения 2 проводим как для внецентренно сжатого элемента по СП 63.13330. Приведенное сечение в виде двутавра показано на рисунке 5.5.11, а.
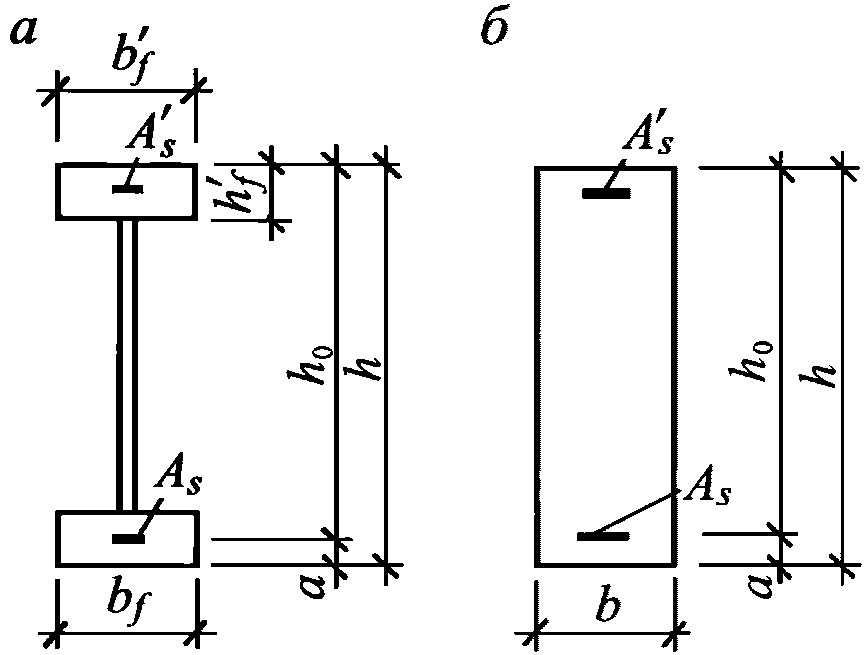
а - двутавровое, б - прямоугольное
шпренгельной системы в сечении 2
Исходные данные: расчетная длина элемента l0 = 7,36 м; геометрические характеристики сечения: h = 135 см;  ;
;  ; a = a' = 17,5 см; h0 = 117,5 см; площадь сечения арматуры
; a = a' = 17,5 см; h0 = 117,5 см; площадь сечения арматуры 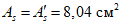
 , усилия M = 267,3 кН·м, N = 547,63 кН.
, усилия M = 267,3 кН·м, N = 547,63 кН.
 ;
;  ; a = a' = 17,5 см; h0 = 117,5 см; площадь сечения арматуры
; a = a' = 17,5 см; h0 = 117,5 см; площадь сечения арматуры 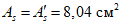
 , усилия M = 267,3 кН·м, N = 547,63 кН.
, усилия M = 267,3 кН·м, N = 547,63 кН.Определяем положение границы сжатой зоны:
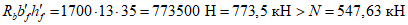 - граница сжатой зоны проходит в полке сечения, поэтому расчет проводим как для прямоугольного сечения шириной
- граница сжатой зоны проходит в полке сечения, поэтому расчет проводим как для прямоугольного сечения шириной 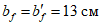 . (рисунок 5.5.11, б).
. (рисунок 5.5.11, б).Определяем высоту сжатой зоны x = 547630/(1700 x 13) = 24,78 см.
Ввиду того, что 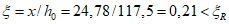 , расчет сечения проводим из условия
, расчет сечения проводим из условия
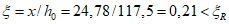 , расчет сечения проводим из условия
, расчет сечения проводим из условияВвиду того, что l0/i = 736/39 = 18,9 > 14, расчет ведем с учетом прогиба элемента (радиус инерции i для квадратного сечения равен i = 0,289h = 0,289·135 = 39 см).
Эксцентриситет e0 = M/N = 267,3/547,63 = 0,49 м.
Условную критическую силу Ncr определяем по 8.1.15 СП 63.13330.2018.
 ;
; 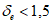 - поэтому для дальнейших расчетов принимаем
- поэтому для дальнейших расчетов принимаем 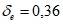 .
.где I - момент инерции сечения: I = bh3/12 = 13·1353/12 = 26,65·105 см4;
Is = 2·8,04(135/2 - 17,5)2 = 40200 см4;
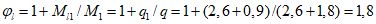 .
.Коэффициент 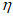 , учитывающий влияние прогиба на значение эксцентриситета e0, определяем по формуле
, учитывающий влияние прогиба на значение эксцентриситета e0, определяем по формуле
 .
.Значение e с учетом прогиба элемента равно
 .
.Проверяем прочность сечения по условию (5.5.24):

Прочность обеспечена.
Расчет сечения 5 (рисунок 5.5.12) проводим как для внецентренно сжатых элементов со случайным эксцентриситетом ea. Приведенное сечение таврового профиля показано на рисунке 5.5.13.
шпренгельной системы в сечении 5

для сечения 5 шпренгельной системы
Исходные данные: расчетная длина элемента l0 = 7,36 м; геометрические характеристики сечения: h = 35 см, b = 13 см, 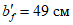 (принята
(принята 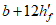 ),
),  , a = a' = 3 см, h0 = 32 см; площадь сечения арматуры
, a = a' = 3 см, h0 = 32 см; площадь сечения арматуры 
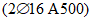 , M = 0, N = N5/2 = 521,86/2 = 260,93 кН (предполагаем, что на два ребра приходится половина силы N5, действующей на все сечение).
, M = 0, N = N5/2 = 521,86/2 = 260,93 кН (предполагаем, что на два ребра приходится половина силы N5, действующей на все сечение).
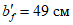 (принята
(принята 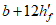 ),
),  , a = a' = 3 см, h0 = 32 см; площадь сечения арматуры
, a = a' = 3 см, h0 = 32 см; площадь сечения арматуры 
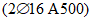 , M = 0, N = N5/2 = 521,86/2 = 260,93 кН (предполагаем, что на два ребра приходится половина силы N5, действующей на все сечение).
, M = 0, N = N5/2 = 521,86/2 = 260,93 кН (предполагаем, что на два ребра приходится половина силы N5, действующей на все сечение).Определяем значение случайного эксцентриситета (по 8.1.7 СП 63.13330.2018).
ea1 = h/30 = 35/30 = 1,16 см, ea2 = l0/600 = 736/600 = 1,23 см. Принимаем большее из значений e0 = ea2 = 1,23 см.
Определяем положение границы сжатой зоны и высоту сжатой зоны x:
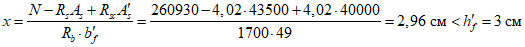 - граница сжатой зоны находится в полке.
- граница сжатой зоны находится в полке.Опуская промежуточные вычисления, приведем для принятого таврового сечения:
- радиус инерции i = 11 см;
- координата центра тяжести y = 19,6 см.
Ввиду того, что l0/i = 736/11 = 66,9 > 14, расчет ведем с учетом гибкости.
Момент инерции относительно оси y:

Is = 4,02(12,42 + 16,62) = 1726 см4.
Коэффициент 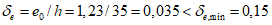 ; принимаем
; принимаем 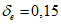 .
.
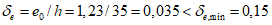 ; принимаем
; принимаем 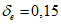 .
.Определяем условную критическую силу Ncr по формуле (5.5.25)
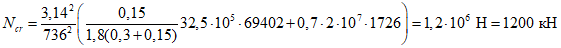 .
.Коэффициент 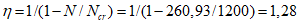 .
.
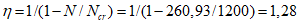 .
.Значение e с учетом прогиба элемента
 .
.Ввиду того, что 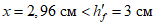 , прочность сечения находим по формуле (5.5.24):
, прочность сечения находим по формуле (5.5.24):
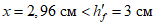 , прочность сечения находим по формуле (5.5.24):
, прочность сечения находим по формуле (5.5.24):1700·49·2,96·(32 - 0,5·2,96) + 40000·4,02(32 - 3,0) = 121,884 кН·м > Ne = 260,93·0,1843 = 48,09 кНм - прочность обеспечена.
Расчет оболочки на действие односторонней снеговой нагрузки (рисунок 5.5.14)
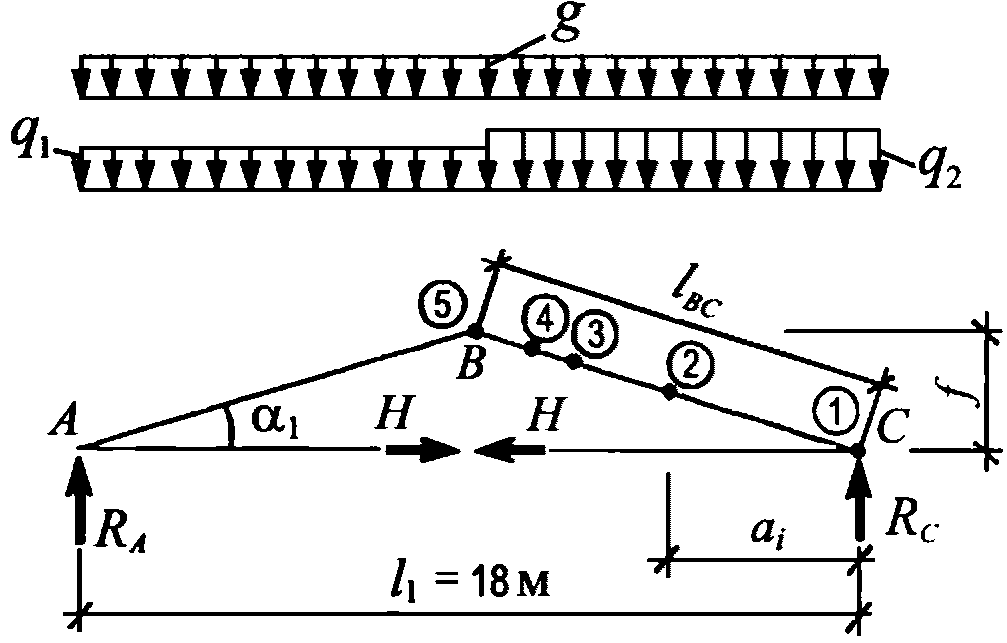
на одностороннюю снеговую нагрузку
Распределенная нагрузка от веса конструкции с кровлей на единицу длины составляет g = q0l2 = 2600·6 = 15600 Н/м = 15,6 кН/м, где q0 - из таблицы 5.5.1 без учета снеговой нагрузки.
Нагрузку от снега с учетом формы покрытия определяем по схеме Б.5 СП 20.13330.2016 для варианта 2 ( ,
, 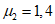 ):
):
 ,
, 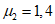 ):
):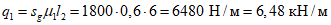 ;
;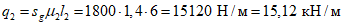 .
.Определяем опорные реакции в шпренгельной системе:
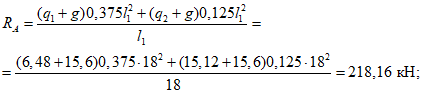
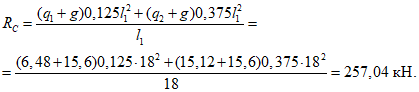
Из уравнений статического равновесия относительно точки B вычисляем изгибающий момент MB и распор H в покрытии:
 ;
;H = MB/f = 1069,2/2 = 534,6 кН.
Определяем нормальные силы N и изгибающие моменты M в сечениях 1 ... 5 правой половины шпренгельной системы, на которую действует большая нагрузка и где усилия будут больше, чем в левой половине шпренгельной системы. В вершину B условно вводим шарнир и рассматриваем конструкцию как балку пролетом l1/2. Характер распределения усилий аналогичен приведенному на рисунке 5.5.9.
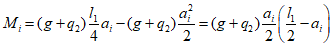 ;
;M1 = 0;  ;
;
 ;
; ;
;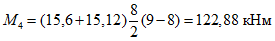 ;
;M5 = 0.
Для определения нормальных сил проектируем все силы на ось BC:
 ;
;N1 = 257,04·0,2169 + 534,6·0,9762 - 0 = 577,63 кН;
N2 = 257,04·0,2169 + 534,6·0,9762 - (15,6 + 15,12)·4,5·0,2169 = 547,65 кН;
N3 = 257,04·0,2169 + 534,6·0,9762 - (15,6 + 15,12)·6,75·0,2169 = 532,65 кН;
N4 = 257,04·0,2169 + 534,6·0,9762 - (15,6 + 15,12)·8·0,2169 = 524,32 кН;
N5 = 257,04·0,2169 + 534,6·0,9762 - (15,6 + 15,12)·9·0,2169 = 517,66 кН.
Проверка несущей способности покрытия в сечениях 1 ... 5 на внецентренное сжатие выполняется аналогично сделанным выше расчетам.
Расчет панели в виде гиперболического параболоида на монтажный случай (рисунок 5.5.15)
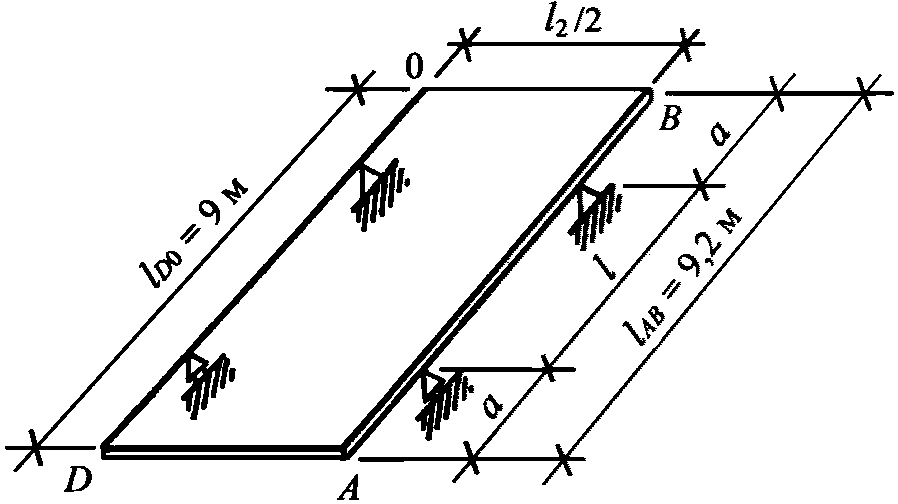
в расчете на монтажные нагрузки
Распределенная монтажная нагрузка на единицу длины
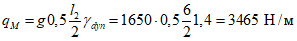 , где g = 1650 Па (таблица 5.5.1);
, где g = 1650 Па (таблица 5.5.1);Расчет панели выполняем как для балочной конструкции, исходя из условия равенства моментов в пролете и на опоре (рисунок 5.5.16)
Mоп = Mпр; Mоп = qMa2/2; Mпр = qM(l2/8 - a2/2).

гиперболической панели на монтажные нагрузки
Приравнивая опорный и пролетный моменты, получаем 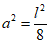 .
.
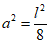 .
.Подставляя значение l = lAB - 2a = (9,2 - 2a) м, получаем a = 1,905 м.
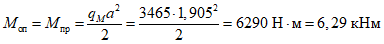 .
.Проверяем сечение ребра AB по формуле 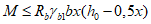 , где b = 6,5 см, h0 = 32 см,
, где b = 6,5 см, h0 = 32 см,  , a = 3 см, площадь сечения арматуры As = 2,011 см2
, a = 3 см, площадь сечения арматуры As = 2,011 см2 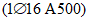 .
.
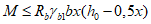 , где b = 6,5 см, h0 = 32 см,
, где b = 6,5 см, h0 = 32 см,  , a = 3 см, площадь сечения арматуры As = 2,011 см2
, a = 3 см, площадь сечения арматуры As = 2,011 см2 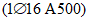 .
.Высота сжатой зоны 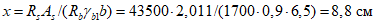 .
.
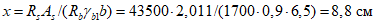 .
.Тогда M = 1700·0,9·6,5·8,8(32 - 0,5·8,8) = 2415000 Н·см = 24,15 кНм > M = 6,29 кНм - прочность обеспечена.
Пример 14
Задание: рассчитать несущую способность четырехлепестковой оболочки покрытия, рассматриваемого в примере 13. Расчетное сопротивление растяжению и площадь сечения арматурного стержня сетки в плите 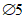 В500 Rs,l = 415 МПа. Размер ячейки арматурной сетки в плите u x u = 200 x 200 мм.
В500 Rs,l = 415 МПа. Размер ячейки арматурной сетки в плите u x u = 200 x 200 мм.
В расчете используем среднюю длину пролета  ;
;
 ;
;По формуле (5.5.2) безразмерные параметры
 ;
; .
.По формуле (5.5.18) в отсутствие углового армирования 

 - нейтральная ось линии излома пересекает коньковую балку.
- нейтральная ось линии излома пересекает коньковую балку.Расстояние от центра тяжести арматуры конькового ребра до его грани
 .
.Ширина конькового ребра 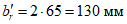 .
.
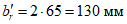 .
. ;
;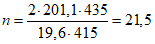 .
. ;
; ;
;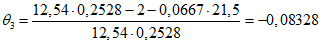 .
.ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
C = 3 + 0,75·0,175{2·0,0667·21,5 + 12,54·0,2528 + 0,08328[4 - 12,54·0,2528(2 + 0,08328)]} = 3 + 0,75·1,75(2,868 + 3,17 + 0,217) = 3,82
Ki = 0,5(3,82 - 1) = 1,41.
Вычисляем предельную нагрузку q по формуле (5.5.3)
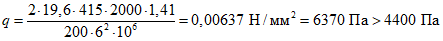 (таблица 5.5.1) - несущая способность оболочки обеспечена.
(таблица 5.5.1) - несущая способность оболочки обеспечена.5.6.1 Цилиндрическими призматическими складками называют тонкостенные конструкции покрытий, состоящие из следующих основных элементов (рисунок 5.6.1):
- тонкой плиты, очерченной по призматической поверхности, вписанной в цилиндрическую (собственно складки);
- бортовых элементов, окаймляющих складку вдоль крайних образующих;
- поперечных диафрагм по криволинейным краям, опирающихся на колонны или стены.
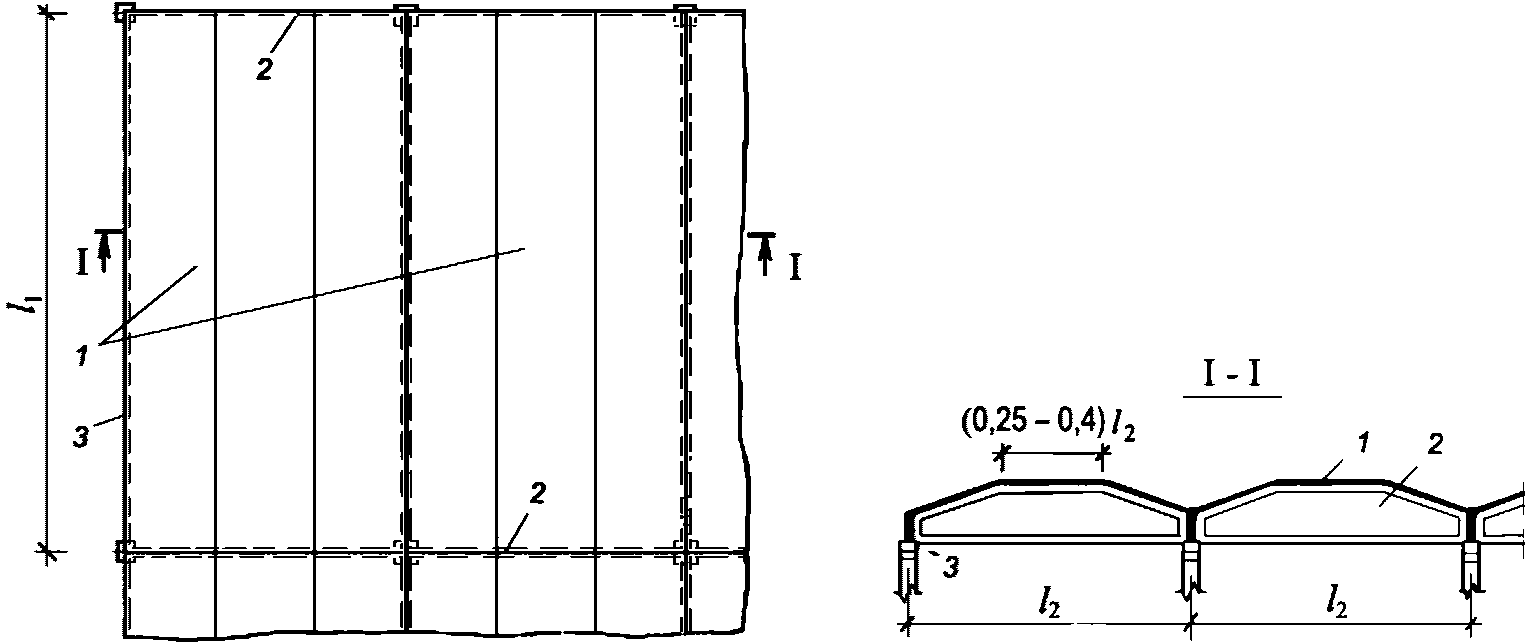
1 - плита; 2 - поперечная диафрагма; 3 - бортовой элемент
с различными типами бортовых элементов
Складки изготавливают гладкими и ребристыми.
Короткими складками называют такие, у которых отношение расстояния между осями опорных диафрагм (пролет оболочки) l1 к расстоянию между бортовыми элементами l2 (длина волны) при l1/l2 <= 1 [6].
5.6.2 Призматические складки рекомендуется применять в покрытиях одноэтажных производственных зданий массового строительства пролетами 18 - 36 м с фонарями и без них.
Складки могут быть одно- и многоволновыми в поперечном направлении, разрезными и неразрезными - в продольном. Короткие призматические складки рекомендуется выполнять сборно-монолитными. Сборные элементы складки сваривают между собой на монтаже, а швы между ними замоноличивают. Плиты к диафрагмам следует приваривать на всех четырех опорах по доступному контуру.
Совместную работу элементов складок рекомендуется обеспечивать:
- устройством бетонных шипов на верхнем поясе диафрагм, пазов на наружных гранях продольных и торцевых ребер плит и бортовых элементов, установкой арматурных каркасов в швах замоноличивания - для неразрезных складок;
- устройством пазов на наружных гранях - для разрезных складок.
Для образования призматической поверхности складки рекомендуется применять плоские ребристые плиты размерами 3 x 6 м или 3 x 12 м.
Очертание верхнего пояса диафрагм должно соответствовать поверхности складки. В неразрезных складках после замоноличивания образуется комплексное сечение верхнего пояса, что позволяет облегчать диафрагму (рисунок 5.6.2).

1 - бетонные шипы на верхнем поясе диафрагмы; 2 - торцевые
ребра плит; 3 - пазы на торцевых ребрах плит; 4 - стержень,
армирующий комплексное сечение; 5 - пазы на продольных
ребрах плит; 6 - каркас в продольном шве между плитами
над диафрагмами; 7 - продольные ребра плит;
8 - верхний пояс диафрагмы
при комплексном сечении верхнего пояса
5.6.3 Сборные железобетонные элементы складчатых покрытий рекомендуется проектировать из тяжелого (классов не ниже B25) или легкого (классов B15 - B20) бетона.
Диафрагмы рекомендуется проектировать из тяжелого бетона (классов не ниже B30).
В качестве предварительно напряженной арматуры продольных ребер плит, бортовых элементов и нижних поясов ферм-диафрагм рекомендуется использовать стержни из арматуры классов А500, А600, А800 и арматурные канаты класса К1400. Полку плит толщиной 30 мм рекомендуется армировать сварными сетками из арматуры класса В500. Ненапрягаемую арматуру ребер плит, элементов диафрагм, а также швов замоноличивания рекомендуется выполнять в виде сварных каркасов из арматуры классов А400, А500.
Ширину швов между плитами рекомендуется назначать не менее:
- 50 мм - для продольных швов;
- 200 мм - для поперечных швов над диафрагмами.
Омоноличивать швы рекомендуется бетоном класса по прочности на сжатие не менее B15, а в зимнее время - не менее B25.
5.6.4 Плиты складок рекомендуется проектировать номинальными размерами 3 x 6 м и 3 x 12 м.
Продольные ребра плит рекомендуется выполнять предварительно напряженными. Высоту продольных ребер рекомендуется принимать в пределах (1/30 - 1/35)l1.
Шаг поперечных ребер рекомендуется принимать равным 1 - 2 м. Высоту поперечных ребер рекомендуется назначать в пределах 1/15 - 1/20 расчетного пролета, равного расстоянию между внутренними гранями продольных ребер.
На наружных гранях продольных ребер предусматривают пазы, обеспечивающие восприятие сдвигающих усилий между плитами. Пазы располагают на длине (1/3 - 1/4)l1 (рисунок 5.6.3).

1 - торцевое ребро; 2 - то же, поперечное; 3 - то же,
продольное; 4 - полка плиты; 5 - арматурная сетка полки;
6 - пазы на продольных ребрах плиты и бортового элемента;
7 - крайний бортовой элемент
При комплексном сечении верхнего пояса диафрагм пазы рекомендуется устраивать также на торцевых ребрах. В этом случае для омоноличивания без устройства опалубки торцевые ребра устраиваются увеличенной высоты (рисунок 5.6.2).
5.6.5 Размеры бортовых элементов, как и плит, определяют по расчету с учетом конструктивных требований. Как правило, бортовые элементы проектируют лоткового сечения с торцевыми ребрами и без промежуточных ребер (рисунок 5.6.3).
Бортовые элементы рекомендуется принимать двух типоразмеров: крайние, устанавливаемые вдоль краев оболочек, и средние, устанавливаемые по всем промежуточным рядам колонн многоволновых складок и соединяющие между собой отдельные волны.
5.6.6 Диафрагмы складчатых покрытий рекомендуется проектировать в виде ферм сегментного очертания, безраскосных ферм или арок с железобетонной или стальной затяжкой.
При стальной затяжке рекомендуется устраивать строительный выгиб узлов нижнего пояса, равный (1/200 - 1/250)l2.
5.6.7 Типовые узлы рекомендуется конструировать в соответствии с рисунком 5.6.4. В складчатых покрытиях допускается устройство аэрационных, светоаэрационных и зенитных фонарей с проемом шириной (1/2 - 1/3)l2. Опирание рам фонарей следует предусматривать на верхний пояс диафрагм.

а - сопряжение диафрагмы с бортовым элементом и плитой
неразрезного складчатого покрытия; б - то же, с плитой
разрезного складчатого покрытия; в - крепление плиты
к фонарной панели; 1 - диафрагма; 2 - плита складки;
3 - бортовой элемент; 4 - арматурный каркас в шве
замоноличивания; 5 - стальной упор; 6 - фонарная
панель; 7 - соединительная планка-подвеска
Проемы для продольных или поперечных зенитных фонарей рекомендуется устраивать с помощью плит-рамок или плит с отверстиями.
Продольные ребра плит, примыкающие к фонарному проему, рекомендуется крепить посредине пролета к стальной фонарной панели (рисунок 5.6.4, в). Фонарная панель при этом должна быть рассчитана на дополнительную нагрузку от покрытия.
5.6.8 Короткие призматические складки состоят из плоских ребристых плит, бортовых элементов и диафрагм (рисунок 5.6.5, а, б). Складки допускается проектировать без бортовых элементов. В этом случае функции бортовых элементов выполняют продольные ребра плит, устанавливаемые вдоль краев покрытия (рисунок 5.6.5, в).
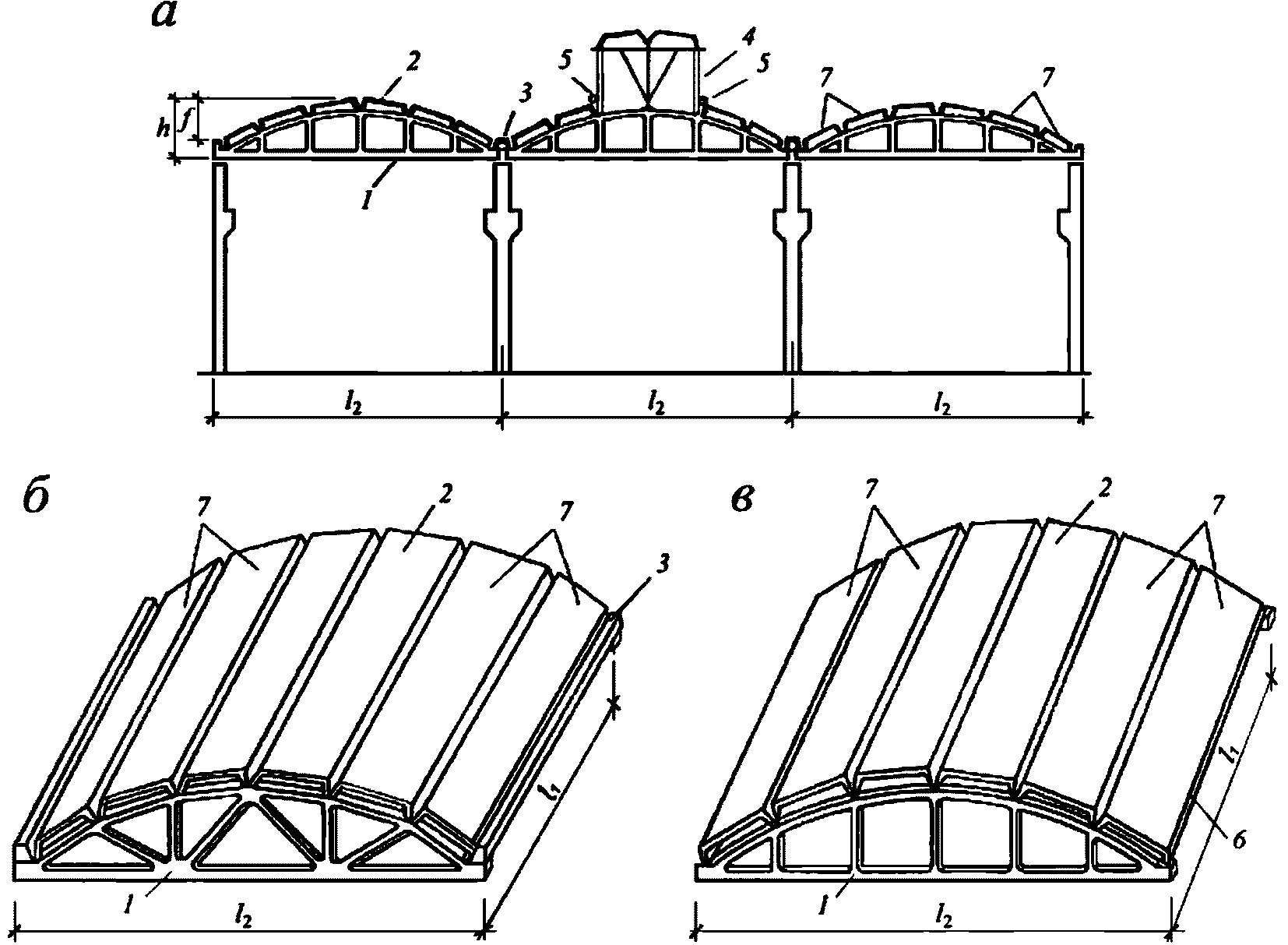
а - конструкция складчатого покрытия; б - складка
с бортовыми элементами; в - то же, без бортовых элементов;
1 - диафрагма; 2 - ребристая плита; 3 - бортовой элемент;
4 - стальной фонарь; 5 - подвеска; 6 - продольное ребро
плиты, выполняющее функции бортового элемента;
7 - крайние грани складки
5.6.9 При определении усилий и расчете оболочек по предельным состояниям следует учитывать СП 63.13330 и 4.2.
Расчет складчатых покрытий выполняют для двух стадий работы конструкции - до и после омоноличивания швов между сборными элементами покрытия.
До замоноличивания швов сборные элементы складок рассчитывают как разрезные конструкции на воздействие нагрузок, возникающих в стадиях изготовления, транспортирования и возведения.
После замоноличивания швов (в стадии эксплуатации) складку рассчитывают на воздействие постоянных и временных нагрузок - как пространственную конструкцию по схемам разрушения, охватывающим одну или две крайние грани складки. Среднюю часть складки, расположенную между четырьмя крайними гранями (по две с каждой стороны), в эксплуатационной стадии рассчитывают только на "местное" разрушение полки, поперечных ребер, а также продольных ребер плит, не закрепленных швами замоноличивания от кручения.
5.6.10 Расчет коротких ребристых призматических складок покрытий для стадии эксплуатации проводят по прочности, жесткости и ширине раскрытия трещин.
Расчет прочности складок покрытий рекомендуется выполнять кинематическим способом метода предельного равновесия - по схемам разрушения, приведенным на рисунках 5.6.6 и 5.6.7.
а, б, в - схемы разрушения для всех плит; г, д - то же,
для крайних плит; 1 - 5 - диски в схемах разрушения
плит от изгиба и продольных ребер от кручения

а - схемы разрушения первой грани складки и бортового
элемента; б - диаграмма скоростей виртуальных перемещений;
в - схема разрушений двух граней складки с изломом бортового
элемента; г - то же, без излома бортового элемента;
д - поперечное сечение складки у края; 1 - 4 - диски
в схемах разрушения; 5 - первые грани складки;
6 - первая и вторая крайние грани складки;
7 - средняя часть складки
Жесткость и ширину раскрытия трещин в полке плиты и в поперечных ребрах определяют согласно СП 63.13330. Требуемая жесткость продольных ребер плит складчатого покрытия, как правило, обеспечивается при условии h/l1 > 1/33, где h - высота ребра; l1 - длина пролета.
Расчет призматических складок покрытий по прочности следует проводить в следующей последовательности: сначала по местным схемам разрушения рассчитывают полку, поперечные и продольные ребра плит (от кручения), затем - складки покрытия и диафрагмы.
5.6.11 Расчет по прочности полки и поперечных ребер плит покрытия следует производить по схемам разрушения, приведенным на рисунке 5.6.6, а, б, в, а крайних плит складок - по схеме разрушения, приведенной на рисунке 5.6.6, г.
Изгибающие моменты в полке на единицу длины линии излома и в поперечных ребрах определяют по "конвертным" схемам разрушения в зависимости от значения параметра
При 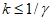 разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, а, и предельное значение изгибающих моментов, воспринимаемых сечением, определяют по формулам:
разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, а, и предельное значение изгибающих моментов, воспринимаемых сечением, определяют по формулам:
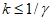 разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, а, и предельное значение изгибающих моментов, воспринимаемых сечением, определяют по формулам:
разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, а, и предельное значение изгибающих моментов, воспринимаемых сечением, определяют по формулам:При  разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, б. В этом случае принимают k1 = 1/k и предельное значение изгибающих моментов определяют по формулам:
разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, б. В этом случае принимают k1 = 1/k и предельное значение изгибающих моментов определяют по формулам:
 разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, б. В этом случае принимают k1 = 1/k и предельное значение изгибающих моментов определяют по формулам:
разрушение полки происходит по схеме, приведенной на рисунке 5.6.6, б. В этом случае принимают k1 = 1/k и предельное значение изгибающих моментов определяют по формулам: (5.6.6)
(5.6.6)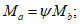 (5.6.7)
(5.6.7)q - равномерно распределенная нагрузка на единицу площади полки с учетом ее веса;
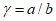 - отношение сторон полки;
- отношение сторон полки;Ma, Mb - изгибающие моменты на единицу длины линии излома, действующие в сечениях полки соответственно в поперечном и продольном направлениях;
qR - нагрузка на единицу длины поперечного ребра, расположенная на ребре и рассчитываемая с учетом его веса;
MR - изгибающий момент, приходящийся на сечение поперечного ребра без полок (рисунок 5.6.6, сечение I-I);
Rsf, RsR - расчетные сопротивления на растяжение арматуры соответственно полки и поперечных ребер;
hf, h0 - соответственно толщина полки и рабочая высота ребра;
- 0,8 - для средних полей средних плит;
- 0,8 при b/a1 < 1,5; 0,9 при 1,5 < b/a1 < 2; 1 при b/a1 > 2 - для крайних полей средних плит и полей крайних плит.
5.6.12 Несущую способность плиты, армированной по результатам расчета по схеме разрушения, приведенной на рисунке 5.6.6, а, б, следует проверять расчетом при схеме разрушения полки и поперечных ребер по рисунку 5.6.6, в.
Изгибающий момент M24, действующий на все поперечные ребра плиты в пролете, определяют по формуле
где q - нагрузка на единицу площади полки с учетом веса поперечных ребер;
b - расстояние в свету между продольными ребрами;
a1 - расстояние в свету между торцевым и поперечным ребрами (рисунок 5.6.6, в, г);
M02 - изгибающий момент, воспринимаемый всеми поперечными ребрами плиты в местах их примыкания к продольным, рассчитывается исходя из установленной в полке арматуры, подобранной по схемам разрушения, приведенным на рисунке 5.6.6, а - г;
c - расстояние между внутренними гранями торцевых ребер.
Подбор арматуры производят по большему значению изгибающего момента в пролете, приходящего на одно поперечное ребро и вычисленного по формуле (5.6.4) или (5.6.8) и (5.6.10).
5.6.13 Расчет поперечных ребер плиты на действие поперечной силы выполняют по СП 63.13330. Максимальное значение поперечной силы в поперечном ребре определяют в зависимости от схемы разрушения, определившей его продольное армирование. При схеме разрушения, приведенной:
на рисунке 5.6.6, а
на рисунке 5.6.6, б
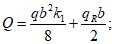 (5.6.12)
(5.6.12)на рисунках 5.6.6, в, г
Q = b(qa + qR)/2. (5.6.13)
При расчете жесткости и ширины раскрытия трещин принимают:
- полное защемление полки в поперечных и продольных ребрах и шарнирное опирание поперечных ребер - если расчет ведется по схемам разрушения, приведенным на рисунке 5.6.6, а, б;
- полное защемление поперечных ребер в продольных - при расчете по схеме разрушения, приведенной на рисунке 5.6.6, в;
- защемление с одной стороны поперечного ребра и шарнирное опирание с другой - при расчете по схеме разрушения, приведенной на рисунке 5.6.6, г.
При определении прогибов поперечных ребер следует принимать тавровое сечение ребра (рисунок 5.6.6, сечение II-II).
5.6.14 В крайних плитах складчатых покрытий, выполняемых без бортовых элементов, и в плитах, примыкающих к фонарным проемам, кроме схем разрушения, приведенных на рисунках 5.6.6, а, б, в, следует рассматривать схему разрушения, приведенную на рисунке 5.6.6, г.
Крутящие моменты M45, действующие в наклонных сечениях концевых участков продольных ребер под углом 45° к их нижней плоскости, воспринимаются сетками, устанавливаемыми на концевых участках продольных ребер, и их значения определяют по формуле
Во всех случаях учитывают, что угловая арматура не воспринимает усилий растяжения, а изгибающий момент M05 принимают равным нулю.
Если в результате расчетов по формуле (5.6.14) значение M45 <= 0, то концевые участки продольных ребер на кручение не армируют.
5.6.15 Короткие призматические складки покрытий на действие равномерно распределенной нагрузки рассчитывают по трем схемам разрушения (рисунок 5.6.7, а, в, г), охватывающим одну или две грани у свободного края.
Предельные значения изгибающих моментов в сечениях определяют на основе кинематического способа теории предельного равновесия.
При изломе двух граней складки работа внутренних сил определяется из пространственной схемы перемещений жестких звеньев - в том числе и перемещения в плоскости одной из граней, излом которой происходит как балки на двух опорах от достижения в наклонных сечениях предельных изгибающих моментов Mult (рисунок 5.6.7, в, г).
5.6.16 При расчете неразрезных складок покрытий армирование продольных ребер плит и бортовых элементов подбирают в соответствии с усилиями от нагрузок, действующих до замоноличивания швов между сборными элементами, а армирование полки и поперечных ребер плит - в соответствии с усилиями от нагрузок, действующих после замоноличивания швов. Опорные моменты M01 и M03 на промежуточных диафрагмах следует определять для стадии эксплуатации (на крайних диафрагмах M01 = 0 и M03 = 0).
Армирование полки, поперечных ребер плит разрезных складок покрытий и продольных ребер первой и второй граней складки подбирают из расчета для стадии эксплуатации. Армирование продольных ребер плит остальных граней складки (в средней части покрытия) определяют из расчета по стадиям изготовления, транспортирования и возведения. В покрытиях зданий с фонарями, а также в покрытиях по фонарям следует подбирать армирование продольных ребер всех плит расчетом для всех стадий их работы.
5.6.17 Максимальные сдвигающие усилия S1 и S2, действующие справа и слева на диафрагмы в плоскости первой грани складки, воспринимаются:
- бетонными шпонками верхнего пояса диафрагм - в неразрезных складчатых покрытиях;
- стальными упорами, приваренными к закладным деталям опорных узлов диафрагм - в разрезных складчатых покрытиях;
- бетоном омоноличивания в узле опирания плит и стойки рамы фонаря на диафрагму - в покрытиях с фонарями.
Проверку наклонных сечений первой грани складки на действие сдвигающих усилий проводят как для балок на действие поперечной силы.
Сварные швы в местах приварки продольных ребер плиты следует рассчитывать на действие сдвигающих усилий S1 или S2 - с учетом того, что у краев покрытия и у температурных швов, где ось первой диафрагмы смещена, сдвигающее усилие S1 или S2 передается на одно продольное ребро.
Для снижения сдвигающих усилий рекомендуется предусматривать связи между плитами первой и второй граней складки по верху торцевых ребер, что обеспечивает передачу части сдвигающего усилия S1 на плиту второй грани покрытия.
5.6.18 В стадии эксплуатации на диафрагмы от складки передается нагрузка в виде нормальных и сдвигающих усилий. Допускается вести расчет диафрагм на вертикальные нагрузки, собираемые с грузовых площадей, приходящихся на соответствующие узлы.
Статический расчет диафрагм проводится с учетом жесткости узлов как многократно статически неопределимой системы.
Пример 15
Задание: запроектировать короткую призматическую складку размерами в плане 12 x 24 м из плоских ребристых панелей 3 x 12 м и железобетонных безраскосных ферм пролетом 24 м. Призматическая складка выполняется сборно-монолитной. Снеговая нагрузка принимается для III снегового района.
Для панелей складки в качестве напрягаемой арматуры используется стержневая термически упрочненная сталь класса А800 с Rs = 695 МПа; Rs,ser = 800 МПа и Es = 200000 МПа.
Класс бетона B20, легкий, плотный на керамзите марки 600 и пористом песке того же вида; марки D1450 по средней плотности с удельным весом 1,45·9,8 = 14,2 кН/м3. Расчетные характеристики бетона: Rb = 11,5 МПа; Rbt = 0,9 МПа; Eb = 13,5·103 МПа.
В качестве ненапрягаемой арматуры используем проволоку периодического профиля 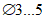 класса Вр500 и стержневую арматуру класса А500. В целях унификации размеры бетонного сечения панелей и граней призматической складки приняты близкими к типовым, как для плит покрытий размерами 3 x 12 м и объемом V = 2,75 м3. Собственный вес керамзитобетонной плиты перекрытия Gser = 2,75·1,45·9,8 = 39 кН.
класса Вр500 и стержневую арматуру класса А500. В целях унификации размеры бетонного сечения панелей и граней призматической складки приняты близкими к типовым, как для плит покрытий размерами 3 x 12 м и объемом V = 2,75 м3. Собственный вес керамзитобетонной плиты перекрытия Gser = 2,75·1,45·9,8 = 39 кН.
Таблица 5.6.1
Нагрузки на покрытие
Наименование нагрузки | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке | Расчетная нагрузка, кН/м2 |
От веса кровли | 1,11 | 1,3 | 1,45 |
От веса плит, в том числе: полки 0,03·14,2 = 0,43 поперечных ребер 0,14 продольных ребер 0,43 торцевых ребер 0,09 | 1,09 | 1,1 | 1,2 |
От снеговой нагрузки, в том числе длительная 0,5S0 | 1,28 <*> | 1,8 | |
ИТОГО | gn + S0 = 3,46 | g + S = 4,45 | |
Расчет полки и поперечных ребер панели.
Исходные данные: нагрузка на полку панели g1 + S = 1,45 + 0,43·1,1 + 1,8 = 3,72 кН/м2;
толщина полки  ;
;
 ;
;размеры сечения поперечного ребра h = 250 мм, b = 50 мм по нижней грани и 80 мм в нижней плоскости полки (рисунок 5.6.8);
расстояние в свету между гранями продольных ребер (рисунок 5.6.9) b1 = 2,95 - 2·0,14 = 2,67 м;
то же, между гранями поперечных ребер, a1 = 1,49 - 0,08 = 1,41 м;
арматура ребра класса А500 с Rs1 = 435 МПа; арматура полки 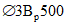 с Rs = 415 МПа.
с Rs = 415 МПа.
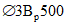 с Rs = 415 МПа.
с Rs = 415 МПа.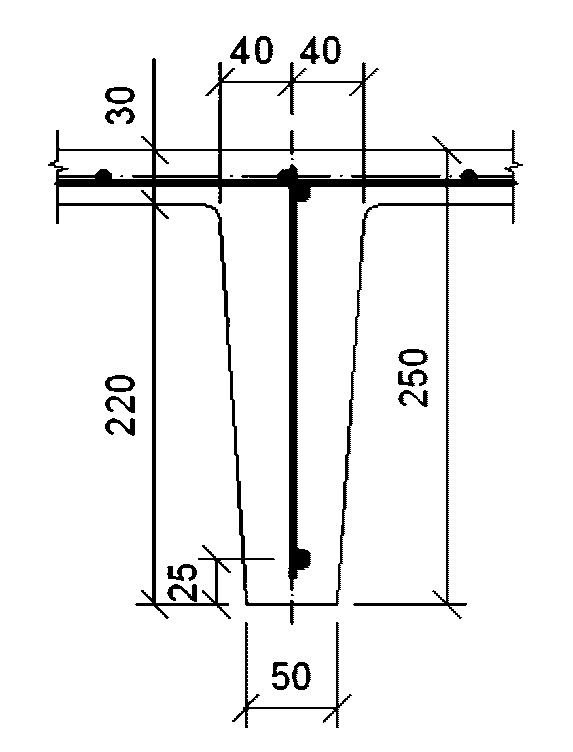

Отношение  , поэтому принимают коэффициент
, поэтому принимают коэффициент  , т.е. при расчете полки нельзя использовать благоприятное влияние распора, возникающего в предельном состоянии при изломе полки.
, т.е. при расчете полки нельзя использовать благоприятное влияние распора, возникающего в предельном состоянии при изломе полки.
 , поэтому принимают коэффициент
, поэтому принимают коэффициент Параметр k по формуле (5.6.1) при h0 = 250 - 25 = 225 мм и отношении 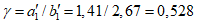 :
:
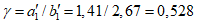 :
:
Излом полки происходит по "конвертной" схеме (рисунок 5.6.6, а). По формуле (5.6.5)
 .
.Изгибающие моменты в сечениях полки панели определяются по формулам (5.6.2) и (5.6.3):
Ma = 3723·1,412·(3 - 0,528·0,46)·0,46/[48(0,46 + 0,528·0,0387)] = 407,1 Нм/м;
Mb = 0,0387·407,1 = 15,8 Нм/м.
Изгибающий момент в сечении поперечного ребра при нагрузке на единицу длины ребра
q1 = 0,14·1,1 + 3,723·0,08 = 0,451 кН/м = 451 Н/м по формуле (5.6.4):
M1 = 3723·1,413(3 - 0,462·0,5282)/(24·0,5282) + 451·2,672/8 = 4587,4 + 401,9 = 4989,3 Нм.
Подбор площади сечения арматуры полки панели
В направлении вдоль панели на 1 м ширины при h0 = 30/2 = 15 мм коэффициент
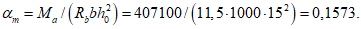
Соответственно  ;
;  ;
;
 ;
;  ;
;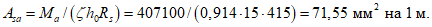
В направлении поперек панели при h0 = 15 - 3 = 12 мм, 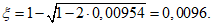
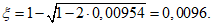
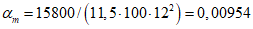 ;
; 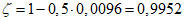 ;
;Asb = 15800/(0,9952·12·415) = 3,2 мм2.
Принимаем арматуру в направлении вдоль панели 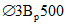 с шагом 100 мм - Asa = 71,0 мм2/м (разница с расчетным значением составляет менее 1%).
с шагом 100 мм - Asa = 71,0 мм2/м (разница с расчетным значением составляет менее 1%).
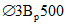 с шагом 100 мм - Asa = 71,0 мм2/м (разница с расчетным значением составляет менее 1%).
с шагом 100 мм - Asa = 71,0 мм2/м (разница с расчетным значением составляет менее 1%).В направлении поперек панели конструктивно  с шагом 200 мм - Asb = 35,5 мм2/м.
с шагом 200 мм - Asb = 35,5 мм2/м.
 с шагом 200 мм - Asb = 35,5 мм2/м.
с шагом 200 мм - Asb = 35,5 мм2/м.Проверка сборной панели на общий излом полки панели (рисунок 5.6.6, б)
Расстояние в свету между внутренними гранями торцевых ребер панели
c = 11,95 - 2·0,275 = 11,4 м (рисунок 5.6.9);
то же, между гранями торцевого и первого поперечного ребра
a2 = 1,505 - 0,275 - 0,04 = 1,19 м.
Приблизительное расстояние между торцевыми линиями излома
l = c - 2·0,1 = 11,4 - 0,2 = 11,2 м.
Арматура полки  с шагом 200 мм на длине линии излома
с шагом 200 мм на длине линии излома
 с шагом 200 мм на длине линии излома
с шагом 200 мм на длине линии изломаAs = 7,1·(11200/200 + 1) = 405 мм2.
Высота сжатой зоны в сечениях семи поперечных ребер по линии излома
x = RsAs/(Rb7b) = 415·405/(11,5·7·50) = 41,76 мм.
Изгибающий момент, воспринимаемый поперечными ребрами в сечении их примыкания к продольному ребру (по линии 0 - 2):
M02 = Madm = RsAs(h0 - 0,5x) = 415·405·(220 - 41,76/2) = 33,47 кНм.
Эксплуатационная нагрузка на панели без учета веса продольных ребер
g2 = (g + S) - 0,43·1,1 = 4,45 - 0,43·1,1 = 3,98 кН/м2.
Изгибающий момент, действующий на все средние поперечные ребра панели, определяем по формуле (5.6.10)
M24 = 3,98·2,672·(3·11,4 - 2·1,19)/24 - 33,47 = 4,15 кНм.
На каждое поперечное ребро, пересекающее линию излома 1 - 3, приходится
M' = M24/7 = 4,15/7 = 0,593 кНм = 593 Нм < M1 = 4989,3 Нм.
При расчетной ширине полки  коэффициент
коэффициент
 коэффициент
коэффициент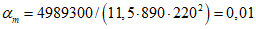 ;
;  ;
;As = 4989300/(0,995·220·415) = 54,92 мм2.
Принимаем для рабочей продольной арматуры поперечного ребра 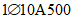 с As = 78 мм2.
с As = 78 мм2.
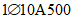 с As = 78 мм2.
с As = 78 мм2.Расчет прочности сечений, наклонных к продольной оси поперечных ребер
Поперечная сила определяется при схеме излома (рисунок 5.6.7, а) по формуле (5.6.11)
Q = 3980(2·2,67 - 1,41·0,46)/8 + 451·2,67/2 = 2935,4 Н.
Сечение ребра b = 50 мм; h0 = 220 мм.
Минимальное усилие, воспринимаемое бетонным сечением, определяем по формуле (8.61) СП 63.13330.2018
Qb1 = Rbtbh0/2 = 0,9·50·220/2 = 4950 Н > 2935,4 Н.
Конструктивно устанавливаем поперечную арматуру 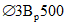 с шагом 150 мм, что меньше предельного значения 0,75h0 по 10.3.13 СП 63.13330.2018.
с шагом 150 мм, что меньше предельного значения 0,75h0 по 10.3.13 СП 63.13330.2018.
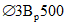 с шагом 150 мм, что меньше предельного значения 0,75h0 по 10.3.13 СП 63.13330.2018.
с шагом 150 мм, что меньше предельного значения 0,75h0 по 10.3.13 СП 63.13330.2018.Предварительный расчет продольных ребер панели в стадии возведения на воздействие собственного веса панели и снеговой нагрузки
(gs + S) = 1,2 + 1,8 = 3,0 кН/м2.
Арматура класса А800 с Rs = 695 МПа. Конструкцию рассчитывают как разрезную с пролетом l0 = 12 - 2·0,1 = 11,8 м.
Изгибающий момент M = (gs + S)l02/8 = 3,0·1,5·11,82/8 = 78,3 кНм.
Ширина полки панели на одно ребро  (рисунок 5.6.10).
(рисунок 5.6.10).
 (рисунок 5.6.10).
(рисунок 5.6.10).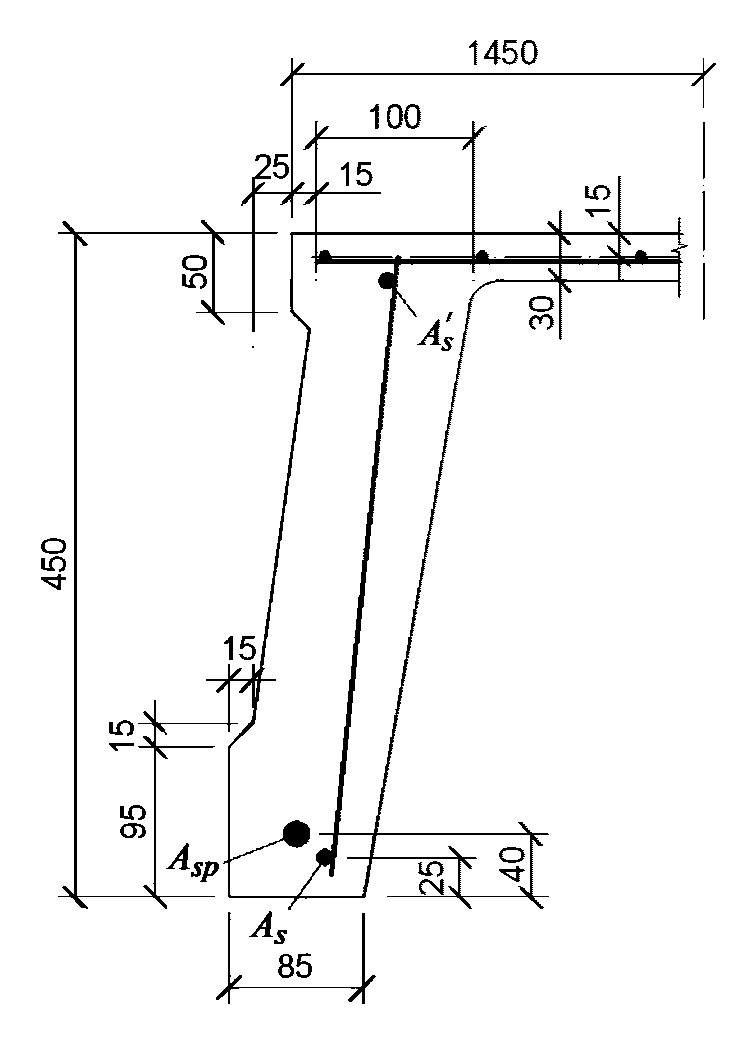
 ;
; 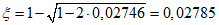 ;
;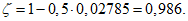
Учитываем в работе арматуры продольного ребра ненапрягаемую арматуру  Rs = 435 МПа, As = 78,5 мм2.
Rs = 435 МПа, As = 78,5 мм2.
 Rs = 435 МПа, As = 78,5 мм2.
Rs = 435 МПа, As = 78,5 мм2.Требуемая площадь сечения напрягаемой арматуры:
Asp = [783·105/(0,986·410) - 435·78,5)]/695 = (193687,23 - 34147,5)/695 = 229,6 мм2.
Принимаем  с Asp = 254,5 мм2.
с Asp = 254,5 мм2.
 с Asp = 254,5 мм2.
с Asp = 254,5 мм2.Расчет продольных ребер на кручение
Крутящий момент находим по формуле (5.6.14):
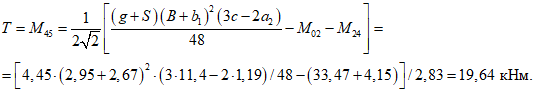
Расчет на кручение таврового сечения приближенно выполняют как прямоугольного с размерами сечения ребра b x h. Вычислим усилие, воспринимаемое арматурой:
продольной растянутой RsAs = 695·254,5 = 176878 Н;
сжатой  ;
;
 ;
;поперечной  с шагом s = 150 мм RswAsw = 300·78,5 = 23550 Н.
с шагом s = 150 мм RswAsw = 300·78,5 = 23550 Н.
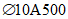 с шагом s = 150 мм RswAsw = 300·78,5 = 23550 Н.
с шагом s = 150 мм RswAsw = 300·78,5 = 23550 Н.Коэффициент, характеризующий соотношение между поперечной и продольной арматурами
 (при M = 0).
(при M = 0).Пониженное значение усилия в продольной арматуре, которое учитывается в расчете:

Высота сжатой зоны бетона при учете сжатой арматуры составляет всего 0,08 мм.
Без учета сжатой арматуры:
x = Rs1As/(Rbb) = 31484/(11,5·100) = 27,4 мм.
Учитывая схему излома, приведенную на рисунке 5.6.7, в, и малую высоту сжатой зоны, при учете сжатой арматуры можно считать, что проекция линии, ограничивающей сжатую зону, на продольную ось элемента не превышает  . Параметры сечения:
. Параметры сечения:
 . Параметры сечения:
. Параметры сечения: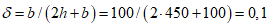 ;
; 
При отсутствии в опорном сечении ребра изгибающего момента коэффициенты k = 0; 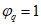 .
.
Несущую способность пространственного сечения найдем по формуле
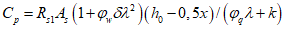 (5.6.15)
(5.6.15)Cp = 31484·(1 + 0,5·0,1·0,32)·(410 - 0,5·27,4)/0,3 = 38,93 кНм > Т = 16,21 кНм.
Прочность элемента на кручение обеспечена.
Расчет разрезной однопролетной складки
Как принято выше, арматура продольных ребер подобрана в соответствии с усилиями от нагрузок, действующих до замоноличивания швов, а арматура полки и поперечных ребер - в соответствии с усилиями от нагрузок, действующих после замоноличивания швов.
Расчет по схеме излома (рисунок 5.6.7, а) с определением изгибающего момента M13 в крайнем бортовом продольном ребре первой грани складки
Работу изгибающих моментов найдем по формуле
Wm = (M02 + M24)/b1 = (33,47 + 4,15)/2,67 = 14,09 кНм/м.
Высота сжатой зоны бетона в поперечном ребре на линии излома 0 - 2:
x1 = RsAs/(Rbb) = 435·78,5/(11,5·50) = 59,4 мм.
Тангенс угла наклона крайней складки к горизонту
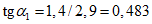 ;
;  ;
; 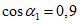 .
.Проявление деформаций учитывается поправочным углом

Угол наклона второй грани: 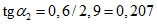 ;
; 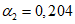 ;
;  .
.
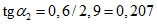 ;
; 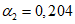 ;
;  .
.Вертикальное перемещение пролетной линии излома 1 - 3
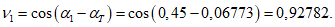
Объем пирамиды вертикальных перемещений
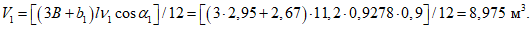
Работа нагрузки 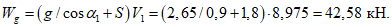
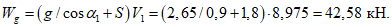
Изгибающий момент в крайнем бортовом продольном ребре первой грани складки найдем по формуле M13 = l(Wg - Wm)/4 = 11,2·(42,58 - 14,09)/4 = 79,77 кНм > M = 78,3 кНм, принятого при предварительном расчете продольных ребер.
Расчет по схеме излома, (рисунок 5.6.7, б) с определением изгибающего момента M13, приходящегося на три продольных ребра двух смежных граней складки
Усилие, воспринимаемое продольной арматурой сетки полки панели, параллельной продольным ребрам ( через 100 мм): q1 = RsAs/s1 = 415·7,1/100 = 29,5 Н/мм.
через 100 мм): q1 = RsAs/s1 = 415·7,1/100 = 29,5 Н/мм.
 через 100 мм): q1 = RsAs/s1 = 415·7,1/100 = 29,5 Н/мм.
через 100 мм): q1 = RsAs/s1 = 415·7,1/100 = 29,5 Н/мм.Высота сжатой зоны бетона в наклонном сечении
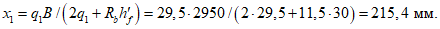
Изгибающий момент, воспринимаемый продольной арматурой сетки полки панели в наклонном сечении
M1 = 0,5q1B(B - x1) = 0,5·29,5·2950·(2950 - 215,4) = 119 кНм.
Усилие, воспринимаемой арматурой сетки полки панели, параллельной поперечным ребрам (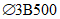 с шагом 200 мм)
с шагом 200 мм)
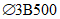 с шагом 200 мм)
с шагом 200 мм)q2 = RsAs/s2 = 415·7,1/200 = 14,73 Н/мм.
Длина проекции наклонного сечения на направлении продольного ребра
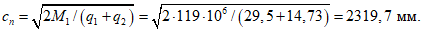
Изгибающий момент, воспринимаемый арматурой сетки, параллельной поперечным ребрам, в наклонном сечении, найдем по формуле
M2 = 0,5q2cn(cn - s2) = 0,5·14,73·2319,7·(2319,7 - 200) = 36,2 кНм.
Усилие, воспринимаемое верхним стержнем каркаса поперечного ребра 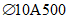 (As = 78 мм2; Rs = 415 МПа):
(As = 78 мм2; Rs = 415 МПа): 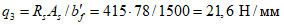 ,
, 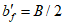 .
.
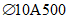 (As = 78 мм2; Rs = 415 МПа):
(As = 78 мм2; Rs = 415 МПа): 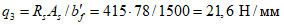 ,
, 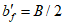 .
.Изгибающий момент, воспринимаемый верхним стержнем каркаса поперечного ребра панели, в наклонном сечении
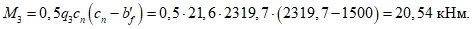
Изгибающий момент, воспринимаемый наклонным сечением первой грани складки в ее плоскости
Mn = M1 + M2 + M3 = 119 + 36,2 + 20,54 = 175,74 кНм.
Виртуальное линейное перемещение

Вертикальное перемещение линии излома 1 - 3
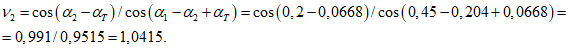
Расстояние от внутренней грани продольного ребра до середины шва замоноличивания r = 140 + 0,5·50 = 165 мм.
Объем пирамиды вертикальных перемещений для первой грани складки
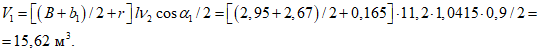
То же, для второй грани складки

Работу нагрузки найдем по формуле
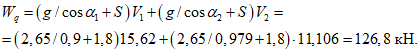
Изгибающий момент, приходящийся на три продольных ребра двух смежных граней складки, определяем по формуле
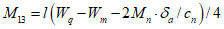 (5.6.16)
(5.6.16)M13 = 11,2(126,8 - 14,09 - 2·175,74·0,3234/2,32)/4 = 178,4 кНм.
На каждое продольное ребро приходится: M = 178,4/3 = 59,47 кНм.
Расчет по схеме излома (рисунок 5.6.7, в) с определением изгибающего момента M13, приходящегося на два смежных продольных ребра граней складки
Вертикальное перемещение линии излома 1 - 3 находим по формуле
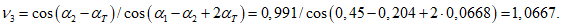
Объем пирамиды вертикальных перемещений для первой грани складки:

То же, для второй грани складки:
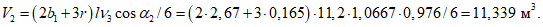
Работу нагрузки найдем по формуле

Изгибающий момент, приходящийся на два смежных продольных ребра граней складки:
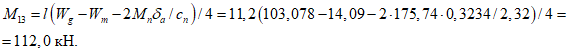
На каждое продольное ребро приходится M = 112/2 = 56 кНм. Наибольший изгибающий момент получается в крайнем бортовом продольном ребре первой грани складки M = 79,77 кНм > 78,3 кНм. Необходимо повторить подбор сечения высокопрочной арматуры при новом значении изгибающего момента:

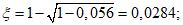
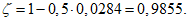
При расчете сечения предварительно напряженной арматуры учитываем работу нижнего стержня арматурного каркаса продольного ребра 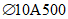 (Rs = 435 МПа, As = 78,5 мм2).
(Rs = 435 МПа, As = 78,5 мм2).
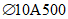 (Rs = 435 МПа, As = 78,5 мм2).
(Rs = 435 МПа, As = 78,5 мм2).Требуемая площадь сечения высокопрочной арматуры класса А800:

Оставляем в качестве напрягаемой арматуры  , а продольное ребро панели может служить бортовым элементом призматической складки.
, а продольное ребро панели может служить бортовым элементом призматической складки.
 , а продольное ребро панели может служить бортовым элементом призматической складки.
, а продольное ребро панели может служить бортовым элементом призматической складки.Из конструктивных соображений в швы замоноличивания между продольными ребрами над диафрагмами рекомендуется устанавливать арматурные каркасы. Они могут учитываться в расчете, и тогда разрезная складка рассматривается как неразрезная. Это становится необходимым, если для обеспечения несущей способности разрезной складки потребуется  площадь сечения рабочей продольной растянутой арматуры, чем при расчете сборных панелей, из которых составлена складка, в стадиях изготовления, транспортирования и возведения.
площадь сечения рабочей продольной растянутой арматуры, чем при расчете сборных панелей, из которых составлена складка, в стадиях изготовления, транспортирования и возведения.
 площадь сечения рабочей продольной растянутой арматуры, чем при расчете сборных панелей, из которых составлена складка, в стадиях изготовления, транспортирования и возведения.
площадь сечения рабочей продольной растянутой арматуры, чем при расчете сборных панелей, из которых составлена складка, в стадиях изготовления, транспортирования и возведения.Расчет на сдвигающее усилие, возникающее в плоской первой (крайней) грани разрезной призматической складки и передаваемое на диафрагму
Максимальное значение сдвигающего усилия определяем по формуле
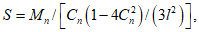 (5.6.17)
(5.6.17)S = 175,74/[2,32(1 - 4·2,322)/(3·11,22)] = 71,416 кН.
В разрезных складчатых покрытиях сдвигающее усилие воспринимается стальными упорами, привариваемыми к закладным деталям опорных узлов диафрагмы и рассчитываемыми согласно СП 16.13330.
Проверка наклонного сечения в плоскости первой грани складки на действие сдвигающего усилия
Расчет производится так же, как балок на действие поперечной силы.
Исходные данные: h0 = 2950 - 50 = 2900 мм; b = 30 мм;  ;
; 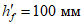 .
.
 ;
; 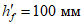 .
.Коэффициент, учитывающий влияние сжатых полок таврового сечения на несущую способность по поперечной силе:
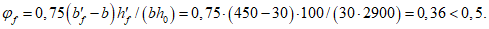
Минимальная поперечная сила, воспринимаемая бетонным сечением:
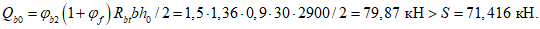
Поперечная арматура устанавливается конструктивно в виде  с шагом sw = 200 мм.
с шагом sw = 200 мм.
 с шагом sw = 200 мм.
с шагом sw = 200 мм.Прочность наклонного сечения обеспечена.
Расчет сечений, наклонных к продольной оси ребра первой грани складки
Нагрузка на единицу длины продольного ребра:
q1 = 0,43·1,5·1,1 + (1,45 + 1,8)·0,2 = 1,36 кН/м.
То же, на единицу площади полки панели,
q2 = 1,45 + 1,2 - 0,43·1,1 + 1,8 = 3,98 кН/м2.
Максимальную величину поперечной силы, воспринимаемую каждым продольным ребром панели, найдем по формуле:
 (5.6.18)
(5.6.18)Q = [1,36·11,2/2 + 3,98·2,67·(11,4 - 1,19)/4]0,9 = 31,26 кН.
До начала расчета вычисляем необходимые геометрические параметры сечения продольного ребра. Напрягаемая арматура 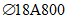 с Asp = 254,5 мм2 (Rs,n = 800 МПа, Es = 2·105 МПа), ненапрягаемая арматура сжатая и растянутая
с Asp = 254,5 мм2 (Rs,n = 800 МПа, Es = 2·105 МПа), ненапрягаемая арматура сжатая и растянутая 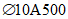 площадью сечения
площадью сечения 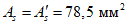 . Передаточная прочность бетона 0,75B = 15 МПа. Способ натяжения арматуры - электротермический, технология изготовления плиты агрегатно-поточная с применением пропаривания; масса плиты - 3,9 т.
. Передаточная прочность бетона 0,75B = 15 МПа. Способ натяжения арматуры - электротермический, технология изготовления плиты агрегатно-поточная с применением пропаривания; масса плиты - 3,9 т.
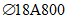 с Asp = 254,5 мм2 (Rs,n = 800 МПа, Es = 2·105 МПа), ненапрягаемая арматура сжатая и растянутая
с Asp = 254,5 мм2 (Rs,n = 800 МПа, Es = 2·105 МПа), ненапрягаемая арматура сжатая и растянутая 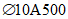 площадью сечения
площадью сечения 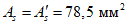 . Передаточная прочность бетона 0,75B = 15 МПа. Способ натяжения арматуры - электротермический, технология изготовления плиты агрегатно-поточная с применением пропаривания; масса плиты - 3,9 т.
. Передаточная прочность бетона 0,75B = 15 МПа. Способ натяжения арматуры - электротермический, технология изготовления плиты агрегатно-поточная с применением пропаривания; масса плиты - 3,9 т.Ввиду симметрии сечения расчет ведем для половины сечения плиты.
Определяем геометрические характеристики приведенного сечения, принимая:

Площадь бетона: A = 145·3 + 7·42/2 + 3·31 + 3,8·31/2 + 1,5·7 + 1,52/2 + 8,5·9,5 + 1,5·5 + 1,52/2 = 435 + 147 + 93 + 58,9 + 10,5 + 2,25 + 80,75 + 7,5 = 834,9 см2 = 83490 мм2.
Приведенная площадь:

Статический момент сечения относительно нижней грани ребра:
S = 435·43,5 + 147·28 + 93·26,5 + 58,9·21,33 + 10,5·10,25 + 1,125·(10 + 39) + 80,75·4,75 + 7,5·42,5 + 36,9·4 + 11,383·(2,5 + 42,5) = 28279,235 см3 = 28279235 мм3.
Расстояние от центра тяжести приведенного сечения до нижней грани ребра:
y = 28279235/89456,7 = 316,122 мм;
ysp = 316,122 - 40 = 276,122 мм;
ys = 316,122 - 25 = 291,122 мм;
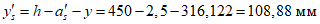 .
.Момент инерции приведенного сечения
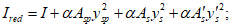
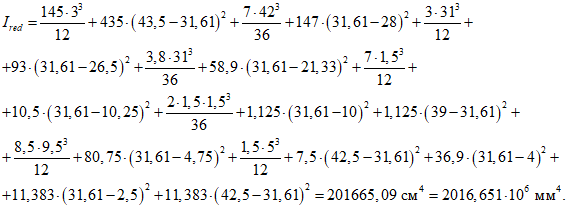
Начальное напряжение в арматуре: 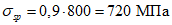 .
.
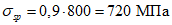 .
.Находим потери в напрягаемой арматуре в соответствии с СП 63.13330.
Первые потери напряжений:
- потери от релаксации напряжений в арматуре равны

При агрегатно-поточной технологии изделие при пропаривании нагревается вместе с формой и упорами, поэтому температурный перепад между ними равен нулю, и, следовательно,  ;
;
 ;
;- потери от деформации формы  и анкеров
и анкеров  при электротермическом натяжении арматуры равны нулю.
при электротермическом натяжении арматуры равны нулю.
Таким образом, сумма первых потерь равна  .
.
 .
.Проверяем максимальные сжимающие напряжения бетона  от действия усилия P(1), вычисляя
от действия усилия P(1), вычисляя 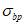 по формуле
по формуле
Здесь e0p1 = ysp = 276,122 мм; ys = y = 316,122 мм.
Момент от собственного веса M = 0.
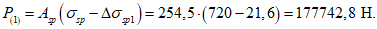
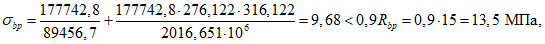
т.е. требование выполняется.
Вторые потери напряжений:
- потери от усадки равны  ;
;
 ;
;- потери от ползучести определяем по формуле

Определяем напряжения в бетоне по (5.6.19) на уровне напрягаемой арматуры, т.е. при ys = ysp = 276,122 мм.
Определяем нагрузку от веса половины плиты:

Момент от этой нагрузки в середине пролета:
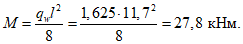
Здесь l = 11,7 м - расстояние между прокладками при хранении плиты; тогда

Напряжения в бетоне на уровне арматуры S' (т.е. при  );
);
 );
);
следовательно, нужно учесть сжимающие напряжения в арматуре 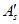 .
.
Потери от ползучести вычисляем по формуле (5.6.20)
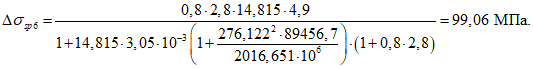
Вторые потери для арматуры S равны:
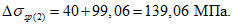
Суммарное значение потерь напряжения:
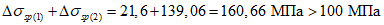 , следовательно, требование СП 63.13330 выполнено, и потери не увеличиваем.
, следовательно, требование СП 63.13330 выполнено, и потери не увеличиваем.Напряжение  с учетом всех потерь равно:
с учетом всех потерь равно:
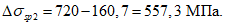
Усилие обжатия с учетом всех потерь напряжений определяем по формуле
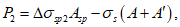 (5.6.21)
(5.6.21)при этом сжимающее напряжение в ненапрягаемой арматуре 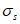 условно принимаем равным вторым потерям напряжений
условно принимаем равным вторым потерям напряжений 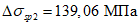 .
.
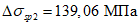 .
.P2 = 557,3·254,5 - 2·78,5·139,06 = 12·104 Н.
Расчет плиты на поперечную силу, приходящуюся на одно продольное ребро плиты
При расчете плиты на поперечную силу рассматриваем прямоугольное сечение без полки шириной b = 85 мм и высотой h0 = 410 мм.
Расчет изгибаемых элементов по бетонной полосе между наклонными сечениями производят по (8.55) СП 63.13330.2018 из условия 0,3Rbbh0 = 0,3·11,5·85·410 = 120,23 кН > Q = 31,26 кН, т.е. прочность бетонной полосы обеспечена.
На погонный метр ребра действует временная нагрузка интенсивностью
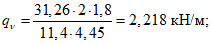
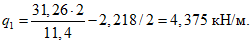
Принимаем первоначально для расчета поперечное армирование в виде арматуры 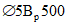 с шагом 200 мм (Asw = 19,6 мм2; Rsw = 300 МПа);
с шагом 200 мм (Asw = 19,6 мм2; Rsw = 300 МПа);
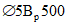 с шагом 200 мм (Asw = 19,6 мм2; Rsw = 300 МПа);
с шагом 200 мм (Asw = 19,6 мм2; Rsw = 300 МПа);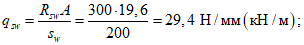
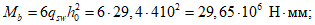
Qb,min = 2qswh0 = 2·29,4·410 = 24108 Н.
Определяем длину проекции невыгодного наклонного сечения

Поскольку 3h0 = 3·410 = 1230 мм < C, то принимаем C = 1230 мм, при этом Qb = Qb,min = 24,1 кН.
Находим значение Q в конце наклонного сечения
Q = Qmax - q1·C = 31,26 - 4,375·1,23 = 25,88 кН.
Поперечную силу, воспринимаемую наклонным сечением, находим по формуле
Q* = Qb + 0,75qswC0 = 24,1 + 0,75·29,4·0,82 = 29,4 + 18,1 = 47,5 кН > 31,26 кН, т.е. прочность любого наклонного сечения обеспечена.
Требуемый по расчету шаг поперечной арматуры
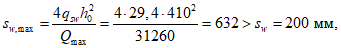
кроме того sw < h0/2 = 410/2 = 20,5 мм, т.е. все требования СП 63.13330 выполнены.
В соответствии с СП 387.1325800 жесткость продольных ребер складчатого покрытия обеспечивается при условии h/l1 > 1/33, где h высота ребра; l1 - длина пролета. В нашем случае l1/h = 11,8/45 = 26,2 < 33, т.е. жесткость продольных ребер плит обеспечена.
5.7.1 К балочным складкам относятся треугольные и трапециевидные складки с жестким поперечным сечением, расчет которых можно выполнять по балочной схеме в предположении линейного распределения продольных деформаций по высоте сечения. Для повышения жесткости граней из их плоскости предусматриваются подкрепляющие ребра или диафрагмы жесткости [7].
Длинными складками условно называют такие, у которых отношение длины пролета l1 к ширине l2 больше 1.
Балочные складки шириной менее 3 м рекомендуется опирать на подстропильные балки, фермы и тому подобные элементы или на стены, а складки шириной 3 м и более допускается опирать непосредственно на колонны.
5.7.2 Складчатые конструкции изготовляют сборными, сборно-монолитными и из монолитного бетона с обычной и предварительно напряженной основной растянутой арматурой, располагаемой в ребрах и поясах. Толщину стенок складок, конструкцию ребер и диафрагм следует принимать в соответствии с 4.4.
5.7.3 Основную растянутую арматуру балочных складок рекомендуется проектировать прямолинейной предварительно напряженной из высокопрочных арматурных стержней классов А600, А800 или арматурных канатов (допускается применять стержни диаметром 20 мм и более из стали класса А540). При этом диаметр стержней и канатов, располагаемых в утолщенных частях складок и в гранях, выбирается, по возможности, наибольшим, но с учетом СП 63.13330.
5.7.4 Грани балочных складок армируются одинарными сварными сетками, расположенными в срединной плоскости граней, если они не подвержены изгибу, или двойными, располагаемыми в соответствии с эпюрой поперечных изгибающих моментов.
В зонах анкеровки предварительно напряженной арматуры около торцов складок рекомендуется предусматривать поперечную арматуру, предотвращающую расслаивание полок или стенок (рисунок 5.7.1).

1 - предварительно напряженная арматура; 2 - сетка;
3 - верхние стержни и их заделка; 4 - поперечные стержни
зоне самозаанкерования предварительно напряженной арматуры
5.7.5 Жесткие узлы сопряжения граней сборных и монолитных складок рекомендуется конструировать как входящие углы железобетонных конструкций с применением пересекающихся стержней или сеток (рисунок 5.7.2) для того, чтобы длина заделки растянутых стержней соответствовала СП 63.13330.
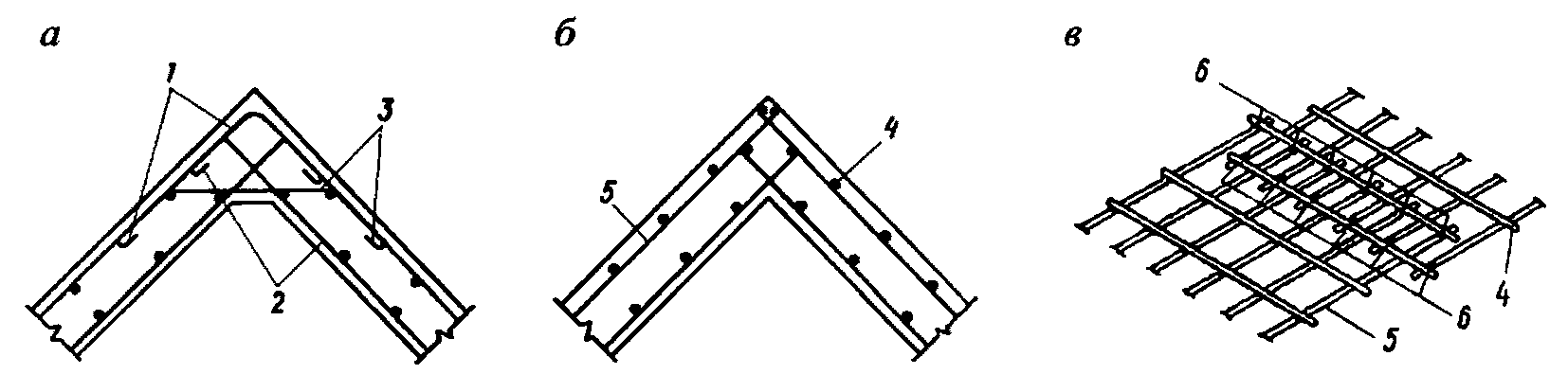
а - отдельными стержнями; б - сварными сетками;
в - положение сеток при сварке; 1 - верхние стержни; 2 - то
же, нижние; 3 - армирование в вутах; 4 - поперечные стержни
пересекающихся сеток; 5 - то же, продольные; 6 - места
точечной сварки
жесткого сопряжения граней треугольной складки
5.7.6 Сборные балочные складки трапециевидной или треугольной формы сечения рекомендуется проектировать из отдельных по длине элементов, соединяемых на месте строительства.
Стыки таких элементов следует предусматривать в наименее напряженных участках складки, в плоскостях, перпендикулярных к продольной оси складки. Минимальная ширина замоноличиваемого шва принимается с учетом диаметра стыкуемых стержней и конструкции их соединения, но не более 250 мм.
Стыки сборных складок с ненапряженной арматурой, расположенные в зонах действия изгибающих моментов, проектируются с применением сварки выпусков арматуры и последующего замоноличивания шва.
Стыки складок с предварительно напряженной арматурой шириной не менее 40 мм и не более шага поперечной арматуры в стенках складки допускается проектировать без выпусков ненапряженной арматуры. При этом продольная предварительно напряженная арматура складки с натяжением на бетон располагается в пазах или каналах с последующим их замоноличиванием или инъецированием.
5.7.7 Формы поперечного сечения призматических складок выбираются из условий производства работ, требований архитектурной выразительности, а также с учетом следующих особенностей:
- трапециевидные складки с горизонтально направленными полками в сжатой зоне меньше склонны к потере устойчивости наклонных стенок и имеют существенно больший момент инерции, чем треугольные той же высоты;
- трапециевидные складки с полками только в растянутой зоне удобнее для их опирания и требуют меньше поперечной арматуры на монтажные усилия; их недостаток - необходимость замоноличивания стыка между складками по низу лотка, отводящего с покрытия воду;
- замоноличенный стык треугольных складок рекомендуется делать только по верхней кромке;
- целесообразно выполнять трапециевидные складки с полками в сжатой и растянутой зонах с замоноличиванием стыка в сжатой зоне.
При выборе наклона и ширины полок рекомендуется учитывать, что оптимальные сечения обеспечивают наибольшую жесткость складки для заданной площади сечения.
При совместном действии полезной равномерно распределенной нагрузки и собственного веса форма оптимального поперечного сечения должна занимать промежуточное положение между очертаниями складок, приведенными на рисунке 5.7.3, соответствующими оптимальным поперечным сечениям только для нагрузки, равномерной по площади покрытия (очертание 1), и для нагрузки собственного веса складки (очертание 2).

а - треугольные сечения; б - трапециевидные сечения;
1 - для нагрузки постоянной интенсивности по ширине складки;
2 - для нагрузки собственного веса складки
складок по жесткости
5.7.8 При расчете призматических складок треугольного и трапециевидного сечений следует различать два случая статической работы конструкции:
- 1 - когда поперечное сечение складки после приложения нагрузки (в том числе и от действия собственного веса) или температурных и других воздействий не испытывает кручения (нет депланации поперечного сечения) и в нем не возникают поперечные симметричные или асимметричные деформации.
В этом случае в средних волнах многоволновой складки или отдельной складки с подкрепляющими ребрами и диафрагмами дополнительных касательных и нормальных усилий в поперечных сечениях не возникает. Тонкостенный элемент такой складчатой конструкции может быть рассчитан и законструирован по схеме простой балки в предположении линейного распределения продольных деформаций по высоте сечения. Стенки и полки, непосредственно нагруженные поперечной нагрузкой, рассчитываются и конструируются с учетом их изгиба. Стыки соседних граней между собой и соединения граней с диафрагмами проектируются так, чтобы обеспечивать конструктивно их совместную работу;
- 2 - когда в складчатой конструкции, нагруженной полосовой или сосредоточенной нагрузкой, или работающей как тонкостенная пространственная складчатая система (в зоне опирания крайних складок на торцевую стену), поперечные сечения изменяют свою форму. В этом случае складчатую систему рекомендуется рассчитывать по технической теории ортотропных оболочек и призматических складок или методом конечных элементов с учетом геометрической нелинейности. Поперечное армирование граней и стыков между ними в этом случае определяется расчетом складок как пространственной системы.
5.7.9 Для подбора продольной арматуры и вычисления прогибов балочных складок допускается приводить сечения складок к тавровому или двутавровому сечению (рисунок 5.7.4) с последующим расчетом их по предельным состояниям согласно СП 63.13330.
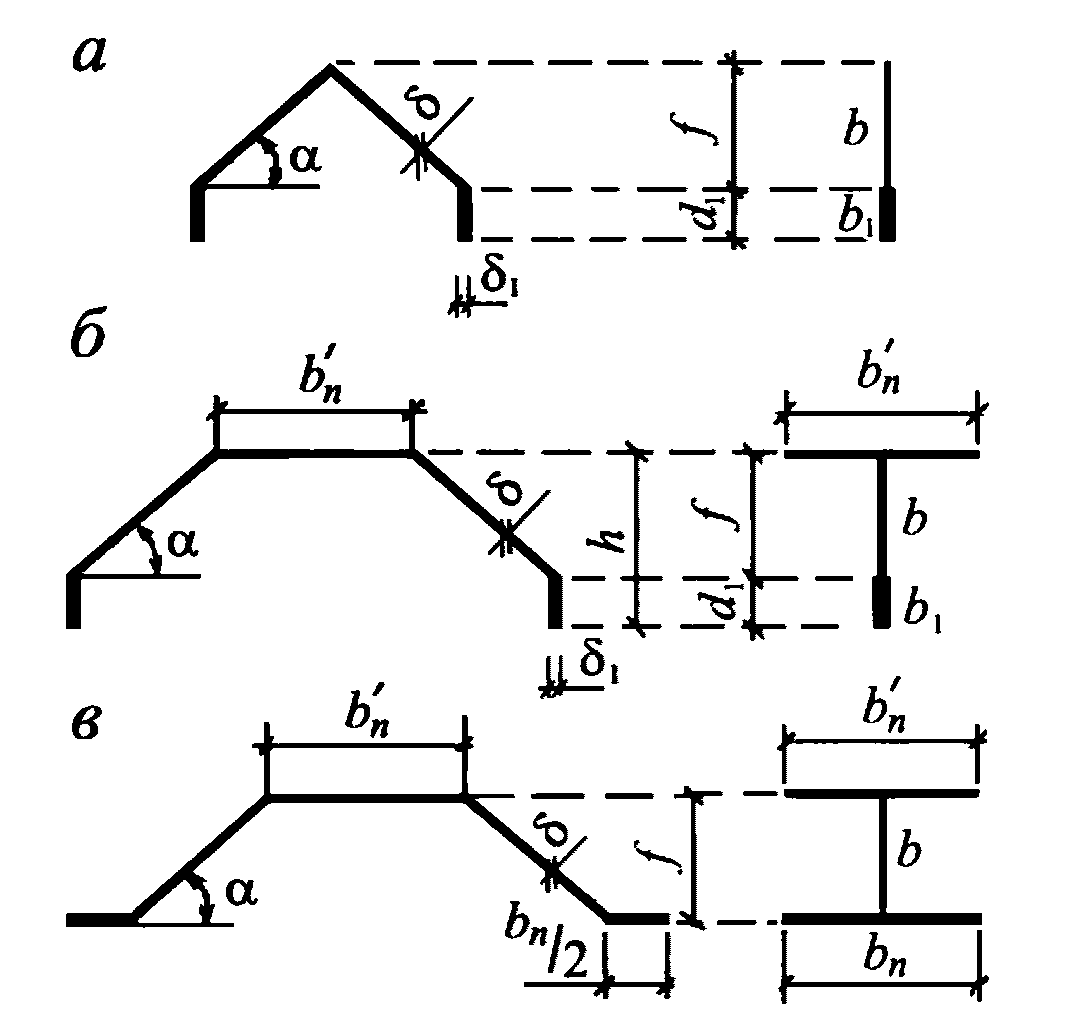
а - к прямоугольным сечениям; б - к тавровым сечениям;
в - к двутавровым сечениям
приведение для расчета
Приведенную толщину бетона стенки b для схем, приведенных на рисунке 5.7.4, следует определять по формуле
 (5.7.1)
(5.7.1)а приведенную толщину b1 (рисунок 5.7.4) - по формуле
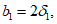 (5.7.2)
(5.7.2)где 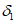 - толщина бортовых элементов;
- толщина бортовых элементов;
При расчете прочности складки по наклонному сечению на действие поперечных сил следует учитывать фактическую толщину наклонных стенок с поправкой на угол наклона.
5.7.10 Для определения поперечных изгибающих моментов в гранях складок, рассматриваемых как балки с недеформируемым поперечным сечением, а также для предварительных расчетов складок в других случаях допускается рассчитывать их как полосу неразрезной плиты на шарнирных опорах. За опоры в этом случае принимаются места сопряжения граней, а за пролет плиты - ширина граней. Число пролетов принимается не менее двух и не более пяти. Соответственно конструктивному решению крайняя опора плиты рассматривается как шарнирная, упруго- или жесткозащемленная.
При этом нормальные усилия для расчета сечений граней допускается определять без учета неразрезности плиты.
5.7.11 Расчет складок открытого профиля рекомендуется выполнять, как правило, с учетом моментов, вызывающих поперечный изгиб граней. Соответственно армирование плит, подкрепляющих ребер граней и их сопряжений рекомендуется проектировать с учетом возможных изгибающих моментов.
Предварительный расчет поперечных моментов в отдельных складках трапециевидного и прямоугольного сечений допускается выполнять как для консольных плит с защемлением по вертикальной плоскости симметрии.
Пример 16
Задание: для покрытия здания пролетом 18 м запроектировать складку размером 3 x 18 м из железобетонных ребристых плит. Снеговая нагрузка принимается для III снегового района.
Материал панелей - тяжелый бетон класса B25 (Rb = 14,5 МПа, Rbt = 1,05 МПа, Eb = 30·103 МПа). Арматура класса А500 (Rs = 435 МПа, Rsc = 400 МПа).
Складка собирается из унифицированных плит П1 и доборных опорных плит П2. Расчет складки выполняем в продольном и поперечном направлениях. Рассматриваем складку как шарнирно-опертую балку постоянного сечения пролетом 18 м (рисунок 5.7.5). Балка подкреплена продольными и поперечными ребрами плит, образующих складку.
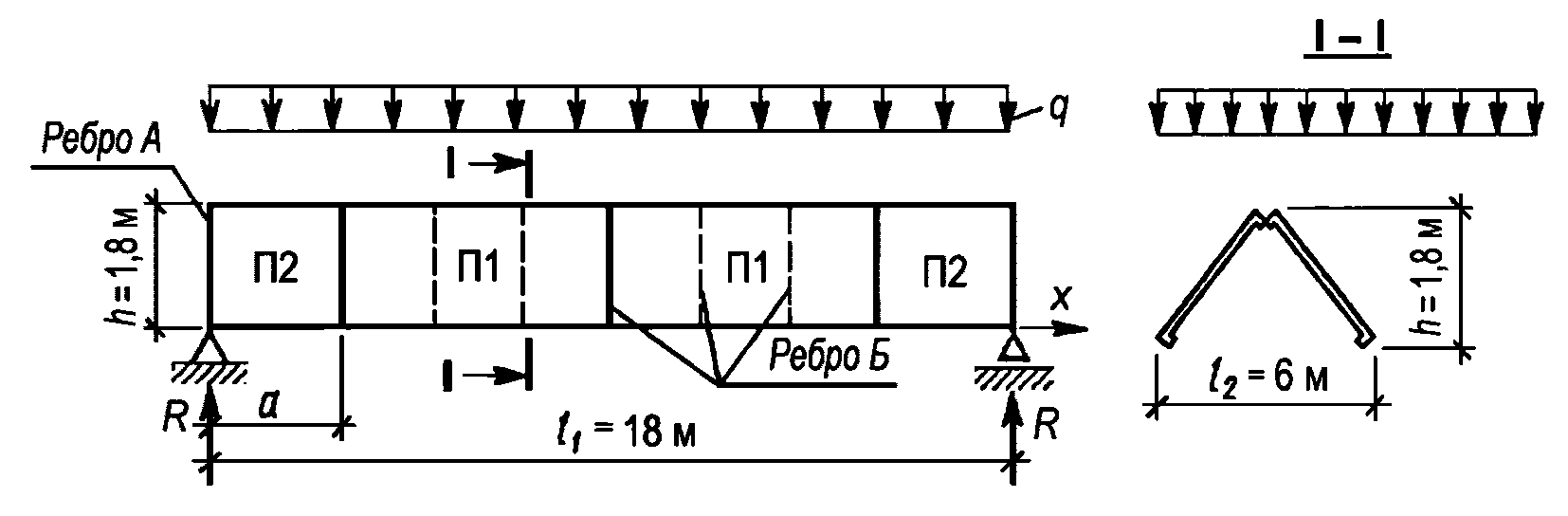
из ребристых плит
Сбор нагрузок на складку
Собственный вес плит в одной складке PП-2 =18 кН, PП-1 = 31 кН.
Общий вес плит в одной складке (расчетный)
 , где
, где 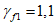 ;
;- бетон замоноличивания швов между плитами:
объем бетона замоноличивания по данным расчета геометрии складки Vb = 2,34 м3;
расчетный полный вес бетона замоноличивания  , где объемный вес бетона
, где объемный вес бетона 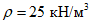 , коэффициент
, коэффициент 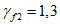 ;
;
 , где объемный вес бетона
, где объемный вес бетона 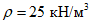 , коэффициент
, коэффициент 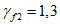 ;
;- полная постоянная нагрузка от собственного веса складки
Pfp = Pp + Pb = 215,6 + 76 = 291,6 кН.
Распределенная нагрузка на 1 м2: 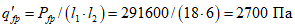 ;
;
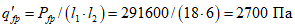 ;
;нагрузка на 1 м длины qfp = Pfp/l1 = 291,6/18 = 16,2 кН/м;
- нагрузка от веса кровли на 1 м2: 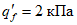 ;
;
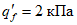 ;
;нагрузка на 1 м длины 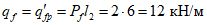 ;
;
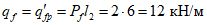 ;
;- снеговая нагрузка: sq = 1,8 кПа;
нагрузка на 1 м длины qs = sql2 = 1800·6 = 10800 Н/м;
- коэффициент динамичности при монтаже принимаем  (предполагается монтаж с предварительным укрупнением в секцию, включающий в себя одну складку шириной 6,0 м).
(предполагается монтаж с предварительным укрупнением в секцию, включающий в себя одну складку шириной 6,0 м).
 (предполагается монтаж с предварительным укрупнением в секцию, включающий в себя одну складку шириной 6,0 м).
(предполагается монтаж с предварительным укрупнением в секцию, включающий в себя одну складку шириной 6,0 м).Расчетная нагрузка:
- в монтажной стадии
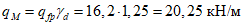 ;
; ;
;- в эксплуатационной стадии
qe = qfp + qf + qs = 16,2 + 12 + 10,8 = 39,0 кН/м;
 ;
;- опорные реакции
RM = qMl1/2 = 20,25·18/2 = 182,25 кН,
Re = qel1/2 = 39,0·18/2 = 351 кН.
Статический расчет складки в продольном направлении
Рассчитываем складку как шарнирно опертую балку, нагруженную равномерно распределенной нагрузкой. Расчетные сечения: для плиты П2 - на расстоянии 3 м от опоры; для плиты П1 - в середине пролета.
Определяем изгибающие моменты в расчетных сечениях для M1 и M2 (рисунок 5.7.6).
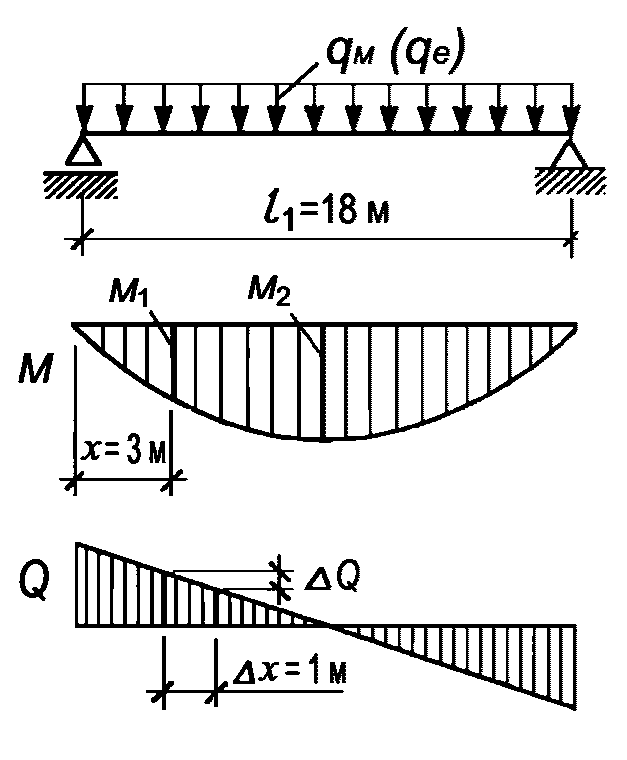
по краю плит П1 и П2
В монтажной стадии
M1M = RMx - qMx2/2 = 182,25·3 - 20,25·32/2 = 455,6 кНм,
M2M = qMl2/8 = 20,25·182/8 = 820 кНм;
в эксплуатационной стадии
Me1 = Rex - qex2/2 = 351·3 - 39,0·32/2 = 877,5 кНм,
Me2 = qel2/8 = 39,0·182/8 = 1579,5 кНм.
Определение армирования продольных ребер плит
Принимаем армирование продольных ребер плит постоянным по длине каждой плиты.
Плита П2

а - в виде двух плит, б - в виде двутавра
Принимаем рабочую высоту сечения h0 = 2100 - 150 = 1950 мм.
Находим необходимую рабочую арматуру в продольных ребрах плит П2, исходя из момента в эксплуатационной стадии работы Me1 = 877,5 кН·м.
Первоначально вычисляем значение 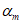 по формуле
по формуле
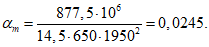
Поскольку 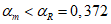 , сжатая арматура по расчету не требуется.
, сжатая арматура по расчету не требуется.
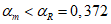 , сжатая арматура по расчету не требуется.
, сжатая арматура по расчету не требуется.При отсутствии сжатой арматуры площадь сечения растянутой арматуры определяется по формуле

Принимаем армирование по  в каждом продольном ребре плиты П2 и еще дополнительно по
в каждом продольном ребре плиты П2 и еще дополнительно по  в шве с каждой стороны складки.
в шве с каждой стороны складки.
 в каждом продольном ребре плиты П2 и еще дополнительно по
в каждом продольном ребре плиты П2 и еще дополнительно по  в шве с каждой стороны складки.
в шве с каждой стороны складки.Таким образом, в шве многопролетной складки устанавливаем по 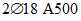 .
.
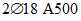 .
.Суммарная площадь сечения арматуры в двух ребрах и шве составляет:
Ase = 4·153,9 + 2·254,5 = 1124,6 мм2 > 1047,5 мм2.
Проверяем арматуру в ребрах складки на монтажные нагрузки с моментом M1M = 455,6 кНм.
Значение  по формуле (5.7.3)
по формуле (5.7.3)
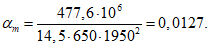
Необходимая арматура в ребрах:

Установленной в ребрах арматуры 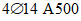 с As = 615,6 мм2 достаточно для восприятия монтажных нагрузок.
с As = 615,6 мм2 достаточно для восприятия монтажных нагрузок.
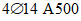 с As = 615,6 мм2 достаточно для восприятия монтажных нагрузок.
с As = 615,6 мм2 достаточно для восприятия монтажных нагрузок.Плита П1
Рассчитываем необходимую рабочую арматуру в продольных ребрах плит П1, исходя из момента в эксплуатационной стадии работы Me2 = 1579,5 кНм.
Вычисляем значение  по формуле (5.7.3)
по формуле (5.7.3)
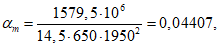
поскольку значение  , сжатой арматуры в плите П1 не требуется.
, сжатой арматуры в плите П1 не требуется.
 , сжатой арматуры в плите П1 не требуется.
, сжатой арматуры в плите П1 не требуется.Определяем необходимую площадь сечения растянутой арматуры по формуле (5.7.4)

Принимаем в ребрах плит П1 арматуру в виде  .
.
 .
.С учетом дополнительной арматуры, устанавливаемой в швах соседних плит в виде 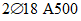 , общее количество арматуры в двух ребрах и шве составляет:
, общее количество арматуры в двух ребрах и шве составляет:
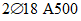 , общее количество арматуры в двух ребрах и шве составляет:
, общее количество арматуры в двух ребрах и шве составляет:As = 4·380,1 + 2·254,5 = 2029,4 мм > 1905 мм2.
Установленной арматуры достаточно для восприятия момента Me2.
Проверяем установленную арматуру в ребрах плит П1  на монтажную нагрузку: As = 4·380,1 = 1520,4 мм2.
на монтажную нагрузку: As = 4·380,1 = 1520,4 мм2.
 на монтажную нагрузку: As = 4·380,1 = 1520,4 мм2.
на монтажную нагрузку: As = 4·380,1 = 1520,4 мм2.Высота сжатой зоны в плите составляет:
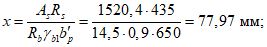

Установленной в ребра плиты П1 арматуры достаточно для восприятия монтажных нагрузок.
Расчет поперечных ребер складки
Проводим расчет поперечных ребер складки на действие изгибающего момента. Рассматриваем вариант многопролетной складки (с учетом бетона замоноличивания швов между складками). Для расчета принимаем сечение складки, приведенное на рисунке 5.7.7.
Определяем изгибающий момент от внешней нагрузки, возникающий в полосе складки шириной 1 м, с учетом поперечной силы, воспринимаемой продольными ребрами складки (рисунок 5.7.8). Для этого определяем приращение касательных напряжений в ребре на участке складки в 1 м. Следует учесть, что касательные напряжения в полке плиты не дают изгибающих моментов вследствие того, что грани складки плоские.
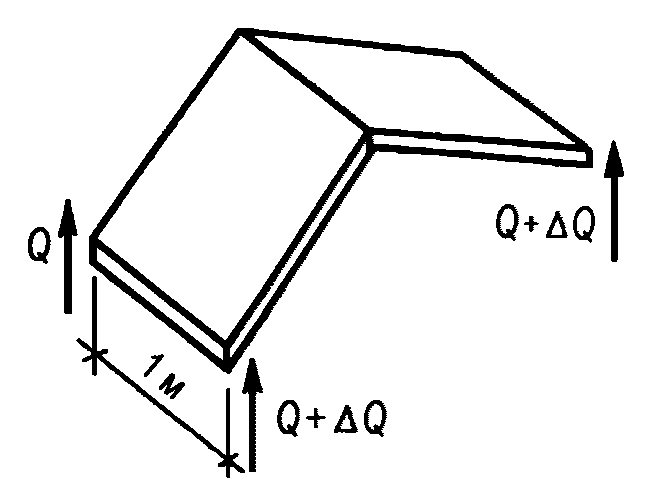
касательных напряжений на участке складки шириной 1 м
Вычисляем геометрические характеристики сечения для определения 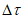 (рисунок 5.7.7).
(рисунок 5.7.7).
Площадь сечения:

Статический момент относительно оси y:
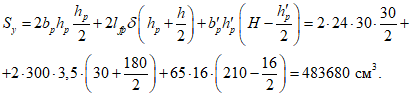
Координата центра тяжести x0 = Sy/A = 483680/4580 = 105,6 см.
Для использования формулы Журавского определяем статический момент отсеченной части плиты выше оси y0

Момент инерции:
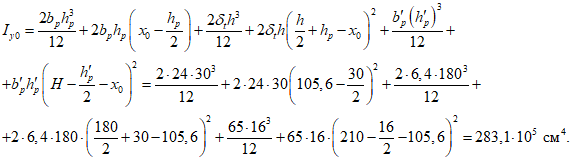
Приращение поперечной силы  на полосу плиты шириной 1 м составляет на 1 м длины
на полосу плиты шириной 1 м составляет на 1 м длины  .
.
 .
.По формуле Журавского на уровне оси x0 вычисляется касательная напряжений 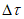
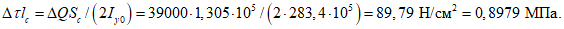
Суммарная поперечная сила Qp, воспринимаемая продольным растянутым ребром (поперечная сила, воспринимаемая частью полки, лежащей ниже оси y0, условно не учитывается):

Расчетный изгибающий момент Mt на 1 м длины в поперечном направлении складывается из момента от внешней нагрузки  и момента, вызванного поперечной силой Qp (рисунок 5.7.9)
и момента, вызванного поперечной силой Qp (рисунок 5.7.9)
 и момента, вызванного поперечной силой Qp (рисунок 5.7.9)
и момента, вызванного поперечной силой Qp (рисунок 5.7.9)
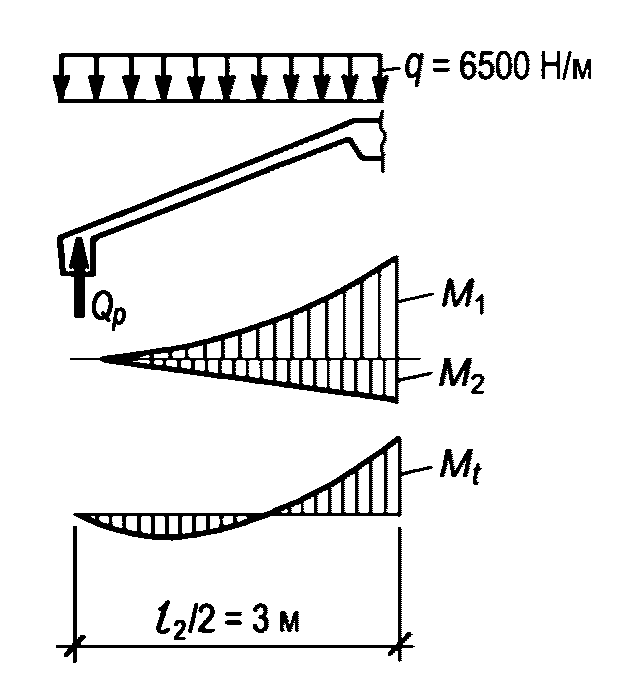
Расчетные моменты для подбора сечений арматуры поперечных ребер (рисунок 5.7.5):
- на одно крайнее поперечное ребро А: MА = Mt·a/2 = 25,21·3/2 = 37,8 кНм;
- на одно промежуточное поперечное ребро Б: MБ = Mt·a = 25,21·3 = 75,63 кНм.
Расчет арматуры выполняется в соответствии с СП 63.13330 и здесь не приводится.
5.8.1 Вспарушенные панели с плоской верхней поверхностью - пространственные элементы покрытий и перекрытий с переменной толщиной, увеличивающейся к контуру, и выпуклой срединной поверхностью, описанной на плоском контуре (рисунок 5.8.1). Панели со ступенчатым изменением толщины называются ступенчато-вспарушенными (рисунок 5.8.2).
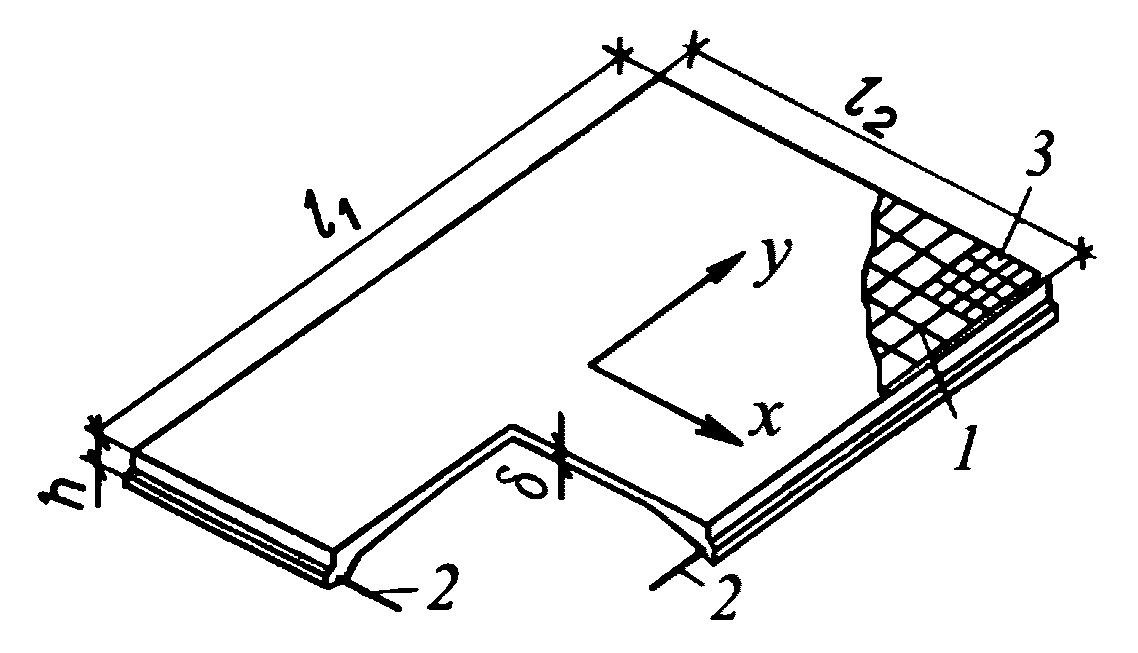
1 - арматурная сетка; 2 - предварительно напряженный
арматурный пояс; 3 - дополнительные сетки в углах панели
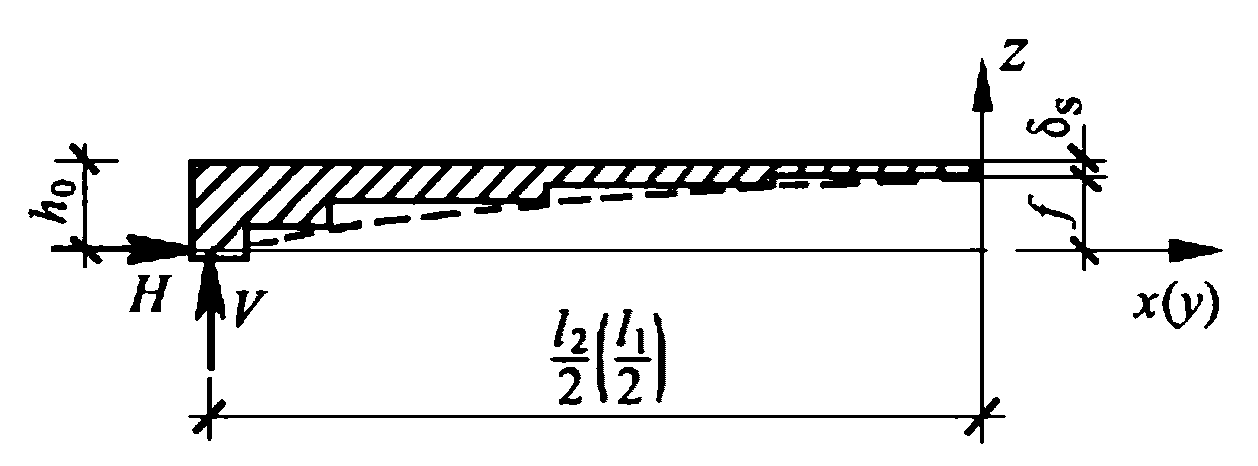
нижней поверхности ступенчато-вспарушенной панели
Панели и конструкции с плоской верхней поверхностью применяют в сборных покрытиях и перекрытиях зданий и сооружений, для которых расчетная нагрузка - равномерно распределенная (или близкая к ней).
Вспарушенные панели и конструкции могут опираться по углам, по контуру, по трем или по двум противоположным сторонам.
Вспарушенные панели проектируют как для однопролетных (разрезных), так и многопролетных (неразрезных) покрытий и перекрытий.
5.8.2 Прямоугольные вспарушенные панели заводского изготовления проектируют длиной l1 <= 7 м, шириной l2 <= 3,6 м и с отношением сторон l1/l2 <= 2. При больших пролетах или полигональном плане перекрываемого помещения применяют сборные вспарушенные конструкции. При этом размеры таких конструкций рекомендуется принимать не более 12 м по длине и 9 м по ширине.
5.8.3 Нижнюю поверхность прямоугольных вспарушенных панелей рекомендуется очерчивать по поверхности положительной гауссовой кривизны, заданной уравнением
где f - стрела подъема поверхности в центре панели по отношению к плоскому контуру;
l1 и l2 - размеры сторон контура (по осям бортовых ребер);
x, y - текущие координаты (рисунки 5.8.1, 5.8.2);
C - параметр, изменяющийся от 0,3 до 0,5 (рекомендуется принимать C = 0,45).
Нижнюю поверхность ступенчато-вспарушенных панелей проектируют таким образом, чтобы в направлении осей x и y (рисунок 5.8.1) она была очерчена дугами поверхности, пересечения которых с внутренними гранями контурных ребер лежали бы в плоскости осей арматурного пояса опорного контура (рисунок 5.8.2). В качестве описывающих дуг в зависимости от технологических и архитектурных требований допускается использовать квадратную параболу или дугу круга со стрелой подъема f. Число ступеней рекомендуется принимать от 2 до 5.
5.8.4 Плиту панелей (рисунок 5.8.1) проектируют из бетона класса B25 и выше и армируют сварной сеткой из проволоки диаметром 3 - 4 мм с ячейкой размерами 200 x 200 мм, а по углам на участках размерами l1/6 и l2/6 - дополнительной сеткой из стержней того же диаметра, располагаемой под основной сеткой.
В средней части вспарушенных и ступенчато-вспарушенных панелей рекомендуется принимать: толщину плиты  - не менее 30 мм, ширину контурных ребер - не менее 100 мм, ширину промежуточных ребер между кессонами панелей - не менее 50 мм. Высоту контурных ребер панелей перекрытий следует принимать не более удвоенной высоты сечения примыкающей к ребру плиты и не менее высоты, требуемой по расчету панели по балочной схеме излома.
- не менее 30 мм, ширину контурных ребер - не менее 100 мм, ширину промежуточных ребер между кессонами панелей - не менее 50 мм. Высоту контурных ребер панелей перекрытий следует принимать не более удвоенной высоты сечения примыкающей к ребру плиты и не менее высоты, требуемой по расчету панели по балочной схеме излома.
Для уменьшения податливости в горизонтальной плоскости в контурных ребрах на длинных сторонах l1 панелей, расположенных по краю здания или сооружения, рекомендуется предусматривать горизонтальные полки у нижней грани ребра, увеличение ширины или соответствующего армирования ребра. Допускается также увеличение толщины или армирования плиты в крайних панелях, или установка связей между панелью и другими несущими конструкциями здания или сооружения.
В плите допускается предусматривать отверстия и проемы. Конструирование и армирование плиты в зоне отверстий должно соответствовать 4.4.24.
5.8.5 Вспарушенные панели и конструкции, как правило, проектируют с предварительно напряженным армированием по контуру.
Контурные ребра панелей армируют предварительно напряженными стержнями или канатами таким образом, чтобы создавался замкнутый арматурный пояс. Заанкеривание стержней в опорной зоне предусматривают путем приварки их к стальным опорным колодкам анкерных устройств и за счет сцепления с бетоном согласно требованиям СП 63.13330. В случае, если стержни или канаты проектируют без анкеров, арматурные элементы следует доводить до наружной грани противоположной стороны панели.
Предварительное напряжение осуществляют натяжением арматуры на бетон в процессе монтажа элементов с последующим обетонированием или натяжением на упоры на заводе-изготовителе (в пределах контурных ребер сборных элементов) с последующим устройством стыков пояса, перекрывающих швы между элементами.
Для компенсации деформаций для сборных вспарушенных конструкций следует предусматривать строительный подъем fc >= fp/5, но не менее 20 мм.
В контурных ребрах кроме основной растянутой арматуры (арматурного пояса) следует предусматривать поперечную арматуру. В ребрах, опертых по всей длине, устанавливают одиночные арматурные каркасы, располагаемые ближе к наружной грани ребра. При этом вблизи углов каркасы должны включать поперечные стержни диаметром 4 - 6 мм с шагом не более 50 мм и нижние стержни диаметром не менее 6 - 8 мм. В контурных ребрах, испытывающих изгиб в вертикальной и горизонтальной плоскостях, вблизи углов на участках размерами l1/6 и l2/6 предусматривают дополнительные арматурные каркасы у внутренней грани ребра.
5.8.6 Сборные вспарушенные конструкции на прямоугольном плане рекомендуется конструировать таким образом, чтобы стыки между монтажными элементами располагались вдоль линий излома расчетной шатровой схемы разрушения.
5.8.7 Ширину опорных площадок при опирании по контуру, по трем или двум сторонам рекомендуется принимать не менее 50 мм, а опорные поверхности панелей, опирающихся по углам, размерами не менее 70 x 70 мм - при опирании на металлические закладные детали, и размерами не менее 100 x 100 мм - при опирании на бетонные поверхности.
5.8.8 В многопролетных покрытиях и перекрытиях из вспарушенных панелей замоноличивание стыков и сварные соединения между ними предусматривают из расчета покрытия или перекрытия как элемента здания в целом на горизонтальные нагрузки и с учетом конструктивных требований. В случае необходимости по контуру панелей предусматривают шпонки, образуемые бетоном замоноличивания стыка.
5.8.9 Расчет вспарушенных панелей следует проводить по предельным состояниям согласно СП 63.13330 и 4.2. При этом несущую способность и сечения рабочей арматуры пояса определяют методом предельного равновесия.
5.8.10 Для прямоугольных вспарушенных и ступенчато-вспарушенных панелей (рисунки 5.8.1, 5.8.2), опертых по контуру, распор H допускается определять, применяя шатровую схему излома (рисунок 5.8.3, б), по формуле
а площадь сечения арматуры предварительно напряженного пояса As - по формуле
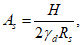 (5.8.3)
(5.8.3)где 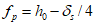 - расчетный подъем панели;
- расчетный подъем панели;
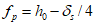 - расчетный подъем панели;
- расчетный подъем панели;l1, l2 - расчетные размеры панели (расстояние между осями опорных площадок);
Rs - расчетное сопротивление предварительно напряженной арматуры пояса;
 , а для крайних панелей покрытий или перекрытий, для которых не выполняются рекомендации 5.8.4,
, а для крайних панелей покрытий или перекрытий, для которых не выполняются рекомендации 5.8.4,  .
.
а - с изломом посредине пролета (балочная схема);
б - с разделением на 5 дисков (шатровая схема излома);
1 - боковые грани; 2 - основная арматура пояса;
H1 и H2 - усилия в поясе
и шатровых складок
Несущую способность панели по сжимающим усилиям в плите допускается проверять как для вспарушенной панели с несмещаемым контуром по 5.8.11.
5.8.11 Для вспарушенных и ступенчато-вспарушенных панелей с несмещаемым контуром предельную нагрузку q или толщину плиты  определяют по формуле
определяют по формуле
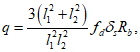 (5.8.4)
(5.8.4)где fd - расчетный подъем панели, определяемый с учетом неупругих деформаций сжатого бетона по формуле
здесь  - средняя толщина вспарушенной или ступенчато-вспарушенной панели;
- средняя толщина вспарушенной или ступенчато-вспарушенной панели;
Eb1 - модуль деформаций бетона, определяемый с учетом длительности действия нагрузки по 5.7 СП 387.1325800.2018.
5.8.12 Для панелей, опертых по двум сторонам или по углам, кроме расчета по шатровой схеме, приведенного в 5.8.10, следует проводить расчет несущей способности панели в одном или при  в двух направлениях по балочной схеме излома как балки П-образного сечения (рисунок 5.8.3, а).
в двух направлениях по балочной схеме излома как балки П-образного сечения (рисунок 5.8.3, а).
Расчет начинают с вычисления геометрических характеристик приведенного сечения и вычисления предельных изгибающих моментов в опорном сечении M0 и в середине пролета Mc.
Значение предельной нагрузки определяют по формуле
 (5.8.6)
(5.8.6)где lx - ширина балки П-образного сечения;
ly - расстояние в свету между колоннами в направлении пролета балки.
В качестве предельной по несущей способности панели перекрытия нагрузки используют меньшую из нагрузок q и qb.
5.8.13 Расчет прогиба поля ступенчато-вспарушенной панели w1 допускается производить приближенно - как для железобетонной опертой по контуру плиты, без трещин в растянутой зоне, по формуле
где p и pl - нормативные значения соответственно полной и длительно действующей на перекрытие нагрузки.
Для панели, опертой по углам, к вычисленному по формуле (5.8.7) значению прогиба плит w1 следует добавлять прогиб ребер w2, вычисленный как для балок Г-образного сечения, и вычесть значение выгиба ребра от обжатия напрягаемой арматурой пояса.
5.8.14 Расчет сборных предварительно напряженных вспарушенных конструкций по предельным состояниям следует выполнять на усилия, возникающие до и после замоноличивания стыков.
5.8.15 Для предварительно напряженных опертых по контуру панелей, удовлетворяющих 5.8.2 и 5.8.4, проверку трещиностойкости допускается не проводить. Проверку трещиностойкости панелей, опертых по двум сторонам или по углам, следует выполнять как для балочных элементов П-образного сечения в одном или в двух направлениях.
Пример 17
Задание: требуется запроектировать сборную ступенчато-вспарушенную панель размерами в осях 3,3 x 5,4 м с опиранием по двум коротким сторонам для междуэтажного перекрытия офисного здания. Временная нагрузка на перекрытии 2,0 кН/м2. Высота этажа 3,6 м.
Принимаем внешние размеры панели в плане 3,28 x 5,38 м (рисунок 5.8.4). Высота контурного ребра панели 270 мм, ширина по нижней грани сечения 100 мм. Плита выполняется с двумя ступенями по толщине. С учетом рекомендаций 5.8.3 по выбору очертания нижней поверхности при расчетной стреле подъема f = 0,1 м (между срединной плоскостью центрального кессона и плоскостью действия распора в контуре) приняты следующие размеры элементов плиты:
- центральный кессон 1,6 x 2,7 м толщиной  ;
;
 ;
;- габариты 1-й ступени 2,28 x 3,8 м с толщиной плиты 50 мм;
- габариты 2-й ступени 3,08 x 5,16 м (до ребер) с толщиной плиты 100 мм.
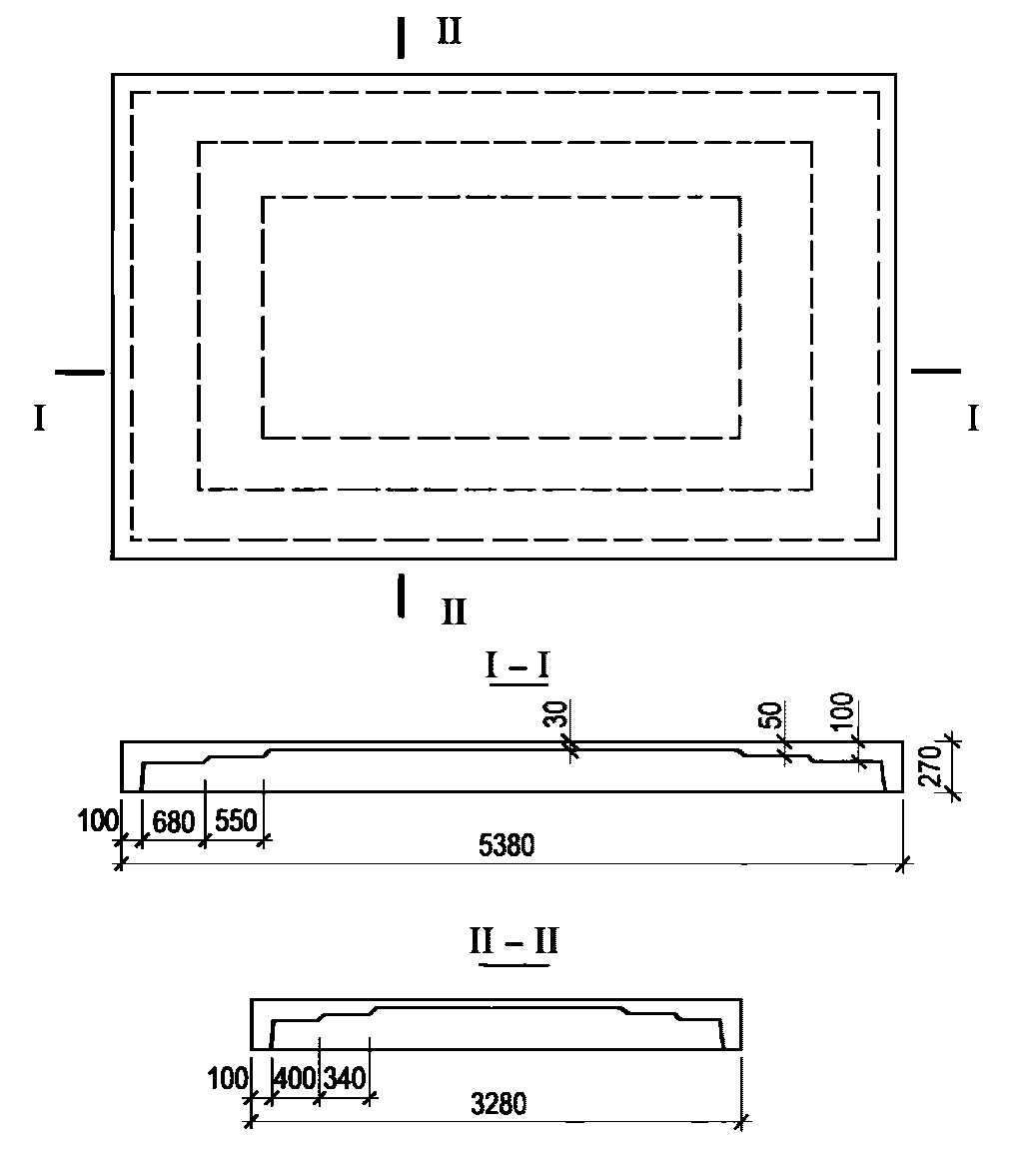
Расчетные пролеты панели: l1 = 5,28 м, l2 = 3,18 м. Расстояние от верха панели до плоскости действия распора в контуре  .
.
 .
.Панель проектируется из тяжелого бетона класса B30 (Rb = 17 МПа; Rbt = 1,15 МПа; Eb = 32500 МПа). В качестве основной арматуры ребер применяется стержневая арматура класса А500 (Rs = 435 МПа).
Для сварных каркасов и сеток применяется арматурная проволока класса Вр500 (Rs = 415 МПа).
Сбор нагрузок приведен в таблицах 5.8.1 и 5.8.2.
Таблица 5.8.1
Вид нагрузки | Нормативная, кН/м2 | Расчетная, кН/м2 | ||
Собственный вес железобетонной плиты без учета веса контурных ребер | 1,68 | 1,1 | 1,85 | |
Вес пола | 0,80 | 1,3 | 1,04 | |
Временная нагрузка 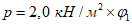 <*> <*> | 1,65 | 1,2 | 1,98 | |
в т.ч. длительная часть временной нагрузки (p x 0,35) | 0,58 | 0,70 | ||
Итого: | Полная нагрузка | 4,13 | 4,87 | |
Длительно действующая нагрузка | 3,06 | 3,59 | ||
<*> В расчетах плиты для временной нагрузки учитывается понижающий коэффициент по формуле (8.1) СП 20.13330.2016 при грузовой площади A = 5,4·3,3 = 17,82 м2: 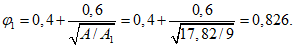 | ||||
Таблица 5.8.2
Вид нагрузки | Нормативная, кН/м | Расчетная, кН/м | |
Собственный вес контурного ребра и вес бетона замоноличивания шва | 0,74 | 1,1 | 0,82 |
Вес половины (по толщине) кирпичной перегородки над ребром с двухсторонней штукатуркой, высотой 3,38 м | 5,11 | 5,92 | |
Итого приложенных непосредственно к ребру: q1 | 5,85 | 6,74 | |
Собственный вес половины ширины плиты | 2,02 | 1,1 | 2,22 |
Вес пола на половине ширины плиты | 1,26 | 1,3 | 1,49 |
Временная нагрузка | 3,14 | 1,16 | 3,77 |
в т.ч. длительная часть временной нагрузки | 1,10 | 1,2 | 1,32 |
Итого передается на ребро плитой: | |||
Полная нагрузка q2 | 6,42 | 7,48 | |
Длительно действующая нагрузка q2,l | 4,38 | 5,03 |
Расчет плиты
Расчетный подъем плиты:  .
.
 .
.Суммарное значение усилий распора H в двух ребрах одного направления по шатровой схеме по формуле (5.8.2):

Требуемая площадь сечения основной арматуры для рядовой панели перекрытия:
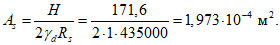
Для крайних панелей перекрытия  ; тогда As = 2,818·10-4 м2.
; тогда As = 2,818·10-4 м2.
 ; тогда As = 2,818·10-4 м2.
; тогда As = 2,818·10-4 м2.Принимаем расположение центра тяжести нижней арматуры на расстоянии 50 мм от нижней грани сечения ребра, верхней арматуры - на расстоянии 30 мм от верхней поверхности (рисунок 5.8.5). Расстояние от плоскости действия распора в контуре до центра тяжести нижней арматуры ребра составляет 105 мм, до центра тяжести верхней арматуры - 85 мм. Тогда требуемое количество нижней арматуры составит As = 1,973·10-4(85/190) = 0,883·10-4 м2, верхней арматуры 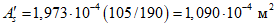 .
.
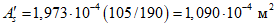 .
.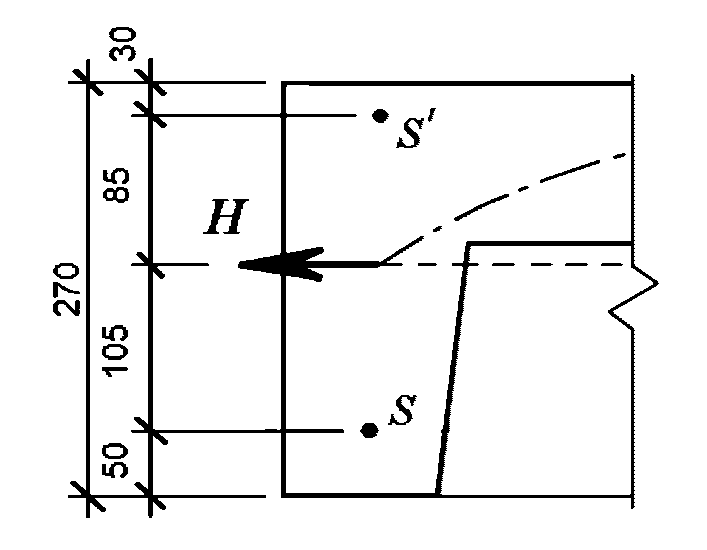
шатрового распора по высоте сечения ребра
Таким образом, в угловых зонах и в пролете коротких (опорных) ребер рядовой панели в качестве нижней арматуры достаточно использовать стержень  (As = 1,131·10-4 м2); в крайних панелях -
(As = 1,131·10-4 м2); в крайних панелях - 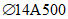 (As = 1,539·10-4 м2). В качестве верхней арматуры могут быть установлены соответственно
(As = 1,539·10-4 м2). В качестве верхней арматуры могут быть установлены соответственно 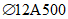 и
и  .
.
 (As = 1,131·10-4 м2); в крайних панелях -
(As = 1,131·10-4 м2); в крайних панелях - 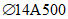 (As = 1,539·10-4 м2). В качестве верхней арматуры могут быть установлены соответственно
(As = 1,539·10-4 м2). В качестве верхней арматуры могут быть установлены соответственно 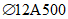 и
и  .
.При проверке плиты на сжимающие усилия расчетный подъем панели с учетом неупругих деформаций сжатого бетона определяется по формуле (5.8.5). При этом в случае продолжительного действия нагрузок учитывается снижение начального модуля деформаций бетона по СП 63.13330

Суммарное значение усилий распора H в двух ребрах одного направления по формуле (5.8.1) при длительно действующей нагрузке 3,59 кН/м2 составляет 126,5 кН.
Средняя толщина плиты ступенчато-вспарушенной панели 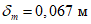 .
.
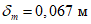 .
.Расчетный подъем панели по формуле (5.8.5)
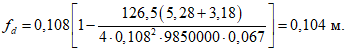
Тогда предельная нагрузка по условию прочности сжатой плиты по формуле (5.8.6)

Аналогично выполняется проверка при непродолжительном действии нагрузки. При этом усилие распора вычисляется от полной расчетной нагрузки 4,87 кН/м2, а расчетный подъем панели - с модулем деформаций Eb1 = 0,85Eb = 0,85·32500 = 27600 МПа (5.7 СП 387.1325800.2018):
H = 171,9 кН; fd = 0,106 м; qu = 19,67 кН/м2 > 5,35 кН/м2.
Армирование плиты панели выполняется конструктивно сеткой с ячейкой 200/200 из проволоки  .
.
 .
.Прогиб плиты вычисляется по формуле (5.8.7) при нормативных значениях нагрузок:
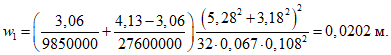
Расчет продольных ребер по прочности
Контурное ребро рассчитывается как балка таврового сечения. В соответствии с требованиями СП 63.13330 расчетная ширина полки в одну сторону от ребра ограничивается значением 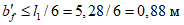 . При этом толщина полки переменна: на участке шириной 0,04 м от края
. При этом толщина полки переменна: на участке шириной 0,04 м от края 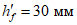 , затем на участке шириной 0,34 м
, затем на участке шириной 0,34 м 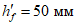 , ближе к ребру на участке 0,40 м -
, ближе к ребру на участке 0,40 м - 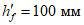 . В запас первый участок не учитываем, считая расчетную ширину полки равной 0,34 + 0,4 + 0,1 = 0,84 м.
. В запас первый участок не учитываем, считая расчетную ширину полки равной 0,34 + 0,4 + 0,1 = 0,84 м.
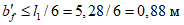 . При этом толщина полки переменна: на участке шириной 0,04 м от края
. При этом толщина полки переменна: на участке шириной 0,04 м от края 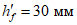 , затем на участке шириной 0,34 м
, затем на участке шириной 0,34 м 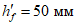 , ближе к ребру на участке 0,40 м -
, ближе к ребру на участке 0,40 м - 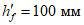 . В запас первый участок не учитываем, считая расчетную ширину полки равной 0,34 + 0,4 + 0,1 = 0,84 м.
. В запас первый участок не учитываем, считая расчетную ширину полки равной 0,34 + 0,4 + 0,1 = 0,84 м.Расчетный изгибающий момент от внешних расчетных нагрузок:
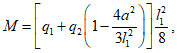 (5.8.8)
(5.8.8)где q1 = 6,74 кН/м - нагрузка веса ребер и веса перегородки (равномерная по длине пролета);
q2 = 7,48 кН/м - нагрузка веса плиты, веса пола и полная временная нагрузка (трапециевидная нагрузка с параметром a = l2/2 = 3,18/2 = 1,59 м - рисунок 5.8.6).
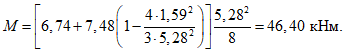

Требуемая арматура по прочности ребра:
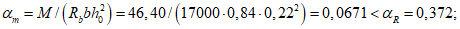
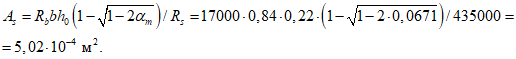
Принимаем 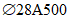 (As = 6,158·10-4 м2).
(As = 6,158·10-4 м2).
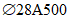 (As = 6,158·10-4 м2).
(As = 6,158·10-4 м2).Поперечная сила на опоре от расчетных нагрузок:
Q = q1l1/2 + q2(l1 - a)/2 = 6,59·5,28/2 + 7,48(5,28 - 1,59)/2 = 31,2 кН.
Проверяем условие прочности по наклонной полосе по формуле (8.55) СП 63.13330.2018
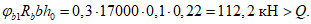
Проверяем условия прочности по поперечной силе для элементов без поперечной арматуры:
Qb,max = 2,5Rbtbh0 = 2,5·1150·0,1·0,22 = 63,3 кН > Q;
Qb,min = 0,5Rbtbh0 = 0,5·1150·0,1·0,22 = 12,65 кН;

При cmax = Mb/Qb,min = 3h0 = 3·0,22 = 0,66 м:
 - поперечная арматура по расчету требуется.
- поперечная арматура по расчету требуется.Ребро армируется каркасом с поперечной арматурой  с шагом s = 120 мм в опорной зоне (s < h0/2 = 0,27/2 = 0,135 м):
с шагом s = 120 мм в опорной зоне (s < h0/2 = 0,27/2 = 0,135 м):
 с шагом s = 120 мм в опорной зоне (s < h0/2 = 0,27/2 = 0,135 м):
с шагом s = 120 мм в опорной зоне (s < h0/2 = 0,27/2 = 0,135 м):qsw = RswAsw/s = 300000·0,0000196/0,12 = 49,0 кН/м.
Длина проекции наклонного сечения, отвечающая несущей способности ребра по поперечной силе
 - принимаем c = 0,44 м.
- принимаем c = 0,44 м.Несущая способность по поперечной силе
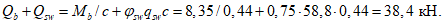
Принятое продольное и поперечное армирование (рисунок 5.8.7) следует проверить расчетом прочности на усилия, возникающие при изготовлении, транспортировании и монтаже панели.

1 - сетки из проволоки 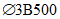 с шагом 200/200; 2 - каркас
с шагом 200/200; 2 - каркас
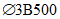 с шагом 200/200; 2 - каркас
с шагом 200/200; 2 - каркасиз проволоки 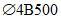 с шагом 120 мм; 3 - каркас из проволоки
с шагом 120 мм; 3 - каркас из проволоки
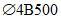 с шагом 120 мм; 3 - каркас из проволоки
с шагом 120 мм; 3 - каркас из проволоки с шагом 120 мм длиной (l1 + l2)/6; 4 - арматурный
с шагом 120 мм длиной (l1 + l2)/6; 4 - арматурныйстержень 

Расчет продольных ребер по раскрытию трещин
Максимальный изгибающий момент от длительно действующих нормативных нагрузок
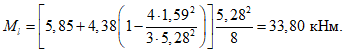
Геометрические характеристики приведенного сечения:
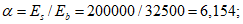
Ared = 0,1·0,27 + 0,4·0,1 + 0,34·0,05 + 0,8·0,03 + 0,0006158·6,154 = 0,1118 м2;
Sred = 0,027·0,135 + 0,04·0,22 + 0,017·0,245 + 0,024·0,255 + 0,00379·0,05 = 0,0229 м3;
yt = Sred/Ared = 0,0229/0,1118 = 0,205 м;
Ired = 0,1·0,273/12 + 0,027(0,135 - 0,065)2 + 0,4·0,13/12 + 0,04(0,065 - 0,05)2 + 0,34·0,053/12 + 0,017(0,065 - 0,025)2 + 0,8·0,033/12 + 0,024(0,065 - 0,015)2 + 0,00379·(0,205 - 0,05)2 = 0,000522 м4;
W = Ired/yt = 0,000522/0,205 = 0,00255 м3.
Упругопластический момент сопротивления таврового сечения по формуле (8.122) СП 63.13330.2018:

Изгибающий момент, воспринимаемый нормальным сечением при образовании трещин, определяем по формуле (8.121) СП 63.13330.2018
Mcrc = Rbt,serWpl = 1750·0,00331 = 5,79 кНм < Ml - трещины образуются, необходим расчет ширины раскрытия трещин.
В соответствии с 8.2.16 СП 63.13330.2018 плечо внутренней пары для таврового сечения с полкой в сжатой зоне и напряжения в растянутой арматуре в сечении с трещиной:
zs = 0,8h0 = 0,8·0,22 = 0,176 м;
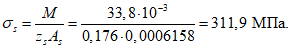
Площадь растянутой зоны бетона при ее высоте 0,5h = 0,135 м < 0,9yt = 0,9·0,205 = 0,185 м и базовое расстояние между трещинами по формуле (8.136) СП 63.13330.2018:
Abt = 0,1·0,135 = 0,0135 м;
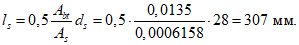
Коэффициент неравномерности распределения относительных деформаций растянутой арматуры между трещинами по формуле (8.137) СП 63.13330.2018
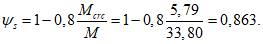
Ширина раскрытия нормальных трещин по формуле (8.128) СП 63.13330.2018 при продолжительном раскрытии

При непродолжительном действии постоянных и временных (длительных и кратковременных) нормативных нагрузок

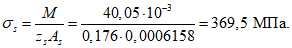
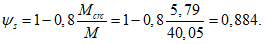

При непродолжительном действии постоянных и временных длительных нормативных нагрузок
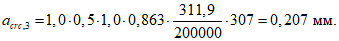
Ширина непродолжительного раскрытия трещин по формуле (8.120) СП 63.13330.2018
acrc = acrc,1 + acrc,2 - acrc,3 = 0,289 + 0,251 - 0,207 = 0,333 мм < acrc,ult = 0,4 мм.
Таким образом, условия обеспечения сохранности арматуры при продолжительном и непродолжительном раскрытии трещин выполняются.
Расчет прогибов продольных ребер
Расчет по прогибам выполняется из условия: f <= fult, где fult - значение предельно допустимого прогиба.
При ограничении прогиба по эстетико-психологическим требованиям (таблица Д.1, пункт 2, перечисление а) СП 20.13330.2016) при l1 = 5,28 м fult = 28 мм. При этом расчет прогиба f выполняется на действие нормативных постоянных и временных длительных нагрузок.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду СП 20.13330.2016, а не СП 20.13330.2018. |
При ограничении прогиба по конструктивным требованиям (Д.1.6 СП 20.13330.2018) fult = 40 мм.
Предельный прогиб по физиологическим требованиям по формуле (Д.1) СП 20.13330.2018 при p = 0,826·0,25·3,3/2 = 0,341 кН/м, p1 + q = 10,23 кН/м и b = 53,6: fult = 53,8 мм.
Расчет прогиба f при ограничениях по конструктивным и физиологическим требованиям выполняется на действие нормативных постоянных и временных длительных и кратковременных нагрузок.
Высота сжатой зоны для таврового сечения по формуле (8.152) СП 63.13330.2018

Здесь: 



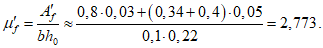
Приведенный модуль деформаций сжатого бетона по формуле (6.9) СП 63.13330.2018 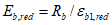 составляет:
составляет:
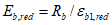 составляет:
составляет:- при непродолжительном действии нагрузки Eb,red = 17/0,0015 = 11300 МПа;
- при продолжительном действии нагрузки Eb,red = 0,9·17/0,0028 = 5500 МПа.
Коэффициент приведения сжатой арматуры к бетону 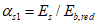 :
:
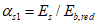 :
:- при непродолжительном действии нагрузки 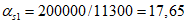 ;
;
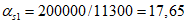 ;
;- при продолжительном действии нагрузки  .
.
 .
.Приведенный модуль деформаций растянутой арматуры с учетом влияния работы растянутого бетона между трещинами  составляет:
составляет:
 составляет:
составляет:- при действии постоянной и временной (длительной и кратковременной) нагрузки
Es,red = 200000/0,884 = 226200 МПа;
- при действии постоянной и временной длительной нагрузки
Es,red = 200000/0,863 = 231800 МПа.
Коэффициент приведения растянутой арматуры к бетону 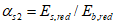 составляет:
составляет:
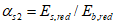 составляет:
составляет:- при действии постоянной и временной (длительной и кратковременной) нагрузки
 ;
;- при действии постоянной и временной длительной нагрузки
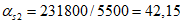 .
.Высота сжатой зоны при непродолжительном действии постоянной и временной (длительной и кратковременной) нагрузки:
xm1 = 0,22·{[(0,028·19,96 + 0,00514·17,65 + 2,773)2 + 2(0,028·19,96 + 0,00514·17,65·0,03/0,22 + 2,773·0,04·0,5/0,22)]1/2 - (0,028·19,96 + 0,00514·17,65 + 2,773)} = 0,0512 м.
Высота сжатой зоны при непродолжительном действии постоянной и временной длительной нагрузки по формуле (5.8.3):
xm2 = 0,22·{[(0,028·42,15 + 0,00514·17,65 +2,773)2 + 2(0,028·42,15 + 0,00514·17,65·0,03/0,22 + 2,773·0,04·0,5/0,22)]1/2 - (0,028·42,15 + 0,00514·17,65 + 2,773)} = 0,0754 м.
Высота сжатой зоны при продолжительном действии постоянной и временной длительной нагрузки:
xm3 = 0,22·{[(0,028·42,15 + 0,00514·36,36 + 2,773)2 + 2(0,028·42,15 + 0,00514·36,36·0,03/0,22 + 2,773·0,04·0,5/0,22)]1/2 - (0,028·42,15 + 0,00514·36,36 + 2,773)} = 0,0744 м.
Плечо внутренней пары: z = 0,8h0 = 0,8·0,22 = 0,176 м.
Жесткость ребра по формуле (8.155) СП 63.13330.2018:
D = Es,redAsz(h0 - xm)
- при непродолжительном действии постоянной и временной (длительной и кратковременной) нагрузки:
D1 = 226200000·0,0006158·0,176·(0,22 - 0,0512) = 4138 кНм;
- при непродолжительном действии постоянной и временной длительной нагрузки:
D2 = 231800000·0,0006158·0,176·(0,22 - 0,0754) = 3633 кНм;
- при продолжительном действии постоянной и временной длительной нагрузки:
D3 = 231800000·0,0006158·0,176·(0,22 - 0,0744) = 3658 кНм.
Кривизна по формуле (8.142) СП 63.13330.2018

- при непродолжительном действии постоянной и временной (длительной и кратковременной) нагрузки:

- при непродолжительном действии постоянной и временной длительной нагрузки:
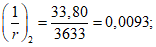
- при продолжительном действии постоянной и временной длительной нагрузки:
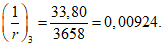
Максимальный прогиб ребра
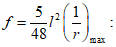
- при продолжительном действии постоянных и временных длительных нагрузок:
f2 = (5/48)·5,282·0,00924 = 0,0268 < fult = 0,028 м;
- по полной кривизне при действии постоянных и временных длительных и кратковременных нагрузок:
f2 = (5/48)·5,282·(0,00968 - 0,0093 + 0,00924) =
= 0,0279 < fult = 0,040 м;
- суммарный прогиб плиты и ребер не превышает предельного прогиба по физиологическим требованиям:
f = f1 + f2 = 0,0202 + 0,0279 = 0,0481 < fult = 0,0538 м.
5.9.1 Рамно-шатровые конструкции представляют собой пространственные плитно-стержневые системы с формой несущей конструкции в виде многогранника на плоском полигональном (как правило, прямоугольном) контуре.
Основная несущая конструкция рамно-шатровых конструкций - пространственная шатровая рама. Продольные оси основных элементов шатровой рамы расположены на пересечениях граней шатра - вдоль ребер шатровой складки (рисунок 5.9.1).

1 - средний диск; 2 - наклонные грани; 3 - контурный
(бортовой) элемент; 4 - ребра шатра
Диагональные рамы сборных рамно-шатровых конструкций в зависимости от длины перекрываемого пролета, строительной высоты перекрытия и уровня действующих нагрузок принимают в виде отдельных сборных элементов - рам с подкосами (рисунок 5.9.2, а), или в составе плит П1 и П2 в виде ребер переменной высоты, увеличивающейся от высоты контура среднего диска до высоты бортового элемента в угловых зонах (рисунок 5.9.2, б). В последнем конструктивном решении контур среднего диска образован внутренними поперечными ребрами плиты П2 и средними частями сопряженных внешних продольных ребер плит П2 и П3. Внешний контур шатровой рамы, в котором размещается основная арматура шатра (затяжка), образован длинными контурными ребрами трапециевидных в плане плит П1. Внутренний контур образован сопряженными ребрами плит П1 и П2.
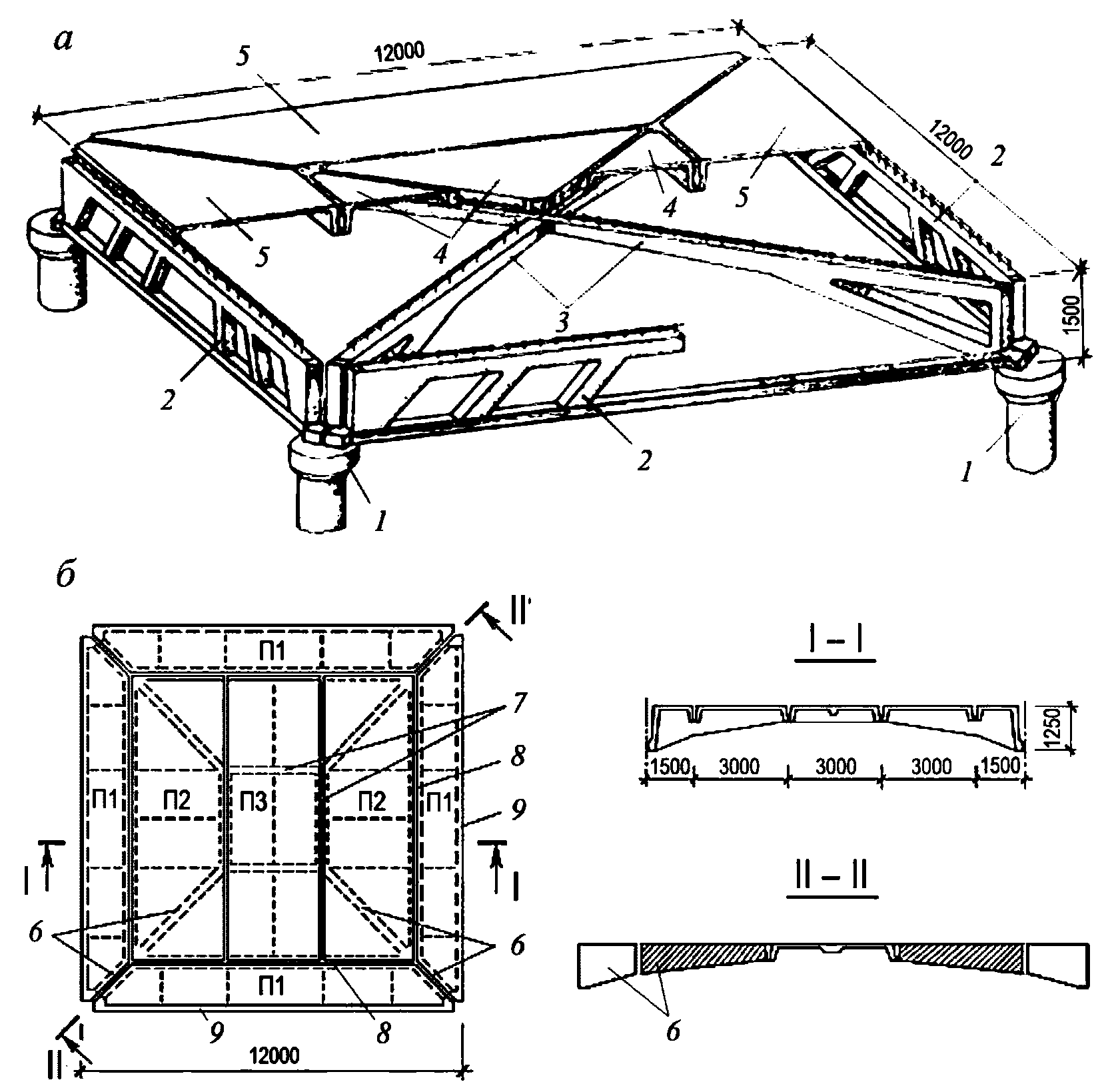
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
а - под нагрузки до 30 кН/м2; б - под нагрузки до 10 кН/м2;
1 - колонны с капителями; 2 - бортовые элементы;
3 - диагональные рамы; 4, 5 - плиты настила; 6 - диагональные
ребра плит (подкос рамы); 7 - контур среднего (центрального)
диска; 9 - внутренний (промежуточный) контур; 10 - внешний
(основной) контур
Пространственная работа конструкций шатрового типа определяется наличием усилий распора. Восприятие усилий распора конструктивно решается устройством замкнутого контура из бортовых элементов по периметру шатра, в которых размещается основная арматура (затяжка) шатра. Значение распора определяется уровнем действующих нагрузок и соотношением основных геометрических размеров конструкции, к которым относятся размеры плана шатра в осях контурных элементов, габариты среднего диска и высота стрелы подъема шатра.
Стрела подъема шатра - расстояние от уровня срединной поверхности среднего диска до уровня пояса затяжки шатра. Строительную высоту шатровых конструкций рекомендуется назначать в пределах 1/8 - 1/12 перекрываемого пролета [8].
5.9.2 Шатровые конструкции проектируют многопролетными и однопролетными (отдельно стоящими), с опиранием по углам на колонны, по нескольким сторонам или по контуру.
5.9.3 Рамно-шатровые конструкции покрытий и перекрытий в зависимости от уровня действующих нагрузок рекомендуется принимать размерами в плане от 6 x 6 м до 18 x 18 м.
Сборные шатровые конструкции, как правило, проектируют из ребристых плит (рисунок 5.9.2). Размеры плит в плане рекомендуется принимать не более 3,6 м по ширине и 12 м по длине. Стыки между сборными элементами шатровых конструкций следует выполнять в соответствии с 4.4.
В шатровых конструкциях могут быть предусмотрены проемы для пропуска коммуникаций, для световых и аэрационных фонарей, а также крепежные приспособления для восприятия сосредоточенных нагрузок от подвесного транспорта, коммуникаций и т.п., которые следует располагать, как правило, в узлах сопряжения ребер.
5.9.4 При проектировании сборных железобетонных элементов рамно-шатровых перекрытий следует использовать бетон классов не ниже B30. Замоноличивание швов между сборными элементами следует выполнять мелкозернистым бетоном класса не ниже класса бетона сборных элементов.
5.9.5 В рамно-шатровых конструкциях всю основную арматуру размещают в бортовом элементе, который при больших усилиях может быть выполнен, например, в виде фермы со сталежелезобетонным нижним поясом (рисунок 5.9.2, а). При устройстве дополнительного внутреннего контура (рисунок 5.9.2, б) площадь сечения основной арматуры шатра в его внешнем контуре допускается снижать в соответствии с расчетным распределением усилия распора между контурами.
5.9.6 При конструировании для предварительного назначения геометрических размеров большепролетных сборных железобетонных рамно-шатровых конструкций перекрытий с элементами шатровой рамы в виде ребер сборных плит (рисунок 5.9.2, б) следует принимать:
а) для рамно-шатровых конструкций при размерах менее 15 x 15 м стрелу подъема шатровой рамы в диапазоне 0,09 ... 0,12 пролета внешнего контурного элемента; при размерах 15 x 15 м и более 0,08 ... 0,11 пролета внешнего контурного элемента;
в) высоту ребер контура центрального диска в пределах 1/6 ... 1/8 размера стороны центрального диска;
д) изменение высоты сечения диагональной рамы рекомендуется принимать линейным от высоты центрального диска до высоты внешнего контура.
При нарушении рекомендуемых соотношений по перечислениям а) и б) рационально повышать несущую способность и жесткость конструкции выполнением в центральной части плана конструкции строительного подъема на величину расчетного прогиба конструкции от собственного веса при пониженном значении модуля деформаций бетона или применять предварительное напряжение нижней арматуры внешнего контура. В последнем случае рекомендуется использовать натяжение канатной арматуры, расположенной в створе колонн, на всю длину и ширину блока здания.
При разработке рамно-шатровых перекрытий для прямоугольных ячеек с соотношением сторон до 1:1,5 (например, 12 x 18 м), следует принимать рекомендуемые соотношения по перечислениям а) - г) по максимальному из размеров.
5.9.7 Рамно-шатровые конструкции для пролетов свыше 18 м следует выполнять монолитными или сборно-монолитными. При разработке конструктивных решений для пролетов более 18 м рекомендуется применение высокопрочной арматуры и предварительного напряжения в ребрах контуров.
5.9.8 Расчет шатровых конструкций выполняют по предельным состояниям как тонкостенной пространственной конструкции в соответствии с 4.2.
Расчеты напряженно-деформированного состояния шатровых конструкций следует выполнять методом конечных элементов с учетом возможного образования трещин и развития неупругих (нелинейных) деформаций в бетоне и арматуре, соответствующих кратковременному и длительному действиям нагрузки. Допускается расчеты выполнять в линейной постановке. При этом в гранях шатровой складки, в элементах шатровой рамы рамно-шатровой конструкции, а также в контурных элементах в первом приближении следует принимать модуль деформаций бетона с понижающим коэффициентом 0,3.
Временную равномерно распределенную нагрузку на большепролетных шатровых перекрытиях допускается учитывать с понижающим коэффициентом  в зависимости от площади конструктивной ячейки перекрытия в соответствии с 8.2.4 СП 20.13330.2016.
в зависимости от площади конструктивной ячейки перекрытия в соответствии с 8.2.4 СП 20.13330.2016.
Предварительные расчеты и расчет по несущей способности шатровых конструкций проводят методом предельного равновесия согласно 5.9.9 - 5.9.12.
- расчета шатра в целом для определения основной растянутой арматуры поясов и нормальных усилий в шарнирно соединяемых гранях складок или элементах диагональных рам;
- определения изгибающих моментов:
в диагональных рамах и контурных элементах с учетом горизонтального усилия распора шатра в опорных узлах;
в плитах настила при опирании их на несущие элементы конструкции.
5.9.10 При расчете отдельно стоящей шатровой конструкции методом предельного равновесия следует рассматривать наиболее опасные схемы излома конструкции.
В общем случае расчет несущей способности шатровых конструкций при действии равномерно распределенной нагрузки может быть выполнен кинематическим методом предельного равновесия с использованием девятидисковой схемы излома, включающей восьмиугольный центральный диск и четыре угловых и четыре пролетных диска, образованные исходящими из углов центрального диска линейными пластическими шарнирами (рисунок 5.9.3).

Несущую способность рамно-шатровой конструкции в зависимости от схемы нагружения и прочностных характеристик элементов конструкции в общем случае находят из условия равенства работ внешних и внутренних сил на виртуальном вертикальном перемещении центрального диска 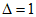 и устанавливают минимумом предельной нагрузки при варьировании трех независимых геометрических параметров Y1, Y2 и Y3 (рисунок 5.9.3), определяющих форму схемы излома (размеры сторон центрального диска, расстояние от угла шатра до ближайшего пластического шарнира на бортовом элементе).
и устанавливают минимумом предельной нагрузки при варьировании трех независимых геометрических параметров Y1, Y2 и Y3 (рисунок 5.9.3), определяющих форму схемы излома (размеры сторон центрального диска, расстояние от угла шатра до ближайшего пластического шарнира на бортовом элементе).
Работа внешней нагрузки Wext на виртуальном перемещении 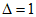 по вертикали центрального диска определяется формулой
по вертикали центрального диска определяется формулой
Wext = qV,
где V - объем эпюры виртуальных перемещений в случае действия нагрузки постоянной интенсивности по всей поверхности ячейки. В общем виде:

где
E = Y1/(Y2 + R); R = (L0 - Y3)/2.
Работа внутренних сил в линиях излома Wint может быть выражена работой предельных моментов на соответствующих углах взаимного поворота дисков в точках пересечения продольных осей ребер конструкции линиями излома. В зависимости от соотношения геометрических размеров конструкции и значений параметров схемы излома может быть рассмотрено 16 расчетных случаев (таблица 5.9.1), где в формулах участвуют следующие предельные моменты:
- M0 и M1 - соответственно во внешнем и внутреннем контурных элементах в точках пересечения их линиями излома (рисунок 5.9.4, а, б, в);
- M2 - в ребре по контуру среднего кессона ячейки в точках пересечения линиями излома (рисунок 5.9.4, а);
- M3 - в пролетном ребре ячейки на участке между внешним контуром и контуром среднего кессона ячейки в точке пересечения линией излома между угловым и пролетным дисками (рисунок 5.9.4, а, б);
- M4 - в том же ребре в точке пересечения линией излома между центральным и пролетным дисками (рисунок 5.9.4, в);
- M5 - в том же ребре в точке пересечения линией излома между центральным и угловым дисками (рисунок 5.9.4, б);
- M6 - в диагональном элементе в точке пересечения линией излома (рисунок 5.9.4, б, в).
Таблица 5.9.1
работы внутренних сил
Расчетный случай | Условия реализации расчетного случая | Расчетные формулы для вычисления Wint | |||
1-A | Y3 <= L2 | Y1 <= A | 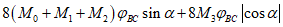 | ||
1-B | Y1 > A |  | |||
2-A1 | L2 < Y3 <= L1 | S0 > 0 | Y1 <= A |  | |
2-A2 | Y1 > A | 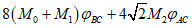 | |||
2-B1 | S0 <= 0 | Y1 <= A | Y2 > A | 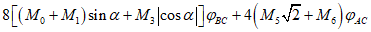 | |
2-B2 | Y2 <= A | 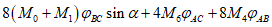 | |||
2-B3 | Y1 > A | Y2 > A | 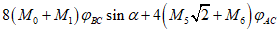 | ||
2-B4 | Y2 <= A | 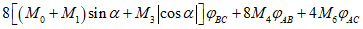 | |||
3-A1 | L1 < Y3 <= L0 | S > 0 | Y1 <= A | Y2 <= A |  |
3-A2 | Y2 > A |  | |||
3-A3 | Y1 > A | Y2 <= A |  | ||
3-A4 | Y2 > A | 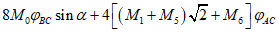 | |||
3-B1 | S <= 0 | Y1 <= A | Y2 <= A |  | |
3-B2 | Y2 > A |  | |||
3-B3 | Y1 > A | Y2 <= A | 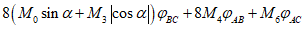 | ||
3-B4 | Y2 > A |  | |||
S = Y2 - (L0 + Y3 - 2L1)/2; S0 = Y2 - (L0 + Y3 - 2L2)/2; A = (L0 - L2)/2, 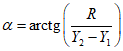 ; ;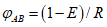 ; ;  ; ; 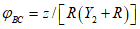 ; ; 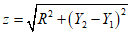 | |||||

вычисления работы внутренних сил
Работа поля плит учитывается тем, что при вычислении моментов M0 ... M6 форма поперечного сечения элементов принимается тавровой. При этом высота полки принимается равной толщине соответствующего поля, а ширина - половине пролета между соседними элементами одного направления. Приближенно моменты M0 ... M6 могут вычисляться как произведение предельного усилия в нижней арматуре RsAs на плечо внутренней пары, с достаточной для расчетов точностью принимаемое как 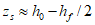 .
.
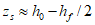 .
.Частными случаями общей девятизвенной схемы являются четырехдисковые балочная (рисунок 5.9.5, а) и конвертная (рисунок 5.9.5, б) схемы, а также пятидисковая шатровая схема (рисунок 5.9.5, в).
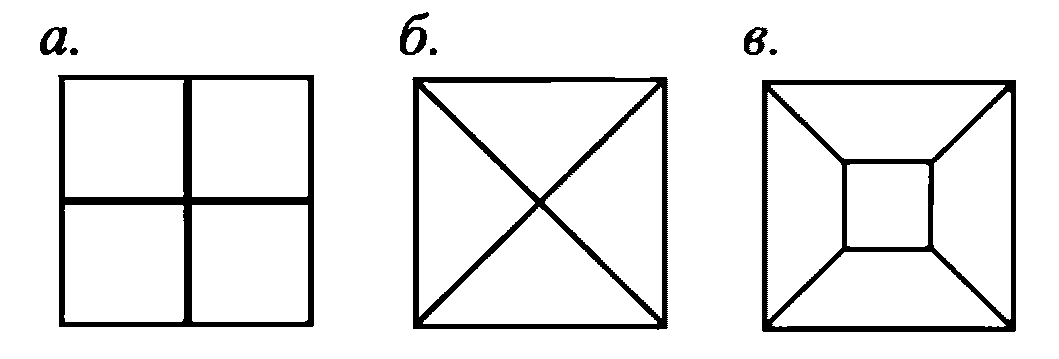
Тип схемы излома | Y1 | Y2 | Y3 |
Балочная | L0/2 | L0/2 | 0 |
Конвертная | 0 | L0/2 | 0 |
Шатровая | 0 | (L0 - Y3)/2 | 0 < Y3 < L0 |
девятизвенной схемы излома
Расчет по балочной схеме производится из условия
Расчет по конвертной схеме производится из условия
Расчет по шатровой схеме для частного случая Y3 = L2 производится из условия
5.9.11 При проектировании рамно-шатровых конструкций до выполнения детального расчета методом конечных элементов следует выполнить расчетную оценку несущей способности рамно-шатрового перекрытия методом предельного равновесия с использованием балочной по формуле (5.9.1) и конвертной по формуле (5.9.2) схем излома для установления требуемых по условию прочности усилий распора шатра соответственно в середине пролета внешнего контура и в его угловой зоне и предварительного подбора сечений соответственно арматурного пояса-затяжки и угловой связи внешнего контура.
5.9.12 В угловой зоне ребра смежных плит П1 (рисунок 5.9.2, б), образующие угол внешнего контура, должны быть соединены сваркой закладных деталей. Усилие в связях и сварных швах в направлении, перпендикулярном к диагонали ячейки,
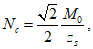
где M0 - предельный момент в угловой зоне внешнего контура из условия разрушения по конвертной схеме;
zs - расстояние по высоте сечения между уровнем усилия в угловой связи и срединной поверхностью полки плиты.
При расчете сборных шатровых конструкций методом предельного равновесия следует учитывать возможность реализации схем излома, включающих, наряду с линейными пластическими шарнирами, конструктивные шарниры по швам сопряжения сборных элементов. Если при таких схемах излома несущая способность конструкции оказывается ниже требуемой, допускается устанавливать учитываемые в расчете связи, препятствующие раскрытию конструктивных шарниров (стальные пластины, соединяющие закладные детали смежных сборных элементов и др.).
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
5.9.12 Угловые зоны шатровых конструкций в месте опирания на капители или колонны следует проверять на прочность при действии в них усилия
где V - вертикальная опорная реакция от нагрузки на шатре;
H - распор шатровой рамы в диагональном направлении от нагрузки на шатре;
Для квадратной в плане шатровой конструкции
 (5.9.6)
(5.9.6)В формулах (5.9.5) - (5.9.7):
q - полная расчетная нагрузка;
l0 - длина пролета внешнего контура шатра;
l1 - длина пролета внутреннего контура (при его наличии в рамно-шатровой конструкции);
l2 - длина пролета среднего диска;
f - стрела подъема шатровой складки или рамы.
При отсутствии внутреннего контура в рамно-шатровой конструкции и для шатровой складки формула (5.9.7) приобретает вид
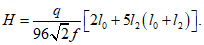 (5.9.8)
(5.9.8)На прочность проверяется сечение опорного подкоса или нижняя по высоте половина опорного сечения диагонального ребра. При этом в расчетном поперечном сечении учитывается продольная арматура.
Для повышения прочности опорного сечения шатра допускается применять косвенное армирование.
Пример 18
Задание: требуется запроектировать междуэтажное перекрытие торгового здания с сеткой колонн 12 x 12 м в виде сборных рамно-шатровых конструкций с опиранием по углам конструктивной ячейки здания на капители колонн. Высота этажа 4,8 м.
Геометрия рамно-шатровой конструкции
Принимаем конструкцию рамно-шатрового перекрытия на ячейку здания из семи сборных элементов в виде ребристых плит трех типоразмеров (рисунок 5.9.6).
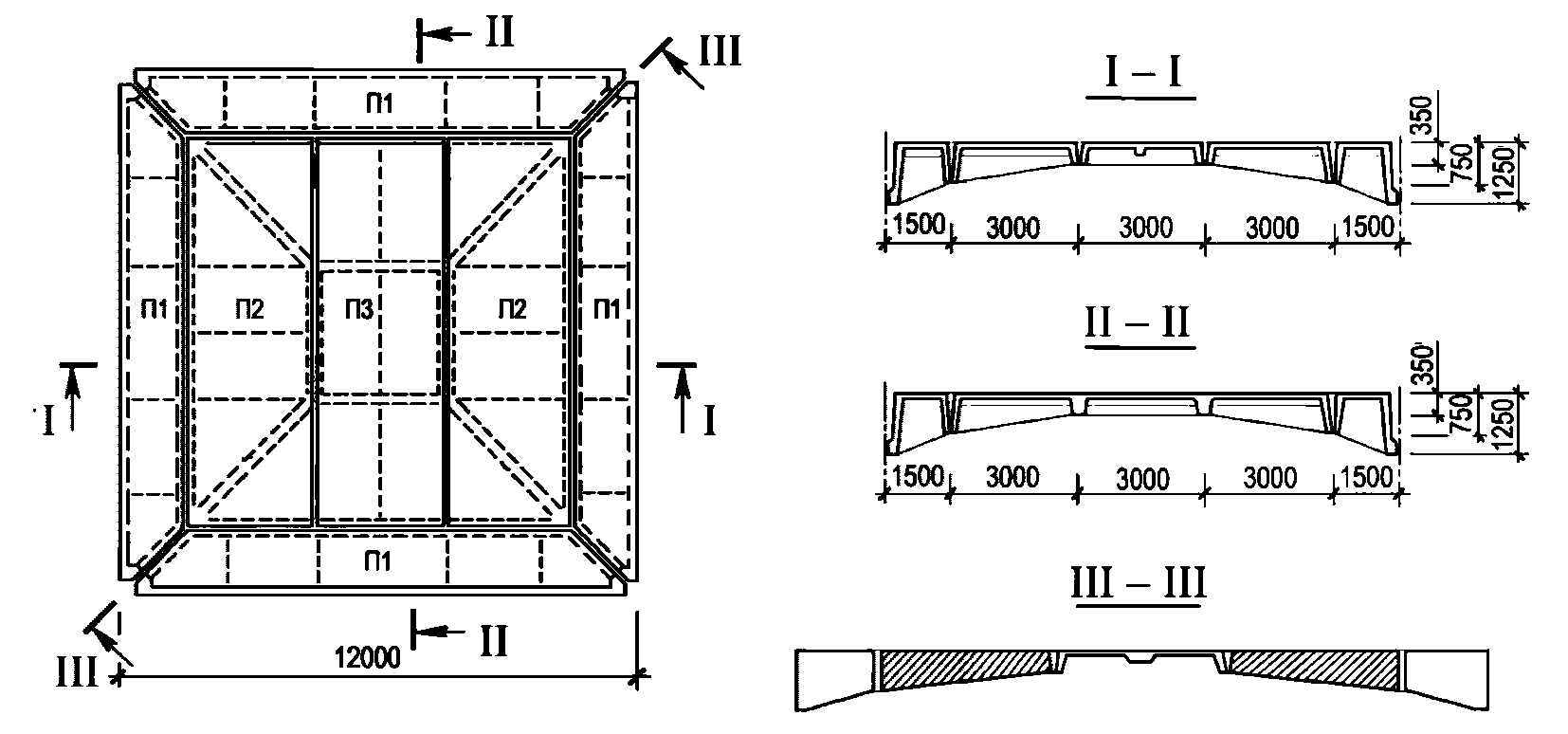
рамно-шатрового перекрытия
Шатровая рама образована диагональными рамами, контуром среднего диска, внешним и внутренним (промежуточным) контурами.
Расчетные пролеты контуров шатровой рамы: L0 = 11,84 м (внешний контур), L1 = 9,0 м (внутренний контур), L2 = 3,0 м (контур среднего диска).
С учетом 5.9.1 по выбору строительной высоты перекрытия при сетке колонн 12 x 12 м принимаем высоту плит П1 по периметру ячейки 1,25 м. При этом расчетная стрела подъема (расстояние по вертикали между срединной плоскостью поля плит и плоскостью действия распора во внешнем контуре в уровне затяжки) составляет f = h0 - hf/2 = 1,185 м, где hf - толщина поля плит (30 мм).
Поперечное сечение ребер жесткости, подкрепляющих поле плит, 0,1 x 0,17(h) м. Ребра жесткости, располагающиеся на линиях продолжения ребер контура среднего диска, выполняются усиленными: в плитах П2 0,24 x 0,32(h) м - равными по размерам сечению контура среднего диска; в плитах П1 0,18 x 0,72(h) м. Сопряженные контурные ребра плит П2 и П3 после замоноличивания шва образуют сечение 0,24 x 0,32(h) м. Сопряженные контурные ребра плит П1 и П2 после замоноличивания шва образуют сечение внутреннего контура 0,26 x 0,72(h) м. Сечение внешнего контура с учетом половины ширины шва замоноличивания между плитами П1 смежных ячеек 0,22 x 1,22(h) м. Диагональные ребра в пределах плит П2 имеют переменное сечение от 0,22 x 0,32(h) м у углов центрального диска до 0,26 x 0,72(h) м у углов внутреннего контура. Диагональные ребра, образованные сопряженными ребрами плит П1, имеют переменные размеры сечения от 0,28 x 0,72(h) м у углов внутреннего контура до 0,30 x 1,22(h) м вблизи колонн. В приведенных выше данных о размерах сечений указаны: высота - без учета толщины поля плит; ширина - средняя по высоте ребра.
Сбор нагрузок на конструкцию приведен в таблице 5.9.2.
Вид нагрузки | Нормативная, кН/м2 | Расчетная, кН/м2 | ||
Собственный вес железобетонных конструкций и бетона замоноличивания швов | 5,46 | 1,1 | 6,01 | |
- то же, в пределах центральной части 10,5 x 10,5 м | 4,30 | 4,73 | ||
Вес пола | 0,80 | 1,3 | 1,04 | |
Вес перегородок | 1,00 | 1,1 | 1,10 | |
Временная нагрузка для расчета элементов | 4,00 | 1,2 | 4,80 | |
- длительная часть временной нагрузки | 1,40 | 1,68 | ||
Временная нагрузка 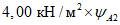 <*> <*> | 3,00 | 1,2 | 3,60 | |
- длительная часть временной нагрузки 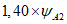 | 1,05 | 1,26 | ||
Итого | - для расчета элементов перекрытия: | |||
Длительно действующая нагрузка | 8,66 | 9,83 | ||
Полная нагрузка | 11,26 | 12,95 | ||
- для расчета ячейки перекрытия в целом <*>: | ||||
Длительно действующая нагрузка | 8,31 | 9,41 | ||
Полная нагрузка | 10,26 | 11,75 | ||
<*> В расчетах ячейки перекрытия в целом при грузовой площади 144,0 м2 временная нагрузка учитывается с понижающим коэффициентом  | ||||
Плиты проектируются из тяжелого бетона класса B30. Бетон замоноличивания швов класса B30. В качестве основной арматуры шатровой рамы используется стержневая арматура класса А500. Для сварных каркасов и сеток применяются стержневая арматура класса А500 и арматурная проволока класса Вр500.
Сборные элементы перекрытия соединяются между собой в узлах сопряжения смежных ребер сваркой закладных деталей через стальные накладки из стали класса С235.
Расчет поля плит и ребер жесткости
В случае равноармированной плиты при расположении сетки в срединной плоскости несущая способность прямоугольной плиты, защемленной по контуру в ребрах, может быть рассчитана методом предельного равновесия по формуле (при b/a < 3)
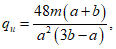
где m - предельный погонный изгибающий момент в линиях излома по конвертной схеме разрушения;
a = 1,33 м и b = 2,76 м - соответственно меньшая и большая стороны прямоугольника максимального по размерам кессона плиты. При армировании плиты сеткой из проволоки  с ячейкой 100/100 мм:
с ячейкой 100/100 мм:
 с ячейкой 100/100 мм:
с ячейкой 100/100 мм:
m = Rbbx(h0 - x/2) = 17000·1·0,00308·(0,015 - 0,00308/2) = 0,7048 кНм/м;
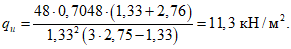
При расчетной нагрузке собственного веса плиты толщиной 30 мм 0,83 кН/м2 полная расчетная нагрузка на плиту составит 0,83 + 1,04 + 1,10 + 4,80 = 7,77 кН/м2 < qu.
Ребра жесткости в плитах П2 и П3 могут быть армированы плоским каркасом с продольной арматурой 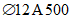 с As = 1,131 см2. При условии достаточности анкеровки верхней арматуры в опорных сечениях несущая способность ребра определяется по формуле
с As = 1,131 см2. При условии достаточности анкеровки верхней арматуры в опорных сечениях несущая способность ребра определяется по формуле
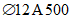 с As = 1,131 см2. При условии достаточности анкеровки верхней арматуры в опорных сечениях несущая способность ребра определяется по формуле
с As = 1,131 см2. При условии достаточности анкеровки верхней арматуры в опорных сечениях несущая способность ребра определяется по формуле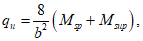
где Msp и Msup - предельные изгибающие моменты соответственно в середине пролета и в опорном сечении ребра. При вычислении Msp как для таврового сечения ширина полки принимается равной 0,10 + 12·0,03 = 0,46 м.
xsp = 435·1,131·10-4/(17,0·0,46) = 0,0063 м;
Msp = 435000·1,131·10-4(0,16 - 0,0063/2) = 7,72 кНм;
xsup = 435·1,131·10-4/(17,0·0,10) = 0,0289 м;
Msup = 435000·1,131·10-4(0,17 - 0,0289/2) = 7,65 кНм;
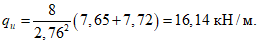
При расчетной нагрузке собственного веса ребра 1,1·25·0,1·0,17 = 0,47 кН/м и ширине грузовой площади ребра b/2 = 1,38 м полная расчетная нагрузка на плиту составляет 0,47 + 7,77·1,38 = 11,2 кН/м < qu.
Расчет несущей способности рамно-шатровой конструкции
Рассмотрим случай равномерно распределенной нагрузки по всей площади перекрытия.
Конструктивно задаемся армированием ребер в пределах внутреннего контура -  (As = 0,000982 м2). В моментах M1 и M2 плечи внутренних пар составят соответственно 0,71 - 0,03/2 = 0,695 м и 0,31 - 0,03/2 = 0,295 м.
(As = 0,000982 м2). В моментах M1 и M2 плечи внутренних пар составят соответственно 0,71 - 0,03/2 = 0,695 м и 0,31 - 0,03/2 = 0,295 м.
 (As = 0,000982 м2). В моментах M1 и M2 плечи внутренних пар составят соответственно 0,71 - 0,03/2 = 0,695 м и 0,31 - 0,03/2 = 0,295 м.
(As = 0,000982 м2). В моментах M1 и M2 плечи внутренних пар составят соответственно 0,71 - 0,03/2 = 0,695 м и 0,31 - 0,03/2 = 0,295 м.Тогда требуемый предельный момент M0 в средней части пролета внешнего контура из условия разрушения по балочной схеме по формуле (5.9.1) составит:
M0 = 11,75·11,842·(12 + 11,84)/32 - 435000·0,000982·(0,695 + 0,295) = 804,3 кНм.
Принимая плечо внутренней пары во внешнем контуре приближенно равным 1,195 - 0,03/2 = 1,18 м, получаем требуемую площадь арматуры класса А500:
As = 804,3/(435000·1,18) = 0,001567 м2.
Принимаем  (As = 0,001609 м2).
(As = 0,001609 м2).
 (As = 0,001609 м2).
(As = 0,001609 м2).Вблизи контура среднего диска в моменте M3 плечо внутренней пары 0,31 - 0,03/2 = 0,295 м.
Требуемый предельный момент M0 в угловой зоне внешнего контура из условия разрушения по конвертной схеме по формуле (5.9.2) составляет:
M0 = 11,75·11,843/24 - 435000·0,000982·(0,695 + 0,295 + 0,295) = 263,7 кНм.
Принимая плечо внутренней пары во внешнем контуре приближенно равным 1,195 - 0,03/2 = 1,18 м, получаем требуемую площадь арматуры класса А500:
As = 263,7/(435000·1,18) = 0,000514 м2.
Конструктивно принимаем  (As = 0,000804 м2).
(As = 0,000804 м2).
 (As = 0,000804 м2).
(As = 0,000804 м2).В угловой зоне ребра смежных плит П1, образующие угол внешнего контура, должны быть соединены сваркой закладных деталей. Усилие в связях и сварных швах в направлении перпендикулярно диагонали ячейки может быть рассчитано как
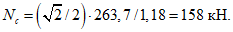
Проверяем несущую способность конструкции по шатровой схеме при принятом армировании. При этом плечо внутренней пары в моментах M4 и M6 вблизи контура среднего диска может быть принято 0,31 - 0,03/2 = 0,295 м. Тогда по формуле (5.9.3) получаем:
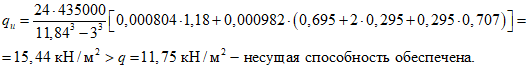
Угловые зоны рамно-шатровых конструкций в месте опирания на капители колонн проверяем по формуле (5.9.4).
Нагрузка на шатре принимается с учетом собственного веса конструкций в пределах центральной части ячейки размерами 10,5 x 10,5 м:
q = 4,73 + 1,04+ 1,10 + 4,80 = 11,67 кН/м2.
Для квадратной в плане конструкции по формулам (5.9.5) - (5.9.7):

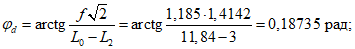
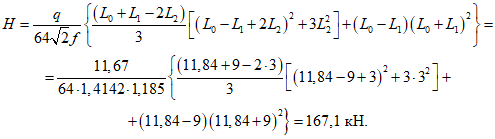
N = 316,7·0,1863 + 167,1·0,9825 = 223,2 кН.
На прочность проверяется нижняя по высоте половина опорного сечения диагонального ребра: 0,3 x 0,6(h) м. При этом в расчетном поперечном сечении учитывается продольная арматура. Несущая способность расчетного сечения на сжатие при установке в нижней зоне диагонального ребра рабочей арматуры  :
:
 :
:Nu = 17000·0,3·0,6 + 435000·0,000982 = 3193 кН > N - прочность обеспечена.
Расчет несущей способности сборных рамно-шатровых перекрытий с учетом конструктивных особенностей
При расчете сборных шатровых конструкций методом предельного равновесия следует учитывать возможность реализации схем излома, включающих, наряду с линейными пластическими шарнирами, конструктивные шарниры по швам сопряжения сборных элементов. Если в этих схемах несущая способность конструкции оказывается ниже требуемой, повысить несущую способность можно установкой и учетом в расчете связей, препятствующих раскрытию конструктивных шарниров (например, стальных пластин, соединяющих закладные детали смежных сборных элементов).
Одна из возможных схем разрушения конструкции - расположение линий излома в швах по периметру внутреннего контура и в диагональных швах между плитами П1 (рисунок 5.9.7).

1, 2 и 3 - связи, работа которых учитывается
предельными моментами - соответственно Mc, Md и Mt
линии излома в швах по периметру внутреннего контура
и между контурными плитами
В этом случае взаимному повороту дисков препятствуют три вида связей, наличие которых может быть учтено следующими предельными моментами: Mc - по угловой связи; Md - по накладкам, соединяющим диагональные ребра плит в продольном направлении; Mt - по накладкам, соединяющим продольные ребра плит в пролете внутреннего контура.
Величина предельной нагрузки определяется по формуле
Требуемое сечение угловой связи может быть определено по полученной выше величине усилия Nc = 158 кН. Для пластины толщиной 10 мм из стали класса С235 требуемая ширина сечения: 158/(0,95·230000·0,01) = 0,072 м. Конструктивно принимаем пластину сечением 10 x 100 мм. Указанная связь - часть арматурного контура, располагается в уровне основной арматуры шатровой рамы. Условно считая плечо внутренней пары в сечении по связи равным плечу внутренней пары внешнего контура вблизи угла 1,18 м, получаем:
Mc = 0,95·230000·0,01·0,1·1,18 = 257,8 кНм.
Накладная пластина связи 2 располагается в уровне нижней поверхности ребра внутреннего контура. Ее прочность должна соответствовать прочности рабочей арматуры диагонального ребра. Для пластины толщиной 10 мм из стали класса С235 требуемая ширина сечения: (435·0,000982)/(0,95·230·0,01) = 0,196 м. Конструктивно принимаем пластину сечением 10 x 220 мм. Находим предельный момент по этой связи:
Md = 0,95·230000·0,01·0,22·0,72 = 346,1 кНм.
Накладная пластина связи 3 также располагается в уровне нижней поверхности ребра внутреннего контура. Конструктивно принимаем пластину сечением 10 x 70 мм из стали класса С235. Находим предельный момент по этой связи:
Mt = 0,95·230000·0,01·0,07·0,72 = 110,1 кНм.
По формуле (5.9.9) находим:
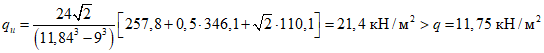 - несущая способность обеспечена.
- несущая способность обеспечена.Специального рассмотрения требует случай, когда разрушение конструкции происходит по линии шва между плитами средней зоны перекрытия с пересечением линией излома плит П1 в поперечном направлении в средней части их пролета (рисунок 5.9.8).
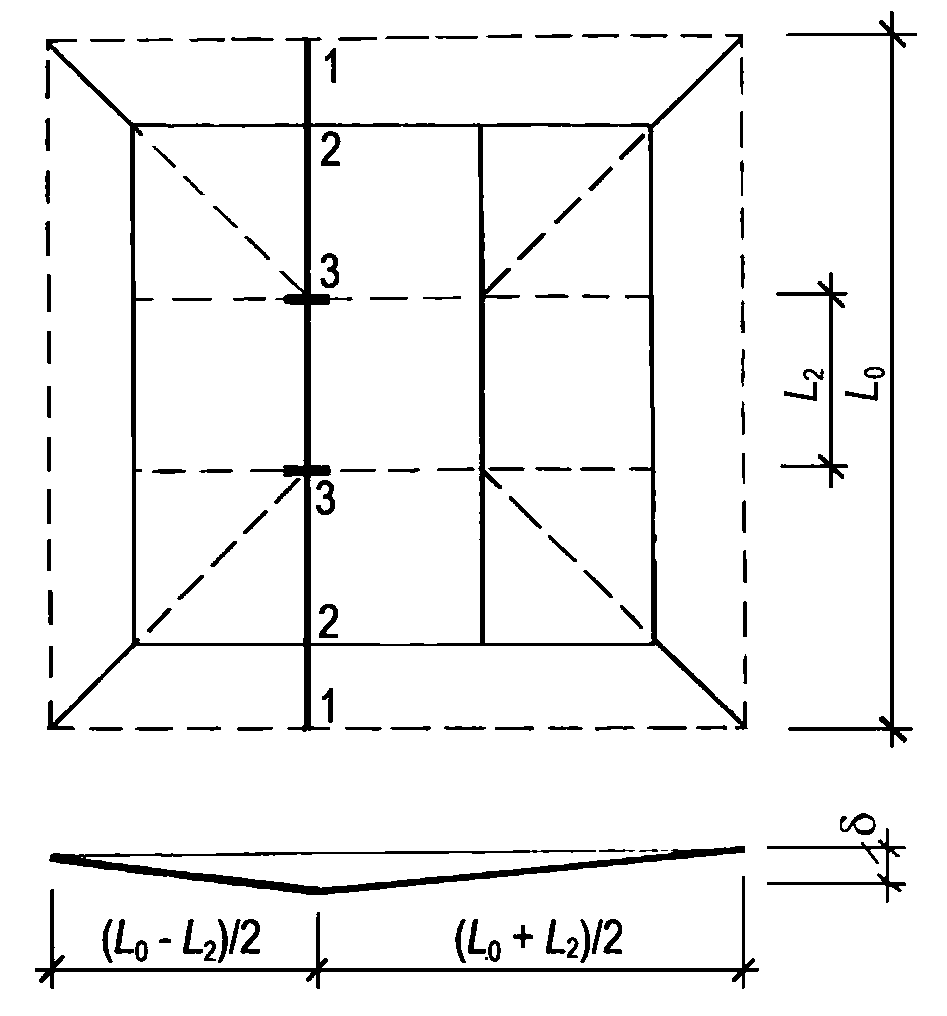
1, 2 и 3 - связи, работа которых учитывается
предельными моментами - соответственно M0, M1 и Ms
линии излома в шве между плитами средней зоны перекрытия
В этом случае взаимному повороту двух дисков препятствует прочность сечений внешнего и внутреннего контуров в точках пересечения их линией излома (соответственно, M0 = 435000·0,001609·1,18 = 825,9 кНм и M1 = 435000·0,000982·0,695 = 296,9 кНм), а такие предельные моменты Ms - по накладкам, соединяющим плиты средней зоны в углах среднего диска. Значение предельной нагрузки для этого случая можно определить по формуле
Накладная пластина связи 3 также располагается в уровне нижней поверхности ребра контура среднего диска. Подберем ее ширину из условия равнопрочности стыка и ребра контура среднего диска:
Ms = M2 = 435000·0,000982·0,295 = 126,0 кНм;
bp = 126,0/(0,95·230000·0,01·0,33) = 0,175 м.
Конструктивно принимаем пластину сечением 10 x 180 мм из стали класса С235. Находим предельный момент по этой связи:
Ms = 0,95·230000·0,01·0,18·0,33 = 129,8 кНм.
По формуле (5.9.10) находим:
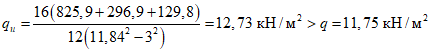 - несущая способность обеспечена.
- несущая способность обеспечена.Строительные нормы для обоснования проектных и конструктивных решений наряду с результатами расчета по предельным состояниям сооружений в целом, их конструктивных элементов и соединений допускают использование данных экспериментальных исследований, в результате которых устанавливают основные параметры строительных объектов, их несущую способность и воспринимаемые ими воздействия (пункт 3.6 ГОСТ 27751-2014). Для зданий и сооружений повышенного уровня ответственности класса КС-3, к числу которых нередко относят большепролетные пространственные конструкции, при проектировании которых использованы не апробированные ранее конструктивные решения или для которых не существует надежных методов расчета, необходимо использовать данные экспериментальных исследований на моделях или натурных конструкциях (пункт 3.7 ГОСТ 27751-2014).
Метод моделирования - эффективное средство исследования железобетонных пространственных конструкций. Проведение расчета таких конструкций с учетом всех их особенностей (сложных граничных условий, наличия ребер, опасности местной потери устойчивости тонкой плиты и т.д.) во многих случаях встречает серьезные затруднения. Метод моделирования позволяет провести качественное и количественное исследование напряженно-деформированного состояния конструкции; оценить достоверность методов ее расчета, распространить результаты единичных опытов на целый класс подобных конструкций.
Разработка многих новых конструкций и решение теоретических вопросов без использования моделирования были бы невозможны, а испытания моделей при исследовании конструкций и сооружений взамен натурных испытаний позволили сэкономить значительные средства.
Исследования железобетонных пространственных конструкций типа оболочек и складок наиболее целесообразно проводить на моделях, изготовленных из армированного мелкозернистого бетона. Как показывает опыт, такие модели, разработанные и изготовленные как подобные прототипу малоразмерные конструкции, обладают прочностными, упругопластическими и конструктивными свойствами, близкими к натурным железобетонным конструкциям. Это позволяет оценить не только работу конструкции в упругой стадии, но и поведение ее после образования трещин вплоть до разрушения. В то же время благодаря небольшим размерам моделей их можно изготовлять и испытывать сериями, что важно для увеличения надежности получаемых экспериментальных данных.
В настоящем разделе обобщен опыт в области исследований железобетонных пространственных конструкций на моделях из армированного бетона [9, 10].
Общий метод моделирования базируется на теории подобия [11, 12]. Два явления называются подобными, если они имеют одинаковую физическую природу и если характеристики одного из них отличаются от характеристик другого только масштабом, одинаковым для всех одноименных характеристик. Одноименными характеристиками называются характеристики с одинаковой размерностью.
При моделировании с применением теорем подобия [11] необходимо знать уравнения, описывающие изучаемое явление в натуре. Например, если изучается работа пространственных конструкций в упругой стадии, можно использовать полную систему дифференциальных уравнений, описывающих их напряженно-деформированное состояние, и соответствующие граничные условия. Применяя указанные теоремы к уравнениям, можно установить соотношения между масштабами различных величин, используемых при моделировании. Затем выбираются значения масштабов, удовлетворяющих найденным соотношениям. При этом необходимо проверять, что изменение масштаба модели не ведет к изменению физической природы протекающего процесса, т.е. не проявляется масштабный эффект.
При моделировании сложных пространственных систем часто невозможно записать уравнения их напряженно-деформированного состояния. В этом случае существенную помощь может оказать теория размерностей [12]. Она позволяет найти рациональные формы построения зависимости между величинами, характеризующими изучаемое явление.
При моделировании строительных конструкций для одноименных характеристик, как правило, выбирается одинаковый масштаб. Такой подход существенно ограничивает применение малых моделей для изучения работы тонкостенных конструкций: их толщина оказывается малой и на практике трудно осуществима. Для преодоления этих трудностей может быть применено аффинное подобие [13], допускающее применение разных масштабов одноименных характеристик.
При моделировании железобетонных пространственных конструкций чаще всего используется простое и расширенное механические подобия [13]. При простом механическом подобии в модели воспроизводятся те же деформации, что и в натурной конструкции. При расширенном механическом подобии деформации модели пропорциональны деформациям натурного образца. В обоих случаях модель должна быть геометрически подобна натуре. Если масштаб модели равен m, то приложенные к модели равномерно распределенные по площади нагрузки остаются такими же, как в натуре; интенсивность распределенной линейной нагрузки меняется в m раз; сосредоточенной силы - в m2 раз.
Вид выбираемых для исследования моделей, их размеры и используемые материалы определяются поставленными целями испытаний железобетонных пространственных конструкций.
ГОСТ 27751-2014 (пункт 11.6) устанавливает, что в случаях, когда при проектировании требуется использование данных экспериментальных исследований реальных строительных конструкций или моделей строительных объектов, подготовку и проведение подобных испытаний, а также оценку полученных результатов следует осуществлять так, чтобы условия эксперимента были подобны условиям работы проектируемой конструкции (во время ее эксплуатации и возведения). При этом условия, которые не моделируются в процессе проведения эксперимента (например, долговременные характеристики), необходимо учитывать при проектировании на основе анализа полученных результатов и, при необходимости, за счет использования коэффициентов надежности.
Исследованиями железобетонных пространственных конструкций на моделях можно решать следующие задачи: контролировать прочность, жесткость и трещиностойкость конструкции; выявлять картину напряженно-деформированного состояния в упругой стадии и после появления трещин; выявлять схему разрушения и оценить несущую способность; проверять особенности технологии монтажа сборных конструкций.
Для получения надежных экспериментальных данных модель должна проектироваться так, чтобы в ней отображались основные конструктивные особенности и особенности возведения натурного образца. В частности, если моделируется сборная конструкция, то и модель в большинстве случаев должна проектироваться сборной. Примером изучения сложной сборной конструкции может служить исследование [14]. В модели фрагмента свода из трех панелей-оболочек КЖС размерами 3 x 18 м (рисунок 6.1) масштабом 1:15 натуральной величины, собранной из 18 моделей панелей-оболочек размерами 200 x 1200 мм, были детально воспроизведены особенности конструктивного решения сводчатой системы, включающего шарнирные узловые соединения сборных элементов и пространственную систему стальных связей свода.

6.2.2 Моделирование узлов конструкций
При моделировании конструкции в целом часто не удается изучить достаточно подробно работу отдельных ее узлов. Это вызвано трудностями, возникающими при моделировании сопряжений элементов. В таких случаях оказывается целесообразным изготовлять узел в натуральную величину и испытывать его, имитируя силовые воздействия на узел, полученные по результатам изучения напряженно-деформированного состояния в предшествующих испытаниях модели в целом или ее расчета.
Для оценки применяемых при проектировании пространственных конструкций методов расчета целесообразно изготовлять модели, которые не являются точной копией какой-либо конструкции. Сохраняется только подобие применяемым конструкциям в целом - форма оболочек, тип контурных элементов, соотношение размеров в плане, отношение стрелы подъема к пролету, характер армирования и т.д. Модели такого типа проектируются так, чтобы они по возможности ближе соответствовали расчетной схеме и в то же время отражали специфические особенности, присущие данному классу конструкций. С помощью моделей рассматриваемого типа можно решать следующие задачи:
- проверять и уточнять методы расчета конструкций в упругой стадии;
- выявлять особенности работы после появления трещин;
- выявлять схему разрушения и проверять расчеты, оценивающие несущую способность конструкции.
6.2.4 Применение моделей для исследования схем излома оболочек при разрушении
Для оценки несущей способности пространственных конструкций широко используется метод предельного равновесия. Его применение требует знания схемы излома. Пространственные конструкции представляют собой сложные многократно статически неопределимые системы, поэтому определение схем излома расчетным путем связано с большими трудностями. Выявление схем излома с помощью опытов на моделях помогает значительно упрощать задачу: снижается степень статической неопределимости конструкции; упрощаются условия записи предельного равновесия; оказывается возможным более точно учесть реологические свойства материала, граничные условия, вид нагрузки и т.п. При проектировании конструкций могут быть использованы типы моделей, описанные в 6.2.1 и 6.2.3.
Цели исследований влияют на размеры испытываемых моделей. Модели реальных конструкций обычно выполняют в масштабе 1/25 - 1/4 натуральной величины. Моделирование узлов конструкций следует стремиться выполнять в натуральную величину. Если же решено узлы уменьшить, их масштаб должен приниматься не менее 1/2. Кроме того, на размер моделей влияют следующие факторы:
- условия передачи нагрузки;
- удобство установки приборов на верхней и нижней поверхностях модели;
- удобство испытания - доступ к приборам, проходы между тяжами нагрузочной системы и т.д.;
- условия изготовления - толщина моделей из бетона не может быть меньше 4 мм;
- наличие испытательного оборудования, помещения и т.д.
Размеры моделей, не являющихся точной копией какой-либо конструкции, назначают с учетом приведенных выше факторов.
Ниже рассматриваются условия подбора модельного материала, при которых выполняются условия простого подобия. Модель должна быть геометрически подобна натурной конструкции.
6.3.1 Критерии подобия
Критерии подобия материалов модели и натуры устанавливают по трем диаграммам (рисунок 6.2), характеризующим процессы деформирования бетона при сжатии и растяжении.
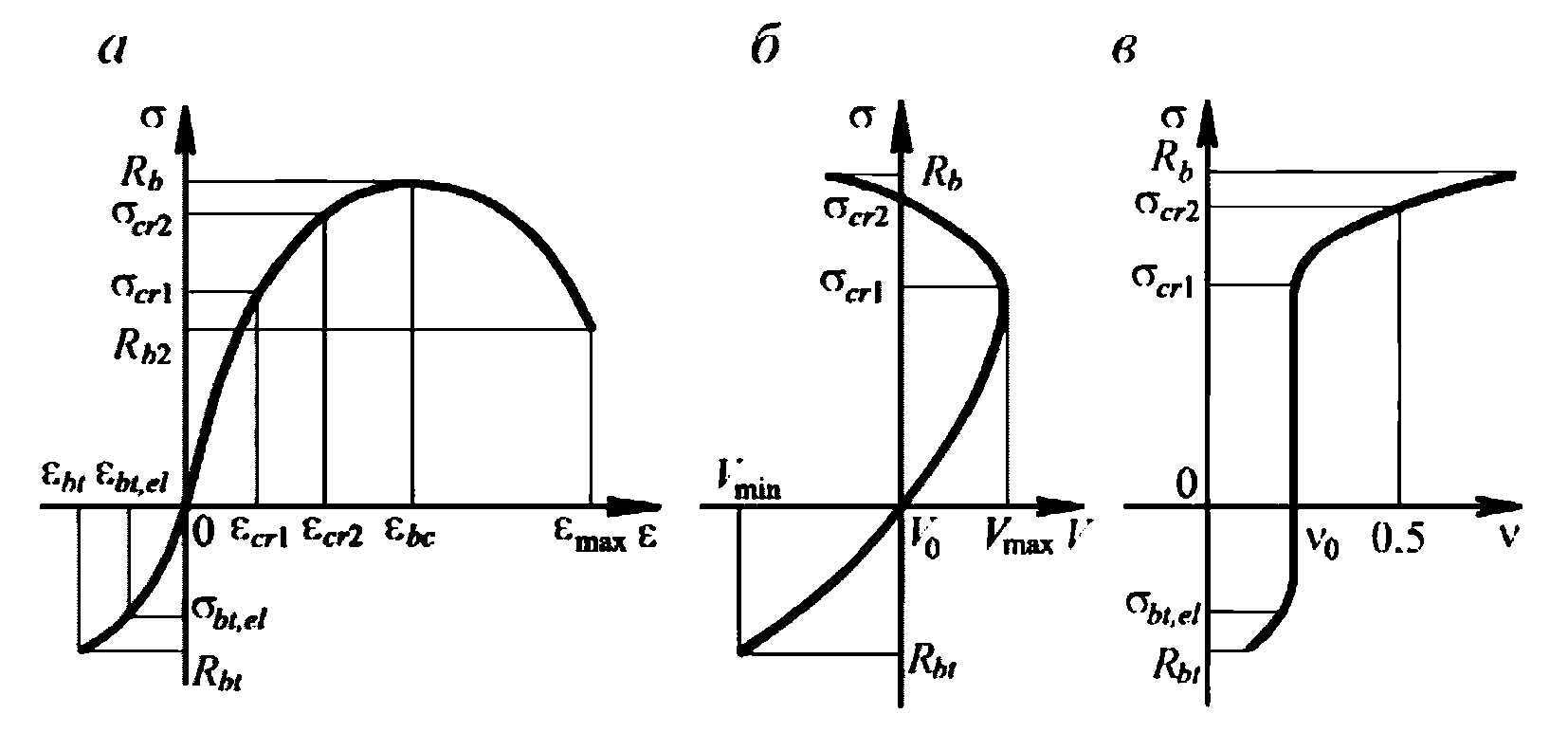
а - диаграмма "напряжение-деформация"  ; б - то же,
; б - то же,
 ; б - то же,
; б - то же,"напряжение-скорость прохождения ультразвука"; в - то же,
"напряжение-изменение коэффициента поперечной деформации"
бетона при нагружении
На диаграммах отмечены характерные точки, называемые параметрическими. Точки характеризуются величиной напряжений, общей для всех трех диаграмм. Таких точек шесть:
Rb - точка максимальных напряжений;
Rb2 - момент окончательного разрушения бетона;
Rbt - момент разрушения бетона от растяжения.
На диаграмме 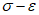 указанным точкам соответствуют деформации
указанным точкам соответствуют деформации 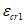 ,
,  ,
, 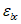 ,
,  ,
,  ,
,  . Некоторые характерные значения V и
. Некоторые характерные значения V и  отмечены соответственно на диаграммах
отмечены соответственно на диаграммах 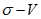 ,
, 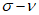 .
.
Для удобства представим диаграмму  в относительных координатах:
в относительных координатах:
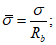
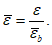
Полное подобие материалов модели и натуры будет обеспечено, если для обоих материалов значения величин  ,
,  ,
,  ,
, 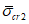 ,
, 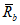 ,
,  ,
, 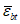 ,
, 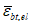 ,
, 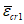 ,
, 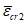 ,
, 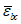 ,
, 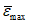 ,
, 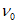 равны. Эти условия представляют собой полную систему критериев подобия бетонов в механическом смысле.
равны. Эти условия представляют собой полную систему критериев подобия бетонов в механическом смысле.
Подобрать модельный материал, для которого выполняются условия полной системы критериев подобия, сложно. В зависимости от конкретных задач механического моделирования из системы критериев подобия могут быть получены неполные, обеспечивающие подобие только в отдельных зонах диаграммы  . Для наиболее характерных задач должны быть равны следующие величины:
. Для наиболее характерных задач должны быть равны следующие величины:
6.3.2 Подбор модельного материала
Система критериев подобия выбирается в зависимости от задач исследования. Значения величин, входящих в критерии подобия, для материала натуры считаются известными. Они могут быть определены по результатам испытаний образцов из бетона натурной конструкции. Задача состоит в выборе материала модели так, чтобы для него выполнялись условия подобия.
В качестве основы модельного материала рекомендуется использовать мелкозернистый бетон, состоящий из смеси цемента, песка, щебня и воды. Применяя различные добавки, можно в довольно широких пределах изменять физико-механические характеристики материала. Данные о направлении изменения физико-механических характеристик материалов от различных добавок приведены в таблице 6.1. Сократить число опытов при подборе материала с нужными свойствами можно, используя методы теории планирования экспериментов [15].
Таблица 6.1
мелкозернистого бетона в зависимости от различных добавок
Вид добавки | Физико-механические характеристики | |||||||
Rb | Rbt | |||||||
Мел молотый | - | - | - | + | + | - | - | - |
Перлитовый песок | - | - | - | - | + | - | - | + |
Графит молотый | - | - | - | - | - | - | + | - |
Щебень, обработанный нитрокраской | - | - | - | - | + | + | + | + |
ПВА с 5%-ной добавкой дибутилфталата | - | - | - | + | + | + | + | + |
Обозначения: знак "+" показывает увеличение, а знак "-" - уменьшение характеристик при введении различных добавок. | ||||||||
Для армирования моделей применяют: стальные тканые и сварные сетки; холоднотянутую проволоку; стержневую арматуру, гладкую и периодического профиля. Количество стержней арматуры и характер армирования в целом сохраняется таким же, как в натурной конструкции. Площадь арматуры подбирается из условий геометрического подобия по прочности.
В случаях исследования исключительно упругой стадии работы конструкции применяют модели из упругих материалов, в частности, из пластмасс.
6.3.3 Контроль механических характеристик материалов
Для определения характеристик бетона моделей тонкостенных конструкций рекомендуется испытывать тонкостенные образцы. Эти образцы по сравнению со сплошными призмами лучше отражают особенности технологии формования тонкостенных конструкций.
В качестве тонкостенного образца рекомендуется использовать полую призму (рисунок 6.3). Призму склеивают эпоксидным клеем из плиток толщиной 10 мм. Торцы ее замоноличивают в металлические оголовники, контролируя ортогональность образца поверхностям оголовников. Из испытания полых призм непосредственно получают Rb, а также модуль деформации, коэффициент поперечного расширения, характеристики ползучести и усадки бетона. При вычислении Rb используют среднее значение фактических толщин пластин по результатам их обмера в испытанном образце.

1 - металлический оголовник; 2 - бетонные пластины;
3 - эпоксидный клей
Для определения характеристик арматуры образцы ее испытывают на разрыв по общепринятой методике.
Для изготовления моделей конструкций используются формы из различных материалов - деревянные, бетонные, стальные, гипсовые, пластмассовые. Выбор материала и конструкций форм определяется удобством их изготовления и количеством изготовляемых моделей. Если предусмотрено изготовление одной-двух моделей, рекомендуется применять деревянные опалубки из брусьев или фанеры. При большом количестве моделей и при использовании термообработки применение деревянных форм не рекомендуется.
Модели оболочек и складок имеют малые размеры сечений элементов. Поэтому к точности изготовления опалубки предъявляются повышенные требования. Контроль осуществляется с помощью шаблонов и нивелирования, отклонения по толщине плиты модели не должны превышать +/- 0,5 мм; кривизна модели должна быть выдержана с точностью +/- 5%. Опалубку необходимо проектировать достаточно жесткой, чтобы при транспортировании и изготовлении в ней не возникало деформаций, искажающих форму изделий. Опалубку рекомендуется выполнять сборно-разборной, чтобы избежать повреждений модели при распалубке.
После изготовления деревянных моделей их поверхность рекомендуется шпаклевать и прокрашивать нитрокраской. При назначении размеров опалубки следует учитывать толщину слоя шпаклевки и краски. Изготовлять бетонные и особенно гипсовые формы следует с учетом процессов усадки и расширения этих материалов при высыхании и увлажнении. Их поверхность рекомендуется окрашивать масляными и полимерными составами. На рабочих поверхностях стальных форм не должно быть следов ржавчины, механических повреждений и тому подобных дефектов. Чтобы исключить сцепление бетона с опалубкой, поверхности форм перед изготовлением в них моделей покрывают слоем смазки (например, разогретой смесью парафина с солидолом или веретенным маслом, смешанным с цементом).
Арматура контурных элементов и ребер выполняется в виде вязаных и сварных каркасов. Каркасы могут изготовляться в деревянных шаблонах. Для армирования полок могут быть использованы заводские плоские сварные или тканые сетки. Если поверхности моделей неразвертывающиеся, сетки для армирования вяжут непосредственно на опалубке. Отдельные проволоки сетки скрепляют между собой вязальной проволокой в местах пересечения (через одну-две ячейки) и привязывают их концы к арматуре контурных элементов.
Защитный слой в ребрах и диафрагмах обеспечивается установкой коротышей арматуры, бетонных или пластмассовых подкладок. В плите под сетку можно укладывать монтажные арматурные стержни, которые удаляют после бетонирования. Для устранения пустот бетон дополнительно уплотняют. Напрягаемую арматуру контурных элементов натягивают на испытательные стенды или на специальные рамы. Усилия натяжения контролируют по манометру на домкрате или механическим динамометром, а также измерением деформаций арматуры тензометрами, индикаторами или тензодатчиками.
Бетон в контурных элементах и ребрах уплотняют глубинными вибраторами сверху и через опалубку снизу и сбоку. Бетон плиты уплотняют виброрейками или площадочными вибраторами. Направляющими виброреек служат стальные полосы или деревянные бруски, крепящиеся к опалубке. После бетонирования полосы и бруски удаляют; оставшиеся углубления затирают бетоном. Толщину моделей при бетонировании контролируют с помощью маяков, крепящихся к опалубке, и шаблонов. Бетонная смесь приготовляется на портландцементе (желательно безусадочном) и должна обладать достаточной удобоукладываемостью.
Бетон моделей может подвергаться термовлажностной обработке либо твердеть в естественных условиях. Бетон естественного твердения через 10 - 12 ч после укладки покрывают слоем опилок и полиэтиленовой пленкой и увлажняют в течение 5 - 28 дней. Это помогает устранить появление усадочных трещин. Распалубку и отпуск натяжения арматуры производят после достижения бетоном необходимой прочности, контролируемой по образцам и неразрушающими методами.
Модели испытывают на стендах. Стенды должны проектироваться так, чтобы на них было удобно производить нагружение модели, монтировать нагрузочную систему и контролировать ее работу, размещать вспомогательные устройства, иметь доступ ко всем элементам модели и приборам, крепить приборы для измерения горизонтальных перемещений модели. Стенды должны обеспечивать безопасность проведения испытаний.
Стенды представляют собой пространственные рамы. Модели опираются на стойки рам, ригели служат для упора нагрузочной системы. На стендах могут укрепляться ходы и подмости. Элементы стенда проектируют стальными или монолитными железобетонными. При размерах модели более 2,5 - 3 м по высоте стенд, как правило, делится на три зоны: внизу размещают нагрузочные устройства (платформы, рычаги, домкраты); над ними устраивают страховочные устройства и сплошной настил для наблюдения за моделью и приборами снизу; на уровне контурных элементов устраивают настил для наблюдения за приборами сверху. Настилы по периметру ограждают перилами. Для безопасности персонала, ведущего испытание, и исключения влияния дополнительной нагрузки хождение по модели при испытании не допускается.
Модели опираются на стенды через шары и катки. Это обеспечивает им свободное перемещение и поворот на опорах. Передача нагрузки с модели на шар или каток осуществляется через металлическую пластину.
Равномерно распределенные и полосовые нагрузки по поверхности моделей рекомендуется заменять системой часто расположенных сосредоточенных сил. Это позволяет устанавливать приборы и наблюдать за появлением и развитием трещин сверху моделей. При назначении расстояния между точками приложения нагрузки учитывается возможность размещения приборов и толщина модели. Это расстояние обычно не должно превышать 25 толщин плиты модели и согласовываться с расположением ребер. В местах приложения нагрузки на поверхности моделей устанавливают подкладки из мягкого материала (например, пенопласта).
В зависимости от величины нагрузки и размеров моделей нагружение выполняют грузом, укладываемым на платформы, или домкратами. Нагрузка на модель передается через систему тяжей, траверс и балок. Платформы с грузом размещают под моделями, ниже моделей устанавливают страховочные подмости (для разгрузки моделей при разрушении). Домкраты также размещают под моделями, а страховочные подмости устанавливают под балки нагрузочной системы. Кроме того, под моделью устанавливаются страховочные леса. Различные схемы нагрузочных систем приведены в [9].
Для измерения деформаций применяют тензодатчики сопротивления с базой 20 - 50 мм, рычажные тензометры с базой не менее 100 мм, индикаторы с ценой деления 0,001 мм. Приборы устанавливают попарно один против другого - на наружной и внутренней гранях элементов. Это позволяет выделять осевые и изгибные деформации.
Прогибы, осадку опор и горизонтальные перемещения элементов модели измеряют индикаторами и прогибомерами с ценой деления 0,01 мм. Приборы укрепляют на специальных рамах, не связанных с подмостями и ходами.
Углы поворота контурных элементов измеряют клинометрами, парными индикаторами или парными прогибомерами, расположенными в одной вертикальной плоскости на разных уровнях.
Для измерения деформаций применяется электротензометрия. При испытании моделей целесообразно применять автоматизированные тензометрические комплексы. В ряде случаев могут оказаться целесообразными оптические и акустические измерительные устройства.
Приборы располагают по основным расчетным сечениям: по середине пролета, в угловых зонах, на контурных элементах. При испытании на сосредоточенные нагрузки приборы концентрируют в зоне нагрузки, где действуют наибольшие усилия.
Для повышения точности оценок параметров натурной конструкции необходимо увеличивать число испытуемых моделей [16]. Для сложных конструкций обычно не удается изготовить более одной-двух моделей. Обычно в применяемых пространственных конструкциях несколько осей симметрии. Это свойство можно использовать для повышения надежности моделирования: постановка приборов в симметричных точках в некоторой степени равнозначна увеличению числа моделей.
Испытания начинают с нескольких пробных нагружений. Их цель - проконтролировать работу всех приборов и устранить имеющиеся неплотности в стыках сборных элементов и опорах. Величина нагрузки выбирается максимальной, при которой в элементах модели не возникает трещин. Пробные нагружения прекращают, когда показания приборов перед нагружением и после разгрузки совпадают.
Затем модели испытывают в упругой стадии их работы. Величину нагрузки выбирают такой же, чтобы деформации были наибольшие без появления трещин. Цикл "нагрузка-разгрузка" повторяют несколько раз. Нагрузку увеличивают этапами, фиксируя на каждом этапе показания всех приборов. Количество повторений циклов зависит от степени разброса показаний и тем больше, чем больше разброс. Увеличение количества нагружений и последующая статистическая обработка опытных данных позволяют повышать достоверность результатов эксперимента. В процессе эксплуатации на оболочку могут действовать несколько различных сочетаний нагрузок. В этом случае модель испытывают на каждое из возможных сочетаний.
При испытании моделей в упругой стадии применяют различные устройства и используют приемы, позволяющие значительно увеличивать объем получаемой информации без значительного усложнения техники проведения эксперимента. Среди них можно отметить устройства, позволяющие изменять граничные условия для изучения многоволновых конструкций на отдельных моделях, изменять жесткости диафрагм одной модели, измерять контактные усилия между плитой и диафрагмой и др.
Модель испытывают до разрушения при невыгоднейшем сочетании нагрузок. Нагрузку увеличивают этапами. На каждом этапе модель осматривают с целью выявления трещин. Обнаружить микротрещины можно в результате смачивания поверхности модели ацетоном - в трещине ацетон высыхает медленнее, четко обозначая ее направление и длину. Трещины очерчивают на поверхности модели, отмечая этап их появления и длину. Ширину раскрытия трещин измеряют микроскопом.
После окончания испытаний необходимо зарисовать и сфотографировать схему разрушения. В местах установки приборов рекомендуется тщательно измерить толщину плиты, высоту и ширину ребер. Эти данные нужны для перехода от деформаций к усилиям. Для оценки несущей способности методом предельного равновесия в линиях излома рекомендуется измерить положение арматуры по высоте сечения.
При обработке опытных данных, полученных при испытании моделей в упругой стадии, используются методы математической статистики. Основная цель статистической обработки состоит в определении доверительного интервала, внутри которого с заданной вероятностью  располагается среднее значение перемещения или усилия.
располагается среднее значение перемещения или усилия.
Различают прямые и косвенные измерения. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно либо с помощью измерительного прибора. При косвенных измерениях измеряемая величина вычисляется из результатов прямых измерений других величин, связанных с измеряемой величиной определенной функциональной зависимостью.
Прямыми измерениями получают, например, следующие данные:
- по показаниям приборов при многократном нагружении моделей - относительные деформации верхних и нижних волокон сечения элементов модели 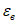 и
и 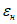 ;
;
- при испытаниях серий призм, изготовленных при бетонировании моделей, - значения начального модуля упругости бетона и его призменной прочности Rb;
- из измерений после разрушения - толщину h моделей и т.д.
Примером косвенных измерений может служить измерение погонных нормальных сил n и погонных изгибающих моментов m в плите модели. Эти величины определяются на основе прямых измерений по формулам:
в которые относительные деформации вводятся со своим знаком.
Прямые измерения обрабатывают следующим образом. Из k измерений ai (i = 1, ..., k) вычисляют среднее значение  и квадраты погрешностей отдельных измерений
и квадраты погрешностей отдельных измерений  . Границы доверительного интервала
. Границы доверительного интервала  находят по формуле
находят по формуле
 . Границы доверительного интервала
. Границы доверительного интервала  находят по формуле
находят по формуле
где Sk - эмпирический стандарт, вычисляемый по формуле

tk - коэффициент Стьюдента при надежности 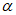 и числе произведенных измерений k (таблица 6.2).
и числе произведенных измерений k (таблица 6.2).
Количество измерений k | Значения коэффициента Стьюдента при надежности | ||||
0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
2 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 |
3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 |
4 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 |
5 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 |
6 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 |
7 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 |
Чтобы выяснить, не является ли измерение k промахом, проверяют условие

Опыт считается бракованным, если условие выполняется.
Доверительный интервал для величин, полученных с помощью косвенных измерений находят следующим образом. Пусть a, b, c, ... полученные прямыми измерениями случайные величины, для каждой из которых известны оценки границ доверительного интервала 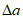 ,
, 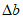 ,
,  , ... при заданной надежности
, ... при заданной надежности 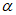 . Границы доверительного интервала для функции f = f(a, b, c, ...) при той же надежности
. Границы доверительного интервала для функции f = f(a, b, c, ...) при той же надежности  оценивают формулой
оценивают формулой
где производные вычисляются при  ,
, 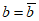 ,
, 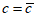 , ... .
, ... .
Применяя, например, формулу (6.2) к формуле (6.1), получим:
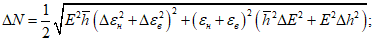

Искомые доверительные интервалы имеют вид

Доверительные интервалы позволяют оценивать достоверность расчета. Его можно считать достоверным, если эпюры расчетных результатов проходят внутри доверительных интервалов, построенных для опытных данных: в этом случае расхождения между опытом и расчетом можно объяснить случайным разбросом опытных данных. В противном случае расчетные данные также не отвергаются, если они идут в запас прочности по сравнению с экспериментом.
Если теоретические данные признают пригодными, расчет может быть использован для оценки работы натурной конструкции в упругой стадии. При испытаниях до разрушения получают величину предельной нагрузки, характеризующей несущую способность моделей. Несущую способность можно определить также из расчета методом предельного равновесия. При достаточно близком совпадении экспериментальных и теоретических данных расчет может быть использован для оценки несущей способности натурной конструкции.
Работу натурной конструкции во всех стадиях можно оценить и непосредственно по результатам испытаний модели. Для этого модель должна быть законструирована подобной натуре. Переход от модели к натуре осуществляется в соответствии с законами геометрического и физического подобия.
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ
Усилия от внешних нагрузок и воздействий
в поперечном сечении элемента
M - изгибающий момент;
N - продольная сила;
Q - поперечная сила;
T - крутящий момент.
Характеристики материалов
Rb,n - нормативное сопротивление бетона осевому сжатию;
Rb, Rb,ser - расчетные сопротивления бетона осевому сжатию для предельных состояний соответственно первой и второй групп;
Rbt,n - нормативное сопротивление бетона осевому растяжению;
Rbt, Rbt,ser - расчетные сопротивления бетона осевому растяжению для предельных состояний соответственно первой и второй групп;
Rb,loc - расчетное сопротивление бетона смятию;
Rbond - расчетное сопротивление сцепления арматуры с бетоном;
Rs, Rs,ser - расчетные сопротивления арматуры растяжению для предельных состояний соответственно первой и второй групп;
Rsw - расчетное сопротивление поперечной арматуры растяжению;
Rsc - расчетное сопротивление арматуры сжатию для предельных состояний первой группы;
Eb - начальный модуль упругости бетона при сжатии и растяжении;
Es - модуль упругости арматуры;
Характеристики положения продольной арматуры
в поперечном сечении элемента
S - обозначение продольной арматуры: при наличии сжатой и растянутой от действия внешней нагрузки зон сечения - расположенной в растянутой зоне; при полностью сжатом от действия внешней нагрузки сечении - расположенной у менее сжатой грани сечения; при полностью растянутом от действия внешней нагрузки сечении: для внецентренно растянутых элементов - расположенной у более растянутой грани сечения; для центрально-растянутых элементов - всей в поперечном сечении элемента;
S' - обозначение продольной арматуры: при наличии сжатой и растянутой от действия внешней нагрузки зон сечения - расположенной в сжатой зоне; при полностью сжатом от действия внешней нагрузки сечении - расположенной у более сжатой грани сечения; при полностью растянутом от действия внешней нагрузки сечении внецентренно растянутых элементов - расположенной у менее растянутой грани сечения.
Геометрические характеристики
b - ширина прямоугольного сечения; ширина ребра таврового и двутаврового сечений;
bf,  - ширина полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
- ширина полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
h - высота прямоугольного, таврового и двутаврового сечений;
hf, 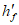 - высота полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
- высота полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
a, a' - расстояние от равнодействующей усилий в арматуре соответственно S и S' до ближайшей грани сечения;
h0, 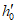 - рабочая высота сечения, равная соответственно h - a и h - a';
- рабочая высота сечения, равная соответственно h - a и h - a';
x - высота сжатой зоны бетона;
Sw - расстояние между хомутами, измеренное по длине элемента;
e0 - эксцентриситет продольной силы N относительно нейтральной оси, проходящей через центр тяжести приведенного сечения;
e, e' - расстояния от точки приложения продольной силы N до равнодействующей усилий в арматуре соответственно S и S';
l1 - пролет конструкции или ее продольный размер;
l2 - длина волны или поперечный размер конструкции;
l0 - расчетная длина элемента, подвергающегося действию сжимающей продольной силы;
f - стрела подъема элемента конструкции;
i - радиус инерции поперечного сечения элемента;
ds, dsw - номинальный диаметр стержней соответственно продольной и поперечной арматуры;
As,  - площади сечения арматуры соответственно S и S';
- площади сечения арматуры соответственно S и S';
Asw - площадь сечения хомутов, расположенных в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение;
A - площадь всего бетона в поперечном сечении;
Ab - площадь сечения бетона сжатой зоны;
Abt - площадь сечения бетона растянутой зоны;
Ared - площадь приведенного сечения элемента;
Aloc - площадь смятия бетона;
I - момент инерции сечения всего бетона относительно нейтральной оси, проходящей через центр тяжести сечения элемента;
Ired - момент инерции приведенного сечения элемента относительно нейтральной оси, проходящей через его центр тяжести;
W - момент сопротивления сечения элемента для крайнего растянутого волокна;
R - радиус кривизны элемента конструкции;
d1 - высота бортового элемента;
qs, 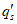 - погонные усилия, воспринимаемые арматурой полки сборного элемента соответственно в растянутой и сжатой зонах.
- погонные усилия, воспринимаемые арматурой полки сборного элемента соответственно в растянутой и сжатой зонах.
Современные пространственные конструкции (железобетон, металл, дерево, пластмассы). Справочник. Под ред. Ю.А. Дыховичного, Э.З. Жуковского. - М.: Высш. шк., 1991 - 543 с. | |
Шугаев В.В. Инженерные методы в нелинейной теории предельного равновесия оболочек. - М.: Готика, 2001 - 368 с. | |
Шугаев В.В., Соколов Б.С. Расчет несущей способности гладких и ребристых железобетонных оболочек методом предельного равновесия в нелинейной постановке./"Строительная механика и расчет сооружений", N 1, 2005 - с. 8 - 13 | |
Виноградов Г.Г. Расчет строительных пространственных конструкций. Л.: Стройиздат, Ленингр. отд-ние, 1990. - 264 с. | |
Горенштейн Б.В. Железобетонные пространственные конструкции для строительства на Севере. - Л.: Стройиздат, Ленингр. отд-ние, 1979 - 160 с. | |
Колчунов В.И., Пятикрестовский К.П., Клюева Н.В. Пространственные конструкции покрытий. - М.: Изд. Ассоциации строительных вузов, 2008 | |
Пространственные покрытия (конструкции и методы возведения). Под общей редакцией Г. Рюле. В 2-х т. Т. I Железобетон, армоцемент. М., Стройиздат, 1973. - 304 с. | |
Соколов Б.С., Пасхин Д.В., Титаев В.А. Исследование конструктивных параметров пространственных перекрытий рамно-шатрового типа. Вестник НИЦ "Строительство" Бетон и железобетон - проблемы и перспективы: Сб. статей. Вып. 4 (15)/под ред. А.И. Звездова - М.: АО "НИЦ "Строительство". 2017. - с. 16 - 27 | |
Стельмах С.И., Хайдуков Г.К. Рекомендации по исследованию железобетонных пространственных конструкций на моделях - В кн.: Пространственные конструкции зданий и сооружений (исследование, проектирование, возведение). М., Стройиздат, 1972. N 1 | |
Хайдуков Г.К., Шугаев В.В., Краковский М.Б. Моделирование при исследовании железобетонных пространственных конструкций. - В кн.: Расчет и конструирование железобетонных конструкций, М., Стройиздат, 1972 | |
Кирпичев М.В. Теория подобия. М., Изд-во АН СССР. 1953 | |
Седов Л.И. Методы подобия и размерности в механике. М., Наука, 1972 | |
Назаров А.Г. О механическом подобии твердых деформируемых тел. Ереван, Изд-во АН Арм. ССР, 1965 | |
Шугаев В.В., Соколов Б.С., Пасхин Д.В. Экспериментально-теоретические исследования сводчатого покрытия из панелей-оболочек КЖС. "Строительная механика и расчет сооружений", N 5, 2007 - с. 67 - 72 | |
Ярмульник Ф.К., Шарапов Г.В., Гайдук В.Г. Методика подбора материала при исследованиях железобетонных конструкций на моделях. Киев, Вища школа, 1974 | |
Мастаченко В.Н. Надежность моделирования строительных конструкций. М., Стройиздат, 1974 |
Ключевые слова: железобетонные пространственные конструкции, оболочка, свод, складка, купол, покрытие, перекрытие, расчет, конструирование, моделирование |

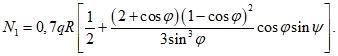

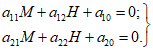


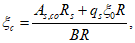
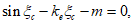
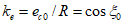 ;
;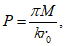

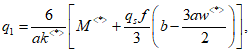


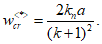
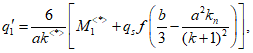

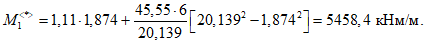

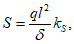
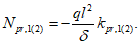

 :
: :
:
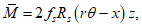

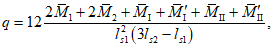


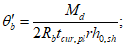

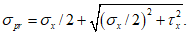
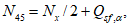
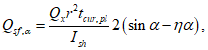
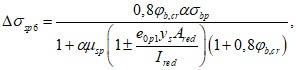
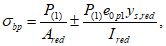
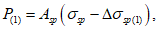
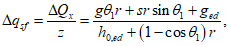
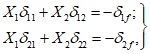


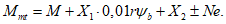
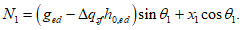
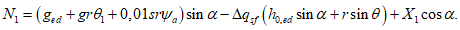
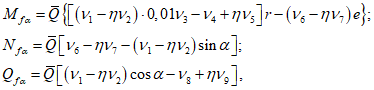
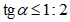 (
(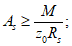
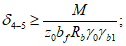
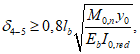


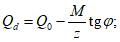
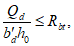
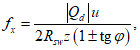
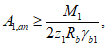
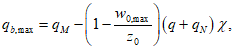

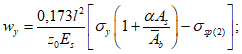
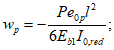
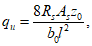

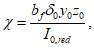
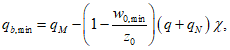

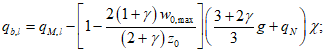
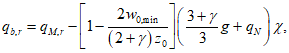
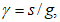




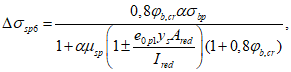
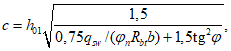

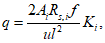
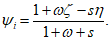


 .
.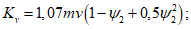
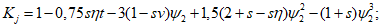
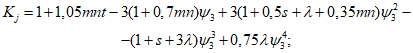
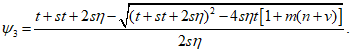

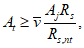

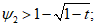 (5.5.16)
(5.5.16)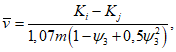
 (5.5.17)
(5.5.17)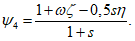

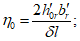
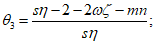 (5.5.23)
(5.5.23)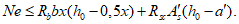
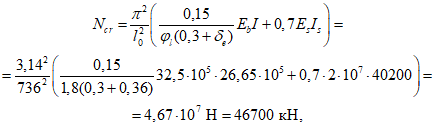
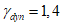 (по
(по 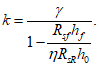




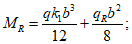
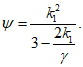


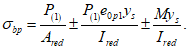
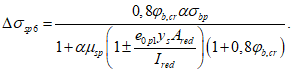
 ;
; 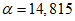 .
.
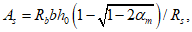


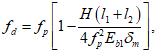
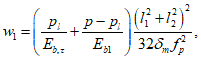
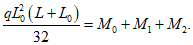

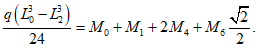

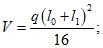

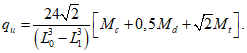

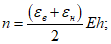
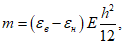 (6.1)
(6.1)