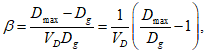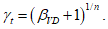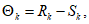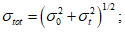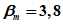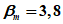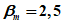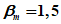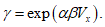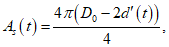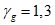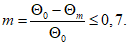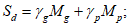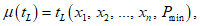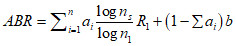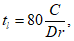СПРАВКА
Источник публикации
М., 2019
Примечание к документу
Название документа
"Методическое пособие по назначению срока службы бетонных и железобетонных конструкций с учетом воздействия среды эксплуатации на их жизненный цикл"
"Методическое пособие по назначению срока службы бетонных и железобетонных конструкций с учетом воздействия среды эксплуатации на их жизненный цикл"
Содержание
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ
"ФЕДЕРАЛЬНЫЙ ЦЕНТР НОРМИРОВАНИЯ, СТАНДАРТИЗАЦИИ
И ТЕХНИЧЕСКОЙ ОЦЕНКИ СООТВЕТСТВИЯ В СТРОИТЕЛЬСТВЕ"
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО НАЗНАЧЕНИЮ СРОКА СЛУЖБЫ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ
КОНСТРУКЦИЙ С УЧЕТОМ ВОЗДЕЙСТВИЯ СРЕДЫ ЭКСПЛУАТАЦИИ
НА ИХ ЖИЗНЕННЫЙ ЦИКЛ
Настоящее методическое пособие разработано во исполнение Поручения Президента Российской Федерации от 19 июля 2018 года N 1235.
Настоящее пособие разработано в развитие положений ГОСТ 27751 (разделы 2 - 5, 9 - 11, 13, 14), а также СП 63.13330, СП 28.13330, СП 20.13330 для реализации проектировщиками требований, заложенных в строительных нормах и правилах, с учетом воздействия среды эксплуатации на их жизненный цикл.
Методическое пособие предназначено для широкого круга специалистов, связанных с проектированием и исследованием железобетона, в том числе проектных организаций, органов экспертизы, надзорных служб, органов лицензирования и сертификации.
При разработке методического пособия были использованы отдельные положения международных стандартов, данные, полученные научно-исследовательскими организациями, техническими комитетами профильных международных организаций РИЛЕМ и ФИБ, а также положения законодательства Российской Федерации о техническом регулировании и о градостроительной деятельности.
Пособие разработано авторским коллективом АО НИЦ "Строительство" - НИИЖБ им. А.А. Гвоздева в составе: д-р техн. наук проф. В.Ф. Степанова, д-р материаловедения В.Р. Фаликман, инженеры А.А. Старостин, О.О. Калашников, Е.Н. Королева.
Основным свойством, определяющим жизненный цикл зданий и сооружений в целом, является безотказность работы конструкций, сохранность заданных эксплуатационных свойств в течение определенного срока службы.
Несмотря на то, что в Техническом регламенте "О безопасности зданий и сооружений" (ФЗ N 384) прямо упоминается необходимость такого подхода, нормативная и доказательная база его в Российской Федерации пока не разработана, что затрудняет переход на применение инновационной продукции и заключение контрактов с учетом "жизненного цикла" в рамках государственно-частного партнерства.
Проектирование долговечности железобетонных конструкций традиционно основывали на установившихся правилах и требованиях к характеристикам материалов, к качеству их составляющих, к условиям работы конструкции, с учетом требований, отраженных в действующих отечественных нормативных документах и ряде документов зарубежных стран.
Сегодня стала очевидной естественная связь между качеством сооружения и его сроком службы. Кроме того, общая стоимость складывается не только из стоимости непосредственного строительства, но и из стоимости эксплуатации и ремонта. В результате в условия контрактов на строительство сложных объектов теперь все чаще включают требования по долговечности сооружения и его сроку службы. Возникает необходимость в новых методах более точного определения проектной долговечности конструкций.
Объем исследований по проблемам долговечности, проведенных в период 1970 - 2000 гг., дал достаточно надежные сведения о процессах разрушения, и сделал возможным включать их в процесс проектирования железобетонных конструкций. При этом достаточно простая математическая модель долговечности, отражающая характер работы конструкции во времени, или модель срока службы как функция соответствующих расчетных параметров, представляют собой весьма ценный инструмент.
На процесс деградации материалов оказывают воздействие многие факторы окружающей среды, однако их математически точное влияние трудно определить, поэтому в пособии принят вероятностный подход к проблемам проектирования, который учитывает реальную природу работы конструкции, что, в свою очередь, обеспечивает надежность результатов ее проектирования.
В настоящем методическом пособии приведены основные принципы проектирования бетонных и железобетонных конструкций с учетом воздействия среды эксплуатации на их жизненный цикл с целью назначения их срока службы.
Задачи разработки пособия - разъяснение особенностей проектирования зданий и сооружений с учетом воздействия среды эксплуатации на их жизненный цикл, а также назначения срока службы бетонных и железобетонных конструкций и обеспечение реализации требований ГОСТ 27751; увеличение срока службы железобетонных конструкций при минимизации затрат в процессе эксплуатации; развитие положений СП 63.13330, СП 28.13330, СП 20.13330 для повышения качества выполняемых проектных работ, сокращения сроков и снижения стоимости проектирования, а также снижения эксплуатационных издержек в процессе эксплуатации зданий и сооружений.
В настоящем методическом пособии использованы ссылки на следующие документы:
ГОСТ 4.212-80 Система показателей качества продукции. Строительство. Бетоны. Номенклатура показателей
ГОСТ 7473-2010 Смеси бетонные. Технические условия
ГОСТ 8829-94 Изделия строительные железобетонные и бетонные заводского изготовления. Методы испытаний нагружением. Правила оценки прочности, жесткости и трещиностойкости
ГОСТ 10060-2012 Бетоны. Методы определения морозостойкости. Основные требования
ГОСТ 10180-2012 Бетоны. Методы определения прочности по контрольным образцам
ГОСТ 10181-2014 Смеси бетонные. Методы испытания
ГОСТ 12730.0-78 Бетоны. Общие требования к методам определения плотности, влажности, водопоглощения, пористости и водонепроницаемости
ГОСТ 12730.1-78 Бетоны. Метод определения плотности
ГОСТ 12730.5-84 Бетоны. Методы определения водонепроницаемости
ГОСТ 13015-2012 Изделия железобетонные и бетонные для строительства. Общие технические требования. Правила приемки, маркировки, транспортирования и хранения
ГОСТ 17624-2012 Бетоны. Ультразвуковой метод определения прочности
ГОСТ 18105-2010 Бетоны. Правила контроля и оценки прочности
ГОСТ 22690-2015 Бетоны. Определение прочности механическими методами неразрушающего контроля
ГОСТ 24211-2008 Добавки для бетонов. Общие технические требования
ГОСТ 25192-2012 Бетоны. Классификация и общие технические требования
ГОСТ 26633-2015 Бетоны тяжелые и мелкозернистые. Технические условия
ГОСТ 27005-2014 Бетоны легкие и ячеистые. Правила контроля средней плотности
ГОСТ 27006-2019 Бетоны. Правила подбора составов
ГОСТ 27751-2014 Надежность строительных конструкций и оснований. Основные положения
ГОСТ 28570-90 Бетоны. Методы определения прочности по образцам, отобранным из конструкций
ГОСТ 31937-2011 Здания и сооружения. Правила обследования и мониторинга технического состояния
ГОСТ 31384-2017 Защита бетонных и железобетонных конструкций от коррозии. Общие технические требования
ГОСТ 34028-2016 Прокат арматурный для железобетонных конструкций. Технические условия
ГОСТ Р ИСО 10005-2007 Менеджмент организации. Руководящие указания по планированию качества
ГОСТ Р 57359-2016 Конструкции бетонные. Правила изготовления
СП 20.13330.2016 "СНиП 2.01.07-85* Нагрузки и воздействия" (с изменениями N 1, N 2)
СП 22.13330.2016 "СНиП 2.02.01-83* Основания зданий и сооружений" (с изменениями N 1, N 2, N 3)
СП 28.13330.2017 "СНиП 2.03.11-85 Защита строительных конструкций от коррозии" (с изменениями N 1, N 2)
СП 48.13330.2019 "СНиП 12-01-2004 Организация строительства"
СП 50.13330.2012 "СНиП 23-02-2003 Тепловая защита зданий" (с изменением N 1)
СП 63.13330.2018 "СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения" (с изменением N 1)
СП 70.13330.2012 "СНиП 3.03.01-87 Несущие и ограждающие конструкции" (с изменениями N 1, N 3)
СП 72.13330.2016 "СНиП 3.04.03-85 Защита строительных конструкций и сооружений от коррозии" (с изменением N 1)
СП 130.13330.2018 "СНиП 3.09.01-85 Производство сборных железобетонных конструкций и изделий"
Примечание - При пользовании настоящим методическим пособием целесообразно проверить действие ссылочных документов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего методического пособия в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде стандартов.
В настоящем методическом пособии применены термины по ГОСТ 25192, ГОСТ 27751, ГОСТ 31384, СП 28.13330, СП 63.13330, СП 72.13330, а также следующие термины с соответствующими определениями:
3.1 безопасность эксплуатации: Способность конструкции с определенной степенью надежности сопротивляться разрушению.
3.2 вероятность разрушения: Вероятность возможного разрушения.
3.3 возраст: Период времени от момента ввода в эксплуатацию до момента осмотра (обследования).
3.4 деградационная модель: Математическая функция, описывающая процесс деградации во времени.
3.5 деградация: Постепенное ухудшение эксплуатационных качеств материала или конструкции.
3.6 долговечность: Способность сооружения, его отдельного узла, элемента, конструкции или изделия сохранять минимально необходимые эксплуатационные качества в течение, по крайней мере, заданного периода времени под воздействием факторов деградации.
3.7 заданный срок службы: Требуемый срок службы, устанавливаемый общими нормативами или заданием заказчика или владельца здания или сооружения.
3.8 квантиль: Значение, которое заданная случайная величина не превышает с фиксированной вероятностью.
Примечание - Если вероятность задана в процентах, то квантиль называется процентилем или перцентилем.
3.9 коэффициент надежности по возрасту: Коэффициент, на который умножают заданный срок службы, чтобы получить проектный срок службы.
3.10 критическое предельное состояние: Состояние, связанное с обрушением или другими подобными формами разрушения конструкции.
3.11 механизм деградации: Последовательность химических, механических или физических изменений, которые ведут к ухудшению одной или нескольких составляющих под воздействием одного из факторов деградации или их комбинации.
3.12 модель долговечности: Математическая модель расчета процесса деградации, работы или продолжительности срока службы.
3.13 модель функциональности: Математическая функция, отражающая изменение эксплуатационных качеств во времени (или с возрастом).
3.14 нарушение долговечности: Превышение максимальной деградации или снижение минимальных эксплуатационных качеств.
3.15 повреждение: Процесс ухудшения качества или снижения стоимости.
3.16 предельное состояние по долговечности: Минимально приемлемое состояние эксплуатационных качеств или максимально приемлемая степень деградации.
Примечание - Это предельное состояние может определяться по пределу эксплуатационных качеств или по предельному состоянию конструкции.
3.17 предельное состояние эксплуатационной пригодности: Состояние, соответствующее условиям, за пределами которых установленные эксплуатационные качества конструкции или ее элемента перестают отвечать необходимым требованиям.
3.18 процесс деградации: Зависящий от времени механизм, ведущий к деградации.
3.19 прочностной расчетный параметр: Свойства материала, геометрические размеры конструкции или ее элемента, или расположение арматуры, которые могут влиять на долговечность конструкции.
3.20 разрушение: Феномен ухудшения состояния ниже предельного уровня (предел эксплуатационных качеств или критическое предельное состояние).
3.21 расчетный параметр долговечности: Характеристика материала, геометрические размеры конструкции или ее элемента, или расположение арматуры, которые могут влиять на долговечность конструкции.
3.22 расчетный срок службы: Срок службы, применяемый в расчете конструкции, учитывающий связанные со временем разбросы значений и обеспечивающий требуемую безопасность против обрушения на протяжении всего заданного периода эксплуатации сооружения.
3.23 риск: Произведение вероятности разрушения на объем ущерба.
3.24 срок службы: Период времени после выпуска изделия или пуска конструкции в эксплуатацию, в течение которого все требуемые качества соответствуют или превышают минимально приемлемые значения при нормально выполняемых мероприятиях по содержанию.
3.25 фактор деградации: Любая из групп внешних факторов, включая климатические условия, биологическое воздействие, напряжения, несовместимость компонентов, характер эксплуатации, оказывающих отрицательное влияние на характеристики строительных материалов и их составляющих.
3.26 функциональность: Степень выполнения конструкцией предназначенных функций.
3.27 эксплуатационная пригодность: Способность сооружения, его отдельного узла, элемента, изделия или конструкции выполнять эксплуатационные функции, для которых объект проектировался и использовался.
4 Основы проектирования бетонных и железобетонных конструкций по срокам их службы с учетом воздействия среды эксплуатации на их жизненный цикл
4.1.1 Работа конструкции и ее деградация
4.1.1.1 Под термином "работа" обычно понимают поведение конструкции на стадии эксплуатации. В принципе, работоспособность конструкции можно связать с ее несущей способностью, устойчивостью, безопасностью эксплуатации, плотностью, гигротермическими и акустическими свойствами, внешним видом и т.д. В контексте пособия под термином "работа" подразумевается только количественная характеристика.
4.1.1.2 Работоспособность - функция времени и, с этой точки зрения, прямо связана с понятием долговечности. Деградация представляет собой процесс постепенного снижения характеристик работоспособности во времени, поэтому описание работоспособности можно осуществлять через степень деградации.
4.1.1.3 Концепции работоспособности и деградации во времени могут применяться на различных уровнях:
- на уровне сооружений;
- на уровне отдельных конструктивных элементов;
- на уровне материалов.
Между этими уровнями возможны взаимосвязи. Так, если, например, определяют несущую способность железобетонной колонны или балки, задача в действительности решается на уровне конструктивного элемента. С другой стороны, в более глубоком смысле, несущая способность будет зависеть от деградации бетона и стали. Таким образом, изменение работоспособности во времени на уровне конструктивного элемента должно вначале оцениваться как скорость изменения работоспособности на уровне материалов.
4.1.1.4 Минимально приемлемые значения работоспособности (или максимально приемлемые значения деградации) называют предельными состояниями по долговечности. Предельное состояние работоспособности - решающий критерий для срока службы. Оно может выражаться как через предел прочности, так и через предел эксплуатационной пригодности.
4.1.2 Срок службы
4.1.2.1 За срок службы принимают период времени, отсчитываемый от пуска объекта в эксплуатацию, в течение которого выполняются требования по его работоспособности. Понятие срока службы также может рассматриваться на различных уровнях. Характер мероприятий, выполняемых в конце срока службы, зависит от выбранного уровня. На уровне сооружения окончание срока службы обычно влечет за собой полное восстановление, реконструкцию или отказ от его использования. На уровне конструктивного элемента или на уровне материала это означает замену или серьезный ремонт элемента или материала.
4.1.2.2 С другой стороны, проблему срока службы можно рассматривать по крайней мере с трех различных точек зрения: технической, функциональной и экономической. В зависимости от выбранной точки зрения можно говорить о техническом, функциональном или экономическом обосновании срока службы. Различные точки зрения заставляют предъявлять к одному и тому же объекту различные требования.
4.1.2.3 Технические требования вызывают необходимость обеспечения технических характеристик работоспособности. В зависимости от уровня рассмотрения к числу таких требований можно отнести конструктивную целостность сооружения, несущую способность конструкции и/или прочность материалов. Значительная часть этих требований включена в состав нормативных документов.
4.1.2.4 Функциональные требования определяют характер нормального использования сооружения или конструкции. Например, ширину и высоту моста назначают в зависимости от потребностей транспорта, движущегося как по мосту, так и под ним. В этом случае продолжительность срока службы будет зависеть, в первую очередь, не столько от технического состояния конструкции, сколько от характера развития транспорта. С точки зрения экономики, сооружение, конструктивный элемент или материал рассматривают как капиталовложение, и требования к сроку службы определяют на основании условия соблюдения прибыльности.
4.1.2.5 В контексте пособия проблемы срока службы рассматриваются, в основном, с точки зрения технического состояния конструкции. Технический подход сосредоточивается на трех аспектах:
- физическая работа конструкции;
- эксплуатационная пригодность и удобство пользования;
- эстетика.
При этом основное внимание уделяется физическим и иным конструктивным функциям железобетонных конструкций.
4.1.2.6 Несущая способность сооружения может быть потеряна из-за деградации бетона и арматуры. Проектирование конструкций должно вестись таким образом, чтобы на протяжении всего заданного срока службы, несмотря на деградацию и старение материалов, обеспечивался бы минимальный уровень безопасности.
4.1.2.7 Дефекты материалов также могут приводить к снижению эксплуатационной пригодности или к возникновению неудобства пользования сооружением. Например, повреждение бетонного покрытия проезжей части дорожного полотна может вызвать неприятную вибрацию автомобиля.
4.1.2.8 Эстетические соображения включают в состав технических требований, если эстетические дефекты возникают из-за деградации или старения материалов. В этом случае эстетические требования могут быть выражены в технических понятиях.
4.1.2.9 Точное определение срока службы конструкции осложняется тем, что в течение этого срока выполняются плановые мероприятия по уходу и обслуживанию. Мероприятия по обслуживанию и уходу за сооружением могут влиять на продолжительность его срока службы, и поэтому они также должны быть включены в рассмотрение. По этой причине в определении термина "срок службы" имеется дополнение: "при условии обеспечения планового обслуживания". Срок службы, заявленный заказчиком или владельцем сооружения при его проектировании, называют заданным сроком службы.
4.1.3 Вероятность разрушения
4.1.3.1 В вероятностном методе проектирования долговечности необходимо иметь в виду не только заданный срок службы, но и определить максимально допустимую вероятность того, что заданный срок службы не будет достигнут. Эту вероятность называют вероятностью разрушения. С другой стороны, вероятность разрушения можно обозначить как вероятность того, что будет превышено некоторое предельное состояние, определяемое предельным состоянием несущей способности или предельным состоянием эксплуатационной пригодности.
4.1.3.2 Если разрушение вызвано деградацией материалов, обычно применяют выражение "нарушение долговечности", чтобы отличить его от "физического разрушения", которое вызывают реальные физические нагрузки. Однако нарушение долговечности может быть одной из причин физического разрушения.
4.1.3.3 Требуемая вероятность разрушения зависит от того, каким образом определяют событие разрушения и какие последствия возможны в результате разрушения. Если разрушение приводит к серьезным последствиям, максимально допустимая вероятность разрушения должна быть, естественно, малой.
4.1.3.4 Для оценки последствий разрушения обычно применяют концепцию риска, под которым понимают произведение вероятности разрушения и объема ущерба.
4.1.3.5 В общем случае, при определении требуемой вероятности разрушения необходимо учитывать социальные и экономические критерии, а также критерии, связанные с сохранением окружающей среды.
4.1.3.6 В состав социальных критериев должны включаться:
- социальное значение сооружения или конструкции;
- последствия разрушения (число возможных жертв и т.д.);
- трудность определения уровня риска.
4.1.3.7 Важность экономических критериев определяется тем, что любой перерыв в работе предприятия, вызванный разрушением, может привести к значительным экономическим потерям, не сравнимым со стоимостью строительства.
4.1.3.8 В подходе, использующем принципы устойчивого развития, необходимо учитывать также природоохранные и экологические критерии. В некоторых случаях авария строительных конструкций может вызвать экологическое бедствие. В обычных зданиях продолжительный и безопасный срок эксплуатации обеспечивается чаще всего тогда, когда их проектируют с соблюдением требований экологии и при экономном расходовании строительных материалов, а сами материалы при их производстве не выделяют и не поглощают большого количества энергии.
4.1.3.9 Неопределенность по поводу конечного качества здания на стадии проектирования значительно выше, чем для уже существующих зданий. Поэтому для существующих зданий требуемый запас прочности может быть меньшим, чем для проектируемых, в то время как вероятность разрушения как для одних, так и для других, в принципе, одинакова. По этой же причине можно утверждать, что при оценке влияния деградации на поведение конструкции в большинстве случаев можно применить одну и ту же теорию как для существующих, так и для проектируемых сооружений. Единственная разница заключается в том, что, в конечном счете, запас прочности для существующих сооружений назначается меньшим, чем для сооружений на стадии проектирования.
4.2.1 Общие положения
4.2.1.1 Теория проектирования долговечности, в принципе, основывается на теории безопасности (или конструктивной надежности), применяемой в проектировании строительных конструкций. В этом контексте под безопасностью эксплуатации понимают способность конструкции с определенной степенью надежности сопротивляться разрушению, сопровождаемому различными потенциально опасными воздействиями, характерными для предназначения конструкции. Однако применение этой теории до сего времени ограничивалось в большей степени задачами, в которых время играло лишь подчиненную роль.
4.2.1.2 В настоящее время проектирование конструкции с обеспеченным запасом надежности подразумевает учет времени, в течение которого должны выполняться требования безопасности эксплуатации. Другими словами, необходимо введение требования на гарантированный срок службы. В практике проектирования конструкций его называют заданным сроком службы. Уровень безопасности при этом выражают как максимально допустимую вероятность разрушения.
4.2.2 Вероятностная теория разрушения и срок службы
4.2.2.1 Простейшая математическая модель, описывающая событие "разрушение", включает переменную нагрузки S и переменную прочности R. В принципе, переменные S и R могут иметь любое значение в любых единицах. Единственной требование, которое при этом должно быть соблюдено, состоит в том, что они должны быть в одной системе единиц.
4.2.2.2 Если R и S не зависят от времени, то событие "разрушение" можно выразить следующим образом
{разрушение} = {R < S}. (4.1)
Другими словами, разрушение наступает тогда, когда прочность становится меньше нагрузки. В этом случае вероятность разрушения Pf теперь определяется условием
Pf = P{R < S}. (4.2)
4.2.2.3 Как прочность R, так и нагрузка S, или они обе могут быть величинами, зависящими от времени. Таким образом, вероятность разрушения также будет зависеть от времени. Принимая R(т) и S(т) за значения прочности и нагрузки в момент т, вероятность разрушения в возрасте t можно выразить как
4.2.2.4 Определение функции Pf(t) из уравнения (4.3а) математически затруднительно. В обычных условиях прочность и нагрузка не могут быть выражены в качестве мгновенных физических величин. Именно поэтому R и S рассматриваются как вероятностные величины с плотностью распределения, либо зависящей от времени, либо постоянной. Отсюда обычно удается выразить вероятность разрушения
4.2.2.5 В соответствии с выражением (4.3б) вероятность разрушения непрерывно увеличивается с ростом времени, как схематично изображено на рисунке 4.1. В начальный момент времени при t = 0 кривые плотностей распределения нагрузки и прочности находятся далеко друг от друга, и вероятность разрушения невелика. С увеличением времени кривые распределения приближаются одна к другой, образуя возрастающую зону перекрывания, которая и представляет собой вероятность разрушения.
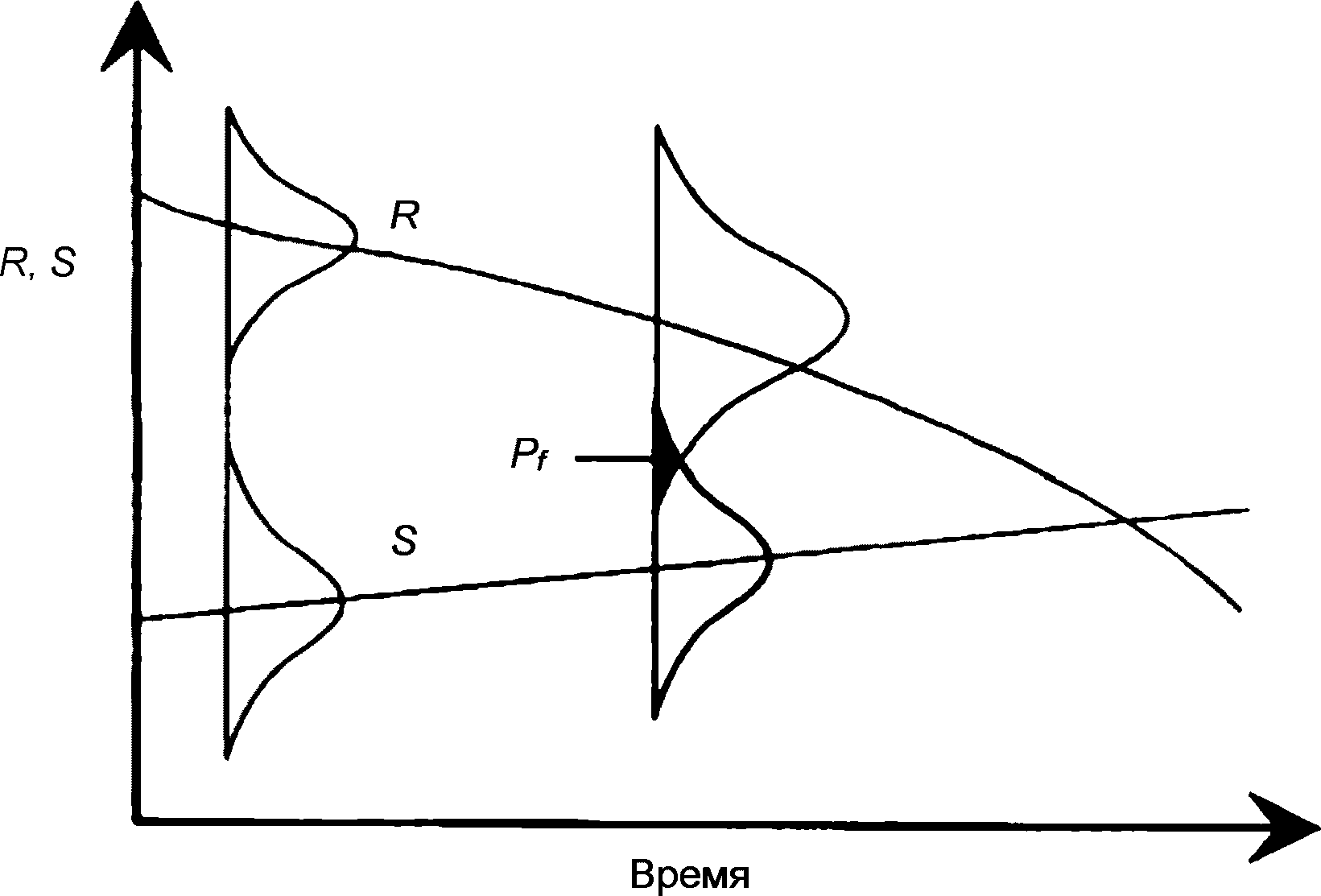
4.2.2.6 Функция Pf(t) имеет характер функции распределения. Если срок службы определяется таким образом, что событие 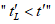 идентично событию "разрушение в возрасте t", то функцию распределения срока службы можно выразить как
идентично событию "разрушение в возрасте t", то функцию распределения срока службы можно выразить как
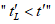 идентично событию "разрушение в возрасте t", то функцию распределения срока службы можно выразить как
идентично событию "разрушение в возрасте t", то функцию распределения срока службы можно выразить какFL(t) = P{tL < t} = Pf(t), (4.4)
где FL - совокупное распределение срока службы.
4.2.2.7 Функцию плотности вероятности можно определить, как производную от функции распределения
 (4.5)
(4.5)4.2.2.8 Вероятность разрушения в некий момент времени можно выразить как сумму произведений двух вероятностей:
- вероятности того, что R < S при S = s, и
- вероятности того, что S = s распространяется на весь диапазон S
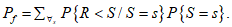 (4.6а)
(4.6а)4.2.2.9 Рассматривая непрерывные распределения вероятности разрушения Pf в некоторый момент времени, можно выразить ее с помощью интегральной свертки
 (4.6б)
(4.6б)где FR(S) - функция распределения R;
fS(S) - функция вероятностной плотности S;
s - общее количество или измеренные значения R и S.
4.2.2.10 Общее решение интегральной свертки, содержащей зависящие от времени распределения R и S, может быть весьма трудоемким. Простое решение этого интеграла возможно только в тех немногочисленных случаях, когда распределения R и S нормальны. Однако интеграл можно решить и упрощенными числовыми методами. Распределение срока службы может быть получено путем расчета значений вероятности разрушения в различные моменты времени, например, при t = 0, 10, 20, 30 и т.д. лет.
4.2.3 Основное формулирование проблемы проектирования долговечности
4.2.3.1 Принципы и методы проектирования
4.2.3.1.1 Основные формулы проектирования долговечности можно записать в соответствии с одним из двух принципов: принципом работы или принципом срока службы.
4.2.3.1.2 При использовании принципа работы основная формула проектирования может быть записана путем введения нагрузки S, взаимосвязанной с работой R. Работа, определенная по модели работы, должна быть большей, чем требуемая нагрузка. При этом имеющаяся в виду работа может относиться к механическим явлениям, физическим, химическим или к эксплуатационным функциям, или к эстетическим требованиям. Что касается нагрузки, то она может иметь механическую природу, или под ней может подразумеваться воздействие окружающей среды.
4.2.3.1.3 При использовании принципа срока службы tL, его величину можно определить с помощью модели срока службы, при этом он должен превышать требуемый заданный срок службы tg.
4.2.3.1.4 Обычно оба принципа дают одинаковые результаты. Выбор того или иного принципа, во многом, зависит от характера поставленной проектной задачи, от типа принятых моделей долговечности и от выбора наиболее простого способа математического решения задачи.
4.2.3.1.5 Метод проектирования долговечности может быть детерминистическим, вероятностным или основанным на факторе безопасного срока службы. Основные положения этих принципов изложены ниже.
4.2.3.2 Детерминистический метод проектирования
4.2.3.2.1 Детерминистический подход - подход к проектированию или конструированию на основе полностью определенных данных о параметрах воздействий и свойствах объекта заведомо в запас безопасности с непревышением установленных в нормативных документах с коэффициентами запаса предельных значений контролируемых параметров. В детерминистическом проектировании долговечности нагрузка, прочность и срок службы понимаются как детерминистические величины, законы распределения этих функций здесь не рассматриваются.
4.2.3.2.2 В соответствии с принципом работы формула принимает вид
где tg - заданный срок службы.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
4.2.3.2.2 Как нагрузка S, так и прочность R - функции, зависящие от времени. Эти функции используют в качестве моделей деградации и работы. Такие параметры проектирования, как конструктивные размеры, характеристики материалов и коэффициенты влияния окружающей среды, включаются в состав этих функций.
4.2.3.2.3 Соответствующая формула проектирования, записанная с учетом принципа срока службы, имеет следующий вид
где tL - функция срока службы. В составе этой функции используют проектные параметры моделей срока службы.
4.2.3.2.4 Проектирование конструкций ведут путем выбора подходящей комбинации значений проектных параметров таким образом, чтобы они удовлетворяли условиям уравнений (4.7) и (4.8).
4.2.3.2.5 При использовании принципа срока службы необходимо иметь в виду, что требования к работоспособности заложены в формулу срока службы. Поэтому подход к решению задачи с использованием понятия работы и подход, основанный на идее срока службы, дают аналогичные проектные формулы, т.е. результаты решения проектных задач одинаковы, независимо от выбранного метода.
4.2.3.3 Вероятностный метод проектирования
4.2.3.3.1 В вероятностном подходе проводится оценка вероятности возникновения события, расчет вероятности того или иного сценария события, анализируются разветвленные и пересекающиеся цепочки событий. Расчетные модели при этом оказываются значительно упрощенными по сравнению с детерминистическим подходом с соответствующими моделями. При вероятностном проектировании долговечности так же, как и при детерминистическом, принимают во внимание распределения нагрузки, реакции и срока службы. Это условие выражается в виде предположения, что проектная формула неверна.
4.2.3.3.2 Проектную формулу можно записать в соответствии с принципом работы или с принципом срока службы, что, как и в случае с детерминистическим методом проектирования, не несет особых отличий. Однако в конечное условие добавляется требование относительно максимально допустимой вероятности разрушения.
4.2.3.3.3 В соответствии с принципом работы необходимо выполнить следующее условие: вероятность того, что прочность конструкции может оказаться меньшей, чем нагрузка в течение срока службы, не должна превышать некую вероятность разрушения.
Математически это требование выглядит как
 (4.9)
(4.9)где  - вероятность разрушения конструкции в течение периода tg;
- вероятность разрушения конструкции в течение периода tg;
 - вероятность разрушения конструкции в течение периода tg;
- вероятность разрушения конструкции в течение периода tg;Pfmax - максимально допустимая вероятность разрушения.
Задача может быть разрешена при известных распределениях нагрузки и прочности. В разделе 5.2 приведено решение для случаев, когда нагрузка и прочность распределены нормально.
4.2.3.3.4 При использовании принципа срока службы требования формулируются следующим образом: вероятность того, что срок службы конструкции может оказаться более коротким, чем заданный срок службы, не должна превышать некую вероятность разрушения. Математически это требование выглядит как
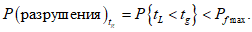 (4.10)
(4.10)Задача может быть решена при известном распределении срока службы. Если форма распределения неизвестна, необходимо следовать какому-либо известному типу распределения. Решение задачи для случаев, когда распределение срока службы предполагается по логарифмически нормальному закону, представлено в 5.3.
4.2.3.4 Метод коэффициента надежности по сроку службы
4.2.3.4.1 Если формулы для нагрузки, прочности и срока службы сложны и на работоспособность конструкции оказывают воздействие многие деградационные факторы, применение вышеприведенного вероятностного метода проектирования может оказаться затруднительным. В подобных случаях целесообразно использовать метод коэффициента надежности по сроку службы. Хотя этот метод основан на теории безопасности и надежности, формулирование процедуры проектирования снова принимает детерминистическую форму. Это осуществляют путем замены требования заданного срока службы на соответствующее требование проектного срока службы. На практике расчетный срок службы определяют перемножением заданного срока службы на коэффициент надежности по сроку службы
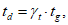 (4.11)
(4.11)где td - расчетный срок службы;
tg - заданный срок службы.
Расчетные формулы теперь можно записать, используя как принцип работы, так и принцип срока службы:
R(td) - S(td) >= 0; (4.12)
tL - td > 0. (4.13)
4.2.3.4.2 Значение коэффициента надежности по сроку службы зависит от максимально допустимой вероятности разрушения. Коэффициент надежности по сроку службы необходимо корректировать в соответствии с результатами вероятностных методов проектирования, как это изложено в разделе 6.
4.2.3.4.3 Методика использования метода коэффициента надежности по сроку службы при проектировании долговечности конструкции приведена в разделе 7. Применение этого метода особенно оправдано при проектировании конструкций, поскольку вероятности нагрузок и прочностей также учитываются с помощью коэффициентов запаса, и в этом данный метод принципиально схож с конструктивными расчетами сооружений.
5.1.1 Для использования вероятностных методов проектирования необходимо сделать несколько допущений, касающихся формы распределений.
5.1.2 К типам распределения, которые можно использовать для оценки срока службы или работоспособности конструкции, относятся:
- нормальное (Гауссово) распределение;
- логарифмически нормальное распределение;
- экспоненциальное распределение;
- распределение Вейбулла;
- гамма-распределение.
5.1.3 В случае применения принципа работы наиболее общее допущение состоит в том, что как нагрузка, так и прочность, или они обе распределены нормально. При применении принципа срока службы распределение срока службы чаще всего принимают по логарифмически нормальному закону, т.е. как нормальное распределение по логарифмической временной шкале.
5.2.1 Теория
5.2.1.1 Если в проектировании долговечности используют принцип работы, а прочность R и нагрузка S являются нормально распределенными величинами, вероятность разрушения можно определить, используя контрольный индекс  :
:
где  - среднее отклонение;
- среднее отклонение;
5.2.1.2 Контрольный индекс 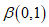 нормально распределен. Вероятности разрушения, соответствующие индексу
нормально распределен. Вероятности разрушения, соответствующие индексу 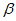 , определяют по таблицам или как функции в современных электронно-вычислительных программах. В конструктивном проектировании контрольный индекс
, определяют по таблицам или как функции в современных электронно-вычислительных программах. В конструктивном проектировании контрольный индекс  также называют индексом безопасности или индексом надежности.
также называют индексом безопасности или индексом надежности.
5.2.1.3 Часто R или S бывают постоянными. Тогда их взаимное отношение в уравнении (5.1) принимает упрощенную форму
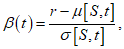 (5.2)
(5.2)или
 (5.3)
(5.3)где r и s - постоянные величины.
5.2.1.4 Если R постоянна, а S - зависящая от времени функция, приближенно определяемая через математическую деградационную модель, задача называется деградационной. Аналогично, если S постоянна, а R - зависящая от времени функция, приближенно определяемая через математическую модель работы, задачу называют рабочей.
5.2.1.5 Поскольку средние и стандартные отклонения зависят от времени, также зависящим от времени оказывается индекс 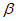 . Для получения распределения срока службы нужно определить вероятности разрушения для различных значений t (например, t = 0, 10, 20 и т.д. лет).
. Для получения распределения срока службы нужно определить вероятности разрушения для различных значений t (например, t = 0, 10, 20 и т.д. лет).
5.2.2 Пример
5.2.2.1 Пусть исследуется процесс карбонизации бетона в наружных слоях железобетонной конструкции. Предположим, что разрушение происходит тогда, когда глубина карбонизации превысит глубину размещения арматуры. В результате происходит депассивация арматуры и начинается процесс ее коррозии. В этом случае возникает деградационная задача с зависящим от времени процессом карбонизации (S) и постоянной величиной защитного слоя бетона (R).
5.2.2.2 Предполагаем, что процесс карбонизации распространяется со скоростью, равной корню квадратному из времени
 (5.4)
(5.4)где  - средняя глубина карбонизации, мм;
- средняя глубина карбонизации, мм;
Kc - коэффициент скорости карбонизации, мм/год;
t - время (или возраст), годы.
5.2.2.3 Значение коэффициента скорости карбонизации зависит от прочности и состава бетона (см. 9.5.3)
Kc = CenvCaira(fck + 8)b, (5.5)
где Cenv - коэффициент воздействия окружающей среды;
Cair - коэффициент содержания воздуха;
fck - нормативная кубиковая прочность на сжатие, МПа;
a, b - константы (зависящие от характеристик вяжущего).
5.2.2.4 Значения параметров и коэффициентов приведены в таблицах 9.3 - 9.5. Предположим, что глубина карбонизации распределена нормально. Коэффициент вариации (отношение стандартного отклонения к среднему) принимаем за постоянную величину.
5.2.2.5 На рисунке 5.1 изображен процесс карбонизации в защитном слое бетона. Если среднее значение глубины карбонизации растет во времени, то и стандартное отклонение также возрастает, оставляя при этом коэффициент вариации постоянным. Та часть распределения глубины карбонизации, которая превышает толщину защитного слоя бетона, показывает вероятность разрушения.
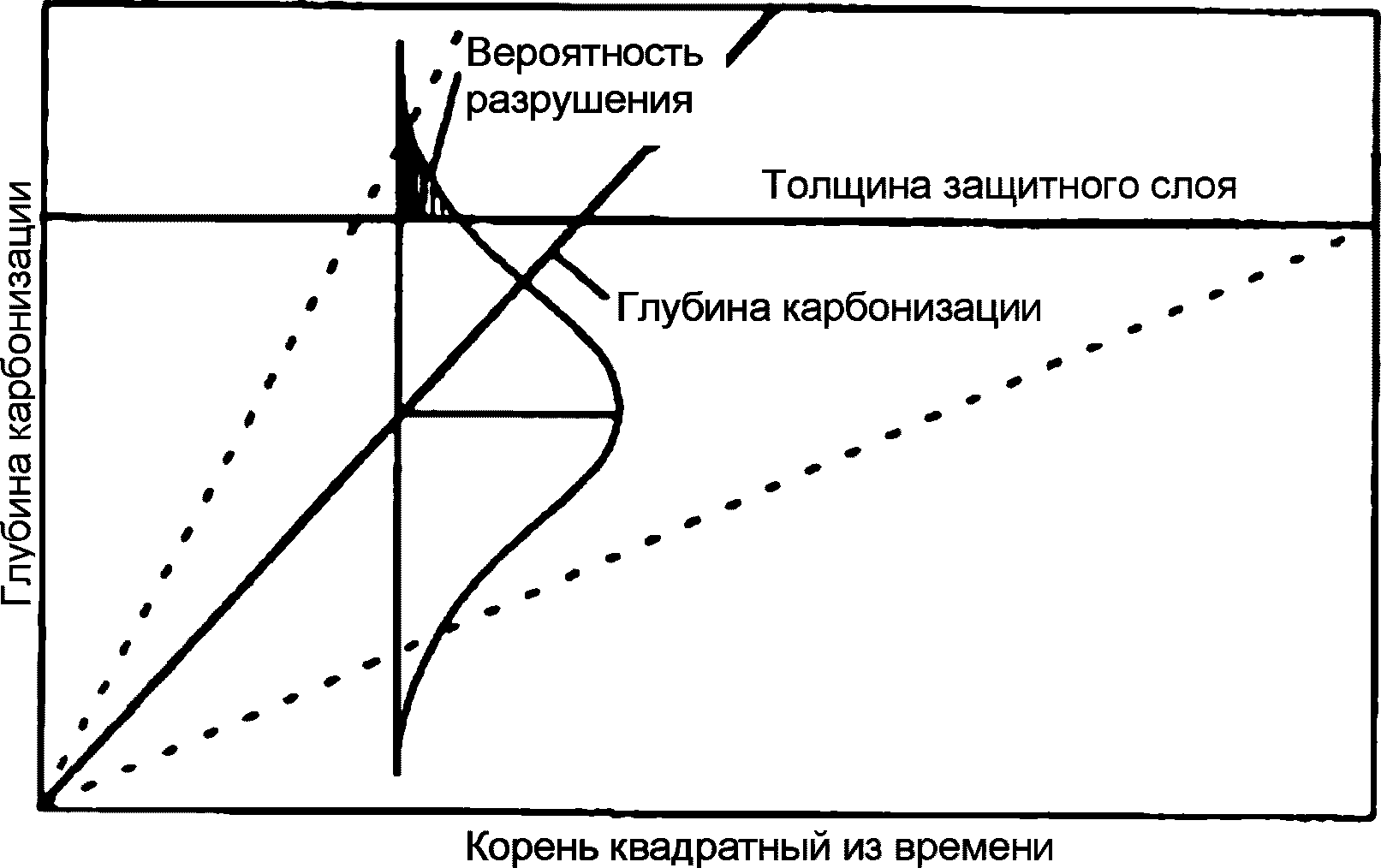
в защитном слое бетона
5.2.2.6 Задание 1. Определить функцию распределения и функцию плотности вероятностей срока службы при условиях:
- конструкция защищена от дождя;
- бетон изготовлен на портландцементе без воздухововлечения;
- нормативная прочность бетона на сжатие 30 МПа;
- толщина защитного слоя бетона 25 мм.
В этом случае предполагаем, что толщина слоя бетона - вероятностная величина. Пусть коэффициент вариации глубины карбонизации равен 0,6, а коэффициент вариации толщины защитного слоя равен 0,2.
Контрольный индекс 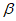 определяем из уравнения (5.1)
определяем из уравнения (5.1)
 (5.6)
(5.6)Функция вероятности распределения и функция плотности вероятности изображены на рисунках 5.2 и 5.3. Следует отметить, что функция вероятности плотности не является нормально распределенной. Плотность вероятности сначала резко возрастает, затем медленно уменьшается с ростом возраста сооружения.
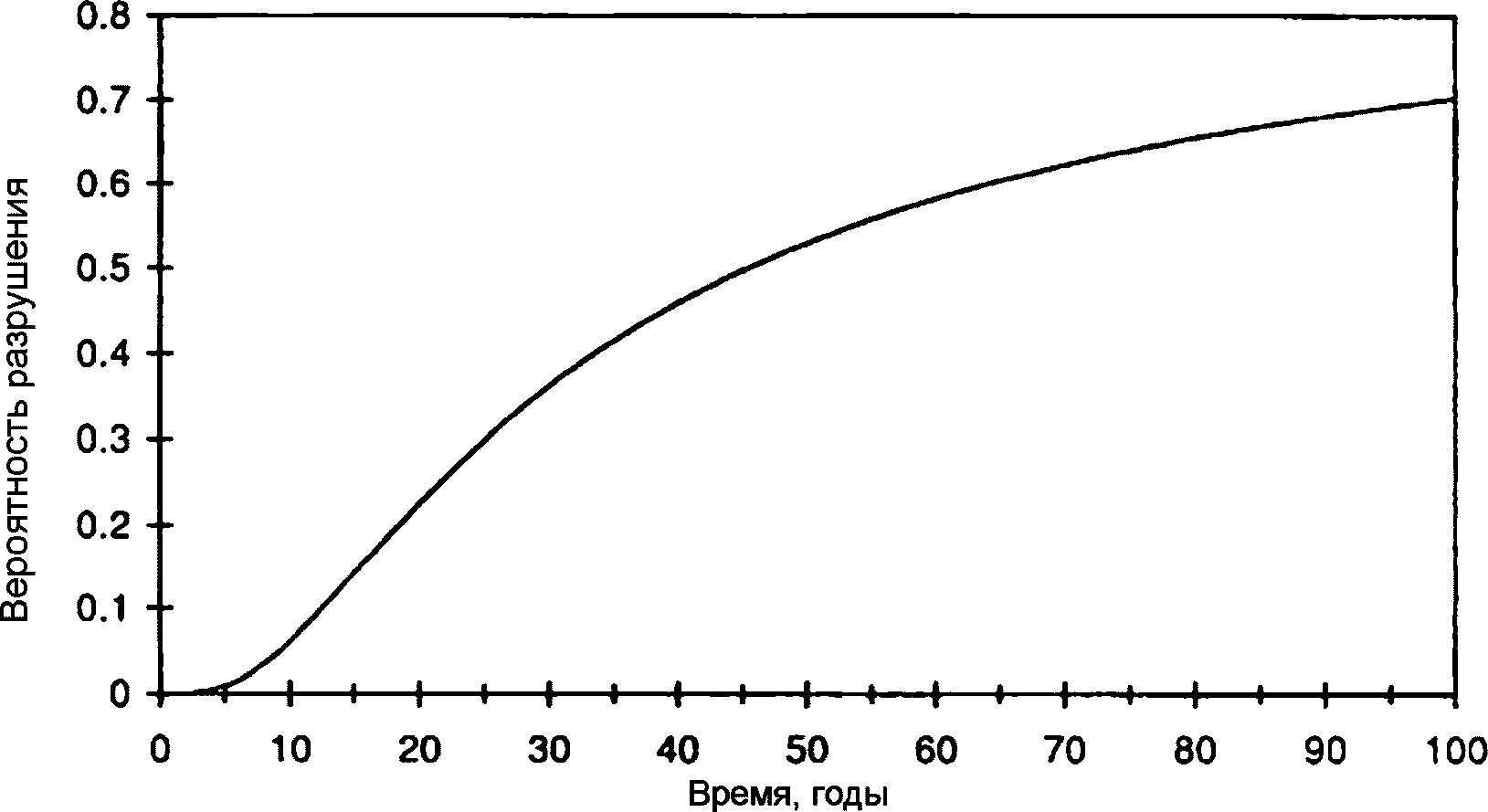
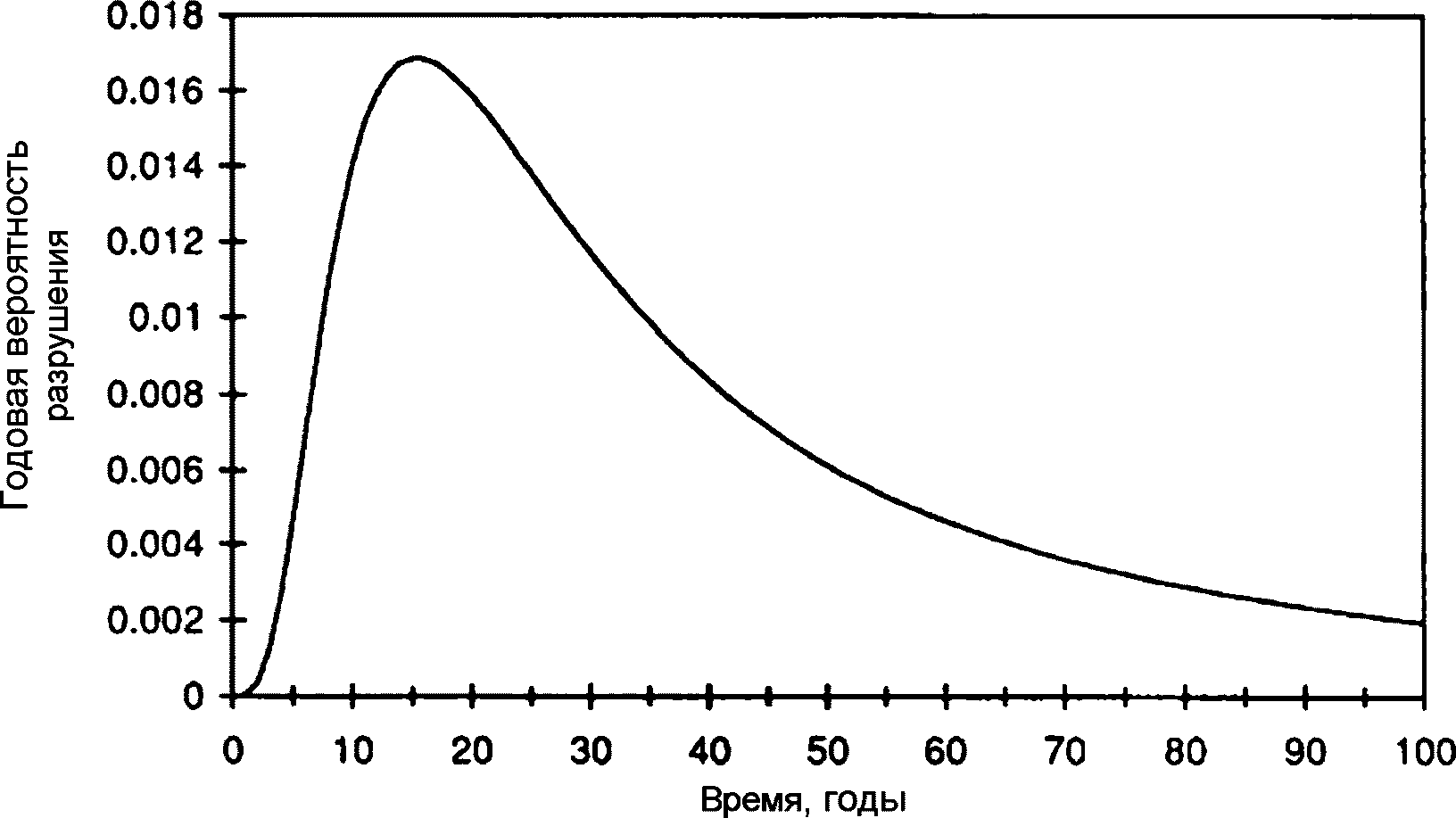
5.2.2.7 Задание 2. Какова требуемая толщина защитного слоя бетона, если заданный срок службы составляет 60 лет с 10%-ной квантилью (вероятность разрушения)?
Для всех вяжущих и для прочностей на сжатие 30, 50 и 70 МПа задача решается по таблице 9.5.
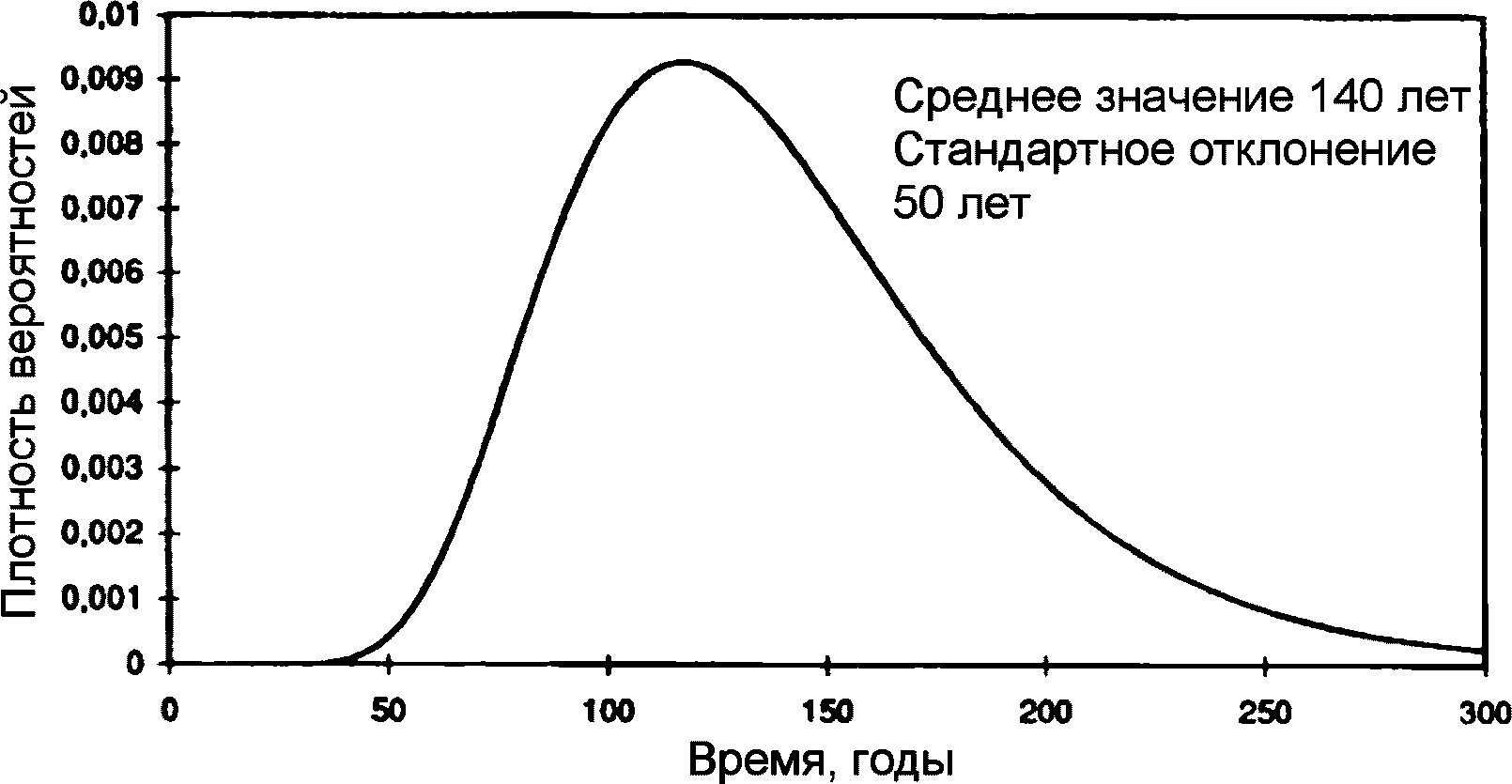
В случае нормального распределения вероятность разрушения, равная 10%, соответствует значению  , равному 1,28. Таким образом, задачу можно сформулировать иначе: какая толщина защитного слоя бетона X даст индекс
, равному 1,28. Таким образом, задачу можно сформулировать иначе: какая толщина защитного слоя бетона X даст индекс  , равный 1,28? Например, для бетона на золе-уноса с прочностью на сжатие 50 МПа значение
, равный 1,28? Например, для бетона на золе-уноса с прочностью на сжатие 50 МПа значение 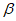 определится из выражения
определится из выражения
 (5.7)
(5.7)Отыскать X не так просто, поскольку эта величина находится как в числителе, так и в знаменателе. Однако задачу можно решить через неравенства. Результаты сведены в таблице 5.1.
Таблица 5.1
Наименование вяжущего | Толщина защитного слоя, мм, при прочности бетона на сжатие, МПа | ||
30 | 50 | 70 | |
Портландцемент | 55 | 27 | 16 |
Портландцемент + 28% золы-уноса | 68 | 41 | 29 |
Портландцемент + 9% микрокремнезема | 75 | 45 | 32 |
Портландцемент + доменный шлак | 68 | 41 | 29 |
5.3.1 Общие положения
5.3.1.1 Как видно из вышеприведенных примеров, несмотря на то, что деградация (глубина карбонизации) была нормально распределена вокруг среднего значения, распределение срока службы обнаружило непрерывное падение в сторону более короткого срока службы. Фактически распределение срока службы чаще всего проявляет именно эту тенденцию. Плотность вероятности резко возрастает, а затем, по мере приближения к бесконечно длительному сроку службы, она плавно опускается, приближаясь к нулю.
5.3.1.2 Для проектирования долговечности часто бывает полезным принять допущение относительно типа распределения срока службы. Его следует выбирать среди кривых, которые имеют опускающуюся ветвь, например, логарифмически нормальное распределение (рисунок 5.4). Логарифмически нормальное распределение означает, что срок службы распределен нормально на логарифмической временной шкале.
срока службы
5.3.1.3 При нормальном распределении (с линейной временной шкалой) уменьшающаяся, но все же конечная вероятность распространяется в обоих направлениях. Из этого следует, что возможен отрицательный срок службы, что, конечно, не может быть принято за действительное решение. То обстоятельство, что на логарифмической временной шкале отрицательные значения невозможны, показывает, что логарифмически нормальное распределение кажется более удобным и наглядным для описания срока службы.
5.3.1.4 Теория логарифмически нормальной аналогии для описания срока службы впервые была применена для решения задач о долговечности бетонных конструкций в [1]. Эта теория содержит кроме того необходимый математический аппарат для определения стандартного отклонения срока службы.
5.3.2 Стандартное отклонение срока службы
5.3.2.1 Стандартное отклонение срока службы определяют с применением модельной формулы для среднего срока службы и стандартных отклонений параметров в формуле. Модельную формулу в общем виде можно записать в следующем виде
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где tL - срок службы;
Xi - параметр материала или условие, или конструктивный размер (i = 1 ... n).
5.3.2.2 Если в уравнение (5.8) вставить средние значения параметров X1, X2, ..., Xn, можно рассчитывать на получение среднеарифметического срока службы 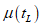 . Стандартное отклонение определяют с помощью формулы
. Стандартное отклонение определяют с помощью формулы
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где  - стандартное отклонение срока службы;
- стандартное отклонение срока службы;
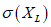 - стандартное отклонение параметра XL;
- стандартное отклонение параметра XL;X1 и n - число переменных.
5.3.3 Вероятности логарифмически нормального распределения срока службы
5.3.3.1 Если распределение срока службы является логарифмически нормальным со средним значением  и стандартным отклонением
и стандартным отклонением  , то функция y = ln(tL) распределена нормально, а ее средняя величина и стандартное отклонение находят по следующим формулам:
, то функция y = ln(tL) распределена нормально, а ее средняя величина и стандартное отклонение находят по следующим формулам:
 (5.10)
(5.10)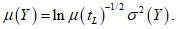 (5.11)
(5.11)Вероятность срока службы, будучи короче некоего времени t, определяется следующим образом
 (5.12)
(5.12)где
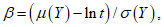 (5.13)
(5.13)а 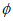 является кумулятивной функцией плотности для стандартного нормального распределения (
является кумулятивной функцией плотности для стандартного нормального распределения (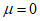 ,
, 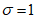 ).
).
5.3.4 Пример
5.3.4.1 Для определения срока службы конструкции по коррозии арматуры применяют уравнение (5.14). Первое выражение в уравнении - время начала коррозии (см. 9.5.3). Второе выражение - время образования трещин, ведущих к коррозии (см. 9.5.4).
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где Cenv - коэффициент воздействия окружающей среды;
Cair - коэффициент содержания воздуха;
C - толщина защитного слоя бетона, мм;
D - диаметр арматурного стержня, мм;
fck - нормативная кубиковая прочность бетона, МПа;
r - скорость коррозии арматуры;
a и b - постоянные.
Значения Cenv, Cair, a и b приведены в таблице 5.2.
Таблица 5.2
и коэффициенты вариации
Обозначение переменной | Среднее значение | Коэффициент вариации | ||||
Cenv | 0,5; 1 | 0,5 | ||||
Cair | 1 | 0,4 | ||||
C, мм | 15; 20; 25; 30; 35 | 0,3 | ||||
D, мм | 25 | 0 | ||||
fck, МПа | 30 | 0,2 | ||||
a | 1800 | 0 | ||||
b | -1,7 | 0 | ||||
| ||||||
r, мкм/год | 16 1 | 0,5 | ||||
5.3.4.2 В формуле стандартного отклонения (уравнение 5.9) неизвестны стандартные отклонения или коэффициенты вариации всех параметров. В таблице 5.2 приведены средние величины и коэффициенты вариации переменных, входящих в состав задачи. Если коэффициенты вариации неизвестны, то их приходится определять приближенно.
Для того, чтобы воспользоваться уравнением (5.9), необходимо выполнить частичное дифференцирование каждой переменной. Если образцовая формула для определения средней величины не слишком сложна, то расчет выполняется алгебраически.
5.3.4.3 Среднее и стандартное отклонения срока службы можно определить подстановкой в формулы средних значений переменных. Таким образом, в нашем примере, если конструкция защищена от дождя (Cenv = 1,  ), а толщина защитного слоя бетона равна 25 мм, мы получаем
), а толщина защитного слоя бетона равна 25 мм, мы получаем
 ), а толщина защитного слоя бетона равна 25 мм, мы получаем
), а толщина защитного слоя бетона равна 25 мм, мы получаем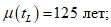
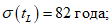
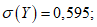
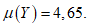
5.3.4.4 Используя таблицы стандартного нормального отклонения и значения 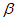 для t = 10, 20, 30 и т.д. лет, можно подсчитать соответствующие вероятности разрушения.
для t = 10, 20, 30 и т.д. лет, можно подсчитать соответствующие вероятности разрушения.
5.3.4.5 На рисунках 5.5 и 5.6 изображены кумулятивные функции вероятности, определенные для различных значений толщины защитного слоя бетона. Из рисунков видно, что вероятность срока службы короче заданного срока службы tg. Требуемую толщину защитного слоя бетона можно определить по графикам как функцию заданного срока службы приемлемой вероятности разрушения.
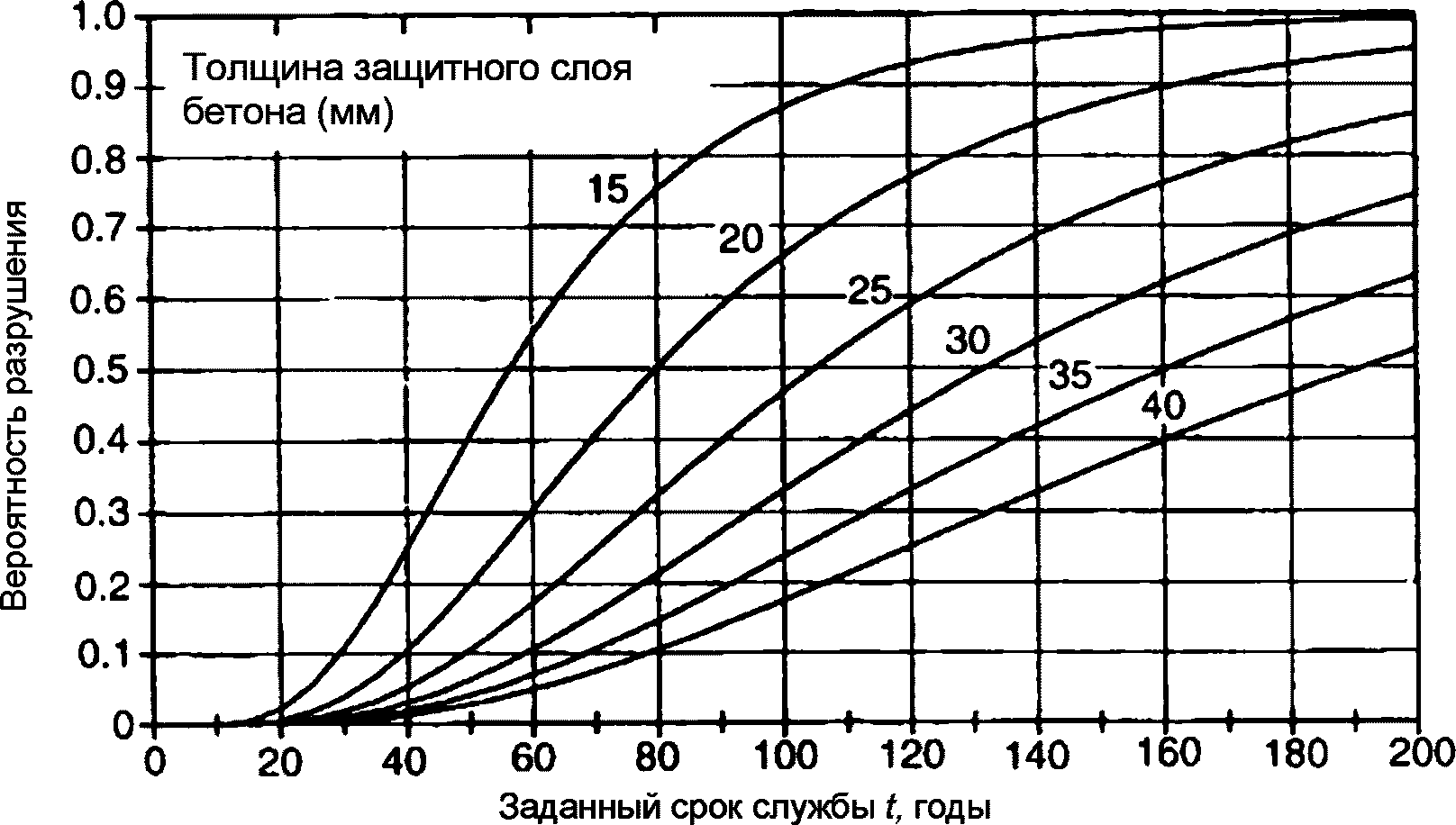
Примечание - Нормативная кубиковая прочность бетона равна 30 МПа, а диаметр арматуры равен 25 мм.
срока службы в случае, когда конструкция защищена от дождя
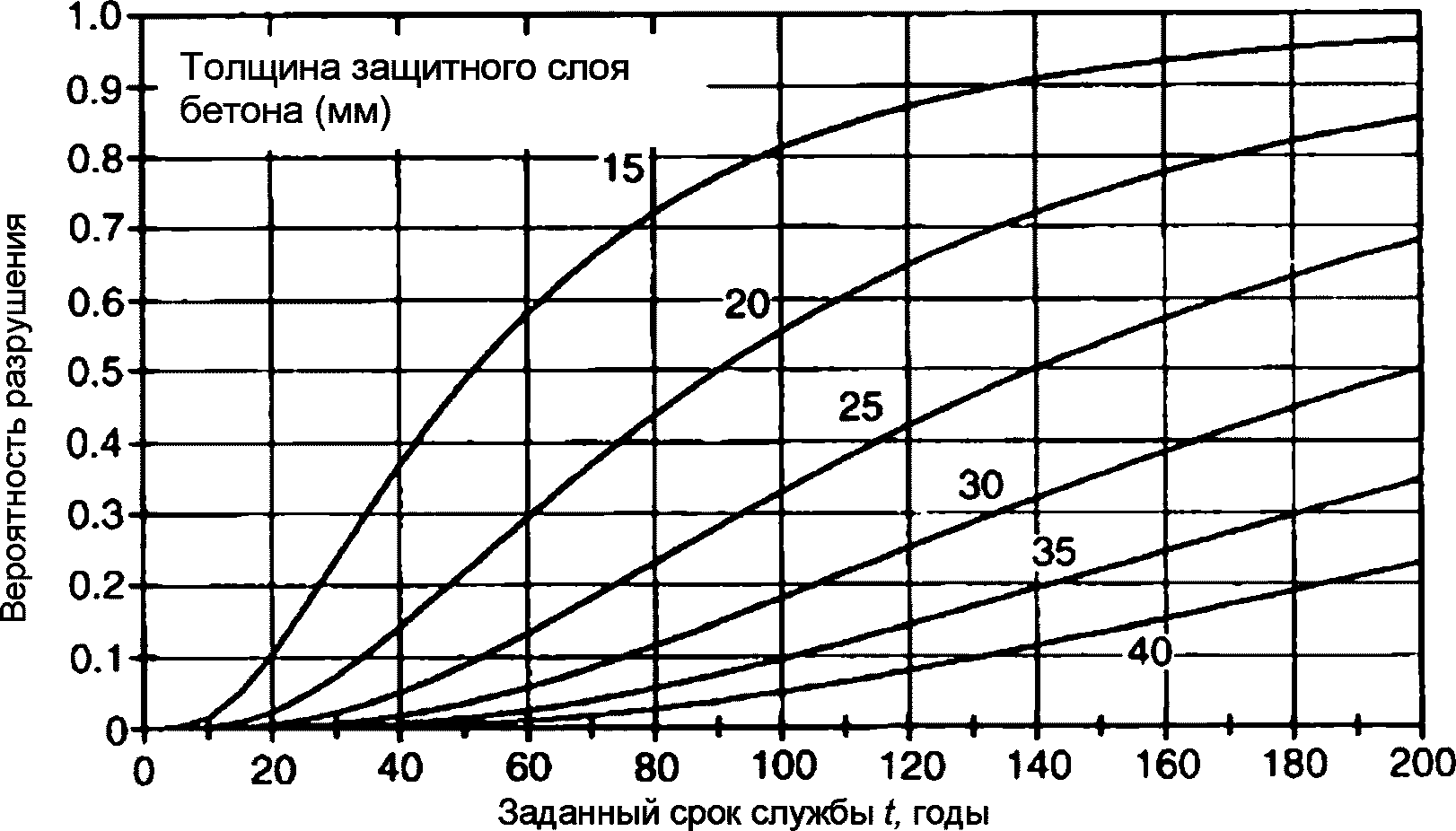
Примечание - Кубиковая прочность бетона равна 30 МПа, а диаметр арматуры равен 25 мм.
срока службы в случае, когда конструкция не защищена
от дождя
5.3.4.6 При работе логарифмически нормальным распределением, прежде чем пользоваться образцовой формулой, нужно установить некоторые дополнительные требования. Одно из таких ограничений состоит в том, что математическая модель срока службы не должна быть слишком сложной, поскольку она должна оставаться дифференциальной относительно любого параметра, входящего в ее состав. Другое условие состоит в том, что эти параметры не должны быть "родственны" один другому; если они будут таковыми, то при определении стандартного отклонения могут проявиться нежелательные взаимосвязи.
6.1.1 В проектировании конструкций метод применения коэффициента надежности по сроку службы основан на тех же принципах безопасности, которые применяют в изложенных выше вероятностных методах. С помощью коэффициента надежности по сроку службы задача снова приобретает форму детерминистического проектирования.
6.1.2 На рисунке 6.1 приведено распределение срока службы и зависимости между заданным сроком службы, вероятностью разрушения и средним сроком службы.
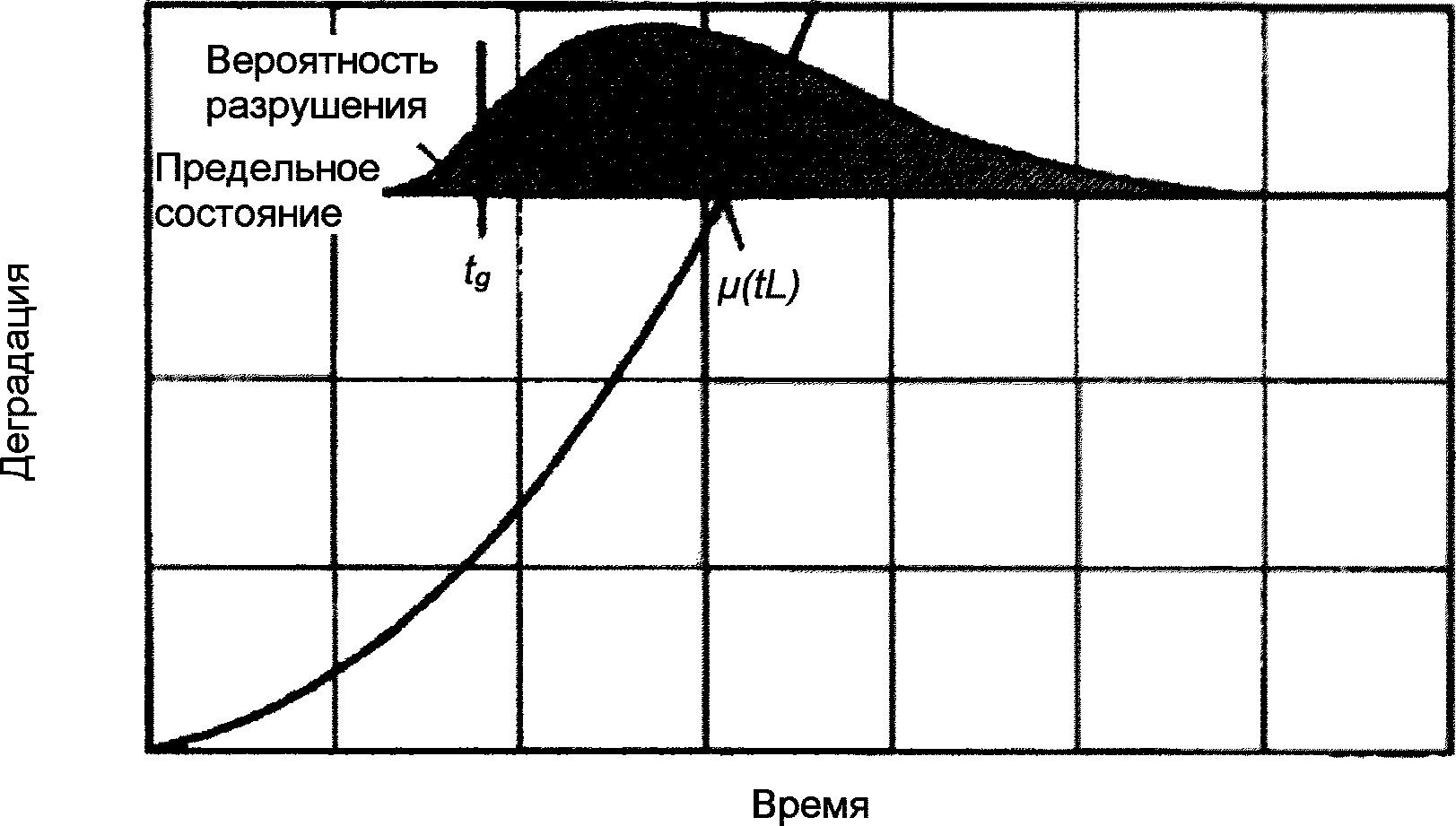
и заданным сроком службы
6.1.3 Коэффициент надежности по сроку службы представляет собой отношение среднего срока службы к заданному сроку службы.
 (6.1)
(6.1)где 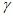 - центральный коэффициент надежности по сроку службы;
- центральный коэффициент надежности по сроку службы;
tg - заданный срок службы.
6.1.4 При использовании коэффициента надежности по сроку службы требование о заданном сроке службы (соответствующее максимально допустимой вероятности разрушения) преобразуется в требование о среднем сроке службы. Причина этого заключается в том, что доступные проектировщикам математические модели долговечности показывают только среднее значение работоспособности, или среднюю величину деградации, или средний срок службы. Поскольку проектировщики имеют дело со средними значениями функций, любое требование по заданному сроку службы должно быть, прежде всего, выражено через соответствующий средний срок службы.
6.1.5 При проектировании долговечности конструкций средний срок службы часто приближенно определяют с помощью математических моделей срока службы как точку пересечения кривой деградации с линией предельного состояния по долговечности (рисунок 6.1). Средний срок службы, определенный по математической модели срока службы, должен превышать или быть равным расчетному сроку службы - произведению коэффициента надежности по сроку службы и заданного срока службы:
 (6.2)
(6.2)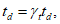 (6.3)
(6.3)где td - расчетный срок службы.
Следует отметить, что средний срок службы не обязательно совпадает с соответствующей 50%-ной вероятностью разрушения - среднестатистическим значением срока службы.
6.1.6 Значение коэффициента надежности по сроку службы зависит от максимально допустимой вероятности разрушения: чем меньше максимально допустимая вероятность разрушения, тем большим будет коэффициент надежности по сроку службы. Кроме того, коэффициент надежности по сроку службы зависит от распределения срока службы.
6.1.7 Рисунок 6.2 иллюстрирует сущность коэффициента надежности по сроку службы в условиях, когда проектирование ведут в соответствии с принципом работы. Кривые на рисунке соответствуют проектной задаче по определению несущей способности. S может представлять собой воздействие на конструкцию нагрузки, а R(t) - несущую способность конструкции, которая во избежание разрушения должна быть больше, чем S. Функцию R(t) - S называют полем безопасности.
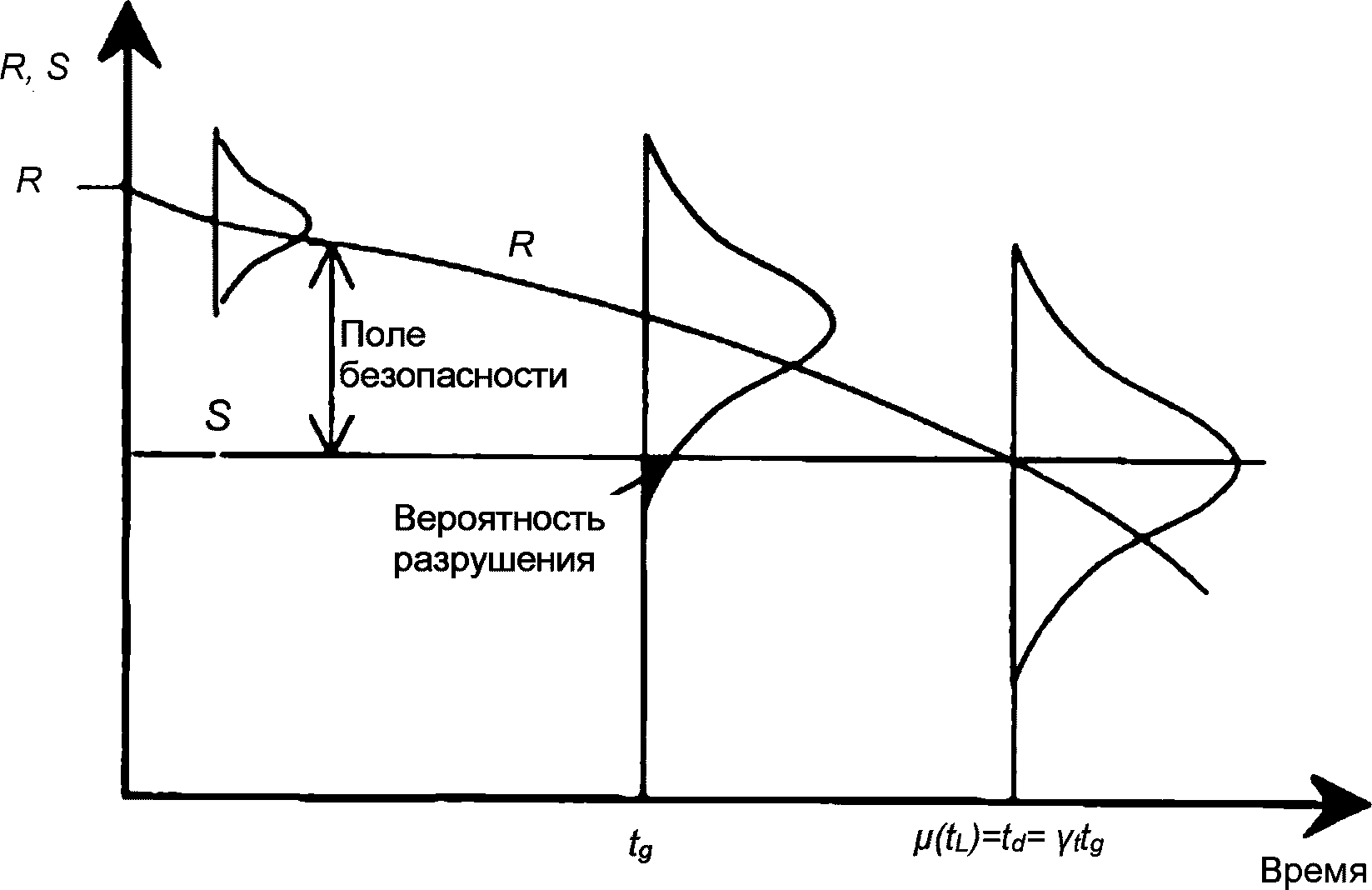
службы в задаче, основанной на принципе работы
6.1.8 Работоспособность конструкции падает со временем из-за деградации материалов. Точка пересечения кривой R(t) с минимальным значением воздействия нагрузки S дает средний срок службы, который равен расчетному сроку службы. Если бы заданный срок службы совпадал с расчетным сроком службы, то, грубо говоря, несущая способность половины всех сооружений оказалась бы ниже, чем действующая на конструкцию нагрузка. Для уменьшения вероятности разрушения при заданном сроке службы, расчетный срок службы должен быть большим, чем заданный срок службы.
6.1.9 В общем случае R(t) представляет собой показатель работоспособности конструкции. S, которая в задаче о работоспособности конструкции отражает воздействие нагрузки, во многих других разделах проектирования долговечности заменяют минимальной работоспособностью конструкции Rmin.
6.1.10 Работоспособность конструкции всегда можно выразить через деградацию. По определению деградация является снижением работоспособности. Переход одной в другую осуществляют путем следующих подстановок
R0 - R(t) = D(t) (6.4)
или
R0 - S = Dmax; (6.5a)
R0 - Rmin = Dmax. (6.5b)
6.1.11 На рисунке 6.3 проиллюстрирован принцип проектирования с применением задачи с деградацией. D(t) представляет собой деградационное влияние нагрузки внешней среды на работоспособность конструкции. Кривая деградации пересекается с максимальной деградацией в точке, соответствующей расчетному сроку службы, причем он должен быть длиннее, чем заданный срок службы. Диапазон Dmax - D(t) - поле безопасности.
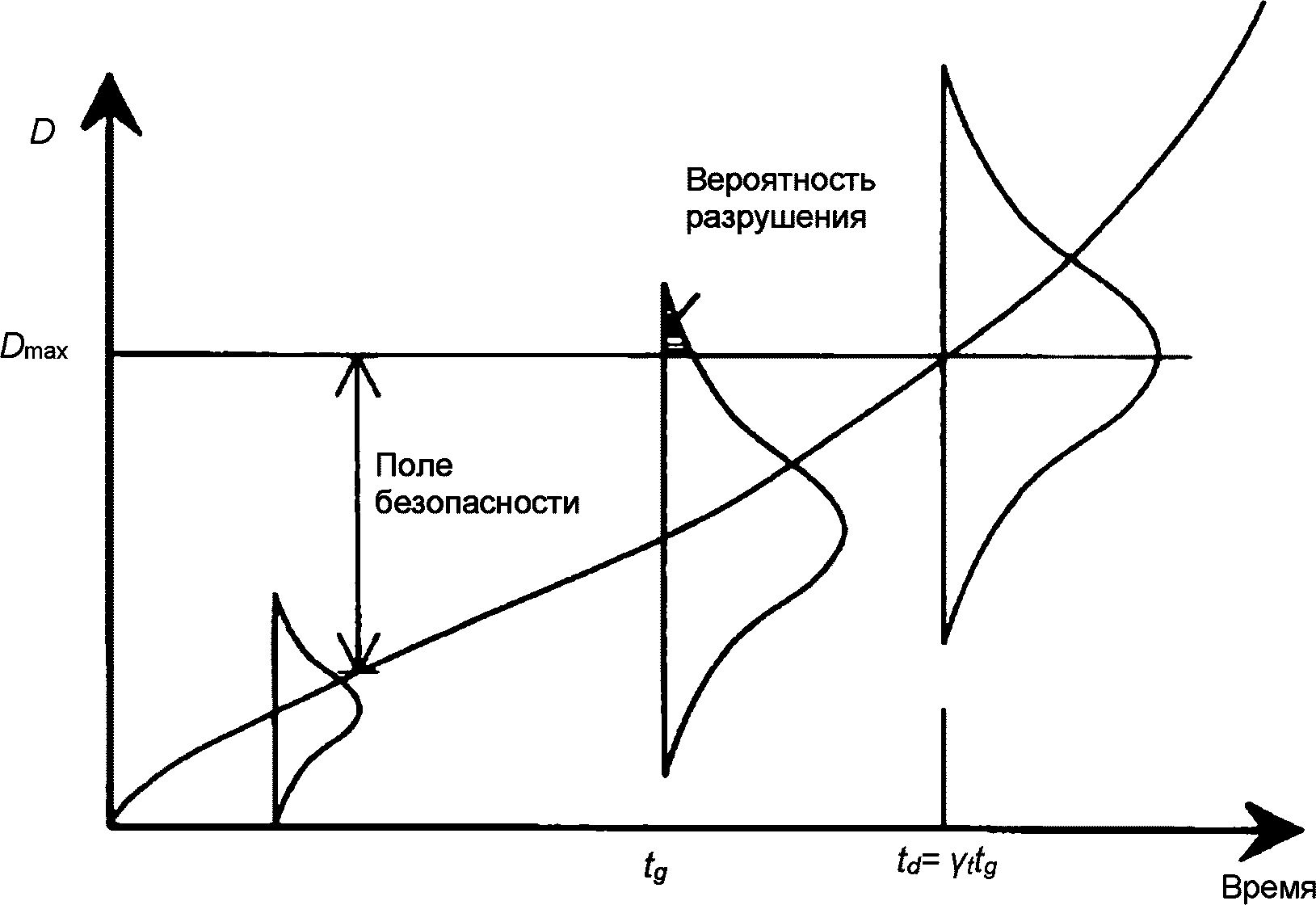
службы в решении задачи о деградации
6.1.12 Обязательное условие применения коэффициента надежности по сроку службы состоит, в конечном счете, в том, что должны быть известны точные значения коэффициентов надежности по сроку службы, поэтому далее рассмотрены вопросы определения коэффициентов надежности по сроку службы различными путями. Практическое применение метода коэффициента надежности по сроку службы изложено в разделе 7.
6.2.1 Определение коэффициента надежности с функцией нормального распределения деградации
6.2.1.1 Предположим, что функция деградации имеет следующий вид
 (6.6)
(6.6)где 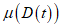 - среднее значение деградации;
- среднее значение деградации;
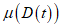 - среднее значение деградации;
- среднее значение деградации;a - постоянный коэффициент;
t - время;
n - экспонента.
6.2.1.2 В принципе, значение экспоненты n может изменяться от  до
до  . Коэффициент a строго определен при известном среднем сроке службы
. Коэффициент a строго определен при известном среднем сроке службы
 (6.7)
(6.7)6.2.1.3 Предположим, что функция деградации нормально распределена вокруг своего среднего значения. Предположим также, что стандартное отклонение D пропорционально средней величине деградации, а коэффициент вариации VD - постоянен.
6.2.1.4 На рисунке 6.4 деградация изображена как функция tn. Значение  можно определить нижеприведенным способом [2]. Индекс
можно определить нижеприведенным способом [2]. Индекс 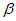 стандартного нормального распределения при tg определяем по формуле
стандартного нормального распределения при tg определяем по формуле
где Dmax - максимальная допустимая деградация;
Dg - среднее значение деградации при tg;
VD - коэффициент вариации деградации.
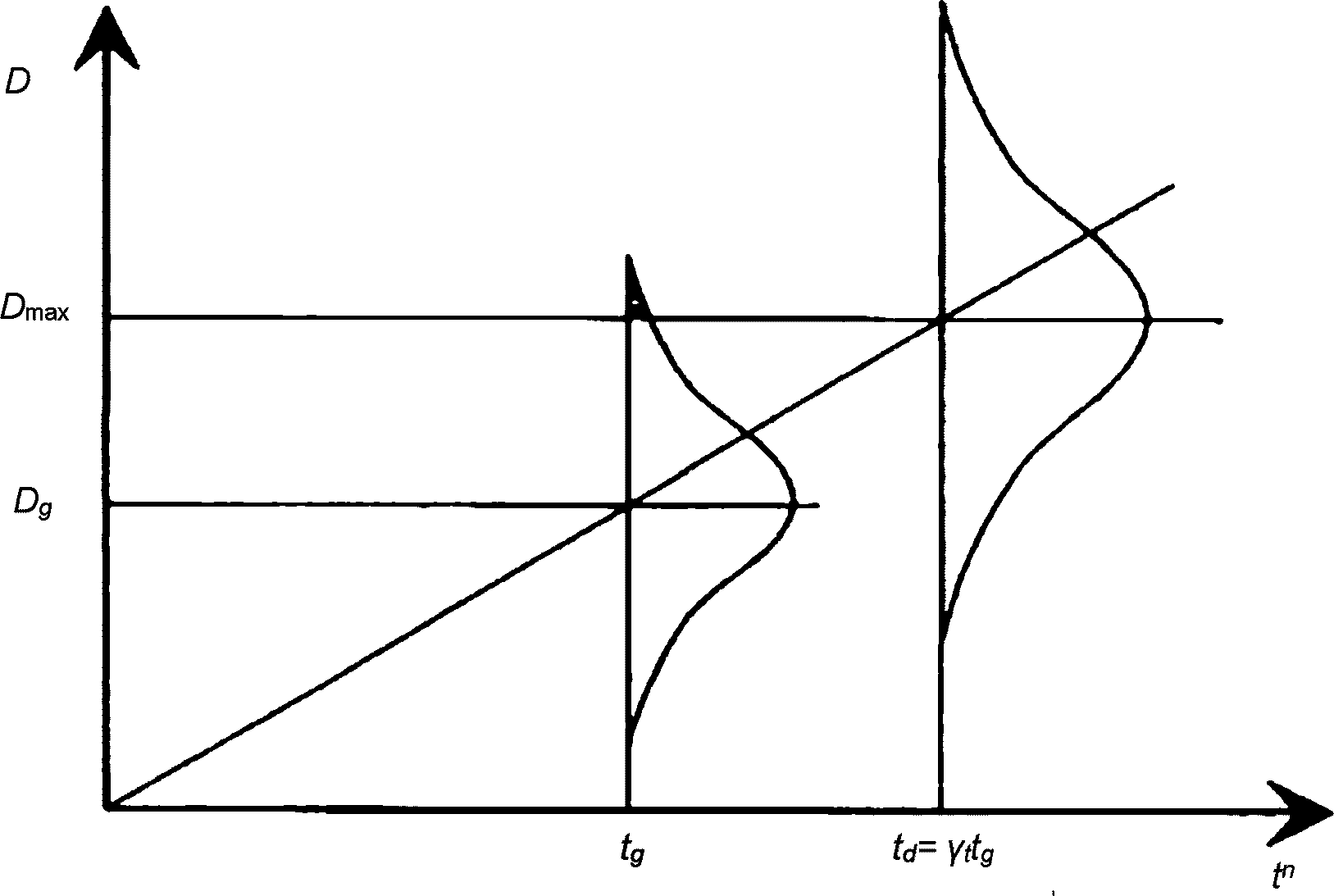
службы при нормальном распределении D
6.2.1.5 По рисунку 6.4 получаем
6.2.1.6 Коэффициент надежности по сроку службы зависит от  (в соответствии с максимально допустимой вероятностью tg), коэффициента вариации VD и экспоненты n. При этом коэффициент надежности по сроку службы напрямую не зависит от tg.
(в соответствии с максимально допустимой вероятностью tg), коэффициента вариации VD и экспоненты n. При этом коэффициент надежности по сроку службы напрямую не зависит от tg.
6.2.1.7 Далее рассмотрим значения  как функцию
как функцию 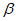 , VD и n. Примем для n: n = 1 (линейная деградация), n = 0,5 (замедленная деградация), n = 2 (ускоренная деградация). В таблицах 6.1 - 6.3 приведены значения коэффициента надежности по сроку службы для значений
, VD и n. Примем для n: n = 1 (линейная деградация), n = 0,5 (замедленная деградация), n = 2 (ускоренная деградация). В таблицах 6.1 - 6.3 приведены значения коэффициента надежности по сроку службы для значений  , соответствующих вероятностям разрушения, равным 1, 5, 10, 20 и 50%.
, соответствующих вероятностям разрушения, равным 1, 5, 10, 20 и 50%.
Таблица 6.1
линейна (n = 1)
Вероятность разрушения, % | Значение | ||
0,5 | 1,0 | ||
1 | 2,33 | 2,16 | 3,33 |
5 | 1,64 | 1,82 | 2,64 |
10 | 1,28 | 1,64 | 2,28 |
50 | 0 | 1,00 | 1,00 |
Таблица 6.2
Значения коэффициента надежности по сроку службы. Деградация
пропорциональна корню квадратному из времени (n = 1/2);
замедленная деградация
Вероятность разрушения, % | Значение | ||
0,5 | 1,0 | ||
1 | 2,33 | 4,64 | 11,06 |
5 | 1,64 | 3,32 | 7,00 |
10 | 1,28 | 2,69 | 5,21 |
50 | 0 | 1,00 | 1,00 |
Таблица 6.3
пропорциональна корню квадратному из времени (n = 2);
ускоренная деградация
Вероятность разрушения, % | Значение | ||
0,5 | 1,0 | ||
1 | 2,33 | 1,47 | 1,82 |
5 | 1,64 | 1,35 | 1,63 |
10 | 1,28 | 1,23 | 1,51 |
50 | 0 | 1,00 | 1,00 |
6.2.2 Определение коэффициента надежности с функцией логарифмически нормального срока службы
6.2.2.1 Предположим, что функция распределения срока службы логарифмически нормальная. Этот вид распределения уже был рассмотрен в 5.3.
6.2.2.2 Подставляя в уравнения (6.10), (6.11) и (6.12) значения t = tg, 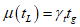 и
и 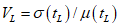 , получим следующее выражение для определения
, получим следующее выражение для определения 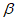
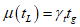 и
и 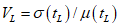 , получим следующее выражение для определения
, получим следующее выражение для определения где  - коэффициент надежности по сроку службы;
- коэффициент надежности по сроку службы;
VL - коэффициент вариации срока службы.
6.2.2.3 Коэффициент надежности по сроку службы получим из выражения
6.2.2.4 Таким образом, коэффициент надежности по сроку службы зависит от индекса  и от коэффициента вариации срока службы, но он непосредственно не зависит от срока службы. В таблице 6.4 приведены коэффициенты надежности по сроку службы, подсчитанные для различных значений
и от коэффициента вариации срока службы, но он непосредственно не зависит от срока службы. В таблице 6.4 приведены коэффициенты надежности по сроку службы, подсчитанные для различных значений 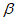 .
.
Таблица 6.4
по методу логарифмически нормального распределения
Вероятность разрушения, % | Коэффициент надежности по сроку службы при коэффициенте вариации VL, равном | |
0,3 | 1,0 | |
1 | 3,36 | 9,81 |
3 | 2,43 | 3,36 |
10 | 2,03 | 4,11 |
30 | 1,12 | 1,41 |
6.3 Определение коэффициентов надежности по сроку службы при проектировании долговечности конструкций
6.3.1 Общие принципы
6.3.1.1 Главную идею процесса проектирования железобетонных конструкций можно выразить следующим образом
Rd - Sd > 0 (6.13)
или
где Rd - расчетное значение несущей способности;
Sd - расчетное значение нагрузки;
6.3.1.2 Расчетное значение несущей способности определяют путем деления значения нормативной прочности бетона на коэффициент надежности по материалу для бетона и нормативной прочности арматурной стали на коэффициент надежности по материалу для стали, а далее пользуясь обычными расчетными формулами для определения несущей способности. Расчетное значение нагрузки получают перемножением величины нормативных нагрузок на их соответствующие коэффициенты надежности.
6.3.1.3 Поскольку частные коэффициенты надежности определяют при условии выполнения требований прочностной безопасности, состояние конструкции, при котором Rd равно Sd, соответствует требуемому уровню безопасности. Если Rd оказывается меньшим, чем Sd, это не означает, что конструкция обрушится или произойдут какие-либо иные физические разрушения. Фактически это означает, что не выполнены требования по соблюдению уровня безопасности. Степень надежности, выраженную в соблюдении условия оставаться выше уровня безопасности, называют надежностью долговечности, и она отличается от прочностной безопасности. Соответственно, термин "нарушение долговечности" необходимо отличать от физического разрушения.
6.3.1.4 Процесс проектирования долговечности конструкции весьма схож с обычным конструктивным проектированием. Однако несущая способность - свойство, зависящее от времени, потому что качество материалов бетона и стали зависит от времени. Возможно, что и нагрузка зависит от времени. Таким образом, основная расчетная формула (6.14) теперь принимает вид
где td - расчетный срок службы.
6.3.1.5 На рисунке 6.5 показано сокращение расчетного поля безопасности во времени. Нулевая линия на рисунке отображает минимальное значение  , которое еще соответствует требованиям уровня безопасности. Начальное значение
, которое еще соответствует требованиям уровня безопасности. Начальное значение  должно быть выше этого значения, потому что оно должно оставаться достаточным и при окончании срока службы сооружения. Анализ изменения значения расчетного поля безопасности во времени показывает, что вероятность опускания ниже уровня безопасности во времени возрастает из-за падения среднего значения
должно быть выше этого значения, потому что оно должно оставаться достаточным и при окончании срока службы сооружения. Анализ изменения значения расчетного поля безопасности во времени показывает, что вероятность опускания ниже уровня безопасности во времени возрастает из-за падения среднего значения  и из-за увеличения разброса.
и из-за увеличения разброса.
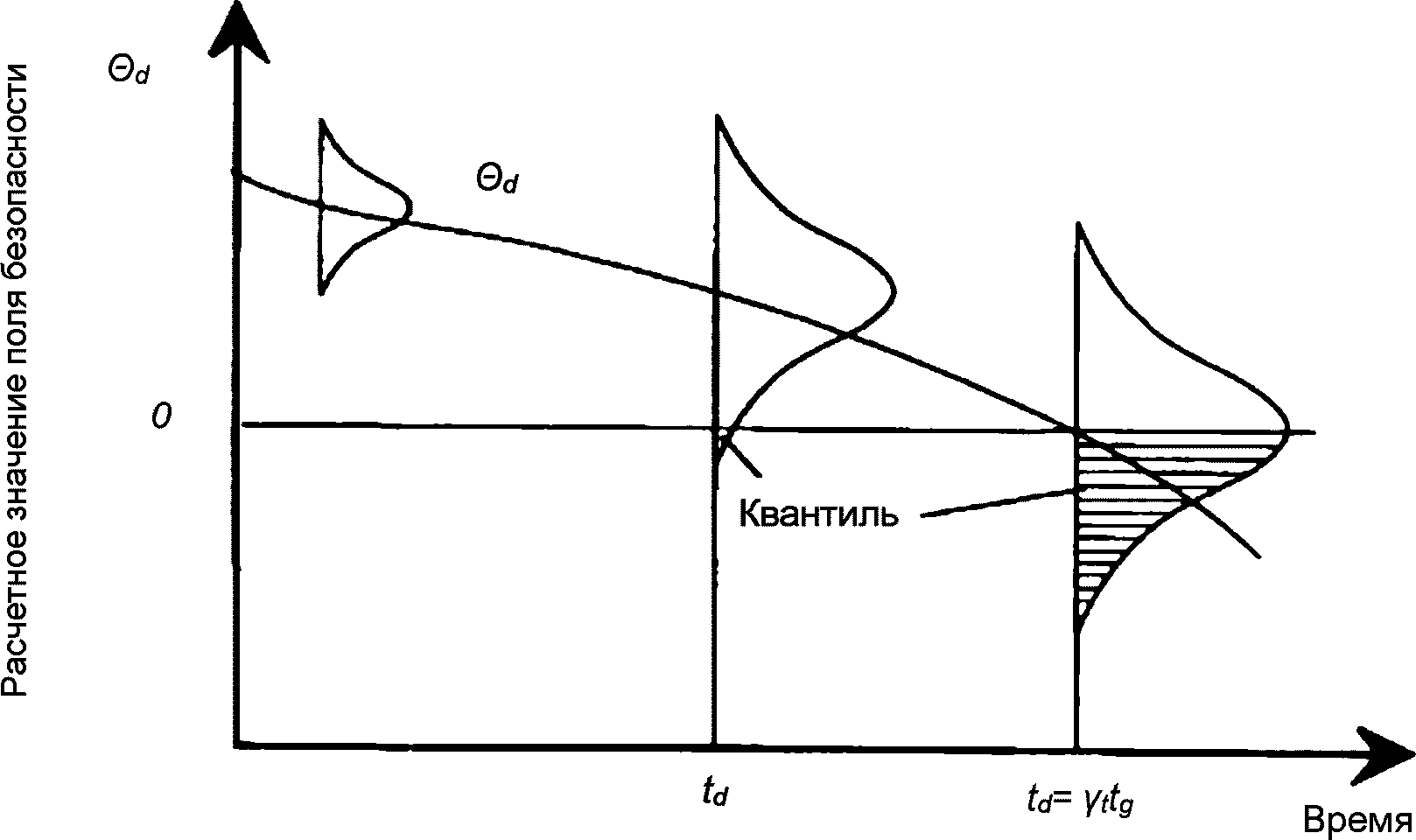
и влияние коэффициента надежности по сроку службы,
определенного по расчетным значениям нагрузок
и несущих способностей
Из рисунка 6.5 также видно, почему в расчетном уравнении (6.15) нужно использовать "расчетный срок службы", а не "заданный срок службы". Если конструкция была бы запроектирована на заданный срок службы tg, то половина сооружений в возрасте, равном заданному сроку службы, не соответствовала бы требованиям по обеспечению необходимого уровня безопасности. Для того, чтобы уменьшить квантиль сооружений, не соответствующих требованиям безопасности к моменту наступления заданного срока службы, в расчетные формулы необходимо закладывать более продолжительный расчетный срок службы.
6.3.1.6 Требуемая разница между расчетным сроком службы и заданным сроком службы определяется коэффициентом надежности по сроку службы. Этот метод в значительной степени напоминает метод обработки вероятностей прочностей и нагрузок в формуле конструктивного расчета. Для получения расчетного срока службы заданный срок службы умножают на коэффициент надежности по сроку службы.
6.3.1.7 Коэффициент надежности по сроку службы должен быть таким, чтобы вероятность снижения ниже требуемого уровня безопасности против разрушения из-за деградации (вероятность потери долговечности) оставалась меньшей, чем требуемая. Чем меньше требуемая вероятность потери долговечности, тем больше коэффициент надежности по сроку службы.
6.3.1.8 Существуют два подхода для определения требуемой вероятности потери долговечности и соответствующего коэффициента надежности по сроку службы: принцип разделенной безопасности и принцип комбинированной безопасности.
В соответствии с принципом разделенной безопасности требование о физической прочности и требование о долговечности налагают раздельно.
Принцип комбинированной безопасности подразумевает, что долговечность - один из нескольких элементов, которые обеспечивают общую прочностную безопасность. Таким образом, требуемая вероятность потери долговечности ассоциируется с требованием о прочностной безопасности.
6.3.2 Определение коэффициентов надежности по сроку службы с использованием принципа разделенной безопасности
6.3.2.1 Принцип разделенной безопасности означает разделение требований по долговечности и по прочностной безопасности. Однако в этом контексте в [3] требования к прочностной безопасности было решено применить также и к безопасности по долговечности. В соответствии с этим требованием надежность против потери долговечности к концу заданного срока службы должна быть такой же, что и кратковременная надежность против физического разрушения в обычном процессе конструктивного проектирования. Некоторые основания для подобного решения приведены в 6.3.3.
6.3.2.2 Требуемые [3] коэффициенты безопасности для обычного проектирования следующие:
- критическое предельное состояние:  (Pf = 7,2 x 10-5)
(Pf = 7,2 x 10-5)
 (Pf = 7,2 x 10-5)
(Pf = 7,2 x 10-5)- предельное состояние по эксплуатационной пригодности:  (Pf = 6,7 x 10-2) [3].
(Pf = 6,7 x 10-2) [3].
 (Pf = 6,7 x 10-2) [3].
(Pf = 6,7 x 10-2) [3].6.3.2.3 Критическое предельное состояние ассоциируется с обрушением или с иными аналогичными формами физического разрушения. Обычно это соответствует максимальному сопротивлению по несущей способности всей конструкции или ее отдельного элемента. Предельные состояния по эксплуатационной пригодности соответствуют условиям, за пределами которых эксплуатационные требования к конструкции или к ее отдельному элементу более не выполняются.
6.3.2.4 Эксплуатационные требования относятся к:
- функционированию конструкции или ее частей;
- удобству эксплуатации;
- внешнему виду [3].
6.3.2.5 Если потеря долговечности в расчетах по предельному состоянию не ведет к серьезным последствиям, можно допустить немного меньшее значение 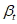 , чем то, которое оговорено в [3] для физической безопасности. С другой стороны, если последствия потери долговечности в расчетах на эксплуатационную пригодность значительны и стоимость возможных ремонтных работ высока, коэффициенту безопасности следует назначать несколько большую величину, чем та, которая предписывается [3]. Таким образом, окончательные требования по обеспечению долговечности приобретают следующие формы:
, чем то, которое оговорено в [3] для физической безопасности. С другой стороны, если последствия потери долговечности в расчетах на эксплуатационную пригодность значительны и стоимость возможных ремонтных работ высока, коэффициенту безопасности следует назначать несколько большую величину, чем та, которая предписывается [3]. Таким образом, окончательные требования по обеспечению долговечности приобретают следующие формы:
1) критическое предельное состояние:
 (серьезные последствия потери долговечности);
(серьезные последствия потери долговечности);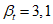 (нет серьезных последствий потери долговечности);
(нет серьезных последствий потери долговечности);2) предельное состояние по эксплуатационной пригодности:
 (последствия потери долговечности значительны, и стоимость ремонта высока);
(последствия потери долговечности значительны, и стоимость ремонта высока);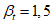 (нет заметных последствий потери долговечности).
(нет заметных последствий потери долговечности).6.3.2.6 Соответствующие коэффициенты надежности по сроку службы определяют из уравнения (6.10). При этом подразумевается линейный характер процесса деградации (n = 1). По таблице 6.5 определяют коэффициенты надежности по сроку службы для разных значений коэффициента вариации (VD).
Таблица 6.5
Предельное состояние | Класс безопасности (последствие потери долговечности) | Вероятность потери долговечности (после времени tg), Pf | Коэффициент безопасности (после времени tg), | Коэффициент надежности по сроку службы | ||
0,4 | 0,6 | 0,8 | ||||
Критическое | 1 (серьезное) | 7,2·10-5 | 3,8 | 2,52 | 3,23 | 4,04 |
Предельное | 2 (не серьезное) | 9,7·10-4 | 3,1 | 2,24 | 2,86 | 3,48 |
Предельное состояние по эксплуатационной пригодности | 1 (заметное) | 6,2·10-3 | 2,5 | 2,00 | 2,50 | 3,00 |
2 (не заметное) | 6,7·10-2 | 1,5 | 1,60 | 1,90 | 2,20 | |
6.3.3 Определение коэффициентов надежности по сроку службы с использованием принципа комбинированной безопасности
6.3.3.1 В соответствии с принципом комбинированной безопасности требование о долговечной безопасности определяют на основании ее влияния на прочностную безопасность. Требуемые коэффициенты надежности по сроку службы определяют на основании расчета по расчетным значениям нагрузок и несущих способностей, в то время, как требования к обеспечению общей прочностной безопасности определяют по расчетным значениям прочностных характеристик. Кроме того, дополнительный разброс, вызванный деградацией (см. рисунок 6.5), накладывается на обычный разброс поля безопасности (обычный разброс по нагрузкам и по несущей способности).
6.3.3.2 Требования традиционного проектирования в [3] относительно прочностной безопасности (см. 6.3.2) ссылаются на поля безопасности, подсчитанные по нормативным значениям характеристик материалов и нагрузок. Это обстоятельство позволяет осуществлять графическую интерпретацию требований безопасности в критическом предельном состоянии, что и показано на рисунке 6.6. Изображенное на рисунке 6.6 и являющееся средним "нормативным" поле безопасности  определяют по формуле
определяют по формуле
где Rk - нормативная несущая способность (по критическому предельному состоянию) или иное состояние конструкции (предельное состояние по эксплуатационной пригодности;
Sk - нормативная нагрузка;
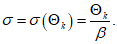 (6.17)
(6.17)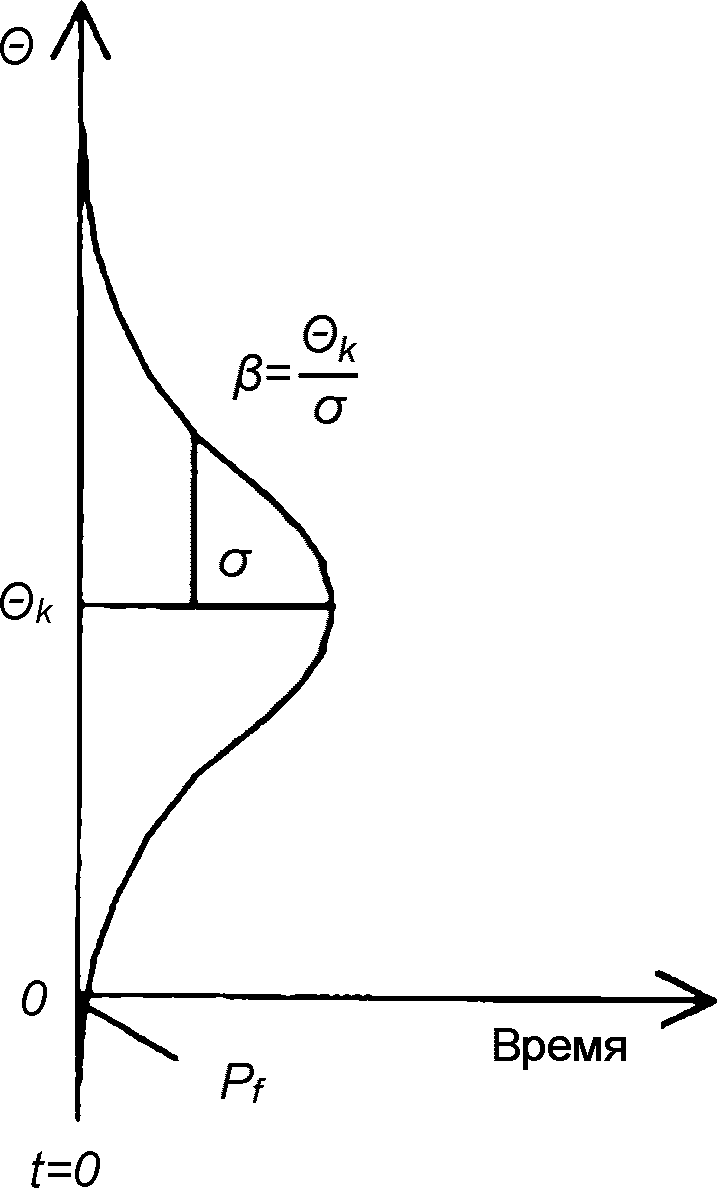
Критическое предельное состояние 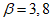 (Pf = 7,2 x 10-5)
(Pf = 7,2 x 10-5)
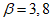 (Pf = 7,2 x 10-5)
(Pf = 7,2 x 10-5)Предельное состояние по эксплуатационной пригодности 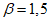 (Pf = 6,7 x 10-2)
(Pf = 6,7 x 10-2)
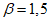 (Pf = 6,7 x 10-2)
(Pf = 6,7 x 10-2)проектировании в соответствии с [3]
6.3.3.3 Определение основных требований проектирования долговечности
6.3.3.3.1 При проектировании долговечности коэффициент прочностной безопасности после истечения срока службы не должен опускаться ниже 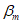 , который, как правило, может быть таким же по значению, что и коэффициент безопасности для критического предельного состояния в обычном конструктивном проектировании. Для случаев, когда при потере прочности конструкции не ожидают каких-либо серьезных последствий, коэффициент безопасности
, который, как правило, может быть таким же по значению, что и коэффициент безопасности для критического предельного состояния в обычном конструктивном проектировании. Для случаев, когда при потере прочности конструкции не ожидают каких-либо серьезных последствий, коэффициент безопасности 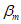 может быть назначен немного меньшим, чем тот, который необходим при обычном проектировании конструкций. Причина этого заключается в том, что в обычном (традиционном) проектировании требования безопасности относят только к начальному периоду срока службы. К концу срока службы в результате деградации фактическая безопасность опускается ниже оговоренного уровня. Таким образом, конструктивные размеры сооружения, запроектированного с учетом критериев по долговечности, но с пониженным коэффициентом безопасности
может быть назначен немного меньшим, чем тот, который необходим при обычном проектировании конструкций. Причина этого заключается в том, что в обычном (традиционном) проектировании требования безопасности относят только к начальному периоду срока службы. К концу срока службы в результате деградации фактическая безопасность опускается ниже оговоренного уровня. Таким образом, конструктивные размеры сооружения, запроектированного с учетом критериев по долговечности, но с пониженным коэффициентом безопасности 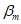 , по-видимому, должны быть близки к размерам традиционно запроектированного. Однако безопасность сооружения, запроектированного с учетом требований по долговечности, находится под контролем на протяжении всего срока службы.
, по-видимому, должны быть близки к размерам традиционно запроектированного. Однако безопасность сооружения, запроектированного с учетом требований по долговечности, находится под контролем на протяжении всего срока службы.
6.3.3.3.2 По перечисленным выше причинам классификацию уровней безопасности, приведенную в 6.3.2, теперь можно применить и к прочностной безопасности:
1) критическое предельное состояние:
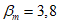 (серьезные последствия потери долговечности);
(серьезные последствия потери долговечности); (нет серьезных последствий потери долговечности);
(нет серьезных последствий потери долговечности);2) предельное состояние по эксплуатационной пригодности:
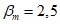 (последствия потери долговечности значительны, и стоимость ремонта высока);
(последствия потери долговечности значительны, и стоимость ремонта высока); (нет заметных последствий потери долговечности).
(нет заметных последствий потери долговечности).6.3.3.3.3 В нижеприведенных расчетах предполагается, что нагрузки и прочностные характеристики материалов остаются неизменными на протяжении всего срока службы сооружения, а их влияние на размеры поля безопасности в основном остается таким же, что и в традиционном проектировании. Предполагается, что деградация материалов оказывает влияние на поперечные размеры элементов (раздел 7) путем снижения значений средних величин и повышением значений стандартных отклонений с влиянием на величину поля безопасности.
6.3.3.3.4 Время или дополнительный разброс, зависящий от деградации, учитывается коэффициентом надежности службы 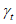
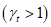 таким образом, что определяющим временем в проектировании является расчетное время td, которое находят путем перемножения заданного срока службы tg на коэффициент надежности по сроку службы. Это означает, что, составляя основные формулы проектирования долговечности для времени t = td, мы не принимаем во внимание дополнительный разброс, зависящий от времени, поскольку влияние разброса уже учтено в коэффициенте надежности
таким образом, что определяющим временем в проектировании является расчетное время td, которое находят путем перемножения заданного срока службы tg на коэффициент надежности по сроку службы. Это означает, что, составляя основные формулы проектирования долговечности для времени t = td, мы не принимаем во внимание дополнительный разброс, зависящий от времени, поскольку влияние разброса уже учтено в коэффициенте надежности 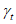 . Коэффициент надежности определяют таким образом, что коэффициент безопасности
. Коэффициент надежности определяют таким образом, что коэффициент безопасности  во время t = td при учете только снижения среднего значения будет таким же, как во время t = tg при учете дополнительного разброса, вызванного деградацией [2].
во время t = td при учете только снижения среднего значения будет таким же, как во время t = tg при учете дополнительного разброса, вызванного деградацией [2].
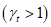 таким образом, что определяющим временем в проектировании является расчетное время td, которое находят путем перемножения заданного срока службы tg на коэффициент надежности по сроку службы. Это означает, что, составляя основные формулы проектирования долговечности для времени t = td, мы не принимаем во внимание дополнительный разброс, зависящий от времени, поскольку влияние разброса уже учтено в коэффициенте надежности
таким образом, что определяющим временем в проектировании является расчетное время td, которое находят путем перемножения заданного срока службы tg на коэффициент надежности по сроку службы. Это означает, что, составляя основные формулы проектирования долговечности для времени t = td, мы не принимаем во внимание дополнительный разброс, зависящий от времени, поскольку влияние разброса уже учтено в коэффициенте надежности 6.3.3.3.5 В приведенных ниже рассуждениях нормативное поле безопасности 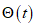 , определенное по формуле (6.16), можно выразить как
, определенное по формуле (6.16), можно выразить как
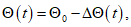 (6.18)
(6.18)где 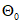 - среднее расчетное поле безопасности при t = 0;
- среднее расчетное поле безопасности при t = 0;
6.3.3.3.6 Стандартное отклонение 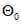 (постоянная величина) обозначено как
(постоянная величина) обозначено как  , а
, а  представляет собой стандартное отклонение
представляет собой стандартное отклонение  (которое из-за наличия деградации соответствует разбросу, изображенному на рисунке 6.5). Далее запишем
(которое из-за наличия деградации соответствует разбросу, изображенному на рисунке 6.5). Далее запишем
где 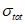 - полное стандартное отклонение
- полное стандартное отклонение  ;
;
6.3.3.3.7 Обозначим также:
6.3.3.3.8 В приведенных далее выражениях нижний индекс t соответствует времени t = tg. Предположим, что среднее значение  возрастает пропорционально росту функции tn, где n представляет собой показатель степени при основании "время", а
возрастает пропорционально росту функции tn, где n представляет собой показатель степени при основании "время", а 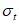 прямо пропорциональна
прямо пропорциональна  .
.
6.3.3.3.9 На рисунке 6.7 показан процесс снижения поля безопасности 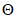 во времени. Вероятность физического разрушения отображается той частью распределений, которые оказались ниже предела
во времени. Вероятность физического разрушения отображается той частью распределений, которые оказались ниже предела  . На вероятность разрушения оказывают влияние как падение среднего значения
. На вероятность разрушения оказывают влияние как падение среднего значения 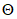 , так и возрастание во времени стандартного отклонения.
, так и возрастание во времени стандартного отклонения.
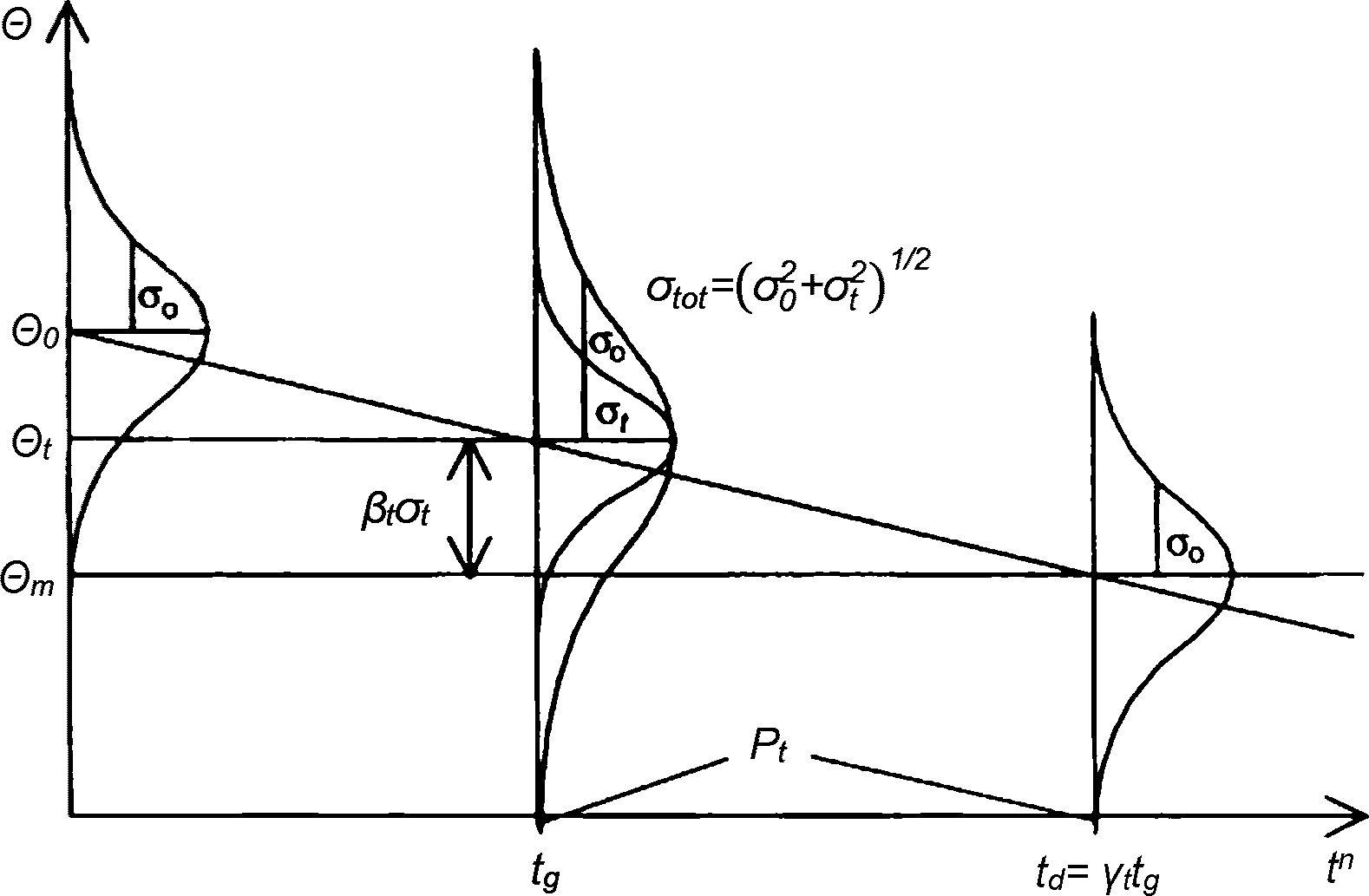
6.3.3.3.10 Как видно из рисунка 6.7, коэффициент безопасности при t = td без учета зависящего от времени разброса равен
 (6.21)
(6.21)В соответствии с вышеупомянутым принципом коэффициент безопасности 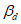 должен равняться коэффициенту безопасности
должен равняться коэффициенту безопасности 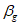 при t = tg, если учитывать также и зависящий от времени разброс. При t = tg среднее значение
при t = tg, если учитывать также и зависящий от времени разброс. При t = tg среднее значение  отклоняется от
отклоняется от 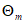 на значение произведения
на значение произведения 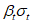 .
.
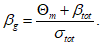 (6.22)
(6.22)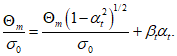
Выполняя далее условие 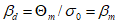 , получаем
, получаем
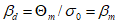 , получаем
, получаемУравнение (6.23) иллюстрирует, насколько отношение требования о полной прочностной безопасности  к требованию о безопасности долговечности
к требованию о безопасности долговечности  зависит от соотношения
зависит от соотношения  .
.
6.3.3.3.12 Следующим образом можно определить 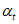 :
:
в соответствии с рисунком 6.7 для 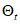 имеем
имеем
 (6.24)
(6.24)где k представляет собой коэффициент снижения 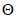 . Таким образом, получаем
. Таким образом, получаем
 (6.25)
(6.25)и
 (6.26)
(6.26)где V0 - коэффициент вариации убывания  .
. 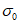 может быть выражена через
может быть выражена через
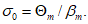 (6.27)
(6.27)6.3.3.3.13 Величину k можно выразить как
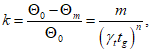 (6.28)
(6.28)где количественная величина m представляет собой относительное снижение  за интервал времени от 0 до tg:
за интервал времени от 0 до tg:
 (6.29)
(6.29) (6.30)
(6.30)6.3.3.3.15 Разделив числитель и знаменатель на 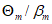 и принимая во внимание, что
и принимая во внимание, что 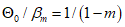 , в конечном итоге получаем:
, в конечном итоге получаем:
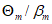 и принимая во внимание, что
и принимая во внимание, что 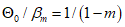 , в конечном итоге получаем:
, в конечном итоге получаем:где
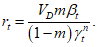 (6.32)
(6.32)6.3.3.3.16 Рассмотрим теперь коэффициент безопасности  . Из рисунка 6.7 получаем
. Из рисунка 6.7 получаем
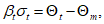
откуда
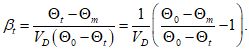
С другой стороны, из рисунка 6.7 видно, что
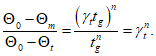
Подставляя последнее выражение в формулу 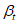 , получим
, получим
Результат оказался таким же, что и в уравнении (6.10).
Подставив выражения (6.31) и (6.33) в уравнение (6.23), мы можем определить значения 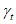 как функцию VD, n и m. Затем из уравнений (6.33) и (6.31) могут быть получены соответствующие значения
как функцию VD, n и m. Затем из уравнений (6.33) и (6.31) могут быть получены соответствующие значения 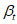 и
и 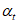 .
.
6.3.3.4 Результаты и их использование
6.3.3.4.1 В таблице 6.6 приведены значения  ,
, 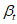 и
и 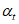 для различных значений m. Значение коэффициента надежности
для различных значений m. Значение коэффициента надежности  равно 3,8. Остальные параметры назначены:
равно 3,8. Остальные параметры назначены:
VD = 0,6;
n = 1.
Таблица 6.6
m | |||
0,001 | 1,00 | 0,00 | 0,00 |
0,1 | 1,23 | 0,39 | 0,20 |
0,2 | 1,44 | 0,73 | 0,37 |
0,3 | 1,63 | 1,05 | 0,51 |
0,4 | 1,83 | 1,38 | 0,64 |
0,5 | 2,02 | 1,71 | 0,75 |
0,6 | 2,23 | 2,06 | 0,84 |
0,7 | 2,46 | 2,43 | 0,91 |
0,8 | 2,70 | 2,84 | 0,96 |
0,9 | 2,97 | 3,29 | 0,99 |
0,999 | 3,28 | 3,79 | 1,00 |
Соответствующие значения при 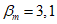 приведены в таблице 6.7, при этом остальные параметры оставлены неизменными.
приведены в таблице 6.7, при этом остальные параметры оставлены неизменными.
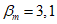 приведены в таблице 6.7, при этом остальные параметры оставлены неизменными.
приведены в таблице 6.7, при этом остальные параметры оставлены неизменными.Таблица 6.7
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
m | |||
0,001 | 1,00 | 0,00 | 0,00 |
0,1 | 1,16 | 0,27 | 0,17 |
0,2 | 1,32 | 0,53 | 0,33 |
0,3 | 1,47 | 0,79 | 0,48 |
0,4 | 1,63 | 1,05 | 0,61 |
0,5 | 1,79 | 1,32 | 0,72 |
0,6 | 1,97 | 1,61 | 0,82 |
0,7 | 2,15 | 1,92 | 0,90 |
0,8 | 2,36 | 2,27 | 0,95 |
0,9 | 2,39 | 2,66 | 0,99 |
0,999 | 2,86 | 3,10 | 1,00 |
6.3.3.4.2 Таблицы 6.8 и 6.9 относятся к проектированию в режиме предельного состояния по эксплуатационной пригодности. Значения 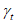 ,
,  и
и  даны для
даны для 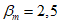 и 1,5. Величины VD и n имеют вышеприведенные значения.
и 1,5. Величины VD и n имеют вышеприведенные значения.
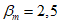 и 1,5. Величины VD и n имеют вышеприведенные значения.
и 1,5. Величины VD и n имеют вышеприведенные значения.Таблица 6.8
m | |||
0,001 | 1,00 | 0,00 | 0,00 |
0,1 | 1,11 | 0,19 | 0,13 |
0,2 | 1,22 | 0,37 | 0,29 |
0,3 | 1,34 | 0,37 | 0,43 |
0,4 | 1,46 | 0,77 | 0,56 |
0,3 | 1,39 | 0,99 | 0,69 |
0,6 | 1,74 | 1,23 | 0,79 |
0,7 | 1,89 | 1,49 | 0,88 |
0,8 | 2,07 | 1,78 | 0,95 |
0,9 | 2,27 | 2,11 | 0,99 |
0,999 | 2,30 | 2,30 | 1,00 |
Таблица 6.9
m | |||
0,001 | 1,00 | 0,00 | 0,00 |
0,1 | 1,04 | 0,07 | 0,10 |
1,2 | 1,09 | 0,15 | 0,20 |
1,3 | 1,13 | 0,25 | 0,32 |
1,4 | 1,21 | 0,33 | 0,44 |
1,5 | 1,28 | 0,47 | 0,37 |
3,6 | 1,37 | 0,62 | 0,70 |
0,7 | 1,47 | 0,78 | 0,82 |
0,8 | 1,59 | 0,98 | 0,92 |
0,9 | 1,73 | 1,21 | 0,98 |
0,999 | 1,90 | 1,50 | 1,00 |
Требуемые значения  и
и  зависят от m (относительное увеличение
зависят от m (относительное увеличение 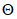 за период времени от 0 до td). В принципе,
за период времени от 0 до td). В принципе, 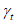 в таблицах 6.6 - 6.9 может иметь любое значение, если оно соответствует реальному m. Величина реального m зависит от степени деградации, проявившейся за срок службы, эта величина должна быть проверена расчетом после завершения проектирования. Величина реального m не должна превышать того m, которое соответствовало
в таблицах 6.6 - 6.9 может иметь любое значение, если оно соответствует реальному m. Величина реального m зависит от степени деградации, проявившейся за срок службы, эта величина должна быть проверена расчетом после завершения проектирования. Величина реального m не должна превышать того m, которое соответствовало  , использованной при проектировании.
, использованной при проектировании.
6.3.3.4.3 В практическом проектировании m принимают равным 0,7 для  , равной 2,46 при
, равной 2,46 при  и для
и для  , равной 2,15 при
, равной 2,15 при  соответственно. После окончания проектирования конструкции величину m проверяют; она не должна быть больше 0,7.
соответственно. После окончания проектирования конструкции величину m проверяют; она не должна быть больше 0,7.
 и для
и для  соответственно. После окончания проектирования конструкции величину m проверяют; она не должна быть больше 0,7.
соответственно. После окончания проектирования конструкции величину m проверяют; она не должна быть больше 0,7.6.3.3.4.4 Назначение m = 0,7 основано на предположении, что поле безопасности в своем диапазоне сокращается, иначе говоря, линейно (приблизительно соответствуя 0,5 в относительном снижении несущей способности R, см. 7.12). Естественно, за период времени от 0 до tg относительное снижение  значительно меньше. Кроме того, разница в несущих способностях конструкции, запроектированной традиционными способами и запроектированной с учетом требований долговечности, была бы слишком большой, если бы m превысило 0,7.
значительно меньше. Кроме того, разница в несущих способностях конструкции, запроектированной традиционными способами и запроектированной с учетом требований долговечности, была бы слишком большой, если бы m превысило 0,7.
6.3.3.4.5 Если окажется, что m > 0,7, проектировщику следует изыскать возможность понизить эту величину путем изменения размеров элементов конструкции, или прочностных характеристик материалов, или путем снижения скорости деградации. Если это не будет сделано, искомый заданный срок службы будет нереалистичным в условиях современной окружающей среды, и его следует сократить. В этом случае проектировщику следует выработать новые требования к величине заданного срока службы.
6.3.3.4.6 Как видно из таблиц 6.6 - 6.9, числовые значения  и
и  , соответствующие максимальному значению m (m = 1), равны критериям безопасности по долговечности, изложенным в 6.3.2. Исходя из этого, можно сделать вывод, что при использовании принципа разделенной безопасности в сочетании с таблицей 6.5, после окончания проектирования проверка величины m не требуется.
, соответствующие максимальному значению m (m = 1), равны критериям безопасности по долговечности, изложенным в 6.3.2. Исходя из этого, можно сделать вывод, что при использовании принципа разделенной безопасности в сочетании с таблицей 6.5, после окончания проектирования проверка величины m не требуется.
6.3.4.1 Если 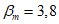 , то в проектировании долговечности используют частные коэффициенты надежности, установленные [3].
, то в проектировании долговечности используют частные коэффициенты надежности, установленные [3].
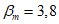 , то в проектировании долговечности используют частные коэффициенты надежности, установленные [3].
, то в проектировании долговечности используют частные коэффициенты надежности, установленные [3].Нагрузки:
 (постоянные нагрузки);
(постоянные нагрузки);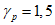 (переменные нагрузки).
(переменные нагрузки).Материалы:
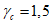 (бетон);
(бетон); (сталь).
(сталь).Если  , то применяют следующие частные коэффициенты надежности.
, то применяют следующие частные коэффициенты надежности.
 , то применяют следующие частные коэффициенты надежности.
, то применяют следующие частные коэффициенты надежности.Нагрузки:
 (постоянные нагрузки);
(постоянные нагрузки); (переменные нагрузки).
(переменные нагрузки).Материалы:
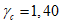 (бетон);
(бетон);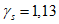 (сталь).
(сталь).6.3.4.2 Частные коэффициенты надежности для  были определены в соответствии с [3, приложение A] с использованием уравнений (6.34) - (6.36). Для постоянных нагрузок предполагают нормальное распределение, а для переменных - распределение вероятностей по Гумбелю. Коэффициенты надежности для материалов определены из предположения логарифмически нормального распределения.
были определены в соответствии с [3, приложение A] с использованием уравнений (6.34) - (6.36). Для постоянных нагрузок предполагают нормальное распределение, а для переменных - распределение вероятностей по Гумбелю. Коэффициенты надежности для материалов определены из предположения логарифмически нормального распределения.
 были определены в соответствии с [3, приложение A] с использованием уравнений (6.34) - (6.36). Для постоянных нагрузок предполагают нормальное распределение, а для переменных - распределение вероятностей по Гумбелю. Коэффициенты надежности для материалов определены из предположения логарифмически нормального распределения.
были определены в соответствии с [3, приложение A] с использованием уравнений (6.34) - (6.36). Для постоянных нагрузок предполагают нормальное распределение, а для переменных - распределение вероятностей по Гумбелю. Коэффициенты надежности для материалов определены из предположения логарифмически нормального распределения.Нормальное распределение
Распределение Гумбеля
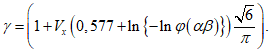 (6.35)
(6.35)Логарифмически нормальное распределение
В уравнениях (6.34) - (6.36):
Vx - коэффициент вариации;
В расчетах были приняты следующие числовые значения:
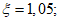
 для нагрузок;
для нагрузок; для прочностных характеристик материалов.
для прочностных характеристик материалов.6.3.4.3 Обратным счетом, подставляя  и соответствующие значения
и соответствующие значения 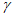 , определяли Vx. Новые значения
, определяли Vx. Новые значения  были определены путем подстановки подсчитанных значений Vx и
были определены путем подстановки подсчитанных значений Vx и 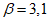 .
.
 и соответствующие значения
и соответствующие значения 6.3.4.4 Если 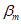 меньше 3,8 (главное условие безопасности по [3]), то необходимо проверить, чтобы поле безопасности
меньше 3,8 (главное условие безопасности по [3]), то необходимо проверить, чтобы поле безопасности  и несущая способность R0 не оказались меньше соответствующих значений, полученных при традиционном проектировании. Если это условие не выполняется, то размеры, установленные при традиционном проектировании, принимают за предельные. Цель этой проверки заключается в обеспечении условия, что окончательная безопасность сооружения ни при каких обстоятельствах не могла бы оказаться более низкой, чем безопасность сооружения, запроектированного традиционными методами.
и несущая способность R0 не оказались меньше соответствующих значений, полученных при традиционном проектировании. Если это условие не выполняется, то размеры, установленные при традиционном проектировании, принимают за предельные. Цель этой проверки заключается в обеспечении условия, что окончательная безопасность сооружения ни при каких обстоятельствах не могла бы оказаться более низкой, чем безопасность сооружения, запроектированного традиционными методами.
7.1.1 Основные принципы
7.1.1.1 На несущую способность бетонных конструкций могут оказывать долговременное влияние следующие факторы деградации:
- коррозия, вызванная проникновением хлоридов;
- коррозия, вызванная карбонизацией;
- механическое истирание;
- воздействие солевых растворов;
- нарушение целостности поверхности;
- воздействие отрицательных температур.
Кроме того, существуют еще некоторые внутренние деградационные процессы, например, реакция щелочей цемента с заполнителем, которая не обязательно вызывается воздействием окружающей среды. Подобные деградационные проблемы не рассматриваются в настоящем методическом пособии, поскольку они могут быть разрешены путем соответствующего выбора исходных материалов и квалифицированного подбора состава бетонной смеси.
7.1.1.2 Факторы деградации воздействуют на бетон, на сталь или на оба этих материала одновременно. В обычных условиях деградация возникает в поверхностной зоне бетона или стали, постепенно разрушая материал.
Основные проявления деградации бетона или стали заключаются в следующем [4]:
- потеря бетона, приводящая к уменьшению поперечного сечения бетонного элемента;
- коррозия арматуры, ведущая к уменьшению площади поперечного сечения стальных стержней.
Коррозия арматуры может возникать:
- в зоне трещин;
- на всех стальных поверхностях, если предположить, что вещества, вызывающие коррозию, могут проникать по порам в бетоне (обычная коррозия в условиях увлажнения);
- в результате отслаивания и шелушения бетона защитного слоя, вызываемого обычным ржавлением арматуры, что приводит к снижению площади поперечного сечения бетона и потере сцепления между арматурой и бетоном.
7.1.1.3 Несущую способность конструкций можно изучать на трех различных уровнях [4]. На первом уровне исследуют только поперечные сечения элементов под влиянием различных силовых воздействий, например, изгибающего момента, поперечной силы, продольной силы и т.д. На втором уровне вводят математическую деградационную модель отдельных конструктивных элементов, например, разрезные балки или колонны, учитывая деформации, проскальзывание и выпучивание арматурных стержней и т.д. И наконец, на третьем уровне рассматривают всю конструкцию целиком, учитывая возможное перераспределение силовых усилий, если это позволяет остаточная пластичность материалов.
7.1.1.4 В разделах методического пособия рассматривается только первый уровень. Несущая способность конструкций оценивается с помощью формул, по которым определяют размеры поперечного сечения элементов. В дополнение к расчетным формулам применяют зависящие от времени деградационные модели для бетона и стали. Эта методика демонстрируется ниже на нескольких примерах.
7.1.2 Примеры расчета процессов деградации
7.1.2.1 Задача настоящего методического пособия заключается в том, чтобы показать, каким образом явление деградации материалов может учитываться при определении несущей способности, и получить представление, как происходит снижение несущей способности во времени.
7.1.2.2 Рассмотрим поперечные сечения статически определимой колонны, находящейся под действием осевой нагрузки, и изогнутой разрезной балки. Предположим, что имеет место деградация бетона и стали, ведущая к уменьшению поперечных размеров бетонной и стальной составляющих элемента. Отслаивание и шелушение бетона вокруг ржавеющей арматуры игнорируем.
7.1.2.2.1 Колонна
Несущая способность центрально загруженной квадратной бетонной колонны, армированной размещенными в углах стержнями (рисунок 7.1), равна
где Rd - несущая способность поперечного сечения на сжатие;
Ac - площадь поперечного сечения бетона;
As - площадь поперечного сечения арматуры;
fck - нормативная прочность бетона на сжатие;
fy - номинальный предел текучести стали;
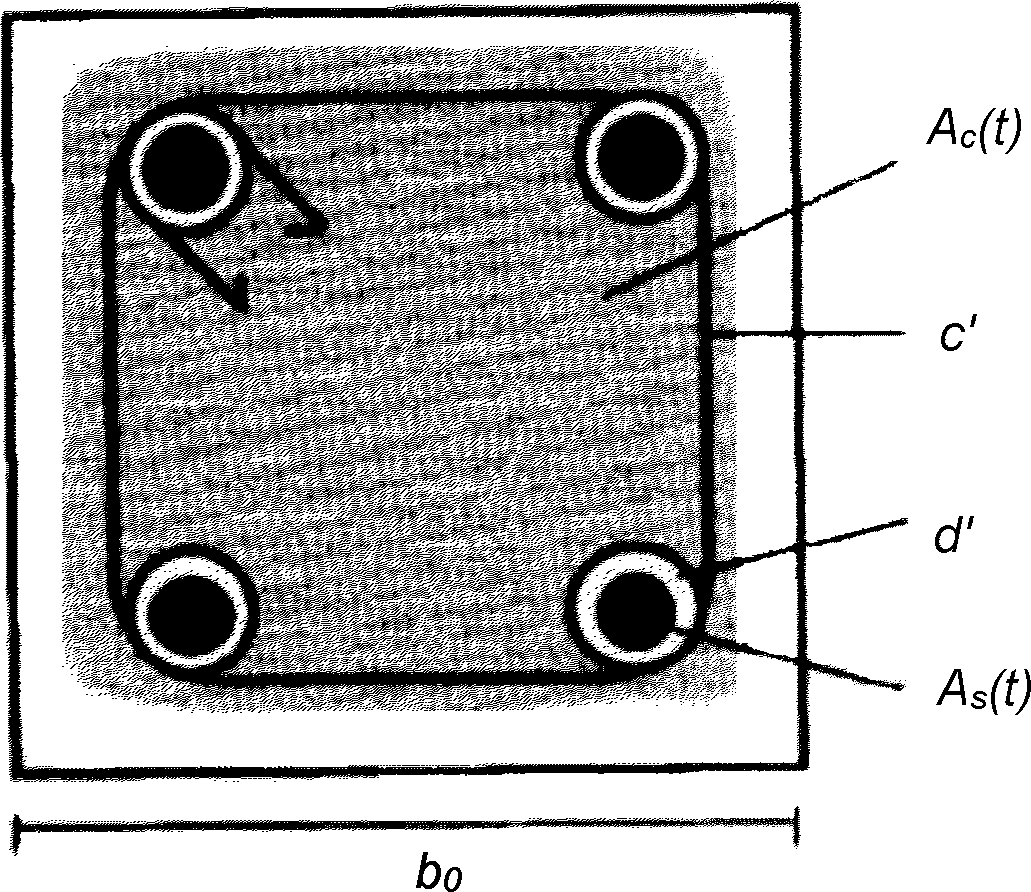
Площади поперечного сечения бетона и арматуры определяют по формулам:
Ac(t) = (b0 - 2c'(t))2; (7.2)
где b0 - первоначальная сторона поперечного сечения стойки;
D0 - первоначальный диаметр арматурных стержней;
c' - деградационная модель для бетона, отражающая глубину разрушения бетона;
d' - деградационная модель для стали, отражающая глубину слоя коррозии стержня.
Если c' мало по сравнению с b0, а d' мало по сравнению с D0, мы можем записать выражение (7.1) в приближенном виде
Из уравнения (7.4) видно, что, по крайней мере, в начальный период срока службы (когда c' и d' сравнительно малы) деградация Rd аналогична процессу деградации в бетоне и стали. Если c' и d' изменяются во времени линейно, то и несущая способность конструкции также будет уменьшаться во времени по линейному закону. Если процесс изменения c' и d' ускоряющийся или замедляющийся, падение несущей способности Rd проявляет такую же тенденцию.
На рисунке 7.2 изображено снижение Ac, As и Rd, выраженное в процентах (в соответствии с уравнениями (7.1) - (7.3), для обычной центрально загруженной колонны в предположении, что c' и d' изменяются во времени по линейному закону. Расчеты выполнены для следующих размеров и прочностных характеристик материалов:
b0 = 500 мм;
D0 = 25 мм;
fck = 40 МПа;
fyk = 400 МПа;
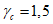 ;
; ;
;c'(t) = 0,4 мм/год;
d'(t) = 0,04 мм/год.
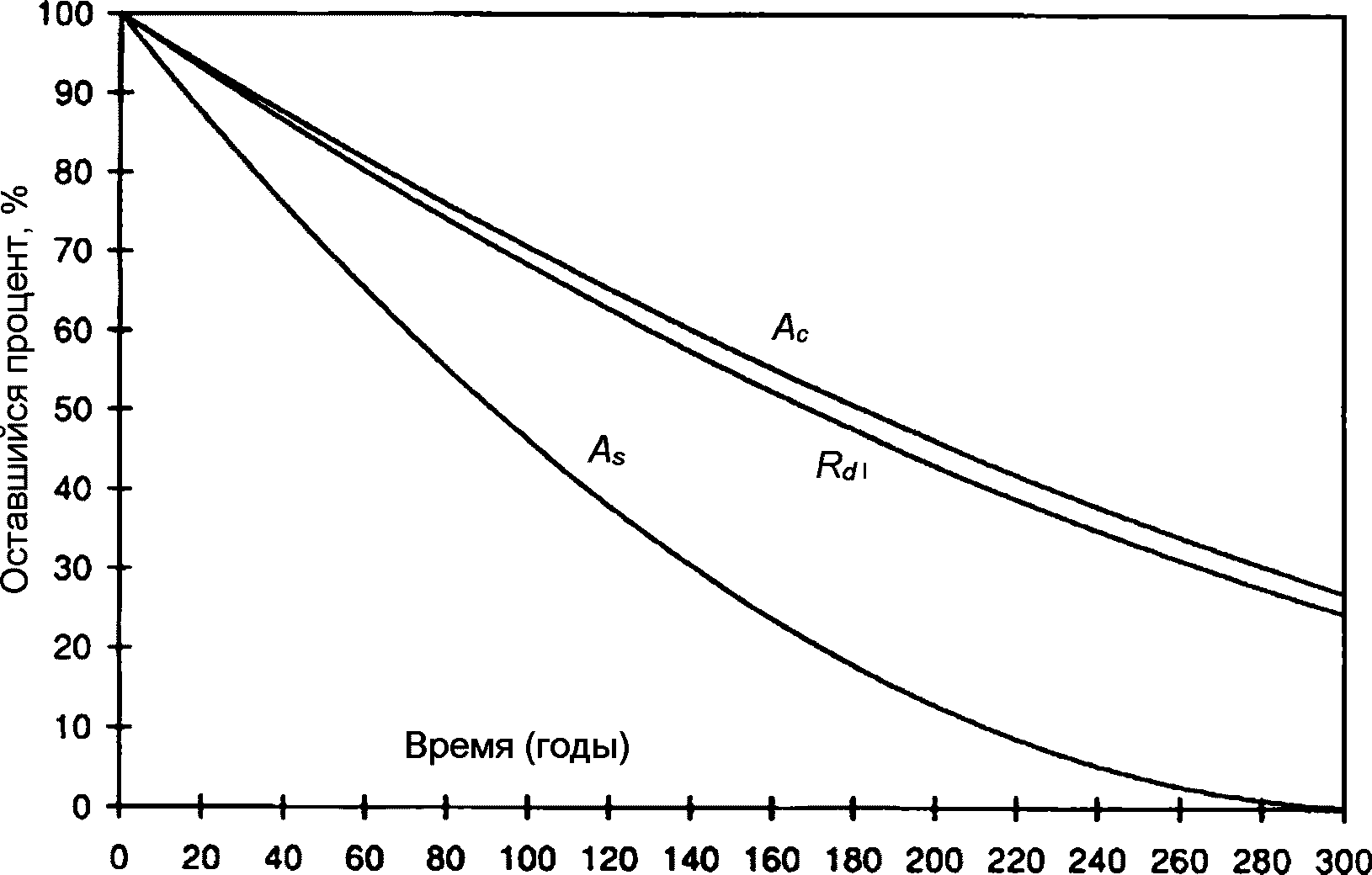
и несущей способности колонны на сжатие
Деградация Rd, как кажется, изменяется во времени приблизительно по прямолинейному закону, и при этом она близко повторяет кривую падения Ac. Коррозия арматуры имеет относительно небольшое влияние на общую несущую способность колонны. Даже при полном исчезновении площади арматуры колонна сохранит некоторую несущую способность.
7.1.2.2.2 Балка
Несущую способность балки определяют по следующим формулам (рисунок 7.3):
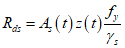 (напряжения в стали - определяющие); (7.5)
(напряжения в стали - определяющие); (7.5)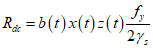 (напряжения в бетоне - определяющие); (7.6)
(напряжения в бетоне - определяющие); (7.6)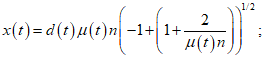 (7.7)
(7.7) (7.8)
(7.8)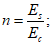 (7.9)
(7.9)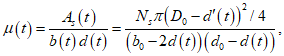 (7.10)
(7.10)где Rds - изгибная несущая способность балки, когда определяющими являются растягивающие напряжения в арматуре;
Rdc - изгибная несущая способность балки, когда определяющими являются сжимающие напряжения в бетоне;
As - площадь поперечного сечения арматуры;
d - рабочая высота сечения балки;
x - расстояние от нейтральной оси до верней грани балки;
z - плечо внутренней пары изгибающего момента;
Es - модуль упругости стали;
Ec - модуль упругости бетона;
c' - деградационная модель, отражающая глубину разрушения в бетоне;
d' - деградационная модель, отражающая глубину коррозии арматуры;
Ns - число стержней арматуры.
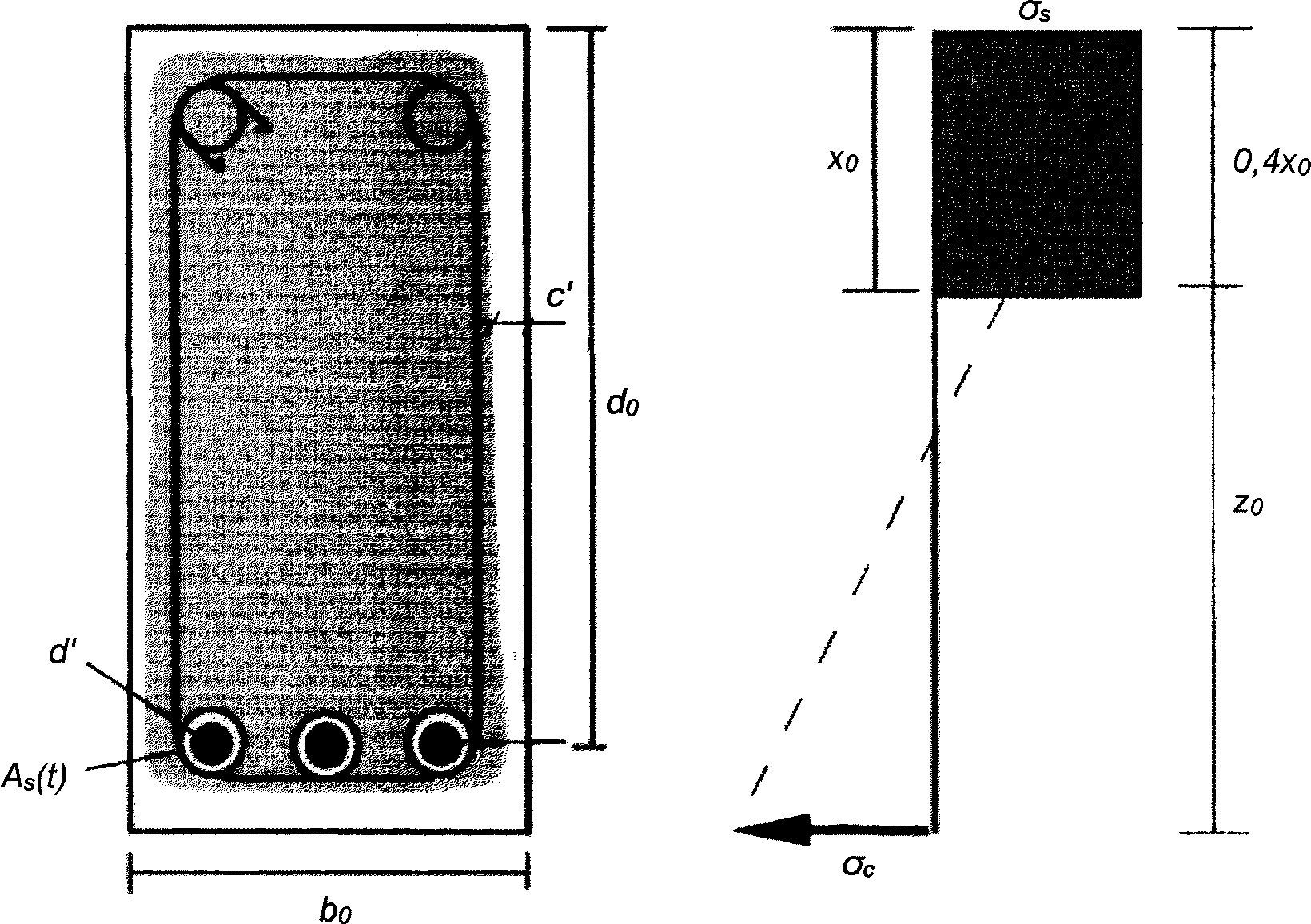
Уменьшение As, z, Rds и Rdc, %, для обычной балки с постоянной скоростью деградации c' и d' изображено на рисунке 7.4. В расчетах приняты следующие размеры и прочностные характеристики материалов:
b0 = 400 мм;
d0 = 700 мм;
D0 = 25 мм;
Ns = 3;
fc = 40 МПа;
fY = 400 МПа;
Es = 200 000 Н/мм2;
Ec = 9500 (fck + 8)1/3 Н/мм2;
 ;
;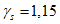 .
.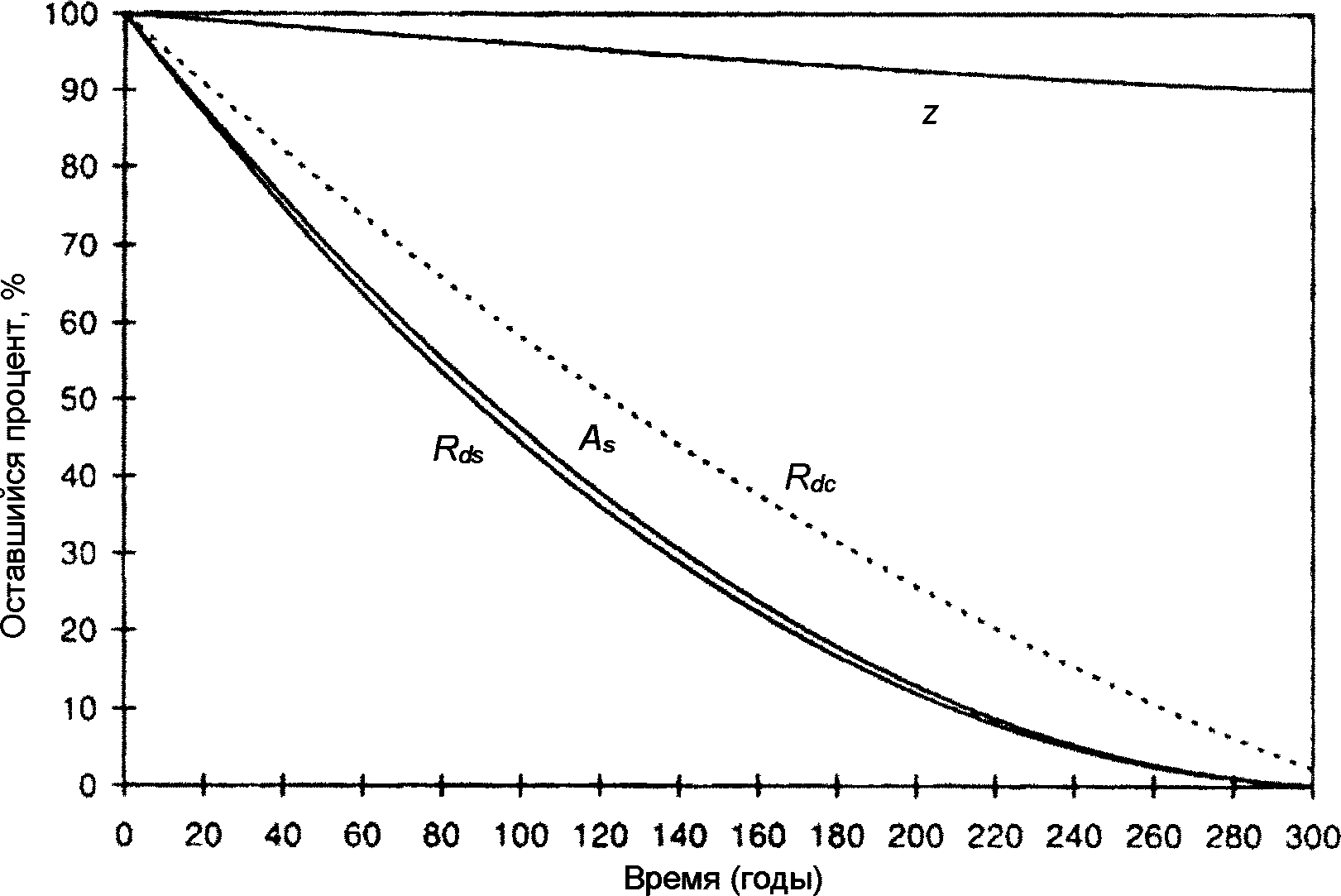
Как видно из рисунка 7.4, кривая снижения Rds близко повторяет закон уменьшения площади поперечного сечения арматуры. Это происходит потому, что уменьшение во времени значения z, как кажется, очень мало, и оно относительно меньше, чем снижение d, поскольку d также уменьшается.
Абсолютная величина Rds меньше, чем абсолютная величина Rdc. Таким образом, Rds в настоящих рассуждениях - определяющий фактор. Кривая Rdc, изображенная на рисунке 7.4, обнаруживает тенденцию к снижению практически по линейному закону.
7.2.1 Предлагаемые приемы проектирования включают в себя следующие фазы:
- традиционное прочностное проектирование;
- проектирование долговечности;
- окончательное проектирование.
- Метод раздельного проектирования, состоящий в простом объединении результатов фазы 1 и фазы 2;
- Метод комбинированного проектирования, в котором прочностное проектирование проводят заново при Rd(td) > Sd(td), используя результаты фазы 2. В этом случае фаза 1 служит, в основном, для проверки, однако в некоторых случаях именно она может оказаться определяющей.
7.2.3 Схема последовательных операций при проектировании приведена на рисунке 7.5.
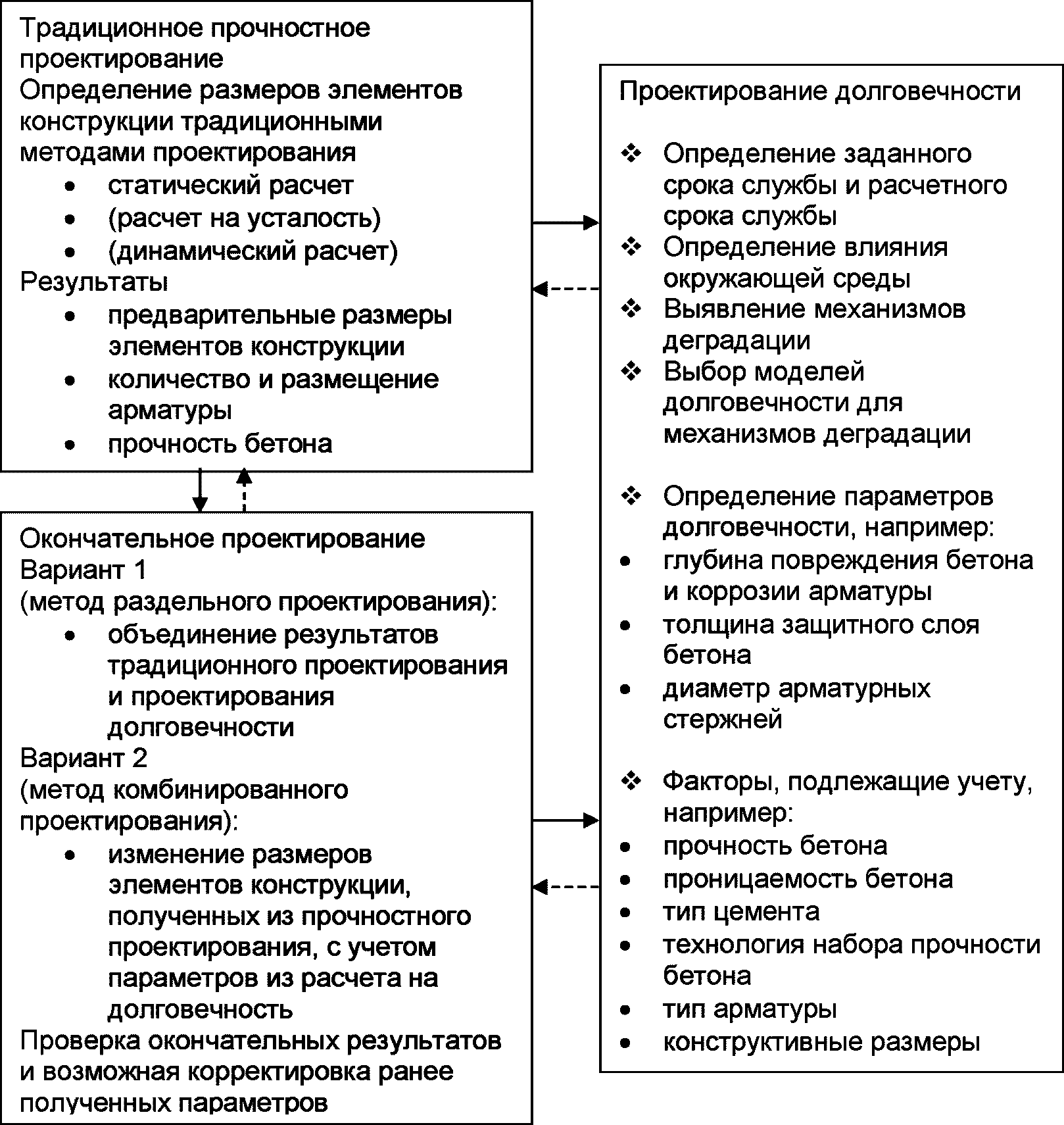
при проектировании долговечности
Традиционное проектирование, при котором размеры сечений железобетонных конструкций определяют из расчета на прочность, выполняют с применением обычных методик. Его задача состоит в определении предварительных размеров элементов конструкции.
7.4.1 Методика проектирования долговечности
Задача проектирования долговечности состоит в обеспечении возможности регулирования долговечности на протяжении всего срока эксплуатации сооружения.
Проектирование долговечности состоит из следующих операций:
- определение заданного срока службы и расчетного срока службы;
- определение влияния окружающей среды;
- выявление факторов долговечности и механизмов деградации;
- выбор моделей долговечности для каждого механизма деградации;
- расчет параметров долговечности с использованием имеющихся расчетных моделей;
- внесение возможных коррективов в расчеты традиционного прочностного проектирования (например, учет собственного веса конструкции);
- перенесение параметров долговечности в окончательный расчет.
7.4.2 Определение заданного срока службы и расчетного срока службы
Заданный срок службы определяют в соответствии с требованиями, приведенными в нормативных документах, в дополнение к возможным специальным требованиям заказчика.
Наиболее часто встречающиеся категории срока службы - 10, 25, 50, 75, 100 лет и т.д. Классификация заданных сроков службы (см. таблицу 7.1) содержится в [3]. Применяется термин "расчетный срок работы" [3], что можно интерпретировать как минимальный требуемый срок службы. В стандарте BS 7543 [5] приводят иную классификацию.
Таблица 7.1
(расчетного срока работы) [3]
Класс | Заданный срок службы (годы) | Примеры |
1 | (1 - 5) | Временные сооружения |
2 | (25) | Заменяемые элементы конструкции, например, крановые стрелы, опорные части |
3 | (50) | Здания и другие сооружения общего назначения |
4 | (100) | Монументальные здания, мосты и другие гражданские сооружения |
Предлагаемая классификация для проектирования долговечности приведена в таблице 7.2. Кроме того, в таблице приведены требования по сроку службы и коэффициенты надежности по нагрузкам и материалам.
Таблица 7.2
и соответствующие коэффициенты надежности по сроку службы
ИС МЕГАНОРМ: примечание. Сноски в таблице даны в соответствии с официальным текстом документа. |
Предельное состояние | Класс безопасности при проектировании долговечности | Раздельное проектирование | Комбинированное проектирование | ||
Коэффициент надежности по сроку службы | Коэффициент надежности по нагрузке и материалу | Коэффициент надежности по сроку службы | Коэффициент надежности по нагрузке и материалу | ||
Критическое предельное состояние | 1 Серьезные социальные, экономические или экологические последствия физического разрушения | 3,3 | нормальные <d> | 2,5 | нормальные |
2 Последствия физического разрушения не серьезны | 2,9 | нормальные <d> | 2,2 | 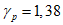 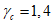 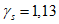 | |
Предельное состояние по эксплуатационной надежности | 1 Заметные последствия и значительные затраты на ремонт | 2,5 | - | 1,9 | - |
2 Незначительные последствия и затраты на ремонт | 1,9 | - | 1,5 | - | |
<a> - необходима проверка на условие: m (относительное снижение поля безопасности за период от 0 до td лет) <= 0,7; <b> - см. таблицу 6.5; <d> - используются коэффициенты надежности по нагрузкам и материалам из прочностного проектирования; <e> - в проектировании долговечности можно использовать пониженные коэффициенты надежности по нагрузке и материалу (см. 6.3.4). Однако надежность в начале срока службы (t = 0) должна быть, по крайней мере, такой же, какую требует традиционное проектирование. | |||||
Расчетный срок службы находят из уравнения (7.11):
где td - расчетный срок службы;
tg - заданный срок службы.
7.4.3 Учет влияния окружающей среды
Анализ влияния окружающей среды подразумевает определение климатических условий, например, колебания температуры и влажности, дожди, конденсация влаги, замерзание, солнечная радиация, воздействие загрязненного воздуха, а также геологических условий, например, уровень грунтовых вод, возможный контакт с морской водой, загрязнение почвы агрессивными реагентами, например, сульфатами или хлоридами. Кроме того, необходимо также выявить и факторы воздействия, связанные с человеческой деятельностью, например, применение солей на дорогах, продукты абразивного действия транспорта и т.д.
7.4.4 Определение факторов деградации и механизмов деградации
Основываясь на анализе характера воздействия окружающей среды, проектировщик определяет факторы, воздействию которых рассматриваемая конструкция вероятнее всего будет подвергаться. На этой стадии работы может оказаться полезным перечень деградационных факторов, приведенных в таблице 8.1.
Если конструкции полностью не защищены от воздействия окружающей среды, обычно предполагают, что имеет место некоторый деградационный процесс как в бетоне, так и в арматуре.
7.4.5 Выбор модели долговечности для каждого деградационного механизма
Задача проектировщика состоит в определении деградационных факторов, которые оказывают решающее влияние на срок службы. Притом может оказаться необходимым сделать предварительную оценку скорости деградации для различных факторов. При подобной оценке можно применить модели, описанные в разделе 8. Для всех типов ухудшения состояния конструкции могут применяться одни и те же расчетные операции и принципы.
Для всех бетонных конструкций, находящихся в обычном, незащищенном от атмосферного воздействия состоянии, механизмы деградации можно классифицировать по следующим конструктивным типам деградации.
1) Коррозия арматуры в зоне расположения трещин в бетоне приводит к уменьшению площади поперечного сечения арматурных стержней. Расчетные модели и прогнозируемая скорость коррозии, которые можно использовать в расчетах, приведены в 9.5.
2) Разрушение поверхностного слоя бетона или замораживание приводят к сокращению площади поперечного сечения бетона. Расчетные модели, приведенные в 9.3 для процесса разрушения поверхностного слоя бетона и в 9.2 для воздействия замораживания, также могут быть непосредственно использованы в расчете.
Расчетные модели для определения срока службы при воздействии общей коррозии, приведенные в разделе 9.5, используют при определении времени появления трещин в защитном слое бетона.
7.4.6 Определения параметров долговечности с помощью расчетных моделей
Глубину коррозии определяют с использованием в качестве расчетного время td. После этого определяют диаметры спиральной арматуры (хомутов) и прочей возможной конструктивной арматуры. Минимальный начальный диаметр стержней D0min равен двойной толщине коррозии, суммированной с минимальным конечным (после окончания срока службы) диаметром стержня. Минимальный конечный диаметр определяет проектировщик (>= 0). При этом первоначальный диаметр должен назначаться с учетом нормативных документов на прокат (D0 >= D0min).
Глубину разрушения бетона определяют, используя в качестве расчетного время td. Минимальную толщину защитного слоя бетона C0min определяют как сумму глубины разрушения бетона и минимальной конечной толщины защитного слоя (после окончания срока службы). Минимальную конечную толщину защитного слоя бетона задает проектировщик (>= 0). Первоначальная толщина защитного слоя бетона, C0, назначается путем округления в большую сторону, при этом должны учитываться требования норм.
Кроме этого, необходимо выполнить проверку на общую коррозию. Задача этой проверки заключается в гарантированном исключении за весь срок службы растрескивания или отслаивания защитного слоя бетона, что привело бы к нарушению сцепления бетона с арматурой. Эту задачу можно выполнить путем применения расчетных моделей срока службы к процессу общей коррозии при условии предварительного назначения размеров толщины защитного слоя бетона и диаметров арматурных стержней в качестве параметров. В качестве арматуры, повышающей сопротивление к образованию трещин и отслаиванию, обычно используют спиральные хомуты.
7.4.7 Возможные пути совершенствования методов расчета в традиционном прочностном проектировании
Некоторые параметры из расчета на долговечность могут оказывать влияние на процесс прочностного проектирования. Таким взаимоактивным влиянием будет, например, увеличение размеров поперечного сечения бетонных элементов, которое увеличивает постоянную нагрузку на горизонтально расположенные элементы, в свою очередь, увеличивая воздействие нагрузки как на горизонтальные, так и на вертикальные элементы. При использовании комбинированного метода эта фаза может отсутствовать.
7.4.8 Перенос параметров долговечности в операции окончательного расчета
Параметры в процессе проектирования долговечности фиксируют и затем переносят на стадии окончательного проектирования в расчеты по определению окончательных размеров поперечного сечения элементов.
7.5.1 Метод раздельного проектирования
В методе раздельного проектирования прочностное проектирование и проектирование долговечности выполняют раздельно друг от друга. Результат традиционного прочностного расчета (фаза 1) - критерии обеспечения прочностной надежности и параметры эксплуатационной пригодности, в то время как в процессе проектирования долговечности (фаза 2) получают параметры долговечности. Обе эти группы параметров затем объединяют в окончательном проектировании конструкции.
В обычных условиях возможную взаимосвязь между параметрами прочностного проектирования и параметрами проектирования долговечности не учитывают. Однако в некоторых случаях эта взаимозависимость может существовать, и тогда возникает необходимость в увязывании параметров прочностных расчетов, о чем говорится в 7.2.2. Довольно часто встречающийся случай состоит в возрастании прочности бетона со временем, что, в свою очередь, оказывает влияние на несущую способность и может снижать размеры поперечного сечения элементов, особенно сжатых.
Предполагается, что размеры поперечных сечений, полученные при традиционном проектировании, представляют собой размеры, необходимые к концу срока службы. Таким образом, эти размеры должны быть увеличены на значения, соответствующие глубине разрушения и коррозии за период срока службы.
Глубину разрушения поверхностного слоя бетона суммируют с конструктивными размерами, полученными в традиционном проектировании. Если воздействию деградационных факторов подвергаются две противоположные стороны конструкции, размеры, полученные при традиционном расчете, увеличивают на двойную глубину разрушения. Окончательный размер получают путем округления в большую сторону.
Диаметры арматурных стержней, полученные из прочностного расчета конструкции, увеличивают на двойную глубину коррозии. Окончательный диаметр получают путем округления в большую сторону, учитывая при этом диаметры стандартов на прокат.
Проверка величины m (относительное уменьшение размеров поля безопасности за время от 0 до td) не требуется.
7.5.2 Метод комбинированного проектирования
В методе комбинированного проектирования прочностной расчет выполняют заново, принимая во внимание результаты расчета долговечности и требуемую степень безопасности к концу срока службы.
Комбинированный метод особенно удобен для тех механизмов деградации, которые непосредственно влияют на несущую способность или на эксплуатационную пригодность конструкций. Кроме того, в некоторых случаях этот метод позволяет применять меньшие коэффициенты надежности по сроку службы, чем те, которые используют в методе раздельного проектирования, поскольку значение m должно проверяться после окончания расчетов. Для класса безопасности 2 (критическое состояние) требуемый коэффициент безопасности по окончании срока службы может быть немного меньшим, чем при традиционном проектировании.
Основные показатели конструкций - их размеры и прочностные характеристики материалов, именно по ним проверяют выполнение следующего условия:
где Rd(td) - расчетная несущая способность конструкции к концу расчетного срока службы;
Sd(td) - расчетная нагрузка на конструкцию к концу расчетного срока службы.
Значения коэффициентов надежности по материалу и по нагрузке зависят от класса безопасности. Для класса безопасности 1 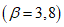 значения коэффициентов надежности по материалу и по нагрузке такие же, что и в традиционном проектировании. Для класса безопасности 2
значения коэффициентов надежности по материалу и по нагрузке такие же, что и в традиционном проектировании. Для класса безопасности 2 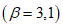 применяют следующие коэффициенты надежности:
применяют следующие коэффициенты надежности:
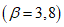 значения коэффициентов надежности по материалу и по нагрузке такие же, что и в традиционном проектировании. Для класса безопасности 2
значения коэффициентов надежности по материалу и по нагрузке такие же, что и в традиционном проектировании. Для класса безопасности 2 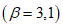 применяют следующие коэффициенты надежности:
применяют следующие коэффициенты надежности: ;
;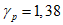 ;
;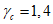 ;
; .
.Окончательные размеры могут быть легко получены с использованием любых расчетных программ.
После решения задачи по определению размеров поперечного сечения элементов конструкции и прочностных характеристик материалов нужно выполнить следующие проверки. Условие на ограничение величины m (относительное снижение размеров поля безопасности за период от 0 до td) выглядит следующим образом
В уравнении (7.13)  представляет собой поле безопасности (равное R - S), которое определяют по нормативным значениям нагрузок и прочностных характеристик материалов. Индекс 0 относится к начальному состоянию конструкции, а m к конечному состоянию по прошествии расчетного периода времени td.
представляет собой поле безопасности (равное R - S), которое определяют по нормативным значениям нагрузок и прочностных характеристик материалов. Индекс 0 относится к начальному состоянию конструкции, а m к конечному состоянию по прошествии расчетного периода времени td.  определяют по окончательному прочностному расчету, назначая коэффициенты надежности по нагрузке и по материалу, равными 1.
определяют по окончательному прочностному расчету, назначая коэффициенты надежности по нагрузке и по материалу, равными 1.  также получена путем подстановки
также получена путем подстановки 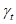 , равного 0. Расчеты легко выполняются в табличной форме (см. примеры в 7.6).
, равного 0. Расчеты легко выполняются в табличной форме (см. примеры в 7.6).
Если m больше 0,7, то требуемая надежность, по-видимому, не обеспечена, поскольку принятый в расчетах коэффициент надежности по сроку службы оказался слишком малым для реальной величины m. Возможно также, что прочность запроектированной конструкции получилась намного большей, чем в соответствующем традиционном прочностном расчете.
Для возвращения в фазу 2 с целью внесения изменений в результаты расчета на долговечность может оказаться необходимым удерживать значение m более низким, чем требуется. Проектировщику может понадобиться ответить на вопрос, не имеется какого-либо способа снизить скорость деградации или как-либо иначе изменить основные предпосылки расчета. Если это невозможно, то прогнозируемый срок службы конструкции может оказаться не реалистичным для предполагаемых условий окружающей среды, в подобных случаях следует рассматривать возможность снижения величины заданного срока службы.
Если в окончательном расчете применены пониженные значения коэффициентов надежности по материалу и по нагрузке, то следует выполнять проверку на то, что размеры поля безопасности 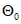 и несущая способность R0 (в начальный период эксплуатации) не меньше этих же величин, полученных в традиционном прочностном расчете. Если это условие не выполнено, то размеры, полученные в традиционном прочностном расчете, являются определяющими. Окончательная надежность сооружения никогда не должна быть меньшей той надежности, полученной из традиционного прочностного расчета.
и несущая способность R0 (в начальный период эксплуатации) не меньше этих же величин, полученных в традиционном прочностном расчете. Если это условие не выполнено, то размеры, полученные в традиционном прочностном расчете, являются определяющими. Окончательная надежность сооружения никогда не должна быть меньшей той надежности, полученной из традиционного прочностного расчета.
7.6.1 Колонна
(a) Постановка задачи проектирования
Определить размеры колонны, находящейся под воздействием следующих нагрузок:
Fg = 1000 кН (постоянная нагрузка);
Fp = 3000 кН (переменная нагрузка).
В квадратном поперечном сечении (со стороной квадрата b) по углам установлены четыре арматурных стержня диаметром D. Предел текучести стали (fy) = 400 МПа.
Предполагается, что в процессе эксплуатации колонны мероприятия по уходу и содержанию не проводятся, поэтому наличие коррозии арматурных стержней в зонах прогнозируемых трещин или разрушение защитного слоя бетона не должны сказаться на обеспечении полноценного использования колонны на протяжении всего срока ее службы. По истечении срока службы косвенная арматура (хомуты) в зоне трещин не должна быть полностью уничтожена. Оставшийся после окончания срока службы защитный слой бетона должен быть толщиной не менее 20 мм, а отслоение, вызванное общей коррозией косвенной арматуры, должно полностью отсутствовать.
(b) Традиционное прочностное проектирование
Традиционный расчет колонны ведем, пользуясь формулами, где
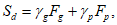 (7.15)
(7.15)а
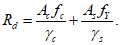 (7.16)
(7.16)Площади поперечного сечения бетона и стали Ac и As определяют по формулам:
Назначая D = 15 мм, из уравнения (7.18) получим As = 707 мм2. Из условия (7.14) находим
Ac = 210155 мм2.
Из уравнения (7.17) определяем b = 453 мм.
Таким образом, получены предварительные размеры по бетону и арматуре.
Заданный срок службы колонны равен 50 годам. Коэффициент надежности по сроку службы равен 3,3 для метода раздельного проектирования и 2,5 для метода комбинированного проектирования срока службы. Таким образом, расчетный срок службы равен
td = 3,3 x 50 = 165 лет (для метода раздельного проектирования)
td = 2,5 x 50 = 125 лет (для комбинированного метода).
Предполагается, что колонна частично погружена в пресную воду, которая замерзает зимой. Таким образом, глубину разрушения поверхностного слоя бетона c' определяют по формуле (см. 9.2):
В этой формуле в качестве параметров приняты следующие величины:
Cenv (фактор воздействия окружающей среды) = 80;
Ccur (фактор технологии набора прочности) = 1;
Cage (фактор возраста) = 1;
a (фактор, отражающий содержание воздуха, %) = 4;
fck (нормативная прочность бетона на сжатие, МПа) = 40.
Подставляя эти значения в уравнение (7.19), получаем толщину деградации поверхностного слоя бетона
c' = 0,135t, мм.
Глубина коррозии стальных стержней в зоне трещин: d' = 0,03t, мм.
В зависимости от расчетного срока службы получаем следующие параметры проектирования долговечности.
Метод раздельного проектирования (td = 165 лет)
Глубина разрушения бетона
c' = 0,135 x 165 = 22,3 мм.
Минимальная толщина защитного слоя Cmin = 20 + 22,3 = 43 мм.
Принимаем C = 45 мм.
Глубина коррозии стальных стержней в зоне трещин d' = 0,03 x 165 = 5,0 мм.
Стержни косвенной арматуры не должны исчезнуть под воздействием коррозии. Тогда минимальный диаметр стержней косвенной арматуры равен
Dh min = 2 x 5,0 = 10 мм.
Назначаем Dh = 10 мм.
Метод комбинированного проектирования (td = 125 лет)
c' = 0,135 x 125 = 16,9 мм, Cmin = 20 + 16,9 = 37 мм.
Принимаем C = 40 мм.
d' = 0,03 x 125 = 3,8 мм, Dh min = 2 x 3,8 = 8 мм.
Принимаем Dh = 10 мм.
Нам еще необходимо выполнить проверку на общую коррозию с уже полученными значениями толщины защитного слоя и диаметров арматурных стержней. Предполагаем, что содержание хлоридов в воде настолько незначительно, что хлоридная коррозия не протекает. Однако арматура в верхней части стойки может подвергаться коррозии из-за карбонизации.
Определяющая арматура в процессе общей коррозии - косвенная арматура. Таким образом, для расчета косвенной арматуры (диаметр ветви спирали вычитаем из толщины защитного слоя рабочей арматуры) применяем уравнения (9.20) и (9.29) (см. 9.5):
 (7.20)
(7.20)где Ch - толщина защитного слоя спирали (Ch = C - Dh);
Dh - диаметр одной ветви спирали;
Cenv - коэффициент воздействия окружающей среды (Cenv = 1);
Cair - коэффициент воздухосодержания (Cair = 0,7);
r - скорость коррозии стали до трещинообразования (~ 12 мкм/год).
В результате получаем 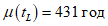 для метода раздельного проектирования, что больше расчетного срока службы (165 лет). Для комбинированного метода проектирования мы получим 322 года, что также превышает расчетный срок службы (125 лет). Таким образом, принятые толщины защитного слоя приемлемы.
для метода раздельного проектирования, что больше расчетного срока службы (165 лет). Для комбинированного метода проектирования мы получим 322 года, что также превышает расчетный срок службы (125 лет). Таким образом, принятые толщины защитного слоя приемлемы.
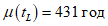 для метода раздельного проектирования, что больше расчетного срока службы (165 лет). Для комбинированного метода проектирования мы получим 322 года, что также превышает расчетный срок службы (125 лет). Таким образом, принятые толщины защитного слоя приемлемы.
для метода раздельного проектирования, что больше расчетного срока службы (165 лет). Для комбинированного метода проектирования мы получим 322 года, что также превышает расчетный срок службы (125 лет). Таким образом, принятые толщины защитного слоя приемлемы.(e) Окончательное проектирование
Метод раздельного проектирования
Длина стороны поперечного сечения колонны в начальный период эксплуатации определена как сумма удвоенной глубины деградации поверхностного слоя бетона и длины, определенной из традиционного расчета (фаза 1):
b0 = b + 2c' = 458 мм + 2 x 22,3 мм = 503 мм.
Диаметр стержней рабочей арматуры определяем таким же путем:
D0 min = 15 мм + 2 x 5,0 мм = 25,0 мм.
Поскольку значение расчетного диаметра соответствует нормативному документу на прокат, принимаем 25 мм.
Примечание - Требуемую толщину защитного слоя Cmin и длину стороны поперечного сечения стойки b0 можно уменьшить за счет повышения прочности бетона на сжатие. Для fck = 50 МПа минимальная толщина защитного слоя бетона будет равна 37 мм, а сторона поперечного сечения стойки - 444 мм.
Метод комбинированного проектирования
При работе с комбинированным методом геометрические характеристики сечения колонны при t = td определяют по формулам прочностного проектирования:
Rd(td) >= Sd, (7.21)
где
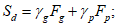 (7.22)
(7.22)Площади поперечного сечения бетона и стали Ac и As определяют по формулам:
Ac(td) = (b0 - 2c'(td))2; (7.24)
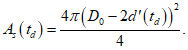 (7.25)
(7.25)ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Из уравнения (7.27) при D0 = 25 мм получим As(td) = 962 мм2.
При выполнении условия уравнения (7.23) получаем Ac(td) = 206826 мм2.
Из уравнения (7.26) получаем
(b0 - 2 x 16,9)2 = 206826 мм2, что дает b0 = 489 мм.
В следующем столбце путем подстановки 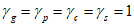 определяем поле безопасности
определяем поле безопасности 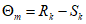 , соответствующее уже полученному решению:
, соответствующее уже полученному решению:
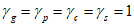 определяем поле безопасности
определяем поле безопасности 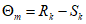 , соответствующее уже полученному решению:
, соответствующее уже полученному решению: .
.Далее, подставляя 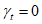 , получим
, получим 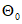 , представляющее собой поле безопасности в начале эксплуатации (t = 0):
, представляющее собой поле безопасности в начале эксплуатации (t = 0):
 .
.Относительное уменьшение R - S (= m)
 , что меньше 0,7.
, что меньше 0,7.Сторона квадратного поперечного сечения колонны из комбинированного расчета немного меньше, чем эта же величина из метода раздельного проектирования.
7.6.2 Балка
Постановка задачи проектирования
Запроектировать балку под следующие нагрузки:
Mg = 10 + 0,1d, кНм (d, мм);
Mp = 50 кНм.
Предполагаем, что балка имеет прямоугольное поперечное сечение шириной b (~= 300 мм) и рабочую высоту d. В нижней зоне балки расположены три арматурные стержня. Предел текучести стали 400 МПа. Нормативная прочность бетона на сжатие 40 МПа, воздухосодержание 2% (без воздухововлечения), вяжущее - портландцемент.
Предполагается, что в процессе эксплуатации балки мероприятия по уходу и содержанию не проводятся, поэтому наличие коррозии арматурных стержней в зонах прогнозируемых трещин или разрушение защитного слоя бетона не должно сказаться на обеспечении полноценного использования балки на протяжении всего срока ее службы. Площадь поперечного сечения косвенной арматуры (хомутов) не должна полностью исчезнуть в результате коррозии в зоне трещин. Толщина оставшегося после окончания срока службы защитного слоя бетона должна быть не менее 20 мм, а отслоение, вызванное общей коррозией косвенной арматуры, должно полностью отсутствовать.
Традиционное прочностное проектирование проводится в соответствии с общепринятыми проектными принципами:
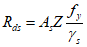 - (определяющее - напряжение в стали); (7.28)
- (определяющее - напряжение в стали); (7.28)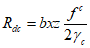 - (определяющее - напряжение в бетоне); (7.29)
- (определяющее - напряжение в бетоне); (7.29) (7.30)
(7.30)z = d - 0,4x; (7.31)
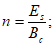
 (7.32)
(7.32)As - площадь поперечного сечения арматурных стержней определяют по формуле
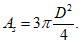 (7.33)
(7.33)ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Принимая 0 = 15 мм, получаем As = 530 мм2.
Подставляя Rds, равное Sd, получаем d = 2083 мм.
Однако увеличение диаметра арматурных стержней ведет к быстрому уменьшению рабочей высоты сечения. Назначая D равным 20 мм, получим As = 942 мм2, d = 543 мм.
Заданный срок службы 50 лет. Коэффициент надежности по сроку службы для раздельного метода проектирования равен 3,3, а для комбинированного метода проектирования - 2,5. Таким образом, расчетный срок службы td для раздельного метода равен 165 годам и 125 годам для комбинированного метода.
Предполагаем, что все стороны балки подвергаются воздействию отрицательных температур. Фактор воздействия окружающей среды при замораживании - Cenv = 40, а прогнозируемое время твердения бетона - 3 дня.
Фактор технологии набора прочности (см. уравнение (8.4), 8.2.2)
 (7.34)
(7.34)Поскольку бетон приготовлен на портландцементе, заключаем что Cage = 1.
Подставляя эти значения в формулу (7.19), получаем
c' = 0,117t, мм. (7.35)
В то же время, в арматурных стержнях в зоне трещин возникает коррозия. Скорость распространения коррозии оценена равной 0,03 мм/год:
d' = 0,03t, мм. (7.36)
Параметры проектирования долговечности приведены ниже (в зависимости от расчетного срока службы).
Метод раздельного проектирования (td = 165 лет)
Глубина разрушения поверхностного слоя c' = 0,117 x 165 = 19,3 мм.
Требуемая толщина защитного слоя бетона Cmin = 20 + 19,3 = 39,3 мм.
Принимаем C = 40 мм.
Глубина коррозии в зоне трещин d' = 0,03 x 165 = 5,0 мм.
Диаметр хомутов не должен быть меньше Dh min = 2 x 5,0 мм = 10,0 мм.
Принимаем Dh = 10 мм.
Комбинированный метод (td = 125 лет)
c' = 0,117 x 125 = 14,6 мм, Cmin = 20 + 14,6 мм = 34,6 мм. Принимаем C = 35 м;
d' = 0,03 x 125 = 3,75 мм, Dh min = 2 x 3,75 мм = 7,5 мм. Принимаем Dh = 10 мм.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: уравнение (8.22) отсутствует. |
Теперь, применяя уравнение (8.22), определяем время появления трещин в защитном слое бетона. Для этого в формулу подставляем следующие значения параметров:
C = 40 мм (метод раздельного проектирования) или 35 мм (комбинированный метод проектирования);
Ch = C - Dh - C - 10 мм;
fck = 40 МПа;
Cenv = 1;
Cair = 1;
Dh = 10 мм;
r = 12 мкм.
По методу раздельного проектирования мы получаем 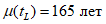 , что равно расчетному сроку службы (165 лет). Таким образом, толщина защитного слоя 40 мм является достаточной. По методу раздельного проектирования мы получаем
, что равно расчетному сроку службы (165 лет). Таким образом, толщина защитного слоя 40 мм является достаточной. По методу раздельного проектирования мы получаем  , что меньше расчетного срока службы (125 лет). Поэтому толщину защитного слоя увеличиваем с 35 до 40 мм. Теперь расчетный срок службы равен 165 годам, поставленная задача выполняется.
, что меньше расчетного срока службы (125 лет). Поэтому толщину защитного слоя увеличиваем с 35 до 40 мм. Теперь расчетный срок службы равен 165 годам, поставленная задача выполняется.
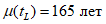 , что равно расчетному сроку службы (165 лет). Таким образом, толщина защитного слоя 40 мм является достаточной. По методу раздельного проектирования мы получаем
, что равно расчетному сроку службы (165 лет). Таким образом, толщина защитного слоя 40 мм является достаточной. По методу раздельного проектирования мы получаем  , что меньше расчетного срока службы (125 лет). Поэтому толщину защитного слоя увеличиваем с 35 до 40 мм. Теперь расчетный срок службы равен 165 годам, поставленная задача выполняется.
, что меньше расчетного срока службы (125 лет). Поэтому толщину защитного слоя увеличиваем с 35 до 40 мм. Теперь расчетный срок службы равен 165 годам, поставленная задача выполняется.Окончательное проектирование
Метод раздельного проектирования
Ширина балки в начальный период эксплуатации равна сумме удвоенного значения глубины деградации поверхностного слоя бетона и ширины балки, полученного из традиционного расчета:
b0 = b + 2b' = 300 + 2 x 19,3 = 339 мм.
Рабочую высоту балки увеличиваем на глубины деградации:
d0 = d + b' = 543 + 19,3 мм = 562 мм. Минимальный диаметр арматурных стержней равен D0 min = 20 + 2 x 5,0 мм = 30,0 мм. Принимаем D0 = 30 мм.
Комбинированный метод проектирования
Определяем геометрические характеристики ведем по следующей формуле
Rd(td) >= Sd, (7.37)
где
 (7.38)
(7.38)а за Rd принимаем меньшую из следующих величин:
 (7.39)
(7.39)(определяющие - напряжения в стали) и
 (7.40)
(7.40)(определяющие - напряжения в бетоне)
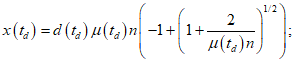 (7.41)
(7.41)z(td) = d(td) - 0,4x(td); (7.42)
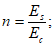
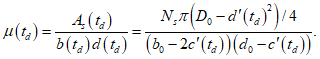 (7.43)
(7.43)As - площадь поперечного сечения арматуры определяется по формуле:
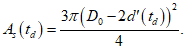 (7.44)
(7.44)При D0 = 28 мм и d'(td) = 3,75 получаем
As(td) = 990 мм2.
Рабочую высоту балки d0 теперь определяем путем приравнивания меньшей из значений Rd, или Rdc к Sd при t = td. Откуда получаем Rds = Sd >= d0 = 531 мм.
Ширина балки равна 300 мм, а толщина защитного слоя для рабочей арматуры - 40 мм.
Рабочая высота балки оказалась немного меньшей, чем при расчете по методу раздельного проектирования. Относительное уменьшение поля безопасности (m = 0,693) не превышает установленный предел - 0,7.
Метод комбинированного проектирования для второго класса безопасности
Для второго класса безопасности (критическое состояние) проектирование долговечности конструкции проводят при 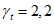 и при пониженных значениях коэффициентов надежности по нагрузке и материалу (см. 6.3.4). Рабочая высота балки равна 414 мм, что явно меньше соответствующей величины при расчете по первому классу безопасности (513 мм); 35 мм достаточно для толщины защитного слоя бетона. Относительное уменьшение
и при пониженных значениях коэффициентов надежности по нагрузке и материалу (см. 6.3.4). Рабочая высота балки равна 414 мм, что явно меньше соответствующей величины при расчете по первому классу безопасности (513 мм); 35 мм достаточно для толщины защитного слоя бетона. Относительное уменьшение 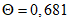 , что меньше 0,7.
, что меньше 0,7.
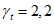 и при пониженных значениях коэффициентов надежности по нагрузке и материалу (см. 6.3.4). Рабочая высота балки равна 414 мм, что явно меньше соответствующей величины при расчете по первому классу безопасности (513 мм); 35 мм достаточно для толщины защитного слоя бетона. Относительное уменьшение
и при пониженных значениях коэффициентов надежности по нагрузке и материалу (см. 6.3.4). Рабочая высота балки равна 414 мм, что явно меньше соответствующей величины при расчете по первому классу безопасности (513 мм); 35 мм достаточно для толщины защитного слоя бетона. Относительное уменьшение 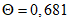 , что меньше 0,7.
, что меньше 0,7.В том случае, когда применяют пониженные значения коэффициентов надежности по нагрузке и материалу, необходимо кроме всего прочего проверить выполнение условия, что несущая способность конструкции и значение поля безопасности, установленные при окончательном проектировании, не меньше соответствующих значений, полученных при традиционном проектировании.
При проектировании долговечности:
Rm = 265 КНм и  .
.
 .
.При традиционном проектировании:
R0 = 186 кНм и  .
.
 .
.В этом случае значения как Rm, так и 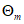 из проектирования долговечности больше этих же значений при традиционном проектировании. Таким образом, определяющими оказались геометрические характеристики, полученные при окончательном проектировании (проектировании долговечности).
из проектирования долговечности больше этих же значений при традиционном проектировании. Таким образом, определяющими оказались геометрические характеристики, полученные при окончательном проектировании (проектировании долговечности).
8.1.1 Модели деградации, работы и срока службы
8.1.1.1 Для проведения проектирования долговечности конструкции в распоряжении проектировщика должны быть математические модели расчета долговечности, с помощью которых он мог бы оценить происходящие во времени изменения характеристик материалов и конструкций. В состав этих моделей входят такие расчетные параметры как геометрические размеры, свойства материалов, параметры воздействия окружающей среды и т.д. Концепция модели долговечности охватывает различные типы моделей, которые более подробно будут рассмотрены ниже.
8.1.1.2 Деградационными моделями называют системы математических уравнений, которые отражают рост деградации во времени (с возрастом) и в процессе изменения соответствующих проектных параметров. Их применяют в проектировании долговечности, когда за предельное состояние принимают максимальную деградацию.
8.1.1.3 Деградацию можно интерпретировать иначе как снижение работоспособности конструкции. Системы математических уравнений, которые интерпретируют снижение работоспособности конструкции как функцию времени и соответствующих проектных параметров, называют моделями работы. Модели работы применяют в проектировании долговечности, когда за предельное состояние принимают минимальную работоспособность.
8.1.1.4 Системы математических уравнений, представляющие срок службы конструкции как функцию различных проектных параметров, называют моделями срока службы. Часто их можно получить из деградационных моделей или из моделей работы, если известны, соответственно, предельные состояния максимальной деградации или минимальной работоспособности. Модели срока службы применяют тогда, когда задача проектирования формулируется в соответствии с принципом срока службы (см. раздел 4).
8.1.1.5 Существуют модели долговечности для разных уровней, например, для материалов, для отдельных элементов конструкции и для целых сооружений. Все они могут быть использованы в проектировании долговечности. Конструктивные уровневые модели, подобные определению несущей способности, применяют в прочностном проектировании. Их обычно создают путем включения моделей деградации материалов в основные расчетные формулы для прочностного проектирования.
8.1.2 Детерминистические и вероятностные модели долговечности
8.1.2.1 Модели долговечности можно разделить на детерминистические и вероятностные (рисунок 8.1). Детерминистические модели долговечности используют при детерминистическом проектировании долговечности, когда не учитывают разброс деградации (или работоспособности, или срока службы). При известных значениях параметров модели позволяют определить только одну величину (деградацию или работоспособность, или срок службы), которая часто оказывается средней величиной. В некоторых случаях детерминистические модели создают для того, чтобы получить не среднее, а верхнее или нижнее квантильное значение.
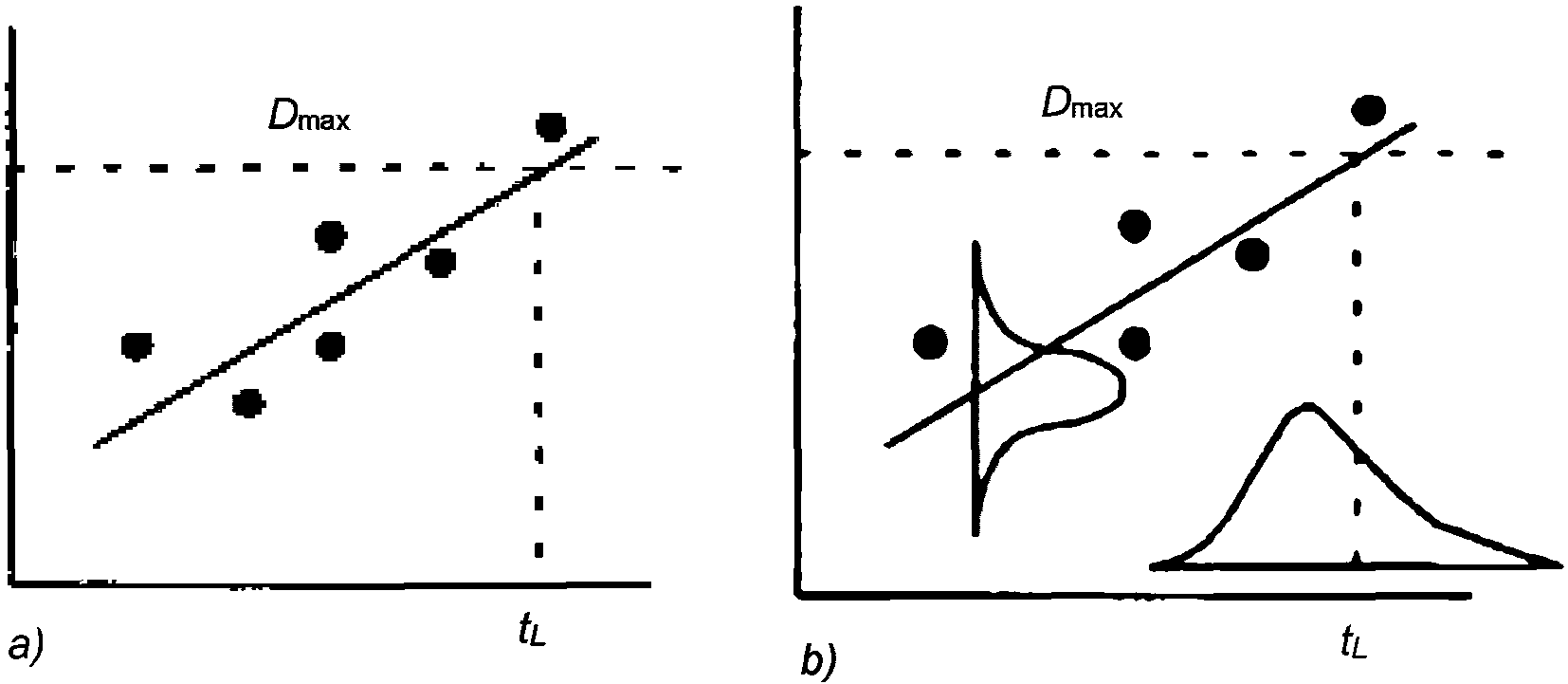
и вероятностная (b) модели
8.1.2.2 Во многих случаях информация, выдаваемая детерминистическими моделями, оказывается недостаточной для оценки риска того, что сооружение не достигнет заданного срока службы. Вероятностные методы проектирования рассматриваются как более полные, особенно в прочностном проектировании конструкций, поскольку разброс, вызываемый деградацией, обычно бывает большим, и степень риска может оказаться довольно высокой.
8.1.2.3 При использовании вероятностных моделей долговечности конструкцию проектируют с обеспечением определенной минимальной надежности по заданному сроку службы. Заданный срок службы не является абсолютной целью, которую нужно достичь любой ценой. Нужно обеспечить выполнение другого требования: вероятность того, что фактический срок службы сооружения может оказаться более коротким, чем заданный срок службы, должна быть меньшей, чем допускаемая вероятность разрушения. Благодаря такой постановке проблемы достигается лучшее понимание природы понятия "срок службы", а процесс проектирования более полно соответствует ожидаемому результату.
8.1.2.4 Вероятностные методы проектирования, кроме того, дают возможность проектировщику оценить чувствительность различных параметров, влияющих на продолжительность срока службы. Таким образом, основное внимание должно быть уделено именно этим параметрам, что может оказаться полезным даже на начальной стадии разработки модели.
8.1.3 Модели долговечности для различных задач
8.1.3.1 Определение потребности в моделировании
8.1.3.1.1 Модели долговечности создают для различных целей. Предпосылки к созданию моделей долговечности, а также стоящие перед ними задачи могут быть различными в зависимости от их конечного предназначения. Модели основывают на различных типах и для различных уровней данных по долговечности. Иногда прогнозирование срока службы может основываться на истории развития конструкции и опыте ее эксплуатации, в то время, как в других случаях для получения информации, позволяющей сделать такой прогноз, необходимо проводить испытания.
8.1.3.1.2 Кроме этого, существуют различия в параметрах моделей, которые зависят от глубины теоретической разработки моделей и от требований заказчика сооружения. Например, параметры проектирования и контроля качества при проведении мероприятий по содержанию сооружения и при его ремонте различны (см. приложение А).
8.1.3.1.3 Для дальнейшего совершенствования моделей долговечности нужно выделить, по крайней мере, следующие направления:
- техническое развитие материалов;
- изучение характера экологического воздействия на материалы;
- создание разноуровневых сетей управления содержанием, ремонтом и реконструкцией сооружений;
- планирование ремонтных работ на уровне объектов;
- анализ рисков, связанных с отдельными сооружениями особого значения;
- проектирование бетонных смесей и обеспечение контроля качества на стройплощадке;
- проектирование долговечности конструкций.
8.1.3.1.4 Не существует каких-либо данных по прогнозированию долговечности новых материалов. Для определения коррозионной стойкости и долговечности новых материалов проводят их ускоренные испытания по искусственному старению. При оценке потенциального срока службы новых материалов полагают, что количество циклов ускоренных испытаний по искусственному старению определенным образом отражает некоторую зависимость со сроком службы материала в реальных условиях.
8.1.3.1.5 Срок службы новых материалов можно пытаться определить сравнением скорости изменения характеристик материалов при ускоренных испытаниях по искусственному старению с результатами, полученными при длительных испытаниях по естественному старению в условиях реальной эксплуатации материала [7]. Сравнительные испытания новых материалов параллельно с известными также могут быть основой для прогнозирования срока службы новых [8].
8.1.3.1.6 Для проведения оценки воздействия окружающей среды на срок службы материалов могут быть использованы ускоренные испытания на старение. Существенное отличие в этом случае состоит в том, что диапазон прогнозирования во времени может растягиваться на длительные сроки. Например, при оценке конечного состояния резервуара для хранения ядерных отходов требуемый срок службы материалов может составлять несколько тысячелетий.
8.1.3.1.7 Для планирования мероприятий по содержанию и эксплуатации существующих сооружений с точки зрения оценки эффективности капиталовложений также необходимы модели долговечности. При этом создаются сетевые многоуровенные системы управления, предназначенные для содержания, ремонта и реконструкции мостов и иных сооружений. Часто модели долговечности таких систем основывают на результатах обследования сооружений, собранных силами официального органа, для которого созданы данные системы. После этого параметры моделей долговечности взаимоувязываются в базе данных системы с результатами проведенных обследований.
8.1.3.1.8 При планировании мероприятий по ремонту отдельных существующих сооружений могут быть использованы другие типы моделей. Зная возраст и современное состояние сооружения, можно использованием экстраполяционной модели прогнозировать будущую работоспособность сооружения и оставшийся срок его службы.
8.1.3.1.9 Для сооружений, связанных с большим социальным, экономическим или экологическим риском, проводят анализы рисков. К таким сооружениям относятся атомные электростанции, платформы для добычи нефти, плотины, мосты и т.д. Для проведения анализов рисков необходимо комбинировать различные вероятностные модели разрушения, по которым определяют критические пути, могущие привести к нарушению безопасности сооружения. В анализе рисков можно применять все возможные виды моделей, даже теоретические.
8.1.3.1.10 Модели долговечности нужны, кроме того, и при проектировании состава бетонных смесей. В число параметров этих моделей входят количество и соотношение составляющих смеси, а также свойства, которые можно определить или оценить по характеристикам бетонной смеси. Эти модели можно применять также и на строительной площадке. Применяя модели долговечности, лицо, контролирующее качество работ, может оценивать будущие характеристики бетона до выдачи разрешения на укладку его в опалубку.
8.1.3.2 Модели для проектирования долговечности конструкций
8.1.3.2.1 Параметры моделей, предполагаемых к использованию при проектировании долговечности конструкций, должны быть доступными инженеру-проектировщику. В этом смысле большее предпочтение отдают не параметрам, относящимся к свежеприготовленной бетонной смеси, а параметрам, которые можно измерять по затвердевшему бетону, например, прочность, пористость и т.д. Они также должны включаться в систему контроля качества проектируемого сооружения.
8.1.3.2.2 Прочностные характеристики материалов в значительной степени влияют на несущую способность сооружения и косвенно на его геометрические размеры, величину пролета, деформации и т.д. Поскольку прочностные характеристики являются неотъемлемыми расчетными параметрами конструктивного проектирования, их весьма удобно принимать за параметры моделей долговечности.
8.1.3.2.3 Если прочностные характеристики не применяют параметры долговечности железобетонных конструкций, то с большой степенью вероятности можно утверждать, что используются другие параметры, так или иначе связанные с прочностью. Это может приводить к опасности возникновения противоречивых требований к расчетным параметрам. По этой причине водоцементное отношение в бетонной смеси, часто используемое в качестве расчетного параметра при проектировании бетонной смеси, не считают пригодным для конструктивных расчетов. Другая причина отказа от него как параметра при конструктивных расчетах состоит в том, что все больше и больше применяемые в бетонных смесях активные минеральные добавки (доменный шлак, зола уноса, микрокремнезем и др.) отодвигают на задний план саму идею водоцементного отношения. Кроме того, определение водоцементного отношения на схватившемся бетоне затруднено, особенно при использовании добавок - заменителей цемента.
8.1.3.2.4 Другой параметр, часто используемый для характеристики качества бетона (наряду с водоцементным отношением) - степень гидратации цемента. Вследствие применения добавок - заменителей цемента понятие "степень гидратации" также стало туманным и его ценность как практического расчетного параметра также упала. Для проектировщика более значимые и достаточно точные для целей расчета параметры - кинетика и продолжительность набора прочности.
8.2.1 Количественный анализ деградации
8.2.1.1 Первый шаг на пути создания моделей деградации является анализ факторов и процессов деградации. В таблице 8.1 системно перечислены все возможные факторы, процессы и последствия деградации. Для удобства все факторы деградации разделены на следующие группы:
1. механические;
2. биологические;
3. химические;
4. физические;
5. связанные с характером эксплуатации.
Таблица 8.1
Деградационный фактор | Процесс | Деградация |
Механические | ||
Статическое загружение | Деформация | Прогибы, трещинообразование, разрушение |
Циклическое загружение | Усталостные напряжения, деформация | Прогибы, трещинообразование, разрушение |
Биологические | ||
Микроорганизмы | Производство кислоты | Выщелачивание |
Химические | ||
"Мягкая" вода | Выщелачивание | Разложение бетона |
Кислота | Выщелачивание | Разложение бетона |
Кислота | Нейтрализация | Депассивация стали <*> |
Кислотные газы | Нейтрализация | Депассизация стали <*> |
Диоксид углерода | Карбонизация | |
Диоксид серы | Сульфатация | |
Диоксид азота | Образование солей | |
Хлориды | Пенетрация, разрушение нейтральной пленки | Депассивация стали <*> |
Депассивация стали, кислород, вода | Коррозия | Разбухание коррозийного слоя стали, потеря диаметра стержней, потеря сцепления |
Сульфаты | Внутрикристаллическое давление | Разрушение бетона |
Силикатные заполнители, щелочи | Силикатная реакция | Увеличение объема, разложение бетона |
Карбонатные заполнители | Карбонатная реакция | Увеличение объема, разложение бетона |
Физические | ||
Изменение температуры | Расширение | Укорочение, удлинение, стесненные деформации |
Изменение относительной влажности | Усадка, набухание | Укорочение, удлинение, стесненные деформации |
Низкие температуры, вода | Образование льда | Разрушение бетона |
Соли-антиобледенители, отрицательные температуры | Перенос теплоты | Отслоение бетона |
Плавающий лед | Абразивное воздействие | Трещинообразование, отслоение |
Воздействие транспорта | Абразивное воздействие | Колееобразование, истирание, износ |
Проточная вода | Эрозия | Повреждение поверхности |
Турбулентный поток | Кавитация | Образование каверн |
8.2.1.2 Этим путем не всегда оказывается возможным четко разграничить факторы деградации. Примером такого явления может служить биогенная сернокислотная коррозия, первопричиной которой являются биологические процессы, а последующая деградация представляет собой химический процесс. В подобных случаях выбор типа деградационного фактора основывают на его происхождении. Классификация деградационных факторов позволяет осуществить их наглядный анализ.
8.2.1.3 Таблица деградационных факторов, подобная таблице 8.1 (первоначально использованная для определения анализа рисков, где она была названа "режимом разрушения и анализом влияния" - FMEA), может быть использована проектировщиком для отбора соответствующих деградационных факторов.
8.2.1.4 Отбор факторов можно проводить двумя путями:
- отбор основан на деградационных факторах, появление которых ожидают в месте расположения будущего сооружения;
- отбор основан на риске; при этом нужно рассматривать лишь те деградационные факторы, которые сопровождаются относительно высокой степенью риска. В этом смысле риск представляет собой вероятность разрушения, помноженную на объем повреждений, вызванных деградацией.
8.2.1.5 На рисунке 8.2 приведена диаграмма, которая иллюстрирует структуру очень сложного механизма, в котором, в свою очередь, участвуют несколько других механизмов, причем влияние одного механизма создает деградационный фактор для другого.
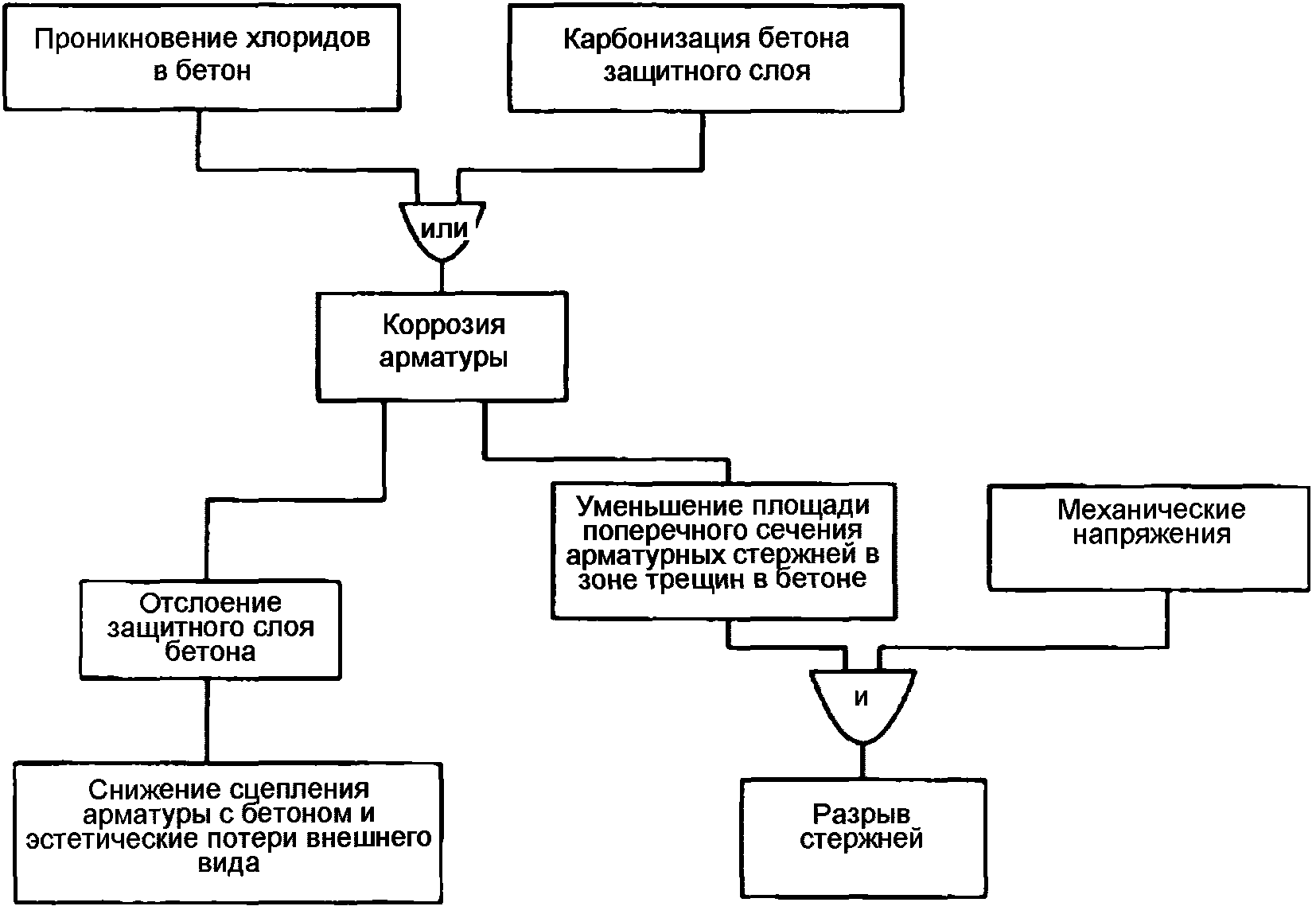
8.2.1.6 Любое воздействие, которому подвергается сооружение, вызывает конкретную ответную реакцию, зависящую от природы рассматриваемого влияния. Для каждого деградационного фактора имеется ответная реакция сооружения, которое пытается воспрепятствовать деградации. Для механического загружения, например, существует определенная несущая способность, разрушению от замораживания противостоит морозостойкость и т.д. Факторы внутренней ответной реакции, в основном, соответствуют свойствам материалов, геометрической форме и размерам.
8.2.1.7 Вообще говоря, ответные реакции можно классифицировать аналогично деградационным факторам:
- механические;
- механо-физические;
- физические;
- механо-химико-физические;
- химические;
- геометрические.
8.2.1.8 При формулировании моделей долговечности необходимо также учитывать возможность человеческой ошибки и другие неопределенные факторы. В эту категорию влияния включают следующие группы [9]:
- неопределенности проектирования;
- ошибки коммуникаций;
- неопределенности при изготовлении и строительстве;
- ошибки математического и статистического моделирования.
8.2.1.9 Если неопределенности проектирования, изготовления и исполнения не обрабатывать особо, то их можно учитывать, как дополнительный разброс в моделях долговечности. Неучет некоторых параметров в моделях долговечности также может приводить к увеличению разброса. Однако обработка грубых погрешностей при наличии разброса невозможна.
8.2.2 Количественное определение деградации, работы и срока службы
8.2.2.1 Заключительный этап в процессе создания моделей долговечности состоит в определении количественных показателей и их состава. Инструментом для выполнения этой задачи служат статистические методы и теоретический анализ. Кроме того, часто приходится прибегать к упрощениям, к отказу от не относящихся напрямую факторов и к ограничению числа факторов, непосредственно относящихся к проблеме.
8.2.2.2 Модели долговечности можно основывать на эмпирическом и на аналитическом фундаменте. Эмпирические модели составляют на основании опыта и результатов экспериментов. Их создают по результатам полевых испытаний и лабораторных исследований с использованием методов корреляции и других статистических методов.
8.2.2.3 Аналитические модели строят на основании законов природы и на фундаментальных научных положениях. Они создаются в результате подробного анализа механизмов деградации и кинетики деградации. До практического применения моделей обычно бывает необходимо проведение испытаний по определению значений некоторых величин, относящихся к свойствам материалов.
8.2.2.4 Весьма часто эмпирические модели представляют точку зрения инженеров, а аналитические модели - точку зрения ученых. Недостаток эмпирических моделей состоит в том, что в них вообще с трудом воспринимается механизм влияния. Вследствие этого любое отклонение за пределы модели становится невозможным без вовлечения некоторого риска.
8.2.2.5 Аналитические модели основаны на более глубоком понимании сути процесса повреждения конструкции, однако их практическое значение может оказаться небольшим, если параметры модели не поддаются непосредственному измерению, или если эти модели не могут быть доведены по какой-либо иной причине до уровня практического применения.
8.2.2.6 При создании моделей долговечности необходимо привлекать как эмпирические, так и аналитические инструменты. Модели могут считаться пригодными, если они основаны на изучении механизмов и факторов, которые способствуют деградации, и в то же время они должны поддаваться проверке в лаборатории и при полевых испытаниях. Условие практической применимости модели для выполнения конструктивных расчетов состоит в том, что она должна быть достаточно проста и поддавалась осмыслению.
8.2.2.7 При разработке эмпирической модели деградации (или работы) обычно необходимы полевые испытания. Их задача состоит в определении степени влияния основных параметров, особенно параметров окружающей среды, на характер протекания деградации во времени. Деградацию (или работу) измеряют в любых подходящих для этого единицах. Для определения средней кривой деградации используют регрессивный анализ и прочие статистические методы (рисунок 8.3).
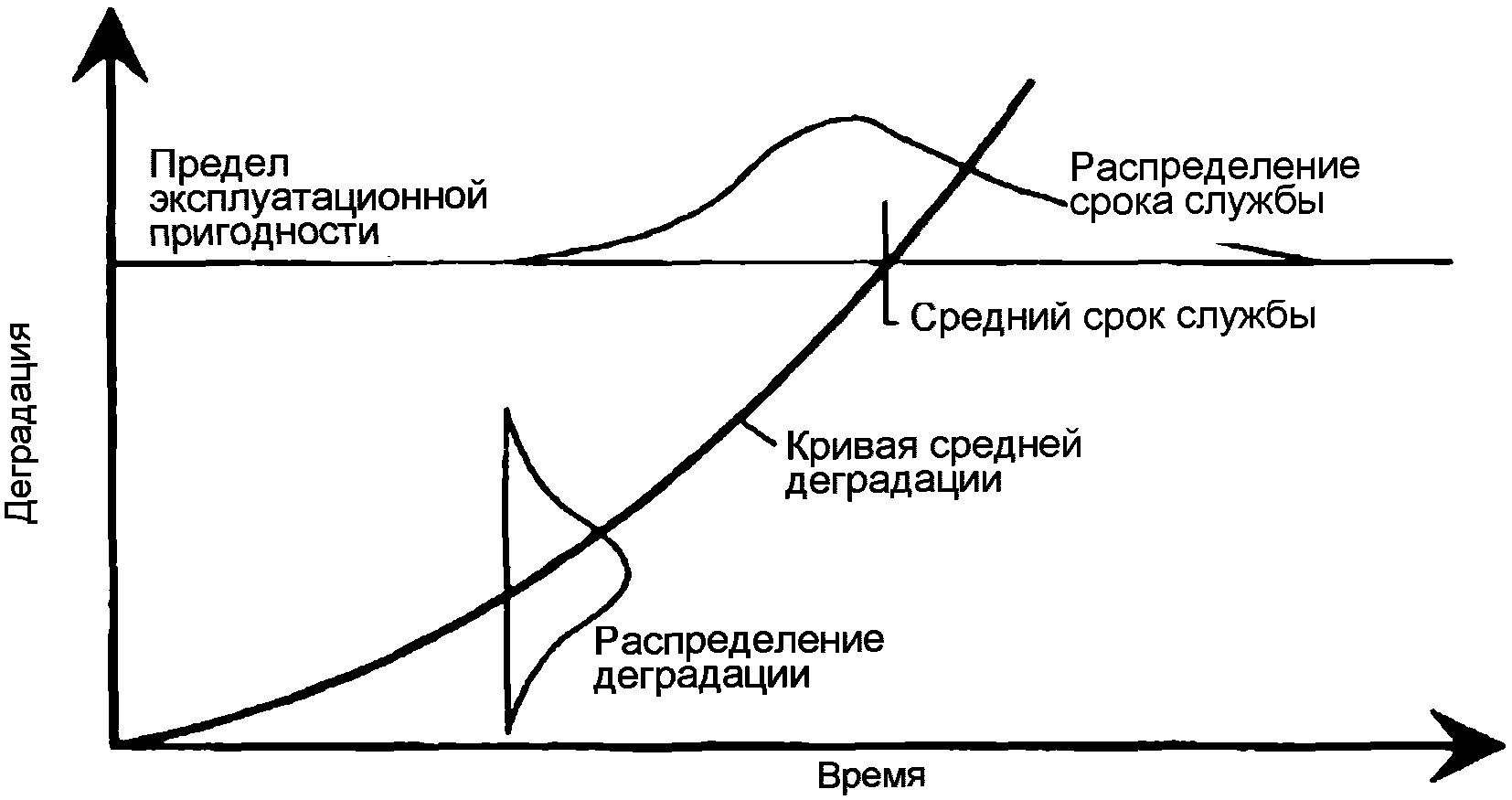
8.2.2.8 Следующий этап создания модели - лабораторные испытания. При этом должна обеспечиваться уверенность в том, что эти лабораторные испытания действительно относятся к изучаемому фактору деградации. После этого изучают влияние различных параметров на скорость деградации; при этом прибегают к серии опытов с меняющимися характеристиками материалов, размерами и т.д. В большинстве случаев информации, полученной из этих испытаний, в сочетании с результатами полевых испытаний, бывает достаточно для построения модели деформации или работы, содержащей несколько параметров:
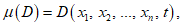 (8.1)
(8.1)где  - средняя деградация;
- средняя деградация;
x1, x2, xn - параметры материала, конструкции и окружающей среды;
t - возраст сооружения.
8.2.2.9 Модели работы можно без труда получить из моделей деградации, поскольку фактически они представляют процесс, противоположный деградации. Например, модель деградации описывает рост глубины карбонизации во времени, соответствующая модель работы отражает изменение во времени толщины некарбонизированного бетона. Некарбонизированная часть бетона защитного слоя, таким образом - своеобразная "способность" конструкции, т.е. характеристика ее работоспособности.
Общий вид модели работы напоминает внешне модель деградации
 (8.2)
(8.2)где  - средняя работоспособность;
- средняя работоспособность;
x1, x2, xn - параметры материала, конструкции и окружающей среды;
t - возраст сооружения.
8.2.2.10 На уровне конструкции работоспособность не всегда является линейной функцией деградации материалов, и в модель работы могут быть включены несколько деградационных факторов. Например, в модели работы несущей способности колонны, несущая способность зависит от величины площади поперечного сечения бетона и стали. Таким образом, модели деградации бетона и стали изображаются математическими функциями площадей поперечного сечения, в которых ширина колонны и диаметр арматурных стержней возведены во вторую степень.
8.2.2.11 Средний срок службы обычно принимают приблизительно равным периоду времени, за который средняя деградация достигнет максимально допустимой суммарной деградации, или за который средняя работоспособность достигнет минимально допустимого состояния работоспособности. При известных максимальной деградации, Dmax, или минимальной работоспособности, Pmin, соответствующий средний срок службы может быть получен из моделей деградации или работы
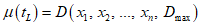 (8.3)
(8.3)или
где  - средний срок службы.
- средний срок службы.
8.2.2.12 Если доступен достаточно большой объем информации по сроку службы, средний срок службы может быть смоделирован непосредственно без необходимости прибегать к моделям деградации или работы. Однако такое случается не часто. Когда средний срок службы определяют по моделям деградации или работы вышеописанным способом, полученный результат не имеет высокой точности, но его часто можно принимать как достаточно близкое среднее значение величины.
8.2.3 От детерминистической к вероятностной модели долговечности
8.2.3.1 В вероятностных моделях содержатся не только средняя деградация (или работа, или срок службы), но и предполагаемая форма распределения, а также методы оценки величины разброса. Вместо получения отдельной конкретной величины по ним можно определить законы распределения каждой комбинации параметрических величин вероятностной модели.
8.2.3.2 При вероятностном проектировании обычно для оценки средней деградации применяют детерминистические расчетные модели. Для оценки характера стандартного отклонения приводится постоянный коэффициент вариации. С увеличением деградации стандартное отклонение также возрастает
 (8.5)
(8.5)где  - стандартное отклонение деградации;
- стандартное отклонение деградации;
8.2.3.3 Оценка стандартного отклонения может также основываться на методе дифференцирования. В соответствии с этим методом детерминистическую модель среднего X дифференцируют по каждому параметру XL модели, а результат умножают на стандартное отклонение этого параметра. Окончательное стандартное отклонение затем определяют по формуле
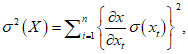 (8.6)
(8.6)где  - стандартное отклонение X (деградация, работа или срок службы);
- стандартное отклонение X (деградация, работа или срок службы);
n - число переменных.
8.2.3.4 Для моделирования типичного вероятностного деградационного процесса железобетонных конструкций можно использовать метод [10]. Этот метод позволяет воспроизвести процесс естественного разрушения, начиная с состояния отличной сохранности с последующей постоянной и случайной деградацией. В течение этого процесса могут быть определены как разброс, так и форма распределения.
8.2.3.5 Процесс по методу [10] начинается также с известной средней кривой. Однако в этом случае не нужны ни параметры, ни предположения о характере распределения.
8.2.3.6 Математическая теория метода [10] находит широкое применение, например, для разработки сетевой системы управления содержанием мостов.
Огромным преимуществом метода [10] является также то, что он позволяет осуществлять линейное программирование. Таким образом, можно проводить анализ по оптимизации затрат на мероприятия по ремонту с целью уменьшения их стоимости, а также планирование ремонта сооружений.
9.1.1 В настоящем разделе приведены несколько примеров моделей долговечности для различных деградационных факторов. Они не являются единственно наиболее вероятными; можно применять другие модели при условии, что они соответствуют формальным требованиям, предъявляемым к моделям долговечности вообще и пригодны для проектирования долговечности. Однако эти модели являются наиболее общепризнанными, хотя на сегодняшний день не существует единого мнения по поводу моделей долговечности.
9.1.2 Поскольку модели предназначены для использования в детерминистическом или полувероятностном проектировании совместно с коэффициентами надежности по сроку службы, в них не содержится какой-либо другой информации относительно вероятностных свойств, кроме средних величин. В формулах моделей поэтому не содержится обозначение  , поскольку предполагается, что модели всегда имеют дело со средними величинами.
, поскольку предполагается, что модели всегда имеют дело со средними величинами.
9.1.3 В связи с вышеизложенным, там, где это необходимо, введению моделей предшествуют несколько вступительных пояснений. Среди них - пояснения, каким образом в состав конструктивного проектирования включают явление деградации. При этом возникают трудно разрешимые задачи, особенно в случае морозного воздействия на бетон и в других случаях разрушения поверхностного слоя, где деградация бетона может принимать различные формы.
9.2.1 Формы повреждений
9.2.1.1 Под морозной агрессией обычно подразумевается нарушение целостности или распад материала на поверхности бетона, которые происходят в результате периодического замораживания и оттаивания. В условиях влажности и замораживания в прилегающих к поверхности слоях происходит снижение прочности бетона с последующим распадом материала и его полной потерей в будущем.
9.2.1.2 Распад бетона происходит в результате замерзания воды в его капиллярных порах. Одна из причин этого заключается в свойстве воды увеличивать свой объем при замерзании примерно на 9%. Другая причина увеличения давления внутри структуры бетона заключается в том, что кристаллы льда имеют тенденцию к росту при замерзании во влажной среде.
9.2.1.3 Морозостойкость бетона следует рассматривать как свойство материала. Способность противостоять повторяющимся циклам замораживания и оттаивания является природным свойством бетона. Морозостойкость зависит от различных характеристик бетона, например, прочности, плотности, содержания воздуха и т.д. Однако скорость разрушения бетона зависит не только от его качества, но также и от степени агрессивности воздействия окружающей среды.
9.2.1.4 Степень агрессивности воздействия окружающей среды во много раз возрастает при использовании солей-антиобледенителей на проезжей части и тротуарах. Соли-антиобледенители не только повышают давление внутри структуры бетона, но и снижают его способность противостоять им. Характерная отличительная черта механизма разрушения "мороз-соль" - непрерывный процесс скалывания тонких слоев бетона (шелушение).
9.2.2.1 В чистом виде морозное повреждение бетона проявляется вначале как снижение прочности на угловых участках бетонных элементов. Уравнение (9.1) представляет собой модель снижения прочности
где fck(d) - нормативная прочность бетона на сжатие на глубине d;
fck - нормативная прочность на сжатие неповрежденного бетона;
d - глубина от поверхности;
H - глубина влияния;
n - коэффициент, относящийся к числу циклов "замораживание-оттаивание" (или ко времени).
9.2.2.2 При конструктивном проектировании снижение прочности бетона в зоне углов можно учесть в виде снижения расчетной прочности, распространяемого по всему поперечному сечению бетонного элемента, или в виде уменьшения размеров поперечного сечения. Последний способ использован в настоящем пособии при введении понятия условной потери бетона.
9.2.2.3 На рисунке 9.1 показано снижение прочности в соответствии с уравнением (9.1) на глубину влияния H. Значение коэффициента n уменьшается от бесконечности (в момент t = 0) до 0 (после бесконечно длительного времени). Условная потеря бетона x определена расчетом. Значение x следует вычесть из ширины поперечного сечения a, что дает эквивалент элемента с неповрежденным бетоном. Таким образом, даже если не происходит реальной потери сколовшегося бетона, будущее повреждение можно учесть путем уменьшения размеров поперечного сечения элементов за счет условной потери бетона. Толщина условно теряемого слоя бетона равна глубине влияния, деленной на зависящий от времени показатель (n + 1).
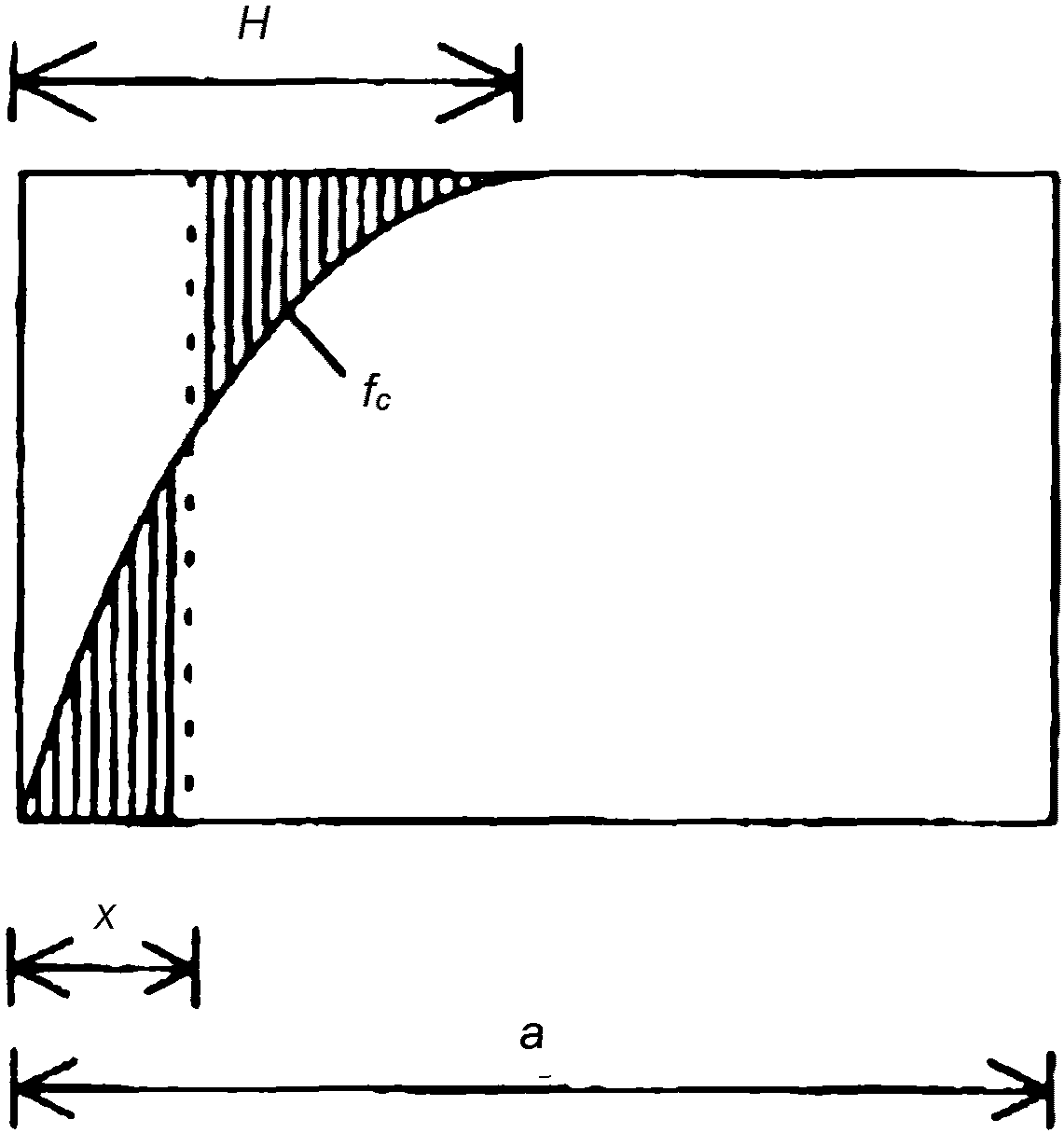 | 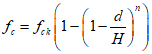 N = fck(a - x) x = H/(n + 1) |
9.2.2.4 Реальное разрушение бетона также имеет место, и оно в не меньшей степени зависит от других возможных воздействий, которым подвергается сооружение. Проточная вода, ледоход, движение транспорта и другие причины часто являются заключительными факторами воздействия, от которого происходит разрушение. В отсутствие подобных воздействий разрушение поверхностного слоя может произойти только после полной потери прочности.
9.2.2.5 Потерю конструктивно работающего бетона как функцию времени можно грубо описать с помощью линейной модели. На рисунке 9.2 приведена подобная модель, в которой действительное отслаивание происходит в несколько этапов. Они могут быть большими или малыми в зависимости от присутствия или отсутствия хлоридов или абразивного воздействия. В этой модели происходит спрямление точек, соответствующих указанным этапам, в плавный линейный процесс. Это явление можно объяснить тем, что в промежутках между этапами в структуре здорового бетона происходит некоторое условное разрушение. Скорость разрушения (потеря конструктивно работающего бетона в вышеописанном процессе) можно определить, применив уравнение (9.2) [11].
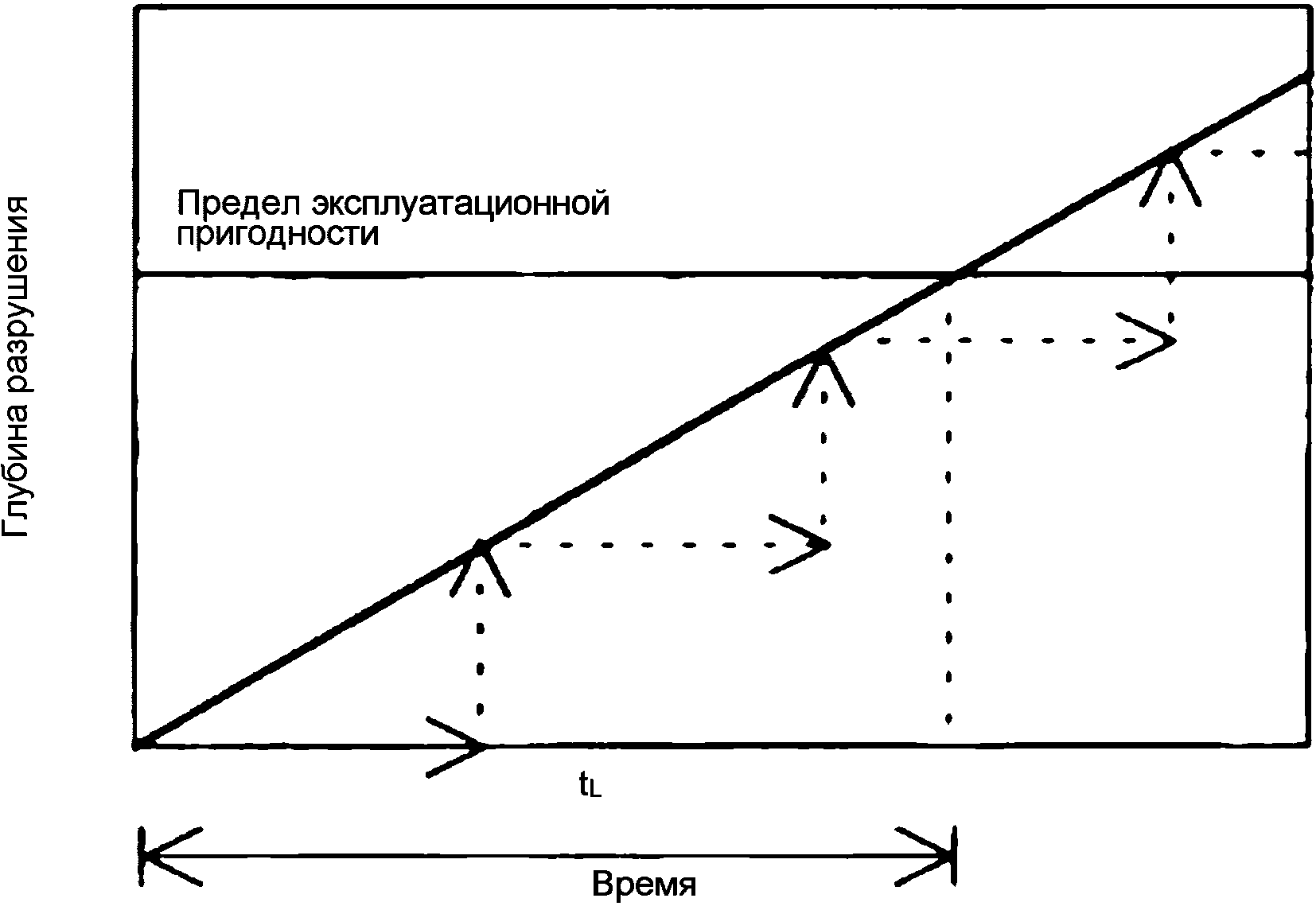
при замораживании
9.2.2.6 Влияние технологии ухода и набора прочности, возраста, содержания воздуха, прочности на сжатие бетона детально изучали в условиях замораживания в солевых растворах [12]. Теория и результаты испытаний были также перенесены на случай чистого замораживания, поскольку скорость потери бетона вряд ли можно измерить, используя методы испытаний на "чистую морозостойкость" (без солевых растворов).
9.2.2.7 Факторы воздействия окружающей среды частично были получены по результатам полевых испытаний [11].
s = rt, (9.3)
где r - скорость разрушения (потеря конструктивно работающего бетона, мм/год);
Cenv - коэффициент воздействия окружающей среды;
Ccur - коэффициент технологии набора прочности;
Cage - коэффициент старения, a = содержание воздуха, %;
fck - нормативная кубиковая прочность бетона на сжатие в возрасте 28 суток, МПа;
s - потеря конструктивно работающего бетона.
9.2.2.8 Формула модели (9.2) является весьма консервативной относительно прочности бетона на сжатие. Сдерживающее влияние прочности на сжатие на скорость разрушения может оказаться большим, чем это предполагает формула. Однако при очень высоких прочностях бетона на сжатие может происходить дополнительное внутреннее трещинообразование, которое не поддается достаточному контролю.
9.2.2.9 Коэффициент технологии набора прочности определяют по формуле
где d - время набора прочности, сутки.
Коэффициент старения определяют по формуле
 (9.5)
(9.5)где psf - доля микрокремнезема в общей массе вяжущего, %;
psl - доля доменного граншлака в общей массе вяжущего;
pfl - доля золы уноса в общей массе вяжущего.
9.2.2.10 Коэффициент воздействия окружающей среды определяют по таблице 9.1.
Таблица 9.1
окружающей среды
Класс | Условия | Значение коэффициента воздействия окружающей среды |
1 | Весьма тяжелые мороз, снег, лед, многократные циклы "замораживание/оттаивание", соленая вода или соли-антиобледенители, колебания температуры и влажности, широты 60° +/- 5° | 80 - 160 |
2 | Тяжелые мороз, снег, лед, многократные циклы "замораживание/оттаивание", постоянный контакт с водой (без хлоридов), колебания температуры и влажности, широты 60° +/- 10° | 40 - 80 |
3 | Умеренные нормальные условия на открытом воздухе, наличие замораживания и оттаивания, широты 60° +/- 10° | 20 - 40 |
4 | Благоприятные отсутствие замораживания и оттаивания | < 20 |
9.3.1 Виды повреждений
9.3.1.1 Под повреждением поверхности бетонных конструкций здесь понимаются различные типы механизмов износа сооружений, находящихся на открытом воздухе, исключая морозную агрессию, которая моделируется независимо. Эти механизмы приводятся в действие под влиянием, например, колебаний температуры и влажности, выщелачивания минералов из структуры бетона и физического солевого износа.
9.3.1.2 Ежедневные колебания температуры, особенно на поверхностях, открытых воздействию солнечной радиации, приводят к постепенному трещинообразованию в бетоне в зонах углов. Циклы увлажнения и высыхания, сопровождаемые климатическими изменениями влажности, также приводят к образованию малых трещин и к небольшим изменениям пористости бетона. Эти явления провоцируются возможным несоответствием качества заполнителей и структуры цементного камня.
9.3.1.3 Вода на контакте с поверхностью бетона вызывает выщелачивание минералов, входящих в состав бетона. Потеря материала возрастает с возникновением химических реакций этих минералов с растворенными в воде газами и ионами, например, CO2, SO2 и Mg2+. Движение воды увеличивает скорость потери материала.
9.3.1.4 Солевое разрушение бетона возникает из-за наличия механизмов, относящихся к явлению кристаллизации солей в порах бетона. К этим механизмам в обычных условиях относят капиллярный подсос соленой воды из грунта или из моря; за этим следует образование солевых кристаллов в порах и кавернах, происходящее при испарении воды. Аналогичный механизм срабатывает при расширении или усадке кристаллов соли, происходящих в результате гидратации или дегидратации, что приводит к образованию трещин и разрушению тела бетона.
9.3.2 Моделирование поверхностных повреждений
9.3.2.1 Понятие условной потери бетона, которое было введено в связи с созданием модели морозной агрессии (см. 9.2.2), применяют также и в модели поверхностных повреждений. Это означает, что ослабление бетона в угловых зонах конструкции учитывают в виде соответствующей условной потери бетона.
9.3.2.2 Снижение несущей способности конструкции определяют не по снижению прочности, а по потерям площади рабочего поперечного сечения.
Проницаемость бетона, возможно, является наиболее важным свойством, влияющим на долговечность конструкций. Скорость проникания воды и растворенных в ней вредных реагентов зависит от проницаемости так же, как и скорость вымывания из бетона важных минералов. Проницаемость бетона, таким образом, оказывает влияние на его прочность на сжатие.
9.3.2.3 Для бетонов средней и высокой прочности (30 - 100 МПа) скорость распада (потеря конструктивно работающего бетона) считается постоянной и обратно пропорциональной показателю степени прочности бетона на сжатие. Использование показателя степени (-3,3) означает, что удвоение прочности снижает скорость потери бетона на одну десятую. Для оценки скорости распада применяют уравнение (9.6) [8]
где r - скорость распада (потеря конструктивно работающего бетона, мм/год);
Cenv - коэффициент воздействия окружающей среды;
Ccur - коэффициент технологии ухода и набора прочности;
fck - нормативная (кубиковая) прочность бетона на сжатие.
9.3.2.4 Скорость распада находится в тесной связи с условиями воздействия окружающей среды. Срок службы высокофункционального бетона в зависимости от окружающих условий может колебаться от 10 лет до 10 миллионов лет. Коэффициент воздействия окружающей среды определяют с использованием таблицы 9.2.
Таблица 9.2
окружающей среды
Класс | Условия | Значение коэффициента воздействия окружающей среды |
1 | Весьма тяжелые "условия Персидского залива", широты 20° +/- 10°, морские сооружения или сооружения в пределах капиллярного подъема соленых грунтовых вод, колебания температуры и влажности | 100000 - 500000 |
2 | Тяжелые морские сооружения или сооружения в пределах капиллярного подъема соленых грунтовых вод, широты 40° +/- 10°, колебания температуры и влажности | 10000 - 100000 |
3 | Нормальные нормальные условия на открытом воздухе, небольшие климатические колебания, широты 40° +/- 10° | 1000 - 10000 |
4 | Благоприятные постоянно сухой воздух, отсутствие прямого солнечного освещения | < 1000 |
9.3.2.5 Формула для отыскания коэффициента технологии ухода и набора прочности такая же, какую использовали в модели морозной агрессии (уравнение 9.4).
9.4.1 Виды повреждений
9.4.1.1 Бетонное прибрежное сооружение в условиях Арктики подвергается воздействию различных деградационных факторов. В зависимости от своей природы, они классифицируются как механические, физические или химические.
9.4.1.2 Среди химических изменений, происходящих под воздействием морской воды, можно назвать проникновение хлоридов и растворение извести. Физические изменения при многократном замораживании и оттаивании сводятся к образованию микротрещин. Однако решающее влияние на процесс разрушения бетона в условиях Арктики почти всегда оказывает абразивное действие льда.
9.4.2 Моделирование абразивного воздействия льда
9.4.2.1 Механизм абразивного воздействия льда, вступающий в действие при ударе ледяных полей о поверхность бетона, состоит из трех элементов: истирание цементного камня (рисунок 9.3 (a)), истирание цементного камня и отрыв выступающего щебня (рисунок 9.3 (b)) и истирание цементного камня при ослабленном сцеплении между крупными зернами щебня и цементным камнем при этом сцепление падает настолько, что щебень выбивается при первом ударе льдины (рисунок 9.3 (c)) [13].
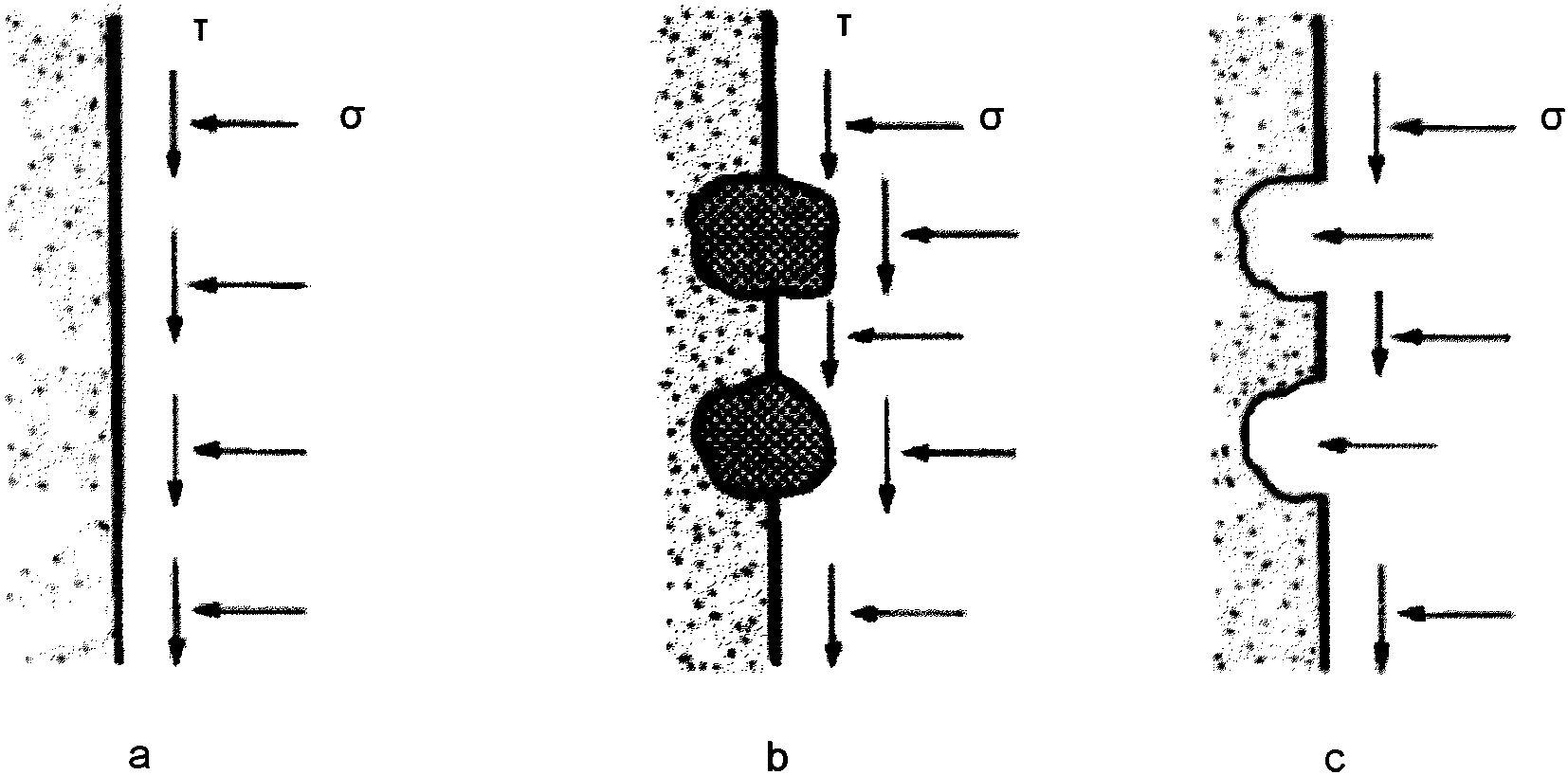
Рисунок 9.3 - Абразивные механизмы [13]
9.4.2.2 Глубину абразивного разрушения бетона арктических морских сооружений можно подсчитать как полную сумму глубины абразивного разрушения цементного камня, определенной на ледокольных испытаниях в открытом море, и размеров щебеночного камня, вырванного с поверхности бетона. Скорость роста глубины абразивного разрушения цементного камня определяют по результатам ледокольных испытаний следующим образом
 (механизм a), (9.7)
(механизм a), (9.7)где s - перемещение ледяного поля, км;
fck - нормативная кубиковая прочность бетона на сжатие, МПа.
9.4.2.3 Полную глубину абразивного разрушения бетона (ABR) можно определить по формуле
где ai - доля камня заполнителя радиусом R в объеме бетона;
ns - число ударов ледяного поля при его перемещении;
n1 - число ударов, отрывающих агрегатный камень (Lcr/R = 1);
b - скорость абразивного разрушения цементного камня, мм.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
9.4.2.3 Абразивное разрушение как функция движения ледяных полей, подсчитанное по формуле (9.8), в виде графика изображено на рисунке 9.4. Кривые абразивного разрушения справедливы при условии нормального распределения заполнителей в бетоне.
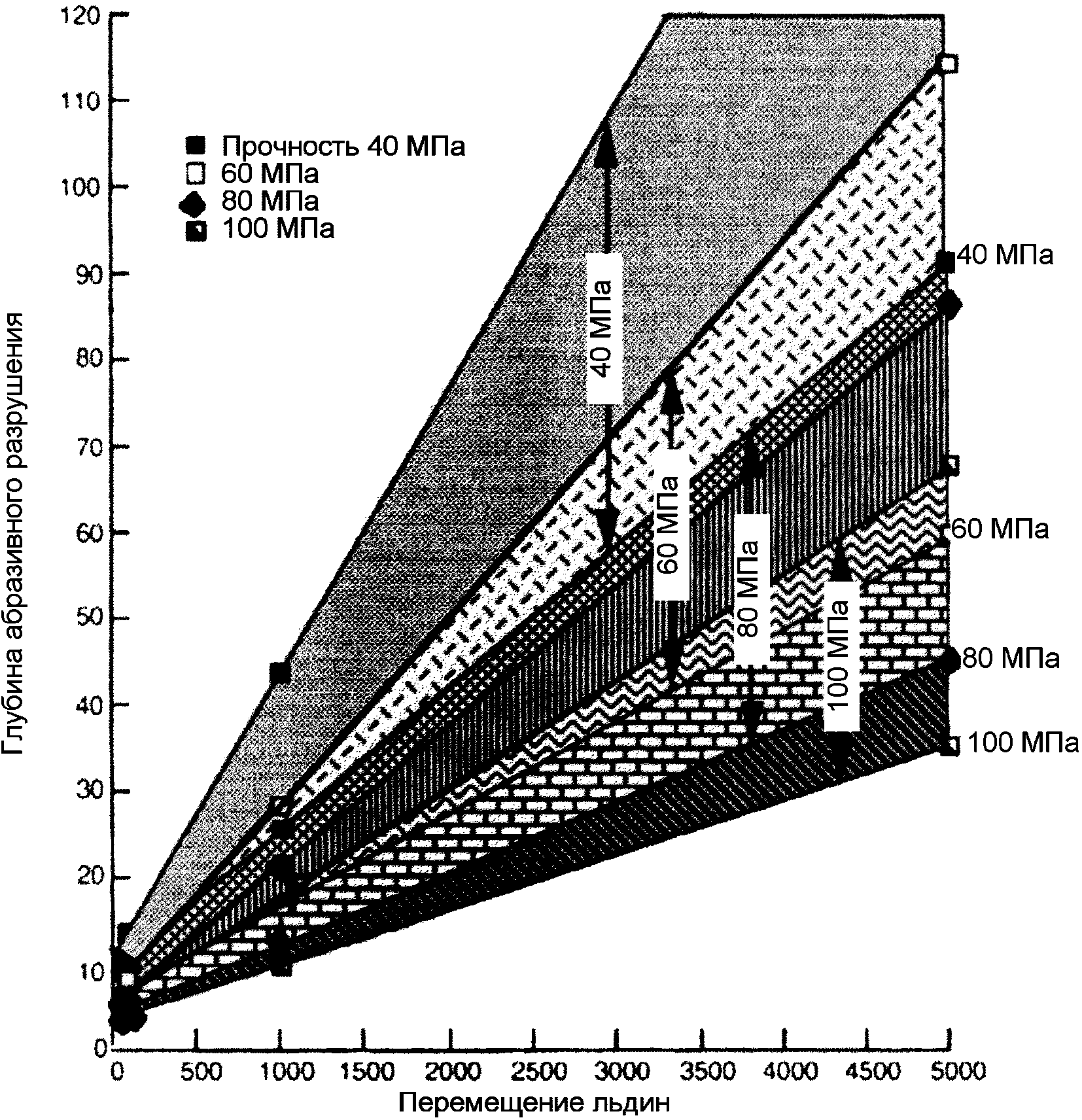
на сжатие fck = 40; 60; 80 и 100 МПа как функция перемещения
ледяных полей [13]
9.4.2.4 Все положения настоящего раздела справедливы для бетонов, обладающих строго определенным сочетанием характеристик. Помимо требований по обеспечению прочности на сжатие fck = 40, 60, 80, 100 МПа, предполагается, что прочность бетона на растяжение fct должна быть не менее 10% прочности на сжатие, а сила сцепления между заполнителями должна быть не менее 90% прочности бетона на растяжение [13]. Из рисунка 9.4 видно, что последний член уравнения (9.8) по мере увеличения перемещений льдин приобретает все более определяющее значение.
9.4.2.5 Если сцепление между заполнителем и цементным камнем нарушено под действием многократных циклов "замораживание/оттаивание", глубину абразивного разрушения можно определять по формуле
 (механизм c), (9.9)
(механизм c), (9.9)где s - перемещение ледяных полей, км;
9.4.2.6 В конструктивном расчете железобетонных сооружений для определения скорости абразивного разрушения можно использовать следующие ориентировочные зависимости:
1) если заполнитель при морозной агрессии не теряется:
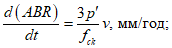 (9.10)
(9.10)2) если заполнитель при морозной агрессии теряется:
 (9.11)
(9.11)где v - перемещение ледяного поля, км/год;
p' - общий пропорциональный объем цементного камня в теле бетона, включая щебень размером до 4 мм (~ 0,4 - 0,6 в зависимости от состава бетонной смеси);
fck - нормативная кубиковая прочность бетона на сжатие, МПа.
Перемещение ледяного поля может достигать в зависимости от скорости ветра и морских течений 10000 км/год.
9.5.1 Роль бетона в защите арматуры
9.5.1.1 Взаимная работа бетона и арматуры частично основывается на том обстоятельстве, что бетон обеспечивает арматуре как химическую, так и физическую защиту против коррозии. Химическое защитное действие бетона обусловливается его щелочностью, которая приводит к образованию на поверхности стали пленки оксидов. Это явление называют пассивацией потому, что пленка оксидов предотвращает распространение коррозии. Кроме этого, бетон обеспечивает физическую защиту стали, служа барьером против реагентов, способствующих возникновению коррозии, например, против воды, кислорода и хлоридов.
9.5.1.2 В обычных железобетонных сооружениях, расположенных на открытом воздухе, коррозия арматуры начинается только тогда, когда начинаются изменения в бетоне, окружающем арматуру. Эти изменения могут иметь физический характер, когда происходит, например, растрескивание бетона и его разрушение с обнажением части стального стержня и оставлением его без физической и химической защиты бетона.
9.5.1.3 В бетоне, окружающем стальной стержень, могут также происходить и химические изменения; наиболее важные из них следующие:
- карбонизация бетона, вызываемая диоксидом углерода, содержащимся в воздухе;
- проникновение в бетон агрессивных анионов, в особенности хлоридов.
Карбонизация представляет собой реакцию диоксида углерода (в воздухе) с гидратированными цементными минералами в бетоне. Это явление происходит на всех открытых поверхностях бетона, вызывая понижение pH в бетоне карбонизированной зоны. В карбонизированном бетоне защитная пассивная пленка на поверхности стали разрушается, открывая путь коррозии. Вредоносное влияние хлоридов основано не на понижении pH, а на их способности иными путями разрушить пассивную пленку.
9.5.2 Моделирование коррозии арматуры
9.5.2.1 Относительно срока службы можно выделить два предельных состояния (рисунок 9.5):
1) Срок службы заканчивается при депассивации стали. Этим правилом обычно пользуются при всех видах хлоридной коррозии, поскольку скорость пенетрации при локальной агрессии все еще довольно трудно определить и степень неопределенности относительно длительности периода распространения коррозии достаточно высока. Таким образом, срок службы ограничен только начальным периодом коррозии (время, когда агрессивный реагент достигнет поверхности стали и начнет процесс депассивации).
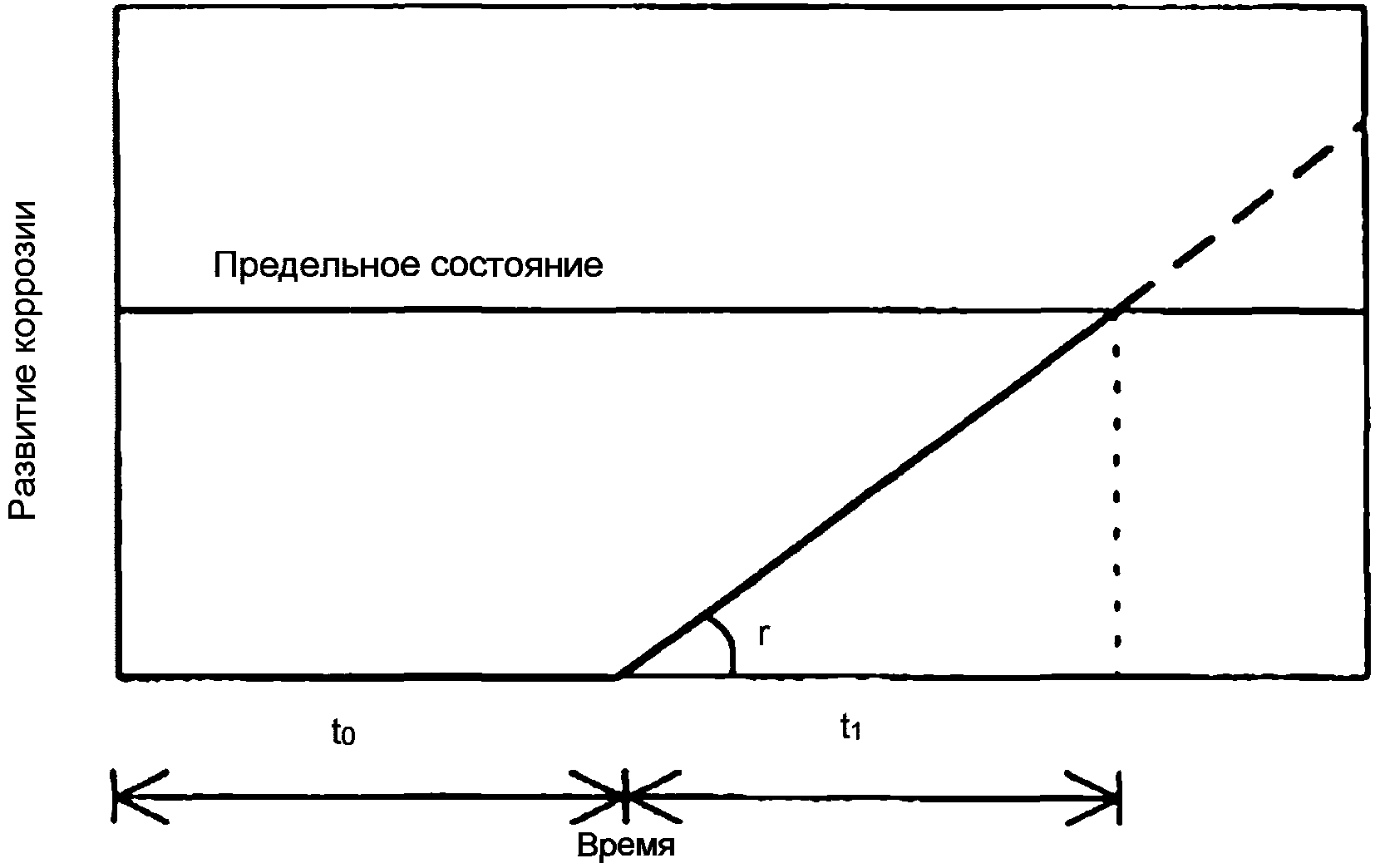
коррозии арматуры
Это же правило применимо для всех видов преднапряженных сталей. Растягивающие напряжения в пучках обычно настолько высоки, что не допускается никакого снижения площади поперечного сечения проволок, поскольку в результате поверхностной коррозии значительно возрастает риск обрыва.
Для тех случаев, когда не допустима никакая коррозия, пользуются формулой
tL = t0, (9.12)
где tL = срок службы;
t0 = время начала коррозии.
2) Предельное состояние определяется растрескиванием защитного слоя бетона, происходящим из-за наличия оксидов, которые образуются в процессе коррозии. В этом случае срок службы включает в себя некоторый период распространения коррозии, в течение которого площадь поперечного сечения арматуры непрерывно сокращается, сцепление между арматурой и бетоном падает, а рабочая площадь поперечного сечения бетона уменьшается из-за отслаивания бетона защитного слоя. Такой подход применяют в тех случаях, когда общая коррозия протекает из-за карбонизации.
9.5.2.2 Срок службы, определяемый по факту растрескивания бетона защитного слоя, находят как сумму времени начала коррозии и времени растрескивания бетона до определенного предела
tL = t0 + tl, (9.13)
где tl - время распространения.
Время распространения tl заканчивается, когда достигается некая максимально допустимая потеря площади поперечного сечения, или происходит потеря сцепления, или ширина раскрытия трещин достигает определенного значения. Числовые значения этих критериев зависят от конкретных деталей и геометрических характеристик каждого элемента.
9.5.2.3 Если трещины образовались в самом начале срока службы, то время начала коррозии t0 будет гораздо более коротким, чем на участках, где трещины отсутствуют, возможно даже, что t0 = 0. В этом случае можно записать:
tL = tl, (9.14)
где tl - время свободной коррозии.
Ниже приведены модели, позволяющие определить t0 и tl. При разработке этих моделей было сделано предположение, что поверхности бетона не имеют какого-либо защитного покрытия и не обработаны герметиками.
9.5.3.1.1 Наиболее общий источник хлоридов - морская вода (прибрежные районы) и соли-антиобледенители. Хлоридные добавки в бетонную смесь здесь не рассматриваются.
9.5.3.1.2 При проникновении хлоридов в бетон их концентрация по мере заглубления падает, образуется градиент. За время начала коррозии принимают время, в течение которого критическая концентрация хлоридов (пороговое значение) достигает поверхности арматуры и депассивирует ее. Градиент концентрации хлоридов часто описывают как функциональную модель ошибки (erf), которая подчиняется условию второго закона диффузии Фика
 (9.15)
(9.15)где Cx - содержание хлоридов на глубине x;
Cs - концентрация хлоридов на поверхности бетона;
x - глубина от поверхности конструкции;
D - коэффициент диффузии;
t - время.
9.5.3.1.3 Время начала коррозии можно получить из формулы
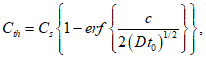 (9.16)
(9.16)где Cth - критическая концентрация хлоридов;
c - толщина защитного слоя;
t0 - время начала коррозии.
Используя параболическую функцию, формулу можно упростить:
 (9.17)
(9.17)после чего формулу для определения времени начала коррозии можно записать в следующем виде:
 (9.18)
(9.18)9.5.3.1.4 Многие стандарты и нормы ограничивают пороговое значение концентрации (Cl-) значением 0,4% массы цемента для обычного железобетона и 0,2% - для предварительно напряженного, что приблизительно соответствует 0,05% - 0,07% массы бетона (0,025% - 0,035% - для преднапряженного бетона).
Практика показывает, что значения Cs на ранней стадии зависят от времени, однако через несколько лет они достигают максимума. Для упрощения расчетов ее обычно принимают постоянной. Нормальные значения лежат в пределах 0,3 - 0,4 массы бетона.
Коэффициент диффузии принимают приблизительно равным 10-7 - 10-8 см2/с.
9.5.3.2 Коррозионное растрескивание напрягаемой арматуры
9.5.3.2.1 К счастью, явление растрескивания при коррозии преднапряженной арматуры достаточно редко. Коррозия может происходить в проволоках преднапряженных пучков, которые подвержены воздействию реагентов, ее вызывающих, что ведет к хрупкому разрушению в условиях почти полного отсутствия каких-либо потерь в площади поперечного сечения. Коррозия напряженных элементов развивается под поверхностными трещинами даже при очень малой ширине раскрытия.
9.5.3.2.2 Для возникновения поверхностных трещин, под которыми может развиваться коррозия напряженных элементов, необходимо, чтобы на отдельных участках произошла ограниченная депассивация стали. Поэтому защита преднапряженной арматуры от воздействия агрессивных реагентов - необходимейшее условие обеспечения ее срока службы, который всегда ограничен временем начала коррозии. Что касается проникновения хлоридов, правила расчета, изложенные в 9.5.3.1, могут быть применены и к преднапряженной арматуре.
9.5.3.3 Коррозия, вызываемая карбонизацией
9.5.3.3.1 Диоксид углерода из воздуха проникает в бетон, нейтрализуя его щелочную среду и образуя фронт карбонизации, который перемещается вглубь тела бетона. Когда этот фронт карбонизации достигает арматуры, пассивная пленка на поверхности арматуры теряет свою стабильность и растворяется, инициируя процесс обычной коррозии. За время начала коррозии принимают время, необходимое для завершения карбонизации защитного слоя бетона.
9.5.3.3.2 Обычно скорость карбонизации считают связанной с квадратным корнем из времени:
d = Kct1/2, (9.19)
где d - глубина карбонизации за время t;
Kc - коэффициент карбонизации;
t - время или возраст.
9.5.3.3.3 Время начала карбонизации можно определить по формуле
9.5.3.3.4 Коэффициент карбонизации зависит от прочности бетона, типа связующего, содержания цемента и от условий окружающей среды (влажность и температура). Для описания скорости карбонизации существует несколько формул. Некоторые из них аналитические, другие - эмпирические.
Основываясь на первом законе Фика, определяют глубину карбонизации [14] по формуле
где x - глубина карбонизации, м;
a - количество щелочных веществ в бетоне;
Dc - эффективный коэффициент диффузии CO2 при данном распределении влажности в порах, м3/с;
C1 - C2 - разность концентрации CO2 в воздухе и по фронту карбонизации, кг/м3;
t - время.
9.5.3.3.5 Этот математический аппарат может быть распространен на случаи переменных циклов смачивания и высыхания [15]. Во влажных условиях фронт карбонизации неподвижен. В период высыхания влага испаряется, чем способствует продвижению фронта карбонизации.
Согласно [15], время t в уравнении (9.21) заменяется на teff, которое определяют следующим образом:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
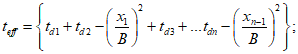 (9.22)
(9.22) (9.23)
(9.23)где xn - глубина карбонизации после n-го цикла смачивания и высыхания, м;
tdn - продолжительность n-ого периода высыхания;
Dv - эффективный коэффициент диффузии для водяных паров при данном распределении влаги в порах, м2/с;
C3 - C4 - разность влажностей в воздухе и по фронту испарения, кг/м3;
b - количество воды, испаряющейся из бетона, кг/м3.
Если продолжительность периодов высыхания и увлажнения одинакова, то время, прошедшее за n циклов, равно
tn = ntd + (n - 1)tw, (9.24)
где tw - продолжительность периодов увлажнения;
td - продолжительность периодов высыхания.
9.5.3.3.6 Теоретическая модель, основанная на принципе "подвижных границ", приведена в [16]. Эта теория рассматривает диффузионные процессы в условиях неустойчивого состояния, где CO2 вступает в реакцию с бетоном таким образом, что бетон выполняет роль "отстойника" для CO2. Еще одна теоретическая модель, описывающая совместное действие морозной агрессии и карбонизации, приведена в [17].
9.5.3.3.7 Экспериментальные модели для оценки глубины карбонизации были предложены Хаккиненом и Парротом. По Хаккинену [18] глубину карбонизации определяют по уравнению (9.20) при коэффициенте карбонизации, отыскиваемом по формуле
где Cenv - коэффициент воздействия окружающей среды;
Cair - показатель содержания воздуха;
fcm - средняя (кубиковая) прочность бетона на сжатие, МПа;
a и b - параметры, зависящие от вида вяжущего.
Вместо средней прочности на сжатие можно применять нормативную прочность по формуле [19]
fcm = fck + 8. (9.26)
9.5.3.3.8 В таблицах 9.3 и 9.4 приведены, соответственно, коэффициент воздействия окружающей среды и показатель содержания воздуха. Параметры a и b формулы (9.25) приведены в таблице 9.5 [20].
Таблица 9.3
скорости карбонизации
Окружающие условия | Cenv |
Конструкции, защищенные от дождя | 1 |
Конструкции, не защищенные от дождя | 0,5 |
Таблица 9.4
скорости карбонизации
Воздушная пористость | Cair |
Воздухововлечение отсутствует | 1 |
Воздухововлечение | 0,7 |
Таблица 9.5
Параметры a и b [20]
Вяжущее | a | b |
Портландцемент | 1800 | -1,7 |
Портландцемент + зола уноса 28% | 360 | -1,2 |
Портландцемент + микрокремнезем 9% | 400 | -1,2 |
Портландцемент + доменный шлак 70% | 360 | -1,2 |
9.5.3.3.9 В соответствии с [21], глубину карбонизации определяют через кислородную проницаемость бетона:
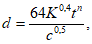 (9.27)
(9.27)где K - кислородная проницаемость бетона при относительной влажности 60%;
t - время;
c - содержание щелочей в цементе;
n - коэффициент затухания (коренная степень).
9.5.4.1 Основное правило
9.5.4.1.1 Коррозия начинается при разрушении защитной пленки, которое наступает в результате падения pH, вызванного карбонизацией, или в результате роста содержания хлоридов, превысившего пороговые значения в зоне расположения арматуры. Объем продуктов коррозии во много раз превышает первоначальный объем металла. Увеличение объема вызывает появление растягивающих напряжений в бетоне вокруг арматурного стержня, что приводит к образованию трещин и отслаиванию бетона защитного слоя.
9.5.4.1.2 Коррозия сопровождается тремя основными явлениями:
- уменьшение площади поперечного сечения арматуры;
- уменьшение сцепления между арматурой и бетоном;
- растрескивание защитного слоя бетона и как следствие уменьшение несущей способности бетонного сечения.
9.5.4.1.3 Для определения продолжительности срока службы необходимо установить численное значение критического порога несущей способности с учетом вышеупомянутых явлений, снижающих долговечность. Указанный критический порог часто удается выразить как вызванное коррозией критическое сокращение радиуса арматурного стержня, поэтому период распространения можно выразить количественно следующим образом [22]
 (9.28)
(9.28)где tl - время распространения коррозии, лет;
r - скорость коррозии.
9.5.4.2 Время появления трещин в защитном слое
9.5.4.2.1 В случае общей коррозии критическое уменьшение радиуса стержня происходит из-за растрескивания бетона защитного слоя. Время распространения трещин можно приближенно определить по следующей формуле [1]
где C - толщина защитного слоя бетона, мм;
D - диаметр арматурного стержня, мм;
r - скорость коррозии в бетоне, мкм/год.
9.5.4.2.2 Скорость коррозии в бетоне в значительной степени зависит от окружающих условий. Среди этих факторов окружающей среды наиболее важными являются относительная влажность и температура. Скорость коррозии арматуры в бетоне можно определить по следующей формуле
где cT - температурный коэффициент;
r0 - скорость коррозии при 20 °C.
9.5.4.2.3 К первостепенным факторам, влияющим на скорость распространения коррозии в бетоне при +20 °C, относят относительную влажность воздуха (или бетона) и содержание хлоридов. Другие факторы, например водоцементное отношение или тип цемента, также могут оказывать некоторое влияние. Числовые значения скорости коррозии в анодных зонах армирования, приведенные в таблице 9.6, можно принять за средние величины. Они определены на основании экспериментальных данных, содержащихся в работе [16].
Таблица 9.6
хлоридами бетоне (анодные зоны)
Относительная влажность, % | Карбонизированный бетон, мкм/год | Насыщенный хлоридами бетон, мкм/год |
99 | 2 | 34 |
95 | 50 | 122 |
90 | 12 | 98 |
85 | 3 | 78 |
80 | 1 | 61 |
75 | 0,1 | 47 |
70 | 0 | 36 |
65 | 0 | 27 |
60 | 0 | 19 |
55 | 0 | 14 |
50 | 0 | 9 |
9.5.4.2.4 Влагосодержание в бетоне, окружающем арматурные стержни, является результатом действия сложного комплекса различных климатических и конструктивных факторов. Равновесие относительной влажности в бетоне конструкции, стоящей на открытом воздухе, зависит от годового и дневного колебания относительной влажности воздуха, конденсации влаги на поверхности, от дождей, брызг и тающей воды, от плотности бетона и глубины залегания рассматриваемого слоя от поверхности (защитный слой).
9.5.4.2.5 Содержание хлоридов также оказывает значительное влияние на содержание влаги и на скорость коррозии в бетоне. Однако время распространения обычно полностью опускают, если присутствуют хлориды. Данные по насыщенному хлоридами бетону, содержащиеся в таблице 9.6, приведены, в основном, для сравнения.
9.5.4.2.6 Среднюю относительную влажность бетона конструкций, не защищенных от дождя, можно считать равной примерно 95% (кроме случаев, когда частота дождей чрезвычайно мала), а бетона конструкций, защищенных от дождя - около 90%. Соответственно, скорость коррозии в карбонизированном бетоне при 20 °C будет равна примерно 50 мкм/год в конструкциях, не защищенных от дождя, и примерно 12 мкм/год в конструкциях, защищенных от дождя.
9.5.4.2.7 Температурные коэффициенты, определенные в [16], и средние дневные температуры для некоторых европейских городов приведены в таблице 9.7. Кроме этого, там же даны скорости коррозии, определенные по формуле (9.30). В таблице 9.7 не учтено влияние прямого солнечного облучения на температуру поверхности конструкций. Однако это влияние может быть значительным. При расчете скорости коррозии следует учитывать также местные микроклиматические особенности.
Таблица 9.7
коррозии для некоторых городов Европы
Город | cT | Скорость коррозии, мкм/год | |
Не защищенные от дождя | Защищенные от дождя | ||
Соданкила (северная Финляндия) | 0,21 | 11 | 2,5 |
Хельсинки | 0,32 | 16 | 4 |
Амстердам | 0,47 | 24 | 6 |
Мадрид | 0,73 | 37 | 9 |
9.5.4.2.8 Широко известно, что скорость коррозии медленно снижается во времени. Однако из-за отсутствия достаточного объема информации по этому вопросу при проектировании долговечности рекомендуется скорость коррозии принимать постоянной.
9.5.4.3 Скорость распространения коррозии под трещинами
9.5.4.3.1 Если трещины в защитном слое бетона появились в самом начале срока службы конструкции (например, из-за усадки, механического воздействия и т.д.) и если ширина раскрытия трещин превышает 0,1 - 0,3 мм, то коррозия обычно начинается немедленно, без какого-либо периода инициации. Если арматурные стержни открыты по всему периметру, коррозию также следует считать круговой.
9.5.4.3.2 Проектировщик может устанавливать предел минимального остаточного диаметра арматурного стержня или соответственно предел максимальной глубины коррозии. Это зависит от типа арматуры - основная рабочая арматура, поперечное армирование, хомуты и т.п., и от фактического напряжения в стержнях. В напрягающих пучках коррозия не допустима вообще.
9.5.4.3.3 Время распространения коррозии под трещиной определяют по формулам:
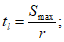 (9.31)
(9.31) (9.32)
(9.32)где tl - время распространения коррозии под трещиной;
r - скорость коррозии под трещиной;
Smax - максимально допустимая глубина коррозии;
Dmin - минимальный диаметр арматурного стержня.
9.5.4.3.4 Коррозия под трещиной представляет собой чрезвычайно сложное явление, которое до сих пор полностью не изучено. При отсутствии более точных сведений пользуются предположением, что средняя скорость коррозии имеет тот же порядок, что и скорость коррозии в бетоне без трещин. В соответствии с этим в расчетах рекомендуется применять следующие значения средних скоростей коррозии [23]:
- если единственное агрессивное воздействие - карбонизация:
при относительной влажности 90 - 98% скорость коррозии - 5 - 10 мкм/год,
при относительной влажности < 85% - <= 2 мкм/год;
- при насыщении хлоридами:
при относительной влажности 100% - <= 10 мкм/год,
при относительной влажности 30 - 93% - 50 - 100 мкм/год,
при относительной влажности < 70% скорость коррозии <= 2 мкм/год.
10 Критерии технического состояния железобетонных конструкций по показателям долговечности и стратегии их эксплуатации применительно к срокам службы
10.1 Анализ большого объема экспериментальных данных, результатов расчетов и численного моделирования, а также опыта эксплуатации зданий и сооружений из бетона и железобетона однозначно показывает, что конструкции разрушаются значительно раньше, чем предусмотрено проектным нормативным сроком, из-за ускоренного физического износа. При этом затраты на ремонт и восстановление сооружений значительно превышают планируемые, а сроки их проведения, объемы и содержание работ часто назначают без учета текущего и будущего состояния элементов конструкций.
10.2 Техническое состояние железобетонных конструкций зданий и сооружений классифицируют в соответствии с таблицей 10.1.
Таблица 10.1
железобетонных конструкций
Категория технического состояния | Характеристика состояния |
1 Исправное | Выполняются требования действующих норм и проектной документации. Необходимости в ремонтных работах нет |
2 Работоспособное | С учетом фактических свойств материалов удовлетворяются требования действующих норм, относящихся к предельным состояниям первой группы; требования норм по предельным состояниям второй группы могут быть нарушены, но обеспечиваются нормальные условия эксплуатации. Защитные свойства бетона по отношению к арматуре на отдельных участках исчерпаны; требуется их восстановление, устройство или восстановление антикоррозионной защиты |
3 Ограниченно работоспособное | Нарушены требования действующих норм, но отсутствуют опасность обрушения и угроза безопасности работающих. Требуется усиление и восстановление эксплуатационных свойств |
4 Недопустимое | Существуют повреждения, свидетельствующие об опасности пребывания людей. Требуются немедленные страховочные мероприятия: с ограничением нагрузок, усиление конструкции |
5 Аварийное | Существуют повреждения, свидетельствующие о возможности обрушения конструкции. Требуются немедленная разгрузка конструкции и устройство временных креплений (стоек, подпорок, накладок и др.) |
10.3 Все конструкции и сооружения выполняют одну или несколько функций, большинство из которых постоянные и активные, хотя некоторые из них могут быть пассивными и реализовываться только по требованию.
10.4 Различают три основные причины потери функциональности (отказа) конструкций, ведущие к снижению прочности, потере внешнего вида или эксплуатационных свойств:
- технические, вызванные старением материала;
- внешние (предусмотренные и непредвиденные), вызванные загрязнением внешней среды: авариями, землетрясениями, вандализмом и т.д.;
- человеческий фактор: ошибки в проектировании, реализации проекта, эксплуатации и т.п.
10.5 Обеспечение долговечности зданий и сооружений на расчетный срок службы - механизм затратный уже на стадии строительства. Окупаемость этих затрат возможна только в процессе эксплуатации. Применительно к разработке стратегии эксплуатации железобетонных конструкций следует иметь в виду известный "закон пяти" Де Ситтера (рисунок 10.1).
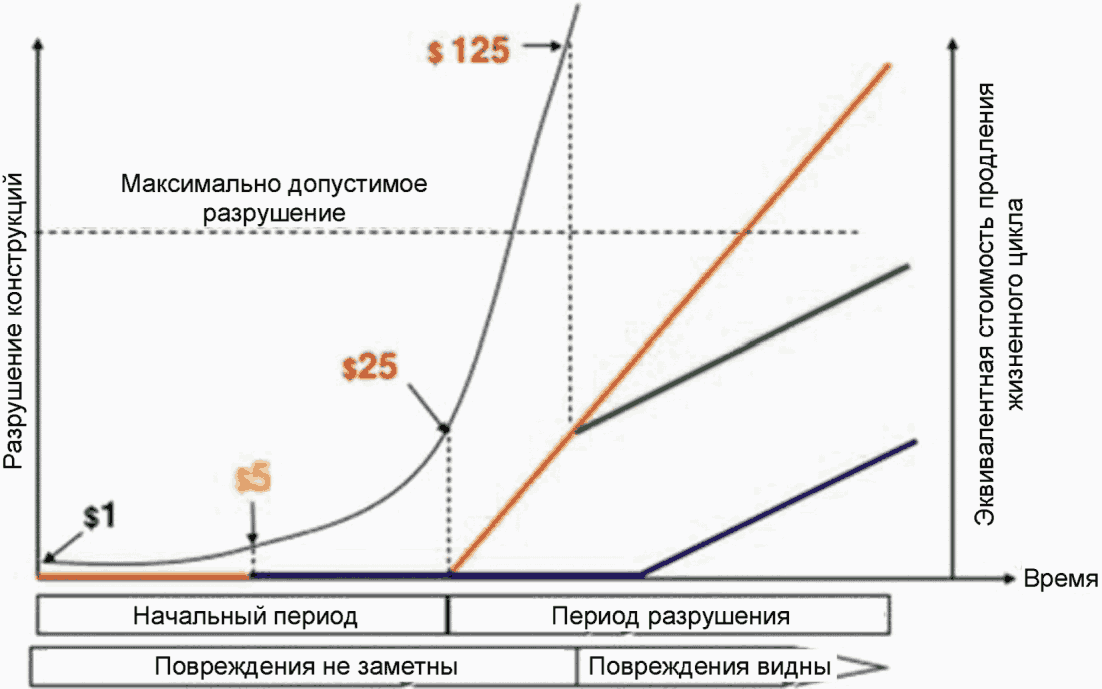
10.6 Срок службы конструкций может быть представлен как сумма двух периодов времени: периода с начала эксплуатации до инициации процесса коррозии и периода непосредственного протекания коррозионного процесса. Срок определяется для отказов двух типов: время трещинообразования защитного слоя бетона; потеря несущей способности. Время инициации определяется либо карбонизацией, либо проникновением хлоридов.
10.7 Возможные последствия потери функциональности (отказа) конструкций оцениваются экономическими и социальными категориями и являются основой при выработке стратегии эксплуатации [24]. Цель стратегии - обеспечение экономически сбалансированных технических мероприятий на уровне отдельных компонентов и конструкции, в целом, позволяющих содержать конструкцию в таком состоянии, когда она может выполнять свои функции в течение определенного периода времени с достаточной надежностью, эксплуатационной пригодностью и надлежащим внешним видом. Приступая к выработке стратегии, следует определить функциональные требования, которым должна отвечать конструкция (компонент), и последствия, к которым может привести преждевременная потеря прочности.
10.8 Известны три принципиально отличные стратегии эксплуатации:
- коррективная;
- по срокам службы;
- по срокам достижения уровня неприемлемости.
В первом случае эксплуатационные действия предпринимают после обнаружения признаков отказа в конструкции; во втором - через определенный период эксплуатации; в последнем случае - после достижения конструкцией или отдельным ее компонентом предельного состояния.
10.9 Эти стратегии применяют на компонентном уровне. Большинство зданий и сооружений представляет собой многокомпонентные системы. Несмотря на безупречное выполнение функций большинством компонентов, сооружение в целом может утратить проектные свойства в результате выхода из строя одного или нескольких компонентов. Поэтому на уровне сооружения для каждой из его функций создается система декомпозиции с использованием принципов системного анализа, разработаны модели их эксплуатации с принятием решения пока только на качественном уровне.
10.10 Цель эксплуатации - минимальная стоимость срока службы. Для оценки используют три типа стоимости: риска, ремонта и инспекции. Поэтому все указанные выше стоимости должны быть привязаны ко времени. Чем дольше выполняет свои функции элемент, тем ниже будет стоимость единицы времени его эксплуатации, но при этом растет риск отказа конструкции, для снижения которого приходится чаще проводить инспекции.
10.11 Существуют упрощенные формулы для количественного определения ожидаемой удельной стоимости эксплуатации для всех трех эксплуатационных стратегий. При этом разработано несколько вариантов компьютерных программ, которые с учетом вероятностных схем деградационных процессов автоматически определяют наиболее экономичную стратегию или выдают стоимость заданной стратегии. В связи с длительным сроком службы строительных конструкций заметную роль в проблемах надежности приобрел фактический банковский процент на вложенный капитал. Возможность количественной оценки стоимости отдельных компонентов и сооружений в целом с учетом эксплуатационных расходов и рисков отказа позволяет оценить целесообразность дальнейшей эксплуатации некоторых сооружений и даже их досрочной замены.
10.12 Создание практической модели поведения конструкции во времени предусматривает проведение мониторинга с момента введения конструкции в эксплуатацию с учетом всех ее фактических характеристик. Предлагаемые модели жизненного цикла конструкций, которые учитывают влияние факторов эксплуатации, позволяют оптимизировать стоимость ремонтов с учетом большого числа параметров: технических и функциональных требований, безопасности, эстетики, экономии, экологии и т.д. Разработаны математические методы сортировки и выбора приоритетов разной степени сложности с учетом большого числа параметров, которые могут быть использованы проектировщиками при выборе оптимальных вариантов эксплуатации. Идентификация и выбор соответствующих методов принятия решений составляет значительную часть системы управления жизненным циклом конструкции, что, в конечном счете, позволяет эффективно продлевать сроки жизни различных зданий и сооружений из бетона. Во всех случаях добавленная "первая" стоимость системы мониторинга и бессрочная стоимость ее обслуживания, как ожидают, сохранят намного большие инвестиции в строительство и эксплуатационные затраты. Международная инициатива "Мониторинг состояния конструкций" может внести значительный вклад в этот процесс, интегрируя растущее разнообразие методов, методик и исследовательских тем в понятный и всесторонний инструмент.
10.13 Неотъемлемая составляющая подобных технологий - полная механизация трудоемких работ, автоматизация контроля и обработки результатов наблюдений, высокий уровень безопасности и комфортности условий труда.
10.14 Количественные показатели долговечности железобетонных конструкций целесообразно разделить на две группы.
Показатели, связанные со сроком службы железобетонной конструкции:
- срок службы - календарная продолжительность эксплуатации железобетонной конструкции от начала эксплуатации объекта (здания, сооружения) или ее возобновление после ремонта до перехода в предельное состояние;
- средний срок службы - математическое ожидание срока службы;
- срок службы до первого капитального ремонта - продолжительность эксплуатации до ремонта, выполняемого для восстановления исправности и полного или близкого к полному восстановлению ресурса конструкции с восстановлением, усилением или заменой любых ее частей;
- срок службы между капитальными ремонтами, зависящий преимущественно от качества ремонта, т.е. от того, в какой степени восстановлен ресурс конструкции;
- суммарный срок службы - календарная продолжительность работы железобетонной конструкции в здании или сооружении от начала эксплуатации до ее выбраковки с учетом времени работы после ремонта;
-  срок службы - календарная продолжительность эксплуатации конструкции, в течение которой железобетонная конструкция не достигнет одного или нескольких предельных состояний с вероятностью
срок службы - календарная продолжительность эксплуатации конструкции, в течение которой железобетонная конструкция не достигнет одного или нескольких предельных состояний с вероятностью 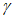 , %.
, %.
 срок службы - календарная продолжительность эксплуатации конструкции, в течение которой железобетонная конструкция не достигнет одного или нескольких предельных состояний с вероятностью
срок службы - календарная продолжительность эксплуатации конструкции, в течение которой железобетонная конструкция не достигнет одного или нескольких предельных состояний с вероятностью Показатели долговечности, выраженные в календарном времени работы, позволяют непосредственно использовать их в планировании сроков организации ремонтов, поставки запасных частей, сроков замены оборудования. Недостаток этих показателей заключается в том, что они не позволяют учитывать интенсивность использования оборудования.
Показатели, связанные с ресурсом конструкции:
- ресурс - суммарная наработка железобетонной конструкции от начала ее эксплуатации или ее возобновление после ремонта до перехода в предельное состояние;
- средний ресурс - математическое ожидание ресурса;
- назначенный ресурс - суммарная наработка, при достижении которой эксплуатация конструкции должна быть прекращена независимо от ее технического состояния;
-  ресурс - суммарная наработка, в течение которой железобетонная конструкция не достигнет предельного состояния с заданной вероятностью
ресурс - суммарная наработка, в течение которой железобетонная конструкция не достигнет предельного состояния с заданной вероятностью  , %.
, %.
 ресурс - суммарная наработка, в течение которой железобетонная конструкция не достигнет предельного состояния с заданной вероятностью
ресурс - суммарная наработка, в течение которой железобетонная конструкция не достигнет предельного состояния с заданной вероятностью В качестве меры продолжительности эксплуатации, как правило, выбирают время эксплуатации конструкции (срок эксплуатации). При этом, по понятным причинам, ресурс может принимать дискретные значения.
10.15 На любой момент времени в процессе эксплуатации (по крайней мере, от 20 и более лет) конструкции зданий и сооружений находятся в различном техническом состоянии и имеют разного рода повреждения. В зависимости от этого выполняемые работы (профилактические и/или ремонтные) по состоянию, в общем случае, относительно любого из уровней надежности во времени будут включать следующие виды: своевременные (профилактика, ремонт); отодвинутые (ремонт); упреждающие (ремонт); а относительно нормируемого уровня надежности (НУН) еще и специальный вид - запоздалые (ремонт).
Затраты на ремонт и восстановление сооружений значительно превышают планируемые, если сроки их проведения, объемы и содержание работ назначают без учета текущего и будущего состояния элементов конструкций.
10.16 Необходимый вид ремонта выбирают в зависимости от технического состояния конструкций и закладываемого нормируемого уровня надежности, резерв которого впоследствии реализуется при эксплуатации.
10.17 Нормируемый уровень надежности обеспечивается использованием рассмотренных видов ремонта при условии их соответствия, как степени коррозионных повреждений, так и вероятностным показателям надежности конструкции по наработке до отказа (таблица 10.2).
Таблица 10.2
состояния конструкций
Группа риска конструкции |  наработка до отказа, % наработка до отказа, % | Степень коррозии (относительно среднего значения), % | Вид ремонта для данной группы риска |
1 | К <= 7 | Своевременный | |
К > 7 | Упреждающий | ||
К <= 7 | Отодвинутый | ||
К > 7 | Упреждающий | ||
2 | К <= 15 | Своевременный | |
К > 15 | Упреждающий | ||
К <= 15 | Отодвинутый | ||
К > 15 | Упреждающий | ||
3 | К <= 25 | Своевременный | |
К > 25 | Упреждающий | ||
К <= 25 | Отодвинутый | ||
К > 25 | Упреждающий |
Условие соответствия требует приспособленности технологических операций, как к условиям выполнения работ, так и текущему состоянию конструкции, что позволяет управлять процессом реализации резерва надежности.
10.18 В соответствии с тремя группами риска, т.е. тремя уровнями надежности, это управление должно обеспечиваться различными, как минимум, тремя технологическими процессами, устраняющими накопленные коррозионные повреждения в конструкции. Количество выполняемых операций, их трудоемкость и техническая сложность выполнения возрастают от одной группы риска к последующим. При этом конструктивные особенности зданий и сооружений также требуют приспособленности технологий ремонта к конкретным условиям. Таким образом, технологии ремонта должны быть "конформативными", т.е. соответствующими, приспособленными.
10.19 Выбор элементной базы конформативных технологий, включая подбор материалов и технологических операций ремонтных работ должен строиться на основе совместимости комплекса показателей, характеризующих состояние ремонтируемого объекта и используемых технических средств.
10.20 Аспекты стратегии эксплуатации зданий и сооружений позволяют:
- планировать ремонтные работы на основе прогнозирования надежности конструкций зданий и сооружений и оценке фактических условий эксплуатации;
- осуществлять разработку конформативных технологических решений на основе принципа многофакторной совместимости, подразумевающего конструктивную, физико-химическую и технологическую совместимость ремонтных операций, материалов и элементов конструкций с целью обеспечения равнокачественных характеристик элементов конструкций в послеремонтный период эксплуатации.
10.21 Большинство проблем, возникающих сегодня при осуществлении ремонтных мероприятий в капитальных сооружениях, связано с недостаточным вниманием к деталям проектирования, технологии и организации работ. Материалы, применяемые для ремонта, хотя и имеют большое значение, доставляют меньше неприятностей. Однако их влияние, а особенно правильный выбор имеют немаловажное значение для увеличения срока службы сооружения и будущего межремонтного периода.
10.22 Ликвидация сооружения или продление эксплуатации, с точки зрения оптимизации расходования средств и интересов устойчивого развития, имеют первостепенное значение. Необоснованные и непланируемые затраты на ремонт и восстановление сооружений, а особенно их подземных частей, наносят ущерб окружающей среде в части потребления ресурсов, изменения условий эксплуатации, загрязнения воды, грунтов и пр. Однако и выполнение ремонтных работ не гарантирует потребителю отсутствие негативных последствий.
Состояние большинства отремонтированных сооружений из железобетона претерпевает серьезное ухудшение спустя уже несколько лет после того, как в них производили ремонтные работы. По данным проведенных исследований, около 75% отказов при ремонте железобетонных конструкций наступает по истечении всего 5 лет.
Уточнение нормативных сроков службы железобетонных конструкций зданий и сооружений - проблема, имеющая большое народнохозяйственное значение, во многом определяющая задачи нового строительства и сохранения существующих основных фондов.
11.1.1 Полный вероятностный метод
11.1.1.1 Предельное состояние - депассивация
11.1.1.1.1 В этом случае должно выполняться следующее условие
p{} = pdep. = p{a - xc(tSL) < 0} < p0, (11.1)
где p{} - вероятность депассивации;
a - толщина защитного слоя, мм;
xc(tSL) - глубина карбонизации во время tSL;
tSL - проектируемый срок службы, лет;
p0 - целевая вероятность отказа.
11.1.1.1.2 Переменные a и xc(tSL) должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.
11.1.1.2 Предельные состояния: трещинообразование, инициированное коррозией, отслаивание и разрушение
11.1.1.2.1 В качестве примера в отношении трещинообразования должны быть использованы следующие основные функции предельного состояния
 (11.2)
(11.2)где p{} - вероятность трещинообразования, инициированного карбонизацией;
 - увеличение радиуса арматурного стержня, обусловленное коррозией;
- увеличение радиуса арматурного стержня, обусловленное коррозией;tSL - проектируемый срок службы, лет;
p0 - целевая вероятность отказа.
11.1.1.2.2 Альтернативное приближение при проектировании определяют по формуле
p{} = pcrac. = p{tSL - tini - tprop < 0} < p0, (11.3)
где p{} - вероятность трещинообразования, инициированного карбонизацией;
tSL - проектируемый срок службы, лет;
tini - индукционный период, лет;
tprop - период развития трещин, лет;
p0 - целевая вероятность отказа.
11.1.1.2.3 Переменные  и
и 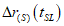 или tini и tprop должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.
или tini и tprop должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.
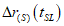 или tini и tprop должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.
или tini и tprop должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.11.1.1.2.4 Большинство существующих на сегодня моделей носят эмпирический характер и часто базируются на крайне ограниченных и не всегда достаточных данных. Корреляции между скоростями коррозии, качеством бетона и влиянием окружающей микросреды в деталях не описаны. Поэтому при верификации расчетов часто используется специальное программное обеспечение, например, Delphic Oracle.
11.1.1.2.5 Для расчетов могут быть использованы методы, описанные в настоящем пособии, а также методы, приведенные в [25].
11.1.2.1 Предельное состояние - депассивация
11.1.2.1.1 В этом случае должно выполняться следующее условие
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
ad - xc,d(tSL) >= 0, (11.5)
где ad - проектное значение толщины защитного слоя, мм;
xc,d(tSL) - проектное значение глубины карбонизации во время tSL, мм.
11.1.2.1.2 Проектное значение толщины защитного слоя вычисляется по формуле
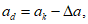 (11.6)
(11.6)где ak - характеристическое значение толщины защитного слоя, мм;
11.1.2.1.3 Проектное значение глубины карбонизации xc,d(tSL) во время tSL вычисляется по формуле
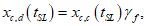 (11.7)
(11.7)где xc,c(tSL) - характеристическое значение глубины карбонизации во время tSL, мм;
11.1.2.1.4 Для расчетов могут быть использованы методы, описанные в настоящем пособии, а также методы, приведенные в [25].
11.1.3.1 В рамках этого приближения устанавливается компромиссное решение относительно геометрических (толщина защитного слоя), материаловедческих (диффузия, характеристики вяжущего и т.п.) и технологических (уход и т.п.) переменных.
11.1.4.1 В общем виде, избежать разрушения можно в том случае, когда депассивация не наблюдается в силу неограниченной сопротивляемости бетона воздействию агрессивных сред или нулевым нагрузкам со стороны окружающей среды.
11.2.1 Полный вероятностный метод
11.2.1.1 Предельное состояние - депассивация
11.2.1.1.1 В этом случае должно выполняться следующее условие
p{} = pdep. = p{CCrit. - C(a, tSL) < 0} < p0, (11.8)
где p{} - вероятность депассивации;
a - толщина защитного слоя, мм;
CCrit. - критическая концентрация хлоридов, % массы вяжущего;
C(a, tSL) - концентрация хлоридов на глубине a за время tSL, % массы вяжущего;
tSL - проектируемый срок службы, лет;
p0 - целевая вероятность отказа.
11.2.1.1.2 Переменные a, CCrit. и C(a, tSL) должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии.
11.2.1.2 Предельные состояния: трещинообразование, инициированное коррозией, отслаивание и разрушение - см. 11.1.1.2.
11.2.2 Метод частных коэффициентов - см. 11.1.2.
11.2.3 Метод "решение, кажущееся удовлетворительным" - см. 11.1.3.
11.2.4 Метод "избежать разрушения" - см. 11.1.4.
11.3.1 Минимальная конструктивная надежность железобетонной конструкции с трещинами должна быть сопоставимой по величине с минимальной надежностью конструкции без трещин, эксплуатируемой в сопоставимых условиях окружающей среды.
11.3.2 Аналогично процедуре, приведенной в 11.1 и 11.2, необходимо идентифицировать нежелательные события в отношении работоспособности/функциональности (предельное состояние по эксплуатационной пригодности - SLS). Кроме того, необходимо проверить, влияют ли на предельные состояния непрерывная коррозия арматуры в зоне трещин или нет.
11.3.3 Если функциональность затронута, рекомендуется избегать подхода "предотвращение ухудшения качества".
11.3.4 В случае нарушения структурной целостности необходимо применять подход "предотвращение ухудшения качества".
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 11.2 отсутствует. |
11.4.1 Следует применять соответствующие правила, приведенные в 11.1, 11.2 и 11.3, и избегать депассивации предварительно напряженной стали на уровне надежности - предельного состояние по несущей способности (ULS) (таблица 11.2).
11.5.1 Полный вероятностный метод
11.5.1.1 Предельное состояние - повреждение при замораживании/оттаивании, вызывающее локальную потерю механических свойств, трещинообразование, откалывание и потери в поперечном сечении
11.5.1.1.1 В этом случае должно выполняться следующее условие
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
p{} = pfreeze/thaw damage = p{SCR - SACT(t < tSL) < 0} <
< p0, (11.9)
где p{} - вероятность повреждения за счет замораживания/оттаивания;
SCR - критическая степень насыщения;
SACT(t) - реальная степень насыщения во время t;
tSL - проектируемый срок службы, лет;
p0 - целевая вероятность отказа, таблица А.5 [25].
11.5.1.1.2 Переменные SCR и SACT(t) должны быть определены количественно в полном вероятностном приближении. Для расчета могут быть использованы методы, описанные в настоящем пособии или приведенные в [25].
11.5.1.2 Предельное состояние - прогиб и обрушение, индуцированные замораживанием/оттаиванием
11.5.1.2.1 Что касается несущей способности и деформаций, традиционное проектирование должно включать локализованные изменения механических свойств из-за повреждения морозом.
11.5.2 Метод частных коэффициентов
11.5.2.1 В этом случае должно выполняться следующее условие
SCR,d - SACT,d(t < tSL) >= 0, (11.10)
где SCR,d - проектное значение критической степени насыщения;
SACT,d(t < tSL) - проектное значение реальной степени насыщения во время t;
tSL - проектируемый срок службы, лет.
11.5.2.2 Проектное значение критической степени насыщения вычисляется по формуле
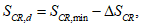 (11.11)
(11.11)где SCR,min - характеристическое значение критической степени насыщения (минимальное значение);
11.5.2.3 Расчетное значение критической степени насыщения рассчитывается по формуле
 (11.12)
(11.12)где SCR,min - характеристическое значение критической степени насыщения (минимальное значение);
11.5.2.4 Расчетное значение фактической степени насыщения в момент времени t SACT,d(t) рассчитывается по формуле
 (11.13)
(11.13)где SACT,d - характеристическое значение критической степени насыщения в момент времени t;
11.5.2.5 В качестве примера процедуры проектирования в [25] приводится применимый метод проектирования. Могут использоваться и другие методы при условии соблюдения основных принципов, сформулированных в настоящем пособии.
11.5.3 Метод "решение, кажущееся удовлетворительным"
11.5.3.1 В рамках этого подхода может быть установлен компромисс между переменными, связанными с имеющимся пространством для расширения (воздухововлечение), материалом (характеристики незамерзающей воды) и старением (карбонизация).
11.5.4 Метод предотвращения ухудшения состояния
11.5.4.1 Как правило, предотвращение ухудшения состояния достигается, если ухудшение морозостойкости не может произойти из-за бесконечного сопротивления материала морозному разрушению или нулевой нагрузки окружающей среды.
11.6.1 Полный вероятностный метод
11.6.1.1 Уравнение предельного состояния для поверхностного отслаивания, вызванного замораживанием/оттаиванием в солях
p{} = pscaling = p{T(t <= tSLCl-) -
- TR(RH(T), T(t), ...) < 0} < p0, (11.14)
где p{} - вероятность отслаивания;
T(t, ...) - температура бетона, град К;
TR(t, ...) - критическая температура замерзания для отслаивания во время t;
tSL - проектируемый срок службы, лет;
p0 - целевая вероятность отказа, таблица А.5 [25].
11.6.1.2 Переменные T и TR должны быть определены в полном вероятностном приближении.
11.6.1.3 Для расчетов могут быть использованы методы, описанные в настоящем пособии, а также методы, приведенные в [25].
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункты 10.5.2 и 10.6.1.1 отсутствуют. |
11.6.2 Предельное состояние - прогиб и обрушение, индуцированные замораживанием/оттаиванием - см. 10.5.2 и 10.6.1.1.
12.1.1 Проектирование железобетонных конструкций по их жизненному циклу в соответствии с настоящим пособием предполагает, что соблюдаются минимальные требования к производству и управлению их качеством, приведенные в СП 70.13330 и СП 130.13330, а также ГОСТ Р 57359, включая дополнения, приведенные ниже.
12.2.1 Спецификация проекта должна содержать технические данные и требования к конкретному проекту, подготовленные для дополнения и уточнения требований указанных выше нормативных документов.
12.2.2 При этом предполагается, что спецификация проекта включает всю необходимую информацию и технические требования для выполнения работ и соглашений, заключенных в ходе строительства. Таким образом, спецификация проекта должна содержать все требования к материалам, производству работ и контролю качества для данного конкретного случая.
12.3.1 Управление качеством производства работ может включать в себя план качества по ГОСТ Р ИСО 10005 и проверку выполненных работ.
12.3.2 План обеспечения качества
12.3.2.1 Если спецификация проекта требует разработку плана качества, то в ней должно быть указано, какие элементы он должен включать.
12.3.2.2 План обеспечения качества может включать такие элементы, как компетентность и надлежащая подготовка персонала, организация проекта и процедуры его выполнения.
12.3.3 Проверка выполненных работ
12.3.3.1 В ходе реализации проекта осуществляется необходимая проверка для оценки соответствия выполненной работы и документируются ее результаты.
12.3.3.2 Спецификация проекта может содержать требования к "встроенной документации" в зависимости от специфики фактического проекта "жизненного цикла". Такой спецификой может быть документирование достигнутых прямых входных параметров, применяемых в моделях проектирования по параметрам долговечности, таких как, например, коэффициенты диффузии, толщина покрытия к арматуре и т.д.
12.3.4 Действия в случае несоответствия
12.3.4.1 Для определения набора минимальных требований к эксплуатационным характеристикам бетона в качестве эталона необходим нормативный документ, подготовленный в соответствии с принципами, изложенными в настоящем пособии. В качестве основы следует использовать требования ГОСТ 25192, ГОСТ 7473, ГОСТ 26663, ГОСТ 31384.
12.3.4.2 Если проектирование по жизненному циклу основывается на эксплуатационных характеристиках бетона, они могут быть заменены требованиями к составу смеси либо на этапе проектирования, основанном на предыдущем опыте, либо на первоначальных испытаниях на этапе строительства. При этом необходимо указывать, являются ли эксплуатационные требования к составу смеси целевыми или характерными значениями.
12.3.4.3 Если проектирование по жизненному циклу основано на других характеристиках материала, чем те, которые рассматриваются в нормативных документах на бетоны, указанных выше (т.е. тип цемента, водовяжущее отношение, содержание цемента, свойства заполнителей и наполнителей и т.д.), и срок службы конструкций зависит от проверки этих характеристик материала во время строительства, спецификация проекта должна ссылаться на соответствующие методы испытаний и статистическую интерпретацию результатов (например, характерные или целевые значения).
13.1.1 Настоящий раздел содержит общую основу для технического обслуживания и контроля состояния в течение срока службы железобетонных конструкций.
13.1.2 В приложении А даются рекомендации относительно степени инспекции/мониторинга конструкции в течение ее срока службы. Таблица А.6 определяет "уровни контроля состояния" в качестве руководства к дифференциации надежности, которая будет использоваться при проектировании конструкций по параметрам долговечности и прогнозировании их срока службы.
13.2.1 В настоящем методическом пособии термин "техническое обслуживание" используется в отношении мероприятий, которые планируется осуществлять в течение срока службы конструкций, с тем чтобы обеспечить выполнение допущений, содержащихся в проекте "жизненного цикла".
13.2.2 В плане технического обслуживания указываются вид и периодичность планируемых мероприятий.
Оценка соответствия может проводиться путем визуальных наблюдений и суждений, сопровождаемых в соответствующих случаях измерениями, испытаниями и измерениями.
Срок службы компонента или структуры всегда связан с одной или несколькими необходимыми функциями этого компонента или структуры.
Поэтому планируемые мероприятия по инспектированию/мониторингу должны быть сосредоточены на оценке проектных данных, применяемых в этих моделях износа.
13.3.1 Осмотр и контроль состояния конструкций в течение их срока службы
13.3.1.1 В настоящем пособии термин "инспекция" означает деятельность по оценке соответствия проектным данным для действий и/или свойств материала и/или продукта, применяемых в проекте жизненного цикла на периодической основе в течение срока службы конструкции, в то время как термин "мониторинг" означает те же самые действия, но на постоянной основе. Основой проведения работ служит ГОСТ 31937.
13.3.2 План контроля состояния конструкций
План контроля состояния должен содержать следующие разделы:
- какие виды инспекций/мониторинга должны проводиться;
- какие компоненты конструкции подлежат проверке/мониторингу;
- периодичность проведения проверок;
- критерии эффективности, которые должны быть выполнены;
- требования к документированию результатов;
- действия в случае несоответствия критериям.
Если проверка/мониторинг показывает, что исходные допущения проектирования по жизненному циклу не выполняются, то должно быть предпринято одно или несколько из следующих действий.
13.4.1 Расширение сферы охвата обследования эффективности для повышения качества и репрезентативности данных.
13.4.2 Выполнение пересчета исходного проекта по параметрам долговечности для оценки остаточного срока службы конструкции. Новый расчет должен быть дополнен данными для воздействий, материалов и продуктов, полученными при анализе состояния конструкций, эксплуатирующихся в конкретных местах. Перепроектирование должно соответствовать процедурам и требованиям, изложенным в разделах настоящего методического пособия.
13.4.3 Конструкция должна быть отремонтирована или усилена для приведения ее характеристик в соответствие с согласованными проектными предположениями. Ремонт должен быть основан на частичном или полном пересчете первоначального проекта жизненного цикла, как указано в 13.4.2.
13.4.4 Конструкция должна быть дополнительно защищена, чтобы уменьшить агрессивные воздействия. Защита должна основываться на пересчете первоначального проекта жизненного цикла.
13.4.5 Конструкция должна быть выведена из эксплуатации.
13.5 Для существующих конструкций затраты на достижение более высокого уровня надежности обычно более высоки по сравнению с вновь проектируемыми конструкциями. По этой причине целевой уровень надежности для перепроектирования срока службы существующих конструкций обычно должен быть ниже.
13.6 Критерии пригодности к эксплуатации, применяемые при оценке жизненного цикла, должны быть определены для проекта и согласованы с будущим владельцем или эксплуатирующей организацией.
(справочное)
КОНСТРУКЦИЙ ПРИ ИХ ПРОЕКТИРОВАНИИ ПО ЖИЗНЕННОМУ ЦИКЛУ
А.1 Особенности применяемых материалов и конструктивных решений требуют более точного подхода к решению задачи установления нормативных сроков службы железобетонных конструкций зданий и сооружений, сложность которой заключается в том, что отдельные элементы зданий и сооружений имеют сильно различающиеся нормативные сроки службы при установленных в ГОСТ 27751 рекомендуемых сроках службы зданий и сооружений, в целом (таблица А.1).
Таблица А.1
Наименование объекта | Примерный срок службы, лет |
Временные здания и сооружения (бытовки строительных рабочих и вахтового персонала, временные склады, летние павильоны и т.п.) | 10 |
Сооружения, эксплуатируемые в условиях сильноагрессивных сред (сосуды и резервуары, трубопроводы предприятий нефтеперерабатывающей, газовой и химической промышленности, сооружения в условиях морской среды и т.п.) | Не менее 25 |
Здания и сооружения массового строительства в обычных условиях эксплуатации (здания жилищно-гражданского и производственного строительства) | Не менее 50 |
Уникальные здания и сооружения (здания основных музеев, хранилищ национальных и культурных ценностей, произведения монументального искусства, стадионы, театры, здания высотой более 75 м, большепролетные сооружения и т.п.) | 100 и более |
А.2 Для каждого сооружения, согласно ГОСТ 27751, необходимо установить его класс (КС-1, КС-2 или КС-3) в зависимости от назначения и социальных, экологических и экономических последствий, повреждений и разрушений. В зависимости от класса сооружений при их проектировании необходимо использовать коэффициенты надежности по ответственности, минимальные значения которых приведены в таблице А.2.
Таблица А.2
по ответственности
Класс сооружений | Уровень ответственности | Минимальные значения коэффициента надежности по ответственности |
КС-3 | Повышенный | 1,1 |
КС-2 | Нормальный | 1,0 |
КС-1 | Пониженный | 0,8 |
Примечание - Для зданий высотой более 250 м и большепролетных сооружений (без промежуточных опор) с пролетом более 120 м коэффициент надежности по ответственности следует принимать не менее 1,2  . . | ||
А.3 Класс и уровень ответственности сооружений, а также численные значения коэффициента надежности по ответственности устанавливаются генпроектировщиком по согласованию с заказчиком в задании на проектирование, но не ниже тех, которые указаны в таблице А.2.
Приведенные классы и уровни ответственности сооружений следует учитывать:
- при оценке долговечности зданий и сооружений;
- при разработке номенклатуры и объема проектных работ, а также проводимых инженерных изысканиях и экспериментальных исследованиях;
- при разработке конструктивных решений надземной и подземной частей сооружений;
- при разработке программ научно-технического сопровождения, при проектировании, изготовлении и монтаже конструкций;
- при разработке правил приемки, испытаний, эксплуатации и технической диагностики строительных объектов [3].
А.4 В [3] содержится классификация заданных сроков службы (таблица А.3), несколько отличающихся от указанных в ГОСТ 27751 (таблица А.1), а также иная дифференциация надежности железобетонных конструкций, где классы последствий (CC) установлены путем рассмотрения последствий отказа или неисправности конструкции (таблица А.4). В [3] применяют термин "расчетный срок работы", что можно интерпретировать как минимальный требуемый срок службы.
Таблица А.3
Категория расчетного срока эксплуатации | Расчетный срок эксплуатации, лет | Примеры |
1 | 10 | Временные конструкции <1> |
2 | От 10 до 25 | Заменяемые конструкции, например, подкрановые балки, некоторые элементы опорных конструкций |
3 | От 15 до 30 | Сооружения сельского хозяйства и аналогичные им |
4 | 50 | Здания и другие сооружения общего назначения |
5 | 100 | Монументальные здания, мосты и другие инженерные сооружения |
Таблица А.4
Класс последствий | Описание | Примеры строительно-монтажных работ |
CC3 | Тяжелые последствия, связанные с человеческими жертвами или очень большие экономические потери, или очень большой ущерб для окружающей среды | Трибуны, общественные здания, где последствия отказа высоки (например, концертный зал) |
CC2 | Последствия, связанные с человеческими жертвами, или значительные экономические потери, или значительный ущерб для окружающей среды | Жилые и офисные здания, общественные здания, где последствия аварии - средние (например, офисное здание) |
CC1 | Низкие последствия для человеческих жизней, а экономические, социальные или экологические последствия небольшие или незначительные | Сельскохозяйственные здания, куда люди обычно не заходят (например, склады и хранилища), "зеленые" дома |
А.5 С тремя классами последствий CC1, CC2 и CC3 [3] связаны три класса надежности RC1, RC2 и RC3, различающиеся по коэффициентам надежности  . В таблице А.5 приведены рекомендуемые минимальные значения коэффициента надежности, связанного с классами надежности.
. В таблице А.5 приведены рекомендуемые минимальные значения коэффициента надежности, связанного с классами надежности.
Таблица А.5
надежности 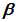 для использования при проектировании
для использования при проектировании
по жизненному циклу (рассчитанные на расчетный срок службы)
Класс эксплуатации - Eurocode 2 | Описание | Класс надежности | SLS <1> | ULS |
Разрушение | ||||
XC <3> | Карбонизация | RC1 | 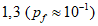 | 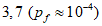 |
RC2 | 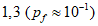 | 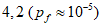 | ||
RC3 | 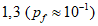 | 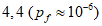 | ||
XD <3> | Соли-антиобледенители | RC1 | 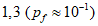 | 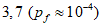 |
RC2 | 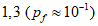 | 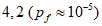 | ||
RC3 | 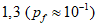 | 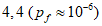 | ||
XS <3> | Морская вода | RC1 | 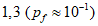 | 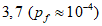 |
RC2 | 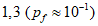 | 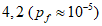 | ||
RC3 | 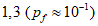 | 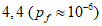 | ||
<1> Надежность предельного состояния по эксплуатационной пригодности (SLS) при коэффициенте  в результате может привести к более низкой надежности предельного состояния по несущей способности (ULS), чем обычно требуется в нормах (см. ISO 2394). Это означает, что для очень агрессивного климата требуются более высокие значения в результате может привести к более низкой надежности предельного состояния по несущей способности (ULS), чем обычно требуется в нормах (см. ISO 2394). Это означает, что для очень агрессивного климата требуются более высокие значения | ||||
А.6 Предлагаемая классификация для проектирования долговечности железобетонных конструкций приведена в таблице 7.2 настоящего пособия. Кроме того, в таблице приведены требования по сроку службы и коэффициенты надежности по нагрузкам и материалам.
Расчетный срок службы находят из уравнения
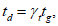 (А.1)
(А.1)где td - расчетный срок службы;
tg - заданный срок службы.
При этом необходима проверка на выполнение условия: m <= 0,7, где m - относительное снижение коэффициента запаса за период от 0 до td лет.
А.7 Анализ влияния окружающей среды подразумевает определение климатических условий, например, учет колебаний температуры и влажности, дождей, конденсации влаги, замерзания, солнечной радиации, воздействия загрязненного воздуха, а также геологических условий, например, уровня грунтовых вод, возможного контакта с морской водой, загрязнения почвы агрессивными реагентами, например, сульфатами или хлоридами. Кроме того, необходимо также выявлять и факторы воздействия, связанные с человеческой деятельностью, например, применение солей-антиобледенителей на дорогах, продукты абразивного воздействия транспорта и т.д.
А.8 В таблице А.6 показаны три возможных уровня контроля разработки проекта (DSL). Уровни надзора за проектированием могут быть привязаны к классу надежности, назначенному или выбранному в соответствии с ответственностью конструкции и в соответствии с национальными требованиями или нормативными документами по проектированию, и реализованы посредством соответствующих мер по управлению качеством.
Таблица А.6
Уровень контроля | Характеристика | Минимальные рекомендуемые требования к проверке расчетов, чертежей и технических условий |
DSL3 (соотносится с RC3) | Расширенный контроль | Проверка третьей стороной: проверка, выполняемая организацией, отличной от той, которая выполнила проект |
DSL2 (соотносится с RC2) | Обычный контроль | Проверка другими лицами, чем те, кто изначально является ответственным в соответствии с процедурой организации |
DSL1 (соотносится с RC1) | Обычный контроль | Самоконтроль: проверка, выполняемая лицом, разработавшим проект |
А.9 Для дифференциации управления качеством строительства могут быть введены три класса выполнения работ (таблица А.7). Классы выполнения могут быть связаны с классами управления качеством, выбранными и реализованными с помощью соответствующих мер и проектов управления качеством.
Таблица А.7
Класс выполнения работ | Характеристика | Требование |
EXC3 (соотносится с RC3) | Расширенное инспектирование | Инспекция третьей стороной |
EXC2 (соотносится с RC2) | Обычное инспектирование | Инспекция в соответствии с процедурой организации |
EXC1 (соотносится с RC1) | Normal inspection | Самоинспекция |
А.10 Для обеспечения срока службы здания, сооружения или их компонентов уровень мониторинга и наблюдений во время эксплуатации - решающий для соответствующего уровня надежности. С этой целью можно использовать уровни контроля состояния (CCL) в течение срока службы, описанные в [26] и приведенные в таблице А.8.
Таблица А.8
Уровень | Характеристика | Требование |
CCL3 | Расширенная инспекция | Систематическая инспекция и мониторинг соответствующих параметров процесса (процессов) ухудшения качества, которые являются критическими при проектировании по жизненному циклу |
CCL2 | Обычная инспекция | Регулярный визуальный осмотр квалифицированным персоналом |
CCL1 | Обычная инспекция | Отсутствие систематического контроля или осмотра |
CCL0 | Отсутствие инспекции | Невозможность инспекции, например, из-за отсутствия доступа |
А.11 Для существующих зданий и сооружений затраты на достижение более высокого уровня надежности обычно более высоки по сравнению с проектируемыми конструкциями. По этой причине целевой уровень для существующих конструкций обычно должен быть ниже.
А.12 Частные коэффициенты безопасности для показателей строительного материала, изделия или прочности конструкции могут быть уменьшены, если применяется класс контроля выше, чем требуется в соответствии с таблицей А.8 и/или применяются другие более строгие требования. Такое уменьшение, которое допускается, например, при неопределенности моделей и размерных отклонений от номинальных значений, не является мерой дифференциации надежности: это только компенсирующая мера для того, чтобы уровень надежности в определенной степени зависел от эффективности мер управления.
[1] Siemes, A., Vrouwenvelder, A. and Beukel, A. van den (1985) Durability of buildings: a reliability analysis. Heron, 30(3), 3 - 48
[2] Vesikari, E. (1995) Betonirakenteiden  (Service life design of concrete structures). Association of Finnish Civil Engineers RIL, Helsinki RIL 183-4.9. (In Finnish, 120 pp.)
(Service life design of concrete structures). Association of Finnish Civil Engineers RIL, Helsinki RIL 183-4.9. (In Finnish, 120 pp.)
 (Service life design of concrete structures). Association of Finnish Civil Engineers RIL, Helsinki RIL 183-4.9. (In Finnish, 120 pp.)
(Service life design of concrete structures). Association of Finnish Civil Engineers RIL, Helsinki RIL 183-4.9. (In Finnish, 120 pp.)[4] Andrade, C., Alonso, C., Gonzales, I.A. and Rodriguez, J. (1989) Remaining service life of corroding structures. Proceedings of the IABSE Symposium Durability of Structures, Lisbon, pp. 359 - 64
[6] CEN, EMV 1991-1. Euro 1, публикация CEN, 1994
[7] Masters, L.W. and Brandt, E. (1989) Systematic methodology for service life prediction of building materials and components. Report of the TC 71-PSL. Prediction of service life of building materials and components. Materials and Structures, 22, 385 - 92
[8] Pihlajavaara, S.E. (1984) The prediction of service life with the aid of multiple testing, reference materials, experience data, and value analysis. VTT Symposium 48, Espoo, Vol. 1, pp. 37 - 64
[9] Kraker, A., de Tichler, J.W. and Vrouwenvelder, A.C.W.M. (1982) Safety, reliability and service life of structures. Heron 27(1), 85 pp.
[10] Jiang, Y., Saito M. and Sinha K.C. (1988) Bridge performance prediction model using Markov chain. Transportation Research Record 1180, pp. 25 - 32. Transportation Research Board Business Office, Washington
[11] Vesikari, E. (1994) Durability design of concrete structures with respect to frost attack. Proceedings of the Fourth International Symposium on Cold Region Development. 13 - 16 June. Association of Finnish Civil Engineers RIL, 2 pp.
[12] Matala, S. (1991) Service life model for frost resistance of concrete based on properties of fresh concrete, Nordisk 
 , Broseminarium,
, Broseminarium,  , Denmark, 18 pp.
, Denmark, 18 pp.
 , Broseminarium,
, Broseminarium, [13] Huovinen, S. (1990) Abrasion of concrete by ice in arctic sea structures (Doctoral thesis). Technical Research Centre of Finland, Espoo. Publications No. 62
[14] Schiessl, P. (1976) Zur Frage der  Rissbreite und der erforderlichen Betondeckung in Stahlbetonbau unter besonderer
Rissbreite und der erforderlichen Betondeckung in Stahlbetonbau unter besonderer  der Karbonatisierung des Betons. Deutscher Ausschuss
der Karbonatisierung des Betons. Deutscher Ausschuss 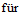 Stahlbeton, Berlin, Vol. 255, 175 pp.
Stahlbeton, Berlin, Vol. 255, 175 pp.
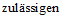 Rissbreite und der erforderlichen Betondeckung in Stahlbetonbau unter besonderer
Rissbreite und der erforderlichen Betondeckung in Stahlbetonbau unter besonderer  der Karbonatisierung des Betons. Deutscher Ausschuss
der Karbonatisierung des Betons. Deutscher Ausschuss [15] Bakker, R. (1993) Model to calculate the rate of carbonation in concrete under different climatic conditions. May. Paper no. 104-CEN TC 104/WGI/TGI/Panel 1. Unpublished
[16] Tuutti, K. (1982) Corrosion of steel in concrete. Swedish Cement and Concrete Research Institute, Stockholm. CBI Research 4:82, 304 pp.
[17] Fagerlund, G., Somerville, G. and Tuutti, K. 'The residual service life of concrete exposed to the combined effect of frost attack and reinforcement corrosion', Proceedings of Int. Conf. Concrete Across Borders 1994. Danish Concrete Association. 1994. p. 351 - 364
[18]  , T. (1993) Influence of high slag content on the basic mechanical properties and carbonation of concrete. Technical Research Centre of Finland, Espoo. Publications 141, 98 pp.+app. 46 pp.
, T. (1993) Influence of high slag content on the basic mechanical properties and carbonation of concrete. Technical Research Centre of Finland, Espoo. Publications 141, 98 pp.+app. 46 pp.
 , T. (1993) Influence of high slag content on the basic mechanical properties and carbonation of concrete. Technical Research Centre of Finland, Espoo. Publications 141, 98 pp.+app. 46 pp.
, T. (1993) Influence of high slag content on the basic mechanical properties and carbonation of concrete. Technical Research Centre of Finland, Espoo. Publications 141, 98 pp.+app. 46 pp.[19] CEB, CEB-FIP Model Code 1990, CEB Bulletin d'information No. 213/214  EuroInternational du
EuroInternational du 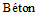 , Lausanne, Switzerland, 1993, 437 p.
, Lausanne, Switzerland, 1993, 437 p.
[20]  , T. (1991) Influence of cementing materials on the permeability of concrete. Technical Research Centre of Finland, Espoo. Research Notes 750, 84 pp.+app. 27 pp.
, T. (1991) Influence of cementing materials on the permeability of concrete. Technical Research Centre of Finland, Espoo. Research Notes 750, 84 pp.+app. 27 pp.
 , T. (1991) Influence of cementing materials on the permeability of concrete. Technical Research Centre of Finland, Espoo. Research Notes 750, 84 pp.+app. 27 pp.
, T. (1991) Influence of cementing materials on the permeability of concrete. Technical Research Centre of Finland, Espoo. Research Notes 750, 84 pp.+app. 27 pp.[21] Parrot, L. (1992) Design for avoiding damage due to carbonation induced corrosion. April. Paper no. 62-CEN TC 104/WGl/TGI/ Panel 1. Unpublished
[22] Alonso, C. and Andrade, C. (1993) Life time of rebars in carbonated concrete. Proceedings of the 10th European Corrosion Congress, Barcelona, Progress in the Understanding and Prevention of Corrosion, Vol. 1, pp. 634 - 41
[23] Andrade, C., Alonso, M.C., Pettersson, K., Somerville, G. and Tuutti, K. (1994) The practical assessment of damage due to corrosion. Proceedings of Int. Conf. Concrete across Borders 1994, Danish Concrete Association, Odense, pp. 337 - 50
[24] Степанова В.Ф., Фаликман В.Р. Современные проблемы обеспечения долговечности железобетонных конструкций. Бетон и железобетон - взгляд в будущее: научные труды III Всероссийской (II Международной) конференции по бетону и железобетону (Москва, 12 - 16 мая 2014 г.). В 7 т. Т. 7. Пленарные доклады. Москва. МГСУ. 2014. 400 с. Стр. 275 - 302
[25] fib bulletin no. 34, Model Code for Service Life Design (MC-SLD), International Federation for Structural Concrete (fib), Lausanne, Switzerland. 2006