СПРАВКА
Источник публикации
М.: Стандартинформ, 2014
Примечание к документу
Документ введен в действие с 01.12.2014.
Название документа
"Р 50.1.086-2013. Рекомендации по стандартизации. Статистические методы. Примеры применения. Часть 6. Анализ выборочных оценок среднего и стандартного отклонения"
(утв. и введены в действие Приказом Росстандарта от 22.11.2013 N 1663-ст)
"Р 50.1.086-2013. Рекомендации по стандартизации. Статистические методы. Примеры применения. Часть 6. Анализ выборочных оценок среднего и стандартного отклонения"
(утв. и введены в действие Приказом Росстандарта от 22.11.2013 N 1663-ст)
Содержание
Приказом Федерального агентства
по техническому регулированию
и метрологии
от 22 ноября 2013 г. N 1663-ст
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
СТАТИСТИЧЕСКИЕ МЕТОДЫ
ПРИМЕРЫ ПРИМЕНЕНИЯ
ЧАСТЬ 6
АНАЛИЗ ВЫБОРОЧНЫХ ОЦЕНОК СРЕДНЕГО И СТАНДАРТНОГО ОТКЛОНЕНИЯ
Statistical methods. Examples of application. Part 6.
Consideration of sample mean and sample standard deviation
Р 50.1.086-2013
Группа Т59
ОКС 03.120.30
Дата введения
1 декабря 2014 года
1 РАЗРАБОТАНЫ Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД")
2 ВНЕСЕНЫ Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 22 ноября 2013 г. N 1663-ст
4 ВВЕДЕНЫ ВПЕРВЫЕ
Информация об изменениях к настоящим рекомендациям публикуется в ежегодном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящих рекомендаций соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Серия рекомендаций по стандартизации "Статистические методы. Примеры применения" включает разъяснения применения статистических методов в простой и доступной форме.
В рекомендациях представлены способы применения простых статистических методов и приемов, показано, как знание процесса производства может способствовать его улучшению, повышению эффективности, производительности и повышению качества изготавливаемой продукции.
Термин "статистический" обычно применяют по отношению к методам, связанным с обработкой числовых данных, относящихся к контролю качества продукции, управлению технологическими процессами, увеличению выпуска продукции и продаж, снижению затрат, и как следствие, стоимости продукции, а также к заработной плате. До применения конкретного статистического метода необходимо четко понимать его назначение.
В настоящих рекомендациях рассмотрены методы статистического анализа оценок среднего и стандартного отклонения, полученных по выборочным данным. В рекомендациях приведены примеры и даны рекомендации по применению этих методов.
В серии рекомендаций "Статистические методы. Примеры применения" приведены пояснения к использованию статистических методов, применяемых в менеджменте, контроле и улучшении процессов с учетом требований ГОСТ Р ИСО/ТО 10017.
В настоящих рекомендациях рассмотрены методы статистического анализа выборочных данных, а также полученных на их основе оценок среднего и стандартного отклонения совокупности.
Применение представленных в настоящих рекомендациях методов позволяет повысить достоверность оценок и таким образом способствует принятию более объективных решений исследуемых параметров.
В настоящих рекомендациях использованы нормативные ссылки на следующие документы:
ГОСТ Р 50779.10-2000 Статистические методы. Вероятность и основы статистики. Термины и определения
ГОСТ Р 50779.11-2000 Статистические методы. Статистическое управление качеством. Термины и определения
ГОСТ Р ИСО 9000-2008 Системы менеджмента качества. Основные положения и словарь
ГОСТ Р ИСО/ТО 10017-2005 Статистические методы. Руководство по применению в соответствии с ГОСТ Р ИСО 9001
ИС МЕГАНОРМ: примечание. Здесь и далее в официальном тексте документа, видимо, допущена опечатка: стандарт имеет номер ГОСТ ИСО 11453-2005, а не ГОСТ Р ИСО 11453-2005. |
ГОСТ Р ИСО 11453-2005 Статистические методы. Статистическое представление данных. Проверка гипотез и доверительные интервалы для пропорций
ИС МЕГАНОРМ: примечание. Взамен ГОСТ Р ИСО 16269-6-2005 Приказом Росстандарта от 12.09.2017 N 1057-ст с 01.12.2018 введен в действие ГОСТ Р 50779.29-2017. |
ГОСТ Р ИСО 16269-6-2005 Статистические методы. Статистическое представление данных. Определение статистических толерантных интервалов
ГОСТ Р ИСО 16269-7-2004 Статистические методы. Статистическое представление данных. Медиана. Определение точечной оценки и доверительных интервалов
ГОСТ Р ИСО 16269-8-2005 Статистические методы. Статистическое представление данных. Определение предикционных интервалов
Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения
Р 50.1.073-2010 Статистические методы. Примеры применения. Часть 2. Анализ данных на соответствие установленным требованиям
Р 50.1.074-2010 Статистические методы. Примеры применения. Часть 3. Анализ данных контроля
Р 50.1.082-2012 Статистические методы. Примеры применения. Часть 4. Прямые статистические приемы анализа данных
Примечание - При пользовании настоящими рекомендациями целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
В настоящих рекомендациях применены термины по ГОСТ Р 50779.10, ГОСТ Р 50779.11, Р 50.1.040 и ГОСТ Р ИСО 9000.
Для обеспечения однозначности трактовки формул и выводов, приведенных в рекомендациях, следует учитывать различия в обозначениях, используемых для характеристик совокупности (партии) и выборки, отобранной из этой совокупности. Обычно для совокупности содержащей N элементов, среднее обозначают  , а стандартное отклонение
, а стандартное отклонение 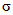 . Для выборки, содержащей n элементов, выборочное среднее обозначают
. Для выборки, содержащей n элементов, выборочное среднее обозначают  , а выборочное стандартное отклонение s. Значения характеристик для различных выборок идентифицируют при помощи нижних индексов, например:
, а выборочное стандартное отклонение s. Значения характеристик для различных выборок идентифицируют при помощи нижних индексов, например:
Если из совокупности отобрано много случайных выборок объема n, то стандартное отклонение выборочных средних  является мерой ошибки при использовании выборочного среднего одной выборки из n элементов в качестве оценки среднего совокупности
является мерой ошибки при использовании выборочного среднего одной выборки из n элементов в качестве оценки среднего совокупности  . Это стандартное отклонение выборок
. Это стандартное отклонение выборок 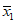 ,
,  и т.д. называют стандартной ошибкой среднего. Аналогично стандартное отклонение выборочных стандартных отклонений s1, s2, ..., и т.д., называют стандартной ошибкой стандартного отклонения при использовании s в качестве оценки
и т.д. называют стандартной ошибкой среднего. Аналогично стандартное отклонение выборочных стандартных отклонений s1, s2, ..., и т.д., называют стандартной ошибкой стандартного отклонения при использовании s в качестве оценки  .
.
Математическая статистика позволяет определить оценки указанных стандартных ошибок по результатам одной выборки. Далее предполагается, что объем выборки n существенно меньше объема совокупности N, например  .
.
 .
.Математическое ожидание (среднее) среднего арифметического (выборочного среднего), рассчитанного по выборке объема n, отобранной из совокупности, равно истинному среднему совокупности, т.е.
Стандартное отклонение выборочного среднего  равно истинному стандартному отклонению совокупности, деленному на корень из n, т.е.
равно истинному стандартному отклонению совокупности, деленному на корень из n, т.е.
В большинстве случаев при n >= 5 распределение выборочных средних может быть аппроксимировано нормальным распределением.
Если предположить, что выборка содержит приблизительно 20 или более элементов, можно сделать следующее заключение. Так как  изменяется в соответствии с нормальным распределением со средним
изменяется в соответствии с нормальным распределением со средним  и стандартным отклонением
и стандартным отклонением  , то маловероятно, что в любой случайной выборке разность
, то маловероятно, что в любой случайной выборке разность  будет больше
будет больше  и почти невероятно, что она будет больше
и почти невероятно, что она будет больше  . Следовательно, скорее всего выборочное среднее не будет отличаться от истинного среднего соответствующей совокупности больше чем на
. Следовательно, скорее всего выборочное среднее не будет отличаться от истинного среднего соответствующей совокупности больше чем на  . В тех случаях, когда стандартное отклонение
. В тех случаях, когда стандартное отклонение  неизвестно, часто используют его оценку, полученную по выборке.
неизвестно, часто используют его оценку, полученную по выборке.
 . В тех случаях, когда стандартное отклонение
. В тех случаях, когда стандартное отклонение Квадрат стандартного отклонения является дисперсией, т.е. s2 - выборочная дисперсия,  - дисперсия совокупности. Математическое ожидание выборочных дисперсий для выборки объема n равно дисперсии совокупности, т.е.
- дисперсия совокупности. Математическое ожидание выборочных дисперсий для выборки объема n равно дисперсии совокупности, т.е.
Однако математическое ожидание выборочного стандартного отклонения s для объема выборки n меньше 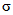 , т.е. s является смещенной оценкой
, т.е. s является смещенной оценкой  . В данном случае смещение отрицательно. Смещение зависит от объема выборки и уменьшается с увеличением объема выборки.
. В данном случае смещение отрицательно. Смещение зависит от объема выборки и уменьшается с увеличением объема выборки.
Таблица 1
доверительных интервалов для среднего и стандартного
отклонения совокупности
Объем выборки | Среднее | Стандартное отклонение | ||||||||||
 , ,  | 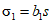 , ,  | |||||||||||
Уровень ошибки | Уровень ошибки | |||||||||||
10% | 5% | 2% | 1% | 10% | 5% | 2% | 1% | |||||
n | a | a | a | a | b1 | b2 | b1 | b2 | b1 | b2 | b1 | b2 |
5 | 0,954 | 1,242 | 1,676 | 2,060 | 0,649 | 2,373 | 0,599 | 2,874 | 0,548 | 3,670 | 0,518 | 4,396 |
6 | 0,823 | 1,050 | 1,374 | 1,647 | 0,672 | 2,090 | 0,624 | 2,453 | 0,575 | 3,004 | 0,546 | 3,485 |
7 | 0,735 | 0,925 | 1,188 | 1,402 | 0,690 | 1,916 | 0,644 | 2,203 | 0,597 | 2,623 | 0,568 | 2,980 |
8 | 0,670 | 0,837 | 1,060 | 1,238 | 0,705 | 1,798 | 0,661 | 2,036 | 0,615 | 2,377 | 0,587 | 2,661 |
9 | 0,620 | 0,769 | 0,966 | 1,119 | 0,718 | 1,712 | 0,675 | 1,916 | 0,631 | 2,205 | 0,603 | 2,440 |
10 | 0,580 | 0,716 | 0,893 | 1,028 | 0,729 | 1,646 | 0,687 | 1,826 | 0,644 | 2,077 | 0,617 | 2,278 |
11 | 0,547 | 0,672 | 0,834 | 0,956 | 0,739 | 1,594 | 0,698 | 1,755 | 0,656 | 1,978 | 0,630 | 2,154 |
12 | 0,519 | 0,636 | 0,785 | 0,897 | 0,747 | 1,551 | 0,708 | 1,698 | 0,667 | 1,899 | 0,641 | 2,056 |
13 | 0,495 | 0,605 | 0,744 | 0,848 | 0,755 | 1,516 | 0,717 | 1,651 | 0,676 | 1,834 | 0,651 | 1,976 |
14 | 0,474 | 0,578 | 0,709 | 0,806 | 0,762 | 1,486 | 0,724 | 1,612 | 0,685 | 1,780 | 0,660 | 1,910 |
15 | 0,455 | 0,554 | 0,678 | 0,769 | 0,768 | 1,460 | 0,732 | 1,578 | 0,693 | 1,734 | 0,668 | 1,854 |
16 | 0,439 | 0,533 | 0,651 | 0,737 | 0,774 | 1,438 | 0,738 | 1,548 | 0,700 | 1,694 | 0,676 | 1,806 |
17 | 0,424 | 0,515 | 0,627 | 0,709 | 0,780 | 1,418 | 0,744 | 1,522 | 0,707 | 1,660 | 0,683 | 1,764 |
18 | 0,411 | 0,498 | 0,606 | 0,684 | 0,785 | 1,401 | 0,750 | 1,500 | 0,713 | 1,629 | 0,689 | 1,728 |
19 | 0.398 | 0,482 | 0,586 | 0,661 | 0,789 | 1,385 | 0,755 | 1,479 | 0,719 | 1,602 | 0,696 | 1,696 |
20 | 0,387 | 0,469 | 0,568 | 0,640 | 0,793 | 1,371 | 0,760 | 1,461 | 0,724 | 1,578 | 0,701 | 1,667 |
21 | 0,377 | 0,456 | 0,552 | 0,621 | 0,797 | 1,358 | 0,765 | 1,445 | 0,729 | 1,557 | 0,707 | 1,641 |
22 | 0,367 | 0,444 | 0,537 | 0,604 | 0,801 | 1,346 | 0,769 | 1,430 | 0,734 | 1,537 | 0,712 | 1,617 |
23 | 0,359 | 0,433 | 0,524 | 0,588 | 0,805 | 1,336 | 0,773 | 1,416 | 0,738 | 1,519 | 0,716 | 1,596 |
24 | 0,350 | 0,423 | 0,511 | 0,574 | 0,808 | 1,326 | 0,777 | 1,403 | 0,743 | 1,502 | 0,721 | 1,576 |
25 | 0,343 | 0,413 | 0,499 | 0,560 | 0,811 | 1,317 | 0,780 | 1,392 | 0,747 | 1,487 | 0,725 | 1,559 |
26 | 0,335 | 0,404 | 0,488 | 0,547 | 0,814 | 1,309 | 0,784 | 1,381 | 0,751 | 1,473 | 0,729 | 1,542 |
27 | 0,329 | 0,396 | 0,478 | 0,535 | 0,817 | 1,301 | 0,787 | 1,371 | 0,754 | 1,460 | 0,733 | 1,527 |
28 | 0,322 | 0,388 | 0,468 | 0,524 | 0,820 | 1,293 | 0,790 | 1,362 | 0,758 | 1,448 | 0,737 | 1,513 |
29 | 0,316 | 0,381 | 0,459 | 0,514 | 0,823 | 1,287 | 0,793 | 1,353 | 0,761 | 1,437 | 0,741 | 1,499 |
30 | 0,311 | 0,374 | 0,450 | 0,504 | 0,825 | 1,280 | 0,796 | 1,345 | 0,764 | 1,427 | 0,744 | 1,487 |
Математическое ожидание выборочного стандартного отклонения по выборке объема n имеет вид:
где c4 - коэффициент, учитывающий смещение и зависящий от n.
Примечание - Соотношение (4) справедливо только в случае, когда наблюдения подчиняются нормальному распределению.
Значения c4 для объемов выборки от 2 до 30 приведены в таблице 2. Значение c4 приблизительно равно 4 (n - l)/(4n - 3).
Таблица 2
выборочных стандартных отклонений
Объем выборки, n | c4 | 1/c4 |
2 | 0,7979 | 1,2533 |
3 | 0,8862 | 1,1284 |
4 | 0,9213 | 1,0854 |
5 | 0,9400 | 1,0638 |
6 | 0,9515 | 1,0509 |
7 | 0,9594 | 1,0424 |
8 | 0,9650 | 1,0362 |
9 | 0,9693 | 1,0317 |
10 | 0,9727 | 1,0281 |
11 | 0,9754 | 1,0253 |
12 | 0,9776 | 1,0230 |
13 | 0,9794 | 1,0210 |
14 | 0,9810 | 1,0194 |
15 | 0,9823 | 1,0180 |
16 | 0,9835 | 1,0168 |
17 | 0,9845 | 1,0157 |
18 | 0,9854 | 1,0148 |
19 | 0,9862 | 1,0140 |
20 | 0,9869 | 1,0132 |
21 | 0,9876 | 1,0126 |
22 | 0,9882 | 1,0120 |
23 | 0,9887 | 1,0114 |
24 | 0,9892 | 1,0109 |
25 | 0,9896 | 1,0105 |
26 | 0,9101 | 1,0100 |
27 | 0,9904 | 1,0097 |
28 | 0,9908 | 1,0093 |
29 | 0,9911 | 1,0090 |
30 | 0,9914 | 1,0087 |
Устранение смещения особенно важно в ситуациях, когда выборочное стандартное отклонение используют в качестве оценки стандартного отклонения совокупности. Для устранения смещения оценку стандартного отклонения определяют по формуле  .
.
 .
.Относительно устранения смещения необходимо учитывать следующее.
а) При малом объеме выборки n смещение является существенным.
б) Если n мало, никакая единственная оценка  не может быть удовлетворительной. Можно лишь получить нижнюю и верхнюю (
не может быть удовлетворительной. Можно лишь получить нижнюю и верхнюю ( и
и  ) границы доверительного интервала для
) границы доверительного интервала для 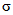 (см. таблицу 1). Этот интервал характеризует неопределенность оценки
(см. таблицу 1). Этот интервал характеризует неопределенность оценки  по малому количеству наблюдений.
по малому количеству наблюдений.
в) Устранение смещения в случае, когда  оценивают по большому количеству малых выборок, позволяет получить объективную несмещенную оценку.
оценивают по большому количеству малых выборок, позволяет получить объективную несмещенную оценку.
В соответствии с (2) существует приближение теоретического выражения для стандартной ошибки стандартного отклонения s (т.е. стандартной ошибки выборочного стандартного отклонения)
Применение этого приближения имеет несколько ограничений:
а) наблюдения x должны подчиняться нормальному распределению или распределению близкому к нормальному;
б) в случае, когда 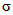 не известно, вместо
не известно, вместо  в правой части (5) используют s, при этом выборка должна состоять не менее чем из тридцати наблюдений.
в правой части (5) используют s, при этом выборка должна состоять не менее чем из тридцати наблюдений.
Пример - Данные таблицы 3 иллюстрируют изменчивость  и s по выборкам из одной и той же совокупности. Через каждые два часа с конвейера отбирают одну банку консервированных томатов и взвешивают ее содержимое. Таким образом, за смену (8 ч) получают четыре результата взвешивания. В таблице 3 приведены результаты наблюдений в течение 40 смен.
и s по выборкам из одной и той же совокупности. Через каждые два часа с конвейера отбирают одну банку консервированных томатов и взвешивают ее содержимое. Таким образом, за смену (8 ч) получают четыре результата взвешивания. В таблице 3 приведены результаты наблюдений в течение 40 смен.
Таблица 3
консервированных томатов, г
Номер смены | Вес содержимого банки, г | |||
1 | 401,5 | 401,5 | 404,8 | 402,8 |
2 | 404,4 | 403,4 | 406,3 | 403,1 |
3 | 405,7 | 405,5 | 406,1 | 404,8 |
4 | 405,0 | 402,6 | 406,6 | 402,9 |
5 | 402,6 | 404,0 | 404,4 | 404,0 |
6 | 404,2 | 403,6 | 403,7 | 407,9 |
7 | 404,4 | 405,2 | 402,5 | 403,5 |
8 | 407,7 | 403,9 | 403,8 | 407,1 |
9 | 409,7 | 400,7 | 405,0 | 405,5 |
10 | 405,7 | 400,4 | 402,3 | 405,4 |
11 | 402,8 | 403,2 | 402,3 | 402,0 |
12 | 400,8 | 406,3 | 403,6 | 402,6 |
13 | 401,0 | 403,9 | 403,0 | 403,4 |
14 | 402,3 | 405,6 | 402,5 | 404,8 |
15 | 403,7 | 404,7 | 405,8 | 403,9 |
16 | 403,9 | 402,2 | 403,7 | 402,7 |
17 | 404,2 | 404,9 | 406,3 | 401,4 |
18 | 403,6 | 404,0 | 401,0 | 400,9 |
19 | 405,9 | 403,8 | 405,6 | 398,4 |
20 | 401,5 | 401,7 | 404,0 | 403,8 |
21 | 405,0 | 405,7 | 404,1 | 404,4 |
22 | 403,8 | 405,4 | 406,5 | 401,3 |
23 | 401,8 | 404,4 | 407,6 | 405,6 |
24 | 402,4 | 401,8 | 403,8 | 401,6 |
25 | 407,3 | 404,1 | 406,3 | 403,1 |
26 | 401,4 | 407,4 | 402,1 | 404,4 |
27 | 402,8 | 403,7 | 405,5 | 402,4 |
28 | 401,6 | 406,5 | 400,8 | 404,1 |
29 | 407,3 | 401,3 | 406,1 | 405,9 |
30 | 401,2 | 405,3 | 405,2 | 403,2 |
31 | 408,4 | 403,3 | 404,1 | 402,9 |
32 | 404,8 | 404,9 | 406,0 | 404,5 |
33 | 403,2 | 402,0 | 403,4 | 404,0 |
34 | 404,9 | 400,9 | 400,9 | 400,4 |
35 | 405,0 | 402,1 | 405,6 | 402,0 |
36 | 402,1 | 403,1 | 403,8 | 404,2 |
37 | 405,3 | 403,9 | 404,7 | 404,3 |
38 | 404,5 | 401,5 | 404,7 | 402,7 |
39 | 405,2 | 399,7 | 405,1 | 406,2 |
40 | 402,0 | 400,7 | 402,6 | 404,9 |
Общий анализ данных таблицы 3 в соответствии с Р 50.1.074 показывает, что изменчивость в выборке от элемента к элементу является устойчивой в течение всего периода наблюдений.
Среднее и стандартное отклонение по 160 наблюдениям составили  и
и 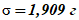 .
.
 и
и 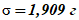 .
.Выборочные средние и стандартные отклонения  и s для сорока выборок по четыре наблюдения в каждой приведены в таблице 4. В таблице 5 они представлены в сгруппированном виде (см. таблицу 6 из Р 50.1.082).
и s для сорока выборок по четыре наблюдения в каждой приведены в таблице 4. В таблице 5 они представлены в сгруппированном виде (см. таблицу 6 из Р 50.1.082).
Таблица 4
средние и стандартные отклонения по четырем
наблюдениям за смену, г
Номер смены | Выборочное среднее | Выборочное стандартное отклонение |
1 | 402,65 | 1,559 |
2 | 404,30 | 1,445 |
3 | 405,52 | 0,544 |
4 | 404,28 | 1,882 |
5 | 403,75 | 0,790 |
6 | 404,85 | 2,050 |
7 | 403,90 | 1,163 |
8 | 405,62 | 2,065 |
9 | 405,22 | 3,680 |
10 | 403,45 | 2,549 |
11 | 402,58 | 0,532 |
12 | 403,32 | 2,297 |
13 | 402,82 | 1,271 |
14 | 403,80 | 1,651 |
15 | 404,52 | 0,954 |
16 | 403,12 | 0,810 |
17 | 404,20 | 2,061 |
18 | 402,38 | 1,654 |
19 | 403,42 | 3,476 |
20 | 402,75 | 1,333 |
21 | 404,80 | 0,707 |
22 | 404,25 | 2,258 |
23 | 404,85 | 2,424 |
24 | 402,40 | 0,993 |
25 | 405,20 | 1,936 |
26 | 403,82 | 2,706 |
27 | 403,60 | 1,378 |
28 | 403,25 | 2,583 |
29 | 405,15 | 2,640 |
30 | 403,72 | 1,941 |
31 | 404,68 | 2,533 |
32 | 405,05 | 0,656 |
33 | 403,15 | 0,839 |
34 | 401,78 | 2,097 |
35 | 403,68 | 1,893 |
36 | 403,30 | 0,920 |
37 | 404,55 | 0,597 |
38 | 403,35 | 1,526 |
39 | 404,05 | 2,942 |
40 | 402,55 | 1,756 |
Таблица 5
появления значений выборочных средних и стандартных
отклонений по четырем наблюдениям
Вес содержимого банки, г | Частота | Выборочное среднее | Частота | Выборочное стандартное отклонение, s, г | Частота |
398,00 - 398,99 | 1 | 400,50 - 400,99 | 1 | 0,500 - 0,999 | 11 |
399,00 - 399,99 | 1 | 401,00 - 401,49 | 2 | 1,000 - 1,499 | 5 |
400,00 - 100,99 | 9 | 401,50 - 401,99 | 5 | 1,500 - 1,999 | 9 |
401,00 - 401,99 | 16 | 402,00 - 402,49 | 8 | 2,000 - 2,499 | 7 |
402,00 - 402,99 | 26 | 402,50 - 402,99 | 7 | 2,500 - 2,999 | 6 |
403,00 - 403,99 | 30 | 403,00 - 403,49 | 5 | 3,000 - 3,499 | 1 |
404,00 - 404,99 | 32 | 403,50 - 403,99 | 6 | 3,500 - 3,999 | 1 |
405,00 - 405,99 | 25 | 404,00 - 404,49 | 4 | ||
406,00 - 406,99 | 11 | 404,50 - 404,99 | 2 | ||
407,00 - 407,99 | 7 | ||||
408,00 - 408,99 | 1 | ||||
409,00 - 409,99 | 1 | ||||
Общее количество | 160 | Общее количество | 40 | Общее количество | 40 |
Если принять среднее и стандартное отклонение по всем (160) имеющимся данным за истинное, можно проверить выполнение соотношений (1), (2), (4) и (5). Результаты приведены в таблице 6.
Таблица 6
полученных результатов с теоретическими
Оцениваемая величина | Результат взвешивания, г | Результат расчета по теоретическим формулам, г |
Среднее значение | 403,84 | 403,84 |
Стандартная ошибка | 0,965 |  |
Среднее значение s, т.е. оценка | 1,727 |  |
Стандартная ошибка s, т.е. оценка | 0,808 |  |
Репрезентативная выборка является важным расширением предыдущих результатов, когда контролируемые элементы отобраны из нескольких источников, каждый из которых находится в статистически управляемом состоянии, но имеет собственное среднее процесса.
Предположим, что совокупность (партия) состоит из большого количества элементов, причем p1 - доля элементов, полученных из первого источника, p2 - из второго и т.д., и pk - из k-го источника. Предположим, что среднее и стандартное отклонение характеристики качества продукции из первого источника  и
и  , из второго источника
, из второго источника  и
и  и т.д. Среднее для всей совокупности в этом случае:
и т.д. Среднее для всей совокупности в этом случае:
 . (6)
. (6)Репрезентативная выборка из n элементов может быть отобрана путем случайного отбора n1 элементов из первого источника, n2 элементов из второго источника, и так далее, где:
n1 + n2 + ... + nk = n,
p1 + p2 + ... + pk = 1.
Если  - среднее характеристики по репрезентативной выборке из n элементов, то это среднее может быть использовано в качестве оценки истинного среднего совокупности
- среднее характеристики по репрезентативной выборке из n элементов, то это среднее может быть использовано в качестве оценки истинного среднего совокупности  . Стандартная ошибка (стандартное отклонение выборочных средних) имеет вид:
. Стандартная ошибка (стандартное отклонение выборочных средних) имеет вид:
На практике часто стандартные отклонения характеристик продукции из различных источников приблизительно совпадают, т.е. 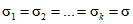 . Тогда (8) принимает вид:
. Тогда (8) принимает вид:
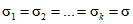 . Тогда (8) принимает вид:
. Тогда (8) принимает вид:Результаты (8) и (9), а также (1) - (3) не зависят от предположений о нормальности распределения и позволяют сделать следующие выводы:
а) если может быть отобрана репрезентативная выборка путем отбора подвыборок, удовлетворяющих условию (7), изменчивость оценки  зависит только от изменчивости наблюдаемой характеристики в пределах каждого источника, а не от различия между средними
зависит только от изменчивости наблюдаемой характеристики в пределах каждого источника, а не от различия между средними  ,
,  , ...,
, ...,  ;
;
б) если значения  ,
,  , ...,
, ...,  неизвестны, их можно оценить в виде выборочных стандартных отклонений по подвыборкам. В частности, если
неизвестны, их можно оценить в виде выборочных стандартных отклонений по подвыборкам. В частности, если  то в качестве оценки
то в качестве оценки  может быть использован размах оценок стандартных отклонений подвыборок;
может быть использован размах оценок стандартных отклонений подвыборок;
 то в качестве оценки
то в качестве оценки в) если нет возможности отобрать репрезентативную выборку, удовлетворяющую условиям (7), то оценка среднего совокупности будет иметь более низкую точность. Всю совокупность элементов в этом случае следует рассматривать как единственную группу, имеющую стандартное отклонение  . Выборочному среднему
. Выборочному среднему  по n наблюдениям выборки, отобранной случайным образом из совокупности, соответствует стандартная ошибка
по n наблюдениям выборки, отобранной случайным образом из совокупности, соответствует стандартная ошибка
В этом случае можно показать, что
Если  , то
, то
 , то
, тоПо величине  больше или равно
больше или равно  . Следовательно, если
. Следовательно, если  ,
,  , ...,
, ...,  не все равны
не все равны  , то среднее процесса меняется от источника к источнику. Оценка общего среднего будет иметь больший разброс и меньшую точность.
, то среднее процесса меняется от источника к источнику. Оценка общего среднего будет иметь больший разброс и меньшую точность.
г) даже при отсутствии попыток определения оценок значений  ,
,  ,...,
,...,  репрезентативную выборку часто используют, чтобы гарантировать, что оценка среднего совокупности максимально достоверна. Другими словами, при отсутствии каких-либо вычислений, отбор репрезентативной выборки фактически спланирован так, что стандартная ошибка соответствует (8) или (9), а не (10), (11) или (12).
репрезентативную выборку часто используют, чтобы гарантировать, что оценка среднего совокупности максимально достоверна. Другими словами, при отсутствии каких-либо вычислений, отбор репрезентативной выборки фактически спланирован так, что стандартная ошибка соответствует (8) или (9), а не (10), (11) или (12).
Изложенное, может быть проиллюстрировано на примере анализа качества кирпичей.
Пример - Свойства кирпича зависят до некоторой степени от его размещения в печи во время обжига. Исследование показало, что в конкретном случае стандартное отклонение прочности всей партии сухих кирпичей, изготовленных в единственной печи, составило:
 .
.Если поперечное сечение печи для обжига разделить на девять секторов, среднее стандартных отклонений прочности кирпича всех секторов печи составляет:
 .
.Из этого следует, что изготовитель, отбирая случайным образом четыре кирпича из каждого сектора, может получить для оценки среднего 36 результатов со стандартной ошибкой
 .
.Примечание - Тот же результат может быть получен следующим образом. Стандартная ошибка для среднего по четырем наблюдениям в каждом секторе печи составляет  . Стандартная ошибка среднего по 36 наблюдениям путем усреднения девяти средних составляет
. Стандартная ошибка среднего по 36 наблюдениям путем усреднения девяти средних составляет  .
.
 . Стандартная ошибка среднего по 36 наблюдениям путем усреднения девяти средних составляет
. Стандартная ошибка среднего по 36 наблюдениям путем усреднения девяти средних составляет  .
.С другой стороны у пользователя нет возможности получить репрезентативную выборку. Чтобы получить оценку среднего с такой же стандартной ошибкой, какая соответствует оценке по 36 кирпичам, пользователь должен проверить n = 110 кирпичей, поскольку:
 .
.Необходимо понимать, что приведенные соображения важны только в случае, когда среднее характеристики используют для управления процессом.
Для некоторых видов продукции на практике не измеряют характеристики каждой единицы продукции в выборке, а записывают единственное значение, которое является общим показателем для всей выборки. Например, определяют общую массу выборки из n элементов, а не результаты взвешивания каждого элемента. Для отбора выборки нештучных материалов, таких как уголь, цемент и нефть, методы отбора выборки могут быть связаны с измерением лишь общей меры. Однако без дополнительной информации невозможно определить достоверность этого показателя. Это вызвано тем, что изменения показателя могут быть следствием изменения среднего, а не ошибками измерений элементов выборки.
Единственный метод, позволяющий оценить процедуры отбора выборки, состоит в независимом повторении процедуры отбора выборки, выполняемой несколько раз на одной и той же партии, что позволяет получить стандартные отклонения этих независимых результатов. Если процесс является устойчивым, то процедура отбора выборки может быть первоначально исследована, а затем периодически проверена. Экономичный метод обеспечения адекватности процесса состоит в независимом отборе повторных выборок. Например, для некоторых видов продукции как описано в Р 50.1.83, на примере отбора выборки железной руды, количество порций руды может быть отобрано равномерно с конвейера и разделено на две части, которые помещают в две отдельные емкости, а затем перемешивают, взвешивают и т.д. Окончательный анализ выполняют независимо два раза.
Предположим, что x1 и x2 - два результата измерений характеристики, используемой для оценки качества продукции. Из статистической теории известно, что стандартное отклонение разности d = x1 - x2 может быть выражено через стандартное отклонение x:
Этот результат справедлив, даже если среднее процесса изменяется от партии к партии при условии, что:
а) изменчивость характеристики вокруг среднего в частях отобранного объема - приблизительно одинакова во всей массе материала;
б) повторные выборки независимы, например, если x1 выше среднего значения, то x2, с равной вероятностью может быть и выше и ниже среднего значения.
Из (13) следует, что если эти условия выполнены,  может быть использовано в качестве оценки
может быть использовано в качестве оценки  , стандартной ошибки оценок x1 и x2. Поскольку известно, что стандартная ошибка среднего x1 и x2 равна
, стандартной ошибки оценок x1 и x2. Поскольку известно, что стандартная ошибка среднего x1 и x2 равна  , то
, то  может быть использовано в качестве стандартной ошибки оценки
может быть использовано в качестве стандартной ошибки оценки  . При контроле процесса последовательные значения d = x1 - x2 могут быть графически показаны на контрольной карте (см. [2]).
. При контроле процесса последовательные значения d = x1 - x2 могут быть графически показаны на контрольной карте (см. [2]).
 . При контроле процесса последовательные значения d = x1 - x2 могут быть графически показаны на контрольной карте (см. [2]).
. При контроле процесса последовательные значения d = x1 - x2 могут быть графически показаны на контрольной карте (см. [2]).9 Пример использования среднего и наименьшего веса в выборке установленного объема стандартных образцов ткани
Ниже приведен пример использования стандартной ошибки среднего, т.е. 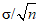 . В примере 2 из Р 50.1.073 приведены веса 128 стандартных образцов ткани, взятых из рулона ткани. Оптовый покупатель обычно сначала изучает качество тканей, а затем определяет свои требования и метод контроля. Например, изготовитель получает штраф, если средний вес образца ткани составляет
. В примере 2 из Р 50.1.073 приведены веса 128 стандартных образцов ткани, взятых из рулона ткани. Оптовый покупатель обычно сначала изучает качество тканей, а затем определяет свои требования и метод контроля. Например, изготовитель получает штраф, если средний вес образца ткани составляет  , а стандартное отклонение
, а стандартное отклонение  . В этом случае изготовитель стремится поднять качество ткани выше этого уровня и получать штрафы реже. Покупатель намерен ввести в контракт положение об отклонении рулона ткани, из которого взята выборка, если образцы не соответствуют этим требованиям. Для этого необходимо определить, сколько образцов (4, 8 или 16) следует отбирать из рулона ткани и каким должен быть минимальный средний вес n образцов, используемый в качестве критерия для отклонения рулона ткани. Проблема состоит в определении этого минимального среднего веса в каждом случае.
. В этом случае изготовитель стремится поднять качество ткани выше этого уровня и получать штрафы реже. Покупатель намерен ввести в контракт положение об отклонении рулона ткани, из которого взята выборка, если образцы не соответствуют этим требованиям. Для этого необходимо определить, сколько образцов (4, 8 или 16) следует отбирать из рулона ткани и каким должен быть минимальный средний вес n образцов, используемый в качестве критерия для отклонения рулона ткани. Проблема состоит в определении этого минимального среднего веса в каждом случае.
 , а стандартное отклонение
, а стандартное отклонение  . В этом случае изготовитель стремится поднять качество ткани выше этого уровня и получать штрафы реже. Покупатель намерен ввести в контракт положение об отклонении рулона ткани, из которого взята выборка, если образцы не соответствуют этим требованиям. Для этого необходимо определить, сколько образцов (4, 8 или 16) следует отбирать из рулона ткани и каким должен быть минимальный средний вес n образцов, используемый в качестве критерия для отклонения рулона ткани. Проблема состоит в определении этого минимального среднего веса в каждом случае.
. В этом случае изготовитель стремится поднять качество ткани выше этого уровня и получать штрафы реже. Покупатель намерен ввести в контракт положение об отклонении рулона ткани, из которого взята выборка, если образцы не соответствуют этим требованиям. Для этого необходимо определить, сколько образцов (4, 8 или 16) следует отбирать из рулона ткани и каким должен быть минимальный средний вес n образцов, используемый в качестве критерия для отклонения рулона ткани. Проблема состоит в определении этого минимального среднего веса в каждом случае.Если производственный процесс находится в состоянии статистической управляемости, выборочные средние по n образцам подчиняются приблизительно нормальному распределению со средним  и стандартным отклонением
и стандартным отклонением  .
.
Таблица 7
Уровень доверия, % | Вероятность ошибки, % | a | Односторонний доверительный интервал u | Двухсторонний доверительный интервал u | |
90 | 10 | 0,10 | 1,2816 | 0,05 | 1,6449 |
95 | 5 | 0,05 | 1,6449 | 0,025 | 1,9600 |
98 | 2 | 0,02 | 2,0537 | 0,01 | 2,3263 |
99 | 1 | 0,01 | 2,3263 | 0,005 | 2,5758 |
Анализ таблицы 7 показывает, что в среднем:
10% выборочных средних (т.е. 1 из 10) будут менее  ;
;
 ;
;5% выборочных средних (т.е. 1 из 20) будут менее  ;
;
 ;
;1% выборочных средних (т.е. 1 из 100) будут менее 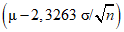 ;
;
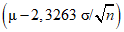 ;
;0,5% выборочных средних (т.е. 1 из 200) будут менее  .
.
 .
.Покупатель решает установить минимум так, чтобы изготовитель, продукция которого соответствует  ,
,  , мог принять только один рулон из 20. В результате установлены следующие приемочные значения:
, мог принять только один рулон из 20. В результате установлены следующие приемочные значения:
 ,
, Для выборок объема 4: 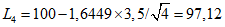 .
.
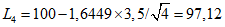 .
.Для выборок объема 8:  .
.
 .
.Для выборок объема 16: 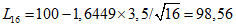 .
.
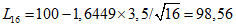 .
.Эти значения приведены в левой стороне таблицы 8 вместе с количеством рулонов, которые были отклонены при проведении контроля.
Если бы было принято решение, что средний вес образца должен быть не менее 103 г со стандартным отклонением не более  , то приемочные значения увеличились бы, они приведены в правой стороне таблицы 8 вместе с количеством принятых рулонов.
, то приемочные значения увеличились бы, они приведены в правой стороне таблицы 8 вместе с количеством принятых рулонов.
 , то приемочные значения увеличились бы, они приведены в правой стороне таблицы 8 вместе с количеством принятых рулонов.
, то приемочные значения увеличились бы, они приведены в правой стороне таблицы 8 вместе с количеством принятых рулонов.Таблица 8
веса образца ткани
Размер выборки |  |  | ||
Приемочное значение L | Количество отклоненных рулонов | Приемочное значение L | Количество принятых рулонов | |
4 | 97,12 | 5 из 32 | 100,12 | 17 из 32 |
8 | 97,96 | 2 из 16 | 100,96 | 3 из 16 |
16 | 98,56 | 1 из 8 | 101,56 | 0 из 8 |
Преимущества изменения приемочного значения для покупателя очевидны. Выборочные среднее и стандартное отклонение для 128 результатов наблюдений равны 99,91 г и 3,49 г соответственно. Изменив правила контроля, покупатель может защитить себя от получения материала низкого качества.
Рассмотрим ситуацию, когда предложенное правило принятия решения применяют к минимальному значению в выборке. Если веса образцов подчиняются нормальному распределению со средним 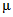 и стандартным отклонением
и стандартным отклонением  , то приемочное значение может быть определено по следующей формуле
, то приемочное значение может быть определено по следующей формуле
 .
.Значение коэффициента k зависит от объема выборки n и вероятности отклонения или принятия партии.
Значения коэффициента k для уровня доверия 95% приведены в таблице 9. В таблице также приведены значения L для  и
и 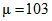 .
.
 и
и 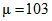 .
.Таблица 9
допустимого веса образца ткани
Объем выборки | k |  | 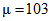 | ||
Приемочное значение L | Количество отклоненных выборок | Приемочное значение L | Количество отклоненных выборок | ||
4 | 2,234 | 92,18 | 2 из 32 | 95,18 | 23 из 32 |
8 | 2,490 | 91,28 | 1 из 16 | 94,28 | 11 из 16 |
16 | 2,726 | 90,46 | 0 из 8 | 93,46 | 6 из 8 |
Сопоставление данных таблиц 8 и 9 является полезным, однако не следует делать общие выводы на основе единственного практического примера.
По выборке могут быть определены оценки для среднего и стандартного отклонения совокупности, из которой отобрана выборка, т.е. оценки 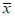 и s для параметров
и s для параметров  и
и  . Если выборка не содержит много элементов, то эти оценки могут быть не очень точны. Погрешность измерений оценивают с помощью стандартных ошибок. Для некоторых практических целей может потребоваться более точный метод определения неопределенности оценки. Этот метод может быть обоснован статистической теорией, но только на основе определенных предположений, которые рассмотрены ниже и должны быть учтены при использовании таблицы 1. Задача и ее решение могут быть представлены в следующей форме.
. Если выборка не содержит много элементов, то эти оценки могут быть не очень точны. Погрешность измерений оценивают с помощью стандартных ошибок. Для некоторых практических целей может потребоваться более точный метод определения неопределенности оценки. Этот метод может быть обоснован статистической теорией, но только на основе определенных предположений, которые рассмотрены ниже и должны быть учтены при использовании таблицы 1. Задача и ее решение могут быть представлены в следующей форме.
На основе выборки из n наблюдений измеримой характеристики определяют выборочные среднее  и стандартное отклонение s, а затем определяют:
и стандартное отклонение s, а затем определяют:
а) границы  и
и  доверительного интервала, который с заданной вероятностью накрывает среднее совокупности
доверительного интервала, который с заданной вероятностью накрывает среднее совокупности  ;
;
б) границы  и
и  доверительного интервала, который с заданной вероятностью накрывает стандартное отклонение совокупности
доверительного интервала, который с заданной вероятностью накрывает стандартное отклонение совокупности  .
.
Доверительные границы вычисляют следующим образом:
для среднего совокупности  ,
,  ; (14)
; (14)
 ,
,  ; (14)
; (14)для стандартного отклонения совокупности  ,
,  . (15)
. (15)
 ,
,  . (15)
. (15)Коэффициенты a, b1 и b2 приведены в таблице 1 для четырех уровней доверия и объемов выборки n от 5 до 30.
Для больших значений n могут быть использованы следующие приближенные формулы

Эти значения соответствуют двусторонним доверительным интервалам для нормированного нормального распределения (см. таблицу 1).
Например, значение u для вероятности ошибки 10% и двустороннего доверительного интервала равно 1,6449. Для выборки объема 30 значения a, b1 и b2 для вероятности ошибки 10%, вычисленные в соответствии с этими формулами, составляют 0,317, 0,825 и 1,282, достаточно близкие к точным значениям 0,311, 0,825 и 1,280. Если, например, мы имеем выборку из 10 элементов и утверждаем, что в выбранной совокупности среднее значение находится в диапазоне от  до
до  , тогда в соответствии с таблицей 1 такой прогноз будет верен с вероятностью 0,90 и ошибочен с вероятностью 0,1. При этом вероятность того, что этот интервал не накроет среднее совокупности
, тогда в соответствии с таблицей 1 такой прогноз будет верен с вероятностью 0,90 и ошибочен с вероятностью 0,1. При этом вероятность того, что этот интервал не накроет среднее совокупности  , равна 0,05.
, равна 0,05.
 до
до  , тогда в соответствии с таблицей 1 такой прогноз будет верен с вероятностью 0,90 и ошибочен с вероятностью 0,1. При этом вероятность того, что этот интервал не накроет среднее совокупности
, тогда в соответствии с таблицей 1 такой прогноз будет верен с вероятностью 0,90 и ошибочен с вероятностью 0,1. При этом вероятность того, что этот интервал не накроет среднее совокупности Таблица 1 разработана для двусторонних доверительных интервалов, но может быть использована для определения границ односторонних интервалов, в этом случае вероятность ошибки необходимо умножить на 2. Например, если необходимо определить верхнюю доверительную границу для уровня доверия 99% и объема выборки 15, то вероятность ошибки (1%) надо удвоить (2%) и определить соответствующее значение b2, которым является 1,734. Таким образом, получен односторонний доверительный интервал для  с уровнем доверия 99%, границу которого определяют по формуле 1,734s.
с уровнем доверия 99%, границу которого определяют по формуле 1,734s.
Приведенные формулы справедливы при следующих предположениях:
1) изменчивость наблюдаемой величины постоянна;
2) наблюдаемая величина подчиняется распределению, близкому к нормальному (см. Р 50.1.82);
3) выборка отобрана случайным образом из совокупности, объем которой существенно больше объема выборки. Это условие обычно удовлетворено, если объем выборки не превосходит 5% объема совокупности. Если из партии, содержащей 20 элементов, отобрана выборка из 10 элементов, то для  и
и  этой партии на основе
этой партии на основе  и s можно определить более узкие интервалы.
и s можно определить более узкие интервалы.
Следующий пример основан на данных взвешивания консервированных томатов, приведенных в таблице 3. Единица измерения - граммы.
Пример - Первая группа из трех выборок дает в общей сложности 12 наблюдений с  и s = 1,681. Если процесс находится в статистически управляемом состоянии, то эти значения можно использовать при определении границ доверительных интервалов для среднего и стандартного отклонения процесса. Для уровня доверия 98% (2% ошибки) в соответствии с таблицей 1: a = 0,785, b1 = 0,667 и b2 = 1,899, что дает следующие значения доверительных границ:
и s = 1,681. Если процесс находится в статистически управляемом состоянии, то эти значения можно использовать при определении границ доверительных интервалов для среднего и стандартного отклонения процесса. Для уровня доверия 98% (2% ошибки) в соответствии с таблицей 1: a = 0,785, b1 = 0,667 и b2 = 1,899, что дает следующие значения доверительных границ:
 и s = 1,681. Если процесс находится в статистически управляемом состоянии, то эти значения можно использовать при определении границ доверительных интервалов для среднего и стандартного отклонения процесса. Для уровня доверия 98% (2% ошибки) в соответствии с таблицей 1: a = 0,785, b1 = 0,667 и b2 = 1,899, что дает следующие значения доверительных границ:
и s = 1,681. Если процесс находится в статистически управляемом состоянии, то эти значения можно использовать при определении границ доверительных интервалов для среднего и стандартного отклонения процесса. Для уровня доверия 98% (2% ошибки) в соответствии с таблицей 1: a = 0,785, b1 = 0,667 и b2 = 1,899, что дает следующие значения доверительных границ:для среднего 404,16 +/- 0,785 x 1,681, т.е. от 402,8 до 405,5 г;
для стандартного отклонения процесса 0,667 x 1,681 и 1,899 x 1,681, т.е. от 1,12 до 3,19 г.
Интервал неопределенности является достаточно большим. Увеличение количества наблюдений в выборке позволяет его сузить. Если первый доверительный интервал построен по шести выборкам (12 наблюдений), то удвоение количества наблюдений (24) позволяет в соответствии с таблицей 3 определить, что  и s = 1,598.
и s = 1,598.
 и s = 1,598.
и s = 1,598.Для уровня доверия 98% в соответствии с таблицей 1: a = 0,511, b1 = 0,743 и b2 = 1,502. Таким образом, границы доверительных интервалов имеют следующий вид:
для среднего: 404,22 +/- 0,511 x 1,598, т.е. от 403,4 до 405,0 г;
для стандартного отклонения: 0,743 x 1,598 и 1,502 x 1,598, т.е. от 1,19 до 2,40 г.
Дополнительная информация позволила сузить доверительные интервалы. В обоих случаях они накрывают значения  и
и  , вычисленные по первым 160 значениям.
, вычисленные по первым 160 значениям.
 и
и  , вычисленные по первым 160 значениям.
, вычисленные по первым 160 значениям.11.1 Терминология
В построении статистических критериев важно точно определить проверяемую гипотезу. Предположения об отсутствии различий или равенстве параметров совокупности обычно принимают в качестве гипотезы и обозначают H0. Гипотезу, которой эту гипотезу противопоставляют, называют альтернативной гипотезой и обозначают H1. Проверку гипотез выполняют на основе статистики, которую вычисляют поданным выборки. Область изменений используемой статистики, соответствующую отклонению нулевой гипотезы, называют критической областью. Вероятность того, что статистика попадает в критическую область в условиях, когда справедлива нулевая гипотеза, (т.е. вероятность ошибочного решения об отклонении нулевой гипотезы в пользу альтернативной гипотезы) называют ошибкой первого рода или уровнем значимости критерия и обозначают  . Вероятность того, что статистика попадает в критическую область в условиях, когда справедлива альтернативная гипотеза, (т.е. вероятность корректного решения об отклонении нулевой гипотезы в пользу альтернативной гипотезы) называют мощностью критерия и обозначают
. Вероятность того, что статистика попадает в критическую область в условиях, когда справедлива альтернативная гипотеза, (т.е. вероятность корректного решения об отклонении нулевой гипотезы в пользу альтернативной гипотезы) называют мощностью критерия и обозначают  . Хорошему критерию соответствует высокая мощность и низкий уровень значимости.
. Хорошему критерию соответствует высокая мощность и низкий уровень значимости.
Вероятность отклонения альтернативной гипотезы в условиях, когда справедлива нулевая гипотеза, называют ошибкой второго рода. Из этого следует, что вероятность  представляет собой ошибку второго рода.
представляет собой ошибку второго рода.
11.2 Гипотеза о равенстве среднего заданному значению
Гипотезу иллюстрирует следующий пример. Предположим, что стандартное отклонение  нормального распределения известно, среднее - неизвестно. Необходимо проверить гипотезу:
нормального распределения известно, среднее - неизвестно. Необходимо проверить гипотезу:
H0: среднее значение нормальной совокупности равно 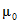 ;
;
против альтернативной гипотезы:
H1: среднее значение нормальной совокупности больше  .
.
Уровень значимости критерия должен составлять 5%. Из совокупности отобрана случайная выборка объема n с выборочным средним  .
.
Интуитивно ясно, что критическая область должна быть расположена справа от  , где c - некоторая константа больше нуля. Для уровня значимости 5% необходимо, чтобы значение
, где c - некоторая константа больше нуля. Для уровня значимости 5% необходимо, чтобы значение  было верхней границей одностороннего доверительного интервала для
было верхней границей одностороннего доверительного интервала для  с доверительной вероятностью 0,95. Соответствующий квантиль нормированного нормального распределения для одностороннего доверительного интервала с доверительной вероятностью 0,95 в соответствии с таблицей 1 равен 1,6449. Поскольку
с доверительной вероятностью 0,95. Соответствующий квантиль нормированного нормального распределения для одностороннего доверительного интервала с доверительной вероятностью 0,95 в соответствии с таблицей 1 равен 1,6449. Поскольку  подчиняется нормальному распределению со средним
подчиняется нормальному распределению со средним  и стандартным отклонением
и стандартным отклонением  , то из этого следует, что
, то из этого следует, что  .
.
 , где c - некоторая константа больше нуля. Для уровня значимости 5% необходимо, чтобы значение
, где c - некоторая константа больше нуля. Для уровня значимости 5% необходимо, чтобы значение  было верхней границей одностороннего доверительного интервала для
было верхней границей одностороннего доверительного интервала для  .
.На рисунке 1 показана критическая область. Область A соответствует ошибке первого рода, в данном случае она равна 0,05. Область (1 - B) соответствует мощности критерия в точке  . Для вычисления мощности критерия вычисляют нормированную разность
. Для вычисления мощности критерия вычисляют нормированную разность  и
и  , т.е.
, т.е.  . Мощности критерия соответствует области справа от Z под плотностью нормированного нормального распределения, которая может быть найдена с помощью таблицы нормированного нормального распределения.
. Мощности критерия соответствует области справа от Z под плотностью нормированного нормального распределения, которая может быть найдена с помощью таблицы нормированного нормального распределения.
 и
и  . Мощности критерия соответствует области справа от Z под плотностью нормированного нормального распределения, которая может быть найдена с помощью таблицы нормированного нормального распределения.
. Мощности критерия соответствует области справа от Z под плотностью нормированного нормального распределения, которая может быть найдена с помощью таблицы нормированного нормального распределения.
В более общем случае среднее и стандартное отклонение совокупности неизвестны. В этом случае множитель  в приведенном выше примере, заменяют на коэффициент
в приведенном выше примере, заменяют на коэффициент  из таблицы 1, определяемый в соответствии с объемом выборки и вероятностью ошибки 0,1. Таким образом, для объема выборки 9 множитель
из таблицы 1, определяемый в соответствии с объемом выборки и вероятностью ошибки 0,1. Таким образом, для объема выборки 9 множитель  можно заменить на 0,620. Увеличение значения множителя отражает увеличение неопределенности, вызванное незнанием значения
можно заменить на 0,620. Увеличение значения множителя отражает увеличение неопределенности, вызванное незнанием значения  .
.
 в приведенном выше примере, заменяют на коэффициент
в приведенном выше примере, заменяют на коэффициент  можно заменить на 0,620. Увеличение значения множителя отражает увеличение неопределенности, вызванное незнанием значения
можно заменить на 0,620. Увеличение значения множителя отражает увеличение неопределенности, вызванное незнанием значения 11.3 Гипотеза о разности двух средних совокупности
Несколько замечаний о понятии числа степеней свободы. Для единственной выборки объема n, не все отклонения от выборочного среднего независимы, поскольку их сумма равна нулю. Если известно (n - 1) отклонение, то n-ое отклонение может быть вычислено. В этом случае число степеней свободы  . Если выборочные значения рассматривать как координаты точки в n-мерном пространстве, то все отклонения от
. Если выборочные значения рассматривать как координаты точки в n-мерном пространстве, то все отклонения от  будут лежать в (n - 1)-мерной плоскости.
будут лежать в (n - 1)-мерной плоскости.
 . Если выборочные значения рассматривать как координаты точки в n-мерном пространстве, то все отклонения от
. Если выборочные значения рассматривать как координаты точки в n-мерном пространстве, то все отклонения от Пример - Самым простым случаем является случай n = 2. Если 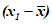 отражать на горизонтальной оси, а
отражать на горизонтальной оси, а  - на вертикальной оси, то любая пара выборочных значений (x1, x2) даст точку, лежащую на прямой линии с угловым коэффициентом минус 1, проходящей через начало координат.
- на вертикальной оси, то любая пара выборочных значений (x1, x2) даст точку, лежащую на прямой линии с угловым коэффициентом минус 1, проходящей через начало координат.
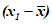 отражать на горизонтальной оси, а
отражать на горизонтальной оси, а  - на вертикальной оси, то любая пара выборочных значений (x1, x2) даст точку, лежащую на прямой линии с угловым коэффициентом минус 1, проходящей через начало координат.
- на вертикальной оси, то любая пара выборочных значений (x1, x2) даст точку, лежащую на прямой линии с угловым коэффициентом минус 1, проходящей через начало координат.Число степеней свободы является параметром многих важных статистических распределений и его часто используют при составлении таблиц распределений. Для рассмотренного случая единственной выборки это не имеет особого значения. Однако использование в таблице распределения числа степеней свободы может облегчить использование таблиц в других случаях, например:
а) в случае единственной выборки, когда количество k независимых ограничений больше 1. В таком случае  ;
;
 ;
;б) в случае k выборок объемов n1, n2, ..., nk с различными средними и равными стандартными отклонениями, которые необходимо объединить для определения оценки стандартного отклонения. В этом случае  , где n = n1 + n2 + ... + nk;
, где n = n1 + n2 + ... + nk;
 , где n = n1 + n2 + ... + nk;
, где n = n1 + n2 + ... + nk;В такой задаче, когда  неизвестно, используют статистику, таблица значений которой приведена в приложении А.
неизвестно, используют статистику, таблица значений которой приведена в приложении А.
Рассмотрим случай б) с k = 2. Это задача сравнения средних двух совокупностей, когда стандартные отклонения совокупностей неизвестны. Предположим, что гипотезы имеют следующий вид:
 против
против 
Данные представляют собой случайную выборку объема n1 из первой совокупности и независимую случайную выборку объема n2 из второй совокупности. Выборочные средние  и
и  . Выборочные дисперсии (т.е. квадраты выборочных стандартных отклонений)
. Выборочные дисперсии (т.е. квадраты выборочных стандартных отклонений)  и
и  :
:
 и
и  .
.Рассмотрим статистическую величину  . Предполагается, что объемы выборок малы по сравнению с объемами соответствующих совокупностей. Очевидно, что
. Предполагается, что объемы выборок малы по сравнению с объемами соответствующих совокупностей. Очевидно, что
 . Предполагается, что объемы выборок малы по сравнению с объемами соответствующих совокупностей. Очевидно, что
. Предполагается, что объемы выборок малы по сравнению с объемами соответствующих совокупностей. Очевидно, что ,
, ,
,где  и
и  - средние совокупностей;
- средние совокупностей;
Рассматриваемые гипотезы можно записать в виде:  и
и  . Гипотеза является двусторонней, поэтому критическая область должна включать положительные и отрицательные значения d.
. Гипотеза является двусторонней, поэтому критическая область должна включать положительные и отрицательные значения d.
 и
и  . Гипотеза является двусторонней, поэтому критическая область должна включать положительные и отрицательные значения d.
. Гипотеза является двусторонней, поэтому критическая область должна включать положительные и отрицательные значения d.Если дисперсии совокупностей совпадают, т.е.  , то
, то
 , то
, тоВ качестве оценки сможет быть использована следующая оценка:
 ,
, .
.Верхний квантиль  , соответствующий двустороннему критерию с необходимым уровнем значимости
, соответствующий двустороннему критерию с необходимым уровнем значимости  , может быть определен по таблице А.1 приложения А. Нулевую гипотезу отклоняют в пользу альтернативной гипотезы, если доверительный интервал для
, может быть определен по таблице А.1 приложения А. Нулевую гипотезу отклоняют в пользу альтернативной гипотезы, если доверительный интервал для  с доверительными границами
с доверительными границами  не включает нуль.
не включает нуль.
 , соответствующий двустороннему критерию с необходимым уровнем значимости
, соответствующий двустороннему критерию с необходимым уровнем значимости  не включает нуль.
не включает нуль.11.4 Мощность критерия
Мощность критерия необходимо оценивать до отбора данных. Часто мощность не анализируют при планировании испытаний, и результаты могут оказаться неокончательными. Если предполагаемая мощность ниже необходимой, для обнаружения различий средних совокупностей следует увеличить один или оба объема выборки. Если это невозможно, может быть принято решение не тратить ресурсы на проведение испытаний или экспериментов, поскольку результат вряд ли даст какую-либо новую информацию. Существует также возможность того, что мощность будет выше, чем необходимо, в этом случае объем испытаний может быть уменьшен.
Во многих случаях определение мощности критерия вызывает существенные трудности, поэтому эти вычисления не всегда выполняют. Однако современные компьютеры позволяют вычислить мощность критерия с применением моделирования.
11.5 Сравнение двух средних в случае парных наблюдений
Увеличение объемов выборки не является единственным способом повышения мощности критерия. Другим способом является устранение или уменьшение влияния различий, вызванных особенностями объектов, на которых выполнялись измерения, или влияния обработки. Например, необходимо сравнить воздействие на урожай зерновых двух видов удобрений A и B. Один из подходов состоит в применении удобрения A к одной случайной выборке из n участков, и удобрения B ко второй случайной выборке из n участков. Обе выборки из n участков отбирают из всего достаточно однородного поля, а затем сравнивают урожаи. Но все отобранные участки неизбежно будут отличаться по дренажу, уровню питательных веществ и т.п. Однако, даже если выборки были аналогичны, изменчивость от участка к участку может быть достаточной для снижения мощности критерия до недопустимого уровня, различия между удобрениями с большой вероятностью могут быть не обнаружены.
Простой способ уменьшить влияние особенностей участка состоит в том, чтобы отбирать смежные пары участков, применяя удобрение A к одному из каждой случайно выбранной пары участков, а удобрение B к другому участку. Предположим, что урожай для i-ой пары участков составил xi для удобрения A и yi - для удобрения B. Затем определяют разности di = (xi - yi) для всех пар, предполагая, что смежные участки почти идентичны по свойствам. Это относится к методу парных сравнений. Если x и y независимы и имеют нормальные распределения, разности d будут подчиняться нормальному распределению с выборочным средним совокупности  и стандартным отклонением совокупности
и стандартным отклонением совокупности  . Выборочные среднее и стандартное отклонение разностей d являются оценками этих параметров.
. Выборочные среднее и стандартное отклонение разностей d являются оценками этих параметров.
Точность критерия не зависит от нулевой и альтернативной гипотез и уровня значимости. Если эти удобрения являются новыми и не апробированными, может возникнуть необходимость определить, какое из них эффективнее. Это может быть сделано с использованием двусторонней гипотезы  против альтернативы
против альтернативы  , что эквивалентно вычислению двустороннего доверительного интервала для d и определения накрывает ли он нулевое значение. С другой стороны удобрение B может быть стандартом, по отношению к которому проводят проверку более дорогостоящего нового удобрения A. Возможно новое удобрение должно повысить урожай больше чем на c, чтобы оправдать затраты на его приобретение. Это можно установить с помощью одностороннего критерия
, что эквивалентно вычислению двустороннего доверительного интервала для d и определения накрывает ли он нулевое значение. С другой стороны удобрение B может быть стандартом, по отношению к которому проводят проверку более дорогостоящего нового удобрения A. Возможно новое удобрение должно повысить урожай больше чем на c, чтобы оправдать затраты на его приобретение. Это можно установить с помощью одностороннего критерия  против альтернативы
против альтернативы  . Удобрение B может быть проверено на отсутствие улучшений. В этом случае следует применять односторонний критерий
. Удобрение B может быть проверено на отсутствие улучшений. В этом случае следует применять односторонний критерий  против альтернативы
против альтернативы 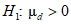 . Во всех этих случаях может быть использована таблица 1.
. Во всех этих случаях может быть использована таблица 1.
 против альтернативы
против альтернативы  , что эквивалентно вычислению двустороннего доверительного интервала для d и определения накрывает ли он нулевое значение. С другой стороны удобрение B может быть стандартом, по отношению к которому проводят проверку более дорогостоящего нового удобрения A. Возможно новое удобрение должно повысить урожай больше чем на c, чтобы оправдать затраты на его приобретение. Это можно установить с помощью одностороннего критерия
, что эквивалентно вычислению двустороннего доверительного интервала для d и определения накрывает ли он нулевое значение. С другой стороны удобрение B может быть стандартом, по отношению к которому проводят проверку более дорогостоящего нового удобрения A. Возможно новое удобрение должно повысить урожай больше чем на c, чтобы оправдать затраты на его приобретение. Это можно установить с помощью одностороннего критерия  против альтернативы
против альтернативы  . Удобрение B может быть проверено на отсутствие улучшений. В этом случае следует применять односторонний критерий
. Удобрение B может быть проверено на отсутствие улучшений. В этом случае следует применять односторонний критерий  против альтернативы
против альтернативы 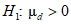 . Во всех этих случаях может быть использована таблица 1.
. Во всех этих случаях может быть использована таблица 1.Метод парных сравнений может быть еще более эффективным, если один и тот же элемент используют для сравнения двух методов испытаний или двух измерительных приборов, или двух лабораторий.
Вся информация о предыдущих испытаниях и оценках  должна быть использована для определения объема выборки n, обеспечивающего достаточную мощность критерия.
должна быть использована для определения объема выборки n, обеспечивающего достаточную мощность критерия.
11.6 Сравнение стандартных отклонений
Проблема определения границ доверительного интервала для стандартного отклонения совокупности  рассмотрена в 10. Проверка гипотезы о равенстве
рассмотрена в 10. Проверка гипотезы о равенстве  заданному значению
заданному значению 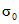 может быть выполнена на основе построения доверительного интервала
может быть выполнена на основе построения доверительного интервала  и определения его положения относительно
и определения его положения относительно  . Рассматриваемая задача представляет собой проверку гипотез о совпадении стандартных отклонений двух совокупностей
. Рассматриваемая задача представляет собой проверку гипотез о совпадении стандартных отклонений двух совокупностей  и
и  . Для решения задачи рассматривают
. Для решения задачи рассматривают  и гипотезу
и гипотезу  против
против 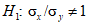 .
.
 и определения его положения относительно
и определения его положения относительно  против
против 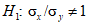 .
.При наличии выборки объема n1 из первой совокупности и выборки объема n2 из второй совокупности определяют выборочные стандартные отклонения sx и sy. Двусторонний доверительный интервал для  , соответствующий доверительной вероятности
, соответствующий доверительной вероятности  , имеет вид:
, имеет вид:
 ,
,где  и
и 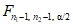 - квантили F-распределения уровней
- квантили F-распределения уровней  и
и  с (n1 - 1) и (n2 - 1) степенями свободы соответственно.
с (n1 - 1) и (n2 - 1) степенями свободы соответственно.
 и
и 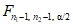 - квантили F-распределения уровней
- квантили F-распределения уровней  и
и Пусть выборка объема 10 из первой совокупности дает sx = 10,5, а выборка объема 16 из второй совокупности дает sy = 6,8, sx/sy = 10,5/6,8 = 1,544. Уровень значимости критерия равен 0,05. В соответствии с таблицами F-распределения F9; 15; 0,975 = 3,12 и F9; 15; 0,025 = 0,265. Доверительный интервал для 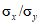 имеет вид
имеет вид  , sx/sy = 10,5/6,8 = 1,544, т.е. (0,874, 3,00).
, sx/sy = 10,5/6,8 = 1,544, т.е. (0,874, 3,00).
 , sx/sy = 10,5/6,8 = 1,544, т.е. (0,874, 3,00).
, sx/sy = 10,5/6,8 = 1,544, т.е. (0,874, 3,00).Так как этот интервал включает значение 1, с вероятностью 0,95 можно утверждать об отсутствии различий между  и
и  .
.
В случае односторонних критериев вычисляют один из односторонних доверительных интервалов:
 или
или 
и определяют, накрывает ли он значение 1.
Для наилучшего представления изменчивости среднего и стандартного отклонения часто используют графическое представление данных в виде точки  для каждой выборки на графике с осями
для каждой выборки на графике с осями 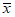 и s. Такое представление данных примера о консервированных томатах показано на рисунке 2, где каждая из 40 точек представляет выборочные среднее и стандартное отклонение по четырем результатам проверки веса содержимого банок. В центре графика в виде треугольника показана точка
и s. Такое представление данных примера о консервированных томатах показано на рисунке 2, где каждая из 40 точек представляет выборочные среднее и стандартное отклонение по четырем результатам проверки веса содержимого банок. В центре графика в виде треугольника показана точка  , представляющая выборочные среднее и стандартное отклонение по всем отобранным элементам с использованием всех 160 исходных данных (
, представляющая выборочные среднее и стандартное отклонение по всем отобранным элементам с использованием всех 160 исходных данных ( ,
,  ).
).
 ,
,  ).
).
консервированных томатов
Точки  окружают точку
окружают точку  . Если производство является стабильным, статистическая теория позволяет спрогнозировать плотность распределения этих точек на различных расстояниях и в различных направлениях от
. Если производство является стабильным, статистическая теория позволяет спрогнозировать плотность распределения этих точек на различных расстояниях и в различных направлениях от  , т.е. оценить вероятность того, что точка
, т.е. оценить вероятность того, что точка  попадет в заданную область.
попадет в заданную область.
Для этого предназначены стандартизованные  карты Канагавы, Аризона и Охота [1]. Эти карты основаны на теории информации и могут быть полезны для определения типа отклонения при рассмотрении
карты Канагавы, Аризона и Охота [1]. Эти карты основаны на теории информации и могут быть полезны для определения типа отклонения при рассмотрении  и s одновременно. Стандартизованная
и s одновременно. Стандартизованная  карта для объема выборки n = 4 с границами, за пределы которых точка
карта для объема выборки n = 4 с границами, за пределы которых точка  может попасть с вероятностью 27/10000, показана на рисунке 3 на примере данных взвешивания консервированных томатов. На карте показано 40 точек
может попасть с вероятностью 27/10000, показана на рисунке 3 на примере данных взвешивания консервированных томатов. На карте показано 40 точек  и целевые значения
и целевые значения  и
и  .
.
 карты Канагавы, Аризона и Охота [1]. Эти карты основаны на теории информации и могут быть полезны для определения типа отклонения при рассмотрении
карты Канагавы, Аризона и Охота [1]. Эти карты основаны на теории информации и могут быть полезны для определения типа отклонения при рассмотрении  карта для объема выборки n = 4 с границами, за пределы которых точка
карта для объема выборки n = 4 с границами, за пределы которых точка  и целевые значения
и целевые значения  и
и  .
.
и стандартного отклонения
Области расположения точек на карте обозначены следующим образом:
A - процесс стабилен;
B - процесс нестабилен вследствие изменения среднего процесса;
C - процесс нестабилен вследствие изменения стандартного отклонения процесса;
D - процесс нестабилен вследствие небольших изменений среднего и стандартного отклонения процесса;
E - процесс нестабилен и по среднему и по стандартному отклонению процесса.
Все 40 точек находятся в области A. Это указывает на то, что вес содержимого банок консервированных томатов соответствует указанной массе нетто и процесс устойчив.
Карта составлена так, чтобы она могла быть использована для любых значений  и
и  . Карта должна быть изменена при изменении объема выборки. Увеличение любого из этих значений приводит к уменьшению границ и приближению их к точке с координатами
. Карта должна быть изменена при изменении объема выборки. Увеличение любого из этих значений приводит к уменьшению границ и приближению их к точке с координатами  ,
,  .
.
 ,
,  .
.Особенно интересна форма области, в которой расположена большая часть точек с координатами  , если процесс находится в статистически управляемом состоянии. При этом чем ближе s к целевому значению
, если процесс находится в статистически управляемом состоянии. При этом чем ближе s к целевому значению  , тем шире область по
, тем шире область по  . Аналогично, чем ближе
. Аналогично, чем ближе  к целевому значению
к целевому значению  , тем большие изменения допустимы для s. Таким образом, существует баланс между отклонениями
, тем большие изменения допустимы для s. Таким образом, существует баланс между отклонениями  от
от 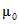 и
и  от
от  . Традиционные контрольные карты в отличие от данных предназначены для независимого контроля
. Традиционные контрольные карты в отличие от данных предназначены для независимого контроля  и s. Таким образом, данный подход является логичным, поскольку для выборок из нормального распределения
и s. Таким образом, данный подход является логичным, поскольку для выборок из нормального распределения  и s должны быть независимыми. Но в нем применена не прямоугольная область отклонений оценок от целевых значений
и s должны быть независимыми. Но в нем применена не прямоугольная область отклонений оценок от целевых значений  и
и  .
.
 , если процесс находится в статистически управляемом состоянии. При этом чем ближе s к целевому значению
, если процесс находится в статистически управляемом состоянии. При этом чем ближе s к целевому значению 13.1 Неколичественные характеристики качества
Многие неколичественные характеристики качества изменяются в соответствии с дискретной шкалой. Например, оценка качества услуг по уборке офисных помещений. Комнаты, выбранные случайным образом, осматривают после уборки, проверяя, что мусорные ведра освобождены, шкафы для хранения документов и столы протерты, ковры вычищены с применением пылесоса. Контролер принимает решение, что уборка помещения соответствует установленным требованиям, если по каждому из перечисленных показателей она признана удовлетворительной.
Характеристика, реализация которой представляет собой одно из нескольких состояний (функционирование-отказ, принадлежность к одной из категорий), является альтернативным признаком.
Для критических характеристик, связанных, например, с безопасностью персонала, все усилия должны быть направлены на то, чтобы доля несоответствующих единиц (продукции) в совокупности была близка к нулю, насколько это возможно. В этом случае обычно используют сплошной контроль с заменой несоответствующих единиц продукции соответствующими, тогда доля несоответствующих единиц в совокупности будет равна нулю.
Для некритических характеристик может быть необходимо определить оценку доли несоответствующих единиц (продукции), границы доверительного интервала для этой доли, проверить гипотезу о соответствии ее заданному значению или сравнить две или более оценок.
13.2 Определение оценки пропорции
Если в примере об уборке помещений выполняют уборку N комнат, то объем совокупности составляет N. В определенный день R комнат не были убраны. Пропорция (доля) совокупности несоответствующих объектов составляет:
P = R/N.
Значение R неизвестно. Случайным образом из совокупности отбирают n комнат и проверяют их уборку. При этом выявлено r комнат с неудовлетворительно выполненной уборкой. Необходимо определить оценку P.
Предположим, что состояние комнаты характеризуется переменной X, принимающей значение 0, если комната убрана удовлетворительно и 1 в противном случае. Совокупность значений X в этом случае состоит из R единиц и (N - R) нулей, а выборка состоит из r единиц и (n - r) нулей. По результатам проверки
 ,
,где xi - значение переменной X для i-ой комнаты.
 . (16)
. (16) .
. . (17)
. (17)Выборочное среднее является несмещенной оценкой среднего совокупности. Если n = 50, а r = 2, то 4% комнат в совокупности являются неудовлетворительно убранными.
13.3 Доверительный интервал для пропорции
На основе выборочных данных (объема выборки n и количества несоответствующих объектов в выборке r) определяют интервал с границами P1 и P2, который с доверительной вероятностью  накрывает значение P. При этом с вероятностью
накрывает значение P. При этом с вероятностью  интервал (P1, P2) не накрывает истинное значение. Предположим вероятности того, что P < P1 и P > P2 равны, т.е.
интервал (P1, P2) не накрывает истинное значение. Предположим вероятности того, что P < P1 и P > P2 равны, т.е.
- если P < P1 то с вероятностью не более  в выборке объема n может быть обнаружено r или более несоответствующих элементов;
в выборке объема n может быть обнаружено r или более несоответствующих элементов;
- если P > P2, то с вероятностью не более 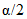 в выборке объема n может быть обнаружено r или менее несоответствующих элементов.
в выборке объема n может быть обнаружено r или менее несоответствующих элементов.
Эти вероятности могут быть вычислены с помощью таблиц биномиального распределения.
Поскольку x принимает значения 0 и 1, то
 .
.Выборочное стандартное отклонение x имеет вид:

Таким образом:

Границы доверительного интервала для P могут быть получены на основе предположения о том, что распределение p близко к нормальному. Двусторонний доверительный интервал для P в этом случае имеет вид (P1, P2)
 ,
,где u - квантиль нормированного нормального распределения уровня  . Если необходим односторонний доверительный интервал, то для определения P1 или P2 необходимо
. Если необходим односторонний доверительный интервал, то для определения P1 или P2 необходимо  заменить на
заменить на  . Нормальное приближение не следует применять, если значение p близко к 0,5 или объем выборки слишком большой.
. Нормальное приближение не следует применять, если значение p близко к 0,5 или объем выборки слишком большой.
 . Если необходим односторонний доверительный интервал, то для определения P1 или P2 необходимо
. Если необходим односторонний доверительный интервал, то для определения P1 или P2 необходимо 13.4 Сравнение пропорции с заданным значением
Задача сводится к определению по выборочным данным соответствия пропорции заданному значению. Например, в выборке объема 30 обнаружено три несоответствующих единицы продукции. С уровнем доверия 0,95 необходимо проверить, что процент несоответствующих единиц продукции в совокупности более 3%. Существует два способа решения этой задачи. Первый способ состоит в определении по выборочным данным нижней границы одностороннего доверительного интервала, соответствующего доверительной вероятности 0,95, для доли несоответствующей продукции в совокупности. Если эта граница будет менее 0,03, то принимают решение о том, что доля несоответствующей продукции в совокупности составляет не менее 3%. Второй способ является своего рода инверсией первого. Необходимо определить вероятность обнаружения трех или более несоответствующих единиц продукции в выборке объема 30, если их доля в совокупности составляет 3%. Если эта вероятность менее 0,05, принимают решение о том, что доля несоответствующих единиц продукции в совокупности составляет не менее 3%. Оба метода эквивалентны.
Для решения задачи первым способом в соответствии с ГОСТ Р ИСО 11453 определяют нижнюю границу одностороннего доверительного интервала, соответствующего доверительной вероятности 0,95, для доли несоответствующих единиц продукции (0,027). Поскольку 0,027 < 0,03 следует принять решение о том, что доля несоответствующих единиц продукции в совокупности составляет не менее 3%. И наоборот вероятность того, что в случайной выборке из 30 элементов будет обнаружено три или более несоответствующих единиц продукции, если их доля в совокупности составляет 3%, равна 0,06. Поскольку это значение больше 0,05, то данные выборки не обеспечивают достаточных доказательств для того, чтобы с уровнем доверия 0,95 утверждать, что доля несоответствующих единиц продукции в совокупности превышает 3%. Фактически можно делать такие выводы лишь с вероятностью 0,94.
Данный пример показывает, насколько большое значение имеет объем выборки в подобных задачах.
13.5 Сравнение двух пропорций
Задача состоит в принятии решения о совпадении (или различии) двух долей в двух совокупностях на основе выборочных данных (см. также ГОСТ Р ИСО 11453). Предположим, что из одной совокупности отобрана случайная выборка объема n1, а из другой совокупности случайная выборка объема n2. В первой выборке обнаружено r1 несоответствующих единиц продукции, а во второй - r2. Таким образом, p1 = r1/n1 и p2 = r2/n2. Если P1 и P2 - неизвестные доли совокупностей, то по выборочным данным можно найти ответы на следующие вопросы:
Если p1 < p2 в случае б) или p1 > p2 в случае в), то на вопросы б) и в) следует ответить, что это маловероятно (без выполнения статистических вычислений). То же можно утверждать, если p1 ~= p2 в случае а). Во всех других ситуациях ответ может быть получен на основе таблиц гипергеометрического распределения. Специальные таблицы разработаны для определения различий между p1 и p2, если n1 и n2 малы. Для больших значений n1 и n2 применяют приближенные методы.
13.6 Определение необходимого объема выборки
Для проверки гипотез о пропорциях важно учитывать мощность критерия. Если объем выборки уменьшен под влиянием технических или экономических причин, следует учитывать влияние сокращения объема выборки на мощность критерия. Совместное рассмотрение необходимых мощности и уровня значимости критерия позволяет определить необходимый объем выборки по соответствующим таблицам или формулам.
Например, необходимо проверить гипотезу H0: P1 = P2 против альтернативы H1: P1 > P2 с равными объемами выборок из обеих совокупностей. Объем выборки должен обеспечить вероятность  принятия гипотезы, когда она верна, и мощность критерия
принятия гипотезы, когда она верна, и мощность критерия  , т.е. вероятность принятия альтернативы, когда P1 > P2. Приближенный объем выборки может быть найден, как решение следующего уравнения
, т.е. вероятность принятия альтернативы, когда P1 > P2. Приближенный объем выборки может быть найден, как решение следующего уравнения
где  и
и  - квантили нормированного нормального распределения уровней
- квантили нормированного нормального распределения уровней  и
и 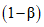 соответственно. Пусть P1 = 0,8, P2 = 0,6,
соответственно. Пусть P1 = 0,8, P2 = 0,6,  ,
,  . Подставляя в (18) значения квантилей получим:
. Подставляя в (18) значения квантилей получим:
 ,
,  . Подставляя в (18) значения квантилей получим:
. Подставляя в (18) значения квантилей получим:Уравнение (19) решают итеративным методом. Сначала задают значения n, а затем вычисляют правую часть, новое значение n и повторяют расчеты до тех пор, пока значения n на предыдущем и последующем шаге не будут близки друг к другу.
Предположим, что начальное значение n = 50. Последовательные итерации в соответствии с (19) дают значения n: 109, 96, 98, 98. Дальнейшие расчеты не нужны. Таким образом, n = 98 соответствует установленным требованиям и является необходимым объемом случайной выборки из каждой совокупности.
Данный приближенный метод обеспечивает быстрое получение решения с хорошей точностью. Формулу (18) можно также использовать для двусторонних гипотез. Для этого  необходимо заменить на
необходимо заменить на  .
.
14.1 Односторонний предикционный интервал для следующих m наблюдений
Иногда необходимо определить такое значение TU на основе данных случайной выборки объема n из нормальной совокупности, для которого с заданным уровнем доверия ни одно из следующих m случайных наблюдений (из той же нормальной совокупности) не превышает TU. (TU - верхняя граница предикционного интервала в соответствии с ГОСТ Р ИСО 16269-8).
Это значение определяют по формуле
 ,
,где  и s - выборочные среднее и стандартное отклонения;
и s - выборочные среднее и стандартное отклонения;
q - коэффициент, который зависит от объема выборки n, количества m следующих наблюдений и уровня доверия.
В таблице 10 приведены значения этого коэффициента для диапазона значений n и m от 5 до 200 и уровня доверия 0,95.
Таблица 10
предикционных интервалов с уровнем доверия 0,95
Объем выборки n | Количество будущих наблюдений m | |||||||
5 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 | |
5 | 3,7879 | 4,4178 | 5,0288 | 5,7938 | 6,3375 | 6,8525 | 7,4934 | 7,9515 |
10 | 2,8868 | 3,2841 | 3,6699 | 4,1593 | 4,5125 | 4,8510 | 5,2769 | 5,5838 |
20 | 2,5744 | 2,8907 | 3,1940 | 3,5777 | 3,8557 | 4,1237 | 4,4632 | 4,7097 |
50 | 2,4153 | 2,6898 | 2,9488 | 3,2720 | 3,5044 | 3,7278 | 4,0112 | 4,2175 |
100 | 2,3661 | 2,6277 | 2,8727 | 3,1759 | 3,3925 | 3,5998 | 3,8616 | 4,0517 |
200 | 2,3422 | 2,5976 | 2,8357 | 3,1290 | 3,3376 | 3,5365 | 3,7869 | 3,9680 |
Значения q убывают с увеличением n и m (вследствие уменьшения информации для прогноза).
Из симметрии нормального распределения следует, что значения q должны быть симметричны для верхней и нижней границ предикционного интервала одного и того же уровня доверия и одинаковых значений n и m:
 .
.Пример - Продавец предъявил претензию поставщику, что 12 женских джемперов определенного фасона имели размер объема груди выше номинала (92,5 см). У поставщика осталось 1100 джемперов в партии этого размера и фасона, причем все были изготовлены в одних и тех же условиях. Поставщик решает проверить размер объема груди джемперов в случайной выборке объема 100. Ни один из этих 100 джемперов не имел объем груди более 92,5 см. Данные прошлых проверок поставщика показывают, что размер объема груди джемперов подчиняется приблизительно нормальному распределению. Выборочные среднее и стандартное отклонения составили  и s = 0,4 см соответственно. Коэффициент q для одностороннего предикционного интервала с n = 100 и m = 1000 в соответствии с таблицей 10 равен 4,0517. Поставщик, таким образом, может быть уверен с вероятностью 0,95, что ни один из оставшихся 1000 джемперов не имеет размер объема груди более 90,1 + 4,0517 x 0,4 = 91,7 см.
и s = 0,4 см соответственно. Коэффициент q для одностороннего предикционного интервала с n = 100 и m = 1000 в соответствии с таблицей 10 равен 4,0517. Поставщик, таким образом, может быть уверен с вероятностью 0,95, что ни один из оставшихся 1000 джемперов не имеет размер объема груди более 90,1 + 4,0517 x 0,4 = 91,7 см.
 и s = 0,4 см соответственно. Коэффициент q для одностороннего предикционного интервала с n = 100 и m = 1000 в соответствии с таблицей 10 равен 4,0517. Поставщик, таким образом, может быть уверен с вероятностью 0,95, что ни один из оставшихся 1000 джемперов не имеет размер объема груди более 90,1 + 4,0517 x 0,4 = 91,7 см.
и s = 0,4 см соответственно. Коэффициент q для одностороннего предикционного интервала с n = 100 и m = 1000 в соответствии с таблицей 10 равен 4,0517. Поставщик, таким образом, может быть уверен с вероятностью 0,95, что ни один из оставшихся 1000 джемперов не имеет размер объема груди более 90,1 + 4,0517 x 0,4 = 91,7 см.Так как 91,7 см < 92,5 см поставщик продолжает поставлять в розничную сеть джемперы этой партии.
14.2 Двусторонний предикционный интервал для следующих m наблюдений
Двусторонний предикционный интервал для следующих m наблюдений представляет собой интервал с границами TL и TU, построенный на основе выборки из n наблюдений так, что с заданным уровнем доверия ни одно из следующих m наблюдений не окажется вне интервала (TL, TU). Границы двустороннего предикционного интервала имеют вид:
 ,
, ,
,где r - коэффициент, который зависит от n, m и уровня доверия. В таблице 11 приведены значения r для двусторонних предикционных интервалов и уровня доверия 0,95.
Таблица 11
предикционных интервалов с уровнем доверия 0,95
Объем выборки, n | Количество будущих наблюдений m | |||||||
5 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 | |
5 | 4,5773 | 5,2286 | 5,8517 | 6,6240 | 7,1698 | 7,6854 | 8,3261 | 8,7837 |
10 | 3,3210 | 3,7173 | 4,1025 | 4,5905 | 4,9424 | 5,2793 | 5,7029 | 6,0082 |
20 | 2,9021 | 3,2076 | 3,5029 | 3,8784 | 4,1514 | 4,4151 | 4,7498 | 4,9929 |
50 | 2,6934 | 2,9523 | 3,1989 | 3,5090 | 3,7335 | 3,9502 | 4,2260 | 4,4273 |
100 | 2,6298 | 2,8743 | 3,1055 | 3,3941 | 3,6016 | 3,8012 | 4,0543 | 4,2386 |
200 | 2,5990 | 2,8366 | 3,0603 | 3,3383 | 3,5372 | 3,7279 | 3,9689 | 4,1440 |
Пример - Необходимо проверить по выборочным данным, что в партии из 250 мужских брюк размера L, поставляемых в комплекте с ремнем, длина ремня составляет от 86 до 92 см. Случайная выборка из 50 брюк дала  и s = 0,78 см. При этом не было обнаружено ремней, длина которых выходила бы за указанный диапазон. В соответствии с таблицей 11 для n = 50 и m = 200 r = 3,9502. Поскольку длина ремня подчиняется нормальному распределению, то двусторонний предикционный интервал имеет вид (88,8 +/- 3,9502 x 0,78), т.е. составляет от 85,7 см до 91,9 см. Так как нижняя граница этого интервала не соответствует допустимым размерам (85,7 < 86), поставщик решает проверить оставшиеся 200 брюк до их поставки.
и s = 0,78 см. При этом не было обнаружено ремней, длина которых выходила бы за указанный диапазон. В соответствии с таблицей 11 для n = 50 и m = 200 r = 3,9502. Поскольку длина ремня подчиняется нормальному распределению, то двусторонний предикционный интервал имеет вид (88,8 +/- 3,9502 x 0,78), т.е. составляет от 85,7 см до 91,9 см. Так как нижняя граница этого интервала не соответствует допустимым размерам (85,7 < 86), поставщик решает проверить оставшиеся 200 брюк до их поставки.
 и s = 0,78 см. При этом не было обнаружено ремней, длина которых выходила бы за указанный диапазон. В соответствии с таблицей 11 для n = 50 и m = 200 r = 3,9502. Поскольку длина ремня подчиняется нормальному распределению, то двусторонний предикционный интервал имеет вид (88,8 +/- 3,9502 x 0,78), т.е. составляет от 85,7 см до 91,9 см. Так как нижняя граница этого интервала не соответствует допустимым размерам (85,7 < 86), поставщик решает проверить оставшиеся 200 брюк до их поставки.
и s = 0,78 см. При этом не было обнаружено ремней, длина которых выходила бы за указанный диапазон. В соответствии с таблицей 11 для n = 50 и m = 200 r = 3,9502. Поскольку длина ремня подчиняется нормальному распределению, то двусторонний предикционный интервал имеет вид (88,8 +/- 3,9502 x 0,78), т.е. составляет от 85,7 см до 91,9 см. Так как нижняя граница этого интервала не соответствует допустимым размерам (85,7 < 86), поставщик решает проверить оставшиеся 200 брюк до их поставки.Более подробная информация о предикционных интервалах приведена в ГОСТ Р ИСО 16269-8.
14.3 Односторонние и двусторонние предикционные интервалы для среднего следующих m наблюдений
Предикционные интервалы для среднего следующих m наблюдений могут быть определены с помощью стандартных таблиц, поскольку они основаны на t-распределении. Верхняя граница одностороннего предикционного интервала для среднего с уровнем доверия  имеет вид:
имеет вид:
 ,
,где  - квантиль t-распределения уровня
- квантиль t-распределения уровня  с (n - 1) степенями свободы. Соответствующая нижняя граница одностороннего предикционного интервала для среднего следующих m наблюдений имеет вид:
с (n - 1) степенями свободы. Соответствующая нижняя граница одностороннего предикционного интервала для среднего следующих m наблюдений имеет вид:
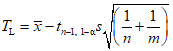 .
.Следует заметить, что  зависит только от двух величин (объема выборки и уровня доверия). Границы двусторонних предикционных интервалов для среднего (TL, TU) имеют вид:
зависит только от двух величин (объема выборки и уровня доверия). Границы двусторонних предикционных интервалов для среднего (TL, TU) имеют вид:
 ,
, .
.Следует помнить, что при отклонении распределения от нормального применение приведенных формул может привести к существенным ошибкам, особенно когда прогноз распространяется на область, расположенную далеко за диапазоном выборочных данных.
15.1 Статистические толерантные интервалы для нормальной совокупности
Статистический толерантный интервал определяют по выборке. Он представляет собой интервал, в пределах которого указанная доля значений совокупности находится с заданной вероятностью.
Границы статистического толерантного интервала изменяются от выборки к выборке. Поскольку статистический толерантный интервал накрывает долю совокупности, альтернативное его наименование, которое иногда используют - статистический интервал покрытия.
Для совокупностей, имеющих нормальное распределение, границы толерантных интервалов определяют аналогично границам предикционных интервалов. Границы толерантных интервалов могут быть четырех видов:
а) границы односторонних толерантных интервалов при известном стандартном отклонении вида  или
или 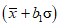 ;
;
 или
или 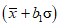 ;
;б) границы двусторонних толерантных интервалов при известном стандартном отклонении вида  ;
;
 ;
;в) границы односторонних толерантных интервалов при неизвестном стандартном отклонении вида 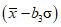 или
или  ;
;
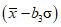 или
или  ;
;г) границы двусторонних толерантных интервалов при неизвестном стандартном отклонении вида  , где константы b1, b2, b3 и b4 зависят от объема выборки и уровня доверия.
, где константы b1, b2, b3 и b4 зависят от объема выборки и уровня доверия.
 , где константы b1, b2, b3 и b4 зависят от объема выборки и уровня доверия.
, где константы b1, b2, b3 и b4 зависят от объема выборки и уровня доверия.Пример - Потребитель приобрел 12000 бобин хлопковой пряжи и намерен проверить распределение ее разрывной нагрузки. Для этого он отбирает случайную выборку из 24 бобин и вырезает из каждой образец нити для испытаний длиной 50 см на расстоянии приблизительно 5 м от свободного конца. Центральную часть каждого образца испытывают на разрывную нагрузку. Единицы измерения - сантиньютон. Выборочные среднее и стандартное отклонения составили  и s = 31,4 сН. Из предыдущего опыта известно, что распределение разрывной нагрузки близко к нормальному распределению. В соответствии с таблицей константа для определения одностороннего статистического толерантного интервала для объема выборки 24, уровня охвата 95% и уровня доверия 95% имеет вид b3 = 2,310. Нижняя граница толерантного интервала 249,8 - 2,310 x 31,4 = 177,3. Потребитель с вероятностью 0,95 может быть уверен, что не менее 95% бобин имеют разрывную нагрузку нити выше 177,3 сН.
и s = 31,4 сН. Из предыдущего опыта известно, что распределение разрывной нагрузки близко к нормальному распределению. В соответствии с таблицей константа для определения одностороннего статистического толерантного интервала для объема выборки 24, уровня охвата 95% и уровня доверия 95% имеет вид b3 = 2,310. Нижняя граница толерантного интервала 249,8 - 2,310 x 31,4 = 177,3. Потребитель с вероятностью 0,95 может быть уверен, что не менее 95% бобин имеют разрывную нагрузку нити выше 177,3 сН.
 и s = 31,4 сН. Из предыдущего опыта известно, что распределение разрывной нагрузки близко к нормальному распределению. В соответствии с таблицей константа для определения одностороннего статистического толерантного интервала для объема выборки 24, уровня охвата 95% и уровня доверия 95% имеет вид b3 = 2,310. Нижняя граница толерантного интервала 249,8 - 2,310 x 31,4 = 177,3. Потребитель с вероятностью 0,95 может быть уверен, что не менее 95% бобин имеют разрывную нагрузку нити выше 177,3 сН.
и s = 31,4 сН. Из предыдущего опыта известно, что распределение разрывной нагрузки близко к нормальному распределению. В соответствии с таблицей константа для определения одностороннего статистического толерантного интервала для объема выборки 24, уровня охвата 95% и уровня доверия 95% имеет вид b3 = 2,310. Нижняя граница толерантного интервала 249,8 - 2,310 x 31,4 = 177,3. Потребитель с вероятностью 0,95 может быть уверен, что не менее 95% бобин имеют разрывную нагрузку нити выше 177,3 сН.Потребитель знает на основе предыдущего опыта, что среднее изменяется от партии к партии и, что разрывная нагрузка хлопковой нити имеет постоянное стандартное отклонение. Таким образом, соответствующая константа b1 = 1,981. Это значение существенно меньше, чем соответствующее значение b3 (2,310) для случая неизвестного стандартного отклонения. Предположим, что  . Тогда граница статистического толерантного интервала 249,8 - 1,981 x 33,2 = 184,0. Потребитель теперь с вероятностью 0,95 может утверждать, что не менее 95% разрывных нагрузок превосходят 184,0 сН.
. Тогда граница статистического толерантного интервала 249,8 - 1,981 x 33,2 = 184,0. Потребитель теперь с вероятностью 0,95 может утверждать, что не менее 95% разрывных нагрузок превосходят 184,0 сН.
 . Тогда граница статистического толерантного интервала 249,8 - 1,981 x 33,2 = 184,0. Потребитель теперь с вероятностью 0,95 может утверждать, что не менее 95% разрывных нагрузок превосходят 184,0 сН.
. Тогда граница статистического толерантного интервала 249,8 - 1,981 x 33,2 = 184,0. Потребитель теперь с вероятностью 0,95 может утверждать, что не менее 95% разрывных нагрузок превосходят 184,0 сН.Если имеются сомнения относительно постоянства  , следует считать
, следует считать  неизвестным и применять соответствующий алгоритм.
неизвестным и применять соответствующий алгоритм.
15.2 Статистические толерантные интервалы для совокупностей с неизвестным видом распределения
Для определения толерантных интервалов для среднего или дисперсии при неизвестном виде распределения применяют порядковые статистики, т.е. отдельные выборочные значения после их расположения в порядке возрастания. Любая единственная пара порядковых статистик может быть использована для определения статистического толерантного интервала, но наибольшее и наименьшее значения охватывают наибольшую долю совокупности. При неизвестном виде распределения статистический толерантный интервал является более широким, чем в ситуации, когда вид распределения известен. Например, чтобы быть уверенным с вероятностью 0,95, что интервал, сформированный из наибольшего и наименьшего наблюдений, накрывает 95% совокупности, необходима выборка из 93 наблюдений. Для охвата 99% совокупности необходимо 473 наблюдения, а для охвата 99,9% совокупности - 4742 наблюдения.
Таблицы значений коэффициентов для определения границ толерантных интервалов приведены в ГОСТ Р ИСО 16269-6.
Методы оценки характеристик совокупности при неизвестном виде функции распределения называют непараметрическими. Преимущество этих методов состоит в том, что их можно применять, когда имеются сомнения в виде функции распределения. Недостатком метода является то, что при равных объемах выборок непараметрические статистические интервалы существенно шире параметрических.
При определении доверительного интервала для медианы непараметрическим методом элементы случайной выборки объема n располагают в порядке возрастания x[1], x[2], ..., x[n]. Симметрично расположенная пара порядковых статистик (x[k], x[n+1-k]]) может быть использована в качестве доверительных границ для медианы.
Чем меньше значение k, тем больше вероятность того, что медиана совокупности будет накрыта этим интервалом. Например, k = 1 соответствуют доверительные границы x[1] и x[n]. Эти границы не накроют медиану совокупности в случае, когда вся выборка из n наблюдений лежит либо выше, либо ниже медианы. Поскольку для каждого наблюдения вероятность быть меньше медианы совокупности равна 0,5, а вероятность быть больше медианы также равна 0,5, то вероятность того, что медиана не будет накрыта интервалом (x[k], x[n+1-k]]) равна (1/2)n + (1/2)n = (1/2)n-1.
Таким образом, доверительная вероятность, соответствующая данному интервалу, равна 1 - (1/2)n-1. Поскольку n принимает значения 2, 3, 4, 5... и т.д., соответствующая доверительная вероятность равна 0,50, 0,75, 0,875, 0,9375 ... и т.д. Могут быть построены односторонние доверительные интервалы в виде (a, x[n]) или (x[1], b), где a и b - наименьшее и наибольшее наблюдения в совокупности, если они известны.
Очевидно, доверительная вероятность не зависит от вида распределения совокупности. Единственное сделанное предположение: вероятность того, что выборочное значение лежит справа или слева от медианы совокупности равна 0,5. Это означает, что распределение должно быть непрерывно в этой точке. Следует отметить, что с увеличением k длина доверительного интервала уменьшается вместе с уменьшением доверительной вероятности.
В ГОСТ Р ИСО 16269-7 приведены таблицы для объема выборки k от 5 до 100. Для больших выборок используют следующую приближенную формулу для доверительной вероятности 
 ,
,где u - квантиль нормированного нормального распределения для одностороннего доверительного интервала уровня  или двустороннего интервала уровня
или двустороннего интервала уровня  ;
;
 или двустороннего интервала уровня
или двустороннего интервала уровня c - константа, зависящая от u.
Значение k необходимо округлить в меньшую сторону до ближайшего целого числа.
Формула дает корректное значение k для объемов выборки до 280000.
Пример - Необходимо определить двусторонний доверительный интервал с доверительной вероятностью 0,99, u = 2,57582930 и c = 1,74. Таким образом, для выборки с объемом 200 единиц
 .
.После округления в меньшую сторону k = 82. Таким образом, можно утверждать с доверительной вероятностью 0,99, что доверительный интервал (x[82], x[119]) накрывает медиану совокупности.
Восемь десятичных разрядов для u позволяют получить k с высокой точностью для выборки большего объема. Для средних объемов выборки достаточно двух или трех десятичных знаков после запятой.
Аналогичные методы могут быть использованы для определения доверительных интервалов для других квантилей совокупности.
(справочное)
Q = 0,25 | Q = 0,1 | Q = 0,05 | Q = 0,025 | Q = 0,01 | Q = 0,005 | Q = 0,0025 | Q = 0,001 | Q = 0,0005 | |
2Q = 0,5 | 2Q = 0,2 | 2Q = 0,1 | 2Q = 0,05 | 2Q = 0,02 | 2Q = 0,01 | 2Q = 0,005 | 2Q = 0,002 | 2Q = 0,001 | |
1 | 1,0000 | 3,0777 | 6,3138 | 12,7062 | 31,8205 | 63,6567 | 127,3213 | 318,3088 | 636,6192 |
2 | 0,8165 | 1,8866 | 2,9200 | 4,3027 | 6,9646 | 9,9248 | 14,0890 | 22,3271 | 31,5991 |
3 | 0,7649 | 1,6377 | 2,3534 | 3,1824 | 4,5407 | 5,8409 | 7,4533 | 10,2145 | 12,9240 |
4 | 0,7407 | 1,5332 | 2,1318 | 2,7764 | 3,7469 | 4,6041 | 5,5976 | 7,1732 | 8,6103 |
5 | 0,7267 | 1,4759 | 2,0150 | 2,5706 | 3,3649 | 4,0321 | 4,7733 | 5,8934 | 6,8688 |
6 | 0,7176 | 1,4398 | 1,9432 | 2,4469 | 3,1427 | 3,7074 | 4,3168 | 5,2076 | 5,9588 |
7 | 0,7111 | 1,4149 | 1,8946 | 2,3646 | 2,9980 | 3,4995 | 4,0293 | 4,7853 | 5,4079 |
8 | 0,7064 | 1,3968 | 1,8595 | 2,3060 | 2,8965 | 3,3554 | 3,8325 | 4,5008 | 5,0413 |
9 | 0,7027 | 1,3830 | 1,8331 | 2,2622 | 2,8214 | 3,2498 | 3,6897 | 4,2968 | 4,7809 |
10 | 0,6998 | 1,3722 | 1,8125 | 2,2281 | 2,7638 | 3,1693 | 3,5814 | 4,1437 | 4,5869 |
11 | 0,6974 | 1,3634 | 1,7959 | 2,2010 | 2,7181 | 3,1058 | 3,4966 | 4,0247 | 4,4370 |
12 | 0,6955 | 1,3562 | 1,7823 | 2,1788 | 2,6810 | 3,0545 | 3,4284 | 3,9296 | 4,3178 |
13 | 0,6938 | 1,3502 | 1,7709 | 2,1604 | 2,6503 | 3,0123 | 3,3725 | 3,8520 | 4,2208 |
14 | 0,6924 | 1,3450 | 1,7613 | 2,1448 | 2,6245 | 2,9768 | 3,3257 | 3,7874 | 4,1405 |
15 | 0,6912 | 1,3406 | 1,7531 | 2,1314 | 2,6025 | 2,9467 | 3,2860 | 3,7328 | 4,0728 |
16 | 0,6901 | 1,3368 | 1,7459 | 2,1199 | 2,5835 | 2,9208 | 3,2520 | 3,6862 | 4,0150 |
17 | 0,6892 | 1,3334 | 1,7396 | 2,1098 | 2,5669 | 2,8982 | 3,2224 | 3,6458 | 3,9651 |
18 | 0,6884 | 1,3304 | 1,7341 | 2,1009 | 2,5524 | 2,8784 | 3,1966 | 3,6105 | 3,9216 |
19 | 0,6876 | 1,3277 | 1,7291 | 2,0930 | 2,5395 | 2,8609 | 3,1737 | 3,5794 | 3,8834 |
20 | 0,6870 | 1,3253 | 1,7247 | 2,0860 | 2,5280 | 2,8453 | 3,1534 | 3,5518 | 3,8495 |
21 | 0,6864 | 1,3232 | 1,7207 | 2,0796 | 2,5176 | 2,8314 | 3,1352 | 3,5272 | 3,8193 |
22 | 0,6858 | 1,3212 | 1,7171 | 2,0739 | 2,5083 | 2,8188 | 3,1188 | 3,5050 | 3,7921 |
23 | 0,6853 | 1,3195 | 1,7139 | 2,0687 | 2,4999 | 2,8073 | 3,1040 | 3,4850 | 3,7676 |
24 | 0,6848 | 1,3178 | 1,7109 | 2,0639 | 2,4922 | 2,7969 | 3,0905 | 3,4668 | 3,7454 |
25 | 0,6844 | 1,3163 | 1,7081 | 2,0595 | 2,4851 | 2,7874 | 3,0782 | 3,4502 | 3,7251 |
26 | 0,6840 | 1,3150 | 1,7056 | 2,0555 | 2,4786 | 2,7787 | 3,0669 | 3,4350 | 3,7066 |
27 | 0,6837 | 1,3137 | 1,7033 | 2,0518 | 2,4727 | 2,7707 | 3,0565 | 3,4210 | 3,6896 |
28 | 0,6834 | 1,3125 | 1,7011 | 2,0484 | 2,4671 | 2,7633 | 3,0469 | 3,4082 | 3,6739 |
29 | 0,6830 | 1,3114 | 1,6991 | 2,0452 | 2,4620 | 2,7564 | 3,0380 | 3,3962 | 3,6594 |
30 | 0,6828 | 1,3104 | 1,6973 | 2,0423 | 2,4573 | 2,7500 | 3,0298 | 3,3852 | 3,6460 |
40 | 0,6807 | 1,3031 | 1,6839 | 2,0211 | 2,4233 | 2,7045 | 2,9712 | 3,3069 | 3,5510 |
60 | 0,6786 | 1,2958 | 1,6706 | 2,0003 | 2,3901 | 2,6603 | 2,9146 | 3,2317 | 3,4602 |
120 | 0,6765 | 1,2886 | 1,6577 | 1,9799 | 2,3578 | 2,6174 | 2,8599 | 3,1595 | 3,3735 |
0,6745 | 1,2816 | 1,6449 | 1,9600 | 2,3263 | 2,5758 | 2,8070 | 3,0902 | 3,2905 | |
Примечание - Q - верхняя область распределения с | |||||||||
KANAGAWA, A., ARIZONO, I., and OHTA, H. Design of the | |
Р 50.1.087-2013 Статистические методы. Примеры применения. Часть 8. Статистическое управление процессами |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 | Т59 |
Ключевые слова: выборочное среднее, выборочное стандартное отклонение, доверительный интервал, проверка гипотез, предикционный интервал, толерантный интервал | ||











 . Заменяя
. Заменяя 
