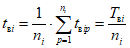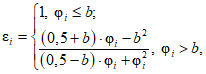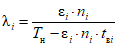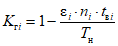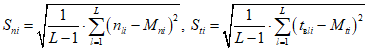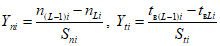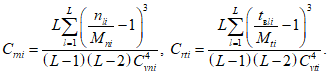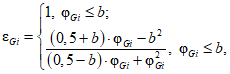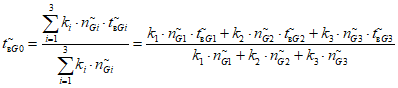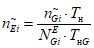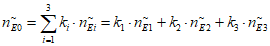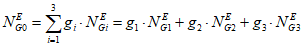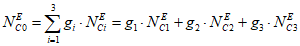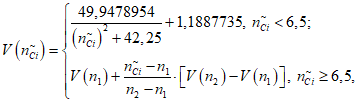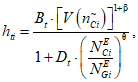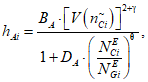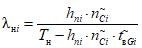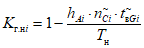СПРАВКА
Источник публикации
Документ опубликован не был
Примечание к документу
Документ введен в действие с 01.01.2020 (Распоряжение ОАО "РЖД" от 06.12.2019 N 2762/р).
Название документа
"Методика расчета и нормирования показателей надежности объектов железнодорожного электроснабжения"
(утв. Распоряжением ОАО "РЖД" от 06.12.2019 N 2762/р)
"Методика расчета и нормирования показателей надежности объектов железнодорожного электроснабжения"
(утв. Распоряжением ОАО "РЖД" от 06.12.2019 N 2762/р)
Содержание
Распоряжением ОАО "РЖД"
от 6 декабря 2019 г. N 2762/р
МЕТОДИКА
РАСЧЕТА И НОРМИРОВАНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ОБЪЕКТОВ ЖЕЛЕЗНОДОРОЖНОГО ЭЛЕКТРОСНАБЖЕНИЯ
1.1. Настоящая Методика определяет порядок расчета и нормирования показателей эксплуатационной надежности объектов железнодорожного электроснабжения ОАО "РЖД" различных видов для заданного полигона обследования и заданного интервала наблюдения.
1.2. Настоящая Методика предназначена для расчета показателей надежности (коэффициента готовности, интенсивности отказов, среднего времени до восстановления) контактной сети, тяговых подстанций, устройств электроснабжения нетяговых потребителей, а также для нормирования показателей надежности указанных объектов железнодорожного электроснабжения.
1.3. Настоящая Методика предназначена для применения подразделениями Трансэнерго и иными структурными подразделениями ОАО "РЖД".
1.4. Применение настоящей Методики сторонними организациями оговаривается в договорах (соглашениях) с ОАО "РЖД".
В настоящей Методике применены термины по ГОСТ 19431-84 "Энергетика и электрификация. Термины и определения", ГОСТ 27.002-2015 "Надежность в технике. Термины и определения", ГОСТ 32192-2013 "Надежность в железнодорожной технике. Основные понятия. Термины и определения", ГОСТ 32895-2014 "Электрификация и электроснабжение железных дорог. Термины и определения", ГОСТ 33947-2016 "Железнодорожное электроснабжение. Номенклатура показателей надежности и функциональной безопасности", ГОСТ Р 50779.21-2004 "Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение", а также следующие термины с соответствующими определениями:
глобальный объект (железнодорожного электроснабжения): условный объект оценки, который включает количество эталонных объектов, эквивалентное всем существующим объектам железнодорожного электроснабжения одного вида (или нескольких видов) и который применяется для определения необходимых параметров модели нормирования показателей надежности на заданном интервале наблюдения;
железнодорожное электроснабжение: подсистема инфраструктуры железнодорожного транспорта, включающая в себя комплекс технических сооружений и устройств, обеспечивающих электроснабжение потребляющих электроэнергию подсистем инфраструктуры железнодорожного транспорта, а также электроснабжение тягового подвижного состава на электрифицированных железных дорогах (Технический регламент Таможенного союза ТРТС 003/2011 "О безопасности инфраструктуры железнодорожного транспорта", статья 2);
интенсивность отказов (объекта железнодорожного электроснабжения): отношение количества отказов объекта железнодорожного электроснабжения, возникших за интервал наблюдения, к разности длительности этого интервала наблюдения и суммарного времени до восстановления объекта за этот интервал наблюдения <1>;
--------------------------------
<1> Данный показатель является обратной величиной по отношению к средней наработке между отказами.
квантиль: значение, которое заданная (случайная) величина не превышает с фиксированной вероятностью;
коэффициент (верхней) доверительной границы: отношение значения верхней границы доверительного интервала к значению показателя, для которого определялась эта верхняя граница;
нормативный (или допустимый) показатель надежности: свойство надежности, выражаемое количественно и получаемое в результате нормирования надежности;
объект оценки: объект (или несколько объектов) железнодорожного электроснабжения одного вида (или нескольких видов), для которого (которых) выполняется расчет фактических показателей надежности и (или) установление нормативных (допустимых) показателей надежности;
суммарное время до восстановления (объекта железнодорожного электроснабжения): сумма времени, затраченного на восстановление объекта (нескольких объектов) за интервал наблюдения;
сценарий принятия (управленческих) решений: рекомендации по принятию управленческих решений о дальнейшей эксплуатации объекта (или объектов) железнодорожного электроснабжения, формируемые в зависимости от соотношения значений фактических и соответствующих им нормативных показателей надежности;
фактический показатель надежности: свойство надежности, выражаемое количественно и получаемое на основе статистических данных эксплуатации объекта (или объектов) железнодорожного электроснабжения;
эталонный объект (железнодорожного электроснабжения): условный объект железнодорожного электроснабжения определенного вида, характеристики которого соответствуют одному реальному объекту данного вида с определенными конструкцией, сроком службы, остаточным ресурсом, условиями эксплуатации и который применяется для определения необходимых параметров модели нормирования показателей надежности.
3.1. Надежность объектов железнодорожного электроснабжения характеризует их способность обеспечивать в расчетных режимах преобразование, распределение и/или передачу электрической энергии тяговым и нетяговым потребителям железнодорожного транспорта в требуемом количестве и нормируемого качества.
3.2. Объекты железнодорожного электроснабжения являются восстанавливаемыми объектами, подвергаемыми техническому обслуживанию и ремонту.
3.3. Настоящая Методика предназначена для применения работниками дистанций электроснабжения, дирекций по энергообеспечению, Трансэнерго, ответственными за организацию работы по обеспечению безопасности движения поездов, повышению надежности технических средств.
3.4. Настоящая Методика предусматривает выполнение автоматизированного расчета показателей в Единой корпоративной платформе Управления Ресурсами, Рисками и Надежностью (ЕКП УРРАН). Рекомендуемая периодичность выполнения расчетов по настоящей Методике составляет:
для расчета фактических показателей надежности - 1 календарный месяц (фактические показатели рассчитываются на 16 число месяца, следующего за месяцем оценки);
для установления нормативных (допустимых) значений показателей надежности - один год (нормативные показатели на следующий год устанавливаются на 01 декабря текущего календарного года).
3.5. Источниками информации о показателях надежности объектов железнодорожного электроснабжения являются комплексная автоматизированная система КАС АНТ и Единая комплексная автоматизированная система ЕК АСУ И.
3.6. В настоящей методике в качестве объектов оценки применяются объекты железнодорожного электроснабжения одного вида (или нескольких видов), расположенные на заданном полигоне обследования.
3.7. Для целей настоящей Методики установлены следующие виды объектов железнодорожного электроснабжения:
- контактная сеть;
- тяговая подстанция;
- линия электропередачи (ЛЭП).
3.8. Надежность линейных устройств электроснабжения учитываются в составе объектов вида "тяговая подстанция". Надежность трансформаторных подстанций учитываются в составе объектов видов "тяговая подстанция" или "ЛЭП", в зависимости от их функциональной принадлежности.
3.9. В качестве полигона обследования для контактной сети могут быть выбраны:
- контактная сеть железнодорожного пути перегона (станции);
- контактная сеть направления;
- контактная сеть в границах района контактной сети (ЭЧК);
- контактная сеть в границах дистанции электроснабжения (ЭЧ);
- контактная сеть в границах дирекции по энергообеспечению;
- контактная сеть в границах Трансэнерго.
3.10. В качестве полигона обследования для тяговой подстанции могут быть выбраны:
- отдельная тяговая подстанция (ЭЧЭ);
- тяговые подстанции в границах ЭЧ;
- тяговые подстанции в границах дирекции по энергообеспечению;
- тяговые подстанции в границах Трансэнерго.
3.11. В качестве полигона обследования для ЛЭП могут быть выбраны:
- ЛЭП в границах перегона (станции);
- ЛЭП направления;
- ЛЭП в границах ЭЧК или района электроснабжения (ЭЧС);
- ЛЭП в границах ЭЧ;
- ЛЭП в границах дирекции по энергообеспечению;
- ЛЭП в границах Трансэнерго.
3.12. В качестве полигона обследования для объектов всех видов могут быть выбраны:
- объекты всех видов в границах ЭЧ;
- объекты всех видов в границах дирекции по энергообеспечению;
- объекты всех видов в границах Трансэнерго.
3.13. Интервал наблюдения для расчета и нормирования показателей устанавливается длительностью не менее одного месяца и не более 12 месяцев с возможностью выбора дат начала и окончания интервала (в формате ДД.ММ.ГГГГ; при этом даты начала и окончания интервала должны принадлежать одному календарному году) с последующим переводом длительности интервала в количество часов.
4.1. В соответствии со спецификой функционирования объектов железнодорожного электроснабжения, для оценки их надежности выбрана следующая номенклатура показателей:
интенсивность отказов 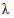 (характеризует безотказность объекта);
(характеризует безотказность объекта);
среднее время до восстановления tв (характеризует ремонтопригодность объекта);
коэффициент готовности Kг (комплексный показатель, характеризует сочетание безотказности и ремонтопригодности объекта).
Данные показатели, применительно к системе железнодорожного электроснабжения, являются ключевыми и позволяют дать оценку эксплуатационной надежности объектов железнодорожного электроснабжения.
4.2. Для принятия обоснованных управленческих решений о текущем состоянии системы железнодорожного электроснабжения на основе показателей надежности требуется установить нормативные значения вышеуказанных показателей. На основании результатов сравнения значений эксплуатационных (фактических) и соответствующих им нормативных показателей надежности может быть получена информация о состоянии надежности объектов.
В связи с вышеизложенным в настоящей Методике, применительно к различным объектам оценки и различным видам объектов, рассматривается нормирование (установление) следующих показателей надежности:
допустимая интенсивность отказов;
допустимое среднее время до восстановления;
допустимый коэффициент готовности.
5.1. На основании анализа существующих объектов железнодорожного электроснабжения, надежность которых рассматривается в настоящей Методике, установлены следующие виды объектов и их номенклатура (таблица 1).
Таблица 1
Виды объектов и их номенклатура
Вид объекта | Номенклатура объектов |
Контактная сеть <1> | Контактная сеть, выполненная по проектам КС-160 для переменного тока |
Контактная сеть, выполненная по проектам КС-160 для постоянного тока | |
Контактная сеть, выполненная по проектам КС-200 (250) для переменного тока | |
Контактная сеть, выполненная по проектам КС-200 (250) для постоянного тока | |
Контактная сеть, выполненная по проектам КС-120 или КС-140 для переменного тока | |
Контактная сеть, выполненная по проектам КС-120 или КС-140 для постоянного тока | |
Тяговая подстанция | Тяговая подстанция переменного тока с высшим напряжением 110 кВ |
Тяговая подстанция переменного тока с высшим напряжением 220 кВ | |
Тяговая подстанция постоянного тока с высшим напряжением 110 кВ | |
Тяговая подстанция постоянного тока с высшим напряжением 220 кВ | |
Тяговая подстанция постоянного и переменного тока с высшим напряжением 110 кВ (стыковая) | |
Тяговая подстанция постоянного и переменного тока с высшим напряжением 220 кВ (стыковая) | |
Тяговая подстанция постоянного тока с высшим напряжением 35 (20) кВ | |
Тяговая подстанция постоянного тока с высшим напряжением 10 (6) кВ | |
ЛЭП | ЛЭП напряжением 10 (6) кВ с защищенными проводами на железобетонных опорах |
ЛЭП напряжением 10 (6) кВ с защищенными проводами на деревянных опорах | |
ЛЭП напряжением 10 (6) кВ с голыми проводами на железобетонных опорах | |
ЛЭП напряжением 10 (6) кВ с голыми проводами на деревянных опорах | |
ЛЭП 35 (20) кВ с защищенными проводами | |
ЛЭП 35 (20) кВ с голыми проводами | |
ЛЭП типа "два провода - рельс", расположенная на опорах контактной сети | |
ЛЭП типа двухцепных линий напряжением 10 (6) кВ с голыми проводами на железобетонных опорах | |
ЛЭП типа двухцепных линий напряжением 10 (6) кВ с голыми проводами на деревянных опорах | |
ЛЭП типа двухцепных линий напряжением 10 (6) кВ с защищенными проводами на железобетонных опорах | |
ЛЭП типа двухцепных линий напряжением 10 (6) кВ с защищенными проводами на деревянных опорах | |
ЛЭП типа двухцепных линий напряжением 35 (20) кВ с голыми проводами | |
ЛЭП типа двухцепных линий напряжением 35 кВ (20) с защищенными проводами | |
ЛЭП напряжением 10 (6) кВ с защищенными проводами, расположенная на опорах контактной сети | |
ЛЭП напряжением 10 (6) кВ с голыми проводами, расположенная на опорах контактной сети |
--------------------------------
<1> Ромбовидная контактная подвеска в настоящей Методике не рассматривается в виду специфики ее применения и малого распространения.
5.2. Исходными данными для расчета показателей надежности являются данные об отказах технических средств КАС АНТ:
1 и 2 категорий (вариант расчета N 1);
1, 2 и 3 категорий (вариант расчета N 2).
Данные об отказах технических средств выбираются:
1) по следующим значениям признака "Группа объектов или укрупненный объект" Классификатора объектов и причин отказов в работе технических средств системы КАС АНТ (Классификатор объектов и причин отказов в работе технических средств системы КАС АНТ, утвержден распоряжением ОАО "РЖД" от 29 декабря 2015 г. N 3126р):
"контактная сеть" (для объекта вида "контактная сеть" настоящей Методики);
"тяговая подстанция" (для объекта вида "тяговая подстанция" настоящей Методики);
"электроснабжение нетяговых потребителей", "линии СЦБ (АБ)" (для объекта вида "ЛЭП" настоящей Методики) <1>;
--------------------------------
<1> Для объекта вида "ЛЭП" данные об отказах технических средств по обоим вышеуказанным признакам "Группа объектов или укрупненный объект" объединяются.
2) только по объектам, принадлежащим заданному объекту оценки (например, контактная сеть направления, ЭЧК, дирекции по энергообеспечению).
В качестве исходных данных из системы КАС АНТ, соответствующих условиям 1) и 2), за заданный интервал наблюдения для варианта расчета N 1 выбирается:
- количество отказов 1 и 2 категории;
- суммарная продолжительность отказов 1 и 2 категории (является суммой разностей времен окончания и начала каждого из рассматриваемых отказов).
В качестве исходных данных из системы КАС АНТ, соответствующих условиям 1) и 2), за заданный интервал наблюдения для варианта расчета N 2 выбирается:
- количество отказов 1, 2 и 3 категории;
- суммарная продолжительность отказов 1, 2 и 3 категории (сумма разностей времен окончания и начала каждого из рассматриваемых отказов).
При расчете фактических показателей надежности к количеству отказов КАС АНТ добавляется (опционально) количество частично работоспособных состояний, взятых с коэффициентом 0,33 (согласно ГОСТ 27.002-2015, частично работоспособное состояние возникает, когда объект может быть способен выполнять одни функции и одновременно не способен выполнять другие).
с учетом реестра объектов
6.1. Учет вида объектов при расчете показателей надежности
Фактические (эксплуатационные) показатели надежности рассчитываются для заданного реального объекта (объекта оценки), по видам объектов в соответствии с реестром объектов, который принят в настоящей Методике. Номенклатура показателей следующая:
фактическая интенсивность отказов  объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки;
объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки;
фактическое среднее время до восстановления tвi объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки;
фактический коэффициент готовности Kгi объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки.
6.2. Расчет фактического среднего времени до восстановления объекта оценки
Фактическое среднее время до восстановления объекта оценки:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); ni - количество отказов объектов вида i (i = 1, 2, 3) по объекту оценки за интервал наблюдения Tн; tвip - время до восстановления после p-го отказа (p = 1...ni) объектов вида i (i = 1, 2, 3) по объекту оценки за интервал наблюдения Tн; Tвi - суммарное время до восстановления объектов вида i (i = 1, 2, 3) по объекту оценки за интервал наблюдения Tн.
Количество отказов объектов вида i (i = 1, 2, 3) включает отказы КАС АНТ 1 и 2 категории (вариант расчета N 1) или 1, 2 и 3 категории (вариант расчета N 2), к которым (опционально) добавляется количество частично работоспособных состояний объектов вида i (i = 1, 2, 3) по объекту оценки, взятое с коэффициентом 0,33.
Для объектов всех видов (i = 0) по объекту оценки фактическое среднее время до восстановления получают путем интеграции, предварительно вычислив "взвешенное" количество отказов n0 для объектов всех видов:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); ki - коэффициент ответственности объектов вида i (i = 1, 2, 3) (таблица 13); ni - количество отказов объектов вида i (i = 1, 2, 3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 1, 2, 3) по объекту оценки за интервал наблюдения Tн.
6.3. Коррекция фактического суммарного времени неготовности
В модели, предусматривающей последовательное соединение объектов, не может быть учтена частичная одновременность восстановлений объектов после отказов. При этом возможна ситуация, когда суммарное время неготовности Tв = n·tв превышает длительность интервала наблюдения Tн. Такая ситуация приводит к некорректному расчету интенсивности отказов и коэффициента готовности, в случае чего указанные параметры имеют отрицательные значения. Для предупреждения такой ситуации применяется специальная коррекция суммарного времени неготовности объекта оценки.
Вычисляется параметр неготовности 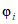 объектов вида i по объекту оценки:
объектов вида i по объекту оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); ni - количество отказов объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 0...3) объекта оценки за интервал наблюдения Tн.
Вычисляется коэффициент 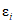 коррекции суммарного времени неготовности объектов вида i объекта оценки:
коррекции суммарного времени неготовности объектов вида i объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); b - порог коррекции суммарного времени неготовности (см. таблицу 13); 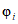 - параметр неготовности объектов вида i (i = 0...3) объекта оценки.
- параметр неготовности объектов вида i (i = 0...3) объекта оценки.
6.4. Расчет фактической интенсивности отказов объекта оценки
Фактическая интенсивность отказов объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i - 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); 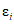 - коэффициент коррекции суммарного времени неготовности объектов вида i (i = 0...3) по объекту оценки; ni - количество отказов объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн.
- коэффициент коррекции суммарного времени неготовности объектов вида i (i = 0...3) по объекту оценки; ni - количество отказов объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн.
6.5. Расчет фактического коэффициента готовности объекта оценки
Фактический коэффициент готовности объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");  - коэффициент коррекции суммарного времени неготовности объектов вида i (i = 0...3) по объекту оценки; ni - количество отказов объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн.
- коэффициент коррекции суммарного времени неготовности объектов вида i (i = 0...3) по объекту оценки; ni - количество отказов объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн; tвi - среднее время до восстановления объектов вида i (i = 0...3) по объекту оценки за интервал наблюдения Tн.
6.6. Порядок округления результатов расчета фактических показателей надежности
Показатели 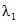 ,
, 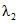 ,
, 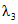 и
и 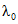 после их вычисления для представления результатов округляются в меньшую сторону до 7 знаков после запятой (десятичные знаки, начиная от 8-го после запятой, отбрасываются).
после их вычисления для представления результатов округляются в меньшую сторону до 7 знаков после запятой (десятичные знаки, начиная от 8-го после запятой, отбрасываются).
Показатели Kг1, Kг2, Kг3 и Kг0 после их вычисления для представления результатов округляются в большую сторону до 6 знаков после запятой (десятичные знаки, начиная от 7-го после запятой, отбрасываются и если результат менее 1, то к полученному значению прибавляется число 0,000001).
Показатели tв1, tв2, tв3 и tв0 (после завершения расчетов фактических интенсивностей отказов и фактических коэффициентов готовности, в которых они используются) для представления результатов округляются в меньшую сторону до 3 знаков после запятой (десятичные знаки, начиная от 4-го после запятой, отбрасываются).
Пример расчета фактических показателей надежности приведен в приложении N 2 к настоящей Методике
Эталонные объекты применяются в целях установления нормативных значений показателей надежности для заданного реального объекта (объекта оценки).
Эталонные объекты позволяют рассматривать различные по характеристикам реальные объекты одного вида в единой оценочной шкале.
Каждому реальному объекту (например, анкерному участку контактной сети) ставится в соответствие эквивалентное количество эталонных объектов, которое зависит от размерности реального объекта и его характеристик.
Для применения в настоящей Методике устанавливаются следующие эталонные объекты:
- эталонный километр развернутой длины контактной сети;
- эталонная тяговая подстанция;
- эталонный километр ЛЭП.
1) Для одного километра развернутой длины контактной сети (вид объекта - 1) эквивалентное количество эталонных объектов определяется по формуле:
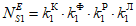 , (8)
, (8)где  - коэффициент конструкции контактной сети (таблица 2);
- коэффициент конструкции контактной сети (таблица 2);  - коэффициент фактического состояния контактной сети (таблица 3);
- коэффициент фактического состояния контактной сети (таблица 3); 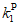 - коэффициент остаточного ресурса анкерного участка контактной сети (таблица 4);
- коэффициент остаточного ресурса анкерного участка контактной сети (таблица 4); 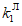 - коэффициент класса железнодорожной линии, на которой эксплуатируется контактная сеть (таблица 5; в соответствии с Методикой расчета технических единиц оборудования, участвующего в процессе передачи электрической энергии, утвержденной распоряжением ОАО "РЖД" от 22 марта 2016 г. N 491р).
- коэффициент класса железнодорожной линии, на которой эксплуатируется контактная сеть (таблица 5; в соответствии с Методикой расчета технических единиц оборудования, участвующего в процессе передачи электрической энергии, утвержденной распоряжением ОАО "РЖД" от 22 марта 2016 г. N 491р).
Таблица 2
Коэффициенты конструкции контактной сети
Конструкция контактной сети | |
1 км развернутой длины контактной сети по проектам КС-160 для переменного тока | 1,0 |
1 км развернутой длины контактной сети по проектам КС-160 для постоянного тока | 1,5 |
1 км развернутой длины контактной сети по проектам КС-200 (250) для переменного тока | 1,3 |
1 км развернутой длины контактной сети по проектам КС-200 (250) для постоянного тока | 1,7 |
1 км развернутой длины контактной сети по проектам КС-120 и КС-140 для переменного тока | 2,0 |
1 км развернутой длины контактной сети по проектам КС-120 и КС-140 для постоянного тока | 2,5 |
Таблица 3
Срок эксплуатации контактной сети | |
Менее 15 лет | 1,0 |
От 15 лет и до 20 лет | 1,1 |
От 20 лет и до 25 лет | 1,2 |
От 25 лет и до 30 лет | 1,3 |
От 30 лет и до 50 лет | 1,5 |
50 лет и более | 1,7 |
Таблица 4
Остаточный срок службы контактной сети | |
5 и более лет (по данным контрольно-оценочной карты) | 1,0 |
от 0 до 5 лет (по данным контрольно-оценочной карты) | 2,0 |
Таблица 5
Классы железнодорожных линий | |
1 | 1,0 |
2 | 0,89 |
3 | 0,8 |
4 | 0,72 |
5 | 0,72 |
2) Для одной тяговой подстанции (вид объекта - 2) эквивалентное количество эталонных объектов определяется по формуле:
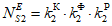 , (9)
, (9)где 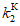 - коэффициент конструкции тяговой подстанции (таблица 6);
- коэффициент конструкции тяговой подстанции (таблица 6);  - коэффициент фактического состояния тяговой подстанции (таблица 7);
- коэффициент фактического состояния тяговой подстанции (таблица 7); 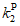 - коэффициент остаточного ресурса тяговой подстанции (таблица 8).
- коэффициент остаточного ресурса тяговой подстанции (таблица 8).
Таблица 6
Коэффициенты конструкции тяговой подстанции
Конструкция тяговой подстанции | |
Тяговая подстанция переменного тока с высшим напряжением 110 кВ | 1,0 |
Тяговая подстанция переменного тока с высшим напряжением 220 кВ | 1,2 |
Тяговая подстанция постоянного тока с высшим напряжением 110 кВ | 1,5 |
Тяговая подстанция постоянного тока с высшим напряжением 220 кВ | 1,7 |
Тяговая подстанция постоянного и переменного тока с высшим напряжением 110 кВ (стыковая) | 2,5 |
Тяговая подстанция постоянного и переменного тока с высшим напряжением 220 кВ (стыковая) | 2,9 |
Тяговая подстанция постоянного тока с высшим напряжением 35 (20) кВ | 1,4 |
Тяговая подстанция постоянного тока с высшим напряжением 10 (6) кВ | 1,3 |
Таблица 7
Срок эксплуатации тяговой подстанции | |
Менее 15 лет | 1,0 |
От 15 лет и до 20 лет | 1,1 |
От 20 лет и до 25 лет | 1,2 |
От 25 лет и до 30 лет | 1,3 |
30 и более лет | 1,4 |
Таблица 8
Остаточный срок службы тяговой подстанции | |
5 и более лет (по данным контрольно-оценочной карты) | 1,0 |
от 0 до 5 лет (по данным контрольно-оценочной карты) | 2,0 |
3) Для одного километра ЛЭП (вид объекта - 3) эквивалентное количество эталонных объектов определяется по формуле:
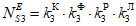 , (10)
, (10)где  - коэффициент конструкции ЛЭП (таблица 9);
- коэффициент конструкции ЛЭП (таблица 9);  - коэффициент фактического состояния ЛЭП (таблица 10);
- коэффициент фактического состояния ЛЭП (таблица 10); 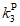 - коэффициент остаточного ресурса ЛЭП (таблица 11);
- коэффициент остаточного ресурса ЛЭП (таблица 11); 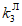 - коэффициент класса железнодорожной линии, на которой эксплуатируется ЛЭП (таблица 12; в соответствии с Методикой расчета технических единиц оборудования, участвующего в процессе передачи электрической энергии, утвержденной распоряжением ОАО "РЖД" от 22 марта 2016 г. N 491р).
- коэффициент класса железнодорожной линии, на которой эксплуатируется ЛЭП (таблица 12; в соответствии с Методикой расчета технических единиц оборудования, участвующего в процессе передачи электрической энергии, утвержденной распоряжением ОАО "РЖД" от 22 марта 2016 г. N 491р).
Таблица 9
Коэффициенты конструкции ЛЭП
Конструкция ЛЭП | |
1 км ЛЭП напряжением 10 (6) кВ с защищенными проводами на железобетонных опорах | 1,0 |
1 км ЛЭП напряжением 10 (6) кВ с защищенными проводами на деревянных опорах | 1,3 |
1 км ЛЭП напряжением 10 (6) кВ с голыми проводами на железобетонных опорах | 3,0 |
1 км ЛЭП напряжением 10 (6) кВ с голыми проводами на деревянных опорах | 3,3 |
1 км ЛЭП 35 (20) кВ с защищенными проводами | 1,5 |
1 км ЛЭП 35 (20) кВ с голыми проводами | 4,0 |
1 км ЛЭП типа "два провода - рельс", расположенная на опорах контактной сети | 1,3 |
1 км ЛЭП типа двухцепных линий напряжением 10 (6) кВ с голыми проводами на железобетонных опорах | 4,0 |
1 км ЛЭП типа двухцепных линий напряжением 10 (6) кВ с голыми проводами на деревянных опорах | 4,3 |
1 км ЛЭП типа двухцепных линий напряжением 10 (6) кВ с защищенными проводами на железобетонных опорах | 1,5 |
1 км ЛЭП типа двухцепных линий напряжением 10 (6) кВ с защищенными проводами на деревянных опорах | 1,8 |
1 км ЛЭП типа двухцепных линий напряжением 35 (20) кВ с голыми проводами | 3,5 |
1 км ЛЭП типа двухцепных линий напряжением 35 (20) кВ с защищенными проводами | 2,0 |
1 км ЛЭП напряжением 10 (6) кВ с защищенными проводами, расположенная на опорах контактной сети | 1,5 |
1 км ЛЭП напряжением 10 (6) кВ с голыми проводами, расположенная на опорах контактной сети | 3,8 |
Таблица 10
Срок эксплуатации ЛЭП | |
Менее 15 лет | 1,0 |
От 15 лет и до 20 лет | 1,1 |
От 20 лет и до 25 лет | 1,2 |
От 25 лет и до 30 лет | 1,3 |
От 30 лет и до 50 лет | 1,5 |
50 лет и более | 1,7 |
Таблица 11
Остаточный срок службы ЛЭП | |
5 и более лет (по данным контрольно-оценочной карты) | 1,0 |
от 0 до 5 лет (по данным контрольно-оценочной карты) | 2,0 |
Таблица 12
Классы железнодорожных линий | |
1 | 1,0 |
2 | 0,89 |
3 | 0,8 |
4 | 0,72 |
5 | 0,72 |
Модель нормирования показателей надежности (далее - Модель), применяемая в настоящей Методике, предусматривает последовательное соединение эталонных объектов на всех иерархических уровнях моделирования (уровень "единичного объекта", уровень "составного объекта", уровень "глобального объекта"). В связи с данным условием уровень "единичного объекта" при моделировании не рассматривается, а "составной объект" является объектом оценки (группой объектов заданного вида, для которой выполняется нормирование показателей надежности).
Применяемая в настоящей Методике Модель (рисунок 1) включает в себя:
модель глобального объекта;
модель эталонного объекта;
модель объекта оценки;
модель коррекции размерности объекта и длительности интервала наблюдения.
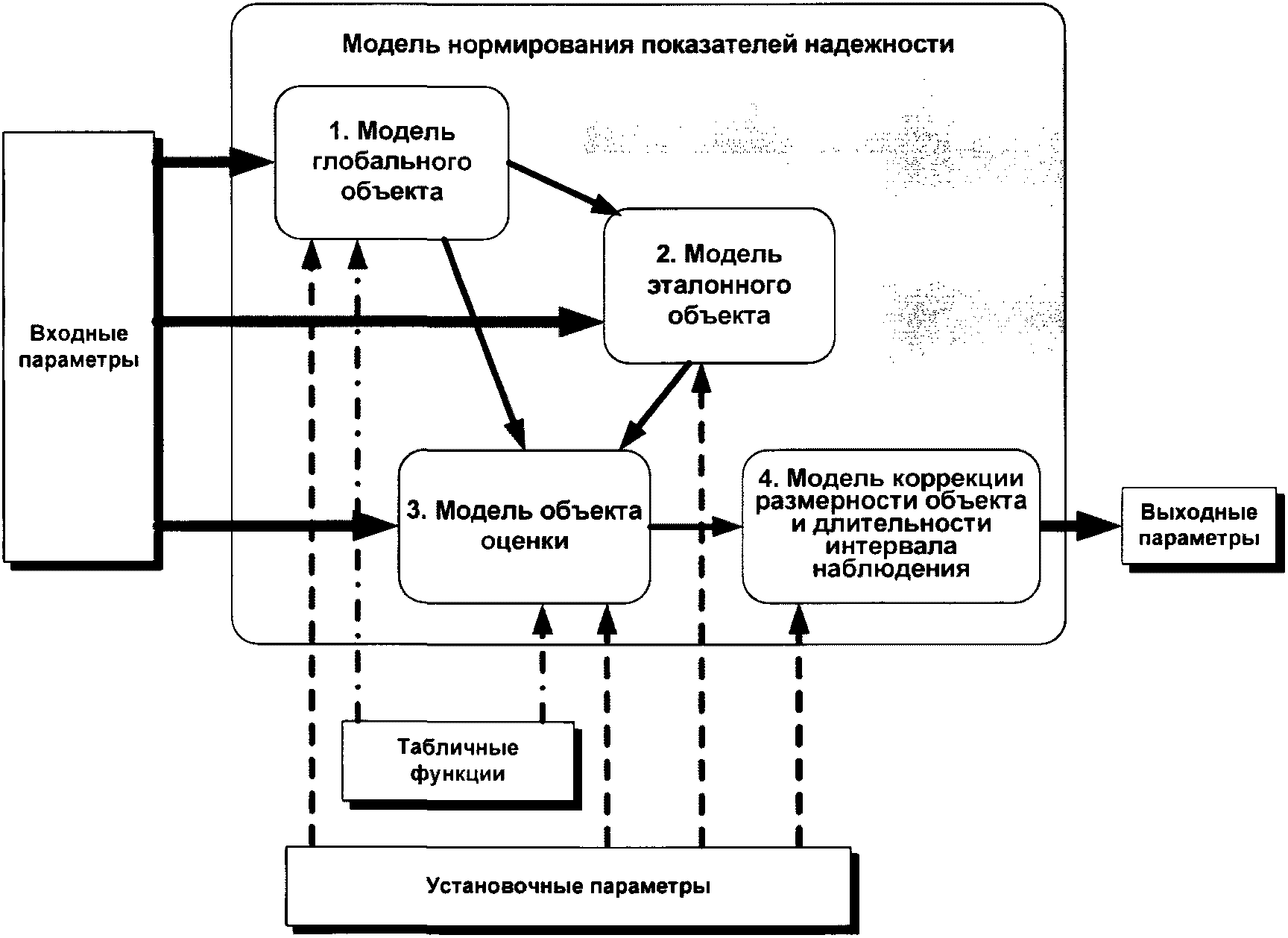
Вышеперечисленные модели, описывающие характеристики объектов по их видам, будут рассмотрены далее.
Входные параметры Модели будут рассмотрены применительно к моделям глобального объекта, эталонного объекта и объекта оценки.
Выходные параметры Модели включают следующие допустимые (нормативные) показатели, применимые к объекту оценки:
допустимый коэффициент готовности;
допустимую интенсивность отказов, 1/ч;
допустимое среднее время до восстановления, ч.
Табличные функции, применяемые в Модели, приведены в приложении N 1 к настоящей Методике. Данные функции определяют:
квантиль теоретического распределения, описывающего ряды количества отказов и среднего времени до восстановления (в модели глобального объекта);
коэффициент доверительного интервала, корректирующий характеристические значения допустимых показателей в зависимости от размерности объекта оценки и длительности заданного интервала наблюдения.
Установочные параметры Модели включают набор параметров, необходимых для настройки применяемых в Модели значений доверительных вероятностей, интервала наблюдения (для модели глобального объекта), коэффициентов ответственности по видам объектов, корректирующих индексов, коэффициентов связности и т.п. Перечень установочных параметров Модели приведен в таблице 13.
Для объединения показателей по видам объектов в интегральный показатель, применяемый к объектам всех видов, в настоящей Методике вводятся коэффициенты ответственности (весовые коэффициенты), отражающие значимость каждого вида объектов (таблица 13).
Таблица 13
N | Обозначение | Характеристика | Возможные значения | Рекомендуемое значение |
1 | an | Доверительная вероятность для оценки верхней границы количества отказов (модель глобального объекта) | 0,8; 0,9; 0,95 | 0,9 |
2 | at | Доверительная вероятность для оценки верхней границы среднего времени до восстановления (модель глобального объекта) | 0,8; 0,9; 0,95 | 0,9 |
3 | TнG | Интервал наблюдения для оценки параметров глобального объекта, ч (модель глобального объекта) | 4380; 8760 | 8760 |
4 | L | Количество интервалов наблюдения для оценки параметров глобального объекта (модель глобального объекта) | 6; 7; 8; 9; 10 | 7 |
5 | k1 | Коэффициент ответственности объектов вида 1 - "контактная сеть" (модели глобального объекта, эталонного объекта, объекта оценки) | 0,35...0,7 | 0,65 |
6 | k2 | Коэффициент ответственности объектов вида 2 - "тяговая подстанция" (модели глобального объекта, эталонного объекта, объекта оценки) | 0,15...0,3 | 0,2 |
7 | k3 | Коэффициент ответственности объектов вида 3 - "ЛЭП" (модели глобального объекта, эталонного объекта, объекта оценки) | 1 - (k1 + k2) | 0,15 |
8 | Корректирующий индекс коэффициента доверительной границы для количества отказов (модель коррекции размерности объекта и длительности интервала наблюдения) | -0,50...0,50 | -0,12 | |
9 | Корректирующий индекс коэффициента доверительной границы для среднего времени до восстановления (модель коррекции размерности объекта и длительности интервала наблюдения) | -0,50...0,50 | -0,25 | |
10 | Корректирующий индекс коэффициента доверительной границы для коэффициента неготовности (модель коррекции размерности объекта и длительности интервала наблюдения) | -1,50...1,00 | -1,25 | |
11 | Bn | Коэффициент связности моделей глобального и эталонного объектов для количества отказов (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,80...3,20 | 1,80 |
12 | Bt | Коэффициент связности моделей глобального и эталонного объектов для среднего времени до восстановления (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,80...3,20 | 1,08 |
13 | BA | Коэффициент связности моделей глобального и эталонного объектов для коэффициента неготовности (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,80...3,20 | 1,78 |
14 | Корректирующий индекс компенсации размерности объекта оценки (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,50...1,50 | 1,10 | |
15 | Dn | Коэффициент компенсации размерности объекта оценки для количества отказов (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,00...0,30 | 0,17 |
16 | Dt | Коэффициент компенсации размерности объекта оценки для среднего времени до восстановления (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,00...0,30 | 0,00 |
17 | DA | Коэффициент компенсации размерности объекта оценки для коэффициента неготовности (модель коррекции размерности объекта и длительности интервала наблюдения) | 0,00...0,30 | 0,08 |
18 | b | Порог коррекции суммарного времени неготовности | 0,1...0,5 | 0,2 |
Модель глобального объекта применяется для описания характеристик надежности объектов электроснабжения заданного вида (или всех видов) по хозяйству электроснабжения в целом ("вся сеть") на основе статистических данных за несколько интервалов наблюдения. Поскольку для хозяйства в целом за интервал наблюдения 4380 или 8760 ч объем выборки, как правило, является достаточным, полученные значения позволяют определить уровень показателей, обеспечиваемый с заданной доверительной вероятностью, путем подбора теоретической функции обеспеченности.
Входные параметры модели глобального объекта:
ряд значений n1i, n2i, ..., nLi количества отказов всех объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") по хозяйству электроснабжения за L последовательных интервалов наблюдения длительностью TнG (отказы КАСАНТ по ответственности Трансэнерго; вариант 1: 1 и 2 категории; вариант 2: 1, 2 и 3 категории) <1>;
ряд значений Tв1i, Tв2i, ..., TвLi суммарного времени до восстановления после отказов всех объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") по хозяйству электроснабжения за L последовательных интервалов наблюдения длительностью TнG (отказы КАСАНТ по ответственности Трансэнерго; вариант 1: 1 и 2 категории; вариант 2: 1, 2 и 3 категории) <1>.
--------------------------------
<1> При нормировании показателей надежности на 01 декабря, данные количества отказов и суммарного времени до восстановления текущего года берутся за 10 месяцев и умножаются на 1,2.
Выходные параметры модели глобального объекта:
характеристическое <1> количество  отказов глобального объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
отказов глобального объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
--------------------------------
<1> Здесь и далее под "характеристическим" показателем понимается показатель, не учитывающий необходимую коррекцию размерности объекта и длительности интервала наблюдения.
характеристическое среднее время 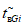 до восстановления глобального объекта вида i (i = 0 - все виды объектов; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП").
до восстановления глобального объекта вида i (i = 0 - все виды объектов; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП").
Расчет выходных параметров модели глобального объекта:
1) Из двух исходных рядов формируется ряд значений среднего времени до восстановления:
где tвli - значение среднего времени до восстановления для l-го интервала наблюдения (l = 1...L) для объектов вида i (i = 1, 2, 3); Tвli - значение суммарного времени до восстановления для l-го интервала наблюдения (l = 1...L) для объектов вида i (i = 1, 2, 3); nli - значение количества отказов для l-го интервала наблюдения (l = 1...L) для объектов вида i (i = 1, 2, 3).
Дальнейшие расчеты выполняются для значений ряда n количества отказов и ряда tв среднего времени до восстановления.
2) Выполняется проверка рядов n и tв на аномальные значения и (при необходимости) коррекция аномальных значений. Для этого оба ряда упорядочиваются по убыванию их значений. Таким образом, в упорядоченном ряду максимальное значение будет у элемента n1i (tв1i), а минимальное - у элемента nLi (tвLi).
Для каждого из двух рядов вычисляется математическое ожидание и среднеквадратическое отклонение по следующим формулам:
Если среднеквадратическое отклонение ряда равно 0, то принимается, что этот ряд не содержит аномальных точек и проверку данного ряда заканчивают.
При среднеквадратическом отклонении больше 0 вычисляют характеристические отклонения Z (для проверки на аномальность элемента упорядоченного ряда с максимальным значением) и Y (для проверки на аномальность элемента упорядоченного ряда с минимальным значением):
Для заданного L рассчитывается функция Ирвина:
Если Zni > I (Zti > I), то значение элемента n1i (tв1i) упорядоченного ряда считается аномальным и для коррекции ряда принимается
n1i = n2i + 0,125·Sni·I (tв1i = tв2i + 0,125·Sti·I). (17)
Если Yni > I (Yti > I), то значение элемента nLi (tвLi) упорядоченного ряда считается аномальным и для коррекции ряда принимается
nLi = n(L-1)i - 0,125·Sni·I
(tвLi = tв(L-1)i - 0,125·Sti·I). (18)
В случае, когда для ряда выполнялась хотя бы одна коррекция аномального значения, следует заново пересчитать его математическое ожидание по формулам (12) для применения в дальнейших расчетах.
3) Для каждого из рядов, прошедших процедуру проверки и коррекции аномальных точек (включая перерасчет математического ожидания), рассчитывается коэффициент вариации:
Если Cvni < 0,1 (Cvti < 0,1), то для дальнейших расчетов принимают Cvni = 0,1 (Cvti = 0,1).
4) Для каждого из рядов, прошедших процедуру проверки и коррекции аномальных точек (включая перерасчет математического ожидания), рассчитывается отношение Cr коэффициента асимметрии к коэффициенту вариации:
5) После расчета Cvni, Cvti, Crni, Crti выполняем их округление по следующим правилам.
Результат Cvni (Cvti) округляется до ближайшего значения, кратного 0,1 (0,1; 0,2; 0,3 и т.д.).
Результат Crni (Crti) округляется до ближайшего значения, кратного 0,5 (0; +/- 0,5; +/- 1,0; +/- 1,5 и т.д.); при этом если после такого округления Crni (Crti) превышает 6, то принимается Crni = 6,0 (Crti = 6,0); если после такого округления значение Crni (Crti) менее (-6), то принимается Crni = -6,0 (Crti = -6,0).
6) По табличным значениям функции обеспеченности для трехпараметрического гамма-распределения для заданной вероятности необеспеченности an (at) (приложение N 1, таблица П1.1 для вероятности обеспеченности 0,8; таблица П1.2 для вероятности обеспеченности 0,9; таблица П1.3 для вероятности обеспеченности 0,95) и полученных выше значений Cvni, Crni (Cvti, Crti) определяется соответствующая ордината yn (yt) в виде модульного коэффициента. Для получения оценки допустимого количества отказов (или допустимого среднего времени до восстановления) данную ординату следует умножить на математическое ожидание исходного ряда:
В случае получения значения Crni < -2,0 (Crti < -2,0), а также если -2,0 < Crni < 0 (-2,0 < Crti < 0) и для полученного значения Cvni (Cvti) табличные значения ординат распределения отсутствуют, искомую ординату для заданной вероятности необеспеченности 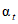 или
или  определяют по модифицированным таблицам (приложение N 1, таблица П1.4 для вероятности обеспеченности 0,8; таблица П1.5 для вероятности обеспеченности 0,9; таблица П1.6 для вероятности обеспеченности 0,95) и полученных выше значений Cvni, Crni (Cvti, Crti). Далее получают оценку допустимого количества отказов (или допустимого среднего времени до восстановления) с помощью преобразования <1>:
определяют по модифицированным таблицам (приложение N 1, таблица П1.4 для вероятности обеспеченности 0,8; таблица П1.5 для вероятности обеспеченности 0,9; таблица П1.6 для вероятности обеспеченности 0,95) и полученных выше значений Cvni, Crni (Cvti, Crti). Далее получают оценку допустимого количества отказов (или допустимого среднего времени до восстановления) с помощью преобразования <1>:
--------------------------------
<1> Данное преобразование требует, чтобы nli/Mni <= 2 и tвli/Mti <= 2 для всех возможных значений l.
7) Коррекция допустимого суммарного времени неготовности
В модели, предусматривающей последовательное соединение объектов, не может быть учтена частичная одновременность восстановлений объектов после отказов. При этом возможна ситуация, когда суммарное время неготовности глобального объекта nGi·tвGi превышает длительность интервала наблюдения TнG. Такая ситуация приводит к некорректному расчету интенсивности отказов и коэффициента готовности, в случае чего указанные параметры имеют отрицательные значения. Для предупреждения такой ситуации применяется специальная коррекция суммарного времени неготовности глобального объекта.
Вычисляется параметр неготовности 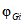 объектов вида i глобального объекта:
объектов вида i глобального объекта:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); nGi - допустимое количество отказов объектов вида i (i = 1, 2, 3) глобального объекта за интервал наблюдения TнG; tвGi - допустимое среднее время до восстановления объектов вида i (i = 1, 2, 3) глобального объекта за интервал наблюдения TнG.
Вычисляется коэффициент 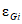 коррекции суммарного времени неготовности объектов вида i глобального объекта:
коррекции суммарного времени неготовности объектов вида i глобального объекта:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); b - порог коррекции суммарного времени неготовности (см. таблицу 13);  - параметр неготовности объектов вида i (i = 0...3) глобального объекта.
- параметр неготовности объектов вида i (i = 0...3) глобального объекта.
8) Полученные выше значения nGi и tвGi учитывают, что интервал наблюдения является конечным и что размерность объекта ограничена. Для обеспечения корректных расчетов эти значения следует преобразовать в характеристические параметры:
где i - вид объектов (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); 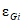 - коэффициент коррекции суммарного времени неготовности объектов вида i (i = 1, 2, 3) глобального объекта; nGi - допустимое количество отказов объектов вида i (i = 0...3) глобального объекта; tвGi - допустимое среднее время до восстановления объектов вида i (i = 1, 2, 3) глобального объекта; W(·) - функция коэффициента доверительных границ от верхней доверительной границы количества отказов:
- коэффициент коррекции суммарного времени неготовности объектов вида i (i = 1, 2, 3) глобального объекта; nGi - допустимое количество отказов объектов вида i (i = 0...3) глобального объекта; tвGi - допустимое среднее время до восстановления объектов вида i (i = 1, 2, 3) глобального объекта; W(·) - функция коэффициента доверительных границ от верхней доверительной границы количества отказов:
где i - вид объектов (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); nв1, nв2 - аргументы табличной функции коэффициента доверительных границ от верхней доверительной границы количества отказов, следующие в таблице друг за другом, причем 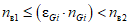 ; W(nв1), W(nв2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ (приложение N 1, таблица П1.7).
; W(nв1), W(nв2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ (приложение N 1, таблица П1.7).
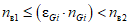 ; W(nв1), W(nв2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ (приложение N 1, таблица П1.7).
; W(nв1), W(nв2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ (приложение N 1, таблица П1.7).9) Рассчитывается характеристическое среднее время до восстановления для глобального объекта по всем видам объектов (i = 0):
где k1, k2, k3 - коэффициенты ответственности для объектов вида 1, 2, 3 соответственно (таблица 13).
Модель эталонного объекта применяется для описания характеристик надежности эталонного объекта заданного вида, который является "измерителем" реальных объектов этого вида.
Входные параметры модели эталонного объекта:
эквивалентное количество 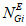 эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для глобального объекта ("вся сеть");
эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для глобального объекта ("вся сеть");
характеристическое количество  отказов глобального объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
отказов глобального объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
интервал наблюдения Tн, для которого нормируются показатели надежности;
Выходные параметры модели эталонного объекта:
характеристическое количество 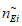 отказов эталонного объекта вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
отказов эталонного объекта вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
коэффициент gi интегрирования эквивалентного количества эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
эквивалентное количество 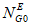 эталонных объектов всех видов (i = 0) для глобального объекта.
эталонных объектов всех видов (i = 0) для глобального объекта.
Расчет выходных параметров модели эталонного объекта:
1) Характеристическое количество отказов эталонного объекта:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");  - характеристическое количество отказов глобального объекта вида i (i = 1, 2, 3); Tн - интервал наблюдения, для которого нормируются показатели надежности;
- характеристическое количество отказов глобального объекта вида i (i = 1, 2, 3); Tн - интервал наблюдения, для которого нормируются показатели надежности;  - эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для глобального объекта; TнG - интервал наблюдения для оценки параметров глобального объекта.
- эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для глобального объекта; TнG - интервал наблюдения для оценки параметров глобального объекта.
Характеристическое количество отказов эталонного объекта для всех видов объектов (i = 0) рассчитывается по формуле:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); ki (k1, k2, k3) - коэффициенты ответственности для объектов вида i (1, 2, 3) соответственно (таблица 13).
2) Коэффициент интеграции эквивалентного количества эталонных объектов:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");  - характеристическое количество отказов эталонного объекта вида i;
- характеристическое количество отказов эталонного объекта вида i;  - характеристическое количество отказов эталонного объекта для всех видов объектов; ki (k1, k2, k3) - коэффициенты ответственности для объектов вида i (1, 2, 3) соответственно (таблица 13).
- характеристическое количество отказов эталонного объекта для всех видов объектов; ki (k1, k2, k3) - коэффициенты ответственности для объектов вида i (1, 2, 3) соответственно (таблица 13).
3) Эквивалентное количество эталонных объектов всех видов (i = 0) для глобального объекта
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); gi - коэффициент интегрирования эквивалентного количества эталонных объектов вида i (i = 1, 2, 3) 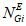 - эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для глобального объекта.
- эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для глобального объекта.
Модель объекта оценки применяется для описания характеристик надежности реального объекта (группы объектов) заданного вида (или всех видов), который представляется как эквивалентное (реальному объекту) количество эталонных объектов.
Входные параметры модели объекта оценки:
количество  единичных (реальных) объектов вида i в составе объекта оценки (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") - анкерных участков контактной сети, тяговых подстанций, километров ЛЭП;
единичных (реальных) объектов вида i в составе объекта оценки (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") - анкерных участков контактной сети, тяговых подстанций, километров ЛЭП;
эквивалентное количество 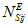 эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для j-го
эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для j-го  единичного (реального) объекта вида i.
единичного (реального) объекта вида i.
 единичного (реального) объекта вида i.
единичного (реального) объекта вида i.Выходные параметры модели объекта оценки:
характеристическое количество 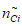 отказов объекта оценки вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
отказов объекта оценки вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП");
коэффициент доверительных границ (функция коэффициента доверительных границ от количества отказов) объекта оценки вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП").
Расчет выходных параметров модели объекта оценки:
1) Для получения характеристического количества отказов объекта оценки сначала определяем эквивалентное количество эталонных объектов в составе объекта оценки <1>:
--------------------------------
<1> Если эквивалентное количество эталонных объектов для объекта оценки является известным, то расчет по данной формуле пропускается.
 , (32)
, (32)где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); 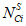 - количество единичных (реальных) объектов вида i в составе объекта оценки;
- количество единичных (реальных) объектов вида i в составе объекта оценки; 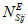 - эквивалентное количество эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для j-го
- эквивалентное количество эталонных объектов вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") для j-го 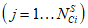 единичного (реального) объекта вида i
единичного (реального) объекта вида i
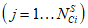 единичного (реального) объекта вида i
единичного (реального) объекта вида iДалее определяем эквивалентное количество эталонных объектов всех видов (i = 0) для объекта оценки:
где i - вид объекта (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); gi - коэффициент интегрирования эквивалентного количества эталонных объектов вида i (i = 1, 2, 3); 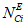 - эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для объекта оценки.
- эквивалентное количество эталонных объектов вида i (i = 1, 2, 3) для объекта оценки.
Характеристическое количество отказов объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); 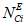 - эквивалентное количество эталонных объектов вида i (i = 0...3) в составе объекта оценки
- эквивалентное количество эталонных объектов вида i (i = 0...3) в составе объекта оценки  - характеристическое количество отказов эталонного объекта вида i (i = 0...3).
- характеристическое количество отказов эталонного объекта вида i (i = 0...3).
2) Коэффициент доверительных границ (функция коэффициента доверительных границ от количества отказов):
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); n1, n2 - аргументы табличной функции коэффициента доверительных границ от количества отказов, следующие в таблице друг за другом, причем 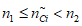 ; V(n1), V(n2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ от количества отказов (приложение N 1, таблица П1.8).
; V(n1), V(n2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ от количества отказов (приложение N 1, таблица П1.8).
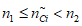 ; V(n1), V(n2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ от количества отказов (приложение N 1, таблица П1.8).
; V(n1), V(n2) - соответствующие этим аргументам значения табличной функции коэффициента доверительных границ от количества отказов (приложение N 1, таблица П1.8).Данная модель реализует функции согласования параметров, полученных с помощью рассмотренных выше моделей, с размерностью объекта оценки, длительностью интервала наблюдения и необходимых масштабных коэффициентов (с учетом специфики эксплуатации и технического обслуживания существующих объектов электроснабжения).
Входные параметры модели коррекции размерности объекта и длительности интервала наблюдения:
коэффициент  доверительных границ для характеристического количества
доверительных границ для характеристического количества  отказов объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки;
отказов объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП") объекта оценки;
эквивалентное количество 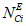 эталонных объектов вида i (i = 0...3) для объекта оценки;
эталонных объектов вида i (i = 0...3) для объекта оценки;
эквивалентное количество 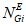 эталонных объектов вида i (i = 0...3) для глобального объекта.
эталонных объектов вида i (i = 0...3) для глобального объекта.
Выходные параметры модели коррекции размерности объекта и длительности интервала наблюдения:
корректирующий коэффициент hni для расчета допустимой (нормативной) интенсивности отказов объекта оценки вида i (i = 0...3);
корректирующий коэффициент hti для расчета допустимого (нормативного) среднего времени до восстановления объекта оценки вида i (i = 0...3);
корректирующий коэффициент hAi для расчета допустимого (нормативного) коэффициента готовности объекта оценки вида i (i = 0...3).
Расчет выходных параметров модели коррекции размерности объекта и длительности интервала наблюдения:
1) Корректирующий коэффициент для расчета допустимой (нормативной) интенсивности отказов объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); Bn - коэффициент связности моделей глобального объекта и эталонного объекта для количества отказов; 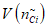 - коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки;
- коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки;  - корректирующий индекс коэффициента доверительной границы для количества отказов; Dn - коэффициент компенсации размерности объекта оценки для количества отказов;
- корректирующий индекс коэффициента доверительной границы для количества отказов; Dn - коэффициент компенсации размерности объекта оценки для количества отказов;  - эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки;  - эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта;  - корректирующий индекс компенсации размерности объекта оценки.
- корректирующий индекс компенсации размерности объекта оценки.
2) Корректирующий коэффициент для расчета допустимого (нормативного) среднего времени до восстановления объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); Bt - коэффициент связности моделей глобального объекта и эталонного объекта для среднего времени до восстановления;  - коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки;
- коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки; 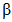 - корректирующий индекс коэффициента доверительной границы для среднего времени до восстановления; Dt - коэффициент компенсации размерности объекта оценки для среднего времени до восстановления;
- корректирующий индекс коэффициента доверительной границы для среднего времени до восстановления; Dt - коэффициент компенсации размерности объекта оценки для среднего времени до восстановления; 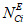 - эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки; 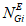 - эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта; 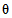 - корректирующий индекс компенсации размерности объекта оценки.
- корректирующий индекс компенсации размерности объекта оценки.
3) Корректирующий коэффициент для расчета допустимого (нормативного) коэффициента готовности объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); BA - коэффициент связности моделей глобального объекта и эталонного объекта для коэффициента неготовности; 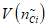 - коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки;
- коэффициент доверительной границы для характеристического количества отказов объектов вида i (i = 0...3) объекта оценки; 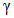 - корректирующий индекс коэффициента доверительной границы для коэффициента неготовности; DA - коэффициент компенсации размерности объекта оценки для коэффициента неготовности;
- корректирующий индекс коэффициента доверительной границы для коэффициента неготовности; DA - коэффициент компенсации размерности объекта оценки для коэффициента неготовности; 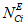 - эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки; 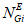 - эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта;
- эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта;  - корректирующий индекс компенсации размерности объекта оценки.
- корректирующий индекс компенсации размерности объекта оценки.
1) Допустимое (нормативное) среднее время до восстановления, ч, объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); hti - корректирующий коэффициент для расчета допустимого (нормативного) среднего времени до восстановления объектов вида i (i = 0...3) объекта оценки; 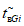 - характеристическое среднее время до восстановления, ч, объектов вида i (i = 0...3) глобального объекта.
- характеристическое среднее время до восстановления, ч, объектов вида i (i = 0...3) глобального объекта.
Показатели tв.н1, tв.н2, tв.н3 и tв.н0 после их вычисления для представления результатов округляются в большую сторону до 3 знаков после запятой (десятичные знаки, начиная от 4-го после запятой, отбрасываются и к полученному значению прибавляется число 0,001).
2) Допустимая (нормативная) интенсивность отказов, 1/ч, объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); hni - корректирующий коэффициент для расчета допустимой (нормативной) интенсивности отказов объекта оценки;  - характеристическое количество отказов объектов вида i (i = 0...3) объекта оценки; Tн - интервал наблюдения, ч;
- характеристическое количество отказов объектов вида i (i = 0...3) объекта оценки; Tн - интервал наблюдения, ч; 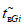 - характеристическое среднее время до восстановления объектов вида i (i = 0...3) глобального объекта.
- характеристическое среднее время до восстановления объектов вида i (i = 0...3) глобального объекта.
Показатели  ,
,  ,
,  и
и 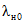 после их вычисления для представления результатов округляются в большую сторону до 7 знаков после запятой (десятичные знаки, начиная от 8-го после запятой, отбрасываются и к полученному значению прибавляется число 0,0000001).
после их вычисления для представления результатов округляются в большую сторону до 7 знаков после запятой (десятичные знаки, начиная от 8-го после запятой, отбрасываются и к полученному значению прибавляется число 0,0000001).
3) Допустимый (нормативный) коэффициент готовности объекта оценки:
где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); hAi - корректирующий коэффициент для расчета допустимого (нормативного) коэффициента готовности объектов вида i (i = 0...3) объекта оценки; 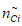 - характеристическое количество отказов объектов вида i (i = 0...3) объекта оценки;
- характеристическое количество отказов объектов вида i (i = 0...3) объекта оценки; 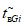 - характеристическое среднее время до восстановления, ч, объектов вида i (i = 0...3) глобального объекта; Tн - интервал наблюдения, ч.
- характеристическое среднее время до восстановления, ч, объектов вида i (i = 0...3) глобального объекта; Tн - интервал наблюдения, ч.
Показатели Kг.н1, Kг.н2, Kг.н3 и Kг.н0 после их вычисления для представления результатов округляются в меньшую сторону до 6 знаков после запятой (десятичные знаки, начиная от 7-го после запятой, отбрасываются).
Пример расчета допустимых (нормативных) показателей надежности приведен в приложении N 3 к настоящей Методике.
Оценка соответствия фактических и нормативных значений показателей надежности выполняется на основе сравнения фактических и нормативных значений с последующим нормированием результата. Результат соответствия выражается в процентах, со знаком "плюс" или "минус" (либо без знака, если результат соответствия равен 0). При этом для среднего времени до восстановления и интенсивности отказов знак "минус" (или нулевой результат) означает, что фактический показатель не хуже допустимого, знак "плюс" - что фактический показатель хуже допустимого. Для коэффициента готовности знак "минус" означает, что фактический показатель хуже допустимого, знак "плюс" (или нулевой результат) - что фактический показатель не хуже допустимого.
Формулы для оценки соответствия:
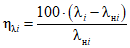 , (43)
, (43)где i - вид объекта (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "ЛЭП"); 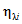 - оценка соответствия фактического и допустимого значений интенсивности отказов;
- оценка соответствия фактического и допустимого значений интенсивности отказов; 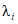 - значение фактической интенсивности отказов;
- значение фактической интенсивности отказов;  - значение допустимой интенсивности отказов;
- значение допустимой интенсивности отказов; 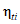 - оценка соответствия фактического и допустимого значений среднего времени до восстановления; tвi - значение фактического среднего времени до восстановления; tв.нi - значение допустимого среднего времени до восстановления;
- оценка соответствия фактического и допустимого значений среднего времени до восстановления; tвi - значение фактического среднего времени до восстановления; tв.нi - значение допустимого среднего времени до восстановления; 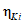 - оценка соответствия фактического и допустимого значений коэффициента готовности; Kгi - значение фактического коэффициента готовности; Kг.нi - значение допустимого коэффициента готовности.
- оценка соответствия фактического и допустимого значений коэффициента готовности; Kгi - значение фактического коэффициента готовности; Kг.нi - значение допустимого коэффициента готовности.
Все расчеты данного пункта применимы к выбранному объекту оценки.
Пример оценки соответствия фактических и допустимых (нормативных) показателей надежности приведен в приложении N 3 к настоящей Методике.
Определение порядка повышения надежности технических средств
В данном разделе содержится порядок принятия решений по повышению надежности технических средств на основе показателей надежности УРРАН с учетом уровней корпоративного управления.
1) Для определения степени соответствия фактических значений показателей надежности допустимым (нормативным) значениям применяется следующий критерий:
если оценка соответствия 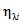
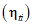 фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) имеет знак "минус" (отрицательное отклонение) или равна 0%, то по данному показателю нормы выполняются (оценка 0 баллов);
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) имеет знак "минус" (отрицательное отклонение) или равна 0%, то по данному показателю нормы выполняются (оценка 0 баллов);
если оценка соответствия 
 фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет более 0%, но менее +20%, то по данному показателю имеется несущественное превышение нормы (оценка 12 баллов);
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет более 0%, но менее +20%, то по данному показателю имеется несущественное превышение нормы (оценка 12 баллов);
если оценка соответствия 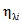
 фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет +20% и более, то по данному показателю имеется существенное превышение нормы (оценка 24 балла).
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет +20% и более, то по данному показателю имеется существенное превышение нормы (оценка 24 балла).
если оценка соответствия 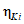 фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) имеет знак "плюс" (положительное отклонение) или равна 0%, то по данному показателю нормы выполняются (оценка 0 баллов);
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) имеет знак "плюс" (положительное отклонение) или равна 0%, то по данному показателю нормы выполняются (оценка 0 баллов);
если оценка соответствия  фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет менее 0%, но не ниже "минус 20%", то по данному показателю имеется несущественное невыполнение нормы (оценка 12 баллов);
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет менее 0%, но не ниже "минус 20%", то по данному показателю имеется несущественное невыполнение нормы (оценка 12 баллов);
если оценка соответствия 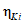 фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет "минус 20%" и ниже, то по данному показателю имеется существенное невыполнение нормы (оценка 24 балла).
фактического и нормативного значений показателя для заданного вида i объектов (i = 0...3) составляет "минус 20%" и ниже, то по данному показателю имеется существенное невыполнение нормы (оценка 24 балла).
Баллы в соответствии с данным критерием суммируются по всем трем показателям надежности для каждого из выбранных объектов оценки (например, дирекции по энергообеспечению) на нескольких (M > 5) одинаковых интервалах наблюдения (например, месяц) и затем усредняются:
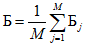 ,
,где Бj - суммарное количество баллов для данного объекта оценки за j-й интервал наблюдения (j = 1...M) по всем трем показателям надежности.
Проблемные объекты железнодорожного электроснабжения по критерию обеспечения заданных показателей надежности выявляются исходя из рейтинга балльных оценок.
Для различных уровней корпоративного управления устанавливаются определенные объекты оценки:
для центрального уровня (Трансэнерго) - дирекции по энергообеспечению;
для регионального уровня (дирекции по энергообеспечению) - ЭЧ (ЭЧК, ЭЧЭ, ЭЧС);
для линейного уровня - направления, участки, отдельные объекты.
После выявления проблемного объекта проводится его "детализация" - выявление конкретных структурных подразделений и конкретных объектов в их подчинении, контрольно-оценочных карт, оснащенности и укомплектованности подразделения персоналом, компетенции персонала, нарушения технологии, несоответствия проектных решений требованиям и других причин, из-за которых возникло несоответствие показателей надежности установленным нормам.
По результатам анализа причин необеспечения заданных показателей надежности, с учетом балльной оценки, принимается одно из следующих решений (таблица 14).
Таблица 14
Сценарии принятия решений
Баллы | Возможные решения |
От 0 и до 12 | - Мониторинг технического состояния объекта в штатном режиме. |
От 12 и до 36 | - Мониторинг технического состояния объекта в штатном режиме; и (или) - Улучшение технического содержания объекта; и (или) - Долгосрочное планирование модернизации и обновления объекта; и (или) - Рассмотрение необходимости капитального ремонта объекта. |
От 36 и до 54 | - Существенное улучшение технического содержания объекта; и (или) - Проверка и существенная корректировка технологического процесса; и (или) - Среднесрочное планирование модернизации и обновления; и (или) - Назначение капитального ремонта объекта. |
От 54 и до 72 | - Оперативное планирование модернизации и обновления объекта; и (или) - Проверка и существенная корректировка технологического процесса; и (или) - Пересмотр кадровой политики, повышение уровня квалификации персонала, уровня технической оснащенности службы эксплуатации. |
к Методике расчета
и нормирования показателей
надежности объектов
железнодорожного
электроснабжения
Таблица П1.1
от параметров Cr и Cv для вероятности обеспеченности 0,8
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-2,0 | 1,09 | 1,17 | 1,27 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,5 | 1,08 | 1,17 | 1,27 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,0 | 1,08 | 1,17 | 1,26 | 1,39 | - | - | - | - | - | - | - | - | - | - | - |
-0,5 | 1,08 | 1,17 | 1,26 | 1,37 | - | - | - | - | - | - | - | - | - | - | - |
0,0 | 1,08 | 1,17 | 1,26 | 1,36 | 1,47 | - | - | - | - | - | - | - | - | - | - |
0,5 | 1,08 | 1,17 | 1,25 | 1,35 | 1,44 | 1,56 | 1,70 | - | - | - | - | - | - | - | - |
1,0 | 1,08 | 1,17 | 1,25 | 1,34 | 1,42 | 1,51 | 1,60 | 1,70 | 1,80 | 1,90 | 2,00 | 2,10 | 2,20 | 2,32 | 2,44 |
1,5 | 1,08 | 1,16 | 1,25 | 1,32 | 1,40 | 1,47 | 1,54 | 1,61 | 1,67 | 1,72 | 1,76 | 1,80 | 1,82 | 1,83 | 1,83 |
2,0 | 1,08 | 1,16 | 1,24 | 1,31 | 1,38 | 1,44 | 1,50 | 1,54 | 1,58 | 1,61 | 1,62 | 1,63 | 1,62 | 1,61 | 1,59 |
2,5 | 1,08 | 1,16 | 1,23 | 1,30 | 1,36 | 1,14 | 1,45 | 1,49 | 1,52 | 1,54 | 1,55 | 1,56 | 1,56 | 1,55 | 1,54 |
3,0 | 1,08 | 1,16 | 1,23 | 1,29 | 1,34 | 1,38 | 1,42 | 1,45 | 1,47 | 1,49 | 1,50 | 1,50 | 1,50 | 1,49 | 1,48 |
3,5 | 1,08 | 1,16 | 1,22 | 1,28 | 1,32 | 1,36 | 1,39 | 1,42 | 1,44 | 1,45 | 1,46 | 1,46 | 1,46 | 1,45 | 1,44 |
4,0 | 1,08 | 1,15 | 1,22 | 1,27 | 1,31 | 1,34 | 1,37 | 1,40 | 1,41 | 1,42 | 1,43 | 1,44 | 1,43 | 1,43 | 1,42 |
4,5 | 1,08 | 1,15 | 1,21 | 1,26 | 1,30 | 1,33 | 1,36 | 1,38 | 1,40 | 1,41 | 1,41 | 1,41 | 1,41 | 1,41 | 1,40 |
5,0 | 1,08 | 1,15 | 1,21 | 1,25 | 1,30 | 1,32 | 1,34 | 1,36 | 1,36 | 1,39 | 1,40 | 1,40 | 1,40 | 1,39 | 1,39 |
5,5 | 1,08 | 1,15 | 1,20 | 1,24 | 1,28 | 1,31 | 1,33 | 1,36 | 1,37 | 1,38 | 1,39 | 1,39 | 1,39 | 1,39 | 1,38 |
6,0 | 1,08 | 1,14 | 1,19 | 1,23 | 1,27 | 1,30 | 1,32 | 1,34 | 1,36 | 1,37 | 1,38 | 1,38 | 1,38 | 1,38 | 1,37 |
Таблица П1.2
от параметров Cr и Cv для вероятности обеспеченности 0,9
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-2,0 | 1,13 | 1,25 | 1,35 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,5 | 1,13 | 1,25 | 1,36 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,0 | 1,13 | 1,25 | 1,37 | 1,49 | - | - | - | - | - | - | - | - | - | - | - |
-0,5 | 1,13 | 1,25 | 1,38 | 1,51 | - | - | - | - | - | - | - | - | - | - | - |
0,0 | 1,13 | 1,26 | 1,39 | 1,52 | 1,66 | - | - | - | - | - | - | - | - | - | - |
0,5 | 1,13 | 1,26 | 1,39 | 1,53 | 1,67 | 1,83 | 2,01 | - | - | - | - | - | - | - | - |
1,0 | 1,13 | 1,26 | 1,40 | 1,54 | 1,68 | 1,83 | 1,99 | 2,16 | 2,35 | 2,55 | 2,78 | 3,03 | 3,26 | 3,46 | 3,64 |
1,5 | 1,13 | 1,26 | 1,40 | 1,54 | 1,68 | 1,82 | 1,97 | 2,11 | 2,26 | 2,41 | 2,56 | 2,71 | 2,86 | 3,00 | 3,13 |
2,0 | 1,13 | 1,26 | 1,40 | 1,54 | 1,67 | 1,80 | 1,94 | 2,06 | 2,19 | 2,30 | 2,40 | 2,50 | 2,57 | 2,64 | 2,70 |
2,5 | 1,13 | 1,26 | 1,40 | 1,53 | 1,66 | 1,78 | 1,90 | 2,01 | 2,12 | 2,22 | 2,31 | 2,39 | 2,46 | 2,53 | 2,59 |
3,0 | 1,13 | 1,26 | 1,40 | 1,52 | 1,65 | 1,76 | 1,87 | 1,97 | 2,06 | 2,15 | 2,23 | 2,30 | 2,36 | 2,42 | 2,47 |
3,5 | 1,13 | 1,26 | 1,39 | 1,52 | 1,63 | 1,74 | 1,84 | 1,93 | 2,02 | 2,10 | 2,17 | 2,23 | 2,29 | 2,34 | 2,38 |
4,0 | 1,13 | 1,26 | 1,39 | 1,51 | 1,62 | 1,72 | 1,81 | 1,90 | 1,98 | 2,05 | 2,12 | 2,18 | 2,24 | 2,28 | 2,32 |
4,5 | 1,13 | 1,26 | 1,39 | 1,50 | 1,60 | 1,70 | 1,79 | 1,88 | 1,95 | 2,02 | 2,09 | 2,09 | 2,19 | 2,24 | 2,28 |
5,0 | 1,13 | 1,26 | 1,37 | 1,49 | 1,60 | 1,70 | 1,79 | 1,86 | 1,94 | 2,00 | 2,06 | 2,11 | 2,16 | 2,20 | 2,24 |
5,5 | 1,13 | 1,26 | 1,38 | 1,48 | 1,58 | 1,68 | 1,76 | 1,84 | 1,91 | 1,98 | 2,04 | 2,09 | 2,14 | 2,18 | 2,22 |
6,0 | 1,14 | 1,26 | 1,37 | 1,47 | 1,56 | 1,66 | 1,73 | 1,82 | 1,90 | 1,96 | 2,02 | 2,07 | 2,12 | 2,16 | 2,20 |
Таблица П1.3
от параметров Cr и Cv для вероятности обеспеченности 0,95
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-2,0 | 1,16 | 1,3 | 1,41 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,5 | 1,16 | 1,31 | 1,43 | - | - | - | - | - | - | - | - | - | - | - | - |
-1,0 | 1,16 | 1,32 | 1,46 | 1,56 | - | - | - | - | - | - | - | - | - | - | - |
-0,5 | 1,16 | 1,32 | 1,47 | 1,61 | - | - | - | - | - | - | - | - | - | - | - |
0,0 | 1,16 | 1,33 | 1,49 | 1,65 | 1,8 | - | - | - | - | - | - | - | - | - | - |
0,5 | 1,17 | 1,33 | 1,51 | 1,68 | 1,86 | 2,03 | 2,22 | - | - | - | - | - | - | - | - |
1,0 | 1,17 | 1,34 | 1,52 | 1,70 | 1,90 | 2,10 | 2,30 | 2,53 | 2,76 | 3,02 | 3,31 | 3,63 | 3,84 | 4,02 | 4,16 |
1,5 | 1,17 | 1,35 | 1,53 | 1,72 | 1,92 | 2,13 | 2,34 | 2,57 | 2,80 | 3,03 | 3,28 | 3,55 | 3,83 | 4,12 | 4,44 |
2,0 | 1,17 | 1,35 | 1,54 | 1,74 | 1,94 | 2,15 | 2,36 | 2,57 | 2,78 | 3,00 | 3,22 | 3,40 | 3,60 | 3,80 | 3,96 |
2,5 | 1,17 | 1,35 | 1,55 | 1,74 | 1,95 | 2,15 | 2,35 | 2,55 | 2,75 | 2,94 | 3,13 | 3,31 | 3,48 | 3,65 | 3,81 |
3,0 | 1,17 | 1,36 | 1,55 | 1,75 | 1,95 | 2,14 | 2,34 | 2,52 | 2,70 | 2,88 | 3,05 | 3,22 | 3,37 | 3,52 | 3,66 |
3,5 | 1,17 | 1,36 | 1,56 | 1,75 | 1,94 | 2,13 | 2,31 | 2,49 | 2,66 | 2,83 | 2,98 | 3,14 | 3,28 | 3,42 | 3,55 |
4,0 | 1,17 | 1,36 | 1,56 | 1,75 | 1,94 | 2,12 | 2,29 | 2,46 | 2,62 | 2,78 | 2,93 | 3,07 | 3,21 | 3,34 | 3,46 |
4,5 | 1,18 | 1,37 | 1,56 | 1,75 | 1,93 | 2,10 | 2,27 | 2,44 | 2,59 | 2,74 | 2,89 | 2,89 | 3,15 | 3,27 | 3,39 |
5,0 | 1,17 | 1,36 | 1,55 | 1,74 | 1,90 | 2,08 | 2,22 | 2,41 | 2,54 | 2,71 | 2,85 | 2,98 | 3,10 | 3,21 | 3,33 |
5,5 | 1,18 | 1,37 | 1,56 | 1,74 | 1,91 | 2,08 | 2,24 | 2,39 | 2,54 | 2,68 | 2,82 | 2,95 | 3,07 | 3,18 | 3,29 |
6,0 | 1,18 | 1,37 | 1,55 | 1,73 | 1,89 | 2,05 | 2,20 | 2,36 | 2,51 | 2,66 | 2,79 | 2,92 | 3,04 | 3,15 | 3,25 |
Таблица П1.4
гамма-распределения от параметров Cr и Cv
для вероятности обеспеченности 0,8
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-0,5 | - | - | - | - | 0,53 | 0,41 | 0,28 | - | - | - | - | - | - | - | - |
-1,0 | - | - | - | - | 0,55 | 0,45 | 0,34 | 0,24 | 0,15 | 0,09 | 0,05 | 0,02 | 0,02 | 0,01 | 0,00 |
-1,5 | - | - | - | 0,65 | 0,56 | 0,47 | 0,38 | 0,30 | 0,22 | 0,16 | 0,15 | 0,07 | 0,04 | 0,02 | 0,01 |
-2,0 | - | - | - | 0,66 | 0,57 | 0,50 | 0,42 | 0,35 | 0,28 | 0,22 | 0,18 | 0,13 | 0,09 | 0,07 | 0,05 |
-2,5 | 0,92 | 0,83 | 0,75 | 0,66 | 0,59 | 0,51 | 0,44 | 0,38 | 0,32 | 0,27 | 0,23 | 0,19 | 0,15 | 0,12 | 0,09 |
-3,0 | 0,92 | 0,83 | 0,75 | 0,67 | 0,60 | 0,53 | 0,47 | 0,41 | 0,35 | 0,31 | 0,26 | 0,22 | 0,19 | 0,16 | 0,13 |
-3,5 | 0,92 | 0,83 | 0,75 | 0,68 | 0,61 | 0,54 | 0,48 | 0,43 | 0,38 | 0,33 | 0,29 | 0,25 | 0,22 | 0,19 | 0,16 |
-4,0 | 0,92 | 0,83 | 0,75 | 0,68 | 0,61 | 0,55 | 0,50 | 0,44 | 0,40 | 0,35 | 0,31 | 0,27 | 0,24 | 0,21 | 0,19 |
-4,5 | 0,92 | 0,83 | 0,76 | 0,69 | 0,62 | 0,56 | 0,51 | 0,46 | 0,41 | 0,37 | 0,33 | 0,33 | 0,26 | 0,23 | 0,20 |
-5,0 | 0,91 | 0,83 | 0,75 | 0,69 | 0,63 | 0,57 | 0,52 | 0,47 | 0,42 | 0,38 | 0,34 | 0,30 | 0,27 | 0,25 | 0,22 |
-5,5 | 0,91 | 0,84 | 0,76 | 0,70 | 0,63 | 0,58 | 0,52 | 0,47 | 0,43 | 0,39 | 0,35 | 0,31 | 0,28 | 0,25 | 0,23 |
-6,0 | 0,91 | 0,84 | 0,77 | 0,70 | 0,64 | 0,58 | 0,53 | 0,48 | 0,44 | 0,40 | 0,36 | 0,32 | 0,29 | 0,26 | 0,24 |
Таблица П1.5
гамма-распределения от параметров Cr и Cv
для вероятности обеспеченности 0,9
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-0,5 | - | - | - | - | 0,34 | 0,22 | 0,12 | - | - | - | - | - | - | - | - |
-1,0 | - | - | - | - | 0,38 | 0,26 | 0,17 | 0,09 | 0,05 | 0,02 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 |
-1,5 | - | - | - | 0,52 | 0,41 | 0,31 | 0,22 | 0,15 | 0,09 | 0,05 | 0,03 | 0,01 | 0,01 | 0,00 | 0,00 |
-2,0 | - | - | - | 0,53 | 0,44 | 0,35 | 0,27 | 0,21 | 0,15 | 0,15 | 0,07 | 0,05 | 0,03 | 0,02 | 0,01 |
-2,5 | 0,88 | 0,76 | 0,65 | 0,55 | 0,46 | 0,38 | 0,31 | 0,25 | 0,20 | 0,16 | 0,12 | 0,09 | 0,07 | 0,05 | 0,03 |
-3,0 | 0,88 | 0,76 | 0,66 | 0,56 | 0,48 | 0,41 | 0,34 | 0,28 | 0,24 | 0,19 | 0,16 | 0,13 | 0,10 | 0,08 | 0,06 |
-3,5 | 0,88 | 0,76 | 0,66 | 0,58 | 0,50 | 0,43 | 0,37 | 0,31 | 0,26 | 0,22 | 0,19 | 0,15 | 0,13 | 0,10 | 0,09 |
-4,0 | 0,88 | 0,77 | 0,67 | 0,59 | 0,51 | 0,44 | 0,38 | 0,33 | 0,28 | 0,24 | 0,21 | 0,18 | 0,15 | 0,13 | 0,10 |
-4,5 | 0,88 | 0,77 | 0,68 | 0,60 | 0,52 | 0,46 | 0,40 | 0,35 | 0,30 | 0,26 | 0,22 | 0,22 | 0,17 | 0,14 | 0,12 |
-5,0 | 0,88 | 0,77 | 0,68 | 0,61 | 0,53 | 0,47 | 0,41 | 0,36 | 0,32 | 0,27 | 0,24 | 0,21 | 0,18 | 0,16 | 0,13 |
-5,5 | 0,88 | 0,78 | 0,69 | 0,61 | 0,54 | 0,48 | 0,42 | 0,37 | 0,33 | 0,28 | 0,25 | 0,22 | 0,19 | 0,16 | 0,14 |
-6,0 | 0,88 | 0,78 | 0,70 | 0,62 | 0,55 | 0,49 | 0,43 | 0,38 | 0,33 | 0,29 | 0,26 | 0,23 | 0,20 | 0,17 | 0,15 |
Таблица П1.6
гамма-распределения от параметров Cr и Cv
для вероятности обеспеченности 0,95
Cr | Cv | ||||||||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | |
-0,5 | - | - | - | - | 0,22 | 0,11 | 0,05 | - | - | - | - | - | - | - | - |
-1,0 | - | - | - | - | 0,26 | 0,16 | 0,08 | 0,04 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
-1,5 | - | - | - | 0,42 | 0,31 | 0,21 | 0,13 | 0,07 | 0,04 | 0,02 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 |
-2,0 | - | - | - | 0,45 | 0,34 | 0,26 | 0,18 | 0,12 | 0,08 | 0,05 | 0,03 | 0,02 | 0,01 | 0,00 | 0,00 |
-2,5 | 0,84 | 0,70 | 0,58 | 0,47 | 0,37 | 0,29 | 0,23 | 0,17 | 0,13 | 0,09 | 0,07 | 0,05 | 0,03 | 0,02 | 0,01 |
-3,0 | 0,84 | 0,71 | 0,59 | 0,49 | 0,40 | 0,33 | 0,26 | 0,21 | 0,17 | 0,13 | 0,10 | 0,08 | 0,06 | 0,04 | 0,03 |
-3,5 | 0,84 | 0,71 | 0,60 | 0,50 | 0,42 | 0,35 | 0,29 | 0,24 | 0,20 | 0,16 | 0,13 | 0,10 | 0,08 | 0,06 | 0,05 |
-4,0 | 0,85 | 0,72 | 0,61 | 0,52 | 0,44 | 0,37 | 0,31 | 0,26 | 0,22 | 0,18 | 0,15 | 0,12 | 0,10 | 0,08 | 0,06 |
-4,5 | 0,85 | 0,72 | 0,62 | 0,53 | 0,46 | 0,39 | 0,33 | 0,28 | 0,24 | 0,20 | 0,17 | 0,17 | 0,11 | 0,09 | 0,08 |
-5,0 | 0,84 | 0,73 | 0,63 | 0,55 | 0,47 | 0,40 | 0,34 | 0,29 | 0,25 | 0,21 | 0,18 | 0,15 | 0,13 | 0,11 | 0,09 |
-5,5 | 0,85 | 0,73 | 0,64 | 0,55 | 0,48 | 0,41 | 0,36 | 0,30 | 0,26 | 0,22 | 0,19 | 0,16 | 0,14 | 0,12 | 0,10 |
-6,0 | 0,85 | 0,74 | 0,65 | 0,56 | 0,49 | 0,43 | 0,37 | 0,32 | 0,27 | 0,23 | 0,20 | 0,17 | 0,15 | 0,12 | 0,11 |
Таблица П1.7
от верхней доверительной границы количества nв отказов
nв | W(nв) | nв | W(nв) | nв | W(nв) | nв | W(nв) | nв | W(nв) |
1,182009 | 2,364018 | 36,29847 | 1,296374 | 261,2361 | 1,088484 | 2058,655 | 1,029327 | 18173,27 | 1,009626 |
2,343638 | 2,343638 | 38,52892 | 1,284297 | 282,0443 | 1,084786 | 2261,451 | 1,027932 | 19177,98 | 1,009367 |
3,466797 | 2,311198 | 40,75235 | 1,273511 | 302,8221 | 1,081508 | 2464,123 | 1,026718 | 20182,57 | 1,009128 |
4,537456 | 2,268728 | 42,96935 | 1,263804 | 323,5728 | 1,078576 | 2666,686 | 1,025648 | 22191,41 | 1,008701 |
5,546568 | 2,218627 | 45,18043 | 1,255012 | 344,2989 | 1,075934 | 2869,152 | 1,024697 | 24199,86 | 1,008328 |
6,490100 | 2,163367 | 47,38606 | 1,247002 | 365,0029 | 1,073538 | 3071,531 | 1,023844 | 26207,97 | 1,007999 |
7,368370 | 2,105249 | 49,58663 | 1,239666 | 385,6865 | 1,071351 | 3273,833 | 1,023073 | 28215,77 | 1,007706 |
8,184992 | 2,046248 | 51,78249 | 1,232916 | 406,3514 | 1,069346 | 3476,064 | 1,022372 | 30223,30 | 1,007443 |
8,945729 | 1,987940 | 53,97395 | 1,226681 | 426,9991 | 1,067498 | 3678,230 | 1,021730 | 32230,58 | 1,007206 |
9,657466 | 1,931493 | 56,16131 | 1,220898 | 447,6309 | 1,065788 | 3880,336 | 1,021141 | 34237,63 | 1,006989 |
10,32740 | 1,877710 | 58,34480 | 1,215517 | 468,2479 | 1,064200 | 4082,388 | 1,020597 | 36244,48 | 1,006791 |
10,96251 | 1,827085 | 60,52466 | 1,210493 | 488,8511 | 1,062720 | 4284,389 | 1,020093 | 38251,15 | 1,006609 |
11,56918 | 1,779873 | 65,95974 | 1,199268 | 509,4413 | 1,061336 | 4486,344 | 1,019624 | 40257,64 | 1,006441 |
12,16921 | 1,738459 | 71,37610 | 1,189602 | 530,0194 | 1,060039 | 4688,254 | 1,019186 | 42263,97 | 1,006285 |
12,76777 | 1,702370 | 76,77597 | 1,181169 | 581,4161 | 1,057120 | 4890,123 | 1,018776 | 44270,15 | 1,006140 |
13,36476 | 1,670596 | 82,16116 | 1,173731 | 632,7507 | 1,054585 | 5091,954 | 1,018391 | 46276,19 | 1,006004 |
13,96014 | 1,642370 | 87,53317 | 1,167109 | 684,0310 | 1,052355 | 5596,376 | 1,017523 | 48282,10 | 1,005877 |
14,55391 | 1,617101 | 92,89326 | 1,161166 | 735,2630 | 1,050376 | 6100,602 | 1,016767 | 50287,89 | 1,005758 |
15,14608 | 1,594324 | 98,24252 | 1,155794 | 786,4519 | 1,048603 | 6604,655 | 1,016101 | 55301,88 | 1,005489 |
15,73668 | 1,573668 | 103,5819 | 1,150909 | 837,6018 | 1,047002 | 7108,554 | 1,015508 | 60315,24 | 1,005254 |
16,91338 | 1,537580 | 108,9121 | 1,146443 | 888,7164 | 1,045549 | 7612,317 | 1,014976 | 65328,06 | 1,005047 |
18,08439 | 1,507032 | 114,2339 | 1,142339 | 939,7987 | 1,044221 | 8115,957 | 1,014495 | 70340,39 | 1,004863 |
19,25010 | 1,480777 | 124,8545 | 1,135041 | 990,8513 | 1,043001 | 8619,484 | 1,014057 | 75352,29 | 1,004697 |
20,41090 | 1,457921 | 135,4480 | 1,128734 | 1041,877 | 1,041877 | 9122,909 | 1,013657 | 80363,80 | 1,004548 |
21,56715 | 1,437810 | 146,0176 | 1,123212 | 1143,853 | 1,039867 | 9626,241 | 1,013289 | 85374,96 | 1,004411 |
22,71917 | 1,419948 | 156,5659 | 1,118328 | 1245,742 | 1,038118 | 10129,49 | 1,012949 | 90385,79 | 1,004287 |
23,86727 | 1,403957 | 167,0952 | 1,113968 | 1347,554 | 1,036580 | 11135,74 | 1,012340 | 95396,32 | 1,004172 |
25,01171 | 1,389539 | 177,6074 | 1,110046 | 1449,297 | 1,035212 | 12141,72 | 1,011810 | 100406,6 | 1,004066 |
26,15273 | 1,376459 | 188,1039 | 1,106493 | 1550,979 | 1,033986 | 13147,45 | 1,011342 | 110426,4 | 1,003876 |
27,29055 | 1,364528 | 198,5861 | 1,103256 | 1652,606 | 1,032879 | 14152,96 | 1,010926 | 120445,3 | 1,003711 |
29,55738 | 1,343517 | 209,0553 | 1,100291 | 1754,183 | 1,031873 | 15158,29 | 1,010552 | 130463,4 | 1,003565 |
31,81358 | 1,325566 | 219,5124 | 1,097562 | 1855,715 | 1,030953 | 16163,43 | 1,010215 | 140480,8 | 1,003435 |
34,06029 | 1,310011 | 240,3937 | 1,092699 | 1957,204 | 1,030107 | 17168,42 | 1,009907 | 150497,7 | 1,003318 |
Таблица П1.8
от количества n отказов
n | V(n) | n | V(n) | n | V(n) | n | V(n) | n | V(n) |
6,5 | 1,779873 | 55 | 1,199268 | 480 | 1,061336 | 4400 | 1,019624 | 40000 | 1,006441 |
7 | 1,738459 | 60 | 1,189602 | 500 | 1,060039 | 4600 | 1,019186 | 42000 | 1,006285 |
7,5 | 1,702370 | 65 | 1,181169 | 550 | 1,057120 | 4800 | 1,018776 | 44000 | 1,006140 |
8 | 1,670596 | 70 | 1,173731 | 600 | 1,054585 | 5000 | 1,018391 | 46000 | 1,006004 |
8,5 | 1,642370 | 75 | 1,167109 | 650 | 1,052355 | 5500 | 1,017523 | 48000 | 1,005877 |
9 | 1,617101 | 80 | 1,161166 | 700 | 1,050376 | 6000 | 1,016767 | 50000 | 1,005758 |
9,5 | 1,594324 | 85 | 1,155794 | 750 | 1,048603 | 6500 | 1,016101 | 55000 | 1,005489 |
10 | 1,573668 | 90 | 1,150909 | 800 | 1,047002 | 7000 | 1,015508 | 60000 | 1,005254 |
11 | 1,537580 | 95 | 1,146443 | 850 | 1,045549 | 7500 | 1,014976 | 65000 | 1,005047 |
12 | 1,507032 | 100 | 1,142339 | 900 | 1,044221 | 8000 | 1,014495 | 70000 | 1,004863 |
13 | 1,480777 | 110 | 1,135041 | 950 | 1,043001 | 8500 | 1,014057 | 75000 | 1,004697 |
14 | 1,457921 | 120 | 1,128734 | 1000 | 1,041877 | 9000 | 1,013657 | 80000 | 1,004548 |
15 | 1,437810 | 130 | 1,123212 | 1100 | 1,039867 | 9500 | 1,013289 | 85000 | 1,004411 |
16 | 1,419948 | 140 | 1,118328 | 1200 | 1,038118 | 10000 | 1,012949 | 90000 | 1,004287 |
17 | 1,403957 | 150 | 1,113968 | 1300 | 1,036580 | 11000 | 1,012340 | 95000 | 1,004172 |
18 | 1,389539 | 160 | 1,110046 | 1400 | 1,035212 | 12000 | 1,011810 | 100000 | 1,004066 |
19 | 1,376459 | 170 | 1,106493 | 1500 | 1,033986 | 13000 | 1,011342 | 110000 | 1,003876 |
20 | 1,364528 | 180 | 1,103256 | 1600 | 1,032879 | 14000 | 1,010926 | 120000 | 1,003711 |
22 | 1,343517 | 190 | 1,100291 | 1700 | 1,031873 | 15000 | 1,010552 | 130000 | 1,003565 |
24 | 1,325566 | 200 | 1,097562 | 1800 | 1,030953 | 16000 | 1,010215 | 140000 | 1,003435 |
26 | 1,310011 | 220 | 1,092699 | 1900 | 1,030107 | 17000 | 1,009907 | 150000 | 1,003318 |
28 | 1,296374 | 240 | 1,088484 | 2000 | 1,029327 | 18000 | 1,009626 | 160000 | 1,003212 |
30 | 1,284297 | 260 | 1,084786 | 2200 | 1,027932 | 19000 | 1,009367 | 170000 | 1,003116 |
32 | 1,273511 | 280 | 1,081508 | 2400 | 1,026718 | 20000 | 1,009128 | 180000 | 1,003028 |
34 | 1,263804 | 300 | 1,078576 | 2600 | 1,025648 | 22000 | 1,008701 | 190000 | 1,002947 |
36 | 1,255012 | 320 | 1,075934 | 2800 | 1,024697 | 24000 | 1,008328 | 200000 | 1,002872 |
38 | 1,247002 | 340 | 1,073538 | 3000 | 1,023844 | 26000 | 1,007999 | 220000 | 1,002738 |
40 | 1,239666 | 360 | 1,071351 | 3200 | 1,023073 | 28000 | 1,007706 | 240000 | 1,002621 |
42 | 1,232916 | 380 | 1,069346 | 3400 | 1,022372 | 30000 | 1,007443 | 260000 | 1,002518 |
44 | 1,226681 | 400 | 1,067498 | 3600 | 1,021730 | 32000 | 1,007206 | 280000 | 1,002427 |
46 | 1,220898 | 420 | 1,065788 | 3800 | 1,021141 | 34000 | 1,006989 | 300000 | 1,002344 |
48 | 1,215517 | 440 | 1,064200 | 4000 | 1,020597 | 36000 | 1,006791 | 320000 | 1,002270 |
50 | 1,210493 | 460 | 1,062720 | 4200 | 1,020093 | 38000 | 1,006609 | 340000 | 1,002202 |
к Методике расчета
и нормирования показателей
надежности объектов
железнодорожного
электроснабжения
1) Объект оценки: ЭЧ-7 Западно-Сибирской ж.д.
2) Интервал наблюдения: Tн = 8760 ч (1 год) - с 01.01.2018 г. по 31.12.2018 г.
3) Коэффициенты ответственности (см. таблицу 13): k1 = 0,65; k2 = 0,2; k3 = 0,15.
4) Данные по количеству отказов и суммарному времени до восстановления по объектам различных видов представлены в таблице П2.1
Таблица П2.1
для объектов видов 1, 2 и 3 по ЭЧ-7 Западно-Сибирской ж.д.
с 01.01.2018 г. по 31.12.2018 г.
Вид объекта, i | ni | Tвi, ч |
1 ("контактная сеть") | 12 | 18,43 |
2 ("тяговая подстанция") | 1 | 0,72 |
3 ("ЛЭП") | 5 | 9,52 |
П2.2. Расчет фактических (эксплуатационных) показателей надежности объекта оценки
1) Фактическое среднее время до восстановления объекта оценки (виды объектов 1, 2, 3) рассчитывается по формуле (1) с применением данных таблицы П2.1:
 .
.2) Для объектов всех видов (i = 0) по объекту оценки фактическое среднее время до восстановления получают путем интеграции. Сначала выполняют интеграцию количества отказов по формуле (2) с применением коэффициентов ответственности (см. п. П2.1):
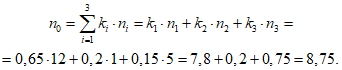
Затем находят среднее время до восстановления по формуле (3):
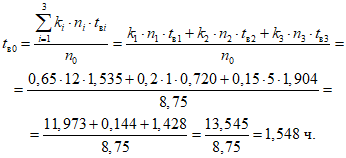
3) Коррекция фактического суммарного времени неготовности выполняется в два этапа. На первом этапе по формуле (4) определяется параметр неготовности:
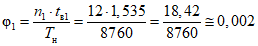 ;
;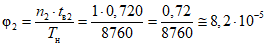 ;
;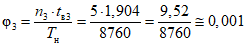 ;
;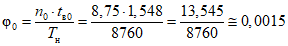 .
.На втором этапе применяется формула (5):
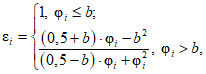
где b = 0,2 (см. таблицу 13).
Поскольку в нашем случае все рассчитанные значения  меньше, чем b, то после применения формулы (5) получим
меньше, чем b, то после применения формулы (5) получим 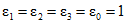 .
.
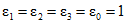 .
.4) Фактическая интенсивность отказов объекта оценки рассчитывается по формуле (6):
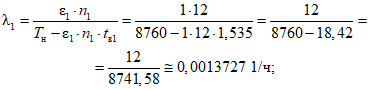
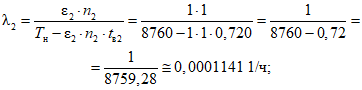
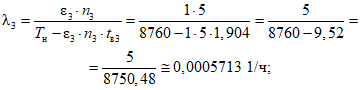
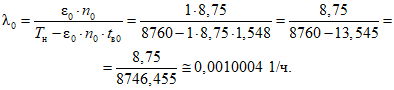
5) Фактический коэффициент готовности объекта оценки вычисляется по формуле (7):
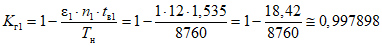 ;
;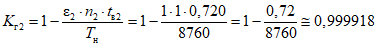 ;
; ;
;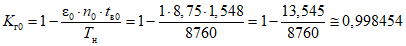 .
.На этом расчет фактических (эксплуатационных) показателей надежности объекта оценки завершен.
к Методике расчета
и нормирования показателей
надежности объектов
железнодорожного
электроснабжения
ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
1) Объект оценки: ЭЧ-7 Западно-Сибирской ж.д.
2) Интервал наблюдения: Tн = 8760 ч (1 год).
3) Данные объекта оценки (получены из ЕКП УРРАН Э):
эквивалентное количество эталонных объектов вида 1 ("контактная сеть"):  ;
;
 ;
;эквивалентное количество эталонных объектов вида 2 ("тяговая подстанция"):  ;
;
 ;
;эквивалентное количество эталонных объектов вида 3 ("ЛЭП"):  .
.
 .
.4) Коэффициенты ответственности (см. п. П3.1): k1 = 0,65; k2 = 0,2; k3 = 0,15.
1) Доверительные вероятности (см. п. П3.1): an = 0,9; at = 0,9.
2) Интервал наблюдения для оценки параметров глобального объекта: TнG = 8760 ч.
3) Количество интервалов наблюдения: L = 7.
4) Данные глобального объекта (получены из ЕКП УРРАН Э):
эквивалентное количество эталонных объектов вида 1 ("контактная сеть"):  ;
;
 ;
;эквивалентное количество эталонных объектов вида 2 ("тяговая подстанция"):  ;
;
 ;
;эквивалентное количество эталонных объектов вида 3 (ЛЭП):  .
.
 .
.П3.2.2 Определение параметров модели глобального объекта
Рассмотрим определение параметров модели на примере глобального объекта вида 1 ("контактная сеть"), при этом в расчетных формулах опустим индекс i. Для объектов остальных видов (i = 2, 3) данная процедура выполняется аналогично.
1) Статистика КАС АНТ по виду 1 для глобального объекта (отказы 1 и 2 кат. за L = 7 интервалов наблюдения - 2012 - 2018 календарные годы) приведена в таблице П3.1.
Таблица П3.1
(продолжительность отказов) для объектов вида 1
Вид объекта, показатель | Год (интервал наблюдения) | |||||||
2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | ||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | nl | 290 | 774 | 754 | 679 | 661 | 629 | 585 |
Tвl | 483,4 | 911,6 | 1065 | 960,1 | 910,9 | 880,6 | 1039 | |
Рассчитаем для пары значений (n1; Tв1) среднее время tв1 до восстановления по формуле (11):
 .
.Для остальных пар значений из таблицы П3.1 (l = 2...7) среднее время tвl до восстановления рассчитывается также, по формуле (11). Результаты расчета представлены в таблице П3.2
Таблица П3.2
Вид объекта, показатель | Год (интервал наблюдения) | |||||||
2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | ||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | tвl | 1,667 | 1,263 | 1,412 | 1,414 | 1,378 | 1,4 | 1,776 |
2) Упорядочим ряды количества отказов из таблицы П3.1 и среднего времени до восстановления из таблицы П3.2 по убыванию значений (в каждом из упорядоченных рядов элемент с номером l = 1 будет иметь максимальное значение, а с номером l = 7 - минимальное). Получим упорядоченные ряды в таблицах П3.3 и П3.4.
Таблица П3.3
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | nl | 774 | 754 | 679 | 661 | 629 | 585 | 290 |
Таблица П3.4
(ряд, упорядоченный по убыванию значений)
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | tвl | 1,776 | 1,667 | 1,414 | 1,412 | 1,4 | 1,378 | 1,263 |
3) Выполним проверку рядов в таблицах П3.3 и П3.4 на наличие "аномальных" точек.
Вычислим математические ожидания обоих рядов по формулам (12):
 ,
, .
.Вычислим среднеквадратические отклонения обоих рядов по формулам (13). Для этого сначала для каждого члена ряда найдем квадрат его разности с математическим ожиданием ряда. Для первых членов рядов:
 ,
,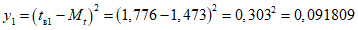 .
.Для остальных членов рядов квадраты их разности с математическим ожиданием ряда вычисляются аналогично. Результаты сведены в таблицы П3.5 и П3.6.
Таблица П3.5
среднеквадратического отклонения ряда количества отказов
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | xl | 22329,3249 | 16752,1249 | 2962,6249 | 1327,1449 | 19,6249 | 1565,7849 | 111937,08 |
Таблица П3.6
отклонения ряда среднего времени до восстановления
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | ql | 0,091809 | 0,037636 | 0,003481 | 0,003721 | 0,005329 | 0,009025 | 0,0441 |
Теперь вычислим среднеквадратические отклонения обоих рядов по формулам (13), суммируя промежуточные данные из таблиц П3.5 и П3.6 с делением сумм на (7 - 1):
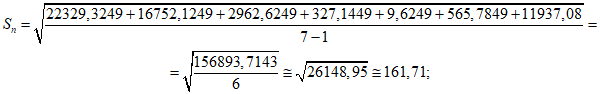

Применяя полученные значения Sn и St, а также данные из таблиц П3.3 и П3.4, найдем характеристические отклонения для рядов по формулам (14) и (15):
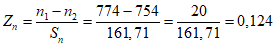 ;
;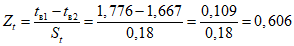 ;
; ;
; .
.Найдем функцию Ирвина для L = 7, где L - количество точек в ряду, по формуле (16):
I = 3,647·(log27)-0,48 = 3,647·(2,81)-0,48 =
= 3,647·0,609 = 2,221.
Как видно, ни одно из характеристических отклонений Zn, Yn, Zt, Yt не превышает I. Значит, аномальные точки в первом и втором рядах отсутствуют, и коррекция значений аномальных точек не требуется. Также не требуется и перерасчет математических ожиданий рядов.
4) Выполним для двух рядов в таблицах П3.3 и П3.4 расчет коэффициентов вариации по формулам (19). Разобьем вычисление на три этапа. На первом этапе найдем значения  и
и  , на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (19). Для первых элементов рядов, соответственно:
, на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (19). Для первых элементов рядов, соответственно:
 и
и  , на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (19). Для первых элементов рядов, соответственно:
, на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (19). Для первых элементов рядов, соответственно: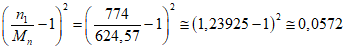 ;
; .
.Для остальных членов ряда расчет выполняется аналогично. Результаты сведены в таблицы П3.7 и П3.8.
Таблица П3.7
коэффициента вариации ряда количества отказов
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | ul | 0,0572405 | 0,0429434 | 0,0075943 | 0,0034019 | 0,0000503 | 0,0040142 | 0,2869548 |
Таблица П3.8
вариации ряда среднего времени до восстановления
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | vl | 0,042362 | 0,017375 | 0,001597 | 0,001707 | 0,00244694 | 0,00414781 | 0,0203014 |
Просуммировав значения в таблицах П3.7 и П3.8, получим соответственно суммы, равные 0,402199 и 0,08994. Подставив их вместо сумм в формулы (19), получим:

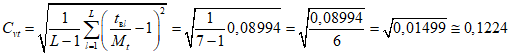 .
.5) Выполним для двух рядов в таблицах П3.3 и П3.4 расчет отношения коэффициента асимметрии к коэффициенту вариации по формулам (20). Разобьем вычисление на три этапа. На первом этапе найдем значения 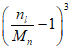 и
и 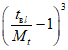 , на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (20). Для первых элементов рядов, соответственно:
, на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (20). Для первых элементов рядов, соответственно:
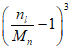 и
и 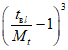 , на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (20). Для первых элементов рядов, соответственно:
, на втором этапе - суммы этих выражений для l = 1...7, а на третьем - выполним остальные вычисления по формулам (20). Для первых элементов рядов, соответственно: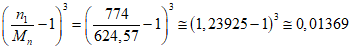 ;
; .
.Для остальных членов ряда расчет выполняется аналогично. Результаты сведены в таблицы П3.9 и П3.10.
Таблица П3.9
коэффициентов асимметрии и вариации ряда количества отказов
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | wl | 0,0136948 | 0,0088991 | 0,0006618 | 0,0001984 | 0,0000004 | -0,0002543 | -0,1537164 |
Таблица П3.10
коэффициентов асимметрии и вариации ряда
среднего времени до восстановления
Вид объекта, показатель | Номер элемента ряда | |||||||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Контактная сеть | zl | 0,008719 | 0,00229 | -0,000064 | -0,000071 | -0,000121 | -0,0002671 | -0,002893 |
Просуммировав значения в таблицах П3.9 и П3.10, получим соответственно суммы, равные -0,13052 и 0,00759. Подставив их вместо сумм в формулы (20), получим:

ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |

6) После расчета Cvn, Cvt, Crn, Crt выполняем их округление по правилам, установленным в настоящей Методике. Коэффициенты вариации округляются до ближайшего значения, кратного 0,1 (в случае нулевого результата принимается значение 0,1):
Cvn = 0,2589 ~= 0,3, Cvt = 0,1224 ~= 0,1.
Отношения коэффициентов асимметрии и вариации округляются до ближайшего значения, кратного 0,5 (в случае нулевого результата принимается значение 0). При превышении Crn (Crt) значения 6 результат ограничивается значением 6, а если значение Crn (Crt) менее (-6), то принимается Crn = -6 (Crt = -6):
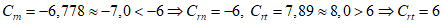 .
.7) Для ряда количества отказов (таблица П3.3), у которого Cvn = 0,3 и Crn = -6, для заданной доверительной вероятности an = 0,9 (см. таблицу 13) выбираем из приложения N 1 таблицу П1.5 модифицированных ординат трехпараметрического гамма-распределения (поскольку значение Crn менее (-2), то требуются модифицированные значения ординат). Для Cvn = 0,3 и Crn = -6 определяем из этой таблицы значение ymod = 0,70.
По формуле (22) для nG с применением значений математического ожидания Mn, полученного выше, находим параметр допустимого количества отказов модели глобального объекта:
nG = Mn·[2 - ymod(an)] = 624,57·(2 - 0,70) = 811,9.
Эта величина характеризует количество отказов глобального объекта (по виду "контактная сеть") в год, которое не будет превышено с вероятностью an = 0,9.
Для ряда среднего времени до восстановления (таблица П3.4), у которого Cvt = 0,1 и Crt = 6, для заданной доверительной вероятности at = 0,9 (см. таблицу 13) выбираем из приложения N 1 таблицу П1.2 ординат трехпараметрического гамма-распределения (поскольку значение Crn неотрицательное, то модифицированные значения ординат не требуются). Для Cvt = 0,1 и Crt = 6 определяем из этой таблицы значение y = 1,14.
По формуле (21) для tвG с применением значений математического ожидания Mt, полученного выше, находим параметр допустимого среднего времени до восстановления модели глобального объекта:
tвG = Mt·y(at) = 1,473·1,14 = 1,679.
Эта величина характеризует среднее время до восстановления глобального объекта (по виду "контактная сеть") в год, которое не будет превышено с вероятностью at = 0,9.
8) Выполним расчет параметров коррекции суммарного времени неготовности. Рассчитаем параметр неготовности по формуле (23):
 .
.Выполним расчет коэффициента коррекции суммарного времени неготовности с использованием параметра b = 0,2 (см. таблицу 13) по формуле (24):

Поскольку 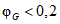 , то принимается
, то принимается  (то есть, фактически, коррекция суммарного времени неготовности для полученных параметров не требуется).
(то есть, фактически, коррекция суммарного времени неготовности для полученных параметров не требуется).
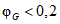 , то принимается
, то принимается 9) Определим характеристическое значение количества отказов глобального объекта (по виду "контактная сеть") для полученного значения 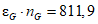 (в соответствии с формулой (25)). Для этого воспользуемся таблицей П1.7 приложения N 1, задающей соответствие между верхней доверительной границей количества отказов и соответствующим коэффициентом доверительных границ W. Из этой таблицы выбираем в левом столбике пару аргументов, между которыми лежит интересующее нас значение 811,9; также выбираем из этой таблицы пару значений W, соответствующих этим двум аргументам. Выбранные значения представлены в таблице П3.11.
(в соответствии с формулой (25)). Для этого воспользуемся таблицей П1.7 приложения N 1, задающей соответствие между верхней доверительной границей количества отказов и соответствующим коэффициентом доверительных границ W. Из этой таблицы выбираем в левом столбике пару аргументов, между которыми лежит интересующее нас значение 811,9; также выбираем из этой таблицы пару значений W, соответствующих этим двум аргументам. Выбранные значения представлены в таблице П3.11.
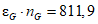 (в соответствии с формулой (25)). Для этого воспользуемся таблицей П1.7 приложения N 1, задающей соответствие между верхней доверительной границей количества отказов и соответствующим коэффициентом доверительных границ W. Из этой таблицы выбираем в левом столбике пару аргументов, между которыми лежит интересующее нас значение 811,9; также выбираем из этой таблицы пару значений W, соответствующих этим двум аргументам. Выбранные значения представлены в таблице П3.11.
(в соответствии с формулой (25)). Для этого воспользуемся таблицей П1.7 приложения N 1, задающей соответствие между верхней доверительной границей количества отказов и соответствующим коэффициентом доверительных границ W. Из этой таблицы выбираем в левом столбике пару аргументов, между которыми лежит интересующее нас значение 811,9; также выбираем из этой таблицы пару значений W, соответствующих этим двум аргументам. Выбранные значения представлены в таблице П3.11.Таблица П3.11
Выбранные аргументы и значения функции коэффициента
доверительных границ от верхней доверительной границы
количества отказов
nв1 | 786,4519 | W(nв1) | 1,048603 |
nв2 | 837,6018 | W(nв2) | 1,047002 |
Далее искомое значение 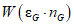 определяется по формуле (26):
определяется по формуле (26):
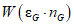 определяется по формуле (26):
определяется по формуле (26):
Характеристическое значение количества отказов и характеристическое среднее время до восстановления глобального объекта (по виду "контактная сеть") рассчитывается по формуле (25):
 ;
; .
.Для объектов вида 1 ("контактная сеть") глобального объекта все необходимые параметры модели определены. По объектам видов 2 ("тяговая подстанция") и 3 ("ЛЭП") расчеты выполняются аналогично. Исходные данные для объектов видов 2 и 3 приведены в таблице П3.12. Результаты расчетов по объектам видов 1, 2 и 3 сведены в таблицу П3.13.
Таблица П3.12
Количество отказов и суммарное время до восстановления
(продолжительность отказов) для объектов видов 2 и 3
Вид объекта, показатель | Год (интервал наблюдения) | |||||||
2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | ||
l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | l = 6 | l = 7 | ||
Тяговая подстанция | nl | 182 | 285 | 276 | 291 | 253 | 265 | 298 |
Tвl | 157,794 | 228,57 | 181,332 | 219,996 | 132,572 | 277,19 | 205,918 | |
ЛЭП | nl | 214 | 681 | 649 | 627 | 389 | 392 | 342 |
Tвl | 242,248 | 1139,994 | 931,964 | 921,063 | 483,916 | 638,96 | 463,068 | |
Таблица П3.13
глобального объекта для объектов видов 1, 2 и 3
Вид объекта, i | ||
1 ("контактная сеть") | 1,602 | 774,9 |
2 ("тяговая подстанция") | 0,888 | 273,4 |
3 ("ЛЭП") | 1,526 | 680,5 |
Расчет характеристического среднего времени до восстановления для глобального объекта по всем видам объектов (i = 0) выполняется по формуле (27) с применением коэффициентов ответственности (см. п. П3.1):

На этом расчет параметров модели глобального объекта завершен.
П3.3.1 Исходные данные
1) Интервал наблюдения для нормирования показателей: Tн = 8760 ч.
2) Эквивалентное количество эталонных объектов для глобального объекта (см. п. П3.2.1):
вида 1 ("контактная сеть"): 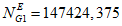 ;
;
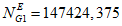 ;
;вида 2 ("тяговая подстанция"): 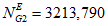 ;
;
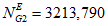 ;
;вида 3 (ЛЭП): 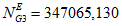 .
.
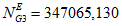 .
.3) характеристическое количество отказов глобального объекта (виды объектов 1, 2 и 3) - см. таблицу П3.13.
П3.3.2 Определение параметров модели эталонного объекта
1) Характеристическое количество 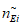 отказов эталонного объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "линия электропередачи") определяется по формуле (28):
отказов эталонного объекта вида i (i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "линия электропередачи") определяется по формуле (28):
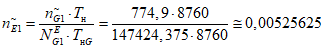 ;
;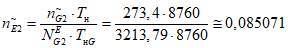 ;
; ;
;2) Характеристическое количество отказов эталонного объекта для всех видов объектов (i = 0) рассчитывается по формуле (29) с применением коэффициентов ответственности (см. п. П3.1):
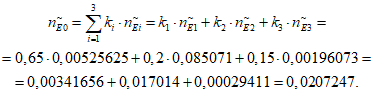
3) Коэффициенты интеграции эквивалентного количества эталонных объектов (для видов 1, 2 и 3) вычисляются по формуле (30) с применением коэффициентов ответственности (см. п. П3.1):
 ;
;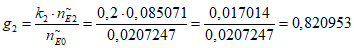 ;
;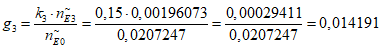 .
.4) Эквивалентное количество эталонных объектов всех видов (i = 0) для глобального объекта рассчитывается по формуле (31):
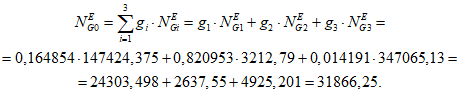
На этом расчет параметров модели эталонного объекта завершен.
П3.4.1 Исходные данные
1) эквивалентное количество эталонных объектов для объекта оценки (см. п. П3.1):
вида 1 ("контактная сеть"):  ;
;
 ;
;вида 2 ("тяговая подстанция"): 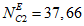 ;
;
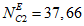 ;
;вида 3 ("ЛЭП"):  .
.
 .
.2) характеристические количества отказов (по видам объектов) - получены выше.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
П3.3.2 Определение параметров модели объекта оценки
1) Эквивалентное количество эталонных объектов всех видов (i = 0) для объекта оценки определяется по формуле (33):

2) Характеристическое количество отказов объекта оценки (для видов 0, 1, 2 и 3) определяется по формуле (34):
 ;
; ;
;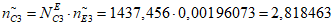 ;
;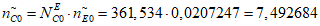 .
.3) Коэффициенты доверительных границ определяются через функцию коэффициента доверительных границ от количества отказов по формуле (35), которая предусматривает применение таблицы П1.8 приложения N 1 в случае, когда аргумент превышает 6,5:
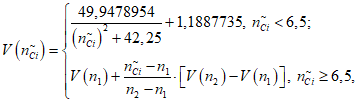
В нашем случае для объектов видов 2 и 3 расчет должен выполняться по верхней из двух формул, а для объектов видов 1 и 0 - по нижней.

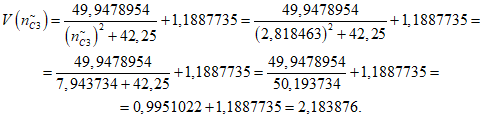
Для объектов вида 1 и 0 воспользуемся таблицей П1.8 приложения N 1, задающей соответствие между количеством отказов и соответствующим коэффициентом доверительных границ V. Из этой таблицы выбираем в левом столбике пару аргументов, между которыми лежит интересующее нас значение 9,89108 (вид 1) и пару аргументов, между которыми лежит интересующее нас значение 7,492684 (вид 0). Также выбираем из этой таблицы две пары значений V, соответствующих этим двум парам аргументам. Выбранные значения представлены в таблицах П3.14 и П3.15.
Таблица П3.14
Выбранные аргументы и значения функции коэффициента
доверительных границ от верхней доверительной границы
количества отказов (для объектов вида 1)
n1 | 9,5 | V(n1) | 1,594324 |
n2 | 10 | V(n2) | 1,573668 |
Таблица П3.15
доверительных границ от верхней доверительной границы
количества отказов (для объектов вида 0)
n1 | 7 | V(n1) | 1,738459 |
n2 | 7,5 | V(n2) | 1,702370 |
Далее находим коэффициенты доверительных границ по формуле:
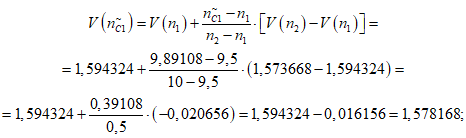
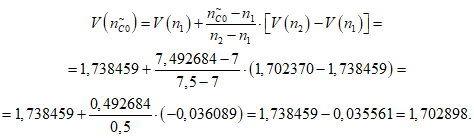
На этом расчет параметров модели объекта оценки завершен.
П3.5.1 Исходные данные
1) Коэффициенты доверительных границ для характеристического количества отказов объектов вида i (i = 0 - все виды; i = 1 - "контактная сеть"; i = 2 - "тяговая подстанция"; i = 3 - "линия электропередачи") объекта оценки - получены выше;
2) Эквивалентное количество эталонных объектов вида i (i = 0...3) для объекта оценки - см. п. П3.2.1;
3) Эквивалентное количество эталонных объектов вида i (i = 0...3) для глобального объекта - см. п. П3.1.
П3.5.2 Определение параметров модели коррекции размерности объекта и длительности интервала наблюдения
1) Корректирующий коэффициент для расчета допустимой (нормативной) интенсивности отказов объекта оценки рассчитывается по формуле (36), при этом значения Bn, Dn, 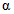 и
и 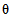 берутся из таблицы 13:
берутся из таблицы 13:


2) Корректирующий коэффициент для расчета допустимого (нормативного) среднего времени до восстановления объекта оценки рассчитывается по формуле (37), при этом значения Bt, Dt,  и
и  берутся из таблицы 13:
берутся из таблицы 13:
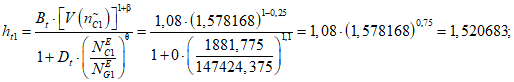
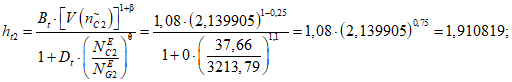
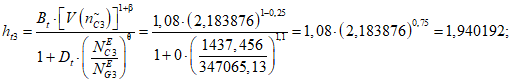

3) Корректирующий коэффициент для расчета допустимого (нормативного) коэффициента готовности объекта оценки рассчитывается по формуле (38), при этом значения BA, DA,  и
и  берутся из таблицы 13:
берутся из таблицы 13:
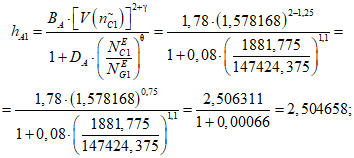
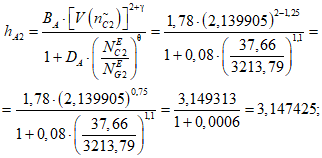
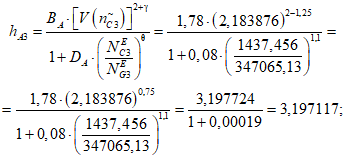

На этом расчет параметров модели коррекции размерности объекта и длительности интервала наблюдения завершен.
1) Допустимое (нормативное) среднее время до восстановления объекта оценки рассчитывается по формуле (39):
 ;
;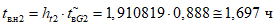 ;
;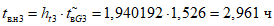 ;
;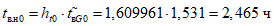 .
.2) Допустимая (нормативная) интенсивность отказов объекта оценки рассчитывается по формуле (40):
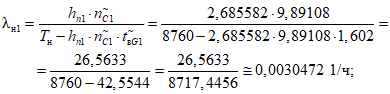

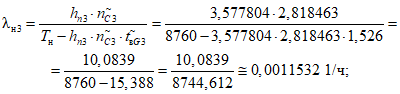

3) Допустимый (нормативный) коэффициент готовности объекта оценки вычисляется по формуле (41):

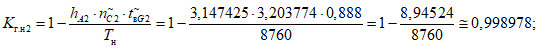
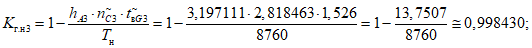
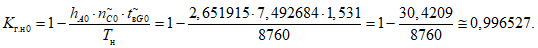
На этом расчет допустимых (нормативных) значений показателей объекта оценки завершен.
Выполним сравнение фактических значений показателей, рассчитанных в примере (приложение N 2) и допустимых (нормативных) значений, полученных выше. Для этого воспользуемся формулами (42) - (44):
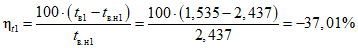 ;
;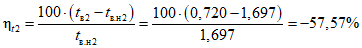 ;
;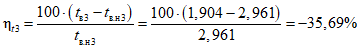 ;
;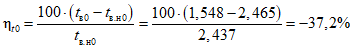 ;
;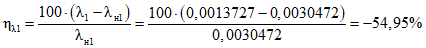 ;
;ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
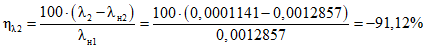 ;
;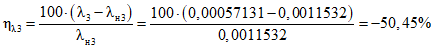 ;
; ;
; ;
;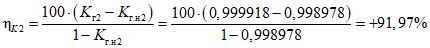 ;
;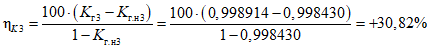 ;
;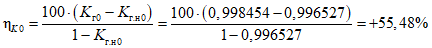 .
.На этом оценка соответствия фактических и нормативных значений показателей надежности завершена.