СПРАВКА
Источник публикации
Обнинск: ФГБУ "ВНИИГМИ-МЦД", 2020
Примечание к документу
Документ введен в действие с 01.11.2020.
Название документа
"РД 52.18.885-2019. Руководящий документ. Определение значений региональных фоновых концентраций органических загрязняющих веществ в почвах"
(введен в действие Приказом Росгидромета от 30.12.2019 N 844)
"РД 52.18.885-2019. Руководящий документ. Определение значений региональных фоновых концентраций органических загрязняющих веществ в почвах"
(введен в действие Приказом Росгидромета от 30.12.2019 N 844)
Руководителем Росгидромета
6 декабря 2019 года
Введен в действие
Приказом Росгидромета
от 30 декабря 2019 г. N 844
РУКОВОДЯЩИЙ ДОКУМЕНТ
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ РЕГИОНАЛЬНЫХ ФОНОВЫХ КОНЦЕНТРАЦИЙ
ОРГАНИЧЕСКИХ ЗАГРЯЗНЯЮЩИХ ВЕЩЕСТВ В ПОЧВАХ
РД 52.18.885-2019
Дата введения
1 ноября 2020 года
1 РАЗРАБОТАН Федеральным государственным бюджетным учреждением "Научно-производственное объединение "Тайфун" (ФГБУ "НПО "Тайфун")
2 РАЗРАБОТЧИКИ В.Е. Попов, канд. с.-х. наук; Н.Н. Лукьянова, канд. хим. наук; М.А. Запевалов, канд. хим. наук
3 СОГЛАСОВАН с Управлением мониторинга состояния и загрязнения окружающей среды (УМСЗ) Росгидромета 05.12.2019
4 УТВЕРЖДЕН Руководителем Росгидромета 06.12.2019
ВВЕДЕН В ДЕЙСТВИЕ приказом Росгидромета от 30.12.2019 N 844
5 ЗАРЕГИСТРИРОВАН головной организацией по стандартизации Росгидромета ФГБУ "НПО "Тайфун" 13.12.2019
ОБОЗНАЧЕНИЕ РУКОВОДЯЩЕГО ДОКУМЕНТА
РД 52.18.885-2019
6 ВВЕДЕН ВПЕРВЫЕ
7 СРОК ПЕРВОЙ ПРОВЕРКИ 2025 год
ПЕРИОДИЧНОСТЬ ПРОВЕРКИ 5 ЛЕТ
1.1 Настоящий руководящий документ устанавливает принципы и методы определения статистических характеристик региональной фоновой концентрации (далее - РФК) органического загрязняющего вещества (далее - ОЗВ): полиароматических углеводородов (далее - ПАУ), нефтяных углеводородов (далее - НУВ) и фенола в почвах региона <*>.
--------------------------------
<*> Помимо административной области или района предлагаемый алгоритм расчета РФК по согласованию с разработчиками руководящего документа может быть использован и для других территорий со строго очерченными границами.
1.2 Для получения достоверных статистических характеристик РФК ОЗВ настоящий руководящий документ дает указания по стратегии выбора фоновых пробных площадок, количеству отбираемых проб почвы, статистической обработке данных измерений.
1.3 Настоящий руководящий документ предназначен для организаций Росгидромета, в том числе оперативно-производственных подразделений, осуществляющих мониторинг почвенного покрова Российской Федерации.
В настоящем руководящем документе использованы ссылки на следующие нормативные документы:
ГОСТ 17.4.4.02-2017 Почвы. Методы отбора и подготовки проб для химического, бактериологического, гельминтологического анализа
ГОСТ Р ИСО 5479-2002 Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения
ГОСТ Р 50779.29-2017 Статистические методы. Статистическое представление данных. Часть 6. Определение статистических толерантных интервалов
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основа статистики. Термины и определения
ISO 11259:1998 Качество почвы. Упрощенное описание почвы (ISO 11259:1998, IDT)
Примечание - При пользовании настоящим руководящим документом целесообразно проверять действие стандартов - в информационной системе общего пользования - на официальном сайте федерального органа исполнительной власти в сфере стандартизации в сети Интернет или по ежегодно издаваемому информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячно издаваемого информационного указателя "Национальные стандарты" за текущий год.
Если ссылочный документ заменен (изменен), то при пользовании настоящим руководящим документом следует руководствоваться замененным (измененным) нормативным документом. Если ссылочный нормативный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
В настоящем руководящем документе применены следующие термины с соответствующими определениями:
3.1 вклад диффузного источника: Вклад ОЗВ, выделяемого перемещающимися источниками, источниками с большой площадью или многочисленными источниками.
3.2 выборка: Часть генеральной совокупности элементов, отобранных для изучения, с целью получения информации о ней.
3.3 выброс: Концентрация химиката, которая является резко выделяющейся по величине по отношению к остальному массиву данных.
3.4 генеральная совокупность: Совокупность всех объектов (единиц), относительно которых предполагается делать выводы при изучении конкретной задачи.
3.5 доверительный интервал: Интервальная оценка параметра распределения с известной вероятностью включения в интервал значений.
Примечание - Например, оценка доверительного интервала 95% среднего значения совокупности представляет собой интервал, который будет содержать истинное значение среднего в 95% всех выборок, которые могут быть выбраны с заданной схемой выборки.
3.7 концептуальная модель: Описание ожидаемого источника поступления загрязняющих веществ и его влияния на окружающую среду, включая пространственную область воздействия, пути поступления, миграцию, трансформацию и сток.
3.8 органическое загрязняющее вещество; ОЗВ: Органическое вещество, которое при превышении некоторой пороговой концентрации (установленного для него норматива) может оказывать негативное воздействие на окружающую среду.
3.9 показатели РФК: Показатели статистически достоверных точечных и интервальных оценок РФК, рассчитанные на основе данных измерений содержания ОЗВ в пробах почвы фоновых территорий, отобранных случайным образом.
3.10 предел обнаружения: Минимальное содержание определяемого ОЗВ в пробе почвы, сигнал от которого можно надежно отличить от шумового сигнала прибора.
Примечание - Обычно предел обнаружения принимают равным утроенному значению стандартного отклонения шумового сигнала.
3.11 простая случайная выборка: Метод выборки, где образцы собираются в случайные моменты времени или местоположения в течение периода выборки или области исследования.
3.12 регион: Территория со строго очерченными границами (административная область или административный район).
3.13 региональная фоновая концентрация; РФК: Истинная средняя концентрация ОЗВ в почвах фоновой части территории региона.
3.14 систематический отбор: Метод определения местоположения выборок, в которых места расположения выборок расположены в узлах геометрической сетки (например, квадрат, прямоугольник, треугольник, шестиугольник).
3.15 случайная величина: Набор наблюдаемых значений переменной.
3.16 статистическая характеристика: Цифровой показатель, вычисленный из случайной величины выбранного параметра совокупности.
3.17 толерантная граница: Граница толерантного интервала. [ГОСТ Р 50779.29-2017, пункт 3.1.2] 3.18 толерантный интервал: Интервал, для которого можно утверждать с данным уровнем доверия, что он содержит, по крайней мере, заданную долю определенной совокупности. [ГОСТ Р 50779.10-2000, пункт 2.61] |
3.19 фоновая территория: Территория региона за исключением территории, подверженной непосредственному воздействию локальных источников ОЗВ, территорий транспортной инфраструктуры и промышленного зонирования.
3.20 экспертная оценка: Использование накопленных научно-технических знаний, опыта работы и знания современных научных исследований для оценки значений регионального фона.
В настоящем руководящем документе введены и применены следующие сокращения:
- ВДГ - верхняя доверительная граница среднего арифметического;
- ВДГ(М) - верхняя доверительная граница медианы;
- МКД - межквартильный диапазон (разница между 25 и 75 персентилями выборки);
- НУВ - общее содержание нефтяных углеводородов;
- ОДК - ориентировочная допустимая концентрация;
- ОЗВ - органическое загрязняющее вещество;
- ПАУ - полиароматические углеводороды;
- ПДК - предельно допустимая концентрация;
- РФК - региональная фоновая концентрация;
- BaPeq - бензапиреновый эквивалент;
- JB - статистический критерий Харке-Бера;
- SF - статистический критерий Шапиро-Франчия;
- SW - статистический критерий Шапиро-Уилкса;
- W/s - критерий отношения диапазона к стандартному отклонению.
5.1 Фоновое содержание ОЗВ в почве может быть обусловлено природными причинами (разложением растительных остатков и гумуса, синтезом микробной биомассы) и антропогенными причинами за счет диффузного загрязнения. Диффузное загрязнение почв возникает в результате рассеяния ОЗВ из крупных точечных источников (например, путем рассеяния переносимых воздухом на большие и малые расстояния выбросов промышленных предприятий и переноса загрязняющих отходов паводком), ОЗВ из менее мощных, но имеющих повсеместное распространение источников (транспортных средств, бытовых отопительных систем, малых предприятий по сжиганию отходов и т.д.), а также осуществления загрязняющих видов деятельности, связанных с землепользованием (например, в результате разноса загрязняющих отходов или операций опрыскивания в сельском хозяйстве). Содержание ОЗВ в почве можно разделить на природную и антропогенную фракции. Отношение этих фракций меняется в широких пределах в зависимости от типа органического вещества, типа почвы и типа землепользования, а также от вида и степени внешнего загрязнения. Содержание стойких ОЗВ, например ПАУ с пятью и более кольцами, в почве чаще всего обусловлено антропогенными источниками. Поэтому фоновое содержание таких ОЗВ в основном обусловлено типом и размером диффузного загрязнения из отдаленных источников.
5.2 Показатели РФК ОЗВ, рассчитанные в соответствии с настоящим РД, могут быть использованы для:
а) определения текущего содержания ОЗВ в почвах региона;
б) оценки динамики РФК ОЗВ с течением времени;
в) оценки степени загрязнения почвы по сравнению с предельно допустимыми концентрациями (ПДК), или ориентировочно допустимыми концентрациями (ОДК);
г) оценки степени загрязнения почв (кратности величины РФК) при отсутствии ПДК и ОДК;
д) расчета риска для человека, вызванного присутствием ОЗВ в почве;
е) идентификации участков территории с повышенным фоновым содержанием из-за особенностей почвенного покрова и рельефа местности;
ж) определения суммарного индекса загрязнения почвы.
5.3 Значения РФК представляют собой статистические характеристики математической обработки выборки из статистической совокупности (где выборка - это массив результатов измерений концентрации ОЗВ в пробах почвы (например, проб массой 1 кг), отобранных на фоновых пробных площадках в пределах территории данного региона, а генеральная совокупность - это масса всего верхнего слоя почвы изучаемого региона).
Математическая статистическая обработка проводится для:
а) отбора данных соответствующих фоновому содержанию в почве (то есть проверка на выпадающие значения (выбросы));
б) характеристики центральности данных и степени их разброса.
Набор статистических характеристик зависит от вида распределения полученных данных:
а) для нормального распределения данных:
1) среднее арифметическое РФК  ;
;
2) стандартное отклонение s;
3) статистически обоснованная верхняя доверительная граница (ВДГ) среднего арифметического РФК  . Значение
. Значение  РФК считается статистически обоснованным, если оно определено с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ;
РФК считается статистически обоснованным, если оно определено с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ;
б) для логнормального распределения данных:
1) среднее арифметическое РФК  ;
;
2) медианная концентрация РФК  ;
;
3) логарифм среднего арифметического  ;
;
 ;
;4) логарифм стандартного отклонения Log(s);
5) верхняя доверительная граница средней величины РФК  считается статистически обоснованной, если она определена с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ;
считается статистически обоснованной, если она определена с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ;
в) для непараметрического распределения данных:
1) среднее арифметическое РФК  ;
;
2) 25, 50 (медианная концентрация CМ), 75 и 95 персентили РФК;
3) статистически обоснованная верхняя доверительная граница медианы РФК 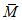 . Значение верхней границы
. Значение верхней границы  РФК считается статистически обоснованным, если оно определено с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ медианы (95% ВДГ(М)).
РФК считается статистически обоснованным, если оно определено с доверительной вероятностью P = 0,95. В настоящем руководящем документе рассчитывается величина 95% ВДГ медианы (95% ВДГ(М)).
5.4 Использование статистических характеристик РФК зависит от конкретной задачи (оценка динамики РФК, оценка загрязнения почвы в результате деятельности локального источника, конкретного ОЗВ).
5.5 Список ОЗВ, для которых требуется рассчитать показатели РФК, определяется организацией в каждом конкретном случае.
5.6 Для расчета используют массив данных химического анализа проб почвы, количество которых достаточно для вычисления статистически обоснованных характеристик РФК.
5.7 Отбор и анализ проб почвы на территории данного региона проводится в соответствии с ГОСТ 17.4.4.02.
5.8 Для контроля динамики диффузного загрязнения окружающей среды региона расчет параметров РФК должен проводиться периодически не реже одного раза в 5 лет.
5.9 Расчетные показатели РФК ОЗВ действительны в течение пяти лет со дня выдачи официального ответа на запрос, после чего подлежат пересмотру. В случае значительного изменения уровней загрязнения в результате ввода или реконструкции крупных предприятий, являющихся источниками диффузного загрязнения ОЗВ на территории региона, показатели РФК независимо от сроков их установления могут быть скорректированы по просьбе субъектов, действующих на территории региона.
Рассчитываемая средняя концентрация РФК (в статистических терминах среднее арифметическое статистической выборки) является только отражением средней величины реальной концентрации ОЗВ (в статистических терминах, генеральной совокупности). При повторном случайном отборе проб почвы эта средняя концентрация ОЗВ будет другой. Поэтому в настоящем руководящем документе за РФК принимают интервал, в который будет попадать средняя РФК при доверительной вероятности 95%. То есть при проведении на данной территории 100 обследований (экспедиций) 95% средних величин РФК будут находиться в некотором интервале от средней величины, рассчитываемой по результатам единственной экспедиции. Таким образом, РФК характеризуется интервалом от нижней границы 95% доверительного интервала среднего арифметического РФК до верхнего 95% доверительного интервала среднего арифметического РФК. Вместе с тем для принятия решений о кратности загрязнения почвы ОЗВ фоновому уровню наиболее часто используемым значением РФК будет являться величина среднего арифметического.
В некоторых случаях для расчета фоновой концентрации ОЗВ в незагрязненных почвах могут использоваться статистически достоверные корреляционные зависимости РФК от содержания органического углерода или содержания глинистых частиц в почве.
6.1 Оценку статистических характеристик РФК ОЗВ проводят по данным выборки. Основными статистическими характеристиками РФК являются математическое ожидание, медиана, среднее квадратическое отклонение или коэффициент вариации истинной средней концентрации ОЗВ в почве. Для оценки статистических характеристик РФК ОЗВ в настоящем руководящем документе используются графические методы и формальные статистические критерии. Графические методы позволяют просматривать данные и улучшить их понимание. Формальные статистические критерии обеспечивают статистическую достоверность оценочным показателям РФК ОЗВ.
6.2 Экспертная оценка является неотъемлемой частью методологии определения РФК ОЗВ. Экспертную оценку проводят при оценке полноты выборки, выборе соответствующего статистического критерия и формулировки заключений об уровне РФК на основе статистического анализа. Экспертная оценка должна быть обоснована, содержать ссылки на действующую нормативную документацию и сопровождаться вспомогательной информацией, на основе которой она была основана.
7.1 Определение РФК ОЗВ охватывает вопросы сбора предварительной информации о фоновых уровнях ОЗВ и вопросы экспериментального определения РФК. Экспериментальное определение РФК включает отбор проб почвы (стратегию и процедуру), химический анализ (предварительную обработку, извлечение и измерение), статистическую обработку и представление данных. Перед началом работ по определению РФК ОЗВ необходимо провести:
а) выбор анализируемых веществ и почвенных параметров (например, сумма ПАУ в почве, содержание бенз(а)пирена или индивидуального ПАУ, содержание в почве органического углерода и/или глинистых частиц);
б) описание территории исследования с четким обозначением ее границ;
в) определение отрезка времени, в течение которого отбирают образцы почвы и периода времени, в течение которого используют полученные показатели РФК.
7.2 РФК определяют для ОЗВ из перечня приоритетных загрязнителей, приведенных в приложении А. С практической точки зрения главный интерес представляют наиболее стойкие и малоподвижные соединения по причине их значительной сорбционной способности и накопления в почве, в то время как их испарение, биодеградация и миграция незначительны.
Кроме концентрации индивидуального загрязнителя для характеристики общего загрязнения ПАУ используют сумму ПАУ 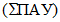 или оценку на основе бензапиренового эквивалента. Для такой оценки используют коэффициенты эквивалентной токсичности BaPeq для наиболее канцерогенных ПАУ, приведенные в приложении Б.
или оценку на основе бензапиренового эквивалента. Для такой оценки используют коэффициенты эквивалентной токсичности BaPeq для наиболее канцерогенных ПАУ, приведенные в приложении Б.
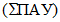 или оценку на основе бензапиренового эквивалента. Для такой оценки используют коэффициенты эквивалентной токсичности BaPeq для наиболее канцерогенных ПАУ, приведенные в приложении Б.
или оценку на основе бензапиренового эквивалента. Для такой оценки используют коэффициенты эквивалентной токсичности BaPeq для наиболее канцерогенных ПАУ, приведенные в приложении Б.В отобранных пробах почвы также определяют почвенные параметры, наиболее важные с точки зрения миграции и трансформации этих ОЗВ:
а) тип почвы в соответствии с классификацией 1977 года [1];
б) pH солевая (1 н KCl);
в) содержание органического углерода;
г) гранулометрический состав.
7.2 РФК определяют для территории региона:
а) территории административной области;
б) территории административного района;
в) другой территории с заданными размерами (по согласованию с разработчиками настоящего руководящего документа).
Примечание - При использовании значений РФК ОЗВ включается название региона. Например, показатели РФК ОЗВ для Калужской области, показатели РФК ОЗВ для муниципального образования "город Обнинск" и т.п.
Обследуемая территория может быть очерчена в соответствии с двумя принципами:
а) географический принцип (на карте очерчивается контур территории обследования по координатам, в пределах которых она находится);
б) принцип стратификации (на карте очерчивается контур территории, и эта территория стратифицируется по типу почвы, типу землепользования или высоты над уровнем моря).
Фоновыми территориями считаются территории, которые могут быть загрязнены за счет диффузных источников загрязнения (глобальных и региональных), за исключением случаев очевидного воздействия локальных источников. Поэтому на карте региона выделяют территории потенциального локального загрязнения и далее эти территории не учитывают при разработке плана отбора проб почвы. При определении РФК не учитывают следующие территории:
а) территория, удаленная на 500 м в обе стороны от дорог с грунтовым или асфальтовым покрытием с числом полос движения не менее 2;
б) территория, эквивалентная трем размерам защитных санитарных зон;
в) при наличии на предприятии трубы, выбрасывающей загрязнители, территория на расстоянии радиусом 40 высот трубы от места расположения трубы;
г) в городах не рассматриваются территории, помеченные на карте границ территориальных зон города как территории, относящиеся к производственно-коммунальным зонам и зонам инженерной и транспортной инфраструктуры.
7.3 При определении времени отбора проб почвы для определения РФК ОЗВ учитывают период, в течение которого РФК может значительно измениться под воздействием человеческой деятельности. Интервал между определениями РФК должен быть основан на:
а) предполагаемой скорости обогащения почвы ОЗВ за счет диффузных источников;
б) предполагаемой скорости потери ОЗВ из почвы за счет вертикальной миграции, биодеградации, испарения и поглощения растениями;
в) величине ошибки определения концентрации ОЗВ при химическом анализе и допустимой статистической погрешности определения средней концентрации РФК.
7.4 Показатели РФК могут быть определены на основании:
а) оценки существующих данных (из различных литературных источников);
б) сбора новых данных на основании соответствующей стратегии экспериментального определения РФК.
8.1 При использовании существующих данных особое внимание необходимо обращать на качество и сравнимость данных, особенно если данные собраны из разных источников. Соответствующая стратегия гармонизации должна охватывать такие вопросы, как
а) проверка полноты набора данных на основании принимаемых минимальных требований;
б) оценка совместимости различных методов отбора проб почвы и методов химического анализа;
в) идентификация и удаление из набора данных, резко выделяющихся наблюдений (выбросов).
В отобранных данных должна содержаться информация:
а) о дате отбора пробы;
б) об использованном принципе выбора месторасположения пробной площадки (метод случайного отбора, метод отбора в узлах сетки и т.д.);
в) о месторасположении пробной площадки (координаты);
г) о глубине отбора пробы почвы;
д) о методе отбора проб почвы;
е) о пробной площадке (типе почвы, типе землепользования);
ж) о методике анализа.
Эта информация может быть использована для отбора литературных данных с точки зрения их пригодности для определения РФК ОЗВ.
8.2 В каждом индивидуальном случае должны оцениваться сопоставимость методик предварительной обработки проб почвы и аналитические методы (степень извлечения, точность измерений).
8.3 РФК в почвах включает некоторую концентрацию ОЗВ за счет диффузного загрязнения. При этом исключаются места, загрязнение которых обусловлено локальными источниками. Поэтому из литературного набора данных необходимо удалить данные, явно связанные с местами локального загрязнения. Для этого применяют как географические, так и статистические методы идентификации выбросов. Способы исключения выбросов приведены в подразделе 11.9.
9.1 Если в результате работы с литературными источниками для определения статистически достоверного уровня РФК ОЗВ данных не хватает, то необходимо проводить отбор проб почвы в фоновых районах данного региона. Содержание ОЗВ в почве состоит из природной компоненты и компоненты, обусловленной диффузным антропогенным загрязнением. Природное содержание ОЗВ во многом зависит от типа почвы, в том числе от содержания органического углерода и глинистых частиц. Тип землепользования и расстояние до источников загрязнения также влияют на фоновое содержание ОЗВ в почве. Отбор проб почвы для характеристики фона должен учитывать динамический характер загрязнения почвы ОЗВ.
Хорошо разработанный план отбора проб почвы играет критически важную роль при обеспечении необходимого количества данных для достоверного определения значений РФК. С помощью соответствующего плана решается вопрос о репрезентативности значений РФК ОЗВ (степени статистической достоверности, с которой значения характеризуют РФК и степень ее изменчивости). План по отбору проб почвы включает объяснение и обоснование числа отбираемых образцов, месторасположение пробных площадок и интервал времени, в течение которого эти пробы должны быть отобраны.
При определении РФК ОЗВ статистической совокупностью служат все единицы, из которых эта статистическая совокупность состоит. Например, площадь территории региона может быть отождествлена с множеством площадей, эквивалентных площади пробной площадки (пробная площадка рассматривается здесь как небольшой участок земли размером 10 x 10 м, с которого методом конверта отбирается смешанный образец почвы массой около 1 кг). Или масса верхнего слоя почвы региона может быть отождествлена с множеством образцов почвы массой 1 кг. Типы планов по отбору проб почвы, которые основаны на использовании статистических методов для последующего анализа результатов и обоснования значений РФК ОЗВ, представлены в 9.1.1 - 9.1.3.
9.1.1 Метод простого случайного отбора основан на теории случайной вероятности отбора единиц выборки (каждая точка отбора имеет равную вероятность выбора). Координаты для отбора образцов почвы выбираются случайным образом (например, с помощью генератора случайных чисел). Метод простого случайного отбора используется в случае более или менее одинакового уровня загрязнения почвы. Главными достоинствами использования этого метода являются:
а) статистически обоснованная оценка среднего арифметического и стандартного отклонения содержания ОЗВ в почве;
б) легкость для понимания;
в) простота оценки количества отбираемых проб почвы.
9.1.2 Систематический отбор проб почвы, также называемый методом отбора по сетке, состоит из отбора проб в узлах квадратной, треугольной или ромбической сетки. Систематический метод отбора проб почвы обеспечивает равномерный охват территории и прост в использовании. При этом важные характеристики определяемой совокупности не будут упущены. Кроме того, отбор образцов, взятый через регулярные интервалы, используют для оценки пространственных или временных корреляций значений РФК ОЗВ. При случайном систематическом отборе проб почвы начальные координаты сетки для отбора проб почвы выбирают случайным образом. Если отбор образцов почвы в данной точке невозможен из-за наличия зданий, водной поверхности или по другим причинам, с помощью систематического подхода может быть выбрана новая пробная площадка.
9.1.3 При стратифицированном случайном отборе образцов территорию региона разделяют на страты (участки), которые являются более однородными, чем исходная территория. Разделение территории региона на страты проводят в соответствии с типом почвы и/или типом землепользования. Для отбора проб почвы из каждой страты можно использовать простой или систематический методы случайного отбора образцов. Этот подход используют при оценке параметров РФК ОЗВ для территории региона со значительным количеством сильно отличающихся типов почвы или типов землепользования. При планировании отбора проб почвы собирают и оценивают информацию о типах почвы и типу землепользования. Рекомендуемые типы землепользования приведены в приложении В (раздел "Факторы почвообразования").
9.2 Достоверность статистических характеристик РФК ОЗВ зависит от количества отбираемых проб почвы. Чтобы определить минимальное число образцов почвы, необходимое для надежной оценки средней концентрации ОЗВ на территории региона, предварительно оценивают величину стандартного отклонения. При этом оценка стандартного отклонения не должна быть меньше истинного стандартного отклонения генеральной совокупности. Предварительная оценка стандартного отклонения РФК может быть основана на предварительном исследовании территории региона или на другом исследовании, проведенном на территории с характеристиками, аналогичными исследуемой территории. В отсутствие предварительной информации можно оценить стандартное отклонение путем деления ожидаемого диапазона изменения РФК ОЗВ на шесть, т.е.

Однако такая оценка является лишь грубым приближением и должна использоваться только при отсутствии других источников информации.
При определении количества отбираемых проб почвы, при которой погрешность средней концентрации не превышает заданной величины (например, если погрешность определения РФК не должна превышать 30%) используют предварительную информацию об ожидаемом типе статистического распределения РФК ОЗВ (нормальное, логнормальное или непараметрическое). Методы, которые могут быть использованы при планировании отбора проб почвы, приведены в 9.2.1 - 9.2.3. Количество отбираемых проб почвы для определения РФК ОЗВ не может быть меньше девяти (в том числе при стратифицированном отборе проб почвы количество отбираемых образцов не может быть меньше девяти на страту).
9.2.1 Если статистическое распределение РФК на территории изучаемого региона может быть охарактеризовано как нормальное, соответствующее количество образцов, необходимое для характеристики РФК, может быть рассчитано с помощью одного из следующих методов.
9.2.1.1 Если в результате исследования литературных источников были определены стандартное отклонение среднего s для числа образцов n, то общее количество отбираемых проб почвы ntot при определении фона можно оценить с помощью отношения лямбда  , которое учитывает максимальное допустимое отклонение от среднего и таблицы Г.1.
, которое учитывает максимальное допустимое отклонение от среднего и таблицы Г.1.
9.2.1.2 При нормальном распределении набора данных соответствующее количество отбираемых проб почвы можно также рассчитать, используя статистику Стьюдента (t-статистику), которая использует t-статистику на уровне значимости  с n - 1 степенями свободы. Число отбираемых образцов почвы ntot для числа степеней свободы литературных данных n - 1 и
с n - 1 степенями свободы. Число отбираемых образцов почвы ntot для числа степеней свободы литературных данных n - 1 и  вычисляют в соответствии с приложением Д.
вычисляют в соответствии с приложением Д.
 вычисляют в соответствии с приложением Д.
вычисляют в соответствии с приложением Д.9.2.2 Для определения числа отбираемых образцов почвы при логнормальном распределении РФК используют метод Лэнда в соответствии с приложением Е.
9.2.3 Если распределение РФК нельзя описать нормальным или логнормальным распределением, то количество отбираемых образцов почвы для такого непараметрического распределения для того, чтобы с 95% вероятностью считать, что РФК находится в интервале, включающем 95% всех измерений, будет не менее 59 в соответствии с ГОСТ Р 50779.29-2017.
9.2.4 В соответствии с рекомендациями комитета по экологической политике Европейской экономической комиссии участки отбора проб почвы не могут находиться на территории площадью более 300 км2 (то есть на территории квадрата со сторонами приблизительно 16 x 16 км) [2].
9.3 Интерпретация фоновых концентраций ОЗВ в почве требует общей информации о территории обследования. Наиболее важные параметры для описания почвы обследуемой территории приведены в приложении В [3].
9.4 Отбор проб почвы осуществляется в соответствии с ГОСТ 17.4.4.02. Пробы почвы отбирают с глубины от 0 до 5 см и от 5 до 20 см.
9.5 Если концентрация ОЗВ не меняется в течение года, то взятие проб почвы можно проводить в любое время года. Практические вопросы отбора проб рассматриваются перед определением периода времени для отбора образцов почвы. Например, во влажный сезон трудно отбирать образцы почвы из-за близкого уровня залегания грунтовых вод. И, наоборот, во время засухи почва становится твердой. Доступ к некоторым участками может быть затруднен из-за растущих сельскохозяйственных культур. В этом случае рекомендуется отбирать пробы вскоре после уборки урожая или сразу после посева.
9.6 Отобранные пробы почвы могут храниться в течение нескольких лет после их отбора для определения концентраций других ОЗВ, которые могут представлять интерес в будущем. Высушенные образцы почвы должны храниться в герметичных контейнерах. Контейнеры должны храниться в комнате с низкой влажностью воздуха, которая защищена от пыли, света и значительных изменений температуры.
10.1 В отобранных образцах почвы измеряют два набора параметров. Первым параметром является концентрация ОЗВ. Вторым параметром является основное почвенное свойство (содержание органического вещества и/или содержание глины). Эти параметры необходимы для оценки статистических характеристик РФК и для расчета с помощью корреляционных зависимостей фонового содержания ОЗВ, если для данной пробной площадки известна величина только основного почвенного свойства.
10.2 Химический анализ ОЗВ выполняют в соответствии с аттестованными методиками измерений. Основным требованием к анализу ОЗВ является достаточно низкий предел обнаружения для того, чтобы количество измерений ниже предела обнаружения было минимальным. Во время анализа проводят процедуры контроля качества анализа.
11.1 Анализ конкретных данных начинают с получения "статистического портрета", т.е. с оценивания основных характеристик распределения содержания ОЗВ в почвах региона. Многие статистические методы основаны на допущении о нормальности такого распределения. Для оценки типа статистического распределения аналитических результатов, которые при условии случайности отбора проб почвы являются статистической выборкой из генеральной совокупности, используются следующее методы:
а) графические методы;
б) формальные статистические критерии.
При стратифицированном отборе при определении типа статистического распределения для каждой страты используют выборку, состоящую как минимум из девяти измерений. Окончательный выбор вида статистического распределения делают на основе одновременной оценки результатов, полученных перечисленными ниже методами:
а) вероятностные графики (графический метод);
б) ящичные графики (графический метод);
в) критерий отношения диапазона данных к величине стандартного отклонения (формальный критерий);
г) критерий Шапиро-Уилкса для выборки с числом данных n <= 50 (формальный критерий);
д) критерий Шапиро-Франчия для выборки с числом данных n > 50 (формальный критерий);
е) критерий Харке-Бера для выборки с числом данных n > 1000 (формальный критерий);
ж) критерий Д'Агостино для выборки с числом данных n > 50 (формальный критерий).
Ввиду того, что практически у каждого формального критерия имеются ограничения при определении типа статистического распределения, при статистическом анализе выборки необходима предварительная проверка исходных данных экспертом. Например, тест Шапиро-Уилкса не эффективен, когда несколько величин в наборе данных одинаковы. Лучше всего он работает для выборки с количеством данных менее 50, но в модификации Шапиро-Франчия может быть использован и для большего числа измерений. Его также нельзя использовать, если в выборке имеются измерения ниже предела обнаружения. Критерий Харке-Бера учитывает асимметрию и эксцесс распределения. Кроме асимметрии и эксцесса критерий Д'Агостино учитывает также и центральность распределения. Однако он не может быть использован для данных с числом измерений менее 50 и более 1000.
11.2 Вероятностный график используют для первоначальной оценки формы распределения данных выборки. Такой график позволяет осуществить визуальный осмотр данных и дать предварительную оценку соответствия нормальному статистическому распределению вероятности. Также с помощью этих графиков можно идентифицировать отклонение данных от нормального распределения. Вероятностные графики строят путем построения зависимости концентраций, упорядоченных в порядке возрастания вдоль оси "y", от соответствующих квантилей стандартного нормального распределения или "величин z" (то есть нормального распределения со средним значением, равным нулю, и стандартным отклонением, равным единице). Если данные выборки подчиняются нормальному распределению, то построенные точки данных лежат вблизи прямой линии. Если данные не являются нормальными, на графике видны перегибы прямой линии или линия искривляется. Кроме того, на полученном графике можно визуально обнаружить данные с необычно высокими значениями (выбросы).
Вероятностные графики могут использовать также для оценки выборки на логнормальность распределения путем построения графика вероятности с использованием преобразования аналитических результатов в натуральные логарифмы вместо исходных (нетрансформированных) результатов аналитических измерений. Для определения наиболее подходящего распределения рекомендуется строить вероятностные графики как для исходных (нетрансформированных), так и для логарифмически преобразованных данных.
Ввиду субъективности интерпретации вероятностных графиков не следует делать выводы относительно статистических распределений, основываясь только на вероятностных графиках. Вероятностные графики следует использовать в сочетании с другими описанными в этом разделе методами. Способ построения вероятностных графиков и примеры их использования приведены в приложении Ж.
11.3 Другим способом визуального представления данных выборки являются ящичные графики с усами. На рисунке 1 представлен ящичный график, построенный на основании исходных данных концентраций 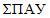 , приведенных в таблице Ж.2. Верхняя и нижняя сторона ящика, соответственно, представляют собой 25 и 75 персентили выборки. Разницу между ними обозначают как межквартильный диапазон (МКД). Горизонтальная линия посередине ящика представляет медиану (50 персентиль). Крест в середине ящика обозначает величину среднего арифметического концентрации. Вертикальные линии, проходящие от концов коробки (усы), рисуют на величину некоторого интервала от 25 персентили вниз и на величину интервала от 75 персентили вверх. Этот интервал обычно равен 1,5*МКД. Этот размер уса полезен тем, что внешние значения, показанные звездочками за пределами верхнего значения уса, являются потенциальными выбросами. Для их идентификации применяют формальные критерии для выбросов. Ящичные графики с усами наиболее полезны при сравнении двух и более наборов данных. Ввиду субъективности интерпретации не следует делать выводы относительно статистических распределений, основываясь только на ящичных графиках. Эти графики используют только в сочетании с другими методами определения формы статистического распределения выборки, а не в качестве единственного определяющего фактора.
, приведенных в таблице Ж.2. Верхняя и нижняя сторона ящика, соответственно, представляют собой 25 и 75 персентили выборки. Разницу между ними обозначают как межквартильный диапазон (МКД). Горизонтальная линия посередине ящика представляет медиану (50 персентиль). Крест в середине ящика обозначает величину среднего арифметического концентрации. Вертикальные линии, проходящие от концов коробки (усы), рисуют на величину некоторого интервала от 25 персентили вниз и на величину интервала от 75 персентили вверх. Этот интервал обычно равен 1,5*МКД. Этот размер уса полезен тем, что внешние значения, показанные звездочками за пределами верхнего значения уса, являются потенциальными выбросами. Для их идентификации применяют формальные критерии для выбросов. Ящичные графики с усами наиболее полезны при сравнении двух и более наборов данных. Ввиду субъективности интерпретации не следует делать выводы относительно статистических распределений, основываясь только на ящичных графиках. Эти графики используют только в сочетании с другими методами определения формы статистического распределения выборки, а не в качестве единственного определяющего фактора.
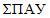 , приведенных в таблице Ж.2. Верхняя и нижняя сторона ящика, соответственно, представляют собой 25 и 75 персентили выборки. Разницу между ними обозначают как межквартильный диапазон (МКД). Горизонтальная линия посередине ящика представляет медиану (50 персентиль). Крест в середине ящика обозначает величину среднего арифметического концентрации. Вертикальные линии, проходящие от концов коробки (усы), рисуют на величину некоторого интервала от 25 персентили вниз и на величину интервала от 75 персентили вверх. Этот интервал обычно равен 1,5*МКД. Этот размер уса полезен тем, что внешние значения, показанные звездочками за пределами верхнего значения уса, являются потенциальными выбросами. Для их идентификации применяют формальные критерии для выбросов. Ящичные графики с усами наиболее полезны при сравнении двух и более наборов данных. Ввиду субъективности интерпретации не следует делать выводы относительно статистических распределений, основываясь только на ящичных графиках. Эти графики используют только в сочетании с другими методами определения формы статистического распределения выборки, а не в качестве единственного определяющего фактора.
, приведенных в таблице Ж.2. Верхняя и нижняя сторона ящика, соответственно, представляют собой 25 и 75 персентили выборки. Разницу между ними обозначают как межквартильный диапазон (МКД). Горизонтальная линия посередине ящика представляет медиану (50 персентиль). Крест в середине ящика обозначает величину среднего арифметического концентрации. Вертикальные линии, проходящие от концов коробки (усы), рисуют на величину некоторого интервала от 25 персентили вниз и на величину интервала от 75 персентили вверх. Этот интервал обычно равен 1,5*МКД. Этот размер уса полезен тем, что внешние значения, показанные звездочками за пределами верхнего значения уса, являются потенциальными выбросами. Для их идентификации применяют формальные критерии для выбросов. Ящичные графики с усами наиболее полезны при сравнении двух и более наборов данных. Ввиду субъективности интерпретации не следует делать выводы относительно статистических распределений, основываясь только на ящичных графиках. Эти графики используют только в сочетании с другими методами определения формы статистического распределения выборки, а не в качестве единственного определяющего фактора.
в почвах
11.4 Для проверки нормальности распределения данных выборки можно использовать формальный критерий отношения величины диапазона массива данных измерений концентрации ОЗВ в почве W и величины стандартного отклонения s. Этот критерий проверяет степень эксцесса распределения выборки. Данный критерий используют только для предварительной оценки нормальности типа распределения выборки. При проверке с помощью критерия W/s используют критический диапазон. Если вычисленная величина попадает внутрь диапазона, тогда данные считают распределенными нормально. Методика и пример использования этого критерия приведены в приложении И. Критические уровни критерии W/s для уровня значимости  0,05 и 0,10 приведены в таблице И.1.
0,05 и 0,10 приведены в таблице И.1.
11.5 При количестве данных в наборе до 50 (n <= 50) рекомендуется использовать в качестве формального критерия проверки нормальности распределения данных критерий Шапиро-Уилкса [4]. Этот критерий нужно применять как для исходных данных, так и для логарифмов данных.
Для применения критерия Шапиро-Уилкса для проверки на логнормальность распределения выборки сначала данные необходимо логарифмировать в соответствии с уравнением y = ln(x). Эти трансформированные данные используют вместо величин нетрансформированных данных x. Данные измерений ниже предела обнаружения (если в массиве данных их было не более 50%) заменяют на половину величины предела обнаружения. Критерий Шапиро-Уилкса применяют к выборке в соответствии с приложением К.
Если результаты свидетельствуют о том, что исходные данные и логарифмы данных соответствуют критерию Шапиро-Уилкса, то при окончательном решении того, к какому типу распределения принадлежит массив данных, руководствуются более высоким значением критерия Шапиро-Уилкса.
11.6 При количестве данных в массиве более 50 (n > 50) для проверки нормальности распределения в качестве формального критерия используют критерий Шапиро-Франчия [5]. Проверку проводят как для исходных данных, так и для натуральных логарифмов данных. Результаты проверки с помощью критерия Шапиро-Франчия подтверждают с помощью анализа вероятностных графиков или ящичных графиков с усами. Причиной отклонения от нормального или логнормального распределения может служить асимметрия данных или наличие большого хвоста (или и то, и другое). Анализ данных с помощью ящичного графика с усами, и в особенности вероятностного графика, может дать представление о том, почему проверка с помощью критерия Шапиро-Франчия не была успешной. Причиной этого может быть наличие в выборке выброса. После удаления выброса из выборки снова применяют критерий Шапиро-Франчия к выборке. Критерий Шапиро-Франчия применяют к выборке в соответствии с приложением Л.
Если результаты статистической проверки свидетельствуют о том, что данные проходят оба типа проверки, то для того чтобы сделать выводы о распределении данных, необходимо учитывать результаты проверки с более высоким значением критерия Шапиро-Франчия.
11.7 При количестве данных в выборке более 1000 проверку нормальности распределения проводят с помощью критерия Харке-Бера. Проверка данных с помощью этого критерия является проверкой того, имеют ли данные выборки асимметрию и эксцесс, соответствующие нормальному распределению. В соответствии с этим критерием сначала вычисляют коэффициент асимметрии и коэффициент эксцесса и рассчитывают критерий Харке-Бера. Затем определяют табличное значение критерия на основе критических значений Пирсона в соответствии с таблицей М.1. Для уровня значимости 0,05 критическая величина Пирсона равна 5,991. Если величина критерия Харке-Бера больше 5,991, то распределение не является нормальным. Если величина критерия Харке-Бера меньше 5,991, то распределение является нормальным.
11.8 При количестве данных в выборке более 50 проверку нормальности распределения можно проводить с помощью критерия Д'Агостино. Этот критерий основан на D-статистике, который определяет постоянное отношение оценки популяции Даунтона к стандартному отношению выборки. Критерий учитывает отклонения от нормальности для эксцесса и асимметрии. Порядок расчета по этому критерию приведен в приложении Н.
11.9 Применение статистических критериев для оценки выбросов является частью процесса первоначальной проверки исходных данных выборки и, таким образом, корректной оценки параметров генеральной совокупности. Выбросы данных могут быть в результате следующих причин:
а) данные могут быть неправильными в результате неправильного отбора образцов, ошибок при лабораторном анализе и вводе данных;
б) резко выделяющимся может быть правильный результат, принадлежащий другой генеральной совокупности (например, загрязненной территории, а не фоновой);
в) резко выделяющейся может быть реально существующая в природе концентрация (представляющая реальную генеральную совокупность фоновой территории).
Статистические методы для выявления выбросов представлены в разделах 11.9.2 - 11.9.5. Однако отнесение измерения к выбросу не означает его автоматического удаления из массива данных.
Формальную проверку на наличие выбросов проводят только в случае подозрений о наличии одного или нескольких выбросов. Основаниями для такого подозрения является высокое значение коэффициента вариации или существенное отличие от нуля коэффициента асимметрии. Особенно если такие результаты получаются не только при использовании исходных данных, но и логарифмов данных. Кроме того, потенциальные выбросы можно легко идентифицировать на графиках (таких как вероятностные графики и ящичные графики с усами). Методы проверки данных на выбросы приведены ниже:
а) вероятностный график;
б) ящичный график;
в) критерий Граббса для одного выброса;
г) критерий Диксона для нескольких выбросов для выборки с числом данных n <= 25;
д) критерий Рознера для нескольких выбросов для выборки с числом данных n > 25.
Если с помощью анализа исходных табличных данных или с помощью использования графических методов появилось подозрение на наличие потенциального выброса, то это наблюдение проверяют с помощью одного из трех формальных критериев. Как правило, для выборок с 50% или более значениями ниже предела обнаружения статистическое распределение данных определить невозможно. Поэтому в этом случае с помощью приведенных выше графических методов выбросы идентифицируют только качественно.
11.9.1 Вероятностные графики используют не только для графической оценки типа распределения данных, но и для выявления потенциальных выбросов. На вероятностном графике потенциальные выбросы будут отображаться как изолированные точки вдали от основной массы точек. Основная масса точек может, например, формировать линию, при этом потенциальные выбросы будут располагаться на некотором расстоянии от этой линии.
На ящичном графике потенциальные точки выбросов представляют точками выше верхней границы усов или ниже нижней границы усов. Однако для классификации измерения как выброс необходимо проверять их с помощью формальных критериев. Кроме того, некоторые формальные критерии для выбросов, представленные в этом разделе (например, критерий Рознера), требуют первоначальной оценки количества выбросов в выборке. Для выбора этого количества также используют вероятностные или ящичные графики.
11.9.2 Для идентификации одиночных выбросов в большинстве массивов данных с числом измерений от 3 до 100 используют критерий Граббса [6]. Применение этого критерия основано на предположении о нормальности распределения выборки, поэтому сначала оценивают форму статистического распределения выборки. Если данные распределены логнормально, то необходимо выполнить логарифмическое преобразование данных и проверить эти преобразованные данные с помощью критерия Граббса. При наличии нескольких потенциальных выбросов необходимо использовать другие критерии (например, критерий Диксона или критерий Рознера). Если в массиве данных количество измерений ниже предела обнаружения не более 50%, то для проверки на выбросы измерения ниже предела обнаружения заменяют на половину величины предела обнаружения. Чтобы проверить данные на выбросы, когда распределение выборки является логарифмически нормальным, сначала рассчитывают y = ln(x) и используют значения y (логарифмически трансформированные данные) вместо значений x. Расчеты по этой методике проводят в соответствии с приложением П.
11.9.3 Критерий Диксона используют для определения выбросов в выборке с количеством измерений не менее 25 [7]. Критерий Диксона основан на предположении о нормальности распределения данных измерений. Поэтому сначала определяют вид статистического распределения. Если данные распределены нормально, то наличие выброса определяют с помощью критерия Диксона. Если в массиве данных количество измерений ниже предела обнаружения не более 50%, то для нормальной формы распределения этот критерий применяют к исходным (нетрансформированным) данным, заменив измерения ниже предела обнаружения на половину величины предела обнаружения. Чтобы проверить данные на выбросы, когда распределение выборки является логарифмически нормальным, сначала рассчитывают величину y = ln(x) и используют значения y (логарифмически трансформированные данные) вместо значений x.
Критерий Диксона используют также для проверки наличия в выборке нескольких потенциальных выбросов. Сначала оценивают наименьшее из потенциальных экстремальных измерений (исключая временно более экстремальные наблюдения из набора данных). Если наименьшее из экстремальных наблюдений идентифицируют как выброс, тогда измерения с большими концентрациями также классифицируют как выбросы. Если потенциальный выброс с самой маленькой концентрацией не классифицируют как таковой, то с помощью этой же процедуры проверяют потенциальный выброс с большей концентрацией. Методика и пример расчетов приведены в приложении Р.
11.9.4 Критерий Рознера применяют для набора данных с числом измерений n > 25, и имеются свидетельства наличия более одного потенциального выброса [8]. С помощью критерия Рознера можно проверить данные как на наличие выбросов с высокими, так и низкими концентрациями. Потенциальные выбросы проверяют группами. Применение критерия Рознера предполагает, что выборка имеет нормальное распределение. Если данные распределены логарифмически, необходимо выполнить логарифмическое преобразование данных и применить критерий Рознера к этим преобразованным данным. Перед проверкой с помощью критерия Рознера необходимо определить общее количество потенциальных выбросов (k). Для предварительной оценки потенциальных выбросов необходимо использовать вероятностные графики, графики ящиков с усами или визуальный осмотр табличных данных.
Процедура применения критерия Рознера основана на процессе итерации. Сначала для всего набора данных вычисляют среднее арифметическое, стандартное отклонение и максимальные значения потенциальных выбросов. Потенциальные выбросы исключают по одному от самого большого до самого маленького. Затем вычисляют первую статистику критерия для проверки того, все ли значения потенциальных выбросов k являются выбросами. Если результат статистически значим, то все k наблюдений классифицируют как выбросы. Если этот результат статистически не значим, то группу возможных выбросов уменьшают на единицу (т.е. наименьший потенциальный выброс возвращают обратно в выборку), и статистику критерия пересчитывают с учетом остальных k - 1 возможных выбросов. Этот процесс повторяют до тех пор, пока не будут определены все выбросы или пока в выборке выбросов не останется.
При нормальном распределении для проверки выбросов используют исходные (нетрансформированные) данные, при этом при наличии до 50% измерений ниже предела обнаружения их заменяют на величину половины предела обнаружения. Для проверки выбросов при логнормальном распределении сначала вычисляют y = ln(x) и эти значения y используют вместо значений x. Расчеты по этой методике проводят в соответствии с приложением С.
11.9.5 В том случае, если распределение данных не подчиняется нормальному или логнормальному распределению, то для выборок с числом данных более 60 для идентификации потенциальных выбросов применяют критерий Уолша в соответствии с приложением Т.
11.9.6 До принятия окончательного решения об использовании идентифицированных с помощью формальных критериев потенциальных выбросов еще раз пересматривают все записи, сделанные как на этапе отбора проб почвы, так и на этапе химического анализа. После исследования всей информации возможны следующие действия.
1) если есть основания полагать, что отобранный образец не является фоновым, то это значение из набора данных удаляют;
2) если значение является репрезентативным для фоновых условий, то это значение в наборе данных сохраняют.
11.10 Одной из статистических характеристик РФК является среднее арифметическое содержания ОЗВ в почве. Среднее арифметическое, являющееся параметром центральности, представляет собой усредненное значение всего массива данных. Другие параметры центральности включают медиану (то есть срединное значение) и моду (то есть наиболее часто встречающееся значение). С точки зрения воздействия на человека среднее арифметическое значение обеспечивает наилучшее представление средних уровней воздействия на данной территории, поскольку оно включает величину всех измерений. Из-за неопределенности в оценке истинной средней арифметической концентрации ОЗВ в почве на данной территории (поскольку такая оценка основана на статистической обработке выборки отобранной случайным образом) часто используют ВДГ арифметического среднего всех измерений. Для представления диапазона неопределенности используют доверительные интервалы вокруг среднего арифметического. При расчете ВДГ для среднего используют уровень значимости  , которую обозначают как 95% ВДГ. В зависимости от вида распределения данных для расчета 95% ВДГ используют следующие методы:
, которую обозначают как 95% ВДГ. В зависимости от вида распределения данных для расчета 95% ВДГ используют следующие методы:
 , которую обозначают как 95% ВДГ. В зависимости от вида распределения данных для расчета 95% ВДГ используют следующие методы:
, которую обозначают как 95% ВДГ. В зависимости от вида распределения данных для расчета 95% ВДГ используют следующие методы:а) для данных, имеющих нормальное распределение, используют t-метод Стьюдента;
б) для данных, имеющих логнормальное распределение, используют метод Лэнда;
в) для наборов данных, не имеющих нормального или логнормального распределения, используют метод для непараметрического распределения.
Процедура выбора подходящего метода для вычисления 95% ВДГ для среднего приведена ниже:
а) сначала рассчитывают процент данных измерений ниже предела обнаружения (например, набор с девятью данными, три из которых ниже предела обнаружения, содержит 33% значений ниже предела обнаружения);
б) для массивов данных с количеством измерений ниже предела обнаружения < 50% определяют форму статистического распределения данных. Этот этап не требуется для выборок с количеством измерений ниже предела обнаружения более 50%;
в) все наборы данных проверяют на наличие выбросов; формальную проверку на выбросы проводят только в том случае, если первоначальная оценка данных (то есть обзор табличных данных и/или графиков) указывает на наличие одного или нескольких потенциальных выбросов;
г) для наборов данных с количеством измерений ниже предела обнаружения < 50% и имеющих нормальное распределение для расчета величины 95% ВДГ для среднего используют метод, приведенный в 11.10.1;
д) для наборов данных с количеством измерений ниже предела обнаружения < 50% и имеющих логнормальное распределение для расчета величины 95% ВДГ для среднего используют метод Лэнда, приведенный в 11.10.2.
11.10.1 При нормальном распределении выборки 95% ВДГ для среднего может быть рассчитана на основе t-распределения Стьюдента. Сначала оценивают статистическое распределение данных с использованием формальных критериев и проводят проверку на наличие выбросов. Верхнюю доверительную границу среднего часто используют для сравнения среднего арифметического РФК с экологическими или санитарно-гигиеническими нормативами. Если критерий 95% ВДГ больше норматива, то делают вывод о том, что среднее арифметическое РФК выше данного норматива. Если 95% ВДГ меньше норматива, то делают заключение, что среднее арифметическое РФК ниже данного норматива. Расчеты проводят в соответствии с приложением У, в котором приведен также пример расчетов.
11.10.2 Для данных, имеющих логнормальное распределение, для вычисления 95% ВДГ используют метод Лэнда в соответствии с приложением Ф. Если полученный 95% ВДГ больше норматива, то делают вывод о том, что средняя РФК выше данного норматива. Если 95% ВДГ меньше норматива, то делают вывод о том, что средняя РФК ниже данного норматива.
11.10.3 Метод t-распределения и метод Лэнда основываются, соответственно, на предположениях о нормальности и логнормальности распределения выборки. Для выборок, которые не являются ни нормальными, ни логнормальными, используют метод расчета в соответствии с приложением Х. При этом ВДГ определяют не для среднего арифметического, а для медианы.
После расчета значений РФК проводят проверку на близость рассчитанных значений РФК типичным значениям РФК для аналогичной климатической зоны. Пределы варьирования фона для Центрального района Российской Федерации приведены в таблице 1.
Таблица 1
Пределы варьирования приоритетных ОЗВ в почве фоновых
районов центра Европейской части РФ
Соединение | Пределы варьирования, мкг/кг |
 | 40 - 300 |
НУВ | 20 000 - 150 000 |
Фенол | 0,1 - 0,5 |
13.1 Знание корреляционных зависимостей значений РФК от ключевых почвенных параметров (содержания органического вещества или содержания глинистых частиц) позволяет сделать оценку РФК ОЗВ для некоторой точки территории без непосредственного измерения концентрации ОЗВ. Если средняя ошибка аппроксимации парной регрессии РФК ОЗВ в почве от почвенного параметра меньше 15%, то следует вычислить пределы изменения почвенного параметра, при котором ошибка прогноза концентрации показателя РФК не будет превышать 30%.
13.2 Для n пар экспериментально определенной в почве концентрации ОЗВ yxi и экспериментально определенного содержания ключевого почвенного параметра xi строят линейную регрессию вида
где Yxp - расчетная концентрация ОЗВ в почве;
xp - задаваемая величина ключевого почвенного параметра.
Для каждого экспериментально определенного значения почвенного параметра xi (i изменяется от 1 до n) с помощью уравнения (1) рассчитывают величину Yxi. Среднюю ошибку аппроксимации  рассчитывают по уравнению
рассчитывают по уравнению
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 (2)
(2)Если средняя ошибка аппроксимации  меньше 15%, то строят график зависимости ошибки прогноза РФК от величины ключевого почвенного параметра. Величину ошибки прогноза РФК D от содержания в почве ключевого почвенного параметра xp рассчитывают по уравнению (3):
меньше 15%, то строят график зависимости ошибки прогноза РФК от величины ключевого почвенного параметра. Величину ошибки прогноза РФК D от содержания в почве ключевого почвенного параметра xp рассчитывают по уравнению (3):
 (3)
(3)где
 (4)
(4)и
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
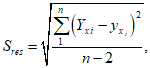 (5)
(5)где n - количество проанализированных образцов;
Sres - величина остаточной дисперсии;
13.3 На рисунке 2 показана зависимость величины ошибки прогноза РФК ОЗВ от содержания физической глины в почвах. Для этой зависимости было получено уравнение линейной регрессии Y(x) = 31,395 + 2,3815(x), R2 = 0,7604. При такой корреляции ошибка прогноза при уровне значимости 0,05 не будет превышать 30% для содержания глины в почве выше 5%. Таким образом, выходными параметрами для регрессионного уравнения, используемого для прогноза зависимости РФК от ключевого почвенного параметра, являются:
а) величина средней ошибки аппроксимации  ;
;
б) коэффициенты регрессионного уравнения (1) a и b;
в) интервал изменения ключевого параметра, для которого величина точечной ошибки прогноза не превышает 30% (для графика, приведенного на рисунке 2, содержание физической глины, при котором ошибка прогноза не превышает 30%, составляет интервал от 5 до 20%).

от содержания в ней физической глины
(справочное)
Таблица А.1
Тип соединения | Соединение | Количество бензольных колец |
ПАУ | Нафталин | 2 |
ПАУ | Аценафтилен | 3 |
ПАУ | Аценафтен | 3 |
ПАУ | Флюорен | 3 |
ПАУ | Фенантрен | 3 |
ПАУ | Антрацен | 3 |
ПАУ | Флуорантен | 4 |
ПАУ | Пирен | 4 |
ПАУ | Бенз[а]антрацен | 4 |
ПАУ | Хризен | 4 |
ПАУ | 5-Метилхризен | 4 |
ПАУ | Бензо[c]флюорен | 4 |
ПАУ | Бензо[b]флуорантен | 5 |
ПАУ | Бензо[j]флуорантен | 5 |
ПАУ | Бензо[k]флуорантен | 5 |
ПАУ | Бензо[а]пирен | 5 |
ПАУ | Бенз[е]пирен | 5 |
ПАУ | Перилен | 5 |
ПАУ | Дибенз[а,h]антрацен | 5 |
ПАУ | Бензо[ghi]перилен | 6 |
ПАУ | Индено[1,2,3-cd]пирен | 6 |
ПАУ | Трифенилен | 4 |
ПАУ | Циклопента[cd]пирен | 6 |
ПАУ | Дибензо[а,е]пирен | 6 |
ПАУ | Дибензо[а,h]пирен | 6 |
ПАУ | Дибензо[а,i]пирен | 6 |
ПАУ | Дибензо[а,l]пирен | 6 |
ПАУ | Коронен | 7 |
ПАУ | 7,12-Диметилбенз[а]антрацен | 4 |
НУВ | Общее содержание нефтяных углеводородов | 0 - 6 |
Фенол | Общее содержание фенола | 1 |
(справочное)
ПАУ | BaPeq |
Бенз[а]антрацен | 0,1 |
Бензо[а]пирен | 1 |
Бензо[bjk]флуорантен | 0,1 |
Бензо[ghi]перилен | 0,01 |
Хризен | 0,01 |
Дибенз[а,h]антрацен | 1 |
Индено[1,2,3-cd]пирен | 0,1 |
(рекомендуемое)
ОПИСАНИЕ МЕСТОПОЛОЖЕНИЯ ПРОБНОЙ ПЛОЩАДКИ И ОПИСАНИЕ ПОЧВЫ
Таблица В.1
Параметры для описания местоположения пробной площадки
и почвы (по ФАО.2012. Руководство по описанию почв)
Тип описания | Параметр |
Общая информация о месте расположения пробной площадки | Номер площадки Тип описания почвенного профиля Описание основного разреза Описание полуямы Описание прикопки Описание буровой скважины Дата описания Авторы Местоположение Координаты Превышение |
Формы и элементы рельефа Основная форма рельефа Положение места заложения разреза в ландшафте Форма склона Прямой Вогнутый Выпуклый Террасированный Со сложным рельефом Угол наклона склона Плоский Ровный Почти ровный Очень пологий Пологий Наклонный Сильно наклонный Умеренно крутой Крутой Очень крутой Землепользование Возделывание сельскохозяйственных культур Однолетние с.-х. культуры Многолетние с.-х. культуры Древесные и кустарниковые насаждения Смешанные системы земледелия Животноводство Лесоводство Естественные лесные массивы Искусственные лесные массивы Природоохранные территории Особо охраняемые природные территории Объекты рекультивации экосистем Населенные пункты и промышленность Жилые территории Промышленные территории Транспортные объекты Рекреационные объекты Отвалы и карьеры Свалки Военные объекты Остальные типы землепользования Растительность Сомкнутый лес Редкостойный лес Кустарниковый лес Полукустарниковый лес Травяные сообщества Верховое болото Низинное болото Сельскохозяйственные культуры Зерновые культуры Кормовые культуры Технические культуры Антропогенное влияние Влияние отсутствует Растительность нарушена слабо Растительность нарушена в средней степени Растительность нарушена сильно Насыпь, дамба, вал Гарь Искусственная терраса Распашка Почвообразующие породы | |
Описание почвы | Характеристики поверхности Переход границы между горизонтами Резкий (0 - 2 см) Ясный (2 - 5 см) Постепенный (5 - 15 см) Диффузный (более 15 см) Форма границы между горизонтами Ровная Волнистая Неровная Прерывистая Первичные компоненты Гранулометрический состав Цвет почвы Пятнистость Восстановительные условия Карбонаты Гипс Легкорастворимые соли Полевое определение pH Содержание органического вещества Организация почвенных компонентов Плотность Пористость Новообразования Биологическая активность Антропогенные включения Влажность почвы Наличие и глубина грунтовых вод Почвенный тип в системе классификации 1997 года |
(рекомендуемое)
ОПРЕДЕЛЕНИЕ ЧИСЛА ОТБИРАЕМЫХ ОБРАЗЦОВ ПОЧВЫ
ПРИ НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ КОНЦЕНТРАЦИИ ОЗВ В ПОЧВЕ
С ПОМОЩЬЮ МЕТОДА ОШИБКИ СРЕДНЕГО (МЕТОД ЛЯМБДА)
С помощью отношения лямбда 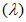 оценивают общее количество отбираемых проб почвы ntot, когда по литературным источникам было рассчитано стандартное отклонение среднего s для числа образцов n (таблица Г.1). Поэтапный метод расчета числа ntot приведен ниже:
оценивают общее количество отбираемых проб почвы ntot, когда по литературным источникам было рассчитано стандартное отклонение среднего s для числа образцов n (таблица Г.1). Поэтапный метод расчета числа ntot приведен ниже:
а) используя n данных из литературных источников вычисляется величина  :
:
 (Г.1)
(Г.1)где  - средняя концентрация ОЗВ;
- средняя концентрация ОЗВ;
Cm - максимальная допустимая величина отклонения от среднего арифметического.
Следует отметить, что меньшее значение  означает, что для поддержания определенного доверительного уровня требуется отобрать большее количество образцов;
означает, что для поддержания определенного доверительного уровня требуется отобрать большее количество образцов;
б) в таблице Г.1 приведена зависимость числа отбираемых образцов ntot для рассчитанных значений  при
при  и статистической мощности
и статистической мощности  .
.
 и статистической мощности
и статистической мощности  .
.Таблица Г.1
и применении одностороннего t-критерия для среднего,
при величине  и
и 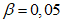
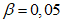
ntot | ntot | ||
0,30 | 119 | 0,90 | 15 |
0,35 | 90 | 0,95 | 14 |
0,40 | 70 | 1,00 | 13 |
0,45 | 55 | 1,1 | 11 |
0,50 | 45 | 1,2 | 10 |
0,55 | 38 | 1,3 | 8 |
0,60 | 32 | 1,4 | 8 |
0,65 | 28 | 1,5 | 7 |
0,70 | 24 | 1,6 | 6 |
0,75 | 21 | 1,7 | 6 |
0,80 | 19 | 1,8 | 6 |
0,85 | 17 | 1,9 | 5 |
Пример - Если величина арифметического среднего содержания нефтяных углеводородов по литературным данным составило 114,5 мг/кг, величина стандартного отклонения 60 мг/кг, а максимальная ошибка среднего не должна превышать 30%, то величина  будет равна (148,85 - 114,5)/60 = 34,35/60 = 0,5725. В соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 32. Если величина стандартного отклонения будет равна 80 мг/кг, то при прочих равных условиях
будет равна (148,85 - 114,5)/60 = 34,35/60 = 0,5725. В соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 32. Если величина стандартного отклонения будет равна 80 мг/кг, то при прочих равных условиях  . Тогда в соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 55.
. Тогда в соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 55.
 . Тогда в соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 55.
. Тогда в соответствии с таблицей Г.1 количество отбираемых образцов должно быть не меньше 55.(обязательное)
РАСПРЕДЕЛЕНИИ КОНЦЕНТРАЦИИ ОЗВ В ПОЧВЕ ПРИ ИСПОЛЬЗОВАНИИ
СТАТИСТИКИ СТЬЮДЕНТА
При нормальном распределении набора данных соответствующее количество отбираемых проб почвы рассчитывают, используя статистику Стьюдента (t-статистику). Эта формула использует t-статистику на уровне значимости  с n - 1 степенями свободы:
с n - 1 степенями свободы:
где  ;
;
 ;
;Cm - максимальная допустимая величина отклонения от среднего арифметического;
s - стандартное отклонение набора данных;
Число отбираемых образцов почвы ntot для числа степеней свободы литературных данных n - 1 и уровня значимости  от 0,001 до 0,3 приведены в таблице Д.1.
от 0,001 до 0,3 приведены в таблице Д.1.
Пример - Для средней концентрации ОЗВ 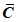 , равной 10, и стандартного отклонения, равного 3 (коэффициент вариации равен 30%), при максимальном отклонении от среднего, равном 15%
, равной 10, и стандартного отклонения, равного 3 (коэффициент вариации равен 30%), при максимальном отклонении от среднего, равном 15% 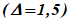 , числе ранее отобранных проб почвы n = 6 и
, числе ранее отобранных проб почвы n = 6 и  количество отбираемых проб почвы ntot, согласно уравнению (Д.1), должно быть равным 26. Если предполагается, что максимальное отклонение от среднего не должно превышать 10%, то количество отбираемых проб почвы необходимо увеличить до 59.
количество отбираемых проб почвы ntot, согласно уравнению (Д.1), должно быть равным 26. Если предполагается, что максимальное отклонение от среднего не должно превышать 10%, то количество отбираемых проб почвы необходимо увеличить до 59.
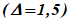 , числе ранее отобранных проб почвы n = 6 и
, числе ранее отобранных проб почвы n = 6 и  количество отбираемых проб почвы ntot, согласно уравнению (Д.1), должно быть равным 26. Если предполагается, что максимальное отклонение от среднего не должно превышать 10%, то количество отбираемых проб почвы необходимо увеличить до 59.
количество отбираемых проб почвы ntot, согласно уравнению (Д.1), должно быть равным 26. Если предполагается, что максимальное отклонение от среднего не должно превышать 10%, то количество отбираемых проб почвы необходимо увеличить до 59.Таблица Д.1
данных df(n - 1) и уровня значимости 
0,15 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 | |
0,30 | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
df(n - 1) | ||||||||
1 | 1,963 | 3,078 | 6,314 | 12,71 | 31,82 | 63,66 | 318,31 | 636,62 |
2 | 1,386 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 | 31,599 |
3 | 1,250 | 1,638 | 2,353 | 3,187 | 4,541 | 5,841 | 10,715 | 12,924 |
4 | 1,190 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 | 8,610 |
5 | 1,156 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 | 6,869 |
6 | 1,134 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 | 5,959 |
7 | 1,119 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 | 5,408 |
8 | 1,108 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 | 5,041 |
9 | 1,100 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 | 4,781 |
10 | 1,093 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 | 4,587 |
11 | 1,088 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 |
12 | 1,083 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 | 4,318 |
13 | 1,079 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 | 4,221 |
14 | 1,076 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4,140 |
15 | 1,074 | 1,341 | 1,753 | 2,131 | 2,607 | 2,947 | 3,733 | 4,073 |
16 | 1,071 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | 3,686 | 4,015 |
17 | 1,069 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,648 | 3,965 |
18 | 1,067 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | 3,610 | 3,922 |
19 | 1,066 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,579 | 3,883 |
20 | 1,064 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,552 | 3,850 |
21 | 1,063 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | 3,527 | 3,819 |
22 | 1,061 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | 3,505 | 3,792 |
23 | 1,060 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | 3,485 | 3,768 |
24 | 1,059 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | 3,467 | 3,745 |
25 | 1,058 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | 3,450 | 3,725 |
26 | 1,058 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | 3,435 | 3,707 |
27 | 1,057 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | 3,421 | 3,690 |
28 | 1,056 | 1,313 | 1,7401 | 2,048 | 2,467 | 2,763 | 3,408 | 3,674 |
29 | 1,055 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | 3,396 | 3,659 |
30 | 1,055 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | 3,385 | 3,646 |
40 | 1,050 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | 3,307 | 3,551 |
60 | 1,045 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | 3,232 | 3,460 |
80 | 1,043 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 | 3,195 | 3,416 |
100 | 1,042 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 | 3,174 | 3,390 |
1000 | 1,037 | 1,282 | 1,646 | 1,962 | 2,330 | 2,581 | 3,098 | 3,300 |
(обязательное)
ПРИ ЛОГНОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ КОНЦЕНТРАЦИИ ОЗВ В ПОЧВЕ
Для расчета числа независимых наблюдений, ntot, необходимых для оценки статистически достоверной величины медианы логнормального распределения, используется уравнение (Е.1)
где
 (Е.2)
(Е.2)и
 (Е.3)
(Е.3)где d - ожидаемая допустимая ошибка в оценке медианы. Следует отметить, что относительный коэффициент ошибок должен быть указан в исходной нетрансформированной шкале (ошибка среднего (%)/100);
 - процент доверия, при котором ошибка медианы не превышает d;
- процент доверия, при котором ошибка медианы не превышает d;n - количество литературных данных, на основе которых рассчитывались 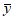 и
и  ;
;
N - количество данных в генеральной совокупности.
Примеры
1 Предположим, что величина d равна 0,10 (относительная ошибка 10%) и  равна 0,05 и предварительные данные дают величину
равна 0,05 и предварительные данные дают величину  , равной 2,0. Если предположить, что величина N генеральной совокупности очень большая, тогда уравнение (Е.1) дает
, равной 2,0. Если предположить, что величина N генеральной совокупности очень большая, тогда уравнение (Е.1) дает

Для уменьшения количества отбираемых проб почвы необходимо увеличить допустимую ошибку медианы или уменьшить уровень доверия (то есть увеличить значение  ). Например, если принять величину d, равной 0,50 (относительная ошибка 50%), и
). Например, если принять величину d, равной 0,50 (относительная ошибка 50%), и  , равной 0,05, то количество отбираемых проб уменьшится до n = 47. Если принять величину d, равной 0,30 (относительная ошибка 30%), и
, равной 0,05, то количество отбираемых проб уменьшится до n = 47. Если принять величину d, равной 0,30 (относительная ошибка 30%), и  , равной 0,05, то количество отбираемых проб n будет равно 112.
, равной 0,05, то количество отбираемых проб n будет равно 112.
2 Предположим, что на некоторой территории в 24 образцах были измерены фоновые концентрации суммы ПАУ, мкг/кг. Исходные данные в порядке возрастания составляют: 1 - 14,57; 2 - 16,05; 3 - 19,3; 4 - 24,8; 5 - 27,5; 6 - 27,8; 7 - 32,4; 8 - 33,4; 9 - 33,8; 10 - 33,9; 11 - 35,1; 12 - 50,9; 13 - 54,85; 14 - 63,95; 15 - 68,3; 16 - 70,9; 17 - 96; 18 - 109,75; 19 - 135,8; 20 - 141,8; 21 - 160; 22 - 184,3; 23 - 296,9; 24 - 728,9.
Если использовать весь приведенный массив данных, то величина  будет равна 0,9463. Поэтому в соответствии с уравнением Е.1 количество отбираемых проб для надежного определения медианы не должно быть меньше 53.
будет равна 0,9463. Поэтому в соответствии с уравнением Е.1 количество отбираемых проб для надежного определения медианы не должно быть меньше 53.
Если последние два значения рассматривать как выбросы, то величина  для массива данных будет равна 0,5776. Поэтому в соответствии с уравнением Е.1 количество отбираемых проб для надежного определения медианы будет составлять 32.
для массива данных будет равна 0,5776. Поэтому в соответствии с уравнением Е.1 количество отбираемых проб для надежного определения медианы будет составлять 32.
(рекомендуемое)
Для проверки формы распределения концентраций ОЗВ выборки на нормальность с помощью вероятностного графика необходимо использовать исходные данные. А для проверки логнормальности сначала необходимо преобразовать исходные данные в соответствии с выражением y = ln(x), и в дальнейшем использовать эти трансформированные значения y вместо исходных значений x. Если в выборке есть измерения ниже предела обнаружения, то их необходимо заменить числом, равным половине предела обнаружения. Порядок построения вероятностного графика по [10] следующий:
а) расположите исходные данные по порядку от самого маленького значения к самому большому (xi, i = 1, ..., n);
б) вычислите кумулятивную вероятность pi, соответствующую каждой величине xi, с помощью уравнения (Ж.1)
где n - это число образцов проб почвы;
i - это ранг упорядоченного массива данных;
в) определите квантиль стандартного нормального распределения соответствующую кумулятивной вероятности в соответствии с уравнением (Ж.2).
где Ф-1 означает обратную величину кумулятивного нормального распределения.
Затем постройте зависимость zi от xi. Если набор данных приблизительно соответствует нормальному распределению, то нанесенные точки будут располагаться вдоль воображаемой прямой линии. Кривые линии или линии с изгибом указывают на то, что данные распределены не нормально или выборка отобрана на территории, представляющей две совокупности, например природную компоненту и компоненту значительного локального загрязнения. Логнормальность набора данных может быть оценена путем построения логарифмически преобразованных значений y вместо исходных значений x. Если выборка распределена приблизительно логарифмически нормально, а вероятностный график построен с использованием данных, преобразованных в логарифмы, то нанесенные точки должны находиться на прямой линии или располагаться вблизи нее.
Примеры
1 На некоторой территории были отобраны 23 образца почвы, в которых были измерены  , нг/г. Во втором столбце таблицы Ж.1 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi.
, нг/г. Во втором столбце таблицы Ж.1 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi.
 , нг/г. Во втором столбце таблицы Ж.1 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi.
, нг/г. Во втором столбце таблицы Ж.1 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi.Таблица Ж.1
для исходных данных содержания  в почвах территории
в почвах территории
 в почвах территории
в почвах территорииi | xi | pi | zi | i | xi | pi | zi |
1 | 16,05 | 0,04167 | -1,7317 | 13 | 80,8 | 0,54167 | 0,10463 |
2 | 17 | 0,08333 | -1,383 | 14 | 95 | 0,58333 | 0,21043 |
3 | 18,25 | 0,125 | -1,1503 | 15 | 104,25 | 0,625 | 0,31864 |
4 | 26,25 | 0,16667 | -0,9674 | 16 | 119,5 | 0,66667 | 0,43073 |
5 | 26,495 | 0,20833 | -0,8122 | 17 | 129,8 | 0,70833 | 0,54852 |
6 | 27,65 | 0,25 | -0,6745 | 18 | 138,4 | 0,75 | 0,67449 |
7 | 31,21 | 0,29167 | -0,5485 | 19 | 160,5 | 0,79167 | 0,81222 |
8 | 33 | 0,33333 | -0,4307 | 20 | 165 | 0,83333 | 0,96742 |
9 | 43,4 | 0,375 | -0,3186 | 21 | 179,9 | 0,875 | 1,15035 |
10 | 45,1 | 0,41667 | -0,2104 | 22 | 190,5 | 0,91667 | 1,38299 |
11 | 58 | 0,45833 | -0,1046 | 23 | 196,6 | 0,95833 | 1,73166 |
12 | 78,3 | 0,5 | -1E-16 | ||||
Полученный вероятностный график приведен на рисунке Ж.1.

для некоторой территории
При использовании исходных (нетрансформированных) данных, экспериментальные точки приблизительно формируют две прямые линии. Это отражает или наличие двух популяций  в почвах, формирующих региональный фон, или то, что почвы были отобраны в фоновых районах и в районах, подверженных загрязнению.
в почвах, формирующих региональный фон, или то, что почвы были отобраны в фоновых районах и в районах, подверженных загрязнению.
 в почвах, формирующих региональный фон, или то, что почвы были отобраны в фоновых районах и в районах, подверженных загрязнению.
в почвах, формирующих региональный фон, или то, что почвы были отобраны в фоновых районах и в районах, подверженных загрязнению.2 На некоторой территории были отобраны 24 образца почвы, в которых были измерены  , нг/г. Во втором столбце таблицы Ж.2 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi. Полученный вероятностный график приведен на рисунке Ж.2.
, нг/г. Во втором столбце таблицы Ж.2 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi. Полученный вероятностный график приведен на рисунке Ж.2.
 , нг/г. Во втором столбце таблицы Ж.2 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi. Полученный вероятностный график приведен на рисунке Ж.2.
, нг/г. Во втором столбце таблицы Ж.2 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi. Полученный вероятностный график приведен на рисунке Ж.2.Таблица Ж.2
для исходных данных содержания  в почвах
в почвах
 в почвах
в почвахнекоторой территории
i | xi | pi | zi | i | xi | pi | zi |
1 | 14,57 | 0,04 | -1,75069 | 13 | 54,85 | 0,52 | 0,050154 |
2 | 16,05 | 0,08 | -1,40507 | 14 | 63,95 | 0,56 | 0,150969 |
3 | 19,3 | 0,12 | -1,17499 | 15 | 68,3 | 0,6 | 0,253347 |
4 | 24,8 | 0,16 | -0,99446 | 16 | 70,9 | 0,64 | 0,358459 |
5 | 27,5 | 0,2 | -0,84162 | 17 | 96 | 0,68 | 0,467699 |
6 | 27,8 | 0,24 | -0,7063 | 18 | 109,75 | 0,72 | 0,582842 |
7 | 32,4 | 0,28 | -0,58284 | 19 | 135,8 | 0,76 | 0,706303 |
8 | 33,4 | 0,32 | -0,4677 | 20 | 141,8 | 0,8 | 0,841621 |
9 | 33,8 | 0,36 | -0,35846 | 21 | 160 | 0,84 | 0,994458 |
10 | 33,9 | 0,4 | -0,25335 | 22 | 184,3 | 0,88 | 1,174987 |
11 | 35,1 | 0,44 | -0,15097 | 23 | 296,9 | 0,92 | 1,405072 |
12 | 50,9 | 0,48 | -0,05015 | 24 | 728,9 | 0,96 | 1,750686 |

для некоторой территории для исходных
нетрансформированных данных
При использовании исходных (нетрансформированных) данных две точки с экстремально высокими концентрациями суммы ПАУ отклоняются от прямой линии. Это указывает на то, что или это распределение логнормально, или эти две точки являются выбросами.
3 Вместо исходных данных, приведенных в примере 2, были использованы логарифмически трансформированные данные. Во втором столбце таблицы Ж.3 расположены исходные данные xi. В третьем столбце приведены рассчитанные с помощью уравнения (Ж.1) величины pi. В четвертом столбце приведены рассчитанные с помощью уравнения (Ж.2) величины zi. Полученный вероятностный график приведен на рисунке Ж.3.
Таблица Ж.3
для натуральных логарифмов данных содержания 

в почвах некоторой территории
i | Ln(xi) | pi | zi | i | Ln(xi) | pi | zi |
1 | 2,678965 | 0,04 | -1,75069 | 13 | 4,004602 | 0,52 | 0,050154 |
2 | 2,775709 | 0,08 | -1,40507 | 14 | 4,158102 | 0,56 | 0,150969 |
3 | 2,960105 | 0,12 | -1,17499 | 15 | 4,22391 | 0,6 | 0,253347 |
4 | 3,210844 | 0,16 | -0,99446 | 16 | 4,26127 | 0,64 | 0,358459 |
5 | 3,314186 | 0,2 | -0,84162 | 17 | 4,564348 | 0,68 | 0,467699 |
6 | 3,325036 | 0,24 | -0,7063 | 18 | 4,698205 | 0,72 | 0,582842 |
7 | 3,478158 | 0,28 | -0,58284 | 19 | 4,911183 | 0,76 | 0,706303 |
8 | 3,508556 | 0,32 | -0,4677 | 20 | 4,954418 | 0,8 | 0,841621 |
9 | 3,520461 | 0,36 | -0,35846 | 21 | 5,075174 | 0,84 | 0,994458 |
10 | 3,523415 | 0,4 | -0,25335 | 22 | 5,216565 | 0,88 | 1,174987 |
11 | 3,558201 | 0,44 | -0,15097 | 23 | 5,693395 | 0,92 | 1,405072 |
12 | 3,929863 | 0,48 | -0,05015 | 24 | 6,591537 | 0,96 | 1,750686 |

для некоторой территории для натуральных логарифмов
исходных данных
Если сравнить рисунок Ж.2 с рисунком, построенным с использованием данных, преобразованных в логарифмы (рисунок Ж.3), то при использовании логарифмически преобразованных данных точки концентрации  лежат на прямой линии. Поскольку логарифмически преобразованные данные являются приблизительно нормальными, можно сделать вывод, что исходная (нетрансформированная) выборка является логнормальной.
лежат на прямой линии. Поскольку логарифмически преобразованные данные являются приблизительно нормальными, можно сделать вывод, что исходная (нетрансформированная) выборка является логнормальной.
 лежат на прямой линии. Поскольку логарифмически преобразованные данные являются приблизительно нормальными, можно сделать вывод, что исходная (нетрансформированная) выборка является логнормальной.
лежат на прямой линии. Поскольку логарифмически преобразованные данные являются приблизительно нормальными, можно сделать вывод, что исходная (нетрансформированная) выборка является логнормальной.(рекомендуемое)
ПО ВЕЛИЧИНЕ ОТНОШЕНИЯ ДИАПАЗОНА К СТАНДАРТНОМУ ОТКЛОНЕНИЮ
Для проверки статистического критерия q необходимо знание только величины диапазона данных измерений РФК ОЗВ в почвах W и величины стандартного отклонения s. Этот критерий проверяет степень эксцесса распределения выборки. Статистика критерия q вычисляется в соответствии с уравнением (И.1)
При проверке с помощью критерия W/s используется критический диапазон. Если вычисленная величина попадает внутрь диапазона, тогда данные считаются распределенными нормально. Критические уровни критерия W/s для уровня значимости  0,05 и 0,10 приведены в таблице И.1.
0,05 и 0,10 приведены в таблице И.1.
Таблица И.1
Столбцы a и b обозначают критический уровень слева и справа
n | Уровень значимости | n | Уровень значимости | ||||||
0,05 | 0,10 | 0,05 | 0,10 | ||||||
a | b | a | b | a | b | a | b | ||
3 | 1,758 | 1,999 | 1,782 | 1,997 | 85 | 4,20 | 5,78 | 4,33 | 5,56 |
4 | 1,98 | 2,429 | 2,04 | 2,409 | 90 | 4,24 | 5,82 | 4,36 | 5,60 |
5 | 2,15 | 2,753 | 2,22 | 2,712 | 95 | 4,27 | 5,86 | 4,450 | 5,64 |
6 | 2,28 | 3,012 | 2,37 | 2,949 | 100 | 4,31 | 5,90 | 4,44 | 5,68 |
7 | 2,450 | 3,222 | 2,49 | 3,143 | 150 | 4,59 | 6,18 | 4,72 | 5,96 |
8 | 2,50 | 3,399 | 2,59 | 3,308 | 200 | 4,78 | 6,39 | 4,90 | 6,15 |
9 | 2,59 | 3,552 | 2,68 | 3,449 | 500 | 5,47 | 6,94 | 5,49 | 6,72 |
10 | 2,67 | 3,685 | 2,76 | 3,57 | 1000 | 5,79 | 7,33 | 5,92 | 7,11 |
11 | 2,74 | 3,80 | 2,84 | 3,68 | |||||
12 | 2,80 | 3,91 | 2,90 | 3,78 | |||||
13 | 2,86 | 4,00 | 2,96 | 3,87 | |||||
14 | 2,92 | 4,09 | 3,02 | 3,95 | |||||
15 | 2,97 | 4,17 | 3,07 | 4,02 | |||||
16 | 3,01 | 4,24 | 3,12 | 4,09 | |||||
17 | 3,06 | 4,31 | 3,17 | 4,15 | |||||
18 | 3,10 | 4,37 | 3,21 | 5,21 | |||||
19 | 3,14 | 4,43 | 3,25 | 4,27 | |||||
20 | 3,18 | 4,49 | 3,29 | 4,32 | |||||
25 | 3,34 | 4,71 | 3,45 | 4,53 | |||||
30 | 3,47 | 4,89 | 3,59 | 4,70 | |||||
35 | 3,58 | 5,04 | 3,70 | 4,84 | |||||
40 | 3,67 | 5,16 | 3,79 | 4,96 | |||||
45 | 3,75 | 5,26 | 3,88 | 5,06 | |||||
50 | 3,83 | 5,35 | 3,95 | 5,14 | |||||
55 | 3,90 | 5,43 | 4,02 | 5,22 | |||||
60 | 3,96 | 5,51 | 4,08 | 5,29 | |||||
65 | 4,01 | 5,57 | 4,14 | 5,35 | |||||
70 | 4,06 | 5,63 | 4,19 | 5,41 | |||||
75 | 4,11 | 5,68 | 4,24 | 5,46 | |||||
80 | 4,16 | 5,73 | 4,28 | 5,51 | |||||
Пример - На некоторой территории в 100 образцах были измерены фоновые концентрации нефтяных углеводородов, мг/кг. Исходные данные в порядке возрастания составляют: 1 - 26,8; 2 - 38,7; 3 - 43,7; 4 - 68,3; 5 - 88,9; 6 - 90,9; 7 - 91,6; 8 - 93,2; 9 - 96,5; 10 - 104,4; 11 - 105,7; 12 - 107,0; 13 - 114,0; 14 - 121,8; 15 - 122,5; 16 - 123,2; 17 - 129,94; 18 - 130,2; 19 - 131,3; 20 - 134,3; 21 - 140,4; 22 - 147,6; 23 - 148,5; 24 - 151,6; 25 - 154,2; 26 - 155,4; 27 - 155,8; 28 - 156,6; 29 - 157,9; 30 - 172,7; 31 - 173,2; 32 - 175,5; 33 - 175,8; 34 - 176,5; 35 - 176,5; 36 - 176,8; 37 - 181,0; 38 - 182,0; 39 - 183,5; 40 - 183,8; 41 - 185,4; 42 - 185,5; 43 - 188,5; 44 - 189,0; 45 - 189,2; 46 - 189,8; 47 - 189,8; 48 - 190,7; 49 - 191,1; 50 - 195,2; 51 - 195,2; 52 - 195,5; 53 - 198,9; 54 - 199,4; 55 - 202,6; 56 - 205,1; 57 - 209,2; 58 - 210,2; 59 - 211,0; 60 - 211,3; 61 - 214,3; 62 - 214,9; 63 - 217,3; 64 - 219,1; 65 - 220,0; 66 - 220,9; 67 - 222,1; 68 - 224,3; 69 - 225,0; 70 - 225,4; 71 - 230,6; 72 - 233,6; 73 - 235,2; 74 - 237,3; 75 - 238,4; 76 - 238,9; 77 - 239,6; 78 - 240,0; 79 - 245,9; 80 - 246,1; 81 - 246,2; 82 - 247,8; 83 - 253,4; 84 - 256,7; 85 - 260,4; 86 - 267,0; 87 - 270,9; 88 - 273,4; 89 - 282,1; 90 - 289,0; 91 - 292,2; 92 - 310,4; 93 - 311,8; 94 - 312,7; 95 - 328,1; 96 - 335,8; 97 - 346,0; 98 - 348,2; 99 - 348,5; 100 - 366,2.
Величина стандартного отклонения s для приведенного выше массива данных равна 70,44 мг/кг. Диапазон концентраций W равен 366,2 - 26,8 = 339,4 мг/кг. Отношение W/s = 4,82. Для величины  критические величины критерия на нормальность W/s для n = 100 составляют: a = 4,31 и b = 5,90. Таким образом, 4,31 < 4,82 < 5,90 и рассчитанное отношение W/s расположено внутри диапазона критических уровней a и b, и данные выборки распределены в соответствии с нормальным законом.
критические величины критерия на нормальность W/s для n = 100 составляют: a = 4,31 и b = 5,90. Таким образом, 4,31 < 4,82 < 5,90 и рассчитанное отношение W/s расположено внутри диапазона критических уровней a и b, и данные выборки распределены в соответствии с нормальным законом.
 критические величины критерия на нормальность W/s для n = 100 составляют: a = 4,31 и b = 5,90. Таким образом, 4,31 < 4,82 < 5,90 и рассчитанное отношение W/s расположено внутри диапазона критических уровней a и b, и данные выборки распределены в соответствии с нормальным законом.
критические величины критерия на нормальность W/s для n = 100 составляют: a = 4,31 и b = 5,90. Таким образом, 4,31 < 4,82 < 5,90 и рассчитанное отношение W/s расположено внутри диапазона критических уровней a и b, и данные выборки распределены в соответствии с нормальным законом.(обязательное)
РАСПРЕДЕЛЕНИЯ ШАПИРО-УИЛКСА ДЛЯ ЧИСЛА ОБРАЗЦОВ МЕНЕЕ 50
Для применения критерия Шапиро-Уилкса для проверки на нормальность распределения данных используют исходные нетрансформированные данные. Для проверки на логнормальность распределения выборки с помощью этого критерия сначала данные логарифмируют в соответствии с уравнением y = ln(x). Эти трансформированные данные используют вместо величин нетрансформированных данных x. Данные измерений ниже предела обнаружения (если в массиве данных их было не более 50%) заменяют на половину величины предела обнаружения. Критерий Шапиро-Уилкса (SW) к выборке применяют следующим образом:
а) данные рассортировывают в порядке возрастания от самого маленького к самому большому значению, где x(1) - самая маленькая величина, x(2) - большая величина и x(n) - самая большая величина;
б) принимают, что величина k равна самому большому целому числу, меньшему или равному (n/2) для четного числа n и (n - 1)/2 для нечетного числа n, где n обозначает количество данных;
в) для каждого i = 1, 2, ..., k вычисляют разницу [x(n - i + 1) - x(i)];
г) с помощью таблицы К.1 находят коэффициент ai для i = 1, 2, ..., k;
д) величину b вычисляют в соответствии с выражением (К.1):
 (К.1)
(К.1)е) для выборки вычисляют стандартное отклонение s;
ж) затем, согласно уравнению (К.2), вычисляют статистику критерия Шапиро-Уилкса
и) для выборки с количеством образцов n и уровнем значимости 0,05 с помощью таблицы К.2 вычисляют критическую величину критерия Шапиро-Уилкса  и сравнивают эту величину с вычисленным критерием SW;
и сравнивают эту величину с вычисленным критерием SW;
к) если величина SW больше или равна  , то делают заключение о том, что выборка имеет нормальное или логнормальное (если использовались величины y) распределение;
, то делают заключение о том, что выборка имеет нормальное или логнормальное (если использовались величины y) распределение;
л) если величина SW меньше  , то делают заключение о том, что распределение данных выборки не является нормальным или логнормальным (если использовались величины y).
, то делают заключение о том, что распределение данных выборки не является нормальным или логнормальным (если использовались величины y).
Таблица К.1
на нормальность для различного числа образцов (n)
i | n | ||||||||
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 0,7071 | 0,7071 | 0,6872 | 0,6646 | 0,6431 | 0,6233 | 0,6052 | 0,5888 | 0,5739 |
2 | 0,0000 | 0,1677 | 0,2413 | 0,2806 | 0,3031 | 0,3164 | 0,3244 | 0,3291 | |
3 | 0,0000 | 0,0875 | 0,1401 | 0,1743 | 0,1975 | 0,2141 | |||
4 | 0,0000 | 0,0561 | 0,0947 | 0,1224 | |||||
5 | 0,0000 | 0,0399 | |||||||
i | n | |||||||||
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
1 | 0,5601 | 0,5475 | 0,5359 | 0,5251 | 0,5150 | 0,5056 | 0,4968 | 0,4886 | 0,4808 | 0,4734 |
2 | 0,3315 | 0,3325 | 0,3325 | 0,3318 | 0,3306 | 0,3290 | 0,3273 | 0,3253 | 0,3232 | 0,3211 |
3 | 0,2260 | 0,2347 | 0,2412 | 0,2460 | 0,2495 | 0,2521 | 0,2540 | 0,2553 | 0,2561 | 0,2565 |
4 | 0,1429 | 0,1586 | 0,1707 | 0,1802 | 0,1878 | 0,1939 | 0,1988 | 0,2027 | 0,2059 | 0,2085 |
5 | 0,0695 | 0,0922 | 0,1099 | 0,1240 | 0,1353 | 0,1447 | 0,1524 | 0,1587 | 0,1641 | 0,1686 |
6 | 0,0000 | 0,0303 | 0,0539 | 0,0727 | 0,0880 | 0,1005 | 0,1109 | 0,1197 | 0,1271 | 0,1334 |
7 | 0,0000 | 0,0240 | 0,0433 | 0,0593 | 0,0725 | 0,0837 | 0,0932 | 0,1013 | ||
8 | 0,0000 | 0,0196 | 0,0359 | 0,0496 | 0,0612 | 0,0711 | ||||
9 | 0,0000 | 0,0163 | 0,0303 | 0,0422 | ||||||
10 | 0,0000 | 0,0140 | ||||||||
i | n | |||||||||
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
1 | 0,4643 | 0,4590 | 0,4542 | 0,4493 | 0,4450 | 0,4407 | 0,4366 | 0,4328 | 0,4291 | 0,4254 |
2 | 0,3185 | 0,3156 | 0,3126 | 0,3098 | 0,3069 | 0,3043 | 0,3018 | 0,2992 | 0,2968 | 0,2944 |
3 | 0,2578 | 0,2571 | 0,2563 | 0,2554 | 0,2543 | 0,2533 | 0,2522 | 0,2510 | 0,2499 | 0,2487 |
4 | 0,2119 | 0,2131 | 0,2139 | 0,2145 | 0,2148 | 0,2151 | 0,2152 | 0,2151 | 0,2150 | 0,2148 |
5 | 0,1736 | 0,1764 | 0,1787 | 0,1807 | 0,1822 | 0,1836 | 0,1848 | 0,1857 | 0,1864 | 0,1870 |
6 | 0,1399 | 0,1443 | 0,1480 | 0,1512 | 0,1539 | 0,1563 | 0,1584 | 0,1601 | 0,1616 | 0,1630 |
7 | 0,1092 | 0,1150 | 0,1201 | 0,1245 | 0,1283 | 0,1316 | 0,1346 | 0,1372 | 0,1395 | 0,1415 |
8 | 0,0804 | 0,0878 | 0,0941 | 0,0997 | 0,1046 | 0,1089 | 0,1128 | 0,1162 | 0,1192 | 0,1219 |
9 | 0,0530 | 0,0618 | 0,0696 | 0,0764 | 0,0823 | 0,0876 | 0,0923 | 0,0965 | 0,1002 | 0,1036 |
10 | 0,0263 | 0,0368 | 0,0459 | 0,0539 | 0,0610 | 0,0672 | 0,0728 | 0,0778 | 0,0822 | 0,0862 |
11 | 0,0422 | 0,0122 | 0,0228 | 0,0321 | 0,0403 | 0,0476 | 0,0540 | 0,0598 | 0,0065 | 0,0697 |
12 | 0,0000 | 0,0107 | 0,0200 | 0,0284 | 0,0358 | 0,0424 | 0,0483 | 0,0537 | ||
13 | 0,0000 | 0,0094 | 0,0178 | 0,0253 | 0,0320 | 0,0381 | ||||
14 | 0,0000 | 0,0084 | 0,0159 | 0,0227 | ||||||
15 | 0,0000 | 0,0076 | ||||||||
i | n | |||||||||
31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |
1 | 0,4220 | 0,4188 | 0,4156 | 0,4127 | 0,4096 | 0,4068 | 0,4040 | 0,4015 | 0,3989 | 0,3964 |
2 | 0,2921 | 0,2898 | 0,2876 | 0,2854 | 0,2834 | 0,2813 | 0,2794 | 0,2774 | 0,2755 | 0,2737 |
3 | 0,2475 | 0,2462 | 0,2451 | 0,2439 | 0,2427 | 0,2415 | 0,2403 | 0,2391 | 0,2380 | 0,2368 |
4 | 0,2145 | 0,2141 | 0,2137 | 0,2132 | 0,2127 | 0,2121 | 0,2116 | 0,2110 | 0,2104 | 0,2098 |
5 | 0,1874 | 0,1878 | 0,1880 | 0,1882 | 0,1883 | 0,1883 | 0,1883 | 0,1881 | 0,1880 | 0,1878 |
6 | 0,1641 | 0,1651 | 0,1660 | 0,1667 | 0,1673 | 0,1678 | 0,1683 | 0,1686 | 0,1689 | 0,1691 |
7 | 0,1433 | 0,1449 | 0,1463 | 0,1475 | 0,1487 | 0,1496 | 0,1505 | 0,1513 | 0,1520 | 0,1526 |
8 | 0,1243 | 0,1265 | 0,1284 | 0,1301 | 0,1317 | 0,1331 | 0,1344 | 0,1356 | 0,1366 | 0,1376 |
9 | 0,1066 | 0,1093 | 0,1118 | 0,1140 | 0,1160 | 0,1179 | 0,1196 | 0,1211 | 0,1225 | 0,1237 |
10 | 0,0899 | 0,0931 | 0,0961 | 0,0988 | 0,1013 | 0,1036 | 0,1056 | 0,1075 | 0,1092 | 0,1108 |
11 | 0,0739 | 0,0777 | 0,0812 | 0,0844 | 0,0873 | 0,0900 | 0,0924 | 0,0947 | 0,0967 | 0,0986 |
12 | 0,0585 | 0,0629 | 0,0669 | 0,0706 | 0,0739 | 0,0770 | 0,0798 | 0,0824 | 0,0848 | 0,0870 |
13 | 0,0435 | 0,0485 | 0,0530 | 0,0572 | 0,0610 | 0,0645 | 0,0677 | 0,0706 | 0,0733 | 0,0759 |
14 | 0,0289 | 0,0344 | 0,0395 | 0,0441 | 0,0484 | 0,0523 | 0,0559 | 0,0592 | 0,0622 | 0,0651 |
15 | 0,0144 | 0,0206 | 0,0262 | 0,0314 | 0,0361 | 0,0404 | 0,0444 | 0,0481 | 0,0515 | 0,0546 |
16 | 0,0000 | 0,0068 | 0,0131 | 0,0187 | 0,0239 | 0,0287 | 0,0331 | 0,0372 | 0,0409 | 0,0444 |
17 | - | - | 0,0000 | 0,0062 | 0,0119 | 0,0172 | 0,0220 | 0,0264 | 0,0305 | 0,0343 |
18 | - | - | - | - | 0,0000 | 0,0057 | 0,0110 | 0,0158 | 0,0203 | 0,0244 |
19 | - | - | - | - | - | - | 0,0000 | 0,0053 | 0,0101 | 0,0146 |
20 | - | - | - | - | - | - | - | - | 0,0000 | 0,0049 |
i | n | |||||||||
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | |
1 | 0,3940 | 0,3917 | 0,3894 | 0,3872 | 0,3850 | 0,3830 | 0,3808 | 0,3789 | 0,3770 | 0,3751 |
2 | 0,2719 | 0,2701 | 0,2684 | 0,2667 | 0,2651 | 0,2635 | 0,2620 | 0,2604 | 0,2589 | 0,2574 |
3 | 0,2357 | 0,2345 | 0,2334 | 0,2323 | 0,2313 | 0,2302 | 0,2291 | 0,2281 | 0,2271 | 0,2260 |
4 | 0,2091 | 0,2085 | 0,2078 | 0,2072 | 0,2065 | 0,2058 | 0,2052 | 0,2045 | 0,2038 | 0,2032 |
5 | 0,1876 | 0,1874 | 0,1871 | 0,1868 | 0,1865 | 0,1862 | 0,1859 | 0,1855 | 0,1851 | 0,1847 |
6 | 0,1693 | 0,1694 | 0,1695 | 0,1695 | 0,1695 | 0,1695 | 0,1695 | 0,1693 | 0,1692 | 0,1691 |
7 | 0,1531 | 0,1535 | 0,1539 | 0,1542 | 0,1545 | 0,1548 | 0,1550 | 0,1551 | 0,1553 | 0,1554 |
8 | 0,1384 | 0,1392 | 0,1398 | 0,1405 | 0,1410 | 0,1415 | 0,1420 | 0,1423 | 0,1427 | 0,1430 |
9 | 0,1249 | 0,1259 | 0,1269 | 0,1278 | 0,1286 | 0,1293 | 0,1300 | 0,1306 | 0,1312 | 0,1317 |
10 | 0,1123 | 0,1136 | 0,1149 | 0,1160 | 0,1170 | 0,1180 | 0,1189 | 0,1197 | 0,1205 | 0,1212 |
15 | 0,1004 | 0,1020 | 0,1035 | 0,1049 | 0,1062 | 0,1073 | 0,1085 | 0,1095 | 0,1105 | 0,1113 |
16 | 0,0891 | 0,0909 | 0,0927 | 0,0943 | 0,0959 | 0,0972 | 0,0986 | 0,9980 | 0,1010 | 0,1020 |
17 | 0,0782 | 0,0804 | 0,0824 | 0,0842 | 0,0860 | 0,0876 | 0,0892 | 0,0906 | 0,0919 | 0,0932 |
18 | 0,0677 | 0,0701 | 0,0724 | 0,0745 | 0,0765 | 0,0783 | 0,0801 | 0,0817 | 0,0832 | 0,0846 |
19 | 0,0575 | 0,0602 | 0,0628 | 0,0651 | 0,0673 | 0,0694 | 0,0713 | 0,0731 | 0,0748 | 0,0764 |
20 | 0,0476 | 0,0506 | 0,0534 | 0,0560 | 0,0584 | 0,0607 | 0,0628 | 0,0648 | 0,0667 | 0,0685 |
21 | 0,0379 | 0,0411 | 0,0442 | 0,0471 | 0,0497 | 0,0522 | 0,0546 | 0,0568 | 0,0588 | 0,0608 |
22 | 0,0283 | 0,0318 | 0,0352 | 0,0383 | 0,0412 | 0,0439 | 0,0465 | 0,0489 | 0,0511 | 0,0532 |
23 | 0,0188 | 0,0227 | 0,0263 | 0,0296 | 0,0328 | 0,0357 | 0,0385 | 0,0411 | 0,0436 | 0,0459 |
24 | 0,0094 | 0,0136 | 0,0175 | 0,0211 | 0,0245 | 0,0277 | 0,0307 | 0,0335 | 0,0361 | 0,0386 |
25 | 0,0000 | 0,0045 | 0,0087 | 0,0126 | 0,0163 | 0,0197 | 0,0229 | 0,0259 | 0,0288 | 0,0314 |
Пример - Предположим, что для некоторой территории в 20 образцах были измерены фоновые концентрации ОЗВ. В порядке возрастания исходные данные, мг/кг, равны: 1 - 1,0; 2 - 3,1; 3 - 8,7; 4 - 10; 5 - 14; 6 - 19; 7 - 21,4; 8 - 27; 9 - 39; 10 - 56; 11 - 58,8; 12 - 64,4; 13 - 81,5; 14 - 85,6; 15 - 151; 16 - 262; 17 - 331; 18 - 578; 19 - 637; 20 - 942. В соответствии с пунктом 2 величина n = 20, а величина k = 10. Для каждой величины i = 1, 2, ..., k с помощью таблицы К.1 находят коэффициент ai. Затем с помощью уравнения И.1 рассчитывают величину bi. Для положительных величин разницы [x(n - i + 1) - x(i)] рассчитывают величину b. Для этого примера b составила величину 932,88. Стандартное отклонение для этого массива измерений составило 259,7 мг/кг. С помощью уравнения (К.2) для уровня значимости 0,05 вычисляют величину критерия Шапиро-Уилкса SW = 0,679. С помощью таблицы К.2 находят критическую величину критерия Шапиро-Уилкса (SW0,05). Эта величина для 20 образцов равна 0,905. Поскольку вычисленная величина SW < SW0,05 (0,679 < 0,905), делают заключение, что исходные данные не имеют нормального распределения. Однако если провести аналогичные вычисления, используя натуральные логарифмы исходных данных, то вычисленная величина SW > SW0,05 (0,980 > 0,905), и можно сделать заключение, что логтрансформированные данные имеют нормальное распределение.
Таблица К.2
для критерия Шапиро-Уилкса на нормальность распределения
n | SW0,05 | SW0,10 | n | SW0,05 | SW0,10 |
3 | 0,767 | 0,789 | 27 | 0,923 | 0,935 |
4 | 0,748 | 0,792 | 28 | 0,924 | 0,936 |
5 | 0,762 | 0,806 | 29 | 0,926 | 0,937 |
6 | 0,788 | 0,826 | 30 | 0,927 | 0,939 |
7 | 0,803 | 0,838 | 31 | 0,929 | 0,940 |
8 | 0,818 | 0,851 | 32 | 0,930 | 0,941 |
9 | 0,829 | 0,859 | 33 | 0,931 | 0,942 |
10 | 0,842 | 0,869 | 34 | 0,933 | 0,943 |
11 | 0,850 | 0,876 | 35 | 0,934 | 0,944 |
12 | 0,859 | 0,883 | 36 | 0,935 | 0,945 |
13 | 0,866 | 0,889 | 37 | 0,936 | 0,946 |
14 | 0,874 | 0,895 | 38 | 0,938 | 0,947 |
15 | 0,881 | 0,901 | 39 | 0,939 | 0,948 |
16 | 0,887 | 0,906 | 40 | 0,940 | 0,949 |
17 | 0,892 | 0,910 | 41 | 0,941 | 0,950 |
18 | 0,897 | 0,914 | 42 | 0,942 | 0,951 |
19 | 0,901 | 0,917 | 43 | 0,943 | 0,951 |
20 | 0,905 | 0,920 | 44 | 0,944 | 0,952 |
21 | 0,908 | 0,923 | 45 | 0,945 | 0,953 |
22 | 0,911 | 0,926 | 46 | 0,945 | 0,953 |
23 | 0,914 | 0,928 | 47 | 0,946 | 0,954 |
24 | 0,916 | 0,930 | 48 | 0,947 | 0,954 |
25 | 0,918 | 0,931 | 49 | 0,947 | 0,955 |
26 | 0,920 | 0,933 | 50 | 0,947 | 0,955 |
(обязательное)
РАСПРЕДЕЛЕНИЯ ШАПИРО-ФРАНЧИЯ ДЛЯ ЧИСЛА ОБРАЗЦОВ БОЛЕЕ 50
При количестве данных в массиве более 50 (n > 50) для проверки нормальности распределения в качестве формального критерия используют критерий Шапиро-Франчия. Для того чтобы применить этот критерий к проверке выборки на логнормальность, сначала вычисляют y = ln(x) и используют эти трансформированные данные вместо величин x. Данные измерений ниже предела обнаружения (если в массиве данных их было не более 50%) заменяют на половину величины предела обнаружения. Для определения того, какое из двух типов распределения данных лучше описывает данную выборку, следует сравнить результаты применения критерия к исходным и логарифмированным данным:
а) данные рассортировывают в порядке возрастания от самого маленького к самому большому значению, где x(1) - самая маленькая величина, x(2) - большая величина и x(n) - самая большая величина;
б) затем вычисляют величину стандартного отклонения для массива данных и возводят ее в квадрат (s2);
в) затем вычисляют mi или i-ую нормальную квантиль (величина z) в соответствии с выражением (Л.1):
 (Л.1)
(Л.1)где Ф-1 означает обратную величину кумулятивного стандартного нормального распределения;
г) величину критерия Шапиро-Франчия (SF) вычисляют в соответствии с уравнением (Л.2):
д) с помощью таблицы Л.1 на основании числа наблюдений n, принимая доверительный уровень 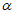 , равный 0,05, определяют критическую величину критерия Шапиро-Франчия
, равный 0,05, определяют критическую величину критерия Шапиро-Франчия  и сравнивают с расчетной величиной SF;
и сравнивают с расчетной величиной SF;
е) если  , делают заключение о том, что массив данных распределен нормально (или логнормально, если используют величины y);
, делают заключение о том, что массив данных распределен нормально (или логнормально, если используют величины y);
 , делают заключение о том, что массив данных распределен нормально (или логнормально, если используют величины y);
, делают заключение о том, что массив данных распределен нормально (или логнормально, если используют величины y);ж) если  , делают заключение о том, что массив данных не распределен нормально (или логнормально, если используют величины y).
, делают заключение о том, что массив данных не распределен нормально (или логнормально, если используют величины y).
 , делают заключение о том, что массив данных не распределен нормально (или логнормально, если используют величины y).
, делают заключение о том, что массив данных не распределен нормально (или логнормально, если используют величины y).Таблица Л.1
Шапиро-Франчия проверки на нормальность распределения
n | SW0,05 | n | SW0,05 |
50 | 0,953 | 75 | 0,969 |
51 | 0,954 | 77 | 0,969 |
53 | 0,957 | 79 | 0,970 |
55 | 0,958 | 81 | 0,970 |
57 | 0,961 | 83 | 0,971 |
59 | 0,962 | 85 | 0,972 |
61 | 0,963 | 87 | 0,972 |
63 | 0,964 | 89 | 0,972 |
65 | 0,965 | 91 | 0,973 |
67 | 0,966 | 93 | 0,973 |
69 | 0,966 | 95 | 0,974 |
71 | 0,967 | 97 | 0,975 |
73 | 0,968 | 99 | 0,976 |
Если результаты статистической проверки свидетельствуют о том, что данные проходят оба типа проверки, то для того, чтобы сделать выводы о распределении данных, необходимо учитывать результаты проверки с более высоким значением SF.
Пример - Предположим, что на некоторой территории в 52 образцах были измерены фоновые ОЗВ. Исходные данные в порядке возрастания составляют (в мг/кг): 1 - 1,07; 2 - 1,43; 3 - 1,51; 4 - 1,84; 5 - 1,99; 6 - 2,08; 7 - 2,20; 8 - 2,36; 9 - 2,51; 10 - 2,83; 11 - 3,25; 12 - 3,56; 13 - 3,90; 14 - 4,14; 15 - 4,26; 16 - 4,39; 17 - 4,53; 18 - 4,81; 19 - 5,0; 20 - 5,05; 21 - 5,47; 22 - 5,53; 23 - 5,58; 24 - 5,64; 25 - 5,64; 26 - 5,75; 27 - 5,81; 28 - 5,87; 29 - 6,17; 30 - 6,42; 31 - 6,96; 32 - 6,96; 33 - 7,24; 34 - 7,54; 35 - 8,17; 36 - 8,85; 37 - 11,02; 38 - 12,30; 39 - 13,07; 40 - 14,15; 41 - 14,59; 42 - 16,78; 43 - 18,17; 44 - 19,30; 45 - 20,29; 46 - 21,98; 47 - 25,79; 48 - 27,11; 49 - 31,19; 50 - 32,46; 51 - 38,47; 52 - 43,82.
С помощью вероятностных графиков можно предположить, что этот массив данных имеет логарифмически нормальное распределение. Для формального подтверждения этой гипотезы к этому массиву данных применяют критерий Шапиро-Франчия. Величина критерия Шапиро-Франчия SFLN для логарифмов исходных данных, рассчитанная с помощью уравнения (Л.2), равняется 0,9763. Величина критерия Шапиро-Франчия для исходных (нетрансформированных данных) равна только 0,7682. Для числа образцов 52 и уровня значимости 0,05 величина SF0,05 равняется 0,955. Поскольку SWLN > SW0,05, можно сделать заключение, что массив данных для ОЗВ имеет логнормальное распределение.
(рекомендуемое)
ФОРМАЛЬНЫЙ СТАТИСТИЧЕСКИЙ КРИТЕРИЙ ПРОВЕРКИ НОРМАЛЬНОСТИ
РАСПРЕДЕЛЕНИЯ ХАРКЕ-БЕРА ДЛЯ ЧИСЛА ОБРАЗЦОВ БОЛЕЕ 1 000
С помощью критерия Харке-Бера проверяют соответствие асимметрии и эксцесса выборки нормальному распределению:
а) сначала выдвигают гипотезу Ho о нормальном распределении выборки;
б) затем вычисляют фактическое значение критерия. В соответствии с этим критерием сначала вычисляют коэффициент асимметрии k3 в соответствии с уравнением (М.1)
затем - коэффициент эксцесса k4 в соответствии с уравнением (М.2)
 (М.2)
(М.2)и величину критерия Харке-Бера JB в соответствии с уравнением (М.3)
Затем определяют табличное значение критерия на основе таблицы М.1 критических значений Пирсона на уровне значимости 0,05 и числе степеней свободы 2. Это значение равно 5,991. Уровень значимости - это вероятность ошибки при утверждении, что распределение является ненормальным. Общепринятой является вероятность ошибки, не превышающая 5%. Число степеней свободы в данном случае отвечает за количество параметров в формуле критерия, а ими являются асимметрия и эксцесс.
Таблица М.1
0,1 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | |
4,605 | 5,991 | 7,378 | 9,210 | 10,597 | 13,816 |
Таким образом, если величина JB > 5,991, то распределение не является нормальным, а если величина JB < 5,991, то распределение является нормальным.
Пример - Предположим, что на некоторой территории в 24 образцах были измерены фоновые концентрации суммы ПАУ, мкг/кг. Исходные данные в порядке возрастания составляют: 1 - 14,57; 2 - 16,05; 3 - 19,3; 4 - 24,8; 5 - 27,5; 6 - 27,8; 7 - 32,4; 8 - 33,4; 9 - 33,8; 10 - 33,9; 11 - 35,1; 12 - 50,9; 13 - 54,85; 14 - 63,95; 15 - 68,3; 16 - 70,9; 17 - 96; 18 - 109,75; 19 - 135,8; 20 - 141,8; 21 - 160; 22 - 184,3; 23 - 296,9; 24 - 728,9.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: уравнение 33 отсутствует. Возможно, имеется в виду уравнение (М.3). |
Если использовать весь приведенный массив данных, то коэффициент асимметрии k3 в соответствии с уравнением (М.1) равняется 3,10, а коэффициент эксцесса k4 равняется 9,971. Рассчитанная по уравнению 33 величина критерия Харке-Бера JB равняется 137,8. Таким образом, 137,8 более 5,991 и распределение массива данных не является нормальным.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: уравнение 33 отсутствует. Возможно, имеется в виду уравнение (М.3). |
Если отбросить два максимальных измерения (296,9 и 728,9 мкг/кг), то коэффициент асимметрии k3 в соответствии с уравнением (М.1) равняется 0,973, а коэффициент эксцесса k4 равняется минус 0,410. Рассчитанная по уравнению 33 величина критерия Харке-Бера JB равняется 3,63. Таким образом, 3,63 менее 5,991 и распределение массива данных является нормальным.
(рекомендуемое)
РАСПРЕДЕЛЕНИЯ Д'АГОСТИНО ДЛЯ ЧИСЛА ОБРАЗЦОВ БОЛЕЕ 50
Критерий Д'Агостино основан на D-статистике, который определяет постоянное отношение оценки популяции Даунтона к стандартному отношению выборки. Критерий учитывает отклонения от нормальности для эксцесса и асимметрии. Порядок расчета по этому критерию приведен ниже:
а) необходимо рассортировать данные в порядке возрастания от самого маленького к самому большому значению, где x(1) - самая маленькая величина, x(2) - следующая большая величина и x(n) - самая большая величина;
б) затем вычисляют величину критерия D в соответствии с уравнением (Н.1)
 (Н.1)
(Н.1)где n - количество данных в массиве;
 (Н.2)
(Н.2)и
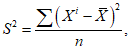 (Н.3)
(Н.3)где  - величина среднего арифметического выборки;
- величина среднего арифметического выборки;
i - порядок (или ранг) наблюдения x;
в) затем вычисляют критерий Y в соответствии с уравнением
 (Н.4)
(Н.4)г) находят величину критерия Д'Агостино в таблице Н.1. Если число образцов не перечислено в таблице, следует использовать следующую графу для более низкого значения n. Для каждого уровня значимости в таблице даны два критических значения. Если вычисленное значение Y меньше или равно первому члену пары (критической величине  ) или больше или равно второму члену пары (критической величине
) или больше или равно второму члену пары (критической величине  ), то распределение концентраций в массиве данных не является нормальным.
), то распределение концентраций в массиве данных не является нормальным.
Таблица Н.1
нормальности выборки
n | 0,005 | 0,001 | 0,025 | 0,05 | 0,1 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 |
50 | -3,949 | -3,442 | 2,757 | -2,220 | -1,661 | 0,759 | 0,923 | 1,038 | 1,140 | 1,192 |
60 | -3,846 | -3,360 | -2,699 | -2,179 | -1,634 | 0,807 | 0,986 | 1,115 | 1,236 | 1,301 |
70 | -3,762 | -3,293 | -2,652 | -2,146 | -1,612 | 0,844 | 1,036 | 1,176 | 1,312 | 1,388 |
80 | -3,693 | -3,237 | -2,613 | -2,118 | -1,594 | 0,874 | 1,076 | 1,226 | 1,374 | 1,459 |
90 | -3,635 | -3,100 | -2,580 | -2,095 | -1,579 | 0,899 | 1,109 | 1,268 | 1,426 | 1,518 |
100 | -3,584 | -3,150 | -2,552 | -2,075 | -1,566 | 0,920 | 1,137 | 1,303 | 1,470 | 1,569 |
150 | -3,409 | -3,009 | -2,452 | -2,004 | -1,520 | 0,990 | 1,233 | 1,423 | 1,623 | 1,746 |
200 | -3,302 | -2,922 | -2,391 | -1,960 | -1,491 | 1,032 | 1,290 | 1,496 | 1,715 | 1,853 |
250 | -3,227 | -2,861 | -2,348 | -1,926 | -1,471 | 1,060 | 1,328 | 1,545 | 1,779 | 1,927 |
300 | -3,172 | -2,816 | -2,316 | -1,906 | -1,456 | 1,080 | 1,357 | 1,528 | 1,826 | 1,983 |
350 | -3,129 | -2,781 | -2,291 | -1,888 | -1,444 | 1,096 | 1,379 | 1,610 | 1,863 | 2,026 |
400 | -3,094 | -2,753 | -2,270 | -1,873 | -1,434 | 1,108 | 1,396 | 1,633 | 1,893 | 2,061 |
450 | -3,064 | -2,729 | -2,253 | -1,861 | -1,426 | 1,119 | 1,411 | 1,652 | 1,918 | 2,090 |
500 | -3,040 | -2,709 | -2,239 | -1,850 | -1,419 | 1,127 | 1,423 | 1,668 | 1,938 | 2,114 |
550 | -3,019 | -2,691 | -2,226 | -1,841 | -1,413 | 1,135 | 1,434 | 1,682 | 1,957 | 2,136 |
600 | -3,000 | -2,676 | -2,215 | -1,833 | -1,408 | 1,141 | 1,443 | 1,694 | 1,972 | 2,154 |
650 | -2,984 | -2,663 | -2,206 | -1,826 | -1,403 | 1,147 | 1,451 | 1,704 | 1,986 | 2,171 |
700 | -2,969 | -2,651 | -2,197 | -1,820 | -1,399 | 1,152 | 1,458 | 1,714 | 1,999 | 2,185 |
750 | -2,956 | -2,640 | -2,189 | -1,814 | -1,395 | 1,157 | 1,465 | 1,722 | 2,010 | 2,199 |
800 | -2,933 | -2,621 | -2,176 | -1,804 | -1,389 | 1,165 | 1,476 | 1,737 | 2,029 | 2,221 |
850 | -2,933 | -2,621 | -2,176 | -1,804 | -1,389 | 1,165 | 1,476 | 1,737 | 2,029 | 2,221 |
900 | -2,923 | -2,613 | -2,170 | -1,800 | -1,386 | 1,168 | 1,481 | 1,743 | 2,037 | 2,231 |
950 | -2,914 | -2,605 | -2,164 | -1,796 | -1,383 | 1,171 | 1,485 | 1,749 | 2,045 | 2,241 |
1000 | -2,906 | -2,599 | -2,159 | -1,792 | -1,381 | 1,174 | 1,489 | 1,754 | 2,052 | 2,249 |
Пример - На некоторой территории в 100 образцах были измерены фоновые концентрации нефтяных углеводородов, мкг/кг. Исходные данные в порядке возрастания составляют: 1 - 26,8; 2 - 38,7; 3 - 43,7; 4 - 68,3; 5 - 88,9; 6 - 90,9; 7 - 91,6; 8 - 93,2; 9 - 96,5; 10 - 104,4; 11 - 105,7; 12 - 107,0; 13 - 114,0; 14 - 121,8; 15 - 122,5; 16 - 123,2; 17 - 129,94; 18 - 130,2; 19 - 131,3; 20 - 134,3; 21 - 140,4; 22 - 147,6; 23 - 148,5; 24 - 151,6; 25 - 154,2; 26 - 155,4; 27 - 155,8; 28 - 156,6; 29 - 157,9; 30 - 172,7; 31 - 173,2; 32 - 175,5; 33 - 175,8; 34 - 176,5; 35 - 176,5; 36 - 176,8; 37 - 181,0; 38 - 182,0; 39 - 183,5; 40 - 183,8; 41 - 185,4; 42 - 185,5; 43 - 188,5; 44 - 189,0; 45 - 189,2; 46 - 189,8; 47 - 189,8; 48 - 190,7; 49 - 191,1; 50 - 195,2; 51 - 195,2; 52 - 195,5; 53 - 198,9; 54 - 199,4; 55 - 202,6; 56 - 205,1; 57 - 209,2; 58 - 210,2; 59 - 211,0; 60 - 211,3; 61 - 214,3; 62 - 214,9; 63 - 217,3; 64 - 219,1; 65 - 220,0; 66 - 220,9; 67 - 222,1; 68 - 224,3; 69 - 225,0; 70 - 225,4; 71 - 230,6; 72 - 233,6; 73 - 235,2; 74 - 237,3; 75 - 238,4; 76 - 238,9; 77 - 239,6; 78 - 240,0; 79 - 245,9; 80 - 246,1; 81 - 246,2; 82 - 247,8; 83 - 253,4; 84 - 256,7; 85 - 260,4; 86 - 267,0; 87 - 270,9; 88 - 273,4; 89 - 282,1; 90 - 289,0; 91 - 292,2; 92 - 310,4; 93 - 311,8; 94 - 312,7; 95 - 328,1; 96 - 335,8; 97 - 346,0; 98 - 348,2; 99 - 348,5; 100 - 366,2.
Предположим, что необходимая величина  равна 0,05.
равна 0,05.
Вычисляем величину S, которая равна

Вычисляем величину T:

Величина D = 195886/(1002·70,1) = 0,279502.
Рассчитываем: Y = 1001/2(0,279502 - 0,282094)/0,02998798 = -0,86459.
Поскольку минус 0,86459 больше, чем минус 2,522, и меньше, чем 1,303, нельзя сделать заключение, что измерения в массиве данных распределены не в соответствии с нормальным законом распределения.
(обязательное)
(ВЫБРОСА) С ПОМОЩЬЮ КРИТЕРИЯ ГРАББСА ДЛЯ ЧИСЛА ОБРАЗЦОВ
ОТ 3 ДО 100
Для идентификации одиночных выбросов в массиве данных с числом измерений от 3 до 100 используется критерий Граббса. Вычисления проводят в соответствии с методикой, приведенной ниже:
а) используя все значения измерений, включая предполагаемый выброс, вычисляют среднее арифметическое  и стандартное отклонение (s) массива данных;
и стандартное отклонение (s) массива данных;
б) предполагаемый выброс (то есть максимальное значение) обозначается как xn, и с помощью уравнения (П.1) вычисляют величину критерия Граббса TG:
 (П.1)
(П.1)в) полученное значение TG сравнивают с критическим значением 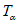 в таблице Н.1 на основании размера выборки (n) и доверительного уровня 95% (то есть
в таблице Н.1 на основании размера выборки (n) и доверительного уровня 95% (то есть  );
);
 );
);г) если  , делают вывод о том, что измерение является выбросом.
, делают вывод о том, что измерение является выбросом.
 , делают вывод о том, что измерение является выбросом.
, делают вывод о том, что измерение является выбросом.Пример - Предположим, что для некоторой территории в 10 образцах были измерены фоновые концентрации ОЗВ, мг/кг. Исходные данные составляют: 1 - 21,2; 2 - 26,0; 3-9,1; 4 - 28,7; 5 - 13,6; 6 - 52,6; 7 - 18,8; 8 - 25,5; 9 - 18,5; 10 - 26,4. Предположим, что оценка показала, что набор данных распределен нормально, за исключением одного максимального значения (одного потенциального выброса в 52,6 мг/кг).
При использовании всех 10 измерений вычисленная величина TG равна 2,42, а критическая величина  из таблицы П.1 при
из таблицы П.1 при  равной 0,05 составляет 2,176. Поскольку TG больше
равной 0,05 составляет 2,176. Поскольку TG больше  (2,42 больше 2,176), можно сделать заключение, что измерение с концентрацией 52,6 мг/кг является выбросом.
(2,42 больше 2,176), можно сделать заключение, что измерение с концентрацией 52,6 мг/кг является выбросом.
Таблица П.1
Критические величины критерия Граббса ( ,
,  )
)
 )
)n | n | n | |||
3 | 1,153 | 36 | 2,823 | 68 | 3,071 |
4 | 1,463 | 37 | 2,835 | 69 | 3,076 |
5 | 1,672 | 38 | 2,846 | 70 | 3,082 |
6 | 1,822 | 39 | 2,857 | 71 | 3,087 |
7 | 1,938 | 40 | 2,866 | 72 | 3,092 |
8 | 2,032 | 41 | 2,877 | 73 | 3,098 |
9 | 2,110 | 42 | 2,887 | 74 | 3,102 |
10 | 2,176 | 43 | 2,896 | 75 | 3,107 |
11 | 2,234 | 44 | 2,905 | 76 | 3,111 |
12 | 2,285 | 45 | 2,914 | 77 | 3,117 |
13 | 2,331 | 46 | 2,923 | 78 | 3,121 |
14 | 2,371 | 47 | 2,931 | 79 | 3,125 |
15 | 2,409 | 48 | 2,940 | 80 | 3,130 |
16 | 2,443 | 49 | 2,948 | 81 | 3,134 |
17 | 2,475 | 50 | 2,956 | 82 | 3,139 |
18 | 2,504 | 51 | 2,964 | 83 | 3,143 |
19 | 2,532 | 52 | 2,971 | 84 | 3,147 |
20 | 2,557 | 53 | 2,978 | 85 | 3,151 |
21 | 2,580 | 54 | 2,986 | 86 | 3,155 |
22 | 2,603 | 55 | 2,992 | 87 | 3,160 |
23 | 2,624 | 56 | 3,000 | 88 | 3,163 |
24 | 2,644 | 57 | 3,006 | 89 | 3,167 |
25 | 2,663 | 58 | 3,013 | 90 | 3,171 |
26 | 2,681 | 59 | 3,019 | 91 | 3,174 |
27 | 2,698 | 60 | 3,025 | 92 | 3,179 |
28 | 2,714 | 61 | 3,032 | 93 | 3,182 |
29 | 2,730 | 62 | 3,037 | 94 | 3,186 |
30 | 2,745 | 63 | 3,044 | 95 | 3,189 |
31 | 2,759 | 64 | 3,049 | 96 | 3,193 |
32 | 2,773 | 65 | 3,055 | 97 | 3,196 |
33 | 2,786 | 66 | 3,061 | 98 | 3,201 |
34 | 2,799 | 67 | 3,066 | 99 | 3,204 |
35 | 2,811 | 68 | 3,071 | 100 | 3,207 |
Окончание таблицы П.1
n | n | n | |||
101 | 3,210 | 116 | 3,257 | 131 | 3,296 |
102 | 3,214 | 117 | 3,259 | 132 | 3,298 |
103 | 3,217 | 118 | 3,262 | 133 | 3,302 |
104 | 3,220 | 119 | 3,265 | 134 | 3,304 |
105 | 3,224 | 120 | 3,267 | 135 | 3,306 |
106 | 3,227 | 121 | 3,270 | 136 | 3,309 |
107 | 3,230 | 122 | 3,274 | 137 | 3,311 |
108 | 3,233 | 123 | 3,276 | 138 | 3,313 |
109 | 3,236 | 124 | 3,279 | 139 | 3,315 |
110 | 3,239 | 125 | 3,281 | 140 | 3,318 |
111 | 3,242 | 126 | 3,284 | 141 | 3,320 |
112 | 3,245 | 127 | 3,286 | 142 | 3,322 |
113 | 3,248 | 128 | 3,289 | 143 | 3,324 |
114 | 3,251 | 129 | 3,291 | 144 | 3,326 |
115 | 3,254 | 130 | 3,294 | 145 | 3,328 |
(рекомендуемое)
С ПОМОЩЬЮ КРИТЕРИЯ ДИКСОНА ДЛЯ ЧИСЛА ОБРАЗЦОВ МЕНЕЕ 25
Если есть подозрения, что в массиве данных с числом измерений n <= 25 имеются несколько выбросов, то для проверки этого используют критерий Диксона. Причем если количество данных ниже предела обнаружения составляют не более 50%, то, заменив измерения ниже предела обнаружения на половину величины предела обнаружения при нормальной форме распределения, этот критерий применяют к исходным (нетрансформированным) данным. Для проверки данных на выбросы при логарифмически нормальном распределении сначала рассчитывают величину y = ln(x) и используют значения y (логарифмически трансформированные данные) вместо значений исходных значений x по приведенной ниже методике:
а) располагают набор данных от наименьшего значения до наибольшего значения и отмечают наблюдения как x(1), x(2) ... x(n), где x(1) является наименьшим значением и x(n) является наибольшим значением;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: уравнения 12 - 15 отсутствуют. |
б) основываясь на размере выборки (n), используют одно из уравнений (12) - (15) для расчета контрольной статистики TD;
n | Статистика критерия Диксона | |
3 - 7 | (x(n) - x(n-1))/(x(n) - x(1)) | Уравнение (Р.1) |
8 - 10 | (x(n) - x(n-1))/(x(n) - x(2)) | Уравнение (Р.2) |
11 - 13 | (x(п) - x(n-2))/(x(п) - x(2)) | |
14 - 25 | (x(п) - x(n-2))/(x(n) - x(3)) | Уравнение (Р.4) |
в) в таблице Р.1 находят критическое значение критерия Диксона  для количества измерений (n) и уровня достоверности 95% (то есть
для количества измерений (n) и уровня достоверности 95% (то есть 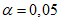 );
);
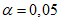 );
);г) сравнивают TD с  . Если TD больше
. Если TD больше  , то измерение (и все потенциальные выбросы, превышающие это значение) можно классифицировать как выбросы.
, то измерение (и все потенциальные выбросы, превышающие это значение) можно классифицировать как выбросы.
Таблица Р.1
n | T | n | T | n | T |
3 | 0,941 | 11 | 0,576 | 19 | 0,462 |
4 | 0,765 | 12 | 0,546 | 20 | 0,450 |
5 | 0,642 | 13 | 0,521 | 21 | 0,440 |
6 | 0,560 | 14 | 0,546 | 22 | 0,430 |
7 | 0,507 | 15 | 0,525 | 23 | 0,421 |
8 | 0,554 | 16 | 0,507 | 24 | 0,413 |
9 | 0,512 | 17 | 0,490 | 25 | 0,406 |
10 | 0,477 | 18 | 0,475 |
Пример - Предположим, что для некоторой территории в 14 образцах были измерены фоновые концентрации бенз(а)пирена. Исходные данные составляют, нг/г: 1 - 1,9; 2 - 2,1; 3 - 2,2; 4 - 2,4; 5 - 2,5; 6 - 2,5; 7 - 2,7; 8 - 2,8; 9 - 2,9; 10 - 3,1; 11 - 3,2; 12 - 3,9; 13 - 4,5; 14 - 4,6. В соответствии с разделом о выбросах можно считать, что, за исключением последних трех данных, эти данные распределены нормально. Сначала оценивается первый потенциальный выброс (3,9 нг/г). Наблюдения с большими значениями (4,5 и 4,6 нг/г) временно не рассматриваются при вычислении критерия Диксона. Поэтому для проведения вычислений число образцов изменяется до 12. Поэтому для вычислений используется уравнение (Р.3). Для n = 12 вычисленная с помощью уравнения (Р.3) величина TD равна 0,444, а критическая величина  для
для  составляет 0,546 (таблица Р.1). Поскольку 0,444 < 0,546, можно сделать заключение, что измерение с концентрацией 3,9 нг/г не является выбросом. Затем количество наблюдений увеличивается до 13. При этом наблюдение с концентрацией 4,5 нг/г считается выбросом. Наблюдение N 14 с максимальной концентрацией 4,6 нг/г при проведении этого расчета не учитывается. Для n, равного 13, вычисленная с помощью уравнения (Р.3) величина TD равна 0,542, а критическая величина
составляет 0,546 (таблица Р.1). Поскольку 0,444 < 0,546, можно сделать заключение, что измерение с концентрацией 3,9 нг/г не является выбросом. Затем количество наблюдений увеличивается до 13. При этом наблюдение с концентрацией 4,5 нг/г считается выбросом. Наблюдение N 14 с максимальной концентрацией 4,6 нг/г при проведении этого расчета не учитывается. Для n, равного 13, вычисленная с помощью уравнения (Р.3) величина TD равна 0,542, а критическая величина 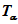 для
для  , равной 0,05, и n, равного 13, составляет 0,521 (таблица Р.1). Поскольку 0,542 больше 0,521, можно сделать заключение, что измерение с концентрацией 4,5 нг/г является выбросом. Поскольку неучтенное измерение с концентрацией 4,6 нг/г больше, чем величина 4,5 нг/г, то можно считать, что оба этих измерения являются выбросами.
, равной 0,05, и n, равного 13, составляет 0,521 (таблица Р.1). Поскольку 0,542 больше 0,521, можно сделать заключение, что измерение с концентрацией 4,5 нг/г является выбросом. Поскольку неучтенное измерение с концентрацией 4,6 нг/г больше, чем величина 4,5 нг/г, то можно считать, что оба этих измерения являются выбросами.
 составляет 0,546 (таблица Р.1). Поскольку 0,444 < 0,546, можно сделать заключение, что измерение с концентрацией 3,9 нг/г не является выбросом. Затем количество наблюдений увеличивается до 13. При этом наблюдение с концентрацией 4,5 нг/г считается выбросом. Наблюдение N 14 с максимальной концентрацией 4,6 нг/г при проведении этого расчета не учитывается. Для n, равного 13, вычисленная с помощью уравнения (Р.3) величина TD равна 0,542, а критическая величина
составляет 0,546 (таблица Р.1). Поскольку 0,444 < 0,546, можно сделать заключение, что измерение с концентрацией 3,9 нг/г не является выбросом. Затем количество наблюдений увеличивается до 13. При этом наблюдение с концентрацией 4,5 нг/г считается выбросом. Наблюдение N 14 с максимальной концентрацией 4,6 нг/г при проведении этого расчета не учитывается. Для n, равного 13, вычисленная с помощью уравнения (Р.3) величина TD равна 0,542, а критическая величина (обязательное)
КРИТЕРИЯ РОЗНЕРА ДЛЯ ЧИСЛА ОБРАЗЦОВ БОЛЕЕ 25
При нормальном распределении для проверки выбросов используются исходные (нетрансформированные) данные, при этом при наличии до 50% измерений ниже предела обнаружения их заменяют на величину половины предела обнаружения. Для проверки выбросов при логнормальном распределении сначала вычисляется y = ln(x), и эти значения y используются вместо значений x. Вычисления проводятся помощью методики, приведенной ниже:
а) данные массива располагают в ряд от наименьшего значения до наибольшего, и наблюдения помечаются как x(1), x(2) ... x(n), где x(1) является наименьшей величиной и x(n) является наибольшей. Предварительно число потенциальных выбросов k определяют из графиков или анализа табличных данных;
б) принимают i = 0 и используют следующие уравнения для расчета среднего арифметического значения  :
:
и стандартного отклонения (s) для полной выборки (то есть, для i = 0).
 (С.2)
(С.2)Необходимо обозначить эти значения как  и s(0). Затем находят величину измерения, наиболее отличающуюся от
и s(0). Затем находят величину измерения, наиболее отличающуюся от  , и обозначают его как y(0);
, и обозначают его как y(0);
в) затем удаляют это экстремальное наблюдение из данных выборки и пересчитывают  и s, обозначив их как
и s, обозначив их как 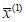 и s(1) (то есть для i = 1). Затем находят величину измерения, наиболее далекую от
и s(1) (то есть для i = 1). Затем находят величину измерения, наиболее далекую от 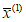 , и обозначают его как
, и обозначают его как 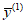 ;
;
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
г) затем удаляют это наблюдение из набора данных и пересчитывают  и s, обозначив их как
и s, обозначив их как  и s21) (то есть для i = 2). Следует отметить, что i относится к числу измерений, которые были удалены из набора данных;
и s21) (то есть для i = 2). Следует отметить, что i относится к числу измерений, которые были удалены из набора данных;
д) повторяют этапы 3 и 4 до тех пор, пока потенциальные выбросы не будут удалены. Эта процедура должна привести к набору результатов в соответствии с выражением
 (С.3)
(С.3)е) затем применяют критерий Рознера для всех возможных выбросов k. Чтобы проверить наличие выбросов, необходимо вычислить статистику критерия в соответствии с уравнением (С.4)
 (С.4)
(С.4)Необходимо найти критическое значение  из таблицы М.1, учитывая число измерений (n) и уровень достоверности 95%
из таблицы М.1, учитывая число измерений (n) и уровень достоверности 95%  . Если
. Если  , то делается заключение о существовании k выбросов. Если нет, процедуру проверки повторяют для k - 1 выбросов. Эта процедура продолжается так до тех пор, пока не будет идентифицирована вся группа выбросов или пока с помощью этого критерия выбросов в выборке обнаружено не будет.
, то делается заключение о существовании k выбросов. Если нет, процедуру проверки повторяют для k - 1 выбросов. Эта процедура продолжается так до тех пор, пока не будет идентифицирована вся группа выбросов или пока с помощью этого критерия выбросов в выборке обнаружено не будет.
 . Если
. Если  , то делается заключение о существовании k выбросов. Если нет, процедуру проверки повторяют для k - 1 выбросов. Эта процедура продолжается так до тех пор, пока не будет идентифицирована вся группа выбросов или пока с помощью этого критерия выбросов в выборке обнаружено не будет.
, то делается заключение о существовании k выбросов. Если нет, процедуру проверки повторяют для k - 1 выбросов. Эта процедура продолжается так до тех пор, пока не будет идентифицирована вся группа выбросов или пока с помощью этого критерия выбросов в выборке обнаружено не будет.Таблица С.1
равной 0,05
n | k | R | n | k | R | n | k | R |
25 | 1 | 2,82 | 35 | 1 | 2,98 | 45 | 1 | 3,09 |
2 | 2,80 | 2 | 2,97 | 2 | 3,08 | |||
3 | 2,78 | 3 | 2,95 | 3 | 3,07 | |||
4 | 2,76 | 4 | 2,94 | 4 | 3,06 | |||
5 | 2,73 | 5 | 2,92 | 5 | 3,05 | |||
10 | 2,59 | 10 | 2,84 | 10 | 2,99 | |||
26 | 1 | 2,84 | 36 | 1 | 2,99 | 46 | 1 | 3,09 |
2 | 2,82 | 2 | 2,98 | 2 | 3,09 | |||
3 | 2,80 | 3 | 2,97 | 3 | 3,08 | |||
4 | 2,78 | 4 | 2,95 | 4 | 3,07 | |||
5 | 2,76 | 5 | 2,94 | 5 | 3,06 | |||
10 | 2,62 | 10 | 2,86 | 10 | 3,00 | |||
27 | 1 | 2,86 | 37 | 1 | 3,00 | 47 | 1 | 3,10 |
2 | 2,84 | 2 | 2,99 | 2 | 3,09 | |||
3 | 2,82 | 3 | 2,98 | 3 | 3,09 | |||
4 | 2,80 | 4 | 2,97 | 4 | 3,08 | |||
5 | 2,78 | 5 | 2,95 | 5 | 3,07 | |||
10 | 2,65 | 10 | 2,88 | 10 | 3,01 | |||
28 | 1 | 2,88 | 38 | 1 | 3,01 | 48 | 1 | 3,11 |
2 | 2,86 | 2 | 3,00 | 2 | 3,10 | |||
3 | 2,84 | 3 | 2,99 | 3 | 3,09 | |||
4 | 2,82 | 4 | 2,98 | 4 | 3,09 | |||
5 | 2,80 | 5 | 2,97 | 5 | 3,08 | |||
10 | 2,68 | 10 | 2,91 | 10 | 3,03 | |||
29 | 1 | 2,89 | 39 | 1 | 3,03 | 49 | 1 | 3,12 |
2 | 2,88 | 2 | 3,01 | 2 | 3,11 | |||
3 | 2,86 | 3 | 3,00 | 3 | 3,10 | |||
4 | 2,84 | 4 | 2,99 | 4 | 3,09 | |||
5 | 2,82 | 5 | 2,98 | 5 | 3,09 | |||
10 | 2,71 | 10 | 2,91 | 10 | 3,04 | |||
30 | 1 | 2,91 | 40 | 1 | 3,04 | 50 | 1 | 3,13 |
2 | 2,89 | 2 | 3,03 | 2 | 3,12 | |||
3 | 2,88 | 3 | 3,01 | 3 | 3,11 | |||
4 | 2,86 | 4 | 3,00 | 4 | 3,10 | |||
5 | 2,84 | 5 | 2,99 | 5 | 3,09 | |||
10 | 2,73 | 10 | 2,92 | 10 | 3,05 | |||
31 | 1 | 2,92 | 41 | 1 | 3,05 | 60 | 1 | 3,20 |
2 | 2,91 | 2 | 3,04 | 2 | 3,19 | |||
3 | 2,89 | 3 | 3,03 | 3 | 3,19 | |||
4 | 2,88 | 4 | 3,01 | 4 | 3,18 | |||
5 | 2,86 | 5 | 3,00 | 5 | 3,17 | |||
10 | 2,76 | 10 | 2,94 | 10 | 3,14 | |||
32 | 1 | 2,94 | 42 | 1 | 3,06 | 70 | 1 | 3,26 |
2 | 2,92 | 2 | 3,05 | 2 | 3,25 | |||
3 | 2,91 | 3 | 3,04 | 3 | 3,25 | |||
4 | 2,89 | 4 | 3,03 | 4 | 3,24 | |||
5 | 2,88 | 5 | 3,01 | 5 | 3,24 | |||
10 | 2,78 | 10 | 2,95 | 10 | 3,21 | |||
33 | 1 | 2,95 | 43 | 1 | 3,07 | 80 | 1 | 3,31 |
2 | 2,94 | 2 | 3,06 | 2 | 3,30 | |||
3 | 2,92 | 3 | 3,05 | 3 | 3,30 | |||
4 | 2,91 | 4 | 3,04 | 4 | 3,29 | |||
5 | 2,89 | 5 | 3,03 | 5 | 3,29 | |||
10 | 2,80 | 10 | 2,97 | 10 | 3,26 | |||
34 | 1 | 2,97 | 44 | 1 | 3,08 | 100 | 1 | 3,38 |
2 | 2,95 | 2 | 3,07 | 2 | 3,38 | |||
3 | 2,94 | 3 | 3,06 | 3 | 3,38 | |||
4 | 2,92 | 4 | 3,05 | 4 | 3,37 | |||
5 | 2,91 | 5 | 3,04 | 5 | 3,37 | |||
10 | 2,82 | 10 | 2,98 | 10 | 3,35 |
Пример - Предположим, что для некоторой территории в 30 образцах были измерены фоновые концентрации ОЗВ. С помощью оценки формы распределения было показано, что эти данные имеют логнормальное распределение. Представленные в порядке возрастания логтрансформированные данные (в виде натуральных логарифмов концентраций, выраженных в мг/кг) составляют: 1 - минус 0,90; 2 - минус 0,85; 3 - минус 0,70; 4 - минус 0,59; 5 - минус 0,57; 6 - минус 0,57; 7 - 0,40; 8 - минус 0,29; 9 - минус 0,23; 10 - минус 0,23; 11 - минус 0,20; 12 - минус 0,19; 13 - 0,13; 14 - минус 0,10; 15 - минус 0,03; 16 - минус 0,003; 17 - 0,03; 18 - 0,10; 19 - 0,11; 20 - 0,13; 21 - 0,16; 22 - 0,25; 23 - 0,25; 24 - 0,30; 25 - 0,36; 26 - 0,55; 27 - 0,60; 28 - 1,50; 29 - 1,60; 30 - 2,00.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 6.1.1 отсутствует. |
На основании вероятностного графика, описанного в пункте 6.1.1 раздела 6, было предположено, что три измерения с самыми высокими концентрациями являются потенциальными выбросами. В соответствии с описанной выше процедурой для i, равной 0, величина R равна 2,87, а R критическая равна 2,91; для i, равной 1, величина R равна 2,77, а R критическая равна 2,89; для i, равной 2, величина R равна 3,13, а R критическая равна 2,88. Поскольку результаты проверки показывают, что величина критерия Рознера для n, равным 30, и числа потенциальных выбросов, равных 3, составила 3,13 и была больше, чем критическая величина критерия Рознера в 2,88, можно сделать заключение, что все три максимальных значения логарифмов содержания ОЗВ в почве (1,5, 1,6 и 2,0) являются выбросами.
(обязательное)
ПРИ НЕПАРАМЕТРИЧЕСКОМ РАСПРЕДЕЛЕНИИ ДАННЫХ
В том случае, если распределение данных не подчиняется нормальному или логнормальному распределению, то для выборок с числом данных более 60 для идентификации потенциальных выбросов применяют следующий критерий (методология проверки данных такой выборки на выбросы приведена ниже):
а) располагают данные выборки в ряд от наименьшего значения до наибольшего и помечают измерения x(1), x(2) ... x(n), где x(1) является наименьшей концентрацией и x(n) является наибольшей концентрацией. Если n менее 60, то проверку с помощью этого критерия проводить нельзя;
б) из графиков или анализа табличных данных сначала определяют количество потенциальных выбросов r более или равно 1.
Затем вычисляют следующие параметры:
k = r + c, (Т.2)
 (Т.4)
(Т.4)где ceiling обозначает округление величин до следующего самого большого целого числа;
в) если Xr - (1 + a)Xr+1 + aXk < 0, то количество r самых маленьких концентраций являются выбросами (при уровне значимости  );
);
г) если Xn+1-r - (1 + a)Xn-r + aXn+1-k > 0, то количество r самых больших концентраций являются выбросами (при уровне значимости  ).
).
Пример - Предположим, что для некоторой территории в 61 образце были измерены фоновые концентрации ОЗВ. Исходные данные, мг/кг: 1 - 14,57; 2 - 16,05; 3 - 19,3; 4 - 24,8; 5 - 27,5; 6 - 27,8; 7 - 32,4; 8 - 33,4; 9 - 33,8; 10 - 33,9; 11 - 35,1; 12 - 50,9; 13 - 54,85; 14 - 63,95; 15 - 68,3; 16 - 70,9; 17 - 96; 18 - 109,75; 19 - 135,8; 20 - 141,8; 21 - 160; 22 - 184,3; 23 - 14,57; 24 - 16,05; 25 - 17,05; 26 - 18,05; 27 - 19,05; 28 - 20,05; 29 - 21,05; 30 - 33,4; 31 - 33,8; 32 - 33,9; 33 - 35,1; 34 - 50,9; 35 - 54,85; 36 - 63,95; 37 - 68,3; 38 - 70,9; 39 - 96; 40 - 109,75; 41 - 135,8; 42 - 141,8; 43 - 160; 44 - 184,3; 45 - 16,05; 46 - 17,05; 47 - 18,05; 48 - 19,05; 49 - 14,57; 50 - 16,05; 51 - 19,3; 52 - 24,8; 53 - 27,5; 53 - 27,5; 54 - 27,8; 55 - 32,4; 56 - 16,05; 57 - 17,05; 58 - 18,05; 59 - 296,9; 60 - 728,9; 61 - 105,2.
Анализируя исходные данные, можно предположить, что число потенциальных выбросов r равно 1 (измерение 60 (728,9 мг/кг)). В соответствии с уравнением (Т.1) величина c равна 12, величина k равна 13. Если принять уровень значимости 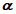 , равным 0,1, то величина b2 равна 10. В соответствии с уравнением (Т.3) величина b равна 3,16, а величина a равна 2,35.
, равным 0,1, то величина b2 равна 10. В соответствии с уравнением (Т.3) величина b равна 3,16, а величина a равна 2,35.
Используя уравнение в пункте г), получаем, что Xn+1-r - (1 + a)Xn-r + aXn+1-k равно минус 18,1, что меньше 0. Таким образом, измерение с самым высоким значением не является выбросом.
(обязательное)
РФК, ИМЕЮЩЕЙ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПРИ УРОВНЕ ЗНАЧИМОСТИ
0,05, С ПОМОЩЬЮ КРИТЕРИЯ СТЬЮДЕНТА [9]
При нормальном распределении выборки ВДГ для среднего рассчитывают на основе t-распределения Стьюдента. Предварительно оценивают статистическое распределение данных с использованием формальных критериев и проводят проверку на наличие выбросов:
а) сначала вычисляют среднее арифметическое значение выборки  и ее стандартное отклонение s;
и ее стандартное отклонение s;
б) используя таблицу С.1, находят t-величину Стьюдента для уровня доверия  (необходимо принимать
(необходимо принимать  , равной 0,05) и степени свободы n - 1. Эта величина обозначается
, равной 0,05) и степени свободы n - 1. Эта величина обозначается  ;
;
 (необходимо принимать
(необходимо принимать в) затем вычисляют одностороннюю  ВДГ для среднего арифметического в соответствии с уравнением
ВДГ для среднего арифметического в соответствии с уравнением
 ВДГ для среднего арифметического в соответствии с уравнением
ВДГ для среднего арифметического в соответствии с уравнениемПример - Предположим, что на некоторой территории в 24 образцах были измерены фоновые концентрации суммы ПАУ, мкг/кг. Исходные данные в порядке возрастания составляют: 1 - 14,57; 2 - 16,05; 3 - 19,3; 4 - 24,8; 5 - 27,5; 6 - 27,8; 7 - 32,4; 8 - 33,4; 9 - 33,8; 10 - 33,9; 11 - 35,1; 12 - 50,9; 13 - 54,85; 14 - 63,95; 15 - 68,3; 16 - 70,9; 17 - 96; 18 - 109,75; 19 - 135,8; 20 - 141,8; 21 - 160; 22 - 184,3; 23 - 296,9; 24 - 728,9. Вычисленная на основе этого массива данных величина среднего арифметического равна 102,54 мкг/кг. При этом величина стандартного отклонения равна 149,54 мг/кг. Величина коэффициента Стьюдента для уровня доверия 95%, найденная в таблице У.1 для 23 степеней свободы, равна 1,714. В соответствии с выражением С.1 величина 95% ВДГ равна 154,87 мкг/кг. Если из исходного массива данных удалить два самых максимальных значения, которые можно рассматривать как выбросы, то величина коэффициента Стьюдента для уровня доверия 95%, найденная в таблице У.1 для 23 степеней свободы, равна 1,721. В соответствии с уравнением (У.1) величина 95% ВДК равна 83,83 мкг/кг.
Таблица У.1
df(n - 1) |  | df(n - 1) |  | df(n - 1) |  |
1 | 6,314 | 13 | 1,771 | 25 | 1,708 |
2 | 2,920 | 14 | 1,761 | 26 | 1,706 |
3 | 2,353 | 15 | 1,753 | 27 | 1,703 |
4 | 2,132 | 16 | 1,746 | 28 | 1,701 |
5 | 2,015 | 17 | 1,740 | 29 | 1,699 |
6 | 1,943 | 18 | 1,734 | 30 | 1,697 |
7 | 1,895 | 19 | 1,729 | 40 | 1,684 |
8 | 1,860 | 20 | 1,725 | 60 | 1,671 |
9 | 1,833 | 21 | 1,721 | 120 | 1,658 |
10 | 1,812 | 22 | 1,717 | > 120 | 1,645 |
11 | 1,796 | 23 | 1,714 | ||
12 | 1,782 | 24 | 1,711 | ||
(обязательное)
АРИФМЕТИЧЕСКОГО РФК, ИМЕЮЩЕЙ ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
ПРИ УРОВНЕ ЗНАЧИМОСТИ 0,05, С ПОМОЩЬЮ МЕТОДА ЛЭНДА
Процедура вычисления ВДГ по методу Лэнда [10] приведена ниже:
а) если в выборке имеются измерения ниже предела обнаружения, то их заменяют на величину половины предела обнаружения (если количество измерений ниже предела обнаружения не достигает 50%). Затем вычисляют натуральный логарифм каждого измерения, при этом трансформированное значение y будет равно ln(x);
б) затем вычисляют среднее значение  и стандартное отклонение (sy) логарифмически преобразованного набора данных;
и стандартное отклонение (sy) логарифмически преобразованного набора данных;
в) в таблице Ф.1 для  находят
находят  . Это значение зависит от размера выборки (n) и стандартного отклонения логарифмически преобразованных данных (sy). Если число измерений и стандартное отклонение не показаны в таблице, то величину
. Это значение зависит от размера выборки (n) и стандартного отклонения логарифмически преобразованных данных (sy). Если число измерений и стандартное отклонение не показаны в таблице, то величину 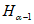 интерполируют, используя соседние ячейки таблицы;
интерполируют, используя соседние ячейки таблицы;
 находят
находят г) для вычисления  ВДГ среднего используется следующее уравнение:
ВДГ среднего используется следующее уравнение:
 ВДГ среднего используется следующее уравнение:
ВДГ среднего используется следующее уравнение:Таблица Ф.1
n | ||||||||||
sy | 3 | 5 | 7 | 10 | 12 | 15 | 21 | 31 | 51 | 101 |
0,10 | 2,750 | 2,035 | 1,886 | 1,802 | 1,775 | 1,749 | 1,722 | 1,701 | 1,684 | 1,670 |
0,20 | 3,295 | 2,198 | 1,992 | 1,881 | 1,843 | 1,809 | 1,771 | 1,742 | 1,718 | 1,697 |
0,30 | 4,109 | 2,402 | 2,125 | 1,977 | 1,927 | 1,882 | 1,833 | 1,793 | 1,761 | 1,733 |
0,40 | 5,220 | 2,651 | 2,282 | 2,089 | 2,026 | 1,968 | 1,905 | 1,856 | 1,813 | 1,777 |
0,50 | 6,495 | 2,947 | 2,465 | 2,220 | 2,141 | 2,068 | 1,989 | 1,928 | 1,876 | 1,830 |
0,60 | 7,807 | 3,287 | 2,673 | 2,368 | 2,271 | 2,181 | 2,085 | 2,010 | 1,946 | 1,891 |
0,70 | 9,120 | 3,662 | 2,904 | 2,532 | 2,414 | 2,306 | 2,191 | 2,102 | 2,025 | 1,960 |
0,80 | 10,43 | 4,062 | 3,155 | 2,710 | 2,570 | 2,443 | 2,307 | 2,202 | 2,112 | 2,035 |
0,90 | 11,74 | 4,478 | 3,420 | 2,902 | 2,738 | 2,589 | 2,432 | 2,310 | 2,206 | 2,117 |
1,00 | 13,05 | 4,905 | 3,698 | 3,103 | 2,915 | 2,744 | 2,564 | 2,423 | 2,306 | 2,205 |
1,25 | 16,33 | 6,001 | 4,426 | 3,639 | 3,389 | 3,163 | 2,923 | 2,737 | 2,580 | 2,447 |
1,50 | 19,60 | 7,120 | 5,184 | 4,207 | 3,896 | 3,612 | 3,311 | 3,077 | 2,881 | 2,713 |
1,75 | 22,87 | 8,250 | 5,960 | 4,795 | 4,422 | 4,081 | 3,719 | 3,437 | 3,200 | 2,997 |
2,00 | 26,14 | 9,387 | 6,747 | 5,396 | 4,962 | 4,564 | 4,141 | 3,812 | 3,533 | 3,295 |
2,50 | 32,69 | 11,67 | 8,339 | 6,621 | 6,067 | 5,557 | 5,013 | 4,588 | 4,228 | 3,920 |
3,00 | 39,23 | 13,97 | 9,945 | 7,864 | 7,191 | 6,570 | 5,907 | 5,388 | 4,947 | 4,569 |
3,50 | 45,77 | 16,27 | 11,56 | 9,118 | 8,326 | 7,596 | 6,815 | 6,201 | 5,681 | 5,233 |
4,00 | 52,31 | 18,58 | 13,18 | 10,38 | 9,469 | 8,630 | 7,731 | 7,024 | 6,424 | 5,908 |
4,50 | 58,85 | 20,88 | 14,80 | 11,64 | 10,62 | 9,669 | 8,652 | 7,854 | 7,174 | 6,590 |
5,00 | 65,39 | 23,19 | 16,43 | 12,91 | 11,77 | 10,71 | 9,579 | 8,688 | 7,929 | 7,277 |
6,00 | 78,47 | 27,81 | 19,68 | 15,45 | 14,08 | 12,81 | 11,44 | 10,36 | 9,449 | 8,661 |
7,00 | 91,55 | 32,43 | 22,94 | 18,00 | 16,39 | 14,90 | 13,31 | 12,05 | 10,98 | 10,05 |
8,00 | 104,60 | 37,06 | 26,20 | 20,55 | 18,71 | 17,01 | 15,18 | 13,74 | 12,51 | 11,45 |
9,00 | 117,70 | 41,68 | 29,46 | 23,10 | 21,03 | 19,11 | 17,05 | 15,43 | 14,05 | 12,85 |
10,00 | 130,800 | 46,31 | 32,73 | 25,66 | 23,35 | 21,22 | 18,93 | 17,13 | 15,59 | 14,26 |
Если полученный ВДГ больше норматива, то необходимо сделать вывод о том, что среднее РФК выше данного норматива. Если ВДГ меньше норматива, то необходимо сделать заключение, что среднее РФК ниже данного норматива.
Пример - Предположим, что для некоторой территории в 15 образцах были измерены фоновые концентрации ОЗВ, мг/кг. Исходные данные: 1 - 3,20; 2 - 27,70; 3 - 2,57; 4 - 9,98; 5 - 6,38; 6 - 2,12; 7 - 2,80; 8 - 12,11; 9 - 6,92; 10 - 5,38; 11 - 23,19; 12 - 7,02; 13 - 7,32; 14 - 28,62; 15 - 2,59. Предположим, что оценка показала, что этот набор данных распределен логнормально. Применяя методологию Лэнда получаем:  равным 1,92;
равным 1,92;  равным 0,76; sy равным 0,87; H0,95 равным 2,545. С помощью уравнения (Ф.1) вычисляем 95% ВДГ: величина в квадратных скобках уравнения (Ф.1) равна 2,90, а величина экспоненты этой величины (то есть величина 95% ВДГ) составляет 18,2 мг/кг.
равным 0,76; sy равным 0,87; H0,95 равным 2,545. С помощью уравнения (Ф.1) вычисляем 95% ВДГ: величина в квадратных скобках уравнения (Ф.1) равна 2,90, а величина экспоненты этой величины (то есть величина 95% ВДГ) составляет 18,2 мг/кг.
(обязательное)
ДЛЯ ВЫБОРКИ, ИМЕЮЩЕЙ НЕПАРАМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Для выборок, которые не являются ни нормальными, ни логнормальными, используют следующий метод вычисления ВДГ. При этом доверительную границу определяют не для среднего, а для медианы. Чтобы построить доверительные границы для медианы при непараметрическом распределении данных по доверительной вероятности p находят U(p). U(p) - число, заданное равенством Ф(U(p)) = (1 + p)/2, где Ф(x) - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Например, при p, равной 95% (т.е. при p равной 0,95), имеем U(p), равным 1,96.
Чтобы построить доверительные границы для медианы, по доверительной вероятности p находят U(p). Затем вычисляют натуральное число 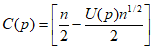 , где [,] - знак целой части числа. Нижняя доверительная граница для медианы имеет вид (при C(p) более 1; если p равно 0,95 и U(p) равно 1,96, то C(p) более 1 при n более 8)
, где [,] - знак целой части числа. Нижняя доверительная граница для медианы имеет вид (при C(p) более 1; если p равно 0,95 и U(p) равно 1,96, то C(p) более 1 при n более 8)
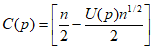 , где [,] - знак целой части числа. Нижняя доверительная граница для медианы имеет вид (при C(p) более 1; если p равно 0,95 и U(p) равно 1,96, то C(p) более 1 при n более 8)
, где [,] - знак целой части числа. Нижняя доверительная граница для медианы имеет вид (при C(p) более 1; если p равно 0,95 и U(p) равно 1,96, то C(p) более 1 при n более 8)Xi = XC(p),
где Xi - член с номером i вариационного ряда, построенного по исходной выборке (т.е. i-я порядковая статистика).
Верхняя доверительная граница для медианы имеет вид
Xi = Xn+1-C(p).
Пример - Предположим, что на некоторой территории в 50 образцах были измерены фоновые концентрации суммы ПАУ, мкг/кг. Расчет проводят в следующей последовательности:
а) располагаем данные выборки в ряд от наименьшего значения до наибольшего и помечаем измерения x(1), x(2) ... x(n), где x(1) является наименьшим измерением и x(n) является наибольшим.
Исходные данные в порядке возрастания составляют: 1 - 9; 2 - 17,5; 3 - 21; 4 - 26,5; 5 - 27,5; 6 - 31; 7 - 32,5; 8 - 34; 9 - 36; 10 - 36,5; 11 - 39; 12 - 40; 13 - 41; 14 - 42,5; 15 - 43; 16 - 45; 17 - 46; 18 - 47,5; 19 - 48; 20 - 50; 21 - 51; 22 - 53,5; 23 - 55; 24 - 56; 25 - 56; 26 - 56,5; 27 - 57,5; 28 - 58; 29 - 59; 30 - 59; 31 - 60; 32 - 61; 33 - 61,5; 34 - 62; 35 - 63; 36 - 64,5; 37 - 65; 38 - 67,5; 39 - 68,5; 40 - 70; 41 - 72,5; 42 - 77,5; 43 - 81; 44 - 82,5; 45 - 90; 46 - 96; 47 - 101,5; 48 - 117,5; 49 - 127,5; 50 - 130;
б) находим медиану выборки численностью n, которая равна 56,25;
в) для доверительной вероятности p, равной 0,95, рассчитываем

Отсчитываем от упорядоченного набора данных число рангов, равное 18. Это и будет нижней 95% доверительной границей медианы. То есть нижняя доверительная граница медианы является X(18), которая равна 47,5 мкг/кг;
г) для верхней 95% доверительной границы медианы рассчитываем: X(50 + 1 - 18) = X(33). И получаем 95% ВДГ, равную 61,5 мкг/кг.
Егоров В.В., Иванова Е.Н., Фридланд В.М. Классификация и диагностика почв СССР. М.: Колос, 1977. 221 с. | |
ООН. Экономический и социальный совет. Европейская экономическая комиссия. Комитет по экологической политике. Рабочая группа по мониторингу и оценке окружающей среды. Руководящие принципы разработки национальных стратегий использования мониторинга загрязнения почв в качестве инструмента экологической политики. 2014. - GE.14-10435 (R) 190914 190914. 30 с. | |
Руководство по описанию почв. Четвертое издание. Рим: Продовольственная и сельскохозяйственная организация объединенных наций, 2012. 114 с. | |
Shapiro S.S., Wilk M.B. An analysis of variance test for normality (complete samples) // Biometrika. 1965. Vol. 52. P. 591 - 611. | |
Shapiro S.S., Francia R.S. An approximate analysis of variance test for normality // Journal of the American Statistical Association. 1972. Vol. 63. P. 1343 - 1372. | |
Grubbs F.E. Procedures for Detecting Outlying Observations in Samples // Technometrics. 1969. Vol. 11, No 1. P. 1 - 21. | |
Dixon W.J. Processing data for outliers// Biometrics. 1953. Vol. 9. P. 74 - 89. | |
Rosner B. Percentage points for a generalized ESD many-outlier procedure // Technometrics. 1983. Vol. 25. P. 165 - 172. | |
Guidance for Comparing Background and Chemical Concentrations in Soil for CERCLA Sites. EPA 540-R-01-003 OSWER 9285.7-41 // Washington, DC: Office of Emergency and Remedial Response U.S. Environmental Protection Agency. 2002. 89 p. | |
Gilbert R.L. Statistical methods for environmental monitoring // New York: Van Nostrand Reinold Company, 1987. 334 p. |
Ключевые слова: региональный фон, органические загрязнители, почва, статистические характеристики |



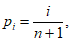




 и
и 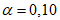 )
)
 ) для критерия
) для критерия