СПРАВКА
Источник публикации
М., 2015
Примечание к документу
Документ рекомендован к применению с 4 декабря 2015 года Распоряжением Росавтодора от 04.12.2015 N 2333-р.
Название документа
"ОДМ 218.3.051-2015. Отраслевой дорожный методический документ. Рекомендации по определению напряженно-деформированного состояния многослойных дорожных одежд"
(издан на основании Распоряжения Росавтодора от 04.12.2015 N 2333-р)
"ОДМ 218.3.051-2015. Отраслевой дорожный методический документ. Рекомендации по определению напряженно-деформированного состояния многослойных дорожных одежд"
(издан на основании Распоряжения Росавтодора от 04.12.2015 N 2333-р)
Содержание
7.1. Расчетное положение транспортной нагрузки на жестком покрытии, усиленном в поперечных швах стальными штырями
9. Конечно-элементная модель для исследования продольной устойчивости плит жестких дорожных покрытий при нестационарном температурном воздействии
Распоряжения Федерального
дорожного агентства
от 4 декабря 2015 г. N 2333-р
ОТРАСЛЕВОЙ ДОРОЖНЫЙ МЕТОДИЧЕСКИЙ ДОКУМЕНТ
РЕКОМЕНДАЦИИ ПО ОПРЕДЕЛЕНИЮ
НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
МНОГОСЛОЙНЫХ ДОРОЖНЫХ ОДЕЖД
ОДМ 218.3.051-2015
ОКС 93080
1 РАЗРАБОТАН ФГБОУ ВПО "Московский автомобильно-дорожный государственный технический университет (МАДИ)"
Руководитель разработки: д-р техн. наук, профессор И.В. Демьянушко
Исполнители: канд. техн. наук, профессор В.М. Стаин, канд. техн. наук, А.В. Стаин.
2 ВНЕСЕН Управлением научно-технических исследований и информационного обеспечения
3 ИЗДАН на основании распоряжения Федерального дорожного агентства от 04.12.2015 N 2333-р
4 ИМЕЕТ РЕКОМЕНДАТЕЛЬНЫЙ ХАРАКТЕР
5 ВВЕДЕН ВПЕРВЫЕ
Настоящий ОДМ устанавливает рекомендации по применению метода конечных элементов для расчета многослойных дорожных одежд с использованием мультидисциплинарных конечно-элементных комплексов.
В настоящем ОДМ использованы нормативные ссылки на следующие документы:
ГОСТ Р 52748-2007 Дороги автомобильные общего пользования. Нормативные нагрузки, расчетные схемы нагружения и габариты приближения.
ГОСТ Р 52398-2005 Классификация автомобильных дорог. Основные параметры и требования.
ГОСТ 26633-2012 Бетоны тяжелые и мелкозернистые. Технические условия
ГОСТ 25192-2012 Межгосударственный стандарт. Бетоны. Классификация и общие технические требования.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: нормативная ссылка упоминается дважды. |
ГОСТ Р 52748-2007 Дороги автомобильные общего пользования. Нормативные нагрузки, расчетные схемы нагружения и габариты приближения.
ГОСТ 23558-94 Смеси щебеночно-гравийно-песчаные и грунты, обработанные неорганическими вяжущими материалами для дорожного и аэродромного строительства. Технические условия.
ГОСТ 25607-2009 Смеси щебеночно-гравийно-песчаные для покрытий и оснований автомобильных дорог и аэродромов. Технические условия.
СП 121.13330.2012 Свод правил. Аэродромы. Актуализированная редакция СНиП 32-03-96.
В настоящем ОДМ применены следующие термины с соответствующими определениями и сокращения:
1 покрытие: Верхняя часть дорожной одежды, воспринимающая непосредственно усилия от колес автомобилей и подвергающаяся непосредственному воздействию атмосферных факторов.
2 основание покрытия: Конструктивный слой дорожной одежды, расположенный под покрытием, и обеспечивающий совместно с покрытием перераспределение и снижение давления на нижележащие дополнительные слои или грунт земляного полотна.
3 искусственное укрепленное основание: Основание покрытия, выполненное из обработанных вяжущим материалов, для которых нормировано расчетное сопротивление растяжению при изгибе.
4 искусственное неукрепленное основание: Слои между искусственным укрепленным основанием и грунтом земляного полотна, выполняющие морозозащитную, дренирующую и теплоизолирующую функции.
5 жесткое покрытие: Покрытие, выполненное из цементобетона, а также асфальтобетонное покрытие на цементобетонном основании.
6 предельное состояние: Состояние конструкции, при наступлении которого она становится неспособной сопротивляться внешним воздействиям или получает недопустимые по условиям эксплуатации повреждения.
7 нормативная нагрузка: Установленное нормами значение веса транспортного средства или его категории.
8 расчетная нагрузка: Нагрузка, учитывающая условия эксплуатации и конфигурацию транспортного средства или категории.
9 МКЭ: Метод конечных элементов.
10 КЭ: Конечный элемент.
11 цементопесок: Песок, укрепленный цементом.
12 НДС: Напряженно-деформированное состояние.
До настоящего времени в практике отечественного проектирования расчеты конструкций дорожных одежд проводятся с использованием устаревших полуэмпирических нормативных методик. Эти методики в основном базируются на таких упрощенных способах определения напряженно-деформированного состояния дорожных одежд, которые не позволяют рассмотреть особенности работы новых конструкций и материалов, неупругое и конструктивно и геометрически нелинейное поведение слоистых конструкций дорожных одежд при нестационарных температурных воздействиях и нагрузках. В то же время, задача создания новых прогрессивных технологий строительства дорог требует разработки новых методов расчетно-проектировочного анализа, основанных на компьютерных технологиях и современных методах механики, учитывающих сложный, физически и геометрически нелинейный характер решаемых задач, особенности работы многослойных конструкций дорог и циклический характер транспортных нагрузок. Исследования по применению метода конечных элементов (МКЭ) для расчета дорожных одежд, выполненные в МАДИ, показали эффективность этого метода для расчета дорожных покрытий, учета реальной работы оснований, особенностей конструкций продольных и поперечных швов и т.д. Данные исследования позволили выявить такие особенности поведения дорожных конструкций, которые не могли быть описаны существующими инженерными методиками.
Таким образом, в настоящее время существует необходимость разработки рекомендаций, которые обеспечат широкое применение МКЭ при расчетах и проектировании дорожных одежд.
Дорожные одежды являются сложной многослойной композитной конструкцией, включающей в себя слои материалов различной толщины, свойства которых могут быть как линейными, так и нелинейными. Воздействия на плиты дорожных покрытий могут включать в себя подвижную и неподвижную нагрузки, сезонные и суточные изменения температуры, осадки основания и т.д. В настоящее время расчет таких конструкций за рубежом выполняется либо с помощью проблемно-ориентированных КЭ пакетов, таких как, например ISLAB2000 [15], либо с использованием мультидисциплинарных конечно-элементных и конечно-разностных комплексов, таких как ABAQUS, ANSYS, FLAC_3D и др. В России конечно-элементные комплексы для расчета конструкций дорожных покрытий используются эпизодически, как правило, в рамках диссертационных работ для решения конкретных задач.
В рамках данной ОДМ даются рекомендации по разработке конечно-элементных моделей для расчета многослойных дорожных покрытий с учетом упруго-пластических свойств основания, возможности отрыва плит покрытия от основания, усилении швов между плитами покрытия с помощью стальных штырей, стационарных и нестационарных температурных воздействиях и т.д. Эти рекомендации могут быть использованы при разработке конечно-элементных моделей дорожных одежд в любом мультидисциплинарном конечно-элементном комплексе.
многослойных дорожных одежд
Для исследования поведения жестких дорожных покрытий при различных внешних воздействиях в настоящее время используются либо проблемно-ориентированные КЭ пакеты, такие например, как ISLAB2000, EverFE 2.23 и другие, либо мультидисциплинарные КЭ пакеты, такие как "ABAQUS", "ANSYS", "MSC.Nastran", "MSC.Marc" и другие.
Проблемно-ориентированные пакеты, созданные с целью охватить как можно больше видов воздействий на дорожное покрытие, грешат избыточным упрощением расчетной схемы конструкции.
Так, например:
- в них рассматриваются, как правило, только стационарные процессы теплообмена;
- радиационный и конвективный теплообмен с окружающей средой учитывается с помощью эмпирических формул и сводится к заданию температуры на поверхности покрытия;
- распределение температуры по толщине дорожной одежды принимается, как правило, линейным, тогда как экспериментальные данные свидетельствуют о том, что оно может быть существенно нелинейным;
- не учитывается возможность отрыва цементобетонного покрытия от основания, что является одним из главных факторов при расчете покрытия на продольную устойчивость.
Этих и многих других недостатков лишены мультидисциплинарные КЭ комплексы.
Таким образом, для создания конечно-элементных моделей многослойного дорожного покрытия, позволяющих учесть процессы его взаимодействия с окружающей средой, а также с транспортными нагрузками, в большей степени подходят мультидисциплинарные КЭ пакеты программ.
Учитывая то, что наиболее популярные в мире мультидисциплинарные КЭ пакеты "ABAQUS", "ANSYS" и "MSC.MARC" по своим возможностям не имеют принципиальных отличий, для расчетов многослойных дорожных одежд может быть использован любой из них.
В США и Канаде для расчета конструкций дорожных одежд чаще используют пакет "ABAQUS", в России - пакеты "ANSYS" или "MSC.MARC".
жесткого дорожного покрытия
Предлагаемая в этом разделе КЭ модель жесткого дорожного покрытия позволяет определить напряженно-деформированное состояние как плиты, так и основания, которое может быть:
- основанием Винклера;
- упругим или упруго-пластическим слоем;
- упругим или упруго-пластическим полупространством.
На примере конструкции плиты, имеющей типовые размеры, и основание из относительно слабого грунта, в качестве которого принята супесь, показано, что прогибы плиты и максимальные растягивающие напряжения в ней существенно различаются в зависимости от модели основания, принятой для реального грунта.
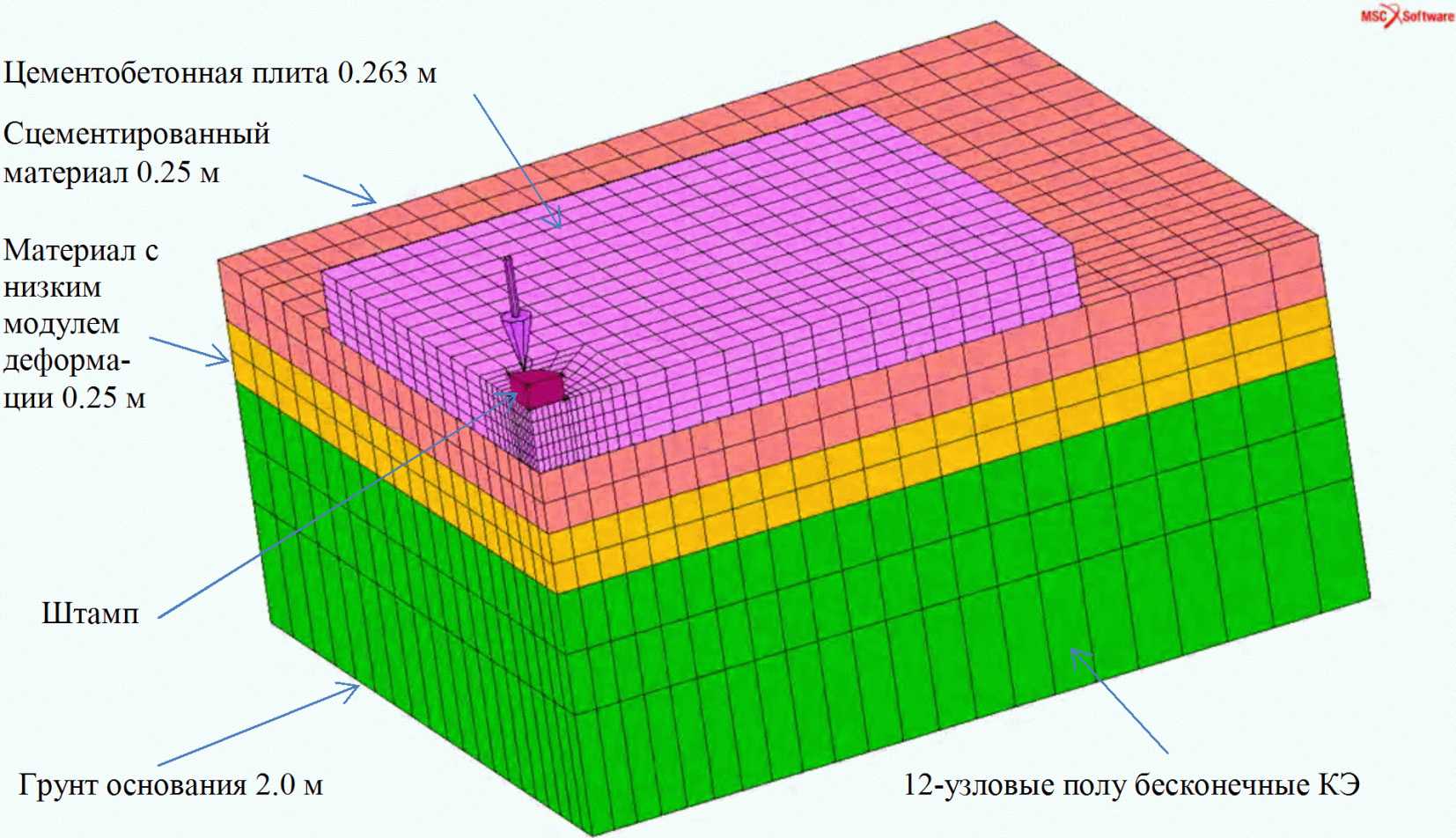
Чтобы иметь возможность сравнить результаты расчетов с результатами, полученными с помощью альтернативных моделей, в соответствии с практикой проектирования цементобетонных плит жестких автомобильно-дорожных покрытий [1], размеры плиты приняты равными вдоль осей X, Y и Z соответственно 5, 0,25 и 3,75 м (рисунок 1).
Как известно, время решения конечно-элементной задачи на персональном компьютере пропорционально кубу размерности задачи. Поэтому желательно, для ускорения процесса решения рассматриваемых задач, уменьшить, насколько это возможно, их размерность. С этой целью в предлагаемой далее конечно-элементной модели жесткого дорожного покрытия (рисунок 1) нижняя часть основания ограничивается двухметровым слоем грунта, включающем в себя полубесконечные КЭ толщиной 0,5 м.
При выборе размеров расчетной области грунта в горизонтальном направлении было принято во внимание быстрое затухание деформаций и усилий в грунте по мере удаления от места приложения нагрузки. Расстояние от краев плиты до краев грунтового массива было принято равным 1 м. При этом, чтобы компенсировать влияние удаленного грунтового массива на рассматриваемую модель, на ее боковых гранях смоделировано основание Винклера. Таким образом, размеры грунтового основания получились равными вдоль осей X, Y и Z соответственно 7,0, 2,0 и 5,75 м (рисунок 1).

Нагрузка на колесо величиной 50 кН прикладывается к плите в виде равномерно распределенного по отпечатку колеса давления. Если принять размер отпечатка равным размеру грани конечного элемента плиты, то есть 25 x 25 см, то величина давления на отпечаток составит 800 кН/м2.
При расчетах толщины бетонных покрытий исходят из наиболее опасных для прочности положений автомобильного колеса на плите. Возможны три расчетные схемы действия нагрузки от колеса на прямоугольную плиту: в центре плиты, на угол и на край плиты. Наиболее опасными являются нагрузки, действующие на край и на угол плиты. Эта схема действия является наиболее сложной для теоретического анализа. Поэтому до сих пор при проектировании толщину бетонных покрытий рассчитывают для случая приложения нагрузки в центральной части плиты, а величины моментов, возникающих при угловом и краевом приложении нагрузок, учитывают с помощью поправочных коэффициентов.
6.2. Использование предлагаемой КЭ модели для оценки влияния модели основания на напряженно-деформированное состояние дорожной конструкции
До сих пор, при расчете плит совместно с грунтовым основанием применяются главным образом две теории, которые в соответствии с классификацией Н.А. Цытовича [13] называются:
- теория местных упругих деформаций, основанная на гипотезе Винклера-Циммермана;
- теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
Обе теории не учитывают неупругих свойств основания, которые в некоторых случаях могут существенно изменить напряженно-деформированное состояние конструкции дорожного покрытия.
В качестве примера использования предлагаемой в данном ОДМ конечно-элементной модели дорожной конструкции исследуем влияние модели основания дорожного покрытия на распределение деформаций и напряжений в дорожной конструкции.
В данной ОДМ рассмотрены три модели основания:
- модель Винклера;
- модель упругого полупространства;
- упруго-пластическая модель Кулона-Мора (в "MSC.MARC" используется ее модифицированный вариант - модель Друкера-Прагера).
Физико-механические характеристики материалов плиты и основания принимались в соответствии с нормативным документом [1]. В качестве грунта основания рассматривалась супесь с модулем упругости Eгр = 27000 кН/м2, коэффициентом Пуассона  , плотностью
, плотностью  , коэффициентом сцепления c = 3 кПа и углом внутреннего трения
, коэффициентом сцепления c = 3 кПа и углом внутреннего трения  . Материал плиты - цементобетон класса Btb4,4 имел модуль упругости E = 3,6*107 кН/м2, коэффициент Пуассона
. Материал плиты - цементобетон класса Btb4,4 имел модуль упругости E = 3,6*107 кН/м2, коэффициент Пуассона  и плотность
и плотность  .
.
 , плотностью
, плотностью  , коэффициентом сцепления c = 3 кПа и углом внутреннего трения
, коэффициентом сцепления c = 3 кПа и углом внутреннего трения  . Материал плиты - цементобетон класса Btb4,4 имел модуль упругости E = 3,6*107 кН/м2, коэффициент Пуассона
. Материал плиты - цементобетон класса Btb4,4 имел модуль упругости E = 3,6*107 кН/м2, коэффициент Пуассона  и плотность
и плотность  .
.При расчете плиты на прочность интерес представляют максимальные растягивающие напряжения в плите, а при расчете по деформациям - максимальные прогибы плиты. Поэтому сравнение результатов расчетов для различных видов загрузки плиты и различных видов оснований выполняется именно по этим параметрам.
Результаты проведенных исследований для всех трех моделей основания иллюстрируются рисунками 2 - 6 и сведены в таблицу 1.

Рисунок 2 - Распределение главных растягивающих
напряжений  в КЭ модели дорожного покрытия
в КЭ модели дорожного покрытия
для основания в виде упруго-пластического
полупространства при нагрузке в углу плиты
Вышеприведенные результаты показывают, что при нагрузке, приложенной в углу плиты, область максимальных растягивающих напряжений расположена на верхней грани плиты на расстоянии порядка одного метра от загруженного угла. Именно в этой области должно произойти разрушение плиты в случае, если нагрузка будет равна предельной.
График распределения вертикальных перемещений конечно-элементной модели в сечении по краю плиты перпендикулярном оси X, изображенный на рисунке 3, показывает, что при упруго-пластической модели основания на границе между плитой и основанием возникает разрыв прогиба, связанный с необратимыми деформациями грунта.

перемещений поверхности основания плиты в сечении
между узлами 2355 и 2377 (рисунок 1) при нагрузке,
приложенной в углу плиты для упруго-пластического основания
Из рисунков 4 - 5, изображающих распределение полных эквивалентных пластических деформаций в грунте в среднем сечении модели, перпендикулярном оси X, видно, что пластические деформации в грунте могут распространяться на глубину порядка полутора метров. И хотя в горизонтальном направлении это сравнительно узкая, до одного метра шириной область, неучет возникающих в ней необратимых деформаций может исказить реальную картину работы основания.
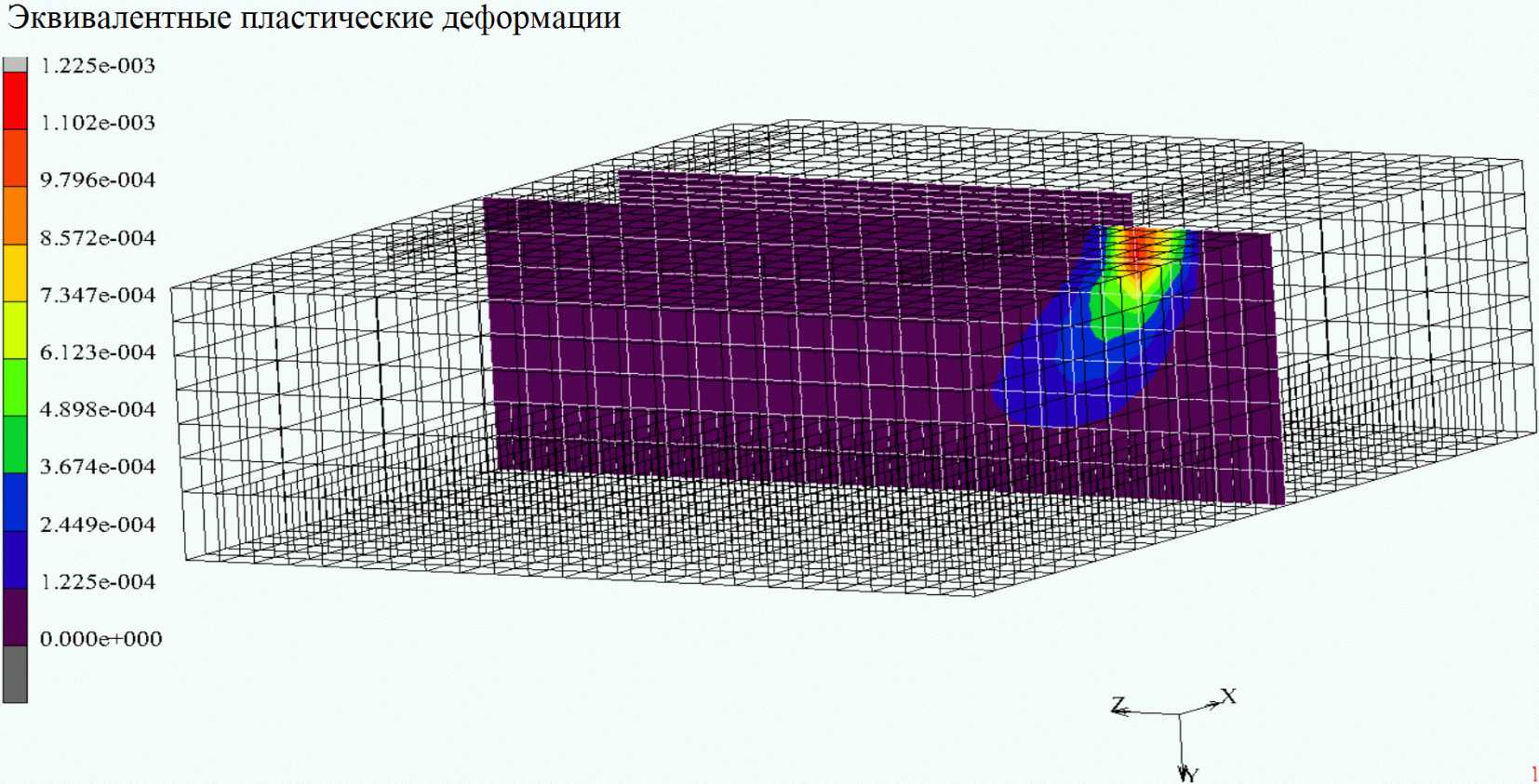
деформаций в упруго-пластическом основании в вертикальном
сечении между узлами 2585 и 2607 (рисунок 1) при нагрузке,
приложенной в середине длинного края плиты
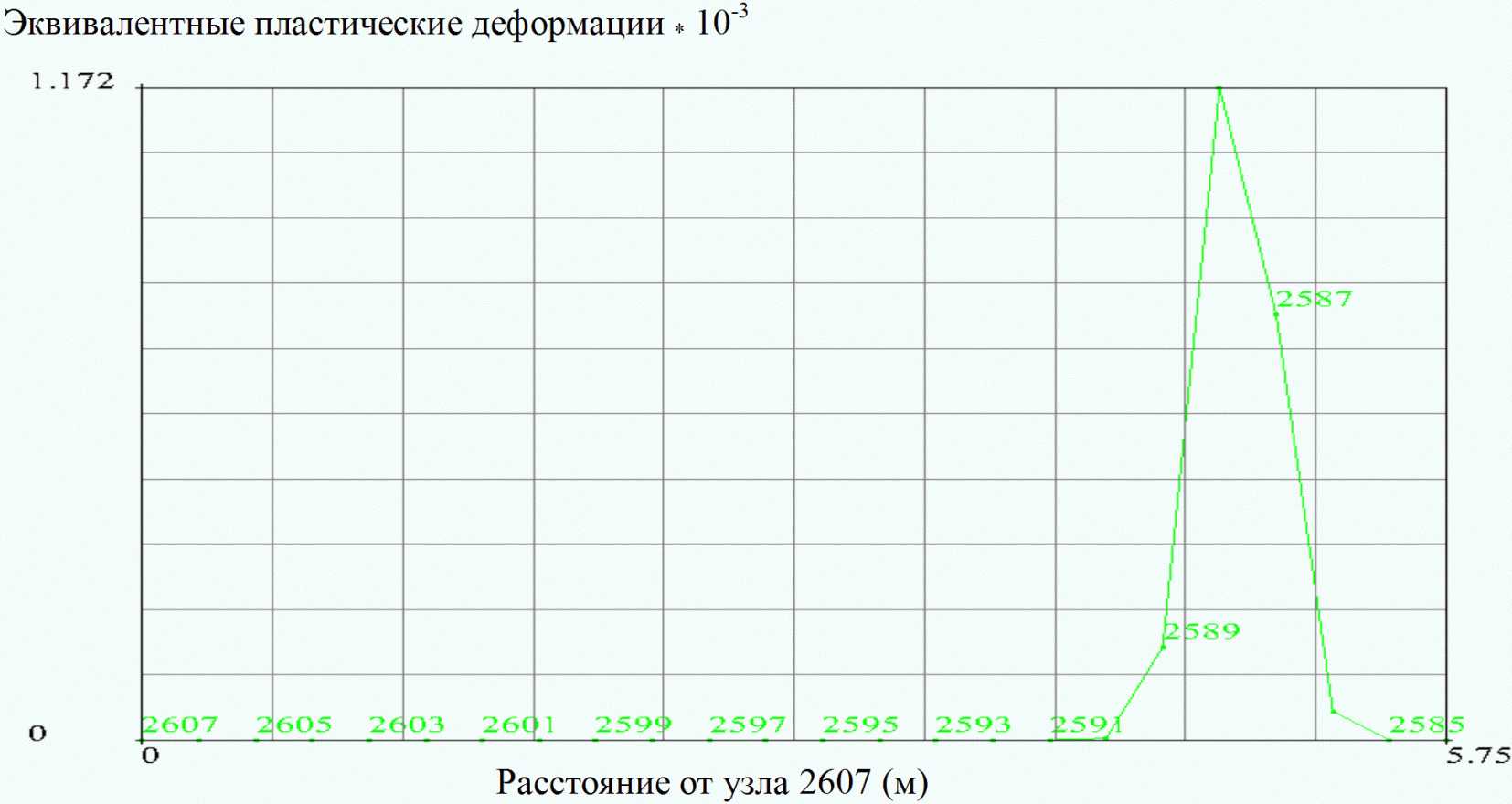
деформаций в упруго-пластическом основании в вертикальном
сечении между узлами 2585 и 2607 (рисунок 1) при нагрузке,
приложенной в середине длинного края плиты
Таблица 1
и максимальные растягивающие напряжения в плите  (МПа)
(МПа)
в зависимости от положения нагрузки и вида основания

Анализируя результаты, приведенные в таблице 1, приходим к следующим выводам:
- при нагрузке в середине плиты для всех трех моделей основания прогибы и максимальные растягивающие напряжения получаются примерно одинаковыми;
- для нагрузки на краю плиты в середине ее длинной грани основание Винклера дает прогибы на 34% большие, а упругое полупространство на 12% меньшие, чем упруго-пластическое полупространство. Такой результат соответствует физическим представлениям о работе данных конструкций;
- наиболее опасным, с точки зрения прочности конструкции, следует считать загружение плиты нагрузкой на ее краю в середине длинной грани, так как именно в этом случае все три модели основания дают самые большие максимальные растягивающие напряжения;
- при расчете по деформациям наиболее опасным следует считать загружение плиты в углу, в этом случае для всех трех моделей основания возникли максимальные прогибы плиты.
Таким образом, в зависимости от выбора модели основания плиты, для слабого грунта, каковым является супесь, разница в прогибах может составить около 34%, а разница в максимальных растягивающих напряжениях около 27,5%. Окончательное решение о выборе той или иной модели основания должно основываться на сравнении результатов расчета с результатами натурного эксперимента.
Для тестирования предлагаемых в данном ОДМ, КЭ моделей дорожных покрытий, созданных в КЭ комплексе "MARC-MENTAT" были использованы результаты, полученные в работе [17]. В этой работе экспериментальные значения прогибов покрытия определялись с помощью оборудования FallingWeightDeflectometer (FWD), а теоретические исследования работы дорожного покрытия выполнялись с помощью КЭ комплекса "ABAQUS". Расположение конструктивных слоев в покрытии, рассмотренном в работе [17], представлено на рисунке 6. Механические свойства слоев жесткого дорожного покрытия, в соответствии с рисунком 6, представлены в таблице 4.
Как и в работе [18], размеры плиты покрытия в плане составляли 4,6 x 3,7 м. Толщина плиты равнялась 0,263 м. Размеры расчетной области в плане были приняты 6,3 x 5,7 м. Толщины конструктивных слоев покрытия и их механические характеристики назначались в соответствии с таблицей 2.
Нагрузка к плите прикладывалась через бесконечно жесткий штамп диаметром 0,3 м.
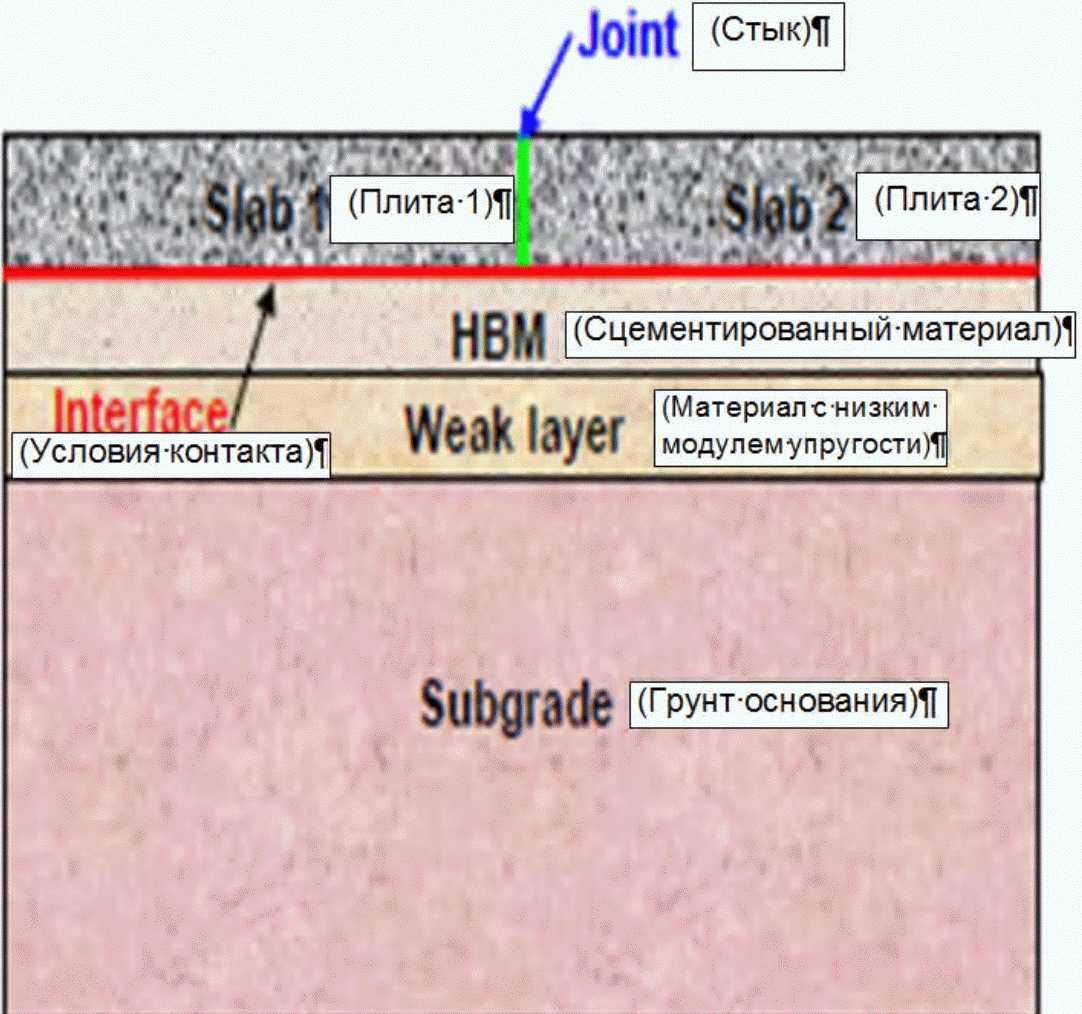
рассмотренного в работе [18]
Средствами "MARC-MENTAT" нами была разработана КЭ модель для этого покрытия, изображенная на рисунке 7.
созданная в КЭ комплексе "MARC-MENTAT"
Таблица 2
дорожного покрытия, исследованного в работе [18]

Для уменьшения размерности задачи и более точного приближения КЭ модели к реальным условиям, грунт, расположенный в основании модели, включал в себя слой 12-узловых полубесконечных конечных элементов. С этой же целью, на боковых гранях модели было смоделировано упругое основание Винклера, а не условия отсутствия горизонтальных перемещений, как это было принято в работе [18]. В силу симметрии задачи относительно двух вертикальных плоскостей, появилась возможность рассмотреть только четверть расчетной области (рисунок 7). В плоскостях симметрии были поставлены условия отсутствия горизонтальных перемещений.
Нагрузка к штампу прикладывалась в два этапа:
- вначале (при t = 0) прикладывался только собственный вес плиты, который далее оставался постоянным;
- затем (при t = 0,01 сек) прикладывалась нагрузка к штампу, которая возрастала до 75 кН (при t = 0,02 сек) и затем уменьшалась до нуля (при t = 0,03 сек).
Для сравнения полученных результатов с результатами работы [18], прогибы плиты от совместного действия ее собственного веса и нагрузки на штамп должны быть уменьшены на величину прогибов от действия собственного веса плиты. Полученный при этом график был построен в одном масштабе с графиками, взятыми из работы [18] (рисунок 8).
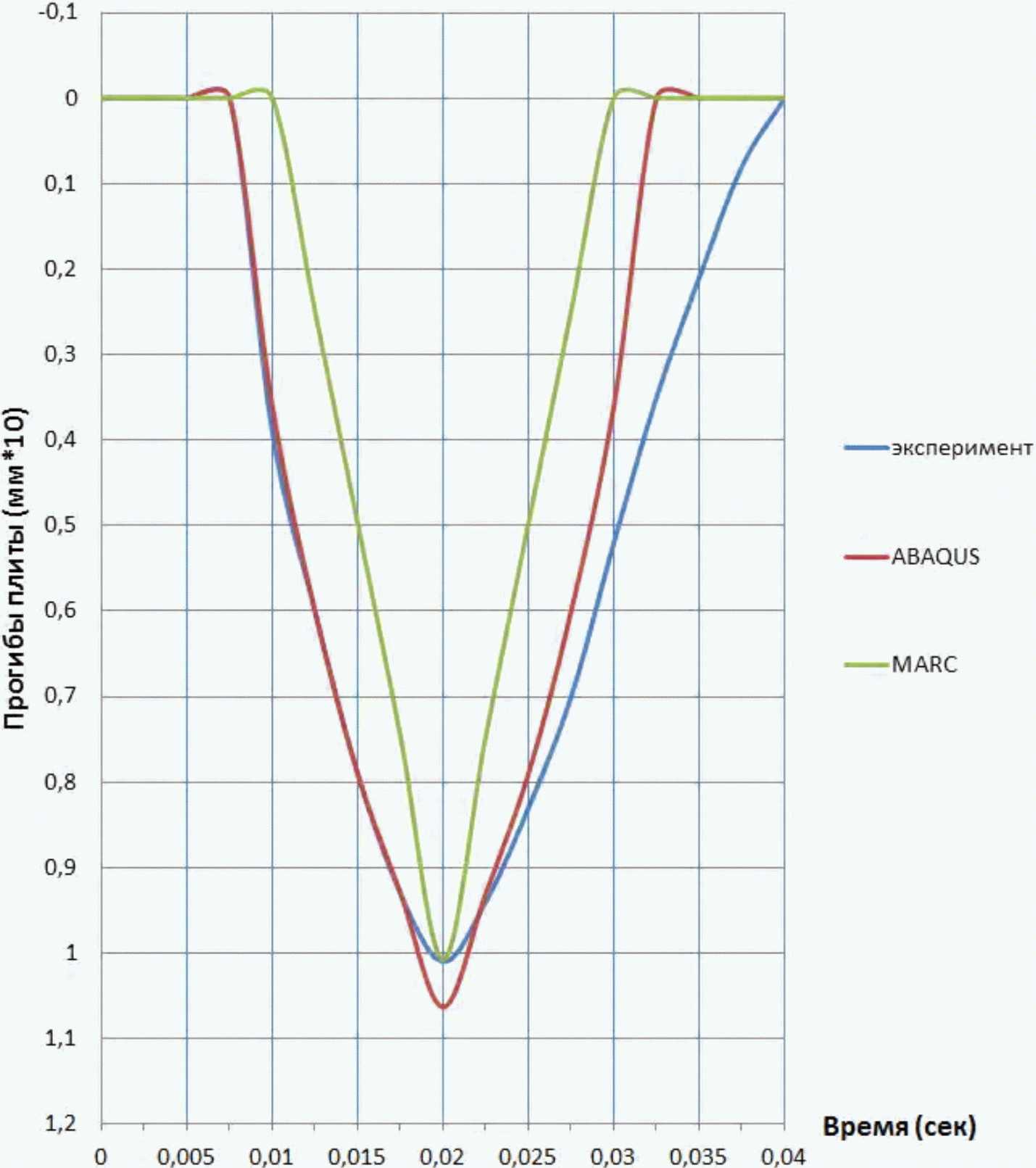
верхней грани плиты в зависимости от времени,
найденных в работе [18] и вычисленное
с помощью КЭ комплекса "MARC-MENTAT"
Из рисунка 8 видно, что максимальный прогиб плиты, полученный на основе модели, построенной в КЭ комплексе "MARC-MENTAT", практически совпадает с результатом экспериментального исследования приведенным в работе [18]. Следовательно, построенные нами в рамках данной ОДМ конечно-элементные модели могут успешно применяться для расчета жестких дорожных покрытий.
6.4. Рекомендации по использованию полученных результатов на стадии проектирования жестких дорожных одежд
При расчете конструкции жесткого многослойного дорожного покрытия методом конечных элементов на стадии его проектирования следует придерживаться следующих рекомендаций:
- Чтобы уменьшить размерность конечно-элементной модели покрытия, а этого требует ограниченность вычислительных ресурсов проектных организаций, нужно в первую очередь уменьшить размеры области основания. Достигается это за счет использования полубесконечных конечных элементов на внешней границе модели покрытия. Такие элементы присутствуют в библиотеках КЭ любого мультидисциплинарного КЭ комплекса;
- Уменьшить размерность конечно-элементной модели покрытия можно также использованием для основания покрытия модели Винклера, вместо модели упругого слоя или модели упругого полупространства;
- Если в расчетной схеме покрытия присутствуют плоскости симметрии, то следует создавать КЭ модель только для части покрытия, расположенную по одну сторону от оси симметрии;
- Для учета неупругих свойств основания лучше всего подходит модель Друкера-Прагера, так как значения угла внутреннего трения и коэффициента сцепления, которые используются в этой модели, для различных видов грунтов можно найти в существующей нормативной документации.
конструкций швов жестких дорожных покрытий
Наиболее ответственными и сложными элементами конструкции цементобетонного покрытия являются продольные и поперечные швы. От правильности проектирования продольных и поперечных швов и соблюдения технологии производства работ при их устройстве, в значительной степени зависит прочность всего покрытия.
При анализе различных вариантов конструкций швов, весьма полезной является параметрическая форма представления КЭ модели. Она позволяет автоматизировать процесс преобразования одной КЭ модели в другую с измененными размерами, свойствами материалов, граничными условиями и густотой КЭ сетки. Создание параметрической модели более трудоемко, чем создание модели с фиксированными числовыми значениями свойств модели и требует, к тому же, более высокой квалификации разработчиков КЭ модели. Однако, на стадии расчетов, при изменении конструкций швов дорожных покрытий, эти недостатки компенсируются за счет полной автоматизации при создании новых моделей конструкций швов с помощью параметрической КЭ модели. Таким образом, рассмотрев с помощью параметрической КЭ модели результаты расчетов для различных вариантов конструкций швов жесткого дорожного покрытия, можно выбрать наиболее оптимальный, удовлетворяющий требованиям технического задания.
Чтобы создать параметрическую модель в КЭ комплексе MARC-MENTAT, нужно все операции, выполняемые при задании размеров КЭ модели, свойств ее материалов, типа контакта между слоями дорожной одежды, выбор решателя системы алгебраических уравнений и так далее, записать в виде процедурного текстового файла с расширением ".proc".
В рамках данной ОДМ разработан процедурный файл, позволяющий построить параметрическую модель для конструкций поперечных швов жестких дорожных покрытий. Фрагмент этого файла, отражающий способ задания геометрических параметров КЭ модели и свойств ее материалов, приведен на рисунке 9.
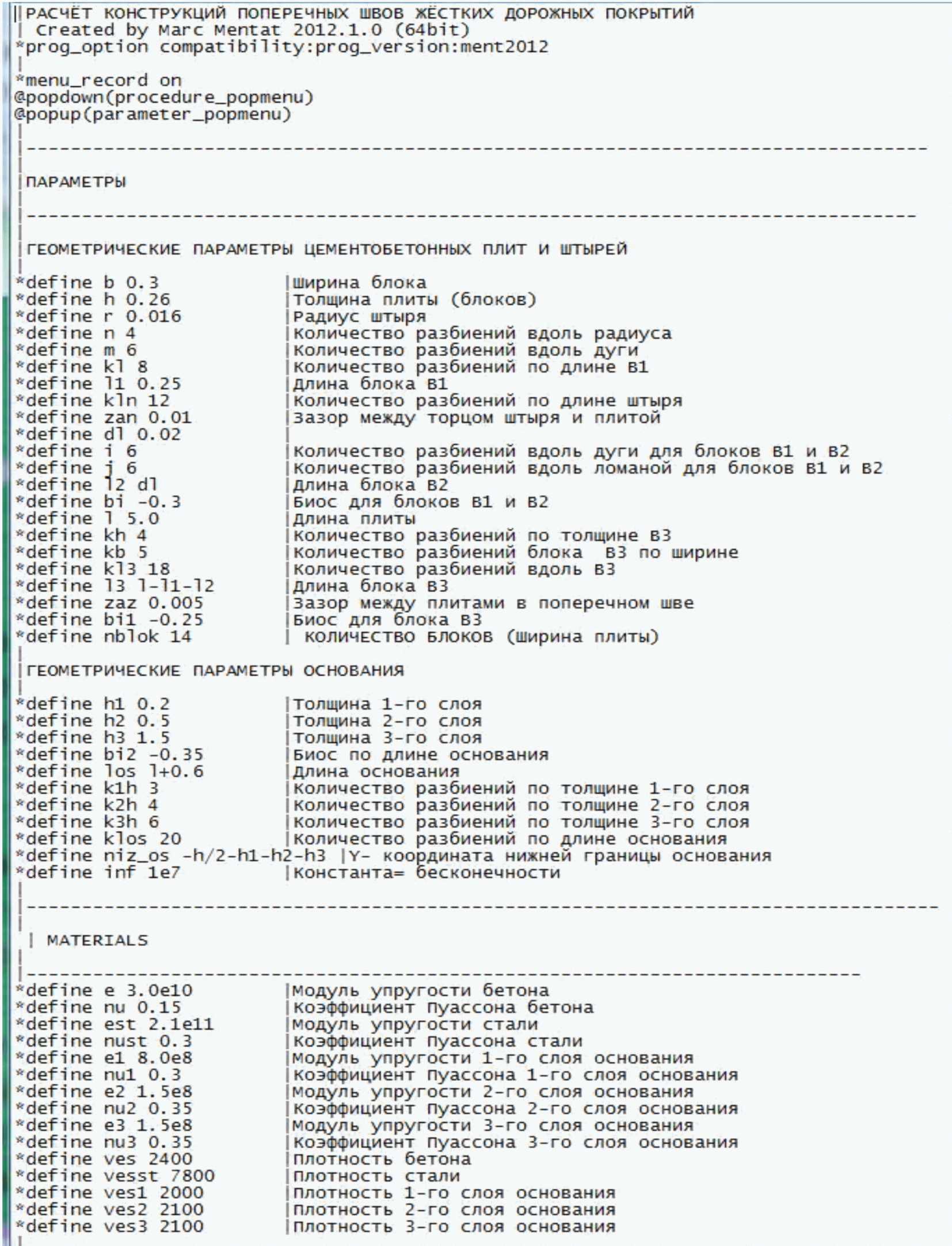
конструкций поперечных швов жестких дорожных покрытий
7.1. Расчетное положение транспортной нагрузки на жестком покрытии, усиленном в поперечных швах стальными штырями
Самые большие напряжения в плите возникают при нагрузке, расположенной посредине ее свободного края. Они возникают по подошве плиты [1]. Поэтому, согласно ГОСТ Р 52748-2007, пункт 5.1.3, такое положение нагрузки считается расчетным. Однако, повторяемость приложения таких нагрузок гораздо меньше, порядка нескольких процентов от расчетного числа проездов для центральной части плиты. В методе расчета, предложенном PortlandCementAssociation (PCA) [19], принято, что она составляет 6%.
В то же время, разрушение цементобетонных дорожных покрытий, усиленных в поперечных швах стальными штырями, начинается, как правило, с разрушения бетона в окрестности поперечных швов [20].
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду рисунок 10, а не рисунок 12. |
Стальные штыри создают в бетоне очаги концентрации напряжений, которые провоцируют образование и развитие трещин в бетоне при повторяющихся транспортных нагрузках и климатических воздействиях (рисунок 12) [17].

в окрестности стального штыря
Поэтому, в качестве расчетного положения оси транспортного средства, при расчете конструкций поперечных швов, очевидно, следует принять положение, предлагаемое в работе [15] и изображенное на рисунке 11.

транспортного средства, принятое в конечно-элементном
пакете ISLAB2000 [15]
Для проверки работоспособности параметрической модели жесткого дорожного покрытия, предлагаемой в рамках данной ОДМ, были использованы экспериментальные результаты, приведенные в работе [17].
В этой работе рассматривалась конструкция дорожного покрытия, состоящая из двух плит, каждая из которых имела длину (в направлении движения транспорта) 5 м и ширину 4,5 м. Толщина плиты составляла 0,26 м.
Плиты в поперечном шве были связаны между собой стальными штырями диаметром 32 мм, длиной 500 мм и с расстоянием между осями штырей равным 300 мм.
Основание для плит состояло из двух слоев: слоя песка, укрепленного цементным раствором толщиной 0,2 м и слоя грунта толщиной 2 м. Размеры основания в плане для проведения тестовых расчетов были приняты 11,2 x 6,2 м.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 3, а не таблица 3. |
Физико-механические свойства материалов приведены в таблице 2.
Таблица 3
Физико-механические свойства материалов

Общий вид конечно-элементной модели, рассмотренной в работе [17], представлен на рисунке 12.

исследованного в работе [17]
Для создания тестовой модели была использована разработанная в рамках данной ОДМ параметрическая конечно-элементная модель конструкции поперечного шва, усиленного стальными штырями. В процедурном файле, соответствующем этой модели (рисунок 9), произвольным параметрам, определяющим свойства модели, были присвоены численные значения, соответствующие тестовой модели (рисунок 12). Общий вид конечно-элементной модели жесткого дорожного покрытия, состоящей из двух плит, соединенных между собой в поперечном шве стальными штырями и нагруженной давлением от четырех колес оси транспортного средства, показан на рисунке 13.

дорожного покрытия, усиленного стальными штырями,
на трехслойном основании
Фрагмент конструкции поперечного шва плиты показан на рисунке 14.

дорожного покрытия, усиленного стальными штырями,
на трехслойном основании
Конечно-элементная модель сдержала 130400 8-узловых объемных конечных элемента и 158243 узла. Воздействия на плиту прикладывались в течение трех шагов по времени:
- вначале, при изменении расчетного времени от 0 до 1 к плите прикладывалась гравитационная нагрузка от собственного веса плиты (рисунок 15). В течение двух последующих шагов по времени от 1 до 3 эта нагрузка оставалась постоянной;
- в начале второго временного шага к плитам покрытия может быть приложено температурное воздействие, которое в течение промежутка времени от 1 до 2 возрастает от нуля до заданных в процедурном файле значений. При этом определяется также закон изменения температуры по толщине плиты (рисунок 16);
- в начале третьего временного шага прикладывается транспортная нагрузка в виде давления на покрытие от четырех колес оси транспортного средства (рисунок 17).
от собственного веса плит в функции от времени

на плиты покрытия в функции от времени и по толщине плиты

на плиты покрытия в функции от времени
Между плитами покрытия и основанием реализован контакт - касание с коэффициентом трения, как и в работе [17], равным 0,05.
Коэффициент трения между стальными штырями и бетоном плиты равнялся 0,1 [17].
Результаты расчетов на действие транспортной нагрузки представлены на рисунках 18 - 27.
На рисунке 18 показано распределение вертикальных перемещений плит покрытия и основания. Как и следовало ожидать, наибольшие перемещения возникают в окрестности поперечного шва - там, где приложена транспортная нагрузка.
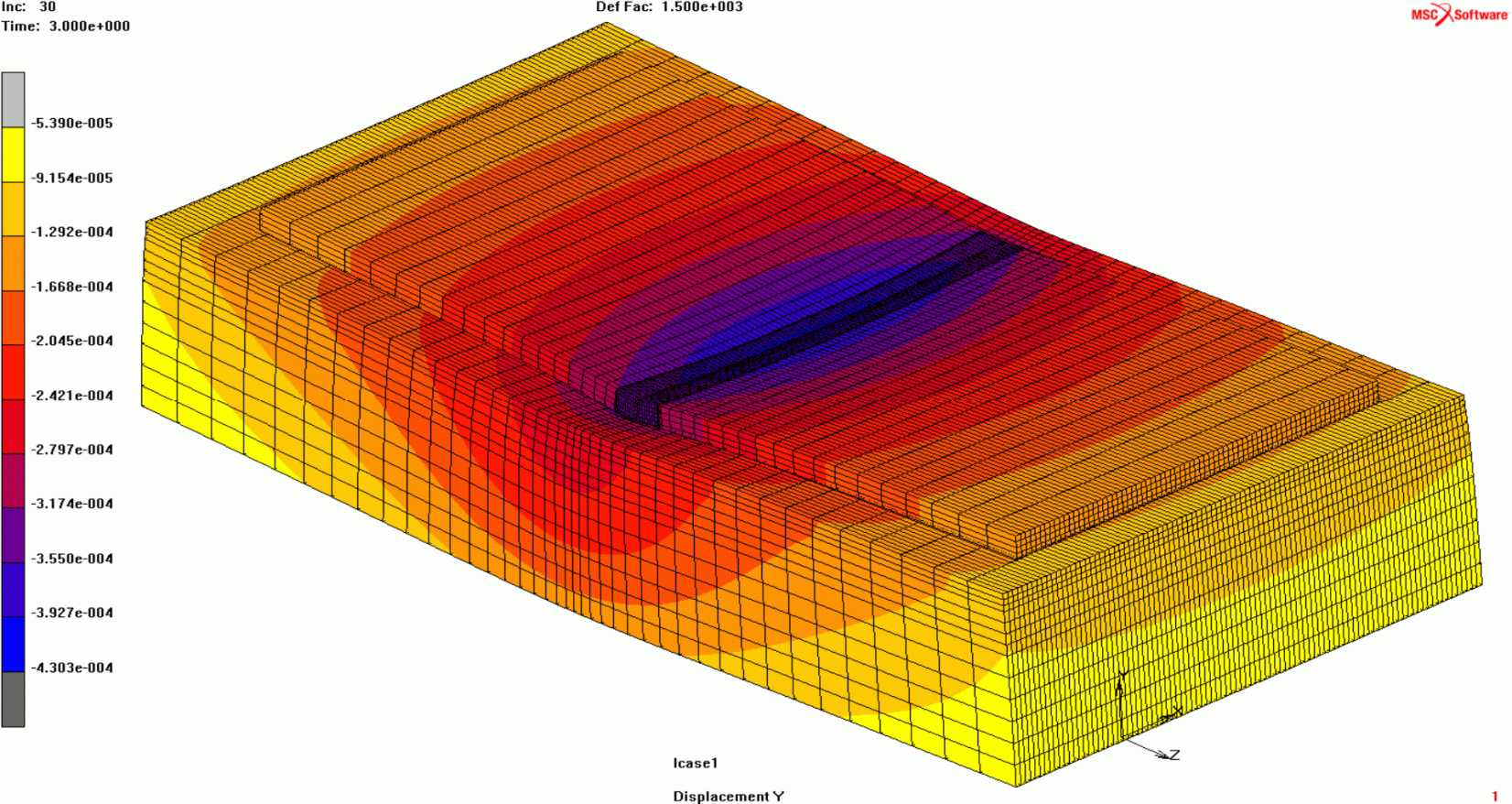
и основания от собственного веса и транспортной нагрузки
в м (для наглядности перемещения увеличены в 1500 раз)
Вертикальные перемещения укрупненного фрагмента плиты и стальных штырей показаны на рисунке 19. При этом, как видно из рисунков 19 и 20, штыри подвергаются деформациям изгиба и среза.

Рисунок 19 - Вертикальные перемещения укрупненного
фрагмента плиты и стальных штырей в м

(для наглядности перемещения увеличены в 1500 раз)
Из рисунков 21 и 22 следует, что в окрестности штырей в бетоне возникают значительные растягивающие напряжения, как на вертикальных, так и на горизонтальных площадках. Эти напряжения могут привести к образованию горизонтальных и вертикальных трещин в бетоне, что соответствует результатам экспериментальных исследований, представленных на рисунке 10.

Рисунок 21 - Распределение нормальных напряжений
в бетоне на горизонтальных площадках

в бетоне на вертикальных площадках
Значительные напряжения в окрестности поперечного шва возникают не только в плитах покрытия, но и в основании (рисунок 23).
Поэтому, влияние свойств основания на прочность и деформации конструкций поперечных швов также должно стать предметом теоретических и экспериментальных исследований.

Рисунок 23 - Распределение эквивалентных напряжений
в основании плиты покрытия
Для сравнения результатов расчетов, выполненных с помощью параметрической конечно-элементной модели дорожного покрытия, разработанной в рамках данной ОДМ, с результатами экспериментов, приведенных в работе [17], были построены графики, изображенные на рисунках 24 и 26. Эти графики показывают изменения вертикальных перемещений узлов, расположенных над стальными штырями на верхних гранях плит, в окрестности поперечного шва, в зависимости от времени (последовательности приложения собственного веса плит покрытия и транспортной нагрузки).
Положение узлов, в которых экспериментально и теоретически определялись вертикальные перемещения плит покрытия, показано на рисунке 25.

узлов, расположенных на верхней грани плиты,
нагруженной транспортной нагрузкой

и теоретически определялись вертикальные перемещения
плит покрытия

узлов, расположенных на верхней грани плиты,
не нагруженной транспортной нагрузкой
На основе графиков, изображенных на рисунках 24, 26, построены графики, изображенные на рис. 27 - 28, на которых приводится сравнение результатов, полученных с помощью параметрической модели конструкции поперечного шва, с результатами экспериментальных исследований, отраженных в работе [17].
Из этих графиков следует, что расчетные значения перемещений верхней грани плиты, полученные с помощью параметрической конечно-элементной модели конструкций поперечного шва жесткого дорожного покрытия, достаточно хорошо соответствуют результатам экспериментальных исследований, представленных в работе [17].

верхней грани плиты, нагруженной транспортной нагрузкой
в окрестности поперечного шва
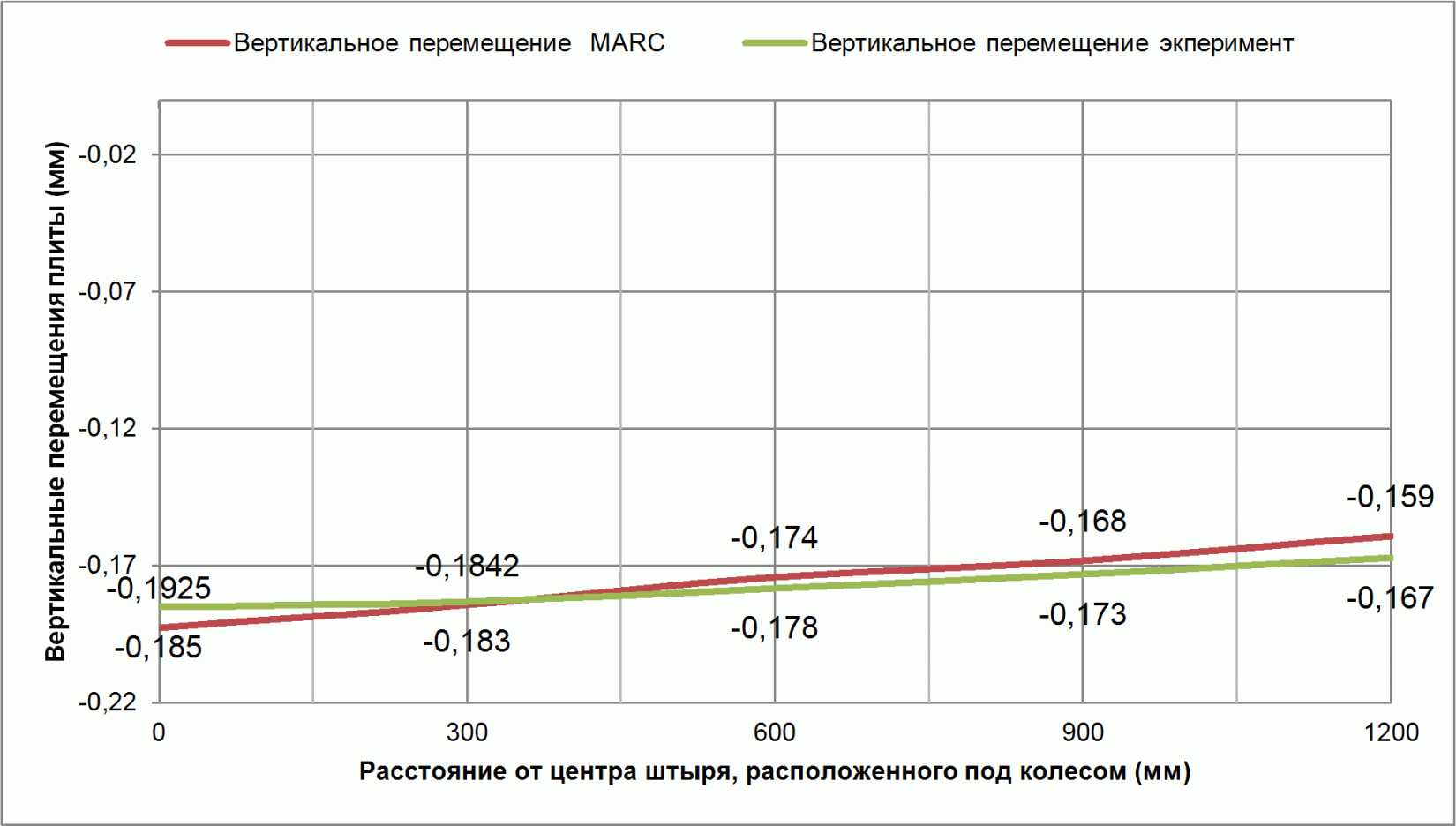
верхней грани плиты, нагруженной транспортной нагрузкой
в окрестности поперечного шва
Как уже отмечалось ранее, в начале второго временного шага к плитам покрытия может быть приложено температурное воздействие, которое в течение промежутка времени от 1 до 2 возрастает от нуля до заданных в процедурном файле значений (рисунок 8). При этом определяется также закон изменения температуры по толщине плиты. Значения температуры на верхней и нижней гранях плит покрытия могут быть заданы любыми.
Рассмотрим вначале случай высоких летних температур, когда при разрушении бетона плит покрытия в окрестности поперечных швов и заполнения швов несжимаемыми материалами покрытие может потерять продольную устойчивость [6].
Будем предполагать наиболее неблагоприятное сочетание технологических и климатических условий: укладка бетона в покрытие выполнялась при температуре 0 °C, а в летний период времени верхняя грань плиты нагрелась до 50 °C, а нижняя до 35 °C, как это представлено на рисунке 8.
Полученное в результате расчетов распределение температуры по толщине плиты покрытия показано на рисунке 29.

Рисунок 29 - Распределение температуры
в плите покрытия в летний период времени
На рисунке 30 изображены вертикальные перемещения плит покрытия при нагреве в летний период времени, на рисунке 31 - продольные перемещения одной плиты, а на рисунке 32 - ее поперечные перемещения.

Рисунок 30 - Вертикальные перемещения плит покрытия
при нагреве в летний период времени
(перемещения увеличены в 50 раз)
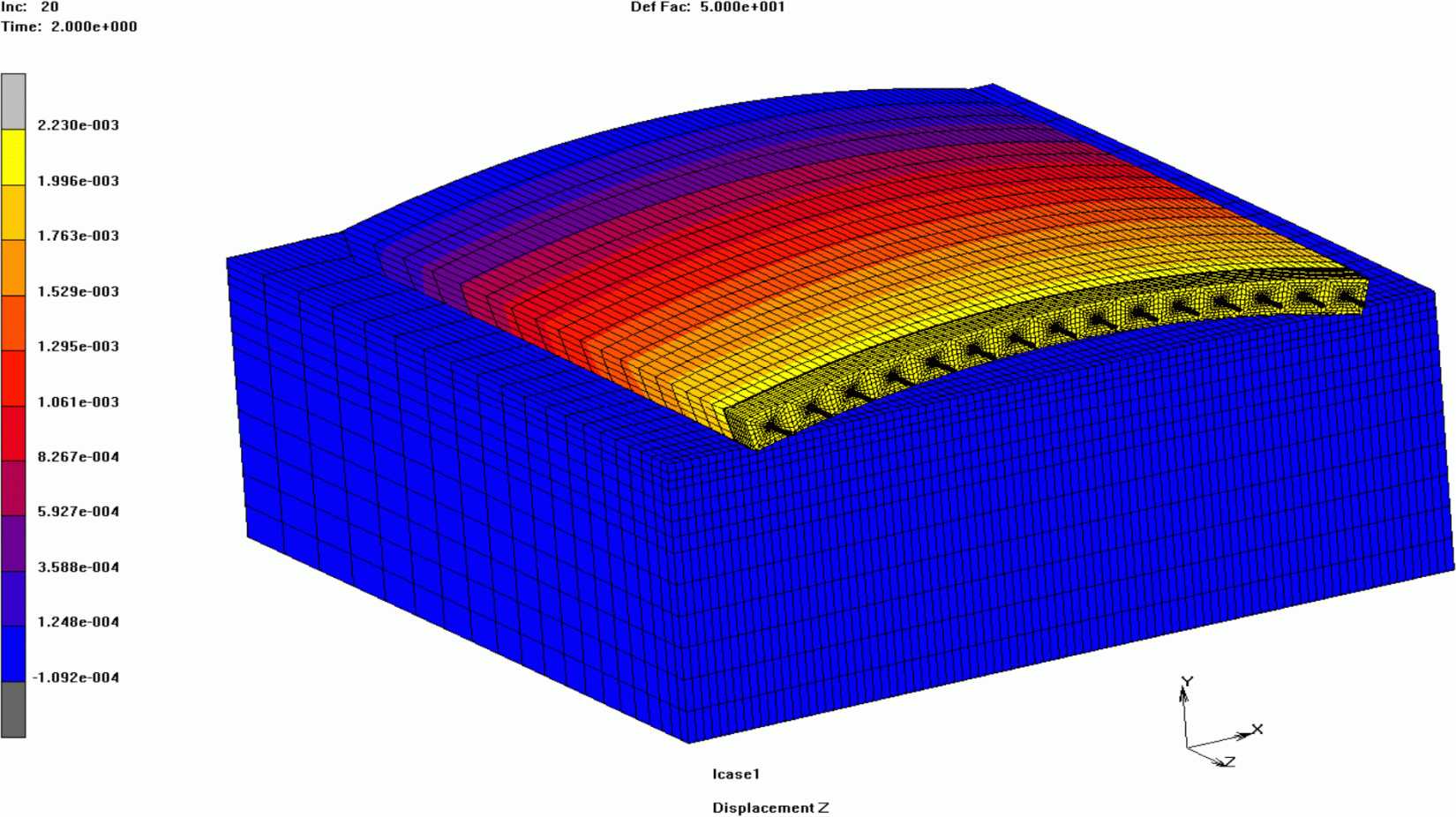
покрытия при нагреве в летний период времени
(перемещения увеличены в 50 раз)
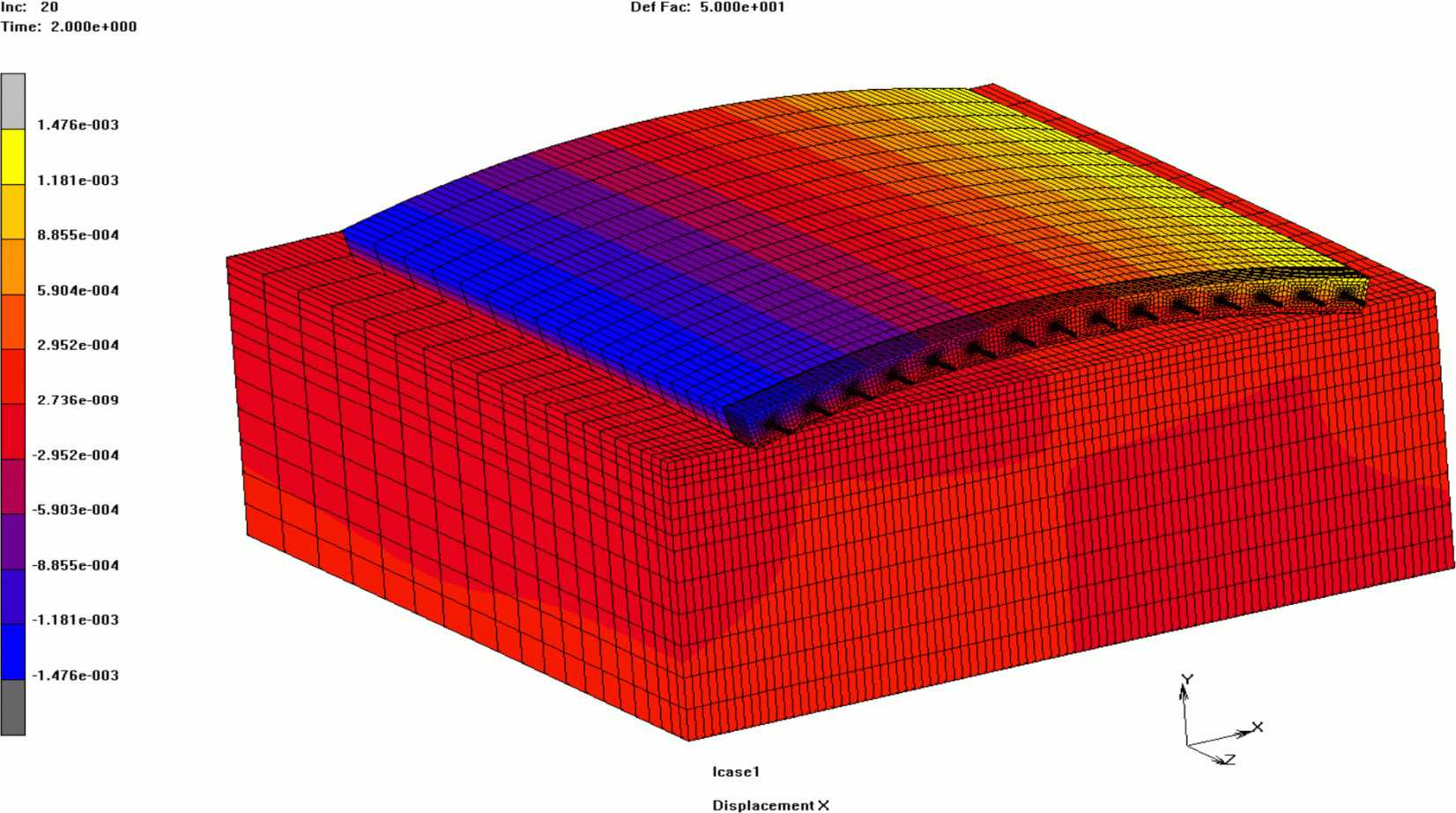
в летний период времени в поперечном направлении
(перемещения увеличены в 50 раз)
Из рисунка 33 видно, что температурное воздействие создает в бетоне плиты в окрестности стальных штырей значительные растягивающие напряжения на горизонтальных площадках, что может спровоцировать образование горизонтальных трещин в бетоне.

Рисунок 33 - Распределение нормальных напряжений
на горизонтальных площадках в бетоне плиты
в окрестности стальных штырей
Если к покрытию, которое уже находится под действием собственного веса и экстремальных летних температур, приложить транспортную нагрузку от оси автомобиля, равную 100 кН, в соответствии с рисунками 13 и 14, то напряженно-деформированное состояние покрытия изменится.
Вертикальные, продольные и поперечные перемещения плит покрытия для этого случая показаны на рисунках 34 - 36.
А распределение максимальных растягивающих напряжений в бетоне в окрестности стальных штырей изображено на рисунках 37 - 40. Из этих рисунков следует, что в бетоне в окрестности стальных штырей возникает высокая концентрация напряжений, которая неизбежно приведет к образованию горизонтальных и вертикальных трещин (рисунок 10).

при нагреве в летний период времени
(перемещения увеличены в 50 раз)

Рисунок 35 - Продольные перемещения одной из плит
покрытия при нагреве в летний период времени
(перемещения увеличены в 50 раз)

при нагреве в летний период времени в поперечном
направлении (перемещения увеличены в 50 раз)
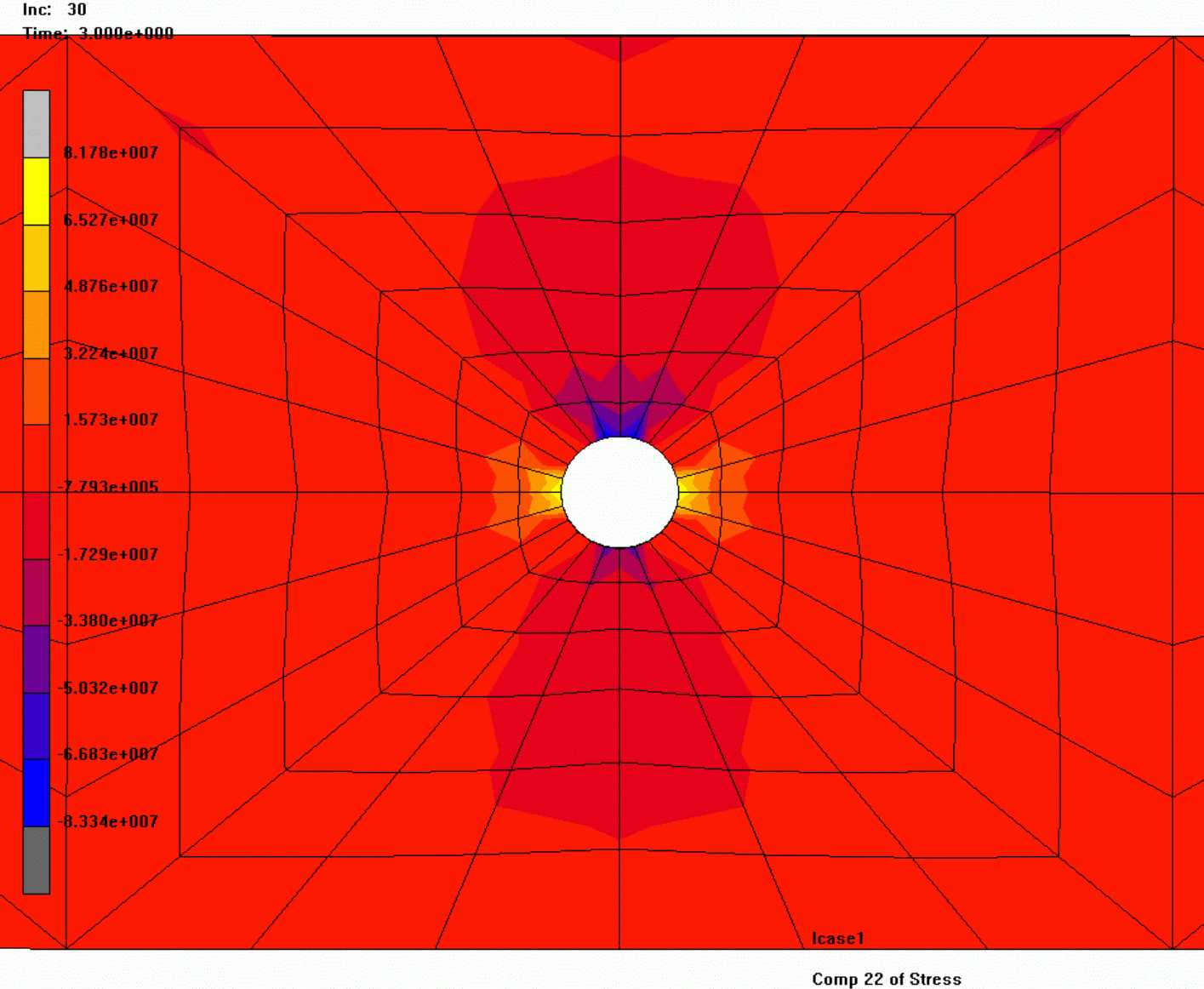
на горизонтальных площадках в бетоне плиты
в окрестности стальных штырей

Рисунок 38 - График распределения нормальных напряжений
на горизонтальных площадках в бетоне плиты
между двумя стальными штырями

Рисунок 39 - Распределение нормальных напряжений
на вертикальных площадках в бетоне плиты
в окрестности стальных штырей
на вертикальных площадках в бетоне плиты в сечении,
проходящем через середину стального штыря
Если к покрытию приложены экстремально низкие температурные воздействия, то деформации покрытия и распределение напряжений в нем будут существенно иными, чем при положительных температурных воздействиях.
Предполагая наиболее неблагоприятное сочетание технологических и климатических условий, рассмотрим, в качестве примера, результаты расчета покрытия в случае температуры на его верхней грани равной -30 °C, температуре на нижней грани равной -20 °C, и при условии, что укладка бетона в покрытие выполнялась при температуре 0 °C.
Полученное в результате расчетов распределение температуры по толщине плиты покрытия показано на рисунке 41.

Рисунок 41 - Распределение температуры в плите покрытия
Распределение вертикальных, продольных и поперечных перемещений плиты покрытия, а также распределение нормальных напряжений в бетоне плиты на вертикальных и горизонтальных площадках в окрестности стального штыря от действия собственного веса и отрицательных температур показаны на рисунках 42 - 47.

Рисунок 42 - Распределение вертикальных перемещений плиты
покрытия от действия собственного веса и отрицательных
температур (перемещения увеличены в 70 раз)

Рисунок 43 - Распределение перемещений плиты покрытия
в продольном направлении от действия собственного веса
и отрицательных температур (перемещения увеличены в 70 раз)
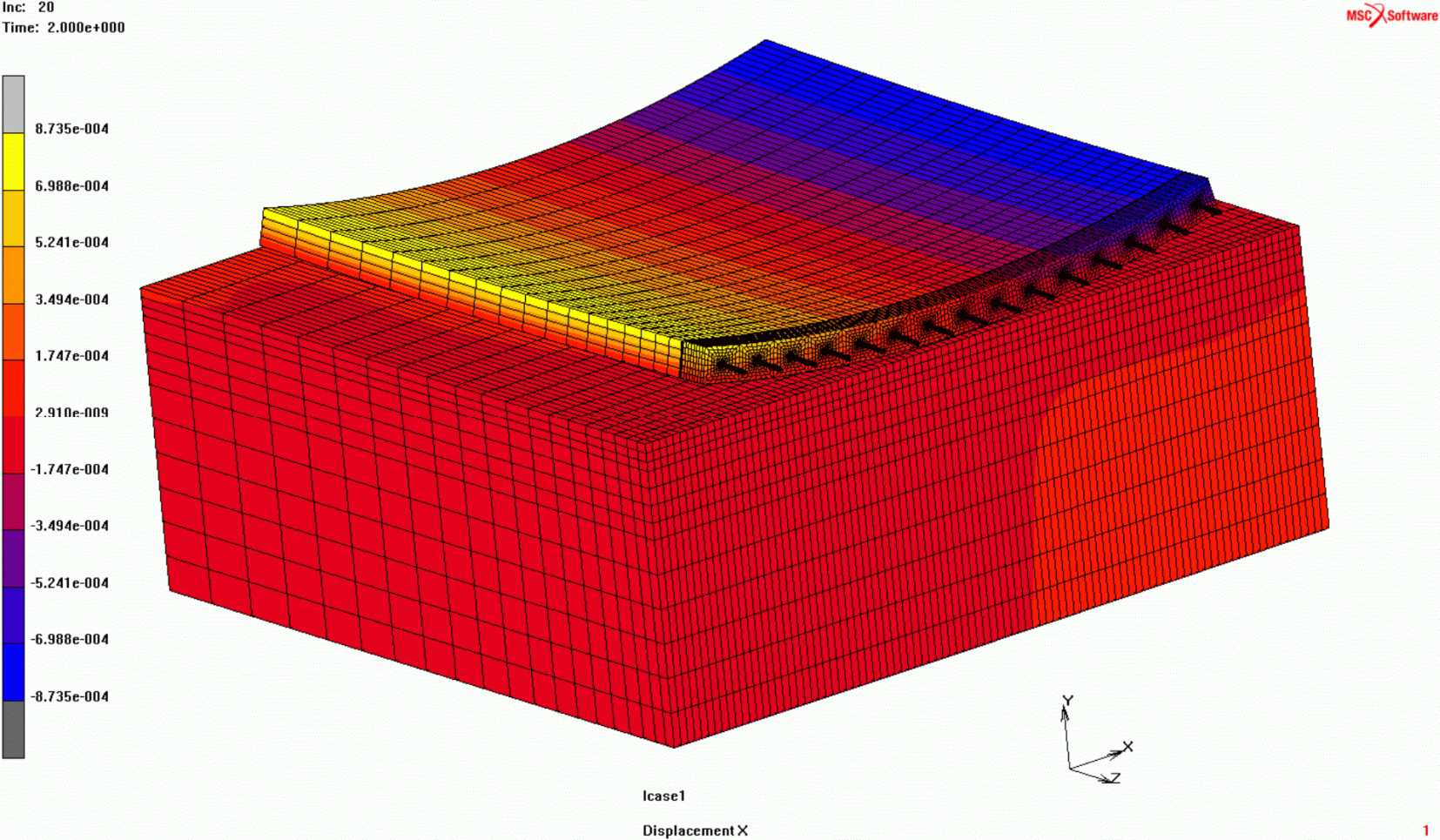
Рисунок 44 - Распределение перемещений плиты покрытия
в поперечном направлении от действия собственного веса
и отрицательных температур (перемещения увеличены в 70 раз)

Рисунок 45 - Вертикальные перемещения плиты
покрытия в поперечном шве от собственного веса
и воздействия температуры

Рисунок 46 - Распределение нормальных напряжений
в бетоне плиты на вертикальных площадках
в окрестности стального штыря

в бетоне плиты на горизонтальных площадках
в окрестности стального штыря
Добавление к нагрузкам на покрытие, которое уже находится под действием собственного веса и экстремальных низких температур, транспортной нагрузки от оси автомобиля, равной 100 кН в соответствии с рисунками 13 и 14, приведет к существенному изменению напряженно-деформированного состояния покрытия.
Вертикальные, продольные и поперечные перемещения покрытия для этого случая показаны соответственно на рисунках 48 - 52, а графики вертикальных перемещений узлов, расположенных над стальными штырями на верхней грани плиты (рисунок 25), в зависимости от времени представлены на рисунке 53.
Формы деформаций дорожного покрытия вполне соответствуют физическим представлениям о том, какими они должны быть при отрицательных температурных воздействиях.

покрытия от действия собственного веса, отрицательных
температур и транспортной нагрузки
(перемещения увеличены в 70 раз)

Рисунок 49 - Распределение вертикальных перемещений
загруженной плиты покрытия от действия собственного веса,
отрицательных температур и транспортной нагрузки
(перемещения увеличены в 70 раз)

Рисунок 50 - График вертикальных перемещений верхней грани
нагруженной плиты в поперечном шве от действия собственного
веса, отрицательных температур и осевой нагрузки

Рисунок 51 - Распределение вертикальных перемещений
нагруженной плиты от действия собственного веса,
отрицательных температур и осевой нагрузки
(перемещения увеличены в 70 раз)

в поперечном направлении от действия собственного веса,
отрицательных температур и осевой нагрузки
(перемещения увеличены в 70 раз)

узлов, расположенных на верхней грани плиты (рис. 25),
в зависимости от времени
Из рис. 54 - 57 следует, что в окрестности стальных штырей в бетоне возникает высокая концентрация напряжений, которая может привести к образованию как горизонтальных, так и вертикальных трещин.

Рисунок 54 - Распределение нормальных напряжений в бетоне
плиты на горизонтальных площадках в окрестности
стального штыря

Рисунок 55 - Распределение нормальных напряжений
в бетоне плиты на горизонтальных площадках
в окрестности стального штыря

Рисунок 56 - Распределение нормальных напряжений
в бетоне плиты на вертикальных площадках в окрестности
стального штыря

в бетоне плиты в вертикальном сечении, проходящем
через середину стального штыря
7.8. Рекомендации по использованию параметрических КЭ моделей при проектировании швов сжатия, усиленных стальными штырями, в жестких дорожных покрытиях
Параметрическая модель конструкции поперечного шва жесткого дорожного покрытия имеет следующие достоинства:
- позволяет исследовать напряженно-деформированное состояние поперечного шва жесткого дорожного покрытия при любых размерах цементобетонных плит, толщин упругих слоев основания, диаметров и длин стальных штырей;
- полученные с ее помощью результаты расчетов конструкций поперечного шва жесткого дорожного покрытия достаточно хорошо соответствуют результатам экспериментальных исследований;
- значительные напряжения в окрестности поперечного шва возникают не только в плитах покрытия, но и в основании, поэтому влияние свойств основания на прочность и деформации конструкций поперечных швов также должно стать предметом теоретических и экспериментальных исследований.
Создание в параметрической модели жесткого дорожного покрытия граничных условий, учитывающих влияние температурных воздействий на напряженно-деформированное состояние дорожных одежд позволяет:
- рассчитывать конструкции цементобетонных дорожных покрытий, усиленных стальными штырями, на действие, как транспортных нагрузок, так и сезонных колебаний температуры окружающей среды;
- прикладывать к конструкции транспортную нагрузку и температурное воздействие по отдельности и в любой последовательности;
- исследовать напряженно-деформированное состояние покрытия как при низких зимних температурах, так и при высоких летних.
дорожных покрытий на продольную устойчивость
В зарубежных и российских источниках отмечается, что разрушение жестких покрытий дорог и аэродромов в виде внезапного выпучивания покрытий в области поперечных швов и трещин является самым опасным видом разрушения, так как может привести к аварийной ситуации, связанной с человеческими жертвами.
Возникают такие разрушения обычно через 3 - 4 года после начала эксплуатации дорожного покрытия при высоких летних температурах и характерны для регионов с резко континентальным климатом, к каковым относится, в частности, большая часть областей Российской Федерации.
Современные исследования этой проблемы ограничиваются главным образом констатацией фактов разрушения покрытий в результате потери ими устойчивости в различных странах мира. Рекомендации по предотвращению этого явления являются либо чисто эмпирическими, либо основанными на простейших моделях теоретической механики и сопротивления материалов.
Исследования показали, что в 80% случаев вспучивание покрытия произошло при температуре более 50 °C.
Причиной вспучивания покрытия может быть не только высокая температура летом, но и низкая температура зимой, которая способствует значительному раскрытию поперечных швов и трещин и попаданию в них несжимаемых материалов.
Устройство асфальтобетонного покрытия поверх цементобетонного покрытия, при ремонте последнего, приводит к уменьшению отражательной способности покрытия и увеличению его температуры.
Коэффициент температурного расширения бетона, очевидно, является одним из главных факторов. Он пропорционален коэффициентам температурного расширения цементного геля, мелкого заполнителя и крупного заполнителя и их соотношению в бетоне. Для предотвращения потери устойчивости желателен низкий коэффициент температурного расширения.
Значительное увлажнение бетона дорожного покрытия в комбинации с высокими температурами входят в число главных причин потери устойчивости дорожным покрытием.
Попеременное замораживание и оттаивание бетона покрытия уменьшает прочность его структурных связей и увеличивает влажность, что также провоцирует вспучивания покрытия.
Вероятность появления и частота возникновения потери продольной устойчивости покрытием увеличивается с возрастом покрытия. Должно пройти от трех до девяти лет, чтобы на дороге возникли случаи потери устойчивости покрытием. Однако известны примеры, когда потеря устойчивости покрытием возникала через год после строительства дороги.
Склонность дорожного покрытия к потере устойчивости зависит от состояния поперечных швов и наличия поперечных трещин.
При исследовании влияния швов необходимо ответить на следующие вопросы:
- присутствуют ли в покрытии швы расширения?
- каково расстояние между швами?
- возможно ли попадание твердых частиц (песок, гравий) в швы?
- есть ли какие-либо повреждения швов?
Анализ опытных данных показал, что потеря устойчивости покрытием чаще возникает на тех дорогах, где нет швов расширения.
Уменьшение расстояния между швами уменьшает вероятность возникновения потери устойчивости покрытием.
Попадание несжимаемых материалов в швы является одной из главных причин потери устойчивости покрытием.
В случае отсутствия в швах уплотняющей мастики, в раскрытые швы и трещины попадают несжимаемые материалы, которые препятствуют свободному расширению покрытия, создавая в нем критические сжимающие напряжения. Последние могут вызвать как разрушение бетона в окрестности швов и трещин, так и потерю устойчивости покрытием.
Кроме того, в швы, не заполненные мастикой, попадает атмосферная влага, которая при движении автотранспорта выбрасывается на поверхность покрытия вместе с твердыми частицами основания. В результате под плитами покрытия образуются полости, а швы в нижней своей части заполняются несжимаемым материалом, что способствует как скалыванию бетона в нижней части покрытия, так и возникновению потери устойчивости.
Попадание антигололедных реагентов в швы и трещины приводит к интенсивному разрушению бетона жестких покрытий в областях, расположенных под швами и трещинами. В результате поперечные сечения покрытия ослабляются. Ослабление сечений может спровоцировать либо скалывание бетона покрытия в швах или трещинах, либо потерю устойчивости покрытием.
Если грунты условно разделить на три группы: пески, супеси и глины, то было установлено, что песчаные основания в наибольшей степени способствуют возникновению потери устойчивости покрытием. Хотя, по сравнению с другими факторами, вид грунтов основания мало влияет на возможность возникновения потери устойчивости покрытием.
Установлено, что влияние величины транспортных нагрузок на возникновение потери устойчивости покрытием имеет вторичное значение по сравнению с остальными факторами. Потеря устойчивости покрытием возникала, как на дорогах с большими нагрузками, так и на дорогах с малой интенсивностью движения.
Виды теплообмена дорожного покрытия с окружающей средой иллюстрируются на рисунке 58.
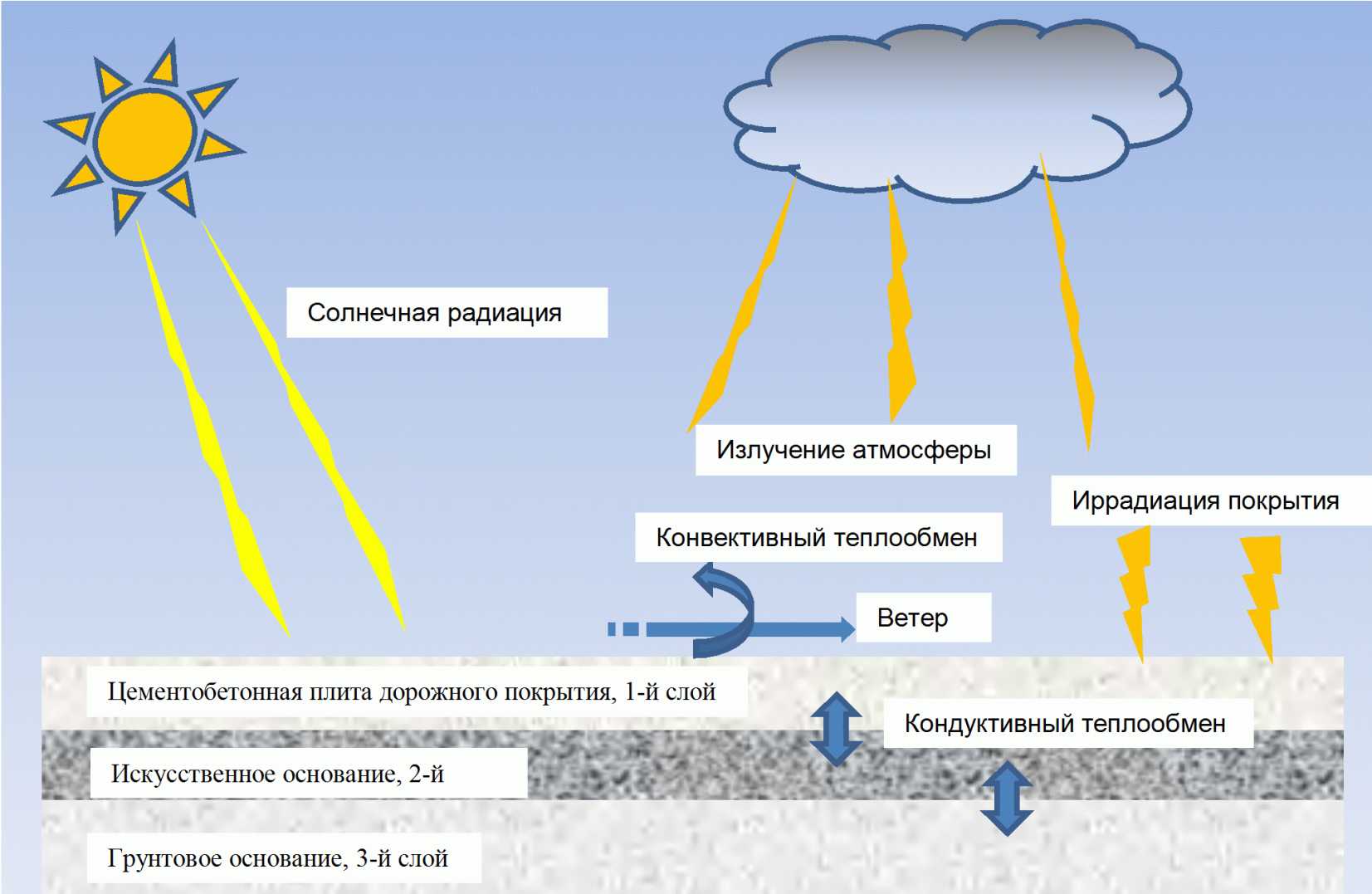
дорожного покрытия с окружающей средой
Согласно этому рисунку, теплообмен цементобетонного дорожного покрытия включает в себя кондуктивную, конвективную и радиационную теплопередачи.
Кондуктивная теплопередача между конструктивными слоями дорожного покрытия определяется приближенно законом Фурье:

где T(y, t) - функция распределения температуры по толщине покрытия во времени;
Конвективная теплопередача Qв между поверхностью покрытия и воздухом выражается законом Ньютона:

где Tп, Tв - температура соответственно поверхности покрытия и воздуха;
 .
.Радиационная теплопередача R выражается радиационным балансом и является мерой притока лучистой энергии к поверхности покрытия
R = (Qп + Qр)(1 - A) - Jэф,
где Qп, Qр - потоки тепла соответственно от прямой и рассеянной коротковолновой радиации солнца;
A - величина, характеризующая отражение тепла в зависимости от цвета поверхности, называемая коэффициентом альбедо поверхности;
Jэф - эффективное излучение покрытия,
Jэф = Jп - Jа,
где Jп - длинноволновое излучение покрытия; Jа - длинноволновое излучение атмосферы.
8.3.1. Разработка и тестирование конечно-элементной модели теплового взаимодействия дорожного покрытия с окружающей средой
Существенным фактором, от которого зависит поведение дорожного покрытия при его эксплуатации, является температура окружающей среды. Для тестирования конечно-элементной модели теплового взаимодействия дорожного покрытия с окружающей средой, созданной в рамках данной ОДМ, использованы результаты, опубликованные в работе [19]. В этой работе исследовался одномерный теплообмен асфальтобетонного покрытия с окружающей средой в течение трех суток. Решение, полученное методом конечных разностей, сравнивалось с результатами эксперимента.
Предлагаемая в данном ОДМ конечно-элементная модель для решения этой же задачи может быть использована при исследовании теплового взаимодействия дорожного покрытия с окружающей средой в плоской и пространственной постановках.
Конечно-элементная модель дорожного покрытия в одномерной постановке изображена на рисунке 59.
Покрытие состоит из двух слоев асфальтобетона - старого, расположенного на грунтовом основании, и нового, уложенного поверх старого. Свойства материалов покрытия и грунта определяются в таблице 4.

асфальтобетонного покрытия для расчета теплообмена
покрытия с окружающей средой
Таблица 4
Слои | Материал | Теплотехнические свойства |
1-й слой Покрытие | Асфальтобетон | Плотность  Удельная теплоемкость c = 921 Дж кг-1 C-1 Теплопроводность k = 1,21 Вт м-1 C-1 Альбедо  Эмиссия  Термическое сопротивление между слоями 1 и 2 Rc = 0 |
2-й слой Основание | Старый асфальтобетон | Плотность  Удельная теплоемкость c = 921 Дж кг-1 C-1 Теплопроводность k = 1,21 Вт м-1 C-1 Термическое сопротивление между слоями 2 и 3 Rc = 0 |
3-й слой Грунтовое основание | Сухой грунт | Плотность  Удельная теплоемкость c =1900 Дж кг-1 C-1 Теплопроводность k = 1,0 Вт м-1 C-1 |
На покрытие, как показано на рисунке 58, действует солнечная и атмосферная радиация. Нагретое покрытие излучает тепло в атмосферу, охлаждается потоками ветра и обменивается теплом с нижележащими слоями покрытия и основанием. Все эти воздействия моделируются с помощью соответствующих начальных и граничных условий.
В качестве начального условия задавалось распределение температуры в покрытии и основании - предполагалось, что от поверхности покрытия до глубины 3,048 м температура постоянна и равна 33,5 °C [19].
Поток тепла от солнечной и атмосферной радиации определялся экспериментально, его изменение в течение суток представлено в таблице 5.
Иррадиация дорожного покрытия описывается уравнением [19]:

где qrad - тепловой поток, излучаемый поверхностью покрытия в атмосферу (Вт м-2, задается в табл. 5);
Ts - температура поверхности дорожного покрытия (вычисляется);
Tsky - температура неба, вычисляется по формуле [20]:
 .
.Здесь  - температура воздуха (температура атмосферы), (°C) и Tdew - точка росы (задаются в таблице 5).
- температура воздуха (температура атмосферы), (°C) и Tdew - точка росы (задаются в таблице 5).
Теплоотдача покрытия, обусловленная конвекцией, определяется законом Ньютона [18]:

где hconv - коэффициент конвекции, который может быть найден по формулам [20]:
hconv = 5,6 + 4,0*vwind, при скорости ветра vwind <= 5 м/сек.
и
 , при скорости ветра vwind > 5 м/сек
, при скорости ветра vwind > 5 м/секКондуктивная теплопередача между слоями дорожного покрытия описывается законом Фурье [19]:

где k - коэффициент теплопроводности, заданный для материалов покрытия в табл. 1; T(y, t) - функция распределения температуры по толщине покрытия в зависимости от времени, которая должна удовлетворять уравнению теплопроводности [19]

ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 5, а не таблица 2. |
Температура атмосферы, точка росы, уровень солнечной радиации, скорость ветра и температура покрытия на глубине 12,7 мм от его поверхности в течение суток определялись экспериментально. Их значения приведены в таблице 2. Скорость ветра, как и в работе [19], по экспериментальным значениям, приведенным в таблице 5, аппроксимировалась кубической линией тренда (красная кривая на рисунке 60). Там же дано уравнение линии тренда.

Рисунок 60 - График экспериментальных значений скорости
ветра в течение суток (синяя линия) и их аппроксимация
кубической линией тренда (красная кривая)
При решении задачи о теплообмене дорожного покрытия с окружающей средой в течение трех суток экспериментальные значения, полученные для первых суток, принимались такими же для вторых и третьих суток.
Таблица 5
параметров покрытия [19]
Время | Температура атмосферы °C | Точка росы °F, °C | Солнечная радиация, Вт/м2 | Скорость ветра м/сек | Время | Эксперимент | МКР | МКЭ | |
12:00 AM | 30,00 | 46 | 7,78 | 0 | 0 | 0:00 | 36,5 | 37,5 | 36,7 |
1:00 AM | 28,90 | 46 | 7,78 | 0 | 0 | 3:00 | 33,75 | 35,5 | 32 |
2:00 AM | 31,1 | 45 | 7,22 | 0 | 1 | 6:00 | 31,25 | 32,2 | 30,8 |
3:00 AM | 30,00 | 44 | 6,67 | 0 | 1 | 9:00 | 46,25 | 45 | 46 |
4:00 AM | 28,30 | 44 | 6,67 | 0 | 0 | 12:00 | 63,75 | 61,25 | 62,5 |
5:00 AM | 26,70 | 46 | 7,78 | 0 | 0 | 15:00 | 65 | 65,6 | 65,5 |
6:00 AM | 26,10 | 48 | 8,89 | 0 | 0 | 18:00 | 53,75 | 53,75 | 53,5 |
7:00 AM | 31,70 | 49 | 9,44 | 132 | 0 | 21:00 | 40 | 41,75 | 40,5 |
8:00 AM | 33,30 | 47 | 8,33 | 385 | 0 | 0:00 | 35,5 | 36,5 | 37 |
9:00 AM | 32,80 | 39 | 3,89 | 582 | 1 | 3:00 | 32,5 | 33,75 | 34 |
10:00 AM | 33,90 | 42 | 5,56 | 720 | 3 | 6:00 | 31,75 | 31,75 | 33,5 |
11:00 AM | 36,70 | 43 | 6,11 | 824 | 0 | 9:00 | 48,75 | 48,75 | 47,5 |
12:00 PM | 37,80 | 44 | 6,67 | 879 | 2 | 12:00 | 65 | 66,25 | 64 |
1:00 PM | 38,90 | 45 | 7,22 | 885 | 3 | 15:00 | 67,5 | 70 | 67 |
2:00 PM | 40,00 | 45 | 7,22 | 835 | 6 | 18:00 | 55 | 58,75 | 54,5 |
3:00 PM | 41,10 | 45 | 7,22 | 736 | 5 | 21:00 | 41,25 | 45,5 | 42 |
4:00 PM | 41,10 | 43 | 6,11 | 582 | 4 | 0:00 | 37 | 40,5 | 37,5 |
5:00 PM | 41,10 | 43 | 6,11 | 390 | 4 | 3:00 | 33,75 | 36,3 | 35 |
6:00 PM | 40,60 | 43 | 6,11 | 181 | 5 | 6:00 | 32 | 33,8 | 33,5 |
7:00 PM | 39,40 | 43 | 6,11 | 5 | 3 | 9:00 | 46,25 | 45,25 | 44 |
8:00 PM | 36,70 | 43 | 6,11 | 0 | 3 | 12:00 | 61,25 | 60,25 | 65 |
9:00 PM | 34,40 | 42 | 5,56 | 0 | 3 | 15:00 | 65 | 67,5 | 67,5 |
10:00 PM | 33,30 | 41 | 5 | 0 | 2 | 18:00 | 52,5 | 55,7 | 55 |
11:00 PM | 31,10 | 40 | 4,44 | 0 | 0 | 21:00 | 38,75 | 43 | 42 |
12:00 PM | 28,90 | 40 | 4,44 | 0 | 0 | 0:00 | 35 | 37,5 | 38 |
Примечание - AM - аббревиатура слов "ante meridiem", то есть "до полудня", а PM - аббревиатура слов "post meridiem", или "после полудня".
В трех последних столбцах таблицы 5 приведены экспериментальные значения температуры на глубине 12,7 мм от поверхности покрытия [19], а также расчетные значения этой же температуры, полученные в работе [19] методом конечных разностей (МКР) и в данном исследовании методом конечных элементов (МКЭ). Эти результаты иллюстрируются графиками, изображенными на рисунке 61. Как видно из сравнения этих графиков, результаты, полученные в данной работе методом конечных элементов (МКЭ), хорошо согласуются как с результатами эксперимента [19], так и с результатами, полученными в работе [19] методом конечных разностей (МКР).

Рисунок 61 - Графики изменения температуры на глубине
12,7 мм от поверхности покрытия в течение трех суток,
полученные экспериментально [19], методом конечных
разностей (МКР) [19] и методом конечных элементов (МКЭ)
Еще одной иллюстрацией результатов, полученных с помощью конечно-элементной модели, предлагаемой в данной ОДМ, является рисунок 62, на котором представлены графики распределения температуры по глубине покрытия и основания в разное время в течение третьих суток.

и основания в течение третьих суток до глубины 0,9 м
8.3.2. Использование конечно-элементной модели теплового взаимодействия дорожного покрытия с окружающей средой для предсказания температуры на поверхности покрытия
При исследовании температурного воздействия на конструкции дорожных одежд можно представить это воздействие в виде стационарного или нестационарного. Если предполагать, что распределение температуры по толщине покрытия известно, а распределение температуры в основании не учитывать, то такое температурное воздействие будем рассматривать как стационарное. Если же известен закон изменения температуры на поверхности покрытия, а распределение температуры по толщине дорожных одежд определяется уравнениями теплопередачи, то такое температурное воздействие будем рассматривать как нестационарное.
Таким образом, чтобы смоделировать нестационарное температурное воздействие на дорожные одежды, нужно знать закон изменения температуры на поверхности покрытия.
Закон изменения температуры на поверхности покрытия может быть установлен в том случае, если в нем установлены датчики измерения температуры (рисунок 63).

Рисунок 63 - Пример установки датчиков
температуры в дорожном покрытии [20]
В дорожных метеорологических станциях используют датчик температуры поверхности и датчик температуры на глубине 30 см (под покрытием), а также контроллер и GPRS модуль для передачи данных в информационные центры.
В тех местах, где дорожные метеорологические станции отсутствуют, приходится использовать данные, которые могут предоставить обычные метеостанции. Такими данными являются: температура воздуха, скорость ветра, уровень солнечной радиации и так далее. Используя эти данные необходимо установить закономерности изменения температуры на поверхности дорожного покрытия и по его толщине.

Рисунок 64 - Дорожная метеорологическая
станция RWS 4030 [14]
Для решения этой задачи может быть использована конечно-элементная модель дорожного покрытия, рассмотренная в разделе 8.3.1 данного ОДМ и изображенная на рисунке 59.
Практика эксплуатации жестких дорожных покрытий показала, что новые дорожные покрытия, при сооружении которых соблюдались нормы производства работ, даже при экстремальных температурных воздействиях устойчивости не теряют. Потеря продольной устойчивости возникает обычно через 3 - 4 года эксплуатации дорожного покрытия, когда от различного вида воздействий на покрытие возникают такие его повреждения, которые при экстремальных летних температурах провоцируют либо значительные разрушения бетона покрытия в окрестности поперечных швов и трещин, либо потерю продольной устойчивости.
В плите, без разрушения бетона в поперечных швах, сжимающие силы P (рисунок 65), возникающие при нагреве плиты, направлены вдоль прямой и даже при короблении плиты в результате неравномерного нагрева не создают таких моментов, которые могли бы привести к потере продольной устойчивости плитой.

Рисунок 65 - Схема продольных усилий, действующих
на плиту при неравномерном нагреве
Если же герметизация поперечных швов была нарушена и в верхнюю часть раскрывшихся зимой швов попали частицы песка, гравия и других жестких материалов, то при нагреве плит в летний период передача продольных усилий между ними будет происходить в узкой области поперечного шва, заполненной этими жесткими материалами. Такое распределение продольных усилий может привести к разрушению бетона в поперечных швах или трещинах по схеме, изображенной на рисунке 66. В этом случае равнодействующая продольных сил смещается вниз и создает момент Mn = P*en.
Ранней весной и поздней осенью, при температурах близких к нулю в поперечные трещины и швы с нарушенной герметизацией попадает влага, как от атмосферных осадков, так и от полива покрытий антигололедными растворами. Эта влага скапливается внизу покрытия, перемешивается с твердыми частицами, попавшими в швы в зимний период, а также с частицами, образовавшимися в результате коррозии бетона от антигололедных растворов, и при движении автотранспорта выбрасывается вверх на поверхность покрытия.

при неравномерном нагреве и разрушении верхней части
одной из плит в поперечном шве
При этом более крупные твердые частицы застревают в нижней части толщины плиты, образуя узкую жесткую область внизу плиты, через которую в летний период передаются продольные силы между соседними плитами. В результате концентрации сжимающих напряжений в нижней части плит может произойти разрушение бетона в поперечных швах и трещинах по схеме, изображенной на рисунке 67.

Рисунок 67 - Схема продольных усилий, действующих на плиту
при неравномерном нагреве и разрушении нижней части
одной из плит в поперечном шве
Равнодействующая продольных сил при этом смещается в верхнюю часть плиты и создает момент Mv = P*ev.
В наиболее опасное положение, с точки зрения потери устойчивости, попадают плиты, у которых на одном конце происходит разрушение бетона в верхней части шва, а на другом конце - в нижней (рисунок 68). В этом случае моменты Mn и Mv суммируются и могут привести к потере устойчивости плитой покрытия.

при неравномерном нагреве и разрушении нижней части плиты
в одном из поперечных швов и верхней части плиты
в другом поперечном шве
Из рисунка 68 следует, что в наибольшей степени вероятность потери продольной устойчивости плитой жесткого покрытия возникает при разрушении нижней части плиты в одном из поперечных швов и верхней части плиты в другом поперечном шве. Поэтому для дальнейших исследований явления потери продольной устойчивости жестким цементобетонным покрытием при экстремальных температурных воздействиях была выбрана именно эта модель покрытия.
На первом этапе исследований, для выяснения основных качественных закономерностей исследуемого явления можно ограничиться расчетными схемами в рамках задачи о плоской деформации и стационарным температурным воздействием с линейным законом изменения температуры по толщине покрытия.
На рисунке 69 изображен один из вариантов такой модели вместе с конечно-элементной сеткой и распределением материалов по толщине дорожной одежды.

Рисунок 69 - Конечно-элементная модель
конструкции покрытия и основания
Величины предполагаемых экстремальных температурных воздействий для различных географических регионов известны, поэтому, рассмотрим в качестве примера случай, когда температура на верхней грани плиты равна 50 °C, а на нижней 35 °C, что соответствует градиенту температур рекомендованному, в частности, в документах [1, 2].
Конечно-элементная сетка во всех областях модели принята равномерной и прямоугольной, за исключением областей, примыкающих к поперечным швам, где в силу концентрации напряжений требуется более густая сетка, чем в остальных областях.
Между плитой покрытия и основанием моделировался контакт "касание", а по торцам плита касалась жестких плоскостей, которые соответствовали условиям контакта рассматриваемой плиты с соседними плитами.
Конечно-элементная сетка в области поперечного шва представлена на рисунке 70.

Рисунок 70 - Конечно-элементная сетка
в области поперечного шва
Материал всех слоев предполагался линейно упругим с модулями упругости и коэффициентами Пуассона, определенными в таблице 6.
Таблица 6
Характеристики | Модуль упругости E (Па) | Коэффициент Пуассона | Плотность |
Бетон плиты покрытия | 3,6*1010 | 0,2 | 2400 |
Песок, укрепленный цементом | 5,5*108 | 0,25 | 2200 |
Песок | 1,2*108 | 0,3 | 2000 |
Супесь | 2,7*107 | 0,32 | 1900 |
Результаты расчетов для плиты толщиной 22 см иллюстрируются рисунками 71 - 73.
В тех случаях, когда величина ослабления плиты составляет 9 см (0.409 от толщины плиты) и менее, потери продольной устойчивости покрытия не происходит (рисунок 71).

в конце итерационного процесса при глубине разрушения
поперечных швов 9 см
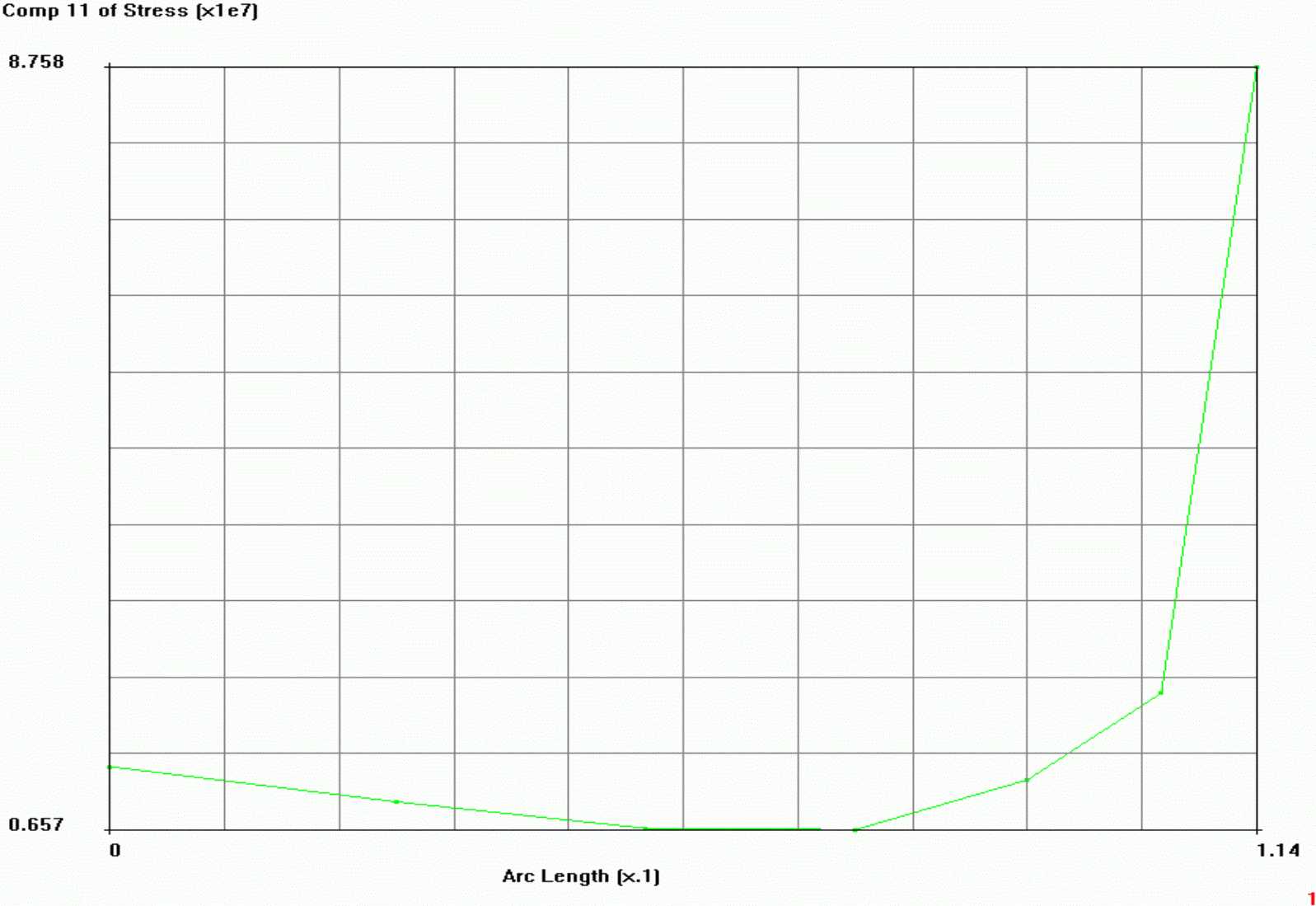
Наибольшие перемещения плиты возникают на ее правом конце, там, где разрушение бетона произошло в нижней части поперечного шва и составляют, как это видно из рисунка 8, 1,16 мм.
При увеличении глубины разрушения поперечных швов до 10 см (0.455 от толщины плиты) плита теряет продольную устойчивость (рисунок 72).
Наибольшие перемещения плиты возникают на ее правом конце, там, где разрушение бетона произошло в нижней части поперечного шва и составляют, как это видно из рисунка 9, 15,2 см.

Рисунок 72 - Вертикальные перемещения плиты
в конце итерационного процесса при глубине разрушения
поперечных швов 10 см
Максимальные сжимающие напряжения возникают в области поперечного шва и в соответствии с рисунком 73 составляют 75.8 МПа.
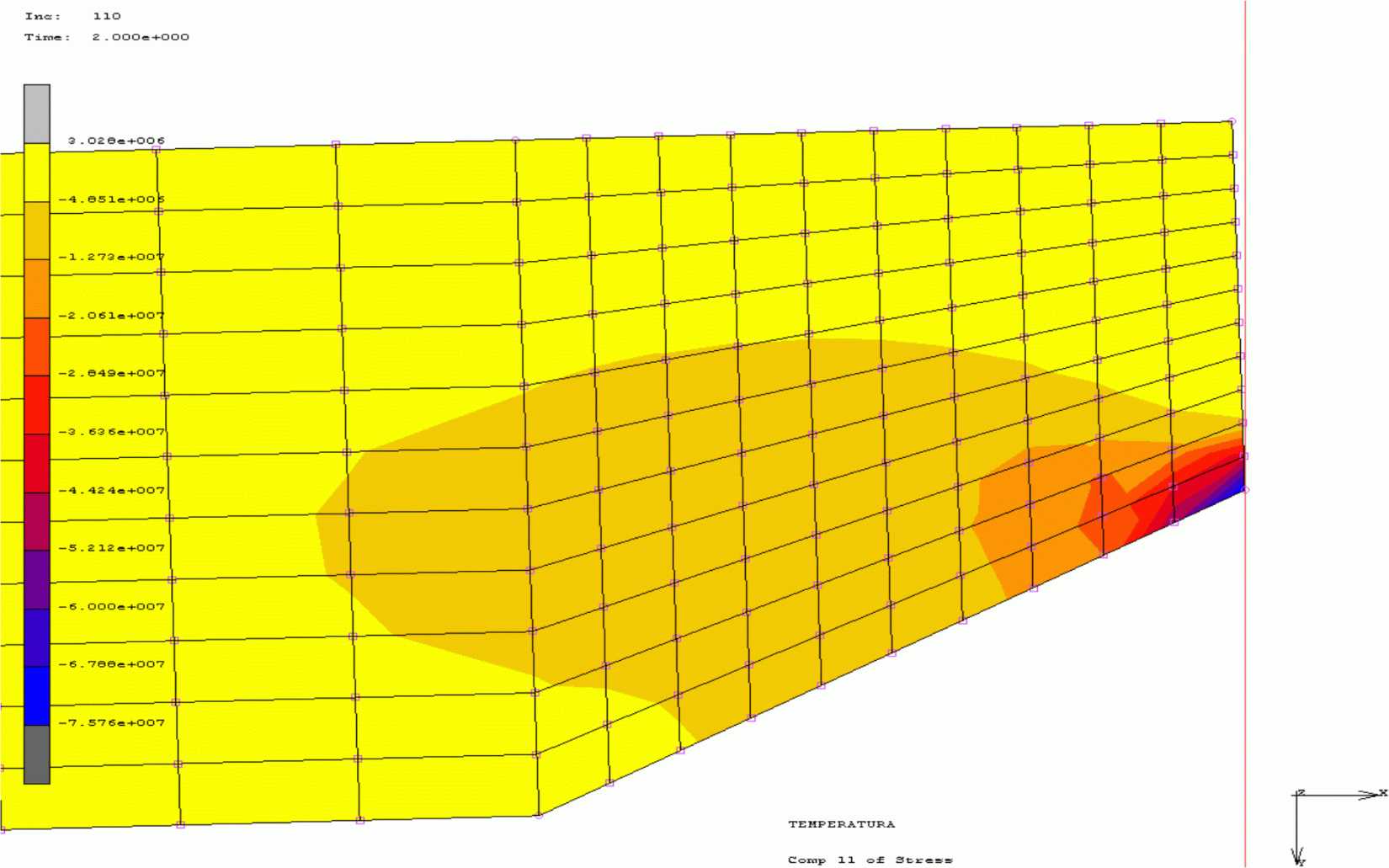
в бетоне плиты покрытия в области поперечного шва
8.6. Анализ результатов, полученных с помощью плоской КЭ модели дорожной одежды при стационарном температурном воздействии
Оценим влияние на продольную устойчивость покрытия таких параметров, как отношение толщины плиты к ее длине, глубины разрушения плиты к ее толщине, а также наличие поперечных трещин в плите.
Влияние толщины плиты покрытия на допустимую глубину разрушения ее торцов в поперечных швах:
- наиболее устойчивыми являются плиты толщиной от 18 до 20 см, они не теряют устойчивость при глубине разрушения, меньшей 0,5 толщины плиты (рисунок 74);
- плиты толщиной от 20 до 24 см не теряют устойчивости при глубине разрушения, меньшей 0,455 толщины плиты;
- наименее устойчивыми являются тонкие плиты толщиной от 16 до 20 см, они имеют допустимую глубину разрушения менее 0,438 толщины плиты.

и относительной глубиной ее разрушения,
при потере покрытием устойчивости
Влияние длины плиты покрытия на допустимую глубину разрушения ее торцов в поперечных швах:
- в наибольшей степени подвержены потере устойчивости плиты длиной от 3 до 5 м. Они имеют допустимую глубину разрушения до 0,455 от толщины плиты (рисунок 75);
- если плита длиннее 5 м, то чем больше длина плиты, тем в меньшей степени (при прочих равных условиях) она подвержена потере устойчивости, из рисунка 75 видно, что, например, при длине плиты 8 м допустимая глубина разрушения составляет 0,591 толщины плиты;
- при длине плиты менее 3 м способность плиты сопротивляться потере устойчивости несколько возрастает по сравнению с длиной от 3 до 5 м, при длине плиты 2 м допустимая глубина разрушения составляет 0,5 от толщины плиты.

ее ослаблением в поперечном шве, при котором происходит
потеря устойчивости дорожным покрытием
Наличие в покрытии поперечных сквозных трещин можно рассматривать как деление плиты покрытия на несколько коротких плит с длиной, равной расстоянию между поперечными трещинами или трещиной и поперечным швом.
продольной устойчивости плит жестких дорожных покрытий
при нестационарном температурном воздействии
Предложенная в разделе 8 модель взаимодействия покрытия с основанием не учитывала такие факторы, как суточное изменение температуры окружающей среды, теплообмен между бетонными плитами покрытия и основанием, возможность изменения режима теплообмена при отрыве плиты от основания. В данном разделе в рамках плоской задачи исследована продольная устойчивость жесткого дорожного покрытия с учетом вышеперечисленных факторов.
Если, в соответствии с документами [1 - 2], расчетную амплитуду колебаний температуры за сутки на поверхности цементобетонного покрытия принять равной 15 °C, а закон изменения температуры близким к синусоидальному, то при ясном небе (облачность 0 - 2 балла) максимальная температура поверхности покрытия наблюдается к 14 - 15 часам, а минимальная - в 4 - 6 часов, что соответствует наибольшей и наименьшей температуре воздуха в эти часы.
Предполагая, как это сделано в исследовании [19], что деформации и напряжения в покрытии при начальной температуре равны нулю, можно вычислить те деформации и напряжения, которые возникают в результате изменений температуры покрытия и основания по отношению к начальной температуре. В соответствии с работой [19], можно допустить, что стабилизация тепловых и соответствующих им деформационных процессов наступает в течение 3-х суток, поэтому именно этот временной период рассматривался при создании КЭ модели (рисунок 76).
Расчеты показали, что устойчивость покрытия в значительной мере зависит от начальной температуры, то есть температуры, при которой происходила укладка бетона покрытия, поэтому тепловое воздействие на покрытие моделируется в виде приращений температуры по отношению к начальной температуре.
Решение рассматривается в рамках задачи о плоской деформации. Конечно-элементная модель конструкции покрытия и основания представлена на рисунке 14.

на поверхности покрытия в течение трех суток
Предполагается симметричная форма потери устойчивости двух соседних плит, поэтому исследуется только часть модели, расположенная слева от плоскости симметрии (рисунок 77). В плоскости симметрии модели запрещались горизонтальные перемещения, а на ее левой и нижней гранях - вертикальные и горизонтальные перемещения.
Радиационный и конвективный теплообмен на поверхности покрытия моделируются переменной по времени температурой, изменяющейся в соответствии с результатами натурных наблюдений так, как это представлено на рисунке 76.
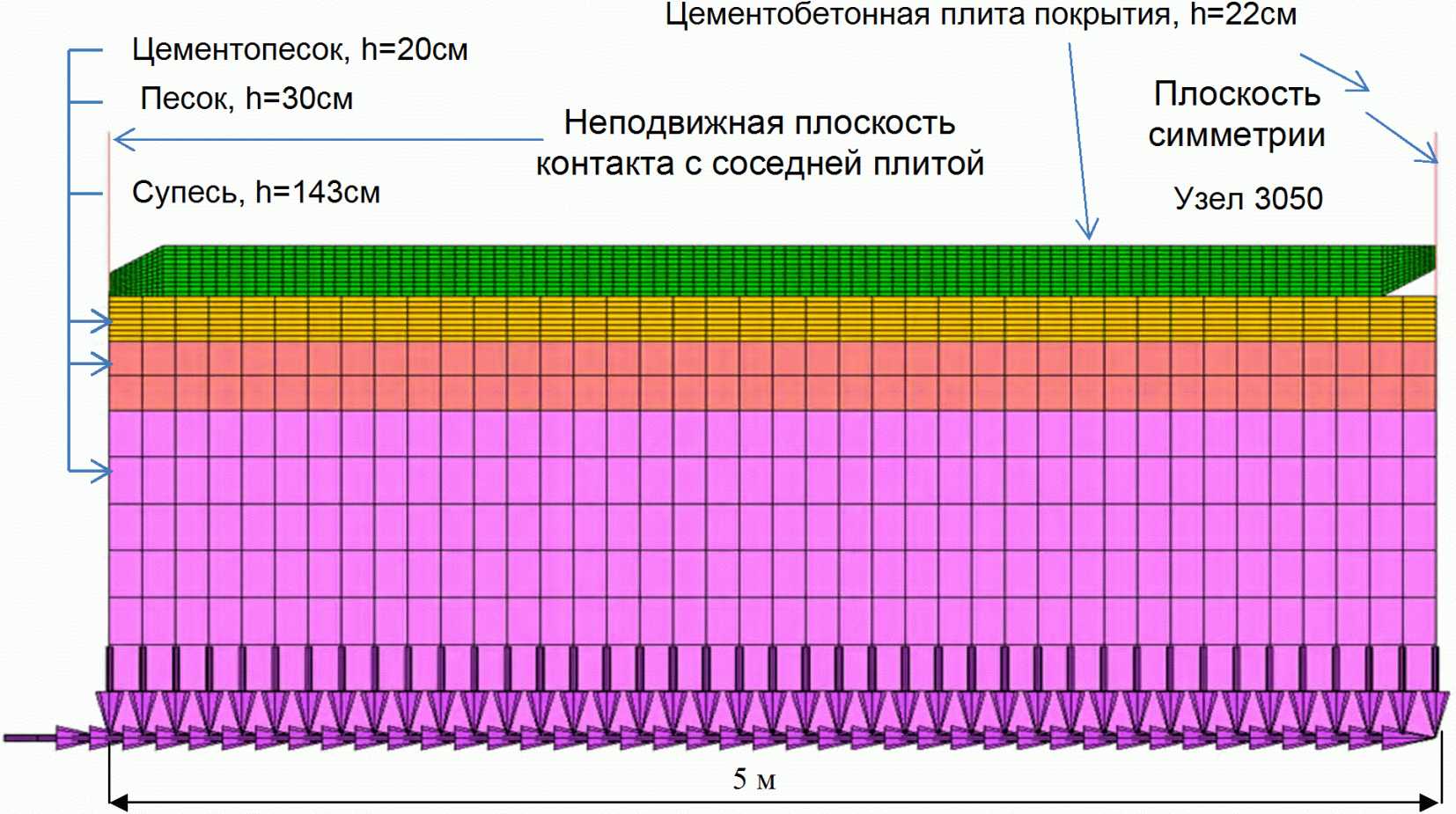
конструкции покрытия и основания
Теплофизические характеристики материалов конструктивных слоев покрытия определены в таблице 7.
Таблица 7
Теплофизические характеристики материалов
конструктивных слоев покрытия
Материал | Плотность (Кгм-3) | Теплопроводность (Вт м-10C-1) | Теплоемкость (Дж кг-10C-1) | Излучение тепла (-) | Поглощение тепла (-) | Модуль деформации (Па) | Коэффициент Пуассона (-) |
Бетон | 2400 | 1,74 | 1000 | 0,8 | 0,8 | 3,6·1010 | 0,2 |
Песок, укрепленный цементом | 2200 | 1,7 | 800 | - | - | 5,5·108 | 0,25 |
Песок | 2000 | 1,8 | 800 | - | - | 1,2·108 | 0,3 |
Супесь | 1900 | 1,5 | 700 | - | - | 2,7·107 | 0,3 |
В плоскости контакта бетонной плиты покрытия с основанием моделируются условия термомеханического контакта. Это означает, что пока плита находится в механическом контакте с основанием, в плоскости контакта реализуется кондуктивная теплопередача. При отрыве плиты от основания и образования прослойки воздуха между ними, кондуктивная теплопередача между плитой и основанием заменяется на радиационную и конвективную. В этом случае реализуется только термический контакт.
Рисунок 78 иллюстрирует эти три случая реализации контакта:
- в крайней левой части модели реализуется полный термомеханический контакт;
- далее на двух третьих ширины модели возникает только термический контакт;
- в правой части модели отсутствует любой контакт.

между бетонной плитой покрытия и основанием
В качестве примера расчета с помощью предлагаемой КЭ модели, рассмотрим наиболее опасный для потери устойчивости дорожным покрытием случай, когда температура укладки бетона в покрытие (начальная температура на поверхности покрытия) равна 0 °C, и, следовательно, разница между температурой укладки бетона и экстремальной летней температурой будет наибольшей. В этом случае покрытие теряет устойчивость в первые сутки нагружения в 17 часов 40 мин (рис. 4) при глубине разрушения поперечного шва = 10 см (0,455 от толщины покрытия). Отметим, что этот результат совпадает с результатом, полученным в работе [6]. Из этого же рисунка видно, что уже на вторые сутки величина максимального перемещения в 17 часов 50 мин достигла 16,24 см и практически такой же осталась в 17 часов 50 мин на третьи сутки. Это свидетельствует о стабилизации процесса деформаций в течение трех суток.
В этом случае покрытие теряет устойчивость в первые сутки нагружения в 12 часов 00 минут при глубине разрушения поперечного шва равной 11 см (рисунки 79, 80).

Рисунок 79 - Распределение вертикальных перемещений
в модели покрытия в момент потери устойчивости
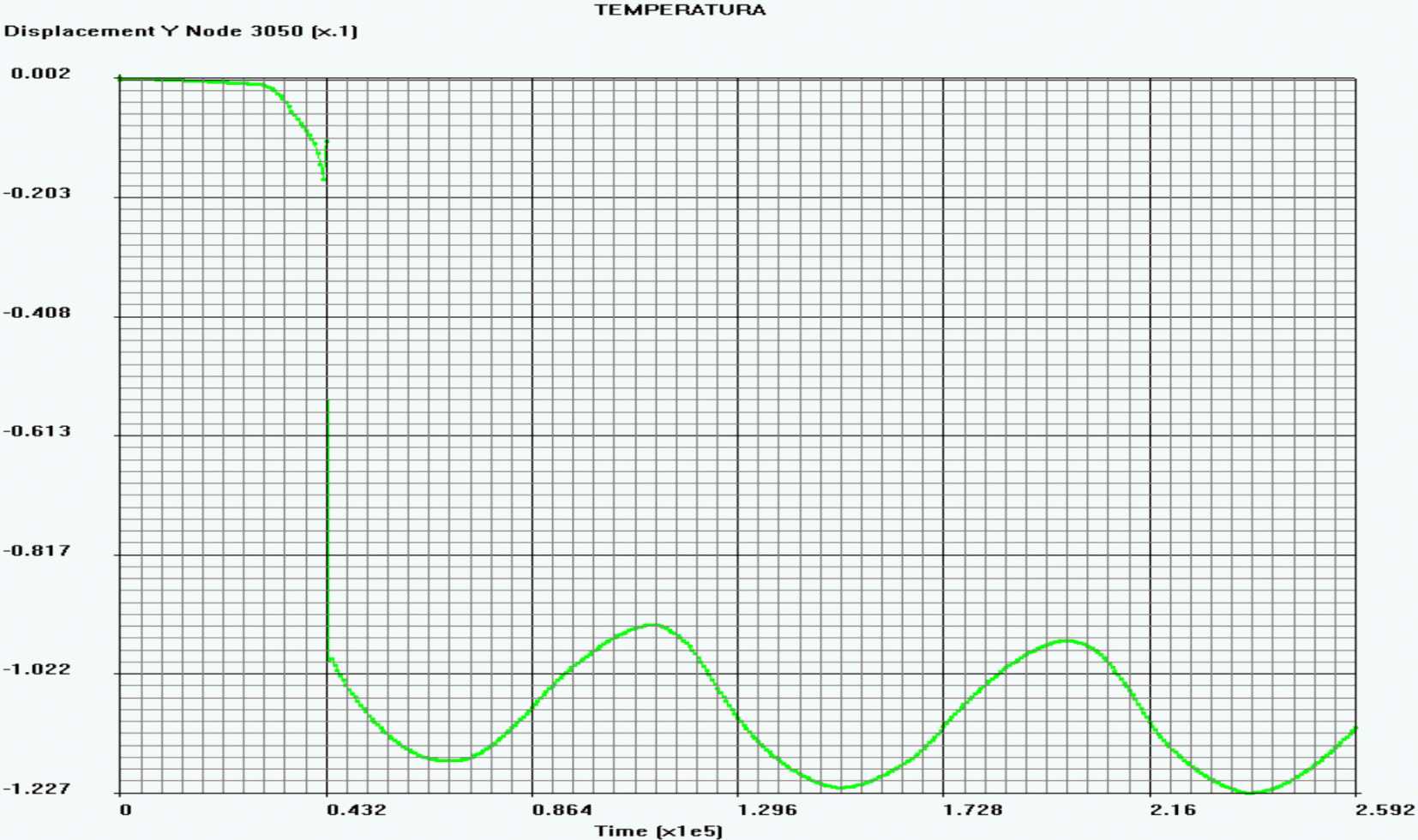
перемещений плиты покрытия в течение 3-х суток
Величина максимального перемещения в этот момент, как это видно из рисунка 80, составила 10 см. Из этого же рисунка видно, что уже на вторые сутки величина максимального перемещения в 18 часов достигла 12,27 см и практически такой же осталась в 18 часов на третьи сутки. Это свидетельствует о стабилизации процесса деформаций от температурного воздействия в течение трех суток.
Распределение температуры в КЭ модели покрытия на третьи сутки в 18 часов 00 минут показано на рисунке 81. Из этого рисунка видно, что в области, где контакт между бетонной плитой покрытия и основанием отсутствует, основание нагревается в меньшей степени, чем там, где контакт сохраняется.
Изменения температуры на верхней и нижней гранях плиты показаны на рисунке 82.
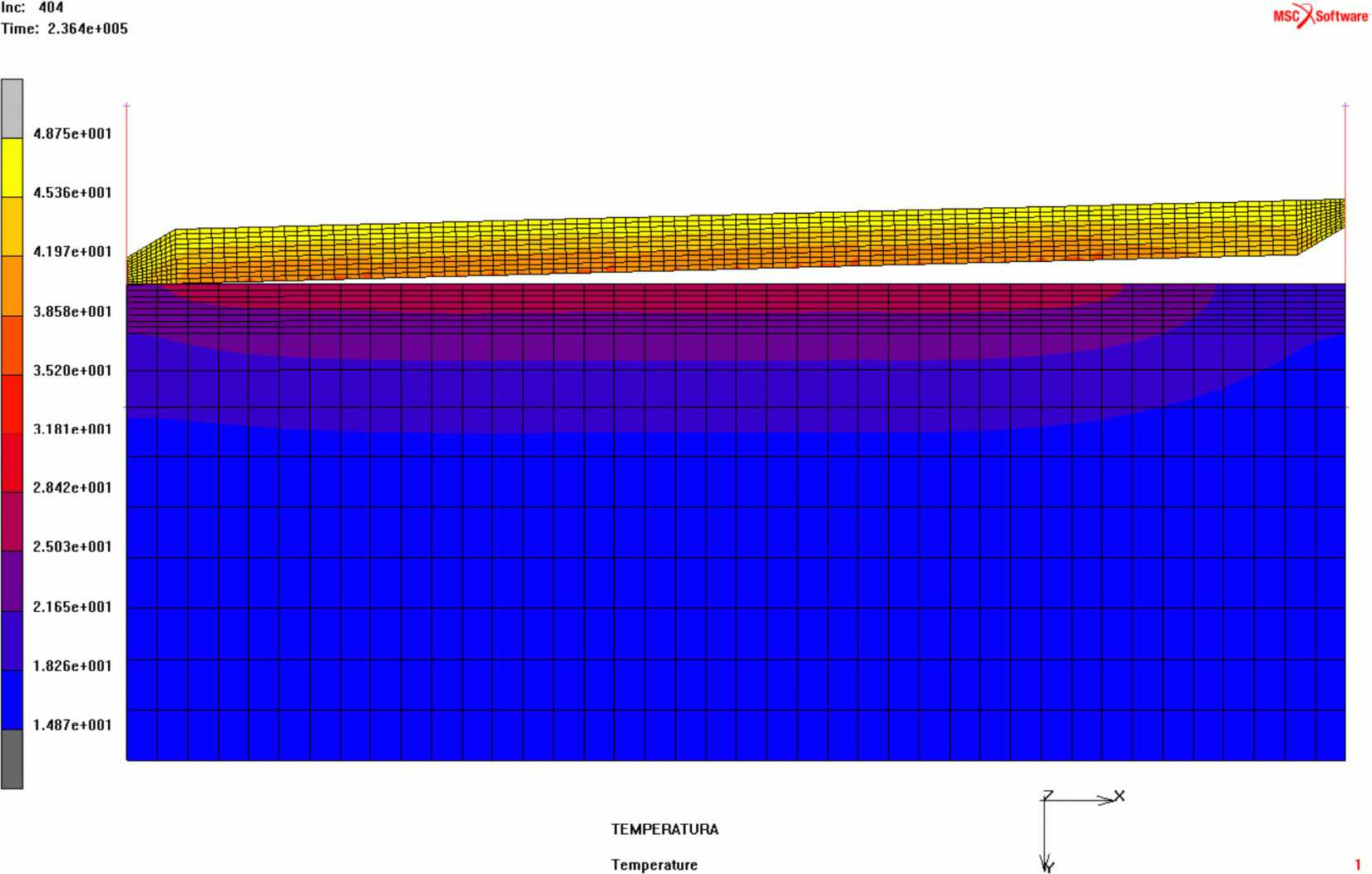
на третьи сутки в 18 часов 00 мин

и нижней гранях плиты в течение трех суток
Отметим отставание экстремальной температуры на нижней грани плиты на 6 часов по сравнению с экстремальной температурой на верхней грани плиты, что соответствует результатам натурных наблюдений, изложенным в документе [2].
Изменение напряжений на верхней и нижней гранях плиты в течение трех суток происходило в соответствии с графиком, изображенным на рисунке 83. Из рисунка 83 следует, что в момент потери покрытием устойчивости происходит его разгрузка в виде скачкообразного падения напряжений, как на верхней, так и на нижней гранях плиты.

Рисунок 83 - Изменение нормальных напряжений
в поперечном сечении плиты на верхней
и нижней гранях в течение трех суток
Предложенная КЭ модель покрытия и основания позволяет определить напряженно-деформированное состояние и распределение температуры не только в дорожном покрытии, но и в основании. В качестве примера такого расчета, на рисунке 84 показано распределение температуры по глубине покрытия и основания для различных моментов времени в течение трех суток, при начальной температуре на поверхности покрытия равной 0 °C.
Из рисунка 84 видно, что существенные изменения температуры в течение суток наблюдаются только в плите, в основании же, с увеличением глубины, быстро стабилизируются, стремясь к начальному распределению температуры.

покрытия и основания для различных моментов
времени в течение трех суток
1. Для более полного учета тех факторов, от которых зависит продольная устойчивость жестких дорожных покрытий необходимо использовать модель нестационарного теплового режима.
2. В течение трех суток процессы теплообмена между плитой и основанием стабилизируются. Это позволяет, при анализе нестационарного теплового режима, ограничиться временным промежутком, равным трем суткам.
На рисунке 85 изображена построенная по результатам расчетов диаграмма зависимости между относительной глубиной разрушения плиты, при которой происходит потеря продольной устойчивости покрытием, и температурой укладки бетона в покрытие (начальной температурой).

Рисунок 85 - Диаграмма зависимости между относительной
глубиной разрушения плиты, при которой происходит потеря
продольной устойчивости покрытием, и температурой укладки
бетона в покрытие (начальной температурой)
Анализируя эту диаграмму, можно сделать следующие выводы:
- потеря устойчивости в значительной мере связана с начальной температурой (температурой укладки бетона в дорожное покрытие);
- для плиты толщиной 22 см при начальной температуре от 5 до 15 °C, глубина разрушения покрытия, при которой происходит потеря продольной устойчивости покрытия, примерно одинакова и составляет 0,5 толщины плиты;
- при начальной температуре от 0 до 5 °C допустимая глубина разрушения покрытия снижается до 0,455 толщины плиты;
- при начальной температуре от 15 до 20 °C она возрастает до 0,545, а при начальной температуре 25 °C и выше покрытие не теряет устойчивости при любой глубине разрушения плиты.
для расчета жестких дорожных покрытий
на продольную устойчивость
Пространственная модель покрытия позволяет:
- оценить точность результатов, полученных с помощью плоской модели;
- учесть влияние транспортной нагрузки на устойчивость покрытия (ее несимметричное расположение на плите покрытия);
- оценить влияние местных повреждений покрытия и основания (частичное разрушение плиты в поперечном шве, образование полостей в основании под плитой и т.п.).
Общий вид модели представлен на рисунке 86.

Рисунок 86 - Конечно-элементная модель
жесткого цементобетонного дорожного покрытия
Воздействие на покрытие собственного веса и температуры моделировалось в следующей последовательности:
- вначале прикладывался собственный вес покрытия, который в течение одной секунды возрастал от нуля до своего полного значения и затем оставался постоянным (рисунок 87);
- затем, в начале второй секунды прикладывалось температурное воздействие, которое в течение этой секунды возрастало от 0 до 50 °C на верхней грани покрытия и от 0 до 35 °C на нижней грани, а затем оставалось постоянным (рисунок 88).


температуры по толщине плиты и во времени
10.2. Влияние состояния продольных швов покрытия на граничные условия для его конечно-элементной модели
Для плит покрытия в продольных швах можно сформулировать три предельных случая граничных условий:
- отсутствие горизонтальных перемещений в направлении перпендикулярном продольным швам. Такой случай реализуется для плит расположенных во внутренней полосе многополосного дорожного покрытия в жаркое летнее время, когда продольные швы оказываются закрытыми (рисунок 89);
- продольные швы в результате температурного воздействия не закрылись и плиты покрытия могут свободно перемещаться в поперечном направлении (рисунок 90);
- перемещения плит в направлении перпендикулярном продольным швам ограничено только с одной стороны, а на противоположной стороне перемещения покрытия ничем не ограничены. Близкий к этому случай возникает, для плит, примыкающих к обочине дорожного покрытия, когда продольные швы закрыты, а обочина не оказывает существенного сопротивления перемещению плит покрытия в ее направлении (рисунок 91).

в продольных швах от горизонтальных смещений

с незакрепленными краями плит в продольных швах

с закрепленными краями плит в продольных швах
и свободными краями со стороны обочины
Реальные граничные условия, в зависимости от полосы движения расположены между этими тремя предельными условиями.
10.2.1. Плиты средней полосы многополосного дорожного покрытия (случай закрепления плит покрытия в продольных швах)
В этом случае граничные условия близки к тем, что возникают в условиях плоской деформации. Это подтверждается результатами расчетов, представленными на рисунках 92 - 95. Результаты получены при толщине плиты 22 см и глубине ослабления равной 11 см (0,5 от толщины плиты).

Рисунок 92 - Распределение вертикальных перемещений плит
покрытия в момент потери устойчивости

Рисунок 93 - Распределение вертикальных перемещений плит
покрытия в момент потери устойчивости (вид сбоку)

Рисунок 94 - Распределение вертикальных перемещений плит
покрытия в момент потери устойчивости (вид сверху)
плиты покрытия в момент потери устойчивости (вид сверху)
Потеря устойчивости покрытием в случае пространственной модели произошла при ослаблении плит покрытия в поперечных швах на глубину равную 11 см (0.5 от толщины плиты), а в случае плоской модели - при ослаблении плит покрытия в поперечных швах на глубину равную 10 см (0.455 от толщины плиты). Такое, несущественное в рамках данной задачи расхождение между результатами (около 9%) обусловлено возможностью деформаций плит между продольными швами в поперечном направлении в рамках пространственной задачи.
Основываясь на этом сравнении, можно прийти к заключению, что результаты, полученные ранее в рамках задачи о плоской деформации, вполне адекватно отражают реальную работу конструкции покрытия при потере продольной устойчивости. При этом, уменьшение глубины разрушения плит покрытия в поперечных швах при потере устойчивости по сравнению с пространственной моделью составляет не более 9%.
При отсутствии закрепления плит в продольных швах, то же самое покрытие толщиной 22 см и с глубиной разрушения плит в поперечных швах равной 11 см устойчивости не теряет. Результаты соответствующего расчета приведены на рисунках 96 - 97.

Рисунок 96 - Распределение вертикальных перемещений
покрытия при отсутствии потери устойчивости

перемещений правой плиты
При отсутствии значительных вертикальных перемещений покрытия, возникающих при потере устойчивости, больший удельный вес в полных перемещениях приобретают перемещения вызванные короблением плит от температурного воздействия в поперечном направлении. Этот факт иллюстрируется рисунками 11 - 12.
Так как в реальных конструкциях жестких дорожных покрытий, даже при частичном заполнении продольных швов несжимаемыми материалами, возможны некоторые горизонтальные перемещения, то критическая глубина разрушения плит покрытия в поперечных швах, а именно та, при которой происходит потеря устойчивости, всегда будет больше, чем при двустороннем ограничении перемещений плит покрытия в продольных швах и меньше, чем при отсутствии этих ограничений.
В этом случае (при закреплении плит покрытия в одном продольном шве и возможности их свободного перемещения на противоположном краю (рисунок 6)) граничные условия близки к тем, что возникают для плит, примыкающих к обочине.
Перемещения, соответствующие короблению плит от температурного воздействия в этом случае не симметричны относительно продольной оси покрытия (рисунки 98 и 99). Большие значения перемещений смещены в сторону закрепления плит в продольном шве.

Рисунок 98 - Вертикальные перемещения плит
от температурного воздействия при запрете горизонтальных
перемещений в продольном шве

от температурного воздействия при запрете горизонтальных
перемещений в продольном шве (для наглядности перемещения
увеличены в 60 раз)
Потери устойчивости в этом случае не произошло, как и в случае с двумя свободными краями, но максимальное значение вертикального перемещения (1,13 см) больше, чем для плиты с двумя свободными краями (1,024 см), то есть напряженно-деформированное состояние в этой плите ближе к потере устойчивости, чем в плите с двумя свободными краями.
Потеря устойчивости покрытием с незакрепленными продольными краями произошла при увеличении разрушения плит в поперечных швах на глубину 13 см (0.591 от толщины плиты).
На рисунке 100 показано распределение вертикальных перемещений плит покрытия в момент потери устойчивости.

покрытия в момент потери устойчивости
Максимальное вертикальное перемещение плит покрытия возникло в поперечном шве и составило 10,01 см.
Потеря устойчивости покрытием с краями, закрепленными в продольном шве и свободных перемещениях в направлении обочины, произошла при увеличении разрушения плит в поперечных швах на глубину 12,5 см (0,568 от толщины плиты).
Полученные результаты иллюстрируются рисунком 101.
Максимальные перемещения покрытия в момент потери устойчивости равные 10,35 см (рисунок 101) в этом случае немного больше, чем для покрытия со свободными краями (10,01 см, рисунок 100).

Рисунок 101 - Распределение вертикальных перемещений
плит покрытия в момент потери устойчивости
Таким образом, подводя итоги анализа, выполненного в разделах 10.2 - 10.4, приходим к следующим выводам:
- из трех предельных случаев граничных условий для плит покрытия в продольных и поперечных швах наиболее опасным является случай с закреплением плит от горизонтальных перемещений в продольных и поперечных швах (этот случай соответствует плитам, расположенным в средних полосах многополосного дорожного покрытия при условии, что продольные и поперечные швы заполнены несжимаемыми материалами и в поперечных швах произошло разрушение плит на глубину не менее половины толщины плиты). Результаты расчетов в этом случае близки к тем, что были получены для аналогичных покрытий при моделировании их в условиях плоской деформации. Поэтому, расчет таких плит допустимо проводить в рамках задач о плоской деформации, что существенно снизит размерность модели и соответственно ускорит время расчетов;
- плиты с краями незакрепленными в поперечных и продольных швах соответствуют новому покрытию, в котором плиты имеют возможность свободно перемещаться в горизонтальном направлении. Опыт эксплуатации жестких дорожных покрытий показывает, что новые покрытия в течение 3 - 5 лет устойчивости не теряют. Из приведенных выше результатов следует, что для потери устойчивости таким покрытием необходимо, чтобы его разрушение в поперечных швах составило не менее чем 0.591 от толщины плиты;
- плиты, примыкающие к обочине дорожного покрытия, при закрытых продольных и поперечных швах, работают в условиях пространственного напряженно-деформированного состояния, поэтому для их расчета необходимо использовать пространственные конечно-элементные модели.
10.5. Влияние различных факторов на продольную устойчивость пространственной конечно-элементной модели жесткого дорожного покрытия
В этом разделе исследуем влияние различных факторов, которые могут способствовать потере продольной устойчивости жестким дорожным покрытием, и учет которых возможен только в рамках пространственной КЭ модели.
При определении транспортной нагрузки предполагалось, что:
- расчетная нагрузка на ось - 115 кН;
- коэффициент динамичности - 1,3;
- расчетная нагрузка на колесо - 57,5·1,3 = 74,75 кН.
Нагрузка на колесо величиной 74,75 кН прикладывается к плите в виде равномерно распределенного по отпечатку колеса давления. Если принять размер отпечатка кратным размеру грани конечного элемента плиты, то есть 20 x 15 x 3 = 900 см2, что приблизительно равно площади круга диаметром 34 см - 908 см2, то величина давления на отпечаток составит 74750 Н/0,09 м2 = 0,831 МПа.
Давление от одного колеса
Если приложить давление от колеса автомобиля в углу плиты покрытия, примыкающей к обочине (рисунок 102), которая при прочих равных условиях, ближе к потере устойчивости, чем плита со свободными краями, то покрытие устойчивости не потеряет. Максимальная величина прогиба плиты в этом случае составит 1,604 см (рисунки 103 - 104), что примерно в полтора раза больше, чем при отсутствии колесной нагрузки.

Рисунок 102 - Загружение плиты, примыкающей к обочине,
давлением от колеса в углу плиты
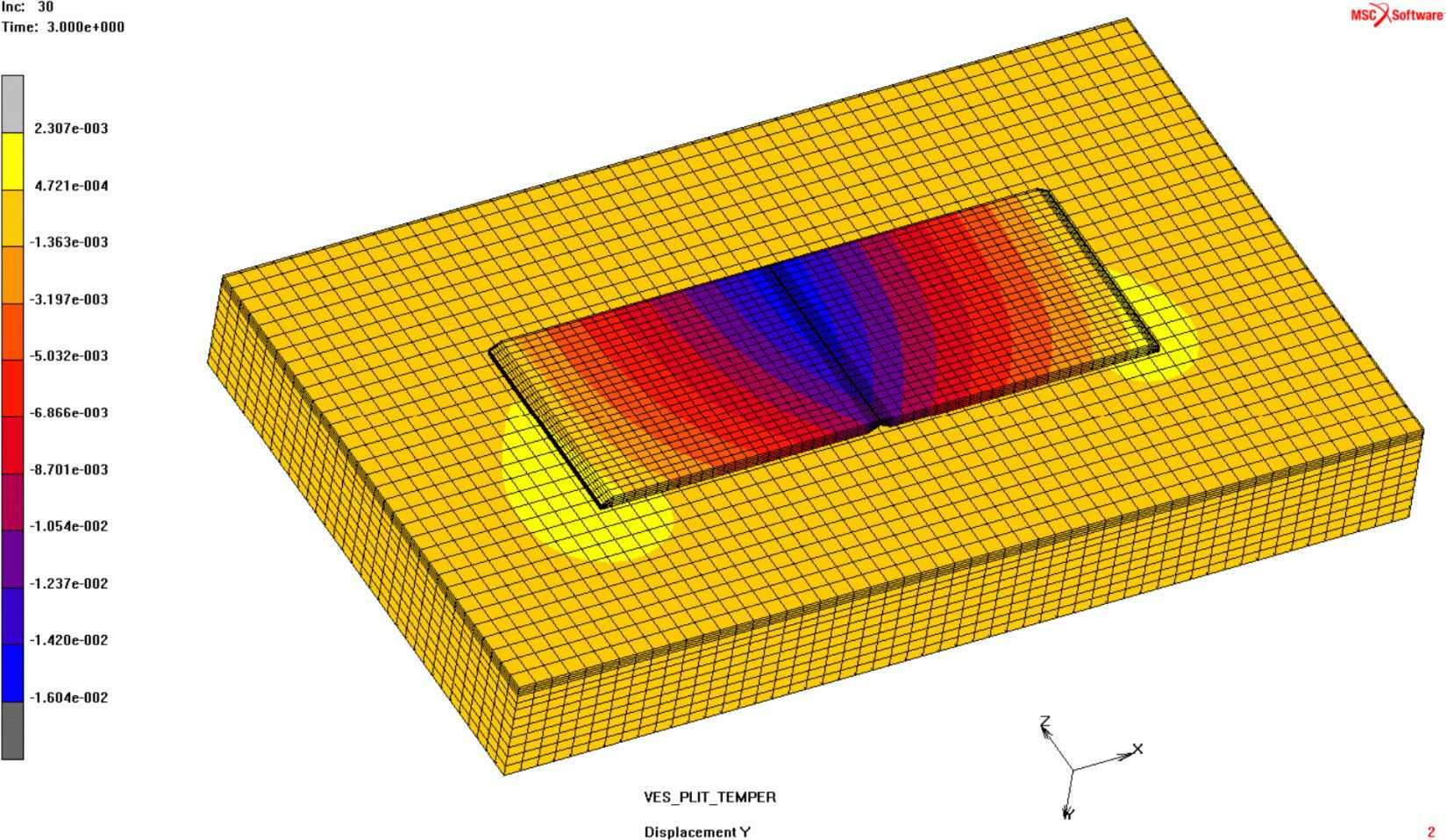
от температурного воздействия и давления
от колеса в углу плиты

от температурного воздействия при закреплении
их в продольном шве
Из рисунков 103 - 104 следует, что одноразовое нагружение давлением от колеса автомобиля незначительно изменяет стремление плиты к потере устойчивости.
Состояние продольных швов влияет на устойчивость покрытия в значительно большей степени, чем транспортная нагрузка.
Давление от оси автомобиля
Схема такого загружения показана на рисунке 105.
При загружении плит покрытия давлением от оси автомобиля, расстояние между центрами отпечатков колес примем равным 1,9 м.
Устойчивости в этом случае покрытие также не потеряло, а максимально перемещение плиты даже стало меньше (1,055 см, рисунок 106), чем при загружении одним колесом, что можно объяснить более близким расположением к продольному шву, чем к обочине второго отпечатка колеса.
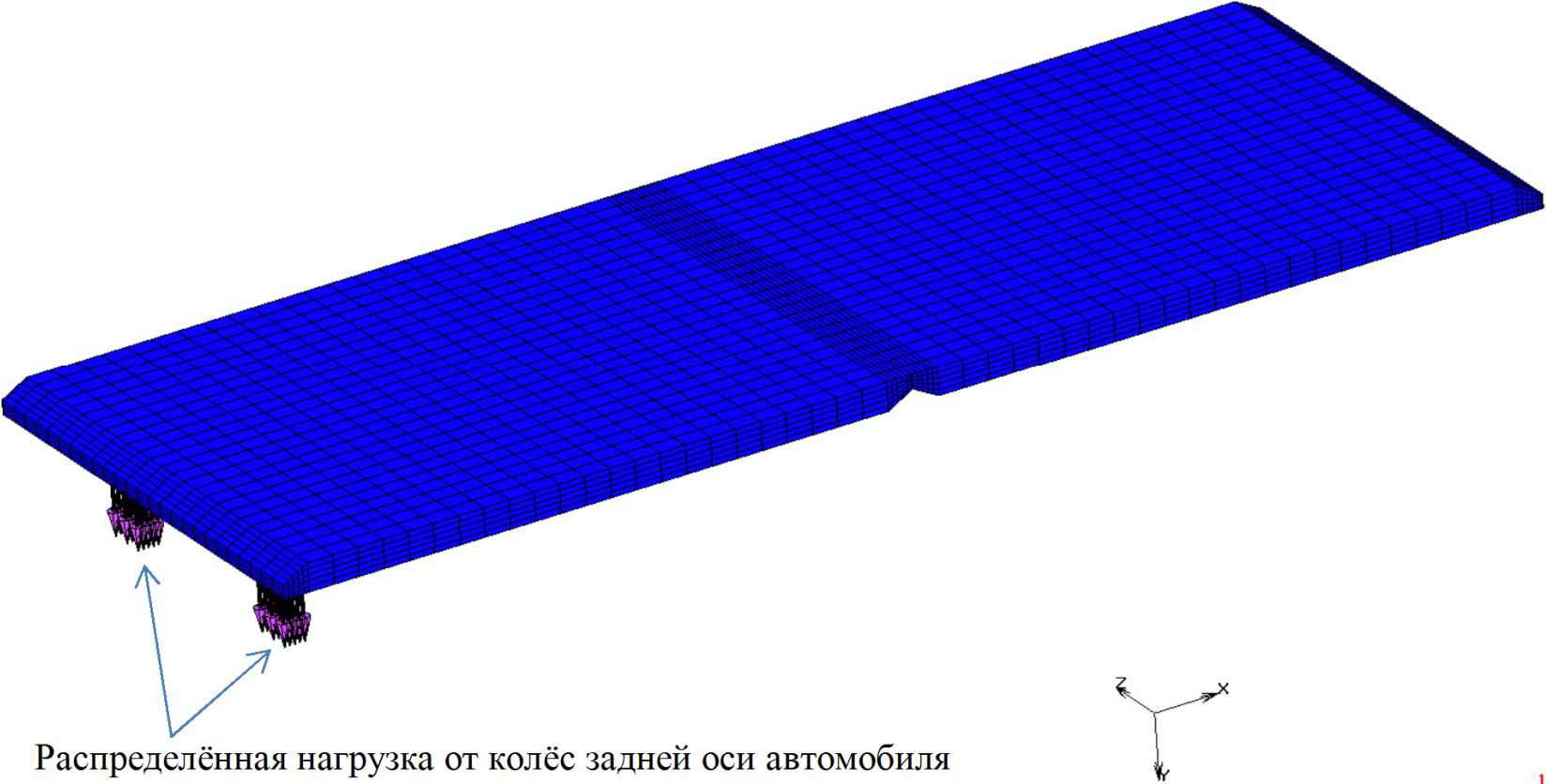
к обочине, давлением от задней оси автомобиля
(два колеса)

от температурного воздействия и давления
от колес задней оси автомобиля
Таким образом, при однократном приложении нагрузки от оси транспортного средства, влияние ее на потерю устойчивости по сравнению с влиянием способов закрепления плит покрытия в продольных швах, можно считать несущественным.
Если в результате внешних воздействий часть плиты в поперечном шве оказывается разрушенной (рисунки 107 - 108), то это приводит к уменьшению продольной жесткости плиты, что в свою очередь уменьшает ее максимальные прогибы от температурного воздействия и снижает вероятность потери продольной устойчивости.
Передача продольных усилий между плитами в этом случае происходит не по всей плоскости шва, а только по неразрушенной части плиты (рисунок 109), что приводит к увеличению сжимающих напряжений в плитах со стороны неразрушенной части (рисунок 110).
Из рисунка 109 следует, что максимальный прогиб уменьшился с 1,604 см для плиты без разрушения (рисунок 106) до 1,099 см для плиты с разрушением ее части (рисунок 109).


угловой частью левой плиты

при полном разрушении угловой части одной из них

в плитах покрытия в результате полного разрушения
одной из них в угловой части
Рассмотрим, насколько существенно влияние закрепления основания слоем песка, перемешанного с цементом, на продольную устойчивость жесткого дорожного покрытия. Конечно-элементная модель жесткого цементобетонного дорожного покрытия без слоя песка, укрепленного цементом, изображена на рисунке 111.
Без нагрузки от оси автомобиля
Если исключить влияние нагрузки на покрытие от колес автомобиля, то при отсутствии в основании слоя песка, закрепленного цементом, покрытие устойчивости не теряет, а максимальное вертикальное перемещение плиты покрытия составляет 1,097 см (рисунок 112).

цементобетонного дорожного покрытия без слоя песка,
укрепленного цементом

на неукрепленном слое песка
С нагрузкой от оси автомобиля
Нагрузка, приложенная от оси автомобиля (рисунок 105), также не привела к потере устойчивости покрытием. Максимальное вертикальное перемещение плиты покрытия составило 1,055 см (рисунок 113), что всего лишь в 1,025 раза больше, чем для плиты со слоем песка, закрепленным цементом.

Рисунок 113 - Вертикальные перемещения покрытия
от температурного воздействия при запрете горизонтальных
перемещений в продольном шве (для наглядности
перемещения увеличены в 60 раз)
Если герметизация поперечных швов нарушена, то в них проникает атмосферная влага и противогололедные реагенты, которые подвергают основание цементобетонных плит покрытия коррозии. В результате разрушения основания и вымывания его частиц из-под плит покрытия могут образоваться полости. Эти полости в сочетании с транспортной нагрузкой могут спровоцировать потерю устойчивости плитами покрытия. На рисунках 114, 115 изображена конечно-элементная модель покрытия с полостью глубиной 5 см под поперечным швом левой плиты.
Без нагрузки от оси автомобиля
Расчеты показали, что плиты покрытия, примыкающие к обочине, которые при отсутствии полости устойчивости не теряли, в результате образования полости потеряли устойчивость (рисунок 116). При этом максимальное вертикальное перемещение плиты покрытия составило 7,708 см.
цементобетонного дорожного покрытия с полостью
между плитой и основанием

цементобетонного дорожного покрытия с полостью
между плитой и основанием
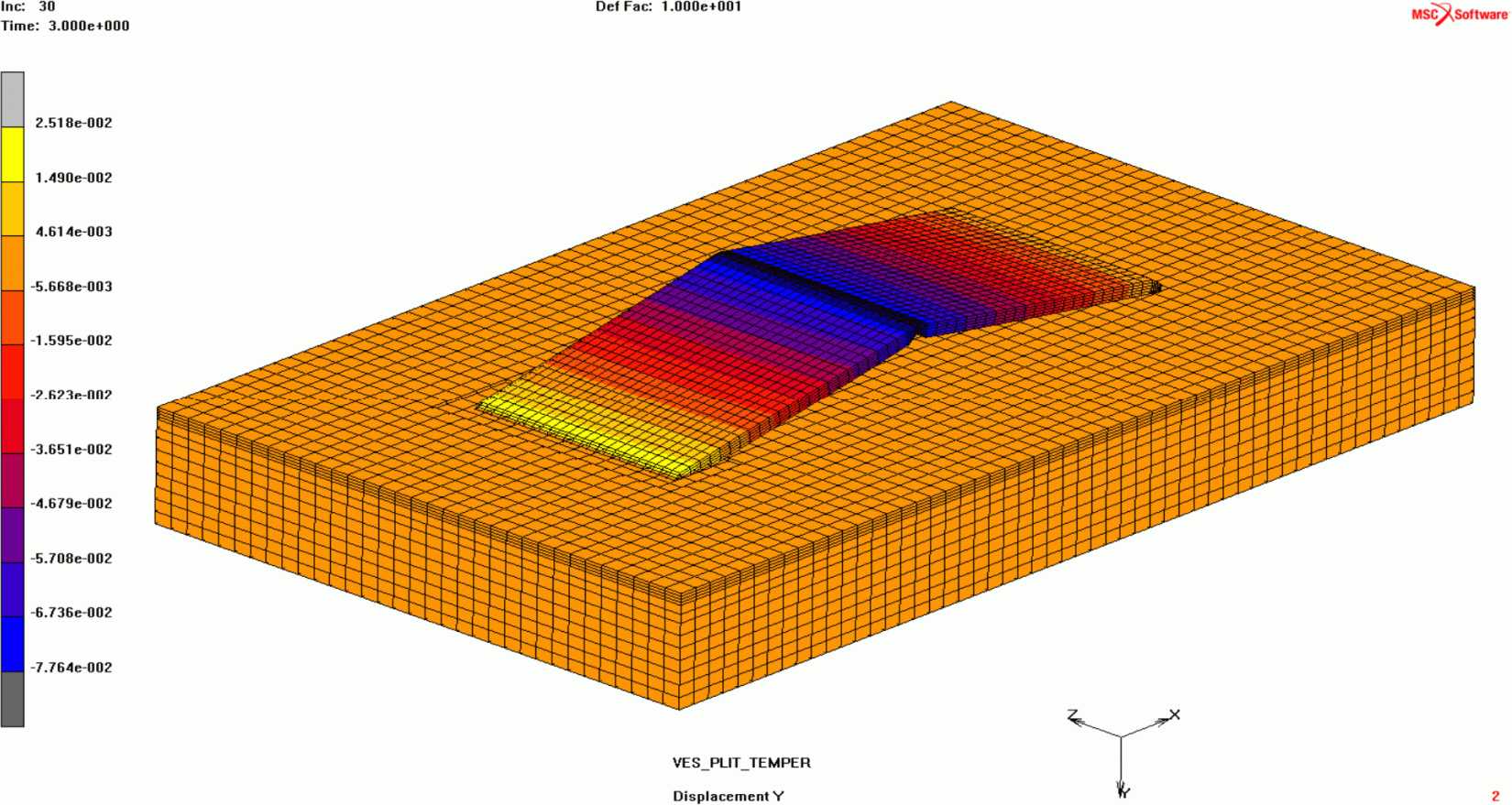
покрытия в момент потери устойчивости
без транспортной нагрузки
С нагрузкой от оси автомобиля
Добавление нагрузки от оси автомобиля, при наличии полости под левой плитой, привело к увеличению максимального вертикального перемещения плиты покрытия до 22,44 см (рисунки 117 - 119).
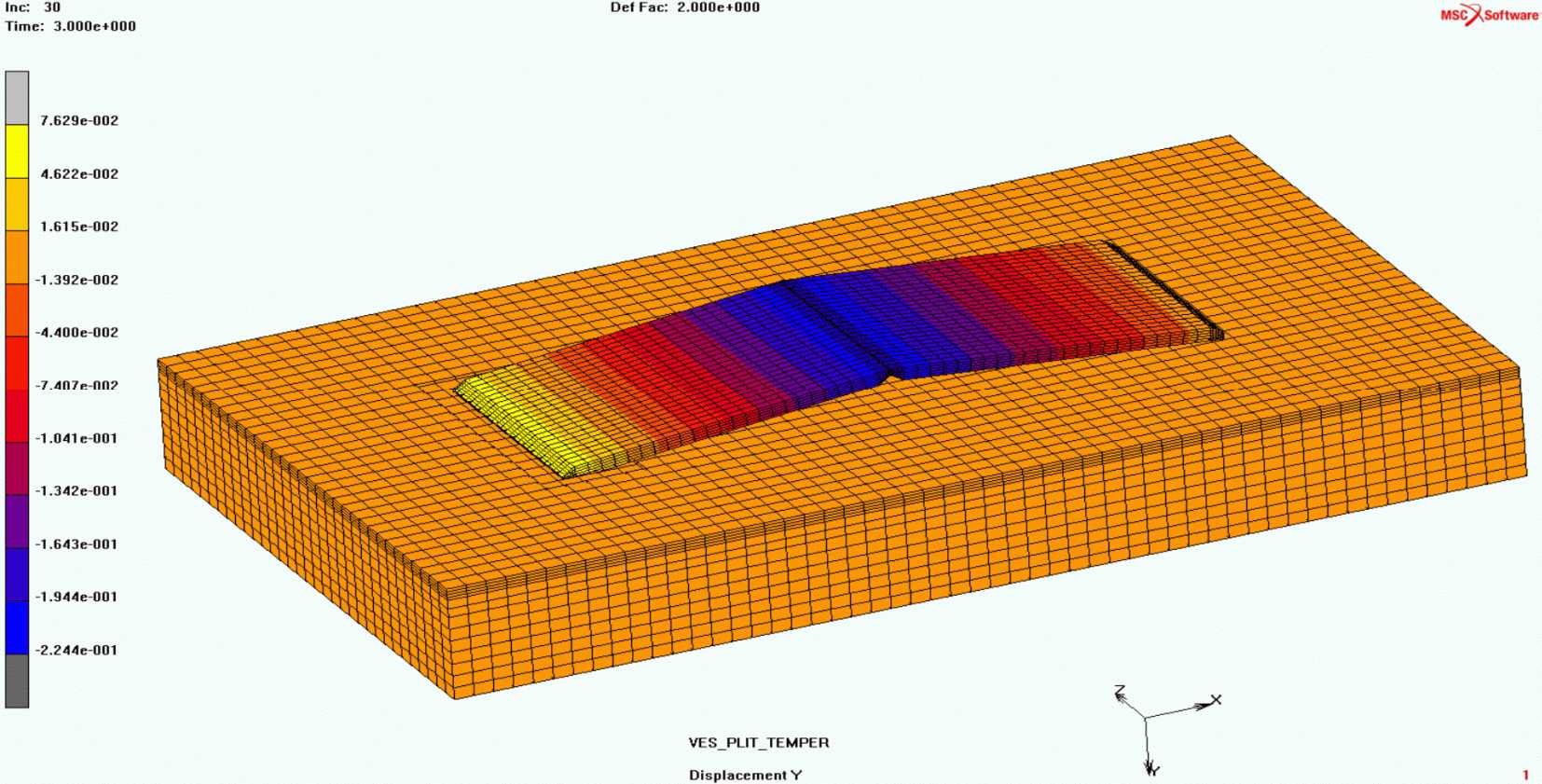
Рисунок 117 - Вертикальные перемещения плит покрытия
при наличии полости под левым поперечным швом левой плиты
и нагрузки от колес автомобиля

Рисунок 118 - Распределение вертикальных перемещений плит
покрытия в момент потери устойчивости
с транспортной нагрузкой

перемещений плит покрытия в момент потери устойчивости
с транспортной нагрузкой
Рассмотрим случай, когда сквозная поперечная трещина образовалась в левой плите на расстоянии 1 м от поперечного шва (рисунок 120).

Рисунок 120 - Конечно-элементная модель жесткого
цементобетонного дорожного покрытия со сквозной
поперечной трещиной
В этом случае, при разрушении плит в поперечных швах на глубину 11 см (0,5 от толщины плиты), покрытие устойчивости не потеряло, а максимальные вертикальные перемещения плиты незначительно возросли (рисунки 121 - 122) (от 1,134 до 1,143 см), по сравнению со случаем отсутствия трещины.

Рисунок 121 - Вертикальные перемещения покрытия
от температурного воздействия при запрете горизонтальных
перемещений в продольном шве (для наглядности перемещения
увеличены в 40 раз)

от температурного воздействия при запрете горизонтальных
перемещений в продольном шве (для наглядности перемещения
увеличены в 40 раз)
Покрытие с трещиной потеряет устойчивость, если глубина разрушения плит будет увеличена до 12 см (0,545 от толщины плиты).
Соответствующий результат представлен на рисунке 123.
Максимальное вертикальное перемещение плит покрытия в поперечном шве составило в этом случае 13,34 см.
Таким образом, приходим к выводу, что наличие сквозной поперечной трещины в покрытии может спровоцировать потерю им продольной устойчивости, но при глубине разрушения плит покрытия в поперечных швах более 0,5 от толщины плиты.

от температурного воздействия при запрете горизонтальных
перемещений в продольном шве и наличии поперечной трещины
(для наглядности перемещения увеличены в 4 раза)
Использование пространственной КЭ модели позволило установить следующее:
- результаты, полученные в рамках задачи о плоской деформации, вполне адекватно отражают реальную работу конструкции покрытия при потере продольной устойчивости;
- уменьшение глубины разрушения плит покрытия в поперечных швах при потере устойчивости в плоской конечно-элементной модели, по сравнению с пространственной моделью, составляет не более 9%.
Наибольшее влияние на возможность потери продольной устойчивости жестким дорожным покрытием оказывают три фактора:
- глубина разрушения поперечных швов - при действии только температуры для потери устойчивости покрытием необходимо разрушение плит покрытия в поперечных швах на глубину не менее 0,5 от толщины плиты;
- состояние продольных швов - при заполнении продольных швов несжимаемыми материалами вероятность потери устойчивости существенно возрастает - для плит покрытия с незакрытыми продольными швами глубина разрушения плит в поперечных швах для потери продольной устойчивости покрытием составляет 0,591 от толщины плиты, а для плит покрытия с закрытыми продольными швами 0,5 от толщины плиты;
- образование полостей между бетонными плитами покрытия и основанием, происходящее в результате разрушения основания и вымывания его частиц из под плит покрытия (в этом случае возможна потеря устойчивости даже плитами покрытия, примыкающим к обочине, которые находятся в более благоприятных, с точки зрения потери устойчивости, условиях, чем плиты средних полос многополосного дорожного покрытия).
10.7. Рекомендации по использованию конечно-элементных моделей для расчета продольной устойчивости плит конструкций дорожной одежды жесткого типа и профилактике нарушения продольной устойчивости плит
В рамках данной ОДМ были разработаны и использовались для исследования продольной устойчивости плит жестких дорожных покрытий три конечно-элементные модели:
- модель плоского деформированного состояния и стационарного распределения температуры по толщине цементобетонных плит покрытия;
- модель плоского деформированного состояния и нестационарного распределения температуры по толщине цементобетонных плит покрытия и основания;
- пространственная модель цементобетонных плит покрытия и основания при стационарном распределении температуры по толщине цементобетонных плит покрытия.
Первая модель является наиболее простой, требует наименьших ресурсов вычислительной техники и позволяет определить наиболее важные факторы, от которых зависит продольная устойчивость плит жестких дорожных покрытий. Она может быть рекомендована при исследовании устойчивости плит покрытия, когда температурный режим в основании покрытия мало влияет на распределение температуры в цементобетонных плитах покрытия.
Однако модель плоского деформированного состояния предполагает запрет перемещений в горизонтальной плоскости в направлении перпендикулярном продольным швам. В результате дорожное покрытие теряет устойчивость при меньших глубинах разрушения плит покрытия в поперечных швах, чем в реальных условиях, когда даже при заполнении продольных швов несжимаемыми материалами, у покрытия остается возможность некоторых горизонтальных смещений в направлении перпендикулярном продольным швам.
Если материалы основания обладают высокой теплопроводностью, то, вероятно, необходимо учитывать влияние теплового баланса в основании на распределение температуры в плитах жесткого дорожного покрытия. С этой задачей справляется вторая конечно-элементная модель дорожного покрытия.
Вторая модель является более сложной, чем первая, так как в ней реализована возможность расчета термомеханического взаимодействия цементобетонных плит покрытия с многослойным основанием. Здесь распределение температуры в плите зависит не только от ее распределения в основании, но и от степени контакта плит покрытия с основанием.
Так же как и первая, вторая модель соответствует задаче о плоской деформации, поэтому, подобно ей, дает заниженные, по сравнению с реальными, глубины разрушения цементобетонных плит покрытия в поперечных швах, при которых происходит потеря продольной устойчивости покрытия.
Если закон изменения температуры на поверхности дорожного покрытия известен, что возможно при наличии на объекте исследования дорожной метеорологической станции, то модель получается более простой. Если же этот закон неизвестен, то к этой модели необходимо добавить конечно-элементную модель теплового взаимодействия дорожного покрытия с окружающей средой для предсказания температуры на поверхности покрытия (раздел 8.3).
Пространственная конечно-элементная модель дорожного покрытия, естественно, является более сложной, чем первые две, требует существенно больших ресурсов вычислительной техники, но зато позволяет решать такие задачи, для которых модели плоской деформации неприменимы. К таковым относятся: расчет дорожного покрытия на совместное действие температуры и транспортной нагрузки; учет влияния заполнения продольных швов несжимаемыми материалами; расчет плит, примыкающих к обочине и так далее (раздел 10).
Методы профилактики нарушения продольной устойчивости плит дорожной одежды жесткого типа достаточно подробно рассмотрены в документах [1 - 3] и работах [9 - 12]. Поэтому приведем здесь лишь наиболее важные положения из этих источников.
Как уже было установлено в данной ОДМ, основными причинами потери продольной устойчивости плитами жесткого дорожного покрытия при экстремальных летних температурах являются:
- разрушение плит в поперечных швах, приводящее к эксцентричной передаче сжимающих усилий между ними и возникновению выпирающих моментов;
- заполнение продольных швов несжимаемыми материалами, препятствующими свободным горизонтальным перемещениям плит в продольных швах, в результате чего возрастают сжимающие усилия, действующие на плиты в поперечных швах;
- образование полостей между цементобетонными плитами покрытия и основанием в окрестности поперечных швов, что создает отсутствие препятствия для перемещения концов плит в вертикальном направлении и, таким образом, способствует увеличению эксцентриситета сжимающих усилий, а, следовательно, и увеличению выпирающего момента.
Так как потеря продольной устойчивости плитами жесткого дорожного покрытия возникает, как правило, через 3 - 4 года после начала эксплуатации дорожного покрытия, то очевидно, что в течение данного промежутка времени произошло накопление таких повреждений плит покрытия, которые в итоге и привели к потере им устойчивости.
Для обнаружения дефектов покрытия, приводящих к потере им продольной устойчивости, должна быть выполнена своевременная диагностика состояния покрытия.
Затраты на эксплуатационное содержание и ремонт цементобетонных покрытий могут быть весьма небольшими, если эти мероприятия проводятся своевременно, правильно проведена диагностика и определены технические решения. Стоимость "отложенного" ремонта возрастает быстрее времени отсрочки [9].
Разрушению плит в поперечных и продольных швах обычно предшествует разрушение герметика, заполняющего эти швы. Установить разрушение герметика в швах можно простым визуальным исследованием.
Наличие полостей между цементобетонными плитами покрытия и основанием можно обнаружить, постукивая по плите вблизи шва. Глухой звук позволяет определить, что плита приподнялась над основанием [11].
В документе [3] при определении очередности работ по ремонту цементобетонных покрытий автомобильных дорог рекомендуется в первую очередь выполнить "устройство швов расширения (при их отсутствии) или устройство дополнительных швов при неработоспособности существующих". Очевидно, что такое мероприятие устранит чрезмерные сжимающие напряжения в поперечных швах и трещинах и снизит риск потери продольной устойчивости покрытием.
Нарезка компенсационных швов возможна как по имеющимся швам сжатия, так и в средней части плиты.
Как было отмечено выше, разрушение плит в поперечных швах происходит в результате попадания в них несжимаемых материалов и противогололедных реагентов. Последнее становится возможным в результате разрушения герметизации швов. Таким образом, чтобы исключить возможность потери устойчивости плитами жесткого дорожного покрытия, необходимо в течение всего срока эксплуатации покрытия обеспечить полную герметизацию его швов, как поперечных, так и продольных. Сквозные поперечные трещины, образующиеся в покрытии в процессе его эксплуатации, также должны быть вовремя загерметезированы. В противном случае они, так же как и поперечные швы, могут стать источником местного разрушения плит покрытия, приводящего к потере им устойчивости.
При недостаточной ширине шва, по сравнению со швами рекомендуемой расчетом ширины, очень велики растягивающие напряжения в мастике. При одних и тех же температурных перемещениях плит в узких швах относительное удлинение больше. Многократное сжатие-растяжение мастики в таких швах приводит к ее разрушению до окончания гарантийного срока. Таким образом, ширина шва играет весьма важную роль в обеспечении сохранности мастики [3]. Расчеты и имеющаяся практика, в том числе международная, показывают, что для климатических условий большинства районов стран СНГ ширина шва должна быть не менее 8 - 10 мм для плит небольших размеров [3].
При выборе типа герметика следует учитывать возможные максимальные отрицательные и положительные температуры воздуха региона, где расположено покрытие. Большую роль на эффективность работы герметика в швах и его срок службы оказывает деформативность герметизирующих материалов.
Все вышеизложенное по технологии герметизации деформационных швов можно отнести к герметизации трещин в покрытиях, особенно тех, которые работают как швы, т.е. изменяют ширину раскрытия под действием температуры [3].
В тех случаях, когда покрытие потеряло устойчивость, требуется полная замена разрушенных участков плит [1].
многополосных жестких дорожных покрытий
Очевидно, что напряженно-деформированное состояние одиночной плиты дорожного покрытия (раздел 6) или двух плит, соединенных штырями в поперечном шве (раздел 7), будет отличаться от напряженно-деформированного состояния системы связанных между собою плит, образующих реальное дорожное покрытие.
Поэтому в данном разделе ОДМ рассмотрена конечно-элементная модель многополосного жесткого дорожного покрытия для расчета его на действие транспортных нагрузок и температуры.
Работа этой модели иллюстрируется примерами расчетов трехполосного жесткого дорожного покрытия при различных положениях транспортной нагрузки, различных диаметрах штырей, соединяющих плиты между собой и различных температурных воздействиях на покрытие.
Модель состоит из девяти прямоугольных в плане плит с размерами 500 x 375 x 22 см (рисунок 124).
Далее, для удобства описания модели и обсуждения результатов расчетов, плитам присвоены номера в соответствии с рисунком 125. На этом же рисунке показано расположение штырей в поперечных и продольных швах.
Параметры дорожного полотна были приняты следующими [1]:
- категория автомобильной дороги - II;
- число полос движения - 3;
- ширина полосы движения - 3,75 м;
- длина плиты - 5,0 м;
- срок службы дорожной одежды - 25 лет;
- расчетная нагрузка на ось - 115 кН;
- коэффициент динамичности - 1,3;
- расчетная нагрузка на колесо - 57,5·1,3 = 74,75 кН.
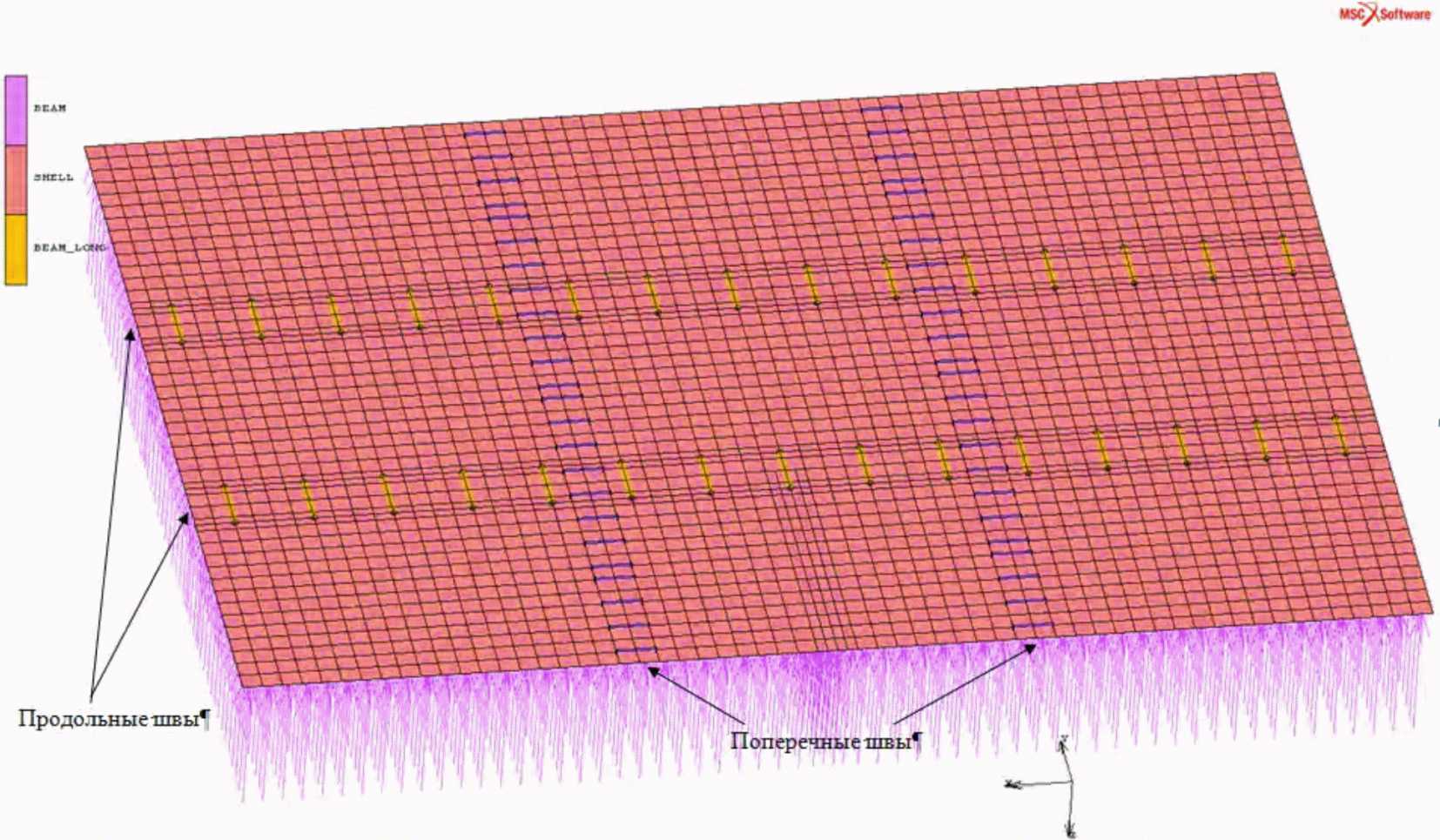
жесткого автомобильно-дорожного покрытия

в поперечных и продольных швах трехполосного
автомобильно-дорожного покрытия
Плиты изготовлены из бетона класса Btb4,4, для которого приняты [1]:
- модуль упругости E = 3,6*107 кПа;
- коэффициент Пуассона  ;
;
 ;
;- плотность  .
.
 .
.Соединительные штыри в поперечных и продольных швах изготовлены из гладких арматурных стержней с модулем упругости Eст = 2,1*108 кПа, коэффициентом Пуассона  и плотностью
и плотностью  .
.
 и плотностью
и плотностью  .
.Длина штырей в поперечных швах в соответствии с нормами [1] составляла 50 см и расстояние между ними принималось равным 50 см.
Длина штырей в продольных швах принималась равной 75 см и расстояние между ними составляло 100 см.
Отпечаток колеса принимается кратным сетке конечно-элементной модели и равным 0,25·0,50 м.
При расчетной нагрузке на ось - 115 кН и коэффициенте динамичности - 1,3 величина расчетной нагрузки на колесо составит - 57,5·1,3 = 74,75 кН, а интенсивность равномерно распределенной нагрузки на отпечатке колеса = 74,75/(0,25·0,5) = 598 кН/м2.
В случае моделирования плит покрытия объемными 8-узловыми конечными элементами размерность задачи становилась недопустимо большой, поэтому выбор был сделан в пользу плоских 4-узловых конечных элементов типа "shell".
В этом случае конечно-элементная модель включала в себя 3050 четырехузловых конечных элемента типа "shell" и 3310 узлов.
Для основания плиты была принята модель Винклера с коэффициентом постели равным 40000 кН/м3.
Рассматривались два варианта загрузки покрытия нагрузкой, передаваемой от оси автомобиля:
- нагрузка в середине плиты с отпечатком одного из колес на краю плиты (рисунок 126);
- нагрузка от двух осей, приложенная на краях плиты (рисунок 127).

автомобиля, для определения максимальных растягивающих
напряжений на нижней грани 2-й плиты в ее средней части

автомобиля, для определения максимальных растягивающих
напряжений на нижней грани 2-й плиты в ее средней части
Предполагается, что при первом варианте загрузки возникают максимальные растягивающие напряжения на нижней грани плиты, а при втором варианте загрузки возникают наибольшие растягивающие напряжения на верхней грани плиты.
В качестве одного из примеров использования созданной в рамках данной ОДМ конечно-элементной модели для расчета многополосного дорожного покрытия, ниже представлены некоторые результаты расчетов трехполосного жесткого дорожного покрытия при расположении оси автомобиля в средней части плиты и диаметре штырей равном 0,04 м.
На рисунках 128 и 129 изображены вертикальные перемещения плит покрытия. Из этих рисунков следует, что значимые значения прогибов плиты возникают только в той плите, к которой приложена нагрузка от колес автомобиля. При этом максимальное значение прогиба возникло в середине нагруженного края плиты и составило 1,124 мм.

Рисунок 128 - Вертикальные перемещения 3-полосного
жесткого автомобильно-дорожного покрытия

передней грани второй и третьей плит
На рисунках 130 и 131 показано распределение максимальных растягивающих напряжений. Из этих рисунков видно, что существенные максимальные растягивающие напряжения возникают только в той плите, к которой приложена нагрузка от колес автомобиля.

Рисунок 130 - Распределение нормальных напряжений 
в нижнем слое жесткого автомобильно-дорожного покрытия

При этом максимальные растягивающие напряжения возникли на нижней грани плиты и составили 2,923 МПа.
На рисунках 132 и 133 показано распределение поперечных сил и изгибающих моментов в штырях, соединяющих плиты покрытия.
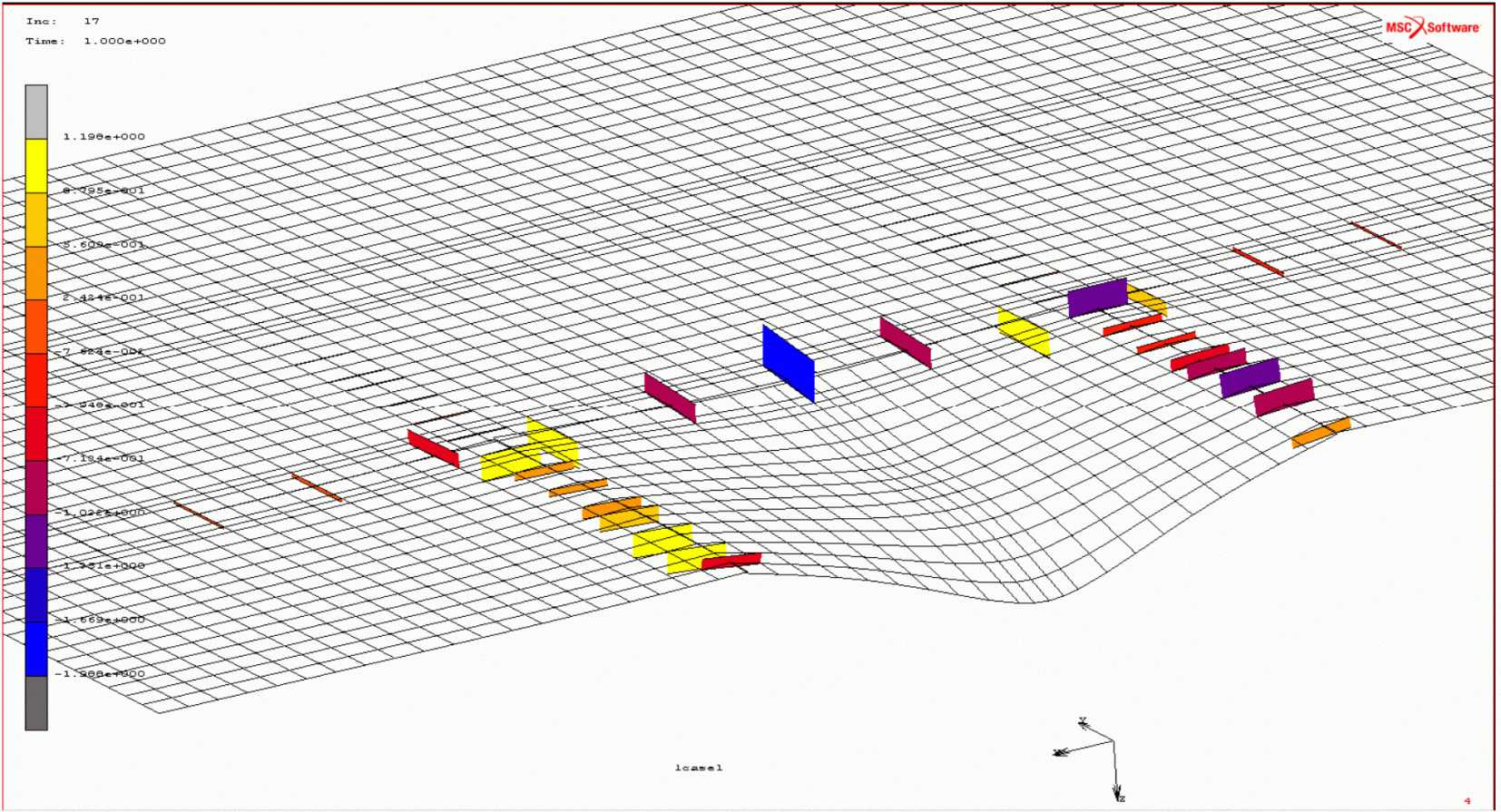
расположенных в поперечных и продольных швах покрытия

расположенных в поперечных и продольных швах покрытия
Из рисунка 132 следует, что наибольшая поперечная сила возникла в штыре продольного шва между 2-й и 5-й плитами, ее величина составила 1,900 кПа.
Соответствующие касательные напряжения среза в штыре можно определить по формуле (1)
где Q - поперечная сила, а F - площадь поперечного сечения штыря.
Так как F = 3,14*0,022 = 12,56*10-4 м2, то
 .
.Максимальные изгибающие моменты, как это видно из рисунка 133, возникли в штырях поперечных швов между плитами 1 - 2 и 2 - 3. Величина их равнялась 1,722*10-3 кН*м.
Максимальные нормальные напряжения при изгибе штырей определим по формуле (2)
где Mx - изгибающий момент, а Wx - осевой момент сопротивления поперечного сечения штыря.
Так как
 ,
,то
 .
.Таким образом, в рассмотренном случае, как нормальные, так и касательные напряжения в штырях значительно меньше соответствующих расчетных сопротивлений для стали, из которой изготавливаются штыри.
Другой пример иллюстрирует применение конечно-элементной модели многополосного дорожного покрытия для расчета трехполосного покрытия при нагрузке, приложенной по краям плиты. Соответствующий случай загружения покрытия показан на рисунке 127.
Результаты расчетов представлены на рисунках 134 - 139.
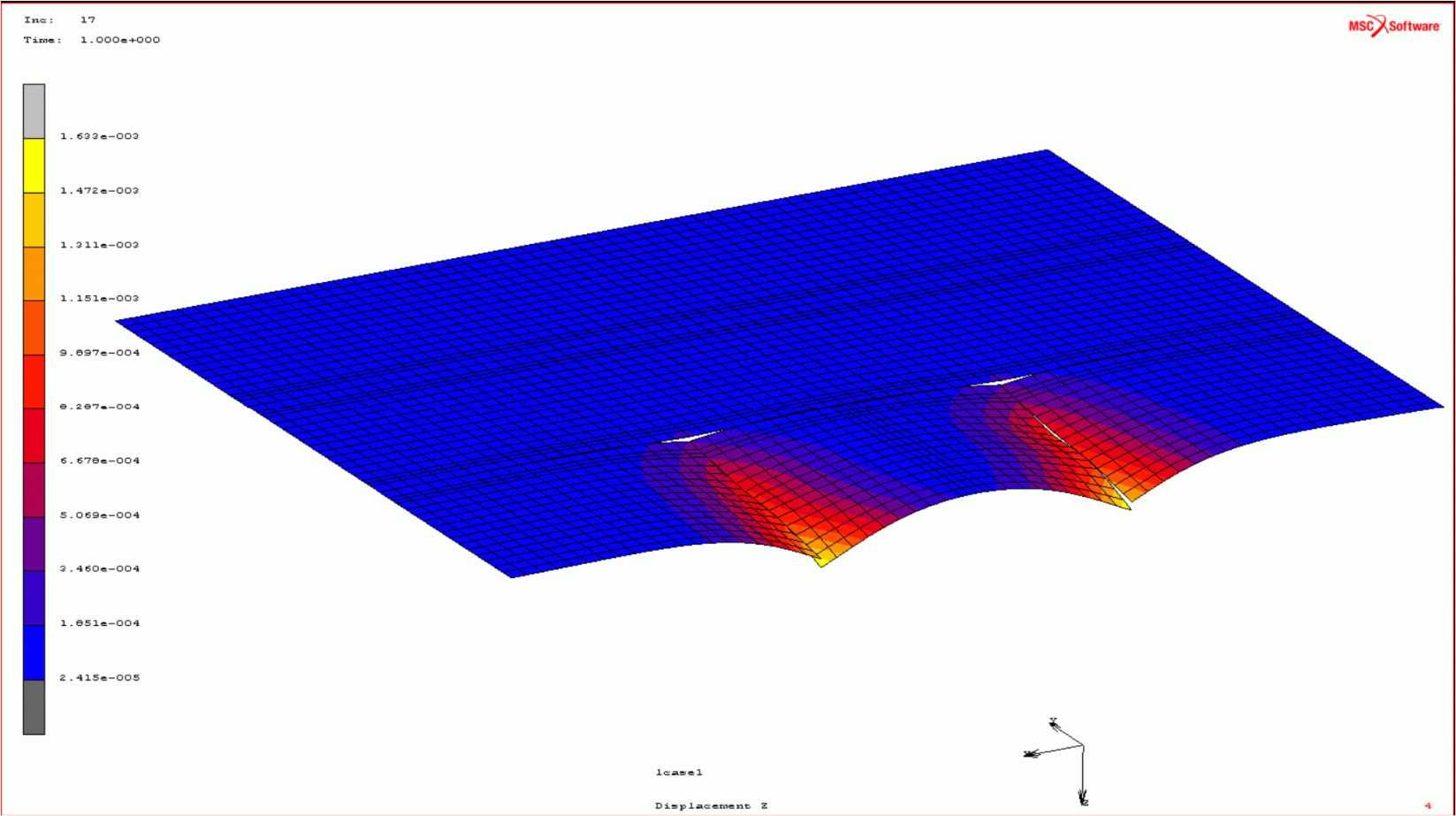
Рисунок 134 - Вертикальные перемещения 3-полосного
жесткого автомобильно-дорожного покрытия
Из рисунка 134 следует, что значимые значения прогибов плиты, возникают не только в той плите, к которой приложена нагрузка от колес автомобиля, но и в соседних с ней плитах одной полосы движения. При этом максимальные значения прогибов возникли по краям нагруженной плиты и составили 1,633 мм.
В этом случае существенными были взаимные смещения соседних плит. Как видно из рисунка 135, в углах плит их взаимное вертикальное смещение составило 0,28 мм. При этом взаимное вертикальное смещение плит в соседних полосах движения, как это следует из рисунка 136, составило 0,17 мм.

жесткого автомобильно-дорожного покрытия в поперечном шве

жесткого автомобильно-дорожного покрытия в продольном шве
Максимальные растягивающие напряжения возникли в местах соединения штырей с плитой, что обусловлено концентрацией напряжений в этих местах (рисунок 137).

Рисунок 137 - Распределение главных растягивающих
напряжений  в верхнем слое жесткого
в верхнем слое жесткого
автомобильно-дорожного покрытия
На рисунке 138 показано распределение поперечных сил в штырях, соединяющих плиты между собой. Из этого рисунка следует, что наибольшие поперечные силы возникли в крайних штырях поперечных швов между первой и второй, а также второй и третьей плитами, ее величина составила 25,56 кПа.

Рисунок 138 - Фрагмент распределения поперечных сил
в штырях, расположенных в поперечных
и продольных швах покрытия
Соответствующие касательные напряжения среза  можно определить по формуле (1).
можно определить по формуле (1).
Так как F = 3,14*0,022 = 12,56*10-4 м2, то
 .
.Максимальные изгибающие моменты, как это видно из рисунка 139, возникли в штырях поперечных швов между плитами 1 - 2 и 2 - 3. Величина их равнялась 89,31*10-3 кН*м.
Максимальные нормальные напряжения в штырях определим по формуле (2).
Так как
 , то
, то .
.
в штырях, расположенных в поперечных
и продольных швах покрытия
Таким образом, и в этом случае, как нормальные, так и касательные напряжения в штырях значительно меньше соответствующих расчетных сопротивлений для стали, из которой изготавливаются штыри.
11.4. Влияние жесткости штыревых связей в поперечных швах на напряженно-деформированное состояние покрытия
Для каждого из двух случаев загрузки плиты рассматривались три варианта диаметров стыковочных штырей:
- диаметр штырей = 0,02 м;
- диаметр штырей = 0,04 м;
- диаметр штырей = 0,08 м.
Штыри диаметром от 0,02 до 0,04 м широко используются в практике строительства жестких автомобильно-дорожных покрытий. Нереальный случай штырей диаметром 0,08 м был рассмотрен только для того, чтобы исследовать влияние увеличения жесткости стыков на напряженно-деформированное состояние дорожного покрытия, при минимальных изменениях в построенной конечно-элементной модели.
Результаты расчетов для различных положений нагрузки и различных диаметров штырей сведены в таблицу 8.
Таблица 8
и различных диаметров штырей
Вид нагрузки | Параметры | Диаметры штырей | ||
0.02 м | 0.04 м | 0.08 м | ||
Нагрузка в середине плиты с отпечатком одного из колес на краю плиты (рисунок 126) | Vmax, мм | 1.126 | 1.124 | 1.118 |
0.023 | 0.014 | 0.005 | ||
0.321 | 0.234 | 0.105 | ||
2.923 | 2.923 | 2.921 | ||
4.47 | 1.51 | 0.109 | ||
1.39 | 0.274 | 0.095 | ||
Нагрузка от двух осей автомобиля, приложенная на краях плиты (рисунок 127) | Vmax, мм | 1.794 | 1.633 | 1.512 |
0.58 | 0.28 | 0.14 | ||
0.21 | 0.17 | 0.11 | ||
1.505 | 1.081 | 1.002 | ||
62.7 | 15.67 | 0.126 | ||
7.19 | 14.22 | 24.8 | ||
В таблице 8 используются следующие обозначения:
- Vmax - максимальный прогиб покрытия;
-  - разница в прогибах между соседними плитами в поперечном шве;
- разница в прогибах между соседними плитами в поперечном шве;
-  - разница в прогибах между соседними плитами в продольном шве;
- разница в прогибах между соседними плитами в продольном шве;
-  - максимальные растягивающие напряжения в бетоне плит покрытия;
- максимальные растягивающие напряжения в бетоне плит покрытия;
-  - касательные напряжения среза в штырях, расположенных в поперечных швах;
- касательные напряжения среза в штырях, расположенных в поперечных швах;
-  - максимальные нормальные напряжения при изгибе в штырях, расположенных в поперечных швах.
- максимальные нормальные напряжения при изгибе в штырях, расположенных в поперечных швах.
Из таблицы 2 следует, что при нагрузке, расположенной в середине плиты:
- максимальные прогибы покрытия мало зависят от диаметра штырей;
- диаметры штырей существенно влияют на разницу в прогибах между соседними плитами (нагруженной и ненагруженной), как в продольных, так и в поперечных швах;
- максимальные растягивающие напряжения в бетоне плиты практически не зависят от диаметра штырей;
- касательные и нормальные напряжения в штырях резко уменьшаются при изменении диаметра штырей.
Из этой же таблицы следует, что при нагрузке, приложенной на краях плиты:
- максимальные прогибы покрытия, а также разница в прогибах между соседними плитами (нагруженной и ненагруженной), как в продольных, так и в поперечных швах, в значительной степени зависит от диаметра штырей;
- разница в максимальных растягивающих напряжениях в бетоне для различных диаметров штырей также значительна;
- наибольшее влияние диаметры штырей оказывают на напряжения в штырях, которые, к тому же, существенно больше, чем при нагрузке приложенной в середине плиты.
и транспортных нагрузок
Добавление к транспортным нагрузкам экстремального температурного воздействия может существенно изменить напряженно-деформированное состояние многополосного жесткого дорожного покрытия.
Для учета температурного воздействия в конечно-элементную модель многополосного жесткого дорожного покрытия, разработанную для расчетов действия транспортных нагрузок, нужно добавить граничные условия, соответствующие температурному воздействию.
В качестве примера, рассмотрим случай, когда температура нижней грани плит покрытия равна 20 °C, а температура верхней грани равна 50 °C. Коэффициент линейного расширения для бетона плит покрытия примем равным 1*10-5 1/град. По толщине плиты температура изменяется по линейному закону.
Транспортные нагрузки, как и раньше, рассмотрим в двух вариантах: ось автомобиля в середине крайней плиты покрытия (рисунок 126) и две оси по краям плиты (рисунок 127). Диаметры штырей в поперечных и продольных швах также будем варьировать от 0,02 м до 0,08 м.
12.1. Нагрузка в середине плиты, с отпечатком одного из колес на краю плиты, и температурное воздействие
Некоторые результаты расчетов для диаметров штырей в поперечных и продольных швах равных 0,02 м показаны на рисунках 140 - 143. Результаты расчетов для диаметров штырей 0,04 и 0,08 м сведены в таблицу 8.
Из рисунка 140 видно, что преобладающее влияние на вертикальные перемещения в данном случае оказывает температурное воздействие. Положение и величина главных растягивающих напряжений зависят главным образом от положения нагрузки на плиту (рисунок 141).

трехполосного жесткого дорожного покрытия, возникающих
от транспортной нагрузки в середине плиты
и температурного воздействия

напряжений  в нижнем слое жесткого автомобильно-дорожного
в нижнем слое жесткого автомобильно-дорожного
покрытия, возникающих от транспортной нагрузки
в середине плиты и температурного воздействия
Значительные поперечные силы возникают только в штырях, соединяющих нагруженную плиту с соседними плитами (рисунок 142), в остальных местах они пренебрежимо малы.
А вот влияние транспортной нагрузки на распределение изгибающих моментов в штырях по сравнению с температурным воздействием пренебрежимо мало (рисунок 143).

в штырях, расположенных в поперечных и продольных
швах покрытия

расположенных в поперечных и продольных швах покрытия
Некоторые результаты расчетов для диаметров штырей в поперечных и продольных швах равных 0,02 м показаны на рисунках 144 - 147.
Результаты расчетов для температурного воздействия, транспортной нагрузки на краях плиты и различных диаметров штырей сведены в таблицу 9.
Из рисунка 144 видно, что максимальные вертикальные перемещения возникают на краях нагруженной плиты, там, где приложена нагрузка.
Максимальные растягивающие напряжения в покрытии возникают от температурного воздействия, а нагрузка, приложенная по краям плиты, уменьшает их значение (рисунок 145).

трехполосного жесткого дорожного покрытия, возникающих
от транспортной нагрузки на краях плиты
и температурного воздействия

в нижнем слое жесткого автомобильно-дорожного покрытия,
возникающих от транспортной нагрузки на краях плиты
и температурного воздействия
Значительные поперечные силы возникают только в штырях, соединяющих нагруженную плиту с соседними плитами в поперечных швах (рисунок 146), в остальных местах они пренебрежимо малы.

Рисунок 146 - Фрагмент распределения поперечных сил
в штырях, расположенных в поперечных и продольных швах
покрытия, возникающих от транспортной нагрузки на краях
плиты и температурного воздействия
Влияние транспортной нагрузки на распределение изгибающих моментов в штырях существенно только для штырей в поперечных швах, соединяющих нагруженную плиту с соседними плитами, в остальных швах распределение изгибающих моментов в штырях зависит главным образом от величины температурного воздействия (рисунок 147).

расположенных в поперечных и продольных швах покрытия,
возникающих от транспортной нагрузки на краях плиты
и температурного воздействия
Результаты расчетов для температурного воздействия, двух видов транспортной нагрузки и различных диаметров штырей сведены в таблицу 9. В таблице 9 используются те же обозначения, что и в таблице 8.
Таблица 9
температурного воздействия и диаметров штырей
Вид нагрузки | Параметры | Диаметры штырей | ||
0.02 м | 0.04 м | 0.08 м | ||
Нагрузка в середине плиты с отпечатком одного из колес на краю плиты (рисунок 3) | Vmax, мм | 2.116 | 2.125 | 2.119 |
5.785 | 5.786 | 5.807 | ||
3.03 | 1.11 | 0.073 | ||
11.3 | 22.3 | 75.5 | ||
Нагрузка от двух осей автомобиля, приложенная на краях плиты (рисунок 4) | Vmax, мм | 3.785 | 3.616 | 3.377 |
3.171 | 3.174 | 3.209 | ||
62.7 | 20.3 | 1.41 | ||
18 | 35.6 | 122.2 | ||
Из таблицы 9 следует, что при нагрузке, расположенной в середине плиты:
- максимальные прогибы покрытия мало зависят от диаметра штырей;
- максимальные растягивающие напряжения в бетоне плиты практически не зависят от диаметра штырей;
- касательные напряжения в штырях резко уменьшаются при увеличении диаметра штырей, что объясняется небольшими поперечными силами, возникающими в штырях от экстремального температурного воздействия по сравнению с нагрузкой, приложенной в середине плиты;
- нормальные напряжения в штырях резко увеличиваются при увеличении диаметра штырей, что объясняется большим влиянием на деформации изгиба штырей экстремального температурного воздействия по сравнению с нагрузкой, приложенной в середине плиты.
Из этой же таблицы следует, что при нагрузке, приложенной на краях плиты:
- максимальные прогибы покрытия, а также максимальные растягивающие напряжения в плите мало зависят от диаметра штырей;
- наибольшее влияние диаметры штырей оказывают на напряжения в штырях, которые, к тому же, существенно больше, чем при нагрузке приложенной в середине плиты.
12.3. Рекомендации по созданию конечно-элементных моделей для многополосных жестких дорожных покрытий, усиленных в продольных и поперечных швах стальными штырями
1. В случае моделирования плит многополосного жесткого дорожного покрытия объемными 8-узловыми конечными элементами размерность задачи становится недопустимо большой и недоступной для решения на обычном персональном компьютере. Поэтому такие задачи следует решать используя для создания конечно-элементной модели покрытия плоские 4-узловые конечные элементы типа "shell".
2. Для моделирования стальных штырей, соединяющих плиты между собой в продольных и поперечных швах необходимо использовать балочные конечные элементы типа "beam".
3. В качестве модели основания рекомендуется использовать модель Винклера.
4. Нагрузка от колеса транспортного средства может быть представлена равномерно распределенным давлением на плиту покрытия в пределах области отпечатка колеса.
5. Задание различных температур на верхней и нижней гранях плиты позволяет смоделировать температурное воздействие на покрытие.
В данной ОДМ "Рекомендации по определению напряженно-деформированного состояния многослойных дорожных одежд" на основании современных конечно-элементных решений предлагаются методы создания конечно-элементных моделей многослойных дорожных одежд, которые позволяют:
- разрабатывать конечно-элементные модели для расчета плит жесткого дорожного покрытия на действие различных транспортных нагрузок и температурных воздействий (разделы 6 - 12);
- оценить влияние модели основания на напряженно-деформированное состояние дорожной конструкции (раздел 6.2);
- создавать конечно-элементные модели для расчета конструкций швов жестких дорожных покрытий, усиленных стальными штырями (разделы 7, 7.1 - 7.7);
- определить вероятность потери продольной устойчивости жестким дорожным покрытием при экстремальных летних температурах (разделы 8 - 10);
- автоматизировать процесс создания новых конечно-элементных моделей многослойных дорожных одежд с помощью параметрической формы представления моделей в мультидисциплинарных конечно-элементных комплексах (раздел 7);
- создавать упрощенные конечно-элементные модели для расчета конструкций многополосных жестких дорожных покрытий (разделы 11 - 12);
- верифицировать уже разработанные и вновь создаваемые конечно-элементные модели дорожных одежд (разделы 6.3, 7.2, 8.3.1).
Предлагаемый проект ОДМ "Рекомендации по определению напряженно-деформированного состояния многослойных дорожных одежд" должен способствовать внедрению современных методов расчета напряженно-деформированного состояния многослойных конструкций дорожных одежд, основанных на использовании мультидисциплинарных конечно-элементных комплексов, в отечественную практику проектирования новых и реконструкции существующих дорог.
Методические рекомендации по проектированию жестких дорожных одежд (взамен ВСН 197-91)/Минтранс России, Госслужба дор. хоз-ва (Росавтодор). - М.: ФГПУ "Информавтодор", 2004. - 135 с. | |
Методические рекомендации по расчету температурных полей, напряжений и деформаций в цементобетонных покрытиях/М.: "Союздорнии", 1976, 132 с. | |
Методические рекомендации по ремонту цементобетонных покрытий автомобильных дорог. Минтранс России, Росавтодор, 2003. | |
[4] | СНиП 23-01-99* Строительная климатология и геофизика |
Демьянушко И.В., Носов В.П., В.М. Стаин, А.В. Стаин. Конечно-элементные модели для расчета плиты жесткого дорожного покрытия//Транспортное строительство. - 2012. - N 4. - с. 5 - 8. | |
Демьянушко И.В., Попов В.А., Стаин В.М., Стаин А.В. Продольная устойчивость жесткого дорожного покрытия при температурном воздействии//Транспортное строительство. - 2012. - N 5. - с. 4 - 7. | |
[7] | Демьянушко И.В., Стаин В.М., Стаин А.В. Моделирование теплового взаимодействия дорожного покрытия с окружающей средой с использованием метода конечных элементов//Транспортное строительство. - 2013. - N 8. - с. 14 - 16. |
Демьянушко И.В., Стаин В.М., Стаин А.В. Современные методы расчета напряженно-деформированного состояния конструкций жестких дорожных одежд//Автомобильные дороги - 2014. - N 8. - с. 14 - 16. | |
Лещицкая Т.П., Попов В.А. Современные методы ремонта аэродромных покрытий. МАДИ, М., 1999. - 129 с. | |
[10] | Попов В.А. Долговечность эксплуатируемых бетонных покрытий аэродромов. - М., Техполиграфцентр, 2007. |
Радовский Б.С. Цементобетонные покрытия в США. http://library.stroit.ru/ | |
Ушаков В.В. Ремонт цементобетонных покрытий автомобильных дорог. - М., 2002. - (Автомоб. дороги: Обзорн. информ./Информавтодор; Вып. 6). | |
Цытович Н.А., Березанцев В.Г., Далматов Б.И. Основания и фундаменты. - М., "Высшая школа", 1970. - 384 с. | |
Дорожная метеорологическая станция RWS 4030 http://www.infomarcompany.com/arws_aws.htm | |
Khazanovich, L., H.T. Yu, S. Rao, K. Galasova, E. Shats, and R. Jones. (2000), "ISLAB2000 - Finite Element Analysis Program for Rigid and Composite Pavements, User's Guide," ERESConsultants, Champaign, Illinois. | |
[16] | Khazanovich, Lev. Dowel and Tie Bars in Concrete Pavement Joints: Theory and Practice. 2nd International Conference on Best Practices for Concrete Pavements. November 2, 2011. |
LI Luoke, TAN Yiqiu, GONG Xiangbing, LI Yunliang. Characterization of Contact Stresses Between Dowels and Surrounding Concrete in Jointed Concrete Pavement. International Journal of Civil & Environmental Engineering IJCEE-IJENS Vol: 12 No: 05. October 2012. | |
Nesnas K., R. Isola, B. Ferne, A finite element investigation of the FWD response of the joints of rigid pavements, Published Project Report Ppr. 405, Transport Research Laboratory, December, 2009. | |
The Thermal and Radiative Characteristics of Concrete Pavements in Mitigating Urban Heat Island Effects/Kamil E. Kaloush, Joby D. Carlson, Jay S. Golden and Patrick E. Phelan; Portland Cement Association. - 2008. | |
Schlangen E. Online Help/Manual module HEAT of FEMMASSE, 1990 - 2000, FEMMASSE b.v. - The Netherlands, 2000. | |
[21] | Kamil E. Kaloush, Joby D. Carlson, Jay S. Golden, and Patrick E. Phelan. The Thermal and Radiative Characteristics of Concrete Pavements in Mitigating Urban Heat Island Effects. Portland Cement Association 2008. |
[22] | MSC.Software.MSC.MARC, 2012. |
Руководитель
организации-разработчика
ФГБОУ ВПО "Московский
автомобильно-дорожный
государственный технический
университет (МАДИ)"
Проректор по научной работе
А.М.ИВАНОВ

