СПРАВКА
Источник публикации
М.: Стройиздат, 1975
Примечание к документу
Название документа
"Руководство по расчету статически неопределимых железобетонных конструкций"
"Руководство по расчету статически неопределимых железобетонных конструкций"
ПО РАСЧЕТУ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
В Руководстве приведены основные методы расчета балочных плит, плит, работающих в двух направлениях, неразрезных балок и рам, монолитных и сборных безбалочных перекрытий и фундаментов под отдельно стоящие сооружения башенного типа.
Методы расчета учитывают неупругие свойства железобетона, воздействие температуры внешней среды и иллюстрируются примерами расчета.
Руководство предназначено для инженерно-технических работников проектных организаций, научных работников, преподавателей строительных вузов, аспирантов и студентов.
Настоящее Руководство содержит рекомендации по расчету статически неопределимых железобетонных конструкций с учетом перераспределения усилий вследствие неупругих деформаций материалов, образования трещин и других факторов, вызывающих в конструкциях необратимые изменения. Рекомендации по расчету, где это целесообразно, ориентированы на использование современной вычислительной техники и математического программирования. Так, приведены методы расчета с использованием ЭВМ опертых по контуру плит и рам на эксплуатационные нагрузки, а также плитных и рамных конструкций по несущей способности с применением статического принципа метода предельного равновесия.
Руководство распространяется на сборные, сборно-монолитные и монолитные обычные и предварительно-напряженные железобетонные конструкции производственных и гражданских зданий и сооружений. В Руководстве изложены вопросы расчета балочных плит и плит, работающих в двух направлениях, неразрезных балок и рам, монолитных и сборных безбалочных перекрытий, фундаментов под дымовые трубы и фундаментов под отдельно стоящие (круглые в плане) сооружения башенного типа.
Впервые в Руководстве рассмотрены вопросы расчета конструкций и сооружений на температурно-климатические воздействия как в процессе возведения, так и в период эксплуатации.
Руководство разработано Научно-исследовательским институтом бетона и железобетона Госстроя СССР (доктора техн. наук, профессора А.А. Гвоздев, С.М. Крылов, кандидаты техн. наук Л.Н. Зайцев, А.М. Проценко, Н.И. Карпенко, В.Н. Самойленко) при участии ЦНИИпромзданий (инженеры Б.Ф. Васильев и А.Я. Розенблюм), Харьковского ПромстройНИИпроекта (канд. техн. наук И.Л. Забелло), ЦНИИСК имени Кучеренко (инж. И.А. Белышев) и др.
При составлении Руководства использованы материалы КиевЗНИИЭПа, ЦНИИЭПСельстроя, ЦНИПИАССа, Института строительной механики и сейсмостойкости АН Грузинской ССР, Полтавского инженерно-строительного института, Белорусского института железнодорожного транспорта и др.
Замечания по содержанию Руководства просьба направлять по адресу: 109389, Москва, Ж-389, 2-я Институтская ул., д. 6, НИИ бетона и железобетона.
Дирекция НИИЖБ
1.1. Расчет статически неопределимых железобетонных конструкций по первой и второй группам предельных состояний следует производить с учетом перераспределения усилий, вызываемого проявлением неупругих деформаций бетона и арматуры и образованием трещин. В случае когда геометрические факторы (продольный изгиб элементов конструкций, изменение геометрической формы конструкций и т.п.) существенно сказываются на условиях равновесия, а следовательно, и на распределении усилий, статический расчет производится по деформированной схеме.
1.2. Учет перераспределения усилий рекомендуется производить для более правильной оценки прочности, трещиностойкости и деформативности конструкций, более рационального их проектирования и получения производственного и экономического эффекта.
1.3. Настоящее Руководство распространяется на статические расчеты конструкций. Динамические расчеты и расчет на выносливость, когда они необходимы, выполняются согласно специальным указаниям.
1.4. По усилиям, вычисленным с учетом перераспределения, сечение элементов конструкций, их армирование, трещиностойкость (и ширина раскрытия трещин) и деформативность (прогибы) определяются согласно указаниям и рекомендациям действующих строительных норм и правил на проектирование железобетонных конструкций и развивающих их руководств.
При отсутствии разработанных методов определения действительного распределения усилий в конструкции, а также с целью упрощения допускается расчет ее по первой и второй группам предельных состояний производить достаточно обоснованными приближенными методами.
1.5. Расчет распределения усилий в упругой системе (в конструкциях без трещин) требуется в случаях, когда:
а) трещины недопустимы (предварительно-напряженные конструкции первой категории трещиностойкости) или требуется проверить при длительно действующей нагрузке закрытие трещин, образовавшихся при кратковременно действовавших нагрузках (предварительно-напряженные конструкции второй категории трещиностойкости);
б) требуется расчет жесткости, но заранее неизвестно, нужно ли рассматривать конструкцию как имеющую трещины или нет (например, при учете совместной работы основания и сооружения);
в) требуется расчет прогибов конструкции при наличии трещин, но в расчет прогибов конструкции с трещинами входит величина прогиба к моменту образования первых трещин (случай плит, работающих в двух направлениях, пп. 1.8, 2.15).
При расчете трещиностойкости статически неопределимых конструкций, испытывающих помимо внешних нагрузок воздействие на конструкцию усилий обжатия предварительно-напряженной арматуры, последние следует учитывать расчетом. Усилия обжатия рассматриваются как внешние силы, равные контролируемым усилиям за вычетом первых потерь и приложенные в центре тяжести напрягаемой арматуры. Потери определяются согласно рекомендациям действующих строительных норм и правил на проектирование железобетонных конструкций.
а) когда требуется оценить прогиб конструкций, работающих в условиях эксплуатации без трещин;
б) когда требуется определить прогиб конструкции, работающей в условиях эксплуатаций с трещинами, но в расчет прогибов ее входит величина прогиба конструкций к моменту образования трещин (пп. 1.8, 2.15).
При расчете общих деформаций сборных стержневых конструкций, пригруженных (обжатых) до омоноличивания стыков, следует учитывать прогиб до омоноличивания, в том числе и с учетом реализовавшейся за этот период ползучести бетона (см. п. 1.10).
1.7. Если в статически неопределимых балках, рамах или других конструкциях, состоящих из стержней, требуется найти прогиб при наличии трещин или проверить ширину раскрытия трещин, либо определить условия образования трещин на определенных участках конструкций при наличии трещин на других участках, то при нахождении усилий в системе следует пользоваться жесткостями, определяемыми для треснувших и нетреснувших сечений.
Оценку прочности, деформативности и трещиностойкости в статически неопределимых системах целесообразно ориентировать на использование математических методов и вычислительной техники.
1.8. Деформативность работающих в двух направлениях железобетонных плит с трещинами следует определять с учетом тех особенностей, которые вносят трещины в работу плит. Плиту при этом следует рассматривать как анизотропную пластинку; анизотропия в данном случае определяется армированием, наличием и наклоном по отношению к арматуре трещин (п. 2.16).
Приближенно максимальный прогиб плит может быть определен по линейной интерполяции между прогибом, отвечающим образованию первых трещин, и прогибом, непосредственно предшествующим исчерпанию несущей способности плит (п. 2.15).
1.9. Ширина раскрытия трещин в плитах определяется по усилиям (изгибающие и крутящие моменты), полученным из расчета плиты как анизотропной пластинки (п. 2.16).
Приближенно ширина раскрытия трещин может быть определена по напряжениям в арматуре, определенным по линейной интерполяции между напряжением в момент образования трещин и нормативным сопротивлением арматуры (п. 2.15).
1.10. При расчете статически неопределимых железобетонных конструкций может в отдельных случаях потребоваться учет влияния ползучести бетона на распределение усилий в системе (пп. 1.5 и 1.6).
Усилия, вызванные при возрасте бетона  смещением опор, усадкой, температурой, а также другими длительными воздействиями, за исключением нагрузок, смягчаются со временем
смещением опор, усадкой, температурой, а также другими длительными воздействиями, за исключением нагрузок, смягчаются со временем  под влиянием ползучести бетона.
под влиянием ползучести бетона.
Степень уменьшения (релаксация) этих вынужденных для системы усилий зависит от соотношения между деформациями ползучести и упругими деформациями армированного бетона и приближенно может быть оценена при помощи множителя (коэффициента релаксации вынужденного усилия)
где Cа - коэффициент, учитывающий деформации ползучести армированного бетона в произвольный момент времени  при нагружении его в возрасте
при нагружении его в возрасте  , определяемый по формуле
, определяемый по формуле
Cб - коэффициент, учитывающий деформации ползучести бетона.
Для конструкций из бетона марки 200 и выше, загружаемых в возрасте более 15 сут., коэффициент Cб допускается определять по формуле
 ,
, ,
,где  - предельная величина меры ползучести бетона, равная:
- предельная величина меры ползучести бетона, равная:
 ,
,R - проектная марка бетона;
Kс - коэффициент, принимаемый по табл. 1;
Вид бетона | Kс |
Обычный тяжелый (с крупным заполнителем) естественного твердения | 0,55 |
То же, подвергнутый пропариванию | 0,5 |
Легкий (с крупным заполнителем) естественного твердения | 0,6 |
То же, подвергнутый пропариванию | 0,55 |
Kп - коэффициент, учитывающий подвижность (удобоукладываемость) бетонной смеси. Если в проекте подвижность смеси не оговаривается, Kп = 1. В остальных случаях принимается по табл. 2;
Таблица 2
Подвижность (удобоукладываемость) бетонной смеси | Kп |
Осадка конуса 5 - 6 см | 1,2 |
Осадка конуса 1 - 2 см (жесткость 20 - 15 с) | 1 |
Жесткость смеси 35 - 50 с | 0,8 |
 ,
,uкр - относительная критическая влажность бетона;
 ,
,hпр - приведенная высота элемента, равная площади сечения, деленной на половину его периметра, соприкасающегося с атмосферой; для элементов, высыхающих со всех сторон
 ,
,b, h - ширина и высота элемента в см;
uс - средняя относительная равновесная влажность бетона элемента;
 ,
,1.11. Если при расчете конструкций необходимо знать величину усадки бетона, то в этом случае ее величину в момент времени t допускается определять по формуле
где  - предельная величина усадки бетона, равная:
- предельная величина усадки бетона, равная:
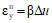 ,
,Вид бетона | |
Обычный тяжелый (с крупным заполнителем) естественного твердения | 0,03 |
То же, подвергнутый пропариванию | 0,025 |
Легкий (с крупным заполнителем) естественного твердения | 0,035 |
То же, подвергнутый пропариванию | 0,03 |
1.12. Если замыкание некоторых или всех связей осуществляется после частичного или полного загружения конструкции, то деформации (прогибы, углы поворота сечений на опорах), приобретенные при работе по разрезной схеме, можно рассматривать как вынужденные перемещения, введенные в неразрезную систему и зафиксированные при замыкании связей. Релаксация усилий, вызванных вынужденными перемещениями, в данном случае может быть оценена коэффициентом релаксации по формуле (1). Под усилиями, вызванными вынужденными перемещениями, следует понимать разность между усилием от внешней нагрузки при работе конструкции по неразрезной схеме и усилием при работе конструкции по разрезной схеме.
При отсутствии необходимых данных (в отношении реологических свойств бетона конструкции, возраста его в момент введения вынужденных деформаций и т.д.) можно (на основании опытных данных) значение коэффициента Cб приближенно принять по формуле (139), используя табл. 4.
Режим эксплуатации конструкций | C |
При средней относительной влажности воздуха 40% и ниже | 3 |
При средней относительной влажности воздуха выше 40% | 2 |
Примечание. Для конструкций, подвергнутых тепловой обработке, значение C (табл. 4) уменьшается путем умножения на коэффициент 0,85.
Если статически неопределимая конструкция (например, сборно-монолитная) состоит из элементов, бетон которых существенно различается по возрасту и по составу, а также если часть элементов имеет особо сильное армирование (например, обетонированные стальные элементы), рекомендуется оценить влияние ползучести на распределение усилий расчетом, как для упругой системы, но с различным для разных элементов или групп элементов снижением их жесткости ( ;
; 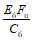 ) вследствие ползучести.
) вследствие ползучести.
Рекомендации настоящего пункта могут быть применены для анализа распределения усилий в конструкциях, имеющих, а также не имеющих трещин в растянутой зоне бетона.
1.13. Особого подхода требуют случаи, когда сборные железобетонные балочные конструкции замоноличиваются после того, как на них некоторое время действовала нагрузка (а для предварительно-напряженных и усилия обжатия). При расчетах нужно учитывать, что ползучесть частично протекает до замыкания. Это ведет к ослаблению релаксационных явлений. В частном случае для неразрезных конструкций балочного типа это может быть учтено следующим образом.
Действующий опорный момент от нагрузки, приложенной до замыкания,
 , (4)
, (4)где Mнер - опорный момент от нагрузки (или усилий обжатия), приложенной до замыкания связей в неразрезной системе, не имеющей трещин в опорном сечении;
Коэффициент релаксации  можно подсчитать по следующей формуле:
можно подсчитать по следующей формуле:
 , (5)
, (5)где t - рассматриваемый момент времени;
Эти коэффициенты определяются по формуле (1).
1.14. Несущая способность статически неопределимой конструкции может быть исчерпана либо при хрупком разрушении одного из ее элементов ранее, чем общие деформации станут слишком велики, либо за счет чрезмерного роста общих необратимых деформаций без полного разрушения какой-либо из частей конструкции.
Расчет несущей способности, если предел ее характеризуется резким возрастанием общих необратимых деформаций, может быть выполнен методом предельного равновесия.
Для расчета несущей способности конструкции при хрупком разрушении следует прослеживать перераспределение усилий до тех пор, пока не выявятся условия хрупкого разрушения одного из элементов конструкции.
деформации конструкции до исчерпания ее несущей способности должны быть достаточно малы для того, чтобы можно было пренебречь изменениями геометрических величин, входящих в условия равновесия;
усилия в элементах конструкции (особенно в тех из них, которые фактически определяют ее несущую способность) должны быть ограничены предельными условиями, с достижением которых деформации этих элементов могут достаточно сильно возрастать.
1.16. Предельными условиями называются неравенства, определяющие для усилий определенную границу. Когда такое неравенство переходит в равенство, элемент конструкции, к которому рассматриваемое усилие относится, вступает в новую область поведения. Примерами предельных условий могут служить: для растянутого стержня арматуры  , для изгибающего момента в балке
, для изгибающего момента в балке  , где z - плечо внутренней пары.
, где z - плечо внутренней пары.
 , где z - плечо внутренней пары.
, где z - плечо внутренней пары.В более общем случае, что необходимо для решения ряда задач, предельные условия по прочности могут быть заданы в виде системы неравенств - ограничений. Такая система неравенств задает некоторую выпуклую область, описывающую прочность сечения для рассматриваемого вида напряженного состояния. Для прямоугольных сечений (в частности, для стержневых конструкций) такую область удобно представить в координатах продольная сила - момент относительно геометрического центра сечения.
На рис. 1 показана область прочности  для прямоугольного сечения с симметричным и несимметричным армированием. Точки D - соответствуют центральному сжатию, точки A - центральному растяжению. Точки Mи и
для прямоугольного сечения с симметричным и несимметричным армированием. Точки D - соответствуют центральному сжатию, точки A - центральному растяжению. Точки Mи и  соответствуют изгибу сечения. Точки выпуклой области, описывающей прочность сечения для рассматриваемого вида напряженного состояния (рис. 1) вычислены согласно действующим нормам и соответствующим руководствам.
соответствуют изгибу сечения. Точки выпуклой области, описывающей прочность сечения для рассматриваемого вида напряженного состояния (рис. 1) вычислены согласно действующим нормам и соответствующим руководствам.

Рис. 1. Область прочности прямоугольного сечения
1 - несимметричное армирование; 2 - симметричное армирование
Таким образом, в области  лежат точки, в которых для внецентренно нагруженного сечения при любом направлении действия момента и силы, прочность сечения обеспечена. Заменив для удобства счета криволинейные участки области прямыми (что практически не ведет к ощутимому снижению прочности сечения и идет в запас), можно записать шесть предельных ограничений вида
лежат точки, в которых для внецентренно нагруженного сечения при любом направлении действия момента и силы, прочность сечения обеспечена. Заменив для удобства счета криволинейные участки области прямыми (что практически не ведет к ощутимому снижению прочности сечения и идет в запас), можно записать шесть предельных ограничений вида
где коэффициенты aiM, aiN, ai вычисляются по соответствующим формулам действующих норм и руководств при характеристиках материалов Ra, Rпр.
1.17. Для выполнения первой из указанных предпосылок конструкции должны быть достаточно жестки, однако признаком достаточности служат здесь не эксплуатационные требования, а чувствительность условий равновесия к возникающим деформациям. Так, для элемента, испытывающего простой изгиб, деформации мало влияют на плечи усилий. Между тем при наличии продольной силы прогибы непосредственно прибавляются к эксцентрицитету или вычитаются из него и могут тем сильнее сказаться на уравнениях равновесия, чем меньше начальный (до деформации) эксцентрицитет.
При выполнении обеих предпосылок, указанных выше, нагрузка, отвечающая пределу несущей способности конструкции, будет наибольшей, при которой еще возможно одновременное соблюдение как условий равновесия, так и предельных условий для всех элементов системы (статический способ).
Одновременно ее величина равна наименьшему из значений, определяемых равенством работ внешних сил и предельных внутренних усилий на каких-либо возможных перемещениях. Возможное перемещение, приводящее к этому наименьшему значению, определяет схему излома конструкции при исчерпании ее несущей способности (кинематический способ).
В каждом отдельном случае, в зависимости от вида конструкции, может быть применен как статический, так и кинематический способы. Как показывает практика, последний наиболее рационален для плитных конструкций.
При расчетах на ЭВМ рациональнее статический способ, который позволяет решить вопросы прочности широкого класса конструкций. При этом статический способ не требует для расчета знания схемы излома конструкции. Она получается как результат расчета совместно с несущей способностью.
1.18. Для обеспечения условий, отвечающих второй предпосылке метода предельного равновесия, т.е. возможности развития достаточных местных деформаций при достижении предельных условий элементов конструкций, следует соблюдать нижеперечисленные правила.
1. Проектировать конструкции так, чтобы причиной разрушения не могли быть срез сжатой зоны или (особенно в элементах двутаврового и таврового сечения) раздавливание бетона от главных сжимающих напряжений.
Учитывая, что изменение величин лишних неизвестных в процессе перераспределения усилий может вызвать как уменьшение, так и увеличение поперечных сил, следует с этим считаться и проводить необходимые расчетные проверки и соответствующие конструктивные мероприятия.
2. Применять для армирования конструкций стали, допускающие достаточно большие деформации в пластических шарнирах.
Этому условию удовлетворяют стали классов A-I - A-V и стали, подвергнутые термическому упрочнению, а также сварные сетки из холоднотянутой проволоки, высокопрочные проволоки, подвергнутые низкотемпературному отпуску.
3. Не допускается в статически неопределимых конструкциях, рассчитываемых с учетом перераспределения усилий, применять обычную и предварительно-напряженную арматуру, не имеющую сцепления с бетоном (пучки, пряди, стержни и канаты в каналах без инъецирования раствором, шпренгельные конструкции, оттянутые стержни и т.п.).
4. Подбирать основные расчетные сечения, а также места обрыва арматуры в элементах, работающих на поперечную нагрузку (балок, настилов), а также стоек, сжатых с большим эксцентрицитетом (рассчитываемых по первому случаю внецентренного сжатия), таким образом, чтобы относительная высота сжатой зоны по прочности отвечала граничным значениям строительных норм и правил.
Это ограничение не распространяется на стойки, не несущие крановых или иных консольных нагрузок и сжатые с небольшим эксцентрицитетом (рассчитанные по второму случаю внецентренного сжатия).
Вышеуказанное изъятие обосновывается тем, что в стойках при достаточной их длине и отсутствии нагрузок на консолях поперечные силы невелики, а поэтому изгибающие моменты изменяются по высоте медленно. В связи с этим, если предельное условие в наиболее опасном сечении обратится в равенство, то и на довольно значительном прилежащем участке возникают весьма ощутимые местные деформации. Накопляясь на относительно большой длине, эти деформации в состоянии будут обеспечивать достаточный взаимный угол поворота между сечениями, ограничивающими область больших деформаций на стойке. Наоборот, в элементах, работающих на поперечную нагрузку или на нагрузку, приложенную к консолям, в местах максимальных моментов часто действуют и значительные поперечные силы.
1.19. Зоны чрезмерных деформаций в состоянии предельного равновесия называются пластическими шарнирами, а в плитах - линиями излома.
Пластические шарниры и линии излома обращают статически неопределимую конструкцию в изменяемую, в которой становится возможным рост деформаций без возрастания нагрузки.
Расчетная схема конструкций, снабженная пластическими шарнирами и линиями излома, называется схемой излома конструкции.
В зависимости от рассматриваемой задачи в дальнейших разделах Руководства даются указания по использованию метода предельного равновесия в статической или кинематической постановке для оценки несущей способности и по выбору метода расчета для оценки эксплуатационных свойств.
В случае если необходимо учитывать деформации конструкции, развивающиеся перед исчерпанием несущей способности, то следует эти деформации определять расчетом и для оценки прочности конструкций применять метод предельного равновесия к деформированной (с измененной геометрией) системе.
Иными словами, следует рассматривать предельное равновесие не первоначальной (до приложения нагрузки) конструкции, а предельное равновесие новой конструкции, геометрические характеристики которой изменились в результате проявившихся деформаций.
Методы расчета ориентированы как на ручной счет или средства малой механизации, так и на использование электронно-вычислительных машин.
Методы расчета
2.1. Плоские плиты делятся на балочные и работающие в двух направлениях.
К балочным относятся прямоугольные равномерно нагруженные плоские плиты, опертые по двум противоположным сторонам и опертые по контуру с соотношением сторон  .
.
Балочные плиты рассматриваются при расчете как полосы шириною 1 м, вырезанные из плиты параллельно ее коротким сторонам.
Прямоугольные плиты при неравномерной нагрузке, равномерно нагруженные, прямоугольные, опертые по контуру, плиты при отношении сторон, равном трем или менее, плиты круглые и кольцевые, плиты более сложных форм, а также безбалочные перекрытия рассматриваются как работающие в двух направлениях.
Сборные настилы и плиты представляют собой обычно многопустотные или ребристые конструкции. В ребристых конструкциях сопротивление плит действию местных нагрузок рассчитывается, как правило, по методам, принятым для плит, работающих в двух направлениях.
В случаях когда конструкции покрытия или перекрытия придается неразрезность, расчет их как целого должен быть произведен дважды: на нагрузки, действующие до создания неразрезности, и на воздействия, которым они подвергаются после осуществления всех предусмотренных проектом связей. При этом для более правильной оценки эксплуатационных свойств целесообразно производить (согласно п. 1.10) учет перераспределения возникших при работе по разрезной схеме усилий за счет ползучести бетона. В нужных случаях следует учитывать и длительность работы плит по разрезной схеме согласно п. 1.10.
Если предусматривается создание предварительного напряжения, следует производить также и расчет на усилия, возникающие при обжатии конструкции.
2.2. Расчет несущей способности балочных плит железобетонных перекрытий с отношением сторон  при равномерно распределенной нагрузке рекомендуется производить, принимая соотношение между пролетным и опорным моментами из условия, чтобы полусумма опорных моментов плюс момент в середине пролета составляла
при равномерно распределенной нагрузке рекомендуется производить, принимая соотношение между пролетным и опорным моментами из условия, чтобы полусумма опорных моментов плюс момент в середине пролета составляла
Опорный момент на крайней свободной опоре принимается равным нулю. В остальных расчетных сечениях величина изгибающего момента принимается не меньшей, чем
В формулах (7) и (8) приняты следующие обозначения:
p = g + q - полная равномерно распределенная расчетная нагрузка;
g - постоянная равномерно распределенная расчетная нагрузка с коэффициентом перегрузки n > 1;
q - временная равномерно распределенная расчетная нагрузка с коэффициентом перегрузки n > 1;
l - расчетный пролет плиты.
Для пролетов плит, поддерживаемых с обеих сторон монолитно с ними связанными ребрами или балками, расчетный пролет l принимается равным пролету в свету.
При свободном опирании одного конца плиты на катковые или иные фиксированные опоры расчетный пролет принимается равным расстоянию свободной опоры от боковой поверхности противоположного ребра или балки. В случае плоского свободного опирания расчетный пролет увеличивается против пролета в свету на половину толщины плиты.
Расчет несущей способности балочных плит с неравными пролетами рекомендуется производить следующим образом:
а) начинать расчет с большого пролета; величину пролетного момента для этого пролета плиты принимать:
1) если больший пролет плиты является крайним - в пределах
 ; (9)
; (9)2) если больший пролет плиты является средним - в пределах
 ; (10)
; (10)б) в соответствии с принятой величиной расчетного пролетного момента определяются для того же большего пролета плиты значения опорных моментов из условия (7), чтобы полусумма опорных моментов плюс момент в середине пролета составила
в) полученные значения опорных моментов, откорректированные в соответствии с фактическим армированием на опорах, принимаются как заданные при определении расчетных моментов в соседних пролетах;
г) определение значений расчетных моментов (пролетных и опорных) рекомендуется производить в соответствии с табл. 5, в которой приведены числовые значения коэффициентов nx для вычисления максимальных значений пролетного момента балочных плит. Максимальное значение пролетного момента в каждом пролете  . Значения nx определяются по заданным nлев и nправ соответственно заданным значениям левого и правого опорных моментов (
. Значения nx определяются по заданным nлев и nправ соответственно заданным значениям левого и правого опорных моментов ( ,
,  ).
).
 . Значения nx определяются по заданным nлев и nправ соответственно заданным значениям левого и правого опорных моментов (
. Значения nx определяются по заданным nлев и nправ соответственно заданным значениям левого и правого опорных моментов ( ,
,  ).
).Таблица 5
nправ | nлев | |||||||||||||||||
8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | ||
14,2 | 13 | 12,5 | 11,9 | 11,5 | 11,2 | 11 | 10,7 | 10,4 | 10,3 | 10,1 | 10 | 9,9 | 9,8 | 9,7 | 9,6 | 9,5 | 8 | |
24 | 22,2 | 19,6 | 18 | 17 | 15,8 | 15,1 | 14,6 | 14,1 | 13,7 | 13,3 | 13,1 | 12,9 | 12,6 | 12,5 | 12,3 | 12,1 | 12 | 9,5 |
23 | 22,7 | 20 | 18,2 | 17,1 | 16,1 | 15,3 | 14,8 | 14,3 | 13,9 | 13,5 | 13,2 | 13,1 | 12,8 | 12,6 | 12,4 | 12,2 | 12,1 | 9,6 |
22 | 23,2 | 20,4 | 18,5 | 17,2 | 16,3 | 15,6 | 14,9 | 14,5 | 14 | 13,7 | 13,4 | 13,2 | 13 | 12,8 | 12,6 | 12,4 | 12,3 | 9,7 |
21 | 23,8 | 21 | 18,9 | 17,7 | 16,6 | 15,9 | 15,2 | 14,7 | 14,3 | 13,9 | 13,6 | 13,3 | 13,1 | 12,9 | 12,8 | 12,6 | 12,5 | 9,8 |
20 | - | 21,7 | 19,6 | 18,2 | 17 | 16,2 | 15,5 | 15 | 14,6 | 14,3 | 13,9 | 13,6 | 13,3 | 13,1 | 13 | 12,8 | 12,6 | 9,9 |
19 | - | 22,6 | 20,1 | 18,7 | 17,3 | 16,6 | 16 | 15,3 | 14,8 | 14,4 | 14,1 | 13,8 | 13,6 | 13,3 | 13,2 | 13,1 | 12,9 | 10 |
18 | - | 23,3 | 20,6 | 19,2 | 17,8 | 17 | 16,2 | 15,6 | 15,1 | 14,8 | 14,4 | 14,1 | 13,9 | 13,6 | 13,4 | 13,2 | 13,1 | 10,1 |
17 | - | 24 | 21,6 | 19,8 | 18,5 | 17,5 | 16,8 | 16,1 | 15,6 | 15,1 | 14,8 | 14,4 | 14,3 | 13,9 | 13,7 | 13,5 | 13,3 | 10,3 |
16 | - | - | 22,6 | 20,6 | 19,1 | 18,2 | 17,3 | 16,5 | 16 | 15,6 | 15,1 | 14,8 | 14,6 | 14,3 | 14 | 13,9 | 13,7 | 10,4 |
15 | - | - | 23,8 | 21,7 | 20 | 18,8 | 18 | 17,1 | 16,5 | 16,1 | 15,6 | 15,3 | 15 | 14,7 | 14,5 | 14,3 | 14,1 | 10,7 |
14 | - | - | - | 22,8 | 21,3 | 19,6 | 18,7 | 18 | 17,3 | 16,8 | 16,2 | 16 | 15,5 | 15,2 | 14,9 | 14,8 | 14,6 | 11 |
13 | - | - | - | 23,4 | 22,2 | 20,8 | 19,6 | 18,8 | 18,2 | 17,5 | 17 | 16,6 | 16,2 | 15,9 | 15,6 | 15,3 | 15,1 | 11,2 |
12 | - | - | - | - | 24 | 22,2 | 21,3 | 20 | 19,1 | 18,5 | 17,8 | 17,3 | 17 | 16,6 | 16,3 | 16,1 | 15,8 | 11,5 |
11 | - | - | - | - | - | 23,4 | 22,8 | 21,7 | 20,6 | 19,8 | 19,2 | 18,7 | 18,2 | 17,7 | 17,2 | 17,1 | 17 | 11,9 |
10 | - | - | - | - | - | - | - | 23,8 | 22,6 | 21,6 | 20,6 | 20,1 | 19,6 | 18,9 | 18,5 | 18,2 | 18 | 12,6 |
9 | - | - | - | - | - | - | - | - | - | 24 | 23,3 | 22,6 | 21,7 | 21 | 20,4 | 20 | 19,6 | 13 |
8 | - | - | - | - | - | - | - | - | - | - | - | - | - | 23,8 | 23,2 | 22,7 | 22,2 | 14,2 |
Расчет балочных плит с равными пролетами при армировании рулонными сетками рекомендуется производить следующим образом:
а) величину пролетных моментов в средних пролетах принимать по формуле
 ; (11)
; (11)б) величину опорных моментов на средних опорах, кроме вторых от края перекрытия, принимать по формуле
 ; (12)
; (12)в) величины пролетных моментов в крайних пролетах и над вторыми от края опорами перекрытия принимать по формуле
 . (13)
. (13)Примечание. Величины опорных моментов, вычисленные согласно рекомендациям пп. "б" и "в", относятся к сечениям плит на гранях опор.
Расчет балочных плит с равными пролетами при армировании плоскими сетками или отдельными стержнями рекомендуется производить по формулам как для равнопролетных второстепенных балок с равномерно распределенной нагрузкой (см. п. 3.2).
2.3. После появления трещин в местах защемлений и в пролете возникает удлинение геометрической оси элемента или срединной поверхности в плитах.
При наличии связей, препятствующих горизонтальным перемещениям (балки, плиты и др.), возникает усилие распора, которое повышает несущую способность и снижает деформативность элемента.
В случае отсутствия данных по определению податливости контура снижение арматуры в балочных плитах с  , окаймленных по всему контуру ребрами или балками, монолитно связанными с плитами, производится на 20% против найденной из расчета без учета распора.
, окаймленных по всему контуру ребрами или балками, монолитно связанными с плитами, производится на 20% против найденной из расчета без учета распора.
В крайних пролетах и над вторыми от края перекрытия опорами балочных плит уменьшение сечения арматуры против данных расчета без учета распора не производится.
Для оценки повышения несущей способности за счет влияния распора может быть использована следующая методика, которая предусматривает:
а) сохранение схемы излома конструкции в стадии предельного равновесия;
б) учет величины предельного прогиба при определении несущей способности конструкции;
в) определение внутренних предельных усилий с учетом как армирования, так и влияния усилий распора.
Увеличение высоты сжатой зоны за счет сил распора
 , (14)
, (14)где hб = 0,85h0 - xоп - xпр и xоп - xпр - высоты сжатой зоны на опоре и в пролете, определяемые из условия прочности и армирования;
 - относительный коэффициент податливости контура при жесткости его на растяжение EкFк;
- относительный коэффициент податливости контура при жесткости его на растяжение EкFк; ;
;  .
.Предельный прогиб конструкции с податливостью  равен:
равен:
 . (15)
. (15)Усилие распора равно: H = xнbRпр, а величина относительного момента от действия распора равна:
Предельная несущая способность конструкции определяется по методу предельного равновесия с учетом действия арочного момента  .
.
Так, для защемленной с двух сторон балочной плиты несущая способность с учетом распора будет:
 . (17)
. (17)2.4. Расчет трещиностойкости и прогибов неразрезных балочных плит производится в соответствии с требованиями п. 1.7 настоящего Руководства и указаниями действующих норм и руководств по проектированию бетонных и железобетонных конструкций.
Для определения распределения усилий с учетом трещинообразования и других неупругих свойств целесообразно использовать итерационные методы и вычислительную технику (см. п. 3.9).
Для приближенной оценки ширины раскрытия трещин и прогибов может быть использован следующий способ определения распределения усилий. Опорные моменты в неразрезных балочных плитах, вычисленные для однородной упругой системы, умножаются на поправочные коэффициенты  , принимаемые согласно рекомендациям п. 3.11 для неразрезных второстепенных балок.
, принимаемые согласно рекомендациям п. 3.11 для неразрезных второстепенных балок.
Пролетные моменты вычисляются по скорректированным опорным моментам методом подвески балочных эпюр.
2.5. Несущая способность плит, работающих в двух направлениях, определяется, как правило, по методу предельного равновесия.
При расчете методом предельного равновесия предполагается, что плита разламывается на плоские звенья, соединенные друг с другом по линиям излома линейными пластическими шарнирами. В зависимости от того, раскрываются ли трещины по линиям излома на нижней или верхней стороне плиты, эти линии излома называются положительными или отрицательными. Схема излома, образуемая линиями излома и опорными шарнирами плиты, должна удовлетворять следующим условиям:
а) сеть положительных или отрицательных линий излома, а если обе эти сети образуются на одной и той же плите, то каждая из них в отдельности должна разделять плиту на выпуклые фигуры (выпуклые многоугольники);
б) схема излома представляет собой однократно изменяемую систему, причем возможные перемещения ее согласуются с условиями закрепления плиты.
Для суждения о степени изменяемости схемы излома плиты можно пользоваться аналогией между нею, с одной стороны, и шарнирно-стержневой фермой той же конфигурации - с другой. При этом как стержни фермы рассматриваются все линии излома (независимо от их знака) и опорные шарниры плиты. Однократной изменяемости схемы излома плиты отвечает однократная статическая неопределенность соответствующей фермы.
Для данной схемы излома плиты соответствующая интенсивность нагрузки, заданной по ее конфигурации, определяется либо из равенства работ внешних и предельных внутренних сил на бесконечно малом возможном перемещении, обусловленном изменяемостью системы, либо из условий равновесия и условий прочности (п. 1.16). В последнем случае при расчетах на ЭВМ можно и не располагать схемой излома. Она получается наряду с величиной несущей способности как результат расчета.
Равенство виртуальных работ может быть записано в виде
где Pi - величина сосредоточенных грузов с коэффициентом перегрузки n > 1;
p - интенсивность (вообще зависящая от координат) распределенной нагрузки (см. п. 2.2);
yi - скорость возможных перемещений точек приложения сосредоточенных грузов;
y - скорость возможных перемещений точек плиты в области действия распределенных нагрузок;
Mк - предельный изгибающий момент на длине каждого линейного пластического шарнира (линии излома);
dF - дифференциал площади плиты.
В случае когда нагрузка на плите только равномерно распределенная, левую часть уравнения виртуальных работ можно записать в виде
 , (19)
, (19)где p - интенсивность равномерно распределенной нагрузки (п. 2.2), имеет то же значение, что и в формуле (18);
V - объем, описанный при виртуальном перемещении той частью плиты, на которой действует равномерно распределенная нагрузка.
Правую часть равенства виртуальных работ (18) можно также представить в виде
 , (20)
, (20)где Mj - предельный изгибающий момент, отвечающий всем стержням арматуры какой-либо группы;
При этом вся арматура плиты разбивается на группы стержней, характеризуемые следующими условиями:
а) все стержни одной группы взаимно параллельны;
б) оба конца каждого стержня группы закреплены в одной и той же паре звеньев схемы излома плиты.
Суммирование распространяется на все группы стержней.
При равномерной нагрузке равенство виртуальных работ может быть, следовательно, записано в виде
 . (21)
. (21)Из всевозможных схем излома плиты наиболее опасной является та, которой отвечает наименьшая интенсивность предельной нагрузки.
2.6. Сумма пролетных и опорных моментов (рис. 2) в панели прямоугольной, работающей в двух направлениях железобетонной плиты, должна удовлетворять условию
где p - имеет то же значение, что и в формулах (7) и (8);
l1 и l2 - меньший и больший расчетные пролеты плиты, значения которых в зависимости от условия опирания плиты принимаются согласно п. 2.2.

предельных моментов прямоугольной плиты
В основу расчета прямоугольных плит, имеющих опоры по всем четырем сторонам, при соотношении большого пролета к меньшему  положено предельное состояние, характеризуемое образованием линейных пластических шарниров, указанных в схеме плиты, изображенной на рис. 3, а.
положено предельное состояние, характеризуемое образованием линейных пластических шарниров, указанных в схеме плиты, изображенной на рис. 3, а.

а - расположение пластических шарниров;
б - план скоростей вращения жестких звеньев при скорости
поступательного перемещения центра плиты, равного 1:
1 - пролетные шарниры; 2 - опорные шарниры
При скорости поступательного перемещения линий излома AB (рис. 3, а), равной 1, работа на возможном перемещении равномерной внешней нагрузки согласно п. 2.5 составляет:
 .
.Скорости вращения каждого из четырех звеньев схемы излома относительно опор равны 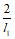 , а диаграмма скоростей имеет вид, показанный на рис. 3, б. Отсюда для моментов, отвечающих нижней арматуре, проходящей из звена 1 в звено 3 (момент
, а диаграмма скоростей имеет вид, показанный на рис. 3, б. Отсюда для моментов, отвечающих нижней арматуре, проходящей из звена 1 в звено 3 (момент  , рис. 3, а) и из звена 2 в звено 4 (момент
, рис. 3, а) и из звена 2 в звено 4 (момент  ), множителем в уравнении работ является величина
), множителем в уравнении работ является величина  . Для моментов, отвечающих каждой группе стержней верхней арматуры, которая пересекает на контуре одну из отрицательных линий излома (моменты с римскими индексами, рис. 2), множитель равен
. Для моментов, отвечающих каждой группе стержней верхней арматуры, которая пересекает на контуре одну из отрицательных линий излома (моменты с римскими индексами, рис. 2), множитель равен  . Работа внутренних сил составляет:
. Работа внутренних сил составляет:
 .
.Приравняв работу внешних и внутренних сил на возможном перемещении и произведя соответствующие преобразования, получим формулу (22).
Величины пролетных и опорных моментов  ,
,  ,
,  ,
,  ,
,  ,
,  , входящих в формулу (22), определяются путем умножения соответствующих площадей сечений арматуры
, входящих в формулу (22), определяются путем умножения соответствующих площадей сечений арматуры  ,
,  ,
,  ,
,  ,
, 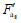 на их расчетные сопротивления и на плечо внутренней пары z:
на их расчетные сопротивления и на плечо внутренней пары z:
 (23)
(23)где z - плечо внутренней пары сил для соответствующего сечения плиты;
Ra - расчетное сопротивление арматуры;
Стержни, отогнутые или обрываемые до пересечения с пролетным пластическим шарниром (рис. 4), в общую площадь  и
и  не включают (т.е. не включают те из стержней, обрываемых или отогнутых на расстоянии a от опор, которые расположены на участке плиты b = a от краев панели).
не включают (т.е. не включают те из стержней, обрываемых или отогнутых на расстоянии a от опор, которые расположены на участке плиты b = a от краев панели).

Рис. 4. Место обрыва части продольных и поперечных
стержней прямоугольной плиты
Площадь сечения стержней, которые расположены на участках b, но отгибаются или обрываются лишь у одной из опор и пересекают пролетный пластический шарнир одним своим концом, включают в общую площадь сечения арматуры  и
и 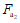 , в размере только 50%.
, в размере только 50%.
2. При наличии у плиты свободных опор значения опорных моментов 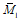 ,
,  ,
,  ,
,  для свободной (незащемленной) опоры принимают равными нулю.
для свободной (незащемленной) опоры принимают равными нулю.
3. Значения опорных отрицательных моментов принимаются по формулам (22), (25), (26) по их абсолютной величине без учета знака момента.
Если нижняя арматура обрывается, частью или полностью не доходя до опор, на расстояниях a2 от коротких сторон и a1 от длинных сторон плиты, то кроме расчета по схеме излома плиты (см. рис. 3) и формуле (22) следует произвести проверку допустимости обрыва или отгиба стержней исходя из схемы излома плиты (рис. 5), пользуясь формулой (24):
где

прямоугольника по месту обрыва пролетной арматуры
Формула (24) выведена на основании тех же соображений, что и формула (22), из условия одновременно возможного образования при разрушении схемы излома по рис. 5.
Допустимость мест обрыва верхней арматуры может быть проверена приближенно (в запас прочности), учитывая в формуле (22) только нижнюю арматуру и вводя вместо пролетов плиты длины тех частей пролетов, на которых верхняя арматура отсутствует.
По экономическим и конструктивным соображениям при подборе сечения необходимо руководствоваться следующими рекомендациями.
1. При армировании плит отдельными стержнями или плоскими сварными сетками соотношение  между площадями сечения арматур, укладываемых на 1 м ширины плиты, назначать в зависимости от отношения пролетов плиты
между площадями сечения арматур, укладываемых на 1 м ширины плиты, назначать в зависимости от отношения пролетов плиты  согласно табл. 6.
согласно табл. 6.
1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2 - 3 | |
1 - 0,8 | 0,9 - 0,7 | 0,8 - 0,6 | 0,7 - 0,5 | 0,6 - 0,4 | 0,65 - 0,35 | 0,5 - 0,3 | 0,45 - 0,25 | 0,4 - 0,2 | 0,35 - 0,2 | 0,2 - 0,15 |
2. При армировании плит рулонными сварными сетками применять для отношения сторон панелей  сетки с квадратными ячейками и одинаковыми диаметрами стержней обоих направлений, а для отношения сторон панелей
сетки с квадратными ячейками и одинаковыми диаметрами стержней обоих направлений, а для отношения сторон панелей  принимать соотношение
принимать соотношение  между площадями сечения арматур, укладываемых на 1 м ширины плиты, согласно табл. 6.
между площадями сечения арматур, укладываемых на 1 м ширины плиты, согласно табл. 6.
3. Соотношение между площадями сечения опорной и пролетной арматур, укладываемых на 1 м плиты:
назначать в пределах 1 - 2,5; при этом для средних пролетов рекомендуется принимать эти соотношения ближе к 2,5.
2.7. Для плит, работающих в двух направлениях и окаймленных по контуру балками, а также для средних полей неразрезных плит величина относительного коэффициента  (см. п. 2.3), учитывающего влияние распора, устанавливается расчетом. При этом предельные прогибы плиты определяются по методике, изложенной в п. 2.15 настоящего Руководства. Для среднего поля неразрезной плиты значение
(см. п. 2.3), учитывающего влияние распора, устанавливается расчетом. При этом предельные прогибы плиты определяются по методике, изложенной в п. 2.15 настоящего Руководства. Для среднего поля неразрезной плиты значение  может быть принято:
может быть принято:
а) для монолитных плит без учета окаймляющих балок  ;
;
б) для плит с учетом окаймляющих балок  . Общая несущая способность плит с распором определяется из условия сохранения постоянного значения арочного момента
. Общая несущая способность плит с распором определяется из условия сохранения постоянного значения арочного момента  [формула (16)] вдоль защемленных сторон.
[формула (16)] вдоль защемленных сторон.
Так, для прямоугольной плиты, защемленной по четырем сторонам, при равномерно распределенной нагрузке предельная несущая способность с учетом влияния распора равна:
При отсутствии данных о податливости контура можно принять следующее снижение расчетного сечения арматуры. Для плит, окаймленных со всех сторон балками или ребрами, благоприятное влияние распора оценивается для средних полей плит и над средними опорами снижением сечения арматуры на 20%.
В крайних полях плит и над вторыми от края перекрытия опорами
при  - на 20%;
- на 20%;
при  - на 10%;
- на 10%;
 - на 10%;
- на 10%;при  снижения сечения арматуры не производится.
снижения сечения арматуры не производится.
Здесь l - величина расчетного пролета в направлении, перпендикулярном краю перекрытия;
lк - величина пролета крайнего поля, измеряемая вдоль края перекрытия.
Соответственно этому в надлежащих случаях в левую часть уравнения работ (22) вводится понижающий коэффициент  , равный 0,8 или 0,9.
, равный 0,8 или 0,9.
2.8. При расчете несущей способности плит, загруженных сосредоточенным грузом, схема излома может определяться из условий минимума несущей способности плиты. К реальной ближе будет та схема излома, которой соответствует меньшая несущая способность. Иными словами, схема излома может быть определена из условий минимума несущей способности. Это положение будет справедливо для любой конфигурации плит и при различных видах и схемах загружений.
Для определения схемы излома плиты при одном сосредоточенном грузе можно воспользоваться формулой, определяющей характер трещин излома в углах плиты (рис. 6), которая имеет вид:

Рис. 6. Характер трещин излома в углах плиты
при сосредоточенном грузе
1 - груз; 2 - биссектриса
2.9. Для свободно опертых и симметрично защемленных прямоугольных и квадратных плит, ослабленных квадратными отверстиями, при равномерной нагрузке и равномерном по пролету плиты армировании схема излома плиты может быть принята с расположением пластических шарниров по тем же направлениям, что и в плитах без отверстий. Наличие отверстий следует учитывать как при вычислении работ внутренних, так и внешних сил.
Для квадратной плиты (с квадратным отверстием в центре) несущая способность при равномерной нагрузке и одинаковом в обоих направлениях армировании нагрузка может вычисляться по следующей формуле:
 , (29)
, (29)где m - предельный момент на единицу длины пластического шарнира;
l - сторона плиты;
Для прямоугольной плиты с квадратным отверстием в центре плиты несущая способность при равномерной нагрузке может вычисляться по следующей формуле:
 , (30)
, (30)где m1 - момент на единицу длины в сечении, параллельном длинной стороне плиты;
m2 - момент на единицу длины в сечении, параллельном короткой стороне;
Для круглых свободно опертых плит, армированных равномерной квадратной сеткой, расчет на равномерную нагрузку производится по формуле
 , (31)
, (31)где fa - сечение арматуры каждого из направлений стержней сетки, отнесенное к единице длины, перпендикулярного стержням сечения;
r - радиус плиты.
Для таких же плит, ослабленных круглым отверстием, не выходящим на контур и расположенным как в центре плиты, так и на радиусе, расчет несущей способности производится по формуле
 , (32)
, (32)где m - предельный момент на единицу длины пластического шарнира;
r - радиус плиты;
2.10. В том случае когда схема излома плиты неизвестна и назначение ее затруднительно (при сложных формах загружений и конфигураций плит), требующих сложных и громоздких вычислений, определение несущей способности плиты можно производить методами математического программирования, ориентированными на использование ЭВМ.
При этом задачи могут быть сформулированы следующим образом:
Первая задача. При заданных внешних силах, геометрических размерах плиты и ее армировании найти такое распределение внутренних сил в плите (изгибающих и крутящих моментов), которые одновременно удовлетворяют уравнениям равновесия и условиям прочности. При этом должны соблюдаться граничные условия, определяемые способом опирания плиты.
Если такая задача имеет решение, то несущая способность плиты не исчерпана действующей нагрузкой. В противном случае нагрузка выше предельной.
Как правило, решение такой задачи связано с большим объемом вычислений.
Вторая задача. Выделяется некоторая характерная нагрузка, а остальные нагрузки считаются постоянными, причем принимается, что характерная нагрузка изменяется пропорционально параметру p, а постоянная нагрузка задана по своей величине. При этих предположениях требуется определить максимальную несущую способность плиты, т.е. максимальное значение параметра p. Геометрия плит и армирование считаются заданными.
Для решения задач целесообразно воспользоваться статическим принципом метода предельного равновесия, который заключается в следующем: определить максимально возможную нагрузку p*, которая может быть уравновешена (в соответствии с уравнениями равновесия) внутренними силами, не нарушающими условия прочности. При этом соблюдение граничных условий обязательно.
Эта задача сводится к задаче математического (выпуклого) программирования следующим образом.
Условия равновесия пластин
заменяются конечно-разностной системой уравнений
где Mxx, Myy и Mxy - изгибающие и крутящие моменты; r(x, y) - интенсивность характерной нагрузки; p - параметр характерной нагрузки; G(x, y) - постоянная нагрузка.
Уравнение (34) есть конечно-разностный (сеточный) аналог уравнения (33), учитывающий граничные условия.
Условия прочности принимаются в виде системы нелинейных неравенств, которые в случае произвольного армирования записываются в виде:
где  и
и  - предельные значения положительных изгибающих моментов;
- предельные значения положительных изгибающих моментов;
Эти предельные значения изгибающих моментов определяются согласно рекомендациям руководства по проектированию бетонных и железобетонных конструкций.
Уравнения (34) вместе с неравенствами (35) или (36) составляют условия, накладываемые на переменные в точках выбранной сетки, и при этих условиях требуется определить p* = pmax(M).
Последнее может быть реализовано методами выпуклого программирования или, если неравенства (35) или (36) линеаризовать, то можно использовать алгоритм симплекс-метода, решающий задачу со смешанными ограничениями - равенствами и неравенствами.
В результате решения этой задачи получается предельная величина характерной нагрузки p*.
Если заданная нагрузка p0 <= p*, то для фиксированной остальной нагрузки несущая способность плиты обеспечена.
2.11. Для численного решения задачи могут быть использованы стандартные программы математического программирования.
Переменные решаемой задачи есть  ,
,  и
и  , где верхние индексы i, j обозначают номер узла сетки. Эти переменные могут быть любого знака, тогда как большинство стандартных программ ориентировано только на неотрицательные переменные.
, где верхние индексы i, j обозначают номер узла сетки. Эти переменные могут быть любого знака, тогда как большинство стандартных программ ориентировано только на неотрицательные переменные.
Условия прочности (35) позволяют внести новые переменные, которые оказываются несвободными и уменьшают число условий:
 ;
;  ;
;  .
.Использование переменных z не меняет уравнения равновесия (33) или (34) и упрощает систему неравенств (35).
При использовании алгоритмов программ симплекс-метода рекомендуется выбирать такие стандартные программы, которые позволяют вводить матрицы условий в "плотной" записи, т.е. без нулевых элементов.
Обычно система уравнений (34) и линеаризованная система неравенств (35) имеет заполнение матрицы условий прочности ненулевыми элементами порядка 10 - 15%.
При численной реализации задачи симплекс-методом возможно явление зацикливания на оптимальных планах. Это объясняется неединственностью распределения внутренних сил в предельном состоянии. Поэтому необходимо предусматривать специальные приемы, защищающие вычислительный процесс от зацикливания.
К ним относятся: а) специальные программы-приставки, анализирующие процесс на зацикливание и выдающие (на печать ЭВМ) один из оптимальных планов; б) программы симплекс-метода с возможностью расщепления при зацикливании; в) использование алгоритмов с регуляризацией, заключающейся в изменении целевой функции. Если в исходной задаче определяется максимум p(M) или p(z), то в регуляризованной задаче следует определять максимум квадратичной формы
 , (37)
, (37)где  - суммирование производится по всем узлам сетки;
- суммирование производится по всем узлам сетки;  - малый параметр регуляризации. Обычно
- малый параметр регуляризации. Обычно  назначается из условия, что для оптимального плана задачи
назначается из условия, что для оптимального плана задачи  .
.
 - суммирование производится по всем узлам сетки;
- суммирование производится по всем узлам сетки;  .
.Для решения задачи методами нелинейного программирования не рекомендуются стандартные программы алгоритмов градиентного типа. Наиболее подходящими в этом случае являются алгоритмы случайного поиска, метод конфигураций и метод проекции градиента.
При использовании ЭВМ с высокой скоростью счета рекомендуется задачу свести к задаче определения безусловного максимума функции многих переменных.
2.12. В расчете учитываются постоянная нагрузка G(x, y) и единичная характерная нагрузка pr(x, y) при p = 1.
Для заданной таким образом нагрузки определяются единичные решения  ,
,  ,
,  и
и  ,
,  ,
,  . Эти решения определяются обычными методами теории упругости. Решение Mp - только для нагрузки r(x, y), а решение MG - только для нагрузки G(x, y).
. Эти решения определяются обычными методами теории упругости. Решение Mp - только для нагрузки r(x, y), а решение MG - только для нагрузки G(x, y).
Общее решение задачи о несущей способности является суммой единичных решений и самоуравновешенного
 , (38)
, (38)ИС МЕГАНОРМ: примечание. Экспликация дана в соответствии с официальным текстом документа. |
где MG и Mp - полученные ранее решения;
p - параметр изменения характерной нагрузки;
Mo - самоуравновешенные внутренние силы, удовлетворяющие однородным уравнениям равновесия:
Граничные условия для самоуравновешенных внутренних сил следующие. Если на части контура плиты заданы граничные условия для внутренних сил, то для самоуравновешенных внутренних сил эти граничные условия аналогичные. Например, если опирание шарнирное, то граничное условие Mxx = 0 распространяется и на самоуравновешенный момент -  .
.
Если граничные условия формулируются в перемещениях, то для самоуравновешенных внутренних сил граничные условия не ставятся.
Однородное уравнение (39) допускает введение функции напряжений, которая должна удовлетворять граничным условиям:
 ;
;  ;
;  . (40)
. (40)Тогда общее выражение для внутренних сил
где
 ;
;  ;
; 
тождественно удовлетворяет уравнениям равновесия (33). Это выражение вводится в условия прочности (35) или (36). В итоге задача сводится к системе неравенств (35), в которой используются новые переменные p и Ф(x, y), причем необходимо произвести подстановку выражения (41) в (35) или (36), что легко осуществляется вложением процедур.
Условия (35) приводятся к такому виду. Вводятся новые переменные:
Тогда (35) записывается так:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
Далее, для переменных p и Ф подстановкой (41) в (42) и результата в (43) формируется система неравенств относительно этих переменных. При этих условиях требуется определить
p* = max p(Ф).
Для решения задачи о безусловном максимуме вводится функция f(p, Ф):
Затем составляется функция со штрафом
где  - цена штрафа;
- цена штрафа;
m >= 0 - показатель штрафа;

Те значения  и
и  , которые доставляют максимум функции (45), практически и есть полное решение задачи предельного равновесия. Переход от функции напряжений
, которые доставляют максимум функции (45), практически и есть полное решение задачи предельного равновесия. Переход от функции напряжений  к внутренним силам производится по формуле (41).
к внутренним силам производится по формуле (41).
2.13. Наиболее распространенный прием представления функции напряжений в виде конечных разностей. Если для плиты назначена некоторая сетка с узлами, пронумерованными в определенном порядке от 1 до N, причем n узлов граничные, в которых функция напряжения задана (рамная аналогия здесь в полной мере сохраняет силу), тогда имеется всего N1 = N - n внутренних узлов в поле плиты, для которых должны быть составлены условия (43).
Обозначим  i-ю функцию из (43) для j-го узла.
i-ю функцию из (43) для j-го узла.
 i-ю функцию из (43) для j-го узла.
i-ю функцию из (43) для j-го узла.Тогда функция (44) принимает вид
Здесь всего 1 + N1, переменных p и Фj(j = 1, ..., N1), где Фj - значение функции напряжений в j-м узле.
Решение задачи осуществляется в четыре этапа.
Этап 1. Решается упругая задача, в которой определяются MG и Mp. Решение можно осуществлять любым известным методом.
Этап 2. Приняв в качестве исходных значений p = 1 и Фj = 0 (j = 1, ..., N1), а также  , решается задача о безусловном экстремуме функции N1 + 1 аргумента (45). Как правило, в результате этого решения получается величина p0 и остается Фj = 0 (j = 1, ..., N), что характеризует максимально допустимое упругое решение.
, решается задача о безусловном экстремуме функции N1 + 1 аргумента (45). Как правило, в результате этого решения получается величина p0 и остается Фj = 0 (j = 1, ..., N), что характеризует максимально допустимое упругое решение.
Этап 3. Составляется стабилизирующий функционал
где  - сеточный оператор Лапласа.
- сеточный оператор Лапласа.
Используя в качестве начального значения p0 и Фj, полученные на предыдущем этапе, решается задача о максимуме функции
где  определяется по (45);
определяется по (45);
 определяется по (45);
определяется по (45);u(Ф) определяется по (47);
В результате решения этой задачи получаются p1 и Фj, доставляющие максимум функции (48).
Этап 4. Если условия (49) для полученных на предыдущем этапе значений Фj выполняются с точностью до 30%, то  остается без изменения. В противном случае принимается новое значение
остается без изменения. В противном случае принимается новое значение
 .
.Затем решается задача о безусловном максимуме функционала
 . (50)
. (50)В результате получаются решения p2 и Фj. Если абсолютная величина разности 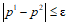 - заданной точности, то задача считается решенной. В противном случае следует уменьшить
- заданной точности, то задача считается решенной. В противном случае следует уменьшить  в два раза и снова повторить расчет, начиная с этапа 3. Если условие точности выполнено, то переход от Фj к внутренним силам по формуле (41) дает действительное распределение внутренних сил в состоянии предельного равновесия.
в два раза и снова повторить расчет, начиная с этапа 3. Если условие точности выполнено, то переход от Фj к внутренним силам по формуле (41) дает действительное распределение внутренних сил в состоянии предельного равновесия.
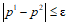 - заданной точности, то задача считается решенной. В противном случае следует уменьшить
- заданной точности, то задача считается решенной. В противном случае следует уменьшить Примечания: 1. Выбор цены и штрафа  не обязателен, а может быть назначен из других соображений. Обычно это соответствует величине
не обязателен, а может быть назначен из других соображений. Обычно это соответствует величине  , где p* - предельное значение параметра нагрузки,
, где p* - предельное значение параметра нагрузки,  - заданная точность выполнения условий прочности (43).
- заданная точность выполнения условий прочности (43).
 , где p* - предельное значение параметра нагрузки,
, где p* - предельное значение параметра нагрузки, 2. При сомнениях относительно назначения цены штрафа 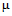 следует повторить расчет, приняв новое значение
следует повторить расчет, приняв новое значение  увеличенным в 10 раз.
увеличенным в 10 раз.
3. Показатель степени m рекомендуется применять m = 1 в случае применения алгоритмов поиска максимума, не связанных с вычислением градиента, и принимать m > 1 (обычно m = 2) в случае градиентных способов поиска максимума. Однако в силу специфических особенностей задачи эти методы следует применять с большей осторожностью, учитывая, что функция (46) не является непрерывно дифференцируемой.
Изложенный выше метод выгодно отличается от всех предыдущих существенно меньшим числом переменных (уменьшение в 3 раза и исключение из ограничений задачи системы уравнений).
Вследствие этого существенно уменьшается объем вычислений и решение можно осуществлять методами нелинейного программирования.
2.14. Если на плиту действует система внешних нагрузок Q1, Q2, ..., Q8 и требуется производить расчет на различные их сочетания, то рекомендуется следующий прием.
Зафиксируем все нагрузки, кроме i-той, в каком-то их сочетании и будем эти нагрузки рассматривать как постоянные. Нагрузку с номером i рассматриваем как изменяющуюся пропорционально параметру pi.
Решив задачу о несущей способности при характерной нагрузке pi и постоянной  ,
,  , ...,
, ...,  получаем первый вектор
получаем первый вектор
 .
.Выбрав другое значение j и при необходимости изменив остальные нагрузки 
 , которые считаются постоянными, снова решаем задачу о несущей способности. Получаем вектор
, которые считаются постоянными, снова решаем задачу о несущей способности. Получаем вектор
 .
.Произведя несколько таких расчетов и получив t векторов Ak (k = i1, i2, ..., it), допустимая область для нагрузок строится как выпуклая линейная оболочка векторов Ak. Это значит, что любое сочетание нагрузок вида  , будет допустимым, если найдутся t положительных чисел
, будет допустимым, если найдутся t положительных чисел  и выполняются следующие неравенства:
и выполняются следующие неравенства:
 , будет допустимым, если найдутся t положительных чисел
, будет допустимым, если найдутся t положительных чисел  ;
;  .
.Эти неравенства понимаются покомпонентно
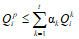 ,
,где  - i-тая компонента вектора Ak.
- i-тая компонента вектора Ak.
Примечание. Решение задач предельного равновесия для различных нагрузок отличается только упругими решениями, составляющими выражение (41). Реализация этих задач возможна по единой ведущей программе, в которой указывается только номер нагрузки, принимаемой в качестве характерной.
2.15. Приближенная оценка прогибов плит, работающих в двух направлениях (п. 1.8), производится по формуле
где pт < p < pп;
fт и pт - прогиб и нагрузка при образовании трещин;
fп и pп - прогиб и нагрузка, соответствующие предельному состоянию по прочности при характеристиках материалов RaII, RпрII;
p - расчетная равномерно распределенная нагрузка с коэффициентом перегрузки, равным единице.
Для шарнирно опертых плит прогиб fт определяется как для упругой плиты по формулам строительной механики.
Для защемленных по контуру плит за прогиб fт следует принимать прогиб при образовании трещин в пролете, когда трещины в защемлениях уже имеются. Поэтому формулами строительной механики для определения fт пользоваться не рекомендуется. Расчетная схема плиты в данном случае может быть представлена в виде шарнирно опертой плиты, загруженной заданной нагрузкой и неизвестными моментами вдоль защемленных сторон. Неизвестные моменты могут быть определены из условия, что сумма углов поворота опорного сечения в местах заделки от действия внешней нагрузки и от действия неизвестных моментов равна величине угла, определяемой из условий ширины раскрытия трещин. Жесткость заделки B уменьшается с увеличением момента в заделке.
Для определения усилий и прогибов в момент образования трещин в пролете плиты после образования трещин в местах защемления можно воспользоваться следующим приближенным расчетом. Усилия и прогибы в плите на приращение нагрузки после образования трещин в местах защемления и до образования трещин в пролете определяются как в свободно опертой плите. Прогиб fп при исчерпании несущей способности определяется из условия, что перемещения точек плиты пропорциональны соответствующим скоростям вращения жестких звеньев схемы излома плиты, а наименьший угол перелома между соседними звеньями в схеме излома равен  , где
, где  - ширина полосы вдоль линии излома, на которой предполагается достижение арматурой предельных сопротивлений. Величина кривизны принимается равной:
- ширина полосы вдоль линии излома, на которой предполагается достижение арматурой предельных сопротивлений. Величина кривизны принимается равной:
 и
и  .
.В плите с максимальным действием распора
 . (53)
. (53)Предельный прогиб равен:
 , (54)
, (54)где  - наименьший угол перелома в пролете плиты между дисками n и m;
- наименьший угол перелома в пролете плиты между дисками n и m;
Методика определения прогиба плиты fп основана на том, что при достижении текучести арматуры на линии излома, где угол перелома наименьший, конструкция плиты становится изменяемой и несущая способность ее исчерпывается.
Учитывая, что ширина наиболее деформируемой зоны  близко соответствует ширине зоны образования трещин, а образование трещин незначительно меняет величины моментов, ширину наиболее деформируемой зоны можно определять по зонам трещинообразования, определенным по данным расчета упругих плит.
близко соответствует ширине зоны образования трещин, а образование трещин незначительно меняет величины моментов, ширину наиболее деформируемой зоны можно определять по зонам трещинообразования, определенным по данным расчета упругих плит.
В табл. 7 приведены выражения предельных прогибов fп для некоторых видов плит и видов загружений.
N схемы | Нагрузка | Вид плиты | Формулы для определения предельного прогиба |
I | Равномерно-распределенная |  | При  |
 | |||
II | То же |  | При  |
 , где , где | |||
III | " |  | При  |
 | |||
IV | " |  | При  |
 | |||
V | " |  | При  |
 | |||
VI | " |  | При  |
 | |||
VII | " |  | |
VIII | " |  |  |
IX | Сосредоточенный груз в центре плиты |  | При  |
 | |||
X | Сосредоточенный груз в одной четверти диагонали |  | При  |
 |
Примечание. l1 - короткая сторона; fп - максимальный прогиб под грузом; a - расстояние от опорного контура до кольцевой трещины, определяемое при расчете несущей способности.
Приближенная оценка прогибов плит с отверстиями, не выходящими на контур, может быть произведена как для плит без отверстий для той же интенсивности нагрузки.
Для приближенной оценки ширины раскрытия трещин в плитах рекомендуется напряжение в арматуре определять по формуле
 . (55)
. (55)Здесь  - напряжение в арматуре в момент образования трещин, определяемое по формуле
- напряжение в арматуре в момент образования трещин, определяемое по формуле
 , (56)
, (56)где Mт - момент на единицу ширины плиты при образовании трещин  ;
;
Fa - площадь растянутой арматуры на той же ширине;
2.16. Более полную и более точную оценку эксплуатационных свойств работающих в двух направлениях железобетонных плит с трещинами можно производить на основе теории деформирования плит, учитывающей анизотропию, создаваемую как направлением трещин, так и направлением армирования. Такая оценка может быть выполнена только при использовании современных ЭВМ. Это может потребоваться при создании типовых конструкций массового изготовления, плит сложной конфигурации при создании конструкций специального назначения, у которых вопросы деформативности и трещиностойкости могут играть решающую роль и при проведении исследований взамен постановки дорогостоящих экспериментальных исследований. В остальных случаях достаточной оказывается приближенная оценка деформативности и трещиностойкости плит, изложенная выше (см. п. 2.15).
Рассматриваются пластинки, подвергнутые пропорциональному нагружению силами, нормальными к срединной поверхности.
Обозначим: h - толщина плиты; R, RпрII, RрII - соответственно марка бетона, расчетная прочность бетона при сжатии и растяжении; Eб - начальный модуль упругости бетона. Полагаем, что пластина армирована прямоугольными сетками, располагаемыми близ ее поверхностей. Стержни сеток (верхних и нижних) ориентированы вдоль координатных осей x и y (рис. 7). Характеристики, связанные или относящиеся к стержням x и y направлений, снабжаются соответственно нижними индексами x и y. Обозначим: fai(i = x, y) - коэффициенты нижнего армирования (fai = Fai/Si, где Fai - площадь стержня, а Si - шаг стержней в сетке); hi - полезные высоты плиты (расстояния от центра тяжести нижней арматуры до верхней поверхности плиты); h0 = 0,5(hx + hy); di - диаметры стержней;  - пределы упругости;
- пределы упругости;  - пределы текучести, а
- пределы текучести, а  - пределы прочности стержней; Ea - модуль упругости арматуры. Аналогичные характеристики для верхней арматуры будем снабжать верхними штрихами (например, fai,
- пределы прочности стержней; Ea - модуль упругости арматуры. Аналогичные характеристики для верхней арматуры будем снабжать верхними штрихами (например, fai,  , h0 и т.д.).
, h0 и т.д.).

1 - плита; 2 - нижняя сетка; 3 - верхняя сетка
Метод расчета изложен в виде, удобном для использования ЭВМ.
Рассматривается расчет пластин без учета нормальных сил и при кратковременном действии нагрузки.
Изучение характера деформирования плит позволяет выделить четыре основные стадии работы железобетона малых ее элементов (сокращенно у отдельных ее точек);
1) упругая стадия без трещин;
2) упругопластическая стадия без трещин (связанная с развитием пластических деформаций в бетоне растянутой зоны);
3) стадия с трещинами при упругой работе арматуры в трещинах;
4) стадия с трещинами после появления пластических деформаций в растянутой арматуре (применительно к оценке деформаций).
Система уравнений, описывающая поведение железобетонных плит при всех указанных стадиях, может быть записана в виде:
где W - функция прогибов; Bik - жесткостные коэффициенты; Mx, My, Mxy - моменты; p(x, y) - нагрузка.
Уравнение равновесия справедливо для всех стадий, изменяются лишь уравнения (57).
1-я стадия. Для упругой стадии без трещин справедлива теория упругих изотропных пластинок, при этом в (57) следует принять:
где D - цилиндрическая жесткость; 0,2 - коэффициент поперечной деформации.
Упругая стадия может считаться справедливой, если абсолютная величина главных моментов
|Mмакс| <= 0,5 Mт; |Mмин| <= 0,5 Mт, (60)
где Mт - упругопластический момент трещинообразования, равный для полосы плиты b = 1 см;
Mт = h2RрII/3,5. (61)
2-я стадия может ограничиваться неравенствами:
0,5 Mт < |Mмакс| <= Mт или 0,5 Mт < |Mмин| <= Mт. (62)
Для этой стадии характерно постепенное падение жесткости за счет развития неупругих деформаций растянутой зоны бетона. В расчетах можно использовать скорректированные выражения (59), где цилиндрическая жесткость D заменяется значением жесткости D1, представленной в виде
 , (63)
, (63)где  - максимальная из двух величин |Mмакс| и |Mмин|.
- максимальная из двух величин |Mмакс| и |Mмин|.
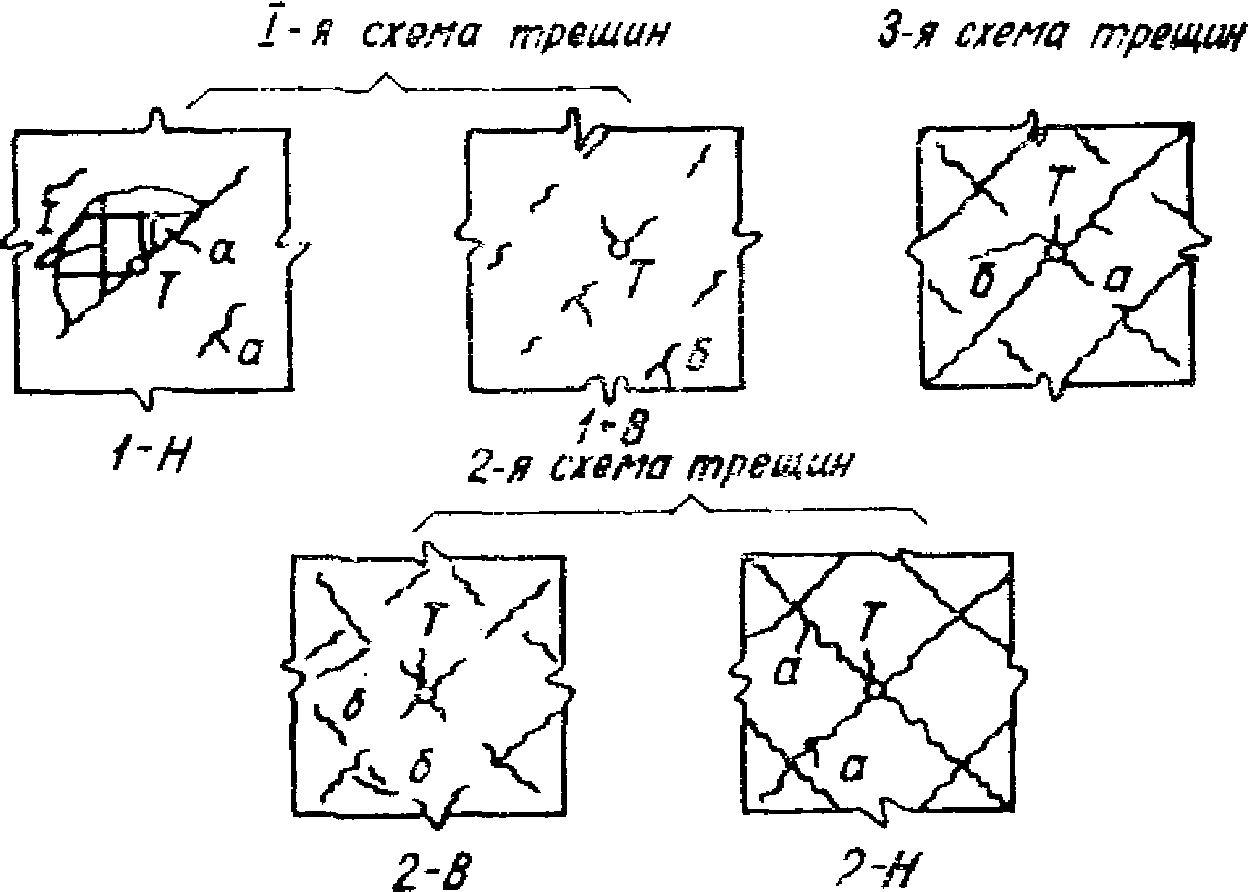
3-я стадия. Для стадии с трещинами выражения (57) зависят от схемы трещин. Можно выделить три основные схемы трещин (рис. 8): 1 - схема наклонных к арматуре и непересекающихся между собой трещин; 2 - схема пересекающихся между собой трещин на одной из поверхностей пластины; 3 - схема двух групп наклонных к арматуре трещин, одна из которых расположена на верхней поверхности плиты, а другая - на нижней.
а - трещины на нижней поверхности плиты;
б - трещины на верхней поверхности плиты;
1 - стержни арматурной сетки; Т - рассматриваемая точка;
Н - нижняя поверхность;  - верхняя поверхность
- верхняя поверхность
Для выявления точек с трещинами необходимо задаться условиями трещинообразования. При решении задач методом конечных разностей (это метод принят в качестве основного) условия трещинообразования и возникновение определенных схем трещин можно рассматривать лишь для отдельных точек поля плиты. При этом схемы 1 и 2 могут образовываться либо на нижней, либо на верхней поверхностях плиты. При этом, если
Mмакс > Mт, |Mмин| < Mт, (64)
то на нижней поверхности у рассматриваемой точки образуется одна трещина (схема 1-Н), которая пройдет по площадке Mмакс. Угол наклона трещины к оси x определяется по формуле
 или
или  . (65)
. (65)При расчетах на ЭВМ рекомендуется принимать
 . (66)
. (66)Если
Mмаст > Mт, Mмин > Mт, (67)
у рассматриваемой точки образуются трещины по схеме 2-Н.
Если
Mмакс > Mт, -Mмин > Mт, (68)
будут возникать трещины на нижней и верхней поверхностях (схема 3). Угол наклона верхних трещин к оси x будет равен:
 . (69)
. (69)Если
|Mмакс| < Mт, -Mмин > Mт, (70)
реализуется первая схема (1-В) на верхней поверхности, если
-Mмакс > Mт, -Mмин > M, (71)
на верхней поверхности реализуется схема 2-В.
Выявленные для точек схемы трещин запоминаются и в дальнейшем фигурируют как известные. В проведенных расчетах учитывается лишь возможный вариант их изменения (так, в процессе нагружения в точках поля плиты с одной трещиной могли образоваться две трещины). В данном случае гипотеза трещинообразования по главным площадкам используется лишь для выявления схем трещин. В процессе нагружения (вследствие перераспределения усилий) площадки трещин могут отклоняться от главных площадок.
В упругопластической стадии работы арматуры указанное разделение схем трещин сохраняется, изменяются лишь параметры, характеризующие величины жесткостей Bij в уравнениях (57).
Прежде чем переходить к определению обобщенных коэффициентов жесткости Bij в (57) при различных схемах трещин, рассмотрим определение основных параметров, от которых будут зависеть указанные обобщенные жесткости.
Определим некоторые предварительные величины. Для схем трещин 1-Н и частично 3:
где  - обобщенный коэффициент армирования перпендикулярно трещине;
- обобщенный коэффициент армирования перпендикулярно трещине;
Nт.п - проекция усилий текучести на нормаль к трещине;
Mп - изгибающий момент на площадке трещины.
Для схемы трещин 2-Н:
Подставляя в (72) и (73) вместо fx, fy,  величины
величины  ,
,  и
и  , получим соответственно величины
, получим соответственно величины  ,
,  ,
,  для верхнего армирования (т.е. для схем трещин 1-В, частично 3 и 2-В).
для верхнего армирования (т.е. для схем трещин 1-В, частично 3 и 2-В).
Определение высот сжатой зоны над трещинами нижней зоны плиты можно производить по формуле
 , (74)
, (74)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: Библиография отсутствует. |
 .
.При
 ;
;  ;
;  ;
;  ;
; величина
 ; (к = 1, 2 и 3). (75)
; (к = 1, 2 и 3). (75)Если  , то c = 3, иначе c = 5.
, то c = 3, иначе c = 5.
Определение относительных высот  сжатой зоны под верхними трещинами
сжатой зоны под верхними трещинами 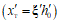 производится также по приведенным выше формулам, где лишь вместо величин
производится также по приведенным выше формулам, где лишь вместо величин  , Nт.п и Mп следует вводить величины
, Nт.п и Mп следует вводить величины  ,
,  и
и  .
.
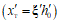 производится также по приведенным выше формулам, где лишь вместо величин
производится также по приведенным выше формулам, где лишь вместо величин В данном случае с целью унификации расчетных формул для схем трещин 2 определяются средние высоты сжатой зоны бетона над (или под) трещинами двух пересекающихся направлений.
Плечи внутренних пар усилий по сечению трещин определяем по формулам:
z = (h0 - 0,5xт);  . (76)
. (76)
 . (76)
. (76)Принято, что бетон сжатой зоны над (или под) наклонными трещинами деформируется как некоторый ортотропный материал, оси ортотропии которого проходят вдоль и перпендикулярно линиям трещин.
Средний модуль деформации бетона перпендикулярно трещинам можно определять из выражения
 , (77)
, (77)где
 ;
;  ;
; ;
; ;
; .
.Заменяя в этих формулах Mп и xт,  и z на аналогичные величины для верхних трещин, получим выражение для модуля деформации
и z на аналогичные величины для верхних трещин, получим выражение для модуля деформации  бетона под верхними трещинами. Для схем трещин 2 вводится усредненный по двум направлениям модуль
бетона под верхними трещинами. Для схем трещин 2 вводится усредненный по двум направлениям модуль  (при этом
(при этом  ).
).
Модуль деформации полос бетона вдоль трещин Eп для 1-й схемы трещин можно определить из выражения
 ,
,  , (78)
, (78)где M принимается равной минимальной по модулю из двух величин |Mмакс| и |Mмин|.
Определены коэффициенты  и
и  , учитывающие влияние касательных напряжений в арматуре в трещинах:
, учитывающие влияние касательных напряжений в арматуре в трещинах:
где  ;
;  - поправочные коэффициенты для упругопластической стадии работы арматуры. В упругой стадии работы арматуры m1 = m2 = 1. Итеративный процесс подсчета напряжений в арматуре также начинается при m1 = m2 = 1.
- поправочные коэффициенты для упругопластической стадии работы арматуры. В упругой стадии работы арматуры m1 = m2 = 1. Итеративный процесс подсчета напряжений в арматуре также начинается при m1 = m2 = 1.
 ;
;  - поправочные коэффициенты для упругопластической стадии работы арматуры. В упругой стадии работы арматуры m1 = m2 = 1. Итеративный процесс подсчета напряжений в арматуре также начинается при m1 = m2 = 1.
- поправочные коэффициенты для упругопластической стадии работы арматуры. В упругой стадии работы арматуры m1 = m2 = 1. Итеративный процесс подсчета напряжений в арматуре также начинается при m1 = m2 = 1.Определяем величины Max и May, от которых будут зависеть напряжения арматуры в трещинах  ,
,  (для верхней арматуры
(для верхней арматуры  и
и  ).
).
Для схемы трещин 1-Н и 3:
 ;
; .
.Для схемы трещин 1-В и 3:
 ;
; .
.Для схемы трещин 2:
Max = Mx; May = My;  ; May = -My.
; May = -My.
 ; May = -My.
; May = -My.Напряжения в арматуре:
 (80)
(80)Средние модули деформаций нижней арматуры в общем виде (как в упругой, так и в упругопластической стадии работы арматур) можно определить из выражения
 (i = x, y), (81)
(i = x, y), (81)где

 ;
;при
 ;
;при 

 ;
; ;
; 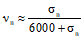 ;
;при 

 ;
;
(где  ;
;  ; lт - расстояние между трещинами).
; lт - расстояние между трещинами).
 ;
;  ; lт - расстояние между трещинами).
; lт - расстояние между трещинами).Заменяя в указанных выражениях Mai на  и подставляя упругие характеристики верхнего армирования, получим средние модули деформаций верхней арматуры
и подставляя упругие характеристики верхнего армирования, получим средние модули деформаций верхней арматуры  .
.
2.17. Ширина раскрытия трещин  представлена в виде
представлена в виде
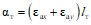 , (82)
, (82)где  ,
,  .
.
 ,
,  .
.В качестве величины lт принимается максимальное из двух значений, определяемых по формулам:
 ,
,  , (83)
, (83)где для стержней периодического профиля  ; для гладких горячекатаных стержней
; для гладких горячекатаных стержней  ; для обыкновенной арматурной проволоки
; для обыкновенной арматурной проволоки  .
.
Аналогичным образом также определяется ширина раскрытия трещин на верхней поверхности плит.
Жесткостные коэффициенты, выведенные для различных схем трещин, несмотря на различие, состоят из повторяющихся в различных комбинациях следующих параметров:
Присваивая величинам, входящим в правые части выражений (84), значения для верхних трещин, получим соответственно значения величин  ,
,  ,
,  и
и  . При этом выражение b3 оставляется без изменения.
. При этом выражение b3 оставляется без изменения.
Выражения коэффициентов Bik для схемы трещин 1-Н:
Для получения Bik для схемы трещин 1-В в выражениях (85) следует заменить a1, b1, a2, b2,  соответственно на
соответственно на  ,
,  ,
,  ,
,  ,
,  . Обозначим эти коэффициенты соответственно через
. Обозначим эти коэффициенты соответственно через  ,
, 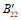 ,
, 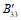 ,
,  и
и  .
.
Жесткостные коэффициенты для схемы трещин 3 являются суммой одноименных коэффициентов, вычисленных для схем трещин 1-Н и 1-В (т.е. равны  ). При этом следует принять b3 = 0.
). При этом следует принять b3 = 0.
Выражения жесткостных коэффициентов для схемы трещин 2-Н имеют вид:
Заменяя в (86) a1, b1, a2, b2 соответственно на  ,
,  ,
,  и
и 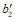 и учитывая, что при этом
и учитывая, что при этом  ,
,  и
и  , получим значения
, получим значения  и
и  для схемы трещин 1-В.
для схемы трещин 1-В.
 ,
,  и
и  , получим значения
, получим значения Для схемы трещин 2 приближенно можно принимать
Однако выражениями (87) не всегда удобно пользоваться в практических расчетах; использование (87) связано с модификацией матрицы уравнений в процессе расчета, кроме этого допускается погрешность в связи с неточностью (87), поэтому и для схемы 2-Н можно учесть некоторую жесткость B33 на кручение (при этом  ), определив ее следующим образом. Полагая поочередно
), определив ее следующим образом. Полагая поочередно  и
и  , определяем, как для схемы 1-Н [по формулам (84) и (85)], две величины B33 при b3 = 0. Жесткость B33 для схемы трещин 2-Н будет равна сумме этих двух величин. Аналогичным образом можно также определить жесткость B33 и для схемы трещины 2-В.
, определяем, как для схемы 1-Н [по формулам (84) и (85)], две величины B33 при b3 = 0. Жесткость B33 для схемы трещин 2-Н будет равна сумме этих двух величин. Аналогичным образом можно также определить жесткость B33 и для схемы трещины 2-В.
2.18. Могут быть использованы два варианта алгоритмов.
В первом варианте алгоритма, чтобы исключить дифференцирование переменных по полю плиты жесткостных коэффициентов, система уравнений (57) и (58) не сводится к одному разрешающему уравнению, как это делается в теории упругих пластинок, а используется в представленном виде. Плита разбивается разностной сеткой, и уравнения (57) и (58) представляются в конечных разностях.
Уравнения равновесия (58) пригодны для любой стадии работы плиты. Уравнения (57) изменяются в зависимости от того, в какой стадии работы находится та или иная точка плиты. В качестве метода решения применяется шагово-итерационный метод с такими особенностями. В качестве начальной (первый шаг) принимается нагрузка, соответствующая упругой работе плиты без трещин. Для первой итерации следующего шага нагрузки по упругому полю жесткостей вычисляется поле моментов (назовем его  ) и поле прогибов. По этому решению анализируются условия трещинообразования в точках и вычисляется новое поле жесткостных коэффициентов в зависимости от установленной стадии работы плиты. По новому полю жесткостей вновь определяется поле моментов и прогибов на следующей итерации
) и поле прогибов. По этому решению анализируются условия трещинообразования в точках и вычисляется новое поле жесткостных коэффициентов в зависимости от установленной стадии работы плиты. По новому полю жесткостей вновь определяется поле моментов и прогибов на следующей итерации  . Если решение
. Если решение  отличается от решения
отличается от решения  на величину,
на величину,  заранее заданной точности, то переходим к следующей итерации. При этом матрицу жесткостей
заранее заданной точности, то переходим к следующей итерации. При этом матрицу жесткостей  нужно вычислить по полусумме решений
нужно вычислить по полусумме решений  и
и  , сглаживая этим процесс возмущения поля моментов, возникающий вследствие того, что непрерывный физический процесс образования трещин моделируется итеративным методом. Процесс считается сошедшимся, если усилия и прогибы на очередных итерациях отличаются во всех точках не более чем на 3%.
, сглаживая этим процесс возмущения поля моментов, возникающий вследствие того, что непрерывный физический процесс образования трещин моделируется итеративным методом. Процесс считается сошедшимся, если усилия и прогибы на очередных итерациях отличаются во всех точках не более чем на 3%.
 заранее заданной точности, то переходим к следующей итерации. При этом матрицу жесткостей
заранее заданной точности, то переходим к следующей итерации. При этом матрицу жесткостей Пусть  и
и  - окончательное поле моментов и жесткостных коэффициентов для данного шага нагрузки. Для сокращения количества итераций на очередном шаге к наиболее рациональным оказывается такой переход, когда жесткостные коэффициенты
- окончательное поле моментов и жесткостных коэффициентов для данного шага нагрузки. Для сокращения количества итераций на очередном шаге к наиболее рациональным оказывается такой переход, когда жесткостные коэффициенты 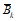 (для первой итерации к-го шага) определяются по значениям моментов
(для первой итерации к-го шага) определяются по значениям моментов  , умноженных на коэффициент нагрузки C.
, умноженных на коэффициент нагрузки C.
 , (88)
, (88)где  - нагрузка данного шага;
- нагрузка данного шага;
pп - нагрузка предыдущего шага.
Для оценки прогибов и ширины раскрытия трещин возрастание нагрузки ведется до нормативной. При дальнейшем повышении нагрузки в точках, где арматура работает в упругопластической стадии, принимается  .
.
 .
.На каждом шаге величины коэффициентов Bjk сравниваются с величинами, полученными по предыдущему решению, и запоминаются  (чем больше Bjk, тем меньше жесткость плиты в точке). В результате при локальных разгрузках, которые могут иметь место при рассматриваемом простом нагружении в процессе трещинообразования, восстановления жесткостных коэффициентов не происходит.
(чем больше Bjk, тем меньше жесткость плиты в точке). В результате при локальных разгрузках, которые могут иметь место при рассматриваемом простом нагружении в процессе трещинообразования, восстановления жесткостных коэффициентов не происходит.
 (чем больше Bjk, тем меньше жесткость плиты в точке). В результате при локальных разгрузках, которые могут иметь место при рассматриваемом простом нагружении в процессе трещинообразования, восстановления жесткостных коэффициентов не происходит.
(чем больше Bjk, тем меньше жесткость плиты в точке). В результате при локальных разгрузках, которые могут иметь место при рассматриваемом простом нагружении в процессе трещинообразования, восстановления жесткостных коэффициентов не происходит.При решении задач в конечных разностях с использованием уравнений (57) и (58) приходится сталкиваться с системой линейных уравнений довольно высокого порядка, что при шагово-итерационном методе решения задачи требует больших затрат машинного времени.
Второй алгоритм, основанный на решении разрешающих уравнений, требует значительно меньших затрат машинного времени. Идея этого алгоритма состоит в следующем. Уравнения (57) представляются в виде:
где жесткости Dik получены путем обращения матрицы жесткостных коэффициентов Bjk. Записывая уравнение (58) в конечных разностях и подставляя в него значения моментов (89), также записанные через конечные разности, приходим к разрешающему (относительно прогибов) уравнению для точки плиты. При этом процедура дифференцирования жесткостей исключается.
При таком подходе получаем систему уравнений, эквивалентную той, которая получается при использовании четырех уравнений (57) и (58). При этом число уравнений сокращается в четыре раза. Решением системы уравнений на каждой итерации будут прогибы в узлах разностной сетки. Значения моментов вычисляются по формулам (89).
В остальном второй алгоритм ничем не отличается от первого. Блок-схема решения задач представлена на рис. 9 и 10. Запись граничных условий при расчете плит с трещинами производится так же, как при расчете анизотропных пластин.

Рис. 9. Блок-схема решения задач при 


а - при расчете по первому алгоритму;
б - при расчете по второму алгоритму
3.1. При расчетах пространственная система каркаса здания расчленяется обычно на плоские поперечные и продольные рамы. В одноэтажных зданиях плоские поперечные рамы (рис. 11, а) образуются из колонн и строительных конструкций, а продольные рамы (рис. 11, б) - из колонн, плит покрытия, подстропильных конструкций связей (решетчатых и в виде распорок) и подкрановых балок. Аналогично расчленяется и каркас многоэтажного здания на поперечные рамы (рис. 11, в), образуемые из колонн и ригелей, и продольные рамы (рис. 11, г), образуемые из колонн, плит перекрытий и продольных ригелей и связей.

а, б - одноэтажных; в, г - многоэтажных
Статический расчет рам правильнее всего производить на совместное действие всех нагрузок и воздействий по деформируемой схеме как нелинейно деформируемых систем с учетом непосредственного влияния продольного изгиба колонн, а также трещин и неупругих деформаций бетона на кривизну и соответственно жесткость элементов.
Однако такой расчет достаточно сложен; в большинстве случаев оказывается возможным с достаточной для практики точностью расчет рам производить упрощенными методами. Методика упрощенного расчета на все воздействия, за исключением вынужденных перемещений (типа температурных), хорошо известна (жесткость колонн принимается без учета трещин, влияние продольного изгиба и неупругих деформаций бетона учитывается коэффициентами  и kдл рекомендуемыми строительными нормами и правилами).
и kдл рекомендуемыми строительными нормами и правилами).
В расчетной схеме рамы оси стержней принимаются совпадающими с геометрическими осями. При шарнирном сопряжении ригеля со стойкой участок ригеля (по вертикали по оси опирания) между его осью и низом принимается бесконечно жестким (рис, 12, а). В случае опирания ригеля по площадке lоп (т.е. при условном шарнире) считается, что шарнир расположен на расстоянии трети длины lоп этой площадки от внутренней ее грани. Участки стержней в пределах жестких узлов учитываются в расчете с повышенной жесткостью; при отсутствии необходимых данных жесткость этих участков принимается равной бесконечности. Величина участка повышенной жесткости принимается по рис. 12, б.

а - конструктивная и расчетная схемы шарнирного узла;
б - конструктивная и расчетная схемы жесткого узла;
1 - участок повышенной жесткости;
l - расстояние от оси колонны до оси опирания ригеля;
hр - высота ригеля; hк - ширина колонны;
hв - высота вута; lк - вылет консоли
При расчете рам (когда это необходимо) по деформированной схеме, который может производиться любым методом статики упругих систем (методом сил, методом перемещений и т.д.) геометрическая нелинейность учитывается путем нахождения в основной системе соответствующего метода статики перемещений от единичных усилий или реакций от единичных перемещений по формулам продольно-поперечного изгиба, т.е. с учетом влияния прогибов стержней на моменты в них. При этом в стойках учитываются продольные силы от совместного действия всех внешних нагрузок; в ригелях наличие продольных сил можно не учитывать.
После раскрытия статической неопределимости усилия в стойках определяются также по формулам продольно-поперечного изгиба.
3.2. Расчет прочности разнопролетных второстепенных балок с равномерно распределенной нагрузкой рекомендуется производить следующим образом:
а) величины пролетных моментов в средних пролетах принимать по формуле
б) величины опорных моментов на средних опорах принимать по формуле
в) величины пролетных моментов в крайних пролетах принимать по формуле
 ; (92)
; (92)г) величины опорных моментов на вторых от конца опорах принимать по формуле
где, как и в формулах (7) и (8),
p = g + q - полная равномерно распределенная расчетная нагрузка;
g - полная равномерно распределенная расчетная нагрузка с коэффициентом перегрузки n > 1;
q - временная равномерно распределенная расчетная нагрузка с коэффициентом перегрузки n > 1;
l - расчетный пролет, принимаемый:
1) для средних пролетов равным расстоянию между прогонами в свету;
2) в крайних пролетах при опирании балок на стену равным расстоянию от боковой поверхности прогона до центра опоры на стене;
3) в крайних пролетах при наличии по контуру перекрытия обвязочных балок равным расстоянию в свету между прогоном и обвязочной балкой.
Примечания: 1. Величины расчетных опорных моментов, вычисленные по формулам (91) и (93), относятся к сечениям балок на гранях опор.
2. Неравнопролетные второстепенные балки монолитных железобетонных перекрытий с пролетами, отличающимися друг от друга не более чем на 10%, разрешается рассчитывать по формулам (90) - (93), как и равнопролетные; при этом опорные моменты следует определить по большему смежному пролету.
Эпюры изгибающих моментов пролетных второстепенных равнопролетных неразрезных балок строятся следующим образом:
а) минимальные - во всех средних пролетах по параболам, отвечающим действию приведенной постоянной нагрузки
 ,
,проходящим через вершины расчетных опорных ординат, а в крайних пролетах - по прямым, определяемым максимальной опорной и нулевой точкой, отстающей от грани опоры на расстоянии от нее, равном
 .
.Введение приведенной постоянной нагрузки учитывает приближенно изменение отрицательных моментов в пролете второстепенных балок, обусловленное сопротивлением главных балок кручению.
Расстояние нулевой точки от грани опоры в крайнем пролете определено таким образом, чтобы при загружении соседнего пролета нагрузкой и величине опорного момента  обеспечивалось восприятие отрицательных моментов в рассматриваемом крайнем пролете, загруженном приведенной постоянной нагрузкой;
обеспечивалось восприятие отрицательных моментов в рассматриваемом крайнем пролете, загруженном приведенной постоянной нагрузкой;
 обеспечивалось восприятие отрицательных моментов в рассматриваемом крайнем пролете, загруженном приведенной постоянной нагрузкой;
обеспечивалось восприятие отрицательных моментов в рассматриваемом крайнем пролете, загруженном приведенной постоянной нагрузкой;б) максимальные - по параболам, отвечающим действию постоянной и временной нагрузок и имеющим вершины на максимальных ординатах положительного момента, а именно: в крайних пролетах на 0,425l от свободного конца, а в остальных пролетах - посередине пролета.
Эпюры моментов для равнопролетных балок при соотношениях полезной расчетной нагрузки к расчетной нагрузке от собственного веса g/q, равное 0,5 - 5, построенные в соответствии с приведенными выше указаниями, даны на рис. 13.

Рис. 13. Эпюры расчетных моментов для равнопролетных
неразрезных второстепенных балок
Значения коэффициентов 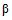 , необходимых для определения ординат отрицательных моментов
, необходимых для определения ординат отрицательных моментов  , в средних пролетах балок в зависимости от соотношения q/g приведены в табл. 8.
, в средних пролетах балок в зависимости от соотношения q/g приведены в табл. 8.
 , в средних пролетах балок в зависимости от соотношения q/g приведены в табл. 8.
, в средних пролетах балок в зависимости от соотношения q/g приведены в табл. 8.Таблица 8
q/g | Номера точек | ||||||||||
5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
0,5 | -0,0715 | -0,01 | +0,022 | +0,024 | -0,004 | -0,0625 | -0,003 | +0,028 | +0,028 | -0,003 | -0,0625 |
1 | -0,0715 | -0,02 | +0,016 | +0,009 | -0,014 | -0,0625 | -0,013 | +0,013 | +0,013 | -0,013 | -0,0625 |
1,5 | -0,0715 | -0,026 | -0,003 | +/- 0 | -0,02 | -0,0625 | -0,019 | -0,004 | +0,004 | -0,019 | -0,0625 |
2 | -0,0715 | -0,03 | -0,009 | -0,006 | -0,024 | -0,0625 | -0,023 | -0,003 | -0,003 | -0,023 | -0,0625 |
2,5 | -0,0715 | -0,033 | -0,012 | -0,009 | -0,027 | -0,0625 | -0,025 | -0,006 | -0,006 | -0,025 | -0,0625 |
3 | -0,0715 | -0,035 | -0,016 | -0,014 | -0,029 | -0,0625 | -0,028 | -0,01 | -0,01 | -0,028 | -0,0625 |
3,5 | -0,0715 | -0,037 | -0,019 | -0,017 | -0,031 | -0,0625 | -0,029 | -0,013 | -0,013 | -0,029 | -0,0625 |
4 | -0,0715 | -0,038 | -0,021 | -0,018 | -0,032 | -0,0625 | -0,03 | -0,015 | -0,015 | -0,03 | -0,0625 |
4,5 | -0,0715 | -0,039 | -0,022 | -0,02 | -0,033 | -0,0625 | -0,032 | -0,016 | -0,016 | -0,032 | -0,0625 |
5 | -0,0715 | -0,04 | -0,024 | -0,021 | -0,034 | -0,0625 | -0,033 | -0,018 | -0,018 | -0,033 | -0,0625 |
3.3. Процент армирования сечений балок и рам должен быть не менее минимального процента, требуемого нормативными документами и руководствами, а для балок, ригелей и стоек рам, работающих по первому случаю внецентренного сжатия, должен также удовлетворять п. 1.18.
Максимальный процент армирования стоек рам ограничивается требованиями соответствующих руководств.
3.4. Для учета пластических деформаций при расчете прочности главных неразрезных балок, неразрезных балок с неравными пролетами, а также рам следует располагать расчетом их как упругих систем. Затем производится перераспределение усилий и по измененным усилиям подбирается арматура. Границы перераспределения усилий, а следовательно, и армирования могут определяться требованиями эксплуатационных свойств (деформативность и трещиностойкость). При отсутствии методов прямого проектирования по эксплуатационной стадии приходится пользоваться методикой повторных и корректирующих расчетов с использованием рекомендаций п. 3.9 настоящего руководства.
Для сокращения труда при ручном счете можно пользоваться достаточно обоснованными приближенными методами оценки распределения усилий с учетом неупругих свойств железобетона в эксплуатационной стадии (например, метод поправочных коэффициентов  п. 3.11 настоящего Руководства).
п. 3.11 настоящего Руководства).
3.5. Перераспределение усилий, обусловленное обстоятельствами, охарактеризованными в п. 1.1 настоящего Руководства, в расчетах по первой группе предельных состояний всегда может быть учтено, как изменение величин лишних неизвестных метода сил по сравнению с величинами, отвечающими упругой системе. При проектировании следует использовать перераспределение сил в статически неопределимых системах для достижения экономического и производственного эффекта: уменьшения расхода материалов, увеличения повторяемости элементов опалубки и арматуры, облегчения условий бетонирования и т.п.
Стойки, работающие по второму случаю внецентренного сжатия, должны быть рассчитаны на усилия, принятые в результате перераспределения, однако они должны иметь достаточное сечение, чтобы воспринять полную продольную силу и по крайней мере половину изгибающего момента, отвечающего упругой системе.
3.6. Для расчета статически неопределимой конструкции с учетом перераспределения усилий можно сначала рассчитать статически неопределенную упругую систему любым эффективным методом на действие расчетной нагрузки от собственного веса и различных случаев невыгодного расположения расчетной полезной нагрузки. Усилия от каждого случая расположения расчетной полезной нагрузки складываются с усилиями от расчетной нагрузки собственного веса. К каждой из полученных таким образом эпюр прибавляются эпюры усилий от лишних неизвестных любой статически определимой основной системы, умножаемые на произвольные положительные или отрицательные множители, подбираемые так, чтобы возможно полнее выполнять рекомендации, приведенные в п. 3.5. Перераспределение усилий, осуществляемое указанным способом, производится для каждого из рассматриваемых невыгодных расположений расчетной полезной нагрузки независимо.
При расчете неразрезных балок к эпюрам моментов от отдельных невыгодно расположенных нагрузок, сложенным от расчетной постоянной нагрузки, прибавляются с произвольным по знаку и величине надопорными ординатами треугольные эпюры (рис. 14).

Рис. 14. Надопорные эпюры моментов,
используемые для перераспределения усилий
В дальнейшем при подборе сечений эпюрами усилий, построенными с учетом перераспределения усилий, пользуются так же, как эпюрами от отдельных нагрузок в упругой системе.
Подбор сечений может быть произведен на ЭВМ с использованием методов математического программирования и принципов оптимального проектирования с удовлетворением требований всех предельных состояний.
3.7. Определение несущей способности статически неопределимых стержневых систем (неразрезные балки, рамы, арки и т.д.) (при проверочных расчетах) можно производить статическим способом метода предельного равновесия. Наиболее целесообразно это делать с привлечением аппарата математического, как правило, линейного программирования и с использованием ЭВМ.
Основной объем работ при использовании ЭВМ состоит в формировании исходной информации для решения задачи программирования. В общем случае эта задача выглядит следующим образом.
В конструкции назначается m' опасных сечений, в которых может возникнуть предельное состояние. Очевидно, что в этих сечениях действует m = 2m' внутренних сил.
Обозначив m-мерный вектор внутренних сил (изгибающие моменты и нормальные силы) t, например,
t = (M1, N1, M2, N2, ..., Mm', Nm'),
можно составить уравнения равновесия этой системы
H't - r - g = 0.
Здесь использована матричная запись уравнений, число которых n = m - s, где s - степень статической неопределимости всей конструкции;
H' - транспонированная кинематическая матрица размером n x m;
r и g - временная и постоянная нагрузки в виде вектора размером n.
Составление уравнений равновесия для различных стержневых систем, т.е. формирование матрицы H и векторов r и g производится по обычным правилам строительной механики с учетом способов дискретизации и назначения системы перемещений характерных точек конструкции.
Условия прочности принимаются в виде системы 6 x m' = k' линейных неравенств, что соответствует шести неравенствам для каждого из m' опасных сечений (см. п. 1.15). Если знаки действующих усилий заранее известны, то число неравенств может быть сокращено в два раза. Эти неравенства могут быть записаны в матричной форме
At + a >= 0,
где A - матрица k x m (k <= k'), имеющая блочную структуру;
a - k-мерный вектор.
Элементы матрицы A и вектора a состоят из коэффициентов неравенств (6) п. 1.16. Принимается, что временная нагрузка p0 изменяется пропорционально одному параметру p, при этом вектор r представляется в виде pr, а задача определения несущей способности заключается в определении максимального значения параметра нагрузки p* = pmax(t) при выполнении ограничений в виде уравнений равновесия и условий прочности одновременно:
Если в результате решения такой задачи окажется, что p* >= 1, то несущая способность конструкции не ниже заданной нагрузки. Если p* < 1, то несущая способность недостаточная.
Эта задача решается методами линейного программирования как задача со смешанными ограничениями (равенства и неравенства) и свободными переменными (не наложены условия неотрицательности компонент вектора t).
Для реализации этой задачи с помощью ЭВМ целесообразно использовать стандартные программы линейного программирования, в которых учитывается слабая заполненность нулевыми элементами матриц H и A в условиях (94).
3.8. Статический метод предельного равновесия имеет следующие модификации, несколько усложняющие подготовку исходной информации, но облегчающие математическую сторону задачи (снижается существенно число переменных задачи и улучшается устойчивость математической части задачи к различного рода помехам, погрешностям вычислений и т.п.).
Метод основной системы. Как при расчете обычной упругой системы, методом сил отбрасываются s связей (s - степень статической неопределимости конструкции) и вместо них вводятся столько же "лишних" неизвестных сил x1, x2, ..., xs, которые в дальнейшем обозначаются s-мерным вектором x. Изгибающий момент и нормальная сила в любом из назначенных опасных сечений из общего числа m' выражаются в виде следующей линейной комбинации:
 ,
,где  и
и  - усилия в основной системе в сечении i от внешних сил g и r (постоянных и временных нагрузок);
- усилия в основной системе в сечении i от внешних сил g и r (постоянных и временных нагрузок);
p - параметр изменения внешней нагрузки;
Lij - усилие в i-том сечении основной системы от единичного j-го лишнего неизвестного.
Эти соотношения можно записать в матричной форме в виде следующего линейного преобразования:
t = tg + ptr + Lx,
где tg и tr - m-мерные векторы, составленные из элементов 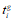 и
и  соответственно;
соответственно;
L - матрица m x s, составленная нз элементов Lij;
x - s-мерный вектор лишних неизвестных.
Подстановка этого преобразования в уравнение равновесия (94) тождественно ему удовлетворяет, а подстановка в неравенства приводит к аналогичным неравенствам относительно новых неизвестных x:
где C = AL - матрица k x s;
f = Atr - k-мерный вектор;
d = a + Atg - также k-мерный вектор.
Определение p* = pmax(x) при ограничениях (95) аналогично решению предыдущей задачи определения p* = pmax(t), однако здесь не фигурируют уравнения равновесия, которые обязательно выполняются, а число неизвестных равно s + 1 - степени статической неопределимости конструкции плюс параметр нагрузки p, который также считается неизвестной величиной. Это значительно меньше числа неизвестных m в предыдущей задаче.
При реализации задачи с помощью ЭВМ можно пользоваться стандартными программами для решения задач линейного программирования в канонической форме, т.е. когда ограничения заданы только в виде системы неравенств.
Как показывает опыт, подобный подход существенно снижает объем перерабатываемой числовой информации.
Модифицированный метод сил. Исходная информация для этого метода в основном составляется как для описанного выше метода сил с той только разницей, что предварительно решается задача в упругой постановке и сохраняется для дальнейшего использования каноническая матрица коэффициентов метода сил  .
.
Усилия в элементах конструкции представляются так:
где tge и tre - усилия в статически неопределимой упругой конструкции, определяемые обычными методами строительной механики. Условия по формуле (95) останутся без изменения, а f = Atre.
d = a + Atge.
Задача может быть поставлена двояко:
а) определить максимальную нагрузку, т.е. определить максимальное значение параметров нагрузки p* = pmax(x). Эта задача ничем существенно не отличается от предыдущих, за исключением, может быть, улучшения показателей устойчивости к погрешностям вычисления;
б) определить действительное распределение внутренних сил для заданной нагрузки. В этой задаче принимается p = 1 и определяется при условиях (95) минимум квадратичной формы
 ,
,где  - элементы канонической матрицы метода сил.
- элементы канонической матрицы метода сил.
Если решение системы неравенств (95) при p = 1 существует, то конструкция не достигает предельного состояния. Те значения x*, которые доставляют минимум U(x), подставленные в выражение (96), дают действительное распределение внутренних сил, ограниченное тем выбором жесткостей, который был принят при вычислении матрицы  .
.
Такая задача, в отличие от предыдущих, является задачей квадратичного программирования, которая сложнее задачи линейного программирования, но, в отличие от последней, имеет единственное решение. Для реализации с помощью ЭВМ подходят любые стандартные программы квадратичного программирования.
Возможно приведение задачи модифицированного метода сил к канонической форме, если предварительно вычислить собственные значения и собственные векторы матрицы  . Пусть
. Пусть  (i = 1, 2, ..., s) - собственные значения, а матрица T составлена из собственных векторов как столбцов. Тогда преобразование переменных по формуле
(i = 1, 2, ..., s) - собственные значения, а матрица T составлена из собственных векторов как столбцов. Тогда преобразование переменных по формуле
 ,
,где  - диагональная матрица s x s приводит к линейной системе неравенств типа (95);
- диагональная матрица s x s приводит к линейной системе неравенств типа (95);
где  и при этих условиях квадратичная форма U(x) преобразуется к нормальной квадратичной форме
и при этих условиях квадратичная форма U(x) преобразуется к нормальной квадратичной форме
 и при этих условиях квадратичная форма U(x) преобразуется к нормальной квадратичной форме
и при этих условиях квадратичная форма U(x) преобразуется к нормальной квадратичной форме .
.Определение минимума такой квадратичной формы при условии (97) эквивалентно предыдущей задаче, но дает существенные преимущества по объему перерабатываемой числовой информации при решении задачи квадратичного программирования и малочувствительна к погрешностям вычислений.
3.9. Распределение усилий в балках и рамах для подсчета деформаций и ширины раскрытия трещин следует определять согласно п. 1.7 настоящего Руководства.
Как при расчете рамных конструкций, так и балочных систем оценку распределения усилий в стадии эксплуатации целесообразно ориентировать на использование современных электронно-вычислительных машин и итерационные методы расчета.
Применительно к рамным конструкциям вычислительный процесс (алгоритм расчета) может быть построен следующим образом.
Для составления программы расчета может быть принята последовательность вычислений, принимаемая обычно при расчете упругих систем как по деформированной, так и по недеформированной схемам. Основная система может быть принята состоящей из однопролетных балок переменной жесткости, решаемых методом сил. Расчет системы в целом целесообразно вести методом деформаций. За неизвестные метода деформаций могут быть приняты углы поворота и горизонтальные смещения отдельных ярусов рамы. Ригели могут быть расположены со сдвижкой по высоте и с пропусками.
Учет неупругих свойств железобетона производится многократным повторением расчета, при котором величина жесткости элементов рамы корректируется в процессе счета. Для учета неупругих свойств железобетона применение для расчета балок основной системы метода сил следует считать целесообразным.
Для корректировки жесткостей по длине элемента каждый стержень рамы разбивается на достаточно большое число участков. Достаточную точность дает разделение на 20 участков. При постоянном по длине сечении и армировании в пределах зоны трещин возможно разделение на меньшее число участков (до 10).
Первоначально рама рассчитывается как упругая система с постоянными жесткостями по длине элемента. По полученным усилиям определяются жесткости участков элемента с учетом возможного трещинообразования и проявления неупругих деформаций бетона.
Для определения жесткостных характеристик при совместном действии изгибающего момента и продольной силы можно воспользоваться либо рекомендациями руководств по проектированию бетонных и железобетонных конструкций, либо принципом эквивалентного изгиба.
Площадь эквивалентной арматуры (для рассматриваемого сечения) определяется по формуле
 , (98)
, (98)где M и N - изгибающий момент и нормальная сила, действующие в сечении от нормативной нагрузки;
z1 - расстояние от центра тяжести сечения всей арматуры, расположенной в растянутой зоне, до точки приложения равнодействующей усилий в сжатой зоне сечения (над трещиной), определяемое согласно соответствующим руководствам.
Жесткость сечений стержней можно представить как произведение изгибающего момента в сечении, вычисленного относительно геометрической оси на радиус кривизны изогнутой оси стержня  . Радиус кривизны
. Радиус кривизны  определяется по расчетным характеристикам материалов (бетона и арматуры) с учетом наличия трещин.
определяется по расчетным характеристикам материалов (бетона и арматуры) с учетом наличия трещин.
В рассматриваемом в настоящем пункте алгоритме расчета использован принцип эквивалентного изгиба. В рамных каркасах стойки, как правило, работают без трещин и жесткость с учетом трещинообразования определяется главным образом для ригелей. В ригелях продольные силы сравнительно невелики и по характеру своей работы эти элементы близки к изгибаемым. Исходя из этого коэффициент 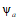 может определяться как для изгибаемых элементов по формуле
может определяться как для изгибаемых элементов по формуле
 . (99)
. (99)Для случаев, когда итерационный процесс сходится медленно, ускорение сходимости процесса может быть достигнуто нахождением среднего между соседними итерациями.
Для каждого участка стержня вычисляется момент, вызывающий образование трещин, и сравнивается с действующим моментом (для первой итерации со значением 0). Если M > Mт, то жесткость вычисляется с учетом образования трещин, а если M < Mт, то без трещин. Далее производится перемножение единичных и грузовых эпюр моментов для участка балки с использованием полученной ранее жесткости. Эти вычисления проводятся с накоплением так, что в момент окончания цикла вычислении для участков данного стержня имеются уже готовые значения коэффициентов системы уравнений метода сил для защемленной балки. Значения полученных неизвестных (моментов защемления от нагрузки) засылаются в специальный массив и хранятся там для дальнейшего использования.
Коэффициенты  , получаемые перемножением эпюр моментов балки, дают возможность определить и реактивные усилия от единичных деформаций концов защемленной балки. На этом заканчивается часть программы, учитывающая специфику работы железобетона.
, получаемые перемножением эпюр моментов балки, дают возможность определить и реактивные усилия от единичных деформаций концов защемленной балки. На этом заканчивается часть программы, учитывающая специфику работы железобетона.
Полученные реактивные усилия засылаются в массив коэффициентов системы уравнений метода деформаций (с накоплением). После окончания вычислений для данного стержня осуществляется переход к следующему стержню и т.д.
В результате оказывается сформированным массив коэффициентов системы уравнений метода деформаций.
После вычисления свободных членов и решения системы происходит обработка заново всех стержней. Повторная обработка всех стержней производится для вычисления эпюр моментов. Этого можно было бы и не делать, но тогда для вычисления эпюры моментов пришлось бы дополнительно хранить в памяти машины результаты расчета всех защемленных балок основной системы (реактивные усилия от единичных деформаций их концов). Для экономии памяти удобнее повторить некоторые вычисления.
После определения жесткости на участке стержня прежнее значение изгибающего момента больше уже не потребуется и на его место засылается новая величина - ордината эпюры моментов свободно опертой балки. К полученной таким образом эпюре добавляются ординаты эпюры вновь вычисленных опорных моментов защемленной балки, а затем и моментов от неизвестных систем уравнений, и так для всех стержней.
В результате получаем в массиве M новую эпюру моментов на границах участков стержней. Затем обычно производится выборка значений моментов через определенное количество участков и засылка их в новый массив моментов, который вместе с массивом нормальных сил выводится на печать. На этом заканчивается одна итерация. Цикл повторяется до тех пор, пока не будет выполнено условие сходимости итерационного процесса (заданное число итераций или разность между предыдущей и последующей итерациями).
3.10. Расчет многоэтажных и многопролетных регулярных рам в силу идентичности в распределении изгибающих моментов в средней области рам можно заменять расчетом более простой рамы. В качестве более простой рамы может быть принята трехэтажная и трехпролетная рама. По данным расчета первого и второго ярусов среднего пролета можно принимать распределение усилий во всех ригелях внутренней области рамы. По моментам в ригелях первого и второго ярусов крайних пролетов и среднего пролета верхнего яруса заполняются моменты в ригелях по всему контуру рамы. Соответственно по моментам в стойках среднего яруса и среднего пролета заполняются моменты во всех стойках рамы. Перерезывающие и нормальные силы в ригелях заполняются аналогично изгибающим моментам. Нормальные силы в стойках заполняются с учетом нагрузки по этажам.
В регулярных рамах образование трещин мало влияет на перерезывающие силы в ригелях и нормальные силы в стойках, а поэтому их можно принимать по данным первой итерации, т.е. по расчету упругой системы. На нормальные силы в ригелях образование трещин влияет больше, но сами силы невелики, а потому и их можно принимать, как и в упругой системе.
Учитывая, что в регулярных рамах после появления трещин состояние соседних пролетов мало влияет на распределение усилий в этом пролете, можно принимать, что все ригели рамы загружены нагрузкой такой же интенсивности.
3.11. При расчете многопролетных балок с равными пролетами при равномерной нагрузке можно ограничиться расчетом пятипролетной балки.
Для приближенной оценки распределения усилий в стадии эксплуатации может быть использован следующий упрощенный способ. Опорные моменты в неразрезных балках, вычисленные как для однородной упругой системы, умножаются на поправочные коэффициенты  , оценивающие неодинаковую жесткость опорных и пролетных сечений.
, оценивающие неодинаковую жесткость опорных и пролетных сечений.
При  по следующим формулам:
по следующим формулам:
 по следующим формулам:
по следующим формулам:а) средние одинаковые пролеты при одном грузе посредине каждого пролета
б) средние одинаковые пролеты, загруженные распределенной нагрузкой или несколькими сосредоточенными грузами
в) для двухпролетной неразрезной балки при распределенной или сосредоточенной нагрузке
Для первых промежуточных опор многопролетных неразрезных балок принимается значение коэффициента  - среднее из двух значений, вычисленного для второго пролета по формуле (101) или (100) и вычисленного по формуле (102).
- среднее из двух значений, вычисленного для второго пролета по формуле (101) или (100) и вычисленного по формуле (102).
При  для всех случаев нагружения по следующей формуле
для всех случаев нагружения по следующей формуле
 для всех случаев нагружения по следующей формуле
для всех случаев нагружения по следующей формуле - отношение опорного момента к пролетному по расчету упругой балки;
- отношение опорного момента к пролетному по расчету упругой балки;По измененным опорным моментам методом подвески балочных эпюр строятся пролетные моменты.
3.12. При расчете зданий на климатические температурные воздействия расстояния между температурными швами устанавливаются на основании расчета каркаса здания на совместное действие внешних нагрузок и перемещений конструкций, вызываемых изменением температуры окружающей среды, усадкой бетона и удлинением нижних граней ригеля каркаса от внешней нагрузки.
При этом расчетная схема каркаса принимается в виде поперечных и продольных статически неопределимых плоских систем (рис. 11).
При точном расчете сложных рам на действие температуры окружающей среды, усадки бетона и удлинения нижней поверхности ригелей рекомендуется использовать синтез метода деформаций и метода сил, как это указано в п. 3.9, используя ЭВМ. В этом случае определение реакций связей, вызванных их единичными перемещениями, а также реакций дополнительных связей, вызванных воздействием температуры, усадки и удлинением нижних граней ригелей, производится методом сил. Величина перемещений принимается согласно п. 3.13. При определении реакции следует учитывать действительное распределение жесткости по длине железобетонных элементов. Учет действительного распределения жесткости рекомендуется производить путем разбивки длины каждого элемента на достаточное число участков и принятия на каждом участке величины жесткости в зависимости от всех действующих усилий. Величину жесткости допускается определять по формулам, приведенным в п. 3.17. Учитывая, что действующие в сечении усилия зависят от жесткости сечения, расчет следует выполнять методом последовательных приближений.
Один из возможных вариантов блок-схемы программы расчета рамной конструкции точным способом на ЭВМ приведен на рис. 15.

Примечание: A = 0, 1 и 2 - признаки, по которым регулируется ход выполнения программы.
Рис. 15. Блок-схема программы расчета
При использовании малых ЭВМ и настольных вычислительных машин допускается в расчет вводить следующие упрощения:
а) жесткость железобетонных элементов рамы с трещинами в растянутой зоне принимать постоянной по всей их длине, равной:
где Kп - коэффициент приведения, равный:
 , (105)
, (105)K - коэффициент, равный K = 1,25 при однозначной и K = 1,5 при двухзначной эпюре моментов по длине элемента;
Mт - момент появления трещин в сечении железобетонного элемента, определяемый согласно п. 3.17;
Mм - максимальная величина изгибающего момента в элементе. Допускается величину Mм принимать Mм = M, где M - расчетный изгибающий момент, который воспринимает сечение при достижении арматуры и бетона расчетных характеристик (см. п. 3.16);
Bбт - жесткость сечений элемента без трещин (см. п. 3.18);
Bст - жесткость сечений элемента с трещиной в растянутой зоне, определяемая согласно п. 3.18 при действии в сечении момента M;
б) при шарнирном сопряжении ригелей и колонн одноэтажных промзданий без мостовых кранов (рис. 11) величину изгибающего момента в заделке колонн допускается определять по формуле
Максимально возможная длина температурного блока указанных одноэтажных зданий определяется по формуле
 ; (108)
; (108) , (109)
, (109)где B - приведенная жесткость колонн, определяемая по формуле (104);
Hк - высота колонн;
Mд и M - изгибающие моменты, соответственно действующие в месте заделки колонн от внешней нагрузки и расчетный, который может воспринять нижняя часть колонн (согласно п. 3.16);
yк - перемещение верха крайней колонны от температурных перемещений;
N - вертикальное усилие, действующее на колонну.
Определение длины температурного блока по формуле (107) производится методом последовательных приближений. В первом приближении длина блока определяется без учета смещения верха колонн (yк = 0);
в) при шарнирном сопряжении ригелей и подкрановых балок с двухъярусными колоннами одноэтажных промышленных зданий (рис. 11, б) усилия в колоннах от вынужденных перемещений допускается определять по формулам:
 ,
,где Mн, Mв - изгибающий момент соответственно в нижней и верхней части крайних колонн;
Bн, Bв - приведенная жесткость соответственно нижней и верхней части колонны, определяемая по формуле (104);
Hн, Hв - высота соответственно нижней и верхней части колонны;
г) при расчете многоэтажных железобетонных каркасных зданий на температурное воздействие допускается усилия определять по формулам:
для колонн нижнего этажа в местах их заделки
 , (112)
, (112)на уровне перекрытия первого этажа
M1 = Mн k, (113)
на уровне перекрытия n-го этажа
 . (114)
. (114)Величина коэффициента k определяется по формулам для двухэтажного здания
 , (115)
, (115)для многоэтажных зданий
 , (116)
, (116)где i1 и i2 - жесткости соответственно колонны нижнего этажа и колонны второго этажа, отнесенные к их длине;
iр - полусумма жесткостей ригелей, примыкающих к колонне в плоскости рассматриваемой рамы; при шарнирном опирании ригелей iр = 0;
Hзд - высота здания;
Hn - расстояние от верха здания до n-го этажа;
H1 - высота первого этажа.
где  - свободные относительные температурные деформации конструкции;
- свободные относительные температурные деформации конструкции;
y - расстояние от точки каркаса, не смещающейся при температурных воздействиях, до рассматриваемой колонны (рис. 11);
Kу - коэффициент, учитывающий податливость ригеля рамы;
Kс - коэффициент, учитывающий податливость сопряжений в узлах рамы.
Свободные относительные температурные деформации конструкции определяются по формуле
где  - расчетное изменение температуры конструкций, определяемое согласно п. 3.14;
- расчетное изменение температуры конструкций, определяемое согласно п. 3.14;
Свободное относительное удлинение нижних граней несущих конструкций покрытия от вертикальной нагрузки равно:
где  - относительное удлинение нижней грани несущей конструкции, принимается: для ферм из низколегированной стали
- относительное удлинение нижней грани несущей конструкции, принимается: для ферм из низколегированной стали  ; для ферм из углеродистой стали
; для ферм из углеродистой стали  ; для железобетонных конструкций допускаются при расчете расстояния между температурными швами промышленных зданий не учитывать удлинения нижних граней, т.е.
; для железобетонных конструкций допускаются при расчете расстояния между температурными швами промышленных зданий не учитывать удлинения нижних граней, т.е. 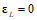 ;
;
 ; для ферм из углеродистой стали
; для ферм из углеродистой стали  ; для железобетонных конструкций допускаются при расчете расстояния между температурными швами промышленных зданий не учитывать удлинения нижних граней, т.е.
; для железобетонных конструкций допускаются при расчете расстояния между температурными швами промышленных зданий не учитывать удлинения нижних граней, т.е. kL - коэффициент, учитывающий влияние вида нагрузки, принимаемый согласно Руководству по проектированию сборных железобетонных колонн одноэтажных промышленных зданий (ЦНИИпромзданий). При расчете колонн с учетом снеговой нагрузки допускается принимать kL = 1, при расчете колонн без снеговой нагрузки - по формуле
 , (120)
, (120)gп - расчетная нагрузка от массы покрытия, включая собственную массу конструкции с коэффициентом перегрузки n = 1;
gс - расчетная снеговая нагрузка с коэффициентом перегрузки n = 1.
При наличии в здании подвесных кран-балок величина коэффициента kL умножается на 0,8.
Величина коэффициента Kу, учитывающего податливость ригеля рамы, принимается по формуле
где Mн - изгибающий момент в нижней части колонн от перемещений, определяемых по формуле (106) или (110), принимая  по формуле (117) без коэффициента Kу. При этом величина Mн не должна быть больше расчетного изгибающего момента, который может воспринимать нижнее сечение колонны [формулы (129) - (131)];
по формуле (117) без коэффициента Kу. При этом величина Mн не должна быть больше расчетного изгибающего момента, который может воспринимать нижнее сечение колонны [формулы (129) - (131)];
Fф - площадь сечения нижнего пояса фермы или ригеля;
E - модуль упругости материала ригеля;
Hк - высота колонны.
Расстояние от точки каркаса, не смещающейся при температурных воздействиях, принимается:
а) в плоскости продольной рамы при отсутствии вертикальных связей по колоннам - по оси рамы, а при наличии вертикальных связей по колоннам - по оси связевой панели;
б) в плоскости поперечной рамы при симметричных (по моменту инерции сечения) колоннах относительно оси рамы - по оси рамы, а при несимметричных колоннах - по формуле
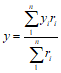 , (122)
, (122)где yi - расстояние от оси крайней колонны, относительно которой определяется расстояние y до i-той колонны;
ri - реакция верхней опоры i-той колонны при ее единичном смещении;
n - число колонн в раме.
Значение коэффициента Kс, учитывающего податливость сопряжений в узлах рамы, принимается, если расчет рамы выполняется точным методом и податливость сопряжений учитывается, то Kс = 1, а в остальных случаях принимается равным:
для сжатых узлов ферм и балок покрытия с колоннами в поперечном направлении рамы
в продольном направлении рамы
для узлов сопряжения подкрановых балок с колоннами
Однако вводимая в расчет величина коэффициента Kс не должна быть меньше 0,6.
В формулах (123) - (125)
где Lбл - длина температурного блока;
d - шаг колонн в блоке.
Для остальных типов сжатых узлов величину коэффициента Kс допускается принимать равным 0,8.
Для растянутых узлов двухъярусных колонн (рис. 12, б) величина коэффициента Kc принимается равной 1/Kc.
3.14. Определение расчетных изменений температур каркасов производственных зданий и сооружений производится по методике раздела СНиП II-6-74 "Температурные климатические воздействия".
Расчетные изменения средних температур конструкций  и
и  в теплое (июль, индекс "т") и холодное (январь, индекс "х") время года определяются по формулам табл. 9.
в теплое (июль, индекс "т") и холодное (январь, индекс "х") время года определяются по формулам табл. 9.
Таблица 9
ИС МЕГАНОРМ: примечание. Текст в шапке таблицы дан в соответствии с официальным текстом документа. |
Конструкции | Здания и сооружения | ||
а) в стадии возведения - все здания и сооружения б) в стадии эксплуатации - открытые сооружения и неотапливаемые здания без технологических источников тепла | в стадии эксплуатации | ||
все отапливаемые в холодное время года здания | а) в стадии воз- кусственным климатом б) в стадии экс- янными технологическими источниками тепла | ||
Не защищенные от воздействия солнечной радиации (в том числе наружные ограждающие конструкции) |  |  | |
 |  | ||
Защищенные от воздействия солнечной радиации (в том числе внутренние конструкции зданий) |  |  | |
 |  | ||
ИС МЕГАНОРМ: примечание. Взамен СНиП II-А.6-72 Постановлением Госстроя СССР от 21.07.1982 N 188 с 01.01.1984 введены в действие СНиП 2.01.01-82. |
Примечания: 1. Расчетные значения tт и tх допускается принимать равными температуре наиболее жарких и наиболее холодных суток по главе СНиП II-А.6-72.
2. В стадии эксплуатации отапливаемых производственных зданий для внутренних конструкций допускается принимать tт = tVII + 3 °C.
Расчетные значения температуры наружного воздуха в теплое tт и холодное tх время года определяются по формулам:
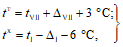 (126)
(126)где tVII, tI - многолетние среднемесячные июльская и январская температуры воздуха, принимаемые по картам 5 и 6 главы СНиП II-6-74 или по главе СНиП II-А.6-72 "Строительная климатология и геофизика";
 ;
; Расчетные значения температуры внутреннего воздуха помещений в теплое tвт и холодное tвх время года определяются по формулам:
 (127)
(127)где 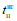 ,
,  - нормативные значения температуры внутреннего воздуха помещений, принимаемые по нормам проектирования зданий или по заданию на проектирование;
- нормативные значения температуры внутреннего воздуха помещений, принимаемые по нормам проектирования зданий или по заданию на проектирование;
Примечание. В стадии эксплуатации отапливаемых производственных зданий без технологических источников тепла расчетные значения температуры воздуха должны приниматься:
а) в теплое время года - не выше 28 °C;
б) в холодное время года - равной температуре дежурного отопления, но не ниже 5 °C.
Расчетное значение T1, учитывающее солнечную радиацию и суточные амплитуды температуры наружного воздуха, должно приниматься равным:
при толщине конструкций в см:
менее 15 - 15 °C;
от 15 до 39 - 10 °C;
более 40 - 5 °C.
Начальная температура, соответствующая замыканию конструкции или ее части в законченную систему, в теплое  и холодное
и холодное  время года, принимается равной:
время года, принимается равной:

Примечание. В необходимых случаях при наличии данных о календарном сроке замыкания конструкции, порядке производства работ и т.д. начальная температура может уточняться в соответствии с этими данными.
Для расчетов каркасов производственных зданий и сооружений расчетные изменения средней температуры  и
и  допускается принимать:
допускается принимать:
а) в стадии эксплуатации - по табл. 10;
Районы СССР, принимаемые по табл. 11 | Расчетные изменения температур, °C | |||||
Открытые сооружения и сооружения в стадии возведения | Неотапливаемые здания | Отапливаемые здания | ||||
+35 | -25 | +25 | -25 | +20 | -5 | |
-10 | ||||||
-15 | ||||||
+40 | -30 | +30 | -30 | +25 | -5 | |
-10 | ||||||
-15 | ||||||
+40 | -35 | +30 | -35 | +25 | -5 | |
-10 | ||||||
-15 | ||||||
+40 | -40 | +30 | -40 | +25 | 0 | |
-5 | ||||||
-10 | ||||||
+45 | +35 | +30 | -15 | |||
-20 | ||||||
+45 | -45 | +35 | -45 | +30 | 0 | |
-5 | ||||||
-10 | ||||||
-15 | ||||||
+50 | -50 | +40 | -50 | +35 | 0 | |
-5 | ||||||
-10 | ||||||
+55 | -55 | +45 | -55 | +40 | 0 | |
-5 | ||||||
+60 | -60 | +50 | -60 | +45 | -5 | |
N района | Описание района | Примечание |
Курильские острова | ||
Черноморское побережье Грузинской ССР | ||
Юго-восточное побережье Азербайджанской ССР | Включая Апшеронский п-в | |
Юго-восточное побережье Камчатского п-ва | Включая Петропавловск-Камчатский | |
Южный берег Крыма, Черноморское побережье Краснодарского края | ||
Грузинская ССР | Исключая Iб | |
Азербайджанская ССР | Исключая Iв | |
Северо-восточное побережье Кольского п-ва | До полярного круга | |
Побережье Белого моря, побережье Приморского края | ||
Южный Сахалин | Южнее Ильинского | |
Предгорья Большого и Малого Кавказских хребтов | ||
Новая Земля | ||
Остров Сахалин | ||
Латвийская и Эстонская ССР | ||
Белорусская, Литовская, Молдавская и Украинская ССР | ||
Краснодарский край | ||
Дагестанская, Кабардино-Балкарская, Северо-Осетинская и Чечено-Ингушская АССР, Карачаево-Черкесская АО | Исключая IIIв | |
Узбекская ССР | Исключая Vг | |
Таджикская и Туркменская ССР | ||
Северная Земля, Ненецкий нац. округ | ||
Камчатская обл. | ||
Владимирская, Вологодская, Горьковская, Ивановская, Калининская, Костромская, Ленинградская, Московская, Новгородская, Псковская и Ярославская области РСФСР | ||
Кольский п-в | ||
Карельская АССР | ||
Приморский край | Исключая IIIб | |
Северный Сахалин | Севернее Катангли | |
Белгородская, Брянская, Волгоградская, Воронежская, Калужская, Курская, Липецкая, Орловская, Пензенская, Рязанская, Саратовская, Смоленская, Тамбовская, Тульская обл. РСФСР, Мордовская АССР | ||
Ставропольский край, Астраханская и Ростовская обл. РСФСР, Калмыцкая и Каракалпакская АССР, Алма-Атинская, Гурьевская, Джамбулская, Кзыл-Ординская, Талды-Курганская, Чимкентская обл. Казахской ССР | ||
Ямало-Ненецкий нац. округ | Территория за Полярным кругом | |
Чукотский п-в, Корякский нац. округ | ||
Архангельская, Кировская, Пермская и Свердловская обл. РСФСР, Коми, Марийская и Удмуртская АССР | ||
Куйбышевская, Курганская, Оренбургская, Ульяновская и Челябинская обл. РСФСР, Актюбинская, Восточно-Казахстанская, Карагандинская, Кокчетавская, Кустанайская, Павлодарская, Северо-Казахстанская, Семипалатинская, Тургайская, Уральская и Целиноградская обл. Казахской ССР, Башкирская, Татарская и Чувашская АССР | ||
Таймырский (Долгано-Ненецкий) нац. округ | ||
Чукотский нац. округ | Исключая VIа | |
Ямало-Ненецкий нац. округ | Исключая VIа | |
Красноярский край | ||
Алтайский и Хабаровский края, Ханты-Мансийский нац. округ, Амурская, Иркутская, Новосибирская, Омская, Томская и Тюменская обл. РСФСР | ||
Магаданская обл., Якутская АССР, Эвенкийский нац. округ |
Примечания: 1. Районирование не распространяется на горные районы.
2. Для береговой полосы морей (за исключением особо оговоренных участков) шириной до 100 км или до ближайшего горного хребта районы принимаются на одну ступень ниже, чем на данной территории суши.
б) в стадии возведения равными  и
и  для неотапливаемых зданий и сооружений, в стадии их эксплуатации, умноженными на коэффициент 0,8.
для неотапливаемых зданий и сооружений, в стадии их эксплуатации, умноженными на коэффициент 0,8.
Примечание. При пользовании табл. 10 абсолютные значения  и
и  получаются завышенными (до 5 °C) по сравнению с результатами, получаемыми по методике СНиП II-6-74.
получаются завышенными (до 5 °C) по сравнению с результатами, получаемыми по методике СНиП II-6-74.
Нормативные значения  и
и  , а также расчетные значения
, а также расчетные значения  и
и  для горных районов во всех случаях определяются по методике СНиП II-6-74.
для горных районов во всех случаях определяются по методике СНиП II-6-74.
3.15. Значения коэффициентов температурного расширения допускается принимать для бетонных и железобетонных конструкций в зависимости от состава бетона и условий эксплуатации по табл. 12.
Таблица 12
Вид бетона | Относительная влажность воздуха в % | ||
< 40 | 40 - 80 | > 80 | |
Обычный тяжелый бетон | 8·10-6 | 10·10-6 | 11·10-6 |
Легкий бетон | 7·10-6 | 8·10-6 | 9·10-6 |
Значения коэффициентов температурного расширения стали принимаются равными:
для углеродистой стали  ;
;
 ;
;для низколегированной стали  .
.
 .
.3.16. Изгибающий момент, который могут воспринять внецентренно сжатые колонны рамы, определяется в зависимости от высоты сжатой зоны сечения.
 , (128)
, (128)а) при 

б) при 
 , (130)
, (130)в) при x >= xпр
В формулах (129) - (131):
 ;
;Значение граничной относительной высоты сжатой зоны колонн из обычного бетона допускается определять по формуле
 , (132)
, (132)Rпр - расчетное сопротивление бетона сжатию (призменная прочность).
3.17. Изгибающий момент при появлении трещин в железобетонных внецентренно сжатых элементах определяется по формуле
Wт - момент сопротивления растянутой грани колонн допускается принимать равным:
rяд - расстояние от ядровой точки, наиболее удаленной от грани, растянутой внешними нагрузками, до центра приведенного сечения:
Fпр = Fаn + bh; (136)
e - расстояние от точки приложения равнодействующей всей вертикальной нагрузки до центра тяжести приведенного сечения.
а) для сечений, в которых при расчетных нагрузках и температурных усилиях появление трещин в растянутой зоне маловероятно,
где Iпр = Iб + nIаCб;
Cб - коэффициент, учитывающий влияние деформаций ползучести бетона, принимаемый по формуле (2).
При отсутствии точных данных о моменте замыкания конструкции допускается величину Cб определять по формуле
где величина C принимается по табл. 4;
б) для сечений, в которых возможно появление трещин в растянутой зоне, жесткость сечения определяется:
для изгибаемых элементов
 , (140)
, (140)для внецентренно сжатых колонн
где
 ; (142)
; (142)Величина относительной высоты сжатой зоны бетона  и коэффициента
и коэффициента  определяется по методике, приведенной в действующих Строительных нормах и правилах.
определяется по методике, приведенной в действующих Строительных нормах и правилах.
Если e0 >= 0,4h, допускается  определять по формуле
определять по формуле
 , (145)
, (145)но не более 1;
где Mт - изгибающий момент при появлении трещин, вычисленный по формуле (133);
M - действующий изгибающий момент относительно центра тяжести сечения;
Sg - коэффициент, характеризующий профиль арматурных стержней, принимаемый для арматуры периодического профиля равным 0,95, для гладкой арматуры Sg = 0,9;
 .
.Для конструкций, подверженных тепловой обработке, значение  умножается на коэффициент 1,15.
умножается на коэффициент 1,15.
При расчете температурных швов без использования ЭВМ допускается жесткость элементов с трещинами в растянутой зоне определять приближенным методом:
для изгибаемых элементов - по формуле
 , (146)
, (146)для внецентренно сжатых колонн прямоугольной формы с процентом армирования  и e0 >= 0,5h - по формуле
и e0 >= 0,5h - по формуле
 и e0 >= 0,5h - по формуле
и e0 >= 0,5h - по формулеВеличины K1, K2, K3 для расчета жесткости внецентренно сжатых колонн с трещинами в растянутой зоне определяются по табл. 13 в зависимости от  и
и  [формулы (143) и (144)];
[формулы (143) и (144)];
M - момент всех сил относительно центра тяжести сечения колонны;
rяд - по формуле (135).
Коэффициенты K1/K3 при | K2 | ||||
0,04 | 0,07 | 0,1 | 0,15 | ||
0 | 0,48 ------ 1,04 | 0,44 ------ 0,92 | 0,4 ------ 0,88 | 0,34 ------ 0,80 | 0,17 |
0,2 | 0,6 ------ 1,08 | 0,55 ------ 0,96 | 0,5 ------ 0,88 | 0,44 ------ 0,82 | 0,2 |
0,6 | 0,68 ------ 1,11 | 0,66 ------ 0,96 | 0,62 ------ 0,89 | 0,56 ------ 0,82 | 0,26 |
3.19. Ширина раскрытия трещин aт, мм, нормальных к оси колонн на уровне центра тяжести растянутой арматуры, определяется по формуле
где C0 - коэффициент, учитывающий длительность действия нагрузки и принимаемый равным 1,25;
d - диаметр стержней растянутой арматуры в миллиметрах; при различных диаметрах стержней значение допускается принимать равным приведенному диаметру
Напряжения в растянутой арматуре  определяются по методике, приведенной в Строительных нормах и правилах.
определяются по методике, приведенной в Строительных нормах и правилах.
3.20. Величина температурно-усадочных напряжений в сплошных бетонных или железобетонных сооружениях определяется по формуле
 , (150)
, (150)где  - относительные усадочные деформации, определяемые по формуле (3);
- относительные усадочные деформации, определяемые по формуле (3);
 ,
,где  - расчетное изменение средних температур железобетонных конструкций промышленных зданий в холодное время согласно п. 3.14;
- расчетное изменение средних температур железобетонных конструкций промышленных зданий в холодное время согласно п. 3.14;
Если  , то сооружение может быть запроектировано без устройства усадочных швов.
, то сооружение может быть запроектировано без устройства усадочных швов.
Если  и появление трещин в сооружении нежелательно, то необходимо устройство температурно-усадочных швов.
и появление трещин в сооружении нежелательно, то необходимо устройство температурно-усадочных швов.
Расстояние между швами допускается определять по формуле
где Fп - приведенная площадь поперечного сечения железобетонной конструкции;
g - вертикальная нагрузка на сооружение, в том числе и собственный вес фундамента;
fт - коэффициент трения бетона по грунту допускается принимать по табл. 14.
Таблица 14
Вид грунта | fт |
Глина, глинистые известняки, глинистые сланцы | 0,5 |
Суглинки, супеси | 0,6 |
Песчаные, гравийные | 0,75 |
Скальные | 0,9 |
Примечание: В случае если бетонные и железобетонные сооружения выполняются в монолитном бетоне, расстояние между швами [формула (151)] должно быть уменьшено на коэффициент 0,8.
Если появление трещин в сооружении допустимо, а устройство температурно-усадочных швов нежелательно, то в этом случае должна быть установлена противоусадочная арматура. Минимальный процент противоусадочной арматуры определяется по формуле
 . (152)
. (152)Максимально возможная ширина раскрытия температурно-усадочных трещин (в момент их появления) определяется по формуле (149), принимая C0 = 1 и  .
.
Ширина раскрытия температурно-усадочных трещин при эксплуатации конструкций равна:
 ; (153)
; (153)4.1. Безбалочными называются плоские железобетонные перекрытия, образованные гладкой плитой, которая жестко сопрягается с поддерживающими ее колоннами посредством местных утолщений, называемых капителями. При возведении зданий методом подъема перекрытий (этажей) перекрытия выполняются не только безбалочными, но и бескапительными (для нагрузок до 2 тс/м2).
4.2. Назначение капителей безбалочных перекрытий состоит в том, чтобы:
а) увеличить прочность плиты на излом;
б) обеспечить плиту от продавливания в месте ее опирания на колонны;
в) увеличить жесткость перекрытия.
В бескапительных перекрытиях для увеличения жесткости, прочности на излом и особенно на продавливание в месте примыкания плит к колоннам устраиваются металлические воротники, размеры которых назначаются из условий прочности на продавливание.
4.3. В настоящем Руководстве даны рекомендации по расчету и проектированию безбалочных перекрытий при расположении колонн по углам квадратной или прямоугольной сетки с равными или неравными пролетами при отношении большей стороны панели к меньшей до 3/2 и отношении величин пролетов не более 4/3.
На краях плит предусматривается возможность:
а) устройства консольного свеса плиты, выступающего за крайний ряд колонн;
б) сопряжения крайнего ряда колонн с плитой при помощи полукапителей и воротников;
в) сопряжения края плиты с окаймляющей балкой, поддерживаемой крайним рядом колонн;
г) опирания края плиты на массивную стену.
4.4. Безбалочное перекрытие следует рассчитывать на нагрузки, равномерно распределенные по всему перекрытию или по его части.
4.5. Арматура в безбалочных перекрытиях состоит из сваренных в сетки или связанных между собой стержней двух взаимно перпендикулярных направлений, параллельных рядам сетки колонн.
4.6. Перекрытия следует рассчитывать на прочность, на возможность образования трещин и на жесткость. В случаях, указанных в п. 4.18, производится также проверка величины раскрытия трещин.
4.7. Расчет прочности плиты и капителей должен предусматривать:
а) расчет на продавливание;
б) расчет на излом полосы панелей вдоль или поперек перекрытия (рис. 16);
в) расчет на одновременный излом смежных панелей разных рядов.

Рис. 16. Схема полосового излома панелей
а - излом поперечной полосы панелей;
б - излом продольной полосы панелей
Расчета на излом отдельной панели Руководство не требует.
Хотя перегрузку одной панели, а также накопление дефектов материала или производства работ в пределах отдельной панели и следует считать наиболее вероятными, все же излом одной панели практически не является опасным, поскольку благодаря связи с окружающими панелями, прочность которых еще не исчерпана, неизбежно должен возникать распор, повышающий прочность угрожаемой панели.
4.8. Расчет на продавливание плиты производится по периметру капители или воротника. Капители рассчитываются на продавливание в наиболее слабых местах, например там, где очертание образует входящие узлы. Проверка на продавливание производится также в местах приложения значительных грузов, распределенных на небольшой площади.
Предполагается, что продавливание происходит по поверхности пирамиды или конуса, боковые стороны или образующая которых наклонены под углом 45° к вертикали (рис. 17).

Рис. 17. Схема продавливания плиты безбалочного перекрытия
а - в плите; б - в капители
Проверка производится по формуле
P <= kRрh0b, (154)
где k = 1 для тяжелых бетонов; k = 0,8 на пористых заполнителях;
P - расчетная продавливающая сила с коэффициентом перегрузки n > 1;
h0 - полезная высота на проверяемом участке;
Rр - расчетное сопротивление бетона на растяжение;
b - среднее арифметическое между периметрами верхнего и нижнего оснований пирамиды, образующейся при продавливании в пределах полезной высоты.
При расчете на продавливание капителей или полукапителей, а также плиты по периметру капителей и полукапителей величина силы P принимается равной сумме сил, передающихся через перекрытие на рассматриваемую колонну, за вычетом нагрузок, приложенных к верхнему основанию пирамиды продавливания.
В частности, при проверке прочности на продавливание квадратной или прямоугольной капители с размерами нижнего основания пирамиды продавливания 2x (2y), размерами в плане грузовой площади колонны lx и ly и при равномерной на окружающих колонну панелях нагрузке p:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
P = p [lxly - 4(x + h0)(y + h0), (155)
где h0 - полезная высота капители или плиты на контуре нижнего основания пирамиды продавливания, при этом
b = 4(x + y + h0). (156)
В бескапительных перекрытиях для повышения несущей способности на продавливание по периметру воротников устанавливается поперечная арматура.
4.9. Расчет на излом отдельной поперечной или продольной полосы панелей является основным и во всех случаях обязательным. Он производится в предположении, что в рассматриваемой полосе панелей образуются линейные пластические шарниры, параллельные оси этой полосы: один линейный пластический шарнир в пролете с раскрытием трещин снизу и по одному линейному пластическому шарниру у опор с раскрытием трещин сверху. В зависимости от положения опорных пластических шарниров сжатая зона может размещаться целиком в плите либо частью или полностью в капителях (рис. 18).

Рис. 18. Положение сжатой зоны в пластических шарнирах
у опор (при раскрытии трещин сверху)
а - в плите; б - в капители
Для бескапительных перекрытий сжатая зона всегда располагается в плите.
В крайней полосе панелей при свободном опирании ее на массивную стену образуются всего два линейных пластических шарнира: один в пролете и один на опоре, вблизи первого ряда колонн; поворот конца плиты, опирающегося на стену, осуществляется свободно.
Требуемая нормами прочность перекрытия должна обеспечиваться при любом, удовлетворяющем вышеуказанным условиям, расположении линейных пластических шарниров на рассчитываемой полосе.
Расчет средних панелей ведется по формуле
где L - расстояние между крайними линейными пластическими шарнирами полосы;
ly - расстояние между рядами колонн в направлении вдоль полосы;
x - расстояние между левым и средним линейными пластическими шарнирами;
p - интенсивность полной расчетной с коэффициентом перегрузки n > 1 нагрузки, равномерно распределенной по полосе;
Fк - площадь верхней арматуры в левом пластическом шарнире в пределах одной панели;
Fп - площадь нижней арматуры в среднем пластическом шарнире в пределах одной панели;

zк, zп,  - плечи внутренней пары в левом, среднем и правом пластических шарнирах соответственно.
- плечи внутренней пары в левом, среднем и правом пластических шарнирах соответственно.
Для конструкций, симметричных относительно середины рассматриваемой полосы, формула (157) приобретает вид
где cx - расстояние крайних пластических шарниров от ближайших к ним рядов колонн;
lx - размер панели в направлении, перпендикулярном рассматриваемой полосе.
Расчет крайних панелей при окаймлении их консолями производится также по формуле (157). В этом случае необходимо произвести дополнительно расчет на излом консоли с образованием одного параллельного краю перекрытия линейного пластического шарнира (рис. 19, а), а также на излом полосы консоли с образованием в пределах одной панели трех перпендикулярных краю перекрытия линейных пластических шарниров: одного в пролете с раскрытием трещин снизу и двух - ближе к линиям колонн с раскрытием трещин вверху (рис. 19, б).

а - с образованием параллельного краю пластического шарнира;
б - то же, перпендикулярных краю пластических шарниров
В случае когда край перекрытия поддерживается полукапителями, расчет крайних панелей по формуле (157) или (158) производится в предположениях:
а) излом полосы панелей, параллельной краю;
б) излом полосы панелей, перпендикулярной краю.
Если край перекрытия поддерживается окаймляющей балкой, расчет крайней панели на излом полосы панелей, параллельной краю, производится по-прежнему по формуле (157), а расчет на излом полосы, перпендикулярной краю, должен производиться в двух вариантах:
а) с изломом окаймляющей балки в тех местах, где происходит излом плиты;
б) без излома окаймляющей балки, но с раздвоением трещины, раскрывающейся внизу (рис. 20).

с поддерживающей балкой
а - с изломом поддерживающей балки; б - то же, без излома
При этом расчет ведется с помощью неравенства:
В формулах (159) и (160) обозначено:
cx - расстояние от линии колонн до ближайшего линейного пластического шарнира
 ;
;b - ширина обвязочной балки;
Fоп - сечение верхней арматуры в крайних линейных пластических шарнирах на протяжении панели;
Fп - сечение нижней арматуры, параллельной краю перекрытия, в среднем линейном пластическом шарнире (схема а) или суммарное сечение той же арматуры в среднем и косом пластических шарнирах (схема б на протяжении панели);
Fy - полное сечение нижней арматуры, перпендикулярной краю перекрытия, в косых линейных пластических шарнирах;
zоп, zп,  ,
,  - плечи внутренней пары для усилий в арматуре, на которое они умножаются в формулах (159) и (160).
- плечи внутренней пары для усилий в арматуре, на которое они умножаются в формулах (159) и (160).
При определении плеча z внутренней пары для верхней арматуры, параллельной краю плиты, следует учитывать, что сжатая зона, соответствующая этой арматуре в верхней арматуре балки, может оказаться целиком вне плиты (в капители безбалочного перекрытия и в обвязочной балке).
Сечение арматуры  , вводимое в расчет по формуле (160), ограничивается условием, что окаймляющая балка в состоянии была воспринять крутящий момент:
, вводимое в расчет по формуле (160), ограничивается условием, что окаймляющая балка в состоянии была воспринять крутящий момент:
 . (161)
. (161)В случае когда край перекрытия свободно опирается на массивную стену, расчет крайней панели должен быть произведен по формуле (157) для случая излома пристенной полосы и для случая излома полосы, перпендикулярной стене по схеме, аналогичной рис. 19, б, и по формуле (160) с учетом, однако, отсутствия окаймляющей балки и верхней арматуры плиты, заделываемой в эту балку.
Величину x в формуле (157) достаточно принять равной:
а) величине L/2 для всех средних панелей, для крайних панелей при изломе полосы, перпендикулярной краю перекрытия при любой его конструкции, а также при изломе полосы, параллельной краю перекрытия для крайних панелей с консолями и для крайних панелей с полукапителями в случае значительной жесткости наружных колонн (см. п. 4.13);
б) 0,55L при изломе полосы, параллельной краю перекрытия, для крайних панелей с окаймляющей балкой, а также для крайних панелей с полукапителями при незначительной (см. п. 4.13) жесткости наружных колонн;
в) 0,65L при изломе полосы, параллельной краю перекрытия, для крайних панелей, свободно опирающихся на наружную стену.
В случаях б и в величина x представляет собой расстояние пролетного пластического шарнира от опорного пластического шарнира, расположенного у внутренней стороны крайней панели.
Величину  по формуле (160) достаточно принять равной: в случае окаймляющей балки по краю перекрытия - 0,5, а в случае опирания края плиты на стену - 0,6.
по формуле (160) достаточно принять равной: в случае окаймляющей балки по краю перекрытия - 0,5, а в случае опирания края плиты на стену - 0,6.
В общем случае следует производить расчет при разном положении опорных пластических шарниров как в пределах капителей - для выявления необходимой арматуры в основных сечениях, так и в плите - для проверки допустимости мест обрыва стержней верхней арматуры.
4.10. Расчет перекрытия на одновременный излом смежных панелей разных рядов следует вести с учетом распора, создаваемого колоннами. Когда распор колонн в явной форме не учитывается, сечение арматуры может быть уменьшено против величин, предусмотренных расчетом, на 10%, если между рассчитываемой панелью и краем перекрытия имеются два ряда колонн или более; на 5% - если между рассчитываемой панелью и краем перекрытия имеется один ряд колонн.
Для консольных свесов плит, а также для панелей, свободно опертых на стены, уменьшение армирования за счет распора колонн не производится.
В случаях, указанных в п. 4.11, расчет перекрытий на одновременный излом смежных панелей разных рядов может не производиться.
При расчете на излом смежных панелей разных рядов принимается, что в пролете средних панелей образуются взаимно перпендикулярные и взаимно параллельные рядам колонн линейные пластические шарниры с раскрытием трещин внизу. Каждая панель разделяется этими пластическими шарнирами на четыре звена, вращающиеся вокруг опорных линейных пластических шарниров, оси которых расположены в зоне капителей, как правило, ниже плиты, под углом к рядам колонн. При этом трещины над опорными пластическими шарнирами раскрываются вверху, а по линии колонн, развиваясь сверху вниз, трещины прорезают всю толщу плиты.
Направления осей опорных пластических шарниров попарно пересекаются на вертикальных плоскостях, в которых лежат оси пролетных пластических шарниров (рис. 21).

Рис. 21. Направление осей опорных пластических шарниров
при одновременном изломе смежных панелей
Когда схема излома панели симметрична относительно обеих осей, направления опорных пластических шарниров образуют с рядами колонн углы, равные 45°.
Если по краю перекрытия плита выступает за колонны в виде консоли, то схема разрушения крайних пролетов и консолей имеет тот же характер, что в средних пролетах.
В крайних панелях перекрытий, имеющих полукапители на крайних колоннах, характер схемы разрушения тот же, что в средних панелях.
Если край перекрытия поддерживается окаймляющей балкой, следует произвести расчет по той же схеме, как и для случая полукапителей, полагая, что окаймляющая балка ломается. Кроме того, должен быть произведен расчет и в предположении, что окаймляющая балка не ломается, а пролетные линии излома в крайней полуполосе имеют косое направление от центра панели к наружным колоннам (рис. 22). При этом в отношении верхней арматуры, связывающей плиту с обвязочной балкой, делаются те же ограничения, как и в п. 4.9.

Рис. 22. Схема излома крайних панелей
с поддерживающей балкой
Если край плиты имеет опору, расчет ведется по схеме рис. 23.

Рис. 23. Схема излома крайних панелей
при опирании их на стену
Для излома смежных панелей разных рядов применительно к схеме излома, симметричной относительно обеих осей панелей, расчет ведется по формуле (162):
При квадратной панели, одинаково армированной в обоих направлениях, это неравенство упрощается и принимает вид
ИС МЕГАНОРМ: примечание. Экспликация дана в соответствии с официальным текстом документа. |
lx, ly, l - пролеты панели;
Fxк, Fyк, Fк - сечение верхней арматуры на ширину панели:
Fxп, Fyп, Fп - сечение нижней арматуры в пролете на ширину панели;
F - сумма сечений арматуры одного направления в пролете и на опоре на ширину панели в случае одинакового армирования в обоих направлениях;
zк - плечо внутренней пары для верхней арматуры;
zп - плечо внутренней пары для нижней арматуры:
4.11. При применении квадратных или прямоугольных в плане капителей ломаного очертания по рис. 24 рекомендуется принимать: величину отношений  и
и  - в пределах от 0,08 до 0,12;
- в пределах от 0,08 до 0,12;

Рис. 24. Капитель ломаного очертания
отношение высоты hк капители в месте перелома ее очертания к толщине плиты hп в пределах от  до
до  ;
;
полуширину капители rx и ry соответственно в направлении пролетов lx и ly не меньшей, чем
 . (164)
. (164)Наклон нижней части капители - не положе, чем под 45°.
При соблюдении этих рекомендаций, а также дальнейших рекомендаций настоящего пункта и п. 4.15 разрешается при проектировании не производить расчет на излом смежных панелей разных рядов, а при расчете на излом полос панелей принимать расположение опорных пластических шарниров только по месту перелома очертания, капителей.
При этом полезная высота плиты h0п и полезная высота капители h0к по обоим направлениям принимаются равными соответственно полной толщине плиты или капители минус диаметр арматуры и минус 1 см.
Плечо внутренней пары для сечений плиты может быть принято равным:
zп = 0,96h0п. (165)
Для плеча внутренней пары верхней арматуры принимается
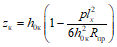 . (166)
. (166)Для средней панели рекомендуется принимать в формуле (157) величины
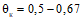
и соответственно
 ,
,а по ширине панели располагать арматуру равномерно.
Для крайних панелей при устройстве консолей принимать в направлении, параллельном краю пролета и консоли, то же распределение арматуры, как для средних панелей, а в направлении, перпендикулярном краю, при тех же значениях  и
и  оставить под наружным рядом колонн и на консоли 2/3 арматуры в надколонных полосах и 1/3 в пролетных полосах. Нижнюю арматуру крайнего пролета и верхнюю над первым внутренним рядом колонн располагать по-прежнему равномерно.
оставить под наружным рядом колонн и на консоли 2/3 арматуры в надколонных полосах и 1/3 в пролетных полосах. Нижнюю арматуру крайнего пролета и верхнюю над первым внутренним рядом колонн располагать по-прежнему равномерно.
При устройстве полукапителей на крайних колоннах в случае большой жесткости последних (см. п. 4.13) армировать крайние панели так же, как средние, с той разницей, что у наружного края вся требуемая расчетом верхняя арматура, перпендикулярная ему, ставится в надколонной полосе.
При меньшей жесткости крайних колонн по сравнению со средними рекомендуется арматуру, параллельную краю, принимать такую же, как для средних панелей. Для направления, перпендикулярного краю, армирование принимать:
 ;
;  .
.Примечание. Надколонными полосами называются части плиты, расположенные в пределах 1/4 пролета в каждую сторону и от оси ряда колонн. Пролетная полоса занимает оставшуюся между надколонными полосами ширину, равную половине пролета.
В случае когда край плиты поддерживается обвязочной балкой, рекомендуется, независимо от жесткости крайних колонн, принимать для направления арматуры перпендикулярно краю коэффициенты распределения:
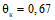 ;
; 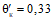 .
.В месте сопряжения плиты с обвязочной балкой не менее двух третей верхней арматуры размещать в пределах надколонной полосы.
Арматуру, параллельную краю плиты, рекомендуется распределять между опорными и пролетными сечениями так же, как для средних панелей, а по ширине панели размещать в полосе шириной в полпролета, примыкающей к внутренним колоннам, две трети необходимой по расчету арматуры, а в полосе, примыкающей к окаймляющей балке, - остальную треть.
При опирании плиты крайних панелей на стену для арматуры, перпендикулярной краю, рекомендуются коэффициенты распределения:
Величина  в этом случае равна нулю.
в этом случае равна нулю.
В направлении, параллельном краю, арматура размещается так же, как при наличии обвязочной балки по крайним колоннам.
По конструктивным соображениям указанные в настоящем пункте значения коэффициентов 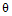 могут быть изменены в ту или иную сторону в пределах до 10%, однако с тем, чтобы удовлетворялось условие
могут быть изменены в ту или иную сторону в пределах до 10%, однако с тем, чтобы удовлетворялось условие
 .
.4.12. Для расчета колонн принимается наиболее опасное состояние, когда по одну сторону от колонны происходит излом полосы, тогда как по другую сторону колонны полоса загружена только нагрузкой от собственной массы. В расчете колонн следует принимать случаи излома как продольных, так и поперечных полос панелей. Для средней колонны момент, передающийся на узел, может быть подсчитан по формуле
где  - суммарное сечение арматуры в загруженном пролете;
- суммарное сечение арматуры в загруженном пролете;
 - суммарное сечение арматуры в загруженном пролете;
- суммарное сечение арматуры в загруженном пролете;Fк,  , Fп - сечения рабочей арматуры на опорах и в средней части загруженного пролета;
, Fп - сечения рабочей арматуры на опорах и в средней части загруженного пролета;
zк, zп,  - плечи внутренней пары на опорах и в пролете для загруженной полосы;
- плечи внутренней пары на опорах и в пролете для загруженной полосы;
l - загруженный пролет;
lс - соседний незагруженный пролет;
p - полная расчетная нагрузка, коэффициент перегрузки n > 1;
g - расчетная нагрузка от собственного веса;
c и c' - расстояния опорных пластических шарниров от осей ближайших колонн.
Величины со штрихами относятся к опоре, противоположной рассчитываемой колонне.
В случае симметричной конструкции загруженной полосы формула (167) принимает вид
Изгибающий момент в нижнем сечении колонны, расположенной над рассматриваемым перекрытием, принимается равным:
 . (169)
. (169)Изгибающий момент для колонны, поддерживающей рассматриваемое перекрытие, в сечении у низа капители
 . (170)
. (170)Здесь iв, iн - жесткости верхней и нижней колонны, отнесенные к расчетной высоте колонны, равной расстоянию от поверхности плиты нижележащего этажа до низа капители следующего этажа, а iпл - жесткость плиты шириной в одну панель, отнесенная к длине пролета lс, за вычетом капителей.
При расчете крайних колонн изгибающий момент в нижнем сечении расположенной над рассматриваемым перекрытием колонны принимается равным:
 , (171)
, (171)а для сечения у низа капители колонны, поддерживающей рассматриваемое перекрытие:
 , (172)
, (172)при этом момент, передающийся на узле, определяется по следующим формулам:
а) для перекрытия с консольным вылетом плиты за крайние колонны
где lк - вылет консоли, считая от оси крайнего ряда колонн;
б) при крайних колоннах с полукапителями или с окаймляющей балкой
Правая часть формулы (174), а также первые слагаемые правой части формулы (173) и первые сомножители правой части (167) и (168) представляют собой изгибающие моменты загруженного пролета у оси рассчитываемых колонн, выраженные через предельные изгибающие моменты в трех линейных пластических шарнирах этого пролета. Дополнительные множители в формулах (167) и (168) оценивают разгружающее действие соседнего пролета, а вычитаемое в формуле (173) - разгружающее действие консоли плиты.
 , (175)
, (175)где iв, iн, iпл имеют значения, указанные в п. 4.12, то крайние колонны считаются имеющими значительную жесткость, а при несоблюдении указанного неравенства - менее жесткими, в соответствии с чем и производится расчет крайних панелей согласно п. 4.11.
4.14. При расчете перекрытия на излом смежных панелей может быть учтен распор наружного ряда колонн, а при расчете средних панелей - распор двух ближайших к краю рядов колонн. При расчете перекрытия может учитываться распор как поддерживающих его колонн, так и колонн, расположенных непосредственно над рассчитываемым перекрытием. Величина распора от каждой колонны принимается равной разделенному на две трети ее расчетной высоты наибольшему изгибающему моменту, который может воспринять сечение колонны в плоскости, перпендикулярной краю перекрытия, при наличии данной продольной силы.
Величина распора определяется по формуле
 , (176)
, (176)где Hi - распор от данной колонны;
hp - высота колонны, считая от плиты нижеследующего перекрытия до низа капителей этой колонны;
Mmax - наибольший возможный расчетный момент в сечении колонны при наличии расчетной продольной силы N.
Величину предельного момента в сечении колонны следует определять как при наибольшей, так и при наименьшей для данного состояния продольной силе и принимать в расчет меньший из полученных моментов.
Величина расчетного распора H на панель определяется для крайних панелей промежуточных перекрытий как сумма распора вышележащей и нижележащей крайних колонн, а для средних перекрытий - как сумма распоров четырех колонн: вышележащих и нижележащих крайних колонн первого промежуточного ряда.
При расчете панели перекрытия распор колонн учитывается путем добавления к правой части неравенства (162) или (163) величины Hzp,
где H - расчетный распор для данной панели;
zp - плечо сил, равное:
 , (177)
, (177)hк - высота капители в месте расположения опорного пластического шарнира;
xк - высота сжатой зоны в опорном пластическом шарнире без учета распора;
xп - высота сжатой зоны в пролетных пластических шарнирах без учета распора;
xкр и xпр - увеличение высоты сжатой зоны соответственно в опорном и пролетном пластических шарнирах под влиянием распора;
lx и ly - пролеты рассматриваемой панели.
4.15. В перекрытиях, спроектированных в соответствии с п. 4.11, должны соблюдаться следующие требования относительно мест обрыва арматуры.
1. В средних панелях:
полное расчетное сечение верхней арматуры должно быть сохранено в каждую сторону от линии колонн не менее чем на длину
а не менее половины этой арматуры должно доходить до сечения, отстоящего от линии колонн, на величину
Сечение нижней арматуры должно быть сохранено полностью в каждую сторону от середины пролета не менее чем на длину
 , (180)
, (180)а половина этой арматуры должна быть заведена за линию края капители не менее чем на длину, требуемую нормами для заделки растянутых стержней.
c - расстояние от оси колонны до места перелома очертания капители;
2. В крайних панелях и консольных выступах арматура, параллельная краю, обрывается в тех же местах, как и в средних панелях.
Для арматуры, перпендикулярной краю, принимаются те же места обрыва, как и в средних панелях в случае устройства полукапителей с достаточно жесткими колоннами (см. п. 4.11). В остальных случаях места обрыва стержней назначаются в соответствии со следующими рекомендациями.
Полное расчетное сечение верхней арматуры над первым промежуточным рядом колонн следует продолжить полностью в крайний пролет не меньше чем на длину:
 , (181)
, (181)а не менее половины этой арматуры следует продолжить до сечения, отстоящего от оси первого промежуточного ряда колонн на величину
 ; (182)
; (182)полное расчетное сечение верхней арматуры над крайними колоннами следует продолжить полностью в крайний пролет не меньше чем на длину
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 , (183)
, (183)а не менее половины этой арматуры следует продолжить до сечения, отстоящего от оси крайнего ряда колонн на величину
 . (184)
. (184)Сечение нижней арматуры на средней части пролета следует сохранить полностью. Половина пролетной арматуры может быть оборвана на расстоянии от оси первого промежуточного ряда колонн не большем чем
 , (185)
, (185)и от оси крайнего ряда колонн, не большем чем
 . (186)
. (186)Половину нижней арматуры следует завести за линию края капителей не менее чем на длину, требуемую для заделки стержней, а в случае окаймляющей балки или опирания на стену довести до края плиты.
4.16. Для выбора стадии работы конструкции, по которой должна производиться проверка прогиба перекрытия, следует проверять условия образования трещин.
Изгибающие моменты M, отнесенные к единице длины рассчитываемого сечения, могут быть определены методами теории упругости.
В случае если перекрытие запроектировано в соответствии с п. 4.11, опасным явится сечение над капителью под углом 45° к линии колонн. При этом величина момента, вызывающего образование трещин, может быть найдена, учитывая форму сечения, образованную двумя трапециями, по формуле
а соответствующая нагрузка - по формуле
Если расчетная нагрузка (n = 1) менее величины pт, проверку прогибов следует производить в предположении, что трещины отсутствуют. Проверка ширины раскрытия трещин при этом отпадает.
4.17. Прогибы перекрытий, определяемые в предположениях об отсутствии трещин, могут быть вычислены методами теории упругости.
Для перекрытий, спроектированных в соответствии с п. 4.11, величину прогиба середины панели при отсутствии трещин в конструкции рекомендуется определять по формуле
Прогиб безбалочных перекрытий обычных складских помещений, подсчитанный в предположении, что трещин в конструкции нет, не должен превышать 1/1000 пролета.
В случае если, согласно п. 4.16, прогиб перекрытия следует определять в предположении о наличии трещин, расчет производится исходя из положений пп. 1.8 и 2.7 настоящего Руководства.
Величина нагрузки pт и прогиб fт при появлении трещин могут быть определены по формулам (188) и (189), где величина M принимается по формуле (187).
Если при назначении армирования производился учет влияния распора, то оно должно быть учтено и при вычислении нагрузки при исчерпании несущей способности.
Для случая безбалочных перекрытий с квадратной сеткой колонн и квадратными капителями прогиб, предшествующий исчерпанию несущей способности fп, может быть выражен формулой
 , (190)
, (190)где l1 - пролет перекрытия по осям колонн;
l - пролет плиты в чистоте между капителями;
4.18. Если конструкция подвергается действию агрессивной среды, а с образованием трещин, согласно п. 4.16, необходимо считаться, то следует проверить ширину раскрытия трещин, которая не должна превышать 0,2 мм.
Проверка величины раскрытия трещин производится для сечений над капителью, при этом величину напряжений в арматуре  принимают в соответствии с рекомендациями действующих строительных норм и правил на проектирование железобетонных конструкций.
принимают в соответствии с рекомендациями действующих строительных норм и правил на проектирование железобетонных конструкций.
4.19. Сборные безбалочные перекрытия образуются из плит, капителей и колонн. Плиты разделяются на межколонные и пролетные. Межколонные плиты опираются на капители и поддерживают пролетные плиты. Они могут быть уложены в одном или двух направлениях (рис. 25). Пролетные плиты опираются в первом случае своими концами на капители и межколонные плиты, а во втором - на межколонные плиты по четырем сторонам. Толщина пролетных плит меньше толщины межколонных на высоту четверти, на которую ложатся пролетные плиты.

Рис. 25. Конструктивная схема сборных безбалочных перекрытий
Пролетные плиты сборных перекрытий с надколонными плитами двух направлений рассчитываются на прочность в соответствии с рекомендациями разд. 2.
Межколонные плиты должны иметь на концевых участках верхнюю арматуру, надежно соединяемую сваркой с арматурой, воспринимающей отрицательные моменты в зоне капителей, которые должны быть тщательно замоноличены конструктивным бетоном. При соблюдении этих условий колонны с капителями и межколонными плитами рассчитываются как рамы согласно рекомендациям разд. 3.
Учитывая возможность одновременного разрушения межколонных и пролетных плит, необходимо производить расчет прочности перекрытия в целом на полосовое разрушение, руководствуясь рекомендациями настоящего раздела для монолитных безбалочных перекрытий.
При качественном заполнении швов по контуру пролетных плит, опертых по четырем сторонам, прогиб этих плит может быть определен следующим образом:
а) вычисляется изгибающий момент на единицу длины при образовании трещин для сплошных гладких плит по формуле
 , (191)
, (191)где h - толщина пролетной плиты.
Нагрузка, отвечающая образованию трещин, определяется как для защемленной плиты по формуле
 , (192)
, (192)а прогиб плиты к моменту трещинообразования - по формуле
 , (193)
, (193)где Eб - модуль упругости бетона.
Связь межколонных плит друг с другом и заливка контура пролетной плиты препятствуют удлинению ее нижней поверхности и при качественном выполнении создают, по крайней мере до образования трещин в пролетной плите, условия, близкие к полному защемлению ее краев;
б) определяется методом предельного равновесия несущая способность свободно опертой плиты p по расчетным характеристикам материалов (RаII, RпрII) учитывается распор, создаваемый контуром, образованным межколонными полосами повышением найденной величины на 20%.
По рекомендациям разд. 2 определяют прогиб плиты при исчерпании ее несущей способности и по формуле (51) - прогиб при расчетной нагрузке с коэффициентом перегрузки n = 1.
СТОЯЩИЕ КРУГЛЫЕ В ПЛАНЕ СООРУЖЕНИЯ БАШЕННОГО ТИПА
5.1. Рекомендации настоящего раздела относятся к круглым или восьмиугольным, а также к кольцевым фундаментам. В пределах нижнего основания трубы или башни толщина круглых и восьмиугольных фундаментов предполагается постоянной, а за его пределами - линейно убывающей по направлению к наружному краю, где она должна составлять не менее одной четверти толщины средней части фундаментной плиты. Толщина фундамента в пределах консольных выступов может убывать также ступенями, назначаемыми так, чтобы толщина консоли ни в одном ее сечении не была меньше, чем при трапецеидальном сечении ее (рис. 26). При кольцевых фундаментах наружная часть кольца предполагается очерченной так же, как указано выше для круглых фундаментов, а внутренняя имеет постоянную толщину, если, согласно п. 5.11, она должна иметь верхнюю арматуру, либо, если верхней арматуры по условиям п. 5.11 не требуется, толщину, убывающую к внутреннему краю по правилам, указанным для наружного консольного выступа.

консольного выступа
Фундамент следует изолировать от воздействия высокой неравномерной температуры, вызванной технологическим теплом. В противном случае расчет и конструирование его производятся по специальным указаниям.
5.2. Сплошные фундаменты рекомендуется осуществлять восьмиугольными и армировать равномерными сетками: в пределах консолей и прилежащих к ним участках внутренней части плиты - нижними сетками, а по всей внутренней части плиты - верхними сетками (рис. 27).

Рис. 27. Схема армирования фундаментов
а - схема раскладки одного из двух рядов верхних сеток,
второй ряд сеток укладывается перпендикулярно первому;
б - схема раскладки одного из двух рядов нижних сеток,
второй ряд сеток укладывается перпендикулярно первому;
1 - верхние сетки; 2 - нижние сетки
Во время бетонирования верхние сетки должны удерживаться в проектном положении специальными сварными элементами, предусмотренными спецификацией арматуры.
Для расчета восьмиугольный фундамент заменяется равновеликим ему по площади круглым.
5.3. Фундамент, подвергающийся совместному действию центрально приложенной нагрузки от веса конструкции и ветрового момента, условно рассчитывается на равномерную нагрузку снизу, интенсивность которой равна наибольшему напряжению, подсчитанному по формулам сопротивления материалов для середины консольного выступа фундамента:
 , (194)
, (194)где r1 - внешний радиус нижнего сечения трубы или башни (рис. 28);
r2 - радиус окружности, ограничивающей равновеликий восьмиугольный круглый фундамент;
p - условно принимаемая для расчета фундамента величина равномерного расчетного реактивного давления на него снизу.

при расчете на отлом консоли
Если следует учесть концентрацию напряжений у края фундамента, то определяется распределение реакций под фундаментом от условной вертикальной силы N = pF.
При этом реактивная сила, приходящаяся на среднюю часть фундамента в пределах площади основания трубы или башни, распределяется по этой части плиты равномерно.
5.4. Толщина плиты должна проверяться по условию скалывания с тем, чтобы поперечная арматура по расчету не требовалась. Проверку следует производить для кольцевых сечений, расположенных вблизи основания стенки трубы или башни с наружной и внутренней стороны этой стенки.
Чтобы удовлетворить вышеуказанному условию, не увеличивая чрезмерно толщину плиты, можно в случае необходимости повысить проектную прочность бетона фундамента, но не свыше марки 200.
Для определения сечения арматуры нижних сеток принимается схема излома плиты по рис. 28. Кольцо консольного выступа распадается при этом на звенья с центральными углами  . Длина линии сопряжения такого звена с центральной цепью равна r1d. Момент реактивной нагрузки, стремящейся повернуть звено, равен
. Длина линии сопряжения такого звена с центральной цепью равна r1d. Момент реактивной нагрузки, стремящейся повернуть звено, равен  . Арматура, пересекающая кольцевую и радиальные трещины, сопротивляется повороту звена. Усилие текучести в этой арматуре на единицу длины линии излома любого направления равно fаRа.
. Арматура, пересекающая кольцевую и радиальные трещины, сопротивляется повороту звена. Усилие текучести в этой арматуре на единицу длины линии излома любого направления равно fаRа.
Равнодействующая усилий текучести на участке кольцевой линии излома и двух радиальных линий излома, выделяющих рассматриваемое звено, равна:
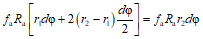 .
.Сжатая зона располагается только на участке кольцевой линии излома длиной  . Усилие сжатия на единицу длины этой линии излома равно:
. Усилие сжатия на единицу длины этой линии излома равно:
Высота сжатой зоны x при этом равна:
 ,
,а плечо внутренней пары равно:
 ,
,тогда момент сил, сопротивляющихся повороту звена, равен:
 .
.Он должен быть больше, чем момент  , стремящийся повернуть это звено, откуда вытекает неравенство (195).
, стремящийся повернуть это звено, откуда вытекает неравенство (195).
Площадь fа стержней нижних сеток, приходящихся на единицу длины перпендикулярного к этим стержням сечения плиты, определяется из неравенства
где Rа - расчетное сопротивление арматуры;
Rпр - расчетная прочность бетона на сжатие;
h0 - полезная высота фундаментной плиты в месте заделки в нее стенок трубы или башни;
m - момент внешних сил, приложенных к консоли, отнесенный к единице длины внешнего контура основания трубы или башни.
Момент m, если это нужно, определяется с учетом концентрации напряжений грунта у краев фундаментной плиты. Если концентрацией напряжений у контура фундамента можно пренебречь, то
При равномерно распределенной реактивной нагрузке
 ,
,откуда получается равенство (196).
5.6. Для определения места теоретического обрыва сеток в зоне постоянной толщины плиты рассматривается схема разрушения, отличающаяся от предыдущих тем, что кольцевая трещина не цилиндрическая, а коническая и обходит внутренние концы сеток (рис. 29).

теоретического обрыва стержней
В этом случае сопротивление повороту звена оказывает только арматура, пересекающая радиальные трещины. Усилие текучести этой арматуры дает равнодействующую
 .
.Длина линии излома звена, на которой имеется сжатие бетона, равна  . Поэтому усилие сжатия на единицу длины этой линии излома есть
. Поэтому усилие сжатия на единицу длины этой линии излома есть
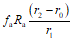 ,
,и высота сжатой зоны
 .
.Поэтому момент от усилий текучести в арматуре равен:
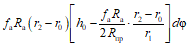 .
.Момент от нагрузки на консольном выступе равен по предыдущему  , а от равномерной нагрузки p, расположенной между радиусами r0 и r1:
, а от равномерной нагрузки p, расположенной между радиусами r0 и r1:
 .
.Условие, что звено не будет поворачиваться, выразится неравенством:
 .
.Плечо внутренней пары в этом случае не точно такое же, как в предыдущем, однако различаются они незначительно.
Пренебрегая этим и полагая плечи внутренней пары в указанных случаях одинаковыми, можно предыдущее условие упростить. Перепишем его в формуле
 .
.Из формулы (195)  ; заменяя в запас прочности в предпоследнем неравенстве fаRаz правой частью последнего неравенства, имеем
; заменяя в запас прочности в предпоследнем неравенстве fаRаz правой частью последнего неравенства, имеем
 ; заменяя в запас прочности в предпоследнем неравенстве fаRаz правой частью последнего неравенства, имеем
; заменяя в запас прочности в предпоследнем неравенстве fаRаz правой частью последнего неравенства, имеем .
.Проверка места теоретического обрыва нижних сеток внутри контура труб производится согласно неравенству:
где p1 - равномерная нагрузка на плиту фундамента в пределах площади нижнего основания трубы. Если концентрация напряжений на контуре фундамента не учитывается, p1 = p;
r0 - расстояние от оси сооружения до места теоретического обрыва сеток арматуры (рис. 29).
5.7. Для случая равномерной нагрузки место теоретического обрыва сеток определяется по приближенной формуле
Заменив в формуле (197) величину момента m его выражением по формуле (196), имеем

или
 ;
;из формулы (198) имеем
 ,
,а при этом условии предыдущее неравенство удовлетворяется.
Стержни сеток следует продолжить за место теоретического обрыва на длину, необходимую для их заанкеривания.
5.8. Сечение верхней арматуры определяется из предположения, что средняя часть плиты под влиянием реактивной нагрузки продавливается вверх с образованием радиальных трещин, раскрывающихся на верхней стороне плиты.
Консольные выступы при этом могут:
а) опускаться при подъеме средней части плиты, а нагрузка, приложенная к консольным выступам, совершает при этом отрицательную работу;
б) поворачиваться за счет образования раскрывающихся снизу кольцевой цилиндрической трещины и радиальных трещин согласно рис. 28;
в) поворачиваться вследствие образования трещин по рис. 29.
Однако сечение нижних сеток и места их обрыва подбираются так, чтобы соответствующие (рис. 28 и 29) схемы разрушения не могли реализоваться. Так как наиболее опасным оказывается случай "а", то для него составляется условие прочности.
Усилие текучести верхней арматуры вдоль одной радиальной трещины равно  .
.
Длина сжатой зоны вдоль этой трещины равна r2, поэтому высота сжатой зоны
 ,
,а плечо внутренней пары равно:
 .
.Условие прочности клиновидного элемента плиты с центральным углом 
 .
.Сечение  стержней верхней сетки, приходящееся на 1 м перпендикулярного к ним сечения, определяется из неравенства:
стержней верхней сетки, приходящееся на 1 м перпендикулярного к ним сечения, определяется из неравенства:
Если реактивная нагрузка по всей площади плиты может быть принята равномерной, то при замене p1 на p неравенство (199) переходит в неравенство
 . (200)
. (200)5.9. Для кольцевых фундаментов (рис. 30) расчет сечения нижней сетки, препятствующей отколу наружного консольного выступа, производится по той же формуле (195), (196), как для сплошных фундаментов.

Рис. 30. Схема кольцевого фундамента
Место теоретического обрыва нижней арматуры определяется по формуле (198). Однако если по расчету расстояние r0 от центра плиты до теоретического обрыва оказывается меньше внутреннего радиуса r3 кольцевого фундамента, то необходимо произвести перерасчет согласно п. 5.10.
5.10. Для кольцевого фундамента при r3 > 2r1 - r2 возможна схема излома, характеризующаяся тем, что наружная консольная часть плиты поднимается, а внутренняя консольная часть плиты опускается, причем реактивная нагрузка на наружной консоли совершает положительную, а на внутренней - отрицательную работу.
Рассуждая так же, как в п. 5.5, но не заменяя радиус r0 (место теоретического обрыва арматуры) внутренним радиусом кольцевой плиты, а также учитывая концентрацию напряжений на внутреннем контуре, находим неравенство (201).
Из условия
при r3 > 2r1 - r2 должно быть определено усиленное против требований п. 5.9 сечение fа нижней арматуры фундамента, где m' - момент реактивных сил, действующих на внутреннем выступе плиты, отнесенной к единице длины дуги радиусом r1.
Если концентрация напряжений на краях плиты может не учитываться, то величина m выражается формулой (196), а величина m' - формулой
 ,
,выводимой так же, как в п. 5.6.
При равномерно распределенной реактивной нагрузке условие (201) приобретает вид
Заменив приближенно, как в п. 5.6, левую часть предыдущей формулы через

и произведя преобразования, можно видеть, что условие выполняется всегда, если
r3 < 2r1 - r2.
5.11. Сечение верхней арматуры кольцевой плиты определяется из рассмотрения схемы излома, при которой внутренняя часть кольцевой плиты поднимается, а наружная опускается.
Усилие верхней арматуры вдоль одной радиальной трещины равно:
 .
.Длина сжатой зоны вдоль этой трещины равна r2 - r3, отсюда высота сжатой зоны
 ,
,а плечо внутренней пары равно:
 .
.Сечение верхней арматуры  должно удовлетворять условию предельного равновесия клиновидного элемента плиты
должно удовлетворять условию предельного равновесия клиновидного элемента плиты
где m' и m - отнесенные к единице длины дуги радиуса r1 моменты реактивных сил, действующих на внутренней и соответственно на внешней части кольцевой плиты.
Если реактивная нагрузка по площади плиты может быть принята равномерной, то неравенство (203) принимает вид
 .
.Если  , то верхняя арматура не требуется.
, то верхняя арматура не требуется.
 , то верхняя арматура не требуется.
, то верхняя арматура не требуется.ПРИМЕРЫ РАСЧЕТА <*>
--------------------------------
<*> В приведенных примерах расчетные характеристики бетона и арматуры приняты по одной из редакций главы СНиП II-21.
Пример 1. Требуется рассчитать П-образную предварительно-напряженную железобетонную раму покрытия пролетом l = 24 м при возвышении оси ригеля над опорными шарнирами на h = 6 м (п. 1.10).
Расчетная нагрузка полная (n = 1) g = 2825 кгс/м
То же, без снега и утеплителя .... q = 1745 "
Расчетная нагрузка полная ........ p = 3340 "
Бетон марки ...................... 400
ИС МЕГАНОРМ: примечание. Взамен ГОСТ 7348-63 Постановлением Госстандарта СССР от 21.01.1981 N 138 с 01.01.1983 введен в действие ГОСТ 7348-81. |
Напрягаемая арматура - гладкая проволока диаметром 5 мм по ГОСТ 7348-63.
Схема напрягаемой арматуры показана на рис. 31.

Рис. 31. Расположение напрягаемой арматуры в П-образной раме
Расчет прочности производится методом предельного равновесия, расчет трещиностойкости - с учетом естественного и искусственного перераспределения усилий.
Характер распределения усилий в стадии эксплуатации, близкий к принятому для стадии исчерпания несущей способности, создается искусственным регулированием величины лишней неизвестной.
Для облегчения ригеля целесообразно иметь на опоре момент, близкий по абсолютной величине к пролетному.
Приняв высоту сечения стоек hс = 80 см, оценивают по расположению пучков соотношение моментов: пролетный момент составит около 52%, а момент у грани стойки - около 48% их суммы.
В силу этого расчетный пролетный момент равен:
 .
.Момент в сечении ригеля у грани стойки
Мгр = 0,48·0,125·3,34·23,22 = 108 тс·м.
Теоретический опорный момент (по оси стойки)
Моп = 0,125·3,34·242 - Мп = 240 - 117 = 123 тс·м.
Распор рамы
 .
.Вертикальная реакция
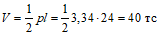 .
.Приняв высоту ригеля hр = 120 см, находят изгибающий момент в стойке в уровне низа ригеля
 .
.Эксцентрицитет продольной силы e0:
в пролетном сечении ригеля
 ;
;в сечении ригеля у грани стойки
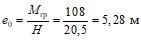 ;
;в сечении стойки в уровне низа ригеля
 .
.Проверка сечений по прочности.
Сечение стойки у ригеля прямоугольное размером 60 x 80 см, с восемью пучками по  , расположенными в два ряда на расстояниях 7,5 и 16,5 см от наружного края стойки. Центр тяжести пучков отстоит от края сечения на 12 см. Сечение арматуры Fa = 18,8 см2 = 0,00188 м2.
, расположенными в два ряда на расстояниях 7,5 и 16,5 см от наружного края стойки. Центр тяжести пучков отстоит от края сечения на 12 см. Сечение арматуры Fa = 18,8 см2 = 0,00188 м2.
 , расположенными в два ряда на расстояниях 7,5 и 16,5 см от наружного края стойки. Центр тяжести пучков отстоит от края сечения на 12 см. Сечение арматуры Fa = 18,8 см2 = 0,00188 м2.
, расположенными в два ряда на расстояниях 7,5 и 16,5 см от наружного края стойки. Центр тяжести пучков отстоит от края сечения на 12 см. Сечение арматуры Fa = 18,8 см2 = 0,00188 м2.Высоту сжатой зоны x определяют из уравнения моментов относительно равнодействующей силы в сечении. При расчетном сопротивлении арматуры Ra = 9500 кгс/см2 = 9,5 тс/см2 и расчетном сопротивлении бетона на сжатие Rпр = 185 кгс/см2 = 1850 тс/м2 уравнение моментов записывается
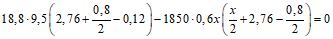
или x2 + 4,72x - 1,05 = 0; x = 0,215 м.
Расчетная несущая способность сечения
N = 1850·0,6·0,215 - 9,5·18,8 = 232 - 179 = 53 тс > 40 тс.
Ригель двутавровый высотой 120 см со стенкой 14 см, шириной полок 60 см и толщиной их по краям 15 см и у сопряжений со стенкой 19 см. Сечение армировано семью пучками по  , из которых четыре расположены прямолинейно в полках на расстоянии 6 см от верхней и нижней грани сечения. Криволинейные пучки расположены в вертикальной плоскости симметрии сечения.
, из которых четыре расположены прямолинейно в полках на расстоянии 6 см от верхней и нижней грани сечения. Криволинейные пучки расположены в вертикальной плоскости симметрии сечения.
 , из которых четыре расположены прямолинейно в полках на расстоянии 6 см от верхней и нижней грани сечения. Криволинейные пучки расположены в вертикальной плоскости симметрии сечения.
, из которых четыре расположены прямолинейно в полках на расстоянии 6 см от верхней и нижней грани сечения. Криволинейные пучки расположены в вертикальной плоскости симметрии сечения.В пролетном сечении расстояния криволинейных пучков от нижней грани составляют 6, 15 и 24 см. Центр тяжести нижней арматуры отстоит от нижней грани на расстоянии
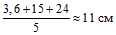 .
. Сечение нижних пучков 11,8  ........ 0,00118
........ 0,00118 
Сечение верхних пучков 4,69 " ........ 0,000469 "
Полное сечение арматуры 16,49 " ........ 0,001649 "
Для среднего сечения ригеля полная величина потерь, оцененная согласно Руководству по проектированию предварительно-напряженных железобетонных конструкций из тяжелого бетона, составляет 2050 кгс/см2. Величина натяжения без учета потерь 11000 кгс/см2.
Согласно Руководству по проектированию предварительно-напряженных железобетонных конструкций из тяжелого бетона, напряжение верхней арматуры при исчерпании прочности принимается равным:  (растяжение).
(растяжение).
 (растяжение).
(растяжение).Высоту сжатой зоны определяют из уравнения моментов относительно равнодействующей силы в сечении
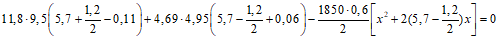 ;
;x2 + 10,2x - 1,51 = 0; x = 0,146 м;
N = 18500·0,6·0,146 - 11,8·9,5 - 4,69·4,95 =
= 22,5 тс > 20,5 тс.
В сечении ригеля у грани стойки расстояния криволинейных пучков от верхней грани составляют 17, 26 и 35 см. Расстояние центра тяжести верхней арматуры от верхней грани
 .
.Величина полных потерь в этом сечении равна 1550 кгс/см2;  (растяжение).
(растяжение).
 (растяжение).
(растяжение).Уравнение для определения высоты сжатой зоны:
 ;
;x2 + 9,36x - 1,41 = 0; x = 0,148 м;
N = 1850·0,6·0,148 - 11,8·9,5 - 4,69·5,45 =
= 22,2 тс > 20,5 тс.
При расчете трещиностойкости сечений принимают распределение усилий такое же, как для расчета несущей способности. Тогда усилия уменьшаются в отношении нагрузок
 .
.Проверяют сечение стойки на уровне нижней грани ригеля. Ввиду малого процента армирования геометрические характеристики сечения при оценке трещиностойкости определяют без учета арматуры.
Ядровое расстояние
 .
.Момент сопротивления с учетом пластических свойств бетона
 .
.Ядровый момент от внешних сил
 .
.Потери в рассматриваемом сечении оценены в 1550 кгс/см2.
Напряжение арматуры с учетом коэффициента точности натяжения
0,9 (11000 - 1550) = 8500 кгс/см2.
Ядровый момент от сил натяжения
8,5·18,8 (0,28 + 0,13) = 65,5 тс·м.
Расчетное сопротивление растяжению RрII = 19 кгс/см2:
RрIIWт = 190·0,12 = 22,5 тс·м;
65,6 + 22,5 = 88 тс·м < 89,2 тс·м,
т.е. условие трещиностойкости не выполняется. Чтобы выполнить условие трещиностойкости, принимают иное распределение усилий, а именно: уменьшают распор на 5%.
Величина ядрового момента от внешних сил становится равной:
 .
.При этом 88 тс·м > 78,5 тс·м. Условие трещиностойкости выполнено.
Проверяют трещиностойкость ригеля в середине пролета.
Величина распора
 .
.Эксцентрицитет сжимающей силы в пролетном сечении
 .
.Момент инерции сечения (пренебрегая арматурой)
 .
.Площадь сечения
F = 1,2·0,14 + 2·0,46·0,17 = 0,32 м2;
 .
.Ядровое расстояние
 .
.Ядровый момент внешней силы
 .
.Расстояние центра тяжести всей арматуры от низа сечения
 .
.Напряжение арматуры с учетом точности натяжения
 .
.Ядровый момент от сил натяжения:
 ;
;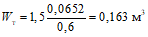 ;
; ;
; .
.Условие трещиностойкости выполнено.
Сечение ригеля у грани стойки находится в более благоприятных условиях в силу меньшей величины момента при выбранном значении распора и меньшей величины потерь, чем в середине пролета. Поэтому условие трещиностойкости ригеля у грани стойки соблюдается.
Для создания в системе желаемого распределения усилий сопряжение одной из стоек с ригелем во время монтажа устраивается шарнирным, причем ось шарнира смещена с оси стойки внутрь пролета на 25 см. Момент в шарнире создается натяжением арматуры стоек. После заделки шарнира бетоном дается дополнительная подтяжка арматуры для обжатия бетона, после чего каналы инъецируются.
Распор рамы при естественном и искусственном распределении усилий определяется с учетом ползучести бетона и наличия арматуры в сечениях ригеля и стойки и фактического ее расположения.
Расстояние центра тяжести арматурных пучков стойки от ее оси по высоте стойки
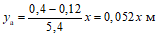 ,
,где x изменяется от 0 до  ; при x = 0 yа = 0;
; при x = 0 yа = 0;
 ; при x = 0 yа = 0;
; при x = 0 yа = 0;при x = 5,4 м yа = 0,28 м, что соответствует
 .
.Расстояние центра тяжести криволинейных арматурных пучков ригеля от его оси по длине ригеля ya = (-0,45 + 0,00587x2) м, где x изменяется от 0 (в середине пролета) до  . При x = 0 ya = -0,45 м, что соответствует удалению центра тяжести криволинейной арматуры от оси ригеля в середине его пролета:
. При x = 0 ya = -0,45 м, что соответствует удалению центра тяжести криволинейной арматуры от оси ригеля в середине его пролета:
 . При x = 0 ya = -0,45 м, что соответствует удалению центра тяжести криволинейной арматуры от оси ригеля в середине его пролета:
. При x = 0 ya = -0,45 м, что соответствует удалению центра тяжести криволинейной арматуры от оси ригеля в середине его пролета: ;
;при
 , yа = 0,34 м,
, yа = 0,34 м,соответствует удалению криволинейной арматуры от оси ригеля y грани стойки
 .
.Средний момент инерции сечений арматуры стойки относительно ее оси по всей высоте до грани ригеля, представляющий собой среднее арифметическое значение моментов инерции арматуры в бесконечном множестве сечений стойки,
 .
.Средний интегральный момент инерции сечений арматуры ригеля относительно его оси по всему пролету в свету

Модульное отношение
 .
.Средний интегральный момент инерции приведенных сечений стойки относительно ее оси по всей высоте до грани ригеля
 .
.Средний интегральный момент инерции приведенных сечений ригеля относительно его оси по всему пролету в свету:
 .
. .
.Для определения коэффициента релаксации вынужденных усилий определяется приведенная высота стоек и ригеля (п. 1.10)
 ;
; ;
; ;
; .
.Относительная критическая влажность бетона стоек и ригеля:
 ;
; .
.Средняя относительная равновесная влажность бетона стоек и ригеля:
 ;
; .
.Расчетное изменение относительной влажности бетона стоек и ригеля:
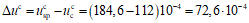 ;
;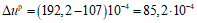 .
.Предельная величина меры ползучести бетона в стойках и ригеле (при условии загружения элемента в возрасте  , R = 400, kп = 1,3, kс = 0,55, см. табл. 1):
, R = 400, kп = 1,3, kс = 0,55, см. табл. 1):
 , R = 400, kп = 1,3, kс = 0,55, см. табл. 1):
, R = 400, kп = 1,3, kс = 0,55, см. табл. 1): ;
; .
.Процент армирования стоек и ригеля
 ;
; .
.Определяется коэффициент, учитывающий деформацию ползучести бетона стоек и ригеля рамы:
 ;
; .
.Коэффициент, учитывающий деформации ползучести железобетонных стоек и ригеля [формула (2)]:
 .
. .
.Коэффициент релаксации вынужденных усилий:
 ;
;  .
.В упругой стадии распор от нагрузки g равен:
 .
.Распор рамы от нагрузки g при естественном распределении усилий с учетом ползучести бетона при  , согласно п. 1.10, равен:
, согласно п. 1.10, равен:
 .
.Регулирование распора производится без утеплителя и снега при нагрузке q = 1,745 тс·м.
Прирост распора от утеплителя и снега
 .
.Для полной расчетной нагрузки g была принята величина распора 16,5 т.
При отсутствии утеплителя и снега распор должен составлять
Hтреб = 16,5 - 6,05 = 10,45 тс.
При естественном распределении усилий с учетом ползучести бетона
 .
.Следовательно, за счет регулирования распор должен быть уменьшен на
 .
.При этом необходимо учесть релаксацию вынужденных усилий за счет ползучести бетона согласно п. 1.10. Распор должен быть увеличен на величину
 ,
,где
 -
-коэффициент релаксации вынужденных усилий;
 -
-перемещение от единичного распора по направлению распора в упругой основной системе, увеличенное в Bб раз:
 -
-перемещение от единичного распора по направлению распора в основной системе с учетом ползучести бетона при  , увеличенное в Eб:
, увеличенное в Eб:
 .
.Если бы  , то
, то  .
.
 , то
, то  .
. .
.Отсюда
 .
.При наличии шарнира в стойке, смещенного с ее оси, распор в статически определимой системе составляет:
 .
.Натяжением арматуры должен быть создан распор
HS = Hзад - H0 = 10,64 - 0,979 = 9,65 тс.
Натяжение арматуры усилием S1 в статически определимой системе создаст распор
 .
.Омоноличивание шарнирного стыка рамы бетоном на высокопрочном быстротвердеющем расширяющемся цементе произведено сразу же после натяжения арматуры стоек усилием S1. После приобретения бетоном омоноличивания проектной прочности дополнительное усилие натяжения в арматуре стоек S2 создает добавочный распор. Усилие S2 не вызывает вынужденных перемещений в раме с замоноличенным стыком и поэтому относится к разряду нагрузок. Поскольку разрыв во времени между натяжением арматуры стоек усилиями S1 и S2 незначителен, то предельные характеристики ползучести армированного бетона ригеля и стоек при оценке добавочного распора от S2 принимаем неизменными.
В основной системе натяжение арматуры стоек усилием S2 вызывает эпюры моментов, возрастающие от нуля у пят рамы до максимума на оси ригеля. Расстояние от центра тяжести арматуры стоек до их оси в уровне оси ригеля равно 0,33 м. Эпюра моментов в раме, вызванная силами S2, показана на рис. 32, а. Эпюра моментов единичного распора приведена на рис. 32, б.

Рис. 32. Эпюры моментов, вызванные
а - силами S2; б - силами распора
Перемещение 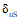 по направлению распора в основной системе под влиянием сил S2 с учетом ползучести бетона равно:
по направлению распора в основной системе под влиянием сил S2 с учетом ползучести бетона равно:
 ;
;перемещение по направлению распора от единичного распора с учетом ползучести бетона
 .
.Распор H2S, вызванный силами S2, равен:
 ;
;HS = H1S + H2S = 0,098S1 + 0,0163S2 = 9,65 тс.
С другой стороны, сумма сил S1 и S2 должна равняться усилиям натяжения арматуры за вычетом потерь, происходящих до окончания регулирования.
Эти потери (включая часть релаксации напряжений арматуры) оценивают величиной 600 кгс/см2:
S1 + S2 = 18,8 (11000 - 600) = 195,5 тс.
Из двух последних уравнений
S1 = 78 тс и S2 = 117,5 тс.
Учитывая упомянутые потери в процессе регулирования усилий, в раме должно быть создано натяжение арматуры стоек, равное:
 ;
; .
.Пример 2. Определение трещиностойкости сечений предварительно-напряженной рамной конструкции с учетом усилий, вызываемых в статически неопределимой системе силами обжатия.
Конструкция рамы приведена на рис. 33. Сечения всех элементов одинаковы и имеют размеры: h = 20 см, b = 12 см. Принят бетон марки 400. Все элементы рамы армированы прядями по  в каждом элементе. В ригелях пряди расположены с эксцентрицитетом равнодействующей сил натяжения: в верхнем ригеле с e0 = 4 см, в нижнем ригеле с e0 = 2 см. В стойках равнодействующая сил обжатия проходит по оси элемента.
в каждом элементе. В ригелях пряди расположены с эксцентрицитетом равнодействующей сил натяжения: в верхнем ригеле с e0 = 4 см, в нижнем ригеле с e0 = 2 см. В стойках равнодействующая сил обжатия проходит по оси элемента.

Контролируемое усилие предварительного натяжения одной пряди составляет 3000 кгс  ; суммарные потери усилия одной пряди определены величиной 500 кгс.
; суммарные потери усилия одной пряди определены величиной 500 кгс.
 ; суммарные потери усилия одной пряди определены величиной 500 кгс.
; суммарные потери усилия одной пряди определены величиной 500 кгс.В соответствии с п. 1.5 произведем расчет рамы на силы обжатия от предварительно-напряженной арматуры и определим возникающие при этом в элементах рамы изгибающие моменты Mоб и нормальные силы Nоб.
С учетом Mоб и Nоб трещиностойкость сечений элементов рамы Mт может быть оценена по формуле:
Mт = RаIIWт + Nобry + Mоб.
Для определения величины Mоб и Nоб произведем расчет рамной системы на действие двух факторов: сил натяжения арматуры Nоi, приложенных по оси элементов, и сосредоточенных моментов Mоi = Nоieоi, приложенных к узлам A, C, D и F (под индексом понимается номер элемента).
1. Расчет рамы на действие сил Nоi.
В общем случае целесообразно рассчитывать раму на независимое действие единичных сил Nоi = 1. При этом от действия сил Nо вдоль ригеля AC во всех элементах рамы возникают усилия за счет смещения и поворота узлов A и C, вызванных укорочением ригеля при неизменном положении D и F. Аналогично при действии сил вдоль крайней стойки AD во всех элементах рамы возникают усилия за счет смешения и поворота узлов A и D, вызванных укорочением стойки при неизменном положении остальных узлов, и т.д.
В нашем случае можно принять, что благодаря симметрии конструкции, равенству параллельных сил обжатия Nоi, а также площадей сечения параллельных элементов одновременное приложение всех сил по оси элементов вызывает одинаковые укорочения параллельных элементов рамы, в результате чего изгибающие моменты в системе не возникают. Нормальная сила в каждом элементе равна внешней силе (обжатия), действующей вдоль этого элемента. Эпюра нормальных сил от единичных сил Nоi = 1 представлена на рис. 34, а.

а - от единичных сил; б - от единичных сосредоточенных
моментов; в - суммарные эпюры от сил обжатия
2. Расчет рамы на действие сосредоточенных моментов.
Моменты в рамной системе, вызываемые внецентренным размещением напрягаемой арматуры в каком-либо элементе рамы, в силу статической неопределимости системы возникают не только в этом элементе, но и во всех элементах системы. При этом в общем случае момент не остается постоянным по длине элемента, а может меняться как по величине, так и по знаку.
Для выявления картины распределения моментов в элементах рамы рассчитываем систему на действие сосредоточенных моментов Mоi = Nоieоi, приложенных к узлам A, C, D и F.
Расчет рамы производим в предположении отсутствия трещин в элементах (т.е. как однородной упругой системы) методом сил.
При этом результаты расчета целесообразно представить в виде эпюр изгибающих моментов и нормальных сил от единичных сосредоточенных моментов (рис. 34, б).
3. Суммарные усилия (нормальные силы Nоб и изгибающие моменты Mоб) определяем по формулам:
 ;
; ,
,где Mok = Nokeok, eok - эксцентрицитет равнодействующей сил натяжения в k-том элементе рамы;
В нашем случае  , так как в каждом элементе возникает нормальная сила только от силы обжатия, приложенной к этому элементу. Величина нормальной силы, как сказано выше, равна силе обжатия;
, так как в каждом элементе возникает нормальная сила только от силы обжатия, приложенной к этому элементу. Величина нормальной силы, как сказано выше, равна силе обжатия;
 , так как в каждом элементе возникает нормальная сила только от силы обжатия, приложенной к этому элементу. Величина нормальной силы, как сказано выше, равна силе обжатия;
, так как в каждом элементе возникает нормальная сила только от силы обжатия, приложенной к этому элементу. Величина нормальной силы, как сказано выше, равна силе обжатия;nik - нормальная сила от действия единичного сосредоточенного момента, приложенного к k-тому узлу рамы;
В нашем случае  ;
;
 ;
;mjk - изгибающий момент от действия единичного сосредоточенного момента, приложенного к k-тому узлу рамы.
Подсчет моментов трещинообразования Mт характерных сечений рамы с учетом усилий от обжатия.
Подсчет проведен на примере верхнего ригеля.
Суммарная нормальная сила обжатия в верхнем ригеле рамы (элементы AB и BC) равна (см. рис. 34, а, б) при Nо = 20 тс
Nоб(AB) = Nоб(BC) = 1·20 - 0,37·20·0,04 -
- 0,37·20·0,02 = 19,55 тс.
Суммарный изгибающий момент в сечении ригеля 1 - 1 (если принять, что момент по оси стойки равен моменту по ее грани):
Mоб1 = 0,28·20·0,04 - 0,21·20·0,02 = 0,14 тс·м.
В соответствии с приведенной выше формулой трещиностойкость Mт сечения 1 - 1 верхнего ригеля при

и

составит:
для верхней грани
 ,
,для нижней грани
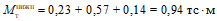 .
.Суммарные эпюры усилий в элементах рамы от фактически действующих сил натяжения арматуры представлены на рис. 34, в.
Сопротивления трещинообразованию характерных сечений рамы, вычисленные по приведенной выше методике, приведены на рис. 35.

Рис. 35. Моменты трещинообразования в сечениях рамы
(в т·см), подсчитанные с учетом усилий от обжатия
(цифры поставлены у той грани, относительно
которой определена трещиностойкость)
Пример 3. Требуется рассчитать плиту монолитного железобетонного перекрытия (рис. 36, пп. 2.5, 2.7).

Рис. 36. Размеры монолитного железобетонного перекрытия
Данные проектирования:
нагрузка от массы конструкции g = 400 кгс/м2 (коэффициент перегрузки n1 = 1,1);
полезная нагрузка на перекрытие p = 1500 кгс/м2 (коэффициент перегрузки n2 = 1,2);
бетон марки 200:
Rпр = 95 кгс/см2 (mбд = 0,85);
RрII = 12 кгс/см2;
Eб = 2,4·105 кгс/см2;
арматура из горячекатаной стали класса A-III:
Rа = 3500 кгс/см2;
Eа = 2·106 кгс/см2.
Расчет.
1. Расчетная нагрузка
p = 400·1,1 + 15000·1,2 = 2240 кгс/м2.
2. Расчетные пролеты:
для средней панели и для крайних в направлении, параллельном краю перекрытия:
l2 = 5 - 0,25 = 4,75 м;
l1 = 4 - 0,25 = 3,75 ";
для крайних панелей в направлении, перпендикулярном краю перекрытия:
l2 = 4,65 + 0,06 = 4,75 м;
l1 = 3,65 + 0,06 = 3,75 ".
3. Отношение сторон панелей плиты
 ;
;все панели рассчитываются как плиты, работающие в двух направлениях.
4. Полезная высота сечения плиты:
в направлении l1
h01 = 12 - (1,5 + 0,4) = 10,1 см = 0,101 м;
в направлении l2
h02 = 12 - (1,5 + 0,8 + 0,4) = 9,3 см = 0,093 м.
5. В соответствии с табл. 6 и указаниями п. 2.5 приняты следующие соотношения между площадями сечения арматур различных направлений:
 ;
;  ;
; 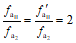 .
.6. Так как 50% стержней обрывается на растяжении  от опор, то площади сечения арматуры
от опор, то площади сечения арматуры  и
и  определяются из условий:
определяются из условий:
 ,
,где величина  выражена в см2, а величина
выражена в см2, а величина  - в см2/м.
- в см2/м.
 ;
;так как согласно принятому выше 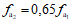 ,
,
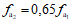 ,
, .
.7. Площадь сечения арматуры  , (на опорах Г/В) определяется из условия
, (на опорах Г/В) определяется из условия
 .
.8. Площадь сечения арматуры  равна:
равна:
 равна:
равна: .
.9. Величины опорных и пролетных моментов определяются по формулам




10. Определяется значение  из условия предельного равновесия
из условия предельного равновесия
 ,
,так как расчет панели ведется без учета влияния распора 
 ;
;ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 ,
,откуда  .
.
 .
.11. Распределение рабочей арматуры в плите панели Г:
 .
. .
. ;
; .
.12. Определение прогиба панели Г.
В момент появления трещин в месте заделки (l1 = 375 см; l2 = 475 см) моменты и соответствующий прогиб в середине пролета по таблицам Справочника-проектировщика равны:
 ;
;  .
.При  , где
, где  ;
;
 , где
, где  ;
;и нагрузка, соответствующая такому виду трещинообразования,
 .
.При нагрузке  моменты в пролете достигнут величины
моменты в пролете достигнут величины

и
 .
.Момент образования трещин в пролете равен: Mт = 453 кгс·см, тогда, согласно п. 2.7 настоящего Руководства, возможно определить усилия и прогиб из представления работы плиты как свободно опертой на приращении нагрузки.
Так 

и
 .
.Общая нагрузка в момент образования трещин в пролете от  будет равна:
будет равна:
 .
.Прогиб в центре плиты, соответствующий образованию трещин в местах защемления,
 ; где
; где 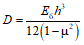 ,
,и при 
 .
.Прогиб на приращение нагрузки  , как в свободно опертой плите, равен:
, как в свободно опертой плите, равен:
 .
.Полный прогиб в центре плиты в момент образования трещин в пролете равен:
 .
.Предельный прогиб в центре плиты - по табл. 7
 ,
,где
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.Расчетная нагрузка на перекрытие
p = 400 + 1500 = 1900 кгс/м2 = 0,19 кгс/см2.
При такой нагрузке в плите имеются трещины в местах защемления и в пролете, а прогиб при расчетной нагрузке может быть определен по формуле (51):
 ;
; .
.В рассматриваемом приближенном способе расчета прогибов опертых по контуру плит длительность действия нагрузки может быть учтена следующей приближенной формулой:
 .
.Относительный прогиб
 .
.13. Определение ширины раскрытия трещин в пролете панели Г.
Согласно Руководству по проектированию бетонных и железобетонных конструкций из тяжелого бетона (без предварительного напряжения),

где k = 1; 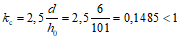 ,
,
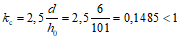 ,
,тогда kc = 1.
Согласно п. 2.7 настоящего Руководства:
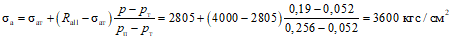 ;
;
 на 1 см ширины плиты;
на 1 см ширины плиты; .
. ;
;  .
.14. Расчет панели Г с учетом влияния распора.
Предельный прогиб конструкции с податливостью  по формуле (согласно указаниям п. 2.7, величина коэффициента
по формуле (согласно указаниям п. 2.7, величина коэффициента  принимается 0,5):
принимается 0,5):
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.15. Величины дополнительных моментов в пролете от действия распора по формуле (16):
в направлении l2:
 , где
, где ;
; ;
; ;
;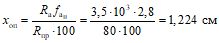 ;
;в направлении l1:
 ,
,где 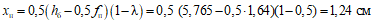 ;
;
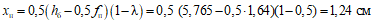 ;
; ;
; ;
; .
.16. Определение значения  по формуле (27)
по формуле (27)
 ;
;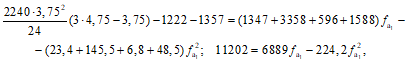
откуда  .
.
 .
.Таким образом, расчет с учетом влияния распора дает снижение армирования на
 .
.Ограничившись одним приближением, принимаем:
 ;
;ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
 ;
;  ;
; ;
; .
.17. Прогиб панели при p = 0,19 кгс/см2
 ;
;с учетом (см. расчет панели Г без распора) длительности нагрузки:
 .
. .
.Панель А
18. Соотношение между площадями сечения арматур:
 ;
; 19. Значение  из условия предельного равновесия (22)
из условия предельного равновесия (22)
 ,
,где  , так как панель угловая;
, так как панель угловая;
 , так как панель угловая;
, так как панель угловая; ;
; ,
,откуда
 .
.20. Распределение рабочей арматуры в плите панели А:
 ;
; ;
; ;
;ИС МЕГАНОРМ: примечание. Единицы измерения даны в соответствии с официальным текстом документа. |
 .
.21. Определение прогиба панели А.
Как для плиты, защемленной по двум сторонам и шарнирно опертой по двум другим, находятся изгибающие моменты и прогиб для случая работы плиты в момент образования трещин в местах защемления:
 ;
; 
и  .
.
 .
.При  ;
;
 ;
; ;
; .
.На приращение нагрузки до образования трещин в пролете плита работает как свободно опертая:
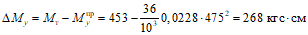 ;
; ;
; .
.Полный прогиб в центре плиты в момент образования трещин в пролете равен:

и соответствующая нагрузка pт = 0,0432 кгс/см2.
Предельный прогиб:
 ;
;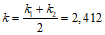 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.Прогиб при нагрузке p = 0,19 кгс/см2 по формуле (51):
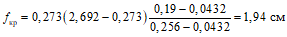 ;
; .
.Относительный прогиб:
 .
.ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Увеличиваем армирование  и соответственно
и соответственно  ,
,  :
:
 и соответственно
и соответственно  ,
,  :
: ;
; .
.Предельный прогиб при принятом армировании
 .
.Из условия предельного равновесия при принятом армировании
 и
и 
и прогиб при расчетной нагрузке
 .
.При длительной нагрузке (см. расчет панели Г)
 ;
; .
.22. Определение ширины раскрытия трещин в пролете панели А

 ,
,где k = 1; 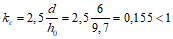 ;
;
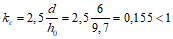 ;
;принимаем kc = 1;
 .
.Здесь:
 ;
;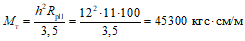 ;
; .
.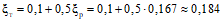 ;
; .
.Пример 4. Расчет плиты, свободно опертой по контуру.
Пусть плита нагружена равномерно распределенной кратковременно действующей нагрузкой q, расчетное значение которой равно 0,45 кгс/см2.
Для проведения расчета используем следующие характеристики плиты (рис. 37):
a = 400 см; b = 200 см; h = 12,1 см;
h0 = 10,18 см; fax = fay = 0,0385 см2/см;
 ; R = 265 кгс/см2; RпрII = 200 кгс/см2;
; R = 265 кгс/см2; RпрII = 200 кгс/см2;RрII = 18,9 кгс/см2; Eб = 298000 кгс/см2; RaII = 4279 кгс/см2.

При использовании данной методики в целях исследования вводятся реальные характеристики бетона и арматуры. Кроме этого, при проведении расчетов для упругопластической стадии с трещинами кроме предела текучести арматуры  вводится еще дополнительно временное сопротивление арматуры растяжению
вводится еще дополнительно временное сопротивление арматуры растяжению  .
.
Кроме перечисленных характеристик плиты необходимо задаться определенным шагом разностной сетки. В данном примере, учитывая симметрию, рассматривается 1/4 часть плиты, которая разбивается разностной сеткой с шагом  ,
,  . Если углы плиты не закреплены от подъема, необходимо учесть подъем углов. При данном отношении a/b = 2 можно принять, что
. Если углы плиты не закреплены от подъема, необходимо учесть подъем углов. При данном отношении a/b = 2 можно принять, что
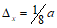 ,
,  . Если углы плиты не закреплены от подъема, необходимо учесть подъем углов. При данном отношении a/b = 2 можно принять, что
. Если углы плиты не закреплены от подъема, необходимо учесть подъем углов. При данном отношении a/b = 2 можно принять, чтоW55 = -0,1W11; W45 = W54 = -0,03W11;
для квадратных плит можно принимать:
W55 = -0,16W11; W45 = W54 = -0,05W11.
Поясним процедуру составления разрешающих уравнений на примере точки 33:
Аналогичным образом составляются уравнения и для других точек. Прежде чем выразить уравнения типа (*) через прогибы, необходимо учесть, что  ; кроме этого, W15 = W25 = W35 = W51 = W52 = W53 = 0.
; кроме этого, W15 = W25 = W35 = W51 = W52 = W53 = 0.
 ; кроме этого, W15 = W25 = W35 = W51 = W52 = W53 = 0.
; кроме этого, W15 = W25 = W35 = W51 = W52 = W53 = 0.Затем значения моментов, входящие в уравнения типа (*), выражаются через конечные разности через прогибы на основании (89). Значения моментов Mxy для точек, лежащих на линиях опирания, записываются в односторонних разностях. Например, для точки 53 первая и вторая производные функции W53 записываются так:
 ;
;  .
.Это несколько сокращает систему линейных уравнений, и в данном случае система сводится к 16 уравнениям. Итерационный процесс считался законченным на каждом шаге нагружения, если последующее поле усилий прогибов отличалось от предыдущего не более чем на 5%. Задача решалась на ЭВМ "Минск-22" по второму алгоритму Руководства (п. 2.8).
На рис. 38 показаны графики прогибов точек плиты по линиям 11 - 15, 11 - 55, 11 - 51 при нормативной нагрузке g = 0,45 кгс/см2.

Рис. 38. Прогибы плиты по линиям
а - 11 - 51; б - 11 - 15; в - 11 - 55
Для оценки напряжений в арматуре могут быть использованы эпюры моментов, построенные при расчетной нагрузке (рис. 39).

Рис. 39. Эпюры моментов в плите по линиям
а - 11 - 51; б - 11 - 15; в - 11 - 55
Образование трещин по полю плиты, ширина их раскрытия и ориентация определяются по рекомендациям п. 2.8 настоящего Руководства и сравниваются с допустимыми значениями, предусмотренными нормативными документами.
Пример 5. Требуется рассчитать для гражданского здания трехпролетную балку рис. 40 с пролетами 4,5; 6 и 4,5 м с целью определения армирования по прочности и определения усилий для оценки деформативности и трещиностойкости балки.

Рис. 40. Трехпролетная неразрезная балка
Даны: нагрузка от собственного веса конструкции g = 750 кгс/м; равномерно распределенная полезная нагрузка q = 1500 кгс/м; коэффициент перегрузки n1 = 1,1; n2 = 1,2.
Расчет.
а) Методами расчета упругих систем определяют эпюры изгибающих моментов для различных случаев загружения:
a11 = 2(l1 + l2) = 2(4,5 + 6) = 21; a12 = l2 = 6;
a22 = 2(l1 + l2) = 2(4,5 + 6) = 21;
1) первое загружение - постоянная нагрузка
 ;
;2) второе загружение - полезная нагрузка в левом пролете
 ; a2g = 0;
; a2g = 0;3) третье загружение - полезная нагрузка в среднем пролете
 ;
;4) четвертое загружение - полезная нагрузка в правом пролете:
a2g = 40,8 (зеркально второму); a1g = 0;
5) полученная система уравнений и ее решение приведены в табл. 15;
Таблица 15
M1 | M2 | Загружения | |||
I | II | III | IV | ||
(1) 21 | 6 | 63,3 | 40,8 | 97,2 | 0;  |
(2) | 21 | 63,3 | 0 | 97,2 | 40,8 |
-1,21 | -18,2 | -11,7 | -27,8 | 0 | |
 | 19,29 | 45,2 | -11,7 | 69,4 | 40,8 |
M2 = | -2,34 | 0,61 | -3,6 | -2,12 | |
= 6 M2 | -14,05 | 3,64 | -21,6 | -12,71 | |
21 M1 | 49,25 | 44,44 | 75,6 | -12,71 | |
M1 = | -2,34 | -2,12 | -3,6 | 0,61 | |
6) строим эпюры моментов (рис. 41) для невыгоднейших комбинаций нагрузок, ординаты которых сведены в табл. 16.

при невыгоднейшей комбинации нагрузок
а - сочетание I и III, б - сочетание I, II и IV;
в - сочетание I и III
Сочетание нагрузок | Сечения | ||||||||
1 | 2 | 3 | 4 | 5 | |||||
| |||||||||
1 сочетание I, II, II загружений | 2,62 | -8,06 | 5,1 | -5,33 | -0,57 | ||||
2 сочетание I, II, IV загружений | 4,72 | -3,85 | -0,14 | -3,85 | 4,72 | ||||
3 сочетание I и III загружений | -0,88 | -5,94 | 5,86 | -5,94 | -0,88 | ||||
4 сочетание I, III и IV загружений | -0,57 | -5,33 | 5,1 | -8,06 | 2,62 | ||||
Максимальные ординаты | 4,85 | -8,06 | 5,86 | -8,06 | 4,85 | ||||
б) Производим перераспределение усилий (согласно п. 3.6) путем прибавления подобранных треугольных эпюр:
1) уменьшаем значение моментов в среднем пролете, для чего к эпюре моментов от сочетания 3 нагрузок добавляем две треугольные эпюры (рис. 42, а) с надопорными ординатами, равными 1,76 тс·м;

2) уменьшаем значение моментов в крайних пролетах, для чего к эпюре моментов от сочетания 2 прибавляем две треугольные эпюры (рис. 42, б) с надопорными ординатами, равными 1,6 тс·м;
3) уменьшаем значение расчетного момента на средних опорах и уравниваем их между собой путем сложения эпюры моментов от сочетания 1 нагрузок и двух треугольных эпюр разных знаков (рис. 42, в) с надопорными ординатами, равными:
на левой опоре - 0,36 тс·м;
на правой опоре - 2,37 "
Полученные в результате перераспределения усилий эпюры моментов для различных сочетаний нагрузок показаны на рис. 43.

Рис. 43. Измененные в результате перераспределения усилий
эпюры моментов
В случае необходимости уменьшения моментов на опорах возможен другой способ перераспределения усилий:
1) уменьшаем значение опорного момента и выравниваем их на эпюре сочетания 1, для чего к ней добавляем две треугольные эпюры с надопорными ординатами:
на левой опоре - +2,12 тс·м;
на правой опоре - -0,61 "
2) уменьшаем пролетный момент в крайних пролетах путем прибавления к эпюре сочетания 2 двух треугольных эпюр с надопорными ординатами 1,6;
3) момент в среднем пролете оставляем тем же.
Эпюры моментов, полученные в результате перераспределения усилий по второму способу, показаны на рис. 44.

Рис. 44. Эпюры моментов в неразрезной балке,
полученные в результате перераспределения усилий
по второму способу
в) Для проверки прогибов и ширины раскрытия трещин в среднем пролете наиболее выгодным сочетанием (см. рис. 41) является сочетание 3 (нагрузка по схемам I и III).
Сечения в среднем пролете и на вторых от края опорах с учетом перераспределения усилий по первому варианту заармированы арматурой периодического профиля из стали класса А-II общей площадью при b = 20 см, h = 40 см и марке бетона 200:
Fап = 5,05 см2;  ; Fа0 = 10,3 см2.
; Fа0 = 10,3 см2.
 ; Fа0 = 10,3 см2.
; Fа0 = 10,3 см2.Соответственно жесткость сечений как  при
при  = 1 равна:
= 1 равна:
Bпр = 8,7·109 кгс·см2 = 870 тс·м2;
Bоп = 13,5·109 кгс·см2 = 1350 тс·м2.
Расчет упругой системы дает следующее значение моментов; в среднем пролете Mпр = 5,86 тс·м; на второй от края опоре Mоп = 5,94 тс·м.
За моменты от нормативной нагрузки с некоторым приближением можно принять:
 ;
; ,
,где gн + qн = 2250 кгс/м - полная нормативная нагрузка; g + q = 2625 кгс/м - полная расчетная нагрузка.
Значения моментов для определения прогибов равны:
 ;
;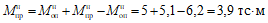 .
.Далее в соответствии с рекомендациями действующих норм подсчитываются прогибы и ширина раскрытия трещин в наиболее напряженных сечениях.
Пример 6. Проверить несущую способность трехпролетной неразрезной балки, нагруженной постоянной нагрузкой g = 0,133 тс, сосредоточенной силой P1 = 0,533 тс и временной нагрузкой q = 0,133 тс/м с использованием ЭВМ (п. 3.7). Схема балки, распределение нагрузки и предельные изгибающие моменты показаны на рис. 45.

В качестве опасных точек для балки выберем сечения в серединах пролетов и над средними опорами и пронумеруем их, как на рис. 45, а.
Применим метод основной системы. Эта основная система показана на рис. 45, б. Для выбранной таким образом системы получаем число опасных сечений m = 5, число неизвестных s = 2, в общем случае условия прочности записываются в виде двух неравенств для каждого момента:
 ,
,где Mi - изгибающий момент в выбранном сечении;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 53, б отсутствует. |
Составляющие для вектора t - векторы tg и tr и матрица L получаются из эпюр усилий в основной системе (рис. 53, б):
 ,
,  ,
,  .
.Для заданной нагрузки можно заранее определить, что в сечениях 1 и 3 изгибающие моменты положительные, а в сечениях 2 и 4 - отрицательные. В сечении 5 знак момента определить сложнее, поэтому будем считать возможным оба знака.
Тогда условия прочности с учетом знака запишутся так:
 ;
;  ;
;  ;
; ;
;  ;
;  .
.Число неравенств равно шести, следовательно, k = 6.
Или в форме (94) будет:
 ,
,  .
.Определим элементы неравенств (95):
 ,
,  ,
,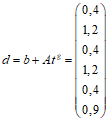 .
.Теперь задача заключается в определении p* = max p(x) при ограничениях (95) полученными числовыми значениями. Решение такой задачи методом линейного программирования приводит к следующему ответу:
p* = 1,25;  , а для
, а для  однозначного решения не существует, но можно обнаружить, что без нарушения условий прочности x может изменяться в пределах от -0,45 до 1,2 (размерность - тс·м).
однозначного решения не существует, но можно обнаружить, что без нарушения условий прочности x может изменяться в пределах от -0,45 до 1,2 (размерность - тс·м).
В данном случае параметр нагрузки p* больше 1 и, следовательно, несущая способность обеспечивается с коэффициентом запаса 1,25. Что же касается действительного распределения внутренних сил, то из решения задачи оказываются известными точно значения моментов в точках 1 и 2; если бы полезная нагрузка возросла в 1,25 раза, в точке 1 было бы M1 = 1 тс·м, а в точке 2 M2 = -1,2 тс·м, т.е. были бы предельные значения моментов.
Определение действительного распределения изгибающих моментов для заданной расчетной нагрузки (p = 1) возможно производить модифицированным методом основной системы. Оставив ту же основную систему и предположив, что жесткость пролетов одинакова и постоянна, получим решение для заданной нагрузки обычным методом сил (см. рис. 45, в).
Здесь оказывается, что момент в точке 2, равный -1,4 тс·м, больше по абсолютной величине предельного момента, равного - 1,2 тс·м, следовательно, необходимо произвести расчет этой балки под заданную нагрузку, но с учетом перераспределения усилий и того, что при расчетной нагрузке еще не достигнуто состояние предельного равновесия.
Каноническая матрица метода сил с точностью до несущественного постоянного множителя такая:
 .
.ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 15, в отсутствует. Вероятно, имеется в виду рисунок 45, в. |
 .
.Вектор f + d в неравенстве (95) записывается так:
 .
.Матрица C остается без изменения. Собственные значения матрицы  есть
есть  и
и  , а матрица собственных векторов с точностью до множителя
, а матрица собственных векторов с точностью до множителя  такая:
такая:
 .
.Поэтому нормальное преобразование переменных производится по формуле
 .
.Применяя это преобразование для матрицы C, получаем матрицу в условиях (96):
 .
.Таким образом, все элементы системы неравенств сформированы, и остается определить минимум для квадратичной функции  при соблюдении этих неравенств.
при соблюдении этих неравенств.
 при соблюдении этих неравенств.
при соблюдении этих неравенств.Такая задача решается методом квадратичного программирования, и ее ответ  ,
,  .
.
 ,
,  .
.По формуле преобразования переменных получаем  ;
;  (размерность тс·м сохраняется).
(размерность тс·м сохраняется).
 ;
;  (размерность тс·м сохраняется).
(размерность тс·м сохраняется).После этого наложением эпюры рис. 45, г на эпюру рис. 45, в получаем окончательное распределение усилий при расчетной нагрузке (рис. 45, г).
Проделанный расчет был осуществлен в предположении, что жесткость сечений в пролетах остается постоянной. Если необходимо учесть изменение жесткости вследствие образования трещин, то, приняв эпюру рис. 45, д за эпюру первого приближения, можно определить новые жесткости, затем вычислить новую каноническую матрицу метода сил и повторить весь расчет заново.
Примечание. Эпюра, представленная на рис. 45, г, есть эпюра остаточных изгибающих моментов, которые возникнут, если все нагрузки (постоянная и временная) будут сняты.
Пример 7. Требуется рассчитать для промышленного здания четырехэтажную трехпролетную раму (рис. 46) с учетом действительных жесткостей элементов конструкций (п. 3.8).

(в кружках указана марка узлов)
Все узлы рамы принимаются жесткими, учитывается наличие жестких участков в местах примыкания ригелей к колоннам.
Для каждого типа нагрузки рама рассчитывается на несколько комбинаций загружения временной, длительно действующей нагрузкой, каждая из которых определяет невыгодное сочетание усилий в одном из сечений ригелей перекрытий.
Комбинация загружений включает также постоянную и горизонтальную (ветровую) нагрузки.
Расчет на каждую комбинацию загружений производится в двух вариантах:
I вариант - все элементы рамы принимаются работающими в упругой стадии, жесткость элементов принимается равной EI;
II вариант - расчет производится с учетом действительных жесткостей конструкций, причем колонны принимаются III категории трещиностойкости, ригели в опорных сечениях (верхняя зона) - III категории, а в пролетных (нижняя зона) II категория трещиностойкости (трещины не допускаются).
В табл. 17 приведены расчетные значения нагрузок, причем в первом случае ветровые нагрузки приняты с k = 0,3. Схема приложения нагрузок дана на рис. 46.
Таблица 17
Тип нагрузки | Постоянная, кгс/м | Временная длительная на перекрытии p1, кгс/м | Кратковременная | |||||
на перекрытии q1 | на покрытии q2 | p2, кгс/м | W1, кгс | W2, кгс | W3, кгс | W4, кгс | ||
Расчетная с n = 1 | 4200 | 4470 | 3000 | 2460 | 957 | 1077 | 1254 | 1152 |
Расчетная с n = 1,1 | 4620 | 5100 | 3600 | 3000 | 3190 | 3590 | 4180 | 3840 |
Попролетные загружения временной длительной нагрузкой приведены в табл. 18. Расчет ведется на 15 загружений.
Таблица 18
N ригеля | N загружения | Номера пролетов, загруженных временной длительной нагрузкой | |||||
1 | 5 - 6 | 9 - 10 | 14 - 15 | 7 - 8 | 11 - 12 | 1 - 2 | |
5 - 6 | 2 | 5 - 6 | 9 - 10 | 13 - 14 | 6 - 7 | 14 - 15 | - |
3 | 5 - 6 | 13 - 14 | 10 - 11 | 7 - 8 | 15 - 16 | - | |
4 | 5 - 6 | 13 - 14 | 6 - 7 | 10 - 11 | 11 - 12 | - | |
6 - 7 | 5 | 9 - 10 | 6 - 7 | 14 - 15 | 11 - 12 | - | - |
6 | 5 - 6 | 9 - 10 | 13 - 14 | 7 - 8 | 11 - 12 | 15 - 16 | |
9 - 10 | 7 | 5 - 6 | 9 - 10 | 13 - 14 | 10 - 11 | 7 - 8 | - |
8 | 9 - 10 | 6 - 7 | 14 - 15 | 11 - 12 | - | - | |
10 - 11 | 9 | 9 - 10 | 6 - 7 | 10 - 11 | 14 - 15 | 15 - 16 | - |
10 | 5 - 6 | 13 - 14 | 10 - 11 | 7 - 8 | 15 - 16 | - | |
11 | 9 - 10 | 13 - 14 | 6 - 7 | 11 - 12 | 15 - 16 | - | |
13 - 14 | 12 | 9 - 10 | 13 - 14 | 6 - 7 | 14 - 15 | 11 - 12 | - |
13 | 5 - 6 | 13 - 14 | 10 - 11 | 7 - 8 | 15 - 16 | - | |
14 - 15 | 14 | 5 - 6 | 13 - 14 | 10 - 11 | 14 - 15 | 11 - 12 | 15 - 16 |
15 | 9 - 10 | 6 - 7 | 14 - 15 | 11 - 12 | - | - | |
Данные о геометрических размерах ригелей, колонн и их армировании приведены на рис. 47, б и в табл. 19.

Рис. 47. Геометрические размеры и армирование
а - ригелей; б - колонн
Марка колонны в каждом этаже | Размер поперечного сечения H·b, см | Количество и диаметр арматуры |
К - 1 | 40 x 40 | |
К - 2 | 40 x 40 | |
К - 3 - а | 40 x 40 | |
К - 3 | 40 x 60 |  |
К - 4 - а | 40 x 60 | |
К - 4 | 40 x 60 |  |
Арматура в пролете ригелей - предварительно-напряженная, остальная арматура класса A-III. Ригели и колонны марки К-4 (см. рис. 46) из бетона марки 400, остальные колонны - из бетона марки 300.
Описание алгоритма расчета распределения усилий приведено в п. 3.8.
Для расчета используются специализированные программы, учитывающие неупругие деформации железобетонных конструкций. Каждый стержень разбивается на заданное количество участков (обычно 20), что позволяет реализовать переменную по длине жесткость. В процессе итерационного расчета происходит стабилизация напряженно-деформированного состояния конструкции.
На предварительно-напряженные зоны ригелей накладывается условие, по которому трещины в этих зонах не образуются при любых значениях усилий.
Результатом расчета в данном примере являются:
для ригелей при всех типах нагрузок - значение изгибающих моментов и поперечных сил на опорах по грани жестких участков, а также максимальные значения моментов; кроме того, для ригелей при расчетных (n1 = 1) нагрузках - величина раскрытия трещин на опорах (верхняя зона) по грани консолей колонн.
В результате обработки результатов машинного счета получаются таблицы усилий, используемые в дальнейших расчетах. Для ригеля 9 - 10 в табл. 20 приведены усилия при расчетной нагрузке.
Таблица 20
N загружения | N сечения | По расчету упругой системы | С учетом трещин | Приращение | |||||||||
в осях | на грани жестких участков | в осях | на грани жестких участков | ||||||||||
My, тс·м | Qy, тс | Ny, тс | M, тс·м | Q, тс | N, тс | M*, тс·м | Q*, тс |  , % , % | |||||
6 | 10 | -37,64 | 29,65 | - | -22,42 | 25,69 | -37,56 | 29,95 | - | -22,18 | 25,99 | -0,2 | 1 |
11 | 23,11 | - | 4,68 | - | - | 24,51 | - | 4,46 | - | - | 6,1 | - | |
12 | -55,52 | -33,71 | - | -38,07 | -29,75 | -52,82 | -33,41 | - | 35,53 | -29,45 | -4,9 | -0,9 | |
7 | 10 | -34,61 | 28,34 | - | -20,11 | 24,38 | -35,76 | 29,15 | - | -20,82 | 25,19 | 3,3 | 2,9 |
11 | 20,38 | - | 4,21 | - | - | 22,82 | - | 4.1 | - | - | 12 | - | |
12 | -64,02 | -35,02 | - | -45,85 | -31,06 | -57,99 | -34,21 | - | -40,26 | -30,25 | -9,4 | -2,3 | |
8 | 10 | -35,9 | 29,89 | - | -20,55 | 25,93 | -36,03 | 30,15 | - | -20,54 | 26,19 | 0,4 | 0,9 |
11 | 25,91 | - | 5,9 | - | - | 26,93 | - | 5,75 | - | - | 3,9 | - | |
12 | -51,68 | -33,47 | - | -34,36 | -29,51 | -49,51 | -33,21 | - | -32,33 | -29,25 | -4,2 | - | |
Огибающие | 10 | -37,64 | 29,89 | - | -22,42 | 25,93 | -37,56 | 30,15 | - | 22,18 | 26,19 | -0,2 | 0,9 |
11 | 25,91 | - | 5.9 | - | - | 26,93 | - | 5,75 | - | - | 3,9 | - | |
12 | -64,02 | -35,02 | - | -45,85 | -31,06 | -57,99 | -34,21 | - | -40,26 | -30,25 | -9,4 | -2,3 | |
Ширина раскрытия трещин для ригелей перекрытий по данным расчета упругой системы  и с учетом неупругих свойств железобетона
и с учетом неупругих свойств железобетона  приведена в табл. 21.
приведена в табл. 21.
N элемента | N загружения | N сечения | ||
5 - 6 | 1, 2, 3 | 19 | 0,102 | 0,009 |
20 | - | - | ||
21 | 0,26 | 0,206 | ||
6 - 7 | 4, 5 | 22 | 0,365 | 0,287 |
23 | - | - | ||
24 | 0,141 | 0,12 | ||
9 - 10 | 6, 7, 8 | 10 | 0,156 | 0,154 |
11 | - | - | ||
12 | 0,269 | 0,213 | ||
10 - 11 | 9, 10 | 13 | 0,332 | 0,27 |
14 | - | - | ||
15 | 0,157 | 0,146 | ||
13 - 14 | 11, 12, 13 | 1 | 0,179 | 0,17 |
2 | - | - | ||
3 | 0,272 | 0,215 | ||
14 - 15 | 14, 15 | 4 | 0,302 | 0,254 |
5 | - | - | ||
6 | 0,225 | 0,192 |
В связи с образованием трещин на опорах ригелей и падением жесткости опорных сечений увеличение моментов в пролете ригелей происходит до 25% при соответствующем снижении момента на опорах по сравнению с результатами расчета упругой системы.
В табл. 22 приведено увеличение в % величин пролетных моментов и уменьшение в % величин суммарных моментов для различных ригелей. Следует отметить, что за счет неупругой работы материалов суммарные моменты в огибающей эпюре снижаются до 6%.
Таблица 22
N ригеля | Пролетные моменты | Суммарные моменты | ||
расчетная нагрузка с n1 = 1 | расчетная нагрузка | расчетная нагрузка с n1 = 1 | расчетная нагрузка | |
5 - 6 | 11,4 | 13,1 | 4,6 | 5 |
6 - 7 | 17,2 | 18 | 4,7 | 5,7 |
9 - 10 | 12 | 14,8 | 5,6 | 5,8 |
10 - 11 | 15,1 | 16,7 | 5 | 5,2 |
13 - 14 | 14,6 | 18 | 5,5 | 6,1 |
14 - 15 | 21,7 | 25 | 0,5 | 1,4 |
Данные табл. 21 показывают, что если по данным расчета упругой системы трещины в сечениях 4, 13 и 22 превысили допустимые, то при учете неупругих свойств материалов они оказывались в допустимых пределах.
Пример 8. Определить усилия в колоннах продольной рамы одноэтажного отапливаемого производственного здания от температурных воздействий и удлинения нижних поясов подстропильных ферм. Схема рамы представлена на рис. 48.

Рис. 48. Расчетная схема рамы
Здание с подвесными кран-балками. Пролеты по 24 м. Шаг колонн 12 м с подстропильными фермами из стали марки Ст3 по серии ПК-01-125, вып. 1. Марка фермы ПФ-95. Площадь нижнего пояса фермы Fф = 22,6 см2. Длина температурного блока 216 м. Высота колонн 6,65 м. Сечение колонны h x b = 0,5 x 0,6 м. Марка бетона 200.  . Толщина защитного слоя a' = 0,05 м.
. Толщина защитного слоя a' = 0,05 м.
 . Толщина защитного слоя a' = 0,05 м.
. Толщина защитного слоя a' = 0,05 м.Влажностный режим - нормальный в месте строительства. Расчетная величина изменения температуры  (по опытным данным). Равномерно распределенная нормативная нагрузка от массы покрытия 320 кгс/м2, снеговая нагрузка 100 кгс/м2. Наибольшая расчетная нагрузка на колонну (с учетом снеговой нагрузки) Nmax = 172 тс, наименьшая (без снеговой нагрузки) Nmin = 97 тс.
(по опытным данным). Равномерно распределенная нормативная нагрузка от массы покрытия 320 кгс/м2, снеговая нагрузка 100 кгс/м2. Наибольшая расчетная нагрузка на колонну (с учетом снеговой нагрузки) Nmax = 172 тс, наименьшая (без снеговой нагрузки) Nmin = 97 тс.
 (по опытным данным). Равномерно распределенная нормативная нагрузка от массы покрытия 320 кгс/м2, снеговая нагрузка 100 кгс/м2. Наибольшая расчетная нагрузка на колонну (с учетом снеговой нагрузки) Nmax = 172 тс, наименьшая (без снеговой нагрузки) Nmin = 97 тс.
(по опытным данным). Равномерно распределенная нормативная нагрузка от массы покрытия 320 кгс/м2, снеговая нагрузка 100 кгс/м2. Наибольшая расчетная нагрузка на колонну (с учетом снеговой нагрузки) Nmax = 172 тс, наименьшая (без снеговой нагрузки) Nmin = 97 тс.Требуется определить изгибающие моменты в заделке крайних колонн, расположенных по среднему ряду, при наибольшей и наименьшей продольной силе в колонне.
Свободное относительное температурное перемещение подстропильных конструкций составит [формула (118)]
 .
.Коэффициент, учитывающий влияние нагрузки на величину удлинения нижнего пояса подстропильных ферм, при наличии в цехе подвесного крана будет:
при учете снеговой нагрузки
KL = 1·0,8 = 0,8;
без учета снеговой нагрузки
 .
.Свободное относительное удлинение нижних поясов подстропильных ферм составит [формула (119)]:
при учете снеговой нагрузки
 ;
;без учета снеговой нагрузки
 .
.Коэффициент податливости стыков [формула (124)]
 .
.Определяем величину момента, который может воспринять колонна при максимальной и минимальной расчетной продольной силе.
Высота сжатой зоны сечения равна:
 ;
; ;
;
 ;
; ,
,поэтому можно применить приближенный метод расчета жесткости сечений с трещинами по формуле (147)
 ;
; ;
; .
.K1 = 0,5; K2 = 0,195; K3 = 0,91.
Вычисляем значения Iпр, Fпр, rяд [формулы (135) - (137)]:
 ;
; ;
; .
.Жесткости для сечений с трещинами равны:
а) для колонн с продольной силой Nmax = 172 тс

б) для колонн с Nmin = 97 тс
 .
.Жесткость сечения колонн без трещин [формулы (138); (139)]
Cб = 0,5(1 + C) = 0,5(1 + 2) = 1,5;
 .
.Для определения приведенной жесткости вычислим, момент сопротивления растянутой грани и момент появления трещин в колоннах
 .
.При действии продольной силы Nmax = 172 тс.

при Nmin = 97 тс;
Mт = 62300·12 + 97000·9,35 = 1650000 кгс·см.
Приведенная жесткость равна (104):
 ;
; ;
;Определяем изгибающий момент в заделке колонн от температурного воздействия и удлинения нижних поясов подстропильных ферм при условии Ky = 1 (первое приближение):
y = 0,5Lб = 0,5·21600 = 10800 см;
 ;
;при учете снеговой нагрузки
 ;
;без учета снеговой нагрузки
 ;
; .
.Определяем значение коэффициентов Ky, учитывающего податливость ригеля по формуле (121):
при учете снеговой нагрузки
 ;
;без учета снеговой нагрузки
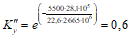 .
.Окончательный изгибающий момент в заделке колонн:
при учете снеговой нагрузки
 ;
;без учета снеговой нагрузки
 .
.Пример 9. Определить расстояния между температурными швами типовой эстакады под технологические трубопроводы (рис. 49) при следующих исходных данных:
расчетная высота стоек 7,2 м, расстояние между стойками 12 м.

Рис. 49. Расчетная схема эстакады
Постоянная вертикальная нагрузка на стойки 40 тс.
Изгибающий момент от внешней нагрузки в нижнем сечении стойки M = 9 тс·м.
Сечения стоек b x h = 60 x 40 см.
Бетон стоек обычный марки 300; RпрII = 180; Rпр = 140; RрII = 16; Eб = 2,6·105; арматура класса А-III; Ra = 3400; Eа = 2·106; 
 ; a' = 4 см.
; a' = 4 см.

Условия эксплуатации - влажность воздуха 50 - 70% (нормальная).
Определяем величину коэффициента Cб, учитывающего пластические свойства бетона при длительном действии нагрузки (139), и расчетную величину изменения температуры  (табл. 10).
(табл. 10).
Учитывая, что конструкция типовая и может быть возведена в любом районе СССР, принимаем:
C = 2;  ; Cб = 0,5(1 + c) = 0,5(1 + 2) = 1,5.
; Cб = 0,5(1 + c) = 0,5(1 + 2) = 1,5.
 ; Cб = 0,5(1 + c) = 0,5(1 + 2) = 1,5.
; Cб = 0,5(1 + c) = 0,5(1 + 2) = 1,5.Для определения момента сопротивления Wт, расстояния от ядровой точки до центра тяжести сечения rяд, длительной жесткости сечений без трещин Bб.т, момента появления трещин Mт вычисляем геометрические характеристики сечения:
 ; yц = 20 см;
; yц = 20 см;Fп = Fп + 2nFа = 40·60 + 2·6,9·27 = 2400 + 372 = 2772 см2;
 ;
; ;
;Iп = Iб + Iа = (3,2 + 0,95)105 = 4,15·105;
 ;
; .
. ;
; .
.Mт = WтRрII + Nrяд = 40500·16 + 32000·7,5 = 8,05·105.
Определяем момент, который могут воспринять внецентренно сжатые колонны при расчетных характеристиках материала
 , так как x < 2a
, так как x < 2aM = (RаFа + 0,5N)(h0 - a') = (27·3400 + 0,5·40000)(36 - 4) =
= 34,5·105 кгс·см.
Ширину раскрытия трещин, нормальных к оси колонн на уровне центра тяжести растянутой арматуры в сечении действия максимального момента M, производим по формуле (148)
 .
.Определяем жесткость сечения стоек с трещинами при действии силы N = 40 тс и расчетного момента Mр = 34,5 тс·м по формуле (141), для чего вычисляем:
 ;
; ;
; ;
;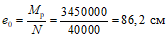 ;
;e = e0 + (0,5h0 - a) = 86,2 + (0,5·40 - 4) = 102,5 см;
Mз = Ne = 40000·102,5 = 4090000 кгс·см;
 ;
; ;
; ;
;Sд = 0,95;  (п. 3.15);
(п. 3.15);
 (п. 3.15);
(п. 3.15); ;
;принимаем  .
.
Жесткость сечений колонн с трещинами в растянутой зоне равна:

Приведенная жесткость колонн равна:
 .
.Максимально возможное расстояние между температурными швами эстакады определяем по формулам:
Mр = M - Mн = 34,5 - 9 = 25,5 тс·м;
 ;
; .
.Перемещение верха крайней колонны
 .
.Выполняем второе приближение с учетом влияния гибкости колонн на их несущую способность:
Mр = M - Mн - Nyк = 34,5 - 9 - 40·0,1 = 21,5 тс·м,
 ;
; ;
; .
.Учитывая, что расстояние между колоннами равно 12 м, длина температурного блока должна быть не более 372 м.
Пример 10. Рассчитать продольный каркас цеха, представляющий собой двухъярусную рамную конструкцию (рис. 50), на температурное воздействие окружающей среды. Здание длиной 240 м проектируется без температурных швов. Подкрановые балки проектируются из металла, покрытие цеха и колонны из железобетона марки 300. Сечение подкрановой части двухветвевых колонн принято 70 x 50, надкрановой 58 x 50 см. Арматура колонны соответственно Fан = 27 см2 и Fав = 20 см2 из класса А-II. Вертикальное усилие в колонне равно: Nн = 142 тс, Nв = 116 тс.

Требуется определить в стадии эксплуатации здания изгибающие моменты в крайних колоннах от изменения климатической температуры.
Расчетное изменение температуры определено по заданию на проектирование
 .
.Определяем величину изгибающего момента, который может воспринять верхняя часть двухъярусной колонны.
Высота сжатой зоны:
 ;
; ;
;Mв = Nв(h0 - 0,5xв) + (RаFав - 0,5Nв)(h0 - a') =
= 116000(46 - 0,5·14·3) + (3400·20 - 0,5·116000)(46 - 4) =
= 4920000 кгс·см.
Нижняя часть колонн (в месте заделки):
 .
.Mн = 142000(46 - 0,5·14,5) + (3400·27 -
- 0,5·142000)(46 - 4) = 6380000 кгс·см,
 ;
; .
.Значения 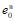 и
и  больше 0,5 сечений колонн.
больше 0,5 сечений колонн.
Поэтому можно применить приближенный метод расчета жесткости сечений с трещинами (п. 3.14), для чего определяем:
 ;
; ;
; ;
; ;
;ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 .
.По табл. 13 определяем значения коэффициентов:
 ;
;  ;
;  ;
; ;
;  ;
;  .
.Вычисляем значения Iпр, Fпр, rяд [формулы (135) - (137)]:
 ;
; ;
;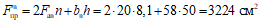 ;
; ;
; ;
; ;
;
 .
.Определяем жесткость сечений колонн без трещин [формулы (138) и (139)]:
Cб = 0,5(1 + C) = 0,5(1 + 2) = 1,5;
 ;
; ;
; ;
; .
.Момент появления трещин:
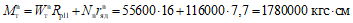 ;
; .
.Приведенная жесткость верхней и нижней части двухъярусных колонн равна (104):
 ;
;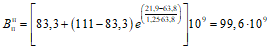 .
.Определяем величину перемещений колонн в плоскости покрытия и подкрановых балок (117):
 ;
; .
.Свободное относительное температурное перемещение железобетонного покрытия равно (п. 3.14):
 .
.Металлических подкрановых балок
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 .
.Относительное удлинение железобетонных элементов покрытия от действия внешней нагрузки (п. 3.10)
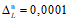 ,
,подкрановых балок  .
.
Расстояние от несмещающейся точки каркаса равно:
 .
.Величину коэффициентов, учитывающих податливость ригелей, принимаем равными:
 .
.Величину коэффициента, учитывающего податливость сжатых стыков подкрановых балок с колоннами, принимаем равным:  . Учитывая, что от действия климатических температур верхние стыки будут растянуты (п. 3.13):
. Учитывая, что от действия климатических температур верхние стыки будут растянуты (п. 3.13):
 . Учитывая, что от действия климатических температур верхние стыки будут растянуты (п. 3.13):
. Учитывая, что от действия климатических температур верхние стыки будут растянуты (п. 3.13): ;
; ;
;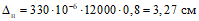 ;
; .
.Усилия в нижней и верхней части двухъярусных колонн от вынужденных перемещений определяем по формулам (110) и (111):

ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |

Пример 11. Рассчитать железобетонную подпорную стенку (стенку подвала машзала прокатного цеха) на действие температуры окружающей среды. Подпорная стенка запроектирована по оси продольного ряда колонн цеха и жестко связана с подколонниками (рис. 51).

Рис. 51. Подпорная стенка по оси продольного ряда колонн
Так как подколонники нагружены значительной вертикальной нагрузкой, то всякое перемещение их в горизонтальном направлении исключено. В этом случае величина температурно-усадочных напряжений в подпорной стенке не зависит от длины сооружения, и поэтому подпорная стенка запроектирована без температурно-усадочных швов при длине 480 м. Стенка проектируется из бетона М200.
Цех возводится в г. Калинине. Относительная влажность воздуха 70%. Ориентировочное время строительства два года.
Расчет стенки в стадии строительства. Согласно табл. 10, для конструкций цеха принимаются расчетные изменения температур в период строительства цеха, равные:
 ;
;  .
.Определяем величину относительной деформации усадки бетона в элементах подпорной стенки (п. 1.10), для этого определяем.
приведенную высоту стенки
 ;
;относительную критическую влажность бетона
 ;
;относительную равновесную влажность бетона
 .
.расчетное изменение относительной влажности бетона
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 .
.Предельная величина усадки бетона в стенке
 .
.Величина усадки бетона через два года после начала строительства:
t = 2·360 = 720 сут.
 .
.Коэффициент релаксации внутренних усилий определяем по формуле (1)  .
.
Предельная величина меры ползучести бетона
 .
.Мера ползучести при t = 720 сут (два года)
 .
.Коэффициент C, учитывающий деформации ползучести бетона,
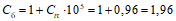 .
.Коэффициент релаксации (1)
 .
.Температурно-усадочные напряжения в плите определяем для стадии охлаждения конструкции. В этом случае:
 ;
;Eб = 240000 кг/см2;  (табл. 11);
(табл. 11);
 (табл. 11);
(табл. 11); .
.Напряжения в плите превышают прочность бетона на растяжение, поэтому в процессе строительства возможно появление в плите температурно-усадочных трещин. В плите необходимо установить противоусадочную арматуру.
Принимаем арматуру класса А-II Ra = 2600 кгс/см2.
Минимальный процент армирования определяем по формуле
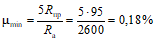 .
.Площадь арматуры на 1 м плиты
 .
.Принимаем  (с шагом 20 см).
(с шагом 20 см).
Максимальная ширина раскрытия трещин в момент их образования [формула (148)] (Cд = 1,  ,
,  , Ea = 2,1·106):
, Ea = 2,1·106):
 .
.Ширина раскрытия температурно-усадочных трещин при эксплуатации конструкций (при C0 = 1,5 и  )
)
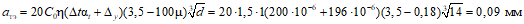 .
.









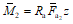 , (25)
, (25)


 и
и  и условия прочности
и условия прочности 



 ;
;  ;
;  ;
;  . (42)
. (42)










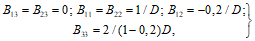


 ;
;  . (73)
. (73) , определяемое по рекомендациям руководства [31], как для балки с
, определяемое по рекомендациям руководства [31], как для балки с 


 ,
,  и
и 














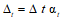













 .
.

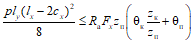





















 равен:
равен: