СПРАВКА
Источник публикации
М.: НИИСК Госстроя СССР, 1989
Примечание к документу
Название документа
"Рекомендации по проектированию покрытий производственных зданий с железобетонными панелями-оболочками КСО"
(одобрены Протоколом Госстроя СССР от 28.12.1987 N 31)
"Рекомендации по проектированию покрытий производственных зданий с железобетонными панелями-оболочками КСО"
(одобрены Протоколом Госстроя СССР от 28.12.1987 N 31)
Содержание
Протоколом секции N 1
Научно-технического совета
НИИСК Госстроя СССР
от 28 декабря 1987 г. N 31
РЕКОМЕНДАЦИИ
ПО ПРОЕКТИРОВАНИЮ ПОКРЫТИЙ ПРОИЗВОДСТВЕННЫХ ЗДАНИЙ
С ЖЕЛЕЗОБЕТОННЫМИ ПАНЕЛЯМИ-ОБОЛОЧКАМИ КСО
Приведены рекомендации по расчету и конструированию панелей-оболочек на пролет типа КСО и гибких предварительно напряженных пластин для покрытий производственных зданий.
Основаны на результатах экспериментально-теоретических исследований, проводившихся в НИИСК (г. Киев) и БТИСМ им. Гришманова (г. Белгород) и опыта внедрения панелей КСО разм. 3 x 24 и 3 x 18 м в г. Белгороде и г. Киеве.
Рассчитаны на инженерно-технических работников проектных и научно-исследовательских организаций, аспирантов и студентов вузов строительного профиля.
Рекомендации разработаны канд. техн. наук Е.И. Стаковиченко, канд. техн. наук В.И. Колчуновым, инж. Е.В. Осовских.
Раздел, относящийся к технологии заводского изготовления панелей КСО и гибких пластин, разработан инж. С.И. Матюшенко совместно с канд. техн. наук А.Д. Либерманом.
Научный редактор - канд. техн. наук А.Д. Либерман.
Рецензенты: д-р техн. наук, проф. И.Е. Милейковский /ЦНИИСК им. В.А. Кучеренко/, ст. науч. сотр., канд. техн. наук Г.В. Шарапов /НИИСК/.
Настоящие рекомендации составлены на основании экспериментально-теоретических исследований покрытий производственных зданий, состоящих из панелей-оболочек на пролет типа КСО и гибких пластин, проводившихся в НИИСК Госстроя СССР и Белгородском технологическом институте строительных материалов им. И.А. Гришманова (БТИСМ).
Приведены сведения, позволяющие законструировать, рассчитать панели-оболочки типа КСО и гибкие пластины по прочности методами предельного равновесия, а также по жесткости и трещиностойкости методом конечных элементов или вариационным методом В.З. Власова.
Особенность применения панелей КСО - возможность пропуска в межферменном пространстве технологических коммуникаций как вдоль пролета, так и из пролета в пролет.
В рекомендациях рассматриваются два основных конструктивных решения покрытия - рядовое и комбинированное. В рядовом варианте покрытия панели-оболочки устанавливаются вплотную друг к другу. В комбинированном - с промежутком 3 м между ними, который затем перекрывается гибкими предварительно напряженными пластинами. В обоих вариантах покрытий панели-оболочки устанавливаются на продольные конструкции: при шаге колонн 6 м - на балки; 12 м - на подстропильные фермы треугольного очертания или балки с горизонтальным верхним поясом.
При расчете безраскосных ферм-диафрагм предусмотрена возможность регулирования усилий в их поясах.
Несущая способность гибкой пластины определяется по деформированной схеме.
Расчет жесткости и трещиностойкости панели-оболочки КСО и гибкой пластины выполняется с применением пластинчато-стержневой аппроксимации конструктивных элементов и программных комплексов, реализующих метод конечных элементов для пространственных систем, например, ППП АПЖБК, "ПРОКРУСТ-81" и др. При учете неупругих деформаций и трещин в элементах панели КСО рекомендовано использование специально разработанных (на основе метода конечных элементов) итерационных алгоритмов и программ. Для нелинейного расчета пластин (пологих оболочек) рекомендовано применение итерационного алгоритма и программы, составленных на основе вариационного метода В.З. Власова.
В Рекомендациях приведены особенности технологии изготовления панелей-оболочек КСО и гибких пластин.
Панели-оболочки КСО размером 3 x 24 и 3 x 18 м внедрены при строительстве промышленных объектов в Белгородской и Киевской областях для зданий различного назначения.
Опыт проектирования и возведения покрытий из панелей КСО показал, что по сравнению с типовыми решениями из плит и ферм снижение расхода бетона и стали составляет 15 - 20%, трудозатрат на монтаже в 1,8 - 2 раза, приведенных затрат на 5 - 8 р./м2 площади здания. В комбинированных покрытиях расход стали и бетона снижается на 20 - 30%, а приведенные затраты по 8 - 10 р./м2.
Экспериментальные исследования натурных образцов конструкций размером 3 x 24,3 x 18 м и разработка заводской технологии изготовления проводились НИИСК Госстроя СССР, БТИСМ им. И.А. Гришманова и Территориальным строительным объединением (ТСО) "Белгородстрой".
1.1. Панели-оболочки КСО (крупноразмерная складчатая оболочка) предназначаются для покрытий промышленных, общественных и других зданий с пролетами 18 и 24 м. Применение панелей КСО предусматривается в покрытиях однопролетных и многопролетных зданий с фонарями (светоаэрационными и зенитными) и без них в бескрановых зданиях, а также оборудованных мостовыми кранами грузоподъемностью 30/5 т или подвесным транспортом грузоподъемностью до 5 т (рис. 1). В покрытиях из панелей КСО возможны установка крышных вентиляторов, вытяжных шахт, а также устройство легкосбрасываемой кровли. Панели КСО могут быть в комплексном исполнении (с утеплителем).
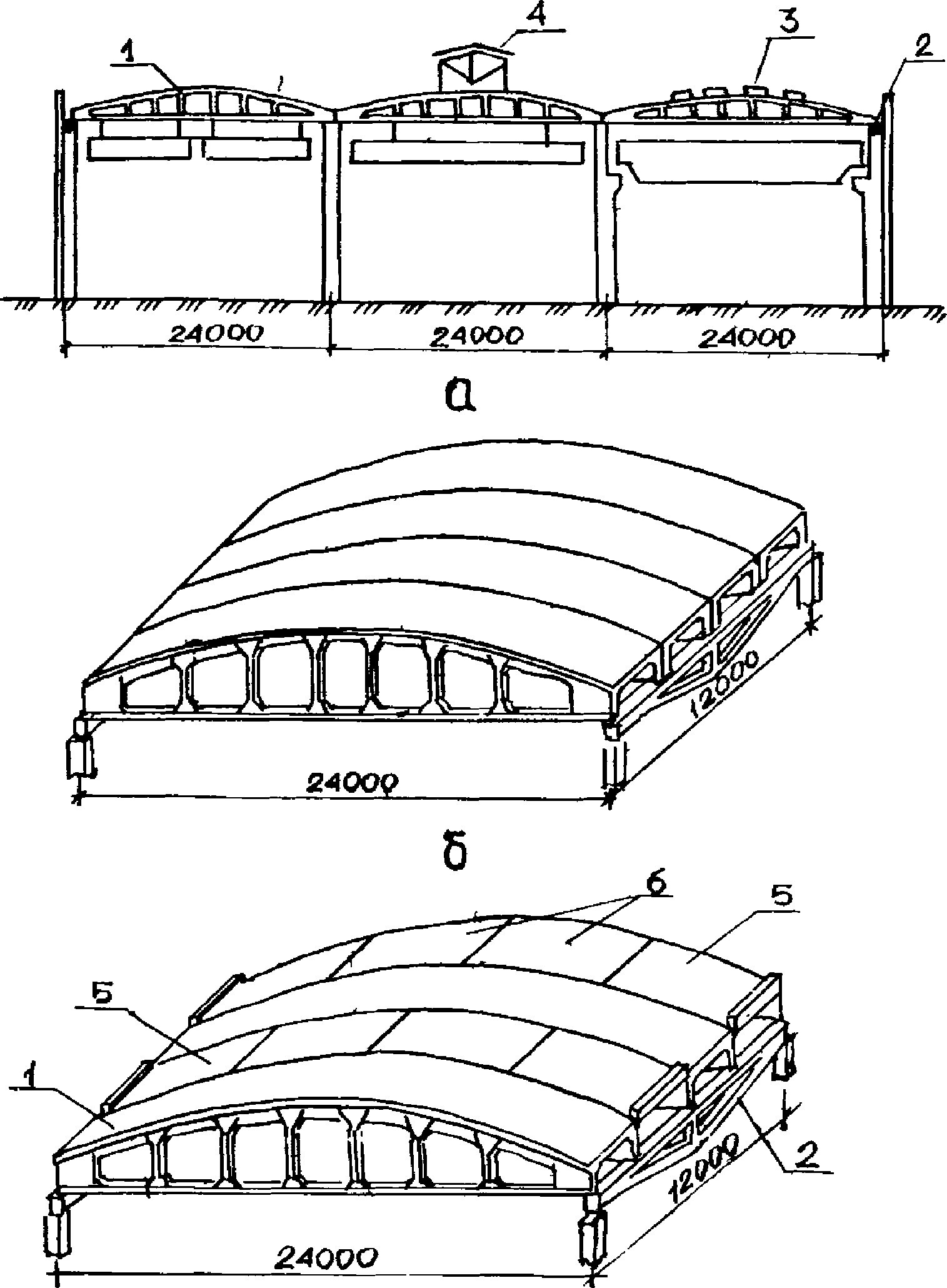
КСО и гибких пластин
а - конструкция покрытия с панелями-оболочками КСО;
б - рядовое покрытие; в - комбинированное покрытие;
1 - панель-оболочка КСО; 2 - подстропильная конструкция;
3 - зенитный фонарь; 4 - светоаэрационный фонарь;
5 - гибкая пластина, крайняя; 6 - гибкая пластина, средняя
1.2. Как установлено анализом, до 30% промышленных зданий выполняются с развитой сетью технологических коммуникаций, размещаемых в межферменном пространстве.
В покрытиях с панелями КСО возможен пропуск коммуникаций как вдоль пролета диаметром до 1,2 - 1,6 м, так и из пролета в пролет диаметром до 0,6 м. В этом состоит существенное отличие панелей КСО от известных панелей на пролет типа КЖС и П.
1.3. НИИСК и Киевским Промстройпроектом разработана рабочая документация серии КП-206 в составе 11 выпусков, предназначенная для строительства зданий из панелей-оболочек КСО в 1,2 и 3 районах снеговых нагрузок под расчетные нагрузки 4,42 - 8,34 кН/м2, в том числе для слабо- и среднеагрессивной среды.
Институтом "Центрогипроруда" Минчермета СССР, БТИСМ и НИИСК разработана рабочая документация панелей-оболочек КСО со схемой расположения стоек с шагом 3 м, а также рабочие чертежи комплексных панелей-оболочек полной заводской готовности с эффективным утеплителем из полистиролбетона.
1.5. Железобетонные конструкции панелей-оболочек КСО и гибких пластин-оболочек рассчитывают по прочности (предельные состояния первой группы), а также по жесткости (предельные состояния второй группы).
Расчет прочности складчатой панели-оболочки КСО производят статическим способом метода предельного равновесия, а расчет прочности гибкой пластины - пологой цилиндрической оболочки - кинематическим способом метода предельного равновесия с учетом деформированной схемы по методу итераций.
1.6. Расчет панелей КСО и пластин-оболочек по жесткости и трещиностойкости производят методом конечных элементов с использованием расчетных моделей различных уровней и существующих общих универсальных программ для расчета пространственных систем.
При необходимости учета неупругих деформаций и трещин в железобетоне (а для гибких пластин-оболочек и деформированной схемы) целесообразно применение специально разработанных для рассматриваемых конструкций алгоритмов и конкретных программ, обеспечивающих не только рациональное использование ЭВМ, но и существенно сокращающих объем вводимой и выходной информации, а также улучшающих инженерную обозримость получаемых при этом решений.
1.7. Изготовление панелей-оболочек целесообразно организовать по стендовой технологии на полигоне или специально оборудованных цехах. Технологическая линия по производству КСО может включать 1 - 3 форм-стендов. Обслуживание такой линии осуществляется двумя мостовыми или козловыми кранами грузоподъемностью 20 - 30/5 т [23].
1.8. Изготовление гибких пластин рекомендуется осуществлять по поточно-агрегатной технологии с применением обычных силовых форм, виброплощадок и ямных камер пропаривания. Предварительное натяжение рекомендуется производить механическим способом с одновременным натяжением всех проволок каждого из взаимно ортогональных направлений. При небольших объемах выпуска изделий допускается применение и электротермического способа натяжения.
1.9. Транспортирование панелей-оболочек КСО рекомендуется проводить, как правило, специализированным автотранспортом, имеющим жесткую платформу и оборудованным опорно-крепежными приспособлениями, например, полуприцепом-площадкой ПЛ 26-24 с тягачом КрАЗ-258, разработанной НИИСК или полуприцепом-площадкой, запроектированным Тульским ПКТИ и изготовленным на заводе нестандартного оборудования ТСО "Белгородстрой".
В качестве автотранспортного средства для перевозки гибких пластин также используется специализированный транспорт с жесткой платформой. Допускается применение одноосного полуприцепа грузоподъемностью 12 т с управляемой задней тележкой.
1.10. Съем панелей-оболочек КСО с формы и монтаж покрытия на объекте строительства рекомендуется вести специально запроектированными траверсами. Желательно, чтобы тросы траверс располагались под углом 80 - 90° к поверхности панели.
Разопалубливание и монтаж с изгибом пластин также осуществляют специальными траверсами. Траверса представляет собой сочетание горизонтальной рамы с блоками, тросами, прогонами и площадками для установки пригрузов с блочно-рычажной системой, осуществляющей прижатие гибкой плиты 3 x 6 м к швеллерам-упорам по торцам горизонтальной рамы. Примерами конструктивного решения таких траверс могут быть траверсы, разработанные и изготовленные ЭКБ НИИСК и ЗЖБИ-1 ТСО "Белгородстрой".
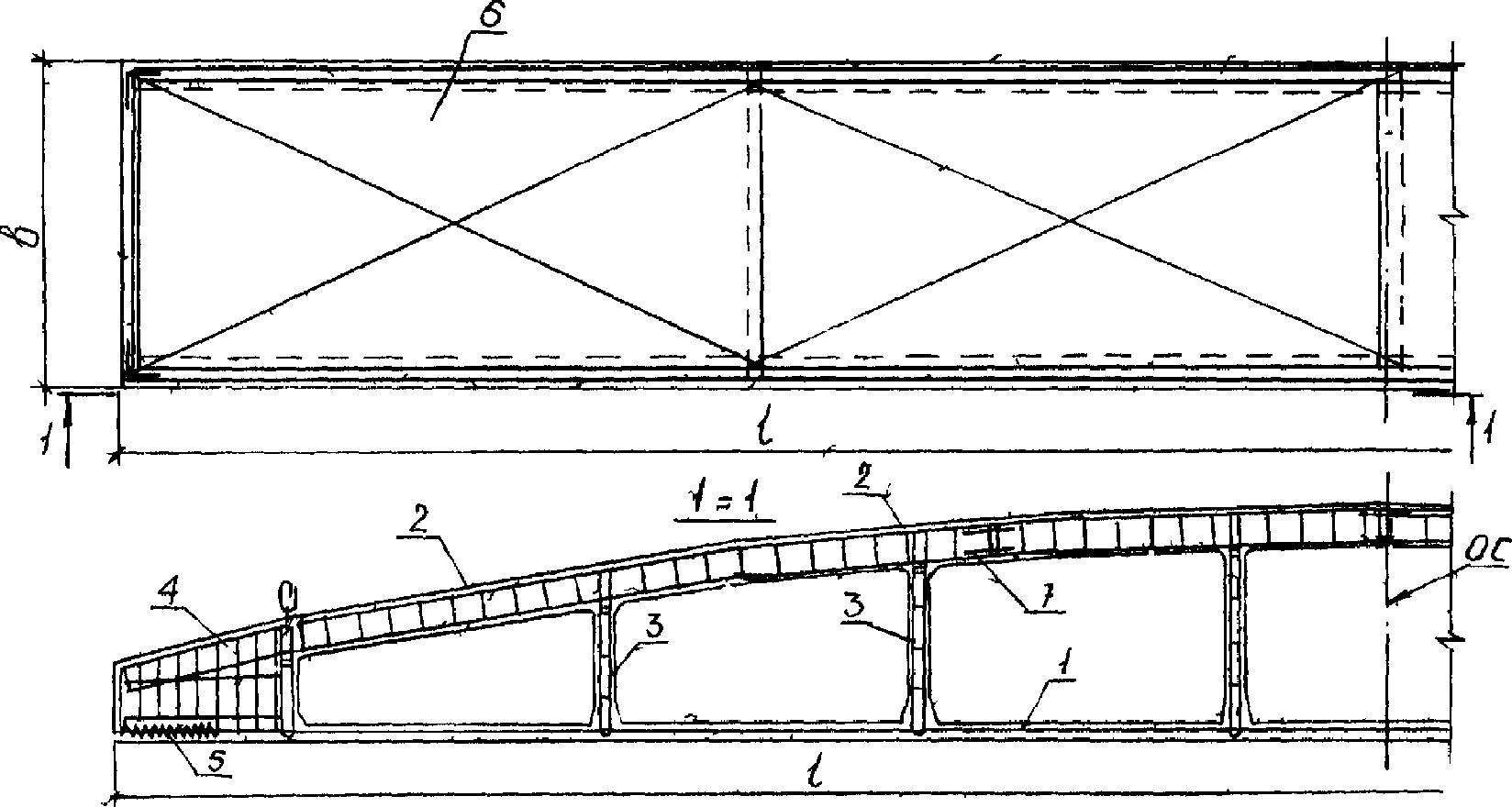
2.1. Панель-оболочку КСО (рис. 2) конструируют в виде пространственной конструкции, состоящей из двух предварительно напряженных безраскосных ферм-диафрагм, соединенных по верху складчатой вутовой полкой. Опорные узлы диафрагм и полку соединяют торцовыми вутами [22].
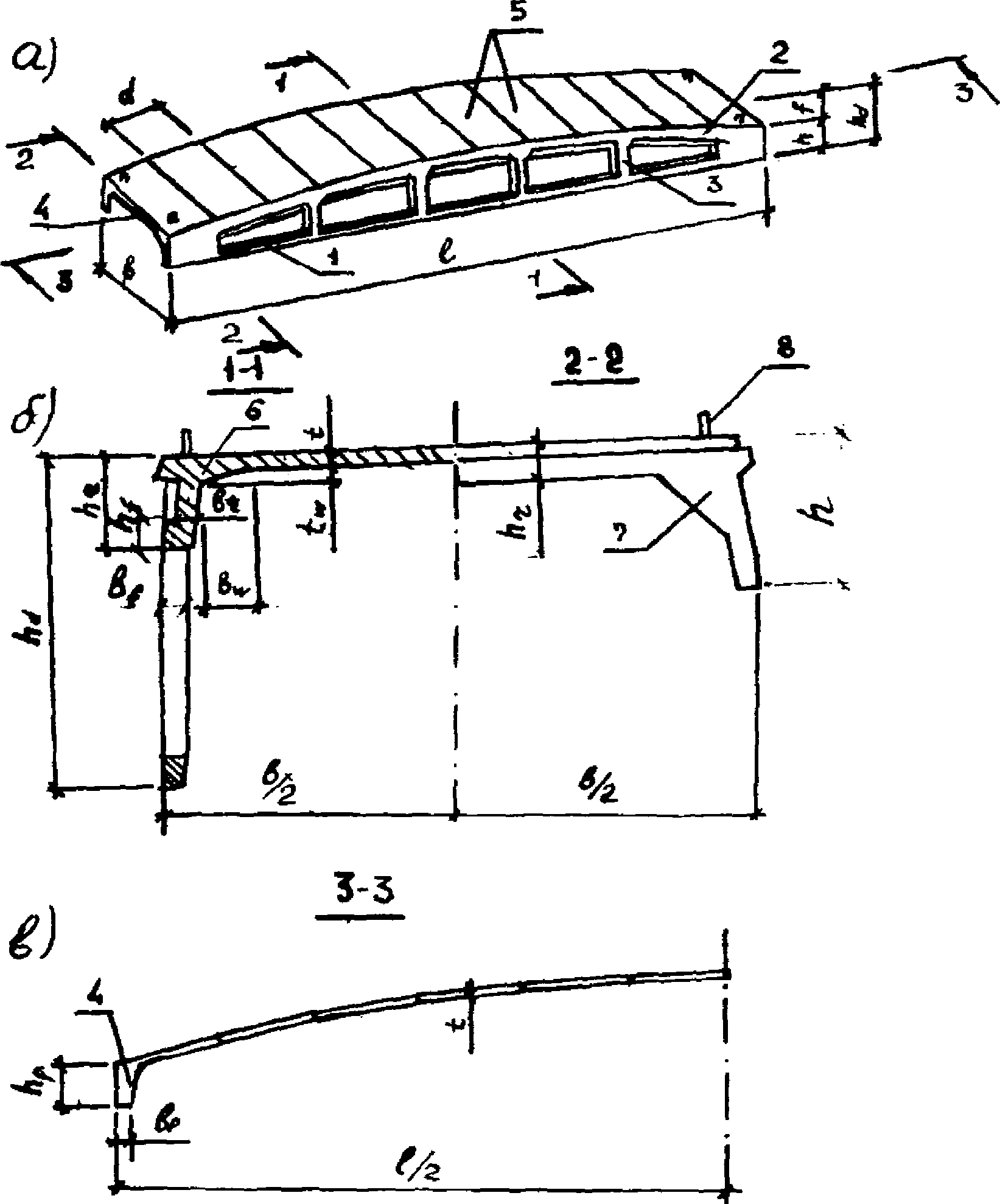
а - общий вид; б и в - соответственно поперечное
и продольное сечения; 1, 2 и 3 - соответственно нижний,
верхний пояса и стойки диафрагмы; 4 - торцовое ребро;
5 - грань складчатой полки; 6 - вутовая часть полки;
7 - торцовые вуты; 8 - падающие петли для подъема
2.2. Номинальные размеры панелей-оболочек в плане b x l, исходя из существующих в промышленном строительстве конструктивных схем, а также из условия транспортирования, принимаются 3 x 18 и 3 x 24 м.
2.3. Высоту поперечного сечения у торца h рекомендуется назначать постоянной для обоих пролетов и равной 750 мм. Высоту поперечного сечения в середине пролета определяют исходя из стрелы подъема f, которую рекомендуется принимать равной 1/15 - 1/20 пролета.
2.4. Очертание верхней поверхности панели (полки) принимается в виде призматической складки, при этом для упрощения конструирования опалубки складчатую поверхность целесообразно получать на базе окружности. Ширину грани полки d назначают 1,5 м, толщину полки t принимают 1/70 - 1/100, а ширину вутовой части полки bw - 1/10 - 1/12 ее пролета. Максимальная высота вутового утолщения tw не должна превышать 1,5 толщины полки.
2.5. Верхний пояс безраскосных ферм-диафрагм допускается выполнять по длине переменного сечения. Высоту верхнего пояса в середине пролета hz рекомендуется принимать 1/4 - 1/6 максимальной высоты диафрагмы hd, а у опорных узлов - на 100 - 120 мм больше. Ширину сечения верхнего пояса диафрагм br также проектируют переменной (с учетом наклона внутренней грани верхнего пояса к вертикали для обеспечения распалубки изделия) и принимают в пределах 1/4 - 1/6 его высоты. Размеры нижней части сечения верхнего пояса bf и hf назначают из условия размещения арматуры.
Расстояние между двумя средними стойками в диафрагмах следует принимать 2,6 м (из условия крепления к ним путей подвесного транспорта), а шаг остальных стоек - 3 м. Возможно также решение диафрагм с шагом всех стоек равным 3 м при расположении одной стойки по середине пролета.
Поперечное сечение нижних поясов и стоек диафрагм панели-оболочки следует назначать в пределах 120 - 160 мм.
Уклоны внутренних граней верхнего, нижнего поясов и опорных узлов рекомендуется предусматривать равными 1:10.
2.6. Торцовые ребра следует проектировать трапециевидного сечения с плавными вутовыми сопряжениями с полкой и верхними поясами диафрагм. Высоту торцового ребра hp следует назначать 1/15 - 1/20 пролета, а ширину по низу bp равной (0,8 - 1,0)hp.
2.7. В качестве аналога при конструировании панели-оболочки КСО могут быть использованы примеры конструктивных решений панелей, приведенные на рис. 3 и 4 применительно к пролетам 24 и 18 м. В то же время исследованиями [7] установлено, что рекомендованные в пп. 2.1 - 2.6 топология, геометрия и параметры элементов являются лишь основой для постановки проектной задачи, ее исходным уровнем. Различные ограничения, накладываемые на поведение конструкции, приводят к неравнозначным запасам несущей способности, жесткости и трещиностойкости конструктивных элементов панели КСО и имеются существенные резервы для их рационального проектирования с позиций структурного синтеза [8].
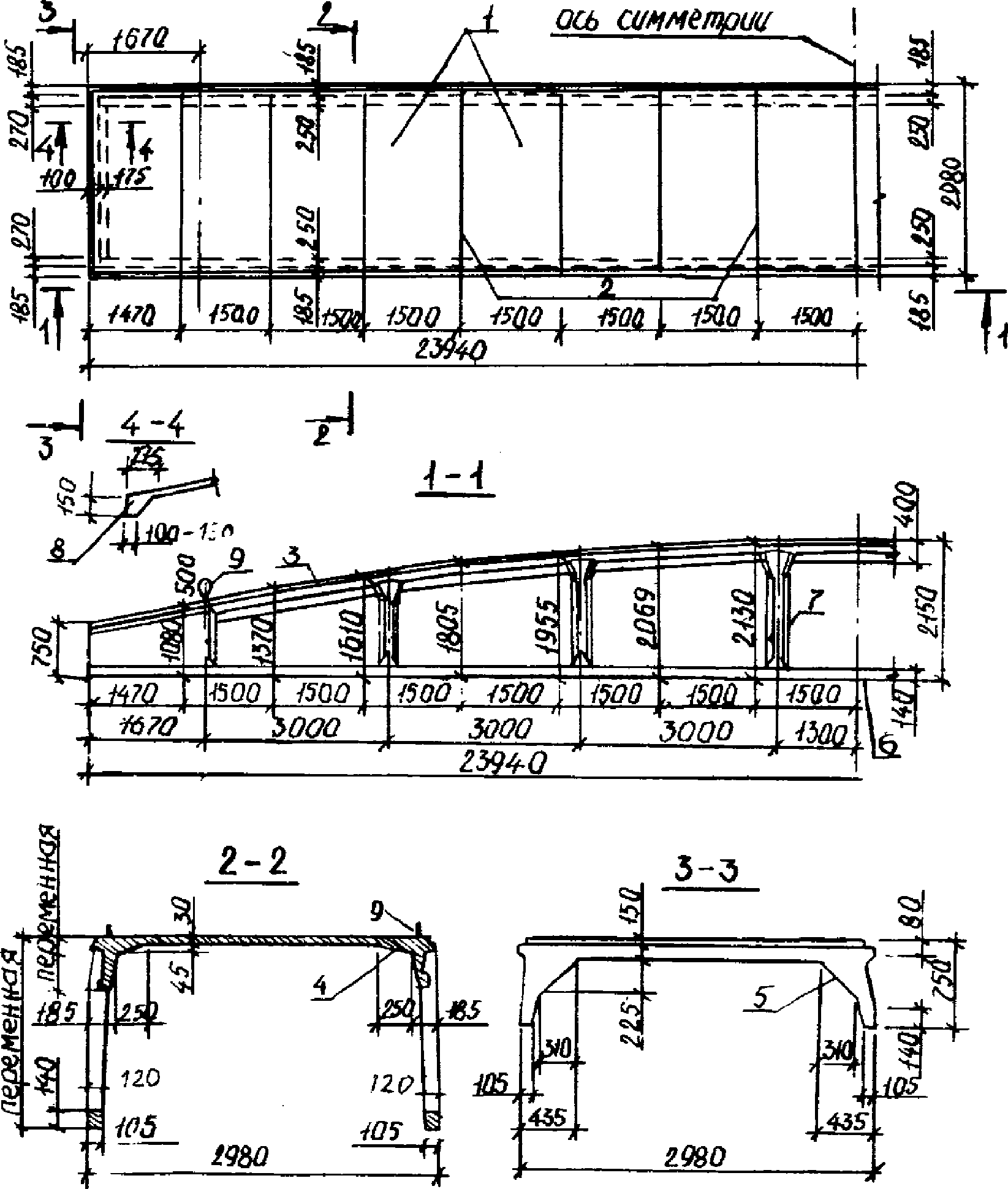
1 - грани складчатой полки; 2 - ребра складчатой полки;
3 - безраскосная ферма-диафрагма; 4 - вутовая часть
полки; 5 - торцовые вуты; 6 - нижний пояс; 7 - стойки;
8 - торцовые ребра; 9 - падающие петли для подъема
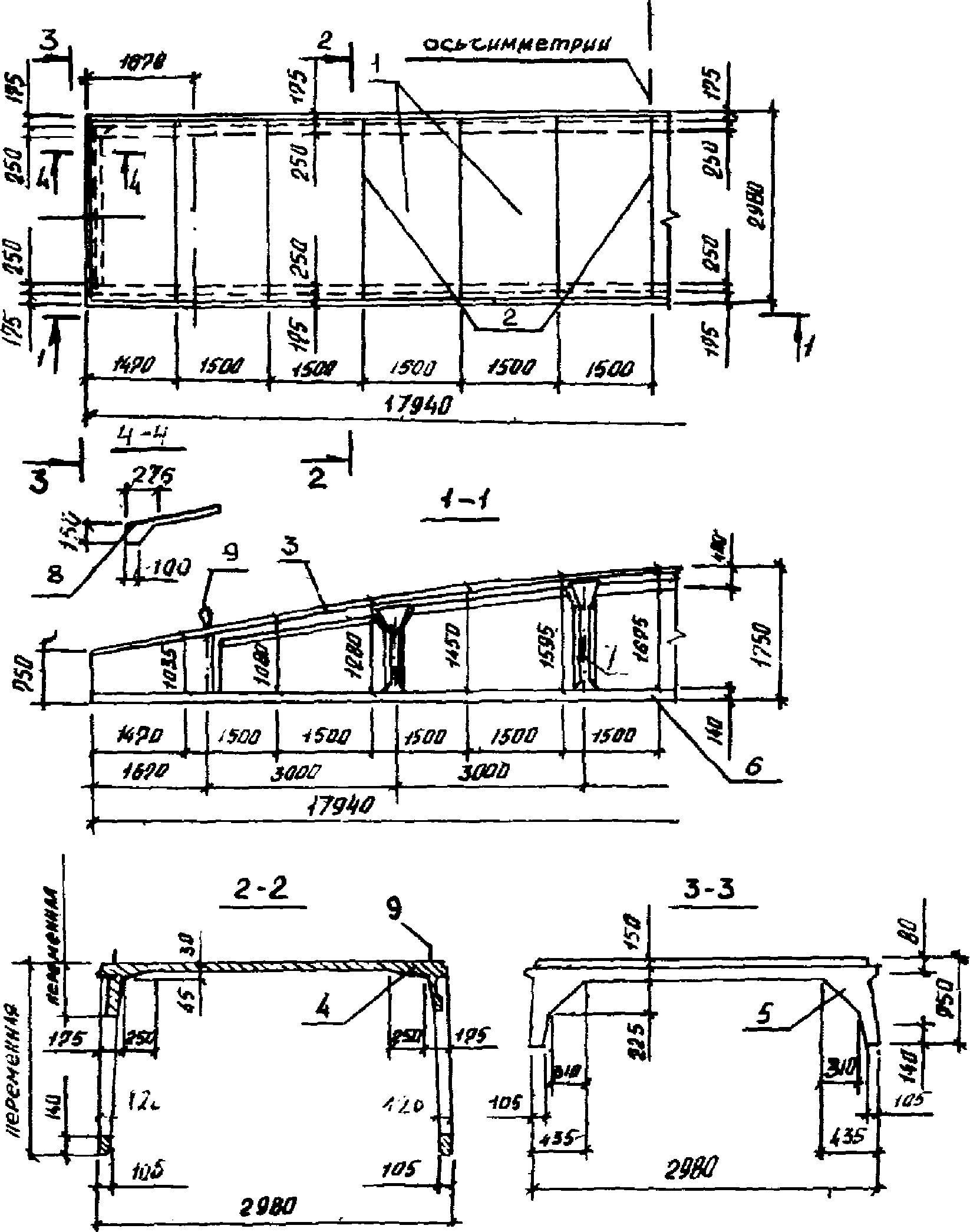
1 - грани складчатой полки; 2 - ребра складчатой полки;
3 - безраскосная ферма-диафрагма; 4 - вутовая часть полки;
5 - торцовые вуты; 6 - нижний пояс; 7 - стойки; 8 - торцовые
ребра; 9 - падающие петли для подъема
2.8. При наличии вентиляционных шахт и крышных вентиляторов следует предусматривать изготовление панелей с проемами диаметром 400, 700, 1000 и 1450 мм, расположенными во второй грани панели на расстоянии 2220 мм от торца у одного из концов панели (рис. 5, а). При этом вторая грань панели утолщается до 100 мм и соответственно армируется.
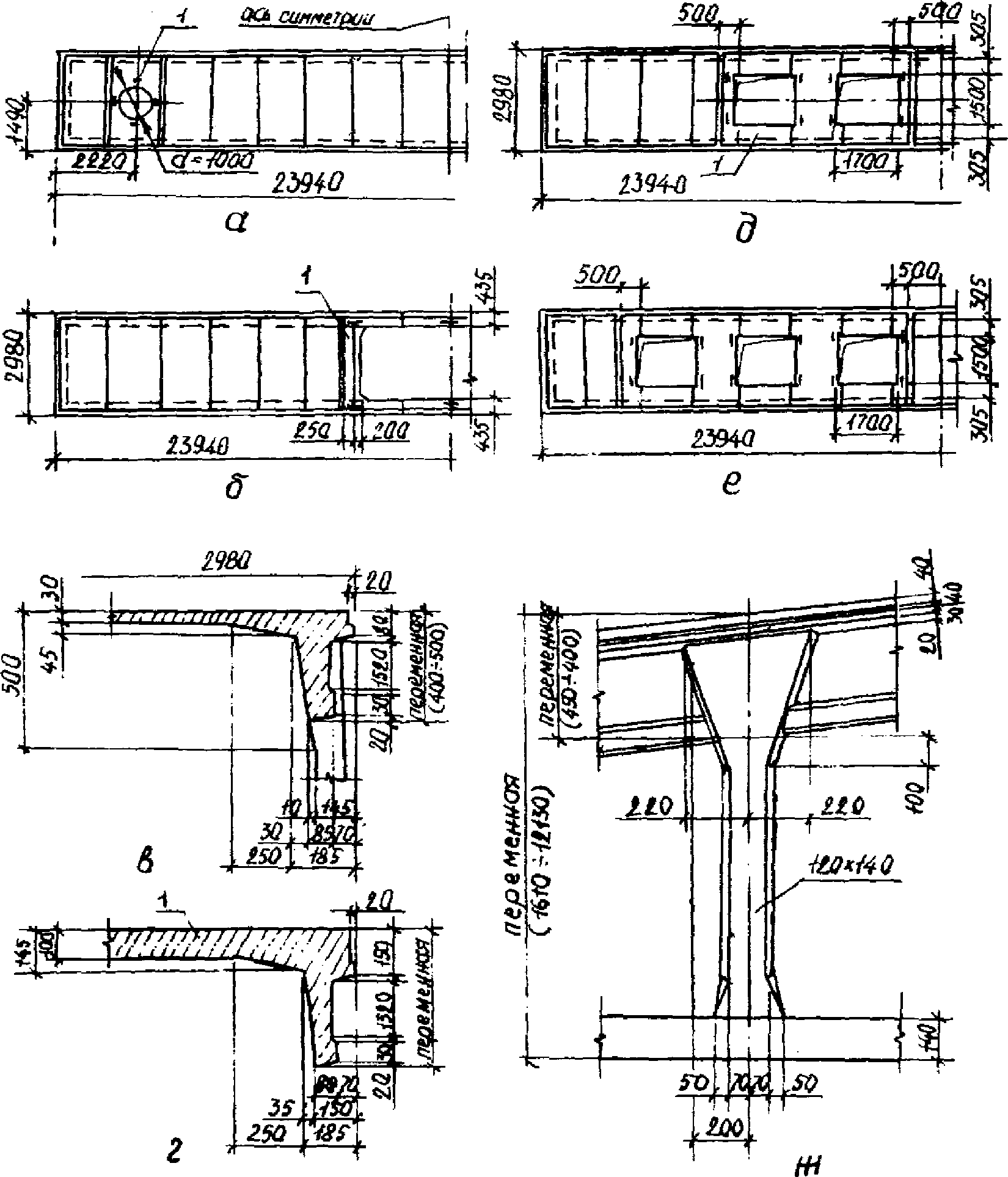
а - с пролетом для воздуховода или крышного вентилятора;
б, д - с проемами для зенитных и светоаэрационного фонарей;
в - поперечное сечение верхнего пояса арочной диафрагмы;
г - то же, с утолщенной полкой у проемов; е - с проемами
для легкосбрасываемой кровли; ж - конструкция стоек
фермы-диафрагмы; 1 - утолщения полки у проемов
2.9. При наличии светоаэрационных фонарей панели следует проектировать с проемом 2000 x 5600 мм (рис. 5, б). При устройстве зенитных фонарей панели КСО размерами 3 x 18 м следует проектировать с двумя проемами размером 1,5 x 1,7 м, а панели размером 3 x 24 м - с четырьмя проемами (рис. 5, д). В панелях размером 3 x 18 м полка у проемов утолщается до 100 мм и соответственно армируется. В панелях размером 3 x 24 м полка утолщается у каждой пары проемов.
2.10. Для устройства легкосбрасываемой кровли в полке панелей-оболочек проектируются проемы, которые размещаются в зависимости от заданной их площади (рис. 5, е).
2.11. Панели-оболочки КСО рекомендуется проектировать из бетонов классов B25 - B45 по прочности на сжатие в зависимости от размера пролета и нагрузок.
2.12. Напрягаемую рабочую арматуру панелей рекомендуется проектировать из стержневой свариваемой стали классов А-V, А-VI и, как правило, выполнять из одного стержня в нижнем поясе каждой диафрагмы (рис. 6). Допускается также применение арматуры класса А-IIIв. При слабо- и среднеагрессивных средах количество стержней в нижнем поясе диафрагмы может быть увеличено до 2 или 4 меньшего диаметра.
1 - предварительно напряженная арматура; 2 - сварная сетка
верхнего пояса фермы-диафрагмы; 3 - арматурный каркас
стойки панели-оболочки; 4 - сварная сетка опорного узла;
5 - спираль; 6 - сварная сетка полки панели-оболочки;
7 - сварной стык сеток верхнего пояса фермы-диафрагмы
2.13. В качестве ненапрягаемой арматуры для сварных каркасов, сеток и отдельных стержней рекомендуется применять стержневую арматуру классов А-I и А-III, а также арматурную проволоку класса Вр-1 (см. рис. 6, 7).
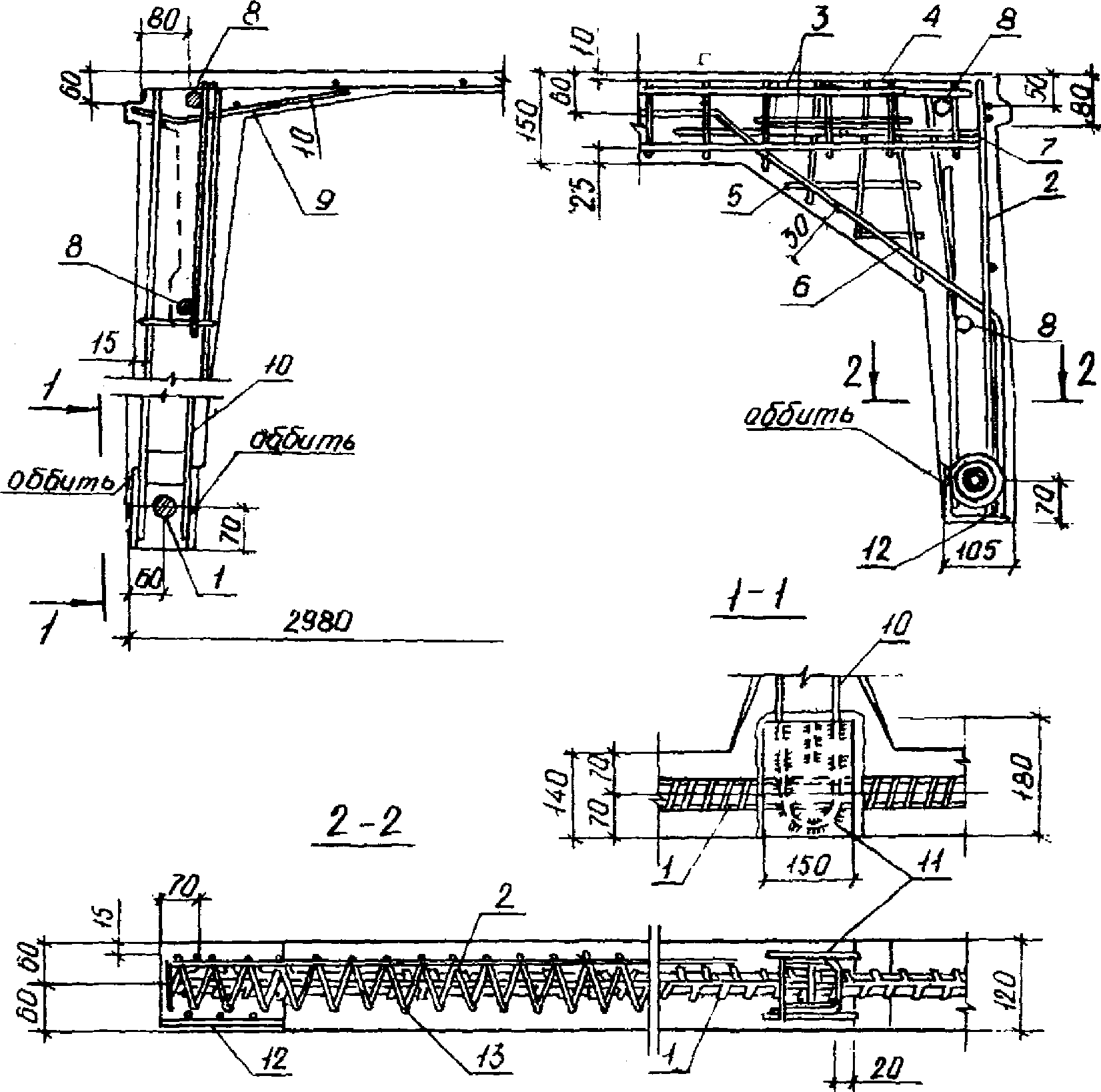
1 - стержневая предварительно напряженная арматура;
2 - сварная сетка опорного узла; 3 - арматурная сварная
сетка торцового ребра; 4 - сварная сетка полки; 5 - сварная
сетка торцового вута; 6 - одиночный стержень; 7 - угловой
стержень; 8 - рабочие стержни сварной сетки верхнего пояса
диафрагмы; 9 - сварная сетка вутовой части полки панели;
10 - арматурный каркас стойки фермы-диафрагмы;
11 - закладная деталь для крепления подвесного транспорта;
12 - опорная закладная деталь; 13 - спираль
Полку панели и вутовой участок армируют сварными сетками из стержней класса Вр-1.
Верхние пояса диафрагм, опорные узлы и торцовые ребра армируют сварными сетками из арматуры класса А-III, стойки диафрагм - пространственными каркасами из арматуры класса А-III.
При номинальной длине сварных сеток верхних поясов и полки равной 6 м, для панели КСО 3 x 24 м устраивают 8 каркасов и 4 сетки, а для панели 3 x 18 - соответственно 6 и 3.
Для предупреждения раскалывания бетона при передаче напряжений с арматуры на бетон в опорных узлах необходимо предусматривать спирали.
Монтажные петли следует проектировать падающими, изготавливаемыми из арматуры класса А-I и привариваемыми к арматурным каркасам, установленным в опорных узлах на расстоянии 1,67 м от торцов панели-оболочки (возможно устройство монтажных петель по концам опорных узлов с креплением анкерных стержней к опорному закладному уголку).
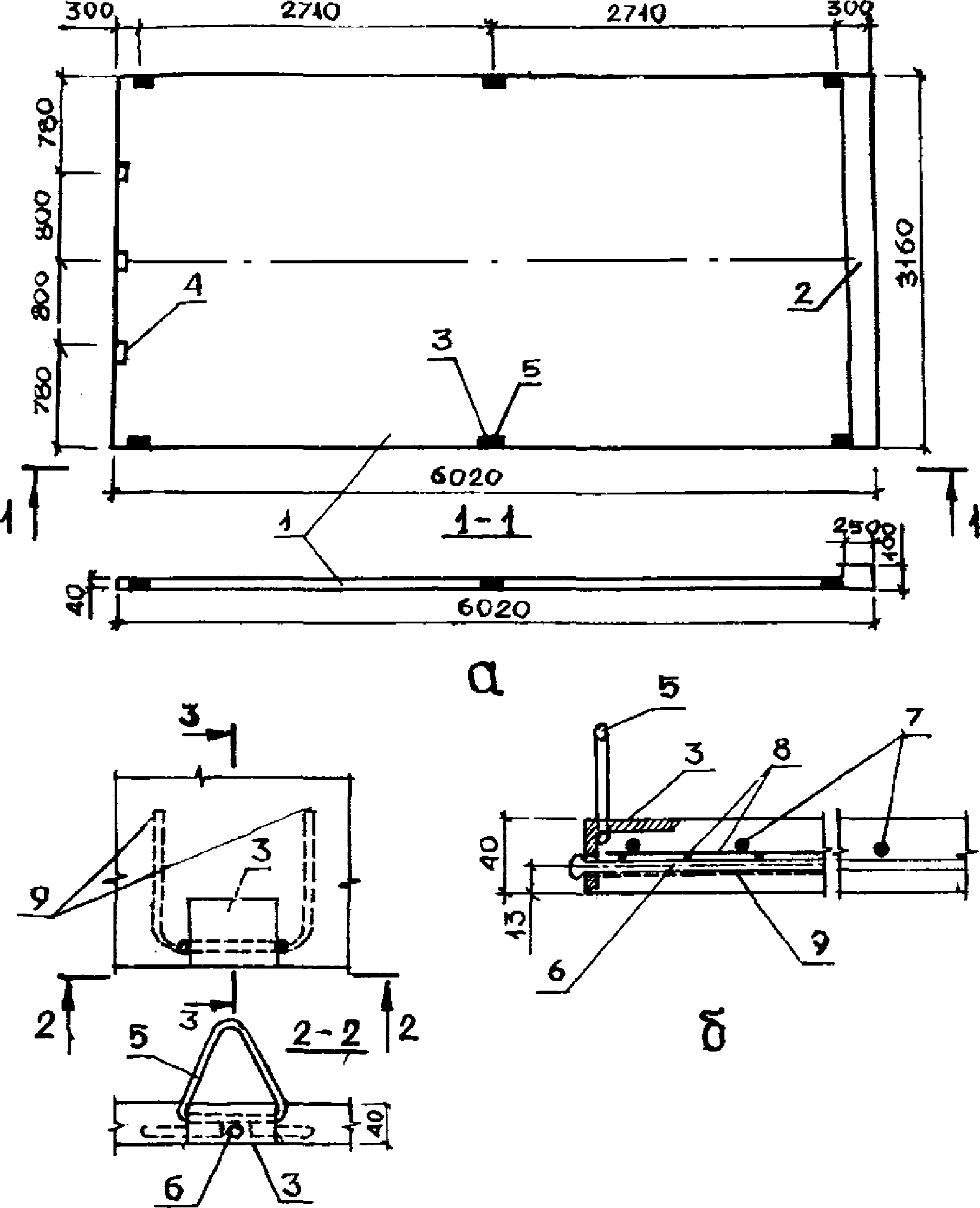
2.14. Предварительно напряженная в двух направлениях гибкая пластина представляет собой тонкостенную железобетонную конструкцию с номинальными размерами 3 x 6 x 0,04 м. Действительные размеры гибкой плиты 3,16 x 6,02 x 0,04 м (рис. 8, 9).
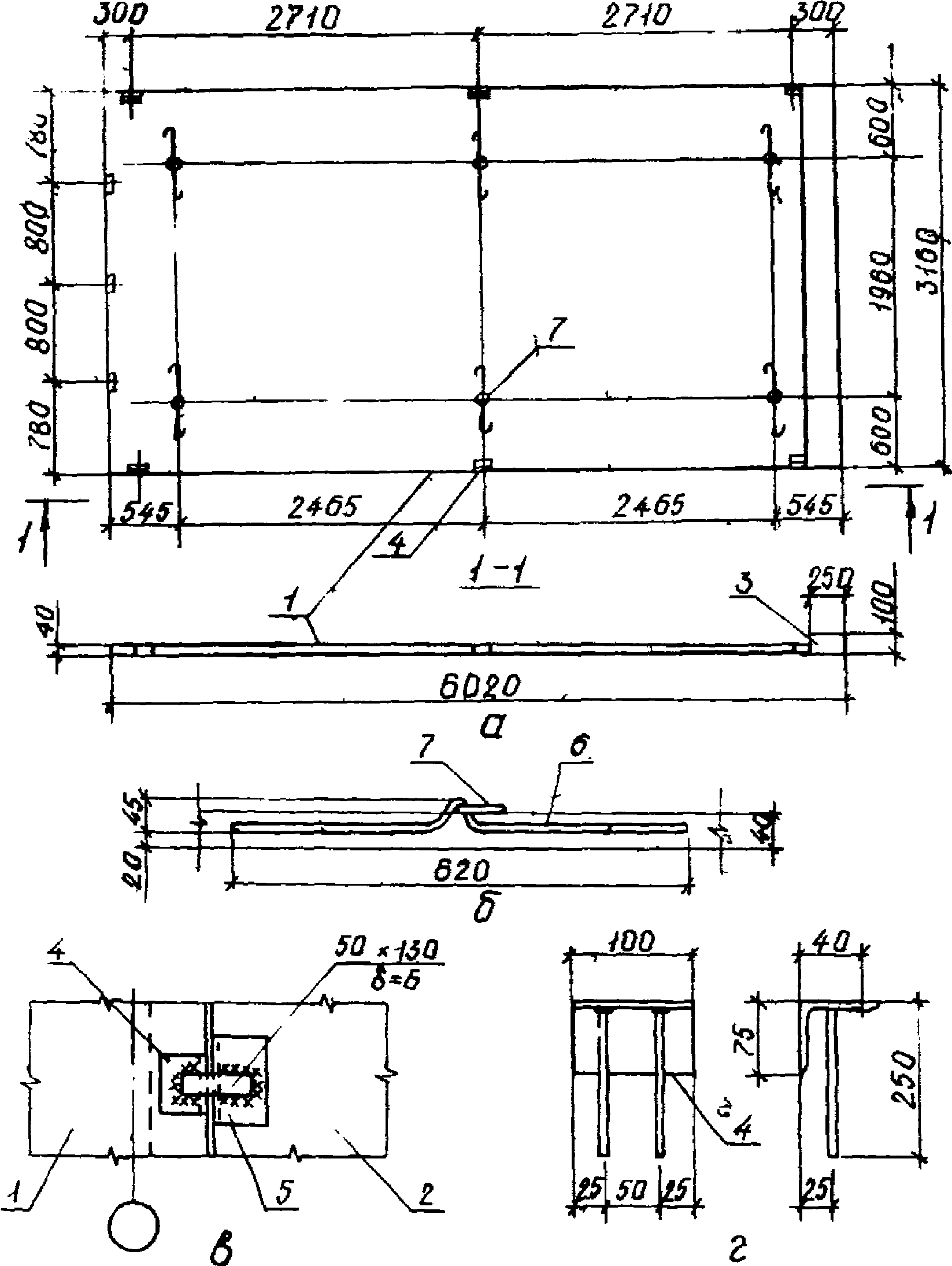
гибкая пластина 3 x 6 x 0,04 м
а - опалубочный чертеж пластины, располагаемый у ендовы;
б - деталь крепления падающей петли; в - деталь крепления
гибкой пластины к панели-оболочке КСО;
г - закладной элемент гибкой пластины;
1 - гибкая пластина; 2 - панель-оболочка КСО 3 x 24 м;
3 - утолщение гибкой пластины у ендовы;
4 - закладная деталь гибкой пластины;
5 - закладная деталь панели-оболочки; 6 - арматурный
стержень; 7 - кольцо для подъема гибкой пластины
пластины с совмещенными соединительными и монтажными
закладными деталями
а - опалубочный чертеж пластины; б - деталь установки
совмещенной закладной детали; 1 - гибкая пластина;
2 - утолщение у ендовы; 3, 4 - закладные детали
для соединения пластины с оболочкой КСО; 5 - закладная
деталь (падающая петля) для подъема пластины;
6 - предварительно напрягаемый арматурный элемент
с высаженными головками; 7 - предварительно напрягаемая
арматура продольного направления; 8 - сварная сетка
для дополнительной анкеровки закладной детали;
9 - анкера закладной детали
Гибкие пластины, устанавливаемые у ендов, имеют у одного из торцов утолщение до 150 мм при ширине 250 мм. Гибкие пластины, устанавливаемые в средней части панелей, проектируются без утолщений.
Для крепления гибких пластин к панелям-оболочкам КСО по их длинным и коротким сторонам проектируются закладные элементы по 3 на сторону (кроме ендовой стороны).
1) установка 6 падающих петель на верхней поверхности пластины симметрично (на некотором расстоянии) от краев. Петлю цепляют за анкерный арматурный стержень, вводимый в бетон и перекрываемый сверху сварной сеткой, для улучшения анкеровки стержня;
2) совмещенная установка 6 падающих петель с соединительными монтажными закладными деталями из уголков, располагаемых по продольным краям пластины. Для обеспечения надежной анкеровки таких элементов в тонкостенной пластине закладная деталь (помимо установки в ней обычных анкерных арматурных стержней) прижимается к бетонной поверхности с помощью предварительно напряженного элемента, имеющего по две высаженных головки на его концах: одну для натяжения, другую для обжатия (см. рис. 9, б).
Возможны и другие схемы установки закладных деталей в гибких пластинах. При этом любые изменения схемы и количество устанавливаемых закладных деталей должны иметь соответствующее надежное теоретическое и опытное обоснование и взаимоувязку с применяемыми монтажными приспособлениями.
2.15. Армирование гибких пластин осуществляется проволочной арматурой класса Вр-П в двух направлениях. В поперечном направлении арматура расположена по низу с защитным слоем 10 ... 15 мм, в продольном направлении - с защитным слоем 10 мм по верху. У краев гибкой пластины (расстояние в пределах 1 м от краев) арматура расположена чаще, в средней части - реже (рис. 10).
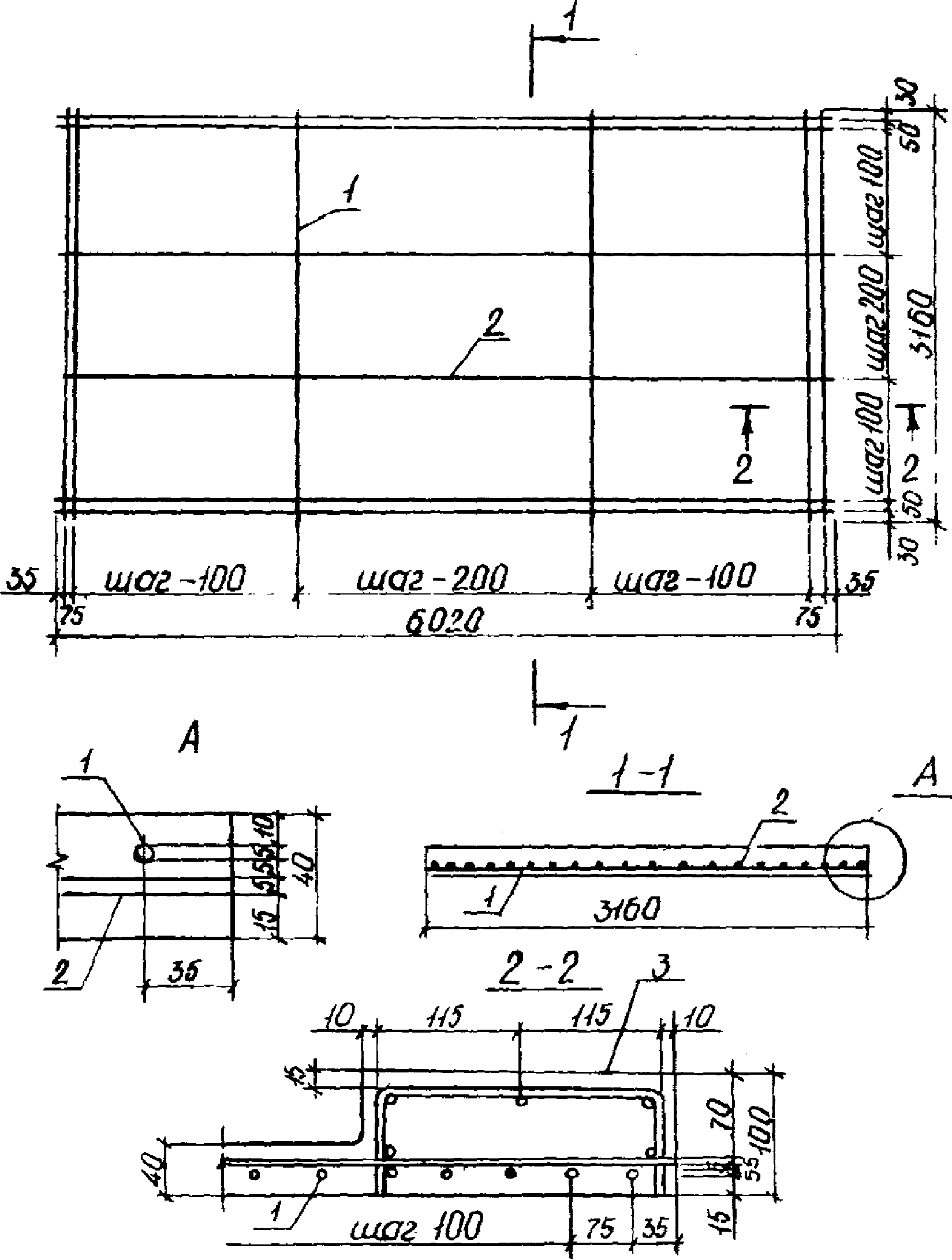
напряженной гибкой пластины
1 - предварительно напряженная проволока поперечная;
2 - то же, продольная; 3 - утолщение
гибкой пластины у ендовы
2.16. Гибкие пластины рекомендуется проектировать из бетона класса B30 - B45 по прочности на сжатие в зависимости от радиуса продольного изгиба и нагрузок.
И ГИБКИХ ПЛАСТИН
3.1. Рассматриваемые покрытия проектируются из панелей-оболочек КСО и поддерживающих продольных конструкций. При невысоких зданиях сельскохозяйственного или общественного строительства, невысоких складских зданиях панели опираются на продольные несущие стены.
В промышленном строительстве при шаге колонн 6 м панели опираются на продольные железобетонные балки (рис. 11, а). Для крайних рядов колонн устанавливают балки прямоугольного сечения с параллельными поясами шириной 250 и высотой 600 мм, для средних рядов колонн - балки трапециевидного сечения с шириной по верху 500 и по низу 250 мм (например, серии 1.462.1-18).
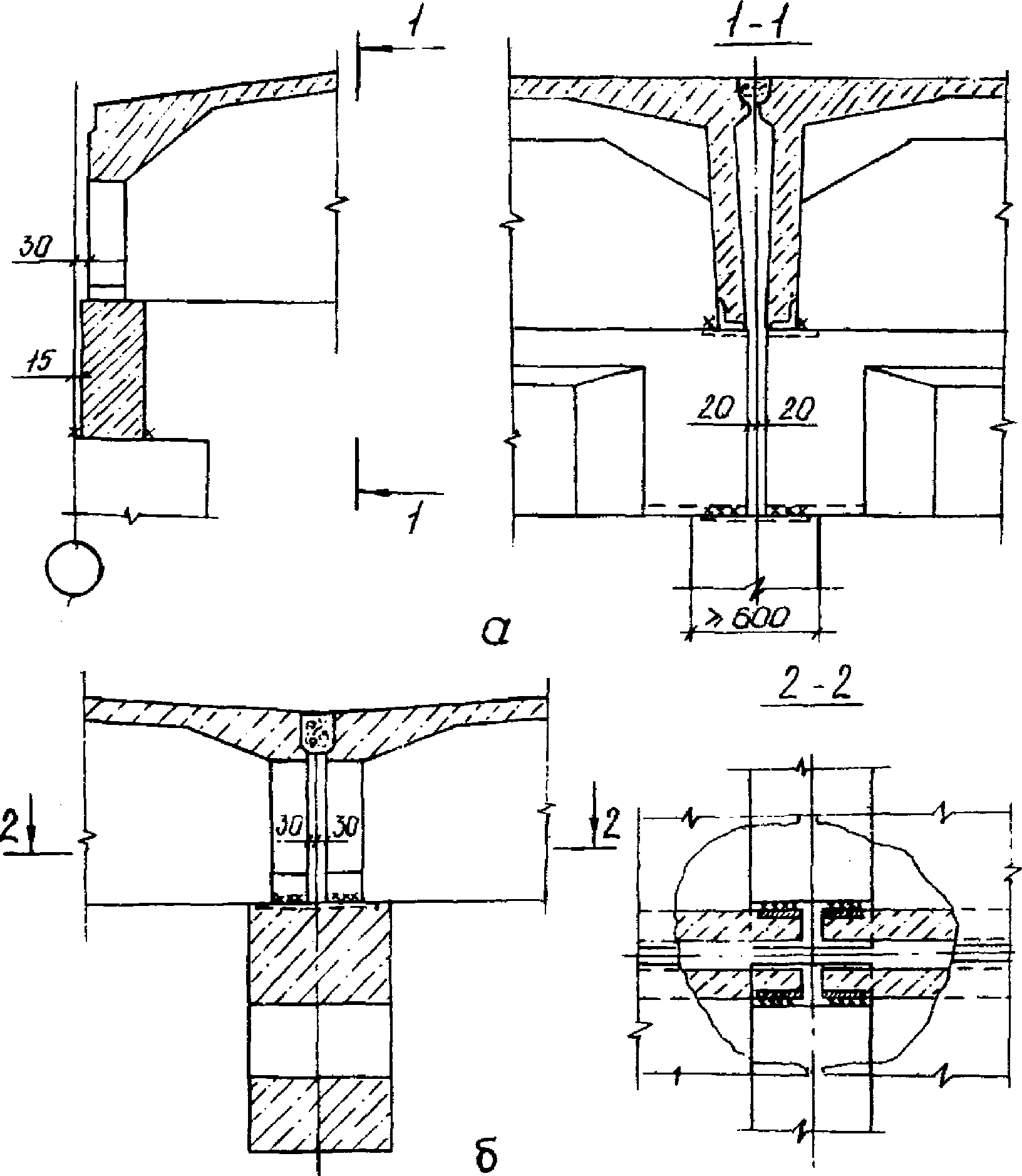
к продольным конструкциям
а - к балкам крайнего ряда колонн; б - к подстропильным
фермам или балкам среднего ряда колонн
При шаге колонн 12 м применяют предварительно напряженные подстропильные фермы пролетом 12 м с горизонтальным верхним поясом и с раздельным армированием нижнего пояса (см. рис. 11, б). Сечения верхнего и нижнего поясов 500 x 350 мм, стойки - 500 x 200 мм. Высота фермы в середине пролета 1910 мм (серия КП-206, вып. II Киевского ПСП и НИИСК). Могут применяться также предварительно напряженные подстропильные балки переменного двутаврового сечения с горизонтальным верхним поясом, разработанные ЦНИИпромзданий.
3.2. Совместная работа покрытия из панелей КСО с каркасом здания (жесткость диска покрытия) обеспечивается креплением панелей изнутри к продольным несущим конструкциям путем сварки закладных деталей во всех углах, а также замоноличиванием швов между панелями.
В комбинированных покрытиях (между панелями КСО устанавливаются гибкие пластины) совместная работа с каркасом здания обеспечивается креплением панелей по всем четырем углам к продольным конструкциям и креплением гибких пластин к панелям в трех местах с каждой стороны путем сварки закладных деталей. Между собой гибкие пластины крепятся также в трех местах (см. рис. 8 и 9).
3.3. Балки крановых путей подвесного транспорта рекомендуется проектировать типовыми, подвешиваемыми к узлам нижнего пояса и опорным узлам диафрагм (рис. 12). Для трехопорных подвесных кранов при расстоянии между средними стойками диафрагм, равном 2,6 м, предусматривают распределительные балки.
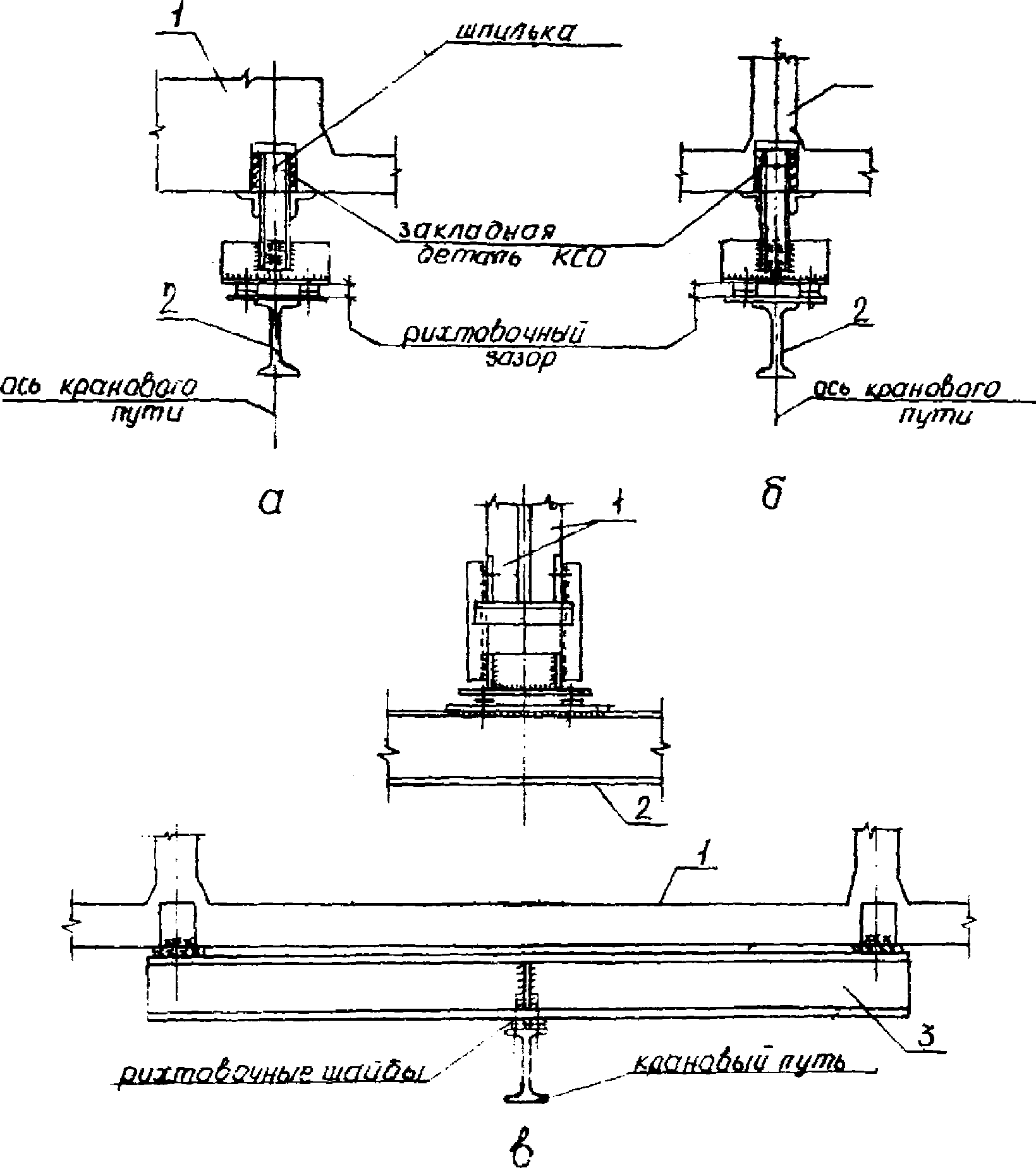
к нижним поясам ферм-диафрагм
1 - нижний пояс панели КСО; 2 - крановый путь;
3 - распределительная балка
3.4. Каркас блочного светоаэрационного фонаря шириной 6 м с опиранием стоек через 3 м с одним ярусом переплетов для покрытий из панелей-оболочек типа КСО рекомендуется выполнять по рабочей документации БВ НИИСК БВ-122-80. Стойки каркаса привариваются к закладным деталям панелей, расположенным у углов фонарных проемов.
3.5. Крепление стакана типового зенитного фонаря серии 1.464-14 к железобетонной панели КСО производится посредством приварки к закладным деталям, расположенным у углов проема полки.
В комбинированных покрытиях проемы для зенитных фонарей устраиваются в панелях КСО, а гибкие пластины проектируются глухими, без проемов. При светоаэрационных фонарях покрытие монтируется из панелей-оболочек с проемом 2 x 5,6 м в середине пролета, гибкую пластину в коньковой части не устанавливают, образуя проем 3 x 6 м.
3.6. Стыки между панелями вдоль верхнего пояса диафрагм рекомендуется замоноличивать бетоном класса B15 на мелком гравии или крупном песке. Стыки гибких пластин с панелями-оболочками КСО допускается не замоноличивать.
3.7. На участках комбинированных покрытий со снеговыми нагрузками от перепадов высот зданий и нагрузками от подвесного транспорта рекомендуется устраивать рядовое расположение панелей.
3.8. Железобетонные стаканы для дефлекторов, зонтов и крышных вентиляторов крепятся к панелям-оболочкам КСО посредством сварки закладных деталей.
РАСЧЕТ ПО НЕСУЩЕЙ СПОСОБНОСТИ
4.1. Расчет панелей-оболочек КСО по несущей способности целесообразно производить по методу предельного равновесия, получившему надежное обоснование при проведении испытаний на натурных образцах конструкций [22].
4.2. При расчете прочности пространственная конструкция панели-оболочки разделяется на такие системы:
безраскосные фермы-диафрагмы со стояками-подвесками, шарнирно прикрепленными к их верхним и нижним поясам;
складчатая полка, защемленная в верхних поясах и торцовых ребрах панели;
торцовые ребра с примыкающими к ним участками полки.
Расчет безраскосной фермы-диафрагмы
4.3. Геометрическую схему фермы-диафрагмы следует образовывать осевыми линиями, проведенными по центрам тяжести бетонных сечений ее конструктивных элементов (верхнего и нижнего поясов, стоек), и жесткими дисками опорных узлов (рис. 13, а).
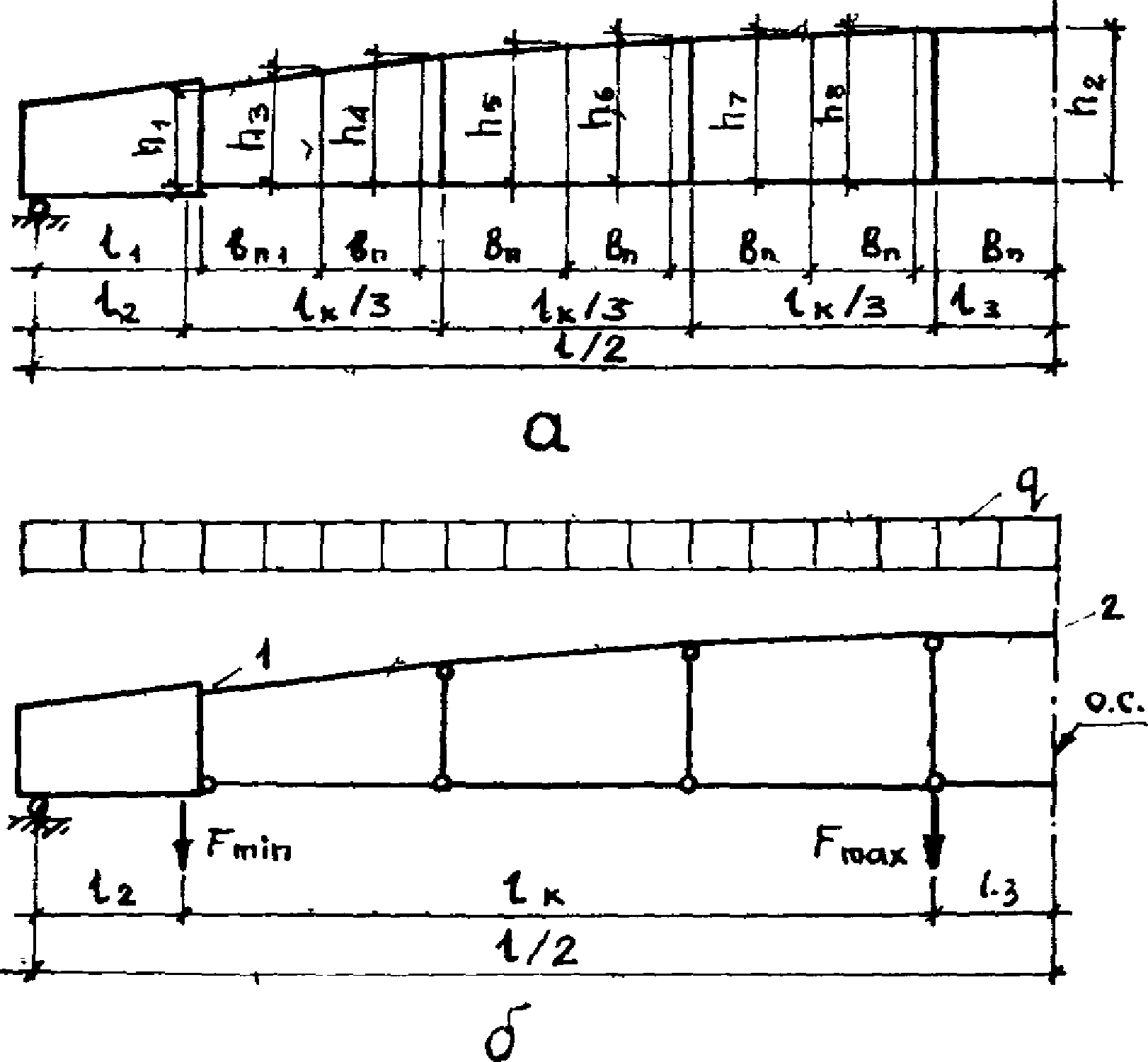
а - геометрическая схема; б - расчетная схема
4.4. Расчетную схему фермы-диафрагмы рекомендуется представлять в виде арки с жесткими дисками у опор с шарнирно прикрепленной затяжкой и стойками (с одиночным шарниром по верху и двойным по низу). Система один раз статически неопределима (см. рис. 13, б). Такая расчетная схема соответствует работе фермы-диафрагмы в стадии предельного равновесия.
4.5. Если в расчетной схеме фермы-диафрагмы (один раз статически неопределимой системе) за неизвестное X1 принять усилие в затяжке, то изгибающие моменты, нормальные и поперечные силы в верхнем поясе фермы-диафрагмы определяются из уравнений:
где  - изгибающий момент в i-ом сечении основной системы от внешней нагрузки;
- изгибающий момент в i-ом сечении основной системы от внешней нагрузки;
Qi0 - поперечная сила (балочная) в i-ом сечении основной системы от внешней нагрузки;
4.6. В верхнем поясе арочной диафрагмы при действии равномерно распределенной нагрузки и сосредоточенных сил от подвесного транспорта следует рассматривать два расчетных сечения - в середине пролета, где по эпюре изгибающих моментов имеет место максимальный положительный момент и у опорного узла, где имеется максимальный отрицательный момент. Если эти изгибающие моменты обозначить соответственно через M2 и M1, а их соотношение через
 (2)
(2)то усилие X1 - определится по формуле
где  ,
,  - пролетный и опорный изгибающие моменты в основной системе от усилия X1 = 1;
- пролетный и опорный изгибающие моменты в основной системе от усилия X1 = 1;
M2p, M1p - то же, от внешней нагрузки;
Из двух рассматриваемых сечений более опасно опорное, так как оно имеет небольшую сжатую зону бетона по низу, в связи с чем в этом сечении обычно ставится дополнительная сжатая арматура.
В первом приближении принимается  . Если в результате подбора арматуры в расчетных сечениях окажется, что в одном из них невозможно расположить арматуру по конструктивным соображениям, то, изменяя коэффициент
. Если в результате подбора арматуры в расчетных сечениях окажется, что в одном из них невозможно расположить арматуру по конструктивным соображениям, то, изменяя коэффициент  , можно перераспределить изгибающие моменты так, чтобы уменьшить значение момента в одном сечении и увеличить во втором. Так, например, если нужно уменьшить количество арматуры в сечении 1, а увеличить в сечении 2, то коэффициенту
, можно перераспределить изгибающие моменты так, чтобы уменьшить значение момента в одном сечении и увеличить во втором. Так, например, если нужно уменьшить количество арматуры в сечении 1, а увеличить в сечении 2, то коэффициенту  придают значение больше единицы (1,1 или 1,2 и т.д.).
придают значение больше единицы (1,1 или 1,2 и т.д.).
4.7. В работе опорного момента кроме растянутой арматуры собственно верхнего пояса надо учитывать арматуру, расположенную в полке.
4.8. Значение ширины сжатой полки, вводимое в расчет при работе положительного пролетного момента, принимается равным половине ширины полки в глухих панелях и расстоянию до проема в панелях с зенитными или светоаэрационным фонарями.
4.9. Задавшись величиной  и определив по формуле (3) усилие в затяжке X1 по формулам (1) находят изгибающие моменты, нормальные и поперечные силы в расчетных сечениях верхнего пояса ферм-диафрагм.
и определив по формуле (3) усилие в затяжке X1 по формулам (1) находят изгибающие моменты, нормальные и поперечные силы в расчетных сечениях верхнего пояса ферм-диафрагм.
Влияние длительности действия нагрузок на прочность бетона рекомендуется оценивать условием
где FI - усилия от нагрузок постоянных, длительных и кратковременных, кроме непродолжительного действия (крановых, возникающих при транспортировании, возведении и т.п.);
FII - усилия от всех нагрузок, включая нагрузки непродолжительного действия.
Принимаемые в этом случае расчетные сопротивления бетона сжатию и растяжению RB и RBt назначаются по [1, табл. 15].
4.10. Площадь сечения растянутой арматуры в расчетном пролетном сечении 2 фермы-диафрагмы рекомендуется определять из уравнения
Высота сжатой зоны бетона этого сечения (по полке) находится по формуле
где h01, h02, h03 - расстояния от центров тяжести арматур;
S1, S2, S3 - до верха полки;
S1 - арматура, расположенная по низу сечения верхнего пояса;
S2 - по верху сечения, определяемая из условия транспортирования панели (см. п. 4.20);
S3 - арматура полки, определяемая согласно п. 4.16;
M2, N2 - усилия в пролетном сечении верхнего пояса фермы-диафрагмы;
Напряжения в стержнях арматуры рекомендуется определять по формуле
где
см. [1, формула (67)].
Задавшись высотой сжатой зоны  , по формуле (7) вычисляют напряжения в арматурах As1, As2, As3. Подставив напряжения
, по формуле (7) вычисляют напряжения в арматурах As1, As2, As3. Подставив напряжения  и
и  в формулу (6), находят высоту сжатой зоны x. Величина сжатой зоны считается вычисленной при
в формулу (6), находят высоту сжатой зоны x. Величина сжатой зоны считается вычисленной при  .
.
4.11. Площади сечений арматуры As2 и As3 в расчетном опорном сечении 1 фермы-диафрагмы (полка - в растянутой зоне сечения) рекомендуется определять из выражений:
где As1 - площадь сечения арматуры, расположенной в полке;
As2, As3 - площади сечений арматуры, расположенные в верхней и нижней зонах сечения верхнего пояса;
h01, h02, h03 - расстояния от центров тяжести арматур S1, S2, S3 до низа сечения;
AB - площадь сечения сжатой зоны бетона;
SB - статический момент сечения сжатой зоны бетона относительно оси, расположенной на расстоянии  от низа сечения верхнего пояса.
от низа сечения верхнего пояса.
Задавшись высотой сжатой зоны  , вычисляют значения AB и SB, напряжения в арматуре - по формуле (7).
, вычисляют значения AB и SB, напряжения в арматуре - по формуле (7).
 , вычисляют значения AB и SB, напряжения в арматуре - по формуле (7).
, вычисляют значения AB и SB, напряжения в арматуре - по формуле (7).4.12. При расчете нижнего пояса арочной диафрагмы по прочности на растяжение следует учитывать коэффициент  , определяемый по [1, п. 3.43].
, определяемый по [1, п. 3.43].
4.13. Усилия в стойках арочных диафрагм, шарнирно прикрепленных к верхнему поясу, при отсутствии подвесных кранов близки к нулю. При наличии подвесного транспорта усилия растяжения в стойках, к которым подвешен крановый путь, определяют с помощью линии влияния опорных реакций в точках подвесок при наиневыгоднейшем расположении кранов.
Расчет стоек арочных диафрагм на действие сосредоточенных сил от подвесного транспорта производится по предельным состояниям как первой, так и второй группы.
Армируются стойки пространственными каркасами, включающими не менее четырех продольных стержней диаметром 12 мм из арматуры класса А-III.
4.14. Расчет опорных узлов панелей-оболочек КСО с наклонными сжатыми гранями, а также промежуточных панелей верхнего пояса арочных диафрагм на действие поперечной силы производится согласно [1, пп. 3.31, 3.32 и 3.33].
Расчет складчатой полки
4.15. Экспериментальными исследованиями установлены три характерных области напряженного состояния полки по ее длине при нагружении: две области по 0,25 у опорных узлов и третья область длиной, равной 0,5l в средней части панели. Полка у опорных узлов в стадии, предшествующей ее разрушению, испытывает, кроме изгиба, усилия растяжения от отрицательных моментов в арочных диафрагмах, а в средней части панели - сжатие от положительных изгибающих моментов.
4.16. Расчет областей полки у опорных узлов по двум ее взаимно перпендикулярным направлениям при регулярной сетке армирования может производиться по формуле
где p - равномерно распределенная расчетная нагрузка на м2 полки.
Расчет полки, расположенной в средней части панели, допускается не производить. При этом, в поперечном направления полка армируется так же, как и полка у опорных узлов, а в продольном принимается шаг стержней арматуры, равный 200 мм.
4.17. Утолщенные до 100 мм участки полки у зенитных фонарей рассчитывают по балочной шарнирной схеме с пролетом, равным расстоянию между верхними поясами арочных диафрагм в свету.
Утолщения у прямоугольных проемов для зенитных и светоаэрационных фонарей, а также круглые проемы, подкрышные вентиляторы и воздуховоды окаймляются конструктивной арматурой (1 стержень диаметром 12 мм класса А-III).
Расчет торцового ребра
4.18. Торцовое ребро с пролетом, равным расстоянию между торцовыми вутами, защемлено в конструкциях опорных узлов. Расчет торцового ребра производится на равномерно распределенную нагрузку, приложенную непосредственно на ребро, а также на нагрузку треугольного очертания, передающуюся с полки панели-оболочки.
Пролетный и опорный изгибающие моменты в торцовом ребре определяются из выражения (см. рис. 18, в)
 (11)
(11)где P1 - равномерно распределенная погонная нагрузка собственно на торцовое ребро;
P2 - максимальная ордината треугольной нагрузки на торцовое ребро;
lр - пролет торцового ребра.
Расчет панелей-оболочек на нагрузки,
возникающие при перевозке автотранспортом
4.19. Расчет панели-оболочки КСО на вертикальные нагрузки, возникающие при транспортировании, можно не производить так как эти нагрузки меньше статических.
4.20. Расчет панелей-оболочек на горизонтальные нагрузки, возникающие при транспортировании, производится как для балки на двух опорах на изгибающий момент в пролете
где g - масса панели-оболочки КСО;
l - длина панели.
По изгибающему моменту определяется расчетное значение площади растянутой арматуры, располагаемой в верхней зоне верхнего пояса ферм-диафрагм.
4.21. Расчет стоек ферм-диафрагм на горизонтальные нагрузки, возникающие при транспортировании, действующие в поперечном направлении панели, производят по изгибающему моменту
где gс, gп - масса погонного метра стойки и нижнего пояса арочной диафрагмы;
hс - высота стойки (расстояние от низа нижнего до низа верхнего пояса);
hп - высота нижнего пояса фермы-диафрагмы;
lп - часть длины нижнего пояса, приходящейся на стойку.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: г) на рисунке 2 отсутствует. |
4.22. Расчет поперечника торцовой рамы (см. рис. 2, в, г) с расчетной высотой ht (торцовое ребро шириной Bр и две стойки с вутами - участки опорных узлов шириной  ) производится на изгибающий момент в стойке
) производится на изгибающий момент в стойке
 ) производится на изгибающий момент в стойке
) производится на изгибающий момент в стойке (14)
(14)и изгибающий момент в торцовом ребре
 (15)
(15)где h1 - расстояние на стойке от низа опорного узла до сечения у торцового вута;
h2 - расчетная высота торцового вута (h1 + h2 = ht);
h3 - расстояние от торцового ребра до горизонтального центра тяжести панели (для панели КСО пролетом 24 м при принятых на рис. 5 геометрических размерах h3 = 0,99 м, а для панели пролетом 18 м (рис. 4) - 0,69 м;
lр - расстояние между осями опорных узлов;
l1 - расстояние от оси опорного узла до конца торцового вута на торцовом ребре.
Примечание. Пример расчета несущей способности панели-оболочки КСО 3 x 24 м комбинированного покрытия производственного здания приведен в приложении 1.
Расчет поперечников зданий с покрытиями из панелей КСО
4.23. Приведенные в настоящих Рекомендациях методы расчета элементов дисков покрытий из панелей-оболочек КСО и комбинированных покрытий с панелями КСО и гибкими предварительно напряженными пластинами - пологими цилиндрическими оболочками ориентированы на расчет конструкций покрытия без учета их работы в пространственной системе здания в целом.
4.24. При рассмотрении каркаса одноэтажного промышленного здания как пространственной системы, включающей элементы диска покрытия, продольные конструкции, колонны, а в некоторых случаях и стеновые панели, расчет панелей-оболочек КСО и гибких преднапряженных пластин может выполняться с использованием методов, изложенных в Рекомендациях. Однако при этом должны быть дополнительно учтены усилия, возникающие в конструкциях диска покрытия при действии на пространственный каркас здания горизонтальных и крановых нагрузок. Наряду с указанной особенностью расчета для такого случая в сборных элементах диска покрытия должны быть предусмотрены специальные конструктивные мероприятия по соединению сборных элементов покрытия между собой и другими конструкциями каркаса, обеспечивающие их совместную работу в соответствии с расчетом.
РАСЧЕТ ПО ДЕФОРМАЦИЯМ
4.25. Расчет панелей-оболочек КСО и покрытий из них по предельным состояниям второй группы согласно действующим нормам [1] допускается производить по усилиям, полученным в предположении линейно-упругого деформирования рассматриваемых сложных пластинчато-стержневых систем при раскрытии их статической неопределимости. При этом могут быть использованы различные численные методы и имеющиеся стандартные программы для ЭВМ.
Рекомендации к построению расчетных схем панелей-оболочек КСО методом конечных элементов с использованием стандартных программ приведены в пп. 4.44 - 4.48.
4.26. Практический расчет панелей-оболочек КСО по предельным состояниям второй группы с учетом неупругих деформаций и трещин в железобетоне, так же как и расчет по несущей способности (см. п. 4.2) можно производить с применением метода декомпозиции (см. п. 4.27 - 4.43). Пространственная пластинчато-стержневая конструкция расчленяется на более простые системы: безраскосные фермы-диафрагмы, складчатую полку, защемленную в верхних поясах и торцовые ребра с примыкающими к ним участкам полки. При этом соответствующими коэффициентами рекомендуется учитывать влияние совместной пространственной работы элементов конструкций КСО, используя данные расчета всей пространственной системы методом конечных элементов. Для определения указанных коэффициентов, применительно к конструкциям КСО с геометрическими параметрами, приведенными на рис. 3 и 4, могут быть использованы рекомендации пп. 4.29, 4.33, 4.36, 4.37, 4.39, 4.41.
Расчет безраскосной фермы-диафрагмы
4.27. Геометрическую схему фермы-диафрагмы следует образовывать осевыми линиями, соединяющими центры тяжести поперечных сечений ее конструктивных элементов (верхнего и нижнего поясов, стоек), и жесткими дисками опорных узлов (рис. 14).
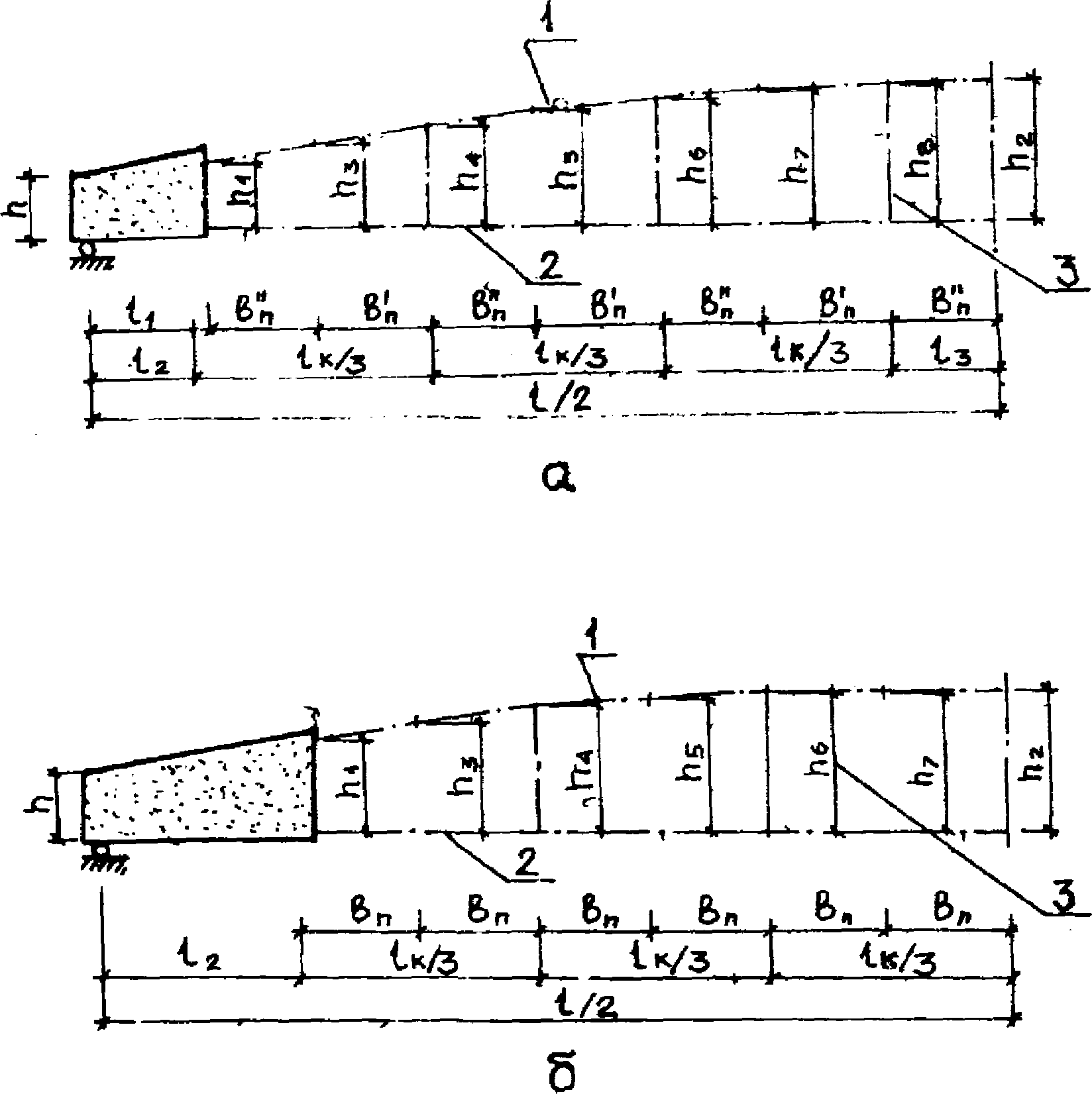
а, б - геометрические схемы для различных типов
панелей-оболочек КСО 3 x 24 м; 1 - линия, соединяющая
центры тяжести сечений верхнего пояса; 2 и 3 - то же,
сечений нижнего пояса и стоек
Геометрические схемы разработанных конструктивных решений панелей КСО (рабочие чертежи серии КП-206 Киевского ПСП, НИИСК и рабочие чертежи института "Центрогипроруда", БТИСМ и НИИСК) отличаются расположением стоек и длиной жестких дисков опорных узлов (см. рис. 14, а, б).
4.28. Расчетную схему фермы-диафрагмы КСО при расчете по второй группе предельных состояний рекомендуется представлять в виде консольной пластинчато-стержневой системы с жесткими рамными узлами соединения стержней между собой и с жесткими дисками (пластинами) опорных узлов (рис. 15, а). Степень статической неопределимости диафрагм зависит от количества стоек, принятого в конструктивном решении (см. рис. 14).
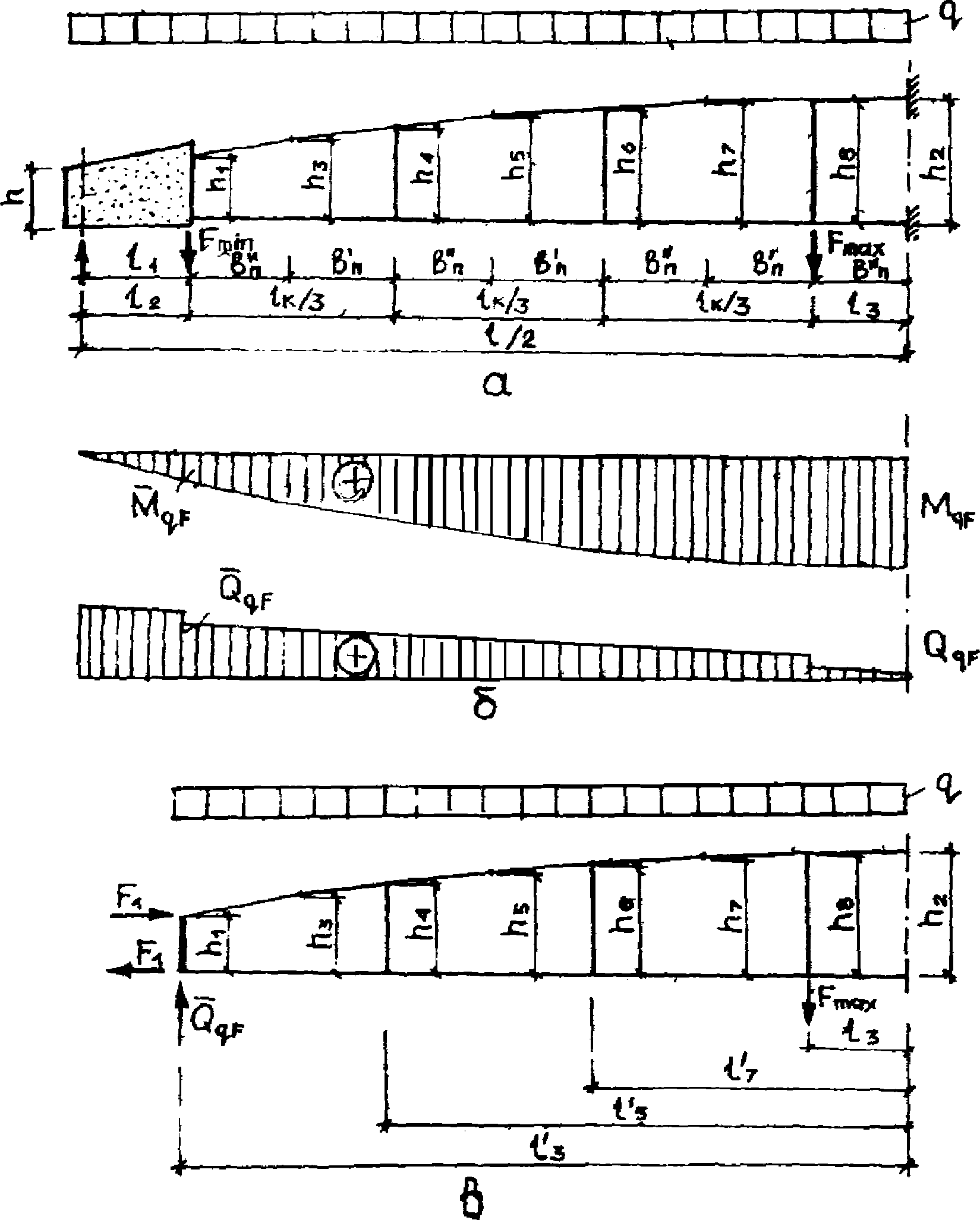
по предельным состояниям второй группы
а - расчетная схема с использованием пластинчато-стержневой
аппроксимации; б - эпюры балочных усилий; в - расчетная
схема с применением стержневой аппроксимации
4.29. С целью сокращения объема вычислений при расчете фермы-диафрагмы (что особенно существенно при нелинейном расчете) возможны также следующие упрощения в расчетной схеме.
Переломы контура верхнего пояса, смещенные в принятом конструктивном решении панели-оболочки по отношению к осям стоек (см. рис. 3 и 4), совмещаются с осями стоек.
Опорный сплошной участок диафрагмы моделируется в виде жесткого вертикально расположенного стержня-вставки, ось которого проходит на расстоянии l2 от опоры (см. рис. 15, а). При этом поперечная сила  и изгибающий момент
и изгибающий момент  , действующие в сечении, расположенном на расстоянии l2 от опоры, рассматриваются как внешние нагрузки. Поперечная сила
, действующие в сечении, расположенном на расстоянии l2 от опоры, рассматриваются как внешние нагрузки. Поперечная сила  считается приложенной вдоль оси вертикально расположенного стержня-вставки, а действие изгибающего момента заменяется парой сил F1, приложенных в центре тяжести верхнего и нижнего поясов рамы (см. рис. 15, в). Значения этих сил вычисляют по формуле
считается приложенной вдоль оси вертикально расположенного стержня-вставки, а действие изгибающего момента заменяется парой сил F1, приложенных в центре тяжести верхнего и нижнего поясов рамы (см. рис. 15, в). Значения этих сил вычисляют по формуле
4.30. Расчет диафрагмы панели КСО с учетом неупругих деформаций и трещин в железобетоне рекомендуется производить методом последовательных нагружений [9]. Раскрытие статической неопределимости и определение неизвестных усилий для плоской рамно-стержневой системы на каждой итерации может выполняться любым из известных методов строительной механики. Рекомендуется применение специально разработанной программы для расчета панелей КСО (см. п. 4.43). Возможно и использование имеющихся стандартных программ для расчета стержневых систем (например: SSP, SYSTERG и др.).
4.31. Жесткостные характеристики приведенных сечений элементов диафрагмы B11, B12, B22 (согласно обозначений действующих норм [1]) определяют в зависимости от уровня нагружения конструкции и наличия трещин. При нелинейном расчете системы методом последовательных нагружений на первых этапах нагружения изгибную жесткость сечений элементов диафрагмы B11 и жесткость на растяжение-сжатие B22 определяют как для сплошного приведенного бетонного сечения в стадии 1 напряженно-деформированного состояния с учетом коэффициентов  и
и 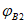 [1].
[1].
Жесткостные характеристики диафрагмы после появления трещин B11, B22, B12 и B21 определяют по формулам [1] (п. 4.35), используя при этом значения усилий в элементах системы, полученные на предыдущем этапе нагружения.
Для определения жесткостных характеристик верхних поясов диафрагм значение ширины сжатой полки сечения, вводимое в расчет, принимается таким же, как и при расчете диафрагмы КСО по несущей способности (см. п. 4.8).
Поскольку в большинстве имеющихся на сегодня стандартных программ для расчета стержневых систем в качестве исходных данных используется изгибная жесткость B11 и жесткость на растяжение-сжатие B22, то при применении этих программ для каждого стержневого элемента диафрагмы на каждой итерации следует определять такое положение оси Y в расчетном сечении, при котором жесткости B12 и B21 обращаются в нуль (рис. 16). При этом допускается на каждом участке стержня в пределах которого изгибающий момент не меняет знак, положение оси Y вычислять для наиболее и наименее напряженного сечений, принимая ее для остальных сечений по линейной интерполяции.
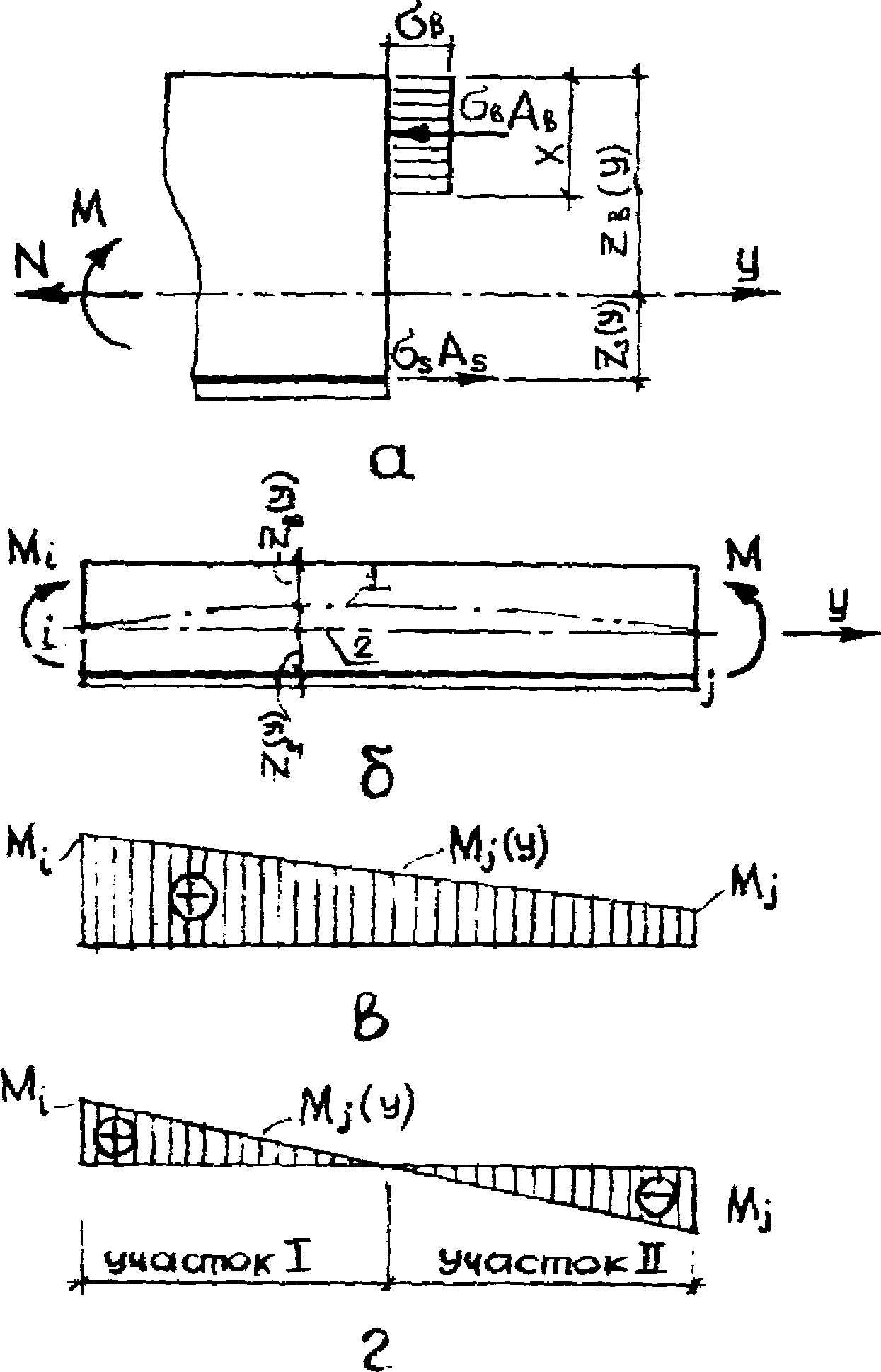
с трещинами при расчете по деформациям
а - схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси элемента; б - положение расчетной оси
по длине элемента; в, г - эпюры изгибающих
моментов; 1 - определено по формулам [1];
2 - принимаемое для расчета диафрагмы
4.32. Максимальный прогиб диафрагмы Ymax (рис. 17) можно вычислять как сумму двух перемещений: первое перемещение определяется перемножением окончательной эпюры моментов в статически неопределимой системе MqF, определенной согласно рекомендациям п. 4.30, на единичную эпюру  , а второе - перемножением грузовых эпюр моментов MQ и Mq на единичную эпюру
, а второе - перемножением грузовых эпюр моментов MQ и Mq на единичную эпюру  , построенных для опорного сплошного участка диафрагмы как для консольно защемленной балки
, построенных для опорного сплошного участка диафрагмы как для консольно защемленной балки
где  - эквивалентная изгибная жесткость j-ого стержня нижнего пояса диафрагмы или опорного сплошного участка, учитывающая неравномерность распределения трещин или переменную геометрию сечений по длине этого стержня.
- эквивалентная изгибная жесткость j-ого стержня нижнего пояса диафрагмы или опорного сплошного участка, учитывающая неравномерность распределения трещин или переменную геометрию сечений по длине этого стержня.
Примечание. Вычисление первого перемещения (первого слагаемого в уравнении для определения Ymax) обычно не требуется, так как при применении стандартных программ для расчета стержневых систем как правило предусматривается процедура распечатки перемещений для всех узлов диафрагмы, включая и узел 2 (см. рис. 17).
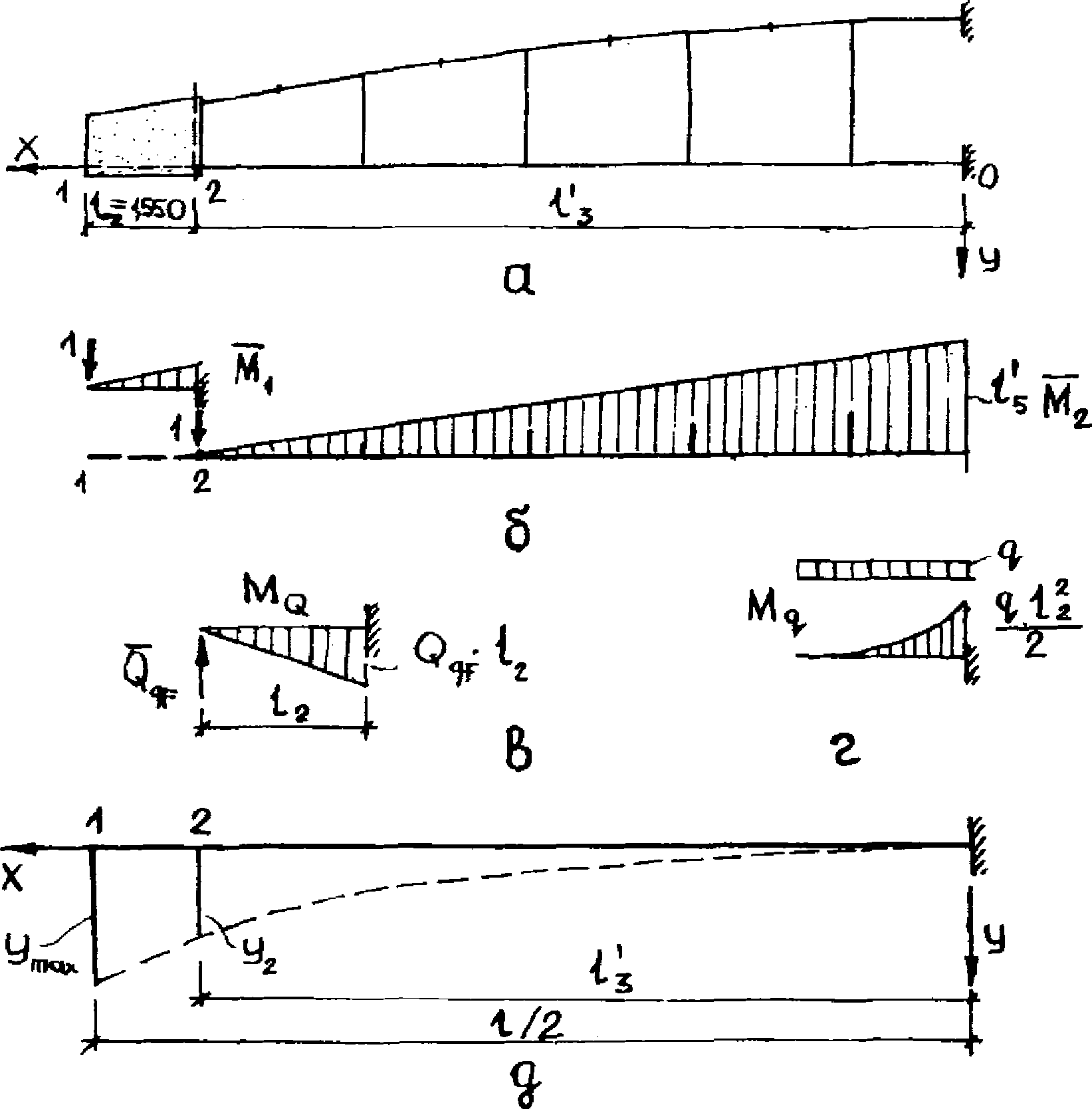
а - геометрическая схема; б, в, г - эпюры моментов
соответственно от единичных сил, нагрузки QqF
и поперечной нагрузки q, приложенной в пределах
опорного сплошного участка диафрагмы; д - схема
прогибов; 1, 2 - номера узлов
4.33. Эквивалентную изгибную жесткость  стержней нижнего пояса и опорного сплошного участка диафрагмы допускается определять в предположении линейного закона изменения изгибающего момента и жесткости Bj в пределах длины j-ого стержня (см. рис. 16, б, в). В этом случае численное значение эквивалентной изгибной жесткости может быть определено по формуле
стержней нижнего пояса и опорного сплошного участка диафрагмы допускается определять в предположении линейного закона изменения изгибающего момента и жесткости Bj в пределах длины j-ого стержня (см. рис. 16, б, в). В этом случае численное значение эквивалентной изгибной жесткости может быть определено по формуле
где  и
и  принимаются по модулю, при этом j = i + 1;
принимаются по модулю, при этом j = i + 1;
 и
и  принимаются по модулю, при этом j = i + 1;
принимаются по модулю, при этом j = i + 1;Mj и Mi - изгибающие моменты в точках j и i соответственно (см. рис. 16, в);
Bj и Bi - жесткости сечений стержня, вычисленные соответственно в начале и в конце стержня.
Если эпюра поперечных изгибающих моментов в пределах длины j-ого стержня двузначна (см. рис. 16, г), то значение эквивалентной жесткости допускается определять как среднее между значениями жесткостей  и
и  , вычисленных по формуле (18) для участков с однозначной эпюрой моментов.
, вычисленных по формуле (18) для участков с однозначной эпюрой моментов.
4.34. Алгоритм итерационного расчета диафрагмы панели-оболочки КСО строится следующим образом.
В качестве начальной (первый шаг) принимают нагрузку, соответствующую упругой работе диафрагмы без трещин (0,4 ... 0,5 от величины нормативной нагрузки), и производят определение неизвестных усилий (раскрытие статической неопределимости) в соответствии с рекомендациями п. 4.30.
Для первой итерации следующего шага нагрузки по вычисленным на первом шаге усилиям M и N на основании зависимостей [1] (п. 4.5) проверяют условия трещинообразования, выявляют элементы с трещинами, и по установленной стадии работы элементов складки, в соответствии с рекомендациями п. 4.31, вычисляют новые значения жесткостей B11 и B22 для каждого из стержней диафрагмы. При этих значениях жесткостей вновь производится статический расчет статически неопределимой диафрагмы на следующей итерации рассматриваемого шага нагрузки. Процесс продолжается до достижения заданной точности. Затем аналогичная процедура выполняется на следующем шаге нагружения системы.
Расчет складчатой полки и торцового ребра
4.35. Расчет полки панели-оболочки КСО по деформациям и трещиностойкости допускается производить на местный изгиб поперечного направления без учета усилий продольного направления.
4.36. Пролетный Mq1 и опорный Mq2 поперечные изгибающие моменты для поперечной полоски единичной ширины (см. рис. 18 а, б) определяют по схеме защемленной в продольных диафрагмах балки по формулам:
где q - равномерно распределенная расчетная нагрузка на м полки при  ;
;
B, B11 - соответственно ширина полки и ширина сечения верхнего пояса диафрагмы (см. рис. 18, а).
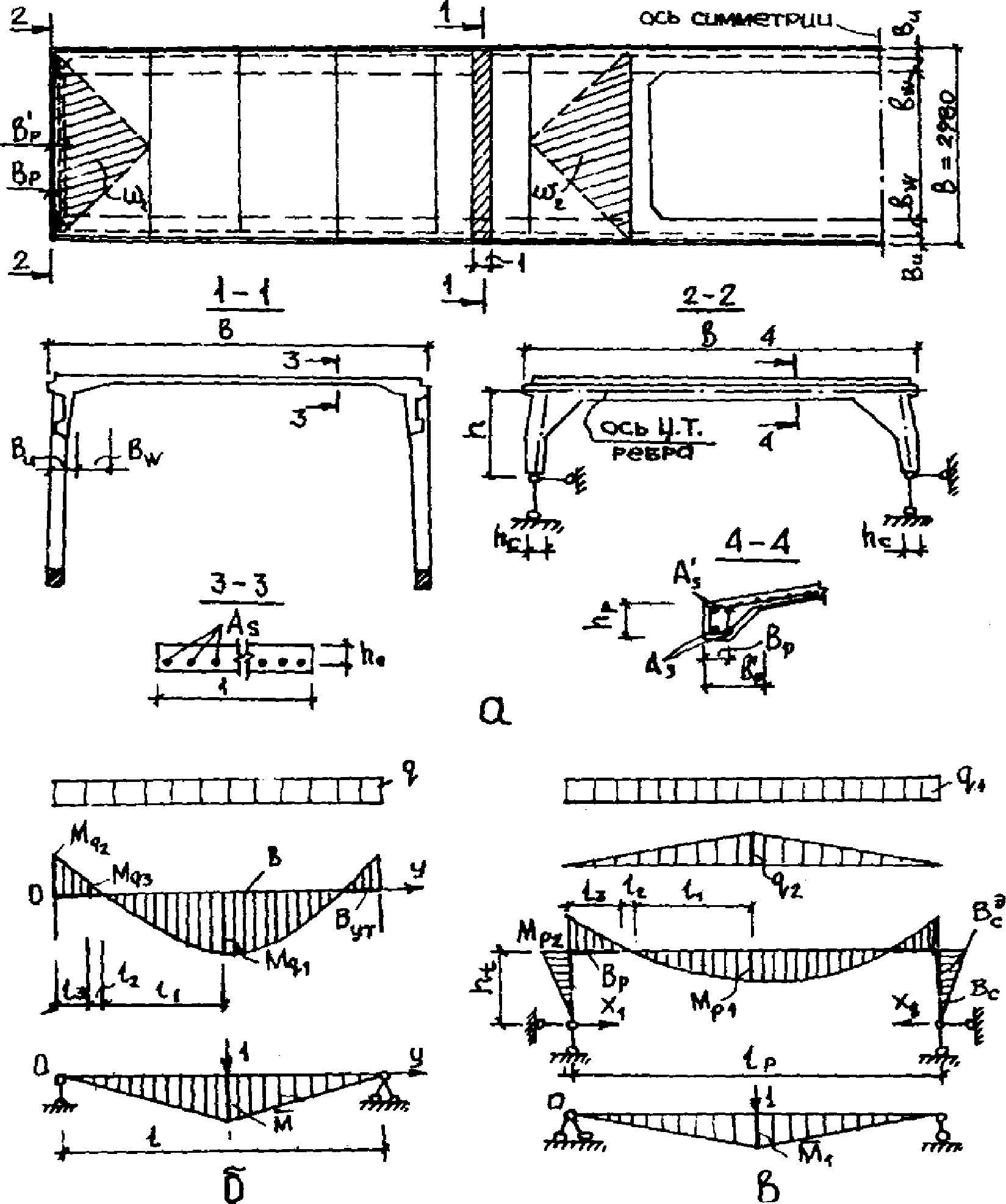
а - план и сечения панели КСО; б - расчетная схема полки;
в - то же, торцового ребра
где Mq - изгибающий момент на j-том участке полки от действия заданной внешней нагрузки q;
B11,j - изгибная жесткость j-ого участка поперечной полоски единичной ширины, определяемая для приведенного сечения (см. рис. 18, а, сеч. 3-3) при расчетной нагрузке  [1, формула (178)].
[1, формула (178)].
Поскольку в местах примыкания к верхним поясам диафрагм полка имеет переменное сечение (Bgm) на длине Bw, то при вычислении прогиба по формуле (21) жесткость этого участка допускается принимать равной значению эквивалентной жесткости, определяемой по формуле (18).
4.38. Количество участков длиной lj, на которые разбивается полка при интегрировании выражения (21) с учетом симметрии эпюр Mq и  , равно трем: первый - длиной l1 (от середины пролета до точки, где Mq изменяет знак), второй - l2 (от указанной точки до точки изменения жесткости полки), третий - l3 (равен ширине вута Bw).
, равно трем: первый - длиной l1 (от середины пролета до точки, где Mq изменяет знак), второй - l2 (от указанной точки до точки изменения жесткости полки), третий - l3 (равен ширине вута Bw).
4.39. Утолщенные до 100 мм участки полки прямоугольных проемов для зенитных и светоаэрационных фонарей, так же как и при определении несущей способности (см. п. 4.17), рассчитывают по схеме однопролетной шарнирно опертой балки. При этом учитывают равномерно распределенную нагрузку, приложенную непосредственно на утолщение, нагрузку, передающуюся от рамы фонаря, а также нагрузку треугольного очертания, передающуюся с примыкающей треугольной грузовой площади w2 (см. рис. 18, а).
4.40. Максимальный прогиб утолщенного участка полки, примыкающего к фонарю, вычисляется по формуле (21), но с тем отличием, что при однозначной эпюре Mq количество участков интегрирования уменьшается до двух: пролетного с жесткостью B11,1 и приопорного с жесткостью  .
.
4.41. Расчет торцового ребра по деформациям производят по расчетной схеме однопролетной рамы с шарнирно закрепленными стойками (см. рис. 18, в) на расчетные нагрузки q = q1 + q2, (см. п. 4.18 настоящих методических рекомендаций) при коэффициенте надежности  .
.
При выборе основной системы по методу сил с введением неизвестного усилия x1 расчетный момент по середине торцового ребра определяется из выражения
где  - изгибающий момент в произвольном сечении j-того стержня основной системы от x1 = 1;
- изгибающий момент в произвольном сечении j-того стержня основной системы от x1 = 1;
Mр - то же, от внесшей нагрузки q;
ht - расчетная высота стойки;
lр - расчетный пролет ребра.
Количество участков интегрирования в пределах ребра определяется аналогично, как и для полки (см. п. 4.38).
Ширина сечения стоек, вводимая в расчет, принимается согласно указаниям п. 4.22.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 4 в СНиП 2.03.01-84 [1] отсутствует. |
4.42. Значения максимальных прогибов для диафрагм, полки и торцового ребра панели-оболочки КСО, вычисленных соответственно по п. 4.32, 4.37 и 4.41 настоящих рекомендаций, не должны превышать максимально допустимых значений, указанных в [1] (табл. 4).
4.43. Для численной реализации методики расчета панелей-оболочек КСО по предельным состояниям первой и второй групп рекомендуется использовать специально разработанную программу К50-88 на языке ФОРТРАН-1У. Программа построена по блочному принципу и включает следующие блоки: "прочность", "статика", "жесткость". С помощью программы можно производить определение несущей способности панели КСО, определять усилия в элементах панели и жесткостные характеристики этих элементов с учетом неупругих деформаций и трещин в железобетоне.
Примечание. Текст программы имеется в вычислительном центре БТИСМ.
Расчет панелей-оболочек КСО методом конечных элементов
с использованием стандартных программ
4.44. Расчет панелей-оболочек КСО по предельным состояниям второй группы может быть выполнен с применением метода конечных элементов и стандартных программ для расчета пространственных дискретно-континуальных систем. Это целесообразно при наличии у проектировщика соответствующих стандартных программ и в предположении упругой работы материала конструкции в пределах эксплуатационной нагрузки.
В настоящее время имеются разработки на основе численных методов, позволяющие выполнить расчет пространственных конструкций с учетом физической и геометрической нелинейности. Однако практическая реализация такого подхода в практике проектирования таких достаточно сложных оболочек как панели КСО на сегодня пока трудновыполнима. Связано это не только со значительными затратами машинного времени на многократное решение больших систем алгебраических уравнений и другими сложностями технического плана при использовании численных методов и ЭВМ, но и с имеющимися неясностями в теоретическом аспекте (критерии трещиностойкости, условия пластичности различных материалов и др.).
4.45. Использование для расчета панелей-оболочек (равно как и пространственных систем покрытий из них) метода конечных элементов требует дискретизации расчетной схемы и представления панели в виде совокупности отдельных конструктивных элементов, соединенных конечным числом шарнирных и жестких узлов. Информация о конструкции представляется в численном виде и должна описывать ее характеристики в расчетных сечениях.
4.46. Для расчета панель-оболочку рекомендуется представлять комбинацией двух вертикально расположенных элементов-диафрагм и соединяющей их верхние пояса складчатой полки. Структура диафрагмы достаточно корректно может быть описана конечными элементами в виде стержня, а опорный сплошной участок диафрагмы - треугольными плоскими конечными элементами (КЭ). Складчатая полка также может быть смоделирована плоскими КЭ, соединенными по узлам верхних поясов с диафрагмами.
4.47. При построении расчетной схемы панели КСО методом конечных элементов могут быть использованы следующие рекомендации.
Размеры элементов (густота расчетной сетки) назначаются в зависимости от предполагаемой величины градиента напряжений и усилий и определяются, с одной стороны, стремлением к наиболее полному описанию реальной конструкции, с другой - существующими возможностями вычислительного комплекса и временем решения задачи.
При расчете рядовой панели на нагрузки, симметричные относительно продольной оси панели, для получения усилий в элементах диафрагм с точностью, достаточной для рабочего проектирования, может быть использована расчетная схема в виде плоской пластинчато-стержневой системы (см. рис. 15, а).
При несимметричных относительно продольной оси нагрузках (например, крановые, полосовые, приложенные вдоль диафрагм и пр.) рекомендуется выполнять расчет панели КСО в целом как пространственно работающей конструкции. За основу может быть принята расчетная схема, приведенная на рис. 19. В зависимости от характера действующих нагрузок, конструктивной схемы покрытия и целей расчета в расчетную схему могут быть включены смежные панели-оболочки и пластины-вставки, или же их влияние следует смоделировать соответствующими граничными условиями по граням панелей КСО.
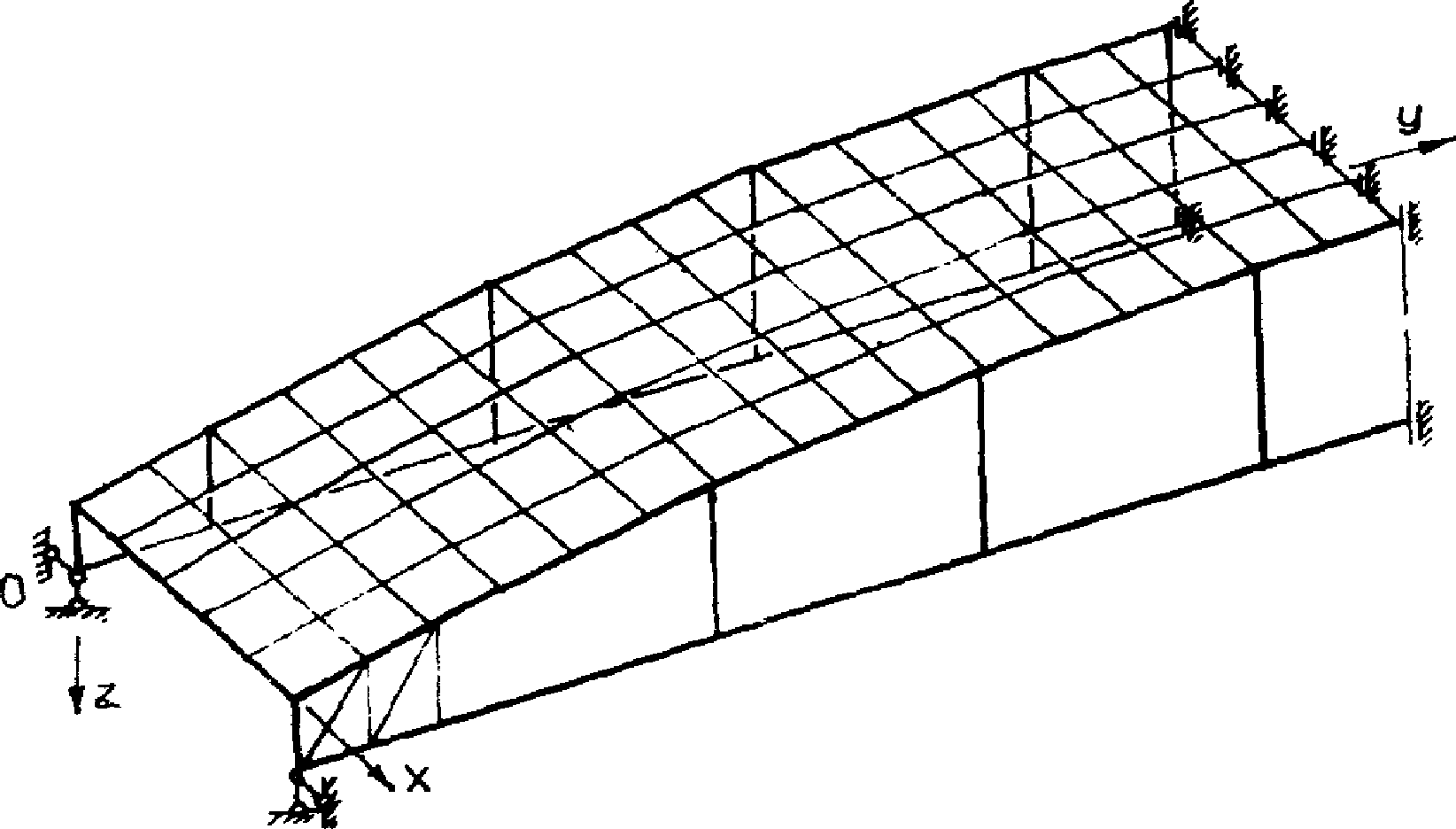
по методу конечных элементов
При нагрузках, несимметричных относительно середины пролета панели-оболочки КСО (например, из-за перепадов высот рассматриваемого и примыкающего пролетов), в расчетную схему панелей КСО следует включать элементы не до оси симметрии посередине пролета (см. рис. 19), а для всей панели, симметрично достраивая вторую половину конструкции.
Следует стремиться к равномерной густоте расчетной сетки при разбивке конструкции на конечные элементы. Нарушение этого условия может вызвать трудности, связанные с ухудшением обусловленности системы уравнений [10]. Равномерная же разбивка существенно облегчает составление исходных данных и их последующую проверку, несмотря на то, что общий объем исходных данных при этом может увеличиться. Наконец, расчетная схема с равномерной густотой сетки достаточно универсальна и может служить основой для расчета панелей-оболочек с отверстиями, проемами, утолщениями, ребрами и другими элементами конструктивной анизотропии. Принятая при этом сетка узлов должна совпадать или быть достаточно близкой к форме и размерам проемов, ребер и утолщений. Учет перечисленных элементов конструктивной анизотропии в этом случае достаточно прост и сводится к исключению (при наличии проемов из расчетной схемы соответствующих КЭ при сохранении всех узлов или постановке (при наличии утолщений и ребер дополнительных стержней, а в некоторых случаях просто к изменению жесткостных характеристик прилегающих к проему элементов. Изменение топологии системы при сохранении принятой геометрической схемы должно сопровождаться наложением связей на узлы, исключенные из расчетной схемы.
Нагрузки, действующие на конструкцию, рекомендуется приводить к узловым. Это вносит известные упрощения при изменении варианта загружения системы.
Учет предварительного напряжения нижнего пояса панели КСО может выполняться двумя способами. Первый способ - в торцы панели вдоль оси нижнего пояса задается сосредоточенная сила, равная величине предварительного напряжения (с учетом потерь), прикладываемая как внешняя нагрузка. Второй способ - нижние пояса панели КСО задаются дважды стержневыми элементами по одним и тем же узлам, причем характеристики одного соответствуют бетонному сечению, а другого - арматурному стержню. Предварительное напряжение задается отрицательным температурным воздействием на стержни, моделирующие арматуру. Как в первом, так и во втором способе наложенные на торцы панелей КСО связи не должны препятствовать перемещению их вдоль осей нижних поясов.
4.48. На стадии предварительных оценочных расчетов для назначения и вычисления приведенных жесткостей конечных элементов могут быть использованы линии влияния усилий в основных расчетных сечениях диафрагм панелей-оболочек КСО 3 x 18 и 3 x 24 м, построенные применительно к разработанным опалубочным формам и размерам сечений конструкции серии КП-206 (рис. 20 и 21).
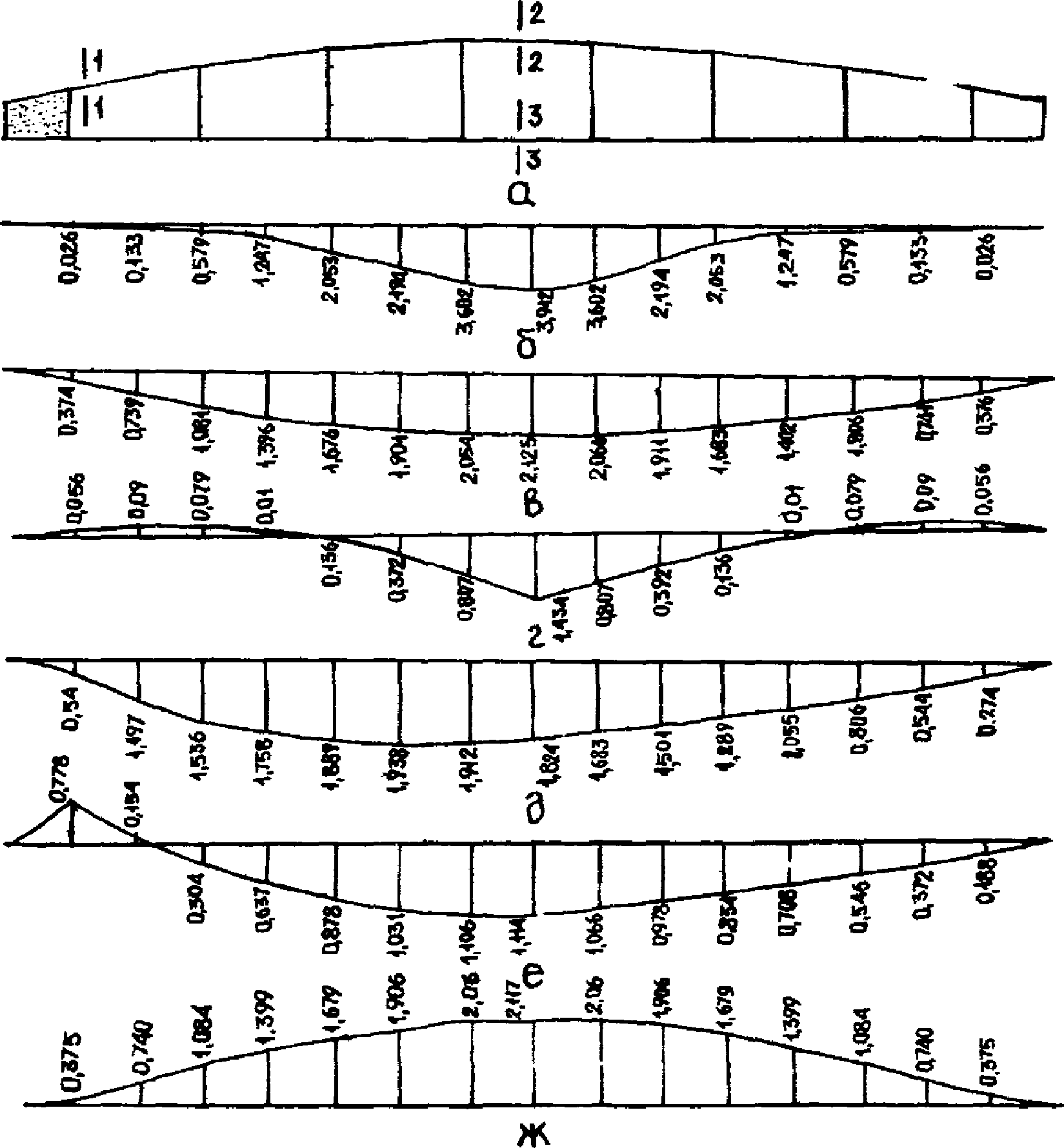
панели-оболочки КСО 3 x 24 м
а - геометрическая схема; б - линия влияния прогиба
в сечении 3-3, см 10-2/кН; в - линия влияния продольной
силы в сечении 2-2; г - то же, в сечении 1-1; д - линия
влияния изгибающего момента в сечении 2-2; е - то же,
в сечении 1-1; ж - линия влияния продольной силы
в сечении 3-3
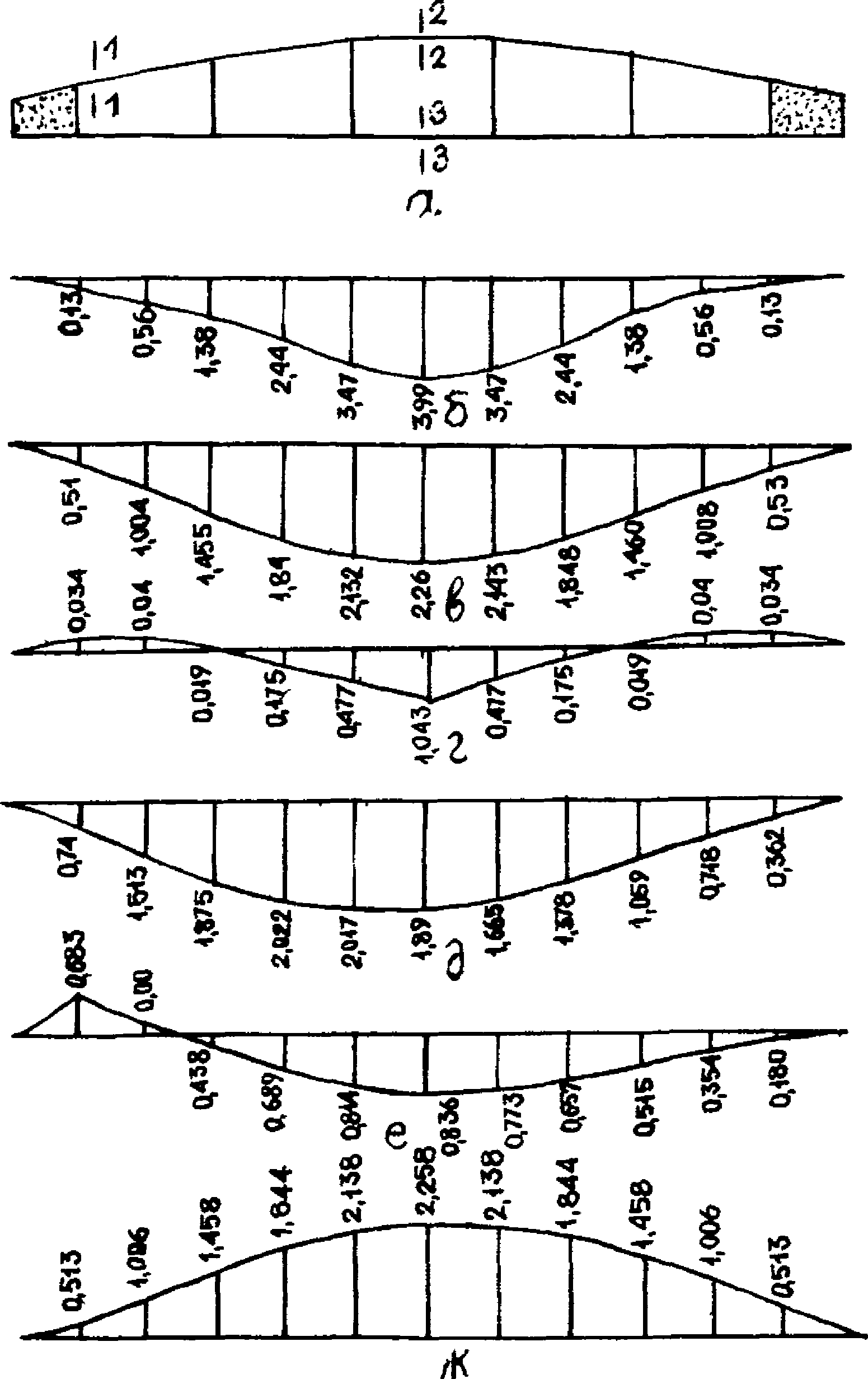
панели-оболочки КСО 3 x 18 м
а - геометрическая схема; б - линия влияния прогиба
в сечении 3-3, см 10-2/кН; в - линия влияния продольной
силы в сечении 2-2; г - то же, в сечении 1-1; д - линия
влияния изгибающего момента в сечении 2-2; е - то же,
в сечении 1-1; ж - линия влияния продольной силы
в сечении 3-3
РАСЧЕТ ПО ОБРАЗОВАНИЮ И РАСКРЫТИЮ ТРЕЩИН
4.49. В элементах панели-оболочки КСО при действии распределенных и сосредоточенных нагрузок, приложенных к диафрагмам, и равномерно распределенной нагрузки, приложенной к полке, следует выполнять проверку на образование следующих типов трещин (рис. 22):
продольных (1, 2) на нижней и верхней поверхности складчатой полки от действия поперечных изгибающих моментов;
нормальных (3, 4) во внецентренно растянутых элементах нижнего пояса и стоек;
нормальных (5) в растянутой зоне торцового ребра от действия изгибающего момента;
наклонных к продольной оси (6) в приопорных сплошных участках диафрагм КСО от действия главных растягивающих напряжений.
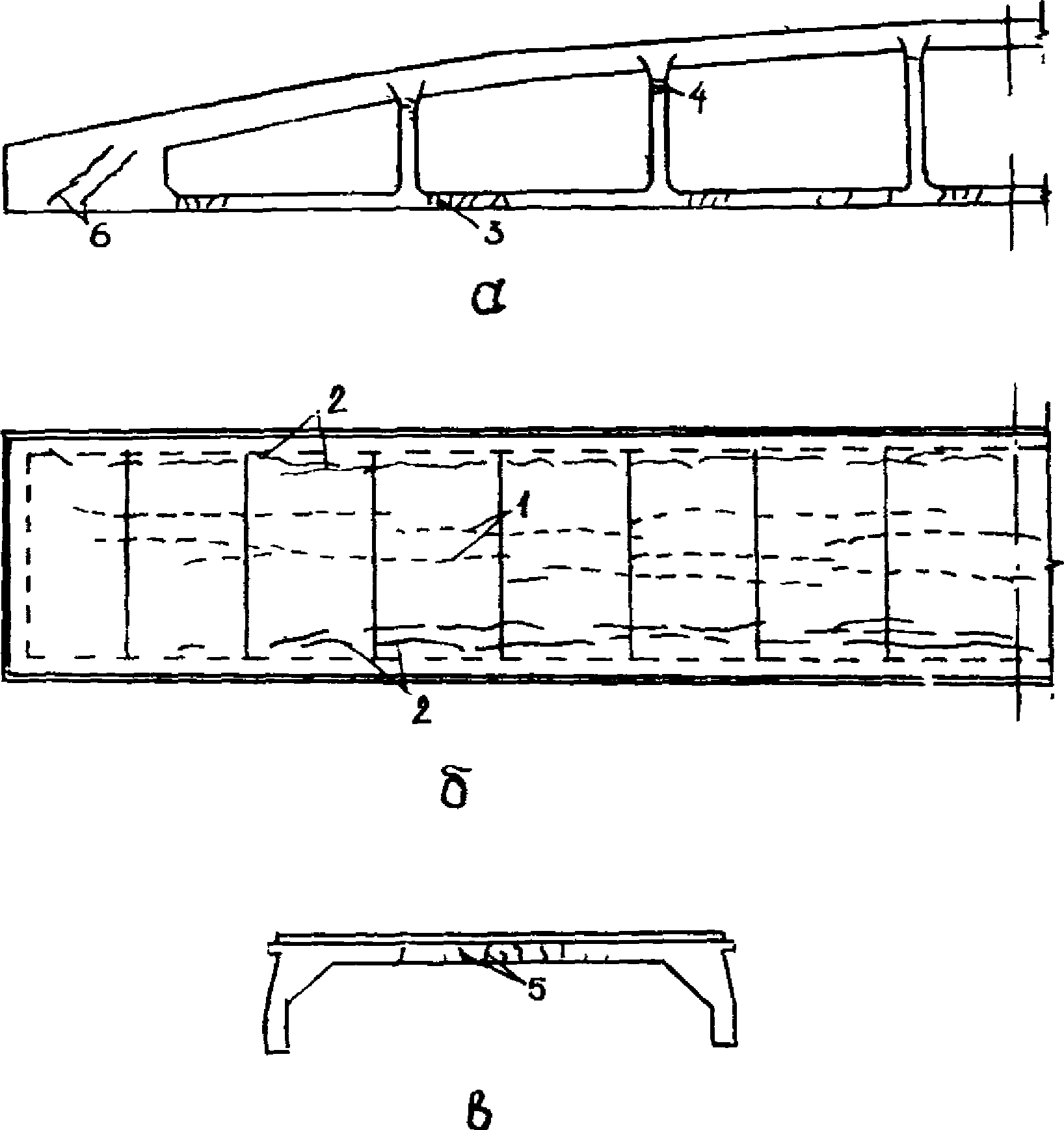
трещиностойкости панели-оболочки КСО
а - диафрагм; б - полки; в - торцового ребра;
1 и 2 - продольные трещины соответственно на нижней
и верхней поверхности полки; 3 и 4 - нормальные трещины
в нижнем поясе и стойках; 5 - нормальные трещины
в торцовом ребре; 6 - наклонные трещины
в приопорном сплошном участке
4.50. Расчет по образованию продольных трещин снизу и сверху в складчатой полке на действие поперечных изгибающих моментов допускается производить без учета влияния усилий продольного направления по методике [1] (п. 4.5). При этом может быть использован алгоритм, приведенный в [11] (табл. 4.2).
4.51. Расчет по образованию нормальных трещин во внецентренно растянутых элементах нижнего пояса и стойках диафрагмы панели-оболочки КСО производят на действие расчетных  усилий (изгибающего момента и продольной силы) при основных сочетаниях нагрузок, действующих на оболочку, согласно указаний [1] (п. 4.5). При этом может быть использован алгоритм, приведенный в [11] (табл. 4.2).
усилий (изгибающего момента и продольной силы) при основных сочетаниях нагрузок, действующих на оболочку, согласно указаний [1] (п. 4.5). При этом может быть использован алгоритм, приведенный в [11] (табл. 4.2).
4.52. Расчет по образованию нормальных трещин в растянутой зоне торцового ребра производят на действие изгибающего момента MР1 (см. п. 4.41 настоящих рекомендаций) согласно указаниям [1 (п. 4.5)].
4.53. Проверку по образованию наклонных трещин в приопорных участках диафрагм панелей-оболочек необходимо производить при действии сосредоточенных нагрузок (например, от подвесных кранов) в пределах рассматриваемого участка.
4.54. Расчет на ограниченное раскрытие трещин в панели-оболочке КСО следует производить для нижнего и верхнего пояса диафрагмы, складчатой полки и торцового ребра, к которым предъявляют требования третьей категории трещиностойкости. Расчет выполняют на непродолжительное и на продолжительное раскрытие трещин.
4.55. Ширину непродолжительного и продолжительного раскрытия трещин определяют в соответствии с указаниями [1] (пп. 4.14, 4.15), применительно к конкретным напряженным состояниям элементов панели-оболочки КСО, и сравнивают с предельно допустимыми значениями ширины непродолжительного и продолжительного раскрытия трещин [1] (табл. 2).
4.56. Проверку трещиностойкости и ширины раскрытия трещин элементов панелей КСО необходимо производить не только на действие эксплуатационных нагрузок, но и на возникающие в стадиях изготовления, транспортирования и монтажа. Расчетные нагрузки в стадиях транспортирования и монтажа можно определять согласно [1] (п. 1.13).
Примечание. Пример расчета панели-оболочки КСО 3 x 24 м комбинированного покрытия производственного здания по предельным состояниям второй группы приведен в приложении 2.
ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
РАСЧЕТ ПО НЕСУЩЕЙ СПОСОБНОСТИ
5.1. Гибкие пластины, уложенные на монтаже на криволинейные по верху панели-оболочки КСО, образуют пологие цилиндрические оболочки средней длины и могут рассматриваться как шарнирно опертые по всему опорному контуру.
При воздействии равномерно распределенной нагрузки пологая цилиндрическая оболочка разрушается по пятидисковой схеме (рис. 23).
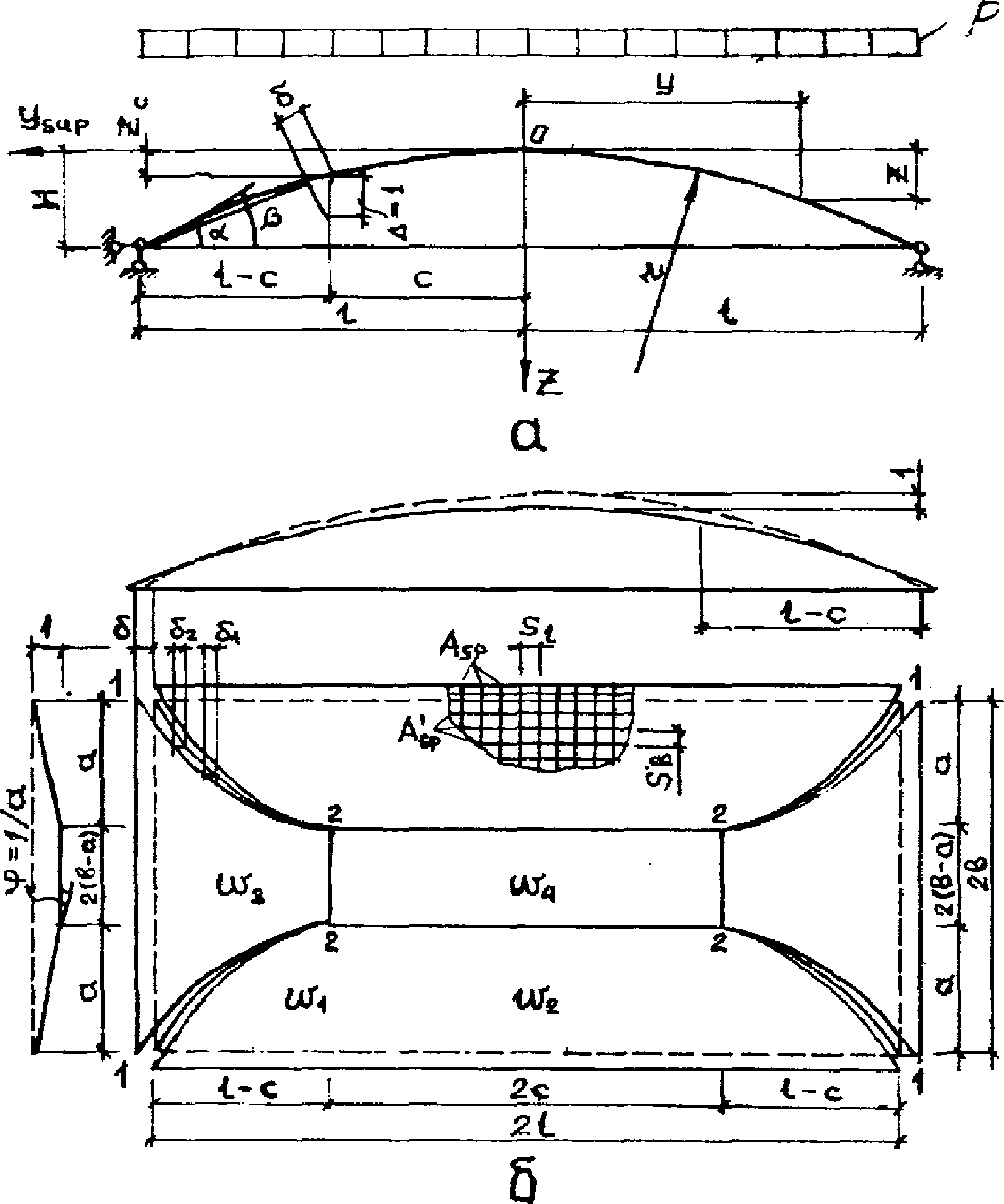
цилиндрической оболочки
а - геометрические параметры конструкции;
б - схема разрушения и виртуальные перемещения
жестких дисков оболочки
Пятидисковая схема разрушения пологой цилиндрической оболочки представляет собой перекрестную систему, в коротком направлении которой осуществляется балочная схема излома по линиям 1-2 - 2-1, а в длинном - растяжение между дисками по линиям излома 1-2 (поворот сечений по линиям излома 2-2 между дисками 3-4 происходит без образования трещин, так как деформации растяжения бетона на этих линиях не компенсируют обжатия от предварительного натяжения и изгиба пластины при монтаже).
Расчет пологой цилиндрической оболочки по несущей способности производится путем последовательных приближений.
В первом приближении пологая оболочка рассчитывается по недеформированной схеме. По найденным параметрам схемы излома и внутренним усилиям определяется прогиб середины оболочки к моменту исчерпания несущей способности.
Во втором и окончательном приближении несущую способность определяют по деформированной схеме, отличающейся от недеформированной радиусом кривизны нижней поверхности оболочки.
При виртуальном перемещении центрального диска на единицу угол поворота  по линии излома 2-2 составит величину 1/a. При этом диски коротких сторон переместятся наружу пролета на величину
по линии излома 2-2 составит величину 1/a. При этом диски коротких сторон переместятся наружу пролета на величину  , а осуществляемое виртуальное растяжение продольной арматуры на участках a - lB и lB будет
, а осуществляемое виртуальное растяжение продольной арматуры на участках a - lB и lB будет  и
и  (рис. 23 и 24).
(рис. 23 и 24).
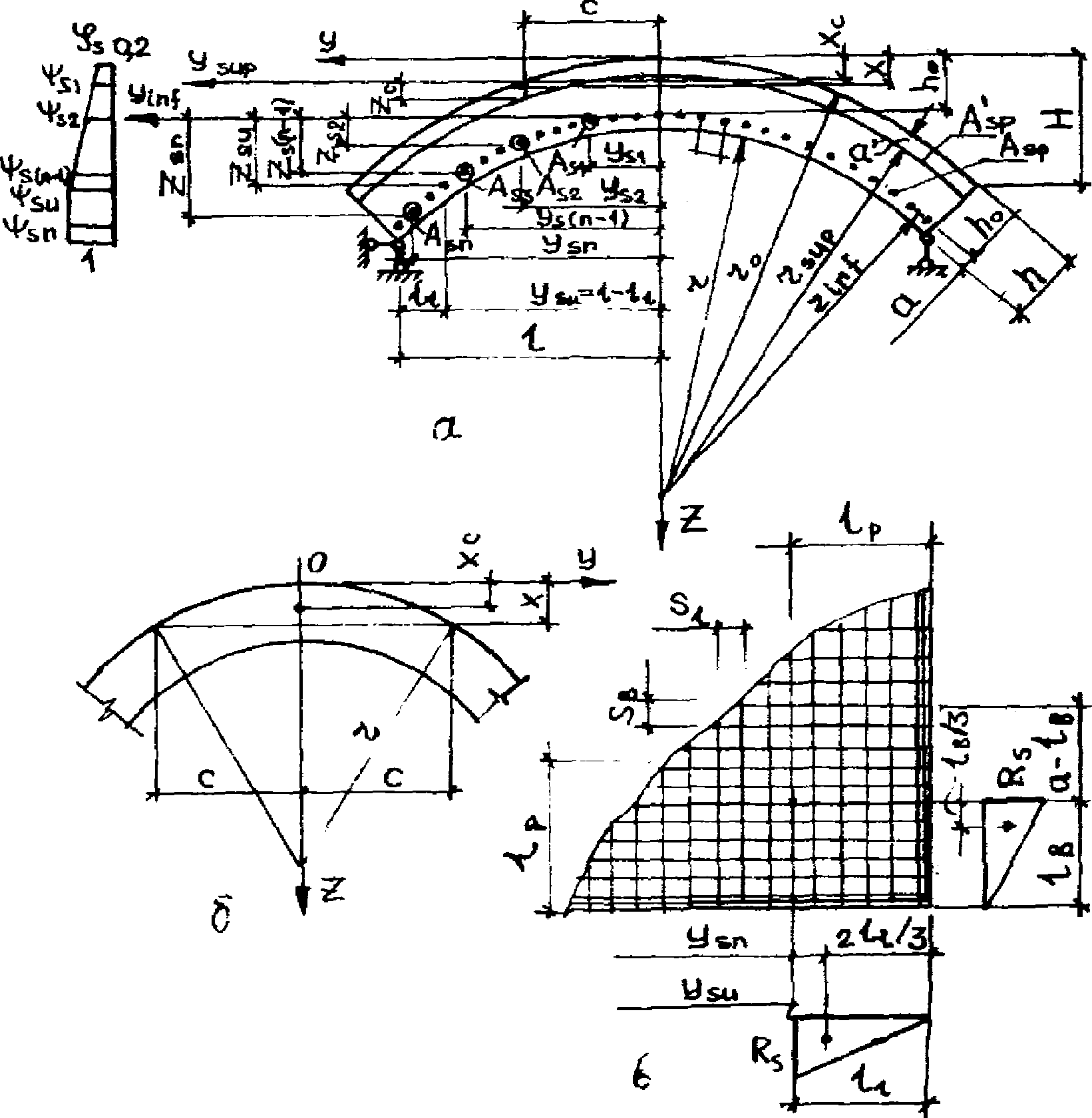
цилиндрической оболочки
а - сечение оболочки по линии излома 1-2 - 2-1;
б - параметры сегмента высотой X; в - длина зон передачи
напряжений и напряжения в арматуре угловых зон оболочки
5.2. Исходя из принципа виртуальных перемещений несущая способность оболочки по стадии предельного равновесия определяется из условия равенства работ внешних нагрузок и внутренних усилий
где Mи - предельный изгибающий момент на линиях излома 1-2 - 2-1;
N1и - усилие растяжения в продольной арматуре на линии излома 1-2, собираемой с длины участка a - lB;
N2и - то же, с длины участка lB;
w - виртуальный объем.
Изгибающий момент Mи, действующий на линии излома 1-2 - 2-1 относительно оси yinf, определяется по формуле
а высоту сжатой зоны x и напряжения  путем последовательных приближений находят по формулам (66) и (67) СНиП 2.03.01-84.
путем последовательных приближений находят по формулам (66) и (67) СНиП 2.03.01-84.
Для вычисления изгибающего момента сетку арматуры короткого направления на длине половины криволинейного сечения разобьем на n участков так, чтобы n-й участок соответствовал длине ll, равной длине зоны передачи напряжений lp, определяемой по формуле (11) СНиП 2.03.01-84. Количество арматуры Asi на этих участках (см. рис. 24) с двух сторон определяется по формуле
Asi = 2Aspli/sl, (25)
где Asp - поперечное сечение одного стержня предварительно напряженной арматуры;
sl - шаг стержней;
li - длина участков с равномерным шагом стержней.
Рекомендуется принимать на длине половины криволинейного сечения около 5 - 6 участков.
Ординаты центров тяжестей zsi усилий в арматуре на участках оболочки определяются по формуле
где ysi - расстояние от оси z до центров тяжести усилий zsi.
Высоту сжатой зоны x определяем из выражения
путем последовательных приближений.
В первом приближении высоту сжатой зоны бетона можно найти, если принять  или принять ее значение из расчета по недеформированной схеме.
или принять ее значение из расчета по недеформированной схеме.
 или принять ее значение из расчета по недеформированной схеме.
или принять ее значение из расчета по недеформированной схеме.Во втором приближении, определив напряжения  по формуле (67) СНиП 2.03.01-84, находим новое значение x. Если сходимость удовлетворительная, значение высоты сжатой зоны считается подобранным.
по формуле (67) СНиП 2.03.01-84, находим новое значение x. Если сходимость удовлетворительная, значение высоты сжатой зоны считается подобранным.
Расстояние до центра тяжести сжатой зоны Xс определяется по формуле
Xс = 5X/8, (28)
а площадь сжатой зоны бетона по формуле
 (29)
(29)где половина ширины сжатой зоны
Усилия растяжения, действующие на линиях излома 1-2 при исчерпании несущей способности, представляются двумя компонентами:
N1и = qB(a - lB); (31)
 (32)
(32)где
Виртуальные перемещения  и
и  определяются по формулам:
определяются по формулам:
 (35)
(35)где
а ордината линии излома 2-2
Неизвестный параметр a схемы излома оболочки определяется по формуле
 (38)
(38)где
Виртуальный угол перелома принимают по выражению
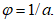
Виртуальный объем определяется по формуле
Подставив найденные значения внутренних усилий, виртуальных перемещений и виртуального объема в формулу (23), найдем несущую способность пологой цилиндрической оболочки по недеформированной схеме.
Оценка прогиба пластины - пологой цилиндрической
оболочки к моменту исчерпания несущей способности
5.3. Оценка деформированного состояния пологой цилиндрической оболочки производится по прогибу конструкции к моменту достижения на линиях излома 1-2 - 2-1 предельного изгибающего момента Mи по формуле
где (1/r)и - кривизна оболочки по сечению 1-2 - 2-1 при предельном изгибающем моменте Mи
где My - изгибающий момент, воспринимаемый сечением 1-2 - 2-1 к моменту проявления текучести в поперечной арматуре, расположенной на расстоянии ll от края оболочки (см. рис. 24, в);
(1/r)y - кривизна оболочки по сечению 1-2 - 2-1 при изгибающем моменте My
Изгибающий момент My рекомендуется определять по формуле
а высоту сжатой зоны x при появлении текучести в арматуре с ординатой дуги zsu - из уравнений
 (48)
(48)где  - напряжение в бетоне верхней кромки сечения от преднапряжения.
- напряжение в бетоне верхней кромки сечения от преднапряжения.
Средние деформации крайнего сжатого волокна бетона
 (49)
(49)Деформации растяжения арматуры с абсциссой ysu = l - ll к моменту появления в ней текучести определяются по формуле
 (50)
(50)где  - полные деформации удлинения арматуры к моменту появления в ней текучести;
- полные деформации удлинения арматуры к моменту появления в ней текучести;
 (51)
(51)Коэффициент  , характеризующий упругопластическое состояние бетона сжатой зоны, определяется по формуле
, характеризующий упругопластическое состояние бетона сжатой зоны, определяется по формуле
 (52)
(52)где P1 - полная нагрузка на 1 м2 оболочки;
P2 - длительная часть нагрузки.
Для арматуры, в которой фиксируется появление текучести (с ординатой zsu от оси yinf), коэффициент  принимается равным единице (см. рис. 20), для арматуры на участке ll - также равным единице. На уровне нейтральной оси X
принимается равным единице (см. рис. 20), для арматуры на участке ll - также равным единице. На уровне нейтральной оси X  . На уровне арматуры zsi определяется по формуле
. На уровне арматуры zsi определяется по формуле
 . На уровне арматуры zsi определяется по формуле
. На уровне арматуры zsi определяется по формулеЗначение  , определяемое по формуле (53) и равное меньше 0,2, принимается равным единице.
, определяемое по формуле (53) и равное меньше 0,2, принимается равным единице.
5.4. Определив по формуле (41) настоящих рекомендаций прогиб оболочки к моменту исчерпания несущей способности, находят стрелу подъема для расчета по деформированной схеме
Hд = H - fи (54)
и радиус кривизны низа оболочки
 (55)
(55)Радиусы кривизны арматуры оболочки:
нижней
rinf = r + a; (56)
верхней
rsup = r + h - a'. (57)
Расчет гибкой пластины по раскрытию трещин
при изгибе на монтаже
5.5. При монтаже гибких пластин с помощью траверс-формообразователей на их верхней поверхности образуются трещины, которые при приложении нагрузки закрываются.
Ширину раскрытия трещин acrc, мм, образующихся при изгибе гибкой пластины, нормальных к продольной оси, рекомендуется определять по формуле (144) СНиП 2.03.01-84, а изгибающий момент, воспринимаемый при этом гибкой пластиной, определяется по формуле
где
 (59)
(59)Напряжения в арматуре и бетоне определяются по формулам:
 (60)
(60) (61)
(61)Относительная высота сжатой зоны бетона определяется из выражения
Коэффициент  определяется согласно п. 4.27 в СНиП 2.03.01-84, а коэффициент
определяется согласно п. 4.27 в СНиП 2.03.01-84, а коэффициент  - согласно формуле (167) СНиП 2.03.01-84, в которой коэффициент
- согласно формуле (167) СНиП 2.03.01-84, в которой коэффициент  рекомендуется определять по формуле
рекомендуется определять по формуле
 (63)
(63)где изгибающие моменты Mcrc и Mr определяются по выражениям (65) и (58) настоящих рекомендаций, а эксцентриситет es,tot - по формуле
es,tot = Mr/P, (64)
где P - усилие предварительного обжатия с учетом полных потерь.
В первом приближении рекомендуется принимать  .
.
 .
.5.6. При определении изгибающих моментов, воспринимаемых нормальными к продольной оси сечениями гибкой пластины при образовании трещин, рекомендуется исходить из следующих соображений:
сечения после деформации остаются плоскими;
наибольшее относительное удлинение крайнего растянутого волокна бетона равно 2RBt,ser/EB;
напряжения в бетоне сжатой зоны определяются с учетом упругих деформаций бетона;
напряжения в бетоне растянутой зоны распределяются по трапециевидной эпюре и равны по величине RBt,ser;
напряжения в напрягаемой арматуре равны алгебраической сумме предварительного напряжения (с учетом всех потерь) и напряжения, отвечающего приращению деформаций окружающего бетона.
5.7. Изгибающий момент, воспринимаемый сечением, нормальным к продольной оси гибкой пластины, при образовании трещин определяется по формуле
где
 (66)
(66) (69)
(69)где
 (71)
(71) (72)
(72)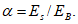
РАСЧЕТ ПО ДЕФОРМАЦИЯМ
5.8. Расчет гибкой пластины - пологой цилиндрической оболочки по предельным состояниям второй группы рекомендуется производить по усилиям, деформациям и перемещениям, вычисленным, как правило, с учетом физической и геометрической нелинейности. При эксплуатационных равномерно распределенных нагрузках и принятых вариантах армирования максимальные прогибы в пластинах не превышают половины их толщины, а трещины при нормативных нагрузках не образуются или образуются на сравнительно небольших участках поверхности [12, 20]. Поэтому в первом приближении расчет пластины-оболочки допускается выполнять в линейно-упругой постановке по недеформированной схеме.
5.9. Определение усилий и перемещений гибкой пластины при силовых и деформационных воздействиях в стадии изготовления и монтажа может быть выполнено с применением численных методов, например, метода конечных разностей, метода конечных элементов и др., в предположении упругой работы железобетона. При этом целесообразно использование существующих стандартных программ для статического расчета таких конструкций, например, "ППП АПЖБК" [13], "Прокруст" [14] и др.
5.10. Определение усилий и перемещений гибкой пластины - пологой цилиндрической оболочки при эксплуатационных нагрузках может быть выполнено аналитическими или численными методами.
При применении аналитических методов, в частности вариационного метода В.З. Власова [15], могут быть использованы рекомендации к построению расчетных схем пластины-оболочки, приведенные в п. 5.12. Особенности построения расчетных схем таких конструкций методом конечных элементов приведены в п. 5.14.
5.11. Практический расчет пластин - пологих цилиндрических оболочек по предельным состояниям второй группы может производиться вариационным методом В.З. Власова [15]. Применение этого метода особенно целесообразно в случае использования персональных ЭВМ, поскольку обеспечивает значительное снижение объема входной и выходной информации и затрат машинного времени по сравнению с численными методами. Кроме того этот метод, в случае необходимости, позволяет выполнить расчеты вручную без использования ЭВМ (см. приложение 2).
5.12. При построении расчетных схем и расчете пластины-оболочки вариационным методом могут быть использованы следующие рекомендации.
Расчет рекомендуется производить с использованием нового варианта смешанного метода в наиболее общей форме [16].
Для расчета цилиндрическая поверхность заменяется вписанной призматической складчатой системой с конечным сравнительно небольшим числом граней (рис. 25). Применительно к рассматриваемой конструкции короткой цилиндрической оболочки с размерами в плане 3 x 6 м для получения результатов, приемлемых в практическом расчете, необходимо принимать 6 - 8 граней.
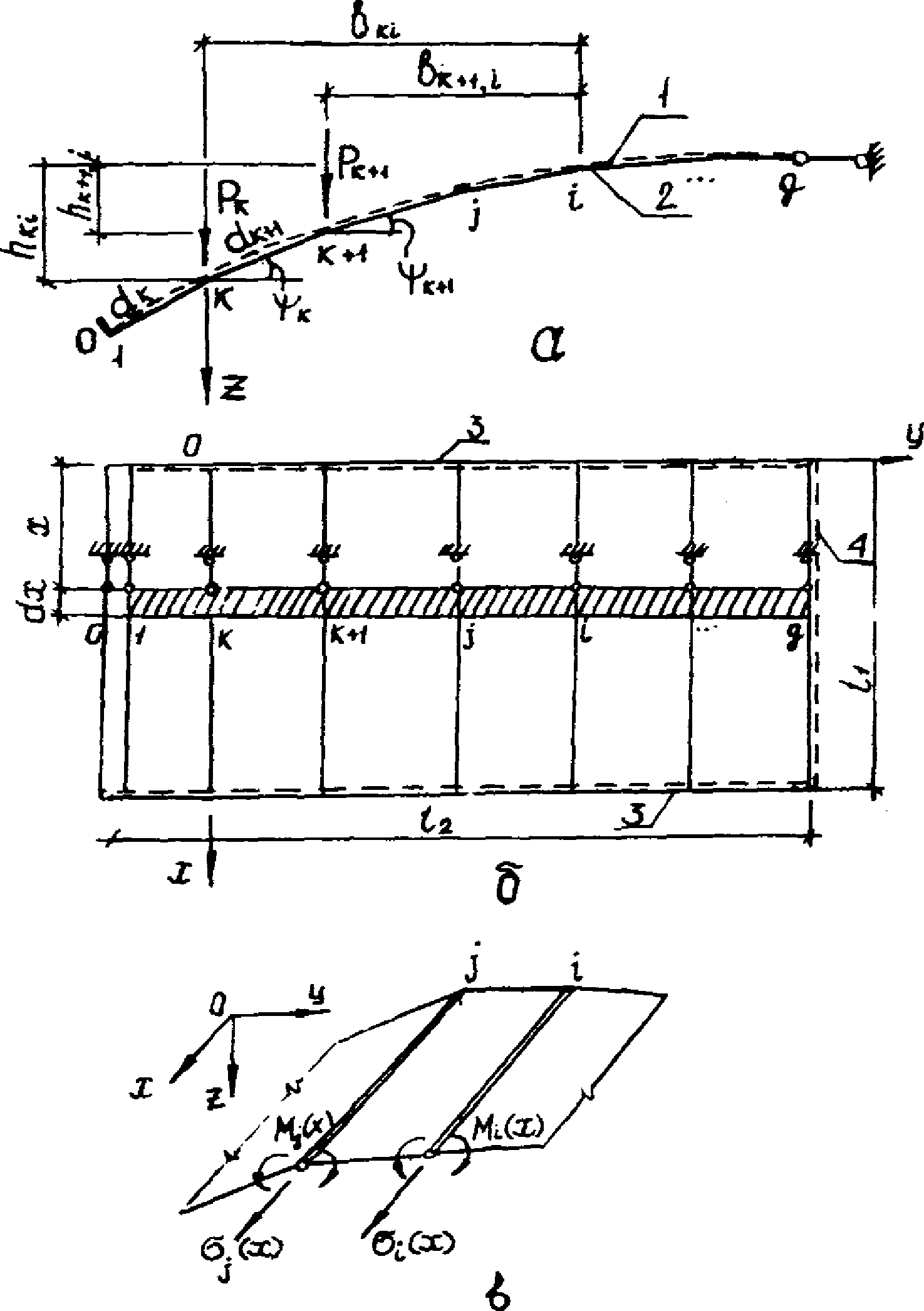
вариационным смешанным методом
а - поперечное сечение и нагрузки; б - план и элементарная
поперечная полоска; в - схема неизвестных усилий;
1 - заданное сечение; 2 - расчетное; 3 - шарнирное
опирание на панель КСО; 4 - шарнирное сопряжение
со смежной пластиной
Имеющееся в крайних пластинах утолщение у одного из торцов в расчетной схеме может быть аппроксимировано в виде дополнительной бортовой грани (см. рис. 25). Допускается также замена указанного утолщения сосредоточенным стрингером с жесткостными характеристиками - определяемыми согласно рекомендациям [6].
При расчете короткой оболочки (отношение пролета к длине волны l1/2l <= 1) предполагается, что ее напряженно-деформированное состояние определяется в основном нормальными силами, сдвигающими усилиями и поперечными изгибающими моментами M. Это позволяет использовать для расчета таких конструкций уравнения полубезмоментной теории цилиндрических оболочек.
Продольные изгибающие моменты могут быть дополнительно учтены введением в расчетную схему вспомогательных фиктивных граней согласно предложениям [12].
В соответствии с принятыми гипотезами о характере напряженного состояния в используемых разрешающих уравнениях для пластины-оболочки в качестве неизвестных в разрешающих дифференциальных уравнениях [16, формула (2.30)] выступают функции продольных напряжений в ребрах складчатой системы  и поперечные изгибающие моменты Mk(x) (см. рис. 25, в).
и поперечные изгибающие моменты Mk(x) (см. рис. 25, в).
Для определения искомых функций напряжений и моментов необходимо вычислить коэффициенты  ,
,  разложений этих функций в ряды по фундаментальным функциям свободных колебаний балки.
разложений этих функций в ряды по фундаментальным функциям свободных колебаний балки.
Вычисление коэффициентов  ,
,  для каждого m-ого числа разложений выполняется решением следующей системы алгебраических уравнений:
для каждого m-ого числа разложений выполняется решением следующей системы алгебраических уравнений:
(j, i = 0, 1, 2, ..., g; k, h = 2, 3, ..., g - 2),
где Ik - момент инерции продольного сечения единичной длины для k-той грани,  , tk - толщина k-ой грани складки;
, tk - толщина k-ой грани складки;
 , tk - толщина k-ой грани складки;
, tk - толщина k-ой грани складки; (75, б)
(75, б)здесь  - произвольный множитель;
- произвольный множитель;
Am - коэффициенты разложений, зависящие от вида граничных условий и нагрузки и определяемые по табл. 3.2 [6];
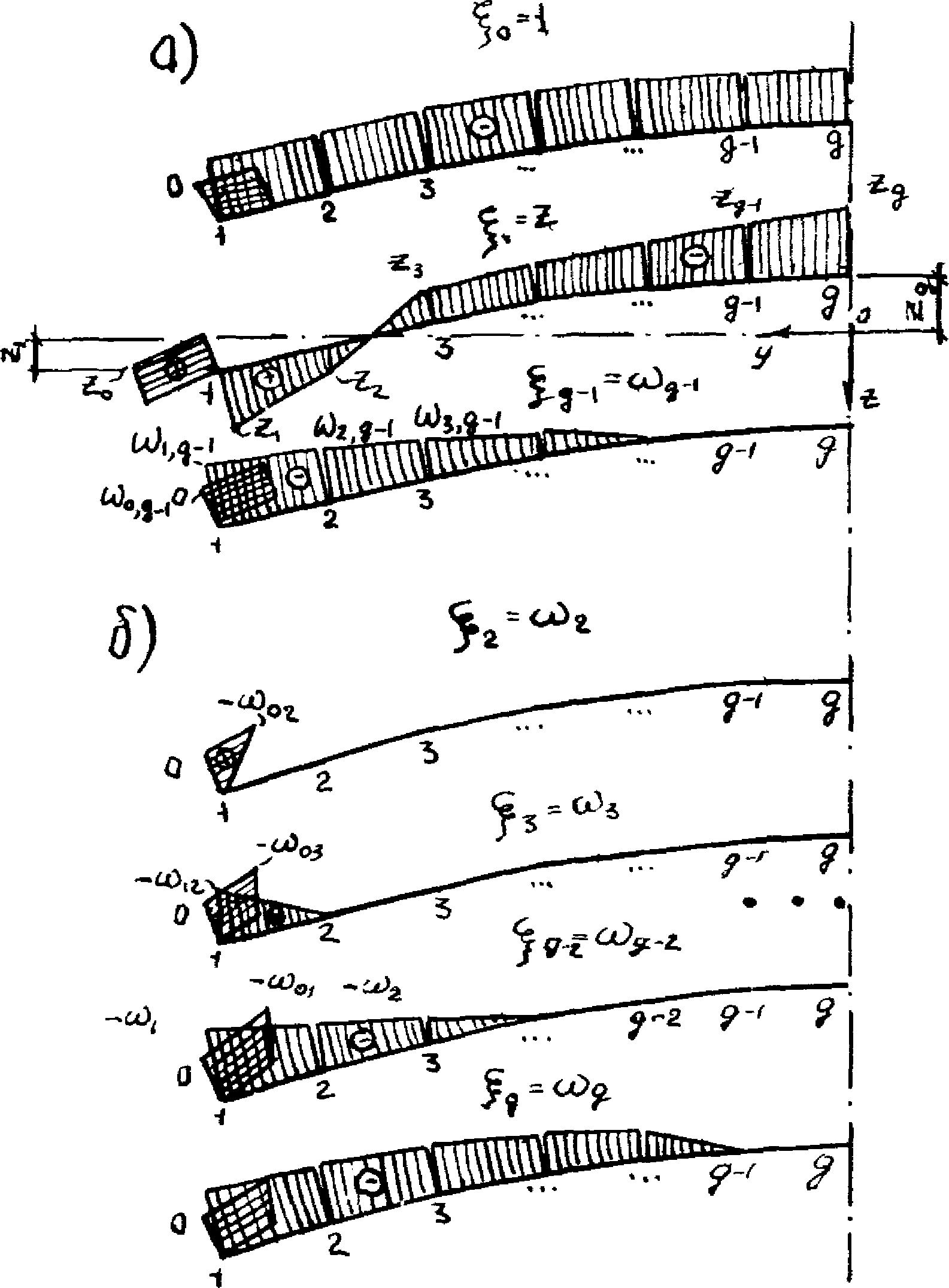
пластины-оболочки g-гранной складкой
а - первой группы; б - второй группы
Функции  первой группы общим числом, равным четырем (i = 0; 1; g - 1; g) принимают согласно изменению продольных перемещений по закону плоских сечений и секториальных площадей для всего поперечного сечения складки как для тонкостенного стержня с недеформируемым контуром:
первой группы общим числом, равным четырем (i = 0; 1; g - 1; g) принимают согласно изменению продольных перемещений по закону плоских сечений и секториальных площадей для всего поперечного сечения складки как для тонкостенного стержня с недеформируемым контуром:
где  ,
,  ,
,  - произвольные множители. Эти множители могут быть приняты равными единице, но могут приниматься и отличными от единицы, и такими, чтобы все коэффициенты aji в (73) были бы одного порядка.
- произвольные множители. Эти множители могут быть приняты равными единице, но могут приниматься и отличными от единицы, и такими, чтобы все коэффициенты aji в (73) были бы одного порядка.
Примечание. Поскольку расчет пластины оболочки производим на действие только вертикальной нагрузки, то в (77)  принимается равным нулю.
принимается равным нулю.
Единичные функции  (i = 2, 3, ..., g - 2) второй группы общим числом g - 4 учитывают деформацию и депланацию контура поперечного сечения складки. Их выбирают в виде эпюр секриториальных площадей
(i = 2, 3, ..., g - 2) второй группы общим числом g - 4 учитывают деформацию и депланацию контура поперечного сечения складки. Их выбирают в виде эпюр секриториальных площадей  , построенных только для части поперечного сечения, расположенного слева от ребра i (i = 2, 3, ..., g - 2), при этом полюс и начало отсчета эпюры секриториальных площадей выбирают в i-ной вершине поперечного сечения складки.
, построенных только для части поперечного сечения, расположенного слева от ребра i (i = 2, 3, ..., g - 2), при этом полюс и начало отсчета эпюры секриториальных площадей выбирают в i-ной вершине поперечного сечения складки.
 , построенных только для части поперечного сечения, расположенного слева от ребра i (i = 2, 3, ..., g - 2), при этом полюс и начало отсчета эпюры секриториальных площадей выбирают в i-ной вершине поперечного сечения складки.
, построенных только для части поперечного сечения, расположенного слева от ребра i (i = 2, 3, ..., g - 2), при этом полюс и начало отсчета эпюры секриториальных площадей выбирают в i-ной вершине поперечного сечения складки.Значения ординат wi(s) в вершинах контура складки
при
при
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 (78, б)
(78, б)Знак плюс перед  принимают в том случае, когда радиус-вектор, проведенный из точки i в точку k + 1, при переходе к точке k для отсчета секриториальной площади поворачивается по часовой стрелке, а знак минус - при повороте против часовой стрелки.
принимают в том случае, когда радиус-вектор, проведенный из точки i в точку k + 1, при переходе к точке k для отсчета секриториальной площади поворачивается по часовой стрелке, а знак минус - при повороте против часовой стрелки.
Система разрешающих уравнений (73) может иметь следующий вид (табл. 1).
Таблица 1
цилиндрической оболочки, аппроксимированной g-гранной
складкой при вертикальной распределенной вдоль
ребер нагрузке (см. рис. 25)
j, k | ... | ... | Свободные члены | |||||||||||
2 | 0 | ... | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | ||
3 | ... | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | |||
4 | 0 | ... | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | ||
... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
g - 2 | 0 | 0 | 0 | ... | 0 | 0 | 0 | ... | 1 | 0 | 0 | 0 | ||
g - 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | ... | 0 | 1 | 0 | 0 | ||
0 | 0 | 0 | 0 | ... | 0 | 0 | ... | 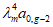 | 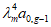 | Amq0 | ||||
1 | 0 | 0 | 0 | ... | 0 | 0 | ... | 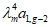 | Amq1 | |||||
2 | 1 | 0 | 0 | ... | 0 | 0 | ... | 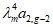 | 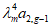 | Amq2 | ||||
... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
g - 2 | 0 | 0 | 0 | ... | 1 | 0 | ... | 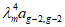 | 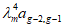 | 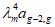 | Amqg-2 | |||
g - 1 | 0 | 0 | 0 | ... | 0 | 1 | ... | 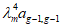 | 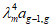 | Amqg-1 | ||||
g | 0 | 0 | 0 | ... | 0 | 0 | ... | Amqg |
Напряжения усилия и перемещения по ребрам складки k = 0, 1, ..., g для каждого m-го члена ряда определяется по следующим формулам.
Для нормальных напряжений
zm(x) - фундаментальная функция свободных колебаний балки, численные значения которой могут быть определены по данным руководства [6] (табл. 3.8 и 3.9).
Для поперечных моментов
 (80)
(80)Для сдвигающих усилий
 (81)
(81)где Sk-1,m(x) - сдвигающая сила по ребру k - 1 в рассматриваемой складке со свободным краем.
Для суммарных сдвигающих усилий  в пределах k-той складки
в пределах k-той складки
 в пределах k-той складки
в пределах k-той складки (82)
(82)Для поперечных сил Qkm на участке k-той грани складки
 (83)
(83)Примечание 1. К вычисленным значениям поперечных сил и поперечных моментов призматических складок добавляют значения поперечных сил и поперечных моментов от местной, нормальной нагрузки как в однопролетной балке со свободно опертыми краями.
Примечание 2. Полные значения усилий и перемещений по ребрам складки определяются суммированием значений для всех рассмотренных в конкретном расчете членов ряда m = 0, 1, 2, ..., m1.
Для нормальных усилий Nk,k-1 и Nk,k+1 по продольным сечениям (рис. 27)
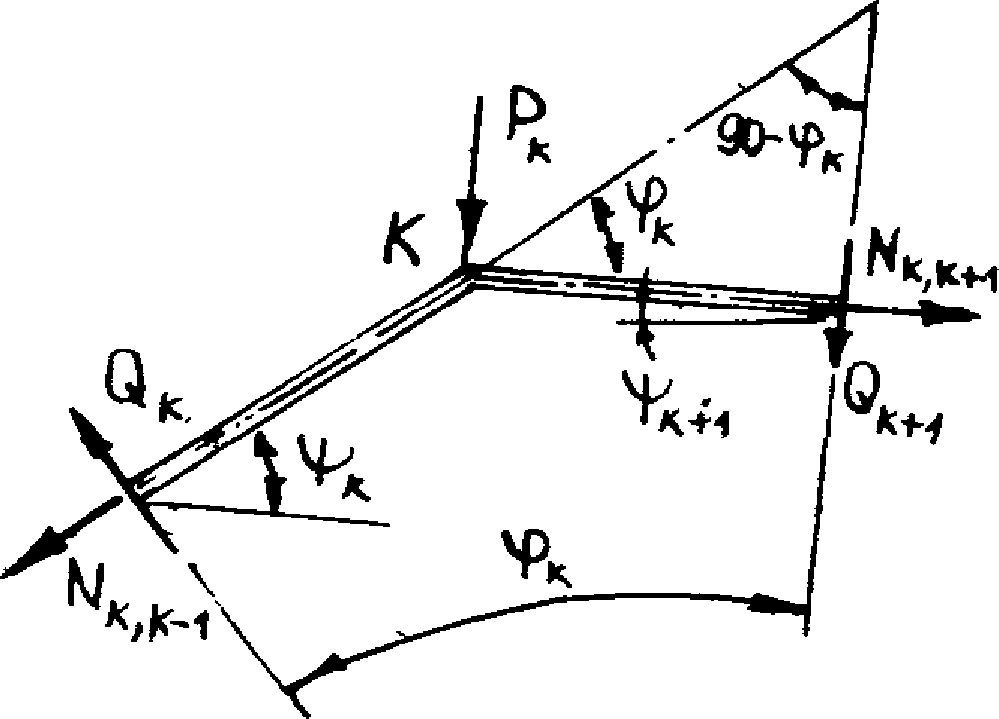
поперечного направления
Формулы (84) в отличие от остальных приводятся для суммы всех удерживаемых в разложения членов ряда, поэтому значения Qk и Qk+1 здесь соответствуют их суммарным значениям:
 (85)
(85)Для вертикальных прогибов vkm точек k-го ребра
где  - значение вертикальных перемещений от единичных функций
- значение вертикальных перемещений от единичных функций  первой и второй группы; для принятых единичных эпюр
первой и второй группы; для принятых единичных эпюр  первой группы
первой группы
 (87, а)
(87, а)для единичных эпюр  второй группы
второй группы
 (i = 2, 3, ..., g - 3). (87, б)
(i = 2, 3, ..., g - 3). (87, б)Знак минус соответствует перемещению точки вверх.
Расчет гибкой пластины-оболочки должен сопровождаться следующими проверками.
1. Проверку вычисления коэффициентов aji и свободных членов qj системы уравнений (73) выполняют сложением по отдельности единичных функций  ,
,  . Суммарные функции соответственно обозначают
. Суммарные функции соответственно обозначают  и
и  . Интегрируя эти эпюры сами на себя по правилу Верещагина, получают контрольные выражения:
. Интегрируя эти эпюры сами на себя по правилу Верещагина, получают контрольные выражения:
 (89)
(89)В первых членах стоят суммы коэффициентов и свободных членов.
2. Полная эпюра продольных растягивающих усилий по поперечному сечению (например, по среднему x = l1/2) при отсутствии продольной нагрузки должна равняться эпюре сжимающих усилий
Nr = Nc, (90)
где Nr и Nc определяют суммированием продольных сжимающих сил в каждой грани Nk, вычисляемых по значениям нормальных напряжений в гранях.
3. Проекция суммарных сил Tk в двух опорных сечениях оболочки на вертикальную ось должна равняться равнодействующей вертикальной нагрузки.
5.13. Расчет гибкой пластины - пологой цилиндрической оболочки - по предельным состояниям второй группы при эксплуатационных нагрузках с учетом неупругих деформаций и трещин в железобетоне целесообразно выполнять вариационным методом В.З. Власова в сочетании с методом последовательных нагружений.
При этом могут быть использованы рекомендации к построению расчетных схем и алгоритмов расчета, приведенные в [12, 16], а также разрешающие уравнения полубезмоментной теории для ортотропной складки с трещинами, учитывающие деформации сдвига [17].
5.14. При построении расчетных схем пластины-оболочки методом конечных элементов могут быть использованы следующие рекомендации.
Один из возможных путей расчета гибкой пластины при силовых и деформационных воздействиях в период распалубки и монтажа конструкции состоит в том, что решение строится методом последовательных приближений.
Первоначально (первый шаг нагружения) плоская пластина рассчитывается без учета собственного веса как пространственно работающий элемент на действия заданных перемещений по направлениям строп траверсы или других точек передачи усилий плите в момент ее подъема и изгиба при монтаже. Полученные в результате такого расчета перемещения узлов расчетной схемы используют для назначения новых координат узлов при расчете на действие нагрузки от собственного веса (второй шаг нагружения). При этом связи накладывают на узлы, соответствующие расположению монтажных петель. Найденные на первом и втором этапах расчета значения усилий в расчетных сечениях суммируют.
При расчете в стадии эксплуатации граничные условия для средних и крайних пластин принимают одинаковыми, за исключением граничных условий по короткой стороне крайней пластины. В обоих случаях пластины принимают шарнирно опертыми по продольным криволинейным краям (рис. 28). Сдвигающие усилия, передающиеся с пластины на КСО, воспринимаются горизонтальными связями, расположенными в местах установки закладных деталей. Взаимодействие со смежными пластинами-вставками может учитываться, например, постановкой по касательной к пластине стержневых элементов соответствующей жесткости.
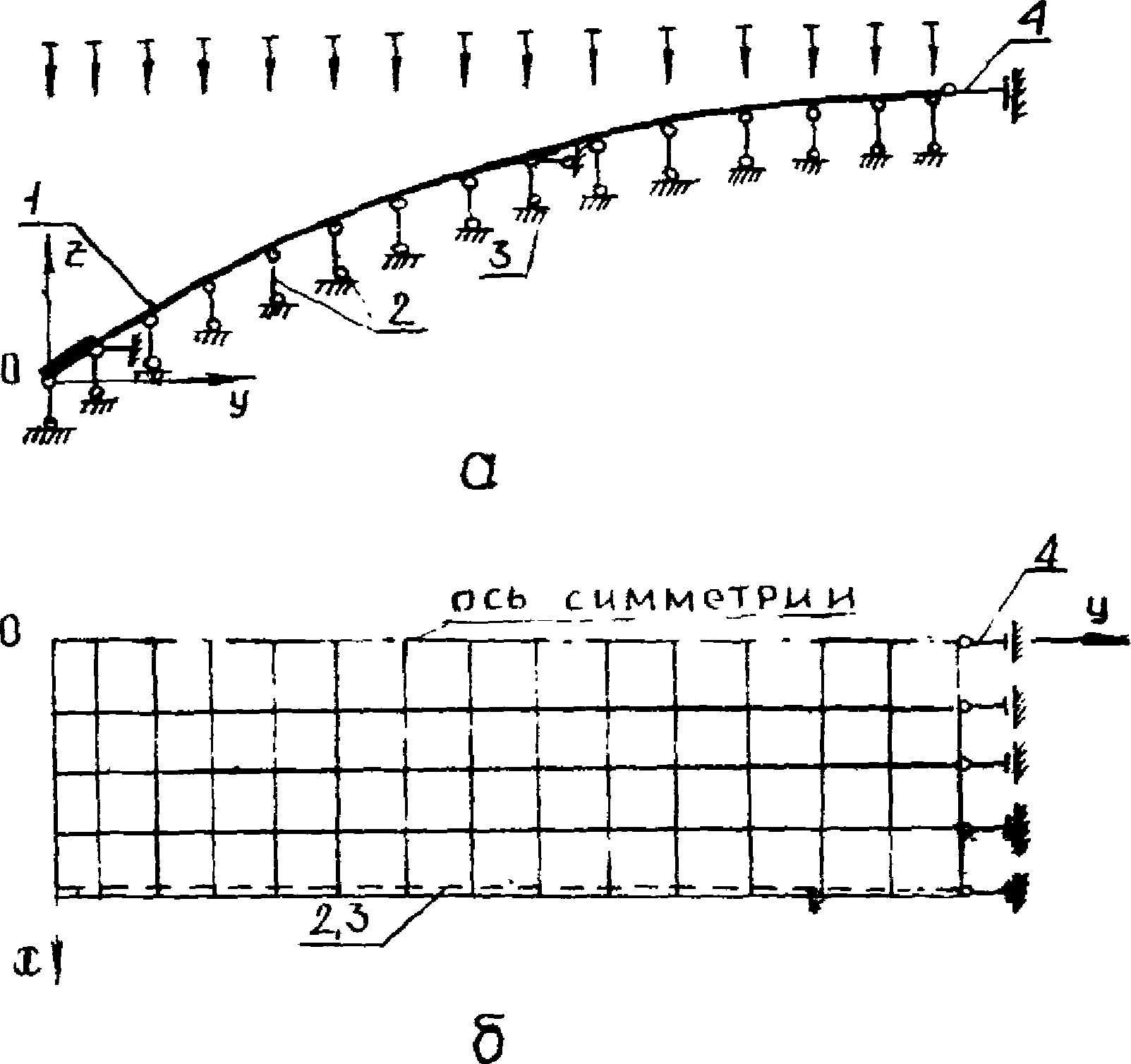
оболочки по методу конечных элементов в стадии эксплуатации
а - продольный разрез; б - план; 1 - пластина;
2 и 3 - вертикальные и горизонтальные связи;
4 - стержневые соединительные элементы
В торцовой части крайней пластины однопролетного покрытия вертикальные связи не вводят.
Во всех случаях симметричного относительно продольной оси нагружения целесообразно использовать для расчета половину пластины. При этом влияние отброшенной части учитывают введением связей по оси симметрии, препятствующих несимметричным перемещениям.
Утолщение пластины у свободного края может моделироваться конечными элементами оболочки нулевой кривизны или постановкой стержневых элементов.
При разбивке на конечные элементы, назначении густоты расчетной сетки, описании нагрузок и учете предварительного напряжения можно руководствоваться указаниями п. 4.47 настоящих рекомендаций.
РАСЧЕТ ГИБКОЙ ПЛАСТИНЫ - ПОЛОГОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
ПО ТРЕЩИНОСТОЙКОСТИ
5.15. При равномерно распределенной эксплуатационной нагрузке и граничных условиях, соответствующих сопряжению пластин-оболочек с панелями-оболочками КСО в составном покрытии (шарнирном опирании по всему опорному контуру или шарнирном опирании по криволинейным краям и упруго-податливом опирании по коротким прямолинейным краям в пологой оболочке), могут образоваться два типа трещин [12] (рис. 29):
косые сквозные 1 от совместного действия нормальных и сдвигающих усилий в угловых зонах;
нормальные 2, располагающиеся на нижней поверхности пластины-оболочки, и вызванные действием изгибающих моментов Mq и растягивающих усилий Ny.
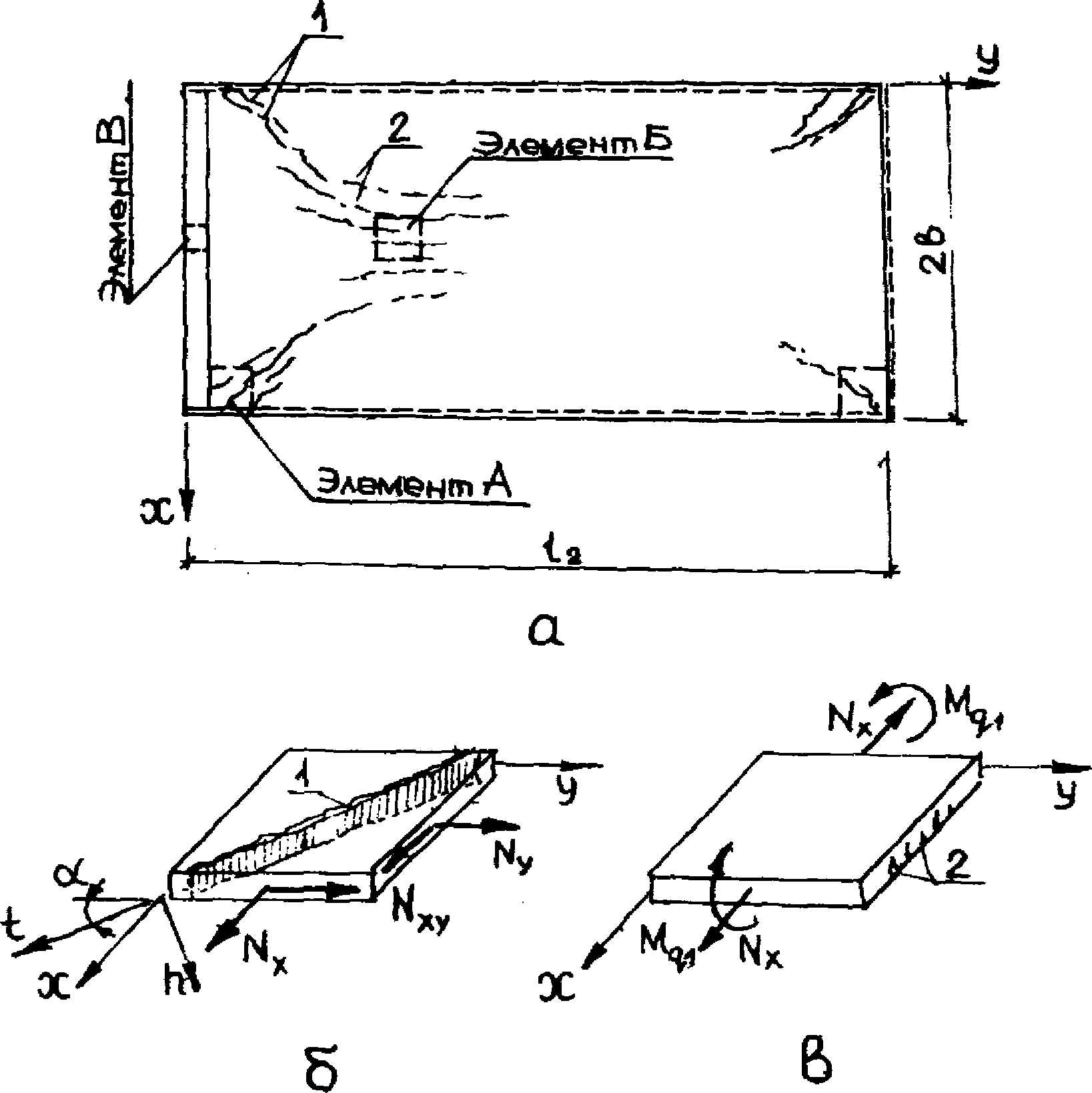
цилиндрической оболочки
а - схема трещин (вид сверху); б - схема усилий
и трещин в элементе А; в - то же, в элементе Б (В);
1 - косые трещины; 2 - нормальные трещины
5.16. Для проверки пластины-оболочки в стадии эксплуатации из полученной распечатки результатов численного расчета принимают мембранные усилия в приопорных угловых зонах пластины Nx, Ny, Nxy (см. рис. 29, элемент А), максимальный погонный изгибающий момент Mq1 и растягивающую силу Ny в среднем продольном сечении (элемент Б), а также изгибающий момент в приопорном утолщении Mp (элемент В).
5.17. Проверка по образованию косых трещин в угловых зонах (см. рис. 29, элемент А) производится из условия
где Nm1 - главные растягивающие усилия
Ncrc - усилие, воспринимаемое сечением двухкомпонентной среды при образовании трещин, которое определяется согласно [1] (п. 4.4). При этом для учета влияния плоского напряженного состояния в правую часть выражения [1, формула (123)] вводится коэффициент Kq, определяемый по формуле (1.8) [18]. При напряженном состоянии "растяжение-растяжение" можно принимать Kq = 1.
Примечание. Усилия  и
и  в расчетных элементах пластины-оболочки принимают с учетом усилий преднапряжения и их изменений в пределах длины зоны передачи напряжений у краев конструкции.
в расчетных элементах пластины-оболочки принимают с учетом усилий преднапряжения и их изменений в пределах длины зоны передачи напряжений у краев конструкции.
5.18. Проверка по образованию нормальных трещин в пластине-оболочке и приопорном утолщении производится соответственно на действие максимальных усилий Mq1, Nx и Mp согласно требованиям [1] (п. 4.5, 4.6). Другие усилия, действующие на элементы Б и В при рассматриваемых граничных условиях и действии равномерно распределенной нагрузки, незначительно влияют на трещиностойкость пластины-оболочки при эксплуатационных нагрузках и для упрощения расчета ими можно пренебречь.
Примечание. При определении усилий в гибкой пластине-оболочке вариационным методом изгибающий момент в приопорном утолщении можно не определять, а проверку трещиностойкости элемента В делать по максимальным растягивающим усилиям, полученным в бортовой грани 0-1 (см. рис. 25).
Проверку трещиностойкости элемента Б в этом случае производят также по максимальным растягивающим усилиям в среднем продольном сечении пластины-оболочки.
5.19. Проверку трещиностойкости пластины-оболочки при монтажных нагрузках допускается производить по методике, приведенной в п. 5.5 - 5.7 на действие только продольного изгибающего момента, возникающего от изгиба пластины.
При определении усилий от монтажных нагрузок по методу конечных элементов проверку по образованию трещин рекомендуется производить как для внецентренно растянутых элементов с учетом взаимного влияния усилий продольного и поперечного направлений с использованием методики [18].
5.20. Расчет по раскрытию косых трещин в угловых зонах пластины-оболочки (см. рис. 29, элемент А) при эксплуатационных нагрузках рекомендуется производить по методике [19] в соответствии с указаниями, изложенными в п. 5.21 - 5.30.
5.21. Деформации железобетонного элемента А с трещинами (см. рис. 29) в осях X, Y при плоском напряженном состоянии определяют по формулам:
где  ,
,  ,
,  - деформации элемента в осях n, t, выбранных соответственно перпендикулярно и параллельно трещине (рис. 30)
- деформации элемента в осях n, t, выбранных соответственно перпендикулярно и параллельно трещине (рис. 30)
acrc - ширина раскрытия трещины;
dcrc - сдвиг берегов трещины;
lcrc - расстояние между трещинами;
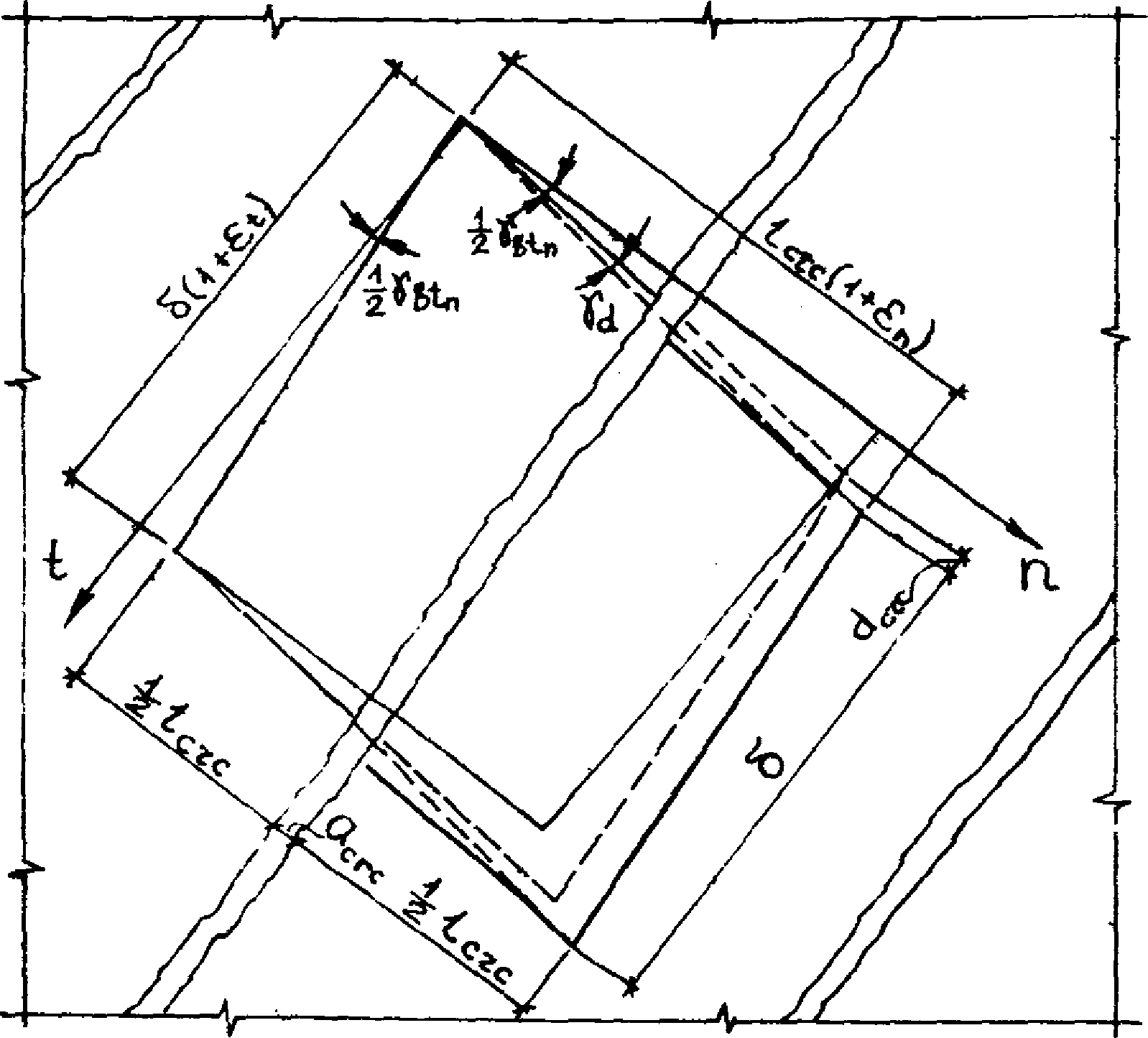
железобетонного элемента пластины с трещинами
5.22. Ширину раскрытия трещин и величину сдвига их берегов вычисляют по формулам (рис. 31):
где ux, uy - смещения арматурных стержней относительно берега трещины.
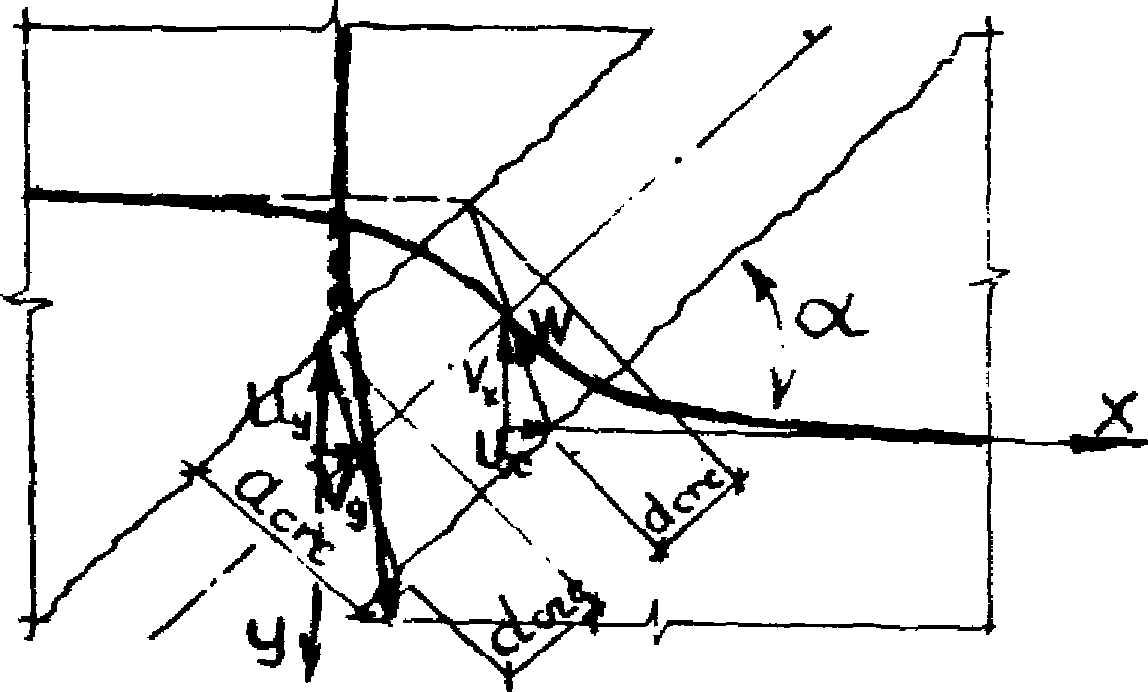
в трещине между берегами бетонной матрицы
5.23. Величины осевых смещений арматурных стержней относительно берега трещины ux и uy определяют по формулам:
 (98)
(98)где  ,
,  - относительные деформации арматуры в трещине соответственно в направлении оси X и Y;
- относительные деформации арматуры в трещине соответственно в направлении оси X и Y;
msx, msy - параметры армирования, равные отношению площади поперечного сечения стержней арматуры соответствующего направления;
Psx, Psy - параметры армирования, равные отношению площади поверхности сцепления арматуры соответствующего направления с бетоном на единице длины;
Gx, Gy - модули деформаций сцепления арматуры соответствующего направления с бетоном;
Esx, Esy - модули упругости стержней арматуры;
5.24. Величину разности деформаций арматуры и бетона в среднем сечении между трещинами соответственно в направлении осей X и Y вычисляют по формулам:
где  - угол наклона трещины (см. рис. 31);
- угол наклона трещины (см. рис. 31);
5.25. Величина расстояния между трещинами (рис. 32) принимается равной максимальному из значений, получаемых по формулам:
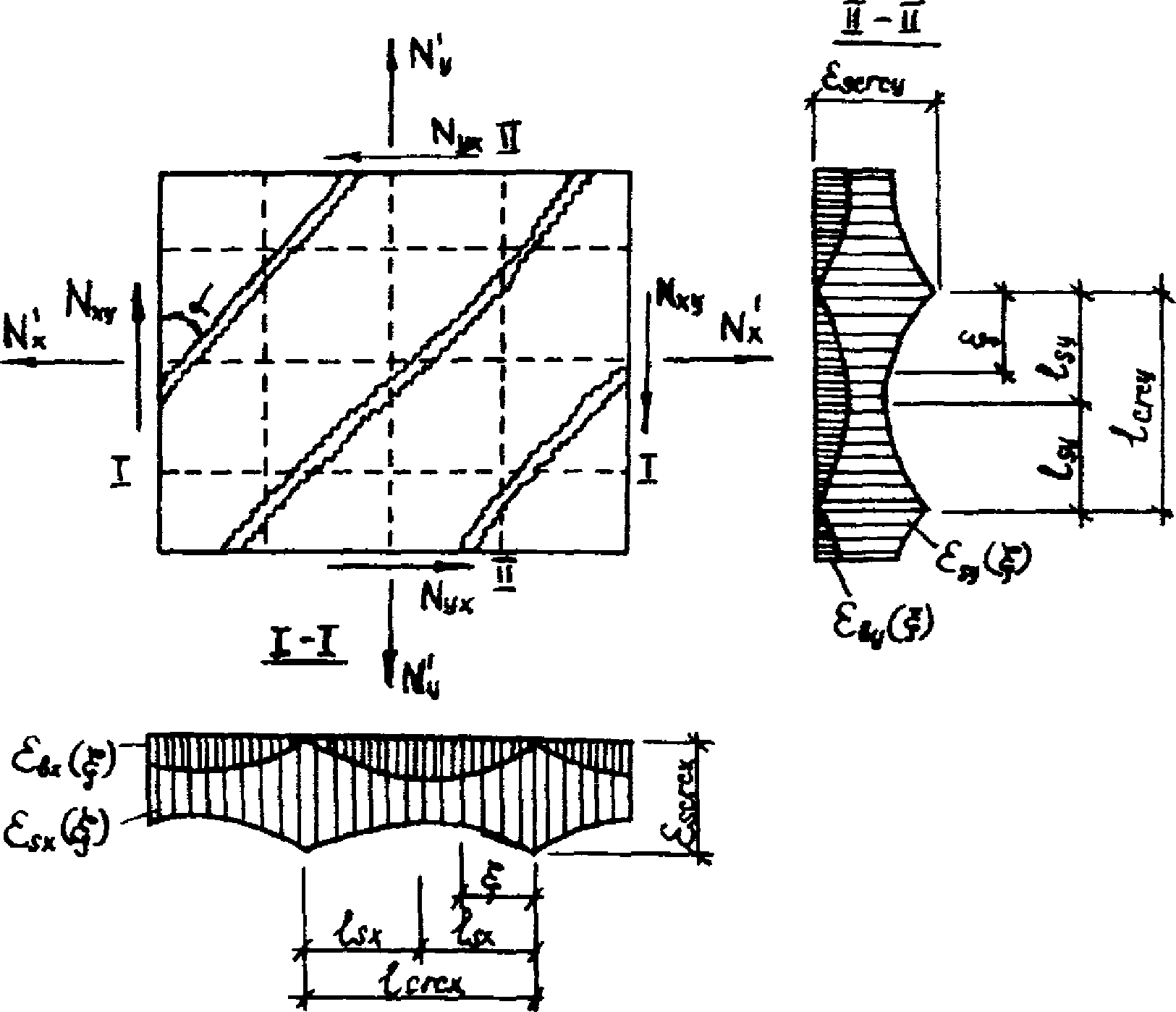
и ширины раскрытия трещин
5.26. Средние относительные деформации полос бетона между трещинами определяются по формулам:
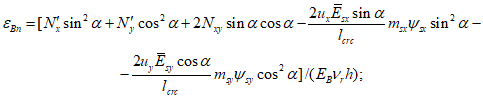
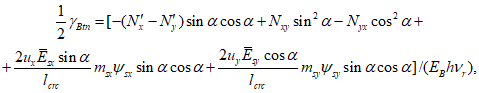
где  ,
,  - средние модули деформации арматуры;
- средние модули деформации арматуры;
 (107)
(107)где  ,
,  - коэффициенты оценки средних пластических деформаций арматуры на участках между трещинами;
- коэффициенты оценки средних пластических деформаций арматуры на участках между трещинами;
5.28. Ширину раскрытия косых трещин в угловых зонах пластины-оболочки можно определять также через относительные деформации элемента
Значение acrc должно совпадать со значением acrc, определенным через осевые смещения арматурных стержней по формуле (95) настоящих рекомендаций. Это условие может быть дополнительной проверкой расчета ширины раскрытия трещин.
5.29. Ширину раскрытия продольных трещин в пластине-оболочке (элемент Б, см. рис. 29) от действия растягивающих усилий Ny и изгибающих моментов Mq1 и ширину раскрытия трещин в растянутой зоне приопорного ребра-утолщения (элемент В) от действия изгибающего момента Mp допускается определять по [1] (п. 4.14 и 4.15).
5.30. Ширина непродолжительного раскрытия трещин, определяемая в соответствии с указаниями п. 5.27 и 5.28 настоящих рекомендаций, должна быть вычислена от действия постоянных, длительных и кратковременных нагрузок, а ширина продолжительного раскрытия трещин определяется по указаниям этих же пунктов, но от действия постоянных и длительных нагрузок. Вычисленные непродолжительное и продолжительное раскрытия трещин не должны превышать ограничений, указанных в [1] (табл. 2).
5.31. Для вычисленной реализации методики расчета гибкой пластины - пологой цилиндрической оболочки по предельным состояниям первой и второй групп, изложенной в пятом разделе рекомендаций, может быть использована специально разработанная программа KSO-88 на языке Фортран-IV.
Программа позволяет определять несущую способность пластины-оболочки, усилия в ней при эксплуатационных нагрузках (на основе вариационного метода [15] и методики [16], [17]) в линейной постановке, а также с учетом неупругих деформаций и трещин в железобетоне, и производить проверку трещиностойкости конструкции.
Примечание. Текст программы имеется в вычислительном центре БТИСМ.
ПАНЕЛЕЙ-ОБОЛОЧЕК КСО И ГИБКИХ ПЛАСТИН
6.1. Изготовление панелей-оболочек КСО в условиях ЗЖБИ организуется по стендовой технологии на полигоне или в цехе. В последнем случае цех должен иметь соответствующую высоту и краны грузоподъемностью 20 - 30 т. Технологическая линия по производству КСО может включать 2 - 4 формы-опалубки (рис. 33).
панелей-оболочек КСО
1 - кран козловой; 2 - бетоноукладчик; 3 - машина
стыковая; 4 - станок для резки арматурной стали;
5 - насосный агрегат; 6 - форма для КСО; 7 - форма
для подсводных ферм; 8 - рольганг l = 27,5 м;
9 - рольганг l = 9 м; 10 - траверса г/п 16 т;
11 - бадья для бетона; 12 - склад готовой продукции
КСО; 13 - склад арматурных сеток КСО; 14 - склад
готовой продукции подвесных ферм;
15 - складирование арматуры
6.2. Панели-оболочки следует изготовлять в металлических формах-опалубках.
Металлическая силовая форма включает поддон, продольные и торцовые борта, захватные и анкерные устройства для открывания и закрывания продольных бортов, паровую рубашку.
6.3. Процесс изготовления панелей-оболочек заключается в следующем:
подготавливается предварительно напрягаемая арматура, изготавливаются арматурные сетки каркасов и закладных деталей;
подготавливаются формы, укладывается и натягивается арматура;
приготавливается бетонная смесь;
формируется изделие;
тепловлажностная обработка;
осуществляется распалубка изделия и доставка на склад готовой продукции.
6.4. Изготовление арматурных каркасов и закладных деталей производится согласно рабочим чертежам.
6.5. Стержни класса А-IIIв подлежат вытяжке на заданное усилие и длину, на концах стержней устраиваются высаженные головки. До высадки на стержнях закрепляются анкерные плиты, закладные детали и спираль (см. рис. 7).
Выдержка стержня под нагрузкой при упрочнении должна быть не менее трех минут.
6.6. На рабочей поверхности форм не должно быть неровностей, она должна быть тщательно очищена от остатков бетона и равномерно покрыта смазкой (например "прямая эмульсия" на основе эмульсола "ЭКС"). Для участков формы со сложной конфигурацией (сопряжения верхнего пояса со стойками, полки с торцовым ребром и др.) рекомендуется использовать смазку следующего состава: машинное масло; соляровое масло (1:0,5); петролатум; керосин (1:0,5), а также смазки мыльно-парафиновую или парафиново-петролатумную в горячем виде. Можно рекомендовать эмалевые и другие смазки многоразового использования.
6.7. Армирование панели-оболочки КСО рекомендуется выполнять в такой последовательности:
установка опорных закладных деталей, выполненных заодно с монтажными петлями и откидными кольцами для строповки изделий;
установка сварных сеток опорного узла и закладных деталей нижнего пояса для крепления подвесного транспорта;
установка напрягаемых арматурных элементов в нижнем поясе с подтяжкой стержней до 30% проектного значения;
установка арматурных каркасов сеток, верхнего пояса и полки.
Для обеспечения проектного положения сварных сеток вутовой части диафрагмы, сетки торцового вута, каркасов стоек и сеток верхнего пояса выполняются сварные работы и устанавливаются фиксаторы для обеспечения защитного слоя.
Стержни и сетки арочной диафрагмы свариваются двусторонним швом длиной не менее 150 мм.
Примечания: 1. Торцовые и продольные борта опалубки устанавливаются после предварительной подтяжки напрягаемой арматуры.
Большая часть операций выполняется с помощью крана и траверсы.
После закрытия бортов арматура нижнего пояса натягивается до проектной величины.
2. При применении арматуры класса А-IIIв стержень натягивают до напряжения 500 МПа с выдержкой в течение 3 - 5 мин.
Для арматуры класса А-V величина преднапряжения 720 МПа.
6.8. Приготовление бетонной смеси для производства панелей-оболочек и гибких преднапряженных пластин производится по общепринятой технологии. Крупность зерен щебня не должна превышать 1/3 толщины полки КСО. Допускается применять щебень с крупностью до 1/2 толщины полки в количестве, не превышающем 25% общего объема щебня. Бетонная смесь должна быть средней жесткости с осадкой конуса 3 - 5 см. Повышение ее пластичности (ОК = 10 - 15 см) для бетонирования нижнего пояса, стоек, приопорного сплошного участка и диафрагмы достигается введением пластифицирующих добавок типа С-3, ЛСТМ-2 и др.
Класс тяжелого бетона для изготовления панелей-оболочек рекомендуется принимать не ниже B30.
6.9. Укладка и уплотнение бетонной смеси (формование) производится в следующем порядке: нижний пояс, стойки, опорные узлы, верхний пояс, полка.
Укладка бетона в нижний пояс производится с помощью вибробадьи и откидного виброжелоба бетонной смесью повышенной пластичности.
Бетонирование стоек фермы-диафрагмы рекомендуется производить бетоном повышенной пластичности с использованием глубинных вибраторов.
Укладку и уплотнение бетона верхнего пояса диафрагм, торцовых ребер и полки панели-оболочки при использовании металлоформ с открывающимися бортами рекомендуется производить с применением специального вибропрофилера, разработанного ЭКБ НИИСК, позволяющего механизировать укладку и уплотнение бетонной смеси в полке панели-оболочки. Уплотнение бетонной смеси в верхних поясах диафрагм и торцовых ребрах производится глубинными или навесными вибраторами, установленными на форме непосредственно в этих зонах.
Скорость формирования устанавливают в зависимости от жесткости бетонной смеси (0,35 - 1,0 м/мин).
Окончательное заглаживание производится с помощью виброшаблона или вращающегося валика, расположенного на бетоноукладчике.
6.10. Тепловлажностная обработка бетона производится контактным способом. Режим тепловой обработки при производстве в условиях полигона зависит от наружной температуры воздуха.
В летний период можно применять следующий режим тепловой обработки, ч.: предварительная выдержка при температуре 20 °C - 2; повышение температуры от 20 до 50 °C - 2; выдержка при температуре 50 °C - 3; подъем температуры до 80 °C - 2; изотермический прогрев при температуре 80 °C - 10 ... 12; снижение температуры от 80 до 20 °C - 2 ... 3.
В зимний период до начала укладки бетона производится предварительный подогрев формы до температуры 25 - 30 °C. Время изотермического прогрева бетона рекомендуется увеличивать до 18 - 24 ч.
Сокращение продолжительности термообработки без перерасхода цемента возможно путем применения специальных комплексных добавок (например, сульфата натрия с пластификатором "ускоритель твердости - пластификатор").
6.11. Тепловая обработка панели-оболочки должна производиться под укрытием складывающейся теплоизоляционной шторой (в зимний период), прорезиненной тканью или полиэтиленовой пленкой. Температуру и влажность среды под пленкой необходимо контролировать каждые 0,5 ч. Процесс теплообработки желательно автоматизировать (например, путем применения программного электронного регулятора температуры "Пуск 3" и др.).
Цикл изготовления панели КСО 36 - 48 ч., 36 ч. - в летнее время: 48 ч. - в зимнее время года.
6.12. Тепловая обработка панели-оболочки осуществляется до достижения бетоном прочности не менее 70% в летнее и 90% в зимнее время. Образцы бетона, используемые для контроля прочности, при пропаривании укладывают на полку панели-оболочки (под паронепроницаемой пленкой).
6.13. Распалубку панелей-оболочек с формы рекомендуется производить в таком порядке: снятие преднапряжения путем постепенной обрезки напрягаемых стержней арматуры; открывание бортов с помощью гидродомкратов или винтовых устройств; отрыв изделия от формы поочередно для обоих торцов панели-оболочки; съем изделия с формы.
6.14. Съем изделий панелей-оболочек с формы, их складирование и последующий монтаж рекомендуется производить специальной траверсой. Траверса (рис. 34) представляет собой балку или ферму с поперечно расположенными по концам двухсторонними консолями, оборудованными блоками и траверсами. Длина траверсы назначается с таким расчетом, чтобы угол наклона строп к горизонту при монтаже изделия составлял не менее 60°.
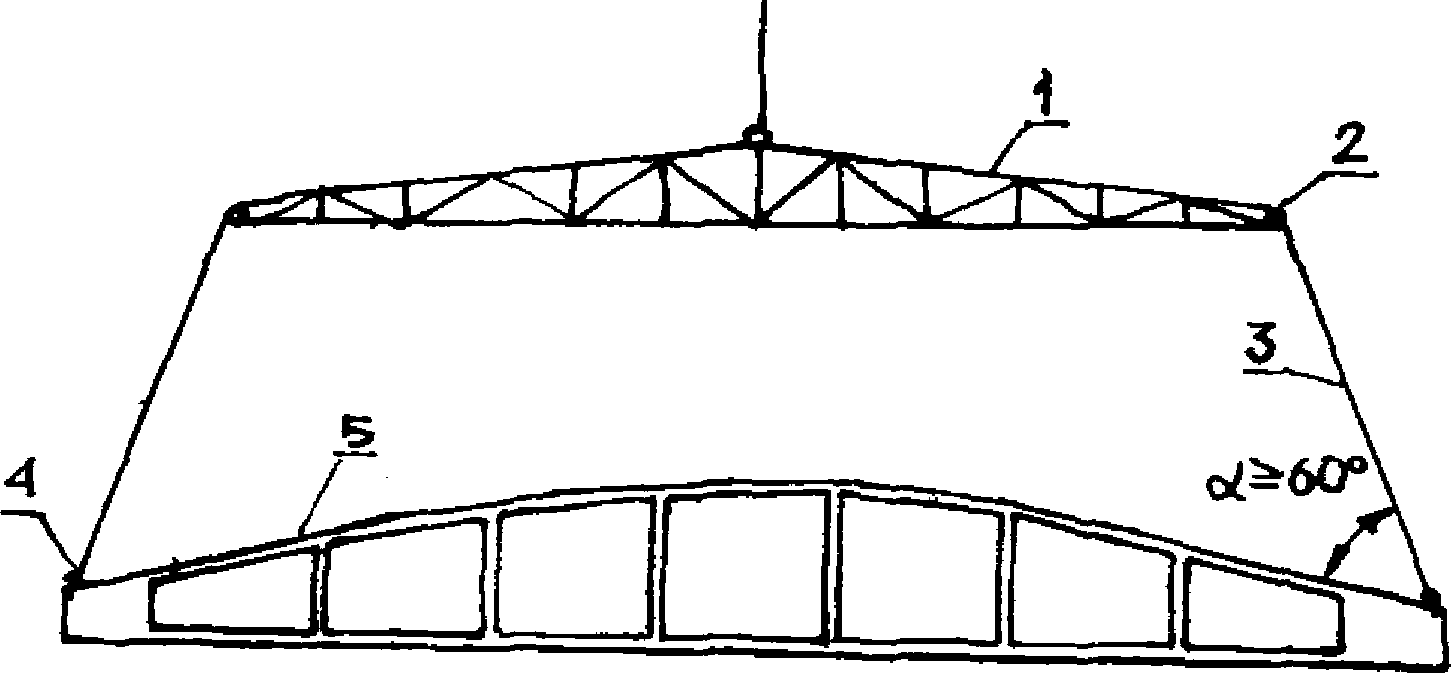
изделия с формы и складировании
1 - несущая конструкция траверсы; 2 - консоли с блоками;
3 - тросы; 4 - монтажная петля с откидным кольцом;
5 - панель КСО
6.15. Гибкие преднапряженные пластины рекомендуется изготовлять размерами 3 x 6 x 0,04 м из бетона классов B25 - B30 с применением высокопрочной проволоки класса ВрП диаметром 3 - 5 мм.
Пластины применяют в сочетании с панелями КСО с укладкой их в промежутках между панелями с шагом 3 м.
Пластины готовят цельными. Необходимые проемы устраивают в панелях КСО.
6.16. Изготовление пластин целесообразно организовать по поточно-агрегатной технологии в цехе или на полигоне завода, оборудованном виброплощадкой и камерами пропаривания. Пластины готовят с использованием силовых металлических форм.
Величина предварительного напряжения определяется способом натяжения и способом образования анкерных головок на концах стержней и составляет 0,6 - 0,8 от нормативного сопротивления растяжению арматуры.
6.17. Изготовление гибких предварительно напряженных пластин размерами 3 x 6 x 0,04 м может быть организовано по поточно-агрегатной технологии в цехе или на полигоне завода с применением металлических силовых форм в количестве 4 - 6 шт.
6.18. Металлическая силовая форма представляет собой плоскую сварную конструкцию в виде балочной клетки, обшитой стальным листом, упоров для натяжения арматуры и ограничителей изделия.
В зависимости от способа напряжения упоры для восприятия усилий преднапряжения могут устанавливаться либо непосредственно на силовой раме - при электротермическом или электротермомеханическом способе натяжения (рис. 35), либо с одной стороны на раме, а с другой стороны на неподвижной силовой траверсе - при механическом способе натяжения (см. рис. 35, б).
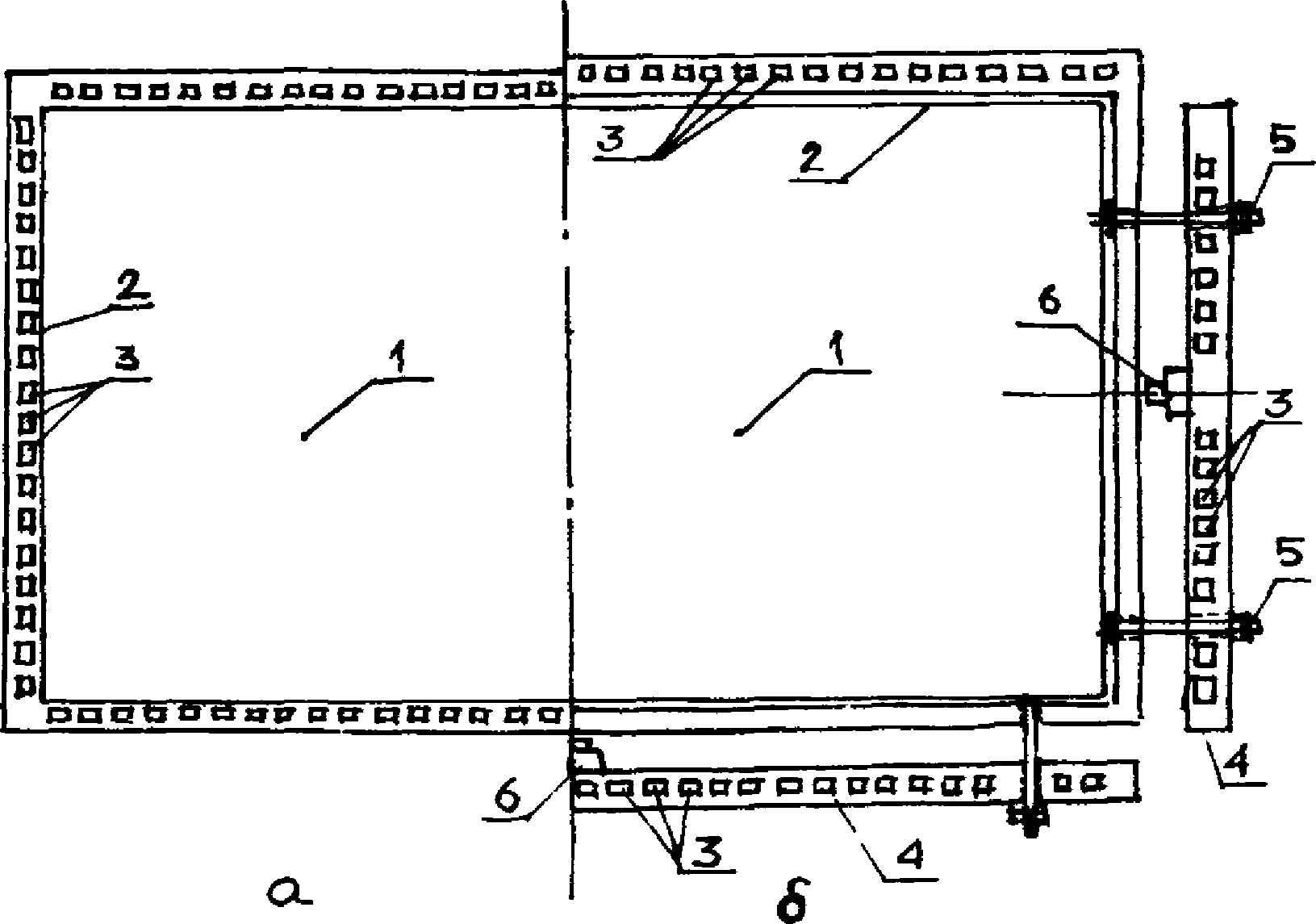
гибких преднапряженных пластин
а - при электротермическом способе натяжения;
б - при механическом способе натяжения; 1 - силовой поддон;
2 - ограничители размеров изделия; 3 - неподвижные упоры
для натяжения; 4 - подвижная силовая балка;
5 - направляющие с элементами крепления;
6 - гидродомкрат
Конструкция силовой формы должна надежно обеспечивать проектное положение арматуры, преднапряжение всех арматурных проволок с одинаковым усилием и иметь соответствующие ограждения, обеспечивающие безопасность работающих.
6.19. Изготовление анкерных головок напрягаемых арматурных элементов рекомендуется производить методом холодного или горячего прессования на специально разработанных автоматах. Изготовление высаженных головок с подогревом концов стержня до 600 - 700° менее трудоемко и обеспечивает более стабильную величину контролируемого напряжения при натяжении, но при назначении контролируемой величины преднапряжения следует учитывать некоторое снижение прочности проволоки на разрыв в зоне головок, определяемое экспериментальным путем.
6.20. Предварительное напряжение пластин с точки зрения уменьшения трудозатрат целесообразно производить механическим способом с одновременным напряжением всех стержней одного направления. При этом упоры для восприятия усилия натяжения должны быть выполнены из высокопрочной стали, обеспечивающей надежную анкеровку и исключение местных пластических деформаций.
6.21. Укладка бетонной смеси при изготовлении гибкой пластины производится с помощью универсальной бадьи, а уплотнение - с помощью виброрейки или виброшаблона с вращающимся валом на всю ширину изделия. При этом, как показал опыт изготовления таких конструкций, оптимальными являются следующие параметры виброрейки: частота - 50 - 60 Гц; амплитуда колебаний - 0,2 - 0,3 мин; скорость передвижения 0,3 - 0,5 м/мин.
Уплотнение выполняется в два прохода (прямой и обратный). При обратном проходе скорость движения виброрейки рекомендуется увеличивать до 1 м/мин.
6.22. Тепловлажностную обработку пластин рекомендуется осуществлять в пропарочных камерах периодического действия при следующем режиме тепловой обработки, ч.: предварительная выдержка изделия при температуре 20 °C - 1,5 ... 2; повышение температуры от 20 до 50 °C - 2; выдержка при температуре 50 °C - 1,5 ... 2; подъем температуры до 80 °C - 1,5 ... 2; изотермический прогрев при температуре 80 °C - 6 ... 8; снижение температуры до 20 °C - 2.
6.23. Съем пластин с формы и изгиб пластин по заданному радиусу рекомендуется производить с помощью самобалансирующей траверсы, разработанной БТИСМ им. Гришманова или НИИСК, представляющей собой горизонтальную сварную раму с блоками, тросами и рычажно-винтовыми прижимами для изгиба пластины.
Подъем изделия производится за шесть строп, идущих от блоков траверсы. При этом из-за различной длины строп (30 - 50 мм) уже при подъеме под действием собственной массы обеспечивается частичный изгиб пластины по цилиндрической поверхности в продольном направлении и повышение ее изгибной жесткости в поперечном направлении.
Цикл изготовления гибкой пластины составляет 24 ч.
Полный изгиб пластин (прижатие к упорам-выступам панелей-оболочек КСО) по заданной кривизне осуществляется при их монтаже с помощью рычажно-винтовых прижимов, установленных на траверсе.
6.24. Окончательная фиксация пластин производится после приварки закладных частей и замоноличивания швов в покрытии.
И ГИБКОЙ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПЛАСТИНЫ - ПОЛОГОЙ
ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ КОМБИНИРОВАННОГО ПОКРЫТИЯ
ПРОИЗВОДСТВЕННОГО ЗДАНИЯ
Отапливаемое производственное здание возводят во II районе снеговых нагрузок. Влажностный режим здания нормальный, среда неагрессивная. По ответственности здание относится к классу II. Здание оборудовано четырьмя подвесными кранами грузоподъемностью 3,2 т.
Габаритные размеры панелей-оболочек КСО 3 x 24 м приняты согласно рис. 2 и 3 настоящих рекомендаций. Армирование полки панели осуществляется сварной рулонной сеткой из арматурной проволоки класса Вр-I. Плоские сетки верхних поясов ферм-диафрагм, торцовые ребра, опорные узлы, пространственные каркасы стоек ферм-диафрагм - из горячекатаной арматурной стали класса А-III. Напрягаемая арматура - из горячекатаной арматурной стали класса А-V.
Для изготовления панели предусмотрен бетон класса B45.
Расчетные характеристики материала панели-оболочки: бетон класса B45, подвергнутый тепловой обработке при атмосферном давлении - RB = 25 МПа; RBt = 1,45 МПа; RB,ser = 32 МПа; RBt,ser = 2,2 МПа; EB = 34·103 МПа; арматура класса А-V - Rs = 680 МПа; Rs,ser = 785 МПа; Es = 190·103 МПа; А-III - Rs = Rsc = 365 МПа; Es = 200·103 МПа;  ; Es = 170·103 МПа.
; Es = 170·103 МПа.
 ; Es = 170·103 МПа.
; Es = 170·103 МПа.Для изготовления гибкой пластины принят бетон класса B30. Армирование осуществляется напрягаемой в двух направлениях проволочной арматурой класса Вр-II.
Расчетные характеристики материала: бетон класса B30, подвергнутый тепловой обработке при атмосферном давлении - RB = 17 МПа; RBt = 1,2 МПа; RB,ser = 22 МПа; Rbt,ser = 1,8 МПа; Eb = 29·103 МПа; арматура класса  ; Es = 200·103 МПа.
; Es = 200·103 МПа.
 ; Es = 200·103 МПа.
; Es = 200·103 МПа.Нагрузки на 1 м2 поверхности покрытия приведены в табл. 1. Все расчетные нагрузки определены с учетом коэффициента надежности по назначению конструкций  .
.
 .
.Вид равномерно распределенной нагрузки | Нагрузка, кПа | Коэффициент надежности по нагрузке | Расчетная нагрузка при | |
нормативная | расчетная при | |||
1 | 2 | 3 | 4 | 5 |
на панель-оболочку: | ||||
постоянная | 3,007 | 2,857 | - | 3,353 |
в т.ч. водоизоляционный ковер | 0,1 | 0,095 | 1,3 | 0,124 |
цементная стяжка 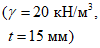 | 0,3 | 0,285 | 1,3 | 0,371 |
утеплитель пенобетон 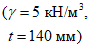 | 0,7 | 0,665 | 1,3 | 0,865 |
вес панели-оболочки | 1,907 | 1,812 | 1,1 | 1,993 |
временная | 0,7 | 0,665 | 1,4 | 0,931 |
снеговая нагрузка | 0,7 | 0,665 | 1,4 | 0,931 |
в т.ч. длительная | 0 | 0 | - | 0 |
кратковременная | 0,7 | 0,665 | 1,4 | 0,931 |
полная | 3,707 | 3,522 | - | 4,284 |
на гибкую пластину: | ||||
постоянная | 2,1 | 1,995 | - | 2,404 |
в т.ч. водотеплоизоляционный ковер | 1,1 | 1,045 | 1,3 | 1,359 |
вес пластины | 1 | 0,95 | 1,1 | 1,045 |
временная | 0,7 | 0,665 | 1,4 | 0,931 |
снеговая нагрузка | 0,7 | 0,665 | 1,4 | 0,931 |
в т.ч. длительная | 0 | 0 | - | 0 |
кратковременная | 0,7 | 0,665 | 1,4 | 0,931 |
полная | 2,8 | 2,66 | - | 3,335 |
Подвесные электрические краны грузоподъемностью 3,2 т создают сосредоточенные нагрузки на диафрагмы панели-оболочки. Максимальное нормативное давление Pmax на тележку составляет 21,36, а минимальное Pmin - 5,46 кН.
Длительные сосредоточенные нагрузки определяют по линии влияния (рис. 1) от действия одного подвесного крана с учетом коэффициента 0,5
F1max = 21,36·0,5·(1 + 0,4) + 4,71 = 19,662 кН,
где 4,71 кН - нагрузка от крановой балки,
F1min = 5,46·0,5·(1 + 0,4) + 4,71 = 8,532 кН.
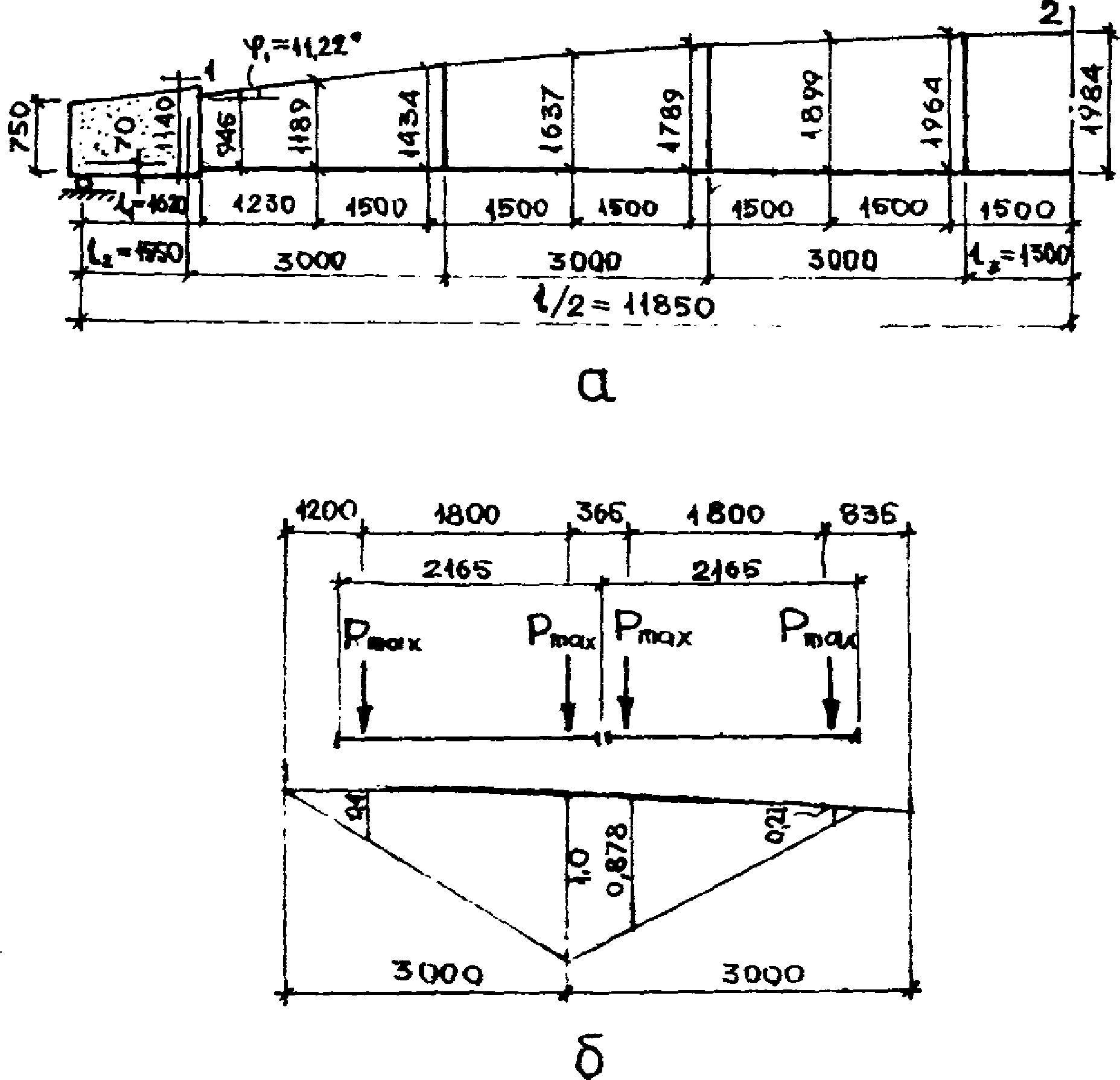
а - геометрическая основа; б - линия влияния давления
на диафрагму и установка нагрузки в невыгодное положение
Кратковременные сосредоточенные нагрузки определяют от действия остальных трех подвесных кранов:
F1max = 21,36·(1 + 0,4) + 4,71 = 34,614 кН;
F1min = 5,46·(1 + 0,4) + 4,71 = 12,354 кН;
F2max = 21,36·(1 + 0,4 + 0,878 + 0,278) + 4,71 = 59,306;
F2min = 5,46·2,556 + 4,71 = 18,666 кН.
Расчет панели-оболочки по несущей способности
Расчет полки. Расчетная нагрузка на полку от веса водотеплоизоляционного слоя - 1,36 кПа; от веса полки - 0,03·2,5·1,1·0,95·9,81 = 0,769 кПа; от снега - 0,931 кПа; полная - P = 1,36 + 0,769 + 0,931 = 3,06 кПа.
Рабочая высота сечения - 1,5 см, бетон тяжелый класса B45 с учетом коэффициента  , арматура класса
, арматура класса 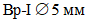 Rs = 36 кН/см2.
Rs = 36 кН/см2.
 , арматура класса
, арматура класса 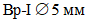 Rs = 36 кН/см2.
Rs = 36 кН/см2.Расчет полки у опорных узлов. По формуле (10) настоящих рекомендаций
M = 0,2P = 0,2·3,06 = 0,612 кН·м/м = 61,2 кН·см/м.
По формуле [6] вычисляем:
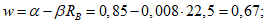
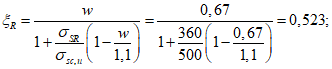
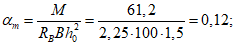
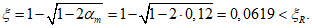
По таблицам пособия [7] значение функции  . Требуемая площадь сечения арматуры на 1 пог. м полки у опорных узлов в продольном и поперечном направлениях
. Требуемая площадь сечения арматуры на 1 пог. м полки у опорных узлов в продольном и поперечном направлениях
 . Требуемая площадь сечения арматуры на 1 пог. м полки у опорных узлов в продольном и поперечном направлениях
. Требуемая площадь сечения арматуры на 1 пог. м полки у опорных узлов в продольном и поперечном направлениях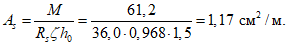
Принимаем шаг стержней 15 см, тогда As = 1,31 см2/м.
В средней части панели устанавливаем в поперечном направлении полки  , шаг 15 см, а в продольном -
, шаг 15 см, а в продольном -  , шаг 20 см.
, шаг 20 см.
Расчет фермы-диафрагмы
Основные сочетания нагрузок на ферму-диафрагму состоят из двух групп. К первой группе относится постоянная нагрузка и одна кратковременная от снега. Ко второй относится постоянная нагрузка и две временных - от снега и от подвесных кранов.
Чтобы определить по какой группе нагрузок вести расчет, найдем усилия в нижнем поясе диафрагмы от этих групп нагрузок, воспользовавшись соотношением (4) настоящих рекомендаций.
Усилие в нижнем поясе диафрагмы от первой группы нагрузок. Полная равномерно распределенная расчетная нагрузка на 1 пог. м диафрагмы P = (4,284 + 3,335)·1,5 = 11,429 кН/м.
Изгибающие моменты в основной системе от этой нагрузки:
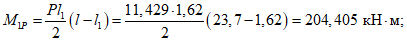
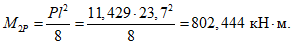
Изгибающие моменты в основной системе от нагрузки
X1 = 1; M11 = -0,945 м; M21 = -1,984 м.
Задавшись в первом приближении  , по формуле (3) настоящих рекомендаций получим усилия в нижнем поясе диафрагмы
, по формуле (3) настоящих рекомендаций получим усилия в нижнем поясе диафрагмы
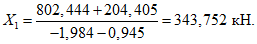
Усилие в нижнем поясе диафрагмы от второй группы нагрузок. Нагрузка на 1 пог. м диафрагмы P = (3,353 + 0,931·0,9 + 2,404 + 0,931·0,9)1,5 = 11,149 кПа.
Сосредоточенные нагрузки учитываются с коэффициентами: надежности по назначению  ; надежности по нагрузке
; надежности по нагрузке  ; сочетаний
; сочетаний  ,
,  для длительной части нагрузки и
для длительной части нагрузки и  для кратковременной. Определим величины нагрузок:
для кратковременной. Определим величины нагрузок:
 ; надежности по нагрузке
; надежности по нагрузке  ; сочетаний
; сочетаний  ,
,  для длительной части нагрузки и
для длительной части нагрузки и  для кратковременной. Определим величины нагрузок:
для кратковременной. Определим величины нагрузок:F1max = 19,662·0,95·1,1·0,7·0,95 + 34,614·0,95·1,1·0,7·0,9 = 37,718 кН;
F1min = 8,532·0,95·1,1·0,7·0,95 + 12,354·0,95·1,1·0,7·0,9 = 14,514 кн;
F2max = 59,306·0,95·1,1·0,7·0,9 = 41,213 кН;
F2min = 18,666·0,95·1,1·0,7·0,9 = 12,971 кН.
Сведем действующие нагрузки к симметричным:
Fmax = (37,718 + 41,213)·0,5 = 39,466 кН;
Fmin = (14,514 + 12,971)·0,5 = 13,743 кН.
Изгибающие моменты в основной системе от второй группы нагрузок составят (рис. 2)
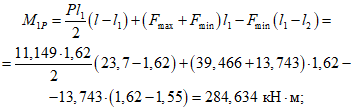
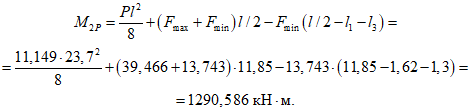
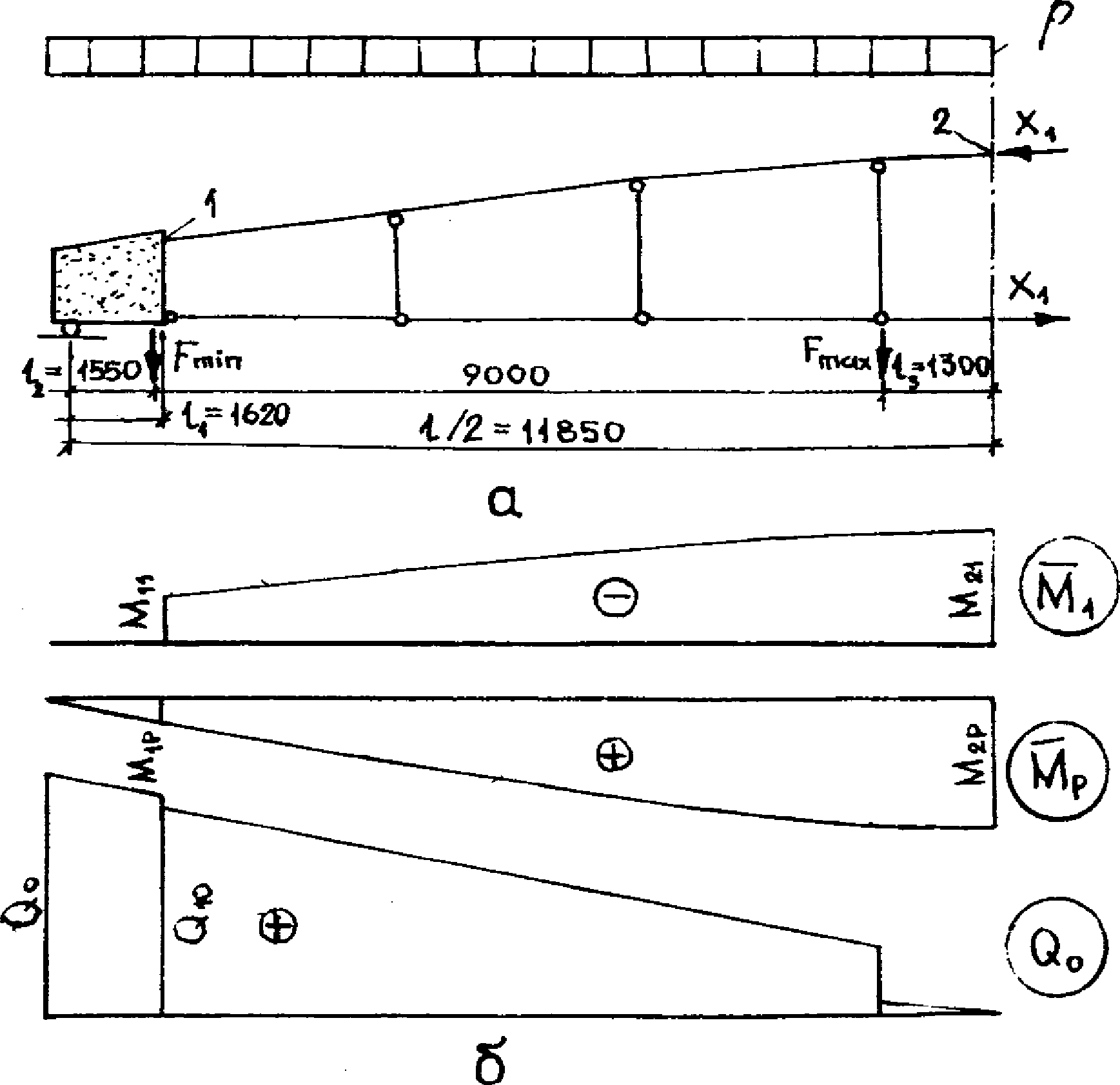
а - расчетная схема и нагрузки; б - единичная: грузовые
эпюры моментов и поперечных сил в верхнем поясе
Вычисляем усилия в нижнем поясе диафрагмы
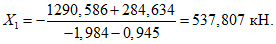
Так как усилие X1 = 343,752 кН < 0,82·537,802 = 440,998 кН, то расчет прочности ведем по второй группе нагрузок.
Изгибающие моменты, нормальные и поперечные силы в сечениях 1 и 2 верхнего пояса диафрагмы определяются по формулам (1) настоящих рекомендаций, учитывая, что  :
:
 :
: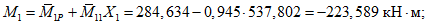
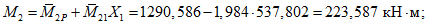
Q0 = Pl/2 + Fmin + Fmax = 11,149·11,85 + 13,743 + 39,466 =
= 185,325 кН;
Q10 = Q0 - Pl1 - Fmin = 185,325 - 11,149·1,62 - 13,743 =
= 160,433 кН;
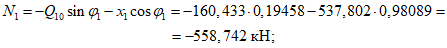
N2 = -X1 = -537,802 кН;
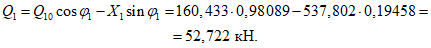
Подбор сечений арматуры в элементах фермы-диафрагмы
Нижний пояс диафрагмы. Площадь сечения предварительно напряженной арматуры класса А-V определяем по формуле (3.196) [7].
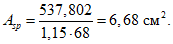
Принимаем  А-V (Asp = 8,043 см2).
А-V (Asp = 8,043 см2).
Верхний пояс диафрагмы имеет два расчетных сечения (см. рис. 2, б): у опорного узла - сечение 1; посередине пролета - сечение 2.
Подбор арматуры в сечении 1 (рис. 3). Геометрические параметры сечения: высота h = 49,5 см; ширина переменная. Изгибающий момент и нормальная сила, действующая в сечении: M1 = 223,589 кН·м; N1 = 558,742 кН. Для бетона класса B45 с учетом коэффициента 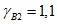
 , для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, h01 = 49,5 - 1,5 = 48 см, h02 = 46,5 см, h03 = 6 см, As1 = 1,31·1,4 = 1,834 см2.
, для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, h01 = 49,5 - 1,5 = 48 см, h02 = 46,5 см, h03 = 6 см, As1 = 1,31·1,4 = 1,834 см2.
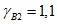
 , для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, h01 = 49,5 - 1,5 = 48 см, h02 = 46,5 см, h03 = 6 см, As1 = 1,31·1,4 = 1,834 см2.
, для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, h01 = 49,5 - 1,5 = 48 см, h02 = 46,5 см, h03 = 6 см, As1 = 1,31·1,4 = 1,834 см2.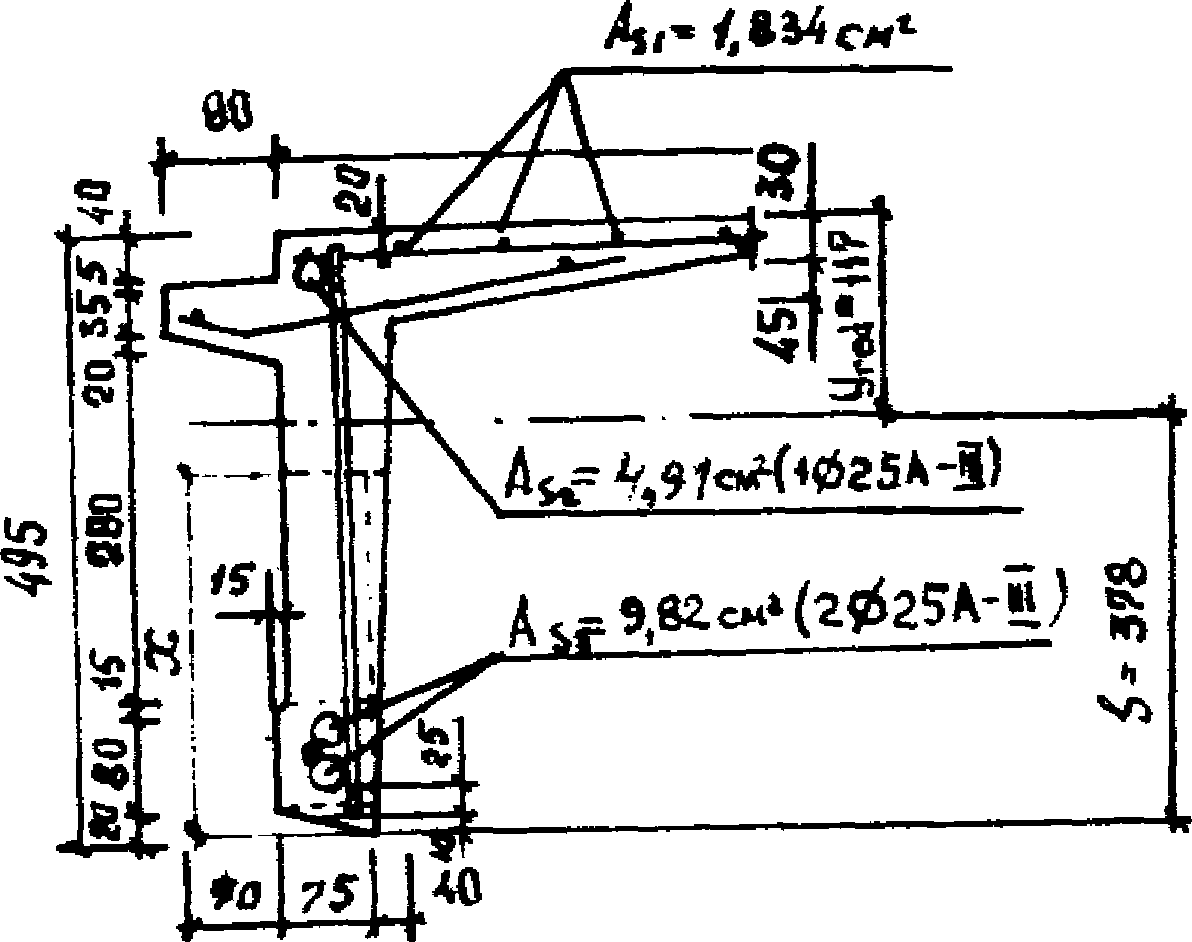
арочной диафрагмы
По формуле (25) СНиП 2.03.01-84 находим граничное значение относительной высоты сжатой зоны бетона, при котором предельное состояние сечения наступает одновременно с достижением в растянутой арматуре напряжений, равных расчетному сопротивлению Rs
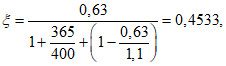
где w = 0,85 - 0,008·27,5 = 0,63.
Высота сжатой зоны сечения определяется по формуле
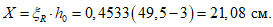
Чтобы определять площадь сечения растянутой и сжатой арматуры по формулам (7) и (9) настоящих рекомендаций, найдем значения площади сжатой зоны бетона AB и ее статического момента SB относительно центра тяжести сечения. Для этого площадь сжатой зоны бетона разобьем на участки (см. рис. 3). Определяем площадь сжатой зоны бетона
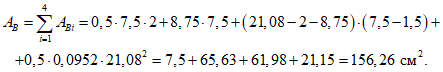
Статический момент сжатой зоны бетона
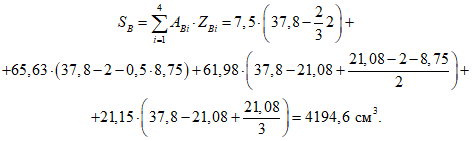
По формуле (7, а) вычисляем
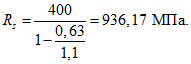
По формуле (7) определяем напряжения в арматуре
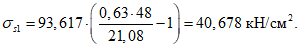
Принимаем  ;
;
 ;
;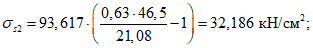
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
принимаем  ;
;
 ;
;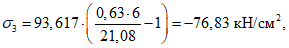
принимаем  .
.
 .
.Количество растянутой и сжатой арматуры определяем по формулам (8) и (9)
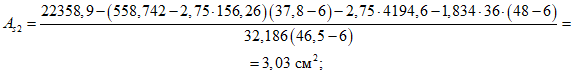
принимаем  А-III (As2 = 3,14 см2);
А-III (As2 = 3,14 см2);
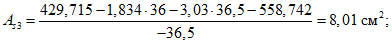
принимаем  А-III (As3 = 7,6 см2).
А-III (As3 = 7,6 см2).
Подбор арматуры в сечении 2 (рис. 4). Геометрические параметры сечения: высота h = 40 см; ширина сжатой зоны сечения B'f = 140 см; рабочая высота h0 = h - a = 40 - 6,3 = 33,7 см. Изгибающий момент и нормальная сила, действующие в сечении, соответственно: M2 = 223,587 кН·м, N2 = 537,802 кН. Для бетона класса B45 с учетом коэффициента 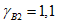
 ; для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, арматура полки As2 = (0,196/20)140 = 1,372 см, Rs = 36 кН/см2.
; для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, арматура полки As2 = (0,196/20)140 = 1,372 см, Rs = 36 кН/см2.
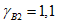
 ; для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, арматура полки As2 = (0,196/20)140 = 1,372 см, Rs = 36 кН/см2.
; для арматуры класса А-III Rs = 365 МПа = 36,5 кН/см2, арматура полки As2 = (0,196/20)140 = 1,372 см, Rs = 36 кН/см2.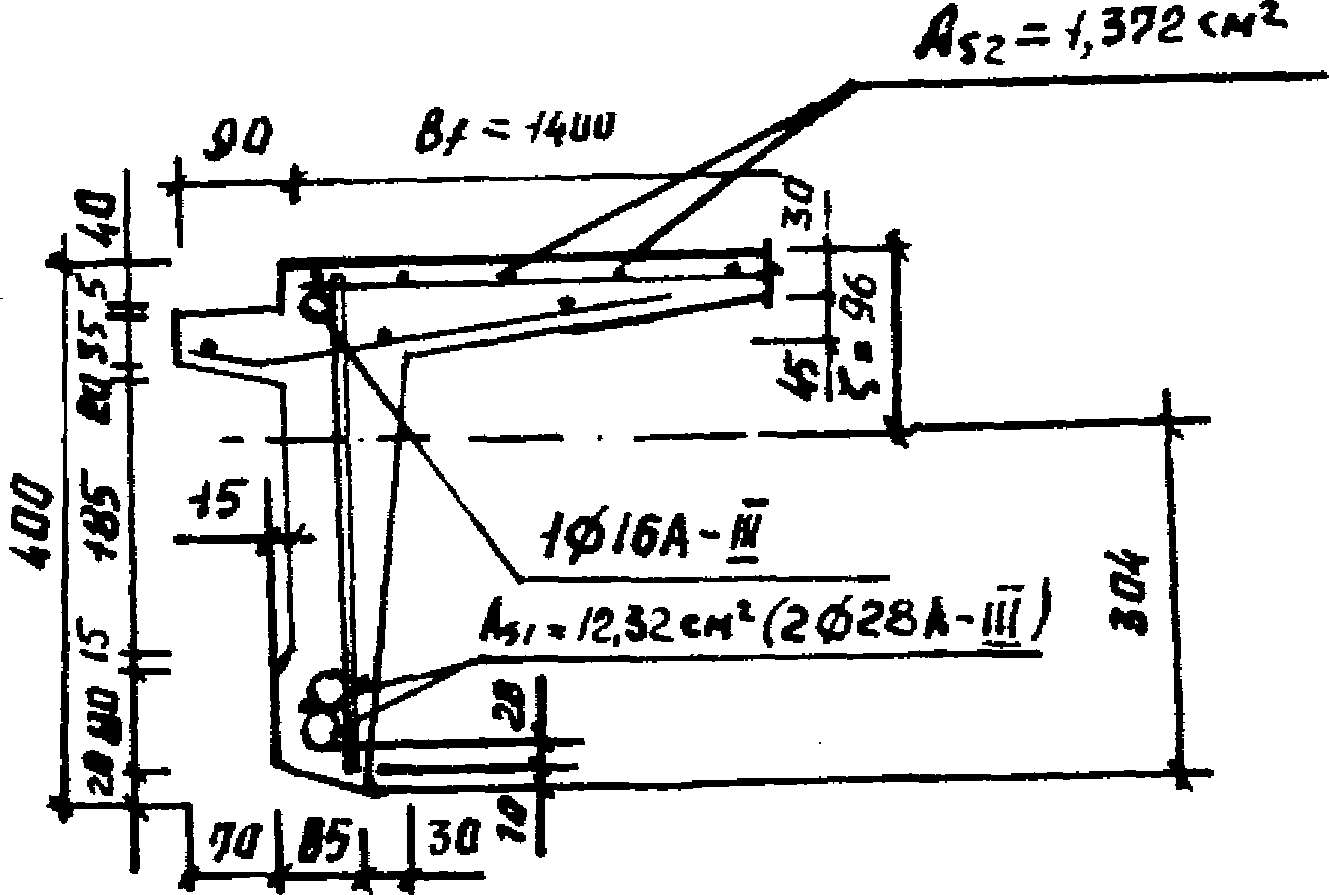
арочной диафрагмы
По формуле (6) настоящих рекомендаций, задавшись высотой сжатой зоны бетона  и определив по формуле (7) напряжения в арматурах As1, As2, As3, определяем высоту сжатой зоны бетона
и определив по формуле (7) напряжения в арматурах As1, As2, As3, определяем высоту сжатой зоны бетона  . Задавшись несколькими значениями высоты сжатой зоны находим, что при
. Задавшись несколькими значениями высоты сжатой зоны находим, что при 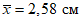
 ,
,  ,
,  .
.
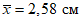
 ,
,  ,
,  .
.Высота сжатой зоны сечения
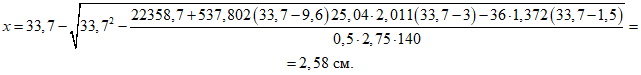
Требуемую площадь сечения растянутой арматуры определим по формуле (5) настоящих рекомендаций
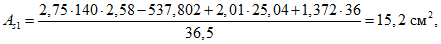
которой удовлетворяют  . Однако диаметр 32 мм не удовлетворяет условию по защитному слою, так как 32·3 = 96 мм, а ширина сечения верхнего пояса по низу равна 85 мм.
. Однако диаметр 32 мм не удовлетворяет условию по защитному слою, так как 32·3 = 96 мм, а ширина сечения верхнего пояса по низу равна 85 мм.
 . Однако диаметр 32 мм не удовлетворяет условию по защитному слою, так как 32·3 = 96 мм, а ширина сечения верхнего пояса по низу равна 85 мм.
. Однако диаметр 32 мм не удовлетворяет условию по защитному слою, так как 32·3 = 96 мм, а ширина сечения верхнего пояса по низу равна 85 мм.Перераспределим часть пролетного момента в сечении 2 на сечение 1. Задаемся коэффициентом перераспределения внутренних усилий  . Тогда
. Тогда
 . Тогда
. Тогда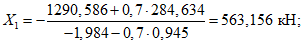
усилия в верхнем поясе диафрагмы
M1 = 284,634 - 0,945·563,156 = -247,548 кН·м;
M2 = 1290,586 - 1,984·563,156 = 173,284 кН·м;
Q0 = 185,325 кН;
Q10 = 160,433 кН;
N1 = -160,433·0,19458 - 563,156·0,98089 = -583,611 кН;
N2 = -X1 = -563,156 кН;
Q1 = 160,433·0,98089 - 563,156·0,19458 = 47,788 кН.
Подбор арматуры в сечении 1:
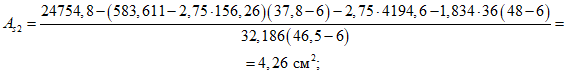
принимаем  А-III (As = 4,91 см2)
А-III (As = 4,91 см2)
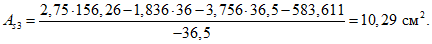
Принимаем  А-III (As = 9,82 см2).
А-III (As = 9,82 см2).
Подбор арматуры в сечении 2. Высота сжатой зоны сечения при  и
и  ,
,  ,
,  ;
;
 и
и  ,
,  ,
,  ;
;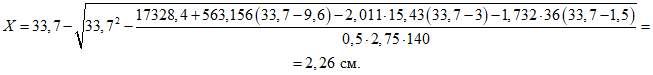
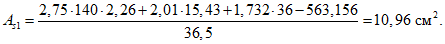
Принимаем  А-III (As = 12632 см2).
А-III (As = 12632 см2).
Стойки диафрагмы. Геометрические параметры сечения стоек: b = 0,14 м: h = 0,12 м: длина средней стойки hc = 2,15 - 0,4 - 0,14 = 1,61 м; рабочая высота сечения ho = h - a = 0,12 - 0,026 = 0,094 м. Бетон класса B45 с учетом коэффициента 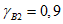
 , RBt,ser = 0,22·0,9 = 0,198 кН/см2. Арматура класса А-III Rs = 36,5 кН/см2. Максимальная нормативная нагрузка Nt,ser = F2max = 59,306 кН. Длина нижнего пояса, учитываемого в расчете средней стойки диафрагмы, ln = 1,5 + 1,3 = 2,8 м. Масса 1 пог. м стойки: gc = 0,155·0,12·2,5·9,81·1,1 = 0,502 кН/м; масса 1 пог. м нижнего пояса gn = 0,14·0,12·2,5·9,81·1,1 = 0,453 кН/м.
, RBt,ser = 0,22·0,9 = 0,198 кН/см2. Арматура класса А-III Rs = 36,5 кН/см2. Максимальная нормативная нагрузка Nt,ser = F2max = 59,306 кН. Длина нижнего пояса, учитываемого в расчете средней стойки диафрагмы, ln = 1,5 + 1,3 = 2,8 м. Масса 1 пог. м стойки: gc = 0,155·0,12·2,5·9,81·1,1 = 0,502 кН/м; масса 1 пог. м нижнего пояса gn = 0,14·0,12·2,5·9,81·1,1 = 0,453 кН/м.
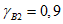
 , RBt,ser = 0,22·0,9 = 0,198 кН/см2. Арматура класса А-III Rs = 36,5 кН/см2. Максимальная нормативная нагрузка Nt,ser = F2max = 59,306 кН. Длина нижнего пояса, учитываемого в расчете средней стойки диафрагмы, ln = 1,5 + 1,3 = 2,8 м. Масса 1 пог. м стойки: gc = 0,155·0,12·2,5·9,81·1,1 = 0,502 кН/м; масса 1 пог. м нижнего пояса gn = 0,14·0,12·2,5·9,81·1,1 = 0,453 кН/м.
, RBt,ser = 0,22·0,9 = 0,198 кН/см2. Арматура класса А-III Rs = 36,5 кН/см2. Максимальная нормативная нагрузка Nt,ser = F2max = 59,306 кН. Длина нижнего пояса, учитываемого в расчете средней стойки диафрагмы, ln = 1,5 + 1,3 = 2,8 м. Масса 1 пог. м стойки: gc = 0,155·0,12·2,5·9,81·1,1 = 0,502 кН/м; масса 1 пог. м нижнего пояса gn = 0,14·0,12·2,5·9,81·1,1 = 0,453 кН/м.Расчет на нагрузки от подвесного транспорта. Нагрузка на среднюю стойку  .
.
 .
.Требуемая площадь сечения арматуры стойки  .
.
 .
.Расчет на горизонтальные нагрузки, возникающие при транспортировании. Изгибающий момент, возникающий в месте примыкания стойки к верхнему поясу, с учетом коэффициента надежности по назначению  , вычисляется по формуле (13) настоящих рекомендаций
, вычисляется по формуле (13) настоящих рекомендаций
 , вычисляется по формуле (13) настоящих рекомендаций
, вычисляется по формуле (13) настоящих рекомендаций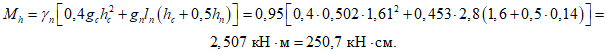
Вычисляем значения:  ;
;
 ;
;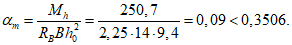
Сжатая арматура не учитывается. Значение функции  . Требуемая площадь сечения арматуры
. Требуемая площадь сечения арматуры
 . Требуемая площадь сечения арматуры
. Требуемая площадь сечения арматуры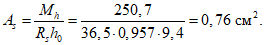
Конструктивно принимаем  А-III (As = 2,26 см2). Стойка армируется пространственным каркасом
А-III (As = 2,26 см2). Стойка армируется пространственным каркасом  А-III (As = 4,52 см2).
А-III (As = 4,52 см2).
Расчет по раскрытию трещин. Напряжение в стержнях арматуры стойки
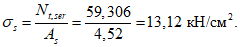
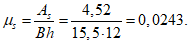
Ширина раскрытия трещин
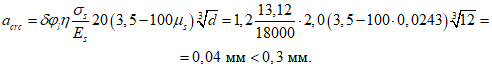
Таким образом, конструктивные соображения стали определяющими при подборе арматуры стоек.
Опорный узел. Расчет по прочности наклонных сечений. Геометрические параметры опорного узла с плавно меняющейся высотой: длина l1 = 162 см; переменная высота h1 = 75 см, h2 = 114 см; средняя ширина B = 13 см (см. рис. 5). Расчетное сопротивление бетона с учетом коэффициента 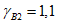
 ,
,  . Расчетное сопротивление растяжению для предельного состояния второй группы предварительно напряженной арматуры класса А-V Rs,ser = 785 МПа, расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы
. Расчетное сопротивление растяжению для предельного состояния второй группы предварительно напряженной арматуры класса А-V Rs,ser = 785 МПа, расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы 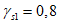
 .
.
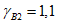
 ,
,  . Расчетное сопротивление растяжению для предельного состояния второй группы предварительно напряженной арматуры класса А-V Rs,ser = 785 МПа, расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы
. Расчетное сопротивление растяжению для предельного состояния второй группы предварительно напряженной арматуры класса А-V Rs,ser = 785 МПа, расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы 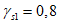
 .
.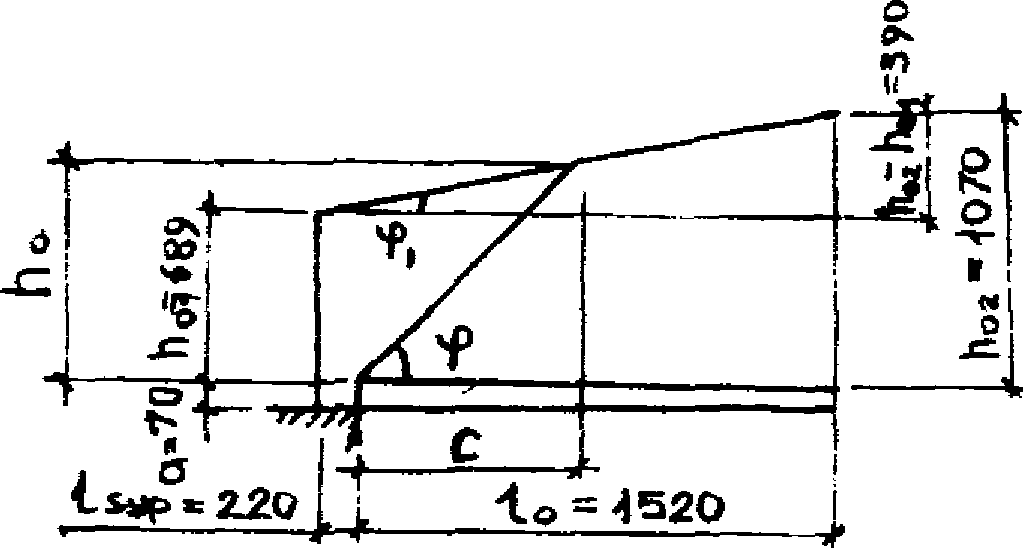
Требуется определить диаметр хомутов и их шаг. В опорном узле устанавливается одна плоская сетка арматуры.
Расчет ведем путем последовательных приближений, задавая 2 - 3 значения угла наклонной трещине, определяя в каждом случае поперечную силу, воспринимаемую бетоном и арматурой в наклонном сечении и сравнивая с действующей поперечной силой. Диаметр хомутов и их шаг задаем из условий:
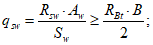
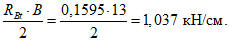
Принимаем хомуты  с шагом Sw = 20 см. Тогда
с шагом Sw = 20 см. Тогда  .
.
 .
.Расчет по первому приближению. Наклонное сечение располагаем под углом  . Вычисляем
. Вычисляем
 . Вычисляем
. ВычисляемИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
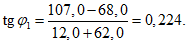
Рабочая высота сечения
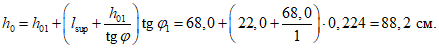
Длина проекции наклонного сечения
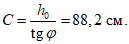
По формулам СНиП 2.03.01-84 ведем дальнейшие вычисления.
Определяем коэффициент
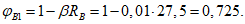
Вычисляем:
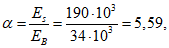
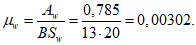
Коэффициент
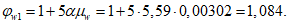
Находим поперечную силу, действующую на расстоянии C = 88,2 см от опоры
Q = Q0 - Ph0 = 185,325 - 11,149·0,882 = 175,49 кН.
Проверяем неравенство
0,3·1,084·0,725·2,75·13·88,2 = 743,42 кН > 175,49 кН.
Неравенство выполняется.
Для вычисления коэффициента  найдем силу предварительного обжатия арочной диафрагмы P.
найдем силу предварительного обжатия арочной диафрагмы P.
При электротермическом способе натяжения
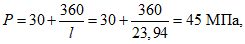
максимально допустимое напряжение
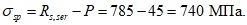
Определяем первые потери напряжений по табл. 5 СНиП 2.03.01-84. Потери от релаксации напряжений
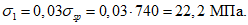
Потери от деформации анкеров при  и l = 23940 мм
и l = 23940 мм
 и l = 23940 мм
и l = 23940 мм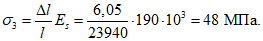
Усилие обжатия панели-оболочки с учетом первых потерь
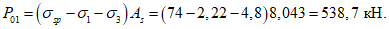
Для определения потерь от быстронатекающей ползучести вычисляем напряжения в бетоне  в нижнем поясе диафрагмы. Приведенная площадь сечения нижнего пояса
в нижнем поясе диафрагмы. Приведенная площадь сечения нижнего пояса
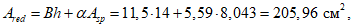
тогда
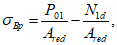
где N1d - усилие в нижнем поясе от веса панели
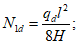
H - расстояние между центрами тяжести верхнего и нижнего поясов в середине панели. Так как qd = 1,907·1,5·0,9 = 2,57 кН/м, то
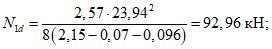
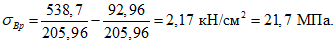
При передаточной прочности бетона RBp = 0,7·45 = 31,5 МПа, коэффициент  , RBp = 0,25 + 0,025·31,5 = 1,038, а
, RBp = 0,25 + 0,025·31,5 = 1,038, а
 , RBp = 0,25 + 0,025·31,5 = 1,038, а
, RBp = 0,25 + 0,025·31,5 = 1,038, а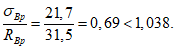
Потери от быстронатекающей ползучести
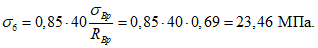
Вторые потери напряжений.
Потери от усадки бетона  . Потери от ползучести бетона при усилии обжатия с учетом потерь от быстронатекающей ползучести при:
. Потери от ползучести бетона при усилии обжатия с учетом потерь от быстронатекающей ползучести при:
 . Потери от ползучести бетона при усилии обжатия с учетом потерь от быстронатекающей ползучести при:
. Потери от ползучести бетона при усилии обжатия с учетом потерь от быстронатекающей ползучести при:P0 = 538,7 - 2,346·8,043 = 519,83 кН;
напряжении в бетоне нижнего пояса
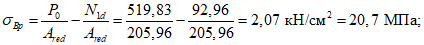
отношении
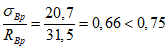
составят
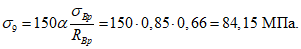
Напряжение в арматуре с учетом всех потерь
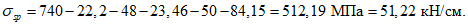
Усилие предварительного обжатия
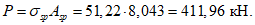
Коэффициент
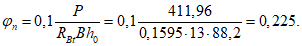
Коэффициент
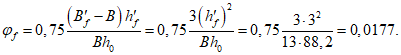
Поперечная сила, воспринимаемая бетоном
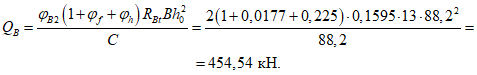
Поперечная сила, воспринимаемая хомутами
Qsw = qsw·C = 1,146·88,2 = 101,08 кН.
Поперечная сила, воспринимаемая бетоном и хомутами
Q = QB + Qsw = 454,54 + 101,08 = 555,62 кН,
что выше действующей на наклонное сечение поперечной силы Q = 175,49 кН.
Расчет по второму приближению. Наклонное сечение располагаем под углом  (чтобы оно не вышло за пределы опорного узла):
(чтобы оно не вышло за пределы опорного узла):
 (чтобы оно не вышло за пределы опорного узла):
(чтобы оно не вышло за пределы опорного узла):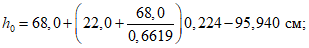
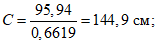
Q = 185,325 - 11,149·1,449 = 169,2 кН;
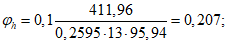
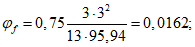
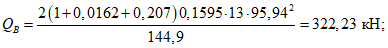
Qw = 1,146·144,9 = 166,1 кН;
Q = 322,23 + 166,1 = 488,33 кН,
что больше действующей на наклонное сечение поперечной силы Q = 169,2 кН.
Таким образом расчет наклонных сечений опорного узла диафрагмы на поперечную силу показал достаточность принятого армирования (хомуты  , шаг 200 мм).
, шаг 200 мм).
Расчет наклонных сечений на действие изгибающего момента. Наклонное сечение под углом  .
.
 .
.Изгибающий момент, действующий в сечении
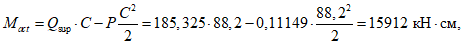
а воспринимаемый наклонным сечением
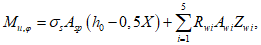
где  - напряжение в предварительно напряженной арматуре нижнего пояса диафрагмы без анкеров в сечении, расположенном в пределах длины анкеровки, на расстоянии lsup от ее торца; X - высота сжатой зоны наклонного сечения, расположенная на расстоянии C от грани опоры; Zwi - расстояние i-ого хомута, расположенного в пределах длины проекции наклонного сечения, до сечения на расстоянии C от грани опоры.
- напряжение в предварительно напряженной арматуре нижнего пояса диафрагмы без анкеров в сечении, расположенном в пределах длины анкеровки, на расстоянии lsup от ее торца; X - высота сжатой зоны наклонного сечения, расположенная на расстоянии C от грани опоры; Zwi - расстояние i-ого хомута, расположенного в пределах длины проекции наклонного сечения, до сечения на расстоянии C от грани опоры.
Определим длину зоны передачи напряжений
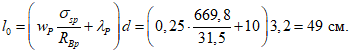
Напряжение в предварительно напряженной арматуре на расстоянии lsup = 22 см от торца диафрагмы
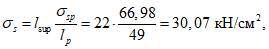
значение высоты сжатой зоны бетона
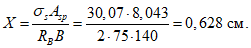
Вычисляем изгибающий момент, воспринимаемый наклонным сечением,
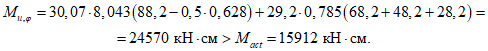
Наклонное сечение под углом  . Определяем изгибающий момент, действующий в сечении,
. Определяем изгибающий момент, действующий в сечении,
 . Определяем изгибающий момент, действующий в сечении,
. Определяем изгибающий момент, действующий в сечении,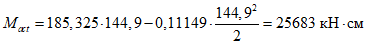
и изгибающий момент, воспринимаемый наклонным сечением,
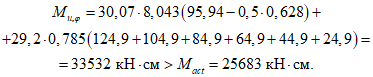
Прочность опорного узла по изгибающему моменту также обеспечена.
Панель верхнего пояса диафрагмы (первая от опорного узла)
Расчет наклонного сечения на поперечную силу Q1 = 47,788 кН. Продольная сжимающая сила N1 = 583,611 кН. Геометрические параметры: высота сечения 49,5 см, ширина по низу (в сжатой зоне сечения) 7,5 см. Расчетное сопротивление бетона с учетом коэффициента 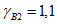
 ,
,  . Расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы
. Расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы 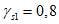
 .
.
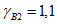
 ,
,  . Расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы
. Расчетное сопротивление арматуры хомутов класса А-III с учетом коэффициента условий работы 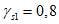
 .
.Требуется определить диаметр хомутов и их шаг.
При диаметре стержней арматуры 25 мм, установленных в рассматриваемом участке верхнего пояса, наименьший допустимый диаметр хомутов - 8 мм. Шаг хомутов принимаем из условия
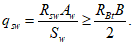
В нашем случае
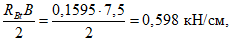
а неравенство выполняется при шаге хомутов 20 см

Дальнейшие вычисления ведем до формулам СНиП 2.03.01-84:
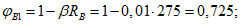
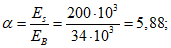
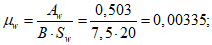
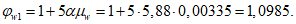
Проверяем неравенство 

0,3·1,0985·0,725·2,75·7,5(49,5 - 6) = 213,676 кН > 47,788 кН.
Условие выполняется.
Коэффициент
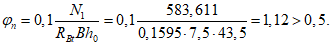
Принимаем  .
.
 .
.Вычисляем значение

Проверяем условие
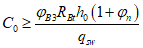
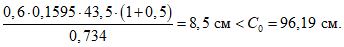
Условие выполняется.
Наименьшее значение поперечного усилия, воспринимаемого бетоном,
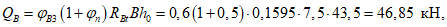
поперечное усилие, воспринимаемое хомутами,
Qw = qsw·C = 2qswh0 = 2·0,734·43,5 = 63,86 кН.
Поперечная сила, воспринимаемая бетоном и хомутами,
Q = QB + Qw = 46,85 + 63,86 = 110,71 кН > 47,788 кН.
Принятые хомуты  с шагом 200 мм удовлетворяют расчету. На остальных участках верхнего пояса устанавливаются такие же хомуты.
с шагом 200 мм удовлетворяют расчету. На остальных участках верхнего пояса устанавливаются такие же хомуты.
Расчет панели-оболочки на горизонтальную нагрузку,
возникающую при транспортировании
Масса панели g = 14 т. Бетон класса B45 с учетом коэффициента 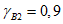
 .
.
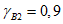
 .
.Арматура класса А-III Rs = 365 МПа = 36,5 кН/см2. Геометрические параметры сечения: h = 294 см, B = 8 см; h0 = 285 см.
Изгибающий момент, действующий в середине пролета в горизонтальном направлении, принимается согласно формуле (12) настоящих рекомендаций
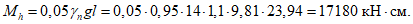
Вычисляем значение
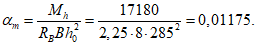
Значение функции  . Площадь сечения растянутой арматуры
. Площадь сечения растянутой арматуры
 . Площадь сечения растянутой арматуры
. Площадь сечения растянутой арматуры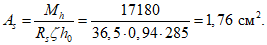
Принимаем  (As = 2,011 см2).
(As = 2,011 см2).
Расчет торцового ребра
Геометрические параметры: высота h = 150 мм; ширина по верху B' = 27,5 см, по низу B = 10 см. Пролет l = 211 см. Ребро защемлено в опорных конструкциях панели и загружено равномерно распределенной нагрузкой, которая приложена непосредственно на ребре, и треугольной нагрузкой, передающейся от полки панели-оболочки (табл. 2).
Таблица 2
Вид нагрузки | Нагрузка, кН/м | Коэффициент надежности по нагрузке | Расчетная нагрузка при | |
Нормативная | Расчетная при | |||
Постоянная равномерно распределенная, | 0,8899 | 0,8219 | - | 1,0025 |
в т.ч. водоизоляционный ковер | 0,0275 | 0,0261 | 1,3 | 0,0339 |
цементная стяжка (  , ,t = 15 мм) | 0,0825 | 0,0784 | 1,3 | 0,1019 |
уголок цементной стяжки (85 x 85 мм) | 0,0354 | 0,0336 | 1,3 | 0,0437 |
утеплитель (пенобетон) (  , t = 140 мм) , t = 140 мм) | 0,1925 | 0,1829 | 1,3 | 0,2378 |
слой гравия, утопленный в мастику | 0,044 | 0,0418 | 1,3 | 0,0543 |
вес торцового ребра | 0,508 | 0,4826 | 1,3 | 0,5309 |
Временная равномерно распределенная снеговая нагрузка (коэффициент C = 1,2) | 0,231 | 0,2195 | 1,4 | 0,3072 |
Полная | 1,1209 | 1,0414 | - | 1,3097 |
Состав нагрузки, передающейся от полки панели на торцовое ребро в виде треугольника, за исключением веса панели-оболочки и снеговой нагрузки, приведен в табл. 1. Расчетная нагрузка при коэффициенте  составляет 0,124 + 0,371 + 0,865 + 0,075·9,81·0,95·1,1 + 0,931·1,2 = 3,247 кН/м2, нагрузка в вершине треугольника - 3,247·2,11·0,5 = 3,425 кН/м.
составляет 0,124 + 0,371 + 0,865 + 0,075·9,81·0,95·1,1 + 0,931·1,2 = 3,247 кН/м2, нагрузка в вершине треугольника - 3,247·2,11·0,5 = 3,425 кН/м.
Максимальный балочный изгибающий момент от суммы нагрузок
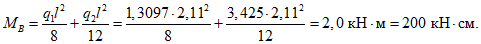
Распределим этот момент поровну между опорами и пролетом, тогда Msup = 100 кН·см
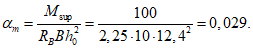
Значение функции  . Площадь сечения растянутой арматуры
. Площадь сечения растянутой арматуры
 . Площадь сечения растянутой арматуры
. Площадь сечения растянутой арматуры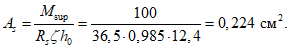
Принимаем  (As = 1,131 см2).
(As = 1,131 см2).
Из расчета по пролетному изгибающему моменту Msup = 100 кН·см получим такое же количество арматуры  .
.
Расчет опорного поперечника торцовой рамы панели-оболочки
на нагрузку, возникающую при транспортировании
Геометрические параметры: высота сечения стоек hc = 12 см, h0 = 9 см; принятая ширина Bc = 30 см; ширина сечения ригеля по верху B'p = 27,5 см, по низу Bp = 15 см; высота сечения ригеля hp = 15 см: h0 = 12,4 см; расстояния до расчетных сечений h1 = 37,5 см, h2 = 30,0 см, h3 = 99 см; l1 = 37,5 см, lр = 286 см. Масса панели q = 14 т. Бетон класса B45 RB = 2,5·0,9 = 2,25 кН/см2. Арматура класса А-III Rs = 36,5 кн/см2 (рис. 6).
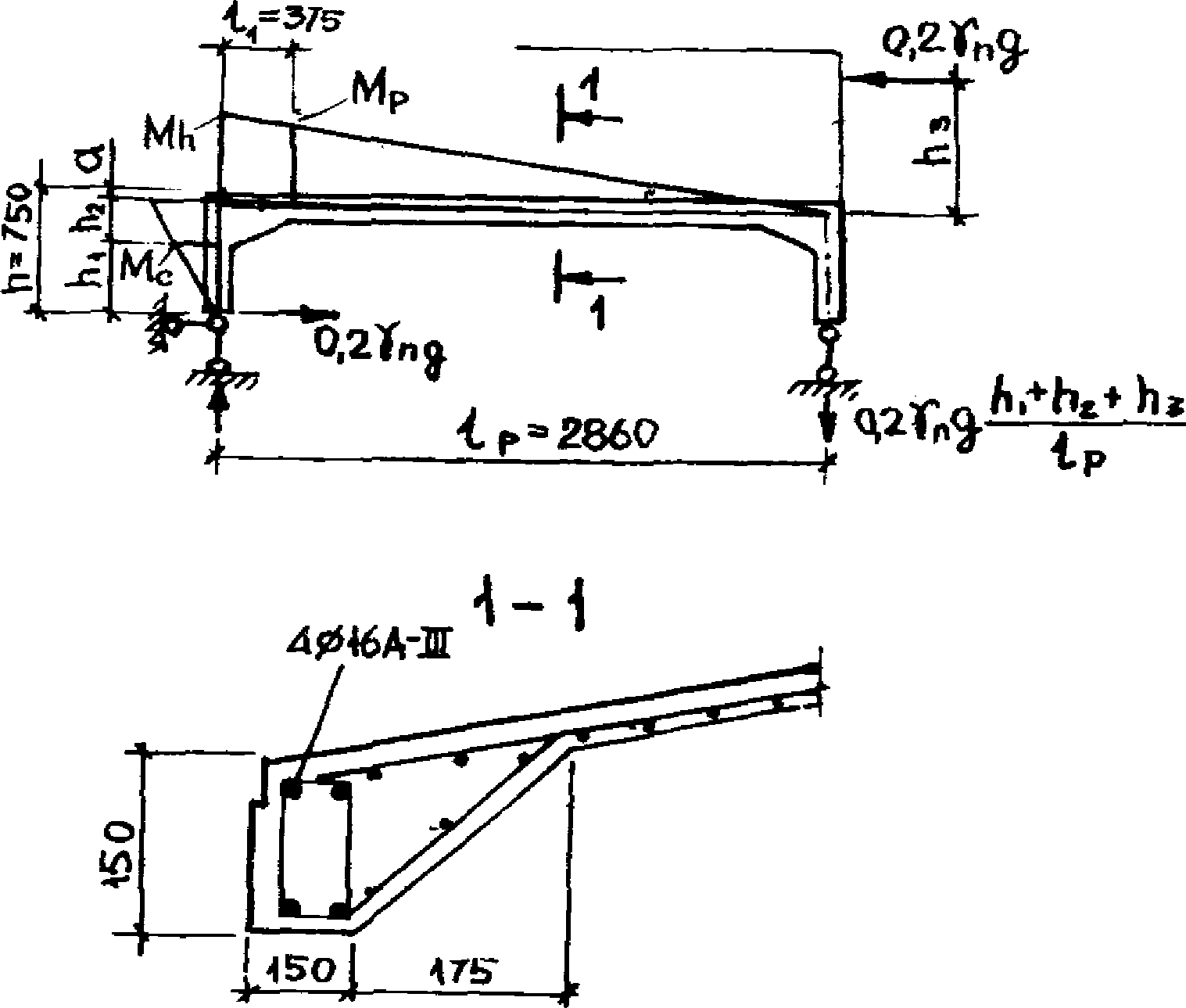
панели-оболочки на нагрузки, возникающие
при транспортировании
а - вид на опорный поперечник торцовой рамы; б - поперечное
сечение торцового ребра
Вычисляем максимальную горизонтальную нагрузку, действующую на опорный контур при транспортировании
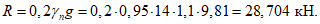
Определяем количество арматуры в стойках опорного поперечника торцовой рамы. Изгибающий момент Mc = Rh1 = 28,704·37,5 = 1076,4 кН·см
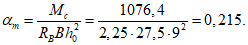
Значение функции  . Количество растянутой арматуры
. Количество растянутой арматуры
 . Количество растянутой арматуры
. Количество растянутой арматуры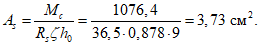
Принимаем  (As = 3,39 см2). В опорном узле в арматурной сетке, запроектированной по расчету опорного узла арочной диафрагмы на поперечную силу, первые три стержня
(As = 3,39 см2). В опорном узле в арматурной сетке, запроектированной по расчету опорного узла арочной диафрагмы на поперечную силу, первые три стержня  (от торца опорного узла) устанавливают с шагом 100 мм.
(от торца опорного узла) устанавливают с шагом 100 мм.
Определение количества арматуры в ригеле опорного контура.
Изгибающий момент
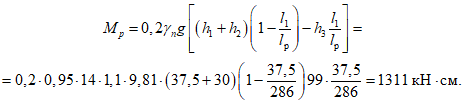
Вычисляем значение
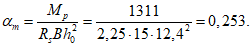
Значение функции  . Определяем количество растянутой арматуры
. Определяем количество растянутой арматуры
 . Определяем количество растянутой арматуры
. Определяем количество растянутой арматуры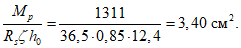
Принимаем  (As = 4,02 см2). По низу ригеля также устанавливаем
(As = 4,02 см2). По низу ригеля также устанавливаем  в связи со знакопеременным изгибающим моментом.
в связи со знакопеременным изгибающим моментом.
Расчет гибкой предварительно напряженной пластины - пологой
цилиндрической оболочки по несущей способности
Геометрические параметры пластины: половина длины пластины - 3,01 м, половина ширины пластины - 1,58 м, толщина пластины - 0,04 м, пролет короткого направления пластины - 3,02 м, длинного - 6,02 м. Материал пластины: бетон тяжелый класса B30, подвергнутый тепловой обработке при атмосферном давлении, с учетом коэффициента 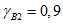 RB = 17 x 0,9 = 15,3 МПа = 1,53 кН/см2, RBt,ser = 1,8·0,9 = 1,62 МПа = 0,162 кН/см2, EB = 29·103 МПа. Арматура класса Вр-II диаметром 5 мм, Rs = 1045 МПа = 104,5 кН/см2, Rs,ser = 1255 МПа = 125,5 кН/см2, Es = 200·103 МПа. Способ натяжения - электротермический.
RB = 17 x 0,9 = 15,3 МПа = 1,53 кН/см2, RBt,ser = 1,8·0,9 = 1,62 МПа = 0,162 кН/см2, EB = 29·103 МПа. Арматура класса Вр-II диаметром 5 мм, Rs = 1045 МПа = 104,5 кН/см2, Rs,ser = 1255 МПа = 125,5 кН/см2, Es = 200·103 МПа. Способ натяжения - электротермический.
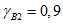 RB = 17 x 0,9 = 15,3 МПа = 1,53 кН/см2, RBt,ser = 1,8·0,9 = 1,62 МПа = 0,162 кН/см2, EB = 29·103 МПа. Арматура класса Вр-II диаметром 5 мм, Rs = 1045 МПа = 104,5 кН/см2, Rs,ser = 1255 МПа = 125,5 кН/см2, Es = 200·103 МПа. Способ натяжения - электротермический.
RB = 17 x 0,9 = 15,3 МПа = 1,53 кН/см2, RBt,ser = 1,8·0,9 = 1,62 МПа = 0,162 кН/см2, EB = 29·103 МПа. Арматура класса Вр-II диаметром 5 мм, Rs = 1045 МПа = 104,5 кН/см2, Rs,ser = 1255 МПа = 125,5 кН/см2, Es = 200·103 МПа. Способ натяжения - электротермический.Гибкая пластина, уложенная длинными сторонами на панели-оболочки КСО, образует пологую цилиндрическую оболочку средней длины. Рассчитываем гибкую пластину, уложенную в средней части панели КСО.
Радиус кривизны верхнего пояса панели-оболочки КСО 3 x 24 м и нижней поверхности пластины определим по формуле
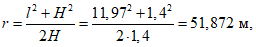
где l - длина половины панели-оболочки, H - стрела подъема криволинейной части панели-оболочки.
Вычисляем радиус кривизны кривой расположения нижней арматуры пластины
rinf = 51,872 + 0,017 = 51,889 м, верхней арматуры rsup = 51,899 м и верхней плоскости пластины r0 = 51,912 м.
Стрела подъема гибкой пластины - пологой оболочки составляет
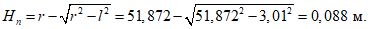
Равномерно распределенная расчетная нагрузка на гибкую пластину составляет 3,335 КПа = 3,335 кН/м2.
Требуется определить количество и расположение арматуры двух направлений пластины.
Определим значение предварительного напряжения в проволочной арматуре класса Вр-II короткого и длинного направлений пластины, учитывая предельную температуру нагрева стержней, равную 400 °C
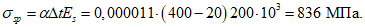
Определим значение напряжений в проволочной арматуре пластины после всех потерь.
Короткое направление, шаг стержней 200 мм
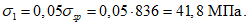
При  и l = 3740 мм
и l = 3740 мм
 и l = 3740 мм
и l = 3740 мм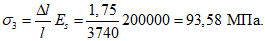
Усилие обжатия после первых потерь
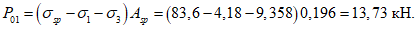
Определяем напряжения в бетоне на уровне нижней арматуры
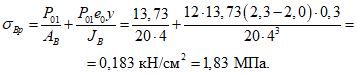
Вычисляем соотношение
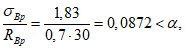
здесь  ; RBp = 0,25 + 0,025·21 = 0,775;
; RBp = 0,25 + 0,025·21 = 0,775;
 ; RBp = 0,25 + 0,025·21 = 0,775;
; RBp = 0,25 + 0,025·21 = 0,775; ;
;  ;
; .
.Определяем напряжение в проволоке с учетом всех потерь
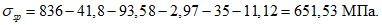
При аналогичном расчете напряжение в проволоке короткого направления с шагом стержней 100 мм составляет 637,5 МПа, в проволоке длинного направления с шагом стержней 200 мм - 687,81 МПа, и с шагом 100 мм - 668,68 МПа.
Расчет гибкой пластины состоит из последовательных приближений.
В первом приближении задается армирование короткого и длинного направлений пластины и оценивается несущая способность по недеформированной схеме. Затем во втором приближении расчет ведем по деформированной схеме. Если заданное армирование удовлетворяет несущей способности, переходим к расчету по образованию и ширине раскрытия трещин при изгибе на монтаже.
Первое приближение - расчет по недеформированной схеме. Задаемся схемой и количеством арматуры в гибкой плите согласно рис. 7.
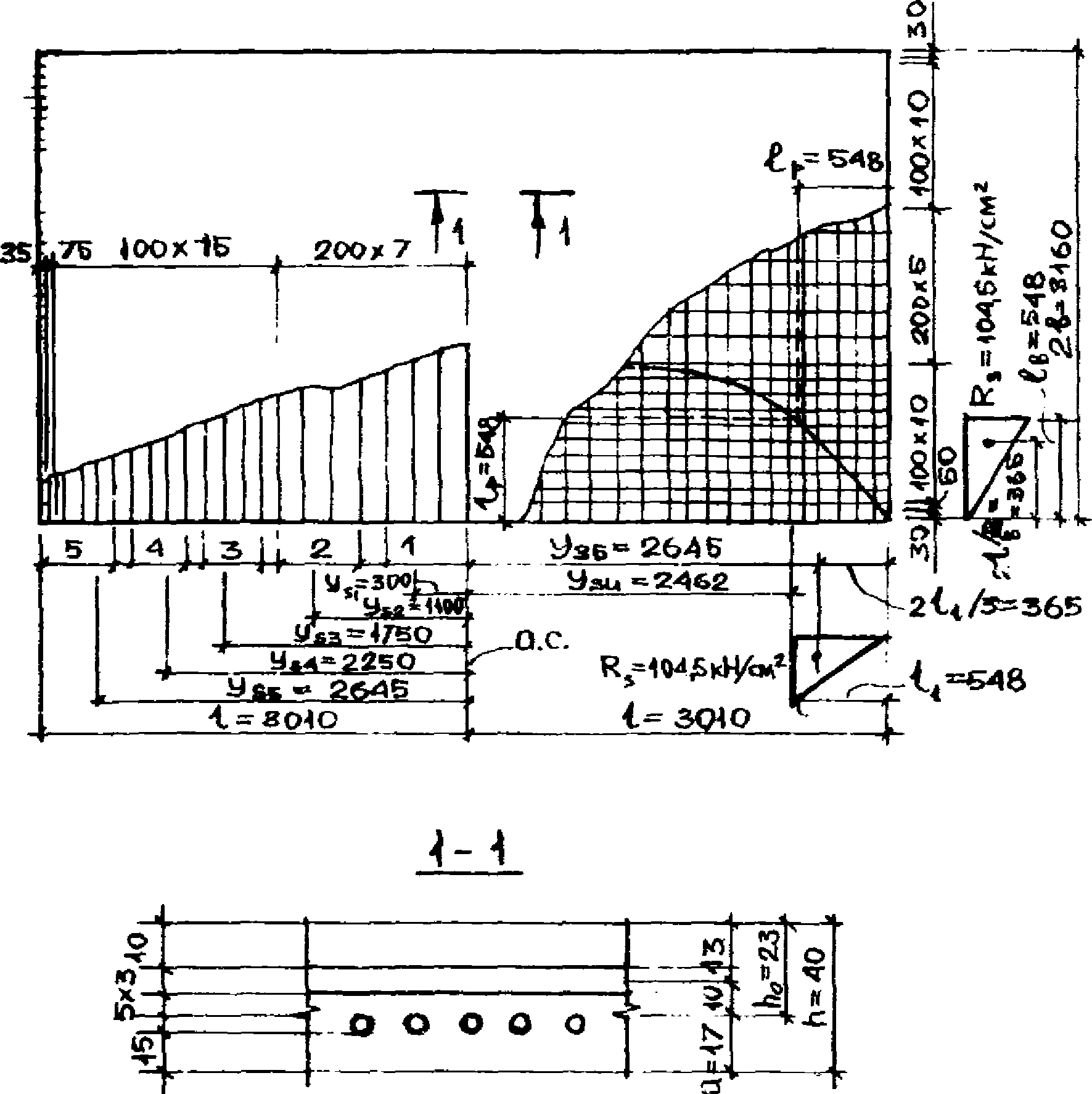
цилиндрической оболочки
Определим длину зоны передачи напряжений при передаточной прочности бетона RBp = 0,7·30 = 21 МПа и Rs = 1045 МПа > 836 МПа
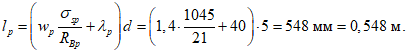
Предполагая, что диагональная трещина войдет в угол пологой оболочки под углом 45°, принимаем значения ll = lB = lp = 0,548 м.
Разделим каждую половину количества арматуры короткого направления на 5 групп (см. рис. 7). Первые и вторые группы состоят из 4 стержней  , As1 = As2 = 0,196·4·2 = 1,568 см2. Третьи и четвертые группы состоят из 5 стержней
, As1 = As2 = 0,196·4·2 = 1,568 см2. Третьи и четвертые группы состоят из 5 стержней  , As3 = As4 = 0,196·5·2 = 1,96 см2. Пятые группы являются зонами передачи напряжений, As5 = 2·0,196·54,8/10 = 2,148 см2. Напряжения в арматуре пятой группы равны нулю на контуре оболочки, а на расстоянии ll = lp равны расчетному сопротивлению арматуры Rs = 104,5 кН/см2. Центр тяжести предельного усилия на этом участке находится на расстоянии 2ll/3 = 0,365 м от контура оболочки.
, As3 = As4 = 0,196·5·2 = 1,96 см2. Пятые группы являются зонами передачи напряжений, As5 = 2·0,196·54,8/10 = 2,148 см2. Напряжения в арматуре пятой группы равны нулю на контуре оболочки, а на расстоянии ll = lp равны расчетному сопротивлению арматуры Rs = 104,5 кН/см2. Центр тяжести предельного усилия на этом участке находится на расстоянии 2ll/3 = 0,365 м от контура оболочки.
Расстояния до центров тяжести всех групп арматуры от середины оболочки Ysi указаны на рис. 7. Ординаты центров тяжести групп арматуры определены по формуле (26) настоящих рекомендаций, рабочая высота - по формуле h01 = Zsi + h0, тогда:
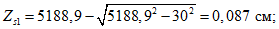
h01 = 0,087 + 2,3 = 2,39 см;
Zs2 = 1,17 см; | h02 = 3,47 см; |
Zs3 = 2,95 см; | h03 = 5,25 см; |
Zs4 = 4,88 см; | h04 = 7,18 см; |
Zsu = 5,84 см; | |
Zs5 = 6,89 см; | h05 = 9,19 см. |
Найдем приближенную высоту сжатой зоны бетона по формуле (27) настоящих рекомендаций

Характеристика сжатой зоны бетона
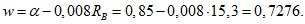
Напряжения в первой группе стержней
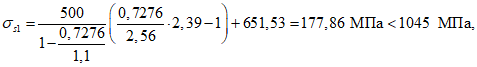
во второй
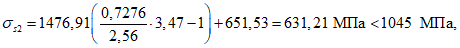
в третьей
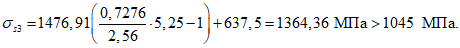
Напряжения в третьей, четвертой и пятой группах стержней принимаем равными расчетному сопротивлению
Rs = 1045 МПа.
Уточняем высоту зоны

Вычисляем напряжения в группах стержней:
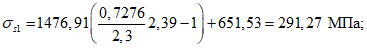
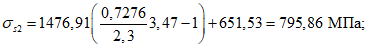
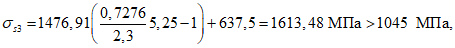
тогда

Окончательно напряжения в группах стержней:
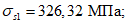
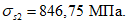
Напряжения в третьей, четвертой и пятой группах стержней принимаем равными Rs = 1045 МПа.
Определяем расстояние до центра тяжести сжатой зоны
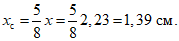
Площадь сжатой зоны бетона
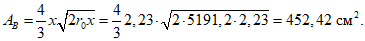
Изгибающий момент относительно оси Yinf определяем по формуле (24) настоящих рекомендаций
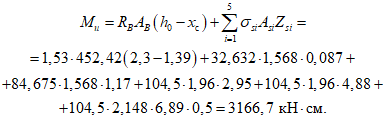
По формуле (33) настоящих рекомендаций найдем погонное усилие
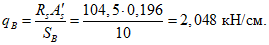
Определив по формуле (30) настоящих рекомендаций значение половины ширины сжатой зоны бетона  и по формуле (37) ординату линии излома 2-2.
и по формуле (37) ординату линии излома 2-2.
 и по формуле (37) ординату линии излома 2-2.
и по формуле (37) ординату линии излома 2-2.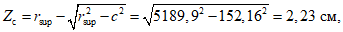
найдем по формуле (36) виртуальное перемещение
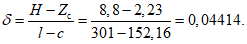
Определяем параметр a схемы излома:
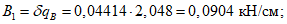
B2 = B(l + c) = 151·(301 + 152,16) = 68427,16 см2;
B3 = (0,58335l + 1,41665C)/2 =
= (0,58335·301 + 1,41665·152,16)/2 = 195,57 см2;
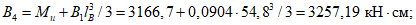
B5 = B2 - B3lB = 68427,16 - 195,57·54,8 = 57709,9 см2;
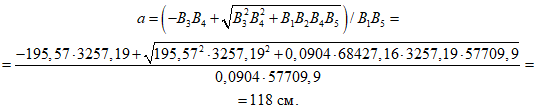
Усилия растяжения:
N1 = qB(a - lB) = 2,048(118 - 54,8) = 129,43 кН;
N2 = (1/2)qBlB = 0,5·2,048·54,8 = 56,12 кН.
Виртуальные перемещения:
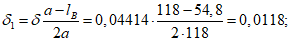
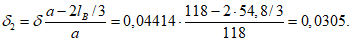
Виртуальный угол перелома
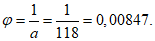
Виртуальный объем
w = 2B(l + c) - a(0,58335l + 1,41665c) =
= 2·151(301 + 152,16) - 118(0,58335·301 + 1,41665·152,16) =
= 90699 см3/см.
Несущая способность по недеформированной схеме
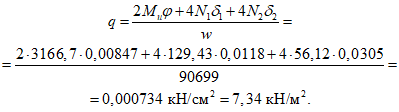
Определим прогиб середины гибкой пластины - пологой оболочки к моменту исчерпания несущей способности. Для этого путем последовательных приближений из уравнения (45) настоящих рекомендаций определим значение X. Задаемся в первом приближении каким-либо значением высоты сжатой зоны бетона. Например, возьмем его из расчета гибкой пластины по несущей способности. Определив по формулам (46), (47) и (53) напряжения в бетоне и арматуре и подставив все известные значения в уравнение (45), получим в левой части уравнения две компоненты - положительную и отрицательную. Если по абсолютной величине они разнятся между собой более, чем на 3%, задаются новым значением высоты сжатой зоны бетона и расчет повторяется. В нашем случае после нескольких приближений X = 3,2 см. По формуле (53) настоящих рекомендаций вычисляем:
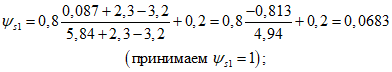
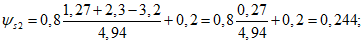
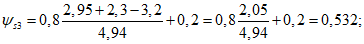
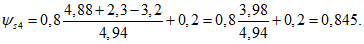
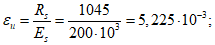
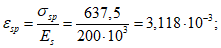
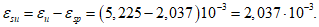
Коэффициент  .
.
 .
.Вычисляем:
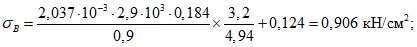
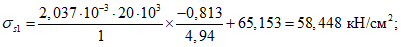
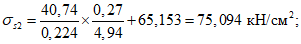
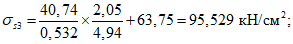
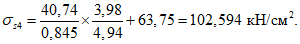
Найденные значения напряжений подставляем в уравнение (45) настоящих рекомендаций
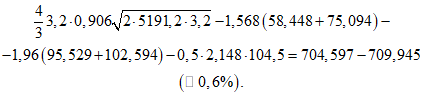
Определим изгибающий момент
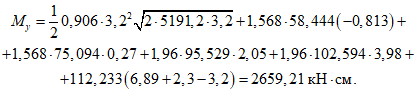
Вычисляем значение
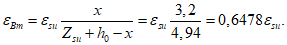
Кривизна к моменту появления текучести в арматуре вычисляется по формуле (43) настоящих рекомендаций
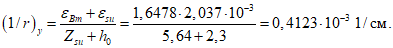
Кривизна к моменту исчерпания несущей способности вычисляется по формуле (42)
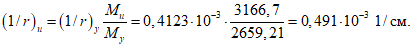
Прогиб к моменту исчерпания несущей способности - по формуле (41)
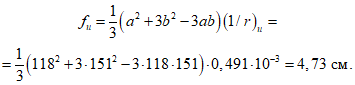
Второе приближение
Расчет по деформированной схеме. Определяем стрелу подъема оболочки в деформированном состоянии:
Hд = H - fu = 8,8 - 4,73 - 4,07 см;
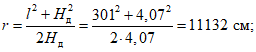
rinf = r + a = 11132 + 1,7 = 11134 см;
rsup = r + h - a' = 11132 + 4 - 1,3 = 11135 см.
Ординаты центров тяжести групп арматуры и рабочие высоты арматуры участков:
Zs1 = 0,04 см; | h01 = 2,34 см; |
Zs2 = 0,54 см; | h02 = 2,84 см; |
Zs3 = 1,38 см; | h03 = 3,68 см; |
Zs4 = 2,27 см; | h04 = 4,57 см; |
Zsu = 2,72 см; | |
Zs5 = 3,21 см; | h05 = 5,51 см. |
Определение высоты сжатой зоны бетона ведем путем последовательных приближений. В первом приближении высоту сжатой зоны можно принять из расчета прочности по недеформированной схеме X = 2,23 см. По формуле (67) СНиП 2.03.01-84 определяем напряжения в группах стержней:
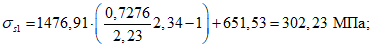
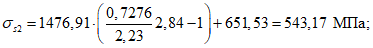
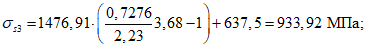
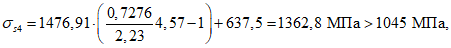
а высоту сжатой зоны бетона по формуле (27)

После ряда приближений значение высоты сжатой зоны будет равно 1,93 см, а напряжения в стержнях:  ,
,  ,
,  .
.
 ,
,  ,
,  .
.Расстояние до центра тяжести сжатой зоны
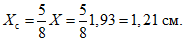
Площадь сжатой зоны бетона
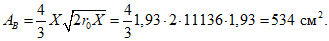
Изгибающий момент относительно оси Yinf
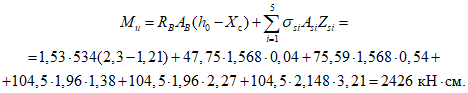
Половина ширины сжатой зоны бетона
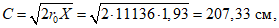
ордината линии излома 2-2
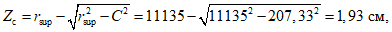
виртуальное перемещение
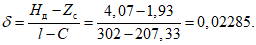
Вычисляем значения:
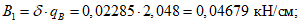
B2 = B(l + C) = 151(301 + 207,33) = 76758 см2;
B3 = (0,58335·l + 1,41665·C)/2 =
= (0,58335·301 + 1,41665·207,33)/2 = 234,65 см,
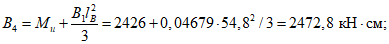
B5 = B2 - B3lB = 76758 - 234,65·54,8 = 63899,2 см2.
Параметр
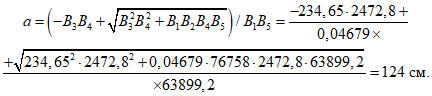
Находим усилия растяжения:
N1 = qB(a - lB) = 2,048(124 - 54,8) = 141,72 кН;
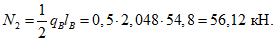
Виртуальные перемещения:
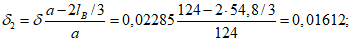
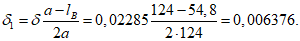
Виртуальный угол перелома
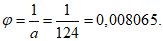
Виртуальный объем
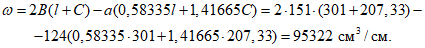
Несущая способность, вычисленная по деформированной схеме
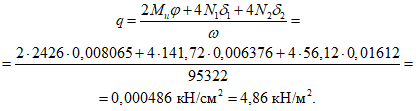
Расчет гибкой пластины по раскрытию трещин при изгибе на монтаже
Определим изгибающий момент, образующий трещины в гибкой пластине при изгибе ее на монтаже на панелях-оболочках КСО 3 x 24 м. Ширина гибкой пластины b = 3,16 м, высота - 0,04 м. Продольная арматура класса Вр-II состоит из 28 проволок диаметром 5 мм площадью Asp = 28·0,196 = 5,488 см2 с рабочей высотой h = 2,7 см (см. рис. 7).
Вычисляем:  ;
;  ;
;  . Среднее значение предварительного напряжения в проволоках в поперечном сечении гибкой пластины
. Среднее значение предварительного напряжения в проволоках в поперечном сечении гибкой пластины
 ;
;  ;
;  . Среднее значение предварительного напряжения в проволоках в поперечном сечении гибкой пластины
. Среднее значение предварительного напряжения в проволоках в поперечном сечении гибкой пластины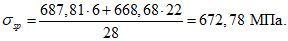
По формулам (39) и (40) настоящих рекомендаций вычисляем:
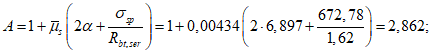
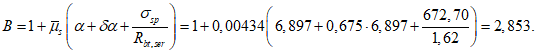
Относительную высоту упругого ядра сечения определяем по формуле (70) настоящих рекомендаций
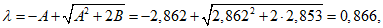
наибольшее напряжение в сжатой зоне бетона - по формуле (67)
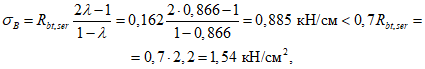
напряжение в растянутой арматуре - по формуле (68)
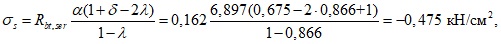
значение mcrc - по формуле (34)
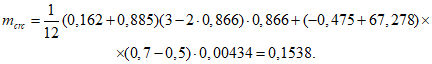
Момент, воспринимаемый сечением при образовании трещин
Mcrc = mcrcbh2 = 0,1538·316·42 = 777,58 кН·см.
Для оценки ширины раскрытия трещин в гибкой пластине при монтаже ее на панели-оболочки КСО 3 x 24 м с кривизной поверху
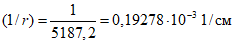
необходимо определить напряжения в верхней продольной арматуре плиты. Определение напряжений ведется путем последовательных приближений, задавшись в первом приближении коэффициентом  , равным, например, 0,3. Тогда по формуле (62) настоящих рекомендаций
, равным, например, 0,3. Тогда по формуле (62) настоящих рекомендаций
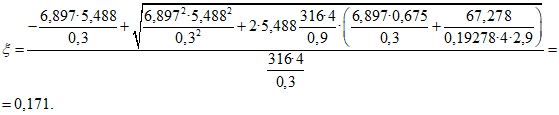
Напряжения в бетоне и арматуре по формулам (44) и (45) настоящих рекомендаций:
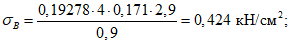
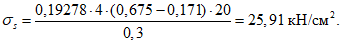
Значение mr вычисляем по формуле (43)
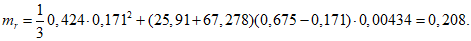
Изгибающий момент
Mr = mrbh2 = 0,208·316·42 = 1052,44 кН·см.
Коэффициент
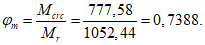
Усилие предварительного обжатия гибкой пластины в продольном направлении
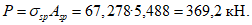
Эксцентриситет
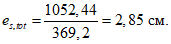
Коэффициент 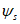 вычисляется по формуле (167) СНиП 2.03.01-84
вычисляется по формуле (167) СНиП 2.03.01-84
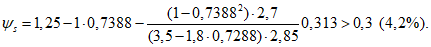
Уточняем
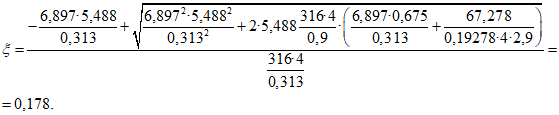
Напряжения в арматуре и бетоне:
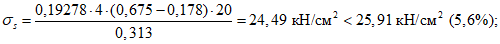
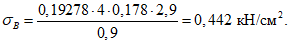
Значение величины
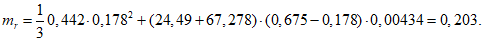
Изгибающий момент
Mr = 0,203·316·42 = 1024,4 кН·см.
Коэффициент
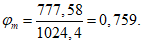
Эксцентриситет
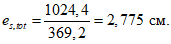
Коэффициент
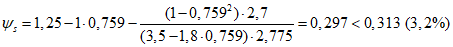
Уточняем:
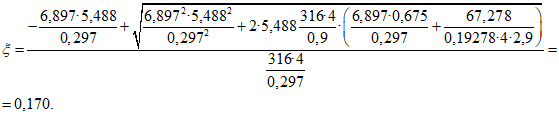
Напряжения в бетоне и арматуре:
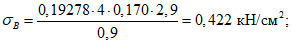
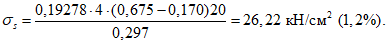
Учитывая, что напряжение в арматуре на этом приближении мало (на 1,2%) отличается от предыдущего, прекращаем шаги приближений и принимаем для расчета напряжения в арматуре  .
.
 .
.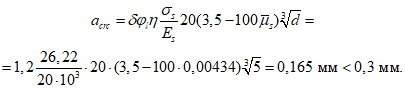
При заданной сетке предварительно напряженной арматуры расчетная несущая способность ее с учетом собственного веса и влияния прогиба равна 4,86 кН/м2, что выше действующей расчетной нагрузки, равной 3,335 кН/м2. Ширина раскрытия трещин в гибких плитах после установки их в комбинированное покрытие с панелями-оболочками КСО 3 x 24 м составляет 0,165 мм, что меньше допустимой величины 0,3 мм.
Результаты расчета свидетельствуют о том, что в гибкой плите можно снизить количество арматуры. Это рекомендуется производить путем уменьшения армирования по краям плиты с шагом стержней 100 мм. В приведенной схеме расположения арматуры (см. рис. 7) участки 3 - 4 поперечной арматуры можно задать с шагом 200 мм. Выполненное уменьшение интенсивности армирования должно быть проверено повторным расчетом.
НАПРЯЖЕННОЙ ПЛАСТИНЫ - ПОЛОГОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
Расчет панели-оболочки по деформациям и трещиностойкости
Данные для расчета панели-оболочки КСО 3 x 24 м и гибкой пластины размером 3 x 6 x 0,04 м приняты такими же, как и при расчете по несущей способности (см. приложение 1).
Статический расчет фермы-диафрагмы
Значения расчетных нагрузок и усилий определим, используя данные табл. 1.
Полная расчетная равномерно распределенная нагрузка первого сочетания при 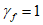 (рис. 8)
(рис. 8)
qI = (3,522 + 2,660)1,5 = 9,270 кН/м.
Изгибающий момент и поперечная сила на расстоянии l2 от опоры от этой нагрузки (см. рис. 8, б):
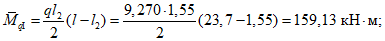
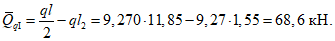
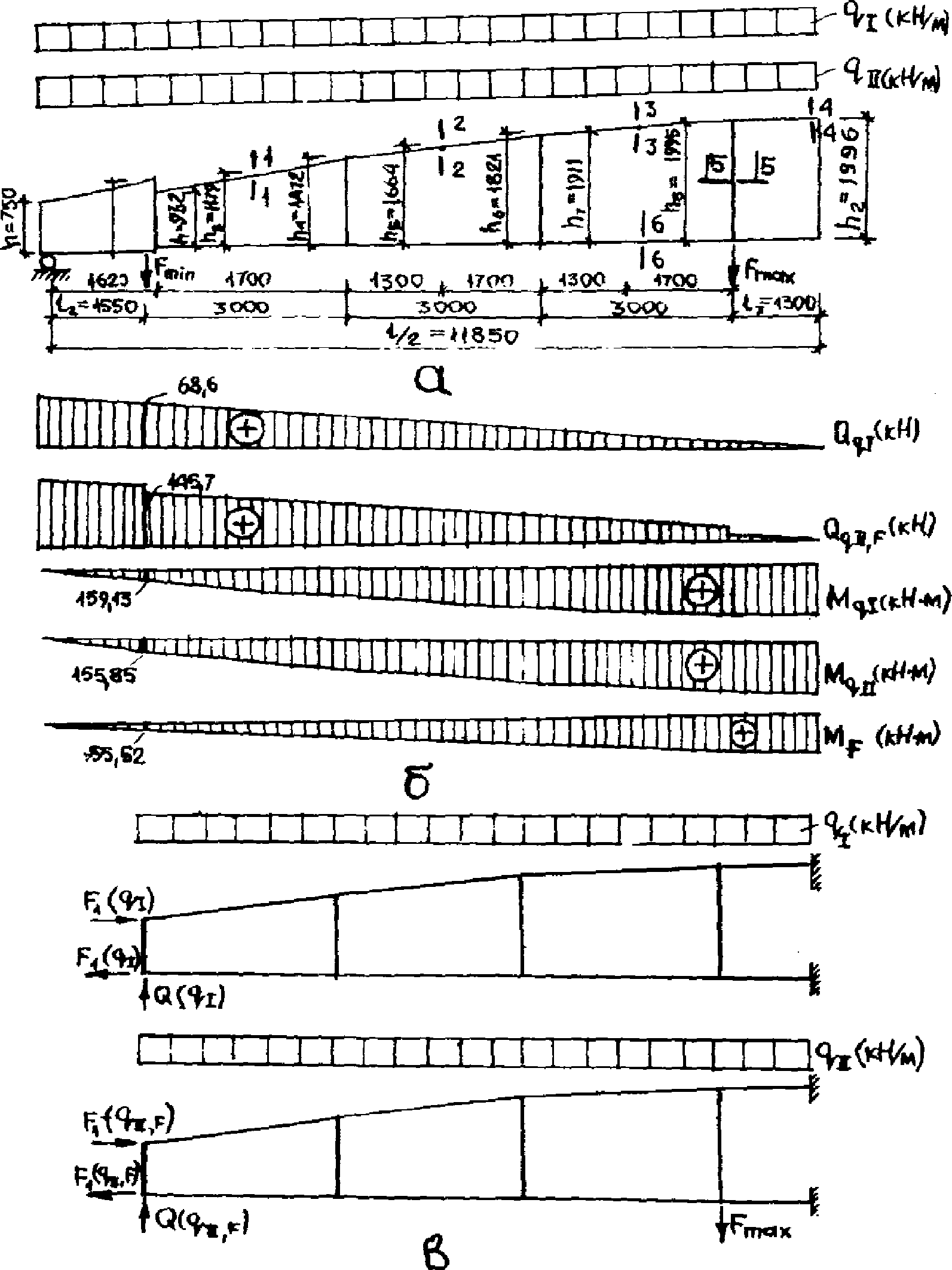
по деформациям
а - расчетная схема с использованием пластинчато-стержневой
аппроксимации; б - эпюры балочных усилий; в - упрощенный
вариант расчетной схемы (стержневая аппроксимация)
Аналогично вычисляем значения расчетной нагрузки, изгибающего момента и поперечной силы для второго основного сочетания:
распределенная нагрузка
qII = (2,857 + 0,665·0,9 + 1,995 + 0,665·0,9)1,5 = 9,078 кН/м;
сосредоточенные нагрузки от кранов при 
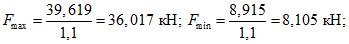
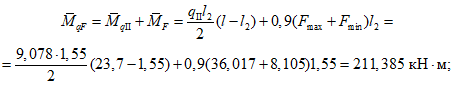
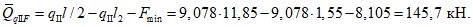
По формуле (16) настоящих рекомендаций вычисляем значение F1 от расчетных нагрузок первого и второго основных сочетаний:
F1(qI) = MgI/h3 = 159,13/0,932 = 170,740 кН;
F1(qII) = MgII/h3 = 11,385/0,932 = 233,246 кН.
Вычисление геометрических характеристик приведенных сечений элементов диафрагмы производим в соответствии с указаниями [1]. Поскольку сечение верхнего пояса диафрагмы имеет переменную высоту, то геометрические характеристики верхнего пояса определим для четырех сечений 1-1 ... 4-4, сделанных по середине участков между стойками (см. рис. 8).
Площадь приведенного сечения 1-1 верхнего пояса диафрагмы, разбитого на шесть участков (рис. 9 и 10),
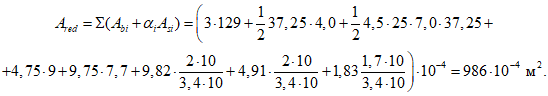
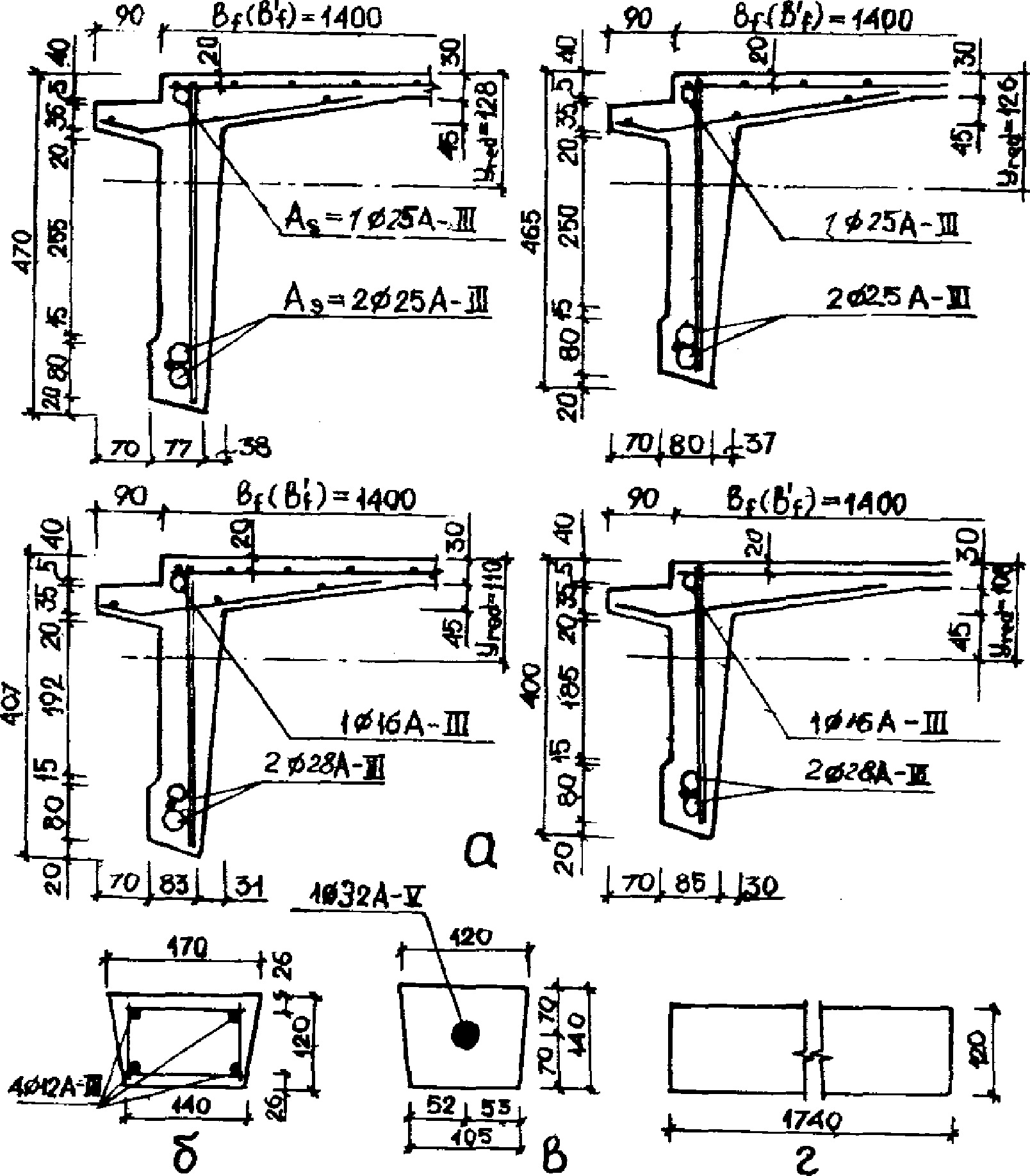
пояса (в) и поперечной сплошной панели (г) диафрагмы КСО
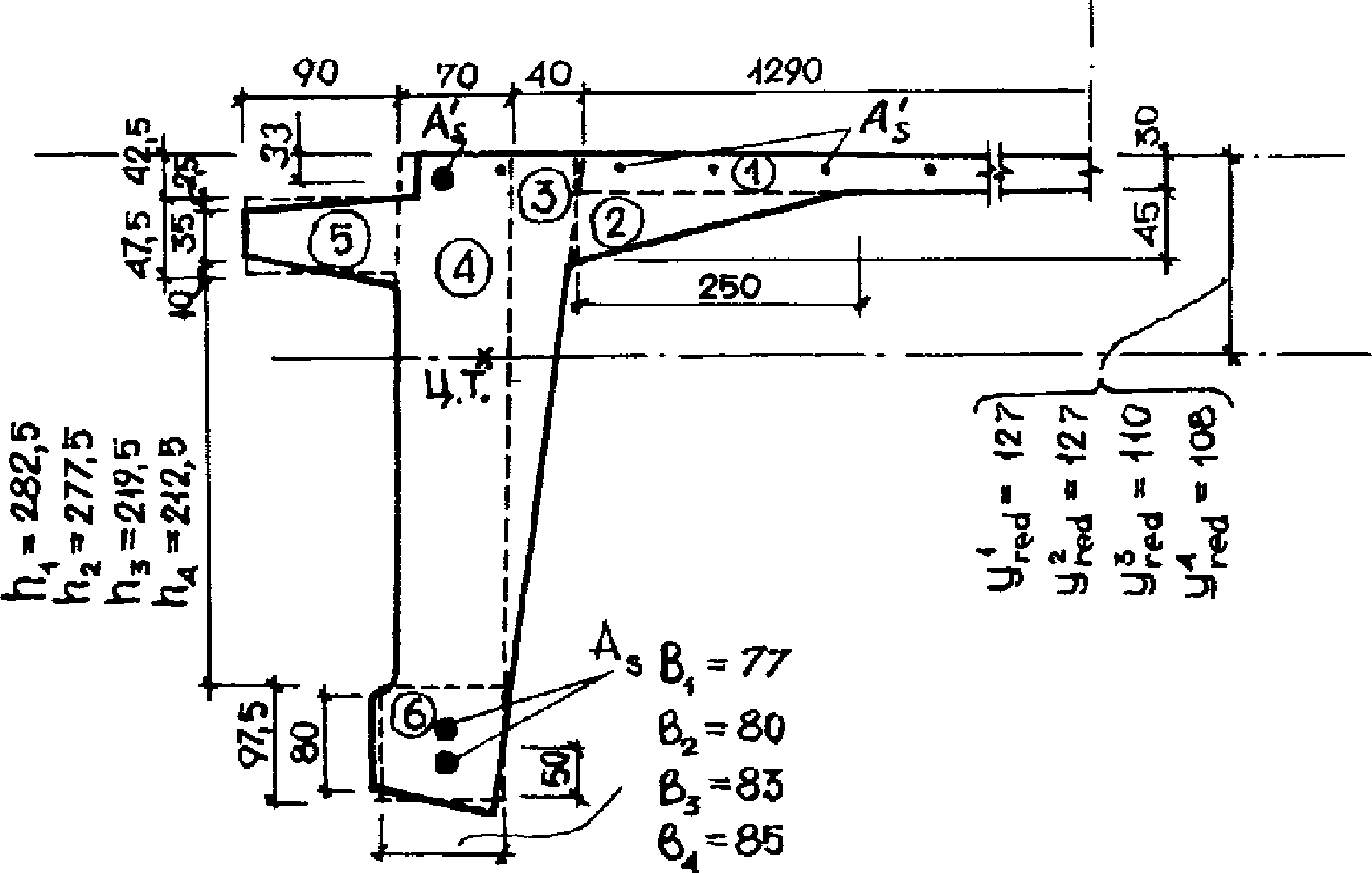
Статический момент рассматриваемого сечения относительно его верхней грани
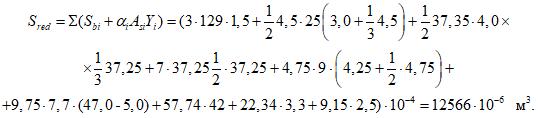
Расстояние от центра тяжести до верхней грани этого же сечения
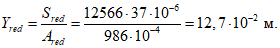
Отметим, что h1, h2, ..., h8 на расчетной схеме диафрагмы (см. рис. 8) в соответствии с п. 4.27 настоящих рекомендаций вычислены с учетом того, что осевая линия верхнего пояса проходит через центры тяжести сечений верхнего пояса.
Момент инерции сечения относительно его центра тяжести
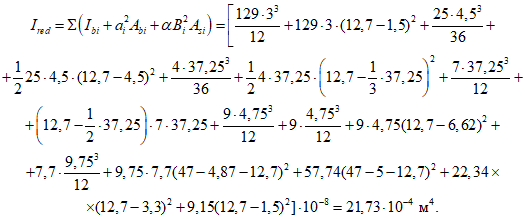
Аналогично определены геометрические характеристики для других расчетных сечений верхнего пояса стоек, нижнего пояса и стержня-вставки диафрагмы. Результаты вычислений сведены в табл. 3 (графы 3 - 6).
Наименование элемента | Сечение | Ared·10-4, м | Sred·10-4, м | Yred·10-2, м | Ired·10-4, м | B11, МПа·м2 | B22, МПа·м2 |
1 | 2 | 4 | 5 | ||||
Верхний пояс | 1 - 1 | 986 | 125,6 | 12,7 | 21,73 | 73,88 | 3352 |
2 - 2 | 984 | 124,9 | 12,7 | 21,39 | 72,73 | 3346 | |
3 - 3 | 937 | 103 | 11 | 14,44 | 49,1 | 3185 | |
4 - 4 | 933 | 100,5 | 10,8 | 12,78 | 43,4 | 3172 | |
Стойки | 5 - 5 | 192 | 14,78 | 7,7 | 0,32 | 1,09 | 652 |
Нижний пояс | 6 - 6 | 216 | 15,12 | 7 | 0,38 | 1,29 | 734 |
Стержень-вставка | 7 - 7 | 2040 | 1816,6 | 87 | 1165 | 6682 | 6936 |
Жесткости приведенных сечений элементов диафрагмы B11 и B22 (для первой итерации) вычислены как для сплошного приведенного сечения в предположении линейно-упругой работы элементов диафрагмы и приведены в табл. 3 (графы 7 и 8).
Примечание. Вычисление геометрических и жесткостных характеристик, приведенных в табл. 3, как и значений изгибающих моментов MqI,  и поперечных QqI, QqII,F в опорном сплошном участке необходимо в случае использования для раскрытия статической неопределимости имеющихся стандартных программ расчета стержневых систем (например, SSP, SYSTERG и др.). При применении программы "KSO-88" вычисление указанных величин не требуется, в качестве исходных данных вводятся только значения нагрузок qI, qII, F, физических и геометрических характеристик диафрагмы и ее сечений.
и поперечных QqI, QqII,F в опорном сплошном участке необходимо в случае использования для раскрытия статической неопределимости имеющихся стандартных программ расчета стержневых систем (например, SSP, SYSTERG и др.). При применении программы "KSO-88" вычисление указанных величин не требуется, в качестве исходных данных вводятся только значения нагрузок qI, qII, F, физических и геометрических характеристик диафрагмы и ее сечений.
Статический расчет стержневой системы диафрагмы выполнен на ЕС ЭВМ ДВК-3 с использованием программы "KSO-88". Результаты расчета в виде усилий и перемещений представлены на рис. 11 (кривая 1 - расчет в линейно-упругой постановке, кривая 2 - расчет с учетом неупругих деформаций и трещин).
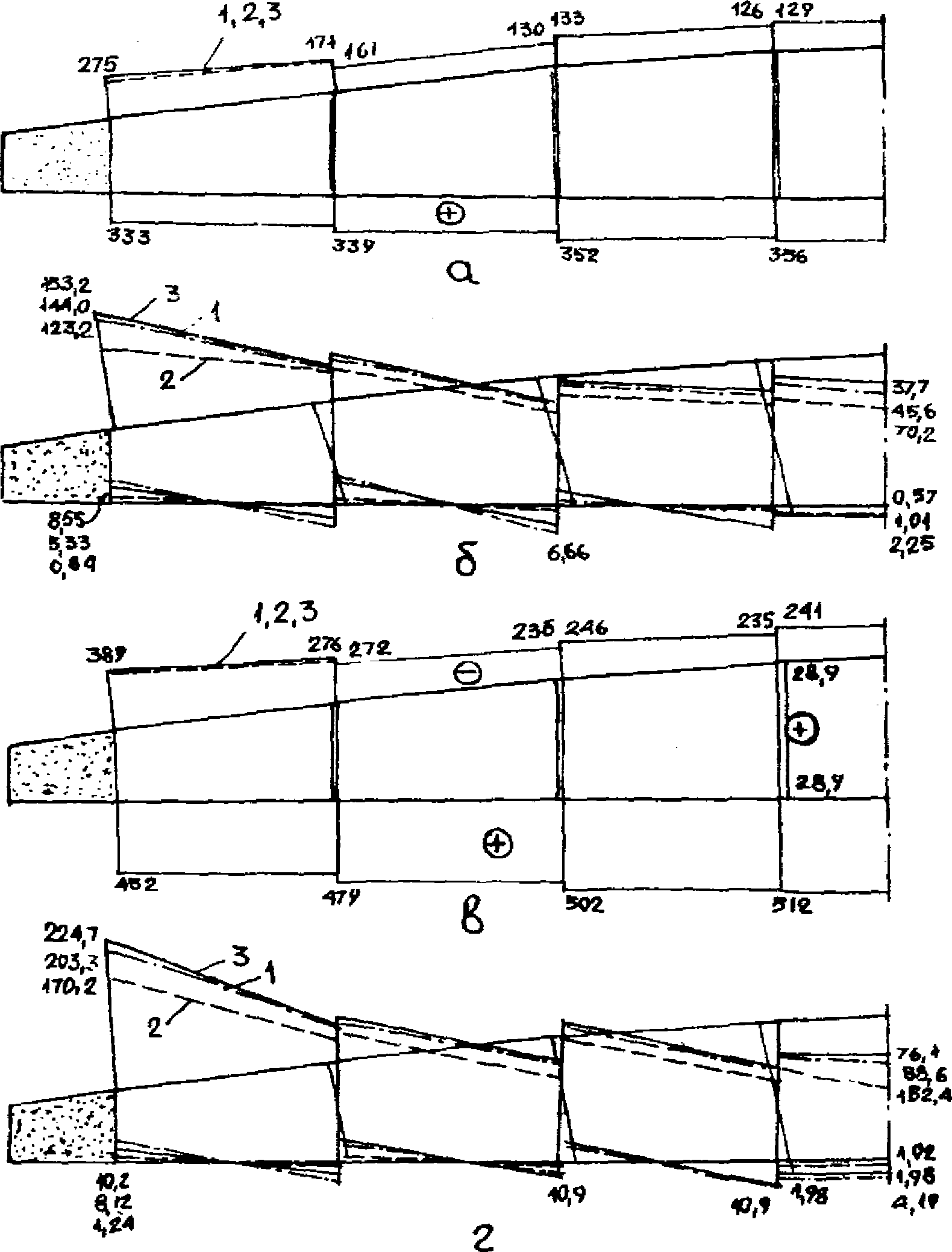
а и б - продольные силы в диафрагме от первого и второго
загружения; в и г - изгибающие моменты в диафрагме КСО
от первого и второго загружения; 1 - расчет
по практической приближенной методике настоящих
рекомендаций; 2 - расчет с учетом неупругих деформаций
и трещин; 3 - расчет методом конечных элементов
Максимальный прогиб диафрагмы с учетом перемещений опорного сплошного участка можно вычислить по формуле (17). Для этого предварительно по формуле (18) определим
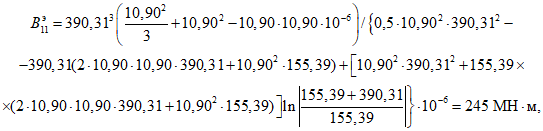
где
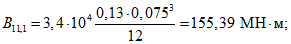
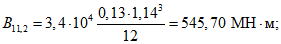
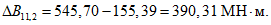
Изгибающие моменты от распределенной нагрузки первого загружения в начале и в конце рассматриваемого участка (см. расчетную схему на рис. 17, г настоящих рекомендаций), и приращение момента соответственно:
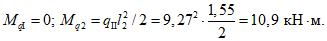
Тогда  .
.
 .
.С учетом значения перемещения узла 2, равного 34,7 мм (см. рис. 17, г) полученного из статического расчета диафрагмы по практической методике, значение максимального прогиба диафрагмы составит
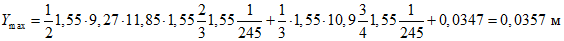
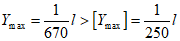
Итерационным расчетом на ЭВМ с учетом изменения жесткостных характеристик при неупругих деформациях и трещинах в железобетоне и нагрузках первого основного сочетания получен максимальный прогиб диафрагмы, равный 51 мм или 1/470 пролета, а при нагрузках второго основного сочетания - соответственно 83 мм и (1/280) пролета. Кривые прогибов диафрагмы приведены на рис. 12, б и в).
Определение усилий и перемещений в панели-оболочке методом конечных элементов с использованием пространственной дискретно-континуальной расчетной схемы
С целью оценки корректности практического метода расчета методом декомпозиции проведен статический расчет панели-оболочки КСО 3 x 24 методом конечных элементов с использованием пространственной дискретно-континуальной расчетной схемы (рис. 12, а) по программе "Прокруст-81" [14].
Расчет выполнен на указанные выше два основные сочетания внешних нагрузок в предположении упругой работы материала. Использованы конечные элементы (КЭ) следующих типов: элемент с библиотечным номером 1 - "стержень общего вида" для моделирования верхних поясов диафрагм, а также стоек, локальных утолщений глухой приопорной части и торцового ребра панели; элемент с библиотечным номером 8 - "прямоугольный элемент оболочки нулевой кривизны" для моделирования полки панели; элемент с библиотечным номером 10 - "треугольный элемент оболочки нулевой кривизны" для глухой приопорной части диафрагм.
Расчетная схема принята симметричной относительно среднего поперечного сечения панели. В узлы 1 и 2 введены линейные связи по направлениям X и Z общей системы координат, а в узлы 129 ... 136 - линейные связи по направлению оси Y и угловые относительно осей X и Z.
В расчетной схеме внешние нагрузки прикладывали следующим образом: полосовые нагрузки, передающиеся на панель-оболочку от гибких пластин-вставок к узлам 3-131 и 8-136 верхних поясов диафрагм, крановые, найденные по линии влияния (см. рис. 1 приложения 1), - к узлам 17, 18, 113 и 114 нижних поясов диафрагм, все остальные - к узлам конечных элементов по полке панели-оболочки.
Время счета задачи на ЭВМ ЕС-1022 составило 22 мин.
Усилия и перемещения в элементах панели-оболочки, полученные из расчета методом конечных элементов, показаны кривыми 3 на рис. 11 и 12 б - к.
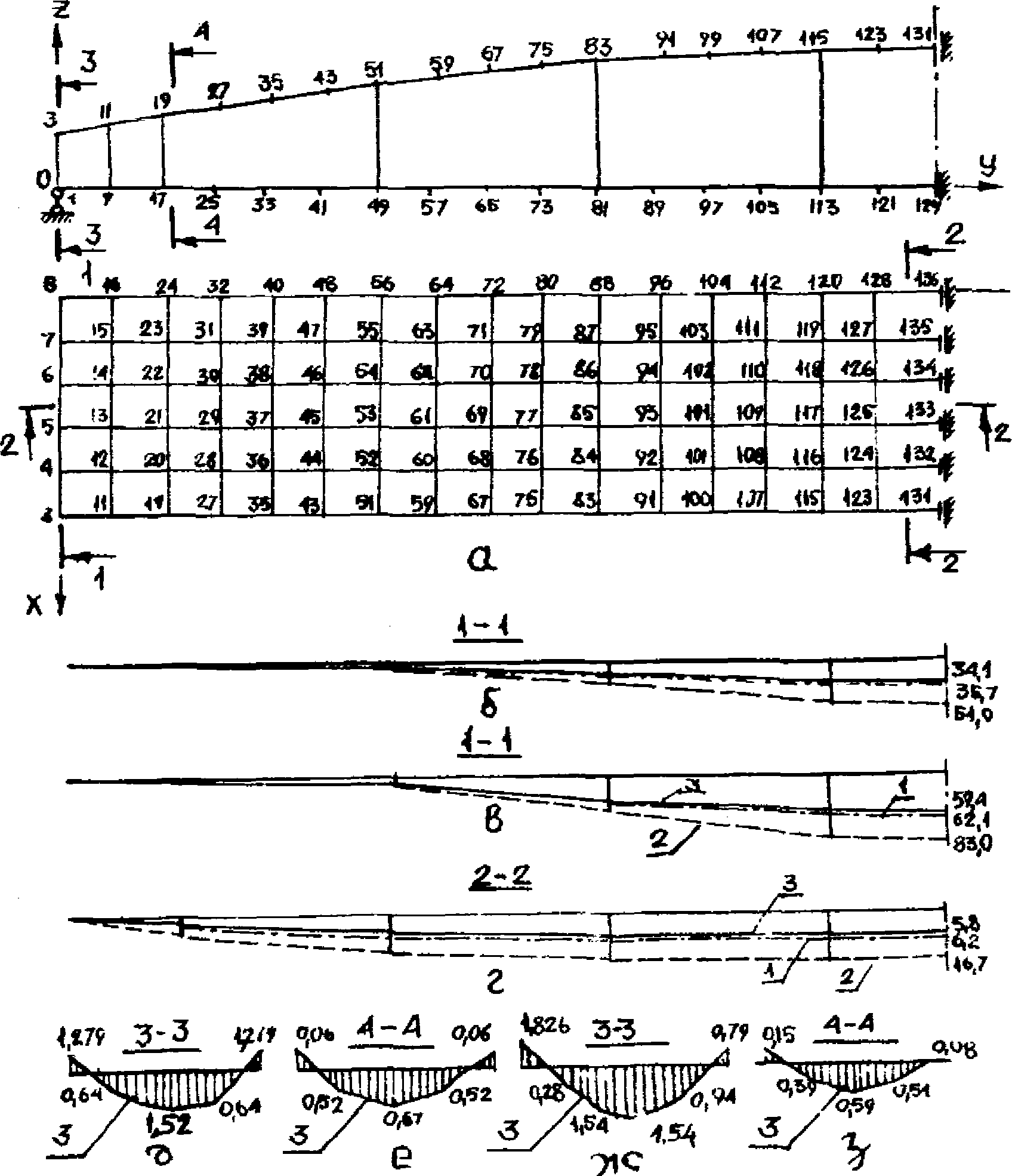
а - расчетная схема по методу конечных элементов;
б и в - прогибы диафрагмы от первого и второго
загружения (мм); г - прогибы полки от первого
загружения (мм); д и ж - изгибающие элементы в торцовом
ребре от первого и второго загружения;
е и з - то же в полке
Расчет диафрагмы панели-оболочки по образованию и раскрытию трещин
Упругопластический момент сопротивления сечения нижнего пояса диафрагмы
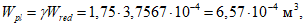
где
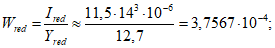
Эксцентриситет приложения продольной силы (см. эпюры M и N рис. 11 в, г)
eo = M/N = 10,9/502 = 0,0217 м.
Поскольку имеем N = 502 > P2 (P2 = 411,96 кН, см. пример расчета по несущей способности в Приложении 1 настоящих рекомендаций), то расстояние от центра тяжести приведенного сечения до ядровой точки вычисляем по формуле (133) [1]
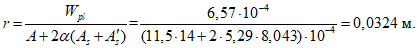
Момент внешних сил в сечении определяем по формуле (128) [1]
M = N(eo + r) = 502(0,0324 + 0,0217) = 26,65 кН·м.
Поскольку усилие обжатия приложено симметрично по сечению нижнего пояса, то eop = 0, а момент от усилия обжатия определяется по формуле (129) [1]
Mrp = P2(eop + r) = 411,96·0,0324 = 13,35 кН·м.
Момент, воспринимаемый сечением при образовании трещин, определяется по формуле (125) [1]
Mcrc = RBt,ser·Wpl + Mrp = 2,2·6,57·10-1 + 13,35 =
= 14,80 кН·м.
Так как Mr = 26,65 кН·м > Mr = 14,89 кН·м, то, следовательно, трещины в стадии эксплуатации образуются.
Ширину непродолжительного и продолжительного раскрытия трещин в нижнем поясе диафрагмы определяем в соответствии с указаниями п. 4.14, 4.15, 1.16 [1].
Эксцентриситет равнодействующей продольных сил
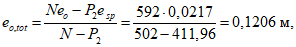
но так как
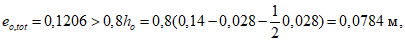
то приращение напряжения в арматуре вычисляем по формуле (148) [1].
Предварительно вычисляем следующие расчетные характеристики:
es = eo = 0,0217 м;
esp = 0;
Ms = Nes = 502·0,0217 = 10,9 кН·м;
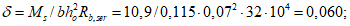
Ntot = N - P2 = 502,0 - 411,96 = 90,04 кН;
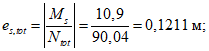
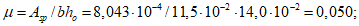
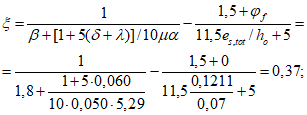
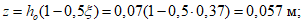
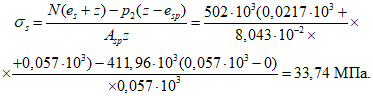
Ширина раскрытия трещин acrc1 от непродолжительного действия всей нагрузки
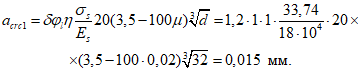
Определим ширину раскрытия трещин acrc2 от непродолжительного действия постоянной и длительной нагрузки. Для этого вычисляем усилия от этих нагрузок, исходя из следующих соотношений (см. табл. 1, Приложение 1):
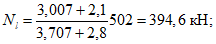
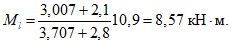
Для определения приращений напряжений в арматуре предварительно вычисляем:
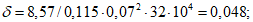
Ntot = 394,60 - 411,96 = -17,36 кН;
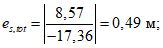
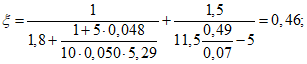
z = 0,07(1 - 0,5·0,46) = 0,054 м.
Приращение напряжений в арматуре при
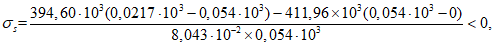
следовательно трещины в нижнем поясе диафрагмы при постоянных и длительных нагрузках не образуются.
Полная ширина раскрытия трещин в нижнем поясе диафрагмы
acrc = acrc1 - acrc2 + acrc3 = 0,015,
что меньше предельно допустимого значения [acrc1] = 0,4 мм.
Расчет перемещений складчатой полки с учетом неупругих деформаций и трещин
Расчет выполняем по практической методике, изложенной в п. 4.35 ... 4.43 настоящих рекомендаций. Расчетная нагрузка на полку (см. табл. 1 Приложения 1) при  составляет q = 1,045 + 0,71 + 0,665 = 2,42 кПа, в т.ч. длительно действующая ql = 1,045 + 0,71 = 1,76 кПа.
составляет q = 1,045 + 0,71 + 0,665 = 2,42 кПа, в т.ч. длительно действующая ql = 1,045 + 0,71 = 1,76 кПа.
Пролетный и опорный расчетные моменты - соответственно при кратковременном и длительном действии нагрузки (согласно формулам (19) и (20) настоящих рекомендаций):
Mq1 = 2,42(2,98 - 2·0,185)2/24 = 0,69 кН·м;
Mql1 = 1,76(2,98 - 2·0,185)2/24 = 0,50 кН·м;
Mq2 = 2,42(2,98 - 2·0,185)2/12 = 1,37 кН·м;
Mql2 = 1,76(2,98 - 2·0,185)2/12 = 1,01 кН·м.
Полка в направлении ее пролета имеет три участка различной жесткости: средний - толщиной 30 мм и жесткостью B1 и два приопорных - с переменной толщиной от 30 до 75 мм и с жесткостями B2 и B3. Значения этих жесткостей в первом приближении (при отсутствии трещин в полке) вычисляем по формулам:
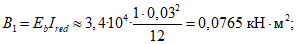
B2 = B1; 

Эквивалентную жесткость приопорного участка Bэ определяем по формуле (18) настоящих рекомендаций, для чего предварительно вычисляют момент в точке сопряжения участков полки различной жесткости Mq3 (см. рис. 18, б)
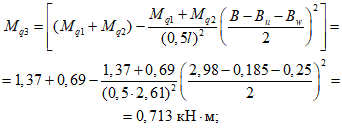
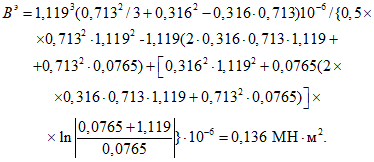
Максимальный прогиб полки от полной нагрузки при ее непродолжительном действии с учетом коэффициентов  и
и 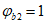 п. 4.24 [1] определяем по формуле (21) настоящих рекомендаций перемножением эпюр Mq и
п. 4.24 [1] определяем по формуле (21) настоящих рекомендаций перемножением эпюр Mq и  (см. рис. 18, б)
(см. рис. 18, б)
 и
и ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
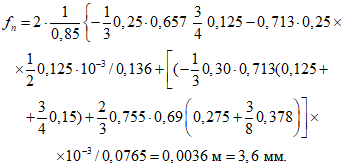
Аналогично вычисляем прогиб от постоянных и длительных нагрузок при продолжительном их действии. В результате прогиб от полной нагрузки в полке при условии отсутствия в ней трещин составил fn = 6,2 мм.
Поскольку при нормативной нагрузке q = 2,42 кПа в полке панели-оболочки появляются трещины в зоне действия максимального пролетного момента (см. расчет полки по трещиностойкости в настоящем приложении), то уточним значение максимального прогиба с учетом наличия трещин на среднем участке полки. Из-за изменения соотношения жесткостей пролетного и опорного участков полки итерационным расчетом определены новые значения пролетного и опорного моментов от полной нагрузки и от длительно действующих нагрузок. Их величины соответственно составили:
Mq1 = 0,472 кН·м; Mql1 = 0,342 кН·м; Mq2 = 1,589 кН·м;
Mql2 = 1,153 кН·м.
Жесткость среднего участка полки с трещинами в наиболее напряженном сечении вычисляем согласно п. 4.27 [1]
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
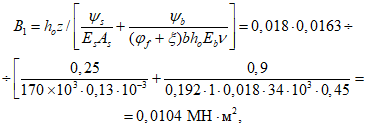
где 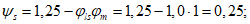

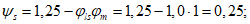

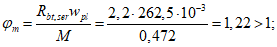
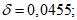
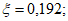 z = 16,3 мм.
z = 16,3 мм.Прогиб балки от непродолжительного действия всей нагрузки
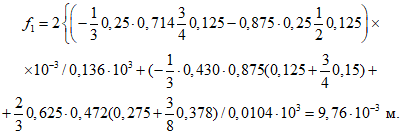
Аналогично определяем прогибы от непродолжительного f2 и продолжительного f3 действия постоянных и длительных нагрузок, для чего предварительно вычисляем значения:
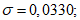
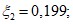 z = 16,2 мм; B1 = 0,0105 МН·м2;
z = 16,2 мм; B1 = 0,0105 МН·м2;ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
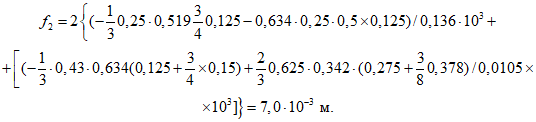
Прогиб f3 при  и B = 0,0049 МН·м2
и B = 0,0049 МН·м2
 и B = 0,0049 МН·м2
и B = 0,0049 МН·м2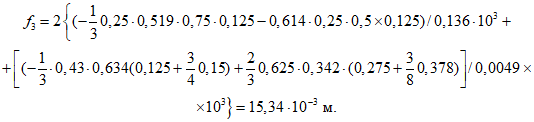
Полный прогиб полки с трещинами
fn = f1 - f2 + f3 = (9,76 - 7,0 + 15,34)·10-3 = 18,1·10-3 м,
или
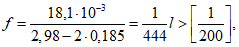
следовательно из условия обеспечения жесткости полки требованиям п. 1.20 [1] необходимо уменьшить расчетную нагрузку на полку или же увеличить интенсивность ее армирования и выполнить повторный расчет прогибов.
Расчет торцового ребра, стойки фермы-диафрагмы и складчатой полки по образованию и раскрытию трещин
Расчетный изгибающий момент в середине пролета торцового ребра, определенный из расчета панели-оболочки по пространственной расчетной схеме методом конечных элементов, при нагрузке первого основного сочетания составил 1,52 кН·м.
Этот же момент может быть определен и по практической методике поэлементного расчета в соответствии с указаниями п. 4.41 настоящих рекомендаций. В этом случае, как показали проведенные вычисления, значение момента Mp1, вычисленного по формуле (22), получается несколько большим, чем при расчете по МКЭ, что идет в запас жесткости и трещиностойкости ребра.
Геометрические параметры и армирование ребра приняты такими же, как и в расчете по несущей способности (см. расчет торцового ребра, Приложение 1). Геометрические характеристики приведенного сечения ребра при принятых размерах и армировании:
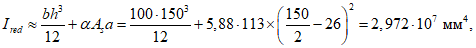
где 

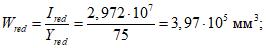
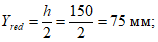
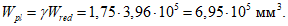
Изгибающий момент, воспринимаемый сечением при образовании трещин, определяют по формуле (125) [1]
Mcrc = Rbt,serWpl = 2,2·6,95·105 = 1,53·106 Н·мм = 1,53 кН·м.
Так как Mcrc = 1,53 кН·м > 1,52 кН·м, то трещины в торцовом ребре не образуются.
Стойка диафрагмы внецентренно растянута и при нагрузках второго сочетания расчетные усилия, определенные из расчета методом конечных элементов, составили: M = 5,1 кН·м; N = 28,9 кН.
Геометрические характеристики приведенного сечения при принятых размерах и армировании:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
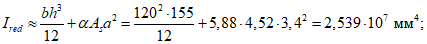
Wred = Ired/Yred = 2,539·107/60 = 4,23·105 мм4;
eo = M/N = 5,1/28,9 = 0,176 м;
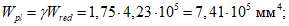
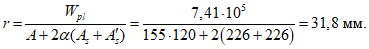
Момент, воспринимаемый сечением перед образованием трещин:
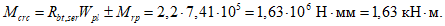
Момент внешних сил
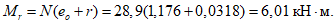
Так как Mr > Mcrc, то трещины в стойке образуются.
Ширину раскрытия трещин определяем по указаниям п. 1.16 и п. 4.13 [1]. В результате вычислений, аналогичных расчету нижнего пояса:
acrc1 = 0,161 мм; acrc2 = 0,128 мм; acrc3 = 0,166 мм.
Полная ширина раскрытия трещин в стойке
acrc = 0,161 - 0,128 + 0,166 = 0,199 мм < [0,4 мм].
Заметим также, что ширина раскрытия трещин, определенная расчетом по усилию растяжения, возникающему в стойке от нагрузки подвесного транспорта, приложенного непосредственно к стойке, собственной массы стойки и примыкающего участка нижнего пояса диафрагм (см. приложение 1), составила 0,0274 мм. Таким образом в обоих случаях конструктивные соображения выступают в качестве определяющих при подборе арматуры стоек.
Расчет полки при армировании, назначенном исходя из обеспечения несущей способности (см. приложение 1), показал, что ширина раскрытия трещин превышает допустимую по требованиям норм [1], поэтому принимаем  Вр-1 с шагом 100 мм.
Вр-1 с шагом 100 мм.
Геометрические характеристики приведенного сечения полки-полоски единичной ширины.
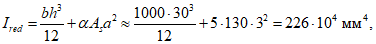
Yo = 0,5h = 1,5 мм;
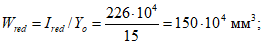
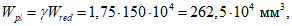
где a = 3 мм - расстояние от центра тяжести арматуры до центра тяжести площади приведенного сечения;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 4.1 в СНиП 2.03.01-84 [1] отсутствует. |
Mcrc = Rbt,serWpl +/- Mrp = 2,2·262,5·103 = 5,8·105 Н·мм =
= 0,58 кН·м.
Следовательно, в стадии эксплуатации в полке КСО появятся трещины, так как Mr = 0,67 > 0,58 кН·м, где Mr = Mq1 = 0,67 (см. рис. 12, е).
Аналогично выполняется проверка трещиностойкости приопорной зоны полки на действие изгибающего момента Mq2 (см. рис. 18, б настоящих рекомендаций). В результате расчета установлено, что трещины в указанной зоне полки при действии заданной нагрузки q = 2,42 кПа не образуются.
Ширину раскрытия трещин в середине пролета полки определим по формулам п. 4.14 и 4.15 [1], для чего вычисляем следующие величины:
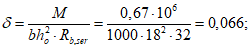
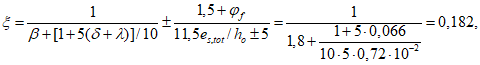
где 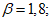

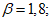

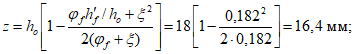
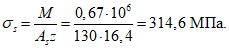
Ширина непродолжительного раскрытия трещин от неполной нагрузки
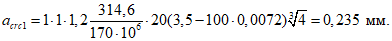
Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки
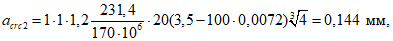
где 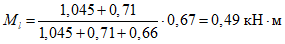 (см. табл. 1);
(см. табл. 1);
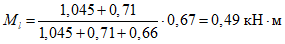 (см. табл. 1);
(см. табл. 1);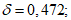
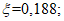 z = 16,3 мм;
z = 16,3 мм; 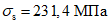 .
.Ширина раскрытия трещин от непродолжительного действия постоянных и длительных нагрузок при 

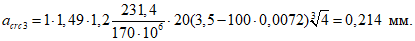
Полная ширина раскрытия трещин в полке панели-оболочки
acrc = 0,235 - 0,144 + 0,214 = 0,305 мм < [0,4 мм].
Расчет гибкой пластины - пологой цилиндрической
оболочки по деформациям и трещиностойкости
Определение усилий и перемещений на основе полубезмоментной теории и вариационного смешанного метода В.З. Власова (см. п. 5.12 настоящих рекомендаций)
Рассчитываем крайнюю пластину-оболочку с утолщением у свободного края 100 x 250 мм (рис. 13, а). Данные для проектирования пластины - пологой цилиндрической оболочки приняты такими же, как и для средней пластины-оболочки при расчете по несущей способности (см. приложение 1).
Расчетный пролет пластины-оболочки в направлении оси принят равным расстоянию в свету между панелями КСО l1 = 3,0 м. Расчетная нагрузка на пластину-оболочку (см. табл. 1 Приложения 1) при  составляет q = 1,045 + 0,95 + 0,665 = 2,660 кПа, в т.ч. длительно действующая q1 = 1,045 + 0,95 = 1,995 кПа.
составляет q = 1,045 + 0,95 + 0,665 = 2,660 кПа, в т.ч. длительно действующая q1 = 1,045 + 0,95 = 1,995 кПа.
В соответствии с рекомендациями п. 5.12 настоящих методических рекомендаций цилиндрическую поверхность следует заменить 6 - 8-гранной вписанной призматической складкой. С целью сокращения объема настоящего примера проиллюстрируем содержание вычислений при замене оболочки четырехгранной (g = 4) складкой, включая бортовую грань, аппроксимирующую утолщение пластины-оболочки у одного из торцов (рис. 13, б).
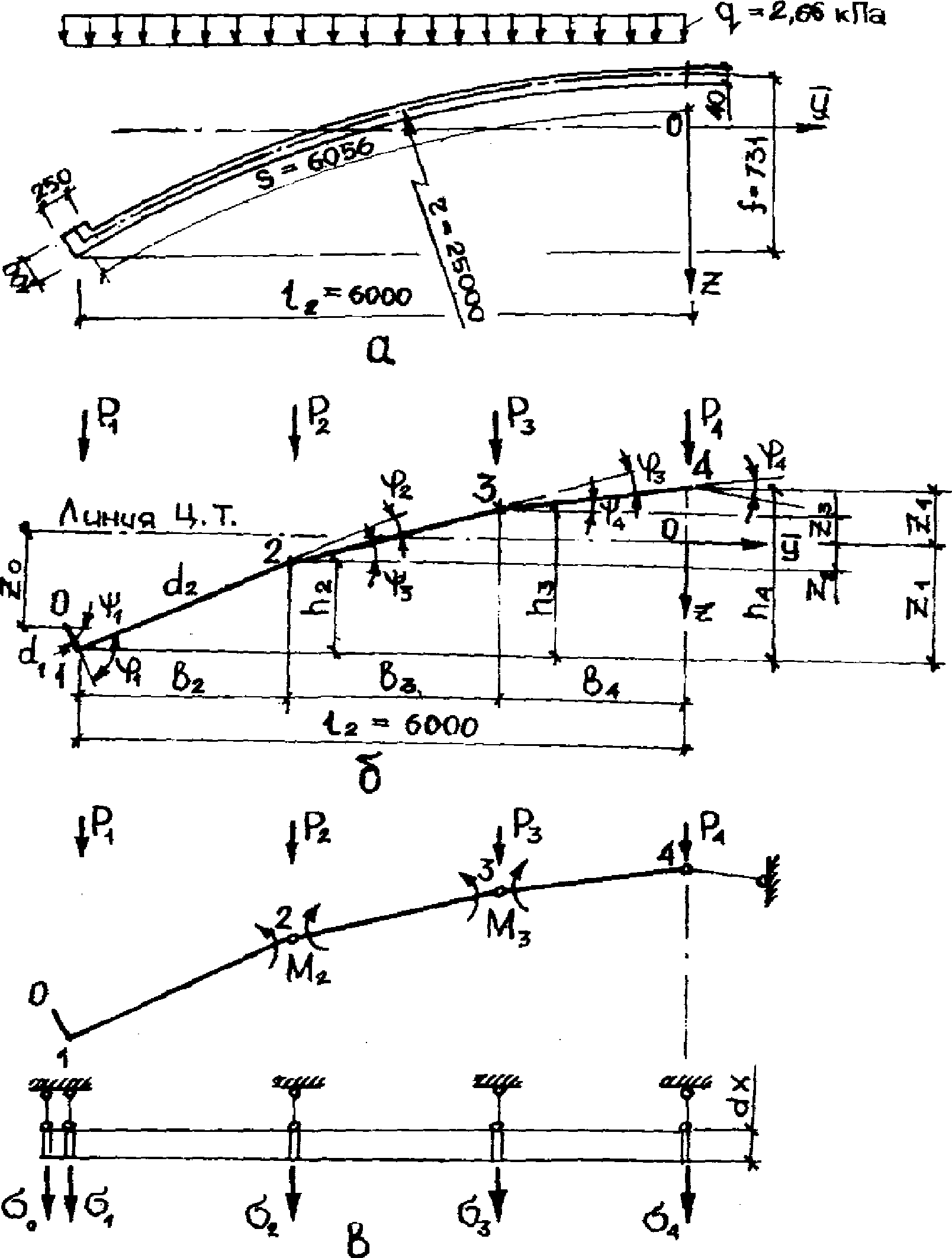
а - геометрическая схема поперечного сечения оболочки
и схема поверхностной нагрузки; б - схема вписанной
складки с полосовыми нагрузками вдоль ребер;
в - основная система смешанного метода
Координаты Z ребер вписанной складки hi (i = 1, 2, ... g) могут быть определены по известным уравнениям окружности:
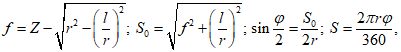
где f, r, l - соответственно стрела подъема, радиус кривизны и пролет панели-оболочки, см. п. 2.3 и рис. 2 настоящих методических рекомендаций; S, S0 и  - соответственно длина дуги образующей оболочки и длина хорды, соединяющей начало и конец этой дуги и угол между двумя радиусами, проведенными через начало и конец хорды, или же из уравнения квадратной параболы Z = -0,0097Y2 + 0,233Y, которое также с достаточной для практического расчета точностью согласуется с геометрией верхнего пояса диафрагмы панели КСО. В результате вычислений по указанным зависимостям при разбивке цилиндрической поверхности на три грани, одинаковые по ширине (d2 = d3 = d4 = 2,0183 м), получены следующие геометрические характеристики складчатой поверхности (см. рис. 13, б):
- соответственно длина дуги образующей оболочки и длина хорды, соединяющей начало и конец этой дуги и угол между двумя радиусами, проведенными через начало и конец хорды, или же из уравнения квадратной параболы Z = -0,0097Y2 + 0,233Y, которое также с достаточной для практического расчета точностью согласуется с геометрией верхнего пояса диафрагмы панели КСО. В результате вычислений по указанным зависимостям при разбивке цилиндрической поверхности на три грани, одинаковые по ширине (d2 = d3 = d4 = 2,0183 м), получены следующие геометрические характеристики складчатой поверхности (см. рис. 13, б):
h1 = 0; h2 = 0,3488 м; h3 = 0,7006 м;
h4 = 0,9747 м; B1 = 0,01608 м; B2 = 1,97218 м;
B3 = 1,98737 м; B4 = 1,99960 м;  ;
;
 ;
;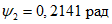 ;
; 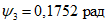 ;
; 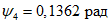 ;
; , толщины всех граней складки (кроме бортовой) приняты одинаковыми t2 = t3 = t4 = 0,04 м; размеры бортовой грани складки приняты по заданным размерам утолщения пластины; d1 = 0,08 м; t1 = 0,25 м.
, толщины всех граней складки (кроме бортовой) приняты одинаковыми t2 = t3 = t4 = 0,04 м; размеры бортовой грани складки приняты по заданным размерам утолщения пластины; d1 = 0,08 м; t1 = 0,25 м.Основная система при расчете рассматриваемой четырехгранной складки смешанным методом приведена на рис. 13, в. Число неизвестных напряжений в ребрах складчатой системы  равно числу ребер i = 0, 1, 2, 3, 4, а число неизвестных моментов MK(X) равно двум (поскольку сопряжение рассматриваемой конструкции крайней пластины-оболочки с примыкающей к ней по ребру 4 средней пластиной-оболочкой принято шарнирным, то M4 в качестве лишнего неизвестного не вводится в расчетной схеме). Влияние соседней пластины-оболочки на напряженно-деформированное состояние рассчитываемой конструкции учитывается введением в расчетную схему шарнирно-сопряженной грани-связи (см. рис. 13, в).
равно числу ребер i = 0, 1, 2, 3, 4, а число неизвестных моментов MK(X) равно двум (поскольку сопряжение рассматриваемой конструкции крайней пластины-оболочки с примыкающей к ней по ребру 4 средней пластиной-оболочкой принято шарнирным, то M4 в качестве лишнего неизвестного не вводится в расчетной схеме). Влияние соседней пластины-оболочки на напряженно-деформированное состояние рассчитываемой конструкции учитывается введением в расчетную схему шарнирно-сопряженной грани-связи (см. рис. 13, в).
В соответствии с рекомендациями п. 5.12 эпюры единичных функций  для рассматриваемой четырехгранной складки имеют вид, показанный на рис. 14. Значение ординат этих эпюр вычисляем по формулам (77) и (78) настоящих рекомендаций:
для рассматриваемой четырехгранной складки имеют вид, показанный на рис. 14. Значение ординат этих эпюр вычисляем по формулам (77) и (78) настоящих рекомендаций:
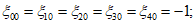
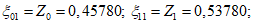
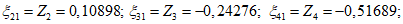
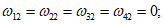
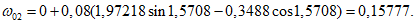
Аналогично вычислены остальные ординаты эпюр единичных функций и получены следующие их значения
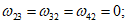
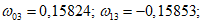
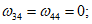
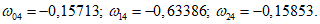
Коэффициенты aji определяем интегрированием эпюр по формуле (75, а) настоящих рекомендаций:
a00 = (2·1·1 + 2·1·1 + 1·1 + 1·1)·0,25·0,08/6 + (2·1 + 2·1 +
+ 1·1 + 1·1)·0,04·2,0183·3/6 = 0,31530;
a01 = a10 =(-2·1·0,45780 - 2·1·0,53780 - 0,45780·1 - 0,53780·1) x
x 0,25·0,08/6 + (-2·0,53780·1 - 2·1·0,10898 - 0,10898·1 -
- 0,53780·1)·0,04·2,0183/6 + (-2·0,10898 - 2·0,24276 -
- 0,10898·1 - 0,24276·1)·0,04·2,0183/6 + (-2·0,10898 -
- 2·0,51689 - 0,10898·1 - 0,51689·1)·0,04·2,0183/6 = 0,00000.
Аналогично вычислены остальные коэффициенты aji и получены следующие их значения:
a02 = a20 = -0,0018974; a03 = a30 = 0,0076987;
a04 = a40 = 0,0556726;
a11 = 0,0306634; a21 = a12 = 0,0009192;
a13 = a31 = -0,0030911; a14 = a41 = -0,0188363;
a22 = 0,0001996; a23 = a32 = 0,0000999;
a24 = a42 = -0,0005997;
a33 = 0,0010144; a34 = a43 = 0,0039625;
a44 = 0,0220985.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: выражение (88 а) отсутствует. Возможно, имеется в виду выражение (88). |
Выполняем проверку правильности вычисления коэффициентов aji, пользуясь выражением (88 а) настоящих методических рекомендаций. Для этого сложением всех единичных эпюр  строим суммарную эпюру
строим суммарную эпюру  (см. рис. 14, б) и интегрируем ее саму на себя по правилу Верещагина
(см. рис. 14, б) и интегрируем ее саму на себя по правилу Верещагина
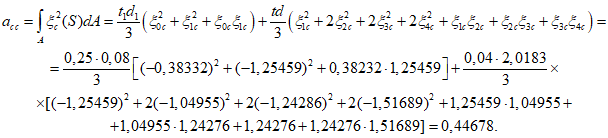
 , т.е. проверка выполняется.
, т.е. проверка выполняется.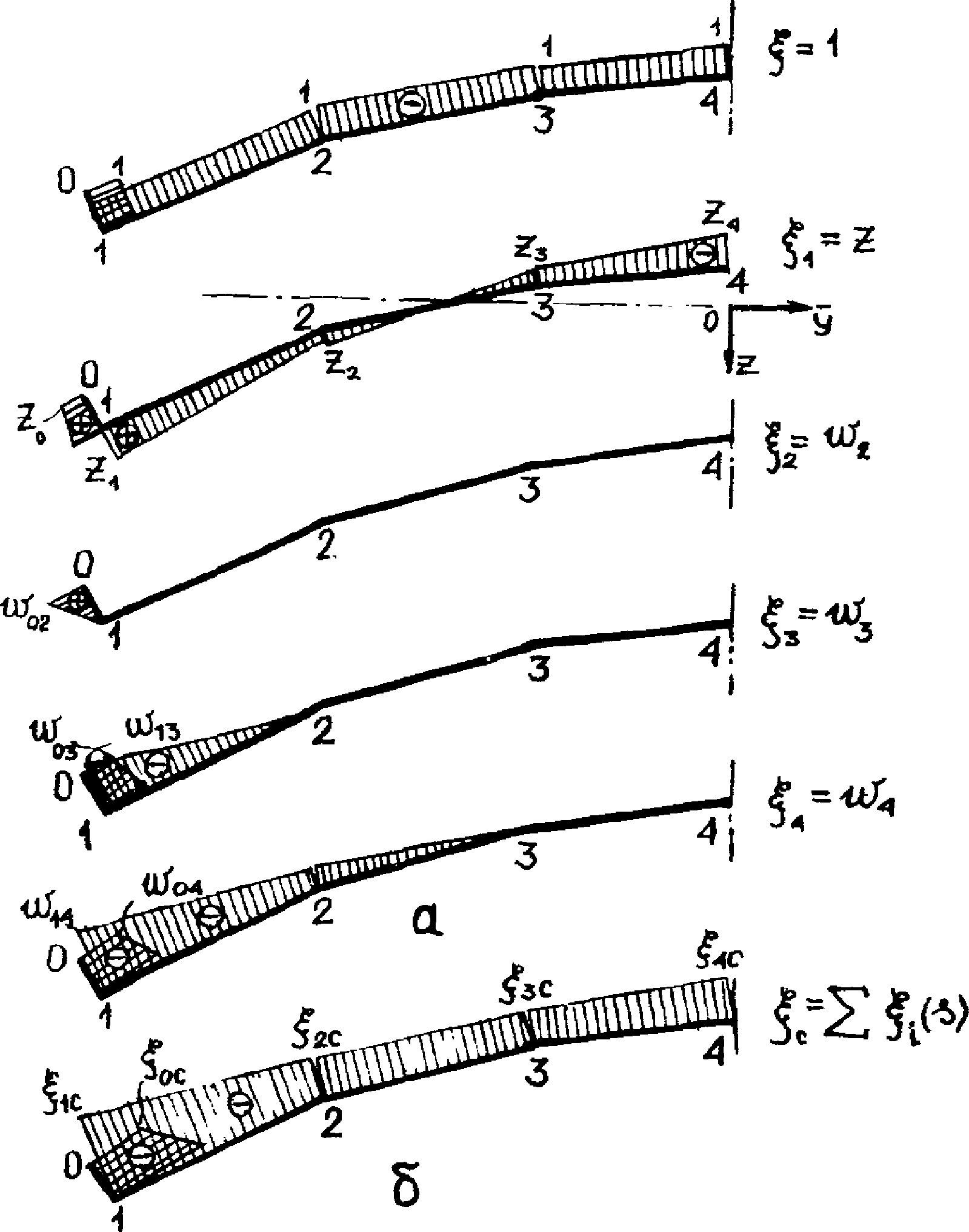
а - при замене оболочки четырехгранной складкой;
б - суммарная
Погрешность вычисления коэффициентов aji составляет
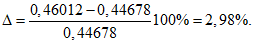
Коэффициенты 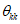 вычисляем по формуле (74):
вычисляем по формуле (74):
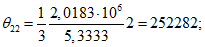
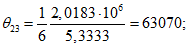
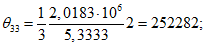
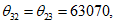
где 5,3333·10 - численное значение момента инерции продольного сечения единичной длины для k-той грани, найденное из выражений
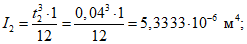
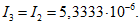
Грузовые коэффициенты qj (j = 1, ..., 4) разрешающих уравнений определяем по формуле (76), принимая интенсивность распределенной нагрузки q = 2,66 кПа.
Значения узловой нагрузки будут равны:
PK = (BK,K-1 + BK,K+1)q/2; (K = 1, ..., 4);
P1 = (0,01608 + 1,97218)·2,66/2 = 2,6230;
P2 = 5,2662; B3 = 5,3026; P4 = 2,6594,
а значения грузовых коэффициентов соответственно составят:
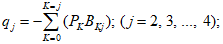
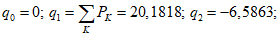
q3 = -26,5485; q4 = -60,1327.
По табл. 3.2 [6] при шарнирном опирании складки и равномерно распределенной вдоль ребер нагрузке для первого члена ряда находим A1 = 1,2732, а по табл. 3.8 [6]  .
.
 .
.Вычисляем значения  и
и  :
:
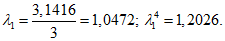
Систему разрешающих алгебраических уравнений для рассматриваемой складки при g = 4 записываем в форме табл. 3.
Таблица 3
j, K | Свободные члены | |||||||
2 | -2523 | -6307 | 0 | 1 | 0 | 0 | 0 | 0 |
3 | -2523 | 0 | 0 | 1 | 0 | 0 | 0 | |
0 | 0 | 0 | 0,3153 | 0,000 | -0,001897 | 0,007699 | 0,05567 | 0 |
1 | 0 | 0 | 0,03366 | 0,0009192 | -0,003091 | -0,01884 | 20,1818 | |
2 | 1 | 0 | 0,0001996 | 0,0000999 | -0,0005997 | -6,5863 | ||
3 | 0 | 1 | 0,001014 | 0,003963 | -26,5485 | |||
4 | 0 | 0 | 0,02210 | -60,1327 |
Решением системы уравнений по методу Гаусса получаем следующие значения параметров  и
и  (K = 2,3; i = 0, 1, ..., 4):
(K = 2,3; i = 0, 1, ..., 4):
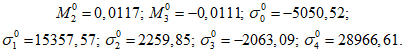
Напряжения усилия и перемещения по ребрам складки при удержании одного члена ряда (m = 1) определяем по формулам (79) - (86).
Нормальные напряжения в ребрах складки при X = 0,5l1 и заданной интенсивности нагрузки q = 2,66 кПа и  соответственно составят (рис. 15):
соответственно составят (рис. 15):
 соответственно составят (рис. 15):
соответственно составят (рис. 15):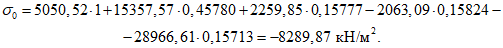
Аналогично вычислены
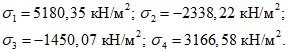
Сдвигающие усилия в опорном сечении X = 0 (рис. 15, б):
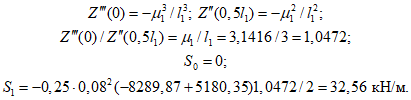
Аналогично вычислены:
S2 = -87,58 кН/м; S3 = 72,56 кН/м; S4 = 0,00004 ~= 0.
Суммарные сдвигающие усилия в пределах K-й грани (рис. 15, г)
T1 = -0,25·0,082[2·(-8289,87) + 5180,35]·1,0472/6 = 3,18 кН.
Аналогично вычислены:
T2 = -162,42 кН; T3 = -2,53 кН; T4 = 138,86 кН.
Для вычисления прогибов ребер складки находим значения ординат эпюр вертикальных перемещений (рис. 16, а) исходя из следующих соотношений:
fKi = 1 при i = 1, K = 0, 1, 2, 3, 4
и
 при i = 2, 3, 4, K = 0, 1, 2.
при i = 2, 3, 4, K = 0, 1, 2.Прогибы ребер складчатой системы в середине пролета при X = 0,5l1 (рис. 16, б) соответственно составят
V1 = 3,31·10-3 м; V2 = 1,77·10-3 м; V3 = 0,53·10-3 м.
Аналогично: 

На рис. 15 и 16, б приведены также эпюры усилий и перемещений пластины-оболочки при аппроксимации ее шести- и семигранной складкой (кривые 2 и 3). Анализ этих кривых показывает, что даже достаточно грубая аппроксимация оболочки четырехгранной складкой позволяет (исходя из максимальных значений усилий и перемещений) произвести оценку жесткости и трещиностойкости такой конструкции.
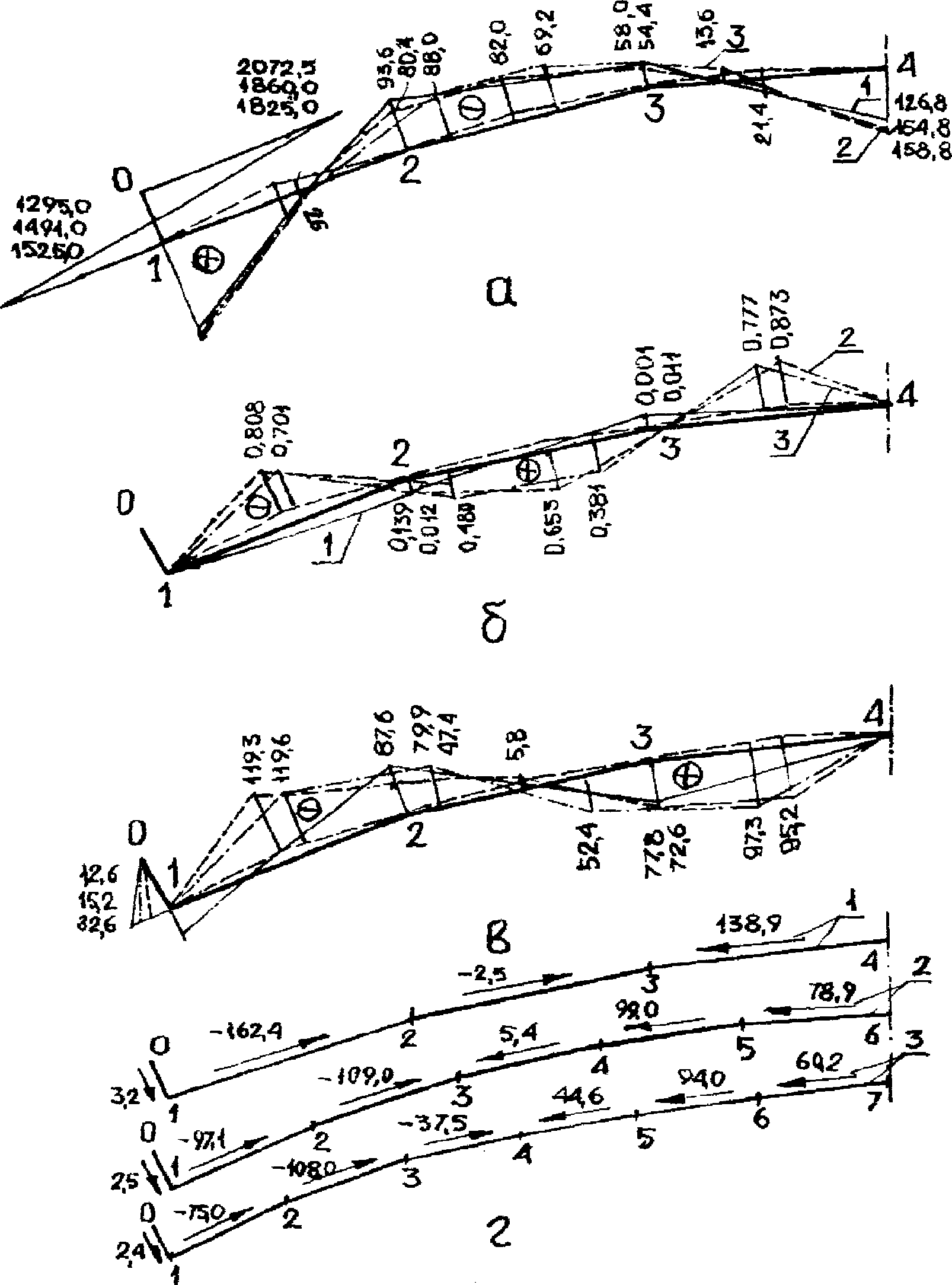
а, б - нормальные усилия Nx (кН/м) и поперечные
изгибающие моменты My (кН·м), в сечении X = 0,5l1;
в, г - соответственно сдвигающие усилия Sx (кН/м)
и суммарные сдвигающие усилия Nx, кН, в опорном сечении
X = 0; 1, 2 и 3 - при аппроксимации оболочки соответственно
четырех-, шести- и семигранной складкой
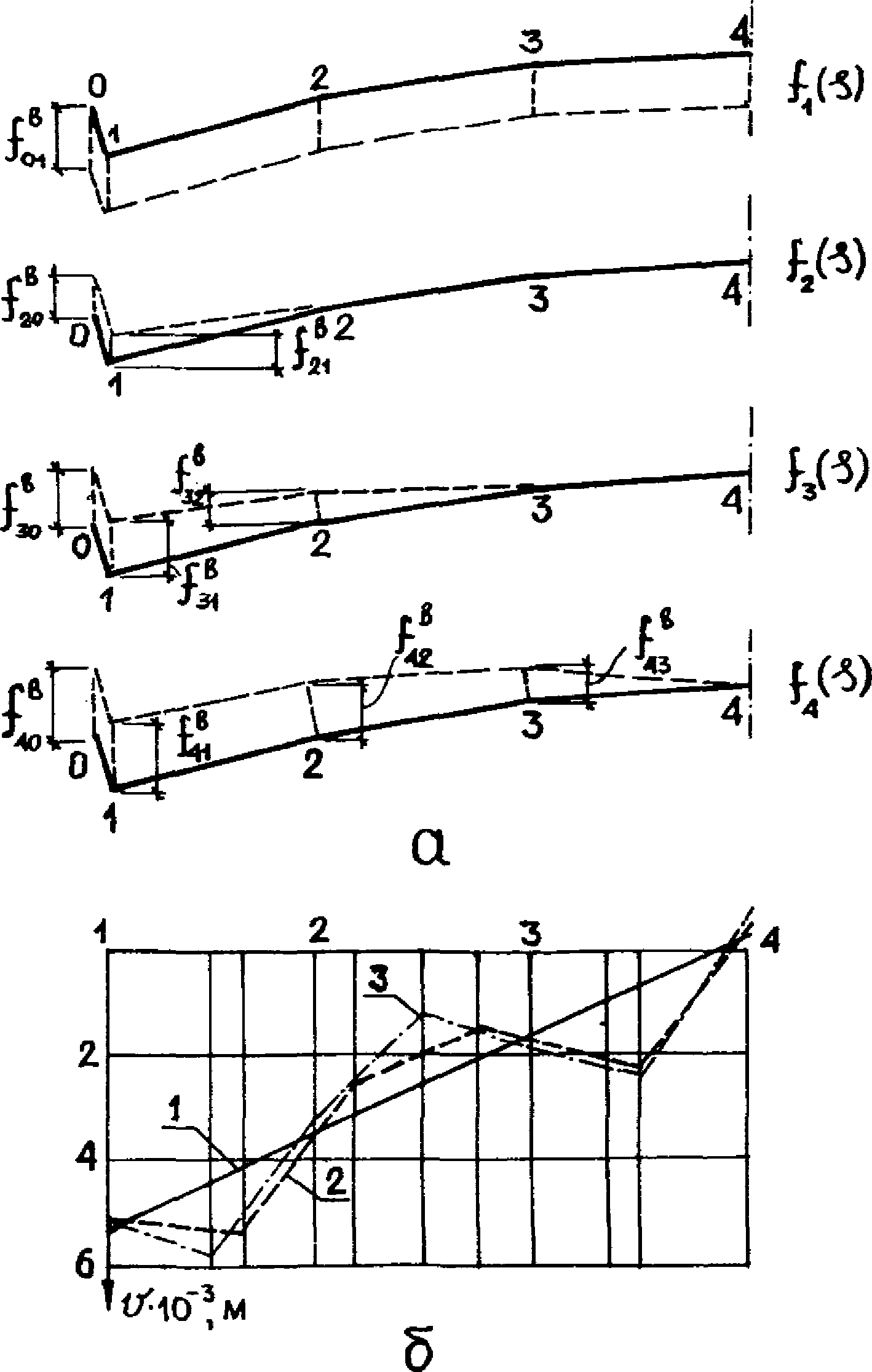
поперечной полоски основной системы (а) и эпюры прогибов
складки в сечении X = 0,5l1 (б); 1, 2 и 3 - соответственно
при аппроксимации оболочки 4-, 6- и 7-гранной складкой
Для оценки жесткости рассматриваемой конструкции пластины-оболочки в соответствии с требованиями [1] определим значение полного расчетного прогиба от всех соответствующих нагрузок. Поскольку согласно эпюре распределения прогибов по сечению складки (см. рис. 16, б) максимальный прогиб возникает в ребре 1 (при аппроксимации четырехгранной складкой), то расчет полного прогиба выполним для этого ребра. Проверка условий трещинообразования показала (см. расчет по трещиностойкости в настоящем Приложении), что при действии нормальной нагрузки q = 2,66 МПа нормальные трещины в пластине-оболочке не образуются и определение прогибов производим как для конструкции без трещин в растянутых зонах.
Вычисляем составляющие полного прогиба пластины-оболочки V11, V12 соответственно от действия кратковременной постоянной и длительной нагрузок:
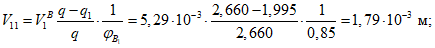
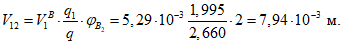
Для определения выгибов пластины от предварительного обжатия в поперечном направлении в соответствии с указаниями [1] предварительно вычисляем следующие величины:
усилие обжатия поперечного направления при схеме армирования и напряжениях в арматуре, принятых при расчете по несущей способности (см. приложение 1)
P2 = 2·651,53·16·0,196·10-1 + 637,5·15·0,196·10-1 = 596,05 кН;
геометрические характеристики приведенного сечения пластины

Sred = 0,2408·0,02 + 0,006353·0,017 = 0,4924·10-2 м3;
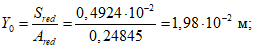
eop2 = [2,3 - (4 - 1,98)]·10-2 м;
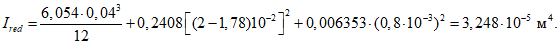
Выгибы V13 и V14 соответственно от непродолжительного действия усилия предварительного обжатия и от усадки и ползучести бетона, вызванных влиянием усилия предварительного обжатия
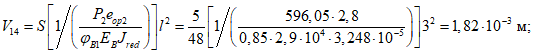
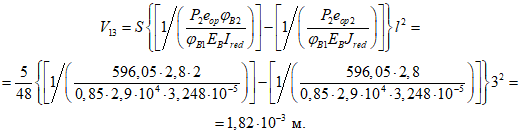
V1 = V11 + V12 - V13 - V14 = 1,79·10-3 + 7,94·10-3 -
- 1,82·10-3 - 1,82·10-3 = 6,11 мм
или
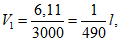
что меньше предельно допустимого значения  .
.
 .
.Расчет по образованию трещин
Для проверки по образованию косых трещин в угловых зонах пластины (см. рис. 29, элемент А) предварительно определим следующие расчетные параметры:
длину зоны передачи напряжений при передаточной прочности RBp = 0,7·30 = 21 МПа соответственно для поперечной и продольной арматуры (рис. 17)
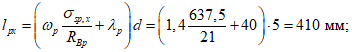
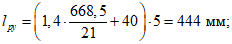
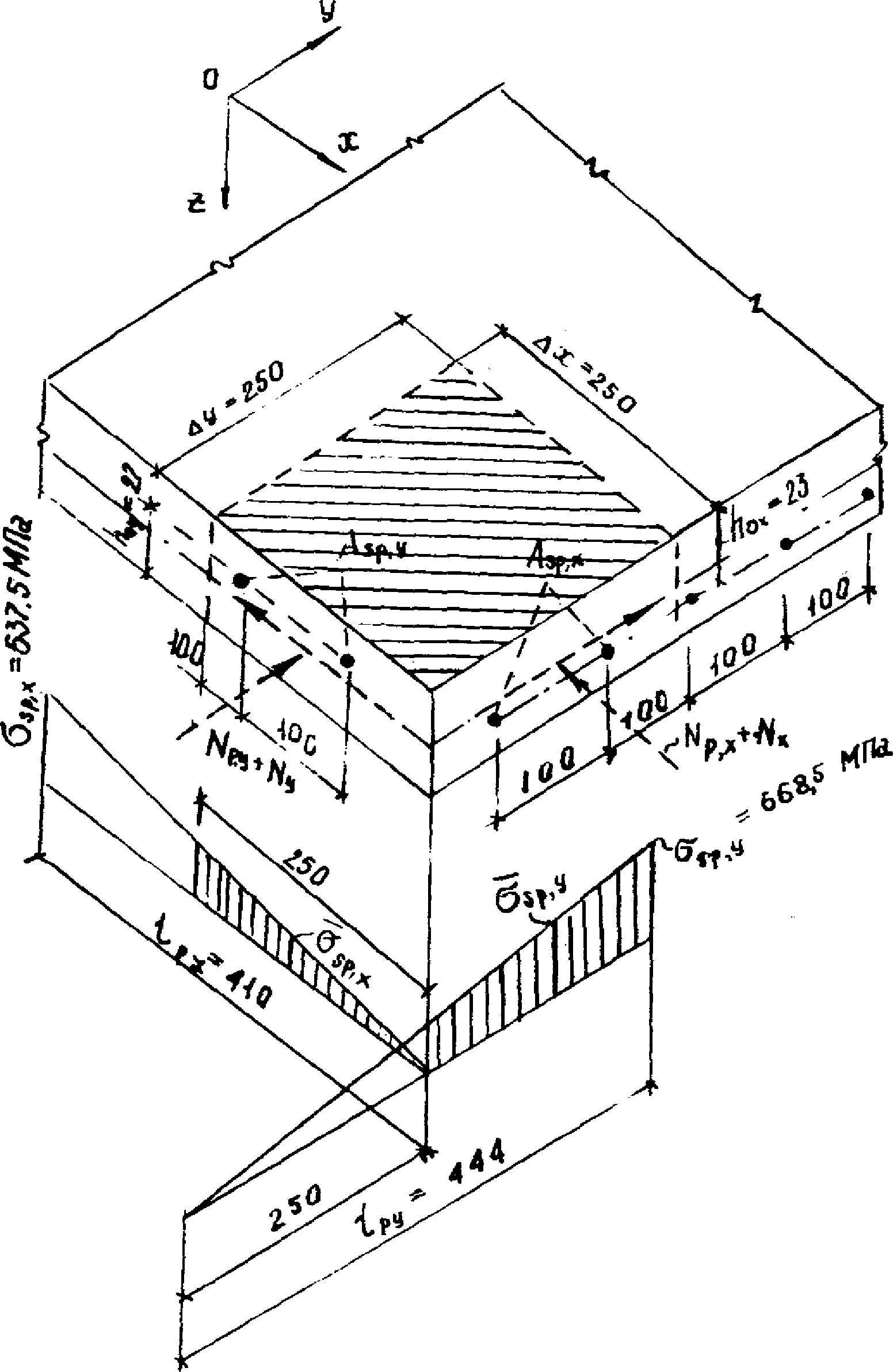
в угловых зонах (элемент А)
площади поперечного сечения предварительно напряженной арматуры в расчетном элементе
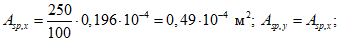
усилия предварительного обжатия, приходящиеся на единицу длины расчетного элемента (с учетом их изменений в пределах длины зоны передачи напряжений) соответственно по оси X и Y
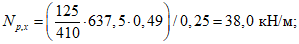
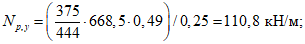
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 19 в Приложении 2 отсутствует. |
нормальные погонные усилия в центре расчетного элемента от действия внешней нагрузки в соответствии с полученными результатами расчета (см. эпюру рис. 15, а) и их изменения в направлении оси X по закону квадратной параболы (рис. 19, а)
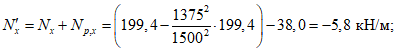
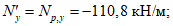
погонные сдвигающие усилия, действующие на расчетные элементы, определим в предположении, что при принятой схеме постановки закладных деталей (см. рис. 18) суммарная сдвигающая сила T2 приходится на крайнюю грань складки (поровну распределяется между соседними закладными деталями и линейно изменяется в направлении оси X):

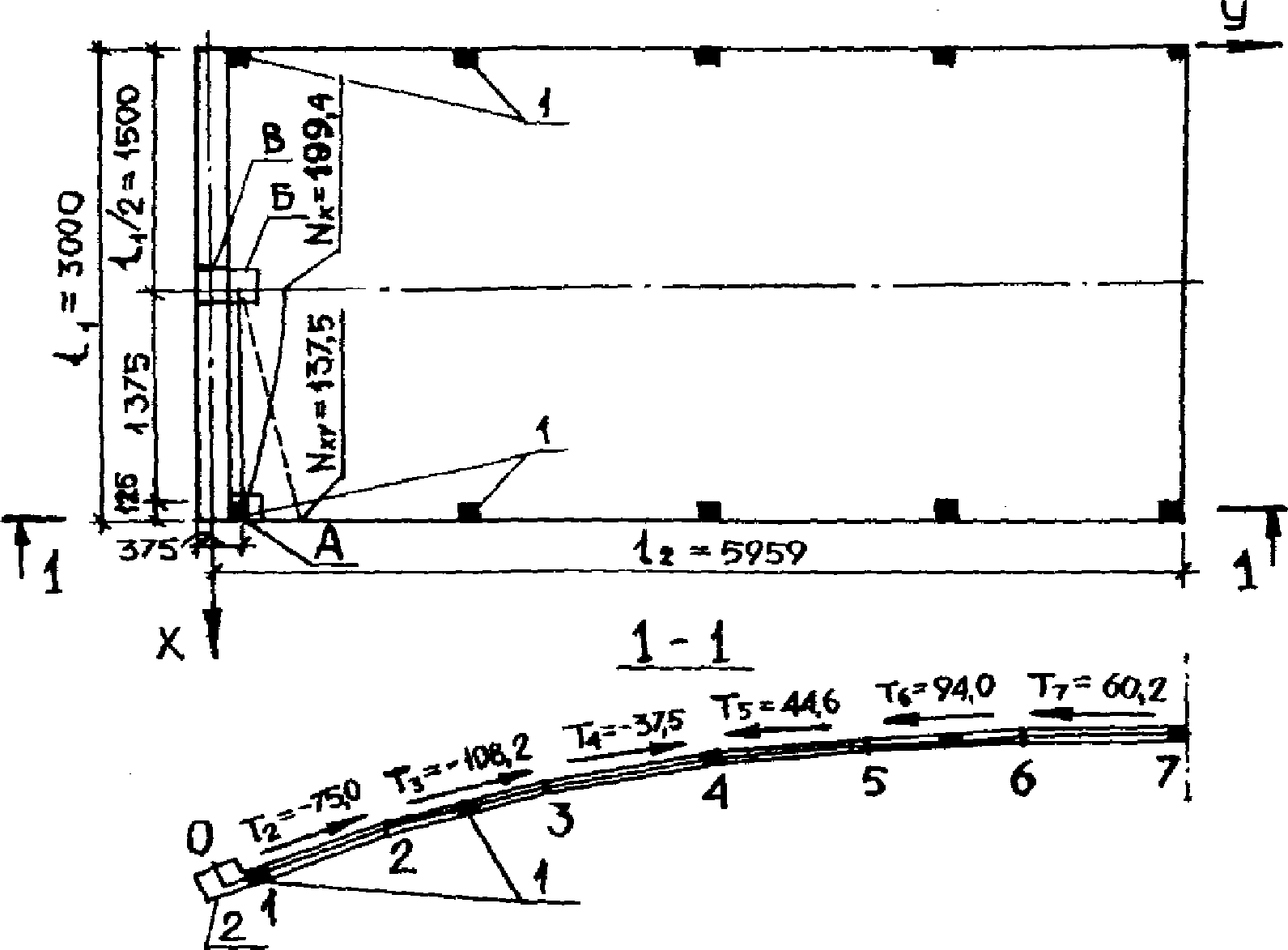
в расчетных элементах А, Б и В
1 - закладная деталь; 2 - приопорное утолщение
Главные усилия, действующие в расчетном элементе, вычисляем по формуле (92) настоящих рекомендаций:
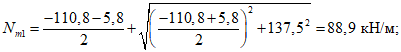
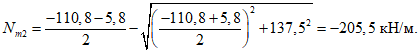
Значение коэффициента Kq определяем по формуле
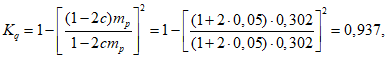
где
mp = |Nm2|/(hRB,scr) = 205,5/(0,04·22) = 0,234.
Погонное усилие воспринимаемое сечением расчетного элемента при образовании трещин, определяем согласно указаниям действующих норм [1] с учетом влияния плоского напряженного состояния
Ncrc = KqRBf,scr·t = 0,937·1,8·103·0,04 = 67,4 кН/м.
Проверку по образованию косых трещин в угловых зонах производим по условию (91) настоящих рекомендаций
Nm1 = 88,9 кН/м >= Ncrc = 67,4 кН/м,
следовательно при нормативной нагрузке в угловых зонах пластины образуются трещины.
Расчет по раскрытию трещин
Определяем угол наклона трещин к оси X по известной формуле теории упругости
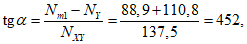
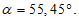
Параметр армирования элемента при заданной арматуре  Вр-II
Вр-II
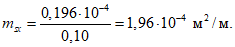
Поскольку интенсивность армирования в направлении оси Y такая же, как и в направлении оси X, то
msy = msx = 1,96·10-4 м2/м.
Вычисляем напряжения в арматуре элемента, соответственно в продольных и поперечных стержнях:
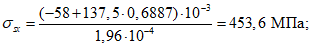
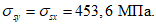
Поскольку  и
и  , то коэффициенты
, то коэффициенты  и
и  и Psx = 1, Psy = 1.
и Psx = 1, Psy = 1.
 и
и  , то коэффициенты
, то коэффициенты Коэффициенты, учитывающие работу растянутого бетона, определяем по формуле (1.92) [18]:
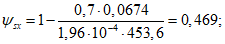
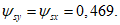
Средние модуль деформаций арматуры на участках между трещинами вычисляем по формулам (106) настоящих рекомендаций:
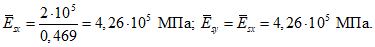
Деформации арматуры в трещине соответственно составят:
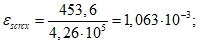
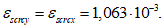
По формулам (101) и (102) настоящих рекомендаций определяем величины разности деформаций арматуры и бетона в среднем сечении между трещинами:
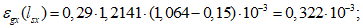
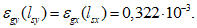
По формулам (99) и (100) настоящих рекомендаций определяем значения расчетных коэффициентов:
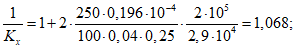
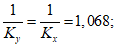
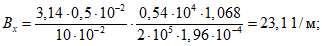
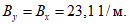
Расстояние между трещинами согласно формулам (103) и (104) настоящих рекомендаций:
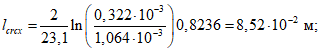
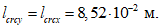
Величину lcrc принимаем равной 8,52·10-2 м.
Смещения арматурных стержней относительно берега трещины вычисляем по формулам (97) настоящих рекомендаций:
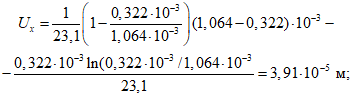
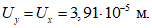
Ширину раскрытия трещин и сдвиг ее берегов определяем соответственно по формулам (95) и (96) настоящих рекомендаций:
acrc = 2·(3,91·0,5671 + 3,91·0,8236)·10-5 = 10,9·10-5 м;
dcrc = 2·(3,91·0,8236 - 3,91·0,5671)·10-5 = 2·10-5 м.
Полагая, что для ортогональности армирования можно применить формулу (1.52) [18], и учитывая равенство коэффициентов  и
и  , определим коэффициент неупругих деформаций полос бетона вдоль трещин
, определим коэффициент неупругих деформаций полос бетона вдоль трещин
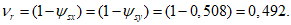
Средние относительные деформации полос бетона между трещинами определяем по формулам (105) настоящих рекомендаций:
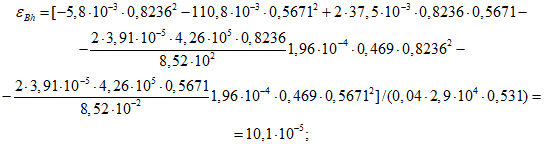
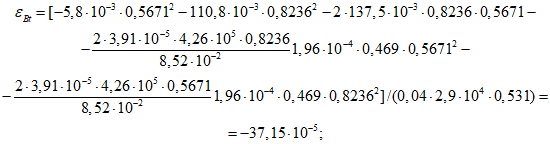
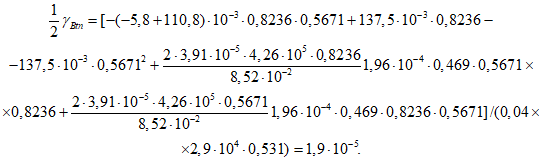
Деформации элемента в осях n, t согласно формулам (94) настоящих рекомендаций:
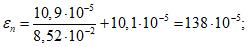
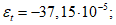
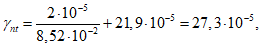
а деформации железобетонного элемента в осях X, Y определяем по формулам (93) настоящих рекомендаций:
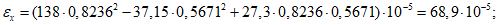
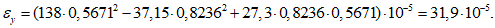
Вычисляем ширину раскрытия трещин через деформации элемента по формуле (108) настоящих рекомендаций:
acrc = (68,9 + 31,9 + 37,15 - 10,1)·10-5 · 8,52·10-2 = 10,9·10-5 м.
Аналогично ведется расчет ширины раскрытия трещин от постоянных и длительных нагрузок.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 19 в Приложении 2 отсутствует. |
Расчет по образованию нормальных трещин в пластине-оболочке (см. рис. 19, элемент Б) производим на действие максимальных растягивающих усилий Nx (изгиб пластины-оболочки в направлении оси X при расчете вариационным методом не учитывается). Согласно результатам статического расчета (см. рис. 15, а) элемент Б с максимальными растягивающими усилиями расположен в сечении X = 0,5l1 у приопорного утолщения пластины-оболочки.
Погонные усилия в рассматриваемом расчетном элементе с учетом усилий обжатия от предварительного напряжения
N'x = Nx - Np,x = 199,4 - 637,5·103·0,5·10-4/0,25 = 71,4 кН/м.
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Погонное воспринимаемое сечением расчетного элемента перед образованием трещин
Ncrc = RBt,scr·t = 1,8·103·0,04 = 72 кН/м.
Поскольку Ncrc = 72 кН/м > N'x = 71,4 кН/м, то нормальные трещины в пластине-оболочке при нормальной нагрузке не образуются.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 19 в Приложении 2 отсутствует. |
Расчет по трещиностойкости приопорного ребра-утолщения (см. рис. 19, элемент Б) производится на действие изгибающего момента в сечении X = 0,5l1 с учетом усилия обжатия от предварительного напряжения по методике действующих норм [1]. Поскольку примеры такого расчета широко освещены в имеющейся справочной литературе (см. например [11]), то в настоящем приложении пример такого расчета не рассматривается.
1. СНиП 2.03.01-84. Бетонные и железобетонные конструкции. - М.: ЦИТП Госстроя СССР, 1985. - 79 с.
2. СНиП 2.01.07-85. Нагрузки и воздействия. - М.: Стройиздат, 1986.
3. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Ч. I / ЦНИИПромзданий, НИИЖБ. - М.: ЦИТП Госстроя СССР, 1988. - 188 с.
4. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Ч. II / ЦНИИПромзданий, НИИЖБ. - М.: ЦИТП Госстроя СССР, 1988. - 144 с.
5. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84). / ЦНИИПромзданий, НИИЖБ. - М.: ЦИТП Госстроя СССР, 1989. - 192 с.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: документ имеет название "Руководство по проектированию железобетонных пространственных конструкций покрытий и перекрытий", а не "Руководство по проектированию железобетонных пространственных покрытий и перекрытий". |
6. Руководство по проектированию железобетонных пространственных покрытий и перекрытий. - М.: Стройиздат, 1979. - 421 с.
7. Колчунов В.И. Деформирование и трещиностойкость железобетонных панелей-оболочек на пролет коммуникационного типа. - В кн.: Нелинейные методы расчета пространственных конструкций. - М.: МИСИ, БТИСМ, 1988. - С. 146 - 157.
8. Юрьев А.Г. Вариационные постановки задач структурного синтеза в статике сооружений. - М.: МИСИ, БТИСМ, 1987. - 94 с.
10. Фрид И. Обусловленность конечноэлементных матриц, полученных на неравномерной сетке // Ракетная техника и космонавтика. 1972. N 2. с. 152 - 154.
11. Голышев А.Б., Бачинский В.Я., Полищук В.П. и др. Проектирование железобетонных конструкций, справочное пособие. - Киев: Будiвельник, 1935.
12. Милейковский И.Е., Колчунов В.И., Половнев В.И. Алгоритм расчета, исследование и анализ жесткости и трещиностойкости железобетонных пластин - пологих цилиндрических оболочек // Исследования по расчету пластин и оболочек. - Ростов-на-Дону, 1987, с. 77 - 86.
13. Пакет прикладных программ для автоматизированного проектирования железобетонных конструкций надземных и подземных сооружений в промышленном и гражданском строительстве. - Киев: НИИАСС, 1984. - 152 с.
14. Программный комплекс для расчета упругих систем "Прокруст-81" / Донецкий ПромстройНИИпроект. - Донецк, 1983. - 104 с.
16. Милейковский И.Е., Колчунов В.И., Соколов А.А. Рекомендации по выбору расчетных схем и методов расчета оболочек покрытий. - М.: МИСИ, БТИСМ, 1987. - 177 с.
17. Колчунов В.И., Половнев В.И., Осовских Е.В. Расчет железобетонных складок с учетом физической нелинейности и трещинообразования. - В кн.: Вопросы прочности, деформативности и трещиностойкости железобетона. - Ростов-на-Дону: РИСИ, 1986, с. 167 - 173.
19. Милейковский И.Е., Колчунов В.И., Оспищев П.И. К построению физических зависимостей деформирования железобетонных пластин и оболочек при обобщенном напряженном состоянии. - В кн.: Нелинейные методы расчета пространственных конструкций. - М.: МИСИ, БТИСМ, 1988, с. 59 - 68.
20. Колчунов В.И., Ефимов В.И., Матюшенко С.И., Степанов А.М. Преднапряженные пластины-оболочки для производственных зданий // Бетон и железобетон, 1989, N 5, с. 21 - 23.
21. Либерман А.Д., Катруца Ю.А., Стаковиченко Е.И., Завгородний С.И., Червинская Т.А., Вышинский В.М. Конструкции покрытий одноэтажных производственных зданий с применением панелей-оболочек на пролет коммуникационного типа и гибких предварительно напряженных плит. - В кн.: Исследование пространственных систем и конструкций зданий и сооружений. - М.: ЦНИИСК, НИИСК, 1986.
22. Стаковиченко Е.И. Крупноразмерные панели-оболочки на пролет коммуникационного типа для промышленного строительства. - В кн.: Строительные конструкции, вып. 37 - Киев: Будiвельник, 1984.
23. Колчунов В.И., Матюшенко С.И., Стаковиченко Е.И. Панели-оболочки на пролет // Промышленное строительство, 1987, N 8. - с. 34.







































 ;
; 



















