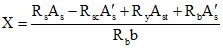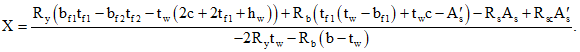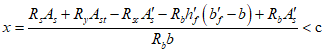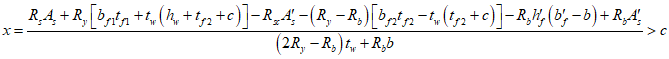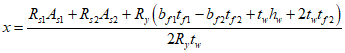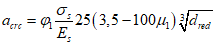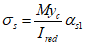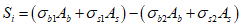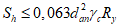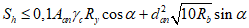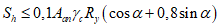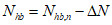СПРАВКА
Источник публикации
М., 2018
Примечание к документу
Название документа
"Методические рекомендации по расчету и проектированию сталежелезобетонных перекрытий"
"Методические рекомендации по расчету и проектированию сталежелезобетонных перекрытий"
Содержание
ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ
"ФЕДЕРАЛЬНЫЙ ЦЕНТР НОРМИРОВАНИЯ, СТАНДАРТИЗАЦИИ
И ОЦЕНКИ СООТВЕТСТВИЯ В СТРОИТЕЛЬСТВЕ"
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ И ПРОЕКТИРОВАНИЮ СТАЛЕЖЕЛЕЗОБЕТОННЫХ ПЕРЕКРЫТИЙ
ОКС 91.080.01;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: Федеральный закон N 123-ФЗ "Технический регламент о требованиях пожарной безопасности" принят 22.07.2008, а не 22.06.2008. |
Настоящие методические рекомендации разработаны в развитие положений к СП 266.1325800.2016 "Конструкции сталежелезобетонные. Правила проектирования" в части конструкций, подверженных изгибу. Методические рекомендации составлены с учетом требований Федеральных законов от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", от 22 июня 2008 г. N 123-ФЗ "Технический регламент о требованиях пожарной безопасности", от 30 декабря 2009 г. N 384-ФЗ "Технический регламент о безопасности зданий и сооружений".
Методические рекомендации разработаны авторским коллективом ЦНИИСК им. В.А. Кучеренко - институт АО "НИЦ "Строительство", НИИЖБ им. А.А. Гвоздева - институт АО "НИЦ "Строительство", ООО "ТЕХСОФТ: к. т. н. Д.В. Конин (руководитель работы); д. т. н. И.И. Ведяков, инженеры А.С. Крылов, Л.С. Рожкова (ЦНИИСК им. В.А. Кучеренко); д. т. н. С.Б. Крылов (НИИЖБ им. А.А. Гвоздева); д. т. н. В.А. Семенов (ООО "ТЕХСОФТ).
Настоящие методические рекомендации разработаны в развитие положений СП 266.1325800.2016 и содержат рекомендации для расчета элементов, подверженных изгибу: сталежелезобетонных плит перекрытий с профилированным настилом, комбинированных балок полностью обетонированных прямоугольного и таврового сечения, сдвиговых соединений. Область применения настоящих рекомендаций ограничивается областью применения сталежелезобетонных конструкций, приведенной в СП 266.1325800.2016 (раздел 1).
В дополнение к нормативным ссылкам, приведенным в СП 266.1325800.2016 (раздел 2) в настоящих рекомендациях использованы нормативные ссылки на следующие документы:
ГОСТ Р 57837-2017 "Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия";
СП 16.13330.2017 "СНиП II-23-81* Стальные конструкции";
СП 20.13330.2016 "СНиП 2.01.07-85* Нагрузки и воздействия";
СП 266.1325800.2016 "Конструкции сталежелезобетонные. Правила проектирования";
СП 294.1325800.2017 "Конструкции стальные. Правила проектирования".
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду СП 266.1325800, а не СП 266.125800. |
В настоящих рекомендациях приведены термины по ГОСТ 27751, ГОСТ Р 1.4, СП 16.13330, СП 63.13330, СП 266.125800. А также следующие термины из СП 266.125800.2016 с измененными определениями:
гибкий упор: конструктивный элемент, объединяющий стальную и железобетонную части сталежелезобетонной конструкции при их совместной работе и возможном незначительном взаимном сдвиге; выполняется в виде арматурных петель, коротышей из арматуры или калиброванной стали, стад-болтов с круглой головкой, гибких уголковых упоров и т.д.;
дюбель: стальной гвоздь для соединения профилированного настила и уголковых гибких упоров к опорной балке с помощью специального порохового пистолета.
Настоящие методические рекомендации разработаны в дополнение к СП 266.1325800.2016 и содержат рекомендации для расчета и проектирования элементов, подверженных изгибу: сталежелезобетонных плит перекрытий с профилированным настилом (рисунок 4.1), комбинированных балок полностью обетонированных прямоугольного и таврового сечения (рисунок 4.2), тавровых балок с опиранием железобетонной плиты на нижний пояс двутавровой балки, сдвиговых соединений.

Рисунок 4.1 - Конструкция сталежелезобетонной плиты,
армированная профилированным настилом:
1 - стальной профилированный настил с рифлеными стенками
гофров; 2 - элемент балочной клетки; 3 - монолитный бетон
плиты; 4 - стержневой упор; 5 - сетка противоусадочного
армирования; 6 - соединение гофрированных профилей
между собой; 7 - рабочая арматура
ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |
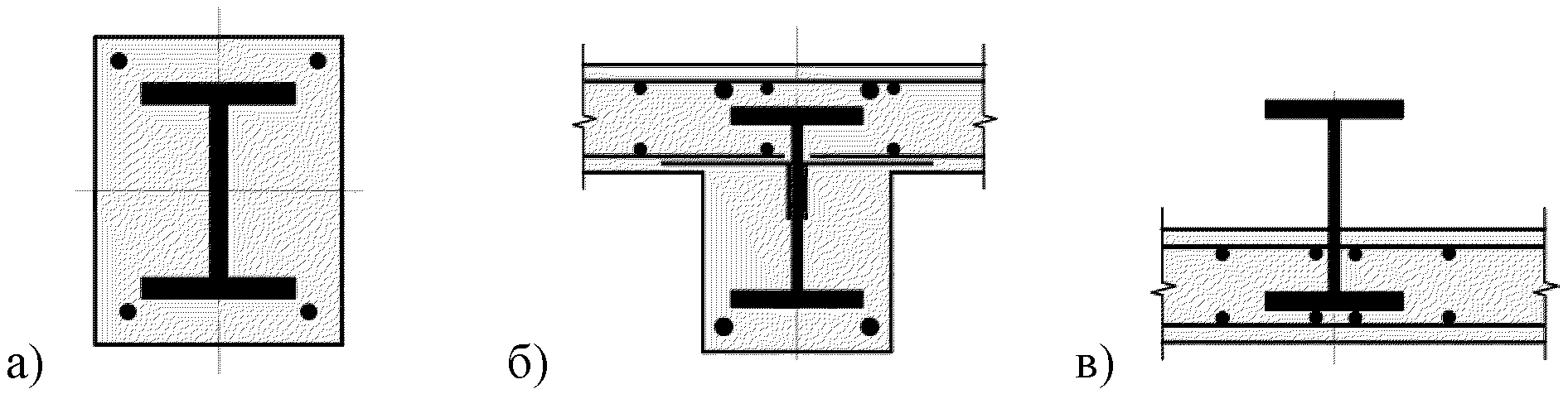
комбинированных балок:
а - полностью обетонированная балка прямоугольного сечения;
б - полностью обетонированная балка таврового сечения;
в - тавровая балка с опиранием железобетонной плиты
на нижний пояс двутавровой балки
Сталежелезобетонные конструкции являются оптимальным видом конструкций при проектировании и возведении многоэтажных, высотных зданий, конструкций зрелищных сооружений, в т.ч. покрытий стадионов и трибун, перекрытий подтрибунных помещений, а также других видах зданий и сооружений, где требуется повышенная прочность конструкций, и малая строительная высота для перекрытий.
4.2.1 Нагрузки и воздействия следует принимать согласно требованиям СП 20.13330, в соответствии со специальными техническими условиями на проектирование данного объекта (если таковые разработаны), а также в соответствие с заданием на проектирование, учитывающим специфические виды нагрузок, данные для которых могут быть приведены в СП 20.13330 не в полном объеме. Для сложных видов нагрузок (снеговые и ветровые) могут использоваться результаты моделирования и продувок в аэродинамических трубах и результаты расчетов нагрузок с использованием специализированных компьютерных программ.
4.2.2 Сочетания нагрузок следует принимать согласно требованиям СП 20.13330.2016 (раздела 6).
4.2.3 Сейсмическое воздействие следует учитывать согласно требованиям СП 14.13330 [3].
4.2.4 Этапы монтажа необходимо учитывать для определения перераспределения усилий и деформаций между элементами конструкции в процессе ее воздействия. Это перераспределение усилий влияет на напряженно-деформированное состояние здания и после его возведения, а также на запас устойчивости конструкций. Особенно сильно это влияние проявляется в зданиях и сооружениях, расчетная схема которых изменяется в процессе возведения из-за использования временных связей, опор и т.д.
Наиболее точно этапы монтажа могут быть учтены с помощью специальных модулей расчетных программных комплексов.
Этапы монтажа учитываются при расчете сталежелезобетонных плит с профилированным настилом согласно СП 266.1325800.2016 (разделу 6.1).
4.2.5 Строительные нагрузки, действующие на конструкцию при монтаже или строительстве (собственный вес, вес подмостей, кранов, работающих людей, инструментов, мелкого оборудования, односторонний распор и др.), а также при изготовлении и транспортировании элементов, следует принимать по проектным данным с учетом предусматриваемых условий производства работ и требований СП 70.13330.
4.3.1 В расчетных схемах фактические эксцентриситеты, не предусмотренные проектом, моделируются с помощью смещения элементов относительно их проектных положений с помощью введения жестких вставок или с помощью введения дополнительных изгибающих моментов в качестве внешней нагрузки в местах эксцентриситетов.
4.3.2 При необходимости выполнения расчета на стойкость против прогрессирующего (цепного) обрушения при проектировании конструкций должна быть предусмотрена конструктивная схема, не допускающая возможности прогрессирующего обрушения в случае локального разрушения несущих конструкций или их элементов, при аварийных воздействиях, не предусмотренных условиями нормальной эксплуатации зданий (пожары, взрывы, ударные воздействия транспортных средств, несанкционированная перепланировка и т.п.).
Соответствующие расчеты конструкций и их элементов следует проводить при учете постоянных и длительных нагрузок и воздействий (при коэффициентах надежности по нагрузке  ). Расчетные прочностные и деформационные характеристики материалов следует принимать равными их нормативным значениям. В случае необходимости учет кратковременных нагрузок и воздействий следует предусматривать в задании на проектирование.
). Расчетные прочностные и деформационные характеристики материалов следует принимать равными их нормативным значениям. В случае необходимости учет кратковременных нагрузок и воздействий следует предусматривать в задании на проектирование.
Расчет в случае локального разрушения конструкций производят только по предельным состояниям первой группы. Развитие неупругих деформаций, перемещения конструкций и раскрытие в них трещин в рассматриваемой чрезвычайной ситуации не ограничивают, если иное не предусмотрено в задании на проектирование.
4.3.3 Помимо расчета элементов перекрытий, должна выполняться проверка устойчивости системы всего каркаса здания, как самостоятельный вид расчета. В этом случае отношение критических нагрузок к расчетным должно быть не менее коэффициента надежности по устойчивости системы 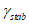 , значения которого указаны в СП 266.1325800.2016 (4.3.6).
, значения которого указаны в СП 266.1325800.2016 (4.3.6).
Для многоэтажных и высотных зданий общая устойчивость должна быть обеспечена в соответствии с требованиями СП 267.1325800.
4.4.1 Рекомендации по учету ползучести, усадки и образования трещин при назначении модуля упругости бетона
4.4.1.1 При выполнении расчетов учет ползучести, усадки и образования трещин осуществляется по-разному, в зависимости от методики расчета и возможностей используемой компьютерной программы.
4.4.1.2 Расчеты с использованием диаграмм деформирования материалов выполняются, как правило, с использованием расчетных программных комплексов. Если программный комплекс допускает непосредственный учет ползучести бетона, то допускается использовать диаграмму деформирования бетона для кратковременных нагрузок, а ползучесть учитывается установкой соответствующих параметров расчета (установка соответствующего указателя в разделе или в окне, отвечающем за организацию счета). При этом, независимо от результатов расчета, все проверки прочности, предписываемые СП 266.1325800, должны быть выполнены отдельно.
Если при расчете с использованием диаграмм деформирования материалов программа не допускает учет ползучести в явном виде, то для расчета следует использовать диаграммы состояния сжатого бетона, соответствующие длительной нагрузке.
При использовании расчетных программных комплексов, ориентированных на зарубежные нормы проектирования, следует иметь в виду, что развитие ползучести в них отличается от отечественных норм. Разница с Еврокодами, например, во времени протекания ползучести приблизительно 10-кратная. Это следует иметь в виду при выборе того или иного способа учета ползучести бетона.
4.4.1.3 Если конструкция рассчитывается как линейно-упругая, то ползучесть и нелинейность работы бетона учитывается снижением модуля упругости бетона. Снижение модуля упругости выполняется по методике СП 63.13330. Если в результате расчета выявляется, что бетон работает с трещинами, то для уточнения результатов выполняется повторный расчет с дополнительным снижением модуля упругости бетона с помощью умножения на коэффициент 0,667 (2/3).
4.4.1.4 Усадка бетона создает в конструкциях напряжения, которые со временем релаксируют в значительной степени. При расчете усадка учитывается по методике [10]. Учет усадки необходим только в случаях, когда она происходит в условиях стеснения деформаций и только в протяженных конструкциях. При использовании программных расчетных комплексов усадку следует учитывать или непосредственно (задавая соответствующий параметр счета) или моделировать ее с помощью температурного воздействия, исходя из коэффициентов температурного расширения материалов.
4.4.2.1 Диаграммы состояния (деформирования) бетона, арматуры и стали используют при расчете сталежелезобетонных элементов по нелинейной деформационной модели.
4.4.2.2 Диаграмма состояния сжатого бетона принимается по СП 63.13330.2012 (6.1.19 - 6.1.26). Рекомендуется использование трехлинейной диаграммы.
4.4.2.4 Диаграмма состояния конструкционной стали принимается по СП 16.13330.2017 (4.2.4 и рисунку В.1 приложения В). Рекомендуется использование двухлинейной диаграммы по точкам OBD (или OACD - с моделированием упруго-пластического перехода) с обязательным ограничением деформаций текучести. Использование "бесконечной" диаграммы Прандтля, в которой деформации текучести не имеют ограничений, при моделировании сталежелезобетонных конструкций не допускается.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду ГОСТ 24045, а не ГОСТ Р 24045. |
4.4.3.1 Размеры сечения профилей профилированного настила для сталежелезобетонных плит с профилированным настилом должны отвечать требованиям ГОСТ Р 24045, СТО 573938459-001-2010 [11], СТО 57398459-30-2008 [12], техническим условиям или другим стандартам организации, утвержденным в установленном порядке.
4.4.3.2 В качестве профилей стальных балок следует применять прокатные профили по ГОСТ Р 57837 [2]. Применение элементов из фасонного проката значительно облегчает конструирование, проектирование и расчет сталежелезобетонных конструкций.
При проектировании изгибаемых элементов следует использовать прокатные двутавры типов Б (балочные нормальные), Ш (широкополочные), ДБ и ДШ (нормальные и широкополочные дополнительных серий) (обозначения по ГОСТ Р 57837-2017). Допускается использовать сечения, усиленные листом со стороны наиболее нагруженной полки. При необходимости минимизации строительной высоты перекрытий, а также при опирании настила перекрытий (монолитного или сборного) на нижнюю полку стальной балки следует использовать двутавры типов К (колонные) или ДК (колонные дополнительных серий).
5.1.1 Проектирование сталежелезобетонных плит с профилированных настилом следует выполнять согласно СП 266.1325800.
5.1.2 Для профилированных листов по СТО 573938459-001-2010 [11] и СТО 57398459-30-2008 [13] ООО "Стальные конструкции - Профлист" разработаны СТО 57398459-035-2014 [14] и СТО 57398459-002-2011 [12] с рекомендациями по проектированию.
При расчете сталежелезобетонных плит перекрытий с профилированным настилом, а также соединительных элементов следует руководствоваться положениями СП 266.1325800, а также возможными другими рекомендациями, утвержденных в установленном порядке с участием предприятия-изготовителя профилированных стальных листов, не противоречащими СП 266.1325800.
В данном подразделе приведены рекомендации по расчету сталежелезобетонных балок с жесткой арматурой в виде двутавра. Для стальной части сечения использованы диаграмма работы как для идеального жесткопластического материала по СП 266.1325800.2016 (6.2.1.6 и 6.2.1.10).
6.1.1 Высота сжатой зоны бетона определяется из условий равновесия усилий, действующих в рассматриваемом нормальном сечении элемента.
В общем случае высота сжатой зоны бетона определяется методом последовательных приближений. При этом, на каждом шаге расчета назначается положение границы сжатой зоны, затем проверяется выполнение условий равновесия. Если относительная погрешность выполнения условий равновесия велика, то выполняется уточнение положения границы сжатой зоны и повторный расчет.
6.1.2 Наиболее точные результаты дает расчет с использованием диаграмм деформирования бетона, стального сердечника и стержневой арматуры. При выполнении расчета в стали сердечника и в стали стержневой арматуры допускаются пластические деформации, не превышающие предельные величины, приведенные в СП 16.13330, СП 63.13330 и СП 266.1325800. Работа растянутого бетона не учитывается.
6.1.3 При определении высоты сжатой зоны допускается вводить следующие упрощающие расчетные допущения.
1) Эпюра напряжений в сжатой зоне бетона принимается постоянной (прямоугольной) с ординатой, равной расчетному сопротивлению бетона.
2) Эпюры напряжений в стальном сердечнике в сжатой и растянутой его частях принимаются постоянными (прямоугольными) с ординатами, равными расчетным сопротивлениям стали при растяжении и сжатии.
3) Напряжения в сжатой части стального сердечника и в сжатой стержневой арматуре принимаются не больше величины, соответствующей условиям совместной работы стали и бетона.
4) Допускается в запас прочности пренебрегать работой стенок стальных сердечников (балок) и учитывать в расчете только полки (это позволяет в большинстве случаев отказаться от многократных пересчетов и определить высоту сжатой зоны на первом шаге расчета).
5) Если по результатам расчета граница сжатой зоны располагается в пределах полки стального сердечника (при изгибе в одной плоскости), то в запас прочности работа этой полки не учитывается.
6) Если сжатая или растянутая полка расположена близко к границе сжатой зоны, то она работает с неполным расчетным сопротивлением и ее в запас прочности можно не учитывать. То же относится к стержневой арматуре. Ориентировочно (с запасом) можно принять, что сталь работает с неполным расчетным сопротивлением на расстоянии 0,25h0 от границы сжатой зоны. Более точно эту величину можно установить, построив в сечении элементы диаграммы деформирования материалов (т.к. это расстояние зависит как от положения границы сжатой зоны, так и от расчетных сопротивлений материалов).
6.1.4 При расчете железобетонных элементов, имеющих полку в сжатой зоне, ширину полки, вводимую в расчет следует принимать в соответствии с указаниями СП 63.13330.2012 (8.1.11).
6.1.5 При расчете по прочности изгибаемых элементов рекомендуется соблюдать условие 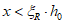 . В случае, когда площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия
. В случае, когда площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия 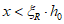 , допускается предельный изгибающий момент Mult определять, принимая значение высоты сжатой зоны
, допускается предельный изгибающий момент Mult определять, принимая значение высоты сжатой зоны 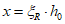 .
.
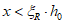 . В случае, когда площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия
. В случае, когда площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия 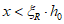 , допускается предельный изгибающий момент Mult определять, принимая значение высоты сжатой зоны
, допускается предельный изгибающий момент Mult определять, принимая значение высоты сжатой зоны 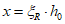 .
.6.1.6 Значение  следует определять по СП 63.13330.2012 (8.1.6).
следует определять по СП 63.13330.2012 (8.1.6).
Далее приведены формулы (6.1) - (6.4) расчета высоты сжатой зоны изгибаемых элементов при 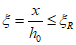 . Все формулы записаны на основании СП 266.1325800.2016 (6.2.1.6).
. Все формулы записаны на основании СП 266.1325800.2016 (6.2.1.6).
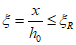 . Все формулы записаны на основании СП 266.1325800.2016 (6.2.1.6).
. Все формулы записаны на основании СП 266.1325800.2016 (6.2.1.6).6.1.7 Случай 1. Нейтральная ось не пересекает профиль жесткой арматуры и находится ниже верхней гибкой арматуры. Весь двутавр расположен в растянутой зоне.
Расчет положения границы сжатой зоны выполняется по формуле:

ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |
Рисунок 3.1 - Случай, когда нейтральная ось не пересекает
профиль жесткой арматуры и находится ниже верхней гибкой
арматуры в обетонированной балке прямоугольного сечения
6.1.8 Случай 2. Нейтральная ось пересекает сжатую (верхнюю) полку жесткой арматуры.
Если при определении величины x по формуле (6.2) окажется, что нейтральная ось не пересекает профиль жесткой арматуры (весь профиль находится в растянутой зоне), а при проверке по формуле (6.1) - пересекает стенку профиля, то расчет следует производить, полагая, что нейтральная ось проходит в пределах толщины верхней (на рисунке) полки профиля жесткой арматуры.

Рисунок 6.2 - Случай, когда нейтральная ось
пересекает сжатую (верхнюю) полку жесткой арматуры
в обетонированной балке прямоугольного сечения
6.1.9 Случай 3. Нейтральная ось пересекает стенку жесткой арматуры.
Расчет положения границы сжатой зоны выполняется по формуле:

Рисунок 6.3 - Случай, когда нейтральная ось пересекает
стенку жесткой арматуры в обетонированной балке
прямоугольного сечения
Расчет балки прямоугольного сечения с жесткой арматурой из двутавра приведен в А.1 (приложения А).
6.2.1 Случай 1. Нейтральная ось не пересекает профиль жесткой арматуры.
Расчет положения границы сжатой зоны выполняется по формуле:
При конструктивном верхнем армировании величину 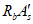 допускается не учитывать.
допускается не учитывать.

Рисунок 6.4 - Случай, когда нейтральная ось
не пересекает профиль жесткой арматуры в полностью
обетонированной балке таврового сечения
6.2.2 Случай 2. Нейтральная ось пересекает стенку жесткой арматуры.
Расчет положения границы сжатой зоны выполняется по формуле:

Рисунок 6.5 - Случай, когда нейтральная ось
пересекает стенку жесткой арматуры в полностью
обетонированной балке таврового сечения
6.2.3 Случай 3. Нейтральная ось пересекает сжатую (верхнюю) полку жесткой арматуры.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеются в виду формулы (6.3) и (6.4), а не формулы (3.3) и (3.4) соответственно. |
Если значение x, определенное по формуле (3.3), больше c (нейтральная ось пересекает профиль жесткой арматуры), а значение x, определенное по формуле (3.4), меньше c (нейтральная ось не пересекает профиль жесткой арматуры), то расчет следует производить, полагая, что нейтральная ось проходит в пределах толщины верхней полки профиля жесткой арматуры.

Рисунок 6.6 - Случай, когда нейтральная ось пересекает
сжатую (верхнюю) полку жесткой арматуры в полностью
обетонированной балке таврового сечения
Расчет балки прямоугольного сечения с жесткой арматурой из двутавра приведен в А.2 (приложения А).
Расчет положения границы сжатой зоны выполняется по формуле:

Рисунок 6.7 - Случай, когда нейтральная ось пересекает
стенку стального профиля жесткой арматуры в комбинированной
балки с опиранием железобетонной плиты на нижний пояс
Расчет балки прямоугольного сечения с жесткой арматурой из двутавра приведен в А.3 (приложения А).
6.4.1 Расчет сталежелезобетонных балок по образованию трещин, нормальных к продольной оси изгибаемого элемента, производят из условия:
где M - изгибающий момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
Mcrc - изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый в соответствии с указаниями СП 63.13330.2012 (подраздел 8.2).
6.4.2 В тех случаях, когда выполняется условие (6.6), выполняют расчет по раскрытию трещин. Расчет производят по непродолжительному и продолжительному раскрытию трещин.
Расчет по раскрытию трещин производят из условия:
acrc <= acrc.ult (6.7)
где acrc - ширина раскрытия трещин от действия внешней нагрузки;
acrc.ult - предельно допустимая ширина раскрытия трещин, определяемая в соответствии с указаниями С СП 63.13330.2012 (подраздел 8.2).
6.4.3 Ширина раскрытия трещин acrc (мм), нормальных к продольной оси изгибаемого элемента, на уровне наиболее растянутых стержней гибкой арматуры определяется по формуле
где 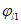 - коэффициент, учитывающий длительность действия нагрузки, принимаемый в соответствии с указаниями 6.4.4;
- коэффициент, учитывающий длительность действия нагрузки, принимаемый в соответствии с указаниями 6.4.4;
Es - модуль упругости арматурной стали;
dred, мм - приведенный диаметр жесткой и гибкой арматуры, расположенной в растянутой зоне сечения, определяемый в соответствии с указаниями 6.4.6.
a) при расчете на действие постоянных и длительных нагрузок
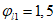 ;
;b) при расчете на действие полной нагрузки
 , (6.9)
, (6.9)где Ml1 и M1 - изгибающие моменты в балке от действия постоянных, а также длительных нагрузок и от полной нагрузки, соответственно.
здесь yc - расстояние от центра тяжести приведенного сечения до центра тяжести наиболее растянутого ряда стержней арматуры;
Ired - момент инерции приведенного поперечного сечения элемента относительно его центра тяжести; определяется по общим правилам сопротивления упругих элементов с учетом площади сечения бетона только сжатой зоны, площадей сечения растянутой и сжатой арматуры с коэффициентом приведения арматуры к бетону 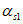 по формуле
по формуле
где Ib, Ist, Is, 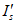 - моменты инерции площадей сечения соответственно сжатой зоны бетона, жесткой арматуры, растянутой и сжатой гибкой арматуры относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения, определяемые с учетом указаний 6.4.7.
- моменты инерции площадей сечения соответственно сжатой зоны бетона, жесткой арматуры, растянутой и сжатой гибкой арматуры относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения, определяемые с учетом указаний 6.4.7.
Значение коэффициента приведения арматуры к бетону 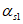 определяется по формуле
определяется по формуле
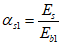 . (6.12)
. (6.12)Значение модуля упругости бетона принимают равными:
- при непродолжительном действии нагрузки
Eb1 = 0,85Eb, (6.13)
- при продолжительном действии нагрузки
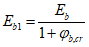 , (6.14)
, (6.14)где 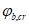 - коэффициент ползучести бетона; принимается по СП 63.13330.2012 (таблица 6.12).
- коэффициент ползучести бетона; принимается по СП 63.13330.2012 (таблица 6.12).
6.4.6 Приведенный диаметр жесткой и гибкой арматуры, расположенной в растянутой зоне, определяется по формуле
где Ps - периметр жесткой и гибкой арматуры, расположенной в растянутой зоне.
6.4.7 Расстояние x от нейтральной линии сечения (центра тяжести приведенного сечения) до сжатой грани для элементов с трещинами в растянутой зоне определяется по формуле
 , (6.16)
, (6.16)где  - сумма приведенных площадей жесткой и гибкой арматуры и площади сжатых свесов бетона;
- сумма приведенных площадей жесткой и гибкой арматуры и площади сжатых свесов бетона;
b - ширина сечения;
6.4.8 Расчет балки по образованию и раскрытию трещин приведен в приведен в А.1 (приложения А).
7.1.1 Гибкие и жесткие упоры обеспечивают совместную работу стального элемента и бетона в сталежелезобетонных конструкциях.
7.1.2 Совместная деформация (работа) профилированного настила с бетоном должна обеспечиваться с помощью устройств для механического сцепления: гибких или жестких упоров, закрепленных на опорах по концам настила или деформированием гофров на концах настила.
Наиболее эффективные устройства для обеспечения совместной деформации (работы) настила с бетоном - упоры двух типов: - стержневые (гибкие упоры) или уголковые (жесткие упоры).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду рисунок 7.1, а не рисунок 5.2. |
7.1.3 Стержневые упоры (стад-болты) выполняют в виде калиброванных стальных стержней диаметром от 10 до 25 мм с круглой головкой, приваренных к стальному опорному элементу (рисунок 5.2). Предел текучести стали стад-болтов - не менее 350 Н/мм2, относительное удлинение при разрыве - не менее 20%.
Упоры в виде шпилек с головкой выполняют по ГОСТ Р 55738.

1 - головка упора; 2 - упор; 3 - сварка;
4 - стальной опорный элемент
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду рисунок 7.2, а не рисунок 5.3. |
7.1.4 Уголковые (гибкие) упоры представляют собой холодноформованный стальной профиль Z-образного сечения (рисунок 5.3), закрепленный одной полкой к стальному опорному элементу с помощью дюбелей.
Материал упоров - оцинкованная сталь толщиной от 2 до 2,5 мм с пределом текучести от 270 до 350 МПа.

1 - уголковый упор; 2 - дюбель; 3 - настил;
4 - опорная балка; 5 - бетон плиты
7.1.5 Расчет сдвиговых соединений выполняется согласно СП 266.1325800.2016 (6.2.4 и разделу 9), а также 7.2 и 7.3, пример расчета приведен в А.4 (приложения А).
7.1.6 Конструктивные требования к расположению упоров приведены в СП 266.1325800.2016 (8.1.3, 8,2, 8.3.9, 8.4.3.2).
7.2.1 Конструкции объединения следует рассчитывать на продольные сдвигающие усилия SQ в объединительном шве от поперечных сил и продольное сдвигающее усилие SN, возникающее от температурных воздействий и усадки бетона, анкеровки высокопрочной арматуры, воздействия примыкающей ванты или раскоса и т.д. Конструкции объединения, расположенные на концевых участках железобетонной плиты, следует рассчитывать, кроме того, на концевые отрывающие усилия Sab.
7.2.2 Сдвигающее усилие по шву объединения железобетонной плиты и стальной балки следует определять для каждого расчетного участка по формуле
где 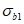 ,
, 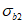 - напряжения в центре тяжести поперечного сечения бетона в правом и левом сечениях расчетного участка плиты длиной ai, соответственно, для сдвигающих усилий от воздействий из п. 7.2.1;
- напряжения в центре тяжести поперечного сечения бетона в правом и левом сечениях расчетного участка плиты длиной ai, соответственно, для сдвигающих усилий от воздействий из п. 7.2.1;
Если растягивающие напряжения в железобетонной плите превышают 0,4Rbt,ser, сдвигающие усилия следует определять в предположении наличия в плите трещин и вычислять напряжения в арматуре 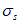 с учетом жесткости плиты при продольной деформации.
с учетом жесткости плиты при продольной деформации.
Полное концевое сдвигающее усилие Se следует определять, принимая на конце  и назначая расчетным поперечное сечение, расположенное на расстоянии от конца плиты равном
и назначая расчетным поперечное сечение, расположенное на расстоянии от конца плиты равном
ae = 0,36(h + bsl), (7.2)
где h - расчетная высота поперечного сечения сталежелезобетонного элемента; bsl - согласно СП 266.1325800.2016 (4.4.4.9).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду п. 7.3.1, а не п. 9.1.1. |
Распределение сдвигающих усилий между железобетонной плитой и стальной балкой в сложных случаях воздействий допускается принимать согласно 9.1.1.
7.2.3 Концевые, отрывающие железобетонную плиту от стальной балки, усилия Sab следует определять по формуле
 , (7.3)
, (7.3)где Zb,st2 - расстояние от центра тяжести поперечного сечения бетона до верхнего волокна стальной балки;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду п. 7.2.2, а не п. 6.2.4.2. |
Se, h, bsl - согласно 6.2.4.2.
Отрывающее усилие Sab следует принимать приложенным на расстоянии ab = 0,024(h + bsl), от конца плиты.
7.2.4 Расчеты конструкции объединения стальной части с железобетонной плитой следует выполнять:
- при жестких упорах - полагая прямоугольной эпюру сжимающих напряжений, передаваемых расчетной сминающей поверхностью упора;
- при вертикальных гибких упорах - исходя из условий работы упора на изгиб со смятием бетона согласно СП.266.1325800.2016 (9.1.2.1) и 7.3.2.1;
- при наклонных упорах - исходя из условий работы упора на сочетание растяжения и изгиба со смятием бетона согласно СП.266.1325800.2016 (9.1.2.2) и 7.3.2.2;
- при закладных деталях плиты, объединенных со стальными поясами высокопрочными болтами, - исходя из расчета фрикционных соединений на высокопрочных болтах согласно СП 16.13330;
- при объединительных швах на высокопрочных болтах, обжимающих железобетон, - исходя из условий работы объединения на трение по контактным поверхностям шва согласно СП.266.1325800.2016 (9.1.3) и 7.3.3;
- при гребенчатых упорах - на действие расчетных сдвигающих и отрывающих усилий с учетом равномерного распределения по длине пролетного строения;
7.2.5 Прочность прикрепления конструкций объединения к стальной части следует рассчитывать согласно СП 16.13330.
Расчеты прочности прикрепления жесткого упора к стальной части конструкции следует выполнять с учетом момента от сдвигающей силы.
Прочность прикрепления уголковых упоров стальной части на дюбелях определяется в НД, разработанных и утвержденных в установленном порядке с участием предприятия-изготовителя упоров.
7.2.6 При одновременном применении в конструкции объединения жестких 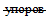 и наклонных упоров допускается учитывать их совместную работу, полагая полное сопротивление объединительного шва равным сумме сопротивлений упоров.
и наклонных упоров допускается учитывать их совместную работу, полагая полное сопротивление объединительного шва равным сумме сопротивлений упоров.
7.3.1 Распределение сдвигающих усилий по шву объединения железобетонной плиты и стальной балки в сложных случаях воздействий
7.3.1.1 Распределение сдвигающих усилий Si, вычисленных по формуле (7.1), между расчетными сечениями следует принимать по треугольной эпюре с длиной основания ai, при этом
где 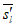 - интенсивность погонных сдвигающих сил.
- интенсивность погонных сдвигающих сил.
7.3.1.2 При распределении околоопорного сдвигающего усилия от поперечных сил SpQ следует принимать, что интенсивность соответствующих погонных сдвигающих сил 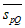 изменяется в обе стороны по прямолинейной эпюре от середины длины околоопорного участка; при этом ордината в середине околоопорного участка равна
изменяется в обе стороны по прямолинейной эпюре от середины длины околоопорного участка; при этом ордината в середине околоопорного участка равна
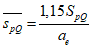 . (7.5)
. (7.5)7.3.1.3 Сдвигающее усилие Sh, приходящееся на один упор на i-м расчетном участке определяется по формуле:
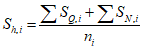 , (7.6)
, (7.6)где SQ,i, SN,i - сдвигающие усилия, определенные по 7.2.1 для i-го участка,
ni - количество упоров i-м расчетном участке.
7.3.2.1 Сдвигающее усилие Sh, приходящееся на один  упор, должно соответствовать следующим условиям прочности:
упор, должно соответствовать следующим условиям прочности:
Sh <= Prd, (7.7)
где Prd - несущая способность упора на сдвиг, кН, принимаемая:
- для упоров в виде прокатных швеллеров, двутавров, уголков без подкрепляющих ребер
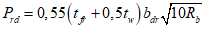 , (7.8)
, (7.8)- для гибких упоров в виде круглых стержней при 2,5 <= l/d <= 4,2
 , (7.9)
, (7.9)- для гибких упоров в виде круглых стержней при l/d > 4,2
для гибких упоров в виде круглых стержней должно быть, кроме того, выполнено условие
где tfr - сумма радиуса закругления и наибольшей толщины полки профиля, см;
tw - толщина стенки профиля, см;
l - длина круглого стержня гибкого упора, см;
dan - диаметр стержня гибкого упора, см;
bdr - ширина площади смятия бетона упором, см;
Ry, Rb - расчетные сопротивления стали упора и бетона соответственно;
- для гибких уголковых упоров Prd принимается на основании НД, разработанных и утвержденных в установленном порядке с участием предприятия-изготовителя упоров.
7.3.2.2 Сдвигающее усилие Sh, кН, приходящееся на один наклонный упор из арматурной стали круглого сечения (гладкого или периодического профиля) или на одну ветвь петлевого упора, должно соответствовать следующим условиям:
где Aan - площадь поперечного сечения стержня упора или ветви упора, см2;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеются в виду формулы (7.12) и (7.13), а не формулы (9.8) и (9.9). |
Для упоров, разведенных в плане, в формулы (9.8) и (9.9) вместо 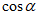 следует подставлять произведение
следует подставлять произведение 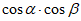 , где
, где 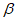 - угол между горизонтальной проекцией упора и направлением действия сдвигающей силы.
- угол между горизонтальной проекцией упора и направлением действия сдвигающей силы.
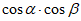 , где
, где Сдвигающее усилие, воспринимаемое сжатыми наклонными упорами, не должно превышать 25% полного сдвигающего усилия, действующего на рассчитываемом участке.
7.3.2.3 При объединении железобетонной части со стальной с помощью наклонных упоров из полосовой стали толщиной tan от 8 до 20 мм и шириной от 20 до 80 мм сдвигающее усилие Sh, приходящееся на один упор или одну ветвь петлевого упора, следует проверять по формуле (7.12), заменяя 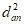 выражением
выражением 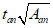 (где tan - см).
(где tan - см).
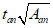 (где tan - см).
(где tan - см).7.3.2.4 Если наклонные или вертикальные упоры находятся в высоком железобетонном ребре и применяются для воспринятия в нем главных растягивающих напряжений, растягивающие усилия в наклонных упорах следует определять как в арматурных отгибах обычного железобетона, а в вертикальных упорах - аналогично усилиям в хомутах обычного железобетона. Допускается достаточность сечения упора для воспринятия им этого растягивающего усилия и сдвигающей силы между железобетоном и сталью проверять независимо и значения усилий не суммировать.
7.3.2.5 Расчет конструкции объединения на жестких упорах следует выполнять из условия
где Sh - сдвигающее усилие, приходящееся на один упор при расчете по прочности;
Ab,dr - площадь поверхности смятия бетона упором.
При сборной железобетонной плите и расположении упоров в проемах плиты расчетное сопротивление Rb следует принимать по классу бетона плиты, а толщину подливки не включать в площадь смятия. При расположении упоров в продольных швах плиты площадь смятия следует учитывать полностью, а расчетные сопротивления принимать по классу бетона замоноличивания швов.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду формула (7.14), а не формула (9.9а). |
Если жесткие упоры расположены в железобетонном ребре или вуте, предельные значения Sh следует уменьшать, умножая правые части формулы (9.9а) на 0,9 при 1,5bdr >= brib > 1,3bdr и на 0,7 при brib <= 1,3bdr, где bdr - ширина площади смятия бетона упором, brib - ширина ребра или вута на уровне центра тяжести расчетной площади смятия бетона упором.
7.3.2.6 Расчет упоров на концевое отрывающее усилие Sab выполняется по СП 16.13330 как конструкции, работающей на растяжение.
7.3.3 Расчеты по прочности объединения железобетона и стали высокопрочными болтами, обжимающими железобетон
7.3.3.1 Значение усилия Nhb натяжения высокопрочного болта следует определять по формуле
где Nhb,n - контролируемое усилие натяжения болта;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду рисунок 7.3, а не рисунок 9.1. |
При конструкции болтового объединения по рисунку 9.1 потери допускается определять по формуле
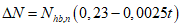 , (7.16)
, (7.16)где t - суммарная толщина плиты и слоя раствора по оси отверстия, принимается в сантиметрах, должна быть не более 50 см.

ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |
1 - высокопрочный болт; 2 - отверстие в бетоне;
3 - арматурный каркас; 4 - распределительная подкладка
7.3.3.2 Во фрикционном соединении железобетонной плиты со стальным поясом (через слой цементно-песчаного раствора или при непосредственном контакте) при условии очистки пояса сдвигающее усилие, приходящееся на один высокопрочный болт, должно соответствовать условию
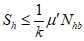 , (7.17)
, (7.17)где Nhb - усилие натяжения высокопрочного болта, определяемое по формуле (7.15);
k = 1,3 - коэффициент безопасности;
0,60 - при омоноличивании шва цементно-песчаным раствором или при монолитной железобетонной плите;
0,45 - при непосредственном контакте сборного железобетона со сталью.
ПРИМЕРЫ РАСЧЕТОВ
А.1 Расчет по прочности и трещиностойкости балки прямоугольного сечения с жесткой арматурой из двутавра
Пример 1. Дано: сталежелезобетонная балка прямоугольного поперечного сечения с размерами по рисунку А.1. Бетон класса по прочности на сжатие B30. Стальной сердечник - двутавр N 30 Б3 по ГОСТ Р 57837-2017 из стали С255. Стержневая арматура верхняя и нижняя -  А500. Суммарный изгибающий момент от внешних нагрузок составляет M = 196.2 кНм. Нагрузка кратковременная. Требуется проверить прочность поперечного сечения и рассчитать балку по образованию и раскрытию трещин, нормальных к продольной оси элемента.
А500. Суммарный изгибающий момент от внешних нагрузок составляет M = 196.2 кНм. Нагрузка кратковременная. Требуется проверить прочность поперечного сечения и рассчитать балку по образованию и раскрытию трещин, нормальных к продольной оси элемента.
 |  |
а) общий вид поперечного сечения | б) поперечное сечение - размеры и материалы |
Рисунок А.1 - К примеру расчета N 1
Запишем геометрические и прочностные характеристики элементов, формирующих поперечное сечение сталежелезобетонной балки:
Rs = 435 МПа, | 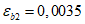 , , |
Rsc = 435 МПа, | As = 157 мм2, |
Rb = 17,0 МПа, |  , , |
Ry = 235 МПа, | Ast = 5874 мм2, |
Es = 2,0·105 МПа, | bf1 = bf2 = 151 мм, |
Rbt,ser = 1,75 МПа, | tf1 = tf2 = 11,5 мм, |
Est = 2,06·105 МПа, | tw = 8 мм, |
Eb = 32500 МПа, | hw = 282 мм. |
Момент инерции одного стержня верхней стержневой арматуры относительно собственной оси 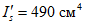 .
.
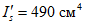 .
.Момент инерции одного стержня нижней стержневой арматуры относительно собственной оси Is = 490 см4.
Момент инерции двутавра относительно горизонтальной оси, проходящей через центр тяжести Ist = 9254,93·104 см4.
1 Расчет прочности поперечного сечения элемента
Вся нагрузка, приложенная к балке является кратковременной, следовательно в расчет вводим полные расчетные сопротивления прочностных характеристик бетона.
Определяем граничную относительную высоту сжатой зоны для стального сердечника и стержневой арматуры:
- для стального сердечника:

где 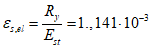 ;
;
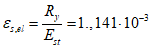 ;
;- для стержневой арматуры:

где  .
.
 .
.В качестве рабочего значения принимаем меньшее, как наиболее опасное: 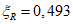 .
.
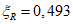 .
.Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.1.7 по формуле (6.1):

Получен противоречивый результат, свидетельствующий о том, что часть стального сердечника сжата, часть - растянута. По формуле (6.1) вся жесткая арматура должна находиться в растянутой зоне. Рассмотренный случай не подходит; переходим к следующему варианту.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.1.9 по формуле (6.2):

Полученная высота сжатой зоны: (c + tf1) < x < (H - c1 - tf2). Нейтральная ось сечения пересекает стенку двутавра, как и предполагалось в формуле (6.2). Вычисленное значение x принимаем для дальнейших расчетов.
Определим расстояние от центра тяжести растянутой арматуры до крайнего растянутого волокна сечения:

где
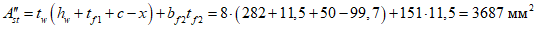 .
.Определим расстояние от центра тяжести сжатого бетона до крайнего сжатого волокна сечения:

где 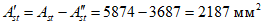 .
.
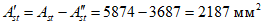 .
.Если сравнить полученную величину a2 = 49,5 мм и 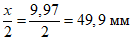 видно, что разница мала (менее 1%). Поэтому при небольших габаритах стального сердечника по отношению к размерам поперечного сечения в расчетах можно упрощенно принимать площадь сжатого бетона, как прямоугольника, без вычета площадей сжатой жесткой и стержневой арматуры. Это сокращает объем вычислений и дает приемлемые результаты для предварительной оценки работоспособности конструкции. В случае необходимости получить точный результат, расчеты следует выполнять без каких-либо сокращений и упрощений.
видно, что разница мала (менее 1%). Поэтому при небольших габаритах стального сердечника по отношению к размерам поперечного сечения в расчетах можно упрощенно принимать площадь сжатого бетона, как прямоугольника, без вычета площадей сжатой жесткой и стержневой арматуры. Это сокращает объем вычислений и дает приемлемые результаты для предварительной оценки работоспособности конструкции. В случае необходимости получить точный результат, расчеты следует выполнять без каких-либо сокращений и упрощений.
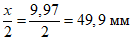 видно, что разница мала (менее 1%). Поэтому при небольших габаритах стального сердечника по отношению к размерам поперечного сечения в расчетах можно упрощенно принимать площадь сжатого бетона, как прямоугольника, без вычета площадей сжатой жесткой и стержневой арматуры. Это сокращает объем вычислений и дает приемлемые результаты для предварительной оценки работоспособности конструкции. В случае необходимости получить точный результат, расчеты следует выполнять без каких-либо сокращений и упрощений.
видно, что разница мала (менее 1%). Поэтому при небольших габаритах стального сердечника по отношению к размерам поперечного сечения в расчетах можно упрощенно принимать площадь сжатого бетона, как прямоугольника, без вычета площадей сжатой жесткой и стержневой арматуры. Это сокращает объем вычислений и дает приемлемые результаты для предварительной оценки работоспособности конструкции. В случае необходимости получить точный результат, расчеты следует выполнять без каких-либо сокращений и упрощений.Рабочая высота сечения h0 = H - a1 = 405 - 119,5 = 285,5 мм.
Определим относительную высоту сжатой зоны  .
.
 .
.Т.к. 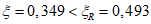 , прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
, прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
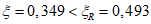 , прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
, прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
Mпр = 216,6 кНм > M = 196,2 кНм.
Прочность сечения обеспечена.
2 Расчет по образованию трещин, нормальных к продольной оси элемента
Требуется определить момент образования трещин с учетом неупругих деформаций растянутого бетона.
Определим коэффициенты приведения арматуры к бетону:
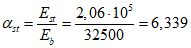 ,
, .
.Определим площадь приведенного к бетону сечения элемента:

где A - площадь поперечного сечения бетона,
 .
.Определим расстояние yt от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента. Для этого вычислим сначала статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона:

 .
.Определим момент инерции приведенного поперечного сечения элемента относительно его центра тяжести:

Определим упругопластический момент сопротивления сечения Wpl для крайнего растянутого волокна бетона. Для прямоугольных сечений и тавровых сечений с полкой, расположенной в сжатой зоне, значение Wpl при действии изгибающего момента в плоскости оси симметрии допускается определять по формуле:
Wpl = 1,3·Wred = 1.3·1.002·107 = 1.302·107 мм3,
где Wred - упругий момент сопротивления приведенного сечения для наиболее растянутого волокна бетонного сечения, определяемый как:
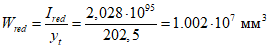 .
.Определяем момент образования трещин с учетом неупругих деформаций растянутого бетона:
Mcrc = Rbt,serWpl = 1,75·1.302·107 = 22784731 Н·мм = 22,78 кНм.
M = 196,2 кНм > Mcrc = 22,78 кНм.
Трещины в растянутой зоне поперечного сечения образуются. Необходимо выполнить расчет по ширине раскрытия трещин.
3 Расчет по раскрытию трещин, нормальных к продольной оси элемента
Определим момент инерции приведенного поперечного сечения элемента относительно его центра тяжести по формуле (6.11). Для этого предварительно вычислим коэффициенты приведения арматуры к бетону 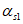 и
и 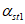 , площадь
, площадь 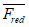 и статический момент
и статический момент 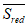 приведенного сечения, а также высоту сжатой зоны x.
приведенного сечения, а также высоту сжатой зоны x.
Eb1 = 0.4·Eb = 0.4·331295 = 1.325·104 МПа.
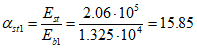 .
.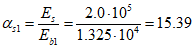 .
.



Определим напряжения в стержнях крайнего ряда растянутой арматуры 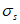 по формуле (6.10):
по формуле (6.10):
 ,
,где yc = H - a - x = 405 - 30 - 166,9 = 208,1 см.
Определим приведенный диаметр жесткой и гибкой арматуры, расположенной в растянутой зоне по формуле (6.15):
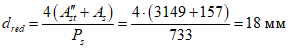 ,
,где
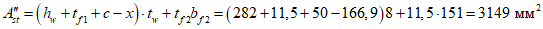 .
.Ps = (282 + 11.5 + 50 - 166,9)·2 + (2·151 - 8) + 2·11,5 + 2·3.14·5·2 = 733 мм.
Определим коэффициент армирования сечения:
 .
.Принимаем 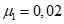 .
.
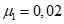 .
.Определяем ширину раскрытия трещин по формуле (6.8):

Полученное значение acrc = 0,218 мм не превышает предельно допустимое значение acrc,ult = 0,3 мм. Требования по трещиностойкости выполнены.
Пример 2. Дано: сталежелезобетонная балка таврового поперечного сечения с размерами по рисунку А.2. Бетон класса по прочности на сжатие B25. Стальной сердечник - двутавр 30 Б3 по ГОСТ Р 57837-2017 из стали С255. Стержневая арматура верхняя - 4 шт. 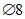 А500, нижняя - 2 шт.
А500, нижняя - 2 шт.  А500. Суммарный изгибающий момент от внешних нагрузок составляет M = 245,3 кНм. Нагрузка кратковременная. Требуется проверить прочность поперечного сечения.
А500. Суммарный изгибающий момент от внешних нагрузок составляет M = 245,3 кНм. Нагрузка кратковременная. Требуется проверить прочность поперечного сечения.
 |  |
а) общий вид поперечного сечения | б) поперечное сечение - размеры и материалы |
Рисунок А.2 - К примеру расчета N 2
Запишем геометрические и прочностные характеристики элементов, формирующих поперечное сечение сталежелезобетонной балки:
Rs = 435 МПа, | 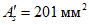 , , |
Rsc = 435 МПа, | Ast = 5874 мм2, |
Rb = 14,5 МПа, | bf1 = bf2 = 151 мм, |
Ry = 235 МПа, | tf1 = tf2 = 11,5 мм, |
Es = 2,0·105 МПа, | tw = 8 мм, |
Est = 2,06·105 МПа, | hw = 282 мм, |
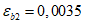 , , | 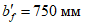 , , |
As = 628 мм2, |  . . |
1 Расчет прочности поперечного сечения элемента
Вся нагрузка, приложенная к балке является кратковременной, следовательно в расчет вводим полные расчетные сопротивления прочностных характеристик бетона.
Определяем граничную относительную высоту сжатой зоны для стального сердечника и стержневой арматуры:
- для стального сердечника:

где 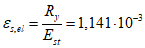
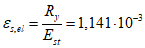
- для стержневой арматуры:

где 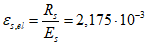 .
.
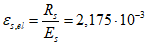 .
.В качестве рабочего значения принимаем меньшее, как наиболее опасное: 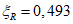 .
.
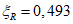 .
.Согласно 6.1.4 в расчет вводится бетонная полка шириной:  .
.
 .
.Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.2.1 по формуле (6.3):
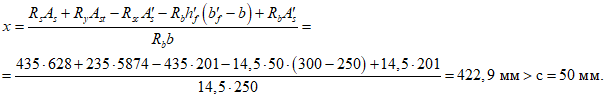
Получен противоречивый результат, свидетельствующий о том, что вся жесткая арматура сжата. По формуле (6.3) вся жесткая арматура должна находиться в растянутой зоне. Рассмотренный случай не подходит; переходим к следующему варианту.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.2.2 по формуле (6.4):

Полученная высота сжатой зоны: (c + tf1) < x < (H - c1 - tf2). Нейтральная ось сечения пересекает стенку двутавра, как и предполагалось в формуле (6.4). Вычисленное значение x принимаем для дальнейших расчетов.
Определим расстояние от центра тяжести растянутой арматуры до крайнего растянутого волокна сечения:

где
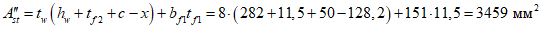 .
.Определим расстояние от центра тяжести сжатого бетона до крайнего сжатого волокна сечения:

где  .
.
 .
.Рабочая высота сечения h0 = H - a1 = 405 - 99,6 = 305,4 мм.
Определим относительную высоту сжатой зоны 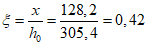 .
.
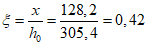 .
.Т.к. 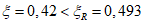 , прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
, прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
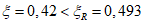 , прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
, прочность сечения проверяем согласно условию СП 266.1325800.2016 (6.2.1.6) (предельный момент, который может быть воспринят поперечным сечением записан относительно центра тяжести растянутой арматуры):
Mпр = 265,8 тм > M = 245,3 тм.
Прочность сечения обеспечена.
Пример 3. Дано: сталежелезобетонная балка таврового поперечного сечения с опиранием железобетонной плиты на нижний пояс стального сечения с размерами по рисунку А.4. Стальные балки расположены с шагом 3,3 м. Длина балки 7 м. Бетон класса по прочности на сжатие B25. Стальной сердечник - двутавр 30 Ш5 по ГОСТ Р 57837-2017 из стали С345. Стержневая арматура верхняя и нижняя - 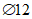 А500 с шагом 0,2 м. Суммарный изгибающий момент от внешних нагрузок составляет M = 588.6 кНм. Нагрузки кратковременные. Требуется проверить прочность поперечного сечения.
А500 с шагом 0,2 м. Суммарный изгибающий момент от внешних нагрузок составляет M = 588.6 кНм. Нагрузки кратковременные. Требуется проверить прочность поперечного сечения.

Рисунок А.3 - К примеру расчета N 3.
Общий вид поперечного сечения

Геометрические размеры поперечного сечения
Запишем геометрические и прочностные характеристики элементов, формирующих рассматриваемое поперечное сечение:
Rs1 = Rs2 = 435 МПа, | bf1 = bf2 = 208 мм, |
Rb = 14.5 МПа, | tf1 = tf2 = 28 мм, |
Ry = 310 МПа, | tw = 16 мм, |
As1 = 452 мм2, | hw = 270 мм, |
As2 = 452 мм2, | bf = 1004 мм, |
Ast = 16246 мм2, | hf = 150 мм. |
1 Расчет прочности поперечного сечения элемента
Согласно СП 266.1325800.2016 (таблица 4.1) в расчет вводится бетонная полка шириной:  , но не более
, но не более 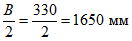 , и не менее
, и не менее 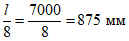 ,
,
 , но не более
, но не более 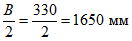 , и не менее
, и не менее 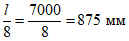 ,
,где l - пролет стальной балки; B - расстояние между осями стальных балок.
Таким образом, принимаем расчетную ширину железобетонной плиты bsl = 1004 мм.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по 6.3 по формуле (6.5), при этом предполагая, что вся железобетонная плита находится в растянутой зоне:

Получено, что нейтральная ось сечения пересекает стенку двутавра и вся железобетонная плита находится в растянутой зоне, как и предполагалось в формуле (6.5). Вычисленное значение x принимаем для дальнейших расчетов.
Проверку прочности сталежелезобетонного сечения выполним по СП 266.1325800.2016 (формула (6.61.)):
 ,
,где ys,i - расстояние от центра тяжести сечения арматуры до оси, относительно которой вычисляются моменты;
yst,i - расстояние от центра тяжести i-го участка стального сечения с одинаковым напряжением до оси, относительно которой вычисляются моменты.
Запишем уравнение равновесия моментов всех сил, действующих в рассматриваемом поперечном сечении, относительно наиболее сжатого волокна стального профиля, при этом не учитывая растянутую бетонную часть:

Mпр = 667 кНм > M = 588,6 кНм.
Прочность сталежелезобетонного сечения обеспечена.
Кроме рассмотренного в примере определения предельного момента, который может быть воспринят поперечным сечением сталежелезобетонной конструкции, необходимо выполнить весь комплекс проверок стальной части балки в соответствии с требованиями СП 16.13330 "Стальные конструкции", включающие в себя проверку устойчивости стенки, поясов и пр.
А.4.1 При выполнении расчетов сдвиговых соединений железобетонной плиты со стальной балкой необходимо руководствоваться указаниями СП 266.1325800.2016 (6.2.4 и 9.1.2), а также раздела 7.
Сдвигающие силы по шву объединения следует определять для каждого расчетного участка. Расчетный участок ограничивается соседними расчетными поперечными сечениями. В соответствии с СП 266.1325800.2016 (4.4.4.1 и 6.2.4) расчетные поперечные сечения, включают также:
- сечения с максимальным изгибающим моментом;
- опоры;
- сечения с нулевым моментом;
- сечения, в которых приложены сосредоточенные нагрузки или реакции;
- сечения с изменением своих размеров, при которых отношение большего момента сопротивления к меньшему превышает 1,2;
- в элементах переменной высоты расчетные сечения выбирают таким образом, чтобы отношение большего значения несущей способности по изгибающему моменту к меньшему (при изгибе в одной плоскости) для любой пары смежных расчетных поперечных сечений не превышало 1,5;
- свободные концы консолей.
Так как расчет сдвиговых соединений является составной частью общего расчета, то ниже приведен полный расчет однопролетной комбинированной балки шарнирно опертой левым торцом и частично защемленной правым торцом. На рисунке А.18 приведена эпюра погонной сдвигающей силы, эпюра несущей способности гибких упоров и схема установки гибких упоров.
А.4.2 Пример 4.
Выполним расчет сдвигового соединения комбинированной балки, состоящей из стального двутавра и железобетонной плиты по верхней полке балки.
Сечение балки приведено на рисунке А.5.

Рисунок А.5 - Сечение рассчитываемой балки, размеры в мм
Стальная часть - двутавр широкополочный 40 Ш2 по ГОСТ Р 57837-2017, сталь С345 по ГОСТ 27772-88.
Плита по профилированному настилу, суммарной толщиной 0,155 м, настил Н75-750-0,8 по ГОСТ 24045-2016 высотой 0,075 м. Гофры профилированного настила ориентированы перпендикулярно оси стальной балки. Расчетная ширина плиты 3,0 м. Бетон тяжелый класса прочности B25. Армирование 15 стержнями диаметром 16 А500, погонная площадь сечения приведенной полосы 10,05 см2/п.м.
Пролет балки 12,15 м. Шарнирное опирание на одной опоре (A) и частичное защемление на 75% на второй опоре. Расчетная схема приведена на рисунке А.6.

Рисунок А.6 - Расчетная схема балки, размеры в м
Характеристики материалов:
Нормативное сопротивление бетона на сжатие Rbn = 18,5 МПа.
Нормативное сопротивление бетона на растяжение Rbt,n = 1,55 МПа.
Нормативное сопротивление растяжению арматуры Rs,n = 500 МПа.
На рисунке А.7 приведена трехлинейная диаграмма состояния сжатого бетона класса B25 с начальным значением модуля упругости Eb = 30.0 ГПа для расчетов по второй группе предельных состояний.

Рисунок А.7 - Трехлинейная диаграмма состояния
сжатого бетона класса B25
На рисунке А.8 приведена двухлинейная диаграмма состояния растянутой арматуры класса А500 с модулем упругости Es = 200 ГПа для расчетов по второй группе предельных состояний.

Рисунок А.8 - Двухлинейная диаграмма состояния
растянутой арматуры класса А500
Расчетное сопротивление стали Ry = 315 МПа.
Модуль упругости стали Est = 206 ГПа.
Предельная деформация стали  .
.
 .
.Изгибная жесткость сечения двутавра при упругой деформации EstIst = 276.13 МНм2
Нагрузки и воздействия
Балка нагружена постоянной равномерно распределенной нагрузкой q = 32,6 кН/м, с учетом коэффициента надежности по нагрузке 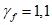 .
.
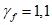 .
.Расчет по прочности и трещиностойкости плиты
При расчете по линейно упругой теории на действие нормативной нагрузки максимальный прогиб составляет 0,017 м, полученные эпюры деформаций и внутренних сил представлены на рисунке А.9.

Рисунок А.9 - Эпюры при расчете балки на действие
нормативной нагрузки: а - прогибы f, мм·10-2; б - изгибающие
моменты Mn, КНм; в - поперечные силы Qn, Нм
При расчете на действие расчетной нагрузки, полученные внутренние усилия: изгибающие моменты Mmax = 408,51 кНм, Mmin = -567,16 кНм, поперечные силы на опорах QA = 171,16 кНм, QB = 240,48 кНм, эпюры и их значения представлены на рисунке А.10 и в таблице А.1.

Рисунок А.10 - Эпюры при расчете балки на действие
расчетной нагрузки: а - изгибающие моменты M, кНм;
б - поперечные силы Q, Нм
Начало участка при расстоянии от опоры "A" li, м | Изгибающий момент в сечении балки M, кНм; | Поперечная сила в сечении Q, Нм |
0,00 | 0,00 | 171,17 |
0,15 | 25,27 | 165,79 |
0,20 | 33,84 | 163,92 |
3,04 | 354,49 | 62,24 |
4,77 | 408,51 | 0,0 |
6,08 | 378,12 | -46,68 |
9,00 | 88,16 | -151,57 |
9,11 | 70,90 | -155,61 |
9,50 | 7,89 | -169,50 |
9,54 | 0,41 | -171,08 |
9,60 | -9,22 | -173,09 |
11,00 | -286,75 | -223,29 |
11,96 | -516,28 | -257,54 |
12,00 | -527,91 | -259,15 |
12,15 | -567,19 | -264,53 |
При помощи САПР был проведен расчет армирования. При действии максимального момента на опоре "B" M = -567,16 кНм, запас по площади арматуры составил 40%, прочность плиты обеспечена.
При расчете по трещиностойкости в САПР из условия обеспечения сохранности арматуры и ширине продолжительного раскрытия трещин acrc1 = 0,3 мм и непродолжительного раскрытия acrc = 0,4 мм получены следующие значения:
Расчет в пролете Mn = 371,4 кНм, Mcrc = 1038,9 кНм, acrc1 = 0,000 мм, acrc = 0,000 мм.
Расчет на опоре "B" Mn = 515,6 кНм, Mcrc = 197,6 кНм, acrc1 = 0,205 мм, acrc = 0,205 мм. Полученная эпюра прогибов с учетом образования трещин представлена на рисунке А.11.

Рисунок А.11 - Эпюра прогибов
с учетом образования трещин, мм
Расчет на сдвигающее усилие
В число расчетных сечений для формирования расчетных участков включаются следующие сечения, где li - удаленность сечения от опоры "A":
1-е сечение - опорное сечение l1 = 0,00 м,
M1 = 0 кНм;
2-е сечение - сечение с максимальным моментом l2 = 4,77 м,
M2 = 408,51 кНм;
3-е сечение - сечение с нулевым моментом l3 = 9,544 м,
M3 = 0 кНм;
4-е сечение - опорное сечение l4 = 12,15 м,
M4 = -567,19 кНм.
Схема расположения расчетных сечений представлена на рисунке А.12.

при расчете на сдвигающее усилие на эпюре моментов
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду СП 266.1325800.2016, а не СП 263.1325800.2016. |
Расчет сдвигающего усилия осуществляется в соответствии с СП 263.1325800.2016 (6.2.4.2, формуле (6.63)), а также 7.2.2:
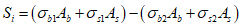 ,
,где 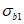 ,
, 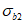 - напряжения в центре тяжести поперечного сечения бетона соответственно в левом и правых сечениях расчетного участка плиты длиной ai;
- напряжения в центре тяжести поперечного сечения бетона соответственно в левом и правых сечениях расчетного участка плиты длиной ai; 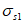 ,
,  - напряжения в продольной арматуре соответственно в тех же сечениях.
- напряжения в продольной арматуре соответственно в тех же сечениях.
В рассматриваемом случае a1 = 4,77 м; a2 = 4,774 м; a3 = 2,606 м (см. рисунок А.12).
Для первого сечения первого расчетного участка M1 = 0 кНм и соответственно  .
.
 .
.Для второго сечения первого расчетного участка M2 = 408,51 кНм.
Ниже приведен расчет сечения для M2 = 408,51 кН/м.
При действии момента M2 = 408,51 кН/м высота сжатой зоны составит x = 0,119 м (рисунок А.13). Полученные значения деформаций и напряжений в материалах приведены в таблице А.2, а также на рисунке А.14. Напряжения и деформации вычисляются в расчетном комплексе (САПР) автоматически.

Рисунок А.13 - Положение нейтральной оси
при действии момента M2
Таблица А.2
Материал | Максимальная относительная деформация | Напряжение при максимальной относительной деформации | Минимальная относительная деформация | Напряжение при минимальной относительной деформации |
Бетон | -0,0006 | -1,74 | -0,01018 | -5,29 |
Арматура | -0,0014 | -28,14 | -0,0014 | -28,14 |
Сталь | -0,0063 | 129,79 | 0,0005 | 10,94 |
Примечание: Знак "+" при растяжении, знак "-" при сжатии | ||||
в частях сечения при действии момента M2:
а - в стали; б - в бетоне
Усилия в железобетонной части сечения относительно ее центра тяжести: Nb2 = -927,4 кН, Mb2 = 5,9 кНм.
Усилия в стальной части относительно ее центра тяжести: Nst2 = -927,4 кН, Mst2 = 114 кНм.
Усилие в железобетонной части (бетоне и арматуре) равно
 .
.Соответственно, сдвигающая сила для этого участка равна
S1 = 927,4 кН.
Для второго расчетного участка первое расчетное сечение совпадает со вторым расчетным сечением первого участка, а во втором расчетном сечении второго участка момент равен нулю. Соответственно, сдвигающая сила для этого участка равна S2 = -927,4 кН.
Для третьего расчетного участка первое расчетное сечение совпадает со вторым расчетным сечением второго участка и момент равен нулю, а во втором расчетном сечении третьего участка момент равен M4 = -567,19 кНм.
Ниже приведен расчет сечения для M4 = -567,19 кНм.
При действии момента M4 = -567,19 кНм высота сжатой зоны составит x = 0,254 м (рисунок А.15). Полученные значения деформаций и напряжений в сечении стальной части рассчитаны в программном комплексе автоматически и приведены в таблице А.3, а также на рисунке А.16.

Рисунок А.15 - Положение нейтральной оси
при действии момента M4
Таблица А.3
Материал | Максимальная относительная деформация | Напряжение при максимальной относительной деформации | Минимальная относительная деформация | Напряжение при минимальной относительной деформации |
Бетон | 0,0127 | 0,00 | 0,0092 | 0,00 |
Арматура | 0,0117 | 233,69 | 0,0117 | 233,69 |
Сталь | 0,0059 | 122,49 | -0,0111 | -223,44 |
Примечание: Знак "+" при растяжении, знак "-" при сжатии | ||||

Усилия в железобетонной части сечения относительно ее центра тяжести: Nb2 = 704,8 кН, Mb2 = -10,4 кНм.
Усилия в стальной части сечения относительно ее центра тяжести: Nst2 = -704,8 кН, Mst2 = -337,4 кНм.
Соответственно, сдвигающая сила для этого участка равна S3 = 704,8 кН.
Для более экономичной расстановки гибких упоров можно построить эпюру погонной сдвигающей силы. Для построения этой эпюры заметим, что при переходе от второго к третьему расчетному участку изгибающий момент меняет знак. Поэтому рассмотрим сечение слева от третьего расчетного сечения (сечения с нулевым моментом) с l3,1 = 9,50 м и сечение справа от третьего расчетного сечения с l3,2 = 9,60 м. Для сечения l3,1 = 9,50 м M3,1 = 7,89 кНм, Q3,1 = -169,5 кН. Для сечения l3,2 = 9,60 м M3,2 = -9,22 кНм, Q3,2 = -173,09 кН. В таблицах А.4 и А.5 представлены расчеты погонных сдвигающих сил для данных сечений.
Погонная сдвигающая сила определена по формуле:
где a - длина расчетного участка,
Si - сдвигающее усилие по шву объединения на заданном участке, определенное по формуле
Si = |Nbi - Nb(i+1)|,
здесь Nbi и Nb(i+1) - продольные силы в железобетонной плите для расчетных сечений i и (i + 1).
Таблица А.4
в сечении l3,1 = 9,50 м при Q3,1 = 169,5 кН
Длина расчетного участка a, м | Изгибающий момент в сечении слева M1, кНм | Изгибающий момент в сечении справа M2, кНм | Продольное усилие в железобетонной части в сечении слева Nb1, кН | Продольное усилие в железобетонной части в сечении справа Nb2, кН | Погонная сдвигающая сила, |
0,002336 | 7,9 | 7,5 | -18,0 | -17,1 | 385,3 |
Таблица А.5
в сечении l3,2 = 9,60 м при Q3,2 = 173,1 кН
Длина расчетного участка a, м | Изгибающий момент в сечении слева M1, кНм | Изгибающий момент в сечении справа M2, кНм | Продольное усилие в железобетонной части в сечении слева Nb1, кН | Продольное усилие в железобетонной части в сечении справа Nb2, кН | Погонная сдвигающая сила, |
0,0028 | -8,7 | -9,2 | 10,8 | 11,4 | 213,9 |
В таблицах А.6 и А.7 представлены расчеты погонных сдвигающих сил в первом и четвертом расчетных сечениях (опорных).
Таблица А.6
Определение погонной сдвигающей силы
в сечении l1 = 0,00 м при Q1 = 171,0 кН
Длина расчетного участка a, м | Изгибающий момент в сечении слева M1, кНм | Изгибающий момент в сечении справа M2, кНм | Продольное усилие в железобетонной части в сечении слева Nb1, кН | Продольное усилие в железобетонной части в сечении справа Nb2, кН | Погонная сдвигающая сила, |
0,150 | 0 | 25,27 | 0 | 57,98 | 386,5 |
Таблица А.7
в сечении l4 = 12,15 м при Q4 = 264.5 кН
Длина расчетного участка a, м | Изгибающий момент в сечении слева M1, кНм | Изгибающий момент в сечении справа M2, кНм | Продольное усилие в железобетонной части в сечении слева Nb1, кН | Продольное усилие в железобетонной части в сечении справа Nb2, кН | Погонная сдвигающая сила, |
0,1071 | -538,8 | -567,2 | 669,6 | 704,8 | 328,7 |
Эпюра погонных сдвигающих сил приведена на рисунке А.17.

Рисунок А.17 - Эпюра погонных сдвигающих сил S, кН/м
Количество гибких упоров и их расстановка определяется из условия, что сдвигающее усилие Sh, приходящееся на один гибкий упор, должно быть меньше, чем несущая способность упора на сдвиг Prd/Sh <= Prd.
В рассматриваемом примере используются гибкие упоры диаметром 19 мм длиной 120 мм и расчетным сопротивлением стали Ry = 350 МПа.
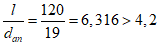 .
.Несущая способность гибкого упора определяется по формуле (7.10) и равна:  , кН.
, кН.
 , кН.
, кН.Также выполнено и условие (7.11)
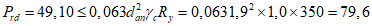 , кН.
, кН.На рисунке А.18 приведена требуемая схема расстановки гибких упоров и эпюра несущей способности соединения по длине балки, без учета фактического шага гофр настила.

а - схема установки гибких упоров для обеспечения требуемой
несущей способности соединения (без учета шага гофр);
б - эпюра сдвигающих сил S и несущей способности соединения
P по длине балки с учетом переменного шага упоров, кН/м
В таблице А.8 приведен расчет несущей способности соединения с учетом переменного шага гибких упоров, шаг упоров приведен требуемый, без учета фактического шага гофр настила.
Таблица А.8
Расчет несущей способности сдвигового соединения
Начало участка при расстоянии от опоры "A" li, м | Погонная сдвигающая сила, S, кН/м | Шаг упоров s, мм | Количество упоров на рассматриваемом участке | Несущая способность соединения P, кН/м |
0,00 | 386,5 | 209 | 1 | 416,0 |
0,21 | 372,5 | 228 | 2 | 381,3 |
0,66 | 335,3 | 247 | 1 | 352,0 |
0,91 | 315,1 | 266 | 1 | 326,8 |
1,18 | 293,4 | 285 | 1 | 305,1 |
1,46 | 270,1 | 304 | 1 | 286,0 |
1,77 | 246,7 | 342 | 1 | 254,2 |
2,11 | 217,4 | 399 | 1 | 217,9 |
2,51 | 184,9 | 456 | 1 | 190,7 |
2,96 | 147,6 | 589 | 1 | 147,6 |
3,55 | 99,6 | 855 | 1 | 101,7 |
4,41 | 29,8 | 1216 | 1 | 71,5 |
5,62 | 69,4 | 684 | 1 | 127,1 |
6,31 | 125,2 | 513 | 1 | 169,5 |
6,8 | 167,1 | 418 | 1 | 208,0 |
7,24 | 201,2 | 36 | 1 | 240,8 |
7,60 | 230,7 | 232 | 1 | 269,2 |
7,92 | 257,0 | 304 | 1 | 286,0 |
8,23 | 281,9 | 285 | 1 | 305,1 |
8,51 | 305,1 | 266 | 1 | 326,8 |
8,78 | 326,8 | 247 | 1 | 352,0 |
9,02 | 347,0 | 228 | 2 | 381,0 |
9,48 | 342,8 | 247 | 10 | 352,0 |
1. | ГОСТ 24045-2016 "Профили стальные листовые гнутые с трапециевидными гофрами для строительства. Технические условия" | ||||
ГОСТ Р 57837-2017 "Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия" | |||||
СП 14.13330.2014 "СНиП II-7-81* Строительство в сейсмических районах" (с изменением N 1) | |||||
4. | СП 16.13330.2017 "СНиП II-23-81* Стальные конструкции" | ||||
5. | СП 20.13330.2016 "СНиП 2.01.07-85* Нагрузки и воздействия" | ||||
6. | СП 63.13330.2012 "СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения" (с изменениями N 1, N 2) | ||||
7. | СП 70.13330.2012 "СНиП 3.03.01-87 Несущие и ограждающие конструкции" | ||||
8. | СП 266.1325800.2016 "Конструкции сталежелезобетонные. Правила проектирования" | ||||
| |||||
9. | СП 267.13330.2016 "Здания и комплексы высотные. Правила проектирования" | ||||
Рекомендации по учету ползучести и усадки бетона при расчете бетонных и железобетонных конструкций. НИИЖБ Госстроя СССР, М.: Стройиздат, 1988, 120 с. | |||||
СТО 573938459-001-2010 Профили стальные листовые гнутые для сталебетонных перекрытий. Технические условия. ООО "Стальные конструкции - Профлист". Рязань, 2010 | |||||
СТО 57398459-002-2011 Перекрытия железобетонные монолитные с несъемной опалубкой из профилированного листа. Общие технические требования. Проектирование и производство работ. ООО "Стальные конструкции - Профлист". Рязань, 2011 | |||||
СТО 57398459-30-2008 (СТП/ПП/30) Профили стальные листовые гнутые для сталебетонных перекрытий. ООО "Стальные конструкции - Профлист". Рязань, 2008 | |||||
СТО 57398459-035-2014 Плиты перекрытий зданий и сооружений сталежелезобетонные с применением стальных профилированных листов. Нормы проектирования. ООО "Стальные конструкции - Профлист". Рязань, 2010 | |||||
УДК 624.012.3/4, 624.014.2 | ОКС 91.080.01; |
Ключевые слова: конструкции сталежелезобетонные, комбинированные балки, сталежелезобетонные плиты, балки, конструкции комбинированные, расчет сталежелезобетонных конструкций, профилированный настил, жесткая арматура, стальной сердечник, внешнее армирование, несъемная опалубка, надежность сталежелезобетонных конструкций, трещиностойкость, гибкий упор, жесткий упор, стад-болт, конструирование сталежелезобетонных конструкций, конструктивные требования, расчет конструкции объединения стальной и железобетонной части сечения | |