СПРАВКА
Источник публикации
М.: Стройиздат, 1983
Примечание к документу
Название документа
"Руководство по проектированию зданий и сооружений на подрабатываемых территориях. Часть I. Исходные данные для проектирования зданий и сооружений на подрабатываемых территориях"
"Руководство по проектированию зданий и сооружений на подрабатываемых территориях. Часть I. Исходные данные для проектирования зданий и сооружений на подрабатываемых территориях"
Содержание
ПО ПРОЕКТИРОВАНИЮ ЗДАНИЙ И СООРУЖЕНИЙ
НА ПОДРАБАТЫВАЕМЫХ ТЕРРИТОРИЯХ
ЧАСТЬ I
ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ ЗДАНИЙ И СООРУЖЕНИЙ
НА ПОДРАБАТЫВАЕМЫХ ТЕРРИТОРИЯХ
Рекомендовано к изданию решением секции N 2 Научно-технического совета НИИСК Госстроя СССР и секции сдвижения горных пород Ученого совета ВНИМИ Минуглепрома СССР.
Разработано к главе СНиП II-8-78 "Здания и сооружения на подрабатываемых территориях".
Содержит рекомендации по расчету деформации земной поверхности. Приведены расчет ожидаемых сдвижений и деформаций земной поверхности для различных условий залегания горных пород и способы выемки угля в конкретных региональных районах угольных месторождений.
Даны примеры расчета сдвижений и деформаций земной поверхности.
Для инженерно-технических работников проектно-изыскательских и проектных организаций.
Разработано НИИСК Госстроя СССР (д-р техн. наук С.К. Клепиков, канд. техн. наук Н.С. Метелюк, инженеры А.Б. Соловьева, Ф.В. Бобров); Донецким ПромстройНИИпроектом Госстроя СССР (кандидаты техн. наук А.А. Петраков, Ю.М. Бучинский); ВНИМИ Минуглепрома (кандидаты техн. наук И.А. Петухов, Р.А. Муллер)
Руководство по проектированию зданий и сооружений на подрабатываемых территориях состоит из трех частей:
часть I - Исходные данные для проектирования зданий и сооружений на подрабатываемых территориях;
часть II - Руководство по проектированию зданий и сооружений на подрабатываемых территориях (промышленные и гражданские здания);
часть III - Руководство по проектированию зданий и сооружений на подрабатываемых территориях.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: раздел 9 отсутствует. |
Часть I Руководства разработана институтом ВНИМИ Минуглепрома СССР: раздел 1 (кандидаты техн. наук В.Н. Земисев, И.А. Петухов); раздел 2 (кандидаты техн. наук А.Г. Акимов, В.Н. Земисев, Р.А. Муллер; И.А. Петухов); раздел 3 (кандидаты техн. наук А.Г. Акимов, В.Н. Земисев, И.А. Петухов); раздел 4 (кандидаты техн. наук В.Н. Земисев, И.А. Петухов); раздел 5 (кандидаты техн. наук Б.Я. Гвирцман, В.Н. Земисев, И.А. Петухов); раздел 6 (кандидаты техн. наук В.Н. Земисев, И.А. Петухов, Ю.Б. Файнштейн); раздел 7 (кандидаты техн. наук Р.А. Муллер, В.Н. Земисев, И.А. Петухов); раздел 8 (кандидаты техн. наук А.Г. Акимов, В.Н. Земисев, М.А. Иофис, Г.А. Нестеров, И.А. Петухов, В.П. Самарин, инженеры Н.И. Митичкина, Н.М. Никольская, А.С. Ягунов); раздел 9 (инж. О.В. Жукова).
Основные понятия, термины и обозначения параметров сдвижения
земной поверхности
1. Ожидаемые сдвижения и деформации - величины сдвижений и деформаций, определяемые в условиях, когда имеются календарные планы развития горных работ и известны необходимые для расчетов исходные данные.
2. Вероятные сдвижения и деформации - величины сдвижений и деформаций, определяемые в условиях, когда отсутствуют календарные планы развития горных работ.
3. Расчетные сдвижения и деформации - величины сдвижений и деформаций, получаемые путем умножения ожидаемых или вероятных сдвижений и деформаций на коэффициенты перегрузки (табл. 4).
Расчетные сдвижения и деформации принимаются для разработки мер охраны зданий и сооружений.
4. Мульда сдвижения земной поверхности - участок земной поверхности, подвергшийся сдвижению под влиянием горных выработок.
5. Оседание земной поверхности 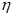 , мм, - вертикальная составляющая векторов сдвижения точек в мульде сдвижения земной поверхности.
, мм, - вертикальная составляющая векторов сдвижения точек в мульде сдвижения земной поверхности.
6. Максимальное оседание 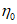 , мм, - наибольшая вертикальная составляющая векторов сдвижения точек при закончившемся процессе сдвижения.
, мм, - наибольшая вертикальная составляющая векторов сдвижения точек при закончившемся процессе сдвижения.
Различают максимальное оседание, мм:
при полной подработке  ,
,
при неполной подработке  .
.
7. Горизонтальное сдвижение земной поверхности 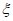 , мм, - горизонтальная составляющая векторов сдвижения точек в мульде сдвижения земной поверхности.
, мм, - горизонтальная составляющая векторов сдвижения точек в мульде сдвижения земной поверхности.
8. Максимальное горизонтальное сдвижение 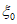 , мм, - наибольшая горизонтальная составляющая векторов сдвижения точек при закончившемся процессе сдвижения.
, мм, - наибольшая горизонтальная составляющая векторов сдвижения точек при закончившемся процессе сдвижения.
9. Главные сечения мульды сдвижения - вертикальные сечения мульды по простиранию и вкрест простирания пласта, проходящие через точки с максимальными оседаниями земной поверхности.
10. Полная подработка земной поверхности - подработка земной поверхности, при которой в мульде сдвижения не происходит увеличения максимального оседания при дальнейшем увеличении длины (ширины) выработанного пространства, и при пологом залегании пластов образуется так называемое плоское дно.
11. Неполная подработка земной поверхности - такая подработка, при которой с увеличением длины (ширины) выработанного пространства увеличивается максимальное оседание.
12. Коэффициент подработанности земной поверхности - отношение фактического размера выработанного пространства к минимальному размеру, при котором наступает полная подработка земной поверхности.
Различают коэффициенты подработанности:
по линии падения пласта - n1,
по простиранию - n2.
При расчетах для удобства используют коэффициенты 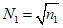 и
и  .
.
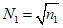 и
и  .
.При полной подработке земной поверхности коэффициенты подработанности по линиям простирания и падения пласта равны или больше единицы.
13. При определении границы влияния подземных разработок приняты следующие значения деформаций земной поверхности: наклон i = 0,5·10-3, растяжение 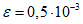 (при среднем интервале 15 - 20 м).
(при среднем интервале 15 - 20 м).
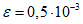 (при среднем интервале 15 - 20 м).
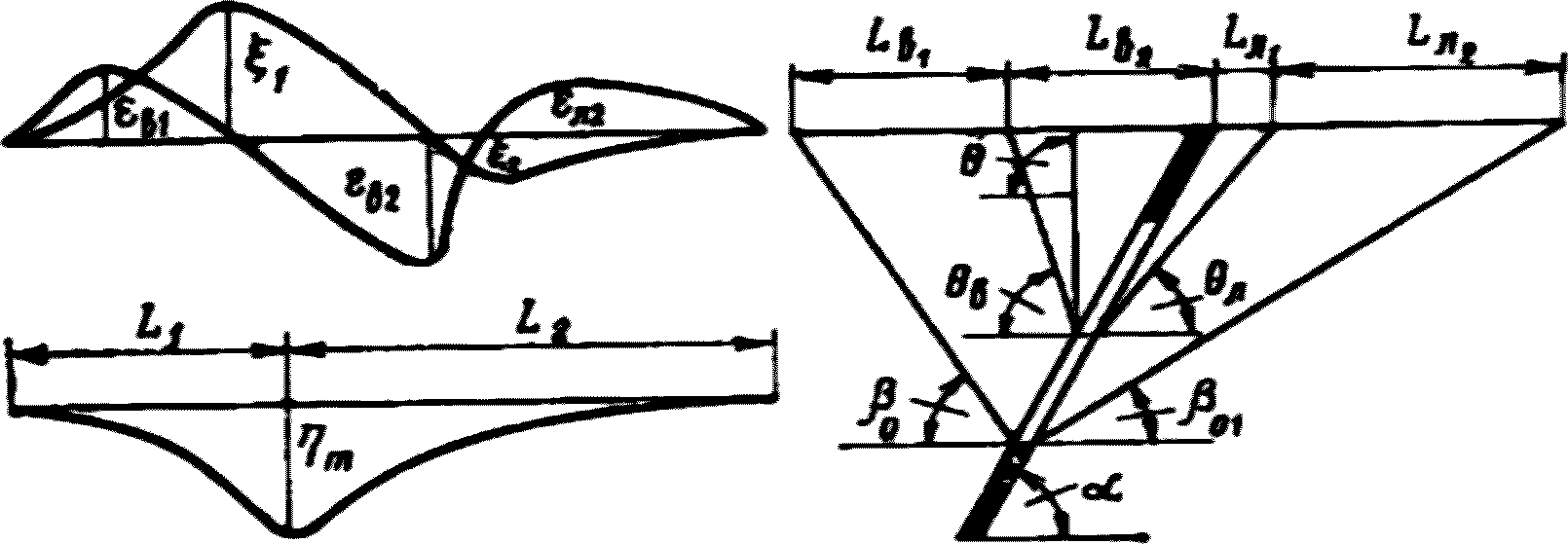
(при среднем интервале 15 - 20 м).Границы зоны влияния подземных разработок определяются граничными углами. Граничными углами называются внешние относительно выработанного пространства углы, образованные на вертикальных разрезах по главным сечениям мульды сдвижения горизонтальными линиями и линиями (последовательно проведенными в коренных породах, мезозойских отложениях и наносах), соединяющими границу выработки с границей зоны влияния подземных разработок на земной поверхности (рис. 1). Различают граничные углы:
в наносах, под которыми понимаются четвертичные и третичные горизонтально залегающие отложения, не вмещающие разрабатываемые пласты - 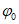 (принимаются одинаковыми во всех направлениях; учитываются при мощности наносов 5 м и более);
(принимаются одинаковыми во всех направлениях; учитываются при мощности наносов 5 м и более);
в мезозойских отложениях на месторождениях палеозойского возраста -  ,
,  ,
, 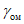 ;
;
в коренных породах, к которым относятся породы того же возраста, что и разрабатываемые пласты, - 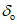 ,
, 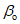 ,
,  .
.
а) | б) |
 |  |
 | |
а - при наклонном залегании пласта; б - при горизонтальном
залегании пласта (по простиранию); в - при крутом залегании
пласта  ; 1 - наносы; 2 - мезозойские отложения;
; 1 - наносы; 2 - мезозойские отложения;
 ; 1 - наносы; 2 - мезозойские отложения;
; 1 - наносы; 2 - мезозойские отложения;3 - коренные породы
Углами 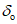 и
и  определяются границы зоны влияния по простиранию пласта; углами
определяются границы зоны влияния по простиранию пласта; углами 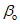 и
и  ,
, 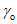 и
и 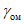 - вкрест простирания пласта соответственно со стороны падения и восстания; углами
- вкрест простирания пласта соответственно со стороны падения и восстания; углами  - граница зоны влияния в лежачем боку пласта при
- граница зоны влияния в лежачем боку пласта при 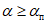 .
.
Величины граничных углов принимаются в соответствии с рекомендациями разд. 8. В подработанной толще на большинстве месторождений граничные углы выполаживаются.
Толща считается подработанной, если линия, проведенная в коренных породах под соответствующим граничным углом от границы данной очистной выработки, пересекает построенные по граничным углам зоны влияния от ранее пройденных очистных выработок по данному пласту, а также по вышележащим и нижележащим пластам.
14. Углы полных сдвижений (градус) - внутренние относительно выработанного пространства углы, образованные на вертикальных разрезах по главным сечениям мульды плоскостью пласта и линиями, соединяющими границы выработки с границами плоского дна мульды сдвижения.
Различают углы полных сдвижений (рис. 1):
у нижней границы выработки - 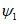 ;
;
у верхней границы выработки - 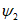 ;
;
у границы выработки по простиранию -  .
.
15. Угол максимального оседания 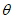 (градус) - угол со стороны падения пласта, образованный на вертикальном разрезе в главном сечении мульды вкрест простирания пласта горизонтальной линией и линией, соединяющей середину очистной выработки с точкой максимального оседания при неполной подработке земной поверхности (см. рис. 1).
(градус) - угол со стороны падения пласта, образованный на вертикальном разрезе в главном сечении мульды вкрест простирания пласта горизонтальной линией и линией, соединяющей середину очистной выработки с точкой максимального оседания при неполной подработке земной поверхности (см. рис. 1).
16. Длина полумульды - расстояние в главном сечении на разрезе вкрест простирания или по простиранию (см. рис. 1) между границей мульды и точкой пересечения с земной поверхностью линии, проведенной под углом полных сдвижений (при полной подработке) или под углом максимального оседания (при неполной подработке). Участок плоского дна при расчете сдвижений и деформаций в длину полумульды не включается.
Различают длины полумульд, м:
по падению - L1;
по восстанию - L2;
по простиранию - L3.
17. Первичная подработка земной поверхности - подработка первым пластом (слоем).
18. Повторная подработка земной поверхности - все последующие подработки другими пластами (слоями).
19. Смежные выработки - выработки, имеющие общую границу по падению, восстанию, простиранию или разделенные целиком такого размера, при котором происходит активизация сдвижения земной поверхности.
20. Активизация сдвижения толщи пород и земной поверхности - изменение характера распределения и величин сдвижений и деформаций земной поверхности и толщи при разработке пласта смежными выработками или при повторных подработках по сравнению со сдвижениями и деформациями от одиночной выработки при первичной подработке.
21. Эффективная мощность пласта mэ (м) - мощность, принимаемая для расчетов сдвижений и деформаций при отработке пластов с закладкой выработанного пространства. Величина mэ определяется с учетом конвергенции боковых пород, полноты заполнения выработанного пространства закладочным массивом и последующего уплотнения материала закладки.
22. Предельные углы падения пластов 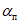 - наименьшие углы падения пластов, при которых возникают опасные сдвижения пород лежачего бока разрабатываемого пласта.
- наименьшие углы падения пластов, при которых возникают опасные сдвижения пород лежачего бока разрабатываемого пласта.
23. Углы максимальных горизонтальных сдвижений (при сдвижении пород лежачего бока) 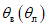 , градус (см. рис. 1) - острые углы, образованные на вертикальном разрезе в главном сечении мульды вкрест простирания пласта горизонтальной линией и линиями, соединяющими середину очистной выработки с точками максимального горизонтального сдвижения в висячем (лежачем) боку.
, градус (см. рис. 1) - острые углы, образованные на вертикальном разрезе в главном сечении мульды вкрест простирания пласта горизонтальной линией и линиями, соединяющими середину очистной выработки с точками максимального горизонтального сдвижения в висячем (лежачем) боку.
24. Относительная величина максимального оседания qо (безразм.) - отношение величины максимального оседания земной поверхности к вынимаемой (считая по нормали) или эффективной мощности пласта при полной подработке, горизонтальном залегании пласта и закончившемся процессе сдвижения.
25. Относительная величина максимального горизонтального сдвижения aо (безразм.) - отношение максимального горизонтального сдвижения к максимальному оседанию при полной подработке, закончившемся процессе сдвижения и горизонтальном залегании пласта.
26. Наклоны - отношение разности оседаний двух соседних точек мульды к расстоянию между ними (безразм. 10-3).
В точке мульды различают наклоны:
в направлении простирания - ix;
в направлении вкрест простирания - iy;
в заданном направлении -  .
.
27. Кривизна - отношение разности наклонов двух соседних интервалов мульды к полусумме длин этих интервалов (10-3 1/м).
Различают кривизну мульды, определенную непосредственно по данным измерений и полученную по сглаженной кривой оседаний.
В точке мульды различают кривизну:
в направлении простирания - Kx;
в направлении вкрест простирания - Ky;
в заданном направлении -  .
.
28. Радиус кривизны - величина, обратная кривизне мульды сдвижения, м или км.
В точке мульды различают радиусы кривизны:
в направлении простирания - Rx;
в направлении вкрест простирания - Ry;
в заданном направлении - 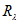 .
.
29. Горизонтальные деформации растяжения или сжатия - отношение разности длин интервала в горизонтальной плоскости к его первоначальной длине (безразм. 10-3).
В точке мульды различают сжатия (растяжения):
в направлении простирания - 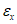 ;
;
в направлении вкрест простирания -  ;
;
в заданном направлении -  .
.
30. Сосредоточенные деформации - деформации (горизонтальные и вертикальные) на небольших (до 5 м) интервалах мульды сдвижения, резко превышающие соответствующие деформации на таких же смежных интервалах. На участках сосредоточенных деформаций обычно возникают трещины и уступы.
31. Уступы - сосредоточенные деформации, проявляющиеся в образовании трещин со сдвигом пород. Уступы возникают вследствие относительных разрывных перемещений смежных участков по напластованию, поверхностям разрывных нарушений, осевым поверхностям складок и т.п.
Различают прямые и обратные уступы. У прямого уступа участок у края трещины, расположенный ближе к точке максимального оседания, оседает больше, чем расположенный дальше от этой точки; у обратного уступа - наоборот.
1.2. При расчетах сдвижений и деформаций земной поверхности в условиях синклинальных складок используются следующие понятия и определения:
1. Синклинальные складки - складки, центральные части которых сложены более молодыми породами по сравнению с породами периферии. Складки называются нормальными, если осевая поверхность занимает вертикальное или наклонное положение, а крылья падают в разные стороны.
2. Ось складки - линия, соединяющая все точки перегиба данной складки (линия 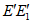 на рис. 2).
на рис. 2).

1 - осевая поверхность складки; 2 - ось складки;
3 - шарнир складки
3. Осевая поверхность складки - поверхность EE1F1E, проходящая через ось и делящая угол складки (V) пополам (рис. 2).
4. Угол складки - двугранный угол, заключенный между крыльями складки.
5. Крылья складки - части складки BAA1B1 и CДД1C1 (рис. 2).
6. Шарнир складки - линия EE1, представляющая собой пересечение продолжения крыльев (рис. 2).
7. Оседание земной поверхности от изгиба слоев  , мм, - часть вертикальной составляющей векторов сдвижения точек в мульде сдвижения, вызванная изгибом слоев подрабатываемого массива по нормали к напластованию.
, мм, - часть вертикальной составляющей векторов сдвижения точек в мульде сдвижения, вызванная изгибом слоев подрабатываемого массива по нормали к напластованию.
8. Оседание земной поверхности от сдвига слоев  , мм, - часть вертикальной составляющей векторов сдвижения точек в мульде, вызванная сдвижением слоев подрабатываемого массива по контактам напластования.
, мм, - часть вертикальной составляющей векторов сдвижения точек в мульде, вызванная сдвижением слоев подрабатываемого массива по контактам напластования.
1.3. Величины сдвижений и деформаций в точках мульды сдвижения могут быть положительными и отрицательными.
При расчете сдвижений и деформаций в главных или параллельных им сечениях мульды знаки их необходимо определять согласно табл. 1.
Сдвижения и деформации | |
Знак положительный | Знак отрицательный |
Оседание | Поднятие |
Горизонтальные сдвижения в сторону восстания и в сторону простирания пласта | Горизонтальные сдвижения в сторону падения и в сторону, обратную простиранию пласта |
Наклоны в сторону восстания и в сторону простирания пласта | Наклоны в сторону падения и в сторону, обратную простиранию пласта |
Кривизна и радиус кривизны выпуклости кривой оседания | Кривизна и радиус кривизны вогнутости кривой оседания |
Растяжение | Сжатие |
Примечания: 1. За направление простирания пласта принимается направление, относительно которого линия падения располагается справа.
2. При построении графиков сдвижений и деформаций положительные величины (кроме оседания) и поднятие откладываются вверх от исходной горизонтальной линии.
2.1. Воздействиями от подработки, учитываемыми при проектировании зданий и сооружений, являются сдвижения и деформации земной поверхности, которые подразделяются на следующие основные виды:
оседание - 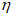 , мм;
, мм;
наклон - (1·10-3);
кривизна (выпуклости, вогнутости) K, К·10-3 1/м, или радиус кривизны 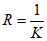 , км;
, км;
горизонтальное сдвижение  , мм;
, мм;
относительная горизонтальная деформация растяжения или сжатия  , 1·10-3;
, 1·10-3;
уступ высотой h, см.
Примечание. Для зданий и сооружений, рассчитываемых с учетом пространственной работы конструкций, дополнительно необходимо определять величины следующих ожидаемых деформаций земной поверхности:
скручивание S, км;
скашивание  , 1·10-3.
, 1·10-3.
2.2. В качестве исходных данных для проектирования зданий и сооружений на подрабатываемых территориях необходимо задавать максимальные величины ожидаемых (нормативных) деформаций земной поверхности на участке строительства в направлениях вкрест и по простиранию пластов (или в направлении главной оси сооружения):
от пластов, намечаемых к отработке в течение всего срока эксплуатации зданий или сооружений, при этом следует предусматривать полный комплекс мер защиты;
от пластов, намечаемых к отработке в течение 20 лет, при этом следует предусматривать сокращенный комплекс мер защиты по согласованию с утверждающей проект инстанцией.
Примечание. Проекты сооружений большой протяженности в плане (трубопроводы и пр.) должны разрабатываться для каждого расчетного участка в отдельности. Разбивка на расчетные участки должна производиться в зависимости от конкретных горно-геологических условий подработки (от их изменений).
2.3. Расчет ожидаемых деформаций земной поверхности должен производиться горными инженерами - маркшейдерами по методам, изложенным в настоящем Руководстве.
Расчет ожидаемых деформаций земной поверхности для неизученных месторождений и для районов с особо сложными горно-геологическими условиями подработки следует производить по методам, разработанным институтами, специализирующимися в этой области.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 2.2.а отсутствует. Возможно, имеется в виду первое перечисление пункта 2.2. |
2.4. В зависимости от максимальных величин ожидаемых (нормативных) деформаций земной поверхности (п. 2.2.а) подрабатываемые территории подразделяются на группы в соответствии с табл. 2.
Группа территории | Ожидаемые деформации земной поверхности | ||
Относительная горизонтальная деформация сжатия или растяжения или | Наклон i, 1·10-3 | Радиус кривизны R, км | |
1 |  | 20 >= i > 10 | 1 <= R < 3 |
2 | 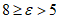 | 10 >= i > 7 | 3 <= R < 7 |
3 |  | 7 >= i > 5 | 7 <= R < 12 |
4 |  | 5 >= i >= 0 | 12 <= R < 20 |
Подрабатываемые территории, на которых при выемке пластов полезного ископаемого образуются уступы земной поверхности, подразделяются в зависимости от ожидаемой высоты уступа на группы в соответствии с табл. 3.
Группа территорий | Ожидаемая высота уступа h, см | Группа территорий | Ожидаемая высота уступа h, см |
I, К | 25 >= h > 15 | III, К | 10 >= h > 5 |
II, К | 15 >= h > 11 | IV, К | 5 >= h > 0 |
2.5. Расчетные сдвижения и деформации земной поверхности, учитываемые при расчете зданий и сооружений как факторы нагрузки, следует определять путем умножения значений ожидаемых (нормативных) деформаций земной поверхности на соответствующие коэффициенты перегрузки n, принимаемые по табл. 4.
Деформации земной поверхности | Коэффициенты перегрузки | Значения коэффициентов перегрузки для расчета сдвижений и деформаций | |
ожидаемых | вероятных | ||
Оседание, | 1,2 | 1,1 (0,9) | |
Горизонтальное сдвижение, | 1,2 | 1,1 (0,9) | |
Относительная горизонтальная деформация растяжения-сжатия, | 1,4 | 1,2 (0,8) | |
Наклон, i | ni | 1,4 | 1,2 (0,8) |
Кривизна, K | nK | 1,8 | 1,4 (0,6) |
Уступ, hу | 1,4 | 1,2 (0,8) | |
Скручивание, S | nS | 1,4 | 1,4 |
Скашивание, | 1,2 | - | |
Примечание. Коэффициенты перегрузки меньше единицы следует учитывать при расчете зданий и сооружений на одновременное действие деформаций земной поверхности двух и более видов, когда уменьшение значения деформаций какого-либо вида может ухудшить условия работы конструкций.
2.6. При расчете конструкций зданий и сооружений на воздействие деформаций земной поверхности необходимо вводить соответствующие коэффициенты условий работы, определяемые по табл. 5 в зависимости от общей длины здания (сооружения) или его отсека.
Деформации земной поверхности | Обозначения | Коэффициенты условий работы при длине здания (сооружения) l, м | ||
менее 15 | 15 - 30 | более 30 | ||
Относительная горизонтальная деформация растяжения или сжатия | 1 | 0,85 | 0,7 | |
Наклон i | mi | 1 | 0,85 | 0,7 |
Кривизна K | mK | 1 | 0,7 | 0,55 |
Скручивание S | mS | 1 | 0,7 | 0,55 |
Скашивание | 1 | 0,85 | 0,7 | |
Примечания: 1. При рассмотрении поперечного сечения здания или сооружения за l принимается его ширина.
2. Для круглых в плане зданий и сооружений за l принимается их внешний диаметр.
3. Для зданий и сооружений башенного типа при l < 15 м следует принимать mi = 1,5.
2.7. Расчетное оседание любой точки основания y относительно центральной оси здания (сооружения) или его отсека (рис. 3), вызванное кривизной земной поверхности, следует определять по формуле:
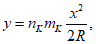 (1)
(1)R - ожидаемый радиус кривизны земной поверхности;
x - расстояние, м, от рассматриваемой точки основания до оси симметрии здания (сооружения) или его отсека (рис. 3).
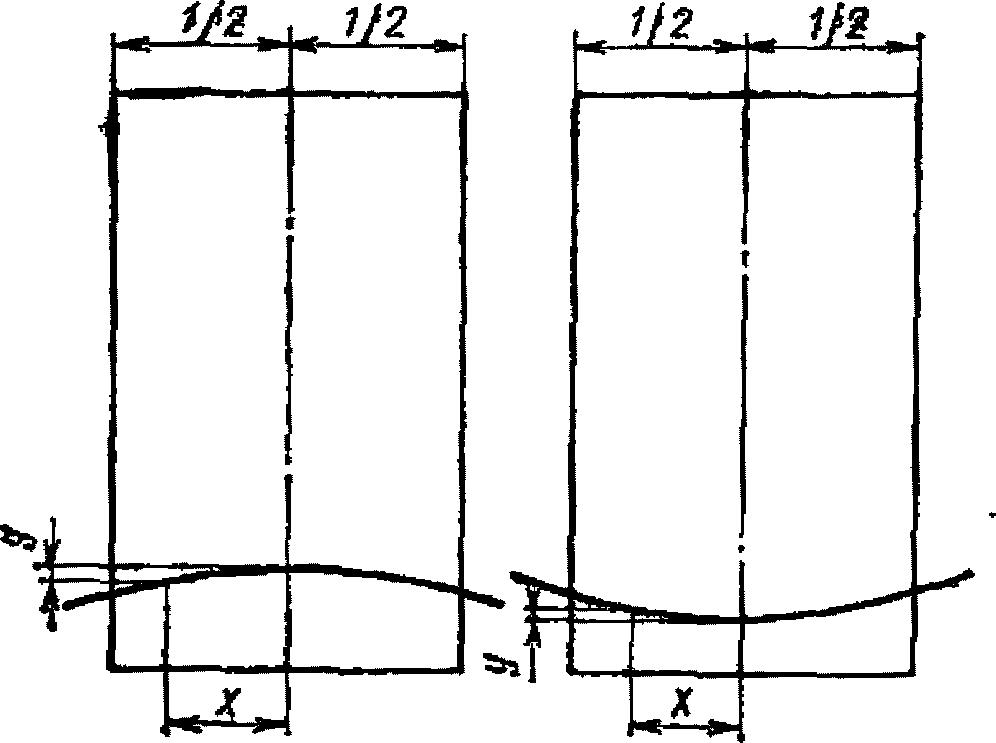
вызванных кривизной земной поверхности
2.8. Расчетную разность оседаний 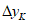 двух точек основания здания (сооружения), вызванную расчетной кривизной земной поверхности, следует определять по формуле
двух точек основания здания (сооружения), вызванную расчетной кривизной земной поверхности, следует определять по формуле
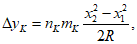 (2)
(2)где x1 и x2 - расстояние от рассматриваемых точек основания до соответствующей центральной оси здания (сооружения) или его отсека;
x1 - от менее удаленной точки;
x2 - от более удаленной точки.
2.9. Расчетную разность оседаний 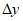 двух точек основания здания (сооружения), вызванную равномерным наклоном i, следует определять по формуле
двух точек основания здания (сооружения), вызванную равномерным наклоном i, следует определять по формуле
 (3)
(3)i - ожидаемый наклон земной поверхности.
2.10. Расчетное перемещение любой точки основания относительно соответствующей центральной оси здания (сооружения) или его отсека (рис. 4), вызванное горизонтальными деформациями (растяжения, сжатия), следует определять по формуле
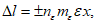 (4)
(4)x - расстояние, м, до соответствующей центральной оси здания (сооружения).
Примечание. В продольной раме каркасного здания или его отсека положение центральной оси принимается в середине жесткого отсека независимо от его расположения относительно оси симметрии.
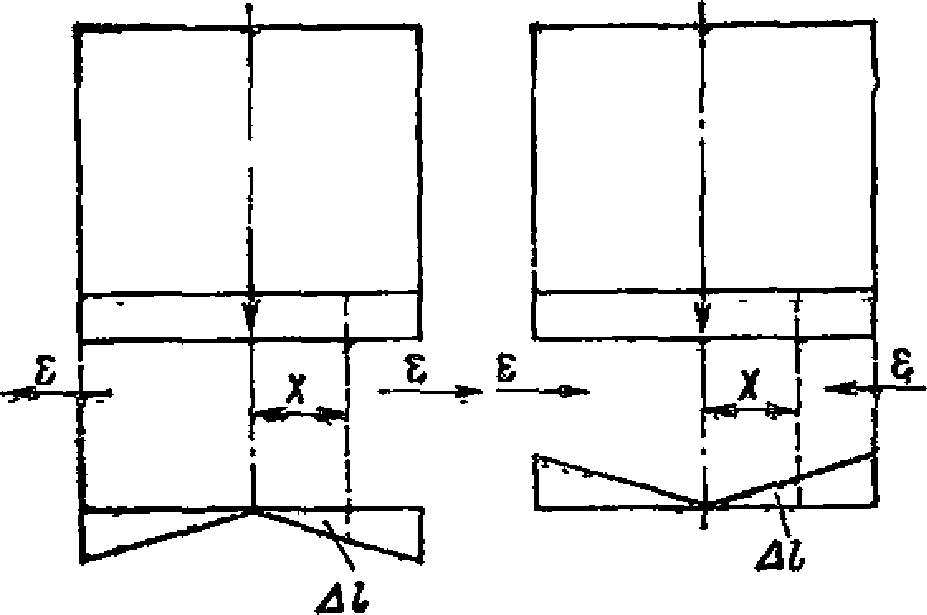
под воздействием горизонтальных деформаций
2.11. Расчетный угол наклона в любой точке основания iK, вызванный деформациями земной поверхности, следует определять по формуле
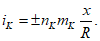 (5)
(5)2.12. Расчетное направление линии уступа следует принимать по простиранию пластов полезных ископаемых.
2.13. Расчетное местоположение уступа в плане зданий и сооружений следует принимать таким, при котором возникающие в несущих конструкциях усилия будут наибольшими.
В тех случаях, когда линии уступов могут быть протрассированы со стороны участка, расположенного рядом с застраиваемой площадкой, расчетное местоположение уступа в плане следует принимать по его наиболее возможному расположению.
3.1. Методика расчета позволяет определять величины сдвижений и деформаций земной поверхности в следующих условиях:
кратность подработки -  (где H - средняя глубина, m - вынимаемая или эффективная мощность пласта) более 20 при углах падения пластов
(где H - средняя глубина, m - вынимаемая или эффективная мощность пласта) более 20 при углах падения пластов 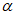 до 55° и более 15 при
до 55° и более 15 при  за пределами зоны провалов и крупных трещин. Глубина разработки до 1200 м;
за пределами зоны провалов и крупных трещин. Глубина разработки до 1200 м;
 за пределами зоны провалов и крупных трещин. Глубина разработки до 1200 м;
за пределами зоны провалов и крупных трещин. Глубина разработки до 1200 м;угол падения пластов от 0 до 90°;
управление кровлей - полное обрушение или закладка выработанного пространства;
закончившийся процесс сдвижения.
3.2. Настоящая методика не применима для расчета сдвижений и деформаций земной поверхности в сложных горно-геологических условиях.
К сложным горно-геологическим условиям относятся:
наличие в толще разрывных геологических нарушений, выходящих под наносы (на земную поверхность);
складчатое залегание пород (кроме складок, приведенных в разд. 6);
гористый рельеф земной поверхности;
наличие древнего оползня в толще;
камерная система разработки;
возможность образования провалов на земной поверхности в результате выноса обводненного песка в горные выработки (Подмосковный бассейн).
3.3. В зависимости от полноты исходных данных определяются ожидаемые или вероятные величины сдвижений и деформаций земной поверхности.
Ожидаемые величины сдвижений и деформаций рассчитываются при наличии календарных планов развития горных работ.
Ожидаемые величины сдвижений и деформаций земной поверхности рассчитываются по одной из приводимых двух методик. Если угол падения пласта 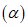 не более величины предельного угла
не более величины предельного угла  , то применяется методика расчета сдвижений и деформаций в условиях отсутствия сдвижения пород лежачего бока. Если
, то применяется методика расчета сдвижений и деформаций в условиях отсутствия сдвижения пород лежачего бока. Если 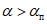 , то расчет производится по методике, учитывающей наличие сдвижения пород лежачего бока.
, то расчет производится по методике, учитывающей наличие сдвижения пород лежачего бока.
Величины 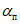 определяются по разд. 8 Руководства. Если в Руководстве не приводится значение
определяются по разд. 8 Руководства. Если в Руководстве не приводится значение 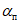 , то применяется методика расчета сдвижений и деформаций земной поверхности при отсутствии сдвижения пород лежачего бока.
, то применяется методика расчета сдвижений и деформаций земной поверхности при отсутствии сдвижения пород лежачего бока.
3.4. Вероятные величины сдвижений и деформаций определяются в условиях выдержанного залегания пород при отсутствии календарных планов горных работ для следующих условий:
при углах падения пластов менее 35°;
при ведении горных работ по горизонтам, положение которых неизвестно, при  или
или  соответственно при отсутствии или при наличии сдвижения пород лежачего бока;
соответственно при отсутствии или при наличии сдвижения пород лежачего бока;
 или
или  соответственно при отсутствии или при наличии сдвижения пород лежачего бока;
соответственно при отсутствии или при наличии сдвижения пород лежачего бока;при расположении границ очистных выработок в свите пластов в одной вертикальной или наклонной плоскости при 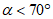 или
или 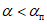 соответственно при наличии или при отсутствии сдвижения пород лежачего бока.
соответственно при наличии или при отсутствии сдвижения пород лежачего бока.
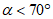 или
или 3.5. По методикам расчета ожидаемых сдвижений и деформаций земной поверхности определяются:
оседания 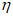 ;
;
горизонтальные сдвижения  ;
;
наклоны i;
горизонтальные деформации - 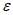 ;
;
кривизна и радиус кривизны R (при  );
);
 );
);величины (hу) обратных уступов в полумульде по падению при выемке двух и более пластов с углом падения более 35° (п. 8.6), а также прямых уступов в полумульде по восстанию при сдвижении пород по напластованию;
В условиях, когда отсутствует сдвижение пород лежачего бока, величины 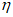 ,
, 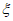 , i, K(R),
, i, K(R), 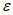 могут определяться в главных сечениях мульды, а также в заданных сечениях, параллельных главным или расположенных под произвольными углами к направлениям простирания пластов.
могут определяться в главных сечениях мульды, а также в заданных сечениях, параллельных главным или расположенных под произвольными углами к направлениям простирания пластов.
В условиях, когда возможно сдвижение пород лежачего бока 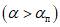 , величины
, величины 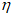 ,
,  , i, K(R) и
, i, K(R) и  могут определяться только в главном сечении мульды сдвижения вкрест простирания пласта.
могут определяться только в главном сечении мульды сдвижения вкрест простирания пласта.
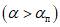 , величины
, величины 3.6. Для решения практических задач по разработке мер охраны объектов применяются расчетные величины сдвижений и деформаций. Используемые для их определения коэффициенты перегрузки (п. 1.1) приведены в табл. 4.
3.7. Расчет сдвижений и деформаций выполняется только для участков мульды, расположенных за пределами зон провалов и крупных трещин с уступами (террас). Границы зон возможных провалов определяются в соответствии с пп. 3.8 - 3.10.
3.8. При разработке пластов с углами падения  на глубине от земной поверхности менее 12m, где m - вынимаемая мощность пласта, на земной поверхности могут образовываться провалы (воронки).
на глубине от земной поверхности менее 12m, где m - вынимаемая мощность пласта, на земной поверхности могут образовываться провалы (воронки).
 на глубине от земной поверхности менее 12m, где m - вынимаемая мощность пласта, на земной поверхности могут образовываться провалы (воронки).
на глубине от земной поверхности менее 12m, где m - вынимаемая мощность пласта, на земной поверхности могут образовываться провалы (воронки).За границу зоны возможных провалов принимается контур, отстоящий в плане от контура очистных выработок на 5 м. Если нижняя граница очистных выработок расположена на глубине более 12m, то за границу зоны провалов со стороны падения пласта принимается контур, отстоящий в плане на 5 м в сторону нижней границы выработки от проекции изогипсы пласта, проведенной на глубине 12m.
К зоне провалов прилегает зона больших трещин, ширина которой принимается равной 10 м. Со стороны падения пласта граница зоны больших трещин располагается в плане не дальше проекции изогипсы пласта, проведенной на глубине 20m.
3.9. При разработке пластов с углами падения более 45° провалы на земной поверхности образуются, если вертикальная высота целиков, оставленных на выходах пластов под наносы, менее hц, а очистные работы под целиками ведутся на глубине менее Hн. Значения hц и Hн для отдельных бассейнов приведены в разд. 8, а для остальных, где они отсутствуют, hц определяется по табл. 6, а Hц принимается равной 400 м.
Мощность пласта, м | 2 и менее | 3 | 4 | 5 | 6 | 7 и более |
hц, м | 60 | 75 | 85 | 90 | 95 | 100 |
Примечание. При разработке мощных пластов слоями hц определяется по суммарной мощности слоев.
3.10. За границы зоны возможных провалов на земной поверхности при разработке пластов с углами падения более 45° принимаются на плане:
по простиранию - линия, проведенная параллельно границе очистной выработки на расстоянии в плане от этой границы, определяемом по формуле:
 но не менее 15 м, (6)
но не менее 15 м, (6)где h - мощность наносов;
со стороны лежачего бока - линия, проведенная на расстоянии в плане lл = lп от выхода почвы пласта под наносы, но не менее 15 м;
со стороны висячего бока - линия, проведенная на расстоянии в плане lв от выхода пласта под наносы, определяемом по формуле
 но не менее 20 м, (7)
но не менее 20 м, (7)где Hв - расстояние по вертикали от земной поверхности до верхней границы выработки, Hв < hц + h (см. п. 3.9);
dв - величина, определяемая по табл. 7.
Мощность пласта, м | 2 и менее | 3 | 4 | 5 | 6 | 7 | 8 и более |
dв, м | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
Примечание. Отклонения от рекомендаций данного пункта допускаются в том случае, когда имеются данные о размерах зоны провалов, обоснованные инструментальными наблюдениями.
К зоне провалов прилегает зона больших трещин, ширина которой принимается со стороны висячего бока равной 30 м, со стороны лежачего бока и по простиранию - 20 м.
ПРИ ОТСУТСТВИИ СДВИЖЕНИЯ ПОРОД ЛЕЖАЧЕГО БОКА
Подготовка исходных горно-геологических данных
и порядок расчета
4.1. Перед началом расчета сдвижений и деформаций строят геологические разрезы по простиранию и вкрест простирания пласта на участке подрабатываемой толщи. На разрезах по данным ближайших скважин выделяют наносы и мезозойские отложения. На разрезы наносят все ранее пройденные и проектируемые очистные выработки с датами (календарным планом) их проходки, определяют глубины разработок, размеры выработок и оставленных (оставляемых) целиков.
4.2. Вынимаемая (вынутая) мощность пласта определяется как суммарная мощность извлекаемых (извлеченных) из очистных выработок слоев угля и вмещающих пород.
При закладке выработанного пространства материалом, доставленным извне участка горных работ, вместо вынимаемой мощности пласта при расчете сдвижений и деформаций принимается эффективная мощность пласта mэ. Для Кузнецкого бассейна величина mэ определяется в соответствии с п. 8.14, для других бассейнов mэ вычисляется по формуле
mэ = (hк + hн)(1 - B1) + B1m, (8)
где m - вынутая мощность пласта;
hк - величины сближения кровли с почвой (конвергенция) до возведения закладочного массива; при отставании закладочного массива от забоя на 8 - 20 м и при отсутствии данных наблюдений принимается hк = 0,15m;
hн - неполнота закладки (среднее расстояние от верха закладочного массива до кровли пласта), определяемая по опыту; B1 - коэффициент усадки закладки, определяемый по фактическим данным, а при отсутствии таких данных - по табл. 8.
Виды закладки | B1 |
Гидравлическая: | |
из песка | 0,05 - 0,15 |
из дробленой породы | 0,15 - 0,30 |
Пневматическая | 0,25 - 0,40 |
Самотечная | |
из дробленой породы | 0,25 - 0,45 |
из рядовой породы | 0,35 - 0,50 |
4.3. Расчет сдвижений и деформаций производится от всех проектируемых очистных выработок, а также от ранее пройденных, которые вызовут активизацию процесса сдвижения на рассматриваемом участке (пп. 4.27 - 4.29).
4.4. Расчет сдвижений и деформаций от проектируемых смежных выработок в зависимости от размера целика между ними и разрыва во времени проведения очистных работ может производиться отдельно от каждой выработки или от нескольких выработок, объединенных в одну суммарного размера (пп. 4.5 и 4.6). Расчет от выработки суммарного размера производится так же, как от отдельной выработки. Сложение соответствующих сдвижений и деформаций от отдельных очистных выработок следует производить в такой же последовательности, в какой намечается их проходка. За окончательные величины ожидаемых сдвижений и деформаций земной поверхности принимаются наибольшие из полученных на различные стадии отработки пластов и горизонтов (рис. 5).
деформаций земной поверхности
1 - от лавы 1 (первая стадия отработки); 2 - от лавы 2;
3 - от лавы 3; 4 - от лав 1 + 2 (вторая стадия отработки);
5 - от лав 1 + 2 + 3 (третья стадия отработки)
4.5. Расчет сдвижений и деформаций отдельно от каждой очистной выработки производится в случаях, когда:
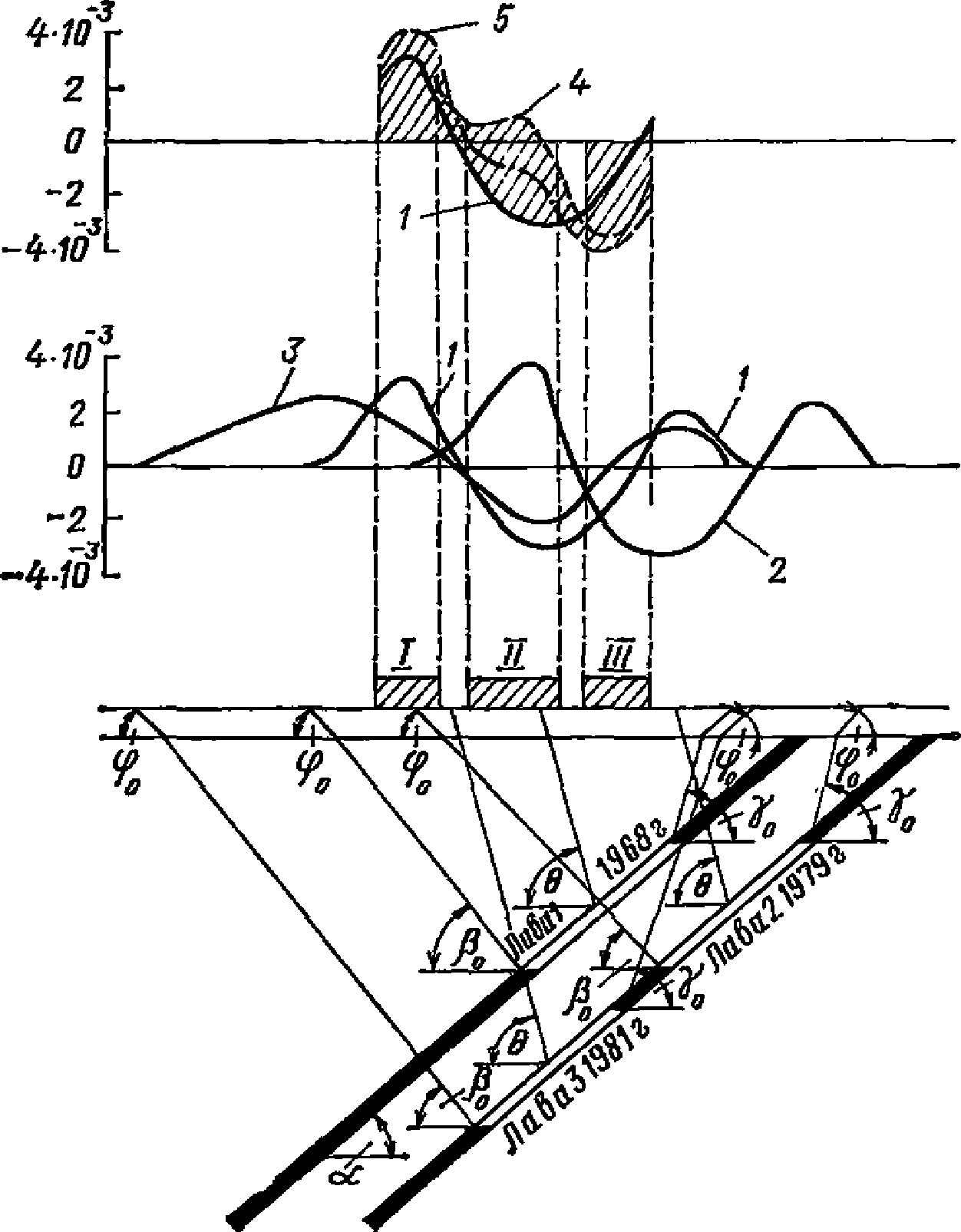
отношение размера целика между смежными выработками l1 к средней глубине его залегания Hц больше 0,1;
отношение 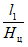 меньше 0,1, если при этом разрыв во времени t между подработками земной поверхности смежными выработками больше или равен продолжительности периода опасных деформаций для смежной выработки, отрабатываемой в первую очередь, tоп (t >= tоп), определяемого по разд. 8 Руководства.
меньше 0,1, если при этом разрыв во времени t между подработками земной поверхности смежными выработками больше или равен продолжительности периода опасных деформаций для смежной выработки, отрабатываемой в первую очередь, tоп (t >= tоп), определяемого по разд. 8 Руководства.
Расчет сдвижений и деформаций от нескольких выработок в пласте производится как от одной выработки суммарных размеров в случаях, когда 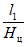 меньше или равно 0,1 и при этом t < tоп для смежной выработки, отрабатываемой в первую очередь.
меньше или равно 0,1 и при этом t < tоп для смежной выработки, отрабатываемой в первую очередь.
Расчеты выполняются от первой выработки, от первой и второй и т.д. Размер такой выработки определяется на разрезе вкрест простирания как сумма длин рассматриваемых выработок, включая межлавные целики.
4.6. При определении сдвижений и деформаций от выемки свиты пластов при 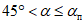 допускается объединять пласты в группы и производить расчеты от эквивалентного (условного) пласта. В группу допускается объединять несколько пластов при одновременном выполнении следующих условий (рис. 6):
допускается объединять пласты в группы и производить расчеты от эквивалентного (условного) пласта. В группу допускается объединять несколько пластов при одновременном выполнении следующих условий (рис. 6):
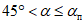 допускается объединять пласты в группы и производить расчеты от эквивалентного (условного) пласта. В группу допускается объединять несколько пластов при одновременном выполнении следующих условий (рис. 6):
допускается объединять пласты в группы и производить расчеты от эквивалентного (условного) пласта. В группу допускается объединять несколько пластов при одновременном выполнении следующих условий (рис. 6):нижние границы выработок находятся на одной глубине Hн (на одном горизонте);
расстояние по нормали между кровлей верхнего и почвой нижнего пласта группы не более 0,2Hн, где Hн - глубина нижней границы выработок.
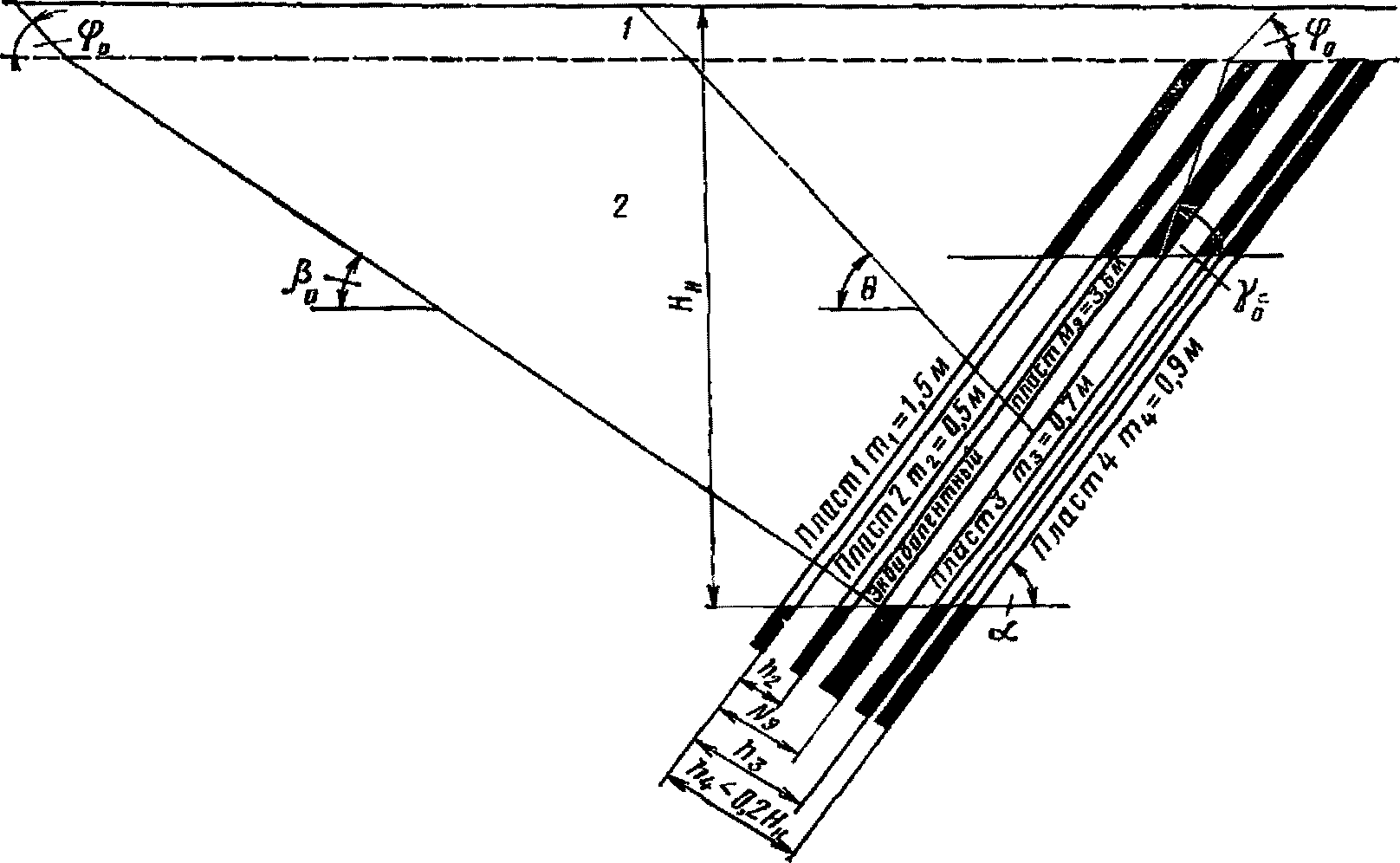
и построения границ мульды сдвижения
1 - наносы; 2 - коренные породы
Мощность эквивалентного пласта Mэ принимается равной суммарной мощности пластов в группе
Mэ = m1 + m2 + ... + mn. (9)
Положение эквивалентного пласта на разрезе определяется расстоянием от почвы верхнего пласта в группе до почвы эквивалентного, которое находится по формуле
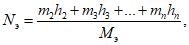 (10)
(10)где m1, m2, ..., mn - соответственно мощности первого (верхнего), второго и т.д. и последнего (нижнего) пластов в группе;
h2, h3, ..., hn - соответственно расстояния по горизонтали (или по нормали) от почвы первого (верхнего) пласта до почвы второго, третьего и т.д. и последнего (нижнего) пластов в группе.
Исходные параметры сдвижения
граничные углы;
угол максимального оседания (при неполной подработке);
углы полных сдвижений (при полной подработке);
относительная величина максимального оседания;
относительная величина максимального горизонтального сдвижения.
Исходные параметры определяются по разд. 8 для соответствующих бассейнов и месторождений.
Примечание. На участках, где проводились инструментальные наблюдения за сдвижением земной поверхности, при расчетах допускается использовать величины исходных параметров процесса сдвижения, полученные в результате этих наблюдений.
4.8. Длины полумульд L1, L2, L3 определяются по граничным углам 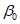 ,
,  ,
, 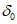 ,
,  и углу максимального оседания
и углу максимального оседания 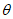 - при неполной подработке или по углам полных сдвижений
- при неполной подработке или по углам полных сдвижений 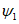 ,
, 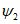 ,
,  - при полной подработке (см. рис. 1).
- при полной подработке (см. рис. 1).
4.9. Если границы очистных выработок в свите пластов расположены в одной плоскости, проведенной под соответствующим углом сдвижения (например, у границы предохранительного целика), то длины полумульд над этими границами определяются следующим образом: все разрабатываемые пласты разделяются на группы таким образом, чтобы расстояние по нормали между вышележащими и нижележащими пластами в каждой группе не превышало 0,2Hн, где Hн - глубина залегания нижней границы выработки в верхнем пласте группы. Границы полумульды от выемки пласта, разрабатываемого первым в группе, определяются по граничным углам, принимаемым в соответствии с разд. 8. Для всех последующих пластов группы граничные углы увеличиваются на 3°. Для других групп пластов определение граничных углов производится аналогично.
Расчет ожидаемых сдвижений и деформаций земной поверхности
от одной очистной выработки
Сдвижения и деформации земной поверхности
в главных сечениях мульды (рис. 7)
а) | б) |
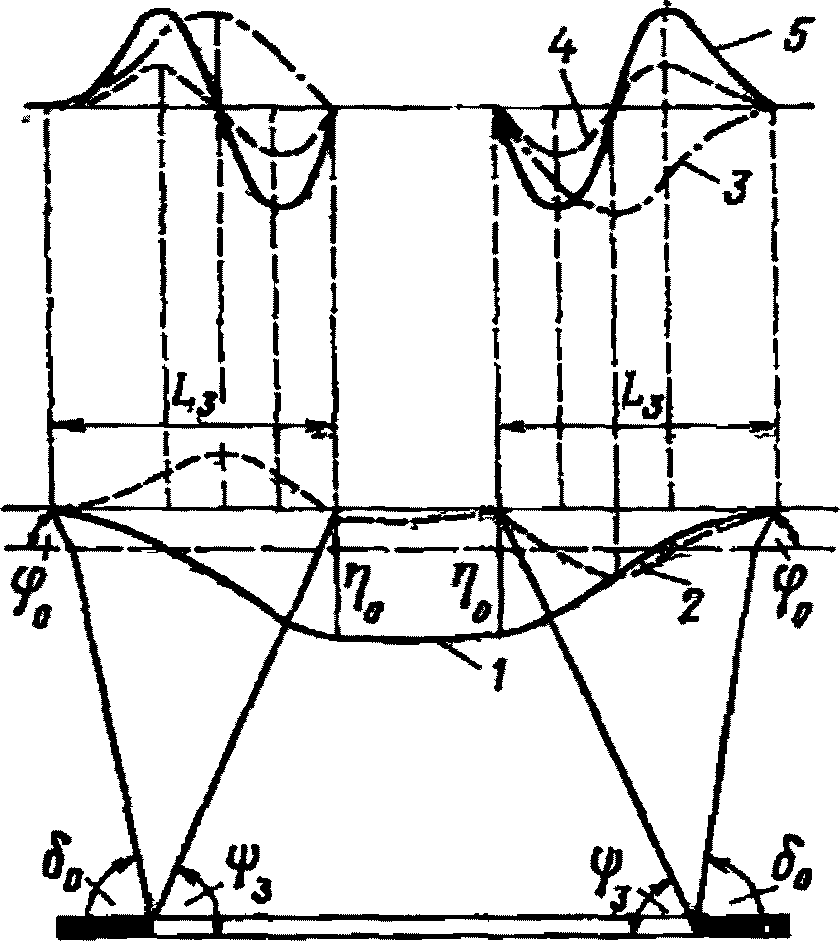 |  |
в точках главных сечений мульды сдвижения
при закончившемся процессе
а - на разрезе по простиранию; б - на разрезе
вкрест простирания; 1 - оседания; 2 - горизонтальные
сдвижения; 3 - наклоны; 4 - кривизна;
5 - горизонтальные деформации
где q0 - определяется по разд. 8 для соответствующих бассейнов и месторождений;
m - вынимаемая мощность пласта;
N1 и N2 - коэффициенты, определяемые по разд. 8.
4.11. Величины оседаний земной поверхности в точках главных сечений мульды сдвижения определяются по формуле
где 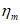 - максимальное оседание земной поверхности в мульде сдвижения;
- максимальное оседание земной поверхности в мульде сдвижения;
S(z) - функция типовой кривой оседания, принимаемая по разд. 8 в зависимости от коэффициента N1 (для точек главного сечения вкрест простирания пластов) и N2 (для точек главного сечения по простиранию пластов);
N1 и N2 - принимаются по разд. 8;
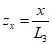 - для точек, расположенных в главном сечении по простиранию пласта;
- для точек, расположенных в главном сечении по простиранию пласта; - для точек, расположенных в полумульде по падению пласта;
- для точек, расположенных в полумульде по падению пласта; - для точек, расположенных в полумульде по восстанию пласта;
- для точек, расположенных в полумульде по восстанию пласта;x, y1, y2 - расстояния от точки максимального оседания (начала координат) до рассматриваемой точки соответственно в полумульдах по простиранию, падению и восстанию;
L1, L2, L3 - длины полумульд (п. 4.8).
в полумульде по простиранию
в полумульде по падению
в полумульде по восстанию
Значения F(zx) определяются по разд. 8 для соответствующих бассейнов и месторождений в зависимости от коэффициентов N2 (п. 4.10) при B = 0. Значения 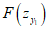 и
и 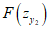 определяются по разд. 8 для соответствующих бассейнов и месторождений в зависимости от коэффициентов N1 (см. п. 4.10) при B = 0.
определяются по разд. 8 для соответствующих бассейнов и месторождений в зависимости от коэффициентов N1 (см. п. 4.10) при B = 0.
в полумульде по простиранию
в полумульде по падению
 (17)
(17)в полумульде по восстанию
Значение F'(z) определяется по разд. 8 для соответствующих бассейнов и месторождений в зависимости от коэффициентов N1 и N2 (см. п. 4.10) при B = 0. При неполной подработке (N < 1) кривизна в точке максимального оседания определяется по средней длине полумульды Lср = 0,5(L1 + L2).
в полумульде по простиранию
в полумульде по падению
в полумульде по восстанию
Значения a0 и F(z) определяются по разд. 8. При этом F(zx) определяется в зависимости от коэффициента N2 при B = 0, а F(zy) - в зависимости от N1 и коэффициента B, определяемого по формуле
где 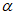 - угол падения пласта;
- угол падения пласта;
h - мощность наносов, м;
hм - мощность горизонтально залегающих  мезозойских отложений, м;
мезозойских отложений, м;
 мезозойских отложений, м;
мезозойских отложений, м;Hср - средняя глубина разработки, м.
в полумульде по простиранию
в полумульде по падению
в полумульде по восстанию
Значения F'(zx) определяются по разд. 8 в зависимости от коэффициента N2 при B = 0, а F'(zy) - в зависимости от коэффициента N1 при B, определяемом по формуле (22). При неполной подработке (N < 1) горизонтальные деформации в точке максимального оседания определяются по средней длине полумульды Lср = 0,5(L1 + L2).
4.16. Для определения функций S(z), F(z) и F'(z) (см. разд. 8) величины коэффициентов N1 и N2 округляются до ближайших значений, приведенных в этих таблицах. Промежуточные значения функций F(z) и F'(z) в зависимости от величины параметра B определяются интерполированием.
Сдвижения и деформации в точках сечений мульды сдвижения,
параллельных главным сечениям (рис. 8)

сдвижений и деформаций земной поверхности
в заданном направлении
1 - граница мульды сдвижения; AB - сечение
мульды сдвижения параллельно главному сечению по простиранию
пласта; CД - то же, вкрест простирания пласта;
P1P2 - сечение мульды сдвижения в произвольном направлении
по отношению к простиранию пласта
4.17. Оседание земной поверхности в точке M определяется по формуле:
 (26)
(26)где S(zx) и S(zy) - функция S(z) при значениях  и
и  - когда точка M расположена в полумульде по падению или
- когда точка M расположена в полумульде по падению или 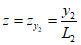 - когда точка M расположена в полумульде по восстанию;
- когда точка M расположена в полумульде по восстанию;
 и
и  - когда точка M расположена в полумульде по падению или
- когда точка M расположена в полумульде по падению или 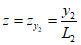 - когда точка M расположена в полумульде по восстанию;
- когда точка M расположена в полумульде по восстанию;x - абсцисса точки M - расстояние от оси y (главного сечения мульды, вкрест простирания пласта) до параллельного ей сечения CД (рис. 8), проходящего через точку M;
y1(y2) - ордината точки M - расстояние от оси x (главного сечения мульды по простиранию пласта) до параллельного ей сечения AB, проходящего через точку M.
Оси координат располагаются в плане следующим образом: началом координат служит точка пересечения главных сечений мульды сдвижения по простиранию и вкрест простирания пласта, проходящих при неполной подработке через точку максимального оседания, а при полной - через начало плоского дна. Ось x совмещается с главным сечением мульды по простиранию, а ось y - с главным сечением мульды вкрест простирания (рис. 8).
Значения S(z) определяются по разд. 8.
4.18. Наклон в точке M по направлению простирания пласта (рис. 8) определяется по формуле
а по направлению вкрест простирания пласта
где ix и iy - наклоны в главном сечении мульды сдвижения, определяемые по формулам (13) - (15).
4.19. Кривизна в точке M по направлению простирания пласта определяется по формуле
а вкрест простирания пласта
где Kx и Ky - кривизна в главных сечениях мульды сдвижения, определяемая по формулам (16) - (18).
4.20. Горизонтальное сдвижение точки M по направлению простирания пласта определяется по формуле
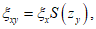 (31)
(31)а вкрест простирания пласта
 (32)
(32)4.21. Горизонтальные деформации (растяжение, сжатие) в точке M по направлению простирания пласта определяются по формуле
а вкрест простирания пласта
Сдвижения и деформации точек земной поверхности
по направлениям, не параллельным главным сечениям мульды
4.22. Сдвижения и деформации в сечениях, не параллельных главным, определяются при установлении мер охраны сооружений, имеющих большую протяженность и расположенных диагонально относительно простирания (падения) пласта: трубопроводы различного назначения, железные дороги, цехи промышленных предприятий и др.
4.23. При расчете знаки сдвижений и деформаций определяются в соответствии со знаками входящих в них параметров и функций.
Начало координат и направления осей показаны на рис. 9.

при расчете скашивания
1 - граница мульды сдвижения
Значения функции F(zx) при B = 0 принимаются отрицательными на участке, где x > 0, и положительными на участке, где x < 0. Значения функции F(zy) при B = 0 принимаются отрицательными в полумульде по восстанию (при y > 0) и положительными в полумульде по падению (при y < 0) (рис. 9). Знаки наклонов ix, входящих в формулы для расчета скручивания, и знаки горизонтальных сдвижений, входящих в формулы для расчета скашиваний, определяются в соответствии с правилами знаков наклонов и горизонтальных сдвижений в главных сечениях мульды.
4.24. Наклон в точке M по направлению P1P2 (см. рис. 8) определяется по формуле
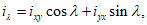 (35)
(35)где  - угол, отсчитываемый против часовой стрелки от направления простирания пласта до заданного направления P1P2;
- угол, отсчитываемый против часовой стрелки от направления простирания пласта до заданного направления P1P2;
ixy и iyx - определяются по формулам (27) и 28).
4.25. Кривизна в точке M по направлению P1P2 определяется по формуле
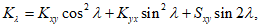 (36)
(36)где Kxy и Kyx определяются по формулам (29) и (30);
Sxy - скручивание, определяемое по формуле  , когда точка M расположена в полумульде по падению, или по формуле
, когда точка M расположена в полумульде по падению, или по формуле  , когда точка M расположена в полумульде по восстанию.
, когда точка M расположена в полумульде по восстанию.
 , когда точка M расположена в полумульде по падению, или по формуле
, когда точка M расположена в полумульде по падению, или по формуле  , когда точка M расположена в полумульде по восстанию.
, когда точка M расположена в полумульде по восстанию.Величины ix и F(zy) определяются в соответствии с п. 4.12.
4.26. Горизонтальные деформации в точке M по направлению P1P2 определяются по формуле
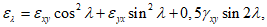 (37)
(37) , когда точка M расположена в полумульде по падению, и
, когда точка M расположена в полумульде по падению, и 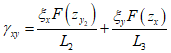 , когда точка M расположена в полумульде по восстанию.
, когда точка M расположена в полумульде по восстанию.Функции F(zx) и F(zy) определяются по разд. 8 при B = 0.
Расчет сдвижений и деформаций от ранее пройденных выработок
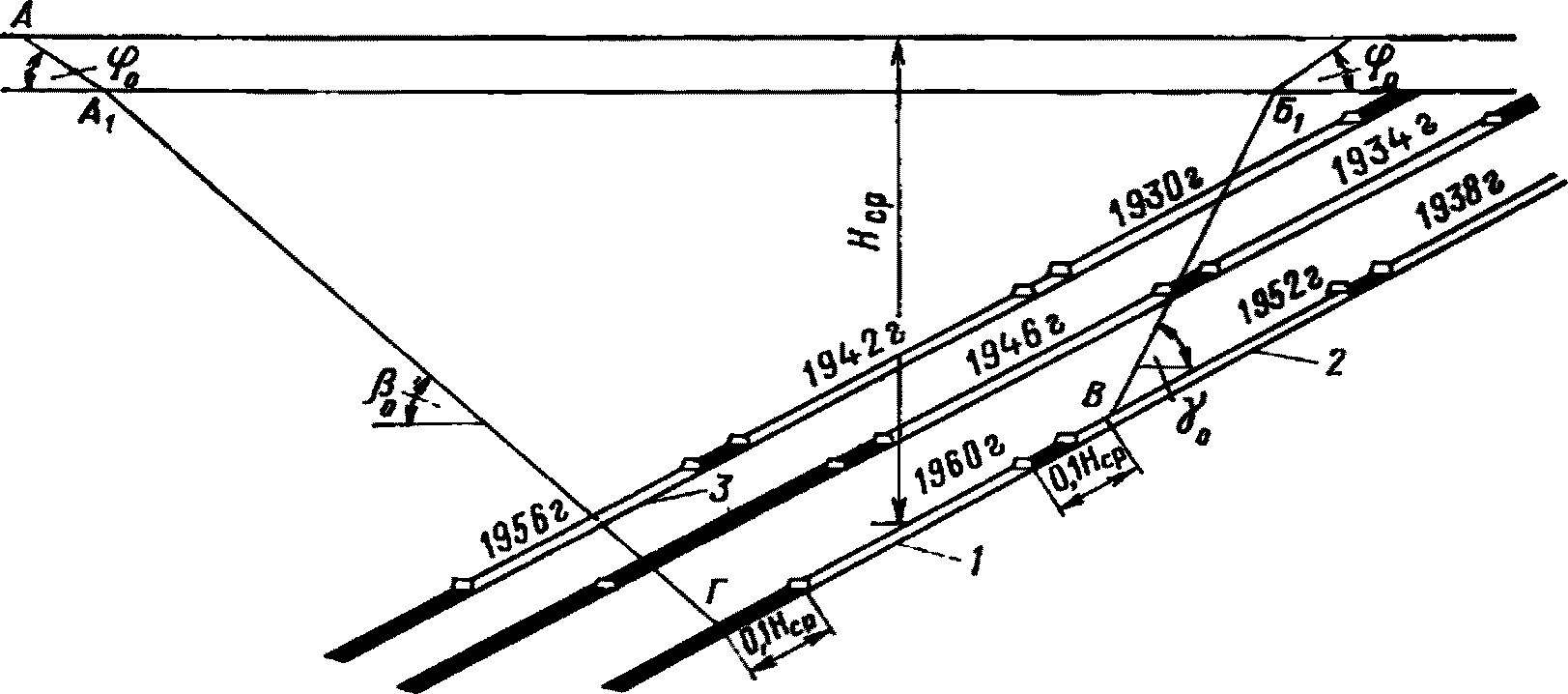
от ранее пройденных выработок
АББ1ВГА1 - зона влияния от действующей выработки;
1 - действующая выработка; 2 - старая выработка
в рассматриваемом пласте, от которого производится расчет;
3 - старая выработка в вышележащем пласте, от которой
производится расчет
4.27. Сдвижения и деформации от ранее пройденных (старых) выработок рассчитываются при одновременном выполнении следующих условий:
граничный угол 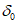 в неподработанной толще равен или более 70°;
в неподработанной толще равен или более 70°;
старая выработка находится в зоне влияния действующих выработок, т.е. выработок, от которых производится расчет сдвижений и деформаций для определения мер охраны (п. 4.28);
старая выработка ранее не подработана, т.е. не попадала в зону влияния от другой старой выработки (п. 4.28);
если от старой выработки были рассчитаны сдвижения и деформации как от действующей выработки и их величины суммированы со сдвижениями и деформациями от других действующих выработок при выборе мер охраны, то расчет от такой выработки как от старой не производится.
4.28. Зона влияния определяется на вертикальных разрезах по простиранию и вкрест простирания пласта линиями, проведенными под соответствующими граничными углами от точек, отстоящих от границ действующих выработок на расстоянии, равном 0,1Hср (Hср - средняя глубина разработки).
4.29. Сдвижения и деформации в точках мульды от старой выработки рассчитываются как от действующей по методике пп. 4.10 - 4.16. При этом максимальное оседание определяется по формуле
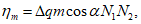 (38)
(38)где 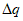 - разность между относительными максимальными оседаниями при повторной и первичной подработках.
- разность между относительными максимальными оседаниями при повторной и первичной подработках.
Полученные величины сдвижений и деформаций от старых выработок суммируются со сдвижениями и деформациями от действующей выработки.
Расчет ожидаемых сдвижений и деформаций, вызванных
сдвижением пород по напластованию (рис. 11)
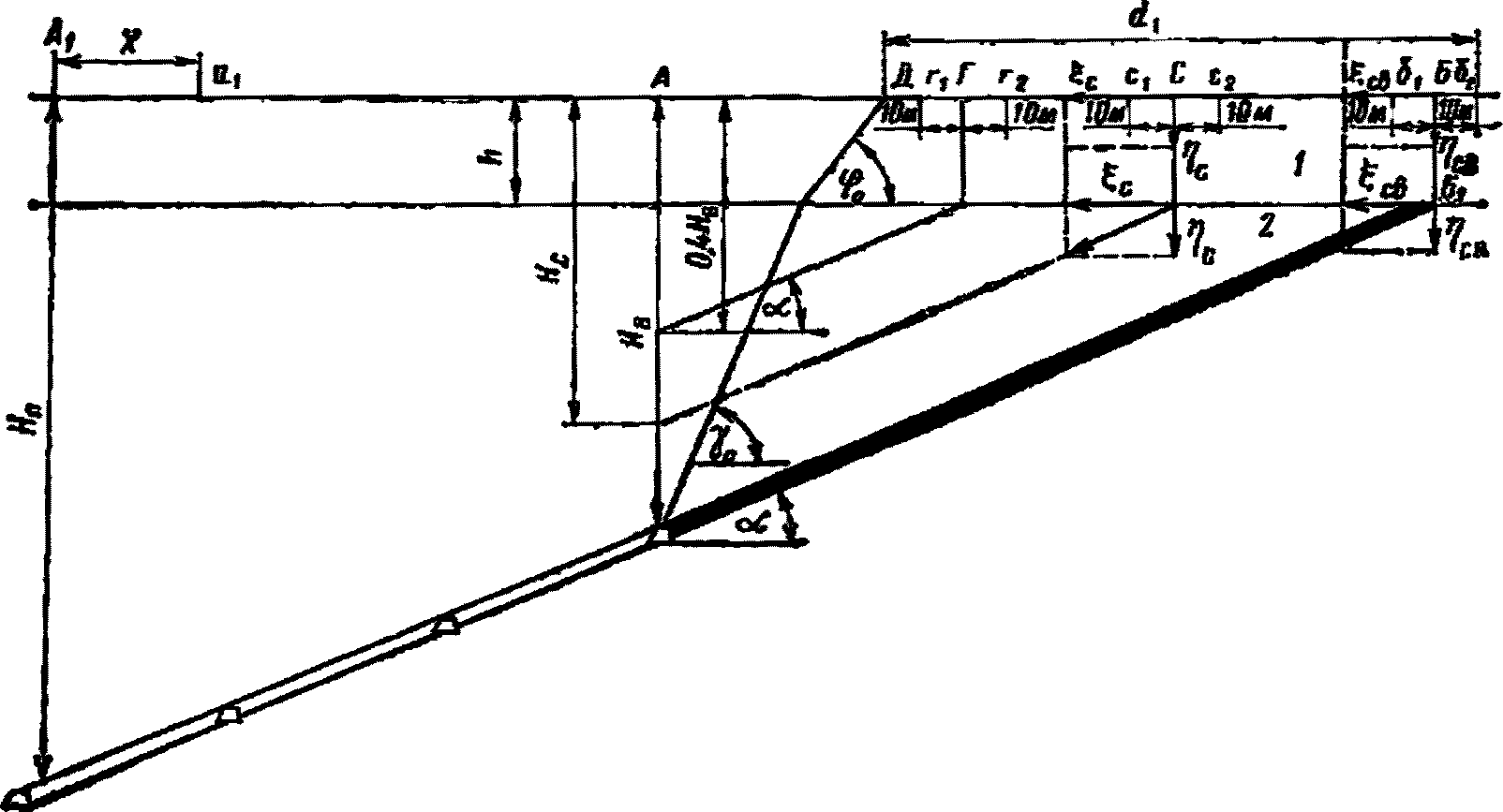
поверхности под влиянием сдвижений по напластованию
1 - наносы; 2 - коренные породы
4.30. Сдвижения и деформации горного массива и земной поверхности, вызванные сдвижением пород по напластованию, возникают в области, ограниченной на разрезе вкрест простирания вертикальной линией, отстоящей от выхода разрабатываемого пласта под наносы на 10 м и линией, проведенной по вертикали от верхней границы выработки при ведении горных работ на первом горизонте (зона 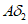 рис. 11). При ведении горных работ на втором и последующих горизонтах область сдвижений по напластованию со стороны падения ограничивается линией, проведенной по вертикали через точку A1 (зона
рис. 11). При ведении горных работ на втором и последующих горизонтах область сдвижений по напластованию со стороны падения ограничивается линией, проведенной по вертикали через точку A1 (зона  ). Положение точки A1 определяется нижней глубиной очистных работ, если эта глубина меньше глубины Hп, и глубиной Hп, если нижняя глубина очистных работ больше глубины Hп.
). Положение точки A1 определяется нижней глубиной очистных работ, если эта глубина меньше глубины Hп, и глубиной Hп, если нижняя глубина очистных работ больше глубины Hп.
Глубина Hп вычисляется по формуле
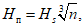 (39)
(39)где Hs - глубина, определяемая в соответствии с табл. 9;
n - количество разрабатываемых пластов (максимальное количество пластов, пересекаемых на разрезе вертикальной линией, проведенной через точки площадки до глубины H = 500 м).
h + hM, м | Угол падения | |||||
15 | 25 | 35 | 45 | 55 | 60 | |
5 | 30 | 60 | 90 | 110 | 140 | 155 |
10 | 30 | 70 | 100 | 130 | 160 | 180 |
15 | 35 | 80 | 115 | 145 | 180 | 200 |
20 и более | 50 | 115 | 160 | 200 | 255 | 285 |
Сдвижение пород по напластованию во всех угольных бассейнах рассчитывается при одновременном выполнении следующих условий:
 (40)
(40)где 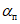 - предельный угол, при котором возникают опасные сдвижения пород лежачего бока; значения
- предельный угол, при котором возникают опасные сдвижения пород лежачего бока; значения 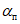 приведены в разд. 8 настоящего Руководства; для Донецкого бассейна вместо угла
приведены в разд. 8 настоящего Руководства; для Донецкого бассейна вместо угла 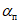 принимается угол, равный 60°;
принимается угол, равный 60°;
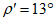 ;
;KH - коэффициент, определяемый по табл. 10 в зависимости от угла падения пласта;
Hв - расстояние по вертикали от земной поверхности до верхней границы выработки разрабатываемого пласта;
h - мощность наносов;
hM - мощность горизонтально залегающих 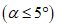 мезозойских отложений при разработке угольных пластов палеозойского возраста; если суммарная мощность (h + hM) менее 5 м или более 20 м, то она принимается равной 20 м;
мезозойских отложений при разработке угольных пластов палеозойского возраста; если суммарная мощность (h + hM) менее 5 м или более 20 м, то она принимается равной 20 м;
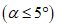 мезозойских отложений при разработке угольных пластов палеозойского возраста; если суммарная мощность (h + hM) менее 5 м или более 20 м, то она принимается равной 20 м;
мезозойских отложений при разработке угольных пластов палеозойского возраста; если суммарная мощность (h + hM) менее 5 м или более 20 м, то она принимается равной 20 м;d1 - расстояние от верхней границы мульды сдвижения до выхода пласта под наносы (отрезок 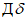 , см. рис. 11);
, см. рис. 11);
14 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
KH | 3,2 | 6,6 | 9,0 | 11,2 | 13,1 | 15,0 | 17,2 | 19,7 | 22,6 | 26,0 |
Примечание. Промежуточные значения коэффициента KH определяются интерполяцией.
4.31. Оседание земной поверхности над выходом разрабатываемого пласта под наносы (точка Б)
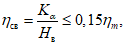 (41)
(41)где 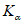 - коэффициент, определяемый по табл. 11 в зависимости от величины граничного угла
- коэффициент, определяемый по табл. 11 в зависимости от величины граничного угла 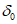 и угла падения пласта;
и угла падения пласта;
Граничный угол | Углы падения | |||||||||
14 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
Менее 60 | 0,10 | 0,62 | 1,24 | 1,85 | 2,47 | 3,08 | 3,91 | 4,94 | 6,17 | 7,73 |
60 - 70 | 0,09 | 0,54 | 1,08 | 1,62 | 2,16 | 2,70 | 3,42 | 4,32 | 5,40 | 6,75 |
Более 70 | 0,08 | 0,46 | 0,91 | 1,36 | 1,83 | 2,28 | 2,88 | 3,64 | 4,55 | 5,70 |
Примечание. Промежуточные значения коэффициента  определяются интерполяцией.
определяются интерполяцией.
4.32. Оседание земной поверхности над выходом под наносы наиболее слабых контактов и неотработанных или отработанных ранее угольных пластов (точка С), залегающих выше рассматриваемого пласта
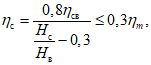 (42)
(42)где Hс - расстояние по вертикали, проходящей через верхнюю границу выработки в разрабатываемом пласте, от земной поверхности до рассматриваемого наиболее слабого контакта; если Hс менее 0,4Hв, то принимается Hс = 0,4Hв.
4.33. Оседание поверхности в точке Г (Hг = 0,4Hв) и А
 (43)
(43)4.34. Оседания в точках на участке АБ, вызванные сдвижением пород по напластованию, определяются по кривой, построенной по величинам оседаний в точках Б, С, Г, А.
4.35. Горизонтальные сдвижения поверхности над выходом разрабатываемого пласта под наносы (точка Б)
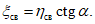 (44)
(44)4.36. Горизонтальные сдвижения поверхности над выходами под наносы наиболее слабых контактов отработанных ранее и неотработанных угольных пластов, расположенных выше разрабатываемого пласта
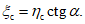 (45)
(45)4.37. Горизонтальное сдвижение в точках Г и А
 (46)
(46)4.38. Горизонтальные сдвижения в точках на участке АБ, вызванные сдвижением пород по напластованию, определяются по кривой, построенной по величинам горизонтальных сдвижений в точках Б, С, Г и А.
4.39. Горизонтальные деформации поверхности над выходом разрабатываемого пласта под наносы (участок  ) (за исключением Донбасса)
) (за исключением Донбасса)
4.40. Горизонтальные деформации поверхности над выходом под наносы наиболее слабых контактов ранее отработанных и неотработанных угольных пластов, расположенных выше разрабатываемого пласта (участок С1С2) (за исключением Донбасса) определяются по формулам (47), в которых вместо 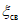 используется разность
используется разность  .
.
4.41. Горизонтальные деформации на участке Г1 и Г2 (за исключением Донбасса) определяются по формулам (47), в которых вместо 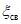 используется разность
используется разность 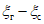 .
.
4.42. В том случае, когда положение наиболее слабых контактов в массиве неизвестно, и в Донецком бассейне, горизонтальные деформации на участке 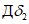 принимаются одинаковыми и определяются по формулам (47), в которых вместо
принимаются одинаковыми и определяются по формулам (47), в которых вместо 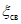 принимается значение
принимается значение  , определяемое по формуле
, определяемое по формуле
где Hв - глубина верхней границы выработки (см. рис. 11).
4.43. Высота прямого уступа над выходом разрабатываемого пласта под наносы (точка Б) (кроме Донбасса)
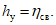 (49)
(49)Высота уступов над выходами вышележащих неотработанных или ранее отработанных пластов и слабых контактов (точка С) (кроме Донбасса)
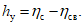 (50)
(50)4.44. В том случае, когда положение слабых контактов, по которым происходит сдвижение по напластованию, неизвестно, и в Донбассе высота прямых уступов на участке БД принимается постоянной и определяется по формуле
 (51)
(51)где Hв - см. п. 4.42.
4.45. При ведении горных работ в одном пласте на втором и последующих горизонтах, а для условий Донбасса во всех случаях, расчет сдвижений, деформаций и прямых уступов производится как при неизвестном положении слабых контактов.
4.46. Наряду с величинами сдвижений и деформаций в зоне  , при ведении горных работ на втором и последующих горизонтах дополнительно определяются величины горизонтальных деформаций и прямых уступов на участке земной поверхности ДА1.
, при ведении горных работ на втором и последующих горизонтах дополнительно определяются величины горизонтальных деформаций и прямых уступов на участке земной поверхности ДА1.
В точке А1 величины горизонтальных деформаций и уступов, вызванные сдвижением пород по напластованию, принимаются равными нулю. Величины горизонтальных деформаций и уступов в точках зоны ДА1 определяются по формулам:
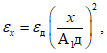 (52)
(52) (53)
(53)где 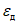 и hд - соответственно горизонтальные деформации и уступы в точке Д, определяемые по приведенным выше формулам;
и hд - соответственно горизонтальные деформации и уступы в точке Д, определяемые по приведенным выше формулам;
x - расстояние от точки А1 до рассматриваемой точки "a" (см. рис. 11).
4.47. На участке А1Д величины оседаний, горизонтальных сдвижений и горизонтальных деформаций рассчитываются также в соответствии с условиями пп. 4.10 - 4.16 (по сглаженным кривым). В расчет принимаются большие из значений, полученных указанным способом и путем расчета сдвижений и деформаций от влияния подвижек по напластованию.
4.48. При разработке свиты пластов, сдвижения и деформации земной поверхности, вызванные сдвижением пород по напластованию, определяются от каждого разрабатываемого пласта в отдельности. Суммарные сдвижения и деформации определяются путем алгебраического сложения сдвижений и деформаций, вызываемых влиянием каждого из пластов.
При этом, если отдельные пласты ранее разработаны на верхних горизонтах до глубины Hот (Hот - глубина по вертикали до нижней границы ранее отработанного горизонта), то при расчетах величин ожидаемых сдвижений и деформаций при ведении горных работ в диапазоне глубин от Hот до Hп, значения величин сдвижений и деформаций от указанных пластов умножаются на коэффициент
 (54)
(54)ПРИ НАЛИЧИИ СДВИЖЕНИЯ ПОРОД ЛЕЖАЧЕГО БОКА
Подготовка исходных данных и порядок расчета
5.1. Подготовка исходных горно-геологических данных к расчету сдвижений и деформаций производится в соответствии с пп. 4.1 и 4.3. Расчет сдвижений и деформаций выполняется только для участков мульды, расположенных за пределами зон провалов и крупных трещин с уступами (террас). Границы зон возможных провалов и крупных трещин с уступами (террас) определяются в соответствии с пп. 3.8 - 3.10.
5.2. Границы мульды сдвижения (см. рис. 1, в) устанавливаются по граничным углам 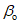 и
и 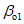 , определяемым по разд. 8 для соответствующих бассейнов и месторождений.
, определяемым по разд. 8 для соответствующих бассейнов и месторождений.
5.3. Длины полумульд L1 и L2 для расчетов оседаний и наклонов определяются углами 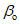 ,
, 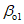 и
и 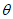 (см. рис. 1, в).
(см. рис. 1, в).
Для расчетов горизонтальных сдвижений и горизонтальных деформаций мульда сдвижения разделяется на четыре части - 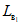 ,
, 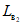 ,
, 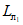 ,
, 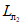 (см. рис. 1, в) плоскостями, проведенными под углами
(см. рис. 1, в) плоскостями, проведенными под углами  ,
, 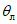 ,
, 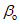 и
и 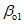 и проекцией на земную поверхность точки выхода почвы пласта под наносы.
и проекцией на земную поверхность точки выхода почвы пласта под наносы.
Начала координат (z = 0) для соответствующих частей мульды располагаются в точках пересечения с земной поверхностью плоскостей, проведенных из середины выработки под углами 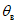 - в висячем боку и
- в висячем боку и 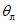 - в лежачем боку (см. рис. 1, в).
- в лежачем боку (см. рис. 1, в).
Расчет сдвижений и деформаций от одной очистной выработки
5.4. Максимальное оседание земной поверхности при отсутствии провалов и крупных трещин с уступами (террас) определяется по формуле
 (55)
(55)где n1 и n2 - коэффициенты подработанности, определяемые по формулам:
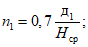 (56)
(56) (57)
(57)но не более 1,0;
Д1 и Д2 - размеры очистной выработки соответственно вкрест простирания и по простиранию пласта;
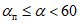 | 60 | 70 | 80 | 90 | |
K3 | 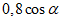 | 0,40 | 0,35 | 0,30 | 0,40 |
Примечание. Промежуточные значения коэффициента K3 определяются интерполяцией.
В Кузнецком бассейне при выемке крутопадающих пластов с закладкой выработанного пространства величина  определяется в соответствии с п. 8.14.
определяется в соответствии с п. 8.14.
При выемке пластов угля с применением закладки, доставляемой извне, вместо вынимаемой мощности пласта m в расчетах используется эффективная мощность mэ, определяемая в соответствии с указаниями п. 4.2.
5.5. Максимальное оседание на границе зоны провалов и крупных трещин с уступами определяется по формулам:
со стороны висячего бока
 (58)
(58)со стороны лежачего бока
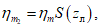 (59)
(59)где S(zв) и S(zл) - значения функции S(z), определяемые по табл. 13) (кроме Кузнецкого бассейна) в зависимости от отношения глубины верхней границы рассматриваемой выработки Hв к вынимаемой мощности и аргументов:
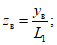 (60)
(60)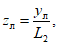 (61)
(61)где yв - расстояние от точки пересечения с земной поверхностью плоскости, проведенной под углом 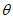 из середины выработки до границы зоны провалов и крупных трещин с уступами со стороны висячего бока;
из середины выработки до границы зоны провалов и крупных трещин с уступами со стороны висячего бока;
yл - то же, со стороны лежачего бока.
Примечание. В Кузнецком бассейне при m >= 6 м и 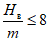 на участках между точками максимального оседания и границами зон провалов сдвижения и деформации определяются в соответствии с п. 8.16.
на участках между точками максимального оседания и границами зон провалов сдвижения и деформации определяются в соответствии с п. 8.16.
 |  |  | ||||||
S(z) | S'(z) | S(z) | S'(z) | S(z) | S'(z) | F(z) | F'(z) | |
0,0 | 1,00 | 0 | 1,00 | 0 | 1,00 | 0 | 1,00 | 0 |
0,1 | 0,32 | 2,6 | 0,96 | 0,8 | 0,98 | 0,5 | 0,97 | 0,2 |
0,2 | 0,17 | 1,0 | 0,83 | 2,2 | 0,90 | 1,0 | 0,93 | 0,4 |
0,3 | 0,09 | 0,6 | 0,52 | 3,2 | 0,77 | 1,6 | 0,88 | 0,6 |
0,4 | 0,05 | 0,4 | 0,30 | 1,5 | 0,58 | 2,0 | 0,81 | 0,8 |
0,5 | 0,04 | 0,25 | 0,20 | 0,9 | 0,39 | 1,9 | 0,71 | 1,0 |
0,6 | 0,03 | 0,15 | 0,12 | 0,6 | 0,22 | 1,4 | 0,60 | 1,2 |
0,7 | 0,02 | 0,07 | 0,07 | 0,4 | 0,10 | 0,9 | 0,47 | 1,4 |
0,8 | 0,01 | 0,03 | 0,03 | 0,3 | 0,04 | 0,4 | 0,32 | 1,6 |
0,9 | 0,005 | 0,01 | 0,01 | 0,2 | 0,01 | 0,2 | 0,17 | 1,7 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1,8 |
Примечание. Промежуточные значения функций S(z), S'(z), F(z) и F'(z) определяются интерполяцией. Значения функций S(z), S'(z), F(z) и F'(z) для Кузнецкого бассейна определяются в соответствии с п. 8.15 (табл. 52).
5.6. Максимальное горизонтальное сдвижение в направлении вкрест простирания пласта при отсутствии провалов и крупных трещин с уступами определяется по формуле
со стороны висячего бока
где  - коэффициент, определяемый по разд. 8, а при отсутствии - по табл. 14 в зависимости от отношения размера целика по падению l1, оставленного у выхода пласта под наносы к соответствующему размеру выработанного пространства по падению Д1;
- коэффициент, определяемый по разд. 8, а при отсутствии - по табл. 14 в зависимости от отношения размера целика по падению l1, оставленного у выхода пласта под наносы к соответствующему размеру выработанного пространства по падению Д1;
со стороны лежачего бока
где Kл - коэффициент, определяемый по табл. 15.
Вынимаемая мощность пласта m, м | |||||
до 70 | 75 | 80 | 90 | ||
до 0,1 | >= 5 | 1,5 | 1,4 | 1,2 | 1,0 |
< 5 | 1,0 | 1,0 | 1,0 | 0,8 | |
> 0,3 | >= 5 | 0,8 | 0,6 | 0,4 | 0,4 |
< 5 | 0,5 | 0,4 | 0,3 | 0,3 | |
Примечание. Промежуточные значения  определяются интерполяцией.
определяются интерполяцией.
50 | 60 | 70 | 75 | 80 | 90 | |
Kл | 0 | 0,1 | 0,15 | 0,4 | 0,7 | 1,0 |
Примечание. Промежуточные значения Kл определяются интерполяцией.
5.7. Максимальное горизонтальное сдвижение в направлении вкрест простирания пласта за пределами зоны провалов и крупных трещин с уступами определяется по формулам:
со стороны висячего бока
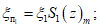 (64)
(64)со стороны лежачего бока
 (65)
(65)где S1(z)m и S2(z)m - максимальные значения функции S(z) соответственно на участках  и
и  за пределами зоны провалов и крупных трещин с уступами, определяемые по табл. 13 в зависимости от отношения
за пределами зоны провалов и крупных трещин с уступами, определяемые по табл. 13 в зависимости от отношения 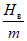 ;
;
5.8. Если суммарная мощность монолитных песчаников и известняков в пределах зоны сдвижения висячего бока более чем в два раза превышает мощность соответствующих пород в зоне сдвижения лежачего бока, то деформации в породах висячего бока умножаются на коэффициент 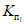 , а в породах лежачего бока - на коэффициент
, а в породах лежачего бока - на коэффициент 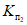 .
.
В тех случаях, когда суммарная мощность монолитных песчаников и известняков в пределах зоны сдвижения лежачего бока более чем в два раза превышает мощность соответствующих пород в зоне сдвижения висячего бока, то деформации в породах висячего бока умножаются на коэффициент  , а в породах лежачего бока - на коэффициент
, а в породах лежачего бока - на коэффициент  .
.
Примечание. Коэффициенты 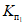 и
и 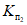 применяются, только если разрабатываются пласты, над выходами которых образуются провалы. При этом в расчет принимаются только слои песчаников и известняков мощностью более 30 м.
применяются, только если разрабатываются пласты, над выходами которых образуются провалы. При этом в расчет принимаются только слои песчаников и известняков мощностью более 30 м.
<= 60 | 70 | 80 | 90 | |
1,0 | 0,9 | 0,7 | 0,5 | |
1,0 | 1,2 | 1,6 | 2,0 |
Примечание. Промежуточные значения коэффициентов 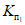 и
и  определяются интерполяцией.
определяются интерполяцией.
5.9. Максимальные наклоны в направлении вкрест простирания пластов определяются по формулам:
со стороны висячего бока
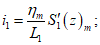 (66)
(66)со стороны лежачего бока
 (67)
(67)При отсутствии провалов за  и
и  принимается максимальное значение функции S'(z), определяемое по табл. 13 в зависимости от значения
принимается максимальное значение функции S'(z), определяемое по табл. 13 в зависимости от значения 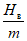 .
.
При наличии провалов за 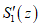 и
и 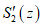 принимаются максимальные значения функции S'(z) соответственно на участках L1 и L2 за пределами зоны провалов и крупных трещин с уступами, определяемое по табл. 13 в зависимости от
принимаются максимальные значения функции S'(z) соответственно на участках L1 и L2 за пределами зоны провалов и крупных трещин с уступами, определяемое по табл. 13 в зависимости от 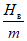 .
.
5.10. Максимальные горизонтальные деформации в направлении вкрест простирания пластов определяются по формулам:
на участке 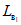
 (68)
(68)на участках  и
и 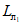 (при
(при 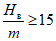 )
)
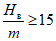 )
)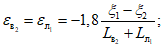 (69)
(69)на участке 
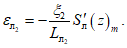 (70)
(70)При отсутствии провалов за 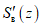 и
и 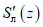 принимается максимальное значение функции S'(z), а при наличии провалов - максимальные значения функции S'(z) соответственно на участках
принимается максимальное значение функции S'(z), а при наличии провалов - максимальные значения функции S'(z) соответственно на участках 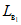 и
и 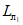 за пределами зоны провалов и крупных трещин с уступами, определяемые по табл. 13 в зависимости от отношения
за пределами зоны провалов и крупных трещин с уступами, определяемые по табл. 13 в зависимости от отношения 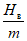 .
.
5.11. Сдвижения и деформации в точках главного сечения мульды сдвижения вкрест простирания пластов определяются по формулам:
величины оседания
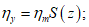 (71)
(71)величины горизонтальных сдвижений
на участке 
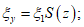 (72)
(72)на участке 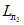
 (73)
(73)на участке 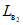 (при
(при 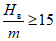 )
)
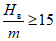 )
)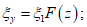 (74)
(74)на участке  (при
(при 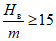 )
)
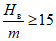 )
)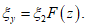 (75)
(75)Величины наклонов:
в полумульде по падению
 (76)
(76)в полумульде по восстанию
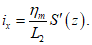 (77)
(77)Величины горизонтальных деформаций:
на участке 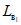
на участках  и
и 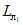 (при
(при 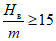 )
)
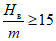 )
) (79)
(79)на участке 
 (80)
(80)где S(z), S'(z), F(z) и F'(z) - значения соответствующих функций, определяемые по табл. 13 в зависимости от отношения 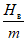 .
.
Примечание. В Кузнецком бассейне на участке  при
при  в формулу (78) вместо величины S'(z) подставляется величина S"(z), определяемая в соответствии с п. 8.16 (табл. 53).
в формулу (78) вместо величины S'(z) подставляется величина S"(z), определяемая в соответствии с п. 8.16 (табл. 53).
Расчет сдвижений и деформаций от нескольких выработок
5.12. Расчет сдвижений и деформаций земной поверхности от нескольких выработок при разработке одного пласта производится следующим образом: при ширине целиков между отрабатываемыми этажами l1 более 0,1Hц (где Hц - средняя глубина залегания целика) расчет производится раздельно от каждой очистной выработки согласно пп. 5.4 - 5.11 с последующим алгебраическим суммированием полученных результатов; при ширине целиков между отрабатываемыми этажами l1, не превышающей 0,1Hц, расчет производится последовательно от одного, двух и более этажей по суммарным размерам выработок, включая размеры междуэтажных целиков l1. При этом положения точек максимального оседания и максимальных горизонтальных сдвижений определяются с помощью плоскостей, которые проводятся под углами  ,
, 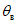 и
и 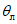 от середины верхнего из суммируемых этажей, а значения функций S(z) и S'(z) определяются по табл. 13, принимая
от середины верхнего из суммируемых этажей, а значения функций S(z) и S'(z) определяются по табл. 13, принимая 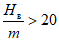 .
.
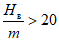 .
.5.13. Расчет сдвижений и деформаций земной поверхности при разработке свиты пластов производится путем алгебраического суммирования соответствующих величин от каждого из пластов.
Последовательность суммирования сдвижений и деформаций от выработок в одном пласте и выработок в свите пластов должна соответствовать последовательности развития очистных работ.
5.14. За окончательные величины сдвижений и деформаций земной поверхности принимаются наибольшие значения из полученных при суммировании соответствующих сдвижений и деформаций от отдельных выработок.
ПОВЕРХНОСТИ ДЛЯ УСЛОВИЙ СИНКЛИНАЛЬНОГО ЗАЛЕГАНИЯ ПОРОД
Условия применения методики расчета
6.1. Методика расчета позволяет определять величины сдвижений и деформаций земной поверхности и высоту уступов в главных сечениях мульды сдвижения на разрезах вкрест простирания при углах падения пород в крыльях складок до 70° в следующих условиях: при отработке симметричных и асимметричных синклинальных складок с наклонным или вертикальным положением осевой поверхности и углами падения пород одного или обоих крыльев на выходах под насосы 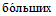 30° (п. 6.2, рис. 12), асимметричных синклинальных складок с углами падения одного крыла больше 30°, а другого меньше 30° (см. п. 6.4, рис. 13 и 14) и шарнирных складок с углами падения пород
30° (п. 6.2, рис. 12), асимметричных синклинальных складок с углами падения одного крыла больше 30°, а другого меньше 30° (см. п. 6.4, рис. 13 и 14) и шарнирных складок с углами падения пород 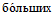 30° (см. п. 6.5, рис. 15).
30° (см. п. 6.5, рис. 15).
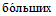 30° (п. 6.2, рис. 12), асимметричных синклинальных складок с углами падения одного крыла больше 30°, а другого меньше 30° (см. п. 6.4, рис. 13 и 14) и шарнирных складок с углами падения пород
30° (п. 6.2, рис. 12), асимметричных синклинальных складок с углами падения одного крыла больше 30°, а другого меньше 30° (см. п. 6.4, рис. 13 и 14) и шарнирных складок с углами падения пород 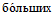 30° (см. п. 6.5, рис. 15).
30° (см. п. 6.5, рис. 15).При отработке складок с углами падения пород обоих крыльев на выходах под наносы меньших 30°, расчет ожидаемых сдвижений и деформаций производится по рекомендациям разд. 4, как для выдержанного залегания пород.
При расположении нижней границы очистной выработки по падению за точкой K - точкой пересечения отрабатываемого пласта с линией, проведенной от точки 0 под углом 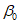 (рис. 16) (
(рис. 16) ( - граничный угол, определяемый по разд. 8 для соответствующих бассейнов и месторождений при
- граничный угол, определяемый по разд. 8 для соответствующих бассейнов и месторождений при  , равном углу падения пород на выходе крыла складки под наносы). В тех случаях, когда нижняя граница очистной выработки располагается по восстанию от точки K, расчет ожидаемых величин сдвижений и деформаций производится по рекомендациям разд. 4 или 5.
, равном углу падения пород на выходе крыла складки под наносы). В тех случаях, когда нижняя граница очистной выработки располагается по восстанию от точки K, расчет ожидаемых величин сдвижений и деформаций производится по рекомендациям разд. 4 или 5.
В главных сечениях мульды сдвижения на разрезах по простиранию расчет ожидаемых сдвижений и деформаций земной поверхности производится в соответствии с рекомендациями разд. 4. При этом максимальное оседание принимается равным максимальному оседанию, рассчитанному для разреза вкрест простирания по рекомендациям п. 6.2. Граничные углы 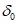 , углы
, углы 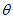 ,
, 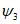 и значения функций S(z), F(z), F'(z) определяются из разд. 8 для соответствующих бассейнов и месторождений.
и значения функций S(z), F(z), F'(z) определяются из разд. 8 для соответствующих бассейнов и месторождений.
Расчет сдвижений и деформаций земной поверхности
6.2. При отработке симметричных и асимметричных нормальных синклинальных складок с наклонным или вертикальным положением осевой поверхности и углами падения крыльев  расчет ожидаемых величин сдвижений земной поверхности производится в следующих характерных точках, показанных на рис. 12:
расчет ожидаемых величин сдвижений земной поверхности производится в следующих характерных точках, показанных на рис. 12:
 расчет ожидаемых величин сдвижений земной поверхности производится в следующих характерных точках, показанных на рис. 12:
расчет ожидаемых величин сдвижений земной поверхности производится в следующих характерных точках, показанных на рис. 12: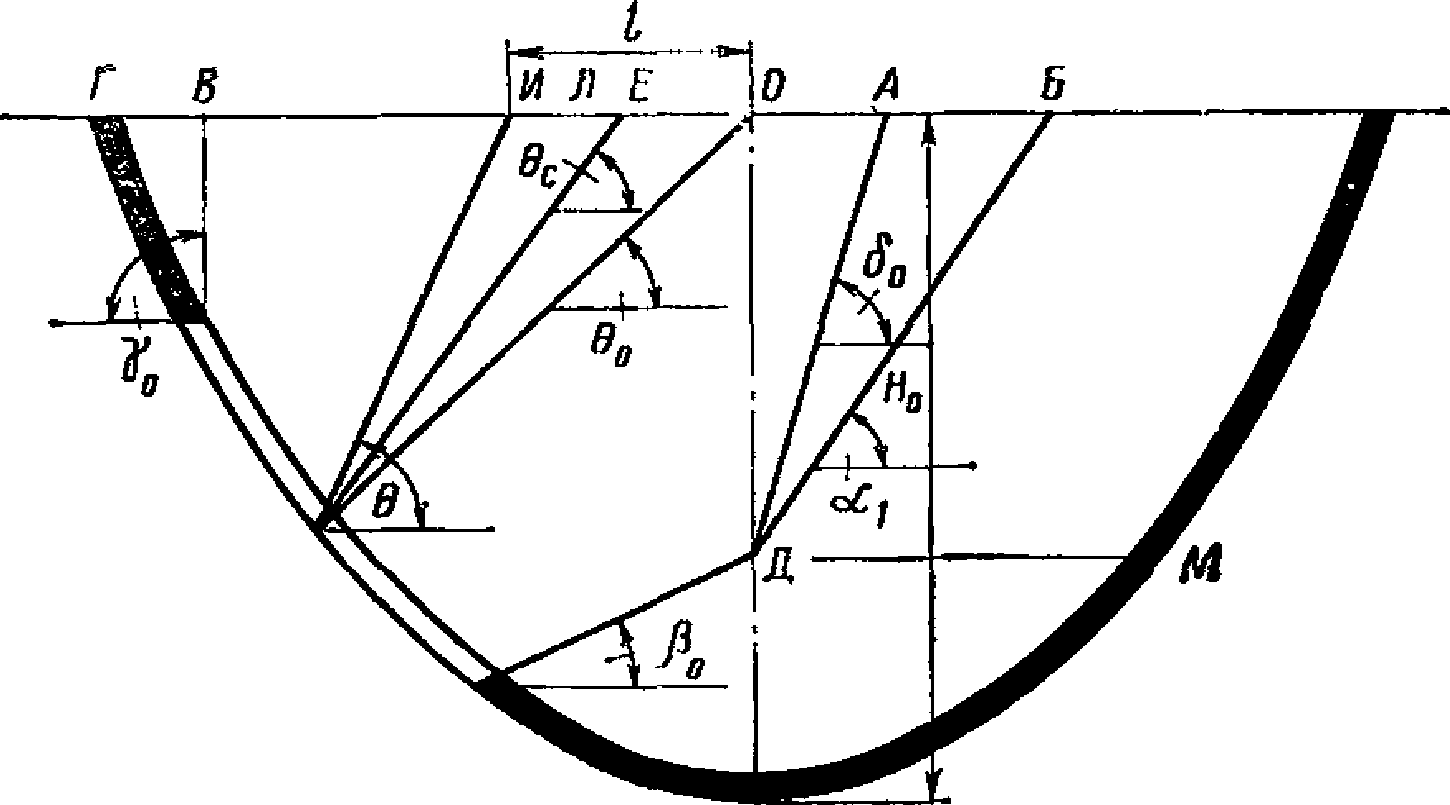
на разрезе вкрест простирания для синклинальных складок
с углами падения обоих крыльев 
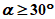
в точках О или Е, в которых определяются величины максимальных оседаний от изгиба слоев по нормали к напластованию 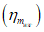 ; точка О определяется пересечением осевой поверхности складки с земной поверхностью; оседание в этой точке рассчитывается в тех случаях, когда линия, проведенная из середины выработки под углом
; точка О определяется пересечением осевой поверхности складки с земной поверхностью; оседание в этой точке рассчитывается в тех случаях, когда линия, проведенная из середины выработки под углом 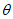 , пересекает осевую поверхность складки; если эта линия не пересекает осевую поверхность, то оседание
, пересекает осевую поверхность складки; если эта линия не пересекает осевую поверхность, то оседание  рассчитывается в точке Е; точка Е определяется пересечением линии, проведенной из середины выработки под углом
рассчитывается в точке Е; точка Е определяется пересечением линии, проведенной из середины выработки под углом  ; угол
; угол  находится по формуле
находится по формуле
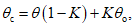 (81)
(81)где  - угол наклона к горизонту линии, соединяющей середину очистной выработки с точкой пересечения земной поверхности осевой поверхностью складки;
- угол наклона к горизонту линии, соединяющей середину очистной выработки с точкой пересечения земной поверхности осевой поверхностью складки;
K - коэффициент, зависящий от отношения  . K = 1 при
. K = 1 при  ; K = 0,9 при
; K = 0,9 при 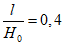 и K = 0,7 при
и K = 0,7 при 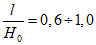 ; при промежуточных значениях коэффициент K определяется интерполированием; l - расстояние от точки О до точки пересечения с земной поверхностью линии, проведенной под углом
; при промежуточных значениях коэффициент K определяется интерполированием; l - расстояние от точки О до точки пересечения с земной поверхностью линии, проведенной под углом  (точка И) (см. рис. 12);
(точка И) (см. рис. 12);
 ; K = 0,9 при
; K = 0,9 при 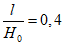 и K = 0,7 при
и K = 0,7 при 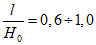 ; при промежуточных значениях коэффициент K определяется интерполированием; l - расстояние от точки О до точки пересечения с земной поверхностью линии, проведенной под углом
; при промежуточных значениях коэффициент K определяется интерполированием; l - расстояние от точки О до точки пересечения с земной поверхностью линии, проведенной под углом в точке А, которая определяет границу зоны изгиба слоев со стороны нижней границы выработки; для определения положения точки А от нижней границы выработки проводится линия под углом 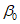 до пересечения с осевой поверхностью складки (точка Д), затем из точки Д проводится линия под углом
до пересечения с осевой поверхностью складки (точка Д), затем из точки Д проводится линия под углом 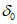 до пересечения с земной поверхностью; значения углов
до пересечения с земной поверхностью; значения углов 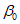 и
и 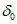 находятся по рекомендациям разд. 8 для соответствующего бассейна. Значения углов
находятся по рекомендациям разд. 8 для соответствующего бассейна. Значения углов 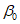 рассчитываются в зависимости от угла падения пласта
рассчитываются в зависимости от угла падения пласта 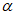 у нижней границы очистной выработки;
у нижней границы очистной выработки;
в точке Б, определяющей границу зоны влияния очистной выработки со стороны ее нижней границы, находится в точке пересечения линии, проведенной под углом  из точки Д, с земной поверхностью
из точки Д, с земной поверхностью  - угол падения пород противолежащего крыла складки; если угол падения пород противолежащего крыла складки переменный, он определяется как средний угол между углом падения пласта у выхода под наносы и углом падения пласта в точке М - в точке пересечения горизонтальной линии, проходящей через точку Д, с пластом (см. рис. 12);
- угол падения пород противолежащего крыла складки; если угол падения пород противолежащего крыла складки переменный, он определяется как средний угол между углом падения пласта у выхода под наносы и углом падения пласта в точке М - в точке пересечения горизонтальной линии, проходящей через точку Д, с пластом (см. рис. 12);
в точке В, определяющей границу зоны изгиба слоев со стороны верхней границы очистной выработки, находится в точке пересечения линии, проведенной от верхней границы очистной выработки под углом 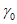 , с земной поверхностью; угол
, с земной поверхностью; угол 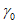 находится по рекомендациям разд. 8 при условии, что
находится по рекомендациям разд. 8 при условии, что 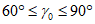 ; значения углов
; значения углов 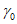 принимаются в зависимости от угла падения пласта
принимаются в зависимости от угла падения пласта  у верхней границы очистной выработки;
у верхней границы очистной выработки;
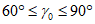 ; значения углов
; значения углов в точке Г - выход пласта на отрабатываемом крыле под наносы;
в точке Л - точке максимального оседания от сдвига по напластованию пород отрабатываемого крыла 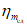 ; находится на расстоянии, равном 0,4 отрезка ОВ (от точки О); в тех случаях, когда максимальное оседание от изгиба
; находится на расстоянии, равном 0,4 отрезка ОВ (от точки О); в тех случаях, когда максимальное оседание от изгиба  находится в точке Е, то и максимальное оседание
находится в точке Е, то и максимальное оседание 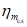 принимается в точке Е, определяемой углом
принимается в точке Е, определяемой углом 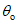 .
.
Оседания и горизонтальные сдвижения в характерных точках земной поверхности рассчитываются по формулам, приведенным в табл. 17.
Точки земной поверхности | Оседания, мм | Горизонтальные сдвижения, мм |
О (ж) | 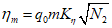 | |
А | 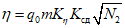 | 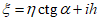 |
Л | 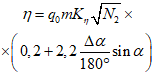 | 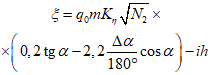 |
В | 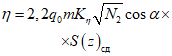 | 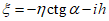 |
Г |  |  |
Е |  | 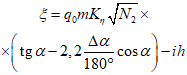 |
Б (р) | 0 | 0 |
При построении графиков горизонтальные сдвижения принимаются с теми знаками, которые получаются по формулам табл. 17.
В выражениях, приведенных в табл. 17, приняты следующие обозначения:
q0 - относительная величина вертикальных сдвижений, определяемая из разд. 8; m - вынимаемая или эффективная мощность пласта, м; 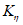 - коэффициент, зависящий от отношения размера выработки (Д1) на разрезе вкрест простирания к глубине залегания оси складки (H0), определяется из табл. 18.
- коэффициент, зависящий от отношения размера выработки (Д1) на разрезе вкрест простирания к глубине залегания оси складки (H0), определяется из табл. 18.
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
0 | 0,25 | 0,35 | 0,45 | 0,60 | 0,8 |
Примечание. Промежуточные значения  определяются интерполированием.
определяются интерполированием.
N2 - коэффициент, определяемый из разд. 8; Kед - коэффициент, определяемый в зависимости от отношения оседания в точке О 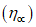 к максимальному оседанию в мульде. Находится из табл. 19;
к максимальному оседанию в мульде. Находится из табл. 19;  - рассчитывается по формулам табл. 17 (точки О и Е).
- рассчитывается по формулам табл. 17 (точки О и Е).
1 | 0,9 | 0,7 | 0,5 | 0,2 | 0,1 | 0 | |
Kсд | 0,5 | 0,35 | 0,30 | 0,20 | 0,15 | 0,1 | 0 |
Примечание. Промежуточные значения Kсд определяются интерполированием.
h - мощность наносов, м;
i - ожидаемый наклон земной поверхности в рассматриваемой точке.
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
S(z)сд | 1 | 0,86 | 0,70 | 0,55 | 0,35 | 0,25 |
Примечание. Промежуточные значения S(z)сд определяются интерполированием.
по формулам табл. 17 рассчитываются величины ожидаемых оседаний в характерных точках мульды сдвижения и строятся графики оседаний. На графиках величины оседаний, отложенные в характерных точках, соединяются прямыми линиями;
определяются величины ожидаемых наклонов на участках мульды сдвижения между характерными точками. Наклоны рассчитываются по отношению разности оседаний в этих точках к расстоянию между ними. Величины наклонов на участке между характерными точками принимаются одинаковыми. К примеру, величины наклонов на участке ОВ будут равны 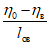 .
.
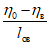 .
.Расчетные величины наклонов на участках между характерными точками определяются по формуле
где i - ожидаемая величина наклонов на рассматриваемом участке;
l - расстояние между характерными точками, принимаемое в пределах 100 м >= l >= 20 м; при l > 100 м l - принимается равным 100 м, а при l < 20 м - принимается равным 20 м.
Наклоны в сторону восстания отрабатываемого пласта принимаются положительными, в обратную сторону - отрицательными.
При использовании для выбора мер охраны расчетных величин наклонов и горизонтальных деформаций, полученных по формулам (82), (83), (86) и (87), коэффициенты перегрузки не вводятся;
ожидаемые величины горизонтальных сдвижений в характерных точках рассчитываются по формулам табл. 17. При этом в выражениях, входящих в эти формулы в качестве наклонов принимаются наибольшие их значения из двух смежных участков, прилегающих к рассматриваемой точке. Величины горизонтальных сдвижений в точке О определяются путем интерполяции между величинами горизонтальных сдвижений, рассчитанных для двух соседних характерных точек;
ожидаемые величины горизонтальных деформаций на участках земной поверхности между характерными точками принимаются одинаковыми на всем участке и рассчитываются по разности горизонтальных сдвижений этих точек, отнесенной к расстоянию между ними.
Расчетные величины горизонтальных деформаций определяются по формуле
где  - ожидаемая величина горизонтальных деформаций на рассматриваемом участке;
- ожидаемая величина горизонтальных деформаций на рассматриваемом участке;
l - расстояние между характерными точками, принимаемое в пределах 100 м >= l >= 20 м; при l > 100 м и l - принимается равным 100 м, а при l < 20 м - принимается равным 20 м.
6.4. Асимметричные нормальные складки с углами падения пород одного крыла 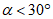 , а другого крыла
, а другого крыла  .
.
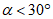 , а другого крыла
, а другого крыла  .
.В том случае, когда очистная выработка расположена в крыле кладки с углом падения  (см. рис. 13), расчет оседаний и горизонтальных сдвижений в точках Ж, (О), А и Б производится по формулам, приведенным в табл. 17. Положение точек А и Б в мульде сдвижения определяется в соответствии с п. 6.2.
(см. рис. 13), расчет оседаний и горизонтальных сдвижений в точках Ж, (О), А и Б производится по формулам, приведенным в табл. 17. Положение точек А и Б в мульде сдвижения определяется в соответствии с п. 6.2.
 (см. рис. 13), расчет оседаний и горизонтальных сдвижений в точках Ж, (О), А и Б производится по формулам, приведенным в табл. 17. Положение точек А и Б в мульде сдвижения определяется в соответствии с п. 6.2.
(см. рис. 13), расчет оседаний и горизонтальных сдвижений в точках Ж, (О), А и Б производится по формулам, приведенным в табл. 17. Положение точек А и Б в мульде сдвижения определяется в соответствии с п. 6.2.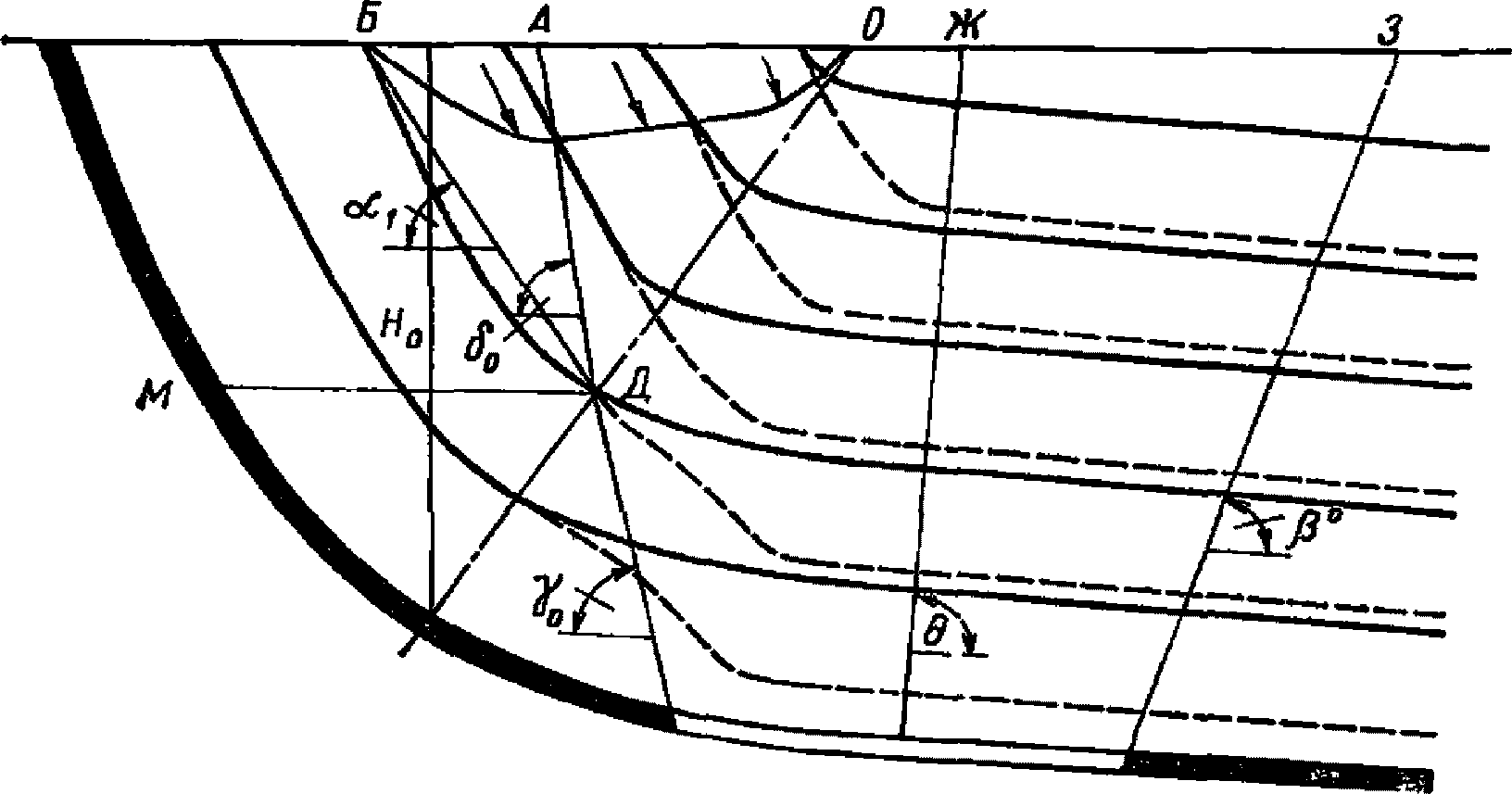
на разрезе вкрест простирания при разработке крыла складки
с углом падения 
Точка с максимальным оседанием от изгиба слоев 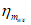 определяется пересечением линий, проведенных от середины выработки под углом
определяется пересечением линий, проведенных от середины выработки под углом 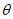 , с земной поверхностью (точка Ж).
, с земной поверхностью (точка Ж). 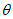 - угол максимального оседания, определяемый в соответствии с рекомендациями разд. 8. В том случае, когда линия, проведенная под углом
- угол максимального оседания, определяемый в соответствии с рекомендациями разд. 8. В том случае, когда линия, проведенная под углом 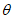 , пересекает осевую поверхность складки, максимальное оседание земной поверхности находится в точке О (см. рис. 13).
, пересекает осевую поверхность складки, максимальное оседание земной поверхности находится в точке О (см. рис. 13).
На участке мульды сдвижения О (Ж), З величины сдвижений и деформаций земной поверхности рассчитываются по методике разд. 4, при этом максимальное оседание рассчитывается по формуле табл. 17 для точки Ж (О).
Ожидаемые величины наклонов и горизонтальных деформаций на участке мульды сдвижения О (Ж), Б рассчитываются, соответственно, по разности оседаний и горизонтальных сдвижений между характерными точками, отнесенной к расстоянию между ними.
Если очистная выработка расположена в крыле складки с углом падения 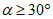 (см. рис. 14), то расчет оседаний и горизонтальных сдвижений земной поверхности производится в точках О (Е), Л, В, Г по формулам, приведенным в табл. 17. Граница мульды сдвижения со стороны нижней границы выработки находится в точке Р.
(см. рис. 14), то расчет оседаний и горизонтальных сдвижений земной поверхности производится в точках О (Е), Л, В, Г по формулам, приведенным в табл. 17. Граница мульды сдвижения со стороны нижней границы выработки находится в точке Р.
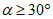 (см. рис. 14), то расчет оседаний и горизонтальных сдвижений земной поверхности производится в точках О (Е), Л, В, Г по формулам, приведенным в табл. 17. Граница мульды сдвижения со стороны нижней границы выработки находится в точке Р.
(см. рис. 14), то расчет оседаний и горизонтальных сдвижений земной поверхности производится в точках О (Е), Л, В, Г по формулам, приведенным в табл. 17. Граница мульды сдвижения со стороны нижней границы выработки находится в точке Р.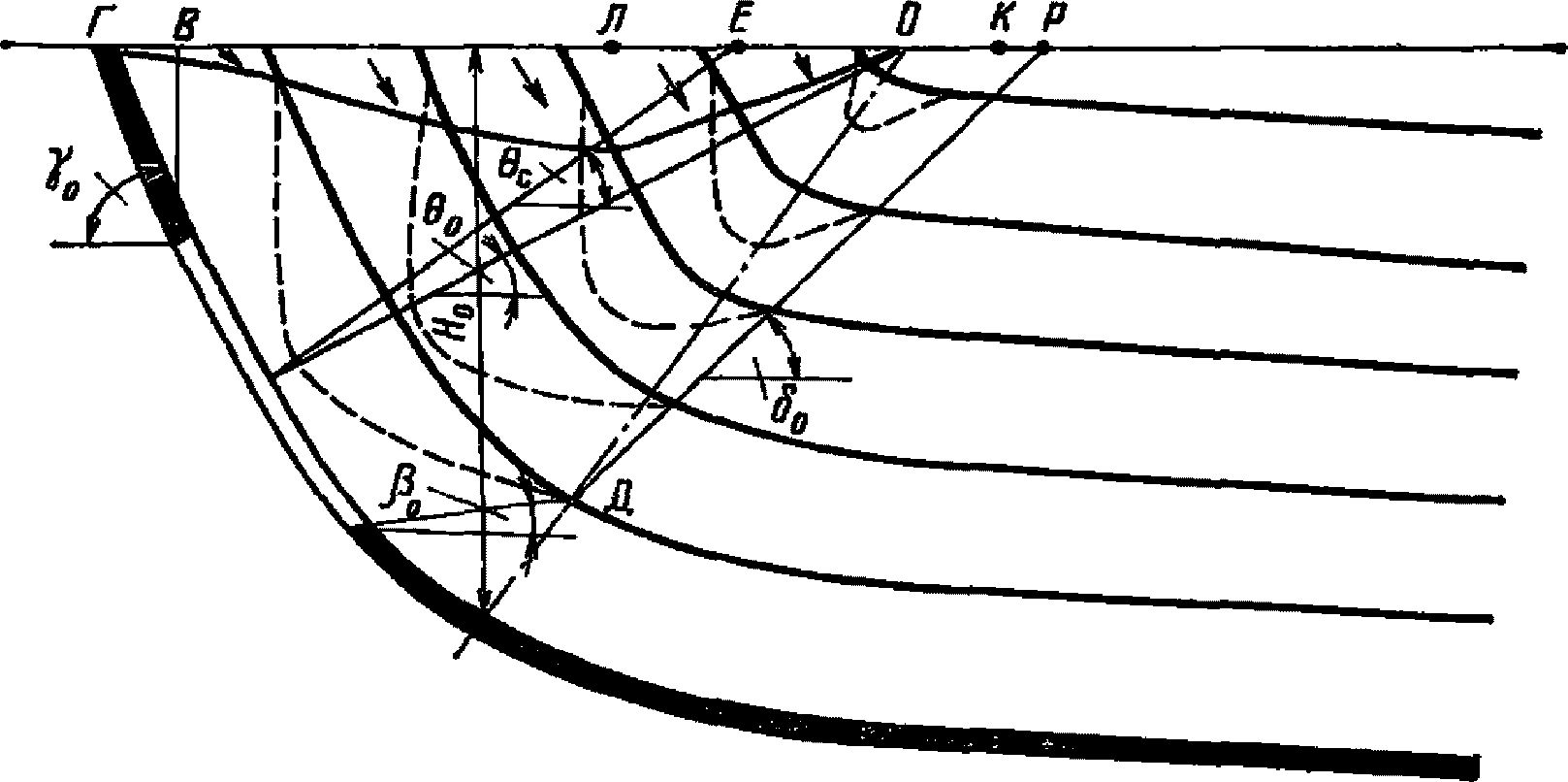
на разрезе вкрест простирания при разработке крыла складки
с углом падения 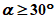
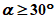
В том случае, когда осевая поверхность складки падает к горизонту под углом, меньшим, чем значение угла 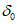 , граница зоны сдвижения на противолежащем крыле находится на расстоянии от осевой поверхности, равном 50 м (точка К).
, граница зоны сдвижения на противолежащем крыле находится на расстоянии от осевой поверхности, равном 50 м (точка К).
Ожидаемые величины наклонов и горизонтальных деформаций земной поверхности на участках мульды сдвижения между характерными точками рассчитываются соответственно по разности оседаний и горизонтальных сдвижений в этих точках, отнесенных к расстоянию между ними.
Расчетные величины наклонов и горизонтальных деформаций определяются по формулам (82) и (83).
6.5. Шарнирные складки. Положение границы зоны сдвижения со стороны нижней границы очистной выработки (точка Б) определяется точкой пересечения с земной поверхностью линии, проведенной от точки Д (см. рис. 15) под углом 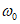 . Угол
. Угол 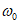 принимается равным 45° при углах падения пород противолежащего крыла складки
принимается равным 45° при углах падения пород противолежащего крыла складки  и равным 55° при углах
и равным 55° при углах  .
.
 и равным 55° при углах
и равным 55° при углах  .
.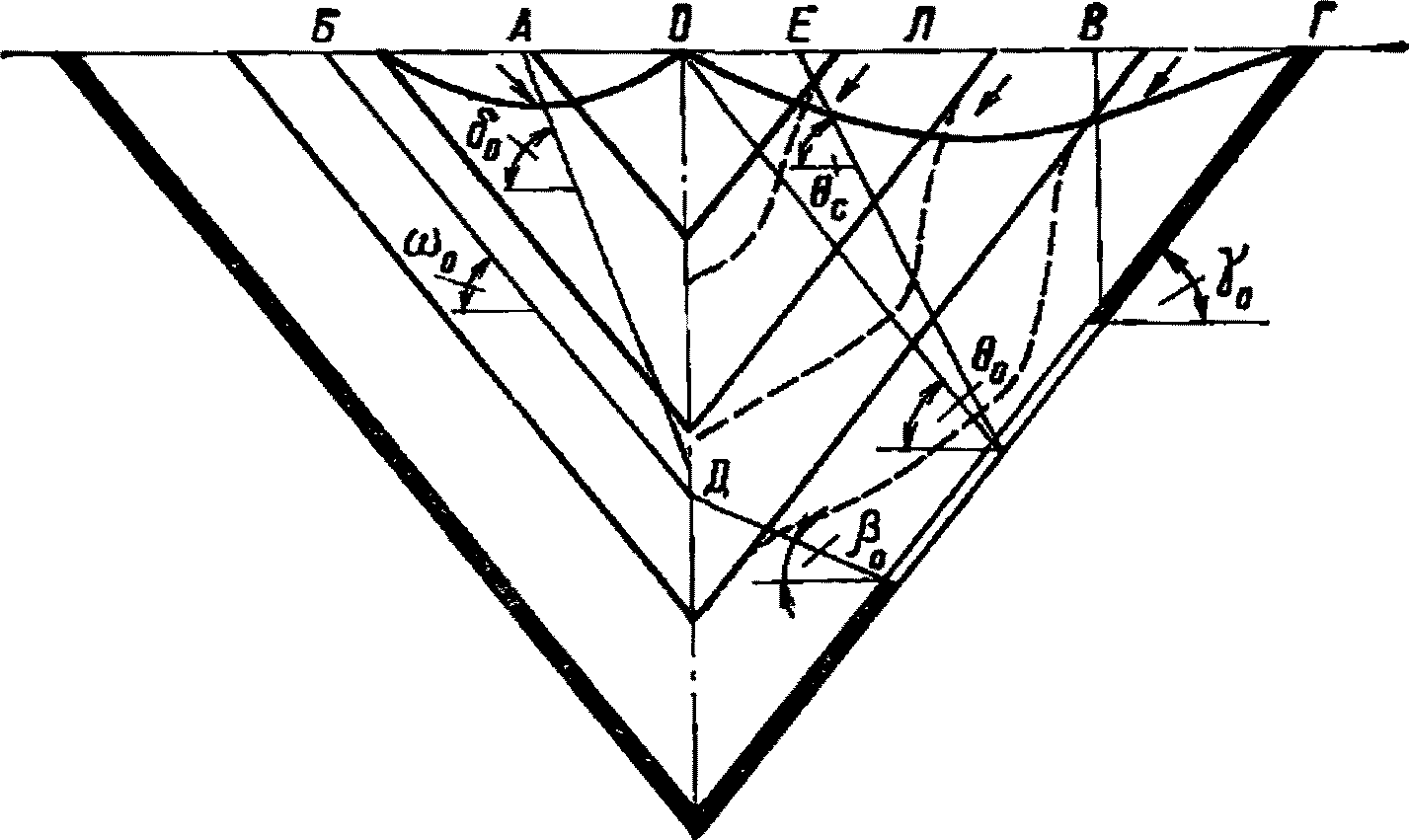
на разрезе вкрест простирания при разработке
шарнирных складок
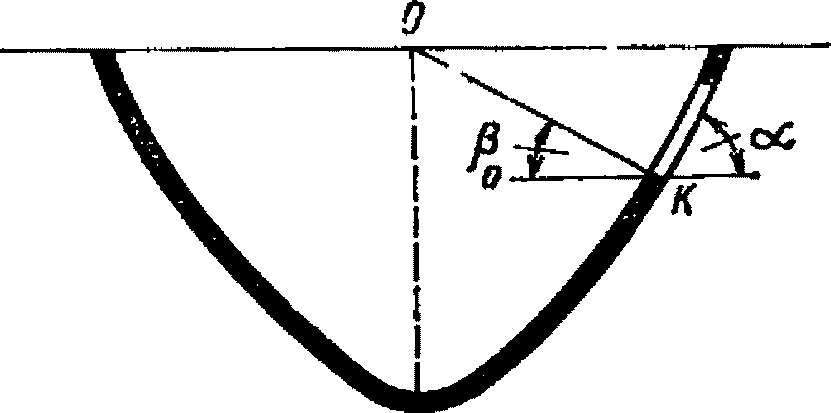
на характер процесса сдвижения
Положение других характерных точек определяется по рекомендациям п. 6.2.
Расчет ожидаемых величин оседаний и горизонтальных сдвижений в характерных точках производится по формулам табл. 21. Обозначения в выражениях табл. 21 соответствуют обозначениям п. 6.2 для табл. 17.
Точка | Оседания, мм | Горизонтальные сдвижения, мм |
0 | 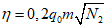 | |
А | 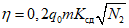 | 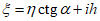 |
Л | 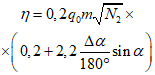 | 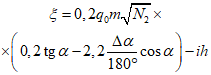 |
В |  | 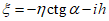 |
Г | 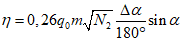 |  |
Е | 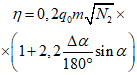 |  |
Б | 0 | 0 |
Значения Kсд для шарнирных складок принимаются равными 0,3 при разработке одиночных пластов и Kсд = 0,15 при отработке свиты пластов.
Значения функции S(z)сд определяются по табл. 22.
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
S(z)сд | 1 | 0,9 | 0,85 | 0,8 | 0,7 | 0,6 |
Примечание. Промежуточные значения S(z)сд определяются интерполированием.
Порядок расчета ожидаемых величин сдвижений и деформаций земной поверхности для условий шарнирных складок аналогичен порядку, рекомендованному в п. 6.3.
В тех случаях, когда угол падения пород противолежащего крыла складки  , ожидаемые величины наклонов и горизонтальных деформаций на участке ОБ (см. рис. 15) рассчитываются по формулам:
, ожидаемые величины наклонов и горизонтальных деформаций на участке ОБ (см. рис. 15) рассчитываются по формулам:
 (84)
(84)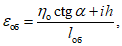 (85)
(85)где  - оседание в точке О;
- оседание в точке О;
lоб - расстояние между точками О и Б, м;
h - мощность наносов;
Расчетные наклоны и горизонтальные деформации земной поверхности на участках между характерными точками рассчитываются по формулам:
где i - ожидаемая величина наклонов на рассматриваемом участке;
l - расстояние между характерными точками, принимаемое в пределах 100 м >= l >= 20 м; при l > 100 м в формуле принимается значение l, равное 100 м, если l < 20 м - принимается значение, равное 20 м.
6.6. Ожидаемые и расчетные величины оседаний, горизонтальных сдвижений, наклонов и горизонтальных деформаций от нескольких выработок в пласте или в свите пластов находятся для условий складчатого залегания путем алгебраического суммирования сдвижений и деформаций, рассчитанных для каждой очистной выработки в отдельности.
6.7. Для нормальных симметричных и асимметричных складок с углами падения крыльев  возможная максимальная высота уступа рассчитывается по формуле
возможная максимальная высота уступа рассчитывается по формуле
 возможная максимальная высота уступа рассчитывается по формуле
возможная максимальная высота уступа рассчитывается по формулегде  - оседание земной поверхности в точке О;
- оседание земной поверхности в точке О;
Участок возможного появления уступа находится между точками А и Л (см. рис. 12).
Для нормальных асимметричных складок с наклонным положением осевой поверхности и углами падения пород одного крыла складки 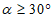 , а другого
, а другого 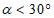 максимальная высота возможного уступа определяется:
максимальная высота возможного уступа определяется:
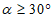 , а другого
, а другого 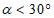 максимальная высота возможного уступа определяется:
максимальная высота возможного уступа определяется:по формуле (88) при разработке крыла складки с углами падения пород 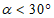 ;
;
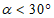 ;
;при разработке крыла складки с углами падения пород 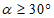 высота уступа принимается равной величине оседания в точке О.
высота уступа принимается равной величине оседания в точке О.
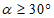 высота уступа принимается равной величине оседания в точке О.
высота уступа принимается равной величине оседания в точке О.В первом случае появление уступа возможно на участке земной поверхности между точками О и А (см. рис. 13), во втором - в районе пересечения осевой поверхности складки с земной поверхностью (по 50 м в обе стороны от точки О, см. рис. 14).
6.8. При разработке шарнирных складок возможная высота уступов определяется по формуле (89) на участке шириной B = 147 - 61V, где V - угол складки в радианах (центр этого участка расположен в точке пересечения земной поверхности осевой поверхностью складки):
где m - вынимаемая мощность пласта, м;
H1 - расстояние от наносов до точки (Д) пересечения осевой поверхности складки линией, проведенной под углом 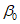 от нижней границы выработки, м;
от нижней границы выработки, м;
Hср - средняя глубина разработки, м;
n = n1n2 - коэффициент подработанности (n2 - коэффициент подработанности по простиранию, n1 - вкрест простирания), определяемые из п. 5.4.
Отношение 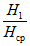 принимается не более 1.
принимается не более 1.
ЗЕМНОЙ ПОВЕРХНОСТИ
7.1. Величины вероятных сдвижений и деформаций при углах падения пластов  , а кривизны при
, а кривизны при 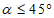 определяются по формулам
определяются по формулам
 , а кривизны при
, а кривизны при 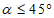 определяются по формулам
определяются по формуламОседание
где m1, m2, m3, ..., mn - мощности разрабатываемых пластов.
При применении закладки выработанного пространства к расчету принимается эффективная мощность, определяемая согласно п. 4.2.
Наклоны
вкрест простирания
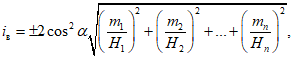 (91)
(91)где H1, H2, ..., Hn - глубины залегания пластов (начиная с верхнего) в точках их пересечения с линией максимального влияния, проведенной из рассматриваемой точки А (границы участка, для которого определяются вероятные сдвижения) под углом  в сторону восстания пластов (рис. 17) на разрезе вкрест простирания
в сторону восстания пластов (рис. 17) на разрезе вкрест простирания
 в сторону восстания пластов (рис. 17) на разрезе вкрест простирания
в сторону восстания пластов (рис. 17) на разрезе вкрест простиранияпо простиранию
где 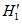 ,
,  , ...,
, ..., 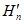 - глубина залегания пластов в точках их пересечения линией, проведенной на разрезе вкрест простирания из рассматриваемой точки А под углом
- глубина залегания пластов в точках их пересечения линией, проведенной на разрезе вкрест простирания из рассматриваемой точки А под углом  (рис. 18);
(рис. 18);
 (рис. 18);
(рис. 18);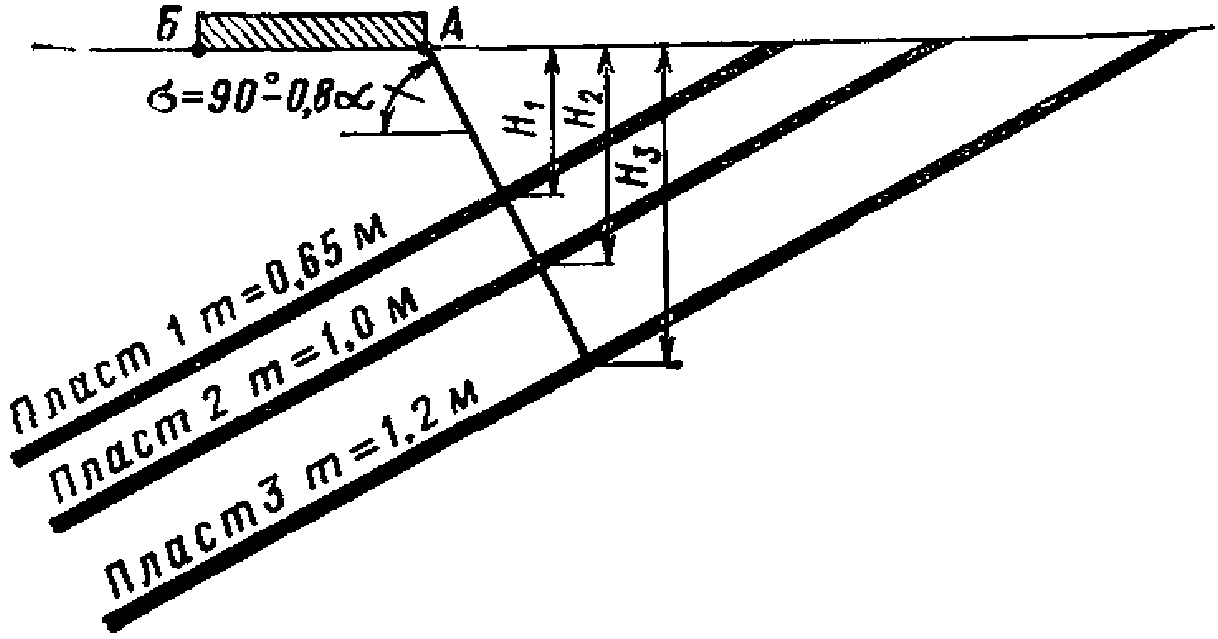
при расчете вероятных сдвижений и деформаций в направлении
вкрест простирания пласта
БА - участок, для которого определяются вероятные величины
сдвижений и деформаций
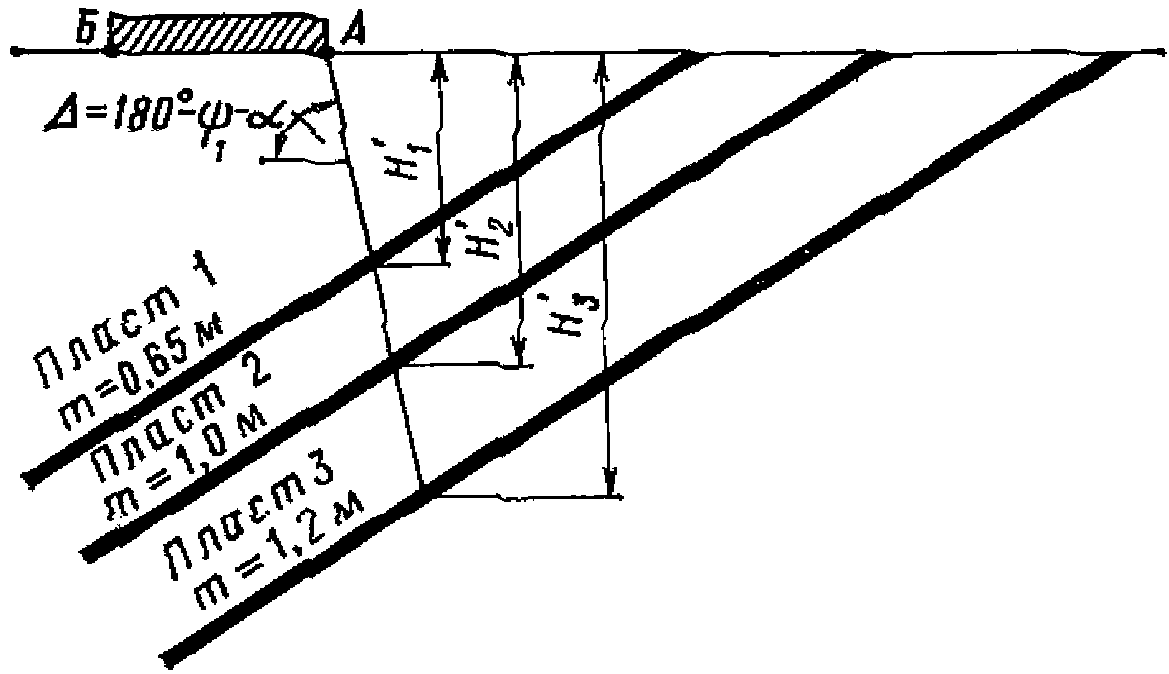
при расчете вероятных сдвижений и деформаций в направлении
простирания пласта
БА - участок, для которого определяются вероятные величины
сдвижений и деформаций
Радиус кривизны:
вкрест простирания
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
по простиранию
Горизонтальные сдвижения:
вкрест простирания
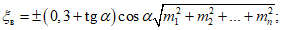 (95)
(95)по простиранию
Горизонтальные деформации:
вкрест простирания
 (97)
(97)по простиранию
7.2. Расчет вероятных сдвижений и деформаций на разрезе вкрест простирания при ведении горных работ по горизонтам при  или
или 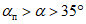 при отсутствии сдвижения пород лежачего бока выполняются с помощью специальной номограммы, которая строится применительно к рассматриваемым условиям (рис. 19).
при отсутствии сдвижения пород лежачего бока выполняются с помощью специальной номограммы, которая строится применительно к рассматриваемым условиям (рис. 19).
 или
или 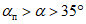 при отсутствии сдвижения пород лежачего бока выполняются с помощью специальной номограммы, которая строится применительно к рассматриваемым условиям (рис. 19).
при отсутствии сдвижения пород лежачего бока выполняются с помощью специальной номограммы, которая строится применительно к рассматриваемым условиям (рис. 19).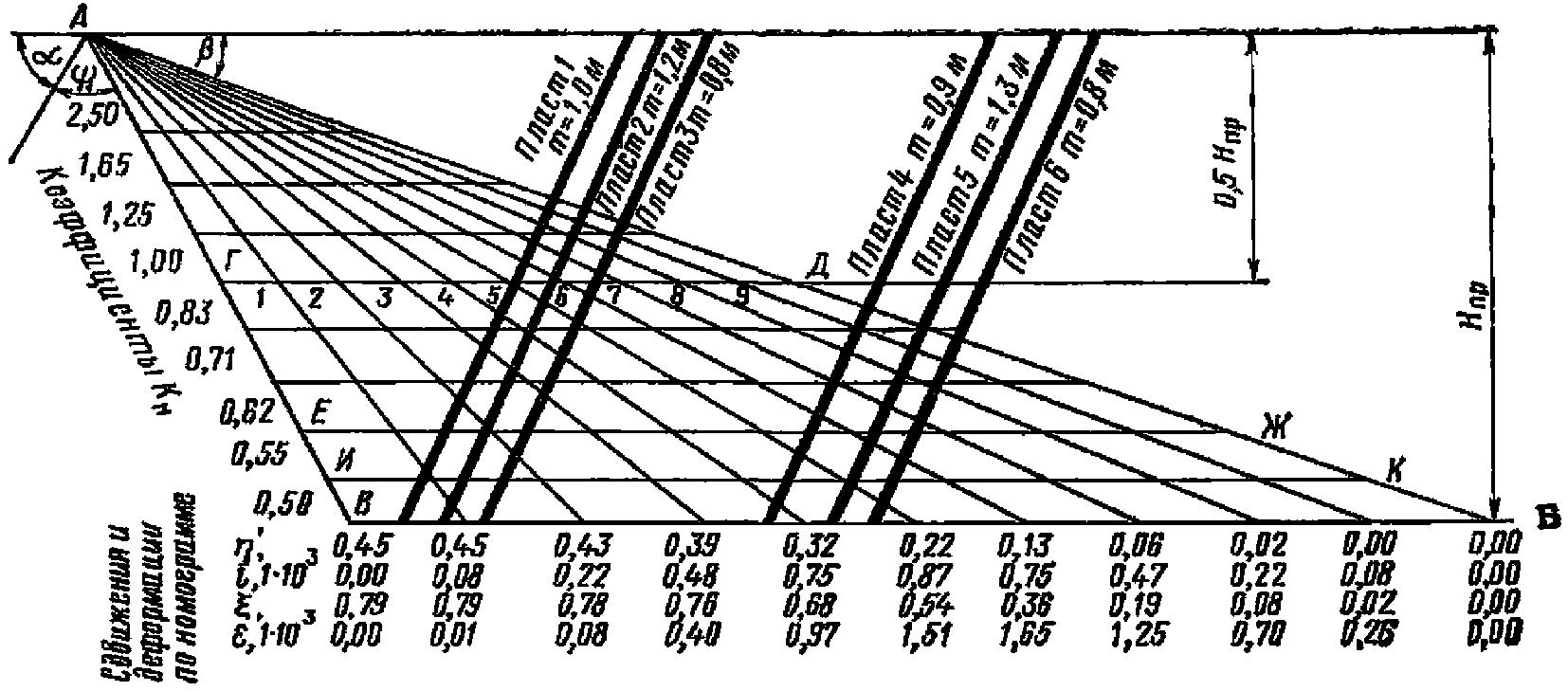
и деформаций на разрезе вкрест простирания
Метод построения номограммы сводится к следующему:
Под граничным углом  к горизонту и углом полных сдвижений
к горизонту и углом полных сдвижений  к пласту на разрезе вкрест простирания из рассматриваемой точки поверхности А проводятся линии АБ и АВ (рис. 19), которые определяют положение границ полумульды при различных глубинах разработки.
к пласту на разрезе вкрест простирания из рассматриваемой точки поверхности А проводятся линии АБ и АВ (рис. 19), которые определяют положение границ полумульды при различных глубинах разработки.
На расстоянии по вертикали от точки А, равном 0,5Hпр проводится горизонтальная линия ГД = L1, которая делится на 10 равных частей (Hпр - проектная глубина разработки).
По формулам (12), (14), (20), (24) в точках деления отрезка ГД соответственно вычисляются величины оседаний, наклонов, горизонтальных сдвижений и горизонтальных деформаций для полумульды по падению пластов. При этом максимальное оседание земной поверхности определяется по формуле
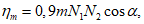 (99)
(99)где 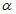 - угол падения пластов.
- угол падения пластов.
При расчетах принимается: m = 1, N1 = N2 = 1,  .
.
 .
.Вычисленные значения оседаний, наклонов, горизонтальных сдвижений и горизонтальных деформаций в точках полумульды по падению ГД = L1 выписываются под соответственными точками отрезка ВБ (см. рис. 19).
Для расчетов наклонов и горизонтальных деформаций от влияния разработки пластов на различных горизонтах зона АБВ разбивается горизонтальными отрезками, отстоящими друг от друга по вертикали на расстоянии 20 - 50 м. Для каждой глубины по формуле (100) вычисляются значения коэффициентов KH
где H - глубина рассматриваемого горизонта.
Значения коэффициентов выписываются около соответствующего положения горизонта (рис. 19).
полюс номограммы помещается в рассматриваемую точку поверхности (точка А на рис. 19);
намечается наиболее неблагоприятное положение горизонта относительно рассматриваемой точки А. Для этой цели находятся точки пересечения линий максимального влияния различных видов сдвижений и деформаций с верхним пластом каждой свиты. В свиту входят пласты, у которых расстояния по горизонтам между кровлей верхнего и почвой нижнего пласта не более 0,3HH, где HH - расстояние от точки пересечения линии максимального влияния с верхним пластом свиты до земной поверхности. Для пластов, которые входят в одну свиту, неблагоприятное положение горизонта определяется точкой пересечения соответствующей линии максимального влияния, проведенной из рассматриваемой точки А с верхним пластом свиты.
Линиями максимального влияния называются линии, соединяющие полюс номограммы и точку с максимальными сдвижениями или деформациями. На рис. 19 линия максимального влияния горизонтальных деформаций - А-6, линия максимального влияния наклонов - А-5, линия максимального влияния оседаний и горизонтальных сдвижений - А-1. Наиболее неблагоприятное положение горизонтов для расчетов горизонтальных деформаций (см. рис. 19) - ГД и ЕЖ, для расчета наклонов - ГД и ИК.
Суммарные вероятные значения сдвижений и деформаций на разрезе вкрест простирания для рассматриваемой точки поверхности А вычисляются по следующим формулам:
оседания
наклоны
горизонтальные сдвижения
 (103)
(103)горизонтальные деформации
Величины обратных уступов и величины раскрытия трещин для условий Донбасса определяются по формулам (107) и (108) разд. 8.
m1, m2, ..., mn - вынимаемые мощности пластов;
Величины сдвижений и деформаций  , i',
, i', 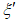 ,
, 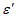 определяются по значениям указанных параметров на луче номограммы, соединяющем рассматриваемую точку с точкой пересечения пласта с наиболее неблагоприятным положением горизонта. Из полученных по формулам (101) - (104) величин сдвижений и деформаций используются их наибольшие значения при различных положениях горизонтов.
определяются по значениям указанных параметров на луче номограммы, соединяющем рассматриваемую точку с точкой пересечения пласта с наиболее неблагоприятным положением горизонта. Из полученных по формулам (101) - (104) величин сдвижений и деформаций используются их наибольшие значения при различных положениях горизонтов.
Если сдвижения и деформации в рассматриваемой точке от различных пластов при наиболее неблагоприятном положении горизонта имеют разные знаки, то для выбора мер защиты объектов используются отдельно суммарные сдвижения и деформации, имеющие положительные и отрицательные значения.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду второе перечисление настоящего пункта, а не пункт 2. |
В тех случаях, когда мощность пород между соседними свитами или группами пластов, определяемыми в соответствии с п. 2, больше, чем расстояние по вертикали между положением наиболее неблагоприятных горизонтов в указанных соседних свитах, для контроля выполняются расчеты вероятных сдвижений и деформаций при положении горизонтов, проходящих через точку пересечения соответствующих линий максимального влияния и середину междупластья.
В тех случаях, когда рассматриваемые пласты отработаны к моменту проектирования мер защиты объектов таким образом, что нижние границы выработок расположены на одном горизонте, а дальнейшая разработка пластов проектируется по горизонтам, расчеты сдвижений и деформаций выполняются следующим образом:
в соответствии с рекомендациями п. 2 определяются суммарные сдвижения и деформации SВ в рассматриваемой точке поверхности от влияния наиболее неблагоприятного положения горизонта (если сдвижения и деформации от отдельных пластов при неблагоприятном положении горизонта имеют разные знаки, то отдельно вычисляются суммарные положительные сдвижения и деформации 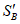 и суммарные отрицательные сдвижения и деформации -
и суммарные отрицательные сдвижения и деформации -  );
);
определяются суммарные сдвижения и деформации в рассматриваемой точке поверхности при отработке пластов до проектной глубины разработок Sпр (если сдвижения и деформации от различных пластов при их разработке до проектной глубины имеют разные знаки, то отдельно вычисляются суммарные положительные сдвижения и деформации - 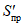 и суммарные отрицательные сдвижения и деформации -
и суммарные отрицательные сдвижения и деформации - 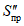 );
);
по номограмме в рассматриваемой точке поверхности рассчитываются суммарные сдвижения и деформации от влияния ранее отработанных (до проектирования мер защиты) участков пластов Sс;
находятся разности 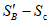 ,
, 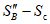 и
и 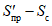 ,
,  , наибольшие из которых по абсолютной величине используются для проектирования мер защиты объектов;
, наибольшие из которых по абсолютной величине используются для проектирования мер защиты объектов;
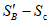 ,
, 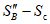 и
и 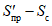 ,
,  , наибольшие из которых по абсолютной величине используются для проектирования мер защиты объектов;
, наибольшие из которых по абсолютной величине используются для проектирования мер защиты объектов;величины уступов в Донбассе рассчитываются с использованием наибольших значений наклонов, полученных в соответствии с изложенными рекомендациями.
В тех случаях, когда рассматриваемые пласты отработаны к моменту проектирования мер защиты до разных горизонтов, расчеты сдвижений и деформаций выполняются следующим образом:
по номограмме выполняются расчеты сдвижений и деформаций от влияния горных выработок, пройденных до момента проектирования мер защиты в каждом пласте 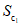 ,
, 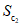 ,
, 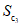 ,
,  ;
;
по номограмме выполняются расчеты сдвижений и деформаций при разработке пластов на различных горизонтах S1, S2, ..., Sn без учета влияния ранее отработанных участков пластов; если сдвижения и деформации от различных пластов имеют разные знаки, то отдельно вычисляются суммарные положительные 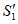 ,
, 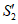 , ...,
, ..., 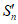 и суммарные отрицательные величины сдвижений и деформаций
и суммарные отрицательные величины сдвижений и деформаций  ,
, 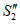 , ...,
, ..., 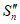 при положениях горных работ на различных горизонтах;
при положениях горных работ на различных горизонтах;
составляются разности между сдвижениями и деформациями 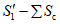 ;
; 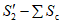 ; ...;
; ...; 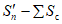 и
и  ;
; 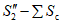 ; ...;
; ...;  , наибольшие из которых по абсолютной величине принимаются для выбора мер защиты объектов (где
, наибольшие из которых по абсолютной величине принимаются для выбора мер защиты объектов (где 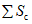 - суммарные сдвижения и деформации от влияния горных выработок, пройденных до проектирования мер защиты). Например (рис. 20), сдвижения и деформации от влияния выработок:
- суммарные сдвижения и деформации от влияния горных выработок, пройденных до проектирования мер защиты). Например (рис. 20), сдвижения и деформации от влияния выработок:
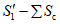 ;
; 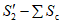 ; ...;
; ...; 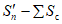 и
и  ;
; 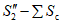 ; ...;
; ...;  , наибольшие из которых по абсолютной величине принимаются для выбора мер защиты объектов (где
, наибольшие из которых по абсолютной величине принимаются для выбора мер защиты объектов (где второго горизонта 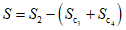 ;
;
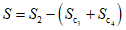 ;
;третьего горизонта 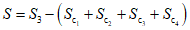 ,
,
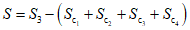 ,
,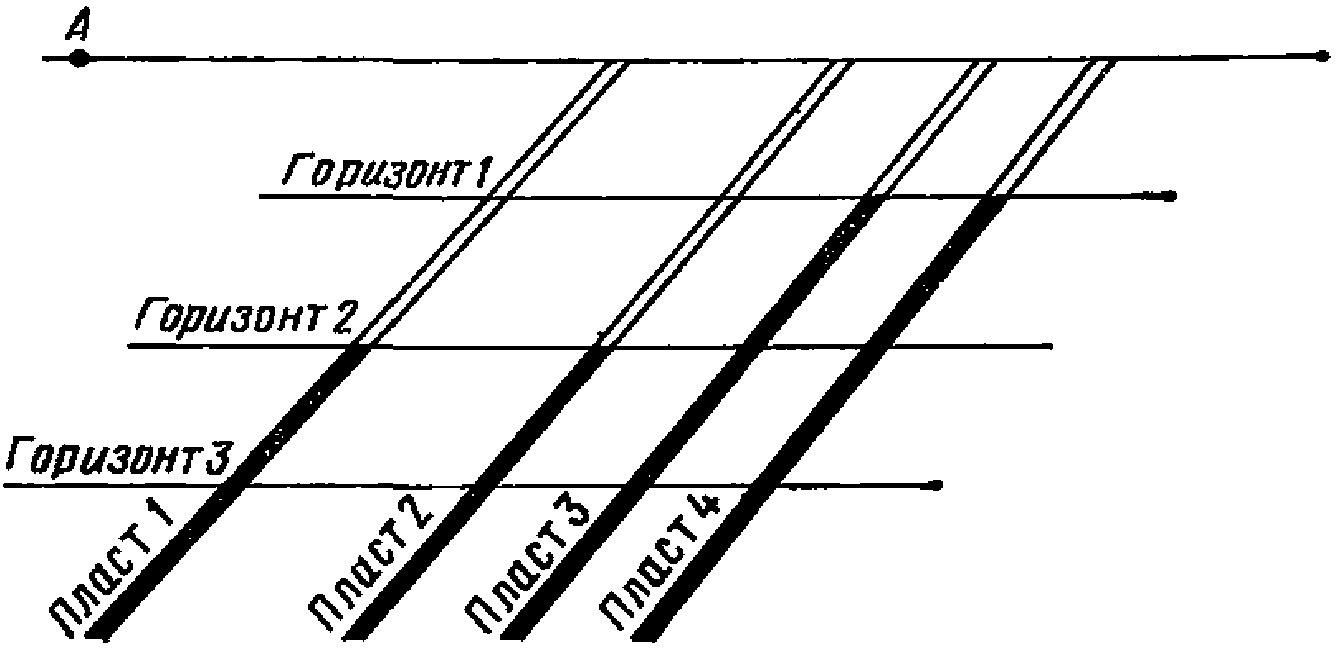
при работах прошлых лет на различных горизонтах
7.4. При ведении горных работ по горизонтам (пп. 7.2 и 7.3) величины вероятных сдвижений и деформаций по простиранию пластов определяются по формулам (90), (92), (94), (96), (98).
7.5. Если известно, что под рассматриваемым участком при разработке свиты пластов границы очистных выработок будут расположены примерно в одной плоскости, проведенной под соответствующим углом сдвижения или в одной вертикальной плоскости (например, у предохранительного целика, границы шахтного поля и т.п.), то расчет сдвижений и деформаций выполняется следующим образом (рис. 21).
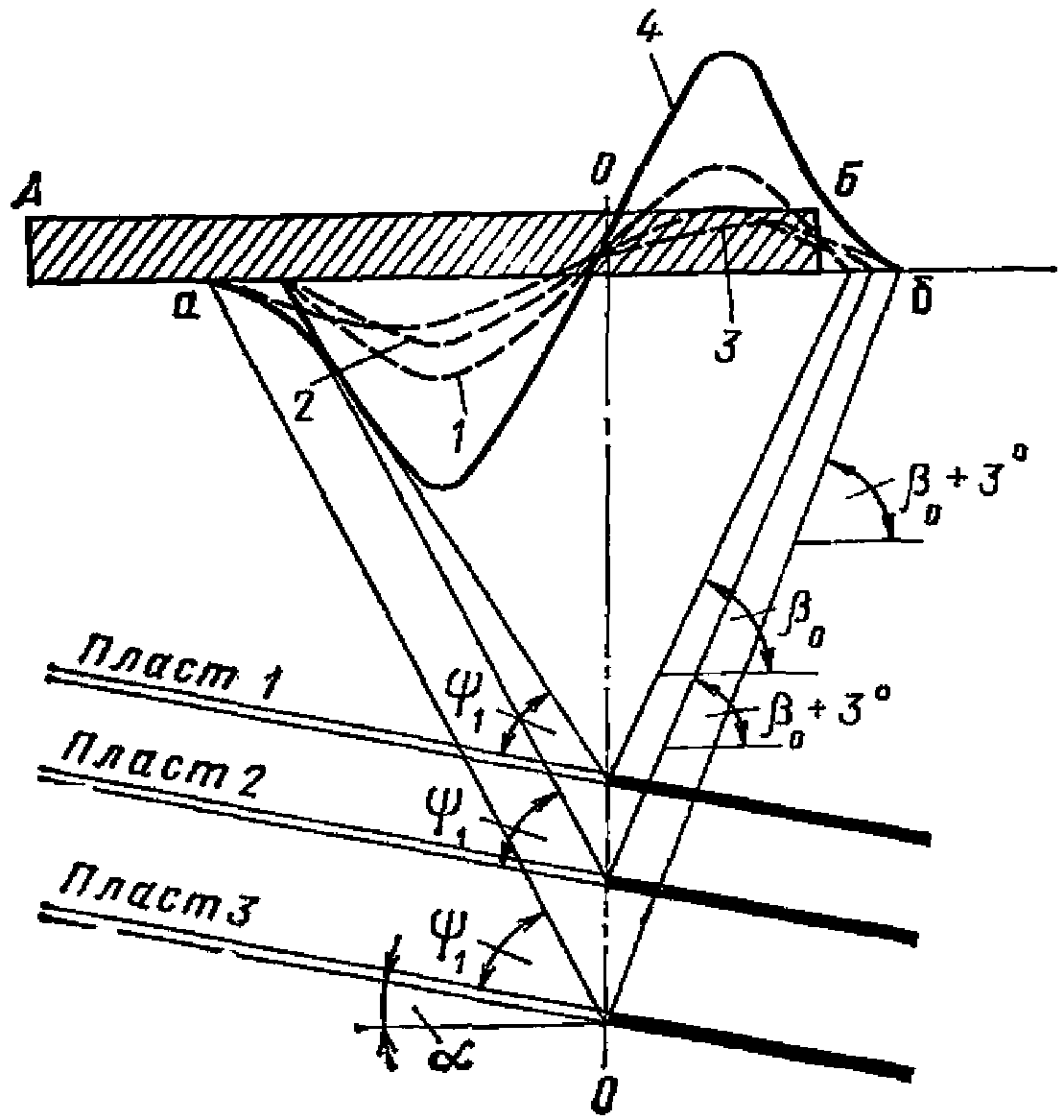
поверхности при расположении границ очистных выработок
в одной вертикальной плоскости
АБ - рассматриваемый участок земной поверхности;
00 - граница шахтного поля; 1 - горизонтальные деформации
при выемке пласта 1; 2 - то же, при выемке пласта 2;
3 - то же, при выемке пласта 3; 4 - суммарные
горизонтальные деформации при выемке пластов 1, 2 и 3
Все разрабатываемые пласты разделяются на группы в соответствии с п. 4.9. От каждого пласта группы устанавливаются границы влияния очистных выработок на земную поверхность с помощью граничных углов и углов полных сдвижений, определяемых по разд. 8 и п. 4.9. Для каждого пласта группы в пределах полученных размеров полумульд рассчитываются величины сдвижений и деформаций в соответствии с указаниями разд. 4 и алгебраически суммируются. Суммарные сдвижения и деформации для остальных групп пластов в свите определяются аналогично.
На участке, равном суммарному размеру полумульды от всех пластов свиты (см. рис. 21) в качестве вероятных сдвижений и деформаций принимаются наибольшие величины из полученных путем суммирования сдвижений и деформаций от выемки всех групп пластов.
На участке, расположенном за линией пересечения земной поверхности с плоскостью, проведенной под углом 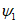 , от границы очистной выработки в нижнем пласте, вероятные сдвижения и деформации рассчитываются в соответствии с указаниями пп. 7.1 - 7.3.
, от границы очистной выработки в нижнем пласте, вероятные сдвижения и деформации рассчитываются в соответствии с указаниями пп. 7.1 - 7.3.
И ДЕФОРМАЦИЙ ЗЕМНОЙ ПОВЕРХНОСТИ
8.1. Граничные углы 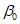 ,
, 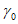 и
и  в неподработанной и подработанной толщах каменноугольных пород во всех районах, кроме Западного Донбасса и районов залегания углей марок ПА и А, принимаются равными:
в неподработанной и подработанной толщах каменноугольных пород во всех районах, кроме Западного Донбасса и районов залегания углей марок ПА и А, принимаются равными: 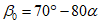 , но не менее 25° в неподработанной толще и 20° - в подработанной толще;
, но не менее 25° в неподработанной толще и 20° - в подработанной толще; 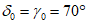 .
.
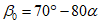 , но не менее 25° в неподработанной толще и 20° - в подработанной толще;
, но не менее 25° в неподработанной толще и 20° - в подработанной толще; 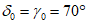 .
.В неподработанной толще каменноугольных пород в районах залегания углей марок ПА и А
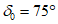 ,
,  , но не более 80°;
, но не более 80°; , но не менее 25°.
, но не менее 25°.В подработанной толще граничные углы в районах залегания углей марок ПА и А принимаются на 5° меньше, чем в неподработанной.
В Западном Донбассе в неподработанной и подработанной толщах каменноугольных пород граничные углы принимаются

Породы | ||
Наносы Донбасса | 55 | - |
Наносы Западного Донбасса | 45 | - |
Меловые отложения | - | 65 |
Примечание. При мощности мезостойких отложений менее 5 м углы 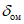 принимаются равными граничным углам в породах, залегающих под этими отложениями.
принимаются равными граничным углам в породах, залегающих под этими отложениями.
8.2. Углы максимального оседания  и полных сдвижений
и полных сдвижений 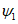 ,
, 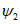 и
и 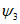 определяются в зависимости от угла падения пласта по табл. 24 (град).
определяются в зависимости от угла падения пласта по табл. 24 (град).
Условия применения | ||||
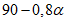 | 55 | 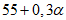 | 55 | |
 | 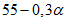 |  | 55 | Верхняя половина лавы и проведенная от ее верхней границы линия под углом |
 |  | 55 | Вся лава и проведенная от ее нижней границы линия под углом | |
90 | 55 | 55 | 55 | В толще меловых отложений |
Примечание: В подработанной толще значение угла  не должно быть менее
не должно быть менее 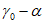 , а значение угла
, а значение угла 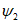 - величины
- величины 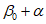 ; при мощности наносов или меловых отложений менее 0,2H их влияние на углы
; при мощности наносов или меловых отложений менее 0,2H их влияние на углы 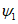 ,
, 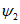 и
и 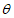 можно не учитывать.
можно не учитывать.

8.3. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 25.
q0 | a0 | Условия применения |
0,75 | 0,3 | В районах залегания углей марок ПА - А |
0,80 | 0,3 | В районах залегания углей марок Д - Г при мощности наносов менее 30% от глубины разработки и марок Ж, К, ОС, Т |
0,85 | 0,4 | В районах залегания углей марок Д - Г при мощности наносов 30% от глубины разработки и более |
При повторных подработках qоп определяется для всех районов Донбасса в зависимости от угла падения пластов
при 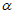 от 0 до 25°
от 0 до 25°
 (105)
(105)где Hср - расстояние по вертикали от середины выработки в разрабатываемом пласте до земной поверхности;
H1 - расстояние от земной поверхности до ранее отработанного пласта, измеренное по вертикали, проведенной через середину выработки в разрабатываемом пласте;
q0 - определяется по табл. 25;
при  от 26° до 70° qоп = 0,95.
от 26° до 70° qоп = 0,95.
Для расчета максимального оседания от ранее пройденных выработок (см. пп. 4.27 - 4.29) принимается qоп = 0,95.
8.4. Коэффициенты N1 и N2 определяются в зависимости от отношения расчетной длины лавы (Др) к средней глубине разработок (H) по табл. 26.
0,05 и менее | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 и более | |
N1 и N2 | 0,22 | 0,30 | 0,43 | 0,52 | 0,60 | 0,67 | 0,74 | 0,80 | 0,85 | 0,90 | 0,94 | 0,98 | 1,0 |
Примечание. При промежуточных значениях  значения N1 и N2 определяются путем интерполяции.
значения N1 и N2 определяются путем интерполяции.
Величина отношения расчетной длины лавы к средней глубине разработок определяется из выражения
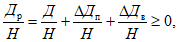 (106)
(106)где Д - фактическая длина лавы;
Значение поправок | ||||||
H, м | ||||||
100 и менее | 200 | 400 | 600 | 800 | 1000 и более | |
Марки угля ПА - А | ||||||
0 | 0,14 | 0,10 | 0,07 | 0,06 | 0,05 | 0,04 |
0,1 | 0,08 | 0,06 | 0,04 | 0,03 | 0,03 | 0,02 |
0,2 | 0,02 | 0,02 | 0,01 | 0,01 | 0,01 | 0,01 |
0,3 | -0,04 | -0,03 | -0,02 | -0,02 | -0,02 | -0,01 |
0,4 | -0,10 | -0,08 | -0,05 | -0,04 | -0,04 | -0,03 |
0,5 | -0,16 | -0,13 | -0,07 | -0,07 | -0,06 | -0,05 |
0,6 и более | -0,22 | -0,18 | -0,10 | -0,09 | -0,08 | -0,07 |
Значения поправок | ||||||
H, м | ||||||
100 и менее | 200 | 400 | 600 | 800 | 1000 и более | |
Марки угля Д - Г (при 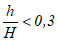 ), Ж, К, ОС, Т ), Ж, К, ОС, Т | ||||||
0 | 0,07 | 0,07 | 0,06 | 0,05 | 0,04 | 0,03 |
0,1 | 0,05 | 0,05 | 0,05 | 0,04 | 0,03 | 0,02 |
0,2 | 0,04 | 0,04 | 0,03 | 0,03 | 0,02 | 0,01 |
0,3 | 0,02 | 0,02 | 0,02 | 0,02 | 0,01 | 0,01 |
0,4 | 0 | 0 | 0 | 0 | 0 | 0 |
0,5 | -0,05 | -0,05 | -0,04 | -0,03 | -0,02 | -0,01 |
0,6 | -0,09 | -0,09 | -0,07 | -0,06 | -0,03 | -0,02 |
0,7 | -0,12 | -0,12 | -0,10 | -0,09 | -0,06 | -0,04 |
0,8 и более | -0,15 | -0,15 | -0,13 | -0,11 | -0,09 | -0,07 |
Марки угля Д - Г при  | ||||||
0 | 0,05 | 0,05 | 0,04 | 0,03 | 0,02 | 0,01 |
0,1 | 0,04 | 0,04 | 0,03 | 0,02 | 0,02 | 0 |
0,2 | 0,03 | 0,03 | 0,02 | 0,01 | 0,01 | 0 |
0,3 | 0,02 | 0,02 | 0,01 | 0,01 | 0 | 0 |
0,4 | 0 | 0 | 0 | 0 | 0 | 0 |
0,5 | -0,03 | -0,03 | -0,01 | -0,01 | -0,01 | 0 |
0,6 | -0,05 | -0,05 | -0,03 | -0,02 | -0,02 | 0 |
0,7 | -0,07 | -0,07 | -0,05 | -0,04 | -0,03 | 0 |
0,8 и более | -0,09 | -0,09 | -0,07 | -0,05 | -0,03 | -0,01 |
При определении поправок 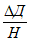 со стороны неотработанной части пласта в районах залегания углей марок ПА - А принимается
со стороны неотработанной части пласта в районах залегания углей марок ПА - А принимается  , в других районах -
, в других районах - 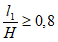 .
.
 , в других районах -
, в других районах - 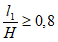 .
.При повторной подработке толщи в районах залегания углей марок ПА - А для определения  отрицательные значения поправок
отрицательные значения поправок 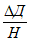 следует принимать уменьшенными по абсолютной величине в два раза по сравнению с приведенными в табл. 27.
следует принимать уменьшенными по абсолютной величине в два раза по сравнению с приведенными в табл. 27.
8.5. Значения функций S(z), F(z) и F'(z) определяются в зависимости от коэффициентов N и B по табл. 29 - 33.
z | Значения функции S(z) | |||
N >= 1 | N = 0,9 | N = 0,8 | N = 0,7 | |
0 | 1,00 | 1,00 | 1,00 | 1,00 |
0,1 | 0,99 | 0,98 | 0,97 | 0,96 |
0,2 | 0,95 | 0,90 | 0,85 | 0,83 |
0,3 | 0,86 | 0,77 | 0,69 | 0,65 |
0,4 | 0,71 | 0,58 | 0,48 | 0,46 |
0,5 | 0,50 | 0,39 | 0,31 | 0,29 |
0,6 | 0,29 | 0,22 | 0,17 | 0,16 |
0,7 | 0,14 | 0,10 | 0,08 | 0,08 |
0,8 | 0,05 | 0,04 | 0,03 | 0,03 |
0,9 | 0,01 | 0,01 | 0,01 | 0,01 |
1 | 0 | 0 | 0 | 0 |
Таблица 30
z | Значения функции F(z) (полумульда по падению пласта) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | 0,19 | 2,17 | 4,15 | 6,13 | 8,11 | 10,09 | 12,07 | 14,05 |
0,2 | 0,56 | 2,46 | 4,36 | 6,26 | 8,16 | 10,06 | 11,96 | 13,86 |
0,3 | 1,20 | 2,92 | 4,64 | 6,36 | 8,08 | 9,80 | 11,52 | 13,24 |
0,4 | 1,89 | 3,31 | 4,73 | 6,15 | 7,57 | 8,99 | 10,41 | 11,83 |
0,5 | 2,20 | 3,20 | 4,20 | 5,20 | 6,20 | 7,20 | 8,20 | 9,20 |
0,6 | 1,89 | 2,47 | 3,05 | 3,63 | 4,21 | 4,79 | 5,37 | 5,95 |
0,7 | 1,20 | 1,48 | 1,76 | 2,04 | 2,32 | 2,60 | 2,88 | 3,16 |
0,8 | 0,56 | 0,66 | 0,76 | 0,86 | 0,96 | 1,06 | 1,16 | 1,26 |
0,9 | 0,19 | 0,21 | 0,23 | 0,25 | 0,27 | 0,29 | 0,31 | 0,33 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | 0,47 | 2,42 | 4,39 | 6,35 | 8,31 | 10,27 | 12,23 | 14,19 |
0,2 | 1,02 | 2,82 | 4,63 | 6,43 | 8,24 | 10,04 | 11,84 | 13,64 |
0,3 | 1,61 | 3,16 | 4,71 | 6,26 | 7,80 | 9,33 | 10,88 | 12,43 |
0,4 | 1,98 | 3,15 | 4,32 | 5,49 | 6,67 | 7,83 | 9,00 | 10,17 |
0,5 | 1,92 | 2,71 | 3,50 | 4,30 | 5,08 | 5,87 | 6,66 | 7,45 |
0,6 | 1,46 | 1,91 | 2,35 | 2,80 | 3,25 | 3,70 | 4,14 | 4,59 |
0,7 | 0,87 | 1,07 | 1,27 | 1,48 | 1,68 | 1,88 | 2,09 | 2,29 |
0,8 | 0,42 | 0,50 | 0,58 | 0,66 | 0,74 | 0,82 | 0,90 | 0,98 |
0,9 | 0,15 | 0,18 | 0,19 | 0,21 | 0,23 | 0,25 | 0,27 | 0,28 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | 0,73 | 2,66 | 4,60 | 6,53 | 8,47 | 10,40 | 12,33 | 14,27 |
0,2 | 1,36 | 3,08 | 4,80 | 6,52 | 8,24 | 9,95 | 11,67 | 13,39 |
0,3 | 1,83 | 3,23 | 4,62 | 6,02 | 7,41 | 8,81 | 10,21 | 11,60 |
0,4 | 1,91 | 2,92 | 3,92 | 4,93 | 5,94 | 6,94 | 7,95 | 8,96 |
0,5 | 1,67 | 2,32 | 2,97 | 3,62 | 4,27 | 4,92 | 5,58 | 6,23 |
0,6 | 1,20 | 1,56 | 1,93 | 2,29 | 2,65 | 3,02 | 3,38 | 3,74 |
0,7 | 0,71 | 0,88 | 1,06 | 1,23 | 1,41 | 1,58 | 1,75 | 1,93 |
0,8 | 0,35 | 0,42 | 0,50 | 0,57 | 0,65 | 0,72 | 0,79 | 0,87 |
0,9 | 0,13 | 0,15 | 0,17 | 0,19 | 0,21 | 0,23 | 0,25 | 0,27 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,7 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | 0,91 | 2,83 | 4,74 | 6,66 | 8,58 | 10,50 | 12,41 | 14,33 |
0,2 | 1,59 | 3,25 | 4,90 | 6,56 | 8,22 | 9,88 | 11,53 | 13,19 |
0,3 | 1,90 | 3,20 | 4,50 | 5,80 | 7,10 | 8,40 | 9,69 | 10,99 |
0,4 | 1,85 | 2,77 | 3,68 | 4,60 | 5,52 | 6,44 | 7,35 | 8,27 |
0,5 | 1,49 | 2,07 | 2,65 | 3,23 | 3,81 | 4,38 | 4,96 | 5,54 |
0,6 | 1,04 | 1,36 | 1,68 | 2,00 | 2,32 | 2,64 | 2,96 | 3,28 |
0,7 | 0,62 | 0,78 | 0,94 | 1,10 | 1,26 | 1,42 | 1,58 | 1,74 |
0,8 | 0,32 | 0,38 | 0,44 | 0,50 | 0,56 | 0,62 | 0,68 | 0,74 |
0,9 | 0,12 | 0,14 | 0,16 | 0,18 | 0,20 | 0,22 | 0,24 | 0,26 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 31
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | -0,19 | 1,79 | 3,77 | 5,75 | 7,73 | 9,71 | 11,69 | 13,67 |
0,2 | -0,56 | 1,34 | 3,24 | 5,14 | 7,04 | 8,94 | 10,84 | 12,74 |
0,3 | -1,20 | 0,52 | 2,24 | 3,96 | 5,68 | 7,40 | 9,12 | 10,84 |
0,4 | -1,89 | -0,47 | 0,95 | 2,37 | 3,79 | 5,21 | 6,63 | 8,05 |
0,5 | -2,20 | -1,20 | -0,20 | 0,80 | 1,80 | 2,80 | 3,80 | 4,80 |
0,6 | -1,89 | -1,31 | -0,73 | -0,15 | 0,43 | 1,01 | 1,59 | 2,17 |
0,7 | -1,20 | -0,92 | -0,64 | -0,36 | -0,08 | 0,20 | 0,48 | 0,76 |
0,8 | -0,56 | -0,46 | -0,36 | -0,26 | -0,16 | -0,06 | 0,04 | 0,14 |
0,9 | -0,19 | -0,17 | -0,15 | -0,13 | -0,11 | -0,09 | -0,07 | -0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | -0,47 | 1,49 | 3,45 | 5,41 | 7,37 | 9,33 | 11,29 | 13,25 |
0,2 | -1,02 | 0,79 | 2,59 | 4,39 | 6,20 | 8,00 | 9,80 | 11,61 |
0,3 | -1,61 | -0,06 | 1,49 | 3,04 | 4,59 | 6,14 | 7,69 | 9,23 |
0,4 | -1,98 | -0,80 | 0,37 | 1,54 | 2,71 | 3,88 | 5,05 | 6,22 |
0,5 | -1,92 | -1,13 | -0,35 | 0,46 | 1,23 | 2,02 | 2,81 | 3,60 |
0,6 | -1,46 | -1,00 | -0,57 | -0,12 | 0,33 | 0,78 | 1,22 | 1,67 |
0,7 | -0,87 | -0,66 | -0,46 | -0,25 | -0,05 | 0,15 | 0,36 | 0,56 |
0,8 | -0,42 | -0,34 | -0,26 | -0,18 | -0,10 | -0,02 | 0,06 | 0,14 |
0,9 | -0,15 | -0,13 | -0,11 | -0,09 | -0,07 | -0,05 | -0,03 | -0,01 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | -0,73 | 1,20 | 3,13 | 5,07 | 7,00 | 8,94 | 10,87 | 12,81 |
0,2 | -1,36 | 0,36 | 2,08 | 3,79 | 5,51 | 7,23 | 8,94 | 10,66 |
0,3 | -1,83 | -0,40 | 1,00 | 2,40 | 3,80 | 5,20 | 6,60 | 8,00 |
0,4 | -1,91 | -0,90 | 0,10 | 1,11 | 2,11 | 3,12 | 4,13 | 5,13 |
0,5 | -1,67 | -1,02 | -0,37 | 0,28 | 0,93 | 1,58 | 2,24 | 2,89 |
0,6 | -1,20 | -0,84 | -0,47 | -0,11 | 0,25 | 0,62 | 0,98 | 1,34 |
0,7 | -0,71 | -0,54 | -0,36 | -0,19 | -0,01 | 0,16 | 0,33 | 0,51 |
0,8 | -0,35 | -0,28 | -0,20 | -0,13 | -0,05 | 0,02 | 0,09 | 0,17 |
0,9 | -0,13 | -0,11 | -0,09 | -0,07 | -0,05 | -0,03 | -0,01 | 0,01 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,7 | ||||||||
0 | 0 | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
0,1 | -0,91 | 1,01 | 2,93 | 4,85 | 6,77 | 8,69 | 10,60 | 12,52 |
0,2 | -1,59 | 0,07 | 1,73 | 3,39 | 5,05 | 6,72 | 8,38 | 10,04 |
0,3 | -1,90 | -0,60 | 0,69 | 1,99 | 3,29 | 4,59 | 5,88 | 7,18 |
0,4 | -1,85 | -0,93 | -1,01 | 0,91 | 1,83 | 2,75 | 3,66 | 4,58 |
0,5 | -1,49 | -0,91 | -0,34 | 0,24 | 0,82 | 1,40 | 1,97 | 2,55 |
0,6 | -1,04 | -0,72 | -0,40 | -0,08 | 0,24 | 0,56 | 0,89 | 1,21 |
0,7 | -0,62 | -0,46 | -0,30 | -0,14 | 0,02 | 0,18 | 0,34 | 0,50 |
0,8 | -0,32 | -0,26 | -0,20 | -0,14 | -0,08 | -0,02 | 0,04 | 0,10 |
0,9 | -0,12 | -0,10 | -0,08 | -0,06 | -0,04 | -0,02 | 0 | 0,02 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 32
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -2,1 | -1,7 | -1,3 | -1,0 | -0,6 | -0,2 | 0,2 | 0,6 |
0,2 | -5,1 | -4,0 | -2,9 | -1,7 | -0,6 | 0,5 | 1,6 | 2,8 |
0,3 | -7,3 | -4,9 | -2,5 | -0,1 | 2,3 | 4,7 | 7,1 | 9,5 |
0,4 | -5,7 | -1,9 | 1,9 | 5,6 | 9,4 | 13,2 | 17,0 | 20,8 |
0,5 | 0 | 4,4 | 8,8 | 13,2 | 17,6 | 22,0 | 26,4 | 30,8 |
0,6 | 5,7 | 9,5 | 13,3 | 17,0 | 20,8 | 24,6 | 28,4 | 32,2 |
0,7 | 7,3 | 9,7 | 12,1 | 14,5 | 16,9 | 19,3 | 21,7 | 24,1 |
0,8 | 5,1 | 6,2 | 7,3 | 8,5 | 9,6 | 10,7 | 11,8 | 13,0 |
0,9 | 2,1 | 2,5 | 2,9 | 3,2 | 3,6 | 4,0 | 4,4 | 4,8 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 |
0,1 | -5,0 | -4,1 | -3,2 | -2,2 | -1,4 | -0,4 | 0,6 | 1,5 |
0,2 | -6,1 | -4,0 | -1,9 | 0 | 2,1 | 4,1 | 6,2 | 8,1 |
0,3 | -5,3 | -2,0 | 1,1 | 4,4 | 7,6 | 10,8 | 14,1 | 17,2 |
0,4 | -1,8 | 2,2 | 6,1 | 10,1 | 14,0 | 18,0 | 22,0 | 25,9 |
0,5 | 2,9 | 6,7 | 10,5 | 14,5 | 18,3 | 22,1 | 25,9 | 29,9 |
0,6 | 5,7 | 8,6 | 11,6 | 14,4 | 17,4 | 20,3 | 23,2 | 26,1 |
0,7 | 5,6 | 7,3 | 9,0 | 10,8 | 12,5 | 14,2 | 16,0 | 17,7 |
0,8 | 3,7 | 4,5 | 5,3 | 6,2 | 7,0 | 7,8 | 8,7 | 9,6 |
0,9 | 1,5 | 1,8 | 2,1 | 2,4 | 2,7 | 3,1 | 3,4 | 3,7 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 |
0,1 | -7,0 | -5,5 | -4,1 | -2,6 | -1,1 | 0,3 | 1,7 | 3,2 |
0,2 | -5,6 | -2,9 | -0,1 | 2,6 | 5,3 | 8,0 | 10,8 | 13,5 |
0,3 | -3,0 | 0,6 | 4,2 | 7,8 | 11,3 | 14,9 | 18,5 | 22,1 |
0,4 | 0,7 | 4,5 | 8,4 | 12,2 | 16,1 | 19,9 | 23,8 | 27,6 |
0,5 | 3,9 | 7,2 | 10,6 | 13,9 | 17,2 | 20,5 | 23,9 | 27,2 |
0,6 | 5,1 | 7,5 | 9,9 | 12,3 | 14,7 | 17,1 | 19,5 | 21,9 |
0,7 | 4,4 | 5,8 | 7,2 | 8,6 | 10,0 | 11,5 | 12,9 | 14,3 |
0,8 | 2,8 | 3,5 | 4,2 | 4,9 | 5,6 | 6,3 | 7,0 | 7,7 |
0,9 | 1,2 | 1,5 | 1,7 | 2,0 | 2,2 | 2,5 | 2,7 | 3,0 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,7 | ||||||||
0 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 |
0,1 | -8,2 | -6,4 | -4,6 | -2,8 | -0,9 | 0,9 | 2,7 | 4,5 |
0,2 | -5,2 | -2,0 | 1,2 | 4,4 | 7 | 10,7 | 13,9 | 17,1 |
0,3 | -1,8 | 2,0 | 5,8 | 9,6 | 13,4 | 17,2 | 21,0 | 24,8 |
0,4 | 2,3 | 6,0 | 9,7 | 13,4 | 17,1 | 20,8 | 24,5 | 28,2 |
0,5 | 4,3 | 7,3 | 10,3 | 13,3 | 16,2 | 19,2 | 22,2 | 25,2 |
0,6 | 4,6 | 6,7 | 8,7 | 10,8 | 12,9 | 15,0 | 17,0 | 19,1 |
0,7 | 3,7 | 4,9 | 6,2 | 7,4 | 8,6 | 9,8 | 11,1 | 12,3 |
0,8 | 2,3 | 2,9 | 3,6 | 4,2 | 4,9 | 5,5 | 6,2 | 6,8 |
0,9 | 1,1 | 1,3 | 1,6 | 1,8 | 2,1 | 2,3 | 2,6 | 2,8 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -2,1 | -2,5 | -2,9 | -3,2 | -3,6 | -4,0 | -4,4 | -4,8 |
0,2 | -5,1 | -6,2 | -7,3 | -8,5 | -9,6 | -10,7 | -11,8 | -13,0 |
0,3 | -7,3 | -9,7 | -12,1 | -14,5 | -16,9 | -19,3 | -21,7 | -24,1 |
0,4 | -5,7 | -9,5 | -13,3 | -17,0 | -20,8 | -24,6 | -28,4 | -32,2 |
0,5 | 0 | -4,4 | -8,8 | -13,2 | -17,6 | -22,0 | -26,4 | -30,8 |
0,6 | 5,7 | 1,9 | -1,9 | -5,6 | -9,4 | -13,2 | -17,0 | -20,8 |
0,7 | 7,3 | 4,9 | 2,5 | 0,1 | -2,3 | -4,7 | -7,1 | -9,5 |
0,8 | 5,1 | 4,0 | 2,9 | 1,7 | 0,6 | -0,5 | -1,6 | -2,8 |
0,9 | 2,1 | 1,7 | 1,3 | 1,0 | 0,6 | 0,2 | -0,2 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 | -4,3 |
0,1 | -5,0 | -6,0 | -6,9 | -7,9 | -8,8 | -9,7 | -10,7 | -11,7 |
0,2 | -6,1 | -8,1 | -10,2 | -12,1 | -14,2 | -16,2 | -18,3 | -20,2 |
0,3 | -5,3 | -8,5 | -11,7 | -15,0 | -18,1 | -21,4 | -24,6 | -27,8 |
0,4 | -1,8 | -5,8 | -9,7 | -14,6 | -17,6 | -21,6 | -25,5 | -29,5 |
0,5 | 2,9 | -1,0 | -4,8 | -8,7 | -12,6 | -16,4 | -20,2 | -24,1 |
0,6 | 5,7 | 2,8 | -0,2 | -3,0 | -5,6 | -8,9 | -11,8 | -14,7 |
0,7 | 5,6 | 3,8 | 2,1 | 0,4 | -1,3 | -3,1 | -4,8 | -2,0 |
0,8 | 3,7 | 2,9 | 2,0 | 1,1 | 0,3 | -0,5 | -1,3 | -2,2 |
0,9 | 1,5 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 | -7,4 |
0,1 | -7,0 | -8,5 | -9,9 | -11,4 | -12,8 | -14,3 | -15,7 | -17,2 |
0,2 | -5,6 | -8,3 | -11,1 | -13,8 | -16,5 | -19,2 | -22,0 | -24,7 |
0,3 | -3,0 | -6,6 | -10,2 | -13,8 | -17,5 | -21,1 | -24,7 | -28,3 |
0,4 | 0,7 | -3,1 | -6,9 | -10,7 | -14,6 | -18,4 | -22,2 | -26,0 |
0,5 | 3,9 | 0,5 | -2,8 | -6,2 | -9,5 | -12,9 | -16,2 | -19,6 |
0,6 | 5,1 | 2,7 | 0,3 | -2,1 | -4,4 | -6,8 | -9,2 | -11,6 |
0,7 | 4,4 | 3,0 | 1,6 | 0,2 | -1,2 | -2,6 | -4,0 | -5,4 |
0,8 | 2,8 | 2,1 | 1,4 | 0,7 | 0 | -0,7 | -1,4 | -2,1 |
0,9 | 1,2 | 1,0 | 0,7 | 0,5 | 0,2 | 0 | -0,3 | -0,5 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,7 | ||||||||
0 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 | -9,4 |
0,1 | -8,2 | -10,0 | -11,9 | -13,7 | -15,5 | -17,3 | -19,1 | -20,9 |
0,2 | -5,2 | -8,4 | -11,5 | -14,7 | -17,9 | -21,0 | -24,2 | -27,4 |
0,3 | -1,8 | -5,6 | -9,4 | -13,2 | -17,0 | -20,8 | -24,6 | -28,4 |
0,4 | 2,3 | -1,4 | -5,0 | -8,7 | -12,4 | -16,1 | -19,8 | -23,5 |
0,5 | 4,3 | 1,3 | -1,7 | -4,7 | -7,6 | -10,6 | -13,6 | -16,6 |
0,6 | 4,6 | 2,6 | 0,5 | -1,6 | -3,7 | -5,8 | -7,8 | -9,9 |
0,7 | 3,7 | 2,4 | 1,2 | 0 | -1,3 | -2,5 | -3,8 | -5,0 |
0,8 | 2,3 | 1,7 | 1,1 | 0,4 | -0,3 | -0,9 | -1,5 | -2,2 |
0,9 | 1,1 | 0,8 | 0,6 | 0,4 | 0,1 | -0,1 | -0,4 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.6. Местоположение и высота обратных уступов (hу) в полумульде по падению при разработке двух и более пластов с углами падения  , величина раскрытия трещин в районе уступа (d) и наклон на участке между уступами (iу) определяются следующим образом:
, величина раскрытия трещин в районе уступа (d) и наклон на участке между уступами (iу) определяются следующим образом:
 , величина раскрытия трещин в районе уступа (d) и наклон на участке между уступами (iу) определяются следующим образом:
, величина раскрытия трещин в районе уступа (d) и наклон на участке между уступами (iу) определяются следующим образом:ожидаемая высота обратного уступа hу при известном положении горных работ рассчитывается по формуле
где lу - расстояние между уступами (определяется из наблюдений или принимается равным 30 м);
i2 - наибольшая величина ожидаемого наклона в районе уступа, рассчитанная на ту же стадию отработки пластов, что и уступы;
C2 - коэффициент, определяемый по табл. 34;
величина раскрытия трещин в районе уступа
где 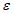 - ожидаемая деформация растяжения на интервале, где возможно возникновение уступа, определяемая в соответствии с указаниями разд. 4. При выемке нескольких пластов для определения d используются суммарные деформации
- ожидаемая деформация растяжения на интервале, где возможно возникновение уступа, определяемая в соответствии с указаниями разд. 4. При выемке нескольких пластов для определения d используются суммарные деформации 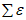 ;
;
наклон iу на участке между уступами определяется по формуле
 (109)
(109)где  - определяется по формуле (14);
- определяется по формуле (14);
местоположение уступов в плане устанавливается либо путем трассировки их с соседних участков шахтного поля, на которых они образовались во время очистных работ, либо путем инструментальных или визуальных наблюдений. В остальных случаях допускается, что уступы могут возникнуть на любом участке полумульды по падению;
вероятная максимальная высота обратных уступов на земной поверхности при отсутствии календарных планов и ведении горных работ определяется по формуле (107), в которой используются значения наклонов, определяемых по формуле (102) при 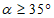 .
.
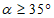 .
.Марки угля | C2 |
Д, Г, Ж | 1,0 |
К, ОС, Т | 0,6 |
ПА - А | 0,3 |
8.7. Период опасных деформаций от отдельной очистной выработки для всех районов бассейна, за исключением Западного Донбасса, в зависимости от средней глубины разработки Hср и скорости подвигания забоя принимается по табл. 35.
Hср, м | Скорость подвигания забоя, м/месяц | ||
30 | 50 | 70 и более | |
До 100 | 3 | 2 | 2 |
300 | 8 | 5 | 4 |
500 | 12 | 7 | 5 |
700 | 16 | 10 | 7 |
Для Западного Донбасса величины периода опасных деформаций, приведенные в табл. 35, следует увеличить в 1,3 раза.
При глубинах разработки свыше 700 м опасные деформации могут проявляться в течение двух лет.
8.8. Граничные углы 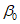 ,
, 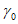 ,
,  и
и 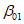 в неподработанной толще каменноугольных пород определяются по табл. 36 (град).
в неподработанной толще каменноугольных пород определяются по табл. 36 (град).
Угол падения | ||||
0 - 5 | 70 | 70 | 70 | - |
6 - 54 | 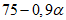 | 70 | 70 | - |
55 - 75 | 25 | - | 70 | 45 |
76 - 80 | 25 | - | 70 | 35 |
81 - 90 | 25 | - | 70 | 25 |
Примечания: 1. При глубине верхней границы выработки менее 50 м величины граничных углов  и
и 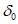 принимаются равными граничному углу в наносах
принимаются равными граничному углу в наносах 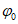 .
.
2. В подработанной толще пород значения граничных углов уменьшаются на 5°.
Граничные углы в наносах  определяются в зависимости от их обводненности по табл. 37 (град).
определяются в зависимости от их обводненности по табл. 37 (град).
Обводненность наносов | Обводненность наносов | ||
Сухие и нормальной влажности | 45 | Обводненные и плывуны | 30 |
Мощность мезозойских отложений hм, м |  | ||
До 100 | 45 | 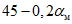 | 45 |
150 | 50 |  | 50 |
200 | 55 | 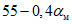 | 55 |
250 и более | 60 | 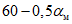 | 60 |
8.9. Углы максимального оседания  и полных сдвижений
и полных сдвижений 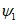 ,
,  и
и 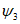 при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта по табл. 39.
при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта по табл. 39.
Углы | Значения углов |
 | |
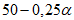 | |
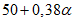 | |
50 |
8.10. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 при первичной и повторных подработках при отсутствии сдвижения пород лежачего бока определяются по табл. 40.
q0 | 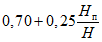 |
a0 | 0,25 |
Примечания: 1. Hп - мощность повторно подрабатываемых пород по линии, соединяющей точку максимального оседания земной поверхности с серединой очистной выработки, от которой производится расчет деформаций; H - мощность всей толщи по указанной линии.
2. Для расчета максимального оседания от ранее пройденных выработок относительное максимальное оседание qоп = 0,95.
8.11. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки (Д) к средней глубине разработки (H) по табл. 41.
1,6 и более | 1,4 | 1,2 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 и менее | |
N1 и N2 | 1,0 | 0,92 | 0,85 | 0,78 | 0,69 | 0,65 | 0,60 | 0,55 | 0,49 | 0,43 |
Примечание. При промежуточных значениях 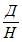 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.12. Значения функций S(z), F(z) и F'(z) при отсутствии сдвижения пород лежачего бока определяются в зависимости от коэффициентов N и B по табл. 42 - 46.
z | Значения функции S(z) | |||
N >= 1 | N = 0,9 | N = 0,8 | N <= 0,7 | |
0 | 1,00 | 1,00 | 1,00 | 1,00 |
0,1 | 0,99 | 0,97 | 0,96 | 0,96 |
0,2 | 0,95 | 0,89 | 0,85 | 0,83 |
0,3 | 0,86 | 0,74 | 0,68 | 0,65 |
0,4 | 0,66 | 0,55 | 0,49 | 0,46 |
0,5 | 0,38 | 0,32 | 0,31 | 0,29 |
0,6 | 0,17 | 0,16 | 0,16 | 0,16 |
0,7 | 0,07 | 0,08 | 0,08 | 0,08 |
0,8 | 0,03 | 0,03 | 0,03 | 0,03 |
0,9 | 0,01 | 0,01 | 0,01 | 0,01 |
1,0 | 0 | 0 | 0 | 0 |
Таблица 43
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициентов B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,2 | 2,2 | 4,6 | 6,4 | 8,2 | 10,2 | 12,1 | 14,1 |
0,2 | 0,5 | 2,5 | 4,5 | 6,3 | 8,2 | 10,1 | 12,0 | 13,9 |
0,3 | 1,6 | 3,2 | 4,9 | 6,6 | 8,4 | 10,0 | 11,8 | 13,5 |
0,4 | 2,6 | 3,6 | 5,1 | 6,5 | 7,9 | 9,4 | 10,8 | 12,2 |
0,5 | 2,3 | 3,6 | 4,6 | 5,6 | 6,6 | 7,6 | 8,6 | 9,6 |
0,6 | 1,5 | 2,8 | 3,4 | 4,0 | 4,6 | 5,2 | 5,8 | 6,3 |
0,7 | 0,6 | 1,7 | 2,0 | 2,3 | 2,5 | 2,8 | 3,1 | 3,4 |
0,8 | 0,3 | 0,8 | 0,8 | 0,9 | 1,1 | 1,2 | 1,3 | 1,4 |
0,9 | 0,1 | 0,2 | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,4 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,6 | 2,5 | 4,5 | 6,4 | 8,4 | 10,4 | 12,3 | 14,3 |
0,2 | 1,1 | 3,1 | 4,9 | 6,7 | 8,5 | 10,3 | 12,1 | 13,9 |
0,3 | 1,7 | 3,4 | 5,0 | 6,6 | 8,1 | 9,6 | 11,2 | 12,7 |
0,4 | 2,2 | 3,6 | 4,7 | 5,9 | 7,0 | 8,2 | 9,4 | 10,6 |
0,5 | 2,0 | 3,1 | 3,9 | 4,7 | 5,4 | 6,2 | 7,0 | 7,8 |
0,6 | 1,2 | 2,2 | 2,6 | 3,1 | 3,5 | 4,0 | 4,4 | 4,8 |
0,7 | 0,7 | 1,2 | 1,4 | 1,6 | 1,9 | 2,1 | 2,2 | 2,4 |
0,8 | 0,3 | 0,6 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,0 |
0,9 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,3 | 0,3 | 0,3 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,7 | 2,6 | 4,7 | 6,6 | 8,6 | 10,5 | 12,4 | 14,4 |
0,2 | 1,4 | 3,3 | 5,1 | 6,8 | 8,5 | 10,2 | 12,0 | 13,7 |
0,3 | 1,8 | 3,5 | 5,0 | 6,4 | 7,8 | 9,2 | 10,6 | 12,0 |
0,4 | 2,0 | 3,3 | 4,4 | 5,4 | 6,5 | 7,5 | 8,5 | 9,6 |
0,5 | 1,7 | 2,8 | 3,5 | 4,1 | 4,8 | 5,5 | 6,2 | 6,8 |
0,6 | 1,1 | 1,9 | 2,4 | 2,7 | 3,1 | 3,4 | 3,8 | 4,2 |
0,7 | 0,7 | 1,1 | 1,3 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
0,8 | 0,3 | 0,5 | 0,6 | 0,6 | 0,7 | 0,8 | 0,9 | 0,9 |
0,9 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,3 | 0,3 | 0,3 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,7 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,8 | 2,8 | 4,9 | 6,8 | 8,7 | 10,6 | 12,6 | 14,5 |
0,2 | 1,6 | 3,6 | 5,2 | 6,9 | 8,5 | 10,2 | 11,9 | 13,5 |
0,3 | 1,9 | 3,6 | 4,9 | 6,2 | 7,5 | 8,8 | 10,1 | 11,4 |
0,4 | 1,8 | 3,1 | 4,0 | 5,0 | 5,9 | 6,8 | 7,7 | 8,6 |
0,5 | 1,4 | 2,4 | 3,0 | 3,6 | 4,2 | 4,8 | 5,4 | 5,9 |
0,6 | 1,0 | 1,6 | 2,1 | 2,4 | 2,6 | 2,9 | 3,2 | 3,5 |
0,7 | 0,7 | 0,9 | 1,1 | 1,2 | 1,4 | 1,6 | 1,7 | 1,9 |
0,8 | 0,3 | 0,5 | 0,6 | 0,6 | 0,6 | 0,7 | 0,8 | 0,8 |
0,9 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,3 | 0,3 | 0,3 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 44
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициентов B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,2 | 1,8 | 3,7 | 5,7 | 7,7 | 10,0 | 12,4 | 14,0 |
0,2 | 0,5 | 1,3 | 3,2 | 5,1 | 6,9 | 8,8 | 10,7 | 12,6 |
0,3 | 1,6 | 0,3 | 2,0 | 3,8 | 5,5 | 7,2 | 8,9 | 10,6 |
0,4 | 2,6 | -0,8 | 0,6 | 2,0 | 3,4 | 4,7 | 6,2 | 7,7 |
0,5 | 2,3 | -1,6 | -0,6 | 0,4 | 1,4 | 2,4 | 3,4 | 4,4 |
0,6 | 1,5 | -1,6 | -1,0 | -0,5 | 0,1 | 0,7 | 1,3 | 1,8 |
0,7 | 0,6 | -1,2 | -0,9 | -0,6 | -0,4 | -0,05 | 0,2 | 0,5 |
0,8 | 0,3 | -0,5 | -0,5 | -0,4 | -0,2 | -0,1 | 0 | 0,1 |
0,9 | 0,1 | -0,2 | -0,2 | -0,2 | -0,2 | -0,1 | -0,1 | -0,1 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,6 | 1,4 | 3,4 | 5,3 | 7,3 | 9,2 | 11,2 | 13,2 |
0,2 | 1,1 | 0,5 | 2,3 | 4,1 | 5,9 | 7,7 | 9,5 | 11,3 |
0,3 | 1,7 | -0,4 | 1,2 | 2,7 | 4,3 | 5,8 | 7,4 | 8,9 |
0,4 | 2,2 | -1,2 | -0,1 | 1,1 | 2,2 | 3,4 | 4,6 | 5,7 |
0,5 | 2,0 | -1,5 | -0,7 | 0,1 | 0,8 | 1,6 | 2,3 | 3,1 |
0,6 | 1,2 | -1,3 | -0,9 | -0,1 | -0,01 | 0,4 | 0,9 | 1,3 |
0,7 | 0,7 | -0,8 | -0,6 | -0,4 | -0,2 | -0,04 | 0,2 | 0,4 |
0,8 | 0,3 | -0,4 | -0,3 | -0,3 | -0,2 | -0,1 | 0 | 0,1 |
0,9 | 0,2 | -0,2 | -0,2 | -0,1 | -0,1 | -0,04 | 0 | 0 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,7 | 1,1 | 3,1 | 5,0 | 6,9 | 8,9 | 10,8 | 12,7 |
0,2 | 1,4 | 0,2 | 1,9 | 3,6 | 5,3 | 7,0 | 10,1 | 10,5 |
0,3 | 1,8 | -0,7 | 0,8 | 2,2 | 3,6 | 5,0 | 6,4 | 7,8 |
0,4 | 2,0 | -1,3 | -0,2 | 0,7 | 1,9 | 2,9 | 3,9 | 5,0 |
0,5 | 1,7 | -1,4 | -0,7 | -0,04 | 0,6 | 1,3 | 2,0 | 2,7 |
0,6 | 1,1 | -1,1 | -0,7 | -0,4 | 0,03 | 0,4 | 0,8 | 1,2 |
0,7 | 0,6 | -0,7 | -0,5 | -0,4 | -0,2 | 0,02 | 0,2 | 0,4 |
0,8 | 0,3 | -0,4 | -0,3 | -0,2 | -0,2 | -0,1 | 0,1 | 0,1 |
0,9 | 0,2 | -0,2 | -0,2 | -0,1 | -0,1 | 0 | 0 | 0 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,7 | ||||||||
0 | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 |
0,1 | 0,8 | 0,8 | 2,8 | 4,7 | 6,6 | 8,5 | 10,4 | 12,4 |
0,2 | 1,6 | -0,1 | 1,4 | 3,0 | 4,7 | 6,4 | 8,04 | 9,6 |
0,3 | 1,9 | -1,0 | 0,3 | 1,6 | 2,9 | 4,2 | 5,5 | 6,8 |
0,4 | 1,8 | -1,3 | -0,4 | 0,4 | 1,5 | 2,4 | 3,3 | 4,2 |
0,5 | 1,4 | -1,3 | -0,7 | -0,1 | 0,5 | 1,1 | 1,6 | 2,2 |
0,6 | 1,0 | -0,9 | -0,6 | -0,3 | 0,1 | 0,4 | 0,7 | 1,0 |
0,7 | 0,6 | -0,6 | -0,4 | -0,3 | -0,1 | 0,1 | 0,2 | 0,4 |
0,8 | 0,3 | -0,3 | -0,2 | -0,2 | -0,2 | 0 | 0,1 | 0,1 |
0,9 | 0,2 | -0,2 | -0,2 | -0,1 | -0,1 | 0 | 0 | 0 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 45
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициентов B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -2,3 | -2,2 | -1,8 | -1,4 | -1,0 | -0,7 | -0,3 | 0,1 |
0,2 | -5,6 | -5,1 | -3,9 | -2,8 | -1,7 | -0,5 | 0,6 | 1,7 |
0,3 | -10,8 | -6,3 | -3,9 | -1,5 | 0,9 | 3,3 | 5,7 | 8,1 |
0,4 | -8,0 | -3,1 | 0,7 | 4,5 | 8,2 | 12,0 | 15,8 | 19,6 |
0,5 | 6,8 | 4,4 | 8,8 | 13,2 | 17,6 | 21,6 | 25,6 | 30,4 |
0,6 | 11,0 | 10,7 | 14,5 | 18,2 | 22,0 | 25,8 | 29,6 | 33,4 |
0,7 | 6,0 | 11,1 | 13,5 | 15,9 | 18,3 | 20,7 | 23,1 | 25,5 |
0,8 | 2,0 | 7,3 | 8,4 | 9,5 | 10,7 | 11,8 | 12,9 | 14,0 |
0,9 | 1,0 | 3,0 | 3,4 | 3,7 | 4,1 | 4,4 | 4,8 | 5,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -4,5 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 |
0,1 | -5,5 | -5,3 | -4,3 | -3,4 | -2,4 | -1,4 | -0,5 | 1,0 |
0,2 | -6,5 | -5,2 | -3,1 | -1,0 | 1,1 | 3,1 | 5,2 | 7,3 |
0,3 | -6,0 | -3,0 | 0,2 | 3,5 | 6,8 | 10,0 | 13,3 | 16,6 |
0,4 | -2,5 | 2,1 | 6,1 | 10,0 | 14,0 | 18,0 | 21,9 | 25,9 |
0,5 | 8,0 | 7,4 | 11,2 | 15,0 | 18,9 | 22,7 | 26,6 | 30,8 |
0,6 | 6,5 | 9,7 | 12,6 | 15,4 | 18,3 | 21,2 | 24,1 | 27,0 |
0,7 | 4,5 | 8,2 | 9,9 | 11,6 | 13,4 | 15,1 | 16,8 | 18,5 |
0,8 | 2,5 | 5,0 | 5,8 | 6,7 | 7,5 | 8,4 | 9,2 | 10,0 |
0,9 | 1,0 | 2,0 | 2,4 | 2,7 | 2,9 | 3,3 | 3,6 | 3,9 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,8 | ||||||||
0 | -6,4 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 |
0,1 | -6,8 | -6,7 | -5,3 | -3,9 | -2,5 | -1,2 | 0,2 | 1,8 |
0,2 | -6,2 | -4,2 | -1,5 | 1,1 | 3,7 | 6,4 | 9,0 | 11,6 |
0,3 | -3,5 | -0,4 | 3,1 | 6,7 | 10,2 | 13,8 | 17,3 | 20,8 |
0,4 | -0,42 | 4,3 | 8,1 | 11,9 | 15,8 | 19,6 | 23,4 | 27,3 |
0,5 | 6,0 | 7,8 | 11,2 | 14,7 | 18,2 | 21,5 | 24,9 | 28,5 |
0,6 | 5,1 | 8,7 | 11,1 | 13,6 | 16,1 | 18,8 | 21,1 | 23,6 |
0,7 | 3,7 | 7,0 | 8,4 | 9,9 | 11,4 | 12,9 | 14,3 | 15,8 |
0,8 | 2,2 | 4,2 | 4,9 | 5,7 | 6,4 | 7,2 | 7,9 | 8,5 |
0,9 | 1,1 | 1,7 | 2,0 | 2,3 | 2,5 | 2,8 | 3,1 | 3,4 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,7 | ||||||||
0 | -8,3 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 |
0,1 | -8,0 | -8,1 | -6,3 | -4,5 | -2,7 | -0,9 | 0,9 | 2,7 |
0,2 | -5,9 | -3,1 | 0,1 | 3,2 | 0,4 | 9,6 | 12,7 | 15,9 |
0,3 | -1,0 | 2,2 | 6,0 | 9,9 | 13,7 | 17,5 | 21,3 | 25,1 |
0,4 | 3,4 | 6,4 | 10,1 | 13,8 | 17,5 | 21,3 | 25,0 | 28,6 |
0,5 | 4,0 | 8,2 | 11,2 | 14,3 | 17,4 | 20,4 | 23,3 | 26,3 |
0,6 | 3,6 | 7,7 | 9,7 | 11,8 | 13,9 | 16,0 | 18,1 | 20,2 |
0,7 | 2,9 | 5,7 | 6,9 | 8,2 | 9,4 | 10,6 | 11,9 | 13,1 |
0,8 | 2,0 | 3,4 | 4,0 | 4,7 | 5,3 | 6,0 | 6,6 | 7,0 |
0,9 | 1,2 | 1,4 | 1,7 | 1,9 | 2,2 | 2,4 | 2,6 | 2,9 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||||||
Значения коэффициентов B | ||||||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
N >= 1 | ||||||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
0,1 | -2,3 | -3,0 | -3,4 | -3,7 | -4,1 | -4,4 | -4,8 | -5,2 | ||||
0,2 | -5,6 | -7,3 | -8,4 | -9,5 | -10,7 | -11,8 | -12,9 | -14,0 | ||||
0,3 | -10,8 | -11,1 | -13,5 | -15,9 | -18,3 | -20,7 | -23,1 | -25,5 | ||||
0,4 | -8,0 | -10,7 | -14,5 | -18,2 | -22,0 | -25,8 | -29,6 | -33,4 | ||||
0,5 | 6,8 | -4,4 | -8,8 | -13,2 | -17,6 | -21,6 | -25,6 | -30,4 | ||||
0,6 | 11,0 | 3,1 | 0,7 | -3,7 | -8,0 | -11,9 | -15,8 | -19,6 | ||||
0,7 | 6,0 | 6,3 | 3,9 | 1,5 | -0,9 | -3,3 | -5,7 | -8,1 | ||||
0,8 | 2,0 | 5,0 | 3,9 | 2,8 | 1,6 | 0,5 | -0,6 | -1,7 | ||||
0,9 | 1,0 | 2,2 | 1,8 | 1,4 | 1,0 | 0,7 | 0,3 | -0,1 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
N = 0,9 | ||||||||||||
0 | -4,5 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 | -5,4 | ||||
0,1 | -5,5 | -7,2 | -8,2 | -9,1 | -10,1 | -11,0 | -12,0 | -13,0 | ||||
0,2 | -6,5 | -9,4 | -11,4 | -13,6 | -15,6 | -17,7 | -19,8 | -21,8 | ||||
0,3 | -6,0 | -9,5 | -12,7 | -16,0 | -19,2 | -22,5 | -25,8 | -29,0 | ||||
0,4 | -2,5 | -5,8 | -9,8 | -13,4 | -17,0 | -21,3 | -25,6 | -29,6 | ||||
0,5 | 8,0 | -0,2 | -4,0 | -7,8 | -11,7 | -15,5 | -19,4 | -23,6 | ||||
0,6 | 6,5 | 3,9 | 1,0 | -1,8 | -4,7 | -7,6 | -10,5 | -13,4 | ||||
0,7 | 4,5 | 4,9 | 3,2 | 1,5 | -0,3 | -2,0 | -3,7 | -5,4 | ||||
0,8 | 2,5 | 3,4 | 2,6 | 1,8 | 1,0 | 0,1 | -0,7 | -1,5 | ||||
0,9 | 1,0 | 1,5 | 1,1 | 0,9 | 0,6 | 0,3 | -0,1 | -0,4 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
N = 0,8 | ||||||||||||
0 | -6,4 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 | -8,3 | ||||
0,1 | -6,8 | -9,5 | -10,9 | -12,2 | -13,6 | -15,0 | -16,3 | -17,7 | ||||
0,2 | -6,2 | -9,4 | -12,1 | -14,6 | -17,3 | -19,9 | -22,3 | -25,0 | ||||
0,3 | -3,5 | -7,4 | -10,9 | -14,5 | -18,0 | -21,6 | -25,1 | -28,6 | ||||
| ||||||||||||
0,4 | -0,4 | -3,4 | -7,2 | -10,9 | -14,6 | -18,6 | -22,6 | -26,! | ||||
0,5 | 6,0 | 1,0 | -2,4 | -5,9 | -9,4 | -12,7 | -16,1 | -19,7 | ||||
0,6 | 5,1 | 3,7 | 1,2 | -1,2 | -3,7 | -6,2 | -8,7 | -11,2 | ||||
0,7 | 3,7 | 4,0 | 2,6 | 1,1 | -0,4 | -1,9 | -3,3 | -4,8 | ||||
0,8 | 2,2 | 2,8 | 2,1 | 1,4 | 0,6 | -0,1 | -0,9 | -1,6 | ||||
0,9 | 1,1 | 1,3 | 1,0 | 0,7 | 0,5 | 0,2 | -0,1 | -0,4 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
N <= 0,7 | ||||||||||||
0 | -8,3 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 | -11,2 | ||||
0,1 | -8,0 | -11,9 | -13,4 | -15,3 | -17,1 | -18,9 | -20,7 | -22,5 | ||||
0,2 | -5,9 | -9,4 | -12,6 | -15,7 | -18,9 | -21,9 | -24,8 | -28,2 | ||||
0,3 | -1,0 | -5,4 | -9,2 | -13,0 | -16,8 | -20,6 | -24,4 | -28,2 | ||||
0,4 | 3,4 | -1,0 | -4,6 | -8,4 | -12,1 | -15,8 | -19,5 | -23,2 | ||||
0,5 | 4,0 | 2,2 | -0,8 | -3,9 | -7,0 | -10,0 | -12,9 | -15,9 | ||||
0,6 | 3,6 | 3,5 | 1,4 | -0,6 | -2,7 | -4,8 | -6,9 | -9,0 | ||||
0,7 | 2,9 | 3,2 | 2,0 | 0,7 | -0,5 | -1,8 | -3,0 | -4,2 | ||||
0,8 | 2,0 | 2,2 | 1,6 | 0,9 | 0,3 | -0,3 | -1,0 | -1,6 | ||||
0,9 | 1,2 | 1,0 | 0,8 | 0,6 | 0,3 | -0,1 | -0,2 | -0,4 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
8.13. Углы максимального оседания 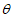 и максимальных горизонтальных сдвижений
и максимальных горизонтальных сдвижений 
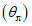 при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 47 (град).
при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 47 (град).
55 | 48 | 48 | 45 |
60 | 50 | 50 | 50 |
70 | 55 | 55 | 55 |
80 | 72 | 67 | 60 |
90 | 90 | 60 | 60 |
Примечание. Для промежуточных значений  углы
углы 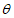 ,
,  и
и  определяются интерполированием.
определяются интерполированием.
8.14. Максимальное оседание при выемке пластов с закладкой выработанного пространства определяется по формуле
 (110)
(110)где Kа - коэффициент, учитывающий активизацию процесса сдвижения горных пород при повторных подработках, определяется по табл. 48;
K3, n1 и n2 - определяются в соответствии с п. 5.4.
Условия подработки на отрабатываемом горизонте (этаже) | Значения коэффициента Kа | |
Пласты на верхних горизонтах (этажах) | ||
не отработаны | отработаны системами с обрушением кровля | |
Первичная | 0,9 | 1,3 |
Повторная | 1,1 | 1,5 |
Эффективная мощность mэ определяется по формуле
mэ = Kр[hк(1 - B1) + B1m], м, (111)
где Kр - коэффициент, определяемый по табл. 49, в зависимости от применяемой системы разработки и вида закладки;
hк - величина сближения кровли с почвой (конвергенция) в зоне опорного давления и на участках между забоем и закладкой, при отсутствии инструментальных данных hк определяется из выражения hк = 0,5B1m;
m - вынимаемая мощность пласта, м;
B1 - коэффициент усадки закладки, определяемый по фактическим данным, а при отсутствии таких данных - по табл. 50 в зависимости от глубины горных работ и угла падения пласта.
Схема разработки | Направление выемки пластов | Вид закладки | Kр |
Поперечно-наклонные и горизонтальные слои | По восстанию | Гидравлическая | 0,7 |
Комбинация поперечно-наклонных, горизонтальных и наклонных слоев | То же | " | 0,8 |
По простиранию | Самотечная | 1,2 | |
Наклонные слои: | |||
короткие полосы | По восстанию | Гидравлическая | 1,3 |
длинные полосы | По простиранию | " | 1,4 |
Самотечная | 1,5 | ||
Щитовая | По падению | " | 1,6 |
Закладочный материал | Коэффициенты усадки закладки B | |||||||||||||||||
Углы падения, град | ||||||||||||||||||
50 | 70 | 90 | ||||||||||||||||
Глубина горных работ, м | ||||||||||||||||||
100 | 200 | 300 | 400 | 500 | 600 | 100 | 200 | 300 | 400 | 500 | 600 | 100 | 200 | 300 | 400 | 500 | 600 | |
Дробленые породы Кузнецкой свиты кл. 0 - 80 мм | 0,235 | 0,280 | 0,300 | 0,315 | 0,330 | 0,335 | 0,220 | 0,270 | 0,290 | 0,305 | 0,320 | 0,330 | 0,215 | 0,265 | 0,285 | 0,300 | 0,310 | 0,325 |
Дробленые горелые породы кл. 0 - 10 мм | 0,070 | 0,102 | 0,125 | 0,141 | 0,159 | 0,173 | 0,065 | 0,090 | 0,111 | 0,130 | 0,143 | 0,158 | 0,060 | 0,083 | 0,107 | 0,125 | 0,138 | 0,150 |
Дробленые песчаники кл. 0 - 10 мм | 0,080 | 0,109 | 0,130 | 0,149 | 0,165 | 0,180 | 0,075 | 0,100 | 0,120 | 0,137 | 0,153 | 0,164 | 0,073 | 0,097 | 0,115 | 0,130 | 0,147 | 0,159 |
Песок ижморский (глинистых частиц) 2 - 12% | 0,031 | 0,030 | 0,064 | 0,075 | 0,085 | 0,093 | 0,028 | 0,045 | 0,056 | 0,068 | 0,076 | 0,085 | 0,025 | 0,042 | 0,053 | 0,064 | 0,072 | 0,080 |
Песок бийский | 0,017 | 0,027 | 0,035 | 0,042 | 0,046 | 0,050 | 0,014 | 0,023 | 0,031 | 0,037 | 0,043 | 0,046 | 0,012 | 0,022 | 0,030 | 0,035 | 0,041 | 0,044 |
Шихта N 1: песок (50%); дробленые породы Кузнецкой свиты кл. 0 - 60 мм (50%) | 0,048 | 0,073 | 0,090 | 0,102 | 0,114 | 0,126 | 0,043 | 0,066 | 0,082 | 0,095 | 0,104 | 0,112 | 0,038 | 0,063 | 0,078 | 0,090 | 0,100 | 0,109 |
Шихта N 2: дробленые горелые породы кл. 0 - 10 мм (50%) и дробленые породы Кузнецкой свиты кл. 0 - 60 мм (50%) | 0,120 | 0,153 | 0,172 | 0,181 | 0,188 | 0,191 | 0,105 | 0,143 | 0,162 | 0,174 | 0,182 | 0,188 | 0,100 | 0,140 | 0,157 | 0,172 | 0,179 | 0,185 |
Упрочненная закладка N 1 | 0,010 | 0,019 | 0,028 | 0,036 | 0,045 | 0,053 | 0,008 | 0,018 | 0,023 | 0,030 | 0,037 | 0,044 | 0,007 | 0,015 | 0,021 | 0,028 | 0,035 | 0,041 |
То же, N 2 | 0,003 | 0,006 | 0,009 | 0,012 | 0,015 | 1,018 | 0,003 | 0,005 | 0,008 | 0,010 | 0,012 | 0,014 | 0,002 | 0,005 | 0,007 | 0,009 | 0,011 | 0,013 |
Номер упрочненной закладки | Дробленые породы Кузнецкой свиты | Молотые гранулированные шлаки КМК или Запсиба | Портландцемент марки М 400 | Вода, м3 | Возраст закладки, сут | |
класса | ||||||
0,6 мм ("отсев") | 0 - 60 мм | |||||
Закладка N 1 | 1100 | - | 300 | 50 | 400 | 28 |
Закладка N 2 | - | 1100 | 385 | 65 | 520 | 45 |
8.15. Значения функций S(z), S'(z), S"(z), F(z) и F'(z) при наличии сдвижения пород лежачего бока определяются по табл. 52.
z | S(z) | S'(z) | S"(z) | F(z) | F'(z) | ||||||||||||||
Полумульда | |||||||||||||||||||
по падению | по восстанию | по падению | по восстанию | по падению | |||||||||||||||
| |||||||||||||||||||
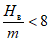 | 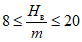 | 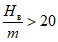 |  |  | 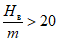 |  | 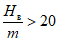 |  |  |  | 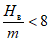 | 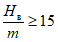 |  | ||||||
0,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 1,0 | 0,0 | ||||
0,05 | - | - | - | - | - | - | 3,5 | - | 0,20 | - | - | - | 2,81 | - | - | ||||
0,10 | 0,57 | 0,96 | 0,94 | 0,32 | 0,96 | 0,98 | 2,94 | 0,8 | 0,40 | 2,60 | 0,8 | 0,5 | 2,58 | 0,97 | 0,2 | ||||
0,20 | 0,39 | 0,83 | 0,83 | 0,17 | 0,83 | 0,90 | 2,20 | 2,2 | 1,05 | 1,00 | 2,2 | 1,0 | 1,88 | 0,93 | 0,4 | ||||
0,30 | 0,28 | 0,52 | 0,73 | 0,09 | 0,52 | 0,77 | 1,83 | 3,2 | 1,55 | 0,60 | 3,2 | 1,6 | 1,28 | 0,88 | 0,6 | ||||
0,40 | 0,22 | 0,30 | 0,55 | 0,05 | 0,30 | 0,58 | 1,40 | 1,5 | 2,10 | 0,40 | 1,5 | 2,0 | 0,90 | 0,81 | 0,8 | ||||
0,50 | 0,16 | 0,20 | 0,43 | 0,04 | 0,20 | 0,39 | 1,07 | 0,9 | 1,85 | 0,25 | 0,9 | 1,9 | 0,54 | 0,71 | 1,0 | ||||
0,60 | 0,10 | 0,12 | 0,29 | 0,03 | 0,12 | 0,22 | 0,65 | 0,6 | 1,15 | 0,15 | 0,6 | 1,4 | 0,38 | 0,60 | 1,2 | ||||
0,70 | 0,05 | 0,07 | 0,21 | 0,02 | 0,07 | 0,10 | 0,28 | 0,4 | 0,90 | 0,07 | 0,4 | 0,9 | 0,30 | 0,47 | 1,4 | ||||
0,80 | 0,02 | 0,03 | 0,13 | 0,01 | 0,03 | 0,04 | 0,16 | 0,3 | 0,70 | 0,03 | 0,3 | 0,4 | 0,24 | 0,32 | 1,6 | ||||
0,90 | 0,01 | 0,01 | 0,04 | 0,005 | 0,01 | 0,01 | 0,07 | 0,2 | 0,38 | 0,01 | 0,2 | 0,2 | 0,12 | 0,17 | 1,7 | ||||
0,95 | 0,02 | 0,15 | 0,05 | ||||||||||||||||
1,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,0 | 0,00 | 0,00 | 0,0 | 0,0 | 0,00 | 0,00 | 1,8 | ||||
8.16. При разработке пластов мощностью более 6 м и 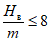 на участках между точками максимального оседания и границами зон провалов сдвижения и деформаций определяются по формулам:
на участках между точками максимального оседания и границами зон провалов сдвижения и деформаций определяются по формулам:
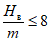 на участках между точками максимального оседания и границами зон провалов сдвижения и деформаций определяются по формулам:
на участках между точками максимального оседания и границами зон провалов сдвижения и деформаций определяются по формулам: | (112) |  | (113) |
 | (114) | 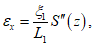 | (115) |
где S(z), S'(z), S"(z) - значения функций на этих участках, определяемые по табл. 53, в зависимости от аргумента 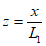 ;
;
x - расстояние, откладываемое от точки максимального оседания до расчетной точки в сторону границы зоны провалов и крупных трещин со стороны висячего бока пласта, м;
L1 - расстояние от точки максимального оседания до выхода пласта под наносы.
z | S(z) | S'(z) | S"(z) |
полумульды по восстанию | |||
0 | 1,0 | 3,7 | 3,1 |
0,05 | - | 3,9 | 3,4 |
0,10 | 1,2 | - | - |
0,15 | - | 4,15 | 3,7 |
0,20 | 1,4 | - | - |
0,25 | - | 4,30 | 4,1 |
0,30 | 1,6 | - | - |
8.17. Период опасных деформаций процесса tоп, мес, сдвижения определяется по табл. 54 в зависимости от среднемесячного продвигания забоя и глубины разработки Hср.
Предельный угол падения пласта, при котором возникают опасные сдвижения лежачего бока, 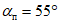 .
.
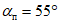 .
.Hср, м | Скорость подвигания очистного забоя, м/мес | ||||
20 | 40 | 60 | 80 | 100 | |
100 | 4 | 3 | 2 | 1 | 1 |
200 | 6 | 4 | 3 | 2 | 2 |
300 | 8 | 5 | 4 | 3 | 3 |
400 | 10 | 6 | 5 | 4 | 3 |
500 | 12 | 7 | 5 | 4 | 4 |
Примечание. Приведенная в табл. 54 продолжительность не распространяется на участки:
подрабатываемые камерами; попадающие в зону провалов; над выходами мощных крутых пластов; при наличии в толще тектонических нарушений.
8.18. Граничные углы 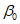 ,
, 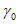 и
и 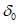 в неподработанной толще каменноугольных пород принимаются:
в неподработанной толще каменноугольных пород принимаются: 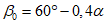 ;
; 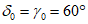 . В подработанной толще значения граничных углов
. В подработанной толще значения граничных углов 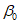 ,
,  и
и 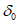 уменьшаются на 5°. Граничные углы в мезозойских отложениях при мощности их 20 м и менее принимаются равными граничным углам в коренных породах. При мощности мезозойских отложений более 20 м граничные углы в мезозойских отложениях принимаются одинаковыми во всех направлениях
уменьшаются на 5°. Граничные углы в мезозойских отложениях при мощности их 20 м и менее принимаются равными граничным углам в коренных породах. При мощности мезозойских отложений более 20 м граничные углы в мезозойских отложениях принимаются одинаковыми во всех направлениях 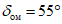 . Граничный угол в наносах
. Граничный угол в наносах 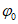 принимается равным 45°.
принимается равным 45°.
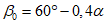 ;
; 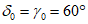 . В подработанной толще значения граничных углов
. В подработанной толще значения граничных углов 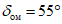 . Граничный угол в наносах
. Граничный угол в наносах 8.19. Углы максимального оседания  и полных сдвижений
и полных сдвижений  ,
, 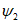 ,
, 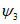 определяются в зависимости от угла падения пласта по табл. 55.
определяются в зависимости от угла падения пласта по табл. 55.
0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
90 | 89 | 88 | 86 | 84 | 82 | 79 | 75 | 71 | 66 | 60 | 52 | 44 | |
55 | 52 | 50 | 48 | 46 | 44 | 43 | 43 | 43 | 44 | 45 | 48 | 53 | |
55 | 58 | 61 | 64 | 66 | 68 | 69 | 71 | 73 | 74 | 75 | 76 | 77 | |
55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 |
8.20. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 56.
Характеристика толщи | q0 | a0 |
Не подработанная ранее толща | 0,75 | 0,30 |
Подработанная толща | 0,85 | 0,30 |
8.21. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к средней глубине разработок H по табл. 57.
1,4 и более | 1,2 | 1,0 | 0,90 | 0,80 | 0,70 | 0,60 | 0,50 | 0,40 | 0,30 | 0,20 | 0,15 и менее | |
N1 и N2 | 1,00 | 0,96 | 0,90 | 0,86 | 0,81 | 0,75 | 0,66 | 0,51 | 0,30 | 0,15 | 0,09 | 0,05 |
Примечание. При промежуточных значениях 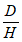 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.22. Значения функций S(z), F(z) и F'(z) в зависимости от коэффициентов N и B определяются по табл. 29 - 33.
8.23. Период опасных деформаций процесса сдвижения определяется по табл. 58 в зависимости от скорости подвигания очистного забоя и от глубины разработки Hср.
Hср, м | Период опасных деформаций tоп, мес | |||
Скорость подвигания очистного забоя, м/мес | ||||
40 | 60 | 80 | 100 | |
100 | 3 | 3 | 2 | 1 |
200 | 4 | 3 | 3 | 2 |
300 | 6 | 5 | 4 | 3 |
400 | 7 | 6 | 5 | 3 |
500 | 7 | 6 | 5 | 4 |
Углы падения пластов, град | |||
0 - 15 | 55 | 55 | 55 |
16 - 50 |  | 55 | 55 |
В подработанной толще граничные углы уменьшаются на 5°. Граничные углы в наносах 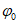 принимаются равными 40°.
принимаются равными 40°.
8.25. Углы максимального оседания 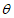 и полных сдвижений
и полных сдвижений 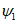 ,
, 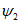 и
и  при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта
при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта  по табл. 60.
по табл. 60.
<= 30 | 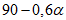 |  |  | 60 |
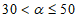 | 70 |  | 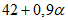 | 60 |
8.26. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 61.
Параметры | Первичная подработка | Повторная подработка |
q0 | 0,85 | 0,90 |
a0 | 0,35 | 0,35 |
8.27. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки (Д1 или Д2) к средней глубине разработок (H) по табл. 62.
ИС МЕГАНОРМ: примечание. Вторая графа шапки таблицы дана в соответствии с официальным текстом документа. |
0,1 и более | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 и менее | |
N1 и N2 | 1,00 | 0,95 | 0,90 | 0,85 | 0,80 | 0,74 | 0,67 | 0,60 | 0,52 | 0,42 |
Примечание. При промежуточных значениях 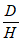 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.28. Значения функций S(z), F(z) и F'(z) при отсутствии сдвижения пород лежачего бока определяются в зависимости от коэффициентов N и B по табл. 63 - 67.
z | Значения функции S(z) | ||
N >= 1 | N = 0,9 | N <= 0,8 | |
0 | 1,00 | 1,00 | 1,00 |
0,1 | 0,95 | 0,93 | 0,91 |
0,2 | 0,81 | 0,78 | 0,76 |
0,3 | 0,60 | 0,58 | 0,57 |
0,4 | 0,40 | 0,38 | 0,37 |
0,5 | 0,24 | 0,24 | 0,24 |
0,6 | 0,14 | 0,14 | 0,14 |
0,7 | 0,08 | 0,08 | 0,08 |
0,8 | 0,04 | 0,04 | 0,04 |
0,9 | 0,02 | 0,02 | 0,02 |
1,0 | 0 | 0 | 0 |
Таблица 64
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | 0,95 | 2,28 | 3,61 | 4,94 | 6,27 | 7,60 | 8,93 | 10,26 |
0,2 | 1,75 | 2,88 | 4,02 | 5,15 | 6,29 | 7,42 | 8,55 | 9,69 |
0,3 | 2,05 | 2,89 | 3,73 | 4,57 | 5,41 | 6,25 | 7,09 | 7,93 |
0,4 | 1,80 | 2,36 | 2,92 | 3,48 | 4,04 | 4,60 | 5,16 | 5,72 |
0,5 | 1,30 | 1,64 | 1,97 | 2,31 | 2,64 | 2,98 | 3,32 | 3,65 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,00 | 7,00 | 8,40 | 9,80 |
0,1 | 1,10 | 2,40 | 3,70 | 5,01 | 6,31 | 7,61 | 8,91 | 10,21 |
0,2 | 1,75 | 2,84 | 3,93 | 5,03 | 6,12 | 7,21 | 8,30 | 9,39 |
0,3 | 2,00 | 2,81 | 3,62 | 4,44 | 5,25 | 6,06 | 6,87 | 7,68 |
0,4 | 1,70 | 2,23 | 2,76 | 3,30 | 3,83 | 4,36 | 4,89 | 5,42 |
0,5 | 1,20 | 1,54 | 1,87 | 2,21 | 2,54 | 2,88 | 3,22 | 3,55 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | 1,20 | 2,47 | 3,75 | 5,02 | 6,30 | 7,57 | 8,84 | 10,12 |
0,2 | 1,70 | 2,76 | 3,83 | 4,89 | 5,96 | 7,02 | 8,08 | 9,15 |
0,3 | 1,95 | 2,75 | 3,55 | 4,34 | 5,14 | 5,94 | 6,74 | 7,54 |
0,4 | 1,65 | 2,17 | 2,69 | 3,20 | 3,72 | 4,24 | 4,74 | 5,28 |
0,5 | 1,15 | 1,49 | 1,82 | 2,16 | 2,49 | 2,83 | 3,17 | 3,50 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 65
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | -0,95 | 0,38 | 1,71 | 3,04 | 4,37 | 5,70 | 7,03 | 8,36 |
0,2 | -1,75 | -0,62 | 0,52 | 1,65 | 2,79 | 3,92 | 5,05 | 6,19 |
0,3 | -2,05 | -1,21 | -0,37 | 0,47 | 1,31 | 2,15 | 2,99 | 3,83 |
0,4 | -1,80 | -1,24 | -0,68 | -0,12 | -0,44 | 1,00 | 1,56 | 2,12 |
0,5 | -1,30 | -0,96 | -0,63 | -0,29 | 0,04 | 1,38 | 0,72 | 1,05 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,06 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,40 |
0,1 | -1,10 | 0,20 | 1,50 | 2,81 | 4,11 | 5,41 | 6,71 | 8,01 |
0,2 | -1,75 | -0,66 | 0,43 | 1,53 | 2,62 | 3,71 | 4,80 | 5,89 |
0,3 | -2,00 | -1,19 | -0,38 | 0,44 | 1,25 | 2,06 | 2,87 | 3,68 |
0,4 | -1,70 | -1,17 | -0,64 | -0,10 | 0,43 | 0,96 | 1,49 | 2,02 |
0,5 | -1,20 | -0,86 | -0,53 | -0,19 | 0,14 | 0,48 | 0,82 | 1,15 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,08 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | -1,20 | 0,07 | 1,35 | 2,62 | 3,90 | 5,17 | 6,44 | 7,72 |
0,2 | -1,70 | 0,63 | 0,43 | 1,49 | 2,56 | 3,62 | 4,68 | 5,75 |
0,3 | -1,95 | -1,15 | -0,35 | 0,44 | 1,24 | 2,04 | 2,84 | 3,64 |
0,4 | -1,65 | -1,13 | -0,61 | -0,10 | 0,42 | 0,94 | 1,46 | 1,98 |
0,5 | -1,15 | -0,81 | -0,48 | -0,14 | 0,19 | 0,53 | 0,87 | 1,20 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,08 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 66
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -8,75 | -7,4 | -6,1 | -4,8 | -3,4 | -2,1 | -0,8 | 0,6 |
0,2 | -5,50 | -3,1 | -0,6 | 1,9 | 4,3 | 6,8 | 9,2 | 11,7 |
0,3 | -0,25 | 2,6 | 5,4 | 8,4 | 11,3 | 14,2 | 17,0 | 19,9 |
0,4 | 3,75 | 6,3 | 8,8 | 11,3 | 13,9 | 16,4 | 18,9 | 21,4 |
0,5 | 5,00 | 6,8 | 8,6 | 10,5 | 12,3 | 14,1 | 15,9 | 17,7 |
0,6 | 4,00 | 6,1 | 6,2 | 7,4 | 8,5 | 9,6 | 10,7 | 11,8 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,3 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 0,7 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 |
0,1 | -8,75 | -7,2 | -5,7 | -4,1 | -2,6 | -1,1 | 0,5 | 2,1 |
0,2 | -4,50 | -2,1 | 0,4 | 2,9 | 5,3 | 7,8 | 10,2 | 12,7 |
0,3 | 0,25 | 3,1 | 5,9 | 8,7 | 11,5 | 14,3 | 17,1 | 19,9 |
0,4 | 4,00 | 6,4 | 8,8 | 11,1 | 13,5 | 15,9 | 18,3 | 20,7 |
0,5 | 4,50 | 6,2 | 7,9 | 9,5 | 11,2 | 12,9 | 14,6 | 16,3 |
0,6 | 3,50 | 4,6 | 5,7 | 6,9 | 8,0 | 9,1 | 10,2 | 11,3 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,6 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -9,00 | -9,00 | -9,00 | -9,0 | -9,00 | -9,00 | -9,00 | -9,00 |
0,1 | -8,50 | -6,8 | -5,1 | -3,5 | -1,8 | -0,1 | 1,6 | 3,3 |
0,2 | -3,75 | -1,4 | 1,0 | 3,4 | 5,8 | 8,2 | 10,6 | 13,0 |
0,3 | 0,25 | 3,0 | 5,7 | 8,4 | 11,2 | 14,0 | 16,7 | 19,4 |
0,4 | 4,00 | 6,3 | 8,6 | 10,9 | 13,2 | 15,6 | 17,9 | 20,5 |
0,5 | 4,25 | 5,9 | 7,5 | 9,1 | 10,7 | 12,3 | 13,9 | 15,5 |
0,6 | 3,25 | 4,4 | 5,5 | 6,6 | 7,7 | 8,9 | 10,0 | 11,1 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,6 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -8,75 | -10,1 | -11,4 | -12,7 | -14,1 | -15,4 | -16,7 | -18,1 |
0,2 | -5,50 | -8,0 | -10,4 | -12,9 | -15,3 | -17,8 | -20,2 | -22,7 |
0,3 | -0,25 | -3,1 | -6,0 | -8,9 | -11,8 | -14,7 | -17,5 | -20,4 |
0,4 | 3,75 | 1,2 | -1,3 | -3,8 | -6,4 | -8,9 | -11,4 | -13,9 |
0,5 | 5,00 | 3,2 | 1,4 | -0,5 | -2,3 | -4,1 | -5,9 | -7,7 |
0,6 | 4,00 | 2,9 | 1,8 | 0,6 | -0,5 | -1,6 | -2,7 | -3,9 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | 0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,5 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 |
0,1 | -8,75 | -10,3 | -11,8 | -13,4 | -14,9 | -16,5 | -18,0 | -19,6 |
0,2 | -4,50 | -7,0 | -9,4 | -11,9 | -14,3 | -16,8 | -19,2 | -21,7 |
0,3 | -0,25 | -2,6 | -5,4 | -8,2 | -11,0 | -13,8 | -16,6 | -19,4 |
0,4 | 4,00 | 1,6 | -0,8 | -3,1 | -5,5 | -7,9 | -10,3 | -12,7 |
0,5 | 4,50 | 2,8 | 1,1 | -0,5 | -2,2 | -3,9 | -5,6 | -7,3 |
0,6 | 3,50 | 2,4 | 1,3 | 0,1 | -1,0 | -2,1 | -3,2 | -4,3 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | 0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,7 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 |
0,1 | -8,50 | -10,2 | -11,9 | -13,5 | -15,2 | -16,9 | -18,6 | -20,3 |
0,2 | -3,75 | -6,1 | -8,5 | -10,9 | -13,3 | -15,7 | -18,1 | -20,5 |
0,3 | 0,25 | -2,5 | -5,2 | -7,9 | -10,7 | -13,5 | -16,2 | -18,9 |
0,4 | 4,00 | 1,7 | -0,6 | -2,9 | -5,2 | -7,6 | -9,9 | -12,2 |
0,5 | 4,25 | 2,6 | 1,0 | -0,6 | -2,2 | -3,8 | -5,4 | -7,1 |
0,6 | 3,24 | 2,1 | 1,0 | -0,1 | -1,2 | -2,4 | -3,5 | -4,6 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | 0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.29. Провалы на земной поверхности при  образуются, если глубина разработки Hн < 200 м, а вертикальная высота целиков, оставляемых на выходах пластов под наносы, менее значений hц, определяемых в зависимости от мощности m по табл. 68.
образуются, если глубина разработки Hн < 200 м, а вертикальная высота целиков, оставляемых на выходах пластов под наносы, менее значений hц, определяемых в зависимости от мощности m по табл. 68.
 образуются, если глубина разработки Hн < 200 м, а вертикальная высота целиков, оставляемых на выходах пластов под наносы, менее значений hц, определяемых в зависимости от мощности m по табл. 68.
образуются, если глубина разработки Hн < 200 м, а вертикальная высота целиков, оставляемых на выходах пластов под наносы, менее значений hц, определяемых в зависимости от мощности m по табл. 68.m, м | 2 и менее | 3 | 4 | 5 | 6 | 7 и более |
hц, м | 30 | 40 | 50 | 60 | 65 | 70 |
8.30. Период опасных деформаций процесса сдвижения определяется по табл. 69 в зависимости от скорости подвигания очистного забоя и от глубины разработки Hср.
Предельный угол падения пласта, при котором возникают опасные сдвижения пород лежачего бока, 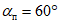 .
.
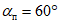 .
.Hср, м | Период опасных деформаций tоп, мес | ||||
Скорость подвигания очистного забоя, м/мес | |||||
20 | 40 | 60 | 80 | 100 | |
100 | 5 | 4 | 3 | 2 | 2 |
200 | 9 | 6 | 5 | 4 | 3 |
300 | 13 | 8 | 6 | 5 | 4 |
400 | 16 | 10 | 7 | 6 | 5 |
500 | 18 | 12 | 8 | 6 | 5 |
Угол падения пласта | ||||
0 - 25 | 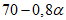 | 70 | - | 70 |
26 - 59 | 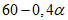 | 70 | - | 70 |
60 и более | 35 | - | 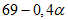 | 70 |
Граничные углы в подработанной толще уменьшаются на 5°. Граничный угол в наносах  принимается равным 45°.
принимается равным 45°.
8.32. Углы максимального оседания 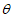 и полных сдвижений
и полных сдвижений 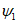 ,
, 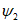 и
и 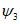 при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта
при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта 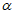 по табл. 71.
по табл. 71.
0 | 90 | 50 | 50 | 50 |
10 | 85 | 48 | 53 | 50 |
20 | 80 | 45 | 56 | 50 |
30 | 75 | 42 | 60 | 50 |
40 | 70 | 40 | 65 | 50 |
50 | 65 | 38 | 70 | 50 |
60 | 60 | 35 | 75 | 50 |
8.33. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 72.
Подработанность массива | q0 | a0 |
А. При наличии в толще известняков | ||
Первичная подработка | 0,4 | 0,3 |
Повторная подработка при закончившемся периоде опасных деформаций от ранее отработанных пластов | 0,8 | 0,3 |
Б. При отсутствии в толще известняков | ||
Первичная и повторная подработка | 0,6 | 0,3 |
8.34. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки (Д) к средней глубине разработок (H) по табл. 73.
1,6 и более | 1,4 | 1,2 | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 и менее | |
N1 и N2 | 1,00 | 0,92 | 0,85 | 0,78 | 0,74 | 0,69 | 0,65 | 0,60 | 0,55 | 0,49 | 0,42 | 0,35 |
Примечание. При промежуточных значениях 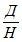 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.35. Значения функций S(z), F(z) и F'(z) при отсутствии сдвижения пород лежачего бока определяются в зависимости от коэффициентов N и B по табл. 74 - 78.
z | Значения функции S(z) | ||
N >= 1 | N = 0,9 | N <= 0,8 | |
0 | 1,00 | 1,00 | 1,00 |
0,1 | 0,97 | 0,96 | 0,95 |
0,2 | 0,89 | 0,87 | 0,86 |
0,3 | 0,76 | 0,73 | 0,71 |
0,4 | 0,58 | 0,56 | 0,54 |
0,5 | 0,40 | 0,37 | 0,35 |
0,6 | 0,24 | 0,22 | 0,20 |
0,7 | 0,12 | 0,11 | 0,10 |
0,8 | 0,05 | 0,05 | 0,04 |
0,9 | 0,01 | 0,01 | 0,01 |
1,0 | 0 | 0 | 0 |
Таблица 75
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,55 | 1,71 | 2,88 | 4,04 | 5,21 | 6,37 | 7,53 | 8,70 |
0,2 | 1,05 | 2,12 | 3,19 | 4,25 | 5,32 | 6,39 | 7,46 | 8,53 |
0,3 | 1,55 | 2,46 | 3,37 | 4,29 | 5,20 | 6,11 | 7,02 | 7,93 |
0,4 | 1,80 | 2,50 | 3,19 | 3,89 | 4,58 | 5,28 | 5,98 | 6,67 |
0,5 | 1,70 | 2,18 | 2,66 | 3,14 | 3,62 | 4,10 | 4,58 | 5,06 |
0,6 | 1,40 | 1,69 | 1,98 | 2,26 | 2,55 | 2,84 | 3,13 | 3,42 |
0,7 | 0,95 | 1,09 | 1,24 | 1,38 | 1,53 | 1,67 | 1,81 | 1,96 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,65 | 1,80 | 2,95 | 4,11 | 5,26 | 6,41 | 7,56 | 8,71 |
0,2 | 1,15 | 2,19 | 3,24 | 4,28 | 5,33 | 6,37 | 7,41 | 8,46 |
0,3 | 1,55 | 2,43 | 3,30 | 4,18 | 5,05 | 5,93 | 6,81 | 7,68 |
0,4 | 1,80 | 2,47 | 3,16 | 3,82 | 4,49 | 5,16 | 5,83 | 6,50 |
0,5 | 1,70 | 2,14 | 2,59 | 3,03 | 3,48 | 3,92 | 4,36 | 4,81 |
0,6 | 1,30 | 1,56 | 1,83 | 2,09 | 2,36 | 2,62 | 2,88 | 3,15 |
0,7 | 0,85 | 0,98 | 1,11 | 1,25 | 1,38 | 1,51 | 1,64 | 1,77 |
0,8 | 0,50 | 0,56 | 0,62 | 0,68 | 0,74 | 0,80 | 0,84 | 0,88 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,70 | 1,84 | 2,98 | 4,12 | 5,26 | 6,40 | 7,54 | 8,68 |
0,2 | 1,20 | 2,23 | 3,26 | 4,30 | 5,33 | 6,36 | 7,39 | 8,42 |
0,3 | 1,60 | 2,45 | 3,30 | 4,16 | 5,01 | 5,86 | 6,71 | 7,56 |
0,4 | 1,80 | 2,45 | 3,10 | 3,74 | 4,39 | 5,04 | 5,69 | 6,34 |
0,5 | 1,70 | 2,12 | 2,54 | 2,96 | 3,38 | 3,80 | 4,22 | 4,64 |
0,6 | 1,25 | 1,49 | 1,73 | 1,97 | 2,21 | 2,45 | 2,69 | 2,93 |
0,7 | 0,80 | 0,92 | 1,04 | 1,16 | 1,28 | 1,40 | 1,52 | 1,64 |
0,8 | 0,45 | 0,50 | 0,55 | 0,59 | 0,65 | 0,70 | 0,75 | 0,80 |
0,9 | 0,20 | 0,21 | 0,22 | 0,23 | 0,24 | 0,25 | 0,26 | 0,27 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 76
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,55 | 0,71 | 1,78 | 2,94 | 4,11 | 5,27 | 6,43 | 7,60 |
0,2 | -1,05 | 0,02 | 1,09 | 2,15 | 3,22 | 4,29 | 5,36 | 6,43 |
0,3 | -1,55 | -0,64 | 0,27 | 1,19 | 2,10 | 3,01 | 3,92 | 4,83 |
0,4 | -1,80 | -1,10 | -0,41 | 0,29 | 0,98 | 1,68 | 2,38 | 3,07 |
0,5 | -1,70 | -1,22 | -0,74 | -0,26 | 0,22 | 0,70 | 1,18 | 1,66 |
0,6 | -1,40 | -1,11 | -0,82 | -0,54 | -0,25 | 0,04 | 0,33 | 0,61 |
0,7 | -0,95 | -0,81 | -0,66 | -0,52 | -0,37 | -0,23 | -0,09 | 0,06 |
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 |
0,9 | -0,25 | -0,24 | -0,23 | -0,21 | -0,20 | -0,19 | -0,18 | -0,17 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,65 | 0,50 | 1,65 | 2,81 | 3,96 | 5,11 | 6,26 | 7,41 |
0,2 | -1,15 | -0,11 | 0,94 | 1,98 | 3,03 | 4,07 | 5,11 | 6,16 |
0,3 | -1,55 | -0,67 | 0,20 | 1,08 | 1,95 | 2,83 | 3,71 | 4,58 |
0,4 | -1,80 | -1,13 | -0,46 | 0,22 | 0,89 | 1,56 | 2,23 | 2,90 |
0,5 | -1,70 | -1,26 | -0,81 | -0,37 | 0,08 | 0,52 | 0,96 | 1,41 |
0,6 | -1,30 | -1,04 | -0,77 | -0,51 | -0,24 | 0,02 | 0,28 | 0,55 |
0,7 | -0,85 | -0,71 | -0,59 | -0,45 | -0,32 | -0,19 | -0,06 | 0,07 |
0,8 | -0,50 | -0,44 | -0,38 | -0,32 | -0,26 | -0,20 | -0,14 | -0,08 |
0,9 | -0,25 | -0,24 | -0,23 | -0,21 | -0,20 | -0,19 | -0,18 | -0,17 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,70 | 0,44 | 1,58 | 2,72 | 3,86 | 5,00 | 6,14 | 7,28 |
0,2 | -1,20 | -0,17 | 0,86 | 1,90 | 2,93 | 3,96 | 4,99 | 6,02 |
0,3 | -1,60 | -0,75 | 0,10 | 0,96 | 1,81 | 2,66 | 3,51 | 4,36 |
0,4 | -1,80 | -1,15 | -0,50 | 0,14 | 0,79 | 1,44 | 2,09 | 2,74 |
0,5 | -1,70 | -1,28 | -0,86 | -0,44 | -0,02 | 0,40 | 0,82 | 1,24 |
0,6 | -1,25 | -1,01 | -0,77 | -0,53 | -0,29 | -0,05 | 0,19 | 0,43 |
0,7 | -0,80 | -0,68 | -0,56 | -0,44 | -0,32 | -0,20 | -0,08 | 0,04 |
0,8 | -0,46 | -0,40 | -0,36 | -0,31 | -0,26 | -0,21 | -0,16 | -0,11 |
0,9 | -0,22 | -0,20 | -0,18 | -0,16 | -0,15 | -0,14 | -0,13 | -0,12 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 77
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -5,25 | -4,6 | -3,9 | -3,3 | -2,6 | -2,0 | -1,3 | -0,6 |
0,2 | -5,00 | -3,7 | -2,5 | -1,2 | 0,0 | 1,3 | 2,6 | 3,8 |
0,3 | -3,75 | -1,9 | -0,0 | 1,8 | 3,7 | 5,6 | 7,5 | 9,3 |
0,4 | -0,75 | 1,4 | 3,6 | 5,7 | 7,9 | 10,1 | 12,3 | 14,4 |
0,5 | 2,00 | 4,0 | 6,1 | 8,1 | 10,2 | 12,2 | 14,2 | 16,3 |
0,6 | 3,75 | 5,4 | 7,1 | 8,8 | 10,5 | 12,2 | 13,9 | 15,6 |
0,7 | 4,25 | 5,4 | 6,5 | 7,7 | 8,8 | 10,0 | 11,1 | 12,2 |
0,8 | 3,50 | 4,2 | 4,8 | 5,5 | 6,1 | 6,8 | 7,5 | 8,1 |
0,9 | 1,75 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 | 3,9 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 |
0,1 | -5,75 | -5,0 | -4,2 | -3,4 | -2,6 | -1,9 | -1,1 | -0,3 |
0,2 | -4,75 | -3,4 | -2,0 | -0,6 | 0,8 | 2,2 | 3,5 | 4,9 |
0,3 | -3,50 | -1,6 | 0,2 | 2,1 | 3,9 | 5,8 | 7,7 | 9,5 |
0,4 | -0,75 | 1,4 | 3,6 | 5,7 | 7,9 | 10,1 | 12,3 | 14,4 |
0,5 | 2,50 | 4,5 | 6,6 | 8,6 | 10,7 | 12,7 | 14,7 | 16,8 |
0,6 | 4,25 | 5,8 | 7,4 | 8,9 | 10,5 | 12,1 | 13,6 | 15,2 |
0,7 | 4,00 | 5,0 | 6,0 | 7,1 | 8,1 | 9,1 | 10,1 | 11,1 |
0,8 | 3,25 | 3,9 | 4,5 | 5,1 | 5,7 | 6,3 | 6,9 | 7,45 |
0,9 | 1,75 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 | 3,9 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 |
0,1 | -6,00 | -5,2 | -4,3 | -3,5 | -2,6 | -1,8 | -1,0 | -0,1 |
0,2 | -4,50 | -3,1 | -6,1 | -0,2 | 1,3 | 2,7 | 4,1 | 5,6 |
0,3 | -3,00 | -1,1 | -0,8 | -2,8 | 4,7 | 6,6 | 8,5 | 10,4 |
0,4 | -0,50 | 1,7 | 3,8 | 6,0 | 8,1 | 10,3 | 12,5 | 14,6 |
0,5 | 2,75 | 4,8 | 6,8 | 8,9 | 10,9 | 13,0 | 15,1 | 17,1 |
0,6 | 4,50 | 6,0 | 7,5 | 9,0 | 10,5 | 12,0 | 13,5 | 15,0 |
0,7 | 4,00 | 5,0 | 5,9 | 6,9 | 7,8 | 8,8 | 9,8 | 10,7 |
0,8 | 3,00 | 3,5 | 4,1 | 4,6 | 5,2 | 5,7 | 6,2 | 6,8 |
0,9 | 1,50 | 1,7 | 2,0 | 2,2 | 2,5 | 2,7 | 2,9 | 3,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -5,25 | -5,91 | -6,6 | -7,2 | -7,9 | -8,6 | -9,2 | -9,9 |
0,2 | -5,00 | -6,3 | -7,5 | -8,8 | -10,0 | -11,3 | -12,6 | -13,8 |
0,3 | -3,75 | -5,6 | -7,5 | -9,3 | -11,2 | -13,1 | -15,0 | -16,8 |
0,4 | -0,75 | -2,9 | -5,1 | -7,2 | -9,4 | -11,6 | -13,8 | -15,9 |
0,5 | 2,00 | -0,04 | -2,1 | -4,1 | -6,2 | -8,2 | -10,2 | -12,3 |
0,6 | 3,75 | 2,1 | 0,4 | -1,3 | -3,0 | -4,7 | -6,4 | -8,1 |
0,7 | 4,25 | 3,1 | 2,0 | 0,8 | -0,3 | -1,5 | -2,6 | -3,7 |
0,8 | 3,50 | 2,8 | 2,2 | 1,5 | 0,9 | 0,2 | -0,5 | -1,1 |
0,9 | 1,75 | 1,5 | 1,2 | 0,9 | 0,6 | 0,3 | -0,1 | -0,4 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 | -5,50 |
0,1 | -5,75 | -6,5 | -7,3 | -8,1 | -8,9 | -9,7 | -10,4 | -11,2 |
0,2 | -4,75 | -6,1 | -7,5 | -8,9 | -10,3 | -11,7 | -13,0 | -14,4 |
0,3 | -3,50 | -5,4 | -7,2 | -9,1 | -10,9 | -12,8 | -14,7 | -16,5 |
0,4 | -0,75 | -2,9 | -5,1 | -7,2 | -9,4 | -11,6 | -13,8 | -15,9 |
0,5 | 2,50 | 0,5 | -1,6 | -3,6 | -5,7 | -7,7 | -9,7 | -11,8 |
0,6 | 4,25 | 2,7 | 1,1 | -0,4 | -2,0 | -3,6 | -5,1 | -6,7 |
0,7 | 4,00 | 3,0 | 2,0 | 0,9 | -0,1 | -1,1 | -2,1 | -3,1 |
0,8 | 3,25 | 2,7 | 2,1 | 1,5 | 0,9 | 0,2 | -0,4 | -1,0 |
0,9 | 1,75 | 1,5 | 1,2 | 0,9 | 0,6 | 0,3 | -0,1 | -0,4 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 | -6,75 |
0,1 | -6,00 | -6,8 | -7,7 | -8,5 | -9,4 | -10,2 | -11,0 | -11,9 |
0,2 | -4,50 | -5,9 | -7,4 | -8,8 | - 10,3 | -11,7 | -13,1 | -14,6 |
0,3 | -3,00 | -4,9 | -6,8 | -8,8 | -10,7 | -12,6 | -14,5 | -16,4 |
0,4 | -0,50 | -2,7 | -4,8 | -7,0 | -9,1 | -11,3 | -13,5 | -15,6 |
0,5 | 2,75 | 0,7 | -1,3 | -3,4 | -5,4 | -7,5 | -9,5 | -11,6 |
0,6 | 4,50 | 3,0 | 1,5 | 0 | -1,5 | -3,0 | -4,5 | -6,0 |
0,7 | 4,00 | 3,0 | 2,1 | 1,1 | 0,2 | -0,8 | -1,8 | -2,7 |
0,8 | 3,00 | 2,5 | 1,9 | 1,4 | 0,8 | 0,3 | -0,2 | -0,8 |
0,9 | 1,50 | 1,3 | 1,0 | 0,8 | 0,5 | 0,3 | 0,1 | -0,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.36. Углы максимального оседания  и максимальных горизонтальных сдвижений
и максимальных горизонтальных сдвижений 
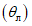 при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 79.
при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 79.
60 | 60 | 50 | 60 |
70 | 55 | 60 | 70 |
80 | 72 | 70 | 80 |
90 | 90 | 80 | 80 |
Примечание. Промежуточные значения 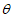 ,
, 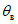 и
и 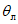 определяются интерполированием.
определяются интерполированием.
8.37. Коэффициенты Kз и  , используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, определяются в зависимости от угла падения пласта по табл. 80.
, используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, определяются в зависимости от угла падения пласта по табл. 80.
60 | 70 | 80 | 90 | |
Kз | 0,35 | 0,26 | 0,18 | 0,10 |
1,50 | 1,50 | 1,50 | 1,50 |
Примечание. Промежуточные значения Kз определяются интерполированием.
8.38. Предельная глубина разработки, при которой возможно появление провалов на земной поверхности, если вертикальная высота целиков hц, оставляемых на выходах пластов, под наносы, принимается Hн = 500 м.
8.39. Период опасных деформаций земной поверхности:
под влиянием выемки одного пласта в зависимости от глубины разработки Hср до 300 м определяется по табл. 81.
Hср, м | Период опасных деформаций tоп, мес | ||
До 100 | 200 | 300 | |
tоп, мес | 4 | 7 | 8 |
При глубинах разработки от 300 до 700 м опасные деформации могут проявляться в течение 1,5 лет после первичной подработки и в течение 0,5 года - после повторной подработки.
8.40. Значения угла трения по наиболее слабому контакту вмещающих пород с угольным пластом принимаются: 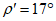 - при отсутствии известняка;
- при отсутствии известняка;  - при наличии известняка.
- при наличии известняка.
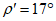 - при отсутствии известняка;
- при отсутствии известняка;  - при наличии известняка.
- при наличии известняка.Предельный угол падения пласта, при котором возникают опасные сдвижения пород лежачего бока,  .
.
 .
.8.41. Граничный угол 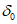 в неподработанной и подработанной толще принимается во всех направлениях равным 55°. Граничный угол в наносах
в неподработанной и подработанной толще принимается во всех направлениях равным 55°. Граничный угол в наносах  принимается равным 45°.
принимается равным 45°.
8.42. Углы максимального оседания и полных сдвижений: 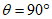 ;
; 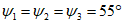 .
.
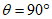 ;
; 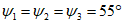 .
.8.43. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 82.
Параметры | Первичная подработка | Повторная подработка |
q0 | 0,80 | 0,90 |
a0 | 0,34 | 0,34 |
8.44. Коэффициенты N1 и N2 определяются в зависимости от отношения расчетной длины лавы Др к средней глубине разработок H по табл. 83.
0,05 и менее | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 и более | |
N1 и N2 | 0,22 | 0,3 | 0,43 | 0,52 | 0,60 | 0,67 | 0,74 | 0,80 | 0,85 | 0,90 | 0,94 | 0,98 | 1,0 |
Примечание. При промежуточных значениях  ,
, 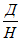 и
и 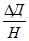 значения N1 и N2 в табл. 83 определяются интерполированием.
значения N1 и N2 в табл. 83 определяются интерполированием.
Отношение расчетной длины лавы к глубине определяется из выражения:

где Д - фактическая длина лавы;
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 и более | |
0,10 | 0,07 | 0,05 | 0,03 | 0 | -0,03 | -0,05 | -0,07 | -0,10 |
При последовательной отработке лав в одном пласте с междулавными целиками шириной менее 0,1H, а также при повторной подработке земной поверхности поправки  и
и 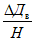 принимаются равными нулю.
принимаются равными нулю.
8.45. Значения функций S(z), F(z) и F'(z) определяются в зависимости от коэффициентов N по табл. 85 - 87.
z | Значения функции S(z) | |||
Коэффициенты подработанности | ||||
N >= 1 | N = 0,9 | N = 0,8 | N <= 0,7 | |
0 | 1,000 | 1,000 | 1,000 | 1,000 |
0,1 | 0,980 | 0,960 | 0,940 | 0,905 |
0,2 | 0,898 | 0,845 | 0,790 | 0,728 |
0,3 | 0,731 | 0,650 | 0,575 | 0,514 |
0,4 | 0,504 | 0,430 | 0,365 | 0,311 |
0,5 | 0,299 | 0,255 | 0,215 | 0,179 |
0,6 | 0,169 | 0,140 | 0,115 | 0,095 |
0,7 | 0,089 | 0,070 | 0,057 | 0,047 |
0,8 | 0,039 | 0,035 | 0,026 | 0,021 |
0,9 | 0,014 | 0,011 | 0,009 | 0,008 |
1,0 | 0 | 0 | 0 | 0 |
Таблица 86
z | Значения функции F(z) | |||
Коэффициенты подработанности | ||||
N >= 1 | N = 0,9 | N = 0,8 | N <= 0,7 | |
0 | 0 | 0 | 0 | 0 |
0,1 | 0,24 | 0,70 | 0,76 | 0,76 |
0,2 | 0,76 | 1,41 | 1,41 | 1,41 |
0,3 | 1,53 | 1,94 | 1,82 | 1,76 |
0,4 | 2,06 | 1,94 | 1,82 | 1,70 |
0,5 | 1,76 | 1,35 | 1,29 | 1,23 |
0,6 | 1,06 | 0,82 | 0,76 | 0,76 |
0,7 | 0,53 | 0,41 | 0,41 | 0,41 |
0,8 | 0,24 | 0,18 | 0,18 | 0,18 |
0,9 | 0,06 | 0,06 | 0,06 | 0,06 |
1,0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) | |||
Коэффициенты подработанности | ||||
N = 1 | N = 0,9 | N = 0,8 | N <= 0,7 | |
0 | 0 | -6,47 | -7,76 | -7,88 |
0,1 | -3,82 | -7,17 | -7,47 | -7,23 |
0,2 | -6,88 | -6,23 | -5,53 | -4,82 |
0,3 | -6,88 | -2,59 | -1,88 | -1,47 |
0,4 | -1,29 | +3,64 | +3,18 | +2,06 |
0,5 | +6,23 | +6,06 | +5,41 | +5,06 |
0,6 | +6,76 | +4,41 | +4,23 | +4,12 |
0,7 | +3,82 | +3,23 | +3,06 | +2,94 |
0,8 | +2,06 | +2,06 | +1,94 | +1,88 |
0,9 | +1,00 | +0,94 | +0,82 | +0,70 |
1,0 | 0 | 0 | 0 | 0 |
8.46. Период опасных деформаций процесса сдвижения определяется по табл. 88 в зависимости от скорости подвигания очистного забоя и от глубины разработки Hср.
Hср, м | Период опасных деформаций tоп, мес | ||||
Скорость подвигания очистного забоя, м/мес | |||||
20 | 40 | 60 | 80 | 100 | |
300 | 16 | 8 | 6 | 5 | 4 |
400 | 21 | 11 | 8 | 6 | 5 |
500 | 26 | 13 | 9 | 8 | 6 |
МЕСТОРОЖДЕНИЯ ПЕЧОРСКОГО БАССЕЙНА
Угол падения пласта | ||||
0 - 59 |  | 70 | 70 | |
60 и более | 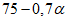 , но не менее 25 , но не менее 25 | 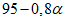 , но не менее 25 , но не менее 25 | 70 |
В подработанной толще граничные углы 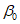 ,
,  ,
,  и
и 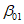 уменьшаются на 5°. Граничный угол в наносах
уменьшаются на 5°. Граничный угол в наносах 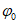 принимается равным 50°.
принимается равным 50°.
8.48. Углы максимального оседания и полных сдвижений при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта по табл. 90.
Параметры | Угол падения пласта, град | ||||||||||||
0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
90 | 87 | 82 | 79 | 76 | 72 | 70 | 68 | 65 | 62 | 60 | 58 | 55 | |
55 | 54 | 54 | 53 | 52 | 51 | 50 | 48 | 47 | 46 | 45 | 43 | 42 | |
55 | 56 | 57 | 58 | 60 | 61 | 63 | 66 | 68 | 71 | 74 | 77 | 80 | |
55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | |
Примечание. В мощных (более 40 м) наносах Воркутинского и Воргашорского месторождений принимаются 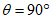 ,
, 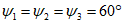 .
.
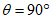 ,
, 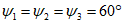 .
.8.49. Относительные величины максимального оседания q0 и горизонтального сдвижения a0 определяются по табл. 91 и 92.
Мощность наносов h, м | Мощность коренных пород в процентах от общей мощности подрабатываемой толщи | a0 | ||
первичная подработка | повторная подработка | |||
До 45 | 40 и более | Менее 25 | 0,9 | 0,9 |
Прочие горно-геологические условия | 0,65 | 0,8 | ||
Мощность наносов h, м | Отношение мощности коренных пород к средней глубине разработки | a0 |
Менее 40 | - | 0,3 |
40 и более | До 0,1 | 0,5 |
0,1 - 0,3 | 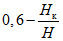 | |
Более 0,3 | 0,3 |
8.50. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к средней глубине разработок H по табл. 93.
1,4 и более | 1,2 | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 и менее | |
N1 и N2 | 1,00 | 0,92 | 0,84 | 0,80 | 0,75 | 0,70 | 0,65 | 0,59 | 0,53 | 0,46 | 0,37 |
8.51. Значения функций S(z), F(z) и F'(z) при отсутствии сдвижения пород лежачего бока определяются в зависимости от коэффициентов N и B по табл. 94 - 98.
z | Значения функции S(z) | ||
N >= 1 | N = 0,9 | N <= 0,8 | |
0 | 1,00 | 1,00 | 1,00 |
0,1 | 0,99 | 0,98 | 0,96 |
0,2 | 0,94 | 0,91 | 0,89 |
0,3 | 0,83 | 0,79 | 0,76 |
0,4 | 0,62 | 0,61 | 0,59 |
0,5 | 0,40 | 0,40 | 0,39 |
0,6 | 0,23 | 0,23 | 0,23 |
0,7 | 0,12 | 0,12 | 0,12 |
0,8 | 0,05 | 0,05 | 0,05 |
0,9 | 0,01 | 0,01 | 0,01 |
1,0 | 0 | 0 | 0 |
Таблица 95
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,30 | 1,49 | 2,68 | 3,86 | 5,05 | 6,24 | 7,43 | 8,62 |
0,2 | 0,80 | 1,93 | 3,06 | 4,18 | 5,31 | 6,44 | 7,57 | 8,70 |
0,3 | 1,60 | 2,60 | 3,59 | 4,59 | 5,58 | 6,58 | 7,58 | 8,57 |
0,4 | 2,15 | 2,89 | 3,64 | 4,38 | 5,13 | 5,87 | 6,61 | 7,36 |
0,5 | 1,95 | 2,43 | 2,91 | 3,39 | 3,87 | 4,35 | 4,83 | 5,31 |
0,6 | 1,40 | 1,68 | 1,95 | 2,23 | 2,50 | 2,78 | 3,06 | 3,33 |
0,7 | 0,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,40 | 1,58 | 2,75 | 3,93 | 5,10 | 6,28 | 7,46 | 8,63 |
0,2 | 0,90 | 1,99 | 3,08 | 4,18 | 5,27 | 6,36 | 7,45 | 8,54 |
0,3 | 1,55 | 2,50 | 3,45 | 4,39 | 5,34 | 6,29 | 7,24 | 8,19 |
0,4 | 2,00 | 2,73 | 3,46 | 4,20 | 4,93 | 5,66 | 6,39 | 7,12 |
0,5 | 1,90 | 2,38 | 2,86 | 3,34 | 3,82 | 4,30 | 4,78 | 5,26 |
0,6 | 1,40 | 1,68 | 1,95 | 2,23 | 2,50 | 2,78 | 3,06 | 3,33 |
0,7 | 0,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,55 | 1,70 | 2,85 | 4,01 | 5,16 | 6,31 | 7,46 | 8,61 |
0,2 | 1,00 | 2,07 | 3,14 | 4,20 | 5,27 | 6,34 | 7,41 | 8,48 |
0,3 | 1,50 | 2,41 | 3,32 | 4,24 | 5,15 | 6,06 | 6,97 | 7,88 |
0,4 | 1,85 | 2,56 | 3,27 | 3,97 | 4,68 | 5,39 | 6,10 | 6,81 |
0,5 | 1,80 | 2,26 | 2,74 | 3,20 | 3,67 | 4,14 | 4,61 | 5,08 |
0,6 | 1,35 | 1,63 | 1,90 | 2,18 | 2,45 | 2,73 | 3,01 | 3,33 |
0,7 | 0,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 96
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,30 | 0,89 | 2,08 | 3,26 | 4,45 | 5,64 | 6,83 | 8,02 |
0,2 | -0,80 | 0,33 | 1,46 | 2,58 | 3,71 | 4,84 | 5,97 | 7,10 |
0,3 | -1,60 | -0,60 | 0,39 | 1,39 | 2,38 | 3,38 | 4,38 | 5,37 |
0,4 | -2,15 | -1,41 | -0,66 | 0,08 | 0,83 | 1,57 | 2,31 | 3,06 |
0,5 | -1,95 | -1,47 | -0,99 | -0,51 | -0,03 | 0,45 | 0,93 | 1,41 |
0,6 | -1,40 | -1,12 | -0,84 | -0,57 | -0,30 | -0,02 | 0,26 | 0,53 |
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 |
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 |
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,40 | 0,78 | 1,95 | 3,13 | 4,30 | 5,48 | 6,66 | 7,83 |
0,2 | -0,90 | 0,19 | 1,28 | 2,38 | 3,46 | 4,56 | 5,65 | 6,74 |
0,3 | -1,55 | -0,60 | 0,35 | 1,29 | 2,24 | 3,19 | 4,14 | 5,09 |
0,4 | -2,00 | -1,27 | -0,54 | 0,20 | 0,93 | 1,66 | 2,39 | 3,12 |
0,5 | -1,90 | -1,42 | -0,94 | -0,46 | 0,02 | 0,50 | 0,98 | 1,46 |
0,6 | -1,40 | -1,12 | -0,85 | -0,57 | -0,30 | -0,02 | 0,26 | 0,53 |
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 |
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 |
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | -0,55 | 0,60 | 1,75 | 2,91 | 4,06 | 5,21 | 6,36 | 7,51 |
0,2 | -1,00 | 0,06 | 1,14 | 2,20 | 3,27 | 4,34 | 5,41 | 6,48 |
0,3 | -1,50 | -0,59 | 0,32 | 1,24 | 2,15 | 3,06 | 3,97 | 4,88 |
0,4 | -1,85 | -1,14 | -0,43 | 0,27 | 0,98 | 1,69 | 2,40 | 3,11 |
0,5 | -1,80 | -1,33 | -0,86 | -0,40 | 0,07 | 0,54 | 1,01 | 1,48 |
0,6 | -1,35 | -1,07 | -0,80 | -0,52 | -0,25 | 0,03 | 0,31 | 0,58 |
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 |
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 |
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 97
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -4,00 | -3,6 | -3,3 | -2,9 | -2,6 | -2,2 | -1,8 | -1,5 |
0,2 | -6,50 | -5,5 | -4,6 | -3,6 | -2,7 | -1,7 | -0,7 | 0,2 |
0,3 | -6,75 | -4,8 | -2,9 | -1,0 | 0,9 | 2,9 | 4,8 | 6,7 |
0,4 | -1,75 | 0,8 | 3,4 | 6,0 | 8,6 | 11,2 | 13,8 | 16,4 |
0,5 | 3,75 | 6,1 | 8,4 | 10,8 | 13,1 | 15,5 | 17,8 | 20,2 |
0,6 | 5,25 | 6,9 | 8,6 | 10,3 | 12,0 | 13,7 | 15,4 | 17,1 |
0,7 | 4,25 | 5,3 | 6,4 | 7,5 | 8,6 | 9,7 | 10,7 | 11,8 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 |
0,1 | -4,50 | -4,0 | -3,5 | -3,1 | -2,6 | -2,1 | -1,6 | -1,1 |
0,2 | -5,75 | -4,7 | -3,6 | -2,5 | -1,4 | -0,4 | 0,7 | 1,8 |
0,3 | -5,50 | -3,6 | -1,8 | 0,1 | 1,9 | 3,8 | 5,7 | 7,5 |
0,4 | -1,75 | 0,7 | 3,1 | 5,5 | 7,9 | 10,3 | 12,7 | 15,1 |
0,5 | 3,00 | 5,3 | 7,6 | 9,8 | 12,1 | 14,4 | 16,7 | 19,0 |
0,6 | 5,00 | 6,7 | 8,4 | 10,0 | 11,7 | 13,4 | 15,1 | 16,8 |
0,7 | 4,25 | 5,3 | 6,4 | 7,5 | 8,6 | 9,7 | 10,7 | 11,8 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 |
0,1 | -5,00 | -4,4 | -3,7 | -3,0 | -2,4 | -1,7 | -1,0 | -0,4 |
0,2 | -4,75 | -3,6 | -2,4 | -1,2 | 0,1 | 1,3 | 2,5 | 3,7 |
0,3 | -3,75 | -2,5 | -0,7 | 1,2 | 3,0 | 4,8 | 6,6 | 8,4 |
0,4 | -1,50 | 0,7 | 2,9 | 5,2 | 7,4 | 9,6 | 11,8 | 14,0 |
0,5 | 2,50 | 4,7 | 6,8 | 9,0 | 11,1 | 13,3 | 15,5 | 17,6 |
0,6 | 4,50 | 6,2 | 7,8 | 9,4 | 11,0 | 12,6 | 14,2 | 15,8 |
0,7 | 4,00 | 5,1 | 6,2 | 7,2 | 8,3 | 9,4 | 10,5 | 11,6 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -4,00 | -4,4 | -4,7 | -5,1 | -5,4 | -5,8 | -6,2 | -6,5 |
0,2 | -6,50 | -7,5 | -8,4 | -9,4 | -10,3 | -11,3 | -12,3 | -13,2 |
0,3 | -6,75 | -8,7 | -10,6 | -12,5 | -14,4 | -16,4 | -18,3 | -20,2 |
0,4 | -1,75 | -4,3 | -6,9 | -9,5 | -12,1 | -14,7 | -17,3 | -19,9 |
0,5 | 3,75 | 1,4 | -0,9 | -3,3 | -5,6 | -8,0 | -10,3 | -12,7 |
0,6 | 5,25 | 3,6 | 1,9 | 0,2 | -1,5 | -3,2 | -4,9 | -6,6 |
0,7 | 4,25 | 3,2 | 2,1 | 1,0 | -0,1 | -1,2 | -2,2 | -3,3 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 |
0,1 | -4,50 | -5,00 | -5,5 | -5,9 | -6,4 | -6,9 | -7,4 | -7,9 |
0,2 | -5,75 | -6,8 | -7,9 | -9,0 | -10,1 | -11,2 | -12,2 | -13,3 |
0,3 | -5,50 | -7,4 | -9,2 | -11,1 | -12,9 | -14,8 | -16,7 | -18,5 |
0,4 | -1,75 | -4,2 | -6,6 | -9,0 | -11,4 | -13,8 | -16,2 | -18,6 |
0,5 | 3,00 | 0,7 | -1,6 | -3,8 | -6,1 | -8,4 | -10,7 | -13,0 |
0,6 | 5,00 | 3,3 | 1,6 | -0,1 | -1,7 | -3,4 | -5,1 | -6,8 |
0,7 | 4,25 | 3,2 | 2,1 | 1,0 | -0,1 | -1,2 | -2,2 | -3,3 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 |
0,1 | -5,00 | -5,7 | -6,3 | -7,0 | -7,6 | -8,3 | -9,0 | -9,6 |
0,2 | -4,75 | -6,0 | -7,2 | -8,4 | -9,6 | -10,8 | -12,0 | -13,2 |
0,3 | -4,25 | -6,1 | -7,9 | -9,7 | -11,5 | -13,3 | -15,1 | -16,9 |
0,4 | -1,50 | -3,7 | -5,9 | -8,2 | -10,4 | -12,6 | -14,8 | -17,0 |
0,5 | 2,50 | 0,3 | -1,8 | -4,0 | -6,1 | -8,3 | -10,5 | -12,6 |
0,6 | 4,50 | 2,9 | 1,3 | -0,4 | -2,0 | -3,6 | -5,2 | -6,8 |
0,7 | 4,00 | 2,9 | 1,8 | 0,8 | -0,3 | -1,4 | -2,5 | -3,6 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.52. Значения углов максимального оседания 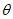 и максимальных горизонтальных сдвижений
и максимальных горизонтальных сдвижений  и
и 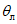 при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 99.
при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта по табл. 99.
60 | 55 | 35 | 60 |
70 | 50 | 30 | 70 |
80 | 70 | 50 | 80 |
90 | 90 | 80 | 80 |
Примечание. Промежуточные значения  ,
,  и
и  определяются интерполированием.
определяются интерполированием.
8.53. Коэффициенты Kз и 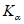 , используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, принимаются равными: Kз = 0,25;
, используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, принимаются равными: Kз = 0,25;  .
.
 .
.8.54. Предельный угол, при котором возникают опасные сдвижения лежачего бока пласта 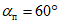 .
.
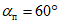 .
.8.55. Период опасных деформаций процесса сдвижения под влиянием одного пласта в зависимости от средней глубины разработки определяется по табл. 100 (tоп, мес).
Hср, м | 100 и менее | 200 | 300 | 400 и более |
tоп, мес | 4 | 6 | 8 | 10 |
Угол падения пласта | |||
0 - 55 |  | 60 | 60 |
Граничные углы  ,
, 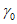 и
и 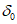 в подработанной толще уменьшаются на 5°. Граничный угол в наносах
в подработанной толще уменьшаются на 5°. Граничный угол в наносах 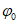 принимается равным 50°.
принимается равным 50°.
8.57. Углы максимального оседания  и полных сдвижений
и полных сдвижений 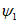 ,
, 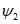 и
и 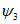 определяются в зависимости от угла падения пласта по табл. 102.
определяются в зависимости от угла падения пласта по табл. 102.
Параметры | Угол падения пластов, град | ||||||
0 | 10 | 20 | 30 | 40 | 50 | 60 | |
90 | 83 | 76 | 70 | 65 | 60 | 55 | |
55 | 54 | 52 | 50 | 47 | 45 | 42 | |
55 | 57 | 60 | 63 | 68 | 74 | 79 | |
55 | 55 | 55 | 55 | 55 | 55 | 55 | |
8.58. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 103.
Параметры | Первичная подработка | Повторная подработка |
q0 | 0,7 | 0,85 |
a0 | 0,3 | 0,3 |
8.59. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к средней глубине разработки H по табл. 104.
1,4 и более | 1,2 | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 и менее | |
N1 и N2 | 1,00 | 0,92 | 0,84 | 0,80 | 0,75 | 0,70 | 0,65 | 0,59 | 0,53 | 0,46 | 0,37 |
Примечание. При промежуточных значениях 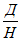 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.60. Значения функций S(z), F(z) и F'(z) определяются в зависимости от коэффициентов N и B по табл. 105 - 109.
z | Значения функции S(z) | ||
N >= 1 | N = 0,9 | N <= 0,8 | |
0 | 1,00 | 1,00 | 1,00 |
0,1 | 0,99 | 0,98 | 0,96 |
0,2 | 0,94 | 0,91 | 0,89 |
0,3 | 0,83 | 0,79 | 0,76 |
0,4 | 0,62 | 0,61 | 0,59 |
0,5 | 0,40 | 0,40 | 0,39 |
0,6 | 0,23 | 0,23 | 0,23 |
0,7 | 0,12 | 0,12 | 0,12 |
0,8 | 0,05 | 0,05 | 0,05 |
0,9 | 0,01 | 0,01 | 0,01 |
1,0 | 0 | 0 | 0 |
Таблица 106
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,30 | 1,49 | 2,68 | 3,86 | 5,05 | 6,24 | 7,43 | 8,62 |
0,2 | 0,80 | 1,93 | 3,06 | 4,18 | 5,31 | 6,44 | 7,57 | 8,70 |
0,3 | 1,60 | 2,60 | 3,59 | 4,59 | 5,58 | 6,58 | 7,58 | 8,57 |
0,4 | 2,15 | 2,89 | 3,64 | 4,38 | 5,13 | 5,87 | 6,61 | 7,36 |
0,5 | 1,95 | 2,43 | 2,91 | 3,39 | 3,87 | 4,35 | 4,83 | 5,31 |
0,6 | 1,40 | 1,68 | 1,95 | 2,23 | 2,50 | 2,78 | 3,06 | 3,33 |
0,7 | 0,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,40 | 1,58 | 2,75 | 3,93 | 5,10 | 6,28 | 7,46 | 8,63 |
0,2 | 0,90 | 1,99 | 3,08 | 4,18 | 5,27 | 6,36 | 7,45 | 8,54 |
0,3 | 1,55 | 2,50 | 3,45 | 4,39 | 5,34 | 6,29 | 7,24 | 8,19 |
0,4 | 2,00 | 2,73 | 3,46 | 4,20 | 4,93 | 5,66 | 6,39 | 7,12 |
0,5 | 1,90 | 2,38 | 2,86 | 3,34 | 3,82 | 4,30 | 4,78 | 5,26 |
0,6 | 1,40 | 1,68 | 1,95 | 2,23 | 2,50 | 2,78 | 3,06 | 3,33 |
0,7 | 0,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 |
0,1 | 0,55 | 1,70 | 2,85 | 4,01 | 5,16 | 6,31 | 7,46 | 8,61 |
0,2 | 1,00 | 2,07 | 3,14 | 4,20 | 5,27 | 6,34 | 7,41 | 8,48 |
0,3 | 1,50 | 2,41 | 3,32 | 4,24 | 5,15 | 6,06 | 6,97 | 7,88 |
0,4 | 1,85 | 2,56 | 3,27 | 3,97 | 4,68 | 5,39 | 6,10 | 6,81 |
0,5 | 1,80 | 2,26 | 2,74 | 3,20 | 3,67 | 4,14 | 4,61 | 5,08 |
0,6 | 1,35 | 1,63 | 1,90 | 2,18 | 2,45 | 2,73 | 3,01 | 3,33 |
0,7 | 6,90 | 1,04 | 1,19 | 1,33 | 1,48 | 1,62 | 1,76 | 1,90 |
0,8 | 0,55 | 0,61 | 0,67 | 0,73 | 0,79 | 0,85 | 0,91 | 0,97 |
0,9 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | 0,32 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 107
z | Значения функции F(z) (полумульда по восстанию) | |||||||||||
Значения коэффициента B | ||||||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
N >= 1 | ||||||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,50 | ||||
0,1 | -0,30 | 0,89 | 2,08 | 3,26 | 4,45 | 5,64 | 6,83 | 8,02 | ||||
0,2 | -0,80 | 0,33 | 1,48 | 2,58 | 3,71 | 4,84 | 5,97 | 7,10 | ||||
0,3 | -1,60 | -0,60 | 0,39 | 1,39 | 2,38 | 3,38 | 4,38 | 5,37 | ||||
0,4 | -2,15 | -1,41 | -0,66 | 0,08 | 0,83 | 1,57 | 2,31 | 3,06 | ||||
0,5 | -1,95 | -1,47 | -0,99 | -0,51 | -0,03 | 0,45 | 0,93 | 1,41 | ||||
0,6 | -1,40 | -1,12 | -0,84 | -0,57 | -0,30 | -0,02 | 0,26 | 0,53 | ||||
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 | ||||
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 | ||||
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 | ||||
1,0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | ||||
N = 0,9 | ||||||||||||
0 | 0 | 1,20 | 2,40 | 3,60 | 4,80 | 6,00 | 7,20 | 8,40 | ||||
0,1 | -0,40 | 0,78 | 1,95 | 3,13 | 4,30 | 5,48 | 6,66 | 7,83 | ||||
0,2 | -0,90 | 0,19 | 1,28 | 2,38 | 3,46 | 4,56 | 5,65 | 6,74 | ||||
0,3 | -1,55 | -0,60 | 0,35 | 1,29 | 2,24 | 3,19 | 4,14 | 5,09 | ||||
0,4 | -2,00 | -1,27 | -0,54 | 0,20 | 0,93 | 1,66 | 2,39 | 3,12 | ||||
0,5 | -1,90 | -1,42 | -0,94 | -0,46 | 0,02 | 0,50 | 0,98 | 1,46 | ||||
0,6 | -1,40 | -1,12 | -0,85 | -0,57 | -0,30 | -0,02 | 0,26 | 0,53 | ||||
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 | ||||
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 | ||||
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
N <= 0,8 | ||||||||||||
| ||||||||||||
0,1 | 0 | 1,20 | 2,40 | 3,60 | 4,06 | 6,00 | 7,20 | 8,58 | ||||
0,1 | -0,55 | 0,60 | 1,75 | 2,91 | 1,06 | 5,21 | 6,36 | 7,51 | ||||
0,2 | -1,00 | 0,06 | 1,14 | 2,20 | 3,27 | 4,34 | 5,41 | 6,48 | ||||
0,3 | -1,50 | -0,59 | 0,32 | 1,24 | 2,15 | 3,06 | 3,97 | 4,80 | ||||
0,4 | -1,85 | -1,14 | -0,43 | 0,27 | 0,98 | 1,69 | 2,40 | 3,11 | ||||
0,5 | -1,80 | -1,33 | -0,86 | -0,40 | 0,07 | 0,54 | 1,01 | 1,48 | ||||
0,6 | -1,35 | -1,07 | -0,80 | -0,52 | -0,25 | 0,03 | 0,31 | 0,58 | ||||
0,7 | -0,90 | -0,76 | -0,61 | -0,47 | -0,32 | -0,18 | -0,04 | 0,11 | ||||
0,8 | -0,55 | -0,49 | -0,43 | -0,37 | -0,31 | -0,25 | -0,19 | -0,13 | ||||
0,9 | -0,25 | -0,24 | -0,23 | -0,22 | -0,21 | -0,20 | -0,18 | -0,17 | ||||
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
Таблица 108
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -4,00 | -3,6 | -3,3 | -2,9 | -2,6 | -2,2 | -1,8 | -1,5 |
0,2 | -6,50 | -5,5 | -4,6 | -3,6 | -2,7 | -1,7 | -0,7 | 0,2 |
0,3 | -6,75 | -4,8 | -2,9 | -1,0 | 0,9 | 2,9 | 4,8 | 6,7 |
0,4 | -1,75 | 0,8 | 3,4 | 6,0 | 8,6 | 11,2 | 13,8 | 16,4 |
0,5 | 3,75 | 6,1 | 8,4 | 10,8 | 13,1 | 15,5 | 17,8 | 20,2 |
0,6 | 5,25 | 6,9 | 8,6 | 10,3 | 12,0 | 13,7 | 15,4 | 17,1 |
0,7 | 4,25 | 5,3 | 6,4 | 7,5 | 8,6 | 9,7 | 10,7 | 11,8 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 |
0,1 | -4,50 | -4,0 | -3,5 | -3,1 | -2,6 | -2,1 | -1,6 | -1,1 |
0,2 | -5,75 | -4,7 | -3,6 | -2,5 | -1,4 | -0,4 | 0,7 | 1,8 |
0,3 | -5,50 | -3,6 | -1,8 | 0,1 | 1,9 | 3,8 | 5,7 | 7,5 |
0,4 | -1,75 | 0,7 | 3,1 | 5,5 | 7,9 | 10,3 | 12,7 | 15,1 |
0,5 | 3,00 | 5,3 | 7,6 | 9,8 | 12,1 | 14,4 | 16,7 | 19,0 |
0,6 | 5,00 | 6,7 | 8,4 | 10,0 | 11,7 | 13,4 | 15,1 | 16,8 |
0,7 | 4,25 | 5,3 | 6,4 | 7,5 | 8,6 | 9,7 | 10,7 | 11,8 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 |
0,1 | -5,00 | -4,4 | -3,7 | -3,0 | -2,4 | -1,7 | -1,0 | -0,4 |
0,2 | -4,75 | -3,6 | -2,4 | -1,2 | 0,1 | 1,3 | 2,5 | 3,7 |
0,3 | -3,75 | -2,5 | -0,7 | 1,2 | 3,0 | 4,8 | 6,6 | 8,4 |
0,4 | -1,50 | 0,7 | 2,9 | 5,2 | 7,4 | 9,6 | 11,8 | 14,0 |
0,5 | 2,50 | 4,7 | 6,8 | 9,0 | 11,1 | 13,3 | 15,5 | 17,6 |
0,6 | 4,50 | 6,2 | 7,8 | 9,4 | 11,0 | 12,6 | 14,2 | 15,8 |
0,7 | 4,00 | 5,1 | 6,2 | 7,2 | 8,3 | 9,4 | 10,5 | 11,5 |
0,8 | 3,00 | 3,7 | 4,3 | 5,0 | 5,6 | 6,3 | 7,0 | 7,6 |
0,9 | 1,50 | 1,8 | 2,1 | 2,4 | 2,7 | 3,0 | 3,3 | 3,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -4,00 | -4,4 | -4,7 | -5,1 | -5,4 | -5,8 | -6,2 | -6,5 |
0,2 | -6,50 | -7,5 | -8,4 | -9,4 | -10,3 | -11,3 | -12,3 | -13,2 |
0,3 | -6,75 | -8,7 | -10,6 | -12,5 | -14,4 | -16,4 | -18,3 | -20,2 |
0,4 | -1,75 | -4,3 | -6,9 | -9,5 | -12,1 | -14,7 | -17,3 | -19,9 |
0,5 | 3,75 | 1,4 | -0,9 | -3,3 | -5,6 | -8,0 | -10,3 | -12,7 |
0,6 | 5,25 | 3,6 | 1,9 | 0,2 | -1,5 | -3,2 | -4,9 | -6,6 |
0,7 | 4,25 | 3,2 | 2,1 | 1,0 | -0,1 | -1,2 | -2,2 | -3,3 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 | -3,25 |
0,1 | -4,50 | -5,0 | -5,5 | -5,9 | -6,4 | -6,9 | -7,4 | -7,9 |
0,2 | -5,75 | -6,8 | -7,9 | -9,0 | -10,1 | -11,2 | -12,2 | -13,3 |
0,3 | -5,50 | -7,4 | -9,2 | -11,1 | -12,9 | -14,8 | -16,7 | -18,5 |
0,4 | -1,75 | -4,2 | -6,6 | -9,0 | -11,4 | -13,8 | -16,2 | -18,6 |
0,5 | 3,00 | 0,7 | -1,6 | -3,8 | -6,1 | -8,4 | -10,7 | -13,0 |
0,6 | 5,00 | 3,3 | 1,6 | -0,1 | -1,7 | -3,4 | -5,1 | -6,8 |
0,7 | 4,25 | 3,2 | 2,1 | 1,0 | -0,1 | -1,2 | -2,2 | -3,3 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 | -5,25 |
0,1 | -5,00 | -5,7 | -6,3 | -7,0 | -7,6 | -8,3 | -9,0 | -9,6 |
0,2 | -4,75 | -6,0 | -7,2 | -8,4 | -9,6 | -10,8 | -12,0 | -13,2 |
0,3 | -4,25 | -6,1 | -7,9 | -9,7 | -11,5 | -13,3 | -15,1 | -16,9 |
0,4 | -1,50 | -3,7 | -5,9 | -8,2 | -10,4 | -12,6 | -14,8 | -17,0 |
0,5 | 2,50 | 0,3 | -1,8 | -4,0 | -6,1 | -8,3 | -10,5 | -12,6 |
0,6 | 4,50 | 2,9 | 1,3 | -0,4 | -2,0 | -3,6 | -5,2 | -6,8 |
0,7 | 4,00 | 2,9 | 1,8 | 0,8 | -0,3 | -1,4 | -2,5 | -3,6 |
0,8 | 3,00 | 2,3 | 1,7 | 1,0 | 0,4 | -0,3 | -1,0 | -1,6 |
0,9 | 1,50 | 1,2 | 0,9 | 0,6 | 0,3 | 0 | -0,3 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.61. Период опасных деформаций процесса сдвижения в зависимости от средней глубины разработки Hср определяется по табл. 110, tоп, мес.
Hср, м | 100 и менее | 200 | 300 | 400 и более |
tоп, мес | 3 | 6 | 7 | 7 |
Таблица 111
Углы падения пластов | ||||
0 - 55 | 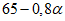 , но не менее 25 , но не менее 25 | 65 | - | 65 |
56 и более | 25 | - |  , но не менее 25 , но не менее 25 | 65 |
В подработанной толще граничные углы 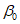 ,
,  ,
, 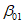 и
и  уменьшаются на 5°. Граничный угол в наносах
уменьшаются на 5°. Граничный угол в наносах 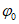 принимается равным 40°.
принимается равным 40°.
8.63. Углы максимального оседания 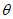 и углы полных сдвижений
и углы полных сдвижений  ,
, 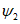 и
и  при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта по табл. 112 - 113.
при отсутствии сдвижения пород лежачего бока определяются в зависимости от угла падения пласта по табл. 112 - 113.
0 - 25 | |
26 - 55 |  |
Примечание. В наносах угол максимального оседания принимается равным 90°.
0 - 10 | 60 | 60 | 60 |
20 | 62 | 60 | 60 |
30 | 60 | 65 | 60 |
40 | 56 | 72 | 60 |
50 | 51 | 78 | 60 |
55 | 49 | 82 | 60 |
Примечание. Промежуточные значения углов полных сдвижений определяются интерполированием.
8.64. Относительные величины максимального оседания q0 и максимального горизонтального сдвижения a0 определяются по табл. 114.
Параметры | Первичная подработка | Повторная подработка |
q0 | 0,85 | 0,95 |
a0 | 0,35 | 0,35 |
8.65. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к средней глубине разработки H по табл. 115.
1,1 и более | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 и менее | |
N1 и N2 | 1,00 | 0,95 | 0,90 | 0,85 | 0,80 | 0,74 | 0,67 | 0,60 | 0,52 | 0,42 |
8.66. Значения функций S(z), F(z) и F'(z) при отсутствии сдвижения пород лежачего бока определяются в зависимости от коэффициентов N и B по табл. 116 - 120.
z | Значения функции S(z) | ||
N >= 1 | N = 0,9 | N <= 0,8 | |
0 | 1,00 | 1,00 | 1,00 |
0,1 | 0,95 | 0,93 | 0,91 |
0,2 | 0,81 | 0,78 | 0,76 |
0,3 | 0,60 | 0,58 | 0,57 |
0,4 | 0,40 | 0,38 | 0,37 |
0,5 | 0,24 | 0,24 | 0,24 |
0,6 | 0,14 | 0,14 | 0,14 |
0,7 | 0,08 | 0,08 | 0,08 |
0,8 | 0,04 | 0,04 | 0,04 |
0,9 | 0,02 | 0,02 | 0,02 |
1,0 | 0 | 0 | 0 |
Таблица 117
z | Значения функции F(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | 0,95 | 2,28 | 3,61 | 4,94 | 6,27 | 7,60 | 8,93 | 10,26 |
0,2 | 1,75 | 2,88 | 4,02 | 5,15 | 6,29 | 7,42 | 8,55 | 9,69 |
0,3 | 2,05 | 2,89 | 3,73 | 4,57 | 5,41 | 6,25 | 7,09 | 7,93 |
0,4 | 1,80 | 2,36 | 2,92 | 3,48 | 4,04 | 4,60 | 5,16 | 5,72 |
0,5 | 1,30 | 1,64 | 1,97 | 2,31 | 2,64 | 2,98 | 3,32 | 3,65 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | 1,10 | 2,40 | 3,70 | 5,01 | 6,31 | 7,61 | 8,91 | 10,21 |
0,2 | 1,75 | 2,84 | 3,93 | 5,03 | 6,12 | 7,21 | 8,30 | 9,39 |
0,3 | 2,00 | 2,81 | 3,62 | 4,44 | 5,25 | 6,06 | 6,87 | 7,68 |
0,4 | 1,70 | 2,23 | 2,76 | 3,30 | 3,83 | 4,36 | 4,89 | 5,42 |
0,5 | 1,20 | 1,54 | 1,87 | 2,21 | 2,54 | 2,88 | 3,22 | 3,55 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | 1,20 | 2,47 | 3,75 | 5,02 | 6,30 | 7,57 | 8,84 | 10,12 |
0,2 | 1,70 | 2,76 | 3,83 | 4,89 | 5,96 | 7,02 | 8,08 | 9,15 |
0,3 | 1,95 | 2,75 | 3,55 | 4,34 | 5,14 | 5,94 | 6,74 | 7,54 |
0,4 | 1,65 | 2,17 | 2,69 | 3,20 | 3,72 | 4,24 | 4,74 | 5,28 |
0,5 | 1,15 | 1,49 | 1,82 | 2,16 | 2,49 | 2,83 | 3,17 | 3,50 |
0,6 | 0,80 | 1,00 | 1,19 | 1,39 | 1,58 | 1,78 | 1,98 | 2,17 |
0,7 | 0,50 | 0,61 | 0,72 | 0,84 | 0,95 | 1,06 | 1,17 | 1,28 |
0,8 | 0,30 | 0,36 | 0,41 | 0,47 | 0,52 | 0,58 | 0,64 | 0,69 |
0,9 | 0,15 | 0,18 | 0,21 | 0,23 | 0,26 | 0,29 | 0,32 | 0,35 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 118
z | Значения функции F(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | -0,95 | 0,38 | 1,71 | 3,04 | 4,37 | 5,70 | 7,03 | 8,36 |
0,2 | -1,75 | -0,62 | 0,52 | 1,65 | 2,79 | 3,92 | 5,05 | 6,19 |
0,3 | -2,05 | -1,21 | -0,37 | 0,47 | 1,31 | 2,15 | 2,99 | 3,83 |
0,4 | -1,80 | -1,24 | -0,68 | -0,12 | 0,44 | 1,00 | 1,56 | 2,12 |
0,5 | -1,30 | -0,96 | -0,63 | -0,29 | 0,04 | 0,38 | 0,72 | 1,05 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,08 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | -1,10 | 0,20 | 1,50 | 2,81 | 4,11 | 5,41 | 6,71 | 8,01 |
0,2 | -1,75 | -0,66 | 0,43 | 1,53 | 2,62 | 3,71 | 4,80 | 5,89 |
0,3 | -2,00 | -1,19 | -0,38 | 0,41 | 1,25 | 2,06 | 2,87 | 3,68 |
0,4 | -1,70 | -1,17 | -0,64 | -0,10 | 0,43 | 0,96 | 1,49 | 2,02 |
0,5 | -1,20 | -0,86 | -0,53 | -0,19 | 0,14 | 0,48 | 0,82 | 1,15 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,08 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | 0 | 1,40 | 2,80 | 4,20 | 5,60 | 7,00 | 8,40 | 9,80 |
0,1 | -1,20 | 0,07 | 1,35 | 2,62 | 3,90 | 5,17 | 6,44 | 7,72 |
0,2 | -1,70 | -0,63 | 0,43 | 1,49 | 2,56 | 3,62 | 4,68 | 5,75 |
0,3 | -1,95 | -1,15 | -0,35 | 0,44 | 1,24 | 2,04 | 2,84 | 3,64 |
0,4 | -1,65 | -1,13 | -0,61 | -0,10 | 0,42 | 0,94 | 1,46 | 1,98 |
0,5 | -1,15 | -0,81 | -0,48 | -0,14 | 0,19 | 0,53 | 0,87 | 1,20 |
0,6 | -0,80 | -0,60 | -0,41 | -0,21 | -0,02 | 0,18 | 0,38 | 0,57 |
0,7 | -0,50 | -0,39 | -0,28 | -0,16 | -0,05 | 0,06 | 0,17 | 0,28 |
0,8 | -0,30 | -0,24 | -0,19 | -0,13 | -0,08 | -0,02 | 0,04 | 0,09 |
0,9 | -0,15 | -0,12 | -0,09 | -0,07 | -0,04 | -0,01 | 0,02 | 0,05 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 119
z | Значения функции F'(z) (полумульда по падению) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -8,75 | -7,4 | -6,1 | -4,8 | -3,4 | -2,1 | -0,8 | 0,6 |
0,2 | -5,50 | -3,1 | -0,6 | 1,9 | 4,3 | 6,8 | 9,2 | 11,7 |
0,3 | -0,25 | 2,6 | 5,4 | 8,4 | 11,3 | 14,2 | 17,0 | 19,9 |
0,4 | 3,75 | 6,3 | 8,8 | 11,3 | 13,9 | 16,4 | 18,9 | 21,4 |
0,5 | 5,00 | 6,8 | 8,6 | 10,5 | 12,3 | 14,1 | 15,9 | 17,7 |
0,6 | 4,00 | 5,1 | 6,2 | 7,4 | 8,5 | 9,6 | 10,7 | 11,8 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,3 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 0,7 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 | -6,00 |
0,1 | -8,75 | -7,2 | -5,7 | -4,1 | -2,6 | -1,1 | 0,5 | 2,1 |
0,2 | -4,50 | -2,1 | 0,4 | 2,9 | 5,3 | 7,8 | 10,2 | 12,7 |
0,3 | 0,25 | 3,1 | 5,9 | 8,7 | 11,5 | 14,3 | 17,1 | 19,9 |
0,4 | 4,00 | 6,4 | 8,8 | 11,1 | 13,5 | 15,9 | 18,3 | 20,7 |
0,5 | 4,50 | 6,2 | 7,9 | 9,5 | 11,2 | 12,9 | 14,6 | 16,3 |
0,6 | 3,50 | 4,6 | 5,7 | 6,9 | 8,0 | 9,1 | 10,2 | 11,3 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,6 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 |
0,1 | -8,50 | -6,8 | -5,1 | -3,5 | -1,8 | -0,1 | 1,6 | 3,3 |
0,2 | -3,75 | -1,4 | 1,0 | 3,4 | 5,8 | 8,2 | 10,6 | 13,0 |
0,3 | 0,25 | 3,0 | 5,7 | 8,4 | 11,2 | 14,0 | 16,7 | 19,4 |
0,4 | 4,00 | 6,3 | 8,6 | 10,9 | 13,2 | 15,6 | 17,9 | 20,2 |
0,5 | 4,25 | 5,9 | 7,5 | 9,1 | 10,7 | 12,3 | 13,9 | 15,5 |
0,6 | 3,25 | 4,4 | 5,5 | 6,6 | 7,7 | 8,9 | 10,0 | 11,1 |
0,7 | 2,50 | 3,2 | 3,9 | 4,6 | 5,3 | 6,0 | 6,7 | 7,4 |
0,8 | 1,75 | 2,2 | 2,6 | 3,0 | 3,4 | 3,9 | 4,3 | 4,7 |
0,9 | 0,75 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
z | Значения функции F'(z) (полумульда по восстанию) | |||||||
Значения коэффициента B | ||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
N >= 1 | ||||||||
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | -8,75 | -10,1 | -11,4 | -12,7 | -14,1 | -15,4 | -16,7 | -18,1 |
0,2 | -5,50 | -8,0 | -10,4 | -12,9 | -15,3 | -17,8 | -20,2 | -22,7 |
0,3 | -0,25 | -3,1 | -6,6 | -8,9 | -11,8 | -14,7 | -17,5 | -20,4 |
0,4 | 3,75 | 1,2 | -1,3 | -3,8 | -6,4 | -8,9 | -11,4 | -13,9 |
0,5 | 5,00 | 3,2 | 1,4 | -0,5 | -2,3 | -4,1 | -5,9 | -7,7 |
0,6 | 4,00 | 2,9 | 1,8 | 0,6 | -0,5 | -1,6 | -2,7 | -3,8 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | -0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,7 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N = 0,9 | ||||||||
0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 | -6,0 |
0,1 | -8,75 | -10,3 | -11,8 | -13,4 | -14,9 | -16,5 | -18,0 | -19,6 |
0,2 | -4,50 | -7,0 | -9,4 | -11,9 | -14,3 | -16,8 | -19,2 | -21,7 |
0,3 | -0,25 | -2,6 | -5,4 | -8,2 | -11,0 | -13,8 | -16,6 | -19,4 |
0,4 | 4,00 | 1,6 | -0,8 | -3,1 | -5,5 | -7,9 | -10,3 | -12,7 |
0,5 | 4,50 | 2,8 | 1,1 | -0,5 | -2,2 | -3,9 | -5,6 | -7,3 |
0,6 | 3,50 | 2,4 | 1,3 | 0,1 | -1,0 | -2,1 | -3,2 | -4,3 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | -0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,7 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
N <= 0,8 | ||||||||
0 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 | -9,00 |
0,1 | -8,50 | -10,2 | -11,9 | -13,5 | -15,2 | -16,9 | -18,6 | -20,3 |
0,2 | -3,75 | -6,1 | -8,5 | -10,9 | -13,3 | -15,7 | -18,1 | -20,5 |
0,3 | 0,25 | -2,5 | -5,2 | -7,9 | -10,7 | -13,5 | -16,2 | -18,9 |
0,4 | 4,00 | 1,7 | -0,6 | -2,9 | -5,2 | -7,6 | -9,9 | -12,2 |
0,5 | 4,25 | 2,6 | 1,0 | -0,6 | -2,2 | -3,8 | -5,4 | -7,1 |
0,6 | 3,24 | 2,1 | 1,0 | -0,1 | -1,2 | -2,4 | -3,5 | -4,6 |
0,7 | 2,50 | 1,8 | 1,1 | 0,4 | -0,3 | -1,0 | -1,7 | -2,4 |
0,8 | 1,75 | 1,3 | 0,9 | 0,5 | -0,1 | -0,4 | -0,8 | -1,2 |
0,9 | 0,75 | 0,5 | 0,3 | 0,1 | -0,1 | -0,3 | -0,5 | -0,6 |
1,0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
8.67. Углы максимального оседания 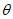 и максимального горизонтальных сдвижений
и максимального горизонтальных сдвижений 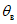 и
и 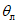 при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта, град, по табл. 121.
при сдвижении пород лежачего бока определяются в зависимости от угла падения пласта, град, по табл. 121.
55 | 56 | 35 | 50 |
60 | 61 | 42 | 54 |
70 | 70 | 55 | 62 |
80 | 80 | 68 | 71 |
90 | 90 | 80 | 80 |
8.68. Коэффициенты Kз и  , используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, определяются в зависимости от угла падения пласта, табл. 122.
, используемые для расчета максимального оседания и горизонтального сдвижения при сдвижении пород лежачего бока, определяются в зависимости от угла падения пласта, табл. 122.
55 - 60 | 70 | 80 | 90 | |
Kз | 0,60 | 0,57 | 0,53 | 0,50 |
0,50 | 0,50 | 0,50 | 0,50 |
Примечание. Промежуточные значения Kз определяются путем интерполяции.
8.69. Период опасных деформаций процесса сдвижения tоп, мес, в зависимости от скорости подвигания очистного забоя и глубины разработки Hср определяется по табл. 123.
Hср, м | Скорость подвигания очистного забоя, м/мес | ||||
20 | 40 | 60 | 80 | 100 | |
100 | 5 | 4 | 3 | 2 | 2 |
200 | 9 | 6 | 5 | 4 | 3 |
300 | 13 | 8 | 6 | 5 | 4 |
8.70. Значение угла трения по наиболее слабому контакту вмещающих пород с угольным пластом принимается 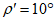 .
.
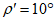 .
.Предельный угол падения пласта, при котором возникает опасное сдвижение пород лежачего бока, 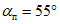 .
.
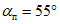 .
.8.71. Граничные углы в неподработанной и подработанной толще принимаются одинаковыми по всей покрывающей толще и равными во всех направлениях  .
.
 .
.8.72. Значения параметров, используемых для расчета сдвижений и деформаций земной поверхности: угол максимального оседания 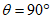 ; угол полных сдвижений
; угол полных сдвижений  ; относительное максимальное оседание q0 = 0,9; относительное максимальное горизонтальное сдвижение a0 = 0,32; коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к глубине разработок H по табл. 124.
; относительное максимальное оседание q0 = 0,9; относительное максимальное горизонтальное сдвижение a0 = 0,32; коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к глубине разработок H по табл. 124.
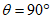 ; угол полных сдвижений
; угол полных сдвижений  ; относительное максимальное оседание q0 = 0,9; относительное максимальное горизонтальное сдвижение a0 = 0,32; коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к глубине разработок H по табл. 124.
; относительное максимальное оседание q0 = 0,9; относительное максимальное горизонтальное сдвижение a0 = 0,32; коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к глубине разработок H по табл. 124.1,1 и более | 1,0 | 0,9 | 0,8 | 0,7 | |
N1 и N2 | 1 | 0,95 | 0,90 | 0,85 | 0,80 |
8.73. Значения функций S(z), F(z) и F'(z) определяются для всех значений коэффициентов N по табл. 125.
z | S(z) | F(z) | F'(z) |
0 | 1,00 | 0 | 0 |
0,1 | 0,98 | 0,53 | -6,5 |
0,2 | 0,88 | 1,60 | -13,1 |
0,3 | 0,66 | 2,76 | -6,4 |
0,35 | - | 2,85 | - |
0,4 | 0,38 | 2,65 | 7,1 |
0,5 | 0,16 | 1,57 | 10,1 |
0,6 | 0,05 | 0,70 | 7,5 |
0,7 | 0,01 | 0,20 | 2,9 |
0,8 | 0,005 | 0,04 | 0,6 |
0,9 | 0,002 | 0,02 | 0,1 |
1,0 | 0 | 0 | 0 |
8.74. Продолжительность опасного периода деформаций процесса сдвижения принимается равной 6 мес.
ХАРАКТЕРОМ СДВИЖЕНИЯ ГОРНЫХ ПОРОД
8.75. Параметры процесса сдвижения, необходимые для расчета сдвижений и деформаций земной поверхности, определяются для месторождений с неизученным или недостаточно изученным характером процесса сдвижения в зависимости от принадлежности их к одной из групп, приведенных в табл. 126.
Бассейн, месторождение, геолого-промышленный район, шахта | Группа |
Александрийское месторождение | I |
Ахалцихское месторождение; шахты "Шебунино" и N 10/13 объединения Сахалинуголь | II |
Ангренское месторождение | III |
Артемовское и Тавричанское месторождения (объединение Приморскуголь); Ленгерское и Кызыл-Кийское месторождения (объединение Средазуголь); Анадырское месторождение (шахта "Анадырская" N 3-бис) | IV |
Шурабское, Таш-Кумырское, Сулюктинское, Кок-Янгакское, Джергаланское, Согутинское месторождения (объединение Средазуголь); Липовецкое месторождение (объединение Приморскуголь); месторождение бухты "Угольной" (шахта "Беринговская" N 2); Галимовское месторождение (шахта "Омсукчанская") | V |
Ткибульское и Ткварчельское месторождения (объединение Грузуголь); Черемховское месторождение; Сангарское месторождение (шахта "Сангарская"); шахта "Джебарики-Хая", Нижне-Аркагалинское месторождение (шахты "Кадыкчанская" и "Кедровская") | VI |
Шахты объединения Сахалинуголь (кроме "Шебунино" и N 10/13); Черногорское месторождение | VII |
Сучанский бассейн; Подгородненское месторождение (объединение Приморскуголь) | VIII |
8.76. Предельный угол падения пласта, при котором возникают опасные сдвижения пород висячего бока, определяются по табл. 127.
Бассейн, месторождение | Мощность пласта, м | ||
4 и более | менее 4 | ||
1. | 50 | 55 | |
Сучанский бассейн (Старый Сучан), Сахалинское месторождение, месторождения VI группы | 55 | 60 | |
Сучанский бассейн (Северный Сучан), месторождения Средней Азии (кроме Ленгерского и Кызыл-Кийского), месторождения VII группы (кроме Сахалинского) | 60 | 60 | |
4. | Месторождения VIII группы (кроме Сучанского бассейна) | 65 | 65 |
8.77. Граничные углы 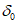 ,
,  ,
, 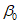 и
и  , град, в неподработанной толще коренных пород определяются по табл. 128 - 130 в зависимости от группы, к которой относится месторождение.
, град, в неподработанной толще коренных пород определяются по табл. 128 - 130 в зависимости от группы, к которой относится месторождение.
Группы месторождений | I | II | III | IV | V | VI | VII | VIII |
40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 |
Таблица 129
Граничные углы | |||||||||||||||||||
Угол падения | m, м | ||||||||||||||||||
0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 80 | 85 | 90 | ||
45 | 45 | 41 | 38 | 35 | 34 | 32 | 32 | 31 | 31 | 30 | 29 | 29 | 28 | 27 | 26 | 25 | 25 | 25 | - |
50 | 50 | 46 | 43 | 40 | 38 | 36 | 35 | 33 | 32 | 31 | 31 | 30 | 29 | 28 | 27 | 25 | 25 | 25 | - |
55 | 55 | 50 | 47 | 44 | 42 | 40 | 39 | 35 | 34 | 32 | 31 | 30 | 29 | 28 | 27 | 25 | 27 | 28 | до 4 |
25 | 25 | 25 | 4 и более | ||||||||||||||||
60 | 60 | 55 | 52 | 49 | 46 | 43 | 41 | 39 | 37 | 34 | 33 | 31 | 28 | 26 | 25 | 25 | 27 | 28 | до 4 |
25 | 25 | 25 | 4 и более | ||||||||||||||||
65 | 65 | 60 | 57 | 53 | 50 | 46 | 43 | 41 | 40 | 36 | 33 | 29 | 26 | 25 | 25 | 25 | 28 | 30 | до 4 |
25 | 27 | 28 | 4 и более | ||||||||||||||||
70 | 70 | 65 | 61 | 57 | 54 | 50 | 46 | 42 | 40 | 36 | 33 | 29 | 25 | 25 | 25 | 25 | 31 | 35 | до 4 |
25 | 28 | 30 | 4 и более | ||||||||||||||||
75 | 75 | 70 | 66 | 61 | 57 | 53 | 50 | 45 | 41 | 36 | 33 | 29 | 25 | 25 | 25 | 28 | 31 | 35 | до 4 |
25 | 28 | 30 | 4 и более | ||||||||||||||||
Группы VIII и IX при C > 50% и M >= 30 м | |||||||||||||||||||
70 | 70 | 65 | 62 | 58 | 55 | 52 | 50 | 47 | 46 | 43 | 41 | 39 | 35 | 32 | 30 | 30 | 32 | 35 | до 4 |
30 | 30 | 30 | 4 и более | ||||||||||||||||
75 | 75 | 70 | 67 | 63 | 60 | 56 | 54 | 51 | 49 | 46 | 43 | 41 | 38 | 35 | 35 | 35 | 35 | 35 | |
Примечание. При промежуточных значениях 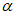 угол
угол  определяется интерполированием.
определяется интерполированием.
50 | 55 - 80 | 85 | 90 | |
35 | 40 | 35 | 25 |
В подработанной толще граничные углы в коренных породах принимаются на 5° меньше.
Граничные углы в наносах  определяются в зависимости от мощности наносов по табл. 131.
определяются в зависимости от мощности наносов по табл. 131.
Мощность наносов h, м | |
Менее 40 | 45 |
40 - 60 | 50 |
Более 60 | 55 |
Примечания: 1. Если в толще наносов преобладают обводненные отложения, то значения угла 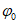 уменьшаются на 5°.
уменьшаются на 5°.
2. На месторождениях, относящихся к I и II группам (табл. 126), угол 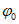 принимается равным соответствующему граничному углу в коренных породах.
принимается равным соответствующему граничному углу в коренных породах.
Граничные углы 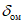 и
и  , град, в мезозойских отложениях, не являющихся коренными породами (залегающих над палеозойскими отложениями с угловым несогласием более 5°), при любом количестве подработок определяются в зависимости от мощности мезозойских отложений по табл. 132.
, град, в мезозойских отложениях, не являющихся коренными породами (залегающих над палеозойскими отложениями с угловым несогласием более 5°), при любом количестве подработок определяются в зависимости от мощности мезозойских отложений по табл. 132.
Мощность мезозойских отложений hм, м | |||
Менее 50 | 60 | ||
51 - 100 | 65 | , но не более граничного угла в коренных породах | |
Более 100 | 70 | ||
Граничный угол 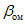 при любом количестве подработок определяется в зависимости от угла
при любом количестве подработок определяется в зависимости от угла  , град, и угла падения мезозойских отложений по табл. 133.
, град, и угла падения мезозойских отложений по табл. 133.
Граничные углы | |||||||
0 | 10 | 20 | 30 | 40 | 50 | 60 | |
60 | 60 | 55 | 50 | 45 | 40 | 35 | 30 |
65 | 65 | 60 | 55 | 50 | 45 | 40 | 35 |
70 | 70 | 65 | 60 | 55 | 50 | 45 | 40 |
8.78. Угол максимального оседания 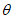 определяется по формуле
определяется по формуле
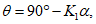
где K1 - коэффициент, определяемый по табл. 134 в зависимости от группы месторождения и величины отношения суммарной мощности наносов h и горизонтально залегающих мезозойских отложений hм к средней глубине разработки H. Если 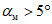 , то K1 определяется по величине
, то K1 определяется по величине  .
.
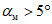 , то K1 определяется по величине
, то K1 определяется по величине Группы месторождений | Значения коэффициента K1 | |||||||||
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 и более | |
I - II | 0,68 | 0,61 | 0,54 | 0,47 | 0,40 | 0,34 | 0,27 | 0,20 | 0,14 | 0 |
III - IV | 0,72 | 0,65 | 0,58 | 0,50 | 0,43 | 0,36 | 0,29 | 0,22 | 0,14 | 0 |
V | 0,78 | 0,71 | 0,63 | 0,55 | 0,47 | 0,39 | 0,31 | 0,24 | 0,16 | 0 |
VI | 0,86 | 0,77 | 0,69 | 0,60 | 0,52 | 0,43 | 0,35 | 0,26 | 0,17 | 0 |
VII | 0,91 | 0,82 | 0,73 | 0,64 | 0,55 | 0,46 | 0,36 | 0,27 | 0,18 | 0 |
VIII | 1,00 | 0,91 | 0,81 | 0,71 | 0,60 | 0,50 | 0,40 | 0,30 | 0,20 | 0 |
Примечание. При промежуточных значениях 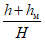 значение коэффициента K1 определяется интерполированием.
значение коэффициента K1 определяется интерполированием.
Для всех групп месторождений при 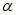 более 50° для расчета угла
более 50° для расчета угла 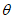 используется
используется 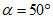 .
.
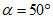 .
.Углы полных сдвижений определяются следующим образом:
по простиранию пласта углы 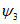 определяются по табл. 135 в зависимости от группы месторождений и средней глубины разработки;
определяются по табл. 135 в зависимости от группы месторождений и средней глубины разработки;
Группы месторождений | Значения углов | ||||||
H, м | |||||||
100 и менее | 200 | 400 | 600 | 800 | 900 | 1000 и более | |
I - II | 64 | 64 | 65 | 65 | 65 | 65 | 65 |
III - IV | 62 | 63 | 63 | 64 | 64 | 65 | 65 |
V | 60 | 61 | 62 | 63 | 64 | 64 | 65 |
VI | 57 | 58 | 60 | 61 | 62 | 64 | 65 |
VII | 55 | 56 | 58 | 60 | 62 | 64 | 65 |
VIII | 51 | 53 | 55 | 58 | 61 | 63 | 65 |
Величины углов | ||||||||||||||||||||
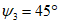 |  |  | ||||||||||||||||||
0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 0 | 10 | 20 | 30 | |
90 - 85 | 45 --- 45 | 40 --- 50 | 35 --- 55 | 30 --- 60 | 50 --- 50 | 44 --- 56 | 38 --- 62 | 33 --- 69 | 55 --- 55 | 48 --- 62 | 42 --- 69 | 36 --- 77 | ||||||||
84 - 75 | 45 --- 45 | 40 --- 50 | 35 --- 56 | 30 --- 61 | 50 --- 50 | 44 --- 56 | 39 --- 63 | 33 --- 69 | 55 --- 55 | 49 --- 62 | 42 --- 70 | |||||||||
74 - 65 | 47 --- 47 | 41 --- 52 | 36 --- 58 | 31 --- 63 | 52 --- 52 | 46 --- 58 | 40 --- 64 | 34 --- 72 | 57 --- 57 | 50 --- 64 | ||||||||||
64 - 55 | 49 --- 49 | 43 --- 55 | 38 --- 61 | 32 --- 67 | 54 --- 54 | 48 --- 61 | 41 --- 68 | 35 --- 75 | 59 --- 59 | |||||||||||
54 - 45 | 52 --- 52 | 46 --- 59 | 40 --- 66 | 34 --- 73 | 57 --- 57 | 50 --- 64 | 44 --- 72 | 37 --- 81 | ||||||||||||
44 - 35 | 57 --- 57 | 50 --- 64 | 44 --- 72 | 62 --- 62 | 54 --- 70 | 47 --- 78 | ||||||||||||||
34 - 25 | 63 --- 63 | 56 --- 72 | 67 --- 67 | 59 --- 76 | ||||||||||||||||
Продолжение табл. 136
Величины углов | ||||||||||||||||||||
 | 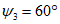 | 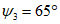 | ||||||||||||||||||
40 | 50 | 60 | 70 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | |
90 - 85 | 60 --- 60 | 53 --- 68 | 46 --- 76 | 39 --- 85 | 65 --- 65 | 57 --- 73 | 49 --- 82 | 42 --- 92 | ||||||||||||
84 - 75 | 36 --- 78 | 60 --- 60 | 53 --- 68 | 46 --- 76 | 39 --- 85 | 65 --- 65 | 57 --- 74 | 50 --- 83 | 42 --- 93 | |||||||||||
74 - 65 | 43 --- 71 | 37 --- 80 | 62 --- 62 | 54 --- 69 | 47 --- 78 | 40 --- 87 | 66 --- 66 | 58 --- 75 | 50 --- 84 | 43 --- 94 | ||||||||||
64 - 55 | 52 --- 66 | 45 --- 74 | 38 --- 83 | 63 --- 63 | 56 --- 72 | 48 --- 80 | 41 --- 90 | 68 --- 68 | 60 --- 77 | 52 --- 86 | 44 --- 96 | |||||||||
54 - 45 | 62 --- 62 | 54 --- 70 | 47 --- 78 | 40 --- 88 | 66 --- 66 | 58 --- 75 | 50 --- 84 | 42 --- 94 | 70 --- 70 | 62 --- 79 | 53 --- 89 | 45 --- 99 | ||||||||
44 - 35 | 66 --- 66 | 58 --- 74 | 50 --- 83 | 70 --- 70 | 61 --- 79 | 53 --- 88 | 73 --- 73 | 64 --- 83 | 56 --- 92 | |||||||||||
34 - 25 | 71 --- 71 | 62 --- 80 | 74 --- 74 | 65 --- 83 | 77 --- 77 | 66 --- 86 | ||||||||||||||
Примечания: 1. При промежуточных значениях углов 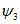 принимаются ближайшие значения, приведенные в таблице. 2. При промежуточных значениях
принимаются ближайшие значения, приведенные в таблице. 2. При промежуточных значениях 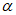 значения углов
значения углов 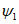 и
и 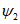 определяются интерполированием.
определяются интерполированием.
8.79. Относительное максимальное оседание земной поверхности q0 определяется:
при первичной подработке - по табл. 137 в зависимости от группы месторождений, средней глубины выработки H и отношения 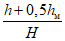 ;
;
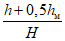 ;
;при повторной подработке
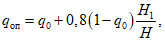
где q0 - относительное максимальное оседание от разрабатываемого пласта, определяемое по табл. 137;
H - расстояние по вертикали от середины выработки в разрабатываемом пласте до земной поверхности;
H1 - расстояние между земной поверхностью и ранее отработанным пластом, измеряемое по вертикали, проведенной через середину выработки в разрабатываемом пласте.
Примечания: 1. При  принимается
принимается  ; 2. Если вертикаль, проведенная из середины выработки, пересекает несколько ранее отработанных пластов, то к расчету принимается максимальное значение H1. 3. При расчете деформаций от свиты пластов (3 и более) или от эквивалентного пласта принимается qоп = 0,9 для всех пластов.
; 2. Если вертикаль, проведенная из середины выработки, пересекает несколько ранее отработанных пластов, то к расчету принимается максимальное значение H1. 3. При расчете деформаций от свиты пластов (3 и более) или от эквивалентного пласта принимается qоп = 0,9 для всех пластов.
Группы месторождений | Относительное максимальное оседание q0 | ||||||
H, м | 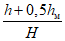 | ||||||
менее 0,20 | 0,20 - 0,40 | 0,41 - 0,60 | 0,01 - 0,70 | 0,71 - 0,80 | более 0,80 | ||
I | Все глубины | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
II | Все глубины | 0,85 | 0,95 | 0,95 | 0,95 | 0,95 | 0,95 |
III | 0,85 | 0,85 | 0,90 | 0,90 | 0,95 | 0,95 | |
IV - V | 0,75 | 0,80 | 0,85 | 0,90 | 0,95 | 0,95 | |
VI - VIII | До 200 | 0,70 | 0,75 | 0,80 | 0,90 | 0,90 | 0,95 |
200 и более | 0,75 | 0,80 | 0,85 | 0,95 | 0,95 | 0,95 | |
Относительное максимальное горизонтальное сдвижение a0 при первичной и повторной подработках определяется по табл. 138 в зависимости от группы месторождений и величины отношения

Группы месторождений | Относительное максимальное горизонтальное сдвижение | ||||
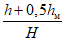 | |||||
<= 0,10 | 0,11 - 0,20 | 0,21 - 0,30 | 0,31 - 0,40 | > 0,40 | |
I | 0,45 | 0,45 | 0,45 | 0,45 | 0,45 |
II | 0,40 | 0,40 | 0,45 | 0,45 | 0,45 |
III | 0,35 | 0,35 | 0,40 | 0,45 | 0,45 |
IV, V | 0,30 | 0,35 | 0,40 | 0,45 | 0,45 |
VI, VII | 0,30 | 0,30 | 0,35 | 0,40 | 0,45 |
VIII | 0,30 | 0,30 | 0,30 | 0,35 | 0,40 |
8.80. Коэффициенты N1 и N2 определяются в зависимости от отношения размера выработки Д к средней глубине разработки H по табл. 139.
Группы месторождений | Значения коэффициентов N1 и N2 | ||||||||||||
2 и более | 1,6 | 1,2 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,25 | 0,2 | 0,15 и менее | |
I - II | 1 | 1 | 1 | 0,95 | 0,85 | 0,75 | 0,70 | 0,60 | 0,45 | 0,35 | 0,25 | 0,20 | 0,10 |
III - IV | 1 | 1 | 1 | 0,95 | 0,80 | 0,75 | 0,65 | 0,55 | 0,45 | 0,30 | 0,25 | 0,15 | 0,10 |
V - VI | 1 | 1 | 0,95 | 0,85 | 0,70 | 0,65 | 0,55 | 0,45 | 0,35 | 0,25 | 0,20 | 0,15 | 0,10 |
VII - VIII | 1 | 1 | 0,90 | 0,80 | 0,65 | 0,60 | 0,50 | 0,40 | 0,30 | 0,20 | 0,15 | 0,10 | 0,10 |
Примечание. При промежуточных значениях 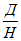 коэффициенты N1 и N2 определяются интерполированием.
коэффициенты N1 и N2 определяются интерполированием.
8.81. Значения функций S(z), F(z) и F'(z) определяются в зависимости от коэффициентов N и B по табл. 29 - 33 (см. п. 8.5).
8.82. Угол максимального оседания 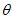 при сдвижении пород лежачего бока определяется по формуле
при сдвижении пород лежачего бока определяется по формуле
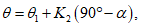
где 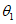 - угол, определяемый по табл. 140;
- угол, определяемый по табл. 140;
K2 - коэффициент, определяемый по табл. 141 в зависимости от процентного содержания C слоев песчаников и известняков мощностью более 15 м, в толще пород висячего бока, затронутой сдвижением. Размер толщи, затронутой сдвижением, определяется длиной мульды сдвижения на земной поверхности.
Группы месторождений | Значения угла | |||
до 60 | 70 | 80 | 90 | |
I - IV | 55 | 60 | 75 | 90 |
V - VII | 40 | 50 | 70 | 90 |
VIII | 30 | 45 | 70 | 90 |
Примечание. Промежуточные значения  определяются интерполированием.
определяются интерполированием.
Группы месторождений | Значения коэффициента K2 | ||||
C (%) | |||||
до 20 | 30 | 40 | 50 | 60 и более | |
V - VII | 0,1 | 0,2 | 0,25 | 0,3 | 0,5 |
VIII | 0,3 | 0,3 | 0,4 | 0,5 | 0,9 |
Примечания: 1. Для месторождений I - IV групп принимается K2 = 0.
2. Промежуточные значения коэффициента определяются интерполированием.
Угол максимального горизонтального сдвижения в висячем боку  определяется в зависимости от угла максимального оседания
определяется в зависимости от угла максимального оседания  , град, по табл. 142.
, град, по табл. 142.
<= 60 | 70 | 75 | 80 | 85 | 90 | |
65 | 70 | 75 | 70 | 60 |
Примечание. Промежуточные значения 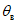 определяются интерполированием.
определяются интерполированием.
Угол максимального горизонтального сдвижения в лежачем боку  определяется в зависимости от угла падения
определяется в зависимости от угла падения 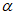 , град, по табл. 143.
, град, по табл. 143.
50 | 60 | 70 | 80 и более | |
40 | 50 | 55 | 60 |
Примечание. Промежуточные значения 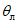 определяются интерполированием.
определяются интерполированием.
8.83. Период опасных деформаций процесса сдвижения определяется по табл. 144 в зависимости от глубин разработки и от скорости подвигания забоя лавы.
Период опасных деформаций tоп, мес | ||||
Hср, м | Скорость подвигания забоя лавы, м/мес | |||
30 | 50 | 70 | 100 | |
50 | 2 | 2 | 1 | 1 |
100 | 4 | 3 | 2 | 2 |
200 | 6 | 5 | 4 | 3 |
300 | 7 | 6 | 5 | 4 |
400 | 8 | 7 | 5 | 4 |
500 | 7 | 5 | 4 | 3 |
Примечание. Для промежуточных значений Hср искомые величины определяются путем интерполирования, а скорости подвигания забоя округляются до ближайших значений.
ПРИМЕРЫ РАСЧЕТА СДВИЖЕНИЙ И ДЕФОРМАЦИЙ ЗЕМНОЙ ПОВЕРХНОСТИ
Пример 1. Расчет ожидаемых величин сдвижений и деформаций земной поверхности на площадке, подлежащей застройке (рис. 23).

ожидаемых сдвижений и деформаций
1 - наносы; 2 - коренные породы
На поле действующей шахты N 5 в Донбассе, разрабатывающей угли марки К, выбрана площадка АБ для застройки жилыми зданиями. Под площадкой залегают два пласта: l5 и l4. Мощность наносов 20 м. Верхний горизонт в обоих пластах отработан до начала строительства. Календарный план отработки пластов под застраиваемыми площадками имеется. Ниже горизонта 320 м горные работы по обоим пластам производиться не будут. Здания расположены длинными сторонами вкрест простирания, поэтому расчет деформаций произведен только на разрезе вкрест простирания. Расположение выработок под площадкой показано на рис. 23. Скорость подвигания забоя 30 м/мес.
Границы отрабатываемых пластов на выбранном участке земной поверхности определим по углам 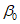 и
и 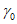 . Согласно п. 8.1,
. Согласно п. 8.1, 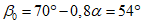 ;
;  ;
;  согласно табл. 23.
согласно табл. 23.
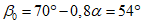 ;
;  ;
;  согласно табл. 23.
согласно табл. 23.От границ площадки проводим линии под углами 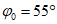 и продолжаем их в коренных породах под углами
и продолжаем их в коренных породах под углами 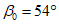 и
и 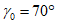 до пересечения с почвой нижнего пласта l4. Таким образом, на застраиваемый участок земной поверхности окажут влияние работы в лавах 15 и 17 в пласте l5 и в лавах 27 и 29 в пласте l4.
до пересечения с почвой нижнего пласта l4. Таким образом, на застраиваемый участок земной поверхности окажут влияние работы в лавах 15 и 17 в пласте l5 и в лавах 27 и 29 в пласте l4.
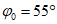 и продолжаем их в коренных породах под углами
и продолжаем их в коренных породах под углами 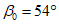 и
и 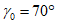 до пересечения с почвой нижнего пласта l4. Таким образом, на застраиваемый участок земной поверхности окажут влияние работы в лавах 15 и 17 в пласте l5 и в лавах 27 и 29 в пласте l4.
до пересечения с почвой нижнего пласта l4. Таким образом, на застраиваемый участок земной поверхности окажут влияние работы в лавах 15 и 17 в пласте l5 и в лавах 27 и 29 в пласте l4.Для назначения мер охраны возводимых зданий необходимо определить ожидаемые величины наклонов, кривизны и горизонтальных деформаций земной поверхности на участке расположения строительной площадки АБ при подработке ее двумя пластами между горизонтами 160 - 320 м.
Необходимые для расчетов величины горно-геологических параметров приведены в табл. 145.
Параметры | Пласт l5 | Пласт l4 | ||||||
Номера лав | ||||||||
15 | 17 | 7, 15 | 15, 17 | 27 | 29 | 19, 27 | 27, 29 | |
m, м | 1,50 | 1,50 | - | - | 1,20 | 1,20 | - | - |
20 | 20 | - | - | 20 | 20 | - | - | |
h, м | 20 | 20 | - | - | 20 | 20 | - | - |
Д1, м | 200 | 200 | - | - | 200 | 200 | - | - |
Д2, м | 750 | 750 | - | - | 750 | 750 | - | - |
Hср, м | 200 | 280 | - | - | 200 | 280 | - | - |
l1, м | - | - | 20 | 30 | - | - | 20 | 20 |
Hц, м | - | - | 160 | 240 | - | - | 160 | 240 |
Величины ожидаемых наклонов, кривизны и горизонтальных деформаций на площадке АБ необходимо рассчитывать в такой же последовательности, в какой намечается проходка очистных выработок (см. п. 4.4).
Поскольку в пласте l5 отношение размера целика между лавами 15 и 17 к глубине его залегания 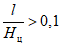 , то, согласно п. 4.5, расчет производим отдельно от каждой очистной выработки.
, то, согласно п. 4.5, расчет производим отдельно от каждой очистной выработки.
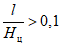 , то, согласно п. 4.5, расчет производим отдельно от каждой очистной выработки.
, то, согласно п. 4.5, расчет производим отдельно от каждой очистной выработки.В пласте l4 отношение размера целика между лавами 27 и 29 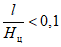 и разрыв во времени t между подработками участка смежными выработками меньше продолжительности периода опасных деформаций tоп(t < tоп), определяемого по п. 8.7. В соответствии с п. 4.5, расчет должен производиться как от одной лавы суммарного размера.
и разрыв во времени t между подработками участка смежными выработками меньше продолжительности периода опасных деформаций tоп(t < tоп), определяемого по п. 8.7. В соответствии с п. 4.5, расчет должен производиться как от одной лавы суммарного размера.
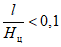 и разрыв во времени t между подработками участка смежными выработками меньше продолжительности периода опасных деформаций tоп(t < tоп), определяемого по п. 8.7. В соответствии с п. 4.5, расчет должен производиться как от одной лавы суммарного размера.
и разрыв во времени t между подработками участка смежными выработками меньше продолжительности периода опасных деформаций tоп(t < tоп), определяемого по п. 8.7. В соответствии с п. 4.5, расчет должен производиться как от одной лавы суммарного размера.Согласно календарному плану работ, расчет ожидаемых величин деформаций производим по следующим этапам:
отработка лавы 15 с учетом смежной лавы 7;
отработка лавы 17 с учетом смежной лавы 15 (сумма деформаций лав 15 и 17);
отработка лавы 27 с учетом смежной лавы 19 (сумма деформаций лав 15, 17 и 27);
отработка лавы 29 (сумма деформаций от лав 15, 17 и от лав 27 и 29 как от одной выработки).
Для определения наибольших деформаций полученные значения деформаций на каждом этапе последовательно суммируются.
Исходные параметры для расчета ожидаемых деформаций вычисляем в соответствии с пп. 4.7 - 4.9. Определяем исходные параметры для расчета ожидаемых деформаций при разработке пластов l5 и l4.
Отработка лавы 15.
Граничные углы, согласно п. 8.1, в подработанной и неподработанной толще данной марки угля принимаем:  ;
;  . Граничные углы в наносах
. Граничные углы в наносах  принимаем согласно табл. 23.
принимаем согласно табл. 23.
 ;
;  . Граничные углы в наносах
. Граничные углы в наносах  принимаем согласно табл. 23.
принимаем согласно табл. 23.Угол максимального оседания, согласно табл. 24, при наличии горных работ в данном пласте на вышележащем горизонте, принимаем: 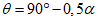 ;
; 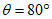 .
.
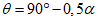 ;
; 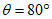 .
.Максимальное оседание (см. п. 4.10):

Определяем значение коэффициентов N1, N2 (см. п. 8.4).
Вкрест простирания:
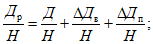

По табл. 26 находим N1 = 0,9.
По простиранию 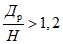 , следовательно, N2 = 1.
, следовательно, N2 = 1.
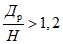 , следовательно, N2 = 1.
, следовательно, N2 = 1.Относительные величины максимального оседания и максимального горизонтального сдвижения находим по табл. 25:
q0 = 0,8; a0 = 0,3;
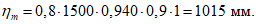
Длина полумульд (см. п. 4.8): L1 = 230 м; L2 = 198 м.
Наклоны (см. п. 4.12):
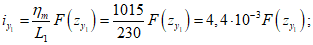
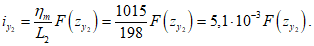
Кривизна (см. п. 4.3):

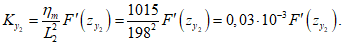
Горизонтальные деформации (см. п. 4.15):

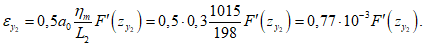
Находим B (см. п. 4.14):
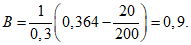
Отработка лавы 17.
Исходные данные для расчета ожидаемых деформаций земной поверхности от отработки этой лавы определяем вышеизложенным способом (табл. 146).
Параметры | Лава 15 | Лава 17 | Лава 27 | Лавы 27 + 29 |
70 | 70 | 70 | 70 | |
54 | 54 | 54 | 54 | |
55 | 55 | 55 | 55 | |
80 | 80 | 80 | - | |
- | - | - | 55 | |
- | - | - | 61 | |
q0 | 0,8 | 0,8 | - | - |
qоп | - | - | 0,94 | 0,94 |
a0 | 0,3 | 0,3 | 0,3 | 0,3 |
0,9 | 0,6 | 0,9 | 1,2 | |
N1 | 0,9 | 0,74 | 0,9 | 1,0 |
B | 0,9 | 1,0 | 0,9 | 0,9 |
L1, м | 230 | 279 | 234 | 310 |
L2, м | 198 | 242 | 197 | 266 |
1015 | 935 | 954 | 1060 | |
 | 4,4 | - | 4,2 | 3,4 |
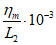 | 5,1 | 3,4 | - | 4,0 |
 | 0,02 | - | 0,02 | 0,011 |
 | 0,03 | 0,01 | - | 0,015 |
 | 0,66 | - | 0,61 | 0,51 |
 | 0,77 | 0,52 | - | 0,60 |
Отработка лавы 27.
Граничные углы (см. п. 8.1) принимаем: 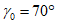 ;
; 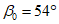 . Граничные углы в наносах принимаем по табл. 23
. Граничные углы в наносах принимаем по табл. 23  . Угол максимального оседания принимаем по табл. 24
. Угол максимального оседания принимаем по табл. 24  . Относительные величины максимального оседания и горизонтального сдвижения принимаем по табл. 25: q0 = 0,8; a0 = 0,3.
. Относительные величины максимального оседания и горизонтального сдвижения принимаем по табл. 25: q0 = 0,8; a0 = 0,3.
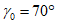 ;
; 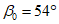 . Граничные углы в наносах принимаем по табл. 23
. Граничные углы в наносах принимаем по табл. 23  . Угол максимального оседания принимаем по табл. 24
. Угол максимального оседания принимаем по табл. 24  . Относительные величины максимального оседания и горизонтального сдвижения принимаем по табл. 25: q0 = 0,8; a0 = 0,3.
. Относительные величины максимального оседания и горизонтального сдвижения принимаем по табл. 25: q0 = 0,8; a0 = 0,3.Длины полумульд (см. п. 4.8): L1 = 234 м; L2 = 197 м.
Максимальное оседание (см. п. 4.10):
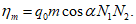
Определяем коэффициенты N1 и N2 (см. п. 8.4).
Вкрест простирания:
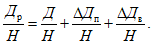

Из табл. 26 находим N1 = 0,9.
По простиранию отношение 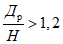 , следовательно, из табл. 26 N2 = 1.
, следовательно, из табл. 26 N2 = 1.
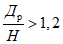 , следовательно, из табл. 26 N2 = 1.
, следовательно, из табл. 26 N2 = 1.Относительное максимальное оседание при повторной подработке (см. п. 8.3):

Тогда

Наклоны (см. п. 4.12):

Кривизна (см. п. 4.13):

Горизонтальные деформации (см. п. 4.15):
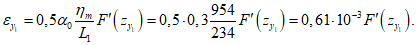
Далее, согласно п. 4.5, производим расчет от лав 27 и 29 как от одной суммарного размера.
Размер суммарной лавы согласно п. 4.5:
Д27+29 = 200 + 20 + 200 = 420 м.
Расчет деформаций производим обычным способом.
Все рассчитанные параметры сведены в табл. 146. Используя величины, приведенные в таблице, определяем значения наклонов, кривизн и горизонтальных деформаций в точках главных сечений мульд сдвижения от каждой лавы в районе застраиваемой площадки.
Полученные величины деформаций приведены в табл. 147.
Таблица 147
от отработки лав
z | Лава 15 | Лава 17 | Лава 27 | Лава 27 + 29 | ||||||||||||||
i1·10-3 | i2·10-3 | K1·10-3 | K2·10-3 |  | i2·10-3 | K2·10-3 | 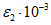 | i1·10-3 | K1·10-3 | i1·10-3 | i2·10-3 | K1·10-3 | K2·10-3 | 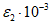 | ||||
0 | 0 | 0 | 0,11 | 0,11 | -3,07 | -3,07 | 0 | -0,09 | -4,89 | 0 | -0,09 | -2,62 | 0 | 0 | 0 | 0 | 0 | 0 |
0,1 | 2,07 | -2,40 | -0,10 | -0,15 | -2,77 | -4,54 | -3,09 | -0,08 | -5,20 | 1,93 | -0,10 | -2,56 | 0,51 | -0,65 | -0,02 | -0,02 | -0,70 | -1,28 |
0,2 | 4,49 | -5,20 | -0,12 | -0,18 | -2,77 | -6,08 | -5,41 | -0,05 | -4,37 | 4,18 | -0,12 | -2,56 | 1,51 | -1,90 | -0,05 | -0,05 | -1,68 | -3,11 |
0,3 | 7,08 | -8,21 | -0,11 | -0,16 | -1,52 | -6,31 | -6,46 | -0,02 | -2,91 | 6,60 | -0,11 | -1,40 | 3,24 | -4,08 | -0,07 | -0,07 | -2,09 | -4,84 |
0,4 | 8,71 | -10,10 | -0,04 | -0,05 | 1,19 | -4,16 | -6,29 | 0,02 | -0,73 | 8,12 | -0,04 | +1,10 | 5,10 | -6,43 | -0,06 | -0,06 | -0,94 | -4,64 |
0,5 | 8,45 | -9,79 | +0,06 | 0,09 | 4,16 | -0,46 | -5,07 | 0,04 | 0,68 | 7,87 | 0,06 | 3,84 | 5,94 | -7,48 | 0 | 0 | 1,64 | -2,04 |
0,6 | 6,42 | -7,45 | +0,11 | 0,17 | 5,48 | 2,39 | -3,54 | 0,05 | 1,35 | 6,00 | 0,11 | 5,06 | 5,10 | -6,43 | 0,06 | 0,06 | 3,73 | 1,17 |
0,7 | 3,83 | -4,44 | +0,11 | 0,17 | 4,69 | 3,08 | -2,11 | 0,04 | 1,25 | 3,57 | 0,11 | 4,33 | 3,24 | -4,08 | 0,07 | 0,07 | 3,90 | 2,65 |
0,8 | 1,85 | -2,14 | +0,07 | 0,11 | 2,90 | 2,31 | -1,09 | 0,02 | 0,88 | 1,72 | 0,07 | 2,68 | 1,51 | -1,90 | 0,05 | 0,05 | 2,50 | 2,09 |
0,9 | 0,66 | -0,76 | +0,03 | 0,04 | 1,19 | 0,92 | -0,41 | 0,01 | 0,42 | 0,61 | 0,03 | 1,10 | 0,51 | -0,65 | 0,02 | 0,02 | 1,02 | 0,87 |
1,0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Для назначения мер охраны необходимо знать наибольшие деформации, которые могут возникнуть на различных этапах отработки пластов. Эти величины определяем следующим образом.
На графики (рис. 24, а, б, в) наносим рассчитанные величины наклонов, кривизны и горизонтальных деформаций от лавы 15 (кривые 1), от лавы 17 (кривые 2), от лавы 27 (кривые 3), от лав 27 + 29, рассчитанных как от одной лавы суммарного размера (кривые 4).
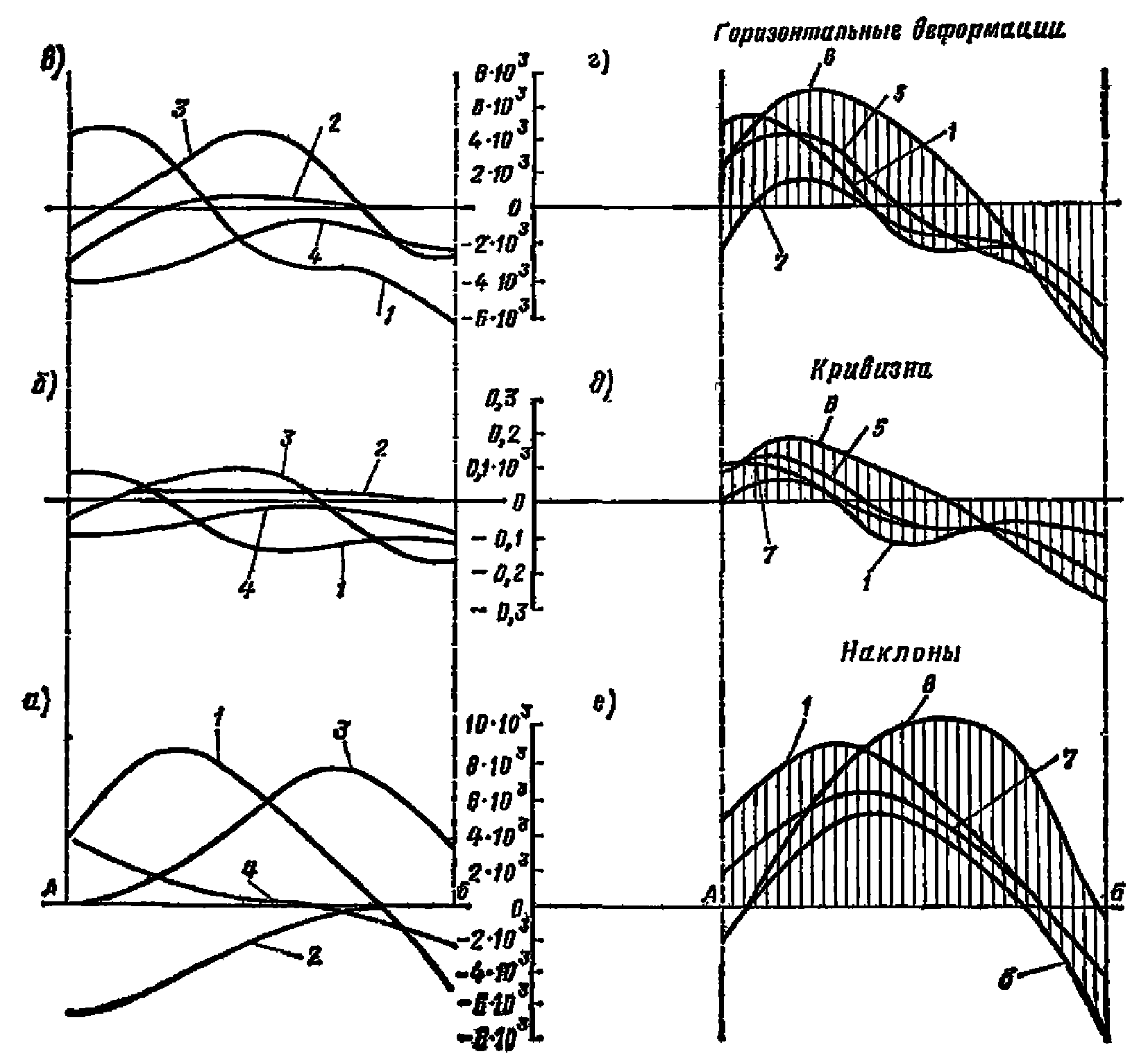
а, е - наклонов; б, д - кривизны; в, г - горизонтальных
деформаций; а, б, в - от отдельной выработки: 1 - от лавы
15; 2 - от лавы 17; 3 - от лавы 27; 4 - от лав 27 + 29;
г, д, е - суммарные величины; 5 - от лав 15 + 17;
6 - от лав 15 + 17 + 27; 7 - от лав 15 + 17 + 27 + 29
На графиках рис. 24, г, д, е откладываем величины наклонов, кривизны и горизонтальных деформаций от лавы 15 (кривые 1), суммируя которые с соответствующими значениями от лавы 17, получим на графиках г, д, е кривые 5 - суммарные величины от обеих лав.
Деформации от лав 15 и 17 (кривые 5) суммируем со значениями деформаций от лавы 27. Получим суммарные деформации от лав 15, 17 и 27 (кривые 6).
Затем величины деформаций от отработки лав 27 и 29 (кривые 4), рассчитанные как от одной лавы суммарной длины, складываем с суммарными значениями деформаций от лав 15 и 17 (кривые 5), получаем суммарные кривые 7.
На графиках рис. 24, г, д, е вертикальной штриховкой выделены максимальные значения наклонов, кривизны и горизонтальных деформаций, ожидаемые в точках площадки АБ.
Величины наклонов, кривизны и горизонтальных деформаций на застраиваемой площадке АБ достигают следующих значений: наклоны i = +10·10-3; кривизна K = -0,3·10-3; растяжение 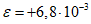 ; сжатие
; сжатие  .
.
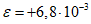 ; сжатие
; сжатие  .
.При выборе мер охраны для отдельных зданий на площадке АБ следует пользоваться наибольшими значениями наклонов, кривизны и горизонтальных деформаций непосредственно в основании рассматриваемых зданий, с учетом коэффициентов перегрузки и условий работы.
Пример 2. Расчет величин вероятных сдвижений и деформаций земной поверхности (рис. 25).
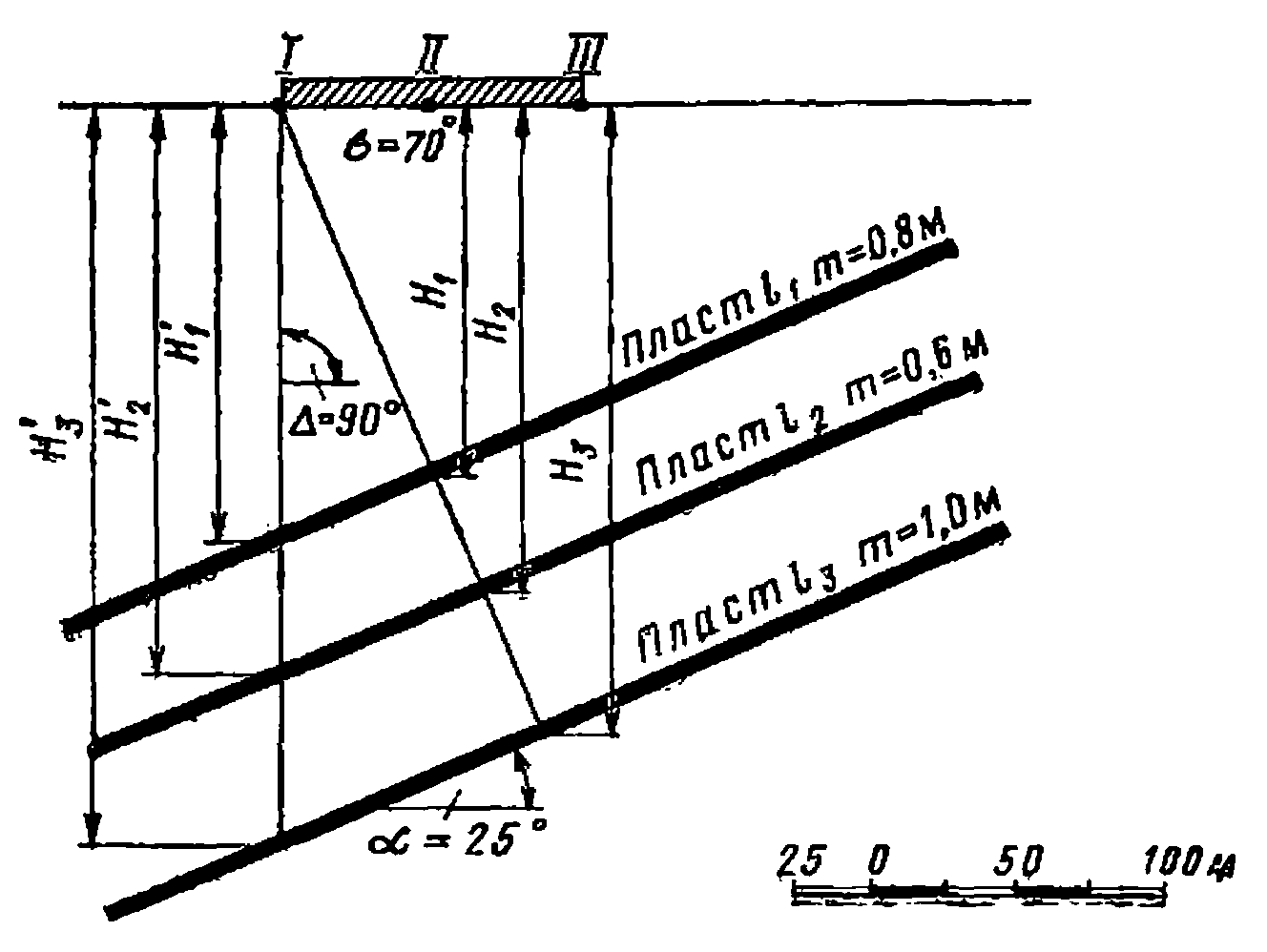
земной поверхности
В Донецком бассейне над свитой пластов расположена площадка для строительства. Необходимо определить деформации земной поверхности в пределах площадки при ее подработке свитой трех пластов: l1, l2, l3. Календарный план развития горных работ отсутствует и нельзя наметить горизонты отработки пластов. В данном случае можно определить только вероятные величины деформаций земной поверхности.
Угол падения пластов 25°, мощности пластов даны в табл. 148. Поскольку протяженность площадки невелика (150 м), для расчета сдвижений и деформаций земной поверхности достаточно взять три точки (I, II, III).
Наименование пласта | Мощность пласта, м | Глубина залегания пласта, м | |||||
Точка I | Точка II | Точка III | |||||
H | H' | H | H' | H | H' | ||
l1 | 0,8 | 140 | 165 | 120 | 140 | 100 | 116 |
l2 | 0,6 | 182 | 215 | 162 | 190 | 142 | 168 |
l3 | 1,0 | 238 | 280 | 218 | 255 | 198 | 232 |
Расчет величин вероятных сдвижений и деформаций производим в соответствии с разд. 7. Строим разрез вкрест простирания пластов и наносим на него точки I, II и III (см. рис. 25).
Для расчета величин деформаций в точке I по направлению вкрест простирания из этой точки проводим линию в сторону восстания пластов под углом  и определяем глубину залегания H1, H2 и H3 - точек пересечения этой линии с пластами.
и определяем глубину залегания H1, H2 и H3 - точек пересечения этой линии с пластами.
 и определяем глубину залегания H1, H2 и H3 - точек пересечения этой линии с пластами.
и определяем глубину залегания H1, H2 и H3 - точек пересечения этой линии с пластами.Для расчета величин деформаций в направлении по простиранию из точки I проводим линию под углом  . Согласно п. 8.2, в условиях неподработанной толщи
. Согласно п. 8.2, в условиях неподработанной толщи  . При
. При 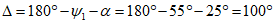 , т.е. большем 90°, принимаем
, т.е. большем 90°, принимаем 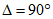 , а затем определяем глубину залегания
, а затем определяем глубину залегания  ,
,  и
и 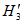 точек пересечения проведенной линии с пластами.
точек пересечения проведенной линии с пластами.
 . При
. При 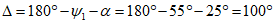 , т.е. большем 90°, принимаем
, т.е. большем 90°, принимаем 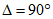 , а затем определяем глубину залегания
, а затем определяем глубину залегания Аналогичным образом проводим линии из точек II и III и получаем для них глубины H и H'. Численные значения H и H' для точек I, II и III приведены в табл. 148.
По полученным значениям H и H' вычисляем по формулам (90) - (98) величины вероятных сдвижений и деформаций для точки 1:
оседание
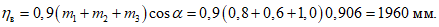
Наклоны:
вкрест простирания
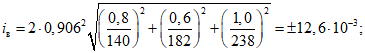
по простиранию

Радиус кривизны:
вкрест простирания
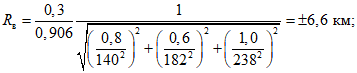
по простиранию
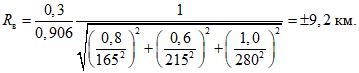
Горизонтальные сдвижения:
вкрест простирания

по простиранию

Горизонтальные деформации:
вкрест простирания

по простиранию
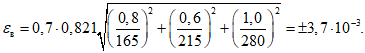
Аналогично определяем вероятные сдвижения и деформации для точек II и III.
Вычисленные значения вероятных сдвижений и деформаций приведены в табл. 149.
Наименование сдвижений и деформаций | Вкрест простирания | По простиранию | ||||
Точки | ||||||
I | II | III | I | II | III | |
1960 | 1960 | 1960 | 1960 | 1960 | 1960 | |
i, 1·10-3 | 12,6 | 15,0 | 17,5 | 10,7 | 12,5 | 14,6 |
R, км | 6,6 | 4,7 | 3,4 | 9,2 | 6,9 | 4,8 |
980 | 980 | 980 | 390 | 390 | 390 | |
8,5 | 10,0 | 10,9 | 3,7 | 6,2 | 7,3 | |
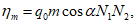





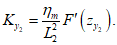
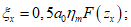
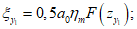
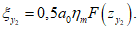
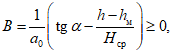
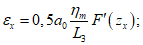
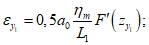
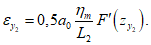
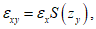


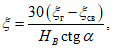
 , то в
, то в 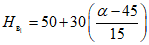 при
при 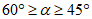 .
.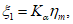


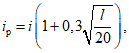
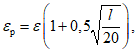
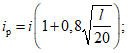


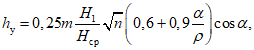
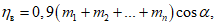


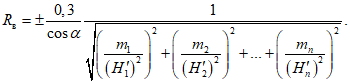
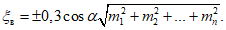
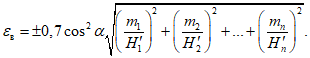
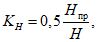
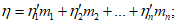
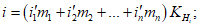
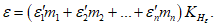
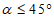 рассчитываются по
рассчитываются по 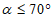 )
)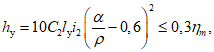

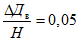 ;
;  ;
;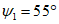 ;
;  .
.