СПРАВКА
Источник публикации
М.: Стройиздат, 1978
Примечание к документу
Название документа
"Рекомендации по проектированию гасителей колебаний для защиты зданий и сооружений, подверженных горизонтальным динамическим воздействиям от технологического оборудования и ветра"
"Рекомендации по проектированию гасителей колебаний для защиты зданий и сооружений, подверженных горизонтальным динамическим воздействиям от технологического оборудования и ветра"
Содержание
ПО ПРОЕКТИРОВАНИЮ ГАСИТЕЛЕЙ КОЛЕБАНИЙ ДЛЯ ЗАЩИТЫ ЗДАНИЙ
И СООРУЖЕНИЙ, ПОДВЕРЖЕННЫХ ГОРИЗОНТАЛЬНЫМ ДИНАМИЧЕСКИМ
ВОЗДЕЙСТВИЯМ ОТ ТЕХНОЛОГИЧЕСКОГО ОБОРУДОВАНИЯ И ВЕТРА
Рекомендованы к изданию секцией динамики сооружений Ученого совета ЦНИИСК им. Кучеренко.
Рекомендации содержат практические указания по проектированию динамических и ударных гасителей колебаний, устанавливаемых на отдельных конструкциях, зданиях и сооружениях для защиты их от динамических воздействий, возбуждаемых при работе технологического оборудования и действии ветра.
Предназначены для работников проектных и строительно-монтажных организаций.
Гасители колебаний являются эффективным средствам уменьшения колебаний строительных конструкций, зданий и сооружений при действии на них динамических нагрузок от машин или ветровой нагрузки.
Рекомендации по проектированию гасителей колебаний, предназначенные для проектных и строительно-монтажных организаций, должны способствовать более широкому применению гасителей колебаний в строительстве. Они содержат расчетные данные и примеры конструкций гасителей колебаний.
Рекомендации разработаны отделением динамики сооружений Центрального научно-исследовательского института строительных конструкций им. В.А. Кучеренко (д-р техн. наук, проф. Б.Г. Коренев, кандидаты техн. наук В.И. Сысоев, М.Я. Волоцкий). При составлении рекомендаций использованы материалы, представленные Казанским инженерно-строительным институтом (д-р техн. наук, проф. Н.А. Пикулев), институтом Днепрпроектстальконструкция (канд. техн. наук М.Я. Волоцкий и инж. О.М. Фукс), Московским инженерно-строительным институтом им. В.В. Куйбышева и институтом Уралпромстройниипроект (инж. А.Н. Эрделевский). Общее редактирование рекомендаций выполнено д-ром техн. наук А.И. Цейтлиным и д-ром техн. наук, проф. Б.Г. Кореневым.
1.1. Гасители колебаний являются одним из наиболее эффективных методов борьбы с вибрациями сооружений, получивших в последние годы широкое применение в практике строительства. Настоящие Рекомендации обобщают накопленный опыт применения гасителей и основываются на теоретических и экспериментальных исследованиях, выполненных в ЦНИИСКе, Днепрпроектстальконструкции и других перечисленных в предисловии организациях.
1.2. В Рекомендациях рассматриваются только ударные и динамические гасители колебаний. Применение управляемых гасителей колебаний, электродинамических гасителей и других устройств, связанных с использованием источников энергии, здесь не обсуждается.
1.3. В данных Рекомендациях рассматривается применение гасителей колебаний для виброзащиты высоких и гибких зданий и инженерных сооружений (дымовых труб, телевизионных башен и др.) при горизонтальных колебаниях. Отдельные положения Рекомендаций могут быть использованы при расчете и проектировании некоторых других сооружений или их конструктивных элементов.
Область применения Рекомендаций охватывает главным образом следующие важнейшие типы сооружений:
здания с металлическим каркасом;
стальные дымовые трубы;
решетчатые и сплошные металлические башни;
железобетонные башенные сооружения с гибкой металлической верхней частью (например, железобетонные телевизионные башни с металлической верхней частью).
1.4. Опыт применения гасителей колебаний показал, что они наиболее эффективны при гашении колебаний, которые носят резонансный характер и возникают в конструкциях, обладающих малым демпфированием.
Применение гасителей колебаний с целью снижения уровня колебаний железобетонных сооружений является, как правило, значительно менее эффективным, но в тех случаях, когда оно будет признано целесообразным, для расчета также можно пользоваться формулами, графиками и таблицами настоящих Рекомендаций. Эффективность применения гасителей колебаний особенно велика в сооружениях, верхняя часть которых имеет сравнительно большую гибкость.
1.5. Наиболее часто гасители применяются для защиты от колебаний, вызванных действием машин и ветра. В Рекомендациях основное внимание уделено учету влияния периодических воздействий, более кратко рассматривается влияние непериодических сил и автоколебаний.
1.6. Вопрос об использовании гасителей колебаний решается так же, как и все остальные вопросы проектирования виброзащитных устройств, с учетом технико-экономических соображений. При этом должно быть обращено внимание на стабильность параметров гасителя в процессе эксплуатации и на сведение к минимуму затрат на наблюдение и уход за гасителями колебаний.
1.7. Применение тех или иных гасителей колебаний и назначение их параметров должно быть обосновано расчетом, проведенным на основании настоящих Рекомендаций с учетом действующих руководств по учету динамических воздействий.
1.8. В разд. 2 рассматриваются линейные динамические гасители колебаний, в разд. 3 - ударные гасители колебаний. В большинстве случаев необходимый эффект виброгашения может быть достигнут применением гасителей одного из названных типов. Вопрос в том, каким из типов гасителей следует воспользоваться в конкретном случае, решается на основе технико-экономических соображений.
2.1. Динамическим гасителем колебаний называется устройство, состоящее из сравнительно жесткого элемента, называемого далее массой, присоединенного с помощью упругой связи (или связи, соединенной параллельно с демпфирующим элементом) к защищаемой конструкции. Параметры гасителя - масса, квазиупругий коэффициент и коэффициент демпфирования - определяются в результате расчета или назначаются по конструктивным соображениям. Если парциальная частота гасителя близка к частоте вынужденных колебаний конструкции, то масса гасителя совершает колебания, амплитуда которых, как правило, значительно превышает амплитуду колебаний конструкции. Возникающие при этом упругие и диссипативные силы в элементах гасителя, воздействуя на защищаемую конструкцию, уменьшают ее колебания.
2.2. Динамические гасители колебаний в зависимости от конструктивной схемы делятся на три группы: гасители с гибким элементом (пружинные), маятниковые и комбинированные гасители.
Принципиальная схема гасителя, состоящего из "массы", квазиупругого элемента и демпфирующего устройства, во всех указанных трех случаях одинакова. "Масса" представляет, как правило, призматический или цилиндрический стальной или чугунный груз. В отдельных случаях возможно применение железобетонных грузов.
Пружинный гаситель содержит упругий элемент в виде стальной пружины, системы стальных пружин или специальных резин.
2.3. Для гашения горизонтальных колебаний дымовых труб и башенных сооружений рекомендуется использовать успешно применяемые на практике гасители маятникового типа, принципиальная схема такого гасителя изображена на рис. 1. Маятниковые гасители следует применять в основном при гашении низкочастотных колебаний с частотой 1 - 3 Гц.

Рис. 1. Схема маятникового гасителя
Для виброгашения зданий часто оказывается целесообразным использование схемы гасителя колебаний, разработанного в Уральском Промстройниипроекте (рис. 2); такие гасители позволяют одновременно гасить как горизонтальные, так и вертикальные колебания.

Рис. 2. Схема гасителя конструкции Уралпромниипроекта
2.4. Если гаситель находится в закрытом и отапливаемом помещении, то в качестве демпфирующих элементов могут быть использованы вязкие демпферы, описанные в "Руководстве по проектированию виброизоляции машин и оборудования".
Для гасителей, находящихся в условиях, которые исключают возможность частых осмотров, а также размещенных на открытых площадках или в неотапливаемых помещениях, рекомендуется применение демпфирующих устройств, основанных на использовании сухого трения (для пружинных гасителей) или внутреннего трения для маятниковых гасителей колебаний.
Неоднократно применявшаяся для виброгашения металлических башен конструкция <1> маятникового гасителя колебаний, использующего внутреннее трение в элементе, показана на рис. 3. Трение создается за счет деформирования верхней части троса (рис. 3). Для повышения уровня демпфирования рекомендуется конструкция, в которой используется изгиб нижней части троса (рис. 4).
--------------------------------
<1> Конструкция предложена Б.Г. Кореневым и А.Н. Блехерманом.
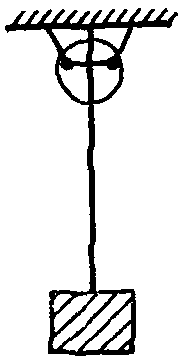
Рис. 3. Маятниковый гаситель с повышенным
демпфированием в верхней части каната

демпфированием в верхней и нижней частях каната
2.5. В тех случаях, когда по конструктивным соображениям вместо одиночного применяется группа одинаковых гасителей, необходимо обращать внимание на то, чтобы все гасители, входящие в одну группу, имели одинаковую частоту.
2.6. По характеру зависимости реакции гасителя от амплитуд колебаний следует различать линейные и нелинейные динамические гасители. В настоящих Рекомендациях рассматриваются в основном линейные гасители, которые применяются значительно чаще.
Принципиальная схема линейного гасителя изображена на рис. 5.

Рис. 5. Схема гасителя с демпфером вязкого трения
Диссипативные свойства гасителя, как уже отмечалось, могут быть обусловлены не только наличием демпфера вязкого трения, как показано на рис. 5, но и большим внутренним неупругим сопротивлением пружины или иной связи.
2.7. Гасители могут использоваться для различных целей, например для уменьшения амплитуд колебаний или ускорений перекрытий в связи с необходимостью удовлетворения требованиям санитарных норм, для уменьшения амплитуд внутренних усилий в конструкциях исходя из требований прочности и повышения надежности.
2.8. В зависимости от цели применения гасителей и от характера внешнего воздействия устанавливается критерий качества виброгашения, по степени уменьшения которого можно судить об эффективности гасителей. Эффективность гашения колебаний следует определять для гасителей с оптимальными параметрами.
Массу гасителей обычно не оптимизируют - увеличение массы всегда приводит к увеличению эффективности виброгашения. Хотя выбор массы гасителей (как и решение вопроса о целесообразности использования тех или иных гасителей) производится на основе технико-экономического анализа, опыт виброгашения строительных конструкций показал, что применять гасители целесообразно лишь в тех случаях, когда необходимый эффект достигается при общей относительной массе гасителей 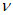 , не превышающей 5%.
, не превышающей 5%.
2.9. В пп. 2.16 - 2.37 рассматриваются наиболее часто встречающиеся случаи, когда моделью защищаемого сооружения может служить система с одной степенью свободы. Такой моделью можно пользоваться, если при изменении собственных частот сооружения в 1,5 - 2 раза резонансные явления возможны лишь для одной собственной частоты сооружения, а при ветровом резонансе - когда лишь одна критическая скорость ветра меньше 25 м/с. Чтобы воспользоваться Рекомендациями пп. 2.16 - 2.37, следует предварительно определить собственную частоту p, для которой возможны резонансные явления, соответствующую ей форму колебаний w(x) и вычислить приведенную массу M и обобщенную жесткость k:
 ;
;  , (1)
, (1)где m(x) - погонная масса сооружения;
форма колебаний w(x) нормирована так, что ордината в точке подвеса гасителя равна 1;
h - общая высота сооружения;
n - общее количество сосредоточенных масс.
2.10. В тех случаях, когда эффективность виброгашения оценивается по результатам, полученным для защищаемой системы с одной степенью свободы, необходимо учитывать следующее. Если коэффициент внутреннего неупругого сопротивления  сооружения, например металлической башни, мал, то перемещения и усилия, соответствующие резонирующей форме колебаний, настолько увеличиваются, что влиянием остальных форм колебаний можно пренебречь. Оценки эффективности виброгашения, приведенные в пп. 2.16 - 2.37, оказываются в этих случаях достаточно точными. Если значение
сооружения, например металлической башни, мал, то перемещения и усилия, соответствующие резонирующей форме колебаний, настолько увеличиваются, что влиянием остальных форм колебаний можно пренебречь. Оценки эффективности виброгашения, приведенные в пп. 2.16 - 2.37, оказываются в этих случаях достаточно точными. Если значение  велико или имеет место нерезонансный случай, то при оценке эффективности следует учесть влияние других форм колебаний, особенно если критерием качества виброгашения служит изгибающий момент или другое внутреннее усилие. В наиболее часто встречающихся случаях, когда резонансные явления возможны для первой собственной частоты сооружения, следует сначала вычислить усилия или перемещения, полагая, что внешняя нагрузка действует как статическая, а затем добавить усилия или перемещения, соответствующие учету вклада резонирующей формы колебаний, с коэффициентом r:
велико или имеет место нерезонансный случай, то при оценке эффективности следует учесть влияние других форм колебаний, особенно если критерием качества виброгашения служит изгибающий момент или другое внутреннее усилие. В наиболее часто встречающихся случаях, когда резонансные явления возможны для первой собственной частоты сооружения, следует сначала вычислить усилия или перемещения, полагая, что внешняя нагрузка действует как статическая, а затем добавить усилия или перемещения, соответствующие учету вклада резонирующей формы колебаний, с коэффициентом r:
 ; (2)
; (2) ,
,где 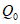 - обобщенная сила;
- обобщенная сила;
q(x) - интенсивность внешней нагрузки;
k - обобщенная жесткость;
2.11. В случаях когда возможность использования результатов, полученных для модели с одной степенью свободы, вызывает сомнение, следует подобрать оптимальные параметры гасителей по формулам, приведенным в пп. 2.16 - 2.37, а затем определить эффективность виброгашения по программе, описанной в Прил. 1.
Если сооружение обладает густым спектром собственных частот и резонансные явления наблюдаются для двух и более собственных частот, особенно при установке гасителей в различных уровнях, следует подбирать параметры гасителей, пользуясь программой, помещенной в Прил. 1. Некоторые рекомендации для таких случаев даны в п. 2.38.
2.12. Классификация расчетных случаев и назначение критерия качества виброгашения зависят от характера внешнего воздействия. Необходимо различать следующие воздействия.
Гармоническое воздействие с мало (до +/- 5%) изменяющейся частотой. Источником такого воздействия может быть, например, синхронный электродвигатель. Для борьбы с возникающими при этом вибрациями могут быть использованы гасители без дополнительных демпфирующих элементов. Диссипативные свойства таких гасителей обычно не учитываются. Рекомендации по подбору параметров гасителей без демпфирования даны в пп. 2.16 - 2.19.
Гармоническое воздействие с нестабильной частотой. Источником такого воздействия могут быть, например, асинхронные электродвигатели и другие двигатели с изменяющимся числом оборотов. Применение гасителей без демпфирования в подобных случаях не дает эффекта.
Присоединяя такие гасители, можно несколько изменить собственные частоты, обычно вместо резонансной собственной частоты p возникают две близкие (отличающиеся менее чем на 15 - 20%) собственные частоты системы с гасителем  ,
,  , причем
, причем  . Такой раздвижки оказывается недостаточно, чтобы собственные частоты оказались вне пределов диапазона изменения частоты воздействия, поэтому резонанс возникает, но лишь на других частотах. В подобных случаях следует использовать гасители с повышенными диссипативными свойствами либо применять систему виброзащиты в виде большого числа по-разному настроенных гасителей. В настоящем выпуске даны в основном рекомендации по подбору гасителей с демпфированием.
. Такой раздвижки оказывается недостаточно, чтобы собственные частоты оказались вне пределов диапазона изменения частоты воздействия, поэтому резонанс возникает, но лишь на других частотах. В подобных случаях следует использовать гасители с повышенными диссипативными свойствами либо применять систему виброзащиты в виде большого числа по-разному настроенных гасителей. В настоящем выпуске даны в основном рекомендации по подбору гасителей с демпфированием.
 . Такой раздвижки оказывается недостаточно, чтобы собственные частоты оказались вне пределов диапазона изменения частоты воздействия, поэтому резонанс возникает, но лишь на других частотах. В подобных случаях следует использовать гасители с повышенными диссипативными свойствами либо применять систему виброзащиты в виде большого числа по-разному настроенных гасителей. В настоящем выпуске даны в основном рекомендации по подбору гасителей с демпфированием.
. Такой раздвижки оказывается недостаточно, чтобы собственные частоты оказались вне пределов диапазона изменения частоты воздействия, поэтому резонанс возникает, но лишь на других частотах. В подобных случаях следует использовать гасители с повышенными диссипативными свойствами либо применять систему виброзащиты в виде большого числа по-разному настроенных гасителей. В настоящем выпуске даны в основном рекомендации по подбору гасителей с демпфированием.Периодические импульсные воздействия и нагрузки при прохождении через резонанс по своему характеру близки к гармоническому воздействию с нестабильной частотой. В этих случаях необходимо применять гасители с демпфированием.
Воздействие ветра может возбудить автоколебания типа "ветровой резонанс" или "галопирование", а также вызвать стационарные случайные колебания от пульсаций ветрового напора. Во всех этих случаях должны использоваться гасители с повышенными диссипативными свойствами, так как пульсации ветра представляют собой воздействие с широким спектром частот, а в режиме автоколебаний диапазон резонансно-опасных частот не ограничен, по крайней мере, снизу (если при некоторой критической скорости ветра, соответствующей p, возбуждаются автоколебания, то при меньшей критической скорости ветра, соответствующей 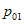 , тоже будут возбуждаться автоколебания).
, тоже будут возбуждаться автоколебания).
2.13. Необходимо учитывать, что гасители с демпфированием, оптимизированные из условия снижения уровня вибраций при каком-либо воздействии, будут эффективно гасить колебания и при других воздействиях. Однако, если определенный тип воздействия преобладает (вносит наибольший вклад в нежелательный для конструкции эффект), следует выбирать соответствующие этому воздействию оптимальные параметры, при которых гаситель наиболее эффективен.
2.14. Если габариты сооружения позволяют установить большое число (не менее 6 - 10) гасителей в одном уровне, то вместо одного или нескольких одинаково настроенных гасителей с повышенным демпфированием можно использовать большую группу по-разному настроенных гасителей со слабыми диссипативными свойствами <1>.
--------------------------------
<1> Такая система виброзащиты, по предложению Н.А. Пикулева, впервые была использована для борьбы с колебаниями здания Казанского университета.
При проектировании такой виброзащитной системы рекомендуется обеспечить расстройку парциальных частот гасителей не более чем на 3% с равномерным заполнением всего диапазона изменения частот воздействия. Амплитуды перемещений масс таких гасителей значительно превышают амплитуды колебаний обычных гасителей с демпфированием; это следует учитывать при определении габаритов помещений, предназначенных для размещения гасителей, и расчете связи гасителя на прочность. При проектировании такой системы виброзащиты обязательно следует учитывать возможность непреднамеренных расстроек гасителей.
Расчет групповых гасителей рекомендуется выполнять по программе, приведенной в Прил. 1.
2.15. При проектировании гасителей следует учитывать, что в процессе эксплуатации сооружения возможно изменение массы и других характеристик, влияющих на собственные частоты сооружения, в частности, при нестабильной частоте гармонического воздействия гаситель без демпфирования может оказаться неэффективным, если масса конструкции будет существенно изменяться.
и оценка их эффективности
2.16. При гармоническом воздействии с мало изменяющейся частотой (см. п. 2.12) рекомендуется применять гасители без специальных демпфирующих элементов. Диссипативные свойства таких гасителей при оценке эффективности виброгашения в пп. 2.17 - 2.20 не учитываются, так же как и диссипативные свойства защищаемой системы.
Критерием качества виброгашения R для случаев, рассмотренных в пп. 2.17 - 2.20, является максимальная в заданном диапазоне изменения частоты воздействия (от  до
до 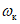 ) амплитуда перемещений или ускорений главной (приведенной) массы M. Параметры гасителя
) амплитуда перемещений или ускорений главной (приведенной) массы M. Параметры гасителя  и f подбираются так, чтобы уменьшить критерий качества виброгашения до допустимого значения
и f подбираются так, чтобы уменьшить критерий качества виброгашения до допустимого значения 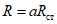 .
.
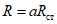 .
. ;
; 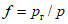 ;
;  ;
;  ,
,где  - масса гасителя;
- масса гасителя;
f - настройка гасителя;
p - собственная частота защищаемой системы;
R - значение критерия качества виброгашения, соответствующее единичной обобщенной силе 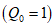 ;
;
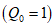 ;
; ; если R соответствует ускорению главной массы - условно принято
; если R соответствует ускорению главной массы - условно принято  .
.При оптимальной настройке  допустимые значения R достигаются на концах интервала изменения частоты воздействия, как показано на рис. 6.
допустимые значения R достигаются на концах интервала изменения частоты воздействия, как показано на рис. 6.

Рис. 6. Амплитудно-частотные характеристики системы
без гасителя (1) и с гасителем (2)
2.17. При гармоническом воздействии с мало изменяющейся частотой и постоянной амплитудой внешней силы  в случае, когда критерием качества является максимальная в диапазоне от
в случае, когда критерием качества является максимальная в диапазоне от  до
до  амплитуда перемещений главной массы, параметры гасителя подбираются по формулам:
амплитуда перемещений главной массы, параметры гасителя подбираются по формулам:
 в случае, когда критерием качества является максимальная в диапазоне от
в случае, когда критерием качества является максимальная в диапазоне от  (3)
(3)где  - относительная частота вынужденных колебаний
- относительная частота вынужденных колебаний 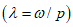 ;
;
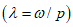 ;
;2.18. При воздействии, рассматриваемом в п. 2.17, и критерии качества - максимальной амплитуде ускорения главной массы - параметры гасителя рекомендуется определять по формулам:
 (4)
(4)Формулы (4) пригодны также в случае, когда амплитуда силы пропорциональна квадрату частоты возбуждения  , а критерий качества - максимальная амплитуда колебаний главной массы.
, а критерий качества - максимальная амплитуда колебаний главной массы.
 , а критерий качества - максимальная амплитуда колебаний главной массы.
, а критерий качества - максимальная амплитуда колебаний главной массы.2.19. При гармоническом воздействии с мало изменяющейся частотой и амплитудой силы, пропорциональной квадрату частоты возбуждения 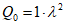 , в случае, когда критерием качества является максимальная амплитуда ускорения главной массы, оптимальные параметры гасителей рекомендуется принимать по формулам:
, в случае, когда критерием качества является максимальная амплитуда ускорения главной массы, оптимальные параметры гасителей рекомендуется принимать по формулам:
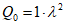 , в случае, когда критерием качества является максимальная амплитуда ускорения главной массы, оптимальные параметры гасителей рекомендуется принимать по формулам:
, в случае, когда критерием качества является максимальная амплитуда ускорения главной массы, оптимальные параметры гасителей рекомендуется принимать по формулам: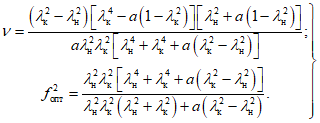 (5)
(5)2.20. Определение амплитуд перемещений и ускорений при произвольных значениях  и, в частности, при
и, в частности, при 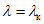 или
или  , выполняется по формулам:
, выполняется по формулам:
 ;
; 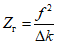 ;
;  ;
;  , (6)
, (6)где  ;
;
 ;
;2.21. При гармоническом воздействии с нестабильной частотой (см. п. 2.12) рекомендуется применять гасители с демпфирующими элементами. Амплитудно-частотная характеристика  в этом случае имеет такой вид, какой показан на рис. 7.
в этом случае имеет такой вид, какой показан на рис. 7.
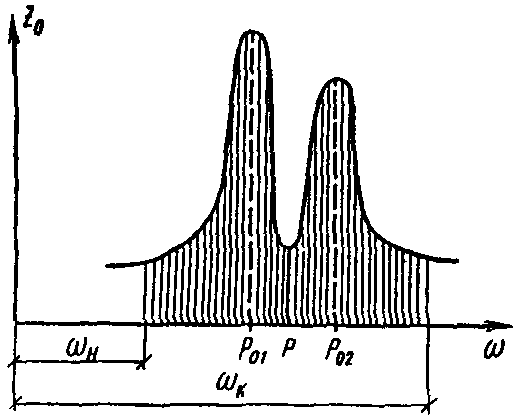
Рис. 7. Амплитудно-частотная характеристика
в диапазоне изменения частоты воздействия
При оптимальных параметрах гасителя минимизируется наибольшая из ординат 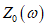 , обычно при этом оба максимума амплитудно-частотной характеристики становятся одинаковыми.
, обычно при этом оба максимума амплитудно-частотной характеристики становятся одинаковыми.
Далее приведены результаты для гасителей двух типов: с демпфером вязкого трения (тип первый) и со связью, обладающей повышенным неупругим сопротивлением (тип второй), причем даны формулы для определения не только оптимальных параметров гасителей, но и соответствующих значений критерия качества и максимальных амплитуд удлинений связи (для маятниковых гасителей - амплитуд перемещений массы маятника относительно точки подвеса) гасителя. Для гасителей с демпфирующими элементами оптимизируются настройка гасителей и безразмерные коэффициенты  или
или 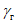 , характеризующие диссипативные свойства гасителей. Учтено внутреннее неупругое сопротивление защищаемой системы, характеризуемое коэффициентом потерь
, характеризующие диссипативные свойства гасителей. Учтено внутреннее неупругое сопротивление защищаемой системы, характеризуемое коэффициентом потерь 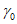 .
.
Здесь и далее:
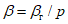 ;
;  ;
;  ;
; ;
;  ;
;  ;
;  ,
,где  - коэффициент вязкого трения демпфера в гасителе первого типа;
- коэффициент вязкого трения демпфера в гасителе первого типа;
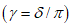 .
.--------------------------------
<1> Вследствие того, что большинство приведенных здесь результатов были получены с использованием указанных констант u, v, этот способ описания затухания сохранен в настоящих Рекомендациях.
2.22. При гармоническом воздействии с нестабильной частотой и постоянной амплитудой силы  , если критерием качества является максимальная амплитуда перемещений главной массы при произвольном изменении частоты воздействия, оптимальные параметры гасителей определяются по формулам (7) и (8).
, если критерием качества является максимальная амплитуда перемещений главной массы при произвольном изменении частоты воздействия, оптимальные параметры гасителей определяются по формулам (7) и (8).
Для гасителей первого типа оптимальные параметры определяются по формуле:
 ;
;  , (7)
, (7)при этом:
 ;
; .
.Для гасителей второго типа оптимальные параметры определяются по формулам:
при этом:
 ;
; .
.2.23. При том же критерии качества, какой рассматривался в п. 2.22, если амплитуда силы пропорциональна квадрату частоты возбуждения  , оптимальные параметры гасителей рекомендуется назначать по формулам:
, оптимальные параметры гасителей рекомендуется назначать по формулам:
 , оптимальные параметры гасителей рекомендуется назначать по формулам:
, оптимальные параметры гасителей рекомендуется назначать по формулам:для гасителей первого типа:
для гасителей второго типа:
2.24. При гармоническом воздействии с нестабильной частотой и постоянной амплитудой силы  , если критерием качества является максимальная амплитуда ускорения главной массы при произвольном изменении частоты воздействия, оптимальные параметры гасителей рекомендуется определять по формулам:
, если критерием качества является максимальная амплитуда ускорения главной массы при произвольном изменении частоты воздействия, оптимальные параметры гасителей рекомендуется определять по формулам:
для гасителей первого типа:
 (11)
(11)для гасителей второго типа:
 (12)
(12)2.25. При критерии качества, рассматриваемом в п. 2.24, если амплитуда силы пропорциональна квадрату частоты возбуждения  , оптимальные параметры гасителей определяются по формулам:
, оптимальные параметры гасителей определяются по формулам:
 , оптимальные параметры гасителей определяются по формулам:
, оптимальные параметры гасителей определяются по формулам:для гасителей первого типа:
 (13)
(13)для гасителей второго типа:
 (14)
(14)2.26. В случае, если частота возбуждающей силы при номинальном числе оборотов двигателя больше p и во время пуска и остановок возникает режим прохождения через резонанс, параметры гасителей рекомендуется подбирать как для гармонического воздействия с нестабильной частотой. В действительности оптимальные параметры для обоих указанных случаев несколько отличаются друг от друга, но разница в эффективности (например, если критерием качества является наибольшая амплитуда главной массы в процессе прохождения через резонанс) невелика.
2.27. При работе паровоздушных, гидравлических простого действия и механических фрикционных молотов, а также копров и других механизмов на сооружение могут действовать периодические (с периодом T) импульсы одного направления и одинаковые по величине, например s = 1. Если период T и соответственно частота  нестабильны, а критерием качества является наибольшая (при различных T) амплитуда перемещений главной массы, то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам:
нестабильны, а критерием качества является наибольшая (при различных T) амплитуда перемещений главной массы, то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам:
 нестабильны, а критерием качества является наибольшая (при различных T) амплитуда перемещений главной массы, то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам:
нестабильны, а критерием качества является наибольшая (при различных T) амплитуда перемещений главной массы, то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам: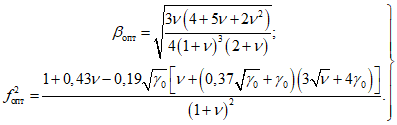 (15)
(15)Значение критерия качества R следует определять по табл. 1 для промежуточных значений  ,
,  допускается использовать интерполяцию.
допускается использовать интерполяцию.
Таблица 1
главной массы при различных значениях  и
и 
Для s = 1 | Для  | |||||||
Rk | Rk | |||||||
0,025 | 0 | 0,188 | 0,962 | 9,62 | 0,19 | 0,974 | 9,57 | |
0,05 | 0,188 | 0,957 | 7,13 | 0,19 | 0,98 | 7,1 | ||
0,1 | 0,188 | 0,95 | 5,74 | 0,19 | 0,99 | 5,71 | ||
0,05 | 0 | 0,259 | 0,927 | 6,99 | 0,264 | 0,95 | 6,92 | |
0,05 | 0,259 | 0,92 | 5,66 | 0,264 | 0,958 | 5,6 | ||
0,1 | 0,259 | 0,911 | 4,81 | 0,264 | 0,97 | 4,76 | ||
0,075 | 0 | 0,309 | 0,893 | 5,84 | 0,318 | 0,927 | 5,74 | |
0,05 | 0,309 | 0,886 | 4,92 | 0,318 | 0,937 | 4,85 | ||
0,1 | 0,309 | 0,876 | 4,3 | 0,318 | 0,951 | 4,23 | ||
0,1 | 0 | 0,348 | 0,862 | 5,15 | 0,36 | 0,905 | 5,04 | |
0,05 | 0,348 | 0,853 | 4,45 | 0,36 | 0,917 | 4,36 | ||
0,1 | 0,348 | 0,843 | 3,95 | 0,36 | 0,932 | 3,88 | ||
2.28. При работе механизмов с зубчатыми передачами, машин ударного действия с кривошипно-шатунным приводом и др. на сооружение действуют периодические (с периодом T, частотой  , безразмерной частотой
, безразмерной частотой  ) импульсы одного направления, величина которых пропорциональна частоте, например
) импульсы одного направления, величина которых пропорциональна частоте, например  . Если критерием качества виброгашения является наибольшая амплитуда перемещений главной массы при нестабильной частоте
. Если критерием качества виброгашения является наибольшая амплитуда перемещений главной массы при нестабильной частоте  , то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам:
, то для гасителей первого типа оптимальные параметры рекомендуется определять по формулам:
 , безразмерной частотой
, безразмерной частотой  ) импульсы одного направления, величина которых пропорциональна частоте, например
) импульсы одного направления, величина которых пропорциональна частоте, например  (16)
(16)Величина R определяется по табл. 1.
2.29. Если гасители используются для борьбы с колебаниями сооружений, подверженных действию одиночных импульсов, оптимальные параметры гасителей можно подбирать из условия скорейшего затухания переходного процесса. В системе с оптимальными гасителями обеим собственным частотам -  и
и  - будут соответствовать одинаковые значения декремента колебаний
- будут соответствовать одинаковые значения декремента колебаний  и коэффициента неупругого сопротивления
и коэффициента неупругого сопротивления 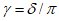 .
.
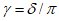 .
.Для гасителей первого типа:
(величины  для некоторых значений
для некоторых значений  и
и  приведены в табл. 2).
приведены в табл. 2).
Таблица 2
Значение логарифмических декрементов колебаний
системы с гасителем
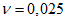 |  |  | ||||||||||
0 | 0,305 | 0,952 | 0,497 | 0,416 | 0,907 | 0,685 | 0,491 | 0,865 | 0,83 | 0,548 | 0,827 | 0,95 |
0,025 | 0,328 | 0,948 | 0,57 | 0,438 | 0,902 | 0,761 | 0,512 | 0,86 | 0,905 | 0,567 | 0,82 | 1,018 |
0,05 | 0,352 | 0,945 | 0,648 | 0,458 | 0,898 | 0,834 | 0,532 | 0,854 | 0,985 | 0,585 | 0,814 | 1,09 |
0,075 | 0,374 | 0,941 | 0,72 | 0,48 | 0,892 | 0,908 | 0,551 | 0,848 | 1,05 | 0,603 | 0,808 | 1,16 |
0,1 | 0,394 | 0,937 | 0,79 | 0,5 | 0,888 | 0,984 | 0,571 | 0,844 | 1,125 | 0,621 | 0,803 | 1,23 |
Для гасителей второго типа:
2.30. В тех случаях, когда динамические гасители применяются для борьбы с ветровым резонансом, рекомендуется назначать оптимальные параметры гасителя как для гармонического воздействия с нестабильной частотой и амплитудой силы, пропорциональной квадрату частоты возбуждения (см. пп. 2.23 и 2.25). Для определения истинных значений R и  следует задать амплитуду обобщенной силы в соответствии с главой СНиП II-6-74 "Нагрузки и воздействия".
следует задать амплитуду обобщенной силы в соответствии с главой СНиП II-6-74 "Нагрузки и воздействия".
2.31. Гасители, предназначенные для борьбы с ветровым резонансом, одновременно могут эффективно гасить колебания, вызванные пульсациями ветрового напора. Эффективность их в этом случае можно оценить по формулам, приведенным в п. 2.37.
Поскольку в настоящее время нет точных данных об оптимальных параметрах гасителей и эффективности гашения колебаний, вызванных пульсациями ветра для различных фиксированных значений p, рекомендуется максимально повышать диссипативные свойства системы с гасителем; для системы с увеличившимся декрементом колебаний, согласно главе СНиП II-6-74, можно принимать более низкие значения коэффициента динамичности.
Поскольку оптимальные параметры гасителей в рассматриваемом здесь случае получаются такими же, как и в случае, рассмотренном в п. 2.29, оптимальные параметры гасителей и значения декрементов колебаний для системы с гасителями рекомендуется определять по формулам (17) и (18).
2.32. Для борьбы с галопированием сооружений, имеющих аэродинамически неустойчивую форму сечения (прямоугольник, ромб и т.п.), оптимальные параметры подбираются из условия максимального увеличения критической скорости потока, при которой возникают автоколебания.
Для гасителей первого типа оптимальные параметры определяются по формулам:
 ;
;  . (19)
. (19)В результате установки гасителя с такими параметрами критическая скорость ветра увеличивается в  раз.
раз.
 раз.
раз.Параметры, вычисленные по формулам (19), являются оптимальными и при скоростях потока выше критической, так как им соответствуют наименьшие амплитуды автоколебаний.
оптимальных гасителей колебаний
при ограниченном демпфировании
2.33. В тех случаях, когда не удается реализовать на практике оптимальное демпфирование в гасителях и по конструктивным соображениям приходится назначать демпфирование меньше оптимального (особенно это относится к гасителям второго типа), рекомендуется определять оптимальную настройку гасителей при фиксированном (предельно допустимом) значении  .
.
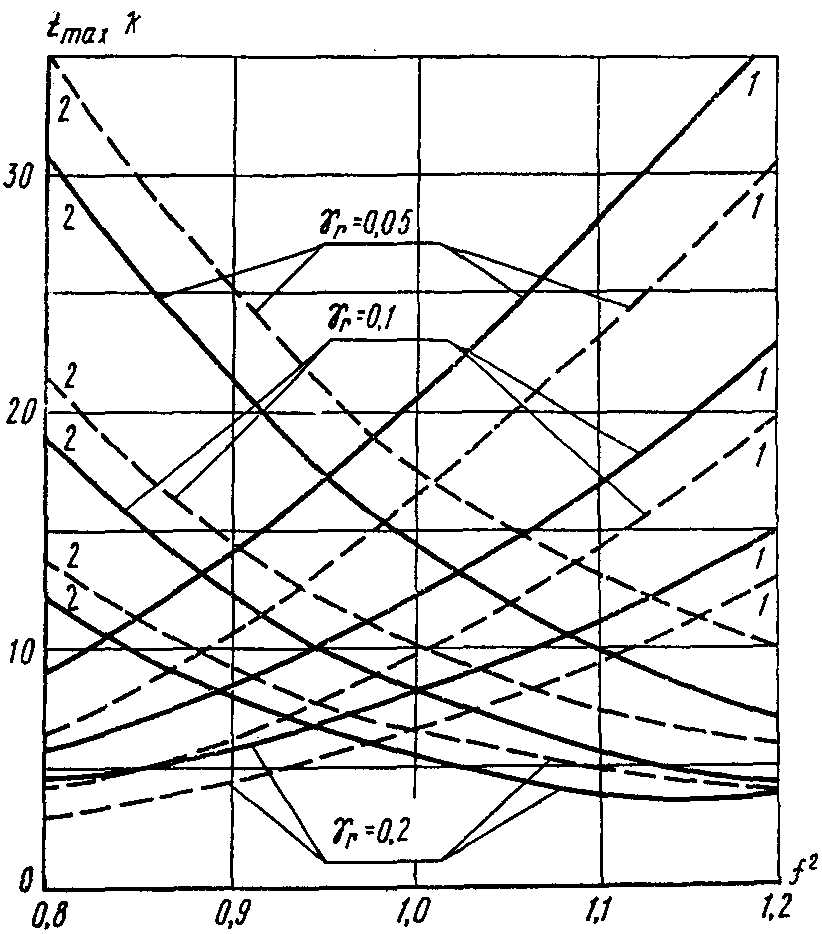
2.34. При гармоническом воздействии с нестабильной частотой, если критерием качества является максимальная амплитуда перемещений главной массы, оптимальную настройку и эффективность виброгашения для фиксированных значений  следует определять по графикам рис. 8 - 15.
следует определять по графикам рис. 8 - 15.
при 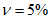 ,
, 
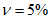 ,
, 

при  ,
, 
 ,
, 
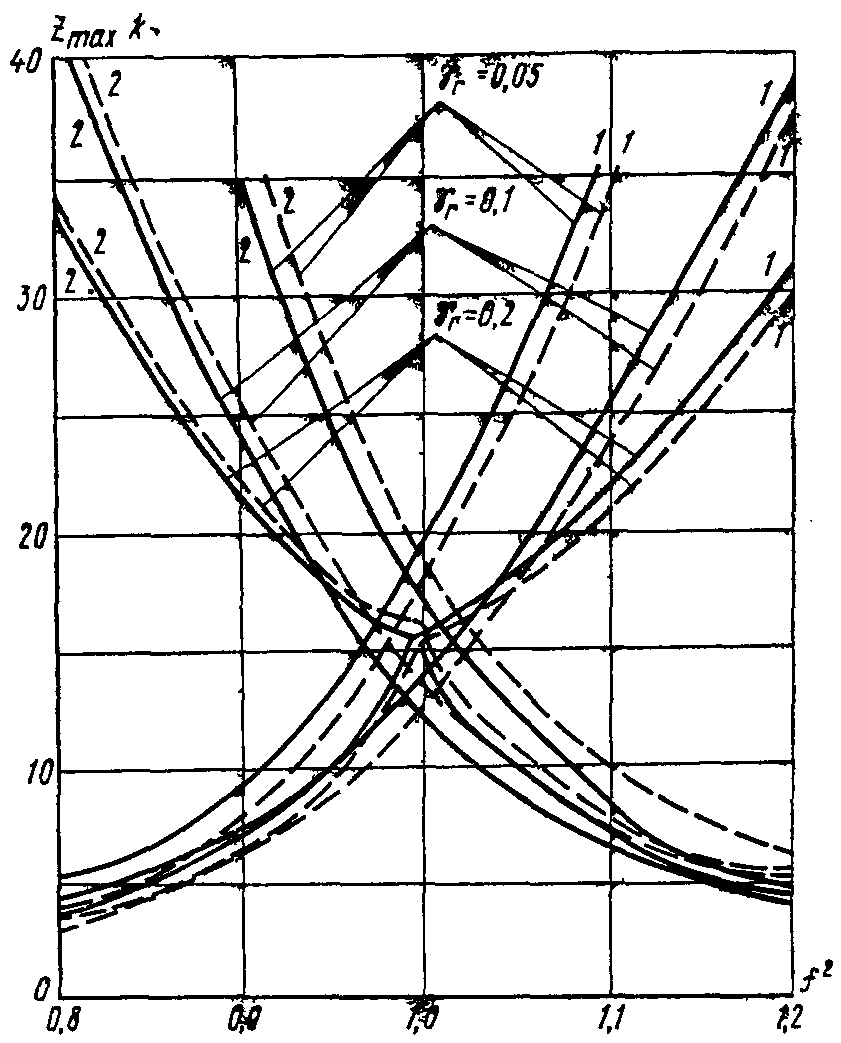
Рис. 10. Влияние настройки на величину 
при  ,
, 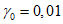
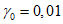

Рис. 11. Влияние настройки на величину 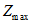
при  ,
, 
 ,
, 
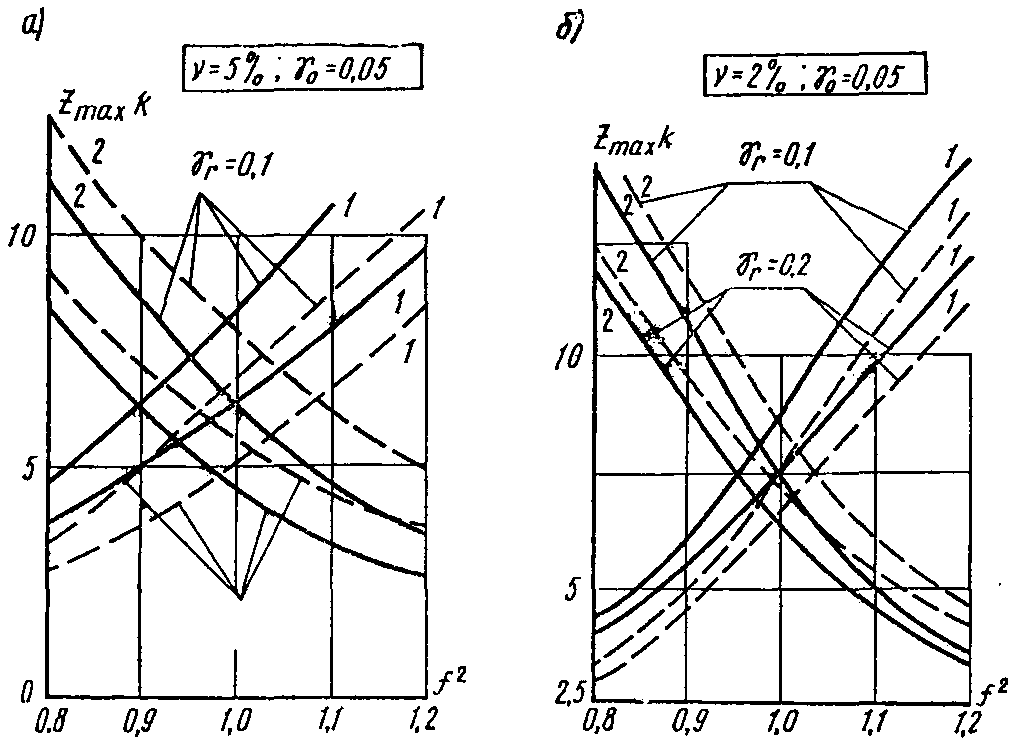
Рис. 12. Влияние настройки на величину 

Рис. 13. Влияние настройки на величину 

Рис. 14. Влияние настройки на величину 

Оптимальная настройка определяется из условия равенства максимальных амплитуд перемещений главной массы, соответствующих частотам  и
и  .
.
На рис. 8 - 15 показано, как в зависимости от настройки гасителей изменяются значения максимальных амплитуд колебаний  главной массы, соответствующие первой (кривые 1) и второй (кривые 2) собственным частотам системы с гасителем. Оптимальные значения
главной массы, соответствующие первой (кривые 1) и второй (кривые 2) собственным частотам системы с гасителем. Оптимальные значения 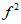 соответствуют точке пересечения кривых 1 и 2. Пунктирные линии на графиках соответствуют силе, амплитуда которой пропорциональна квадрату частоты
соответствуют точке пересечения кривых 1 и 2. Пунктирные линии на графиках соответствуют силе, амплитуда которой пропорциональна квадрату частоты  (этими графиками можно пользоваться для подбора гасителей при ветровом резонансе), сплошные линии соответствуют силе с постоянной амплитудой
(этими графиками можно пользоваться для подбора гасителей при ветровом резонансе), сплошные линии соответствуют силе с постоянной амплитудой  .
.
 (этими графиками можно пользоваться для подбора гасителей при ветровом резонансе), сплошные линии соответствуют силе с постоянной амплитудой
(этими графиками можно пользоваться для подбора гасителей при ветровом резонансе), сплошные линии соответствуют силе с постоянной амплитудой Графики построены для нескольких значений  и коэффициента неупругого сопротивления гасителя
и коэффициента неупругого сопротивления гасителя 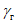 ; для промежуточных значений
; для промежуточных значений 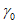 ,
,  ,
,  приближенные результаты можно получить по интерполяции.
приближенные результаты можно получить по интерполяции.
2.35. Если критерием качества виброгашения является величина, обратная наименьшему декременту колебаний системы с гасителем (аналогично пп. 2.29 и 2.31), то оптимальная настройка гасителя не зависит от величины 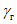 . В системе с оптимально настроенным гасителем так же, как и в случае, рассмотренном в п. 2.29, обеим частотам
. В системе с оптимально настроенным гасителем так же, как и в случае, рассмотренном в п. 2.29, обеим частотам  и
и  - соответствуют одинаковые значения декремента колебаний
- соответствуют одинаковые значения декремента колебаний  и коэффициента неупругого сопротивления
и коэффициента неупругого сопротивления  .
.
Значения  ,
,  определяются по формулам:
определяются по формулам:
 ;
;  . (20)
. (20)от оптимальных значений на эффективность виброгашения
2.36. При создании гасителей и их эксплуатации могут возникнуть небольшие отклонения их параметров от проектных и, в частности, от оптимальных значений. Особенно сильно сказываются на эффективности виброгашения изменения настройки; отклонения в демпфировании сравнительно мало влияют на эффективность гашения колебаний.
Если действительная настройка f несколько отличается от оптимального значения  , то измененный критерий качества
, то измененный критерий качества  для гармонического воздействия с нестабильной частотой рекомендуется вычислять по формуле:
для гармонического воздействия с нестабильной частотой рекомендуется вычислять по формуле:
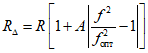 , (21)
, (21)где R - значение критерия качества при оптимальной настройке;
 - для случая, рассмотренного в п. 2.22;
- для случая, рассмотренного в п. 2.22; - для случая, рассмотренного в п. 2.25.
- для случая, рассмотренного в п. 2.25.Для случаев, рассмотренных в п. 2.34, влияние отклонений f от оптимального значения можно оценить по графикам, представленным на рис. 8 - 15. Для произвольного (неоптимального) значения  следует взять наибольшую (по кривой 1 или 2) ординату
следует взять наибольшую (по кривой 1 или 2) ординату  .
.
 .
.при фиксированных (неоптимальных) параметрах гасителя
2.37. Если гасители подобраны для одного преобладающего воздействия, то для прочих воздействий они будут неоптимальными. Для оценки эффективности виброгашения в подобных случаях следует пользоваться приведенными ниже формулами, по которым также более точно, чем в п. 2.36, можно оценить эффективность расстроенных гасителей второго типа. Приближенные результаты для гасителей первого типа можно получить, приняв  .
.
Дополнительные обозначения:
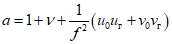 ;
;  ;
; ;
; ;
; ;
; ;
; ;
;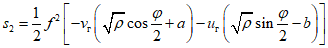 .
.Частотам  и
и 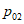 соответствуют два значения
соответствуют два значения  :
:
 :
: (22)
(22)Максимальные амплитуды главной массы (соответствующие частотам 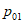 ,
, 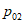 ) определяются по следующим формулам:
) определяются по следующим формулам:
для гармонического воздействия с нестабильной частотой и постоянной амплитудой силы  :
:
 (23)
(23)для гармонического воздействия с нестабильной частотой и амплитудой силы, пропорциональной квадрату частоты:
 (24)
(24)Амплитуды удлинений связи гасителя соответственно равны:
для  :
:
 (25)
(25)для  :
:
 :
: (26)
(26)когда моделью сооружения не может служить
система с одной степенью свободы
2.38. В случаях, не отвечающих условиям п. 2.9, модель защищаемого гибкого сооружения должна быть более сложной, чем система с одной степенью свободы, при этом рекомендуется пользоваться программой, приведенной в Прил. 1. Программа составлена на языке "Алгол" и отлажена для транслятора ТА-1М, используемого в машинах типа М-220, М-222, БЭСМ-4 и др.
Для расчета по программе расчетная схема сооружения должна быть задана, как показано на рис. 28, в виде многоступенчатого стержня с дополнительными связями, обладающими упругими и диссипативными свойствами. В разных уровнях к защищаемой системе могут быть присоединены по одному или несколько гасителей (первого или второго типа). Более подробные сведения о системе с гасителями содержатся в инструкции к программе, помещенной в Прил. 1. Ясно, что выбранная расчетная схема может отразить особенности работы большинства сооружений с гасителями при горизонтальных динамических воздействиях и вполне отвечает целям настоящих рекомендаций, хотя нетрудно привести примеры гашения колебаний (в основном вертикальных или комбинированных) континуальных систем типа сложных рам, складок, оболочек, когда указанная модель не может отразить особенности работы защищаемой системы.
При расчете по программе могут быть заданы два типа воздействий. Первое - гармоническое воздействие с нестабильной частотой и амплитудой, практически произвольно зависящей от частоты. Второе воздействие, рассмотренное в пп. 2.16 - 2.20, - стационарный случайный процесс (пульсации ветра) при фиксированном распределении интенсивности нагрузки по высоте сооружения.
Программа позволяет для заданных параметров гасителей вычислить максимальные в заданном диапазоне частот воздействия амплитуды перемещений и усилий в стержне (для воздействий первого типа) или определить нормы (корень квадратный из дисперсии) перемещений и усилий в стержне - для воздействия второго типа.
Чтобы облегчить оптимизацию, предусмотрена возможность одновременно задать несколько вариантов исходных данных по гасителям, для каждого варианта будут получены результаты, оценив которые конструктор может назначать параметры гасителей, либо задать новые исходные данные для повторного счета.
Целесообразно предварительно вычислить приближенно оптимальные параметры гасителей как для системы с одной степенью свободы.
и исходные данные для расчета
3.1. Ударные гасители колебаний простейшей конструкции подразделяются по типу на маятниковые, пружинные и плавающие, по числу соударений - на гасители одностороннего действия (одноударные) и двустороннего действия (двухударные). В одноударном гасителе за каждый период колебаний системы происходит один удар гасителя о систему, в двухударном гасителе - два удара. Между массой маятникового и пружинного одноударного гасителя, с одной стороны, и системой, с другой, может быть "отрицательный", нулевой и положительный зазор. В плавающем гасителе возможен только положительный зазор. В зависимости от направления колебаний гасители могут быть вертикальные и горизонтальные.
3.2. Тип гасителя выбирается в зависимости от частоты гасимых колебаний. Ориентировочно можно считать, что маятниковые ударные гасители применяются для гашения колебаний с частотой от 0,4 до 2 Гц, пружинные - от 2 до 10 Гц и плавающие - выше 10 Гц.
3.3. Одноударные гасители применяются для гашения колебаний, амплитуда которых с течением времени может изменяться в широких пределах. Двухударные гасители применяются для гашения колебаний с постоянной амплитудой.
3.4. Выбор зазора между массой гасителя и системой в одноударных гасителях производится в зависимости от величины той минимальной амплитуды колебаний системы, при которой начинается гашение. С точки зрения эффективности гашения в одноударных гасителях наиболее выгодным является нулевой зазор. "Отрицательный" зазор применяется часто в случае гашения постоянно действующих колебаний системы с определенной амплитудой. Положительный зазор применяется в случае необходимости гашения колебаний при прохождении через резонанс и устранения гашения в рабочем режиме.
3.5. Исходными данными для расчета гасителя колебаний являются:
а) данные по системе (схема, распределение масс и их величины, частоты и формы собственных колебаний, амплитуды вынужденных колебаний, которые необходимо погасить, коэффициент поглощения энергии колебаний <1> и динамические нагрузки, возбуждающие колебания данной системы);
б) расчетная схема гасителя (его тип, направление действия и главные конструктивные особенности);
в) требуемая эффективность, т.е. отношение амплитуды колебаний системы без гасителя к той же величине с гасителем;
г) материалы, из которых предполагается изготовить гаситель, в частности свойства соударяющихся тел - бойной части гасителя, смонтированной на системе, и ударника массы гасителя.
--------------------------------
<1> Коэффициент поглощения энергии колебаний  ,
,  - коэффициент сопротивления, равный c/2M, где c - коэффициент, учитывающий неупругие сопротивления в дифференциальном уравнении колебаний, M - масса системы;
- коэффициент сопротивления, равный c/2M, где c - коэффициент, учитывающий неупругие сопротивления в дифференциальном уравнении колебаний, M - масса системы;  - частота собственных колебаний системы с учетом затухания) равен удвоенному логарифмическому декременту колебаний
- частота собственных колебаний системы с учетом затухания) равен удвоенному логарифмическому декременту колебаний  или коэффициенту неупругого сопротивления
или коэффициенту неупругого сопротивления  (коэффициенту внутреннего трения), который дается в Инструкции по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки;
(коэффициенту внутреннего трения), который дается в Инструкции по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки; 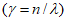 , умноженному на
, умноженному на  .
.
 ,
,  или коэффициенту неупругого сопротивления
или коэффициенту неупругого сопротивления 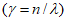 , умноженному на
, умноженному на 3.6. Время соударения ударного гасителя колебаний и сооружения  по сравнению с периодом колебаний сооружения и поэтому не учитывается, а весь процесс соударения оценивается коэффициентом восстановления скорости при ударе, который может иметь значение от 0 до 1. Величину коэффициента восстановления скорости при ударе, зависящего от свойств соударяющихся тел, при отсутствии более точных данных рекомендуется принимать по табл. 3.
по сравнению с периодом колебаний сооружения и поэтому не учитывается, а весь процесс соударения оценивается коэффициентом восстановления скорости при ударе, который может иметь значение от 0 до 1. Величину коэффициента восстановления скорости при ударе, зависящего от свойств соударяющихся тел, при отсутствии более точных данных рекомендуется принимать по табл. 3.
Таблица 3
Материал поверхности конструкции, воспринимающей удар | Материал ударяющего тела | |
твердые металлы (стали, чугуны, сплавы и т.п.) | медь, алюминий, дерево, твердые пластмассы и т.п. | |
Сталь | 0,6 | 0,4 |
Дерево | 0,55 | 0,4 |
Камень | 0,4 | 0,3 |
Бетон | 0,35 | 0,25 |
3.7. Проектирование ударного гасителя колебаний производится в следующем порядке:
а) обосновывается выбор типа гасителя с главными конструктивными особенностями;
б) выбирается материал, из которого будет изготовлена бойная часть, и определяется коэффициент восстановления скорости при ударе;
в) подбирается величина массы гасителя в зависимости от требуемой эффективности;
г) составляются чертежи гасителя колебаний.
3.8. Настройка маятникового или пружинного ударного гасителя одностороннего действия, расположенного на системе с одной степенью свободы, производится из условий:
 ;
;  , (27)
, (27)где 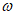 - частота возмущающей силы;
- частота возмущающей силы;
T - период соударений;
3.9. Определение длины маятника маятникового гасителя колебаний рекомендуется производить из условия
 , (28)
, (28)где  - круговая частота собственных колебаний свободного маятника;
- круговая частота собственных колебаний свободного маятника;
3.10. Для того чтобы ось привеса маятника гасителя не испытывала ударов, точка контакта маятника и системы должна совпадать с так называемым центром удара. Для обычно применяемых маятников, плоскость материальной симметрии которых перпендикулярна к оси привеса, реакции в точке привеса равны нулю при соблюдении следующих условий:
а) удар должен происходить в плоскости материальной симметрии маятника;
б) точка контакта должна совпадать с так называемой осью качания, соответствующей оси привеса маятника, т.е. должно выполняться условие
где l - расстояние от оси привеса до точки контакта (длина эквивалентного математического маятника);
3.11. Настройка плавающего ударного гасителя двустороннего действия, расположенного на системе с одной степенью свободы, производится из условия
 , (30)
, (30)где  - частота возмущающей силы;
- частота возмущающей силы;
T - период соударений.
на системе с одной степенью свободы
3.12. Расчетные схемы маятникового гасителя на системе с одной степенью свободы представлены на рис. 16, где приняты следующие обозначения: M и  - массы системы и гасителя; k - коэффициент жесткости; c - коэффициент, учитывающий неупругие сопротивления в системе; l - длина маятника гасителя;
- массы системы и гасителя; k - коэффициент жесткости; c - коэффициент, учитывающий неупругие сопротивления в системе; l - длина маятника гасителя;
 ,
,где P,  и
и  - амплитуда, частота и начальная фаза внешней возмущающей силы.
- амплитуда, частота и начальная фаза внешней возмущающей силы.
а - без затухания; б - с затуханием в системе
 (31)
(31)где x и  - перемещение системы и угол поворота маятника гасителя.
- перемещение системы и угол поворота маятника гасителя.
В случае пренебрежимо малых неупругих сопротивлений в системе, предварительный подбор параметров маятникового гасителя рекомендуется производить без учета инерционной силы гасителя по формулам (32), а затем, при необходимости, для сконструированного гасителя производить определение параметров гасителя по более точным формулам (33). В случае, если неупругие сопротивления в системе достаточно велики и ими пренебречь нельзя, подбор параметров маятникового гасителя рекомендуется производить по формулам (35).
3.13. Для схемы, изображенной на рис. 16, а, если не учитывать инерционную силу гасителя, в случае резонанса величины  и
и  определяются по формулам:
определяются по формулам:
3.14. Наряду с формулами (32) для выбора параметров  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  и
и  от
от  и r, приведенными на рис. 17.
и r, приведенными на рис. 17.

Рис. 17. Графики зависимости  и
и  от
от  и r
и r
при расчете гасителя по схеме, изображенной на рис. 16, а,
если не учитывать силу инерции гасителя
3.15. Для схемы, изображенной на рис. 16, а, при учете инерционной силы гасителя в резонансном режиме:
где
 (34)
(34)3.16. Наряду с формулами (33) для выбора параметров  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  и
и  от
от  и r, приведенными на рис. 18.
и r, приведенными на рис. 18.

при расчете гасителя по схеме, изображенной на рис. 16, а,
если сила инерции гасителя учитывается
3.17. Для схемы, изображенной на рис. 16, б, если не учитывать инерционную силу гасителя, в случае резонанса:
где
 (36)
(36)3.18. Наряду с формулами (35) для выбора параметров  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  и
и  от
от  и
и 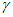 , приведенными на рис. 19, для случая r = 0,5.
, приведенными на рис. 19, для случая r = 0,5.

для случая r = 0,5 при расчете гасителя по схеме,
изображенной на рис. 18, б,
если не учитывать силу инерции гасителя
с одной степенью свободы
3.19. Расчетные схемы пружинного гасителя на системе с одной степенью свободы представлены на рис. 20, где приняты следующие обозначения: M и  - массы системы и гасителя; k,
- массы системы и гасителя; k,  ,
, 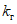 - коэффициенты жесткости; c и
- коэффициенты жесткости; c и 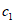 - коэффициенты, учитывающие неупругие сопротивления соответственно в системе и в гасителе;
- коэффициенты, учитывающие неупругие сопротивления соответственно в системе и в гасителе;
 , где P,
, где P, 
а - без затухания (гаситель связан упругой связью только
с основанием); б - с затуханием в системе и гасителе
(гаситель связан упругой связью только с основанием);
в - без затухания (гаситель связан упругими связями
с системой и основанием)
В пп. 3.20 - 3.26 принято:
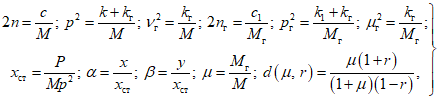 (37)
(37)где x и y - перемещения масс системы и гасителя.
3.20. Для схемы, изображенной на рис. 20, а, в случае резонанса:
 (38)
(38)3.21. Наряду с формулами (38) для выбора  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  и
и 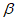 от
от  и r, приведенными на рис. 21.
и r, приведенными на рис. 21.

при расчете гасителя по схеме, изображенной на рис. 20, а
3.22. Для схемы, изображенной на рис. 20, б, в случае резонанса:
 (39)
(39)где
 (40)
(40)3.23. Наряду с формулами (39) для выбора параметров гасителя колебаний в случае  и r = 0,5 можно пользоваться графиками зависимости
и r = 0,5 можно пользоваться графиками зависимости 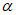 и
и  от
от  и
и  , приведенными на рис. 22; на этих графиках
, приведенными на рис. 22; на этих графиках  изменяется в пределах от 0,01 до 0,1, а
изменяется в пределах от 0,01 до 0,1, а  - от 0 до 0,1. Для других значений
- от 0 до 0,1. Для других значений 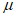 и r при вычислениях, производимых на ЭВМ, эти графики могут служить контрольным счетом при выверке программы.
и r при вычислениях, производимых на ЭВМ, эти графики могут служить контрольным счетом при выверке программы.
 и r = 0,5 можно пользоваться графиками зависимости
и r = 0,5 можно пользоваться графиками зависимости 
для случая 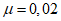 и r = 0,5 при расчете гасителя
и r = 0,5 при расчете гасителя
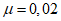 и r = 0,5 при расчете гасителя
и r = 0,5 при расчете гасителяпо схеме, изображенной на рис. 20, б
3.24. Для схемы, изображенной на рис. 20, в, в случае резонанса:
 (41)
(41)где
 (42)
(42)3.25. Для выбора параметров гасителя колебаний в случаях  , равных 0,02; 0,03; 0,04; 0,05; 0,1; 0,25 и 0,5, графики зависимости
, равных 0,02; 0,03; 0,04; 0,05; 0,1; 0,25 и 0,5, графики зависимости  и
и 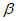 от v при r = 0,5 приведены на рис. 23.
от v при r = 0,5 приведены на рис. 23.

Рис. 23. Графики зависимости 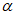 и
и  от v для
от v для 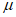 ,
,
равных 0,02; 0,03; 0,04; 0,05; 0,1; 0,25 и 0,5 и r = 0,5
при расчете гасителя по схеме, изображенной на рис. 20, в
 ;
; 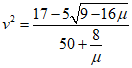 , (43)
, (43)графики зависимости 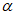 и
и 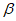 от
от 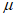 и r приведены на рис. 24.
и r приведены на рис. 24.

при расчете гасителя по схеме, изображенной на рис. 20, в,
в случае когда нет связи гасителя с неподвижным основанием
на системе с одной степенью свободы
3.27. Расчетные схемы плавающего гасителя колебаний на системе с одной степенью свободы представлены на рис. 25, где приняты следующие обозначения: M и  - массы системы и гасителя; k - коэффициент жесткости; c - коэффициент, учитывающий неупругие сопротивления в системе;
- массы системы и гасителя; k - коэффициент жесткости; c - коэффициент, учитывающий неупругие сопротивления в системе;  - величина зазора;
- величина зазора; 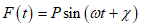 , где P,
, где P, 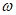 и
и  - амплитуда, частота и начальная фаза возмущающей силы.
- амплитуда, частота и начальная фаза возмущающей силы.
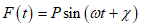 , где P,
, где P, 
а - без затухания, б - с затуханием в системе
В пп. 3.28 - 3.33 принято:
 (44)
(44)где x и y - перемещения масс системы и гасителя.
3.28. Для схемы, изображенной на рис. 25, а в случае резонанса:
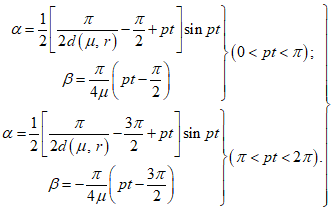 (45)
(45)3.29. Величина относительного зазора должна быть равна
3.30. Наряду с формулами (45) и (46) для выбора  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  от
от  и r и b от
и r и b от  , приведенными на рис. 26.
, приведенными на рис. 26.
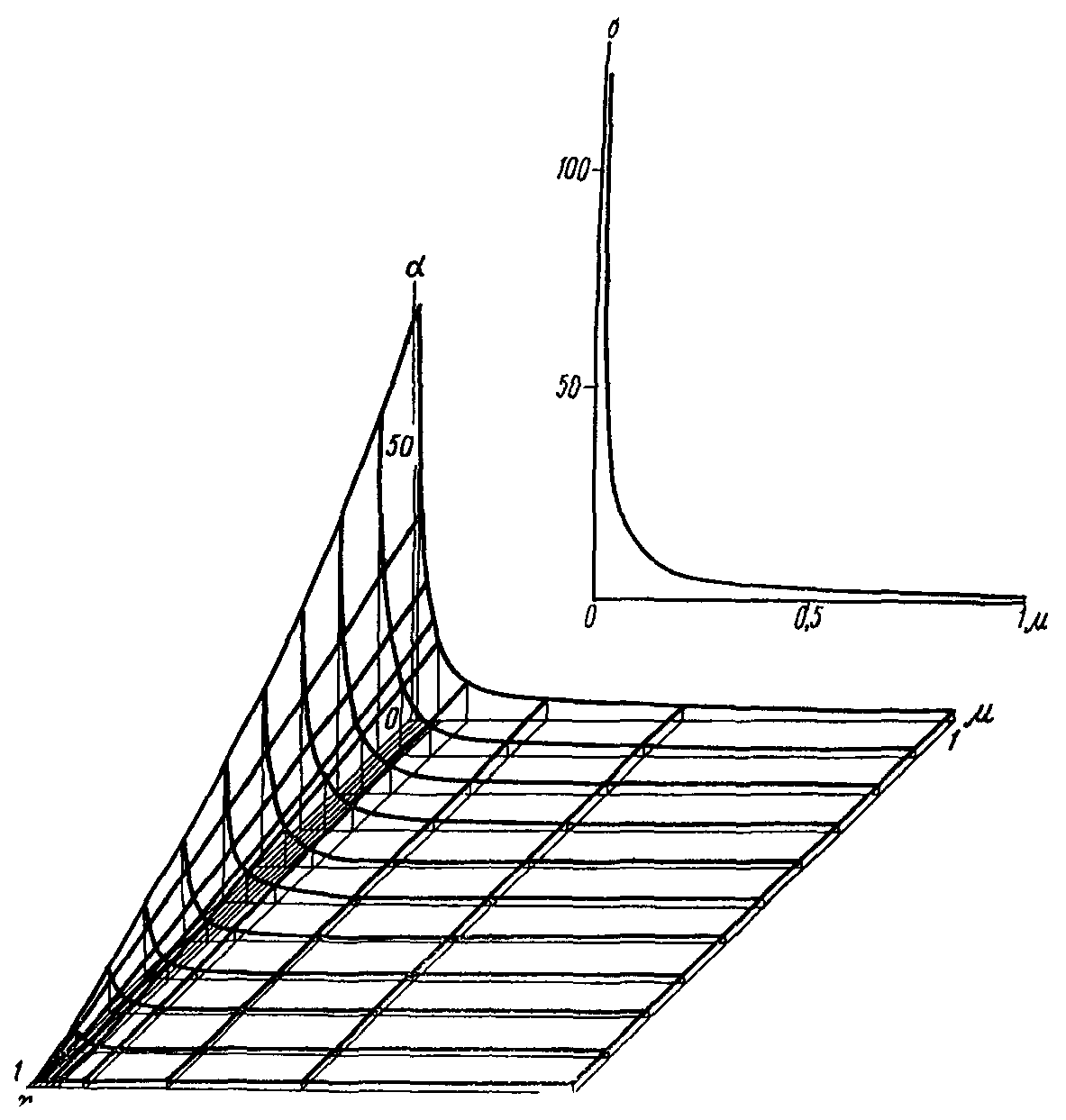
Рис. 26. Графики зависимости  от
от  и r и b от
и r и b от 
при расчете гасителя по схеме, изображенной на рис. 25, а
3.31. Для схемы, изображенной на рис. 25, б, в случае резонанса:
 ;
;где
 (48)
(48)3.32. Величина относительного зазора должна быть равна
 . (49)
. (49)3.33. Наряду с формулами (47) и (49) для выбора  и r можно пользоваться графиками зависимости
и r можно пользоваться графиками зависимости  и b от
и b от  ,
,  и r, приведенными на рис. 27.
и r, приведенными на рис. 27.

Рис. 27. Графики зависимости  и b от
и b от  и
и 
для случая r = 0,5 при расчете гасителя по схеме,
изображенной на рис. 25, б
ПОВЕРОЧНОГО РАСЧЕТА СООРУЖЕНИЯ С ДИНАМИЧЕСКИМИ
ГАСИТЕЛЯМИ КОЛЕБАНИЙ (ДЛЯ ЭВМ М-222 И М-220)




Инструкция к программе
1. Программа предназначена для оценки эффективности линейных динамических гасителей, установленных на многоэтажных зданиях, башнях или мачтах, при горизонтальных динамических воздействиях от технологического оборудования и пульсаций ветра.
2. Расчетной моделью сооружения является многоступенчатый стержень с присоединенными по границам участков гасителями колебаний и податливыми связями, препятствующими поворотам (рис. 28, а) или горизонтальным перемещениям (рис. 28, б) сечений.

Многоступенчатый стержень может иметь различные условия опирания по концам, как показано в табл. 4. Коэффициент внутреннего неупругого сопротивления стержня 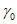 должен быть одинаковым для всех участков; константы Е.С. Сорокина
должен быть одинаковым для всех участков; константы Е.С. Сорокина  , характеризующие диссипативные свойства присоединенных в конце участка j связей, могут быть различными. Число гасителей, присоединенных в конце любого участка, может быть произвольным. Погонная масса стержня, жесткость при изгибе и продольная сила должны быть постоянными в пределах участка.
, характеризующие диссипативные свойства присоединенных в конце участка j связей, могут быть различными. Число гасителей, присоединенных в конце любого участка, может быть произвольным. Погонная масса стержня, жесткость при изгибе и продольная сила должны быть постоянными в пределах участка.
Верхний узел - N | Коэффициенты к концевым параметрам | |||
1 | 0 | 1 | 0 | |
1 | 1 | 0 | 0 | |
0 | 0 | 1 | 1 | |
0 | 1 | 0 | 1 | |
Продолжение прил. 1
Нижний узел - O | Начальные параметры | ||
M0 | Q0 | ||
1 | 0 | 1 | |
0 | 1 | 1 | |
 | 1 | 1 | |
1 | 0 | -k0 | |
 | 1 | -k0 | |
3. Каждый участок j (j = 1, 2,..., n) рассчитываемой системы характеризуют следующие параметры:
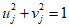 );
);4. Каждый присоединяемый в конце участка j гаситель характеризуют следующие параметры:
5. Воздействие на систему должно соответствовать представлению в виде произведения двух функций, одна из которых  зависит лишь от координат системы, вторая
зависит лишь от координат системы, вторая  - лишь от времени.
- лишь от времени.
6. Функцию нагрузок  в пределах участка стержня j характеризуют следующие параметры:
в пределах участка стержня j характеризуют следующие параметры:
7. Функция  задается спектральным представлением, т.е. должны быть заданы границы частотных интервалов, в пределах которых находятся ординаты спектра воздействия, и функция
задается спектральным представлением, т.е. должны быть заданы границы частотных интервалов, в пределах которых находятся ординаты спектра воздействия, и функция  (рис. 29), представляющая собой или нормированную спектральную плотность стационарного случайного процесса (для пульсаций ветра), или амплитудно-частотный коэффициент к нагрузке (для гармонического воздействия с нестабильной частотой от технологического оборудования).
(рис. 29), представляющая собой или нормированную спектральную плотность стационарного случайного процесса (для пульсаций ветра), или амплитудно-частотный коэффициент к нагрузке (для гармонического воздействия с нестабильной частотой от технологического оборудования).
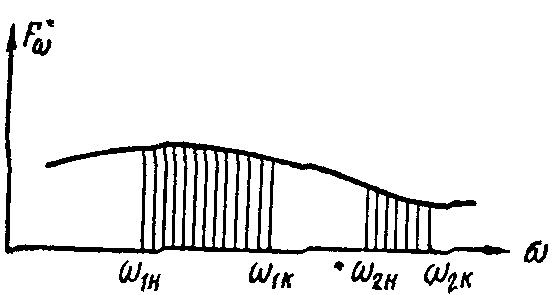
Рис. 29. Функция 
8. Каждый частотный интервал t характеризуется параметрами:
 ;
;9. Функция  может иметь вид:
может иметь вид:
 - для гармонического воздействия с нестабильной частотой;
- для гармонического воздействия с нестабильной частотой; - для стационарного случайного процесса,
- для стационарного случайного процесса,где  ;
; 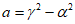 .
.
 ;
; 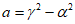 .
.Здесь  ,
,  ,
, 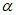 - произвольные постоянные, например для гармонического воздействия с нестабильной частотой и постоянной амплитудой сил нагрузки следует принять
- произвольные постоянные, например для гармонического воздействия с нестабильной частотой и постоянной амплитудой сил нагрузки следует принять 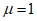 ;
;  ;
; 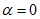 , если амплитуды сил пропорциональны квадрату частоты, -
, если амплитуды сил пропорциональны квадрату частоты, -  ;
;  ;
;  . Для пульсаций ветра обычно полагают
. Для пульсаций ветра обычно полагают  ;
;  ;
;  .
.
 ;
;  .
.10. В результате расчета для каждого сечения s, расположенного в начале либо в конце какого-нибудь участка стержня, вычисляются:
а) при стационарном случайном воздействии - нормы (корень квадратный из дисперсии) внутренних усилий и перемещений 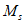 ,
,  ,
,  ,
, 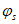 ;
;
б) при гармоническом воздействии с нестабильной частотой - максимальные для всех заданных частотных интервалов амплитудные значения каждой из величин  ,
,  ,
,  ,
,  . Следует отметить, что значения
. Следует отметить, что значения  ,
,  ,
, 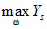 ,
, 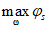 могут соответствовать разным частотам. Здесь
могут соответствовать разным частотам. Здесь 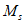 ,
,  ,
,  ,
,  - амплитудные значения изгибающего момента, поперечной силы, прогиба и угла поворота соответственно.
- амплитудные значения изгибающего момента, поперечной силы, прогиба и угла поворота соответственно.
 ,
, 11. Поскольку все интервалы частот разбиты на участки длиной  , значение
, значение 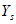 например, определяется в процессе счета на машине по формулам:
например, определяется в процессе счета на машине по формулам:
а)  ;
;
 ;
;б)  ,
,
 ,
,где  ,
,  , - передаточная и комплексно сопряженная с ней функции;
, - передаточная и комплексно сопряженная с ней функции;
 ,
, 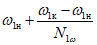 ,...,
,..., 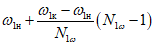 ;
;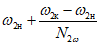 ,...,
,...,  ;
; Уменьшение числа точек деления интервалов частот  приводит к сокращению времени счета, но одновременно и к потере точности вычислений. Форма задания частотного диапазона по интервалам с разными отрезками деления позволяет сократить число точек
приводит к сокращению времени счета, но одновременно и к потере точности вычислений. Форма задания частотного диапазона по интервалам с разными отрезками деления позволяет сократить число точек  и одновременно не пропустить важных для точности счета ординат функций
и одновременно не пропустить важных для точности счета ординат функций  ,
,  .
.
 ,
, 12. Чтобы оценить эффективность гасителей, все указанные выше результаты получаются по программе и для системы без гасителей.
Исходные данные
13. Исходные данные для расчета записываются и набиваются на перфокартах в виде массивов (таблиц) в следующем порядке:
1. Табл. A (числа N,  ,
,  );
);
2. Табл. B (характеристика стержня и присоединенных связей);
3. Табл. E (спектральная характеристика воздействия);
4. Табл. V (характеристика нагрузки и гасителей) - этих таблиц может быть несколько.
Здесь: N - общее количество участков стержня;

Исходные данные, (в безразмерной форме)

14. К приведенным выше обозначениям следует добавить следующее.
В табл. B начальные параметры 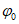 ,
,  ,
,  и коэффициенты к концевым параметрам
и коэффициенты к концевым параметрам  ,
,  ,
,  ,
,  назначаются в соответствии с табл. 4; константа Е.С. Сорокина
назначаются в соответствии с табл. 4; константа Е.С. Сорокина 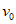 характеризует диссипативные свойства связей, моделирующих основание.
характеризует диссипативные свойства связей, моделирующих основание.
В табл. E первое число назначается равным:
1 - если воздействие гармоническое с нестабильной частотой;
-1 - если воздействие - стационарный случайный процесс.
В табл. V первое число назначается равным:
1 - если необходимо получить результаты также и для системы без гасителей;
2 - если необходимо получить результаты только для системы с гасителями.
В каждой последующей группе из четырех цифр первое число имеет абсолютную величину, равную номеру участка стержня, в конце которого расположены гаситель или внешние силы, и следующие знаки: знак "+", если три последующих числа характеризуют гаситель: знак "-", если три последующих числа характеризуют нагрузку.
Значения трех последующих чисел в группе ясны из обозначений, приведенных выше.
15. Часто возникает необходимость проверить эффективность гасителей при различных параметрах. В этих случаях следует задавать одновременно несколько таблиц V. В первой табл. V целесообразно назначать первое число равным 1, в последующих - равным 2 (для сокращения счета). Количество чисел  во всех табл. V должно быть одинаковым.
во всех табл. V должно быть одинаковым.
16. При заполнении табл. B, V, E может быть принята любая увязанная система размерностей, например, силы - т, длины - м, времени - с. Предусмотрена возможность задавать все величины в безразмерной форме, как указано в соответствующих таблицах. Если положить  ,
,  ,
,  ,
, 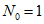 , числа в таблицах исходных данных в размерной и безразмерной форме будут совпадать.
, числа в таблицах исходных данных в размерной и безразмерной форме будут совпадать.
17. Следует отметить, что массу стержня 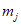 и параметры гасителей
и параметры гасителей  ,
,  нельзя назначать равными нулю.
нельзя назначать равными нулю.
Результаты расчета
18. В результате счета вычисляются значения  ,
, 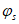 ,
,  ,
, 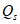 для сечений s, расположенных в начале и в конце каждого участка стержня.
для сечений s, расположенных в начале и в конце каждого участка стержня.
Результаты расположены в табл. Y в следующем порядке:  ,
, 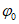 ,
,  ,
,  ,
, 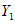 ,
,  ,
, 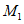 ,
,  ,...,
,...,  ,
,  ,
, 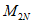 ,
, 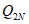 . Нумерация сечений снизу вверх.
. Нумерация сечений снизу вверх.
19. Связи и гасители считаются расположенными между концом предыдущего (снизу) и началом следующего (сверху) участков стержня.
20. В процессе счета на печать выдаются последовательно: 1. Табл. A; 2. Табл. B; 3. Табл. E; 4. Табл. V; 5. Табл. Y (для системы с гасителями); 6. Табл. Y (для системы без гасителей; если это предусмотрено заданием); 7. Табл. V, 8. Табл. Y (для гасителей с измененными параметрами).
Если исходные данные были заданы в безразмерной форме, вместо значений  ,
,  ,
,  ,
,  получаются соответственно
получаются соответственно  ,
,  ,
,  ,
, 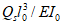 .
.
 ,
,  .
.Работа за пультом
21. Работа за пультом производится в соответствии с инструкцией к транслятору. Рекомендуется фиксировать процедуры в памяти машины.
Контрольный пример
В качестве примера ниже приведены результаты расчета для системы, изображенной на рис. 30. Нагрузка, изображенная на рис. 30, а, является гармонической с нестабильной частотой, на рис. 30, б изображена нагрузка, действующая как стационарный случайный процесс. Дополнительно обозначены:  ;
;  - жесткость ригеля при изгибе,
- жесткость ригеля при изгибе,  - длина ригеля. Исходные данные приведены в табл. 5; параметры нагрузок следующие: для варианта а) -
- длина ригеля. Исходные данные приведены в табл. 5; параметры нагрузок следующие: для варианта а) -  ,
,  ,
,  ,
,  ,
,  ; для варианта б) -
; для варианта б) -  ,
,  ,
,  ,
,  ,
,  .
.
 ;
;  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Номер участка | Nj, т | mj, т·с2/м2 | Flj, тм2 | lj, м | vj | kj, т/м | kj, тм/рад | ||||
1 | 40 | 0,025 | 1800 | 6 | 0,02 | - | 500 | 2 | 0,02 | 0,1 | 2,3 |
2 | 20 | 0,02 | 1000 | 4 | 0,02 | - | 300 | 1 | - | - | - |
3 | 10 | 0,02 | 1000 | 4 | 0,02 | - | 300 | 1 | 0,05 | 0,1 | 2,3 |
Результаты счета выдаются на печать в нормализованном виде (мантисса числа, опущенная десятка, порядок числа).
Результаты расчета сооружения (к рис. 30, а)
+.3000000010+01 | +.1600000010+02 | +.1300000010+02 | Табл. A | |||||||
Исходные данные | Табл. B | +.0000000010-00 | +.4000000010+02 | +.2000000010+02 | +.1000000010+02 | +.0000000010-00 | +.0000000010-00 | +.3000000010+01 | Табл. E | |
+.2000000010-01 | +.2499999910-01 | +.2000000010-01 | +.2000000010-01 | +.0000000010-00 | +.1500000010+01 | +.5000000010+01 | ||||
+.1000000010+01 | +.1800000010+04 | +.1000000010+04 | +.1000000010+04 | +.1000000010+01 | +.2300000010+01 | |||||
+.1000000010+01 | +.6000000010+01 | +.4000000010+01 | +.4000000010+01 | +.1000000010+01 | +.1000000010+02 | |||||
+.0000000010-00 | +.2000000010-01 | +.20000000 -01 | +.2000000010-01 | +.2250000010+01 | ||||||
+.1000000010+01 | +.0000000010+00 | +.0000000010+00 | +.0000000010+00 | +.1000000010+01 | +.2500000010+02 | |||||
+.1000000010+01 | +.5000000010+03 | +.3000000010+03 | +.3000000010+03 | +.1000000010+01 | +.2000000010+01 | |||||
+.0000000010-00 | +.2000000010+01 | +.1000000010+01 | +.1000000010+01 | +.0000000010-00 | +.2500000010+01 | |||||
+.1000000010+01 | +.5000000010+01 | +.0000000010-00 | +.1000000010+01 | +.2000000010-01 | -.9999999910-01 | Табл. V | ||||
-.1000000010+01 | +.2000000010+01 | +.5000000010+01 | +.2300000010+01 | +.3000000010+01 | +.4999999910+01 | |||||
+.0000000010-00 | -.3000000010+01 | +.2000000010+01 | -.9999999910-01 | +.2300000010+01 | ||||||
Результаты расчета сооружения | с гасителями | Y | M | Q | ||||||
+.0000000010-00 | +.0000000010-00 | +.969758910+03 | +.1717724010+03 | |||||||
+.5769305610+01 | +.1213896310+01 | +.2893477510+03 | +.1704385310+03 | |||||||
+.5769305610+01 | +.1213896310+01 | +.3182981710+03 | +.1254934310+03 | |||||||
+.1153739510+02 | +.1259589810+01 | +.2942164010+03 | +.122784810+03 | |||||||
+.1153739510+02 | +.1259589810+01 | +.8358844210+02 | +.7756677410+02 | |||||||
+.1629199210+02 | +.8840306110+00 | +.2659129210+03 | +.7316480810+02 | |||||||
без гасителей | +.0000000010-00 | +.0000000010-00 | +.2163614110+04 | +.3859607810+03 | ||||||
+.1281968510+02 | +.2683043710+01 | +.6594421710+03 | +.3827475410+03 | |||||||
+.1281968510+02 | +.2683043710+01 | +.6821993710+03 | +.2748351410+03 | |||||||
+.2542996210+02 | +.2723538710+01 | +.6581562110+03 | +.2684492710+03 | |||||||
+.2542996210+02 | +.2723538710+01 | +.1588267610+03 | +.1605874310+03 | |||||||
+.3561493110+02 | +.1884589610+01 | +.5656383810+03 | +.1501372910+03 | |||||||
Результаты расчета сооружения (к рис. 30, б)
+.3000000010+01 | +.2000000010+02 | +.1000000010+02 | Табл. A | |||||||
Исходные данные | Табл. B | +.0000000010-00 | +.0000000010-00 | +.5000000010+03 | +.0000000010-00 | +.2000000010-01 | +.1000000010+01 | +.3000000010+01 | Табл. E | |
+.2000000010-01 | +.4000000010+02 | +.2000000010+01 | +.3000000010+03 | +.0000000010-00 | +.2000000010+02 | |||||
+.1000000010+01 | +.2499999910-01 | +.2000000010+02 | +.1000000010+01 | +.3000000010+03 | -.1000000010+01 | +.3000000010+01 | ||||
+.1000000010+01 | +.1800000010+04 | +.2000000010-01 | +.1000000010+02 | +.1000000010+01 | +.0000000010-00 | +.1000000010+02 | ||||
+.0000000010-00 | +.6000000010+01 | +.1000000010+04 | +.2000000010-01 | +.0000000010-00 | +.4200000010-00 | +.1000000010+02 | ||||
+.1000000010+01 | +.2000000010-01 | +.4000000010+01 | +.1000000010+04 | +.0000000010-00 | +.2250000010+01 | |||||
+.1000000010+01 | +.0000000010-00 | +.2000000010-01 | +.4000000010+01 | +.1000000010+01 | +.9999999910-01 | |||||
+.1000000010+01 | +.0000000010-00 | +.9999999910-01 | -.3000000010+01 | +.0000000010-00 | -.9999999910-01 | +.2300000010+01 | Табл. V | |||
-.1000000010+01 | +.0000000010-00 | +.0000000010-00 | +.1140000010-00 | +.1000000010+01 | +.2000000010-01 | -.9999999910-01 | ||||
+.9999999910-01 | -.2000000010+01 | +.0000000010-00 | +.0000000010-00 | +.2300000010+01 | +.3000000010+01 | +.4999999910-01 | ||||
Результаты расчета сооружения | с гасителями | Y | M | Q | ||||||
+.0000000010-00 | +.0000000010-00 | +.2537996710+02 | +.4442565910+01 | |||||||
+.1516108910-00 | +.3195932410-01 | +.7609226810+01 | +.4530988610+01 | |||||||
+.1516108910-00 | +.3195032410-01 | +.8390514910+01 | +.3251937310+01 | |||||||
+.3037754110-00 | +.3336938110-01 | +.7724945310+01 | +.3279080310+01 | |||||||
+.3037754110-00 | +.3336938110-01 | +.2341408310+01 | +.2030045210+01 | |||||||
+.4302339410-00 | +.2366322010-01 | +.7097546810+01 | +.2053972110+01 | |||||||
без гасителей | +.0000000010-00 | +.0000000010-00 | +.3090525010+02 | +.5461639610+01 | ||||||
+.1837519910-00 | +.3853870210-01 | +.9416631410+01 | +.5520419910+01 | |||||||
+.1837519910-00 | +.3853870210-01 | +.9859287210+01 | +.3919022410+01 | |||||||
+.3654271410-00 | +.3938720510-01 | +.9438641910+01 | +.3907948410+01 | |||||||
+.3654271410-00 | +.3938720510-01 | +.2395685610+01 | +.2307280110+01 | |||||||
+.5132226410+00 | +.2745606610-01 | +.8235173210+01 | +.2270640910+01 | |||||||
ПРИМЕРЫ РАСЧЕТОВ ДИНАМИЧЕСКИХ ГАСИТЕЛЕЙ КОЛЕБАНИЙ
ДЛЯ СЛУЧАЕВ, КОГДА МОДЕЛЬЮ СООРУЖЕНИЯ МОЖЕТ СЛУЖИТЬ
СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Пример 1
Подобрать оптимальные параметры динамического гасителя и оценить эффективность гашения колебаний здания, расчетная схема которого изображена на рис. 31. Источником возбуждения является вентилятор с номинальным числом оборотов n = 400 об/мин 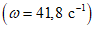 , установленный на перекрытии на отметке 9 м.
, установленный на перекрытии на отметке 9 м.
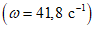 , установленный на перекрытии на отметке 9 м.
, установленный на перекрытии на отметке 9 м.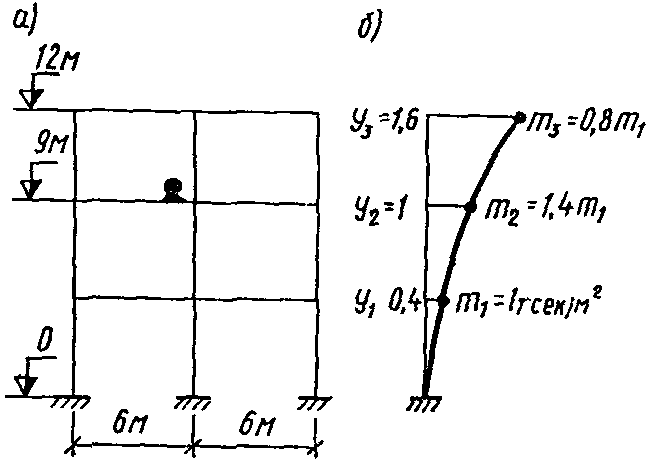
Рис. 31 Схема сооружения и первая форма свободных колебаний
Амплитуда возбуждающей силы, возникающей в результате вращения эксцентрика, пропорциональна квадрату частоты 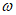 . Диссипативные свойства сооружения характеризуются коэффициентом
. Диссипативные свойства сооружения характеризуются коэффициентом 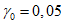 .
.
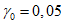 .
.Для простоты при определении форм колебаний масса сооружения считалась сосредоточенной в уровнях ригелей и таким образом форма колебаний характеризуется ординатами  ,
, 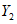 ,
,  . В соответствии с п. 2.9, форма колебаний нормирована по ординате
. В соответствии с п. 2.9, форма колебаний нормирована по ординате 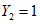 . Первая частота собственных колебаний здания оказалась равной
. Первая частота собственных колебаний здания оказалась равной 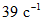 ; вторая частота -
; вторая частота -  ; в соответствии с п. 2.9 можно (так как
; в соответствии с п. 2.9 можно (так как  ) в данном случае пользоваться формулами п. 2.16 - 2.37. Поскольку число оборотов вентилятора может изменяться в процессе работы и, кроме того, при пусках и остановках возникает режим прохождения через резонанс (см. п. 2.26), оптимальные параметры гасителя следует подбирать как для гармонического воздействия с нестабильной частотой по формулам п. 2.23.
) в данном случае пользоваться формулами п. 2.16 - 2.37. Поскольку число оборотов вентилятора может изменяться в процессе работы и, кроме того, при пусках и остановках возникает режим прохождения через резонанс (см. п. 2.26), оптимальные параметры гасителя следует подбирать как для гармонического воздействия с нестабильной частотой по формулам п. 2.23.
 ) в данном случае пользоваться формулами п. 2.16 - 2.37. Поскольку число оборотов вентилятора может изменяться в процессе работы и, кроме того, при пусках и остановках возникает режим прохождения через резонанс (см. п. 2.26), оптимальные параметры гасителя следует подбирать как для гармонического воздействия с нестабильной частотой по формулам п. 2.23.
) в данном случае пользоваться формулами п. 2.16 - 2.37. Поскольку число оборотов вентилятора может изменяться в процессе работы и, кроме того, при пусках и остановках возникает режим прохождения через резонанс (см. п. 2.26), оптимальные параметры гасителя следует подбирать как для гармонического воздействия с нестабильной частотой по формулам п. 2.23.Из конструктивных соображений выбран гаситель с вязким демпфером и массой  , который устанавливается на перекрытии на отметке 9 м.
, который устанавливается на перекрытии на отметке 9 м.
 , который устанавливается на перекрытии на отметке 9 м.
, который устанавливается на перекрытии на отметке 9 м.В соответствии с п. 2.9 приведенная масса и обобщенная жесткость сооружения равны
 ;
; .
.Относительная масса гасителя составляет
 .
.Оптимальные параметры гасителя определяем по формулам (9):
 ;
; ;
;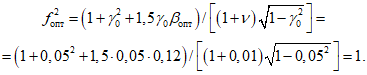
Относительная амплитуда перемещений сооружения с гасителем равна
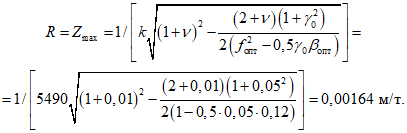
Относительная амплитуда удлинений связи гасителя соответственно равна
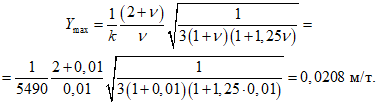
До установки гасителя относительная амплитуда перемещений сооружения составляла
 .
.Следовательно, в результате присоединения гасителя амплитуда колебаний сооружения уменьшилась более чем вдвое.
Пример 2
Подобрать оптимальные параметры гасителей колебаний и определить эффективность виброгашения металлической башни-трубы. Поперечное сечение трубы и места установки маятниковых динамических гасителей (помечены крестиками) показаны на рис. 32.

Рис. 32. Сечение башни-трубы
1 - газоотводящие стволы
Особенностями этого примера являются необходимость учета двух эксплуатационных режимов - с тремя (вариант 1) и с двумя (вариант 2) газоотводящими стволами и, кроме того, невозможность увеличения  более чем до 0,1. Каждому варианту соответствует своя приведенная масса и своя первая частота свободных колебаний (
более чем до 0,1. Каждому варианту соответствует своя приведенная масса и своя первая частота свободных колебаний (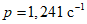 для варианта 1,
для варианта 1,  для варианта 2). Формы колебаний отличаются незначительно.
для варианта 2). Формы колебаний отличаются незначительно.
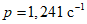 для варианта 1,
для варианта 1,  для варианта 2). Формы колебаний отличаются незначительно.
для варианта 2). Формы колебаний отличаются незначительно.При обтекании трубы ветровым потоком возникает ветровой резонанс, который, как показал расчет сооружения с учетом усталости, создает наибольшую опасность для сооружения.
По варианту 1 первая и вторая критические скорости ветра соответственно равны (см. главу СНиП II-6-74, п. 6.21):
 ;
; .
.По варианту 2 критические скорости ветра равны соответственно  и
и  .
.
 и
и  .
.Поскольку в обоих вариантах  больше 25 м/с, в данном случае в соответствии с п. 2.9 можно пользоваться формулами пп. 2.23 и 2.30.
больше 25 м/с, в данном случае в соответствии с п. 2.9 можно пользоваться формулами пп. 2.23 и 2.30.
Ввиду того что при различных эксплуатационных режимах башни-трубы работают одни и те же гасители, их общая относительная приведенная масса  и настройка f оказываются различными для вариантов 1 и 2. Для упрощения примера (в отличие от реального случая - расчета башни-трубы Норильского ГМК) будем полагать
и настройка f оказываются различными для вариантов 1 и 2. Для упрощения примера (в отличие от реального случая - расчета башни-трубы Норильского ГМК) будем полагать  для варианта 1 и
для варианта 1 и  для варианта 2. Коэффициент внутреннего неупругого сопротивления защищаемой конструкции
для варианта 2. Коэффициент внутреннего неупругого сопротивления защищаемой конструкции  примем равным 0,01.
примем равным 0,01.
 для варианта 1 и
для варианта 1 и  для варианта 2. Коэффициент внутреннего неупругого сопротивления защищаемой конструкции
для варианта 2. Коэффициент внутреннего неупругого сопротивления защищаемой конструкции Оптимальное затухание в гасителе  , вычисленное по формуле (10), больше, чем предельно допустимое значение
, вычисленное по формуле (10), больше, чем предельно допустимое значение 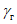 (для варианта 1
(для варианта 1 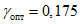 ; для варианта 2
; для варианта 2  ), поэтому в дальнейших расчетах ограничиваемся максимально возможным значением
), поэтому в дальнейших расчетах ограничиваемся максимально возможным значением 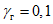 и оптимальную настройку гасителя определяем в соответствии с рекомендациями п. 2.34.
и оптимальную настройку гасителя определяем в соответствии с рекомендациями п. 2.34.
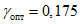 ; для варианта 2
; для варианта 2  ), поэтому в дальнейших расчетах ограничиваемся максимально возможным значением
), поэтому в дальнейших расчетах ограничиваемся максимально возможным значением 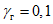 и оптимальную настройку гасителя определяем в соответствии с рекомендациями п. 2.34.
и оптимальную настройку гасителя определяем в соответствии с рекомендациями п. 2.34.Чтобы выбрать оптимальное значение  , строим (используя рис. 9) графики зависимости
, строим (используя рис. 9) графики зависимости  от
от  для варианта 1 (на рис. 33 они показаны сплошными линиями). Затем с помощью рис. 8 и 9 определяем ординаты графиков зависимости
для варианта 1 (на рис. 33 они показаны сплошными линиями). Затем с помощью рис. 8 и 9 определяем ординаты графиков зависимости  от
от  для варианта 2 и строим графики, показанные пунктиром на рис. 33, увеличивая при этом значения
для варианта 2 и строим графики, показанные пунктиром на рис. 33, увеличивая при этом значения 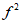 в
в  раз, для того, чтобы настройка
раз, для того, чтобы настройка  определялась относительно одной и той же частоты p, соответствующей варианту с тремя газоотводящими стволами.
определялась относительно одной и той же частоты p, соответствующей варианту с тремя газоотводящими стволами.
 раз, для того, чтобы настройка
раз, для того, чтобы настройка  определялась относительно одной и той же частоты p, соответствующей варианту с тремя газоотводящими стволами.
определялась относительно одной и той же частоты p, соответствующей варианту с тремя газоотводящими стволами.
Рис. 33. Влияние изменения настройки на величину 
Оптимальным можно считать значение  , при котором для любых частот значение
, при котором для любых частот значение  не превышает 16,2.
не превышает 16,2.
 , при котором для любых частот значение
, при котором для любых частот значение В процессе эксплуатации гасителей квадрат настройки, который пропорционален жесткости связи гасителя, может измениться до 5%, но и при этом значение  не превышает 20.
не превышает 20.
Таким образом, подобранные гасители уменьшают амплитуды колебаний (внутренних усилий) башни-трубы при ветровом резонансе примерно в пять раз.
КОНСТРУКТИВНЫЕ ФОРМЫ УДАРНЫХ ГАСИТЕЛЕЙ КОЛЕБАНИЙ
Пример 1. Маятниковый ударный гаситель колебаний
стальной футерованной дымовой трубы высотой 80 м
Гаситель рассчитан по схеме рис. 16, б. Масса дымовой трубы равна 330 т. Первая круговая частота собственных колебаний  . После приведения сооружения к расчетной системе получено M = 64,7 т. Для указанной дымовой трубы n = 0,05, следовательно, коэффициент неупругого сопротивления
. После приведения сооружения к расчетной системе получено M = 64,7 т. Для указанной дымовой трубы n = 0,05, следовательно, коэффициент неупругого сопротивления  . При
. При 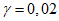 относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы в 3,5 раза, необходимо иметь
относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы в 3,5 раза, необходимо иметь  . При r = 0,5 и
. При r = 0,5 и  по рис. 19 величине
по рис. 19 величине  соответствует
соответствует 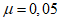 . При этом
. При этом  . Длина маятников гасителя равна 6,46 м.
. Длина маятников гасителя равна 6,46 м.
 . После приведения сооружения к расчетной системе получено M = 64,7 т. Для указанной дымовой трубы n = 0,05, следовательно, коэффициент неупругого сопротивления
. После приведения сооружения к расчетной системе получено M = 64,7 т. Для указанной дымовой трубы n = 0,05, следовательно, коэффициент неупругого сопротивления  . При
. При 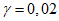 относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы в 3,5 раза, необходимо иметь
относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы в 3,5 раза, необходимо иметь  по рис. 19 величине
по рис. 19 величине 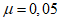 . При этом
. При этом В соответствии с приведенным расчетом было принято восемь маятников, подвешенных по периметру в верхней части трубы на листовых шарнирах. При колебаниях трубы в каком-либо горизонтальном направлении будут работать не все восемь маятников, а лишь часть их. Если, например, колебания трубы происходят в направлении, проходящем через какие-либо два диаметрально противоположных маятника, то из восьми маятников эти два маятника работают с эффективностью 100%, четыре - 70% и два совершенно не работают, так как первые два совершают удары перпендикулярно касательной к бойному приспособлению, четыре следующие - под углом 45° и последние два вообще не совершают ударов, поскольку движутся по касательным к нему. Учитывая это, принято, что каждый маятник имеет массу 650 кг. Подвеска маятников осуществлена на кронштейнах. Удары маятников воспринимаются стальным кольцом, жестко прикрепленным к кожуху трубы. Стальное кольцо снабжено деревянными прокладками и стальным кожухом. Общий вид гасителя представлен на рис. 34. Для того чтобы листовые шарниры не испытывали ударов, место удара маятника (поясок) поднято выше центра массы маятника на 6,3 см.

Рис. 34. Маятниковый ударный гаситель
колебаний дымовой трубы
Для повышения эффективности маятникового гасителя колебаний дымовой трубы рекомендуется на стальном кольце бойного приспособления устанавливать вогнутые стальные цилиндрические оболочки с ребрами жесткости, снабженные прокладками (рис. 35). В ударном гасителе, состоящем из восьми маятников, четыре маятника, работающие с эффективностью 70%, будут при новом бойном устройстве работать с эффективностью 90 - 95%, а два неработающих маятника - 25 - 30%.
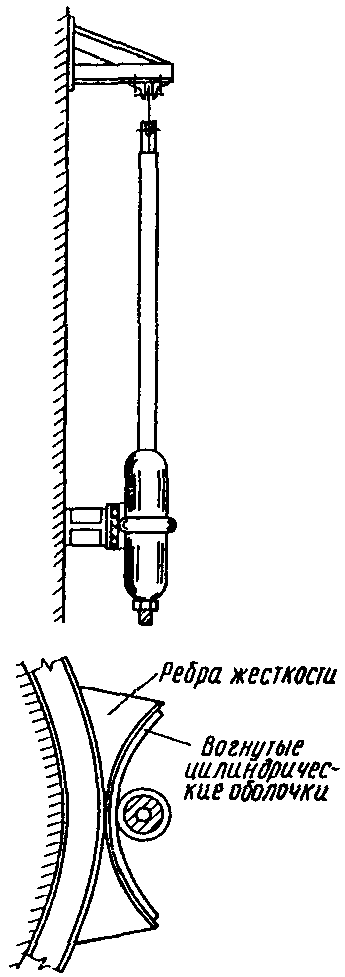
Рис. 35. Вогнутые цилиндрические оболочки бойной части,
повышающие эффективность гасителя
Пример 2. Маятниковый ударный гаситель колебаний
стальной радиобашни высотой 100 м
Гаситель рассчитывается по схеме рис. 16, б, масса радиобашни равна 50 т. Первая круговая частота собственных колебаний 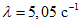 . После приведения сооружения к расчетной схеме получено M = 7,32 т. Для данной радиобашни n = 0,1, следовательно,
. После приведения сооружения к расчетной схеме получено M = 7,32 т. Для данной радиобашни n = 0,1, следовательно, 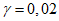 . При
. При  относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы, например, в пять раз, необходимо иметь
относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы, например, в пять раз, необходимо иметь 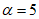 . При r = 0,5 и
. При r = 0,5 и  по рис. 19 величине
по рис. 19 величине 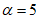 соответствует
соответствует 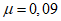 . При этом
. При этом  . Длина маятников гасителя равна 1,42 м.
. Длина маятников гасителя равна 1,42 м.
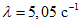 . После приведения сооружения к расчетной схеме получено M = 7,32 т. Для данной радиобашни n = 0,1, следовательно,
. После приведения сооружения к расчетной схеме получено M = 7,32 т. Для данной радиобашни n = 0,1, следовательно, 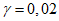 . При
. При  относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы, например, в пять раз, необходимо иметь
относительная амплитуда колебаний системы без гасителя равна 25. Для того чтобы снизить амплитуду вынужденных колебаний системы, например, в пять раз, необходимо иметь  по рис. 19 величине
по рис. 19 величине  . При этом
. При этом В соответствии с приведенным расчетом для башни приняты четыре маятника, подвешиваемые внутри решетчатой конструкции верхней части радиобашни на листовых шарнирах. Для того чтобы при колебаниях башни в любом горизонтальном направлении обеспечивалось  , масса маятника принята 250 кг. Пояски маятников выполнены из жесткой резины. Подвеска маятников осуществлена на диагональных связях. Удары маятников воспринимаются диагональными рамными связями.
, масса маятника принята 250 кг. Пояски маятников выполнены из жесткой резины. Подвеска маятников осуществлена на диагональных связях. Удары маятников воспринимаются диагональными рамными связями.
 , масса маятника принята 250 кг. Пояски маятников выполнены из жесткой резины. Подвеска маятников осуществлена на диагональных связях. Удары маятников воспринимаются диагональными рамными связями.
, масса маятника принята 250 кг. Пояски маятников выполнены из жесткой резины. Подвеска маятников осуществлена на диагональных связях. Удары маятников воспринимаются диагональными рамными связями.Пример 3. Пружинный ударный гаситель
колебаний фундамента компрессора
Требуется уменьшить колебания виброизолированного фундамента общей массой 20 т, испытывающего из-за очень малого коэффициента неупругого сопротивления в виброизоляторах большие резонансные колебания при пуске и остановке машины. Считаем, что прохождение через резонанс происходит настолько медленно, что амплитуды можно вычислить по формулам, выведенным для установившихся вынужденных колебаний. Задача состоит в том, чтобы на всем диапазоне частот амплитуда колебаний машины с фундаментом не превышала некоторой конечной величины. Для стальных пружинных виброизоляторов  , поэтому относительная амплитуда колебаний системы без гасителя равна 50. Чтобы снизить амплитуду резонансных колебаний системы в 3 раза, необходимо иметь
, поэтому относительная амплитуда колебаний системы без гасителя равна 50. Чтобы снизить амплитуду резонансных колебаний системы в 3 раза, необходимо иметь  . При r = 0,5 по рис. 24 величине
. При r = 0,5 по рис. 24 величине  соответствует
соответствует  . При этом
. При этом  . В этом случае масса гасителя равна 400 кг.
. В этом случае масса гасителя равна 400 кг.
 , поэтому относительная амплитуда колебаний системы без гасителя равна 50. Чтобы снизить амплитуду резонансных колебаний системы в 3 раза, необходимо иметь
, поэтому относительная амплитуда колебаний системы без гасителя равна 50. Чтобы снизить амплитуду резонансных колебаний системы в 3 раза, необходимо иметь  . При этом
. При этом  . В этом случае масса гасителя равна 400 кг.
. В этом случае масса гасителя равна 400 кг.В соответствии с приведенным расчетом принято, что по двум боковым сторонам фундамента симметрично располагаются две массы, каждая на своих направляющих и со своими пружинами. Вес каждой массы 200 кг. На рис. 36 представлен эскиз установки гасителя на фундаменте. Бойная часть на боковой плоскости фундамента выполняется из стального элемента, прикрепленного к фундаменту. Для возможности регулировки частоты собственных колебаний гасителя массы в верхней части снабжены загрузочными углублениями.
Рис. 36. Установка гасителя
на виброизолированном фундаменте

 ;
; 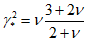 , (8)
, (8)



 - для случаев, рассмотренных в
- для случаев, рассмотренных в 


