СПРАВКА
Источник публикации
М.: Издательство стандартов, 1986
Примечание к документу
Документ введен в действие с 01.07.1987.
Название документа
"РД 50-25645.210-85. Руководящий нормативный документ. Методические указания. Безопасность радиационная экипажа космического аппарата в космическом полете. Методика расчета энергетической плотности потоков протонов и нейтронов в космическом аппарате"
(утв. и введены в действие Постановлением Госстандарта СССР от 10.12.1985 N 3881)
"РД 50-25645.210-85. Руководящий нормативный документ. Методические указания. Безопасность радиационная экипажа космического аппарата в космическом полете. Методика расчета энергетической плотности потоков протонов и нейтронов в космическом аппарате"
(утв. и введены в действие Постановлением Госстандарта СССР от 10.12.1985 N 3881)
Содержание
Постановлением Государственного
комитета СССР по стандартам
от 10 декабря 1985 г. N 3881
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
БЕЗОПАСНОСТЬ РАДИАЦИОННАЯ ЭКИПАЖА КОСМИЧЕСКОГО АППАРАТА
В КОСМИЧЕСКОМ ПОЛЕТЕ. МЕТОДИКА РАСЧЕТА ЭНЕРГЕТИЧЕСКОЙ
ПЛОТНОСТИ ПОТОКОВ ПРОТОНОВ И НЕЙТРОНОВ
В КОСМИЧЕСКОМ АППАРАТЕ
РД 50-25645.210-85
Группа Ф40
ОКСТУ 6968
Срок введения
с 1 июля 1987 года
ИСПОЛНИТЕЛИ:
В.Б. Хвостов, канд. физ.-мат. наук; О.Е. Адамов, канд. техн. наук; А.И. Григорьев, д-р мед. наук; А.В. Губарев; В.П. Демин, канд. техн. наук; Е.Е. Ковалев, д-р техн. наук; Г.В. Красильников; Е.Н. Лесновский, канд. техн. наук; А.П. Лобаков; И.И. Максимов; В.Н. Никитинский; А.А. Оглоблин, д-р техн. наук; В.А. Панин; С.М. Перфильева; И.Я. Ремизов, канд. техн. наук; В.А. Сакович, канд. техн. наук; В.М. Сахаров, канд. техн. наук; В.И. Степакин, канд. техн. наук; И.Ф. Усольцев, канд. техн. наук.
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ постановлением Государственного комитета СССР по стандартам от 10.12.85 г. N 3881
Введены впервые
Утверждены постановлением Госстандарта от 10 декабря 1985 г. N 3881, срок введения установлен с 01.07.1987 г.
Настоящие методические указания устанавливают алгоритмы расчета энергетической плотности потоков первичных протонов, а также вторичных протонов и нейтронов (нуклонов) внутри космического аппарата (КА) в диапазоне энергий от 1 до 1000 МэВ, учитывающие пространственное распределение вещества в КА, средняя толщина защиты которого, выраженная в массовых единицах длины, не превышает 15 г/см2.
1.1. Расчет энергетической плотности потоков протонов и вторичных нейтронов внутри КА осуществляют в приближении однократного ядерного взаимодействия первичных протонов с веществом защиты КА.
1.2. В расчетах прохождения космических лучей через защиту КА ядерные взаимодействия протонов с энергией E < 20 МэВ не учитывают.
1.3. Учет потерь энергии протонов на ионизацию осуществляют в приближении непрерывного замедления с использованием ионизационных потерь энергии протона S(E) и ионизационных пробегов R(E), определяемых по РД 50-25645.206-84.
1.4. Ослабление флюенса нуклонов с энергией E0 за счет ядерных взаимодействий в однородном веществе на геометрическом расстоянии t, см, определяют функцией
 (1)
(1)где  - оптическое расстояние в веществе, т.е. расстояние, выраженное в долях среднего пробега нуклона до ядерного взаимодействия
- оптическое расстояние в веществе, т.е. расстояние, выраженное в долях среднего пробега нуклона до ядерного взаимодействия  , определяемого по ГОСТ 25645.211-85.
, определяемого по ГОСТ 25645.211-85.
 - оптическое расстояние в веществе, т.е. расстояние, выраженное в долях среднего пробега нуклона до ядерного взаимодействия
- оптическое расстояние в веществе, т.е. расстояние, выраженное в долях среднего пробега нуклона до ядерного взаимодействия 1.4.1. Оптическое расстояние для нейтронов с энергией E0 вычисляют по формуле
 (2)
(2)где  - плотность вещества, г/см3.
- плотность вещества, г/см3.
1.4.2. Оптическое расстояние для протонов с начальной энергией E0 вычисляют по формуле
 (3)
(3)где  (4)
(4)
 (4)
(4)Остаточную энергию протона E после прохождения в веществе расстояния t вычисляют из соотношения
 (5)
(5)1.4.3. Для объекта, состоящего из зон с различными веществами, оптическое расстояние вычисляют как сумму оптических расстояний, пройденных нуклоном в каждой из зон.
1.5. Энергетическое распределение плотности потоков протонов  и нейтронов
и нейтронов  вычисляют в фиксированных точках
вычисляют в фиксированных точках  внутри КА в энергетических узлах Ej (j = 1, ..., J), заданных в диапазоне энергий от 1 до 1000 МэВ в порядке возрастания энергии.
внутри КА в энергетических узлах Ej (j = 1, ..., J), заданных в диапазоне энергий от 1 до 1000 МэВ в порядке возрастания энергии.
 и нейтронов
и нейтронов  вычисляют в фиксированных точках
вычисляют в фиксированных точках Примечание. Выбор узловых значений Ej и количество узлов J должны обеспечить вычисление интегрального по энергии флюенса нуклонов с погрешностью не более 20%. Для энергетических узлов при J > 20 следует принять логарифмическую сетку.
ПОТОКОВ ПРОТОНОВ И НЕЙТРОНОВ
2.1. Геометрию и состав вещества КА задают по ГОСТ 25645.204-83, причем в качестве внешней границы объекта принимают описанную сферу радиуса R0. Начало неподвижной системы координат совмещают с центром сферы (см. рисунок).

и нейтронов в космическом аппарате:
1 - космический аппарат (КА); 2 - сфера радиуса R0;
сферы; 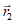 - точка внутри КА
- точка внутри КА
2.2. Каждой зоне K космического аппарата ставят в соответствие индекс вещества l(k), заполняющего эту зону. Пустым зонам присваивают значение индекса l = 0.
2.3. Для каждого вещества с индексом l(k), отличным от нуля, определяют следующие характеристики:
ионизационные потери энергии протонов Sl(E) по РД 50-25645.206-84;
ионизационные пробеги протонов Rl(E) по РД 50-25645.206-84;
средние пробеги нуклонов до ядерного взаимодействия  и
и  по ГОСТ 25645.211-85;
по ГОСТ 25645.211-85;
 и
и двойные дифференциальные распределения вторичных нуклонов  (m = пр, н - протон или нейтрон, соответственно) по ГОСТ 25645.211-85.
(m = пр, н - протон или нейтрон, соответственно) по ГОСТ 25645.211-85.
 (m = пр, н - протон или нейтрон, соответственно) по ГОСТ 25645.211-85.
(m = пр, н - протон или нейтрон, соответственно) по ГОСТ 25645.211-85.Примечание. Средние пробеги нейтронов с энергией E < 20 МэВ определяют в соответствии с рекомендуемым приложением.
2.4. Источник первичных протонов задают плотностью тока протонов через поверхность сферы радиуса R0 в каждой точке  (см. рисунок), равной
(см. рисунок), равной
 (см. рисунок), равной
(см. рисунок), равной (6)
(6)где  - изотропная в
- изотропная в  плотность потока протонов космических лучей;
плотность потока протонов космических лучей;
 - единичный вектор направления в точке
- единичный вектор направления в точке Примечание. Угол  отсчитывается от нормали
отсчитывается от нормали  в точке
в точке  .
.
 отсчитывается от нормали
отсчитывается от нормали  (7)
(7)где  - начальный статистический вес истории;
- начальный статистический вес истории;
 - начальный статистический вес истории;
- начальный статистический вес истории; - функция плотности вероятности для энергетического распределения протонов;
- функция плотности вероятности для энергетического распределения протонов; , где
, где  - функция плотности вероятности распределения
- функция плотности вероятности распределения  ;
; - функция плотности вероятности распределения
- функция плотности вероятности распределения  ;
;Emin и Emax - минимальное и максимальное значения энергии в спектре протонов космических лучей, равные соответственно 30 и 1000 МэВ.
ПЕРВИЧНЫХ ПРОТОНОВ
3.1. Декартовы координаты точки вылета протона  (см. рисунок) с поверхности сферы радиусом R0 моделируют для каждой i-ой истории (i = 1, ..., I) по следующей схеме.
(см. рисунок) с поверхности сферы радиусом R0 моделируют для каждой i-ой истории (i = 1, ..., I) по следующей схеме.
 (см. рисунок) с поверхности сферы радиусом R0 моделируют для каждой i-ой истории (i = 1, ..., I) по следующей схеме.
(см. рисунок) с поверхности сферы радиусом R0 моделируют для каждой i-ой истории (i = 1, ..., I) по следующей схеме.3.1.1. Направление  моделируют из изотропного в
моделируют из изотропного в  распределения для
распределения для  :
:
 моделируют из изотропного в
моделируют из изотропного в  (8)
(8)где  и
и  - случайные числа, равномерно распределенные в интервале 0, 1).
- случайные числа, равномерно распределенные в интервале 0, 1).
3.1.2. Направляющие косинусы в декартовой системе координат  вычисляют по формулам
вычисляют по формулам
 вычисляют по формулам
вычисляют по формулам (9)
(9)3.1.3. Декартовы координаты точки  вычисляют по формулам
вычисляют по формулам
 вычисляют по формулам
вычисляют по формулам (10)
(10) (11)
(11)3.3. Направляющие косинусы в неподвижной декартовой системе координат для направления  из точки
из точки  на точку
на точку  вычисляют по формулам
вычисляют по формулам
 из точки
из точки  (12)
(12)3.4. Вычисляют косинус угла  между внешней нормалью к сферической поверхности в точке
между внешней нормалью к сферической поверхности в точке  и направлением
и направлением  по формуле
по формуле
 и направлением
и направлением  по формуле
по формуле (13)
(13)причем  ,
,
 ,
,т.е.
3.5. Значения энергии протона в точке  принимают равным Ej (j = 1, ..., J) и вычисляют значения энергии первичного протона
принимают равным Ej (j = 1, ..., J) и вычисляют значения энергии первичного протона  в точке
в точке  по следующему алгоритму.
по следующему алгоритму.
 в точке
в точке 3.5.1. Направляют луч из точки  в направлении
в направлении  и вычисляют длины отрезков
и вычисляют длины отрезков  , (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых зон
, (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых зон  , (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
, (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
 , (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых зон
, (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых зон  , (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
, (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.Примечание. Далее в формулах аргументы при tn и kn опущены.
3.5.2. Значения энергии протона E'n (n = 1, ..., N0 - 1) на границах пересекаемых зон kn вычисляют из рекуррентного соотношения для пробегов протона:
 (15)
(15)полагая E'0 = Ej.
3.5.3. Если значение энергии протона E'n при n <= N0 - 1 превышает Emax = 1000 МэВ, т.е. попадание в точку  протонов с энергией Ej из источника невозможно, то для всех j' >= j дальнейшее вычисление энергетического распределения не производится.
протонов с энергией Ej из источника невозможно, то для всех j' >= j дальнейшее вычисление энергетического распределения не производится.
3.5.4. Значение энергии первичного протона  принимают равным значению энергии протона
принимают равным значению энергии протона 
 (16)
(16)3.6. Оптическое расстояние для протона с энергией  между точками
между точками  и
и  в направлении
в направлении  вычисляют по формуле
вычисляют по формуле
 (17)
(17)где


Значения E'n - по п. 3.5.2.
3.7. Значение энергетической плотности потока первичных протонов в точке  при энергии Ej вычисляют по формуле
при энергии Ej вычисляют по формуле
 (18)
(18) (19)
(19)3.9. Для получения статистически обеспеченной оценки  , (j = 1, ..., F) вычисления по пп. 3.1 - 3.8 следует выполнить I раз (для сложной геометрии космического аппарата I >= 104).
, (j = 1, ..., F) вычисления по пп. 3.1 - 3.8 следует выполнить I раз (для сложной геометрии космического аппарата I >= 104).
 , (j = 1, ..., F) вычисления по пп. 3.1 - 3.8 следует выполнить I раз (для сложной геометрии космического аппарата I >= 104).
, (j = 1, ..., F) вычисления по пп. 3.1 - 3.8 следует выполнить I раз (для сложной геометрии космического аппарата I >= 104).3.10. Значение  , нормированное на единичную плотность потока первичных протонов
, нормированное на единичную плотность потока первичных протонов  , вычисляют по формуле
, вычисляют по формуле
 , нормированное на единичную плотность потока первичных протонов
, нормированное на единичную плотность потока первичных протонов  , вычисляют по формуле
, вычисляют по формуле (20)
(20)ВТОРИЧНЫХ НУКЛОНОВ
4.1. Декартовы координаты вылета протона r1 = {x1, y1, z1} - по п. 3.1.
4.2. Протонной истории присваивают статистический вес W = W0, где W0 определяют по п. 2.5.
4.3. Направление вылета протона из источника (см. рисунок) моделируют по следующему алгоритму.
4.3.1. Подвижную систему координат помещают в точку  , направив ось z1 по внешней к сферической поверхности нормали
, направив ось z1 по внешней к сферической поверхности нормали  , направляющие косинусы которой в неподвижной системе координат nx, ny, nz вычисляют по формулам (14).
, направляющие косинусы которой в неподвижной системе координат nx, ny, nz вычисляют по формулам (14).
 , направляющие косинусы которой в неподвижной системе координат nx, ny, nz вычисляют по формулам (14).
, направляющие косинусы которой в неподвижной системе координат nx, ny, nz вычисляют по формулам (14).4.3.2. Направление вылета протона  в подвижной системе координат моделируют, используя
в подвижной системе координат моделируют, используя  ,
,  , определяемые по формулам п. 2.5, причем
, определяемые по формулам п. 2.5, причем
 в подвижной системе координат моделируют, используя
в подвижной системе координат моделируют, используя  ,
,  (21)
(21)где  ,
,  - случайные числа, равномерно распределенные в интервале (0, 1).
- случайные числа, равномерно распределенные в интервале (0, 1).
4.3.3. Значения направляющих косинусов вектора  в неподвижной системе координат
в неподвижной системе координат  , вычисляют по формулам
, вычисляют по формулам
 , вычисляют по формулам
, вычисляют по формуламИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 (22)
(22)4.4. Значение энергии первичного протона E*1 моделируют из распределения f1(E0), определяемого по п. 2.5, полагая
 (23)
(23)где  - случайное число, равномерно распределенное в интервале (0, 1).
- случайное число, равномерно распределенное в интервале (0, 1).
4.5. Оптическое расстояние в КА для протона с энергией E*1, выходящего из точки  в направлении
в направлении  , вычисляют по следующему алгоритму.
, вычисляют по следующему алгоритму.
 , вычисляют по следующему алгоритму.
, вычисляют по следующему алгоритму.4.5.1. Направляют луч из точки  в направлении
в направлении  и вычисляют длины отрезков
и вычисляют длины отрезков  , (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон
, (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  , (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
, (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
 , (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон
, (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  , (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
, (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.4.5.2. Если на пути луча встречаются только пустые зоны, т.е. l(kn) = 0 для всех n = 1, ..., N0 - 1, то история прерывается.
4.5.3. Если на пути луча есть заполненные веществом зоны, то вычисляют значения энергии протона E'n на границах зон из рекуррентного соотношения для пробегов протона:
 (24)
(24)полагая E'0 = E*1.
4.5.4. Если  , то в последовательности пересекаемых зон (n = 1, ..., N0 - 1) определяют номер n0, при котором
, то в последовательности пересекаемых зон (n = 1, ..., N0 - 1) определяют номер n0, при котором 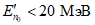 .
.
 , то в последовательности пересекаемых зон (n = 1, ..., N0 - 1) определяют номер n0, при котором
, то в последовательности пересекаемых зон (n = 1, ..., N0 - 1) определяют номер n0, при котором 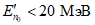 .
.Примечание. Данное условие означает, что протон из-за ионизационных потерь достигает энергии 20 МэВ в зоне с номером  .
.
 (25)
(25)где  ;
;
 ;
; - геометрическое расстояние от точки
- геометрическое расстояние от точки 4.6. Оптическое расстояние, пройденное протоном в КА до ядерного взаимодействия в точке  , вычисляют по формуле
, вычисляют по формуле
 (26)
(26)где  - геометрическое расстояние между точками
- геометрическое расстояние между точками  и
и  ;
;
 - геометрическое расстояние между точками
- геометрическое расстояние между точками 4.7. Новый статистический вес протонной истории, компенсирующий смещенность оценки пробега протона до ядерного взаимодействия вычисляют по формуле
 (27)
(27)4.8. В последовательности пересекаемых зон (n = 1, ..., N0 - 1) вычисляют номер n1, для которого выполняется неравенство
 (28)
(28)где  - значения оптических расстояний протона в пересекаемых зонах КА, определенные по п. 4.5.5.
- значения оптических расстояний протона в пересекаемых зонах КА, определенные по п. 4.5.5.
 - значения оптических расстояний протона в пересекаемых зонах КА, определенные по п. 4.5.5.
- значения оптических расстояний протона в пересекаемых зонах КА, определенные по п. 4.5.5.Примечание. Точка  находится в зоне с номером
находится в зоне с номером  .
.
4.9. Энергию протона E*2 в точке  вычисляют по следующему алгоритму.
вычисляют по следующему алгоритму.
4.9.1. Вычисляют оптическое расстояние, пройденное протоном в зоне с номером  :
:
 (29)
(29)4.9.2. Значение оптического расстояния для протона с энергией E*2 в веществе зоны n1 вычисляют по формуле
4.9.3. Значение энергии протона E*2 вычисляют путем обратной интерполяции из зависимости Ql(E) для значения Ql, определяемого по формуле (30).
4.10. Вычисляют геометрическое расстояние T12 по следующему алгоритму.
4.10.1. Расстояние  , пройденное протоном в зоне с номером
, пройденное протоном в зоне с номером  , вычисляют по формуле
, вычисляют по формуле
 (31)
(31)4.10.2. Расстояние T12 вычисляют по формуле
 (32)
(32)4.11. Декартовы координаты точки ядерного взаимодействия протона  вычисляют по формулам
вычисляют по формулам
 вычисляют по формулам
вычисляют по формулам (33)
(33)4.14. Угол между векторами  и
и  вычисляют по формуле
вычисляют по формуле
 (34)
(34)4.15. Направляют луч из точки  в направлении
в направлении  и вычисляют длины отрезков
и вычисляют длины отрезков  (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон
(n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
(n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
 (n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон
(n = 1, ..., N0 - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  (n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.
(n = 1, ..., N0 - 1) по ГОСТ 25645.204-83.4.16. В последовательности пересекаемых зон (n = 1, ..., N0 - 1) определяют номер n2, для которого справедливо неравенство
 (35)
(35)Примечание. Точка  расположена в зоне с номером
расположена в зоне с номером  .
.
4.17. Длину отрезка  , проходимую нуклоном в зоне
, проходимую нуклоном в зоне  , вычисляют из соотношения
, вычисляют из соотношения
 (36)
(36)4.18. Длину отрезка  полагают равной
полагают равной  .
.
4.19. Оптическое расстояние между точками  и
и  для нейтронов с энергией Ej <= E*2 (j = 1, ..., J) вычисляют по формуле
для нейтронов с энергией Ej <= E*2 (j = 1, ..., J) вычисляют по формуле
 (37)
(37)4.20. Значение энергетической плотности потока вторичных нейтронов в точке  при энергии Ej вычисляют по формуле
при энергии Ej вычисляют по формуле
 (38)
(38)4.21. Значение  заносят в сумматор
заносят в сумматор 
 заносят в сумматор
заносят в сумматор 
 (39)
(39)4.22. Энергию вторичного протона  , с которой он должен вылететь из точки
, с которой он должен вылететь из точки  , чтобы прийти в точку
, чтобы прийти в точку  с энергией Ej (j = 1, ..., J) вычисляют по следующему алгоритму.
с энергией Ej (j = 1, ..., J) вычисляют по следующему алгоритму.
4.22.1. Определяют энергии протонов на границах пересекаемых зон из рекуррентного соотношения для ионизационных пробегов протона
 (40)
(40)полагая E'0 = Ej.
4.22.2. Если значение энергии протона E'n превышает значение E*2, т.е. попадание в точку  протонов с энергией Ej невозможно, то для всех j' >= j дальнейшее вычисление энергетического распределения не производится.
протонов с энергией Ej невозможно, то для всех j' >= j дальнейшее вычисление энергетического распределения не производится.
4.22.3. Значение энергии вторичного протона  , образующегося в протон-ядерном взаимодействии в точке
, образующегося в протон-ядерном взаимодействии в точке  , принимают равным
, принимают равным  .
.
4.23. Оптическое расстояние для протона с энергией  (j = 1, ..., J) между точками
(j = 1, ..., J) между точками  и
и  вычисляют по формуле
вычисляют по формуле
 (41)
(41)4.24. Значение энергетической плотности потока протонов в точке  при энергии Ej вычисляют по формуле
при энергии Ej вычисляют по формуле
 (42)
(42) (43)
(43)4.26. Для получения статистически обеспеченной оценки  и
и  , (j = 1, ..., J) вычисления по п. 4.1 - 4.25 следует выполнить I раз (I >= 104).
, (j = 1, ..., J) вычисления по п. 4.1 - 4.25 следует выполнить I раз (I >= 104).
 и
и  , (j = 1, ..., J) вычисления по п. 4.1 - 4.25 следует выполнить I раз (I >= 104).
, (j = 1, ..., J) вычисления по п. 4.1 - 4.25 следует выполнить I раз (I >= 104).4.27. Значения  и
и  , (j = 1, ..., J), нормированные на единичную плотность потока первичных протонов, вычисляют по формулам
, (j = 1, ..., J), нормированные на единичную плотность потока первичных протонов, вычисляют по формулам
 и
и  , (j = 1, ..., J), нормированные на единичную плотность потока первичных протонов, вычисляют по формулам
, (j = 1, ..., J), нормированные на единичную плотность потока первичных протонов, вычисляют по формулам (44)
(44)Рекомендуемое
1. Средние пробеги нейтронов до ядерного взаимодействия с энергией E < 20 МэВ вычисляют по формуле:

где  - полное микроскопическое сечение ядерного взаимодействия нейтронов, барн.
- полное микроскопическое сечение ядерного взаимодействия нейтронов, барн.
2. Полные микроскопические сечения ядерного взаимодействия нейтронов с E < 20 МэВ рекомендуется брать из справочника <*>.
--------------------------------
<*> Медведев Ю.А., Степанов Б.М., Труханов Г.Я. Ядерно-физические константы взаимодействия нейтронов с элементами, входящими в состав атмосферы и земной коры: Справочник. - М.: Энергоиздат, 1981.
 задают в виде
задают в виде и точкой
и точкой  вычисляют по формуле
вычисляют по формуле
 заносят в сумматор
заносят в сумматор  :
: вычисляют по формуле
вычисляют по формуле
 из точки
из точки  заносят в сумматор
заносят в сумматор  :
: