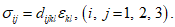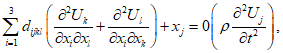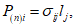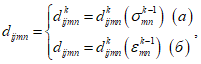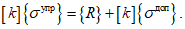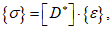СПРАВКА
Источник публикации
М., 2019
Примечание к документу
Название документа
"Методическое пособие. Автоматизированные методы расчета массивных железобетонных конструкций при объемном напряженном состоянии"
"Методическое пособие. Автоматизированные методы расчета массивных железобетонных конструкций при объемном напряженном состоянии"
ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ
"ФЕДЕРАЛЬНЫЙ ЦЕНТР НОРМИРОВАНИЯ, СТАНДАРТИЗАЦИИ
И ТЕХНИЧЕСКОЙ ОЦЕНКИ СООТВЕТСТВИЯ В СТРОИТЕЛЬСТВЕ"
МЕТОДИЧЕСКОЕ ПОСОБИЕ
АВТОМАТИЗИРОВАННЫЕ МЕТОДЫ РАСЧЕТА МАССИВНЫХ ЖЕЛЕЗОБЕТОННЫХ
КОНСТРУКЦИЙ ПРИ ОБЪЕМНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
В настоящее время в связи с интенсивным развитием вычислительной техники остро встает проблема перевода методов расчета и проектирования строительных конструкций на полностью автоматизированную компьютерную основу. Весьма перспективным и назревшим представляется решение этой проблемы и для конструкций, работающих в условиях объемных напряженных состояний. Среди них - массивные фундаментальные плиты толщиной до 4 м и более, массивные колонны под высокой нагрузкой, стены ядер жесткости высотных зданий, защитные оболочки, плотины и др.
В основу автоматизированных методов, как правило, закладываются современные вычислительные методы и в первую очередь метод конечных элементов (МКЭ). Однако в вопросах применения современных вычислительных методов к расчетам массивных железобетонных конструкций наблюдаются негативные тенденции, которые могут свести на нет все выгоды, связанные с автоматизацией. Речь идет о полном или частичном игнорировании факторов нелинейности бетона и железобетона и связанного с ним перераспределения усилий в программах расчета конструкций методом конечных элементов и другими методами. Это может привести к количественным, а иногда и к качественным искажениям реальной картины деформирования конструкций под нагрузкой, а в итоге - к понижению надежности конструктивных решений в одних случаях и неоправданному перерасходу материалов в других.
Разработка методического пособия направлена на развитие и совершенствование современных ЭВМ-программ расчета массивных конструкций с учетом в них сложных физико-механических свойств бетона и железобетона при объемных напряженных состояниях (особенностей прочности и нелинейных связей между напряжениями и относительными деформациями, влияния образования трещин по различным схемам, приобретаемой в процессе деформирования и трещинообразования анизотропии, ползучести, усадки, особенностей сцепления арматуры с бетоном и других факторов).
Известно, что каждый материал "входит" в механику с набором только ему присущих соотношений. К таким соотношениям относят связи между напряжениями и деформациями (физические соотношения), а также общие критерии оценки прочности и трещиностойкости бетона и железобетона. В целом они образуют систему определяющих соотношений материала.
В методическом пособии обобщены многолетние исследования, выполненные в НИИЖБ, НИИСФ РААСН и в других институтах страны и за рубежом по конструированию и экспериментальной проверке определяющих соотношений для бетона и железобетона. Рассматривается самый общий случай - объемное напряженное состояние. Это отвечает поставленной задаче расчета массивных конструкций. В виде частных случаев из полученных соотношений следуют соотношения для плоского и одноосного напряженных состояний, что существенно раздвигает возможности использования представленных зависимостей для расчета различных (не только массивных) конструкций.
Методическое пособие разработано для применения специалистами, чья деятельность связана с проектированием и оценкой надежности массивных железобетонных конструкций современных зданий и сооружений, включая:
- специалистов проектных организаций;
- органов лицензирования сертификации, а также проверки безопасности конструктивных решений.
Методическое пособие разработано авторским коллективом НИИСФ РААСН, членами и советниками РААСН (руководитель работы - д-р техн. наук Н.И. Карпенко (разделы 1 - 11); д-р техн. наук В.И. Травуш (разделы 1 - 5, 11), С.Н. Карпенко (разделы 4 - 11), В.И. Корсун (разделы 6 - 7), А.Н. Петров (разделы 6, 8), В.А. Ерышев (раздел 6), Л.И. Ярин (раздел 11); канд. техн. наук И.Г. Чепизубов (разделы 5, 6); научные сотрудники: Г.А. Моисеенко (разделы 5, 6), М.В. Степанов (разделы 5, 6), Н.Г. Семенова (оформление разделов 1 - 11).
Пособие предназначено для расчета массивных железобетонных конструкций, работающих в условиях трехосного напряженного состояния (толстых плит, массивных стержней, массивных стен и ядер жесткости, например, высотных зданий, защитных оболочек, толстостенных сосудов и др.), а также, в частных случаях, немассивных конструкций (например, плит перекрытий и монолитных стен жесткости сложной конфигурации), отдельные области которых деформируются в условиях объемного напряженного состояния, на статические (или приводимые к ним) нагрузки, вынужденные деформации или перемещения вследствие внутренних и внешних силовых воздействий. Однако методы расчета и проектирования таких конструкций практически не нашли отражения в СП 63.13330.2018 "СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения". Разработка данного методического пособия в дополнение к СП 63.13330 направлена на устранение этого недостатка.
В методическом пособии обобщены физические модели и математические методы, ориентированные, в основном, на использование в программах и программных комплексах расчета конструкций современными вычислительными средствами.
Пособие может компенсировать отсутствие нормативных документов по составлению алгоритмов и программ расчета массивных и традиционных железобетонных конструкций с полным учетом физической нелинейности применительно к современным математическим методам.
По мере увеличения скорости вычислительных средств по объемным моделям с использованием МКЭ можно будет рассчитывать все виды железобетонных конструкций вплоть до балок и колонн.
Методическое пособие включает современные методы расчета и проектирования, основанные на использовании современных объемных моделей деформирования и исчерпания прочности бетона и железобетона с учетом различных факторов физической нелинейности, влияния трещинообразования, приобретаемой и конструктивной анизотропии при трехосных напряженных состояниях.
Методическое пособие включает методы, направленные на решение задач расчета массивных железобетонных монолитных и сборных конструкций малозатратными слабоитерационными и безитерационными способами расчета.
В настоящем методическом пособии использованы ссылки на следующие нормативные документы:
СП 63.13330.2018 "СНиП 52-01-2003 "Бетонные и железобетонные конструкции. Основные положения" (с изменением N 1);
ГОСТ 27751-2014 "Надежность строительных конструкций и оснований. Основные положения и требования".
В настоящем методическом пособии применяются следующие термины с соответствующими определениями:
3.1 объемное напряженное состояние: Напряженное состояние, характеризующееся у каждой точки в декартовых осях координат x, y, z шестью компонентами тензора напряжений  ,
,  ,
, 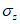 ,
, 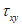 ,
,  ,
,  (в бетоне
(в бетоне 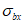 ,
,  ,
, 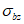 ,
,  ,
, 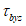 ,
,  ).
).
3.2 главные напряжения: Объемное напряженное состояние характеризуется главными напряжениями  ,
,  ,
,  (в бетоне
(в бетоне  ,
,  ,
,  ). Рассматривается напряженное состояние у точки в осях n, m, l (или 1, 2, 3), повернутых относительно осей x, y, z на определенные углы, приводящие к условиям, когда касательные напряжения (
). Рассматривается напряженное состояние у точки в осях n, m, l (или 1, 2, 3), повернутых относительно осей x, y, z на определенные углы, приводящие к условиям, когда касательные напряжения (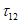 ,
,  ,
,  ) становятся равными нулю, а нормальные напряжения, обозначаемые
) становятся равными нулю, а нормальные напряжения, обозначаемые  ,
,  ,
, 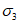 , становятся главными.
, становятся главными.
3.3 инварианты напряженного состояния: Главные напряжения и отдельные соотношения между напряжениями, не зависящие от поворота осей координат.
3.4 диаграммы деформирования материалов: Связи между напряжениями и относительными деформациями бетона и арматуры при одноосном напряженном состоянии, которые претерпевают существенные изменения (трансформацию) при объемном напряженном состоянии.
3.5 исходные характеристики бетона и арматуры: Нормативные (Rbn, Rbtn) и расчетные (Rb, Rbt) характеристики бетона; нормативные (Rsn) и расчетные (Rs) характеристики арматуры; начальные модули упругости бетона Eb и арматуры Es.
3.6 прочность бетона при объемном напряженном состоянии: Прочность бетонных элементов считается обеспеченной, если соблюдается критерий прочности.
3.7 критерий прочности: Определенная функция между главными напряжениями, их инвариантами и исходными характеристиками бетона, которая должна быть меньше или равна нулю (<= 0); при нарушении этого условия (при > 0) наступает разрушение бетона.
3.8 схемы исчерпания прочности бетона: Различают четыре схемы исчерпания прочности бетона (схема 0 - разрушение элемента по всему объему; схема 1 - образование трещин вдоль площадок приложения напряжений  ; схема 2 - образование трещин по двум ортогональным направлениям - вдоль площадок приложения
; схема 2 - образование трещин по двум ортогональным направлениям - вдоль площадок приложения  и
и  ; схема 3 - образование трещин по трем ортогональным направлениям.
; схема 3 - образование трещин по трем ортогональным направлениям.
3.9 деформированные состояния бетона при объемном напряженном состоянии: Деформированные состояния бетонного элемента при объемном напряженном состоянии в главных осях 1, 2, 3 представляются тремя относительными главными деформациями  ,
,  ,
, 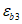 и тремя сдвиговыми деформациями
и тремя сдвиговыми деформациями 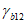 ,
, 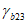 ,
,  , которые равны нулю. Они остаются для удобства матричных преобразований.
, которые равны нулю. Они остаются для удобства матричных преобразований.
3.10 физические соотношения для бетонных элементов: Связь между напряжениями и относительными деформациями. Физические соотношения устанавливаются в главных осях 1, 2, 3 как для нелинейного ортотропного материала, а затем переводятся в глобальную систему координат x, y, z.
3.11 ортогональное (ортотропное) армирование: Армирование с расположением арматуры по трем ортогональным направлениям (вдоль осей x, y, z).
3.12 коэффициенты армирования 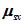 ,
,  ,
, 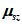 : Площади стержней, приходящиеся на единицу площади плоскости, проведенной к направлениям стержней.
: Площади стержней, приходящиеся на единицу площади плоскости, проведенной к направлениям стержней.
3.13 косоугольное армирование: дисперсное армирование стержнями, расположенными под произвольным углом к осям координат; 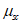 - коэффициент косоугольного армирования.
- коэффициент косоугольного армирования.
3.14 виды критериев прочности железобетонных элементов: Используются два вида критериев прочности - для железобетонных элементов без трещин и для железобетонных элементов с трещинами. В первом случае используются прочностные характеристики бетона и арматуры, а во втором - прочностные характеристики арматуры в сечениях с трещинами и отдельно (в отдельном условии) прочностные характеристики бетона между трещинами.
3.15 физические соотношения для железобетонных элементов: Связи между напряжениями и относительными деформациями до и после образования трещин по различным схемам.
3.16 методы решения физически нелинейных задач железобетона: Метод упругих решений, метод переменных параметров упругости, метод начальных напряжений, метод конечных разностей, метод конечных элементов, новый слабоитерационный метод конечных элементов с представлением физических соотношений в конечных приращениях.
Представленные модели и методы расчета массивных железобетонных конструкций основываются на следующих предпосылках:
4.1 Рассматриваются конструкции, работающие в условиях объемного напряженного состояния.
4.2 Расчет конструкций по предельным состояниям первой и второй групп производят по напряжениям (усилиям), деформациям и перемещениям, вычисляемым с учетом физической нелинейности и анизотропии бетона и железобетона, а в необходимых случаях - ползучести, термоползучести и накопления повреждений (в длительных процессах).
Примечание - Анизотропия - неодинаковость свойств (здесь - механических) по разным направлениям. Ортотропия - вид анизотропии, при котором имеются три взаимно перпендикулярные плоскости симметрии свойств.
4.3 Физическую нелинейность, анизотропию и ползучесть учитывают в физических соотношениях, связывающих между собой напряжения и относительные деформации. При этом следует выделять две стадии деформирования элементов - до и после образования трещин. Особенности разрушения бетона и железобетона учитывают в условиях (критериях) прочности, ограничивающих область безопасных (не вызывающих разрушение) напряжений.
4.4 Общие физические соотношения базируются на исходных одноосных диаграммах связи между напряжениями и деформациями в бетоне и арматуре и их трансформациях в зависимости от знака напряжений (сжатие "-", растяжение "+"), длительности действия напряжений, режима их приложения (мягкий, жесткий), влияния влажностных и других факторов.
4.5 До образования трещин для бетона используют нелинейные физические соотношения ортотропной модели, позволяющие учитывать неоднородность деформирования при сжатии и растяжении и влияние на деформации направленного развития в структуре бетона множества микротрещин, а также трещин большей протяженности (дефектов отрыва) в зависимости от напряженного состояния.
Для железобетона в стадии до образования трещин исходят из совместности осевых деформаций арматуры и окружающего бетона за исключением концевых участков арматуры, не снабженных специальными анкерами.
При опасности выпучивания арматуры следует ограничивать ее предельные сжимающие напряжения.
4.6 В общих условиях прочности бетона учитывают сочетание напряжений на площадках разных ортогональных направлений, в силу которых, в частности, его сопротивление двух- и трехосному сжатию превышает прочность при одноосном сжатии, а при комбинациях сжатия и растяжения может быть меньше, чем при действии одного из них. В необходимых случаях должна приниматься во внимание длительность действия напряжений.
Геометрическая интерпретация условия прочности в пространстве трех главных напряжений - поверхность, которая должна удовлетворять как традиционным требованиям (выпуклость, непрерывность, симметрия относительно гидростатической оси), так и обладать следующими специфическими свойствами:
быть функцией инвариантов тензора напряжений;
характеризоваться девиаторными кривыми, которые меняют форму при переходе от трехосного растяжения к сжатию-растяжению и трехосному сжатию, отображая этим различные механизмы разрушения бетона (отрывной; смешанный отрывно-сдвиговый; сдвиговый);
являться в области трехосного равномерного сжатия разомкнутой для плотных бетонов и замкнутой - для пористых (однако для плотных бетонов на величины напряжений трехосного равномерного сжатия ставится дополнительное ограничение, связанное с соблюдением целостности бетона как материала после разгрузки).
Условие прочности железобетона без трещин составляют, исходя из условий прочности составляющих материала (бетона и арматуры), как двухкомпонентной среды.
4.7 В качестве условия трещинообразования используют условия прочности бетона двухкомпонентной среды с учетом влияния физической нелинейности и в некоторых случаях, в основном в изгибаемых элементах, влияния градиентов деформаций и напряжений.
4.8 Для железобетона после образования трещин в бетоне используют нелинейные физические соотношения анизотропного тела общего вида, устанавливаемые с учетом следующих факторов:
- углов наклона трещин к арматуре и схем пересечения трещин;
- раскрытия трещин и сдвига их берегов;
- жесткости арматуры при осевых деформациях под действием напряжений в трещинах с учетом влияния на деформации сил сцепления арматуры с полосами или блоками бетона между трещинами;
- жесткости арматуры при тангенциальных перемещениях ее у берегов трещины под действием касательных напряжений в арматуре в трещинах с учетом податливости бетонного основания у берегов трещин;
- жесткостей бетона между трещинами при продольных (вдоль трещин) и сдвиговых (по нормали к трещинам) деформациях под действием соответствующих нормальных и касательных напряжений и снижения этих жесткостей для схем пересекающихся трещин;
- жесткостей остаточных бетонных связей зацепления берегов трещин при сдвигах берегов при достаточно малой ширине раскрытия трещин;
- нарушения совместности осевых деформаций арматуры и бетона между трещинами с сохранением лишь условия совместности перемещений арматуры и бетона по середине полос или блоков между трещинами.
В физических соотношениях для бетонных элементов с трещинами учитывается лишь жесткость бетона между трещинами и жесткость связей зацепления берегов трещин (при малом их раскрытии).
4.9 Ширину раскрытия трещин и взаимный сдвиг их берегов определяют исходя из смещений стержней различных направлений относительно пересекаемых ими берегов трещин с учетом расстояний между трещинами и при соблюдении условия совместности этих смещений в трещине.
4.10 Условия прочности плоских и объемных элементов с трещинами основывают на следующих предпосылках:
- сопротивление бетона сжатию снижается из-за возникновения растяжений в перпендикулярном направлении, создаваемого силами сцепления с растянутой арматурой, а также при образовании пересекающихся трещин;
- при определении прочности арматуры учитываются схемы образования трещин и углы наклона трещин к арматуре;
- в стержнях арматуры учитываются, как правило, нормальные напряжения, направленные вдоль их оси; допускается учитывать касательные напряжения в арматуре в местах трещин (нагельный эффект), принимая, что стержни не изменяют своей ориентации;
- принимается, что в трещине разрушения все пересекающие ее стержни арматуры, имеющие площадку текучести, достигают расчетных сопротивлений на растяжение; для стержней арматуры, не имеющих предела текучести, напряжения должны контролироваться в процессе деформационного расчета (или вводиться в виде расчетных сопротивлений с соответствующими коэффициентами условия работы).
Прочность бетона в различных его зонах оценивают по напряжениям в нем как в компоненте двухкомпонентной среды (за вычетом приведенных напряжений в арматуре между трещинами, определяемых с учетом напряжений в трещинах, сцепления и частичного нарушения совместности осевых деформаций арматуры с бетоном).
4.11 Физические соотношения для железобетона, а также известные уравнения равновесия, совместности деформаций, геометрические соотношения и граничные условия составляют системы определяющих уравнений механики бетона и железобетона. Поскольку элементы матриц жесткости физических соотношений (условной жесткости) не являются константами, а представляются функциями напряжений, деформаций или неаналитическими зависимостями типа вычислительного оператора, то решение задач, в основном, выполняется численными методами. Разрешающие уравнения в основном конструируются с помощью метода конечных элементов (МКЭ). Могут использоваться и другие методы: граничных элементов (МГЭ), конечных разностей (МКР) и вариационно-разностный (ВРМ). Решение разрешающих уравнений осуществляется шагово-итерационными методами, в основе которых, как правило, лежат различные модификации метода упругих решений применительно к железобетону.
4.12 Несущую способность железобетонных конструкций, способных претерпевать достаточные пластические деформации, допускается определять методом предельного равновесия, используя в качестве условий текучести соответствующие условия прочности железобетонных элементов (в основном с арматурой, имеющей достаточно протяженную площадку текучести).
4.13 Статический расчет конструкций выполняют отдельно на действие расчетных нагрузок (для оценки предельных состояний первой группы) и отдельно на действие эксплуатационных нагрузок (для оценки предельных состояний второй группы) с использованием, за некоторыми исключениями (они оговорены в разделах), соответствующих этим предельным состояниям значений характеристик бетона и арматуры по СП 63.13330. Значения этих характеристик умножаются на значения дополнительных коэффициентов условий работы, учитывающие особенности свойств бетона и арматуры при неодноосных и неоднородных напряженных состояниях. В отдельные формулы введены значения нормативных характеристик материалов (например, бетона Rbn, Rbtn). Условно принято, что таким образом обозначенные величины не должны изменяться при расчетах по предельным состояниям обеих групп.
4.14 Расчет конструкций с учетом физической нелинейности, как правило, выполняют на каждую комбинацию (сочетание) нагрузок совместно с подбором соответствующего армирования сечений или его проверкой, если армирование задано. По подобранным коэффициентам армирования строится огибающая эпюра армирования для всех комбинаций нагрузок и по ней проводится окончательное конструирование. При наличии данных учитывается последовательность приложения комбинаций нагрузок и их взаимное влияние.
4.15 Помимо внешних и внутренних нагрузок учитывают усилия обжатия их предварительно напряженной арматурой. Усилия обжатия могут учитываться как внутренние силы (начальные напряжения), вводимые в физические соотношения, и как внешние силы, равные контролируемым усилиям за вычетом первых потерь и приложенные на уровне центра тяжести напрягаемой арматуры в виде некоторой равнодействующей или в виде распределенных по длине зон анкеровки следящих сил (или в виде того и другого в зависимости от вида преднапряжения).
4.16 При расчете конструкций по прочности, деформациям, образованию и раскрытию трещин методом конечных элементов должны быть проверены условия прочности и трещиностойкости для всех конечных элементов, составляющих конструкцию, а также условия возникновения чрезмерных перемещений конструкции.
4.17 При оценке предельного состояния по прочности на экстремальные внутренние и внешние воздействия допускается учитывать возможную работу отдельных конечных элементов на нисходящих ветвях деформирования с развитием больших пластических деформаций, если это не влечет за собой потери конструкцией своих эксплуатационных и защитных свойств и развитие прогрессирующего разрушения и по истечении действия рассматриваемой нагрузки возникающие при этом повреждения могут быть устранены без риска для здоровья людей и загрязнения окружающей среды. В других случаях эти факторы моделируют лишь с тем, чтобы выявить действительные прочностные и деформативные свойства сооружений.
4.18 Общие принципы расчета и проектирования массивных железобетонных конструкций основаны на развитии принципов расчета, изложенных в методическом пособии "Статически неопределимые железобетонные конструкции. Диаграммные методы автоматизированного расчета и проектирования", на более общий класс железобетонных конструкций, работающих в условиях объемного напряженного состояния. Таким образом они становятся применимыми для различных железобетонных конструкций.
5 Соотношения теории напряжений и теории деформаций, характеризующие трехосное (объемное) напряженно-деформированное состояние элементов
5.1 Напряженное состояние объемного (трехмерного) элемента в ортогональных осях x, y, z характеризуется шестью компонентами тензора напряжений 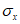 ,
,  ,
, 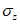 ,
, 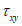 ,
,  ,
, 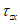 (рисунок 5.1). При рассмотрении общих вопросов предлагается использовать тензорные обозначения, которые позволяют записывать ряд формул в компактном виде. При использовании тензорной символики декартовы координаты x, y, z обозначают x1, x2, x3 или в общем виде xi, где индекс i принимает значения 1, 2, 3.
(рисунок 5.1). При рассмотрении общих вопросов предлагается использовать тензорные обозначения, которые позволяют записывать ряд формул в компактном виде. При использовании тензорной символики декартовы координаты x, y, z обозначают x1, x2, x3 или в общем виде xi, где индекс i принимает значения 1, 2, 3.

а - в произвольных осях;
б - в осях главных напряжений 1, 2, 3
Нормальные напряжения обозначают  ,
, 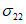 ,
,  , а касательные
, а касательные 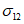 ,
, 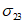 ,
,  . Общий компонент записывают в виде
. Общий компонент записывают в виде  (i, j = 1, 2, 3). Отдельные компоненты получаются из общего заменой букв i и j цифрами 1, 2 и 3. В дальнейшем под
(i, j = 1, 2, 3). Отдельные компоненты получаются из общего заменой букв i и j цифрами 1, 2 и 3. В дальнейшем под 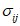 будем понимать также совокупность всех девяти компонентов тензора напряжений.
будем понимать также совокупность всех девяти компонентов тензора напряжений.
5.2 Напряженное состояние можно также характеризовать главными нормальными напряжениями  ,
,  ,
,  . Кроме этого используются следующие инвариантные характеристики напряженного состояния:
. Кроме этого используются следующие инвариантные характеристики напряженного состояния:
 - второй инвариант девиатора напряжений;
- второй инвариант девиатора напряжений; - третий инвариант девиатора напряжений.
- третий инвариант девиатора напряжений.Эти характеристики связаны с компонентами тензора напряжений соотношениями:
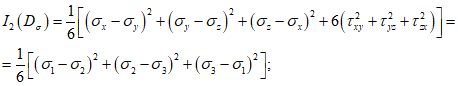 (5.2)
(5.2) (5.3)
(5.3)Производными второго инварианта девиатора напряжений служат:
T - интенсивность касательных напряжений;
 (5.4)
(5.4) (5.5)
(5.5)Характеристики напряженного состояния, связанные со вторым и третьим инвариантами девиатора напряжений:
Эти характеристики определяются соотношениями:
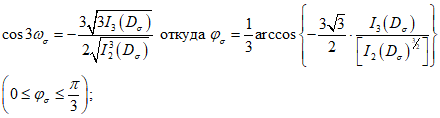 (5.6)
(5.6) (5.7)
(5.7)Параметр  , выраженный через главные напряжения, записывается в виде
, выраженный через главные напряжения, записывается в виде
Главные напряжения определяются формулами:
при использовании инвариантов  , T и
, T и 
 (5.9)
(5.9)при использовании инвариантов  ,
,  и
и 
5.3 Направляющие косинусы между главными напряжениями и осями координат i = x, y, z определяются выражениями
lei = Aei/Ae, (5.11)
где lei - направляющие косинусы между рассматриваемым главным напряжением  и i-й осью координат (i = x = 1; i = y = 2; i = z = 3), причем
и i-й осью координат (i = x = 1; i = y = 2; i = z = 3), причем  ;
;
 ;
;Aei - адъюнкта i-го элемента строки e матрицы  ;
;
 ;
;E - единичная матрица (e = 1, 2, 3);
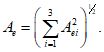 (5.12)
(5.12)Например, при e = 1, i = 1, 2, 3 (или i = x, y, z)
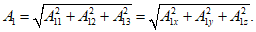
В развернутом виде адъюнкты записываются выражениями
 (5.13)
(5.13)Если Ac = 0, то
при  lex = 1, ley = lez = 0;
lex = 1, ley = lez = 0;
 lex = 1, ley = lez = 0;
lex = 1, ley = lez = 0;при 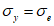 ley = 1, lex = lez = 0;
ley = 1, lex = lez = 0;
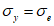 ley = 1, lex = lez = 0;
ley = 1, lex = lez = 0;при 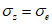 lez = 1, lex = ley = 0.
lez = 1, lex = ley = 0.
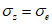 lez = 1, lex = ley = 0.
lez = 1, lex = ley = 0.5.4 Деформированное состояние объемного (трехмерного) элемента в ортогональных осях x, y, z характеризуется шестью компонентами деформаций  ,
,  ,
,  ,
,  ,
,  ,
, 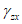 .
.
Компоненты 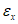 ,
,  ,
,  ,
, 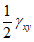 ,
,  ,
, 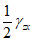 образуют симметричный тензор деформаций. Подобно компонентам тензора напряжения
образуют симметричный тензор деформаций. Подобно компонентам тензора напряжения  под символом
под символом  понимают соответствующий компонент тензора деформаций или совокупность всех девяти компонентов тензора деформаций.
понимают соответствующий компонент тензора деформаций или совокупность всех девяти компонентов тензора деформаций.
Деформированное состояние можно также характеризовать главными линейными деформациями  ,
,  ,
, 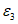 , а также инвариантами типа (5.1) - (5.10), где
, а также инвариантами типа (5.1) - (5.10), где  заменяется на
заменяется на  , а
, а 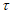 на
на  .
.
5.5 Углы между направлениями главных напряжений и осями координат могут быть представлены в виде частного случая угла поворота осей x, y, z в положение x', y', z' (или n, m, l). При этом тензор напряжений  преобразуется в тензор
преобразуется в тензор 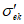 по формуле
по формуле
где lij - направляющие косинусы углов между старыми и новыми осями (рисунок 5.2) определяются тремя строками таблицы 5.1.
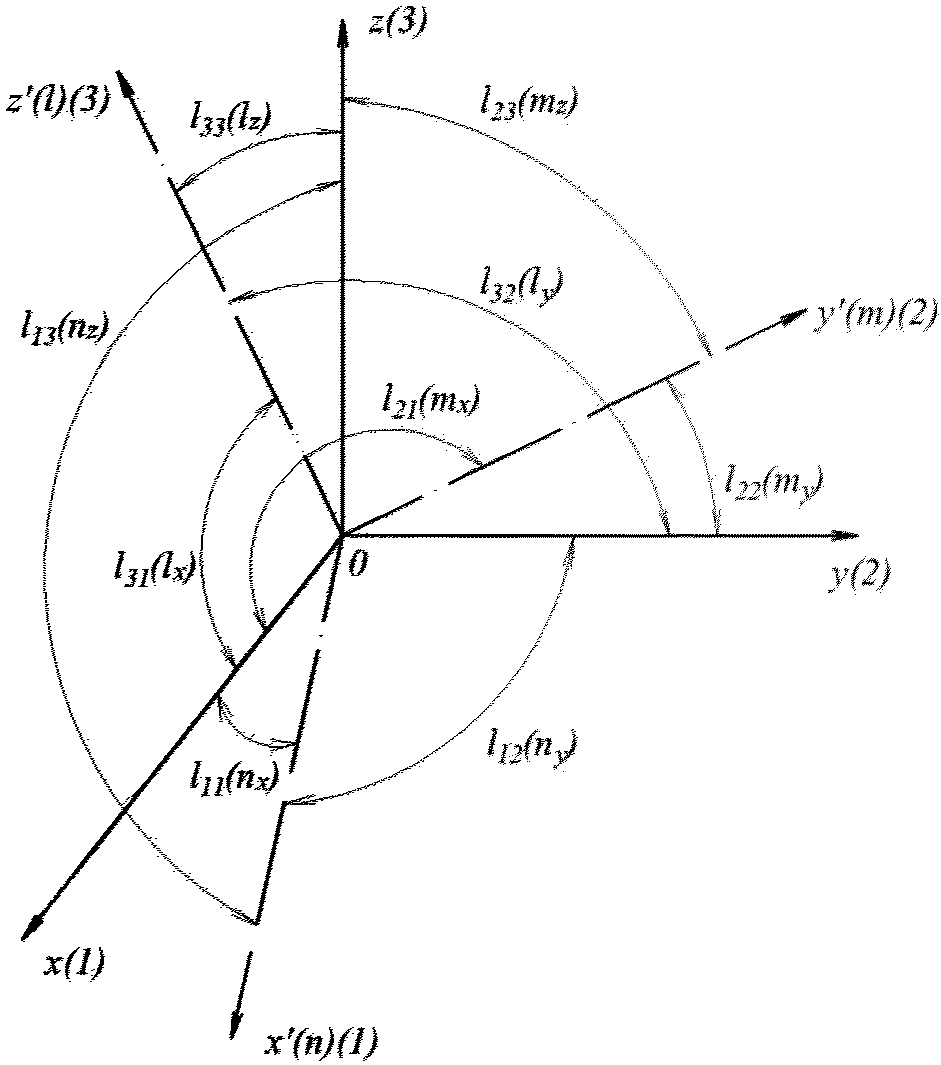
углов поворота осей координат
x | y | z | |
x'(n) | l11(nx) | l12(ny) | l13(nz) |
y'(m) | l21(mx) | l22(my) | l23(mz) |
x'(l) | l31(lx) | l32(ly) | l33(lz) |
lj1 | lj2 | lj3 |
Первый индекс при l обозначает номер новой оси, второй - номер старой оси координат.
Формула (5.14) представляет собой сокращенную запись двойного суммирования, которое производится по повторяющимся индексам i, j = 1, 2, 3. Индексы e, k, стоящие в правой и левой частях формулы, - неповторяющиеся или свободные. Для примера приведем отдельные компоненты тензора  в развернутом виде:
в развернутом виде:
 (5.15)
(5.15)Обратное преобразование от осей x', y', z' к осям x, y, z осуществляется по формуле
Используют также обозначения направляющих косинусов в виде ni, mi, li (таблица 1; i = x, y, z).
Для компонентов тензора деформаций 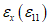 ,
, 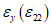 ,
, 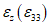 ,
,  ,
, 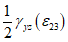 ,
, 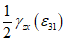 формулы преобразования (5.14) и (5.16) аналогичны при замене в них
формулы преобразования (5.14) и (5.16) аналогичны при замене в них 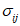 на
на  .
.
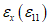 ,
, 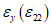 ,
, 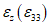 ,
,  ,
, 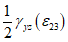 ,
, 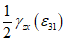 формулы преобразования (5.14) и (5.16) аналогичны при замене в них
формулы преобразования (5.14) и (5.16) аналогичны при замене в них 6 Диаграммы деформирования материалов применительно к моделированию объемного напряженного состояния
Диаграммы деформирования бетона и арматуры - исходная база для построения общих моделей и методов расчета массивных железобетонных конструкций. Начальными являются диаграммы деформирования бетона и арматуры при кратковременном нагружении. Их аналитические зависимости трансформируются на предмет учета деформаций ползучести бетона и влияния повышенных температур в диаграммы изохроны. Условно к разделу диаграмм также относятся нормируемые меры ползучести и усадки бетона.
Аналитические выражения диаграмм подобраны таким образом, что они, в последующих разделах, удобно входят в матрицы жесткости железобетона, представляются как через напряжения так и деформации (исходя из решения задач в напряжениях или деформациях), а также сравнительно просто трансформируются при учете неодноосных напряженных состояний.
Аналитические выражения для диаграмм записаны применительно к расчету конструкций по предельным состояниям второй группы. Если расчет ведется по предельным состояниям первой группы, то во всех формулах характеристики бетона Rb.ser, Rbt.ser и арматуры Rs.ser заменяются на Rb, Rbt, Rs.
6.1.1 Характеристики бетонов
Характеристики бетонов, используемых в расчетах статически неопределимых железобетонных конструкций, приведены в пунктах 6.1.1 - 6.1.12 СП 63.13330.2018. Основными прочностными характеристиками бетона являются нормативные значения сопротивления бетона осевому сжатию Rbn и сопротивление осевому растяжению Rbtn, устанавливаемые с обеспеченностью 0,95. По ним определяются расчетные характеристики бетона сжатию (с индексом b) и растяжению (с индексом bt) по предельным состояниям первой (Rb, Rbt) и второй (Rb.ser, Rbt.ser) групп. Эти характеристики приведены в СП 63.13330.
6.1.2 Виды диаграмм
В расчетах статически неопределимых конструкций используются следующие виды диаграмм деформирования бетона при кратковременном действии нагрузок:
- нормативных - при расчете на кратковременное действие нагрузок;
- расчетных.
Нормативные диаграммы используются для расчета конструкций по предельным состояниям второй группы.
Диаграмма имеет две ветви: одна ветвь относится к сжатию (рисунок 6.1, а), а вторая - к растяжению (рисунок 6.1, б). Напряжения и деформации сжатия принимаются отрицательными, а растяжения - положительными.
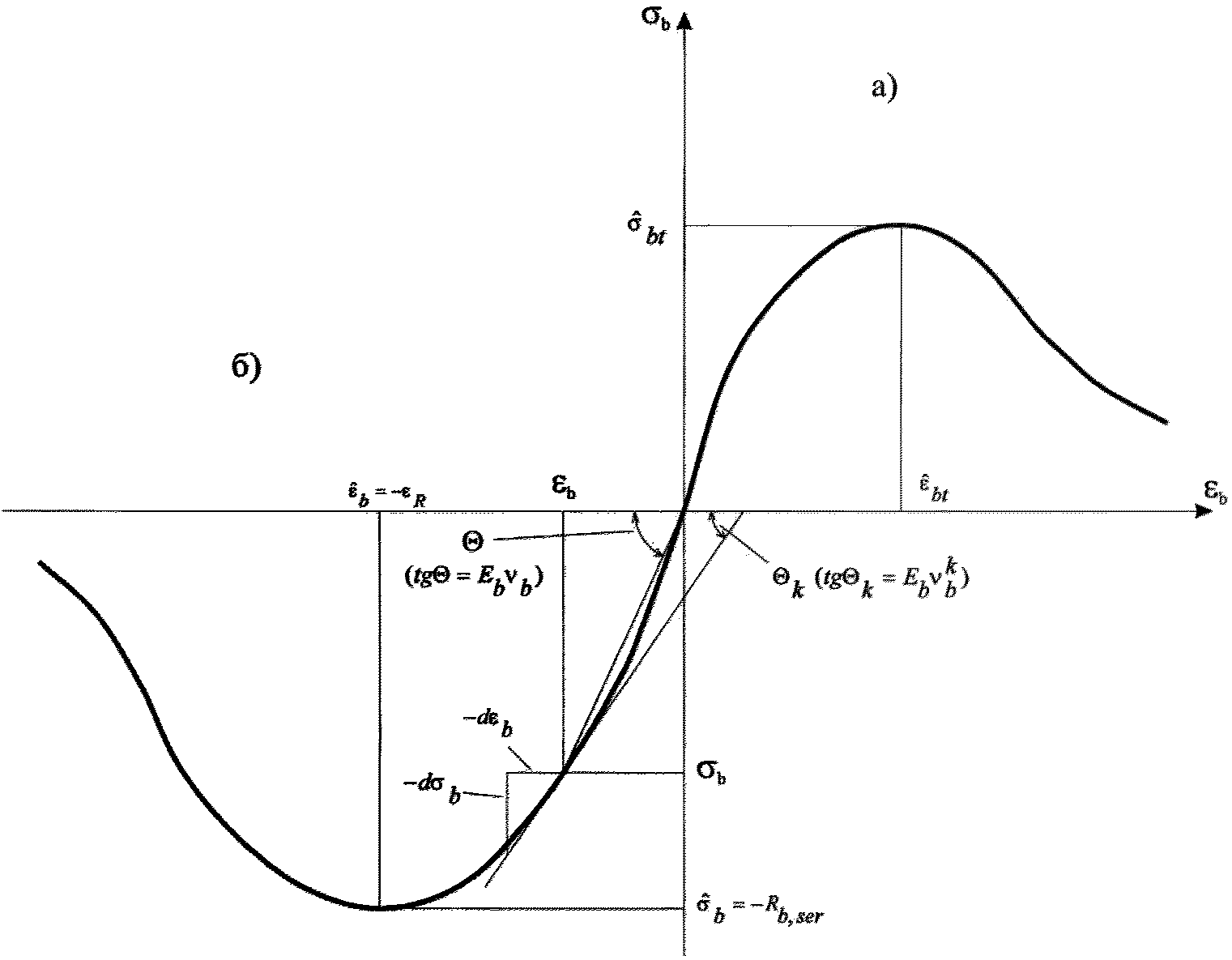
при растяжении (а) и сжатии (б)
Аналитическую зависимость описания диаграммы сжатия бетона  (рисунок 6.1, а) рекомендуется принимать по формуле:
(рисунок 6.1, а) рекомендуется принимать по формуле:
 (рисунок 6.1, а) рекомендуется принимать по формуле:
(рисунок 6.1, а) рекомендуется принимать по формуле:где Eb - начальный модуль упругости бетона (назначается по таблице 6.11 СП 63.13330.2018);
(для восходящей ветви диаграммы применяется знак плюс "+", а нисходящий - минус "-"),
где  - уровень напряжений в бетоне (положительная величина)
- уровень напряжений в бетоне (положительная величина)
 (6.3)
(6.3)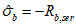 ;
;здесь 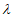 - безразмерный коэффициент, зависящий от вида бетона, принимаемый равным:
- безразмерный коэффициент, зависящий от вида бетона, принимаемый равным:
для тяжелого и мелкозернистого бетона 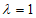 ;
;
для легкого и поризованного бетона средней плотности D (кг/м3) 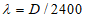 ;
;
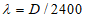 ;
;для ячеистого бетона  ;
;
 ;
;для восходящей ветви диаграммы в зависимости (6.2)
для нисходящей ветви диаграммы в зависимости (6.2)
здесь B* - фиксированный класс бетона, начиная с которого ниспадающая ветвь бетона исключается из расчета (B* = 105 МПа).
При определении значений  для сжатой зоны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов при условии, что ее высота x удовлетворяет условию
для сжатой зоны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов при условии, что ее высота x удовлетворяет условию
значения  допускается определять:
допускается определять:
для восходящей ветви  ,
,
 ,
,для нисходящей ветви  ;
;
 ;
;h0 - полезная высота сечения, если высота сжатой зоны располагается в нижней части сечения h0 заменяется на  .
.
Коэффициент 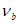 также определяется через уровень деформаций
также определяется через уровень деформаций 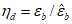 из решения квадратного уравнения
из решения квадратного уравнения
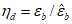 из решения квадратного уравнения
из решения квадратного уравнениягде
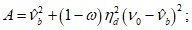
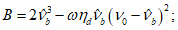
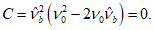
При решении (6.9) перед квадратным корнем принимается знак плюс.
Аналитическую зависимость описания диаграммы растяжения бетона  (рисунок 6.1 б) рекомендуется принимать в виде формул (6.1), (6.2), (6.6) - (6.9), где
(рисунок 6.1 б) рекомендуется принимать в виде формул (6.1), (6.2), (6.6) - (6.9), где 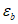 ,
,  ,
,  ,
,  ,
, 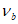 ,
, 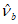 заменяются соответственно на
заменяются соответственно на  ,
,  ,
,  ,
,  ,
, 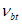 ,
, 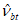
 (рисунок 6.1 б) рекомендуется принимать в виде формул (6.1), (6.2), (6.6) - (6.9), где
(рисунок 6.1 б) рекомендуется принимать в виде формул (6.1), (6.2), (6.6) - (6.9), где ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
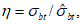 (6.10)
(6.10)где  ,
,  - напряжение и относительные деформации в вершине диаграммы растяжения, для нормативной диаграммы
- напряжение и относительные деформации в вершине диаграммы растяжения, для нормативной диаграммы
ИС МЕГАНОРМ: примечание. Формулы даны в соответствии с официальным текстом документа. |
здесь R0,bt = 2,5 МПа,
здесь hэ = 0,3 м - некоторая эталонная высота сечения,
в остальных случаях  .
.
Коэффициенты 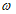 определяются по формулам (6.6), (6.7) с учетом их корректировок при выполнении условия (6.8).
определяются по формулам (6.6), (6.7) с учетом их корректировок при выполнении условия (6.8).
Допускается для изгибаемых элементов из тяжелого бетона значение  определять по зависимости
определять по зависимости
где r/r0t >= 1, r - кривизна элемента; r0t - некоторая эталонная кривизна,
 , R0 = 2 МПа, L = 105 м.
, R0 = 2 МПа, L = 105 м.Как для сжатого, так и для растянутого бетонов нисходящая ветвь при двухзначной эпюре напряжений используется до уровня напряжений  (рисунок 6.1). После этого уровня соответствующий элемент бетона принимается выключенным из работы. Для бетонов класса выше B80 ниспадающая ветвь не учитывается.
(рисунок 6.1). После этого уровня соответствующий элемент бетона принимается выключенным из работы. Для бетонов класса выше B80 ниспадающая ветвь не учитывается.
 (рисунок 6.1). После этого уровня соответствующий элемент бетона принимается выключенным из работы. Для бетонов класса выше B80 ниспадающая ветвь не учитывается.
(рисунок 6.1). После этого уровня соответствующий элемент бетона принимается выключенным из работы. Для бетонов класса выше B80 ниспадающая ветвь не учитывается.За максимальное принимается усилие, которое может быть воспринято сечением с учетом выключения из работы отдельных слоев бетона, деформации которых превышают предельные значения.
6.1.5 Запись диаграмм в конечных приращениях
Эта форма записи диаграмм используется при расчете конструкции путем последовательного шагового нагружения. В этом случае переход от точки i на диаграмме к точке i + 1 осуществляется по хорде 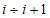 (рисунок 6.2) с использованием зависимости
(рисунок 6.2) с использованием зависимости
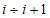 (рисунок 6.2) с использованием зависимости
(рисунок 6.2) с использованием зависимости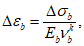 (6.14)
(6.14)где (применительно к рисунку 6.2)
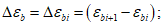
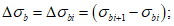
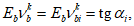
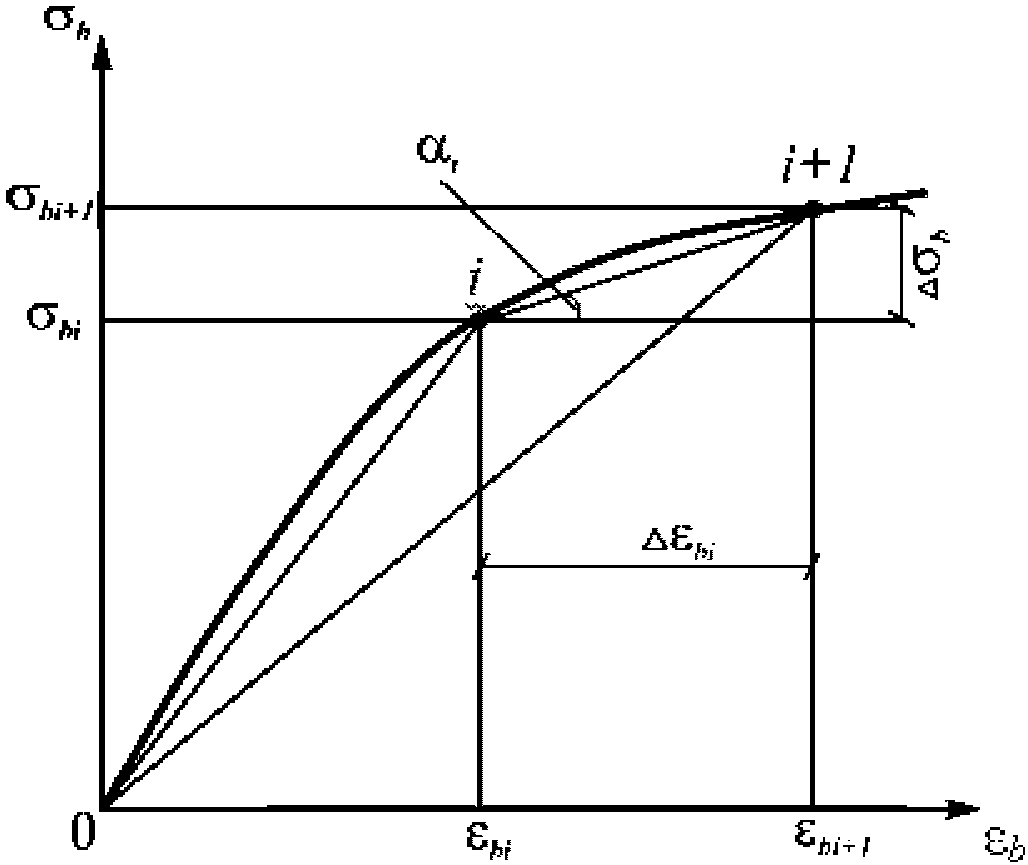
напряжений и приращениями деформаций
При этом коэффициент  (условно касательный коэффициент) может определяться по формулам
(условно касательный коэффициент) может определяться по формулам
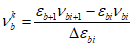 | |
или | |
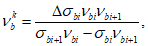 |
где 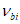 ,
, 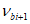 - определяются по формуле (6.2) с учетом п. 6.1.3, 6.1.4 в зависимости от ветви диаграммы (сжатия или растяжения).
- определяются по формуле (6.2) с учетом п. 6.1.3, 6.1.4 в зависимости от ветви диаграммы (сжатия или растяжения).
6.1.6 Расчетные диаграммы деформирования бетона
Расчетные диаграммы бетона формируются по формулам (6.1) - (6.15), где нормативные значения Rb.ser, Rbt.ser заменяются соответственно на расчетные Rb, Rbt.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблицы 6.1.13, 6.1.14 и 6.1.15 в СП 63.13330.2018 отсутствуют. Возможно, имеются в виду таблицы 6.13, 6.14 и 6.15 соответственно. |
Характеристики арматуры, используемые в расчетах статически неопределимых конструкций, приведены в пп. 6.2.1 - 6.2.11 СП 63.13330.2018. Основные прочностные характеристики арматуры - нормативные сопротивления растяжению Rs.n, устанавливаемые с обеспеченностью 0,95. По ним определяются расчетные характеристики арматуры растяжению предельным состояниям по второй группе (Rs.ser) и предельным состояниям первой группы (Rs). Для предельных состояний первой группы дополнительно вводятся расчетные характеристики сжатию Rsc (исходя из возможности выпучивания сжатой арматуры в конструкциях) и расчетные сопротивления Rsw поперечной арматуры (хомутов и отогнутых стержней). Эти характеристики приведены в таблицах 6.1.13, 6.1.14 и 6.1.15 СП 63.13330.2018.
Диаграммы деформирования арматуры  , связывающие относительные деформации
, связывающие относительные деформации  с напряжениями
с напряжениями 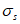 , используют при расчете статически неопределимых конструкций по нелинейной диаграммной модели.
, используют при расчете статически неопределимых конструкций по нелинейной диаграммной модели.
 , связывающие относительные деформации
, связывающие относительные деформации Диаграммы деформирования арматуры разделяются на два вида:
- на рисунке 6.3 а - без физической площадки текучести (согласно СП 63.13330.2018 для арматуры A600 - A1000, Bp500, Bp1200 - 1600, K1400 - 1700);
- на рисунке 6.3 б - с физической площадкой текучести (согласно СП 63.13330.2018 для арматуры A240, A400, A500, B500).

а - арматуры без физической площадки текучести;
б - арматуры с физической площадкой текучести
На диаграммах (рисунок 6.3) выделены следующие характерные точки:
e - точка конца линейного участка диаграммы с напряжениями  и деформациями
и деформациями
a - точка соответствующая нелинейному отрезку диаграммы с напряжением  , которым соответствуют относительные деформации
, которым соответствуют относительные деформации
 (6.17)
(6.17)u - точка, соответствующая разрыву арматуры с напряжениями 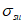 и деформациями
и деформациями 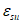 .
.
Кроме этого для диаграммы с площадкой текучести вводятся две дополнительные точки - точка p, соответствующая концу площадки текучести с напряжениями 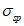 и деформациями
и деформациями  , и промежуточная точка k на ветви упрочнения с напряжениями
, и промежуточная точка k на ветви упрочнения с напряжениями  и относительными деформациями
и относительными деформациями 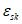 . Напряжения и недостающие относительные деформации в точках определяются по формулам:
. Напряжения и недостающие относительные деформации в точках определяются по формулам:
Коэффициенты  ,
, 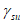 ,
,  , а также относительные деформации
, а также относительные деформации  , соответствующие напряжениям, приведены в таблицах 6.1 и 6.2.
, соответствующие напряжениям, приведены в таблицах 6.1 и 6.2.
Таблица 6.1
Класс арматуры | Номинальный диаметр арматуры, мм | |||
A600 | 10 - 40 | 0,7 | 1,35 | 0,06 |
A800 | 10 - 32 | 0,7 | 1,28 | 0,07 |
A1000 | 10 - 32 | 0,7 | 1,23 | 0,06 |
Bp500 | 3 - 5 | 0,7 | 1,08 | 0,025 |
Bp1200 | 8 | 0,85 | 1,05 | 0,04 |
Bp1300 | 7 | 0,85 | 1,05 | 0,04 |
Bp1400 | 4 - 6 | 0,85 | 1,1 | 0,05 |
Bp1500 | 3 | 0,85 | 1,2 | 0,06 |
Bp1600 | 3 - 5 | 0,85 | 1,2 | 0,06 |
K1400 | 15 | 0,8 | 1,07 | 0,05 |
K1500 | 6 - 18 | 0,8 | 1,07 | 0,05 |
K1600 | 6, 9, 11, 12, 15 | 0,8 | 1,07 | 0,05 |
K1700 | 6 - 9 | 0,8 | 1,07 | 0,05 |
Таблица 6.2
Класс арматуры | Номинальный диаметр арматуры, мм | |||||
A240 | 6 - 40 | 0,97 | 1,01 | 0,015 | 2,0 | 0,19 |
A400 | 6 - 40 | 0,9 | 1,05 | 0,012 | 1,45 | 0,14 |
A500 | 10 - 40 | 0,85 | 1,07 | 0,008 | 1,3 | 0,10 |
B500 | 3 - 16 | 0,8 | 1,04 | 0,005 | 1,1 | 0,03 |
Диаграмма разделяется на два участка: линейный от  до
до 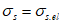 и нелинейный от
и нелинейный от  до
до  .
.
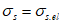 и нелинейный от
и нелинейный от  до
до  .
.Нормативная диаграмма используется при расчете конструкций по предельным состояниям второй группы. При этом
 (6.22)
(6.22)На линейном отрезке (при 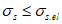 )
)
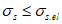 )
)где Es - модуль упругости арматуры.
На нелинейном отрезке (при 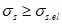 )
)
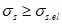 )
)где 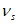 - коэффициент изменения секущего модуля арматуры, определяемый по формуле
- коэффициент изменения секущего модуля арматуры, определяемый по формуле
где 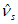 - коэффициент изменения секущего модуля в вершине диаграммы (при
- коэффициент изменения секущего модуля в вершине диаграммы (при 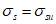 );
);
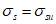 );
);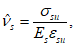 (6.27)
(6.27)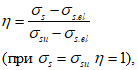 (6.28)
(6.28)
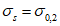 .
.Если оказывается, что вычисленные по формуле (6.29) значения 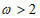 , то зависимость (6.30) становится справедливой только до уровней
, то зависимость (6.30) становится справедливой только до уровней 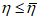 , где
, где
от 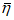 до
до 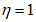 используется линейный участок диаграммы.
используется линейный участок диаграммы.
Коэффициент изменения секущего модуля также может определяться через уровень деформаций 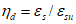 из решения квадратного уравнения
из решения квадратного уравнения
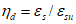 из решения квадратного уравнения
из решения квадратного уравнения(в решении уравнения (6.32) перед квадратным корнем принимается знак плюс).
Линейный участок диаграммы описывается формулой (6.23). В диаграмму включается два нелинейных отрезка (рисунок 6.2 б):
- от точки e (конца линейного участка) до точки p (конца площадки текучести);
- от точки p до точки u (соответствующей разрыву арматуры).
Для описания первого нелинейного отрезка (ep) используются формулы (6.24) - (6.31), где 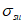 заменяется
заменяется 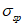 ,
, 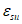 на
на 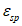 ;
;  определяется по формуле (6.20), а значение
определяется по формуле (6.20), а значение 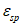 назначается по таблице 6.2.
назначается по таблице 6.2.
Для описания второго нелинейного участка (pku) - участка упрочнения арматуры, также используются формулы (6.24) - (6.32), в которых следует заменить
 (6.33)
(6.33)и принять
Эта диаграмма используется для расчета конструкций по предельным состояниям первой группы. Она описывается зависимостями (6.16) - (6.34), где следует принимать
 (6.35)
(6.35)Относительные деформации  ,
, 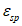 , а также переходные коэффициенты
, а также переходные коэффициенты 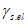 ,
,  ,
,  , приведенные в таблицах 6.1 и 6.2, остаются без изменения. Согласно СП 63.13330 при расчете ответственных конструкций диаграмму без физической площадки текучести разрешается использовать до
, приведенные в таблицах 6.1 и 6.2, остаются без изменения. Согласно СП 63.13330 при расчете ответственных конструкций диаграмму без физической площадки текучести разрешается использовать до  , а для арматуры с физической площадкой текучести
, а для арматуры с физической площадкой текучести  . После этого арматура исключается из расчета.
. После этого арматура исключается из расчета.
 , а для арматуры с физической площадкой текучести
, а для арматуры с физической площадкой текучести  . После этого арматура исключается из расчета.
. После этого арматура исключается из расчета.Напряжения в арматуре, соответствующие 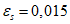 ,
,  , представляются в виде
, представляются в виде 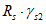 , где
, где  - коэффициент увеличения прочности. При этом разрешается принимать
- коэффициент увеличения прочности. При этом разрешается принимать  .
.
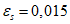 ,
,  , представляются в виде
, представляются в виде  .
.Используются два вида диаграмм. Первая диаграмма связывает напряжения 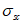 относительными деформациями
относительными деформациями  в трещине, она записывается как для свободной арматуры по указаниям СП 63.13330.
в трещине, она записывается как для свободной арматуры по указаниям СП 63.13330.
Вторая диаграмма связывает напряжения в арматуре в трещине  со средними деформациями
со средними деформациями 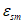 арматуры на участках между трещинами, которые из-за влияния сцепления арматуры с бетоном на участках между трещинами оказываются меньше деформаций
арматуры на участках между трещинами, которые из-за влияния сцепления арматуры с бетоном на участках между трещинами оказываются меньше деформаций  свободной арматуры. Средняя диаграмма имеет два участка. Первый участок (при
свободной арматуры. Средняя диаграмма имеет два участка. Первый участок (при  ) соответствует линейной стадии деформирования арматуры в трещинах. На этом участке
) соответствует линейной стадии деформирования арматуры в трещинах. На этом участке
 ) соответствует линейной стадии деформирования арматуры в трещинах. На этом участке
) соответствует линейной стадии деформирования арматуры в трещинах. На этом участкегде
или
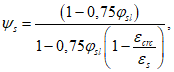 (6.39)
(6.39)где 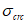 - напряжения в арматуре в трещине в момент трещинообразования (в момент после образования трещины);
- напряжения в арматуре в трещине в момент трещинообразования (в момент после образования трещины);
 - при длительном действии напряжений.
- при длительном действии напряжений.Второй участок диаграммы (при 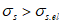 ) представляется в виде
) представляется в виде
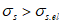 ) представляется в виде
) представляется в виде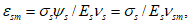 (6.40)
(6.40)где параметр 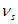 секущего модуля определяется по указаниям СП 63.13330.2018,
секущего модуля определяется по указаниям СП 63.13330.2018,
6.3.2 Связи между конечными приращениями напряжений и относительных деформаций арматуры
Эти связи используются при расчете железобетонных конструкций в приращениях слабоитерационными и безитерационными методами.
При этом используются два вида связей:
- для арматуры в элементах без трещин (рисунок 6.4);
- для арматуры в элементах с трещинами (рисунок 6.5).
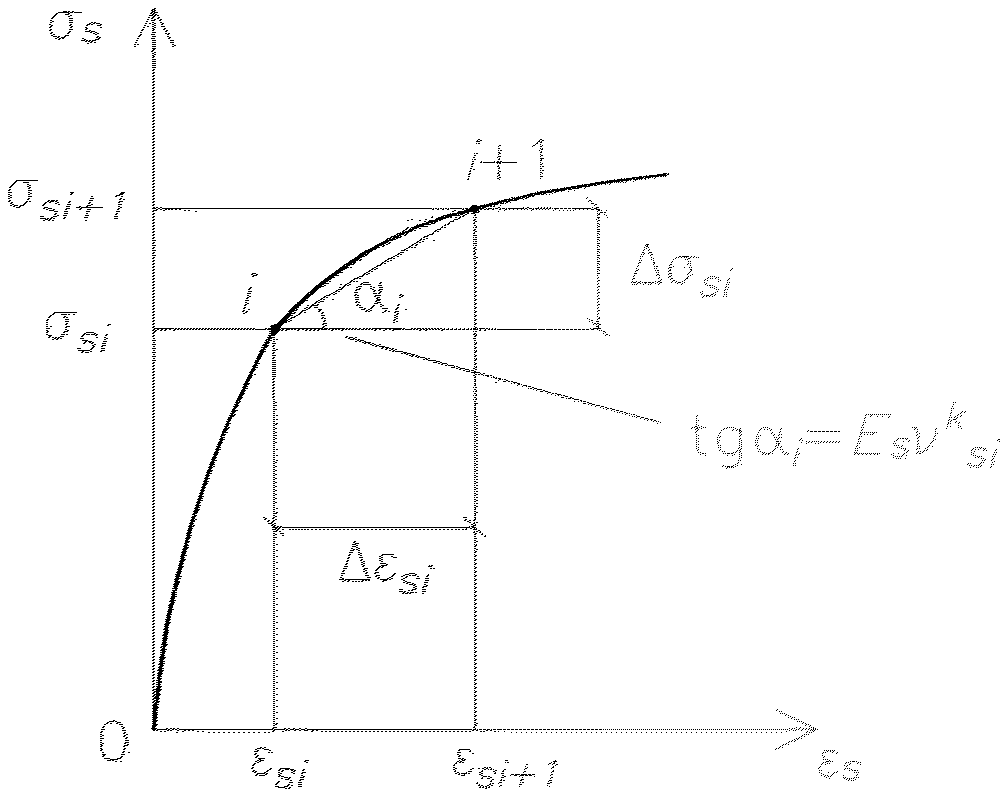
напряжений и относительных деформаций на отрезках 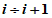
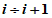
диаграммы арматуры в пластической стадии ее деформирования
в элементах без трещин
напряжений и относительных деформаций на отрезках 
диаграммы арматуры в элементах с трещинами (0-1 - отрезок
диаграммы деформирования арматуры до образования трещины;
1-2 - отрезок средней диаграммы арматуры в элементах
с трещинами)
Для арматуры в элементах без трещин связи между напряжениями и деформациями арматуры описываются диаграммами деформирования свободной арматуры, которые представлены в 6.2.1 - 6.2.4. В этом случае переход от точки i в точку i + 1 на диаграмме (рисунок 6.4) осуществляется по хорде  в виде:
в виде:
 в виде:
в виде:где 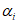 - угол наклона хорды
- угол наклона хорды 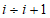 к оси
к оси  ;
;
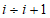 к оси
к оси  (6.44)
(6.44)здесь  ,
, 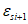 - относительные деформации, соответствующие точкам i и i + 1 на диаграмме;
- относительные деформации, соответствующие точкам i и i + 1 на диаграмме;
Коэффициенты  выражаются через следующие модули диаграммы в начале (в точке i) и в конце (в точке i + 1) шага нагружения по формуле
выражаются через следующие модули диаграммы в начале (в точке i) и в конце (в точке i + 1) шага нагружения по формуле
 (6.45)
(6.45)или
 (6.46)
(6.46)где  ,
, 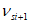 - коэффициенты секущего модуля в точке i и i + 1, определяемые по формулам (6.25). На линейном участке диаграммы
- коэффициенты секущего модуля в точке i и i + 1, определяемые по формулам (6.25). На линейном участке диаграммы  .
.
 .
.Для арматуры в элементах с трещинами используется средняя диаграмма (рисунок 6.5), связывающая напряжения в арматуре в трещинах  с ее средними деформациями
с ее средними деформациями 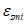 между трещинами, которая описывается формулами (6.36) - (6.41). По аналогии с (6.42), (6.43) зависимости, описывающие переход от точки i к точке i + 1 на средней диаграмме, представляются в виде:
между трещинами, которая описывается формулами (6.36) - (6.41). По аналогии с (6.42), (6.43) зависимости, описывающие переход от точки i к точке i + 1 на средней диаграмме, представляются в виде:
 (6.47)
(6.47) (6.48)
(6.48)где 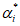 - угол наклона хорды
- угол наклона хорды 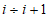 к оси средних относительных деформаций
к оси средних относительных деформаций  ;
;
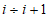 к оси средних относительных деформаций
к оси средних относительных деформаций  (6.49)
(6.49)здесь 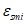 ,
, 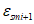 - средние относительные деформации арматуры, соответствующие точкам i и i + 1 на средней диаграмме;
- средние относительные деформации арматуры, соответствующие точкам i и i + 1 на средней диаграмме;
При этом коэффициенты  определяются по формуле
определяются по формуле
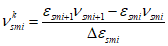 (6.50)
(6.50)или
 (6.51)
(6.51)где  ,
,  - коэффициенты секущего модуля средней диаграммы в точках i и i + 1, определяемые по формулам (6.37), (6.41). На линейном участке диаграммы деформирования арматуры в трещинах
- коэффициенты секущего модуля средней диаграммы в точках i и i + 1, определяемые по формулам (6.37), (6.41). На линейном участке диаграммы деформирования арматуры в трещинах
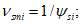
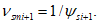 (6.52)
(6.52)Для учета влияния на процесс деформирования элементов длительного действия нагрузок рекомендуется использовать два типа диаграмм-изохрон:
- диаграммы-изохроны 1 на рисунке 6.6, а, соответствующие ступенчатым режимам нагружения (далее такие режимы называются жесткими), когда нагрузка 3 мгновенно прикладывается в возрасте бетона t0 с последующей выдержкой в течение времени t - t0;
- диаграммы-изохроны 2, 3 на рисунке 6.6, б, соответствующие режиму нагружения бетона в возрасте t0 возрастающими напряжениями 4 или деформациями 5 (далее такие режимы называют мягкими), причем скорость роста напряжений или деформаций, в течение времени нагружения остается в среднем близкой к постоянной (например, при учете стадии возведения зданий и сооружений).
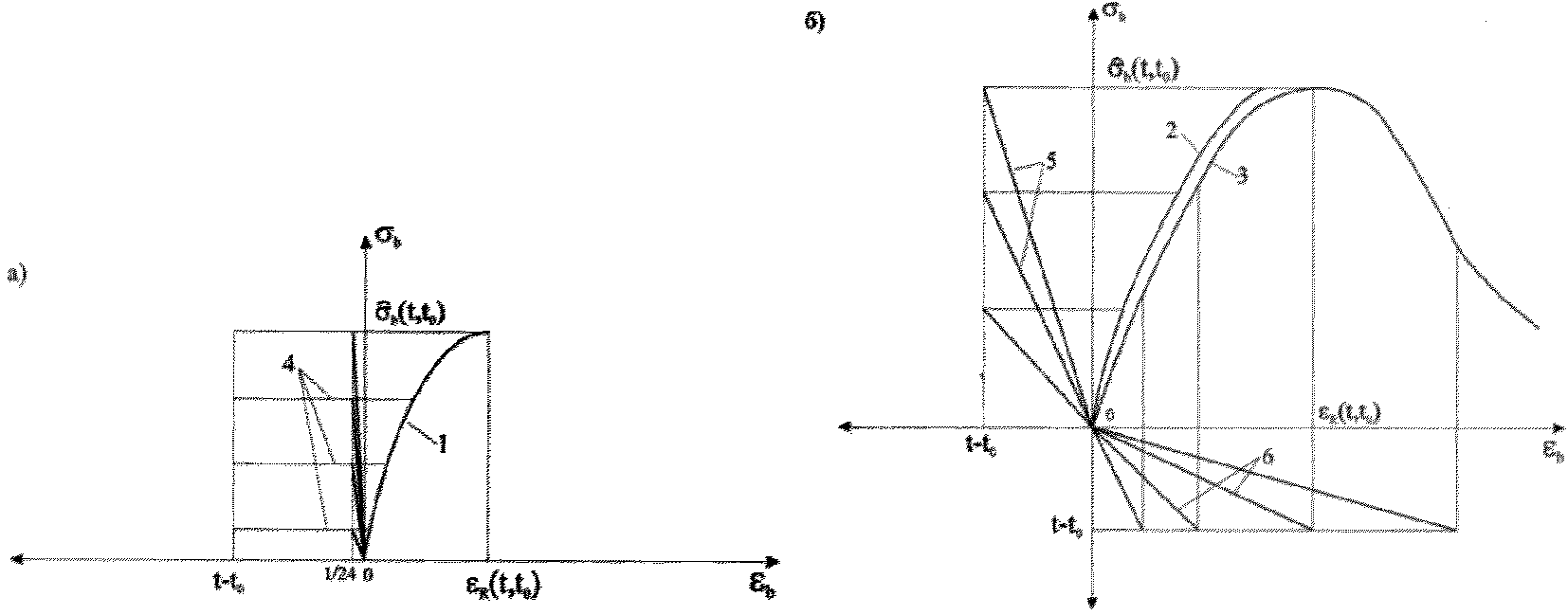
а - жестком, б - мягком режимах нагружения
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Для каждой точки диаграммы-изохроны время натекания деформаций константа и равная времени загружения t - t0. Вершина диаграммы-изохроны имеет координаты 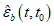 ,
,  . В случае одноосного сжатия
. В случае одноосного сжатия  или Rb(t,t0).
или Rb(t,t0).
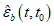 ,
,  . В случае одноосного сжатия
. В случае одноосного сжатия  или Rb(t,t0).
или Rb(t,t0).Аналитическая зависимость для описания диаграмм-изохрон принимается в виде (6.1) - (6.12), где значения величин  ,
,  ,
,  ,
,  ,
, 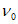 определяют с учетом возраста бетона в момент загружения t0, времени загружения t - t0 и режима нагружения.
определяют с учетом возраста бетона в момент загружения t0, времени загружения t - t0 и режима нагружения.
Параметры аналитической зависимости (6.1) для описания диаграмм-изохрон бетона при жестком режиме нагружения и времени  определяют по формулам (6.2) - (6.13), в которые необходимо вносить следующие изменения:
определяют по формулам (6.2) - (6.13), в которые необходимо вносить следующие изменения:
 определяют по формулам (6.2) - (6.13), в которые необходимо вносить следующие изменения:
определяют по формулам (6.2) - (6.13), в которые необходимо вносить следующие изменения:вместо 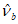 используется значение
используется значение  , определяемое по формуле
, определяемое по формуле
вместо 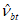 используется значение
используется значение 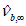 , определяемое по формуле (6.53) при замене
, определяемое по формуле (6.53) при замене 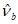 на
на 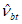 , здесь
, здесь 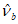 вычисляют по формуле (6.4), а
вычисляют по формуле (6.4), а 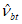 - по формуле (6.12);
- по формуле (6.12);
на восходящей ветви 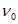 заменяется на
заменяется на 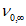 , определяемое по формуле
, определяемое по формуле
fc - функция, учитывающая нелинейность деформаций ползучести, равная
t0 - возраст бетона в момент приложения нагрузки, в сут, причем здесь и далее t0 >= 7 сут - при естественном твердении бетона и t0 >= 28Rbp/Rbn - при твердении с тепловой обработкой, причем Rbp - отпускная (передаточная) прочность бетона после пропаривания; Rbn - проектная прочность бетона.
Обозначение параметра | Значение параметра для класса бетона | |||||||
B12,5 | B15 | B20 | B30 | B40 | B50 | >= B60 | ||
Тяжелый бетон | 3,34 | 3,29 | 3,1 | 2,73 | 2,41 | 1,95 | 1,56 | |
Мелкозернистый бетон | 3,26 | 3,0 | 2,82 | 2,44 | 2,14 | 1,7 | 1,38 | |
2,24 | 1,87 | 1,41 | 0,97 | 0,74 | 0,74 | 0,74 | ||
Обозначение параметра | Значение параметра для модуля открытой поверхности M0, м-1, элемента | ||||
10 и менее | 20 | 30 | 40 и более | ||
0,004 | 0,006 | 0,08 | 0,01 | ||
d | t0 = 7 сут | 0,752 | 0,842 | 0,942 | 1,052 |
t0 >= 28 сут | 0,625 | 0,7 | 0,785 | 0,875 | |
Примечания.
1 Для бетонов классов B12,5 - B50, с осадкой конуса 1 - 2 см или жесткостью 10 - 15 с, значение 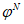 умножают на коэффициент 0,9, при 7 сут < t0 < 28 сут, значение d принимают по линейной интерполяции.
умножают на коэффициент 0,9, при 7 сут < t0 < 28 сут, значение d принимают по линейной интерполяции.
2 Для бетонов, подвергнутых тепловой обработке, значение 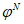 следует умножать на 0,8.
следует умножать на 0,8.
Относительная влажность среды | Коэффициент |
40 и менее | 1,27 |
50 | 1,13 |
60 | 1,00 |
70 | 0,87 |
80 | 0,73 |
90 | 0,60 |
100 | 0,47 |
Модуль открытой поверхности M0, м-1, элемента | Коэффициенты | |
0 | 0,51 | 0,89 |
5 | 0,65 | 0,89 |
10 | 0,76 | 0,89 |
20 | 0,93 | 1,00 |
30 | 1,00 | 1,13 |
40 | 1,22 | 1,27 |
60 и более | 1,27 | 1,27 |
При мягком режиме нагружения следует использовать зависимости (6.53) - (6.56), заменяя в формулах (6.53) - (6.54) 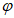 на
на 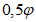 и полагая в формуле (6.55)
и полагая в формуле (6.55)
k = [0,74 + 0,18t0/t2]4. (6.57)
При двухосном сжатии относительное снижение ползучести бетона учитывается заменой в формуле (6.53) параметра  на
на  :
:
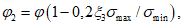 (6.58)
(6.58)Параметры аналитической зависимости (6.1), (6.2) для описания диаграмм-изохрон сжатого бетона в течение времени t - t0 определяют по 6.1.3, подставляя вместо Rb,ser, Eb,  ,
, 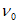 ,
,  ,
,  значения Rb,ser(t,t0), Eb(t,t0),
значения Rb,ser(t,t0), Eb(t,t0),  ,
, 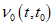 ,
,  ,
, 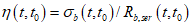 .
.
 ,
, 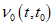 ,
,  ,
, 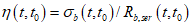 .
.При растяжении учитывают особенности перехода к диаграммам растяжения, указанные в п. 6.1.4, при этом величины Rb,ser(Rb) заменяют на Rbt,ser(Rbt).
Параметры  ,
,  вычисляют по формулам (6.53), (6.54), заменяя
вычисляют по формулам (6.53), (6.54), заменяя  на
на  и подставляя вместо
и подставляя вместо  и fc соответственно значения
и fc соответственно значения  и fc(t,t0), вычисляемые по формулам:
и fc(t,t0), вычисляемые по формулам:
 ,
,  вычисляют по формулам (6.53), (6.54), заменяя
вычисляют по формулам (6.53), (6.54), заменяя  и подставляя вместо
и подставляя вместо  и fc(t,t0), вычисляемые по формулам:
и fc(t,t0), вычисляемые по формулам: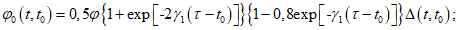
t, t0 - принимают в сутках;
 (6.60)
(6.60)В формуле (6.54) следует принимать 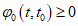 .
.
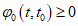 .
.Прочность бетона с учетом возраста, режима и времени его нагружения определяют по формуле
где для мягкого режима нагружения
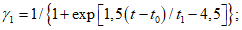 (6.62)
(6.62)t1 = 365{1 - exp(-8·10-4t0)}; (6.63)
для жесткого режима нагружения 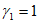 , кроме этого, для момента времени (t - t0) > 365 сут принимают t - t0 = 365 сут.
, кроме этого, для момента времени (t - t0) > 365 сут принимают t - t0 = 365 сут.
Значение Rb,ser(t0) равно Rb,ser, определяемому для заданного возраста бетона t0 в момент начала загружения. Если характеристики прочности бетона заданы в возрасте 28 сут, то Rb,ser(t0) вычисляют по формуле (6.69) с учетом условий внешней среды.
Значение коэффициента  в формуле (6.61) принимают: при условиях эксплуатации конструкций, благоприятных для нарастания прочности бетона (под водой, во влажном грунте или при влажности окружающей среды выше 75%)
в формуле (6.61) принимают: при условиях эксплуатации конструкций, благоприятных для нарастания прочности бетона (под водой, во влажном грунте или при влажности окружающей среды выше 75%)
 (6.64)
(6.64)в остальных случаях
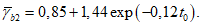 (6.65)
(6.65)Для ячеистого бетона принимают  .
.
 .
.Начальный модуль упругости бетона с учетом возраста и времени нагружения определяют по формуле
где Rbn(t) = max[Rb,ser(t0); Rb,ser(t,t0)] - большее из двух значений, указанных в скобках; значение Rb,ser(t,t0) определяют по формуле (6.61); при расчете конструкций по предельным состояниям первой группы структура формулы (6.66) не изменяется (допускается вместо Rb,ser(t0), Rb,ser(t,t0) вводить средние значения сопротивлений бетона, тогда в знаменателе 14 МПа заменяется на 18 МПа). При тепловой обработке значение Eb(t,t0), вычисляемое по формуле (6.66), снижается на 10%.
При описании ниспадающей ветви полной диаграммы бетона в формуле (6.7) при определении  значение
значение  заменяется на
заменяется на  .
.
 .
.Деформации ползучести могут определяться на основании нелинейных теорий ползучести с использованием мер ползучести. При этом общие деформации суммируются из кратковременных и длительных (деформаций ползучести). В частном случае общие деформации сжатого или растянутого бетонного призматического элемента в момент времени t, нагруженного в момент t0 постоянными напряжениями  , определяются по формуле
, определяются по формуле
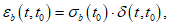 (6.67)
(6.67)где
где Eb(t0) - модуль упругости (определяют по формуле (6.66) при t = t0);
C(t,t0) - линейные деформации ползучести при действии постоянного единичного напряжения - линейная составляющая меры ползучести;
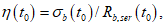
где Rb,ser(t0) определяется с учетом влияния внешней среды по формуле
где B - класс бетона в возрасте 28 сут;
Rb,ser(28) - определяется по СП 63.13330.2018 как Rb,ser.
При внешней среде, благоприятной для нарастания прочности бетона (согласно 6.4.3), формула (6.68) справедлива для t0 >= 7 сут. В противном случае в формуле (6.68) принимают 7 <= t0 <= 28 сут.
Значения линейной меры ползучести бетона к моменту времени t, загруженного в момент времени t0, принимают в виде
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 (6.70)
(6.70)где  - предельное значение меры ползучести,
- предельное значение меры ползучести,
 - предельное значение меры ползучести,
- предельное значение меры ползучести,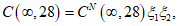 (6.71)
(6.71)
где c = 0,5, коэффициенты d и  принимают по таблице 6.4;
принимают по таблице 6.4;
f(t - t0) - функция, учитывающая развитие деформаций ползучести во времени:
 (6.72)
(6.72)Предельное значение меры ползучести  бетона, загруженного в возрасте t0 = 28 сут и твердеющего в естественных условиях при влажности окружающей среды W = 60%, принимают по таблице 6.7, а значение коэффициентов
бетона, загруженного в возрасте t0 = 28 сут и твердеющего в естественных условиях при влажности окружающей среды W = 60%, принимают по таблице 6.7, а значение коэффициентов 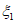 и
и  , учитывающих влияние размеров поперечного сечения и влажность среды, по таблицам 6.5 и 6.6.
, учитывающих влияние размеров поперечного сечения и влажность среды, по таблицам 6.5 и 6.6.
 бетона, загруженного в возрасте t0 = 28 сут и твердеющего в естественных условиях при влажности окружающей среды W = 60%, принимают по таблице 6.7, а значение коэффициентов
бетона, загруженного в возрасте t0 = 28 сут и твердеющего в естественных условиях при влажности окружающей среды W = 60%, принимают по таблице 6.7, а значение коэффициентов Вид бетона |  , МПа, для бетона класса , МПа, для бетона класса | ||||||
B12,5 | B15 | B20 | B30 | B40 | B50 | >= B60 | |
Обычный тяжелый и мелкозернистый на кварцевом песке | 163 | 143 | 115 | 84 | 67 | 50 <*> | 39 <**> |
Примечания. 1 Для бетонов B12,5 - B50, с осадкой конуса 1 - 2 см или жесткостью бетонной смеси 15 - 10 с, значения 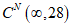 следует умножать на коэффициент 0,9. следует умножать на коэффициент 0,9.2 Для бетонов, изготовленных на шлакопортландцементе, значения  надо умножать на 1,15; для бетонов, изготовленных на пуццолановом портландцементе, - на 1,35; для бетонов, изготовленных на крупном заполнителе из известняка, - на 0,85. надо умножать на 1,15; для бетонов, изготовленных на пуццолановом портландцементе, - на 1,35; для бетонов, изготовленных на крупном заполнителе из известняка, - на 0,85.3 Для бетонов, подвергнутых тепловой обработке, значения Eb(t) и 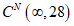 следует умножать на коэффициент 0,9. следует умножать на коэффициент 0,9. | |||||||
Предельное значение усадки тяжелого бетона при окончании его хранения в момент времени tW определяют по выражению
 (6.73)
(6.73)принимая значения 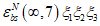 по таблице 6.8.
по таблице 6.8.
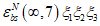 по таблице 6.8.
по таблице 6.8.Характеристики | Значения для класса обычного тяжелого бетона | |||||||||||
B12,5 | B15 | B20 | B30 | B40 | B50 | B60 | ||||||
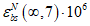 | 350 | 350 | 400 | 400 | 400 | 400 | 400 | |||||
Для возраста бетона в момент окончания влажного хранения tW, сут | ||||||||||||
7 и менее | 28 | 60 | 90 | 180 | 360 и более | |||||||
1 | 0,95 | 0,93 | 0,92 | 0,91 | 0,90 | |||||||
При относительной влажности и среды W, % | ||||||||||||
40 и менее | 50 | 60 | 70 | 80 | 90 | |||||||
1,29 | 1,14 | 1 | 0,87 | 0,73 | 0,56 | |||||||
Модуль открытой поверхности образца M0, м-1 | ||||||||||||
0 | 5 | 10 | 20 | 40 | 60 | 80 и более | ||||||
0,22 | 0,65 | 0,83 | 0,95 | 1,09 | 1,13 | 1,15 | ||||||
0,004 | 0,004 | 0,004 | 0,008 | 0,016 | 0,025 | 0,033 | ||||||
Примечания. 1 Для бетонных смесей, с осадкой конуса 1 - 2 см или жесткостью 15 - 40 с, значения  , приведенные в таблице, умножают на коэффициент 0,85. , приведенные в таблице, умножают на коэффициент 0,85.2 Для конструкций, эксплуатируемых на открытом воздухе в районах, относящихся к IV климатической зоне, указанные в настоящей таблице значения 3 Для мелкозернистого бетона значения  , приведенные в настоящей таблице, умножают на коэффициент 1,6. , приведенные в настоящей таблице, умножают на коэффициент 1,6.4 Для бетонных смесей с пластифицирующими добавками значения  , приведенные в настоящей таблице, умножают на коэффициент 1,15. , приведенные в настоящей таблице, умножают на коэффициент 1,15. | ||||||||||||
Значения деформаций усадки бетона к моменту t определяют по формуле
 (6.74)
(6.74)где 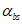 принимают по таблице 6.8.
принимают по таблице 6.8.
7 Определение прочности бетонных элементов при различных объемных напряженных состояниях. Условия образования трещин по различным схемам
7.1.1 Прочность бетонных элементов массивных конструкций, работающих в условиях трехосных напряженных состояний, должна оцениваться на основании условия прочности бетонов.
Условие прочности должно согласовываться с результатами экспериментальных исследований при различных напряжениях бетона и соответствовать требованиям 4.5. Компонентам напряжений в бетоне присваиваются индексы "b" по типу 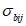 . Положительными считаются растягивающие напряжения. В координатах главных напряжений
. Положительными считаются растягивающие напряжения. В координатах главных напряжений  ,
, 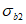 ,
, 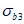 в бетоне критерий прочности представляется поверхностью общего вида, которая является разомкнутой в области всестороннего равномерного сжатия (рисунок 7.1, а) для плотных бетонов и замкнутой для пористых (рисунок 7.2, б). Построение поверхности прочности (рисунок 7.1, а - в) удобно осуществлять в цилиндрических координатах нормального
в бетоне критерий прочности представляется поверхностью общего вида, которая является разомкнутой в области всестороннего равномерного сжатия (рисунок 7.1, а) для плотных бетонов и замкнутой для пористых (рисунок 7.2, б). Построение поверхности прочности (рисунок 7.1, а - в) удобно осуществлять в цилиндрических координатах нормального 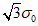 и касательного
и касательного 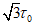 октаэдрических напряжений и угла вида напряженного состояния (или параметра Лоде-Надаи
октаэдрических напряжений и угла вида напряженного состояния (или параметра Лоде-Надаи 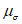 согласно 5.2).
согласно 5.2).
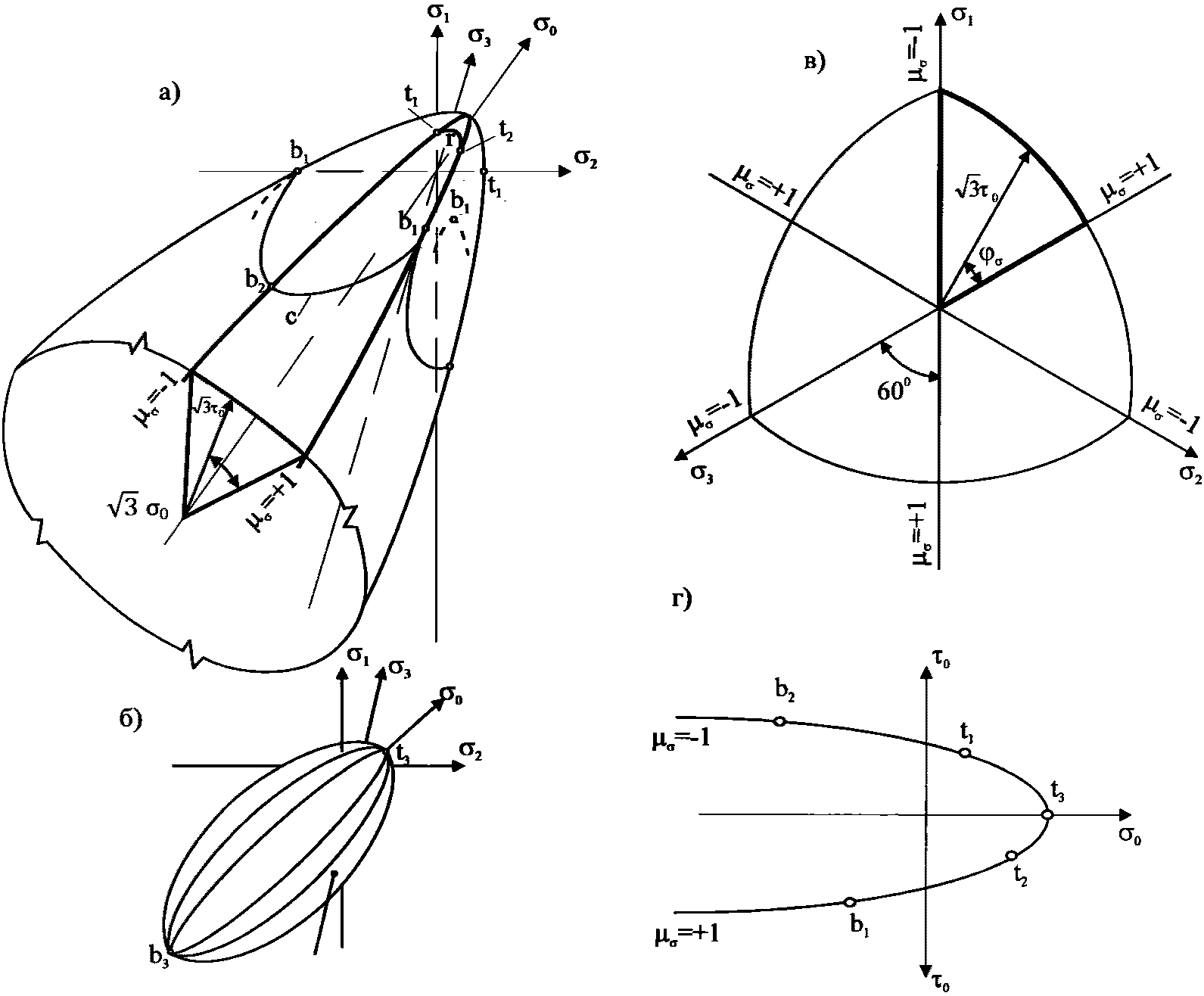
Поверхность прочности состоит из шести одинаковых частей (лепестков), которые располагаются между сечениями  и
и 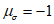 . Каждому
. Каждому  соответствует своя меридиональная линия (рисунок 7.1, а, г). На линии
соответствует своя меридиональная линия (рисунок 7.1, а, г). На линии 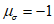 находятся точки одноосного растяжения t1 и двухосного равномерного сжатия b2, а на линии
находятся точки одноосного растяжения t1 и двухосного равномерного сжатия b2, а на линии 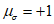 - двухосного равномерного растяжения t2 и одноосного сжатия b2. Кроме этого на рисунке 7.1, а, б, г приведены: t3 - точка, соответствующая трехосному равномерному растяжению; b3 - точка соответствующая трехосному равномерному сжатию; r - линия, соответствующая двухосному растяжению; C - линия, соответствующая двухосному сжатию. Формы девиаторных кривых (рисунок 7.2) зависят от вида бетона и изменяются в различных областях напряженных состояний (неравномерного растяжения, смешанных, неравномерного сжатия).
- двухосного равномерного растяжения t2 и одноосного сжатия b2. Кроме этого на рисунке 7.1, а, б, г приведены: t3 - точка, соответствующая трехосному равномерному растяжению; b3 - точка соответствующая трехосному равномерному сжатию; r - линия, соответствующая двухосному растяжению; C - линия, соответствующая двухосному сжатию. Формы девиаторных кривых (рисунок 7.2) зависят от вида бетона и изменяются в различных областях напряженных состояний (неравномерного растяжения, смешанных, неравномерного сжатия).
 и
и 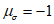 . Каждому
. Каждому 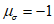 находятся точки одноосного растяжения t1 и двухосного равномерного сжатия b2, а на линии
находятся точки одноосного растяжения t1 и двухосного равномерного сжатия b2, а на линии 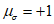 - двухосного равномерного растяжения t2 и одноосного сжатия b2. Кроме этого на рисунке 7.1, а, б, г приведены: t3 - точка, соответствующая трехосному равномерному растяжению; b3 - точка соответствующая трехосному равномерному сжатию; r - линия, соответствующая двухосному растяжению; C - линия, соответствующая двухосному сжатию. Формы девиаторных кривых (рисунок 7.2) зависят от вида бетона и изменяются в различных областях напряженных состояний (неравномерного растяжения, смешанных, неравномерного сжатия).
- двухосного равномерного растяжения t2 и одноосного сжатия b2. Кроме этого на рисунке 7.1, а, б, г приведены: t3 - точка, соответствующая трехосному равномерному растяжению; b3 - точка соответствующая трехосному равномерному сжатию; r - линия, соответствующая двухосному растяжению; C - линия, соответствующая двухосному сжатию. Формы девиаторных кривых (рисунок 7.2) зависят от вида бетона и изменяются в различных областях напряженных состояний (неравномерного растяжения, смешанных, неравномерного сжатия).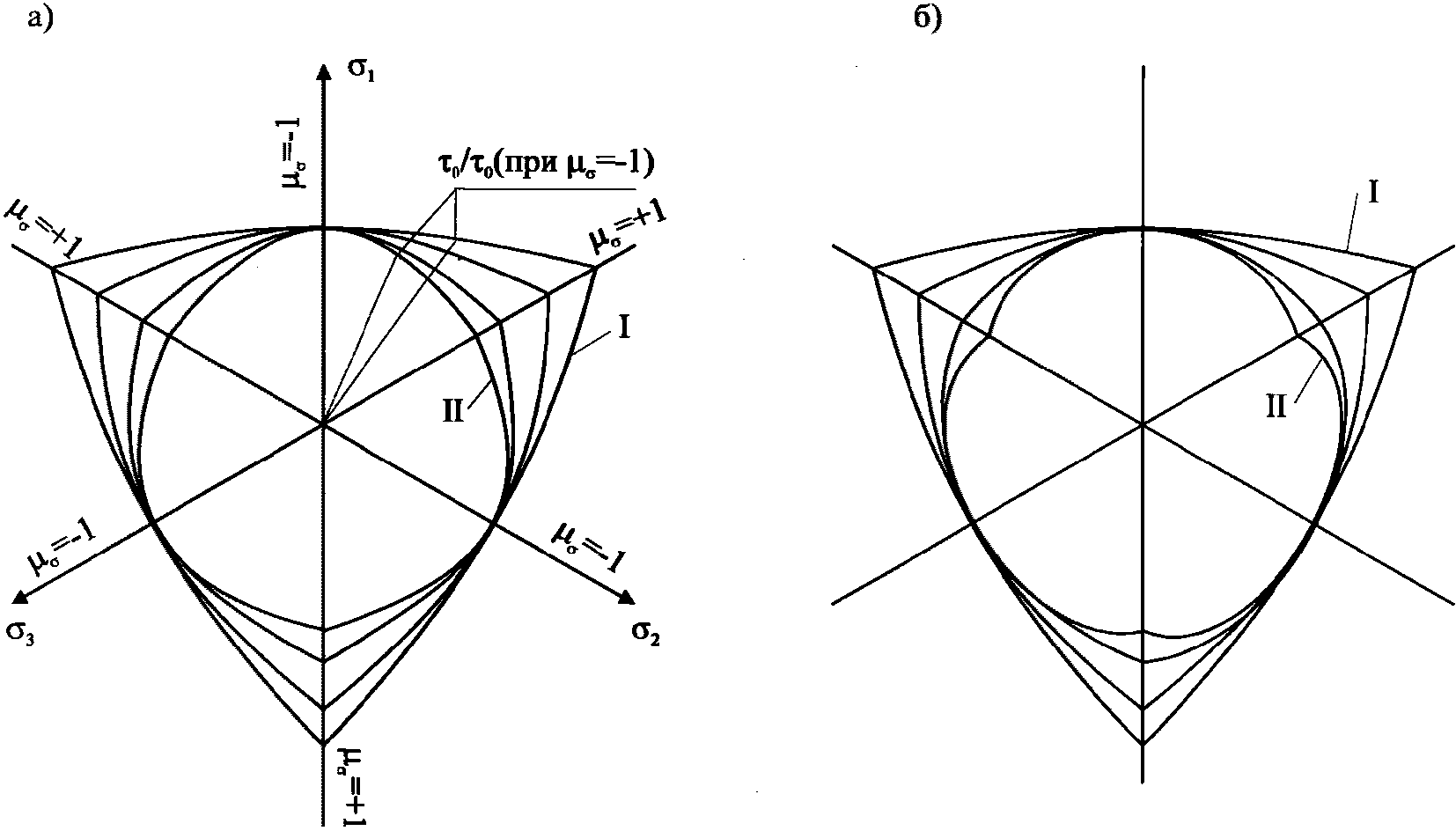
и их изменение при изменении напряженных состояний
(от неравномерного растяжения - I до высоких уровней
неравномерного сжатия - II); а) - для высокопрочного
бетона (Rb = 50 МПа), б) - для низкопрочного бетона
(Rb = 10 МПа)
Прочность бетонных элементов считается обеспеченной при выполнении условия прочности, записанного в виде неравенства
при  (7.2)
(7.2)
 (7.2)
(7.2)7.1.2 Коэффициентом 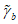 в условии (7.1) учитывается влияние вида напряженного состояния (по параметру
в условии (7.1) учитывается влияние вида напряженного состояния (по параметру 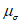 Лоде-Надаи) на изменение прочности бетона в области трехосного или двухосного (плоского) сжатия (при
Лоде-Надаи) на изменение прочности бетона в области трехосного или двухосного (плоского) сжатия (при 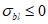 ). Этот коэффициент определяют по формуле
). Этот коэффициент определяют по формуле
 (7.3)
(7.3)где

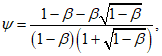 (7.4)
(7.4)Rbn, Rbtn - вычисляют по таблице 6.7 СП 63.13330.2018 (Rbn = Rb,ser, Rbtn = Rbt,ser).
Коэффициент  устанавливают на основании обработки экспериментальных исследований при плоском сжатии. В этом случае он характеризует влияние среднего напряжения
устанавливают на основании обработки экспериментальных исследований при плоском сжатии. В этом случае он характеризует влияние среднего напряжения 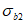 на увеличение прочности бетона при двухосном сжатии (на увеличение предельного значения
на увеличение прочности бетона при двухосном сжатии (на увеличение предельного значения  по модулю; в случае двухосного сжатия
по модулю; в случае двухосного сжатия  ).
).
 ).
).7.1.3 Коэффициент  в условии (7.1) учитывает влияние вида напряженного состояния на изменение прочности бетона в области всестороннего трехосного или двухосного (плоского) растяжения (при
в условии (7.1) учитывает влияние вида напряженного состояния на изменение прочности бетона в области всестороннего трехосного или двухосного (плоского) растяжения (при  ). Этот коэффициент определяют по формуле
). Этот коэффициент определяют по формуле
 ). Этот коэффициент определяют по формуле
). Этот коэффициент определяют по формулегде
 (7.7)
(7.7)p - коэффициент, влияющий на характер изменения прочности в области двуосного растяжения (p = (-1) - (2); в расчетах следует принимать p = 0);
Коэффициенты f и n зависят от вида бетона и принимаются по таблице 7.1; f <= 1; при f = 1 поверхность прочности разомкнута в области трехосного равномерного сжатия (рисунок 7.1 а), а в случае f > 1 - замкнута (рисунок 7.1 б);
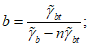 a = nb. (7.9)
a = nb. (7.9)Вид бетона | Значение коэффициента | |
f | n | |
Тяжелый бетон | 1,0 | 1,0 |
Мелкозернистый бетон | 1,05 | -3,0 |
Шлакопемзобетон | 1,1 | 0,7 |
Бетон на зольном гравии | 1,1 | 1,0 |
Керамзитобетон | 1,1 | 1,2 |
На значения параметра a накладывается ограничение
которое, однако, при рекомендуемых параметрах удовлетворяется автоматически.
7.1.4 Условие прочности (7.1) может быть представлено в ином виде - в зависимости от октаэдрического касательного напряжения в бетоне 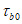 , среднего напряжения
, среднего напряжения 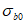 и параметра Лоде-Надаи по напряжениям
и параметра Лоде-Надаи по напряжениям  ,
,
Параметры 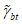 ,
, 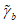 , a, b, f,
, a, b, f,  вычисляют по 7.2, 7.3. При этом формулу (7.8) для параметра
вычисляют по 7.2, 7.3. При этом формулу (7.8) для параметра 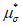 , входящего в формулу (7.5) по определению
, входящего в формулу (7.5) по определению 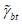 , удобно использовать в виде:
, удобно использовать в виде:
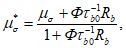 (7.12)
(7.12)где
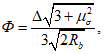 (7.13)
(7.13)здесь  - см. 7.1.3.
- см. 7.1.3.
Зависимость (7.11) в виде равенства равна нулю (= 0) удобно использовать при анализе геометрии рекомендуемой поверхности прочности, которая заключает внутри себя области безопасных напряженных состояний (выход за поверхность прочности приводит к разрушению). Фиксируя  , строят меридиональные кривые (функции
, строят меридиональные кривые (функции  ,
,  - образующие поверхности прочности, рисунок 7.1 г); фиксируя
- образующие поверхности прочности, рисунок 7.1 г); фиксируя  - строят девиаторные кривые (функции
- строят девиаторные кривые (функции 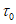 ,
,  - направляющие поверхности прочности, рисунок 7.1 в). Соблюдение условия (7.10) обеспечивает выпуклость поверхности (7.11).
- направляющие поверхности прочности, рисунок 7.1 в). Соблюдение условия (7.10) обеспечивает выпуклость поверхности (7.11).
7.2.1 Основной для оценки прочности - критерий (7.1), однако, в ряде случае удобно использовать коэффициенты запаса прочности, которые устанавливают на основе критерия (7.1). Коэффициентом запаса прочности элемента конструкции называют величину 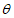 , на которую следует умножать соответствующие расчетной нагрузке напряжения
, на которую следует умножать соответствующие расчетной нагрузке напряжения 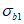 ,
, 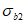 ,
,  в элементе (или некоторые из напряжений
в элементе (или некоторые из напряжений 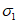 ,
, 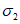 ,
, 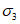 (в зависимости от режима нагружения), чтобы таким образом увеличенные напряжения
(в зависимости от режима нагружения), чтобы таким образом увеличенные напряжения  ,
,  ,
, 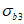 (они обозначаются
(они обозначаются  ,
,  ,
,  ) удовлетворяли условию (7.1) в виде равенства нулю. Напряжения
) удовлетворяли условию (7.1) в виде равенства нулю. Напряжения  ,
, 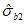 ,
, 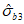 называют предельными.
называют предельными.
Вместо  при определении деформаций используют уровень напряжений
при определении деформаций используют уровень напряжений  , где
, где
 (7.14)
(7.14)Значение  вычисляют по 7.2.2. Прочность элемента обеспечена, если
вычисляют по 7.2.2. Прочность элемента обеспечена, если
в других случаях элемент считается разрушенным.
7.2.2 В случае простого нагружения, когда все напряжения увеличиваются пропорционально одному параметру (в нашем случае в качестве такого параметра используется уровень 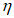 ),
),
В случае одностороннего догружения главным напряжением  , когда
, когда
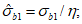
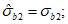
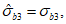 (7.18)
(7.18)но так, чтобы
 (7.19)
(7.19)Коэффициент 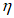 находят из решения квадратного уравнения
находят из решения квадратного уравнения
или непосредственно определяют  из решения квадратного уравнения (7.1) при известных значениях
из решения квадратного уравнения (7.1) при известных значениях  и
и  , а затем уже вычисляют
, а затем уже вычисляют 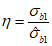 . Указанными способами вычислять
. Указанными способами вычислять 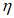 рекомендуется при
рекомендуется при  .
.
 и
и  , а затем уже вычисляют
, а затем уже вычисляют 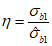 . Указанными способами вычислять
. Указанными способами вычислять  .
.В случае одностороннего догружения напряжениями  , когда
, когда


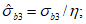 (7.21)
(7.21) (7.22)
(7.22)коэффициент  находят из решения квадратного уравнения
находят из решения квадратного уравнения
или непосредственно определяют  из решения квадратного уравнения (7.1) при известных значениях
из решения квадратного уравнения (7.1) при известных значениях  ;
; 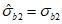 , а затем уже вычисляют
, а затем уже вычисляют  . Указанными способами рекомендуется вычислять
. Указанными способами рекомендуется вычислять 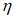 при
при  .
.
 ;
; 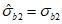 , а затем уже вычисляют
, а затем уже вычисляют  . Указанными способами рекомендуется вычислять
. Указанными способами рекомендуется вычислять  .
.Различают случай трехосного неравномерного сжатия  и случай смешанных напряжений (
и случай смешанных напряжений ( ,
, 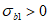 ). Если режим возможного догружения конструкции неизвестен, то в случае смешанных напряжений
). Если режим возможного догружения конструкции неизвестен, то в случае смешанных напряжений  вычисляют дважды - из решения уравнений (7.17) и (7.20) и из двух значений выбирают большее. В случае трехосного сжатия используют уравнение (7.23), которое приводит к большему значению
вычисляют дважды - из решения уравнений (7.17) и (7.20) и из двух значений выбирают большее. В случае трехосного сжатия используют уравнение (7.23), которое приводит к большему значению  .
.
 и случай смешанных напряжений (
и случай смешанных напряжений ( ,
, 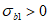 ). Если режим возможного догружения конструкции неизвестен, то в случае смешанных напряжений
). Если режим возможного догружения конструкции неизвестен, то в случае смешанных напряжений 7.3.1 Если прочностные характеристики бетона известны в возрасте t0 = 28 сут (Rb = Rb(28), Rbt = Rbt(28)), а бетон нагружается в более позднем возрасте t0, то вместо величин Rb(28) и Rbt(28) вводят в условие (7.1) и формулу (7.6) величины Rb(t0), Rbt(t0), соответствующие действительному возрасту t0 и определяемые по формуле (6.69).
7.3.2 При учете длительности действия напряжений в условии (7.1) и формуле (7.6) величины Rb и Rbt заменяют соответственно на величины Rb(t,t0), Rbt(t,t0), определяемые по формуле (6.61).
7.3.3 При учете других факторов величины Rb и Rbt вводятся в условие (7.1) после умножения на коэффициенты условия работы 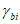 (i = 1, 3, 5), принимаемые по пункту 6.1.12 СП 63.13330.2018.
(i = 1, 3, 5), принимаемые по пункту 6.1.12 СП 63.13330.2018.
7.4.1 Различают четыре схемы исчерпания прочности бетонных элементов (рисунок 7.3) при нарушении условия (7.1) и его преобразований (7.17), (7.20) и (7.23):
0 - схемы разрушения элемента по всему объему вследствие трехосного, двухосного или одноосного сжатия;
1 - образование трещин, плоскость которых ортогональна направлению главного напряжения 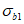 ;
;
2 - образование двух взаимно перпендикулярных трещин, плоскости которых ортогональны направлениям главных напряжений  и
и  ;
;
3 - образование трех взаимно ортогональных трещин.
Эти схемы реализуются при следующих комбинациях напряжений:
 ,
,  - схема 0;
- схема 0;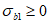 ,
,  ,
, 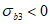 - схема 0, 1;
- схема 0, 1; ,
, 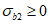 ,
, 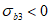 - схема 0, 1, 2;
- схема 0, 1, 2;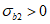 ,
,  - схема 1, 2, 3.
- схема 1, 2, 3.
Для схемы 0 возможны две ситуации:
- происходит полное разрушение бетона и элемент полностью выключается из работы;
- напряжения в элементе начинают уменьшаться при работе его на ниспадающей ветви диаграмм 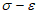 и разрушение носит постепенный характер.
и разрушение носит постепенный характер.
Для схем 1 и 2 допускается возможность полагать лишь образование трещин и учитывать сопротивление бетона по направлениям главных напряжений 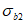 и
и 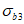 .
.
Для схемы 3 при появлении трех взаимно ортогональных трещин бетон элемента полностью выключается из работы (за исключением некоторых сил зацепления).
Все ситуации должны быть рассмотрены в процессе деформационных расчетов конструкции с разрушенными элементами и должен быть решен вопрос о потере прочности конструкции в целом при соответствующем распределении усилий между отдельными элементами или частями конструкции.
7.5.1 Главные относительные деформации бетона в момент исчерпания прочности бетона называют предельными. Эти деформации при кратковременном действии напряжений определяют по формулам:
где если 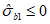 (случай трехосного сжатия), то
(случай трехосного сжатия), то
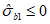 (случай трехосного сжатия), то
(случай трехосного сжатия), то (7.26)
(7.26)(ek = 12, 13, 23),
здесь  ,
,  - соответственно коэффициент изменения секущего модуля и относительные деформации в вершине диаграммы одноосного сжатия:
- соответственно коэффициент изменения секущего модуля и относительные деформации в вершине диаграммы одноосного сжатия:  ,
, 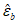 определяют по формуле (6.5);
определяют по формуле (6.5);
 ,
,  (7.27)
(7.27) ;
; ;
;s = 1 для тяжелого бетона, s = 2 для мелкозернистого.
7.5.2 Если  (область смешанных напряжений и всестороннего растяжения), то предварительно выполняется сортировка напряжений
(область смешанных напряжений и всестороннего растяжения), то предварительно выполняется сортировка напряжений  (e = 1, 2, 3) на положительные
(e = 1, 2, 3) на положительные 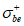 и отрицательные
и отрицательные  напряжения (например, если
напряжения (например, если 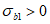 , то
, то  ,
,  ; если
; если  , то
, то  ,
, 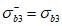 ), затем определяются соответствующие им величины
), затем определяются соответствующие им величины
 (область смешанных напряжений и всестороннего растяжения), то предварительно выполняется сортировка напряжений
(область смешанных напряжений и всестороннего растяжения), то предварительно выполняется сортировка напряжений 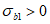 , то
, то  ,
,  ; если
; если  , то
, то  ,
, 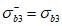 ), затем определяются соответствующие им величины
), затем определяются соответствующие им величины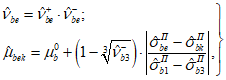 (7.28)
(7.28)(ek = 13, 23, 12);
здесь величины  ,
,  ,
,  - меньше или равны единице,
- меньше или равны единице,

причем 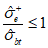 ;
;  вычисляют по формуле (6.11);
вычисляют по формуле (6.11);  - прочность бетона в вершине диаграммы одноосного сжатия
- прочность бетона в вершине диаграммы одноосного сжатия 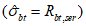 ; если
; если 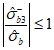 , то
, то
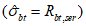 ; если
; если 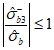 , то
, то7.5.3 Если 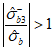 , то
, то  вычисляют по формуле (7.25),
вычисляют по формуле (7.25),  или
или 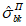 (e, k = 1, 2, 3,
(e, k = 1, 2, 3,  ) - приведенные главные напряжения, причем
) - приведенные главные напряжения, причем  ; если
; если 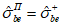 (напряжения положительны);
(напряжения положительны); 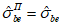 , если
, если 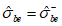 (напряжения отрицательны);
(напряжения отрицательны); 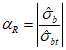 .
.
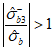 , то
, то  ; если
; если 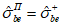 (напряжения положительны);
(напряжения положительны); 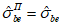 , если
, если 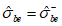 (напряжения отрицательны);
(напряжения отрицательны); 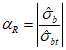 .
.8 Связи между напряжениями и деформациями (физические соотношения) для бетонных элементов при объемном напряженном состоянии
8.1.1 Исходные физические соотношения для бетонных элементов записывают в виде: связей между главными напряжениями и главными относительными деформациями (первый вид записи, согласно 8.2, 8.5); связей между приращениями главных напряжений и деформаций (второй вид записи, согласно 8.3, 8.5). В этих соотношениях учитывается физическая нелинейность (коэффициенты жесткости или податливости зависят от напряжений или деформаций) и приобретаемая в процессе деформирования ортотропия. Ортотропия обусловлена возникновением и направленным развитием микротрещин (в основном вдоль площадок максимальных растягивающих и минимальных по модулю сжимающих главных напряжений) в процессе увеличения напряжений, а также различными диаграммами деформирования бетона при сжатии и растяжении.
При длительном приложении напряжений учитывается ползучесть на основе использования диаграмм-изохрон. Соотношения, учитывающие ползучесть приведены в 8.5.
8.1.2 Вводимые в физические соотношения главные напряжения в бетоне ( ,
, 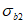 ,
,  ), как и при рассмотрении условий прочности полагаются расположенными в последовательности:
), как и при рассмотрении условий прочности полагаются расположенными в последовательности:  . Если при этом направлении главные напряжения
. Если при этом направлении главные напряжения 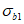 ,
,  ,
, 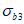 в процессе нагружения не меняются, то такие напряжения называются главными с фиксированными направлениями. Положительные - напряжения растяжения. Отдаленность (или близость) главных напряжений к их предельным значениям, характеризующим начало разрушения бетонного элемента, оцениваются согласно указаниям пункта 7.2 по уровню напряжений
в процессе нагружения не меняются, то такие напряжения называются главными с фиксированными направлениями. Положительные - напряжения растяжения. Отдаленность (или близость) главных напряжений к их предельным значениям, характеризующим начало разрушения бетонного элемента, оцениваются согласно указаниям пункта 7.2 по уровню напряжений  .
.
 . Если при этом направлении главные напряжения
. Если при этом направлении главные напряжения Модули деформации физических соотношений зависят от уровня  и программы (режима) нагружения.
и программы (режима) нагружения.
8.1.3 Под простой нагрузкой (разгрузкой) подразумевают нагрузку (разгрузку), в результате которой все три главных напряжения с фиксированными направлениями увеличиваются (уменьшаются) пропорционально одному параметру. В случае, если главные напряжения остаются фиксированными, но при этом их значения изменяются не пропорционально одному параметру, однако так, что уровень 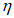 возрастает, то такое нагружение называют активным (при убывании уровня получают случай активной разгрузки). Остальные случаи нагрузки (разгрузки) относятся к сложным.
возрастает, то такое нагружение называют активным (при убывании уровня получают случай активной разгрузки). Остальные случаи нагрузки (разгрузки) относятся к сложным.
8.1.4 Сформированные для каждого элемента физические соотношения в локальных осях n, m, l главных напряжений затем переводятся в глобальную (общую для всей конструкции) систему координат по 8.6.
Связи между приращениями напряжений и деформаций представлены в двух видах:
- между конечными приращениями главных напряжений и деформаций;
- между малыми приращениями (дифференциалами) главных напряжений и деформаций.
8.2.1 Главные относительные деформации в физических соотношениях обозначают:  ,
, 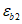 ,
,  ,
,  ,
, 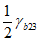 ,
, 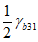 , а главные напряжения:
, а главные напряжения: 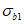 ,
,  ,
,  ,
,  ,
,  ,
, 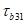 . Они образуют два вектор-столбца:
. Они образуют два вектор-столбца:
где T - знак транспонирования.
Касательные компоненты напряжений и деформаций - симметричны (т.е.  ,
, 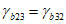 ,
, 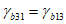 ,
,  ,
, 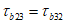 ,
,  ). Кроме этого в осях главных напряжений и деформаций все касательные компоненты равны нулю. Однако они остаются в приведенных ниже выражениях с целью использования стандартных матричных преобразований при переводе физических соотношений из локальной системы координат в глобальную (п. 8.6).
). Кроме этого в осях главных напряжений и деформаций все касательные компоненты равны нулю. Однако они остаются в приведенных ниже выражениях с целью использования стандартных матричных преобразований при переводе физических соотношений из локальной системы координат в глобальную (п. 8.6).
 ,
, 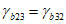 ,
, 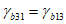 ,
,  ,
, 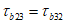 ,
,  ). Кроме этого в осях главных напряжений и деформаций все касательные компоненты равны нулю. Однако они остаются в приведенных ниже выражениях с целью использования стандартных матричных преобразований при переводе физических соотношений из локальной системы координат в глобальную (п. 8.6).
). Кроме этого в осях главных напряжений и деформаций все касательные компоненты равны нулю. Однако они остаются в приведенных ниже выражениях с целью использования стандартных матричных преобразований при переводе физических соотношений из локальной системы координат в глобальную (п. 8.6).Связи между полными напряжениями и деформациями в случае простой и активной нагрузок представляются в виде
где [Cb]n - матрица податливости бетона.
Матрица податливости бетона определяется:
здесь и ниже из двух знаков выбирается знак плюс (знак минус вводится при учете деформирования элемента на нисходящей ветви, т.е. после выхода напряжений на поверхность прочности);
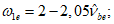
 (8.5)
(8.5)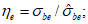
здесь значения  вычисляют по п. 7.5 (на восходящей ветке
вычисляют по п. 7.5 (на восходящей ветке  , где
, где 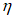 указаны в п. 7.2). Остальные значения, входящие в формулу (8.4), конкретизируются ниже в зависимости от области напряженного состояния;
указаны в п. 7.2). Остальные значения, входящие в формулу (8.4), конкретизируются ниже в зависимости от области напряженного состояния;
(ek = 12, 23, 13),
(ek = 12, 23, 13).
8.2.2 Область напряжений 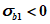 (случай трехосного сжатия)
(случай трехосного сжатия)
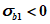 (случай трехосного сжатия)
(случай трехосного сжатия)Принимают
 (8.8)
(8.8)где коэффициент 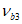 вычисляют по формуле (8.4), полагая
вычисляют по формуле (8.4), полагая
здесь 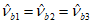 определяют по указаниям пункта 7.5;
определяют по указаниям пункта 7.5;
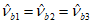 определяют по указаниям пункта 7.5;
определяют по указаниям пункта 7.5; - на нисходящей; на восходящей ветви
- на нисходящей; на восходящей ветвиR1, R2 - импирические величины
на нисходящей ветви c = 0;
Коэффициенты  (e = 1, 2, 3) вычисляют по формуле (8.4), полагая
(e = 1, 2, 3) вычисляют по формуле (8.4), полагая 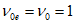 на восходящей ветви и
на восходящей ветви и  - на нисходящей и назначая
- на нисходящей и назначая  по п. 7.5.
по п. 7.5.
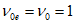 на восходящей ветви и
на восходящей ветви и  - на нисходящей и назначая
- на нисходящей и назначая Коэффициент  вычисляют по формуле (8.4), заменяя в ней
вычисляют по формуле (8.4), заменяя в ней  на
на  ;
; 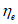 на
на 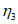 ;
; 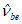 на
на 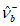 , значения
, значения  указаны в п. 7.5 и полагая
указаны в п. 7.5 и полагая 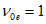 на восходящей ветви и
на восходящей ветви и  - на нисходящей (при
- на нисходящей (при  в случае трехосного растяжения эти вычисления можно не выполнять, принимая
в случае трехосного растяжения эти вычисления можно не выполнять, принимая 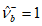 ).
).
 - на нисходящей (при
- на нисходящей (при  в случае трехосного растяжения эти вычисления можно не выполнять, принимая
в случае трехосного растяжения эти вычисления можно не выполнять, принимая Если история активной нагрузки заранее не известна, то она может заменяться последовательным рассмотрением простых нагрузок на шагах. При этом на каждом шаге нагрузки фиксируют главные напряжения  (e = 1, 2, 3), принимают их как компоненты простого нагружения для данного шага и переходят к формированию матрицы податливости бетона (8.3) по представленным выше указаниям и формулам.
(e = 1, 2, 3), принимают их как компоненты простого нагружения для данного шага и переходят к формированию матрицы податливости бетона (8.3) по представленным выше указаниям и формулам.
8.3.1 Пусть теперь простая или активная нагрузка в некоторой точке A (при напряжениях  и относительных деформациях
и относительных деформациях  ) сменяется простой или активной разгрузкой;
) сменяется простой или активной разгрузкой;  ,
,  - текущие (на шагах) напряжения и деформации на ветви разгрузки.
- текущие (на шагах) напряжения и деформации на ветви разгрузки.
Приращения напряжений и деформаций, отсчитываемые от точки A - конечные (в принципе любые, в отличие от бесконечно малых); эти приращения составляют:
Физические соотношения на ветви разгрузки записываются в приращениях:
где  - вектор-столбец приращений деформаций
- вектор-столбец приращений деформаций
 (8.14)
(8.14)вектор-столбец приращений напряжений
Коэффициенты  (e = 1, 2, 3), входящие в матрицу (8.16), вычисляют двояким способом. При первом способе
(e = 1, 2, 3), входящие в матрицу (8.16), вычисляют двояким способом. При первом способе
где  - коэффициенты, вычисляемые по текущим (на шагах) напряжениям
- коэффициенты, вычисляемые по текущим (на шагах) напряжениям  как при простой нагрузке;
как при простой нагрузке;
Во втором способе коэффициенты 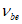 вычисляют по формуле (8.4), полагая в ней
вычисляют по формуле (8.4), полагая в ней
и заменяя  на
на  ;
;
 ;
;8.3.2 Повторная нагрузка
Если в процессе разгрузки переходят из области напряженного состояния  в область
в область 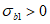 и наоборот, то начало перехода в другую область относится к началу нагрузки в этой области.
и наоборот, то начало перехода в другую область относится к началу нагрузки в этой области.
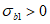 и наоборот, то начало перехода в другую область относится к началу нагрузки в этой области.
и наоборот, то начало перехода в другую область относится к началу нагрузки в этой области.Теперь пусть разгрузка в одной области напряжений следует до точки B, а затем начинается повторная нагрузка. В точке B фиксируются значения величины 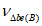 , вычисляемые по формуле (8.17) или (8.18), в которых коэффициент 0,2 заменяется на 0,25. Физические соотношения записываются в виде (8.13), где приращения напряжений и деформаций вычисляются по формулам (8.12) после замены в этих формулах индекса A на индекс B. Матрицу податливости
, вычисляемые по формуле (8.17) или (8.18), в которых коэффициент 0,2 заменяется на 0,25. Физические соотношения записываются в виде (8.13), где приращения напряжений и деформаций вычисляются по формулам (8.12) после замены в этих формулах индекса A на индекс B. Матрицу податливости 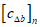 представляют в виде (8.16), заменяя
представляют в виде (8.16), заменяя 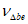 на
на  . Эти соотношения используют до тех пор, пока текущие уровни
. Эти соотношения используют до тех пор, пока текущие уровни 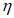 не достигнут величины
не достигнут величины 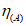 - уровня напряжений, соответствующего началу разгрузки в точке A. После этого переходят к определению деформаций по первоначальным соотношениям (8.2) - (8.11).
- уровня напряжений, соответствующего началу разгрузки в точке A. После этого переходят к определению деформаций по первоначальным соотношениям (8.2) - (8.11).
8.4.1 В практических расчетах не всегда удобно одновременно использовать деформационные (типа (8.2)) и инкрементальные (типа (8.13)) формулировки физических соотношений, а встает задача приведения соотношений к единому виду. Это приведение следует осуществлять по указанным ниже правилам. Пусть на линии нагружения, изображенной в координатах главных напряжений 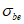 (e = 1, 2, 3), намечены три точки 0, 1, 2 и записаны соотношения с индексами (p-s) = (1-0), (2-1), (2-0), в виде
(e = 1, 2, 3), намечены три точки 0, 1, 2 и записаны соотношения с индексами (p-s) = (1-0), (2-1), (2-0), в виде
где вторые индексы s = 0, 1, 0 в круглых скобках указывают на точку, от которой отсчитываются приращения напряжений и деформаций, а также значения секущих модулей, а первые p = 1, 2, 2 - на точку, для которой устанавливаются связи между таким образом найденными приращениями напряжений и деформаций. Если точка 0 помещена в начало координат, то, естественно, приращения на участках (1-0) и (2-0) переходят в общие величины напряжений и деформаций для точек 1, 2 и лишь на участке (2-1) они выступают как приращения.
Вектор-столбец приращений напряжений и относительных деформаций на участке (p-s),
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
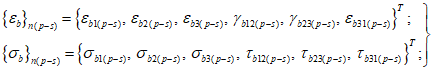 (8.20)
(8.20) - матрица податливости бетона на приращениях напряжений и деформаций на участке (p-s)
- матрица податливости бетона на приращениях напряжений и деформаций на участке (p-s)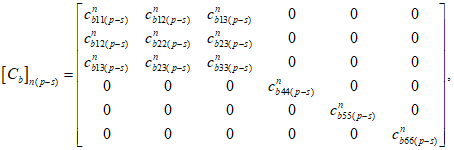 (8.21)
(8.21)(ke = 11, 12, 13, 22, 23, 33),
Формулы (8.22) связывают коэффициенты податливости на трех участках деформирования (1-0), (2-1) и (2-0). Значения податливостей на двух участках ((1-0), (2-0) - на ветви нагрузки и (1-0), (2-1) - в случае, если в точке 1 нагрузка сменяется разгрузкой) вычисляют по п. 8.2, 8.3, а на третьем участке их находят, используя соотношения (8.22).
Например, на указанном выше пути нагружения 0-A-B с разгрузкой (которой является одним из вариантов пути нагружения 0-1-2) коэффициенты cke(A-0) вычисляют по п. 8.2, коэффициенты cke(B-A) - по п. 8.3, коэффициенты cke(B-0) находят, используя соотношения (8.22), (8.23). Внося коэффициенты cke(B-0) в матрицу (8.3), можно на ветви разгрузки (если она является частичной) вместо соотношений (8.19), записанных в конечных приращениях, использовать деформационные соотношения (8.2). И, наоборот, путь нагружения до точки A можно пройти, используя вместо (8.2) соотношение (8.19) на отрезке типа 2-1, при этом на отрезках (1-0) и (2-0) жесткости cke вычисляются по формулам (8.4) - (8.11), а на отрезке 2-1 они находятся из соотношений (8.22) или (8.23).
Записывая физические соотношения относительно небольших конечных приращений, можно, с некоторым приближением, использовать эти соотношения и для описания сложного нагружения при изменении нумерации и ориентации осей главных напряжений.
8.5.1 Деформации ползучести учитываются на основе приведенных в п. 6.4.1 - 6.4.3 диаграмм-изохрон с учетом указанных в настоящем пункте дополнительных особенностей "натекания" таких деформаций в условиях длительного трехосного напряжения. Изохронами описываются жесткие режимы ступенчатого нагружения, когда напряжения  ,
, 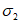 ,
, 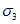 прикладываются в возрасте t0 в течение непродолжительного периода времени (одного часа), а затем выдерживаются в течение времени t-t0 практически постоянными (допускаемое изменение напряжений в течение t-t0 составляет 10%).
прикладываются в возрасте t0 в течение непродолжительного периода времени (одного часа), а затем выдерживаются в течение времени t-t0 практически постоянными (допускаемое изменение напряжений в течение t-t0 составляет 10%).
Физические соотношения представляются формулами (8.1) - (8.10), (7.24) - (7.29) и п. 7.5 и 8.2.1, в которые вносят следующие изменения:
- функции напряжений, а также константы, входящие в формулы п. 7.5 и 8.2.1 за исключением констант 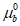 , R1, R2 (они не изменяются), становятся зависимыми еще и от времени действия напряжений (t-t0) и возраста бетона t0 к моменту приложения напряжений, что сказывается формально на их обозначениях, например,
, R1, R2 (они не изменяются), становятся зависимыми еще и от времени действия напряжений (t-t0) и возраста бетона t0 к моменту приложения напряжений, что сказывается формально на их обозначениях, например, 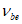 ,
, 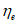 ,
, 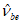 ,
, 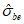 (e = 1, 2, 3),
(e = 1, 2, 3),  ,
, 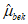 ,
,  (ek = 12, 23, 13),
(ek = 12, 23, 13), 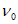 ,
,  ,
,  , Rb,ser, Rbt,ser, Eb и др. заменяются соответственно на
, Rb,ser, Rbt,ser, Eb и др. заменяются соответственно на  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , Rb,ser(t,t0), Rbt,ser(t,t0), Eb(t,t0) и т.д.;
, Rb,ser(t,t0), Rbt,ser(t,t0), Eb(t,t0) и т.д.;
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , Rb,ser(t,t0), Rbt,ser(t,t0), Eb(t,t0) и т.д.;
, Rb,ser(t,t0), Rbt,ser(t,t0), Eb(t,t0) и т.д.; (8.24)
(8.24)допускается заменять  на
на 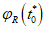 , где
, где
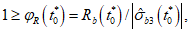 (8.25)
(8.25)( ;
;  в области смешанных напряжений сжатия-растяжения и трехосного растяжения; здесь и ниже
в области смешанных напряжений сжатия-растяжения и трехосного растяжения; здесь и ниже 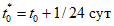 ); предельные напряжения
); предельные напряжения 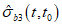 - вычисляют по п. 7.3;
- вычисляют по п. 7.3; 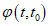 - определяется формулой (6.59));
- определяется формулой (6.59));
 ;
;  в области смешанных напряжений сжатия-растяжения и трехосного растяжения; здесь и ниже
в области смешанных напряжений сжатия-растяжения и трехосного растяжения; здесь и ниже 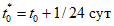 ); предельные напряжения
); предельные напряжения 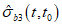 - вычисляют по п. 7.3;
- вычисляют по п. 7.3; 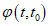 - определяется формулой (6.59));
- определяется формулой (6.59));- функции 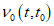 ,
, 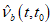 ,
, 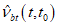 , Rb,ser(t,t0), Eb(t,t0) вычисляют по пп. 6.4.1 - 6.4.3, заменяя в формулах (6.55) и (6.59) коэффициент k на
, Rb,ser(t,t0), Eb(t,t0) вычисляют по пп. 6.4.1 - 6.4.3, заменяя в формулах (6.55) и (6.59) коэффициент k на 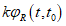 (допускается заменять k на
(допускается заменять k на 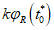 );
);
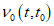 ,
, 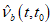 ,
, 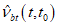 , Rb,ser(t,t0), Eb(t,t0) вычисляют по пп. 6.4.1 - 6.4.3, заменяя в формулах (6.55) и (6.59) коэффициент k на
, Rb,ser(t,t0), Eb(t,t0) вычисляют по пп. 6.4.1 - 6.4.3, заменяя в формулах (6.55) и (6.59) коэффициент k на 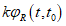 (допускается заменять k на
(допускается заменять k на 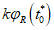 );
);- коэффициент c в формуле (8.9), который теперь может обозначаться c(t,t0), на восходящей ветви определяют по формуле
 (8.26)
(8.26)здесь s вычисляют по формуле (8.10).
На нисходящей ветви c(t,t0) = 0.
Физические соотношения (8.2), (8.13), (8.19) для бетона записаны в локальных осях координат n, m, l в виде связей относительных деформаций (или их конечных приращений) с напряжениями (или их приращениями) через матрицу податливости. Прежде чем использовать эти соотношения в зависимостях метода конечных элементов, выполняют две операции:
- операция обращения соотношений к виду, связывающему наоборот напряжения с деформациями через матрицу жесткости и
- операция перевода полученных соотношений из локальных осей координат n, m, l (или 1, 2, 3, или x', y', z', как они еще иначе обозначены в п. 5.5) в глобальную (общую для всей конструкции) систему x, y, z. В некоторых случаях физические соотношения используют в виде (8.2) и выполняют лишь одну процедуру перевода этих соотношений в глобальную систему координат x, y, z.
В результате операции обращения соотношений (8.2) получают
где
 (8.28)
(8.28)здесь [db]n - матрица жесткости.
Преобразованные к координатам x, y, z соотношения (8.3) и (8.27) соответственно записываются
 (8.29)
(8.29)где 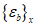 ,
,  - вектор-столбцы соответственно относительных деформаций и напряжений в осях координат
- вектор-столбцы соответственно относительных деформаций и напряжений в осях координат
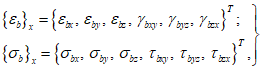 (8.30)
(8.30){Cb}x - матрица податливости материала размером 6 x 6 с элементами cbji = cbij в координатах x, y, z (i, j = 1, 2, 3, 4, 5, 6); здесь и далее первый индекс - номер строки в матрице, второй - номер столбца, на пересечении которых расположен конкретный элемент;
 - матрица жесткости материала размером 6 x 6 с элементами dbij = dbji
- матрица жесткости материала размером 6 x 6 с элементами dbij = dbji Между вектор-столбцами напряжений и деформаций в осях n, m, l и x, y, z имеются связи:
где T - знак транспонирования матрицы,
Направляющие косинусы lij фиксируются согласно таблице 5.1; преобразования (8.31) и (8.32) устанавливаются по п. 5.5. В этом случае компоненты 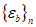 и
и  не образуют симметричный тензор, поскольку касательные компоненты
не образуют симметричный тензор, поскольку касательные компоненты 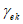 применяются без коэффициента
применяются без коэффициента  , поэтому их преобразования сводятся к формулам (8.32). Если коэффициент
, поэтому их преобразования сводятся к формулам (8.32). Если коэффициент 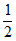 , если
, если  вводится, тогда компоненты деформаций преобразовываются по формулам типа (8.31). При этом
вводится, тогда компоненты деформаций преобразовываются по формулам типа (8.31). При этом  заменяется на
заменяется на 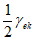 .
.
Несимметричные компоненты  ,
,  вводятся для того, чтобы при повороте осей координат можно было сохранять симметрию матриц жесткости и податливости материала относительно главной диагонали.
вводятся для того, чтобы при повороте осей координат можно было сохранять симметрию матриц жесткости и податливости материала относительно главной диагонали.
Используются вторые обозначения направляющих косинусов согласно таблице 5.1 матрицу (8.33), можно также представить в виде:
 (8.34)
(8.34)Матрицы жесткости и податливости при повороте осей координат преобразовываются в виде
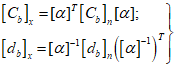 (8.35)
(8.35)и наоборот
Соотношения (8.13), (8.19) преобразовывают таким же образом.
9 Оценка прочности железобетонных элементов без трещин и с трещинами при различных напряженных состояниях
Рассматривается элемент, с взаимно ортогональным (ортотропным) армированием, совпадающим с осями координат x, y, z в виде объемных (рисунок 9.1 а) каркасов, а также, возможно, дисперсным армированием арматурными стержнями i-го направления, расположенными под произвольным углом к осям координат (рисунок 9.1 б). Каждое направление стержней (i = x, y, z, j) характеризуется коэффициентом армирования  , который равен площади Ai стержней, приходящейся на единицу площади плоскости, проведенной нормально к направлению стержней. Согласно рисунку 9.1 а
, который равен площади Ai стержней, приходящейся на единицу площади плоскости, проведенной нормально к направлению стержней. Согласно рисунку 9.1 а
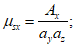
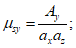
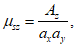 (9.1)
(9.1)где ai(i = x, y, z) - расстояния между стержнями.
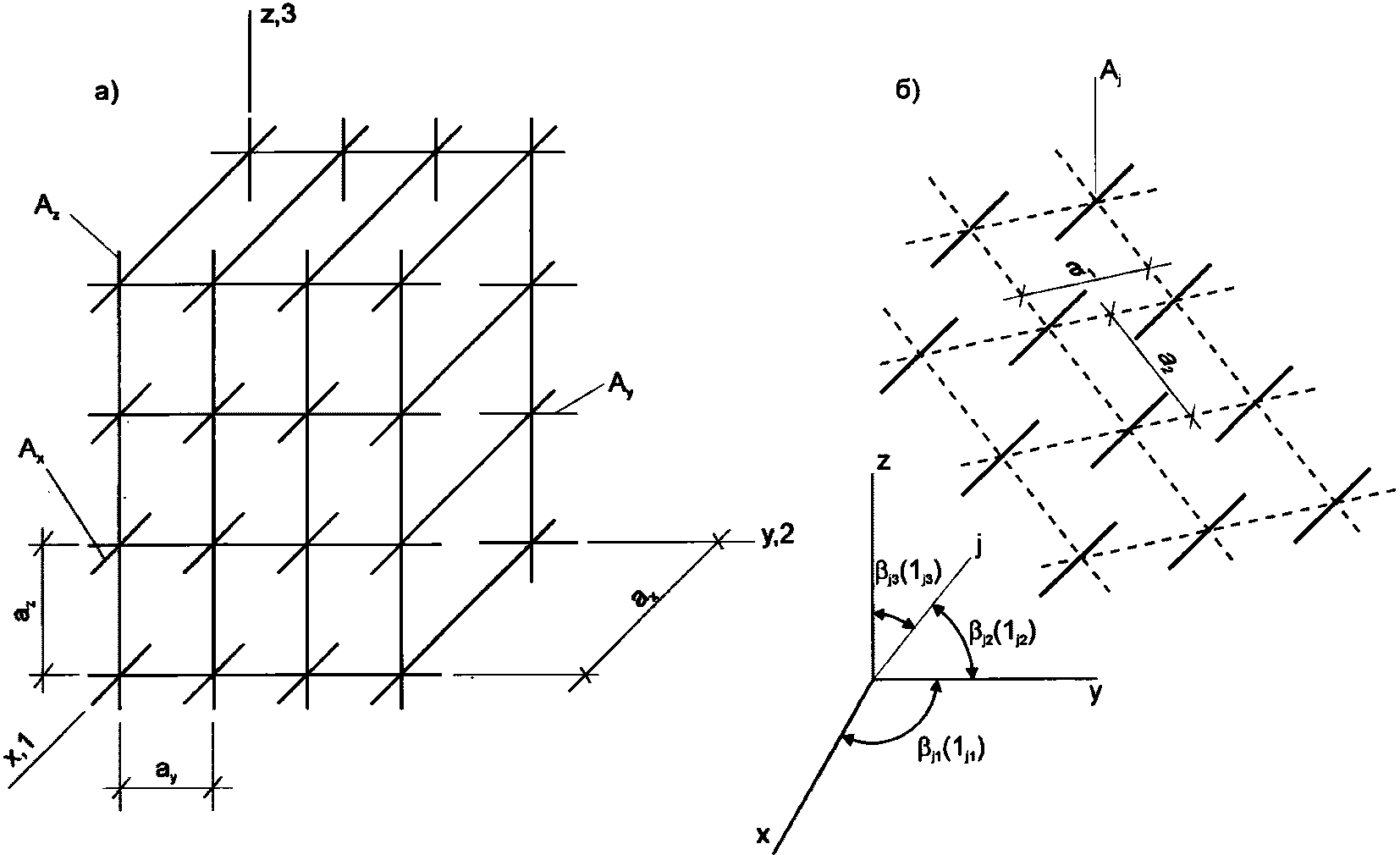
Согласно рисунку 9.1 б
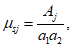 (9.2)
(9.2)где Aj - площади отдельных стержней j направлений;
a1, a2 - расстояния между стержнями.
Если к некоторому направлению i дисперсно устанавливаемой арматуры добавляются отдельные дискретные стержни, то
 (9.3)
(9.3)где Asi(1) - площадь одиночного стержня i-го направления;
Si(1) - максимальное сечение конечного элемента, нормальное к направлению стержня i.
В ряде случаев (например, при расчете конструкций методом конечных элементов) коэффициент армирования удобно вычислять по формуле
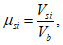 (9.4)
(9.4)где Vsi - суммарный объем арматурных стержней i-го направления в элементе;
Vb - объем конечного элемента.
Для произвольно расположенных стержней каждое направление армирования, кроме коэффициента 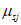 , характеризуется углами
, характеризуется углами  наклона стержней j к осям i = x(1), y(2), z(3) или их косинусами lji (согласно таблице 5.1).
наклона стержней j к осям i = x(1), y(2), z(3) или их косинусами lji (согласно таблице 5.1).
9.2.1 Условия прочности трехмерных железобетонных элементов без трещин устанавливаются исходя из следующих предпосылок:
- осевые деформации арматуры и деформации бетона по направлениям армирования принимаются равными (за исключением концевых участков арматуры, не снабженных специальными анкерами);
- напряжения в элементе  - суммарные величины, состоящие из напряжений в бетоне
- суммарные величины, состоящие из напряжений в бетоне  и приведенных нормальных напряжений в арматуре (
и приведенных нормальных напряжений в арматуре (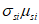 , где
, где  - нормальные напряжения в арматуре);
- нормальные напряжения в арматуре);
- касательными напряжениями в арматурных стержнях можно пренебречь, хотя их учет допускается выполнять по п. 9.3;
- арматурные стержни в процессе деформирования не изменяют своей первоначальной ориентации;
- прочность железобетонного элемента считается исчерпанной, если для составляющих напряжений в бетоне  не обеспечивается выполнение принятых в разделе 7 условий прочности бетона при ограничениях, накладываемых СП 63.13330.2018 на расчетные сопротивления арматуры сжатию.
не обеспечивается выполнение принятых в разделе 7 условий прочности бетона при ограничениях, накладываемых СП 63.13330.2018 на расчетные сопротивления арматуры сжатию.
Из второй и четвертой предпосылок следует:
для ортогонального армирования
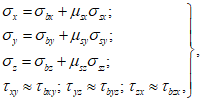 (9.5)
(9.5)для произвольного армирования
 (9.6)
(9.6)где lji - направляющие косинусы углов произвольного армирования (согласно таблице 5.1);
В момент исчерпывания прочности бетона (т.е. выхода на поверхность прочности) полагают, что напряжения в арматуре 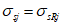 ; главные напряжения в бетоне
; главные напряжения в бетоне  (e = 1, 2, 3). Значения величин
(e = 1, 2, 3). Значения величин 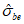 вычисляют по 7.1 - 7.3, а величины
вычисляют по 7.1 - 7.3, а величины  - по п. 9.2.3.
- по п. 9.2.3.
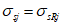 ; главные напряжения в бетоне
; главные напряжения в бетоне  (e = 1, 2, 3). Значения величин
(e = 1, 2, 3). Значения величин 9.2.2 Прочность ортогонально армированного железобетонного конечного элемента считается обеспеченной, если выполняются условия прочности:
(в виде равенства или не равенства нулю определителя), где  ,
, 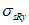 ,
, 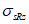 - напряжения в арматуре трех ортогональных направлений в момент исчерпания прочности бетона;
- напряжения в арматуре трех ортогональных направлений в момент исчерпания прочности бетона;  (i, j = x, y, z) - касательные напряжения в арматуре в момент исчерпания прочности элемента, которые допускается принимать равными нулю, или учитывать по п. 9.3.2.
(i, j = x, y, z) - касательные напряжения в арматуре в момент исчерпания прочности элемента, которые допускается принимать равными нулю, или учитывать по п. 9.3.2.
Наряду с условием (9.7) должны выполняться дополнительные условия:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
Знаки (+/-) перед элементами определителя (9.7), стоящими на главной диагонали (главными элементами), не синхронизированы с аналогичными знаками, стоящими перед побочными элементами. Для касательных (побочных) элементов (9.7)
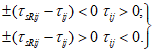 (9.9)
(9.9)Знаки перед элементами определителя и величины назначают исходя из схемы напряженного состояния. Различают три схемы:
1 - всестороннего сжатия бетона  ;
;
 ;
;2 - смешанных напряжений (положительных и отрицательных, 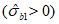 ,
, 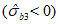 ;
;
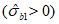 ,
, 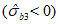 ;
;3 - всестороннего растяжения 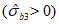 .
.
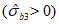 .
.Схема 1. Условие прочности (9.7) при 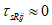 преобразуется к виду:
преобразуется к виду:
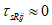 преобразуется к виду:
преобразуется к виду:Дополнительные условия (9.8) также преобразуются
Значения величин  вычисляют по разделу 7.
вычисляют по разделу 7.
Схема 2. Проверку прочности проводят дважды. Один раз проверяют выполнимость условий (9.7) - (9.8), ограничивая величину  , найденную по разделу 7.5 (пункты 7.5.1 - 7.5.2), неравенством
, найденную по разделу 7.5 (пункты 7.5.1 - 7.5.2), неравенством 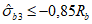 (или
(или  ). Второй раз проводят проверку выполнимости условия (9.7), записанного виде:
). Второй раз проводят проверку выполнимости условия (9.7), записанного виде:
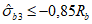 (или
(или  ). Второй раз проводят проверку выполнимости условия (9.7), записанного виде:
). Второй раз проводят проверку выполнимости условия (9.7), записанного виде:Кроме этого должны выполняться условия
Нарушение хотя бы одного из условий (9.12), (9.13) указывает на образование трещин в массивном элементе. Если образование трещин не допускается, то нарушение (9.12), (9.13) фактически указывает на исчерпание прочности. Если трещины допускаются, тогда после проверки (9.12), (9.13) переходят к проверке прочности элемента с трещинами по п. 9.3.2.
Для ответственных элементов, случайное образование трещин в которых может привести к прогрессирующему разрушению, проверку по п. 9.3.2 выполняют и в случае, когда условия (9.12), (9.13) выполняются.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 9.8 отсутствует. |
Схема 3. Проверяют выполнимость условий (9.12), (9.13). Нарушение хотя бы одного из условий (9.12), (9.13) указывает на образование трещин и на разрушение в случае, если образование трещин не допускается. Если трещины допускаются, то чтобы выяснить вопрос прочности элемента, переходят к проверке условий прочности, по п. 9.8.
Для ответственных элементов, случайное образование трещин в которых может привести к прогрессирующему разрушению, проверку по п. 9.8 выполняют и в случае, когда условия (9.12), (9.13) выполняются.
9.2.3 Напряжения  ,
,  ,
,  для элементов без трещин вычисляют по деформациям арматуры
для элементов без трещин вычисляют по деформациям арматуры  ,
,  ,
,  , которые приравниваются к соответствующим деформациям бетона
, которые приравниваются к соответствующим деформациям бетона  ,
,  ,
, 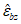 по соответствующим направлениям укладки арматуры в момент исчерпания прочности бетона. Деформации в осях
по соответствующим направлениям укладки арматуры в момент исчерпания прочности бетона. Деформации в осях  в момент исчерпания прочности бетона вычисляют через главные деформации
в момент исчерпания прочности бетона вычисляют через главные деформации 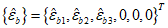 , используя преобразование п. 8.6
, используя преобразование п. 8.6
 в момент исчерпания прочности бетона вычисляют через главные деформации
в момент исчерпания прочности бетона вычисляют через главные деформации 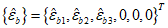 , используя преобразование п. 8.6
, используя преобразование п. 8.6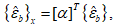 (9.14)
(9.14)где  - матрица направляющих косинусов lei главных площадок (формируется в виде (8.36), направляющие косинусы lei определяют по 5.3); главные деформации
- матрица направляющих косинусов lei главных площадок (формируется в виде (8.36), направляющие косинусы lei определяют по 5.3); главные деформации  вычисляют по формулам (7.24).
вычисляют по формулам (7.24).
Переход от деформаций к напряжениям в арматуре осуществляется на основании диаграмм деформирования арматуры, приведенных в п. 6.2.2 - 6.2.4. Вычисленные напряжения в сжатой арматуре, если есть опасность выпучивания стержней, ограничиваются по абсолютной величине сопротивления Rsc согласно СП 63.13330.2018 (в нашем случае Rsc обозначают Rsci, где i = x, y, z). Для стержней в массивах, где нет опасности выпучивания, ограничение по Rsc допускается не вводить.
9.2.4 Прочность железобетонного элемента, с неортогональной арматурой (косо устанавливаемой к направлениям декартовых координат x, y, z, согласно рисунку 9.1, б), так же как и в случае ортогонального армирования, зависит от схемы напряженного состояния бетона. Для проверки прочности используют соответственно условия (9.10) - (9.13), в которых предварительно заменяют:
где lji - направляющие косинусы арматуры j-го направления к декартовым осям x (i = 1), y (i = 2), z (i = 3);
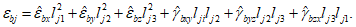 (9.17)
(9.17)Переход от деформаций 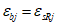 к напряжениям
к напряжениям 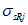 в арматуре осуществляется на основе приведенных в п. 6.2.2 - 6.2.4 диаграмм деформирования арматурных сталей.
в арматуре осуществляется на основе приведенных в п. 6.2.2 - 6.2.4 диаграмм деформирования арматурных сталей.
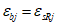 к напряжениям
к напряжениям Дополнительную проверку элементов, в которых возможно образование трещин, следует проводить по п. 9.5. Дополнительную проверку по п. 9.5 для ответственных элементов (согласно п. 9.4) необходимо выполнять и в случае, когда условия прочности (9.15), (9.16) выполняются.
9.3.1 Элемент считается работающим с трещинами, если нарушаются условия п. 9.2.3 - 9.2.4 при схемах напряжений 2 и 3.
Прочность железобетонных элементов с трещинами зависит от схемы трещин (согласно 7.4) и считается обеспеченной, если одновременно удовлетворяются условия прочности сжатого бетона между трещинами (в виде блоков или пластин в случае схемы 1, или полос в случае схемы 2, согласно 9.3.4). При схеме трещинообразования 3 достаточно лишь проверки прочности растянутой арматуры.
Условия прочности растянутой арматуры в трещинах устанавливаются на основе предпосылок, изложенных в разделе 4 "Общие положения". Применительно к трехмерным элементам эти предпосылки конкретизируются следующим образом:
- прочность элемента исчерпывается вследствие чрезмерных пластических деформаций или разрыва арматуры по некоторым трещинам (трещины разрушения), которые расположены в общем случае наклонно к стержням арматуры;
- в трещинах разрушения (текучести, если используется арматура с площадкой текучести) напряжения во всех пересекающих ее стержнях достигают расчетных сопротивлений на растяжение Rsi, вводимых с коэффициентами неравномерности напряжений арматуры  по направлениям i (для арматуры с площадкой текучести
по направлениям i (для арматуры с площадкой текучести  );
);
- в стадии исчерпания прочности элемента по арматуре учитываются, как правило, нормальные напряжения в арматурных стержнях (направленные вдоль их осей). Допускается учитывать касательные напряжения в арматуре в местах пересечения ее трещинами (нагельный эффект), предполагая при этом, что стержни не изменяют своей ориентации (направляющих косинусов).
В тех случаях, когда необходимо избегать преждевременного разрушения от сжатия блоков (пластин) и полос бетона между трещинами, напряжения в арматуре в трещинах должны быть ограничены значениями  . В зонах, где действуют большие касательные напряжения в бетоне и трещины косо располагаются к стержням арматуры, напряжения в арматуре ограничиваются условиями
. В зонах, где действуют большие касательные напряжения в бетоне и трещины косо располагаются к стержням арматуры, напряжения в арматуре ограничиваются условиями  , где Rswi указаны в 6.2.9 СП 63.13330.2018.
, где Rswi указаны в 6.2.9 СП 63.13330.2018.
 . В зонах, где действуют большие касательные напряжения в бетоне и трещины косо располагаются к стержням арматуры, напряжения в арматуре ограничиваются условиями
. В зонах, где действуют большие касательные напряжения в бетоне и трещины косо располагаются к стержням арматуры, напряжения в арматуре ограничиваются условиями  , где Rswi указаны в 6.2.9 СП 63.13330.2018.
, где Rswi указаны в 6.2.9 СП 63.13330.2018.9.3.2 Прочность ортогонально армированного железобетонного элемента по растянутой арматуре считается обеспеченной, если выполняется условие (в виде равенства и неравенства нулю определителя)
(при этом выражения в круглых скобках не должны быть отрицательны). Условие (9.18) можно представить (при  ;
;  ;
; 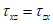 ) в виде
) в виде
 ;
;  ;
; 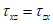 ) в виде
) в видегде 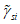 - коэффициент условия работы растянутой арматуры в трещинах. Для ответственных сооружений
- коэффициент условия работы растянутой арматуры в трещинах. Для ответственных сооружений  , допускается величину этого коэффициента принимать равной
, допускается величину этого коэффициента принимать равной
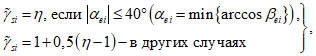 (9.20)
(9.20)где  - угол наклона трещины (нормали к плоскости трещины) к рассматриваемому направлению стержней арматуры;
- угол наклона трещины (нормали к плоскости трещины) к рассматриваемому направлению стержней арматуры;
(i = 1(x), 2(y), 3(z)); 

lei - направляющие косинусы главных растягивающих напряжений 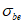 к осям x, y, z, которые вычисляются по 5.3,
к осям x, y, z, которые вычисляются по 5.3,  .
.
Допускается учитывать влияние касательных напряжений в арматуре (нагельного эффекта) на прочность трехмерного элемента по арматуре. При учете этого эффекта в условиях прочности (9.19) заменяются:
 (i = x, y, z),
(i = x, y, z),где значения величины  определяются по формулам 9.3.4.
определяются по формулам 9.3.4.
9.3.3 Прочность растянутой арматуры произвольно армированных трехмерных железобетонных элементов с трещинами считается обеспеченной, если выполняется условие
Условие (9.21) получают вычисляя определитель типа (9.18). Коэффициенты 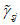 определяют по 9.3.2, заменяя
определяют по 9.3.2, заменяя 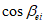 на
на  , где
, где
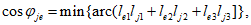 (9.22)
(9.22)e - индексы главных растягивающих напряжений (e = 1, 2, 3).
9.3.4 Согласно 9.3.1 наряду с проверкой прочности по растянутой арматуре в трещинах должна проводиться проверка прочности сжатых блоков (пластин) или полос бетона между трещинами по предлагаемым в настоящем пункте условиям. Выделяют случай ортогонального расположения арматуры в трех направлениях и случай произвольного (косоугольного) расположения стержней.
Последовательность вычислений в случае ортотропного армирования предлагается в виде
- определяются коэффициенты  по формуле
по формуле
 (9.23)
(9.23)- вычисляются напряжения в арматуре
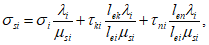 (9.24)
(9.24)где i = x, y, z (1, 2, 3), причем k = y(2), n = z(3);
при i = x величина k = y(2), n = z(3);
при i = y; k = x(1); n = z(3);
при i = z; k = x(1); n = y(2)
(1, 2, 3 вместо x, y, z принимаются при записи направляющих косинусов lek, len, lei);
- определяются коэффициенты В.И. Мурашева 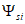 по 6.3.1;
по 6.3.1;
- определяется стадия работы арматурных стержней каждого i-го направления (i = x, y, z);
если  - упругая,
- упругая,
 - упругая,
- упругая,- вычисляются средние относительные деформации арматуры всех трех направлений в зависимости от установленной стадии деформирования:
для упругой  ,
,
 ,
,где Esi - модуль упругости арматуры по пункту 6.2.12 СП 63.13330.2018;
для упруго-пластической стадии деформирования арматуры средние деформации  определяются по диаграммам 6.3.1 в зависимости от напряжений
определяются по диаграммам 6.3.1 в зависимости от напряжений  ;
;
 ;
;- вычисляется деформация 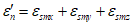 ;
;
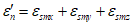 ;
;- определяется коэффициент условия работы бетона в пластинах или полосах бетона между трещинами по формуле
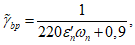 (9.25)
(9.25)где  - коэффициент влияния размеров конструкции на степень повреждаемости полос бетона между трещинами
- коэффициент влияния размеров конструкции на степень повреждаемости полос бетона между трещинами
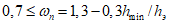 ,
,hmin - минимальный размер поперечного сечения конструкции в плоскости трещины,
hэ - эталонная толщина (hэ = 0,1 м).
Коэффициент  вводится к прочностной характеристике бетона в виде
вводится к прочностной характеристике бетона в виде
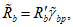 (9.26)
(9.26)где  - прочность бетона, определяемая в зависимости от схемы трещин и схемы напряжений: если реализуется схема трещин 1 и
- прочность бетона, определяемая в зависимости от схемы трещин и схемы напряжений: если реализуется схема трещин 1 и  ;
;  , то величина
, то величина  , где предельные напряжения
, где предельные напряжения  вычисляют по 7.2.2; в других случаях
вычисляют по 7.2.2; в других случаях 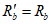 .
.
 , где предельные напряжения
, где предельные напряжения 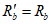 .
.Если проверка прочности выполняется в одном блоке с деформационным расчетом конструкции согласно разделу 10, то значения величин  ,
,  ,
,  допускается назначать по этому расчету.
допускается назначать по этому расчету.
Прочность бетона между трещинами на сжатие в ортотропно армированных элементах считается обеспеченной, если выполняются условия:
где обозначены
 (9.28)
(9.28)В случае косоугольного армирования прочность бетона между трещинами считается обеспеченной, если выполняются условия (9.27), где однако следует принимать:
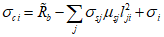
(i = x, y, z или 1, 2, 3),
 (9.29)
(9.29)Напряжения 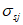 в арматуре вычисляют в процессе деформационного расчета по разделу 10. Допускается принимать
в арматуре вычисляют в процессе деформационного расчета по разделу 10. Допускается принимать 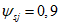 ;
;  , где значения
, где значения 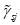 назначают по 9.3.2.
назначают по 9.3.2.
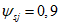 ;
;  , где значения
, где значения 9.4.1 Подбор арматуры, устанавливаемой вдоль осей x, y, z в элементах без трещин, производят по формулам:
где lei - направляющие косинусы напряжений 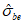 к осям координат x, y, z (i = 1, 2, 3), которые вычисляются по 5.3 и таблице 5.1.
к осям координат x, y, z (i = 1, 2, 3), которые вычисляются по 5.3 и таблице 5.1.
Если трещины в элементе не допускаются, то по формулам (9.30) арматура подбирается дважды (при e = 1 и e = 3) и из двух одинаковых значений коэффициентов армирования выбирается большее.
В ответственных элементах, в которых реализуется схема напряжений 2 и 3 (согласно п. 9.22) и в которых при этом случайное образование трещин может привести к разрушению конструкции или ее основных частей, дополнительно к указанным выше формулам (9.30), подбирается арматура по модифицированным формулам (9.30), полагая в них 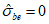 и заменяя
и заменяя  на Rsi - расчетные сопротивления арматуры согласно СП 63.13330.2018. Из получаемых таким образом трех значений каждого коэффициента выбирается большее.
на Rsi - расчетные сопротивления арматуры согласно СП 63.13330.2018. Из получаемых таким образом трех значений каждого коэффициента выбирается большее.
В схеме 1 напряжений (согласно п. 9.2.2) арматура подбирается при 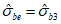 (e = 3).
(e = 3).
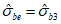 (e = 3).
(e = 3).Если коэффициенты армирования, определяемые по формулам (9.30), получаются отрицательными, то возможны две ситуации: 1 - арматура по расчету не требуется, 2 - при этой схеме армирования добавление арматуры не может обеспечивать прочность элемента по бетону и необходимо изменять схему армирования, добавив косо устанавливаемые вдоль e стержни или изменять класс бетона (или то и другое). Вторая ситуация встречается: при e = 1, если числитель хотя бы одного из выражений (9.30) больше нуля, а значение  (i = x, y, z) в этом выражении меньше нуля; при e = 3, если числитель хотя бы одного выражения (9.30) меньше нуля, а значение
(i = x, y, z) в этом выражении меньше нуля; при e = 3, если числитель хотя бы одного выражения (9.30) меньше нуля, а значение  в этом выражении положительно.
в этом выражении положительно.
После подбора арматуры должны быть проверены условия (9.10), (9.11). Если хотя бы одно из них нарушается, то следует коэффициенты армирования  увеличить до выполнения этого условия.
увеличить до выполнения этого условия.
Если трещины не допускаются, то аналогичная процедура проделывается и с условиями (9.12), (9.13).
9.4.2 Подбор растянутой арматуры в элементах с трещинами, устанавливаемой вдоль осей x, y, z рекомендуется производить по формулам:
где lei - направляющие косинусы главных растягивающих напряжений, вычисляемые по 5.3. Формулы (9.31) используют в зависимости от схемы напряжений. В случае, если  ,
, 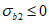 ,
,  , коэффициенты
, коэффициенты  вычисляют при индексе e = 1. В случае, если
вычисляют при индексе e = 1. В случае, если 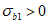 ,
,  ,
,  , коэффициенты
, коэффициенты  по формулам (9.31) вычисляют дважды - при e = 1 и e = 2 и из двух одноименных значений выбирают большее. В случае, если
по формулам (9.31) вычисляют дважды - при e = 1 и e = 2 и из двух одноименных значений выбирают большее. В случае, если 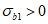 , коэффициенты
, коэффициенты 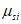 по формуле (9.31) вычисляют трижды при e = 1, 2, 3 и из трех значений каждого коэффициента выбирают большее. Значения
по формуле (9.31) вычисляют трижды при e = 1, 2, 3 и из трех значений каждого коэффициента выбирают большее. Значения  (i = x, y, z) принимают по 9.3.2. Значения величины lei вычисляют по 5.3. При этом допускается углы, соответствующие значениям lei, изменять до 15° (с последующим изменением lei), если это приводит к более низкой сумме
(i = x, y, z) принимают по 9.3.2. Значения величины lei вычисляют по 5.3. При этом допускается углы, соответствующие значениям lei, изменять до 15° (с последующим изменением lei), если это приводит к более низкой сумме 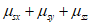 .
.
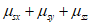 .
.После подбора арматуры должно быть проверено условие (9.18). Если это условие не выполняется, то коэффициенты армирования должны быть увеличены до значений, необходимых для выполнения этого условия.
10 Связи между напряжениями и деформациями (физические соотношения) для железобетонных элементов при объемном напряженном состоянии. Учет влияния образования и развития трещин по различным схемам
Основные предпосылки, заложенные при выводе физических соотношений, приведены в п. 9.2. Согласно этим предпосылкам общие напряжения элемента  суммируются из приведенных напряжений бетона и приведенных напряжений арматуры
суммируются из приведенных напряжений бетона и приведенных напряжений арматуры
 суммируются из приведенных напряжений бетона и приведенных напряжений арматуры
суммируются из приведенных напряжений бетона и приведенных напряжений арматуры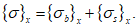
Общие связи между напряжениями и деформациями железобетона имеют вид
где [d]x - матрица жесткости железобетона.
Матрица жесткости железобетона представляется в виде:
 (10.2)
(10.2)где [Cb]x - матрица податливости бетона (8.3), преобразованная по указаниям п. 8.6 к осям x, y, z;
[ds]x - матрица жесткости арматуры, которая при ортотропном армировании имеет вид:
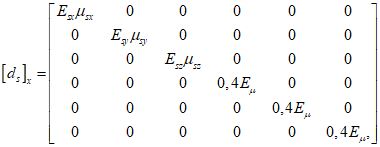 (10.3)
(10.3)здесь  ;
;
 ;
; - коэффициенты армирования, определяемые по 9.1;
- коэффициенты армирования, определяемые по 9.1;Esi - начальные модули деформации арматуры, определяемые по СП 63.13330.2018.
Если арматура деформируется за пределом упругости, то вместо Esi вводят величины Esi, 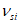 , где
, где  - коэффициенты изменения начального модуля, определяемые по 6.2.3 - 6.2.5.
- коэффициенты изменения начального модуля, определяемые по 6.2.3 - 6.2.5.
10.2.1 В соответствии с 7.4 в элементе предполагается три схемы образования трещин (согласно рисунку 7.3):
1 - элемент с одной трещиной;
2 - элемент с двумя взаимно перпендикулярными трещинами;
3 - элемент с тремя взаимно перпендикулярными трещинами.
Элементы без трещин относятся условно к схеме 0 (эта схема вводится здесь для того, чтобы представить универсальную запись физических соотношений, пригодных как для стадии с трещинами, так и стадии без трещин).
Условия образования трещин определяются напряженным состоянием в бетоне и охарактеризованы в 7.4.
При появлении трещин (схема 1) считается, что элемент разделен на отдельные пластины, соединенные стержнями арматуры. В элементе нарушается совместность осевых деформаций арматуры и бетона, вследствие взаимных смещений, что приводит к раскрытию трещин. Косое (в общем случае) пересечение трещин стержнями арматуры приводит кроме разъединения пластин, вследствие раскрытия трещин, к взаимному сдвигу пластин вдоль трещин (сдвигу берегов трещин). Пластины бетона между трещинами способны сопротивляться двухосному действию усилий вдоль плоскости трещин. В трещинах все усилия (за исключением некоторых сил зацепления берегов трещин) воспринимаются арматурой, в которой возникают осевые и касательные (за счет нагельного эффекта) напряжения. В пластинах между трещинами напряжения в арматуре уменьшаются за счет ее сцепления с бетоном, что сказывается на средних относительных деформациях всего элемента.
При реализации схемы 2 бетон разделяется трещинами на отдельные полосы бетона, которые сопротивляются осевому сжатию (растяжению) или сжатию со сдвигом. Особенности работы арматуры, пересекающей трещины, сохраняются как в схеме 1. При пересекающейся системе трещин (схема 3) бетон выключается из самостоятельной работы, но продолжает оказывать влияние на уменьшение средних деформаций арматуры.
10.2.2 Относительные деформации
Под относительными деформациями элемента с трещинами подразумеваются деформации, которые складываются из двух частей:
- относительные деформации, связанные с трещинообразованием;
- относительные деформации бетона между трещинами.
В системе координат n, m, l, совпадающих с возможным образованием ортогональных трещин (рисунок 7.3), относительные деформации элемента составляют:
- при схеме 1 (рисунок 10.1)
- при схеме 2
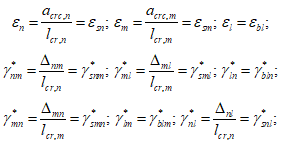 (10.6)
(10.6)- при схеме 3
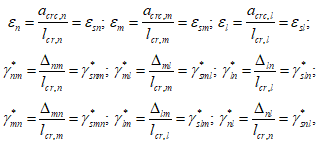 (10.7)
(10.7)где acrc,l - ширина раскрытия трещин, ортогональных к осям n, m, l (e = n, m, l);
lcr,l - расстояния между трещинами в направлениях n, m, l.
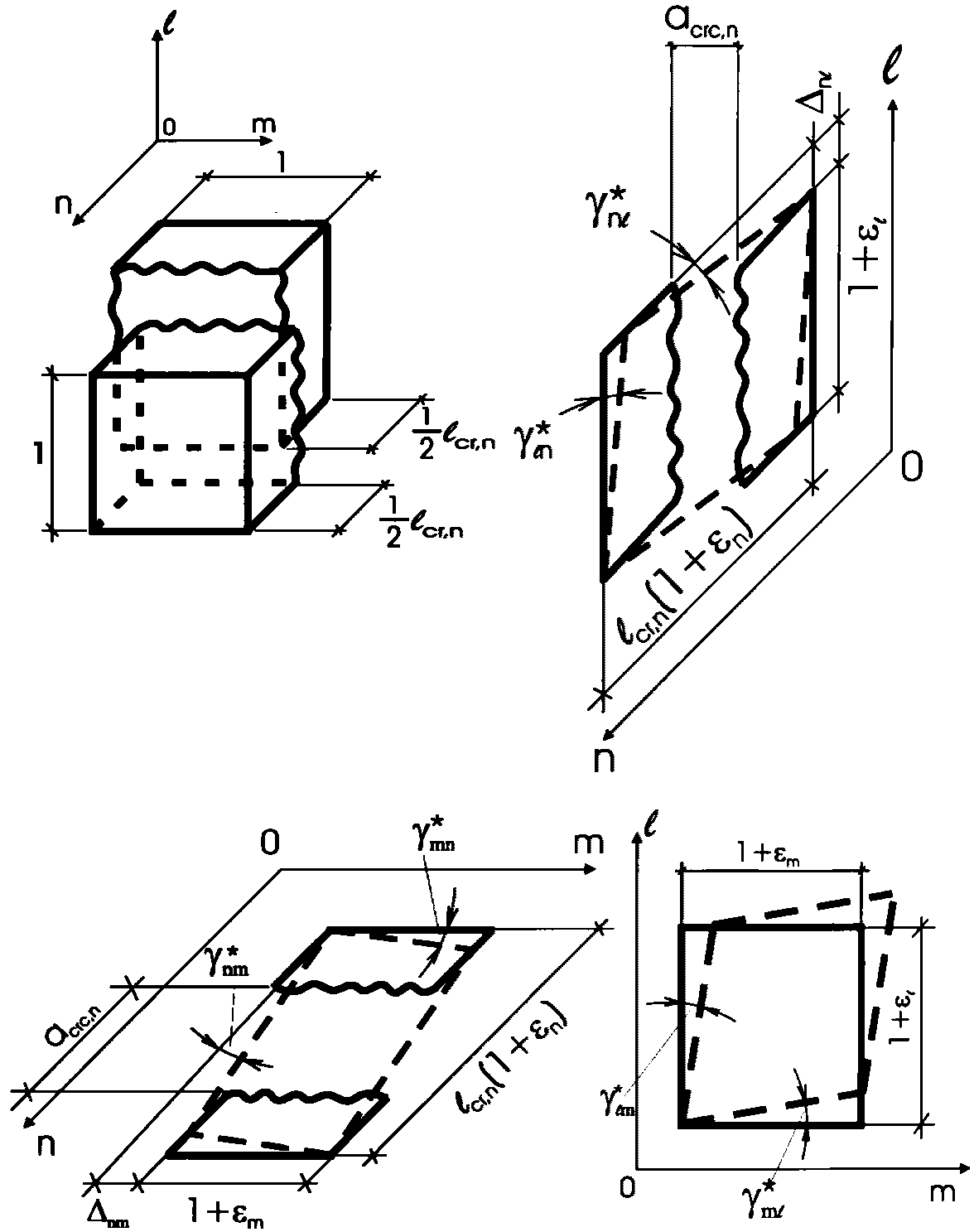
деформаций элементов с трещинами
Деформации элемента с трещинами представляются в виде девятикомпонентного столбца
В окончательные расчеты вводятся суммарные углы сдвига

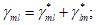
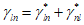 (10.9)
(10.9)в результате вектор-столбец (10.8) преобразуется к виду
 (10.10)
(10.10)Деформации элемента без трещин получают из соотношений (10.5), полагая acrc,n = 0;  , кроме этого
, кроме этого
 , кроме этого
, кроме этого ; (e, k = n, m, l;
; (e, k = n, m, l; 10.2.3 Напряжения
Напряжения в элементе складываются в осях n, m, l из напряжений в бетоне  и приведенных (с учетом коэффициентов армирования
и приведенных (с учетом коэффициентов армирования  и углов наклона арматуры к осям n, m, l) напряжений в арматуре
и углов наклона арматуры к осям n, m, l) напряжений в арматуре  . Причем на площадках трещин основными являются приведенные напряжения в арматуре, а напряжения в бетоне практически (за исключением некоторых напряжений в связях защемления) равны нулю. На площадках, нормальных к трещинам, напряжения в бетоне и приведенные напряжения в арматуре выступают как равнозначные. Чтобы учесть указанный фактор выключения бетона по тем или иным направлениям (в зависимости от расположения трещин), вводятся девятикомпонентные вектор-столбцы напряжений: бетона между трещинами
. Причем на площадках трещин основными являются приведенные напряжения в арматуре, а напряжения в бетоне практически (за исключением некоторых напряжений в связях защемления) равны нулю. На площадках, нормальных к трещинам, напряжения в бетоне и приведенные напряжения в арматуре выступают как равнозначные. Чтобы учесть указанный фактор выключения бетона по тем или иным направлениям (в зависимости от расположения трещин), вводятся девятикомпонентные вектор-столбцы напряжений: бетона между трещинами 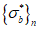 ; связей зацепления
; связей зацепления 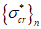 и арматуры
и арматуры  ;
;
где
Формальные множители  фиксируют условие, что на площадках-трещинах напряжения зацепления совпадают с напряжениями в бетоне, а на остальных площадках напряжения зацепления равны нулю.
фиксируют условие, что на площадках-трещинах напряжения зацепления совпадают с напряжениями в бетоне, а на остальных площадках напряжения зацепления равны нулю.
 фиксируют условие, что на площадках-трещинах напряжения зацепления совпадают с напряжениями в бетоне, а на остальных площадках напряжения зацепления равны нулю.
фиксируют условие, что на площадках-трещинах напряжения зацепления совпадают с напряжениями в бетоне, а на остальных площадках напряжения зацепления равны нулю.Общие напряжения обозначаются:
причем
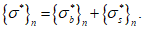 (10.15)
(10.15)Учитывается парность общих касательных напряжений,
хотя парность составляющих касательных компонентов отдельно арматуры и отдельно бетона может нарушаться. В силу парности девятикомпонентный вектор-столбец (10.14) преобразовывается к шестикомпонентному
 (10.17)
(10.17)Компоненты вектор-столбца (10.12) напряжений арматуры вычисляются по формулам:
(e, k = n, m, l; 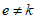 ; i, j = x, y, z;
; i, j = x, y, z; 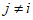 ),
),
где li, lj, ki, kj (ni, mi, li) - направляющие косинусы осей n, m, l к осям x, y, z, определяемые согласно таблице 5.1;
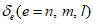 - коэффициенты, вычисляемые по формулам (10.13), кроме этого:
- коэффициенты, вычисляемые по формулам (10.13), кроме этого:Например, полагая e = n и k = m при схеме 1 трещин из (10.18) получают:
 (10.20)
(10.20) (10.21)
(10.21)Полагая e = m, k = m при схеме 1 трещин из (10.18) получают:

Реальные напряжения арматуры i - направлений ( - нормальные в трещинах,
- нормальные в трещинах,  - средние между трещинами,
- средние между трещинами, 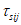 - касательные в трещинах) вычисляют по формулам:
- касательные в трещинах) вычисляют по формулам:
 (10.22)
(10.22)(j, i = x, y, z),  , (p = n, m, l).
, (p = n, m, l).
Искусственно введенные параметры  ,
, 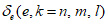 принимают следующие значения (в зависимости от схемы трещин).
принимают следующие значения (в зависимости от схемы трещин).
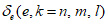 принимают следующие значения (в зависимости от схемы трещин).
принимают следующие значения (в зависимости от схемы трещин).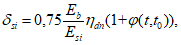
где  - уровень деформаций;
- уровень деформаций;
 - уровень деформаций;
- уровень деформаций;Нормальные напряжения арматуры в трещинах допускается вычислять по упрощенным формулам. В случае схемы 1 трещин упрощенные формулы записываются:
при i = x: j = y, e = z; при i = y: j = x, e = z; при i = z: j = x, e = y;
Ecrn, Ecrnm, Ecrnl - модули деформации связей зацепления берегов трещины определяются по формулам:
В случаях схемы 2 трещин дополнительно записываются модифицированные формулы (10.24), (10.25) для второго направления трещин, в которых направляющие косинусы ni, nj, ne заменяются соответственно на косинусы mi, mj, me и кроме этого  заменяются на
заменяются на 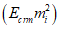 ,
,  на
на  ,
,  на
на  . Из вычисленных по формуле (10.24) и модифицированной формуле (10.25) двух напряжений
. Из вычисленных по формуле (10.24) и модифицированной формуле (10.25) двух напряжений  принимается большее.
принимается большее.
 заменяются на
заменяются на 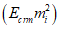 ,
,  на
на  ,
,  на
на  . Из вычисленных по формуле (10.24) и модифицированной формуле (10.25) двух напряжений
. Из вычисленных по формуле (10.24) и модифицированной формуле (10.25) двух напряжений В случае схемы 3 трещин дополнительно записываются модифицированные формулы (10.24), (10.25) для третьего направления трещин, в которых направляющие косинусы ni, mj, ne заменяются соответственно на косинусы li, lj, le, кроме этого заменяются: 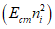 на
на  ,
, 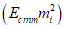 на
на  ,
, 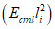 на
на  . Напряжения
. Напряжения 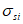 вычисляются по таким образом модифицированной формуле и формулам, рекомендованным для схемы 2 и из трех значений
вычисляются по таким образом модифицированной формуле и формулам, рекомендованным для схемы 2 и из трех значений  выбирается большее.
выбирается большее.
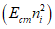 на
на  ,
, 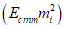 на
на  ,
, 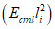 на
на  . Напряжения
. Напряжения После вычисления напряжений арматуры по формулам (10.16) - (10.25) и заполнения вектор-столбца (10.12) с использованием формул (10.16) переходят к определению первого вектор-столбца напряжений из (10.11):
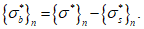 (10.26)
(10.26)Отдельно формируется вектор-столбец (10.12) с использованием формул (10.18), в которых полагают 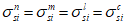 ;
; 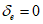 . Таким образом заполненный вектор-столбец (10.18) обозначается
. Таким образом заполненный вектор-столбец (10.18) обозначается 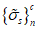 . Затем определяют средние напряжения бетона в пластинах или полосах между трещинами
. Затем определяют средние напряжения бетона в пластинах или полосах между трещинами
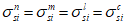 ;
;  (10.27)
(10.27)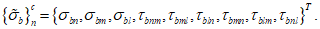 (10.28)
(10.28)10.2.5 Запись соотношений между напряжениями и деформациями бетона до появления трещин применительно к рассмотрению элементов с трещинами
При этом соотношения (8.2), (8.3) представляются в виде:
здесь согласно пунктам 8.2.1 - 8.2.3
Коэффициенты (10.30) вычисляются по 8.2, полагая n = 1; m = 2; l = 3; ek = 12, 23, 31, 21, 32, 13, используя компоненты напряжений бетона (10.28); при этом входящая в эти формулы призменная прочность Rb умножается на коэффициент, вычисляемый согласно  п. 9.3.4, а значения величины
п. 9.3.4, а значения величины  , вычисляемые по п. 6.1.3, умножаются на коэффициент, принимаемый равным меньшему из значений двух величин: 1,2 и
, вычисляемые по п. 6.1.3, умножаются на коэффициент, принимаемый равным меньшему из значений двух величин: 1,2 и  .
.
 .
.Условия (10.29) можно представить в виде
ИС МЕГАНОРМ: примечание. Обозначения даны в соответствии с официальным текстом документа. |
где 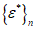 формируется в виде (10.8),
формируется в виде (10.8), 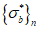 - в виде (10.11), матрица
- в виде (10.11), матрица  , представленная в (10.29) согласно (10.31), является матрицей податливости бетона.
, представленная в (10.29) согласно (10.31), является матрицей податливости бетона.
В обращенном виде условие (10.31) записывается
где коэффициенты матрицы жесткости  в развернутом виде записываются
в развернутом виде записываются
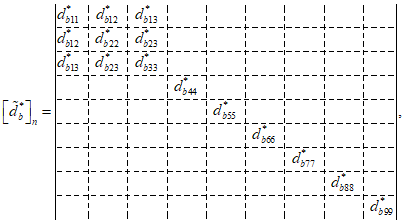 (10.33)
(10.33)При этом сохраняются зависимости (10.34), однако коэффициенты матрицы  корректируются следующим образом:
корректируются следующим образом:
- для первой схемы трещин
- для второй схемы трещин дополнительно к указанным равенствам добавляются равенства
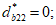
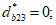
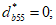
 (10.34)
(10.34)- для третьей схемы трещин к указанным равенствам добавляются новые равенства
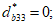
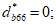
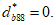 (10.34)
(10.34)Формально для бетона с трещинами с учетом указанных выше факторов матрица 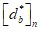 может быть представлена в виде:
может быть представлена в виде:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где
 (10.36)
(10.36)Кроме этого для элементов с трещинами вводится матрица жесткости зацеплений берегов трещин
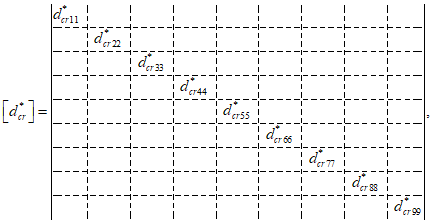 (10.37)
(10.37)где
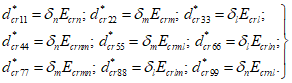 (10.38)
(10.38)Модулями зацепления Ecrn, Ecrm, Ecnl и другие формируются по 10.2.4.
Таким образом для элементов с трещинами зависимости (10.32) корректируются с учетом (10.35), (10.47). Откорректированные зависимости представляются в виде
 (10.39)
(10.39)где
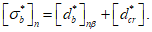 (10.40)
(10.40)10.2.7 Зависимости между напряжениями и деформациями арматуры
Вектор-столбец напряжений арматуры записывают в виде (10.12) и вычисляют по формулам
где
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
Элементы матрицы  вычисляют по формулам:
вычисляют по формулам:
 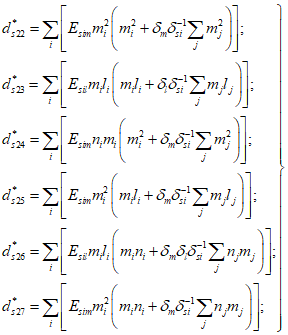  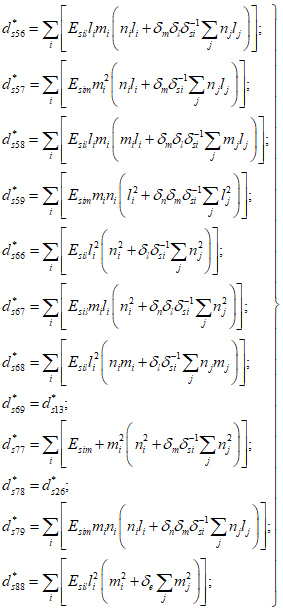 | (10.43) |
 (10.44)
(10.44)Из формул (10.42) получают коэффициенты 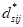 любой схемы трещин, а также элементов без трещин (схема 0), присваивая параметрам
любой схемы трещин, а также элементов без трещин (схема 0), присваивая параметрам 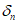 ,
, 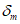 ,
,  ,
,  ,
, 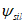 ,
,  значения, указанные в формулах (10.13), (10.19), (10.23).
значения, указанные в формулах (10.13), (10.19), (10.23).
10.2.8 Общие зависимости между напряжениями бетона и арматуры и деформациями
Эти соотношения следуют из суммирования соотношений (10.32) и (10.41)
где 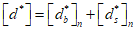 .
.
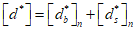 .
.Соотношения (10.45) связаны со сдвиговыми компонентами типа  и
и  несимметричного тензора деформаций. Для выполнения практических расчетов девятикомпонентные соотношения (10.45) сводятся к шестикомпонентным, используя условие парности касательных компонент
несимметричного тензора деформаций. Для выполнения практических расчетов девятикомпонентные соотношения (10.45) сводятся к шестикомпонентным, используя условие парности касательных компонент
и общие углы сдвига
Для перехода от девятикомпонентных соотношений к шестикомпонентным.
Соотношения (10.45) преобразовываются к виду
где  .
.
 .
.В развернутом виде соотношения (10.48) записываются
Используя соотношения (10.46), (10.47) сводим девятикомпонентную систему (10.49) к шестикомпонентной
или в сокращенном виде
где
В практических расчетах соотношения (10.49) преобразовываются к соотношениям в общих осях x, y, z. Компоненты напряжений и относительных деформаций преобразовываются по формулам:
где
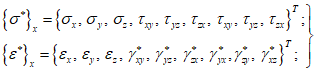 (10.54)
(10.54) (10.55)
(10.55)Учитывая (10.53) зависимости (10.48) преобразовываются к виду:
где
 (10.57)
(10.57)В развернутом виде соотношения (10.56) представляются в виде (10.49), где индексы n, m, l заменяются соответственно на индексы x, y, z, естественно изменяются значения параметров податливости  , которые обозначаются
, которые обозначаются 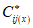 .
.
Используя условие парности касательных напряжений и общие углы сдвига в осях x, y, z:
 (10.58)
(10.58)девятикомпонентная система (10.56) сводится по аналогии с (10.49) к шестикомпонентной
или в сокращенном виде
Коэффициенты матрицы [C]x выражаются через коэффициенты матрицы [Cx] по формулам (10.51) - (10.52), в которых нижний индекс (n) заменяется на индекс (x).
В практических расчетах соотношения (10.59) можно непосредственно получать из соотношений (10.50), полагая
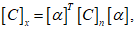 (10.61)
(10.61)где 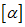 - шестикомпонентная матрица преобразования (8.33).
- шестикомпонентная матрица преобразования (8.33).
В практических расчетах также используются соотношения (10.60) в обращенном виде
где  .
.
 .
.При рассмотрении железобетонных элементов, армированных вдоль ортогональных осей x, y, z, повернутые оси x', y', z' могут обозначаться n, m, l (рисунок 5.1). При этом вводятся новые обозначения направляющих косинусов ni, mi, li (i = x, y, z) согласно таблице 5.1.
Пусть i - произвольные направления стержней, которые не совпадают с направлениями осей x, y, z и не ортогональны между собой. Каждое направление i характеризуется коэффициентом армирования  , а также декартовой системой координат i, i(a), i(r), где ось i совпадает с направлением осей, а остальные могут располагаться произвольно; ni, mi, li - направляющие косинусы направления i к осям n, m, l, аналогично nj, mj, lj (j = i(a), i(r)) - направляющие косинусы двух других осей к осям n, m, l. Такая трактовка направляющих косинусов позволяет распространять приведенные в п. 10.2.1 - 10.2.6 формулы на случай произвольного армирования. Однако при этом теряют силу формулы (10.24) - (10.25) по определению напряжений арматуры в трещинах при ортотропном армировании.
, а также декартовой системой координат i, i(a), i(r), где ось i совпадает с направлением осей, а остальные могут располагаться произвольно; ni, mi, li - направляющие косинусы направления i к осям n, m, l, аналогично nj, mj, lj (j = i(a), i(r)) - направляющие косинусы двух других осей к осям n, m, l. Такая трактовка направляющих косинусов позволяет распространять приведенные в п. 10.2.1 - 10.2.6 формулы на случай произвольного армирования. Однако при этом теряют силу формулы (10.24) - (10.25) по определению напряжений арматуры в трещинах при ортотропном армировании.
10.4.1 При определении ширины раскрытия трещин рассматривают три схемы трещин (схема 1, схема 2, схема 3), которые указаны в пункте 7.4. В случае схемы 1 трещин ширину раскрытия следует определять по формуле
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
где 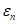 - относительные удлинения элемента по нормали к трещинам, определяемые на основании физических соотношений (10.50);
- относительные удлинения элемента по нормали к трещинам, определяемые на основании физических соотношений (10.50);
lcr - расстояние между трещинами, которое вычисляется в зависимости от схемы трещин и схемы армирования.
Случай армирования стержнями арматуры трех ортогональных направлений, расположенных вдоль осей x, y, z, которые пересекает наклонная трещина n (или x' согласно рисунку 5.2), где n - нормаль к наклонной трещине, nx(l11), ny(l12), nz(l13) - направляющие косинусы углов наклона n к осям x, y, z сокращенно ni(i = x, y, z). В этом случае расстояние между трещинами определяется по зависимости формуле
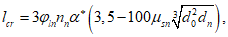 (10.65)
(10.65)где 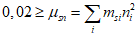 ;
;
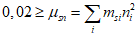 ;
; ;
; ;
; ,
,здесь  - коэффициенты армирования, определяемые по п. 9.1;
- коэффициенты армирования, определяемые по п. 9.1;
di - диаметры в мм арматурных стержней, i-направлений (i = x, y, z), 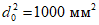 ;
;
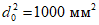 ;
;- при стержневой арматуре периодического профиля | 1,0; |
- стержневой гладкой арматуре | 1,3; |
- проволочной арматуре периодического профиля и канатов | 1,2; |
- гладкой проволочной арматуре | 1,4; |
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок | 1,0 |
многократно повторяющейся нагрузки, а также продолжительного действия постоянных и длительных нагрузок для конструкций из бетона: | |
тяжелого: | |
естественной влажности | 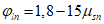 |
в водонасыщенном состоянии | 1,2; |
при попеременном водонасыщении и высушивании | 1,75; |
- Мелкозернистого групп | |
А | 1,75; |
Б | 1,5; |
- Легкого и поризованного не менее | 1,5; |
Ячеистого | 2,5. |
Значения  для легкого, мелкозернистого, поризованного и ячеистого бетонов в водонасыщенном состоянии умножаются на коэффициент 0,8, а при попеременном водонасыщении и высушивании - на коэффициент 1,2.
для легкого, мелкозернистого, поризованного и ячеистого бетонов в водонасыщенном состоянии умножаются на коэффициент 0,8, а при попеременном водонасыщении и высушивании - на коэффициент 1,2.
Указанные выше рекомендации действуют, если деформации 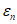 в формуле (10.64) вычислены при продолжительном действии нагрузок без учета влияния деформаций ползучести, в других случаях
в формуле (10.64) вычислены при продолжительном действии нагрузок без учета влияния деформаций ползучести, в других случаях 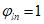 .
.
Если элемент армируется косоугольной сеткой, то для определения lcr в случае непересекающихся трещин следует использовать более общую формулу
где d0 = 10 мм;
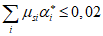
иначе
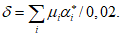
10.4.2 В случае образования новых трещин, направленных нормально к осям n, m, l по схемам 2 и 3, дополнительно вычисляется ширина раскрытия трещин по направлениям m и l, при этом в формулах (10.64)  заменяется соответственно на
заменяется соответственно на  и
и  , которые вычисляются по системе (10.50). При этом в формулах (10.64), (10.66), (10.67) ni заменяется на mi и li. Вычисленные по формулам (10.64) и (10.66) значения
, которые вычисляются по системе (10.50). При этом в формулах (10.64), (10.66), (10.67) ni заменяется на mi и li. Вычисленные по формулам (10.64) и (10.66) значения 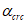 и
и  умножаются на коэффициент 0,8 и в расчет вводится
умножаются на коэффициент 0,8 и в расчет вводится  из двух уменьшенных величин.
из двух уменьшенных величин.
 из двух уменьшенных величин.
из двух уменьшенных величин.11 Математические методы расчета массивных железобетонных конструкций с учетом физической нелинейности
Настоящий раздел посвящен методам решения задач по определению напряженно-деформированного состояния массивных железобетонных конструкций с учетом физической нелинейности. Физическая нелинейность или нелинейность деформирования заключается в отсутствии пропорциональной связи между напряжениями и деформациями. Это относится как к упруго-мгновенным деформациям, так и к деформациям ползучести.
В теории железобетона специфические нелинейные связи между напряжениями и деформациями определяют физическую модель объекта. С этой точки зрения в настоящем разделе основное внимание уделено применению в качестве деформационной модели железобетона, модели с учетом трещин, подробно рассмотренных в предыдущих разделах, однако предлагаемые методы решения обладают достаточной общностью и могут рассматриваться как общие методы решения задач нелинейной теории железобетона.
Для решения любой инженерной задачи о прочности, жесткости и устойчивости необходимо знать поле перемещений, которое для железобетонного континиуума характеризуется тремя функциями:
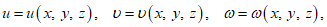
поле деформаций, характеризуемое шестью функциями:
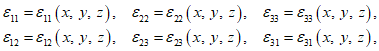
поле напряжений, характеризуемое шестью функциями:
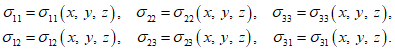
Определяющая система уравнений для нахождения указанных пятнадцати функций может быть получена одним из двух эквивалентных способов: из рассмотрения равновесия бесконечно малого элемента континиуума или с помощью вариационных принципов. Представим уравнения первого способа в матричной форме
- три уравнения равновесия статики (динамики)
где точки обозначают взятие производной по времени;
- шесть геометрических уравнений (формулы Коши)
шесть физических уравнений, которые в соответствии с соотношениями (10.1), (10.62) представляем:
Обозначим матрицы дифференцирования через [D] в уравнение (11.1) и 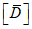 в уравнении (11.2). Тогда, подставив (11.3) в уравнения равновесия (11.1) и учитывая (11.2), получим разрешающие уравнения для малых деформаций континиуума
в уравнении (11.2). Тогда, подставив (11.3) в уравнения равновесия (11.1) и учитывая (11.2), получим разрешающие уравнения для малых деформаций континиуума
Уравнение (11.4) можно получить в более компактной форме, если рассматриваемые величины представить в тензорных обозначениях. Действительно, уравнения (11.1), (11.2) можем записать соответственно как:
Причем 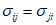 ;
;  .
.
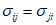 ;
;  .
.Шесть физических уравнений записываются как
Здесь и ниже применяется соглашение о суммировании по повторяющемуся индексу. Подставив (11.7) в уравнение равновесия (11.5) и учитывая (11.6), получим систему разрешающих уравнений, эквивалентную (11.4)
к которой необходимо присоединять граничные условия, задаваемые в напряжениях на части S1 боковой поверхности континиуума
в перемещениях на части S2, поверхности S континиуума
где Us2i - проекции вектора перемещения, принимающего постоянные значения в точках S2 поверхности. Например, Us2i = 0 в точках закрепления.
Прежде чем сформулировать разрешающие уравнения вторым способом, введем некоторые понятия. Для этого рассмотрим тело с объемом V, ограниченного поверхностью S и находящегося под действием внешних объемных F и поверхностных p(n) сил в равновесии. Условия на поверхности тела определяются соотношениями (11.9) и (11.10) для части S1 и S2 соответственно.
Перемещения Ui, при которых тело находится в равновесии, назовем истинными перемещениями. Наряду с истинными перемещениями имеют место геометрически возможные перемещения, подчиняющиеся граничным условиям (11.10). Очевидно существует бесконечное множество систем геометрически возможных перемещений, причем каждой такой системе перемещений соответствует некоторое напряженное состояние с тензором напряжений  , который можно определить по уравнению (11.6). Любой тензор
, который можно определить по уравнению (11.6). Любой тензор  , компоненты которого удовлетворяют внутри объема V, занятого телом, уравнениям равновесия (11.5) и граничным условиям (11.9) на части S1 поверхности, назовем тензором статически возможных напряжений. Очевидно, что множество тензоров статически возможных напряжений содержит в себе и тензор
, компоненты которого удовлетворяют внутри объема V, занятого телом, уравнениям равновесия (11.5) и граничным условиям (11.9) на части S1 поверхности, назовем тензором статически возможных напряжений. Очевидно, что множество тензоров статически возможных напряжений содержит в себе и тензор  , которому соответствует система истинных перемещений. Если компоненты тензора напряжений
, которому соответствует система истинных перемещений. Если компоненты тензора напряжений  удовлетворяют уравнениям равновесия (11.5), граничным уравнениям (11.9), а также уравнениям совместности деформаций (при использовании деформационной модели железобетона), тогда тензор
удовлетворяют уравнениям равновесия (11.5), граничным уравнениям (11.9), а также уравнениям совместности деформаций (при использовании деформационной модели железобетона), тогда тензор  назовем тензором истинных напряжений.
назовем тензором истинных напряжений.
Составляем интеграл 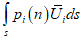 , распространенный по поверхности S тела, в котором
, распространенный по поверхности S тела, в котором  геометрически возможные перемещения. В силу (11.9) можем записать:
геометрически возможные перемещения. В силу (11.9) можем записать:
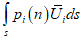 , распространенный по поверхности S тела, в котором
, распространенный по поверхности S тела, в котором 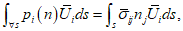
где nj - нормаль к поверхности тела.
Учитывая преобразование
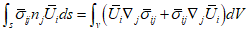
и уравнения равновесия (11.5), получим равенство
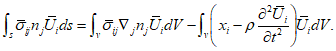
В результате приходим к интегральному соотношению
Соотношение (11.11) лежит в основе формулировки вариационных принципов. Теперь представим геометрически возможное перемещение в виде
где Ui - истинные перемещения, SUi - произвольные геометрически возможные бесконечно малые их изменения (вариации перемещений). Так как Ui удовлетворяют граничным условиям (11.10), то на части S2 поверхности SUi = 0. Подставив (11.12) в (11.11), получим разрешающие уравнения второго способа в виде
При рассмотрении статических задач соотношение (11.13) принимает вид
в котором левая часть представляет собой изменение энергии деформации континиуума
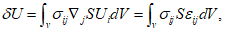
а правая часть - работа внешних сил. Полученное уравнение (11.14) указывает на то, что сумма работ внешних сил на произвольных возможных вариациях перемещений равна вариации полной энергии деформаций континиуума, соответствующей вариациям перемещений.
Полученные разрешающие уравнения (11.4), (11.8) и (11.13) можно записать в другом виде, выбрав в качестве основных неизвестных функций - напряжения. Однако изложение настоящего раздела построено на рассмотрении решения в перемещениях, как наиболее распространенного в настоящее время, хотя это не исключает применение рекомендуемых приемов для методов типа метода сил.
Для большинства практических задач решения (11.4), (11.8) или (11.13) в замкнутом виде получить трудно, а иногда и просто невозможно, так как помимо чисто математических проблем, связанных с решением систем дифференциальных уравнений в частных производных, возникает проблема нелинейности таких уравнений, обусловленная зависимостью (11.3).
Как следует из разделов 8 и 10, эти зависимости являются неаналитическими зависимостями нелинейного вычислительного оператора, который позволяет записать элементы матрицы жесткости для железобетона в виде матрицы упругости анизотропного материала. Однако элементы этой матрицы не являются константами, а зависят, в общем случае, от достигнутого уровня напряженно-деформированного состояния и схемы трещин. Кроме того, следует помнить, что в отличие от упруго-пластического тела, деформирование железобетонного континиуума не подчиняется гипотезам простого нагружения, единой кривой, активного и равновесного нагружения. Все это определяет специфику методов решения нелинейных задач железобетонного континиуума.
Для получения замкнутых решений (11.4), (11.8) или (11.13) с использованием нелинейной зависимости (11.3) применяют различные варианты метода последовательных приближений. Решение нелинейных задач теории железобетона сводится к решению последовательности линейных задач, каждая из которых может быть интерпретирована как некоторая задача теории упругости (метод упругих решений).
Последовательность линейных задач, к которым сводится исходная нелинейная задача, решается, как правило, численными методами: методом конечных элементов (МКЭ), методом конечных разностей (МКР) или вариационно-разностным методом (ВРМ). Применение численных методов вызвано неаналитическим характером зависимости (11.3), а также анизотропными свойствами железобетонного массива. В настоящем разделе наибольшее внимание уделено (МКЭ), хотя принципиального значения выбор метода решения линейной задачи не имеет, важно, чтобы он учитывал особенности принятой для расчета физической модели материала.
Один из основных методов решения нелинейных задач теории железобетона - метод упругих решений. Под этим термином здесь понимается совокупность методов, в которых решение нелинейной задачи ищется в виде сходящейся последовательности линейных решений. Поставленную выше задачу для систем уравнений (11.4), (11.8) или (11.13) запишем, введя в рассмотрение номер итерации "k".
где
т.е. на каждой итерации матрица жесткости материала вычисляется по результатам предыдущего решения, что позволяет рассматривать компоненты матрицы жесткости постоянными в пределах одной итерации. В рамках метода упругих решений уравнение (11.15) - запись физических соотношений (11.3) или (11.7). С учетом этого, системы (11.4), (11.8) или (11.13) можно формально представить в виде
где  - некоторые операторы от указанных функций.
- некоторые операторы от указанных функций.
В рамках метода упругих решений разрешающее уравнение (11.17) - система линейных дифференциальных уравнений упругой задачи. На каждой итерации необходимо решать задачу о деформировании анизотропного континиуума. В сочетании с неаналитической зависимостью для жесткостей это определяет применение в основном дискретных методов решения задач: метода конечных элементов, метода конечных разностей и др.
Общий алгоритм решения задач методом упругих решений основан на аналогии между деформированием железобетона и упруго-пластических тел. Для последних доказано, что при соблюдении некоторых гипотез решение неупругой (нелинейной) задачи может быть заменено решением нелинейной упругой задачи. В свою очередь решение нелинейно упругой задачи можно получить как решением линейной: с переменными модулями упругости, начальными напряжениями и др. Соответственно и модификации метода упругих решений носят такие же наименования.
Для упруго-пластических тел при одноосном деформировании получено доказательство сходимости метода упругих решений при определенных ограничениях на кривизну кривой деформирования и при условии ее непрерывности и дифференцируемости. Сходимость метода упругих решений для железобетона с трещинами основывается на практике применения этого метода для решения задач и на применении ряда приемов ускорения сходимости, изложенных далее.
11.5 Метод переменных параметров упругости. Слабоитерационный метод переменных параметров упругости на приращениях нагрузки
Решение задачи сводится к процессу последовательных приближений с переменными параметрами упругости, определяемыми по формулам (11.16). В первом приближении полагают, что переменные параметры упругости равны начальным значениям и решение задачи сводится к решению обычной линейной задачи теории упругости. По решению линейной задачи определяются компоненты тензора напряжений  и деформаций
и деформаций  в первом приближении. Затем по формулам (11.16) в каждой точке континиуума определяются параметры
в первом приближении. Затем по формулам (11.16) в каждой точке континиуума определяются параметры  . Зная эти параметры, решают задачу во втором приближении с использованием полученных значений
. Зная эти параметры, решают задачу во втором приближении с использованием полученных значений  и определяют напряжения
и определяют напряжения 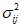 и деформации
и деформации  .
.
Расчеты продолжают до тех пор, пока полученные результаты расчетов n-го приближения не будут отличаться от результатов расчетов (n - 1)-го приближения на заданную величину с требуемой точностью.
Для упруго-пластического деформирования доказана сходимость такой процедуры, причем при выражении переменных параметров через деформации процесс последовательных приближений дает приближение сверху, и при пересчете параметров через напряжения процесс сходится к двухсторонним приближениям.
К недостаткам метода переменных параметров упругости относится то, что на каждой итерации приходится каждый раз решать системы линейных уравнений, а это самая трудоемкая операция в алгоритме. Улучшить сходимость этого метода можно также, применив его модификацию, известную в литературе под названием метода дополнительных нагрузок.
Для улучшения сходимости и снижения числа итераций можно использовать метод упругих решений на конечных приращениях. В этом случае нагрузка разбивается на несколько частей с точками 0, 1, 2, ..., 5. Сначала находится решение для начального отрезка 0-1. При слабой нелинейности на этом отрезке итерации практически исключаются. Состояние в точке 1 принимается за исходное. Затем рассматривается дополнительное напряженное состояние на отрезке 1-2. Расчет на приращении нагрузки 1-2 сводится к слабоитерационной или безитерационной процедуре. Затем за начальное состояние принимается нагружение приращением нагрузки в точке 2 на приращении 2-3. Решение на 2-3 тоже сводится к слабоитерационной процедуре (1-2 итерации). Таким образом доходим до полной нагрузки (условно в точке 5). Для этого метода физические соотношения сводятся к физическим соотношениям на соответствующих приращениях нагрузки (к физическим соотношениям на приращениях).
Этот метод применяется, когда разрешающая система уравнений составлена в напряжениях и компоненты матрицы жесткости материала выражены через деформации, т.е. в виде (11.16, а). В этом случае искомые напряжения представляются в виде разности
где 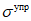 - напряжения в соответствующей упругой задаче;
- напряжения в соответствующей упругой задаче;
Дискретизированную разрешающую систему уравнений, полученную аппроксимацией систем (11.4), (11.8) или (11.13) конечными элементами или конечными разностями, можем записать:
где {x} - вектор-столбец неизвестных усилий или перемещений, определяется спецификой выбранного метода;
[k(x)] - матрица коэффициентов разрешающей системы уравнений;
{R} - вектор-столбец усилий.
Если принять, что слагаемые, возникшие из-за наличия дополнительных членов в (11.18) и перенесенных в правую часть (11.20), известны, то получим как бы систему уравнений теории упругости с дополнительными усилиями. В первом приближении полагаем, что все дополнительные усилия равны нулю. Тогда приходим к обычной задаче теории упругости, при решении которой определяются упругие напряжения (точка 1 на рисунке 11.1).
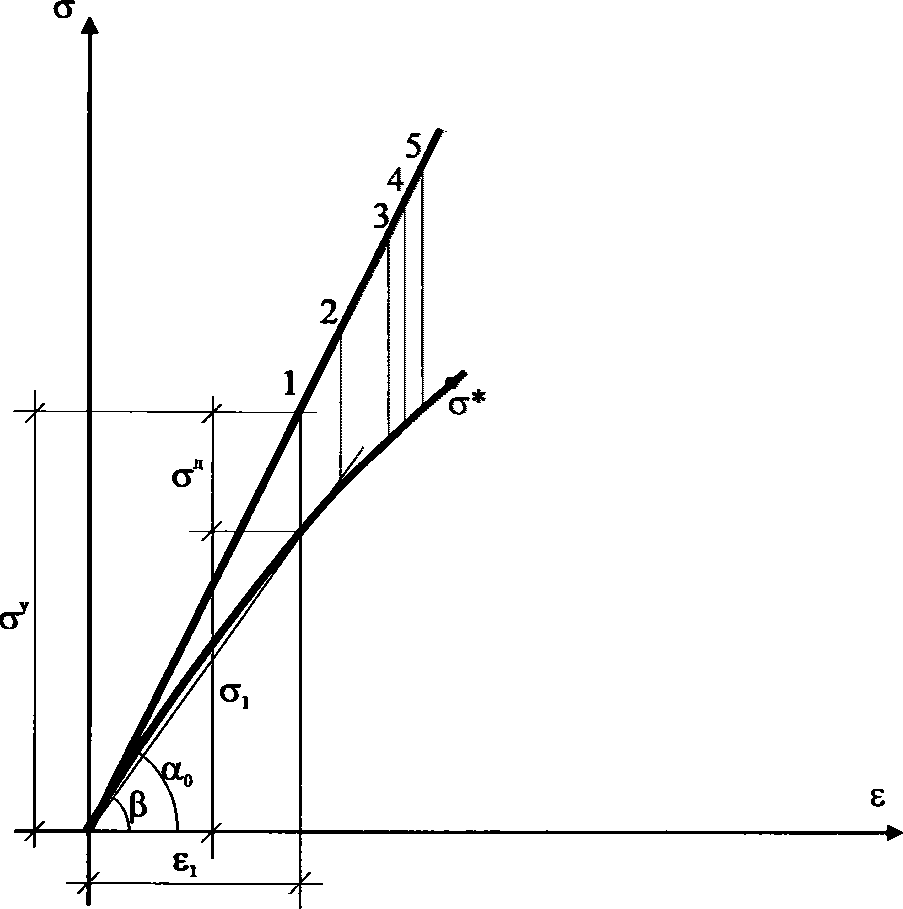
По начальным значениям матрицы жесткости и упругим напряжениям вычисляются деформации, одинаковые как для упругого, так и неупругого тела (на рисунке 11.1). По значениям полученных деформаций подсчитываются компоненты матрицы жесткости железобетона, а по ним вычисляются напряжения в неупругом состоянии.
Полученные значения напряжений, вообще говоря, и есть искомое решение задачи, однако эти напряжения не решение разрешающей системы, поэтому процесс последовательных приближений продолжается до удовлетворительной сходимости (точки 2-5 на рисунке 11.1). Таким образом, процедуру метода можно представить
 (11.21)
(11.21)С вычислительной точки зрения метод начальных напряжений значительно экономней метода переменных параметров упругости. При решении разрешающего уравнения один раз образуется матрица [k] и запоминается. Все дальнейшие решения получаются умножением обращенной матрицы на столбец свободных членов, при формировании которого производятся операции только с матрицами жесткости материала. Для упруго-пластических тел процесс сходится к искомому решению снизу. Для железобетонного континиуума (при использовании модели с трещинами) процесс может расходиться.
Для улучшения сходимости можно предложить следующее. При нагрузках, больших нагрузок образования трещин, в процессе решения необходимо проводить пересчет начальной матрицы [K]. Таким образом процедура будет содержать некоторую комбинацию методов начальных напряжений и переменных параметров упругости.
Процесс последовательных приближений считается законченным, если его результаты соответствуют некоторому критерию сходимости. В методе упругих решений основной критерий - критерий по перемещению. Так как критерий сходимости - величина безразмерная, он приводится к безразмерному виду делением на эталонную величину:
 (11.22)
(11.22)где max|ri| - максимальная величина перемещения;
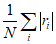 - средняя абсолютная величина.
- средняя абсолютная величина.Такой прием позволяет применять единые значения погрешностей.
Проверка сходимости может быть записана так:
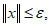
где ||x|| - норма невязки;
 .
.В качестве нормы невязки могут выступать:
- октаэдрическая норма
 (11.23)
(11.23)- евклидова норма
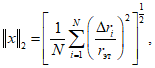 (11.24)
(11.24)- Чебышевская норма
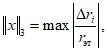 (11.25)
(11.25)здесь 1 <= i <= N - номер компоненты решения;
Если процесс сходится по одной норме, то он сходится и по любой другой норме. Выбор нормы определяет скорость сходимости. При равных условиях наибольшую скорость сходимости дает Евклидова норма, наименьшую - Чебышевская норма.
Могут быть выделены четыре основных метода: метод конечных разностей (МКР). Вариационно-разностный метод (ВРМ), метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). В расчетах железобетонных конструкций наибольшее распространение получили два метода: МКР и МКЭ.
Метод конечных разностей связан с непосредственной реализацией разностного оператора, соответствующего исходному дифференциальному уравнению задач. Эта процедура осуществляется на множестве точек (узлов) внутри области конструкции, в результате формируется система уравнений с матрицей коэффициентов, на полученную систему накладываются и граничные условия. Эти уравнения решаются прямым методом, если задача линейная, после чего итерациями для нелинейных случаев.
Применяемые разностные схемы должны соответствовать следующим требованиям: иметь определенный порядок аппроксимации, сходиться к решению исходных дифференциальных уравнений, быть устойчивыми и однородными.
Особенности применения МКР к расчету железобетонных элементов - нелинейный и разрывной характер их жесткости, что приводит к нелинейным и разрывным коэффициентам в дифференциальных уравнениях и их аппроксимациях. При этих условиях определяющее значение приобретает построение устойчивых, сходящихся и однородных разностных операторов. Под однородностью разностной схемы, когда для всех узлов разрешающее уравнение формируется по единообразному оператору, даже если эти узлы находятся вблизи функции жесткости.
Решение методом конечных разностей предлагает следующие этапы:
- формирование разностной сетки;
- формирование разностных операторов разрешающих уравнений;
- учет граничных условий;
- решение системы уравнений;
- вычисление усилий по перемещениям.
Для расчета с помощью МКР на рассматриваемый континиуум наносится разностная сетка.
Рассмотрим функцию f(x, y, z) и запишем выражения для производных этой функции через ее значения в узлах сетки с помощью конечных разностей. При этом могут потребоваться, в зависимости от конкретных условий, кроме основных узлов, еще и вспомогательные узлы. Хотя при применении таких узлов порядок погрешности 0(h2) не изменяется, но ошибка при этом будет меньше. Разности могут быть односторонние и центральные. Для примера приведем отдельные формулы для конечных разностей в виде (11.26), соответствующие рисунку 11.2.
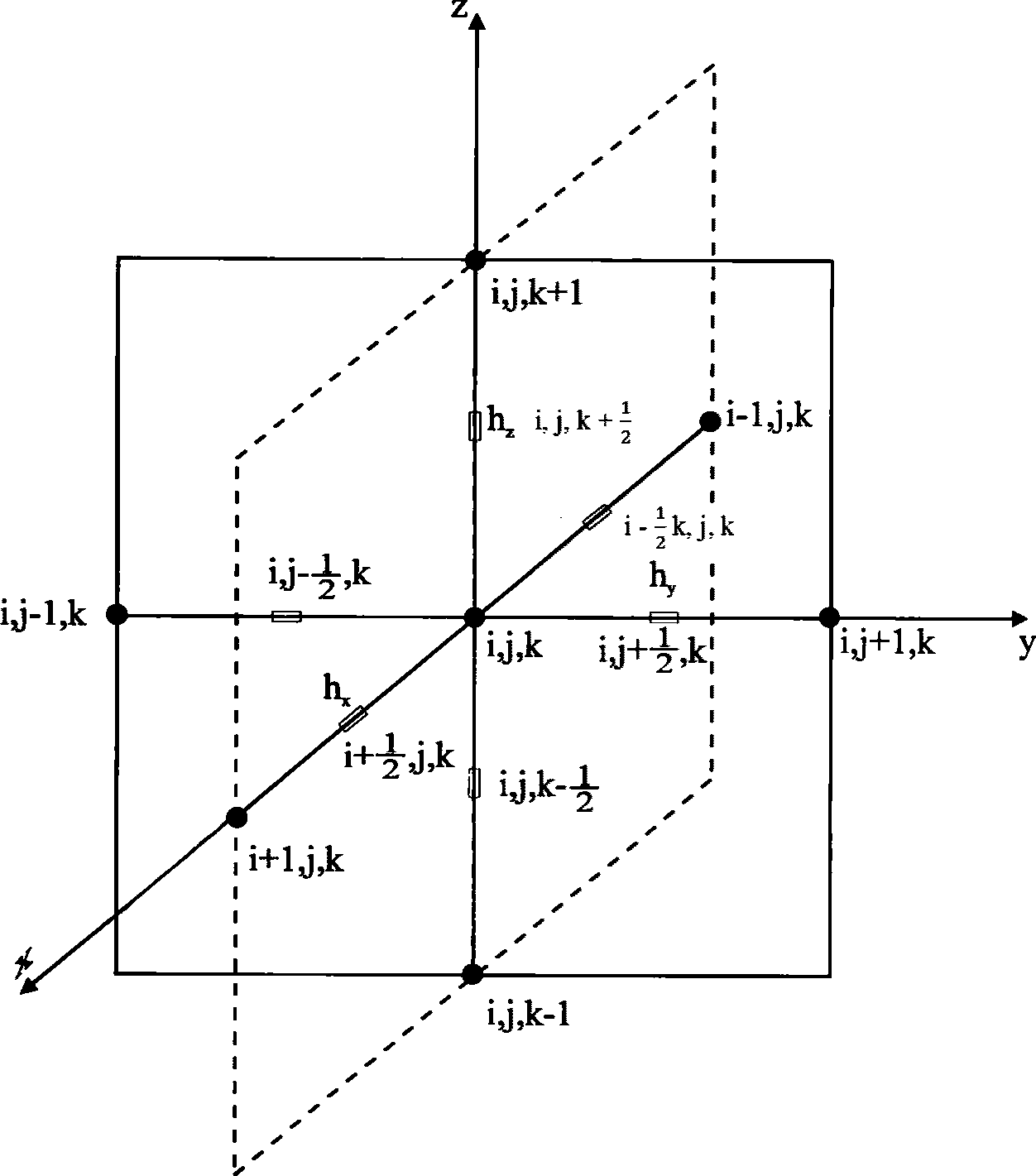
где 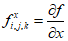 ,
, 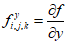 ,
, 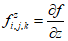 .
.
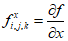 ,
, 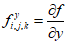 ,
, 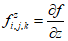 .
.В случае использования вспомогательных узлов преобразуются к виду
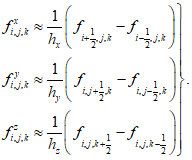 (11.27)
(11.27)Таким же образом выводятся частные производные высших порядков.
Существуют два способа построения системы разрешающих уравнений с использованием законтурных узлов и без них. При первом методе разрешающее уравнение составляется для всех узлов, включая контурные, для контурных же узлов записываются дополнительные граничные условия. Достоинство использования законтурных точек - однородность всей системы и, как следствие, меньшая трудоемкость при программировании. Недостаток такого подхода - увеличение размерности решаемых задач. Если отказаться от использования законтурных узлов, то разрешающие уравнения записываются только для внутриконтурных узлов, причем для предконтурных узлов приходится применять односторонние разности. Для контурных узлов записываются граничные условия. Такой подход, при уменьшении размерности, требует большей трудоемкости, нарушается однородность схемы, а также ухудшается обусловленность разрешающей системы уравнений. Поэтому метод с применением законтурных неизвестных представляется более предпочтительным.
Для построения устойчивой разностной схемы используется метод последовательного дифференцирования. Определяющее дифференциальное уравнение (уравнения равновесия для метода перемещений, уравнение совместности деформаций для метода сил) расписывается в конечных разностях для характерного узла сетки. Затем значение функций разрешающих уравнений в узлах заменяется их разностным представлением из физических уравнений. Получается разностный оператор, аппроксимирующий исходное дифференциальное уравнение. Совокупность узлов конечно-элементной сетки, разностного оператора называется шаблоном. При построении разностных схем для заданного порядка аппроксимации следует использовать минимальный шаблон, т.е. включать в разрешающее уравнение минимальное число узлов.
Принципиальная сущность конечно-элементарного анализа континуального тела заключается в следующем:
- исследуемая область делится воображаемой сеткой дискретизации на некоторое число конечных элементов, которые предполагаются взаимосвязанными в конечном числе узловых точек, расположенных на границах элементов. Обобщенные перемещения этих точек (их число неразрывно связано с принятым числом степеней свободы каждой узловой точки) представляют собой основные неизвестные параметры решаемой задачи, по аналогии с классическим методом перемещений;
- вводятся функции обобщенных перемещений, определяющие их распределение внутри каждого элемента через узловые обобщенные перемещения. Указанные функции однозначно определяют поле деформаций и усилий внутри элемента, в том числе на границах;
- на основании принципа возможных перемещений строится так называемая матрица жесткости элемента, посредством которой сосредоточенные реакции в узлах элемента, уравновешивающие распределенные нагрузки и усилия на его границах, выражаются через обобщенные узловые перемещения;
- матрицы жесткости отдельных элементов позволяют сформировать матрицу жесткости конструкции в целом, в результате чего задача сводится к решению системы линейных алгебраических уравнений относительно неизвестных узловых перемещений, определяющих вместе с выбранными функциями перемещений отдельных элементов напряженно-деформированное состояние всей конструкции.
Таким образом решение задачи нахождения напряженно-деформированного состояния тела легко алгоритмизируется с помощью МКЭ. Этим и объясняется широкое распространение МКЭ, вычислительные операции которого легко программируются и сводятся к решению системы линейных алгебраических уравнений.
11.13 Выбор функций формы, построение матрицы жесткости конечных элементов (КЭ) и разрешающей системы уравнений
Выбор функций формы зависит от ряда факторов, в том числе от формы КЭ и их размеров. Форма и размеры КЭ определяются размерами и формой рассчитываемого тела, условиями его закрепления, характером нагрузки и особенностями самого тела: наличием отверстий, щелей, вырезов и т.д.
Определяем вектор перемещений элемента {q}e в виде совокупности векторов перемещений каждого узла {g}i, i = 1, 2, ..., n. Перемещение 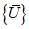 точек КЭ выражаем через узловые перемещения посредством функций формы
точек КЭ выражаем через узловые перемещения посредством функций формы
 (11.28)
(11.28)Функция формы должна соответствовать ряду требований, в том числе она должна быть такой, чтобы обеспечивать непрерывность деформаций по совокупности элементов и быть равной узловому перемещению при подстановке в нее координат узла.
Деформации точек внутри элемента с помощью функций формы выражаются через узловые перемещения
Вектор обобщенных напряжений выражается через деформации стандартным образом при отсутствии начальных деформаций и напряжений
где [D*] - матрица жесткости материала, определенная для железобетона в самом общем случае как матрица анизотропного материала с коэффициентами, зависящими от усилий, однако в пределах упругого расчета по одному из методов упругих решений, эти коэффициенты принимаются постоянными в пределах каждого КЭ (или меняются по заданному закону, зависящему от числа точек КЭ, в которых вычисляются 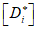 ).
).
Для объединения конечных элементов в ансамбль, отражающий совместность перемещений во всех узлах системы необходимо для каждого элемента уметь вычислять реакцию в любом узле по любой степени свободы от любого единичного узлового перемещения. Эти единичные реакции - коэффициенты матрицы жесткости элемента. Эта матрица строится на основе вариационных принципов и имеет вид
Для каждого конечного элемента между перемещениями узлов и узловыми усилиями существует следующая связь
{R}e = [K]e{q}e, (11.32)
где {R}e - вектор узловых сил по структуре аналогичный вектору узловых перемещений.
Вектор {R}e зависит от характера нагрузки и выбранной функции формы и вычисляется по формуле
 (11.33)
(11.33)где {P}e - внешняя нагрузка.
Далее следует процедура объединения КЭ (ансамблирование), суть которой сводится к приравниванию работы внутренних и внешних сил в узлах. При этом получается глобальная матрица жесткости:
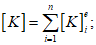 (11.34)
(11.34) (11.35)
(11.35)где n - число КЭ.
В итоге получается разрешающая система уравнений МКЭ
Учет кинематических граничных условий проводится после составления разрешающей системы уравнений. Если какое-то перемещение в каком-либо узле задано (в частности равно нулю), то система уравнений (11.36) соответственно модифицируется.
После решения (11.36), по (11.29) вычисляются деформации, по (11.30) напряжения в КЭ. Эти величины - решение задачи на K - итерации метода упругих решений, если речь идет о расчете железобетонных конструкций.
Чем больше степеней свободы имеет конструктивная система (в частности элементы принимаются более мелкие), тем точнее будет приближенное решение. Такое решение в пределе стремится к точному, соответствующему истинному равновесию. Число степеней свободы не ограничивается функцией формы [H]. Чтобы гарантировать сходимость процесса к точному, необходимо удовлетворять определенным критериям сходимости:
- функция формы должна быть выбрана, чтобы при смещении тела как жесткого целого в нем отсутствовали бы деформации;
- функция формы должна обеспечивать постоянство деформаций при соответствующих перемещениях;
- на границах элементов должна быть обеспечена непрерывность перемещений и их производных на порядок ниже, чем производные, входящие в формулу (11.31).
Пусть m - число узлов, которые аппроксимируют перемещения точек КЭ, а n - число узлов, определяющих геометрию КЭ. Конечные элементы классифицируют по этим двум параметрам следующим образом:
m = n - изопараметрический КЭ (рисунок 11.3, а);
m > n - субпараметрический КЭ (рисунок 11.3, б);
m < n - субпараметрический КЭ (рисунок 11.3, в).

Наиболее распространенные из этих КЭ - изопараметрические, ввиду простоты их реализации.
Вводятся две системы координат: локальная (r, s, t) или (x, y, z) и глобальная (X, Y, Z). Координаты и перемещения изопараметрических элементов могут быть определены в форме:
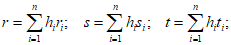 (11.37)
(11.37) (11.38)
(11.38)где ri, si, ti - локальные координаты узлов;
hi - интерполяционные функции;
Ui, Vi, Wi - перемещения узлов.
Заметим, что обычно функции hi задаются в локальной системе координат. В формулу (11.31) величина dV была введена безотносительно системы координат. Теперь уточним, что
 (11.40)
(11.40)где U - матрица Якоби.
где
[B] = [B1, B2, ..., Bn] (11.42)
здесь
Примеры объемных изопараметрических КЭ приведены на рисунке 11.4.

a - 4-узловой, b - 20-узловой
r0 = rir, s0 = sis, t0 = tit,
где r, s, t - текущие координаты,
ri, si, ti - координаты узлов
Из базового КЭ могут быть получены путем простого совмещения узлов другие виды КЭ, что особенно важно. Примеры КЭ приведены на рисунке 11.4. При этом пределы интегрирования остаются теми же. Функции формы совмещенных узлов складываются. Покажем на примере. Возьмем элемент из рисунка 11.4 и совместим попарно узлы 1-5, 2-6, 3-7, 4-8. В результате получается:
Легко заметить, значения Hi в (11.44) представляют функции формы для плоского изопараметрического КЭ. Более того, совместив H1 и H2, H3 и H4, получим функции формы одномерного двухузлового изопараметрического КЭ
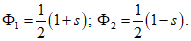 (11.45)
(11.45)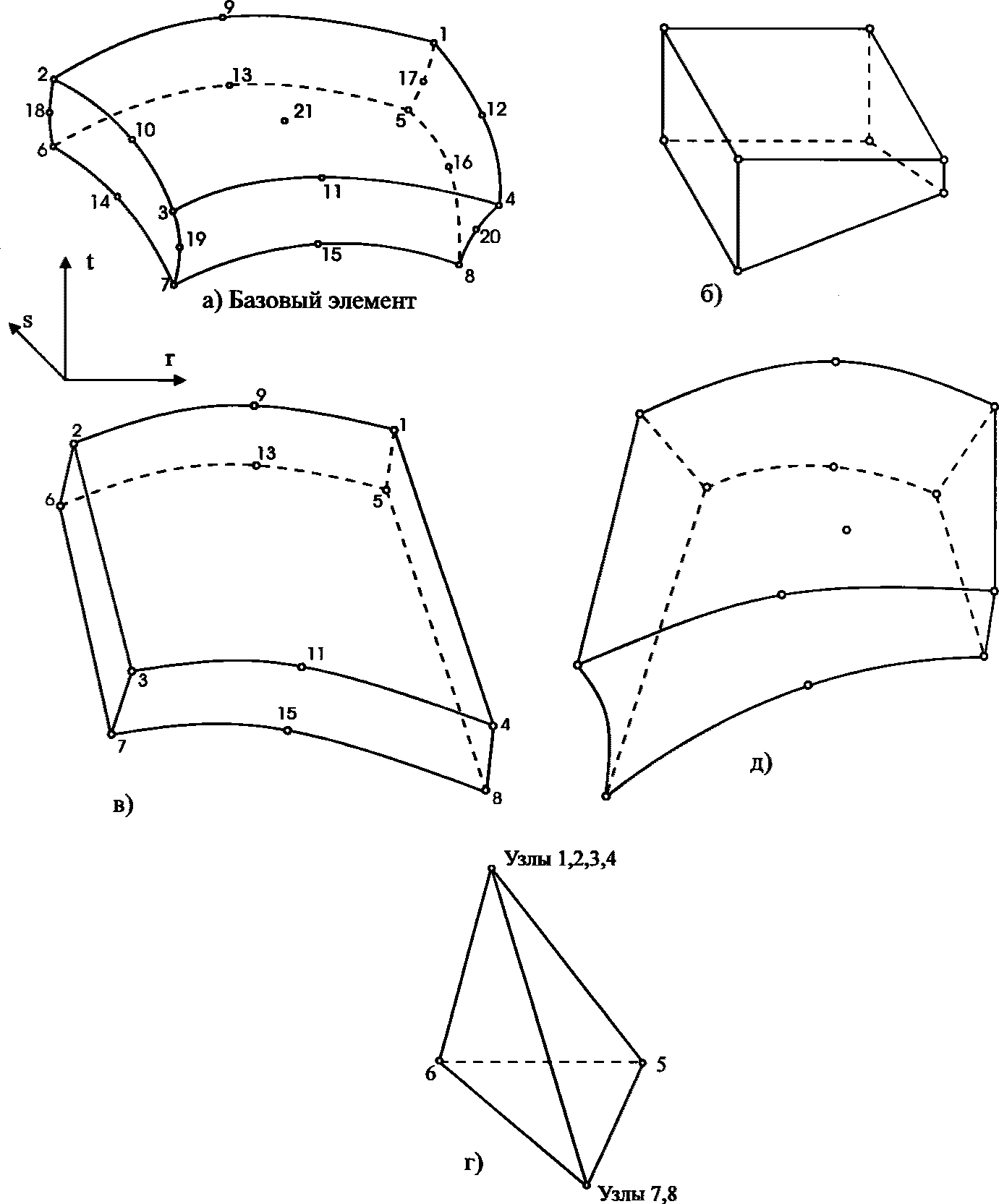
ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |
Рисунок 11.3 - Виды трехмерных элементов
Заметим, что вычисление интеграла (11.41) в явном виде в большинстве случаев затруднительно или невозможно. Обычно это интегрирование производят численно.
Одна из эффективных процедур численного интегрирования - использование квадратурных формул Гаусса. В этом случае применяется n неравноотстоящих узлов (точек) интегрирования, позволяющих строить точные интегралы полиномов (2n-1)-й степени. Коэффициенты полиномов численного интегрирования (коэффициенты Гаусса-Лежандра) для числа точек интегрирования вдоль каждой из осей r, s, t от одной до четырех приведены в таблице 11.1.
Число точек интегрирования на грани элемента | Абсциссы квадратур Гаусса-Лежандра | Весовые коэффициенты квадратур Гаусса-Лежандра | ||||||
1 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 |
2 | -0,57735027 | +0,57735027 | 0 | 0 | 1 | 1 | 0 | 0 |
3 | -0,77459667 | +0,77459667 | 0 | 0,55555556 | 0,88888889 | 0,55555556 | 0 | |
4 | -0,86113631 | -0,33998104 | +0,33998104 | +0,86113631 | 0,34785485 | 0,65214515 | 0,65214515 | 0,34785485 |
Алгоритм численного интегрирования выражения (11.41) - это алгоритм вычисления тройного интеграла: раскрытие формулы начинается с внутреннего интеграла, считая переменные, соответствующие внешним интегралам, константами. При этом из (11.41) получаем
Установив порядок интегрирования (общее количество точек интегрирования вдоль осей r, s, t) и координаты i-й точки интегрирования в локальных координатных осях как абсциссы квадратуры Гаусса-Лежандра, вычисляем матрицу Bi (11.43). Аналогично вычисляются матрицы Bj для j-й точки интегрирования. Определив веса квадратуры (согласно таблице 11.1) и определитель "detU" по формуле (11.46), будем иметь подматрицу Кij матрицы жесткости элемента. Пробегая по всем точкам интегрирования, сформируем полную матрицу K. Глобальная матрица жесткости системы образуется суммированием
 (11.47)
(11.47)где Ki - матрица жесткости i-го элемента.
Выбор коэффициентов в таблице 11.1 определяется принятым порядком интегрирования. Следует иметь в виду, что порядок интегрирования заметно влияет на результаты расчета. Применяя полиномы высокого порядка, можно получать точные значения матриц. Однако, с ростом точек интегрирования увеличиваются и затраты на вычисления. Приемлемые решения можно получить и при более низких порядках интегрирования, допуская некоторые погрешности.
11.17 Пример формирования матрицы жесткости прямоугольного восьмиузлового изопараметрического элемента
Функции формы восьми узлового конечного элемента (рисунок 11.4 а) запишем согласно выражениям:
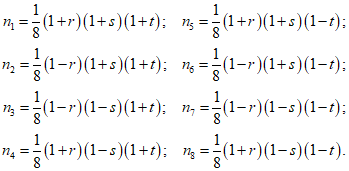 (11.48)
(11.48)Для принятого в форме прямоугольного параллелепипеда элемента положим соотношения сторон a = b = c = 1. В этом случае определитель матрицы Якоби detU = 1, а соотношения между локальными и глобальными координатами запишутся как:
r = x/a = x; s = y/b = y; t = z/c = z. (11.49)
Матрицу дифференциальных операторов (11.43) для первой точки интегрирования представим в виде:
 (11.50)
(11.50)Принимая порядок интегрирования (nrnsnt = 2 x 2 x 2), согласно таблице 11.1 записываем координаты точек интегрирования:
r = x = -0,5773502691896; s = y = -0,5773502691896;
t = z = -0,5773502691896.
Подставляя эти координаты в (11.50), получим матрицу B1. Матрица дифференциальных операторов (11.43) для второй точки интегрирования запишется:
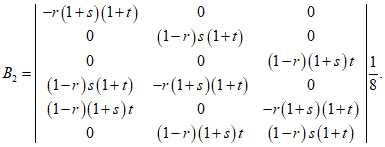 (11.51)
(11.51)Координаты второй точки интегрирования равны:
r = x = -0,5773502691869; s = y = -0,5773502691896;
t = z = -0,5773502691896.
Аналогично вычисляются матрицы Bi для всех точек интегрирования. Имея матрицы дифференциальных операторов, вычисляются подматрицы для точек интегрирования по формуле уравнения
 (11.52)
(11.52)где WtN - произведение весовых коэффициентов для соответствующих порядков интегрирования.
Произведения Wt для рассматриваемого случая представим в виде:
 (11.53)
(11.53)Таким образом формируется глобальная матрица жесткости системы.
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
Абсциссы и весовые коэффициенты квадратурных формул Гаусса-Лежандра
[1] СНиП 2.03.01-84 Бетонные и железобетонные конструкции. М. 1988.
[2] Пособие по расчету статически неопределимых железобетонных конструкций. - М.: Стройиздат, 1994.
[3] Кодекс-образец ЕКБ-ФИБ для норм по железобетонным конструкциям, 2004, 2010.
[4] Методическое пособие "Статически неопределимые железобетонные конструкции. Диаграммные методы автоматизированного расчета и проектирования". Федеральный центр нормирования, стандартизации и оценки соответствия в строительстве, М. 2017.
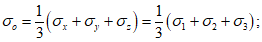
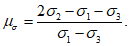


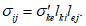

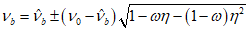

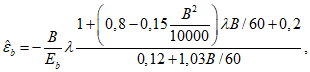
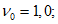
 (6.6)
(6.6)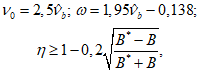








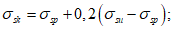
 (6.21)
(6.21)

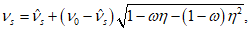
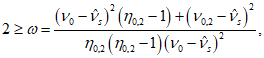
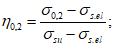
 (6.30)
(6.30)



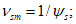
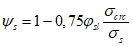
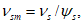


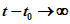
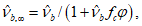
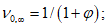
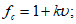

 ,
, 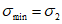 - главные напряжения.
- главные напряжения.
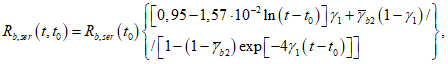
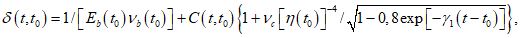



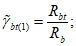

 ;
; 
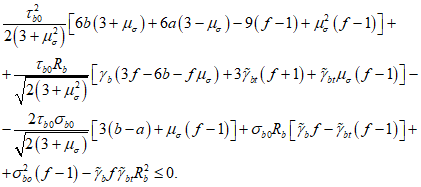
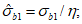
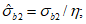
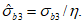 (7.16)
(7.16)

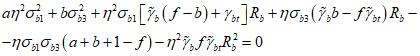



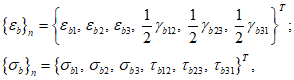

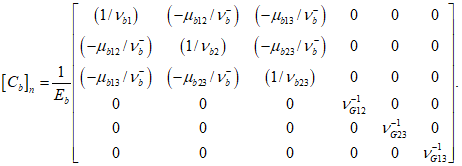

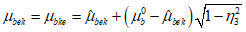
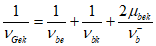
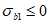 и область
и область  .
.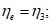
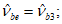
 (8.9)
(8.9)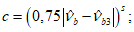
 (8.10)
(8.10)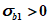 (смешанных напряжений и всестороннего растяжения)
(смешанных напряжений и всестороннего растяжения)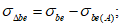
 (e = 1, 2, 3). (8.12)
(e = 1, 2, 3). (8.12)



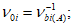
 (8.18)
(8.18)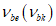 на
на  ,
, 
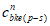 - элементы матрицы, определяемые через элементы
- элементы матрицы, определяемые через элементы 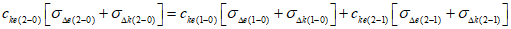
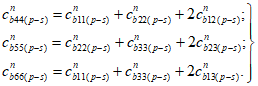
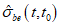 вычисляют по
вычисляют по  , где
, где
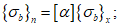
 (8.31)
(8.31)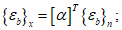
 (8.32)
(8.32)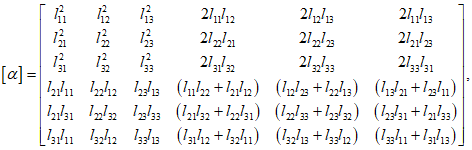



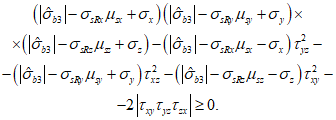
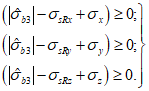



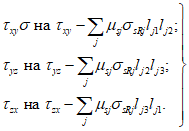



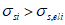 - упруго-пластическая (величины
- упруго-пластическая (величины 
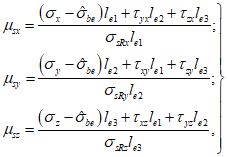
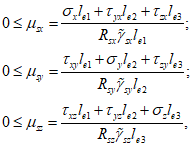




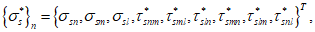


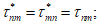
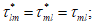
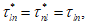 (10.16)
(10.16)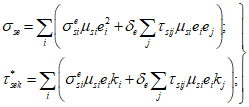
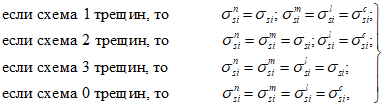



 (10.25)
(10.25)
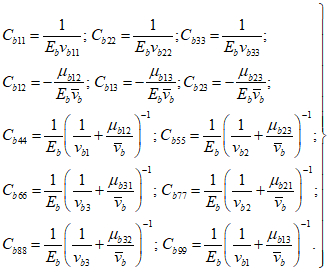


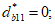
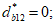
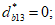
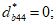
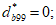 (10.34)
(10.34)
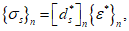



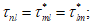
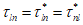 (10.46)
(10.46)
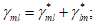
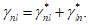 (10.47)
(10.47)


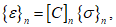


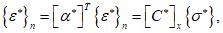







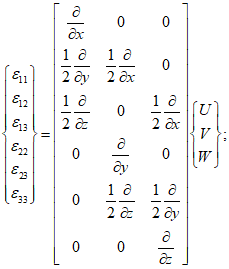
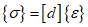
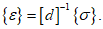 (11.3)
(11.3)