СПРАВКА
Источник публикации
Документ опубликован не был
Примечание к документу
Название документа
"МИ 860-85. Методические указания. Государственная система обеспечения единства измерений. Вольтметры цифровые. Алгоритмы автоматизированной поверки"
(утв. ВНИИМИУС 15.05.1985)
"МИ 860-85. Методические указания. Государственная система обеспечения единства измерений. Вольтметры цифровые. Алгоритмы автоматизированной поверки"
(утв. ВНИИМИУС 15.05.1985)
Содержание
ВНИИМИУС
15 мая 1985 года
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
ВОЛЬТМЕТРЫ ЦИФРОВЫЕ.
АЛГОРИТМЫ АВТОМАТИЗИРОВАННОЙ ПОВЕРКИ
МИ 860-85
РАЗРАБОТАНЫ Всесоюзным научно-исследовательским институтом метрологии измерительных и управляющих систем (ВНИИМИУС) НПО "Система"
ИСПОЛНИТЕЛИ:
Владимиров В.Л. (руководитель темы), Кривохиж И.Ю., Лапичак И.Е., Янишевский И.В.
ПОДГОТОВЛЕНЫ К УТВЕРЖДЕНИЮ Отделом автоматизации поверочных работ ВНИИМИУС
Начальник отдела Г.В. Кучеров, начальник сектора В.Л. Владимиров, инженер И.Ю. Кривохиж
УТВЕРЖДЕНЫ ВНИИМИУС 15 мая 1985 г.
Настоящие методические указания распространяются на программное обеспечение автоматизированных систем поверки средств измерений (АСП СИ), предназначенных для поверки цифровых вольтметров (ЦВ) и (или) комбинированных (универсальных) цифровых измерительных приборов, имеющих цифровой выход (выходной код) и измеряющих постоянные напряжение и (или) силу тока, действующие (эффективные, средние квадратические) и средневыпрямленные значения переменного напряжения и (или) силы тока, активное сопротивление постоянному току.
1.1. Настоящие методические указания допускается использовать для автоматизации процесса метрологической аттестации перечисленных выше цифровых СИ.
1.2. Рекомендации методических указаний не распространяются на программное обеспечение АСП следующих СИ, не имеющих выходного кода; с нормированной вариацией показаний, со ступенью квантования, меньшей десятикратного значения ступени квантования образцовой меры - средства поверки.
1.3. Результаты поверки по настоящим методическим указаниям действительны лишь в случае использования аттестованной (поверенной) АСП СИ.
1.4. Настоящие методические указания устанавливают методику проведения тех операций первичной (при выпуске из производства и ремонта), периодической и внеочередной поверки, которые могут быть автоматизированы на базе применения входящих в состав АСП СИ средств вычислительной техники.
1.5. В методические указания не включены описания операций поверки, производимых вручную (внешний осмотр, опробование и др.), а также выбора средств поверки и контролируемых точек, поэтому разработчики программного обеспечения АСП должны использовать, кроме настоящих методических указаний, НТД на поверяемые ЦВ, а также ГОСТ 14014-82, МИ 118-77.
1.6. Использованные в методических указаниях термины соответствуют ГОСТ 14014-82, ГОСТ 15895-77 (СТ СЭВ 547-77), ГОСТ 8.042-83, ГОСТ 8.207-76, ГОСТ 8.061-80.
ИС МЕГАНОРМ: примечание. Взамен ГОСТ 22261-82 Постановлением Госстандарта России от 15.05.1995 N 250 с 01.01.1996 введен в действие ГОСТ 22261-94. |
2.1. При проведении автоматизированной поверки ЦВ следует соблюдать условия, указанные в ГОСТ 22261-82, ГОСТ 14014-82, эксплуатационной документации на АСП СИ, стандартах и (или) технических условиях на поверяемые цифровые средства измерений.
2.2. Перед проведением автоматизированной поверки оператор АСП СИ должен ввести в оперативную память ЭВМ тип поверяемого ЦВ. После этого все ручные операции поверки должны выполняться оператором по командам ЭВМ, высвечиваемым на экране дисплея. Указанные команды, записанные в машинной программе поверки данного типа ЦВ, должны раскрывать содержание ручных операций таким образом, чтобы исключить необходимость пользования эксплуатационной документацией на поверяемый ЦВ и сделать поверку безбумажной.
Комплект машинных программ поверки конкретных типов ЦВ хранится в долговременной памяти ЭВМ, входящей в состав АСП СИ.
2.3. Машинная программа поверки конкретного типа ЦВ должна включать (кроме содержания ручных и автоматических операций поверки) данные о типе ЦВ и данные о средстве его поверки (программно-управляемой многозначной мере, входящей в состав АСП СИ).
обозначение типа, наименование поверяемого прибора;
вид зависимости систематической составляющей погрешности ЦВ от измеряемой величины (непрерывная или с разрывами);
содержание всех ручных операций (ввода данных о конкретном экземпляре ЦВ, внешнего осмотра, опробования с проверкой отсчетного устройства и выходного разъема, проверки электрической прочности изоляции, установки органов управления ЦВ - при необходимости);
виды измерений (измеряемые физические величины);
диапазоны измерений с указанием основного (основных);
способы управления выбором вида и диапазона измерений (ручной, автоматический или дистанционный);
значения уровней основных входных сигналов в контролируемых точках (для положительной и отрицательной полярностей или для различных частот измеряемой величины);
значение напряжения калибровки ЦВ;
значения частот входных сигналов для поверки на переменном токе;
формула расчета основной допускаемой погрешности со значениями коэффициентов для всех диапазонов и частот;
формула расчета коэффициента Стьюдента со значениями коэффициентов (для оценки погрешности в контролируемой точке);
значения ступени квантования для всех пределов измерений;
формулы расчета контрольного допуска и его коэффициентов для равномерного и трапециевидного распределений;
максимальное значение времени измерения (преобразования);
формы выходных документов поверки;
тип средства поверки данного ЦВ.
2.3.2. Основные данные о средствах поверки:
обозначение типа;
пределы воспроизведения физической величины;
частоты воспроизводимых сигналов;
максимальное значение времени установления выходных сигналов;
формула расчета основной допускаемой погрешности со значениями коэффициентов для всех диапазонов и частот;
способы управления выбором вида и предела воспроизводимой величины (ручной, автоматический или дистанционный).
2.4. О завершении каждой ручной операции оператор должен сообщать ЭВМ путем подачи сигнала через клавиатуру дисплея ЭВМ или выносной пульт оператора.
Следующая (после ручной) операция может выполняться только после того, как ЭВМ примет упомянутый сигнал оператора.
2.5. В случае отрицательных результатов выполнения очередной ручной операции (внешнего осмотра, опробования или проверки электрической прочности изоляции) оператор должен подать соответствующий сигнал ("Брак по внешнему осмотру", "Брак по опробованию" или "Брак по проверке изоляции") в закодированной форме, после чего ЭВМ автоматически выдаст справку установленного образца с указанием причины бракования.
2.6. Определение метрологических характеристик, обработка результатов наблюдений и оформление результатов поверки производятся автоматически.
2.7. Перед выполнением автоматических операций ЭВМ должна запросить оператора, в каком из трех возможных режимов будет производиться работа:
с выдачей протокола поверки на печать и на экран дисплея;
с выдачей протокола только на экран дисплея;
без выдачи протокола.
Оператор задает режим путем подачи соответствующего сигнала в кодированной форме.
2.8. Перед выполнением автоматических операций ЭВМ должна сделать запрос, в каком из двух следующих режимов будет производиться поверка:
до первой контролируемой точки, в которой будет обнаружен брак;
во всех контролируемых точках всех диапазонов измерений.
Оператор задает режим путем подачи соответствующего сигнала в кодированной форме.
2.9. Вмешательство оператора в ход поверки недопустимо, за исключением случая сбоя по вине оператора или большого числа отказов какого-либо одного диапазона измерений при поверке партии однотипных приборов. В последнем случае оператор должен иметь возможность прервать поверку и начать ее с определенного диапазона измерений в целях экономии времени поверки.
2.10. При использовании настоящих методических указаний для автоматизации процессов метрологической аттестации цифровых приборов следует предусмотреть возможность останова программы оператором в любой момент времени, повтора испытаний в данной контролируемой точке, перехода на любую другую контролируемую точку любого диапазона и вида измерений.
2.11. Состояние поверяемого ЦВ оценивают путем автоматического осуществления статистического приемочного контроля по альтернативному и количественному признакам (ГОСТ 15895-77). При этом используются последовательный контроль (ПК) и трехступенчатый контроль (ТК).
Примечание. Определения основных терминов статистического контроля качества продукции, использованных в настоящих методических указаниях, приведены в справочном приложении 1.
2.12. В качестве МХ поверяемого ЦВ используются характеристики его погрешности  , а также систематической
, а также систематической 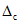 и случайной
и случайной 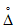 составляющих погрешности ЦВ.
составляющих погрешности ЦВ.
Погрешность поверяемого ЦВ определяют методом прямых измерений с многократными наблюдениями физической величины, воспроизводимой программно-управляемой образцовой многозначной мерой, входящей в состав АСП СИ.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: стандарт имеет номер ГОСТ 15895-77, а не ГОСТ 15995-77. |
усиленный контроль (УК);
нормальный контроль (НК);
ослабленный контроль (ОК).
По запросу ЭВМ оператор задает один из этих трех режимов перед осуществлением автоматических операций поверки путем подачи соответствующего сигнала в кодированной форме.
Рекомендации по применению режимов статистического приемочного контроля:
Режимы метрологического обеспечения ЦВ | Режимы статистического приемочного контроля |
Поверка исходных образцовых СИ . . . . . . . . . . . . . . . . . . . . | УК |
То же, образцовых СИ . . . . . . . . . . . | УК |
" , рабочих СИ, связанных с проведением ответственных измерений . . . . . . | УК |
" , рабочих СИ . . . . . . . . . . . . | НК |
Предремонтная проверка состояния ЦВ и настройка ЦВ . . | ОК |
2.14. Усиленный контроль по п. 2.13 - это последовательный контроль, в основу которого положено значение P = 0,99 доверительной вероятности определения доверительных границ погрешности результата измерений напряжения поверяемым ЦВ (см. справочное приложение 2).
УК производится одновременно и по альтернативному, и по количественному признакам. Это означает, что при УК осуществляется и ПК, и сравнение вычисленной оценки погрешности измерений в данной контролируемой точке с контрольным допуском. Если результаты ПК ("Годен" или "Брак") и контроля по количественному признаку ("Годен" или "Брак") не совпадают, УК в данной точке повторяется. Результат повтора считается окончательным, и ЦВ признается годным только при результатах "Годен-Годен". Таким образом ослабляется влияние случайных импульсных помех и сбоев в цифровой аппаратуре АСП СИ на результат поверки.
При УК гарантируется высокая достоверность результатов поверки (вероятность правильного вывода о состоянии поверяемого ЦВ, оцениваемая с учетом неидеальности методики и средств поверки), которая в любой контролируемой точке будет не менее 96%.
2.15. Нормальный контроль по п. 2.13 - это последовательный контроль, в основу которого положено значение P = 0,95 доверительной вероятности определения доверительных границ погрешности результата измерения напряжения поверяемым ЦВ (см. приложение 2). В остальном НК не отличается от УК по п. 2.14.
При НК гарантируется достоверность результатов поверки в любой контролируемой точке не менее 72%.
2.16. Ослабленный контроль по п. 2.13 - это статистический приемочный контроль поверяемого ЦВ, характеризующийся тем, что при наличии у ЦВ существенной случайной составляющей погрешности используется последовательный контроль для случая P = 0,95, а при отсутствии у ЦВ существенной случайной составляющей погрешности используется трехступенчатый контроль (всего три наблюдения погрешности в контролируемой точке).
При ОК достоверность результатов поверки - не менее 72%.
2.17. В каждой контролируемой точке при применении любого из трех режимов статистического приемочного контроля (УК, НК или ОК) автоматическое определение МХ начинается с осуществления следующих вспомогательных автоматических операций поверки:
подачи входного сигнала;
оценки окончания переходного процесса.
2.18. В справочном приложении 3 приведен пример блок-схемы общего алгоритма автоматизированной поверки.
3.1. Для учета погрешности квантования и возможной вариации показаний ЦВ на его вход с выхода программно-управляемой образцовой меры подается сигнал Ai (далее называемый "Входным сигналом"), который в каждой контролируемой точке изменяется в пределах 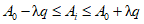 сначала в сторону увеличения, затем в сторону уменьшения, в каждом наблюдении изменяя свой уровень (на +/- 0,1q - для режима ПК и на +/- 0,5q - для режима ТК), где Ai - текущее значение входного сигнала в i-м наблюдении; A0 - значение основного входного сигнала в контролируемой точке; q - значение ступени квантования диапазона, которому принадлежит контролируемая точка;
сначала в сторону увеличения, затем в сторону уменьшения, в каждом наблюдении изменяя свой уровень (на +/- 0,1q - для режима ПК и на +/- 0,5q - для режима ТК), где Ai - текущее значение входного сигнала в i-м наблюдении; A0 - значение основного входного сигнала в контролируемой точке; q - значение ступени квантования диапазона, которому принадлежит контролируемая точка; 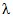 - постоянный коэффициент, равный 1,1 - для УК, 1,0 - для НК и 0,5 - для ТК.
- постоянный коэффициент, равный 1,1 - для УК, 1,0 - для НК и 0,5 - для ТК.
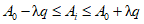 сначала в сторону увеличения, затем в сторону уменьшения, в каждом наблюдении изменяя свой уровень (на +/- 0,1q - для режима ПК и на +/- 0,5q - для режима ТК), где Ai - текущее значение входного сигнала в i-м наблюдении; A0 - значение основного входного сигнала в контролируемой точке; q - значение ступени квантования диапазона, которому принадлежит контролируемая точка;
сначала в сторону увеличения, затем в сторону уменьшения, в каждом наблюдении изменяя свой уровень (на +/- 0,1q - для режима ПК и на +/- 0,5q - для режима ТК), где Ai - текущее значение входного сигнала в i-м наблюдении; A0 - значение основного входного сигнала в контролируемой точке; q - значение ступени квантования диапазона, которому принадлежит контролируемая точка; 3.2. Значение A0 основного входного сигнала в конкретной контролируемой точке по п. 3.1 для ЦВ с непрерывной зависимостью систематической составляющей погрешности от измеряемой величины равно непосредственно тому значению уровня входного сигнала, которое указано в основных данных о типе ЦВ по п. 2.3.1 и соответствует требованиям НТД на ЦВ.
3.3. Значение A0 основного входного сигнала в контролируемой точке по п. 3.1 для ЦВ с зависимостью систематической составляющей погрешности от измеряемой величины, имеющей разрывы, определяется следующим образом.
Вначале на вход ЦВ подается так называемый пробный сигнал, значение 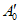 которого определяется указанным в НТД на ЦВ числом единиц младшего десятичного разряда. Например, если в контролируемой точке показание ЦВ должно быть равным 9995, а значение ступени квантования для контролируемого диапазона равно 10-6 В, то искомый выходной десятичный код в контролируемой точке равен B0 = 9995·10-6 В = 9,995 мВ, и значение пробного сигнала равно A0 = 9,995 мВ.
которого определяется указанным в НТД на ЦВ числом единиц младшего десятичного разряда. Например, если в контролируемой точке показание ЦВ должно быть равным 9995, а значение ступени квантования для контролируемого диапазона равно 10-6 В, то искомый выходной десятичный код в контролируемой точке равен B0 = 9995·10-6 В = 9,995 мВ, и значение пробного сигнала равно A0 = 9,995 мВ.
После подачи на вход ЦВ пробного сигнала уровня 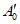 производится оценка окончания переходного процесса в цепи "выход образцовой меры - вход поверяемого ЦВ" в соответствии с указаниями разд. 4. Как только переходный процесс практически завершится, считывается реальный выходной десятичный код
производится оценка окончания переходного процесса в цепи "выход образцовой меры - вход поверяемого ЦВ" в соответствии с указаниями разд. 4. Как только переходный процесс практически завершится, считывается реальный выходной десятичный код 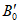 поверяемого ЦВ и сравнивается с искомым кодом B0. Если эти коды не равны, на вход ЦВ подается (один раз) исправленный на значение разности
поверяемого ЦВ и сравнивается с искомым кодом B0. Если эти коды не равны, на вход ЦВ подается (один раз) исправленный на значение разности 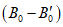 сигнал
сигнал 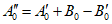 .
.
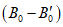 сигнал
сигнал 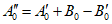 .
.Если потребуется, коррекция входного сигнала повторяется несколько раз. Процесс поиска значения A0 путем последовательного приближения к искомому выходному коду останавливается, как только код на выходе ЦВ станет равным B0. Соответствующее этому наблюдению значение выходного сигнала принимается равным основному входному сигналу A0.
Если процесс поиска значения A0 не завершится в течение времени, равного значению времени задержки по п. 4.3, значение искомого выходного кода принимается равным B0, уменьшенному на одну единицу младшего разряда.
Пример. Определяется значение A0 основного входного сигнала для ЦВ типа Щ1412 в точке B0 = 0010. По команде ЭВМ с выхода программно-управляемого калибратора на вход ЦВ многократно подается пробный сигнал уровня 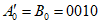 . После практического окончания переходного процесса с выхода ЦВ считан код B0 = 0012. Затем на вход ЦВ с выхода калибратора однократно подается исправленный сигнал уровня
. После практического окончания переходного процесса с выхода ЦВ считан код B0 = 0012. Затем на вход ЦВ с выхода калибратора однократно подается исправленный сигнал уровня 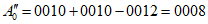 .
.
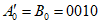 . После практического окончания переходного процесса с выхода ЦВ считан код B0 = 0012. Затем на вход ЦВ с выхода калибратора однократно подается исправленный сигнал уровня
. После практического окончания переходного процесса с выхода ЦВ считан код B0 = 0012. Затем на вход ЦВ с выхода калибратора однократно подается исправленный сигнал уровня 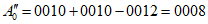 .
.Вторично оценивать окончание переходного процесса не требуется. Теперь на выходе ЦВ получен искомый код B0 = 0010. Следовательно, 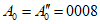 .
.
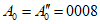 .
.3.4. Текущие значения входного сигнала для режима УК рассчитываются по формуле
где i = 1, 2, ..., 44.
3.5. Текущие значения входного сигнала для режима НК рассчитываются по формуле
где i = 1, 2, ..., 40.
3.6. Текущие значения входного сигнала для режима ТК рассчитываются по формуле
где i = 1, 2, 3.
3.7. В справочном приложении 4 приведен пример блок-схемы алгоритма подачи входного сигнала при автоматизированной поверке ЦВ.
4.1. При автоматизированной поверке изменение входного сигнала для перехода в новую контролируемую точку осуществляется скачкообразно. При этом код на выходе ЦВ, соответствующий данной контролируемой точке, устанавливается не сразу. Это объясняется наличием определенного времени установления сигнала у образцовой меры и инерционностью ЦВ.
Для уменьшения вероятности ошибки при поверке в каждой контролируемой точке после подачи основного входного сигнала A0 (для ЦВ с непрерывной зависимостью систематической составляющей погрешности от измеряемой величины) или пробного входного сигнала 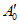 (для ЦВ с зависимостью систематической составляющей погрешности от измеряемой величины) нужно использовать задержку во времени или производить оценку окончания переходного процесса в цепи "выход образцовой меры - вход ЦВ".
(для ЦВ с зависимостью систематической составляющей погрешности от измеряемой величины) нужно использовать задержку во времени или производить оценку окончания переходного процесса в цепи "выход образцовой меры - вход ЦВ".
4.2. Одновременно с подачей основного входного сигнала A0 по п. 3.2 или пробного сигнала 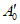 по п. 3.3 включается таймер, входящий в состав АСП СИ.
по п. 3.3 включается таймер, входящий в состав АСП СИ.
максимальному значению времени установления Tу сигналов на выходе образцовой меры, если максимальное значение времени измерения Tи поверяемым ЦВ не превышает 1/3 от Tу,
полуторакратному значению Tу, если значение Tи равно или превышает 1/3 от Tу.
4.4. Для уменьшения времени автоматизированной поверки допускается производить оценку реального времени переходного процесса в цепи "выход образцовой меры - вход поверяемого ЦВ". Оценивать окончание переходного процесса можно следующим образом.
С выхода ЦВ после подачи на его вход сигнала A0 или 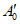 считываются коды. Считывание производится до тех пор, пока не будут выявлены три следующих друг за другом кода B1, B2 и B3, у которых модули разностей |B2 - B1|, |B3 - B2| и |B3 - B1| не превышают nед младшего разряда (nед >= 0). Значение nед устанавливается для каждого конкретного типа ЦВ. Рекомендуется принимать nед = 0 при поверке ЦВ на постоянном токе и nед = 1 при поверке ЦВ на переменном токе. Для ЦВ с нормированной случайной составляющей погрешности допускается устанавливать другие значения nед.
считываются коды. Считывание производится до тех пор, пока не будут выявлены три следующих друг за другом кода B1, B2 и B3, у которых модули разностей |B2 - B1|, |B3 - B2| и |B3 - B1| не превышают nед младшего разряда (nед >= 0). Значение nед устанавливается для каждого конкретного типа ЦВ. Рекомендуется принимать nед = 0 при поверке ЦВ на постоянном токе и nед = 1 при поверке ЦВ на переменном токе. Для ЦВ с нормированной случайной составляющей погрешности допускается устанавливать другие значения nед.
Переходный процесс в данной контролируемой точке считается законченным после считывания последнего из трех упомянутых кодов, т.е. B3. Если время на поиск этих трех кодов достигло значения времени задержки из п. 4.3, переходный процесс считается законченным.
4.5. После окончания переходного процесса на вход ЦВ для реализации ПК подаются изменяющиеся в соответствии с формулами (3.1), (3.2) и (3.3) текущие значения сигналов Ai, нумерация которых в каждой точке начинается с i = 1.
4.6. В процессе измерения МХ (с многократными наблюдениями в каждой контролируемой точке) изменения входных сигналов по уровню должны осуществляться таким образом, чтобы при переходе от Ai к Ai+1 ко входу ЦВ было постоянно приложено напряжение с уровнем, не меньшим A1. Сброс этого напряжения привел бы к необходимости оценки окончания переходного процесса при каждом наблюдении, что снизило бы эффективность автоматизированной поверки.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
4.6. В справочном приложении 5 приведен пример блок-схемы алгоритма оценки окончания переходного процесса.
После окончания переходного процесса в режиме усиленного и нормального контроля в каждой контролируемой точке осуществляется ПК. Ниже описан процесс ПК в одной контролируемой точке.
где Bi - текущее значение выходного кода ЦВ.
5.2. В каждом i-м наблюдении вычисляются и запоминаются суммы 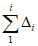 и
и 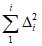 текущих значений и квадратов текущих значений погрешности.
текущих значений и квадратов текущих значений погрешности.
где 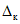 - контрольный допуск, значение которого высчитывается ЭВМ для каждой контролируемой точки.
- контрольный допуск, значение которого высчитывается ЭВМ для каждой контролируемой точки.
5.4. Значение контрольного допуска из п. 5.3 определяется по формуле
где 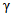 - коэффициент контрольного допуска (см. пп. 5.5, 5.6 и 5.19);
- коэффициент контрольного допуска (см. пп. 5.5, 5.6 и 5.19); 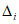 - значение допускаемой абсолютной погрешности ЦВ, высчитываемое ЭВМ для каждой контролируемой точки на основании данных о типе ЦВ.
- значение допускаемой абсолютной погрешности ЦВ, высчитываемое ЭВМ для каждой контролируемой точки на основании данных о типе ЦВ.
Примечание. Если в данных о типе ЦВ допускаемая погрешность задана в виде формулы для относительной погрешности, значение допускаемой абсолютной погрешности определяется как произведение значений относительной погрешности (в относительных единицах) и измеряемого напряжения.
для трапециевидной функции распределения систематической и случайной составляющих погрешности измерений по формуле
для равномерной функции распределения систематической составляющей погрешности измерений по формуле
где 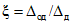 - отношение допускаемой абсолютной (или относительной) погрешности образцового средства поверки (меры) к допускаемой абсолютной (или относительной) погрешности поверяемого ЦВ.
- отношение допускаемой абсолютной (или относительной) погрешности образцового средства поверки (меры) к допускаемой абсолютной (или относительной) погрешности поверяемого ЦВ.
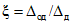 - отношение допускаемой абсолютной (или относительной) погрешности образцового средства поверки (меры) к допускаемой абсолютной (или относительной) погрешности поверяемого ЦВ.
- отношение допускаемой абсолютной (или относительной) погрешности образцового средства поверки (меры) к допускаемой абсолютной (или относительной) погрешности поверяемого ЦВ.для трапециевидной функции распределения систематической и случайной составляющих погрешности измерения по формуле
для равномерной функции распределения систематической составляющей погрешности измерения по формуле
5.7. В методе ПК организуется счетчик числа X выходов текущих значений погрешности по п. 5.1 за значения контрольного допуска по п. 5.4.
Для этого в каждом наблюдении, в котором не выполняется неравенство (5.2) из п. 5.3, число X увеличивается на единицу. Если неравенство (5.2) соблюдается, число X остается неизменным.
5.8. Число X по п. 5.7 характеризует состояние МХ поверяемого ЦВ и является статистическим показателем качества последнего. Этот показатель в ходе ПК сравнивается с контрольными нормативами ПК: приемочным числом C и браковочным числом R (ГОСТ 15895-77).
5.9. Приемочное число по п. 5.8 является функцией числа проведенных наблюдений и на каждом i-м наблюдении определяется:
для усиленного контроля по формуле
для нормального контроля по формуле
5.10. Браковочное число по п. 5.8 является функцией числа проведенных наблюдений и на каждом i-м наблюдении определяется:
для усиленного контроля по формуле
для нормального контроля по формуле
5.11. В каждом наблюдении, в котором выполняется неравенство (5.2) из п. 5.3, по формулам (5.8) или (5.9) п. 5.9 вычисляется приемочное число и проверяется справедливость неравенства
Если неравенство (5.12) соблюдается, ПК заканчивается с результатом "Годен по ПК". При невыполнении неравенства (5.12) ПК продолжается.
5.12. В каждом наблюдении, в котором неравенство (5.2) из п. 5.3 не выполняется, по формулам (5.10) или (5.11) п. 5.10 вычисляется браковочное число и проверяется справедливость неравенства
Если неравенство (5.13) соблюдается, ПК заканчивается с результатом "Брак по ПК". При невыполнении неравенства (5.13) ПК продолжается.
5.13. Если при усиленном контроле число наблюдений возросло до i = 44 и при этом C < X < R, производится усечение ПК.
При X <= 2 контроль считается законченным с результатом "Годен по ПК", при X >= 3 - с результатом "Брак по ПК".
5.14. Если при нормальном контроле число наблюдений возросло до i = 40 и при этом C < X < R, производится усечение ПК. При X <= 4 контроль считается законченным с результатом "Годен по ПК", при X >= 5 - с результатом "Брак по ПК".
5.15. При УК и НК после завершения ПК по его результатам осуществляется контроль по количественному признаку - расчетному значению  доверительной погрешности ЦВ в данной точке, которое определяется по формуле
доверительной погрешности ЦВ в данной точке, которое определяется по формуле
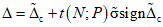 , (5.14)
, (5.14)где 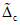 - оценка систематической составляющей (среднего значения) погрешности;
- оценка систематической составляющей (среднего значения) погрешности; 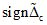 - знак
- знак 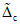 ;
; 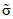 - оценка среднего квадратического отклонения погрешности; t(N; P) - значение коэффициента Стьюдента, зависящее от числа N наблюдений (номера i последнего наблюдения) ПК в данной точке и принятого значения доверительной вероятности P.
- оценка среднего квадратического отклонения погрешности; t(N; P) - значение коэффициента Стьюдента, зависящее от числа N наблюдений (номера i последнего наблюдения) ПК в данной точке и принятого значения доверительной вероятности P.
5.16. Оценка систематической составляющей погрешности по п. 5.15 осуществляется по формуле
5.17. Оценка среднего квадратического отклонения погрешности по п. 5.15 осуществляется по формуле
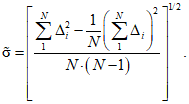 (5.16)
(5.16)5.18. Значение коэффициента Стьюдента по п. 5.15 определяется для P = 0,999 по формуле
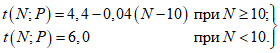 (5.17)
(5.17)5.19. Контроль по количественному признаку (ККП) осуществляется в каждой контролируемой точке путем проверки выполнения неравенства
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
Если неравенство (5.18) выполняется, результатом ККП считается "Годен по ККП", если не выполняется - "Брак по ККП".
5.20. Результаты ПК по пп. 5.11 - 5.14 сравниваются с результатами ККП по п. 5.19. В данной контролируемой точке поверяемый прибор признается:
годным - при результатах "Годен по ПК" и "Годен по ККП";
бракованным - при результатах "Брак по ПК" и "Брак по ККП".
Если результаты ПК и ККП не совпадают ("Годен по ПК" и "Брак по ККП" или "Брак по ПК" и "Годен по ККП"), поверка в данной точке повторяется. Результаты повторной поверки считаются окончательными.
При повторной поверке ЦВ признается в данной точке годным только при получении результатов "Годен по ПК" и "Годен по ККП". При других результатах повторной поверки ЦВ бракуется.
5.21. Если для поверяемого типа ЦВ кроме погрешности нормируется систематическая или случайная составляющая погрешности, проверяется выполнение неравенства
или неравенства
где 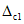 и
и 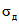 - допускаемые значения систематической составляющей и среднего квадратического отклонения случайной составляющей погрешности, соответственно, коэффициент
- допускаемые значения систематической составляющей и среднего квадратического отклонения случайной составляющей погрешности, соответственно, коэффициент 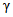 определяется (см. п. 5.22) по одной из формул (5.4) - (5.7).
определяется (см. п. 5.22) по одной из формул (5.4) - (5.7).
5.22. Значение коэффициента 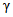 , подставляемого в формулы (5.3), (5.19) и (5.20), зависит от наличия или отсутствия существенной случайной составляющей погрешности ЦВ. Поэтому в каждой контролируемой точке в конце поверки рассматривается выполнение неравенства
, подставляемого в формулы (5.3), (5.19) и (5.20), зависит от наличия или отсутствия существенной случайной составляющей погрешности ЦВ. Поэтому в каждой контролируемой точке в конце поверки рассматривается выполнение неравенства
Если неравенство (5.21) выполняется, то случайной составляющей по сравнению с систематической составляющей погрешности можно пренебречь. Тогда в следующей контролируемой точке (и в данной точке - если необходима повторная поверка) следует исходить из равномерной функции распределения погрешности измерения ЦВ, и коэффициент 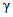 следует определять по формулам (5.5) или (5.7).
следует определять по формулам (5.5) или (5.7).
Если неравенство (5.21) не выполняется, случайной составляющей погрешности пренебречь нельзя. Тогда в следующей контролируемой точке (и в данной точке - если необходима повторная поверка) следует исходить из трапециевидной функции распределения погрешности измерения ЦВ, и коэффициент 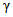 следует определять по формулам (5.4) или (5.6).
следует определять по формулам (5.4) или (5.6).
В начале поверки (в первой контролируемой точке ЦВ), когда информация о случайной составляющей погрешности отсутствует, коэффициент 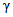 следует определять по формулам (5.4) или (5.6).
следует определять по формулам (5.4) или (5.6).
5.23. Пример блок-схемы алгоритма усиленного (нормального) контроля приведен в справочном приложении 6.
5.24. Пример формы протокола усиленного (нормального) контроля приведен в справочном приложении 7. В случае, если в контролируемой точке противоречивые результаты ПК и ККП приводят к необходимости повторной поверки, в протокол вносятся результаты окончательной, т.е. повторной поверки. Кроме результатов повторной поверки, в протоколе указываются выводы первой поверки (отдельно по ПК и ККП).
Если же поверка в данной точке производилась один раз, в протокол заносятся ее данные. Тогда графа "Выводы 1-й поверки" остается незаполненной.
6.1. При ослабленном контроле поверка в первой контролируемой точке производится в режиме нормального контроля по разд. 5 (без ККП). Ход поверки в следующей контролируемой точке зависит от анализа выполнения неравенства (5.21) по п. 5.19. Если неравенство (5.21) для данной точки не выполняется, случайной составляющей погрешности пренебречь нельзя, и в следующей после рассматриваемой (не обязательно второй) контролируемой точке поверка тоже должна производиться в режиме НК по разд. 5.
Если неравенство (5.21) для данной (первой или любой другой) точки выполняется, считаем, что и в этой, и в следующей контролируемой точке случайной составляющей погрешности можно пренебречь. Тогда поверка в следующей точке должна производиться методом трехступенчатого контроля.
6.2. При поверке методом ТК на вход ЦВ подается сигнал по разд. 3, производится оценка окончания переходного процесса по разд. 4, затем на вход ЦВ последовательно во времени подаются три сигнала, значения уровней которых определяются формулой (3.3) по 3.6.
6.3. В каждом из трех наблюдений метода ТК по формуле (5.1) из п. 5.1 определяется текущая абсолютная погрешность и производится проверка неравенства
Если хотя бы в одном из трех наблюдений неравенство (6.1) не соблюдается, поверка методом ТК прекращается и повторяется в данной точке в режиме НК, результаты которого считаются окончательными. При этом в следующей контролируемой точке поверка должна производиться тоже в режиме НК.
Примечание. При переходе от поверки методом ТК к поверке в режиме НК в конкретной точке входной сигнал не должен изменяться более чем на +/- q. Тогда повторная оценка окончания переходного процесса не требуется.
6.4. Если во всех трех наблюдениях метода ТК неравенство (6.1) соблюдается, ЦВ считается годным в данной точке. Тогда в следующей контролируемой точке поверка должна производиться тоже методом ТК.
Для данной точки рассчитывается среднее значение погрешности по формуле (5.15) п. 5.16 для N = 3.
6.5. В справочном приложении 8 приведен пример блок-схемы алгоритма ослабленного контроля.
6.6. В справочном приложении 9 приведен пример формы протокола автоматизированной поверки ЦВ в режиме ослабленного контроля. В случае, если результаты метода ТК привели к выводу "Брак", в данной точке производится повторная поверка. Тогда в графе "Сколько раз проводилась поверка" указывается "два".
В режиме ОК в протокол выводится меньше данных, чем в режиме УК и НК. Графы "Число выходов погрешности..." и "Доверительная погрешность" в случае поверки по методу ТК не заполняются. Оценкой погрешности по методу ТК считается ее среднее значение (систематическая составляющая) трех наблюдений.
В справочном приложении 10 приведены примеры автоматизированной поверки ЦВ.
Справочное
В НАСТОЯЩИХ МЕТОДИЧЕСКИХ УКАЗАНИЯХ
1. Автоматизированная система поверки средств измерений (АСП СИ) - это функционально и конструктивно организованный и метрологически аттестованный комплекс образцовых средств измерений, средств вычислительной техники, каналов связи и вспомогательного оборудования, снабженный методиками и программами поверки, который выполняет автоматически хотя бы одну из следующих операций:
подача сигналов на вход поверяемого средства измерений,
съем сигналов с выхода поверяемого средства,
обработка результатов измерений и вынесение документированного суждения о пригодности к эксплуатации поверяемого средства,
ввод результатов поверки (при необходимости) в АСУ поверочной деятельностью.
2. Последовательный контроль (ПК) - метод автоматизированной поверки цифровых СИ с существенной случайной составляющей погрешности, характеризующийся тем, что решение относительно годности поверяемого средства в контролируемой точке принимают по результатам ряда наблюдений погрешности в этой точке, максимальное число которых заранее не установлено, причем необходимость следующего наблюдения зависит от результатов предыдущих наблюдений.
3. Трехступенчатый контроль (ТК) - метод автоматизированной поверки цифровых СИ без существенной случайной составляющей погрешности, характеризующийся тем, что решение относительно годности поверяемого средства в контролируемой точке принимают по результатам нескольких наблюдений, максимальное число которых установлено заранее и равно трем, причем необходимость следующего наблюдения погрешности зависит от результатов предыдущих наблюдений.
4. Контроль по количественному признаку (ККП) - метод автоматизированной поверки цифровых СИ, в ходе которого с помощью статистической обработки ряда наблюдений погрешности в контролируемой точке расчетным путем определяют значение доверительной погрешности, а последующее решение о годности СИ в этой точке принимают в зависимости от этого значения.
5. Контрольный норматив - значение показателя качества поверяемого СИ, представляющее собой критерий для принятия решений о годности СИ по результатам поверки.
6. Нормальный контроль (НК) - режим поверки цифровых СИ с существенной случайной составляющей погрешности, применяемый при поверке СИ, не несущих ответственности за здоровье людей, у которых допускаемая погрешность значительно превышает ступень квантования.
7. Усиленный контроль (УК) - режим поверки цифровых СИ с существенной случайной составляющей погрешности, характеризующийся более строгими контрольными нормативами, чем при нормальном контроле, применяемый при поверке высокоточных СИ и СИ, ответственных за здоровье людей.
8. Ослабленный контроль (ОК) - режим поверки цифровых СИ без существенной случайной составляющей погрешности, характеризующийся по сравнению с нормальным контролем меньшим объемом выборки.
9. Контрольный допуск - контрольный норматив, обеспечивающий заданное предельное значение вероятности принять в качестве годного в действительности бракованное СИ, равный максимальному разрешенному значению погрешности в одном наблюдении или измерении в контролируемой точке в случае статистического приемочного контроля по количественному признаку.
10. Приемочное число - контрольный норматив, являющийся критерием для приемки поверяемого СИ в качестве годного в контролируемой точке, равный максимальному разрешенному числу выходов значений погрешности в отдельных наблюдениях за контрольный допуск при последовательном контроле.
11. Браковочное число - контрольный норматив, являющийся критерием для забракования СИ в контролируемой точке и равный минимальному числу выходов погрешности в отдельных наблюдениях за контрольный допуск при последовательном контроле.
12. Усеченный контроль - последовательный контроль, который подлежит прекращению при достижении определенного заранее заданного числа наблюдений, при котором объем информации достаточен для принятия решения о состоянии поверяемого СИ.
13. Достоверность результатов поверки - вероятность принятия в ходе поверки правильного решения о состоянии поверяемого СИ.
14. Оперативная характеристика - выраженная уравнением, графиком или таблицей и обусловленная определенным режимом поверки зависимость вероятности приемки поверяемого СИ в качестве годного от величины, характеризующей качество этого СИ.
Справочное
1. Специфика последовательного контроля, примененного в методических указаниях.
Последовательный контроль (ПК) является одним из статистических методов качества продукции.
Специфика метода ПК, использованного в настоящих методических указаниях, заключается в следующем:
метод ПК привязан к стандартным значениям доверительной вероятности определения доверительных границ погрешности результатов измерений по ГОСТ 8.207-76;
последовательный контроль при необходимости становится усеченным, причем методы замыкания схем контроля гарантируют заданное качество контроля;
предусмотрены три режима контроля: нормальный, усиленный и ослабленный, - выбор которых зависит от функционального назначения и метрологических характеристик поверяемого прибора.
При статистическом приемочном контроле продукции по альтернативному признаку (партия из M изделий годна или дефектна) основной характеристикой партии изделия является генеральная доля дефектных изделий G/M, где G - число дефектных изделий в партии из M изделий.
На практике эта генеральная доля не известна, и решение о качестве всей партии принимается по результатам контроля случайной выборки объемом N (N << M) изделий, из которых X дефектных.
В случае поверки средства измерений всю совокупность измерений, которые выполняются данным прибором за срок его службы, можно рассматривать как "партию" из M погрешностей. При поверке в конкретной контролируемой точке производится N наблюдений погрешности, которые расцениваются как выборочная совокупность из генеральной совокупности M погрешностей. По полученным при поверке выборочным значениям погрешностей (в том числе и тем X значениям, которые вышли за контрольный допуск) судят об истинных значениях погрешности. Поэтому всегда существует риск, что в случайной выборке окажется большое число вышедших за контрольный допуск погрешностей, тогда как во всем множестве {M} погрешностей доля таких погрешностей допустима. В этом случае годный прибор будет ошибочно забракован в результате ошибки поверки 1-го рода 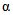 .
.
С другой стороны, в выборке может оказаться малое число погрешностей, превышающих контрольный допуск, тогда как во множестве {M} они встречаются недопустимо часто. В этом случае бракованный прибор будет ошибочно признан годным в результате ошибки поверки 2-го рода 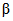 .
.
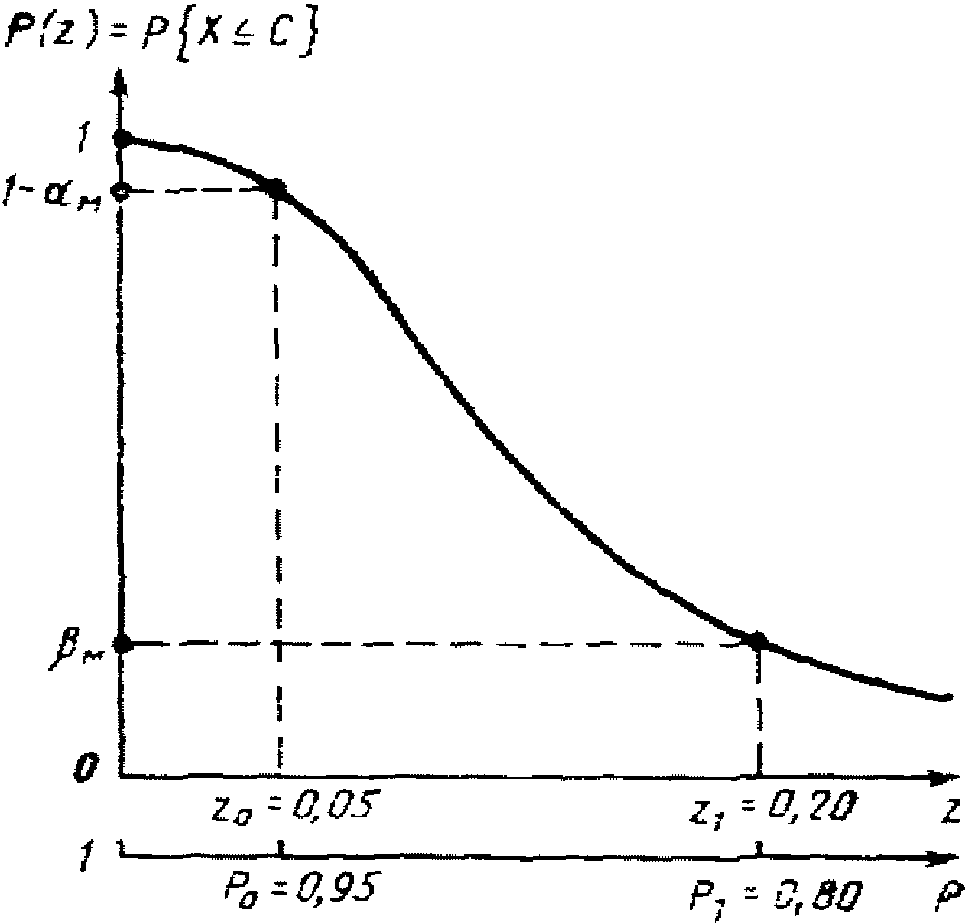
а
б
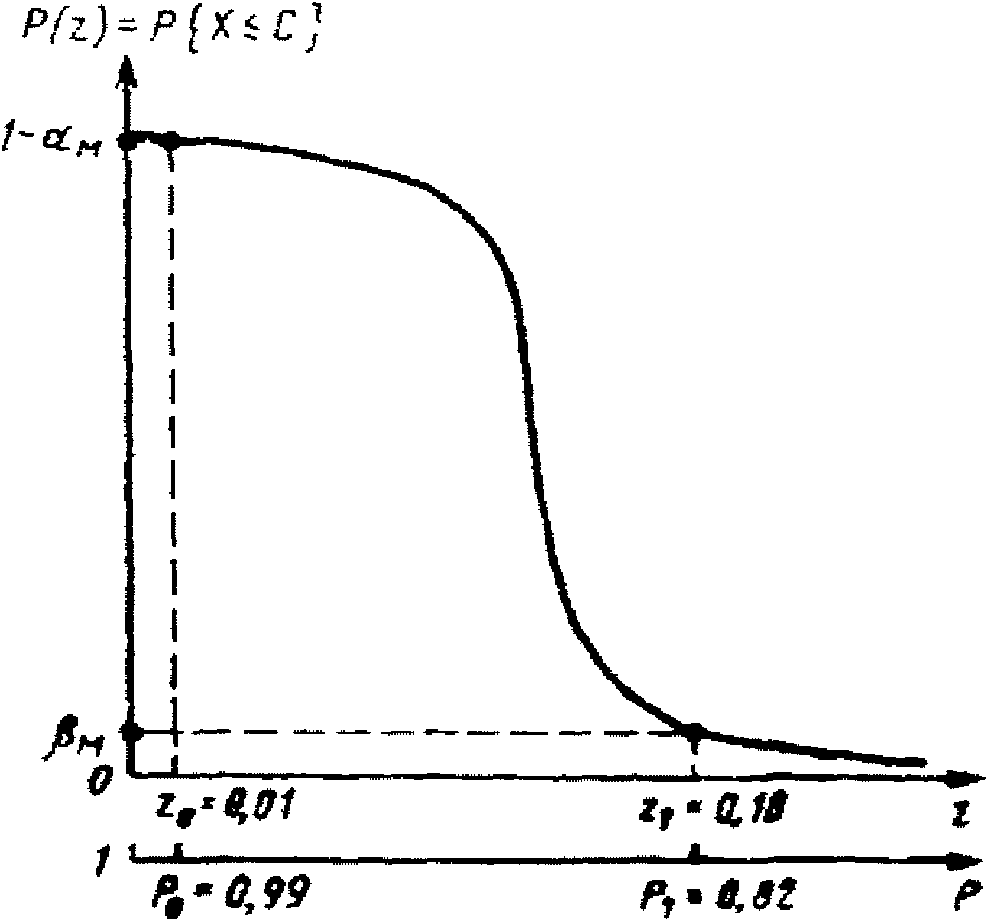
а - нормальный контроль; б - усиленный контроль
Любой статистический контроль производится по плану контроля, под которым понимают систему правил, устанавливающих, как производится выборка, каковы условия принятия и забракования партии, в каком случае контроль следует продолжить. План статистического контроля, в том числе и последовательного контроля, выбирается таким образом, чтобы сделать маловероятными ошибки 1-го и 2-го рода 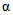 и
и 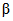 .
.
Основным вероятностным показателем плана статистического контроля является его оперативная характеристика, изображенная на рис. 1. Оперативной характеристикой называется функция P(z), в случае поверки равная вероятности принять СИ как годное с долей вышедших за контрольный допуск погрешностей z = X/N.
При выборочном контроле изделий партии разделяют на хорошие и плохие с помощью двух чисел z0 и z1 (z0 < z1), где z0 - приемлемая, а z1 - браковочная доля дефектных единиц продукции (ГОСТ 15895-77). Партии считаются хорошими при z <= z0 и плохими при z >= z1. При z0 < z < z1 качество партии считается еще допустимым. К плану контроля обычно предъявляются следующие требования
Точно так же при поверке будем считать ЦВ годным, если относительная частота z' события 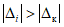 (назовем такое событие "неудачей" в отличие от события
(назовем такое событие "неудачей" в отличие от события 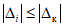 - "успех") не превышает
- "успех") не превышает 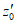 , и будем считать ЦВ бракованным, если
, и будем считать ЦВ бракованным, если 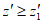 . Кроме того, примем, что при неограниченном увеличении числа наблюдений в контролируемой точке относительная частота
. Кроме того, примем, что при неограниченном увеличении числа наблюдений в контролируемой точке относительная частота 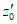 стремится к вероятности события "неудача" в одном наблюдении для годного ЦВ z0 = 1 - P0, а относительная частота
стремится к вероятности события "неудача" в одном наблюдении для годного ЦВ z0 = 1 - P0, а относительная частота 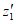 - к вероятности того же события для бракованного ЦВ z1 = 1 - P1, где P0 и P1 - граничные значения вероятности события "успех" в одном наблюдении для годного и бракованного ЦВ соответственно.
- к вероятности того же события для бракованного ЦВ z1 = 1 - P1, где P0 и P1 - граничные значения вероятности события "успех" в одном наблюдении для годного и бракованного ЦВ соответственно.
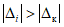 (назовем такое событие "неудачей" в отличие от события
(назовем такое событие "неудачей" в отличие от события 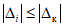 - "успех") не превышает
- "успех") не превышает 2. Последовательный критерий отношения вероятностей и сущность метода ПК.
В основе метода ПК лежит вычисление отношения вероятностей [1, 2] (в отечественной литературе эту величину называют также отношением правдоподобия [3, 4].
Критерий отношения вероятностей указывает конкретные пути выбора одной из двух альтернативных гипотез H. Первая гипотеза H0 - о том, что z = z0 (ЦВ годен), вторая H1 - о том, что z = z1 (ЦВ бракован):
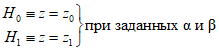 .
.Рассмотрим кратко основное содержание последовательного критерия отношения вероятностей на основе анализа оперативной характеристики.
Используем значения отношений вероятностей P(z1)/P(z0) и [1 - P(z1)]/[1 - P(z0)], соответствующие неравенствам (1) и двум действительным состояниям поверяемого ЦВ: годен и бракован. Эти значения сведены в таблицу.
Вероятность правильно оценить действительное состояние согласно гипотезе | Отношения вероятностей (правдоподобия) | Требования к отношениям вероятностей (правдоподобия) | ||
H1 | H0 | |||
Годен | 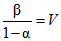 | 0 < V < 1 | ||
Бракован | 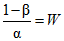 | 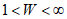 | ||
Для годного в действительности ЦВ используется отношение вероятностей принять прибор в качестве годного, а для бракованного в действительности ЦВ - отношение вероятностей забраковать его. В первом случае (ЦВ на самом деле годен) правдоподобнее должна быть гипотеза H0 (ЦВ признается при поверке годным). Тогда 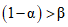 , отношение правдоподобия для этого случая, равное
, отношение правдоподобия для этого случая, равное 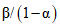 , меньше единицы. Обозначив это отношение через V, можем записать, что 0 < V < 1. Во втором случае (ЦВ на самом деле бракован) правдоподобнее должна быть гипотеза H1 (ЦВ забракуется при поверке). Тогда
, меньше единицы. Обозначив это отношение через V, можем записать, что 0 < V < 1. Во втором случае (ЦВ на самом деле бракован) правдоподобнее должна быть гипотеза H1 (ЦВ забракуется при поверке). Тогда 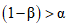 , и отношение правдоподобия
, и отношение правдоподобия 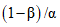 больше единицы. Обозначив его через W, получим
больше единицы. Обозначив его через W, получим 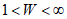 .
.
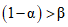 , отношение правдоподобия для этого случая, равное
, отношение правдоподобия для этого случая, равное 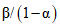 , меньше единицы. Обозначив это отношение через V, можем записать, что 0 < V < 1. Во втором случае (ЦВ на самом деле бракован) правдоподобнее должна быть гипотеза H1 (ЦВ забракуется при поверке). Тогда
, меньше единицы. Обозначив это отношение через V, можем записать, что 0 < V < 1. Во втором случае (ЦВ на самом деле бракован) правдоподобнее должна быть гипотеза H1 (ЦВ забракуется при поверке). Тогда 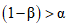 , и отношение правдоподобия
, и отношение правдоподобия 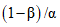 больше единицы. Обозначив его через W, получим
больше единицы. Обозначив его через W, получим 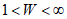 .
.Отметим, что вероятности элементарных событий "успех" и "неудача" в каждом наблюдении погрешности в контролируемой точке составляют полную группу несовместимых событий. Принимается, что каждая из этих двух вероятностей является постоянной величиной, а реализации погрешностей независимы друг от друга. При необходимости корреляция между результатами соседних наблюдений может устраняться с помощью таймера, реализующего задержку отсчетов кодов с выхода ЦВ.
При указанных допущениях распределение вероятностей события "неудача" (или события "успех") в серии из N наблюдений является биномиальным (распределение Бернулли). Найдем выражения для приемочного и браковочного чисел в случае биномиального распределения, наиболее часто используемого при контроле технического состояния изделий, на основе последовательного критерия отношения вероятностей.
Выше было предложено использовать прерывную случайную величину X - число "неудач" в серии из N наблюдений, равное
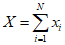 ,
,где xi - характеристическая случайная величина для события "неудача" в i-м наблюдении с двумя возможными значениями: "1" - с вероятностью z и "0" - с вероятностью 1 - z. Таким образом, "z" является неизвестным параметром распределения. Распределение X задается функцией f(x, z), которая определена только для двух значений x, а именно f(1, z) = z и f(0, z) = 1 - z.
Пусть произведено N независимых наблюдений, представленных последовательностью x1, x2, ..., xN. Вероятность получения выборки, совпадающей с указанной, определяется произведением f(x1, z)f(x2, z)...f(xN, z). Если справедлива гипотеза H0, то вероятность получения такой выборки равна z0N = f(x1, z0)f(x2, z0)...f(xN, z0), а если справедлива альтернативная гипотеза H1, то эта вероятность равна z1N = f(x1, z1)f(x2, z1)...f(xN, z1).
При каждом текущем N-м наблюдении вычисляется отношение вероятностей z10/z0N. Если при N-м наблюдении (z1N/z0N) > W, то процесс заканчивается отклонением гипотезы H0. Очевидно, что в этом случае ЦВ бракован (см. таблицу). Если (z1N/z0N) <= V, процесс заканчивается принятием гипотезы H0. Если же V < (z1N/z0N) < W, производится дополнительное наблюдение.
Вместо отношения вероятностей удобнее использовать его логарифм
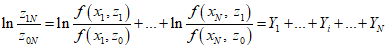 .
.Текущий член суммы в правой части последнего выражения равен
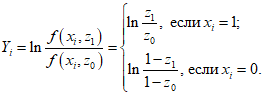
поскольку выше мы приняли, что значению xi = 1 соответствует вероятность z, а значению xi = 0 - вероятность 1 - z. Тогда при X "неудач" и N - X "успехов" имеем
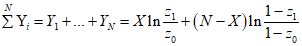 . (2)
. (2)Если 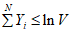 , принимается гипотеза H0, а если
, принимается гипотеза H0, а если 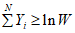 , гипотеза H0 опровергается. Подставив значения V и W из таблицы с учетом принятых выше равенств (1 - z0) = P0 и (1 - z1) = P1, получаем условия принятия гипотезы H0 или ее альтернативы,
, гипотеза H0 опровергается. Подставив значения V и W из таблицы с учетом принятых выше равенств (1 - z0) = P0 и (1 - z1) = P1, получаем условия принятия гипотезы H0 или ее альтернативы,
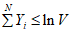 , принимается гипотеза H0, а если
, принимается гипотеза H0, а если 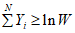 , гипотеза H0 опровергается. Подставив значения V и W из таблицы с учетом принятых выше равенств (1 - z0) = P0 и (1 - z1) = P1, получаем условия принятия гипотезы H0 или ее альтернативы,
, гипотеза H0 опровергается. Подставив значения V и W из таблицы с учетом принятых выше равенств (1 - z0) = P0 и (1 - z1) = P1, получаем условия принятия гипотезы H0 или ее альтернативы,Из неравенства (3), представленного в виде X <= C, находим выражение для приемочного числа:
Из неравенства (4), представленного в виде X >= R, находим выражение для браковочного числа:
Таким образом, вместо того, чтобы при каждом наблюдении контролировать значение отношения вероятностей, сравнивают при каждом наблюдении число "неудач" X с числами C и R по формулам (5) и (6). В этом сущность метода ПК: при X <= C поверяемый ЦВ признается годным, при X >= C - бракуется, а при C < X < R контроль продолжается.
Приемочное и браковочное числа являются функциями от параметров 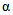 ,
, 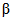 , P0, P1 и числа произведенных наблюдений N. Рассмотрим, каким образом осуществлен выбор указанных параметров в настоящих методических указаниях.
, P0, P1 и числа произведенных наблюдений N. Рассмотрим, каким образом осуществлен выбор указанных параметров в настоящих методических указаниях.
3. Выбор значений параметров 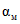 , P0 и P1.
, P0 и P1.
Следует различать оперативную характеристику методики поверки [5] и оперативную характеристику средств поверки. Неидеальность первой объясняется конечным числом наблюдений при наличии существенной случайной погрешности ЦВ, неидеальность второй - наличием неизвестной погрешности у средств поверки. Здесь мы рассмотрим параметры оперативной характеристики методики поверки. При этом средство поверки считаем идеальным.
Сначала осуществим выбор значений параметров P0, 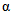 и P1. Значение
и P1. Значение 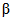 выберем в последнюю очередь, исходя из необходимости усечения последовательного контроля.
выберем в последнюю очередь, исходя из необходимости усечения последовательного контроля.
Для выбора P0 используем, как это сделано в [6, 7], стандартные значения доверительной вероятности определения доверительных границ погрешности результата измерения (0,95 для обычных случаев и 0,99 при измерениях, результаты которых имеют значение для здоровья людей).
Считаем, что в серии многократных наблюдений в каждом наблюдении на вход ЦВ подается образцовый сигнал A0 (будем считать его идеальным). В общем случае ЦВ имеет существенную случайную составляющую погрешности, за счет которой значению A0 входного сигнала будут соответствовать интервалы выходных кодов ЦВ 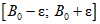 и значений погрешности измерения
и значений погрешности измерения 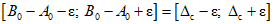 .
.
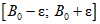 и значений погрешности измерения
и значений погрешности измерения 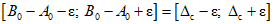 .
.Пусть измерения, совершающиеся с помощью поверяемого ЦВ, не имеют значения для здоровья людей. Тогда границы последнего интервала можно считать доверительными границами погрешности результата измерения, определенными, как того требует стандарт, с доверительной вероятностью P0 = 0,95. Это значит, что в любом i-м наблюдении с вероятностью 95% будет получена погрешность измерения 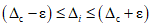 , ограничения для значений которой могут быть записаны в виде
, ограничения для значений которой могут быть записаны в виде 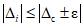 .
.
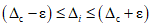 , ограничения для значений которой могут быть записаны в виде
, ограничения для значений которой могут быть записаны в виде 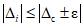 .
.Допустим, что поверке подвергся заведомо годный ЦВ. Тогда 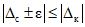 , т.е. доверительные границы погрешности должны уложиться в контрольный допуск. Иначе,
, т.е. доверительные границы погрешности должны уложиться в контрольный допуск. Иначе, 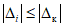 с доверительной вероятностью 0,95:
с доверительной вероятностью 0,95:
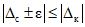 , т.е. доверительные границы погрешности должны уложиться в контрольный допуск. Иначе,
, т.е. доверительные границы погрешности должны уложиться в контрольный допуск. Иначе, 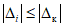 с доверительной вероятностью 0,95:
с доверительной вероятностью 0,95: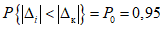 .
.Следовательно, 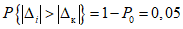 , т.е. вероятность элементарного события "неудача" в каждом из наблюдений равна 5%. Целесообразно предположить, что вероятность забракования в данной точке рассматриваемого заведомо годного ПВ должна быть по возможности не больше вероятности "неудачи" в каждом из N наблюдений в этой точке. Поскольку в большинстве отечественных планов контроля, согласно ГОСТ 18242-72, ошибка 1-го рода
, т.е. вероятность элементарного события "неудача" в каждом из наблюдений равна 5%. Целесообразно предположить, что вероятность забракования в данной точке рассматриваемого заведомо годного ПВ должна быть по возможности не больше вероятности "неудачи" в каждом из N наблюдений в этой точке. Поскольку в большинстве отечественных планов контроля, согласно ГОСТ 18242-72, ошибка 1-го рода 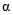 не превышает 0,05, на основании вышеприведенных соображений принимаем, что
не превышает 0,05, на основании вышеприведенных соображений принимаем, что 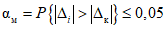 .
.
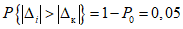 , т.е. вероятность элементарного события "неудача" в каждом из наблюдений равна 5%. Целесообразно предположить, что вероятность забракования в данной точке рассматриваемого заведомо годного ПВ должна быть по возможности не больше вероятности "неудачи" в каждом из N наблюдений в этой точке. Поскольку в большинстве отечественных планов контроля, согласно ГОСТ 18242-72, ошибка 1-го рода
, т.е. вероятность элементарного события "неудача" в каждом из наблюдений равна 5%. Целесообразно предположить, что вероятность забракования в данной точке рассматриваемого заведомо годного ПВ должна быть по возможности не больше вероятности "неудачи" в каждом из N наблюдений в этой точке. Поскольку в большинстве отечественных планов контроля, согласно ГОСТ 18242-72, ошибка 1-го рода 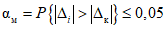 .
.Рассуждая аналогично, приходим к значению 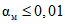 для случая P0 = 0,99.
для случая P0 = 0,99.
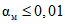 для случая P0 = 0,99.
для случая P0 = 0,99.Итак, верхний уровень качества P0 поверяемого ЦВ нами выбран: это стандартное значение доверительной вероятности определения доверительных границ погрешности ЦВ. Перейдем к выбору нижнего уровня качества P1, обычно произвольному. Попытаемся все же обосновать этот выбор на основании анализа физического смысла P1 для случая поверки. В основе рассуждений по-прежнему лежит модель заведомо годного ЦВ, для которой P0 - это вероятность события "успех" в каждом из многократных наблюдений погрешности в контролируемой точке.
Как известно, относительная частота события "успех" может принимать значения и большие, и меньшие, чем вероятность этого события. Методика приближенного определения доверительных границ для вероятности события "успех" в случае биномиального распределения описана в [8]. Обозначим границы доверительного интервала через Pmin и Pmax и выберем значение доверительной вероятности 0,95:
P {Pmin < P0 < Pmax} = 0,95.
Считаем, что вероятности попадания частоты левее и правее доверительного интервала примерно одинаковы и подчиняются неравенствам:
P{0 <= P0 <= Pmin} >= 0,5(1 - 0,95) = 0,025;
P{Pmax <= P0 <= 1} >= 0,5(1 - 0,95) = 0,025.
Введем обозначения nmin = PminN и nmax = PmaxN, где 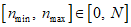 . Из свойств биномиального распределения следует
. Из свойств биномиального распределения следует
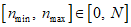 . Из свойств биномиального распределения следует
. Из свойств биномиального распределения следуетЭти два неравенства, решенные относительно nmin и nmax на ЭВМ БЭСМ-6 [6], для P0 = 0,95 дали результаты, показанные на рис. 2, а. Верхняя граница доверительного интервала для вероятности P0 - это прямая Pmax = 1. Нижняя граница доверительного интервала существенно зависит от числа наблюдений. Вследствие того, что N принимает только целочисленные значения, зависимость Pmin (N), асимптотически стремящаяся к прямой P0 = 0,95, имеет характерный "пилообразный" вид. При N >= 10 эта "пила" практически не опускается ниже уровня 0,8.
Как показали исследования на БЭСМ-6 [7], среднее число наблюдений в методе ПК примерно равно 22. Случаи поверки с N < 10 методом ПК не типичны. Поэтому принимаем нижнюю границу доверительного интервала вероятности P0 равной Pmin = 0,8.
Итак, считаем, что у годного ЦВ частота событий "успех" 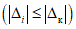 не должна быть меньше значения 0,8. На основании этого осуществляем выбор нижнего уровня качества поверяемого прибора P1 = 0,80 для нормального контроля.
не должна быть меньше значения 0,8. На основании этого осуществляем выбор нижнего уровня качества поверяемого прибора P1 = 0,80 для нормального контроля.
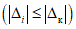 не должна быть меньше значения 0,8. На основании этого осуществляем выбор нижнего уровня качества поверяемого прибора P1 = 0,80 для нормального контроля.
не должна быть меньше значения 0,8. На основании этого осуществляем выбор нижнего уровня качества поверяемого прибора P1 = 0,80 для нормального контроля.Решение неравенств (7), (8) для P0 = 0,99 и аналогичные рассуждения приводят к значению P1 = 0,82 для усиленного контроля (см. рис. 2, б).
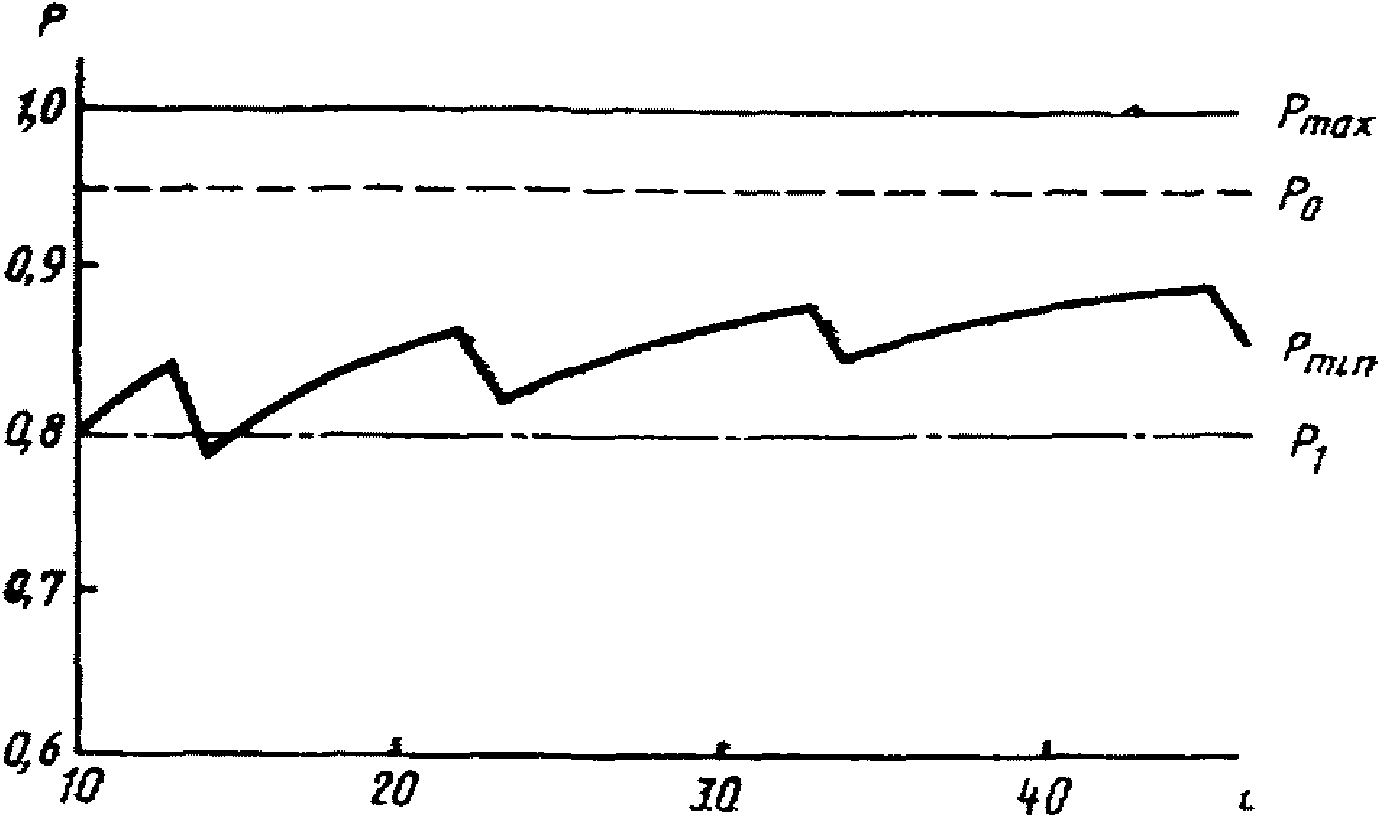
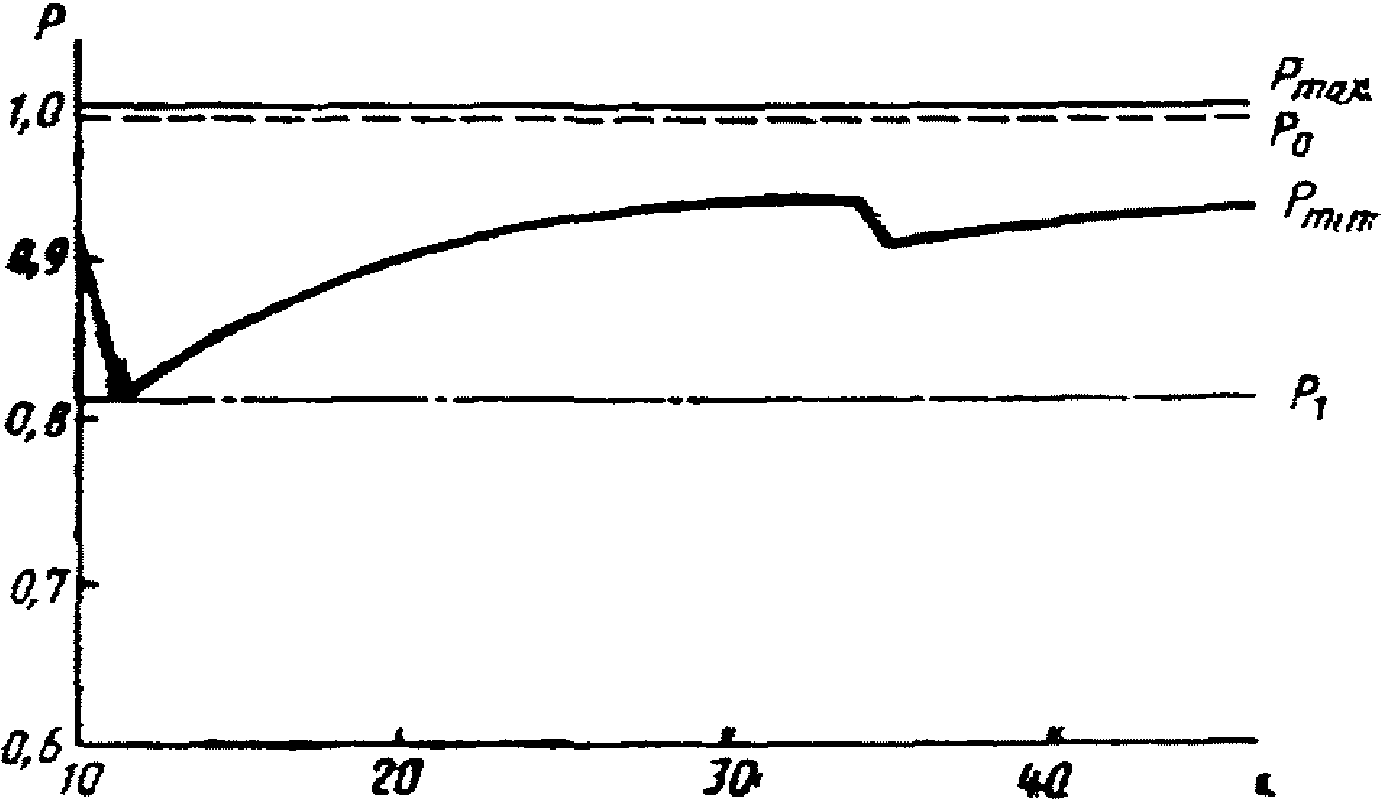
Рис. 2. Доверительный интервал [Pmin; Pmax], отвечающий
стандартному значению вероятности P0 с доверительной
вероятностью 0,95:
а - нормальный контроль; б - усиленный контроль
4. Выбор значения 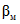 и переход к усеченному контролю.
и переход к усеченному контролю.
Для выбора значения вероятности методической ошибки 2-го рода 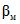 применен известный принцип Неймана-Пирсона, рекомендующий для проверки статистических гипотез при фиксированном уровне ошибки 1-го рода выбирать в качестве критической наиболее мощную область этого уровня, т.е. область с максимальным значением
применен известный принцип Неймана-Пирсона, рекомендующий для проверки статистических гипотез при фиксированном уровне ошибки 1-го рода выбирать в качестве критической наиболее мощную область этого уровня, т.е. область с максимальным значением 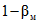 или минимальным значением
или минимальным значением 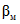 . В соответствии с рис. 1 и принятым выше допущением о биномиальном распределении вероятностей событий "успех-неудача", запишем выражения для подсчета вероятностей методических ошибок поверки:
. В соответствии с рис. 1 и принятым выше допущением о биномиальном распределении вероятностей событий "успех-неудача", запишем выражения для подсчета вероятностей методических ошибок поверки:
С помощью ЭВМ по формуле (9) рассчитаны "ступенчатые" зависимости приемочного числа от числа наблюдений C(N) для случаев P0 = 0,95 (рис. 3, а) и P0 = 0,99 (рис. 3, б), удовлетворяющие условиям 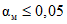 и
и 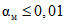 соответственно. Использование этих зависимостей позволило также рассчитать по формуле (10) "пилообразные" кривые
соответственно. Использование этих зависимостей позволило также рассчитать по формуле (10) "пилообразные" кривые 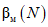 , асимптотически стремящиеся к нулю при
, асимптотически стремящиеся к нулю при 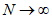 , для P0 = 0,95 (рис. 3, а) и P0 = 0,99 (рис. 3, б).
, для P0 = 0,95 (рис. 3, а) и P0 = 0,99 (рис. 3, б).
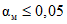 и
и 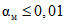 соответственно. Использование этих зависимостей позволило также рассчитать по формуле (10) "пилообразные" кривые
соответственно. Использование этих зависимостей позволило также рассчитать по формуле (10) "пилообразные" кривые 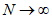 , для P0 = 0,95 (рис. 3, а) и P0 = 0,99 (рис. 3, б).
, для P0 = 0,95 (рис. 3, а) и P0 = 0,99 (рис. 3, б).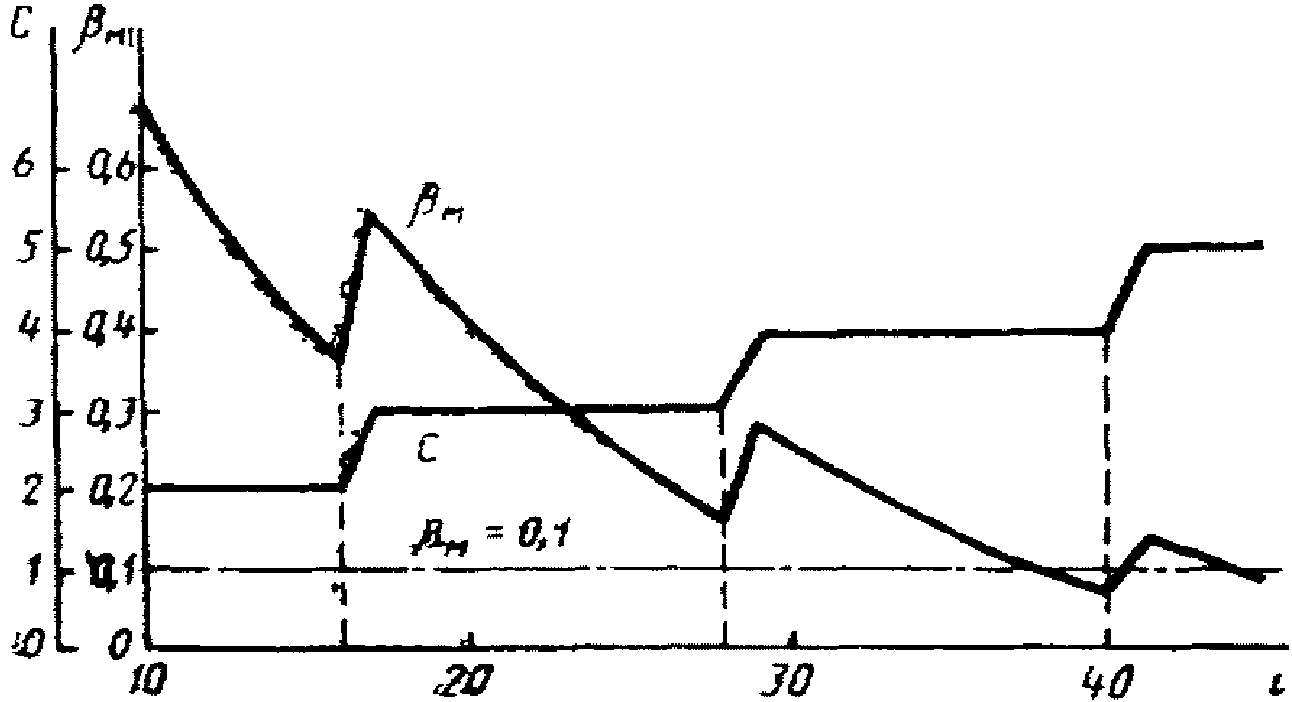
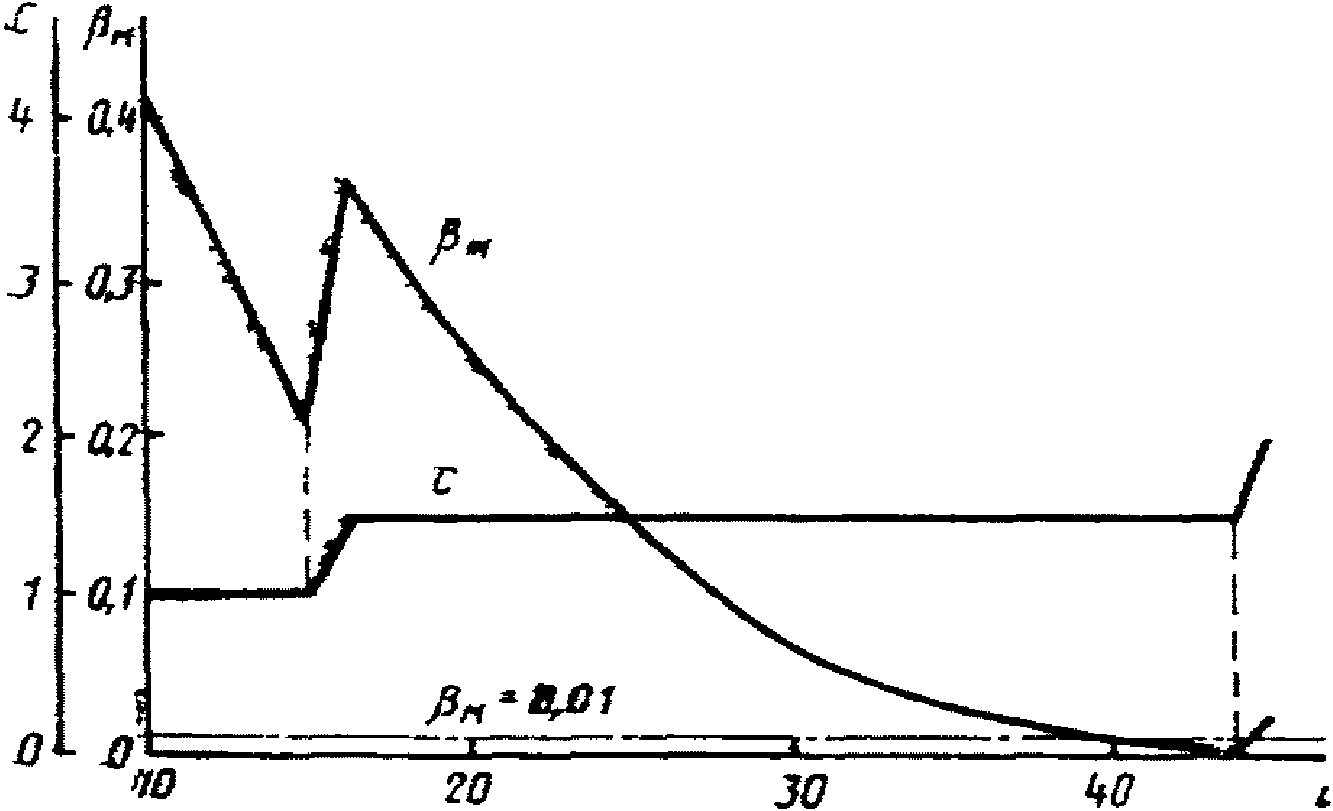
Рис. 3. Графики зависимостей приемочного числа и вероятности
методической ошибки поверки 2-го рода от числа наблюдений
для фиксированной методической ошибки поверки 1-го рода:
а - нормальный контроль; б - усиленный контроль
Чем больше N, тем меньше 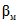 . Но выше отмечалось, что, как показывает практика, неограниченное увеличение числа наблюдений делает автоматизированную поверку неэффективной. Поэтому для выбора
. Но выше отмечалось, что, как показывает практика, неограниченное увеличение числа наблюдений делает автоматизированную поверку неэффективной. Поэтому для выбора 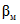 учтем еще и необходимость усечения ПК, характеризующегося наличием нежелательной "зоны безразличия" между зонами годности и бракования.
учтем еще и необходимость усечения ПК, характеризующегося наличием нежелательной "зоны безразличия" между зонами годности и бракования.
К выбору режима усеченного контроля проще всего подойти следующим образом [7]. Следует использовать одни и те же параметры как для режима ПК, так и для вспомогательного режима одноступенчатого контроля. В последнем под "одной ступенью" понимается не одно наблюдение, а одна выборка с фиксированным объемом Nmax. Если в режиме ПК число наблюдений достигло Nmax, поверка прекращается. При этом используется постоянное (не зависящее от N) значение Cmax приемочного числа, выбранное для одноступенчатого контроля.
Одноступенчатому контролю с параметрами 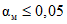 , P0 = 0,95 и P1 = 0,80 соответствует кривая
, P0 = 0,95 и P1 = 0,80 соответствует кривая 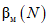 на рис 3, а. Для минимизации
на рис 3, а. Для минимизации 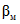 (в соответствии с критерием Неймана-Пирсона) учтем то обстоятельство, что в указанной кривой имеется ряд локальных минимумов, соответствующих значениям N = 16, 28, 40, 53, ... Значения рисков выбирают обычно из ряда 0,01; 0,05, 0,10, ... Вполне достаточному условию
(в соответствии с критерием Неймана-Пирсона) учтем то обстоятельство, что в указанной кривой имеется ряд локальных минимумов, соответствующих значениям N = 16, 28, 40, 53, ... Значения рисков выбирают обычно из ряда 0,01; 0,05, 0,10, ... Вполне достаточному условию 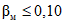 соответствует локальный минимум кривой
соответствует локальный минимум кривой 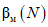 , в котором Nmax = 40,
, в котором Nmax = 40, 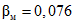 . На кривой C(N) рис. 3, а числу наблюдений N = 40 соответствует Cmax = 4. Подставив эти параметры в формулу (9), получаем уточненное значение
. На кривой C(N) рис. 3, а числу наблюдений N = 40 соответствует Cmax = 4. Подставив эти параметры в формулу (9), получаем уточненное значение 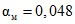 .
.
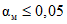 , P0 = 0,95 и P1 = 0,80 соответствует кривая
, P0 = 0,95 и P1 = 0,80 соответствует кривая 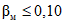 соответствует локальный минимум кривой
соответствует локальный минимум кривой 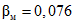 . На кривой C(N) рис. 3, а числу наблюдений N = 40 соответствует Cmax = 4. Подставив эти параметры в формулу (9), получаем уточненное значение
. На кривой C(N) рис. 3, а числу наблюдений N = 40 соответствует Cmax = 4. Подставив эти параметры в формулу (9), получаем уточненное значение 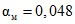 .
.Отметим, что усеченному контролю соответствует несколько увеличенные значения рисков. Теоретические и практические исследования показали [7], что при усеченном контроле, соответствующем вышеописанному одноступенчатому контролю для P0 = 0,95, справедливы значения 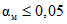 и
и 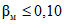 .
.
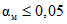 и
и 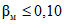 .
.Анализ рис 3, б и аналогичные рассуждения для случая P0 = 0,99 приводят к значениям 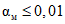 ,
, 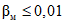 , Nmax = 44, Cmax = 2.
, Nmax = 44, Cmax = 2.
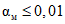 ,
, 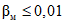 , Nmax = 44, Cmax = 2.
, Nmax = 44, Cmax = 2.Таким образом, в выражения для R и C в режиме усиленного контроля подставлялись значения 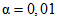 ,
, 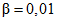 , P0 = 0,99, P1 = 0,82, а в режиме нормального контроля - значения
, P0 = 0,99, P1 = 0,82, а в режиме нормального контроля - значения 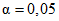 ,
, 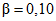 , P0 = 0,95, P1 = 0,80.
, P0 = 0,95, P1 = 0,80.
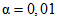 ,
, 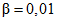 , P0 = 0,99, P1 = 0,82, а в режиме нормального контроля - значения
, P0 = 0,99, P1 = 0,82, а в режиме нормального контроля - значения 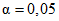 ,
, 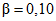 , P0 = 0,95, P1 = 0,80.
, P0 = 0,95, P1 = 0,80.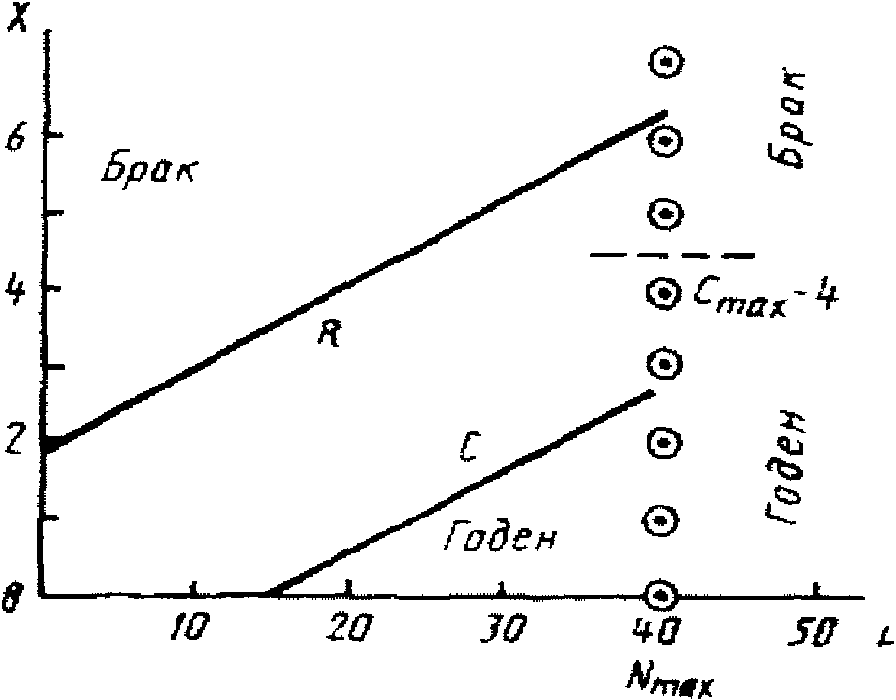
а
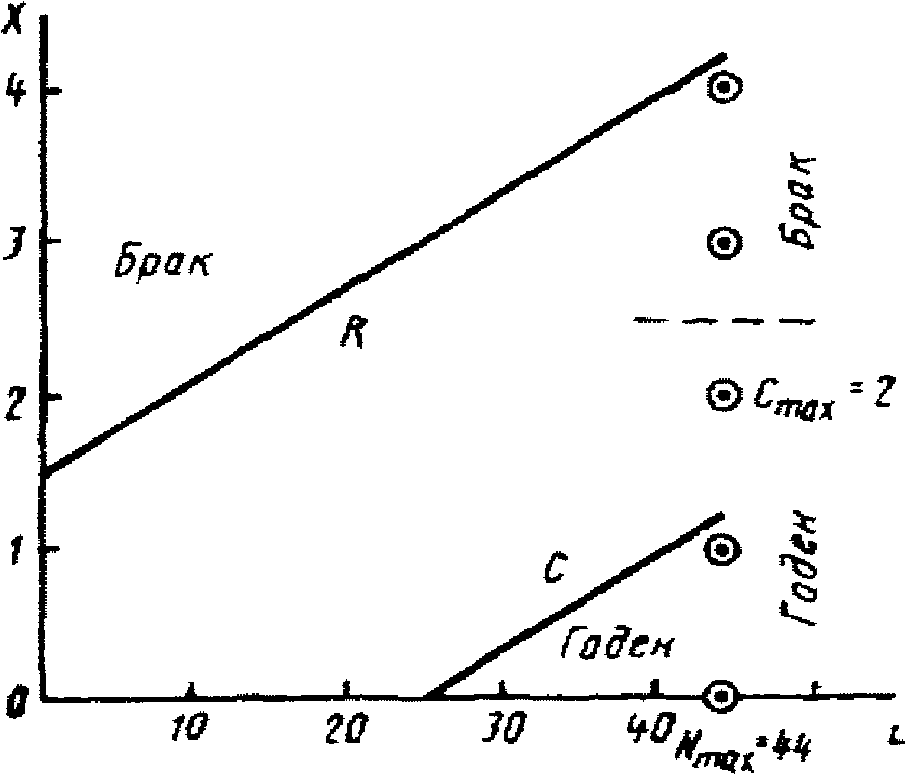
б
а - нормальный контроль; б - усиленный контроль
В режиме усиленного контроля усечение производится при N = 44 и C = 2, а в режиме нормального контроля - при N = 40, C = 4 (рис. 4).
5. Контрольный допуск и достоверность результатов ПК.
В настоящих методических указаниях для повышения достоверности результатов поверки, как и в [9] и МИ 118-77, предусмотрено сужение допускаемой погрешности за счет введения в выражение для контрольного допуска множителя 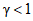 , тем меньшего, чем больше отношение
, тем меньшего, чем больше отношение 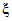 допускаемых погрешностей образцовой меры и поверяемого ЦВ. Значение
допускаемых погрешностей образцовой меры и поверяемого ЦВ. Значение 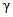 получено из известной формулы для вероятности инструментальной ошибки поверки 2-го рода.
получено из известной формулы для вероятности инструментальной ошибки поверки 2-го рода.
где 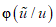 - условная плотность распределения нормализованной оценки
- условная плотность распределения нормализованной оценки 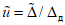 при условии, что u = 1.
при условии, что u = 1.
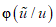 - условная плотность распределения нормализованной оценки
- условная плотность распределения нормализованной оценки 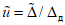 при условии, что u = 1.
при условии, что u = 1.Ни вид, ни параметры закона распределения оценки 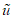 не известны. Поэтому в самой первой контролируемой точке предполагаем, что погрешность ЦВ имеет существенную случайную составляющую, а для определения значения
не известны. Поэтому в самой первой контролируемой точке предполагаем, что погрешность ЦВ имеет существенную случайную составляющую, а для определения значения 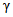 из формулы (11) используем трапециевидную функцию распределения
из формулы (11) используем трапециевидную функцию распределения 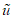 с отношением верхнего основания к нижнему, равным 0,5, как это рекомендуется в п. 3.4.1 МИ 187-79.
с отношением верхнего основания к нижнему, равным 0,5, как это рекомендуется в п. 3.4.1 МИ 187-79.
В этой (как и в любой другой) контролируемой точке оценивается существенность случайной составляющей погрешности по критерию, описанному в п. 5.1 ГОСТ 8.207-76. Если систематическая составляющая превышает случайную более, чем в 8 раз, случайной составляющей погрешности можно пренебречь. Тогда в следующей контролируемой точке используется наихудший (с точки зрения влияния 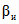 на значение
на значение 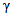 ) вариант распределения
) вариант распределения 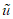 - равномерное распределение [5] с размахом, равным удвоенному значению
- равномерное распределение [5] с размахом, равным удвоенному значению 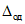 [9, 10].
[9, 10].
Если в какой-либо точке отношение 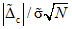 станет меньше (равным) восьми, в следующей точке снова будет использовано трапециевидное распределение.
станет меньше (равным) восьми, в следующей точке снова будет использовано трапециевидное распределение.
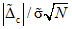 станет меньше (равным) восьми, в следующей точке снова будет использовано трапециевидное распределение.
станет меньше (равным) восьми, в следующей точке снова будет использовано трапециевидное распределение.Из формулы (11) находим значение 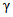 :
:
для трапециевидного распределения
для равномерного распределения
Таким образом, при поверке гарантируется неизменное максимальное значение 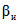 , тогда как
, тогда как 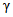 меняется в зависимости от значений
меняется в зависимости от значений 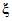 в контролируемых точках.
в контролируемых точках.
В методических указаниях принято, что максимальные значения вероятностей инструментальных ошибок поверки равны максимальным значениям вероятностей методических ошибок поверки, т.е. 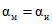 ,
, 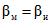 . Это значит, что оперативная характеристика средств поверки совпадает с оперативной характеристикой методики поверки, а инструментальная и методическая достоверности результатов равны. Следовательно, в формулы (12) и (13) для усиленного контроля подставлено значение
. Это значит, что оперативная характеристика средств поверки совпадает с оперативной характеристикой методики поверки, а инструментальная и методическая достоверности результатов равны. Следовательно, в формулы (12) и (13) для усиленного контроля подставлено значение 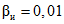 , а для нормального -
, а для нормального - 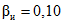 .
.
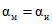 ,
, 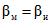 . Это значит, что оперативная характеристика средств поверки совпадает с оперативной характеристикой методики поверки, а инструментальная и методическая достоверности результатов равны. Следовательно, в формулы (12) и (13) для усиленного контроля подставлено значение
. Это значит, что оперативная характеристика средств поверки совпадает с оперативной характеристикой методики поверки, а инструментальная и методическая достоверности результатов равны. Следовательно, в формулы (12) и (13) для усиленного контроля подставлено значение 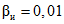 , а для нормального -
, а для нормального - 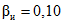 .
.Достоверность результатов метода ПК равна произведению методической и инструментальной достоверности результатов
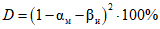 , (14)
, (14)откуда для УК получаем D = 96%, а для НК - D = 72%.
6. Контроль по количественному признаку (ККП).
По результатам N наблюдений усиленного или нормального контроля определяется доверительная погрешность ЦВ в контролируемой точке и производится ее сравнение с контрольным допуском. Результат ККП должен совпасть с результатом ПК. При несовпадения результатов ПК повторяется. Такое дублирование позволяет существенно повысить помехоустойчивость результатов поверки. Если помехи (сбои), которые привели к несовпадению результатов первой поверки, носили случайный характер, маловероятно, что во время повторной поверки они появятся снова. Таким образом, годный ЦВ будет признан годным, даже если во время поверки АСП СИ подвержена действию помех или сбоев.
Маловероятно также, что помехи (сбои) повлияют и на результат ПК, и на результат ККП. Это возможно лишь при воздействии большого количества мощных помех. Одна-две сильные помехи практически не окажут влияния на результат ПК, поскольку этот метод накапливает, интегрирует "неудачи" отдельных наблюдений. Три-четыре и более слабых помех (даже соизмеримых со ступенью квантования ЦВ) могут исказить результат ПК, но не скажутся на результатах ККП. Последний метод как бы дифференцирует помехи, выделяет наиболее мощные и при их наличии дает результат "Брак".
Доверительная погрешность необходима не только для повышения помехоустойчивости поверки. Значения погрешности в контролируемых точках, записанные в протокол поверки, нужны при ремонте бракованного ЦВ, а также при прогнозировании состояния ЦВ по результатам автоматизированной поверки, делающей вполне реальной такую перспективу.
Цифровое моделирование процесса поверки ЦВ показало, что, учитывая высокую достоверность результатов метода ПК, при вычислении доверительной погрешности в методе ККП следует выбрать высокое значение доверительной вероятности. Вот почему в полиноме, аппроксимирующем зависимость коэффициента Стьюдента от числа наблюдений, данную в [11], принято P = 0,999.
Отметим, что вычисление доверительной погрешности практически не увеличивает времени поверки, так как при каждом наблюдении накапливаются значения суммы текущих погрешностей и суммы квадратов этих погрешностей.
7. Метод трехступенчатого контроля (ТК)
Метод ТК применяется только в режиме ослабленного контроля. Покажем, что этот метод, как и метод ПК, тоже обладает высокой достоверностью результатов.
Трехступенчатый контроль заключается в трехразовом сравнении последовательных текущих значений погрешности 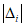 (i = 1, 2, 3) с контрольным допуском
(i = 1, 2, 3) с контрольным допуском 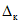 , уменьшенным на половину ступени квантования ЦВ. Таким образом, допускаемая погрешность
, уменьшенным на половину ступени квантования ЦВ. Таким образом, допускаемая погрешность 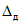 в методе ПК сужена до значения
в методе ПК сужена до значения 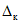 так, чтобы учесть влияние погрешности образцовой меры на результаты поверки, а затем в методе ТК уменьшена еще на 0,5q - максимальное значение погрешности квантования. Напомним по результатам поверки в предыдущей точке сделано предположение, что случайная составляющая погрешности у данного экземпляра ЦВ пренебрежимо мала. Если при всех этих ограничениях три наблюдения подряд приводят к результату "успех", поверяемый прибор считается годным в данной точке.
так, чтобы учесть влияние погрешности образцовой меры на результаты поверки, а затем в методе ТК уменьшена еще на 0,5q - максимальное значение погрешности квантования. Напомним по результатам поверки в предыдущей точке сделано предположение, что случайная составляющая погрешности у данного экземпляра ЦВ пренебрежимо мала. Если при всех этих ограничениях три наблюдения подряд приводят к результату "успех", поверяемый прибор считается годным в данной точке.
Если хотя бы одно наблюдение из трех привело к исходу "неудача", в данной контролируемой точке поверка повторяется в режиме НК, с гарантированным значением достоверности результатов.
5. Карташева А.Н. Достоверность измерений и критерии качества испытаний приборов. М.: Изд-во стандартов, 1967.
6. Владимиров В.Л. Выбор параметров автоматизированной поверки средств измерений с электрическим выходом // Материалы Всесоюзной конф. по измерительным информационным системам "ИИС-81" / ВНИИМИУС, Львов, 1982, ч. 1, с. 123 - 132.
7. Владимиров В.Л., Таранова Н.Г. Применение статистического моделирования для оценки качества метода автоматизированной поверки средств измерений // Системы автоматизации метрологических исследований. Львов, 1983, с. 37 - 44 (Труды ВНИИМИУС).
9. Вострокнутов Н.Н. Испытания и поверка цифровых измерительных устройств. М.: Изд-во стандартов, 1977.
10. Вострокнутов Н.Н., Земельман М.А., Кашлаков В.М. Выбор образцовых средств для периодической поверки с использованием вероятностных критериев // Измерительная техника, 1977, N 7, с. 19 - 22.
Справочное
АВТОМАТИЗИРОВАННОЙ ПОВЕРКИ
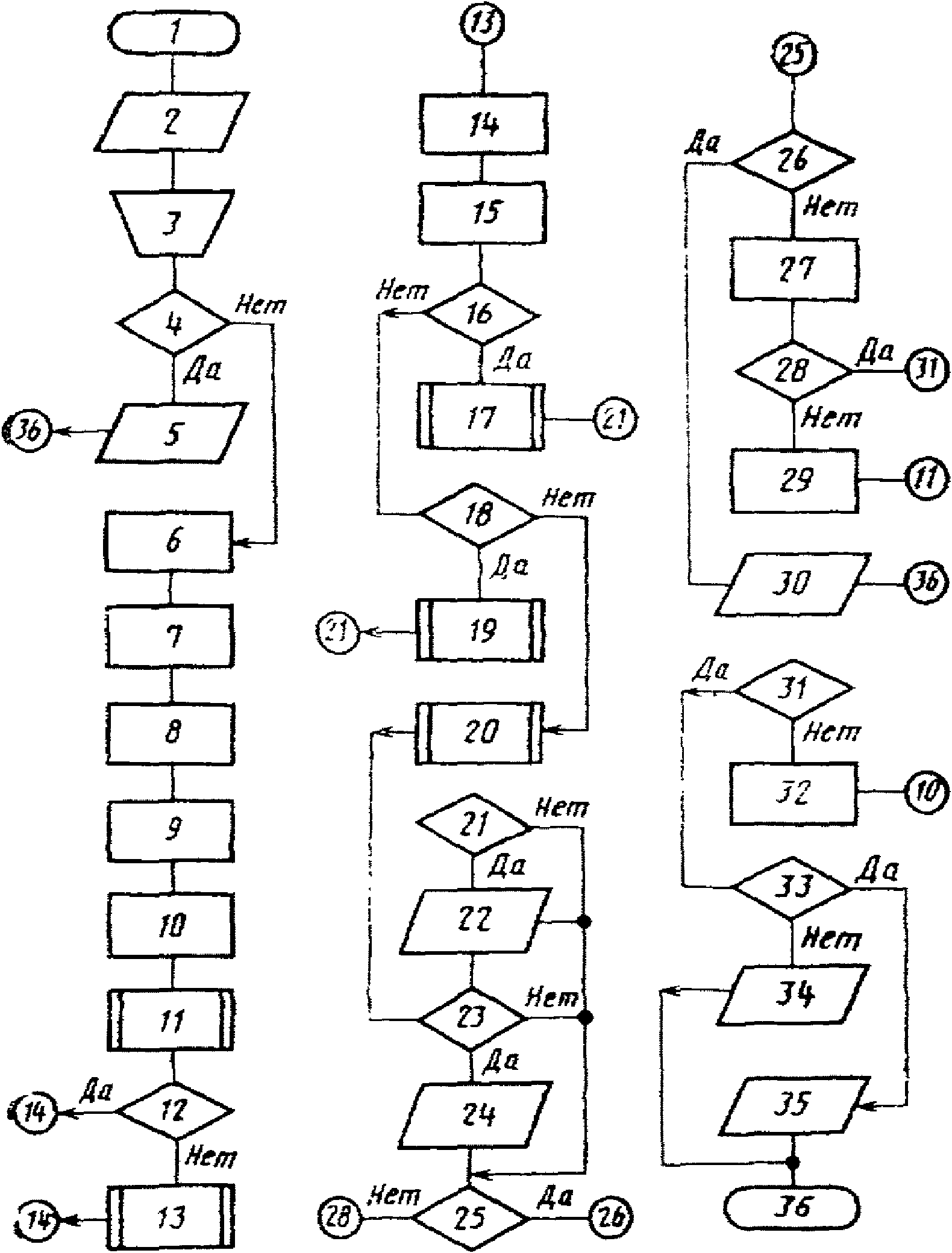
Описание блок-схемы общего алгоритма
автоматизированной поверки
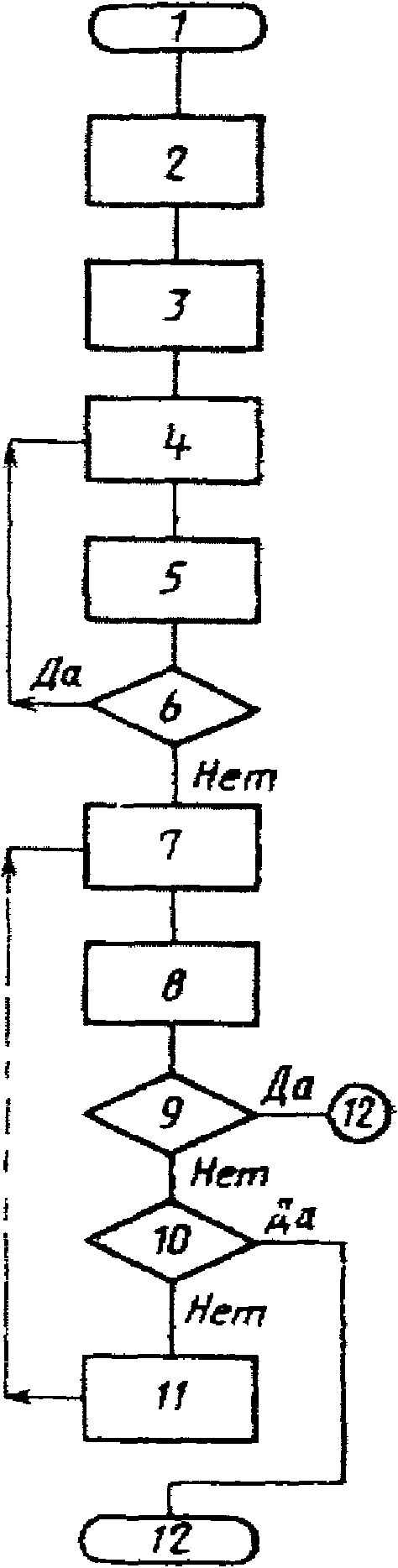
1. Начало.
2. Введение в оперативную память типа ЦВ и данных поверки (заводской номер и принадлежность ЦВ, дата поверки, фамилия поверителя).
3. Проведение ручных операций поверки, в том числе подключение ЦВ к АСП.
4. Есть ли признак брака по результатам ручных операций?
5. Выдача справки о непригодности к эксплуатации по результатам ручных операций.
6. Выбор режимов поверки: УК, НК или ОК.
7. Выбор режима поверки: до первой точки, в которой ЦВ бракуется, или нет.
8. Выбор режима поверки: с выдачей протокола поверки или нет.
9. Присвоение значений признаку наличия случайной составляющей погрешности и признаку использования метода ПК: 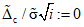 , NR := 2.
, NR := 2.
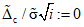 , NR := 2.
, NR := 2.10. Выход в первую контролируемую точку.
11. Алгоритм подачи входного сигнала.
12. Поверяется ЦВ с зависимостью систематической составляющей погрешности от измеряемой величины, имеющей разрывы?
13. Алгоритм оценки окончания переходного процесса.
14. Вычисление 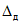 .
.
15. Вычисление 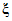 .
.
16. Режим УК?
17. Алгоритм режима УК.
18. Режим НК?
19. Алгоритм режима НК.
20. Алгоритм режима ОК.
21. Есть ли признак печати протокола?
22. Выдача протокола в режиме УК (НК).
23. Есть ли признак печати протокола?
24. Выдача протокола в режиме ОК.
25. Есть ли признак брака?
26. Есть ли признак поверки до первой точки, в которой ЦВ бракуется?
27. Запоминание признака брака в данной точке.
28. Все ли точки диапазона проверены?
29. Переход на следующую контролируемую точку.
30. Выдача справки о непригодности к эксплуатации.
31. Все ли диапазоны проверены?
32. Изменение диапазона.
33. Есть ли хоть одна точка, в которой ЦВ бракуется?
34. Выдача свидетельства о поверке.
35. Выдача справки о непригодности к эксплуатации по точкам, в которых ЦВ бракуется.
36. Конец.
Справочное
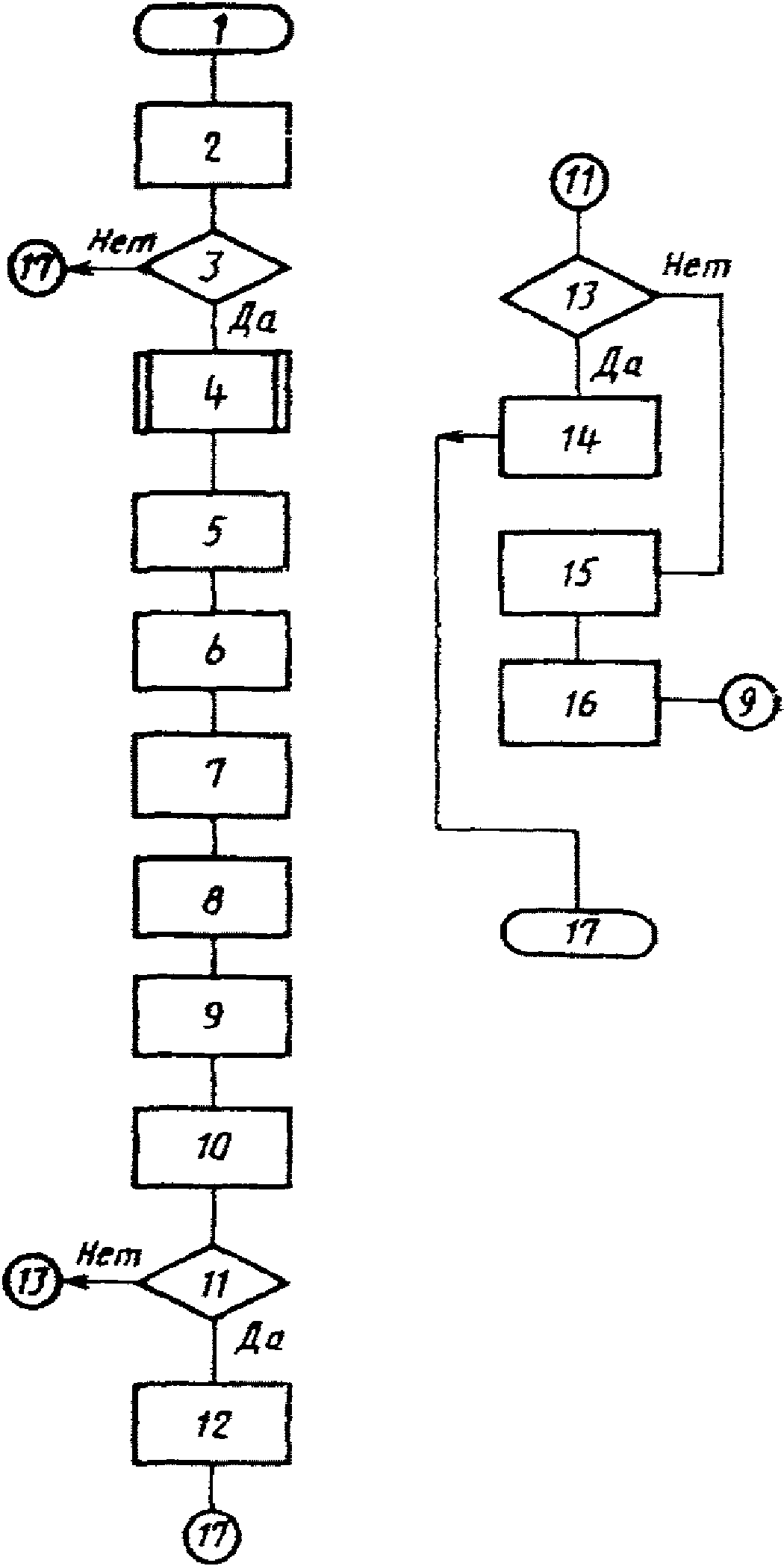
Описание блок-схемы алгоритма подачи входного сигнала
1. Начало.
2. Подача с образцовой меры пробного входного сигнала 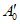 .
.
3. Поверяется ЦВ с зависимостью систематической составляющей погрешности от измеряемой величины, имеющей разрывы?
4. Алгоритмы оценки окончания переходного процесса.
5. Фиксация значения выходного кода B0.
6. Запоминание начального момента времени T0.
7. i := 1.
8. Подача входного сигнала A0i = B0.
9. Считывание выходного сигнала B0i.
10. Фиксация текущего времени T.
11. T - T0 >= Tз? (Tз - время задержки по п. 4.3).
12. Подача основного входного сигнала A0 = B0 - q.
13. B0 - B0i = 0?
14. Подача основного входного сигнала A0 = A0i.
15. Изменение входного сигнала по формуле A0i+1 = A0i + B0 - B0i.
16. i := i + 1.
17. Конец.
Справочное
ОКОНЧАНИЯ ПЕРЕХОДНОГО ПРОЦЕССА
Описание блок-схемы алгоритма оценки
окончания переходного процесса
1. Начало.
2. Фиксация начального момента времени T0.
3. i := 1.
4. Считывание и запоминание значения выходного сигнала Bi.
5. i := i + 1.
6. i < 3?
7. Считывание и запоминание значения выходного сигнала Bi.
8. Фиксация текущего момента времени T.
9. T - T0 >= Tз? (Tз - время задержки по п. 4.3).
10. Выполняются ли условия окончания переходного процесса |Bi - 1 - Bi - 2| <= nед; |Bi - Bi - 1| <= nед; |Bi - Bi - 2| <= nед?
11. Присвоение Bi - 2 := Bi - 1; Bi - 1 = Bi.
12. Конец.
Справочное
УСИЛЕННОГО (НОРМАЛЬНОГО) КОНТРОЛЯ
Описание блок-схемы алгоритма усиленного
(нормального) контроля
1. Начало.
2. MPK := 1, MKP := 1 (MPK и MKP - признаки наличия или отсутствия брака в промежуточных выводах методов ПК и ККП соответственно).
3. Есть ли признак наличия случайной составляющей погрешности:
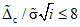 ?
?4. Вычисление 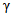 для равномерного распределения погрешности:
для равномерного распределения погрешности:
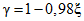 (
(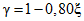 для НК)
для НК)5. Вычисление 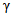 для трапециевидного распределения погрешности:
для трапециевидного распределения погрешности:
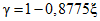 (
(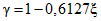 для НК)
для НК)6. Вычисление 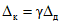 .
.
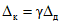 .
.7. X := 0, 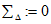 ,
, 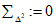 , i := 1, LKP = 1, LPK = 1 (LPK и LKP - признаки наличия или отсутствия брака в окончательных выводах методов ПК и ККП соответственно).
, i := 1, LKP = 1, LPK = 1 (LPK и LKP - признаки наличия или отсутствия брака в окончательных выводах методов ПК и ККП соответственно).
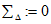 ,
, 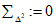 , i := 1, LKP = 1, LPK = 1 (LPK и LKP - признаки наличия или отсутствия брака в окончательных выводах методов ПК и ККП соответственно).
, i := 1, LKP = 1, LPK = 1 (LPK и LKP - признаки наличия или отсутствия брака в окончательных выводах методов ПК и ККП соответственно).8. Подача входного сигнала:
Ai = A0 + q(1,1 - 0,1·|22 - i|)
(Ai = A0 + q(1,0 - 0,1·|20 - i|) для НК).
9. Считывание выходного сигнала Bi.
10. Вычисление 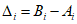 ;
; 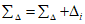 ;
; 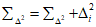 .
.
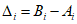 ;
; 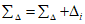 ;
; 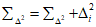 .
.11. 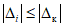 ?
?
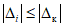 ?
?12. Вычисление приемочного числа C = - 1,4925 + i·0,0612
(C = - 1,6223 + i·0,1103 для НК).
13. X <= C?
14. X := X + 1.
15. Вычисление браковочного числа R = 1,4925 + i·0,0612
(R = 1,8981 + i·0,1103 для НК).
16. X >= R?
17. i < 44? (i < 40? - для НК).
18. i := i + 1.
19. X <= 2? (X <= 4? - для НК).
20. Запоминание признака годности по ПК: LPK = 0.
21. Запоминание признака брака по ПК: LPK = 1.
22. Вычисление 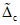 ,
, 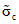 ,
, 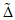 ,
, 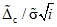 и запоминание их.
и запоминание их.
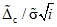 и запоминание их.
и запоминание их.23. 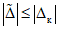 ?
?
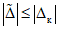 ?
?24. Запоминание признака годности по ККП: LKP = 0.
25. Запоминание признака брака по ККП: LKP = 1.
26. LPK + LKP = 1?
27. MPK + MKP = 1?
28. MPK := LPK, MKP := LKP.
29. 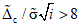 ?
?
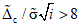 ?
?30. LKP + LPK = 2?
31. Запоминание признака брака в контролируемой точке.
32. Запоминание признака годности в контролируемой точке.
33. Конец.
Справочное
ПРИ УСИЛЕННОМ ИЛИ НОРМАЛЬНОМ КОНТРОЛЕ
ПРОТОКОЛ N _______ автоматизированной поверки вольтметра цифрового типа _______________, принадлежащего _______________, заводской номер ____________________ Режим контроля _________________________ усиленный, нормальный Диапазон измерений, В ____________ Контролируемая точка, В ___________ Сколько раз производилась поверка в точке _____________ один, два | |
ПК _______________________, годен, брак | ККП _______________________ годен, брак |
Число наблюдений _______________. Браковочное число _______________ Приемочное число _______________ Число выходов погрешности за контрольный допуск ____________________ Вывод последовательного контроля __________________________________ годен по ПК, брак по ПК Контрольный допуск, В ________. Доверительная погрешность, В ________ Вывод контроля по количественному признаку ________________________ годен по ККП, брак по ККП Систематическая составляющая погрешности, В _______________________ Отношение систематической составляющей к случайной ________________ Заключение по контролируемой точке ________________________________ годен, брак Заключение по состоянию ЦВ ______________________ годен, брак Достоверность результатов поверки, %, не менее _______________________ Начальник поверочной лаборатории _________________ (И.О. Фамилия) подпись Оператор-поверитель _____________________________ (И.О. Фамилия) подпись Дата поверки "__" _______________ 19__ г. МП | |
Справочное
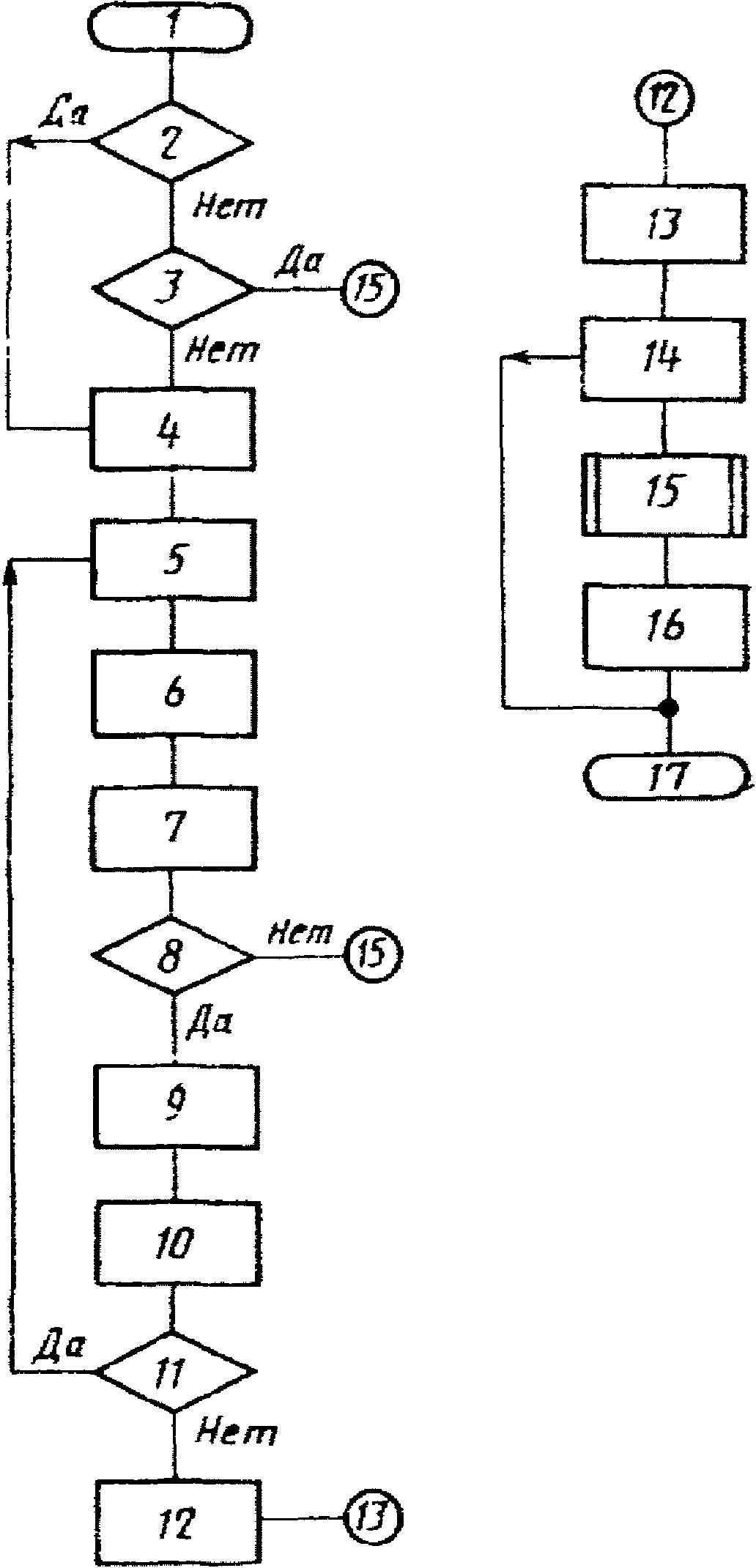
Описание блок-схемы алгоритма ослабленного контроля
1. Начало.
2. Есть ли признак использования метода ТК: NR = 1?
3. Есть ли признак наличия случайной составляющей погрешностей
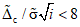 ?
?4. i := 1; 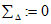 ;
; 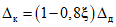 .
.
 ;
; 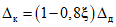 .
.5. Подача входного сигнала Ai = A0 + q(0,5i - 1).
6. Считывание значения выходного сигнала Bi.
7. Вычисление и запоминание 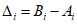 .
.
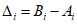 .
.8. 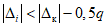 ?
?
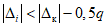 ?
?9. 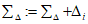 .
.
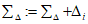 .
.10. i := i + 1.
11. i <= 3?
12. Вычисление и запоминание 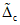 .
.
13. Запоминание признака использования ТК: NR = 1.
14. Запоминание результата поверки в данной точке.
15. Алгоритм режима НК.
16. Запоминание признака использования НК.
17. Конец.
Справочное
ПРИ ОСЛАБЛЕННОМ КОНТРОЛЕ
ПРОТОКОЛ N ________ автоматизированной поверки вольтметра цифрового типа ________________ принадлежащего ______________, заводской номер ______________________ Режим контроля: ослабленный Диапазон измерений, В _____________________________________________ Контролируемая точка, В _________________ один, два Число наблюдений ____________. Контрольный допуск, В ____________ Систематическая составляющая погрешности, В ________________________ Заключение по контролируемой точке ________________________________ годен, брак Заключение по состоянию ЦВ _______________________________________ годен, брак Начальник поверочной лаборатории _________________ (И.О. Фамилия) подпись Оператор-поверитель _____________________________ (И.О. Фамилия) подпись Дата поверки "__" _______________ 19__ г. МП |
Справочное
ПО НАСТОЯЩИМ МЕТОДИЧЕСКИМ УКАЗАНИЯМ И ИХ АНАЛИЗ
Был проведен ряд машинных экспериментов, демонстрирующих возможности методов ПК, ККП и ТК в режимах усиленного, нормального и ослабленного контроля. Результаты экспериментов сведены в пять таблиц.
В табл. 1 и 2 приведены текущие значения 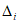 погрешностей, значения браковочного R и приемочного C чисел для режимов УК и НК соответственно. Значения
погрешностей, значения браковочного R и приемочного C чисел для режимов УК и НК соответственно. Значения 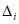 подсчитаны по известной формуле <*>
подсчитаны по известной формуле <*>
--------------------------------
<*> Вострокнутов Н.Н. Испытание и поверка цифровых измерительных устройств. М.: Изд-во стандартов, 1977.
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
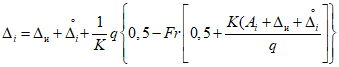 ,
,где 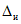 - систематическая составляющая инструментальной погрешности, в большинстве примеров поверки принятая равной двум значениям: 1,3 и 4 ступени квантования (погрешности в примерах указаны в относительных единицах по отношению к q);
- систематическая составляющая инструментальной погрешности, в большинстве примеров поверки принятая равной двум значениям: 1,3 и 4 ступени квантования (погрешности в примерах указаны в относительных единицах по отношению к q); 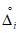 - случайные импульсные помехи; K - коэффициент преобразования квантователя, принятый равным K = 1; Fr[...] - дробная часть числа [...].
- случайные импульсные помехи; K - коэффициент преобразования квантователя, принятый равным K = 1; Fr[...] - дробная часть числа [...].
Таблица 1
i | R | C | ||
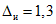 | 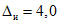 | |||
1 | 1,0 | 4,0 | 1,5 | -1,4 |
2 | 0,9 | 3,9 | 1,6 | -1,38 |
3 | 1,8 | 3,8 | 1,7 | -1,3 |
4 | 1,7 | 3,7 | 1,74 | -1,2 |
5 | 1,6 | 3,6 | 1,8 | -1,18 |
6 | 1,5 | 4,5 | 1,86 | -1,12 |
7 | 1,4 | 4,4 | 1,92 | -1,06 |
8 | 1,3 | 4,3 | 1,98 | -1,0 |
9 | 1,2 | 4,2 | 2,04 | -0,9 |
10 | 1,1 | 4,1 | 2,1 | -0,88 |
11 | 1,0 | 4,0 | 2,17 | -0,8 |
12 | 0,9 | 3,9 | 2,23 | -0,76 |
13 | 1,8 | 3,8 | 2,29 | -0,7 |
14 | 1,7 | 3,7 | 2,35 | -0,64 |
15 | 1,6 | 3,6 | 2,41 | -0,57 |
16 | 1,5 | 4,5 | 2,47 | -0,5 |
17 | 1,4 | 4,4 | 2,53 | -0,45 |
18 | 1,3 | 4,3 | 2,59 | -0,39 |
19 | 1,2 | 4,2 | 2,65 | -0,33 |
20 | 1,1 | 4,1 | 2,72 | -0,27 |
21 | 1,0 | 4,0 | 2,78 | -0,21 |
22 | 0,9 | 3,9 | 2,84 | -0,15 |
23 | 1,0 | 4,0 | 2,9 | -0,08 |
24 | 1,1 | 4,1 | 2,96 | -0,02 |
25 | 1,2 | 4,2 | 3,02 | 0,04 |
26 | 1,3 | 4,3 | 3,08 | 0,09 |
27 | 1,4 | 4,4 | 3,14 | 0,16 |
28 | 1,5 | 4,5 | 3,2 | 0,22 |
29 | 1,6 | 3,6 | 3,26 | 0,38 |
30 | 1,7 | 3,7 | 3,3 | 0,34 |
31 | 1,8 | 3,8 | 3,39 | 0,40 |
32 | 0,9 | 3,9 | 3,45 | 0,46 |
33 | 1,0 | 4,0 | 3,51 | 0,53 |
34 | 1,1 | 4,1 | 3,57 | 0,59 |
35 | 1,2 | 4,2 | 3,63 | 0,65 |
36 | 1,3 | 4,3 | 3,69 | 0,7 |
37 | 1,4 | 4,4 | 3,76 | 0,77 |
38 | 1,5 | 4,5 | 3,82 | 0,83 |
39 | 1,6 | 3,6 | 3,88 | 0,89 |
40 | 1,7 | 3,7 | 3,94 | 0,9 |
41 | 1,8 | 3,8 | 4,001 | 1,02 |
42 | 0,9 | 3,9 | 4,06 | 1,08 |
43 | 1,0 | 4,0 | 4,12 | 1,14 |
44 | 1,1 | 4,1 | 4,18 | 1,2 |
Таблица 2
i | R | C | ||
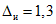 | 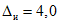 | |||
1 | 0,9 | 3,9 | 2,0 | -1,5 |
2 | 1,8 | 3,8 | 2,1 | -1,4 |
3 | 1,7 | 3,7 | 2,2 | -1,3 |
4 | 1,6 | 3,6 | 2,3 | -1,2 |
5 | 1,5 | 4,5 | 2,4 | -1,1 |
6 | 1,4 | 4,4 | 2,6 | -0,9 |
7 | 1,3 | 4,3 | 2,7 | -0,8 |
8 | 1,2 | 4,2 | 2,8 | -0,7 |
9 | 1,1 | 4,1 | 2,9 | -0,6 |
10 | 1,0 | 4,0 | 3,01 | -0,5 |
11 | 0,9 | 3,9 | 3,1 | -0,4 |
12 | 1,8 | 3,8 | 3,2 | -0,3 |
13 | 1,7 | 3,7 | 3,3 | -0,2 |
14 | 1,6 | 3,6 | 3,4 | -0,1 |
15 | 1,5 | 4,5 | 3,5 | 0,03 |
16 | 1,4 | 4,4 | 3,7 | 0,1 |
17 | 1,3 | 4,3 | 3,8 | 0,2 |
18 | 1,2 | 4,2 | 3,9 | 0,3 |
19 | 1,1 | 4,1 | 3,99 | 0,5 |
20 | 1,0 | 4,0 | 4,1 | 0,6 |
21 | 0,9 | 3,9 | 4,2 | 0,7 |
22 | 1,8 | 3,8 | 4,3 | 0,8 |
23 | 1,7 | 3,7 | 4,4 | 0,9 |
24 | 1,6 | 3,6 | 4,5 | 1,02 |
25 | 1,5 | 4,5 | 4,7 | 1,1 |
26 | 1,4 | 4,4 | 4,8 | 1,2 |
27 | 1,3 | 4,3 | 4,87 | 1,3 |
28 | 1,2 | 4,2 | 4,9 | 1,4 |
29 | 1,1 | 4,1 | 5,1 | 1,6 |
30 | 1,0 | 4,0 | 5,2 | 1,7 |
31 | 0,9 | 3,9 | 5,3 | 1,8 |
32 | 1,8 | 3,8 | 5,4 | 1,9 |
33 | 1,7 | 3,7 | 5,5 | 2,0 |
34 | 1,6 | 3,6 | 5,6 | 2,1 |
35 | 1,5 | 4,5 | 5,8 | 2,2 |
36 | 1,4 | 4,4 | 5,87 | 2,3 |
37 | 1,3 | 4,3 | 5,9 | 2,5 |
38 | 1,2 | 4,2 | 6,1 | 2,6 |
39 | 1,1 | 4,1 | 6,2 | 2,7 |
40 | 1,0 | 4,1 | 6,3 | 2,8 |
При отсутствии импульсных помех и 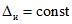 зависимость
зависимость  от Ai имеет характерный "пилообразный" характер, показанный на рис. 1, объясняющийся дискретностью выходных кодов ЦВ, т.е. наличием у ЦВ погрешности квантования. Импульсные помехи (рис. 2) и разрывы в зависимости систематической составляющей погрешности от входного сигнала (рис. 3) искажают этот характер кривой.
от Ai имеет характерный "пилообразный" характер, показанный на рис. 1, объясняющийся дискретностью выходных кодов ЦВ, т.е. наличием у ЦВ погрешности квантования. Импульсные помехи (рис. 2) и разрывы в зависимости систематической составляющей погрешности от входного сигнала (рис. 3) искажают этот характер кривой.
 зависимость
зависимость 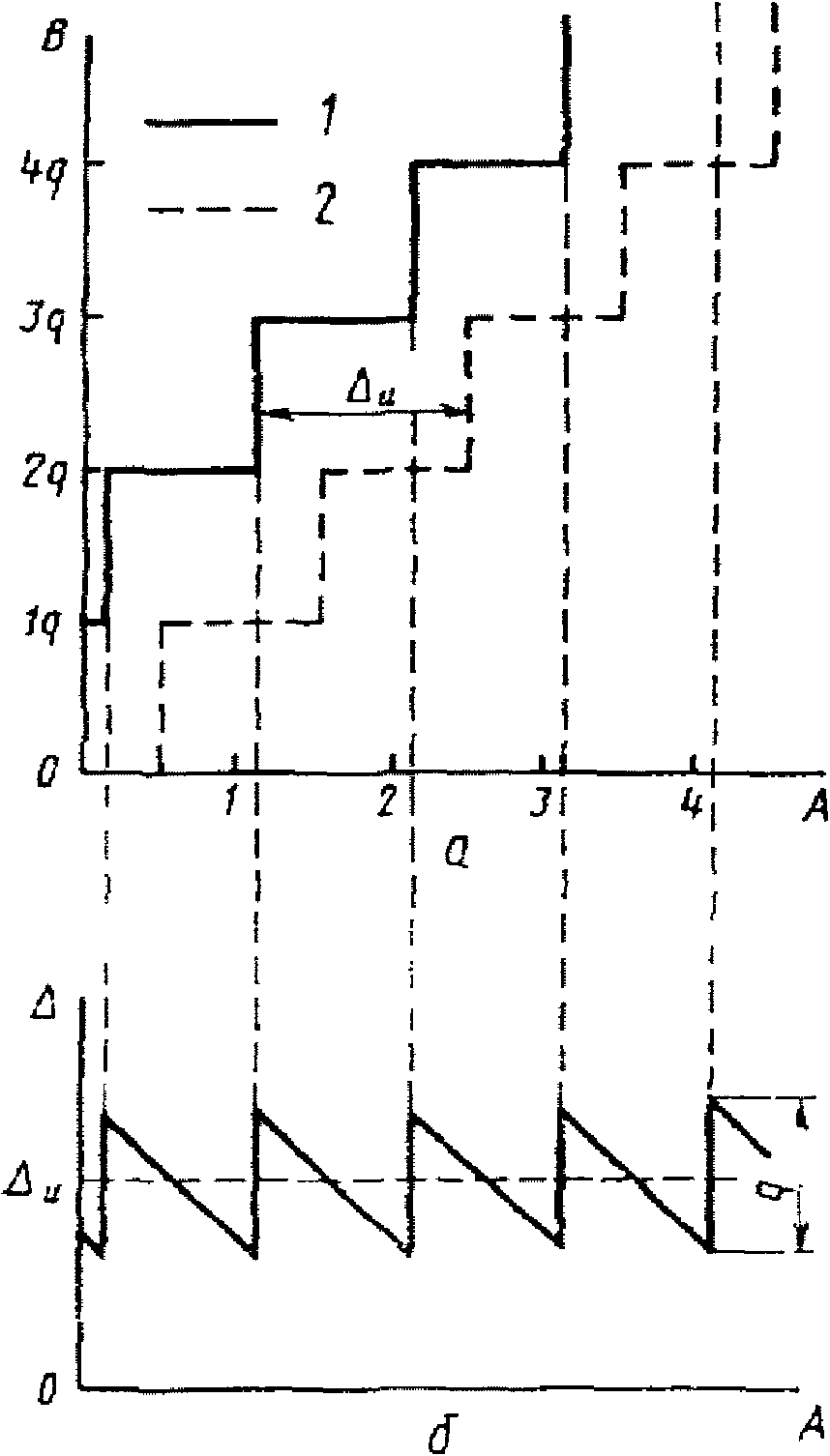
погрешности (б) ЦВ.
1 - функция преобразования ЦВ, имеющего инструментальную
погрешность, 2 - функция преобразования идеального
квантователя
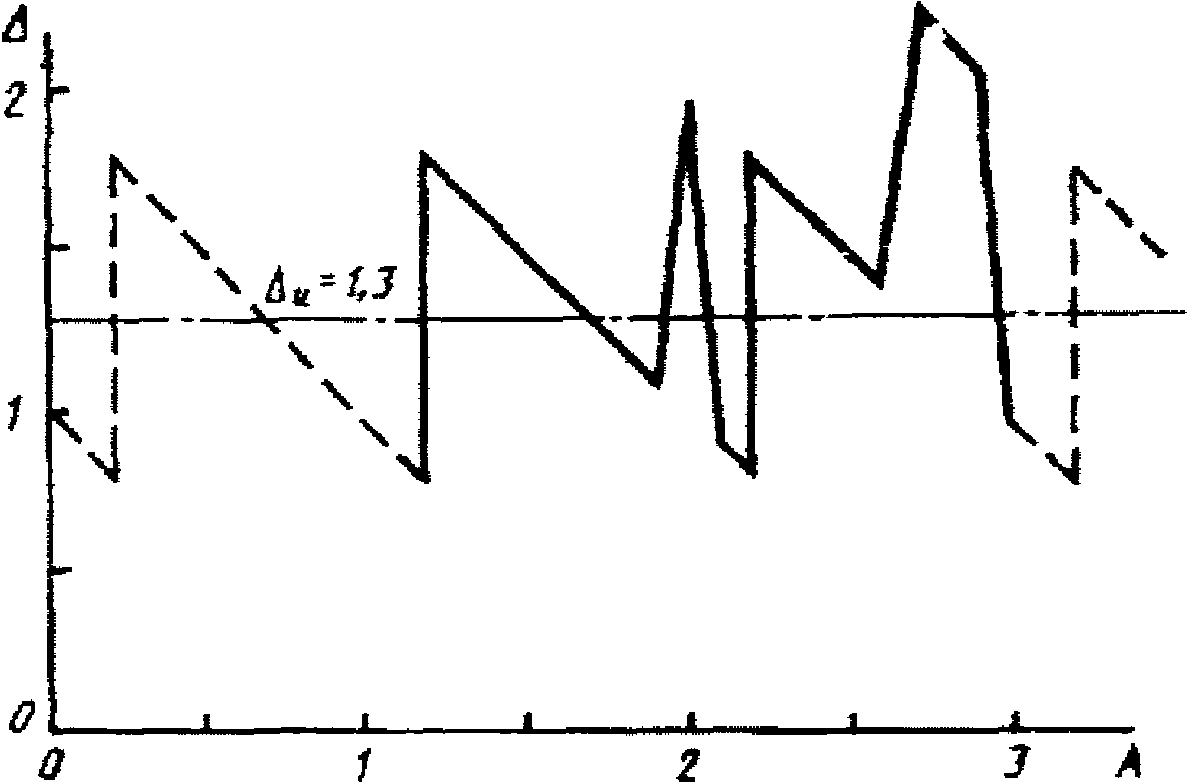
от входного сигнала и случайных импульсных помех
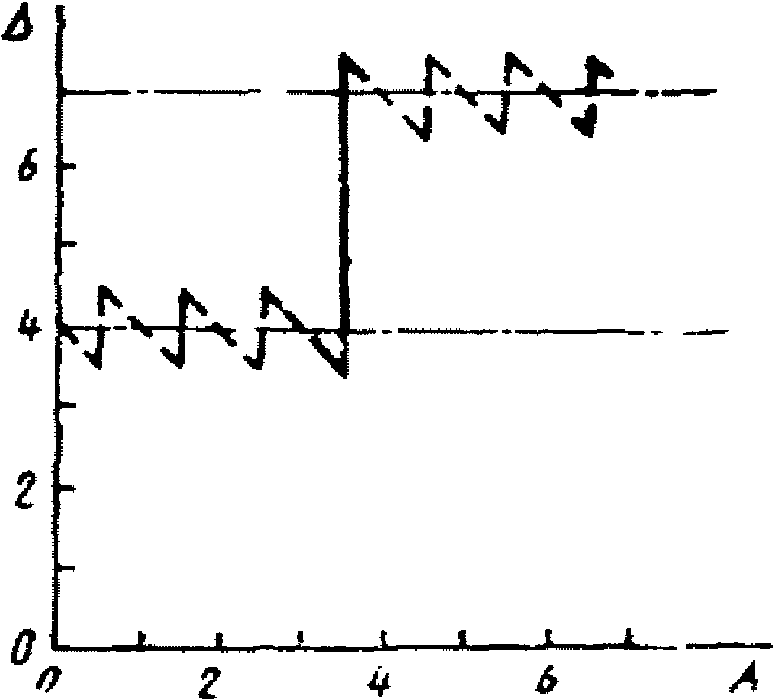
от входного сигнала при наличии разрывов
в систематической составляющей инструментальной
погрешности для примера 14 табл. 4
В табл. 3 представлены результаты усиленного контроля, основанные на обработке и анализе данных табл. 1.
Таблица 3
Номер примера | Задано | N | Оценка наличия существенной | Функция наличия брака | |||||||
ПК | ККП | Результат | |||||||||
функция наличия | |||||||||||
1,3 | 2,0 | 1:5 | 1,65 | 4 | 2,7 | 3,0 | 1 | 1 | 1 | 1 | |
1,3 | 2,1 | 1:5 | 1,73 | 44 | 1,46 | 4,4 | 1 | 1 | 0 | - | |
1,73 | 44 | 1,46 | 4,4 | 1 | 1 | 0 | 1 | ||||
1,3 | 2,2 | 1:5 | 1,81 | 25 | 1,55 | 4,3 | 1 | 0 | 0 | 0 | |
1,3 | 4,5 | 1:1,5 | 1,86 | 25 | 1,55 | 4,3 | 1 | 0 | 0 | 0 | |
4,0 | 5,2 | 1:5 | 4,29 | 7 | 4,77 | 30,7 | 0 | 1 | 1 | 1 | |
4,0 | 5,4 | 1:5 | 4,45 | 38 | 4,23 | 14,6 | 0 | 1 | 0 | - | |
4,34 | 7 | 4,77 | 11,7 | 0 | 1 | 1 | 1 | ||||
4,0 | 5,5 | 1:5 | 4,53 | 25 | 4,26 | 14,9 | 0 | 0 | 0 | 0 | |
4,0 | 8,1 | 1:2 | 4,55 | 25 | 4,26 | 14,9 | 0 | 0 | 0 | 0 | |
8,0 | 10,5 | 1:5 | 8,66 | 25 | 8,25 | 30,2 | 0 | 0 | 0 | 0 | |
10,0 | 12,7 | 1:5 | 10,47 | 38 | 10,23 | 36,0 | 0 | 1 | 0 | - | |
10,21 | 7 | 10,8 | 29,4 | 0 | 1 | 1 | 1 | ||||
В примерах 1 - 4 табл. 3 задана очень малая 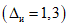 систематическая составляющая инструментальной погрешности. Допускаемая погрешность
систематическая составляющая инструментальной погрешности. Допускаемая погрешность 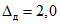 в 1-м примере превышает
в 1-м примере превышает 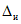 более чем на 0,5q - максимальное значение погрешности квантования. Но за счет погрешности образцовой меры (
более чем на 0,5q - максимальное значение погрешности квантования. Но за счет погрешности образцовой меры (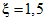 ,
, 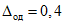 ) текущие значения погрешности из табл. 1 сравниваются при поверке не с
) текущие значения погрешности из табл. 1 сравниваются при поверке не с 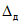 , а с контрольным допуском
, а с контрольным допуском 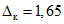 . Достаточно всего N = 4 (
. Достаточно всего N = 4 (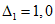 ;
; 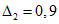 ;
; 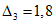 ;
; 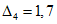 ) наблюдения, чтобы по методу ПК получить X = 2 при R = 1,74, т.е. вывод "Брак" (см. функцию наличия брака при ПК, равную 1). Расчет оценки погрешности показал, что
) наблюдения, чтобы по методу ПК получить X = 2 при R = 1,74, т.е. вывод "Брак" (см. функцию наличия брака при ПК, равную 1). Расчет оценки погрешности показал, что 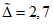 , причем
, причем 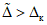 . Следовательно, функция наличия брака по ККП также равна 1, и в результате поверки получаем "Брак", так как выводы по ПК и ККП совпали. Отметим, что в следующей контролируемой точке ЭВМ тоже должна использовать при расчете
. Следовательно, функция наличия брака по ККП также равна 1, и в результате поверки получаем "Брак", так как выводы по ПК и ККП совпали. Отметим, что в следующей контролируемой точке ЭВМ тоже должна использовать при расчете 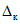 трапециевидную функцию распределения погрешностей, поскольку в этом примере
трапециевидную функцию распределения погрешностей, поскольку в этом примере 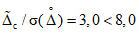 , и функция наличия
, и функция наличия 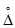 равна 1. Напомним, что случайной здесь считается (при неизвестном входном сигнале) методическая погрешность квантования.
равна 1. Напомним, что случайной здесь считается (при неизвестном входном сигнале) методическая погрешность квантования.
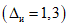 систематическая составляющая инструментальной погрешности. Допускаемая погрешность
систематическая составляющая инструментальной погрешности. Допускаемая погрешность 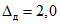 в 1-м примере превышает
в 1-м примере превышает 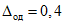 ) текущие значения погрешности из табл. 1 сравниваются при поверке не с
) текущие значения погрешности из табл. 1 сравниваются при поверке не с 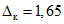 . Достаточно всего N = 4 (
. Достаточно всего N = 4 (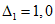 ;
; 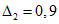 ;
; 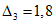 ;
; 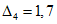 ) наблюдения, чтобы по методу ПК получить X = 2 при R = 1,74, т.е. вывод "Брак" (см. функцию наличия брака при ПК, равную 1). Расчет оценки погрешности показал, что
) наблюдения, чтобы по методу ПК получить X = 2 при R = 1,74, т.е. вывод "Брак" (см. функцию наличия брака при ПК, равную 1). Расчет оценки погрешности показал, что 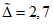 , причем
, причем 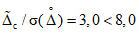 , и функция наличия
, и функция наличия В примере 2 табл. 3 допускаемая погрешность увеличена всего на 0,1 и равна 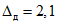 . Однако в методе ПК это привело к резкому увеличению числа наблюдений и к усечению контроля при N = 44. Только за счет того, что было получено X = 4 (при Cmax = 2,0 - см. рис. 4 приложения 2), вывод по ПК - "Брак". Но
. Однако в методе ПК это привело к резкому увеличению числа наблюдений и к усечению контроля при N = 44. Только за счет того, что было получено X = 4 (при Cmax = 2,0 - см. рис. 4 приложения 2), вывод по ПК - "Брак". Но 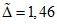 при
при 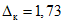 , т.е. вывод по ККП иной - "Годен" (функция наличия брака в табл. 3 равна 0). Следовательно, результат первой поверки неясен, должна проводиться повторная поверка. Поскольку случайные помехи в этом примере отсутствуют, повторная поверка, как показано в таблице, повторила первую. Результаты повторной поверки окончательны, они повторили вывод более "строгого" метода ПК - "Брак".
, т.е. вывод по ККП иной - "Годен" (функция наличия брака в табл. 3 равна 0). Следовательно, результат первой поверки неясен, должна проводиться повторная поверка. Поскольку случайные помехи в этом примере отсутствуют, повторная поверка, как показано в таблице, повторила первую. Результаты повторной поверки окончательны, они повторили вывод более "строгого" метода ПК - "Брак".
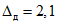 . Однако в методе ПК это привело к резкому увеличению числа наблюдений и к усечению контроля при N = 44. Только за счет того, что было получено X = 4 (при Cmax = 2,0 - см. рис. 4 приложения 2), вывод по ПК - "Брак". Но
. Однако в методе ПК это привело к резкому увеличению числа наблюдений и к усечению контроля при N = 44. Только за счет того, что было получено X = 4 (при Cmax = 2,0 - см. рис. 4 приложения 2), вывод по ПК - "Брак". Но 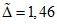 при
при 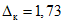 , т.е. вывод по ККП иной - "Годен" (функция наличия брака в табл. 3 равна 0). Следовательно, результат первой поверки неясен, должна проводиться повторная поверка. Поскольку случайные помехи в этом примере отсутствуют, повторная поверка, как показано в таблице, повторила первую. Результаты повторной поверки окончательны, они повторили вывод более "строгого" метода ПК - "Брак".
, т.е. вывод по ККП иной - "Годен" (функция наличия брака в табл. 3 равна 0). Следовательно, результат первой поверки неясен, должна проводиться повторная поверка. Поскольку случайные помехи в этом примере отсутствуют, повторная поверка, как показано в таблице, повторила первую. Результаты повторной поверки окончательны, они повторили вывод более "строгого" метода ПК - "Брак".В примере 3 табл. 3 допускаемая погрешность увеличена еще на 0,1 и равна 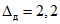 . В итоге при N = 25 ЦВ признается годным и по ПК, и по ККП.
. В итоге при N = 25 ЦВ признается годным и по ПК, и по ККП.
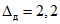 . В итоге при N = 25 ЦВ признается годным и по ПК, и по ККП.
. В итоге при N = 25 ЦВ признается годным и по ПК, и по ККП.В примере 4 табл. 3 показано, что поверка в режиме УК может привести к результату "Годен" даже при "плохом" соотношении допускаемых погрешностей 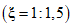 , если допускаемая погрешность ЦВ существенно превышает
, если допускаемая погрешность ЦВ существенно превышает 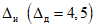 .
.
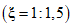 , если допускаемая погрешность ЦВ существенно превышает
, если допускаемая погрешность ЦВ существенно превышает 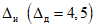 .
.В примерах 5 - 8 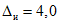 . Эти примеры по своему характеру аналогичны примерам 1 - 4. Если в примере 5 получен четкий "Брак", то в примере 6 поверяемый прибор находится как бы на грани между бракованным и годным, но все же бракуется при повторной поверке методом ПК. В примере 7 получен четкий результат "Годен". Таков же результат примера 8, хотя соотношение допускаемых погрешностей равно здесь 1:2, но
. Эти примеры по своему характеру аналогичны примерам 1 - 4. Если в примере 5 получен четкий "Брак", то в примере 6 поверяемый прибор находится как бы на грани между бракованным и годным, но все же бракуется при повторной поверке методом ПК. В примере 7 получен четкий результат "Годен". Таков же результат примера 8, хотя соотношение допускаемых погрешностей равно здесь 1:2, но 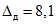 . Отличие примеров 5 - 8 в том, что в них оценка систематической составляющей погрешности немного больше оценки среднего квадратического отклонения результатов наблюдений от погрешности квантования. Следовательно, при реальной поверке в следующих контролируемых точках для подсчета
. Отличие примеров 5 - 8 в том, что в них оценка систематической составляющей погрешности немного больше оценки среднего квадратического отклонения результатов наблюдений от погрешности квантования. Следовательно, при реальной поверке в следующих контролируемых точках для подсчета 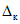 использовалось бы равномерное распределение (функция наличия
использовалось бы равномерное распределение (функция наличия  равна нулю). В этом факте причина того, что при повторной поверке в примере 6 значение
равна нулю). В этом факте причина того, что при повторной поверке в примере 6 значение 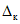 уменьшилось с 4,45 до 4,34, а число наблюдений уменьшилось с 38 до 7.
уменьшилось с 4,45 до 4,34, а число наблюдений уменьшилось с 38 до 7.
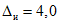 . Эти примеры по своему характеру аналогичны примерам 1 - 4. Если в примере 5 получен четкий "Брак", то в примере 6 поверяемый прибор находится как бы на грани между бракованным и годным, но все же бракуется при повторной поверке методом ПК. В примере 7 получен четкий результат "Годен". Таков же результат примера 8, хотя соотношение допускаемых погрешностей равно здесь 1:2, но
. Эти примеры по своему характеру аналогичны примерам 1 - 4. Если в примере 5 получен четкий "Брак", то в примере 6 поверяемый прибор находится как бы на грани между бракованным и годным, но все же бракуется при повторной поверке методом ПК. В примере 7 получен четкий результат "Годен". Таков же результат примера 8, хотя соотношение допускаемых погрешностей равно здесь 1:2, но 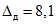 . Отличие примеров 5 - 8 в том, что в них оценка систематической составляющей погрешности немного больше оценки среднего квадратического отклонения результатов наблюдений от погрешности квантования. Следовательно, при реальной поверке в следующих контролируемых точках для подсчета
. Отличие примеров 5 - 8 в том, что в них оценка систематической составляющей погрешности немного больше оценки среднего квадратического отклонения результатов наблюдений от погрешности квантования. Следовательно, при реальной поверке в следующих контролируемых точках для подсчета Методика дает правильные результаты поверки и при сравнительно больших значениях 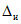 .
.
В примере 10 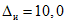 , а
, а 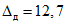 . Первая поверка приводит к бракованию только по методу ПК. При повторной поверке ЦВ бракуется и по ПК, и по ККП, поскольку вместо трапециевидного распределения использовано равномерное (
. Первая поверка приводит к бракованию только по методу ПК. При повторной поверке ЦВ бракуется и по ПК, и по ККП, поскольку вместо трапециевидного распределения использовано равномерное (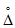 практически отсутствует), значение
практически отсутствует), значение 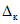 уменьшилось, а значение
уменьшилось, а значение 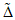 возросло. Число наблюдений, как и в примере 6, уменьшилось при повторной поверке с 38 до 7.
возросло. Число наблюдений, как и в примере 6, уменьшилось при повторной поверке с 38 до 7.
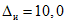 , а
, а 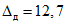 . Первая поверка приводит к бракованию только по методу ПК. При повторной поверке ЦВ бракуется и по ПК, и по ККП, поскольку вместо трапециевидного распределения использовано равномерное (
. Первая поверка приводит к бракованию только по методу ПК. При повторной поверке ЦВ бракуется и по ПК, и по ККП, поскольку вместо трапециевидного распределения использовано равномерное (Таблица 4
Номер примера | Задано | N | Оценка наличия существенной | Функция наличия брака | ||||||||
ПК | ККП | Результат | ||||||||||
Функция наличия | ||||||||||||
1,3 | 2,0 | 1:5 | - | 1,76 | 40 | 1,5 | 4,6 | 1 | 0 | 0 | 0 | |
1,3 | 1,82 | 1:5 | - | 1,6 | 13 | 1,78 | 4,2 | 1 | 1 | 1 | 1 | |
1,3 | 2,0 | 1:2 | - | 1,39 | 4 | 2,7 | 3,8 | 1 | 1 | 1 | 1 | |
1,3 | 3,1 | 1:1,5 | - | 1,83 | 15 | 1,74 | 4,4 | 1 | 0 | 0 | 0 | |
4,0 | 5,2 | 1:5 | - | 4,6 | 15 | 4,36 | 12,5 | 0 | 0 | 0 | 0 | |
4,0 | 5,0 | 1:5 | - | 4,39 | 16 | 4,36 | 12,5 | 0 | 1 | 0 | - | |
4,2 | 7 | 4,86 | 11,2 | 0 | 1 | 1 | 1 | |||||
4,0 | 5,0 | 1:3,3 | - | 4,09 | 7 | 4,85 | 12,6 | 0 | 1 | 1 | 1 | |
4,0 | 8,0 | 1:1,5 | - | 4,7 | 15 | 4,36 | 12,5 | 0 | 0 | 0 | 0 | |
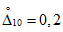 | ||||||||||||
1,3 | 2,25 | 1:5 | 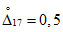 | 1,97 | 19 | 1,95 | 3,95 | 1 | 1 | 0 | - | |
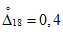 | 1,97 | 15 | 1,74 | 4,4 | 1 | 0 | 0 | 0 | ||||
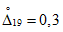 | ||||||||||||
1,3 | 2,1 | 1:5 | 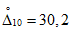 | 1,84 | 24 | 7,6 | 0,6 | 1 | 0 | 1 | - | |
1,84 | 15 | 1,74 | 4,4 | 1 | 0 | 0 | 0 | |||||
8,0 | 9,55 | 1:5 | - | 8,38 | 16 | 8,36 | 25,1 | 0 | 1 | 0 | - | |
8,022 | 7 | 8,85 | 22,3 | 0 | 1 | 1 | 1 | |||||
10,0 | 12,0 | 1:5 | - | 10,53 | 15 | 10,34 | 31,25 | 0 | 0 | 0 | 0 | |
4,0 | i = 1 - 4, i = 36 - 40 | |||||||||||
7,0 | 8,5 | 1:5 | 7,46 | 40 | 7,06 | 6,53 | 1 | 0 | 0 | 0 | ||
4,0 | i = 5 - 35 i = 1 - 4, i = 36 - 40 | |||||||||||
7,0 | 6,0 | 1:5 | i = 5 - 35 | 5,3 | 7 | 9,7 | 2,7 | 1 | 1 | 1 | 1 | |
В примерах 1 - 4 табл. 4 задано 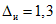 . В примере 1 исходные параметры точно те же, что и в примере 1 табл 3. Но если режим УК дает результат "Брак", то НК приводит к результату "Годен", поскольку гарантированная достоверность результатов при НК (72%) меньше чем при УК (96%). Кстати, здесь контроль при N = 40 становится усеченным и X = 4 = Cmax (см. рис. 4 приложения 2), т.е. число выходов погрешности за контрольный допуск предельно возможное для годного ЦВ. Но метод ККП подтвердил вывод ПК:
. В примере 1 исходные параметры точно те же, что и в примере 1 табл 3. Но если режим УК дает результат "Брак", то НК приводит к результату "Годен", поскольку гарантированная достоверность результатов при НК (72%) меньше чем при УК (96%). Кстати, здесь контроль при N = 40 становится усеченным и X = 4 = Cmax (см. рис. 4 приложения 2), т.е. число выходов погрешности за контрольный допуск предельно возможное для годного ЦВ. Но метод ККП подтвердил вывод ПК: 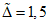 при
при 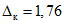 .
.
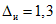 . В примере 1 исходные параметры точно те же, что и в примере 1 табл 3. Но если режим УК дает результат "Брак", то НК приводит к результату "Годен", поскольку гарантированная достоверность результатов при НК (72%) меньше чем при УК (96%). Кстати, здесь контроль при N = 40 становится усеченным и X = 4 = Cmax (см. рис. 4 приложения 2), т.е. число выходов погрешности за контрольный допуск предельно возможное для годного ЦВ. Но метод ККП подтвердил вывод ПК:
. В примере 1 исходные параметры точно те же, что и в примере 1 табл 3. Но если режим УК дает результат "Брак", то НК приводит к результату "Годен", поскольку гарантированная достоверность результатов при НК (72%) меньше чем при УК (96%). Кстати, здесь контроль при N = 40 становится усеченным и X = 4 = Cmax (см. рис. 4 приложения 2), т.е. число выходов погрешности за контрольный допуск предельно возможное для годного ЦВ. Но метод ККП подтвердил вывод ПК: 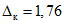 .
.Уменьшив в примере 2 табл. 4 допускаемую погрешность до 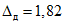 , получаем результат поверки "Брак".
, получаем результат поверки "Брак".
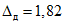 , получаем результат поверки "Брак".
, получаем результат поверки "Брак".В примере 3 по сравнению с примером 1 изменено только соотношение допускаемых погрешностей (1:2 вместо 1:5). Результат поверки также изменяется. "Брак" объясняется уменьшением точности образцовой меры, при котором достоверность результатов падает ниже установленной для НК нормы (72%).
Пример 5 табл. 4 аналогичен примеру 5 табл. 3, только НК дает результат "Годен" для того же ЦВ, который бракуется при УК.
Примеры 6 таблиц 3 и 4 также аналогичны. В обоих случаях повторная поверка приводит к "Браку". Но для НК задано 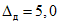 , тогда как для УК
, тогда как для УК 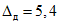 .
.
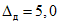 , тогда как для УК
, тогда как для УК 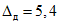 .
.Пример 7 табл. 4 по сравнению с примером 6 из той же таблицы отличается только худшим соотношением погрешностей (1:3,3 вместо 1:5) и отсутствием необходимости производить повторную поверку для того же результата ("Брак") при N = 7.
Если же увеличить допускаемую погрешность до 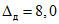 , как это сделано в примере 8, то даже при соотношении погрешностей 1:1,5 получаем результат "Годен".
, как это сделано в примере 8, то даже при соотношении погрешностей 1:1,5 получаем результат "Годен".
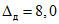 , как это сделано в примере 8, то даже при соотношении погрешностей 1:1,5 получаем результат "Годен".
, как это сделано в примере 8, то даже при соотношении погрешностей 1:1,5 получаем результат "Годен".В примерах 9 и 10 на результаты первой поверки оказывают влияние случайные импульсные помехи 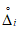 (см. рис. 2). Считаем, что при повторной поверке помехи отсутствуют. Поэтому в обоих примерах повторная поверка дала результат "Годен". Четыре импульсных помехи примера 9 (в наблюдениях i = 10, 17, 18 и 19) имеют малые амплитуды, не превышающие 0,5. Поэтому на результате метода ККП они не сказались. Но по методу ПК в первой поверке получен "Брак". А в примере 10 действует одна помеха (i = 10), но с большой амплитудой: 30,2. Она не повлияла на результат ПК, но в методе ККП при первой поверке дала четкий "Брак":
(см. рис. 2). Считаем, что при повторной поверке помехи отсутствуют. Поэтому в обоих примерах повторная поверка дала результат "Годен". Четыре импульсных помехи примера 9 (в наблюдениях i = 10, 17, 18 и 19) имеют малые амплитуды, не превышающие 0,5. Поэтому на результате метода ККП они не сказались. Но по методу ПК в первой поверке получен "Брак". А в примере 10 действует одна помеха (i = 10), но с большой амплитудой: 30,2. Она не повлияла на результат ПК, но в методе ККП при первой поверке дала четкий "Брак": 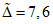 при
при 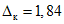 . Если бы помехи не были случайными и снова возникли при повторной поверке, ЦВ был бы забракован. Таким образом, методика "фильтрует" случайные помехи.
. Если бы помехи не были случайными и снова возникли при повторной поверке, ЦВ был бы забракован. Таким образом, методика "фильтрует" случайные помехи.
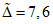 при
при 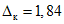 . Если бы помехи не были случайными и снова возникли при повторной поверке, ЦВ был бы забракован. Таким образом, методика "фильтрует" случайные помехи.
. Если бы помехи не были случайными и снова возникли при повторной поверке, ЦВ был бы забракован. Таким образом, методика "фильтрует" случайные помехи.Примеры 11 и 12 демонстрируют возможности методики при больших 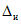 , когда число наблюдений обычно уменьшается за счет снижения "веса" погрешности квантования. Отметим, что во всех случаях получения противоречивых результатов по методам ПК и ККП при отсутствии случайных помех (в том числе и в примере 11) вывод "Брак" дает метод ПК, а не ККП. Именно этот более "строгий" метод поверки определяет достоверность ее результатов.
, когда число наблюдений обычно уменьшается за счет снижения "веса" погрешности квантования. Отметим, что во всех случаях получения противоречивых результатов по методам ПК и ККП при отсутствии случайных помех (в том числе и в примере 11) вывод "Брак" дает метод ПК, а не ККП. Именно этот более "строгий" метод поверки определяет достоверность ее результатов.
Примеры 13 и 14 характерны наличием разрыва в систематической составляющей погрешности (см. рис. 3), принимающей два значения: 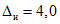 и
и 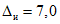 . При
. При 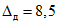 (пример 13) усеченный контроль (при N = 40) дает совместно с ККП результат "Годен". Уменьшение допускаемой погрешности в примере 14 до значения
(пример 13) усеченный контроль (при N = 40) дает совместно с ККП результат "Годен". Уменьшение допускаемой погрешности в примере 14 до значения 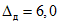 уже на седьмом наблюдении приводит к бракованию ЦВ. Методика, следовательно, дает надежные результаты и при поверке ЦВ с разрывами в характеристике (функции) преобразования квантователя.
уже на седьмом наблюдении приводит к бракованию ЦВ. Методика, следовательно, дает надежные результаты и при поверке ЦВ с разрывами в характеристике (функции) преобразования квантователя.
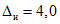 и
и 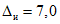 . При
. При 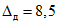 (пример 13) усеченный контроль (при N = 40) дает совместно с ККП результат "Годен". Уменьшение допускаемой погрешности в примере 14 до значения
(пример 13) усеченный контроль (при N = 40) дает совместно с ККП результат "Годен". Уменьшение допускаемой погрешности в примере 14 до значения 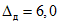 уже на седьмом наблюдении приводит к бракованию ЦВ. Методика, следовательно, дает надежные результаты и при поверке ЦВ с разрывами в характеристике (функции) преобразования квантователя.
уже на седьмом наблюдении приводит к бракованию ЦВ. Методика, следовательно, дает надежные результаты и при поверке ЦВ с разрывами в характеристике (функции) преобразования квантователя.В табл. 5 представлены результаты поверки в режиме ослабленного контроля по методу ТК.
Номер примера | Задано | Вычислено | Функция брака (при невыполнении условия 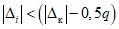 для для | Функция брака в результате ТК | |||||||
1,3 | 2,0 | 1:5 | 1,68 | 1,5 | 1,0 | 1,5 | 1 | 0 | 1 | 1 | |
2 | 4,0 | 6,0 | 1:5 | 5,04 | 4,5 | 4,0 | 4,5 | 0 | 0 | 0 | 0 |
3 | 1,3 | 3,0 | 1:5 | 2,52 | 1,5 | 1,0 | 1,5 | 0 | 0 | 0 | 0 |
Исходные данные примера 1 здесь совпадают с данными примера 1 из табл. 4. Метод ТК (см. табл. 5) дает "Брак", но при переходе, как того требует методика, к режиму НК и методу ПК получаем "Годен" (табл. 4). Следовательно, "жесткость" метода ТК не приводит к ошибке поверки 1-го рода.
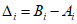
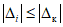
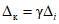
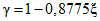
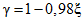
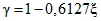
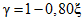
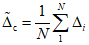
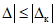
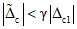
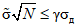
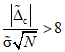
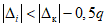
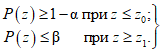
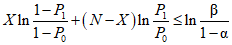
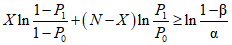
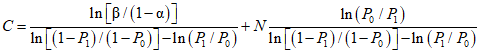
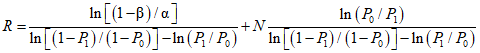
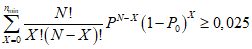
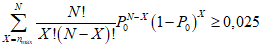
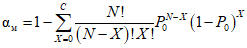
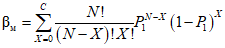
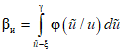
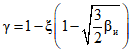
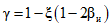
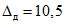 получаем "Годен".
получаем "Годен".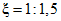 за счет увеличения
за счет увеличения 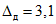 .
.