СПРАВКА
Источник публикации
М.: Издательство стандартов, 1987
Примечание к документу
Документ введен в действие с 01.07.1987.
Название документа
"МИ 1453-86. Методические указания. Оценка достоверности данных о физико-механических свойствах металлов и сплавов"
(утв. Протоколом НТС ВНИЦ ПВ от 19.12.1985 N 25)
"МИ 1453-86. Методические указания. Оценка достоверности данных о физико-механических свойствах металлов и сплавов"
(утв. Протоколом НТС ВНИЦ ПВ от 19.12.1985 N 25)
Утверждены
Протоколом секции N 3
научно-технического Совета
Всесоюзного научно-исследовательского
центра по изучению свойств
поверхности и вакуума
от 19 декабря 1985 г. N 25
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ОЦЕНКА ДОСТОВЕРНОСТИ ДАННЫХ
О ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВАХ МЕТАЛЛОВ И СПЛАВОВ
МИ 1453-86
Введены в действие
с 1 июля 1987 года
РАЗРАБОТАНЫ Всесоюзным научно-исследовательским центром по материалам и веществам Госстандарта СССР (ВНИЦ МВ Госстандарта СССР), Московским институтом стали и сплавов
ИСПОЛНИТЕЛИ
Л.В. Кобликова; Г.А. Карпова; М.И. Орлов, канд. физ.-мат. наук
ПОДГОТОВЛЕНЫ К УТВЕРЖДЕНИЮ Всесоюзным научно-исследовательским институтом метрологической службы (ВНИИМС)
Начальник отдела стандартизации Г.П. Сафаров
УТВЕРЖДЕНЫ секцией N 3 научно-технического Совета Всесоюзного научно-исследовательского центра по изучению свойств поверхности и вакуума 19 декабря 1985 г. (протокол N 25).
Настоящие методические указания устанавливают основные принципы оценки достоверности результатов измерений физико-механических свойств металлов и сплавов.
Методические указания рассчитаны на инженерно-технических и научных работников лабораторий физико-механических испытаний.
Излагаемые методы оценки достоверности данных предусматривают возможность использования ЭВМ.
Методические указания разработаны в дополнение к государственным стандартам на методы определения физико-механических свойств металлов и сплавов.
1.1. Методы определения данных о физико-механических свойствах металлов и сплавов <*> регламентируются действующими государственными стандартами. Настоящие методические указания устанавливают основные принципы оценки достоверности результатов измерений физико-механических свойств металлов и сплавов <**>.
--------------------------------
<*> В дальнейшем - данные.
<**> В дальнейшем - результаты измерения.
1.2. Методические указания распространяются на данные, полученные методами измерений макроскопически изотропного материала в зоне температур и внешних физических воздействий, не приводящих к изменению его химического состава и структуры.
1.3. Определение данных в различных областях науки и техники проводится с разных физических позиций:
в математических теориях упругости, пластичности и ползучести, исходя из представлений о сплошной среде;
в физике твердого тела с учетом атомной структуры и ее нарушений на основе теории дислокаций и вакансий;
в металловедении с учетом микроструктуры и ее изменений;
в физико-химической механике с учетом воздействий окружающей среды на деформируемое тело.
1.4. Оценка достоверности данных должна проводиться на основе обеспечения и оценки точности определения данных конкретным методом определения и сравнительного анализа и сопоставления результатов измерения с оцененными данными, полученными в других лабораториях, с помощью методов и средств измерения, основанных на других физических предпосылках и позициях. Поскольку данные об одном и том же свойстве в большей или меньшей степени согласованы, основной задачей при проведении сравнительного анализа является оценка согласованности данных между собой.
О ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВАХ МЕТАЛЛОВ И СПЛАВОВ
2.1. Большое число методов получения данных о физико-механических свойствах металлов и сплавов основано на выполнении косвенных измерений, то есть измерений, при которых значения измеряемой величины A находят путем согласованных измерений других величин - аргументов Ai, связанных с измеряемой величиной известной зависимостью
где A - искомое значение косвенно измеряемой величины; f - функциональная зависимость, форма которой и природа связанных ею величин заранее известны; A1, ..., Am - значения величин Ai.
По виду функциональной зависимости (1) необходимо различать косвенные измерения с линейной зависимостью (линейные) с нелинейной зависимостью (нелинейные) между измеряемой величиной и аргументами.
2.2. Так как аргументы Ai, содержащие случайные и систематические погрешности измерений, являются случайными величинами, измеряемую величину A следует рассматривать функцией случайных величин с нормальным распределением вероятностей.
2.3. В качестве оценки истинного значения косвенно измеряемой величины A необходимо принимать значение, получаемое подстановкой в (1) средних арифметических значений аргументов.
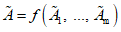 . (2)
. (2)2.4. Результаты измерения величин A, A1, ..., Am должны быть представлены совокупностью следующих данных:
S, Si - оценка среднего квадратического отклонения результата измерения;
n - число наблюдений, использованных для нахождения S, Si.
2.5. Систематические погрешности, возникающие при измерении физико-механических свойств металлов и сплавов, обусловлены многими причинами, как то:
несоответствием представлений о структуре и физических свойствах материала образца, положенных в основу теоретического соотношения;
несоответствием геометрии образца (формы, размеров), принятым в модели;
несоответствием условий внешнего воздействия на образец, принятым при проведении измерений (его закреплении в измерительной установке, воздействие агрессивных сред, неучтенное воздействие температур, воздушных потоков, атмосферного давления, влажности воздуха, вибраций, магнитных и электрических полей, ионизирующих излучений и др.);
неточностью показаний измерительных приборов из-за их конструкционных недостатков или технологического несовершенства изготовления (наличием люфтов и мертвых ходов в подвижных частях, неравномерным трением в опорах, неточностью градуировки средств измерения, старением (износом) деталей, элементов узлов измерительных приборов, а также нарушением их регулировки и т.д.);
несовершенством метода измерения, как следствие некоторых допущений и упрощений, применением эмпирических формул и функциональных зависимостей вместо точных, неполным знанием всех свойств наблюдаемых явлений и т.п.;
индивидуальными особенностями наблюдателя.
2.5.1. Поскольку невыявленные систематические погрешности могут быть причиной ошибочных выводов, установления ложных законов, неудовлетворительной конструкции устройства и массового брака на производстве, для обеспечения достоверности получения данных необходимо проводить тщательный анализ и учет возможных причин появления систематических погрешностей.
2.5.2. Учет систематических погрешностей заключается в их обнаружении и максимально возможном исключении путем введения компенсирующей поправки.
2.5.3. При прямых измерениях Ai с точным оцениванием систематических погрешностей необходимо различать средства измерения, показания которых дают оценку измеряемой величины (основные) и средства измерения влияющих величин (дополнительные). Для основных средств измерения необходимо установить индивидуальные систематические погрешности, для дополнительных можно ограничиться данными нормативных документов. Далее необходимо найти функции влияния тех влияющих величин, которые при измерении могут оказаться за пределами области их нормальных значений.
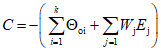 (3)
(3)где C - поправка; 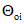 - оценка систематической погрешности основных средств измерения; Ej - оценка влияющей величины; Wj - коэффициент влияния.
- оценка систематической погрешности основных средств измерения; Ej - оценка влияющей величины; Wj - коэффициент влияния.
2.5.4. Неисключенные систематические погрешности должны учитываться при определении погрешности аргументов Ai.
Например, причинами неисключенных остатков систематических погрешностей могут быть:
систематические погрешности образцовых средств, с помощью которых оценивались погрешности основных средств измерения;
погрешности оценки влияющей величины и определения коэффициента влияния;
возможная динамическая погрешность и т.п.
2.5.5. Для вычисления неисключенных систематических погрешностей их необходимо рассматривать как случайные величины с равномерной плотностью распределения 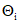 , принимая, что распределение
, принимая, что распределение 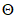 изменяется в зависимости от числа слагаемых
изменяется в зависимости от числа слагаемых 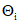 от равномерного до нормального.
от равномерного до нормального.
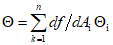 , (4)
, (4)где df/dAi - частная производная в точке измерения или коэффициент влияния 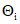 на
на 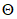 .
.
2.5.6. В случае линейных косвенных измерений, когда 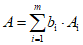 , для оценки границ систематической погрешности следует пользоваться следующими правилами.
, для оценки границ систематической погрешности следует пользоваться следующими правилами.
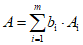 , для оценки границ систематической погрешности следует пользоваться следующими правилами.
, для оценки границ систематической погрешности следует пользоваться следующими правилами.2.5.6.1. Если число m мало и 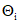 можно считать равномерно распределенными в пределах границ
можно считать равномерно распределенными в пределах границ 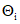 , то
, то
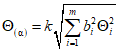 . (5)
. (5)Значения коэффициента k приведены в ГОСТ 8.207-76.
При m <= 3 следует также оценить сумму 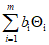 , и если
, и если 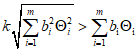 , то за границы неисключенной систематической погрешности нужно принять
, то за границы неисключенной систематической погрешности нужно принять
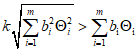 , то за границы неисключенной систематической погрешности нужно принять
, то за границы неисключенной систематической погрешности нужно принять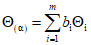 . (6)
. (6)2.5.6.2. Если составляющие 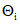 образованы большим числом слагаемых и все границы
образованы большим числом слагаемых и все границы 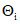 вычислены для одной и той же доверительной вероятности
вычислены для одной и той же доверительной вероятности 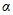 , то
, то
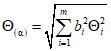 , (7)
, (7)Если k слагаемых 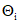 имеют нормальное распределение и l-равномерное, то
имеют нормальное распределение и l-равномерное, то
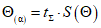 , (8)
, (8)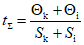 , (9)
, (9)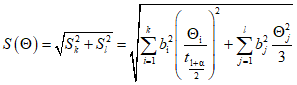 , (10)
, (10)2.5.7. В случае нелинейных косвенных измерений, когда 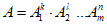 , расчет систематической погрешности результата измерения необходимо производить в относительной форме
, расчет систематической погрешности результата измерения необходимо производить в относительной форме
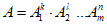 , расчет систематической погрешности результата измерения необходимо производить в относительной форме
, расчет систематической погрешности результата измерения необходимо производить в относительной формеВместо абсолютных погрешностей измерений аргументов во всех формулах следует оперировать их относительными погрешностями. Коэффициенты влияния для относительных погрешностей аргументов оказываются равными показателями степеней соответствующих аргументов.
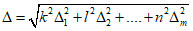 . (12)
. (12)Для расчета границ систематической погрешности результата измерения необходимо пользоваться теми же правилами, что и в п. 2.5.6, границы систематических погрешностей 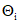 заменить на
заменить на  , а коэффициенты bi на коэффициенты влияния в относительной форме.
, а коэффициенты bi на коэффициенты влияния в относительной форме.
2.5.8. В случае нелинейной зависимости смешанного типа уравнение принимает вид
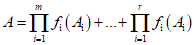 . (13)
. (13)2.6. Случайная погрешность результата косвенного измерения, образующаяся путем сложения случайных погрешностей аргументов Ai с большим основанием может считаться нормально распределенной величиной.
2.6.1. Оценка среднего квадратического отклонения случайной погрешности определяется соотношением
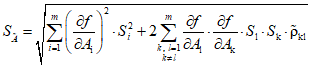 , (14)
, (14)где df/dAi - частная производная в точке измерения, вычисляемая при средних арифметических значениях аргументов; Sl, Sk - оценки средних квадратических отклонений результатов измерений величин Al и Ak соответственно; 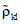 - оценка коэффициента корреляции между случайными погрешностями l и k-аргументов; m - количество аргументов.
- оценка коэффициента корреляции между случайными погрешностями l и k-аргументов; m - количество аргументов.
2.6.2. При линейных косвенных измерениях
где 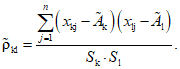 (16)
(16)
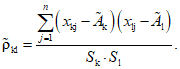 (16)
(16)Корреляция между погрешностями измерений аргументов возникает тогда, когда измерения выполняются одновременно на однотипных средствах измерений и изменение величин оказывает воздействие на результаты наблюдений.
Если же аргументы измеряют в разное время и для их измерений применяют разные по устройству средства измерений, то нет оснований ожидать появление корреляции между погрешностями этих измерений, в этом случае формула (15) принимает вид
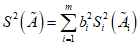 . (17)
. (17)2.6.3. В случае нелинейных косвенных измерений
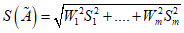 , (18)
, (18)где Wi - коэффициенты влияния
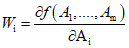 . (19)
. (19)В случае, если 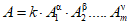 , расчет
, расчет 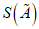 необходимо производить в относительной форме
необходимо производить в относительной форме
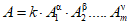 , расчет
, расчет 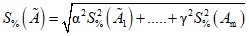 . (20)
. (20)2.6.4. Доверительные границы случайной погрешности определения вычисляются, исходя из нормального закона распределения случайных погрешностей по формуле
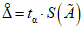 , (21)
, (21)где 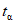 - квантиль нормального распределения.
- квантиль нормального распределения.
О ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВАХ МЕТАЛЛОВ И СПЛАВОВ
3.1. Оценка достоверности данных, полученных в процессе проведенного эксперимента, заключается в проведении сопоставительного анализа результатов измерения с данными, полученными принципиально различными путями в других экспериментах и лабораториях.
3.2. Важной задачей в процедуре оценки достоверности является комплектование наиболее представительного массива имеющихся экспериментальных данных измеренной величины или величин, связанных с ней функционально, и выбора из всего массива экспериментальных данных наилучших по точности определения и достоверности. Необходимо отличать ситуации, когда сличение результатов оправдано и когда оно недопустимо.
Например, лишено смысла сопоставление таких результатов измерений, при которых по существу измерялись разные по размерам величины или оценка точности определения сопоставляемых данных сомнительна и т.п.
3.3. Достоверность полученных в процессе эксперимента данных подтверждается (не подтверждается) при проведении анализа их согласованности между собой.
3.4. Математически задача сводится к проверке принадлежности массивов сопоставляемых данных одной и той же генеральной совокупности с одним центром и дисперсией рассеивания. Методы проверки однородности массива состоят в анализе значимых смещений относительно друг друга средних значений 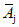 и их дисперсий D[Aj].
и их дисперсий D[Aj].
3.5. Для проведения сопоставительного анализа делается ряд допущений:
возможное множество результатов измерений и случайные погрешности 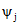 распределены по нормальному закону;
распределены по нормальному закону;
систематическая погрешность 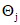 конкретной реализации способа измерений принимается случайной, равномерно распределенной величиной;
конкретной реализации способа измерений принимается случайной, равномерно распределенной величиной;
весовые коэффициенты j массива данных определяются дисперсиями результатов измерений
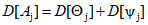 . (22)
. (22)3.5.1. Проверка однородности массива, образованного из полученных при эксперименте и сопоставимых данных, выполняется с использованием статистических методов Стьюдента, Фишера, Аббе, а также корреляционного и регрессионного анализа.
4. В случае невозможности применения методов статистического анализа для оценки сопоставимости научных результатов оценка достоверности проводится авторами в пределах их компетенции и с использованием методов квалиметрии (экспертных оценок).
Необходимость применения этих методов должна быть аргументирована и процедура их применения тщательно описана.
УДК 661 : 620.178 |