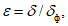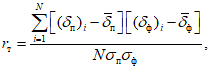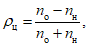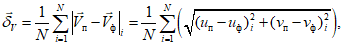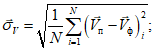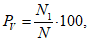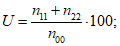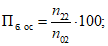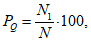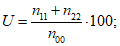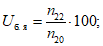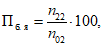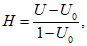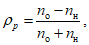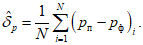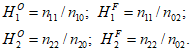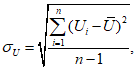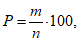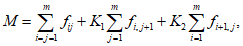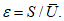СПРАВКА
Источник публикации
М.: Госгидромет СССР, 1991
Примечание к документу
Документ введен в действие с 1 января 1992 года.
Взамен Методических указаний по проведению оперативных испытаний новых методов гидрометеорологических прогнозов, 1977 г. и Временных указаний по проведению оперативных испытаний методов долгосрочных прогнозов погоды, 1983 г.
Название документа
"РД 52.27.284-91. Руководящий документ. Методические указания. Проведение производственных (оперативных) испытаний новых и усовершенствованных методов гидрометеорологических и гелиогеофизических прогнозов"
(утв. ГУГМС СССР 25.01.1991)
"РД 52.27.284-91. Руководящий документ. Методические указания. Проведение производственных (оперативных) испытаний новых и усовершенствованных методов гидрометеорологических и гелиогеофизических прогнозов"
(утв. ГУГМС СССР 25.01.1991)
Комитетом гидрометеорологии
при Кабинете Министров СССР
25 января 1991 года
РУКОВОДЯЩИЙ ДОКУМЕНТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПРОВЕДЕНИЕ ПРОИЗВОДСТВЕННЫХ (ОПЕРАТИВНЫХ) ИСПЫТАНИЙ
НОВЫХ И УСОВЕРШЕНСТВОВАННЫХ МЕТОДОВ ГИДРОМЕТЕОРОЛОГИЧЕСКИХ
И ГЕЛИОГЕОФИЗИЧЕСКИХ ПРОГНОЗОВ
РД 52.27.284-91
Группа Т58
Дата введения
1 января 1992 года
Настоящий руководящий документ (РД) устанавливает общие правила проведения производственных (оперативных) испытаний новых и усовершенствованных методов гидрометеорологических и гелиогеофизических прогнозов и их оценки.
Положения РД обязательны для организаций Росгидромета СССР, проводящих производственные испытания методов гидрометеорологических и гелиогеофизических прогнозов, для Центральной методической комиссии по гидрометеорологическим прогнозам (ЦМКП) и Методической комиссии по снеголавинным прогнозам (МКПЛ).
Производственные (оперативные) испытания новых и усовершенствованных методов гидрометеорологических прогнозов являются неотъемлемой частью процесса их внедрения в оперативную практику учреждений Госгидромета СССР.
Производственные испытания преследуют две основные цели:
определение степени надежности испытываемых методов или численных схем прогноза в сравнении с имеющимися и установление возможности их внедрения в оперативную практику;
анализ ошибок прогнозов и выработка рекомендаций по дальнейшему усовершенствованию методов прогнозов.
Вопросы организации производственных испытаний, порядок их проведения и подведение итогов определены Положением Госгидромета СССР [1].
Результаты производственных испытаний новых и усовершенствованных методов прогнозов, разработанных для крупных физико-географических и экономических районов, для сельскохозяйственных зон, акваторий морей и океанов, методов прогнозов стихийных гидрометеорологических явлений, а также методов среднесрочных, долгосрочных, краткосрочных, сверхкраткосрочных прогнозов погоды и методов гелиогеофизических прогнозов рассматриваются Центральной методической комиссией по гидрометеорологическим прогнозам Госгидромета СССР. Результаты производственных испытаний методов, имеющих локальное значение, рассматриваются на Технических советах управлений-заказчиков.
Результаты производственных испытаний новых и усовершенствованных методов (способов) прогнозов снеголавинной опасности рассматриваются Методической комиссией по снеголавинным прогнозам, организованной Госгидрометом СССР при САНИГМИ.
Решения о целесообразности внедрения в оперативную практику организаций Госгидромета СССР новых и усовершенствованных методов прогнозов принимаются при положительных результатах их производственных испытаний.
Установлена следующая продолжительность испытания различных видов прогнозов:
для численных схем прогноза метеорологических элементов - не более шести месяцев (на оперативном материале или с использованием стандартных архивов метеорологических полей);
для краткосрочных и среднесрочных прогнозов погоды, гидрологических и морских прогнозов - до одного года;
для долгосрочных прогнозов погоды, гидрологических, морских и агрометеорологических прогнозов - до двух лет.
Для сокращения сроков испытания и получения статистически надежных выводов о надежности методов прогноза гидрометеорологических явлений с малой природной повторяемостью (опасных и стихийных), а также долгосрочных прогнозов в период производственных испытаний рекомендуется использовать независимый ряд наблюдений по архивам прошлых лет.
На основании рассмотрения результатов испытаний ЦМКП и Технические (Ученые) советы принимают решение о целесообразности внедрения разработанного метода в качестве основного, вспомогательного или консультативного, а также о нецелесообразности внедрения в связи с низкой надежностью метода, в случае необходимости - о дальнейшем усовершенствовании метода.
В качестве основного для внедрения рекомендуется метод прогноза, являющийся лучшим в сравнении с применяемыми методами по надежности или технологичности (при одинаковом уровне надежности).
В качестве вспомогательного рекомендуется метод прогноза, являющийся лучшим в сравнении с применяемыми методами по надежности в отдельные периоды, в отдельных районах (пунктах, водных объектах), при определенных гидрометеорологических условиях или дающий объективную основу при составлении прогнозов.
В качестве консультативных могут быть рекомендованы отдельные методы прогнозов, имеющие невысокую надежность, но являющиеся единственными для определенных гидрометеорологических условий, районов или заблаговременностей.
Накопленный ранее опыт оперативных испытаний в Гидрометцентре СССР, других НИУ, республиканских и территориальных управлениях по гидрометеорологии Росгидромета СССР был обобщен в [2, 3], а также в наставлениях по оценке различных видов прогнозов и в отдельных публикациях, помещаемых в ежегодных информационных сборниках о результатах испытаний новых методов гидрометеорологических прогнозов, подготавливаемых лабораторией испытания новых методов прогнозов Гидрометцентра СССР.
В последние годы появились новые направления в разработке методов гидрометеорологических прогнозов, новые виды прогнозов, дальнейшее развитие получили методы проведения испытаний, разработаны некоторые характеристики оценки качества прогнозов. Эти обстоятельства явились причиной подготовки настоящих методических указаний по проведению производственных (оперативных) испытаний, в которых учтен опыт, накопленный при использовании методических указаний, изданных в 1977 г. [2], а также международный опыт. В настоящие методические указания включены современные системы оценок и методики проведения производственных испытаний различных видов гидрометеорологических и гелиогеофизических прогнозов.
В основу приводимых ниже оценок различных видов прогнозов положены принципы, изложенные в соответствующих наставлениях по службе прогнозов, учтены рекомендации ВМО по оценке численных схем и рекомендации ИКАО по оценке авиационных прогнозов. Как показала практика проведения производственных испытаний, анализа и обобщения их результатов, одних этих оценок бывает недостаточно для всесторонней характеристики метода. Поэтому для различных видов прогнозов рекомендуются еще дополнительные характеристики качества.
Учитывая сложность организации и проведения производственных испытаний в различных подразделениях Госгидромета, их следует считать ответственным научным экспериментом, имеющим существенное значение не только для быстрейшего внедрения новых научных достижений, но и для дальнейшего усовершенствования испытываемых методов прогноза.
Современный уровень развития гидродинамических, физико-статистических и синоптических методов прогноза дает возможность количественного прогноза различных метеорологических элементов и явлений погоды (атмосферного давления, температуры, осадков, скорости и направления ветра, опасных и стихийных явлений и др.) как в отдельных пунктах, так и на больших территориях. Большое количество прогнозируемых элементов и методов их предвычисления диктует необходимость унификации и автоматизации процесса испытаний.
Принципиально важными при проведении испытаний являются:
правильный выбор территории, по которой необходимо проводить оценку;
выбор и контроль фактических данных наблюдений или объективного анализа, используемых для сравнения;
типы синоптических процессов, содержащие случаи с большой и малой изменчивостью фактических полей метеорологических элементов для различных сезонов года;
количество случаев для испытаний, обеспечивающее статистическую достоверность выводов;
единообразие используемых оценок, позволяющее установить надежность проверяемых численных схем и расчетных методов прогноза.
Выполнение указанных требований обеспечит методически правильное проведение производственных испытаний и сравнимость оценок в прогностических подразделениях, проводящих испытания.
анализа полей метеорологических элементов и явлений
и объективного анализа полей метеорологических элементов
1.1.1.1. Испытание численных схем прогноза и объективного анализа полей метеорологических элементов и явлений погоды обычно проводится в Гидрометцентре СССР, региональных или территориальных центрах, располагающих электронно-вычислительной техникой и обеспечивающих составление численных прогнозов. При испытании новых численных схем должно проводиться определение их эффективности в сравнении с используемыми численными схемами в данном центре.
1.1.1.2. Численный прогноз полей метеорологических элементов (давления, геопотенциала, температуры, ветра и др.) рассчитывается для различных уровней атмосферы в узлах регулярной сетки по территориям от региона до полушария, с заблаговременностью до 72 ч (краткосрочные прогнозы) и от 72 ч до 10 суток (среднесрочные прогнозы).
1.1.1.3. При испытании численных схем прогноза и объективного анализа метеорологических элементов необходимо руководствоваться следующими основными положениями:
1) оценка должна производиться для каждой изобарической поверхности и для каждого срока прогноза отдельно;
2) территория для оценки прогнозов выбирается в зависимости от назначения численных прогнозов. Оценка надежности численной схемы производится по всей области прогноза, а также по территории, обслуживаемой данным прогностическим центром;
3) сравнение испытываемой численной модели с используемыми в оперативной работе производится на одном и том же материале, т.е. по одинаковым территориям, регулярным сеткам, срокам прогноза, изобарическим поверхностям, периодам и количеству прогнозов;
4) испытания численных схем могут проводиться либо в оперативном (полуоперативном) режиме, либо на материале специально разработанного автоматизированного архива стандартных синоптических ситуаций;
5) случаи для испытания численных схем прогноза метеорологических явлений должны содержать разнообразные типы синоптических положений за различные сезоны года с большой и малой фактической изменчивостью полей. При испытании численных схем прогноза барического поля и ветра должны использоваться случаи углубляющихся и заполняющихся циклонов, усиливающихся и разрушающихся антициклонов, стационарных и быстро смещающихся в различных направлениях, случаи появления новых барических образований, при испытании численных схем прогноза температуры воздуха и точки росы - случаи их интенсивной и слабой адвекции, трансформации, выделения теплоты конденсации при выпадении осадков, наличие или отсутствие интенсивных вертикальных движений;
6) для определения качества численного прогноза метеорологических элементов необходимо рассчитывать статистические оценки. При этом в качестве исходных и фактических данных используются результаты объективного анализа соответствующих полей, применяющихся в данной численной схеме.
Для оценки качества численного прогноза давления и геопотенциала для центров барических образований (циклонов, антициклонов) рассчитываются синоптико-статистические характеристики путем использования исходных, прогностических и фактических синоптических карт и карт барической топографии;
7) при оценке качества схемы объективного анализа метеорологических элементов рассчитывают статистические и синоптико-статистические характеристики. Испытываемая схема объективного анализа сравнивается с "ручным" анализом, выполненным синоптиками, с ранее внедренными объективными анализами и с данными метеорологических станций. Приемлемой методикой испытания различных схем объективного анализа является также сравнение качества численных прогнозов, рассчитанных на основе одной прогностической модели, использующей в качестве исходной информации данные сравниваемых объективных анализов;
8) статистические показатели успешности численных прогнозов и объективного анализа имеют реальный смысл лишь при наличии достаточно длинных рядов испытываемых переменных (расчетных точек), которые обеспечивают необходимый доверительный интервал и репрезентативность рассчитываемых оценок.
Влияние количества расчетных точек на доверительный интервал коэффициента корреляции r и относительной ошибки  можно оценить по следующим формулам:
можно оценить по следующим формулам:
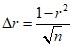 ,
,  ,
,где  .
.
 .
.В табл. 1 приведены доверительные интервалы для различных значений r и  в зависимости от количества расчетных точек (n).
в зависимости от количества расчетных точек (n).
Таблица 1
и относительной ошибки 
r | |||||||
n = 30 | n = 143 | n = 841 | n = 30 | n = 143 | n = 841 | ||
0,3 | 0,95 | 0,17 | 0,08 | 0,03 | 0,05 | 0,02 | 0,01 |
0,4 | 0,92 | 0,15 | 0,07 | 0,03 | 0,06 | 0,03 | 0,01 |
0,5 | 0,87 | 0,14 | 0,06 | 0,02 | 0,08 | 0,03 | 0,01 |
0,6 | 0,80 | 0,12 | 0,05 | 0,02 | 0,09 | 0,04 | 0,02 |
0,7 | 0,71 | 0,09 | 0,04 | 0,02 | 0,09 | 0,04 | 0,02 |
0,8 | 0,60 | 0,06 | 0,03 | 0,01 | 0,08 | 0,04 | 0,02 |
0,9 | 0,44 | 0,03 | 0,02 | 0,01 | 0,06 | 0,04 | 0,02 |
Принимая во внимание данные табл. 1 и то, что значения r и 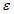 рассчитываются с точностью до 0,01, количество расчетных узлов должно в совокупности составлять 1000 или более. Зная количество расчетных точек по территории одного численного прогноза, легко определить минимальное количество прогнозов, необходимое для получения достоверных значений статистических оценок полей метеорологических элементов. Так, для региона размером 11 x 13 точек количество оцениваемых прогнозов должно быть не менее 6 - 7. Однако для обеспечения достаточной репрезентативности оценок прогноза особых точек барических образований (центров циклонов и антициклонов) объем выборки (исходных сроков прогноза) должен быть
рассчитываются с точностью до 0,01, количество расчетных узлов должно в совокупности составлять 1000 или более. Зная количество расчетных точек по территории одного численного прогноза, легко определить минимальное количество прогнозов, необходимое для получения достоверных значений статистических оценок полей метеорологических элементов. Так, для региона размером 11 x 13 точек количество оцениваемых прогнозов должно быть не менее 6 - 7. Однако для обеспечения достаточной репрезентативности оценок прогноза особых точек барических образований (центров циклонов и антициклонов) объем выборки (исходных сроков прогноза) должен быть 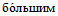 : для полусферных прогнозов - не менее 16 случаев, а для региональных прогнозов (территория 11 x 13 точек) - не менее 32 случаев;
: для полусферных прогнозов - не менее 16 случаев, а для региональных прогнозов (территория 11 x 13 точек) - не менее 32 случаев;
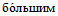 : для полусферных прогнозов - не менее 16 случаев, а для региональных прогнозов (территория 11 x 13 точек) - не менее 32 случаев;
: для полусферных прогнозов - не менее 16 случаев, а для региональных прогнозов (территория 11 x 13 точек) - не менее 32 случаев;9) принимая во внимание, что слишком густая сетка точек увеличивает взаимную корреляцию между исходными данными, используемыми при расчете статистических оценок, расстояние между точками регулярной сетки около 600 км можно считать близким к оптимальному.
1.1.1.4. Численные прогнозы метеорологических явлений (осадки, шквалы, гололед, град и др.) рассчитываются либо для узлов регулярной сетки, либо непосредственно для пунктов региона с заблаговременностью 12 и 36 ч (день), 24 и 48 ч (ночь).
1.1.1.5. При испытании численных схем прогноза метеорологических явлений необходимо руководствоваться следующими условиями:
1) оценка производится для каждого срока прогноза отдельно: для дневных прогнозов - по данным наблюдений о явлениях в период с 9 до 21 ч, для ночных прогнозов - по данным наблюдений в период с 21 до 9 ч;
2) оценка оправдываемости прогнозов метеорологических явлений производится по пунктам и по районам. Если прогнозы рассчитываются для узлов регулярной сетки, то при оценке оправдываемости прогнозов по пунктам используется выбранная для испытаний сеть метеорологических станций, расположенных на расстоянии не более 50 км от узлов сетки.
Оценка оправдываемости прогнозов по району производится по данным метеорологических станций, находящихся в радиусе, составляющем половину шага сетки (например, радиус 150 км при шаге сетки 300 км). При этом используется вся имеющаяся информация о явлениях погоды в данной зоне на картах погоды за все сроки наблюдений и из донесений об опасных и стихийных явлениях погоды, относящихся к периоду действия прогноза;
3) при испытании численных схем прогноза метеорологических явлений в выборку должны входить случаи с явлениями и без явлений за соответствующие сезоны;
4) количество случаев (прогнозов) при испытании указанных численных схем должно составлять не менее 60. Так, для испытания численных схем прогноза осадков, гроз и града можно ограничиться одним летним сезоном, если повторяемость данного явления по территории региона достаточно велика. В некоторых случаях для обеспечения репрезентативности оценок успешности для различных сезонов года период испытания схем прогноза метеорологических явлений может быть продлен до одного года.
Для сокращения сроков испытаний и получения статистически надежных выводов об успешности схем прогноза явлений с малой природной повторяемостью рекомендуется использовать независимый ряд наблюдений по архивам прошлых лет;
5) при испытании численных схем прогноза метеорологических явлений, а также полей температуры (точки росы) и ветра с привлечением к испытанию прогностических подразделений эффективность новой схемы выявляется на основании результатов ее сравнения с применяемыми численными моделями, а также расчетными и синоптическими методами прогноза, согласно действующему Наставлению [4] и статистическим оценкам, приведенным ниже;
6) при отсутствии аналогичных методов и численных схем прогнозов метеорологических явлений следует производить сопоставление качества методических прогнозов с качеством "псевдопрогнозов": инерционных, случайных и климатических прогнозов (последние - при оценке среднесрочных численных прогнозов). В этих случаях методические прогнозы могут быть признаны удовлетворительными лишь в том случае, когда рассчитанные оценки (или хотя бы часть из них) для этих прогнозов будут выше, чем соответствующие оценки для "псевдопрогнозов".
полей давления воздуха у поверхности Земли и геопотенциала
на изобарических поверхностях
Для наиболее полной оценки качества численных схем прогноза и анализа барического поля необходимо использовать статистические и синоптико-статистические характеристики успешности, взаимно дополняющие друг друга. Статистические оценки качества прогнозов, объективно рассчитываемые на ЭВМ, позволяют установить успешность прогнозов в целом и произвести сопоставление различных схем прогноза с целью отбора наилучшей.
Синоптико-статистические характеристики успешности позволяют установить, насколько успешно та или другая численная схема прогнозирует положение, скорость и направление перемещения и эволюцию основных барических образований (циклонов, антициклонов). Расчет синоптико-статистических характеристик успешности производится в основном вручную с использованием исходных, прогностических и фактических карт и поэтому является весьма трудоемким.
прогноза барического поля с заблаговременностью до 48 ч
Для оценки качества полушарных и региональных численных прогнозов на срок до 48 ч следует рассчитывать следующие статистические характеристики:
1) средняя абсолютная ошибка прогноза (с точностью до 0,1)
2) средняя относительная ошибка прогноза (с точность до 0,01)
где  - средняя абсолютная фактическая изменчивость.
- средняя абсолютная фактическая изменчивость.
 - средняя абсолютная фактическая изменчивость.
- средняя абсолютная фактическая изменчивость.В формулах (1) и (2) N - общее число точек регулярной сетки по территории прогноза (i = 1, 2, ..., N), Hп, Hф, Hи - соответственно прогностическое, фактическое (в срок прогноза) и исходное значения давления (геопотенциала).
Чем меньше  и
и  , тем лучше прогноз. При значении
, тем лучше прогноз. При значении 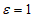 качество методических прогнозов находится на уровне инерционных прогнозов, а при
качество методических прогнозов находится на уровне инерционных прогнозов, а при 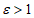 методические прогнозы барического поля хуже инерционных;
методические прогнозы барического поля хуже инерционных;
3) средняя квадратическая ошибка прогноза (с точностью до 0,1)
Чем меньше  , тем выше качество прогноза. По сравнению со средней абсолютной ошибкой прогноза
, тем выше качество прогноза. По сравнению со средней абсолютной ошибкой прогноза  в среднюю квадратическую ошибку
в среднюю квадратическую ошибку 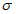 наибольший вклад вносят значительные разности (Hп - Hф). При нормальном распределении ошибок
наибольший вклад вносят значительные разности (Hп - Hф). При нормальном распределении ошибок 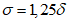 . В реальных условиях значения
. В реальных условиях значения 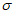 примерно на 20% превышают значения
примерно на 20% превышают значения  ;
;
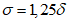 . В реальных условиях значения
. В реальных условиях значения 4) средняя арифметическая (систематическая) ошибка прогноза (с точностью до 0,1)
Систематическая ошибка позволяет судить о так называемой фоновой погрешности, т.е. о методическом среднем смещении прогностического поля давления или геопотенциала. Положительные значения 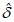 указывают на систематическое завышение прогностических значений давления или геопотенциала, отрицательные
указывают на систематическое завышение прогностических значений давления или геопотенциала, отрицательные  - на их занижение;
- на их занижение;
5) среднее квадратическое отклонение ошибки прогноза (стандартная ошибка), с точностью до 0,1
По сравнению с  , величина
, величина 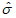 учитывает вклад систематических ошибок, что помогает автору вносить необходимую коррекцию в численную модель прогноза;
учитывает вклад систематических ошибок, что помогает автору вносить необходимую коррекцию в численную модель прогноза;
6) корреляция тенденций - коэффициент корреляции между прогностическими и фактическими изменениями давления (геопотенциала), с точностью до 0,01
где
 ;
; 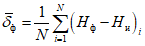 ;
;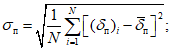

При точном прогнозе r = 1, при плохом r = 0. Следует отметить, что значения 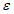 и r при нормальном распределении проверяемых величин связаны между собой соотношением
и r при нормальном распределении проверяемых величин связаны между собой соотношением  , или
, или  . Отсюда следует, что с уменьшением (увеличением)
. Отсюда следует, что с уменьшением (увеличением) 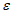 должен увеличиваться (уменьшаться) коэффициент корреляции r;
должен увеличиваться (уменьшаться) коэффициент корреляции r;
 , или
, или  . Отсюда следует, что с уменьшением (увеличением)
. Отсюда следует, что с уменьшением (увеличением) 7) оценка прогнозов с учетом градиентов давления (геопотенциала)
где числитель указывает ошибку в прогнозе разности давления (геопотенциала) в i-й паре точек, а знаменатель - фактическую или прогностическую изменчивость в той же паре точек (наибольшую по значению), N - число пар точек.
Критерий S1 позволяет дать оценку подобия градиентов сравниваемых барических полей. При идеальном прогнозе S1 = 0.
При современном уровне развития гидродинамических прогнозов прогноз приземного давления можно считать отличным при S1 <= 20, хорошим при 20 < S1 <= 40, удовлетворительным при 40 < S1 <= 70 и бесполезным при S1 > 70; прогноз высотного барического поля можно считать отличным при S1 <= 15 и бесполезным при S1 > 60.
Рассчитанные для каждой изобарической поверхности (чаще у поверхности Земли и для 500 гПа) статистические характеристики приводятся в виде таблицы осредненных по месяцам и за период испытаний значений оценок, в которой также указывается для каждой испытываемой модели территория оценки, период испытаний, заблаговременность прогнозов, количество прогнозов.
барического поля с заблаговременностью до 48 ч
Синоптико-статистические оценки численных прогнозов барического поля включают:
оценку оправдываемости прогноза давления (геопотенциала) в центре барических образований и их эволюции;
оценку оправдываемости прогнозов положения и траекторий барических образований за период, соответствующий заблаговременности прогноза;
оценку прогнозов факта возникновения (исчезновения) барических образований.
Для расчета указанных оценок исходные данные снимаются с исходных, фактических и прогностических карт в центрах циклонов и антициклонов. Циклоны и антициклоны включаются в выборку, если они имеют хотя бы одну замкнутую изобару (изогипсу) на фактической или прогностической карте.
Примечание. Принимая во внимание, что современные отечественные численные модели по точности прогноза барического поля приближаются к точности передовых зарубежных численных схем, а также большую трудоемкость и невысокую точность расчета синоптико-статистических оценок, их следует рассматривать как дополнительные и в некоторых случаях ограничиваться расчетом только статистических оценок, приведенных в п. 1.1.2.1. Такое ограничение может быть принято Ученым советом института-разработчика с учетом результатов авторских испытаний и обязательно должно быть отражено в программе испытаний.
(геопотенциала) в центре барических образований
и их эволюции
Для оценки оправдываемости прогноза значений давления (геопотенциала) в центрах барических образований и его эволюции рассчитываются средние абсолютные 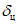 по формуле (1), средние арифметические
по формуле (1), средние арифметические 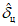 по формуле (4) ошибки прогноза давления (геопотенциала), относительные ошибки
по формуле (4) ошибки прогноза давления (геопотенциала), относительные ошибки 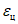 по формуле (2) и оправдываемость прогнозов знака эволюции давления (геопотенциала)
по формуле (2) и оправдываемость прогнозов знака эволюции давления (геопотенциала) 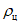 по формуле (8). Указанные характеристики успешности рассчитываются для всех барических образований, а также отдельно для циклонов и антициклонов.
по формуле (8). Указанные характеристики успешности рассчитываются для всех барических образований, а также отдельно для циклонов и антициклонов.
Для расчета  и
и 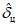 значения давления (геопотенциала) снимаются с прогностических и фактических карт в центрах барических образований с точностью 1 - 2 гПа. Положительные значения
значения давления (геопотенциала) снимаются с прогностических и фактических карт в центрах барических образований с точностью 1 - 2 гПа. Положительные значения  указывают на систематическое завышение давления в центре барического образования, а отрицательные значения
указывают на систематическое завышение давления в центре барического образования, а отрицательные значения  - на занижение.
- на занижение.
Расчет относительной ошибки прогноза давления (геопотенциала) в центрах барических образований  определяется по формуле (2), где N - общее количество барических образований либо количество циклонов или антициклонов.
определяется по формуле (2), где N - общее количество барических образований либо количество циклонов или антициклонов.
Оправдываемость прогнозов знака эволюции давления (геопотенциала) оценивается с помощью величины:
где nо и nн - соответственно число центров, в которых прогноз знака изменения давления (геопотенциала) оправдался или не оправдался.
При вычислении 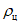 необходимо для каждого центра найти значения фактической изменчивости
необходимо для каждого центра найти значения фактической изменчивости 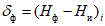 и прогностической изменчивости
и прогностической изменчивости 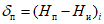 за соответствующий заблаговременности прогноза интервал времени и произвести их сравнение. В случае если знаки
за соответствующий заблаговременности прогноза интервал времени и произвести их сравнение. В случае если знаки 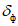 и
и  в центре циклона (антициклона) совпадают, прогноз считается оправдавшимся и получает оценку со знаком "+". В случае если знаки
в центре циклона (антициклона) совпадают, прогноз считается оправдавшимся и получает оценку со знаком "+". В случае если знаки 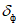 и
и  оказались противоположными, прогноз эволюции не оправдался и получает оценку со знаком "-". Затем определяются nо и nн, а также рассчитывается среднее значение
оказались противоположными, прогноз эволюции не оправдался и получает оценку со знаком "-". Затем определяются nо и nн, а также рассчитывается среднее значение  для каждой заблаговременности прогноза и испытываемой численной модели.
для каждой заблаговременности прогноза и испытываемой численной модели.
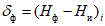 и прогностической изменчивости
и прогностической изменчивости 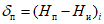 за соответствующий заблаговременности прогноза интервал времени и произвести их сравнение. В случае если знаки
за соответствующий заблаговременности прогноза интервал времени и произвести их сравнение. В случае если знаки Для более детального анализа знака эволюции давления в центрах барических образований на разных стадиях их развития желательно рассчитывать  для случаев фактического углубления (усиления), заполнения (ослабления) циклонов (антициклонов) и для случаев, когда давление (геопотенциал) в их центрах не менялось.
для случаев фактического углубления (усиления), заполнения (ослабления) циклонов (антициклонов) и для случаев, когда давление (геопотенциал) в их центрах не менялось.
Вычисленные средние значения 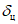 ,
,  ,
, 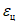 и
и 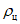 представляются в виде табл. 2.
представляются в виде табл. 2.
Таблица 2
(геопотенциала) в центрах барических образований
и их эволюции у поверхности Земли и на различных
изобарических поверхностях
Схема | Заблаговременность, ч | Число барических образований | Средняя изменчивость | Средняя ошибка | Оправдываемость по знаку | |||
фактическая | прогностическая | абсолютная | арифметическая | относительная | ||||
У поверхности Земли | ||||||||
1 | 24 | 155 | 4,74 | 3,98 | 4,68 | -2,15 | 0,83 | 0,14 |
2 | 24 | 155 | 4,65 | 4,37 | 5,58 | -1,05 | 0,90 | 0,07 |
1 | 48 | 129 | 6,25 | 4,85 | 5,75 | -2,01 | 0,91 | 0,26 |
2 | 48 | 129 | 6,30 | 5,01 | 6,34 | 1,52 | 1,00 | 0,06 |
Поверхность 500 гПа | ||||||||
1 | 24 | 139 | 3,37 | 3,00 | 3,61 | 0,52 | 0,79 | 0,15 |
2 | 24 | 139 | 3,37 | 3,04 | 3,67 | -1,64 | 0,84 | 0,02 |
1 | 48 | 120 | 4,77 | 4,72 | 5,05 | 1,00 | 0,85 | 0,10 |
2 | 48 | 120 | 5,09 | 4,53 | 5,47 | -1,85 | 0,93 | 0,00 |
В приведенном примере оценки численных схем (табл. 2) схема 1 имеет более высокие характеристики успешности по сравнению со схемой 2.
и траектории барических образований
Для определения качества прогноза перемещения барических образований вычисляются:
ошибка в прогнозе положения барических образований (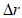 , км);
, км);
ошибка в прогнозе траектории барических образований за период, соответствующий заблаговременности прогноза (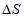 , км);
, км);
ошибка в прогнозе направления перемещения  .
.
Величина 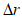 определяется как расстояние между прогностическим и фактическим положениями центров барических образований с точностью до 10 км. Значения
определяется как расстояние между прогностическим и фактическим положениями центров барических образований с точностью до 10 км. Значения  рассчитываются как отдельно для циклонов и антициклонов, так и для тех и других вместе.
рассчитываются как отдельно для циклонов и антициклонов, так и для тех и других вместе.
Ошибка в прогнозе траектории циклонов и антициклонов определяется как разность между прогностическим и фактическим перемещениями центров циклонов (антициклонов) за период заблаговременности прогноза с точностью до 10 км. 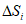 рассчитывается как разность протяженностей фактической и прогностической траекторий барических центров, считая их прямолинейными за период заблаговременности прогноза. Затем для всех барических образований и отдельно для циклонов и антициклонов рассчитываются средние значения
рассчитывается как разность протяженностей фактической и прогностической траекторий барических центров, считая их прямолинейными за период заблаговременности прогноза. Затем для всех барических образований и отдельно для циклонов и антициклонов рассчитываются средние значения 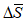 по модулю и средние значения
по модулю и средние значения 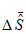 с учетом знака.
с учетом знака. 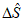 указывает на систематическое замедление или ускорение перемещения прогностических центров циклонов (антициклонов), так как траектории численно равны средней скорости перемещения барических центров за период заблаговременности прогноза.
указывает на систематическое замедление или ускорение перемещения прогностических центров циклонов (антициклонов), так как траектории численно равны средней скорости перемещения барических центров за период заблаговременности прогноза.
Ошибка в прогнозе направления перемещения циклонов и антициклонов 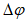 определяется значением угла между прогностической и фактической траекториями движения циклонов (антициклонов) с точностью до 1°. При этом выделяются случаи отклонения прогностической траектории от фактической влево (вл.) и вправо (вп.). Вычисляются средние значения
определяется значением угла между прогностической и фактической траекториями движения циклонов (антициклонов) с точностью до 1°. При этом выделяются случаи отклонения прогностической траектории от фактической влево (вл.) и вправо (вп.). Вычисляются средние значения  для всех барических образований, отдельно для циклонов и антициклонов, а также для случаев отклонения траекторий влево и вправо. Значения средних оценок, рассчитанные отдельно для циклонов и антициклонов, приводятся в тексте отчета по результатам испытания.
для всех барических образований, отдельно для циклонов и антициклонов, а также для случаев отклонения траекторий влево и вправо. Значения средних оценок, рассчитанные отдельно для циклонов и антициклонов, приводятся в тексте отчета по результатам испытания.
Опыт работы по испытанию численных прогнозов барического поля показал, что допустимыми ошибками при прогнозах заблаговременностью до 36 ч являются 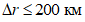 ,
,  ,
,  при хорошем прогнозе;
при хорошем прогнозе; 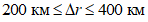 ,
, 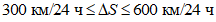 ;
;  при удовлетворительном;
при удовлетворительном;  ,
, 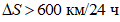 ,
,  при плохом.
при плохом.
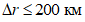 ,
,  ,
,  при хорошем прогнозе;
при хорошем прогнозе; 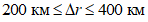 ,
, 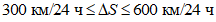 ;
;  при удовлетворительном;
при удовлетворительном;  ,
, 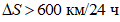 ,
,  при плохом.
при плохом.(исчезновения) барических образований
Для полной характеристики качества численной схемы очень важно оценить прогноз возникновения новых барических образований, а также прогноз заполнения циклонов и разрушения антициклонов, существовавших в исходный срок.
Используя исходные, фактические и прогностические карты, подсчитывается количество оправдавшихся новых центров (a); количество оправдавшихся исчезнувших центров (b); количество предсказанных, но не наблюдавшихся (ложных) новых центров (c); количество наблюдавшихся, но не предсказанных (сглаженных) центров (d). Используя эти данные, рассчитываются следующие характеристики:
оправдываемость в процентах прогноза возникновения новых центров

оправдываемость в процентах прогноза исчезновения центров

общая оправдываемость в процентах новообразования и исчезновения барических центров
 (9)
(9)Результаты проверки прогнозов положения, скорости перемещения, возникновения и исчезновения барических образований следует представить по форме 1.
Сопоставление статистических и синоптико-статистических характеристик позволит оценить надежность проверяемой численной схемы прогноза барического поля в сравнении с использующимися в оперативной практике. При этом предпочтение отдается той из них, оценки которой являются лучшими. При решении вопроса о внедрении учитывается также технологичность и экономичность численных схем, принимаются во внимание количество и качество прогнозов различных метеорологических элементов, рассчитываемых той или иной численной схемой.
Для установления успешности прогнозов по проверяемой численной схеме в различных физико-географических районах и выявления областей систематических ошибок прогноза необходим анализ рассчитанных статистических характеристик по территории прогноза. Показательными в этом отношении являются карты распределения  ,
,  ,
,  и
и 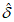 , осредненных для каждого узла регулярной сетки по месяцам и сезонам. Очень полезным является выделение и анализ статистических характеристик для определенных синоптических ситуаций, в особенности тех, которые приводят к резким изменениям и неблагоприятным условиям погоды в различные сезоны года.
, осредненных для каждого узла регулярной сетки по месяцам и сезонам. Очень полезным является выделение и анализ статистических характеристик для определенных синоптических ситуаций, в особенности тех, которые приводят к резким изменениям и неблагоприятным условиям погоды в различные сезоны года.
Для установления источников ошибок проверяемой численной схемы можно провести дополнительный анализ статистических характеристик в районах, занимаемых циклонами и антициклонами. В этих случаях область оценки является переменной и ее следует смещать в направлении перемещения барических образований, а полученные при этом статистические характеристики несравнимы с характеристиками для всей области прогноза. Такие оценки представляют определенную ценность, так как дают возможность установления применимости численной схемы в определенных синоптических ситуациях и физико-географических условиях. Это важно как для синоптиков, использующих численные прогнозы в оперативной работе, так и для авторов, работающих над усовершенствованием численных схем.
возникновения и исчезновения барических образований
Численная схема (автор) | Заблаговременность, ч | Количество барических образований | Количество оправдавшихся новых центров (a) | Количество оправдавшихся исчезнувших центров (b) | Количество ложных центров (c) | Количество сглаженных центров (d) | Qн | Qи | Q | ||||||
вл. | вп. | ||||||||||||||
У поверхности Земли | |||||||||||||||
Уровень 500 гПа | |||||||||||||||
анализа полей метеорологических элементов
Главной трудностью, с которой приходится сталкиваться при оценке надежности новых численных схем объективного анализа (ОА) полей метеорологических элементов, является получение исходных данных, которые можно уверенно использовать в качестве "эталонных" для сравнения с данными испытываемой схемы ОА.
Предлагаются следующие четыре способа возможной оценки ОА, каждый из которых может использоваться с учетом имеющихся возможностей и имеет свои преимущества и недостатки:
1) сравнение испытываемой схемы ОА с анализом полей метеорологических элементов, выполненным вручную синоптиком, полагая, что последний наиболее близок к истине. Способ этот используется для оценки ОА барического поля. Понятно, что синоптический (субъективный) анализ обладает определенными недостатками, тем не менее синоптик при анализе использует историю развития синоптических процессов, а также наблюдения за ветром, что позволяет в некоторых случаях восстанавливать целые барические образования особенно над малоосвещенными районами. Одновременно производится сравнение с синоптическим анализом и схемы ОА, ранее внедренной в оперативную практику.
При сопоставлении численной схемы ОА барического поля с синоптическим анализом на картах вручную выделяются экстремальные точки барических полей (центры циклонов и антициклонов) и рассчитываются следующие синоптико-статистические характеристики:
Ошибки 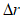 ,
,  и
и  рассчитываются как отдельно для циклонов и антициклонов, так и для тех и других вместе.
рассчитываются как отдельно для циклонов и антициклонов, так и для тех и других вместе.
При использовании схем объективного анализа барического поля важно также оценить, насколько правильно испытываемая схема ОА представляет количество барических центров, т.е. оценить сглаживания наблюдавшихся барических центров либо представления ложных центров. С этой целью определяется количество центров на картах испытываемой схемы ОА (n1) и количество центров на картах синоптического ОА (n2) и рассчитывается величина Q = n1/n2. Если Q > 1, то испытываемая схема ОА имеет тенденцию к диагнозу ложных центров, если Q < 1, то происходит сглаживание центров. Величину Q желательно рассчитывать как отдельно для циклонов и антициклонов, так и для тех и других вместе.
Синоптико-статистические оценки ОА барического поля представляются по форме 2;
2) сравнение данных в узлах регулярной сетки, полученных по испытываемой схеме ОА, с данными наблюдений на станциях. Для этой цели предварительно выбираются станции, совпадающие с узлами регулярной сетки ОА либо отстоящими от них не более чем на 50 км;
3) сравнение испытываемой схемы ОА с объективными анализами лучших зарубежных центров (например, НМЦ США или ЕЦСПП), принимая во внимание, что в настоящее время успешность ОА зарубежных центров выше успешности отечественных схем ОА.
При проведении сравнения испытываемой схемы ОА с данными метеорологических станций или ОА зарубежных центров в автоматизированном режиме рассчитываются следующие оценки: средние абсолютные ошибки 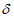 , средние систематические ошибки
, средние систематические ошибки  , средние квадратические ошибки
, средние квадратические ошибки  и коэффициент корреляции r между значениями метеорологических элементов в узлах сетки сравниваемых объективных анализов. Лучшим считается объективный анализ, имеющий более высокие оценки успешности;
и коэффициент корреляции r между значениями метеорологических элементов в узлах сетки сравниваемых объективных анализов. Лучшим считается объективный анализ, имеющий более высокие оценки успешности;
4) сравнение качества численных прогнозов, рассчитанных по одной и той же численной прогностической модели, но с использованием в качестве исходных данные в узлах регулярной сетки, полученные с помощью сравниваемых численных схем ОА. В автоматизированном режиме рассчитываются статистические оценки получаемых прогнозов (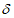 ,
, 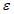 ,
, 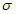 ,
,  , r, S1), расчетные формулы которых приведены в п. 1.1.2. Сравнение статистических характеристик прогнозов, полученных по разным схемам ОА, позволяет сделать вывод о качестве сравниваемых объективных анализов: вариант прогноза с ОА лучшего качества имеет лучшие показатели успешности.
, r, S1), расчетные формулы которых приведены в п. 1.1.2. Сравнение статистических характеристик прогнозов, полученных по разным схемам ОА, позволяет сделать вывод о качестве сравниваемых объективных анализов: вариант прогноза с ОА лучшего качества имеет лучшие показатели успешности.
Сопоставление объективных анализов производится по территории северного полушария либо для отдельных регионов, например, для Европы (10° з.д. - 50° в.д., 35 - 75° с.ш.), Азии (60 - 140° в.д., 0 - 75° с.ш.), Африки (10° з.д. - 50° в.д., 0 - 30° с.ш.), Тихого океана (150° в.д. - 140° з.д.), Северной Америки (130° в.д. - 70° з.д.), Атлантического океана (60 - 20° з.д.), Приполярного района (80 - 90° с.ш.).
Уровень, гПа | Число барических образований | n1 | n2 | Q = n1/n2 | |||||||||||||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
Земля | |||||||||||||||||||||
850 | |||||||||||||||||||||
700 | |||||||||||||||||||||
500 | |||||||||||||||||||||
300 | |||||||||||||||||||||
... | |||||||||||||||||||||
... | |||||||||||||||||||||
... | |||||||||||||||||||||
Примечание. 1 - циклоны, 2 - антициклоны, 3 - все барические образования.
анализа полей температуры воздуха, влажности
(точка росы), ветра и осадков
Оценка надежности численных схем ОА полей температуры, влажности (точки росы) и ветра у поверхности Земли и на изобарических поверхностях производится путем сравнения данных ОА в узлах регулярной сетки с данными измерений на станциях, совпадающих с узлами сетки или расположенных от них в радиусе не более 50 км. При этом рассчитываются и анализируются следующие статистические оценки:
средняя абсолютная ошибка температуры (точки росы) 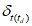 , средняя квадратическая ошибка
, средняя квадратическая ошибка  , средняя систематическая ошибка
, средняя систематическая ошибка  (формулы (1), (3), (4), в которые подставляются соответствующие значения t и td);
(формулы (1), (3), (4), в которые подставляются соответствующие значения t и td);
средняя абсолютная ошибка анализа вектора ветра  , средняя квадратическая ошибка вектора ветра
, средняя квадратическая ошибка вектора ветра 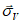 , средняя абсолютная ошибка скорости ветра
, средняя абсолютная ошибка скорости ветра 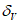 , средняя систематическая ошибка скорости ветра
, средняя систематическая ошибка скорости ветра 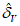 , средняя абсолютная ошибка направления ветра
, средняя абсолютная ошибка направления ветра  . Для вычисления этих статистических характеристик используются формулы (17) - (21).
. Для вычисления этих статистических характеристик используются формулы (17) - (21).
Качество схем ОА осадков устанавливается по двум показателям: по факту их наличия или отсутствия и количеству путем сравнения данных об осадках в узлах регулярной сетки ОА с данными на станциях, отстоящих от узлов сетки не далее 50 км либо совпадающих с ними. При оценке объективного анализа осадков по факту (по аналогии с прогнозом) рассчитывается общая оправдываемость анализа (u), оправдываемость факта наличия осадков (uос), предупрежденность осадков (Пос), оправдываемость факта отсутствия осадков (uб. ос), предупрежденность факта отсутствия осадков (Пб. ос), критерий качества Пирси - Обухова.
При оценке количества осадков рассчитываются средняя абсолютная ошибка  , средняя систематическая ошибка
, средняя систематическая ошибка  и повторяемость ошибок анализа количества осадков (PQ) при заданных значениях градаций (<= 1, <= 2, <= 3, > 3 мм за 12 ч в холодный период года и <= 1, <= 2, <= 3, <= 5, <= 8, > 8 мм за 12 в теплый период года).
и повторяемость ошибок анализа количества осадков (PQ) при заданных значениях градаций (<= 1, <= 2, <= 3, > 3 мм за 12 ч в холодный период года и <= 1, <= 2, <= 3, <= 5, <= 8, > 8 мм за 12 в теплый период года).
Для расчета указанных выше характеристик качества ОА осадков по факту и по количеству следует использовать формулы (22) - (30) и рекомендации, изложенные в п. 1.1.5, подставляя в формулы вместо прогностических значений осадков данные объективного анализа.
В заключение отметим, что при необходимости сравнения двух или более конкурирующих схем ОА температуры, влажности (точки росы), ветра или осадков возможно использование способов, описанных выше для оценки успешности ОА барического поля.
численного прогноза барического поля на 3 - 10 суток
1.1.2.4.1. Гидродинамические прогнозы барического поля, рассчитанные с заблаговременностью 3 - 10 суток, охватывают характерный масштаб существования барических образований (около 5 суток). Это обстоятельство диктует необходимость при установлении успешности этих прогнозов проводить их сравнение с климатологическими прогнозами, в отличие от краткосрочных численных прогнозов, которые сравниваются с инерционными прогнозами. В этом состоит отличительная особенность испытания прогнозов барического поля на средние сроки.
1.1.2.4.2. Для оценки качества численных прогнозов барического поля на средние сроки следует рассчитывать следующие статистические характеристики:  ,
, 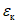 (нормирование производится по отношению к климатическому прогнозу),
(нормирование производится по отношению к климатическому прогнозу), 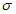 ,
, 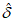 ,
, 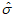 ; rт - коэффициент корреляции тенденций; rа - коэффициент корреляции аномалий, rаи - коэффициент корреляции аномалий для инерционного прогноза, S1 - параметр оценки геометрического подобия прогнозируемых и фактических полей геопотенциала.
; rт - коэффициент корреляции тенденций; rа - коэффициент корреляции аномалий, rаи - коэффициент корреляции аномалий для инерционного прогноза, S1 - параметр оценки геометрического подобия прогнозируемых и фактических полей геопотенциала.
1.1.2.4.3. Аналитические выражения для  ,
, 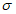 ,
,  ,
,  , rт и S1 приведены в формулах (1) - (7). Остальные статистические характеристики имеют следующий вид:
, rт и S1 приведены в формулах (1) - (7). Остальные статистические характеристики имеют следующий вид:
средняя относительная ошибка прогноза (с точностью до 0,01)
 (10)
(10)где  - средняя абсолютная климатическая изменчивость;
- средняя абсолютная климатическая изменчивость;
 - средняя абсолютная климатическая изменчивость;
- средняя абсолютная климатическая изменчивость;коэффициент корреляций аномалий (с точностью до 0,01)
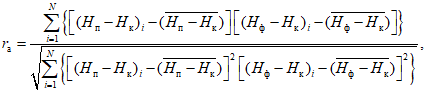 (11)
(11)где Hк - климатическое значение геопотенциала (давления).
Значения rт и rа изменяются от -1 до 1. Для идеального прогноза rт = rа = 1, для случайного прогноза rт = rа = 0;
коэффициент корреляции аномалий для инерционного прогноза
 (12)
(12)численного прогноза барического поля на 3 - 10 суток
1.1.2.5.1. В качестве синоптико-статистических характеристик данных прогнозов рассчитываются следующие оценки, отражающие положение планетарной высотной фронтальной зоны (ПВФЗ) в прогнозируемый период: абсолютная 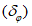 и относительная
и относительная  ошибки положения характерной для ПВФЗ (для данного сезона) изогипсы на прогностической карте в сравнении с фактической.
ошибки положения характерной для ПВФЗ (для данного сезона) изогипсы на прогностической карте в сравнении с фактической.
1.1.2.5.2. Характерными изогипсами для различных сезонов года являются следующие: для зимы 536 гПа, для весны 544 гПа, для первой и второй половины лета соответственно 560 и 572 гПа, для осени 566 гПа и для предзимья 544 гПа [2]. В случае зонального процесса над интересующей территорией оценка производится по одной характерной изогипсе, а в случаях, когда формируются две ветви ПВФЗ, - по двум.
Абсолютная  и относительная
и относительная 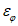 ошибки положения характерной изогипсы ПВФЗ рассчитываются по следующим формулам:
ошибки положения характерной изогипсы ПВФЗ рассчитываются по следующим формулам:
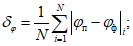 (13)
(13) (14)
(14)где  и
и 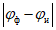 - соответственно отклонение прогностической изогипсы от фактической и ошибка инерционного прогноза в градусах меридиана, вычисленные в точках пересечения указанных изогипс и меридианов с интервалом 20°, а N - общее число точек.
- соответственно отклонение прогностической изогипсы от фактической и ошибка инерционного прогноза в градусах меридиана, вычисленные в точках пересечения указанных изогипс и меридианов с интервалом 20°, а N - общее число точек.
 и
и 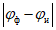 - соответственно отклонение прогностической изогипсы от фактической и ошибка инерционного прогноза в градусах меридиана, вычисленные в точках пересечения указанных изогипс и меридианов с интервалом 20°, а N - общее число точек.
- соответственно отклонение прогностической изогипсы от фактической и ошибка инерционного прогноза в градусах меридиана, вычисленные в точках пересечения указанных изогипс и меридианов с интервалом 20°, а N - общее число точек.1.1.2.5.3. Как показал опыт, численные схемы барического поля с 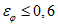 предусматривают перестройку барического поля, т.е. удовлетворительно предсказывают положение и скорость перемещения барических образований, их эволюцию.
предусматривают перестройку барического поля, т.е. удовлетворительно предсказывают положение и скорость перемещения барических образований, их эволюцию.
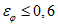 предусматривают перестройку барического поля, т.е. удовлетворительно предсказывают положение и скорость перемещения барических образований, их эволюцию.
предусматривают перестройку барического поля, т.е. удовлетворительно предсказывают положение и скорость перемещения барических образований, их эволюцию.Рабочая и сводная формы представления результатов расчета указанных ошибок приводятся по форме 3 и 4.
Форма записи исходных данных при расчете  и
и 
Меридиан, ...° | Положение характерной изогипсы |  | ||||
40 | ||||||
20 | ||||||
0 | ||||||
Среднее | Среднее | |||||
барического поля на 3 - 10 суток
Схема (автор) | Месяц | Заблаговременность, ч | |||||||||
72 | 96 | 120 | 144 | ... | 72 | 96 | 120 | 144 | ... | ||
Январь | |||||||||||
Февраль | |||||||||||
Март | |||||||||||
... | |||||||||||
... | |||||||||||
... | |||||||||||
Среднее | |||||||||||
При анализе результатов испытания следует выделить и оценить отдельно случаи с резкой перестройкой барического поля.
воздуха и точки росы у поверхности Земли
и на изобарических поверхностях
1.1.3.1. При испытании численных схем прогноза температуры воздуха, точки росы (дефицита точки росы) производится оценка прогнозов данных метеорологических элементов в сравнении с их объективным анализом. При этом вычисляются и анализируются следующие статистические характеристики:
средняя абсолютная ошибка прогноза температуры (точки росы) 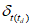 , с точностью до 0,1;
, с точностью до 0,1;
средняя относительная ошибка 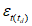 , с точностью до 0,01 (при значении
, с точностью до 0,01 (при значении 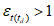 качество прогнозов температуры ниже инерционных);
качество прогнозов температуры ниже инерционных);
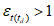 качество прогнозов температуры ниже инерционных);
качество прогнозов температуры ниже инерционных);средняя квадратическая ошибка  , с точностью до 0,1;
, с точностью до 0,1;
средняя систематическая ошибка 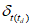 , с точностью до 0,1;
, с точностью до 0,1;
коэффициент корреляции между прогностическими и фактическими изменениями температуры (точки росы) 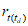 , с точностью до 0,01.
, с точностью до 0,01.
1.1.3.2. Для вычисления указанных статистических характеристик используются соответственно формулы (1) - (4) и (6). При этом вместо прогностических, фактических и исходных значений геопотенциала подставляются соответствующие значения температуры (точки росы).
1.1.3.3. Дополнительно рассчитывается оценка Pt, показывающая процент оправдавшихся прогнозов по заданным градациям ошибок
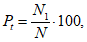 (15)
(15)где N1 - количество узлов сетки, в которых отклонение прогностической величины от фактической не превышает заданного предела, N - общее число узлов. Принимаются следующие градации отклонений прогностических значений от фактических (по абсолютному значению), для которых рассчитывается оценка Pt: <= 1,0, <= 2,0, <= 3,0, <= 4,0, <= 5,0 °C.
Вычисленные статистические характеристики качества прогноза температуры (точки росы) представляются по форме 5. Для анализа повторяемости ошибок по территории прогноза, выявления районов с большими значениями ошибок и установления возможных причин их возникновения рекомендуется строить карты распределения 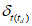 ,
, 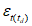 ,
,  ,
,  ,
,  .
.
(точки росы)
Численная схема (автор) | Заблаговременность прогноза, ч | Число случаев | rt | P, % | |||||||||
<= 1° | <= 2° | <= 3° | <= 4° | <= 5° | |||||||||
У поверхности Земли | |||||||||||||
850 гПа | |||||||||||||
700 гПа | |||||||||||||
500 гПа | |||||||||||||
и направления ветра у поверхности Земли
и на изобарических поверхностях
1.1.4.1. При оценке численных прогнозов ветра рассчитываются следующие статистические характеристики, при этом в качестве фактического ветра используется объективный анализ поля ветра:
средняя абсолютная ошибка прогноза вектора ветра (с точностью до 1)
где u и v - зональная и меридиональная составляющие скорости ветра;
средняя квадратическая ошибка прогноза вектора ветра (с точностью до 1)
средняя абсолютная ошибка прогноза скорости ветра (с точностью до 1)
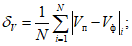 (18)
(18)средняя систематическая ошибка прогноза скорости ветра (с точностью до 1)
 (19)
(19)средняя абсолютная ошибка прогноза направления ветра (с точностью до 1°)
оценка PV (%) для следующих значений отклонения прогностического значения скорости ветра от фактического: <= 5, <= 10, <= 15 м/с
где N1 - число узлов сетки, в которых отклонение прогностических значений скорости ветра от фактических не превышают заданного предела, N - общее число узлов.
1.1.4.2. Оценки 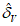 ,
,  и PV рассчитываются как для всего прогностического поля, так и отдельно по градациям прогностического ветра: V < 15, 15 < V <= 25 (ОЯ), V >= 25 м/с (СГЯ).
и PV рассчитываются как для всего прогностического поля, так и отдельно по градациям прогностического ветра: V < 15, 15 < V <= 25 (ОЯ), V >= 25 м/с (СГЯ).
Для представления оценок, полученных при испытании численных схем прогноза ветра, рекомендуется форма 6. Отдельная таблица составляется для PV.
Характеристики успешности прогнозов скорости
и направления ветра
Схема (автор) | Период испытания, месяц | Заблаговременность прогноза, ч | Количество прогнозов | Поверхность, гПа | |||||
Оценка качества прогноза осадков производится по факту наличия (отсутствия) и количеству осадков.
Характеристики оправдываемости прогноза факта осадков вычисляются с помощью таблицы сопряженности (форма 7), где n11 - число оправдавшихся прогнозов факта осадков; n12 - число неоправдавшихся прогнозов факта наличия осадков; n10 - число прогнозов наличия осадков; n21 - число неоправдавшихся прогнозов отсутствия осадков; n22 - число оправдавшихся прогнозов отсутствия осадков; n20 - число прогнозов отсутствия осадков; n01 - число случаев с осадками; n02 - число случаев без осадков; n00 - общее число прогнозов факта наличия и отсутствия осадков для данной выборки.
Примечание. Для численных прогнозов nij обозначает соответственно число узлов регулярной сетки.
Прогноз | Наблюдалось | Сумма | |
Осадки | Без осадков | ||
Осадки | n11 | n12 | n10 |
Без осадков | n21 | n22 | n20 |
Сумма | n01 | n02 | n00 |
Рассчитываются следующие характеристики успешности прогноза факта наличия (отсутствия) осадков (%):
общая оправдываемость прогноза осадков
оправдываемость прогноза наличия осадков
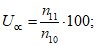 (23)
(23)предупрежденность факта наличия осадков
 (24)
(24)оправдываемость прогноза факта отсутствия осадков
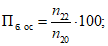 (25)
(25)предупрежденность факта отсутствия осадков
критерий качества прогноза (критерий Пирси - Обухова)
Величина T принимает значения от -1,0 до 1,0. Для идеального прогноза T = 1,0.
При вычислении оценок за факт осадков принимается осредненное в пункте или районе (в узлах сетки) количество осадков >= 0,1 мм/12 ч. Осредненное количество осадков < 0,1 мм/12 ч принимается за факт отсутствия осадков.
Рассчитываются следующие статистические характеристики:
средняя абсолютная ошибка
средняя (систематическая) ошибка
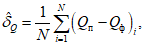 (29)
(29)где N - общее количество прогнозов (узлов сетки); Qп и Qф - соответственно прогностическое и фактическое значения количества осадков в пункте (узле сетки);
оправдываемость в процентах прогноза осадков при заданных градациях ошибок
где N1 - количество узлов сетки (прогноз по пункту, территории), в которых отклонение прогностических значений количества осадков от фактических не превышает заданного предела. Принимаются следующие градации отклонений прогностических значений количества осадков от фактических (по абсолютному значению), для которых рассчитывается оценка PQ: <= 3,0; <= 8,0; <= 15,0; <= 30,0 мм/12 ч (или мм/24 ч).
При оценке численных прогнозов осадков в узлах регулярной сетки производится сравнение прогноза осадков с данными объективного анализа осадков в узлах сетки либо метеорологических станций.
вертикальных движений воздуха
В современных численных схемах прогноза вертикальных движений воздуха [5] предусмотрены, как правило, расчет и выдача в узлах регулярной сетки на изобарических поверхностях 850, 700 и 500 гПа и выше значений вертикальных компонентов  скорости ветра (вертикальных движений) в гПа/12 ч на день (от 9 ч до 21 ч) и на ночь (от 21 ч до 9 ч). Поскольку вертикальный компонент скорости ветра инструментально не измеряется, осуществить непосредственную оценку вертикальных движений не представляется возможным.
скорости ветра (вертикальных движений) в гПа/12 ч на день (от 9 ч до 21 ч) и на ночь (от 21 ч до 9 ч). Поскольку вертикальный компонент скорости ветра инструментально не измеряется, осуществить непосредственную оценку вертикальных движений не представляется возможным.
1.1.6.1. Предлагаются следующие две методики оценки вертикальных движений:
1) сопоставление рассчитанных вертикальных движений с фактическим распределением тех метеорологических элементов, в формировании которых вертикальные движения играют существенную роль (осадки, вертикальное распределение температуры и влажности воздуха, облачность);
2) сравнение прогностических вертикальных движений воздуха с "эталонными" полями, заранее рассчитанными по качественным исходным данным.
1.1.6.2. Испытание численных схем прогноза вертикальных движений целесообразно проводить в холодный период года, когда отсутствует конвекция и синоптические процессы отличаются активностью.
1.1.6.3. При использовании первого вида оценки качество прогноза 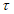 устанавливается по совпадению зон интенсивных восходящих движений с зонами облачности слоистых форм и с зонами обложных осадков, а также путем сравнения фактических кривых вертикального распределения температуры Tф и точки росы Td ф с прогностическими Tп и Td п, рассчитанных с учетом их адвективных (
устанавливается по совпадению зон интенсивных восходящих движений с зонами облачности слоистых форм и с зонами обложных осадков, а также путем сравнения фактических кривых вертикального распределения температуры Tф и точки росы Td ф с прогностическими Tп и Td п, рассчитанных с учетом их адвективных ( и
и  ) и адиабатических (
) и адиабатических ( и
и  ) изменений за счет подъема или опускания воздуха вследствие восходящих или нисходящих вертикальных движений и трансформационных изменений (в холодный период года). Для оценки прогноза вертикальных движений по оправдываемости прогноза температуры, влажности и количества осадков необходимо использовать выбранную для испытаний стандартную сеть станций и для отдельных станций (вручную) рассчитать вертикальное распределение T и Td с учетом основных факторов, действующих в атмосфере, а также количество обложных осадков по Руководству [5]. Для исключения ошибок в расчетах, обусловленных учетом адвекции, целесообразно использовать диагностические траектории движения воздушных частиц, т.е. траектории, построенные по фактическим картам барической топографии. Далее путем сопоставления рассчитанных значений T, Td и Qобл соответственно на день и на ночь с фактическими их значениями в пункте (осадков в радиусе 100 км) необходимо вычислить ошибки, указанные в п. 1.1.5.
) изменений за счет подъема или опускания воздуха вследствие восходящих или нисходящих вертикальных движений и трансформационных изменений (в холодный период года). Для оценки прогноза вертикальных движений по оправдываемости прогноза температуры, влажности и количества осадков необходимо использовать выбранную для испытаний стандартную сеть станций и для отдельных станций (вручную) рассчитать вертикальное распределение T и Td с учетом основных факторов, действующих в атмосфере, а также количество обложных осадков по Руководству [5]. Для исключения ошибок в расчетах, обусловленных учетом адвекции, целесообразно использовать диагностические траектории движения воздушных частиц, т.е. траектории, построенные по фактическим картам барической топографии. Далее путем сопоставления рассчитанных значений T, Td и Qобл соответственно на день и на ночь с фактическими их значениями в пункте (осадков в радиусе 100 км) необходимо вычислить ошибки, указанные в п. 1.1.5.
1.1.6.4. При сопоставлении зон восходящих движений с зонами облачности и обложных осадков вычисляются средние расхождения между границами зон и повторяемость этих значений по градациям (<= 200, 201 - 400, > 400 км).
1.1.6.5. Прогноз вертикальных движений считается удовлетворительным, если применение их в расчетах T, Td и Qобл дает удовлетворительные результаты, а различие в положении зон обложных осадков и восходящих вертикальных движений в преобладающем числе случаев составляет не более 200 км.
1.1.6.6. При использовании второго вида оценки качества прогноза  в теоретическом отношении наиболее совершенным ("эталонным") может быть метод расчета вертикальных движений по данным наблюдений за ветром [5]. Основное его преимущество состоит в том, что расчетные формулы получены непосредственно из уравнения неразрывности без привлечения дополнительных гипотез. При использовании фактического ветра нет необходимости вводить поправку на трение. Поэтому расчет дает вполне удовлетворительные результаты в районах, достаточно хорошо освещенных сведениями о ветре.
в теоретическом отношении наиболее совершенным ("эталонным") может быть метод расчета вертикальных движений по данным наблюдений за ветром [5]. Основное его преимущество состоит в том, что расчетные формулы получены непосредственно из уравнения неразрывности без привлечения дополнительных гипотез. При использовании фактического ветра нет необходимости вводить поправку на трение. Поэтому расчет дает вполне удовлетворительные результаты в районах, достаточно хорошо освещенных сведениями о ветре.
1.1.6.7. В лаборатории испытания новых методов прогнозов погоды Гидрометцентра СССР "эталонные" вертикальные движения могут быть рассчитаны по данным ПГЭП, входящим в автоматизированный архив оценки качества численных схем прогноза.
Тем не менее качество "эталонных" вертикальных движений необходимо оценить с использованием первого варианта.
1.1.6.8. При установлении качества  , предвычисленных новыми методами прогноза путем сравнения с "эталонными"
, предвычисленных новыми методами прогноза путем сравнения с "эталонными"  , следует исходить из того, что они должны совпадать по знаку и иметь небольшие (10 - 20 гПа/12 ч) различия в значениях скорости вертикальных движений воздуха.
, следует исходить из того, что они должны совпадать по знаку и иметь небольшие (10 - 20 гПа/12 ч) различия в значениях скорости вертикальных движений воздуха.
Оценка численных прогнозов метеорологических явлений (шквалов, гроз, гололеда, града и др.), рассчитанных для узлов регулярной сетки, производится путем сравнения с данными наблюдений по территории в радиусе, составляющем половину шага сетки. Для альтернативных прогнозов явлений рассчитываются характеристики оправдываемости по формулам (22) - (27), приведенным в п. 1.1.5. Кроме того, вычисляются критерии надежности Н.А. Багрова (H)
ИС МЕГАНОРМ: примечание. Обозначения даны в соответствии с официальным текстом документа. |
где 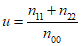 ;
;  - оправдываемость случайных прогнозов (
- оправдываемость случайных прогнозов (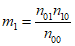 ,
, 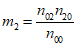 ) и критерий точности А.М. Обухова (Q)
) и критерий точности А.М. Обухова (Q)
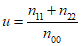 ;
;  - оправдываемость случайных прогнозов (
- оправдываемость случайных прогнозов (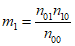 ,
, 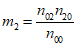 ) и критерий точности А.М. Обухова (Q)
) и критерий точности А.М. Обухова (Q) (32)
(32)где 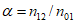 ,
,  . Чем больше H и Q, тем лучше качество прогнозов. Здесь используются те же условные обозначения, что и в п. 1.1.5.
. Чем больше H и Q, тем лучше качество прогнозов. Здесь используются те же условные обозначения, что и в п. 1.1.5.
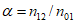 ,
,  . Чем больше H и Q, тем лучше качество прогнозов. Здесь используются те же условные обозначения, что и в п. 1.1.5.
. Чем больше H и Q, тем лучше качество прогнозов. Здесь используются те же условные обозначения, что и в п. 1.1.5.Результаты испытания представляются по форме 8.
метеорологических явлений
Численная схема (автор) | Заблаговременность прогноза | Количество прогнозов | Оправдываемость | T | H | Q | ||||
общая (U) | наличия явления (Uя) | отсутствия явления (Uб. я) | предупрежденность явления (Пя) | предупрежденность отсутствия явления (Пб. я) | ||||||
элементов и явлений с заблаговременностью до 48 ч
методов прогноза погоды
1.2.1.1. Расчетные методы краткосрочных прогнозов погоды предназначены, как правило, для предвычисления какого-либо метеорологического элемента или явления погоды по пункту или по территории с примерным радиусом 100 - 150 км, соизмеримым с территорией области или республики. Заблаговременность этих прогнозов составляет от 1 ч (авиационные или сверхкраткосрочные прогнозы) до 48 ч (прогнозы общего пользования, специализированные прогнозы).
1.2.1.2. Расчетные методы краткосрочных прогнозов погоды позволяют прогнозировать либо факт возникновения отдельных метеорологических явлений (гроза, гололед, заморозки и т.д.), либо количественные характеристики метеорологических элементов или явлений погоды (температуры, осадков, скорости ветра, а также видимости при туманах, размера града, отложения гололеда и т.д.). При этом последние можно подразделить по интенсивности прогнозируемых метеорологических элементов и явлений на три группы:
методы, предусматривающие прогноз метеорологических элементов любых значений и явлений погоды различной интенсивности (температура, осадки, ветер, гололед, град, туман, метель и т.д.);
методы, предусматривающие в прогнозе определенный диапазон метеорологических элементов или определенную интенсивность явлений погоды (значительные дожди, сильный ветер, включая шквал, умеренный и сильный град, умеренная и сильная болтанка и т.д.). Это прежде всего методы прогноза метеорологических элементов, отнесенных к категории стихийных и представляющих наибольшую важность для организаций народного хозяйства;
методы, предусматривающие прогноз комплекса метеорологических элементов или явлений погоды (два или более), наблюдающихся одновременно (например сильный ветер и сильный дождь, дождь с грозой и шквалом). Это методы прогноза метеорологических элементов и явлений погоды, относящихся к категории стихийных, а также имеющих любые количественные значения.
1.2.1.3. Отмеченные особенности методов прогнозов обусловливают различия в методике проведения их оперативных испытаний. А именно, ряд случаев при испытании указанных методов может быть неодинаковым. Так, для получения надежных выводов о качестве методов прогноза первой и третьей групп (при любых значениях метеорологических элементов) необходим ряд в 60 - 100 случаев. При испытании методов прогноза стихийных и редко наблюдающихся явлений погоды или отдельной градации метеорологических элементов объем выборки должен быть не меньше их природной повторяемости или больше ее. Ввиду этого установление природной повторяемости указанных метеорологических элементов и явлений погоды посредством проработки режимного материала является предварительным и очень важным этапом испытания.
Для увеличения ряда случаев с редко наблюдающимися явлениями погоды допускается привлечение независимого (не участвующего в разработке метода) материала прошлых лет. В связи с этим авторам методов целесообразно в проектах методических указаний (программах испытания) указывать продолжительность зависимого ряда наблюдений.
1.2.1.4. При сравнительной оценке нескольких расчетных способов прогноза того или иного метеорологического элемента или явления погоды необходимо выполнять следующие условия:
расчеты по всем способам производить для одних и тех же случаев, с использованием одного и того же исходного материала;
все способы оценивать по одной и той же фактической информации о метеорологических элементах и явлениях погоды в пункте или по территории, с применением одних и тех же критериев оценки и статистических характеристик;
одновременно оценивать прогнозы данного метеорологического явления или элемента, составленные синоптиками оперативно, а также инерционные прогнозы.
При этом необходимо руководствоваться следующим:
прогнозы различной заблаговременности оценивать отдельно для каждого периода (день, ночь);
прогнозы метеорологических элементов и явлений, составленные для пункта и для территории (области, республики), оценивать отдельно.
1.2.1.5. Как известно, в оперативном режиме прогнозы погоды синоптиком составляются в терминах, соответствующих определенным количественным градациям, и оцениваются с учетом территориального распределения метеорологических элементов (явлений), согласно действующему Наставлению [4]. Отдельные расчетные методы также предвычисляют метеорологические элементы и явления в определенных градациях. В этих случаях сопоставление с прогнозами синоптиков производится, согласно [4], с учетом территориального распределения метеорологических элементов. Другие методы предназначены для прогноза экстремальных (иногда средних) их значений в пункте или по территории (области, республики). В таких случаях необходимо параллельно методическим прогнозам оценивать прогнозы синоптиков по экстремальному значению метеорологического элемента в пункте или по территории. Одинаковая оценка методических и синоптических прогнозов позволит установить возможность и границы применимости проверяемого метода в оперативной практике.
1.2.1.6. При испытании расчетных методов, как и численных схем прогноза метеорологических элементов, необходимо вычислять соответствующие статистические характеристики по формулам подраздела 1.1.
наличия (отсутствия) метеорологических явлений,
в том числе стихийных
1.2.2.1. При установлении надежности расчетных методов прогноза таких метеорологических явлений, как гроза, град, гололед, гололедица, метель, пыльная буря, шквал и смерч, первоначально составляется таблица сопряженности прогноза с фактическими данными о явлениях по форме 9. На основании этих данных рассчитываются оправдываемости в процентах прогнозов общая (U), наличия (Uя) и отсутствия (Uб. я) явления, которые также представляются по форме 9:
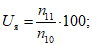 (34)
(34)где n11 и n22 - число оправдавшихся прогнозов с явлением и без явления соответственно, n00 - общее число прогнозов, n10 и n20 - соответственно число прогнозов с явлением и без явления. Кроме того, рассчитывается предупрежденность в процентах случаев с явлением (Пя) и без явлений (Пб. я) по формулам:
где n01 и n02 - соответственно фактическое число дней с явлением и без явления.
1.2.2.2. Для характеристики успешности метода прогнозов с учетом случайных прогнозов необходимо рассчитывать критерий надежности Н.А. Багрова
где  - оправдываемость случайных прогнозов (здесь m1 = n10n01/n00, m2 = n20n02/n00).
- оправдываемость случайных прогнозов (здесь m1 = n10n01/n00, m2 = n20n02/n00).
 - оправдываемость случайных прогнозов (здесь m1 = n10n01/n00, m2 = n20n02/n00).
- оправдываемость случайных прогнозов (здесь m1 = n10n01/n00, m2 = n20n02/n00).Установлено, что прогнозы с H < 0,33 являются ненадежными. Для того чтобы значение критерия надежности было показательным, вероятность осуществления прогнозируемого явления должна превышать его природную повторяемость.
1.2.2.3. Для оценки качества альтернативных прогнозов может быть применен и критерий качества прогнозов Пирси - Обухова
Значение T может изменяться от -1 до 1. Отрицательное значение T свидетельствует о том, что отношение ошибочных прогнозов явления к фактическому числу дней без явления превышает отношение оправдавшихся прогнозов явления к фактическому числу дней с явлением (Пя). Положительные значения T свидетельствуют о том, что предупрежденность явления (Пя) превышает отношение ошибочных прогнозов явления к фактическому числу дней без явления. При идеальном прогнозе T = 1.
1.2.2.4. Приведенные различного вида оправдываемости прогнозов и статистические показатели при испытании того или иного метода прогноза могут оказаться в разнообразных соотношениях (одни высокие, другие низкие даже при сравнительно высокой общей оправдываемости прогнозов). Это обстоятельство довольно часто затрудняет правильное заключение о надежности методов краткосрочных прогнозов явлений погоды.
В решении данного вопроса вполне эффективным может быть суммарный показатель (uя + Пя), характеризующий наиболее важные стороны метода. По данным [2], величина uя + Пя >= 130% характеризует удовлетворительное качество прогнозов. Чем больше каждый из показателей, тем выше качество прогнозов и успешность проверяемой методики в целом.
Все сведения об успешности методов прогнозов целесообразно представлять по форме 9.
Прогноз | Наблюдалось | Сумма | U | U + П | |
явление | без явления | ||||
Явление | n11 | n12 | n10 | Uя | Uя + Пя |
Без явления | n21 | n22 | n20 | Uб. я | Uб. я + Пб. я |
Сумма | n01 | n02 | n00 | ||
П | Пя | Пб. я | |||
T | H | ||||
прогноза метеорологических элементов и явлений
Оценка оправдываемости прогнозов, содержащих количественные характеристики температуры воздуха, скорости и направления ветра (включая шквалы), осадков, метелей, гололеда и града, производится согласно действующему Наставлению [4]. Помимо этого для температуры воздуха, а также точки росы, ветра и осадков рассчитываются статистические характеристики.
у поверхности Земли
Методы количественного прогноза температуры и влажности воздуха у поверхности Земли могут предусматривать прогноз экстремальной (максимальной и минимальной) температуры воздуха (T) или точки росы (Td), прогноз значений T и Td в отдельные сроки (например, 0 ч или 12 ч СГВ), прогноз средней суточной температуры воздуха (Tсут).
1.2.3.1.1. При установлении надежности методов прогноза той или иной температуры воздуха и точки росы у поверхности Земли необходимо сравнивать прогнозируемые значения T и Td соответственно с фактическими их значениями в те сроки, для которых выполнен расчет. При этом в случае необходимости оценки средней суточной температуры фактическое ее значение определяется по данным о T за восемь сроков по формуле

При оценке прогнозов T и Td помимо оправдываемости (Pн), согласно [4], рассчитываются статистические характеристики 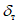 ,
, 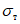 ,
, 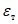 и
и 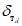 ,
, 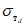 ,
,  , а также средние арифметические ошибки
, а также средние арифметические ошибки 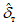 и
и  , характеризующие систематические ошибки метода. Указанные показатели необходимо рассчитывать в соответствии с указаниями п. 1.1.3 и по формулам (1) - (4). В используемых формулах N будет обозначать общее число составленных прогнозов. Кроме того, рассчитывается оправдываемость прогнозов в процентах
, характеризующие систематические ошибки метода. Указанные показатели необходимо рассчитывать в соответствии с указаниями п. 1.1.3 и по формулам (1) - (4). В используемых формулах N будет обозначать общее число составленных прогнозов. Кроме того, рассчитывается оправдываемость прогнозов в процентах

при заданных градациях ошибок: <= 1,0; <= 2,0; <= 3,0; <= 4,0; <= 5,0 °C. Здесь N1 - количество прогнозов, в которых отклонение прогностической величины от фактической не превышает заданную ошибку.
1.2.3.1.2. Результаты испытания следует представлять по форме 10.
Результаты испытания методов прогноза
температуры (точки росы)
Метод (автор) | Заблаговременность прогноза, ч | Количество прогнозов | Статистические характеристики | PH | Pt | ||||||||
<= 1° | <= 2° | <= 3° | <= 4° | <= 5° | |||||||||
слое атмосферы
1.2.3.2.1. В настоящее время разработанные методы прогноза инверсий предусматривают только альтернативный прогноз их наличия и вида (приземная или приподнятая инверсия) без количественных показателей (вертикальная протяженность, температура на верхней и нижней границах). Для установления надежности методов прогноза наличия инверсий рассчитываются оценки, характеризующие качество прогноза факта метеорологических явлений и изложенные в п. 1.2.2. В частности, рассчитываются оправдываемости прогнозов инверсий общая (u), наличия (uя) и отсутствия (uб.я), предупрежденности наличия (Пя) и отсутствия (Пб.я), критерий надежности H и критерий качества Пирси - Обухова T соответственно по формулам (33) - (39). Полученные результаты представляются по форме 9.
1.2.3.2.2. Для установления надежности методов прогноза вида инверсий рассчитывается оправдываемость прогнозов. При этом прогноз следует считать оправдавшимся на 100%, если фактически наблюдался спрогнозированный вид инверсии. В случаях, когда был спрогнозирован один вид инверсий, а наблюдался другой вид, или инверсия отсутствовала (наблюдались нормальный ход распределения температуры воздуха с высотой, изотермия), оправдываемость прогнозов составляет соответственно 50 или 0%. Средние оценки оправдываемости прогнозов вида инверсии следует представлять в виде табл. 3.
Таблица 3
Заблаговременность прогноза, ч | Метод прогноза | Инверсия | Общая оправдываемость | ||||||||||
приземная | приподнятая | ||||||||||||
дано прогнозов | оправдалось | % | дано прогнозов | оправдалось | % | дано прогнозов | оправдалось | % | |||||
12 | Методический | 10 | 9 | 700 | 70 | 13 | 13 | 1200 | 92 | 23 | 22 | 1900 | 83 |
Инерционный | 33 | 27 | 2200 | 67 | 32 | 30 | 2950 | 92 | 65 | 57 | 5150 | 79 | |
24 | Методический | 11 | 10 | 900 | 82 | 13 | 12 | 1000 | 77 | 24 | 22 | 1900 | 79 |
Инерционный | 33 | 25 | 2050 | 62 | 32 | 23 | 2300 | 72 | 65 | 48 | 4350 | 67 | |
1.2.3.2.3. При сравнительной оценке двух или более методов, прогноза инверсий температуры воздуха в табл. 3 приводятся сведения об успешности всех методов. К внедрению в оперативную практику рекомендуется метод, имеющий лучшие показатели успешности.
1.2.3.2.4. При наличии одного расчетного метода прогноза инверсии составленные методические прогнозы сравниваются с инерционными прогнозами, когда прогнозом является наличие (отсутствие) определенного вида инверсии в исходный срок прогноза. Преимущество методических прогнозов перед инерционными по большинству показателей успешности может служить основанием для внедрения метода прогноза инверсий в оперативную прогностическую практику.
включая шквалы
1.2.3.3.1. Расчетные методы прогноза ветра могут предусматривать преобладающую среднюю или максимальную скорость ветра при порывах (включая шквалы), а также направление ветра (преобладающее или в определенный срок). При оценке каждого вида указанных прогнозов ветра необходимо сравнивать прогностическое значение с соответствующим ему фактическим значением за указанный срок или период действия прогноза.
1.2.3.3.2. Надежность методов прогноза, предвычисляющих любые скорости ветра в виде конкретного их значения, устанавливается с помощью статистических характеристик 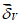 ,
,  ,
,  ,
,  ,
, 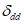 и PV, рассчитанных по формулам (16) - (21) и в соответствии с рекомендациями п. 1.1.4. Кроме того, рассчитываются оправдываемости прогнозов, согласно действующему Наставлению.
и PV, рассчитанных по формулам (16) - (21) и в соответствии с рекомендациями п. 1.1.4. Кроме того, рассчитываются оправдываемости прогнозов, согласно действующему Наставлению.
1.2.3.3.3. Поскольку при испытаниях важно установить практическую значимость методики не только в целом, но и в отдельных диапазонах скорости ветра, все статистические показатели и оправдываемости прогнозов ветра рассчитываются для всей совокупности составленных прогнозов и отдельно для трех следующих градаций: Vп < 15 м/с, 15 м/с <= Vn < 25 м/с (ОЯ), Vn >= 25 м/с (СГЯ). Для побережий и акваторий океанов, арктических и дальневосточных морей критериями ОЯ и СГЯ являются другие значения скорости ветра. Поэтому в этих районах статистические показатели следует рассчитывать для установленных градаций.
1.2.3.3.4. Для градаций ОЯ или СГЯ вычисляется также предупрежденность в процентах по формуле

где n11 - число оправдавшихся прогнозов со значениями скорости ветра в градациях ОЯ или СГЯ, n01 - фактическое число дней с явлением (ветром опасных значений или отнесенным к стихийным гидрометеорологическим явлениям).
1.2.3.3.5. Надежность методов прогноза, предвычисляющих ветер в виде определенной градации (например, >= 15 м/с или >= 25 м/с), устанавливается путем расчета следующих показателей успешности:
оправдываемости прогнозов в данной градации по факту (uя)ф и с допуском Наставления (uя)Н;
оправдываемости прогнозов отсутствия данной градации (uб.я)ф, (uб.я)Н;
общей оправдываемости прогнозов ветра (u)ф, (u)Н;
предупрежденности случаев с ветром данной градации (Пя)ф, (Пя)Н;
предупрежденности случаев отсутствия ветра в данной градации (Пб.я)ф, (Пб.я)Н;
критерия качества Пирси - Обухова (T);
суммарного показателя (uя)ф + (Пя)ф и (uя)Н + (Пя)Н.
1.2.3.3.6. Приведенные показатели успешности прогнозов рассчитываются по формулам (33) - (37) и (39). Полученные результаты представляются в виде табл. 4, в которой в качестве примера приведены данные об успешности прогноза сильных шквалов (>= 25 м/с) на текущий день по территории с использованием спутниковых, радиолокационных и аэросиноптических данных (автор метода В.Ф. Лапчева - Гидрометцентр СССР).
Таблица 4
Результаты испытания метода прогноза сильных шквалов
(>= 25 м/с)
Прогноз | Наблюдалось | Сумма | Uф, % | UН, % | Uф + Пф, % | UН + ПН, % | |
>= 25 м/с | < 25 м/с | ||||||
>= 25 м/с | 14 | 39 | 53 | 26 | 62 | 60 | 143 |
< 25 м/с | 24 | 3738 | 3765 | 99 | 97 | 198 | 194 |
Сумма | 41 | 3777 | 3818 | ||||
Пф, % | 34 | 99 | |||||
ПН, % | 81 | 97 | |||||
Tф = 0,33 TН = 0,80 | |||||||
При оценке прогнозов направления ветра необходимо по формуле (20) вычислять среднюю абсолютную ошибку направления ветра 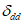 и ее повторяемость в процентах по градациям: 0 - 30, 31 - 60, 61 - 90, > 90°, а результаты представлять в виде табл. 5.
и ее повторяемость в процентах по градациям: 0 - 30, 31 - 60, 61 - 90, > 90°, а результаты представлять в виде табл. 5.
Таблица 5
Результаты сравнительной оценки способов прогноза
направления ветра
Прогноз | Повторяемость, (%) | ||||
0 - 30° | 31 - 60° | 61 - 90° | > 90° | ||
Методический | 20 | 69 | 20 | 11 | - |
Инерционный | 30 | 55 | 24 | 21 | - |
Надежность методов количественного прогноза осадков характеризуется показателями успешности прогнозов как самого факта выпадения осадков, так и их количества.
1.2.3.4.1. Качество прогнозов осадков по факту их выпадения устанавливается с помощью критерия надежности HQ или критерия качества Пирси - Обухова TQ, а также значениями оправдываемости прогнозов (общей, с осадками и без осадков) и их предупрежденности. Эти результаты испытаний представляются в виде табл. 6.
Таблица 6
Прогноз количества осадков | Фактически наблюдались | Сумма | Uф, % | UН, % | Uф + Пф, % | UН + ПН, % | ||
30 <= Q < 50 | Q >= 50 | Q < 30 | ||||||
30 <= Q < 50 | 83 | 61 | 62 | 206 | 71 | 75 | 127 | 127 |
Q >= 50 | 20 | 47 | 4 | 71 | 66 | 75 | 98 | 111 |
Q < 30 | 46 | 39 | 3525 | 3610 | 98 | 98 | 196 | 196 |
Сумма | 149 | 147 | 3591 | 3887 | 94 | 96 | ||
Пф | 56 | 32 | 98 | |||||
ПН | 52 | 36 | 98 | |||||
1.2.3.4.2. При оценке прогнозов количества осадков любых значений помимо их оправдываемости, согласно Наставлению, необходимо вычислять статистические характеристики 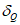 ,
, 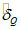 и PQ по формулам (28) - (30) с учетом рекомендаций п. 1.1.5.
и PQ по формулам (28) - (30) с учетом рекомендаций п. 1.1.5.
1.2.3.4.3. Для детальной оценки качества проверяемых способов прогноза осадков различной интенсивности необходимо вычислять статистические характеристики для различных градаций действующего Наставления [4].
1.2.3.4.3.1. В тех случаях, когда метод предусматривает прогноз в отдельных градациях (например, количество осадков >= 30 мм), эти прогнозы оцениваются по факту осадков (u)ф и с допуском Наставления (u)Н, а также рассчитываются их предупрежденности и суммарные показатели аналогично приведенным в табл. 6. В этой таблице приведены сведения об успешности прогнозов сильных осадков в трех градациях (Q < 30 мм, 30 мм <= Q < 50 мм и Q >= 50 мм), рассчитанных для европейской части СССР с использованием радиолокационных, спутниковых и аэросиноптических данных наблюдений (автор метода Н.И. Глушкова).
1.2.3.5.1. При оценке прогнозов этих явлений погоды необходимо вычислять оправдываемости прогнозов по формулам (33) - (35), предупрежденности явлений по формулам (36) - (37), а также критерий качества Пирси - Обухова и критерий надежности Н.А. Багрова по формулам (38), (39). Результаты представляются по форме 8.
1.2.3.5.2. При отсутствии ранее внедренных в оперативную практику расчетных методов прогнозов рассматриваемых явлений погоды производится сравнение с инерционными прогнозами этих явлений. Целесообразность внедрения метода определяется его преимуществами перед инерционными прогнозами.
При сравнительной оценке ряда методов прогнозов предпочтение отдается методу, имеющему лучшие показатели успешности.
Надежность новых методов прогноза метеорологических элементов и явлений погоды, предназначенных для метеорологического обеспечения авиации, устанавливается с использованием показателей успешности, изложенных в пп. 1.1.3 - 1.1.5 и 1.1.7, а также стандартов и рекомендаций ИКАО [6, 7]. При этом учитываются точность различных видов прогнозов и их обеспеченность, желательные с точки зрения эксплуатации воздушных судов. Эти данные приведены в табл. 7. Если точность прогнозов находится в указанных пределах с заданной обеспеченностью, то, согласно международному опыту, влияние возможных ошибок прогноза метеорологических условий на эксплуатацию воздушных судов считается незначительным по сравнению с влиянием навигационных ошибок и других эксплуатационных ошибок и показателей.
Таблица 7
(по данным ИКАО)
Прогнозируемый метеорологический элемент | Желательная точность прогноза | Обеспеченность (P) % |
Прогноз по аэродрому | ||
Направление ветра | +/- 30° | 80 |
Скорость ветра | +/- 3 м/с при скорости до 15 м/с, +/- 20% при скорости более 15 м/с | 80 |
Видимость | +/- 200 м при видимости до 700 м, +/- 30% при видимости от 700 м до 10 км | 80 |
Осадки | Наличие или отсутствие | 80 |
Количество облаков | +/- 2 октанта | 70 |
Высота НГО | +/- 30 м при высоте до 120 м, +/- 30% в интервале 120 - 3000 м | 70 |
Температура воздуха | +/- 1 °C | 70 |
Прогноз для посадки | ||
Направление ветра | +/- 30° | 90 |
Скорость ветра | +/- 3 м/с при скорости до 15 м/с, | 90 |
Видимость | +/- 20% при скорости более 15 м/с +/- 200 м при видимости до 700 м, +/- 30% при видимости от 700 м до 10 км | 90 |
Осадки | Наличие или отсутствие | 90 |
Количество облаков | +/- 2 октанта | 90 |
Высота НГО | +/- 30 м при высоте до 120 м, +/- 30% в интервале 120 - 3000 м | 90 |
Прогноз для взлета | ||
Направление ветра | +/- 30° | 90 |
Скорость ветра | +/- 3 м/с при скорости до 15 м/с, +/- 20% при скорости более 15 м/с | 90 |
Температура воздуха | +/- 1 °C | 90 |
Давление воздуха | +/- 1 гПа | 90 |
Зональный прогноз и прогноз по маршруту | ||
Температура воздуха на высотах | +/- 3 °C (средняя в радиусе 450 км) | 90 |
Скорость ветра на высотах | +/- 30 км/ч до уровня 400 гПа включительно, +/- 40 км/ч выше уровня 400 гПа (модуль векторной разности среднего ветра в радиусе 450 км) | 90 |
Особые явления по маршруту и облачность | Наличие или отсутствие, | 80 |
точность расположения по горизонтали +/- 100 км, | 70 | |
точность расположения по вертикали +/- 600 м | 70 | |
для посадки и взлета воздушных судов
1.2.4.1.1. При испытании методов прогноза метеорологических элементов (направления и скорости ветра, видимости, количества облаков, высоты нижней границы облаков, температуры воздуха) рассчитываются по формулам (1) - (4) следующие характеристики оправдываемости: средняя абсолютная ошибка прогнозов  , средняя систематическая ошибка
, средняя систематическая ошибка 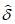 , средняя квадратическая ошибка
, средняя квадратическая ошибка  , средняя относительная ошибка
, средняя относительная ошибка 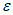 .
.
1.2.4.1.2. Для оценки прогнозов метеорологических элементов и явлений, составляемых в альтернативной форме (наличие или отсутствие осадков, особых явлений), составляется таблица сопряженности (см. форму 7) и по формулам (22) - (26) рассчитывается общая оправдываемость прогноза (u), оправдываемость прогноза явления (uя), предупрежденность явления (Пя), оправдываемость прогноза отсутствия явления (uб.я), предупрежденность отсутствия явления (П)б.я. Рассчитывается также критерий качества T и критерий надежности H соответственно по формулам (27), (31). Анализируя полученные характеристики оправдываемости альтернативных прогнозов, целесообразно принимать во внимание климатическую повторяемость прогнозируемого явления. Так, для редких явлений (климатическая повторяемость K < 0,5) оправдываемость методического прогноза явления Uя должна быть не менее 0,5. В противном случае использование методических прогнозов не имеет смысла, так как их оправдываемость будет ниже оправдываемости климатического прогноза.
1.2.4.1.3. Считается, что критерий надежности Багрова (H) для эффективного метода прогноза должен быть не менее 0,3. Однако это справедливо при климатической повторяемости прогнозируемого явления K >= 0,5. Для более редких явлений погоды, например при K = 0,1 ... 0,2, значения H для методически оправданных прогнозов должны быть не менее 0,5 - 0,6. Для определения климатической повторяемости K может использоваться сравниваемая выборка фактических наблюдений, если она достаточно репрезентативна.
1.2.4.1.4. При испытании новых методов прогнозов метеорологических элементов и явлений определяется также обеспеченность P при заданной точности прогнозов (см. табл. 7). Обеспеченность рассчитывается как процентное отношение количества прогнозов, точность которых отвечает требованиям ИКАО, к общему числу составленных прогнозов. Например, если из 100 составленных прогнозов направления ветра 80 прогнозов имеют точность 30° или менее, то в этом случае обеспеченность прогнозов 80%.
1.2.4.1.5. В процессе испытаний производится сравнение рассчитанных характеристик успешности прогнозов испытываемого метода с успешностью ранее внедренных методов, а также с синоптическими и инерционными прогнозами.
1.2.4.2.1. При оценке успешности авиационных прогнозов температуры и ветра в узлах регулярной сетки на заданных уровнях атмосферы, составляемых на основе численных прогнозов по территории (например, по территории ответственности Московского регионального центра зональных прогнозов), а также в точках маршрутов, рассчитываются следующие характеристики:
абсолютные ошибки прогноза температуры  и вектора ветра
и вектора ветра 
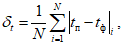 (40)
(40) (41)
(41)относительные ошибки прогноза температуры  и ветра
и ветра 
 (42)
(42) (43)
(43)Здесь индексы "п", "ф", "и" указывают соответственно прогностические, фактические и исходные значения температуры воздуха и вектора ветра;
обеспеченность в процентах прогнозов температуры и ветра при заданной их точности (см. табл. 7)
 (44)
(44)где N - количество узлов регулярной сетки (точек на маршруте), в которых дан прогноз температуры и ветра; N' - количество узлов, в которых разность прогностических и фактических значений температуры не превышала по модулю 3 °C (в качестве фактического значения температуры воздуха в узле сетки принимается среднее значение для круга радиусом 450 км). Для ветра N' означает количество узлов, в которых модуль векторной разности прогностических и фактических значений ветра не превышал 30 км/ч для высот до уровня 400 гПа включительно и 40 км/ч выше уровня 400 гПа (в качестве фактического значения ветра в узле сетки принимается его среднее значение для круга радиусом 450 км).
1.2.4.2.2. В соответствии с требованиями ИКАО, с точки зрения эксплуатации воздушных судов желательно, чтобы значения P для температуры и ветра были не ниже 90%.
1.2.4.2.3. Прогнозы особых явлений по маршруту (турбулентности, обледенения, гроз, града) и облачности оцениваются альтернативно. При этом рассчитываются те же оценки, что и для прогнозов по аэродрому. Прогноз особого явления считается оправдавшимся, если оно осуществилось и точность его местоположения находилась в пределах +/- 100 км по горизонтали и +/- 600 м по вертикали по отношению к точке прогноза.
1.2.4.2.4. Вывод о внедрении испытываемых методов прогноза делается на основании анализа полученных оценок в сравнении с оценками ранее внедренных методов, синоптических прогнозов и с учетом желаемой точности и обеспеченности авиационных прогнозов (см. табл. 7).
1.3.1.1. Современный уровень научных исследований крупномасштабной атмосферной циркуляции в тропической зоне, условий возникновения тропических циклонов (ТЦ) на базе имеющейся информации о возникновении, эволюции и перемещении ТЦ позволяет разрабатывать методы их прогноза. Методы прогноза ТЦ можно разделить на три основных вида: эмпирические, статистические и гидродинамические. Эти методы предусматривают прогноз возникновения, эволюции и перемещения ТЦ.
1.3.1.2. Тропические циклоны (ураганы и тайфуны) в отличие от внетропических циклонов имеют свои отличительные особенности:
они являются локальными образованиями с горизонтальными размерами от 400 до 800 км;
наиболее показательными количественными характеристиками ТЦ являются атмосферное давление в его центре и скорость ветра в зоне его влияния.
1.3.1.3. Вследствие этого прогнозируемые характеристики ТЦ обычно относят к локальному объекту (практически к точке), а не ко всему полю, как это принято при прогнозе будущего положения макромасштабного барического поля.
1.3.1.4. Испытание новых методов прогноза перемещения и эволюции ТЦ производится в сравнении с другими расчетными методами аналогичного прогноза, а также в сравнении с инерционными прогнозами перемещения и эволюции ТЦ. При этом инерционный прогноз (в отличие от тривиального инерционного прогноза других элементов и явлений погоды, соответствующего их значениям в исходный срок) составляется с учетом изменения давления воздуха в центре ТЦ, скорости и направления его перемещения за период времени, предшествующий исходному сроку.
порядка на 24 ч вперед. Прогнозируется движение ТЦ на запад
с постоянной скоростью
В основу инерционного прогноза ТЦ берется гипотеза, согласно которой суммарный эффект всех сил, направляющих ТЦ в течение некоторого прошедшего периода, продолжает действовать в течение такого же будущего периода. В силу указанного предположения инерционный прогноз представляет собой линейную экстраполяцию движения ТЦ на последующий период времени. В зависимости от вида интерполяции различают инерционные прогнозы первого и второго порядка [8]. Инерционному прогнозу первого порядка присущи однородные (постоянные) скорость и направление перемещения ТЦ в течение прошедшего и будущего периодов (черт. 1). Инерционный прогноз второго порядка учитывает изменение (увеличение или уменьшение) скорости, а также изменение направления движения ТЦ в течение прошедшего периода и соответственно этому - изменение в будущий период (черт. 2 и 3). Оба вида инерционных прогнозов не лишены погрешностей, хотя у прогнозов второго порядка на отдельных участках траекторий перемещения погрешности несколько меньше. Однако в оперативных условиях расчет инерционного прогноза высшего порядка затруднен из-за отсутствия информации о положении ТЦ внутри периода, ближайшего к исходному сроку.
Для получения статистически надежных выводов о качестве прогнозов необходимо стремиться к тому, чтобы количество случаев было соизмеримо с природной повторяемостью ТЦ на выбранной акватории океана или превышало ее.
Испытание новых методов прогноза возникновения ТЦ производится в сравнении с имеющимися расчетными методами возникновения ТЦ, а также с климатическим прогнозом.

порядка на 24 ч. Направление движения постоянное, ускорение
движения 1 м/с за предшествующие 12 ч является предиктором
для прогноза скорости перемещения
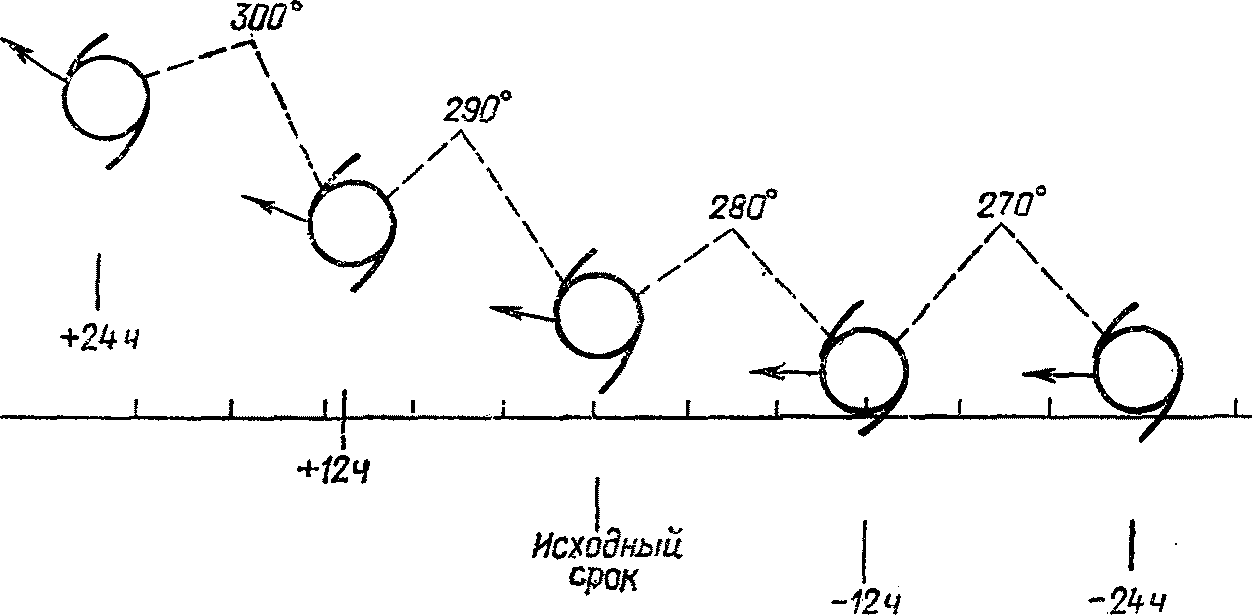
порядка. Скорость движения постоянная, изменение направления
движения ТЦ на 10° за предшествующие 12 ч является
предиктором на последующие 24 ч
1.3.2.1. В настоящее время в оперативной практике прогностических подразделений прогнозы перемещения ТЦ составляются с заблаговременностью 24, 48 и 72 ч. Ввиду этого и разрабатываемые методы предусматривают перемещение ТЦ с указанной заблаговременностью. При испытании таких методов прогнозов для каждой заблаговременности определяются показатели, характеризующие ошибки в положении центров ТЦ, скорости и направления их перемещения. Ошибки в положении ТЦ определяют следующие показатели успешности:
абсолютная ошибка прогнозов положения центра ТЦ (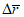 - средняя,
- средняя, 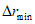 ,
,  - экстремальные), являющаяся расстоянием между фактическим и прогностическим положениями центров в срок прогноза с точностью до 10 км. Повторяемость (%)
- экстремальные), являющаяся расстоянием между фактическим и прогностическим положениями центров в срок прогноза с точностью до 10 км. Повторяемость (%)  рассчитывается по градациям (<= 200, 201 - 400, < 400 км);
рассчитывается по градациям (<= 200, 201 - 400, < 400 км);
относительная ошибка прогнозов положения ТЦ (с точностью до 0,01)
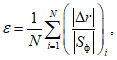
где i - номер ТЦ, N - число случаев,  - модуль векторной ошибки положения ТЦ,
- модуль векторной ошибки положения ТЦ, 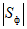 - модуль вектора фактического перемещения ТЦ за период времени, соответствующий заблаговременности прогноза.
- модуль вектора фактического перемещения ТЦ за период времени, соответствующий заблаговременности прогноза.
Успешность прогнозов скорости перемещения ТЦ характеризуют
абсолютная ошибка прогноза скорости перемещения ТЦ

вычисляемая (с точностью до 10 км на 24, 48 и 72 ч) для участков траекторий ТЦ с заблаговременностью 24, 48 и 72 ч (повторяемость 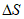 рассчитывается по градациям 0 - 250, 251 - 450 и > 450 км на 24, 48 и 72 ч);
рассчитывается по градациям 0 - 250, 251 - 450 и > 450 км на 24, 48 и 72 ч);
средняя арифметическая (систематическая) ошибка скорости перемещения ТЦ

характеристика завышения или занижения прогностической скорости ТЦ по сравнению с фактической

Погрешности в прогнозах направления перемещения ТЦ характеризует ошибка 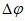 , определяемая значением угла между фактической и прогностической траекториями ТЦ с точностью до 1° (в пределах от 0 до 180° вправо или влево). Рассчитывается повторяемость
, определяемая значением угла между фактической и прогностической траекториями ТЦ с точностью до 1° (в пределах от 0 до 180° вправо или влево). Рассчитывается повторяемость 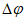 по градациям (< 20, 21 - 35, > 35°). При этом отдельно рассматриваются случаи отклонения прогностической траектории ТЦ от фактической влево и вправо. Вычисляются среднее и экстремальное значения
по градациям (< 20, 21 - 35, > 35°). При этом отдельно рассматриваются случаи отклонения прогностической траектории ТЦ от фактической влево и вправо. Вычисляются среднее и экстремальное значения  .
.
Из всех перечисленных показателей успешности прогнозов перемещения ТЦ основным принято считать ошибки в прогнозе положения ТЦ  . Все указанные выше показатели представляются в отчете об испытаниях метода в виде табл. 8.
. Все указанные выше показатели представляются в отчете об испытаниях метода в виде табл. 8.
1.3.2.1. Для выявления особенностей проверяемого метода и установления возможности его использования для прогноза траекторий ТЦ различной конфигурации помимо средних значений указанных ошибок вычисляются ошибки отдельно для каждого вида траекторий. Так, траектории ТЦ могут быть условно разделены на простые, параболические и сложные. К простым следует относить траектории, имеющие вид прямой или обратной ветви. Параболические траектории совмещают в себе прямую и обратную ветви, а также участок поворота. Простые и параболические траектории обычно соответствуют перемещению ТЦ в поле, где крупномасштабный фоновый поток определен достаточно хорошо. К сложным следует относить траектории ТЦ, имеющие крутые повороты, петли, возвратные движения. Такие перемещения обычно имеют место при взаимодействии двух и более одновременно существующих ТЦ, а также при отсутствии ярко выраженного крупномасштабного фонового потока.
Таким образом, при установлении надежности испытываемого метода прогноза должны быть рассчитаны и проанализированы указанные выше оценки отдельно для прямой ветви траекторий и для обратной ветви, для участка поворота и для сложных траекторий. В качестве примера такого вида оценки в табл. 9 приведены результаты испытания численного метода прогноза траекторий ТЦ в западной части Тихого океана с заблаговременностью до трех суток (авторы И.Г. Ситников, В.А. Зленко).
При анализе результатов испытаний следует иметь в виду, что в зависимости от значений указанных ошибок прогнозы могут интерпретироваться в следующих категориях:
при заблаговременности 24 ч при хорошем прогнозе 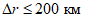 ,
,  ,
,  , при удовлетворительном прогнозе
, при удовлетворительном прогнозе 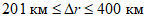 ,
,  ,
,  , при плохом прогнозе
, при плохом прогнозе  ,
,  ,
, 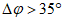 ;
;
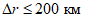 ,
,  ,
,  , при удовлетворительном прогнозе
, при удовлетворительном прогнозе 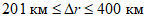 ,
,  ,
,  , при плохом прогнозе
, при плохом прогнозе  ,
,  ,
, 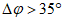 ;
;ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
при заблаговременности 48 ч при хорошем прогнозе 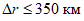 ,
,  ,
, 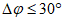 , при удовлетворительном прогнозе
, при удовлетворительном прогнозе  ,
,  ,
,  , при плохом прогнозе
, при плохом прогнозе 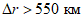 ,
,  ,
, 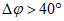 ;
;
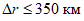 ,
,  ,
, 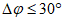 , при удовлетворительном прогнозе
, при удовлетворительном прогнозе  ,
,  ,
,  , при плохом прогнозе
, при плохом прогнозе 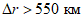 ,
,  ,
, 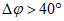 ;
;при заблаговременности 72 ч при хорошем прогнозе 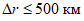 ,
, 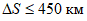 ,
, 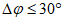 , при удовлетворительном прогнозе
, при удовлетворительном прогнозе  ,
, 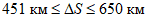 ,
,  , при плохом прогнозе
, при плохом прогнозе  ,
,  ,
,  .
.
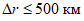 ,
, 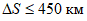 ,
, 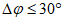 , при удовлетворительном прогнозе
, при удовлетворительном прогнозе  ,
, 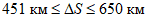 ,
,  , при плохом прогнозе
, при плохом прогнозе  ,
,  ,
,  .
.При сравнительной оценке ряда методов прогноза перемещения ТЦ и решении вопроса о целесообразности внедрения предпочтение отдается методу, имеющему лучшие показатели успешности. Естественно, у одного метода могут быть лучшими одни показатели, у второго - другие. В этом случае приоритет отдается методу по количеству лучших оценок. Однако и такой формальный подход может быть не всегда оправданным. Так, при наличии высоких показателей успешности прогнозов перемещения ТЦ лишь на определенном участке траектории (например, прямая ветвь) метод может быть рекомендован для использования при прогнозировании перемещения ТЦ только на данном участке траекторий.
При отсутствии внедренных методов прогноза перемещения ТЦ испытание нового метода производится в сравнении с инерционными прогнозами. В таком случае новый метод прогноза перемещения ТЦ рекомендуется к внедрению при наличии преимуществ метода перед инерционными прогнозами.
Таблица 8
в западной части Тихого океана за 1987 г.
(метод Гидрометцентра СССР)
Ошибки в прогнозе положения ТЦ
Заблаговременность прогноза, ч | N | Повторяемость (%) | Экстремальное | ||||||
0 - 200 км | 201 - 400 км | 401 - 600 км | > 600 км | min | max | ||||
24 | 82 | 36 | 49 | 11 | 4 | 259 | 44 | 637 | 0,72 |
48 | 66 | 12 | 26 | 36 | 26 | 497 | 145 | 1004 | 0,63 |
72 | 50 | 2 | 22 | 18 | 58 | 699 | 185 | 1619 | 0,53 |
Ошибки в прогнозе скорости перемещения ТЦ
Заблаговременность прогноза, ч | N | Повторяемость (%) | Экстремальное | |||||||
0 - 250 км/сут | 251 - 450 км/сут | > 450 км/сут | min | max | ||||||
24 | 82 | 482 | - | - | - | 171 | 4 | 820 | - | 1,02 |
48 | 66 | 508 | - | - | - | 147 | 4 | 425 | - | 1,02 |
72 | 50 | 502 | - | - | - | 135 | 3 | 478 | - | 0,94 |
Ошибки в прогнозе направления перемещения ТЦ
Заблаговременность прогноза, ч | N | Повторяемость (%) | Число случаев | Экстремальное | |||||||
<= 20° | 21 - 35° | > 35° | вправо | влево | вправо | влево | для всех случаев | min | max | ||
24 | 82 | - | - | - | 50 | 50 | 21 | 28 | 24 | 1 | 138 |
48 | 66 | - | - | - | 58 | 42 | 20 | 26 | 22 | 1 | 72 |
72 | 50 | - | - | - | 69 | 31 | 22 | 28 | 24 | 1 | 76 |
Таблица 9
Тихого океана при различных видах их траекторий
(метод Гидрометцентра СССР, 1987 г.)
Прямая ветвь
Ошибки в прогнозе положения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 200 км | 201 - 400 км | 401 - 600 км | > 600 км | min | max | ||||
24 | 40 | 37 | 53 | 10 | 0 | 252 | 77 | 594 | 0,72 |
48 | 32 | 19 | 28 | 31 | 22 | 449 | 145 | 980 | 0,61 |
72 | 26 | 4 | 35 | 19 | 42 | 613 | 185 | 1429 | 0,53 |
Ошибки в прогнозе скорости перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 250 км/сут | 251 - 450 км/сут | > 450 км/сут | min | max | |||||
24 | 40 | 416 | - | - | - | 148 | 4 | 351 | 0,97 |
48 | 32 | 413 | - | - | - | 117 | 5 | 333 | 1,09 |
72 | 26 | 406 | - | - | - | 85 | 3 | 248 | 1,05 |
Ошибки в прогнозе направления перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Число случаев | Экстремальное | |||||||
<= 20° | 21 - 35° | > 35° | влево | вправо | влево | вправо | min | max | |||
24 | 40 | - | - | - | 23 | 17 | 20 | 34 | 26 | 1 | 63 |
48 | 32 | - | - | - | 16 | 16 | 19 | 33 | 26 | 2 | 72 |
72 | 26 | - | - | - | 11 | 15 | 20 | 33 | 27 | 3 | 76 |
Обратная ветвь
Ошибки в прогнозе положения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 200 км | 201 - 400 км | 401 - 600 км | > 600 км | min | max | ||||
24 | 15 | 33 | 47 | 13 | 7 | 280 | 44 | 637 | 0,37 |
48 | 10 | 10 | 30 | 0 | 60 | 590 | 191 | 901 | 0,31 |
72 | 4 | 0 | 0 | 25 | 75 | 639 | 580 | 877 | 0,32 |
Ошибки в прогнозе скорости перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 250 км/сут | 251 - 450 км/сут | > 450 км/сут | min | max | |||||
24 | 15 | 809 | - | - | - | 211 | 3 | 456 | 1,01 |
48 | 10 | 945 | - | - | - | 181 | 7 | 514 | 0,91 |
72 | 4 | 837 | - | - | - | 216 | 133 | 263 | 0,74 |
Ошибки в прогнозе направления перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Число случаев | Экстремальное | |||||||
<= 20° | 21 - 35° | > 35° | влево | вправо | влево | вправо | min | max | |||
24 | 15 | - | - | - | 4 | 11 | 13 | 13 | 13 | 2 | 37 |
48 | 10 | - | - | - | 5 | 5 | 11 | 14 | 12 | 1 | 25 |
72 | 4 | - | - | - | 2 | 2 | 4 | 12 | 8 | 3 | 15 |
Участок поворота
Ошибки в прогнозе положения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 200 км | 201 - 400 км | 401 - 600 км | > 600 км | min | max | ||||
24 | 23 | 43 | 43 | 9 | 5 | 224 | 69 | 637 | 0,68 |
48 | 22 | 5 | 18 | 59 | 18 | 500 | 187 | 942 | 0,68 |
72 | 19 | 0 | 11 | 16 | 73 | 812 | 206 | 1619 | 0,54 |
Ошибки в прогнозе скорости перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 250 км/сут | 251 - 450 км/сут | > 450 км/сут | min | max | |||||
24 | 23 | 429 | - | - | - | 142 | 6 | 554 | 0,94 |
48 | 22 | 477 | - | - | - | 157 | 4 | 378 | 0,98 |
72 | 19 | 580 | - | - | - | 184 | 4 | 478 | 0,87 |
Ошибки в прогнозе направления перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Число случаев | Экстремальное | |||||||
<= 20° | 21 - 35° | > 35° | влево | вправо | влево | вправо | min | max | |||
24 | 23 | - | - | - | 13 | 10 | 24 | 35 | 28 | 1 | 138 |
48 | 22 | - | - | - | 16 | 6 | 24 | 17 | 22 | 1 | 56 |
72 | 19 | - | - | - | 16 | 3 | 25 | 22 | 24 | 1 | 39 |
Сложные траектории
Ошибки в прогнозе положения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 200 км | 201 - 400 км | 401 - 600 км | > 600 км | min | max | ||||
24 | 4 | 0 | 50 | 25 | 25 | 473 | 284 | 841 | 2,19 |
48 | 2 | 0 | 0 | 50 | 50 | 769 | 534 | 1004 | 1,92 |
72 | 1 | 0 | 0 | 0 | 100 | 610 | 610 | 610 | 0,91 |
Ошибки в прогнозе скорости перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Экстремальное | ||||||
0 - 250 км/сут | 251 - 450 км/сут | > 450 км/сут | min | max | |||||
24 | 4 | 261 | - | - | - | 416 | 298 | 820 | 2,59 |
48 | 2 | 198 | - | - | - | 353 | 254 | 452 | 2,78 |
72 | 1 | 224 | - | - | - | 195 | 195 | 195 | 1,87 |
Ошибки в прогнозе направления перемещения ТЦ
Заблаговременность прогноза, ч | Количество ТЦ | Повторяемость (%) | Число случаев | Экстремальное | |||||||
<= 20° | 21 - 35° | > 35° | влево | вправо | влево | вправо | min | max | |||
24 | 4 | - | - | - | 1 | 3 | 38 | 20 | 25 | 11 | 38 |
48 | 2 | - | - | - | 1 | 1 | 18 | 20 | 19 | 18 | 20 |
72 | 1 | - | - | - | 0 | 1 | - | 11 | 11 | 11 | 11 |
1.3.3.1. Процесс эволюции ТЦ характеризуется не только изменением давления воздуха в его зоне, но и изменением скорости ветра. Последний признак является главным при определении стадии развития ТЦ [5]. Поэтому для установления надежности методов прогноза эволюции ТЦ необходимо использовать статистические показатели успешности, предназначенные для оценки качества прогноза давления и ветра. В частности, для определения успешности прогноза изменения давления в центре ТЦ используются следующие статистические характеристики:
оценка прогноза знака изменения давления в ТЦ
где nо, nн - соответственно количество ТЦ, в которых прогноз знака изменения давления воздуха оправдался или не оправдался.
Значение 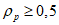 свидетельствует об удовлетворительном, а
свидетельствует об удовлетворительном, а 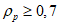 - о хорошем качестве прогноза знака изменения давления в ТЦ;
- о хорошем качестве прогноза знака изменения давления в ТЦ;
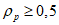 свидетельствует об удовлетворительном, а
свидетельствует об удовлетворительном, а 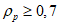 - о хорошем качестве прогноза знака изменения давления в ТЦ;
- о хорошем качестве прогноза знака изменения давления в ТЦ;абсолютная ошибка прогноза давления в ТЦ (с точностью до 0,1)
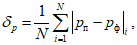 (46)
(46)где N - количество ТЦ, pп и pф - прогностическое и фактическое значения давления в центрах ТЦ;
относительная ошибка прогноза (с точностью до 0,01)
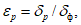 (47)
(47)где
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 (48)
(48)средняя арифметическая (систематическая) ошибка прогноза давления в центрах ТЦ (с точностью до 0,1)
Положительное (отрицательное) значение 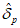 свидетельствует о систематическом завышении (занижении) давления в центрах ТЦ.
свидетельствует о систематическом завышении (занижении) давления в центрах ТЦ.
Формулы (45) - (49) используются также для расчета аналогичных показателей успешности прогнозов изменения скорости ветра:  ,
, 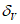 ,
, 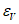 ,
, 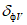 ,
,  . При этом скорость ветра в ТЦ определяется эмпирически по разнице значений приземного давления между периферией и центром ТЦ или с помощью графика, приведенного в [5], согласно изложенным там рекомендациям.
. При этом скорость ветра в ТЦ определяется эмпирически по разнице значений приземного давления между периферией и центром ТЦ или с помощью графика, приведенного в [5], согласно изложенным там рекомендациям.
1.3.3.2. Для выявления возможности практического использования испытываемого метода прогноза эволюции ТЦ на различных стадиях его развития целесообразно рассчитать указанные характеристики успешности отдельно для стадии формирования (тропическая депрессия с Vт < 17 м/с), молодого циклона (тропический шторм с 17 м/с <= Vт <= 33 м/с) и зрелого циклона (урагана или тайфуна с Vт > 33 м/с). Изменение интенсивности ТЦ устанавливается по радиусу кольца максимального ветра или радиусу его глаза в соответствии с рекомендациями [5].
1.3.3.3. Все значения указанных характеристик успешности прогнозов изменения давления воздуха и ветра в ТЦ в среднем для всех ТЦ и отдельных его стадий, а также экстремальные значения 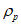 ,
,  ,
,  ,
, 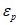 и
и 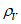 ,
, 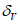 ,
, 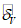 ,
,  следует представлять в виде табл. 10 и 11. При этом в табл. 11 необходимо также привести сведения об оправдываемости прогнозов ветра в соответствие с действующим Наставлением [4].
следует представлять в виде табл. 10 и 11. При этом в табл. 11 необходимо также привести сведения об оправдываемости прогнозов ветра в соответствие с действующим Наставлением [4].
1.3.3.4. При сравнении нового метода прогноза эволюции ТЦ с используемым в оперативной практике предпочтение отдается методу, имеющему лучшие показатели успешности. В случае если один из сравниваемых методов имеет лучшие показатели успешности только на одной из стадий развития ТЦ, такой метод прогноза может быть рекомендован для использования именно на данной стадии развития ТЦ в качестве вспомогательного к другому методу, имеющему более высокие оценки на других стадиях и в целом.
1.3.3.5. При отсутствии в оперативной практике внедренных методов прогноза эволюции ТЦ сравнение испытываемого метода прогноза производится с инерционными прогнозами. При этом прогностическое значение давления, предсказываемое инерционными прогнозами различной заблаговременности, имеет вид:  , где
, где 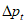 - тенденция изменения давления к исходному сроку за период времени, соответствующий заблаговременности прогноза.
- тенденция изменения давления к исходному сроку за период времени, соответствующий заблаговременности прогноза.
 , где
, где Например,

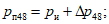

где
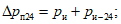

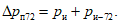
Таблица 10
по статистическому методу ДВНИГМИ в сравнении с инерционными
прогнозами (1986 и 1987 гг.)
Заблаговременность прогноза, ч | Статистический метод | Инерционный прогноз | |||||||||
Число прогнозов | Число прогнозов | ||||||||||
12 | 20 | 7,7 | 5,6 | -0,2 | 1,37 | 0,25 | 20 | 9,1 | 1,63 | 0,35 | |
24 | 21 | 11,5 | 13,0 | -3,5 | 0,88 | 0,24 | 21 | 20,7 | - | 1,59 | 0,38 |
36 | 15 | 10,2 | 16,1 | -3,0 | 0,63 | 0,73 | 14 | 27,4 | - | 1,70 | 0,43 |
48 | 16 | 11,9 | 21,5 | -6,9 | 0,55 | 0,62 | 11 | 28,5 | - | 1,32 | 0,36 |
60 | 11 | 12,9 | 18,4 | -7,6 | 0,70 | 0,73 | 8 | 28,5 | - | 1,54 | 0,62 |
72 | 4 | 14,2 | 30,0 | -10,2 | 0,47 | 1,0 | 3 | 16,6 | - | 0,55 | 1,00 |
Примечание. Для инерционного прогноза значения 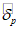 не приведены, так как они не были рассчитаны.
не приведены, так как они не были рассчитаны.
Таблица 11
в тайфунах по статистическому методу ДВНИГМИ
(1986 и 1987 гг.)
Заблаговременность прогноза, ч | Число прогнозов | |||||
12 | 17 | 3,5 | 2,3 | 0,8 | 1,55 | 0,29 |
24 | 18 | 4,9 | 5,3 | 2,3 | 0,93 | 0,28 |
36 | 15 | 4,2 | 6,3 | 2,6 | 0,66 | 0,46 |
48 | 14 | 5,0 | 7,4 | 2,1 | 0,67 | 0,50 |
60 | 11 | 4,0 | 7,2 | 2,9 | 0,55 | 0,73 |
72 | 4 | 3,2 | 10,5 | 3,2 | 0,30 | 1,0 |
Метод прогноза, уступающий в успешности инерционным прогнозам, для внедрения в оперативную практику не пригоден.
1.3.4.1. Для установления надежности методов прогноза возникновения ТЦ используется альтернативная оценка. С помощью формы 11 по наличию (отсутствию) ТЦ на исходных, прогностических и фактических картах прогнозы можно отнести к оправдавшимся ("+") или неоправдавшимся ("-"). На основании полученных данных составляется таблица сопряженности прогностических сведений о возникновении и отсутствии ТЦ (форма 12). В ней n11 и n12 - соответственно количество оправдавшихся и неоправдавшихся прогнозов возникновения ТЦ; n10 - количество составленных прогнозов возникновения ТЦ; n22 и n21 - соответственно количество оправдавшихся и неоправдавшихся прогнозов отсутствия ТЦ; n20 - количество составленных прогнозов отсутствия ТЦ; n00 - общее количество составленных прогнозов; n01 - фактическое число случаев возникновения ТЦ; n02 - фактическое число случаев отсутствия ТЦ (неразвития тропических возмущений). С их помощью рассчитываются оправдываемости в процентах прогнозов возникновения ТЦ: общая (U), наличие ТЦ (Uя), отсутствие ТЦ (Uб.я) соответственно по формулам:
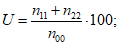
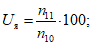

Кроме того, вычисляется предупрежденность возникновения ТЦ (ПТЦ) и критерий качества прогнозов Пирси - Обухова (TТЦ)
ПТЦ = n11/n01; TТЦ = n11/n01 - n12/n02,
а также количество ложных и сглаженных ТЦ.
Прогноз | Наличие ТЦ на картах | ||
исходных | фактических | прогностических | |
Возникновение (реальные центры) | Нет | Есть | Есть (+) нет (-) |
Отсутствие | Нет | Нет | Нет (+) есть (-) |
Ложные центры | Нет | Нет | Есть (-) |
Сглаживание | Есть | Есть | Нет (-) |
тропических циклонов
Прогноз | ТЦ на фактических картах | Сумма | |
есть | нет | ||
Возникновение ТЦ (наличие ТЦ) | n11 | n12 | n10 |
Неразвитие тропических возмущений (отсутствие ТЦ) | n21 | n22 | n20 |
Сумма | n01 | n02 | n00 |
Полученные результаты оценки прогнозов возникновения ТЦ необходимо представлять по форме 13.
Метод (автор) | Заблаговременность прогноза, ч | Количество ТЦ | U | Uя | Uб.я | ПТЦ | TТЦ | ||||
наблюдавшиеся | возникновение | ложные | сглаженные | ||||||||
фактические | предусмотренные прогнозом | ||||||||||
1.3.4.2. При анализе результатов испытания нового метода прогноза возникновения ТЦ в сравнении с ранее внедренным методом предпочтение отдается методу прогноза, имеющему меньшее количество ложных и сглаженных центров, а также более высокие остальные показатели успешности прогнозов. При этом следует иметь в виду, что среди остальных показателей наиболее информативным можно считать критерий качества прогнозов TТЦ, значения которого могут изменяться от -1 до 1. Однако качество прогнозов можно считать удовлетворительным при TТЦ >= 0,3 и хорошим при TТЦ >= 0,5.
1.3.4.3. При отсутствии внедренных методов прогнозы возникновения ТЦ, составленные испытываемым методом, сравниваются по месяцам и сезонам с климатическими прогнозами, повторяемость которых на данной территории (акватории океана) устанавливается путем предварительной обработки климатических данных о возникновении ТЦ в указанные периоды. Результаты сравнения представляются по форме 12 и 13. Уровень успешности, характеризующийся достаточно высокими показателями и превышающий успешность климатических прогнозов, является основанием для рекомендации к внедрению испытываемого метода прогноза возникновения ТЦ в оперативную практику.
элементов и явлений погоды на 3 - 10 суток
на средние сроки
1.4.1.1. В настоящее время разработка методов прогноза метеорологических элементов погоды на средние сроки получила широкое развитие. Многообразие используемых научных подходов и способов их реализации определяет особенности создаваемых методов составления прогнозов на эти сроки. С учетом указанных особенностей методы прогноза погоды на средние сроки можно подразделить на следующие виды:
синоптический метод, основанный на анализе всего имеющегося материала, используется для составления прогнозов погоды до 5 суток;
гидродинамический метод, с помощью которого предвычисляются прогнозы барического поля, поля температуры и влажности воздуха, ветра и осадков;
статистический метод прогноза метеорологических элементов;
гидродинамико-статистический метод, использующий статистическую интерпретацию расчетов гидродинамической модели атмосферы;
синоптико-гидродинамико-статистический метод.
В последние годы особенно широкое распространение получили методы статистической интерпретации гидродинамических прогнозов. С их помощью предвычисляются прогнозы минимальной, максимальной и средней суточной температуры воздуха и суточных сумм осадков до 7 суток, детализированные по дням для отдельных пунктов, а также для отдельных административных и экономических районов, бассейнов рек и энергосистем на территории СССР. Заблаговременность таких прогнозов до 6 суток.
Методы прогнозов на средние сроки, кроме того, предусматривают прогнозирование средней аномалии температуры воздуха на 10 суток. Заблаговременность этих прогнозов нулевая.
Методы среднесрочных прогнозов погоды, за исключением синоптического, являются автоматизированными. Испытание новых методов среднесрочного прогноза производится в сравнении с уже внедренными в оперативную практику методами аналогичного прогноза, а также с синоптическими (составленными синоптиками оперативно) и инерционными прогнозами.
1.4.1.2. Различные сроки прогнозов метеорологических элементов обусловливают также некоторые особенности оценки методов прогноза. Детализированные по дням прогнозы на 3 - 7 суток оцениваются по методике, аналогичной оценке методов краткосрочных прогнозов. При этом прогнозы на третьи, четвертые и пятые сутки сравниваются с синоптическими и инерционными прогнозами, а прогнозы на шестые и седьмые сутки сравниваются с инерционными прогнозами. Инерционным же прогнозом обычно является значение метеорологического элемента в исходный срок (период).
Следует отметить специфику составления инерционных прогнозов экстремальной температуры воздуха, поскольку в исходный срок составления методического и синоптического прогнозов (как правило, ночной или утренний) информация о максимальной температуре (Tmax) исходных суток отсутствует. Поэтому в качестве инерционного прогноза максимальной температуры для каждых суток берется значение Tmax за прошедший день. В результате чего заблаговременность инерционных прогнозов Tmax будет на 24 ч больше, чем у методических и синоптических прогнозов.
1.4.1.3. При составлении же прогноза минимальной температуры в качестве инерционного прогноза на все сроки следует использовать значение Tmin за прошедшую ночь. При этом заблаговременности инерционных, методических и синоптических прогнозов будут одинаковыми. Однако при оценке автоматизированного метода прогноза экстремальной температуры на 3 - 7 суток Гидрометцентра СССР, срок готовности которого (5 ч СГВ) оказался раньше времени поступления информации о Tmin за прошедшую ночь, в качестве инерционного прогноза Tmin бралось значение минимальной температуры за прошедшую ночь. В этом случае заблаговременность инерционных прогнозов Tmin оказалась на 24 ч больше заблаговременности методических и синоптических прогнозов.
Возникающие подобным образом различия в заблаговременности сопоставляемых прогнозов необходимо всегда учитывать при анализе результатов.
1.4.1.4. Многолетняя практика составления прогнозов аномалии температуры воздуха на 10 суток показала оправданной такую оценку, когда прогностические значения аномалии температуры воздуха сравниваются с фактическими, с их климатической изменчивостью и инерцией. При установлении надежности методов прогноза осадков на 10 суток прогнозы следует оценивать по отношению к их климатической декадной норме.
1.4.1.5. Прогнозы на средние сроки составляются, как правило, не для отдельного пункта, а для поля точек или географических пунктов. Более того, для таких величин, как осадки, которые распределяются в пространстве неравномерно, расчеты производятся на основе данных, осредненных по площади. Поэтому новые методы прогноза на средние сроки испытываются на материалах того региона, для которого они разработаны, и оцениваются по полю точек или станций, рекомендованных автором метода.
и явлений погоды на сроки от 3 до 7 суток
и минимальной)
1.4.2.1.1. При оценке методов прогноза температуры воздуха кроме оправдываемости прогнозов (P, %), согласно Наставлению [4], рассчитываются следующие статистические показатели успешности:
средняя абсолютная ошибка (с точностью до 0,1)
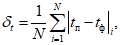 (50)
(50)где tп и tф - прогностическое и фактическое значения температуры воздуха соответственно, N - число прогнозов;
средняя арифметическая (систематическая) ошибка, с точностью до 0,1
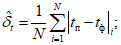 (51)
(51)относительная ошибка (с точностью до 0,01)
 (52)
(52)где 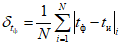 - средняя абсолютная фактическая изменчивость температуры; tи - значение температуры воздуха в исходный срок.
- средняя абсолютная фактическая изменчивость температуры; tи - значение температуры воздуха в исходный срок.
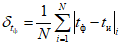 - средняя абсолютная фактическая изменчивость температуры; tи - значение температуры воздуха в исходный срок.
- средняя абсолютная фактическая изменчивость температуры; tи - значение температуры воздуха в исходный срок.Кроме того, рассчитывается оправдываемость прогнозов (Pt) при заданных градациях ошибок: <= 1, <= 2, <= 3, <= 4, <= 5 °C.
Для получения надежных выводов по результатам испытания методов прогноза необходим ряд 100 случаев и более. Он должен включать случаи не только малой изменчивости температуры воздуха, но и случаи резких ее изменений как в сторону повышения, так и понижения.
Результаты испытания представляются в виде таблиц, составленных в среднем за время испытания, а также за отдельные сезоны (форма 14). Отдельно оцениваются случаи резких изменений температуры (+/- 10 °C и более).
Результаты испытания методов прогноза температуры воздуха
на 3 - 7 суток
Заблаговременность прогноза, сутки | N | P, % | Pt, % | |||||||
<= 1° | <= 2° | <= 3° | <= 4° | <= 5° | ||||||
Методический прогноз | ||||||||||
Инерционный прогноз | ||||||||||
Синоптический прогноз | ||||||||||
1.4.2.1.2. Новый метод прогноза температуры на 3 - 7 суток может быть внедрен в практику, если оправдываемость прогнозов, составленных по этому методу, превышает оправдываемость прогнозов, составленных уже внедренным методом. При отсутствии внедренных методов прогноза температуры воздуха на средние сроки успешность методических прогнозов должна превышать успешность инерционных прогнозов и быть на уровне или выше оправдываемости прогнозов, составленных синоптическим методом.
1.4.2.2.1. Для установления надежности методов прогноза осадков на средние сроки, детализированного по дням, необходим ряд для каждой заблаговременности не менее 100 случаев. При этом следует рассчитывать оправдываемость прогнозов осадков каждой заблаговременности отдельно, согласно Наставлению [4]. Качество прогнозов факта выпадения осадков устанавливается с помощью критерия качества Пирси - Обухова, рассчитываемого по формуле
Все обозначения, используемые в этой формуле, приведены в п. 1.1.5. Значения TQ могут изменяться от -1 до 1. Качество прогнозов осадков следует считать удовлетворительным при TQ >= 0,3 и хорошим при TQ >= 0,5. Для идеального прогноза T = 1.
1.4.2.2.2. Для выявления успешности прогнозов количества осадков рассчитываются следующие статистические показатели:
средняя абсолютная ошибка (с точностью 0,1 мм при Qф < 1 мм и с точностью до 1 мм при Qф >= 1 мм)
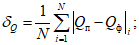 (54)
(54)средняя арифметическая (систематическая) ошибка (с точностью до 0,1 мм)
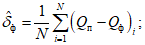 (55)
(55)относительная ошибка прогноза (с точностью до 0,01)
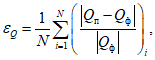 (56)
(56)где Qп и Qф - соответственно прогностическое и фактическое количество осадков за период прогноза; N - количество составленных прогнозов данной заблаговременности.
Указанные статистические показатели успешности прогнозов количества осадков рассчитываются для всей совокупности прогнозов, а также для отдельных их градаций (без осадков, слабые, умеренные, сильные и очень сильные осадки), согласно действующему Наставлению.
1.4.2.2.3. Помимо указанных показателей рассчитываются оправдываемости (%) прогнозов при указанных градациях ошибок
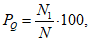
где N1 - количество прогнозов, в которых отклонение прогностических значений от фактических по абсолютным значениям не превышает заданный предел. PQ рекомендуется рассчитывать для следующих градаций ошибок: <= 3,0; <= 8,0; <= 15,0; <= 30,0 мм/сут.
При оценке прогнозов количества осадков по пункту в качестве Qф принимается среднее количество осадков по станциям и постам, расположенным в пределах данного пункта (города). При оценке прогнозов количества осадков по области (району) в качестве Qф берется среднее значение количества осадков по всем станциям и постам в данной области (районе).
1.4.2.2.4. Результаты испытания нового метода прогноза осадков представляются по форме 15 для всего периода испытаний и для отдельных сезонов года.
Результаты испытания метода прогноза осадков на 3 - 7 суток
Заблаговременность прогноза, сутки | Количество составленных прогнозов | PН, % | PQ, % | TQ | ||||||
<= 3 мм/сут | <= 8 мм/сут | <= 15 мм/сут | <= 30 мм/сут | |||||||
туман, гололед, метель, пыльная буря, сильный ветер)
1.4.2.3.1. Поскольку методы прогноза опасных явлений погоды с заблаговременностью от 3 до 7 суток весьма немногочисленны, то опыт испытания таких методов невелик. Поэтому в практической работе рекомендуется руководствоваться опытом испытания методов краткосрочного прогноза явлений погоды (см. п. 1.2.2). Вместе с тем следует иметь в виду, что при малой повторяемости отдельных явлений погоды (град, метель, пыльная буря) ряд случаев с самим явлением должен быть не менее их природной повторяемости. Для часто наблюдающихся явлений погоды рекомендуется число случаев с явлением не менее 60.
Испытание нового метода прогноза явления погоды следует проводить в сравнении с внедренными в оперативную практику методами прогноза этого же явления, а также с инерционными и синоптическими прогнозами.
1.4.2.3.2. Для установления надежности методов прогноза явлений погоды для каждой заблаговременности целесообразно рассчитать показатель качества Пирси - Обухова (T) по формуле (53), а также оправдываемость прогнозов (PН), согласно действующему Наставлению.
Результаты испытания следует представлять по форме 16. К внедрению в оперативную практику следует рекомендовать метод, имеющий более высокие показатели успешности и превышающий успешность инерционных прогнозов.
Результаты испытания метода прогноза опасных явлений погоды
на 3 - 7 суток
Заблаговременность прогноза, сутки | Прогноз | |||||
методический | синоптический | инерционный | ||||
PН, % | T | PН, % | T | PН, % | T | |
и ее аномалии на 10 суток
1.4.3.1. Основное требование, предъявляемое к оценкам прогноза температуры воздуха на 10 суток, должно заключаться в том, чтобы они достаточно объективно и однозначно характеризовали успешность прогноза как при сохранении, так и при изменении температурного режима.
1.4.3.2. Для оценки успешности прогнозов средней температуры на 10 суток в практической работе применяется ряд показателей успешности.
1.4.3.2.1. Первый из них - показатель аналогичности, характеризующий меру совпадения изменений прогнозируемой и фактической температуры воздуха (или ее аномалии) по знаку, рассчитывается по формуле
 (57)
(57)где n+ и n- - соответственно число оправдавшихся и неоправдавшихся изменений температуры воздуха (или ее аномалии) по знаку из общего числа точек (N) на данной территории.
1.4.3.2.2. Второй показатель успешности прогноза температуры - относительная ошибка 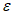 определяется как отношение суммы абсолютных ошибок методического прогноза к сумме абсолютных ошибок климатологического прогноза
определяется как отношение суммы абсолютных ошибок методического прогноза к сумме абсолютных ошибок климатологического прогноза
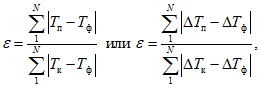 (58)
(58)где Tп, Tф и Tк - прогностическая, фактическая и климатическая температуры, а 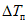 ,
,  и
и 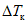 - соответственно прогностическая, фактическая и климатическая аномалии температуры воздуха.
- соответственно прогностическая, фактическая и климатическая аномалии температуры воздуха.
1.4.3.2.3. Третий показатель - общая оправдываемость прогноза
где n - число точек, в которых выполняется следующее условие: относительная ошибка прогноза в данной точке qi не превышает некоторого порогового значения Ci для данного пункта.
Величина P может меняться от 0 (при очень плохом прогнозе) до 1 (при очень хорошем прогнозе), она может быть выражена в процентах.
1.4.3.3. При оценке прогнозов по территории со стандартными точками для каждой точки i находят величину
 (60)
(60)где  - абсолютная ошибка прогноза, равная |Tп - Tф|; Si - средняя многолетняя изменчивость температуры воздуха за 10 суток в данной точке для данного месяца. Пороговое значение Ci, учитывающее климатическую и географическую изменчивость температуры воздуха, определяется из соотношения Ci = 0,846Si.
- абсолютная ошибка прогноза, равная |Tп - Tф|; Si - средняя многолетняя изменчивость температуры воздуха за 10 суток в данной точке для данного месяца. Пороговое значение Ci, учитывающее климатическую и географическую изменчивость температуры воздуха, определяется из соотношения Ci = 0,846Si.
1.4.3.4. Величина P (в процентах) рассчитывается по формуле (59) для точек, в которых qi < 0,9. Она характеризует успешность конкретного прогноза по данной территории, является достаточно жесткой (близка к оценке по  ) и, как показывает практика, хорошо отражает успешность прогноза знака и изменения температуры. Оценку P легко модифицировать, меняя пороговое значение ее по мере усовершенствования методов прогноза.
) и, как показывает практика, хорошо отражает успешность прогноза знака и изменения температуры. Оценку P легко модифицировать, меняя пороговое значение ее по мере усовершенствования методов прогноза.
1.4.3.5. Показатели успешности прогнозов температуры воздуха на 10 суток ( ,
, 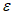 , P и
, P и  ), рассчитанные за весь период испытания, приводятся по форме 17. Отдельно рекомендуется составлять такие таблицы для случаев резких изменений аномалий температуры.
), рассчитанные за весь период испытания, приводятся по форме 17. Отдельно рекомендуется составлять такие таблицы для случаев резких изменений аномалий температуры.
Результаты испытания новых методов прогноза на 10 суток
Месяц | Методический прогноз | Инерционный прогноз | |||||||
P0,9 | P0,9 | ||||||||
Примечание. Такая же таблица составляется для случаев резких изменений аномалии 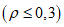 .
.
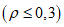 .
.1.4.3.6. Испытание новых методов прогнозов температуры воздуха на 10 суток производится в сравнении с методами, применяемыми в оперативной практике. Метод прогноза, имеющий лучшие показатели успешности, рекомендуется для практического использования.
1.5.1. Вероятностные прогнозы выражают существующую в каждой ситуации неопределенность в знании будущего состояния атмосферы, и поэтому качество вероятностного прогноза связано с точностью предвычисления функции распределения вероятностей, которая сообщается потребителю в качестве прогноза. Ясно, что о качестве предвычисления этой функции невозможно судить по отдельному испытанию, в котором реализуется одно конкретное значение предиктанта, причем совершенно необязательно наиболее вероятное. Оценивать успешность вероятностных прогнозов можно лишь по достаточно представительной их совокупности.
1.5.2. Обычно используемые в статистике методы оценки соответствия предвычисляемых и наблюдаемых частот (подобные критериям, основанным на статистике 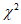 ) дадут высокие оценки для климатологического вероятностного прогноза, когда каждому событию приписывается его климатическая вероятность. Этот прогноз, однако, рассматривается как тривиальный и используется для сравнения с методическими прогнозами. Следовательно, оценки должны содержать меру отклонения предсказанных вероятностей от климатических и их изменчивость от прогноза к прогнозу.
) дадут высокие оценки для климатологического вероятностного прогноза, когда каждому событию приписывается его климатическая вероятность. Этот прогноз, однако, рассматривается как тривиальный и используется для сравнения с методическими прогнозами. Следовательно, оценки должны содержать меру отклонения предсказанных вероятностей от климатических и их изменчивость от прогноза к прогнозу.
1.5.3. В принципе, возможны два подхода к оценке качества вероятностных прогнозов, исходя из поставленной цели. Первый подход связан с оценкой последствий принимаемых потребителем на основе прогностической информации решений с точки зрения полезности прогностической информации (экономическая оценка). Второй подход ориентирован на непосредственную оценку "совершенства" прогнозов, т.е. степени соответствия прогнозов реальным наблюдениям (научная или эмпирическая оценка). Ниже будут рассматриваться только оценки, реализующие второй подход.
1.5.4. Из возможных свойств или атрибутов прогноза, подлежащих оценке, можно выделить три наиболее очевидные:
точность прогнозов - свойство, отражающее среднее по совокупности прогнозов соответствие между ожидаемыми и осуществившимися событиями;
смещение (или надежность) - соответствие средних значений в группе прогнозов реальной группе наблюдений;
категоричность - свойство, отражающее близость вероятностного прогноза категорическому, т.е. близость функции распределения к дельта-функции, когда единичная масса распределения сосредоточена в единственной точке. При этом последнее свойство не связано с соответствием прогноза наблюдению. Однако высокая степень такого соответствия характеризует большую уверенность (меньшую неопределенность) прогноза.
1.5.5. Рассмотрим теперь ряд оценок, касающихся первых двух свойств вероятностного прогноза. Введем основные обозначения. Будем рассматривать совокупность из n фазовых прогнозов с числом фаз k. Предвычисленные вероятности обозначим P1i, P2i, ... Pki, где i изменяется от 1 до n. Положим, что наблюдениям соответствуют распределения вероятностей d1i, ..., dki, где dSi = 1, если в i-м наблюдении осуществилась фаза s, и dri = 0 при 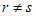 .
.
1.5.5.1. Наиболее распространенной оценкой качества для вероятностных прогнозов является оценка Брайера
которая измеряет точность вероятностного прогноза. При этом "самый плохой" прогноз - это прогноз, дающий вероятность 1 для одной из градаций, которая никогда не осуществляется, а "самый лучший" всегда угадывает градацию в такой же ситуации.
Эта оценка, однако, не учитывает упорядоченности градаций. К примеру, даны два вероятностных прогноза в трех градациях: 0,4; 0,1; 0,5 и 0,1; 0,4; 0,5. Фактически осуществилась третья градация. Несмотря на то что оба прогноза третью градацию спрогнозировали с наибольшей вероятностью и оценка Брайера у них одинаковая, второй прогноз с учетом спрогнозированного распределения градаций все-таки можно считать "лучшим", так как он с меньшей вероятностью дает наиболее удаленную от факта первую градацию. Чтобы учесть упорядоченность категорий, нужно рассчитать следующую оценку, использующую накопленные суммы вероятностей ( и
и  ):
):
 и
и  ):
):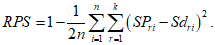 (62)
(62)Помимо квадратичных оценок PS и RPS применяется использующая абсолютные разности оценка APS:
Оценки PS, RPS и APS изменяются в интервале от 0 до 1, причем для идеальных прогнозов эти оценки равны единице, для абсолютно недостоверных - нулю.
Кроме перечисленных, различными авторами использовались другие оценки успешности (в том числе логарифмические и энтропийного типа). Такие оценки и связанные с ними вопросы подробно рассматриваются в [9].
1.5.6. Как уже указывалось раньше, выводы, получаемые на основании различных систем оценок, могут быть неодинаковыми (в том числе принципиально), поскольку ориентированы на различные свойства прогноза. Но и оценки одного свойства могут быть несопоставимы из-за размерности. Для преодоления этого неудобства вместо самой оценки необходимо использовать ее безразмерный аналог, так называемую "меру мастерства"
где S(R) - оценка методического прогноза; S(П) - оценка "стандартного" метода прогноза; S(I) - оценка "идеального", т.е. абсолютно точного прогноза. Мера мастерства SS определяет качество методического прогноза по сравнению со "стандартным". В качестве "стандартного" прогноза можно использовать случайный, климатологический или инерционный прогноз. Для идеальных прогнозов мера мастерства равна 1; если SS(R, П) = 0, то качество методического прогноза находится на уровне "стандартного", и при SS(R, П) < 0 - ниже "стандартного" прогноза.
1.5.7. Для определения второго свойства прогнозов - значения их смещения (надежности) - следует использовать меру смещения, равную алгебраической разности предсказанных вероятностей и фактических частот
 (65)
(65)Практически для этого все прогнозы группируются по градациям значений предсказанных вероятностей Pп (например, через 0,1) и в каждой группе подсчитывается эмпирическая частота осуществления соответствующей градации Pф. Для этих целей удобно использовать двумерную диаграмму.
На черт. 4 в качестве примера приведена такая диаграмма для прогноза приземной температуры воздуха, осредненной по 45 крупным пространственным областям, расположенным в северном полушарии (схема ГРАН - 84, авторы Г.В. Груза, Э.Я. Ранькова - Гидрометцентр СССР). На черт. 4 интервал изменения Pп разделен на 10 градаций. Общее число вероятностей прогнозируемых фаз n = km, где k - число прогнозируемых фаз предиктанта (в данном случае 3), а m - число прогнозов. Из них некоторое число ni попадает в i-ю градацию (i = 1, ..., 10). Кроме того, n'i - число случаев, когда осуществлялась фаза предиктанта, прогностическая вероятность которой также попадала в i-ю градацию. При этом всегда n'i <= ni, а (Pф)i есть n'i/ni. Для идеального вероятностного прогноза градация, предсказанная с вероятностью P, должна в среднем осуществляться с частотой P, т.е. (Pп)i = (Pф)i. Таким образом, точки с координатами (Pп, Pф) должны группироваться около биссектрисы координатного угла. На черт. 4 около каждой точки с координатами (Pп, Pф) приведено число ni. Из чертежа видно, что большинство представленных точек группируется вдоль биссектрисы в пределах 15%-й полосы, т.е. различие предвычисленных и фактических частот в основном не превосходит указанное значение. На наибольшем удалении от биссектрисы находится точка с Pп (80 - 90%) в градации i = 9. Учитывая, что для этой точки ni = 2, ее влияние на оценку прогнозов можно считать несущественным.

соответствия прогностической вероятности (Pп) фактической
повторяемости (Pф), для прогнозов средней месячной
температуры воздуха по схеме ГРАН-84 за период
с декабря 1983 г. по декабрь 1987 г.
1.5.8. На черт. 5 приведена гистограмма предсказанных вероятностей, на основании которой можно судить, например, о "категоричности" оцениваемого прогноза. В данном случае более 50% предсказанных вероятностей находилось в интервале 20 - 40%, однако имелись довольно высокие (70 - 90%) и весьма низкие (20 - 10% и менее) предсказанные вероятности.
1.5.9. Гистограмма и диаграмма, представленные на черт. 4 и 5, содержат довольно много информации: помимо "среднего качества" они показывают, за счет чего это среднее складывается, где соответствие прогноза и факта лучше и где хуже и насколько хуже. Поэтому их вполне можно использовать как удобный и наглядный способ оценки качества вероятностных прогнозов.
1.5.10. Последний вопрос, который нужно упомянуть в связи со статистической оценкой качества вероятностных прогнозов - это вопрос статистической значимости для таких оценок. Следует, однако, отметить, что определение уровня значимости оценок качества методов вероятностных прогнозов - задача крайне сложная в вычислительном отношении и требует больших затрат ресурсов ЭВМ [9]. Поэтому в настоящих методических указаниях эта проблема не рассматривается.

вероятностей (Pп), построенная по данным схемы ГРАН-84
за период с декабря 1983 г. по декабрь 1987 г.
1.5.11. В заключение подробно рассмотрим расчет статистических оценок вероятностных прогнозов на конкретном примере. В табл. 12 представлен пример (искусственный) оценки вероятностного прогноза для трехмерного предиктанта Y = (y1, y2, y3) трех равновероятных градаций при объеме выборки прогнозов n = 10. Прогностические вероятности обозначены P1, P2, P3; реально осуществившаяся фаза - Ф; апостериорные вероятности - d1, d2, d3, т.е. dф = 1, и di = 0 при  ; S обозначает накопленные вероятности, т.е. SP1 = P1, SP2 = P1 + P2, SP3 = P1 + P2 + P3 и аналогично для Sdi. При этом SP3 = Sd3 = 1.
; S обозначает накопленные вероятности, т.е. SP1 = P1, SP2 = P1 + P2, SP3 = P1 + P2 + P3 и аналогично для Sdi. При этом SP3 = Sd3 = 1.
Кроме того, в табл. 12 приведены значения [Pi - di], (Pi - di)2, (SPi - Sdi)2. Заметим здесь, что
(SP1 - Sd1)2 = (P1 - d1)2; (SP3 - Sd3)2 = (1 - 1)2 = 0;
(SP2 - Sd2)2 = [P1 + P2 - (d1 + d2)]2,
но P1 + P2 = 1 - P3, а

так что (SP2 - Sd2)2 = (P3 - d3)2.
Это замечание облегчает расчеты в случае наличия трех фаз.
Кроме того, для 10 заданных градаций (0 <= P < 0,1; 0,1 <= P < 0,2; ..., 0,9 <= P <= 1) приведены частоты попадания в них прогностических вероятностей (n1, n2, ..., n10), а также число случаев, когда соответствующая вероятность относилась к осуществившейся впоследствии фазе (n'1, n'2, ..., n'10).
Таблица 12
Номер прогноза | Прогноз | Факт | Накопленные вероятности | |P2 - d2| | |P3 - d3| | |||||||||||
P1 | P2 | P3 | Ф | d1 | d2 | d3 | SP2 | SP3 | Sd1 | Sd2 | ||||||
y1 | ||||||||||||||||
1 | 0,22 | 0,30 | 0,48 | 2 | 0 | 1 | 0 | 0,22 | 0,52 | 1,0 | 0 | 1 | 1 | 0,22 | 0,70 | 0,48 |
2 | 0,17 | 0,36 | 0,47 | 3 | 0 | 0 | 1 | 0,17 | 0,53 | 1,0 | 0 | 0 | 1 | 0,17 | 0,36 | 0,53 |
3 | 0,40 | 0,20 | 0,40 | 1 | 1 | 0 | 0 | 0,40 | 0,60 | 1,0 | 1 | 1 | 1 | 0,60 | 0,20 | 0,40 |
4 | 0,56 | 0,32 | 0,14 | 1 | 1 | 0 | 0 | 0,56 | 0,88 | 1,0 | 1 | 1 | 1 | 0,44 | 0,32 | 0,14 |
5 | 0,29 | 0,41 | 0,30 | 3 | 0 | 0 | 1 | 0,29 | 0,70 | 1,0 | 0 | 0 | 1 | 0,29 | 0,41 | 0,70 |
6 | 0,30 | 0,50 | 0,20 | 2 | 0 | 1 | 0 | 0,30 | 0,80 | 1,0 | 0 | 1 | 1 | 0,30 | 0,50 | 0,20 |
7 | 0,18 | 0,70 | 0,12 | 2 | 0 | 1 | 0 | 0,18 | 0,88 | 1,0 | 0 | 1 | 1 | 0,18 | 0,30 | 0,12 |
8 | 0,42 | 0,41 | 0,17 | 2 | 0 | 1 | 0 | 0,42 | 0,83 | 1,0 | 0 | 1 | 1 | 0,42 | 0,59 | 0,17 |
9 | 0,16 | 0,13 | 0,71 | 1 | 1 | 0 | 0 | 0,16 | 0,29 | 1,0 | 1 | 1 | 1 | 0,86 | 0,13 | 0,71 |
10 | 0,55 | 0,32 | 0,13 | 1 | 1 | 0 | 0 | 0,55 | 0,87 | 1,0 | 1 | 1 | 1 | 0,45 | 0,32 | 0,13 |
y2 | ||||||||||||||||
1 | 0,21 | 0,28 | 0,51 | 2 | 0 | 1 | 0 | 0,21 | 0,49 | 1,0 | 0 | 1 | 1 | 0,21 | 0,72 | 0,51 |
2 | 0,34 | 0,29 | 0,37 | 3 | 0 | 0 | 1 | 0,34 | 0,63 | 1,0 | 0 | 0 | 1 | 0,34 | 0,29 | 0,63 |
3 | 0,16 | 0,21 | 0,63 | 3 | 0 | 0 | 1 | 0,16 | 0,37 | 1,0 | 0 | 0 | 1 | 0,16 | 0,21 | 0,37 |
4 | 0,41 | 0,33 | 0,26 | 2 | 0 | 1 | 0 | 0,41 | 0,74 | 1,0 | 0 | 1 | 1 | 0,41 | 0,67 | 0,26 |
5 | 0,38 | 0,35 | 0,27 | 1 | 1 | 0 | 0 | 0,38 | 0,73 | 1,0 | 1 | 1 | 1 | 0,62 | 0,35 | 0,27 |
6 | 0,20 | 0,41 | 0,39 | 1 | 1 | 0 | 0 | 0,20 | 0,61 | 1,0 | 1 | 1 | 1 | 0,80 | 0,41 | 0,39 |
7 | 0,46 | 0,18 | 0,36 | 1 | 1 | 0 | 0 | 0,46 | 0,64 | 1,0 | 1 | 1 | 1 | 0,54 | 0,18 | 0,36 |
8 | 0,52 | 0,18 | 0,30 | 3 | 0 | 0 | 1 | 0,52 | 0,70 | 1,0 | 0 | 0 | 1 | 0,52 | 0,18 | 0,70 |
9 | 0,46 | 0,39 | 0,15 | 1 | 1 | 0 | 0 | 0,46 | 0,85 | 1,0 | 1 | 1 | 1 | 0,54 | 0,39 | 0,15 |
10 | 0,42 | 0,17 | 0,41 | 2 | 0 | 1 | 0 | 0,42 | 0,59 | 1,0 | 0 | 1 | 1 | 0,42 | 0,83 | 0,41 |
y3 | ||||||||||||||||
1 | 0,14 | 0,20 | 0,66 | 3 | 0 | 0 | 1 | 0,14 | 0,34 | 1,0 | 0 | 0 | 1 | 0,14 | 0,20 | 0,34 |
2 | 0,06 | 0,55 | 0,39 | 3 | 0 | 0 | 1 | 0,06 | 0,61 | 1,0 | 0 | 0 | 1 | 0,06 | 0,55 | 0,61 |
3 | 0,20 | 0,41 | 0,39 | 2 | 0 | 1 | 0 | 0,20 | 0,61 | 1,0 | 0 | 1 | 1 | 0,20 | 0,59 | 0,39 |
4 | 0,48 | 0,38 | 0,14 | 1 | 1 | 0 | 0 | 0,48 | 0,86 | 1,0 | 1 | 1 | 1 | 0,52 | 0,38 | 0,14 |
5 | 0,38 | 0,45 | 0,17 | 2 | 0 | 1 | 0 | 0,38 | 0,83 | 1,0 | 0 | 1 | 1 | 0,38 | 0,55 | 0,17 |
6 | 0,50 | 0,25 | 0,25 | 1 | 1 | 0 | 0 | 0,50 | 0,75 | 1,0 | 1 | 1 | 1 | 0,50 | 0,25 | 0,25 |
7 | 0,13 | 0,35 | 0,52 | 2 | 0 | 1 | 0 | 0,13 | 0,48 | 1,0 | 0 | 1 | 1 | 0,13 | 0,65 | 0,52 |
8 | 0,42 | 0,17 | 0,41 | 1 | 1 | 0 | 0 | 0,42 | 0,59 | 1,0 | 1 | 1 | 1 | 0,58 | 0,17 | 0,41 |
9 | 0,24 | 0,33 | 0,43 | 2 | 0 | 1 | 0 | 0,24 | 0,57 | 1,0 | 0 | 1 | 1 | 0,24 | 0,67 | 0,43 |
10 | 0,20 | 0,40 | 0,40 | 2 | 0 | 1 | 0 | 0,20 | 0,60 | 1,0 | 0 | 1 | 1 | 0,20 | 0,60 | 0,40 |
11,44 | 12,67 | 11,29 | ||||||||||||||
35,40 | ||||||||||||||||
APS = 0,41 | ||||||||||||||||
Номер прогноза | (P1 - d1)2 | (P2 - d2)2 | (P3 - d3)2 | (SP1 - Sd1)2 | (SP2 - Sd2)2 | Частота попадания в градации | ||||||||||
<= 0,2 | <= 0,3 | <= 0,5 | <= 0,6 | <= 0,7 | <= 0,8 | <= 0,9 | ||||||||||
y1 | ||||||||||||||||
1 | 0,048 | 0,490 | 0,230 | 0,048 | 0,230 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
2 | 0,029 | 0,130 | 0,281 | 0,029 | 0,281 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
3 | 0,360 | 0,040 | 0,160 | 0,360 | 0,160 | 0,0 | 1/0 | 2/1 | ||||||||
4 | 0,194 | 0,102 | 0,020 | 0,194 | 0,014 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
5 | 0,084 | 0,168 | 0,490 | 0,084 | 0,490 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
6 | 0,090 | 0,250 | 0,040 | 0,090 | 0,040 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
7 | 0,032 | 0,090 | 0,014 | 0,032 | 0,014 | 0,0 | 2/0 | 1/1 | ||||||||
8 | 0,176 | 0,348 | 0,029 | 0,176 | 0,029 | 0,0 | 1/0 | 2/1 | ||||||||
9 | 0,740 | 0,017 | 0,504 | 0,740 | 0,504 | 0,0 | 2/1 | 1/0 | ||||||||
10 | 0,203 | 0,102 | 0,017 | 0,203 | 0,017 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
y2 | ||||||||||||||||
1 | 0,044 | 0,518 | 0,260 | 0,044 | 0,260 | 0,0 | 2/1 | 1/0 | ||||||||
2 | 0,116 | 0,084 | 0,397 | 0,116 | 0,397 | 0,0 | 1/0 | 2/1 | ||||||||
3 | 0,026 | 0,044 | 0,137 | 0,026 | 0,137 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
4 | 0,168 | 0,449 | 0,068 | 0,168 | 0,068 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
5 | 0,384 | 0,122 | 0,073 | 0,384 | 0,073 | 0,0 | 1/0 | 2/1 | ||||||||
6 | 0,640 | 0,168 | 0,152 | 0,640 | 0,152 | 0,0 | 1/1 | 1/0 | 1/0 | |||||||
7 | 0,292 | 0,032 | 0,130 | 0,292 | 0,130 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
8 | 0,270 | 0,032 | 0,490 | 0,270 | 0,490 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
9 | 0,292 | 0,152 | 0,022 | 0,292 | 0,022 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
10 | 0,176 | 0,689 | 0,168 | 0,176 | 0,168 | 0,0 | 1/1 | 2/0 | ||||||||
y3 | ||||||||||||||||
1 | 0,020 | 0,040 | 0,116 | 0,020 | 0,116 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
2 | 0,004 | 0,302 | 0,372 | 0,004 | 0,372 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
3 | 0,040 | 0,348 | 0,152 | 0,040 | 0,152 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
4 | 0,270 | 0,144 | 0,020 | 0,270 | 0,020 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
5 | 0,144 | 0,302 | 0,029 | 0,144 | 0,029 | 0,0 | 1/0 | 1/0 | 1/1 | |||||||
6 | 0,250 | 0,062 | 0,062 | 0,250 | 0,062 | 0,0 | 2/0 | 1/1 | ||||||||
7 | 0,017 | 0,422 | 0,270 | 0,017 | 0,270 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
8 | 0,336 | 0,029 | 0,168 | 0,336 | 0,168 | 0,0 | 1/0 | 2/1 | ||||||||
9 | 0,057 | 0,449 | 0,185 | 0,057 | 0,185 | 0,0 | 1/0 | 1/1 | 1/0 | |||||||
10 | 0,040 | 0,360 | 0,160 | 0,040 | 0,160 | 0,0 | 1/0 | 2/1 | ||||||||
5,542 | 6,485 | 5,216 | 5,542 | 5,216 | 0,0 | 1/0 | 19/2 | 16/2 | 21/9 | 21/10 | 8/4 | 2/2 | 2/1 | |||
17,243 | 10,758 | |||||||||||||||
PS = 0,723 | PPS = 0,821 | 0,0 | 0,11 | 0,12 | 0,43 | 0,48 | 0,5 | 1,0 | 0,5 | |||||||
1.5.11.1. Рассмотрим, например, первый прогноз (y1)1 предиктанта y1, имеющий P1 = 0,22, P2 = 0,30, P3 = 0,48 и наблюдавшуюся вторую фазу предиктанта Ф = 2, вследствие чего апостериорные вероятности d1 = 0; d2 = 1; d3 = 0.
Тогда накопленные вероятности (графы 9 - 14 табл. 12) имеют вид:
SP1 = P1 = 0,22, SP2 = P1 + P2 = 0,52, SP3 = 1
и, как замечено выше,
Sd1 = d1 = 0, Sd2 = d1 + d2 = 1, Sd3 = 1.
1.5.11.2. В графах 15 - 23 табл. 12 приведены вычисленные абсолютные значения и квадраты разностей прогностических и фактических вероятностей:
|P1 - d1| = |0,22 - 0| = 0,22;
|P2 - d2| = |0,30 - 1| = |-0,70| = 0,70;
|P3 - d3| = |0,48 - 1| = 0,48;
(P1 - d1)2 = 0,222 = 0,048;
(P2 - d2)2 = 0,702 = 0,490;
(P3 - d3)2 = 0,482 = 0,230;
(SP1 - Sd1)2 = (0,22 - 0)2 = 0,048;
(SP2 - Sd2)2 = (0,52 - 1)2 = 0,482 = 0,230;
(SP3 - Sd3)2 = (1 - 1)2 = 0.
Квадраты разностей (SPi - Sdi)2 можно не вычислять в случае трех фаз предиктанта, так как (SP1 - Sd1)2 = (P1 - d1)2, (SP2 - Sd2)2 = (P3 - d3)2, ((SP3 - Sd3)2 = 0.
1.5.11.3. В графах 24 - 33 табл. 12 представлены частоты попадания в заданные градации. В данном случае у нас по одной прогностической вероятности попадает в градации 3, 4 и 5, так как 0,2 <= P1 < 0,3; 0,3 <= P2 < 0,4 и 0,4 <= P3 < 0,5, и поэтому мы заносим единицы в графы n3, n4 и n5. Реально осуществилась фаза второго предиктанта, для которой прогностическая вероятность P2 = 0,30, и она попадает в 4-ю градацию 0,3 <= P < 0,4, поэтому мы должны занести n'4 = 1 в графу 27 табл. 12.
1.5.11.4. Дополнительно рассмотрим заполнение граф ni, n'i на примере (y1)3, где P1 = P3 = 0,40, P2 = 0,20 и осуществившаяся фаза Ф = 1. Здесь первая и третья прогностические вероятности попадают в градацию 5 (0,4 <= P1 = P3 < 0,5), а вторая - в градацию 3 (0,2 <= P2 < 0,3), так что n5 = 2, а n3 = 1. Так как осуществилась фаза 1, то n'5 = 1. При расчете оценок качества 10 представленных прогнозов для y1, y2 и y3 как 30 независимых прогнозов по формулам (61) - (63) следует вычислить соответствующие суммы (графы 15 - 23 табл. 12)



для i = 1, 2, 3 (эти суммы приведены в табл. 12 в строке  , там же приведены суммарные значения ni, n'i для i = 1, 2, ... 10). Далее для определения оценок APS, PS и RPS следует сложить эти суммы для трех градаций (соответствующие три значения приведены в строке
, там же приведены суммарные значения ni, n'i для i = 1, 2, ... 10). Далее для определения оценок APS, PS и RPS следует сложить эти суммы для трех градаций (соответствующие три значения приведены в строке  ) и воспользоваться формулами (61) - (63) при общем числе прогнозов n = 30:
) и воспользоваться формулами (61) - (63) при общем числе прогнозов n = 30:



Для сравнения рассчитаем указанные оценки для климатологического прогноза в случае трех равновероятных градаций, когда P1 = P2 = P3 = 0,333, |Pi - di| = 0,333 для двух из значений i и 1 - 0,333 = 0,667 для третьего значения. Тогда


RPS = 0,777.
1.5.11.5. Вычисленные значения n'i,/ni и частоты предвычисленных вероятностей ni/n = ni/90 (в нашем случае) нанесены на графики (черт. 6 и 7).

Черт. 6. Диаграмма надежности, построенная по данным

построенная по данным табл. 12
1.5.12. Сравнение средних оценок успешности методических и климатологических вероятностных прогнозов позволяет сделать заключение о предпочтительности методических вероятностных прогнозов для практического использования. Мера мастерства, рассчитанная по формуле (64) с использованием количественных величин APS, PS и RPS для методических и климатологических прогнозов, составила


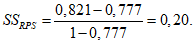
Эти данные свидетельствуют о небольшом преимуществе методических прогнозов над климатическими по всем рассмотренным оценкам качества вероятностных прогнозов.
долгосрочных прогнозов погоды
2.1.1. При испытании методов долгосрочных прогнозов погоды, как правило, решаются две задачи:
определение качества (успешности, оправдываемости) предсказания;
определение ценности (пользы) прогнозов.
В настоящем разделе будут рассматриваться методы, позволяющие реализовать первую задачу. Вторая задача, которая должна определяться методологией принятия решения, выходит за рамки данного раздела, так как она зависит от специфики использования метеорологических прогнозов конкретным потребителем.
2.1.2. Оперативные (производственные) испытания методов долгосрочных прогнозов погоды преследуют следующие основные цели:
определение качества и надежности предлагаемых методов;
сравнение их с методами, использующимися в оперативной работе (если такие методы существуют) и с тривиальными прогнозами (случайным, климатологическим, инерционным и др.);
выработка рекомендаций по внедрению методов прогнозов в производственную практику;
обеспечение потребителей информацией о качестве прогнозов.
2.1.3. Методы долгосрочных прогнозов погоды можно подразделить на три группы:
методы, предусматривающие прогноз двухфазного явления (бинарного признака);
методы, предусматривающие прогноз многофазного гидрометеорологического явления;
методы, предусматривающие прогноз метеорологических элементов по непрерывной шкале.
К первой группе относятся альтернативные прогнозы двухфазного явления (наличия или отсутствия засухи и т.д.).
Вторая группа включает методы прогноза номинальных (дискретных) предиктантов или фазовые прогнозы (больше нормы, норма, меньше нормы и т.д.).
Третью группу составляют прогнозы значений метеорологических элементов по непрерывной шкале (прогноз средней сезонной температуры и т.д.).
Отмеченные особенности методов долгосрочного прогноза обусловливают различия в методике проведения их оперативных испытаний и выборе оценок успешности. На практике определение успешности предполагает процесс сравнения, поскольку абсолютные оценки являются малоинформативными. Чаще приходится оперировать с относительными характеристиками качества, что дает возможность проведения сравнения оценок испытываемого метода с оценками имеющихся методов, а также стандартного метода прогноза (случайного, климатологического, инерционного или другого), имеющего наилучшую оправдываемость.
2.1.4. В программе испытаний автору метода на основе анализа качества прогнозов на зависимом и независимом материале необходимо четко определить время (конкретные месяцы, сезоны и т.д.) и территорию (европейская часть СССР, СССР и т.д.) действия прогноза, а также указать способы определения успешности прогнозов. В течение оперативных испытаний методов долгосрочных прогнозов погоды можно лишь подтвердить или не подтвердить данные авторских испытаний. Делать самостоятельные выводы на материале оперативных испытаний (выделять время года или территорию, на которой метод "работает", рекомендовать к внедрению отдельные компоненты вектора-предиктанта и т.д.) недопустимо ввиду непродолжительности (не более двух лет) периода проведения этих испытаний.
2.1.5. Аналогичные соображения относятся и к перечню показателей качества прогнозов. Если по данным оперативных испытаний некоторые показатели будут свидетельствовать о высокой успешности прогнозов, а другие - об их низкой оправдываемости, то принятие решения о внедрении метода будет затруднено, так как эта ситуация характерна для случайных совпадений. Следовательно, оценивать прогнозы в период оперативных испытаний целесообразно лишь теми показателями, которые по авторским данным доказывают их эффективность. При выборе показателей успешности следует руководствоваться следующими рекомендациями:
для преемственности оценок целесообразно рассчитывать традиционные показатели успешности;
при разработке новых показателей успешности необходимо стремиться к тому, чтобы эти показатели являлись статистиками с известными законами распределения вероятностей. В этом случае надежность метода определяется с помощью проверки статистических предположений;
в случае, когда возникает необходимость сравнить качество долгосрочных прогнозов погоды, рассчитанное с помощью разных процедур оценивания, необходимо использовать меры мастерства.
2.2.1. В общих положениях в качестве отдельной группы были выделены прогнозы явлений, состоящих из двух фаз (градаций, типов, классов, категорий и т.д.). В этом параграфе приведены способы оценки таких прогнозов.
2.2.2. Наиболее полную информацию о совпадении (несовпадении) прогностических и фактических классов явления можно получить, построив таблицу сопряженности (форма 18).
Прогноз | Наблюдалось | Сумма | |
Ф1 | Ф2 | ||
П1 | n11 | n12 | n10 |
П2 | n21 | n22 | n20 |
Сумма | n01 | n02 | n00 |
Примечание. Ф1 и Ф2 - фактическое осуществление первого и второго классов; П1 и П2 - прогнозы этих классов; nij - количество случаев, когда прогнозировался i-й класс, а осуществился j-й класс; n10 = n11 + n12 - общее число прогнозов первого класса; n20 = n21 + n22 - общее число прогнозов второго класса; n01 = n11 + n21 и n02 = n12 + n22 - общее число осуществлений первого и второго классов соответственно; n00 = n10 + n20 = n01 + n02 - общее число прогнозов.
2.2.3. Для определения эффективности разработанного метода прогноза нужно построить таблицу сопряженности для метода стандартного (случайного) прогноза (форма 19).
Элементы n'ij определяются следующим образом:
n'21 = n20n01/n00; n'22 = n20n02/n00. (66)
(случайного) прогноза
Прогноз | Наблюдалось | Сумма | |
Ф1 | Ф2 | ||
П1 | n'11 | n'12 | n10 |
П2 | n'21 | n'22 | n20 |
Сумма | n01 | n02 | n00 |
2.2.4. Проиллюстрируем построение таблиц сопряженности (формы 18 и 19) на примерах. Пусть по некоторой методике прогнозировалось два класса какого-либо явления. Всего составлено 100 прогнозов. Допустим, что первый класс прогнозировался 40 раз (в 30 случаях прогноз оказался успешным, в 10 случаях он не оправдался). Второй класс прогнозировался 60 раз (в 40 случаях прогноз оправдался, в 20 - не оправдался). На основании этих данных строим таблицу сопряженности (табл. 13).
Таблица 13
Прогноз | Наблюдалось | Сумма | |
Ф1 | Ф2 | ||
П1 | 30 | 10 | 40 |
П2 | 20 | 40 | 60 |
Сумма | 50 | 50 | 100 |
Таблица сопряженности (табл. 14) строится на основании данных, полученных с помощью формул (66).
Таблица 14
Прогноз | Наблюдалось | Сумма | |
Ф1 | Ф2 | ||
П1 | 20 | 20 | 40 |
П2 | 30 | 30 | 60 |
Сумма | 50 | 50 | 100 |
2.2.5. Наиболее часто употребляемым показателем качества, основанным на данных таблиц сопряженности, служит величина
характеризующая количество оправдавшихся прогнозов в серии из n00 испытаний.
В данном примере для методического и случайного прогнозов  и
и  соответственно. Таким образом, судя по этому показателю, методический прогноз является эффективным. Вместе с тем существует вероятность того, что достигнутое превышение оправдываемости методических прогнозов над стандартными является случайным. Проверка значимости (достоверности) достигнутого положительного эффекта должна присутствовать при подведении итогов испытаний. В данном случае следует проверить так называемую "нулевую гипотезу" о том, что успешности методического и случайного прогнозов находятся на одном уровне, т.е.
соответственно. Таким образом, судя по этому показателю, методический прогноз является эффективным. Вместе с тем существует вероятность того, что достигнутое превышение оправдываемости методических прогнозов над стандартными является случайным. Проверка значимости (достоверности) достигнутого положительного эффекта должна присутствовать при подведении итогов испытаний. В данном случае следует проверить так называемую "нулевую гипотезу" о том, что успешности методического и случайного прогнозов находятся на одном уровне, т.е.  . Для этой цели можно воспользоваться биномиальным распределением и оценить вероятность, которая покажет, что в серии из n00 = 100 испытаний количество успешных прогнозов (n' = n11 + n22) случайно вместо 50 оказалось равным 70. Используя биномиальное распределение
. Для этой цели можно воспользоваться биномиальным распределением и оценить вероятность, которая покажет, что в серии из n00 = 100 испытаний количество успешных прогнозов (n' = n11 + n22) случайно вместо 50 оказалось равным 70. Используя биномиальное распределение
 и
и  соответственно. Таким образом, судя по этому показателю, методический прогноз является эффективным. Вместе с тем существует вероятность того, что достигнутое превышение оправдываемости методических прогнозов над стандартными является случайным. Проверка значимости (достоверности) достигнутого положительного эффекта должна присутствовать при подведении итогов испытаний. В данном случае следует проверить так называемую "нулевую гипотезу" о том, что успешности методического и случайного прогнозов находятся на одном уровне, т.е.
соответственно. Таким образом, судя по этому показателю, методический прогноз является эффективным. Вместе с тем существует вероятность того, что достигнутое превышение оправдываемости методических прогнозов над стандартными является случайным. Проверка значимости (достоверности) достигнутого положительного эффекта должна присутствовать при подведении итогов испытаний. В данном случае следует проверить так называемую "нулевую гипотезу" о том, что успешности методического и случайного прогнозов находятся на одном уровне, т.е.  . Для этой цели можно воспользоваться биномиальным распределением и оценить вероятность, которая покажет, что в серии из n00 = 100 испытаний количество успешных прогнозов (n' = n11 + n22) случайно вместо 50 оказалось равным 70. Используя биномиальное распределение
. Для этой цели можно воспользоваться биномиальным распределением и оценить вероятность, которая покажет, что в серии из n00 = 100 испытаний количество успешных прогнозов (n' = n11 + n22) случайно вместо 50 оказалось равным 70. Используя биномиальное распределение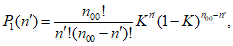 (68)
(68)где n00 = 100, n' = 70, K = 0,5, получим вероятность, которая показывает, что в данной серии зафиксированная успешность  оказалась случайной (эта вероятность называется уровнем значимости). Она составляет
оказалась случайной (эта вероятность называется уровнем значимости). Она составляет
 оказалась случайной (эта вероятность называется уровнем значимости). Она составляет
оказалась случайной (эта вероятность называется уровнем значимости). Она составляет
Следовательно, с вероятностью 0,9997 нулевая гипотеза отвергается и можно утверждать, что преимущество методического прогноза над стандартным действительно существует. Отметим, что в практике метеорологических исследований в области долгосрочных прогнозов погоды в качестве порогового значения принято использовать уровень значимости, равный 0,05.
2.2.6. Можно рекомендовать упрощенный способ проверки нулевой гипотезы. В случае, когда K близко к 0,5, биномиальное распределение приближается к нормальному уже при n00 = 25. Воспользуемся свойствами нормального распределения. Как известно, нормально распределенная случайная величина полностью описывается средним значением n' и средним квадратическим отклонением  , которое рассчитывается с помощью соотношения
, которое рассчитывается с помощью соотношения

Подставляя значения n00 и K для рассматриваемого примера в это соотношение, находим  . Таким образом, следует оценить вероятность события, при котором величина n1 на данном отрезке испытаний случайно изменила свое среднее значение с 50 на 70.
. Таким образом, следует оценить вероятность события, при котором величина n1 на данном отрезке испытаний случайно изменила свое среднее значение с 50 на 70.
Напомним некоторые свойства нормального распределения: вероятность значения, превышающего среднее значение величины более чем на  , составляет около 0,05, а на величину более
, составляет около 0,05, а на величину более  - около 0,001. В анализируемом случае
- около 0,001. В анализируемом случае 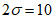 ,
,  . Следовательно, нулевая гипотеза отвергается с уровнем значимости меньше, чем 0,001.
. Следовательно, нулевая гипотеза отвергается с уровнем значимости меньше, чем 0,001.
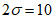 ,
,  . Следовательно, нулевая гипотеза отвергается с уровнем значимости меньше, чем 0,001.
. Следовательно, нулевая гипотеза отвергается с уровнем значимости меньше, чем 0,001.2.2.7. Предположим теперь, что проводились испытания двух конкурирующих методов прогнозов. Таблица сопряженности второго метода представлена табл. 15.
Таблица 15
Прогноз | Наблюдалось | Сумма | |
Ф1 | Ф2 | ||
П1 | 26 | 14 | 40 |
П2 | 24 | 36 | 60 |
Сумма | 50 | 50 | 100 |
В этом случае n11 + n22 = 62, а  . Поскольку
. Поскольку  , уже нельзя с уровнем значимости 0,05 утверждать о преимуществе первого метода (для которого n11 + n12 = 70) над вторым.
, уже нельзя с уровнем значимости 0,05 утверждать о преимуществе первого метода (для которого n11 + n12 = 70) над вторым.
 . Поскольку
. Поскольку  , уже нельзя с уровнем значимости 0,05 утверждать о преимуществе первого метода (для которого n11 + n12 = 70) над вторым.
, уже нельзя с уровнем значимости 0,05 утверждать о преимуществе первого метода (для которого n11 + n12 = 70) над вторым.В случае когда одно из прогнозируемых событий является редким (например, Ф1 - сильная засуха, Ф2 - отсутствие сильной засухи) для проверки нулевых гипотез нужно использовать законы не биномиального (или нормального) распределения, а распределения Пауссона.
2.2.8. Для углубленного анализа качества двухфазного прогноза рекомендуется использовать меры частичной точности относительно индивидуальных событий. К ним относятся две такие характеристики:
мера точности для фактически осуществившегося события;
мера точности относительно числа прогнозов события.
Для i-го события эти меры обозначаются  и
и  . Они называются оправдываемостью прогноза фазы и ее предупрежденностью и записываются следующим образом:
. Они называются оправдываемостью прогноза фазы и ее предупрежденностью и записываются следующим образом:
Оправдываемости прогнозов различных фаз и предупрежденности этих фаз, рассчитанные по данным табл. 13 - 15 с использованием формул (69), приведены в табл. 16.
Таблица 16
фаз и их предупрежденности
Таблица | ||||
13 | 0,70 | 0,60 | 0,67 | 0,80 |
14 | 0,50 | 0,40 | 0,50 | 0,60 |
15 | 0,65 | 0,52 | 0,60 | 0,72 |
Из данных табл. 16 видно, что и оправдываемость, и предупрежденность по первой методике (см. табл. 13) превосходят аналогичные показатели по другим методам.
2.2.9. Информация, содержащаяся в таблице сопряженности прогноза бинарного признака, часто объединяется в один индекс  , определенный в интервале от -1 до 1,
, определенный в интервале от -1 до 1,
Для табл. 13 - 15 этот индекс, часто называемый качественным коэффициентом корреляции, составляет соответственно 0,40, 0,0, 0,24.
Желательно, чтобы компоненты вектора-предиктанта (являющиеся бинарными признаками) были линейно независимы. Тогда таблицы сопряженности могут быть построены для каждого прогноза. По совокупности таких таблиц сопряженности можно рассчитать не только средние значения перечисленных показателей качества, но их изменчивости. Это дает возможность более полно применять методы математической статистики для проверки нулевых гипотез. В частности, по среднему значению  и среднему квадратическому отклонению
и среднему квадратическому отклонению  (учитывая, что при небольших значениях
(учитывая, что при небольших значениях 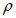 распределение этого индекса подчиняется гауссовскому закону), можно оценить значимость различий
распределение этого индекса подчиняется гауссовскому закону), можно оценить значимость различий  двух методических или методического и стандартного прогнозов. Например, табл. 17 дает возможность проверить гипотезу о несущественности отличия среднего значения
двух методических или методического и стандартного прогнозов. Например, табл. 17 дает возможность проверить гипотезу о несущественности отличия среднего значения 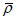 от 0 при 5%-м уровне значимости. В табл. 17 приведены значения
от 0 при 5%-м уровне значимости. В табл. 17 приведены значения  , ниже которых отвергается (с уровнем значимости 5%) гипотеза о несущественности отличия
, ниже которых отвергается (с уровнем значимости 5%) гипотеза о несущественности отличия 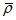 от 0 при данном количестве испытаний n00. Например, если в серии из n00 = 30 испытаний среднее значение
от 0 при данном количестве испытаний n00. Например, если в серии из n00 = 30 испытаний среднее значение  оказалось равным 0,10 и среднее квадратическое отклонение
оказалось равным 0,10 и среднее квадратическое отклонение 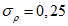 , то оценку
, то оценку  можно с 95%-й вероятностью считать значимой. Если бы при том же объеме выборки
можно с 95%-й вероятностью считать значимой. Если бы при том же объеме выборки  оказалось равным 0,30, то при 5%-м уровне значимости
оказалось равным 0,30, то при 5%-м уровне значимости 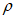 , равное 0,10, статистически не отличается от
, равное 0,10, статистически не отличается от  . Для промежуточных значений
. Для промежуточных значений 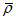 и n00 допустима интерполяция данных табл. 17.
и n00 допустима интерполяция данных табл. 17.
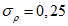 , то оценку
, то оценку Таблица 17
значимости индекса 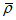 при заданном объеме выборки n00
при заданном объеме выборки n00
n00 | ||||
0,10 | 0,15 | 0,20 | 0,25 | |
30 | 0,28 | 0,42 | 0,56 | 0,71 |
40 | 0,33 | 0,50 | 0,67 | |
50 | 0,36 | 0,54 | 0,73 | |
100 | 0,52 | 0,78 | ||
2.2.10. Другой формой качественного коэффициента корреляции является выражение
 (71)
(71)Качество прогнозов, оцененное с помощью этого показателя по данным табл. 13 - 15, следующее: R1 = 0,38, R2 = 0, R3 = 0,28.
2.2.11. Универсальной характеристикой надежности метода прогноза является мера мастерства
где U и U0 - любые из перечисленных показателей успешности соответственно методических и стандартных прогнозов; Uи - успешность идеального прогноза. Например, при U = P1 (учитывая, что Uи = 1) меры мастерства, рассчитанные по данным табл. 13 - 15, составят:
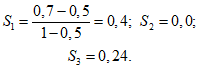
При  меры мастерства будут равны
меры мастерства будут равны
 меры мастерства будут равны
меры мастерства будут равны
Для идеальных прогнозов мера мастерства S = 1, при S = 0 качество методического прогноза находится на уровне стандартного и при S < 0 - ниже стандартного прогноза.
Использование меры мастерства в качестве характеристики качества дает возможность проводить сравнение успешности тех методов прогноза, в которых границы между двумя классами предиктанта (а следовательно, и содержание прогнозов) отличаются друг от друга.
Разумеется, допустимы и другие приемы и оценки для определения качества методов двухфазных прогнозов, основанные на анализе таблиц сопряженности. При этом нужно стремиться к построению таких оценок качества, распределения вероятностей которых аппроксимируются известными законами. В этом случае выводы о значимости показателей качества прогнозов будут статистически обоснованными.
2.2.12. При подведении итогов испытания обязательными показателями качества двухфазных прогнозов являются характеристики P1 и  двумерной таблицы сопряженности, вычисляемые по формулам (67), (70).
двумерной таблицы сопряженности, вычисляемые по формулам (67), (70).
В тех случаях, когда два прогнозируемых класса являются существенно неравновероятными, необходимо определять оправдываемость и предупрежденность прогнозов обоих классов ( ,
,  ,
,  ,
,  ), рассчитанных по формулам (69).
), рассчитанных по формулам (69).
2.2.13. Аналогичные оценки должны быть рассчитаны для определения качества оперативных и стандартных прогнозов. Сравнительный анализ этих оценок позволит сделать вывод об эффективности метода в период испытаний. При этом необходимо рассчитывать меру мастерства Sмет по формуле (72) с использованием перечисленных выше оценок испытываемого (оперативного) стандартного и идеального прогнозов.
2.3.1. Объектами многофазного прогноза являются, как правило, дискретные непересекающиеся классы значений метеорологического элемента. Примеры многофазных прогнозов: классы значений температуры и осадков (норма, больше нормы, меньше нормы), типы атмосферной засушливости (нормальная, слабая, средней интенсивности, сильная) и т.д.
2.3.2. Подходы к оцениванию прогнозов многофазных метеорологических элементов или явлений можно рассмотреть на примерах верификации трехфазных прогнозов.
Построим таблицу (матрицу) сопряженности для методического прогноза для n00 случаев по трем фазам (форма 20).
Для случайного прогноза построим также таблицу (матрицу) сопряженности (форма 21), элементы которой определяются по формуле
Прогноз | Наблюдалось | Сумма | ||
Ф1 | Ф2 | Ф3 | ||
П1 | n11 | n12 | n13 | n10 |
П2 | n21 | n22 | n23 | n20 |
П3 | n31 | n32 | n33 | n30 |
Сумма | n01 | n02 | n03 | n00 |
Прогноз | Наблюдалось | Сумма | ||
Ф1 | Ф2 | Ф3 | ||
П1 | n'11 | n'12 | n'13 | n10 |
П2 | n'21 | n'22 | n'23 | n20 |
П3 | n'31 | n'32 | n'33 | n30 |
Сумма | n01 | n02 | n03 | n00 |
Для того чтобы определить эффективность методических прогнозов, сформулируем нулевую гипотезу: таблицы сопряженности методического и стандартного (например, случайного) прогнозов статистически не отличаются друг от друга. Для проверки этого предположения формируется статистика критерия  следующим образом:
следующим образом:
Заметим, что  можно рассчитывать лишь в том случае, когда ни один из элементов матриц {n} и {n'} не меньше 5.
можно рассчитывать лишь в том случае, когда ни один из элементов матриц {n} и {n'} не меньше 5.
Теоретическое распределение  хорошо известно и затабулировано. Если две сравниваемые матрицы сильно отличаются одна от другой,
хорошо известно и затабулировано. Если две сравниваемые матрицы сильно отличаются одна от другой,  велико. Когда значения
велико. Когда значения  больше заранее определенных пределов, нулевую гипотезу отвергают и делают вывод, что успешность методических прогнозов заметно отличается от успешности случайного прогноза. Уровень
больше заранее определенных пределов, нулевую гипотезу отвергают и делают вывод, что успешность методических прогнозов заметно отличается от успешности случайного прогноза. Уровень 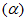 , при котором отклоняется нулевая гипотеза в исследованиях по долгосрочным прогнозам погоды, обычно считается равным 5%. Доверительные границы критерия
, при котором отклоняется нулевая гипотеза в исследованиях по долгосрочным прогнозам погоды, обычно считается равным 5%. Доверительные границы критерия  , при которых отвергается нулевая гипотеза, зависят от числа степеней свободы m, которое равно числу элементов матрицы минус число ограничений. Для данных форм 20 и 21 число ограничений равно 5. Значит число степеней свободы равно m = 9 - 5 = 4. Рассмотрим применение критерия
, при которых отвергается нулевая гипотеза, зависят от числа степеней свободы m, которое равно числу элементов матрицы минус число ограничений. Для данных форм 20 и 21 число ограничений равно 5. Значит число степеней свободы равно m = 9 - 5 = 4. Рассмотрим применение критерия  на примере.
на примере.
2.3.3. Для примера посмотрим таблицу сопряженности для методических прогнозов метеорологического элемента для 100 случаев по трем фазам (табл. 18) и таблицу сопряженности для случайных прогнозов, элементы которой определяются с помощью формулы (73) (табл. 19).
Таблица 18
Прогноз | Наблюдалось | Сумма | ||
Ф1 | Ф2 | Ф3 | ||
П1 | 15 | 15 | 10 | 40 |
П2 | 5 | 10 | 15 | 30 |
П3 | 10 | 5 | 15 | 30 |
Сумма | 30 | 30 | 40 | 100 |
Таблица 19
Прогноз | Наблюдалось | Сумма | ||
Ф1 | Ф2 | Ф3 | ||
П1 | 12 | 12 | 16 | 40 |
П2 | 9 | 9 | 12 | 30 |
П3 | 9 | 9 | 12 | 30 |
Сумма | 30 | 30 | 40 | 100 |
Рассчитаем
Теоретическое значение 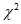 для m = 4 составляет 18,46 при
для m = 4 составляет 18,46 при  ; 13,28 при
; 13,28 при  и 9,49 при
и 9,49 при 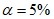 . Таким образом, судя по данным табл. 18 и 19, ни при 5%, ни тем более при 1 и 0,1%-х уровнях значимости нельзя отвергать гипотезу о примерно одинаковой успешности методических и случайных прогнозов.
. Таким образом, судя по данным табл. 18 и 19, ни при 5%, ни тем более при 1 и 0,1%-х уровнях значимости нельзя отвергать гипотезу о примерно одинаковой успешности методических и случайных прогнозов.
 ; 13,28 при
; 13,28 при  и 9,49 при
и 9,49 при 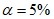 . Таким образом, судя по данным табл. 18 и 19, ни при 5%, ни тем более при 1 и 0,1%-х уровнях значимости нельзя отвергать гипотезу о примерно одинаковой успешности методических и случайных прогнозов.
. Таким образом, судя по данным табл. 18 и 19, ни при 5%, ни тем более при 1 и 0,1%-х уровнях значимости нельзя отвергать гипотезу о примерно одинаковой успешности методических и случайных прогнозов.Для оценки близости данных таблиц сопряженности методических и случайных прогнозов можно использовать нормированный показатель Чупрова - Пирсона
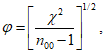 (75)
(75)где  принимает значения от 0 до 1. При
принимает значения от 0 до 1. При  методические прогнозы полностью совпадают со случайными, при
методические прогнозы полностью совпадают со случайными, при  методические прогнозы являются абсолютно точными. Поскольку показатель Чупрова - Пирсона всегда принимает неотрицательные значения даже в случаях заведомо плохих прогнозов, пользоваться им для суждения о качестве прогнозов не очень удобно. Для приведенного примера (табл. 18 и 19)
методические прогнозы являются абсолютно точными. Поскольку показатель Чупрова - Пирсона всегда принимает неотрицательные значения даже в случаях заведомо плохих прогнозов, пользоваться им для суждения о качестве прогнозов не очень удобно. Для приведенного примера (табл. 18 и 19)  .
.
 .
.2.3.4. При сравнительной оценке методов долгосрочного прогноза можно использовать понятие климатического прогноза. Пусть до проведения испытаний известны повторяемости каждой фазы явления. Прогноз наиболее вероятной фазы (если такая существует) ассоциируется с климатологическим прогнозом. Таблица сопряженности климатологического прогноза является матрицей, в которой лишь элементы одной строки (номер которой соответствует номеру наиболее вероятной фазы) являются не нулевыми.
Например, повторяемости трех фаз явления, рассчитанные по архивной выборке, равны f1 = 0,20, f2 = 0,50 и f3 = 0,30. Очевидно, что базирующийся на этой информации стандартный климатологический прогноз заключается в предсказании каждый раз только второй фазы явления. Для серии из 100 испытаний, проведенной на тех же фактических данных, что и в табл. 18, строится таблица сопряженности для климатологического прогноза (табл. 20).
2.3.5. В практике определения успешности долгосрочных прогнозов погоды большое распространение получила методика использования матриц цены прогнозов
 (76)
(76)Таблица 20
Прогноз | Наблюдалось | Сумма | ||
Ф1 | Ф2 | Ф3 | ||
П1 | 0 | 0 | 0 | 0 |
П2 | 30 | 30 | 40 | 100 |
П3 | 0 | 0 | 0 | 0 |
Сумма | 30 | 30 | 40 | 100 |
порядок которой определяется порядком матрицы сопряженности. Оценка качества производится по формуле
2.3.5.1. Матрица C должна строиться с учетом интересов конкретного потребителя. Если стоимость ошибки прогноза неизвестна, то можно рекомендовать матрицу C следующего вида:
Несимметричность этой матрицы обусловлена стремлением получить одинаковую сумму элементов каждой строки и тем самым не допустить, чтобы одна из прогнозируемых фаз была более "выгодна" для оценки, чем остальные.
2.3.5.2. Оценка прогнозов вычисляется с помощью формул (77) и (78). Для матрицы сопряженности методических прогнозов

Для матрицы случайных прогнозов получим Tсл = 0,49. Преимущество методических прогнозов над случайными составляет 6%. Оценка качества для климатологического прогноза, рассчитанная с использованием соотношений (77) и (78), Tкл = 0,48. При этом преимущество методических прогнозов над климатологическими составляет 7%.
2.3.6. При оценке многофазных прогнозов применимы многие критерии, приведенные в п. 2.2. В частности, как правило, указываются значения P1, вычисляемые по формуле (67), характеризующие долю точных прогнозов (отношение суммы диагональных элементов таблицы сопряженности к общему числу прогнозов). Для методических, случайных и климатологических прогнозов (см. табл. 18 - 20)  ,
,  ,
,  соответственно. Меры мастерства, рассчитанные по формуле (72) для различных показателей успешности, не превысили 0,15. Все эти данные не противоречат уже сделанному выводу о том, что качество методических прогнозов (см. табл. 18) мало отличается от качества стандартных прогнозов.
соответственно. Меры мастерства, рассчитанные по формуле (72) для различных показателей успешности, не превысили 0,15. Все эти данные не противоречат уже сделанному выводу о том, что качество методических прогнозов (см. табл. 18) мало отличается от качества стандартных прогнозов.
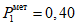 ,
,  ,
,  соответственно. Меры мастерства, рассчитанные по формуле (72) для различных показателей успешности, не превысили 0,15. Все эти данные не противоречат уже сделанному выводу о том, что качество методических прогнозов (см. табл. 18) мало отличается от качества стандартных прогнозов.
соответственно. Меры мастерства, рассчитанные по формуле (72) для различных показателей успешности, не превысили 0,15. Все эти данные не противоречат уже сделанному выводу о том, что качество методических прогнозов (см. табл. 18) мало отличается от качества стандартных прогнозов.2.3.7. В целом можно заключить, что для определения успешности метода многофазных прогнозов рассчитываются с использованием таблицы сопряженности как минимум три показателя:  , P1 и T соответственно по формулам (74), (67), (77). При этом матрица Cij для трехфазного предиктанта имеет вид
, P1 и T соответственно по формулам (74), (67), (77). При этом матрица Cij для трехфазного предиктанта имеет вид

для четырехфазного -

для пятифазного -

Аналогичные оценки рассчитываются по данным таблиц сопряженности официальных и стандартных прогнозов, что позволяет оценить меру мастерства S по формуле (72).
метеорологических элементов
2.4.1. Объектами долгосрочных прогнозов метеорологических элементов нередко являются непрерывные величины (средняя месячная температура, сезонная сумма осадков и т.д.). В этом случае возникает необходимость оценки интенсивности прогнозируемых значений.
2.4.2. Наиболее простой оценкой прогноза в i-й точке поля является систематическая ошибка
 (79)
(79)где Пi (Фi) - прогностическое (фактическое) значение метеорологического элемента; систематическая ошибка прогностического поля (вектора размерности n00) вычисляется с помощью соотношения
а абсолютная ошибка  -
-
 (81)
(81)Относительной ошибкой долгосрочного прогноза полей метеорологических элементов является оценка
 (82)
(82)где 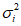 - дисперсия элемента в i-й точке. Следует отметить, что среднее значение
- дисперсия элемента в i-й точке. Следует отметить, что среднее значение 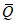 в серии из n испытаний является показательным, если n достаточно велико. Метод, для которого
в серии из n испытаний является показательным, если n достаточно велико. Метод, для которого  , имеет преимущество над климатологическими прогнозами.
, имеет преимущество над климатологическими прогнозами.
Иногда используется показатель K, характеризующий число точек (в процентах), для которых абсолютная ошибка прогноза метеорологического элемента меньше его среднего квадратического отклонения
Здесь  , если
, если  , и
, и  в противном случае. Если распределение вероятностей значений метеорологического элемента описывается нормальным законом, успешным можно считать метод, для которого K > 0,68.
в противном случае. Если распределение вероятностей значений метеорологического элемента описывается нормальным законом, успешным можно считать метод, для которого K > 0,68.
 , и
, и Одной из наиболее популярных, особенно за рубежом, оценок качества является квадратическая погрешность прогноза
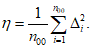 (84)
(84)Представляет интерес тот факт, что 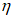 может быть разделено на две составляющие, которые описывают некоторые свойства прогнозов:
может быть разделено на две составляющие, которые описывают некоторые свойства прогнозов:
Первое слагаемое в правой части выражения (85) представляет собой квадрат средней ошибки, второе слагаемое характеризует изменчивость прогностических ошибок.
Важной характеристикой линейной зависимости между прогностическими и фактическими значениями метеорологических элементов является коэффициент корреляции
 (86)
(86)На значение коэффициента корреляции оказывают влияние климатические особенности пространственного распределения элемента. Поэтому рекомендуется рассчитывать r между прогностическими и фактическими аномалиями, т.е. 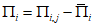 ,
,  . В данном случае индекс i соответствует номеру точки (пункта), j - моменту времени.
. В данном случае индекс i соответствует номеру точки (пункта), j - моменту времени.
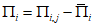 ,
,  . В данном случае индекс i соответствует номеру точки (пункта), j - моменту времени.
. В данном случае индекс i соответствует номеру точки (пункта), j - моменту времени.В то время как выборочные значения коэффициента корреляции не подчиняются известным законам распределения, нормально распределенной является величина
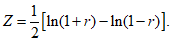 (87)
(87)Среднее квадратическое отклонение  величины Z практически не зависит от истинной корреляции и описывается соотношением
величины Z практически не зависит от истинной корреляции и описывается соотношением
 (88)
(88)Таким образом, для оценки значимости величины Z можно воспользоваться таблицами нормального распределения.
2.4.3. Если рассматривать прогностические и фактические абсолютные значения метеорологических элементов как n00-мерные векторы, то степень близости между двумя такими векторами можно характеризовать косинусом угла между ними
 (89)
(89)или
 (90)
(90)При этом  , являющийся мерой параллельности векторов
, являющийся мерой параллельности векторов  и
и  , изменяется от 0 до 1. Эффективным можно считать прогноз,
, изменяется от 0 до 1. Эффективным можно считать прогноз,  которого (при невозможности определения методически обоснованного порогового значения), по крайней мере, не меньше
которого (при невозможности определения методически обоснованного порогового значения), по крайней мере, не меньше  .
.
 .
.В отчетах об испытаниях следует приводить не только средние, но и экстремальные оценки качества прогнозов за период испытаний.
Для определения мер мастерства методов прогнозов непрерывных величин также может быть использована формула (72). Рассчитаем меру мастерства S на конкретном примере. Пусть среднее значение абсолютной ошибки методических долгосрочных прогнозов температуры  за период испытаний составило 3 °C, в то время как абсолютная ошибка климатологических прогнозов
за период испытаний составило 3 °C, в то время как абсолютная ошибка климатологических прогнозов  равна 2 °C. Очевидно, что для идеального прогноза
равна 2 °C. Очевидно, что для идеального прогноза  . Мера мастерства в этом случае
. Мера мастерства в этом случае 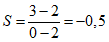 , что свидетельствует о непригодности метода для практического использования. Если на том же материале для другого метода
, что свидетельствует о непригодности метода для практического использования. Если на том же материале для другого метода 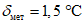 , то мера мастерства такого метода станет равной S = 0,25. Эта величина свидетельствует о преимуществе методического прогноза над климатологическим.
, то мера мастерства такого метода станет равной S = 0,25. Эта величина свидетельствует о преимуществе методического прогноза над климатологическим.
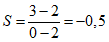 , что свидетельствует о непригодности метода для практического использования. Если на том же материале для другого метода
, что свидетельствует о непригодности метода для практического использования. Если на том же материале для другого метода 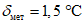 , то мера мастерства такого метода станет равной S = 0,25. Эта величина свидетельствует о преимуществе методического прогноза над климатологическим.
, то мера мастерства такого метода станет равной S = 0,25. Эта величина свидетельствует о преимуществе методического прогноза над климатологическим.2.4.4. Наиболее часто непрерывные значения метеорологических элементов прогнозируются в заданных точках поля. Для верификации такого рода прогнозов в период испытания необходимо рассчитывать следующие оценки:  ,
, 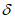 , Q и K соответственно по формулам (80) - (83). Аналогичные оценки необходимо рассчитать для оперативного и наилучшего из стандартных прогнозов. После этого эффективность методических прогнозов определяется с использованием меры мастерства S, рассчитанной по формуле (72).
, Q и K соответственно по формулам (80) - (83). Аналогичные оценки необходимо рассчитать для оперативного и наилучшего из стандартных прогнозов. После этого эффективность методических прогнозов определяется с использованием меры мастерства S, рассчитанной по формуле (72).
2.4.5. В предыдущих параграфах рассмотрен набор показателей качества, которые можно использовать для целей верификации долгосрочных прогнозов погоды. Этот набор можно существенно расширить, так как в принципе какой-либо перечень оценок качества нельзя считать исчерпывающим. Кроме того, можно утверждать, что не существует и какого-либо одного показателя, наилучшим образом характеризующего качество прогностических схем.
Вместе с тем следует учесть, что в большинстве случаев на испытания передаются методы прогнозов, в которых предиктанты представлены в одном и том же виде. В этом случае естественно стремление к регламентации и оценок качества прогнозов.
Агрометеорологические прогнозы являются одним из главных видов обслуживания организаций народного хозяйства.
Существующие методы агрометеорологических прогнозов условно можно разделить на несколько основных групп.
3.1.1. Прогнозы агрометеорологических условий:
прогноз теплообеспеченности вегетационного периода;
прогноз сроков оттаивания и промерзания почвы;
прогноз запасов продуктивной влаги и др.
3.1.2. Фенологические прогнозы:
прогнозы сроков наступления основных фаз развития растений;
прогнозы оптимальных сроков начала весенних полевых работ и др.
3.1.3. Прогнозы урожайности основных сельскохозяйственных культур и качества урожая.
3.1.4. Прогнозы состояния озимых культур в зимний период.
3.1.5. Прогнозы оптимальных режимов орошения, полегания зерновых культур, произрастания пастбищной растительности и др.
3.1.6. Прогнозы сроков появления и распространения болезней и вредителей растений.
Существующие методы агрометеорологических прогнозов предусматривают заблаговременности от одной декады до нескольких месяцев.
агрометеорологических прогнозов
3.2.1. Проведение авторских и производственных испытаний новых и усовершенствованных методов агрометеорологических прогнозов позволяет определить качество проверяемых методов и решить вопрос о целесообразности их внедрения в оперативную практику. Оценка этих методов производится путем сравнения расчетных данных с фактически наблюдаемым значением прогнозируемого элемента. При этом оценивается степень точности расчетов значений прогнозируемых элементов и уточняется территория, в пределах которой можно применять их для оперативного агрометеорологического обслуживания народного хозяйства. Заключение о качестве метода делается на материалах независимой выборки с помощью двух критериев: оправдываемости метода  и его ошибки
и его ошибки 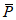 .
.
3.2.2. Оправдываемость метода 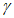 представляет собой выраженное в процентах отношение числа оправдавшихся прогнозов к числу всех прогнозов, составленных по данному методу
представляет собой выраженное в процентах отношение числа оправдавшихся прогнозов к числу всех прогнозов, составленных по данному методу

где n+ - число оправдавшихся прогнозов; N - общее число прогнозов.
Прогноз считается оправдавшимся, если его ошибка не превышает допустимую погрешность, рассчитанную на основании среднего квадратического отклонения прогнозируемого элемента  с учетом заблаговременности составления прогноза.
с учетом заблаговременности составления прогноза.
Если прогноз составляется с заблаговременностью два месяца и меньше, в качестве допустимой погрешности элемента принимается величина, равная  ; при заблаговременности прогноза более двух месяцев, но менее четырех месяцев -
; при заблаговременности прогноза более двух месяцев, но менее четырех месяцев - 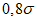 ; при заблаговременности прогнозов свыше четырех месяцев -
; при заблаговременности прогнозов свыше четырех месяцев -  .
.
3.2.3. Среднее квадратическое отклонение 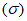 прогнозируемого элемента рассчитывается по формуле
прогнозируемого элемента рассчитывается по формуле
 (91)
(91)где 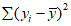 - сумма квадратов разностей значений элемента за каждый отдельный год (yi) и среднего многолетнего их значения
- сумма квадратов разностей значений элемента за каждый отдельный год (yi) и среднего многолетнего их значения 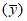 ; n - число случаев данного вариационного ряда.
; n - число случаев данного вариационного ряда.
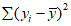 - сумма квадратов разностей значений элемента за каждый отдельный год (yi) и среднего многолетнего их значения
- сумма квадратов разностей значений элемента за каждый отдельный год (yi) и среднего многолетнего их значения 3.2.4. Для тех методов прогноза урожайности, валового сбора урожая и методов прогноза других элементов, в динамике временных рядов которых прослеживается тенденция увеличения или уменьшения его значений (тренд), среднее квадратическое отклонение 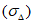 прогнозируемого элемента рассчитывается по формуле:
прогнозируемого элемента рассчитывается по формуле:
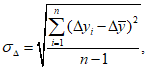 (92)
(92)где  - - разность между предыдущим и последующим значениями агрометеорологических элементов во временном ряду;
- - разность между предыдущим и последующим значениями агрометеорологических элементов во временном ряду; 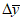 - среднее значение указанной разности.
- среднее значение указанной разности.
3.2.5. Ошибка метода  представляет собой выраженную в процентах среднюю относительную ошибку оправдавшихся прогнозов
представляет собой выраженную в процентах среднюю относительную ошибку оправдавшихся прогнозов

где Pi - относительная ошибка в процентах оправдавшегося прогноза, имеющая вид

где yф - фактическое значение элемента; yп - прогнозируемое значение;  - среднее арифметическое его значение за последние пять лет.
- среднее арифметическое его значение за последние пять лет.
3.2.6. Производственные испытания методов агрометеорологических прогнозов проводятся не менее двух лет. Выводы о приемлемости метода для оперативной работы делаются на основании испытаний в течение 5 - 7 лет, из них авторские испытания в течение 3 - 5 лет и производственные испытания в течение двух лет.
Заключение о целесообразности использования метода в целях оперативного агрометеорологического обслуживания делается на основании сравнения результатов оценки прогнозов, составленных по новому методу, с оправдываемостью прогнозов по имеющимся методам такого же агрометеорологического прогноза аналогичной заблаговременности, в случае отсутствия аналогичных методов - с оправдываемостью инерционного, климатологического прогнозов. Проверка методов производится на одном и том же фактическом материале.
3.2.7. Оправдываемость метода  должна быть выше оправдываемости инерционного и климатологического прогнозов при одной и той же допустимой ошибке, или ошибка метода P должна быть меньше при одной и той же оправдываемости.
должна быть выше оправдываемости инерционного и климатологического прогнозов при одной и той же допустимой ошибке, или ошибка метода P должна быть меньше при одной и той же оправдываемости.
3.2.8. Под инерционным прогнозом подразумевается прогноз, составленный на основании предположения, что прогнозируемое значение элемента будет таким же, как и в прошлом году.
3.2.9. Под климатологическим подразумевается метод прогноза, при котором в качестве прогнозируемого значения принимается среднее многолетнее значение элемента или расчет его по тренду (при наличии последнего). Среднее многолетнее значение рассчитывается по материалам 25 - 30-летнего периода наблюдений за элементом. В качестве прогнозируемого значения элемента по тренду на год прогноза принимается среднее арифметическое из фактических наблюдений за последние пять лет.
3.2.10. Окончательное решение об оперативном использовании нового метода принимается после сопоставления результатов испытаний с существующими методами прогноза аналогичной заблаговременности на одном и том же фактическом материале с учетом достоинств и недостатков сравниваемых методов (новый вид информации, расширение обслуживаемой территории и др.).
3.2.11. Результаты испытания методов прогноза представляются на рассмотрение Технических (Ученых) Советов территориальных и региональных управлений по гидрометеорологии (научно-исследовательских учреждений), а также Центральной методической комиссией (ЦМКП) Госгидромета СССР по форме 22.
Результаты испытаний методов
агрометеорологических прогнозов за период
Территория | Количество составленных прогнозов N (A) | Заблаговременность составления прогноза, месяц | Число оправдавшихся прогнозов n+ (A') | Оправдываемость метода | Оправдываемость инерционных прогнозов | Оправдываемость климатологических прогнозов | Ошибка метода |
агрометеорологических прогнозов по территории
Оценка успешности агрометеорологических прогнозов может производиться как по отдельным пунктам, областям, краям, республикам, так и в целом по территории, для которой рассчитывается уравнение. Метод может быть рекомендован к внедрению в оперативную работу, если не менее чем в 70% пунктов исследуемой территории показатели успешности  и Pтер метода лучше аналогичных показателей инерционного, климатологического и существующего метода прогноза аналогичной заблаговременности.
и Pтер метода лучше аналогичных показателей инерционного, климатологического и существующего метода прогноза аналогичной заблаговременности.
Оправдываемость по территории  представляет собой среднюю оправдываемость метода по всем пунктам
представляет собой среднюю оправдываемость метода по всем пунктам
где A - число пунктов, по которым составлялись прогнозы; 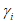 - оправдываемость метода в конкретном пункте.
- оправдываемость метода в конкретном пункте.
Ошибка метода по территории (Pтер) представляет собой среднюю ошибку оправдавшихся прогнозов по всем пунктам, для которых составляется прогноз
где  - средняя относительная ошибка оправдавшихся прогнозов в конкретном пункте; A' - число пунктов, в которых прогноз оправдался.
- средняя относительная ошибка оправдавшихся прогнозов в конкретном пункте; A' - число пунктов, в которых прогноз оправдался.
и валового сбора зерна сельскохозяйственных культур
3.3.1.1. Для расчета критериев успешности методов прогноза урожайности и валового сбора урожая сельскохозяйственных культур используют данные о средней урожайности и валовом сборе урожая, полученные из Госкомстата СССР.
3.3.1.2. Критерием оправдываемости прогнозов в зависимости от заблаговременности их составления ( ,
, 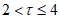 ,
,  месяцев) является допустимая погрешность (
месяцев) является допустимая погрешность ( ,
,  ) с поправочным коэффициентом на заблаговременность (0,67, 0,8, 1,0 соответственно).
) с поправочным коэффициентом на заблаговременность (0,67, 0,8, 1,0 соответственно).
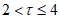 ,
, Среднее квадратическое отклонение (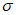 ,
,  ) рассчитывается по материалам наблюдений за последние 15 лет (включая и год прогноза).
) рассчитывается по материалам наблюдений за последние 15 лет (включая и год прогноза).
При определении допустимой погрешности методов прогноза урожайности и валового сбора тех культур, в динамике временных рядов которых есть тренд, расчет среднего квадратического отклонения  необходимо производить не реже одного раза в три года. Для других культур можно использовать величину
необходимо производить не реже одного раза в три года. Для других культур можно использовать величину 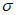 , рассчитанную перед началом авторских испытаний.
, рассчитанную перед началом авторских испытаний.
3.3.1.3. Заключение о целесообразности использования метода в целях оперативного агрометеорологического обслуживания делается на основании сравнения результатов проверки прогнозов, составленных по новому методу, с оценками успешности инерционного, климатологического и существующих методов прогноза аналогичной заблаговременности.
Оценки успешности испытываемого метода должны быть лучше аналогичных показателей сравниваемых методов.
3.3.1.4. Рассмотрим пример оценки метода прогноза урожайности основных зерновых и зернобобовых культур в Башкирской АССР. Исходные данные приведены в табл. 21. Прогноз составлен 20 июля. Заблаговременность прогноза один месяц.
Среднее квадратическое отклонение урожайности 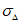 , рассчитанное по материалам наблюдений за последние 15 лет, составляет 4,9 ц/га. Допустимая погрешность
, рассчитанное по материалам наблюдений за последние 15 лет, составляет 4,9 ц/га. Допустимая погрешность  ;
; 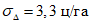 .
.
 ;
; 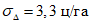 .
.Как следует из данных табл. 21, при такой допустимой погрешности из 11 составленных прогнозов оправдалось 9. Оправдываемость метода

Оправдываемость инерционного прогноза

Таблица 21
зерновых и зернобобовых культур в Башкирской АССР
Год | Фактический урожай (yф), ц/га | Методический прогноз | Инерционный прогноз | Климатологический прогноз | ||||||
прогнозируемый урожай (yп), ц/га | абсолютная ошибка | относительная ошибка (Pi), % | прогнозируемый урожай (y"п), ц/га | абсолютная ошибка | относительная ошибка (P'i), % | прогнозируемый урожай (y"п), ц/га | абсолютная ошибка | относительная ошибка (P"i), % | ||
1978 | 20,3 | 17,2 | 3,1+ | 20 | 15,2 | 5,1- | 33 | 14,1 | 6,2- | 44 |
1979 | 16,0 | 15,6 | 0,4+ | 3 | 20,3 | -4,3- | 28 | 15,2 | 0,8+ | 5 |
1980 | 17,4 | 15,3 | 2,1+ | 12 | 16,0 | 1,4+ | 8 | 15,2 | 2,2+ | 14 |
1981 | 10,5 | 8,4 | 2,1+ | 13 | 17,4 | 6,9- | 43 | 17,3 | -6,8- | 39 |
1982 | 14,0 | 11,7 | 2,3+ | 15 | 10,5 | 3,5- | 22 | 15,9 | -1,9+ | 11 |
1983 | 18,6 | 20,0 | -1,4+ | 9 | 14,0 | 4,6- | 30 | 15,6 | 3,0+ | 19 |
1984 | 14,5 | 14,0 | 0,5+ | 3 | 18,6 | -4,1- | 27 | 15,3 | -0,8+ | 5 |
1985 | 19,8 | 15,8 | 4,0- | 26 | 14,5 | 5,3- | 34 | 15,0 | 4,8- | 32 |
1986 | 22,9 | 17,4 | 5,5- | 31 | 19,8 | 3,1+ | 17 | 15,5 | 7,4- | 48 |
1987 | 8,5 | 10,7 | -2,2+ | 13 | 22,9 | -14,4- | 85 | 18,0 | -9,5- | 53 |
1988 | 12,4 | 12,4 | 0+ | 0 | 8,5 | 3,9- | 25 | 16,9 | -4,5- | 27 |
Примечание. 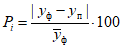 .
.
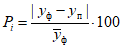 .
.Придерживаясь гипотезы о нормальном распределении случайных ошибок, можно принять, что оправдываемость климатологического прогноза  при допустимой погрешности
при допустимой погрешности 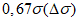 составит примерно 50% (в других случаях при допустимой погрешности
составит примерно 50% (в других случаях при допустимой погрешности  и
и  она составит 58 и 68% соответственно).
она составит 58 и 68% соответственно).
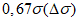 составит примерно 50% (в других случаях при допустимой погрешности
составит примерно 50% (в других случаях при допустимой погрешности  и
и Ошибка метода

ошибка инерционного прогноза
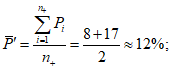
ошибка климатологического прогноза

В данном случае оправдываемость метода существенно выше оправдываемости инерционного и климатологического прогнозов. Предлагаемый метод имеет явные преимущества и может быть рекомендован к использованию в оперативной работе. В том случае, когда оправдываемость сравниваемых прогнозов будет одинакова, предпочтение отдается методу с меньшей ошибкой  .
.
перезимовки озимых зерновых культур
3.3.2.1. При оценке методов прогноза условий перезимовки озимых зерновых культур проводят сравнение ожидаемых размеров площадей с погибшими и поврежденными посевами с фактическими размерами площади пересева по данным Госкомстата СССР, выраженными в процентах общей посевной площади культуры.
3.3.2.2. Допустимой погрешностью прогноза является величина, равная  площади с погибшими посевами в процентах общей посевной площади озимых, рассчитанная за период наблюдений не менее 15 лет.
площади с погибшими посевами в процентах общей посевной площади озимых, рассчитанная за период наблюдений не менее 15 лет.
Допустимая погрешность является критерием, с помощью которого оценивается успешность прогнозов, составленных по испытываемому методу, а также успешности инерционного и климатологического прогнозов.
3.3.2.3. Заключение о возможности практического использования нового метода прогноза перезимовки озимых зерновых культур в оперативной работе делается на основе сравнения показателей успешности всех вышеназванных методов прогноза и имеющегося в оперативной практике, полученных на материалах проверки.
Если показатели успешности нового метода ( , P) позволяют отдать ему предпочтение, то в этом случае новый метод целесообразно использовать для целей оперативного обслуживания народного хозяйства.
, P) позволяют отдать ему предпочтение, то в этом случае новый метод целесообразно использовать для целей оперативного обслуживания народного хозяйства.
3.3.3.1. Основой методов прогноза запасов продуктивной влаги являются закономерности изменения запасов влаги в зависимости от метеорологических условий вегетационного периода, свойств почв и фаз развития растений.
3.3.3.2. Оценка указанных методов производится путем сравнения рассчитанных запасов влаги в почве с фактическими. Допустимая ошибка устанавливается по материалам наблюдений за запасами влаги в почве под сельскохозяйственными культурами за период не менее 15 лет. В зависимости от заблаговременности прогноза она составляет 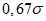 ,
, 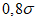 ,
, 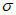 .
.
Метод, оправдываемость которого  на независимом материале выше оправдываемости прогнозов по методу, используемому в оперативной практике, а также выше оправдываемости инерционного и климатологического прогнозов (либо имеющий меньшую ошибку при одинаковой оправдываемости), может быть рекомендован к внедрению в оперативную практику.
на независимом материале выше оправдываемости прогнозов по методу, используемому в оперативной практике, а также выше оправдываемости инерционного и климатологического прогнозов (либо имеющий меньшую ошибку при одинаковой оправдываемости), может быть рекомендован к внедрению в оперативную практику.
3.3.3.3. При необходимости оценить качество рассматриваемых методов прогноза по территории показатели успешности (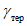 , Pтер) определяются по методике, изложенной в п. 3.2, с использованием формул (93), (94).
, Pтер) определяются по методике, изложенной в п. 3.2, с использованием формул (93), (94).
3.3.4.1. При оценке успешности методов прогноза качества урожая сельскохозяйственных культур проводят сравнение рассчитанного содержания белков, углеводов, крахмала, сахара и других характеристик качества зерна с фактическим содержанием их по данным информационных сообщений Государственной хлебной инспекции и ВНИИ зерна и продуктов его переработки.
3.3.4.2. Допустимая погрешность при оценке прогноза принимается равной 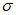 ,
, 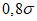 ,
, 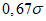 в зависимости от заблаговременности его составления. Этот же критерий используется и при оценке успешности используемого в оперативной работе метода прогноза, а также инерционного и климатологического прогнозов качества урожая на материалах одной и той же выборки.
в зависимости от заблаговременности его составления. Этот же критерий используется и при оценке успешности используемого в оперативной работе метода прогноза, а также инерционного и климатологического прогнозов качества урожая на материалах одной и той же выборки.
3.3.4.3. Заключение о возможности практического использования нового метода в оперативной работе делается на основе сравнения показателей успешности вышеназванных методов прогноза, полученных на материалах проверки.
3.3.5.1. В основу методов рассматриваемых видов прогнозов положены физические и биологические закономерности в формировании агрометеорологического режима орошаемых полей и реакция орошаемых культур на метеорологические условия. Они построены на использовании многофакторных связей, отражающих эти закономерности.
3.3.5.2. Испытания методов проводят на материалах 5 - 7 лет (из которых два года приходятся на производственные испытания метода). Допустимая погрешность метода устанавливается на материале наблюдений за изменчивостью оросительных норм по годам на сети агро- и гидрометеорологических станций за 10 - 15 последних лет. В новых районах орошения европейской части СССР за допустимую погрешность прогноза и расчета оптимальных оросительных норм под яровую пшеницу принимается +/- 400 м3/га, под кукурузу +/- 600 м3/га и для влагозарядковых поливов под озимую пшеницу +/- 300 м3/га.
Допустимая погрешность для сроков полива посевов составляет +/- 3 дня на легких почвах и +/- 5 дней на тяжелых.
Заключение о возможности практического использования нового метода в оперативной работе делается на основе сравнения показателей успешности всех сравниваемых методов прогноза, полученных на материалах проверки.
3.3.6.1. При испытании методов фенологических прогнозов используются наблюдения за датами наступления фаз развития сельскохозяйственных культур в те годы, которые не вошли в статистический материал по разработке метода.
3.3.6.2. За допустимую ошибку принимается величина 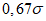 (среднее квадратическое отклонение от средней многолетней даты наступления данной фазы в днях).
(среднее квадратическое отклонение от средней многолетней даты наступления данной фазы в днях).
Если при производственных испытаниях оправдываемость прогнозов  , составленных по новому методу, выше оправдываемости климатологического, используемого в оперативной работе, и инерционного прогнозов (либо его ошибка P меньше при одной и той же оправдываемости), то метод может быть рекомендован к внедрению в оперативную работу.
, составленных по новому методу, выше оправдываемости климатологического, используемого в оперативной работе, и инерционного прогнозов (либо его ошибка P меньше при одной и той же оправдываемости), то метод может быть рекомендован к внедрению в оперативную работу.
3.3.6.3. По этой же методике оцениваются агрометеорологические прогнозы сроков оттаивания и промерзания почвы, сроков появления и распространения болезней и вредителей, а также другие методы прогноза дат наступления тех или иных агрометеорологических явлений.
4.1.1. Оценка качества всех видов гидрологических прогнозов, на основе которой решается вопрос о целесообразности применения данной методики в оперативной практике, регламентируется Наставлением [10]. Согласно Наставлению, методика прогноза считается эффективной, а ее практическое применение оправданным только в том случае, если погрешность прогнозов, составленных по данной методике, существенно меньше равновероятных отклонений от нормы или другого заданного значения предсказываемой переменой, на которую со статистической точки зрения выгоднее всего ориентироваться при отсутствии методики прогноза.
Для краткосрочных прогнозов в качестве такой величины принимается фактическое значение предсказываемой переменной (например, речного стока) на момент прогноза плюс среднее ее изменение за период заблаговременности. Эффективной считается методика, для которой отношение  , где S - средняя квадратическая погрешность проверочных прогнозов;
, где S - средняя квадратическая погрешность проверочных прогнозов;  - среднее квадратическое изменение предсказываемой переменной за период заблаговременности прогноза.
- среднее квадратическое изменение предсказываемой переменной за период заблаговременности прогноза.
 , где S - средняя квадратическая погрешность проверочных прогнозов;
, где S - средняя квадратическая погрешность проверочных прогнозов; 4.1.2. Согласно Наставлению [10], оценка качества методики прогноза является обязательной процедурой при ее разработке. Поэтому, если речь идет о локальных методах прогнозов, основанных на традиционных физически обоснованных подходах, решение о целесообразности использования их в оперативной практике может приниматься на основе анализа оценок, полученных в процессе авторских испытаний на архивном материале. Однако при этом оценки прогнозов должны быть получены в условиях, приближенных к оперативным: если в качестве исходной информации используются неизвестные к моменту выпуска прогноза величины, то должны быть приведены оценки, полученные при определении этих величин теми же способами, которые предполагается использовать при выпуске прогноза. При проведении авторских испытаний таких методик кроме оценки точности на материале, который использовался для построения прогностических зависимостей, необходимо получить также оценку точности на независимом материале (не использованном при разработке прогностических зависимостей). Объем независимой выборки должен составлять не менее 20% объема выборки, использовавшейся при построении прогностических зависимостей.
4.2.1. Как следует из вышесказанного, оперативные испытания целесообразно проводить перед внедрением новых методов краткосрочных и долгосрочных территориальных прогнозов, выпуск которых осуществляется с помощью ЭВМ и базируется на использовании банков данных, функционирующих в оперативном режиме.
4.2.2. Основной целью проведения оперативных испытаний методов долгосрочных территориальных прогнозов является оценка надежности функционирования разработанных расчетных схем в условиях автоматизации процесса усвоения исходной информации и неизбежных при этом потерь данных. Оценку качества прогностических методик в данном случае целесообразно проводить традиционными методами [10]. Из-за очень ограниченного числа прогнозов (1 - 2 случая) в период оперативных испытаний эффективность методики определяется в основном по результатам авторских испытаний.
4.2.3. Значительный интерес представляют оперативные испытания новых методов краткосрочных прогнозов расходов и уровней воды, основанных на использовании математических моделей процессов формирования речного стока. Такие методы дают возможность непрерывного прогнозирования в течение длительного периода времени. При этом образуется достаточный по объему материал, позволяющий получать надежные статистические оценки.
4.3.1. Новые расчетные методы краткосрочных прогнозов водного режима, как правило, связаны с технологическими линиями автоматизированной обработки гидрометеорологической информации, поступающей непосредственно в ЭВМ. Вследствие этого испытания помимо оценки качества методики должны выявить возможности адаптации прогностической схемы при использовании имеющейся технологической линии с учетом реальных потерь информации и ее погрешностей.
Вторым важным моментом является необходимость использования информации краткосрочных метеорологических прогнозов. Поэтому для полного представления о возможностях методики при испытании необходимо производить оценку точности схемы как с использованием информации метеорологических прогнозов, так и по фактическим значениям используемых метеорологических элементов.
4.3.2. При испытании таких методов прогноза необходимо учитывать следующее:
оценки точности должны быть получены для каждой заблаговременности прогнозов независимо;
если прогноз составляется для нескольких пунктов, то оценка производится отдельно для каждого пункта. Для территориально общих методик помимо оценок по каждому пункту даются обобщенные оценки по всей территории;
при прогнозировании расходов (уровней) воды непрерывно в периоды формирования весеннего половодья, дождевых паводков, меженного стока оценки определяются для каждого из этих периодов отдельно. Для крупных рек с четко выраженным одномодальным гидрографом весеннего половодья продолжительностью более 50 - 60 суток целесообразно определять оценки точности отдельно для периодов подъема и спада уровня воды;
при сравнительной оценке нескольких методов прогноза расчеты необходимо производить для одних и тех же случаев с применением одинаковых критериев. При этом помимо основного критерия точности  необходимо привлекать ряд дополнительных оценок, которые будут рассмотрены ниже;
необходимо привлекать ряд дополнительных оценок, которые будут рассмотрены ниже;
продолжительность испытаний, как правило, не должна превышать 1 - 2 года, причем число прогнозов для каждой заблаговременности в период половодья на равнинных реках должно быть не менее 60 - 100, для дождевых паводков и снего-дождевого стока горных рек - не менее 30 - 50.
4.4.1. Как указывалось выше, основным критерием качества и применимости методики является отношение  . Правила вычисления S и
. Правила вычисления S и 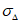 изложены в [1]. Эффективными считаются методы, для которых
изложены в [1]. Эффективными считаются методы, для которых  .
.
 .
.Из-за большой изменчивости гидрографов речного стока от года к году этот критерий можно считать достаточно надежным лишь тогда, когда он определяется по большому числу лет, включающих высокие и низкие паводки. При оперативных испытаниях в течение 1 - 2 лет эти условия не выполняются и для высоких паводков оценки будут завышены, а для низких - занижены. В этом случае величину  необходимо вычислять для каждого года испытания, представив ее как
необходимо вычислять для каждого года испытания, представив ее как 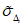 , с учетом вероятностей значений изменения прогнозируемой величины за период заблаговременности:
, с учетом вероятностей значений изменения прогнозируемой величины за период заблаговременности:

где 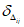 - абсолютное значение фактического изменения прогнозируемой величины за период заблаговременности
- абсолютное значение фактического изменения прогнозируемой величины за период заблаговременности  для i-го года испытания в момент времени j; N - количество выпущенных прогнозов;
для i-го года испытания в момент времени j; N - количество выпущенных прогнозов; 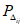 - вероятность величины
- вероятность величины 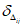 ;
; 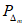 - максимальное значение кривой распределения фактических изменений
- максимальное значение кривой распределения фактических изменений 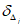 ;
;  - величина изменения (нижняя граница интервала), соответствующая значению
- величина изменения (нижняя граница интервала), соответствующая значению  .
.
4.4.2. Для расчета величины  по формулам (95) необходимо предварительно на архивных данных за 8 - 10 лет, включающих высокие и низкие половодья (паводки), определить кривую распределения фактической изменчивости расходов (уровней) воды для каждой заблаговременности. При построении этой кривой весь диапазон изменения
по формулам (95) необходимо предварительно на архивных данных за 8 - 10 лет, включающих высокие и низкие половодья (паводки), определить кривую распределения фактической изменчивости расходов (уровней) воды для каждой заблаговременности. При построении этой кривой весь диапазон изменения 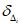 нужно разбить на 10 - 20 равных интервалов. В качестве примера в табл. 22 показан расчет кривой распределения величин
нужно разбить на 10 - 20 равных интервалов. В качестве примера в табл. 22 показан расчет кривой распределения величин  для реки Юг у села Кичменгский Городок при заблаговременности прогноза пять суток.
для реки Юг у села Кичменгский Городок при заблаговременности прогноза пять суток.
Таблица 22
Интервал изменения | Число случаев в интервале (m) | Вероятность попадания в интервал (m/n)·100% |
1000 - 1099 | 2 | 0,6 |
900 - 999 | 2 | 0,6 |
800 - 899 | 3 | 0,9 |
700 - 799 | 4 | 1,2 |
600 - 699 | 6 | 1,8 |
500 - 599 | 9 | 2,8 |
400 - 499 | 16 | 5,0 |
300 - 399 | 22 | 6,8 |
200 - 299 | 50 | 15,5 |
100 - 199 | 74 | 23,0 |
0 - 99 | 134 | 41,6 |
Сумма | 322 | 100 |
По данным табл. 22 можно определить 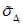 для года, для которого проводятся испытания, учитывая полученные в ней значения
для года, для которого проводятся испытания, учитывая полученные в ней значения 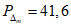 и
и  . В табл. 23 приведен пример расчета
. В табл. 23 приведен пример расчета 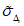 для низкого половодья. Полученная таким образом изменчивость прогнозируемой величины за период заблаговременности
для низкого половодья. Полученная таким образом изменчивость прогнозируемой величины за период заблаговременности  используется при определении оправдываемости прогнозов. Прогноз считается оправдавшимся, если ошибка прогноза не превышает допустимую погрешность, равную
используется при определении оправдываемости прогнозов. Прогноз считается оправдавшимся, если ошибка прогноза не превышает допустимую погрешность, равную 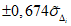 . По результатам выпущенных прогнозов определяется обеспеченность метода в процентах, равная отношению числа оправдавшихся прогнозов к общему числу прогнозов.
. По результатам выпущенных прогнозов определяется обеспеченность метода в процентах, равная отношению числа оправдавшихся прогнозов к общему числу прогнозов.
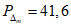 и
и  . В табл. 23 приведен пример расчета
. В табл. 23 приведен пример расчета 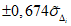 . По результатам выпущенных прогнозов определяется обеспеченность метода в процентах, равная отношению числа оправдавшихся прогнозов к общему числу прогнозов.
. По результатам выпущенных прогнозов определяется обеспеченность метода в процентах, равная отношению числа оправдавшихся прогнозов к общему числу прогнозов.Таблица 23
 | |||||
201 | 0,36 | 0,64 | 40 401 | 1,64 | 66 258 |
203 | 0,36 | 0,64 | 41 209 | 1,64 | 67 583 |
181 | 0,55 | 0,45 | 32 761 | 1,45 | 47 503 |
165 | 0,55 | 0,45 | 27 285 | 1,45 | 39 476 |
135 | 0,55 | 0,45 | 18 225 | 1,45 | 26 326 |
102 | 0,55 | 0,45 | 10 404 | 1,45 | 15 086 |
60 | 1,0 | 0,0 | 3 600 | 1,0 | 3 600 |
76 | 1,0 | 0,0 | 5 776 | 1,0 | 5 776 |
39 | 1,0 | 0,0 | 1 521 | 1,0 | 1 521 |
20 | 1,0 | 0,0 | 400 | 1,0 | 400 |
85 | 1,0 | 0,0 | 7 225 | 1,0 | 7 225 |
138 | 0,55 | 0,45 | 19 044 | 1,45 | 27 614 |
200 | 0,36 | 0,64 | 40 000 | 1,64 | 66 000 |
212 | 0,36 | 0,64 | 44 944 | 1,64 | 74 158 |
152 | 0,55 | 0,45 | 23 104 | 1,45 | 33 501 |
62 | 1,0 | 0,0 | 3 844 | 1,0 | 3 844 |
15 | 1,0 | 0,0 | 225 | 1,0 | 225 |
61 | 1,0 | 0,0 | 3 721 | 1,0 | 3 721 |
110 | 0,55 | 0,45 | 12 100 | 1,45 | 17 545 |
86 | 1,0 | 0,0 | 7 396 | 1,0 | 7 396 |
0 | 1,0 | 0,0 | 0 | 1,0 | 0 |
72 | 1,0 | 0,0 | 5 184 | 1,0 | 5 184 |
126 | 0,55 | 0,45 | 15 876 | 1,45 | 23 020 |
177 | 0,55 | 0,45 | 31 329 | 1,45 | 45 427 |
188 | 0,55 | 0,45 | 35 344 | 1,45 | 51 249 |
166 | 0,55 | 0,45 | 27 556 | 1,45 | 39 956 |
137 | 0,55 | 0,45 | 18 769 | 1,45 | 27 215 |
108 | 0,55 | 0,45 | 11 664 | 1,45 | 16 913 |
87 | 1,0 | 0,0 | 7 569 | 1,0 | 7 569 |
74 | 1,0 | 0,0 | 5 476 | 1,0 | 5 476 |
52 | 1,0 | 0,0 | 2 704 | 1,0 | 2 704 |
39,41 | 739 571 |
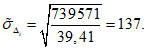
4.4.3. Для более полной оценки метода необходимо использовать еще несколько показателей точности. Это особенно важно при сравнении нового метода с использующимися в оперативной практике методами и при принятии решения о преимуществе одного из них. К таким дополнительным показателям можно отнести
среднюю абсолютную ошибку прогноза
где Qф и Qп - соответственно прогностическое и фактическое значения расхода воды (если прогнозируется уровень воды, то в (96) необходимо подставить значения уровня воды), N - число составленных прогнозов;
среднюю относительную ошибку прогноза
 (97)
(97)где  - средняя абсолютная фактическая изменчивость расходов (уровней) воды
- средняя абсолютная фактическая изменчивость расходов (уровней) воды
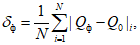 (98)
(98)Q0 - расход (уровень) воды в день выпуска прогноза.
Чем ближе к нулю значение 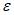 , тем эффективнее методика.
, тем эффективнее методика.
4.5.1. Методы долгосрочных ледовых прогнозов обычно основаны на физико-статистической зависимости сроков ледовых явлений от количественных характеристик предшествующих атмосферных процессов. Физическое обоснование таких зависимостей часто является недостаточным для рекомендаций о применении их в оперативной практике лишь на основании авторских испытаний на материале, использованном при разработке метода. Для испытания устойчивости зависимости во времени необходимо выполнить оценку надежности метода на независимом материале, т.е. по данным наблюдений, не использованных при разработке метода. Такое испытание выполняется двумя способами.
4.5.2. Первый способ состоит в выделении для проверки на независимом материале данных за последние годы. Число лет, выделяемых для этой цели, как указано выше, должно составлять не менее 20% общего числа лет ряда наблюдений, но не менее пяти лет. При отборе этих случаев следует предусматривать, чтобы в их число вошли значительные (превышающие 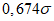 ) отклонения значений предиктанта от средних многолетних значений, а
) отклонения значений предиктанта от средних многолетних значений, а 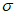 независимого ряда была не меньше
независимого ряда была не меньше 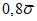 многолетнего ряда, используемого при разработке метода.
многолетнего ряда, используемого при разработке метода.
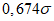 ) отклонения значений предиктанта от средних многолетних значений, а
) отклонения значений предиктанта от средних многолетних значений, а 4.5.3. Второй способ оценки временной устойчивости прогностических зависимостей - способ "выбрасываемых точек", реализуемый на ЭВМ. Он состоит в определении коэффициентов прогностического уравнения при исключении из ряда от одного до пяти лет и в составлении по полученным уравнениям проверочных прогнозов для исключенных лет. Исключая из ряда последовательно каждый следующий год (или группу лет), получаем весь ряд прогнозируемых значений. Последние коррелируются с фактическими значениями за те же годы, и коэффициент корреляции, называемый коэффициентом прогностической информативности (КПИ), служит показателем временной устойчивости зависимостей.
4.5.4. Достаточно устойчивыми и применимыми в практике считаются прогностические зависимости (уравнения), по которым совокупность проверочных прогнозов на независимом ряде имеет удовлетворительную оправдываемость и КПИ > 0,6, причем эта оправдываемость должна отличаться от оправдываемости, подсчитанной по зависимому ряду, не более чем на 10%, а КПИ меньше коэффициента корреляции прогностического уравнения - не более чем на 0,1.
Если метод прогноза разработан без применения ЭВМ, можно ограничиться проверкой по первому способу.
4.5.5. Оперативные испытания методов следует проводить, если необходимо оценить возможность его использования при поступлении исходной информации в реальном масштабе времени. Оправдываемость составленных в ходе этих испытаний одного-двух прогнозов для каждого пункта или участка реки недостаточна для решения вопроса о целесообразности внедрения методики в оперативную практику. Поэтому при решении вопроса о внедрении метода следует учитывать результаты авторских испытаний на независимом материале.
4.5.6. Оценка применимости методов краткосрочных прогнозов сроков ледовых явлений, согласно [10], производится путем вычисления средней квадратической погрешности проверочных прогнозов  и сравнения ее с предельным значением прогнозируемого элемента S1, меняющимся в зависимости от заблаговременности прогноза. В табл. 24 приведены значения S1 и указана качественная оценка методики при условии
и сравнения ее с предельным значением прогнозируемого элемента S1, меняющимся в зависимости от заблаговременности прогноза. В табл. 24 приведены значения S1 и указана качественная оценка методики при условии  .
.
В том случае, если в качестве исходной информации предполагается использование прогнозируемых величин, испытание методов должно включать оценку точности как при расчете по фактическим входным данным, так и по прогнозируемым их величинам. Число проверочных прогнозов на независимом материале с использованием промежуточных прогнозов должно составлять для одного объекта не менее десяти.
4.5.7. Оперативные испытания методов прогноза ледового режима целесообразно проводить для выявления возможности возникновения ошибок из-за неполноты оперативной информации, а также для проверки надежности реализации прогностической схемы при использовании существующей технологической линии. Продолжительность испытаний не должна быть более двух лет.
Таблица 24
сроков появления ледовых явлений с различной
заблаговременностью при условии 
Оценка методики | Средняя заблаговременность прогнозов, сутки | ||||
1 - 3 | 4 - 5 | 6 - 9 | 10 - 13 | 14 - 15 | |
Хорошая | 0,7 | 1,5 | 2,2 | 3,0 | 3,7 |
Удовлетворительная | 1,2 | 2,4 | 3,6 | 4,8 | 5,9 |
морских гидрологических прогнозов
5.1.1. Производственным (оперативным) испытаниям подлежат все новые и усовершенствованные методы прогноза и анализа морских гидрологических элементов и явлений. Испытания проводятся на основании программы испытаний, составленной автором метода.
5.1.2. По продолжительности действия морские гидрологические прогнозы делятся на краткосрочные (менее 3 суток), среднесрочные (от 3 до 14 суток), долгосрочные (от 15 суток до 6 месяцев) и сверхдолгосрочные (более 6 месяцев).
5.1.3. Во время испытаний методов краткосрочных и среднесрочных прогнозов точность метода оценивается на независимом материале, который может быть выбран как по данным, не использованным при разработке метода, так и на основе текущей информации.
5.1.4. Важным условием проверки метода является знание природной изменчивости прогнозируемого элемента (явления). Для каждого элемента (явления) в зависимости от его природной изменчивости устанавливается статистически обоснованное количество проверочных прогнозов, достаточное для объективной оценки метода. Для численных прогнозов полей морских гидрологических элементов (волнение, температура воды и др.) число проверочных прогнозов должно быть не менее 30.
5.1.5. При разработке методов долгосрочных и сверхдолгосрочных морских гидрологических прогнозов обычно приходится использовать данные многолетних наблюдений. Требование проведения оперативных испытаний таких методов на независимом материале может значительно задержать их внедрение в практику. Поэтому для суждения о применимости метода можно в дополнение к результатам производственных испытаний использовать результаты авторских испытаний.
морских гидрологических прогнозов
5.2.1. В соответствии с [11] для определения надежности методов морских гидрологических прогнозов используются два основных критерия точности и эффективности методов.
5.2.2. Одним из них служит отношение средней квадратической ошибки прогнозов S к среднему квадратическому отклонению от нормы  или к среднему квадратическому отклонению изменений того же элемента от среднего его изменения за период заблаговременности прогноза
или к среднему квадратическому отклонению изменений того же элемента от среднего его изменения за период заблаговременности прогноза 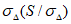 .
.
 или к среднему квадратическому отклонению изменений того же элемента от среднего его изменения за период заблаговременности прогноза
или к среднему квадратическому отклонению изменений того же элемента от среднего его изменения за период заблаговременности прогноза 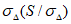 .
.Средняя квадратическая ошибка проверочных прогнозов определяется по формуле
 (99)
(99)где Ui, Uр - соответственно фактические и рассчитанные значения; n - число проверочных прогнозов.
Среднее квадратическое отклонение прогнозируемого элемента от нормы за многолетний ряд наблюдений  рассчитывается по формуле
рассчитывается по формуле
где  - среднее значение элемента за многолетний ряд наблюдений (норма).
- среднее значение элемента за многолетний ряд наблюдений (норма).
Среднее квадратическое отклонение изменений элемента от среднего его изменения за период заблаговременности прогноза  вычисляется по формуле
вычисляется по формуле
 (101)
(101)где  - изменение прогнозируемого элемента за период заблаговременности прогноза,
- изменение прогнозируемого элемента за период заблаговременности прогноза, 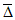 - среднее изменение элемента за тот же период.
- среднее изменение элемента за тот же период.
Чем меньше отношение  , тем выше точность метода.
, тем выше точность метода.
 , тем выше точность метода.
, тем выше точность метода.5.2.3. Другим критерием применимости, тесно связанным с первым (при нормальном распределении ошибок прогноза и отклонений прогнозируемых величин от нормы), является условие превышения обеспеченности метода над природной или инерционной обеспеченностью. Понятие обеспеченности метода в процентах, введенное Наставлением [11] и характеризующее оправдываемость прогнозов, рассчитывается по формуле
где m - количество оправдавшихся прогнозов; n - общее число прогнозов.
При расчете обеспеченности метода (P) за допустимую погрешность принимаются значения, которые составляют для прогнозов заблаговременностью до 2 месяцев  ; для прогнозов заблаговременностью от 2 до 6 месяцев
; для прогнозов заблаговременностью от 2 до 6 месяцев 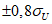 ; для прогнозов заблаговременностью более 6 месяцев
; для прогнозов заблаговременностью более 6 месяцев 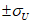 .
.
 ; для прогнозов заблаговременностью от 2 до 6 месяцев
; для прогнозов заблаговременностью от 2 до 6 месяцев 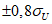 ; для прогнозов заблаговременностью более 6 месяцев
; для прогнозов заблаговременностью более 6 месяцев Метод считается применимым для практического использования, если обеспеченность его превышает природную обеспеченность.
5.2.4. Для определения эффективности метода краткосрочного прогноза обеспеченность метода сравнивается не с климатической обеспеченностью, а с обеспеченностью инерционных прогнозов, которая также рассчитывается по формуле (102). Область сравнения методического прогноза с инерционным определяется временной изменчивостью прогнозируемого элемента, которая устанавливается авторами методов на стадии проведения авторских испытаний. Инерционный и климатический прогнозы будут иметь одинаковую точность при сдвиге во времени  , который соответствует уменьшению вдвое ординаты корреляционной (или ковариационной) функции данного элемента [1]. При
, который соответствует уменьшению вдвое ординаты корреляционной (или ковариационной) функции данного элемента [1]. При 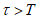 (T - заблаговременность прогноза) инерционный прогноз становится статистически менее точным. Поэтому при
(T - заблаговременность прогноза) инерционный прогноз становится статистически менее точным. Поэтому при  методические прогнозы следует сравнивать с инерционными, а при
методические прогнозы следует сравнивать с инерционными, а при 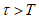 - с климатологическими прогнозами.
- с климатологическими прогнозами.
5.2.5. Для оценки качества численных методов морских гидрологических прогнозов рекомендуется также использовать следующие статистические характеристики: среднюю абсолютную ошибку  , среднюю относительную ошибку
, среднюю относительную ошибку 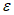 , среднюю арифметическую (систематическую) ошибку
, среднюю арифметическую (систематическую) ошибку  , среднее квадратическое отклонение ошибки (стандартную ошибку)
, среднее квадратическое отклонение ошибки (стандартную ошибку) 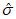 , корреляцию тенденций VT, которые рассчитываются соответственно по формулам (1), (2), (4), (5) и (6).
, корреляцию тенденций VT, которые рассчитываются соответственно по формулам (1), (2), (4), (5) и (6).
методов морских гидрологических прогнозов
5.3.1. Вышеуказанные критерии надежности метода могут быть использованы для оценки большинства методов морских гидрологических прогнозов. Однако в ряде случаев использование этих критериев затруднено и возникает необходимость учета специфических особенностей метода. К таким случаям относятся:
а) оценка расчетных и численных методов прогнозов полей элементов;
б) оценка методов прогнозов, допустимая погрешность которых не связана со средней квадратической величиной ряда  ;
;
в) оценка методов, по которым прогнозы составляются в сроки, находящиеся в пределах многолетней амплитуды элемента (явления).
5.3.2. Оценка успешности расчетных и численных методов прогноза полей гидрометеорологических элементов производится путем определения только обеспеченности метода по формуле (102). В этом случае m - число узлов сетки, в которых отклонение прогностического значения от фактического не превышает допустимой погрешности; n - общее число узлов сетки.
Аналогичным образом оценивается качество методов прогнозов гидрометеорологических элементов, выраженных в виде границ разделов (например, гидрологический фронт, глубина залегания термоклина, кромка дрейфующего льда и т.д.).
5.3.3. Для ряда методов морских гидрологических прогнозов (например, прогноза волнения) допустимая ошибка не связана со средней квадратической величиной ряда  и устанавливается эмпирически. Величина допустимой ошибки для оценки каждого вида таких прогнозов приведена в [11].
и устанавливается эмпирически. Величина допустимой ошибки для оценки каждого вида таких прогнозов приведена в [11].
Оценка применимости таких методов в оперативной практике производится путем определения только обеспеченности метода по формуле (102).
5.3.4. Оценка методов, прогнозы по которым составляются в сроки, находящиеся в пределах многолетней амплитуды элемента (явления), производится по значению отношения  . При этом
. При этом 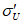 - среднее квадратическое отклонение элемента от его среднего значения, установленного для членов ряда n', находящегося в пределах сокращенной амплитуды Aс, т.е. в пределах дат составления прогноза и самого позднего наступления явления. Величина
- среднее квадратическое отклонение элемента от его среднего значения, установленного для членов ряда n', находящегося в пределах сокращенной амплитуды Aс, т.е. в пределах дат составления прогноза и самого позднего наступления явления. Величина  определяется по формуле (100), где число членов многолетнего ряда n заменяется на n' для сокращенной амплитуды Aс.
определяется по формуле (100), где число членов многолетнего ряда n заменяется на n' для сокращенной амплитуды Aс.
Дальнейшее определение успешности метода производится в соответствии с критериями, изложенными в п. 5.2.
морских гидрометеорологических элементов
5.4.1. В настоящее время оценка качества методов объективного анализа полей морских гидрологических элементов представляет собой трудную задачу в силу существования ряда факторов, в том числе отсутствие на морях и океанах сети регулярных наблюдений, подобной сети метеорологических наблюдений на суше;
неравномерной по пространству и времени частоты измерений, производимых персоналом морских судов на добровольной основе, а также зачастую недостаточной точности и несовершенства методов наблюдений;
значительной пространственной и временной изменчивости параметров океана, приводящей к неоднородности и анизотропности полей гидрометеорологических элементов.
В результате стандартные методы оценки качества объективного анализа, применяемые метеорологами, не могут адекватно применяться в отношении полей морских гидрологических элементов. Так, например, при использовании метода прямой интерполяции искусственно уменьшается плотность данных наблюдений, что приводит к росту ошибок интерполяции, а в районах океана с малой освещенностью наблюдениями получение оценки становится невозможным.
5.4.2. Поэтому в настоящее время процедура испытаний новых методов объективного анализа полей морских гидрологических элементов может быть сведена к следующему:
на первом этапе испытаний сравниваются результаты объективного и ручного анализов, полученные по одним и тем же данным наблюдений. Для уменьшения субъективности оценок ручной анализ должен быть проведен не менее чем двумя специалистами. По результатам сравнения объективного и ручного анализов производится качественная оценка достоверности объективного анализа в отношении общей картины распределения, степени ее детализации, резкости градиентов и т.д.;
количественную оценку результатов объективного анализа (расчет значений среднего абсолютного отклонения, среднего квадратического отклонения и т.д.) целесообразно производить применительно к местам производства надежных и репрезентативных наблюдений (на стационарных и дрейфующих буях, с борта научно-исследовательских судов и кораблей погоды и т.д.). Допустимая погрешность анализа должна быть сравнима с существующей точностью измерений данного гидрометеорологического элемента;
при наличии эффективной численной модели краткосрочного прогноза гидрометеорологического элемента и различных схем объективного анализа заключение о качестве того или иного объективного анализа может быть получено по результатам прогнозов, предвычисленных с использованием различных объективных анализов.
территория действия прогноза - территория, на которой предсказывается сход (или несход), движение и остановка лавины. Оценка прогноза производится только на фактах схода лавин в пределах этой территории;
заблаговременность прогноза - промежуток времени между моментом выдачи прогноза потребителю и моментом начала его действия;
длительность (период) действия прогноза - промежуток времени между моментом начала и моментом окончания его действия. Этот промежуток может иметь фиксированное значение, он может зависеть от каких-либо условий и быть различным по протяженности. Оценка прогноза производится только по фактам схода лавин в течение этого промежутка;
предмет прогноза - лавиноопасный период, обусловленный единым физико-географическим комплексом условий и причин лавинообразования. Прогноз составляется только для случаев, принадлежащих данному комплексу. Такой комплекс может определяться как общими причинами возникновения (генезис), которые определяются согласно той или иной генетической классификации лавин [13], так и конкретными причинами возникновения ("спусковой фактор"). Конкретные причины определяют лавины самопроизвольные (или спонтанные), сходящие без явных видимых причин; лавины, сошедшие от случайных причин (падение камня или шапки снега, землетрясение и т.д.); лавины, сошедшие при искусственном, целенаправленном активном воздействии (АВ).
прогноза лавинной опасности
6.2.1. Альтернативные прогнозы лавинной опасности имеют формулировки "лавиноопасно", "нелавиноопасно". Формулировка "лавиноопасно" означает, что на территории действия прогноза за время его действия прогнозируется сход хотя бы одной лавины объемом не менее некоторого Vmin. Обычно за Vmin принимается значение 10 м3, которое потенциально опасно для жизни одинокого пешехода или лыжника. Но это значение для конкретного метода может быть иным.
6.2.1.1. При оценке каждый случай альтернативного прогноза может попасть в одну из следующих пяти групп:
прогноз "лавиноопасно" оправдался - есть сход лавины;
прогноз "лавиноопасно" не оправдался - нет схода лавины;
прогноз "нелавиноопасно" не оправдался - есть сход лавины;
прогноз "нелавиноопасно" оправдался - нет схода лавины;
прогноз не оценивался независимо от формулировки (например, из-за отсутствия видимости).
6.2.2. Дифференцированные по градациям прогнозы лавинной опасности могут содержать качественные показатели, уточняющие формулировку "лавиноопасно". Например: "слабая лавинная опасность" или "умеренная". Такие показатели должны расшифровываться количественными градациями определяющих параметров: количеством лавин, их объемами и т.п.
6.2.3. На всех этапах авторских и производственных испытаний каждого метода прогноза лавин должно соблюдаться требование полной идентичности объективных правил прогнозирования и оценок.
При определении периода разработки, периодов авторских и производственных испытаний необходимо, чтобы число случаев с явлениями было не меньше ряда их природной повторяемости. Установление ряда природной повторяемости таких случаев, а также ряда природной повторяемости всех случаев, подлежащих прогнозу по данному методу, путем проработки фактического материала о сходе лавин, является предварительным этапом испытаний. Для увеличения числа случаев с редко наблюдающимися явлениями допускаются производственные испытания метода их прогноза на независимом материале прошлых зим.
6.2.4. При сравнительной оценке нескольких методов прогноза необходимо все методы оценивать по одной и той же фактической информации о сходе лавин, на одной и той же территории, за одно и то же время, с применением одних и тех оценок, определенных настоящими методическими указаниями. Если один из сравниваемых методов является более общим по предмету прогноза и (или) территории прогноза, то для него кроме показателей оценки по всему методу должны быть рассчитаны и показатели оценки для более частного (локального) варианта, соответствующего второму из сравниваемых методов. Такую оценку выполняет автор вновь представляемого метода. Если оба метода представляются одновременно, то такую оценку выполняет автор общего метода.
прогнозов лавинной опасности
6.3.1.1. Ряд случаев альтернативного прогноза лавин по проверяемому методу за весь период испытаний n состоит из ряда оцениваемых случаев n00 и ряда неоцениваемых случаев nxx
n = n00 + nxx. (103)
Если ряд оцениваемых случаев n00 меньше ряда природной повторяемости случаев, подлежащих прогнозу, то метод не оценивается.
Весь ряд оцениваемых случаев прогноза n00 разбивается на группы nij по форме 23.
Таблица сопряженности
Прогноз | Наблюдалось | Сумма | |
лавиноопасно | нелавиноопасно | ||
Лавиноопасно | n11 | n12 | n10 |
Нелавиноопасно | n21 | n22 | n20 |
Сумма | n01 | n02 | n00 |
Примечание. n11 - число оправдавшихся прогнозов с формулировкой "лавиноопасно"; n12 - число неоправдавшихся прогнозов с формулировкой "лавиноопасно"; n21 - число неоправдавшихся прогнозов с формулировкой "нелавиноопасно"; n22 - число оправдавшихся прогнозов с формулировкой "нелавиноопасно"; n10 = n11 + n12 - число всех оцениваемых прогнозов с формулировкой "лавиноопасно"; n20 = n21 + n22 - число всех оцениваемых прогнозов с формулировкой "нелавиноопасно"; n01 = n11 + n21 - число всех оцениваемых случаев со сходом лавин; n02 = n12 + n22 - число всех оцениваемых случаев без схода лавин; n00 = n10 + n20 = n01 + n02 - число всех оцениваемых случаев.
6.3.1.2. Основными показателями для оценки прогнозов лавинной опасности являются:
общая оправдываемость прогнозов в процентах (или просто оправдываемость)
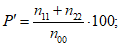 (104)
(104)предупрежденность наличия явления в процентах (или просто предупрежденность)
 (105)
(105)6.3.1.3. Дополнительными показателями для оценки прогнозов лавинной опасности являются:
оправдываемость прогноза наличия явления в процентах
 (106)
(106)оправдываемость прогноза отсутствия явления в процентах
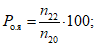 (107)
(107)предупрежденность отсутствия явления в процентах
 (108)
(108)критерий качества прогнозов Пирси - Обухова
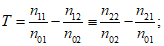 (109)
(109)критерий надежности по Н.А. Багрову
 (110)
(110)где

ошибка риска метода
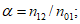 (111)
(111)ошибка страховки метода
 (112)
(112)критерий точности по А.М. Обухову
 (113)
(113)Все показатели успешности метода вычисляются как для всего периода испытаний в целом, так и для каждого зимнего сезона отдельно и представляются по форме 24.
В случае когда знаменатель одного из показателей успешности метода равен нулю, значение этого показателя является неопределенным. В соответствующей графе формы 24 ставится знак ~ или 0/0, и этот показатель не участвует в оценке метода.
метода прогноза ... за период с 19... по 19... г.
Количество зимних сезонов | Число случаев (природная повторяемость) | Число оцениваемых прогнозов | Оценки | P + P', % | Pя + 100, % | ||||||||||||
всех подлежащих прогнозу | со сходом лавин | без схода лавин | неоцениваемых | основные | дополнительные | ||||||||||||
P, % | P', % | Pн.я, % | Pо.я, % | P'о.я, % | T | H | Q | ||||||||||
Если сумма основных показателей надежности метода за весь период испытаний меньше либо равна природной повторяемости случаев с явлениями Pя плюс 100%, т.е. если справедливо неравенство
P + P' <= Pя + 100, (114)
где Pя - природная повторяемость случаев с явлениями в процентах, и (или) критерий надежности по Н.А. Багрову H меньше 0,5, то метод не принимается к рассмотрению.
6.3.1.4. Если на рассматриваемой территории до предлагаемого метода не было других действующих объективных методов прогноза данного явления (предмета прогноза), то в рекомендациях о внедрении метод принимается в качестве основного при условии, что для него неравенства
и
выполняются как за весь период испытаний, так и отдельно за каждый зимний сезон.
6.3.1.5. Метод рекомендуется к внедрению в качестве консультативного, если за весь период испытаний условия неравенств (115) и (116) выполняются, но в один из зимних сезонов какое-либо из указанных условий (или оба) не выполняются. При этом необходимо выявить отличительные особенности этого зимнего сезона от остальных и указать на установленное отличие в методических указаниях с изложением данного метода.
6.3.1.6. Если на данной территории кроме предлагаемого метода существует другой объективный метод прогноза данного явления (предмета прогноза), то необходимо провести сравнение основных показателей успешности прогнозов по этим методам. В случае когда оба основных показателя одного метода больше соответствующих показателей другого метода или один из них больше, а другой равен соответствующему показателю, преимущество должно быть отдано методу с большей суммой основных показателей. Если же соотношение основных показателей окажется различным
 (117)
(117)то могут быть справедливыми два неравенства. При наличии неравенства
|P'1 - P'2| >= |P1 - P2| (118)
предпочтение отдается тому методу, у которого больше величина P'.
При наличии другого соотношения
|P'1 - P'2| < |P1 - P2| (119)
предпочтение отдается методу, у которого больше количество лучших дополнительных показателей.
6.3.1.7. Если при сравнении методов прогноза лавинной опасности по приведенным показателям не выявлен лучший из методов, необходимо рассмотреть их преимущества по заблаговременности, сложности технологии, по лучшим оценкам прогноза лавин больших объемов и по оценкам их экономической эффективности, если такие можно определить [14].
При сравнительной оценке общего метода прогноза лавинной опасности с локальным общий метод, имеющий худшие показатели успешности в области пересечения предмета и (или) территории прогноза, может быть рекомендован к внедрению в качестве дополнительного к локальному.
прогнозов лавинной опасности
6.3.2.1. Для сравнения таких методов прогноза лавинной опасности с методами альтернативного прогноза рассчитываются и применяются одни и те же показатели и правила. При этом все случаи прогнозов, дифференцированных по градациям лавинной опасности, попадают в группу n10.
6.3.2.2. Для оценки сравниваемых прогнозов применяются следующие показатели успешности:
оправдываемость дифференцированных прогнозов в процентах
 (120)
(120)где n1 - число правильных дифференцированных прогнозов (попавших в свою градацию), в том числе прогнозы с формулировкой "нелавиноопасно"; n0 - число всех дифференцированных прогнозов;
предупрежденность дифференцированных прогнозов в процентах
 (121)
(121)где n3 - число правильных и выданных с превышением степени лавинной опасности дифференцированных прогнозов, за исключением прогнозов с формулировкой "нелавиноопасно"; n2 - число всех случаев со сходом лавин;
ошибка риска дифференцированных прогнозов
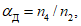 (122)
(122)где n4 - число ошибочных дифференцированных прогнозов, попавших в более сильные по сравнению с предсказывавшимися градациями, в том числе ошибочные прогнозы с формулировкой "нелавиноопасно";
ошибка страховки дифференцированных прогнозов
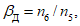 (123)
(123)где n6 - число ошибочных дифференцированных прогнозов, попавших в более слабые по сравнению с предсказывавшимися градациями; n5 - число всех случаев, за исключением числа случаев с лавинами самой сильной градации.
6.3.2.3. При сравнении таких методов друг с другом оправдываемость и предупрежденность дифференцированных прогнозов выступают в качестве основных показателей, а ошибки риска и страховки дифференцированных прогнозов - в качестве дополнительных. Сравнение проводится по тем же правилам, что и для методов альтернативного прогноза.
7.1.1. Настоящий раздел устанавливает порядок использования в прогностических подразделениях гелиогеофизических служб (в главном прогностическом центре ИПГ, в Москве и региональных центрах при УГМ в Мурманске, Ташкенте, Новосибирске и Хабаровске) единой системы критериев оценки качества новых (или усовершенствованных) гелиогеофизических прогнозов, регламентирует процедуры производственных испытаний, а также предназначен для проведения аттестации уже используемых методов и для постоянного контроля качества выпускаемых прогнозов. Она является обязательной для прогностических подразделений гелиогеофизической службы и может в качестве рекомендаций использоваться разработчиками методов. Представленные в п. 7.4 методологические аспекты гелиогеофизических прогнозов имеют познавательный характер и помогают определить процедуру испытания в зависимости от классификации метода.
7.1.2. Целью производственных испытаний являются объективизация и ускорение процесса внедрения новых (или усовершенствованных) методов; унификация производственных испытаний, в первую очередь по составу критериев для определения качества и надежности испытываемых методов, сравнения их между собой как в методическом, так и в практическом аспекте.
7.1.3. Последовательность этапов от разработки до внедрения новых методов, взаимоотношения между авторами методов и прогностическими подразделениями, где проводятся испытания, регламентируются "Положением об испытании и внедрении новых и усовершенствованных методов (способов) гидрометеорологических и гелиогеофизических прогнозов и расчетов", утвержденным Госгидрометом СССР 1 февраля 1989 г. и "Положением об испытании и внедрении новых и усовершенствованных методов (способов) гелиогеофизических прогнозов и расчетов", утвержденным директором ИПГ им. академика Федорова Е.К. как головного научно-исследовательского института по гелиогеофизике, 15 мая 1988 г.
7.2.1. Некоторый гелиогеофизический процесс описывается функцией  , зависящей от времени t, координат
, зависящей от времени t, координат 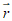 , энергии E, множества параметров
, энергии E, множества параметров 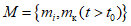 , в том числе и прогнозируемых
, в том числе и прогнозируемых  , определяющих различные явления и процессы. Прогноз этого процесса в самом общем смысле можно рассматривать как вычисление в момент времени t' > t0 значений функции
, определяющих различные явления и процессы. Прогноз этого процесса в самом общем смысле можно рассматривать как вычисление в момент времени t' > t0 значений функции  для времени t > t0 (черт. 8). В дальнейшем прогнозируемые значения функции
для времени t > t0 (черт. 8). В дальнейшем прогнозируемые значения функции  будем обозначать
будем обозначать  . Как правило, вид прогнозируемой функции может существенно отличаться от истинного вида U. Наиболее простой и часто встречающийся вид
. Как правило, вид прогнозируемой функции может существенно отличаться от истинного вида U. Наиболее простой и часто встречающийся вид 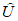 - это дискретная
- это дискретная  или бинарная
или бинарная 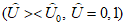 функция. Используются также различные приближения: суперпозиция линейных функций, разложение в ряды Тейлора, Фурье и т.д.
функция. Используются также различные приближения: суперпозиция линейных функций, разложение в ряды Тейлора, Фурье и т.д.
 , зависящей от времени t, координат
, зависящей от времени t, координат 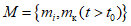 , в том числе и прогнозируемых
, в том числе и прогнозируемых  , определяющих различные явления и процессы. Прогноз этого процесса в самом общем смысле можно рассматривать как вычисление в момент времени t' > t0 значений функции
, определяющих различные явления и процессы. Прогноз этого процесса в самом общем смысле можно рассматривать как вычисление в момент времени t' > t0 значений функции  для времени t > t0 (черт. 8). В дальнейшем прогнозируемые значения функции
для времени t > t0 (черт. 8). В дальнейшем прогнозируемые значения функции 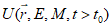 будем обозначать
будем обозначать  или бинарная
или бинарная 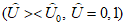 функция. Используются также различные приближения: суперпозиция линейных функций, разложение в ряды Тейлора, Фурье и т.д.
функция. Используются также различные приближения: суперпозиция линейных функций, разложение в ряды Тейлора, Фурье и т.д.
непрерывной функции  (а), дискретной функции
(а), дискретной функции  (б)
(б)
7.2.2. Как правило, процесс составления прогноза состоит из двух этапов: этап накопления исходных данных и этап выполнения прогноза, т.е. вычисление значений  для t > t', где t' - момент выпуска прогноза. Каждый прогноз имеет срок действия [tн, tк], где tн - время начала интервала, для которого составляется прогноз; tк - конец указанного интервала; [t', tн] - интервал времени рассматривается как заблаговременность прогноза; [t', t*н] - условная заблаговременность (черт. 9), т.е. интервал времени от момента выпуска прогноза до момента, когда
для t > t', где t' - момент выпуска прогноза. Каждый прогноз имеет срок действия [tн, tк], где tн - время начала интервала, для которого составляется прогноз; tк - конец указанного интервала; [t', tн] - интервал времени рассматривается как заблаговременность прогноза; [t', t*н] - условная заблаговременность (черт. 9), т.е. интервал времени от момента выпуска прогноза до момента, когда 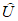 превысит значение условного порога U* (это определение используется в прогнозах развития явлений, когда для вычислений
превысит значение условного порога U* (это определение используется в прогнозах развития явлений, когда для вычислений  привлекаются измеряемые по начальной фазе события значения U).
привлекаются измеряемые по начальной фазе события значения U).
7.2.3. Одной из наиболее важных характеристик прогноза является информативность. Ее часто рассматривают как степень адекватности  прогнозируемого процесса U. Наименьшей адекватностью обладает бинарная функция
прогнозируемого процесса U. Наименьшей адекватностью обладает бинарная функция  как в плане условности прогнозируемой амплитуды процесса, так и в условности временных интервалов.
как в плане условности прогнозируемой амплитуды процесса, так и в условности временных интервалов.
 прогнозируемого процесса U. Наименьшей адекватностью обладает бинарная функция
прогнозируемого процесса U. Наименьшей адекватностью обладает бинарная функция  как в плане условности прогнозируемой амплитуды процесса, так и в условности временных интервалов.
как в плане условности прогнозируемой амплитуды процесса, так и в условности временных интервалов.
прогноза развития явлений  и
и 
7.2.4. Существует два подхода к определению периода действия прогнозов - корреляционный и спектральный. Первый подход, как правило, чаще используется для стационарных случайных процессов, имеющих монотонно убывающую автокорреляционную функцию. Временем корреляции (когерентности) Tк обычно называют отрезок времени сдвига, на котором автокорреляционная функция существенно отличается от нуля. Вне этого отрезка она почти равна нулю. Прогнозы, срок действия которых [tн, tк] <= (0,1 ... 0,2)Tк, относят к краткосрочным. Среднесрочные прогнозы относятся к области 0,2Tк < [tн, tк] <= Tк, прогнозы с [tн, tк] > Tк являются долгосрочными. Поскольку автокорреляционная функция однозначно связана со спектром процесса через преобразование Фурье, то в спектральном определении краткосрочные прогнозы учитывают высшие гармоники, долгосрочные прогнозы - только гармонические составляющие низких и инфранизких частот.
7.2.5. Рассматриваются прогнозы двух типов: однократные (для них используются в качестве исходных данных только данные наблюдений) и многократные (в число исходных данных включаются, кроме того, результаты предыдущих прогнозов). Как правило, многократные прогнозы позволяют решать задачи долгосрочного прогноза на период, значительно превышающий время Tк.
7.2.6. В методическом смысле различные виды гелиогеофизических прогнозов условно делят на два класса: аналого-вероятностный и детерминированный. Их основное отличие заключается в степени изученности природы прогнозируемых процессов. Так, например, при прогнозе случайного процесса (того или иного состояния явления, фазы и т.д.) по аналогии с наблюдавшимися ранее его реализациями или на основе имеющегося в распоряжении априорного распределения этого процесса говорят лишь о вероятности (оправдываемости) соответствия между U и  . Если же процесс достаточно изучен и состояния прогнозируемого явления вычисляются с достаточной вероятностью, в этих случаях наиболее употребим термин "точность прогноза", т.е. значение абсолютного (относительного) отклонения
. Если же процесс достаточно изучен и состояния прогнозируемого явления вычисляются с достаточной вероятностью, в этих случаях наиболее употребим термин "точность прогноза", т.е. значение абсолютного (относительного) отклонения  от U. Под надежностью прогноза для класса аналого-вероятностных методов рассматривается доверительный интервал оправдываемости состояний
от U. Под надежностью прогноза для класса аналого-вероятностных методов рассматривается доверительный интервал оправдываемости состояний  при фиксированном уровне значимости
при фиксированном уровне значимости  (
( - накопленная вероятность). Под надежностью детерминированных прогнозов понимается доверительный интервал для отклонения
- накопленная вероятность). Под надежностью детерминированных прогнозов понимается доверительный интервал для отклонения  от U при соответствующем уровне значимости
от U при соответствующем уровне значимости  .
.
 - накопленная вероятность). Под надежностью детерминированных прогнозов понимается доверительный интервал для отклонения
- накопленная вероятность). Под надежностью детерминированных прогнозов понимается доверительный интервал для отклонения 7.2.7. Особую роль при практическом использовании различных методов прогноза играют такие характеристики, как состав и объем исходных данных, их доступность в оперативном плане, адаптируемость методов к изменениям их состава и качества.
7.2.8. Таким образом, перечисленные характеристики прогнозов определяют собственно формулу прогноза:
используя следующие исходные данные за период [t0, t'] вычисляют по некоторому алгоритму прогнозируемые значения 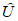 процесса U для периода [tн, tк] с заблаговременностью [t', tн];
процесса U для периода [tн, tк] с заблаговременностью [t', tн];
оправдываемость (вероятность) 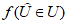 или точность
или точность 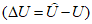 прогноза составит величину
прогноза составит величину  или
или 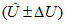 при уровне значимости
при уровне значимости 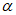 , где
, где  и
и  - доверительные интервалы.
- доверительные интервалы.
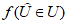 или точность
или точность 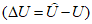 прогноза составит величину
прогноза составит величину  или
или 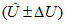 при уровне значимости
при уровне значимости Наиболее актуальной задачей является сравнение различных методов прогноза, которое в первую очередь осуществляется по характеристикам, составляющим формулу прогноза, а затем по оценкам критериев методической и практической значимости.
гелиогеофизических прогнозов
7.3.1.1. В качестве исходных данных для вычисления оценок качества аналого-вероятностных методов используются результаты прогноза и наблюдений, представленные в таблице (матрице) сопряженности {nij} (форма 25).
Для матрицы в форме 25 выполняется условие
 (124)
(124)7.3.1.2. На основе такой матрицы получают следующие основные дифференциальные оценки качества прогнозов:
вероятность i-й фазы прогноза j-го состояния процесса
fij = nij/N;
априорная вероятность j-го состояния процесса (климатологическая вероятность)

вероятность выбора i-й фазы прогноза

условная апостериорная вероятность i-й фазы прогноза, причем  ,
,
 ,
,
Прогноз считается успешным, если выполняется условие
Прогноз | Наблюдалось | Сумма | |||||
U1 | U2 | ... | Uj | ... | Um | ||
n11 | n12 | ... | n1j | ... | n1m | ||
n21 | n22 | ... | n2j | ... | n2m | ||
ni1 | ni2 | ... | nij | ... | nim | ||
. . . | |||||||
nm1 | nm2 | ... | nmj | ... | nmm | ||
Сумма | N1 | N2 | ... | Nj | ... | Nm | N |
Примечание. N - общее число наблюдений (прогнозов); N1, N2, ..., Nm - количество состояний данного процесса (U1, U2, ..., Um);  ,
,  , ...,
, ...,  - количество фаз прогнозов (
- количество фаз прогнозов ( ,
,  , ...,
, ...,  ).
).
7.3.1.3. В качестве основной интегральной оценки качества прогноза рассматривается оправдываемость
где K1 и K2 - веса смежных градаций или значений допусков, необходимых для перехода от дискретной шкалы к непрерывной.
В качестве вспомогательных интегральных оценок используются оценка точности
 (127)
(127)где 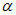 - ошибка риска (пропущенная фаза события);
- ошибка риска (пропущенная фаза события); 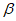 - ошибка страховки (ложный прогноз фазы события);
- ошибка страховки (ложный прогноз фазы события);
оценка предупрежденности о j-й фазе явления
П = nij/Nj. (128)
7.3.1.4. Для сравнения методов прогнозов между собой следует пользоваться мерой успешности
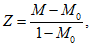 (129)
(129)где M0 - оправдываемость базового или тривиального прогноза.
7.3.1.5. В качестве единой характеристики методической значимости, в том числе и разнородных прогнозов, используется величина J, выражающая долю снятия неопределенности явления. Она является отношением меры количества информации, содержащейся в прогнозах, к мере безусловной энтропии явления
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
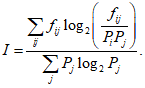 (130)
(130)7.3.1.6. Специальное место в оценке практической значимости прогнозов (оценке эффективности) занимают расчеты величины риска или расходов (доходов) R, связанные с использованием платежной матрицы потребителя прогнозов {Cij}. Средняя эффективность метода оценивается как
7.3.2.1. Для оценок методической значимости детерминированных прогнозов следует использовать величины, являющиеся производными характеристиками абсолютного отклонения 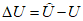 :
:
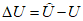 :
:относительное отклонение
 (132)
(132)среднее квадратическое отклонение предсказываемой функции 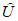 от нормы U за некоторый период наблюдений
от нормы U за некоторый период наблюдений
 (133)
(133)средняя квадратическая ошибка проверочных прогнозов
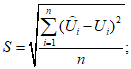 (134)
(134)относительная средняя квадратическая ошибка проверочных прогнозов
Перечисленные величины рассматриваются как характеристики точности метода, а доверительные интервалы для них определяют надежность метода при соответствующем уровне значимости.
7.3.2.2. Сравнение методов данного класса проводится, как правило, по названным характеристикам с тривиальными прогнозами. В случае отсутствия аналогичного метода, в том числе и тривиального, рекомендуется вычисление критерия A
где f2 = n - k - 1; f1 = n - 1; k - число переменных в аппроксимационном выражении
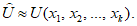 (137)
(137)Метод прогноза считается успешным, если выполняется условие
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
A(f1, f2) > F(f1, f1), (138)
где F(f1, f2) - квантиль распределения Фишера со степенями свободы f1 и f2.
Как правило, для значений f1 и f2 > 30 при A >= 2 метод оказывается достаточно полезным.
Удобным для сравнения методов прогноза между собой является коэффициент корреляции
 (139)
(139)Необходимо отметить, что  и r при нормальном распределении
и r при нормальном распределении 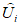 относительно Ui связаны соотношением
относительно Ui связаны соотношением
В тех случаях, когда разброс 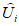 не носит нормального закона, следует пользоваться заменой типа
не носит нормального закона, следует пользоваться заменой типа 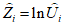 , для которой соотношение (140) будет выполняться.
, для которой соотношение (140) будет выполняться.
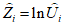 , для которой соотношение (140) будет выполняться.
, для которой соотношение (140) будет выполняться.качества различных видов гелиогеофизических прогнозов
проведения производственных испытаний
7.4.1.1. Как правило, производственные испытания гелиогеофизических прогнозов следует проводить в главном или региональных прогностических центрах гелиогеофизических служб Госгидромета СССР, располагающих необходимым числом данных наблюдений и соответствующими техническими средствами. Испытание каждого нового метода прогноза следует проводить в сравнении с используемым в данном центре.
7.4.1.2. Решение о проведении испытаний новых методов прогнозов принимается при рассмотрении научной ценности и практической значимости метода по результатам авторских испытаний на секции или Ученом совете головного НИИ - ИПГ им. академика Федорова Е.К. Прогностическое подразделение, проводящее испытания, и срок испытаний определяются планом проведения испытаний, который составляется ежегодно.
7.4.1.3. В зависимости от характеристик метода прогноза по продолжительности и заблаговременности периоды испытаний устанавливаются и оговариваются в согласованной с авторами метода программе испытаний, с учетом необходимого статистического объема реализаций прогнозируемого явления (параметра явления). При этом он должен быть не меньше природной повторяемости, в связи с чем для редко наблюдающихся явлений допускается испытание на материале оперативных данных прошлых лет, не участвовавших в разработке метода, и с имитацией условий прогноза.
При проведении испытаний методов краткосрочных прогнозов часто наблюдающихся явлений длина ряда должна составлять не менее 1/3 длины ряда, используемого при разработке метода, причем прогнозируемый параметр должен изменяться в достаточно широком диапазоне.
7.4.1.4. При сравнении разных методов прогноза одного и того же гелиогеофизического параметра необходимо выполнять следующие условия:
прогноз составляется для одних и тех же явлений с использованием одного и того же объема исходных данных (но, возможно различных по составу);
методы оценивать с применением одних и тех же критериев и статистических характеристик;
в качестве базового метода использовать метод, применяемый в прогностическом подразделении, а в случае его отсутствия - тривиальный прогноз.
7.4.1.5. Индивидуальные свойства (специфические требования и т.д.) конкретного метода, учет которых необходим при проведении испытаний, должны оговариваться в программе испытаний, согласование которой осуществляется авторами метода с прогностическим подразделением до начала испытаний.
7.4.1.6. Отчет с результатами производственных испытаний метода прогноза в месячный срок направляется прогностическими подразделениями в адрес Ученого совета (копия авторам) головного НИИ. Метод, имеющий положительные результаты и рекомендованный к внедрению ЦМКП или Ученым (техническим) советом головного НИИ (управления по гидрометеорологии), считается внедренным, если он постоянно используется в практической работе прогностического подразделения гелиогеофизических служб Госгидромета СССР.
гелиогеофизических прогнозов
7.4.2.1.1. В перечень краткосрочных прогнозов, выпускаемых гелиогеофизическими службами Госгидромета СССР, входят:
прогноз интегральных индексов солнечной активности (прогноз числа солнечных пятен W и прогноз потока радиоизлучения Солнца R на  );
);
 );
);прогноз вероятности солнечных вспышек указанного оптического балла;
прогноз степени возмущенности магнитного поля Земли;
прогноз состояния ионосферы Земли для пяти регионов территории СССР (полярная шапка, зона сияний, средние широты, юг, восток);
прогноз радиационной обстановки в околоземном космическом пространстве и на трассах пилотируемых космических аппаратов.
Перечисленные прогнозы выпускаются с заблаговременностью 7 - 8 часов на срок от одних до двух суток.
7.4.2.1.2. Для прогнозов интегральных индексов в качестве исходных используются следующие ряды данных: для прогноза W - ряды базовой обсерватории в Кисловодске, для прогноза R - ряды базовых обсерваторий Симферополя и Оттавы (Канада). Поскольку используемые для прогнозов методы относятся к классу детерминированных, постоянный контроль качества этих методов осуществляется с помощью критериев, представленных в формулах (135) и (136). При испытании новых методов следует пользоваться этими же критериями; период испытания нужно выбирать в зависимости от значений f1 и f2, а исходные данные - в указанных обсерваториях.
7.4.2.1.3. Прогноз вероятности солнечных вспышек указанного оптического балла относится к классу аналого-вероятностных методов, поэтому контроль его качества ведется по критерию (126), причем для термина "возможны вспышки указанного балла" при составлении матрицы сопряженности цена ошибки единичного прогноза равна 1/3, для термина "ожидаются вспышки указанного балла" - 2/3. В качестве исходных данных как для прогноза, так и для оценки оправдываемости используются обобщенные оперативные данные мировой сети, поступающие ежедневно из WWA Boulder. Минимальный период для оценки оправдываемости - 30 суток. Сравнение испытываемого метода рекомендуется вести по результатам анализа матрицы сопряженности с использованием критерия (125).
7.4.2.1.4. Прогноз степени возмущенности магнитного поля Земли составляется на основе рекуррентного прогноза по "коврикам" Бартельса и диагностического прогноза геоэффективности солнечных вспышек по шестибалльной шкале Ap-индекса (или Aк-индекса): 0 <= Ap <= 7; 8 <= Ap <= 14; 15 <= Ap <= 19; 20 <= Ap <= 29; 30 <= Ap <= 49; Ap >= 50. Оценивается прогноз "балл в балл" или "балл +/- 1 балл" по формуле (126), где K1 и K2 выбираются соответствующим образом. Минимальный период для оценки этих прогнозов - 30 суток. При сравнении с новым методом необходимо вычислять оценки апостериорных вероятностей для каждого балла (фазы) прогноза и проверять выполнение условия (125). В качестве Ap-индекса используется его оценка Ap (MOS), оперативно вычисляемая по четырем - шести Aк-индексам среднеширотных обсерваторий в Ленинграде, Москве, Свердловске, Подкаменной Тунгуске, Иркутске, Петропавловске-Камчатском. При анализе результатов прогноза по конкретному региону в качестве прогнозируемого параметра, как правило, используется Aк-индекс базовой обсерватории данного региона.
7.4.2.1.5. Прогноз состояния ионосферы Земли осуществляется для каждого региона на основе оценки отклонений суточного хода критических частот слоя F2 от их медианных значений по семибалльной шкале. Оценки оправдываемости должны вычисляться на основе значений {nij} матрицы сопряженности, составленной за период не менее 30 суток. Однако сравнение нового метода с базовым следует проводить за более длительный период, учитывая сезонный ход в поведении параметров ионосферы. Аналогичные требования по оценке качества прогнозов распространяются и на прогнозы параметров, характеризующих слои F1, E и ES. В тех случаях, когда новый метод относится к классу детерминированных и характеризуемых величиной 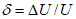 , его сравнение с базовым следует проводить по формуле (126), в которой значения K1 и K2 подбираются так, что позволяют проводить сопоставление значений оправдываемости M (иными словами, осуществляется переход от непрерывной шкалы испытываемого метода к дискретной шкале базового метода).
, его сравнение с базовым следует проводить по формуле (126), в которой значения K1 и K2 подбираются так, что позволяют проводить сопоставление значений оправдываемости M (иными словами, осуществляется переход от непрерывной шкалы испытываемого метода к дискретной шкале базового метода).
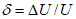 , его сравнение с базовым следует проводить по формуле (126), в которой значения K1 и K2 подбираются так, что позволяют проводить сопоставление значений оправдываемости M (иными словами, осуществляется переход от непрерывной шкалы испытываемого метода к дискретной шкале базового метода).
, его сравнение с базовым следует проводить по формуле (126), в которой значения K1 и K2 подбираются так, что позволяют проводить сопоставление значений оправдываемости M (иными словами, осуществляется переход от непрерывной шкалы испытываемого метода к дискретной шкале базового метода).7.4.2.1.6. Прогноз радиационной обстановки в околоземном космическом пространстве и на трассах пилотируемых космических аппаратов осуществляется только в главном прогностическом центре служб (ИПГ) по аналого-вероятностному методу. В качестве исходных данных используются не только данные наблюдений с ИСЗ "Метеор", но и результаты краткосрочных прогнозов вспышечной активности и возмущенности геомагнитного поля, а также результаты детерминированного прогноза развития событий солнечных космических лучей (СКЛ) и диагностического прогноза радиационных характеристик геоэффективных солнечных вспышек. По результатам окончательного прогноза составляется матрица сопряженности, в которой весь диапазон доз облучения (Д) разбит на четыре уровня (Д <= 12,5; 12,5 < Д <= 100; 100 < Д <= 1000; Д > 1000 мрад). Цены ошибок прогнозов аналогичны ценам прогноза вспышек, поскольку используются термины "возможен", "ожидается" указанный балл радиационной обстановки. Ввиду того что ухудшение радиационных условий наблюдается относительно редко, период проведения производственных испытаний определяется статистической достаточностью событий СКЛ. Для увеличения ряда с указанными условиями возможно использование данных прошлых лет, не вошедших в авторские испытания. Как правило, N в матрице сопряженности должно быть не менее 300, причем для суммы возмущенных состояний явления должно выполняться условие 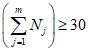 .
.
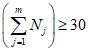 .
.Естественно, что качество данного вида прогноза зависит не только от качества данных наблюдений, но и от качества прогнозов, входящих в него в виде исходных данных. Это определяет возможность оценки практической значимости по формуле (131) для входных прогнозов.
7.4.2.2.1. Среднесрочные прогнозы возмущенности геомагнитного поля и состояния ионосферы составляют на пять суток с заблаговременностью не менее одних суток. Оба вида прогнозов по методической основе и системе оценок качества оправдываемости аналогичны краткосрочным прогнозам, поскольку прогнозы выпускаются как последовательность прогнозируемых параметров на каждые из пяти суток (либо баллы Ap-индекса, либо баллы среднего суточного отклонения критических частот от их медианных значений). Однако минимальный период проведения испытаний таких прогнозов при сравнении с базовым (применяемым в оперативной работе) методом должен быть не менее 150 суток. Это позволит обеспечить равные условия оценок качества обоих методов как по составу исходных данных, так и по идентичности наблюдавшегося спектра возмущений. Матрицы сопряженности рекомендуется составлять для каждых суток отдельно, оценки оправдываемости по критерию (126) сопоставлять с аналогичными по базовому варианту как отдельно, так и в совокупности по всем пяти суткам.
7.4.2.3.1. В настоящее время в прогностических подразделениях гелиогеофизических служб выпускаются следующие прогнозы, относящиеся к категории долгосрочных:
1) еженедельный прогноз на 27 суток с заблаговременностью одни сутки
интегральных индексов активности солнца W и R;
периодов солнечных вспышек указанного оптического балла;
периодов появления событий солнечных космических лучей (СКЛ);
периодов возмущений геомагнитного поля по трехбалльной шкале Ap-индекса (0 <= Ap <= 14; 15 <= Ap <= 29; Ap > 30);
периодов ухудшения радиационной обстановки на трассах пилотируемых космических аппаратов по четырехбалльной шкале;
2) ежемесячный прогноз на 30 - 31 сутки с заблаговременностью одни сутки
возмущенности геомагнитного поля по шестибалльной шкале Ap индекса для каждых суток;
состояния ионосферы Земли по шестибалльной шкале средних суточных отклонений критических частот слоя F2 от медианных значений для каждых суток.
7.4.2.3.2. Анализ оправдываемости прогнозов, указанных во втором пункте, выполняется аналогично анализу краткосрочных или среднесрочных прогнозов; период испытания рекомендуется выбирать на срок не менее одного года или проводить испытания на материале прошлых лет.
7.4.2.3.3. Относительно прогнозов, указанных в первом пункте, необходимо подчеркнуть, что оценки оправдываемости рассчитываются не для суточных интервалов, а для указанных периодов, причем прогноз на период считается оправдавшимся, если в этот период наблюдалось по крайней мере одно событие указанного типа (балла и т.д.). Поскольку прогнозы на 27 суток выпускаются еженедельно, то период проведения производственных испытаний должен быть не менее шести месяцев.
7.4.2.3.4. В целом качество всех видов гелиогеофизических прогнозов может в той или иной мере зависеть от фазы 11-летнего цикла солнечной активности. Именно поэтому следует проводить ежегодную оценку их качества. В случае когда успешность методов падает, следует вносить коррективы в формулу прогноза (решающие правила, аппроксимационные выражения и т.д.). Обязательность таких действий очевидна, если авторами методики указана процедура корректировки формулы прогноза. Эту особенность гелиогеофизических прогнозов необходимо оговаривать в программе испытаний.
используемые при гелиогеофизическом прогнозировании
7.5.1. Специфика проведения испытаний различных методов гелиогеофизических прогнозов в значительной мере зависит от привлекаемого математического аппарата. Его выбор для прогноза конкретного процесса прежде всего определяется степенью исследования последнего.
7.5.2. Любой гелиогеофизический процесс может быть детерминированным U = F(x) или стохастическим U = F(x) + Z, где Z - некоторая случайная величина. Если прогноз стохастического процесса составляется с использованием только априорного распределения (процесс практически не исследован, явление прогнозируется на основе распределения естественной встречаемости состояний данного процесса), то такой метод называется климатологическим. При этом его основной характеристикой оправдываемости является априорная (климатологическая) вероятность. Наличие распределения или совокупности условных распределений (процесс в некоторой степени исследован) позволяет осуществлять с апостериорной (условной) вероятностью более эффективный прогноз отдельных состояний процесса (подразумевается, что она выше, чем климатологическая). Так, известные условия отбора активных областей в атмосфере Солнца по их площади, структуре магнитных полей, предшествующей вспышечной активности увеличивают вероятность "протонных" вспышек в два, три раза по сравнению с априорной вероятностью.
7.5.3. В задачах разработки прогноза детерминированных процессов в качестве тривиальных рассматриваются инерционный и линейный прогнозы. Если некоторый процесс U = F(t) разложить в ряд Тейлора в окрестности t0
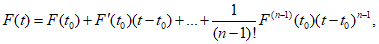 (141)
(141)то прогноз с использованием первого члена разложения представляет собой инерционный прогноз, а с использованием двух первых членов - линейный прогноз. Такой прием часто используется для прогноза процессов, описываемых монотонными функциями изменения чисел Вольфа, фонового потока радиоизлучения Солнца и т.д. По аналогии для квазигармонических процессов (например, для прогноза 11-летнего цикла солнечной активности, суточного хода магнитного поля Земли) применяется разложение в ряд Фурье
 (142)
(142)7.5.4. Методы прогноза развития явлений базируются на процедуре экстраполяции характеристики процесса U, причем в качестве  обычно пользуются либо самим видом U, либо его приближением в виде суперпозиций элементарных функций. При прогнозе развития солнечных протонных событий в качестве
обычно пользуются либо самим видом U, либо его приближением в виде суперпозиций элементарных функций. При прогнозе развития солнечных протонных событий в качестве 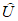 наиболее часто выбирают тот класс функций U, который является решением уравнения переноса протонов (СКЛ) в межпланетной среде.
наиболее часто выбирают тот класс функций U, который является решением уравнения переноса протонов (СКЛ) в межпланетной среде.
Важное место в задачах разработки методов прогноза занимает аппарат автокорреляционного анализа. Он весьма эффективно работает для квазипериодических процессов, таких как рекуррентные геомагнитные возмущения, "активные долготы" Солнца.
7.5.5. Класс методов диагностического прогноза базируется на исследованиях различных проявлений одного и того же процесса, содержащего быстрый и медленный компоненты, между которыми имеется связь. Тогда изменения любого из них позволяют прогнозировать другой. Примером такого метода служит прогноз элементов радиационной обстановки в околоземном космическом пространстве от протонов СКЛ (медленный компонент) по характеристикам электромагнитного излучения солнечных вспышек (быстрый компонент). Основным элементом методов диагностического прогноза является задача поиска связи между измеряемым и прогнозируемым компонентами. В самом общем смысле ее рассматривают как задачу "черного ящика", на входе которого имеются входные параметры 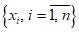 , множество случайных параметров
, множество случайных параметров  и набор выходных параметров
и набор выходных параметров 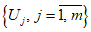 .
.
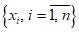 , множество случайных параметров
, множество случайных параметров  и набор выходных параметров
и набор выходных параметров 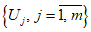 .
.7.5.5.1. Поиск конкретного математического выражения  соответствует первому этапу метода - диагнозу состояния процесса; элементы прогноза определяются на этапе оценки времени возможного упреждения в вычислении
соответствует первому этапу метода - диагнозу состояния процесса; элементы прогноза определяются на этапе оценки времени возможного упреждения в вычислении  и, как правило, условны. Именно поэтому заблаговременность таких прогнозов бывает переменной, а сами прогнозы носят название текущих.
и, как правило, условны. Именно поэтому заблаговременность таких прогнозов бывает переменной, а сами прогнозы носят название текущих.
 соответствует первому этапу метода - диагнозу состояния процесса; элементы прогноза определяются на этапе оценки времени возможного упреждения в вычислении
соответствует первому этапу метода - диагнозу состояния процесса; элементы прогноза определяются на этапе оценки времени возможного упреждения в вычислении 7.5.5.2. Исследование количественных связей ведут в рамках многомерных регрессионных моделей: общей линейной или квадратичной модели МНК (метод главных компонентов, метод дискриминантного анализа) в n-мерном пространстве признаков (предикторов), для которого существуют наборы реализаций входных и выходных значений процесса. Вид функции 
 (143)
(143)критерием качества исследуемой связи (решающего правила) служит математическое ожидание функции риска (штрафа) 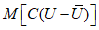 , где в качестве риска выбран квадрат ошибки
, где в качестве риска выбран квадрат ошибки 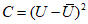 . Процедура построения решающего правила сводится к определению вектора {bij}, реализующего
. Процедура построения решающего правила сводится к определению вектора {bij}, реализующего 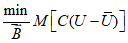 . При этом задача исключения неинформативных предикторов формулируется как выбор из заданного множества
. При этом задача исключения неинформативных предикторов формулируется как выбор из заданного множества  такого подмножества
такого подмножества 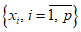 , где p < n, которое обеспечивает требуемую точность прогнозирования.
, где p < n, которое обеспечивает требуемую точность прогнозирования.
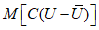 , где в качестве риска выбран квадрат ошибки
, где в качестве риска выбран квадрат ошибки 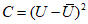 . Процедура построения решающего правила сводится к определению вектора {bij}, реализующего
. Процедура построения решающего правила сводится к определению вектора {bij}, реализующего 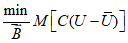 . При этом задача исключения неинформативных предикторов формулируется как выбор из заданного множества
. При этом задача исключения неинформативных предикторов формулируется как выбор из заданного множества 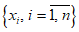 такого подмножества
такого подмножества 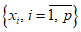 , где p < n, которое обеспечивает требуемую точность прогнозирования.
, где p < n, которое обеспечивает требуемую точность прогнозирования.Реализованная процедура исключения предикторов преобразует обобщенную регрессивную модель в адаптивную.
Методы прогноза, основанные на аппарате моделей МНК, оказываются весьма удобными, поскольку позволяют решать задачи поиска не только качественных, но и количественных связей.
7.5.6. Мощным аппаратом для задач диагностического прогноза являются методы распознавания, позволяющие производить классификацию явлений (объектов), т.е. накапливать априорную информацию и сопоставлять ее с апостериорной. Как правило, система распознавания приспособлена для распознавания только данного вида явлений по набору предикторов, среди которых рассматриваются детерминированные (принимающие конкретные числовые значения), вероятностные (измерения проводятся с большими ошибками), логические ("да", "нет", "О", "1") и структурные. Системы распознавания подразделяются на простые (одноуровневые) и сложные (многоуровневые), без обучения и самообучающиеся.
7.5.6.1. Системы распознавания имеют различную интерпретацию: геометрическую, алгебраическую и т.д. Пусть в априорном словаре признаков содержится набор параметров явлений  (априорное признаковое пространство размерности n), и произведено разбиение явлений на классы
(априорное признаковое пространство размерности n), и произведено разбиение явлений на классы  . Тогда для получения решающего правила требуется выделить в пространстве признаков области
. Тогда для получения решающего правила требуется выделить в пространстве признаков области 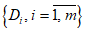 , эквивалентные классам, т.е. характеризуемые необходимой зависимостью: если явление с признаками
, эквивалентные классам, т.е. характеризуемые необходимой зависимостью: если явление с признаками  относится к классу
относится к классу 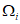 , то представляющая его в признаковом пространстве точка принадлежит области Di. Для алгебраической трактовки решающее правило сводится к построению разделяющих функций
, то представляющая его в признаковом пространстве точка принадлежит области Di. Для алгебраической трактовки решающее правило сводится к построению разделяющих функций 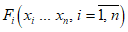 , обладающих следующими свойствами: если явление, имеющее признаки
, обладающих следующими свойствами: если явление, имеющее признаки 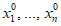 , относится к классу
, относится к классу 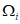 , то значение
, то значение 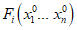 должно быть наибольшим. Таким оно должно быть и для всех других значений признаков явлений, относящихся к классу
должно быть наибольшим. Таким оно должно быть и для всех других значений признаков явлений, относящихся к классу 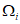 . Если вектор признаков явлений, принадлежащий к
. Если вектор признаков явлений, принадлежащий к  , обозначить xq, то для всех значений вектора
, обозначить xq, то для всех значений вектора 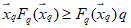 , g = 1 ... m,
, g = 1 ... m, 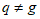 . Таким образом, в признаковом пространстве системы распознавания граница разбиений, называемая решающей границей между областями Di, соответствующими классам
. Таким образом, в признаковом пространстве системы распознавания граница разбиений, называемая решающей границей между областями Di, соответствующими классам  , выражается уравнением
, выражается уравнением
 (априорное признаковое пространство размерности n), и произведено разбиение явлений на классы
(априорное признаковое пространство размерности n), и произведено разбиение явлений на классы 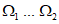 . Тогда для получения решающего правила требуется выделить в пространстве признаков области
. Тогда для получения решающего правила требуется выделить в пространстве признаков области 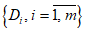 , эквивалентные классам, т.е. характеризуемые необходимой зависимостью: если явление с признаками
, эквивалентные классам, т.е. характеризуемые необходимой зависимостью: если явление с признаками 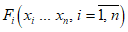 , обладающих следующими свойствами: если явление, имеющее признаки
, обладающих следующими свойствами: если явление, имеющее признаки 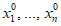 , относится к классу
, относится к классу 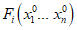 должно быть наибольшим. Таким оно должно быть и для всех других значений признаков явлений, относящихся к классу
должно быть наибольшим. Таким оно должно быть и для всех других значений признаков явлений, относящихся к классу  , обозначить xq, то для всех значений вектора
, обозначить xq, то для всех значений вектора 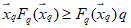 , g = 1 ... m,
, g = 1 ... m,  (144)
(144)7.5.7. В последние годы успешно развиваются некоторые области технической кибернетики, основанные на теории эвристической самоорганизации. Авторы успешно соединяют регрессионный анализ с теорией статических решений в соответствии с некоторыми новыми принципами. Одним из таких принципов является принцип внешних дополнений, число которых не должно быть меньше решаемых вопросов (целей). Например, поиск уравнений для получения оптимальных оценок коэффициентов (первая цель) обычно использует критерий минимума средней квадратической ошибки в узлах интерполяции (обучающей последовательности). Для второй цели - получения уравнений, обладающих хорошими прогнозирующими свойствами, - уже требуется второй критерий, например минимум средней квадратической ошибки, определяемой на другом множестве точек (поверочной последовательности). Для третьей цели - оптимизации разделения имеющихся точек на указанные выше две последовательности - требуется дополнительный критерий (критерий минимума ошибки) на еще одном множестве точек (экзаменационной последовательности) и т.д.
Под термином самоорганизация в широком смысле слова обычно понимается происходящий под действием внешней среды процесс самопроизвольного (спонтанного) увеличения порядка, или организации в системе, состоящей из многих элементов. Математической мерой порядка и организации может быть величина, обратная энтропии, и следовательно, процесс самоорганизации связан с уменьшением энтропии.
При реализации принципов эвристической самоорганизации многорядный регрессионный анализ принимает форму полиномиальных алгоритмов Метода Группового Учета Аргументов (МГУА), а многорядная теория статистических решений - вероятностных алгоритмов МГУА. В их основу положены наиболее общие алгоритмы природы: многорядная селекция, эволюция и адаптация сложных систем. В силу этого любая задача прогноза состояний системы сводится к указанию критерия селекции, состава возможных переменных и перечня опорных функций.
Одним из главных преимуществ алгоритмов МГУА в отличие от алгоритмов распознавания образов, где реализуется выбор единственного решения - жесткое (детерминированное) управление поиска оптимальных связей, является возможность отбора на каждом ряде селекции множества решений, близких к оптимальному.
7.5.8. Вышеизложенные методологические аспекты гелиогеофизического прогнозирования определяют в целом процедуру проведения испытаний методов: в первую очередь это классификация метода как в плане формулы прогноза, так и в плане обеспеченности метода составом и объемом оперативных данных, наличия необходимых технических средств. Далее должен быть определен набор наиболее пригодных критериев оценки качества и надежности метода, установлены сроки проведения испытаний с целью получения достаточного статистического материала и оценена технологичность метода в целом.
1. | УТВЕРЖДЕН | Комитетом гидрометеорологии при Кабинете Министров СССР 25 января 1991 г. |
2. | Разработчики | Г.С. Булдовский Г.К. Веселова Р.М. Вильфанд М.Ю. Бардин В.И. Корень В.А. Волженков В.М. Пасов В.П. Зинченко А.А. Исаев С.Г. Фролов Н.И. Канцерская |
3. | ОДОБРЕН | Центральной методической комиссией по гидрометеорологическим прогнозам Госгидромета СССР 25 октября 1990 г. |
4. | ЗАРЕГИСТРИРОВАН | ЦКБ ГМП 13 февраля 1991 г. |
5. | ВЗАМЕН | Методических указаний по проведению оперативных испытаний новых методов гидрометеорологических прогнозов 1977 г. и Временных указаний по проведению оперативных испытаний методов долгосрочных прогнозов погоды, 1983 г. |
ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
Обозначение НТД, на который дана ссылка | Номер пункта, подпункта | |
Положение об испытании и внедрении новых и усовершенствованных методов (способов) гидрометеорологических и гелиогеофизических прогнозов и расчетов. - М.: Гидрометеоиздат, 1989. - 11 с. | ||
Методические указания по проведению оперативных испытаний новых методов гидрометеорологических прогнозов. - Л.: Гидрометеоиздат, 1977. - 100 с. | ||
Временные указания по проведению оперативных испытаний методов долгосрочных прогнозов погоды/Под ред. А.П. Жидикова. - М.: Гидрометцентр СССР, 1983 - 19 с. | ||
Наставление по службе прогнозов. Раздел 2. Ч. III, IV, V. - М.: Гидрометеоиздат, 1981. - 56 с. | ||
Руководство по краткосрочным прогнозам погоды. Ч. I. - Л.: Гидрометеоиздат, 1986. - 702 с. | ||
Метеорологическое обеспечение международной аэронавигации. Приложение 3 ИКАО. - 10-е изд. - 1986. - 91 с. | ||
Наставление по метеорологическому обеспечению гражданской авиации СССР (НМО ГА-90). - Л.: Гидрометеоиздат, 1990. - 104 с. | ||
WMO Tropical Cyclone Project, Sub-Project N 6. Operational techniques for forecasting tropical cyclone intensity and movement. - WMO pap. - 1979. - N 528. | ||
Груза Г.В., Ранькова Э.Я. Вероятностные метеорологические прогнозы. - Л.: Гидрометеоиздат, 1983. - 271 с. | ||
Наставление по службе прогнозов. Раздел 3. Ч. I. Служба гидрологических прогнозов. Прогнозы режима вод суши. - Л.: Гидрометеоиздат, 1962. - 193 с. | ||
Наставление по службе прогнозов. Раздел 3. Ч. III. Служба морских гидрологических прогнозов. - Л.: Гидрометеоиздат, 1982. - 143 с. | ||
Методические рекомендации по прогнозу лавин в СССР. - М.: Гидрометеоиздат, 1989. | ||
Гляциологический словарь. - Л.: Гидрометеоиздат, 1984. - 527 с. | ||
Жигульский А.А. Методические аспекты количественной оценки надежности и эффективности противолавинных мероприятий и сооружений//Труды II Всесоюз. совещания по лавинам. - Л.: Гидрометеоиздат, 1987. - С. 294 - 304. | ||