СПРАВКА
Источник публикации
Киев: НИИСК Госстроя СССР, 1983
Примечание к документу
Название документа
"Методические рекомендации по расчету сборно-монолитных конструкций по предельным состояниям"
(одобрены Протоколом НИИСК Госстроя СССР от 18.05.1983 N 14)
"Методические рекомендации по расчету сборно-монолитных конструкций по предельным состояниям"
(одобрены Протоколом НИИСК Госстроя СССР от 18.05.1983 N 14)
Содержание
Протоколом НИИСК Госстроя СССР
от 18 мая 1983 г. N 14
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ СБОРНО-МОНОЛИТНЫХ КОНСТРУКЦИЙ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
Одобрены секцией N 1 Научно-технического совета НИИСК Госстроя СССР, Протокол N 14 от 18 мая 1983 года.
Даны рекомендации по расчету прочности, трещиностойкости и деформативности внецентренно сжатых, внецентренно растянутых и изгибаемых сборно-монолитных стержневых конструкций. В качестве иллюстрации даны примеры расчета. Проведено сопоставление расчетных данных, полученных по предлагаемым формулам и нормативной методике, с опытными. Настоящие методические рекомендации распространяются на тяжелый бетон, мелкозернистый бетон и легкий бетон плотной структуры.
Рассчитаны на инженеров-проектировщиков, студентов вузов и факультетов строительного профиля.
Разработаны д-ром техн. наук А.Б. Голышевым (НИИСК Госстроя СССР) и кандидатами техн. наук В.П. Полищуком (Курский ПИ), Я.Г. Сунгатуллиным (Казанский ИСИ), В.Ф. Усмановым (СамГАСИ), А.В. Харченко (НИИСК Госстроя СССР).
Отзывы и замечания направлять по адресу: 252180 Киев, И. Клименко, 5/2, НИИСК Госстроя СССР, лаборатория теории расчета железобетонных конструкций.
1.1. В настоящих методических рекомендациях рассматриваются сборно-монолитные конструкции, состоящие из заранее изготовленных преднапряженных сборных элементов (рассчитаны на восприятие нагрузок, возникающих в период строительства) и дополнительно уложенных на месте использования конструкции монолитного бетона и арматуры (рис. 1).

1 - преднапряженные сборные элементы; 2 - монолитный бетон
1.2. Сборно-монолитные конструкции должны удовлетворять требованиям расчета по прочности, по образованию и раскрытию трещин и по деформациям.
Расчет производится для двух стадий работы конструкции:
а) до приобретения монолитным бетоном заданной прочности - на нагрузки, действующие на данном этапе возведения конструкции (в т.ч. нагрузку от собственного веса сборных элементов и монолитного бетона);
б) после приобретения монолитным бетоном заданной прочности - на нагрузки, действующие на этом этапе возведения и эксплуатации конструкции.
До приобретения монолитным бетоном заданной прочности расчет сборно-монолитных конструкций выполняется по [12], после - в соответствии с настоящими методическими рекомендациями.
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
2.1. Расчет сборно-монолитных конструкций по прочности производится для сечений, нормальных к продольной оси и наклонных наиболее опасного направления, а также для контактного слоя между сборными элементами и монолитным бетоном.
к продольной оси конструкции
2.2. Определение предельных усилий в нормальных сечениях производится исходя из следующих предпосылок:
в расчет вводится "приведенный" бетон с прочностными и деформативными характеристиками, зависящими от предельной сжимаемости исходных бетонов, геометрии и компоновки сечения;
связь между напряжениями и деформациями "приведенного" бетона, а также напряжениями и деформациями арматурной стали принимается в виде диаграмм рис. 2;
для средних деформаций "приведенного" бетона и арматуры считается справедливой гипотеза плоских сечений;
в качестве расчетного принимается сечение со средней высотой сжатой зоны x, соответствующей средним деформациям;
сопротивление расчетного сечения считается исчерпанным, если деформации крайних сжатых волокон "приведенного" бетона или растянутой арматуры достигают предельных значений.
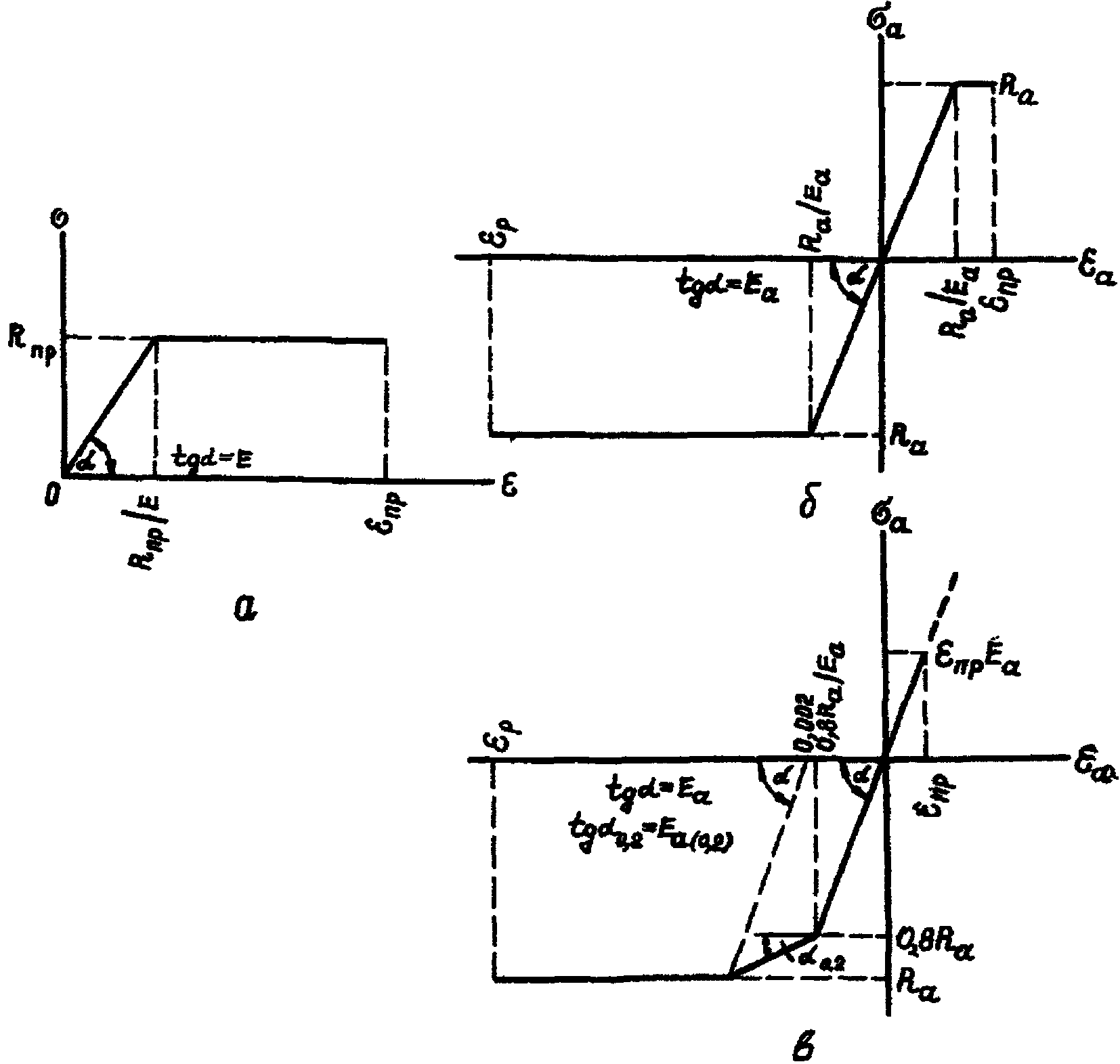
а - для "приведенного" бетона; б - для арматурной стали,
имеющей физический предел текучести; в - для арматурной
стали, не имеющей физического предела текучести
Эпюра нормальных напряжений в бетоне сжатой зоны расчетного сечения имеет вид прямоугольной трапеции с высотой участка постоянных напряжений, равной  , где (см. рис. 2, а):
, где (см. рис. 2, а):
при 

 (1)
(1)при 
 (2)
(2)призменная прочность в случае внецентренного сжатия при eб < eб.я
 (3)
(3)призменная прочность в случае внецентренного сжатия и растяжения при eб >= eб.я и в случае изгиба
модуль упругости
коэффициент пластичности "приведенного" бетона
где S и Sм - статические моменты площади соответственно всей сжатой зоны сечения конструкции и монолитной части указанной зоны относительно нулевой линии при  ;
;
 ;
;eб - расстояние от центра тяжести приведенного сечения конструкции (приведение по прочности арматуры и монолитного бетона к бетону сборных элементов) до точки приложения силы N;
eб.я - то же, до ядровой точки, наиболее удаленной от растянутого (наименее сжатого) края сечения.
При арматурной стали, не имеющей физического предела текучести,
 (7)
(7)а при имеющей физический предел текучести
где nам = Eа/Eм;
Для определения модулей упругости Eс, Eм и E можно пользоваться также табл. 1, а коэффициента  - табл. 2.
- табл. 2.
Вид бетона | Расчетный модуль упругости (Eс, Eм, E) 10-3 при классе бетона по прочности на сжатие | |||||||||||||
B7,5 | B10 | B12,5 | B15 | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 | ||
Тяжелый | Естественного твердения | - | - | 13,0 | 14,5 | 16,5 | 18,0 | 20,0 | 21,1 | 21,8 | 22,8 | 23,3 | 23,6 | 23,9 |
Подвергнутый тепловой обработке при атмосферном давлении | - | - | 12,0 | 13,0 | 14,5 | 16,0 | 18,0 | 19,0 | 19,7 | 20,3 | 20,8 | 21,1 | 21,4 | |
Мелкозернистый | Вида А естественного твердения | - | - | 10,7 | 12,0 | 13,3 | 14,5 | 16,0 | 17,0 | 17,7 | - | - | - | - |
Вида А, подвергнутый тепловой обработке при атмосферном давлении | - | - | 9,7 | 10,5 | 12,0 | 13,0 | 14,0 | 14,8 | 15,5 | - | - | - | - | |
Вида Б естественного твердения | - | - | 9,7 | 10,5 | 12,0 | 13,0 | 14,0 | - | - | - | - | - | - | |
В зависимости от марки до плотности (объемной массе) | ||||||||||||||
Легкий | D 1400 | 5,7 | 6,2 | 6,6 | 7,0 | 7,7 | 8,4 | - | - | - | - | - | - | - |
D 1800 | 7,2 | 7,8 | 8,4 | 9,0 | 10,1 | 10,8 | 11,5 | 12,1 | 12,6 | - | - | - | - | |
D 2200 | - | 10,5 | 10,5 | 11,0 | 12,2 | 13,3 | 14,0 | 14,5 | 15,0 | - | - | - | - | |
Вид бетона | Коэффициент | ||||||||||||
B7,5 | B10 | B12,5 | B15 | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 | |
Тяжелый | - | 0,85 | 0,83 | 0,81 | 0,76 | 0,73 | 0,68 | 0,64 | 0,62 | 0,60 | 0,57 | 0,54 | 0,51 |
Мелкозернистый | - | 0,75 | 0,72 | 0,70 | 0,65 | 0,60 | 0,55 | 0,50 | 0,48 | 0,45 | - | - | - |
Легкий (ориентировочно) | 0,5 | 0,47 | 0,44 | 0,40 | 0,33 | 0,28 | 0,21 | 0,15 | - | - | - | - | - |
2.4. Расчетные значения деформаций предельной растяжимости арматурной стали  допускается принимать равными при:
допускается принимать равными при:
проволочной арматуре .................... 0,01
то же, стержневой ....................... 0,02
При высокопрочной арматурной стали классов А-IV, Ат-IV, А-V, Ат-V, Ат-VI, В-II, Вр-II и К-7 в случае соблюдения условия  расчетное сопротивление арматуры Rа умножается на коэффициент условий работы mа4 [12], где при арматурной стали, не имеющей физического предела текучести,
расчетное сопротивление арматуры Rа умножается на коэффициент условий работы mа4 [12], где при арматурной стали, не имеющей физического предела текучести,
 (9)
(9)а при имеющей физический предел текучести
 (10)
(10)здесь nа = Eа/E.
Внецентренно сжатые конструкции
2.5. Расчет прочности конструкций произвольного сечения с одной осью симметрии, когда внешняя сила действует в плоскости симметрии (рис. 3, б), производится из условия
высота сжатой зоны и напряжения в арматуре определяются в результате совместного решения уравнений
где Fпл и Sпл - соответственно площадь сжатой части сечения, работающей в пластической стадии, и статический момент указанной части относительно центра тяжести сечения стержней наиболее растянутого (наименее сжатого) ряда продольной арматуры;
Sупр и Jупр - статический момент и момент инерции сжатой части сечения, работающей в упругой стадии, относительно нулевой линии;
Sаi - статический момент площади сечения i-го ряда продольной арматуры относительно центра тяжести сечения стержней наиболее растянутого (наименее сжатого) ряда указанной арматуры;
Примечание. При h0i - x > 0 в уравнении (14) ставится знак "плюс", при h0i - x <= 0 - "минус".
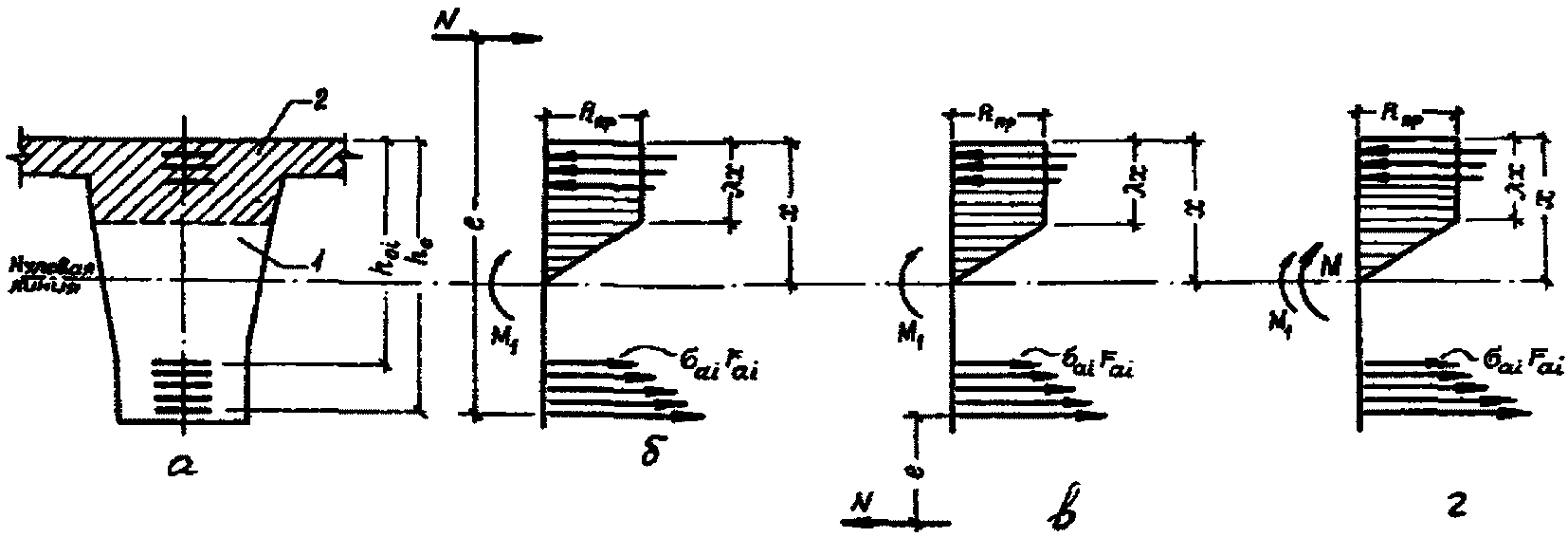
с одной осью симметрии
а - поперечное сечение; б - схема усилий и эпюра напряжений
при внецентренном сжатии; в - то же, при внецентренном
растяжении; г - то же, при изгибе; 1 - площадь сжатой
части сечения, работающей в упругой стадии;
2 - то же, в пластической
Порядок расчета принимается следующий:
а) задается начальное значение высоты сжатой зоны сечения и при заданном значении x вычисляются характеристики Fпл и Sупр;
б) по формуле (13) определяются напряжения в арматуре. Если при этом для стержней из стали, не имеющей физического предела текучести, не соблюдается условие  , напряжения в указанных стержнях пересчитываются по формуле (14). В тех случаях, когда вычисленные по этой формуле напряжения превышают предельное сопротивление Rаi, принимается
, напряжения в указанных стержнях пересчитываются по формуле (14). В тех случаях, когда вычисленные по этой формуле напряжения превышают предельное сопротивление Rаi, принимается  .
.
 , напряжения в указанных стержнях пересчитываются по формуле (14). В тех случаях, когда вычисленные по этой формуле напряжения превышают предельное сопротивление Rаi, принимается
, напряжения в указанных стержнях пересчитываются по формуле (14). В тех случаях, когда вычисленные по этой формуле напряжения превышают предельное сопротивление Rаi, принимается  .
.Для стержней из стали, имеющей физический предел текучести, должно соблюдаться условие  , в противном случае принимается
, в противном случае принимается  ;
;
 , в противном случае принимается
, в противном случае принимается  ;
;в) проверяется условие (12). Если это условие не выполняется, принимается новое значение x и расчет повторяется до тех пор, пока оно не будет выполняться с заданной точностью;
для арматурной стали, не имеющей физического предела текучести, при 

 (16)
(16)для арматурной стали, не имеющей физического предела текучести, при  , а также для стали с физическим пределом текучести
, а также для стали с физическим пределом текучести
 , а также для стали с физическим пределом текучести
, а также для стали с физическим пределом текучести (17)
(17)если рассматриваемое условие не выполняется, расчет повторяется с учетом замены в выражениях (11) - (14)  на
на
 (18)
(18)д) проверяется неравенство (11).
2.6. Расчет прочности конструкций произвольного сечения при любых внешних усилиях (общий случай см. на рис. 4) производится из условия (11), где
e - расстояние от точки приложения силы N до оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения наиболее растянутого (наименее сжатого) стержня продольной арматуры;
Sпл - статический момент площади сжатой части сечения, работающей в пластической стадии, относительно указанной выше оси;
Sаi - статический момент площади сечения i-го стержня продольной арматуры относительно той же оси;
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
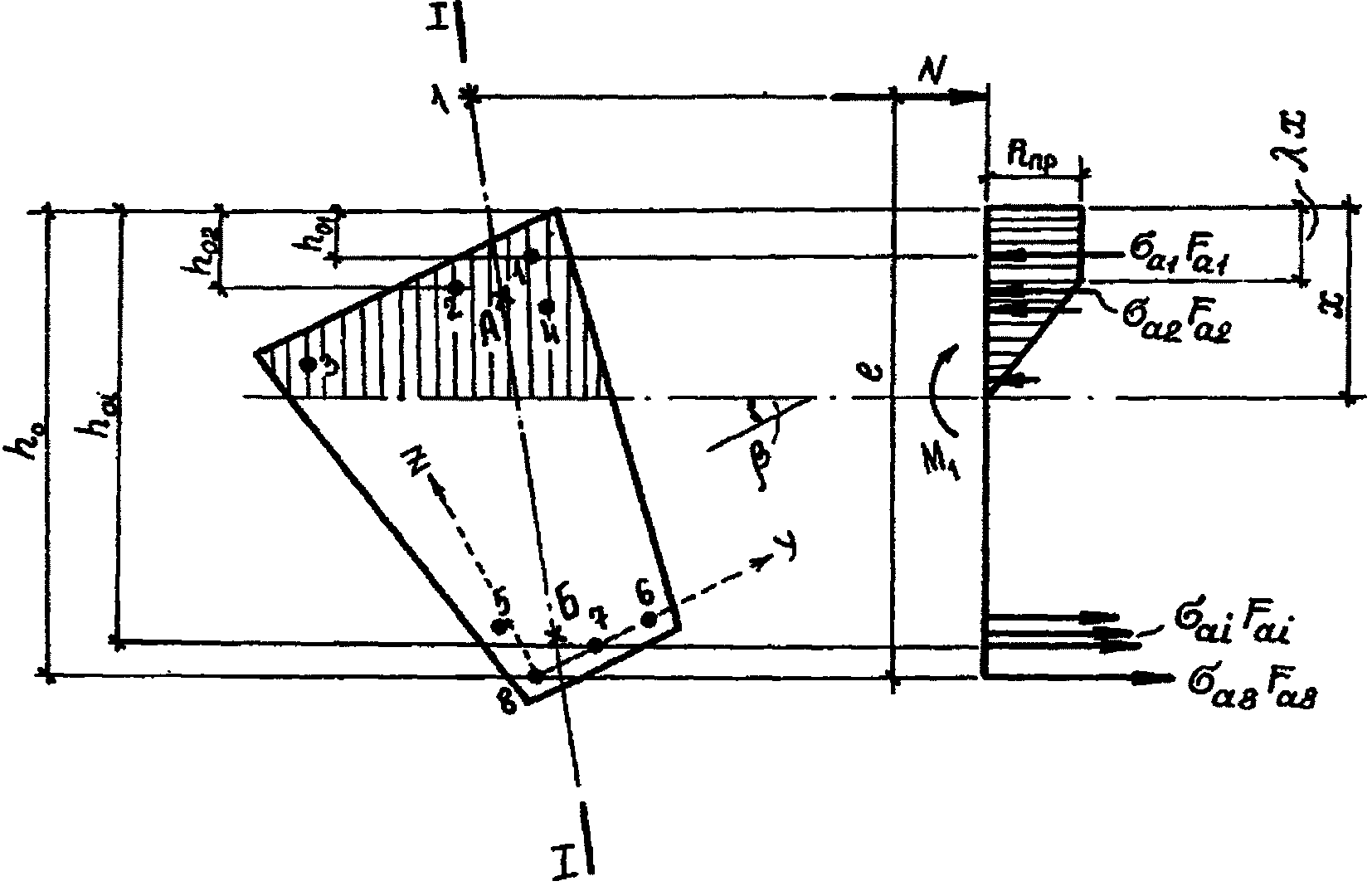
формы на косое внецентренное сжатие (общий случай)
1 - точка приложения продольной силы N; А - точка приложения
равнодействующей усилий в сжатой арматуре и в бетоне
сжатой зоны; Б - точка приложения равнодействующей усилий
в растянутой арматуре; I-I - плоскость, проходящая
через точки приложения продольной силы и равнодействующих
внутренних сжимающих и растягивающих усилий;
1 - 8 - арматурные стержни
Высота сжатой зоны и напряжения в арматуре определяются в результате совместного решения уравнений (12) - (14) и дополнительного условия
обеспечивающего расположение внешней продольной силы и равнодействующих внутренних сжимающих и растягивающих усилий в одной плоскости (см. рис. 4, плоскость I-I).
В формуле (19):
Y и Z - координаты точки приложения продольной силы относительно взаимно перпендикулярных осей, проходящих через центр тяжести сечения наиболее растянутого (наименее сжатого) стержня;
YА и ZА - координаты точки приложения равнодействующей усилий в сжатой арматуре и в бетоне сжатой зоны относительно тех же осей;
YБ и ZБ - то же, усилий в растянутой арматуре.
Порядок расчета:
а) задаются начальные значения высоты сжатой зоны сечения x и угла наклона нулевой линии  и при заданных значениях вычисляются характеристики Fпл и Sупр;
и при заданных значениях вычисляются характеристики Fпл и Sупр;
б) см. с. 9;
в) проверяются условия (12) и (14). Если они не выполняются, принимаются новые значения x и  и расчет повторяется до тех пор, пока все указанные выше условия не будут выполняться с заданной точностью;
и расчет повторяется до тех пор, пока все указанные выше условия не будут выполняться с заданной точностью;
Внецентренно растянутые конструкции
2.7. Расчет по прочности конструкций произвольного сечения с одной осью симметрии, когда внешняя сила действует в плоскости оси симметрии (см. рис. 3, в), производится по формулам (11) - (15) с учетом замены в уравнении (12) величины N на -N. При этом должно выполняться условие
 (20)
(20)Если указанное условие не выполняется, расчет производится по формулам СНиП II-21-75.
2.8. Расчет прочности конструкций в общем случае производится из условия (11). Высота сжатой зоны и напряжения в арматуре определяются в результате совместного решения уравнений (12) - (14) с учетом замены в уравнении (12) величины N на -N и дополнительного условия (19).
Порядок расчета изложен в п. 2.6.
Изгибаемые конструкции
2.9. Расчет по прочности конструкций произвольного сечения с одной осью симметрии, когда внешняя сила действует в плоскости оси симметрии (см. рис. 3, г), производится по формулам (11) - (15) с учетом замены в неравенстве (11) величины Ne на M. В уравнении (12) принимается N = 0.
2.10. Расчет по прочности конструкций в общем случае производится из условия (11) с учетом замены Ne на M. Высота сжатой зоны и напряжения в арматуре определяются в результате совместного решения уравнений (12) - (14), полагая в выражении (12) N = 0, и дополнительного условия
обеспечивающего параллельность плоскости действия моментов внешних и внутренних сил, в котором  - угол наклона плоскости действия изгибающего момента относительно оси Z.
- угол наклона плоскости действия изгибающего момента относительно оси Z.
Порядок расчета:
а) и б) см. п. 2.6;
в) проверяются условия (12) и (21). Если эти условия не выполняются, принимаются новые значения x и  и расчет повторяется до тех пор, пока все указанные выше условия не будут выполняться с заданной точностью;
и расчет повторяется до тех пор, пока все указанные выше условия не будут выполняться с заданной точностью;
г) и д) см. п. 2.6.
к продольной оси конструкции
2.11. При расчете <*> по прочности наклонных сечений должно выполняться условие
где при поперечной арматуре в виде вертикальных стержней (хомутов)
kп1 = 1 + 5nаFx/bux; (23)
при поперечной арматуре в виде наклонных (отогнутых), расположенных под углом 45° к продольной оси конструкции, стержней
--------------------------------
<*> См. Постановление Госстроя СССР от 10 января 1983 г. N 3 "Об изменении главы СНиП II-21-75 "Бетонные и железобетонные конструкции".
Коэффициент kб1 определяется по формуле
kб1 = 1 - 0,006Rпр. (25)
Примечание. В формулах (22) - (24) и во всех последующих в разд. 2 принято: b - ширина прямоугольного сечения или ширина ребра таврового и двутаврового сечений конструкции; при переменной величине b по высоте конструкции в формулы вводится ширина конструкции на уровне середины высоты сечения (без учета полок). Для конструкций с поперечной арматурой рабочую высоту сечения h0 допускается отсчитывать от центра тяжести сечения крайнего продольного ненапрягаемого стержня, анкерующего поперечные стержни (хомуты).
2.12. При расчете по прочности наклонных сечений предельные усилия определяются исходя из следующих предпосылок:
в расчет вводится "приведенный" бетон (см. п. 2.2);
в качестве расчетной принимается схема рис. 5;
связь между напряжениями и деформациями арматурной стали принимается в виде диаграмм рис. 2, б, в; связь между нормальными напряжениями и продольными деформациями "приведенного" бетона - в виде диаграммы рис. 2, а; между касательными напряжениями и деформациями сдвига - в виде диаграммы рис. 6, где при a/h0 <= 2 Rсд = 0,5Rпр, а при a/h0 >= 2,5 соответственно Rсд = 2,2Rр - расчетного сопротивления "приведенного" бетона осевому растяжению (для 2 < a/h0 < 2,5 численные значения Rсд находятся по интерполяции):
для средних деформаций "приведенного" бетона и арматуры на участках между ближайшими к сечению I-I трещинами считается справедливой гипотеза плоских сечений;
считается, что эпюра касательных напряжений в бетоне сжатой зоны сечения I-I ограничивается квадратной параболой с максимальной ординатой, расположенной на уровне вершины наклонной трещины;
напряжения в поперечной арматуре, пересекаемой наклонной трещиной, принимаются равными расчетному сопротивлению Rаx;
в расчет вводится поперечное усилие в продольной растянутой арматуре в месте пересечения ее наклонной трещиной (нагельная сила Qа);
сопротивление расчетного наклонного сечения считается исчерпанным, если деформации "приведенного" бетона в сечении I-I над наклонной трещиной по направлению главных сжимающих напряжений достигают предельных значений.

сечений (lоп - длина участка опирания конструкции),
для плоского напряженного состояния
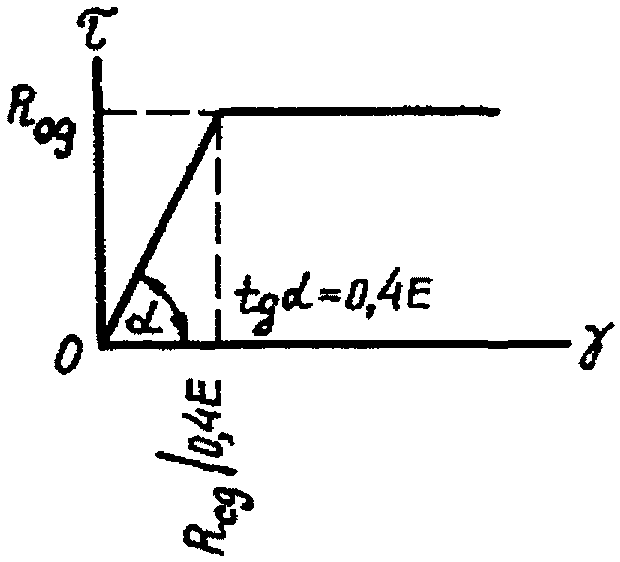
2.13. Расчетные значения коэффициента пластичности "приведенного" бетона  определяются по формуле
определяются по формуле
 (26)
(26)коэффициент k - по графикам рис. 7 при
 (27)
(27)
Значение  расшифровано в п. 2.3.
расшифровано в п. 2.3.
2.14. При расчете статически определимых конструкций в качестве расчетных наклонных трещин рассматриваются:
при действии равномерно распределенной нагрузки - трещины с вершинами, расположенными на расстоянии от осей опор a = 0,25l (рис. 8, а);
при действии нагрузки в виде сосредоточенных сил - трещины с вершинами под силами (рис. 8, б);
при совместном действии сосредоточенных сил и равномерно распределенной нагрузки - трещины с вершинами, расположенными на расстоянии от осей опор a = 0,25l и трещины с вершинами под силами.

При расчете пролетных участков статически неопределимых конструкций в качестве расчетных наклонных трещин рассматриваются:
при действии равномерно распределенной нагрузки - трещины с вершинами, расположенными на расстоянии от нулевых точек на эпюре изгибающих моментов aпр = 0,25lпр (рис. 8, в);
при действии нагрузки в виде сосредоточенных сил - трещины с вершинами под силами (рис. 8, г);
при совместном действии сосредоточенных сил и равномерно распределенной нагрузки - трещины с вершинами, расположенными на расстоянии от нулевых точек на эпюре изгибающих моментов aпр = 0,25lпр и трещины с вершинами под силами.
При расчете надопорных участков статически неопределимых конструкций независимо от вида нагрузки в качестве расчетных наклонных рассматриваются трещины с вершинами у граней опор (см. рис. 8, в, г).
2.15. Расчет прочности наклонных сечений производится в зависимости от положения нулевой линии и вершины расчетной наклонной трещины относительно нижней грани сжатой полки.
При  должно выполняться условие
должно выполняться условие
где MI = M + Ne - момент внешних сил, расположенных по одну сторону от сечения I-I, относительно оси, проходящей через центр тяжести сечения продольной растянутой арматуры;
При арматурной стали, не имеющей физического предела текучести, высота сжатой зоны сечения I-I определяется из уравнения
где
kа = Rа/(Rа + 0,01Eа); (33)
при этом должно выполняться условие
Если условие (34) не выполняется слева, высота сжатой зоны определяется из уравнения (29), коэффициенты A1 - A3 - по формулам (30) - (32) при kа = 1 и 0,008Eа = 0.
В случае невыполнения условия (34) справа
Высота сжатой зоны сечения I-I над наклонной трещиной определяется из уравнения
где
Усилия в продольной растянутой арматуре в месте пересечения ее наклонной трещиной определяются по формулам:
 (40)
(40)где
 (42)
(42)При этом должны выполняться условия
В формулах (38) - (41):
qх = RахFх/uх; (45)
qот = RахFот/uот; (46)
 (47)
(47)В общем случае (совместное действие сосредоточенных сил и равномерно распределенной нагрузки)
В формулах (31), (35), (41) и во всех последующих верхний знак перед силой N ставится, если она сжимающая, нижний - если растягивающая.
При  и
и  должно выполняться условие
должно выполняться условие
 должно выполняться условие
должно выполняться условиеПри арматурной стали, не имеющей физического предела текучести, высота сжатой зоны сечения I-I определяется из уравнения (29), коэффициенты A1 - A3 - по формулам (32) и
При этом должно выполняться условие (34).
Если условие (34) не выполняется слева, высота сжатой зоны определяется из уравнения (36), коэффициенты A1 - A3 - по формулам (50), (51) и (32) при kа = 1 и 0,008Eа = 0.
Если условие (34) не выполняется справа, высота сжатой зоны определяется по формуле
Высота сжатой зоны сечения I-I над наклонной трещиной определяется по формуле (36), коэффициенты B1 - B3 - по формулам (37), (39) и
 (53)
(53)Усилия в продольной растянутой арматуре в месте пересечения ее наклонной трещиной определяются по формулам
При арматурной стали, не имеющей физического предела текучести, высота сжатой зоны сечения I-I определяется из уравнения (29), коэффициенты A1 - A3 - по формулам (50), (51) и (32) с выполнением условия (34).
Если условие (34) не выполняется слева, высота сжатой зоны определяется из уравнения (29), коэффициенты A1 - A3 - по формулам (50), (51) и (32) при kа = 1 и 0,008Eа = 0.
Если условие (34) не выполняется справа, высоту сжатой зоны находим по формуле (52).
Высота сжатой зоны сечения I-I над наклонной трещиной вычисляется по формуле (36) при
B1 = 0,5Rпрb; (55)
 (56)
(56) (57)
(57)Усилия в продольной растянутой арматуре в месте пересечения ее наклонной трещиной определяются по формулам (54) и (41) при
с выполнением условий (43) и (44).
При арматурной стали, имеющей физический предел текучести, высота сжатой зоны сечения I-I определяется из уравнения (29) с учетом выражений (30) - (32) или (50), (51) и (32) при kа = 1 и 0,008Eа = 0, а при  - по формуле (35) или (52) в зависимости от положения нулевой линии относительно нижней грани сжатой полки.
- по формуле (35) или (52) в зависимости от положения нулевой линии относительно нижней грани сжатой полки.
 - по формуле (35) или (52) в зависимости от положения нулевой линии относительно нижней грани сжатой полки.
- по формуле (35) или (52) в зависимости от положения нулевой линии относительно нижней грани сжатой полки.Величина  , вводимая в расчет, принимается такой же, как и при расчете прочности нормальных сечений.
, вводимая в расчет, принимается такой же, как и при расчете прочности нормальных сечений.
При невыполнении условия (43) необходимо изменить интенсивность поперечного армирования в виде вертикальных стержней (увеличить, если нагельная сила Qа больше правой части указанного условия; снизить, если меньше) и уточнить значения xв и Nа.
Интенсивность  поперечного армирования в виде вертикальных стержней, удовлетворяющая условию (43), определяется по формуле
поперечного армирования в виде вертикальных стержней, удовлетворяющая условию (43), определяется по формуле
 (59)
(59)Изменение интенсивности достигается за счет варьирования шага вертикальных стержней или площади их поперечного сечения (или того и другого одновременно).
При невыполнении условия (44) необходимо уменьшить количество обрываемой (отгибаемой) арматуры.
2.16. Проверка прочности конструкций прямоугольного сечения производится по формулам (28) - (48) при  .
.
2.17. При отсутствии поперечной арматуры расчет прочности по наклонным сечениям производится по формулам п. 2.4 при qх = qот = 0 с соблюдением условий (43) и (44). При невыполнении первого условия необходима постановка поперечной арматуры в виде вертикальных стержней, второго - уменьшение количества обрываемой арматуры.
2.18. Длина проекции наклонной трещины на продольную ось конструкции определяется в зависимости от места расположения вершины рассматриваемой расчетной трещины по длине конструкции. Если ее вершина расположена на расстоянии 0,25l от оси опоры
если под силой
Как в том, так и в другом случае должно выполняться условие
h0 <= c <= 2h0. (62)
Численные значение Mт находим по формуле (93) с учетом замены Rс.рII на Rс.р, численные значения Mр(I) - из выражения (28) или (49) в зависимости от положения нулевой линии относительно нижней грани сжатой полки.
Примечание. В формулах (60) и (61) верхние знаки перед rя ставятся, если сила N сжимающая, нижние - если растягивающая.
2.19. Для поперечной арматуры в виде вертикальных стержней, устанавливаемой по расчету в конструкциях с поперечной нагрузкой, в пределах ее пролета должно выполняться условие
 (63)
(63)Расстояние между вертикальными стержнями uх, между опорой и концом наклонного стержня, ближайшего к опоре, а также между концом предыдущего и началом последующего наклонного стержня должно быть не более величины
 (64)
(64)2.20. В конструкциях, рассчитываемых только на фиксированные, в т.ч. и на сплошные распределенные, нагрузки, расчетную поперечную силу Q следует определять с учетом разгружающего влияния нагрузки, приложенной к конструкции в пределах длины проекции расчетной наклонной трещины, если эта нагрузка приложена на грани конструкции и действует в ее сторону.
2.21. Определение предельных усилий в контактном слое производится исходя из следующих предпосылок:
контактный слой рассматривается как дисперсная система, состоящая из нормальных и сдвиговых связей; при этом считается, что нормальные связи абсолютно жесткие, а сдвиговые обладают упруго-пластической податливостью;
в качестве критерия исчерпания сопротивления контактного слоя при поликомпонентных контактах, за исключением шпоночных (пронизанных сквозными поперечными шпонками), принимается нарушение сплошности контактного слоя, при шпоночных контактах - срез бетона шпонок на уровне указанного слоя.
Примечание. Поликомпонентными считаются контакты, сопротивление которых определяется двумя или более компонентами (сцепление, зацепление, трение, поперечные шпонки и пр.).
2.22. Расчет по прочности контактного слоя производится из условия
где Qсд - усилие сдвига;
bсд - ширина ожидаемой поверхности сдвига, по которой производится проверка прочности;
lсд - длина участка сдвига.
При расчете статически определимых конструкций (рис. 9)
где
 (67)
(67) (68)
(68)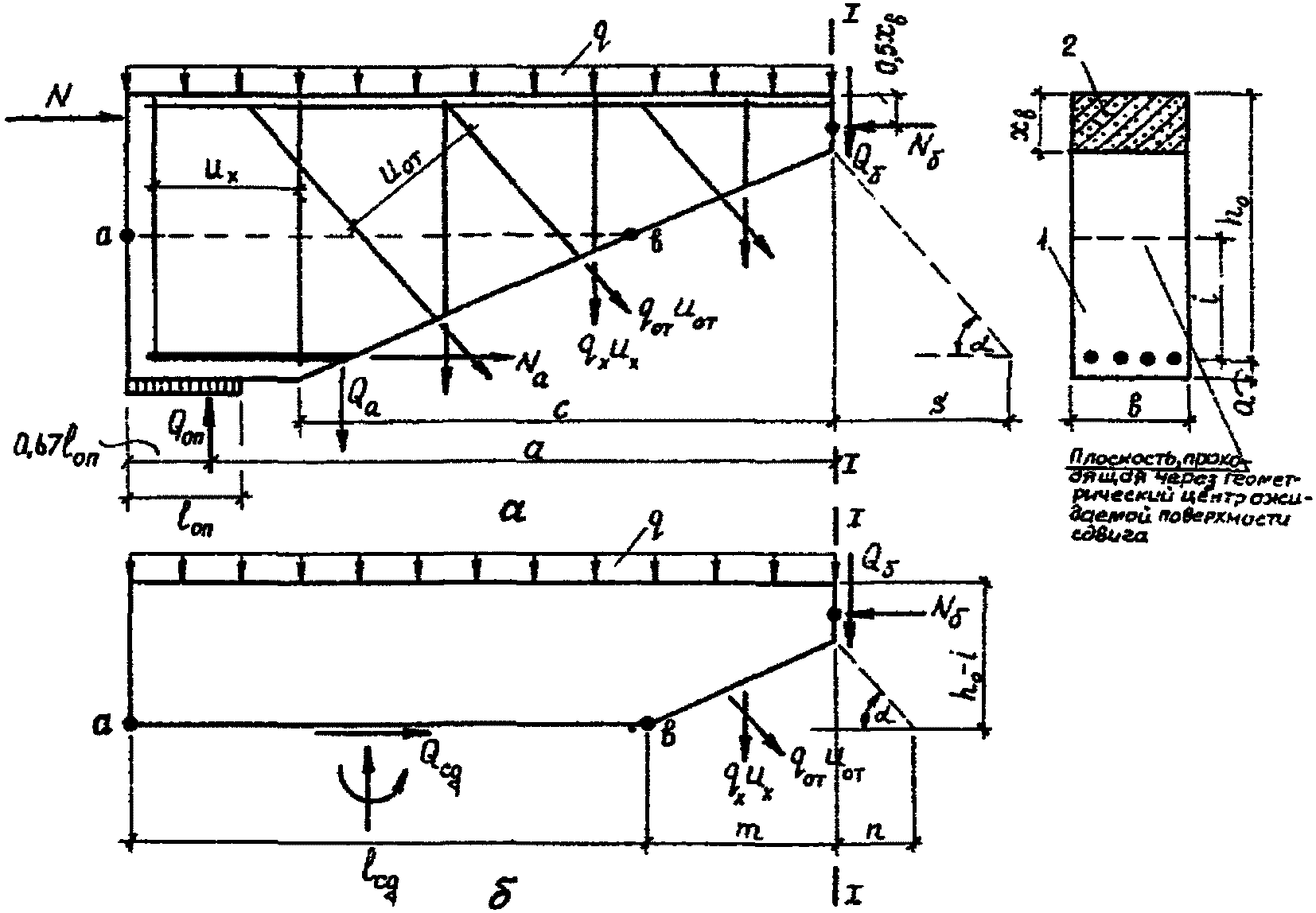
контактного слоя в статически определимых конструкциях
а - схема для определения Nб; б - то же, величины Qсд;
1 - сборный элемент; 2 - монолитный бетон
Если геометрический центр ожидаемой поверхности сдвига расположен над вершиной наклонной трещины (в пределах высоты xв), первую часть формулы (66) необходимо умножить на коэффициент (h0 - i)/xв.
При расчете статически неопределимых конструкций (рис. 10)
где
 (70)
(70) (71)
(71) (72)
(72) (73)
(73) (74)
(74)
статически неопределимых конструкций
а - схема для определения lсд; б - схема
для определения Nб и Nа; в - то же, для определения Qсд
Численные значения Nб.пр, Nб.оп, xв.пр, xв.оп, qот.пр, qот.оп и sпр, sоп определяются по формулам п. 2.15, cпр и cоп - по формулам п. 2.18.
Если геометрический центр ожидаемой поверхности сдвига расположен над вершиной пролетной наклонной трещины (в пределах высоты xв.пр), первый член правой части формулы (69) необходимо умножить на коэффициент (h0.пр - iпр)/xв.пр. Если геометрический центр ожидаемой поверхности сдвига расположен над вершиной надопорной наклонной трещины (в пределах высоты xв.оп), второй член правой части формулы (69) необходимо умножить на коэффициент (h0.оп - iоп)/xв.оп.
2.23. Прочность контактного слоя определяется по ожидаемой поверхности сдвига bсдlсд (поверхность, обладающая минимальным сопротивлением сдвигу).
Для плоских армированных и неармированных контактов это плоскость сопряжения (рис. 11, а), для плоских шпоночных контактов - плоскость, проходящая по бетону более низкого класса (рис. 11, б); для армированных и неармированных контактов с выступающими продольными ребрами сдвиг возможен по четырем плоскостям (см. рис. 11, в - г) с проверкой для всех четырех случаев.
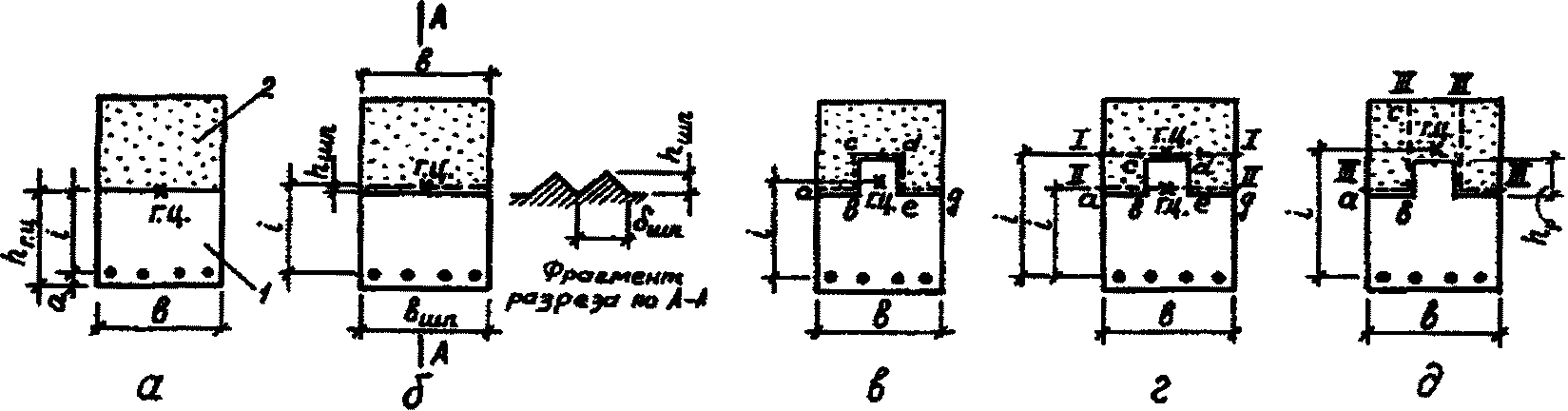
а - контакт плоский (bсд = b); б - с поперечными шпонками
(bсд = b); в - с продольным ребром, bсд = 2ab + bc + cd;
г - с продольным ребром, проверка прочности производится
по плоскостям I-I и II-II (bсд = b); д - контакт
с продольным ребром, проверка прочности производится
по плоскостям III-III, bсд = 2(ab + bc);
1 - сборный элемент; 2 - монолитный бетон
2.24. В статически определимых конструкциях длина участка сдвига lсд принимается равной расстоянию от торца конструкции до точки, в которой ближайшая к торцу расчетная наклонная трещина пересекает плоскость, проходящую через геометрический центр ожидаемой поверхности сдвига (см. рис. 10)
 (75)
(75)В статически неопределимых конструкциях наиболее опасны, с точки зрения прочности, участки, заключенные между ближайшими расчетными наклонными трещинами - пролетной и опорной (см. рис. 10, а).
Длина таких участков
 (76)
(76)2.25. В общем случае (при расчете шпоночного контакта, пронизанного поперечной арматурой) среднее суммарное расчетное сопротивление сдвигу принимается равным
где  - сопротивление за счет сцепления и механического зацепления;
- сопротивление за счет сцепления и механического зацепления;
 (80)
(80)при поперечной арматуре в виде вертикальных стержней
 (81)
(81)в виде наклонных стержней
 (82)
(82)В этих формулах
k1 - характеристика поверхности контакта, определяемая по табл. 3 (для монолитного бетона с 0,65 <= В/Ц <= 0,75);
k2 - характеристика дисперсности поперечного армирования (табл. 4);
k3 - коэффициент трения бетона о бетон, принимаемый равным 0,63;
bг - ширина горизонтального участка ожидаемой поверхности сдвига (на рис. 11, а - г значение bг = b; на рис. 11, в - соответственно bг = 2ab + cd).
Состояние поверхности контакта сборных элементов | Значение k1 для класса монолитного бетона | ||||
B3,5 | B7,5 | B12,5 | B15 | B30 | |
Гладкая, сухая; контакт между бетонами по нескольким плоскостям | 0,4 | 0,6 | 0,9 | 1,2 | 1,0 |
То же, контакт плоский | 0,3 | 0,5 | 0,6 | 0,6 | 0,5 |
Шероховатая, сухая; контакт по нескольким плоскостям | 0,5 | 0,8 | 1,2 | 1,6 | 1,3 |
То же, контакт плоский | 0,4 | 0,7 | 0,8 | 0,8 | 0,6 |
Диаметр поперечных стержней, мм | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | 16 | 25 |
k2 | 2,2 | 2,0 | 1,8 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,1 | 1,0 |
При бесшпоночном контакте в формуле (13) 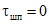 .
.
При отсутствии поперечной арматуры, пронизывающей контакт, в формуле (77) 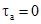 , а в формулах (78) и (79) k2 = 1.
, а в формулах (78) и (79) k2 = 1.
При расчете прочности контактного слоя статически неопределимых конструкций на участках у промежуточных опор независимо от схемы нагружения следует принимать  .
.
2.26. Если в плоском шпоночном контакте (рис. 12) усилия сдвига воспринимаются только шпонками (контакт сухой, полученный как отпечаток от металлической опалубки, поперечная арматура отсутствует), прочность контактного слоя проверяется из условия
где bшп - ширина шпонки;
nшп - число срезов, вводимое в расчет.

а - поперечное сечение конструкции; б, в и д - треугольные,
прямоугольные и трапецеидальные шпонки; г - треугольные
шпонки (сборный элемент) и трапецеидальные (монолитный
бетон); 1 - сборный элемент; 2 - монолитный бетон
Высота шпонки проверяется из условия
При  по условиям (83) и (84) проверяются как шпонки сборных элементов, так и шпонки монолитного бетона (в первом случае Rр = Rс.р и Rпр = Rс.пр, во втором Rр = Rм.р и Rпр = Rм.пр); при
по условиям (83) и (84) проверяются как шпонки сборных элементов, так и шпонки монолитного бетона (в первом случае Rр = Rс.р и Rпр = Rс.пр, во втором Rр = Rм.р и Rпр = Rм.пр); при  проверяются только шпонки монолитного бетона (Rр = Rм.р и Rпр = Rм.пр).
проверяются только шпонки монолитного бетона (Rр = Rм.р и Rпр = Rм.пр).
 по условиям (83) и (84) проверяются как шпонки сборных элементов, так и шпонки монолитного бетона (в первом случае Rр = Rс.р и Rпр = Rс.пр, во втором Rр = Rм.р и Rпр = Rм.пр); при
по условиям (83) и (84) проверяются как шпонки сборных элементов, так и шпонки монолитного бетона (в первом случае Rр = Rс.р и Rпр = Rс.пр, во втором Rр = Rм.р и Rпр = Rм.пр); при  проверяются только шпонки монолитного бетона (Rр = Rм.р и Rпр = Rм.пр).
проверяются только шпонки монолитного бетона (Rр = Rм.р и Rпр = Rм.пр).Для треугольных шпонок число срезов, вводимое в расчет, должно быть не более 6, для прямоугольных и трапецеидальных - не более 3.
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
3.1. Сборно-монолитные конструкции в зависимости от предъявляемых к ним требований по трещиностойкости рассчитываются по образованию трещин в сборных элементах, нормальных к продольной оси конструкции и наклонных - в зоне действия наибольших главных растягивающих напряжений.
Расчет производится в наиболее опасных местах по длине пролета в зависимости от вида эпюры изгибающих моментов, поперечных сил и изменения сечения конструкции.
3.2. При расчете по образованию трещин вводятся сечения, приведенные (по модулю упругости) к более прочному бетону.
нормальных к продольной оси конструкции
3.3. Усилия, вызывающие появление нормальных трещин, определяются исходя из следующих предпосылок:
для деформаций бетона и арматуры считается справедливой гипотеза плоских сечений;
напряжения в бетоне сжатой зоны определяются с учетом упругих, а в необходимых случаях неупругих, деформаций бетона;
напряжения в бетоне растянутой зоны распределяются равномерно и принимаются равными Rс.рII;
наибольшие относительные удлинения крайних растянутых волокон бетона принимаются равными 2Rс.рII/EсII.
 (85)
(85)где  - момент приложенных к конструкции внешних сил относительно оси, проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;
- момент приложенных к конструкции внешних сил относительно оси, проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;
для изгибаемых конструкций (рис. 13, а)
для внецентренно сжатых конструкций (рис. 13, б)
 (87)
(87)для внецентренно растянутых конструкций (рис. 13, в)
rу - расстояние от центра тяжести приведенного сечения конструкции до ядровой (условной) точки указанного сечения, наиболее удаленной от растянутой зоны, трещинообразование которой определяется.

в приведенном сечении конструкции при расчете
по образованию нормальных трещин
а - при изгибе; б - при внецентренном сжатии;
в - то же, растяжении; 1 - ядровая точка;
2 - центр тяжести приведенного сечения
Для внецентренно сжатых и изгибаемых конструкций
 (89)
(89)где
 (90)
(90)при этом должно выполняться условие 0,7 <= kя <= 1.
Для внецентренно растянутых конструкций
 (91)
(91)Численные значения  определяются по формуле
определяются по формуле
 (92)
(92)где  - напряжения в наиболее обжатых волокнах сборных элементов к моменту приобретения монолитным бетоном заданной прочности [12].
- напряжения в наиболее обжатых волокнах сборных элементов к моменту приобретения монолитным бетоном заданной прочности [12].
Момент, воспринимаемый сечением конструкции при образовании нормальных трещин, определяется по формуле
где r1.у - расстояние от центра тяжести приведенного сечения сборных элементов до ядровой (условной) точки указанного сечения, наиболее удаленной от растянутой зоны, трещинообразование которой определяется;
Если сборные элементы попадают в сжатую зону конструкции,
 (94)
(94)где
 (95)
(95)Если сборные элементы не попадают в сжатую зону конструкции,
r1.у = r1.я. (96)
Численные значения  определяются по формуле
определяются по формуле
 (97)
(97)где  - напряжения в наименее обжатых волокнах сборных элементов к моменту приобретения монолитным бетоном заданной прочности [12];
- напряжения в наименее обжатых волокнах сборных элементов к моменту приобретения монолитным бетоном заданной прочности [12];
y' - расстояние от центра тяжести приведенного сечения конструкции до крайних сжатых волокон сечения сборных элементов.
При возрасте бетона сборных элементов к моменту приобретения монолитным бетоном заданной прочности 3 мес. и более в формуле (93) допускается принимать  .
.
 .
.3.5. Величина Wт определяется по формуле
 (98)
(98)Положение нулевой линии приведенного сечения конструкции определяется из условия
 (99)
(99)где Jб.0 - момент инерции площади сжатой зоны сечения конструкции относительно его нулевой линии;
Jа.0 и  - моменты инерции площадей сечения соответственно арматуры А и А' относительно нулевой линии;
- моменты инерции площадей сечения соответственно арматуры А и А' относительно нулевой линии;
Sб.р - статический момент площади растянутой зоны сечения конструкции относительно нулевой линии;
Sб.0 - статический момент площади сжатой зоны сечения конструкции относительно нулевой линии;
Sа.0 и  - статические моменты площадей сечения соответственно арматуры А и А' относительно нулевой линии;
- статические моменты площадей сечения соответственно арматуры А и А' относительно нулевой линии;
Fб.р - площадь растянутого бетона в сечении конструкции.
Если монолитный бетон попадает в растянутую зону конструкции и не выполняется условие
 (100)
(100)численные значения Sб.р и Fб.р определяются без учета монолитного бетона.
наклонных к продольной оси конструкции
при 

 (101)
(101)при 

 (102)
(102)где m1 - коэффициент условий работы, определяемый по табл. 5.
Класс бетона | B15 и ниже | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 | |
Значение m1 для бетона | тяжелого и мелкозернистого | 0,5 | 0,5 | 0,5 | 0,5 | 0,45 | 0,4 | 0,35 | 0,3 | 0,25 | 0,2 |
легкого | 0,5 | 0,4 | 0,3 | 0,2 | 0,2 | 0,2 | - | - | - | - | |
Если сборные элементы попадают в сжатую зону конструкции, проверка по образованию трещин производится на уровне центра тяжести приведенного сечения сборных элементов и центра тяжести приведенного сечения конструкции, а при тавровых и двутавровых элементах и по линии примыкания сжатой полки к ребру. Если сборные элементы не попадают в сжатую зону конструкции, проверка по образованию трещин производится на уровне центра тяжести приведенного сечения сборных элементов.
3.7. Величины главных растягивающих и главных сжимающих напряжений в бетоне сборных элементов  и
и  определяются по формуле
определяются по формуле
где  - нормальные напряжения в бетоне сборных элементов на площадке, перпендикулярной к продольной оси конструкции, от сил предварительного обжатия и внешних нагрузок, действующих к моменту приобретения монолитным бетоном заданной прочности [12];
- нормальные напряжения в бетоне сборных элементов на площадке, перпендикулярной к продольной оси конструкции, от сил предварительного обжатия и внешних нагрузок, действующих к моменту приобретения монолитным бетоном заданной прочности [12];

на площадках, параллельных продольной оси конструкции
1 - сборный элемент; 2 - монолитный бетон
Для уровня центра тяжести приведенного сечения сборных элементов
 (104)
(104)где y0 - расстояние от центра тяжести приведенного сечения конструкции до центра тяжести приведенного сечения сборных элементов.
Для уровня центра тяжести приведенного сечения конструкции
 (105)
(105)При y < 0,4h и x <= 2,5y
 (106)
(106)при y > 0,4h и x <= h
 (107)
(107)Касательные напряжения
 (108)
(108)где Sп - статистический момент части приведенного сечения конструкции, расположенной выше уровня, на котором производится проверка по образованию трещин, относительно оси, проходящей через центр тяжести приведенного сечения;
b - ширина приведенного сечения конструкции на уровне, для которого производится проверка по образованию трещин.
При тавровых и двутавровых сборных элементах при наличии в месте примыкания к ребру скосов следует также проверять  на уровне примыкания к ребру скоса.
на уровне примыкания к ребру скоса.
3.8. Если сборные элементы попадают в сжатую зону приведенного сечения конструкции, а монолитный бетон - как в сжатую, так и растянутую зоны указанного сечения, расчету по образованию наклонных трещин на уровне центра тяжести приведенного сечения конструкции предшествует проверка условий:
при 

 (109)
(109)при 

 (110)
(110)Величины главных растягивающих и главных сжимающих напряжений в монолитном бетоне  и
и  определяются по формуле
определяются по формуле
 (111)
(111)где  - местные сжимающие напряжения в монолитном бетоне на площадке, параллельной продольной оси конструкции, от внешних нагрузок (опорной реакции), приложенных после приобретения монолитным бетоном заданной прочности (см. рис. 14);
- местные сжимающие напряжения в монолитном бетоне на площадке, параллельной продольной оси конструкции, от внешних нагрузок (опорной реакции), приложенных после приобретения монолитным бетоном заданной прочности (см. рис. 14);
при y < 0,4h и x <= 2,5y
при y >= 0,4h и x <= h
 (114)
(114)При невыполнении условий (112) и (113) расчет по образованию трещин производится в соответствии с пп. 3.6 и 3.7 при b = bс.
3.9. Сборно-монолитнне конструкции рассчитываются по раскрытию трещин в сборных элементах, нормальных к продольной оси конструкции, и наклонных - в зоне действия наибольших главных растягивающих напряжений.
Расчет производится для конструкций, к трещиностойкости которых предъявляются требования 2-й категории (ограниченное по ширине кратковременное раскрытие трещин при условии их последующего надежного закрытия), и для конструкций, к трещиностойкости которых предъявляются требования 3-й категории.
Полная ширина раскрытия трещин определяется по формулам:
для конструкций, к трещиностойкости которых предъявляются требования 2-й категории,
aт = aт1; (115)
для конструкций, к трещиностойкости которых предъявляются требования 3-й категории,
aт = aт1 - aт2 + aт3, (116)
где aт1 - ширина раскрытия трещин от кратковременного действия всех нагрузок;
aт2 - ширина раскрытия трещин от постоянных и длительных нагрузок при их кратковременном действии;
aт3 - то же, длительном.
3.10. В основу расчета по раскрытию трещин положены следующие предпосылки:
раскрытие трещин есть накопление относительных взаимных смещений арматуры и бетона на участках активного сцепления, расположенных по обе стороны от трещины (рис. 15), т.е.
напряжения сцепления по поверхности контакта бетона и растянутой арматуры на участках между трещинами изменяются пропорционально относительным взаимным смещениям арматуры и бетона;
относительное удлинение бетона  на уровне растянутой арматуры в сечении "u" принимается равным отношению напряжений в бетоне на указанном уровне к его модулю упруго-пластичности (0,5Eс).
на уровне растянутой арматуры в сечении "u" принимается равным отношению напряжений в бетоне на указанном уровне к его модулю упруго-пластичности (0,5Eс).
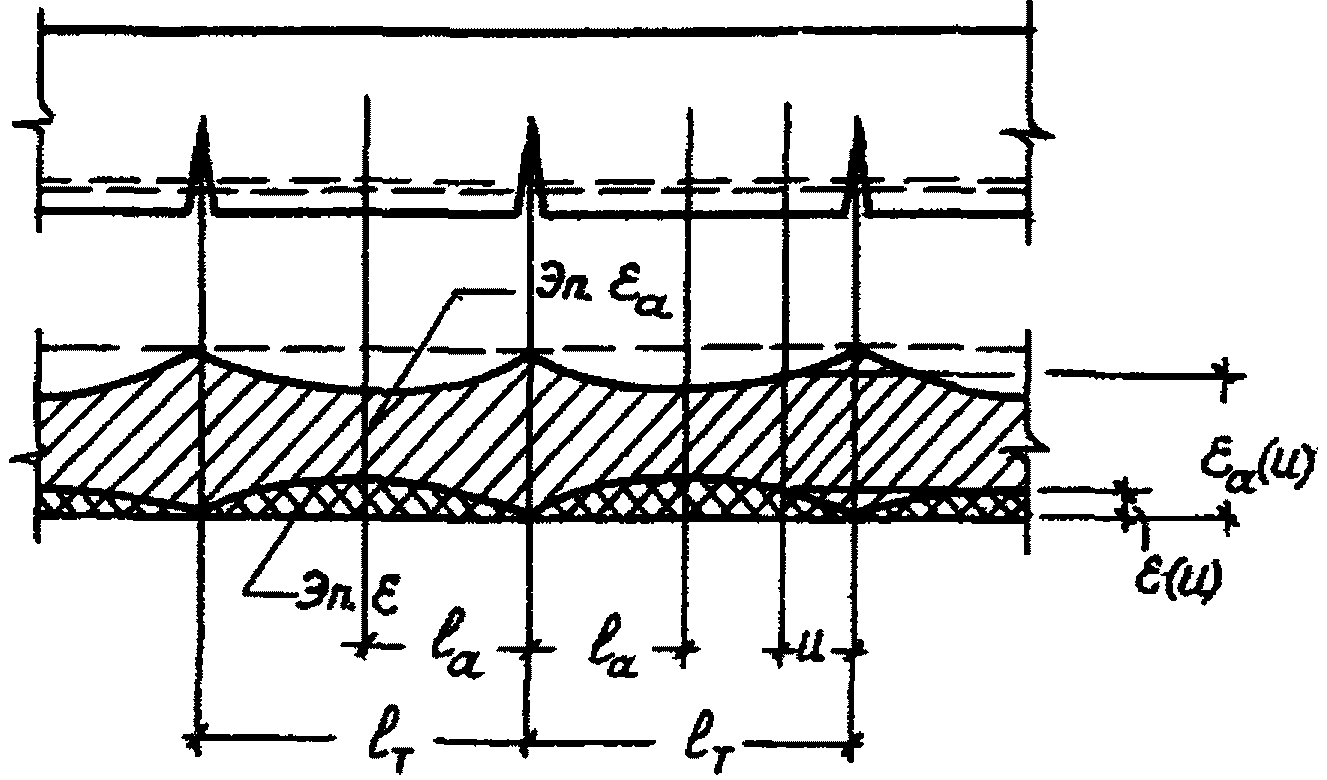
Рис. 15. Расчетная схема к уравнению (117)
3.11. При расчете по раскрытию трещин вводятся сечения, приведенные (по модулю упругости) к более прочному бетону.
нормальных к продольной оси конструкции
3.12. Ширина раскрытия нормальных трещин определяется по формуле
 (118)
(118)где Cд - коэффициент, принимаемый равным:
при учете кратковременных нагрузок и кратковременном действии
постоянных и длительных нагрузок ........................... 1,0
многократно повторяющейся нагрузки, а также длительного
действия постоянных и длительных нагрузок для конструкций
из бетона:
тяжелого естественного твердения ........................... 1,5
тяжелого в водонасыщенном состоянии ........................ 1,2
мелкозернистого вида А (Б) ................................. 1,75 (2,0)
легкого .................................................... 1,5
стержневой периодического профиля .......................... 1,0
гладкой .................................................... 1,3
проволочной периодического профиля и канатах ............... 1,2
гладкой .................................................... 1,4
 (119)
(119) (120)
(120)ИС МЕГАНОРМ: примечание. Обозначения даны в соответствии с официальным текстом документа. |
Gа - модуль взаимного смещения арматуры и бетона сборных элементов на участках между трещинами, принимаемый равным kсцEс, где kсц - коэффициент, определяемый по табл. 6 в зависимости от вида, класса бетона и степени его обжатия;
F - площадь бетона в приведенном сечении конструкции высотой h0 без учета свесов сжатой полки;
b - ширина ребра указанного сечения;
x0 - высота сжатой зоны приведенного сечения конструкции, определяемая по формуле (191).
Вид бетона | Значение kсц при классе бетона | ||||||||
B7,5 | B10 | B15 | B20 | B30 | B40 | B50 | B60 | ||
Тяжелый (Обычный) | 0 | - | 0,58 | 0,51 | 0,48 | 0,42 | 0,40 | 0,38 | 0,37 |
0,2 | - | - | 0,50 | 0,47 | 0,41 | 0,39 | 0,37 | 0,36 | |
0,4 | - | - | 0,44 | 0,41 | 0,35 | 0,33 | 0,31 | 0,30 | |
0,6 | - | - | 0,35 | 0,31 | 0,27 | 0,25 | 0,23 | 0,22 | |
0,8 | - | - | 0,20 | 0,18 | 0,16 | 0,14 | 0,12 | 0,11 | |
Мелкозернистый и легкий (Ориентировочно) | 0 | 0,7 | 0,64 | 0,57 | 0,51 | 0,43 | 0,36 | - | - |
0,2 | - | - | 0,55 | 0,49 | 0,41 | 0,34 | - | - | |
0,4 | - | - | 0,48 | 0,34 | 0,38 | 0,32 | - | - | |
0,6 | - | - | 0,37 | 0,35 | 0,30 | 0,27 | - | - | |
Примечания. 1. Здесь  - сжимающие напряжения в бетоне сборных элементов на уровне центра тяжести сечения арматуры наиболее растянутого ряда в стадии предварительного обжатия [12].
- сжимающие напряжения в бетоне сборных элементов на уровне центра тяжести сечения арматуры наиболее растянутого ряда в стадии предварительного обжатия [12].
2. Численные значения kсц для промежуточных классов бетонов и уровней предварительного обжатия определяются по интерполяции.
Напряжения в растянутой арматуре
где для изгибаемых конструкций (рис. 16, а)
 (122)
(122)Nс = N1.0 + D0; (123)
для внецентренно сжатых конструкций (рис. 16, б)
 (124)
(124)Nс = N + N1.0 + D0; (125)
для внецентренно растянутых конструкций (рис. 16, в)
 (126)
(126)Nс = -N + N1.0 + D0. (127)

в приведенном сечении конструкции при расчете
по раскрытию нормальных трещин
а - при изгибе; б - при внецентренном сжатии;
в - при внецентренном растяжении; 1 - центр тяжести эпюры
нормальных напряжений в бетоне сжатой зоны приведенного
сечения; 2 - центр тяжести площади приведенного сечения
Значения C0 и D0 расшифрованы в п. 3.24.
Значения напряжений  для напрягаемой и
для напрягаемой и  для ненапрягаемой арматуры (см. п. 3.16) не должны превышать RаII для стержневой и 0,8RаII для проволочной.
для ненапрягаемой арматуры (см. п. 3.16) не должны превышать RаII для стержневой и 0,8RаII для проволочной.
 для напрягаемой и
для напрягаемой и  для ненапрягаемой арматуры (см. п. 3.16) не должны превышать RаII для стержневой и 0,8RаII для проволочной.
для ненапрягаемой арматуры (см. п. 3.16) не должны превышать RаII для стержневой и 0,8RаII для проволочной.При dм/h1.0 <= 1 и nмсbм/bс <= 3 напряжения в арматуре допускается определять по формуле
где для изгибаемых конструкций
для внецентренно сжатых
Mз = M1 + N(eа - 0,8h0) - (Mт - Rс.рIIWт) (131)
и внецентренно растянутых конструкций
3.13. При приложении внешних нагрузок до приобретения монолитным бетоном заданной прочности со стороны растянутых волокон допускается образование нормальных трещин в сборных элементах. Ширина их раскрытия при наличии начальных трещин в сборных элементах определяется по формуле
 (133)
(133)где a1.т - ширина раскрытия начальных трещин к моменту приобретения монолитным бетоном заданной прочности [12];
lt - расстояние между начальными трещинами;
 (134)
(134)Напряжения в растянутой арматуре определяются по формулам:
для изгибаемых конструкций
 (135)
(135)для внецентренно сжатых и внецентренно растянутых конструкций
 (136)
(136)где
При dм/h1.0 <= 1 и nмсbм/bс <= 3 в формуле (137) допускается принимать C0 = D0 = 0.
к продольной оси конструкции
3.14. В общем случае (при комбинированном армировании) ширина раскрытия наклонных трещин определяется по формулам:
для вертикальных стержней
для наклонных стержней
где
kх = buх/(buх + 2nасFх); (140)
kот = buот/(buот + 2nасFот); (141)
Gх - модуль взаимного смещения вертикальных стержней и бетона сборных элементов, принимаемый равным 0,55Gа;
Gот - модуль взаимного смещения наклонных стержней и бетона сборных элементов, принимаемый при  равным Gа, при
равным Gа, при  и 60° - соответственно 0,75Gа.
и 60° - соответственно 0,75Gа.
 равным Gа, при
равным Gа, при  и 60° - соответственно 0,75Gа.
и 60° - соответственно 0,75Gа.Напряжения в вертикальных и наклонных стержнях определяются по формулам (рис. 17)
 (142)
(142) (143)
(143)где QI - поперечная сила в сечении I-I;
Qбв - усилие сдвига в бетоне сечения I-I над наклонной трещиной;
Qбн - усилие сдвига в бетоне сечения II-II под наклонной трещиной;
В формулах (144) и (145):
x0 и z0 - высота сжатой зоны сечения I-I и расстояние от центра тяжести сечения арматуры А до центра тяжести эпюры нормальных напряжений в бетоне сжатой зоны; определяются по формулам соответственно (191) и (128), причем при равномерно распределенной нагрузке рассматривается сечение на расстоянии 0,25l от оси опоры, а при сосредоточенной - сечение под первой силой;
x0.в - высота сжатой зоны сечения I-I над наклонной трещиной;
при a < 1,6h0
при a >= 1,6h0
QII - поперечная сила в сечении II-II;
x0.н - высота части сечения II-II под наклонной трещиной;
 (149)
(149) (152)
(152)Sн - статический момент части приведенного сечения II-II высотой x0.н относительно оси, проходящей через центр тяжести указанного сечения;
Sп - статический момент части приведенного сечения конструкции, расположенной по одну сторону от оси, проходящей через центр тяжести указанного сечения;
b и hп - ширина ребра и высота растянутой полки приведенного сечения конструкции;
kв и kн - коэффициенты, учитывающие влияние местных сжимающих напряжений в бетоне;
при действии сосредоточенных сил и при пролете среза a <= 2h0
 (153)
(153)при действии равномерно распределенной нагрузки
 (155)
(155)kн - см. формулу (154).
При действии сосредоточенных сил и пролете среза a > 2h0 коэффициенты kв и kн принимаются равными единице.
При действии сосредоточенных сил и пролете среза a < 1,6h0 расстояние от оси опоры до сечения I-I - a1, которое необходимо иметь при вычислении длины проекции наклонной трещины на продольную ось конструкции c, принимается равным a - расстоянию до первой сосредоточенной силы, а при пролете среза a >= 1,6h0 и при действии равномерно распределенной нагрузки определяется по формуле

в поперечной арматуре
При расчете конструкций двутаврового сечения или таврового сечения с полкой в сжатой зоне в формулы (147), (150) и (151) вводится момент инерции полного приведенного сечения. Если же в результате определения xо.в окажется, что  - высоты сжатой полки, - производится перерасчет xо.в, при этом в указанные выше формулы вводится момент инерции приведенного сечения без учета свесов сжатой полки.
- высоты сжатой полки, - производится перерасчет xо.в, при этом в указанные выше формулы вводится момент инерции приведенного сечения без учета свесов сжатой полки.
 - высоты сжатой полки, - производится перерасчет xо.в, при этом в указанные выше формулы вводится момент инерции приведенного сечения без учета свесов сжатой полки.
- высоты сжатой полки, - производится перерасчет xо.в, при этом в указанные выше формулы вводится момент инерции приведенного сечения без учета свесов сжатой полки.При поперечной арматуре только в виде вертикальных стержней
 (157)
(157)При расчете конструкций таврового сечения с полкой в сжатой зоне или прямоугольного сечения в формулах (146), (148), (150), (151) и (156) принимается hп = 0,25h.
При невыполнении условий (112) и (113) расчет по раскрытию трещин производится при b = bс.
С предельной величиной раскрытия трещин, установленной нормами, сравнивается большее из значений aт, полученных по формулам (138) и (139).
3.15. Сборно-монолитные конструкции рассчитываются по закрытию трещин в сборных элементах, нормальных к продольной оси конструкции, и наклонных - в зоне действия наибольших главных растягивающих напряжений.
Расчет производится для зон конструкции, к трещиностойкости которых предъявляются требования 2-й категории, если в этих зонах при действии постоянных, длительных и кратковременных нагрузок при коэффициенте надежности по нагрузке  трещины образуются.
трещины образуются.
к продольной оси конструкции
3.16. Для обеспечения надежного закрытия нормальных трещин при действии постоянных и длительных нагрузок должны соблюдаться следующие требования:
а) сечение конструкции с трещинами в растянутой зоне от действия постоянных, длительных и кратковременных нагрузок должно оставаться обжатым при действии постоянных и длительных нагрузок, вводимых в расчет с коэффициентом надежности по нагрузке  , с нормальными напряжениями сжатия
, с нормальными напряжениями сжатия
 (158)
(158)на растягиваемой внешними нагрузками грани конструкции не менее 0,5 МПа.
Примечание. Верхний знак перед силой N ставится, если она сжимающая, нижний - если растягивающая.
Данное требование соблюдается, если выполняется условие
 (159)
(159)Mз.т - момент, воспринимаемый сечением конструкции при закрытии трещин и определяемый по формуле
б) в напрягаемой арматуре А от действия постоянных, длительных и кратковременных нагрузок (при коэффициенте надежности по нагрузке  ) не должны возникать необратимые деформации, что обеспечивается соблюдением условия
) не должны возникать необратимые деформации, что обеспечивается соблюдением условия
 (161)
(161)где  - полные напряжения в напрягаемой арматуре к моменту приобретения монолитным бетоном заданной прочности с учетом всех потерь [12];
- полные напряжения в напрягаемой арматуре к моменту приобретения монолитным бетоном заданной прочности с учетом всех потерь [12];
в ненапрягаемой арматуре А не должны возникать необратимые деформации, что обеспечивается соблюдением условия
 (162)
(162)где  - напряжения в ненапрягаемой арматуре от усадки и ползучести бетона сборных элементов, проявившихся к моменту приобретения монолитным бетоном заданной прочности [12].
- напряжения в ненапрягаемой арматуре от усадки и ползучести бетона сборных элементов, проявившихся к моменту приобретения монолитным бетоном заданной прочности [12].
При возрасте бетона сборных элементов к моменту приобретения монолитным бетоном заданной прочности 3 мес и более в формуле (160) допускается принимать  .
.
 .
.к продольной оси конструкции
3.17. Наклонные трещины считаются надежно закрытыми, если оба главных напряжения, определяемые по формуле (103), сжимающие и меньшее из них составляет не менее 0,5 МПа, т.е. если выполняется условие
 (163)
(163)3.18. Деформации (прогибы, углы поворота) сборно-монолитных конструкций вычисляются по формулам строительной механики, определяя входящие в них величины кривизн в соответствии с настоящими методическими рекомендациями.
Величины деформаций сборно-монолитных конструкций отсчитываются от их начального состояния (до обжатия сборных элементов).
3.19. При расчете по деформациям в расчет вводятся сечения, приведенные (по модулю упругости) к более прочному бетону.
3.20. Для участков конструкций, где в растянутой зоне не образуются трещины, нормальные к продольной оси конструкции, либо они закрыты, величины кривизн определяются как для сплошного тела.
Для участков конструкций, где в растянутой зоне имеются трещины, нормальные к продольной оси конструкции, величины кривизн определяются на основе следующих предпосылок:
для средних деформаций арматуры и бетона считается справедливой гипотеза плоских сечений;
напряжения в бетоне сжатой зоны (в сечениях с трещинами) определяются с учетом упругих, а в необходимых случаях неупругих, деформаций бетона.
Конструкции или участки конструкций рассматриваются без трещин в растянутой зоне, если трещины не образуются при действии постоянных, длительных и кратковременных нагрузок или они закрыты при действии постоянных и длительных нагрузок; при этом нагрузки вводятся в расчет с коэффициентом надежности по нагрузке  .
.
в растянутой зоне
3.21. На участках, где не образуются нормальные трещины, полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых конструкций определяется по формуле
 (164)
(164)где  и
и  - кривизны соответственно от действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12];
- кривизны соответственно от действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12];
 - то же, после приобретения монолитным бетоном заданной прочности;
- то же, после приобретения монолитным бетоном заданной прочности; (167)
(167)В общем случае:
 (171)
(171) (172)
(172) (173)
(173) (174)
(174) (175)
(175)При внешней нагрузке в виде изгибающего момента SIII = 0 и  .
.
 .
.За начало отсчета времени при определении  ,
,  ,
,  и
и  в формулах (165), (166) и (169) принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении
в формулах (165), (166) и (169) принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении  и
и  в формуле (168) - момент нагружения конструкции после приобретения монолитным бетоном заданной прочности.
в формуле (168) - момент нагружения конструкции после приобретения монолитным бетоном заданной прочности.
Численные значения коэффициентов  и
и  соответственно в зависимости от
соответственно в зависимости от  и
и  , а также возраста бетона к началу отсчета времени
, а также возраста бетона к началу отсчета времени  определяются по табл. 7.
определяются по табл. 7.
3 | 7 | 14 | 28 | 45 | 60 | 90 | 180 | 365 и более | |
0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
0,5 | 1,34 | 1,35 | 1,36 | 1,38 | 1,4 | 1,41 | 1,43 | 1,45 | 1,5 |
1,0 | 1,68 | 1,71 | 1,73 | 1,75 | 1,79 | 1,82 | 1,86 | 1,91 | 2,0 |
1,5 | 2,02 | 2,06 | 2,09 | 2,13 | 2,19 | 2,24 | 2,29 | 2,36 | 2,5 |
2,0 | 2,36 | 2,42 | 2,46 | 2,5 | 2,58 | 2,65 | 2,72 | 2,82 | 3,0 |
2,5 | 2,7 | 2,77 | 2,82 | 2,88 | 2,98 | 3,06 | 3,14 | 3,27 | 3,5 |
3,0 | 3,04 | 3,12 | 3,18 | 3,25 | 3,37 | 3,47 | 3,57 | 3,73 | 4,0 |
3.23. При отсутствии необходимых данных для определения параметров  ,
,  ,
,  и
и  (сорт цемента, состав бетона, условия изготовления и эксплуатации конструкции и т.п.) в формулах (170) - (176) рекомендуется принимать
(сорт цемента, состав бетона, условия изготовления и эксплуатации конструкции и т.п.) в формулах (170) - (176) рекомендуется принимать  , где C - коэффициент, принимаемый для тяжелого и легкого бетонов, а также мелкозернистого видов А и Б при влажности воздуха, %, соответственно равным:
, где C - коэффициент, принимаемый для тяжелого и легкого бетонов, а также мелкозернистого видов А и Б при влажности воздуха, %, соответственно равным:
 , где C - коэффициент, принимаемый для тяжелого и легкого бетонов, а также мелкозернистого видов А и Б при влажности воздуха, %, соответственно равным:
, где C - коэффициент, принимаемый для тяжелого и легкого бетонов, а также мелкозернистого видов А и Б при влажности воздуха, %, соответственно равным: более 40% ................................ 2,0; 2,6; 3,0
40% и ниже ............................... 3,0; 3,9; 4,5
Кривизна от усадки бетона принимается равной нулю.
в растянутой зоне
3.24. На участках, где образуются нормальные трещины, полная величина кривизны изгибаемых внецентренно сжатых и внецентренно растянутых конструкций определяется по формуле
где  - кривизна (см. п. 3.21) от длительного действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12];
- кривизна (см. п. 3.21) от длительного действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12];
 (178)
(178) (180)
(180) (181)
(181) (184)
(184) (185)
(185) (186)
(186) (187)
(187) (188)
(188)Jо.т.с и Jт.с - моменты инерции площади сечения сжатой зоны бетона сборных элементов относительно нулевой линии соответственно в начальный и рассматриваемый момент времени t;
Jо.т.м и Jт.м - то же, сжатой зоны монолитного бетона;
e1.0x и e1.x - расстояния от точки приложения силы N1.0 до нулевой линии приведенного сечения конструкции соответственно в начальный и рассматриваемый момент времени t;
Высота сжатой зоны приведенного сечения конструкции в начальный момент времени - x0 и в рассматриваемый момент времени t - x отыскивается из уравнений
и
где
Sо.т.с и Sт.с - статические моменты площади сечения сжатой зоны бетона сборных элементов относительно нулевой линии соответственно в начальный и рассматриваемый момент времени t;
Sо.т.м и Sт.м - то же, сжатой зоны монолитного бетона.
Примечание. Знак "плюс" перед силой N в формулах (189) и (190) ставится, если она сжимающая, "минус" - если растягивающая.
В формулах (189), (190) и (193), (194):  и
и  - коэффициенты, учитывающие неравномерность распределения деформации растянутой арматуры на длине участка с трещинами соответственно в начальный и рассматриваемый момент времени t;
- коэффициенты, учитывающие неравномерность распределения деформации растянутой арматуры на длине участка с трещинами соответственно в начальный и рассматриваемый момент времени t;
 (195)
(195) <*> (196)
<*> (196)F - площадь бетона в приведенном сечении конструкции высотой h0 без учета свесов сжатой полки;
b - ширина ребра указанного сечения;
 (197)
(197)--------------------------------
<*> Упрощенная нами формула работы В.М. Бондаренко "Некоторые вопросы нелинейной теории железобетона" (Харьков: Харьк. университет, 1968, 323 с.).
Высота сжатой зоны x0 отыскивается из уравнения (191) при  .
.
Момент Mз допускается определять по формулам (130) - (132).
При dм/h1.0 <= 1 и nмсbм/bс <= 3 в формулах (182), (183) и (191), (192) допускается принимать C0 = C = 0 и D0 = D = 0.
При расчете изгибаемых конструкций (при  ) для определения
) для определения  допускается пользоваться формулой
допускается пользоваться формулой
 ) для определения
) для определения  (198)
(198)а для определения  - формулой
- формулой
 (199)
(199)3.25. При приложении внешней нагрузки до приобретения монолитным бетоном заданной прочности со стороны растянутых волокон допускается образование нормальных трещин в сборных элементах.
Полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых конструкций при наличии начальных трещин в сборных элементах определяются по формуле (177), где  - кривизна от совместного действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12]
- кривизна от совместного действия усилий N1.0 и M1 к моменту приобретения монолитным бетоном заданной прочности [12]
 (200)
(200) (201)
(201)где J1.0.т - момент инерции приведенного сечения сборных элементов относительно нулевой линии при высоте сжатой зоны x1;
x1 - высота сжатой зоны приведенного сечения сборных элементов к моменту приобретения монолитным бетоном заданной прочности [12].
Численные значения m0.т, mт и x0, x определяются по формулам соответственно (182), (183) и (191), (192) при
 (204)
(204) (206)
(206)где
 (208)
(208) (209)
(209)M1.т - сопротивление сборных элементов образованию нормальных трещин [12].
При отсутствии нагрузок, приложенных после приобретения монолитным бетоном заданной прочности  , кривизна равна
, кривизна равна  при
при
 , кривизна равна
, кривизна равна Высота сжатой зоны x отыскивается из уравнения (192) при  , коэффициент
, коэффициент  - по формуле (207) при n1 = 1.
- по формуле (207) при n1 = 1.
За начало отсчета времени при вычислении  и
и  в формулах п. 3.24 принимается момент нагружения конструкции после приобретения монолитным бетоном заданной прочности, а при
в формулах п. 3.24 принимается момент нагружения конструкции после приобретения монолитным бетоном заданной прочности, а при  - момент приобретения монолитным бетоном заданной прочности.
- момент приобретения монолитным бетоном заданной прочности.
3.27. При отсутствии необходимых данных для расчета параметров  и
и  (сорт цемента, состав бетона, условия изготовления и эксплуатации конструкции и пр.) кривизны определяются по формулам (177) - (210) с учетом
(сорт цемента, состав бетона, условия изготовления и эксплуатации конструкции и пр.) кривизны определяются по формулам (177) - (210) с учетом  .
.
 .
.ПРИМЕРЫ РАСЧЕТА
Пример 1. Определить прочность расчетного нормального сечения конструкции (рис. 1), работающей в условиях косого изгиба. Сборный элемент выполнен без предварительного напряжения.

Рис. 1. К примеру 1 (размеры в см)
1 - сборный элемент; 2 - монолитный бетон
Исходные данные. Бетон сборного элемента класса B30; Eс = 2,0·104 МПа; Rс.пр = 17,0 МПа; монолитный бетон класса B12,5; Eм = 1,2·104 МПа; Rм.пр = 7,3 МПа; арматура класса А-III; Eа = 2·105 МПа; Rа = 375 МПа; Fа1 = Fа2 = Fа3 = Fа4 = Fа8 = 1,13 см2  ; Fа5 = Fа6 = Fа7 = 8,04 см2
; Fа5 = Fа6 = Fа7 = 8,04 см2  ; zа1 = zа2 = zа3 = 3 см; zа4 = 6 см; zа5 = 42 см; zа6 = zа7 = zа8 = 46 см; yа1 = yа5 = yа6 = 4 см; yа2 = 27 см; yа3 = yа4 = yа8 = 31 см; yа7 = 17,5 см. Угол наклона плоскости действия моментов внешних сил
; zа1 = zа2 = zа3 = 3 см; zа4 = 6 см; zа5 = 42 см; zа6 = zа7 = zа8 = 46 см; yа1 = yа5 = yа6 = 4 см; yа2 = 27 см; yа3 = yа4 = yа8 = 31 см; yа7 = 17,5 см. Угол наклона плоскости действия моментов внешних сил  .
.
 ; Fа5 = Fа6 = Fа7 = 8,04 см2
; Fа5 = Fа6 = Fа7 = 8,04 см2  ; zа1 = zа2 = zа3 = 3 см; zа4 = 6 см; zа5 = 42 см; zа6 = zа7 = zа8 = 46 см; yа1 = yа5 = yа6 = 4 см; yа2 = 27 см; yа3 = yа4 = yа8 = 31 см; yа7 = 17,5 см. Угол наклона плоскости действия моментов внешних сил
; zа1 = zа2 = zа3 = 3 см; zа4 = 6 см; zа5 = 42 см; zа6 = zа7 = zа8 = 46 см; yа1 = yа5 = yа6 = 4 см; yа2 = 27 см; yа3 = yа4 = yа8 = 31 см; yа7 = 17,5 см. Угол наклона плоскости действия моментов внешних сил  .
.Решение. По табл. 2 настоящих методических рекомендаций для заданных классов бетонов находим:


Угол наклона нулевой линии по "упругому" расчету  , откуда
, откуда  .
.
 , откуда
, откуда  .
.Расстояние h0 от крайнего сжатого волокна сечения до прямой, параллельной нулевой линии и проходящей через центр тяжести наиболее растянутого стержня, вычисляем по формуле

Далее находим Sм = 25180 см3; S = 31870 см3;  .
.
 .
.По формуле (4) вычисляем
Rпр = 17,0(1 - 0,79) + 7,3·0,79 = 9,34 МПа,
а по формулам (5) и (6) - соответственно

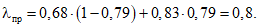
Теперь можем приступить к расчету сопротивления сечения.
Задаемся начальными значениями высоты сжатой зоны сечения и углом наклона нулевой линии: x1 = 35 см;  .
.
 .
.Так как  и
и  , значения Fпл и Sупр вычисляем по формулам:
, значения Fпл и Sупр вычисляем по формулам:
 и
и  , значения Fпл и Sупр вычисляем по формулам:
, значения Fпл и Sупр вычисляем по формулам:
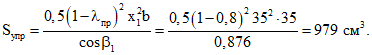
По формуле (13) определяем напряжения в арматурных стержнях. Для случая косого изгиба  , тогда при
, тогда при  по формуле (13) находим
по формуле (13) находим
 , тогда при
, тогда при  по формуле (13) находим
по формуле (13) находим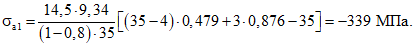
Аналогичным образом для стержней A2 - A8 получим:
 ;
;  ;
;  ;
; 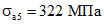 ;
;  ;
; 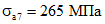 ;
; 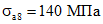 .
.ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
Для стержней A2 - A4 принимаем 
 , а для стержня A6 -
, а для стержня A6 -  .
.

 , а для стержня A6 -
, а для стержня A6 -  .
.Проверяем условие (12):

Так как указанное условие явно не выполняется, принимаем новые величины параметров сжатой зоны: x2 = 25 см;  ; sin 15° = 0,259; cos 15° = 0,966.
; sin 15° = 0,259; cos 15° = 0,966.
 ; sin 15° = 0,259; cos 15° = 0,966.
; sin 15° = 0,259; cos 15° = 0,966.С учетом этого:


Напряжения в арматурных стержнях:
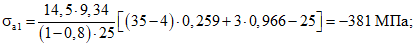
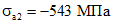 ;
;  ;
;  ;
; 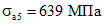 ;
;  ;
;  ;
; 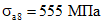 .
.Проверяем условие (12):

Так как указанное условие вновь не выполняется, расчет повторяем в прежней последовательности.
Принимаем: x3 = 28,5 см;  ; sin 8° = 0,140; cos 8° = 0,99. Тогда:
; sin 8° = 0,140; cos 8° = 0,99. Тогда:


Напряжения в арматуре:

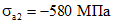 ;
; 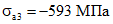 ;
;  ;
;  ;
; 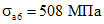 ;
; 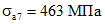 ;
;  .
.Проверяем условие (12):

т.е. можно считать, что условие (12) практически выполняется. Теперь проверяем условие (21). Для этого находим положение равнодействующей усилий в растянутой арматуре:
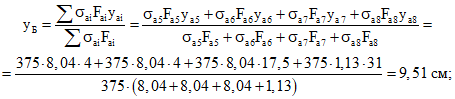
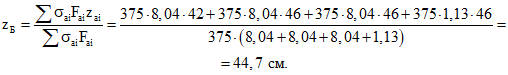
Аналогичным образом вычисляем положение равнодействующей усилий в сжатом бетоне и сжатой арматуре: yА = 18,9 см; zА = 10,7 см.
Окончательно по формуле (21) имеем
 , т.е.
, т.е. 
Таким образом, условие (21) практически выполняется.
Завершается задача оценкой прочности сечения (см. ф-лу (11)).
Для этого находим:
Sпл = Fплrпл = 719·36,2 = 26000 см3;
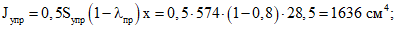

Sа1 = Fа1rа1 = 1,13·42,6 = 48,1 см3;
Sа2 = Fа2rа2 = 1,13·39,7 = 44,9 см3;
Sа3 = Fа3rа3 = 1,13·38,8 = 43,8 см3;
Sа4 = Fа4rа4 = 1,13·35,8 = 40,5 см3;
Sа5 = Fа5rа5 = 8,04·3,96 = 31,8 см3; Sа6 = 0;
Sа7 = Fа7rа7 = 8,04·1,9 = 15,3 см3;
Sа8 = Fа8rа8 = 1,13·3,8 = 4,3 см3.
Здесь rпл - расстояние от центра тяжести бетона, работающего в пластической стадии, до прямой, параллельной нулевой линии и проходящей через центр тяжести сечения наиболее растянутого стержня (A6);
rаi - расстояние от центра тяжести сечения арматуры Ai до той же линии.
Сопротивление сечения:

Пример 2. Определить "кратковременный" прогиб однопролетной свободно опертой сборно-монолитной конструкции (рис. 2) в середине пролета с учетом предварительного загружения сборного элемента.

Рис. 2. К примеру 2 (размеры в см)
1 - сборный элемент; 2 - монолитный бетон
Через месяц после укладки монолитного бетона конструкция загружена равномерно распределенной нагрузкой интенсивностью q = 31 кН/м.
Исходные данные. Бетон сборного элемента класса B40; Eс = 3,6·104 МПа; Rс.рII = 2 МПа; монолитный бетон класса B15; Eм = 2,4·104 МПа; nмс = 0,7; Eа = 1,9·105 МПа; nас = 5,3; W1.т = 27750 см3; r1.я = 18,6 см; расчетный пролет l = 600 см; N1.0 = 400 кН; e1.0н = 7,2 см; e1.ан = 9,4 см; M1 = 180 кН·м;  .
.
 .
.Решение. Проверяем трещиностойкость сборного элемента:
M1.т = N1.0(e1.0н + r1.я) + Rс.рIIW1.т = 40000·(7,2 + 18,6) + 20·27750 = 15,9·105 кгс·см = 159 кН·м.
Так как M1.т < M1 = 180 кН·м, в сборном элементе со стороны растянутых волокон имеются трещины. С учетом этого по формулам [4] находим x1 = 31,7 см; J1.т = 1,4·105 см4;  .
.
 .
.Полный прогиб сборного элемента до укладки монолитного бетона
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
f1 = f1M + f1N = 1,09 - 0,13 = 0,96 см.
Площадь монолитного бетона при высоте x1 + dм - Fм = 1781,8 см2, статический момент указанной площади относительно нулевой линии при высоте сжатой зоны x1 + dм - Sм = 48,2·103 см3, расстояние от центра тяжести площади сечения монолитного бетона до его наиболее сжатого края  - Sм/Fм = 31,7 + 20 - 48,2·103/1781,8 = 24,65 см. Собственный момент инерции площади монолитного бетона Jм = 4,18·105 см4.
- Sм/Fм = 31,7 + 20 - 48,2·103/1781,8 = 24,65 см. Собственный момент инерции площади монолитного бетона Jм = 4,18·105 см4.
 - Sм/Fм = 31,7 + 20 - 48,2·103/1781,8 = 24,65 см. Собственный момент инерции площади монолитного бетона Jм = 4,18·105 см4.
- Sм/Fм = 31,7 + 20 - 48,2·103/1781,8 = 24,65 см. Собственный момент инерции площади монолитного бетона Jм = 4,18·105 см4.По формулам (203) и (205) определяем
C0 = 0,85·3,6·106·0,7·4,18·105·29·10-6 = 25,96·106 Н·см;
D0 = 0,85·3,6·106·0,7·1781,8·(31,7 + 20 - 24,65)·29·10-6 = 3·106 Н, а по формуле (207)
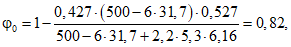
где
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |


По формуле (193) находим
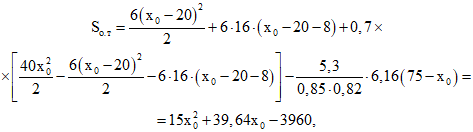
а по формуле (189)

В соответствии с (191)

После некоторых преобразований получим  , откуда x0 = 43,7 см.
, откуда x0 = 43,7 см.
 , откуда x0 = 43,7 см.
, откуда x0 = 43,7 см.Jо.т = 9,93(43,7)3 + 39,64(43,7)2 - 8219·43,7 + 281872 = 8,31·105 см4; e1.0x = h0 - e1.ан - x0 = 75 - 9,4 - 43,7 = 21,9 см.
По формулам (182) и (202) определяем:

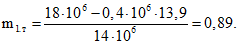
Кривизна конструкции от нагрузок, приложенных после приобретения монолитным бетоном заданной прочности, равна (см. формулу (179)):
 ; прогиб
; прогиб  .
.Полный прогиб конструкции с учетом пригрузки сборного элемента f = f1M - f1N + f2 = 1,09 - 0,13 + 0,48 = 1,44 см.
ЭКСПЕРИМЕНТАЛЬНОЕ ОБОСНОВАНИЕ
На диаграммах рис. 1 - 14 сопоставлены опытные значения прочности (по нормальным сечениям, по контактному слою), трещиностойкости (по образованию и раскрытию нормальных трещин) и деформативности (прогибы) сборно-монолитных конструкций в широком диапазоне изменения основных факторов с теоретическими, подсчитанными по формулам настоящих методических рекомендаций и, по возможности, формулам [11].

Условные обозначения:
 по предлагаемой методике;
по предлагаемой методике; по [11]
по [11]по нормальным сечениям к опытной
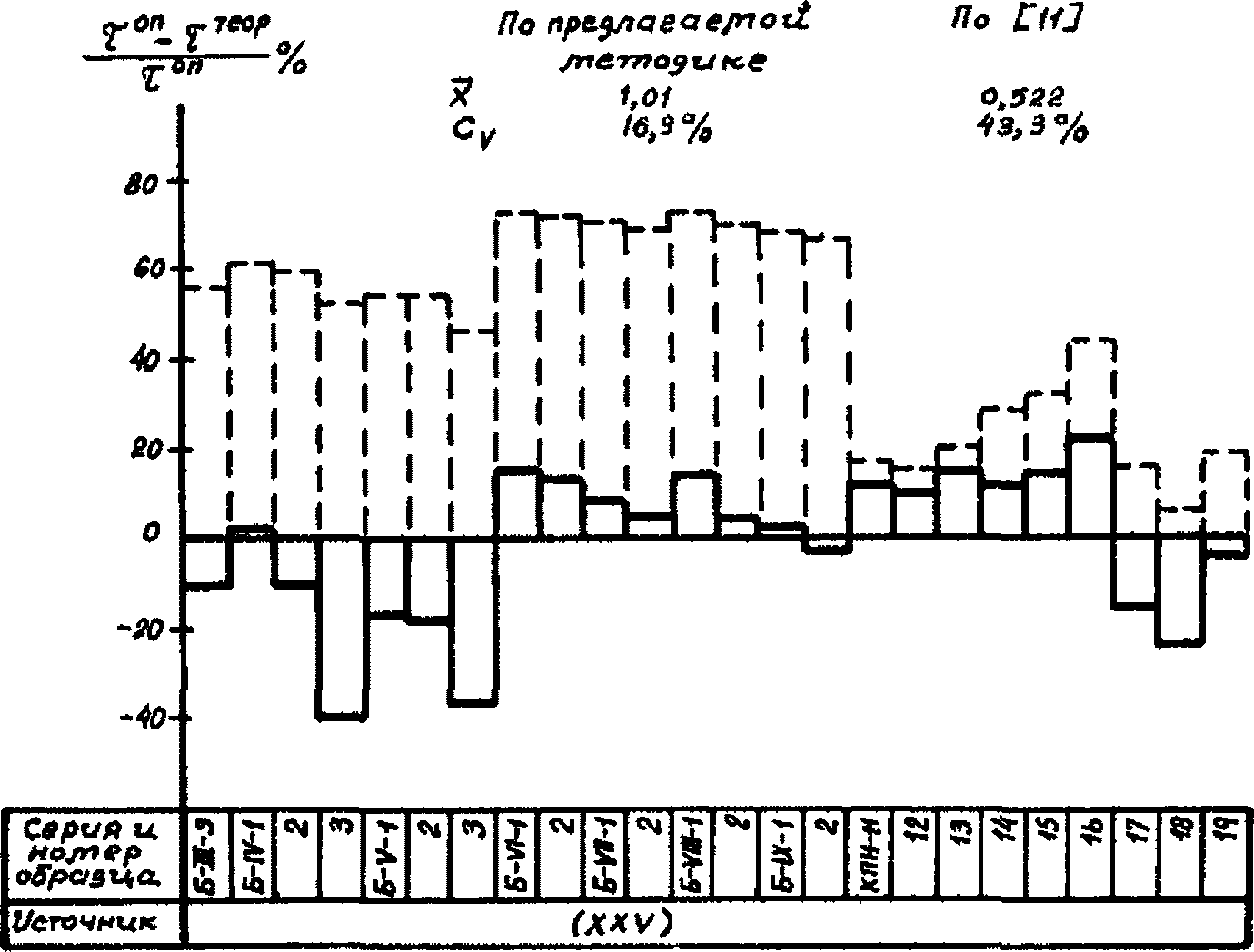
Условные обозначения:
Рис. 2. Отношение теоретической величины действующих
в контактном слое напряжений сдвига к опытной

Условные обозначения:
Рис. 3. Отношение теоретической величины среднего (по длине
участка сдвига) суммарного предельного сопротивления сдвигу
к опытной

Условные обозначения:
 по предлагаемой методике;
по предлагаемой методике; по [11]
по [11]Рис. 4. Отношение теоретического момента образования

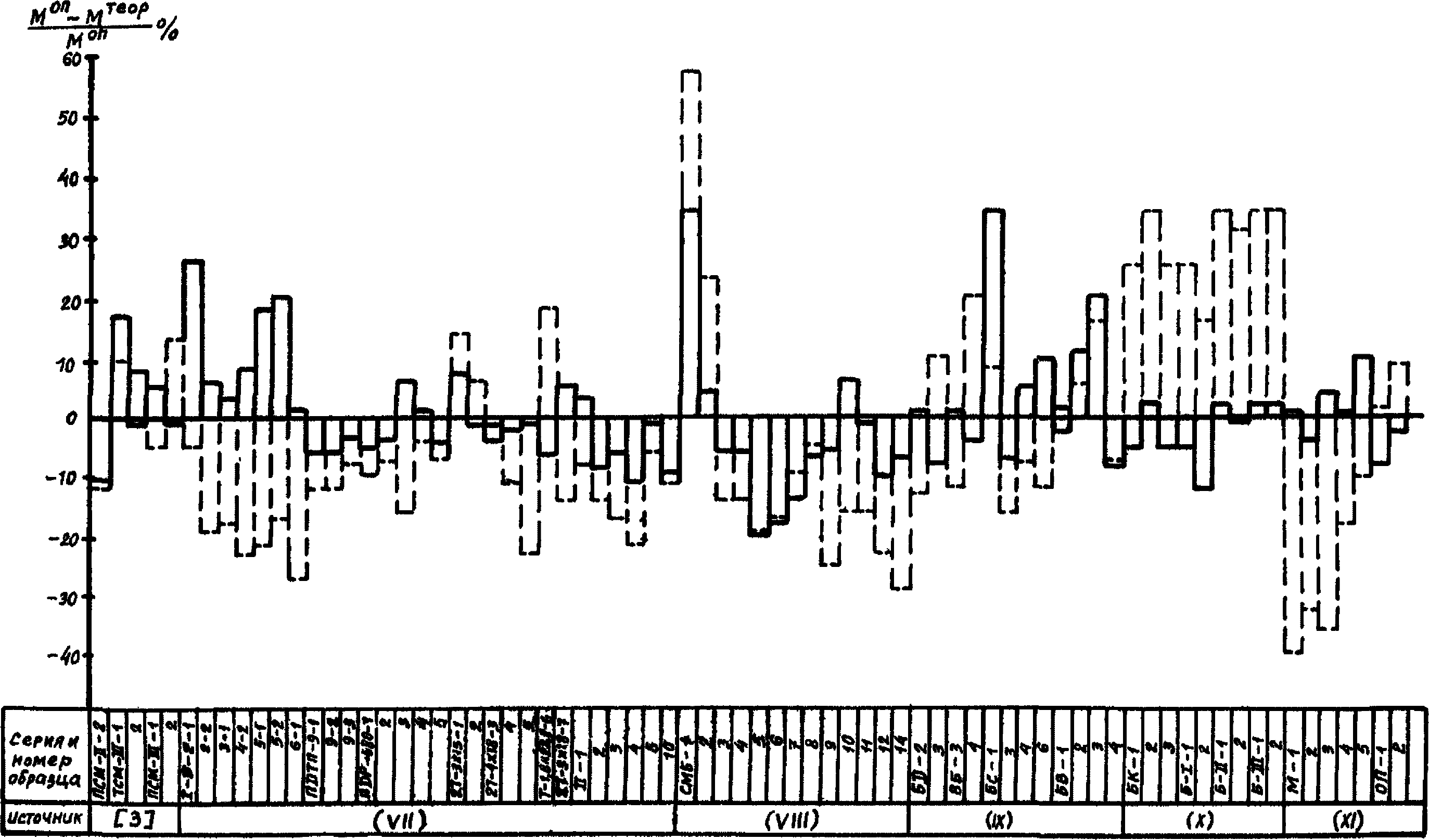
Рис. 6
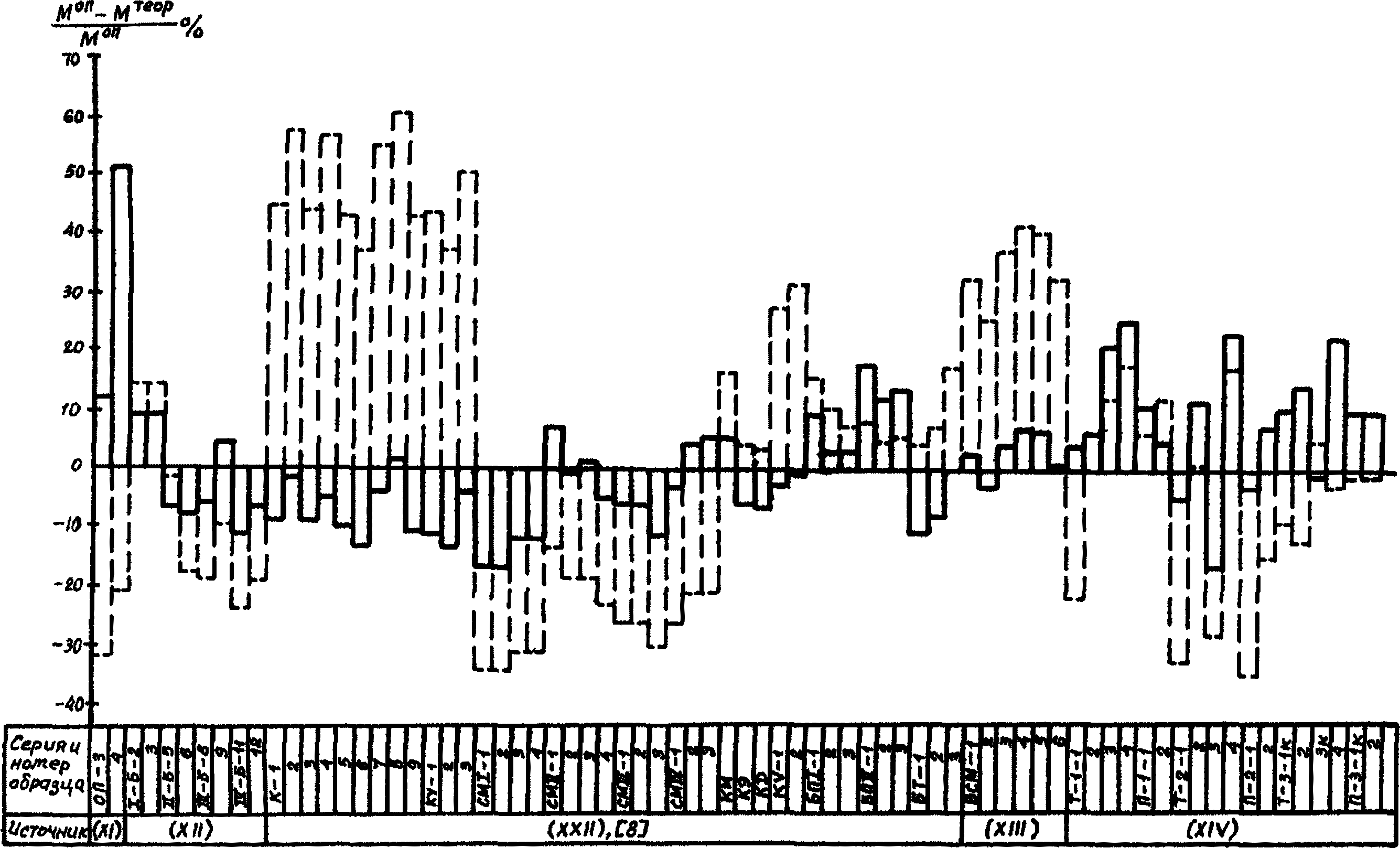
Рис. 7
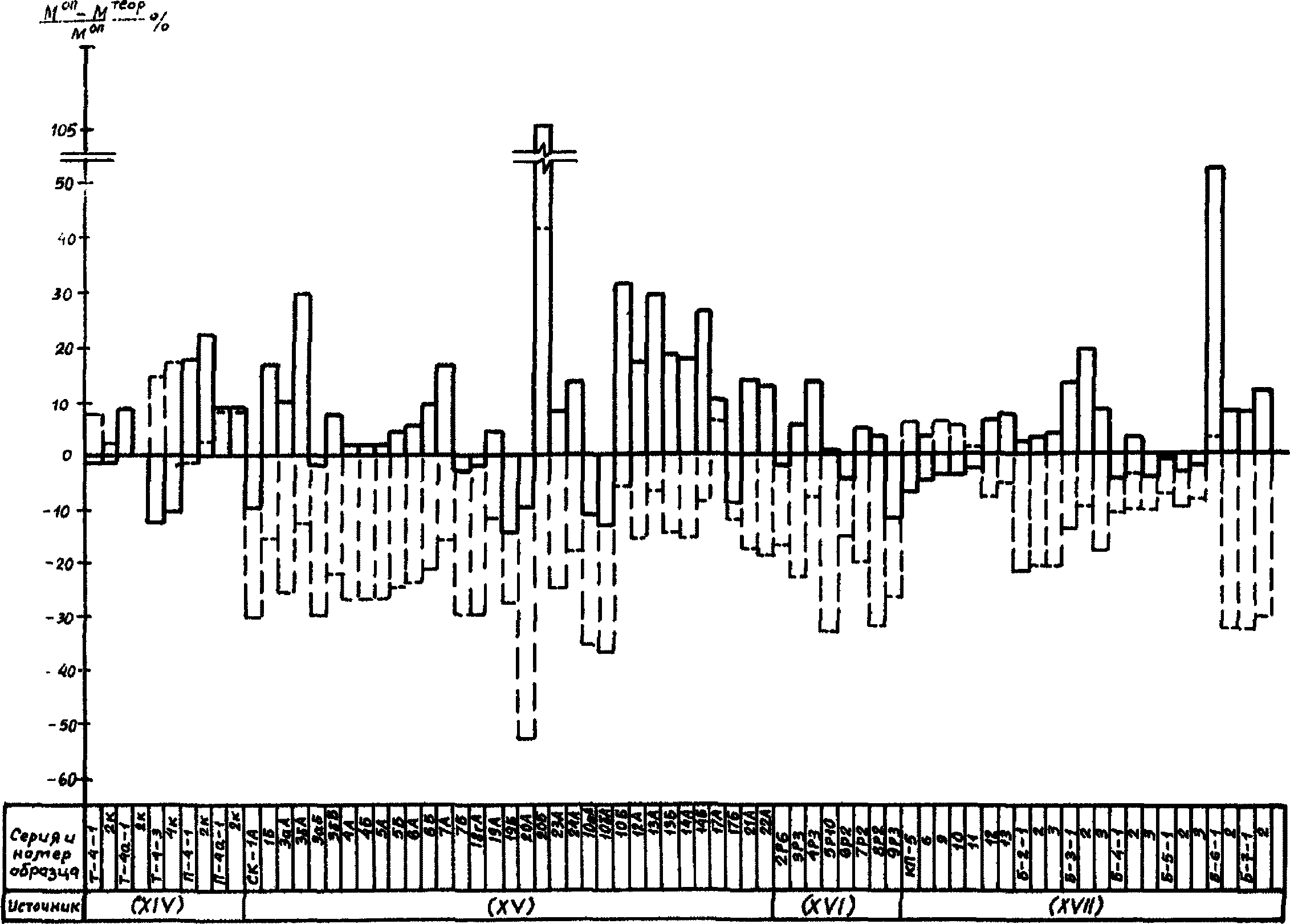
Рис. 8

Рис. 9

Рис. 10
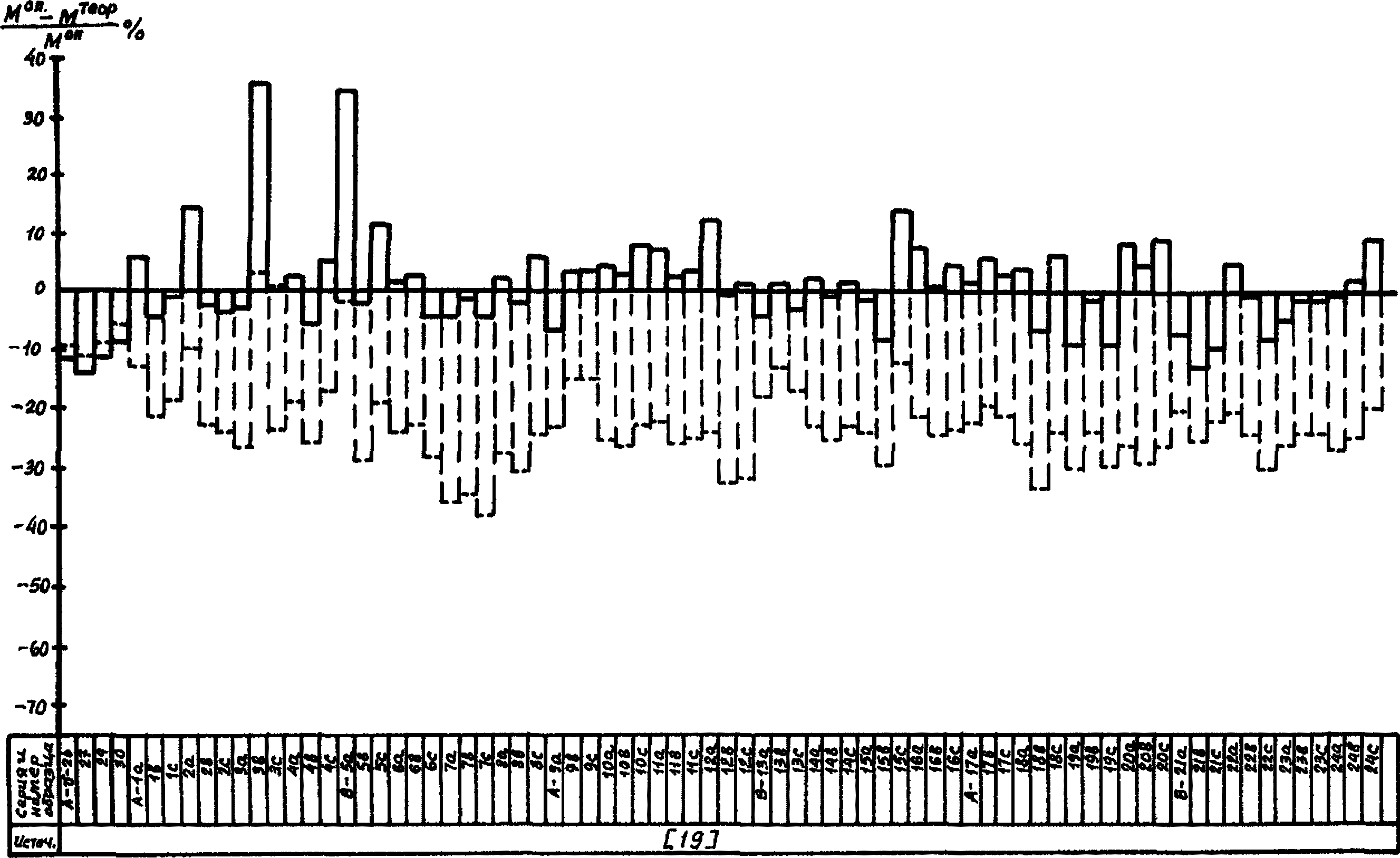
Рис. 11
ИС МЕГАНОРМ: примечание. Рисунок дан в соответствии с официальным текстом документа. |

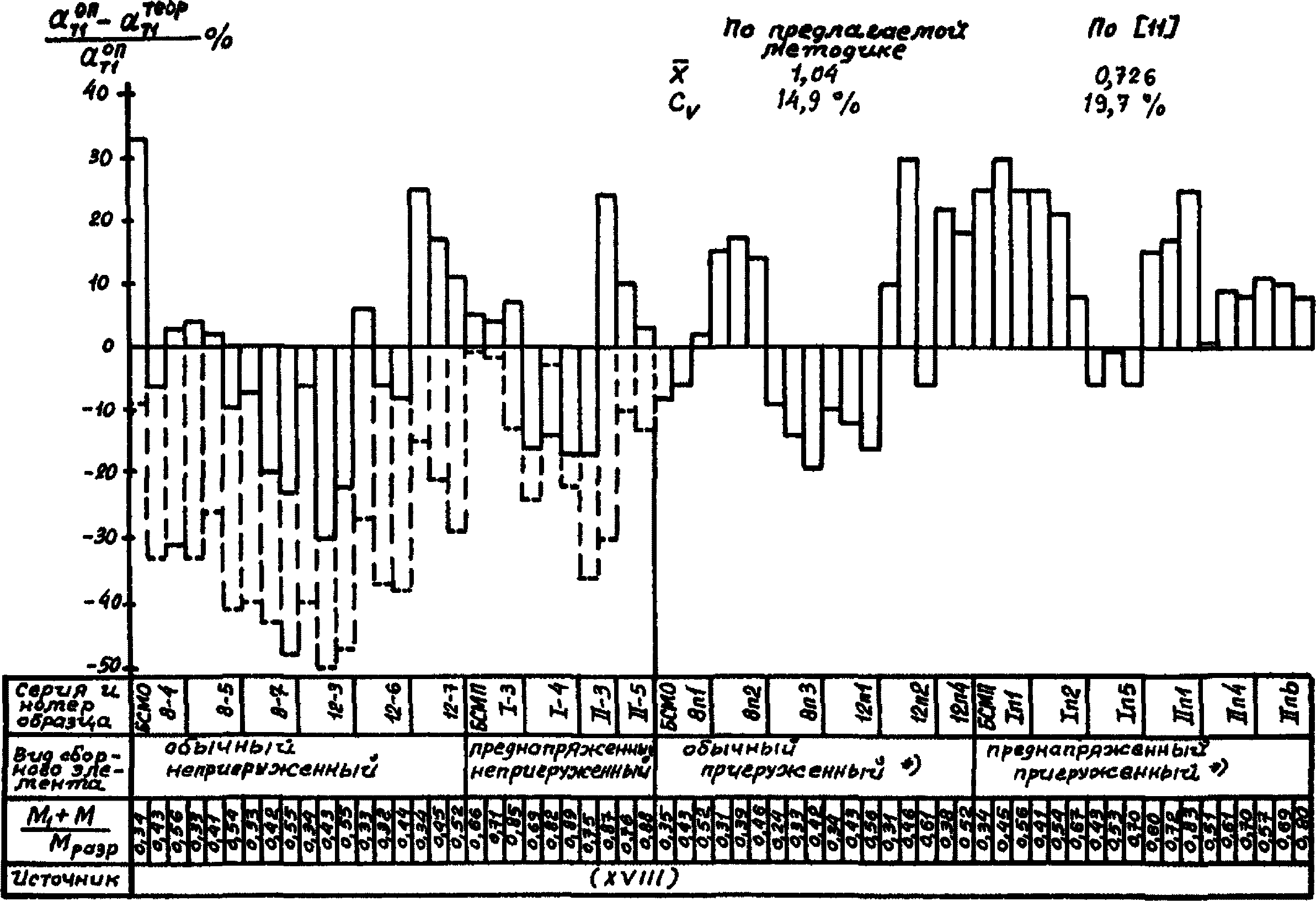
--------------------------------
<*> В [11] расчет отсутствует.
Условные обозначения:
 по предлагаемой методике;
по предлагаемой методике; по [11]
по [11]Рис. 13. Отношение теоретической ширины раскрытия нормальных
трещин к опытной

--------------------------------
<*> В [11] расчет отсутствует.
Условные обозначения:
 по предлагаемой методике;
по предлагаемой методике; по [11]
по [11](без учета выгибов от предварительного напряжения)
В качестве источников опытных данных использовались, помимо приведенных в списке литературы:
диссертации на соискание ученой степени канд. техн. наук Абдель-Кадера Гасана Юсефа "Исследование трещиностойкости и деформативности сборно-монолитных балок"/КИСИ, Киев, 1980 (I); Белавина С.Ф. "Исследование трещиностойкости, жесткости и прочности сборно-монолитных конструкций"/ВНИИ железобетон, Москва, 1964 (II); Городецкого Б.Л. "экспериментально-теоретические исследования прочности контакта в сборно-монолитных преднапряженных железобетонных конструкциях"/КИСИ, Киев - Свердловск, 1969 (III); Кривошеева П.И. "Исследование трещиностойкости комбинированных предварительно напряженных железобетонных изгибаемых конструкции"/НИИСК; Киев, 1971 (IV); Ковтунова Б.П. "Исследование прочности сборно-монолитных балочных конструкций из обычных и преднапряженных сборных элементов"/НИИЖБ, Москва, 1966 (V); Корякина В.П. "Исследование работы внецентренно растянутых сборно-монолитных железобетонных конструкций, армированных преднапряженными элементами"/КуИСИ, Куйбышев, 1963 (VI); Купермана И.Ш. "Исследование железобетонных преднапряженных плит типа Т и ТТ пролетом 12 - 24 м для покрытий одноэтажных производственных зданий"/ВНИИмонтажспецстрой, Москва, 1968 (VII); Медведева С.Н. "Исследование сборно-монолитных преднапряженных железобетонных конструкций"/Горький, 1965 (VIII); Мехди аль Шейх Али "Исследования трещиностойкости сборно-монолитных преднапряженных железобетонных элементов"/НИИЖБ, Москва, 1964 (IX); Мирзаева П.Т. "Исследование деформативности преднапряженных сборно-монолитных керамзитобетонных балок при длительном действии постоянных и переменных нагрузок"/КИСИ, Киев, 1975 (X); Михайлова О.В. "Особенности работы сборно-монолитных конструкций гидротехнических сооружений, армированных преднапряженными элементами"/МИСИ, Москва, 1963 (XI); Нуртаева М.К. "Исследование влияния усадки бетона омоноличивания на напряженно-деформированное состояние и трещиностойкость балочных сборно-монолитных конструкций с преднапряженными элементами"/НИИЖБ, Москва, 1970 (XII); Портянко В.К. "Экспериментально-теоретические исследования прочности статически неопределимых сборно-монолитных балочных конструкций"/Москва, 1967 (XIII); Питулько С.М. "Исследование трещиностойкости и деформативности изгибаемых сборно-монолитных конструкций при кратковременном и длительном действии нагрузок"/НИИЖБ, Москва, 1972 (XIV); Савченко-Бельского В.Г. "Исследование прочности двухслойных преднапряженных железобетонных балок"/НИИСК, Киев, 1960 (XV); Стулия Н.Г. "Исследование несущей способности, трещиностойкости и жесткости двухслойных железобетонных изгибаемых элементов с преднапряженной арматурой"/Харьков, 1953 (XVI); Сунгатуллина Я.Г. "Экспериментальное исследование совместной работы преднапряженных железобетонных элементов с керамзитобетоном"/НИИЖБ, Москва - Свердловск, 1960 (XVII); Усманова В.Ф. "Влияние предварительного загружения сборных элементов на трещиностойкость и деформативность сборно-монолитных конструкций"/НИИСК, Киев, 1980 (XVIII); Фатхуллина В.Ш. "Исследование трещиностойкости по наклонному сечению и прочности по контакту сборно-монолитных балок, армированных поперечными преднапряженными железобетонными элементами"/КазИСИ, Казань, 1972 (XIX); Ху Ли-веня "Перераспределение усилий в сборно-монолитных преднапряженных железобетонных элементах перекрытий многоэтажных промзданий"/МИСИ, Москва, 1960 (XX); Цалалихина М.С. "Исследование сборно-монолитных конструкций плоских покрытий производственных зданий с укрупненной сеткой колонн из преднапряженных элементов механизированного изготовления"/Москва, 1963 (XXI); Юркши А.Б. "Исследование работы преднапряженных сборно-монолитных железобетонных балок при кратковременных статических и многократно повторных нагрузках"/ВИСИ, Вильнюс, 1971 (XXII); Полищука В.П. "Исследование длительных деформаций изгибаемых сборно-монолитных конструкций, работающих без трещин в растянутой зоне"/Уралниистромпроект, Челябинск, 1965 (XXIII); Харченко А.В. "Исследование прочности сборно-монолитных изгибаемых конструкций по нормальным сечениям"/НИИСК, Киев, 1978 (XXIV);
научно-технический отчет "Исследовать прочность и деформативность изгибаемых, внецентренно сжатых и внецентренно растянутых сборно-монолитных конструкций"/КазИСИ, рег. N 81071097, - Казань, 1983 (XXV).
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ
Усилия
p - сосредоточенная нагрузка, приложенная после приобретения монолитным бетоном заданной прочности
q - интенсивность равномерно распределенной нагрузки, приложенной после приобретения монолитным бетоном заданной прочности
P и Qоп - опорные реакции от внешних нагрузок, приложенных после приобретения монолитным бетоном заданной прочности
M, Q и N - изгибающий момент, поперечная сила и продольная сила в сечении конструкции от внешних нагрузок, приложенных после приобретения монолитным бетоном заданной прочности
N1.0 - равнодействующая сил предварительного обжатия сборных элементов с учетом всех потерь, проявившихся до приобретения монолитным бетоном заданной прочности [12]
M1 и Q1 - изгибающий момент и поперечная сила от постоянных нагрузок, действующих в процессе возведения конструкции (в т.ч. от собственного веса сборных элементов и монолитного бетона)
Характеристики материалов
Rс.пр и Rс.пр.II - расчетные сопротивления бетона сборных элементов осевому сжатию для предельных состояний соответственно первой и второй групп
Rс.р и Rс.р.II - то же, осевому растяжению
Rс.о - передаточная прочность бетона сборных элементов
Eс и EсII - расчетные значения начального модуля упругости бетона сборных элементов при сжатии и растяжении для предельных состояний соответственно первой и второй групп
Rм.пр и Rм.пр.II - расчетные сопротивления монолитного бетона осевому сжатию для предельных состояний соответственно первой и второй групп
Rм.р и Rм.р.II - то же, осевому растяжению
Eм и EмII - расчетные значения начального модуля упругости монолитного бетона при сжатии и растяжении для предельных состояний соответственно первой и второй групп
Rа и Rа.II - расчетные сопротивления арматуры сжатию и растяжению для предельных состояний соответственно первой и второй групп
Eа - модуль упругости арматурной стали
nас = Eа/EсII; nмс = EмII/EсII
Геометрические характеристики
F1.п и J1.п - площадь приведенного сечения сборных элементов и момент инерции указанной площади относительно оси, проходящей через его центр тяжести
W1.0 и W1.т - моменты сопротивления приведенного сечения сборных элементов относительно растянутого края указанного сечения, определяемые соответственно как для упругого материала и с учетом неупругих деформаций растянутого бетона
e1.0н и e1.ан - расстояния от точки приложения силы N1.0 до соответственно центра тяжести приведенного сечения сборных элементов и центра тяжести сечения арматуры А
d1.0н - то же, до менее обжатых (растянутых) волокон сборных элементов
i1 - расстояние от центра тяжести приведенного сечения сборных элементов до центра тяжести бетона в указанном сечении
Fс и Jс - площадь всего бетона в поперечном сечении сборных элементов и собственный момент инерции указанной площади
h1.0 - рабочая высота поперечного сечения сборных элементов
bс - суммарная ширина ребер сборных элементов (при элементах таврового или двутаврового сечений) или ширина сечения сборных элементов на уровне его центра тяжести (при других видах сечений)
Fп и Jп - площадь приведенного сечения конструкции и момент инерции указанной площади относительно оси, проходящей через его центр тяжести
W0 и Wт - моменты сопротивления приведенного сечения конструкции относительно растянутого края указанного сечения, определяемые соответственно как для упругого материала и с учетом неупругих деформаций растянутого бетона
e0 и eа - расстояния от точки приложения силы N до соответственно центра тяжести приведенного сечения конструкции и центра тяжести сечения арматуры А
h, h0 и  - полная высота поперечного сечения конструкции, рабочая высота и высота сжатой полки указанного сечения
- полная высота поперечного сечения конструкции, рабочая высота и высота сжатой полки указанного сечения
Fм и Jм - площадь монолитного бетона в поперечном сечении конструкции и собственный момент инерции указанной площади
iсо - то же, до центра тяжести бетона в приведенном сечении сборных элементов
iмо - то же, монолитного бетона
dм - высота слоя монолитного бетона над сборными элементами
hм и bм - высота сечения монолитного бетона и ширина указанного сечения на уровне его центра тяжести
Fа и  - площадь сечения арматуры А и А'
- площадь сечения арматуры А и А'
Pа - периметр сечения арматуры А
Fх и Pх - площадь сечения поперечной арматуры в виде вертикальных стержней (хомутов), расположенной в одной, нормальной к продольной оси конструкции, плоскости, и периметр указанного сечения
Fот и Pот - то же, поперечной арматуры в виде наклонных (отогнутых) стержней, расположенных в одной, наклонной к продольной оси конструкции, плоскости
uх и uот - шаг вертикальных стержней (хомутов) и расстояние между наклонными (отогнутыми) стержнями, измеренное по нормали к ним
1. Буракас А.И. Комбинированные преднапряженные перекрытия промышленных зданий. - Киев:  , 1964. - 113 с.
, 1964. - 113 с.
 , 1964. - 113 с.
, 1964. - 113 с.2. СН 165-76. Инструкция по проектированию бетонных и железобетонных конструкций из плотного силикатного бетона. - М.: Стройиздат, 1977. - 48 с.
3. Кузьмичев А.Е., Магометов Р.О. К расчету элементов сборно-монолитных конструкций по предельным состояниям второй группы. - Бетон и железобетон, 1982, N 1, с. 14 - 16.
4. Методические рекомендации по расчету несущей способности сборно-монолитных конструкций по нормальным сечениям. - Киев: НИИСК, 1980. - 39 с.
5. Методические рекомендации по определению ширины раскрытия трещин в железобетонных элементах. - Киев: НИИСК, 1982. - 27 с.
6. Методические рекомендации по учету влияния ползучести бетонов при расчете железобетонных стержней и стержневых систем. - Киев: НИИСК, 1981. - 73 с.
7. Методические рекомендации по учету влияния ползучести бетонов при расчете сборно-монолитных стержневых конструкций. - Киев: НИИСК, 1983. - 51 с.
8. Полищук В.П. Поведение сборно-монолитных конструкций во времени. - В кн.: железобетонные конструкции/Уралниистромпроект. - Челябинск, 1969, вып. IV, с. 10 - 28.
9. Проектирование и изготовление сборно-монолитных конструкций. - Киев:  , 1982. - 152 с.
, 1982. - 152 с.
 , 1982. - 152 с.
, 1982. - 152 с.10. Рокач В.И. Деформации железобетонных изгибаемых элементов. - Киев:  , 1968. - 96 с.
, 1968. - 96 с.
 , 1968. - 96 с.
, 1968. - 96 с.11. Руководство по проектированию железобетонных сборно-монолитных конструкций. - М.: Стройиздат, 1977. - 62 с.
12. СНиП II-21-75. Бетонные и железобетонные конструкции. Нормы проектирования. - М.: Стройиздат, 1975. - 89 с.
13. Сунгатуллин Я.Г. Экспериментально-теоретические основы расчета сопротивления сдвигу армированного и неармированного контактов сборно-монолитных конструкций. - В кн.: Сборные и сборно-монолитные конструкции. - Казань - Ленинград, 1975. - с. 7 - 24.
14. Честелли-Гуиди К. Предварительно напряженный железобетон. - М.: Госстройиздат, 1960. - 467 с.
15. Abeles P.W. Breaking Tests on Three Size Prestressed Concrete Bridge Beams. "Structural Engineer", vol. 29, 1951, N 5 (p.p. 149 - 160).
16. Abeles P.W. Strain and Fatique Tests on Partially Prestressed Concrete Constructions. Journal of the American Concrete Institute, vol. 26 (Proc. vol. 51), December 1954, N 4 (p.p. 361 - 376).
17. Bryson J.O., Skoda L.F., Watstein D. Flexural behaviour of prestressed split-beam composite concrete section. Journal of the Prestressed Concrete Institute, vol. 10, 1965, N 3.
18. Evans R.H., Parker A.S. Behaviour of Prestressed Concrete Composite Beams. Journal of the American Concrete Institute, vol. 26 (Proc. vol. 51), May 1955, N 9 (p.p. 861 - 878).
19. Graegorzewski W. Obliczanie zelbetowych construkcij zginanych deskami strunobetonowymi. Wydawnictwo "Arkady", Warszawa, 1963.
20. Lyse J. Tests of full-sized prestressed concrete bridge beams. Journal of the American Concrete Institute, vol. 29 (proc. vol. 54), May 1958, N 11.
21. Okada K., Jochioka J. Study on the Differential Shrinkage of Composite Prestressed Concrete Beams. Memories of the Faculty of Engineering Kyoto University. Vol. 30, part 4, October 1968 (p.p. 359 - 370).
22. Ozell A.M. Behaviour of simple-span and continuous composite prestressed concrete beams. Journal of the Prestressed Concrete Institute, vol. 2, June 1957, N 1 (p.p. 18 - 31, 42 - 74).
23. Revesz S. The cracking Load of a Composite Pre-tensioned T-Beam. "Civil Engineering and Public Works-Review." Vol. 47, September 1952, N 555 (p.p. 733 - 735).
24. Khan F.P., Brawn A.J. Load tests of 120-ft precast prestressed bridge girder. Journal of the American Concrete Institute, vol. 30 (proc. vol. 55), July 1958, N 1.
25. Soutter P. Die Verbundwirkung zwischen vorgespannten und nicht vorgespannten Beton und ihre Anwendung aus den Platten-balken mit vorgespannten Steig. "Scheizerische Bauzeitung" Bd 124, 26. August 1944, N 9 (s.s. 103 - 108).
26. Stanger R.H. A Test of a Prestressed Concrete Railway Bridge Girder. "Concrete and Constructional Engineering", vol. 45, August 1950, N 8 (p.p 296 - 299).











 для приведенного бетона
для приведенного бетона
















 проверка прочности производится из
проверка прочности производится из 
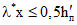 в
в  - соответственно
- соответственно 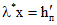 .
.


















































 в
в  имеем
имеем  .
. по предлагаемой методике [
по предлагаемой методике [ по
по  по предлагаемой методике [
по предлагаемой методике [ по
по