СПРАВКА
Источник публикации
М.: Стандартинформ, 2018
Примечание к документу
Документ включен в Перечень стандартов и рекомендаций в области информационной безопасности, применяемых в рамках реализации цифровой повестки Евразийского экономического союза (Рекомендация Коллегии Евразийской экономической комиссии от 12.03.2019 N 9).
Текст данного документа приведен с учетом поправки, опубликованной в "ИУС", N 1, 2021.
Документ введен в действие с 01.06.2019.
Название документа
"ГОСТ 34.11-2018. Межгосударственный стандарт. Информационная технология. Криптографическая защита информации. Функция хэширования"
(введен в действие Приказом Росстандарта от 04.12.2018 N 1060-ст)
"ГОСТ 34.11-2018. Межгосударственный стандарт. Информационная технология. Криптографическая защита информации. Функция хэширования"
(введен в действие Приказом Росстандарта от 04.12.2018 N 1060-ст)
Содержание
Приказом Федерального
агентства по техническому
регулированию и метрологии
от 4 декабря 2018 г. N 1060-ст
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ИНФОРМАЦИОННАЯ ТЕХНОЛОГИЯ
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
ФУНКЦИЯ ХЭШИРОВАНИЯ
Information technology. Cryptographic
data security. Hash-function
ГОСТ 34.11-2018
МКС 35.040
Дата введения
1 июня 2019 года
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2015 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
1 РАЗРАБОТАН Центром защиты информации и специальной связи ФСБ России с участием Открытого акционерного общества "Информационные технологии и коммуникационные системы" (ОАО "ИнфоТеКС")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 26 "Криптографическая защита информации"
3 ПРИНЯТ Межгосударственным советом по метрологии, стандартизации и сертификации (протокол от 29 ноября 2018 г. N 54)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по МК (ИСО 3166) 004-97 | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
Туркмения | TM | Главгосслужба "Туркменстандартлары" |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 4 декабря 2018 г. N 1060-ст межгосударственный стандарт ГОСТ 34.11-2018 введен в действие в качестве национального стандарта Российской Федерации с 1 июня 2019 г.
5 Настоящий стандарт подготовлен на основе применения ГОСТ Р 34.11-2012
6 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Настоящий стандарт содержит описание алгоритма и процедуры вычисления хэш-функции для любой последовательности двоичных символов, которые применяются в криптографических методах защиты информации, в том числе в процессах формирования и проверки электронной цифровой подписи.
Необходимость разработки настоящего стандарта вызвана потребностью в создании на межгосударственном уровне хэш-функции, соответствующей современным требованиям к криптографической стойкости и требованиям межгосударственного стандарта ГОСТ 34.10.
Настоящий стандарт терминологически и концептуально увязан с международным стандартом ИСО 2382 [1], а также международными стандартами серий ИСО/МЭК 9796 [2], [3], ИСО/МЭК 14888 [4] - [6] и ИСО/МЭК 10118 [7] - [10].
Примечание - Основная часть стандарта дополнена приложением А "Контрольные примеры".
Настоящий стандарт определяет алгоритм и процедуру вычисления хэш-функции для любой последовательности двоичных символов, которые применяются в криптографических методах обработки и защиты информации, в том числе для реализации процедур обеспечения целостности, аутентичности, электронной цифровой подписи (ЭЦП) при передаче, обработке и хранении информации в автоматизированных системах.
Определенная в настоящем стандарте функция хэширования используется при реализации систем электронной цифровой подписи на базе асимметричного криптографического алгоритма по ГОСТ 34.10.
Стандарт рекомендуется использовать при создании, эксплуатации и модернизации систем обработки информации различного назначения.
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ 34.10-2018 Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочного стандарта в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1.1 дополнение (padding): Приписывание дополнительных бит к строке бит.
Примечание - Адаптировано из ИСО/МЭК 10118-1 [7].
3.1.2 инициализационный вектор (initializing value): Вектор, определенный как начальная точка работы функции хэширования.
Примечание - Адаптировано из ИСО/МЭК 10118-1 [7].
3.1.3 сообщение (message): Строка бит произвольной конечной длины.
Примечание - Адаптировано из ИСО/МЭК 14888-1 [4].
3.1.4 функция сжатия (round function): Итеративно используемая функция, преобразующая строку бит длиной L1 и полученную на предыдущем шаге строку бит длиной L2 в строку бит длиной L2.
Примечания
1 Адаптировано из ИСО/МЭК 10118-1 [7].
2 В настоящем стандарте понятия "строка бит длиной L" и "двоичный вектор-строка размерности L" считаются тождественными.
3.1.5 хэш-код (hash-code): Строка бит, являющаяся выходным результатом хэш-функции.
Примечание - Адаптировано из ИСО/МЭК 10118-1 [7].
3.1.6 хэш-функция (collision-resistant hash-function): Функция, отображающая строки бит в строки бит фиксированной длины и удовлетворяющая следующим свойствам:
1) по данному значению функции сложно вычислить исходные данные, отображаемые в это значение;
2) для заданных исходных данных сложно вычислить другие исходные данные, отображаемые в то же значение функции;
3) сложно вычислить какую-либо пару исходных данных, отображаемых в одно и то же значение.
Примечания
1 Адаптировано из ИСО/МЭК 10118-1 [7].
2 В настоящем стандарте в целях сохранения терминологической преемственности по отношению к нормативным документам, действующим на территории государства, принявшего настоящий стандарт, и опубликованным ранее на русском языке научно-техническим изданиям установлено, что термины "хэш-функция", "криптографическая хэш-функция", "функция хэширования" и "криптографическая функция хэширования" являются синонимами.
3.1.7 [электронная цифровая] подпись (signature); ЭЦП: Строка бит, полученная в результате процесса формирования подписи.
Примечания
1 Адаптировано из ИСО/МЭК 14888-1 [4].
2 В настоящем стандарте в целях сохранения терминологической преемственности по отношению к нормативным документам, действующим на территории государства, принявшего настоящий стандарт, и опубликованным ранее на русском языке научно-техническим изданиям установлено, что термины "электронная подпись", "цифровая подпись" и "электронная цифровая подпись" являются синонимами.
В настоящем стандарте применены следующие обозначения:
V* - множество всех двоичных векторов-строк конечной размерности (далее - векторы), включая пустую строку;
|A| - размерность (число компонент) вектора  (если A - пустая строка, то |A| = 0);
(если A - пустая строка, то |A| = 0);
Vn - множество всех n-мерных двоичных векторов, где n - целое неотрицательное число; нумерация подвекторов и компонент вектора осуществляется справа налево, начиная с нуля;
A||B - конкатенация векторов  , т.е. вектор из V|A|+|B|, в котором левый подвектор из V|A| совпадает с вектором A, а правый подвектор из V|B| совпадает с вектором B;
, т.е. вектор из V|A|+|B|, в котором левый подвектор из V|A| совпадает с вектором A, а правый подвектор из V|B| совпадает с вектором B;
 , т.е. вектор из V|A|+|B|, в котором левый подвектор из V|A| совпадает с вектором A, а правый подвектор из V|B| совпадает с вектором B;
, т.е. вектор из V|A|+|B|, в котором левый подвектор из V|A| совпадает с вектором A, а правый подвектор из V|B| совпадает с вектором B;An - конкатенация n экземпляров вектора A;
 - биективное отображение, сопоставляющее элементу кольца
- биективное отображение, сопоставляющее элементу кольца  , j = 0, ..., n - 1, выполнено равенство Vecn(z) = zn-1||...||z1||z0;
, j = 0, ..., n - 1, выполнено равенство Vecn(z) = zn-1||...||z1||z0; - отображение, обратное отображению Vecn, т.е.
- отображение, обратное отображению Vecn, т.е.  ;
; - отображение, ставящее в соответствие вектору zk-1||...||z1||z0, k >= n, вектор zk-1||...||zk-n+1||zk-n;
- отображение, ставящее в соответствие вектору zk-1||...||z1||z0, k >= n, вектор zk-1||...||zk-n+1||zk-n;a := b - операция присваивания переменной a значения b;
M - двоичный вектор, подлежащий хэшированию,  , |M| < 2512;
, |M| < 2512;
 , |M| < 2512;
, |M| < 2512; - функция хэширования, отображающая вектор (сообщение) M в вектор (хэш-код) H(M);
- функция хэширования, отображающая вектор (сообщение) M в вектор (хэш-код) H(M);IV - инициализационный вектор функции хэширования,  .
.
 .
.Настоящий стандарт определяет две функции хэширования  с длинами хэш-кода n = 256 бит и n = 512 бит.
с длинами хэш-кода n = 256 бит и n = 512 бит.
 с длинами хэш-кода n = 256 бит и n = 512 бит.
с длинами хэш-кода n = 256 бит и n = 512 бит.Значение инициализационного вектора IV для функции хэширования с длиной хэш-кода 512 бит равно 0512. Значение инициализационного вектора IV для функции хэширования с длиной хэш-кода 256 бит равно (00000001)64.
Нелинейное биективное преобразование множества двоичных векторов V8 задается подстановкой
 , (1)
, (1)где  .
.
 .
.Значения подстановки  записаны ниже в виде массива
записаны ниже в виде массива  :
:
 :
:Значения перестановки 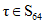 записаны ниже в виде массива
записаны ниже в виде массива  :
:
 :
:Линейное преобразование l множества двоичных векторов V64 задается умножением справа на матрицу A над полем GF(2), строки которой записаны ниже последовательно в шестнадцатеричном виде. Строка матрицы с номером j, j = 0, ..., 63, записанная в виде aj,15 ... aj,0, где  , i = 0, ..., 15, есть Vec4(aj,15)||...||Vec4(aj,0).
, i = 0, ..., 15, есть Vec4(aj,15)||...||Vec4(aj,0).
 , i = 0, ..., 15, есть Vec4(aj,15)||...||Vec4(aj,0).
, i = 0, ..., 15, есть Vec4(aj,15)||...||Vec4(aj,0).8e20faa72ba0b470 | 47107ddd9b505a38 | ad08b0e0c3282d1c | d8045870ef14980e |
6c022c38f90a4c07 | 3601161cf205268d | 1b8e0b0e798c13c8 | 83478b07b2468764 |
a011d380818e8f40 | 5086e740ce47c920 | 2843fd2067adea10 | 14aff010bdd87508 |
0ad97808d06cb404 | 05e23c0468365a02 | 8c711e02341b2d01 | 46b60f011a83988e |
90dab52a387ae76f | 486dd4151c3dfdb9 | 24b86a840e90f0d2 | 125c354207487869 |
092e94218d243cba | 8a174a9ec8121e5d | 4585254f64090fa0 | accc9ca9328a8950 |
9d4df05d5f661451 | c0a878a0a1330aa6 | 60543c50de970553 | 302a1e286fc58ca7 |
18150f14b9ec46dd | 0c84890ad27623e0 | 0642ca05693b9f70 | 0321658cba93c138 |
86275df09ce8aaa8 | 439da0784e745554 | afc0503c273aa42a | d960281e9d1d5215 |
e230140fc0802984 | 71180a8960409a42 | b60c05ca30204d21 | 5b068c651810a89e |
456c34887a3805b9 | ac361a443d1c8cd2 | 561b0d22900e4669 | 2b838811480723ba |
9bcf4486248d9f5d | c3e9224312c8da0 | effa11af0964ee50 | f97d86d98a327728 |
e4fa2054a80b329c | 727d102a548b194e | 39b008152acb8227 | 9258048415eb419d |
492c024284fbaec0 | aa16012142f35760 | 550b8e9e21f7a530 | a48b474f9ef5dc18 |
70a6a56e2440598e | 3853dc371220a247 | 1ca76e95091051ad | 0edd37c48a08a6d8 |
07e095624504536c | 8d70c431ac02a736 | c83862965601dd1b | 641c314b2b8ee083 |
Здесь в одной строке записаны четыре строки матрицы A, при этом в строке с номером i, i = 0, ..., 15, записаны строки матрицы A с номерами 4i + j, j = 0, ..., 3 в следующем порядке (слева направо):
4i + 0, 4i + 1, 4i + 2, 4i + 3.
Результат умножения вектора  на матрицу A есть вектор
на матрицу A есть вектор 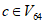 :
:
 на матрицу A есть вектор
на матрицу A есть вектор  , (2)
, (2)где 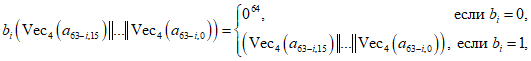
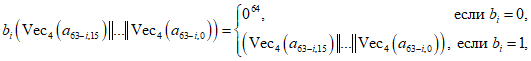
для всех i = 0, ..., 63.
Итерационные константы записаны в шестнадцатеричном виде. Значение константы, записанное в виде a127 ... a0, где  , i = 0, ..., 127, есть Vec4(a127)||...||Vec4(a0):
, i = 0, ..., 127, есть Vec4(a127)||...||Vec4(a0):
 , i = 0, ..., 127, есть Vec4(a127)||...||Vec4(a0):
, i = 0, ..., 127, есть Vec4(a127)||...||Vec4(a0):C1 = b1085bda1ecadae9ebcb2f81c0657df2f6a76432e45d
016714eb88d7585c4fc4b7ce09192676901a2422a08a460d
31505767436cc744d23dd806559f2a64507;
C2 = 6fa3b58aa99d2f1a4fe39d460f70b5d7f3feea720a232
b9861d55e0f16b501319ab5176b12d699585cb561c2db0aa7
ca55dda21bd7cbcd56e679047021b19bb7;
C3 = f574dcac2bce2fc70a39fc286a3d843506f15e5f529c1
f8bf2ea7514b1297b7bd3e20fe490359eb1dc93a376062db09
c2b6f443867adb31991e96f50aba0ab2;
C4 = ef1fdfb3e81566d2f948e1a05d71e4dd488e857e335c3
c7d9d721cad685e353fa9d72c82ed03d675d8b71333935203
be3453eaa193e837f1220cbebc84e3d12e;
C5 = 4bea6bacad4747999a3f410c6ca923637f151df1686104
a359e35d7800fffbdbfcd1747253af5a3dfff00b723271a167a
56a27ea9ea63f5601758fd7c6cfe57;
C6 = ae4faeae1d3ad3d96fa4c33b7a3039c02d66c4f95142a46c187
f9ab49af08ec6cffaa6b71c9ab7b40af21f66c2bec6b6bf71
c57236904f35fa68407a46647d6e;
C7 = f4c70e16eeaac5ec51ac86febf240954399ec6c7e6bf
87c9d3473e33197a93c90992abc52d822c3706476983284a
05043517454ca23c4af38886564d3a14d493;
C8 = 9b1f5b424d93c9a703e7aa020c6e41414eb7f8719c36
de1e89b4443b4ddbc49af4892bcb929b069069d18d2bd1a5c
42f36acc2355951a8d9a47f0dd4bf02e71e;
C9 = 378f5a541631229b944c9ad8ec165fde3a7d3a1b258942243
cd955b7e00d0984800a440bdbb2ceb17b2b8a9aa6079c540
e38dc92cb1f2a607261445183235adb;
C10 = abbedea680056f52382ae548b2e4f3f38941e71cff8a
78db1fffe18a1b3361039fe76702af69334b7a1e6c303b7652
f43698fad1153bb6c374b4c7fb98459ced;
C11 = 7bcd9ed0efc889fb3002c6cd635afe94d8fa6bbbebab
076120018021148466798a1d71efea48b9caefbacd1d7d476
e98dea2594ac06fd85d6bcaa4cd81f32d1b;
C12 = 378ee767f11631bad21380b00449b17acda43c32bcdf
1d77f82012d430219f9b5d80ef9d1891cc86e71da4aa88e12852
faf417d5d9b21b9948bc924af11bd720.
При вычислении хэш-кода H(M) сообщения  используются следующие преобразования:
используются следующие преобразования:
 используются следующие преобразования:
используются следующие преобразования: ; (3)
; (3) , (4)
, (4)где 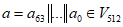 ,
,  , i = 0, ..., 63;
, i = 0, ..., 63;
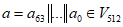 ,
, 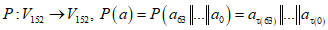 , (5)
, (5)где  ,
,  , i = 0, ..., 63;
, i = 0, ..., 63;
 ,
,  , (6)
, (6)где  ,
,  , i = 0, ..., 7.
, i = 0, ..., 7.
 ,
, Значение хэш-кода сообщения  вычисляется с использованием итерационной процедуры. На каждой итерации вычисления хэш-кода используется функция сжатия:
вычисляется с использованием итерационной процедуры. На каждой итерации вычисления хэш-кода используется функция сжатия:
 вычисляется с использованием итерационной процедуры. На каждой итерации вычисления хэш-кода используется функция сжатия:
вычисляется с использованием итерационной процедуры. На каждой итерации вычисления хэш-кода используется функция сжатия: , (7)
, (7)значение которой вычисляется по формуле
 , (8)
, (8)где E(K, m) = X[K13]LPSX[K12] ... LPSX[K2]LPSX[K1](m).
Значения 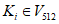 , i = 1, ..., 13 вычисляются следующим образом:
, i = 1, ..., 13 вычисляются следующим образом:
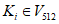 , i = 1, ..., 13 вычисляются следующим образом:
, i = 1, ..., 13 вычисляются следующим образом:K1 = K; (9)
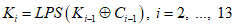 .
.Исходными данными для процедуры вычисления хэш-кода H(M) является подлежащее хэшированию сообщение  и
и  - инициализационный вектор.
- инициализационный вектор.
 и
и  - инициализационный вектор.
- инициализационный вектор.Алгоритм вычисления функции H состоит из следующих этапов.
Присвоить начальные значения текущих величин:
Шаг 1.1 - присвоить h := IV;
Шаг 1.2 - присвоить  ;
;
 ;
;Шаг 1.3 - присвоить  ;
;
 ;
;Шаг 1.4 - перейти к этапу 2.
При положительном исходе перейти к этапу 3.
В противном случае выполнить последовательность вычислений по 2.2 - 2.7;
Шаг 2.2 - вычислить подвектор  сообщения M : M'||m. Далее выполнить последовательность вычислений:
сообщения M : M'||m. Далее выполнить последовательность вычислений:
 сообщения M : M'||m. Далее выполнить последовательность вычислений:
сообщения M : M'||m. Далее выполнить последовательность вычислений:Шаг 2.3 - присвоить h := gN(h, m);
Шаг 2.4 - присвоить  ;
;
 ;
;Шаг 2.5 - присвоить 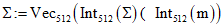 ;
;
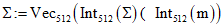 ;
;Шаг 2.6 - присвоить M := M';
Шаг 2.7 - перейти к шагу 2.1.
Шаг 3.1 - присвоить m := 0511-|M|||1||M;
Шаг 3.2 - присвоить h := gN(h, m);
Шаг 3.3 - присвоить 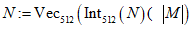 ;
;
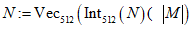 ;
;Шаг 3.4 - присвоить 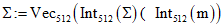 ;
;
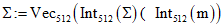 ;
;Шаг 3.5 - присвоить h := g0(h, N);
Шаг 3.7 - конец работы алгоритма.
Значение величины h, полученное на шаге 3.6, является значением функции хэширования H(M).
(справочное)
Настоящее приложение носит справочный характер и не является частью нормативных положений настоящего стандарта.
Векторы из V* записываются в шестнадцатеричном виде. Вектор  , записанный в виде an-1...a0, где
, записанный в виде an-1...a0, где  , i = 0, ..., n - 1, есть Vec4(an-1)||...||Vec4(a0).
, i = 0, ..., n - 1, есть Vec4(an-1)||...||Vec4(a0).
 , i = 0, ..., n - 1, есть Vec4(an-1)||...||Vec4(a0).
, i = 0, ..., n - 1, есть Vec4(an-1)||...||Vec4(a0).Необходимо вычислить хэш-код сообщения
M1 = 323130393837363534333231303938373635343332313
03938373635343332313039383736353433323130393837363
5343332313039383736353433323130.
Присваиваются значения:
h := IV = 0512;
N := 0512;
 .
.Длина сообщения |M1| = 504 < 512, поэтому происходит дополнение неполного блока:
m := 013231303938373635343332313039383736353433323
13039383736353433323130393837363534333231303938373
635343332313039383736353433323130.
Вычисляется значение  .
.
 .
.После преобразования S:
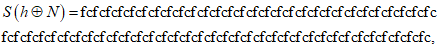
после преобразования P:
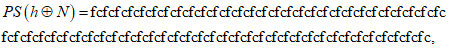
после преобразования L:

Затем выполняется преобразование E(K, m):
Итерация 1
K1 = b383fc2eced4a574b383fc2eced4a574b383fc2eced4a
574b383fc2eced4a574b383fc2eced4a574b383fc2eced4a574
b383fc2eced4a574b383fc2eced4a574,
X[K1](m) = b2b1cd1ef7ec924286b7cf1cffe49c4c84b5c91
afde694448abbcb18fbe0964682b3c516f9e2904080b1cd1ef
7ec924286b7cf1cffe49c4c84b5c91afde69444,
SX[K1](m) = 4645d95fc0beec2c432f8914b62d4efd3e5e37
f14b097aead67de417c220b0482492ac996667e0ebdf45d95
fc0beec2c432f8914b62d4efd3e5e37f14b097aea,
PSX[K1](m) = 46433ed624df433e452f5e7d92452f5ed98937
e4acd989375f14f117995f14f1c0b64bc266c0b64bbe2d092067
be2d09ec4e7ab0e0ec4e7a2cfdea48eb2cfdea,
LPSX[K1](m) = e60059d4d8e0758024c73f6f3183653f56579189602
ae4c21e7953ebc0e212a0ce78a8df475c2fd4fc43fc4b71c01e35
be465fb20dad2cf690cdf65028121bb9,




Итерация 2
K2 = d0b00807642fd78f13f2c3ebc774e80de0e902d23aef2
ee9a73d010807dae9c188be14f0b2da27973569cd2ba051301036
f728bd1d7eec33f4d18af70c46cf1e,
LPSX[K2]LPSX[K1](m) = 18e77571e703d19548075c574ce5
e50e0480c9c5b9f21d45611ab86cf32e352ad91854ea7df8f863
d46333673f62ff2d3efae1cd966f8e2a74ce49902799aad4.
Итерация 3
K3 = 9d4475c7899f2d0bb0e8b7dac6ef6e6b44ecf66716d3a
0f16681105e2d13712a1a9387ecc257930e2d61014a1b5c9fc
9e24e7d636eb1607e816dbaf927b8fca9,
LPSX[K3] ... LPSX[K1](m) = 03dc0a9c64d42543ccdb62960
d58c17e0b5b805d08a07406ece679d5f82b70fea22a7ea56e21814619
e8749b308214575489d4d465539852cd4b0cd3829bef39.
Итерация 4
K4 = 5c283daba5ec1f233b8c833c48e1c670dae2e40cc4c3219
c73e58856bd96a72fdf9f8055ffe3c004c8cde3b8bf78f95f3370
d0a3d6194ac5782487defd83ca0f,
LPSX[K4] ... LPSX[K1](m) = dbee312ea7301b0d6d13e43855e
85db81608c780c43675bc93cfd82db4933b3898a35b13e1878abe
119e4dffb9de4889738ca74d064cd9eb732078c1fb25e04.
Итерация 5
K5 = 109f33262731f9bd569cbc9317baa551d4d2964fa18d42
c41fab4e37225292ec2fd97d7493784779046388469ae195c436
fa7cba93f8239ceb5ffc818826470c,
LPSX[K5] ... LPSX[K1](m) = 7fb3f15718d90e889f9fb7c38f527
bec861c298afb9186934a93c9d96ade20df109379bb9c1a1ffd
0ad81fce7b45ccd54501e7d127e32874b5d7927b032de7a1.
Итерация 6
K6 = b32c9b02667911cf8f8a0877be9a170757e25026ccf41
e67c6b5da70b1b874743e1135cfbefe244237555c676c153d
99459bc382573aee2d85d30d99f286c5e7,
LPSX[K6] ... LPSX[K1](m) = 95efa4e104f235824bae5030fe
2d0f170a38de3c9b8fc6d8fa1a9adc2945c413389a121501fa71a
65067916b0c06f6b87ce18de1a2a98e0a64670985f47d73f1.
Итерация 7
K7 = 8a13c1b195fd0886ac49989e7d84b08bc7b00e4f3f62765
ece6050fcbabdc2346c8207594714e8e9c9c7aad694edc922d6b01
e17285eb7e61502e634559e32f1,
LPSX[K7] ... LPSX[K1](m) = 7ea4385f7e5e40103bfb25c67e404
c7524eec43e33b1d06557469c604985430432b43d941b77ffd
476103338e9bd5145d9c1e18b1f262b58a81dcefff6fc6535.
Итерация 8
K8 = 52cec3b11448bb8617d0ddfbc926f2e88730cb9179d6decea
5acbffd323ec3764c47f7a9e13bb1db56c342034773023d617ff01
cc546728e71dff8de5d128cac,
LPSX[K8] ... LPSX[K1](m) = b2426da0e58d5cfe898c36e797993
f902531579d8ecc59f8dd8a60802241a4561f290cf992eb398894424
bf681636968c167e870967b1dd9047293331956daba.
Итерация 9
K9 = f38c5b7947e7736d502007a05ea64a4eb9c243cb82154aa
138b963bbb7f28e74d4d710445389671291d70103f48fd4d4c01
fc415e3fb7dc61c6088afa1a1e735,
LPSX[K9] ... LPSX[K1](m) = 5e0c9978670b25912dd1ede5bdd1
cf18ed094d14c6d973b731d50570d0a9bca215415a15031fd20
ddefb5bc61b96671d6902f49df4d2fd346ceebda9431cb075.
Итерация 10
K10 = 0740b3faa03ed39b257dd6e3db7c1bf56b6e18e40cdaabd
30617cecbaddd618ea5e61bb4654599581dd30c24dab877ad
0687948286cfefaa7eef99f6068b315,
LPSX[K10] ... LPSX[K1](m) = c1ddd840fe491393a5d460440
e03bf451794e792c0c629e49ab0c1001782dd37691cb6896f3e00
b87f71d37a584c35b9cd8789fad55a46887e5b60e124b51a61.
Итерация 11
K11 = 185811cf3c2633aec8cfdfcae9dbb29347011bf92b95910
a3ad71e5fca678e45e374f088f2e5c29496e9695ce8957837107
bb3aa56441af11a82164893313116,
LPSX[K11] ... LPSX[K1](m) = 3f75beaf2911c35d575088e30542
b689c85b6b1607f8b800405941f5ab7042847b9b08b58b4fbdd6154
ed7b366fd3ee778ce647726ddb3c7d48c8ce8866a8435.
Итерация 12
K12 = 9d46bf66234a7ed06c3b2120d2a3f15e0fedd87189b75
b3cd2f206906b5ee00dC9a1eab800fb8cc5760b251f4db5cdef
427052fa345613fd076451901279ee4c,
LPSX[K12] ... LPSX[K1](m) = f35b0d889eadfcff73b6b17f33413
a97417d96f0c4cc9d30cda8ebb7dcd5d1b061e620bac75b367370605
f474ddc006003bec4c4d7ce59a73fbe6766934c55a2.
Итерация 13
K13 = 0179104026b900d8d768b6e223484c9761e3c585b3a405
a6d2d8565ada926c3f7782ef127cd6b98290bf612558b4b60
aa3cbc28fd94f95460d76b621cb45be70,
X[K13] ... LPSX[K1](m) = fc221dc8b814fc27a4de079d
10097600209e5375776898961f70bded0647bd8f1664cfa8bb8d8ff
1e0df3e621568b66aa075064b0e81cce132c8d1475809ebd2.
Результат выполнения преобразования gN(h, m):
h = fd102cf8812ccb1191ea34af21394f3817a86641445
aa9a626488adb33738ebd2754f6908cbbbac5d3ed0f522c
50815c954135793fb1f5d905fee4736b3bdae2.
Изменяются значения переменных N и  :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
000000000000000000000000000001f8,

Результат выполнения преобразования g0(h, N):
h = 5c881fd924695cf196c2e4fec20d14b642026f2a0b1716
ebaabb7067d4d597523d2db69d6d3794622147a14f19a66e7
f9037e1d662d34501a8901a5de7771d7c.
Результат выполнения преобразования 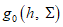 :
:
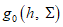 :
:h = 486f64d917879417fef082b3381a4e211c324f074654
c38823a7b76f830ad00fa1fbae42b1285c0352f227524bc9ab
16254288dd6863dccd5b9f54a1ad0541b.
Хэш-кодом сообщения M1 является значение:
H(M1) = 486f64c1917879417fef082b3381a4e211c324f074654
c38823a7b76f830ad00fa1fbae42b1285c0352f227524bc9ab
16254288dd6863dccd5b9f54a1ad0541b.
Присваиваются значения:
h := IV = (00000001)64;
N := 0512;
 .
.Длина сообщения |M1| = 504 < 512, поэтому происходит дополнение неполного блока:
m := 013231303938373635343332313039383736353433323
13039383736353433323130393837363534333231303938373
635343332313039383736353433323130.
Вычисляется значение  .
.
 .
.После преобразования S:

после преобразования P:

после преобразования L:

Затем выполняется преобразование E(K, m):
Итерация 1
K1 = 23c5ee40b07b5f1523c5ee40b07b5f1523c5ee40b07b5
f1523c5ee40b07b5f1523c5ee40b07b5f1523c5ee40b07b5f
1523c5ee40b07b5f1523c5ee40b07b5f15,
X[K1](m) = 22f7df708943682316f1dd72814b662d14f3db
7483496e251afdd976854f6c2712f5d778874d6a2110f7df
708943682316f1dd72814b662d14f3db7483496e25,
SX[K1](m) = 65c061327951f35a99a6d819f5a29a0193d290ffa
92ab25cf14b538aa8cc9d21f0f4fe6dc93a7818e9c061327951
f35a99a6d819f5a29a0193d290ffa92ab25c,
PSX[K1](m) = 659993f1f0e99993c0a6d24bf4c0a6d261d89053
fe61d8903219ff8a6d3219ff79f5a9a8c979f5a951a22acc3a51a
22af39ab29d78f39ab25a015c21185a015c,
LPSX[K1](m) = e549368917a0a2611d5e08c9c2fd5b3c563f18
c0f68c410d84ae9d5fbdfb934055650121b7aa6d7b3e7d09d46
ac4358adaa6ae44fa3b0402c4166d2c3eb2ef02,



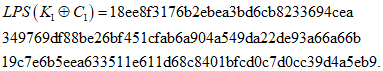
Итерация 2
K2 = 18ee8f3176b2ebea3bd6cb8233694cea349769df88be
26bf451cfab6a904a549da22de93a66a66b19c7e6b5eea633511
e611d68c8401bfcd0c7d0cc39d4a5eb9,
LPSX[K2]LPSX[K1](m) = c502dab7e79eb94013fcd1ba64def
3b916f18b63855d43d22b77fca1452f9866c2b45089c62e9d82
edf1ef45230db9a23c9e1c521113376628a5f6a5dbc041b2.
Итерация 3
K3 = aaa4cf31a265959157aec8ce91e7fd46bf27dee21164c
5e3940bba1a519e9d1fce0913f1253e7757915000cd674be12
cc7f68e73ba26fb00fd74af4101805f2d,
LPSX[K3] ... LPSX[K1](m) = 8e5a4fe41fc790af29944f027
aa2f10105d65cf60a66e442832bb9ab5020dc54772e36b03d4b9aa
471037212cde93375226552392ef4d83010a007e1117a07b5.
Итерация 4
K4 = 61fe0a65cc177af50235e2afadded326a5329a2236747
bf8a54228aeca9c4585cd801ea9dd743a0d98d01ef0602b0e
332067fb5ddd6ad568200311920839286,
LPSX[K4] ... LPSX[K1](m) = dee0b40df69997afef726f03bdc13
cb6ba9287698201296f2fd8284f06d33ea4a850a0ff48026dd47d
e88ec813ed2eb1186059d842d8d17f0bfa259e56655b1.
Итерация 5
K5 = 9983685f4fd3636f1fd5abb75fbf26a8e2934314aa2ecb
3ee4693c86c06c7d4e169bd540af75e1610a546acd63d960bad
595394cc199bf6999a5d5309fe73d5a,
LPSX[K5] ... LPSX[K1](m) = 675ea894d326432e1af7b201bc369
f8ab021f6fa58da09678ffc08ef30db43a37f117347cb77da0f6ba
30c85848896c3bac240ab14144283518b89a33d0caf07.
Итерация 6
K6 = f05772ae2ce7f025156c9a7fbcc6b8fdf1e735d613946
e32922994e52820ffea62615d907eb0551ad170990a86602088
af98c83c22cdb0e2be297c13c0f7a156,
LPSX[K6] ... LPSX[K1](m) = 1bc204bf9506ee9b86bbcf82d254
a112aea6910b6db3805e399cb718d1b3319964459516967cee4e648
e8cfbf81f56dc8da6811c469091be5123e6a1d5e28c73.
Итерация 7
K7 = 5ad144c362546e4e46b3e7688829fbb77453e9c3211974330
b2b8d0e6be2b5acc89eb6b35167f159b7b005a43e5959a651a9b18
cfc8e4098fcf03d9b81cfbb8d,
LPSX[K7] ... LPSX[K1](m) = f30d791ed78bdee819022a3d
78182242124efcdd54e203f23fb2dc7f94338ff955a5afc15ffef
03165263c4fdb36933aa982016471fbac9419f892551e9e568b.
Итерация 8
K8 = 6a6cec9a1ba20a8db64fa840b934352b518c638ed530122
a83332fe0b8efdac9018287e5a9f509c78d6c746adcd5426fb
0a0ad5790dfb73fc1f191a539016daa,
LPSX[K8 ... LPSX[K1](m) = 1fc20f1e91a1801a4293d3f3aa
9e91560fcc3810bb15f3ee9741c9b87452519f67cb9145519884
a24de6db736a5cb1430da7458e5e51b80be5204ba5b2600177.
Итерация 9
K9 = 99217036737aa9b38a8d6643f705bd51f351531f948f0
fc5e35fa35fee9dd8bdbb4c9d580a224e9cd82e0e2069fc49
ed367d5f94374435382b8fb6a8f5dd0409,
LPSX[K9] ... LPSX[K1](m) = 1a52f09d1e81515a36171e0b1a2809
c50359bed90f2e78cbd89b7d4afa6d046655c96bdae6ee97055
cc7e857267c2ccf28c8f5dd95ed58a9a68c12663bb28967.
Итерация 10
K10 = 906763c0fc89fa1ae69288d8ec9e9dda9a7630e8bfd6
c3fed703c35d2e62aeaff0b35d80a7317a7f76f83022f2526791
ca8fdf678fcb337bd74fe5393ccb05d2,
LPSX[K10] ... LPSX[K1](m) = 764043744a0a93687e65aba8cfc25
ec8714fb8e1bdc9ae2271e7205eaaa577c1b3b83e7325e50a19bd2d56
b061b5de39235c9c9fd95e071a1a291a5f24e8c774.
Итерация 11
K11 = 88ce996c63618e6404a5c8e03ee433854e2ae3eee
68991bbbff3c29d38dadb6ed6a1dae9a6dc6ddf52ce34af272
f96d3159c8c624c3fe6e13d695c0bfc89add5,
LPSX[K11] ... LPSX[K1](m) = 9b1ce8ff26b445cb288c0aeccf
84658eea91dbdf14828bf70110a5c9bd146cd9646350cff4e90e7b
63c5cc325e9b441081935f282d4648d9584f71860538f03b.
Итерация 12
K12 = 3e0a281ea9bd46063eec550100576f3a506aa168cf
82915776b978fccaa32f38b55f30c79982ca45628e8365d
8798477e75a49c68199112a1d7b5a0f7655f2db,
LPSX[K12] ... LPSX[K1](m) = 133aeecede251eb81914b8ba48
dcbc0b8a6fc63a292cc49043c3d3346b3f0829a9cb71ecff25ed
2a91bdcf8f649907d10cb76ff2e43100cdd4ba8a147a572f5.
Итерация 13
K13 = f0b273409eb31aebe432fbae1867212262c848422b6a
92f93f6cbab54ed18b8314b21cffc51e3fa319ff433e76ef6
adb0ef9f5e03c907fa1fcf9eca06500bf03,
LPSX[K13] ... LPSX[K1](m) = e3889d8e40960453fd26431450
bb9d29e8a78e78024656697caf698125ee83aabd796d133a3bd
28988428cb112766d1a1e32831f12d36fad21b2440122a5cdf6.
Результат выполнения преобразования gN(h, m):
h = e3bbadbf78af3264c9137127608aa510de90ba4d3075665844965
fb611dbb1998d48552a0c0ce6bcba71bc802a4f5b2d2a07b12c22e
25794178570341096fdc7.
Изменяются значения переменных N и  :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
000000000000000000000000000001f8,
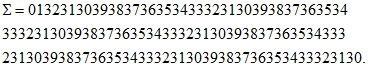
Результат выполнения преобразования g0(h, N):
h = 70f22bada4cfe18a6a56ec4b3f328cd40db8e1bf8a9d5f
711d5efab11191279d715aab7648d07eddbf87dc79c80516e6
ffcbcf5678b0ac29ea00fa85c8173cc6.
Результат выполнения преобразования  :
:
 :
:h = 00557be5e584fd52a449b16b0251d05d27f94ab76cbaa6
da890b59d8ef1e159d2088e482e2acf564e0e9795a51e4dd261
f3f667985a2fcc40ac8631faca1709a.
Хэш-кодом сообщения M1 является значение:
H(M1) = 00557be5e584fd52a449b16b0251d05d27
f94ab76cbaa6da890b59d8ef1e159d.
Пусть необходимо вычислить хэш-код сообщения
M2 = fbe2e5f0eee3c820fbeafaebef20fffbf0e1e0f0f520e
0ed20e8ece0ebe5f0f2f120fff0eeec20f120faf2fee5e2202
ce8f6f3ede220e8e6eee1e8f0f2d1202ce8f0f2e5e220e5d1.
Присваиваются значения:
h := IV = 0512;
N := 0512;
 .
.Длина сообщения |M2| = 576 < 512, поэтому сначала преобразуется часть сообщения
m := fbeafaebef20fffbf0e1e0f0f520e0ed20e8ece0
ebe5f0f2f120fff0eeec20f120faf2fee5e2202ce8f6f3
ede220e8e6eee1e8f0f2d1202ce8f0f2e5e220e5d1.
Вычисляется значение  .
.
 .
.После преобразования S:
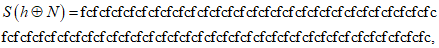
после преобразования P:
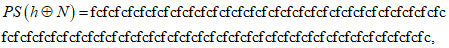
после преобразования L:

Затем выполняется преобразование E(K, m):
Итерация 1
K1 = b383fc2eced4a574b383fc2eced4a574b383fc2eced4a574
b383fc2eced4a574b383fc2eced4a574b383fc2eced4a574b383
fc2eced4a574b383fc2eced4a574,
X[K1](m) = 486906c521f45a8f43621cde3bf44599936b10
ce2531558642a303de2038858593790ed02b3685585b750fc
32cf44d925d6214de3c0585585b730ecb2cf440a5,
SX[K1](m) = f29131ad8e613035196148598e6c8e8de6fe9e
75c840c432c731185f906a8a8de5404e1428fa8bf47354d408
be63aecb79693857f6ea8bf473d04e48be6eb00,
PSX[K1](m) = f251de2cde47b74791966f735435963d3114e
911044d9304ac85e785e14085e418985cf9428b7f8be6e684068
fe66ee613c80ca8a83aa8eb03e843a8bfecbf00,
LPSX[K1](m) = 909aa733e1f52321a2fe35bfb8f67e92fbc
70ef544709d5739d8faaca4acf126e83e273745c25b7b8f4a83
a7436f6353753cbbbe492262cd3a868eace0104af1,




Итерация 2
K2 = d0b00807642fd78f13f2c3ebc774e80de0e902d23aef2ee
9a73d010807dae9c188be14f0b2da27973569cd2ba051301036
f728bd1d7eec33f4d18af70c46cf1e,
LPSX[K2]LPSX[K1](m) = 301aadd761d13df0b473055b14a2f74a45
f408022aecadd4d5f19cab8228883a021ac0b62600a495950c628354
ffce1161c68b7be7e0c58af090ce6b45e49f16.
Итерация 3
K3 = 9d4475c7899f2d0bb0e8b7dac6ef6e6b44ecf66716d3a
0f16681105e2d13712a1a9387ecc257930e2d61014a1b5c9fc
9e24e7d636eb1607e816dbaf927b8fca9,
LPSX[K3] ... LPSX[K1](m) = 9b83492b9860a93cbca1c0d
8e0ce59db04e10500a6ac85d4103304974e78d32259ceff03fbb
353147a9c948786582df78a34c9bde3f72b3ca41b9179c2cceef3.
Итерация 4
K4 = 5c283daba5ec1f233b8c833c48e1c670dae2e40cc4c3219
c73e58856bd96a72fdf9f8055ffe3c004c8cde3b8bf78f95f3370
d0a3d6194ac5782487defd83ca0f,
LPSX[K4] ... LPSX[K1](m) = e638e0a1677cdea107ec3402f70698
a4038450dab44ac7a447e10155aa33ef1bdaf8f49da7b66f3e
05815045fbd39c991cb0dc536e09505fd62d3c2cd00b0f57.
Итерация 5
K5 = 109f33262731f9bd569cbc9317baa551d4d2964fa18d42c
41fab4e37225292ec2fd97d7493784779046388469ae195c436
fa7cba93f8239ceb5ffc818826470c,
LPSX[K5] ... LPSX[K1](m) = 1c7c8e19b2bf443eb3adc0c787a52
a173821a97bc5a8efea58fb8b27861829f6dd5ff9c97865e08dac66
f47392b578e21266e323a0aacedeec3ef0314f517c6.
Итерация 6
K6 = b32c9b02667911cf8f8a0877be9a170757e25026ccf41e
67c6b5da70b1b874743e1135cfbefe244237555c676c153d99459
bc382573aee2d85d30d99f286c5e7,
LPSX[K6] ... LPSX[K1](m) = 48fecfc5b3eb77998fb39bfcccd
128cd42fccb714221be1e675a1c6fdde7e31198b318622412af7e
999a3eff45e6d61609a7f2ae5c2ff1ab7ff3b37be7011ba2.
Итерация 7
K7 = 8a13c1b195fd0886ac49989e7d84b08bc7b00e4f3f62765
ece6050fcbabdc2346c8207594714e8e9c9c7aad694edc922d6
b01e17285eb7e61502e634559e32f1,
LPSX[K7] ... LPSX[K1](m) = a48f8d781c2c5be417ae644cc2e
15a9f01fcead3232e5bd53f18a5ab875cce1b8a1a400cf48521c7ce
27fb1e94452fb54de23118f53b364ee633170a62f5a8a9.
Итерация 8
K8 = 52cec3b11448bb8617d0ddfbc926f2e88730cb9179d6
decea5acbffd323ec3764c47f7a9e13bb1db56c342034773023
d617ff01cc546728e71dff8de5d128cac,
LPSX[K8] ... LPSX[K1](m) = e8a31b2e34bd2ae21b0ecf29cc
4c37c75c4d11d9b82852517515c23e81e906a451b72779c3087141
f1a15ab57f96d7da6c7ee38ed25befbdef631216356ff59c.
Итерация 9
K9 = f38c5b7947e7736d502007a05ea64a4eb9c243cb82154
aa138b963bbb7f28e74d4d710445389671291d70103f48fd4d
4c01fc415e3fb7dc61c6088afa1a1e735,
LPSX[K9] ... LPSX[K1](m) = 34392ed32ea3756e32979cb0a
2247c3918e0b38d6455ca88183356bf8e5877e55d542278a696523
a8036af0f1c2902e9cbc585de803ee4d26649c9e1f00bda31.
Итерация 10
K10 = 0740b3faa03ed39b257dd6e3db7c1bf56b6e18e40cdaabd
30617cecbaddd618ea5e61bb4654599581dd30c24dab877ad
0687948286cfefaa7eef99f6068b315,
LPSX[K10] ... LPSX[K1](m) = 6a82436950177fea74cce6d
507a5a64e54e8a3181458e3bdfbdbc6180c9787de7ccb676dd809
e7cb1eb2c9ebd016561570801a4e9ce17a438b85212f4409bb5e.
Итерация 11
K11 = 185811cf3c2633aec8cfdfcae9dbb29347011bf92b
95910a3ad71e5fca678e45e374f088f2e5c29496e9695ce
8957837107bb3aa56441af11a82164893313116,
LPSX[K11] ... LPSX[K1](m) = 7b97603135e2842189b0c9667596
e96bd70472ccbc73ae89da7d1599c72860c285f5771088f1fb0f943
d949f22f1413c991eafb51ab8e5ad8644770037765aec.
Итерация 12
K12 = 9d46bf66234a7ed06c3b2120d2a3f15e0fedd87189
b75b3cd2f206906b5ee00dC9a1eab800fb8cc5760b251f4
db5cdef427052fa345613fd076451901279ee4c,
LPSX[K12] ... LPSX[K1](m) = 39ec8a88db635b46c4321adf41
fd9527a39a67f6d7510db5044f05efaf721db5Cf976a726ef33
dc4dfcda94033e741a463770861a5b25fefcb07281eed629c0e.
Итерация 13
K13 = 0179104026b900d8d768b6e223484c9761e3c585b3a
405a6d2d8565ada926c3f7782ef127cd6b98290bf612558b4
b60aa3cbc28fd94f95460d76b621cb45be70,
X[K13] ... LPSX[K1](m) = 36959ac8fdda5b9e135aac3d62b
5d9b0c279a27364f50813d69753b575e0718ab8158560122584464
f72c8656b53f7aec0bccaee7cfdcaa9c6719e3f2627227e.
Результат выполнения преобразования gN(h, m):
h = cd7f602312faa465e3bb4ccd9795395de2914e938f10f
8e127b7ac459b0c517b98ef779ef7c7a46aa7843b8889731
f482e5d221e8e2cea852e816cdac407c7af.
Изменяются значения переменных N и  :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000200,

Длина оставшейся части сообщения меньше 512, поэтому происходит дополнение неполного блока.
m := 000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000001fbe2e5f0eee3c820.
Результат выполнения преобразования gN(h, m):
h = c544ae6efdf14404f089c72d5faf8dc6aca1db5e28577fc
07818095f1df70661e8b84d0706811cf92dffb8f96e61493dc
382795c6ed7a17b64685902cbdc878e.
Изменяются значения переменных N и  :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000240,

Результат выполнения преобразования g0(h, N):
h = 4deb6649ffa5caf4163d9d3f9967fbbd6eb3da68f916b6
a09f41f2518b81292b703dc5d74e1ace5bcd3458af43bb456e
837326088f2b5df14bf83997a0b1ad8d.
Результат выполнения преобразования  :
:
 :
:h = 28fbc9bada033b1460642bdcddb90c3fb3e56c497ccd0f6
2b8a2ad4935e85f037613966de4ee00531ae60f3b5a47f8dae
06915d5f2f194996fcabf2622e6881e.
Хэш-кодом сообщения M2 является значение:
H(M2) = 28fbc9bada033b1460642bdcddb90c3fb3e56c497
ccd0f62b8a2ad4935e85f037613966de4ee00531ae60f3b5a
47f8dae06915d5f2f194996fcabf2622e6881e.
Присваиваются значения:
h := IV = (00000001)64;
N := 0512;
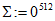 .
.Длина сообщения |M2| = 576 > 512, поэтому сначала преобразуется часть сообщения
m := fbeafaebef20fffbf0e1e0f0f520e0ed20e8ece0ebe5f
0f2f120fff0eeec20f120faf2fee5e2202ce8f6f3ede220e8e
6eee1e8f0f2d1202ce8f0f2e5e220e5d1.
Вычисляется значение  .
.
 .
.После преобразования S:

после преобразования P:

после преобразования L:

Затем выполняется преобразование E(K, m):
Итерация 1
K1 = 23c5ee40b07b5f1523c5ee40b07b5f1523c5ee40b07b5
f1523c5ee40b07b5f1523c5ee40b07b5f1523c5ee40b07b5f
1523c5ee40b07b5f1523c5ee40b07b5f15,
X[K1](m) = d82f14ab5f5ba0eed3240eb0455bbff8032d02a
05b9eafe7d2e511b05e977fe4033f1cbe55997f39cb331dad
525bb7f3cd2406b042aa7f39cb351ca5525bbac4,
SX[K1](m) = 8d4f93828747a76c49e204adc8473bd11101dda
7470a415b832b77ad5dbc572d111f14950ce8570be4aecd9f0
e472fd2d9e231ad2c38570be46a14000e47a586,
PSX[K1](m) = 8d49118311e4d9e44fe2012b1faee26a9304
dd7714cd311482ada7ad959fad0087c8475d0c0e2c0e47470
abce8473847a73b4157572f57a56cd15b2d0bd20b86,
LPSX[K1](m) = a3a72a2e0fb5e6f812681222fec037b0db
972086a395a387a6084508cae13093aa71d352dcbce288e9a
39718a727f6fd4c5da5d0bc10fac3707ccd127fe45475,


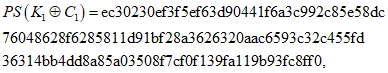
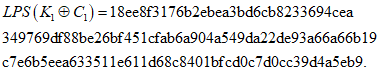
Итерация 2
K2 = 18ee8f3176b2ebea3bd6cb8233694cea349769df88be
26bf451cfab6a904a549da22de93a66a66b19c7e6b5eea
633511e611d68c8401bfcd0c7d0cc39d4a5eb9,
LPSX[K2]LPSX[K1](m) = 9f50697b1d9ce23680db1f4d35629778864
c55780727aa79eb7bb7d648829cba8674afdac5c62ca352d
77556145ca7bc758679fbe1fbd32313ca8268a4a603f1.
Итерация 3
K3 = aaa4cf31a265959157aec8ce91e7fd46bf27dee21164
c5e3940bba1a519e9d1fce0913f1253e7757915000cd674be
12cc7f68e73ba26fb00fd74af4101805f2d,
LPSX[K3] ... LPSX[K1](m) = 4183027975b257e9bc239b75c977
ecc52ddad82c091e694243c9143a945b4d853116eae14fd81b14bb
47f2c06fd283cb6c5e61924edfaf971b78d771858d5310.
Итерация 4
K4 = 61fe0a65cc177af50235e2afadded326a5329a2236747
bf8a54228aeca9c4585cd801ea9dd743a0d98d01ef0602b0e
332067fb5ddd6ad568200311920839286,
LPSX[K4] ... LPSX[K1](m) = 0368c884fcee489207b5b97a133ce
39a1ebfe5a3ae3cccb3241de1e7ad72857e76811d324f01fd7a75e
0b669e8a22a4d056ce6af3e876453a9c3c47c767e5712.
Итерация 5
K5 = 9983685f4fd3636f1fd5abb75fbf26a8e2934314aa2ecb
3ee4693c86c06c7d4e169bd540af75e1610a546acd63d960bad
595394cc199bf6999a5d5309fe73d5a,
LPSX[K5] ... LPSX[K1](m) = c31433ceb8061e46440144e65553
976512e5a9806ac9a2c771d5932d5f6508c5b78e406c4efab98ac
5529be0021b4d58fa26f01621eb10b43de4c4c47b63f615.
Итерация 6
K6 = f05772ae2ce7f025156c9a7fbcc6b8fdf1e735d613946
e32922994e52820ffea62615d907eb0551ad170990a86602088
af98c83c22cdb0e2be297c13c0f7a156,
LPSX[K6] ... LPSX[K1](m) = 5d0ae97f252ad04534503fe5f52e9bd
07f483ee3b3d206beadc6e736c6e754bb713f97ea7339927893eacf2b
474a482cadd9ac2e58f09bcb440cf36c2d14a9b6.
Итерация 7
K7 = 5ad144c362546e4e46b3e7688829fbb77453e9c321197
4330b2b8d0e6be2b5acc89eb6b35167f159b7b005a43e5959a
651a9b18cfc8e4098fcf03d9b81cfbb8d,
LPSX[K7] ... LPSX[K1](m) = a59aa21e6ad3e330deedb9ab9912205
c355b1c479fdfd89a7696d7de66fbf7d3cec25879f7f1a8cca4c793d5
f2888407aecb188bda375eae586a8cfd0245c317.
Итерация 8
K8 = 6a6cec9a1ba20a8db64fa840b934352b518c638ed5301
22a83332fe0b8efdac9018287e5a9f509c78d6c746adcd5426
fb0a0ad5790dfb73fc1f191a539016daa,
LPSX[K8] ... LPSX[K1](m) = 9903145a39d5a8c83d28f70fa1fbd
88f31b82dc7cfe17b54b50e276cb2c4ac682b4434163f214cf7ce
6164a75731bcea5819e6a6a6fea99da9222951d2a28e01.
Итерация 9
K9 = 99217036737aa9b38a8d6643f705bd51f351531f948f0
fc5e35fa35fee9dd8bdbb4c9d580a224e9cd82e0e2069fc49
ed367d5f94374435382b8fb6a8f5dd0409,
LPSX[K9] ... LPSX[K1](m) = 330e6cb1d04961826aa263f2328f15
b4f3370175a6a9fd6505b286efed2d8505f71823337ef71513e57a700
eb1672a685578e45dad298ee2223d4cb3fda8262f.
Итерация 10
K10 = 906763c0fc89fa1ae69288d8ec9e9dda9a7630e8bfd6
c3fed703c35d2e62aeaff0b35d80a7317a7f76f83022f25267
91ca8fdf678fcb337bd74fe5393ccb05d2,
LPSX[K10] ... LPSX[K1](m) = ad347608443ab9c9bbb64f633a
5749ab85c45d4174bfd78f6bc79fc4f4ce9ad1dd71cb2195b1cfab
8dcaaf6f3a65c8bb0079847a0800e4427d3a0a815f40a644.
Итерация 11
K11 = 88ce996c63618e6404a5c8e03ee433854e2ae3eee689
91bbbff3c29d38dadb6ed6a1dae9a6dc6ddf52ce34af272f96
d3159c8c624c3fe6e13d695c0bfc89add5,
LPSX[K11] ... LPSX[K1](m) = a065c55e2168c31576a756c7ecda
9129cd3d207f8f43073076c30e111fd5f119095ca396e9fb78a2bf
4781c44e845e447b8fc75b788284aae27582212ec23ee.
Итерация 12
K12 = 3e0a281ea9bd46063eec550100576f3a506aa168cf82
915776b978fccaa32f38b55f30c79982ca45628e8365d87984
77e75a49c68199112a1d7b5a0f7655f2db,
LPSX[K12] ... LPSX[K1](m) = 2a6549f7a5cd2eb4a271a7c71762c
8683e7a3a906985d60f8fc86f64e35908b29f83b1fe3c704f3c116
bdfe660704f3b9c8a1d0531baaffaa3940ae9090a33ab.
Итерация 13
K13 = f0b273409eb31aebe432fbae1867212262c848422b6a
92f93f6cbab54ed18b8314b21cffc51e3fa319ff433e76ef6
adb0ef9f5e03c907fa1fcf9eca06500bf03,
X[K13] ... LPSX[K1](m) = dad73ab73b7e345f46435c690f05e
94a5cb272d242ef44f6b0a4d5d1ad8883318b31ad01f96e709f08949
cd8169f25e09273e8e50d2ad05b5f6de6496c0a8ca8.
Результат выполнения преобразования gN(h, m):
h = 203cc15dd55fcaa5b7a3bd98fb2408a67d5b9f33a80bb
50540852b204265a2c1aaca5efe1d8d51b2e1636e34f5becc
077d930114fefaf176b69c15ad8f2b6878.
Изменяются значения переменных N и  :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000200,
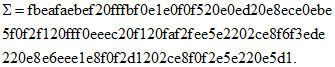
Длина оставшейся части сообщения меньше 512, поэтому происходит дополнение неполного блока:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
0000000000000001fbe2e5f0eee3c820.
Результат выполнения преобразования gN(h, m):
h = a69049e7bd076ab775bc2873af26f098c538b17e39a5c
027d532f0a2b3b56426c96b285fa297b9d39ae6afd8b9001d
97bb718a65fcc53c41b4ebf4991a617227.
Изменяются значения переменных N и 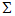 :
:
N = 0000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000240,

Результат выполнения преобразования g0(h, N):
h = aee3bd55ea6f387bcf28c6dcbdbbfb3ddacc67dcc13dbd
8d548c6bf808111d4b75b8e74d2afae960835ae6a5f0357555
9c9fd839783ffcd5cf99bd61566b4818.
Результат выполнения преобразования  :
:
 :
:h = 508f7e553c06501d749a66fc28c6cac0b005746d97537
fa85d9e40904efed29dC345e53d7f84875d5068e4eb743f
0793d673f09741f9578471fb2598cb35c230.
Хэш-кодом сообщения M2 является значение:
H(M2) = 508f7e553c06501d749a66fc28c6cac0b
005746d97537fa85d9e40904efed29d.
Примечание - Оригиналы международных стандартов ИСО и ИСО/МЭК находятся в национальных (государственных) органах по стандартизации <*> государств, принявших настоящий стандарт.
--------------------------------
<*> В Российской Федерации оригиналы международных стандартов ИСО/МЭК находятся в Федеральном информационном фонде стандартов.
ИСО 2382:2015 (ISO 2382:2015) | Информационная технология. Словарь (Information technology - Vocabulary) | |
ИСО/МЭК 9796-2:2010 (ISO/IEC 9796-2:2010) | Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 2. Механизмы на основе целочисленной факторизации (Information technology - Security techniques - Digital signature schemes giving message recovery - Part 2: Integer factorization based mechanisms) | |
ИСО/МЭК 9796-3:2006 (ISO/IEC 9796-3:2006) | Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 3. Механизмы на основе дискретного логарифма (Information technology - Security techniques - Digital signature schemes giving message recovery - Part 3: Discrete logarithm based mechanisms) | |
ИСО/МЭК 14888-1:2008 (ISO/IEC 14888-1:2008) | Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 1. Общие положения (Information technology - Security techniques - Digital signatures with appendix - Part 1: General) | |
[5] | ИСО/МЭК 14888-2:2008 (ISO/IEC 14888-2:2008) | Информационная технология. Методы обеспечения защиты. Цифровые подписи с приложением. Часть 2. Механизмы, основанные на разложении на множители. (Information technology - Security techniques - Digital signatures with appendix - Part 2: Integer factorization based mechanisms) |
ИСО/МЭК 14888-3:2016 (ISO/IEC 14888-3:2016) | Информационная технология. Методы и средства обеспечения безопасности. Цифровые подписи с приложением. Часть 3. Механизмы на основе дискретного логарифма (Information technology - Security techniques - Digital signatures with appendix - Part 3: Discrete logarithm based mechanisms) | |
ИСО/МЭК 10118-1:2016 (ISO/IEC 10118-1:2016) | Информационная технология. Методы защиты информации. Хэш-функции. Часть 1. Общие положения (Information technology - Security techniques - Hash-functions - Part 1: General) | |
[8] | ИСО/МЭК 10118-2:2010 (ISO/IEC 10118-2:2010) | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 2. Хэш-функции с использованием алгоритма шифрования n-битными блоками (Information technology - Security techniques - Hash-functions - Part 2: Hash-functions using an n-bit block cipher) |
[9] | ИСО/МЭК 10118-3:2004 (ISO/IEC 10118-3:2004) | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 3. Выделенные хэш-функции (Information technology - Security techniques - Hash-functions - Part 3: Dedicated hash-functions) |
ИСО/МЭК 10118-4:1998 (ISO/IEC 10118-4:1998) | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 4. Хэш-функции с применением арифметических операций над абсолютными значениями чисел (Information technology - Security techniques - Hash-functions - Part 4: Hash-functions using modular arithmetic) |
