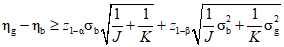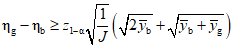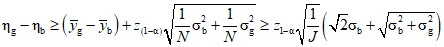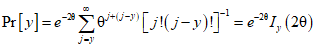СПРАВКА
Источник публикации
М.: Стандартинформ, 2016
Примечание к документу
Документ введен в действие с 01.12.2016.
Название документа
"ГОСТ Р ИСО 11843-6-2015. Национальный стандарт Российской Федерации. Статистические методы. Способность обнаружения. Часть 6. Методология определения критического значения и минимального обнаруживаемого значения с применением аппроксимации распределения Пуассона нормальным распределением"
(утв. и введен в действие Приказом Росстандарта от 06.10.2015 N 1471-ст)
"ГОСТ Р ИСО 11843-6-2015. Национальный стандарт Российской Федерации. Статистические методы. Способность обнаружения. Часть 6. Методология определения критического значения и минимального обнаруживаемого значения с применением аппроксимации распределения Пуассона нормальным распределением"
(утв. и введен в действие Приказом Росстандарта от 06.10.2015 N 1471-ст)
Содержание
Приказом Федерального агентства
по техническому регулированию
и метрологии
от 6 октября 2015 г. N 1471-ст
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАТИСТИЧЕСКИЕ МЕТОДЫ
СПОСОБНОСТЬ ОБНАРУЖЕНИЯ
ЧАСТЬ 6
МЕТОДОЛОГИЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОГО ЗНАЧЕНИЯ И МИНИМАЛЬНОГО
ОБНАРУЖИВАЕМОГО ЗНАЧЕНИЯ С ПРИМЕНЕНИЕМ АППРОКСИМАЦИИ
РАСПРЕДЕЛЕНИЯ ПУАССОНА НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
Statistical methods. Capability of detection. Part 6.
Methodology for the determination of the critical value
and the minimum detectable value in Poisson distributed
measurements by normal approximations
(ISO 11843-6:2013, IDT)
ГОСТ Р ИСО 11843-6-2015
Группа Т59
ОКС 03.120.30
Дата введения
1 декабря 2016 года
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного аутентичного перевода на русский язык англоязычной версии международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 6 октября 2015 г. N 1471-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 11843-6:2013 "Способность обнаружения. Часть 6. Методология определения критического значения и минимального обнаруживаемого значения с применением аппроксимации распределения Пуассона нормальным распределением" (ISO 11843-6:2013 "Capability of detection - Part 6: Methodology for the determination of the critical value and the minimum detectable value in Poisson distributed measurements by normal approximations", IDT).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации и межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
В приборах различного типа для обнаружения сигналов часто используют метод подсчета импульсов (датчик рентгеновской, электронной и ионной спектроскопии, такие как рентгеновские дифрактометры, рентгеновские флуоресцентные спектрометры, рентгеновские фотоэлектронные спектрометры, оже-электронные спектрометры, масс-спектрометры вторичной ионизации, хромато-масс-спектрометры и др.). В этом случае сигналы состоят из серии импульсов, появляющихся случайным образом через нерегулярные интервалы времени. Для их описания может быть применено распределение Пуассона, а методология определения минимального обнаруживаемого значения может быть выведена с применением статистической теории.
Определение минимального обнаруживаемого значения иногда важно в практической работе. Это значение обеспечивает критерий принятия решения, когда "сигнал не обнаружен или когда сигнал значимо отличается от фонового шума" [1 - 8]. Например, это важно, когда измеряемая величина представляет опасные вещества или поверхностное загрязнение полупроводниковых материалов. Ограничения на опасные вещества устанавливают пределы использования шести опасных материалов (шестивалентный хром, свинец, ртуть, кадмий и огнезащитные агенты, пербромодифенил) в производстве электронных компонентов и соответствующих товаров, продаваемых в ЕС. Для проверки используют специальные приборы. Рентгеновские флуоресцентные спектрометры и газохроматографические масс-спектрометры являются такими приборами. Рентгеновские дифрактометры используют для измерения уровня опасности асбеста и кристаллического кремния в окружающей среде или в строительных материалах.
Методы, используемые для определения минимального обнаруживаемого значения, должны в течение некоторого времени широко использоваться в области аналитической химии, но не там, где используют метод подсчета импульсов. Необходимо установить методологию определения минимального обнаруживаемого значения в этой области.
В настоящем стандарте распределение Пуассона аппроксимировано нормальным распределением, обеспечивающим согласованность с подходом IUPAC, лежащем в основе серии стандартов ISO 11843. Обычную аппроксимацию используют для генерации дисперсии, критического значения отклика, критерия способности обнаружения и минимального обнаруживаемого значения [1].
В настоящем стандарте:
Настоящий стандарт полностью согласован с ИСО 11843-1, ИСО 11843-3, ИСО 11843-4.
В настоящем стандарте установлены методики определения критического значения переменной отклика и минимального обнаруживаемого значения по результатам измерений, подчиняющихся распределению Пуассона. Стандарт применим в тех случаях, когда изменчивость фонового шума и сигнала могут быть описаны распределением Пуассона. Обычно для распределения Пуассона используют аппроксимацию в виде нормального распределения (см. ИСО 11843-3 и ИСО 11843-4).
Сопоставление точности результатов при использовании распределения Пуассона и его аппроксимации нормальным распределением приведено в приложении C.
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
Руководство ИСО 30 Термины и определения, используемые в области стандартных образцов (ISO Guide 30 Terms and definitions used in connection with reference materials)
ИСО 3534-1 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах (ISO 3534-1 Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability)
ИСО 11843-1 Способность обнаружения. Часть 1. Термины и определения (ISO 11843-1 Capability of detection - Part 1: Terms and definitions)
ИСО 11843-2 Способность обнаружения. Часть 2. Методология в случае линейной калибровки (ISO 11843-2 Capability of detection - Part 2: Methodology in the linear calibration case)
ИСО 11843-3 Способность обнаружения. Часть 3. Методология определения критического значения отклика без использования данных калибровки (ISO 11843-3 Capability of detection - Part 3: Methodology for determination of the critical value for the response variable when no calibration data are used)
ИСО 11843-4 Способность обнаружения. Часть 4. Метод сравнения заданного значения с минимальным обнаруживаемым значением (ISO 11843-4 Capability of detection - Part 4: Methodology for comparing the minimum detectable value with a given value)
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 11843-1, ИСО 11843-2, ИСО 11843-3, ИСО 11843-4 и Руководству ИСО 30.
Условия использования в расчетах распределения Пуассона обычно определяют экспериментально. Количество обнаруженных импульсов возрастает при увеличении времени наблюдений и ширины области наблюдаемого спектра. Эти два параметра должны быть установлены и сохраняться в процессе измерений.
Для достоверного определения минимального обнаруживаемого значения необходимо выполнение следующих требований:
a) сигнал и фоновый шум подчиняются распределению Пуассона. Сигнал является средним наблюдаемых значений;
b) исходные данные не обработаны и не сглажены;
c) продолжительный непрерывный интервал времени измерений более предпочтителен, чем несколько коротких промежутков времени наблюдений. Измерения продолжительностью в одну секунду предпочтительнее, чем 10 измерений продолжительностью по 100 мс каждое. Аппроксимация распределения Пуассона нормальным распределением дает более точные результаты для более высоких значений среднего;
d) количество измерений. Поскольку в приведенных методах использованы только средние, для их определения необходимо выполнение повторных измерений. Мощность теста возрастает с увеличением количества измерений;
e) количество каналов, используемых датчиком. Не должно быть наложения соседних пиков. Количество используемых каналов для измерения фонового шума и выборочный спектр должны быть идентичными (приложение D, рисунок D.1);
f) ширина пика. Для мониторинга единственного пика рекомендуется использовать полную ширину на половине максимума (FWHM). Это предпочтительно в случае измерения высоты вершины и/или ширины основания пика. Соответствующее значение FWHM должно быть определено заранее на основе результатов измерений стандартной выборки. Идентичное значение FWHM следует использовать и для фонового шума и для измерений элементов выборки.
Дополнительные факторы. Инструмент должен быть поверен (калиброван), датчик должен работать в пределах его линейного диапазона. Не должно быть сигналов, которые не могли бы быть четко идентифицированы, как не являющиеся шумом. Деградация объекта в процессе измерений должна быть незначительной. Должен быть обнаружен, по крайней мере, один сигнал или пик, относящийся к рассматриваемому объекту.
5.1 Критическое значение на основе нормального распределения
Решение о значимости измеренного сигнала (или нет) может быть принято на основе сопоставления среднего арифметического 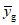 результатов измерений с выбранным значением yc. Значение yc, рассматриваемое как критическое значение, удовлетворяет требованию
результатов измерений с выбранным значением yc. Значение yc, рассматриваемое как критическое значение, удовлетворяет требованию
где вероятность вычислена при условии, что система находится в базовом состоянии (x = 0), а  - заданное значение вероятности.
- заданное значение вероятности.
Формула (1) задает вероятность того, что  при условии, что:
при условии, что:
где 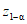 - квантиль нормированного нормального распределения уровня
- квантиль нормированного нормального распределения уровня 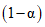 ;
;
J - количество повторных измерений чистой стандартной выборки. Оно представляет значение переменной в базовом состоянии;
K - количество повторных измерений контролируемой выборки. Оно дает значение фактической переменной состояния.
Знак "+" используют в формуле (2), если переменная отклика увеличивается при увеличении переменной состояния.
Знак "-" используют в противоположном случае.
Определение критического значения соответствует ИСО 11843-1 и ИСО 11843-3. Его взаимосвязь с результатами измерений в фактическом и базовом состояниях показана на рисунке 1.

X - отклик; Y - базовое состояние; 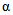 - вероятность ошибки
- вероятность ошибки
первого рода; 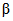 - вероятность ошибки второго рода
- вероятность ошибки второго рода
значения и результатов измерений отклика
в фактическом и базовом состояниях
Если переменная отклика подчиняется распределению Пуассона с достаточно большим средним, оценка стандартного отклонения результатов повторных измерений переменной отклика в базовом состоянии (оценка  ) имеет вид
) имеет вид 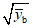 . Стандартное отклонение результатов повторных измерений переменной отклика в фактическом состоянии по выборке имеет вид
. Стандартное отклонение результатов повторных измерений переменной отклика в фактическом состоянии по выборке имеет вид  и является оценкой
и является оценкой  (см. приложение B).
(см. приложение B).
Критическое значение yc переменной отклика, которая подчиняется распределению Пуассона, аппроксимированному нормальным распределением, имеет вид:
где 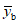 - среднее арифметическое результатов измерений отклика в базовом состоянии.
- среднее арифметическое результатов измерений отклика в базовом состоянии.
5.3 Критерий достаточной способности обнаружения
Критерий достаточной способности обнаружения позволяет принимать решения об обнаружении сигнала на основе сопоставления критического значения вероятности с установленным значением уровня доверия  . Если критерий выполнен, можно принимать решение о том, что минимальное обнаруживаемое значение xd не превосходит значения переменной состояния xg. Минимальное обнаруживаемое значение тогда определяет наименьшее значение переменной отклика
. Если критерий выполнен, можно принимать решение о том, что минимальное обнаруживаемое значение xd не превосходит значения переменной состояния xg. Минимальное обнаруживаемое значение тогда определяет наименьшее значение переменной отклика 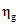 , для которого неправильное решение может быть принято с вероятностью
, для которого неправильное решение может быть принято с вероятностью  . Это значение в ситуации, когда нет сигнала, а только фоновый шум, соответствует ошибке второго рода.
. Это значение в ситуации, когда нет сигнала, а только фоновый шум, соответствует ошибке второго рода.
Если стандартное отклонение отклика для данного значения xg равно  , критерий того, что вероятность больше или равна
, критерий того, что вероятность больше или равна 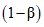 устанавливает неравенство (4), из которого могут быть получены неравенства (5) и (6):
устанавливает неравенство (4), из которого могут быть получены неравенства (5) и (6):
где 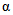 - вероятность ошибки первого рода;
- вероятность ошибки первого рода;
Для 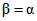 и K = J критерий можно упростить
и K = J критерий можно упростить
Если 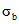 заменить оценкой
заменить оценкой  (см. 5.2), а также
(см. 5.2), а также  заменить оценкой
заменить оценкой  (см. приложение B), критерий превращается в неравенство (7).
(см. приложение B), критерий превращается в неравенство (7).
Примечание - При валидации метода в соответствии с ИСО 11843-4 обычно выбирают K = J = 1.
5.4 Подтверждение критерия достаточной способности обнаружения
Стандартные отклонения и математические ожидания отклика обычно неизвестны, таким образом оценка при использовании неравенства критерия (6), должна быть получена по экспериментальным данным. Левая часть неравенства (6) неизвестна, а правая часть известна.
Доверительный интервал для  определяют по N результатам повторных измерений в базовом состоянии и N повторных измерений выборки с переменной состояния равной xg. Доверительный интервал с уровнем доверия
определяют по N результатам повторных измерений в базовом состоянии и N повторных измерений выборки с переменной состояния равной xg. Доверительный интервал с уровнем доверия  для
для 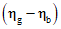 :
:
 для
для 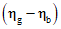 :
: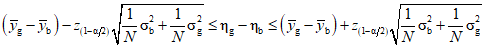 , (8)
, (8)где  - квантиль нормированного нормального распределения уровня
- квантиль нормированного нормального распределения уровня  .
.
 .
.Для подтверждения критерия достаточной способности обнаружения используют односторонний критерий. Нижняя граница одностороннего доверительного интервала для 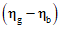 с
с  и уровнем доверия
и уровнем доверия 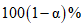 имеет вид:
имеет вид:
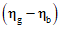 с
с 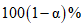 имеет вид:
имеет вид:где N - количество результатов повторных измерений каждого образца сравнения, используемого при определении оценки способности обнаружения;
Нижнюю границу одностороннего доверительного интервала для 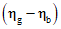 , полученную в соответствии с неравенством (9), сопоставляют с правой частью неравенства (6):
, полученную в соответствии с неравенством (9), сопоставляют с правой частью неравенства (6):
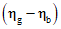 , полученную в соответствии с неравенством (9), сопоставляют с правой частью неравенства (6):
, полученную в соответствии с неравенством (9), сопоставляют с правой частью неравенства (6):Приближенную нижнюю границу T0 доверительного интервала для 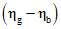 с уровнем доверия
с уровнем доверия  получают, заменяя
получают, заменяя  и
и 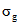 на
на 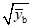 и
и 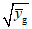 , соответственно (как в (3) и (7)):
, соответственно (как в (3) и (7)):
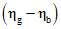 с уровнем доверия
с уровнем доверия  получают, заменяя
получают, заменяя Если T0 удовлетворяет неравенству (7), принимают решение о том, что минимальное среднее обнаруживаемое значение отклика 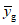 меньше или равно минимальному обнаруживаемому значению отклика yd. Значение xd поэтому меньше или равно xg и, для относительно больших значений N, нижняя доверительная граница в соответствии с формулой (11) является удовлетворительной.
меньше или равно минимальному обнаруживаемому значению отклика yd. Значение xd поэтому меньше или равно xg и, для относительно больших значений N, нижняя доверительная граница в соответствии с формулой (11) является удовлетворительной.
Определение оценки способности обнаружения обычно является частью первичной валидации метода. Отчет должен включать:
a) информацию об образцах сравнения, включая значения xg, для эталонного состояния;
b) количество повторных измерений N для каждого эталонного состояния;
c) средние арифметические  и
и 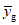 ;
;
d) выбранные значения  ,
,  , J и K;
, J и K;
e) значения левых и правых частей неравенства (7) с использованием оценок, т.е. (yg - yb) или, если это применимо, ( , K = J), значение
, K = J), значение  , соответствующий доверительный интервал и его приемлемую нижнюю границу
, соответствующий доверительный интервал и его приемлемую нижнюю границу
 , соответствующий доверительный интервал и его приемлемую нижнюю границу
, соответствующий доверительный интервал и его приемлемую нижнюю границу ,
,f) заключение относительно способности обнаружения;
g) при необходимости, минимальное обнаруживаемое значение для заданной величины фонового шума. Это значение получают, заменяя N и J бесконечностью и 1, соответственно, в формуле (10).
Наблюдаемые значения должны быть зафиксированы, поскольку они представляют отклик переменной состояния. Тот факт, что наблюдаемые значения используют для проверки истинных значений, не является причиной для замены их верхней границей (равной критическому значению) или минимальным обнаруживаемым значением. В отчете также указывают критическое значение и минимальное обнаруживаемое значение.
(справочное)
ОБОЗНАЧЕНИЯ, ИСПОЛЬЗУЕМЫЕ В ИСО 11843-6
X - параметр состояния;
Y - переменная отклика;
J - количество повторных измерений на образце сравнения, представляющих значения в базовом состоянии (пустая проба);
K - количество повторных измерений в реальном состоянии (контрольная выборка);
N - количество повторных измерений каждого образца сравнения при определении оценки способности обнаружения;
x - значение переменной состояния;
y - значение переменной отклика;
yc - критическое значение переменной отклика в соответствии с ИСО 11843-1 и ИСО 11843-3;
xg - заданное значение, которое проверяют для определения, больше оно минимального обнаруживаемого значения или нет;
xd - минимальное обнаруживаемое значение переменной состояния;
yd - минимальное обнаруживаемое значение отклика с переменной состояния, равной xd;
T0 - нижняя доверительная граница.
(справочное)
РАСПРЕДЕЛЕНИЯ ПУАССОНА НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
Функция вероятности распределения Пуассона 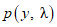 имеет вид:
имеет вид:
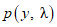 имеет вид:
имеет вид: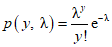 , (B.1)
, (B.1)где  - среднее, соответствующее среднему количеству событий за установленный период времени;
- среднее, соответствующее среднему количеству событий за установленный период времени;
y - фактическое количество событий, зарегистрированных за то же время.
Так как случайная величина Y подчиняется распределению Пуассона с параметром  , математическое ожидание и дисперсия этой случайной величины равны
, математическое ожидание и дисперсия этой случайной величины равны 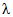 , т.е.
, т.е. 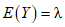 и
и 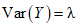 . Таким образом, необходимо определить оценку только параметра
. Таким образом, необходимо определить оценку только параметра  . Эта оценка на основе J независимых результатов измерений имеет вид:
. Эта оценка на основе J независимых результатов измерений имеет вид:
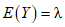 и
и 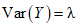 . Таким образом, необходимо определить оценку только параметра
. Таким образом, необходимо определить оценку только параметра 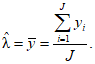 (B.2)
(B.2)При аппроксимации распределения Пуассона нормальным распределением случайную величину Y заменяют случайной величиной Z, которая подчиняется нормальному распределению 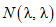 .
.
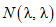 .
.(справочное)
В данном приложении минимальные обнаруживаемые значения отклика, вычисленные с использованием аппроксимации распределения Пуассона нормальным распределением, сопоставлены с минимальными обнаруживаемыми значениями, полученными на основе распределения Пуассона. Это позволяет определить зависимость точности аппроксимации от количества данных.
Минимальное обнаруживаемое значение отклика для распределения Пуассона вычисляют в соответствии со следующей процедурой.
Сумма случайных величин, подчиняющихся распределению Пуассона, также подчиняется распределению Пуассона. Однако это несправедливо для разности случайных величин, подчиняющихся распределению Пуассона. Если эта разность четко описана, используется следующая функция вероятности. Отклик в базовом состоянии соответствует фоновому шуму при измерениях yb и переменная отклика в реальном состоянии yd отражает каждую из двух выборок в условиях нулевой гипотезы.
Это означает, что распределение можно описать формулой (C.1), где y = |yb - yd|.
Распределение можно описать формулой (C.2) в условиях альтернативной гипотезы.
Минимальный обнаруживаемый отклик в фактическом состоянии может быть получен из этих двух уравнений. Альтернативно минимальный обнаруживаемый отклик при использовании аппроксимации может быть получен с помощью формул (7) и (11), если количество повторных измерений N заменить на бесконечность.
В таблице C.1 приведено минимальное обнаруживаемое значение, когда параметр yb соответствует значению в базовом состоянии от 1 до 200, а также разности значений yd, вычисленных с помощью точного и приближенного метода [11].
Таблица C.1
и нормальной аппроксимации
Значение отклика в базовом состоянии | Распределение Пуассона | Нормальное приближение | Разность |
yb | yd | yd | |
1 | 8,2 | 8,4 | - 0,1 |
2 | 11,3 | 11,3 | 0,0 |
3 | 14,1 | 13,8 | 0,3 |
4 | 17,1 | 16,0 | 1,0 |
5 | 18,9 | 18,1 | 0,8 |
6 | 20,8 | 20,1 | 0,7 |
7 | 22,2 | 22,0 | 0,2 |
8 | 24,7 | 23,9 | 0,9 |
9 | 26,1 | 25,7 | 0,4 |
10 | 27,4 | 27,4 | 0,0 |
11 | 29,9 | 29,1 | 0,7 |
12 | 31,2 | 30,8 | 0,3 |
13 | 32,5 | 32,5 | 0,0 |
14 | 34,9 | 34,1 | 0,7 |
15 | 36,1 | 35,7 | 0,4 |
16 | 37,4 | 37,3 | 0,1 |
17 | 39,8 | 38,9 | 0,9 |
18 | 41,0 | 40,4 | 0,6 |
19 | 42,3 | 42,0 | 0,3 |
20 | 43,5 | 43,5 | 0,0 |
21 | 45,8 | 45,0 | 0,8 |
22 | 47,1 | 46,5 | 0,5 |
23 | 48,3 | 48,0 | 0,3 |
24 | 49,5 | 49,5 | 0,0 |
25 | 51,8 | 51,0 | 0,8 |
26 | 53,0 | 52,4 | 0,6 |
27 | 54,2 | 53,9 | 0,3 |
28 | 55,4 | 55,3 | 0,1 |
29 | 57,7 | 56,8 | 1,0 |
30 | 58,9 | 58,2 | 0,7 |
31 | 60,1 | 59,6 | 0,5 |
32 | 61,3 | 61,0 | 0,3 |
33 | 62,5 | 62,4 | 0,0 |
34 | 64,7 | 63,8 | 0,9 |
35 | 65,9 | 65,2 | 0,7 |
36 | 67,1 | 66,6 | 0,5 |
37 | 68,3 | 68,0 | 0,3 |
38 | 69,5 | 69,4 | 0,1 |
39 | 71,7 | 70,8 | 1,0 |
40 | 72,9 | 72,1 | 0,8 |
41 | 74,1 | 73,5 | 0,6 |
42 | 75,2 | 74,9 | 0,4 |
43 | 76,4 | 76,2 | 0,2 |
44 | 77,5 | 77,6 | 0,0 |
45 | 79,8 | 78,9 | 0,9 |
46 | 80,9 | 80,3 | 0,7 |
47 | 82,1 | 81,6 | 0,5 |
48 | 83,3 | 82,9 | 0,3 |
49 | 84,4 | 84,3 | 0,1 |
50 | 85,6 | 85,6 | 0,0 |
51 | 87,8 | 86,9 | 0,9 |
52 | 88,9 | 88,3 | 0,7 |
53 | 90,1 | 89,6 | 0,5 |
54 | 91,2 | 90,9 | 0,3 |
55 | 92,4 | 92,2 | 0,2 |
56 | 93,5 | 93,5 | 0,0 |
57 | 95,7 | 94,8 | 0,9 |
58 | 96,9 | 96,1 | 0,8 |
59 | 98,0 | 97,4 | 0,6 |
60 | 99,2 | 98,7 | 0,4 |
61 | 100,3 | 100,0 | 0,3 |
62 | 101,5 | 101,3 | 0,1 |
63 | 102,6 | 102,6 | 0,0 |
64 | 104,8 | 103,9 | 0,9 |
65 | 105,9 | 105,2 | 0,7 |
66 | 107,1 | 106,5 | 0,6 |
67 | 108,2 | 107,8 | 0,4 |
68 | 109,3 | 109,1 | 0,3 |
69 | 110,5 | 110,4 | 0,1 |
70 | 111,6 | 111,6 | 0,0 |
71 | 113,8 | 112,9 | 0,9 |
72 | 114,9 | 114,2 | 0,7 |
73 | 116,0 | 115,5 | 0,6 |
74 | 117,2 | 116,7 | 0,4 |
75 | 118,3 | 118,0 | 0,3 |
76 | 119,4 | 119,3 | 0,2 |
77 | 120,5 | 120,5 | 0,0 |
78 | 122,7 | 121,8 | 0,9 |
79 | 123,9 | 123,1 | 0,8 |
80 | 125,0 | 124,3 | 0,7 |
81 | 126,1 | 125,6 | 0,5 |
82 | 127,2 | 126,8 | 0,4 |
83 | 128,3 | 128,1 | 0,2 |
84 | 129,5 | 129,3 | 0,1 |
85 | 130,6 | 130,6 | 0,0 |
86 | 132,8 | 131,9 | 0,9 |
87 | 133,9 | 133,1 | 0,8 |
88 | 135,0 | 134,3 | 0,6 |
89 | 136,1 | 135,6 | 0,5 |
90 | 137,2 | 136,8 | 0,4 |
91 | 138,3 | 138,1 | 0,3 |
92 | 139,5 | 139,3 | 0,1 |
93 | 140,6 | 140,6 | 0,0 |
94 | 142,7 | 141,8 | 0,9 |
95 | 143,9 | 143,1 | 0,8 |
96 | 145,0 | 144,3 | 0,7 |
97 | 146,1 | 145,5 | 0,6 |
98 | 147,2 | 146,8 | 0,4 |
99 | 148,3 | 148,0 | 0,3 |
100 | 149,4 | 149,2 | 0,2 |
101 | 150,5 | 150,5 | 0,1 |
102 | 151,6 | 151,7 | -0,1 |
103 | 153,8 | 152,9 | 0,9 |
104 | 154,9 | 154,2 | 0,7 |
105 | 156,0 | 155,4 | 0,6 |
106 | 157,1 | 156,6 | 0,5 |
107 | 158,2 | 157,8 | 0,4 |
108 | 159,3 | 159,1 | 0,3 |
109 | 160,4 | 160,3 | 0,2 |
110 | 161,5 | 161,5 | 0,0 |
111 | 163,7 | 162,7 | 1,0 |
112 | 164,8 | 163,9 | 0,9 |
113 | 165,9 | 165,2 | 0,7 |
114 | 167,0 | 166,4 | 0,6 |
115 | 168,1 | 167,6 | 0,5 |
116 | 169,2 | 168,8 | 0,4 |
117 | 170,3 | 170,0 | 0,3 |
118 | 171,4 | 171,2 | 0,2 |
119 | 172,5 | 172,5 | 0,1 |
120 | 173,6 | 173,7 | 0,0 |
121 | 175,8 | 174,9 | 0,9 |
122 | 176,9 | 176,1 | 0,8 |
123 | 178,0 | 177,3 | 0,7 |
124 | 179,1 | 178,5 | 0,6 |
125 | 180,2 | 179,7 | 0,4 |
126 | 181,3 | 180,9 | 0,3 |
127 | 182,4 | 182,1 | 0,2 |
128 | 183,5 | 183,3 | 0,1 |
129 | 184,6 | 184,5 | 0,0 |
130 | 186,7 | 185,8 | 1,0 |
131 | 187,8 | 187,0 | 0,9 |
132 | 188,9 | 188,2 | 0,8 |
133 | 190,0 | 189,4 | 0,6 |
134 | 191,1 | 190,6 | 0,5 |
135 | 192,2 | 191,8 | 0,4 |
136 | 193,3 | 193,0 | 0,3 |
137 | 194,4 | 194,2 | 0,2 |
138 | 195,5 | 195,4 | 0,1 |
139 | 196,6 | 196,6 | 0,0 |
140 | 198,7 | 197,8 | 1,0 |
141 | 199,8 | 198,9 | 0,9 |
142 | 200,9 | 200,1 | 0,8 |
143 | 202,0 | 201,3 | 0,6 |
144 | 203,1 | 202,5 | 0,6 |
145 | 204,2 | 203,7 | 0,5 |
146 | 205,3 | 204,9 | 0,3 |
147 | 206,4 | 206,1 | 0,2 |
148 | 207,5 | 207,3 | 0,1 |
149 | 208,6 | 208,5 | 0,1 |
150 | 209,6 | 209,7 | 0,0 |
151 | 211,8 | 210,9 | 0,9 |
152 | 212,9 | 212,1 | 0,8 |
153 | 214,0 | 213,3 | 0,7 |
154 | 215,0 | 214,4 | 0,6 |
155 | 216,1 | 215,6 | 0,5 |
156 | 217,2 | 216,8 | 0,4 |
157 | 218,3 | 218,0 | 0,3 |
158 | 219,4 | 219,2 | 0,2 |
159 | 220,5 | 220,4 | 0,1 |
160 | 221,6 | 221,6 | 0,0 |
161 | 223,7 | 222,7 | 1,0 |
162 | 224,8 | 223,9 | 0,9 |
163 | 225,9 | 225,1 | 0,8 |
164 | 227,0 | 226,3 | 0,7 |
165 | 228,1 | 227,5 | 0,6 |
166 | 229,1 | 228,6 | 0,5 |
167 | 230,2 | 229,8 | 0,4 |
168 | 231,3 | 231,0 | 0,3 |
169 | 232,4 | 232,2 | 0,2 |
170 | 233,5 | 233,4 | 0,1 |
171 | 234,6 | 234,5 | 0,0 |
172 | 236,7 | 235,7 | 1,0 |
173 | 237,8 | 236,9 | 0,9 |
174 | 238,9 | 238,1 | 0,8 |
175 | 240,0 | 239,3 | 0,7 |
176 | 241,0 | 240,4 | 0,6 |
177 | 242,1 | 241,6 | 0,5 |
178 | 243,2 | 242,8 | 0,4 |
179 | 244,3 | 244,0 | 0,3 |
180 | 245,4 | 245,1 | 0,2 |
181 | 246,5 | 246,3 | 0,2 |
182 | 247,5 | 247,5 | 0,1 |
183 | 248,6 | 248,6 | 0,0 |
184 | 250,7 | 249,8 | 0,9 |
185 | 251,8 | 251,0 | 0,8 |
186 | 252,9 | 252,2 | 0,8 |
187 | 254,0 | 253,3 | 0,7 |
188 | 255,1 | 254,5 | 0,6 |
189 | 256,2 | 255,7 | 0,5 |
190 | 257,2 | 256,8 | 0,4 |
191 | 258,3 | 258,0 | 0,3 |
192 | 259,4 | 259,2 | 0,2 |
193 | 260,5 | 260,3 | 0,1 |
194 | 261,6 | 261,5 | 0,1 |
195 | 262,6 | 262,7 | 0,0 |
196 | 264,8 | 263,8 | 0,9 |
197 | 265,8 | 265,0 | 0,8 |
198 | 266,9 | 266,2 | 0,7 |
199 | 268,0 | 267,3 | 0,7 |
200 | 269,1 | 268,5 | 0,6 |
Вычисления для распределения Пуассона и при использовании нормальной аппроксимации дают довольно близкие результаты по всему диапазону (см. рисунок C.1).

X - значение yb; Y - разность значений yd, полученных
точным и приближенным методом в %
для распределения Пуассона и с использованием его
аппроксимации нормальным распределением в процентах
Если минимальное обнаруживаемое значение отклика должно быть определено с погрешностью не более 5%, условия измерений должны быть отрегулированы так, чтобы значение yb составляло не менее 18.
(справочное)
ВЫБОР КОЛИЧЕСТВА КАНАЛОВ ДЛЯ ДАТЧИКА
Количество каналов датчика, выбранных для измерений, определяет диапазон, который может быть охвачен в процессе измерений. Важно обеспечить отсутствие наложения соседних пиков и одинаковое количество каналов при измерении фонового шума и выборки.

X - каналы; Y - относительная интенсивность (учитываемых
импульсов); S - область сигнала; B1 - левая фоновая область;
B2 - правая фоновая область
(справочное)
ПРИМЕРЫ РАСЧЕТОВ
E.1 Пример 1. Определение содержания опасных веществ с помощью рентгеновской дифрактометрии
Асбест хризотиловый (опасное вещество) может быть обнаружен при использовании рентгеновской дифрактометрии. Образец асбеста хризотилового массой 0,10 мг был точно взвешен, смешан с чистой водой, осажден на фильтровальную бумагу и проанализирован. Результаты показали содержание асбеста 0,10% или 0,10 мг/100 мг (максимально допустимое значение в строительных материалах). Проводилось пять повторных измерений содержания асбеста в холостой пробе с xb = 0 и в фактической пробе с xg. Результаты исследования порошка асбеста хризотилового, представленные в виде зависимости интенсивности дифрагированного излучения от Брэгговского угла  , приведены на рисунке E.1. Способность обнаружения вычислена для K = J = 1 и
, приведены на рисунке E.1. Способность обнаружения вычислена для K = J = 1 и  .
.
 .
.
X - Брэгговский угол 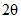 ;
;
Y - относительная интенсивность сигналов
лучей асбеста хризотилового
Условия измерений:
Средство измерений: рентгеновский дифрактометр;
Источник рентгеновского излучения: Cu, обеспечивающий K-альфа монохроматическое рентгеновское излучение с 0,154 нм;
Выходная мощность: 40 кВ, 40 мА;
Ширина канала: 0,02 градуса Брэгговского угла 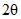 ;
;
Общее количество каналов: 23 (для фонового шума и для пиковой области);
Количество измерений: 5;
Время аккумуляции в каждом канале: 2 с;
Полная ширина на уровне половины максимума (FWHM): 0,46 градуса Брэгговского угла  .
.
E.1.1 Статистический анализ
В результате эксперимента yb = 174, yg = 261. Для этих значений нижняя граница доверительного интервала, вычисленная по формуле (11) для уровня доверия 95% имеет вид:
 .
.Эта нижняя граница больше

(см. формулы (6) и (7)).
Таким образом, с уровнем доверия 95% можно принять решение о том, что в исследованном порошке присутствует 0,1% асбеста хризотилового.
E.1.2 Определение оценки минимальной обнаруживаемой концентрации асбеста
Минимальная обнаруживаемая концентрация асбеста в строительных материалах может быть определена с использованием тех же самых условий. Минимальная обнаруживаемая концентрация может быть улучшена при увеличении количества измерений. Увеличение количества измерений до бесконечности дает предельную минимальную обнаруживаемую концентрацию, как показано в следующих вычислениях:
 ,
,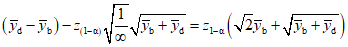 ,
,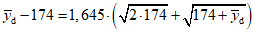 .
.Было получено 238 сигналов для минимального обнаруживаемого значения переменной отклика, по отношению к которому содержание асбеста может быть оценено в процентах следующим образом:
0,1%/(261 - 174) (количество сигналов) = 1,15·10-3%/(количество сигналов).
Предельное минимальное обнаруживаемое содержание асбеста хризотилового получено следующим образом:
1,15·10-3%·(238 - 174) (количество сигналов) = 0,074%.
Таким образом, оценка минимального обнаруживаемого значения содержания асбеста хризотилового составляет 0,074%.
E.2 Пример 2. Определение загрязнения на поверхности кремниевых пластин с помощью рентгеновской фотоэлектронной спектроскопии
Загрязнение поверхности кремниевой пластины веществами органического происхождения определено на основе измерения энергии связи на уровне 1s орбитали углерода, полученной с помощью фотоэлектронной спектроскопии.
Полученные значения для трех повторных измерений в двух областях одного и того же образца, представляющих xb = 0 и неизвестное содержание xg, приведены в таблице E.1 вместе с 1s-спектром углерода (рисунок E.2), полученным на основе фотоэлектронной спектроскопии.
Таблица E.1
и холостой пробы
Фоновый шум | Количество сигналов | Пиковая область | Количество сигналов | ||||||
эВ | n = 1 | n = 2 | n = 3 | Среднее | эВ | n = 1 | n = 2 | n = 3 | Среднее |
291,85 | 102 | 78 | 81 | 283,98 | 111 | 98 | 113 | ||
291,83 | 99 | 77 | 87 | 283,95 | 98 | 103 | 111 | ||
291,80 | 96 | 64 | 88 | 283,93 | 107 | 103 | 128 | ||
291,78 | 112 | 85 | 72 | 283,90 | 99 | 104 | 91 | ||
291,75 | 100 | 86 | 90 | 283,88 | 111 | 95 | 109 | ||
291,73 | 99 | 88 | 63 | 283,85 | 108 | 131 | 110 | ||
291,70 | 109 | 81 | 76 | 283,83 | 103 | 95 | 87 | ||
291,68 | 95 | 76 | 98 | 283,80 | 121 | 115 | 118 | ||
291,65 | 91 | 79 | 75 | 283,78 | 97 | 116 | 91 | ||
291,63 | 107 | 90 | 78 | 283,75 | 102 | 103 | 102 | ||
291,60 | 92 | 90 | 72 | 283,73 | 118 | 95 | 105 | ||
yi (суммарное количество сигналов/канал) | 1102 | 894 | 880 | 959 | yi (суммарное количество сигналов/канал) | 1175 | 1158 | 1165 | 1166 |
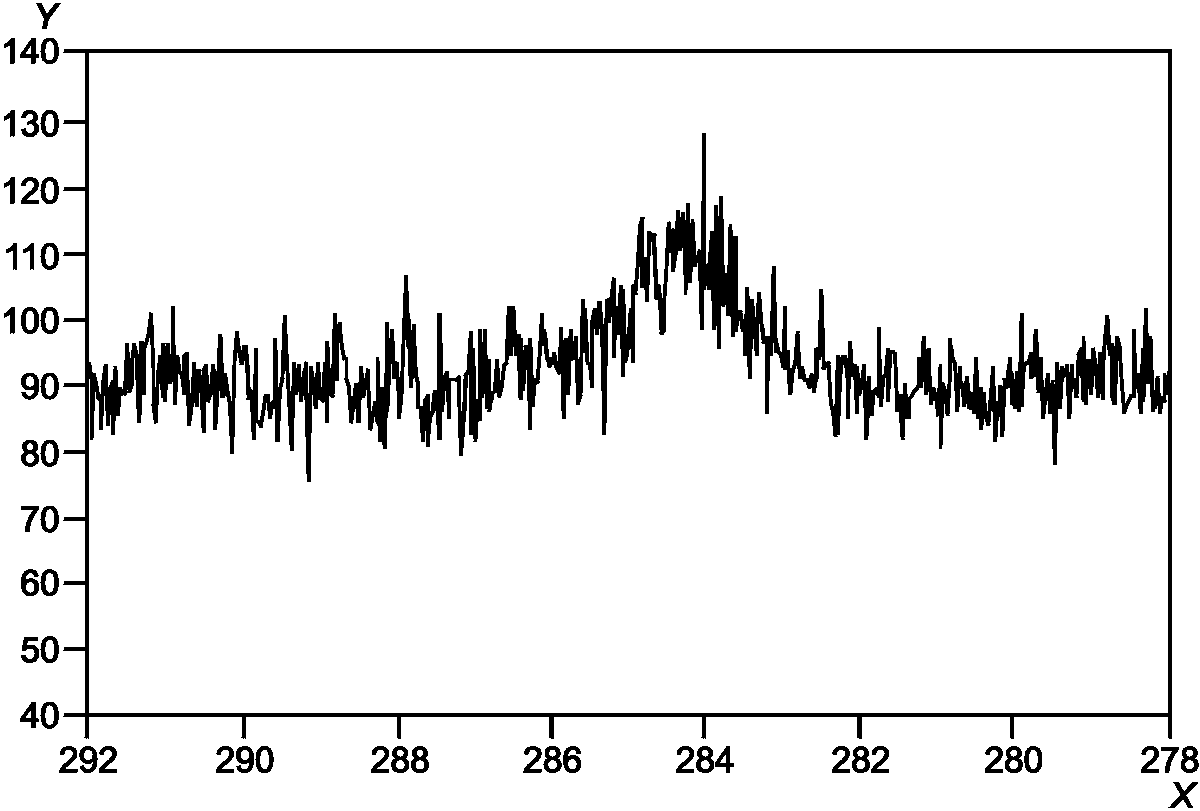
X - энергия связи, эВ; Y - относительная
интенсивность сигналов
на основе фотоэлектронной спектроскопии
При использовании трех повторных измерений способность обнаружения вычислена для K = J = 1 и 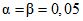 .
.
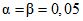 .
.Условия измерений:
Средство измерений: рентгеновский фотоэлектронный спектрометр;
Источник рентгеновского излучения: Al, обеспечивающий K-альфа монохроматическое рентгеновское излучение;
Выходная мощность: 0,9 Вт;
Ширина канала 0,025 эВ;
Количество каналов: 11 (для фонового шума и пиковой области);
Количество измерений: 3;
Время аккумуляции в каждом канале: 100 мс.
E.2.1 Статистический анализ
В результате эксперимента  ,
, 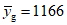 . Используя эти значения по формуле (10), определена нижняя граница доверительного интервала для уровня доверия 95%:
. Используя эти значения по формуле (10), определена нижняя граница доверительного интервала для уровня доверия 95%:
 ,
, 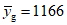 . Используя эти значения по формуле (10), определена нижняя граница доверительного интервала для уровня доверия 95%:
. Используя эти значения по формуле (10), определена нижняя граница доверительного интервала для уровня доверия 95%: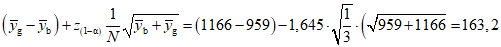 .
.Эта нижняя граница больше

(см. неравенство (6)). Поэтому с уровнем доверия 95% можно утверждать, что поверхность кремниевой пластины загрязнена углеводородом.
E.2.2 Определение минимального обнаруживаемого содержания углеводорода с использованием аппроксимации
Минимальное обнаруживаемое содержание загрязнения углеводородом поверхности кремниевой пластины получено на основе наблюдаемого количества сигналов всех составляющих элементов и факторов чувствительности установленного средства измерений.
(справочное)
НАЦИОНАЛЬНЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ И ДЕЙСТВУЮЩИМ
В ЭТОМ КАЧЕСТВЕ МЕЖГОСУДАРСТВЕННЫМ СТАНДАРТАМ
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального, межгосударственного стандарта |
Руководство ИСО 30 | - | <*> |
ИСО 3534-1:2006 | - | <*> |
ИСО 11843-1:1997 | IDT | ГОСТ Р ИСО 11843-1-2007 "Статистические методы. Способность обнаружения. Часть 1. Термины и определения" |
ИСО 11843-2:2000 | IDT | ГОСТ Р ИСО 11843-2-2007 "Статистические методы. Способность обнаружения. Часть 2. Методология в случае линейной калибровки" |
ИСО 11843-3:2003 | IDT | ГОСТ ИСО 11843-3-2005 "Статистические методы. Способность обнаружения. Методология определения критического значения отклика без использования данных калибровки" |
ИСО 11843-4:2003 | IDT | ГОСТ ИСО 11843-4-2005 "Статистические методы. Способность обнаружения. Метод сравнения минимального обнаруживаемого значения с заданным значением" |
<*> Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: IDT - идентичный стандарт. | ||
Kaiser H. Die berechnung der nachweisempfindlichkeit. Spectrochimica Acta. 1947, 3 pp. 40 - 67 | ||
[2] | Currie L.A. & Svehla G. Limits for qualitative detection and quantitative determination. Application to radiochemistry. Anal. Chem. 1968, 40 pp. 586 - 593 | |
[3] | MacDougall D. & Crummett W.B. Guidelines for data acquisition and data quality evaluation in environmental chemistry. Anal. Chem. 1980, 52 pp. 2242 - 2249 | |
[4] | Currie L.A. The Limitations of Models and Measurements as Revealed Througha Chemometric Intercomparison. J. Res. NBS. 1985, 90 pp. 409 - 422 | |
[5] | Currie L.A., & Svehla G. Nomenclature for the presentation of results of chemical analysis (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66 pp. 595 - 608 | |
[6] | Currie L.A. Nomenclature in evaluation of analytical methods including detection and quantification capabilities (IUPAC Recommendations 1995). Pure Appl. Chem. 1995, 67 pp. 1699 - 1724 | |
[7] | Currie L.A. Detection: International update, and some emerging dilemmas involving calibration, the blank, and multiple detection decisions. Chemom. Intell. Lab. Syst. 1997, 37 pp. 151 - 181 | |
ISO/IEC Guide 98-3 | Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) | |
[9] | Baer D.R. Improving surface-analysis methods for characterization of advanced materials by development of standards, reference data, and interlaboratory comparisons. Surf. Interface Anal. 2007, 39 pp. 283 - 293 | |
[10] | Furukawa Y., Iwasaki M., Tanaka A. A practical method for determining minimum detectable values in pulse-counting measurements. Anal. Sci. 2010, 26 pp. 259 - 265 | |
Tsutsumi Y., Kawamura H., Suzuki T. The estimation of detection capability for Poisson distributed measurements, ANQ Congress, Ho Chi Minh City, 2011 | ||
[12] | ISO 3534-2 | Statistics - Vocabulary and symbols - Part 2: Applied statistics |
[13] | ISO 5479:1997 | Statistical interpretation of data - Tests for departure from the normal distribution |
[14] | ISO 5725-2:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 | Т59 |
Ключевые слова: измерение, отклик, стандартное состояние, базовое состояние, приведенная переменная состояния, калибровка, критическое значение отклика, ошибка первого рода | ||
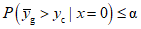



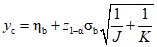 (см.
(см.