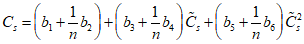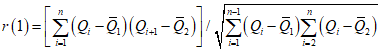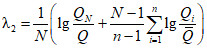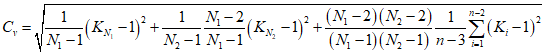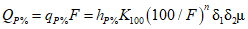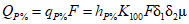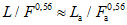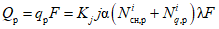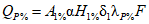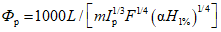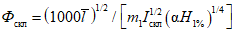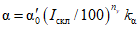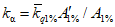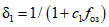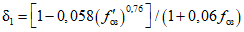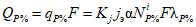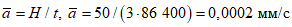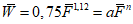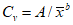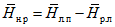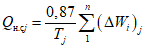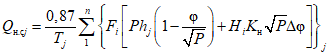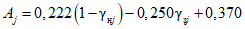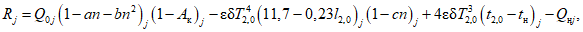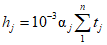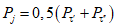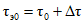СПРАВКА
Источник публикации
Ленинград: Гидрометеоиздат, 1986
Примечание к документу
Название документа
"Практические рекомендации по расчету гидрологических характеристик в зоне хозяйственного освоения БАМа"
"Практические рекомендации по расчету гидрологических характеристик в зоне хозяйственного освоения БАМа"
Итоговой сессией
Ученого Совета Государственного
гидрологического института
13 января 1984 года
ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
В ЗОНЕ ХОЗЯЙСТВЕННОГО ОСВОЕНИЯ БАМа
В рекомендациях приводятся методы расчетов гидрологических характеристик рек зоны БАМа при наличии, недостаточности и отсутствии данных гидрометрических наблюдений.
Рассмотрены методы оценки ресурсов поверхностного стока, расчета годового стока и его внутригодового распределения, максимальных расходов и слоев весеннего половодья и дождевых паводков, минимальных летне-осенних и зимних расходов воды, продолжительности перемерзания рек, наледного регулирования стока.
Рекомендации предназначены для специалистов, работающих в области гидрологии, гидротехники, мелиорации, а также преподавателей и студентов ВУЗов.
В Рекомендациях излагаются методы расчета основных гидрологических характеристик, а также дополнительных характеристик, имеющих большое значение для оценки режима речного стока в зоне хозяйственного освоения БАМа (рис. 1.1) как при наличии данных гидрометрических наблюдений достаточной продолжительности, так и при их недостаточности. Вместе с тем наибольшее внимание уделено методам расчета гидрологических характеристик при отсутствии данных гидрометрических наблюдений. Отдельные главы посвящены вопросам оценки продолжительности перемерзания рек и наледного регулирования стока.
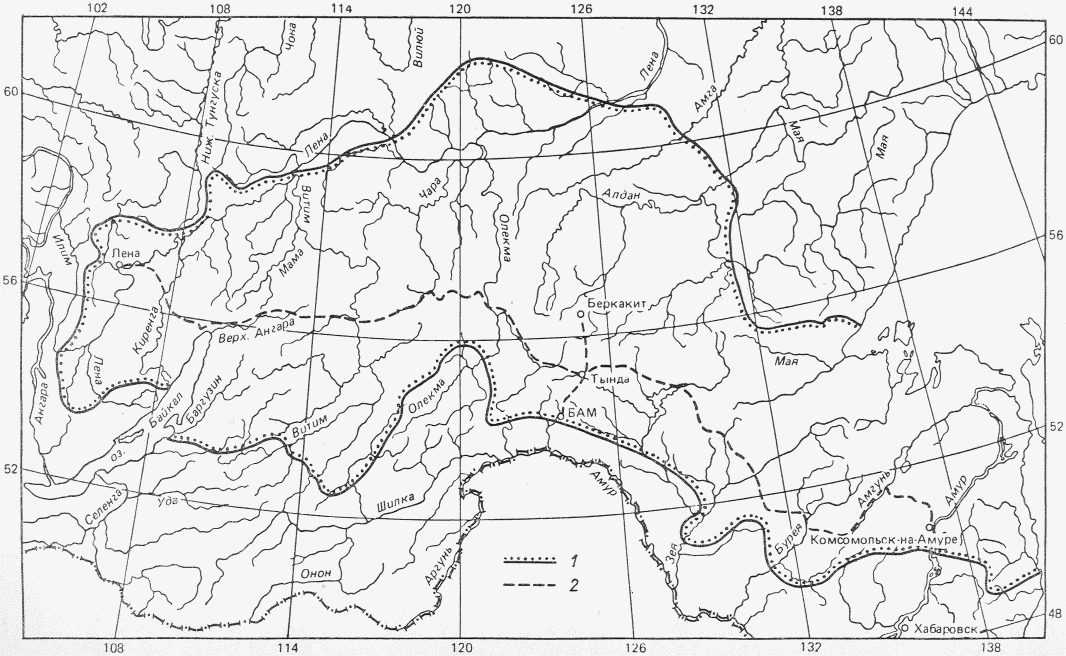
Рис. 1.1. Территория экономического освоения БАМа
1 - граница зоны БАМа, 2 - трасса БАМа
В основу Рекомендаций положены уточненные для зоны хозяйственного освоения БАМ существующие методы расчета основных гидрологических характеристик, изложенные в СНиПе 2.01.14-83, с учетом данных сетевых гидрометеорологических наблюдений последних лет, а также расчетные методы, разработанные по результатам экспедиционных исследований для части территории, занятой многолетней мерзлотой.
Отдельные разделы Рекомендаций разработали:
главу 4 - С.А. Журавин (разд. 4.1, 4.2), Н.И. Горошкова, Н.Г. Василенко (разд. 4.3), М.М. Бабкин, Э.С. Херсонский, Н.Г. Василенко (разд. 4.4), М.М. Бабкин (разд. 4.5), В.П. Юницына, Е.А. Обливанова (разд. 4.6);
главу 5 - Г.А. Любимов;
главу 6 - канд. геогр. наук Б.Л. Соколов, Б.Н. Дейкин, М.Л. Марков.
Редактирование карт гидрологических характеристик осуществлено канд. геогр. наук А.П. Копыловым.
Общее руководство работой осуществлено канд. геогр. наук Б.М. Доброумовым, канд. геогр. наук Б.Л. Соколовым, С.А. Журавиным.
В работе над Рекомендациями принимали участие Ф.А. Лифшиц, Т.В. Чиркова, Ф.Ф. Черная.
Настоящие Рекомендации составлены с целью обеспечения проектных, строительных и других народнохозяйственных организаций методами гидрологических расчетов, позволяющими повысить надежность проектирования и строительства различных гидротехнических и водохозяйственных объектов в зоне БАМа и эффективность их эксплуатации.
При определении расчетных гидрологических характеристик рек зоны БАМа используются данные гидрометеорологических наблюдений, включая стационарные наблюдения за последние годы, опубликованные в официальных документах Государственного комитета СССР по гидрометеорологии и контролю природной среды. В связи с недостаточной гидрометеорологической изученностью исследуемого района дополнительно учитываются данные экспедиционных инженерно-гидрологических изысканий, а также материалы наблюдений за гидрологическими характеристиками по архивным, литературным и другим источникам, относящимся к периоду до начала регулярных наблюдений (при этом делается ссылка на источник информации, оценивается ее достоверность и точность).
Надежность данных гидрометрических наблюдений в необходимых случаях следует подвергать проверке в соответствии с требованиями п. 1.3 "Пособия по определению расчетных гидрологических характеристик" (Л.: Гидрометеоиздат, 1984), обращая особое внимание на полноту и надежность наблюдений за стоком при наличии ледовых явлений, освещенность кривых расходов воды гидрометрическими наблюдениями во всем диапазоне колебаний уровней, полноту учета стока воды на поймах и в протоках. Сомнительные данные в расчетах не используются.
При определении расчетных гидрологических характеристик в зависимости от наличия гидрометрической информации предусмотрены расчетные схемы:
а) при наличии данных гидрометрических наблюдений - непосредственно по этим данным;
б) при недостаточности данных гидрометрических наблюдений - путем приведения их к многолетнему периоду по данным рек-аналогов с более длительными рядами наблюдений;
в) при отсутствии данных гидрометрических наблюдений - по формулам с применением данных рек-аналогов, интерполяцией, основанной на совокупности данных наблюдений всей сети гидрометеорологических станций и постов данного района или более обширной территории, а также по материалам разовых гидрометрических съемок (меженных и по меткам уровней высоких вод).
При этом используется метод гидрологической аналогии и пространственной интерполяции гидрологических характеристик и параметров речного стока с применением карт их пространственного распределения. При построении карт для рек, в бассейнах которых имеет место интенсивное развитие хозяйственной деятельности, существенно влияющее на естественный речной сток, необходимо его восстановление. Оценка антропогенных изменений стока под влиянием хозяйственной деятельности и качества восстановления стока при достаточной длине ряда наблюдений выполняется с применением параметрических критериев однородности Фишера, Стьюдента, Колмогорова-Смирнова, а при малой длине ряда наблюдений - с применением непараметрических критериев однородности Вилкоксона. В табл. 1.1 приведен перечень рек в зоне БАМа и прилегающей территории с неоднородными рядами годового стока. Методы оценки антропогенных изменений стока приведены в работах [12, 40].
Таблица 1.1
Оценка антропогенных изменений годового стока рек
зоны БАМа и прилегающей территории
Река - створ | Период естественный ---------------- нарушенный | Средняя сумма годовых значений за период, мм | Отношение значений естественного периода к значениям нарушенного | ||
осадки | сток | осадки | сток | ||
Ступина - Ступина | 1948 - 61 ------------ 1962 - 70 | 288 ------ 282 | 105 ------ 75 | 1,02 | 1,40 |
Куленга - Белоусово | 1959 - 65 ------------ 1966 - 80 | 262 ------ 292 | 142 ------ 93 | 0,90 | 1,53 |
Манзурка - Зуева | 1953 - 60 ------------ 1961 - 80 | 300 ------ 329 | 73 ------ 100 | 0,91 | 0,73 |
Бирюлька - Бирюлька | 1950 - 75 ------------ 1976 - 80 | 327 ------ 292 | 41 ------ 16 | 1,12 | 2,58 |
Чанчур - Чанчур | 1960 - 64 ------------ 1965 - 80 | 435 ------ 426 | 262 ------ 219 | 1,02 | 1,20 |
Купа - Мука | 1956 - 61, 1973 - 80 ------------ 1962 - 72 | 398 ------ 418 | 252 ------ 215 | 0,95 | 1,17 |
Хамра - Хамра | 1965 - 69 ------------ 1970 - 80 | 320 ------ 396 | 303 ------ 177 | 0,81 | 1,69 |
Заза - Усть-Заза | 1957 - 73 ------------ 1974 - 80 | 314 ------ 268 | 76 ------ 30 | 1,17 | 2,51 |
Олов - Комсомольское | 1954 - 83 ------------ 1964 - 80 | 272 ------ 332 | 72 ------ 29 | 0,82 | 2,46 |
Малый Ольдой - Тахтамыгда | 1960 - 71 ------------ 1972 - 80 | 456 ------ 397 | 188 ------ 146 | 1,15 | 1,29 |
Средний Олонгро - Могоча | 1961 - 63 ------------ 1964 - 79 | 475 ------ 387 | 278 ------ 145 | 1,23 | 1,32 |
Уруша - Уруша | 1955 - 66 ------------ 1967 - 80 | 506 ------ 445 | 285 ------ 210 | 1,14 | 1,36 |
Большой Невер - Сковородино | 1951 - 63 ------------ 1964 - 80 | 455 ------ 419 | 169 ------ 113 | 1,09 | 1,50 |
Большая Хатами - Большая Хатами | 1953 - 65 ------------ 1966 - 80 | 458 ------ 530 | 363 ------ 253 | 0,86 | 1,44 |
Тунгир - Николаевский | 1958 - 64 ------------ 1965 - 80 | 421 ------ 371 | 312 ------ 220 | 1,14 | 1,42 |
Упагда - Упагда | 1963 - 68 ------------ 1969 - 80 | 404 ------ 542 | 155 ------ 268 | 0,74 | 0,58 |
Деп - Рычково | 1949 - 63 ------------ 1964 - 79 | 528 ------ 482 | 315 ------ 241 | 1,10 | 1,31 |
Малая Улунга - Улунга | 1951 - 60 ------------ 1961 - 78 | 516 ------ 520 | 154 ------ 123 | 0,99 | 1,25 |
Гарь - Гарь | 1958 - 64 ------------ 1965 - 78 | 638 ------ 541 | 227 ------ 103 | 1,18 | 2,21 |
Половинка - Болдыревка | 1947 - 63 ------------ 1964 - 80 | 548 ------ 525 | 138 ------ 83 | 1,04 | 1,66 |
Туюн - в 3 км от устья | 1949 - 64 ------------ 1965 - 78 | 680 ------ 702 | 479 ------ 413 | 0,97 | 1,16 |
Сутырь - у ж.-д. моста | 1954 - 65 ------------ 1966 - 74 | 721 ------ 702 | 510 ------ 424 | 1,03 | 1,20 |
Беренджа - Урми | 1955 - 60 ------------ 1961 - 79 | 1150 ------ 806 | 991 ------ 435 | 1,43 | 2,28 |
Силинка - Солнечный | 1965 - 74 ------------ 1975 - 79 | 582 ------ 539 | 564 ------ 710 | 1,08 | 0,79 |
Сукпай - Сукпай | 1950 - 77 ------------ 1978 - 80 | 687 ------ 630 | 413 ------ 267 | 1,09 | 1,54 |
Кия - Марусино | 1953 - 71 ------------ 1972 - 80 | 698 ------ 678 | 365 ------ 277 | 1,03 | 1,32 |
При выборе рек-аналогов должны соблюдаться следующие условия:
- географическая близость расположения водосборов;
- сходство климатических условий;
- однородность условий формирования стока, однотипность почвогрунтов, геокриологических и гидрогеологических условий, близкая степень озерности, залесенности, заболоченности;
- площади водосборов должны различаться не более чем в 10 раз, а их средние высоты (для горных рек) не более чем на 300 м;
- отсутствие факторов, существенно искажающих естественный речной сток (регулирование стока, сбросы и водозаборы и т.п.).
В зависимости от определяемой гидрологической характеристики условия выбора рек-аналогов могут несколько изменяться.
Гидрографические, морфометрические и физико-географические характеристики реки и ее водосбора до расчетного створа или пункта гидрологических наблюдений на реках-аналогах, необходимые при расчетах стока малоизученной или неизученной реки, выражаются в виде:
1) площади водосбора F км2;
2) гидрографической длины водотока L км;
3) средневзвешенного уклона водотока 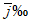 , представляющего собой условный выравненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов профиля водотока. Вычисляется только для незарегулированных водотоков по формуле
, представляющего собой условный выравненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов профиля водотока. Вычисляется только для незарегулированных водотоков по формуле
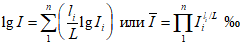 , (1.1)
, (1.1)где Ii - частные средние уклоны отдельных участков продольного профиля водотока, 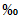 ; li - длина частных участков продольного профиля между точками перегиба, км; L - гидрографическая длина водотока до пункта наблюдений, км;
; li - длина частных участков продольного профиля между точками перегиба, км; L - гидрографическая длина водотока до пункта наблюдений, км;
4) средней высоты водосбора H в метрах над уровнем моря, определяемой либо непосредственно по гипсографической кривой водосбора, либо по формуле
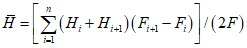 , (1.2)
, (1.2)где Hi - высота поверхности горизонтального сечения (горизонтали), м; Fi+1 - Fi - площадь между двумя соседними горизонталями; F - общая площадь водосбора;
5) относительных величин лесистости и заболоченности водосбора fл и fб, вычисляемых в процентах от общей площади водосбора;
6) относительной озерности водосбора fоз в процентах, представляющей собой отношение суммы площадей всех озер, расположенных на водосборе, к его площади. Средневзвешенная озерность 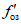 вычисляется по формуле
вычисляется по формуле
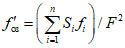 , (1.3)
, (1.3)где Si - площадь зеркала озера, fi - площадь водосбора озера, F - площадь водосбора реки до замыкающего створа;
7) закарстованности бассейна fк в процентах, определяемой по отношению закарстованной площади водосбора ко всей его площади;
8) характеристики почвогрунтов, слагающих поверхность водосбора, определяемой по почвенным картам с выделением по механическому составу глинистых, суглинистых, супесчаных, песчаных и каменистых;
9) средней глубины уровня грунтовых вод, определяемой по гидрогеологическим картам;
10) характеристики зарегулированности речной системы искусственными водоемами (количество, расположение и регулирующие емкости);
11) характеристики рельефа (равнинный - относительное колебание высот в пределах водосбора менее 200 м, горный - более 200 м);
12) при наличии мерзлоты - ее характеристики (островная, прерывистая, сплошная).
Для малых рек (F < 200 км2) дополнительно вычисляются:
1) средний уклон склонов водосбора Iск %, который определяется по картам и планам в горизонталях по формуле
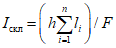 , (1.4)
, (1.4)где h - высота сечения рельефа, м; 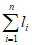 - сумма длин горизонталей в пределах водосбора, км;
- сумма длин горизонталей в пределах водосбора, км;
2) густота речной сети водосбора 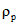 км/км2, определяется по отношению суммарной длины всех водотоков на водосборе к общей площади водосбора по формуле
км/км2, определяется по отношению суммарной длины всех водотоков на водосборе к общей площади водосбора по формуле
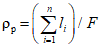 ; (1.5)
; (1.5)3) густота русловой сети водосбора 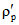 км/км2, определяется как отношение суммарной длины речных долин, сухих русел, оврагов, балок и логов <1> к общей площади водосбора.
км/км2, определяется как отношение суммарной длины речных долин, сухих русел, оврагов, балок и логов <1> к общей площади водосбора.
--------------------------------
<1> На малых горных водосборах в зоне БАМа часть первичной русловой сети скрыта под моховым покровом (так называемые каменные трубы). Поэтому определяемая по картам густота русловой сети для этих водосборов может быть занижена по сравнению с фактической.
Гидрографические характеристики реки и ее водосбора для зоны БАМа определяются по топографическим картам, масштабы которых (от 1:10 000 до 1:100 000) выбираются в зависимости от размера и рельефа водосбора.
Характер почвогрунтов, степень закарстованности, глубина залегания уровня грунтовых вод определяются по специальным картам (почвенно-грунтовым и гидрогеологическим).
ПРИ НАЛИЧИИ ДАННЫХ ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ <1>
--------------------------------
<1> Разделы 2 и 3 являются изложением соответствующих разделов "Пособия по определению расчетных гидрологических характеристик" (Л.: Гидрометеоиздат, 1984) с учетом особенностей гидрологического режима рек зоны БАМа.
Определение расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений достаточной продолжительности осуществляется на основе применения аналитических функций распределения ежегодных вероятностей превышения.
Продолжительность периода наблюдений считается достаточной, если рассматриваемый период репрезентативен (т.е. включает в себя периоды различной водности), а относительная средняя квадратическая ошибка расчетного значения исследуемой гидрологической характеристики не превышает 10%.
Репрезентативность ряда наблюдений за n лет оценивается по рекам-аналогам с наибольшей продолжительностью наблюдений N лет по разностным интегральным кривым речного стока или сопоставлением кривых распределения речного стока по реке-аналогу за периоды n и N лет.
Если относительные средние квадратические ошибки больше 10%, ряд наблюдений является нерепрезентативным и требуется приведение рассматриваемой гидрологической характеристики к многолетнему периоду.
Эмпирическая ежегодная вероятность превышения (Pm %) гидрологических характеристик определяется по формуле
где m - порядковый номер членов ряда гидрологической характеристики, ранжированной в убывающем порядке; n - общее число членов ряда.
Для сглаживания и экстраполяции эмпирических кривых распределения ежегодных вероятностей превышения, как правило, применяется трехпараметрическое гамма-распределение либо, при соответствующем обосновании, другие функции распределения.
Параметры аналитических кривых распределения (среднее многолетнее значение 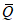 , коэффициенты вариации Cv и асимметрии Cs) определяются по гидрометрическим рядам наблюдений методами наибольшего правдоподобия, моментов (основные методы), графоаналитическим или графическим (вспомогательные методы) способом. Описание перечисленных методов расчета приведено в работе [31].
, коэффициенты вариации Cv и асимметрии Cs) определяются по гидрометрическим рядам наблюдений методами наибольшего правдоподобия, моментов (основные методы), графоаналитическим или графическим (вспомогательные методы) способом. Описание перечисленных методов расчета приведено в работе [31].
Расчет коэффициентов вариации Cv и асимметрии Cs для трехпараметрического гамма-распределения и биномиального распределения методом моментов с учетом внутрирядной корреляции выполняется по формулам:
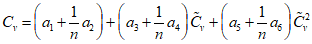 , (2.2)
, (2.2)где a1, ..., a6; b1, ..., b6 - коэффициенты, определяемые по табл. 2.1, 2.2; 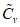 и
и 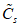 - смещенные оценки коэффициентов вариации и асимметрии, определяемые по формулам:
- смещенные оценки коэффициентов вариации и асимметрии, определяемые по формулам:
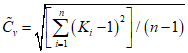 , (2.4)
, (2.4)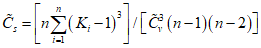 . (2.5)
. (2.5)Таблица 2.1
Значение Cs/Cv | r (1) | a1 | a2 | a3 | a4 | a5 | a6 |
2 | 0 | 0 | 0,19 | 0,99 | -0,88 | 0,01 | 1,54 |
0,3 | 0 | 0,22 | 0,99 | -0,41 | 0,01 | 1,51 | |
0,5 | 0 | 0,18 | 0,98 | 0,41 | 0,02 | 1,47 | |
3 | 0 | 0 | 0,69 | 0,98 | -4,34 | 0,01 | 6,78 |
0,3 | 0 | 1,15 | 1,02 | -7,53 | -0,04 | 12,38 | |
0,5 | 0 | 1,75 | 1,00 | -11,79 | -0,05 | 21,13 | |
4 | 0 | 0 | 1,36 | 1,02 | -9,68 | -0,05 | 15,55 |
0,3 | -0,02 | 2,61 | 1,13 | -19,85 | -0,22 | 34,15 | |
0,5 | -0,02 | 3,47 | 1,18 | -29,71 | -0,41 | 58,08 |
Примечание. Коэффициент автокорреляции между смежными членами ряда r (1) определяется по формуле (2.6).
Таблица 2.2
r (1) | b1 | b2 | b3 | b4 | b5 | b6 |
0 | 0,03 | 2,00 | 0,92 | -5,09 | 0,03 | 8,10 |
0,3 | 0,03 | 1,77 | 0,93 | -3,45 | 0,03 | 8,03 |
0,5 | 0,03 | 1,63 | 0,92 | -0,97 | 0,03 | 7,94 |
Несмещенные оценки Cv и Cs определяются по специальным таблицам, приведенным в работе [27].
Расчетные отношения Cs/Cv, а также r (1) принимаются как средние из значений, установленных по группе рек с наибольшей продолжительностью наблюдений.
При невозможности использовать для расчета основные методы допускается применять вспомогательные, графоаналитический и графический, описанные в работе [31].
где
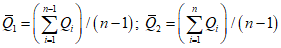 .
.В случае неоднородности исходных данных гидрометрических наблюдений эмпирические и аналитические кривые распределения устанавливаются отдельно для каждой однородной совокупности, после чего рассчитывается обобщенная (составная) кривая распределения при наличии наблюдений за всеми однородными элементами (например, весенними максимумами снегового и снегодождевого происхождения) в каждом году или их чередовании из года в год по следующим формулам:
а) при наличии наблюдений в каждом году за всеми однородными элементами режима (n1 = n2 = n3 = n) ежегодная вероятность превышения P % рассматриваемой гидрологической характеристики при любом ее значении определяется по формуле
где P1, P2, P3 - ежегодные вероятности превышения однородных элементов, выраженные в долях единицы.
При двух однородных гидрологических характеристиках формула (2.7) принимает вид
P = (P1 + P2 - P1P2)·100; (2.8)
б) если в каждом году имеется только одно значение рассматриваемой гидрологической характеристики, используется формула
где n1, n2, n3 - число членов однородных совокупностей.
При двух генетически однородных элементах формула (2.9) приобретает вид
P = (n1P + n2P)/(n1 + n2). (2.10)
При наличии в ряду наблюдений нулевых значений (например, минимальные расходы) расчет выполняется по формуле
Вероятности превышения в формулах (2.9) - (2.11) выражаются в процентах.
Для наибольшего или наименьшего членов ряда гидрометрических наблюдений следует указывать доверительные интервалы эмпирической ежегодной вероятности превышения.
Случайные средние квадратические ошибки выборочных средних при коэффициенте автокорреляции r < 0,5 определяются по приближенной зависимости
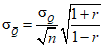 ; (2.12)
; (2.12)при r > 0,5
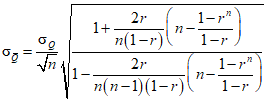 . (2.13)
. (2.13)Случайные средние квадратические ошибки коэффициентов вариации при Cs = 2Cv определяются по формуле
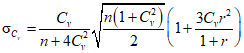 . (2.14)
. (2.14)Подробно случайные средние квадратические ошибки выборочных средних арифметических и коэффициентов вариации, включая закон их распределения, рассматриваются в работе [27].
При наличии обоснованных сведений о выдающихся значениях речного стока параметры кривых распределения гидрологических характеристик определяются следующими методами:
1. При учете одного выдающегося значения гидрологической характеристики, не входящего в n-летний ряд данных гидрометрических наблюдений:
а) методом наибольшего правдоподобия в зависимости от статистик 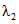 и
и 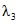 , определяемых по формулам:
, определяемых по формулам:
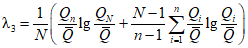 ; (2.16)
; (2.16)б) методом моментов по формулам:
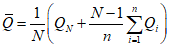 ; (2.17)
; (2.17)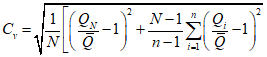 . (2.18)
. (2.18)2. При учете двух выдающихся значений гидрологической характеристики, не входящих в непрерывный n-летний ряд данных гидрометрических наблюдений:
а) методом наибольшего правдоподобия в зависимости от статистик 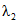 и
и 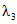 , определяемых по формулам:
, определяемых по формулам:
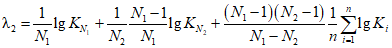 ; (2.19)
; (2.19)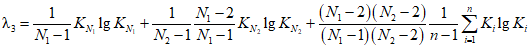 ; (2.20)
; (2.20)б) методом моментов по формулам:
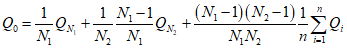 ; (2.21)
; (2.21)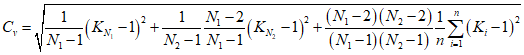 . (2.22)
. (2.22)3. При учете одного выдающегося значения гидрологической характеристики, входящего в n-летний ряд данных гидрометрических наблюдений:
а) методом наибольшего правдоподобия в зависимости от статистик 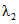 и
и 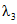 , определяемых по формулам:
, определяемых по формулам:
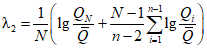 ; (2.23)
; (2.23)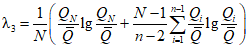 ; (2.24)
; (2.24)б) методом моментов по формулам:
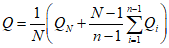 ; (2.25)
; (2.25)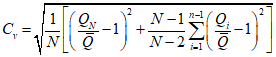 . (2.26)
. (2.26)4. При учете двух выдающихся значений гидрологической характеристики, входящих в n-летний ряд данных гидрометрических наблюдений:
а) методом наибольшего правдоподобия в зависимости от статистик 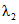 и
и 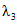 , определяемых по формулам:
, определяемых по формулам:
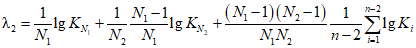 ; (2.27)
; (2.27)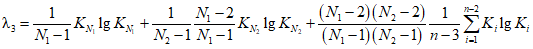 ; (2.28)
; (2.28)б) методом моментов по формулам:
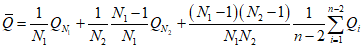 ; (2.29)
; (2.29)В формулах (2.15) - (2.30) 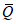 - среднее арифметическое значение, рассчитанное с учетом выдающегося значения расхода воды; n - число лет непрерывных наблюдений; N - число лет, в течение которых выдающееся значение гидрологической характеристики не было превышено. (Эмпирическая ежегодная вероятность превышения выдающегося значения гидрологической характеристики определяется по формуле (2.1) с заменой n на N);
- среднее арифметическое значение, рассчитанное с учетом выдающегося значения расхода воды; n - число лет непрерывных наблюдений; N - число лет, в течение которых выдающееся значение гидрологической характеристики не было превышено. (Эмпирическая ежегодная вероятность превышения выдающегося значения гидрологической характеристики определяется по формуле (2.1) с заменой n на N); 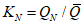 ;
; 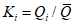 - модульные коэффициенты.
- модульные коэффициенты.
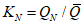 ;
; 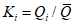 - модульные коэффициенты.
- модульные коэффициенты.Использование формул (2.15) - (2.30) допускается только в том случае, когда исторические сведения о выдающейся гидрологической величине и число лет ее непревышения абсолютно достоверны.
Расчет боковой приточности выполняется в соответствии с рекомендациями СНиПа 2.01.14-83.
Расчет ресурсов речного стока <1> при наличии данных гидрометрических наблюдений выполняется методом линейных уравнений [2] по формуле
--------------------------------
<1> Необходимо иметь в виду, что в зоне БАМа внутригодовое и внутрисезонное распределение ресурсов речного стока для большей части территории является более важной характеристикой, чем их абсолютное значение.
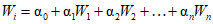 , (2.31)
, (2.31)где 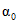 - свободный член уравнения;
- свободный член уравнения; 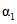 , ...,
, ..., 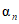 - весовые коэффициенты; W1, ..., Wn - объемы годового стока в створах рек, принятых для оценки водных ресурсов, км3; 1, ..., n - индексы, присвоенные отдельным речным бассейнам, входящим в рассматриваемую территорию; Wi - i-тая характеристика водных ресурсов (местный сток, приток или отток вод) за исследуемый год, км3.
- весовые коэффициенты; W1, ..., Wn - объемы годового стока в створах рек, принятых для оценки водных ресурсов, км3; 1, ..., n - индексы, присвоенные отдельным речным бассейнам, входящим в рассматриваемую территорию; Wi - i-тая характеристика водных ресурсов (местный сток, приток или отток вод) за исследуемый год, км3.
Весовые коэффициенты 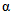 представляют собой отношение площади, с которой осуществляется приток воды на исследуемую территорию или отток с нее, к площади бассейна, сток с которого измеряется. В случае отсутствия данных о стоке с каких-либо площадей используется метод аналогии, причем сток с неизученной территории (Wn) за конкретные годы принимается равным стоку реки-аналога (Wan), с учетом отношения нормы стока
представляют собой отношение площади, с которой осуществляется приток воды на исследуемую территорию или отток с нее, к площади бассейна, сток с которого измеряется. В случае отсутствия данных о стоке с каких-либо площадей используется метод аналогии, причем сток с неизученной территории (Wn) за конкретные годы принимается равным стоку реки-аналога (Wan), с учетом отношения нормы стока 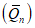 неизученной территории (по карте) к норме стока реки-аналога (Qan):
неизученной территории (по карте) к норме стока реки-аналога (Qan):
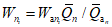 . (2.32)
. (2.32)Уравнения для расчета ресурсов речного стока промышленных районов зоны БАМа приведены в табл. 2.3.
Таблица 2.3
Линейные уравнения для расчета водных ресурсов
речного стока промышленных районов зоны БАМа
Верхнеленский промрайон: W = 1,2W1 - 1,2W2 - 0,6W3 + W4, где 1 - р. Лена - г. Киренск, 2 - р. Лена - пгт Качуг, 3 - р. Киренга - с. Карам, 4 - р. Нижняя Тунгуска - с. Подволошино. |
Южно-Якутский промрайон: W = 1,1W1 - 2,1W2 + 1,7W3 + 1,6W4 + 1,5W5 + W6 + 1,2W7 + 0,9W8, где 1 - р. Олекма - с. Куду-Кель, 2 - р. Олекма - с. Средняя Олекма, 3 - р. Бирюк - пос. Бирюк, 4 - р. Намана - с. Мякинда, 5 - р. Туолба - с. Алексеевка, 6 - р. Ботома - местн. Бролог, 7 - р. Амга - с. Буяга, 8 - р. Алдан - с. Усть-Миль. |
Зейско-Бомнакский промрайон: W = W1 + W2 + 1,4W3, где 1 - р. Гилюй - Перевоз, 2 - р. Зея - с. Бомнак, 3 - р. Деп - с. Рычково. |
Верхнеселемджинский промрайон: W = 1,2W1, где 1 - р. Селемджа - Усть-Ульма. |
Ургальский промрайон: W = 0,9W1 + 0,6W2, где 1 - р. Бурея - с. Каменка, 2 - р. Амгунь - с. Каменка. |
При определении расчетных гидрологических характеристик годового стока при наличии данных гидрометрических наблюдений расчеты выполняются согласно требованиям, приведенным в начале данного раздела (формулы и относящиеся к ним пояснения).
Для определения внутригодового распределения стока воды при наличии данных гидрометрических наблюдений за период не менее 15 лет используются следующие методы:
а) расчет внутригодового распределения стока по аналогии с распределением реального года;
б) метод компоновки сезонов.
Внутригодовое распределение стока следует рассчитывать по водохозяйственным годам, начиная с многоводного сезона, в зависимости от типа режима реки и преобладающего использования стока.
Реки зоны БАМа относятся к восточно-сибирскому (реки бассейна Верхней Лены и Северного Байкала) и дальневосточному (реки бассейна Амура и Северного Приморья) типам, которые характеризуются соответственно высоким половодьем, на шлейф которого накладываются дождевые паводки, высокими летними дождевыми паводками и глубокой зимней меженью. На большинстве рек центральной части зоны сток в зимний период на продолжительное время (4 - 6 мес.) прекращается полностью или исчезающе мал. Для рек бассейна р. Витима в пределах Витимского нагорья весеннее половодье, обусловленное исключительно снеговым питанием, в отдельные годы может быть очень слабо выраженным.
Практически для всей зоны БАМа можно принять следующие основные гидрологические сезоны: весна - лето - IV - IX, осень - X - XI, зима - XII - III.
Лимитирующими периодом и сезоном года для зоны БАМа являются соответственно осень - зима (X - III) и зима XII - III.
Особое внимание при расчетах необходимо уделять распределению стока в первый весенний (IV) и летние (VI - VIII) месяцы с большой внутримесячной изменчивостью стока, связанной с резким переходом стока от нулевого или очень малого к весеннему половодью и чередованием периодов глубокой межени.
Характерное внутригодовое распределение речного стока для различных промрайонов зоны освоения БАМа приведено в табл. 2.4.
Таблица 2.4
Характерное расчетное распределение месячного
и сезонного стока рек зоны БАМа для отдельных
промышленных районов, % годового
Характеристика года по водности | Весна - лето | Осень | Зима | Весна - лето | Осень | Зима | |||||||||
IV | V | VI | VII | VIII | IX | X | XI | XII | I | II | III | IV - IX | X - XI | XII - XIII | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
I. Верхнеленский промрайон | |||||||||||||||
р. Тутура - д. Грехова, F = 7100 км2, n = 42 (1936 - 77 гг.) | |||||||||||||||
Многоводный | 3,4 | 29,2 | 16,6 | 7,1 | 12,2 | 8,7 | 7,3 | 4,7 | 2,0 | 3,7 | 2,8 | 2,3 | 77,2 | 12,0 | 10,8 |
Средний | 3,2 | 38,8 | 13,7 | 9,8 | 7,3 | 6,2 | 6,6 | 3,8 | 4,0 | 2,6 | 2,1 | 1,9 | 79,0 | 10,4 | 10,6 |
Маловодный | 4,3 | 33,7 | 17,7 | 11,3 | 6,4 | 7,8 | 4,6 | 2,8 | 4,7 | 2,6 | 2,3 | 1,8 | 81,2 | 7,4 | 11,4 |
р. Таюра - с. Таюра, F = 5720 км2; n = 22 (1956 - 1977 гг.) | |||||||||||||||
Многоводный | 2,4 | 30,0 | 18,0 | 11,0 | 7,7 | 7,0 | 7,5 | 4,6 | 3,9 | 3,0 | 2,6 | 2,3 | 76,1 | 12,1 | 11,8 |
Средний | 3,9 | 30,4 | 16,1 | 10,3 | 9,4 | 8,2 | 5,6 | 4,7 | 4,1 | 2,8 | 2,3 | 2,2 | 78,3 | 10,3 | 11,4 |
Маловодный | 3,4 | 35,0 | 16,1 | 8,9 | 8,4 | 7,4 | 5,5 | 4,1 | 4,1 | 2,8 | 2,3 | 2,0 | 79,2 | 9,6 | 11,2 |
II. Казачинский промрайон | |||||||||||||||
р. Жуя - с. Светлый, F = 4790 км2, n = 30 (1948 - 77 гг.) | |||||||||||||||
Многоводный | 0,7 | 17,3 | 32,6 | 19,5 | 11,4 | 8,6 | 5,4 | 2,2 | 1,2 | 0,5 | 0,3 | 0,3 | 90,1 | 7,6 | 2,3 |
Средний | 0,4 | 21,8 | 36,3 | 10,7 | 14,3 | 8,1 | 4,5 | 1,8 | 0,9 | 0,5 | 0,4 | 0,3 | 91,6 | 6,3 | 2,1 |
Маловодный | 1,0 | 21,8 | 41,5 | 11,8 | 9,6 | 6,9 | 3,9 | 1,5 | 0,9 | 0,5 | 0,3 | 0,3 | 92,6 | 5,4 | 2,0 |
III. Северо-Бурятский промрайон | |||||||||||||||
р. Гоуджекит - с. Гоуджекит, F = 297 км2, n = 20 (1956 - 67, 1970 - 77 гг.) | |||||||||||||||
Многоводный | 0,8 | 5,2 | 50,2 | 15,8 | 9,8 | 7,2 | 4,9 | 2,2 | 1,4 | 1,0 | 0,8 | 0,7 | 89,0 | 7,1 | 3,9 |
Средний | 1,0 | 6,1 | 49,0 | 14,6 | 10,5 | 9,1 | 3,6 | 2,1 | 1,3 | 1,0 | 0,9 | 0,8 | 90,3 | 5,7 | 4,0 |
Маловодный | 1,0 | 10,6 | 46,1 | 16,9 | 8,4 | 6,6 | 3,4 | 2,2 | 1,6 | 1,2 | 1,0 | 0,9 | 89,7 | 5,6 | 4,7 |
р. Витим - с. Романовка, F = 18 200 км2, n = 34 (1944 - 77 гг.) | |||||||||||||||
Многоводный | 0,2 | 3,9 | 8,1 | 43,6 | 25,6 | 12,5 | 5,6 | 0,4 | 0,1 | 0 | 0 | 0 | 93,9 | 6,0 | 0,1 |
Средний | 0,4 | 10,0 | 6,9 | 40,1 | 22,3 | 15,6 | 4,3 | 0,4 | 0 | 0 | 0 | 0 | 95,3 | 4,7 | 0,0 |
Маловодный | 0,6 | 6,8 | 11,6 | 15,9 | 22,2 | 39,6 | 3,0 | 0,3 | 0 | 0 | 0 | 0 | 96,7 | 3,3 | 0,0 |
р. Конкудера - с. Конкудера, F = 4920 км2, n = 21 (1955, 1958 - 77 гг.) | |||||||||||||||
Многоводный | 0,8 | 8,4 | 31,8 | 19,9 | 13,5 | 4,3 | 6,2 | 2,9 | 2,5 | 1,2 | 0,9 | 0,6 | 85,7 | 9,1 | 5,2 |
Средний | 1,3 | 7,7 | 35,7 | 19,0 | 13,8 | 9,9 | 6,0 | 2,2 | 1,6 | 1,0 | 0,9 | 0,9 | 87,4 | 8,2 | 4,4 |
Маловодный | 1,0 | 6,6 | 36,0 | 18,6 | 14,6 | 11,8 | 5,0 | 2,2 | 1,6 | 2,2 | 0,8 | 0,6 | 88,6 | 7,2 | 4,1 |
IV. Удоканский промрайон | |||||||||||||||
р. Чара - с. Чара, F = 4150 км2, n = 27 (1951 - 77 гг.) | |||||||||||||||
Многоводный | 0,8 | 8,3 | 33,2 | 21,6 | 15,3 | 12,2 | 4,2 | 1,9 | 1,0 | 0,6 | 0,6 | 0,3 | 91,2 | 6,2 | 2,6 |
Средний | 0,6 | 8,1 | 36,2 | 22,2 | 14,1 | 10,4 | 4,2 | 1,7 | 0,9 | 0,6 | 0,6 | 0,4 | 91,6 | 5,8 | 2,6 |
Маловодный | 1,1 | 7,5 | 32,4 | 21,7 | 17,1 | 11,5 | 4,0 | 1,9 | 1,3 | 0,7 | 0,5 | 0,3 | 91,2 | 6,1 | 2,7 |
V. Южно-Якутский промрайон | |||||||||||||||
р. Чульман - с. Чульман, F = 3840 км2, n = 24 (1954 - 77 гг.) | |||||||||||||||
Многоводный | 1,1 | 29,4 | 20,6 | 13,6 | 16,0 | 12,1 | 5,2 | 1,4 | 0,5 | 0,1 | 0 | 0 | 92,8 | 6,6 | 0,6 |
Средний | 0,1 | 32,0 | 24,5 | 17,5 | 12,6 | 8,4 | 3,3 | 1,2 | 0,3 | 0,1 | 0 | 0 | 95,1 | 4,5 | 0,4 |
Маловодный | 1,2 | 38,6 | 7,8 | 21,3 | 15,3 | 11,7 | 3,0 | 0,9 | 0,2 | 0 | 0 | 0 | 95,9 | 3,9 | 0,2 |
р. Тимптон - с. Нагорный, F = 613 км2, n = 18 (1951 - 77 гг.) | |||||||||||||||
Многоводный | 0,3 | 22,0 | 10,2 | 30,1 | 17,7 | 14,7 | 4,4 | 0,6 | 0 | 0 | 0 | 0 | 95,0 | 5,0 | 0,0 |
Средний | 0,1 | 17,9 | 34,4 | 7,0 | 27,3 | 11,5 | 1,7 | 0,1 | 0 | 0 | 0 | 0 | 98,2 | 1,8 | 0,0 |
Маловодный | 0,9 | 21,1 | 14,5 | 16,8 | 32,8 | 10,8 | 3,0 | 0,1 | 0 | 0 | 0 | 0 | 96,9 | 3,1 | 0,0 |
VI. Тындинский промрайон | |||||||||||||||
р. Тында - с. Тында, F = 4060 км2, n = 27 (1951 - 55, 1957 - 78 гг.) | |||||||||||||||
Многоводный | 1,5 | 27,3 | 8,7 | 21,9 | 13,1 | 19,1 | 7,1 | 1,0 | 0,3 | 0 | 0 | 0 | 91,6 | 8,1 | 0,3 |
Средний | 0,6 | 24,3 | 33,9 | 16,5 | 12,0 | 6,9 | 5,0 | 0,7 | 0,1 | 0 | 0 | 0 | 94,2 | 5,7 | 0,1 |
Маловодный | 1,6 | 37,1 | 10,0 | 7,0 | 24,0 | 17,0 | 2,8 | 0,5 | 0 | 0 | 0 | 0 | 96,7 | 3,3 | 0,0 |
VII. Зейско-Бомнакский промрайон | |||||||||||||||
р. Ток - с. Николаевский, F = 3820 км2, n = 33 (1945 - 77 гг.) | |||||||||||||||
Многоводный | 0,6 | 8,1 | 17,9 | 31,9 | 22,3 | 13,6 | 4,3 | 0,9 | 0,4 | 0 | 0 | 0 | 94,4 | 5,2 | 0,4 |
Средний | 1,3 | 22,0 | 13,8 | 31,4 | 9,9 | 17,1 | 3,4 | 0,9 | 0,2 | 0 | 0 | 0 | 95,5 | 4,3 | 0,2 |
Маловодный | 1,3 | 34,5 | 17,3 | 7,3 | 12,4 | 23,2 | 3,2 | 0,9 | 0,1 | 0 | 0 | 0 | 95,8 | 4,1 | 0,1 |
р. Унаха - с. Унаха, F = 1950 км2, n = 17 (1961 - 78 гг.) | |||||||||||||||
Многоводный | 3,4 | 27,8 | 8,3 | 22,8 | 17,2 | 12,7 | 6,2 | 1,2 | 0,4 | 0 | 0 | 0 | 92,2 | 7,4 | 0,4 |
Средний | 1,1 | 34,1 | 16,5 | 22,9 | 12,8 | 6,4 | 4,8 | 1,3 | 0,1 | 0 | 0 | 0 | 93,8 | 6,1 | 0,1 |
Маловодный | 0,9 | 35,8 | 9,4 | 18,1 | 8,3 | 22,8 | 3,6 | 1,1 | 0 | 0 | 0 | 0 | 95,3 | 4,7 | 0,0 |
VIII. Верхнеселемджинский промрайон | |||||||||||||||
р. Нора - устье р. Эльги, F = 9630 км2, n = 21 (1941 - 61 гг.) | |||||||||||||||
Многоводный | 1,2 | 12,8 | 9,0 | 31,2 | 18,9 | 16,1 | 7,9 | 2,0 | 0,7 | 0,1 | 0,1 | 0,0 | 89,2 | 9,9 | 0,9 |
Средний | 1,1 | 16,7 | 22,8 | 6,6 | 31,7 | 13,0 | 5,7 | 1,6 | 0,5 | 0,2 | 0,1 | 0,0 | 91,9 | 7,3 | 0,8 |
Маловодный | 1,8 | 16,5 | 12,9 | 29,0 | 21,9 | 3,3 | 6,2 | 1,6 | 0,4 | 0,2 | 0,1 | 0,1 | 91,4 | 7,8 | 0,8 |
IX. Комсомольско-Амурский промрайон | |||||||||||||||
р. Горин - Бактор, F = 18 300 км2, n = 25 (1951 - 57, 1959, 1960, 1962 - 77 гг.) | |||||||||||||||
Многоводный | 2,9 | 26,2 | 18,4 | 12,0 | 8,7 | 14,3 | 10,9 | 3,8 | 1,6 | 0,7 | 0,3 | 0,2 | 82,5 | 14,7 | 2,8 |
Средний | 3,6 | 25,3 | 19,1 | 8,6 | 12,6 | 15,0 | 10,2 | 3,5 | 1,4 | 0,4 | 0,2 | 0,1 | 84,2 | 13,7 | 2,1 |
Маловодный | 4,7 | 27,2 | 20,0 | 11,5 | 9,2 | 16,2 | 7,0 | 2,3 | 1,1 | 0,4 | 0,2 | 0,2 | 88,8 | 9,3 | 1,9 |
X. Ургальский промрайон | |||||||||||||||
р. Ниман - в 12 км от устья, F = 14 500 км2, n = 28 (1949 - 77 гг.) | |||||||||||||||
Многоводный | 0,8 | 20,8 | 9,2 | 30,1 | 17,4 | 13,8 | 6,5 | 0,9 | 0,3 | 0,1 | 0,1 | 0 | 92,1 | 7,4 | 0,5 |
Средний | 1,2 | 12,2 | 18,0 | 21,9 | 31,6 | 9,2 | 5,3 | 1,1 | 0,3 | 0,1 | 0,1 | 0 | 93,1 | 6,4 | 0,5 |
Многоводный | 2,2 | 29,9 | 21,9 | 8,4 | 13,6 | 17,8 | 4,7 | 1,0 | 0,3 | 0,1 | 0,1 | 0 | 93,8 | 5,7 | 0,5 |
р. Дубликан - в 4,0 км от устья, F = 2220 км2, n = 25 (1949 - 59, 1961 - 70, 1974 - 77 гг.) | |||||||||||||||
Многоводный | 2,1 | 11,5 | 8,3 | 29,8 | 15,1 | 20,5 | 9,9 | 1,9 | 0,6 | 0,2 | 0,1 | 0,0 | 87,3 | 11,8 | 0,9 |
Средний | 2,6 | 20,2 | 13,6 | 17,4 | 23,9 | 10,0 | 9,2 | 2,3 | 0,5 | 0,2 | 0,1 | 0,0 | 87,7 | 11,5 | 0,8 |
Маловодный | 3,7 | 13,0 | 10,4 | 14,6 | 21,6 | 26,3 | 8,0 | 1,7 | 0,5 | 0,1 | 0,1 | 0,0 | 89,6 | 9,7 | 0,7 |
XI. Сов. Гаванский промрайон | |||||||||||||||
р. Тумнин - с. Тумнин, F = 13 900 км2, n = 18 (1949 - 68 гг.) | |||||||||||||||
Многоводный | 1,8 | 24,6 | 19,1 | 12,1 | 7,7 | 14,6 | 12,0 | 4,2 | 1,6 | 1,0 | 0,8 | 0,6 | 79,9 | 16,1 | 4,0 |
Средний | 2,7 | 14,8 | 11,0 | 17,5 | 20,6 | 16,4 | 10,2 | 3,2 | 1,8 | 0,9 | 0,5 | 0,4 | 83,0 | 13,4 | 3,6 |
Маловодный | 4,1 | 28,4 | 17,5 | 8,8 | 10,8 | 14,3 | 9,7 | 3,1 | 1,6 | 0,9 | 0,5 | 0,4 | 83,9 | 12,8 | 3,7 |
р. Мули - с. Джигдаси, F = 1410 км2, n = 20 (1952, 1957, 1964 - 77 гг.) | |||||||||||||||
Многоводный | 3,5 | 15,0 | 18,4 | 25,7 | 11,1 | 7,1 | 11,1 | 3,8 | 1,4 | 0,9 | 0,7 | 0,5 | 81,6 | 14,9 | 5,5 |
Средний | 6,2 | 12,2 | 11,0 | 16,1 | 14,5 | 23,5 | 9,3 | 4,2 | 1,9 | 0,6 | 0,3 | 0,2 | 83,6 | 13,5 | 3,0 |
Маловодный | 4,4 | 27,2 | 19,2 | 16,8 | 12,3 | 7,8 | 6,4 | 3,2 | 1,6 | 0,7 | 0,2 | 0,2 | 87,7 | 9,6 | 2,7 |
XII. Тугурский промрайон | |||||||||||||||
р. Гугинка - с. Гуга, F = 56,5 км2, n = 26 (1951 - 78 гг.) | |||||||||||||||
Многоводный | 2,3 | 33,5 | 20,1 | 11,1 | 8,7 | 6,7 | 12,2 | 4,5 | 0,9 | 0 | 0 | 0 | 82,4 | 16,7 | 0,9 |
Средний | 3,9 | 34,9 | 14,6 | 19,3 | 9,8 | 7,0 | 7,3 | 3,0 | 0,2 | 0 | 0 | 0 | 89,5 | 10,3 | 0,2 |
Маловодный | 4,7 | 31,2 | 14,9 | 9,3 | 7,8 | 24,6 | 5,8 | 1,7 | 0 | 0 | 0 | 0 | 92,5 | 7,5 | 0,0 |
р. Нимелен - с. Тимченко, F = 9950 км2, n = 31 (1947 - 77 гг.) | |||||||||||||||
Многоводный | 1,1 | 12,7 | 19,7 | 27,6 | 15,4 | 9,3 | 9,3 | 2,5 | 1,1 | 0,6 | 0,4 | 0,3 | 85,8 | 11,8 | 2,4 |
Средний | 1,3 | 20,2 | 24,1 | 16,7 | 14,0 | 10,6 | 7,9 | 3,0 | 1,0 | 0,5 | 0,4 | 0,3 | 86,9 | 10,9 | 2,2 |
Маловодный | 1,5 | 15,5 | 25,9 | 20,5 | 12,8 | 9,8 | 8,6 | 2,8 | 1,2 | 0,6 | 0,4 | 0,4 | 86,0 | 11,4 | 2,6 |
Для рек зоны БАМа расчет внутригодового распределения следует выполнять методом компоновки В.Г. Андреянова по упрощенной схеме ввиду того, что здесь не наблюдается зависимости водности лимитирующего периода и от водности лимитирующего сезона.
Сток расчетной вероятности превышения за год, лимитирующие период и сезон определяются по кривым распределения ежегодных вероятностей (эмпирическим или аналитическим).
Распределение стока по аналогии с распределением реального года может быть принято в качестве расчетного, если вероятность превышения стока за этот год, лимитирующие период и сезон, а также минимальный или максимальный (соответственно для оценки распределения стока маловодного и многоводного годов) месячный расход наиболее близки между собой и соответствуют заданной ежегодной вероятности превышения с отклонением от нее не более чем на 20%. При расчете этим методом перечисленные характеристики за все годы наблюдений ранжируются и из числа имеющихся лет выбирается год, отвечающий указанным требованиям.
Для выбранного года устанавливается относительное распределение стока по месяцам и сезонам в процентах от годового стока. Для перехода к средним за интервал времени расходам воды (м3/с) для года заданной вероятности превышения P % с годовым расходом QP% значения относительного распределения умножаются: для месяцев - на 12QP%/100, для сезонов - на 12QP%/(100n), где n - число месяцев в данном сезоне.
Расчет внутригодового распределения стока методом компоновки основывается на условии равнообеспеченности водности года, лимитирующих периода и сезона по следующим градациям: очень многоводный (P = 5%), многоводный (25%), средний (50%), маловодный (75%) и очень маловодный (95%).
Распределение стока по месяцам (внутрисезонное) принимается осредненным для групп лет с обеспеченностью в пределах: P < 33% - для многоводных лет, 33% < P < 66% - для средних лет, P > 66% - для маловодных лет.
Для каждого года определенной группы водности среднемесячные расходы воды ранжируются с указанием календарных месяцев, к которым они относятся, после чего для всех лет каждой градации водности суммируются эти ряды и среднемесячные расходы воды за сезон. Затем устанавливается процентное отношение сумм средних расходов за месяц к сумме за сезон, которое характеризует среднее для данной градации водности относительное распределение стока по месяцам внутри сезона. Значения процентной доли для каждого порядкового номера месяца относят к наиболее часто встречающемуся.
Расчетное распределение стока по месяцам и сезонам в процентах годового устанавливается перемножением значений месячного стока (в процентах сезонного) на относительное значение сезонного стока (в долях годового).
Методики расчета внутригодового распределения стока подробно изложены в работе [25].
и дождевых паводков
Расчетные гидрологические характеристики максимального стока воды определяются согласно требованиям, изложенным в п. 4.3 и 4.4.
Для рек с продолжительностью стояния максимальных расходов воды сутки и более расчет производится по среднесуточным значениям, менее суток - по мгновенным расходам воды. В последнем случае необходимо исследовать связь между среднесуточными и мгновенными расходами воды.
При невозможности разделения максимальных расходов воды на дождевые и талые допускается расчет без учета генетического происхождения максимумов.
Расчетные минимальные расходы воды рек определяются для зимнего и летне-осеннего периода. Они включают в себя: минимальный среднесуточный расход и средний расход воды за 30 сут с наименьшим стоком за оба сезона и средний минимальный расход воды за 10 сут для летне-осеннего периода.
За зимний период принимается время от начала появления ледовых явлений на реках до начала весеннего половодья; за летне-осенний - от конца половодья до начала ледовых явлений на реках.
В случае отсутствия ледовых явлений на реках за конец летне-осеннего и начало зимнего периодов принимается дата устойчивого перехода температуры воздуха через 0 °C. В зоне БАМа такое явление может отмечаться на малых реках горных районов Прибайкалья с очень мощным снежным покровом, перекрывающим русла рек.
Вопросы перемерзания рек зоны БАМа рассматриваются в гл. 5.
ПРИ НЕДОСТАТОЧНОСТИ ДАННЫХ ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ
При недостаточности данных гидрометрических наблюдений приведение параметров кривых распределения ежегодных вероятностей превышения гидрологических характеристик к многолетнему периоду с применением парной и множественной регрессии осуществляется при соблюдении следующих условий:
а) число совместных лет наблюдений в пункте приведения и пунктах-аналогах должно быть равным или более 10 лет (n' >= 10);
б) парные коэффициенты корреляции между значениями стока в приводимом пункте и пунктах-аналогах должны быть равны или превышать 0,7 (r >= 0,7); коэффициент множественной корреляции между стоком в пункте приведения и стоком в пунктах-аналогах должен быть равен или превышать 0,7 (R >= 0,7);
в) отношение каждого из коэффициентов регрессии к его средней квадратической ошибке должно быть равно двум или более 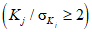 .
.
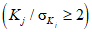 .
.Приведение рассматриваемой гидрологической характеристики производится в случаях, когда средняя квадратическая ошибка расчетного значения гидрологической характеристики превышает 10%.
Математическая основа процедуры, ее алгоритм и примеры приведения рассмотрены в работе [24].
Приведение статистических параметров к многолетнему периоду может быть осуществлено также графическим или графоаналитическим методами.
Графический метод применяется в основном для определения среднего многолетнего стока. Графические зависимости строятся при наличии не менее шести соответственных значений годового стока в расчетном створе и створе реки-аналога и считаются удовлетворительными при коэффициенте корреляции не менее 0,7. При прямолинейной связи норма стока в приводимом створе определяется по норме стока реки-аналога.
Графоаналитическим методом по графику связи стока в приводимом створе и створе-аналоге восстанавливаются опорные координаты Q5%, Q50%, Q95% (расходы воды вероятностью превышения 5, 50 и 95%), соответствующие трем ординатам пункта-аналога Q5%а, Q50%а, Q95%а и определяются коэффициенты скошенности, асимметрии, среднее квадратическое отклонение, среднее многолетнее значение стока по формулам:
S = (Q5% + Q95% - 2Q50%)/(Q5% - Q95%); (3.1)
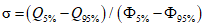 , (3.2)
, (3.2)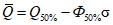 , (3.3)
, (3.3)где 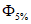 ,
, 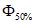 ,
, 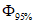 - нормированные ординаты биномиальной кривой распределения, соответствующие вычисленному значению коэффициента скошенности S; таблица значений приведена в работе [31].
- нормированные ординаты биномиальной кривой распределения, соответствующие вычисленному значению коэффициента скошенности S; таблица значений приведена в работе [31].
В случае отсутствия или недостаточности данных наблюдений за речным стоком в пунктах-аналогах для приведения могут быть использованы сведения об осадках, температуре воздуха и других факторах, определяющих рассматриваемую гидрологическую характеристику.
Приведение параметров кривых распределения ежегодных вероятностей превышения рассматриваемой гидрологической характеристики к многолетнему периоду осуществляется двумя способами:
а) при использовании одного аналога среднее многолетнее значение определяется за N лет по формуле
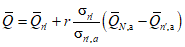 , (3.4)
, (3.4)где индекс n' показывает, что характеристика рассчитана за период совместных наблюдений.
Коэффициент вариации определяется по формуле
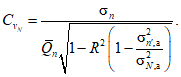 (3.5)
(3.5)Относительная средняя квадратическая ошибка приведенного среднего многолетнего значения годового стока вычисляется по уравнению
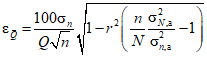 ; (3.6)
; (3.6)б) параметры кривых распределения рассчитываются с учетом погодично восстановленных по уравнениям регрессии значений гидрологической характеристики.
Следует иметь в виду, что при этом размах колебаний рассматриваемой гидрологической характеристики, рассчитанный по уравнениям регрессии, приуменьшается по сравнению с наблюденными (чем выше R, тем меньше занижение дисперсий рассчитанных значений). Систематическое преуменьшение дисперсий исключается путем дополнительного расчета погодичных значений Qi по формуле
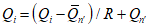 . (3.7)
. (3.7)Приведение параметров к многолетнему периоду осуществляется последовательно по нескольким уравнениям регрессии в порядке убывания коэффициентов парной или множественной корреляции.
По восстановленному ряду совместно с наблюденными данными рассчитываются параметры распределения и коэффициент автокорреляции между стоком смежных лет.
Расчетные отношения Cs/Cv характеристик стока принимаются в соответствии с указаниями гл. 1.
Расчет ресурсов речного стока при недостаточности данных наблюдений выполняется по картам нормы годового стока (приложение 1), а при оценке ресурсов поверхностного стока в маловодные годы - с помощью карты годового стока соответствующей обеспеченности по формуле
W = 31,5·10-6(M1F1 + M2F2 + ... + MnFn), (3.8)
где W - ресурсы речного стока, км3; M1, M2, ..., Mn - средние значения модуля стока между соседними изолиниями, пересекающими территорию, для которой оцениваются ресурсы речного стока; F1, F2, ..., Fn - соответствующие площади между изолиниями модулей стока.
Расчет внутригодового распределения стока при недостаточности данных гидрометрических наблюдений (10 < n < 20 лет) наряду с анализом исходных данных требует оценки репрезентативности имеющегося короткого ряда годового и сезонного стока по двум признакам:
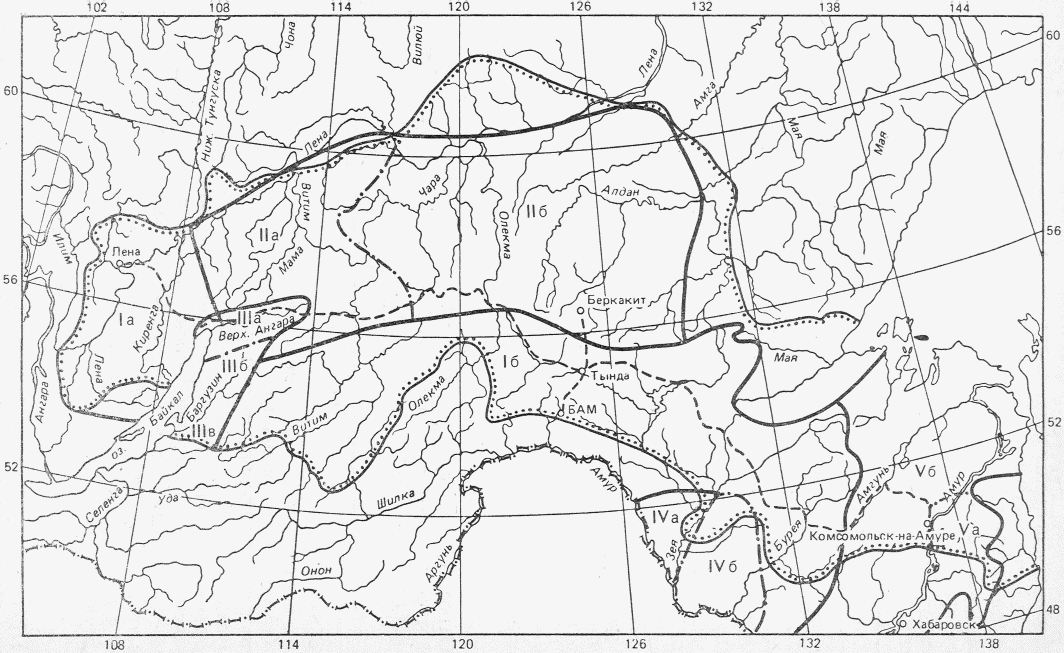
1) по среднему стоку за период распределения, по сезонам года (в долях годового стока) путем сопоставления для длиннорядного опорного пункта в данном гидрологическом районе (рис. 3.1) характеристик распределения стока по сезонам года за весь длинный ряд и за короткий ряд, по которому имеются наблюдения на рассматриваемой реке. При значительном расхождении следует выполнять приведение к многолетнему периоду средних значений стока за год, лимитирующие период и сезон для короткого ряда наблюдений;
распределением стока
1 - граница района, I а - V б - номера подрайонов:
I а - верховье Лены до впадения р. Киренги (включая
ее бассейн); I б - бассейн р. Витима (до впадения
р. Тулдунь), верховье Олекмы, реки бассейнов Верхнего
и Среднего Амура; II а - правобережье Лены от р. Киренги
до р. Большой Патом (включительно); II б - правобережье
Средней Лены (от р. Большой Патом до р. Буотамы), верховья
рек Алдана и Амги; III а - реки, впадающие в северную
часть оз. Байкал; III б - правобережье р. Баргузина;
III в - левобережье р. Баргузина; IV а - реки южной части
Амуро-Зейского плато; IV б - реки Зейско-Буреинской равнины;
V а - правобережье р. Амура между устьями рек Уссури
и Горин; V б - левобережье Нижнего Амура
от р. Биры до устья
2) по эмпирическим кривым обеспеченности стока за год и лимитирующим периоду и сезону на опорном длиннорядном пункте-аналоге. На этих кривых отмечаются точки, соответствующие короткому ряду наблюдений. Если точки располагаются равномерно по всей амплитуде обеспеченности, то короткий ряд является репрезентативным.
ПРИ ОТСУТСТВИИ ДАННЫХ ГИДРОМЕТЕОРОЛОГИЧЕСКИХ НАБЛЮДЕНИЙ
В случае отсутствия данных гидрометрических наблюдений значения среднего многолетнего стока и коэффициента вариации следует определять интерполяцией между значениями, полученными для рек-аналогов по данным наиболее продолжительных рядов гидрометрических наблюдений и приведенными к многолетнему периоду с учетом влияния местных факторов (карста, выходов подземных вод, наличия и характера многолетней мерзлоты и др.).
Для расчета нормы стока и коэффициента вариации следует использовать карты нормы годового стока и коэффициента его изменчивости рек зоны БАМа (приложения I и II), при этом все расчеты выполняются относительно центров тяжести водосборов.
Сток для расчетного пункта равнинной реки определяется прямой интерполяцией, горной - с учетом средней высоты водосбора.
При наличии дополнительной информации для горных районов карты необходимо уточнять.
Допускается определять норму годового стока по картам для рек с площадью водосбора 1 - 50 тыс. км2, а при отсутствии резких изменений в рельефе и климатических условиях и для больших площадей по формуле
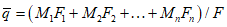 , (4.1)
, (4.1)где M1, M2, ..., Mn - средние значения модуля стока между изолиниями, пересекающими водосбор, л/(с·км2); F1, F2, ..., Fn - соответствующие площади между изолиниями, км2; F - общая площадь водосбора до расчетного створа, км2.
Расчеты ресурсов поверхностного стока неизученных рек или промрайонов, для которых невозможно использовать линейные уравнения (2.3), выполняются по картам нормы стока (приложение I) или с помощью карты годового стока заданной обеспеченности по формуле
W = M1F1 + M2F2 + ... + MnFn, (4.2)
где W - объем годового стока, км3; M1, M2, ..., Mn - средние значения модуля стока между изолиниями, пересекающими водосбор, л/(с·км2); F1, F2, ..., Fn - соответствующие площади между изолиниями, км2.
Обычно для малых рек и рек, сток которых формируется в зонах переменного увлажнения (модуль стока составляет 4 - 0,5 л/(с·км2)); в рассчитанные по карте значения нормы стока вводится поправка на разность в дренировании средними и малыми реками подземных вод. Для рек зоны БАМа такие поправки не выявлены даже в области малых площадей.
Погрешность определения среднего годового стока по карте составляет +/- 10 - 15%.
Для неисследованных малых горных рек норма стока определяется по районным связям модулей среднего годового стока со средней высотой водосборов M = f(Hср) (рис. 4.1). Для горных районов, для которых такие зависимости не установлены из-за недостатка информации, они должны быть получены по мере накопления данных.
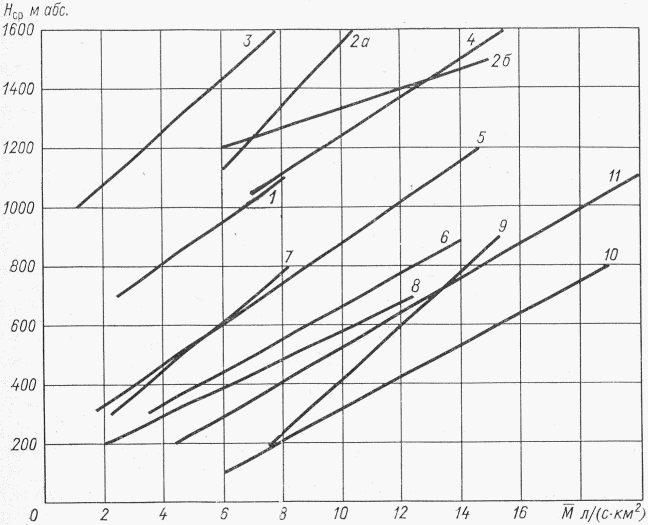
Рис. 4.1. Районные зависимости нормы годового стока
от средней высоты водосбора
1 - Верхняя Лена (Цикур, Илга, Анга, Куленга, Тутура);
2а - р. Баргузин и ее левые притоки; 2б - правые притоки
р. Баргузина; 3 - Верхний и Средний Витим (Витимкан, Чина,
Джилинда, Заза, Конда, Юмурчен, Ципа, Ципикан, Амалат,
Каренга, Багдарин, Тулдунь); 4 - Верхняя Чара (до п. Чара
и притоки - Нижний Ингамакит, Лурбун, Наминга); 5 - притоки
Средней Лены (Кута, Олекма в среднем и нижнем течении, Жуя,
Алдан - верхний и средний, Тимптон, Чара в среднем и нижнем
течении и др.); 6 - р. Зея до п. Бомнак и ее правобережные
притоки (Бомнак, Унаха, Ток, Мульмуга); 7 - Средний Амур
и Средняя Зея (Пикан, Тында, Правый Уркан, Малый Ольдой);
8 - Левобережные притоки р. Зея (Селемджа, Граматуха, Гарь,
Нора, Б. Пера, Томь, Белая, Бурунда); 9 - Бурея и Архара
(Тырма, Туюн, Сутырь, Дубликан, Ниман, Хинган);
10 - Левобережные притоки Нижнего Амура (Кур, Бира,
Горин и др.); 11 - Амгунь, Нимелен
Коэффициент вариации годового стока для неизученных рек может быть определен не только по карте-схеме (приложение II), но и по формуле
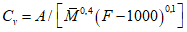 , (4.3)
, (4.3)где A - параметр, определяемый по данным рек-аналогов, л/с; M - средний многолетний модуль стока, л/(с·км2); F - площадь водосбора, км2.
Отношение Cs/Cv принимается равным двум для всей территории, для Приморья Cs/Cv = 3.
Для неизученной реки границы сезонов и лимитирующего периода, среднее распределение стока по сезонам в долях годового, отношения между коэффициентами вариации сезонного и годового стока, распределение стока маловодных сезонов по месяцам для определенной группы водности сезона принимаются по данным реки-аналога или группы аналогов с наиболее продолжительными рядами гидрометрических наблюдений. При выборе аналогов рекомендуется их подбирать в пределах районов, обозначенных на рис. 3.1.
В случае отсутствия надежных аналогов внутригодовое распределение стока рассчитывается по региональным зависимостям статистических параметров сезонного стока от определяющих факторов (площади водосбора, его средней высоты, характера почвогрунтов и др.).
Статистические характеристики зимнего и летне-осеннего, весеннего стока, стока дождевых паводков и их зависимости от площади и средней высоты водосбора приведены в разд. 4.3, 4.4, 4.6 и гл. 5.
Районные отношения Cvсез/Cvгод и Cs/Cv для осенне-зимнего периода и зимнего сезона приведены в работе [6].
В случае отсутствия материалов гидрометеорологических наблюдений расчет максимального весеннего стока выполняется двумя способами:
1) по эмпирическим формулам,
2) методом гидрологической аналогии.
Расчет по эмпирическим формулам. Для расчета максимальных расходов весеннего половодья рекомендуются следующие формулы:
для водосборов F <= 100 км2
где QP% - расчетный мгновенный максимальный расход талых вод вероятностью превышения P %, м3/с; qP% - модуль максимального расчетного расхода воды (QP%/F), м3/(с·км2); F - площадь водосбора до рассматриваемого створа, км2; n - показатель степени редукции q1%/h1% по площади водосбора, равный для рассматриваемого региона 0,17; hP% - расчетный слой суммарного (без срезки грунтового питания) стока половодья той же вероятности превышения P %, что и искомый максимальный расход воды, мм; K100 - параметр, характеризующий дружность весеннего половодья с водосборов площадью 100 км2; 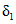 - коэффициент, учитывающий снижение максимальных расходов воды рек, зарегулированных проточными озерами и водохранилищами;
- коэффициент, учитывающий снижение максимальных расходов воды рек, зарегулированных проточными озерами и водохранилищами; 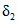 - коэффициент, учитывающий снижение максимальных расходов воды в заболоченных бассейнах;
- коэффициент, учитывающий снижение максимальных расходов воды в заболоченных бассейнах; 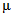 - коэффициент, учитывающий неравенство статистических параметров слоя стока и максимальных расходов воды.
- коэффициент, учитывающий неравенство статистических параметров слоя стока и максимальных расходов воды.
Рекомендуемые формулы применяются для рек с площадями водосборов от элементарно малых (менее 1 км2) до 50 000 км2, за исключением транзитных участков рек, на которых происходит сильное распластывание волны половодья, вызывающее снижение максимальных расходов воды.
При проектировании сооружений на реках с площадями водосборов, превышающих указанные пределы, максимальные расходы талых вод в случае отсутствия гидрометрических данных определяются по результатам полевых гидрологических исследований.
Значения hP% определяются по трем статистическим параметрам: hP% = f(h0, Cvh, Csh). Значения среднего многолетнего слоя весеннего половодья (h0) и коэффициента вариации (Cvh) определяются по картам изолиний как средние взвешенные значения для водосбора (приложения III, IV). Коэффициент асимметрии слоя стока половодья (Csh) принимается равным 2Cvh для первого района и 3Cvh для второго и третьего районов (рис. 4.2).
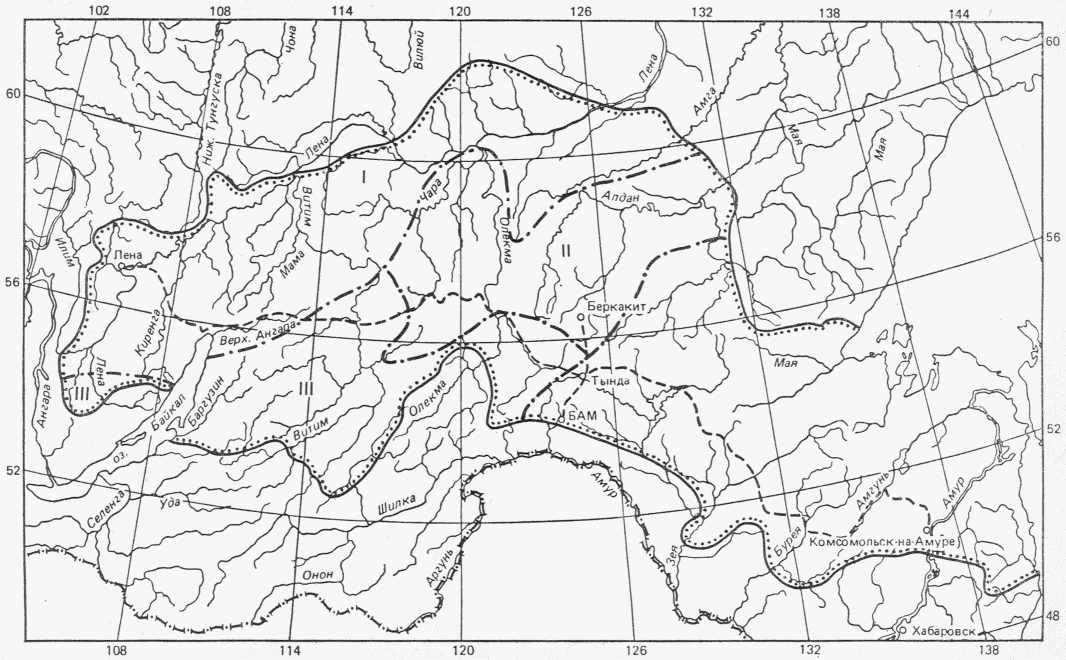
Рис. 4.2. Схема районирования территории по соотношению
максимальных расходов талых и дождевых вод
Римские цифры - номера районов: I - Qмакс.вес > Qмакс.дожд,
II - Qмакс.вес ~= Qмакс.дожд, III - Qмакс.вес < Qмакс.дожд
Выделение районов обосновано соотношением максимальных расходов весеннего половодья и дождевых паводков, а границы их уточнены на основании материалов наблюдений по 1977 г. для всего диапазона площадей водосборов, по которым имеются данные наблюдений. На реках первого района максимальные расходы весеннего половодья (средние за период наблюдений и 1%-ной вероятности превышения) в 2 раза и более превышают соответствующие наибольшие расходы летних паводков. Половодье имеет преимущественно снеговое происхождение и лишь в пределах Байкальского и Чуйского хребтов (реки Киренга, Мама, Мамакан и др.) оно смешанное, снегодождевое, но доля дождевой составляющей относительно невелика. На реках второго района наибольшие максимальные расходы в одни годы бывают в период весеннего половодья, а в другие - во время летних паводков, число таких лет в среднем одинаково, причем на водотоках межгорных впадин и выровненных плато весенние и летние максимальные расходы примерно равны. На реках третьего района максимумы летних паводков в среднем в 1,5 - 2,0 раза превышают наибольшие весенние расходы.
Ординаты кривых обеспеченности hP% для определения расчетного значения слоя стока половодья принимаются по таблицам трехпараметрического гамма-распределения [31].
Коэффициент дружности весеннего половодья при площади водосбора 100 км2 (K100) устанавливается по карте изолиний, как средневзвешенное значение (приложение V) [8, 9].
Озерность большинства речных водосборов 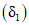 не превышает на рассматриваемой территории 1%. В отдельных случаях, когда озерность больше 2%, ее влияние учитывается согласно рекомендациям [31]. Значение коэффициента
не превышает на рассматриваемой территории 1%. В отдельных случаях, когда озерность больше 2%, ее влияние учитывается согласно рекомендациям [31]. Значение коэффициента 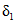 находится по табл. 4.1.
находится по табл. 4.1.
Таблица 4.1
Коэффициент снижения слоя стока половодья
в зависимости от озерности бассейна
Относительная озерность бассейна, % | Коэффициент снижения слоя стока половодья |
2 - 10 | 0,9 - 0,8 |
10 - 20 | 0,8 - 0,7 |
> 20 | 0,7 |
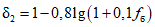 , (4.6)
, (4.6)где fб - степень заболоченности речного бассейна в процентах от его общей площади.
При заболоченности более 50% и преобладании верховых болот значение коэффициента 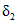 следует увеличить на 30%.
следует увеличить на 30%.
Значения коэффициента 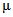 определялись в диапазоне установленных для данного района коэффициентов вариации слоя и максимального расхода. Их значения оказались практически равны значениям, принятым ранее для района Восточной Сибири. Разница в отдельных случаях не выходит за пределы 2 - 3%. Поэтому значения
определялись в диапазоне установленных для данного района коэффициентов вариации слоя и максимального расхода. Их значения оказались практически равны значениям, принятым ранее для района Восточной Сибири. Разница в отдельных случаях не выходит за пределы 2 - 3%. Поэтому значения 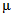 при определении максимальных расходов весеннего половодья вероятностью превышения 0,1 - 25% рекомендуется принимать согласно табл. 4.2.
при определении максимальных расходов весеннего половодья вероятностью превышения 0,1 - 25% рекомендуется принимать согласно табл. 4.2.
Таблица 4.2
Значения коэффициента 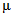 в зависимости от обеспеченности
в зависимости от обеспеченности
максимального расхода воды весеннего половодья
Обеспеченность, % | 0,1 | 1 | 3 | 5 | 10 | 25 |
1,04 | 1,00 | 0,98 | 0,96 | 0,94 | 0,89 |
Расчет методом аналогии. При наличии многолетних наблюдений за стоком в смежных бассейнах максимальный расход может быть вычислен методом гидрологической аналогии.
В качестве аналогов принимаются близко расположенные бассейны с одинаковыми метеорологическими условиями формирования весеннего половодья и сходными факторами подстилающей поверхности.
Исследование зависимостей характеристик максимального стока от факторов подстилающей поверхности показало, что при выборе аналогов в условиях рассматриваемой территории особое внимание следует уделять сходству высотного положения речных водосборов, экспозиции склонов и направленности речных долин.
Площади водосборов расчетной реки и реки-аналога не должны различаться более чем в 5 - 10 раз. При этом форма водосбора реки-аналога должна быть подобна форме водосбора расчетной реки; для этого должны выполняться следующие приближенные равенства:
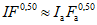 , (4.8)
, (4.8)где L - длина водотока, км; F - площадь водосбора, км2; I - средневзвешенный уклон водотока, 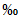 .
.
Показатель степени 0,56 в формуле (4.7) подтвержден и по водосборам данного района.
По общему географическому и высотному положению речных водосборов на рассматриваемой территории выделено 9 районов (рис. 4.3) с присущими каждому из них зависимостями среднего и 1%-ной обеспеченности слоев весеннего половодья и коэффициентов вариации слоев от средней высоты водосбора (рис. 4.4, 4.5) [7]. С помощью таких зависимостей можно уточнить значения параметров с учетом разности средних высот водосборов расчетной реки и реки-аналога. По мере накопления информации такие зависимости подлежат уточнению <1>.
--------------------------------
<1> В районах значительного распространения карста зависимости характеристик максимального стока весеннего половодья от средней высоты водосбора имеют обратную тенденцию. В районах, расположенных в зоне многолетней мерзлоты, влияние карста не сказывается.
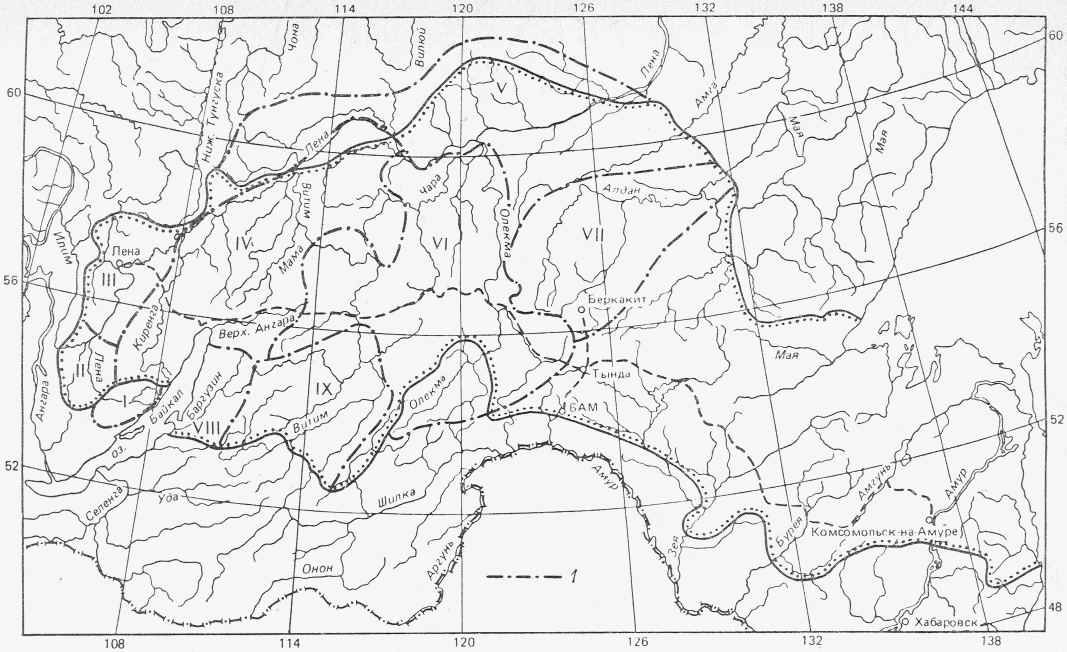
зависимости характеристик слоя весеннего половодья
от средней высоты и местоположения водосбора
1 - граница района. Римские цифры - номера районов
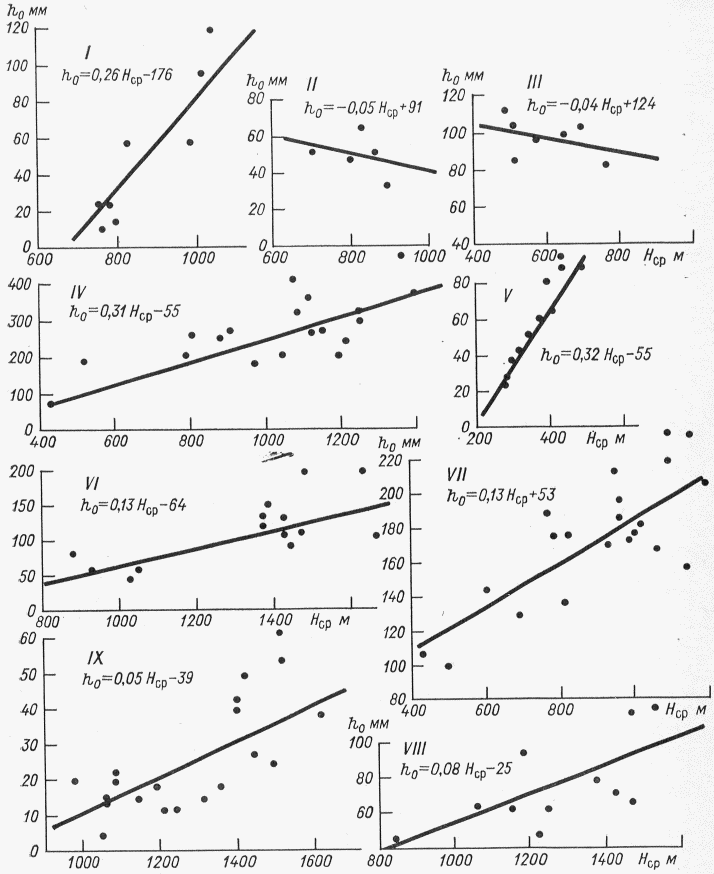
Римские цифры - номера районов
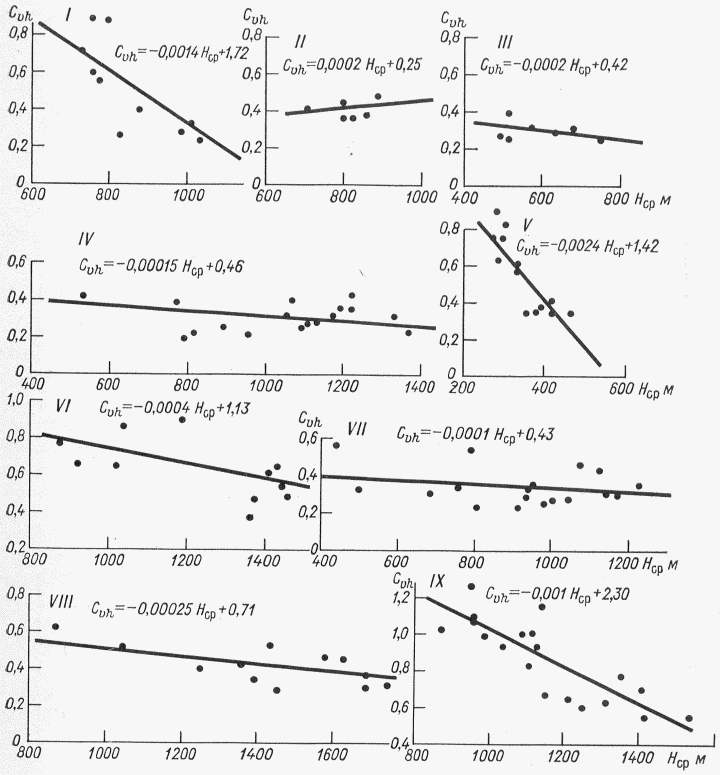
Римские цифры - номера районов
Имея створ-аналог с рядом наблюдений не менее 25 лет, уточненные значения среднего слоя (h0) и коэффициента вариации (Cvh) с учетом разности средних высот водосборов реки-аналога и расчетной реки, соответствующее районное отношение Cs/Cv, при равенстве значений коэффициента дружности весеннего половодья в расчетном створе и створе-аналоге максимальный расход весеннего половодья в расчетном створе заданной вероятности превышения можно вычислить по формуле
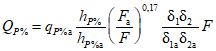 . (4.9)
. (4.9)Для водосборов с F <= 100 км2
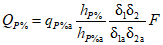 . (4.10)
. (4.10)Значение hP% определяется по изложенной методике с учетом районных зависимостей (см. рис. 4.4, 4.5).
Для правильного выбора аналога рекомендуется производить расчет по двум-трем смежным бассейнам и принимать среднее значение QP% Если значения QP%, полученные по бассейнам-аналогам, существенно (более чем на 20%) различаются, рекомендуется принимать в расчет большее из них.
Для рек Центрального БАМа (рис. 4.6) с площадями водосборов менее 5000 км2 расчет максимальных расходов воды весеннего половодья в случае отсутствия данных гидрометрических наблюдений рекомендуется выполнять по формуле
где QP% - расчетный максимальный расход воды, м3/с; qP% - расчетный модуль стока, м3/(с·км2); F - площадь водосбора, км2; j - "эталонное" значение густоты речной сети, км/км2; определяется по картам м-ба 1:100 000; Kj - коэффициент, учитывающий изменение действующей густоты (длины) речной сети в период половодья; 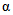 - коэффициент стока половодья; i - уклон водосбора в долях единицы; определяется по топокартам м-ба 1:100 000; Nд.р и Nсн.р - расчетные значения метеорологической силы дождя и снеготаяния периода формирования половодья, определяются как произведение средней интенсивности и слоя эффективной части дождя; соответственно для снеготаяния - произведение средней интенсивности снеготаяния и запаса воды в снеге на начало снеготаяния, мм2/с.
- коэффициент стока половодья; i - уклон водосбора в долях единицы; определяется по топокартам м-ба 1:100 000; Nд.р и Nсн.р - расчетные значения метеорологической силы дождя и снеготаяния периода формирования половодья, определяются как произведение средней интенсивности и слоя эффективной части дождя; соответственно для снеготаяния - произведение средней интенсивности снеготаяния и запаса воды в снеге на начало снеготаяния, мм2/с.
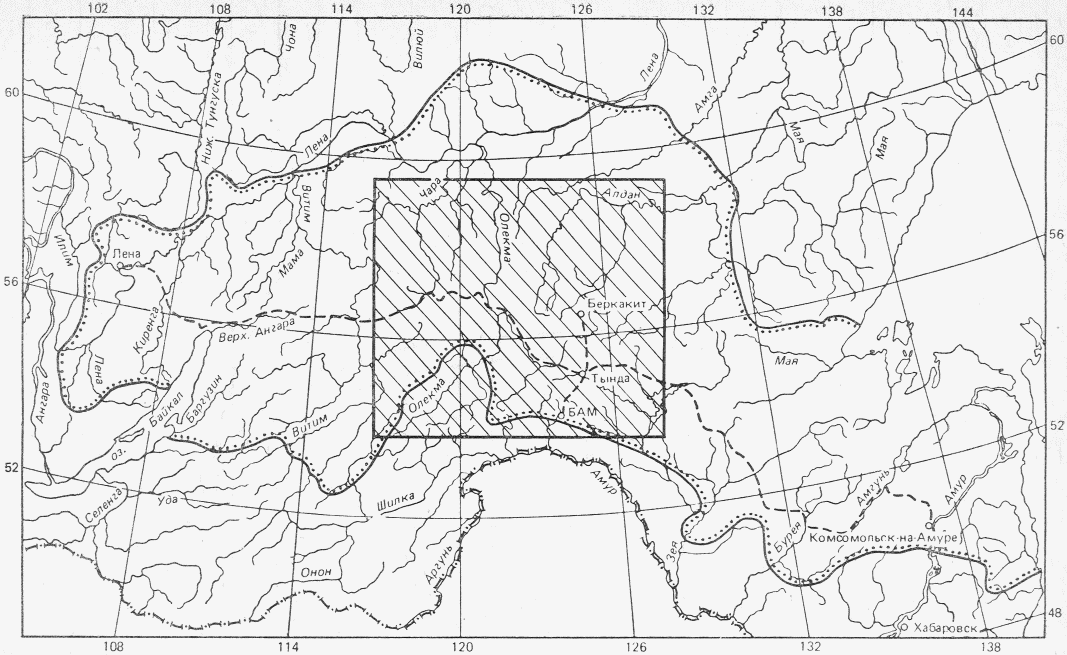
Для расчета фактических максимальных расходов воды весеннего половодья параметры формулы (4.11) определяются следующим образом:
- расчетные значения Nд и Nсн - по данным репрезентативной метеостанции (слой водоподачи H) и гидрометрического створа-аналога (продолжительность половодья t);
- коэффициент стока половодья - по графикам связи 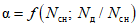 по значениям Nсн% и Nд1% репрезентативных метеостанций (рис. 4.7);
по значениям Nсн% и Nд1% репрезентативных метеостанций (рис. 4.7);
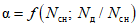 по значениям Nсн% и Nд1% репрезентативных метеостанций (рис. 4.7);
по значениям Nсн% и Nд1% репрезентативных метеостанций (рис. 4.7);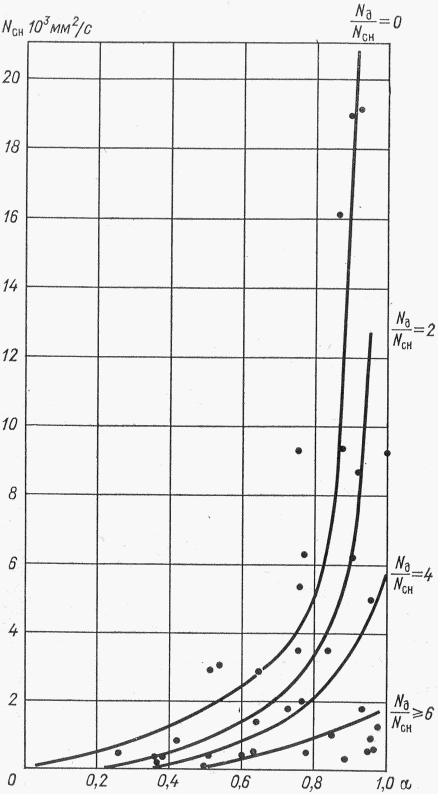
снеготаяния (Nсн) и относительной долей участия дождя Nд/Nсн
- значение коэффициента изменения густоты речной сети в половодье определяется обратным пересчетом по уравнению (4.11), по данным створов-аналогов; при восстановлении пропусков наблюдений в расчет принимаются средние из наблюденных значения Kj; для ориентировочных расчетов Kj можно принять равным 0,5.
Определение расчетных параметров при вычислении расходов воды 1%-ной обеспеченности выполняется следующим образом:
- значения Nсн и Nд 1%-ной обеспеченности за период половодья вычисляются по данным репрезентативных для рассматриваемого водосбора метеостанций графоаналитическим методом;
- значения j и i определяются, как указано выше, по топографическим картам м-ба 1:100 000 в соответствии с существующими методиками;
- коэффициент стока 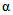 определяется по районному графику
определяется по районному графику 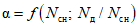 в соответствии со значениями Nсн1%, Nд1% - 1%-ной обеспеченности (см. рис. 4.7);
в соответствии со значениями Nсн1%, Nд1% - 1%-ной обеспеченности (см. рис. 4.7);
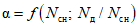 в соответствии со значениями Nсн1%, Nд1% - 1%-ной обеспеченности (см. рис. 4.7);
в соответствии со значениями Nсн1%, Nд1% - 1%-ной обеспеченности (см. рис. 4.7);- коэффициент изменения густоты речной сети Kj за период от половодья при расчете расхода воды 1%-ной обеспеченности рекомендуется принимать равным единице.
Расчетная формула (4.11) в этом случае принимает вид
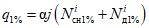 . (4.12)
. (4.12)Переход к расходам воды другой обеспеченности осуществляется по районным переходным коэффициентам 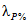 (табл. 4.3).
(табл. 4.3).
Таблица 4.3
Значения переходных коэффициентов 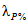
Река, район | Обеспеченность, % | |||
2 | 5 | 10 | 25 | |
Алдан и его притоки, верховье Лены | 0,88 | 0,75 | 0,62 | 0,52 |
Бассейн Верхнего Амура, (Гилюй, Тында, Унаха) | 0,86 | 0,70 | 0,54 | 0,30 |
Средний Амур (бассейн Селемджи, Амгуни, Буреи) | 0,87 | 0,69 | 0,50 | 0,26 |
Для расчета максимальных расходов воды дождевых паводков (QP%) неизученных рек в качестве основного расчетного метода рекомендуется метод аналогии с использованием одного или нескольких ближайших аналогов.
В случае отсутствия надежных рек-аналогов максимальные (мгновенные расходы воды дождевых паводков (QP%) рекомендуется определять:
- для водосборов рек и временных водотоков площадью до 1000 км2 по формуле предельной интенсивности стока;
- для водосборов рек площадью водосбора 1000 - 30 000 км2 по эмпирической редукционной формуле.
В силу слабой изученности малых рек зоны БАМа расчеты по формуле предельной интенсивности стока в диапазоне площадью 200 - 1000 км2 проверяются по эмпирической редукционной формуле.
При проектировании сооружений на реках с площадью водосбора более 30 00 км2 расчетные максимальные расходы воды определяются методом аналогии с обязательным проведением полевых гидрометрических исследований.
Специальные полевые исследования также необходимы в районах интенсивного развития карстовых явлений (Верхняя Лена, Лено-Алданское междуречье и др.).
Расчет максимальных (мгновенных) расходов воды дождевых паводков (QP% м3/с) рек и временных водотоков площадью водосбора до 1000 км2 производится по формуле предельной интенсивности стока:
где A1% - модуль максимального расхода воды 1%-ной обеспеченности, выраженный в долях произведения 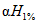 , при
, при 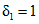
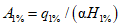 (4.14)
(4.14)и численно равный 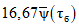 ;
; 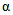 - сборный коэффициент; H1% - суточный слой осадков 1%-ной обеспеченности, мм;
- сборный коэффициент; H1% - суточный слой осадков 1%-ной обеспеченности, мм; 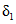 - коэффициент, учитывающий зарегулированность максимальных расходов проточными озерами;
- коэффициент, учитывающий зарегулированность максимальных расходов проточными озерами; 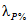 - коэффициент перехода от 1%-ной обеспеченности к другой обеспеченности; F - площадь водосбора реки, км2;
- коэффициент перехода от 1%-ной обеспеченности к другой обеспеченности; F - площадь водосбора реки, км2; 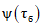 - ордината кривой редукции средней интенсивности осадков за бассейновое время добегания
- ордината кривой редукции средней интенсивности осадков за бассейновое время добегания 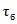 , мин.
, мин.
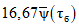 ;
; 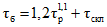 , (4.15)
, (4.15)где 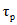 - русловое время добегания, мин;
- русловое время добегания, мин; 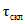 - склоновое время добегания, мин.
- склоновое время добегания, мин.
Относительный модуль максимального расхода воды A1% определяется по табл. 4.4 в зависимости от гидроморфометрической характеристики русла Фр и времени склонового добегания 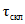 .
.
Таблица 4.4
максимальных расходов воды 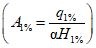
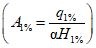
Гидроморфометрическая характеристика русла при | 0 | 1 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
20 мин | 0 0,27 | 1 0,25 | 7 0,20 | 16 0,16 | 35 0,10 | 57 0,074 | 82 0,058 | 109 0,047 | 135 0,040 | 163 0,085 | 190 0,030 | 222 0,027 | 253 0,024 |
60 мин | 0 0,13 | 2 0,125 | 9 0,11 | 18 0,094 | 38 0,071 | 61 0,059 | 86 0,048 | 112 0,040 | 138 0,035 | 167 0,031 | 194 0,027 | 226 0,025 | 257 0,023 |
90 мин | 0 0,093 | 2 0,090 | 9 0,082 | 19 0,074 | 40 0,060 | 63 0,050 | 88 0,042 | 114 0,037 | 140 0,033 | 171 0,029 | 198 0,026 | 929 0,024 | 260 0,022 |
150 мин | 0 0,064 | 2 0,063 | 10 0,059 | 20 0,055 | 43 0,048 | 66 0,041 | 91 0,035 | 117 0,031 | 145 0,028 | 175 0,26 | 203 0,023 | 233 0,022 | 265 0,020 |
200 мин | 0 0,052 | 2 0,051 | 10 0,048 | 21 0,045 | 44 0,040 | 70 0,036 | 96 0,032 | 123 0,028 | 152 0,026 | 178 0,024 | 208 0,022 | 237 0,020 | 270 0,019 |
Гидроморфометрическая характеристика русла при | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 |
20 мин | 418 0,016 | 600 0,012 | 780 0,010 | 980 0,0085 | 1190 0,0074 | 1370 0,0065 | 1850 0,0053 | 2310 0,0045 | 2760 0,0039 | 3270 0,0035 | 3760 0,0031 | 4350 0,0028 | 4850 0,0027 |
60 мин | 420 0,016 | 603 0,012 | 780 0,010 | 980 0,0085 | 1190 0,0074 | 1380 0,0065 | 1860 0,0052 | 2320 0,0045 | 2770 0,0039 | 3280 0,0035 | 3770 0,0031 | 4360 0,0028 | 4860 0,0026 |
90 мин | 422 0,015 | 604 0,012 | 790 0,010 | 990 0,0084 | 1200 0,0073 | 1390 0,0034 | 1870 0,0052 | 2330 0,0044 | 2780 0,0039 | 3290 0,0034 | 3780 0,0030 | 4370 0,0028 | 4870 0,0026 |
150 мин | 425 0,0145 | 607 0,012 | 790 0,0096 | 1000 0,0082 | 1210 0,0072 | 1400 0,0063 | 1880 0,0052 | 2340 0,0044 | 2800 0,0039 | 3310 0,0034 | 3800 0,0030 | 4390 0,0028 | 4890 0,0026 |
200 мин | 428 0,014 | 610 0,011 | 800 0,0094 | 1010 0,0082 | 1220 0,0071 | 1410 0,0063 | 1890 0,0052 | 2350 0,0044 | 2810 0,0039 | 3320 | 3820 | 4400 | 4900 0,0026 |
Для рассматриваемой территории значения ординат кривой редукции осадков представлены в табл. 4.5.
Таблица 4.5
Значения ординат кривой редукции осадков
Характеристика | ||||||||
5 | 10 | 20 | 40 | 60 | 90 | 150 | 300 | |
0,15 | 0,23 | 0,32 | 0,40 | 0,45 | 0,50 | 0,58 | 0,69 | |
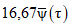 | 0,50 | 0,38 | 0,27 | 0,17 | 0,13 | 0,093 | 0,064 | 0,038 |
Характеристика | |||||||
720 | 1440 | 2880 | 4320 | 5760 | 7200 | 14400 | |
0,87 | 1,06 | 1,29 | 1,45 | 1,59 | 1,73 | 2,16 | |
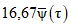 | 0,020 | 0,012 | 0,0075 | 0,0056 | 0,0046 | 0,0040 | 0,0025 |
Гидроморфометрическая характеристика русла реки вычисляется по формуле
где L - длина реки от истока до замыкающего створа, км; Iр - средневзвешенный уклон русла, 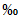 ; m - коэффициент, зависящий от шероховатости русла и поймы; определяется по табл. 4.6.
; m - коэффициент, зависящий от шероховатости русла и поймы; определяется по табл. 4.6.
Таблица 4.6
Значения коэффициента m
Категория русла реки | Характеристика русла и поймы в среднем по всей длине реки - от истока до замыкающего створа | Коэффициент m |
1 | Сравнительно чистые русла постоянных равнинных водотоков. Русла периодических водотоков (сухих логов) в относительно благоприятных условиях | 11 |
2 | Русла (больших и средних) рек, значительно засоренные, извилистые и частично заросшие, каменистые, с неспокойным течением. Периодические водотоки, несущие во время паводка заметное количество наносов, с крупногалечным или покрытым растительностью ложем | 9,0 |
3 | Галечно-валунные русла горного типа, с неправильной поверхностью водного зеркала. Русла периодических водотоков, сильно засоренные и извилистые | 7,0 |
Время склонового добегания устанавливается по табл. 4.7 в зависимости от гидроморфометрической характеристики склона
где 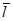 - средняя длина склонов водосбора, км, определяется по формуле
- средняя длина склонов водосбора, км, определяется по формуле
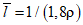 (4.18)
(4.18)(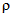 - густота овражно-балочной и русловой сети, км/км2); m1 - коэффициент шероховатости склонов, определяется по табл. 4.8; Iскл - средний уклон склонов водосбора,
- густота овражно-балочной и русловой сети, км/км2); m1 - коэффициент шероховатости склонов, определяется по табл. 4.8; Iскл - средний уклон склонов водосбора, 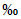 .
.
Таблица 4.7
от гидроморфометрической характеристики склонов водосбора
Гидроморфометрическая характеристика склонов водосбора | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 | 10 | 12 | 15 |
Время склонового добегания, мин | 2,7 | 5,9 | 10 | 14 | 19 | 25 | 38 | 55 | 75 | 95 | 115 | 140 | 170 | 220 | 320 |
Таблица 4.8
Характеристика поверхности склонов | Коэффициент m1 для склонов с травяным покровом | ||
редкий или отсутствует | обычный | густой | |
Гладкие поверхности (асфальт, бетон) | 0,50 | - | - |
Укатанная спланированная грунтовая поверхность такыровидные равнины | 0,40 | 0,30 | 0,25 |
Поверхность хорошо обработанная вспашкой и боронованием; невспаханная без кочек; булыжная мостовая; поверхность в населенных пунктах с застройкой менее 20% | 0,30 | 0,25 | 0,20 |
Грубо обработанная вспашкой поверхность, таежные завалы, кочковатая, а также поверхность в населенных пунктах с застройкой более 20% | 0,2 | 0,15 | 0,10 |
Таблица 4.9
и показателя степени редукции ny
Категория почвогрунтов | Характеристика почвогрунтов | ny | ||
1 | Горно-тундровые структурно-мерзлотные маломощные почвы гольцов (торфянистые, перегнойные, гольцово-дерновые) на элювии кристаллических пород | 0,5 - 0,6 | 1 | |
2 | Горно-таежные мерзлотные почвы (торфянисто-мерзлотные, подзолистые) на элювии кристаллических пород | 0,3 - 0,4 | 1 | |
3 | Горно-таежные мерзлотные оподзоленные почвы на элювии трещиноватых метаморфических и безкарбонатных пород, подзолистые иллювиально-железистые почвы на осадочных породах межгорных впадин | 0,2 - 0,3 | 1 | |
4 | Таежные палевые мерзлотные почвы на лессовидном карбонатном суглинке и суглинистом элювии карбонатных пород, горно-таежные мерзлотные оподзоленные на элювии терригенно-карбонатных пород | 0,15 - 0,25 | 1 | |
5 | Горно-таежные перегнойно-карбонатные почвы Прибайкалья на терригенно-карбонатных породах | 0,07 - 0,1 | 1/2 | |
6 | Серые лесные почвы Забайкалья на делювиальных, сильно щебенистых суглинках, подстилаемых каменисто-щебенистыми отложениями | 0,05 - 0,06 | 1/2 | |
7 | Каменисто-щебенистые, глинистые оподзоленные почвы каменистых россыпей | 0,05 - 0,1 | 1 | |
8 | Почвы, залегающие на мощных толщах рыхлых отложений | 0,02 - 0,03 | 1 | |
9 | Маломощные дерново-подзолистые, торфянистые и торфяные почвы марей в условиях многолетней мерзлоты | 0,3 - 0,4 | 1/2 | |
10 | Дерново-подзолистые, подзолисто-болотные, глееватые почвы равнинной части Амура при отсутствии многолетней мерзлоты | |||
при HP% = | 90... 100 мм | 0,15 | 1/2 | |
100... 120 | 0,25 | 1/2 | ||
130... 140 | 0,35 | 1/2 | ||
150... 180 | 0,45 | 1/2 | ||
Примечания. 1. При хорошей дренированности почвогрунтов (наличие песчаных отложений, повышенная трещиноватость грунтов и т.д.) принимается нижний предел 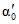 . 2. Карстовые явления для почвогрунтов 4-й и 5-й категорий снижают
. 2. Карстовые явления для почвогрунтов 4-й и 5-й категорий снижают 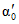 в 2 - 2,5 раза.
в 2 - 2,5 раза.
Таблица 4.10
F км2 | <= 0,3 | 1 | 10 | 50 | 200 | 500 | 1000 | |
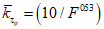 | 6,41 | 3,39 | 1 | 0,426 | 0,204 | 0,126 | 0,087 | |
Бассейн р. Лены | ||||||||
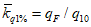 | 1,46 | 1,33 | 1 | 0,800 | 0,600 | 0,492 | 0,400 | |
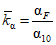 при при | 20 | 0,311 | 0,585 | 1 | 1,55 | 2,06 | 2,43 | 2,63 |
60 | 0,545 | 0,757 | 1 | 1,41 | 1,82 | 2,13 | 2,29 | |
90 | 0,696 | 0,833 | 1 | 1,37 | 1,69 | 1,97 | 2,12 | |
150 | 0,857 | 0,936 | 1 | 1,24 | 1,49 | 1,71 | 1,81 | |
200 | 0,932 | 0,982 | 1 | 1,17 | 1,37 | 1,55 | 1,63 | |
Северное Забайкалье | ||||||||
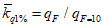 | 1,30 | 1,20 | 1 | 0,779 | 0,600 | 0,441 | 0,355 | |
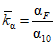 при при | 20 | 0,277 | 0,526 | 1 | 1,51 | 2,06 | 2,18 | 2,33 |
60 | 0,485 | 0,682 | 1 | 1,37 | 1,82 | 1,91 | 2,03 | |
90 | 0,620 | 0,750 | 1 | 1,33 | 1,69 | 1,76 | 1,88 | |
150 | 0,764 | 0,843 | 1 | 1,21 | 1,49 | 1,53 | 1,61 | |
200 | 0,831 | 0,884 | 1 | 1,14 | 1,37 | 1,39 | 1,45 | |
Бассейн р. Амура | ||||||||
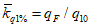 | 1,23 | 1,16 | 1 | 0,823 | 0,650 | 0,520 | 0,428 | |
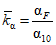 при при | 20 | 0,261 | 0,509 | 1 | 1,60 | 2,24 | 2,57 | 2,81 |
60 | 0,456 | 0,659 | 1 | 1,45 | 1,98 | 2,25 | 2,44 | |
90 | 0,583 | 0,725 | 1 | 1,41 | 1,83 | 2,08 | 2,27 | |
150 | 0,718 | 0,815 | 1 | 1,28 | 1,61 | 1,81 | 1,94 | |
200 | 0,781 | 0,855 | 1 | 1,21 | 1,48 | 1,63 | 1,74 | |
Примечание. Для промежуточных значений площадей водосборов значения 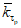 ,
, 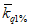 ,
, 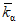 определяются интерполяцией.
определяются интерполяцией.
Сборный коэффициент
где 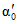 - сборный коэффициент для водосбора площадью 10 км2 и средним уклоном склонов 100% определяется по табл. 4.9 в зависимости от типа почвогрунтов, преобладающих на рассматриваемом водосборе; для почв равнинной части бассейна Амура зависит от H1%; ny - показатель степени редукции
- сборный коэффициент для водосбора площадью 10 км2 и средним уклоном склонов 100% определяется по табл. 4.9 в зависимости от типа почвогрунтов, преобладающих на рассматриваемом водосборе; для почв равнинной части бассейна Амура зависит от H1%; ny - показатель степени редукции 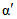 по Iскл, определяется по табл. 4.9;
по Iскл, определяется по табл. 4.9; 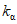 - коэффициент перехода от
- коэффициент перехода от 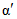 для площади 10 км2 к
для площади 10 км2 к 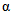 для рассматриваемой площади водосбора F км2; он зависит от вида кривой редукции осадков, кривой редукции стока, времени руслового и склонового добегания и определяется по формуле
для рассматриваемой площади водосбора F км2; он зависит от вида кривой редукции осадков, кривой редукции стока, времени руслового и склонового добегания и определяется по формуле
где 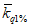 - средний районный коэффициент перехода (коэффициент редукции модулей максимальных расходов воды q 1%-ной обеспеченности от площади водосбора 10 км2 к площади водосбора F км2; определяется по табл. 4.10);
- средний районный коэффициент перехода (коэффициент редукции модулей максимальных расходов воды q 1%-ной обеспеченности от площади водосбора 10 км2 к площади водосбора F км2; определяется по табл. 4.10); 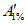 - относительный (в долях
- относительный (в долях 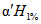 ) модуль максимального расхода для площади водосбора 10 км2 при времени склонового добегания
) модуль максимального расхода для площади водосбора 10 км2 при времени склонового добегания 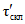 , равном времени склонового добегания для рассчитываемого бассейна площадью F км2 и времени руслового добегания в минутах, определяемого по формуле
, равном времени склонового добегания для рассчитываемого бассейна площадью F км2 и времени руслового добегания в минутах, определяемого по формуле
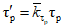 , (4.21)
, (4.21)Поскольку сборный коэффициент 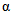 зависит от искомых величин
зависит от искомых величин 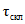 ,
, 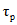 , A1%, он определяется графоаналитически - методом последовательных приближений.
, A1%, он определяется графоаналитически - методом последовательных приближений.
Суточный слой осадков 1%-ной обеспеченности (H1%) определяется по данным ближайших метеостанций, имеющих наибольшую длительность наблюдений, либо по карте (приложение VI).
Коэффициент 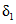 , учитывающий зарегулированность максимальных расходов воды проточными озерами, определяется по формуле
, учитывающий зарегулированность максимальных расходов воды проточными озерами, определяется по формуле
либо при наличии сведений о средневзвешенной озерности
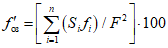 (4.23)
(4.23)по формуле
где fоз - относительная озерность, %; c1 - эмпирический коэффициент, равный 0,11; для случая расположения створов у истока из крупных озер c1 = 0,15; Si - площадь зеркала i-го озера; fi - площадь водосбора i-го озера.
Переходный коэффициент 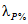 от вероятности превышения P = 1% к другой расчетной вероятности превышения определяется по табл. 4.11.
от вероятности превышения P = 1% к другой расчетной вероятности превышения определяется по табл. 4.11.
Таблица 4.11
Обеспеченность, % | 0,1 | 1 | 3 | 5 | 10 | 25 |
1,42 | 1,00 | 0,80 | 0,70 | 0,57 | 0,40 |
Расчет максимальных (мгновенных) расходов воды по формуле (4.13) производится в следующем порядке:
1. По карте (приложение VI) либо по данным ближайших метеорологических станций определяют средневзвешенные (средние) по водосбору осадки HP% мм.
2. В зависимости от типа преобладающих на водосборе почвогрунтов по табл. 4.9 определяют 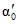 и ny.
и ny.
3. По табл. 4.10, соответствующей площади водосбора F км2 (по бас. р. Лены, Сев. Забайкалья или р. Амура), при 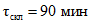 определяют
определяют 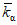 , отвечающий средней районной зависимости времени руслового добегания от площади водосбора и приравниваемый в первом приближении
, отвечающий средней районной зависимости времени руслового добегания от площади водосбора и приравниваемый в первом приближении 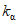 .
.
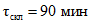 определяют
определяют 4. По формуле (4.19) рассчитывают сборный коэффициент 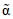 (знак ~ над характеристикой обозначает приближенное значение этой характеристики).
(знак ~ над характеристикой обозначает приближенное значение этой характеристики).
7. По уточненному значению 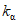 по формуле (4.19) определяют
по формуле (4.19) определяют 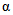 и далее по
и далее по 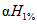 по формулам (4.17) и (4.16) и с помощью табл. 4.7 и 4.4 находят расчетное значение A1%.
по формулам (4.17) и (4.16) и с помощью табл. 4.7 и 4.4 находят расчетное значение A1%.
8. Для рек с площадями водосборов больше 200 км2 в качестве значения 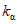 допускается принимать значение
допускается принимать значение 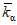 , отвечающее средней районной зависимости времени руслового добегания от площади водосбора при
, отвечающее средней районной зависимости времени руслового добегания от площади водосбора при 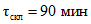 ; при этом п. 4 - 6 из схемы расчета исключают.
; при этом п. 4 - 6 из схемы расчета исключают.
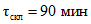 ; при этом п. 4 - 6 из схемы расчета исключают.
; при этом п. 4 - 6 из схемы расчета исключают.9. Величины 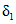 и
и 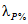 определяют вышеизложенным способом.
определяют вышеизложенным способом.
10. Для мельчайшей ручейковой сети с неясно выраженным тальвегом сборный коэффициент 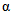 определяют аналогично изложенному в п. 1 - 7, а относительный максимальный модуль стока A1% определяют по табл. 4.4 при Фр = 0 в соответствии с временем склонового добегания
определяют аналогично изложенному в п. 1 - 7, а относительный максимальный модуль стока A1% определяют по табл. 4.4 при Фр = 0 в соответствии с временем склонового добегания 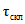 мин.
мин.
В случае наличия данных многолетних наблюдений на реке-аналоге сборный коэффициент 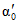 для неизученного водотока может быть определен по формуле
для неизученного водотока может быть определен по формуле
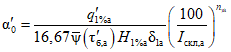 , (4.25)
, (4.25)где
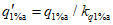 (4.26)
(4.26)- модуль максимального расхода воды реки-аналога, отнесенной к площади 10 км2; 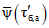 - значение ординаты кривой редукции осадков, соответствующей расчетному времени добегания в бассейне реки-аналога
- значение ординаты кривой редукции осадков, соответствующей расчетному времени добегания в бассейне реки-аналога 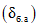 для площади водосбора 10 км2; расчетное время добегания равно
для площади водосбора 10 км2; расчетное время добегания равно
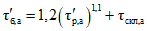 (4.27)
(4.27)здесь
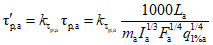 (4.28)
(4.28)находится по табл. 4.7 в зависимости от гидроморфометрической характеристики склонов водосбора-аналога при 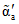 , устанавливаемый в соответствии с п. 1 - 7 разд. 4.4 методом последовательных приближений.
, устанавливаемый в соответствии с п. 1 - 7 разд. 4.4 методом последовательных приближений.
Для площадей водосбора-аналога, 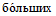 200 км2,
200 км2, 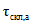 допускается брать равным 90 мин.
допускается брать равным 90 мин.
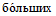 200 км2,
200 км2, Расчетное значение максимального расхода воды для неизученного водосбора при определенных по аналогу значениях коэффициентов 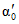 и ny находится по формуле (4.13) в соответствии с п. 1, 3 - 10 настоящего раздела.
и ny находится по формуле (4.13) в соответствии с п. 1, 3 - 10 настоящего раздела.
Примечание. При расчете стока по формуле предельной интенсивности методом аналогии рекой-аналогом является водосбор, имеющий близкие почвенно-геологические и мерзлотные условия. Площади водосборов при этом не должны различаться более чем в 10 раз и быть больше 1000 км2.
Расчет максимальных (мгновенных) расходов воды дождевых паводков QP% (м3/с) для неизученных рек с площадями водосборов 200 - 30 000 км2 при отсутствии рек-аналогов производится по эмпирической редукционной формуле
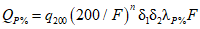 , (4.29)
, (4.29)где q200 - модуль максимального расхода воды 1%-ной обеспеченности, отнесенный к площади водосбора 200 км2 (при 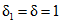 ); n - показатель степени редукции модуля максимального расхода с увеличением площади водосбора;
); n - показатель степени редукции модуля максимального расхода с увеличением площади водосбора; 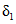 - коэффициент, учитывающий снижение максимального расхода проточными озерами;
- коэффициент, учитывающий снижение максимального расхода проточными озерами; 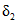 - коэффициент, учитывающий снижение максимального расхода болотами;
- коэффициент, учитывающий снижение максимального расхода болотами; 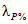 - коэффициент перехода от 1%-ной обеспеченности к другой обеспеченности.
- коэффициент перехода от 1%-ной обеспеченности к другой обеспеченности.
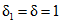 ); n - показатель степени редукции модуля максимального расхода с увеличением площади водосбора;
); n - показатель степени редукции модуля максимального расхода с увеличением площади водосбора; Модуль максимального расхода воды q200 определяется по карте (приложение VII) либо по данным реки-аналога. Коэффициент 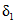 определяется по формулам (4.22) и (4.24). Коэффициент
определяется по формулам (4.22) и (4.24). Коэффициент 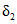 определяется по формуле
определяется по формуле
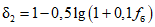 , (4.30)
, (4.30)где fб - степень заболоченности водосбора, %.
Переходные коэффициенты 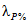 находят по табл. 4.12.
находят по табл. 4.12.
Таблица 4.12
Значения переходного коэффициента 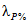
Обеспеченность, % | 0,1 | 1 | 3 | 5 | 10 | 25 |
1,35 | 1,00 | 0,84 | 0,76 | 0,65 | 0,50 |
Для рек, отличающихся большой изменчивостью дождевого стока (равнинные реки Верхней Лены, исключая реки бассейна Киренги, горные реки Амазаро-Ольдойского междуречья, реки предгорий Зеи, Селемджи и Хингано-Буреинского нагорья) значения 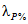 принимаются по табл. 4.13.
принимаются по табл. 4.13.
Таблица 4.13
Значения переходного коэффициента 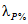
Обеспеченность, % | 0,1 | 1 | 3 | 5 | 10 | 25 |
1,53 | 1,00 | 0,78 | 0,65 | 0,50 | 0,30 |
Для рек площадью водосбора 200 - 1000 км2 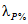 находится по табл. 4.11.
находится по табл. 4.11.
Показатель степени редукции n равен 0,18 для равнинных районов Прибайкалья и левобережья Лены, характеризующихся наличием островной многолетней мерзлоты. Для остальной территории зоны БАМа n = 0,35.
При наличии данных многолетних наблюдений на реке-аналоге расчет максимального расхода производится по формуле
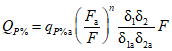 . (4.31)
. (4.31)Для рек-аналогов необходима близость не только в площадях водосбора, почвенно-геологических и мерзлотных условиях, а также в увлажненности бассейнов (т.е. в величинах 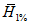 мм) и в условиях стока воды по водосбору, характеризующихся формой водосборов и уклонами рек:
мм) и в условиях стока воды по водосбору, характеризующихся формой водосборов и уклонами рек:
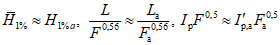 . (4.32)
. (4.32)При | 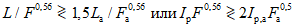 | (4.33) |
расчет максимального расхода методом аналогии рекомендуется производить по редукционной формуле с учетом руслового времени добегания:
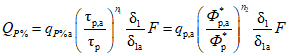 , (4.34)
, (4.34)где 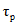 - русловое время добегания, мин,
- русловое время добегания, мин,
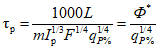 ; (4.35)
; (4.35)Ф* - морфометрическая характеристика русла (вспомогательное время добегания),
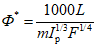 ; (4.36)
; (4.36)L, Iр, m определяются как в формуле (4.16); n1 и n2 - показатели степени редукции модулей максимальных расходов с возрастанием соответственно руслового 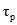 и вспомогательного Ф* времени добегания; n1 = 0,6, n2 = 0,7.
и вспомогательного Ф* времени добегания; n1 = 0,6, n2 = 0,7.
Расчетные значения слоев дождевого паводочного стока определяются по данным изученных рек-аналогов. В связи со сложностью формирования дождевых паводков на реках зоны БАМа, когда трудно, а подчас и невозможно получить генетически однородные выборки слоев паводочного стока по каждой отдельной реке (в выборку включены слои стока как за единичные паводки, так и за целые паводочные периоды большой длительности), рекомендуется расчетные значения (наибольших в году) слоев паводочного стока определять для фиксированных интервалов времени t = 1, 2, 3, 5, 7, 10, 15, 20, 30 сут и т.д. Эти значения, при исключении влияния таких факторов, как озерность, заболоченность, площадь водосбора, являются зональными характеристиками максимального стока и легко поддаются пространственной интерполяции методом аналогии.
Расчетные слои дождевого паводочного стока для неизученной реки определяются при этом методом аналогии для бассейнового времени добегания 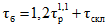 .
.
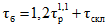 .
.Для ориентировочных расчетов слой дождевого паводочного стока 1%-ной обеспеченности допускается определять по карте (приложение VIII).
Расчет максимального дождевого стока неизученных рек района Центрального БАМа (рис. 4.6) в диапазоне площади водосбора от элементарно малых до 5000 км2 рекомендуется выполнять с использованием следующей формулы:
где QP% - расчетный максимальный расход воды, м3/с; qP% - расчетный максимальный модуль стока, м3/(с·км2); NP% - обобщенный показатель паводкообразующего дождя (метеорологическая сила дождя), определяется как произведение слоя и средней интенсивности эффективной части дождя, мм2/с; Kj - коэффициент увеличения густоты (длины) русловой сети в период дождевых паводков; jэ - густота русловой сети ("эталонное" значение), определенная по картам масштаба 1:100 000, км/км2; 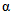 - коэффициент паводочного стока; i - уклон водосбора, в долях единицы, определяется по картам, как и jэ; F - площадь водосбора;
- коэффициент паводочного стока; i - уклон водосбора, в долях единицы, определяется по картам, как и jэ; F - площадь водосбора; 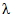 - коэффициент перехода от расчетного расхода 1%-ной обеспеченности к расходам другой вероятности превышения.
- коэффициент перехода от расчетного расхода 1%-ной обеспеченности к расходам другой вероятности превышения.
Для расчета максимальных расходов воды конкретных дождевых паводков параметры формулы (4.37) устанавливаются следующим образом:
1. По данным об осадках выделяется паводкообразующий дождь. Для района Центрального БАМа "паводкообразующими" следует считать дожди, вызывающие существенные паводки на фоне предшествующей межени (10 - 15 сут без осадков), в ходе которых за период от начала дождя до окончания наиболее эффективной части выпадает более 20 мм.
2. Расчетные значения паводкообразующих осадков вычисляются как сумма суточных (часовых) сумм осадков (за вычетом слоя начальных потерь) за период от начала дождя до окончания его наиболее эффективной части. Контроль выделения конца дождя целесообразно проводить по данным о гидрографе стока створа-аналога, как правило, конец эффективной части дождя совпадает с моментом прохождения максимума.
3. Продолжительность дождя рекомендуется принимать по суточным интервалам. Например, на метеостанции зафиксирован дождь 21, 22, 23, 24 VII соответственно 5, 10, 20, 25 мм.
Установлено, что расчетный слой паводкообразующих осадков за вычетом слоя начальных потерь составляет 50 мм, продолжительность 3 сут. Средняя интенсивность дождя определяется как частное от деления суммарного слоя осадков за эффективную часть дождя на его продолжительность:
Соответственно обобщенный параметр дождя Nд составит 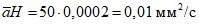 .
.
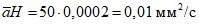 .
.Определение продолжительности дождя в часах или сутках не вносит существенных ошибок в определение модуля максимального дождевого стока, так как в формуле (4.37), превалирующее значение имеют коэффициент стока 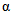 и гидрографические характеристики водосбора (jэKj).
и гидрографические характеристики водосбора (jэKj).
4. Коэффициент стока 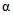 для восстановления фактических максимальных расходов воды дождевых паводков определяется на дату его начала по рекам-аналогам или по районным кривым изменения его величины в сезоне (рис. 4.8).
для восстановления фактических максимальных расходов воды дождевых паводков определяется на дату его начала по рекам-аналогам или по районным кривым изменения его величины в сезоне (рис. 4.8).
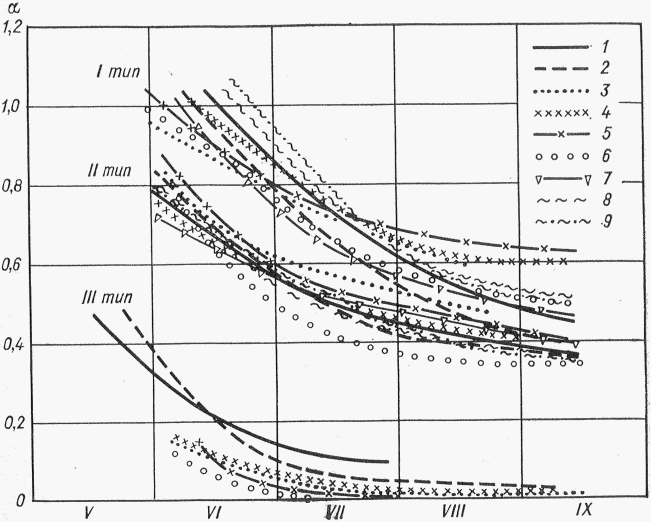
паводочных коэффициентов стока 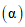
Тип I: 1) р. Малый Амалат, 2) р. Могой - Францевский,
3) р. Уруша - п. Уруша, 4) р. Тимптон - п. Нагорный,
5) р. Иенгра - п. Золотинка, 6) р. Чульман - п. Чульман,
7) р. Тунгир - пр. Николаевский, 8) р. Богдарин -
п. Богдарин, 9) р. Витимкан - пр. Ивановский;
тип II: 1) р. Сутур - ж.-д. мост, 2) р. Бодайбо -
Красноармейск, 3) р. Верхн. Нерюнгри - п. Нерюнгри,
4) р. Унаха - п. Унаха, 5) р. Тында - п. Тында,
6) р. Большой Невер - п. Сковородино, 7) р. Большая
Хатами - п. Хатами, 8) р. Ягдынья - п. Красивый,
9) р. Беренжа - п. Урми; тип III: 1) р. Половинная -
д. Половинная, 2) р. Радио - Уруэйте, 3) р. Яра - Ярская,
4) р. Коршуниха, 5) р. Ступина, 6) р. Казачья
5. Коэффициент увеличения густоты речной сети определяется по районному графику Kj = f(Nд) - рис. 4.9.
и коэффициента густоты речной сети (Kj)
Для определения обеспеченных максимальных модулей дождевого стока параметры, входящие в формулу (4.37), определяются следующим образом:
- значения параметра N 1%-ной обеспеченности рекомендуется вычислять по эмпирическому ряду наблюдений (в условиях северо-востока предпочтительнее включать в ряд все паводки теплого сезона, а не только максимальные в году), графоаналитическим методом;
- Kj - по районному графику Kj = f(N) (рис. 4.9) в зависимости от значения Nд 1%-ной обеспеченности;
- коэффициент стока  - по районным кривым
- по районным кривым 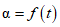 (рис. 4.8) с использованием данных о площади распространения многолетней мерзлоты на водосборе и их уклонов.
(рис. 4.8) с использованием данных о площади распространения многолетней мерзлоты на водосборе и их уклонов.
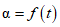 (рис. 4.8) с использованием данных о площади распространения многолетней мерзлоты на водосборе и их уклонов.
(рис. 4.8) с использованием данных о площади распространения многолетней мерзлоты на водосборе и их уклонов.Если распределение предельных значений коэффициентов стока в ходе теплого сезона года происходит по типу кривой I, то при расчете расходов воды 1%-ной обеспеченности целесообразно принимать 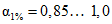 , по типу кривой II - 0,7... 0,3. Характер распределения предельных значений
, по типу кривой II - 0,7... 0,3. Характер распределения предельных значений 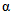 в сезоне проверяется по створам-аналогам.
в сезоне проверяется по створам-аналогам.
 , по типу кривой II - 0,7... 0,3. Характер распределения предельных значений
, по типу кривой II - 0,7... 0,3. Характер распределения предельных значений Переход к расходам другой вероятности превышения выполняется по переходным коэффициентам 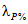 , значения которых приведены в табл. 4.14.
, значения которых приведены в табл. 4.14.
Таблица 4.14
Значения предельных коэффициентов 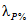
Обеспеченность, % | 0,01 | 0,1 | 1,0 | 2 | 5 | 10 | 25 |
1,82 | 1,46 | 1,0 | 0,86 | 0,68 | 0,55 | 0,36 |
и дождевых паводков
Под расчетным гидрографом понимаются гидрографы, основные элементы которых (максимальный расход, объем стока основной волны и всего половодья или паводка в целом) отвечают заданной вероятности превышения. Выбор метода построения расчетного гидрографа и расчетной модели зависит от задач, для решения которых он используется.
При проектировании гидротехнических объектов с незначительным регулирующим объемом используется модель одновершинного гидрографа с наибольшим максимальным расходом и наименьшим временем подъема гидрографа.
При больших регулирующих объемах, сопоставимых с полным объемом половодий (паводков), используется модель с наибольшим объемом половодья (паводка) и наибольшей сосредоточенностью стока в центральной части гидрографа.
При многовершинном характере гидрографа выбирается модель из числа многоводных лет, в которой наибольшая волна после короткого промежутка времени следует за меньшей волной.
При расчетах регулирования половодий (паводков) каскадом водохранилищ строится расчетный гидрограф притока к верхнему гидроузлу и гидрографы боковой приточности между гидроузлами. При этом выбирается модель сочетания гидрографов, увязанная по объему стока для всех ступеней каскада за календарные интервалы времени.
Гидрографы половодий и паводков, продолжающихся длительные интервалы времени, а также для площадей водосборов более 1000 км2, строятся по максимальным среднесуточным расходам воды. Гидрографы дождевых паводков на реках с площадями водосборов менее 1000 км2 строятся по срочным максимальным расходам воды.
Переход от среднесуточных максимальных расходов воды к срочным и обратно производится с помощью переходных коэффициентов в соответствии с работой [31].
Параметры основных элементов гидрографов - максимальный расход воды, слой стока половодья (паводка), слой стока основной волны, сочетание расчетных гидрографов в каскаде и т.д. - определяются методом гидрологической аналогии по данным рек-аналогов.
Построение расчетных гидрографов производят по модели одного из наблюдавшихся половодий (паводков) в расчетном створе или на реке-аналоге, наиболее неблагоприятной в отношении работы гидроузла.
Переход от модели к расчетному гидрографу производится с помощью переходных коэффициентов для отдельных участков гидрографа-модели [31].
При наличии данных о 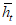 (средних за интервал времени t) и максимальных значениях слоя паводочного стока, переходные коэффициенты определяются для отдельных участков гидрографа по формуле
(средних за интервал времени t) и максимальных значениях слоя паводочного стока, переходные коэффициенты определяются для отдельных участков гидрографа по формуле
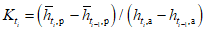 (4.39)
(4.39)при t = 1, 2, 3, 5, 7, 10, 15, 20 сут и т.д., где 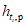 - расчетный слой максимального стока половодья (паводка) обеспеченностью P% за ti сут, приведенный к площади водосбора Fа (иначе, расчетное значение
- расчетный слой максимального стока половодья (паводка) обеспеченностью P% за ti сут, приведенный к площади водосбора Fа (иначе, расчетное значение 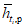 , взятое по реке-аналогу);
, взятое по реке-аналогу); 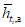 - слой максимального стока половодья (паводка) за ti суток за конкретное половодье (паводок), взятые в качестве расчетной модели по реке-аналогу; i - 1, i - последовательность номеров интегральных интервалов времени.
- слой максимального стока половодья (паводка) за ti суток за конкретное половодье (паводок), взятые в качестве расчетной модели по реке-аналогу; i - 1, i - последовательность номеров интегральных интервалов времени.
Для расчетов регулирования паводочного стока на реках с F < 1000 км2, при проектировании водохранилищ с незначительной регулирующей емкостью, допускается использование в качестве модели типового уравнения одновершинного паводка. Например,
 , (4.40)
, (4.40)где 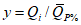 - ординаты расчетного гидрографа Qi, выраженные в долях среднесуточного максимального расхода воды заданной обеспеченности Qi; x = ti/tп - абсциссы расчетного гидрографа, выраженные в долях условной продолжительности подъема паводка tп; a - параметр, зависящий от коэффициента формы гидрографа [31].
- ординаты расчетного гидрографа Qi, выраженные в долях среднесуточного максимального расхода воды заданной обеспеченности Qi; x = ti/tп - абсциссы расчетного гидрографа, выраженные в долях условной продолжительности подъема паводка tп; a - параметр, зависящий от коэффициента формы гидрографа [31].
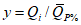 - ординаты расчетного гидрографа Qi, выраженные в долях среднесуточного максимального расхода воды заданной обеспеченности Qi; x = ti/tп - абсциссы расчетного гидрографа, выраженные в долях условной продолжительности подъема паводка tп; a - параметр, зависящий от коэффициента формы гидрографа [31].
- ординаты расчетного гидрографа Qi, выраженные в долях среднесуточного максимального расхода воды заданной обеспеченности Qi; x = ti/tп - абсциссы расчетного гидрографа, выраженные в долях условной продолжительности подъема паводка tп; a - параметр, зависящий от коэффициента формы гидрографа [31].В случае отсутствия материалов гидрометрических наблюдений минимальные 30-суточные расходы воды за зимний и летне-осенний периоды определяются:
а) для средних рек по картам изолиний минимального стока 80%-ной обеспеченности (приложения IX, X); при этом к средним относятся реки с площадью бассейна, превышающей приведенную в табл. 4.15, 4.16 (но не больше 75 000 км2) в зависимости от принадлежности к гидрологическому району согласно рис. 4.10 и 4.11;
б) для малых рек - по эмпирическим зависимостям минимальных расходов воды (модулей стока) от гидрографических характеристик исследуемого водосбора (площади и средней высоты водосбора); к малым относятся реки с площадью бассейна, не превышающей приведенную в табл. 4.15, 4.16.
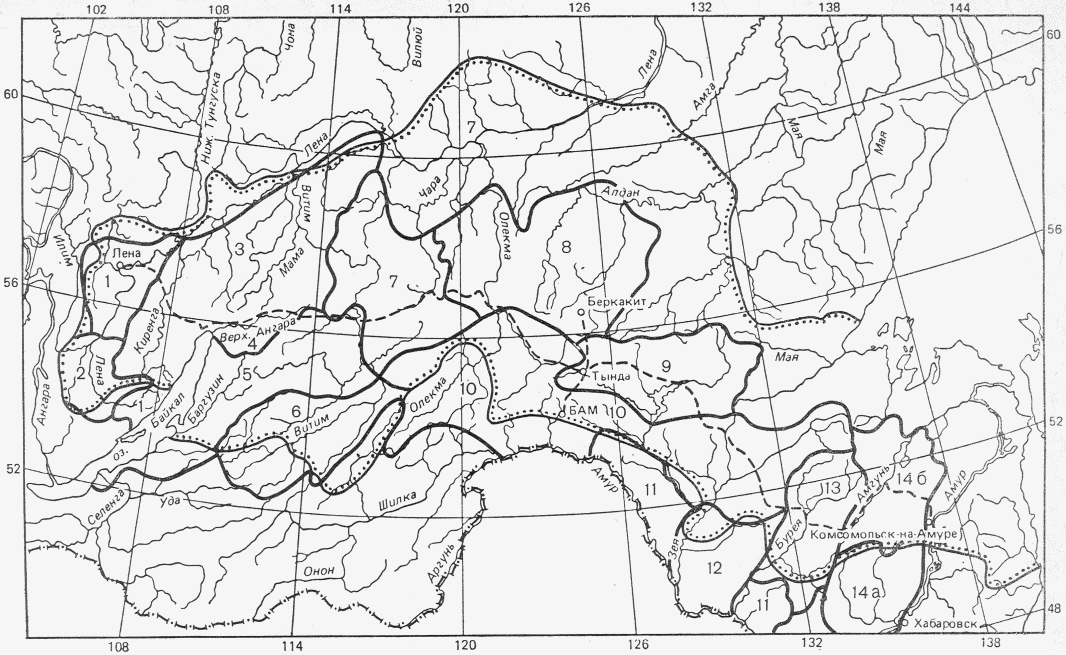
30-суточного расхода воды малых рек обеспеченностью 80%
за период открытого русла
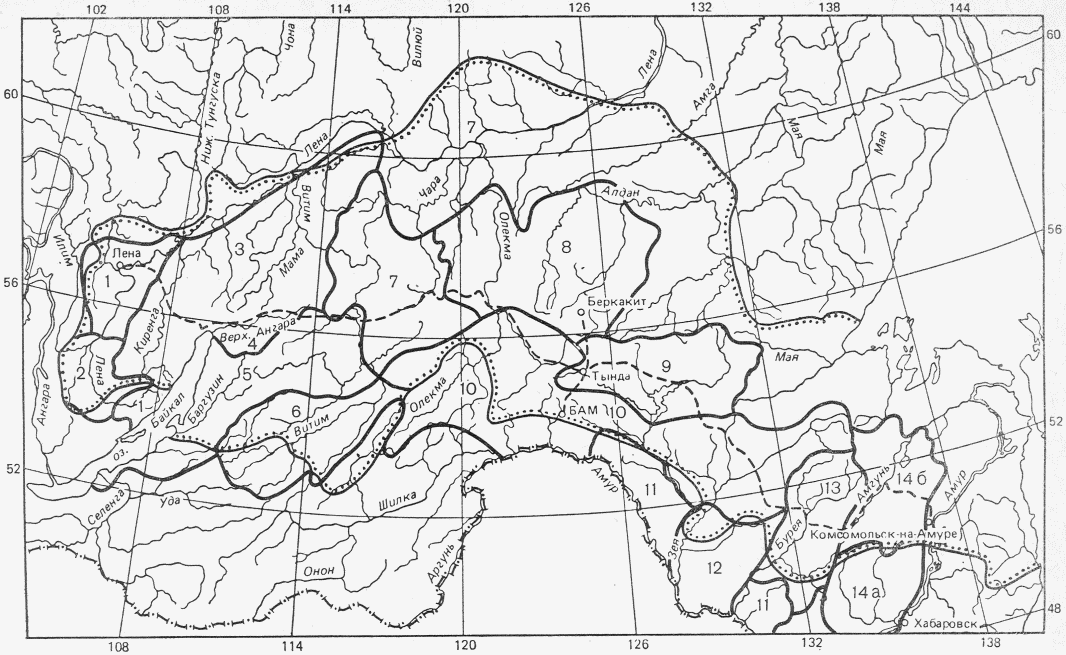
минимального 30-суточного зимнего расхода воды
малых рек обеспеченностью 80%
Таблица 4.15
для периода открытого русла
Районы по карте рис. 4.10 | Наибольшие площади бассейнов малых рек, км2 |
5 | 1000 |
1, 6, 7, 8, 13 | 1500 |
3, 4, 11, 14 | 2000 |
2, 9, 10 | 2500 |
12 | 3000 |
Таблица 4.16
Районы по карте рис. 4.11 | Наибольшие площади бассейнов малых рек, км2 |
1, 4, 5, 10, 15 | 1000 |
11, 16 | 1500 |
2, 3, 8, 14 | 2000 |
6, 7, 12, 13 | 2500 |
9 | 3000 |
Значение минимального 30-суточного стока 80%-ной обеспеченности для неизученного бассейна средней реки определяется путем планиметрирования площадей между изолиниями стока с учетом весовых коэффициентов.
Погрешность определения минимального стока по картам изолиний стока составляет +/- 15 - 20%.
Следует отметить, что карты изолиний не могут быть использованы для определения минимального стока рек, в пределах водосборов которых расположены озера, регулирующие значительную часть стока, а также реки, имеющие на водосборе участки ярко выраженного карста.
Минимальные 10-суточные расходы воды 80%-ной обеспеченности (период открытого русла) для средних рек устанавливается по соотношению
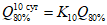 , (4.41)
, (4.41)где Q80% - минимальный 30-суточный расход воды 80%-ной обеспеченности, определяемый по карте приложения IX, м3/с; K10 - коэффициент, принимаемый по табл. 4.17.
Минимальные среднесуточные расходы воды для средних рек устанавливаются по соотношению
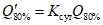 , (4.42)
, (4.42)где Q80% - минимальный 30-суточный расход 80%-ной обеспеченности, определяемый по картам приложений IX, X, м3/с; Kсут - коэффициент, принимаемый по табл. 4.17, 4.18.
Таблица 4.17
среднесуточного и 10-суточного расхода воды (модуля)
80%-ной обеспеченности за период открытого русла
Номер района по карте рис. 4.10 | K10 = q10/q30 | Kсут = qсут/q30 |
Бассейн р. Лены и оз. Байкал | ||
1 | 0,92 | 0,80 |
2 | 0,80 | 0,72 |
3 | 0,77 | 0,60 |
4 | 0,72 | 0,65 |
5 | 0,80 | 0,68 |
6 | 0,59 | 0,54 |
7 | 0,63 | 0,60 |
8 | 0,66 | 0,60 |
0,46 <1> | 0,27 <1> | |
Бассейн р. Амура | ||
9 | 0,65 | 0,36 |
10 | 0,60 | 0,50 |
0,44 <2> | 0,30 <2> | |
11 | 0,83 <3> | 0,74 <3> |
0,64 <4> | 0,52 <4> | |
12 | 0,88 | 0,75 |
13 | 0,60 | 0,42 |
14 | 0,71 | 0,61 |
--------------------------------
Таблица 4.18
среднесуточного расхода воды (модуля) 80%-ной
обеспеченности за период зимней межени
Номер района по карте рис. 4.11 | Kсут = qсут/q30 | Номер района по карте рис. 4.11 | Kсут = qсут/q30 |
1 | 0,87 | 9 | 0,84 |
2 | 0,82 | 10 | 0,80 |
3 | 0,83 | 11 | 0,84 |
4 | 0,85 | 12 | 0,88 |
5 | 0,92 | 13 | 0,85 |
6 | 0,89 | 14 | 0,87 |
7 | 0,88 | 15 | 0,93 |
8 | 0,78 | 16 | 0,84 |
Значения минимального 30-суточного, 10-суточного и суточного стока расчетной обеспеченности определяются путем умножения минимального стока 80%-ной обеспеченности на значения переходных коэффициентов, помещенных в табл. 4.19, 4.20.
Таблица 4.19
Переходные коэффициенты 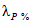 для определения
для определения
минимальных расходов воды различной обеспеченности
за период открытого русла
Номер района по карте рис. 4.10 | 80% | 90% | 95% | 97% | 99% |
Бассейн Лены и оз. Байкал | |||||
1 | 1 | 0,82 | 0,75 | 0,64 | 0,45 |
2 | 1 | 0,82 | 0,75 | 0,64 | 0,50 |
3 | 1 | 0,82 | 0,75 | 0,64 | 0,46 |
4 | 1 | 0,82 | 0,75 | 0,64 | 0,61 |
5 | 1 | 0,82 | 0,75 | 0,64 | 0,56 |
6 | 1 | 0,82 | 0,75 | 0,64 | 0,60 |
1 | 0,64 <*> | 0,43 <*> | 0,38 <*> | 0,33 <*> | |
7 | 1 | 0,86 | 0,80 | 0,78 | 0,70 |
8 | 1 | 0,82 | 0,75 | 0,64 | 0,57 |
0,67 <*> | 0,42 <*> | 0,28 <*> | 0,10 <*> | ||
Бассейн р. Амура | |||||
9 | 1 | 0,76 | 0,64 | 0,54 | 0,41 |
10 | 1 | 0,76 | 0,64 | 0,54 | 0,54 |
11 | 1 | 0,86 | 0,76 | 0,70 | 0,66 |
12 | 1 | 0,82 | 0,69 | 0,63 | 0,62 |
13 | 1 | 0,82 | 0,69 | 0,63 | 0,62 |
14 | 1 | 0,82 | 0,69 | 0,58 | 0,51 |
--------------------------------
Таблица 4.20
минимальных расходов воды различной вероятности
превышения за период зимней межени
Бассейн | 80% | 90% | 95% | 97% | 99% |
р. Лена | 1 | 0,87 | 0,81 | 0,74 | 0,67 |
оз. Байкал | 1 | 0,88 | 0,78 | 0,73 | 0,65 |
р. Амур | 1 | 0,79 | 0,61 | 0,56 | 0,53 |
Минимальные 30-суточные расходы воды 80%-ной обеспеченности для малых рек (с площадью бассейна меньше, чем указано в табл. 4.15, 4.16, но не менее 100 км2) определяются по формулам:
для периода открытого русла
для зимнего периода
где Q80% - минимальный 30-суточный расход воды 80%-ной обеспеченности для периода открытого русла, зимнего периода, м3/с; F - площадь водосбора, км2; H - высота водосбора, км; a, n, f0 - параметры, определяемые по табл. 4.21, 4.22, 4.23, 4.24 для однородных по условиям формирования минимального стока физико-географических районов (см. рис. 4.10, 4.11).
Таблица 4.21
Значения параметров a, n в формуле (4.43)
для периода открытого русла
Номер района по карте рис. 4.10 | Период, сут | a | n | Номер района по карте рис. 4.10 | Период, сут | a | n |
1 | 30 | 0,93 | 1,20 | 10 | 30 | 0,32 | 1,26 |
10 | 0,87 | 1,19 | 10 | 0,062 | 1,39 | ||
1 | 0 66 | 1,21 | 1 | 0,047 | 1,39 | ||
2 | 30 | 0,039 | 1,45 | 11 <1> | 30 | 11,0 | 0,86 |
10 | 0,038 | 1,44 | 10 | 9,57 | 0,86 | ||
1 | 0,029 | 1,45 | 1 | 8,14 | 0,86 | ||
3 | 30 | 17,1 | 0,97 | 11 <2> | 30 | 15,0 | 0,86 |
10 | 12,4 | 0,97 | 10 | 13,0 | 0,86 | ||
1 | 9,40 | 0,97 | 1 | 11,1 | 0,86 | ||
4 | 30 | 17,8 | 0,90 | 11 <3> | 30 | 1,50 | 1,08 |
10 | 13,5 | 0,89 | 10 | 0,96 | 1,08 | ||
1 | 11,5 | 0,90 | 1 | 0,78 | 1,08 | ||
5 | 30 | 3,22 | 1,08 | 11 <4> | 30 | 2,30 | 1,08 |
10 | 2,55 | 1,08 | 10 | 1,47 | 1,08 | ||
1 | 2,24 | 1,07 | 1 | 1,20 | 1,08 | ||
7 | 30 | 11,8 | 0,96 | 12 | 30 | 1,50 | 0,93 |
10 | 10,3 | 0,91 | 10 | 1,32 | 0,93 | ||
1 | 7,13 | 0,96 | 1 | 1,12 | 0,93 | ||
8 | 30 | 5,75 | 1,03 | 13 | 30 | 2,20 | 1,13 |
10 | 0,85 | 1,22 | 10 | 1,32 | 1,13 | ||
1 | 0,028 | 1,63 | 1 | 1,20 | 1,10 |
--------------------------------
Таблица 4.22
Значения параметров a, n в формуле (4.44)
для периода открытого русла
Номер района по карте рис. 4.10 | Период, сут | a | n |
6 | 30 | 0,041 | 8,81 |
10 | 0,025 | 9,24 | |
1 | 0,024 | 7,00 | |
9 | 30 | 9,12 | 2,20 |
10 | 5,93 | 2,20 | |
1 | |||
14а | 30 | 15,8 | 1,45 |
10 | 11,2 | 1,46 | |
1 | 9,6 | 1,46 | |
14б | 30 | 9,33 | 0,84 |
10 | 6,62 | 0,84 | |
1 | 5,70 | 0,84 |
Примечания: 1. Для района 9 qсут определяется по формуле qсут = 6,3H - 2,3. 2. Высота водосбора H принимается в километрах.
Таблица 4.23
Значения параметров a, n, f0 в формуле (4.45)
для периода зимней межени
Номер района по карте рис. 4.11 | Период, сут | a | n | f0 |
1 | 30 | 0,232 | 1,29 | 0 |
1 | 0,296 | 1,23 | 0 | |
2 | 30 | 0,2087 | 1,160 | -280 |
1 | 0,152 | 1,168 | -280 | |
3 | 30 | 0,153 | 1,12 | -768 |
1 | 0,0852 | 1,16 | -768 | |
4 | 30 | 0,437 | 1,13 | 0 |
1 | 0,358 | 1,13 | 0 | |
5 | 30 | 95,5 | 0,63 | 0 |
1 | 46,8 | 0,70 | 0 | |
8 | 30 | 0,00024 | 1,560 | -1090 |
1 | 0,000315 | 1,482 | -1090 | |
9 | 30 | 13,1 | 0,661 | 0 |
1 | 8,1 | 0,711 | 0 | |
10 | 30 | 4,0030 | 1,03 | -193 |
1 | 4,3160 | 0,994 | -193 | |
11 | 30 | 1,73 | 0,86 | -1000 |
1 | 1,45 | 0,86 | -1000 | |
12 | 30 | 0,02002 | 1,426 | 0 |
1 | 0,02778 | 1,375 | 0 | |
13 | 30 | 1,1100 | 0,748 | 0 |
1 | 0,7400 | 0,776 | 0 | |
14 | 30 | 0,1850 | 1,029 | -351 |
1 | 0,1310 | 1,066 | -351 | |
15 | 30 | 0,0283 | 1,251 | 0 |
1 | 0,0323 | 1,227 | 0 | |
16 | 30 | 0,0 | 0,0 | 0 |
1 | 0,0 | 0,0 | 0 |
Таблица 4.24
Значение параметров a, n в формуле (4.46)
для периода зимней межени
Номер района по карте рис. 4.11 | Период, сут | a | n |
6 | 30 | 1,75 | 2,979 |
1 | 1,39 | 3,128 | |
7 | 30 | 6,50 | -7,289 |
1 | 5,71 | -7,29 |
Формулы (4.43) - (4.46) не могут быть использованы для расчета минимального стока рек со значительным озерным регулированием или рек, протекающих в районах резкого локального влияния карста, а также при ярко выраженном влиянии хозяйственной деятельности на сток рек.
По условиям истощения стока в зимний период реки зоны БАМа подразделяются на две категории.
К первой относятся реки, сток которых существует в течение всего зимнего периода. Минимальное расчетное значение его определяется согласно рекомендациям разд. 4.6.
Вторую категорию образуют реки, поверхностный сток которых некоторый промежуток времени бывает равен нулю.
Расчет количественных характеристик перемерзания рек за период отсутствия стока имеет такое же важное практическое значение, как и расчет минимальных значений стока.
Перемерзание характеризуется следующими основными количественными параметрами: 1) повторяемостью в многолетнем цикле колебаний водности реки Pпер, %; 2) датой наступления Дн; 3) датой окончания Д0 и 4) продолжительностью Tпер, сут.
при наличии данных наблюдений
В зависимости от наличия исходных данных возможны два варианта расчета:
1) при наличии данных длительных наблюдений (> 7 лет);
2) при наличии непродолжительных стационарных наблюдений (< 7 лет).
Первый вариант.
Повторяемость перемерзания в многолетнем цикле колебания водности (Pпер%) определяется по формуле
где n1 - число лет с наличием перемерзания; n - общее число лет наблюдений.
Определение значений трех других характеристик перемерзания различной обеспеченности осуществляется по эмпирической кривой распределения. Обеспеченность эмпирических точек определяется по формуле (5.1).
Построение кривой распределения дат наступления перемерзания производится не по ежегодным датам, а по числам, соответствующим разности между наиболее ранней датой в ряду наблюдений и ежегодными значениями. Аналогичные преобразования производятся для дат окончания перемерзания.
При Pпер = 100% построение кривой распределения характеристик перемерзания производится без учета лет, в которые сток воды наблюдался в течение всего зимнего периода, по формуле (5.1). Истинная вероятность превышения P1 определяется по формуле
P1 = n1P/n. (5.2)
где n1 - число лет с перемерзанием; P - вероятность явления, полученная по эмпирической кривой обеспеченности; n - общее число лет наблюдений.
Второй вариант.
Построение эмпирических кривых обеспеченности не производится. Вероятные значения анализируемых характеристик рассчитывают методом гидрологической аналогии. В районе зоны БАМа (рис. 5.1), в котором располагается пункт с непродолжительным периодом наблюдений, находят пункт-аналог с длительным рядом наблюдений, который подбирается не только по общим правилам (гл. 2), но и по сходству значений анализируемой характеристики в годы совместных наблюдений.
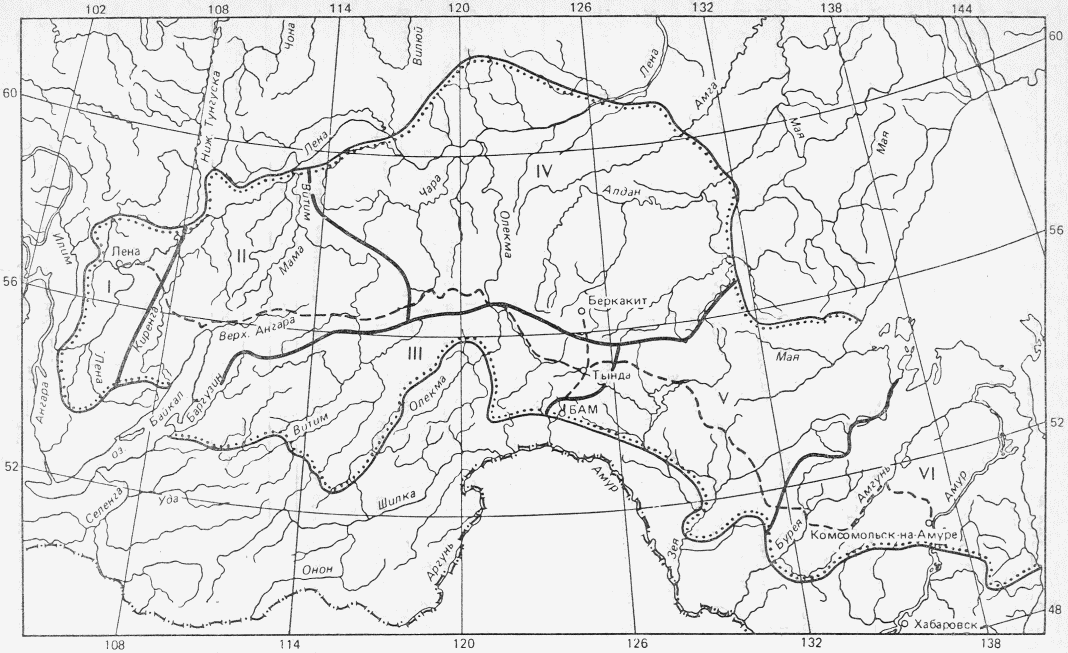
формирования зимнего стока рек
Повторяемость перемерзания на изучаемой реке принимается такой же, как у аналога.
при отсутствии данных наблюдений
Расчет характеристик перемерзания осуществляется на основе их связи с площадью водосбора изучаемой реки, минимальным 30-суточным летне-осенним стоком 80%-ной обеспеченности, определяемым по карте (приложение IX) и схеме районов с однородными условиями формирования зимнего стока (см. рис. 5.1).
Расчеты предусматривается выполнять для двух случаев:
а) при ежегодной (Pпер = 100%) и б) периодической (Pпер < 100%) повторяемости перемерзания. Предельные значения площадей водосборов рек, на которых в различных районах зоны БАМа может наблюдаться первый или второй случай, определяются по табл. 5.1.
Таблица 5.1
Предельные площади водосборов рек
с явлением перемерзания, км2
Номер района по рис. 5.1 | Площади водосборов рек, на которых сток может | ||
прекращаться | не прекращаться | ||
ежегодно | периодически | ||
I | > 50 | > 400 | < 400 |
II | > 50 | > 500 | < 500 |
III | > 50 000 | > 70 000 | < 70 000 |
IV | > 10 000 | > 25 000 | < 25 000 |
V | > 500 | > 20 000 | < 20 000 |
VI | > 500 | > 4 000 | < 4 000 |
При Pпер = 100% дата начала и продолжительность периода перемерзания расчетной 80%-ной обеспеченности определяются по табл. 5.2 по площади водосбора реки.
Таблица 5.2
Дата наступления Дн (числитель) и продолжительность периода
Tпер (знаменатель) отсутствия стока 80%-ной обеспеченности
на ежегодно перемерзающих реках зоны БАМа
Номер района по рис. 5.1 | Площадь водосбора, км2 | ||||||||||
50 | 100 | 500 | 1 000 | 2 000 | 5 000 | 10 000 | 15 000 | 20 000 | 30 000 | 50 000 | |
III | - ----- - | (2,11) -------- (185) | 13,11 -------- 170 | 19,11 ------- 165 | 24,11 ------- 158 | 2,12 ------- 148 | 11,12 ------- 140 | 15,12 ------- 138 | 19,12 ------- 136 | 24,12 ------- 132 | (10,01) -------- (120) |
IV | - ----- - | 26,10 ------- (210) | 31,10 ------- 182 | 4,11 ------- 170 | 12,11 ------- 163 | 17,11 ------- 151 | 25,11 ------- 140 | (15,12) ------- (120) | - ----- - | - ----- - | - ----- - |
V | - ----- - | 15,11 ------- 170 | 25,11 ------- 162 | 5,12 ------- 150 | 20,12 ------- 130 | (10,01) -------- (110) | (2,02) ------- (90) | - ----- - | - ----- - | - ----- - | - ----- - |
VI | 21,11 ------- 155 | 27,11 ------- 145 | (19,12) -------- (130) | - ----- - | - ----- - | - ----- - | - ----- - | - ----- - | - ----- - | - ----- - | - ----- - |
Примечание. В районах I и II ежегодно перемерзают реки с площадью водосбора менее 50 км2.
Дата окончания периода перемерзания (начало стока) связана с интенсивностью развития синоптических процессов весной, что практически исключает ее зависимость от размеров площади водосбора, и определяется так же, как и при Pпер < 100%.
При Pпер < 100% значение Pпер для неизученной реки выбирается из табл. 5.3 по значениям площади водосбора и минимального летне-осеннего стока.
Таблица 5.3
на которых возможно перемерзание, км2
Повторяемость перемерзания, Pпер % | Зональное значение минимальных летне-осенних модулей 30-суточного стока 80%-ной обеспеченности, л/(с·км2) | |||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
100 | 1000 | 320 | 160 | 100 | 75 | 60 | - | - |
80 - 99 | - | 700 | 340 | 220 | 160 | 120 | 90 | 70 |
60 - 79 | - | 1 200 | 600 | 400 | 280 | 200 | 160 | 120 |
40 - 59 | - | 2 600 | 1400 | 900 | 600 | 460 | 340 | 280 |
20 - 39 | - | 6 000 | 3000 | 1800 | 1200 | 900 | 700 | 500 |
0 - 19 | - | 12 000 | 7000 | 4000 | 2000 | 2000 | 1600 | 1200 |
Водотоки с площадью водосбора более 1000 км2 и модулем минимального летне-осеннего стока 80%-ной обеспеченности свыше 9,0 л/(с·км2) имеют постоянный зимний сток. При промежуточных значениях площади водосбора и минимального стока между значениями, указанными в табл. 5.3, определение Pпер производится по прямой интерполяции, причем чем больше исходные значения, тем меньше следует принимать Pпер.
Продолжительность отсутствия стока в сутках на периодически перемерзающих реках 80%-ной обеспеченности определяется по формуле
Tпер = 2Pпер, (5.3)
где Pпер в процентах.
Соответствующую Tпер дату начала перемерзания получают обратным пересчетом от средней даты начала весеннего стока (табл. 5.4).
Таблица 5.4
Даты начала весеннего стока по районам зоны БАМа
Номер района по рис. 5.1 | I | II | III | IV | V | VI |
Дата | 3,05 | 6,05 | 3,05 | 1,05 | 23,04 | 15,04 |
И НАЛЕДНОГО РЕГУЛИРОВАНИЯ РЕЧНОГО СТОКА
С гидрологической точки зрения наибольшее значение имеют наледи подземных и речных вод. Их ежегодное образование зимой и последующее таяние в теплое время года приводит к внутригодовому наледному регулированию ресурсов поверхностных и подземных вод. Кроме того, наледи этих типов оказывают вредное, преимущественно разрушающее воздействие на инженерные сооружения: автомобильные и железные дороги, мостовые переходы, земляное полотно, дорожное покрытие, водопропускные отверстия, санитарно-технические коммуникации, промышленные и гражданские здания и т.п.
Наледное регулирование стока (речного и подземного) заключается в перераспределении во времени части речных и подземных вод, аккумулируемых наледями: внутригодовое - с холодного на теплый сезон; многолетнее - от года к году. Для большинства речных бассейнов в зоне БАМа многолетнее наледное регулирование стока имеет небольшое значение и может не учитываться в гидрологических расчетах.
В результате внутригодового наледного регулирования зимний речной сток уменьшается на объем питания наледей (и образования речного льда), а в теплое время года - увеличивается на объем наледного стока.
характеристик наледей
Основные характеристики наледей следующие:
для наледей подземных вод - площадь 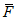 , средняя толщина или мощность
, средняя толщина или мощность 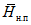 , объем
, объем 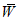 ;
;
для наледей речных вод - средняя толщина или мощность 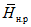 .
.
Перечисленные характеристики определяются на конец зимы, поскольку в это время наледи имеют максимальные размеры.
При этом
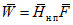 . (6.1)
. (6.1)Основными параметрами кривых распределения, используемыми в практике статистических обобщений и гидрологических расчетов, являются математическое ожидание (среднее значение), среднее квадратическое отклонение (или коэффициент вариации) и коэффициент асимметрии.
6.1.1. Для наледей подземных вод основной исходной характеристикой является их максимальная площадь в конце зимы. Она определяется по данным наземных обследований или по аэрофотосъемкам. В обоих случаях задача состоит в том, чтобы зафиксировать не только контуры наледного массива в год съемки, но главным образом средние многолетние его границы, для чего используются дешифровочные признаки. Методика производства наземных и аэрофотосъемочных работ, перечень и описание используемых при этом дешифровочных признаков, правила обработки полевых материалов по определению площади наледей изложены в работах [1, 13, 23, 33].
Сведения о средних многолетних значениях этой характеристики по отдельным районам содержатся в трех выпусках Каталога наледей зоны БАМа [14 - 16], в работах [11, 19, 23 и др.], а также в фондах организаций различных министерств и ведомств, в первую очередь МИНГЕО СССР.
Массовое определение средней многолетней мощности наледей подземных вод осуществляется по следующим выражениям:
или
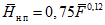 , (6.3)
, (6.3)где 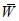 и
и 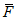 - соответственно в тыс. м3 и тыс. м2, a и n - параметры.
- соответственно в тыс. м3 и тыс. м2, a и n - параметры.
Относительная средняя квадратическая ошибка расчета объема отдельных наледей по выражению (6.2) составляет 34,7%, а суммарного объема совокупности наледей в речном бассейне - 10,5% [36].
Точность расчета повышается в 1,2 - 1,4 раза, если пользоваться районными значениями параметров уравнений (6.2), приведенными в табл. 6.1.
Таблица 6.1
Значения параметров уравнения (6.2)
для отдельных речных бассейнов в зоне БАМа
Бассейн реки | Кол-во наледей | a | n |
Предбайкалье | |||
Тумусун | 36 | 0,603 | 1,241 |
Иркут | 67 | 1,500 | 1,000 |
Ангара | 126 | 1,000 | 1,000 |
Купа | 28 | 0,300 | 1,270 |
Кута | 51 | 0,300 | 1,270 |
Лена (до устья р. Витима) | 83 | 0,300 | 1,270 |
Забайкалье | |||
Верхняя Ангара | 38 | 0,254 | 1,330 |
Муя | 27 | 0,332 | 1,252 |
Куанда | 16 | 0,544 | 1,085 |
Витим | 54 | 0,365 | 1,220 |
Апсат | 16 | 2,153 | 0,927 |
Нижний Ингамакит | 50 | 1,484 | 1,013 |
Чара | 91 | 1,260 | 1,046 |
Хани | 13 | 0,541 | 1,191 |
Нюкжа | 94 | 0,409 | 1,089 |
Южная Якутия | |||
Большой Нимныр | 11 | 0,636 | 1,132 |
Чульман | 98 | 0,894 | 1,118 |
Тимптон | 129 | 0,894 | 1,118 |
Алдан | 166 | 0,894 | 1,118 |
Дальний Восток | |||
Аргунь | 65 | 1,000 | 1,000 |
Онон | 22 | 1,280 | 1,076 |
Шилка | 36 | 1,280 | 1,076 |
Гилюй | 126 | 0,500 | 1,035 |
Зея | 196 | 0,750 | 1,037 |
Бурея | 24 | 0,760 | 1,065 |
Амур | 375 | 0,750 | 1,037 |
Для более точного определения рассматриваемых характеристик наледей подземных вод, например, при проектировании противоналедной борьбы, гидротехнических сооружений, контактирующих с наледными массивами и пр., необходимо проведение детальных полевых работ. Методика их выполнения рассмотрена в работах [1, 13].
Ориентировочные значения коэффициента вариации Cv и коэффициента асимметрии Cs для наледей, морфологические характеристики которых больше или меньше заданного значения, определяются по табл. 6.2.
Таблица 6.2
морфометрических характеристик наледей подземных вод
Группа наледей | Площадь | Мощность | Объем | ||||||
Cv | Cs | Cs/Cv | Cv | Cs | Cs/Cv | Cv | Cs | Cs/Cv | |
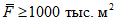 | |||||||||
Первая: | 0,14 | 0 | 0 | 0,16 | 0,1 | 0,6 | |||
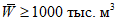 | 0,26 | 0,6 | 2,3 | ||||||
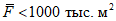 | |||||||||
Вторая: | 0,87 | 1,8 | 2,1 | 1,0 | 2,1 | 2,1 | |||
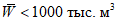 | |||||||||
Более точные результаты могут быть получены при использовании следующего выражения для коэффициента вариации
где 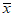 - среднее многолетнее значение характеристики; A и b - параметры.
- среднее многолетнее значение характеристики; A и b - параметры.
Значения параметров уравнения (6.4) приведены в табл. 6.3.
Таблица 6.3
Значения параметров уравнения (6.4) для морфометрических
характеристик наледей подземных вод, корреляционных
отношений и относительных средних квадратических
отклонений от линии регрессии 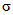
Характеристика | A | b | r | |
Площадь | 2,67 | 0,371 | 0,86 | 32,4 |
Мощность | 0,278 | 1,16 | 0,77 | 46,6 |
Объем | 3,03 | 0,388 | 0,88 | 35,7 |
Коэффициенты асимметрии площади CsF и объема CsW наледей определяются в зависимости от коэффициентов вариации этих характеристик CvF и CvW по следующим выражениям:
CvF = 2,56CvF - 0,35, (6.5)
CsW = 2,27CvW - 0,27 (6.6)
или с учетом формулы (6.4) и табл. 6.3:
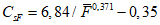 , (6.7)
, (6.7)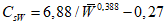 . (6.7')
. (6.7')Коэффициент асимметрии мощности наледных массивов в соответствии с табл. 6.2 принимается равным 0,6. Распределение рассматриваемых характеристик наледей подчиняется биномиальному закону.
Для более полного описания закономерностей многолетних колебаний размеров наледей используются также сведения о продолжительности фаз их развития. Эта характеристика определяется по данным табл. 6.4.
Таблица 6.4
развития наледей подземных вод
Фаза развития наледи | Для площади | Для мощности | Для объема |
Наледи первой группы: | |||
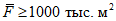 ; ; | 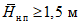 ; ; | 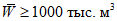 | |
II (0,60 - 0,89 нормы) | 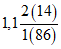 | 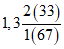 | 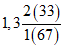 |
III (0,9 - 1,09 нормы) | 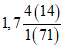 | 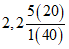 | 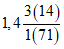 |
IV (1,10 - 1,39 нормы) | 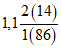 | 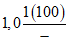 | 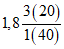 |
Наледи второй группы: | |||
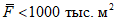 ; ; | 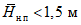 ; ; | 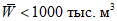 | |
I (0,59 нормы) | 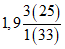 | 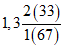 | 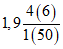 |
II (0,60 - 0,89 нормы) | 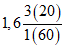 | 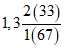 | 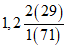 |
III (0,9 - 1,09 нормы) | 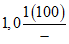 | 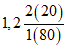 | 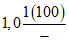 |
IV (1,10 - 1,39 нормы) | 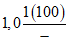 | 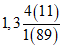 | 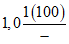 |
V (>= 1,40 нормы) | 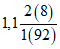 | 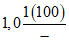 | 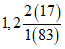 |
Примечание. Перед дробью указано среднее значение продолжительности; в числителе - максимальная продолжительность; в скобках - ее вероятность, %; в знаменателе - минимальная продолжительность; в скобках - ее вероятность, %.
6.1.2. В связи с отсутствием массовых наблюдений средняя многолетняя мощность наледей речных вод может быть определена расчетным способом по уравнению
где 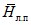 - толщина ледяного покрова рек, измеряемая на сети станций и постов Госкомгидромета, м;
- толщина ледяного покрова рек, измеряемая на сети станций и постов Госкомгидромета, м; 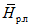 - толщина речного льда, м; ежегодные ее значения рассчитываются по следующему уравнению [20]:
- толщина речного льда, м; ежегодные ее значения рассчитываются по следующему уравнению [20]:
где 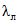 и
и 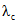 - теплопроводность льда и снега; H0 - толщина льда на начало расчетного периода; t - средняя за расчетный период температура воздуха; L и
- теплопроводность льда и снега; H0 - толщина льда на начало расчетного периода; t - средняя за расчетный период температура воздуха; L и 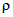 - удельная теплота льдообразования и плотность льда; hс - высота снежного покрова на льду; T - длительность расчетного периода.
- удельная теплота льдообразования и плотность льда; hс - высота снежного покрова на льду; T - длительность расчетного периода.
Принимая теплопроводность и плотность льда, удельную теплоту льдообразования средними для условий Сибири и Дальнего Востока, формулу (6.9) можно привести к следующему виду [39]:
где 0,5 - коэффициент, установленный опытным путем.
При наличии шуги подо льдом в начале зимы, когда интенсивность нарастания льда снизу велика,
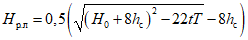 . (6.11)
. (6.11)Если на речном участке имеется значительный приток тепла снизу вследствие выхода подземных вод, то
где q' - слой стаивания льда за счет теплопритока снизу; Hпр - предельная при данной температуре воздуха и высоте снежного покрова толщина льда, определяемая по формуле [20]; Hпр.э - предельная эквивалентная толщина льда.
Предельная эквивалентная толщина льда (Hпр.э) определяется по формуле
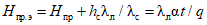 , (6.13)
, (6.13)где q - приток тепла снизу.
Таким образом, расчет ежегодных значений толщины речного льда по формулам (6.10) - (6.12) производится по данным о температуре воздуха и высоте снежного покрова на льду, измеряемым на станциях и постах. Осреднением этих значений в каждом пункте рассчитывают среднюю многолетнюю толщину речного льда 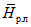 , а по выражению (6.8) определяют
, а по выражению (6.8) определяют 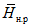 . При этом сведения о толщине ледяного покрова
. При этом сведения о толщине ледяного покрова 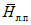 берут из гидрологических ежегодников.
берут из гидрологических ежегодников.
Среднее многолетнее значение толщины наледей речных вод в зоне БАМа более просто, но менее точно может быть определено по карте на рис. 6.1 для рек с площадью водосбора 150 - 250 000 км2. Для этого дополнительно используются графики на рис. 6.2 и 6.3. Порядок расчета следующий. На интересующем речном участке по карте 6.1 определяют мощность наледи в предположении, что площадь водосбора до расчетного створа равна 5000 км2, а высота участка над уровнем моря 500 м абс. Это значение мощности отмечают на графике рис. 6.3 при Hв = 500 м абс., сносят параллельно линии, соответствующей району расположения расчетного пункта (см. рис. 6.1), до высоты этого пункта и по вертикальной шкале определяют новое значение мощности наледи. Последнее отмечают на графике рис. 6.2 при площади водосбора 5000 км2, затем сносят параллельно линии связи до значения площади водосбора, замыкаемого расчетным пунктом, и по вертикальной шкале определяют искомое значение средней многолетней мощности наледи.
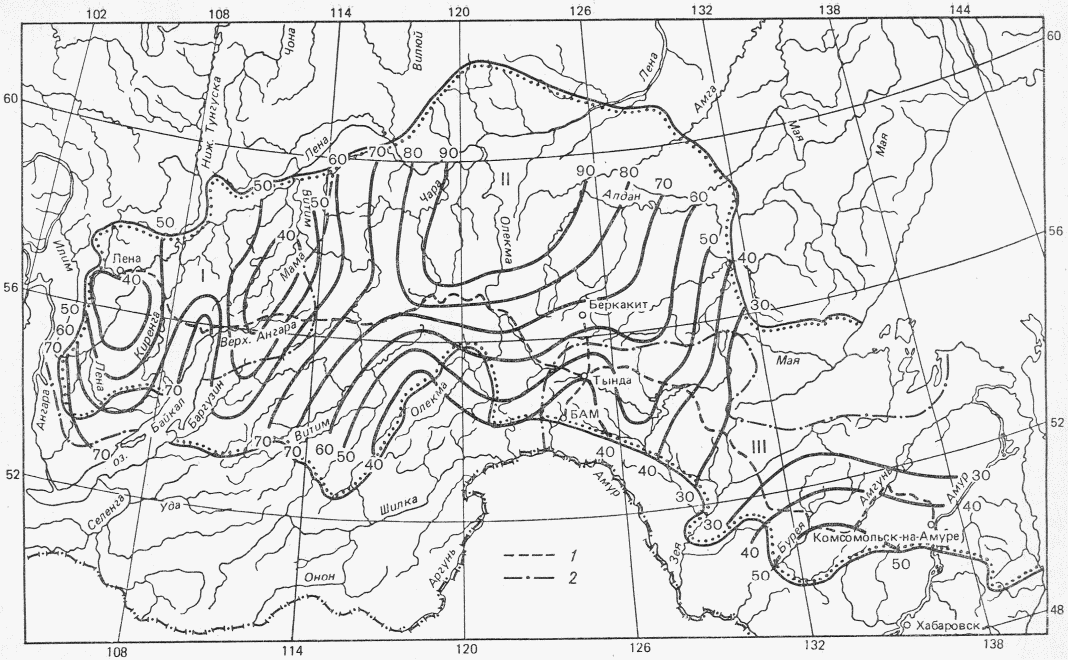
речных вод (см), приведенной к площади водосбора 5000 км2
и высоте местности 500 м абс.
1 - трасса БАМа, 2 - граница района.
Римские цифры - номера районов
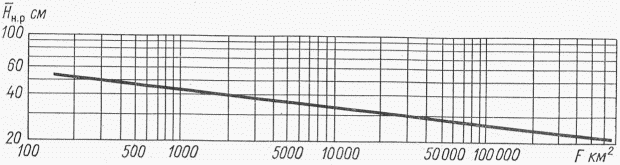
Hн.р в зависимости от площади водосбора F
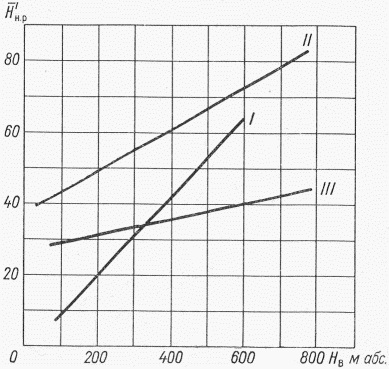
речных вод, приведенной к площади водосбора 5000 км2, 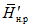
с высотой местности Hв
Цифры у линий связи - номера районов на карте рис. 6.1
Коэффициент вариации этой характеристики рассчитывается по следующему выражению [34]:
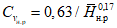 , (6.14)
, (6.14)где 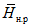 в метрах.
в метрах.
Точность расчета характеризуется следующими данными: корреляционное отношение связи 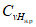 и Hн.р равно 0,92, а относительное среднее квадратическое отклонение от линии регрессии - 24,7%.
и Hн.р равно 0,92, а относительное среднее квадратическое отклонение от линии регрессии - 24,7%.
Коэффициент асимметрии мощности наледей речных вод 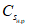 определяется в зависимости от коэффициента вариации этой характеристики по выражению
определяется в зависимости от коэффициента вариации этой характеристики по выражению
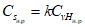 , (6.15)
, (6.15)где 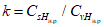 . Значения k снимаются с карты (рис. 6.4).
. Значения k снимаются с карты (рис. 6.4).
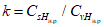 . Значения k снимаются с карты (рис. 6.4).
. Значения k снимаются с карты (рис. 6.4).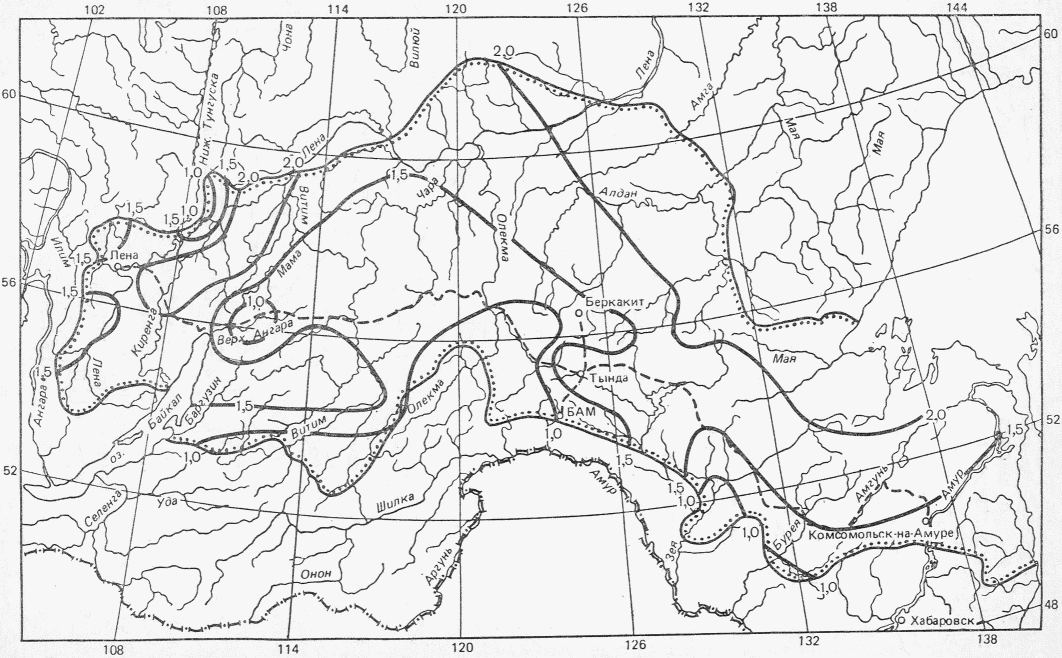
Рис. 6.4. Распределение отношения коэффициента асимметрии
к коэффициенту вариации толщины речных наледей
Распределение ежегодных значений мощности наледей речных вод подчиняется биномиальному закону и, в частности, трехпараметрическому гамма-распределению.
Вероятность (частота) образования наледей по территории и во времени определяется следующим образом:
1) Pт - вероятность образования наледи на случайно выбранном участке реки в зоне БАМа (территориальная) - определяется по табл. 6.5 и карте на рис. 6.5;
Таблица 6.5
образования наледей речных вод Pт
Номер района по карте на рис. 6.5 | Номер подрайона по карте на рис. 6.5 - бассейн главной реки | Pт |
I | Iа - бас. р. Ангары | 0,75 |
Iб - бас. р. Верхней Лены | 0,80 | |
II | IIа - бас. рек Селенги, Баргузина, Верхней Ангары | 0,90 |
IIб - бас. рек Витима, Олекмы | 0,80 | |
III | Бас. р. Алдана | 0,80 |
IV | Бас. р. Среднего и Нижнего Амура | 0,90 |
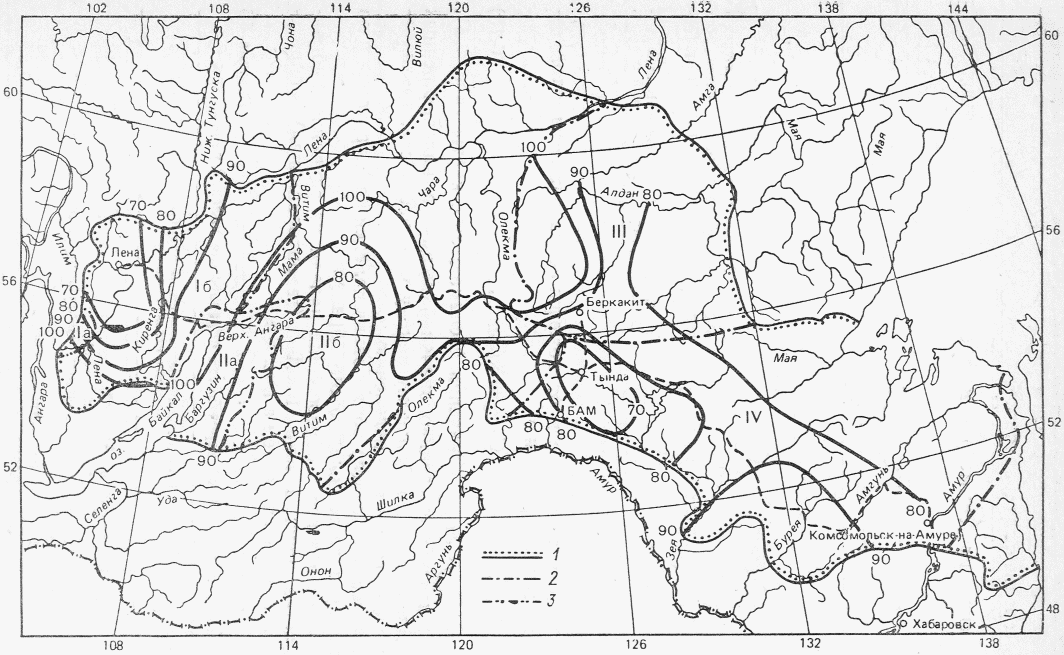
наледей речных вод, %
1 - граница зоны БАМа, 2 - граница района,
3 - граница подрайона. Римские цифры - районы и подрайоны
для определения территориальной вероятности образования
наледей речных вод по табл. 6.4
2) Pе - вероятность ежегодного образования наледи на речном участке с природными условиями, благоприятными для наледеобразования (временная) - определяется по карте на рис. 6.5;
3) Pз - вероятность образования наледи в течение зимы (временная) - определяется по графику на рис. 6.6.
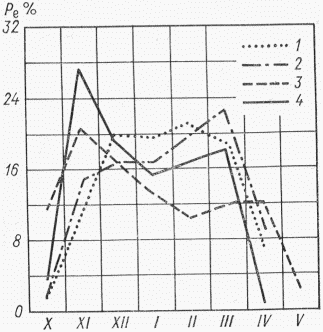
Рис. 6.6. Ежемесячная вероятность (частота) образования
наледей речных вод на средних и крупных реках Pе
1 - Забайкалье, 2 - Дальний Восток, 3 - Южная Якутия
и север Амурской области, 4 - Предбайкалье
Расчетный интервал 10 сут достаточно детально отражает гидрограф питания наледей в зимний период продолжительностью 200 - 210 сут. Средний расход питания наледей за j-тую декаду определяется по формуле
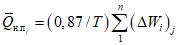 , (6.16)
, (6.16)где 0,87 - коэффициент перехода от объема льда к объему воды;
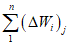 - изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.
- изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.При наличии данных только о максимальных объемах всех наледей в бассейне в конце зимы и материалов наблюдений за режимом одной-двух из них средний расход питания наледей определяется по выражению
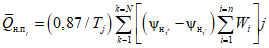 , (6.17)
, (6.17)где 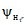 и
и 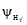 - относительные объемы наледей в долях максимального объема в конце зимы W соответственно в конце
- относительные объемы наледей в долях максимального объема в конце зимы W соответственно в конце 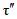 и начале
и начале 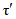 j-й декады; Tj - продолжительность декады, с; k - число задаваемых диапазонов объема наледей.
j-й декады; Tj - продолжительность декады, с; k - число задаваемых диапазонов объема наледей.
Значения 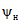 устанавливаются по данным наблюдений.
устанавливаются по данным наблюдений.
При отсутствии сведений о режиме наледеобразования и наличии данных о площади наледей в конце зимы гидрограф питания наледей рассчитывается по следующему выражению [37]:
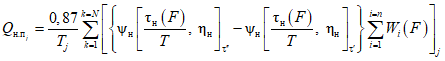 , (6.18)
, (6.18)где 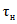 - продолжительность формирования наледей, сут;
- продолжительность формирования наледей, сут; 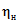 - безразмерное время, равное отношению продолжительности периода от даты начала образования наледей до границ расчетного периода
- безразмерное время, равное отношению продолжительности периода от даты начала образования наледей до границ расчетного периода 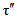 и
и 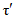 к общей продолжительности наледеобразования
к общей продолжительности наледеобразования 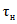 .
.
Определение параметров этого выражения производится следующим образом. Объем каждой наледи W вычисляется по связи с ее площадью - формула (6.2), табл. 6.1. Продолжительность формирования наледей зимой определяется по графику на рис. 6.7 с относительной средней квадратической ошибкой 6,7% среднего многолетнего значения 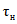 и 19,8% значений за отдельные годы. Значения относительного объема наледей на концах расчетных интервалов времени
и 19,8% значений за отдельные годы. Значения относительного объема наледей на концах расчетных интервалов времени 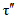 и
и 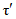 снимаются с кривой на рис. 6.8 или рассчитываются по аппроксимирующему ее уравнению
снимаются с кривой на рис. 6.8 или рассчитываются по аппроксимирующему ее уравнению
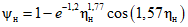 . (6.19)
. (6.19)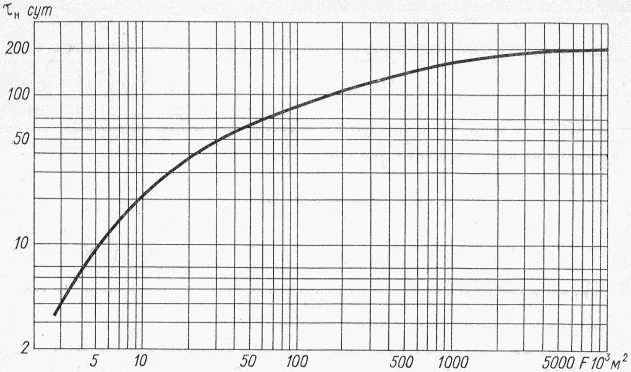
подземных вод зимой в зависимости от размеров их площадей F
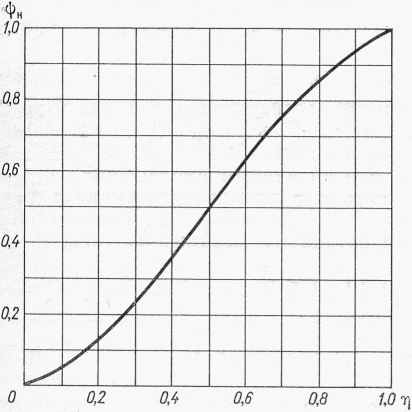
(в долях максимального объема в конце зимы W)
в относительном времени 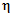 (в долях продолжительности
(в долях продолжительности
формирования наледей зимой 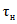 )
)
Расчет ординат гидрографа питания наледей производится в следующей последовательности. С помощью графика на рис. 6.7 по известной площади в конце зимы F определяется продолжительность формирования наледи 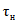 , вычисляется количество расчетных интервалов времени (в данном случае декад):
, вычисляется количество расчетных интервалов времени (в данном случае декад): 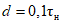 . Затем по графику рис. 6.8 определяются значения
. Затем по графику рис. 6.8 определяются значения 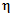 на концах расчетных интервалов времени. При этом конец предыдущей декады является началом последующей. По найденным значениям относительного времени определяются значения
на концах расчетных интервалов времени. При этом конец предыдущей декады является началом последующей. По найденным значениям относительного времени определяются значения 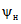 на начало и конец каждой декады, разность между которыми дает приращение объема наледи в относительном выражении на протяжении декады. Умножением полученных разностей на объем наледи вычисляются абсолютные приращения объема наледи на каждую декаду, последующий пересчет которых в средние декадные расходы питания наледи не представляет трудности.
на начало и конец каждой декады, разность между которыми дает приращение объема наледи в относительном выражении на протяжении декады. Умножением полученных разностей на объем наледи вычисляются абсолютные приращения объема наледи на каждую декаду, последующий пересчет которых в средние декадные расходы питания наледи не представляет трудности.
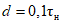 . Затем по графику рис. 6.8 определяются значения
. Затем по графику рис. 6.8 определяются значения Расчеты выполняются для каждой наледи в отдельности. Суммированием средних декадных расходов питания всех наледей в бассейне получают суммарный гидрограф в бассейне. Эти вычисления довольно трудоемки, поэтому массовые расчеты и особенно при большом количестве наледей в бассейне целесообразно производить с помощью электронно-вычислительной техники. В приложении 3 работы [37] приведена программа таких расчетов на ЭВМ по рассмотренному алгоритму.
За начало гидрографа принимается дата образования больших наледей площадью в конце зимы более 0,7 км2.
Дата начала образования больших наледей устанавливается по материалам натурных наблюдений. Если последние в районе наблюдений отсутствуют, то ориентировочно она может быть определена по табл. 6.6. Погрешность расчета суммарных расходов питания совокупностей наледей в речном бассейне по выражению (6.28) составляет 10 - 15%, а одиночных наледей - 30 - 35%.
Таблица 6.6
Средние многолетние даты образования больших наледей
подземных вод (площадью в конце зимы более 0,7 км2)
Район | Дата |
Забайкалье | 30.10 |
Север Амурской области | 15.11 |
Южная Якутия | 20.11 |
Центральная Якутия | 25.10 |
Дальний Восток | 25.11 |
и потерь зимнего стока на образование речного льда
Ледяной покров в зоне БАМа формируется из собственно речного (кристаллического) льда, который нарастает снизу (сверху вниз), и наледного (слоистого) льда, нарастающего сверху (снизу вверх) при прорывах речных вод на поверхность льда.
Гидрограф суммарных потерь зимнего речного (подземного) стока на образование ледяного покрова рек вычисляется по следующему выражению [37]:
где Qр.л - средний расход воды, равный аккумуляции речного стока в ледяном покрове рек бассейна за j-тый расчетный интервал времени, м3/с; Kj - модульный коэффициент, равный отношению приращения объема аккумуляции за расчетный интервал времени к среднему приращению по всем интервалам за весь зимний период; V - объем потерь речного стока за зиму, м3; Tj - продолжительность расчетного интервала времени, с.
Суммарный объем воды в речном льду и наледях речных вод в бассейне определяется по формуле [37]
где n и l - соответственно количество и длина равноудаленных от истоков i-тых участков русловой сети, а их произведение представляет суммарную длину этих участков в бассейне; 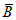 и
и 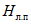 - соответственно средние ширина реки в начале ледостава и толщина ледяного покрова в конце зимы на i-том участке;
- соответственно средние ширина реки в начале ледостава и толщина ледяного покрова в конце зимы на i-том участке; 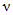 - отношение ширины ледяного покрова в конце зимы на реках с наледями к
- отношение ширины ледяного покрова в конце зимы на реках с наледями к 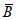 ; L - длина реки; Pт - территориальная вероятность (частота) образования наледи на случайно выбранном участке реки в бассейне.
; L - длина реки; Pт - территориальная вероятность (частота) образования наледи на случайно выбранном участке реки в бассейне.
Значения l задаются в соответствии с данными о составе речной сети бассейнов, приведенными в справочниках "Ресурсы поверхностных вод СССР", согласно которым приняты следующие расстояния от истоков до створов, замыкающих равноудаленные участки рек: 10, 25, 50, 100, 200, 300, 500 и 1000 км. Количество равноудаленных участков рассчитывается по методике Р.Е. Нежиховского [18, 22]. При недостаточности или отсутствии сведений о составе речной сети в справочниках "Ресурсы поверхностных вод СССР" расчет выполняется с использованием соотношения различных характеристик состава речной сети или их связи с гидрографическими характеристиками. Расчет количества и суммарной длины рек в принятых градациях их длин, необходимых для последующего определения числа равноудаленных створов и участков, производится по уравнениям табл. 6.7 для бассейнов рек, расположенных в определенных районах зоны БАМа (рис. 6.9). Ориентировочный расчет количества равноудаленных участков может быть выполнен методом аналогии по данным табл. 6.8.
Таблица 6.7
Nl с длиной реки L (км), суммарной длины рек 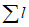 (км) с Nl,
(км) с Nl,
а также относительные средние квадратические отклонения
точек от осредняющих линий на графиках связи
Градации длин рек l км | Nl = f(L) | 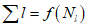 | ||
Бассейны рек района I по карте на рис. 6.9 | ||||
10 | Nl = 0,00796L2,03 | 37,1 | 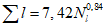 | 13,5 |
10 - 25 | Nl = 0,0000760L2,31 | 30,5 | 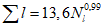 | 5,52 |
26 - 50 | Nl = 0,0000329L2,19 | 33,1 | 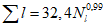 | 7,40 |
51 - 100 | Nl = 0,00000463L2,34 | 29,4 | 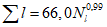 | 6,71 |
101 - 200 | Nl = 0,00000731L2,04 | 55,7 | 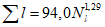 | 15,0 |
201 - 300 | Nl = 0,000165L1,42 | 18,9 | 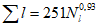 | 6,36 |
301 - 500 | Nl = 0,000489L1,24 | 56,6 | 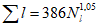 | 19,4 |
501 - 1000 | Nl = 0,0000284L1,62 | 43,1 | 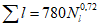 | 20,2 |
1000 | Nl = 0,00000507L1,75 | 83,6 | 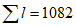 | 6,5 |
Бассейны рек района II по карте на рис. 6.9 | ||||
< 10 | Nl = 1,37L1,28 | 31,8 | 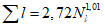 | 11,4 |
10 - 25 | Nl = 0,0598L1,34 | 31,8 | 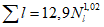 | 1,31 |
26 - 50 | Nl = 0,0110L1,33 | 26,6 | 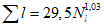 | 2,31 |
51 - 100 | Nl = 0,00197L1,41 | 20,2 | 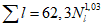 | 6,53 |
101 - 200 | Nl = 0,000380L1,47 | 59,8 | 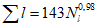 | 6,60 |
201 - 300 | Nl = 0,0000590L1,44 | 70,5 | 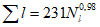 | 6,36 |
301 - 500 | Nl = 0,00000734L1,79 | 60,7 | 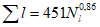 | 10,1 |
501 - 1000 | Nl = 0,00000122L1,92 | 80,0 | 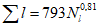 | 15,5 |
> 1000 | Nl = 0,000000102L2,17 | 37,5 | 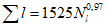 | 19,7 |
Бассейны рек района III по карте на рис. 6.9 | ||||
< 10 | Nl = 0,0024L2,06 | 47,8 | 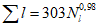 | 10,9 |
10 - 25 | Nl = 0,00014L2,24 | 37,9 | 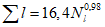 | 2,1 |
26 - 50 | Nl = 0,0000025L2,56 | 43,0 | 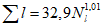 | 3,4 |
51 - 100 | Nl = 0,0000068L2,26 | 35,0 | 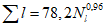 | 3,6 |
101 - 200 | Nl = 0,0000036L2,21 | 76,3 | 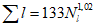 | 9,2 |
201 - 300 | Nl = 0,0000026L2,07 | 32,6 | 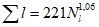 | 8,7 |
301 - 500 | Nl = 0,0000063L1,88 | 49,8 | 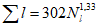 | 7,4 |
501 - 1000 | Nl = 0,0000021L1,95 | 56,7 | 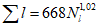 | 14,4 |
> 1000 | Nl = 0,00000088L1,95 | 32,6 | 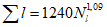 | 14,7 |
Бассейны рек района IV по карте на рис. 6.9 | ||||
< 10 | Nl = 0,0315L1,94 | 56,9 | 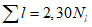 | 22,8 |
10 - 25 | Nl = 0,00335L1,82 | 25,3 | 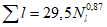 | 7,44 |
26 - 50 | Nl = 0,000400L1,88 | 23,3 | 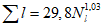 | 5,32 |
51 - 100 | Nl = 0,000148L1,84 | 48,7 | 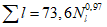 | 7,82 |
101 - 200 | Nl = 0,0000246L1,96 | 75,6 | 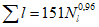 | 7,60 |
201 - 300 | Nl = 0,00000107L2,16 | 76,9 | 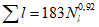 | 12,5 |
301 - 500 | Nl = 0,000000039L2,65 | 61,6 | 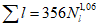 | 10,5 |
501 - 1000 | Nl = 0,00000455L1,84 | 45,3 | 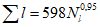 | 8,46 |
> 1000 | Nl = 0,00000022L2,12 | 22,9 | 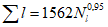 | 16,7 |
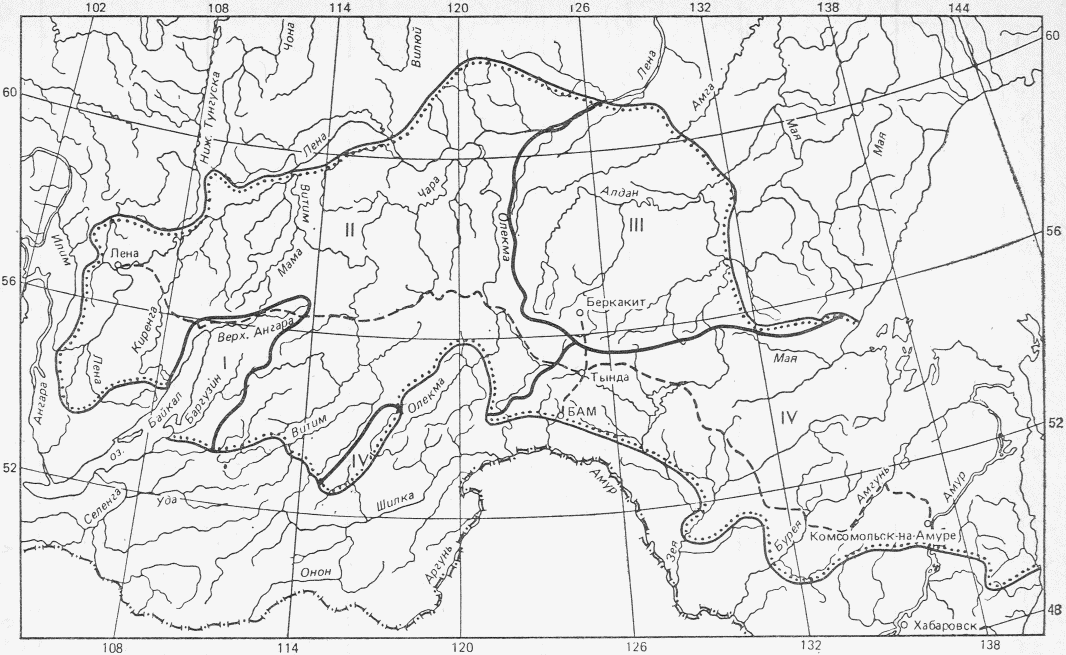
речных бассейнов Ne, 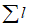 , B, Hр и толщины ледяного
, B, Hр и толщины ледяного
Таблица 6.8
в некоторых бассейнах зоны БАМа
Река - створ | Градации длин участков, км | |||||||||
10 | 0 - 10 | 10 - 25 | 25 - 50 | 50 - 100 | 100 - 200 | 200 - 300 | 300 - 500 | 500 - 1000 | 1000 | |
Туолба - устье | 48,4 | 10,6 | 6,39 | 1,33 | 0,25 | 0,063 | 0,063 | 0,063 | ||
Ботома - устье | 66 6 | 7,62 | 4,76 | 1,11 | 0,16 | 0,079 | 0,079 | 0,079 | ||
Алдан - устье р. Учур | 106 | 7,92 | 4,78 | 1,12 | 0,42 | 0,15 | 0,042 | 0,017 | 0,017 | 0,0083 |
Алдан - устье | 148 | 8,15 | 4,94 | 1,13 | 0,36 | 0,12 | 0,044 | 0,019 | 0,0082 | 0,0041 |
Тимптон - устье | 143 | 8,04 | 4,86 | 1,13 | 0,43 | 0,16 | 0,045 | 0,022 | 0,022 | |
Учур - устье | 135 | 8,88 | 5,30 | 1,10 | 0,23 | 0,11 | 0,053 | 0,035 | 0,018 | |
Витим - устье | 77,1 | 8,52 | 5,09 | 1,08 | 0,33 | 0,098 | 0,044 | 0,027 | 0,0088 | |
Олекма - устье Нюкжи (без Нюкжи) | 137 | 10,0 | 5,91 | 1,12 | 0,32 | 0,11 | 0,038 | 0,025 | 0,012 | 0,0044 |
Олекма - устье | 92,8 | 8,61 | 5,17 | 1,12 | 0,33 | 0,10 | 0,038 | 0,024 | 0,0095 | 0,0047 |
Верхняя Ангара - устье | 98,4 | 8,64 | 5,14 | 1,03 | 0,37 | 0,14 | 0,093 | 0,047 | ||
Баргузин - устье | 111 | 9,52 | 5,78 | 1,42 | 0,47 | 0,19 | 0,095 | 0,047 | ||
Селенга | 35,7 | 2,94 | 1,80 | 0,41 | 0,10 | 0,036 | 0,018 | 0,011 | 0,0044 | 0,0022 |
Джида - устье | 70,9 | 6,55 | 4,25 | 1,19 | 0,38 | 0,17 | 0,085 | 0,085 | 0,042 | |
Чикой | 150 | 6,90 | 4,07 | 0,86 | 0,28 | 0,086 | 0,043 | 0,043 | 0,022 | |
Хилок | 83,2 | 9,09 | 5,79 | 1,48 | 0,31 | 0,10 | 0,052 | 0,052 | 0,026 | |
Уда | 60,8 | 9,22 | 5,55 | 1,15 | 0,29 | 0,14 | 0,057 | 0,029 | ||
Аргунь - устье | 66,2 | 7,02 | 3,99 | 0,61 | 0,20 | 0,10 | 0,061 | 0,041 | 0,020 | |
Шилка - устье | 64,5 | 7,19 | 4,27 | 0,85 | 0,23 | 0,073 | 0,029 | 0,019 | 0,0097 | 0,0048 |
Зея - устье | 121 | 8,06 | 5,00 | 1,31 | 0,48 | 0,18 | 0,054 | 0,026 | 0,0085 | 0,0042 |
Селемджа - устье | 153 | 8,78 | 5,36 | 1,33 | 0,47 | 0,15 | 0,058 | 0,029 | 0,014 | |
Бурея - устье | 224 | 8,92 | 5,36 | 1,20 | 0,45 | 0,17 | 0,042 | 0,028 | 0,014 | |
Уссури - устье | 169 | 6,85 | 4,06 | 0,82 | 0,24 | 0,078 | 0,031 | 0,021 | 0,010 | |
Тунгуска - устье | 216 | 10,3 | 6,16 | 1,29 | 0,46 | 0,20 | 0,066 | 0,066 | 0,033 | |
Горин - устье | 279 | 10,5 | 6,25 | 1,34 | 0,45 | 0,18 | 0,089 | 0,045 | ||
Амгунь - устье | 195 | 10,4 | 6,17 | 1,17 | 0,28 | 0,10 | 0,034 | 0,034 | 0,017 | |
Характеристики состава и протяженности русловой сети бассейна остаются неизменными при расчете и ежегодных, и средних многолетних значений потерь зимнего стока на образование ледяного покрова рек и наледей речных вод.
Значения B и Hл.п для каждого равноудаленного участка в бассейне определяются в зависимости от местоположения его от истока, т.е. от длины реки:
где B и Hл.п - в метрах, L - в километрах.
Параметры выражений (6.22) определяются по материалам наблюдений на сети станций и постов - ежегодных или средних многолетних. Например, в табл. 6.9 приведены значения параметров для ежегодной толщины ледяного покрова по восточной части зоны БАМа (район IV по рис. 6.9) за 1956 - 1979 гг. В отдельные годы связь толщины ледяного покрова с длиной реки отсутствует вследствие более равномерного распределения зимней температуры и толщины снежного покрова по территории. В соответствующей строчке табл. 6.9 параметр n2 = 0, а значения 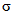 характеризуют среднее квадратическое отклонение толщины ледяного покрова в пунктах наблюдений от средней арифметической толщины по району.
характеризуют среднее квадратическое отклонение толщины ледяного покрова в пунктах наблюдений от средней арифметической толщины по району.
Таблица 6.9
Значения параметров уравнения (6.22) и средние
квадратические отклонения точек от линий регрессии 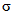
для толщины ледяного покрова в районе III (см. рис. 6.9)
Зима | a2 | n2 | Зима | a2 | n2 | ||
1956 - 57 | 0,88 | 0 | 22 | 1969 - 70 | 0,22 | 0,29 | 44 |
1957 - 58 | 1,05 | 0 | 27 | 1970 - 71 | 0,44 | 0,17 | 20 |
1958 - 59 | 1,05 | 0 | 29 | 1971 - 72 | 0,45 | 0,15 | 28 |
1959 - 60 | 1,00 | 0 | 24 | 1972 - 73 | 0,61 | 0,08 | 34 |
1960 - 61 | 0,47 | 0,16 | 23 | 1973 - 74 | 0,53 | 0,10 | 34 |
1961 - 62 | 0,51 | 0,09 | 15 | 1974 - 75 | 0,75 | 0,06 | 19 |
1962 - 63 | 0,83 | 0,03 | 22 | 1975 - 76 | 0,62 | 0,10 | 30 |
1963 - 64 | 0,83 | 0 | 25 | 1976 - 77 | 0,83 | 0 | 40 |
1964 - 65 | 0,95 | 0 | 18 | 1977 - 78 | 0,95 | 0 | 35 |
1965 - 66 | 0,28 | 0,26 | 29 | 1978 - 79 | 0,85 | 0 | 38 |
1966 - 67 | 0,36 | 0,19 | 28 | ||||
1967 - 68 | 0,42 | 0,18 | 29 | Вес период 1956 - 1979 | 0,54 | 0,10 | 22 |
1968 - 69 | 0,33 | 0,20 | 33 |
При расчетах средних многолетних объемов потерь зимнего стока на образование ледяного покрова рек по всей зоне БАМа значения параметров выражений (6.22) берут из табл. 6.10. Там же приведены уравнения для расчета глубины рек в начале ледостава, которая может быть использована для приближенного определения толщины ледяного покрова при недостаточности или отсутствии сведений об этой характеристике на перемерзающих реках.
Таблица 6.10
суммарной толщины речного льда и наледей речных вод в конце
зимы Hл.п (м) и глубины реки в начале ледостава Hр (м)
с длиной реки L (км), а также относительные средние
квадратические отклонения точек от осредняющих линий
на графиках связи 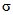 (по средним многолетним данным)
(по средним многолетним данным)
Вид уравнения связи | Бассейны рек р-на I по карте на рис. 6.9 | Бассейны рек р-на II по карте на рис. 6.9 | ||
Уравнение связи | Уравнение связи | |||
B = f(L) | B = 0,28L1,08 | 38,8 | B = 0,12L1,19 | 24,7 |
Hл.п = f(L) | Hл.п = 0,60L0,11 | 30,4 | Hл.п = 0,36L0,16 | 42,0 |
Hр = f(L) | Hр = 0,12L0,94 | 23,8 | Hр = 0,0095L0,84 | 37,7 |
Вид уравнения связи | Бассейны рек р-на III по карте на рис. 6.9 | Бассейны рек р-на IV по карте на рис. 6.9 | ||
Уравнение связи | Уравнение связи | |||
B = f(L) | B = 0,12L1,18 | 46,7 | B = 0,086L1,29 | 30,4 |
Hл.п = f(L) | Hл.п = 0,25L0,20 | 35,2 | Hл.п = 0,60L0,11 | 30,4 |
Hр = f(L) | Hр = 0,016L0,78 | 52,7 | Hр = 0,029L0,71 | 27,6 |
В практических расчетах рекомендуется пользоваться табл. 6.11, где помещены данные о ширине и глубине рек в начале ледостава, а также о толщине ледяного покрова в конце зимы, рассчитанные по уравнениям табл. 6.10 по участкам в принятых градациях длин рек. Эти данные соответствуют расчетным створам, расположенным на середине речных участков.
Таблица 6.11
Ширина 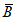 , глубина
, глубина 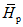 рек в начале ледостава и толщина льда
рек в начале ледостава и толщина льда
в конце зимы 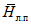 (по средним многолетним данным)
(по средним многолетним данным)
Номер района по карте на рис. 6.9 | Характеристика | Удаленность участка от истока реки, км | |||||||||
10 | 0 - 10 | 10 - 25 | 25 - 50 | 50 - 100 | 100 - 200 | 200 - 300 | 300 - 500 | 500 - 1000 | 1000 | ||
I | 0,28 | 1,50 | 5,80 | 13,7 | 28,5 | 63,0 | 110 | 180 | 360 | ||
0,013 | 0,060 | 0,17 | 0,36 | 0,67 | 1,30 | 2,19 | 3,20 | 5,60 | |||
0,60 | 0,72 | 0,82 | 0,90 | 0,98 | 1,08 | 1,10 | 1,20 | 1,25 | |||
II | 0,17 | 0,85 | 3,60 | 9,20 | 21,0 | 48,0 | 90,0 | 150 | 320 | ||
0,011 | 0,036 | 0,10 | 0,19 | 0,34 | 0,62 | 0,95 | 1,40 | 2,40 | |||
0,19 | 0,28 | 0,41 | 0,50 | 0,62 | 0,75 | 0,88 | 1,00 | 1,20 | |||
III | 0,38 | 0,80 | 3,40 | 8,50 | 18,5 | 42,0 | 75,0 | 130 | 275 | 720 | |
0,12 | 0,13 | 0,18 | 0,26 | 0,39 | 0,65 | 0,92 | 1,30 | 2,30 | 7,0 | ||
0,81 | 0,36 | 0,42 | 0,51 | 0,60 | 0,70 | 0,78 | 0,85 | 0,95 | 1,20 | ||
IV | 0,090 | 0,60 | 3,10 | 8,50 | 22,0 | 55,0 | 110 | 200 | 450 | ||
0,044 | 0,11 | 0,25 | 0,42 | 0,67 | 1,10 | 1,50 | 2,10 | 3,20 | |||
0,60 | 0,72 | 0,82 | 0,90 | 0,98 | 1,08 | 1,10 | 1,20 | 1,25 | |||
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду формула (6.21), а не формула (6.1). |
Параметр 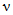 в формуле (6.1), по существу представляющий поправочный коэффициент B в начале ледостава на участках рек с наледными явлениями, определяется по графику рис. 6.10 при расчетах ежегодных и средних многолетних значений потерь зимнего стока.
в формуле (6.1), по существу представляющий поправочный коэффициент B в начале ледостава на участках рек с наледными явлениями, определяется по графику рис. 6.10 при расчетах ежегодных и средних многолетних значений потерь зимнего стока.
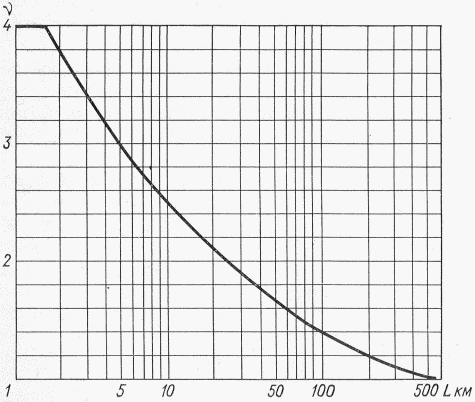
Рис. 6.10. Изменение отношения ширины ледяного покрова
в конце зимы к ширине рек в начале ледостава
Параметр Pт в формуле (6.21) - территориальная вероятность образования наледи на случайно выбранном участке реки - является числовой характеристикой, отражающей и ту часть общего количества рек (и их участков), на которых наблюдаются наледные явления и для которых определяется параметр 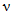 . Значения Pт берут из табл. 6.5 с помощью карты на рис. 6.5. Они определены для средних многолетних условий, но могут быть использованы и при ориентировочных расчетах ежегодных потерь зимнего стока на ледообразование. Погрешность расчета объема потерь рассмотренным методом составляет 35 - 40% [37].
. Значения Pт берут из табл. 6.5 с помощью карты на рис. 6.5. Они определены для средних многолетних условий, но могут быть использованы и при ориентировочных расчетах ежегодных потерь зимнего стока на ледообразование. Погрешность расчета объема потерь рассмотренным методом составляет 35 - 40% [37].
Средний многолетний объем значений V для любого бассейна в зоне БАМа определяется по карте на рис. 6.11 и графику на рис. 6.12 для массовых расчетов при региональных исследованиях. Порядок расчета следующий. По карте на рис. 6.11 в точке, соответствующей центру водосбора (для малых рек), или путем взвешивания площадей между соседними изолиниями в пределах водосбора (для средних и крупных рек) определяют слой потерь зимнего стока, приведенный к площади водосбора 10 000 км2. Это значение потерь отмечают на графике (рис. 6.12), затем сносят параллельно наклонной линии до фактического значения площади водосбора и по вертикальной шкале определяется искомый результат.
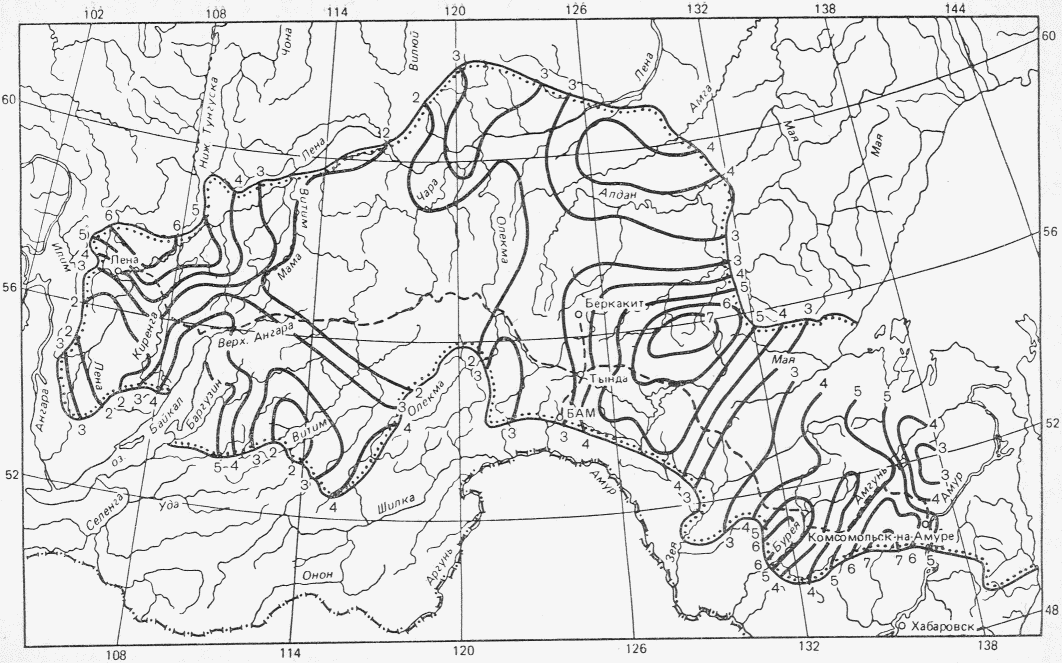
Рис. 6.11. Карта слоя потерь зимнего стока на образование
ледяного покрова рек, приведенного к площади 10 000 км2, мм
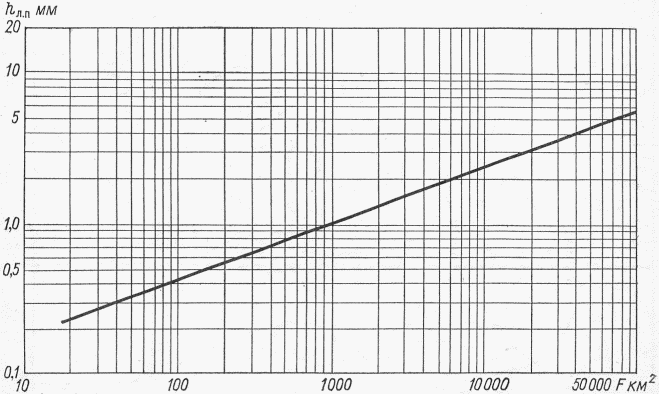
ледяного покрова рек hл.п от площади водосбора.
Гидрограф потерь зимнего стока на образование ледяного покрова рек рассчитывается по выражению (6.20). Учитывая специфику этих расчетов, связанную с использованием осредненных характеристик ледяного покрова и ширины русла по длине рек, а также их еще сравнительно невысокую точность, в качестве расчетного интервала времени целесообразно использовать месяц. Значения Kj устанавливают по материалам наблюдений за интенсивностью нарастания толщины ледяного покрова на сети гидрометеорологических станций и постов: 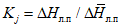 , где
, где 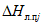 и
и 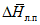 - соответственно приращение толщины льда за j-тый интервал времени и среднее значение по интервалам за весь зимний период.
- соответственно приращение толщины льда за j-тый интервал времени и среднее значение по интервалам за весь зимний период.
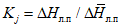 , где
, где Ориентировочные средние значения этого параметра за многолетний период по отдельным районам зоны БАМа приведены в табл. 6.12.
Таблица 6.12
Средние многолетние значения модульных коэффициентов
для расчета гидрографа потерь зимнего речного стока
на образование ледяного покрова рек по выражению (6.20)
Номер района по карте на рис. 6.9 | X | XI | XII | I | II | III | IV |
I | 1,86 | 1,28 | 1,14 | 0,85 | 0,10 | ||
II | 1,88 | 1,88 | 1,09 | 0,94 | 0,78 | 0,31 | 0,16 |
III | 2,02 | 1,60 | 0,93 | 0,71 | 0,42 | 0,18 | |
IV | 1,74 | 1,39 | 1,00 | 0,73 | 0,32 |
Суммарный объем потерь стока рек в бассейне, израсходованного к концу зимы на аккумуляцию в наледях речных вод, рассчитывается по рассмотренной методике. Единственное отличие заключается в том, что вместо Hл.п в уравнение (6.21) подставляется Hн.р - толщина наледей этого типа, средние многолетние значения которой определяют по следующей формуле:
Hн.р = 0,693/L0,214, (6.23)
где Hн.р - в сантиметрах, L - в километрах.
Методика расчета толщины речных наледей заданной обеспеченности рассмотрена в разд. 6.2.
Расчетный интервал 10 сут достаточно детально отражает гидрограф наледного стока при таянии наледей подземных вод в теплое время года продолжительностью 120 - 140 сут. За начало таяния льда, а следовательно, и гидрографа 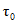 принимается дата устойчивого перехода среднесуточной температуры воздуха через 0 °C к положительным ее значениям. Средний расход наледного стока за j-тую декаду от начала таяния равен
принимается дата устойчивого перехода среднесуточной температуры воздуха через 0 °C к положительным ее значениям. Средний расход наледного стока за j-тую декаду от начала таяния равен
где 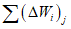 - изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.
- изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.
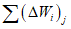 - изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.
- изменение суммарного объема n наледей в бассейне за j-тую декаду продолжительностью T.Формула (6.24) позволяет рассчитать гидрограф наледного стока при наличии данных об объеме каждой наледи в речном бассейне и интенсивности его уменьшения летом как в среднем многолетнем разрезе, так и за конкретные годы. При наличии данных только о площади наледей в бассейне в конце зимы и режиме стаивания и разрушения одной-двух из них гидрограф наледного стока рассчитывается по следующему выражению:
где Fi - площадь каждой из n наледей в бассейне в конце холодного периода года, м2; P - безразмерный параметр, учитывающий динамику уменьшения площади наледи в результате стаивания льда с ее поверхности; hj - слой стаивания льда с поверхности i-той наледи за j-тую декаду, м; 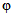 - безразмерный параметр, учитывающий динамику уменьшения площади наледи в результате водной эрозии; Hi - мощность каждой из n наледей в конце зимы, м; Kн - безразмерный параметр, характеризующий изменение средней мощности наледей за теплый период;
- безразмерный параметр, учитывающий динамику уменьшения площади наледи в результате водной эрозии; Hi - мощность каждой из n наледей в конце зимы, м; Kн - безразмерный параметр, характеризующий изменение средней мощности наледей за теплый период; 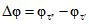 , где
, где 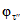 и
и 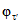 - значения параметра
- значения параметра 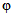 в конце
в конце 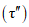 и начале
и начале 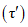 расчетного интервала времени.
расчетного интервала времени.
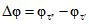 , где
, где Определение параметров в формуле (6.25) производится следующим образом.
Средняя мощность наледей в конце зимы H определяется в соответствии с рекомендациями, приведенными в разд. 6.2.
Расчет hj при наличии данных актинометрических и метеорологических наблюдений на наледи или около нее выполняется по следующей формуле:
где 86 400 - число секунд в сутках;  - плотность льда наледей, равная 870 кг/м3; Lп.л - удельная теплота плавления пресноводного льда при 0 °C и нормальном атмосферном давлении, равная 334 кДж/кг; R - радиационный баланс наледи, Вт/м2; Pа - турбулентный теплообмен с атмосферой, Вт/м2; LE - тепловой эквивалент испарения (-LE) или конденсации (+LE) водяного пара на поверхности наледи, Вт/м2. Здесь L = 2,48·10-3 кДж/кг - удельная теплота фазового перехода процесса испарения (конденсации).
- плотность льда наледей, равная 870 кг/м3; Lп.л - удельная теплота плавления пресноводного льда при 0 °C и нормальном атмосферном давлении, равная 334 кДж/кг; R - радиационный баланс наледи, Вт/м2; Pа - турбулентный теплообмен с атмосферой, Вт/м2; LE - тепловой эквивалент испарения (-LE) или конденсации (+LE) водяного пара на поверхности наледи, Вт/м2. Здесь L = 2,48·10-3 кДж/кг - удельная теплота фазового перехода процесса испарения (конденсации).
Радиационный баланс наледи и его составляющие могут быть определены по исходным данным трех видов: 1) материалам актинометрических и специальных наблюдений на наледи; 2) материалам актинометрических наблюдений вне наледи, в том числе на ближайшей актинометрической станции и 3) метеорологическим данным ближайшей метеостанции.
1. При наличии актинометрических и специальных наблюдений на наледи радиационный баланс рассчитывается по следующей формуле:
Rj = Qj(1 - Aj - Eэфj - Qнj), (6.27)
где Qj - суммарная солнечная радиация, Вт/м2; Aj - альбедо поверхности наледи, в долях единицы; Eэфj - эффективное излучение, Вт/м2; Qнj - часть коротковолновой радиации, поглощенная поверхностью льда и проникшая через толщу наледи Hн.п. Составляющие Qj и Eэфj определяются по методике, изложенной в Руководстве [29].
Альбедо поверхностей наледей не зависит от высоты солнца и условий освещенности, а также от высоты местоположения наледных массивов [10]. В течение теплого сезона оно изменяется закономерным образом в соответствии с изменением соотношения основных типов микрорельефа поверхности наледей.
При наличии материалов наблюдений среднее значение альбедо по площади наледи определяется по формуле (6.28) с погрешностью, не превышающей 3 - 5% [10]:
где 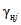 - доля площади наледи с насыщенными талой водой понижениями в середине j-той декады;
- доля площади наледи с насыщенными талой водой понижениями в середине j-той декады; 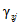 - доля площади наледи на тот же момент времени, загрязненная наносами со склона или при выходе речных вод на лед во время половодья и паводков. Параметры
- доля площади наледи на тот же момент времени, загрязненная наносами со склона или при выходе речных вод на лед во время половодья и паводков. Параметры 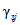 и
и  определяются по материалам специальных наблюдений на наледи или по аэрофотоснимкам.
определяются по материалам специальных наблюдений на наледи или по аэрофотоснимкам.
В случае отсутствия данных натурных наблюдений за микрорельефом поверхности льда среднее по площади наледи альбедо может быть определено двумя способами, в которых не учитывается загрязненность наледи наносами, что несколько снижает точность определения Aj.
В соответствии с первым способом альбедо определяется по табл. 6.13.
Таблица 6.13
занятой насыщенными водой понижениями  , в безразмерном
, в безразмерном
времени, выраженном в долях единицы продолжительности
периода таяния наледи 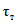 (остальные обозначения в тексте)
(остальные обозначения в тексте)
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
Aj | 0,46 | 0,46 | 0,46 | 0,46 | 0,47 | 0,51 | 0,54 | 0,55 | 0,55 |
0,12 | 0,37 | 0,39 | 0,37 | 0,33 | 0,26 | 0,15 | 0,06 | 0,01 |
Здесь 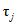 - середина j-той декады в период таяния наледи. Значения
- середина j-той декады в период таяния наледи. Значения 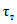 определяются по табл. 6.14 в зависимости от площади наледи в конце зимы.
определяются по табл. 6.14 в зависимости от площади наледи в конце зимы.
Таблица 6.14
Продолжительность таяния и разрушения наледей 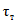 (сут)
(сут)
в зависимости от размеров их площадей F (тыс. м2)
в конце зимы
F | F | F | F | ||||
1 | 49 | 200 | 74 | 700 | 105 | 3 000 | 132 |
10 | 50 | 250 | 79 | 800 | 108 | 4 000 | 134 |
20 | 53 | 300 | 84 | 900 | 112 | 5 000 | 136 |
30 | 55 | 350 | 88 | 1000 | 114 | 6 000 | 137 |
50 | 58 | 400 | 91 | 1200 | 118 | 7 000 | 137 |
75 | 61 | 450 | 94 | 1400 | 121 | 8 000 | 138 |
100 | 64 | 500 | 97 | 1600 | 123 | 9 000 | 138 |
120 | 66 | 550 | 99 | 1800 | 125 | 10 000 | 138 |
140 | 68 | 600 | 102 | 2000 | 127 | 15 000 | 139 |
160 | 71 | 650 | 104 | 2500 | 130 | 20 000 | 140 |
По второму способу альбедо рассчитывается как средневзвешенное по типам микрорельефа поверхности наледи по выражению
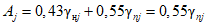 , (6.29)
, (6.29)где 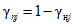 - доля площади наледи с положительными и отрицательными ненасыщенными водой формами микрорельефа поверхности льда. Значения
- доля площади наледи с положительными и отрицательными ненасыщенными водой формами микрорельефа поверхности льда. Значения  определяются по табл. 6.13.
определяются по табл. 6.13.
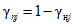 - доля площади наледи с положительными и отрицательными ненасыщенными водой формами микрорельефа поверхности льда. Значения
- доля площади наледи с положительными и отрицательными ненасыщенными водой формами микрорельефа поверхности льда. Значения Прошедшая через наледь радиация определяется по выражению
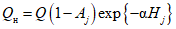 , (6.30)
, (6.30)где 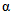 - коэффициент экстинции, характеризующий интенсивность уменьшения поглощенной радиации Q(1 - Aj) в толще наледи, 1/см; Hj - средняя мощность наледи за j-тую декаду, см.
- коэффициент экстинции, характеризующий интенсивность уменьшения поглощенной радиации Q(1 - Aj) в толще наледи, 1/см; Hj - средняя мощность наледи за j-тую декаду, см.
Коэффициент экстинции определяется в зависимости от средней мощности наледи по следующему выражению:
 (6.31)
(6.31)где 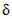 - мощность коры таяния, см; zпр - предельная глубина, ниже которой
- мощность коры таяния, см; zпр - предельная глубина, ниже которой 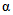 практически не меняется, zпр ~= 100 см; a и n - параметры для средних условий освещенности, равные соответственно 0,16 и 0,41.
практически не меняется, zпр ~= 100 см; a и n - параметры для средних условий освещенности, равные соответственно 0,16 и 0,41.
При средней мощности наледи Hj < 100 см.
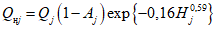 , (6.32)
, (6.32)при Hj >= 100 см
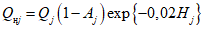 . (6.33)
. (6.33)Глубже 1,0 м в лед проникает менее 10% радиации, поглощенной наледью, поэтому в практических расчетах учет Qн нецелесообразен при средней мощности наледи более 1,0 м.
2. Если актинометрические наблюдения проведены вне наледи, в том числе на ближайшей актинометрической станции, то составляющие радиационного баланса рассчитываются следующим образом. Средняя за j-тую декаду интенсивность суммарной радиации на наледи принимается равной данной характеристике, полученной на актинометрической площадке вне наледи.
Эффективное излучение наледи (в Вт/м2) определяется по формуле
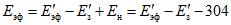 , (6.34)
, (6.34)где 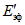 и
и 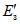 - эффективное излучение и собственное излучение поверхности на площадке актинометрической станции; Eн - собственное длинноволновое излучение наледи, равное 304 Вт/м2 при постоянной абсолютной температуре ее поверхности Tн = 273,16 К и коэффициенте серости льда
- эффективное излучение и собственное излучение поверхности на площадке актинометрической станции; Eн - собственное длинноволновое излучение наледи, равное 304 Вт/м2 при постоянной абсолютной температуре ее поверхности Tн = 273,16 К и коэффициенте серости льда 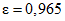 .
.
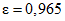 .
.Остальные характеристики радиационного режима наледи определяются по изложенной выше методике.
3. В случае отсутствия актинометрических наблюдений радиационный баланс рассчитывается по метеорологическим данным ближайшей метеостанции по формуле [4]
где Q0j - суммарная радиация при безоблачном небе в j-тую декаду, определяется по табл. 6.15 в зависимости от широты места; n - среднее декадное значение общей облачности, в долях единицы; a, b, c - числовые параметры в поправках на облачность, b = 0,38, a и c определяются по табл. 6.16; 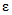 - коэффициент серости тающего льда;
- коэффициент серости тающего льда; 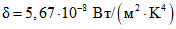 - постоянная Стефана-Больцмана; T2,0 - температура воздуха на уровне 2,0 м, K; t2,0 и tн - средняя декадная температура воздуха в j-тую декаду и температура поверхности наледи, °C; e2,0 - среднее за j-тую декаду парциальное давление водяного пара, гПа.
- постоянная Стефана-Больцмана; T2,0 - температура воздуха на уровне 2,0 м, K; t2,0 и tн - средняя декадная температура воздуха в j-тую декаду и температура поверхности наледи, °C; e2,0 - среднее за j-тую декаду парциальное давление водяного пара, гПа.
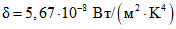 - постоянная Стефана-Больцмана; T2,0 - температура воздуха на уровне 2,0 м, K; t2,0 и tн - средняя декадная температура воздуха в j-тую декаду и температура поверхности наледи, °C; e2,0 - среднее за j-тую декаду парциальное давление водяного пара, гПа.
- постоянная Стефана-Больцмана; T2,0 - температура воздуха на уровне 2,0 м, K; t2,0 и tн - средняя декадная температура воздуха в j-тую декаду и температура поверхности наледи, °C; e2,0 - среднее за j-тую декаду парциальное давление водяного пара, гПа.Таблица 6.15
Суммарная солнечная радиация Q0 на горизонтальную
поверхность на уровне моря при альбедо, равном нулю,
в зависимости от широты местности, Вт/м2
Месяц | Декада | Градусы северной широты | |||||||
48 | 50 | 52 | 54 | 56 | 58 | 60 | 62 | ||
III | 1 | 167 | 157 | 147 | 136 | 128 | 118 | 108 | 98 |
2 | 188 | 179 | 170 | 162 | 152 | 143 | 134 | 124 | |
3 | 214 | 206 | 198 | 190 | 181 | 172 | 163 | 154 | |
IV | 1 | 241 | 233 | 225 | 218 | 210 | 201 | 192 | 183 |
2 | 260 | 255 | 249 | 243 | 237 | 230 | 222 | 215 | |
3 | 282 | 277 | 271 | 264 | 260 | 255 | 250 | 245 | |
V | 1 | 298 | 294 | 290 | 286 | 282 | 279 | 275 | 271 |
2 | 312 | 311 | 307 | 304 | 301 | 299 | 297 | 293 | |
3 | 323 | 321 | 319 | 318 | 316 | 314 | 313 | 311 | |
VI | 1 | 330 | 329 | 328 | 328 | 327 | 327 | 327 | 327 |
2 | 334 | 334 | 333 | 333 | 333 | 333 | 333 | 334 | |
3 | 334 | 334 | 333 | 333 | 333 | 333 | 333 | 334 | |
VII | 1 | 328 | 327 | 325 | 324 | 323 | 323 | 323 | 323 |
2 | 320 | 319 | 317 | 316 | 314 | 313 | 313 | 312 | |
3 | 308 | 305 | 301 | 300 | 297 | 295 | 293 | 291 | |
VIII | 1 | 294 | 290 | 285 | 282 | 278 | 275 | 273 | 271 |
2 | 276 | 272 | 267 | 263 | 258 | 254 | 249 | 243 | |
3 | 257 | 249 | 241 | 236 | 232 | 227 | 222 | 217 | |
IX | 1 | 234 | 228 | 221 | 213 | 205 | 199 | 193 | 187 |
2 | 211 | 204 | 197 | 188 | 180 | 172 | 164 | 155 | |
3 | 185 | 178 | 170 | 161 | 153 | 145 | 137 | 129 | |
X | 1 | 163 | 154 | 145 | 137 | 129 | 121 | 112 | 103 |
2 | 143 | 134 | 124 | 115 | 106 | 97 | 87 | 79 | |
3 | 121 | 111 | 102 | 93 | 83 | 73 | 63 | 53 | |
Таблица 6.16
Значения коэффициентов формулы (6.35)
для расчета поправок на облачность
Параметр | Градусы северной широты | |||||||
48 | 50 | 52 | 54 | 56 | 58 | 60 | 68 | |
a | 0,40 | 0,40 | 0,40 | 0,40 | 0,39 | 0,38 | 0,36 | 0,33 |
c | 0,71 | 0,72 | 0,73 | 0,74 | 0,74 | 0,75 | 0,76 | 0,77 |
При наличии данных об облачности разных ярусов параметр c вычисляется по формуле [3]
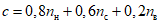 , (6.36)
, (6.36)где nн, nс, nв - количество облаков нижнего, среднего и верхнего ярусов. В случае отсутствия достаточно надежных данных об облачности разных ярусов в расчете могут быть использованы осредненные поправки из табл. 6.17.
Таблица 6.17
Поправка на облачность к эффективному излучению
N = 1 - cn = 1 - (0,8nн + 0,65nс + 0,25nв)n
(по М.В. Завариной [30])
nн | n | ||||||||||
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
0,0 | 1,00 | 1,00 | 0,99 | 0,98 | 0,96 | 0,94 | 0,91 | 0,87 | 0,84 | 0,80 | 0,75 |
0,99 | 0,97 | 0,94 | 0,90 | 0,84 | 0,77 | 0,68 | 0,58 | 0,47 | 0,35 | ||
1,00 | 0,98 | 0,96 | 0,91 | 0,88 | 0,82 | 0,74 | 0,68 | 0,59 | 0,46 | ||
0,1 | 0,98 | 0,96 | 0,94 | 0,91 | 0,88 | 0,84 | 0,79 | 0,75 | 0,70 | ||
0,99 | 0,97 | 0,94 | 0,89 | 0,83 | 0,76 | 0,67 | 0,57 | 0,46 | 0,36 | ||
0,97 | 0,95 | 0,91 | 0,85 | 0,80 | 0,73 | 0,64 | 0,57 | 0,45 | |||
0,2 | 0,95 | 0,92 | 0,88 | 0,84 | 0,80 | 0,75 | 0,69 | 0,64 | |||
0,97 | 0,93 | 0,88 | 0,82 | 0,75 | 0,66 | 0,56 | 0,44 | 0,32 | |||
0,93 | 0,90 | 0,84 | 0,77 | 0,71 | 0,67 | 0,52 | 0,44 | ||||
0,3 | 0,90 | 0,86 | 0,81 | 0,76 | 0,71 | 0,65 | 0,58 | ||||
0,93 | 0,88 | 0,82 | 0,74 | 0,65 | 0,55 | 0,43 | 0,31 | ||||
0,88 | 0,84 | 0,77 | 0,68 | 0,61 | 0,51 | 0,39 | |||||
0,4 | 0,83 | 0,78 | 0,72 | 0,66 | 0,60 | 0,53 | |||||
0,87 | 0,81 | 0,73 | 0,64 | 0,54 | 0,42 | 0,29 | |||||
0,81 | 0,76 | 0,62 | 0,57 | 0,49 | 0,37 | ||||||
0,5 | 0,75 | 0,68 | 0,62 | 0,55 | 0,48 | ||||||
0,80 | 0,72 | 0,63 | 0,52 | 0,41 | 0,28 | ||||||
0,72 | 0,66 | 0,56 | 0,44 | 0,35 | |||||||
0,6 | 0,65 | 0,58 | 0,50 | 0,42 | |||||||
0,71 | 0,62 | 0,51 | 0,39 | 0,26 | |||||||
0,62 | 0,55 | 0,43 | 0,30 | ||||||||
0,7 | 0,54 | 0,45 | 0,36 | ||||||||
0,61 | 0,50 | 0,38 | 0,24 | ||||||||
0,50 | 0,42 | 0,29 | |||||||||
0,8 | 0,41 | 0,31 | |||||||||
0,49 | 0,37 | 0,23 | |||||||||
0,37 | 0,28 | ||||||||||
0,9 | 0,26 | ||||||||||
0,35 | 0,22 | ||||||||||
0,22 | |||||||||||
1,0 | 0,2 | ||||||||||
Примечание. Данными первых строк следует пользоваться при наличии облаков нижнего и верхнего ярусов, данными вторых строк - при наличии облаков нижнего и среднего ярусов, данными третьих строк - при наличии облаков всех трех ярусов.
Расчет Qн и Aj производится по методике, изложенной выше. Турбулентные составляющие УТБ рассчитываются по уравнениям:
Pа = 0,276(1 + 5,6u2,0)t2,0; (6.37)
LE = 2,33(l2,0 - 6,1)u2,0, (6.38)
где u2,0, t2,0, e2,0 - средние декадные значения скорости ветра, температуры воздуха и парциального давления водяного пара на уровне 2,0 м; 6,1 - максимальное давление водяного пара при температуре поверхности 0 °C.
Расчет hj при отсутствии данных наблюдений производится по следующей формуле [33]:
где 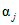 - температурный коэффициент стаивания льда, мм/°C, за декаду;
- температурный коэффициент стаивания льда, мм/°C, за декаду; 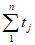 - сумма положительных значений среднесуточной температуры воздуха, °C.
- сумма положительных значений среднесуточной температуры воздуха, °C.
В свою очередь
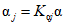 , (6.40)
, (6.40)где 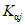 - параметр, учитывающий изменение коэффициента стаивания льда в течение теплого периода года, определяется для каждой j-той декады по рис. 6.13;
- параметр, учитывающий изменение коэффициента стаивания льда в течение теплого периода года, определяется для каждой j-той декады по рис. 6.13; 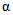 - средний за период таяния с положительными значениями внутрисуточного хода температуры воздуха коэффициент стаивания льда, определяется по выражению
- средний за период таяния с положительными значениями внутрисуточного хода температуры воздуха коэффициент стаивания льда, определяется по выражению
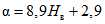 , (6.41)
, (6.41)где Hв - высота местоположения наледи, км.
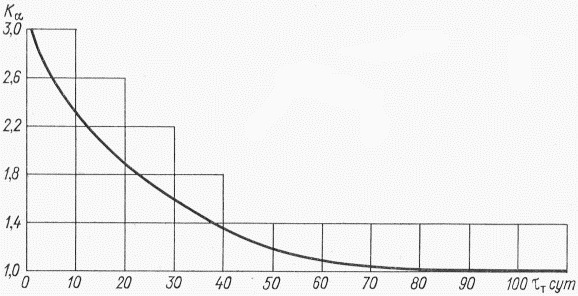
Суммы положительных значений температуры воздуха на j-тую декаду снимаются с графиков на рис. 6.15 в зависимости от высоты местности и местоположения наледи в каком-либо районе однородной связи 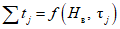 (рис. 6.14).
(рис. 6.14).
 (рис. 6.14).
(рис. 6.14).
положительных значений средней суточной температуры воздуха
от высоты местности, приведенных на рис. 6.15
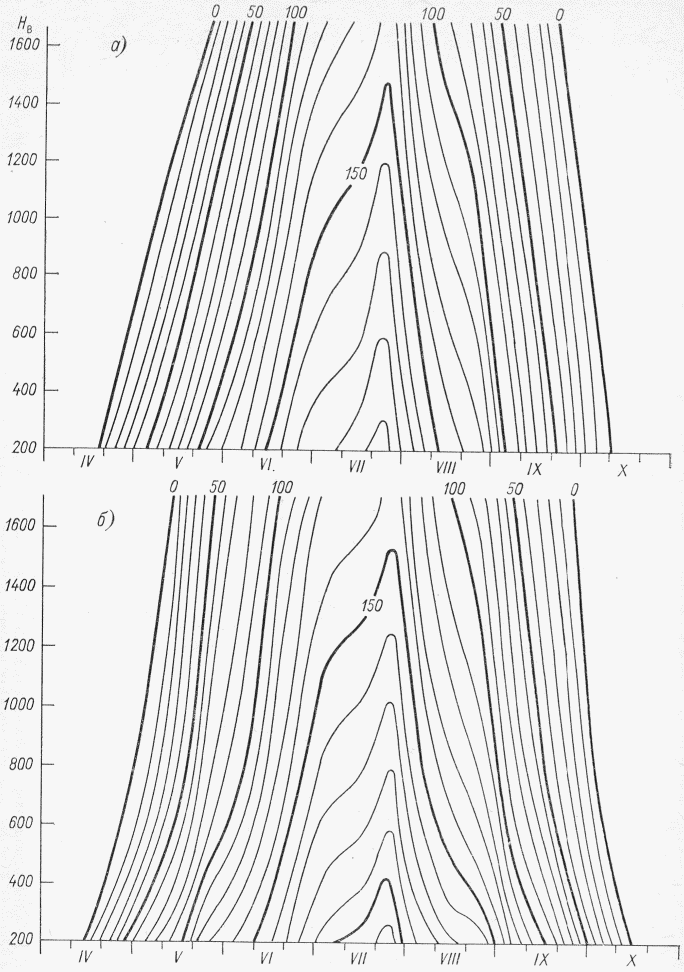
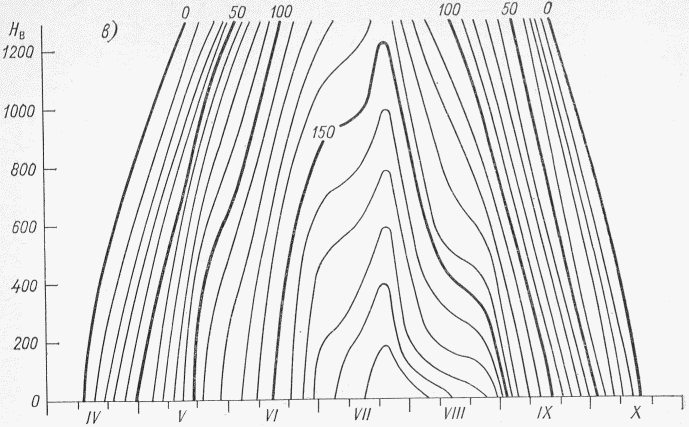
положительных средних суточных температур
воздуха (°C) в зависимости от высоты местности Hв
(по средним многолетним данным)
а - район I на рис. 6.14, б - район II, в - район III
Параметр P за j-тую декаду рассчитывается по уравнению
где 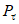 и
и 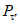 - значения относительной площади наледей соответственно в начале
- значения относительной площади наледей соответственно в начале 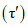 и конце
и конце 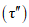 j-той декады в долях максимальных абсолютных значений F в конце зимы.
j-той декады в долях максимальных абсолютных значений F в конце зимы.
На рис. 6.16 приведен график для определения параметра P в зависимости от интенсивности стаивания льда с поверхности наледи, выраженного отношением суммарного слоя стаивания льда за период от начала таяния до заданного момента времени 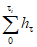 к средней мощности наледи в период ее максимального развития
к средней мощности наледи в период ее максимального развития 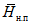 .
.
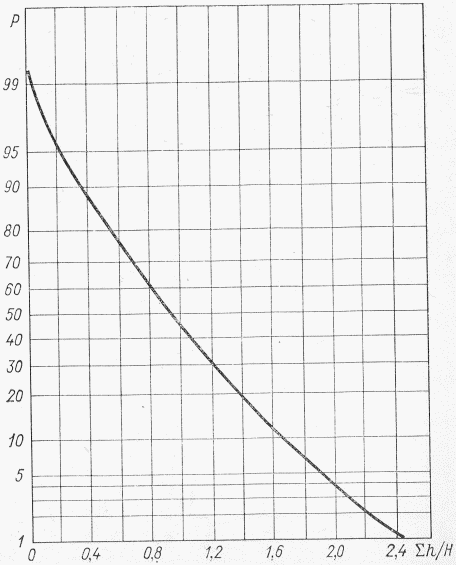
P в зависимости от стаивания льда с их поверхности,
выраженного отношением суммарного слоя стаивания льда
за период от начала таяния до заданного момента
времени 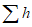 к средней мощности наледи в период
к средней мощности наледи в период
ее максимального развития H
Параметр 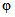 за j-тую декаду рассчитывается по следующему уравнению:
за j-тую декаду рассчитывается по следующему уравнению:
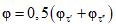 , (6.43)
, (6.43)где 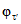 ,
, 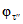 - значения параметра на начало
- значения параметра на начало 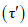 и конец
и конец 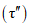 j-той декады.
j-той декады.
На рис. 6.17 приведен график для определения параметра 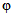 в зависимости от средней ширины наледи в конце зимы
в зависимости от средней ширины наледи в конце зимы  длины водотока от истока до наледи Lр и времени после начала водной эрозии
длины водотока от истока до наледи Lр и времени после начала водной эрозии  . Средняя ширина каждой наледи
. Средняя ширина каждой наледи  рассчитывается как частное от деления площади F на ее длину. За длину наледи принимается расстояние через геометрический центр от верхнего до нижнего ее конца. Длина водотока Lр может быть определена по картам или установлена с помощью справочников "Ресурсы поверхностных вод СССР". В последнем случае по справочникам находится вся длина реки и из нее вычитается расстояние от наледи до устья, которое может быть установлено по каталогам наледей [11, 14, 15, 16] или по картам. Отдельные, особенно большие, наледи иногда пересекают два или несколько водотоков одного порядка. В таких случаях за параметр Lр принимается сумма длин этих водотоков от их истоков до наледи.
рассчитывается как частное от деления площади F на ее длину. За длину наледи принимается расстояние через геометрический центр от верхнего до нижнего ее конца. Длина водотока Lр может быть определена по картам или установлена с помощью справочников "Ресурсы поверхностных вод СССР". В последнем случае по справочникам находится вся длина реки и из нее вычитается расстояние от наледи до устья, которое может быть установлено по каталогам наледей [11, 14, 15, 16] или по картам. Отдельные, особенно большие, наледи иногда пересекают два или несколько водотоков одного порядка. В таких случаях за параметр Lр принимается сумма длин этих водотоков от их истоков до наледи.
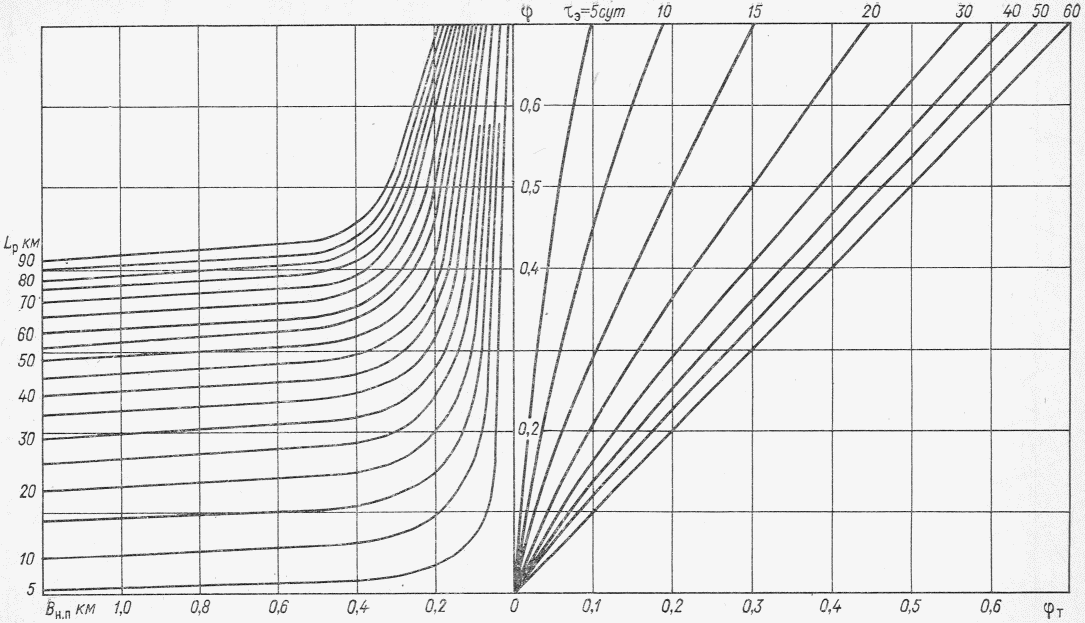
в зависимости от средней ширины наледи в конце зимы Bн.п
и длины водотока от истока до наледи Lр на концах расчетных
интервалов времени после начала водной эрозии 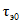
Дата начала водной эрозии 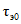 рассчитывается по следующему выражению:
рассчитывается по следующему выражению:
где 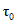 - дата начала таяния наледи;
- дата начала таяния наледи; 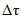 - период от начала таяния до начала процесса эрозии, сут.
- период от начала таяния до начала процесса эрозии, сут.
На рис. 6.18 приведен график для определения 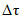 в зависимости от длины водотока от истока до наледи Lр.
в зависимости от длины водотока от истока до наледи Lр.
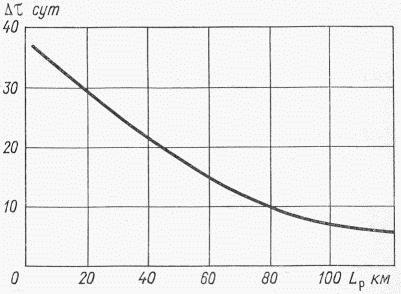
до начала процесса эрозии 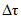 в зависимости от длины
в зависимости от длины
водотока от истока до наледи Lр
Параметр Kн за j-тую декаду определяется по графику на рис. 6.19 в зависимости от параметра Pj, рассчитанного по выражению (6.42).
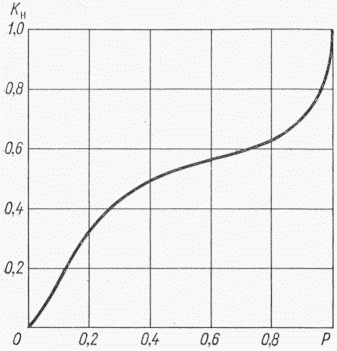
от уменьшения относительной площади наледи P
Расчет ординат гидрографа наледного стока производится для каждой наледи в отдельности в следующей последовательности:
1) теплый период года от даты начала таяния разделяется на расчетные периоды - декады;
2) для каждой декады определяется слой стаивания hj по уравнениям (6.26) и (6.39) или по имеющимся данным режимных наблюдений;
3) на конец каждой декады вычисляется суммарный слой стаивания льда от начала таяния 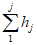 и рассчитывается отношение
и рассчитывается отношение 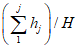 ;
;
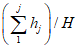 ;
;4) по графику на рис. 6.16 определяется параметр 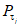 . По найденным значениям
. По найденным значениям 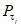 рассчитывается параметр Pj по уравнению (6.42);
рассчитывается параметр Pj по уравнению (6.42);
5) с помощью графика на рис. 6.18 по известной длине водотока Lр определяется период от начала таяния до начала процесса водной эрозии 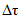 ;
;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду выражение (6.44), а не выражение (6.54). |
6) по выражению (6.54) рассчитывается дата начала водной эрозии 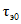 ;
;
7) затем с помощью графика на рис. 6.17 по известным средней ширине наледи 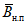 , длине водотока Lр и установленной дате начала эрозии
, длине водотока Lр и установленной дате начала эрозии 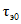 определяется коэффициент
определяется коэффициент 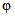 на конец каждой j-той декады;
на конец каждой j-той декады;
8) по найденным значениям 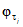 рассчитываются параметры
рассчитываются параметры 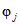 и
и 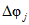 ;
;
9) с помощью графика на рис. 6.19 по известным значениям Pj определяется коэффициент Kн;
10) найденные значения параметров подставляются в формулу (6.25) и вычисляется средний расход наледного стока за j-тую декаду Qн.сj. Суммарный средний декадный расход наледного стока всех наледей в бассейне получается суммированием их расходов.
Ошибки расчета средних декадных расходов наледного стока по формуле (6.25) для отдельных наледей составляют 20 - 25%. При расчете суммарного гидрографа стока воды со всех наледей в бассейне ошибки уменьшаются в 1,5 - 2 раза, поскольку индивидуальные особенности отдельных наледей нивелируются.
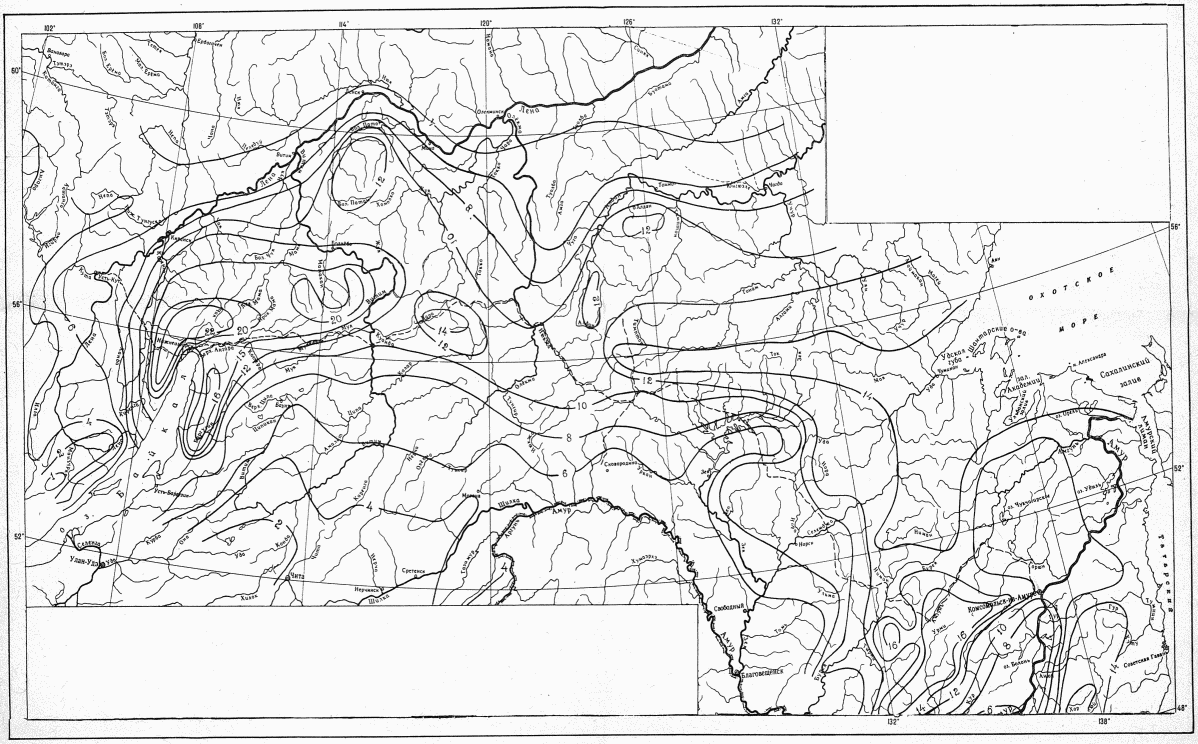
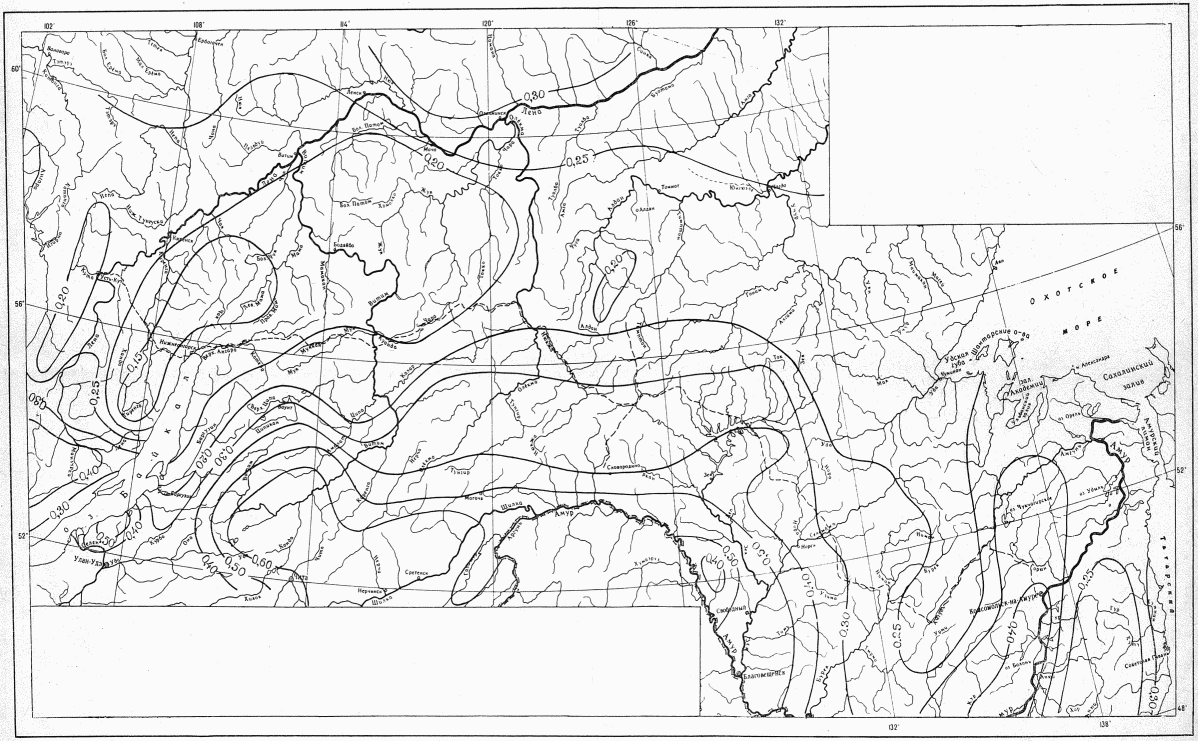
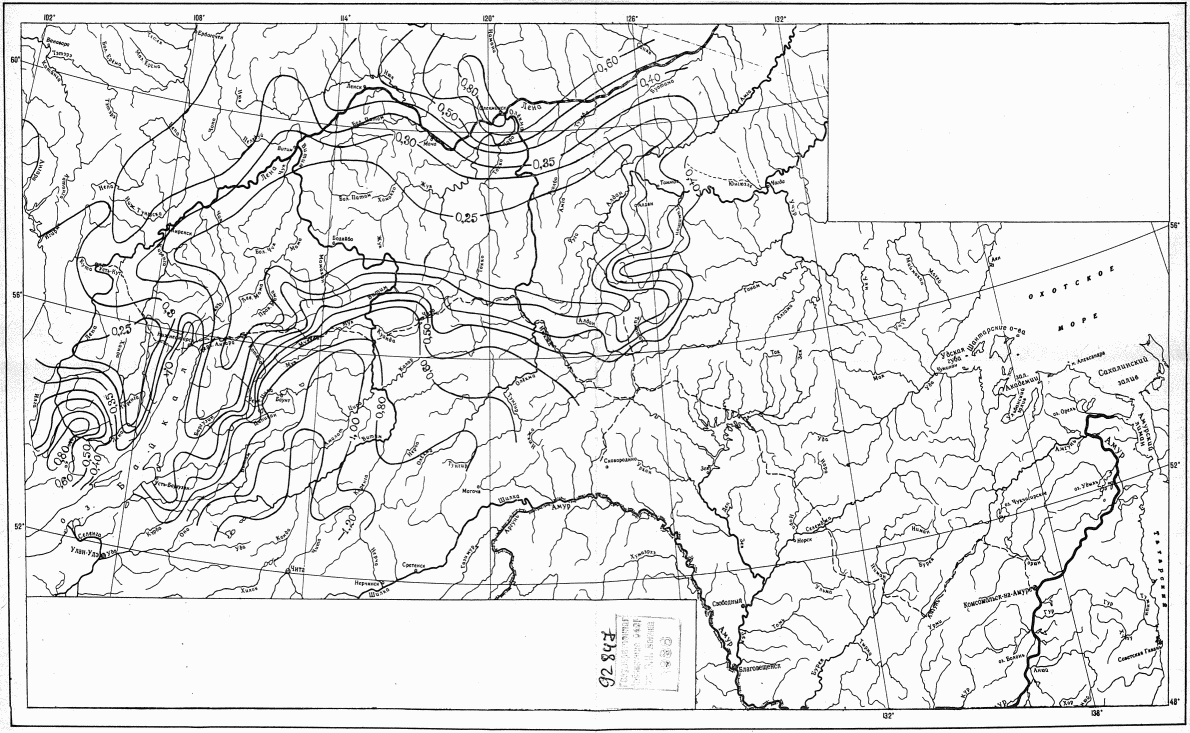
РЕК ЗОНЫ БАМа 1%-НОЙ ОБЕСПЕЧЕННОСТИ ДЛЯ ПЛОЩАДИ
ВОДОСБОРА F = 100 км2
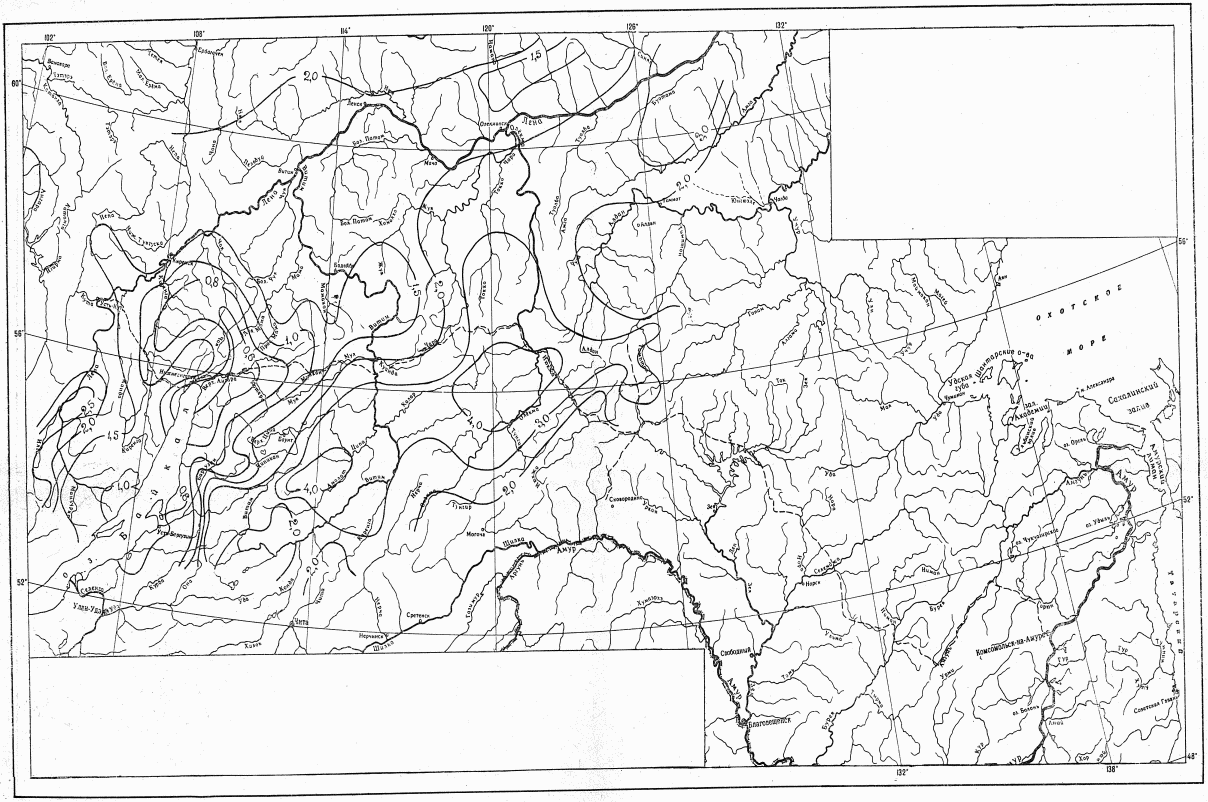
1%-НОЙ ОБЕСПЕЧЕННОСТИ, мм
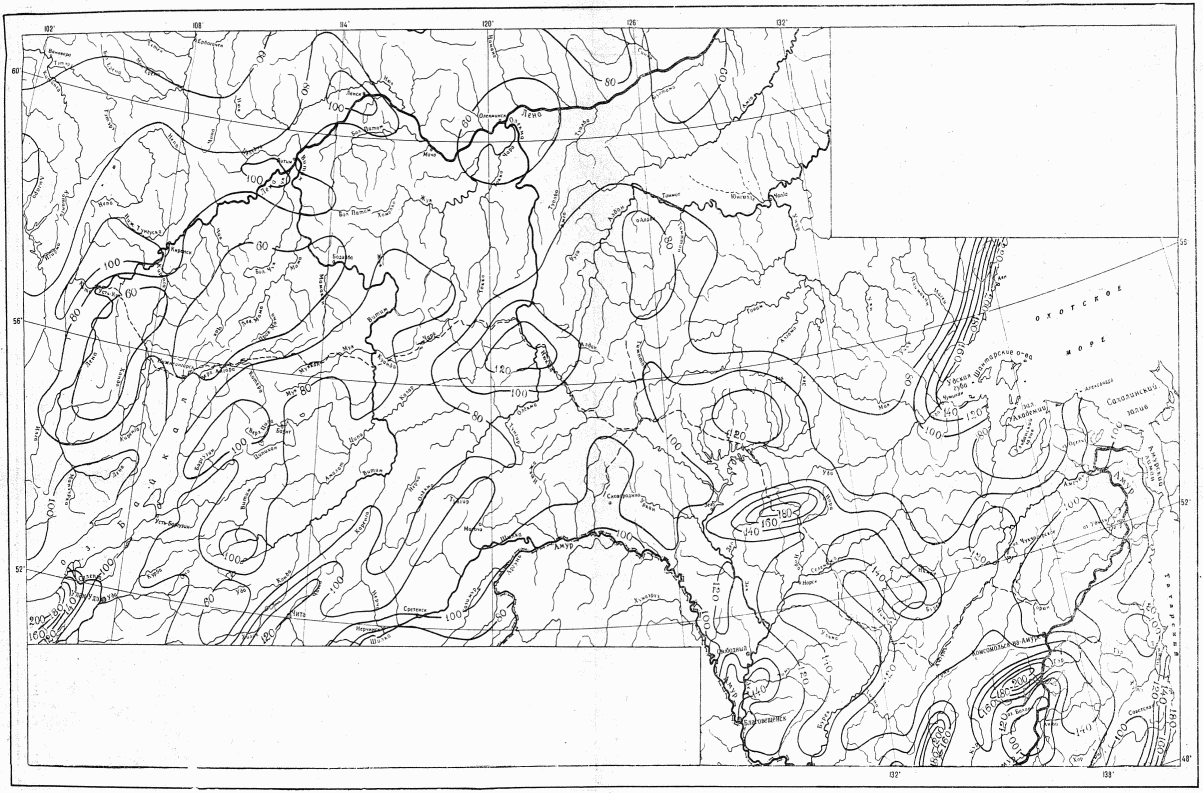
1%-НОЙ ОБЕСПЕЧЕННОСТИ ДЛЯ ПЛОЩАДИ ВОДОСБОРА
F = 200 км2, м3/(с·км2)
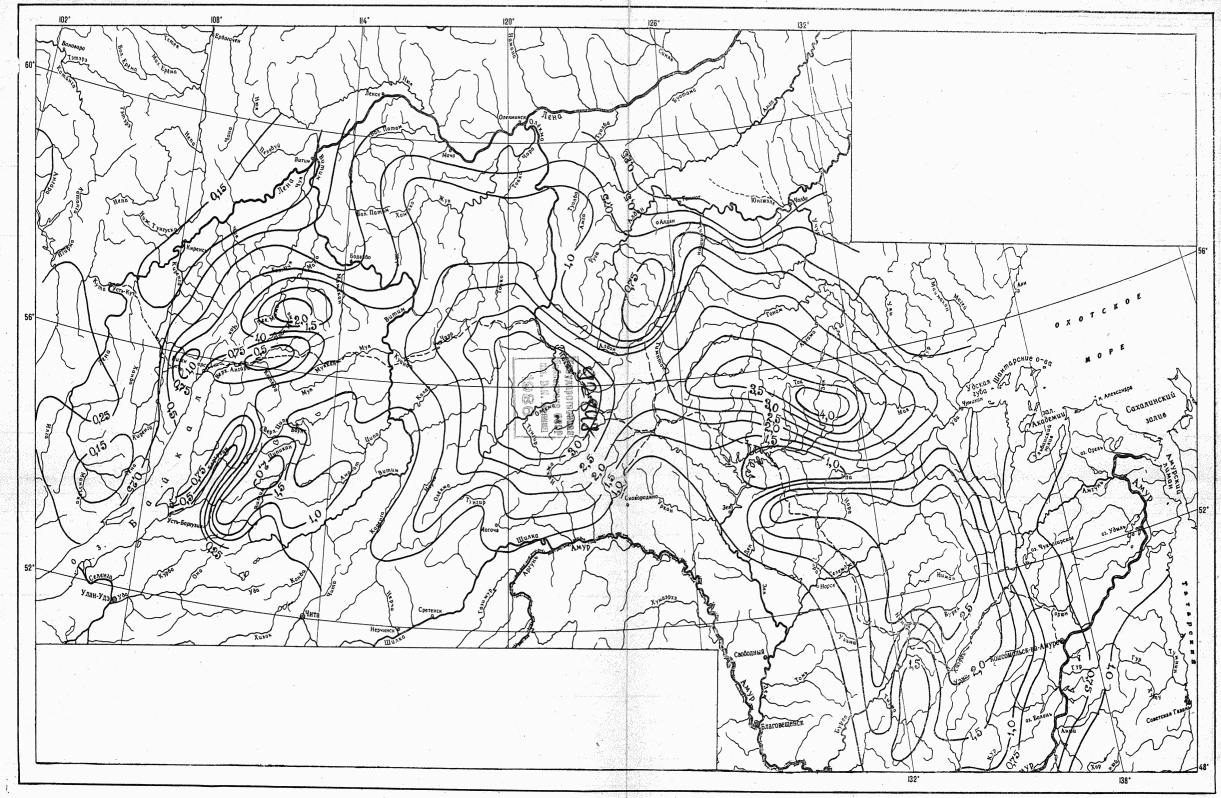
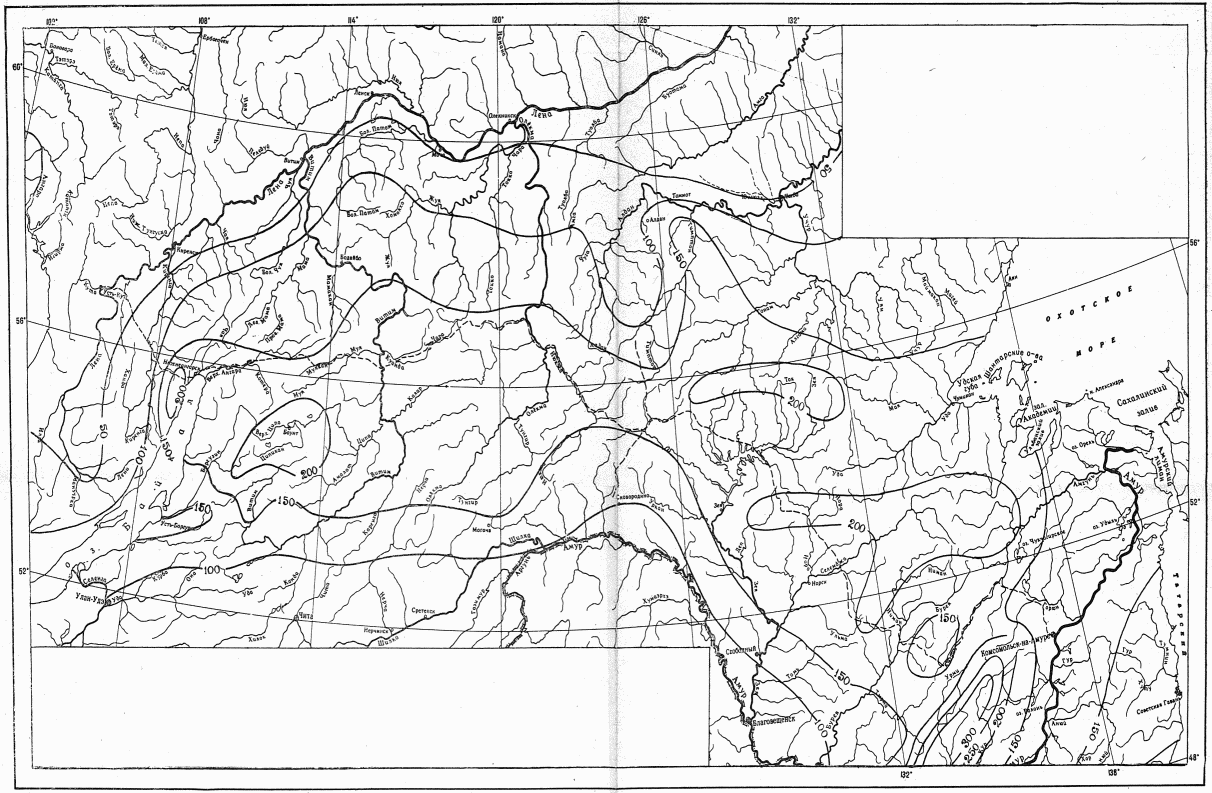
ОБЕСПЕЧЕННОСТИ ЗА ПЕРИОД ОТКРЫТОГО РУСЛА, л/(с·км2)
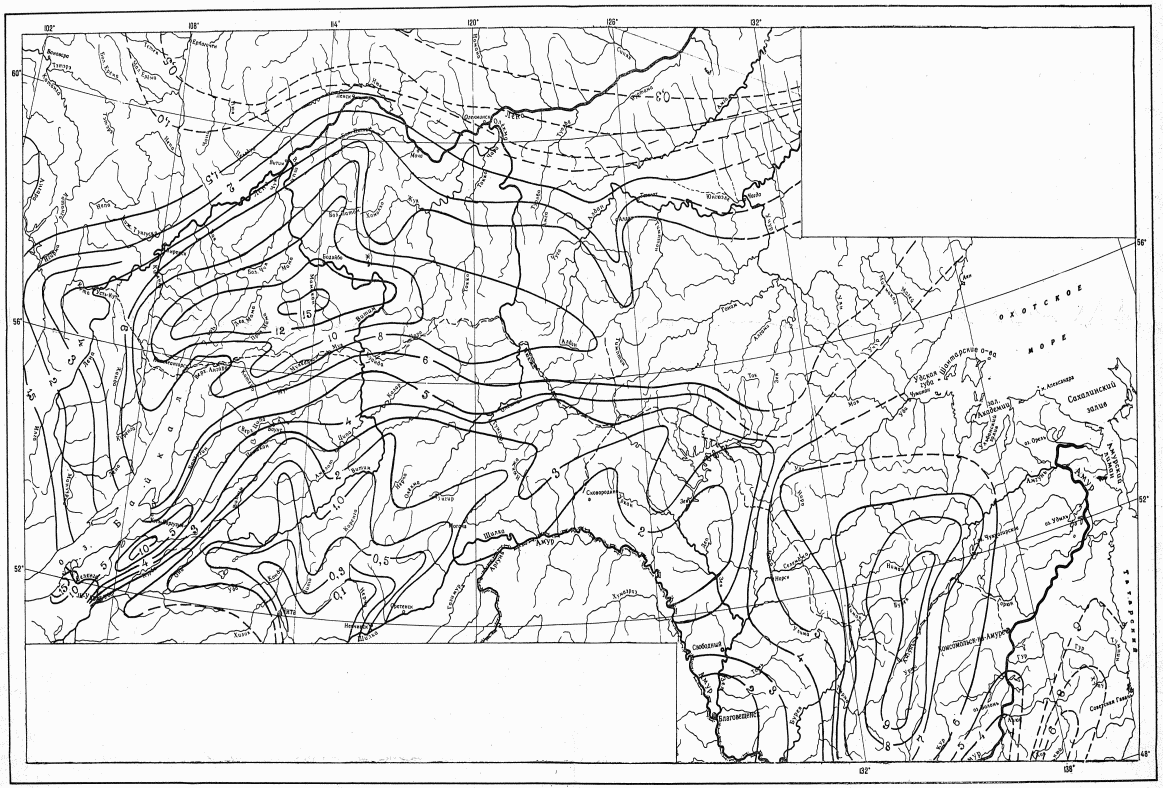
80%-НОЙ ОБЕСПЕЧЕННОСТИ, л/(с·км2)
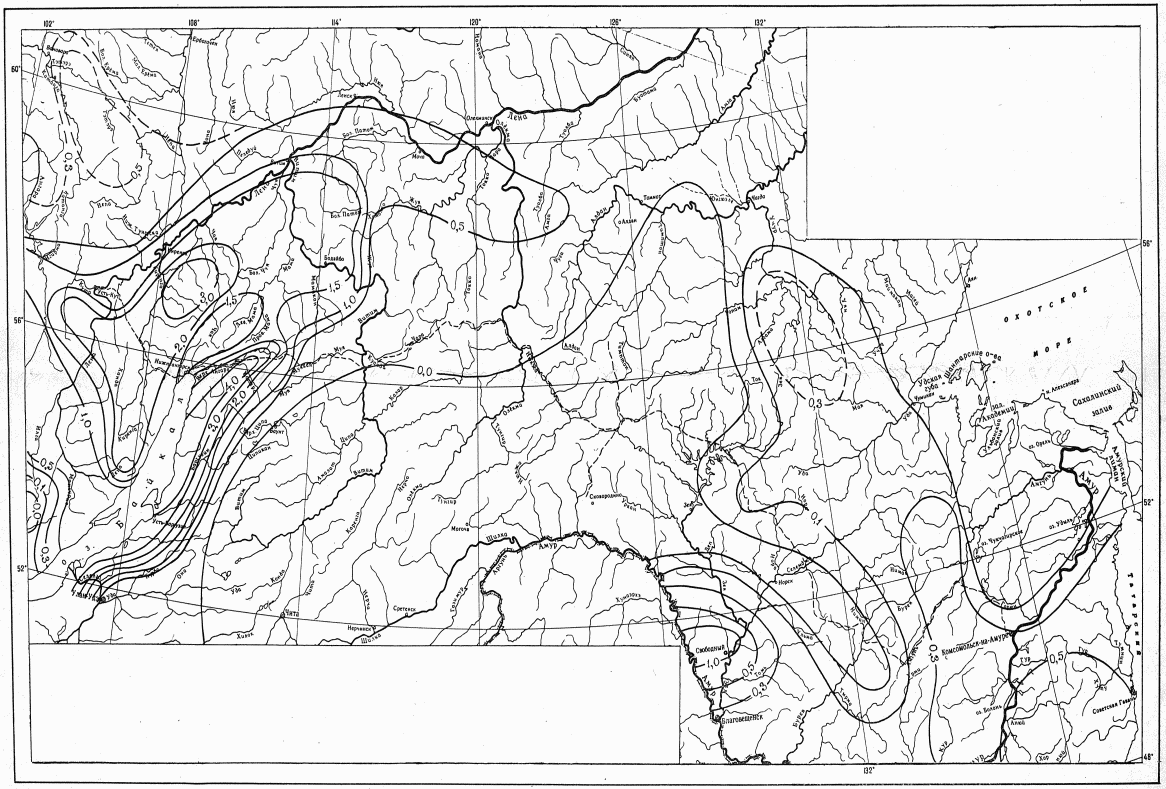
2. Бабкин В.И. и др. Методические основы расчета водных ресурсов и водного баланса территории СССР. - Труды ГГИ, 1977, вып. 241, с. 11 - 28.
3. Берлянд М.Е., Берлянд Т.Г. Определение эффективного излучения Земли с учетом влияния облаков. - Изв. АН СССР. Сер. геофиз., 1952, N 1, с. 64 - 78.
5. Ван дер Варден Б.Л. Математическая статистика. - М.: Изд-во иностр. лит-ры, 1960. - 480 с.
7. Горошкова Н.И. Методика расчета максимального стока весеннего половодья рек западного и центрального участков зоны БАМ. - Труды ГГИ, 1983, вып. 290, с. 11 - 25.
8. Горошкова Н.И. Пример исследования предельной интенсивности стока весеннего половодья (по материалам Колымской воднобалансовой станции). - В кн.: Вопросы гидрологии суши: Доклады конференции молодых ученых и специалистов. Л., 1979, с. 10 - 17.
9. Горошкова Н.И. Редукция предельной интенсивности стока весеннего половодья. - Труды ГГИ, 1980, вып. 275, с. 33 - 43.
10. Дейкин Б.Н. Изменчивость альбедо наледей в период их таяния. - Материалы гляциологических исследований, 1981, вып. 41, с. 80 - 84.
11. Дейкин Б.Н., Марков М.Л. Распространение наледей в бассейне р. Куанды (по результатам аэровизуальных обследований). - Труды ГГИ, 1983, вып. 290, с. 68 - 83.
12. Доброумов Б.М., Устюжанин Б.С. Преобразование водных ресурсов и режима рек центра ЕТС. - Л.: Гидрометеоиздат, 1980. - 224 с.
14. Каталог наледей зоны БАМ. Вып. 1. Наледи верхней части бассейна р. Чары. - Л.: Гидрометеоиздат, 1980. - 62 с.
16. Каталог наледей зоны БАМ. Вып. 3. Наледи бассейна р. Верхней Ангары. - Л.: Гидрометеоиздат, 1982. - 95 с.
17. Линслей Р.К., Колер М.А., Паулюс Д.Х. Прикладная гидрология.- Л.: Гидрометеоиздат, 1962. - 759 с.
18. Нежиховский Р.А. Русловая сеть бассейна и процесс формирования стока воды. - Л.: Гидрометеоиздат, 1971. - 475 с.
19. Оспенников Е.Н. и др. Экзогенные геологические явления и процессы. Южная Якутия. - М.: Изд. МГУ, 1980. - 228 с.
20. Пиотрович В.В. Расчет толщины ледяного покрова на водохранилищах по метеорологическим элементам. - Труды Гидрометцентра СССР, 1968, вып. 18. - 136 с.
21. Попова И.Л. Оценка характеристик речных наледей в зоне БАМ. - В кн.: Вопросы гидрологии суши: Доклады конференции молодых ученых и специалистов. Л., 1980, с. 61 - 66.
22. Пособие по краткосрочным прогнозам поверхностного стока рек. - Л.: Гидрометеоиздат, 1973.- 147 с.
23. Прокачева В.Г., Снищенко Д.В., Усачев В.Ф. Дистанционные методы гидрологического изучения зоны БАМа: Справочно-методическое пособие. - Л.: Гидрометеоиздат, 1982. - 224 с.
24. Рекомендации по приведению рядов речного стока и их параметров к многолетнему периоду. - Л.: Гидрометеоиздат, 1979. - 64 с.
25. Рекомендации по расчетам внутригодового распределения стока при строительном проектировании. - Л.: Гидрометеоиздат, 1975. - 75 с.
26. Репрезентативные и экспериментальные водосборы. Международное руководство по исследованиям и практике. - Л.: Гидрометеоиздат, 1971. - 427 с.
27. Рождественский А.В. Оценка точности кривых распределения гидрологических характеристик. - Л.: Гидрометеоиздат, 1977. - 268 с.
28. Рождественский А.В., Чеботарев А.И. Статистические методы в гидрологии. - Л.: Гидрометеоиздат, 1974. - 422 с.
29. Руководство гидрометеорологическим станциям по актинометрическим наблюдениям. - Л.: Гидрометеоиздат, 1973. - 226 с.
31. СНиП 2.01.14-83 "Определение расчетных гидрологических характеристик". М.: Стройиздат, 1983. - 48 с.
32. Соколов Б.Л. Наледи и речной сток. - Л.: Гидрометеоиздат, 1975. - 190 с.
34. Соколов Б.Л. Приближенная оценка некоторых характеристик стока по данным эпизодических наблюдений. - Труды ГГИ, 1978, вып. 254, с. 64 - 75.
35. Соколов Б.Л. Многолетние колебания размеров наледей подземных вод. - Труды ГГИ, 1982, вып. 286, с. 71 - 94.
36. Соколов Б.Л. Основные итоги изучения наледей зоны БАМа. - Труды ГГИ, 1983, вып. 290, с. 47 - 67.
38. Херсонский Э.С. Методика расчета максимальных расходов воды. - Метеорология и гидрология, 1979, N 6, с. 80 - 89.
39. Чижов А.Н. Исследование механизма наледных явлений на реках. - Труды ГГИ, 1982, вып. 287, с. 15 - 32.
УДК 556.525(571.5/6) |