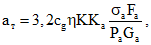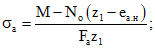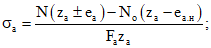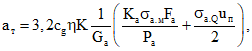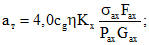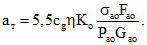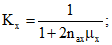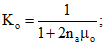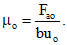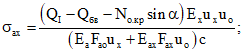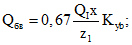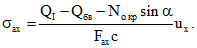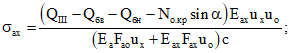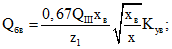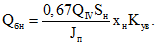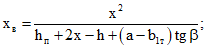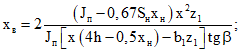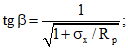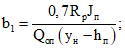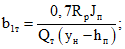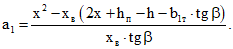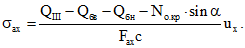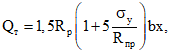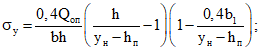СПРАВКА
Источник публикации
Киев: НИИСК Госстроя СССР, 1982
Примечание к документу
Название документа
"Методические рекомендации по определению ширины раскрытия трещин в железобетонных элементах"
(одобрены Протоколом НИИСК Госстроя СССР от 28.04.1982 N 5)
"Методические рекомендации по определению ширины раскрытия трещин в железобетонных элементах"
(одобрены Протоколом НИИСК Госстроя СССР от 28.04.1982 N 5)
Содержание
Научно-технического совета
НИИСК Госстроя СССР
от 28 апреля 1982 г. N 5
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ОПРЕДЕЛЕНИЮ ШИРИНЫ РАСКРЫТИЯ
ТРЕЩИН В ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТАХ
Даны методические рекомендации по определению ширины раскрытия трещин в обычных и предварительно напряженных железобетонных элементах и числовые примеры, иллюстрирующие их использование (приложение 2).
Рекомендации основаны на результатах многолетних теоретических и экспериментальных исследований и могут рассматриваться как шаг в развитии инженерных методов расчета железобетонных элементов.
Распространяются на элементы из тяжелых (обычных), мелкозернистых, легких и плотных силикатных бетонов.
Рассчитаны на инженерно-технических работников проектных и научно-исследовательских организаций, а также студентов и аспирантов вузов и факультетов строительного профиля.
Разработаны инж. Смоляго Г.А., кандидатами техн. наук Усмановым В.Ф., Волковым Ю.А. и докт. техн. наук Голышевым А.Б.
Отзывы и замечания просим направлять по адресу: 252037 Киев-37, ул. И. Клименко, 5/2, НИИСК Госстроя СССР, лаборатория теории расчета железобетонных конструкций.
1.1. Железобетонные элементы рассчитываются на раскрытие трещин, нормальных к продольной оси элемента, наклонных, пересекающих продольную и поперечную арматуру, и наклонных, пересекающих поперечную арматуру (рис. 1).
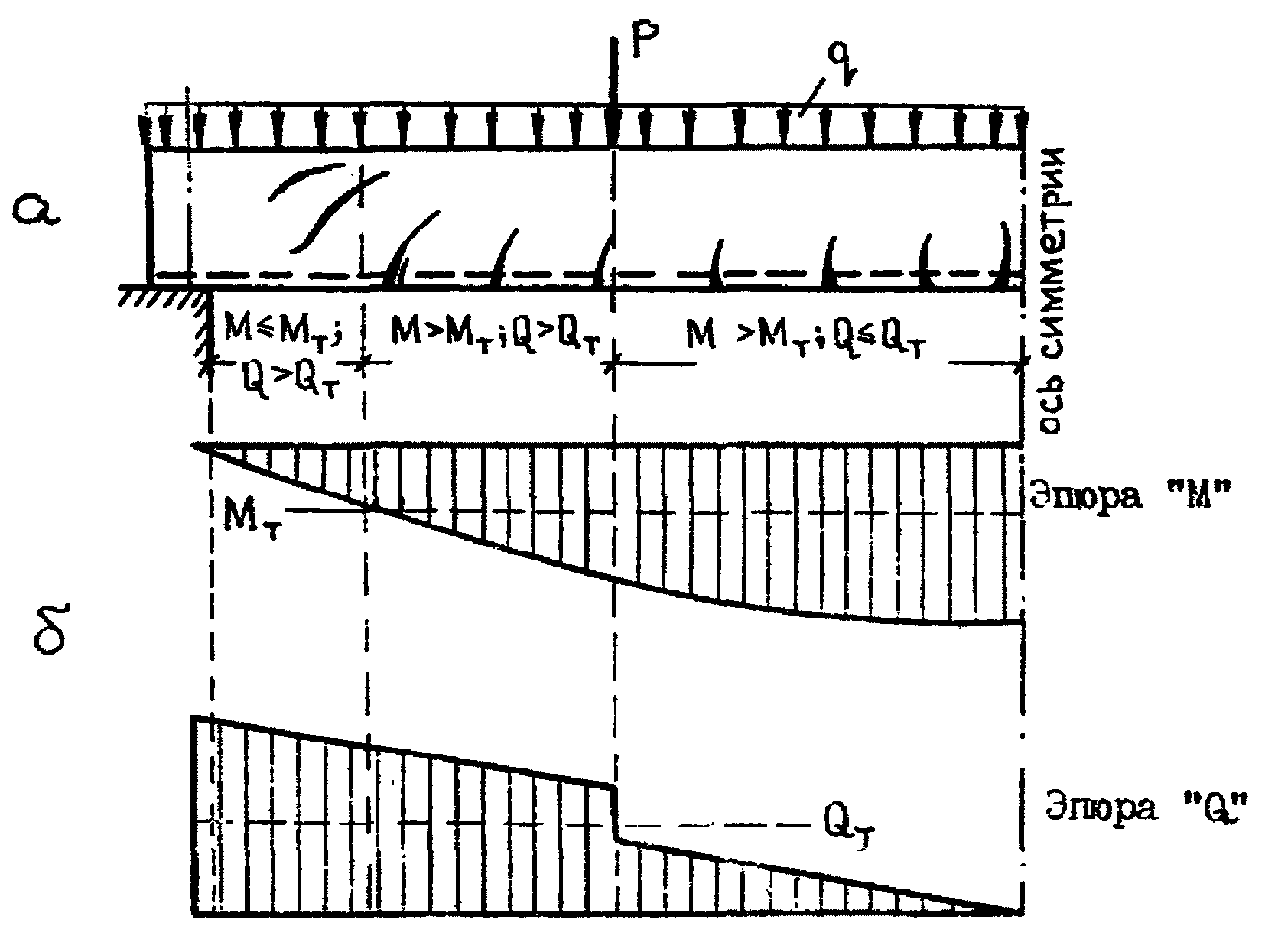
а - типы трещин; б - эпюры моментов и поперечных сил
1.2. Расчет по раскрытию трещин производится для элементов, к трещиностойкости которых предъявляются требования 2-й категории (ограниченное по ширине кратковременное раскрытие трещин при условии их последующего надежного закрытия) и для элементов, к трещиностойкости которых предъявляются требования 3-й категории.
Определение полной ширины раскрытия трещин производится по формулам:
для элементов, к трещиностойкости которых предъявляются требования 2-й категории
aт = aт1; (1)
для элементов, к трещиностойкости которых предъявляются требования 3-й категории
aт = aт1 - aт2 + aт3, (2)
где aт1 - ширина раскрытия трещин от кратковременного действия всех нагрузок;
aт2 - ширина раскрытия трещин от постоянных и длительных нагрузок при их кратковременном действии;
aт3 - то же, от длительного действия указанных нагрузок.
раскрытие трещин есть накопление относительных взаимных смещений арматуры и бетона на участках активного сцепления, расположенных по обе стороны от трещины (рис. 2), то есть
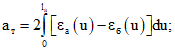 (3)
(3)напряжения сцепления по поверхности контакта бетона и растянутой арматуры на участках между трещинами изменяются пропорционально относительным взаимным смещениям арматуры и бетона;
относительное удлинение бетона на уровне растянутой арматуры в сечении "u" - 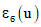 принимается равным отношению напряжений в бетоне на указанном уровне к его модулю упругопластичности;
принимается равным отношению напряжений в бетоне на указанном уровне к его модулю упругопластичности;
сжатый бетон и растянутая арматура работают упруго.

2.1. Расчет по раскрытию нормальных трещин требуется, если на рассматриваемом участке (по длине элемента) при действии кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок M > Mт и Q <= Qт <*>.
--------------------------------
<*> Условные обозначения приведены в приложении 4.
2.2. При расчете по раскрытию нормальных трещин кроме общих предпосылок, изложенных в п. 1.3, используется дополнительная предпосылка о том, что эпюра нормальных напряжений в бетоне растянутой зоны изменяется от треугольной в сечении с трещиной до трапецеидальной в средних сечениях на участке между трещинами с максимальными напряжениями, равными предельному сопротивлению бетона осевому растяжению.
2.3. Ширина раскрытия нормальных трещин определяется на уровне центра тяжести сечения наиболее растянутого ряда арматуры.
2.4. Максимальная ширина раскрытия трещин на уровне центра тяжести сечения наиболее растянутого ряда арматуры определяется по формуле
где cg - коэффициент, принимаемый равным: при учете кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок - 1; многократно повторяющейся нагрузки, а также длительного действия постоянных и длительных нагрузок для элементов из бетонов:
тяжелых естественного твердения - 1,5;
тяжелых в водонасыщенном состоянии - 1,2;
мелкозернистых
вида А - 1,75;
вида Б - 2,0;
вида В - 1,5;
легких плотной структуры - 1,5;
поризованных - 2,0;
ячеистых - 2,5;
для изгибаемых, внецентренно сжатых и внецентренно растянутых элементов:
для центрально растянутых элементов К = 1
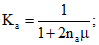 (7)
(7)Gа - модуль взаимного смещения арматуры и бетона на участках между трещинами, принимаемый равным KсцEб, где Kсц - коэффициент, определяемый по таблице в зависимости от вида, марки бетона и степени его обжатия;
Fа и Pа - площадь и периметр поперечного сечения всей арматуры А.
Вид бетона | Проектная марка бетона | |||||||
100 | 150 | 200 | 300 | 400 | 600 | 800 | ||
Тяжелые (обычные) | 0 | - | 0,56 | 0,51 | 0,45 | 0,42 | 0,39 | 0,37 |
0,2 | - | - | 0,50 | 0,44 | 0,41 | 0,38 | 0,36 | |
0,4 | - | - | 0,44 | 0,38 | 0,35 | 0,32 | 0,38 | |
0,6 | - | - | 0,35 | 0,29 | 0,27 | 0,24 | 0,22 | |
0,8 | - | - | 0,20 | 0,18 | 0,16 | 0,13 | 0,11 | |
Мелкозернистые | 0 | - | 0,76 | 0,65 | 0,55 | 0,50 | - | - |
0,2 | - | - | 0,64 | 0,53 | 0,48 | - | - | |
0,4 | - | - | 0,57 | 0,46 | 0,43 | - | - | |
0,6 | - | - | 0,45 | 0,35 | 0,33 | - | - | |
0,8 | - | - | 0,23 | 0,18 | 0,16 | - | - | |
Легкие плотной структуры | 0 | 0,8 | 0,7 | 0,65 | 0,55 | 0,49 | - | - |
0,2 | - | - | 0,64 | 0,53 | 0,48 | - | - | |
0,4 | - | - | 0,57 | 0,46 | 0,43 | - | - | |
0,6 | - | - | 0,44 | 0,35 | 0,33 | - | - | |
0,8 | - | - | 0,23 | 0,18 | 0,16 | - | - | |
Плотные силикатные | 0 | - | 0,97 | 0,79 | 0,65 | 0,57 | - | - |
0,2 | - | - | 0,78 | 0,63 | 0,56 | - | - | |
0,4 | - | - | 0,70 | 0,54 | 0,51 | - | - | |
0,6 | - | - | 0,54 | 0,40 | 0,39 | - | - | |
0,8 | - | - | 0,26 | 0,19 | 0,17 | - | - | |
Примечания. 1. Численные значения коэффициента Kсц для промежуточных марок бетонов и уровней предварительного обжатия определяются по интерполяции. 2.  - напряжения обжатия бетона на уровне центра тяжести сечения наиболее растянутого ряда арматуры А, определяемые в соответствии с п. 1.29 СНиП II-21-75; Rо - передаточная прочность бетона.
- напряжения обжатия бетона на уровне центра тяжести сечения наиболее растянутого ряда арматуры А, определяемые в соответствии с п. 1.29 СНиП II-21-75; Rо - передаточная прочность бетона.
В формулах (5) и (6):
x - высота сжатой зоны бетона над вершиной нормальной трещины в сечении с величиной изгибающего момента, средней для рассматриваемого участка, определяемая в соответствии с п. 4.28 СНиП II-21-75, или по формуле (5.12) [3];
F - площадь бетона в сечении высотой h0 без учета свесов сжатой полки
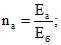 (8)
(8)для прямоугольных, тавровых и двутавровых сечений
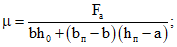 (9)
(9)если во внецентренно растянутых элементах растягивающаяся сила Nс = N - Nо расположена между центрами тяжести арматуры А и А', то при определении 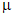 рабочая высота h0 принимается от точки расположения силы Nс до менее растянутой грани, при этом для центрального растяжения
рабочая высота h0 принимается от точки расположения силы Nс до менее растянутой грани, при этом для центрального растяжения
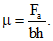 (10)
(10)Величина Qт, которую необходимо иметь при определении границ рассматриваемого участка (при действии равномерно распределенной, а в ряде случаев и смешанной нагрузки) подсчитывается по формуле (1) приложения 1.
Напряжения в растянутой арматуре 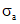 в стадиях транспортирования, возведения и эксплуатации определяются по формулам:
в стадиях транспортирования, возведения и эксплуатации определяются по формулам:
для изгибаемых элементов (рис. 3, а)
для внецентренно сжатых элементов (см. рис. 3, б)
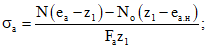 (12)
(12)для внецентренно растянутых элементов (см. рис. 3, в) при
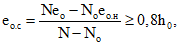 (13)
(13)а также, если N < Nо
для внецентренно растянутых элементов при 0 < eа < 0,8h0 (см. рис. 3, г)
для центрально растянутых элементов
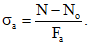 (16)
(16)Здесь:
z1 - расстояние от центра тяжести сечения арматуры А до точки приложения равнодействующей усилий в сжатой зоне сечения элемента, определяемое в соответствии с п. 4.28 СНиП II-21-75, или по формуле (4.7) [3]; zа - расстояние между центрами тяжести сечений арматуры А и А'.

элемента при расчете по раскрытию нормальных трещин
1 - точка приложения равнодействующей усилий в сжатой
или менее растянутой зоне; 2 - центр тяжести площади
арматуры А; 3 - центр тяжести площади приведенного сечения;
прямоугольная эпюра соответствует расчету по СНиП,
треугольная - по формулам работы [3]
В формулах (14) и (15) знак "минус" принимается при расположении растягивающей силы N между центрами тяжести арматуры А и А', знак "плюс" - при расположении силы N вне расстояния между арматурами А и А'.
При сопоставлении средней опытной ширины раскрытия нормальных трещин с вычисленной по формуле (4) ветчину aт, полученную по этой формуле, следует разделить на 1,6.
ПЕРЕСЕКАЮЩИХ ПРОДОЛЬНУЮ И ПОПЕРЕЧНУЮ АРМАТУРУ
3.1. Расчет по раскрытию наклонных трещин, пересекающих продольную и поперечную арматуру, требуется, если на рассматриваемом участке (по длине элемента) при действии кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок M > Mт и Q > Qт.
3.2. Ширина раскрытия трещин, пересекающих продольную и поперечную арматуру, определяется вдоль оси продольной арматуры и вдоль оси поперечной арматуры.
3.3. При определении ширины раскрытия трещин вдоль оси продольной арматуры используются предпосылки пп. 1.3 и 2.2 настоящих методических рекомендаций.
3.4. Ширина раскрытия трещин вдоль оси продольной арматуры определяется на уровне центра тяжести сечения наиболее растянутого ряда указанной арматуры.
3.5. Максимальная ширина раскрытия трещин на уровне центра тяжести сечения наиболее растянутого ряда продольной арматуры определяется по формуле
где 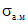 и
и 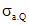 - напряжения или (при наличии предварительного напряжения) приращения напряжений в арматуре А на уровне центра тяжести сечения указанной арматуры от действия, соответственно, изгибающего момента и поперечной силы.
- напряжения или (при наличии предварительного напряжения) приращения напряжений в арматуре А на уровне центра тяжести сечения указанной арматуры от действия, соответственно, изгибающего момента и поперечной силы.
Значения 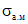 определяются по формуле (11), где M - изгибающий момент в нормальном сечении, проходящем через начало наклонной трещины (левая граница среднего участка на рис. 1), значения
определяются по формуле (11), где M - изгибающий момент в нормальном сечении, проходящем через начало наклонной трещины (левая граница среднего участка на рис. 1), значения  - по формуле
- по формуле
где QII - поперечная сила в нормальном сечении, проходящем через начало наклонной трещины;
Nо.кр - равнодействующая усилий предварительного напряжения наклонных стержней (отогнутой напрягаемой арматуры) в том же сечении с учетом потерь, соответствующих рассматриваемой стадии работы элемента;
Sр - статический момент площади сечения арматуры А, приведенной к бетону, и площади защитного слоя бетона высотой h - h0 относительно оси, проходящей через центр тяжести приведенного сечения элемента;
bа - ширина поперечного сечения элемента на уровне наиболее растянутого ряда арматуры А.
Если начало наклонной трещины расположено между двумя стержнями поперечной арматуры (вертикальными, наклонными или вертикальным и наклонным) uп - расстояние между указанными стержнями, измеренное вдоль оси продольной арматуры на уровне центра тяжести сечения наиболее растянутого ряда, если начало наклонной трещины расположено между опорой и ближайшим к ней наклонным стержнем uп - расстояние между осью опоры и указанным стержнем, измеренное вдоль оси продольной арматуры на уровне центра тяжести сечения наиболее растянутого ряда.
Значения cg, 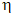 , K, Kа, Pа и Gа расшифрованы в п. 2.4 настоящих методических рекомендаций.
, K, Kа, Pа и Gа расшифрованы в п. 2.4 настоящих методических рекомендаций.
При сопоставлении средней опытной ширины раскрытия наклонных трещин с вычисленной по формуле (17) величину aт, полученную по этой формуле, следует разделить на 1,6.
3.6. При определении ширины раскрытия трещин вдоль оси поперечной арматуры кроме общих предпосылок, изложенных в п. 1.3 настоящих методических рекомендаций, используется дополнительная предпосылка о том, что после образования трещины бетон, вовлекаемый в работу каждым стержнем поперечной арматуры, находится в условиях осевого растяжения. При определении напряжений в поперечной арматуре в качестве расчетной принимается схема, показанная на рис. 4.

в поперечной арматуре на участке M > Mт, Q > Qт
3.7. В общем случае (при комбинированном армировании) максимальная ширина раскрытия наклонных трещин вдоль оси поперечной арматуры определяется по формулам:
для вертикальных стержней
для наклонных стержней
Здесь:
Gаx - модуль взаимного смещения вертикальных стержней и бетона, принимаемый равным 0,55Gа;
Gао - модуль взаимного смещения наклонных стержней и бетона, принимаемый равным: при 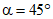 - Gа, при
- Gа, при 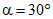 и 60° - 0,75Gа;
и 60° - 0,75Gа;
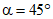 - Gа, при
- Gа, при 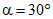 и 60° - 0,75Gа;
и 60° - 0,75Gа;Fаx и Pаx - площадь и периметр поперечного сечения вертикальных стержней, расположенных в одной нормальной к продольной оси элемента плоскости, пересекающей наклонную трещину;
Fао и Pао - то же, наклонных стержней.
В формулах (21) и (22):
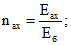 (23)
(23)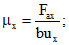 (24)
(24)Напряжения в вертикальных и наклонных стержнях определяются по формулам:
где QI - поперечная сила в сечении I-I, то есть в нормальном сечении, в котором величина Q - Qт меняет знак (при равномерно распределенной нагрузке Q = Qт);
Qбв - усилие сдвига в бетоне сечения I-I над наклонной трещиной;
c - длина участка, ограниченного нормальным сечением, в котором M = Mт и нормальным сечением, в котором величина Q - Qт меняет знак.
В формуле (28):
x - высота сжатой зоны бетона в сечении I-I, определяемая в соответствии с п. 4.28 СНиП II-21-75, или по формуле (5.12) [3] (при равномерно распределенной нагрузке - в сечении, расположенном на расстоянии 0,25l от оси опоры, при сосредоточенной и смешанной нагрузке - в сечении под силой);
Kув - коэффициент, учитывающий влияние местных сжимающих напряжений в бетоне от местного действия сосредоточенных сил и распределенной нагрузки;
при действии сосредоточенных сил и a <= 2h0
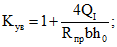 (29)
(29)при действии равномерно распределенной нагрузки
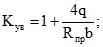 (30)
(30)при действии сосредоточенных сил и Q > 2h0 коэффициент Kув принимается равным единице.
При поперечной арматуре в виде вертикальных стержней и одного наклонного стержня (отогнутая напрягаемая арматура) в формуле (25) принимается uо = 6d, где d - диаметр стержня (каната, пучка), а в формулах (26) и (27) - uо = c.
При поперечной арматуре только в виде вертикальных стержней
Значения cg,  , Ga и z1 расшифрованы в п. 2.4 настоящих методических рекомендаций. Величина Qт определяется по формуле (1) приложения 1.
, Ga и z1 расшифрованы в п. 2.4 настоящих методических рекомендаций. Величина Qт определяется по формуле (1) приложения 1.
С предельной величиной раскрытия трещин, установленной нормами, сравнивается большее из значений aт, полученных по формулам (19) и (20).
При сопоставлении средней опытной ширины раскрытия трещин с вычисленной по формулам (19) и (20) величину aт, полученную по соответствующей формуле, следует разделить на 1,6.
ПЕРЕСЕКАЮЩИХ ПОПЕРЕЧНУЮ АРМАТУРУ
4.1. Расчет ширины раскрытия наклонных трещин, пересекающих поперечную арматуру, требуется если на рассматриваемом участке (по длине элемента) при действии кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок M <= Mт и Q > Qт.
4.2. Ширина раскрытия трещин, пересекающих поперечную арматуру, определяется вдоль оси указанной арматуры.
4.3. При определении ширины раскрытия трещин вдоль оси поперечной арматуры кроме общих предпосылок, изложенных в п. 1.3, используются следующие дополнительные предпосылки:
после образования трещины бетон, вовлекаемый в работу каждым стержнем поперечной арматуры, находится в условиях осевого растяжения;
траектория трещины в сжатой от действия внешней нагрузки зоне элемента представляет собой гиперболу, касательная к которой в точке пересечения с линией, проходящей через центр тяжести сечения, образует с этой линией угол, равный 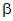 ;
;
траектория трещины в растянутой от действия внешней нагрузки зоне элемента представляет собой прямую линию, переходящую в месте пересечения ребра с полкой в гиперболу, касательная к которой в этом месте образует угол, равный 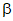 .
.
При определении напряжений в поперечной арматуре в качестве расчетной принимается схема, показанная на рис. 5.
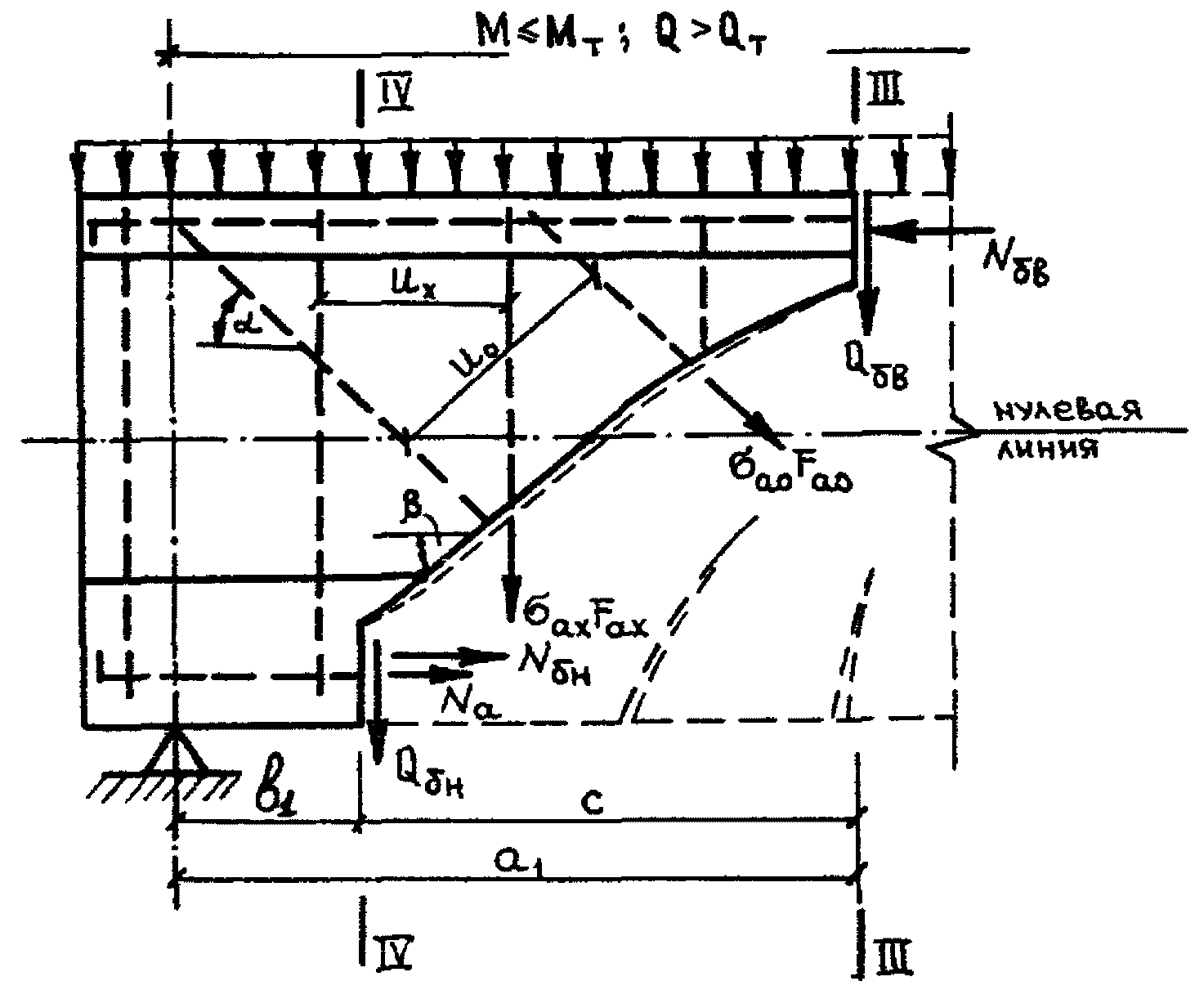
в поперечной арматуре на участке M <= Mт, Q > Qт
4.4. В общем случае (при комбинированном армировании) максимальная ширина раскрытия наклонных трещин вдоль оси поперечной арматуры определяется по формулам (19) и (20), где
В этих формулах:
QIII - поперечная сила в сечении III-III (при действии сосредоточенных сил QIII = QII = QI);
Qбв - усилие сдвига в бетоне сечения III-III над наклонной трещиной
Qбн - усилие сдвига в бетоне сечения IV-IV под наклонной трещиной
В формуле (34):
xв - высота сжатой зоны сечения III-III над наклонной трещиной;
при a < 1,6h0
при a >= 1,6h0
QIV - поперечная сила в сечении IV-IV (при действии сосредоточенных сил QIV = QIII = QII = QI);
xн - высота части сечения IV-IV под наклонной трещиной
Sн - статический момент площади сечения IV-IV высотой xн, растянутой от действия внешней нагрузки, относительно оси, проходящей через центр тяжести указанного сечения;
yн - расстояние от оси, проходящей через центр тяжести сечения IV-IV, до растянутого от действия внешней нагрузки края указанного сечения;
Kун - коэффициент, учитывающий влияние местных сжимающих напряжений в бетоне от местного сжатия, возникающего вблизи приложения опорных реакций; при действии сосредоточенных сил и a <= 2h0, а также при действии равномерно распределенной нагрузки
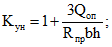 (42)
(42)при действии сосредоточенных сил и a > 2h0 коэффициент Kун принимается равным единице.
При действии сосредоточенных сил и пролете среза a < 1,6h0 расстояние от оси опоры до сечения III-III - a1, которое необходимо иметь при вычислении длины проекции наклонной трещины на продольную ось элемента c, принимается равным a (то есть расстоянию до первой сосредоточенной силы), а при пролете среза a >= 1,6h0 и при действии равномерно распределенной нагрузки определяется по формуле
Значения Gаx, Gао, Fаx, Fао, Nо.кр, Pао, Pаx, x, Kув и z1 расшифрованы, соответственно, в пп. 3.7 и 2.4 настоящих методических рекомендаций.
Величина Qт определяется по формуле (4) приложения 1.
При расчете элементов двутаврового сечения или таврового сечения с полкой в сжатой зоне в формулы (37), (40) и (41) вводится момент инерции полного приведенного сечения. Если в результате определения xв окажется, что  , производится перерасчет xв, при этом в формулы (37), (40) и (41) вводится момент инерции приведенного сечения без учета свесов сжатой полки.
, производится перерасчет xв, при этом в формулы (37), (40) и (41) вводится момент инерции приведенного сечения без учета свесов сжатой полки.
 , производится перерасчет xв, при этом в формулы (37), (40) и (41) вводится момент инерции приведенного сечения без учета свесов сжатой полки.
, производится перерасчет xв, при этом в формулы (37), (40) и (41) вводится момент инерции приведенного сечения без учета свесов сжатой полки.При поперечной арматуре в виде вертикальных стержней и одного наклонного стержня (отогнутой напрягаемой арматуры) в формуле (22) принимается uо = 6d, где d - диаметр стержня (каната, пучка), а в формулах (32) и (33) - uо = c.
При поперечной арматуре только в виде вертикальных стержней
При расчете элементов таврового сечения с полкой в сжатой зоне или прямоугольного сечения в формулах (36), (38), (40), (41), (43) и в формуле (5) приложения 1 принимается hп = 0,25h.
С предельной величиной раскрытия трещин, установленной нормами, сравнивается большее из значений aт, полученных по формулам (19) и (20).
При сопоставлении средней опытной ширины раскрытия трещин с вычисленными по формулам (19) и (20) величину aт, полученную по соответствующей формуле, следует разделить на 1,6.
ОБРАЗУЮТСЯ НАКЛОННЫЕ ТРЕЩИНЫ
Если на рассматриваемом участке (по длине элемента) при действии кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок M > Mт (см. рис. 1), величину Qт рекомендуется определять по формуле
где
при действии сосредоточенных сил
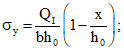 (2)
(2)при действии равномерно-распределенной нагрузки
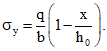 (3)
(3)Значение x расшифровано в п. 3.7 настоящих методических рекомендаций.
Если на рассматриваемом участке (по длине элемента) при действии кратковременных нагрузок и кратковременном действии постоянных и длительных нагрузок M <= Mт (см. рис. 1), величину Qт рекомендуется определять по формуле
где
Sп - статический момент части сечения, расположенной по одну сторону от оси, проходящей через центр тяжести указанного сечения.
Значения 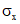 и yн и расшифрованы в п. 4.4 настоящих методических рекомендаций.
и yн и расшифрованы в п. 4.4 настоящих методических рекомендаций.
Определить полную максимальную ширину раскрытия нормальных трещин в предварительно напряженной железобетонной балке (см. рисунок).
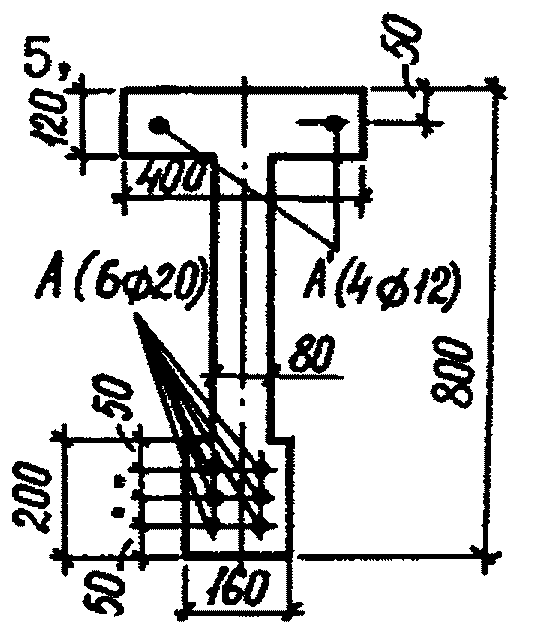
Исходные данные
Балка изготовлена из тяжелого бетона М 500; Eб = 3,6·105 кгс/см2; Rр = 20 кгс/см2. Арматура А преднапряженная из стали класса А-V; Fа = 18,85 см2; Eа = 1,9·106 кгс/см2; Pа = 37,7 см; nа = 5,3. Арматура А' ненапряженная из стали класса А-III;  ; Eа = 2·106 кгс/см2. Характеристики сечения: F = 1184 см2; Fп = 1310 см2; Jп = 105·104 см4. Натяжение арматуры производится на упоры. Усилие предварительного обжатия с учетом всех потерь составляет Nо = 87650 кгс, эксцентриситет его относительно центра тяжести приведенного сечения - eо = 34,6 см. Спуск натяжных устройств производится на 28 сутки. Уровень обжатия бетона
; Eа = 2·106 кгс/см2. Характеристики сечения: F = 1184 см2; Fп = 1310 см2; Jп = 105·104 см4. Натяжение арматуры производится на упоры. Усилие предварительного обжатия с учетом всех потерь составляет Nо = 87650 кгс, эксцентриситет его относительно центра тяжести приведенного сечения - eо = 34,6 см. Спуск натяжных устройств производится на 28 сутки. Уровень обжатия бетона 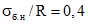 . Балка загружена длительно действующей нагрузкой: равномерно-распределенной интенсивностью q = 3000 кгс/м и двумя сосредоточенными силами P = 4250 кгс, расположенными на расстоянии 400 см от осей опор. Расчетный пролет балки l = 1160 см. Максимальный момент M = 6746000 кгс·см.
. Балка загружена длительно действующей нагрузкой: равномерно-распределенной интенсивностью q = 3000 кгс/м и двумя сосредоточенными силами P = 4250 кгс, расположенными на расстоянии 400 см от осей опор. Расчетный пролет балки l = 1160 см. Максимальный момент M = 6746000 кгс·см.
 ; Eа = 2·106 кгс/см2. Характеристики сечения: F = 1184 см2; Fп = 1310 см2; Jп = 105·104 см4. Натяжение арматуры производится на упоры. Усилие предварительного обжатия с учетом всех потерь составляет Nо = 87650 кгс, эксцентриситет его относительно центра тяжести приведенного сечения - eо = 34,6 см. Спуск натяжных устройств производится на 28 сутки. Уровень обжатия бетона
; Eа = 2·106 кгс/см2. Характеристики сечения: F = 1184 см2; Fп = 1310 см2; Jп = 105·104 см4. Натяжение арматуры производится на упоры. Усилие предварительного обжатия с учетом всех потерь составляет Nо = 87650 кгс, эксцентриситет его относительно центра тяжести приведенного сечения - eо = 34,6 см. Спуск натяжных устройств производится на 28 сутки. Уровень обжатия бетона 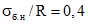 . Балка загружена длительно действующей нагрузкой: равномерно-распределенной интенсивностью q = 3000 кгс/м и двумя сосредоточенными силами P = 4250 кгс, расположенными на расстоянии 400 см от осей опор. Расчетный пролет балки l = 1160 см. Максимальный момент M = 6746000 кгс·см.
. Балка загружена длительно действующей нагрузкой: равномерно-распределенной интенсивностью q = 3000 кгс/м и двумя сосредоточенными силами P = 4250 кгс, расположенными на расстоянии 400 см от осей опор. Расчетный пролет балки l = 1160 см. Максимальный момент M = 6746000 кгс·см.Решение.
По формуле (159) [5] определяем:

то есть  .
.
 .
.По формуле (164) [5] находим:
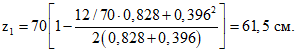
По формулам (5) и (6) вычисляем:
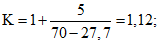
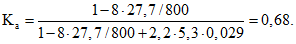
По таблице настоящих методических рекомендаций имеем Kсц = 0,335.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: формула (II) отсутствует. |
Напряжения в продольной арматуре (сверх преднапряжения) на уровне центра тяжести ее сечения [формула (II) настоящих методических рекомендаций]
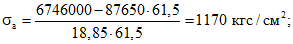
ширина раскрытия трещин [формула (4)]
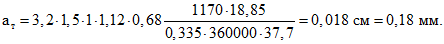
Пример 2.
Определить полную максимальную ширину раскрытия наклонных трещин, пересекающих продольную и поперечную арматуру предварительно напряженной железобетонной балки (см. рис. 4).
Исходные данные
Поперечная арматура в виде вертикальных стержней (хомутов) из стали класса А-III, Fаx = 2,26 см2 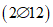 ; Pаx = 7,54 см; ux = 30 см; nаx = 5,55; Gаx = 66400 кгс/см2; a/h0 = 3; Nо = 20000 кг; l = 580 см. Остальные данные приведены в примере 1.
; Pаx = 7,54 см; ux = 30 см; nаx = 5,55; Gаx = 66400 кгс/см2; a/h0 = 3; Nо = 20000 кг; l = 580 см. Остальные данные приведены в примере 1.
 ; Pаx = 7,54 см; ux = 30 см; nаx = 5,55; Gаx = 66400 кгс/см2; a/h0 = 3; Nо = 20000 кг; l = 580 см. Остальные данные приведены в примере 1.
; Pаx = 7,54 см; ux = 30 см; nаx = 5,55; Gаx = 66400 кгс/см2; a/h0 = 3; Nо = 20000 кг; l = 580 см. Остальные данные приведены в примере 1.Решение.
Сначала определим ширину раскрытия трещин на уровне центра тяжести сечения наиболее растянутого ряда продольной арматуры.
По аналогии с примером 1 находим:

x = 0,446·70 = 31,2 см;
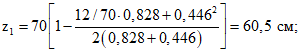
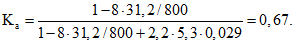
Определяем расстояние от оси опоры до сечения, проходящего через начало наклонной трещины (см. сечения II-II на рис. 4) - b1.
По формуле (120) [5] имеем
Mт = 1 487 640 кгс·см.
Момент в сечении II-II равен
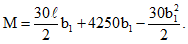
При этом должно выполняться условие (см. рис. 1) M = Mт.
В результате b1 = 136 см.
Поперечная сила в сечении II-II - QII = 8870 кгс, а в сечении I-I (то есть в сечении под сосредоточенной нагрузкой) QI = 6650 кгс.
Величина Qт определяется по формуле (1) приложения 1, где для сосредоточенной нагрузки
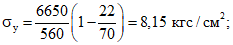
для равномерно распределенной нагрузки
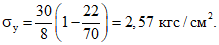
Суммарная величина местных напряжений составляет
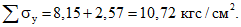
С учетом этого

Напряжения в продольной арматуре в сечении II-II определяются по формулам соответственно (11) и (18) настоящих методических рекомендаций:
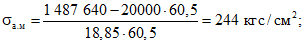
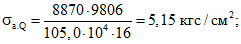
ширина раскрытия трещин - по формуле (17)
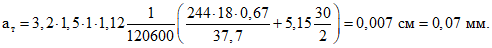
Теперь определим ширину раскрытия трещин вдоль оси поперечной арматуры.
Придерживаясь последовательности, принятой ранее, находим:
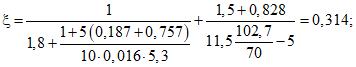
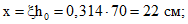
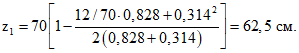
Длина проекции наклонной трещины на горизонтальную ось равна
c = a - b1 = 210 - 136 = 74 см.
Усилие сдвига в бетоне в сечении I-I определяется по формуле (28) настоящих методических рекомендаций, где
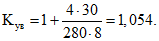
С учетом этого

Напряжение в поперечной арматуре определяется по формуле (31) настоящих методических рекомендаций
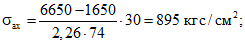
коэффициент Kх - по формуле (21)
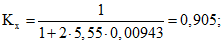
ширина раскрытия трещины - по формуле (19)
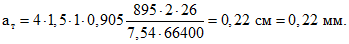
Пример 3.
Определить полную максимальную ширину раскрытия наклонных трещин, пересекающих поперечную арматуру предварительно напряженной железобетонной балки (см. рис. 5 настоящих методических рекомендаций).
Исходные данные
Поперечная арматура в виде вертикальных стержней (хомутов) из стали класса А-III; Fаx = 2,26 см2 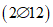 ; Pаx = 7,54 см; ux = 10 см; nаx = 5,55. Балка загружена длительно действующей нагрузкой: равномерно распределенной интенсивностью q = 4500 кгс/м и двумя сосредоточенными силами P = 9000 кгс, расположенными на расстоянии 210 см от осей опор. Остальные данные приведены в примере 1.
; Pаx = 7,54 см; ux = 10 см; nаx = 5,55. Балка загружена длительно действующей нагрузкой: равномерно распределенной интенсивностью q = 4500 кгс/м и двумя сосредоточенными силами P = 9000 кгс, расположенными на расстоянии 210 см от осей опор. Остальные данные приведены в примере 1.
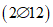 ; Pаx = 7,54 см; ux = 10 см; nаx = 5,55. Балка загружена длительно действующей нагрузкой: равномерно распределенной интенсивностью q = 4500 кгс/м и двумя сосредоточенными силами P = 9000 кгс, расположенными на расстоянии 210 см от осей опор. Остальные данные приведены в примере 1.
; Pаx = 7,54 см; ux = 10 см; nаx = 5,55. Балка загружена длительно действующей нагрузкой: равномерно распределенной интенсивностью q = 4500 кгс/м и двумя сосредоточенными силами P = 9000 кгс, расположенными на расстоянии 210 см от осей опор. Остальные данные приведены в примере 1.Решение.

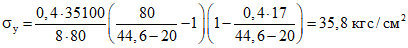
находим
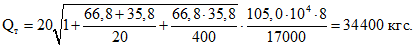
Опорная реакция равна
Qоп = 0,5ql + P = 0,5·45·1160 + 9000 = 35100 кгс.
По формулам (40) и (41) настоящих методических рекомендаций имеем:
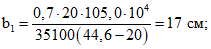
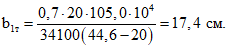
По формуле (39) находим
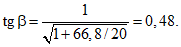
Высота части сечения IV-IV (см. рис. 5) под наклонной трещиной равна
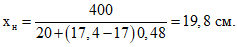
По аналогии с примером 1 находим:
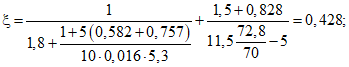
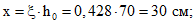
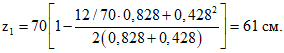
По формуле (37) настоящих методических рекомендаций определяем

Расстояние от оси опоры до вершины наклонной трещины в сжатой зоне

Длина проекции наклонной трещины на горизонтальную ось
c = a1 - b1 = 96,3 - 17 = 79,3 см.
Поперечная сила в сечении III-III (см. рис. 5) - QIII = 30760 кгс, а в сечении IV-IV - QIV = 34335 кгс.
Усилия сдвига в бетоне, соответственно, в сечении III-III и IV-IV определяются по формулам (34), (35) настоящих методических рекомендаций, где

С учетом этого:
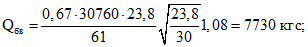
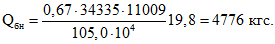
Напряжение в поперечной арматуре определяется по формуле (44) настоящих методических рекомендаций:
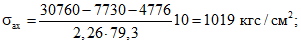
коэффициент Kx - по формуле (21)

ширина раскрытия трещины - по формуле (19)

ЭКСПЕРИМЕНТАЛЬНОЕ ОБОСНОВАНИЕ
На диаграммах рис. 1 - 4 сопоставлены теоретические значения aт в широком диапазоне изменения основных факторов с опытными, полученными в НИИСК Ю.А. Волковым, В.Ф. Усмановым и Смоляго Г.А. под руководством А.Б. Голышева (см. научно-технические отчеты НИИСК Госстроя СССР за 1975 - 1982 гг.).

трещин к средней опытной (опыты НИИСК 1980 - 1982 гг.)

Рис. 2. Отношение теоретической ширины раскрытия наклонных
трещин (пересекающих продольную и поперечную арматуру)
вдоль оси продольной арматуры к средней опытной
(опыты НИИСК 1975 - 1977 гг.)

Рис. 3. Отношение теоретической ширины раскрытия наклонных
трещин (пересекающих продольную и поперечную арматуру)
вдоль оси поперечной арматуры к средней опытной
(опыты НИИСК 1975 - 1977 гг.)

трещин (пересекающих поперечную арматуру) вдоль оси
поперечной арматуры к средней опытной
(опыты НИИСК 1980 - 1982 гг.)
1. Усилия
M, N и Q - изгибающий момент, продольная и поперечная силы;
Qоп - опорная реакция от внешней нагрузки;
q - интенсивность равномерно распределенной нагрузки;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт [9] отсутствует. |
Nо - усилие предварительного обжатия, с учетом потерь напряжения, соответствующих рассматриваемой стадии работы элемента [9];
M - изгибающий момент, воспринимаемый рассматриваемым сечением элемента при образовании нормальной трещины [9];
Qт - поперечная сила, воспринимаемая рассматриваемым сечением элемента при образовании наклонной трещины (см. прил. 1);
Rр - предельное сопротивление бетона осевому растяжению;
Eб - модуль упругости бетона;
Eа - модуль упругости продольной арматуры и поперечной арматуры в виде наклонных (отогнутых) стержней;
Eаx - модуль упругости поперечной арматуры в виде вертикальных стержней.
2. Геометрические характеристики
Jп - момент инерции приведенного сечения элемента относительно оси, проходящей через центр тяжести указанного сечения;
h и h0 - полная и рабочая высота сечения элемента;
b - ширина ребра элемента;
bп и hп - то же, растянутой полки;
a - пролет среза (т.е. расстояние от оси опоры до первой сосредоточенной силы);
l - расчетный пролет элемента.
1. Инструкция по проектированию бетонных и железобетонных конструкций из плотного силикатного бетона. СН 165-76. - М.: Стройиздат, 1977. - 48 с.
2. Кузнецов Л.В. О расчете наклонных сечений предварительно напряженных железобетонных балок по образованию трещин. - В кн.: Прочность и деформативность железобетонных конструкций. - Киев: БудIвельник, 1978. - С. 61 - 66.
3. Методические рекомендации по расчету железобетонных изгибаемых элементов. - Киев: НИИСК, 1979. - 66 с.
4. Проектирование и изготовление сборно-монолитных конструкций. - Киев: БудIвельник, 1975. - 189 с.
5. Строительные нормы и правила, СНиП II-21-75. Бетонные и железобетонные конструкции. - М., 1976.
6. Торяник М.С., Митрофанов В.П. Положение опасных наклонных трещин железобетонных балок. - В кн.: Совершенствование методов расчета и исследование новых типов железобетонных конструкций. Межвузовский тематический сборник, 2 (129). - Ленинград, 1977. - С. 21 - 30.
7. Чупак И.М., Залесов А.С., Корейба С.А. Сопротивление железобетонных элементов действию поперечных сил. - Кишинев: Штиинца, 1981. - 131 с.