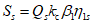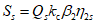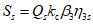СПРАВКА
Источник публикации
М.: Стройиздат, 1969
Примечание к документу
Название документа
"Рекомендации по расчету резервуаров и газгольдеров на сейсмические воздействия"
"Рекомендации по расчету резервуаров и газгольдеров на сейсмические воздействия"
Содержание
РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ РЕЗЕРВУАРОВ И ГАЗГОЛЬДЕРОВ
НА СЕЙСМИЧЕСКИЕ ВОЗДЕЙСТВИЯ
Рекомендации разработаны в Центральной лаборатории сейсмостойкого строительства (руководитель канд. техн. наук В.С. Павлык) ЦНИИ строительных конструкций им. В.А. Кучеренко д-ром техн. наук проф. И.И. Гольденблатом, д-ром техн. наук проф. Н.А. Николаенко, мл. научн. сотр. А.Т. Штоль, инж. В.Р. Тумасовым.
Рекомендации рассчитаны на инженерно-технических работников проектных и научно-исследовательских институтов.
Настоящие Рекомендации составлены в дополнение к СНиП II-А.12-62 "Строительство в сейсмических районах. Нормы проектирования", Стройиздат, М., 1962 и "Инструкции по определению расчетной сейсмической нагрузки на здания и сооружения", М., 1962 и состоят из трех разделов.
В первом разделе даны общие рекомендации по выбору расчетных схем и определению расчетной сейсмической нагрузки для частично заполненных резервуаров и газгольдеров с учетом влияния гидродинамической нагрузки.
Приведен расчет резервуаров с плавающей крышей, даны указания по определению гидродинамического давления при вертикальном сейсмическом толчке.
Во втором разделе даны рекомендации по определению расчетной сейсмической нагрузки на мокрые газгольдеры.
В третьем разделе приведены примеры расчета по определению сейсмической нагрузки для цилиндрических и сферических резервуаров различной емкости, вертикальных газгольдеров постоянного и переменного объемов.
В рекомендациях содержатся данные по определению расчетной сейсмической нагрузки для частично заполненных резервуаров и газгольдеров различной емкости.
Дирекция ЦНИИСК
им. Кучеренко
ДЛЯ ЧАСТИЧНО ЗАПОЛНЕННЫХ РЕЗЕРВУАРОВ
1.1. Настоящие Рекомендации распространяются на расчет вертикальных круговых цилиндрических и сферических резервуаров, частично заполненных жидкостью.
1.2. Предполагается, что резервуар абсолютно жесткий; жидкость, заполняющая резервуар, обладает вязкостью; сейсмическое движение основания является случайным процессом времени или импульсивным; рассматривается переходной процесс колебания жидкости в резервуаре и считается, что длительность землетрясения составляет 30 сек; рассматриваются горизонтальные движения резервуара; даны указания по расчету на вертикальный сейсмический толчок.
1.3. Полная сейсмическая нагрузка, действующая на резервуар, складывается из нагрузки от веса конструкций и от веса заполняющей жидкости.
1.4. Горизонтальные сейсмические силы, приложенные к резервуару и вызванные весом его конструкций, определяются обычным способом по действующему СНиП II-А.12-62, как для жестких конструкций, фундамент которых настолько развит, что поворот сооружения за счет упругости грунта при определении сейсмических воздействий не учитывается.
1.5. Резервуар рассчитывается на горизонтальные и вертикальные гидродинамические силы. Днище резервуара рассчитывается на передаваемое стенками резервуара контурное давление. Указанные нагрузки суммируются с гидростатическим давлением жидкости на стенки и днище.
1.6. Во избежание гидродинамического удара развивающейся в резервуаре волны о покрытие определяется необходимый зазор As между уровнем жидкости и покрытием, если частота волны первой формы больше 1 (1/сек).
1.7. Если балки покрытия разделяют свободную поверхность жидкости на отсеки, то величина зазора As определяется от низа балок до уровня жидкости.
1.8. Если резервуар в силу технологических особенностей заполнен полностью, то жидкость рассматривается как твердое тело.
1.9. Резервуары с одной центральной колонной, радиус которой меньше 0,07 радиуса резервуара, рассчитываются как резервуары без колонны (влиянием колонны можно пренебречь).
1.10. Для резервуара, в котором колонны расположены по концентрическим окружностям, радиус которых меньше 0,07 наименьшего расстояния между колоннами, влиянием колонн можно пренебречь.
ЦИЛИНДРИЧЕСКИЙ РЕЗЕРВУАР
где a - внутренний радиус резервуара;
h - высота резервуара (см. рис. 1);
th - гиперболический тангенс.
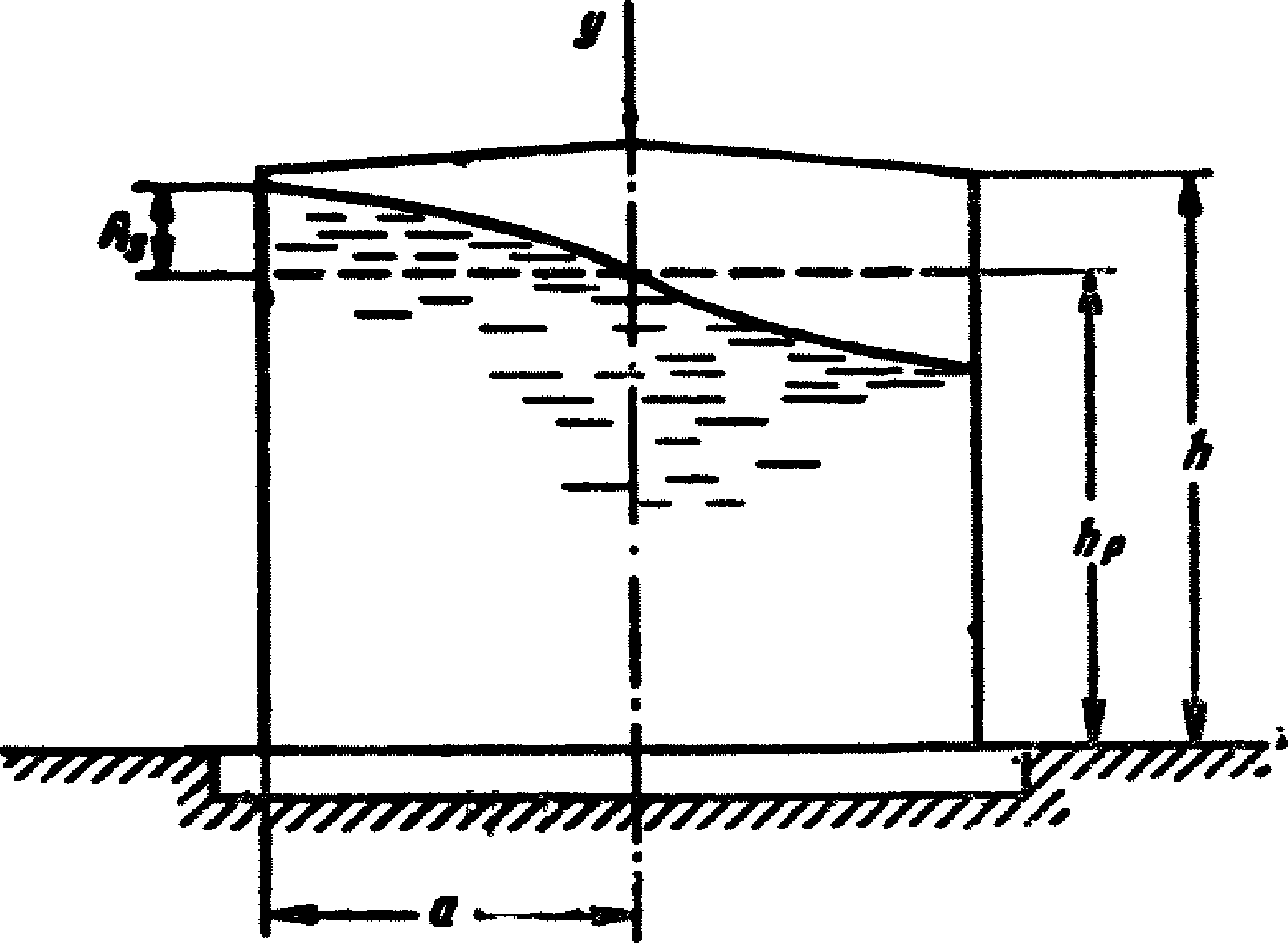
1.12. Величина зазора As (рис. 1) между уровнем жидкости и покрытием резервуара определяется по формуле (1.2):
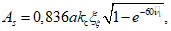 (1.2)
(1.2)где kс - коэффициент сейсмичности, зависящий от балльности района; определяется по СНиП II-А.12-62;
e - основание натурального логарифма;
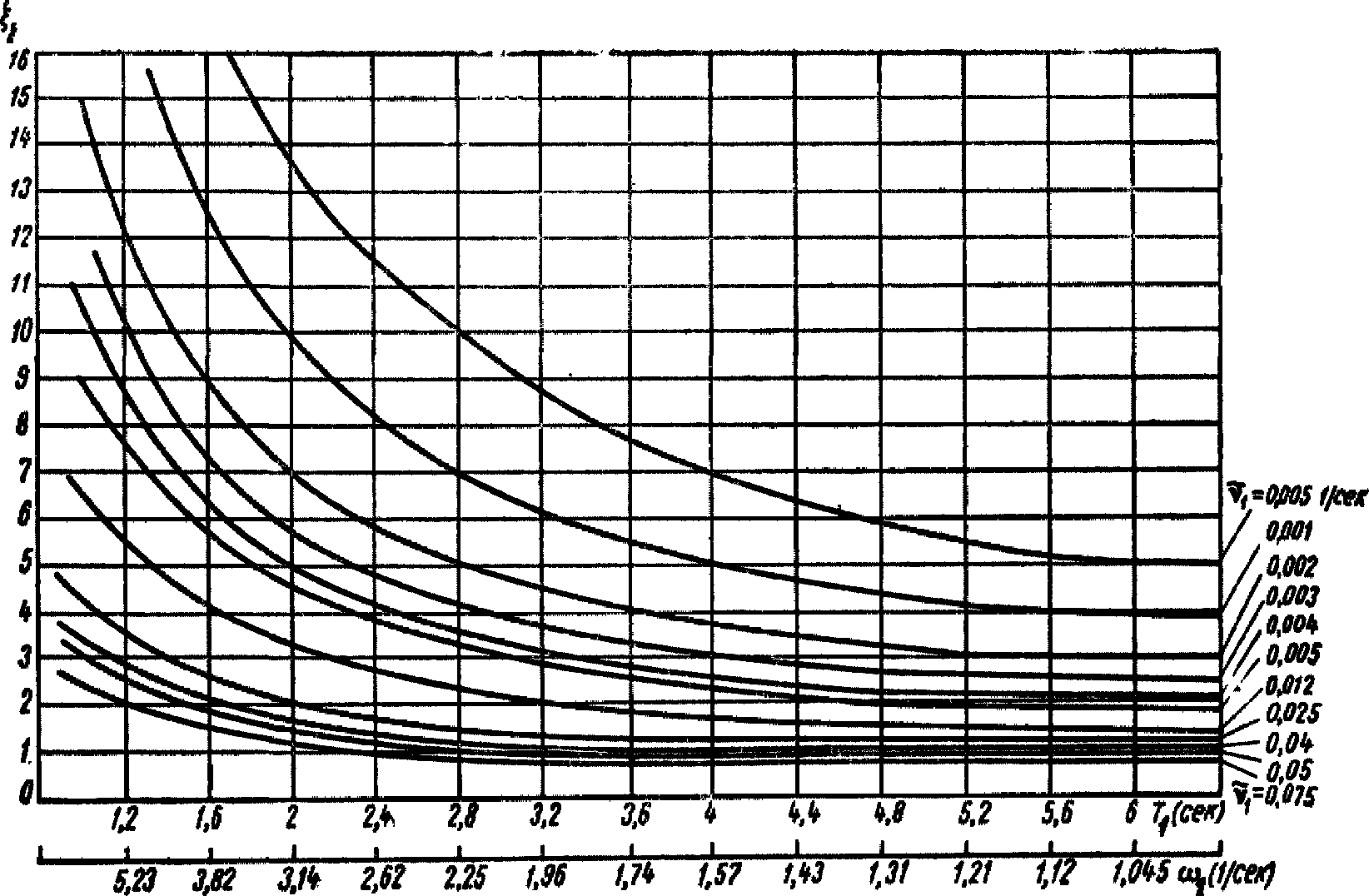
Рис. 2. Графики коэффициента 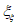 для расчета высоты волны
для расчета высоты волны
в цилиндрическом резервуаре
Для любого отношения 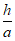
для h > a (h0 > 1)
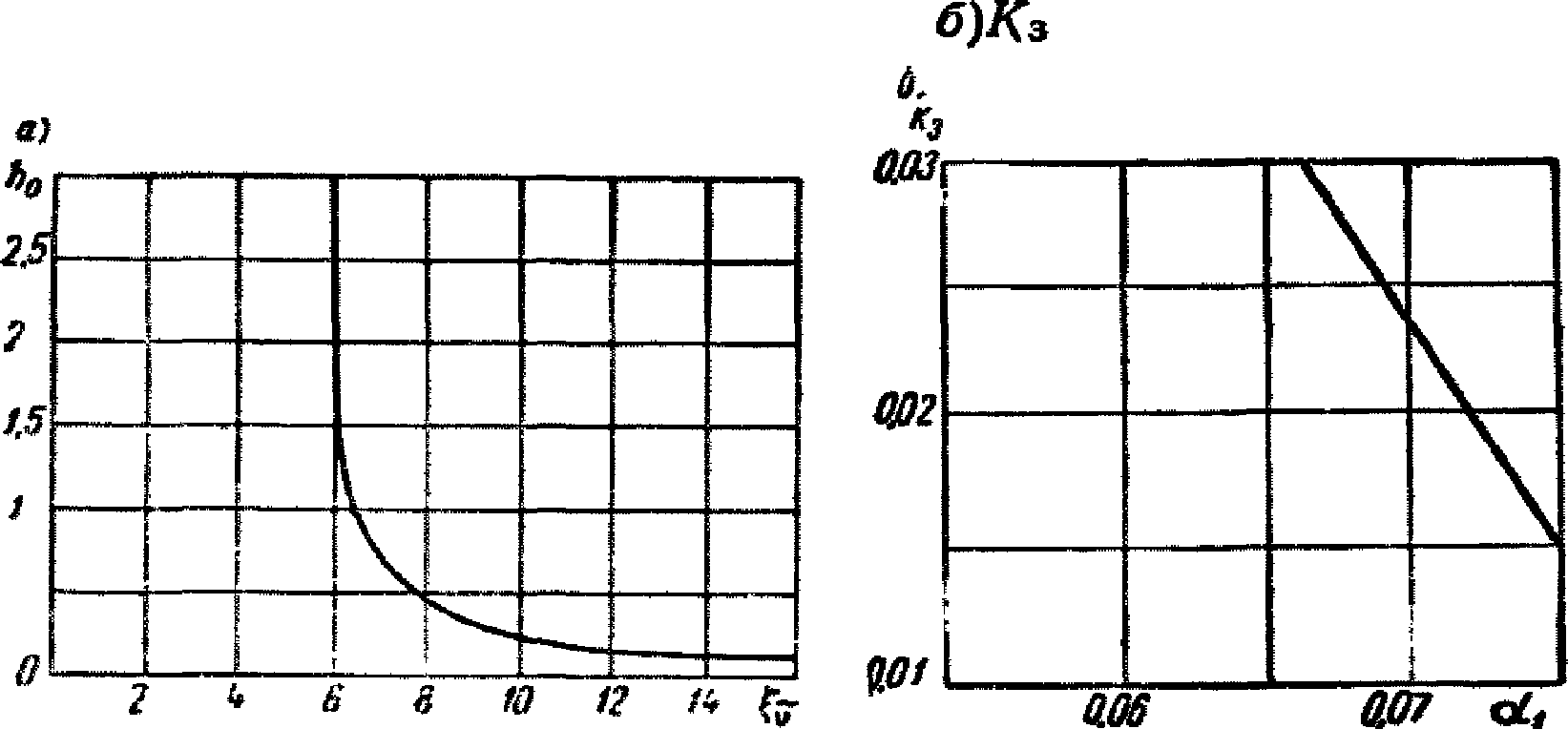
для расчета цилиндрических резервуаров
а - график коэффициента 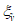 ; б - график коэффициента
; б - график коэффициента 
Некоторые значения коэффициента  приведены в табл. 1.
приведены в табл. 1.
Таблица 1
Температура в град | Кинематическая вязкость в стоксах (см3/сек) | ||||||||||||||
Вода | Масла | Реактивные топлива | |||||||||||||
авиамасло МЗС | автол 18 | автол 10 | трансформаторное | турбинное | автотракторное АС-5 | автотракторное АК-6 | автотракторное АС-9,5 | автотракторное АК-15 | автомобильное АК-10 | Т-1 | Т-5 | ТС-1 | Т-2 | ||
-50 | - | 1,5·105 | 6,5·106 | 1,4·106 | - | - | - | - | - | 6,5·106 | 1,4·108 | 1 500 | 10 000 | 800 | 500 |
-40 | - | 13 600 | 1,9·105 | 36 200 | 99,847 | - | - | - | - | 1,8·105 | 36 200 | 900 | 5 000 | 500 | 430 |
-30 | - | 1 930 | 20 000 | 3 400 | 18,237 | 230,38 | - | - | - | 20 000 | 3 400 | - | - | - | - |
-20 | - | 388 | 2 650 | 540 | 4,812 | 43,57 | - | - | - | 2 650 | 540 | 460 | 1 800 | 280 | 220 |
-10 | - | 111 | 490 | 122 | 1,92 | 12,51 | - | - | - | 490 | 122 | - | - | - | - |
0 | 0,018 | 35,5 | 116 | 39 | 0,91 | 4,6 | 8,673 | 19,34 | 33,69 | 116 | 39,1 | 250 | 600 | 180 | 150 |
10 | 0,013 | - | - | - | 0,49 | 1,99 | - | - | - | - | - | - | - | - | - |
20 | 0,01 | 5,61 | 12,8 | 6 | 0,28 | 1,019 | 1,709 | 2,847 | 4,775 | 12,8 | 6 | 160 | 400 | 130 | 110 |
30 | 0,008 | - | - | - | 0,179 | 0,567 | - | - | - | - | - | - | - | - | - |
40 | 0,0066 | - | - | - | 0,123 | 0,344 | - | - | - | - | - | 120 | 250 | 100 | 90 |
50 | 0,0055 | 0,85 | 1,21 | 0,758 | 0,096 | 0,219 | 0,3219 | 0,4361 | 0,6791 | 1,21 | 0,758 | - | - | - | - |
60 | - | - | - | - | - | - | - | - | - | - | - | 90 | 180 | 80 | 75 |
70 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
80 | - | - | - | - | - | - | - | - | - | - | - | 75 | - | 69 | - |
90 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
100 | - | 0,142 | 0,153 | 0,114 | - | - | 0,0668 | 0,0778 | 0,1063 | 0,153 | 0,114 | 64 | - | 56 | - |
Если 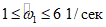 , то As вычисляется по формуле
, то As вычисляется по формуле
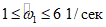 , то As вычисляется по формуле
, то As вычисляется по формуле1.13. Гидродинамическое давление жидкости на стенки резервуара вычисляется по формуле
где
Vоб - объемный вес жидкости, заполняющей резервуар;
ch - гиперболический косинус;
y - ордината (см. рис. 4, а);
Таблица 2
0,4 | 0,3 | 0,2 | 0,1 | 0,05 | 0 | |
 | ||||||
10 | 1,23 | 2,01 | 2,91 | 3,88 | 4,36 | 4,83 |
6 | 0,92 | 1,11 | 1,48 | 1,92 | 2,15 | 2,39 |
4 | 0,85 | 0,84 | 0,97 | 1,21 | 1,35 | 1,49 |
3 | 0,83 | 0,74 | 0,76 | 0,9 | 0,99 | 1,1 |
2,5 | 0,82 | 0,7 | 0,67 | 0,75 | 0,82 | 0,9 |
2 | 0,81 | 0,66 | 0,59 | 0,61 | 0,65 | 0,72 |
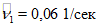 | ||||||
10 | 1,415 | 2,43 | 3,57 | 4,75 | 5,33 | 5,92 |
6 | 0,985 | 1,805 | 1,79 | 2,34 | 2,63 | 2,93 |
4 | 0,876 | 0,94 | 1,165 | 1,475 | 1,65 | 1,84 |
3 | 0,843 | 0,803 | 0,893 | 1,09 | 1,21 | 1,33 |
2,5 | 0,83 | 0,74 | 0,773 | 0,905 | 1 | 1,08 |
2 | 0,82 | 0,695 | 0,66 | 0,729 | 0,8 | 0,88 |
1 | 0,6 | 0,69 | 0,75 | 0,75 | ||
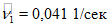 | ||||||
10 | 1,65 | 2,67 | 3,98 | 5,29 | 5,75 | 6,35 |
6 | 1,03 | 1,43 | 2 | 2,62 | 2,95 | 3,27 |
4 | 0,83 | 1 | 1,27 | 1,65 | 1,84 | 2,06 |
3 | 0,85 | 0,79 | 0,99 | 1,21 | 1,32 | 1,5 |
2,5 | 0,82 | 0,73 | 0,84 | 0,99 | 1,11 | 1,21 |
2 | 0,79 | 0,71 | 0,74 | 0,84 | 0,89 | 0,98 |
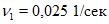 | ||||||
10 | 1,81 | 3,39 | 5,05 | 6,31 | 7,51 | 8,37 |
6 | 1,14 | 1,78 | 2,52 | 3,31 | 3,73 | 4,15 |
4 | 0,91 | 1,22 | 1,59 | 2,03 | 2,33 | 2,58 |
3 | 0,86 | 0,96 | 1,2 | 1,67 | 1,72 | 1,89 |
2,5 | 0,85 | 0,87 | 1,05 | 1,27 | 1,41 | 1,56 |
2 | 0,84 | 0,78 | 0,84 | 1,01 | 1,12 | 1,27 |
 | ||||||
10 | 3,83 | 7,52 | 11,3 | 15 | 16,9 | 18,75 |
6 | 2,01 | 3,74 | 5,66 | 7,4 | 8,34 | 9,27 |
4 | 1,405 | 2,38 | 3,49 | 4,63 | 5,21 | 5,78 |
3 | 1,175 | 1,795 | 2,57 | 3,4 | 3,83 | 4,27 |
2,5 | 1,06 | 1,48 | 2,14 | 2,81 | 3,14 | 3,49 |
2 | 0,973 | 1,26 | 1,71 | 2,26 | 2,51 | 2,77 |
1 | 0,95 | 1,1 | 1,25 | 1,4 | 1,6 | 1,8 |
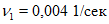 | ||||||
10 | 4,26 | 0,35 | 12,6 | 16,8 | 18,9 | 21 |
6 | 2,22 | 4,18 | 6,21 | 8,28 | 9,32 | 10,32 |
4 | 1,51 | 2,65 | 3,9 | 5,18 | 5,81 | 6,47 |
3 | 1,24 | 1,98 | 2,87 | 3,8 | 4,26 | 4,74 |
2,5 | 1,12 | 1,67 | 2,38 | 3,14 | 3,52 | 3,91 |
2 | 1,01 | 1,36 | 1,9 | 2,49 | 2,8 | 3,1 |
1 | 1,1 | 1,2 | 1,4 | 1,7 | 1,8 | 2,1 |
1 | 1,05 | 1,21 | 1,71 | 2,25 | 2,72 | 3 |
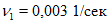 | ||||||
10 | 4,9 | 9,73 | 14,5 | 19,4 | 21,8 | 24,2 |
6 | 2,51 | 4,81 | 7,16 | 9,56 | 10,76 | 11,93 |
4 | 1,69 | 3,04 | 4,49 | 5,95 | 6,7 | 7,45 |
3 | 1,35 | 2,26 | 3,3 | 4,38 | 4,93 | 5,46 |
2,5 | 1,205 | 1,91 | 2,74 | 3,61 | 4,06 | 4,51 |
2 | 1,073 | 1,56 | 2,18 | 2,87 | 3,23 | 3,58 |
1 | 1 | 1,2 | 1,62 | 1,93 | 2,21 | 2,45 |
Продолжение таблицы 2
0,4 | 0,3 | 0,2 | 0,1 | 0,65 | 0 | |
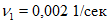 | ||||||
10 | 5,96 | 11,85 | 17,8 | 23,7 | 26,7 | 29,7 |
6 | 3,03 | 5,87 | 8,8 | 11,7 | 13,18 | 14,62 |
4 | 1,99 | 3,7 | 5,49 | 7,32 | 8,24 | 9,14 |
3 | 1,56 | 2,74 | 4,03 | 5,35 | 6,03 | 6,66 |
2,5 | 1,36 | 2,29 | 3,34 | 4,43 | 4,98 | 5,52 |
2 | 1,18 | 1,86 | 2,66 | 3,52 | 3,96 | 4,4 |
1 | 1,05 | 1,21 | 1,71 | 2,25 | 2,72 | 3 |
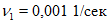 | ||||||
10 | 8,44 | 16,81 | 25,2 | 33,6 | 37,81 | 42 |
6 | 4,22 | 8,29 | 12,42 | 16,58 | 18,65 | 20,71 |
4 | 2,7 | 5,2 | 7,78 | 10,36 | 11,64 | 12,95 |
3 | 2,06 | 3,84 | 5,65 | 7,59 | 8,55 | 9,49 |
2,5 | 1,76 | 3,18 | 4,71 | 6,97 | 7,04 | 7,83 |
2 | 1,47 | 2,56 | 3,75 | 4,25 | 5,59 | 6,21 |
1 | 1,13 | 1,62 | 2,11 | 2,63 | 3,12 | 3,75 |
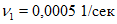 | ||||||
10 | 11,9 | 23,81 | 35,6 | 47,5 | 53,3 | 61 |
6 | 5,9 | 11,84 | 17,58 | 23,4 | 26,3 | 28,8 |
4 | 3,75 | 7,35 | 11 | 14,65 | 16,5 | 18,3 |
3 | 2,8 | 5,4 | 8,05 | 10,71 | 12,15 | 13,15 |
2,5 | 2,36 | 4,47 | 6,65 | 8,86 | 9,95 | 11,06 |
2 | 1,93 | 3,57 | 5,29 | 7,04 | 7,92 | 8,82 |
1 | 1,73 | 2,63 | 3,21 | 38,1 | 4,21 | 4,95 |
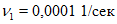 | ||||||
2 | - | - | 7,2 | 9,8 | 11,4 | 13,4 |
1 | - | - | 4,6 | 5,5 | 6 | 6,6 |
жидкости в цилиндрическом резервуаре
Распределенная нагрузка по оси резервуара вычисляется по формуле
Примечания: 1. Значения коэффициента 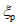 могут вычисляться по линейной интерполяции табл. 2.
могут вычисляться по линейной интерполяции табл. 2.
2. Резервуар на нагрузку P(y) рассчитывается как консольная балка с защемленным концом, по оси которой действует нагрузка Pос(y) [формула (1.9) (см. рис. 4, г)].
1.14. Результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле
где Qж - вес всей жидкости; коэффициент 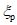 , определяемый по табл. 2 в зависимости от
, определяемый по табл. 2 в зависимости от 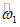 ,
, 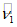 и E1, которое равно:
и E1, которое равно:
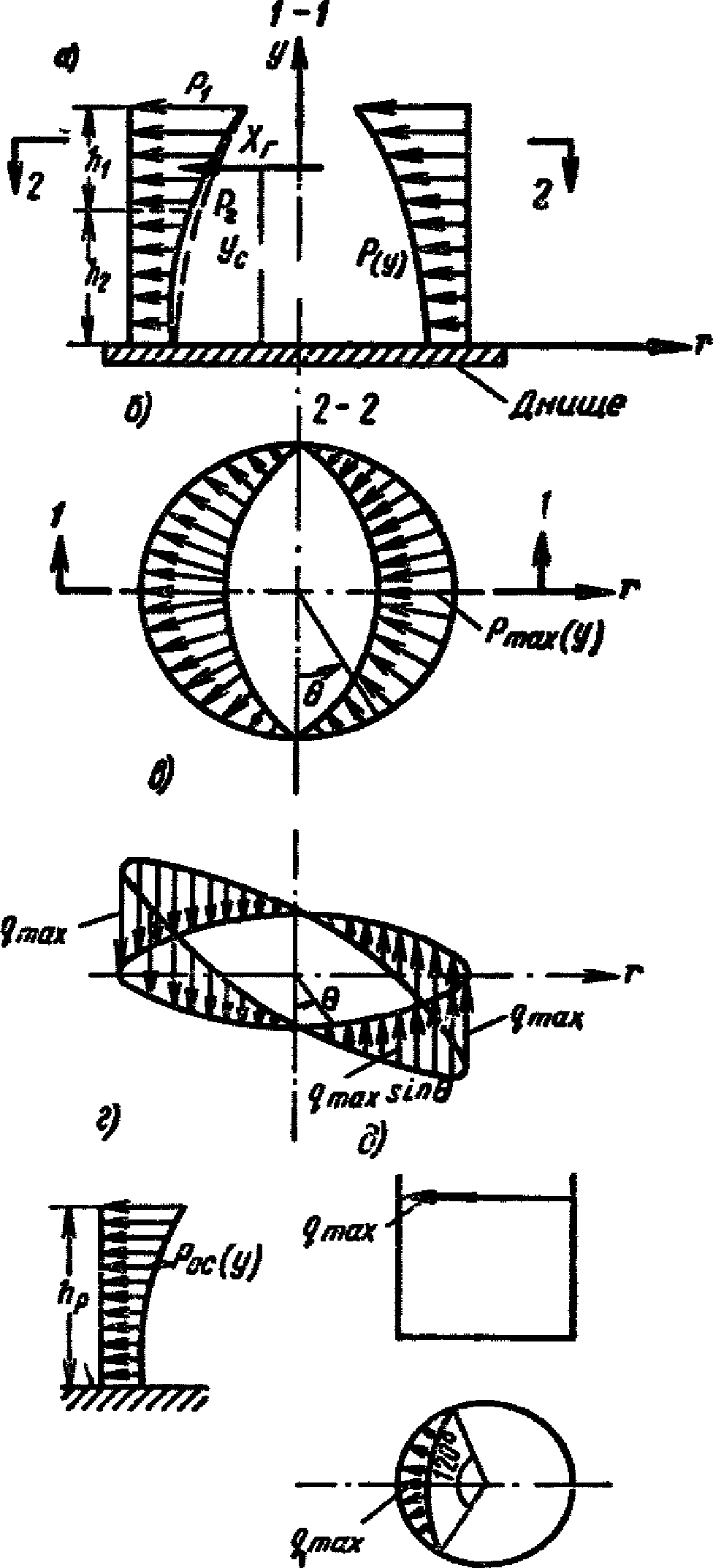
1.15. Координата yс (рис. 4, а), определяющая линию действия силы Xг, соответствует центру тяжести эпюры гидродинамического давления.
Для приближенного определения yс допускается кривую Pmax (y) заменить двумя трапециями (см. рис. 4, а), тогда
1.16. Контурное давление на днище (см. рис. 4, в), вызванное моментом сил, действующих на стенки резервуара, вычисляется по формуле
где
Примечание. Статический расчет днища на контурную нагрузку  производят по формулам, приведенным в Инструкции, опубликованной в сборнике "Исследование по сейсмостойкости зданий и сооружений", Госстройиздат, 1961. Для расчета днища можно использовать практические методы, приведенные в книгах Б.Г. Коренева и Е.И. Черниговской "Расчет плит на упругом основании", Госстройиздат, 1962, И.И. Гольденблата и Н.А. Николаенко "Расчет конструкций на действие сейсмических и импульсивных сил", М., Госстройиздат, 1961.
производят по формулам, приведенным в Инструкции, опубликованной в сборнике "Исследование по сейсмостойкости зданий и сооружений", Госстройиздат, 1961. Для расчета днища можно использовать практические методы, приведенные в книгах Б.Г. Коренева и Е.И. Черниговской "Расчет плит на упругом основании", Госстройиздат, 1962, И.И. Гольденблата и Н.А. Николаенко "Расчет конструкций на действие сейсмических и импульсивных сил", М., Госстройиздат, 1961.
В книге И.И. Гольденблата и Н.А. Николаенко имеются указания по расчету резервуаров на действие нагрузки P(y).
1.17. Распределенная гидродинамическая нагрузка по оси центральной круглой колонны вычисляется по формуле:
где a1 - радиус колонны;
a - радиус резервуара;
Vоб - объемный вес жидкости;
kс - коэффициент сейсмичности;
где 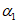 - коэффициент, который берется по графику рис. 3, б в зависимости от
- коэффициент, который берется по графику рис. 3, б в зависимости от 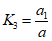 ; остальные величины имеют прежнее значение [см. расшифровку к формуле (1.8)].
; остальные величины имеют прежнее значение [см. расшифровку к формуле (1.8)].
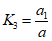 ; остальные величины имеют прежнее значение [см. расшифровку к формуле (1.8)].
; остальные величины имеют прежнее значение [см. расшифровку к формуле (1.8)].1.18. Если частота волны первой формы жидкости, заполняющей резервуар, меньше или равна 1 1/сек  , то расчет высоты волны не производится.
, то расчет высоты волны не производится.
 , то расчет высоты волны не производится.
, то расчет высоты волны не производится.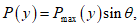 (1.17)
(1.17)где Pmax(y) = VобakсK1, (1.18)
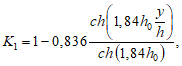 (1.19)
(1.19)Vоб - объемный вес жидкости.
На рис. 5, а для ряда значений 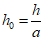 в зависимости от y/h приведены графики коэффициента K1.
в зависимости от y/h приведены графики коэффициента K1.
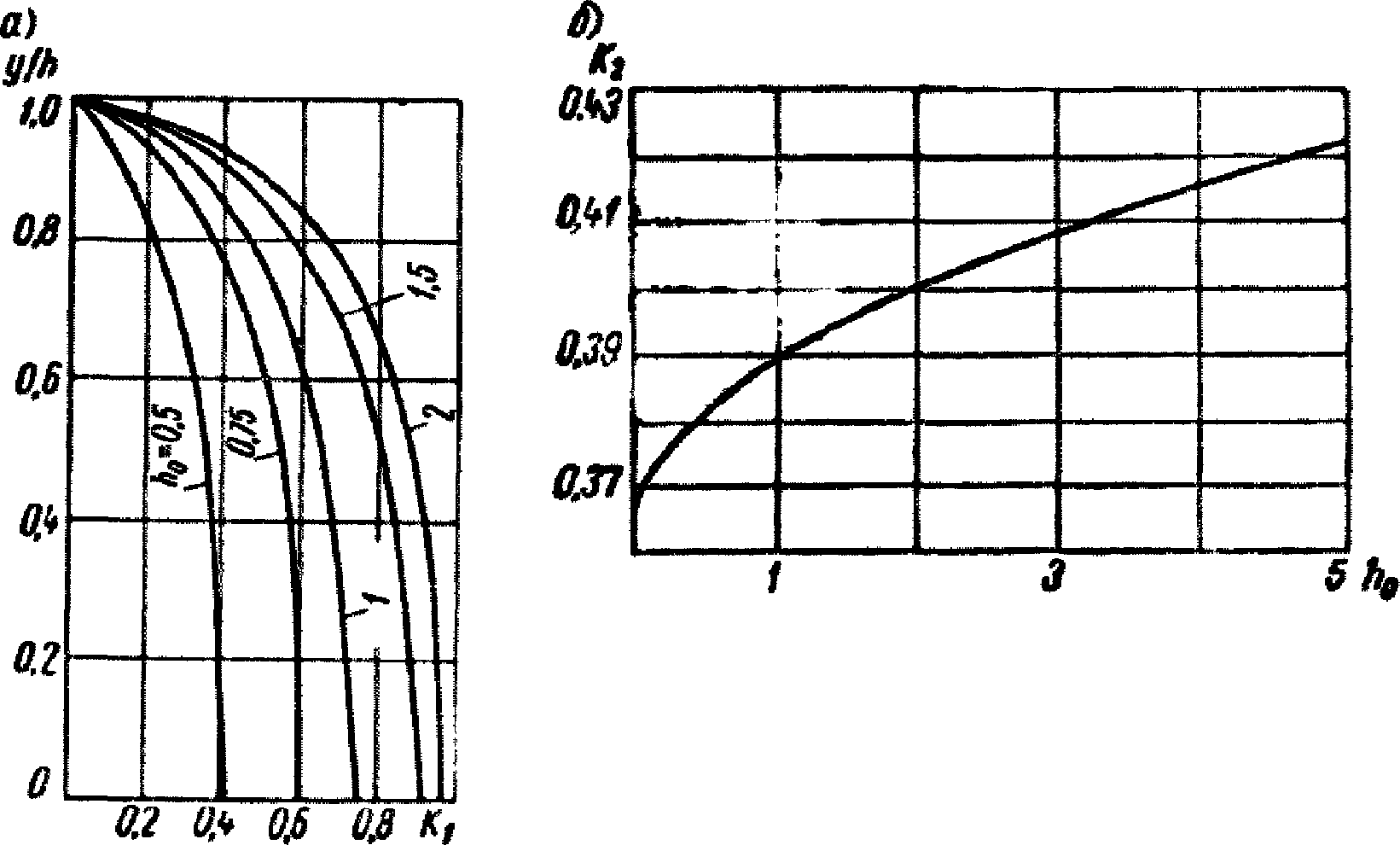
а - график коэффициента K1;
б - график коэффициента K2
1.20. Для  результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле
результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле
 результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле
результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле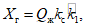 (1.20)
(1.20)где Qж - вес всей жидкости.
Коэффициент  берется по графику 1 рис. 12, а в зависимости от h0.
берется по графику 1 рис. 12, а в зависимости от h0.
Координата yс, определяющая линию действия силы Xг (см. рис. 4, а), вычисляется по формуле
yс = hK2. (1.21)
Коэффициент K2 берется по графику рис. 5, б в зависимости от h0.
1.21. Для 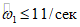 контурное давление на днище (или фундамент), вызванное моментом сил, действующих на стенки резервуара (см. рис. 4, в), вычисляется по формуле
контурное давление на днище (или фундамент), вызванное моментом сил, действующих на стенки резервуара (см. рис. 4, в), вычисляется по формуле
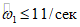 контурное давление на днище (или фундамент), вызванное моментом сил, действующих на стенки резервуара (см. рис. 4, в), вычисляется по формуле
контурное давление на днище (или фундамент), вызванное моментом сил, действующих на стенки резервуара (см. рис. 4, в), вычисляется по формуле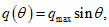 (1.22)
(1.22)где
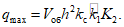 (1.23)
(1.23)Цилиндрический резервуар с плавающей крышей
1.22. Расчет высоты волны в цилиндрическом резервуаре с плавающей крышей не производится.
1.23. Гидродинамическое давление жидкости на стенки резервуара по высоте распределено равномерно, в плане по закону синуса и вычисляется по формуле
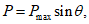 (1.24)
(1.24)где
1.24. Результирующая гидродинамического давления жидкости на стенки резервуара определяется по формуле
Координата yс равна
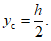 (1.27)
(1.27)1.25. Контурное давление на днище (см. рис. 4, в), вызванное моментом сил, действующих на стенки резервуара, распределено по закону синуса и вычисляется по формуле
где
1.26. Для резервуаров, предназначенных для сейсмических районов, предпочтительна плавающая крыша с мягким затвором. Сейсмическая нагрузка от плавающей крыши распределена по закону синуса, передается на стенки резервуара в крайнем верхнем положении понтона (см. рис. 4, д) и вычисляется по формуле
где
Pп - вес понтона.
1.27. Сейсмическое давление жидкости на стенки резервуара при вертикальном сейсмическом толчке вычисляется по формуле
где Pс - гидростатическое давление жидкости;
Pверт - по высоте распределена так же, как гидростатическая нагрузка, и суммируется с последней.
Если резервуар с плавающей крышей, которая при незаполненном резервуаре опирается на стойки, то необходим расчет на вертикальные силы крыши и стоек. Расчет этих конструкций производится по СНиП II-А.12-62.
Сферический резервуар
[установка на жестком железобетонном стакане (рис. 6)]
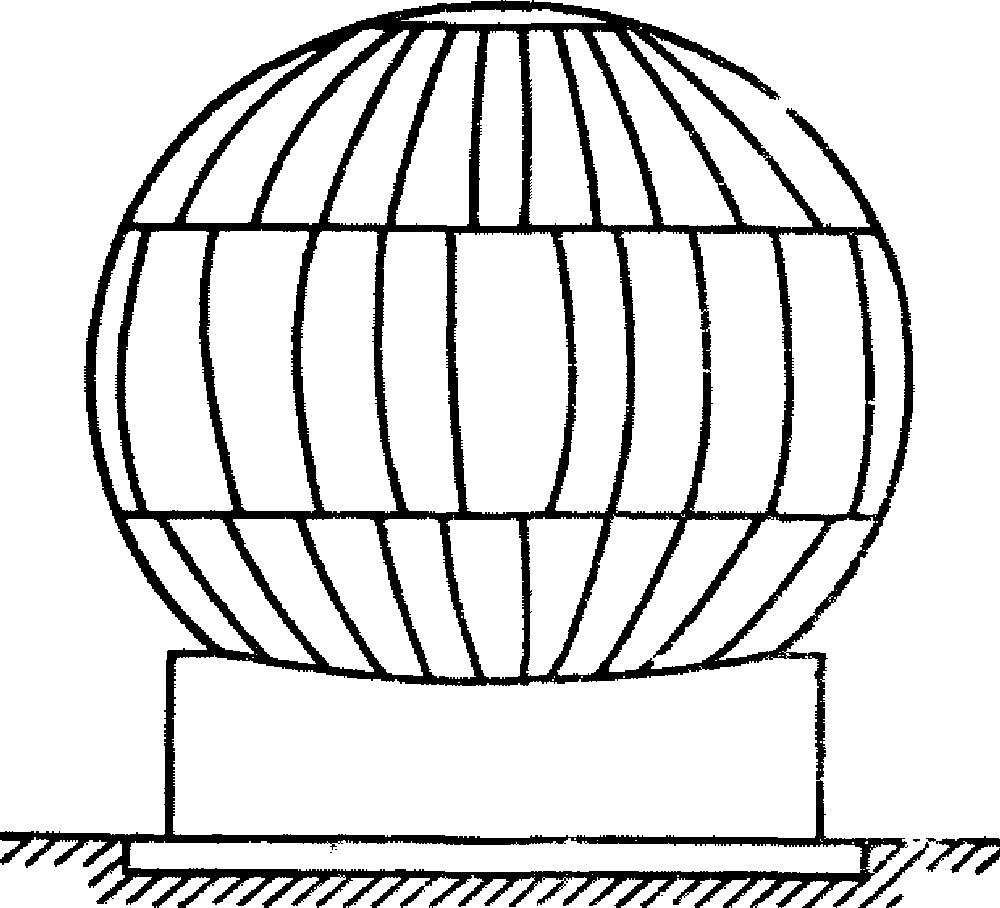
Рис. 6. Установка резервуара на кольцевом
железобетонном "стакане"
1.28. Результирующая гидродинамического давления жидкости на стенки резервуара (полное горизонтальное усилие) определяется по формуле
где
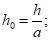
величины h0 и a см. на рис. 8;
 для h0 < 1; (1.35)
для h0 < 1; (1.35)где  и
и 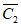 - коэффициенты, которые определяются по графикам рис. 7, а и 7, б в зависимости от h0.
- коэффициенты, которые определяются по графикам рис. 7, а и 7, б в зависимости от h0.
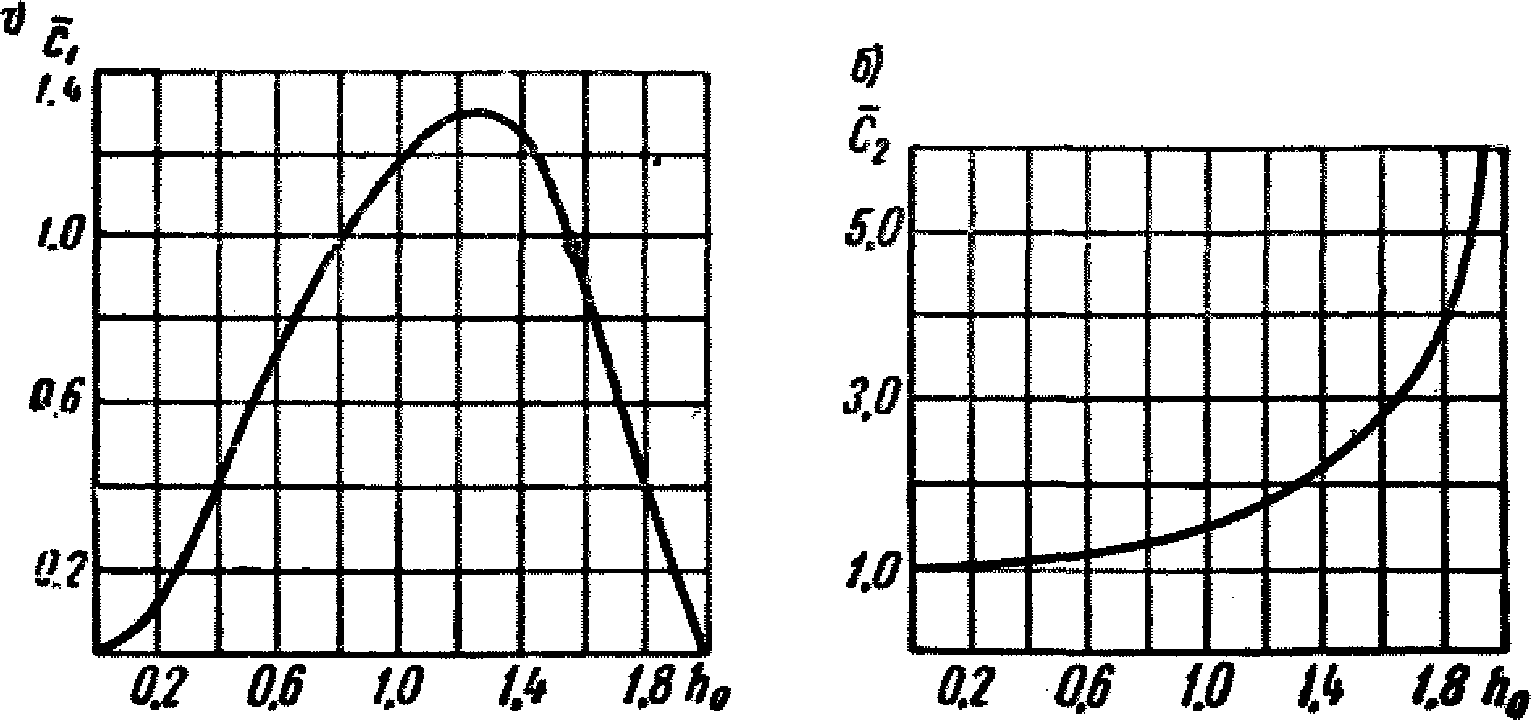
Рис. 7. Графики коэффициентов 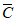
а - график коэффициента 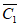 ; б - график коэффициента
; б - график коэффициента 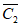
1.29. Координата yс (рис. 8) равна:
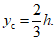 (1.38)
(1.38)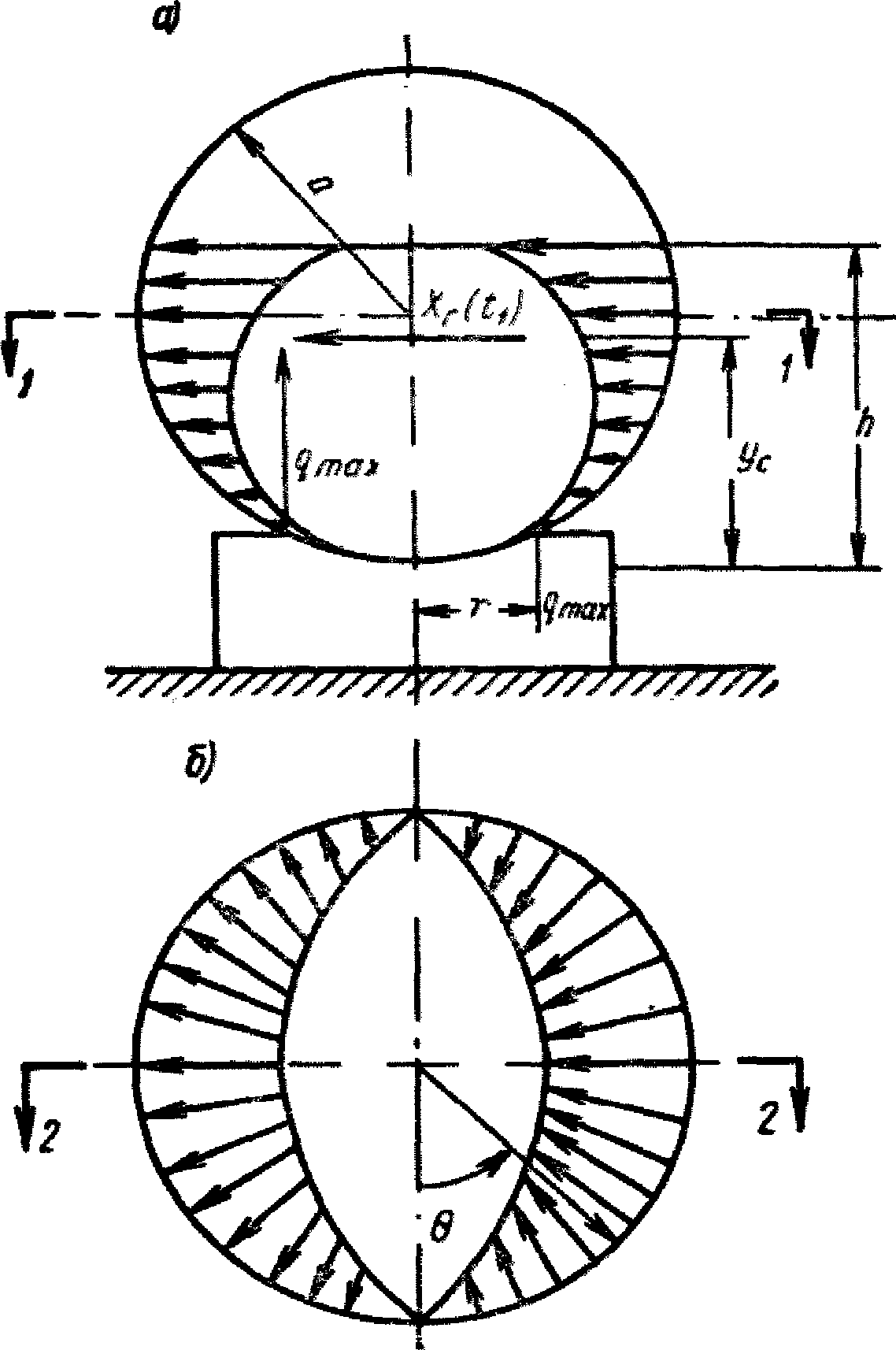
в сферическом резервуаре
1.30. Резервуар рассчитывается на силы реакций от железобетонного стакана (см. рис. 8), которые распределяются по контуру опирания радиуса r, по формуле
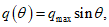 (1.39)
(1.39)где
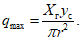 (1.40)
(1.40)Эпюра нагрузки 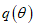 имеет такой же вид, как и контурное давление на днище в случае цилиндрического резервуара (см. рис. 4, в).
имеет такой же вид, как и контурное давление на днище в случае цилиндрического резервуара (см. рис. 4, в).
НА МОКРЫЕ ГАЗГОЛЬДЕРЫ
2.1. Настоящие Рекомендации распространяются на расчет мокрых сферических и цилиндрических газгольдеров, схемы которых показаны на рис. 9, 10, 11, а также на расчет сферических резервуаров, устанавливаемых на стойках.
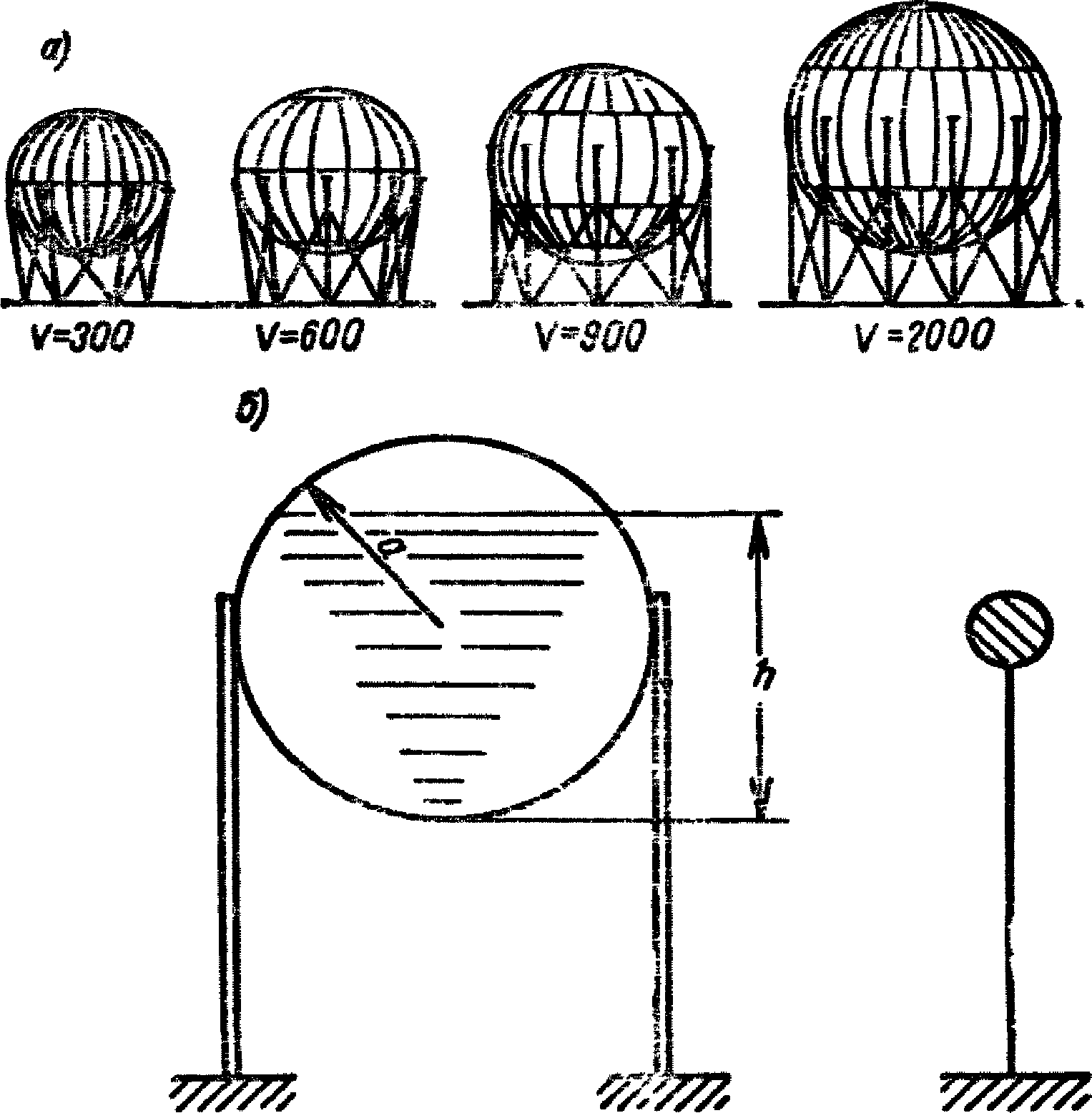
установленного на стойках
а - общий вид; б - расчетная схема
1 - бетонные грузы по всему контуру весом 28 т (колокола);
2 - чугунные грузы по всему контуру весом 55 т (колокола);
3 - резервуар; 4 - песчано-грунтовое основание
2.2. Сейсмическая нагрузка для частично заполненного сферического резервуара [газгольдера, устанавливаемого на стойках (см. рис. 9, а)], определяется по формуле
где Qк - вес конструкции резервуара с учетом половины веса поддерживающих стоек;
Qж - вес жидкости;
h и a - см. на рис. 9, б;
где f11 - горизонтальное перемещение конструкции, несущей резервуар, от силы, равной 1.
Примечания: 1. Вес жидкости, частично заполняющей сферический резервуар, равен: 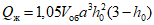 ;
;
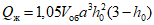 ;
;2. По формуле (2.1) определяется значение сейсмической нагрузки для одноэтажной каркасной конструкции, несущей резервуар. Если резервуар цилиндрический или прямоугольный, то 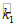 определяется по графику (рис. 12, а). Для прямоугольного резервуара h0 = h/b, где b - ширина резервуара, h - высота налива жидкости.
определяется по графику (рис. 12, а). Для прямоугольного резервуара h0 = h/b, где b - ширина резервуара, h - высота налива жидкости.
3. Коэффициент формы колебаний 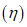 для одномассовых систем равен 1.
для одномассовых систем равен 1.
4. Многоэтажная каркасная конструкция, несущая резервуары, рассчитывается в соответствии с "Инструкцией по определению расчетной сейсмической нагрузки для зданий и сооружений", Госстройиздат, 1962.
5. Конструкции, несущие резервуары, рассчитываются на силу S, вычисленную по формуле (2.1).
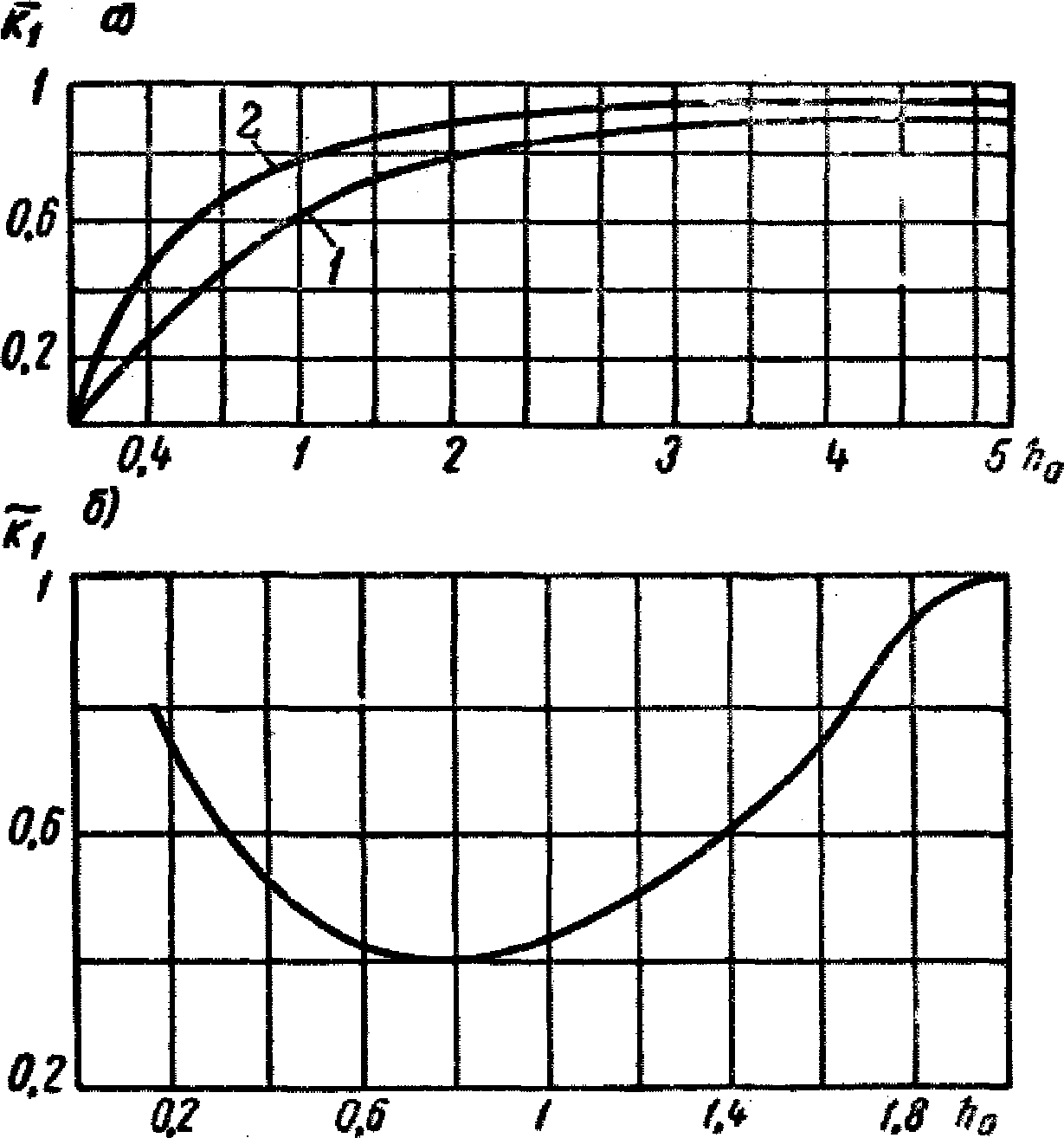
а - цилиндрического (1) и прямоугольного (2);
б - сферического
2.3. Сейсмические нагрузки и высота волны от жидкости в цилиндрическом и сферическом резервуарах, стоящих на каркасе, определяются следующим образом:
а) для сооружений с периодом собственных колебаний до 0,4 сек по формулам (1.10) - (1.29) (рассчитывается как резервуар, стоящий на земле, упругостью каркаса можно пренебречь);
б) для сооружений с периодом собственных колебаний от 0,4 до 1,6 сек все расчетные величины, вычисленные по формулам (1.10) - (1.36), берутся с коэффициентом 1,25.
Примечания: 1. При определении периодов собственных колебаний жидкость можно рассматривать как твердое тело с массой, равной 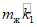 , где mж - масса жидкости, коэффициент
, где mж - масса жидкости, коэффициент 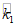 берется в зависимости от резервуара по графикам рис. 12, а.
берется в зависимости от резервуара по графикам рис. 12, а.
2. В некоторых случаях резервуар, стоящий на каркасе, можно на гидродинамические сейсмические силы не рассчитывать, так как напряжения в конструкциях резервуара от этих нагрузок не превышают 10% статических. Подвижность жидкости существенно влияет на сейсмические нагрузки, которые передаются на несущий каркас.
2.4. При расчете круговых вертикальных цилиндрических газгольдеров (см. рис. 10) с отношением 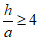 (h - высота налива жидкости от низа днища; a - радиус) жидкость рассматривается как твердое тело и определение сейсмических сил производится обычным образом в соответствии со СНиП II-А.12-62 и Инструкцией, указанной в п. 2.2, или "Указаниями по определению сейсмической нагрузки для вертикальных аппаратов", Госстройиздат, 1961.
(h - высота налива жидкости от низа днища; a - радиус) жидкость рассматривается как твердое тело и определение сейсмических сил производится обычным образом в соответствии со СНиП II-А.12-62 и Инструкцией, указанной в п. 2.2, или "Указаниями по определению сейсмической нагрузки для вертикальных аппаратов", Госстройиздат, 1961.
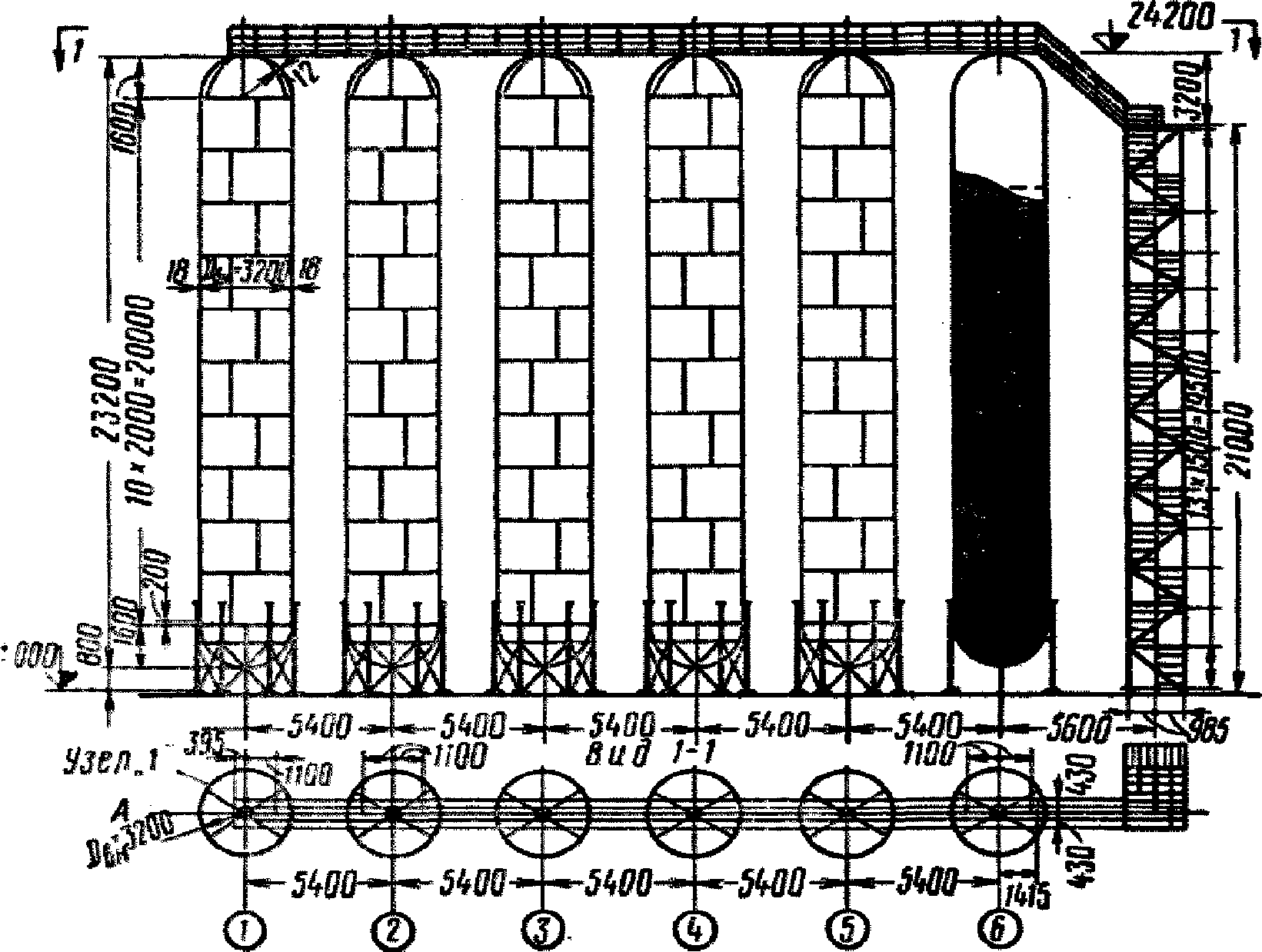
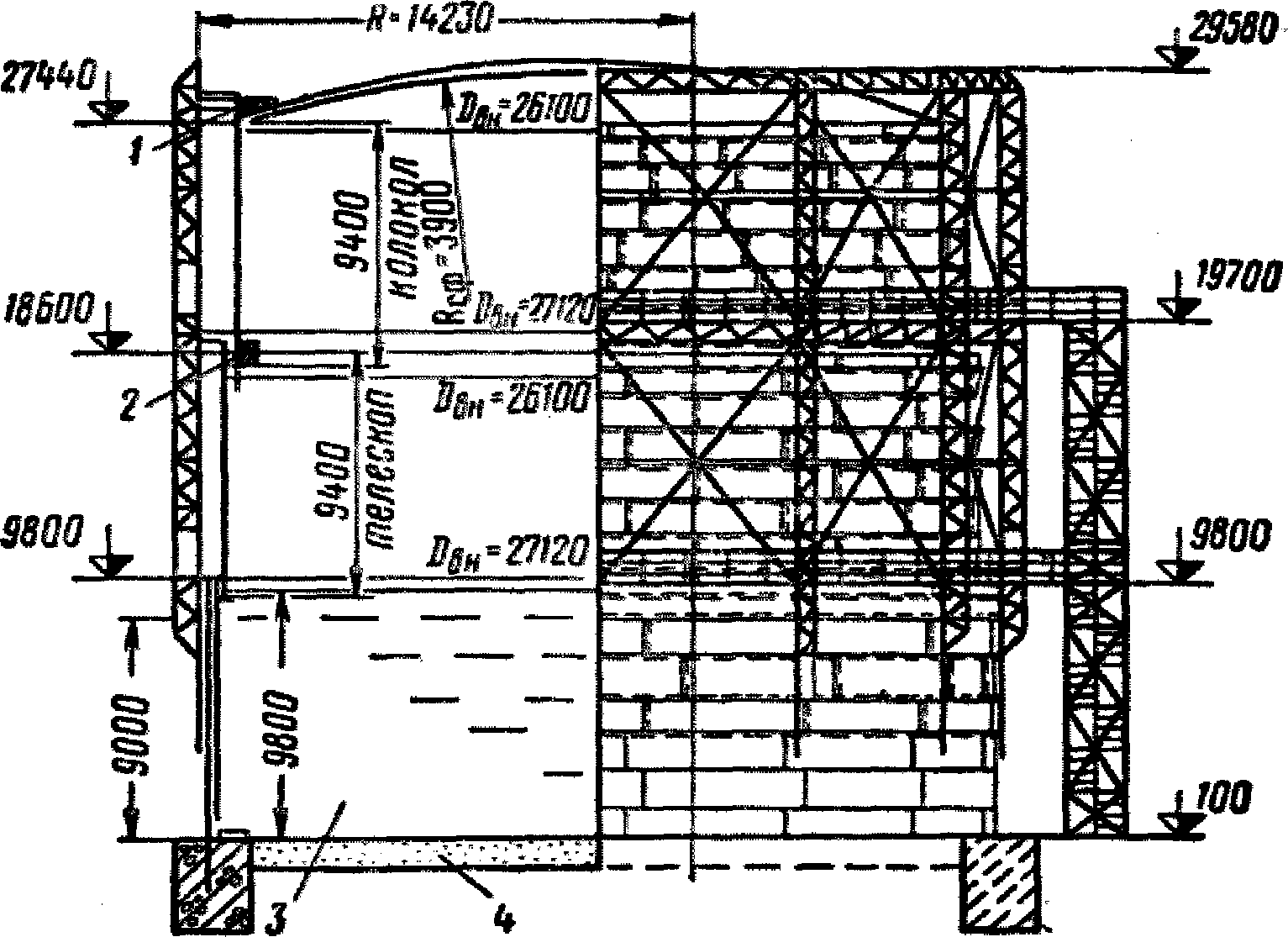
2.5. При расчете цилиндрического газгольдера переменного объема (см. рис. 11) сейсмические нагрузки определяются следующим образом:
б) сейсмические нагрузки от веса телескопа, колокола и решетчатой направляющей конструкции определяются как для жесткой системы по СНиП II-А.12-62, причем рассматривается крайнее верхнее положение колокола;
в) сейсмическая нагрузка от веса телескопа, колокола и других конструкций газгольдера распределяется на 7 стоек направляющей решетчатой конструкции и считается действующей горизонтально в точках, где находятся подвижные ролики (рис. 13 и 14):
где  - значение сейсмической силы в точке
- значение сейсмической силы в точке 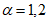 .
.
Примечание. При расчете газгольдера переменного объема (см. рис. 11) рекомендуется принять расчетную схему с двумя степенями свободы, сосредоточив массу на уровне верхнего ролика колокола и верхнего ролика телескопа (см. рис. 14).
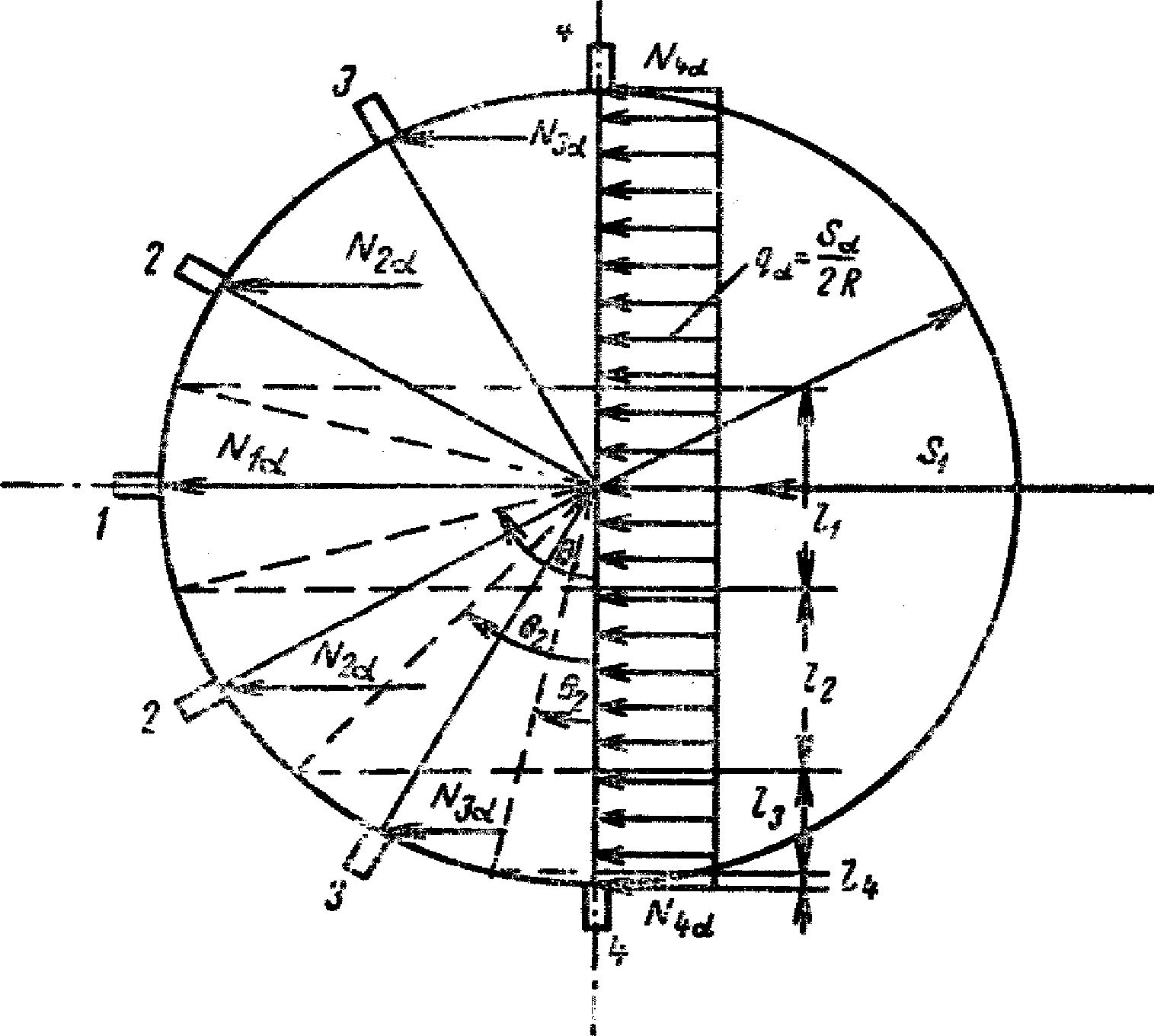
в цилиндрическом газгольдере от веса
телескопа и колокола

Круглый цилиндрический резервуар емкостью 2000 м3
Резервуар предназначен для хранения мазута. Примем, что положительная максимальная температура хранения 20 °C. Основные геометрические параметры резервуара указаны на рис. 15.
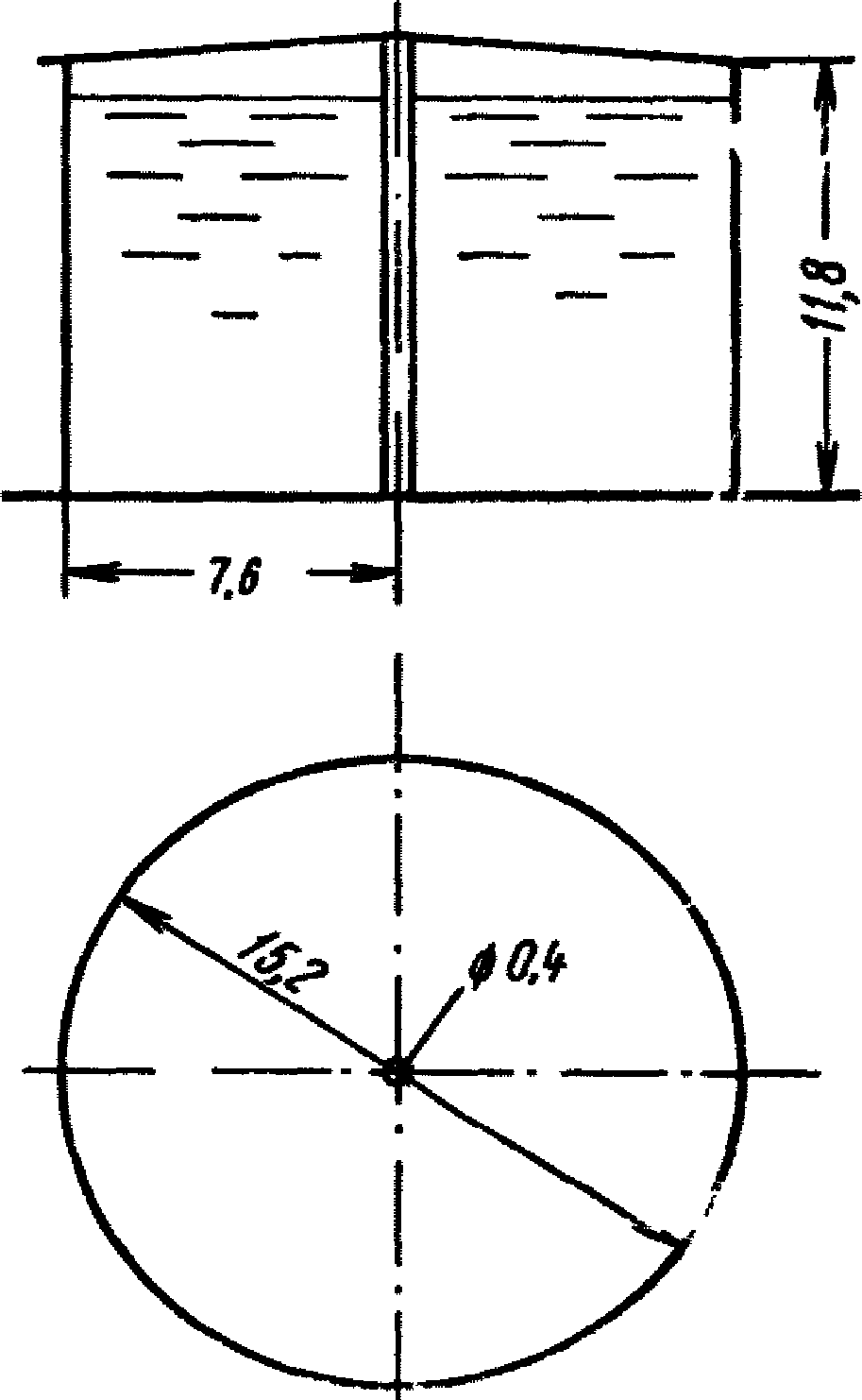
Рис. 15. Схема резервуара емкостью 2000 м3
Радиус резервуара a = 7,6 м, высота до кровли h = 11,8 м, центральная колонна диаметром 0,4 м (a1 = 0,2 м); объемный вес мазута Vоб = 0,8 т/м3, коэффициент кинематической вязкости мазута 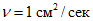 . Считаем, что сейсмическая активность района строительства 9 баллов (kс = 0,1).
. Считаем, что сейсмическая активность района строительства 9 баллов (kс = 0,1).
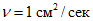 . Считаем, что сейсмическая активность района строительства 9 баллов (kс = 0,1).
. Считаем, что сейсмическая активность района строительства 9 баллов (kс = 0,1).Вычисляем величины h0, 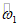 и
и 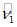 :
:
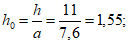
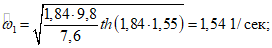
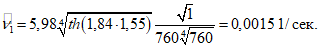
Так как отношение радиуса колонны к радиусу резервуара равно 0,0263, то влиянием колонны на величину амплитуды волны и гидродинамического давления на стенки резервуара можно пренебречь.
Вычислим величину 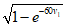 которая понадобится для дальнейших расчетов:
которая понадобится для дальнейших расчетов:  .
.
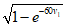 которая понадобится для дальнейших расчетов:
которая понадобится для дальнейших расчетов:  .
.По формуле (1.5) вычисляем As:
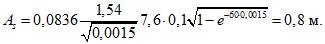
Таким образом, расчетное значение h0 равно:
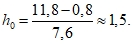
Определяем гидродинамическое давление жидкости на стенки резервуара. Для этого воспользуемся формулами (1.6), (1.8) 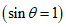 . Результаты всех вычислений приведены в табл. 3.
. Результаты всех вычислений приведены в табл. 3.
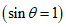 . Результаты всех вычислений приведены в табл. 3.
. Результаты всех вычислений приведены в табл. 3.Таблица 3
y/h | E1(y) по формуле (1.8) | P(y), т/м2, по формуле (1.6) | Pос(y), т/м, по формуле (1.9) | |
0 | 0,384 | 0,886 | 0,184 | 4,4 |
0,2 | 0,376 | 0,905 | 0,187 | 4,47 |
0,4 | 0,35 | 1,03 | 0,214 | 5,11 |
0,6 | 0,301 | 1,29 | 0,268 | 6,4 |
0,8 | 0,201 | 1,94 | 0,403 | 9,65 |
1 | 0 | 3,74 | 0,669 | 16 |
На рис. 16, а построены эпюры гидродинамических давлений.
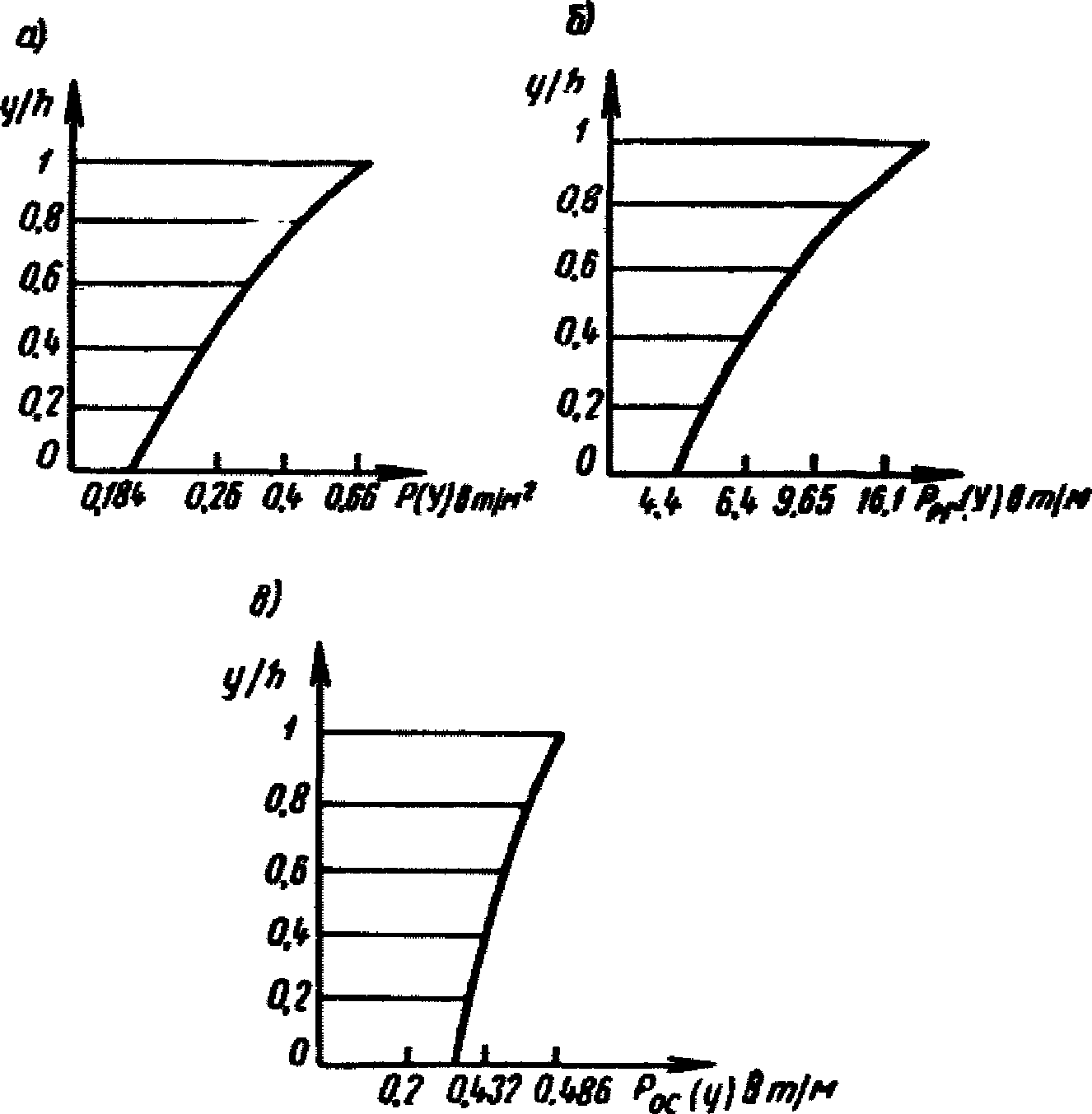
жидкости в цилиндрическом резервуаре
а - эпюра гидродинамического давления жидкости на стенки
резервуара; б - распределение нагрузки по оси резервуара;
в - распределение нагрузки по оси центральной
круглой колонны
Вычислим результирующую гидродинамических сил. По формуле (1.11):
Xг = 1520·0,1·1,61·0,293 = 72 т.
Вычислим величину yс по формуле (1.12):
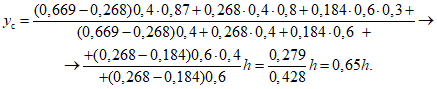
По формуле (1.14) определяем максимальное значение контурного давления на днище резервуара:

Контурное давление на днище распределяется по закону синуса (1.13); эпюра давления 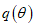 показана на рис. 4, в.
показана на рис. 4, в.
По формуле (1.15) вычисляем распределенную гидродинамическую нагрузку на колонну. Результаты расчета приведены в табл. 4.
Таблица 4
y/h | E1(y) по формуле (1.16) | Pос(y), т/м, по формуле (1.15) | |
0 | 0,0588 | 1,13 | 0,432 |
0,2 | 0,0574 | 1,15 | 0,44 |
0,4 | 0,053 | 1,18 | 0,451 |
0,6 | 0,0444 | 1,21 | 0,462 |
0,8 | 0,0276 | 1,24 | 0,474 |
1 | 0 | 1,27 | 0,486 |
Величина K3 равна:

По графику рис. 3, б определяем 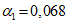 .
.
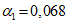 .
.На рис. 16, б приведена эпюра Pос(y).
Сейсмическая нагрузка от веса конструкций резервуара определяется по действующим Нормам и Инструкции, указанной в п. 2.2. Жесткость резервуара в горизонтальном направлении весьма велика (период колебаний его будет мало отличаться от нуля), что дает основание при определении сейсмических сил от веса кровли и корпуса рассматривать резервуар как абсолютно жесткое тело. Тогда в соответствии с принятой методикой расчета сейсмическая нагрузка для резервуара будет равна:
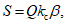
где 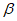 - коэффициент динамичности;
- коэффициент динамичности;
Q - собственный вес конструкции с коэффициентом перегрузки.
Для жестких конструкций 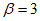 , следовательно, от веса кровли Qкр резервуара
, следовательно, от веса кровли Qкр резервуара
Sкр = 3·0,1Qкр = 0,3Qкр т.
Сейсмическая сила от веса корпуса резервуара равномерно распределена по высоте и равна:
Sс.в = 3·0,1qс.в = 0,3qс.в т/м,
где qс.в - вес 1 м корпуса резервуара.
Круглый цилиндрический резервуар
емкостью 50 000 м3 с плавающим понтоном
Резервуар предназначен для хранения воды. Основные геометрические параметры резервуара указаны на рис. 17, а. Считаем, что сейсмическая активность района строительства 9 баллов (kс = 0,1).
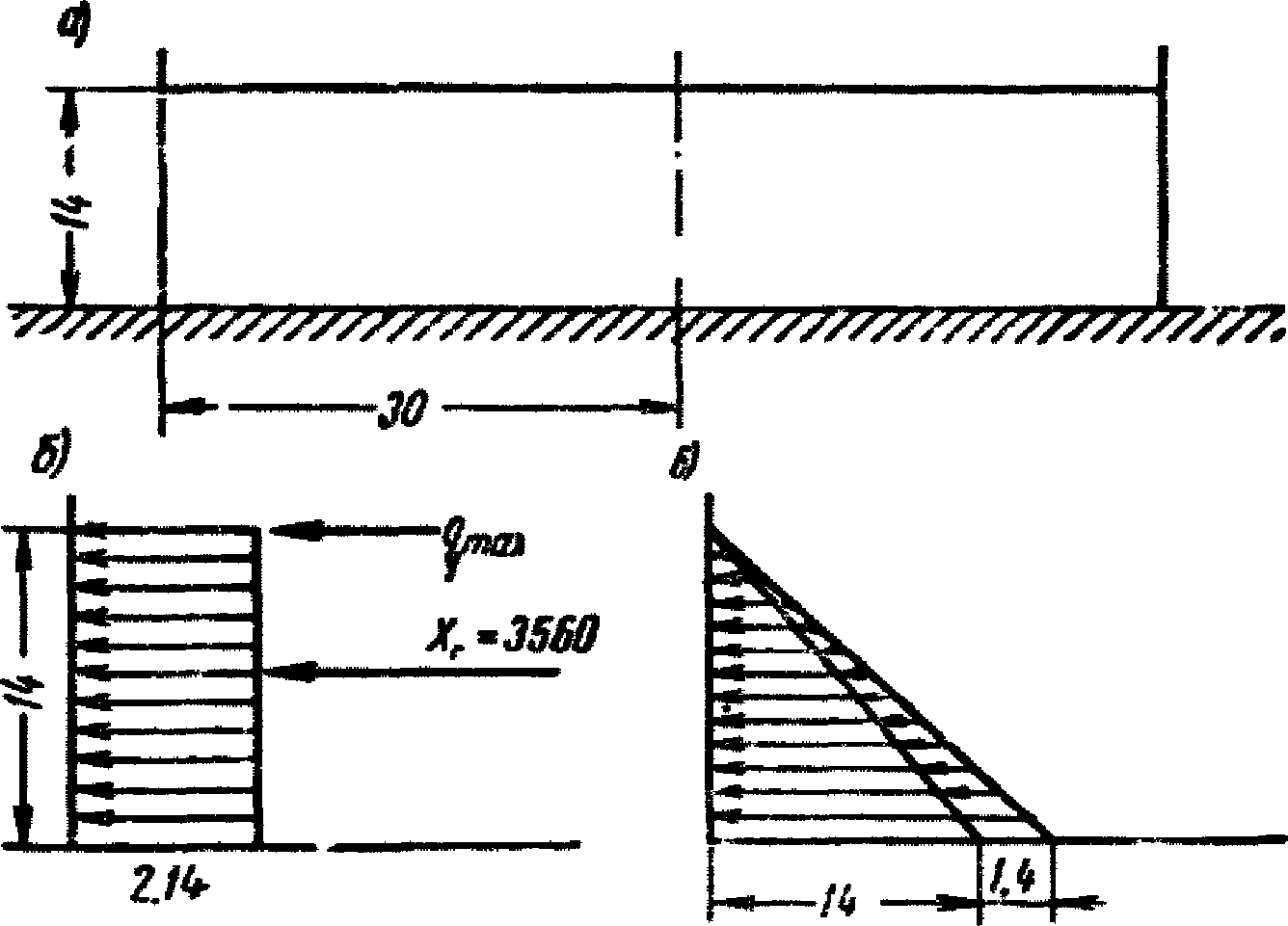
с плавающим понтоном емкостью 50 000 м3
а - схема резервуара; б - распределения давления жидкости
на стенки резервуара; в - сейсмическое давление жидкости
на стенки при вертикальном толчке
По формуле (1.1) вычисляем 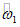 :
:
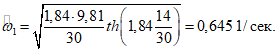
Вычисляем Pmax [см. формулу (1.25)]

Эпюра давления показана на рис. 17, б.
По формуле (1.26) вычисляем результирующую давления
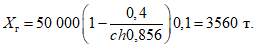
Контурное давление на фундамент вычисляется по формулам (1.28) и (1.29):
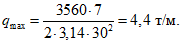
В плане нагрузка распределена по закону синуса (см. рис. 4, в).
Сейсмическая нагрузка от понтона вычисляется по формуле (1.31), (1.30). Вес понтона 180 т,
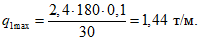
В плане нагрузка распределена по закону синуса (см. рис. 4, д), нагрузка 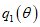 приложена на отметке +1400 (см. рис. 17, б).
приложена на отметке +1400 (см. рис. 17, б).
Сейсмическое давление жидкости на стенки резервуара при вертикальном толчке вычисляем по формуле (1.32):
Pверт = 0,1·14·3 = 4,2 т/м2;
Pс = 14·1 = 14 т/м2.
Если принять, что для вертикального толчка балльность равна 11, то kс = 0,4, тогда
Pверт = 0,4·14·3 = 16,8 т/м2.
Полное давление
Pполное = Pс + Pверт = 14 + 16,8 = 30,8 т/м3.
Сферический резервуар
Схема сферического резервуара, установленного на железобетонном "стакане" с указанием размеров, показана на рис. 18. Резервуар предназначен для хранения сжиженного газа; район строительства с сейсмической активностью 9 баллов (kс = 0,1). Коэффициент кинематической вязкости сжиженного газа примем равным: 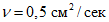 ; объемный вес Vоб = 0,8 т/м3.
; объемный вес Vоб = 0,8 т/м3.
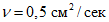 ; объемный вес Vоб = 0,8 т/м3.
; объемный вес Vоб = 0,8 т/м3.
Рис. 18. Схема сферического резервуара,
установленного на железобетонном "стакане"
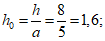
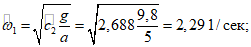
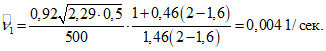
Вычисляем E1 [формула (1.37)]:
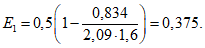
Из табл. 2 определяем 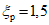 .
.
По формуле (1.33) вычисляем Xг:
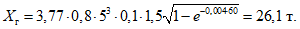
Величину yс примем равной 2/3 h:
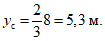
Сейсмическая сила Sс.в от собственного веса резервуара определяется так же, как и в случае цилиндрического резервуара. Примем 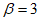 , тогда
, тогда
Sс.в = Q·0,1·3 = 0,3Q,
где Q - вес резервуара.
Контурное давление на днище, на котором устанавливается "стакан", определяется так же, как и для цилиндрического резервуара по формулам (1.13) и (1.14). В формуле (1.14) величина a равна радиусу днища, для данного примера a = 4 м.
Используя формулу (1.14), получим

На эту же нагрузку рассчитывается корпус резервуара.
Расчет конструкций, поддерживающих сферические резервуары
На рис. 19 указаны все основные размеры, необходимые для расчета <1>. Предполагаем, что резервуар заполнен сжиженным газом на высоту 9 м. Объемный вес сжиженного газа 1 т/м3. Коэффициент кинематической вязкости 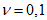 ; район строительства с сейсмической активностью 8 баллов (kс = 0,05). Основными несущими элементами этой конструкции, которые должны рассчитываться на сейсмические силы, являются поддерживающие резервуар стойки. Для определения периода собственных колебаний системы принимаем расчетную схему, показанную на рис. 21, и считаем, что стойки на отметке 9 м заделаны в плиту с бесконечной жесткостью, а внизу заделаны в фундамент. Тяжи между стойками выполнены из круглой стали диаметром 30 мм и могут работать только на растяжение. При горизонтальной нагрузке в работу включаются только 4 тяжа, симметричные относительно диаметра резервуара, вдоль которого действует единичная сила. Предполагается, что стойки испытывают деформации изгиба.
; район строительства с сейсмической активностью 8 баллов (kс = 0,05). Основными несущими элементами этой конструкции, которые должны рассчитываться на сейсмические силы, являются поддерживающие резервуар стойки. Для определения периода собственных колебаний системы принимаем расчетную схему, показанную на рис. 21, и считаем, что стойки на отметке 9 м заделаны в плиту с бесконечной жесткостью, а внизу заделаны в фундамент. Тяжи между стойками выполнены из круглой стали диаметром 30 мм и могут работать только на растяжение. При горизонтальной нагрузке в работу включаются только 4 тяжа, симметричные относительно диаметра резервуара, вдоль которого действует единичная сила. Предполагается, что стойки испытывают деформации изгиба.
--------------------------------

сферического резервуара, установленного на колоннах
а - общий вид резервуара; б - расчетная схема;
в - разрез по 1-1; г - разрез по 2-2; 1 - плита 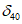 ;
;
2 - низ плоскостей связей; 3 - рифленая сталь 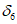
Горизонтальное перемещение f11 от единичной силы 1 т (см. рис. 20) равно: f11 = 0,07 см. Вес резервуара равен 128 т, вес половины стоек и ограждений равен 25 т. Итого полный вес конструктивных элементов
Qк = 128 + 25 = 153 т.
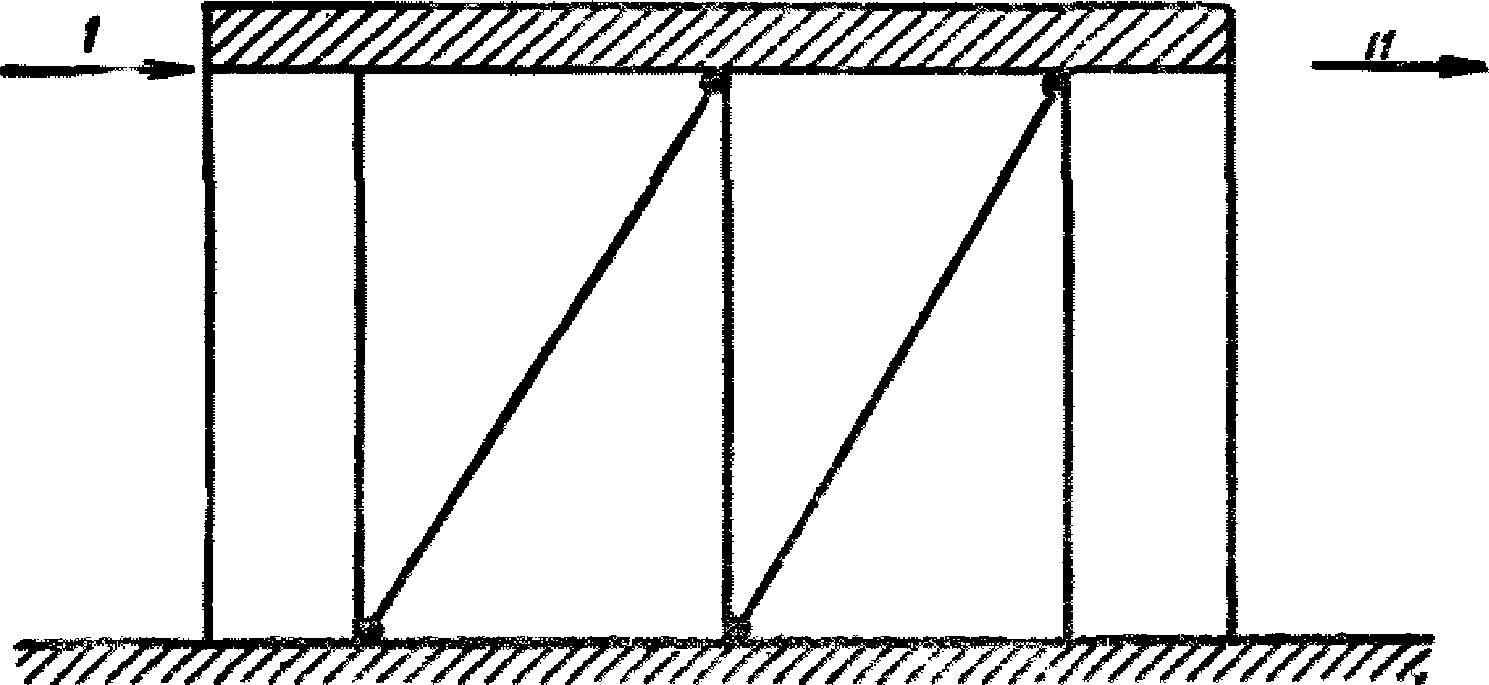
Рис. 20. Схема к определению жесткости конструкций
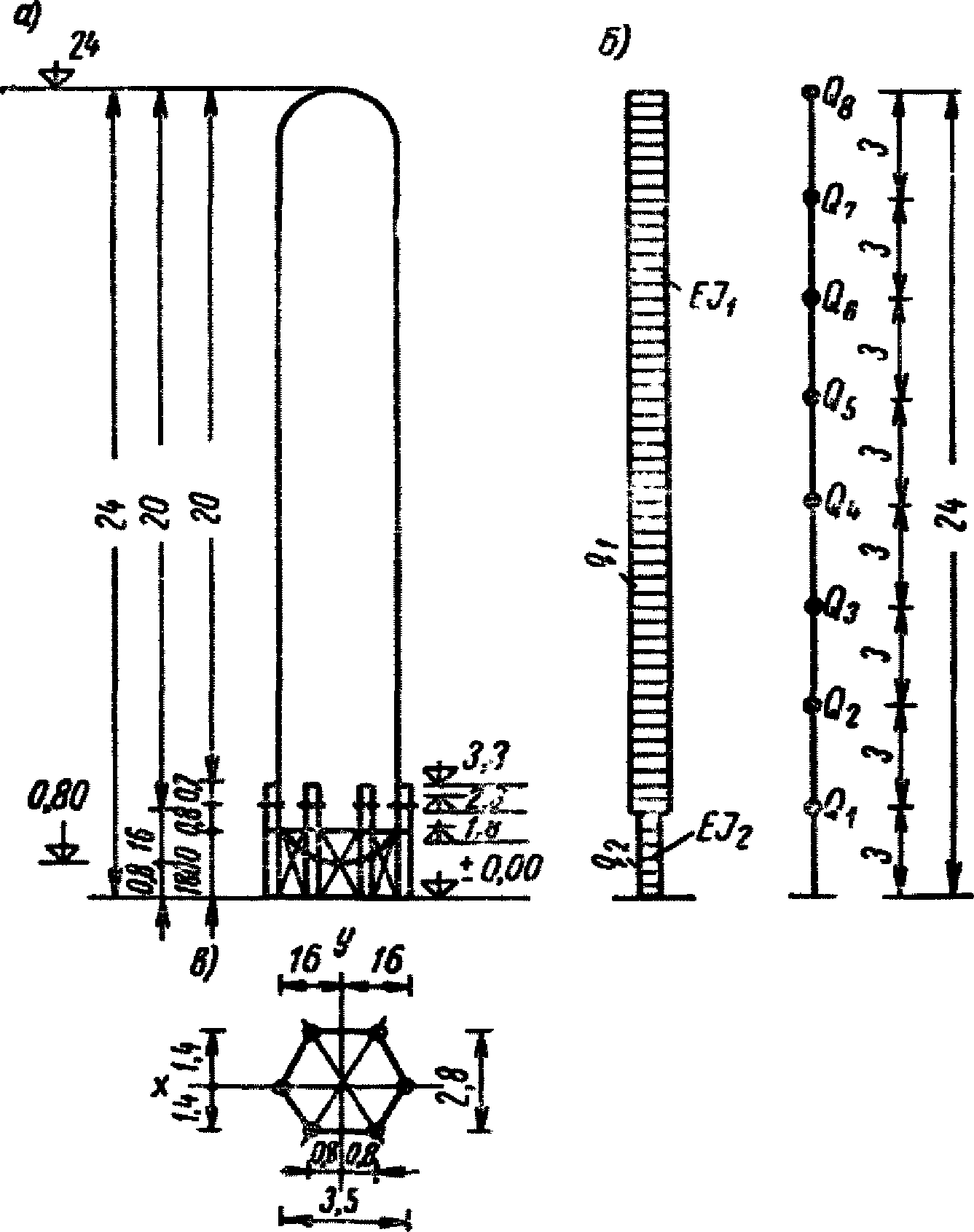
Вес жидкости
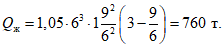

Вычислим величину сейсмической силы S, опираясь на значения коэффициента динамичности, приведенного в СНиП II-А.12-62;  для T = 1,33 сек равна:
для T = 1,33 сек равна:
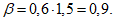
Следовательно:
S = (153 + 760·0,67)0,05·0,9 ~= 30 т.
Для сравнения вычислим величину S1, рассматривая жидкость как твердое тело:
S1 = (153 + 760)·0,05·0,9 = 41 т.
Вертикальный газгольдер постоянного объема
На рис. 10 показана конструкция группы вертикальных газгольдеров с указанием всех необходимых для расчета размеров. Район строительства с сейсмичностью 8 баллов (kс = 0,05). Рассматриваем одиночный газгольдер; жесткостью связывающей конструкции, идущей по верху газгольдеров, пренебрегаем.
На рис. 21 показана расчетная схема с расположением масс (система с 8 степенями свободы). Группа газгольдеров установлена на одном сплошном фундаменте. При данных размерах газгольдера можно предполагать, что превалируют деформации изгиба.
Рассмотрим два варианта расчета газгольдера.
Первый вариант: газгольдер заполнен полностью водой (Vоб = 1 т/м).
Нагрузки:
вес жидкости, заполняющей газгольдер на 1 м высоты:
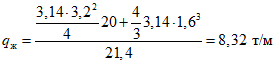
(первый член соответствует цилиндрической, а второй - сферической части газгольдера), вес 1 м оболочки газгольдера
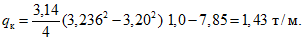
Итого 8,32 + 1,43 = 9,75 т/м.
Вес 1 м опоры: трубы 0,262 т/м; связи 0,18 т/м. Итого 0,44 т/м.
Характеристики жесткости:
момент инерции газгольдера I1 = 21,6·106 см4;
момент инерции опоры (трубы) I0 = 0,151·104 см4;
площадь опоры трубы F = 55,7 см2;
момент инерции системы опор Iу = 4,44·106 см4;
жесткость системы опор EIу = 9,33·102 кГ·см2.
В табл. 5 приведен расчет первых трех периодов и форм колебаний. Периоды вычислялись по формуле (8) "Указаний по определению сейсмической нагрузки для вертикальных аппаратов и примеры расчета", Госстройиздат, 1961:
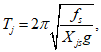
где j - номер формы колебаний;
fs - статическое перемещение в см s-й точки, в которой принята сосредоточенная нагрузка, под действием горизонтальных сил, равных Ps = QsXjs;
Xjs - ордината свободных колебаний, определяемая по табл. 3 приложения II упомянутых Указаний в точке, где вычислено перемещение fs.
N точек S | Вес Qs в т | Расстояние от основания hs в м | Отношение высоты hs/H | Первая форма колебаний | Вторая форма колебаний | Третья форма колебаний | ||||||||||||
условные ординаты | условная горизонтальная нагрузка 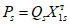 | коэффициент формы колебаний | период колебаний T1 и значение коэффициента | условные ординаты | условная горизонтальная нагрузка 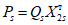 | коэффициент формы колебаний | период колебаний T2 и значение коэффициента | условные ординаты | условная горизонтальная нагрузка 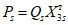 | коэффициент формы колебаний | период колебаний T3 и значение коэффициента | |||||||
8 | 14,7 | 24 | 1 | 1 | 14,7 | 1,54 | T1 = 1,04 сек 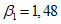 | 3,3 | -1 | -14,7 | -0,69 | T2 = 0,14 сек  | -4,85 | 1 | 14,7 | 0,515 | T3 = 0,124 сек 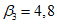 | 3,64 |
7 | 29,4 | 21 | 0,88 | 0,835 | 24,15 | 1,28 | 6,4 | -0,424 | -12,45 | -0,29 | -4,1 | 0,103 | 3,03 | 0,053 | 0,75 | |||
6 | 29,4 | 18 | 0,75 | 0,657 | 22,05 | 1,01 | 4,3 | 0,162 | 4,77 | 0,11 | 1,55 | -0,527 | -15,5 | -0,271 | -3,84 | |||
5 | 29,4 | 15 | 0,63 | 0,5 | 14,7 | 0,77 | 3,3 | 0,508 | 14,92 | 0,35 | 4,95 | -0,529 | -15,53 | -0,272 | -3,85 | |||
4 | 29,4 | 12 | 0,5 | 0,34 | 10 | 0,52 | 2,22 | 0,715 | 21 | 0,5 | 7,05 | 0,02 | 0,59 | 0,0103 | 0,146 | |||
3 | 29,4 | 9 | 0,38 | 0,211 | 6,21 | 0,32 | 1,37 | 0,653 | 19,2 | 0,45 | 6,35 | 0,612 | 18 | 0,315 | 4,45 | |||
2 | 29,4 | 6 | 0,25 | 0,1 | 2,94 | 0,15 | 0,64 | 0,414 | 12,17 | 0,29 | 4,1 | 0,781 | 23 | 0,403 | 5,7 | |||
1 | 16,6 | 3 | 0,125 | 0,029 | 0,48 | 0,045 | 0,11 | 0,145 | 2,41 | 0,1 | 0,8 | 0,319 | 5,3 | 0,164 | 1,31 | |||
В табл. 5 приведены периоды, вычисленные по значению перемещения первой точки.
В табл. 6 приведены значения коэффициентов форм колебаний 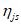 ,
, 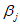 и сейсмических сил Sjs. В графах 9, 14, 19 табл. 5 даны значения сейсмических сил.
и сейсмических сил Sjs. В графах 9, 14, 19 табл. 5 даны значения сейсмических сил.
N точек S | Вес Qs в т | Расстояние от основания hs в м | Отношение высоты hs/H | Первая форма колебаний | Вторая форма колебаний | ||||||||
условные ординаты | условная горизонтальная нагрузка 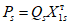 | коэффициент формы колебаний | период колебаний T1 и | сейсмическая сила Ss в т | условные ординаты | условная горизонтальная нагрузка 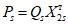 | коэффициент формы колебаний | период колебаний T2 и | сейсмическая сила Ss в т | ||||
8 | 2,22 | 24 | 1 | 1 | 2,22 | 2,18 | T1 = 0,58 сек 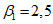 | 1,21 | -1 | -2,22 | -1,53 | T2 = 0,268 сек 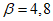 | -1,49 |
7 | 4,44 | 21 | 0,88 | 0,835 | 3,71 | 1,82 | 2,02 | -0,424 | -1,88 | -0,65 | -1,39 | ||
6 | 4,44 | 18 | 0,75 | 0,657 | 2,92 | 1,43 | 1,58 | 0,162 | 0,72 | 0,25 | 5,33 | ||
5 | 29,4 | 15 | 0,63 | 0,5 | 14,7 | 1,09 | 8 | 0,508 | 14,92 | 0,78 | 11 | ||
4 | 29,4 | 12 | 0,5 | 0,34 | 10 | 0,74 | 5,45 | 0,715 | 21 | 1,09 | 15,4 | ||
3 | 29,4 | 9 | 0,38 | 0,211 | 6,21 | 0,46 | 3,38 | 0,653 | 19,2 | 1 | 14,1 | ||
2 | 29,4 | 6 | 0,25 | 0,1 | 2,94 | 0,22 | 1,61 | 0,414 | 12,17 | 0,63 | 8,91 | ||
1 | 16,6 | 3 | 0,12 | 0,029 | 0,48 | 0,063 | 0,26 | 0,145 | 2,41 | 0,22 | 1,76 | ||
Второй вариант: газгольдер заполнен водой до отметки +16,5 м.
Две расчетные схемы показаны на рис. 22. Так как отношение 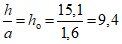 , то всю жидкость можно рассматривать как твердое тело, поскольку коэффициент
, то всю жидкость можно рассматривать как твердое тело, поскольку коэффициент 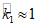 (см. рис. 22, а). Результаты вычислений по расчетной схеме рис. 22, а приведены в табл. 6.
(см. рис. 22, а). Результаты вычислений по расчетной схеме рис. 22, а приведены в табл. 6.
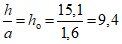 , то всю жидкость можно рассматривать как твердое тело, поскольку коэффициент
, то всю жидкость можно рассматривать как твердое тело, поскольку коэффициент 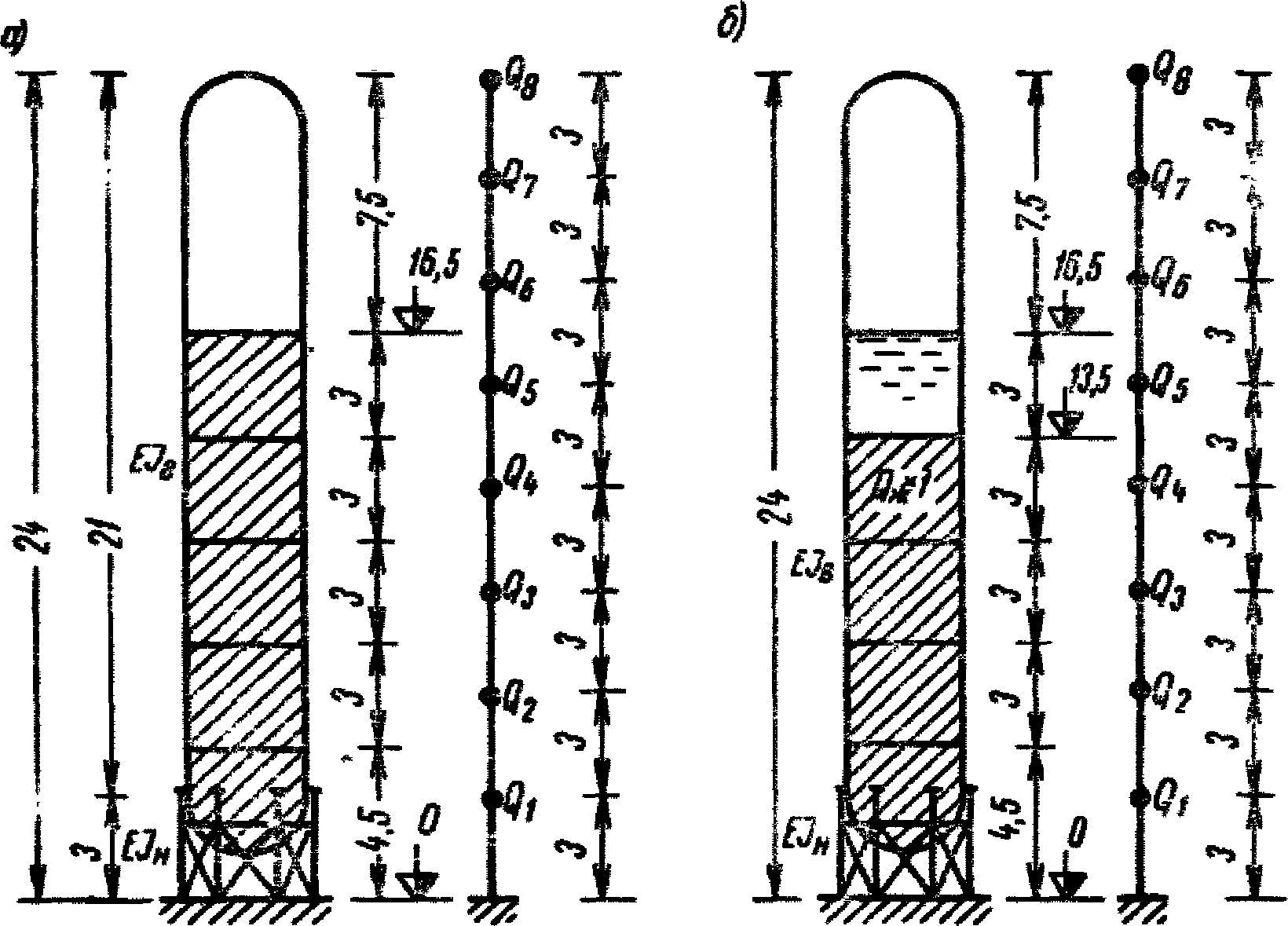
частично заполненного жидкостью
Для сравнения рассмотрим также вариант расчета (см. рис. 22, б), считая, что жидкость только до отметки +13,5 м - твердое тело, так как процесс волнообразования на поверхности жидкости будет весьма слабо сказываться на глубинах ниже отметки +13,5.
Жидкость между отметками 13,5 и 16,5 считаем заключенной в цилиндрическом резервуаре с высотой h = 3 м. Вычислим
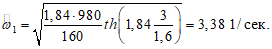
Приведенный вес жидкости между отметками +13,5 и +16,5 в точке 5 для  ;
; 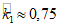 равен
равен
 ;
; 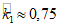 равен
равен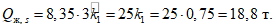
В табл. 7 приведены результаты вычислений по расчетной схеме 22, б.
N точек (S) | Вес Qs в т | Расстояние от основания hs в м | Отношение высоты hs hs/H | Первая форма колебаний | Вторая форма колебаний | ||||||||
условные ординаты | условная горизонтальная нагрузка 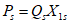 | коэффициент формы колебаний | период колебаний T1 и | сейсмическая сила Ss в т | условные ординаты | условная горизонтальная нагрузка 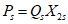 | коэффициент формы колебаний | период колебаний T2 и | сейсмическая сила Ss в т | ||||
8 | 2,22 | 24 | 1 | 1 | 2,22 | 2,22 | T1 = 0,56 сек 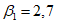 | 1,33 | -1 | -2,22 | -1,51 | T2 = 0,256 сек 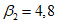 | -1,65 |
7 | 4,44 | 21 | 0,88 | 0,835 | 3,71 | 1,85 | 2,22 | -0,424 | -1,88 | -0,64 | -1,34 | ||
6 | 4,44 | 18 | 0,75 | 0,657 | 2,82 | 1,46 | 1,75 | 0,162 | 0,72 | 0,24 | 0,51 | ||
5 | 23,2 | 15 | 0,63 | 0,5 | 11,6 | 1,11 | 6,95 | 0,508 | 11,79 | 0,77 | 8,6 | ||
4 | 29,4 | 12 | 0,5 | 0,34 | 10 | 0,75 | 5,95 | 0,715 | 21 | 1,08 | 15,3 | ||
3 | 29,4 | 9 | 0,38 | 0,211 | 6,21 | 0,47 | 3,73 | 0,653 | 19,2 | 0,99 | 14 | ||
2 | 29,4 | 6 | 0,25 | 0,1 | 2,94 | 0,22 | 1,75 | 0,414 | 12,17 | 0,63 | 8,92 | ||
1 | 18,6 | 3 | 0,125 | 0,29 | 0,48 | 0,064 | 0,287 | 0,145 | 2,41 | 0,29 | 1,76 | ||
Верхняя часть жидкости рассматривается подвижной.
Как видно из выполненных расчетов (табл. 6 и 7), подвижность жидкости сказывается на величинах сейсмических сил незначительно. Это объясняется тем, что газгольдер представляет собой "резервуар" с очень большим отношением высоты налива к радиусу.
Газгольдер переменного объема
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
На рис. 11 показана схема газгольдера переменного объема <1>. Как видно из рисунка, газгольдер состоит из резервуара, заполненного жидкостью до отметки не более +9 м, телескопа и колокола. Для пригрузки колокола на отметках +27,4 мм и +18,6 м по всему периметру устанавливаются бетонные и чугунные грузы.
--------------------------------
<1> Конструкция газгольдера разработана институтом Проектстальконструкция.
На рис. 11 показано крайнее верхнее положение колокола, в этом положении газгольдер имеет максимальный объем. К резервуару по наружному контуру крепится сквозная решетчатая конструкция, по стойкам которой с помощью роликов перемещается телескоп и колокол. Эта решетчатая конструкция играет роль направляющих для телескопа и колокола и воспринимает сейсмическую нагрузку. Решетчатая направляющая конструкция является жесткой пространственной конструкцией с большим числом связей.
Основные размеры конструкции указаны на рис. 11. Резервуар газгольдера заполнен водой, коэффициент кинематической вязкости 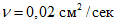 . Район строительства с сейсмической активностью 9 баллов: kс = 0,1.
. Район строительства с сейсмической активностью 9 баллов: kс = 0,1.
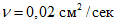 . Район строительства с сейсмической активностью 9 баллов: kс = 0,1.
. Район строительства с сейсмической активностью 9 баллов: kс = 0,1.Для крайнего верхнего положения колокола величина зазора As между уровнем жидкости и покрытием не рассчитывается.
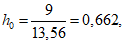
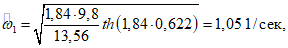
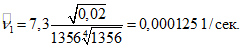
Вычисляем максимальные значения гидродинамического давления для y/h = 0; 0,5; 1 по формулам (1.6), (1.7):
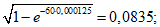
y/h = 0; E1 = 0,19; 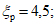
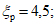
P(0) = 1·13,56·0,1·4,5·0,0835 = 0,509 т/м2;
y/h = 0,5; E1 = 0,153; 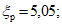
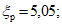
P(0,5h) = 1·13,56·0,1·5,05·0,0835 = 0,572 т/м2;
y/h = 1; E1 = 0; 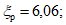
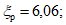
P(1h) = 1·13,56·0,1·6,06·0,0835 = 0,686 т/м2.
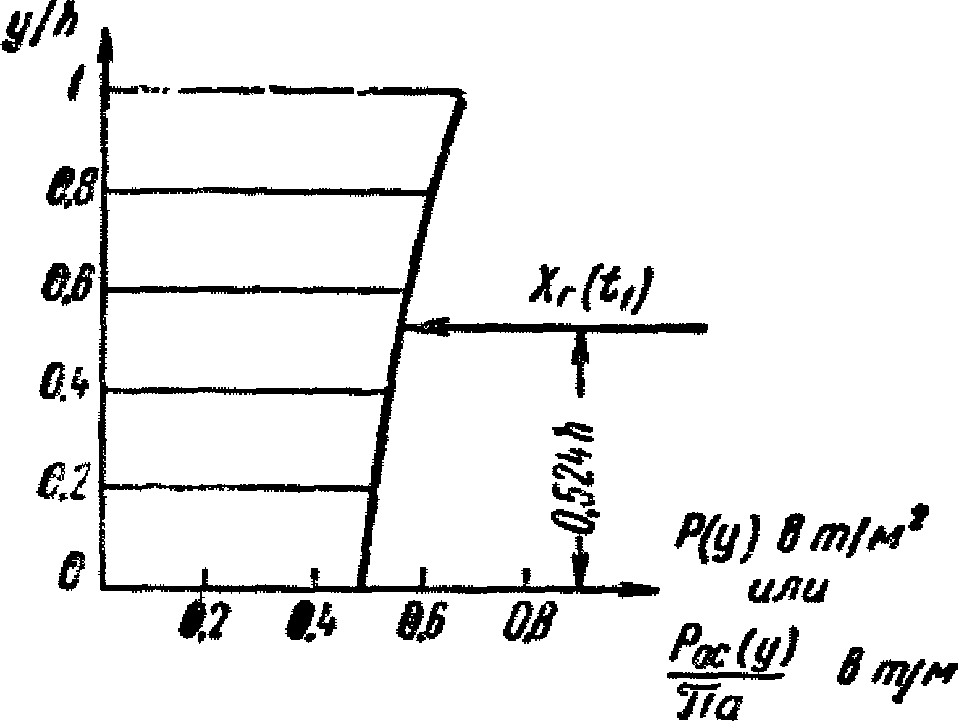
На рис. 23 построена эпюра P(y).
По формуле (1.10) вычисляем Xг

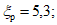
Xг = 3,14·13,562·9·1·0,1·5,3·0,0835 = 230 т.
Величина hс = 0,524 (см. рис. 23). По формуле (1.14) вычисляем qmax:

Давление P(y) в плане распределено по закону синуса (см. рис. 4, б). Контурное давление 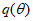 , передаваемое на фундамент газгольдера, также распределяется по закону синуса (см. рис. 4, в).
, передаваемое на фундамент газгольдера, также распределяется по закону синуса (см. рис. 4, в).
Для определения сейсмических сил от веса конструкций газгольдера примем расчетную схему, показанную на рис. 14.
Приближенная оценка периода колебаний решетчатой направляющей конструкции показывает, что он для первой формы равен примерно 0,1 сек. Поэтому для расчета можно принять, что жесткость системы равна бесконечности:
Вес Q2:
вес крыши колокола 3,14·13,052·100 = 53 500 кГ;
вес стенки колокола 2·3,14·13,05·4,4·80 = 28 800 кГ;
вес решетчатой направляющей конструкции 6,28·14·50 + 12,5·50 = 7400 кГ;
вес бетонных грузов: 28 000 кГ
Итого 117 700 кГ = 117,7 т
Вес Q1:
вес стенки колокола 28 800 кГ;
вес телескопа 6,28·13,5·9,4·80 = 6400 кГ;
вес решетчатой направляющей конструкции со смотровой площадкой: 4400 + 8650 + 4400 = 174 500 кГ;
вес чугунных грузов 55 000 кГ
Всего 165 250 кГ = 165 т
Коэффициент динамичности 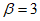 .
.
Сейсмические силы равны:
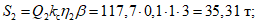
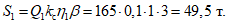
Расчетом определены суммарные значения сейсмических сил S1 и S2, которые должны быть распределены по элементам конструкции. Особенность данной конструкции такова, что силы S1 и S2 передаются на стойки решетчатой направляющей конструкции. Силы 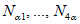 вычисляем по формулам (2.3):
вычисляем по формулам (2.3):
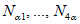 вычисляем по формулам (2.3):
вычисляем по формулам (2.3):На уровне 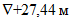 :
:
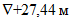 :
:N12 = 0,258·35,2 = 9,1 т;
N22 = 0,224·35,2 = 7,9 т;
N32 = 0,130·35,2 = 4,57 т;
N42 = 0,017·35,8 = 0,6 т.
На уровне 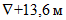 :
:
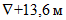 :
:N11 = 0,258·49,5 = 12,8 т.
N21 = 0,224·49,5 = 11,1 т;
N31 = 0,130·49,5 = 6,43 т;
N41 = 0,017·49,5 = 0,842 т.
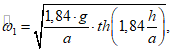
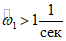 , то весь дальнейший расчет ведется по формулам
, то весь дальнейший расчет ведется по формулам 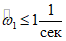 , то расчет ведется по формулам
, то расчет ведется по формулам 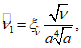
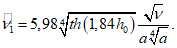
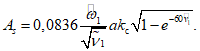
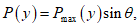
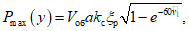
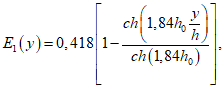
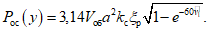
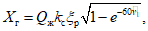
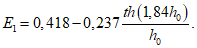

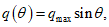
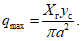

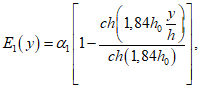
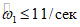 гидродинамическое давление жидкости на стенки резервуара вычисляется по формуле
гидродинамическое давление жидкости на стенки резервуара вычисляется по формуле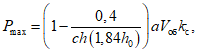
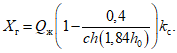
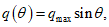
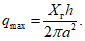
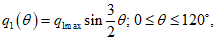
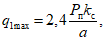
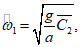
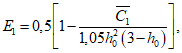
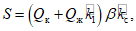
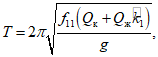
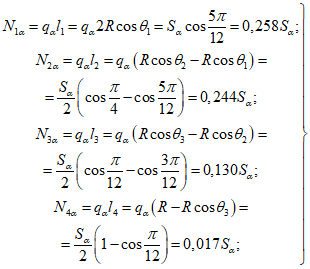
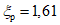
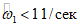 , то расчет ведем по формулам
, то расчет ведем по формулам 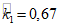 . Период собственных колебаний определяем по
. Период собственных колебаний определяем по