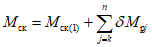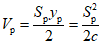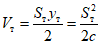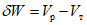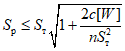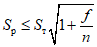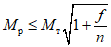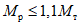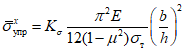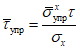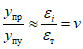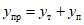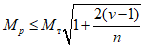СПРАВКА
Источник публикации
М.: Стройиздат, 1974
Примечание к документу
Название документа
"Рекомендации по расчету металлических рамных каркасов на сейсмические воздействия с учетом образования пластических шарниров"
"Рекомендации по расчету металлических рамных каркасов на сейсмические воздействия с учетом образования пластических шарниров"
Содержание
ПО РАСЧЕТУ МЕТАЛЛИЧЕСКИХ РАМНЫХ КАРКАСОВ НА СЕЙСМИЧЕСКИЕ
ВОЗДЕЙСТВИЯ С УЧЕТОМ ОБРАЗОВАНИЯ ПЛАСТИЧЕСКИХ ШАРНИРОВ
Рекомендации составлены в развитие главы СНиП II-А.12-69 и содержат примеры расчета и обоснования по расчету рамных металлических конструкций на сейсмические воздействия. Предназначены для инженеров-проектировщиков.
Рекомендации разработаны сектором динамики и сейсмостойкости ОСДП Центрального научно-исследовательского и проектного института строительных металлоконструкций: д-ром техн. наук, проф. И.Л. Корчинским, канд. техн. наук Л.А. Бородиным, инженерами М.С. Дузинкевичем и Н.А. Короленко.
1.1. Рамные каркасы зданий при учете действия сейсмических сил следует проектировать таким образом, чтобы в наиболее напряженных сечениях в случае, если потеря устойчивости в них не представляет опасности для несущей способности сооружения, обеспечивалось развитие пластических деформаций.
В связи с этим пластические зоны целесообразно предусматривать в ригелях рам, которые не подвержены осевому сжатию, и различные деформации, связанные с потерей местной устойчивости в ригелях, менее опасны для сооружения, чем, например, потеря местной устойчивости в стойках.
Стойки рам подвержены постоянному сжатию от действия осевой нагрузки. Развитие пластических деформаций в стойках может привести к потере не только общей, но и местной устойчивости стоек и к обрушению всего сооружения. Поэтому допускать в них развитие пластических деформаций не рекомендуется.
1.2. Во время землетрясения сооружение подвергается действию многократных повторных загружений. В связи с этим расходование пластических резервов в элементах конструкций при каждом отдельном цикле колебаний должно быть ограничено сравнительно небольшими порциями с тем, чтобы в процессе землетрясения энергия, поглощенная при развитии пластических деформаций в том или ином элементе, не превышала его общей энергоемкости. При таком условии пластические деформации конструкций при каждом цикле загружений должны составлять сравнительно небольшую долю по отношению к упругим деформациям.
Нагрузка, действующая в таком случае на упругопластическую конструкцию, почти не будет отличаться от нагрузки на аналогичную упругую систему. Поэтому определение сейсмической нагрузки на сооружение может производиться в соответствии с нормами главы СНиП II-А.12-69.
1.3. Сечениями элементов рамной конструкции предварительно задаются, руководствуясь обычными принципами проектирования. При этом, согласно п. 1.1, следует соблюдать условия, чтобы напряжения в ригелях рамы от действия основного и дополнительного сочетания нагрузок (т.е. без учета действия сейсмических нагрузок) были не выше расчетных сопротивлений.
Сечения стоек должны подбираться таким образом, чтобы напряжения в них от любых сочетаний нагрузок, включая и действие сейсмических сил, не превышали расчетных сопротивлений.
1.4. При расчете рамной системы с учетом действия сейсмических сил вначале предполагается, что конструкция ведет себя как упругая система. Для этой системы определяются расчетные сейсмические силы 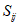 по главным формам колебаний.
по главным формам колебаний.
От действия сейсмических сил находятся эпюры изгибающих моментов по каждой форме. Затем в соответствии с формулой, приведенной в п. 2.9 главы СНиП II-А.12-69, в сечениях элементов рамы определяются значения суммарных моментов M от сейсмической нагрузки:
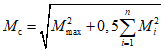 , (1)
, (1)где  - значение максимального момента в сечении по одной из собственных форм;
- значение максимального момента в сечении по одной из собственных форм;
Эти моменты складываются с моментами, возникающими от действия статически приложенной нагрузки (здесь имеется в виду основное сочетание нагрузок). В соответствии с полученными суммарными моментами, учитывающими действие статической и сейсмической нагрузок, производится проверочный расчет и уточнение предварительно заданных сечений элементов рамы.
1.5. При действии сейсмических сил в области опор ригелей возникают максимальные изгибающие моменты. Они могут вызвать значительные напряжения в опорных сечениях ригелей. Для устранения опасности хрупких разрушений в местах сварных соединений ригелей со стойками опорные сечения ригелей следует развивать до таких размеров, чтобы максимальные напряжения в области сварных соединений не превышали расчетных сопротивлений. Развитие опорных сечений ригелей рекомендуется осуществлять за счет увеличения ширины полок (рис. 1). В то же время в месте перехода от основного сечения к его развитому опорному сечению целесообразно создавать условие для возникновения пластического шарнира. С появлением шарнира рост усилий в опорной части ригеля прекратится. Таким образом, пластический шарнир будет выполнять роль предохранителя опорного сварного соединения ригеля со стойкой от хрупких разрушений.
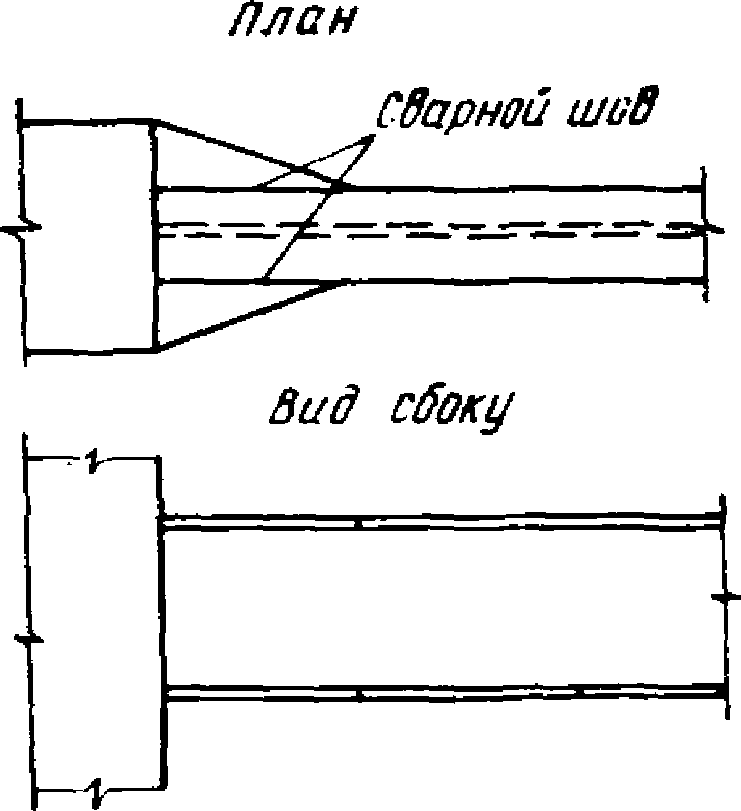
Рис. 1. Конструктивное решение опорной части ригеля
ИС МЕГАНОРМ: примечание. Взамен СНиП II-В.3-62 Постановлением Госстроя СССР от 29.12.1972 N 222 с 1 июля 1973 года введены в действие СНиП II-В.3-72. Взамен СНиП II-В.3-72 Постановлением Госстроя СССР от 14.08.1981 N 144 с 1 января 1982 года введены в действие СНиП II-23-81. |
Условие появления пластического шарнира будет обеспечиваться в том случае, когда момент 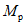 в месте предполагаемого шарнира, вычисленный при расчете рамы как упругой системы, превышает предельный момент
в месте предполагаемого шарнира, вычисленный при расчете рамы как упругой системы, превышает предельный момент 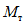 , который фактически может воспринять сечение ригеля в месте образования пластического шарнира. Значение
, который фактически может воспринять сечение ригеля в месте образования пластического шарнира. Значение 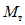 находится согласно обычным правилам расчета по СНиП II-В.3-62*, при этом расчетное сопротивление
находится согласно обычным правилам расчета по СНиП II-В.3-62*, при этом расчетное сопротивление 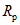 берется умноженным на коэффициент
берется умноженным на коэффициент 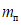 , обеспечивающий образование пластического шарнира. Для конструкций из стали Ст.3 коэффициент
, обеспечивающий образование пластического шарнира. Для конструкций из стали Ст.3 коэффициент 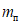 рекомендуется принимать равным 1,5.
рекомендуется принимать равным 1,5.
Соотношение между 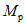 и
и 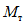 определяется по формуле
определяется по формуле
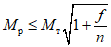 , (2)
, (2)где n - число циклов загружений, ожидаемых при землетрясении; рекомендуется принимать n = 100;
значение f берется меньшим из величин 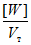 и 2(v - 1);
и 2(v - 1);
[W] - энергия, которая может быть поглощена в пластической зоне ригеля до того момента, пока ригель вследствие потери устойчивости стенки не потеряет несущую способность;
v - отношение максимальной деформации, при которой в зоне пластического шарнира наступает потеря устойчивости в стенке ригеля, к предельной упругой деформации ригеля; значение v находится согласно п. 1.6.
Значение f рекомендуется принимать не более 28.
1.6. Ввиду того, что работа ригелей происходит в пластической стадии, большую опасность для стенок ригелей представляет потеря местной устойчивости стенок. Поэтому, учитывая возможность перегрузок во время землетрясения, при проверочном расчете стенок на местную устойчивость рекомендуется усилия от сейсмической нагрузки увеличивать на 40%.
Проверочный расчет ригеля на местную устойчивость и определение значения v производятся следующим образом.
Вначале определяются касательные напряжения в стенке ригеля:
где Q - поперечная сила в месте образования пластического шарнира;
b и h - толщина и высота стенки.
Затем находятся краевые нормальные напряжения:
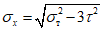 , (4)
, (4)где предел текучести 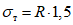 ;
;
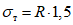 ;
;R - расчетное сопротивление стали.
Далее определяется "относительное" <1> касательное напряжение:
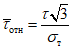 . (5)
. (5)--------------------------------
<1> Под термином "относительное" имеется в виду значение напряжения по отношению к пределу текучести 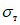 .
.
Затем вычисляется критическое нормальное "относительное" напряжение для упругой стенки <2> по формуле
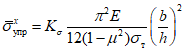 , (6)
, (6)где 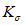 - определяется из табл. 1 в зависимости от
- определяется из табл. 1 в зависимости от 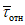 ;
;
E и 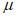 - модуль Юнга
- модуль Юнга 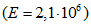 и коэффициент Пуассона
и коэффициент Пуассона 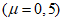 .
.
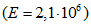 и коэффициент Пуассона
и коэффициент Пуассона 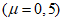 .
.--------------------------------
C | ||
0 | 25,497 | 0,767 |
0,5 | 17,847 | 1,010 |
0,7 | 13,290 | 1,250 |
0,9 | 7,337 | 1,940 |
1 | 0 | 0,708 |
Значения относительных критических касательных напряжений для упругой стенки находятся по формуле
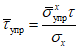 . (7)
. (7)Затем вычисляется интенсивность критических напряжений для упругой стенки:
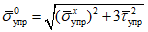 . (8)
. (8)Отношение максимальной деформации, при которой в зоне пластического шарнира наступает потеря устойчивости, к предельной упругой деформации ригеля определяется по формуле
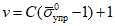 . (9)
. (9)C берется из табл. 1 в зависимости от 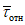 .
.
1.7. Место перехода от основного сечения ригеля к развитому опорному сечению намечается согласно данным расчета, который выполняется в соответствии с пп. 1.5 и 1.6. Кроме того, учитывается унификация элементов рамных каркасов и другие возможные условия конструирования <1>. При этом следует стремиться, чтобы в месте изменения сечений значения ординат эпюры моментов от внешних сил находились в пределах 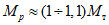 .
.
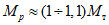 .
.--------------------------------
<1> При экспериментальных исследованиях рамных узлов, проводимых в ЦНИИПроектстальконструкции, расстояние от места изменения сечения до места сопряжения ригеля со стойкой бралось равным утроенной ширине полки.
При условии возникновения в ригеле пластического шарнира величина изгибающего момента 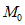 в месте примыкания ригеля к стойке может определяться по формуле
в месте примыкания ригеля к стойке может определяться по формуле
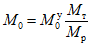 , (10)
, (10)где 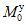 - момент в опорном сечении ригеля, вычисленный при расчете рамы как упругой системы.
- момент в опорном сечении ригеля, вычисленный при расчете рамы как упругой системы.
1.8. При условии образования пластического шарнира в ригеле, как отмечено в предыдущих пунктах, момент 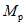 , вычисленный при расчете рамы как упругой системы, превышает предельный момент
, вычисленный при расчете рамы как упругой системы, превышает предельный момент 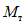 , который может восприниматься ригелем в пластической зоне. Таким образом, в действительности эпюра моментов в области пластического шарнира получается уменьшенной на величину
, который может восприниматься ригелем в пластической зоне. Таким образом, в действительности эпюра моментов в области пластического шарнира получается уменьшенной на величину
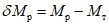 . (11)
. (11)Для практических расчетов рекомендуется пользоваться приближенным методом, в котором предполагается, что изменение момента в ригеле приводит к такому же изменению момента в стойке, примыкающей непосредственно к данному ригелю, и соответственно распространяется на стойки нижерасположенных этажей. Вследствие этого значение максимального изгибающего момента в стойке K-го этажа будет определяться по формуле
где 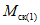 - максимальный момент в сечении стойки K-го этажа, вычисленного при расчете рамы как упругой системы;
- максимальный момент в сечении стойки K-го этажа, вычисленного при расчете рамы как упругой системы;
j = k, k + 1, ..., n - номера вышерасположенных этажей.
По формуле (12) определяются моменты для каждой стойки.
Моменты, полученные в стойке после такого перераспределения, являются расчетными моментами, и по ним проверяются сечения. При этом, как отмечалось в п. 1.3, размеры сечений стоек подбираются из расчета, чтобы напряжения в стойках были не выше расчетных сопротивлений.
1.9. В результате перераспределения усилий за счет смещения эпюр моментов в ригелях может произойти существенное возрастание моментов в стойках, особенно в нижних.
В тех случаях, когда при большой доле перераспределения моментов на стойки требуется значительное увеличение сечений и в результате получается экономически невыгодный вариант, следует обеспечить снижение разницы 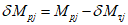 , с тем чтобы ограничить перераспределение усилий на стойки. Уменьшение
, с тем чтобы ограничить перераспределение усилий на стойки. Уменьшение 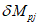 может достигаться двумя способами: либо путем усиления сечения, либо путем переноса пластической зоны в сторону большего удаления от места стыка ригеля со стойкой за счет развития опорного сечения ригеля по длине. Применение того или иного способа следует совмещать с приемами варьирования жесткости элементов каркаса в целях получения наиболее оптимального варианта.
может достигаться двумя способами: либо путем усиления сечения, либо путем переноса пластической зоны в сторону большего удаления от места стыка ригеля со стойкой за счет развития опорного сечения ригеля по длине. Применение того или иного способа следует совмещать с приемами варьирования жесткости элементов каркаса в целях получения наиболее оптимального варианта.
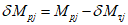 , с тем чтобы ограничить перераспределение усилий на стойки. Уменьшение
, с тем чтобы ограничить перераспределение усилий на стойки. Уменьшение В связи с указанными причинами пластические шарниры могут возникать не во всех ригелях.
РАМЫ НА СЕЙСМИЧЕСКУЮ НАГРУЗКУ
Рассчитать многоэтажное здание санаторного типа (рис. 2, а), проектируемое для района сейсмичностью 9 баллов. Поперечная рама здания выполняется из стали марки Ст.3. Шаг рам в продольном направлении равен 4,5 м. Стойки поперечной рамы здания проектируются с монтажным стыком в уровне четвертого яруса.
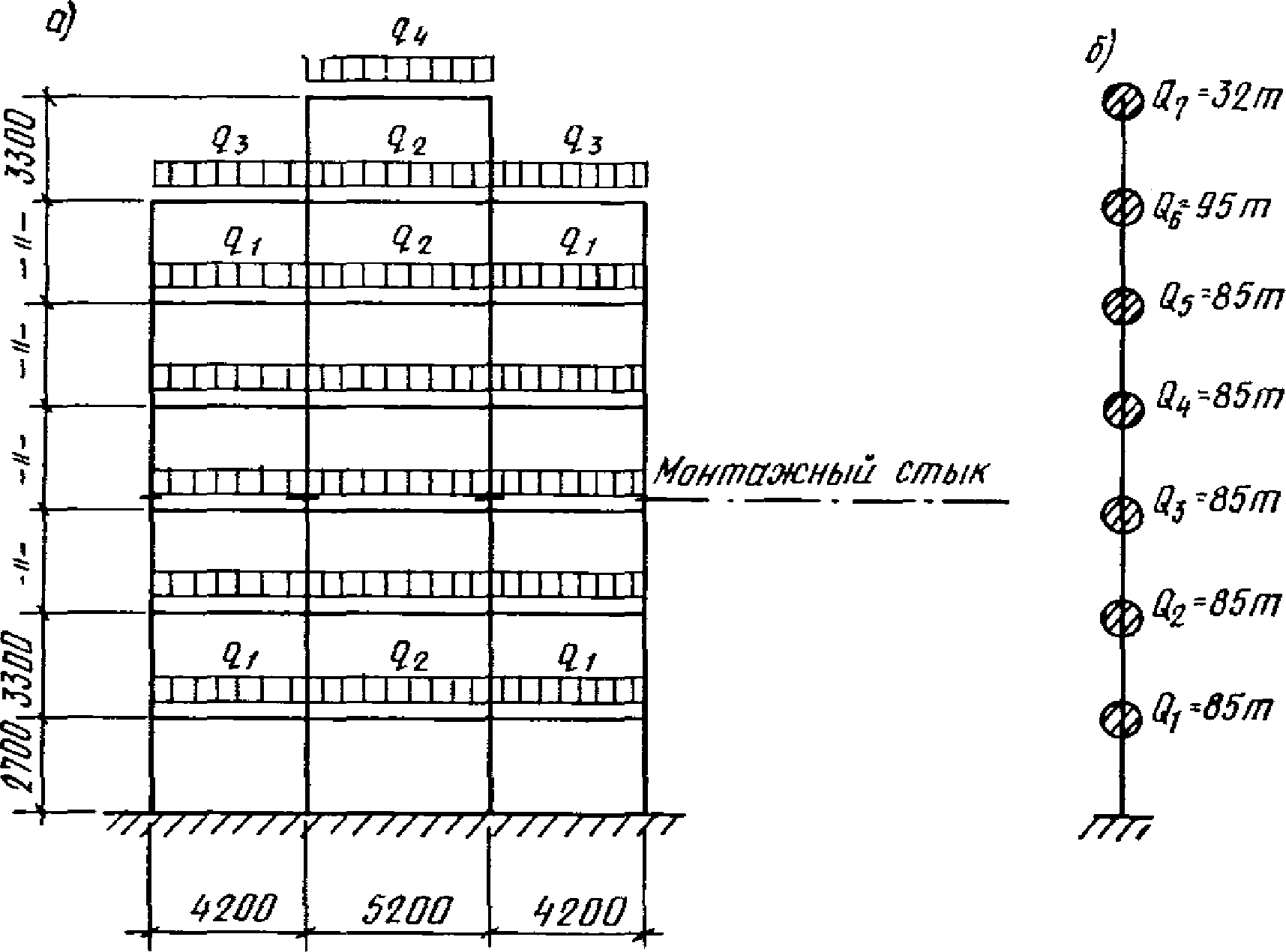
а - схема рамы с распределенными вертикальными нагрузками;
б - значения сосредоточенных нагрузок в раме
Дано: постоянная равномерно распределенная нагрузка на перекрытиях равна: 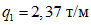 ;
; 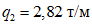 ;
; 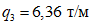 ;
; 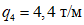 ;
;
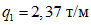 ;
; 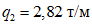 ;
; 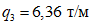 ;
; 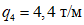 ;
;временная равномерно распределенная нагрузка на перекрытиях равна: 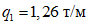 ;
; 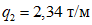 ;
; 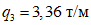 ;
; 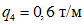 ;
;
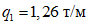 ;
; 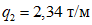 ;
; 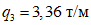 ;
; 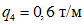 ;
;веса, сосредоточенные в уровнях междуэтажных перекрытий: 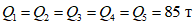 ;
; 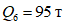 ;
; 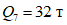 ;
;
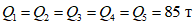 ;
; 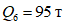 ;
; 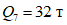 ;
;соответствующие им массы: 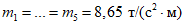 ;
; 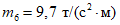 ;
; 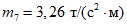 ;
;
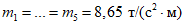 ;
; 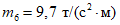 ;
; 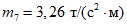 ;
;нормальные сжимающие силы в стойках в уровне низа рамы следующие: 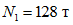 - для крайнего ряда и
- для крайнего ряда и 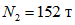 - для среднего ряда стоек. В уровне пола 4-го этажа нормальные сжимающие силы следующие:
- для среднего ряда стоек. В уровне пола 4-го этажа нормальные сжимающие силы следующие: 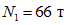 - для крайнего ряда и
- для крайнего ряда и 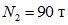 - для среднего ряда стоек.
- для среднего ряда стоек.
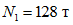 - для крайнего ряда и
- для крайнего ряда и 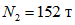 - для среднего ряда стоек. В уровне пола 4-го этажа нормальные сжимающие силы следующие:
- для среднего ряда стоек. В уровне пола 4-го этажа нормальные сжимающие силы следующие: 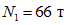 - для крайнего ряда и
- для крайнего ряда и 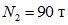 - для среднего ряда стоек.
- для среднего ряда стоек.Здание проектируется в 3-м климатическом районе. Ветровая нагрузка считается приложенной в уровне каждого яруса.
Решение. Расчетная схема здания представляет собой систему с семью степенями свободы (см. рис. 2, б). Сечения элементов рамной конструкции предварительно заданы, руководствуясь обычными принципами проектирования. При этом соблюдалось условие, чтобы напряжения в ригелях рамы от действия основного и дополнительного сочетания нагрузок (т.е. без учета действия сейсмических сил) не превышали расчетных сопротивлений. Заданные сечения стоек и ригелей многоэтажной рамы приведены в табл. 2.
Таблица 2
Элементы рамы | Состав сечения | F, см2 | ||
Ригели | I N 30 | 46,5 | 7080 | 472 |
Крайний ряд стоек: | ||||
верх | 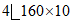 | 125,6 | 20400 | 1270 |
низ | 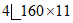 | 137,6 | 22180 | 1390 |
Средний ряд стоек: | ||||
верх | 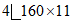 | 137,6 | 22180 | 1390 |
низ | 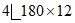 | 168,8 | 34260 | 1900 |
Первый этап расчета рамы с учетом действия сейсмических сил выполняется как расчет обычной упругой системы. Для этой системы находятся частоты и формы собственных колебаний и определяются сейсмические нагрузки, соответствующие первым трем формам собственных колебаний рамы. Для определения частот и форм собственных колебаний рамы решается система канонических уравнений, выражающих условие свободных колебаний системы:
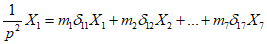 ;
;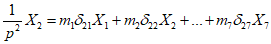 ;
;...............................
...............................
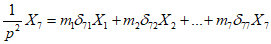 .
.Значения характеристик первой формы колебания получились следующими:
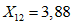 ;
; 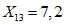 ;
; 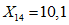 ;
; 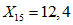 ;
; 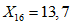 ;
; 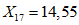 ;
; 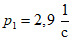 ;
; 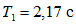 ;
; 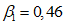 .
.В соответствии с главой СНиП II-А.12-69 принимаем коэффициент динамичности 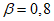 .
.
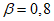 .
.Значения характеристик второй формы:
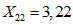 ;
; 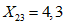 ;
; 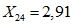 ;
; 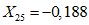 ;
; 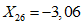 ;
; 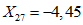 ;
; 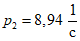 ;
; 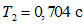 ;
; 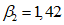 .
.Значения характеристик третьей формы:
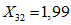 ;
; 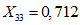 ;
; 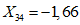 ;
; 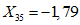 ;
; 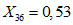 ;
; 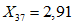 ;
; 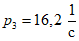 ;
; 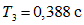 ;
; 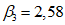 .
.Для данной системы определяются расчетные сейсмические силы, соответствующие главным формам колебаний. Расчетные значения сейсмической нагрузки 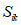 , соответствующие i-му тону собственных колебаний сооружения, находятся по формуле (1) СНиП II-А.12-69, п. 2.4:
, соответствующие i-му тону собственных колебаний сооружения, находятся по формуле (1) СНиП II-А.12-69, п. 2.4:
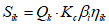 .
.Сейсмическая нагрузка по первой форме колебаний:
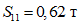 ;
; 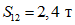 ;
; 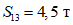 ;
; 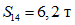 ;
; 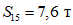 ;
; 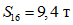 ;
; 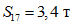 .
.По второй форме колебаний:
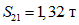 ;
; 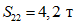 ;
; 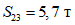 ;
; 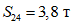 ;
; 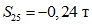 ;
; 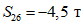 ;
; 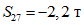 .
.По третьей форме колебаний:
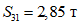 ;
; 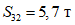 ;
; 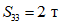 ;
; 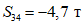 ;
; 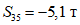 ;
; 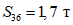 ;
; 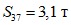 .
.На рис. 3 показаны формы свободных колебаний многоэтажной рамы, которая рассчитана как упругая система, и соответствующие этим формам сейсмические силы.
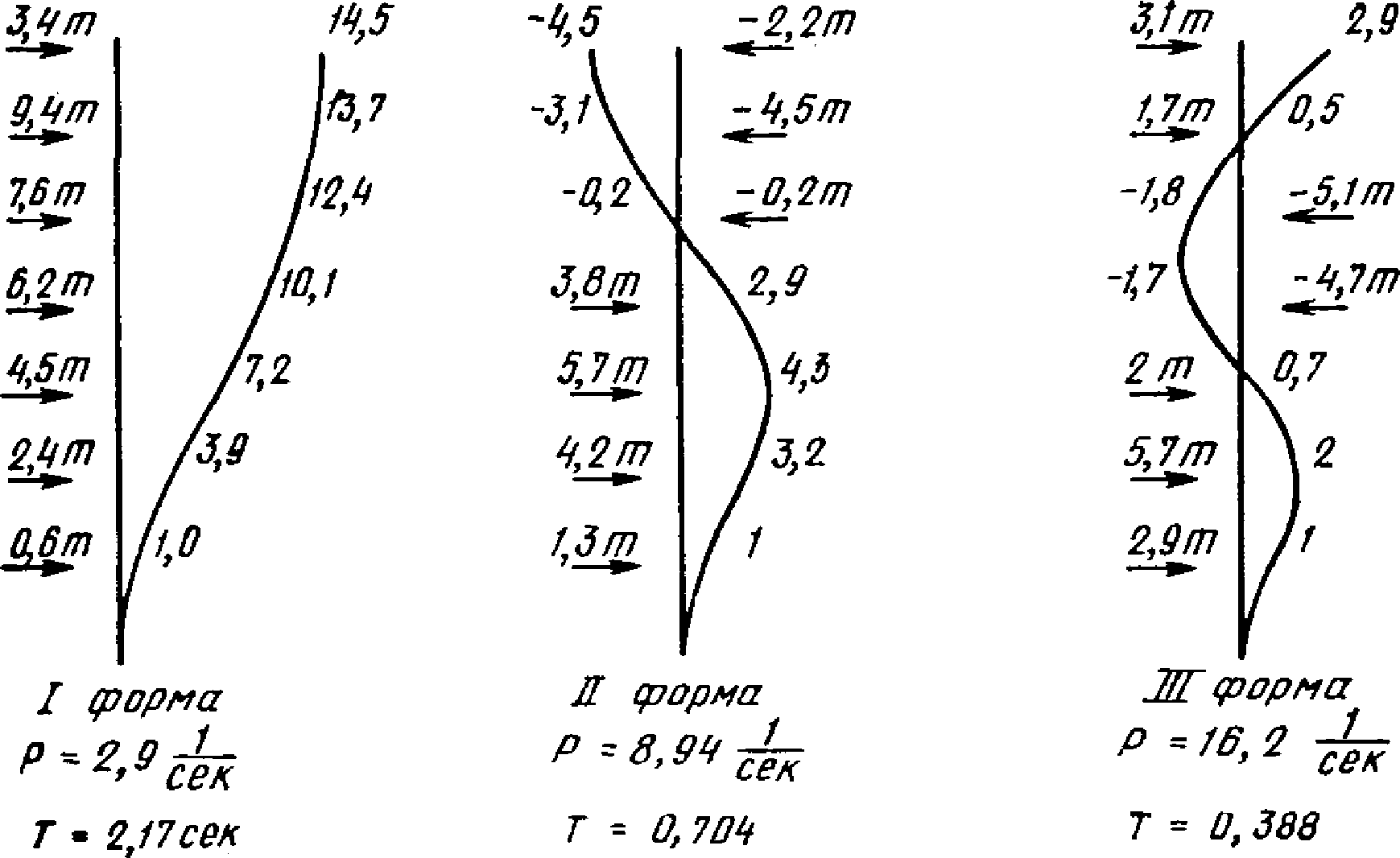
Рис. 3. Расчетные сейсмические нагрузки
на рамную систему по трем формам
Согласно СНиП II-А.12-69, п. 2.6, сейсмическая нагрузка для зданий высотой более 5 этажей должна увеличиваться на некоторый коэффициент, зависящий от числа этажей здания. В данном случае этот коэффициент равен 1,2.
По найденным значениям сейсмических сил построены эпюры изгибающих моментов в раме по каждой форме собственных колебаний и определены значения суммарных моментов 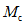 от сейсмической нагрузки с помощью формулы (5) (см. главу СНиП II-А.12-69, п. 2.9):
от сейсмической нагрузки с помощью формулы (5) (см. главу СНиП II-А.12-69, п. 2.9):
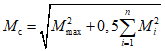 .
.На рис. 4 показана суммарная эпюра изгибающих моментов, вычисленная по трем формам собственных колебаний многоэтажной рамы.
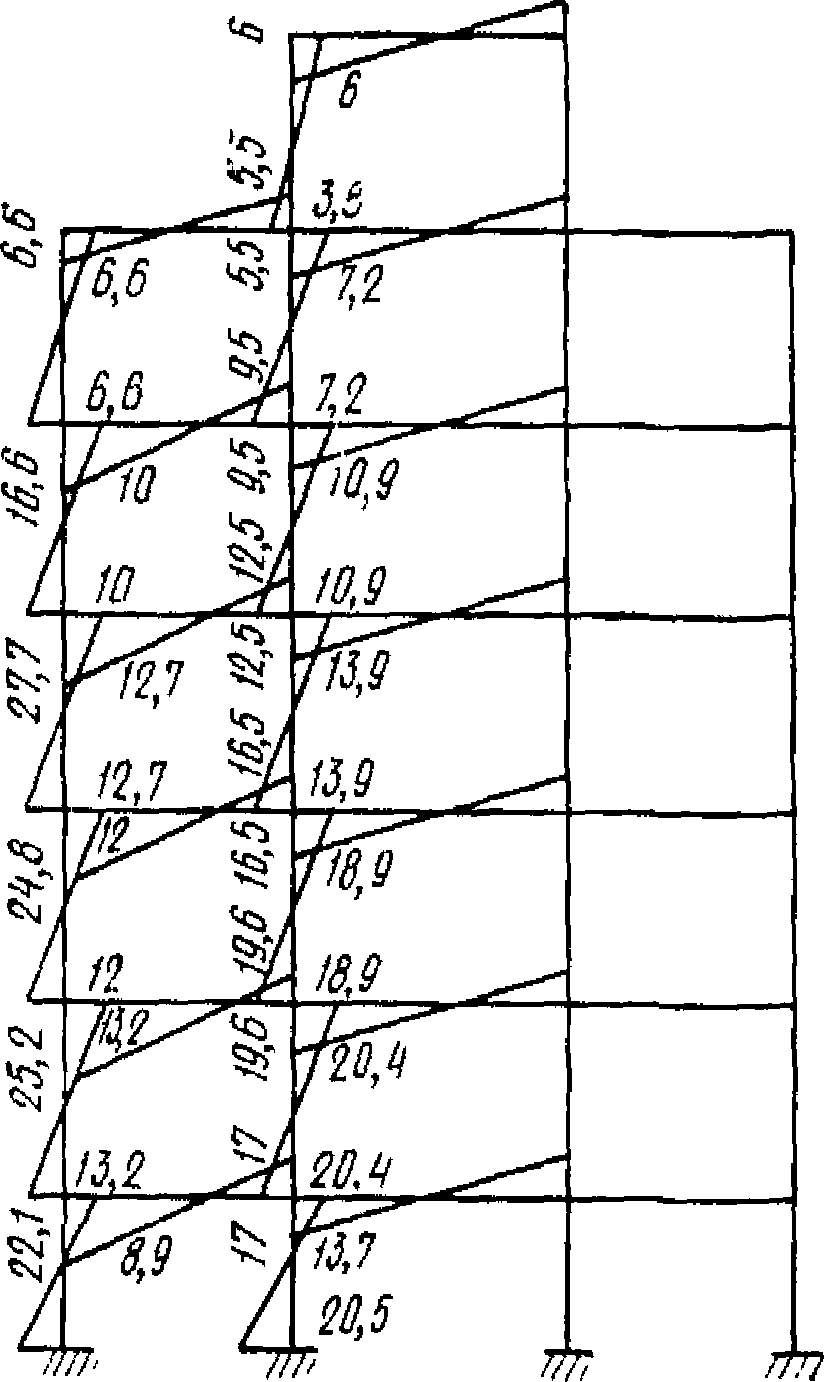
Рис. 4. Эпюра изгибающих моментов
в раме от сейсмических нагрузок
Вычисляем изгибающие моменты в элементах рамы от действия постоянных и временных вертикальных нагрузок. Полученные моменты складываем с моментами эпюры от сейсмической нагрузки.
На рис. 5, а приведена суммарная эпюра изгибающих моментов от вертикальных нагрузок (постоянной и временной). На рис. 5, б показана суммарная эпюра изгибающих моментов при учете действия сейсмической нагрузки.
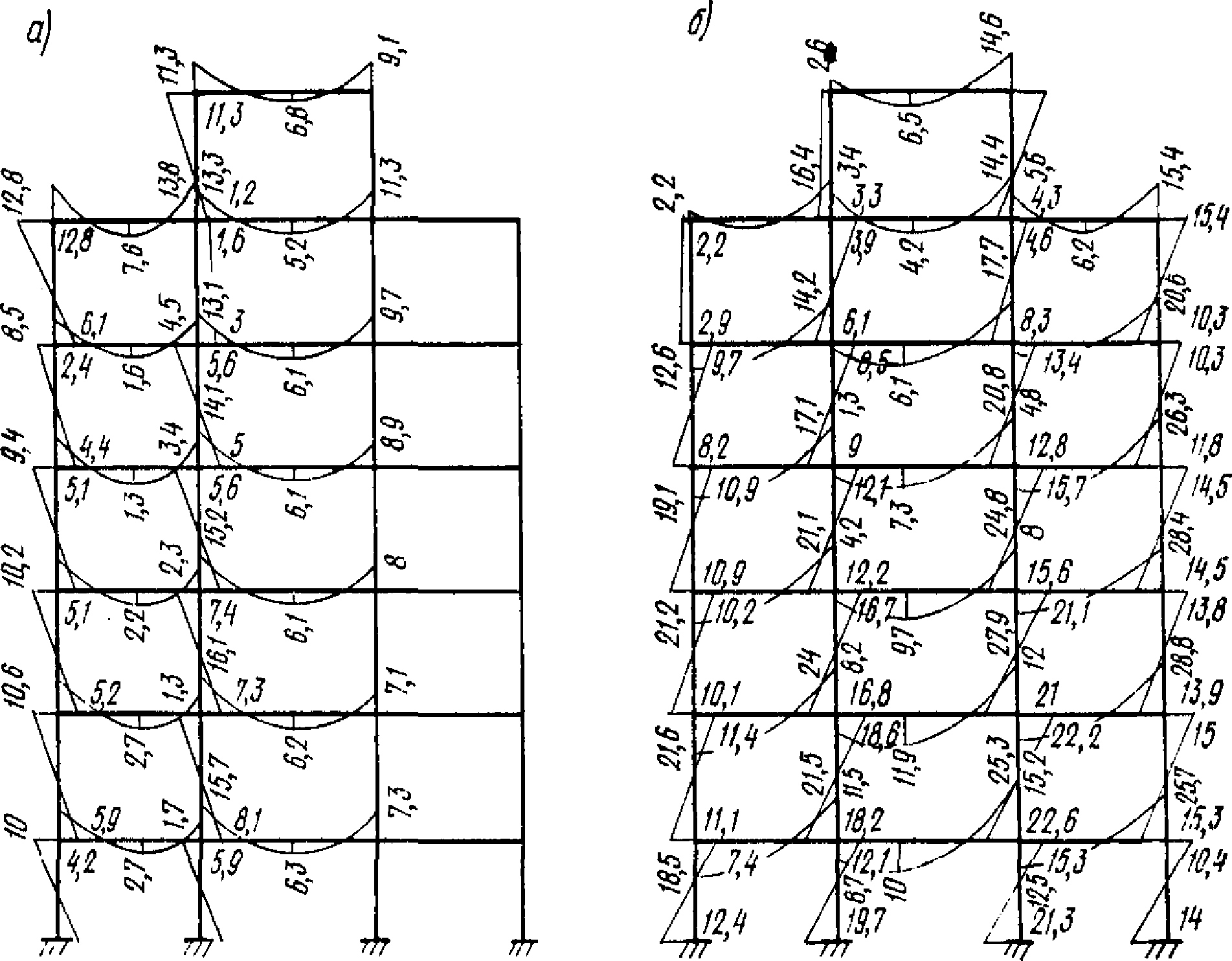
Рис. 5. Эпюры изгибающих моментов в раме
а - от вертикальной нагрузки;
б - от вертикальной и сейсмической нагрузок
В соответствии с полученными суммарными моментами (см. рис. 5, б), включающими действие статической и сейсмической нагрузок, производим поверочный расчет и уточнение предварительно заданных сечений элементов рамы. При этом основное сечение ригелей рамы подбираем с учетом действия максимальных моментов, возникающих в средней части ригеля. В табл. 3 приведены уточненные значения сечений элементов рамы.
Элементы рамы | Состав сечения | F, см2 | J, см4 | N элементов | |
Ригели: | |||||
верхние | I N 27 | 40,2 | 5010 | 371 | 1 |
нижние | I N 33 | 53,8 | 9840 | 597 | 2 |
Стойки: | |||||
крайний ряд | |||||
верх | 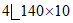 | 109,2 | 13400 | 957 | 3 |
низ | 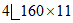 | 137,6 | 22180 | 1390 | 4 |
средний ряд | |||||
верх | 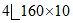 | 125,6 | 20300 | 1270 | 5 |
низ | 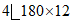 | 168,8 | 34260 | 1900 | 6 |
В связи с тем, что пролетные моменты разные, верхние ригели принимаем из I N 27, а нижние - из I N 33, как показано на рис. 6 (номера элементов на этом рисунке даны в соответствии с табл. 3).
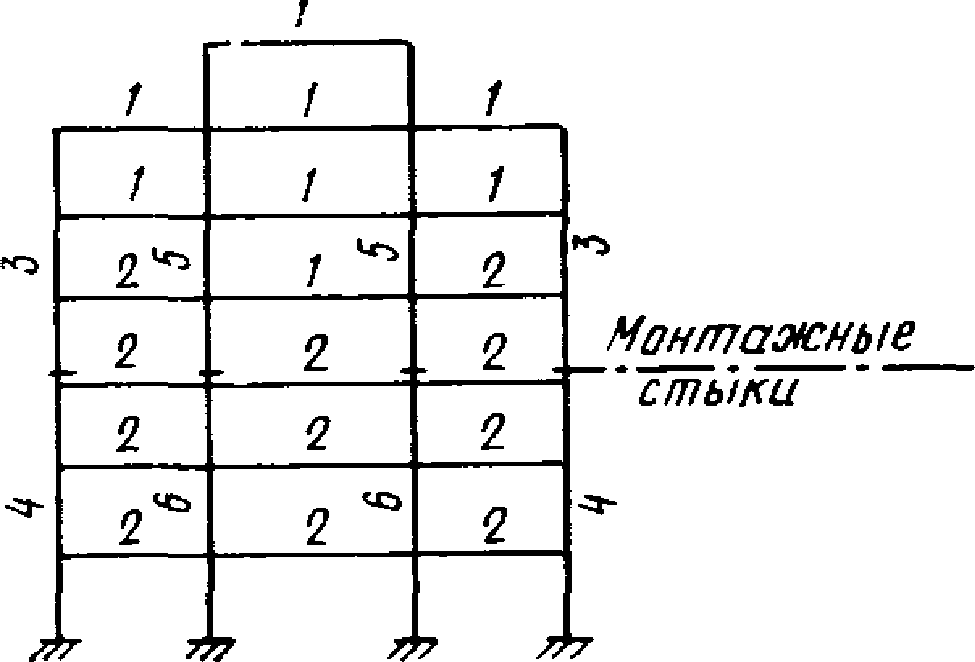
Рис. 6. Схема рамы с номерами ригелей и стоек (см. табл. 3)
Приступим ко второму этапу расчета, связанному с учетом возникновения пластических шарниров в ригелях, и перераспределению моментов в раме. Условие появления пластического шарнира обеспечивается в том случае, когда максимальный момент 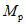 , вычисленный при расчете рамы как упругой системы, превышает момент
, вычисленный при расчете рамы как упругой системы, превышает момент 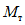 , определяющий предел несущей способности ригеля. Значение
, определяющий предел несущей способности ригеля. Значение 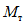 , зависящее от прочности и размеров сечения ригеля, определяется по формуле
, зависящее от прочности и размеров сечения ригеля, определяется по формуле
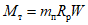 ,
,где коэффициент 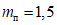 .
.
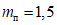 .
.Тогда для верхних ригелей
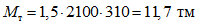 ;
;для нижних ригелей
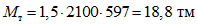 .
.Допустимое соотношение между 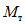 и
и 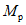 принимаем равным:
принимаем равным:
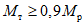 ;
;тогда для верхних ригелей имеем:
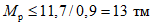 ;
;для нижних ригелей
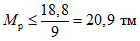 .
.Как видно из эпюры изгибающих моментов, учитывающей действие сейсмических сил, заданное условие может быть обеспечено для всех ригелей многоэтажной рамы.
Дальнейший расчет ведем в предположении, что пластические шарниры возникают во всех ригелях рамы.
Эпюра моментов в области пластического шарнира в ригелях получается уменьшенной на величину 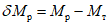 ;
;
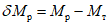 ;
;для верхних ригелей эта разность будет:
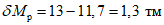 ;
;для нижних ригелей
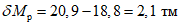 .
.Смещение эпюры моментов в ригелях приводит к соответствующему смещению моментов в стойках.
Находим изгибающий момент для крайней стойки нижнего яруса с учетом смещения эпюры моментов в ригелях:
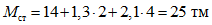 .
.Изгибающие моменты для средних стоек нижнего яруса равны:
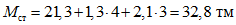 .
.Аналогичное перераспределение моментов выполняем для всех стоек рамы. На рис. 7 показана скорректированная эпюра моментов в многоэтажной раме, полученная после такого перераспределения.
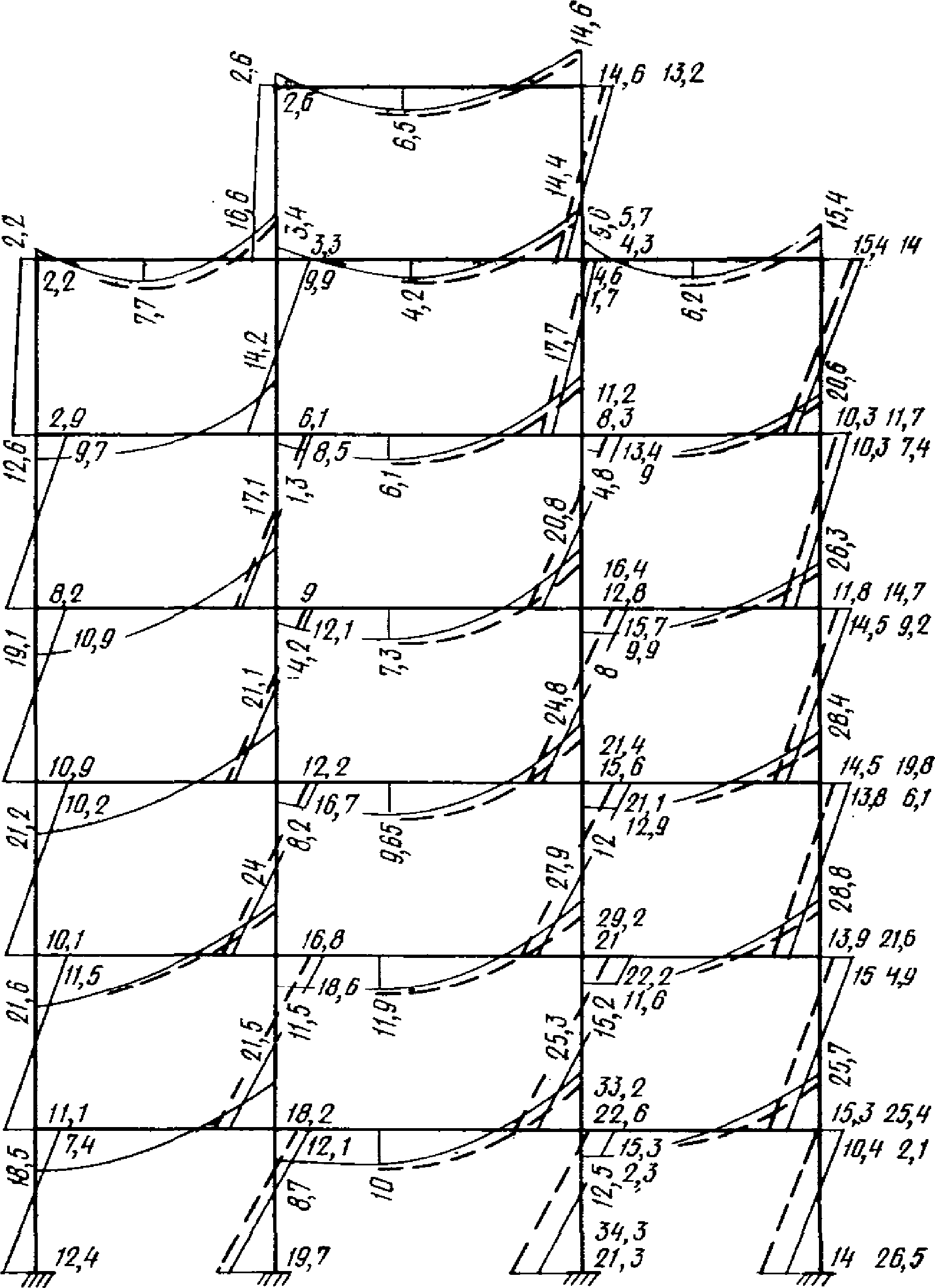
Рис. 7. Перераспределение моментов в раме
при учете образования пластических шарниров
В соответствий с новыми значениями моментов производим подбор сечений стоек как внецентренно-сжатых элементов.
В табл. 4 приведены окончательные значения сечений стоек, полученные после перераспределения моментов в раме.
Таблица 4
Стойки рамы | Состав сечения | F, см2 | ||
Крайний ряд: | ||||
верх | 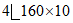 | 125,6 | 20 300 | 1270 |
низ | 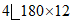 | 168,8 | 34 260 | 1900 |
Средний ряд: | ||||
верх | 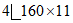 | 137,6 | 22180 | 1390 |
низ | 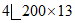 | 203,6 | 51050 | 2550 |
Что касается сечений ригелей, то они остаются неизменными; верхние ригели из I N 27, а нижние - из I N 33.
Исходя из соотношения, что 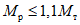 , приближенно находим местоположение пластических шарниров для двух типов ригелей:
, приближенно находим местоположение пластических шарниров для двух типов ригелей:
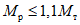 , приближенно находим местоположение пластических шарниров для двух типов ригелей:
, приближенно находим местоположение пластических шарниров для двух типов ригелей:для ригеля среднего ряда 2-го яруса - сечение I N 33;
для ригеля среднего ряда 4-го яруса - сечение I N 27.
Ригель второго яруса среднего пролета имеет наибольшие изгибающие моменты. Изгибающий момент в месте образования пластического шарнира при расчете рамы по упругой схеме 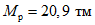 . Это место находится на расстоянии 43 см от оси правой стойки.
. Это место находится на расстоянии 43 см от оси правой стойки.
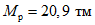 . Это место находится на расстоянии 43 см от оси правой стойки.
. Это место находится на расстоянии 43 см от оси правой стойки.Местоположение пластического шарнира для среднего ригеля на четвертом ярусе согласно расчету находится на расстоянии 59 см от оси правой стойки.
Обратим внимание, что в ригеле 4-го этажа местоположение пластического шарнира отстоит дальше, чем в ригеле 2-го этажа. Это обстоятельство объясняется тем, что основное сечение ригеля 4-го этажа, а соответственно и воспринимаемый им момент меньше, чем во 2-м этаже. Поэтому, чтобы обеспечить необходимое соотношение ординат изгибающих моментов 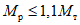 , приходится располагать местоположение пластического шарнира на 4-м этаже несколько дальше, чем на 2-м этаже.
, приходится располагать местоположение пластического шарнира на 4-м этаже несколько дальше, чем на 2-м этаже.
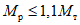 , приходится располагать местоположение пластического шарнира на 4-м этаже несколько дальше, чем на 2-м этаже.
, приходится располагать местоположение пластического шарнира на 4-м этаже несколько дальше, чем на 2-м этаже.Проверим устойчивость стенки среднего ригеля второго яруса в месте появления пластического шарнира. Умножим расчетные усилия от сейсмических сил на коэффициент 1,4. Тогда для среднего ригеля во втором ярусе в месте образования пластического шарнира (рис. 8) имеем следующие расчетные усилия:
M = 27,4 тм; Q = 18,1 т,
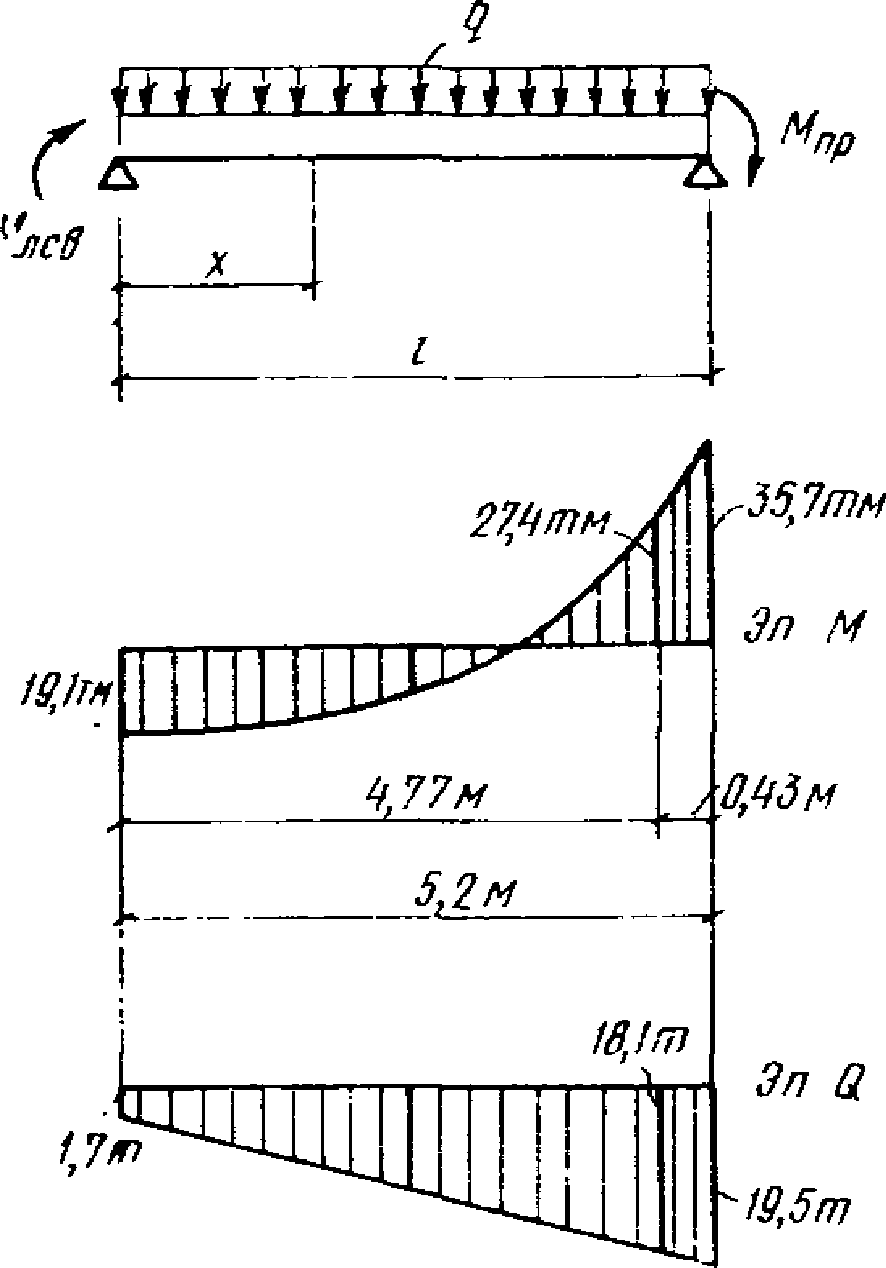
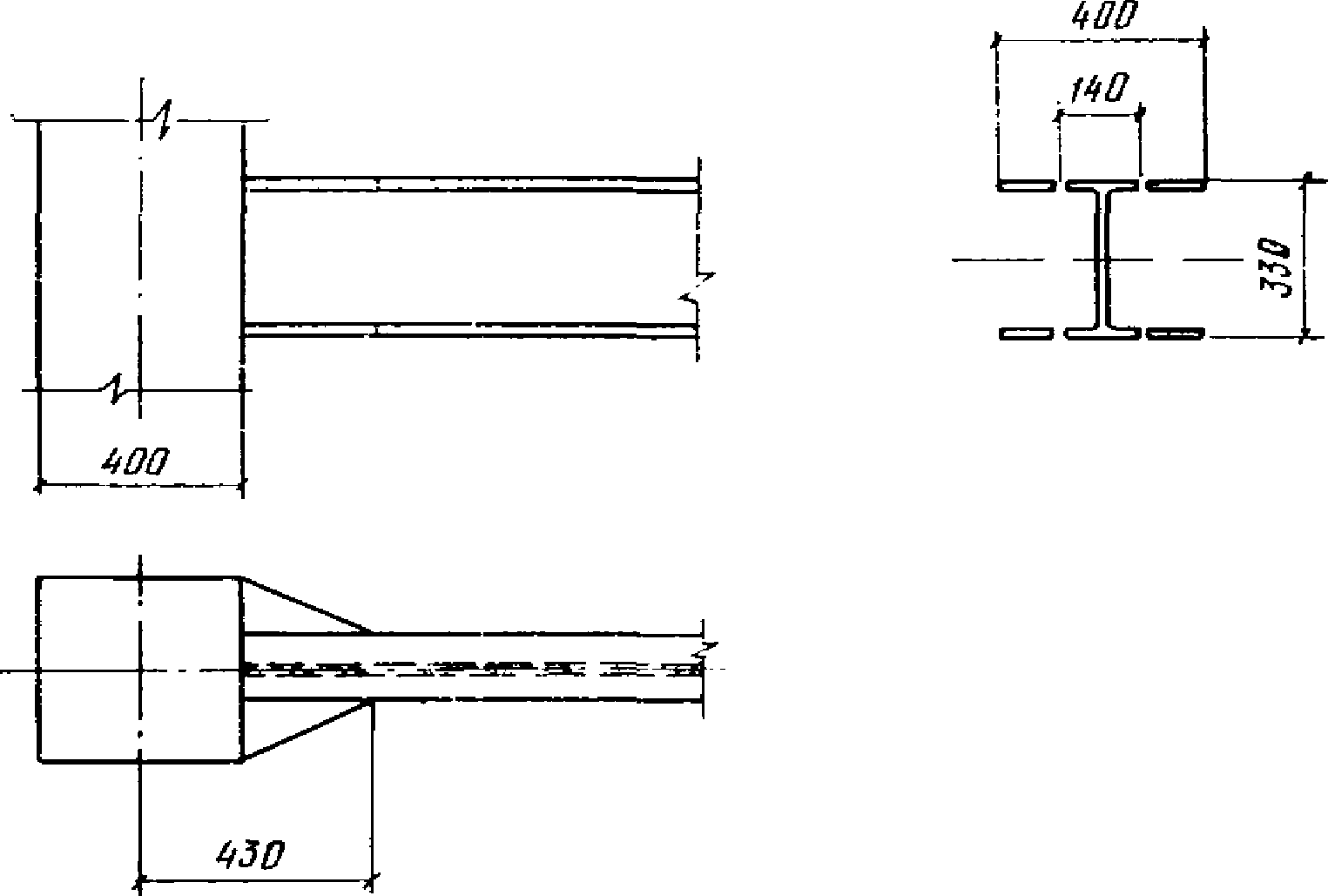
ригель из I N 33, высота стенки h = 29 см, толщина стенки b = 0,7 см. Принятые в соответствии с расчетом размеры опорной части ригеля показаны на рис. 9.
Определим касательные напряжения в стенке ригеля:
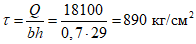 .
.Краевые нормальные напряжения
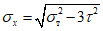 ;
;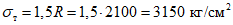 ;
;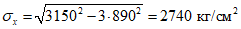 .
.Критическое нормальное напряжение 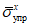 находим, предварительно определив
находим, предварительно определив 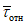 :
:
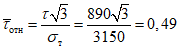 .
.По табл. 1 находим 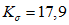 ;
;
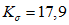 ;
;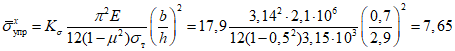 ;
;определяем критические касательные напряжения:
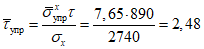 ;
;вычисляем интенсивность критических напряжений:
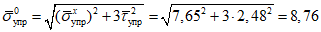 ;
;и, наконец, определяем краевые критические деформации
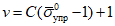 .
.По табл. 1 при 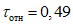 ; C = 1,01
; C = 1,01
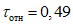 ; C = 1,01
; C = 1,01v = 1,01(8,76 - 1) + 1 = 8,84.
Допустимое соотношение между 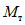 и
и 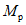 определяем по формуле:
определяем по формуле:
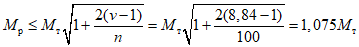 .
.Аналогичный расчет выполняем и для среднего ригеля на четвертом ярусе. Находим, что краевые критические деформации для этого ригеля v = 9,62. А допустимое соотношение между 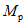 и
и 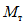 равно:
равно:
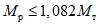 .
.Для найденных соотношений между 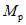 и
и 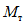 уточняем местоположение пластических шарниров. Находим, что местоположение пластического шарнира для среднего ригеля на втором ярусе при
уточняем местоположение пластических шарниров. Находим, что местоположение пластического шарнира для среднего ригеля на втором ярусе при 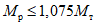 находится на расстоянии x = 47 см от оси стойки. Округлим это значение до 50 см.
находится на расстоянии x = 47 см от оси стойки. Округлим это значение до 50 см.
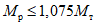 находится на расстоянии x = 47 см от оси стойки. Округлим это значение до 50 см.
находится на расстоянии x = 47 см от оси стойки. Округлим это значение до 50 см.Местоположение пластического шарнира для среднего ригеля на четвертом ярусе при 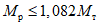 согласно расчету находится на расстоянии x = 60 см от оси стойки. Полученные результаты незначительно отличаются от ранее определенных. Поэтому производить вновь корректировку моментов в элементах рамы нет надобности.
согласно расчету находится на расстоянии x = 60 см от оси стойки. Полученные результаты незначительно отличаются от ранее определенных. Поэтому производить вновь корректировку моментов в элементах рамы нет надобности.
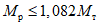 согласно расчету находится на расстоянии x = 60 см от оси стойки. Полученные результаты незначительно отличаются от ранее определенных. Поэтому производить вновь корректировку моментов в элементах рамы нет надобности.
согласно расчету находится на расстоянии x = 60 см от оси стойки. Полученные результаты незначительно отличаются от ранее определенных. Поэтому производить вновь корректировку моментов в элементах рамы нет надобности.Жесткости ригелей и стоек изменились в связи с перераспределением усилий в раме. Проверим, насколько в связи с этим изменилась сейсмическая нагрузка.
Расчет, как и прежде, производим в предположении, что рама работает как упругая система. На рис. 10 приведены формы собственных колебаний рамы и соответствующие им сейсмические силы, полученные в результате проверочного расчета.
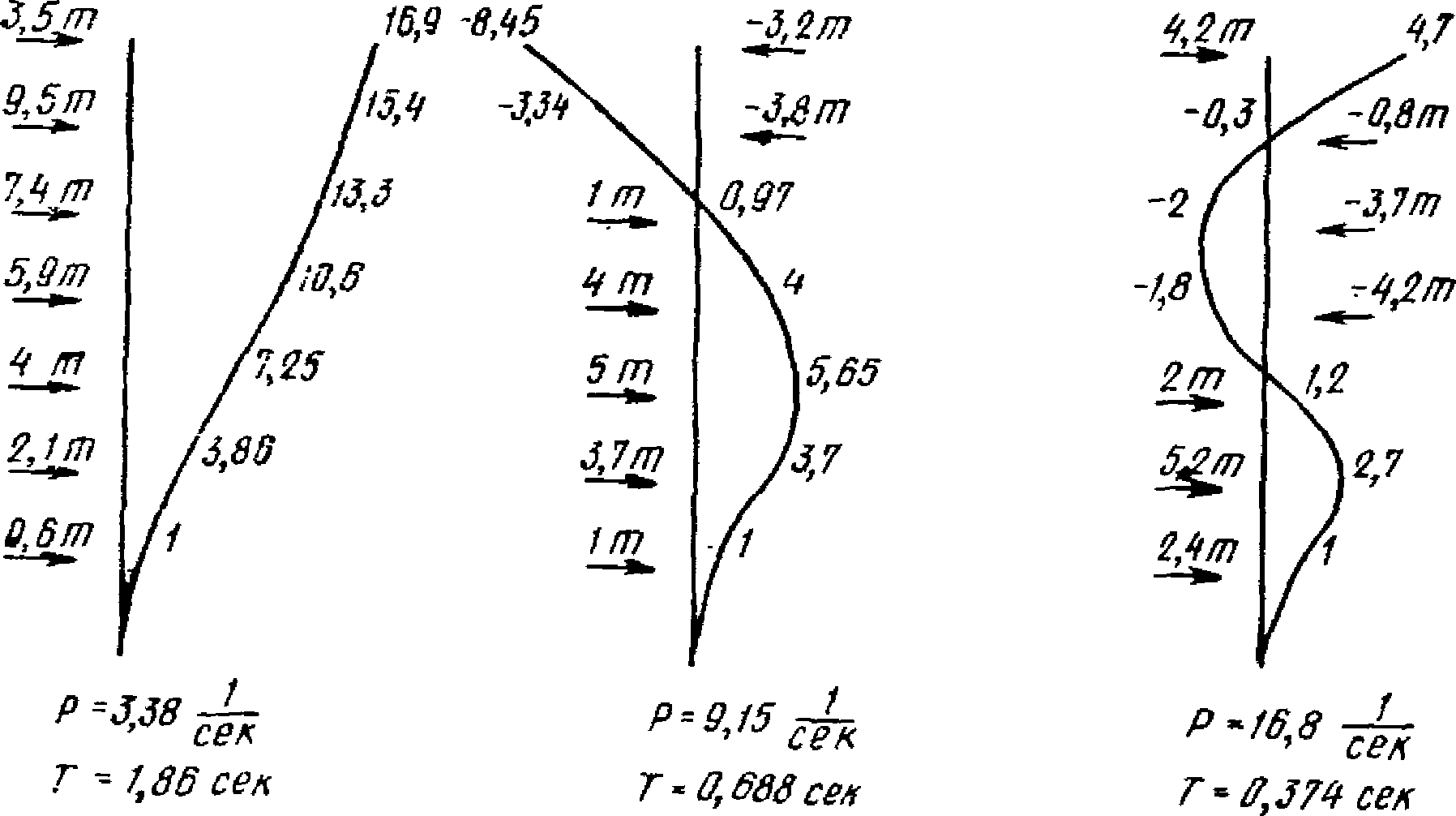
Рис. 10. Расчетные сейсмические нагрузки на рамную
систему при образовании в ригелях пластических шарниров
На рис. 11 приведены значения суммарных поперечных сил в раме по трем формам колебаний, полученных при первоначальном и проверочном расчетах.
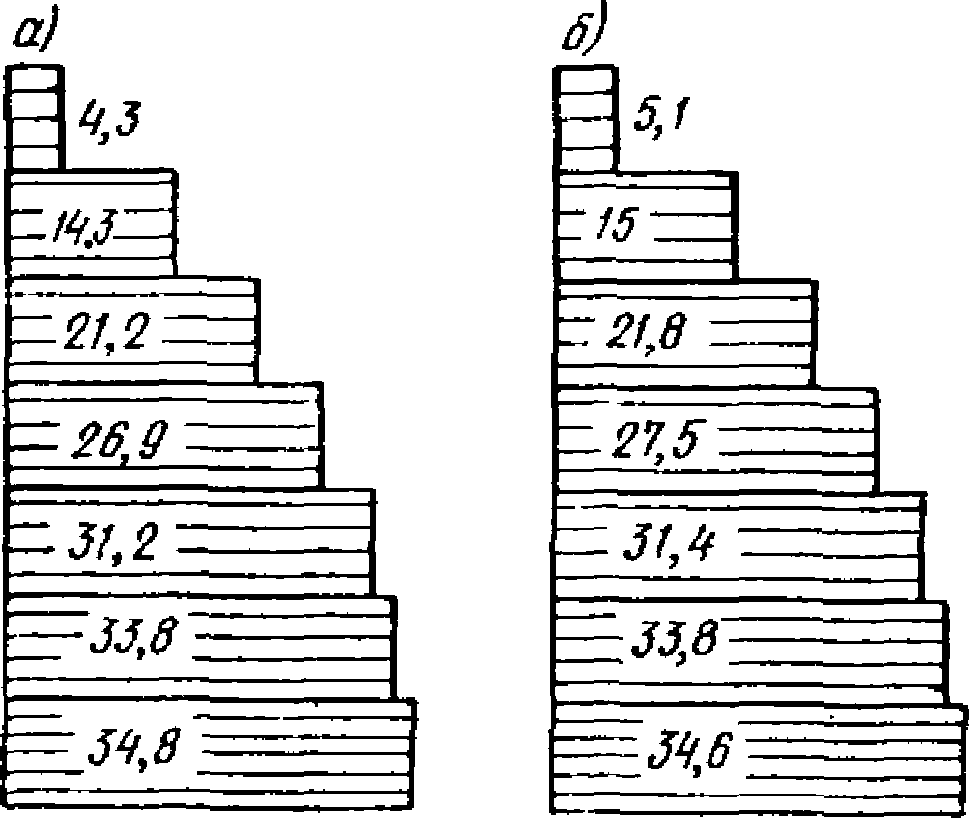
Рис. 11. Эпюра перерезывающих сил в раме
а - при расчете по упругой схеме;
б - при учете образования пластических шарниров
Жесткости элементов рамы, предварительно заданные и вновь полученные, незначительно отличаются друг от друга. Поперечные силы, возникающие в раме от действия сейсмических сил при первоначальном и при повторном расчетах, когда значения жесткостей стоек и ригелей рамы несколько изменились, отличаются также незначительно. Поэтому необходимость в повторном расчете рамы отпадает.
3.1. Сильные землетрясения происходят не так уж часто, и вполне возможно, что многие строения, возведенные в сейсмических районах, за все время своей эксплуатации так и не подвергнутся серьезному сейсмическому воздействию. Поэтому при расчете конструкций на сейсмические нагрузки вряд ли целесообразно будет проектировать их с той же степенью обеспечения сохранности, что и конструкции, несущие обычные статические эксплуатационные нагрузки. Представляется более правильным сейсмические воздействия рассматривать как особые исключительные нагрузки, когда от сооружения не требуется, чтобы оно их перенесло, не получив никаких повреждений. Напротив, экономически будет целесообразней допускать в конструкциях различные повреждения, лишь бы они не вызывали обрушения конструкций и не представляли опасности для людей и для ценного имущества. Если исходить из таких требований, то окажется, что работа конструкций будет происходить в области, граничащей с разрушением, т.е. появится необходимость рассматривать работу материала не только в упругой, но и в пластической стадии.
Учет пластических деформаций позволяет использовать дополнительные резервы несущей способности конструкций, не затрагиваемые в расчетах по упругой стадии [4, 8, 10]. При этом естественно, что чем выше пластические свойства материала конструкции, тем выше будут и дополнительные резервы, которые могут быть рационально использованы.
Большинство металлов, используемых в строительных конструкциях, обладают высокой пластичностью, и поэтому использование таких резервов потенциально может дать практически ощутимый эффект.
Однако не в каждой металлической конструкции, выполненной из высокопластической стали, могут быть использованы запасы ее пластической энергоемкости. Здесь имеется в виду тот факт, что, как правило, все соединения в металлических конструкциях решаются на сварке, а сами сварные соединения и примыкающий к сварным швам металл становятся хрупкими, и пластические свойства здесь очень низки, практически отсутствуют. В то же время обычно именно эти места, т.е. места соединения элементов конструкций, являются областями максимальных напряжений, и именно здесь наступает разрушение. Таким образом, легко может оказаться, что разрушение конструкции произойдет еще до того, когда в других ее частях, способных к пластическому деформированию, напряжения достигнут текучести. Именно так будет протекать работа рамных каркасов при их загружении сейсмической нагрузкой. Действительно, как показано на рис. 12, а, максимальные напряжения в ригеле при типовом конструктивном решении возникают в тех местах, в которых обычно находятся сварные соединения ригелей со стойками. Поскольку сварные соединения обладают хрупкими свойствами, то, по-видимому, в них и произойдут разрушения и никакие пластические деформации при этом не разовьются.
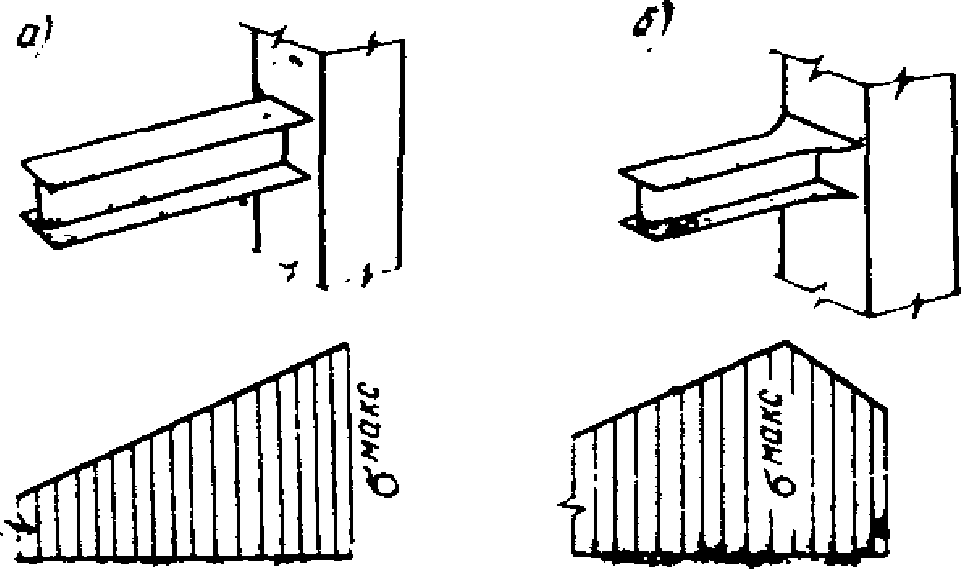
рамного узла и эпюры напряжений в ригеле
а - типового рамного узла; б - узла
с усиленным опорным сечением ригеля
Для того чтобы в рамном каркасе могли развиться пластические деформации, необходимо опасные сечения конструкции вывести из зоны, прилегающей к сварке. Это может быть достигнуто различными путями: например, путем развития сечений элементов в местах их примыкания к узлам; постановкой дополнительных подсобных элементов (типа подкосов), изменяющих характер распределения эпюры изгибающих моментов; включением специальных элементов (вертикальных диагональных связей), предназначенных для восприятия сейсмической нагрузки и работающих в пластической стадии, и т.п.
Ниже будем касаться только первого из названных приемов, а именно случая, когда в металлическом каркасе подкосы или диагональные связи отсутствуют, а развитие пластических деформаций обеспечивается лишь за счет увеличения опорных сечений ригелей (см. рис. 12, б). В этом случае развитие сечений ригелей может быть достигнуто либо путем развития ширины полок, либо путем увеличения высоты стенок, либо путем увеличения размеров тех и других элементов. При этом размеры обычного сечения ригеля и положение места перехода к усиленному сечению следует подбирать из такого расчета, чтобы в то время как в пластической зоне появляется пластический шарнир, напряжения в сварном стыке ригеля со стойкой не превышали расчетных сопротивлений. С появлением пластического шарнира рост усилий в промежутке между шарниром и стыком ригеля со стойкой должен приостановиться. Таким образом, пластический шарнир будет играть роль предохранителя сварного стыка от перенапряжений.
Второй фактор, который тоже может воспрепятствовать использованию пластических резервов конструкции, заключается в опасности потери устойчивости несущих конструкций, которая может наступить ранее стадии, когда напряжения достигнут предела текучести 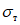 . Для металлических конструкций такая опасность усугубляется тем, что сечения элементов в основном тонкостенны, и поэтому, кроме потери устойчивости всего элемента в целом, появляется опасность также и потери местной устойчивости. Поскольку потеря местной устойчивости может произойти не только в сжатых, но также и в изгибаемых элементах, то задача обеспечения устойчивости работы изгибаемых элементов при высоких напряжениях приобретает большое практическое значение.
. Для металлических конструкций такая опасность усугубляется тем, что сечения элементов в основном тонкостенны, и поэтому, кроме потери устойчивости всего элемента в целом, появляется опасность также и потери местной устойчивости. Поскольку потеря местной устойчивости может произойти не только в сжатых, но также и в изгибаемых элементах, то задача обеспечения устойчивости работы изгибаемых элементов при высоких напряжениях приобретает большое практическое значение.
Таким образом, в зависимости от условий работы того или иного элемента каркаса к каждому из них при проектировании следует предъявлять свои требования, либо связанные с соблюдением устойчивости, либо с обеспечением развития пластических деформаций, либо с ограничением напряжений.
Особое внимание необходимо уделять стойкам, от которых в наибольшей степени зависит сохранность от обрушения всего здания. Поскольку стойки выполнены из тонкостенных элементов и подвержены постоянному сжатию, серьезную опасность для них представляет как местная потеря устойчивости, так и потеря устойчивости в целом. Поэтому допускать пластические деформации в стойках опасно. Следует стремиться, чтобы работа стоек происходила в пределах упругости.
Ригели, напротив, работают в основном на изгиб. Потеря местной устойчивости представляет для них меньшую опасность, чем для стоек. Поэтому в ригелях допустимы пластические деформации. В соответствии с этим при расчете на действие сейсмической нагрузки ригели можно проектировать таким образом, чтобы в них развивались пластические деформации.
При колебании здания, в моменты появления в ригелях пластических деформаций, рост усилий в ригелях будет приостанавливаться. В связи с этим часть сейсмической нагрузки будет перераспределяться на стойки. Чтобы это не приводило к перегрузке стоек, пластические деформации в ригелях должны быть ограничены.
3.2. В связи с тем, что работа каркаса должна происходить в упругопластической области, уместно остановиться на некоторых работах, связанных с исследованием колебаний конструкций при учете пластических деформаций.
В работе [18] Г. Бергом и С. Томайдесом рассмотрены колебания упругопластической системы с одной степенью свободы. Зависимость усилий от деформаций в системе принималась в виде идеальной диаграммы упругопластического деформирования - диаграммы Прандтля. При этом брались различные значения предельной упругой деформации 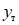 упругопластической системы по отношению к деформациям
упругопластической системы по отношению к деформациям 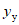 упругой системы. В качестве воздействия на систему использовалась акселерограмма землетрясения в г. Тафте (Калифорния) 21 июля 1952 г. В результате исследований был построен ряд спектров, представляющих собой графики максимальных смещений упругопластических систем при различных периодах их собственных колебаний. Из построенных спектров видно, что у систем, пределы текучести которых достаточно близки к деформациям упругих систем, а характеристики затухания соответствуют реальным конструкциям, смещения за пределы упругости незначительны и спектры смещений таких систем мало отличаются от спектров смещений упругой системы.
упругой системы. В качестве воздействия на систему использовалась акселерограмма землетрясения в г. Тафте (Калифорния) 21 июля 1952 г. В результате исследований был построен ряд спектров, представляющих собой графики максимальных смещений упругопластических систем при различных периодах их собственных колебаний. Из построенных спектров видно, что у систем, пределы текучести которых достаточно близки к деформациям упругих систем, а характеристики затухания соответствуют реальным конструкциям, смещения за пределы упругости незначительны и спектры смещений таких систем мало отличаются от спектров смещений упругой системы.
В работе А. Велетсоса и Н. Ньюмарка [20] также исследовались колебания упругопластических систем с одной степенью свободы. В качестве воздействия использовалась акселерограмма землетрясения Эль-Центро (Калифорния, 18 мая 1940 г.). Показатель пластичности системы определялся величиной 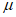 , представляющей собой отношение наибольшей полной деформации упругопластической системы (упругая + пластическая) к наибольшей упругой деформации, т.е.
, представляющей собой отношение наибольшей полной деформации упругопластической системы (упругая + пластическая) к наибольшей упругой деформации, т.е. 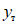 . Значение
. Значение 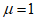 соответствовало чисто упругой работе системы. В результате исследований были построены спектры максимальных ускорений (взятых в отношении к ускорению силы тяжести) для системы с различными периодами собственных колебаний.
соответствовало чисто упругой работе системы. В результате исследований были построены спектры максимальных ускорений (взятых в отношении к ускорению силы тяжести) для системы с различными периодами собственных колебаний.
Характер изменения спектров в зависимости от периодов T при различных 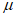 , взятых от
, взятых от 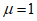 до
до 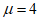 , получился примерно одинаковым, но с возрастанием
, получился примерно одинаковым, но с возрастанием 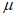 ординаты спектров, представляющие собой относительные ускорения системы
ординаты спектров, представляющие собой относительные ускорения системы 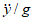 , уменьшаются. Что касается систем, у которых
, уменьшаются. Что касается систем, у которых 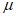 немного больше единицы, отличие ординат спектров по отношению к упругой системе незначительно. Таким образом, в этих случаях как на упругую, так и на упругопластическую систему действуют примерно одинаковые силы.
немного больше единицы, отличие ординат спектров по отношению к упругой системе незначительно. Таким образом, в этих случаях как на упругую, так и на упругопластическую систему действуют примерно одинаковые силы.
В работах [1, 2] приводятся результаты исследований на ЭЦВМ систем с несколькими степенями свободы. Движение основания принималось по синусоидальному закону. Зависимость усилий в стойках от деформаций принималась в виде диаграммы Прандтля.
Величины смещений этажей упругопластической системы 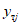 в тот момент, когда в них достигаются пределы текучести, задавались сравнительно близкими к деформациям аналогичной упругой системы, полученной при ее установившихся колебаниях, т.е.
в тот момент, когда в них достигаются пределы текучести, задавались сравнительно близкими к деформациям аналогичной упругой системы, полученной при ее установившихся колебаниях, т.е. 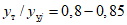 . Исследования показали, что в таких случаях форма перемещений упругопластических систем почти не отличается от формы перемещений упругой системы. При этом величина перемещений упругопластических систем получается несколько меньшей, чем у упругих. Это объясняется тем, что часть энергии колебаний в упругопластической системе расходуется на необратимые пластические деформации.
. Исследования показали, что в таких случаях форма перемещений упругопластических систем почти не отличается от формы перемещений упругой системы. При этом величина перемещений упругопластических систем получается несколько меньшей, чем у упругих. Это объясняется тем, что часть энергии колебаний в упругопластической системе расходуется на необратимые пластические деформации.
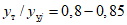 . Исследования показали, что в таких случаях форма перемещений упругопластических систем почти не отличается от формы перемещений упругой системы. При этом величина перемещений упругопластических систем получается несколько меньшей, чем у упругих. Это объясняется тем, что часть энергии колебаний в упругопластической системе расходуется на необратимые пластические деформации.
. Исследования показали, что в таких случаях форма перемещений упругопластических систем почти не отличается от формы перемещений упругой системы. При этом величина перемещений упругопластических систем получается несколько меньшей, чем у упругих. Это объясняется тем, что часть энергии колебаний в упругопластической системе расходуется на необратимые пластические деформации.Подобные исследования системы с двумя степенями свободы были проведены также Е.М. Малинковичем. Он исследовал колебания упругой и упругопластической систем при перемещении основания по синусоидальному закону. Исследования производились как на ЭЦВМ, так и на аналоговой машине. Полученные результаты говорят о том, что в упругопластической системе усилия и деформации меньше, чем в упругой системе.
Оценивая результаты, приведенные в указанных работах, характерно отметить, что при условии, когда пластические деформации, развивающиеся в упругопластической системе за один цикл колебаний, сравнительно невелики, перемещения такой системы близки к перемещениям упругой системы, а сейсмическая нагрузка, прикладываемая к той и другой системам, практически одинакова.
Следует отметить, что такая предпосылка уже использовалась в работе [8], где рассматривалась система с одной степенью свободы, у которой зависимость усилий от деформаций S - y характеризовалась диаграммой Прандтля. В этой работе предполагалось, что сейсмическая нагрузка в упругопластической системе будет такой же, как нагрузка, действующая на упругую систему. Из этого условия вытекает, что элементам упругопластической системы за полцикла колебаний сообщается такое же количество энергии, которое сообщается элементам упругой системы. Такая же предпосылка использовалась и в работе [10], где рассматривались железобетонные многоэтажные рамные каркасы, у которых появление пластических деформаций учитывалось в стойках.
В связи с этим, учитывая принятое условие о необходимости ограничения перемещений конструкций за пределами упругости, сейсмическая нагрузка на сооружение может определяться таким же образом, как при расчете обычной упругой системы, т.е. в этих случаях при определении величины сейсмических нагрузок следует пользоваться нормами главы СНиП II-А.12-69.
3.3. Изложенные выше в пп. 3.1 и 3.2 соображения, касающиеся возможности и целесообразности использования пластических свойств металла при работе конструкций на сейсмические нагрузки, хотя сами по себе являются вполне логичными, но для рекомендации их применения в практических задачах еще не могут рассматриваться как достаточные и требуют подтверждения и количественного обоснования экспериментом. Остановимся поэтому на рассмотрении опытов, проводившихся в этой области.
В 1968 г. Л.Ш. Килимником (ЦНИИСК) были проведены экспериментальные исследования работы узловых сопряжений ригелей с колоннами на действие статической и динамической нагрузок [7]. В качестве объектов испытания были выбраны два типа узлов. Первый из них представлял собой типовое сопряжение, применяемое в настоящее время в конструкциях, возводимых в сейсмических районах (рис. 13, а).
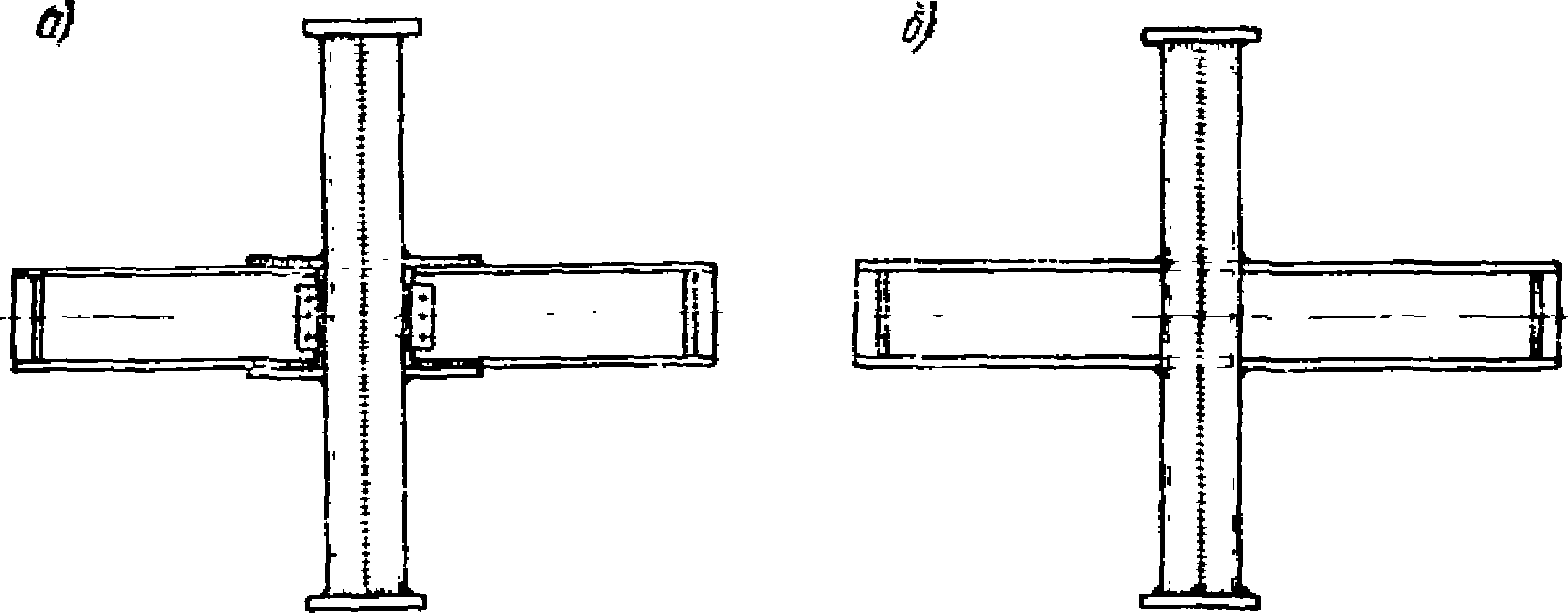
Рис. 13. Схемы образцов рамных узлов, испытанных в ЦНИИСКе
а - типовой узел; б - узел с неразрезной стенкой ригеля
Второй тип узлов (рис. 13, б) был решен несколько по-другому. В этом случае стенка ригеля не обрывалась у колонны, а была пропущена сквозь колонну. Пояса ригелей, имеющие постоянную ширину по всей длине, непосредственно примыкали к колонне, а горизонтальные накладки отсутствовали.
Надо напомнить, что в таких конструкциях наиболее напряженные зоны ригелей находятся вблизи их сопряжения с колоннами, и поэтому эксперимент должен был в основном проходить в упругой стадии и завершаться хрупким разрушением по стыку ригеля со стойкой. Такое обстоятельство исключает возможность использования пластических резервов металла.
Испытание образцов проводилось при статическом и циклическом нагружении колонн и ригелей. Сначала колонны и ригели нагружались статически. Затем к ригелям дополнительно прикладывалась динамическая нагрузка. В завершающей стадии образцы доводились до разрушения. Динамическая нагрузка назначалась различной интенсивности. Количество загружений ограничивалось 1000 циклами с частотой 5,5 Гц. В процессе испытаний велись измерения деформаций в отдельных сечениях ригелей и колонн, а в зонах узлов также измерялись прогибы и углы поворотов ригелей.
Характер разрушений, как и следовало ожидать, показал, что ригели теряли несущую способность в результате разрушения сварных швов, прикрепляющих их к колоннам, или околошовного металла. Никаких сколько-нибудь существенных пластических деформаций в ригелях при этом не наблюдалось. Полученные автором величины прогибов ригелей составляли всего лишь 1/500 - 1/135 их длины.
О неудовлетворительной пластической работе ригелей свидетельствуют также величины отношения энергии упругого деформирования 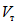 к полной энергии деформирования
к полной энергии деформирования 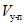 . Это отношение составляло всего 0,7 - 0,9. Обратим внимание, что эти цифры характеризуют величину, обратную той, которая используется нами и представляет собой отношение полной энергии образца к величине только упругой энергии.
. Это отношение составляло всего 0,7 - 0,9. Обратим внимание, что эти цифры характеризуют величину, обратную той, которая используется нами и представляет собой отношение полной энергии образца к величине только упругой энергии.
Более плодотворными оказались эксперименты, проводившиеся Е. Поповым [19], который испытывал четыре типа узловых соединений. В узлах типа F - 1 (рис. 14, а) ригель был непосредственно приварен к колонне. В узлах типа F - 2 (рис. 14, б) были использованы соединительные пластины. В узлах типа F - 3 (рис. 14, в) соединение ригеля с колонной посредством соединительных пластин осуществлялось с помощью высокопрочных болтов. В некоторых образцах типа F - 2 и F - 3 толщины соединительных пластин варьировались.
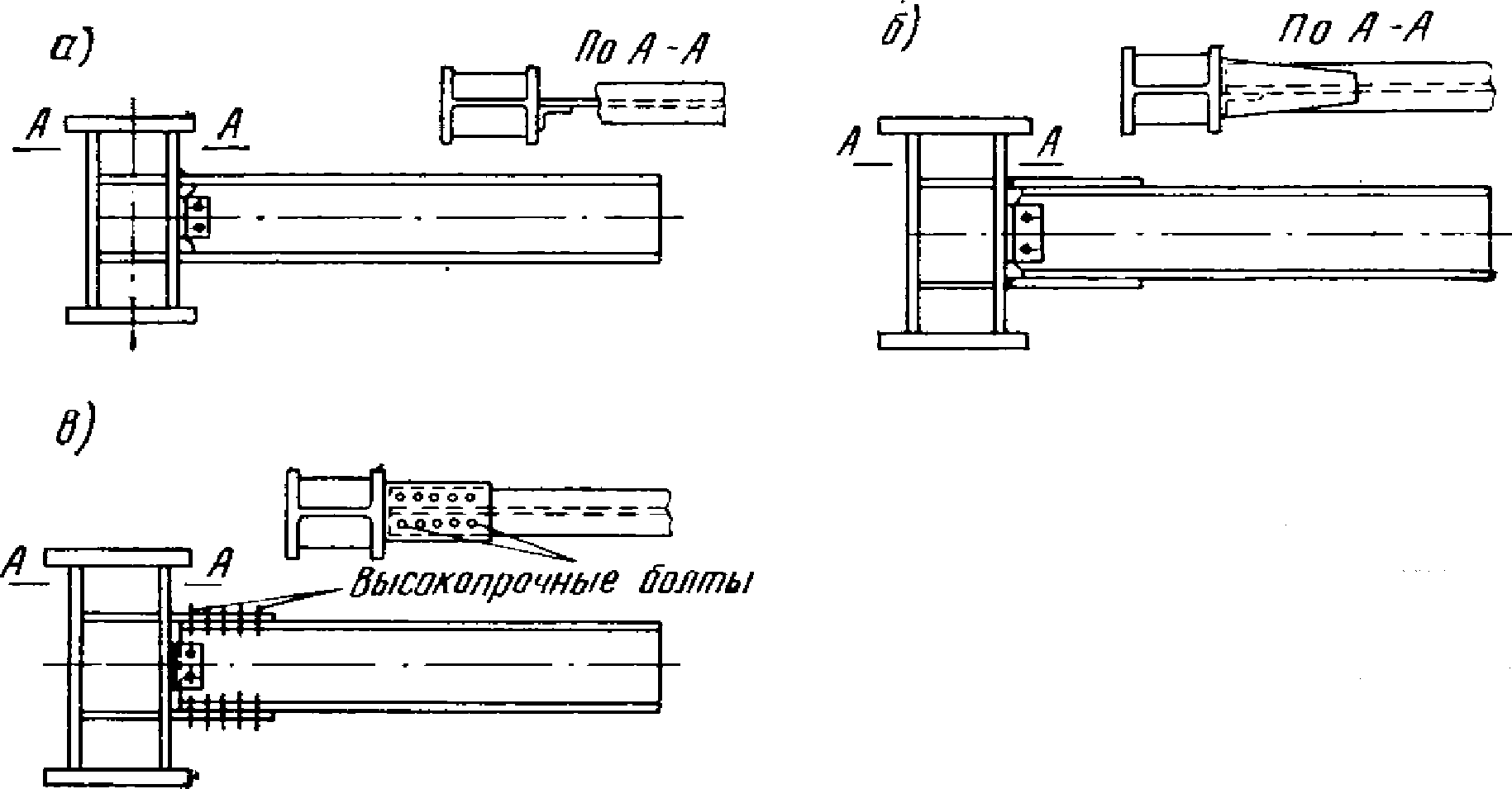
Рис. 14. Схемы образцов рамных узлов,
испытанных Е. Поповым (США)
а - тип F - 1; б - тип F - 2; в - тип F - 3
Совершенное оборудование позволило автору создавать нагрузку, близко отвечающую сейсмическому воздействию. Гидравлический цилиндр двойного действия обеспечивал необходимую величину нагрузки на концы ригелей. В качестве возбудителя гидравлического цилиндра был использован пульсатор с программным управлением. Некоторые типовые программы нагружения представлены на рис. 15.
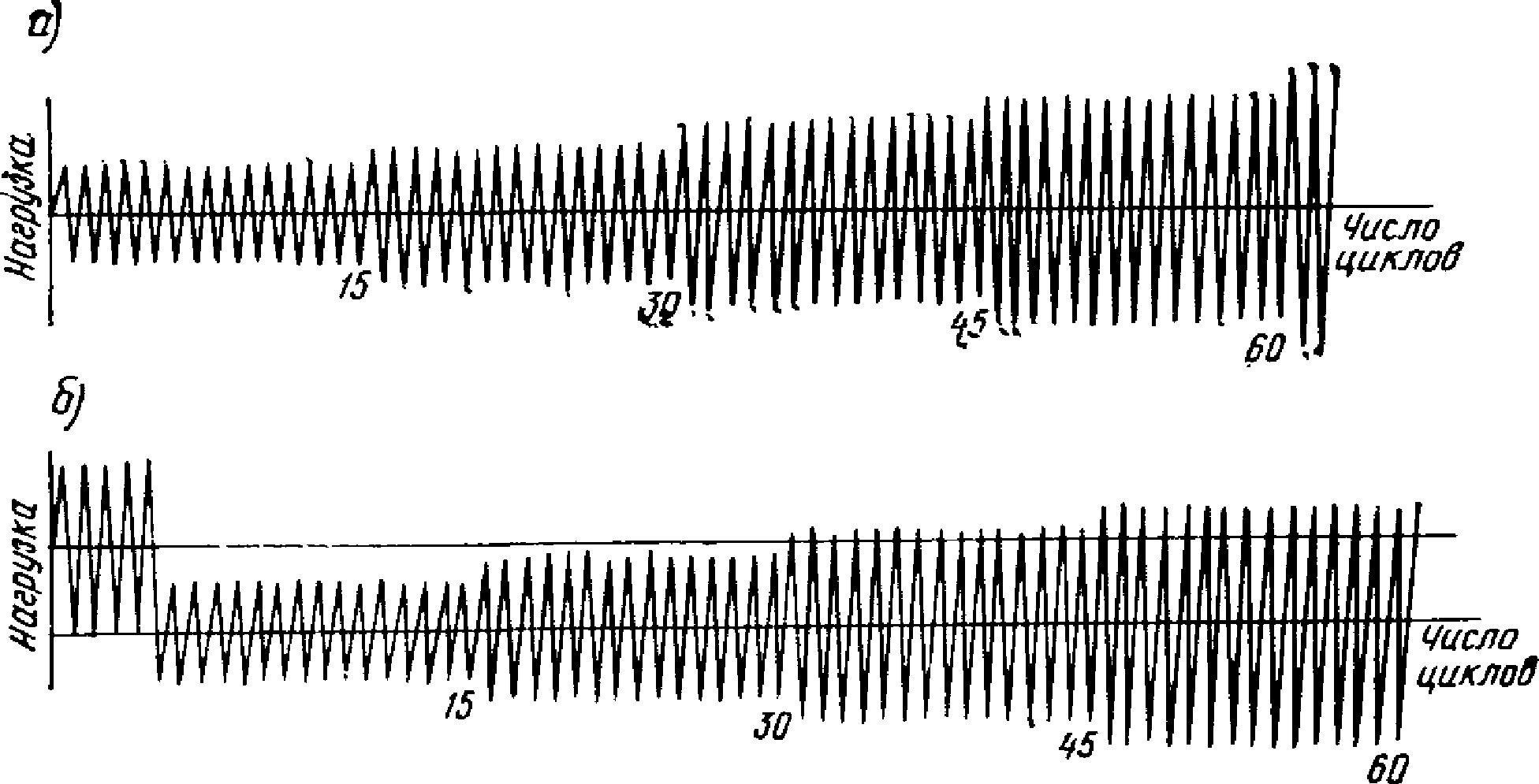
при испытаниях рамных узлов, проводимых Е. Поповым
а - симметричное нагружение; б - асимметричное нагружение
При проведении эксперимента было использовано значительное количество таких программ.
На рис. 15, а показан ступенчатый тип знакопеременной нагрузки. В данном случае амплитуды возрастают постепенно. На рис. 15, б показан пример с несколькими сильными первичными амплитудами и с последующим асимметричным смещением ступенчатой знакопеременной нагрузки.
Конструкция узловых соединений позволяла развиваться пластическим деформациям в ригелях. Задача исследований была дополнена определением количества энергии, затрачиваемой на разрушение ригелей.
Однако использование результатов эксперимента для наших целей оказалось невозможным, поскольку приведенные в источнике [19] данные выражены в абсолютных величинах энергии, которые не привязаны к каким-либо другим механическим характеристикам испытанных конструкций.
Следует сказать также и о некоторых работах зарубежных исследователей, представленных на национальном симпозиуме Японии по сейсмологии и сейсмостойкости, состоявшемся в Токио в 1966 г. [14, 16]. К сожалению, о них можно судить только по имеющимся аннотациям докладов.
В работе Р. Хансона [16] речь идет об исследованиях модели здания со стальным каркасом, в результате которых получены диаграммы усилий от деформаций в здании, характеризующие неупругую работу конструкций, и дается анализ влияния пластических деформаций на реакцию стальных конструкций. Надо отметить, что в этой работе изучалась общая реакция конструкции. При этом не конкретизируется, в каких именно элементах развиваются пластические деформации, что существенно затрудняет использование результатов на практике.
В работе Р. Танабаши и К. Канета [14] приведены результаты экспериментальных исследований прочности и деформативности сварных швов и зоны металла, близкой к шву. Отмечено некоторое возрастание пределов текучести металла в зоне термического влияния, т.е. в зоне сварного соединения, в сравнении с пределом текучести металла вне зоны термического влияния. Характерно отметить, что полученные во время экспериментов диаграммы зависимости усилий от деформаций для растянутых элементов как при однократных, так и при повторных загружениях близки к идеальной диаграмме упругопластического деформирования. Однако в работе не рассматривался вопрос об удалении зон пластичности от сварных соединений, хотя это несомненно позволило бы более эффективно использовать резервы несущей способности конструкций.
Нами была поставлена задача провести экспериментальные исследования с целью не только качественной оценки работы существующих типов рамных узлов и выявления рациональных решений, обеспечивающих более полное использование пластических резервов, но также и с тем, чтобы получить конкретные значения несущей способности и энергоемкости рамных узлов <1>.
--------------------------------
<1> Исследования велись на базе испытательного оборудования ЦНИИСКа им. В.А. Кучеренко.
Испытываемые образцы рамных узлов имели крестообразную форму, представляющую собой пересечение ригелей со стойками. Образцы брались трех типов - А, Б, В. Во всех образцах сечения стоек принимались с запасом, чтобы в них не возникали пластические деформации. Отношения поперечных размеров полок и стенок ригелей брались примерно в той же пропорции, как и в обычных типовых решениях, используемых в проектировании. Величина размеров образцов составляла порядка 1:3 - 1:4 по отношению к размерам реальных конструкций.
Образцы типа А (рис. 16, а) по конструктивной форме были выполнены в соответствии с типовыми решениями. Полки ригелей были соединены со стойками с помощью накладок, которые при этом в местах примыкания к стойкам были несколько уширены с тем, чтобы обеспечить частичное снижение напряжений в сварных стыках.
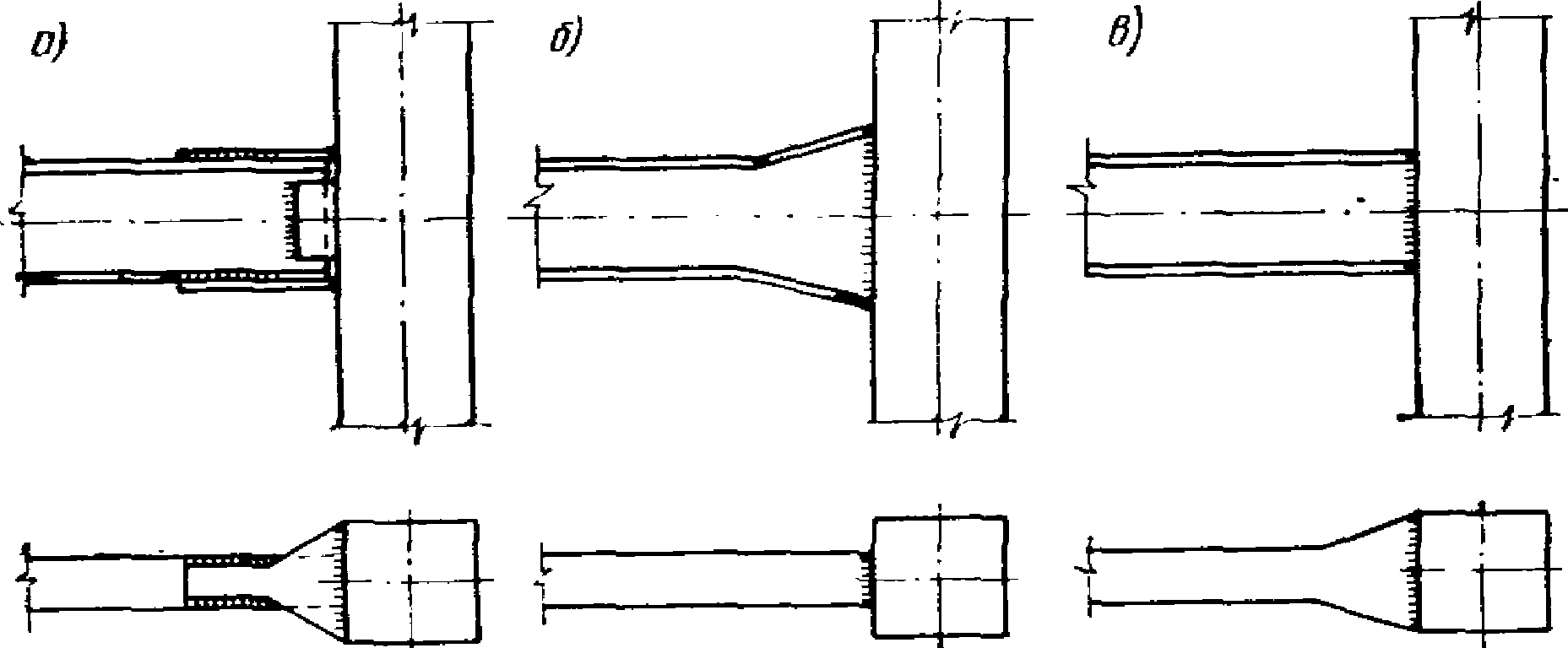
Рис. 16. Схемы образцов рамных узлов,
испытанных в ЦНИИПроектстальконструкции
а - тип А; б - тип Б; в - тип В
Образцы типа Б и В были опытными. У образцов типа Б стенки ригелей в местах их примыкания к стойкам были развиты (рис. 16, б). У образцов типа В были развиты полки ригелей в местах их примыкания к стойкам (рис. 16, в). Эти конструктивные мероприятия применялись с целью удаления зоны максимальных напряжений в ригелях от их сварных стыков со стойками.
Поперечные размеры основных сечений образцов типа Б и В были несколько меньше аналогичных размеров образцов А. Расстояние места перехода от основного сечения до сварного стыка со стойкой у ригелей образцов Б и В бралось равным утроенной ширине полки основного сечения.
К концам ригелей прикладывалась вертикальная нагрузка P, вызывающая в ригелях изгибающие моменты (рис. 17, а). Исследования проводились при статических и динамических загружениях. Динамические загружения были как однозначные, так и знакопеременные.
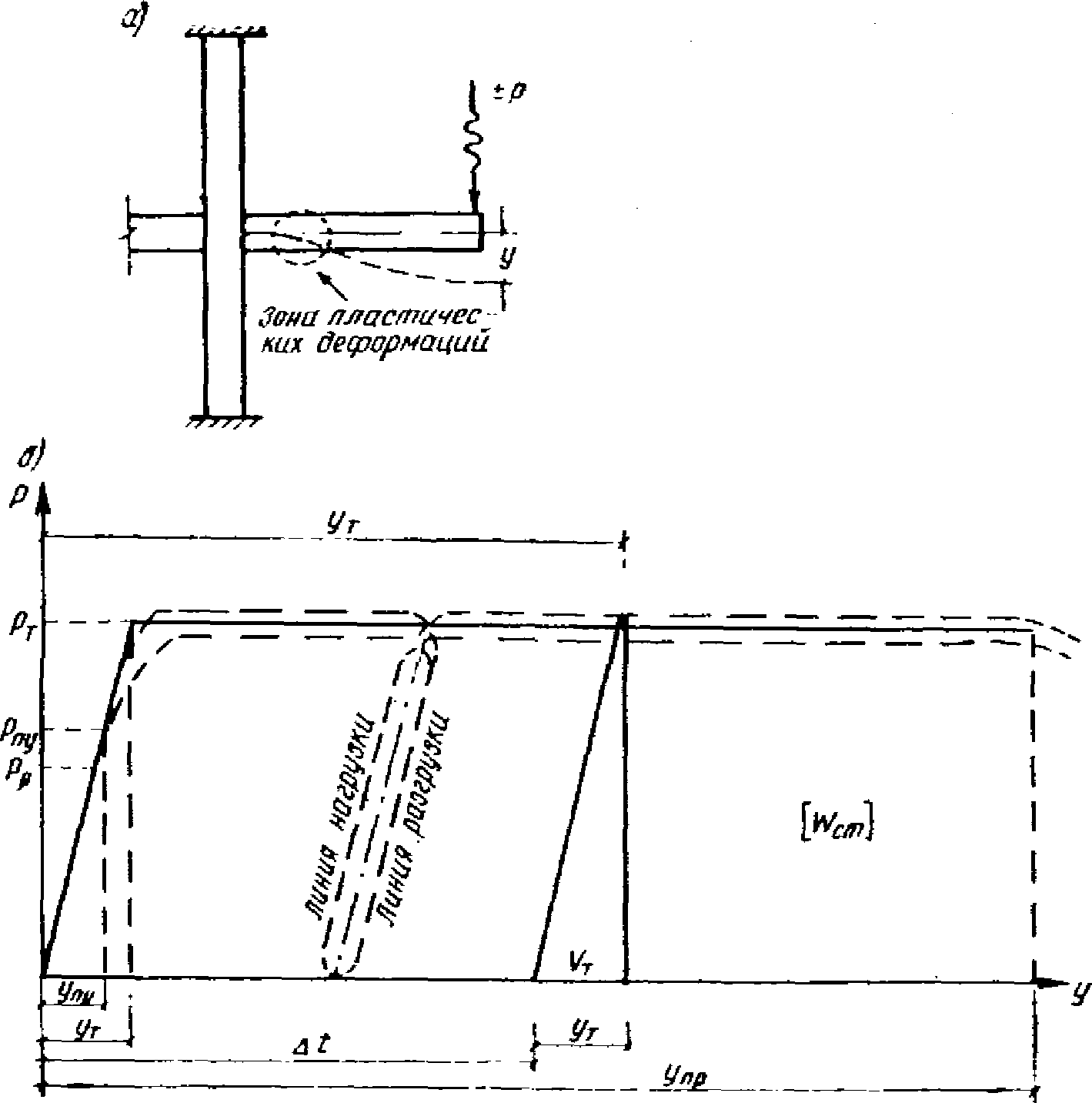
а - схема загружения образцов; б - схема диаграммы P - y,
полученная при испытаниях образцов статической нагрузкой
При испытаниях строились диаграммы зависимости усилий от деформаций (P - y). Площади диаграммы представляют ту энергию, которую испытываемый образец поглощал в процессе загружения.
Диаграммы P - y, построенные при статических испытаниях, по форме получались близкими к идеальной диаграмме упругопластического деформирования - диаграмме Прандтля (рис. 17, б).
Начальные участки полученных диаграмм характеризовали упругую работу ригеля. На этих участках прогиб y находится в прямой пропорциональной зависимости от нагрузки P, т.е. P = cy (c - жесткость образца). Когда прикладываемая к ригелю нагрузка P составляла примерно 0,65 - 0,7 максимальной предельной нагрузки, которую способен воспринимать ригель, зависимость P - y становилась нелинейной. Этот участок диаграммы характеризуется развитием пластических деформаций. С увеличением прогиба y рост усилия P замедлялся, а с достижением некоторого предельного значения 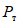 (назовем его пределом несущей способности), по существу, прекращался. С этого момента зона, в которой развиваются пластические деформации, вела себя как пластический шарнир с характерным ростом деформации при относительно неизменном усилии
(назовем его пределом несущей способности), по существу, прекращался. С этого момента зона, в которой развиваются пластические деформации, вела себя как пластический шарнир с характерным ростом деформации при относительно неизменном усилии 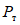 .
.
У образцов типа А зоны пластических деформаций ригелей возникали непосредственно за накладками, соединяющими ригели со стойками.
У образцов типа Б и В, как и предполагалось, зоны пластических деформаций возникали как раз в местах перехода от основного сечения к усиленному. При этом в местах стыков ригелей со стойками не возникало никаких заметных повреждений.
При статических загружениях ни один образец довести до разрушения не удалось, хотя возможности испытательной установки позволяли доводить прогибы до весьма внушительных величин, достигающих примерно 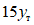 (
(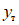 - предельная упругая деформация ригеля).
- предельная упругая деформация ригеля).
Анализ результатов экспериментов и осмотр испытываемых образцов показали, что развитие пластических деформаций в ригелях сопровождалось потерей местной устойчивости в сжатых волокнах ригелей, которая наступала при деформировании в пластической области. Вначале потеря местной устойчивости происходила в сжатой полке ригеля. Однако это не оказывало существенного влияния на величину несущей способности ригеля 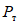 . Затем, когда теряла местную устойчивость стенка, несущая способность ригеля падала.
. Затем, когда теряла местную устойчивость стенка, несущая способность ригеля падала.
Следует при этом указать, что у образцов типа Б, имеющих в опорной части ригеля сравнительно развитую по высоте стенку, ввиду потери ее местной устойчивости снижение несущей способности происходило уже тогда, когда величина прогиба ригеля составляла всего лишь 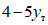 .
.
Что касается образцов А и В, то у них стенки ригелей не были развитыми, благодаря чему их местная устойчивость была выше, чем у образцов Б. Прогибы у этих образцов доводились, как уже отмечалось, до величины, примерно равной 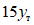 . Однако в них не происходило заметного понижения несущей способности.
. Однако в них не происходило заметного понижения несущей способности.
Энергия, поглощенная при таком прогибе на развитие пластических деформаций, составляла примерно 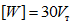 , где
, где 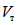 - максимальная потенциальная энергия деформированного ригеля, соответствующая деформации
- максимальная потенциальная энергия деформированного ригеля, соответствующая деформации 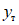 . В дальнейшем значение поглощаемой энергии, как и в данном случае, также будет даваться в отношениях к значению
. В дальнейшем значение поглощаемой энергии, как и в данном случае, также будет даваться в отношениях к значению 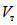 .
.
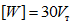 , где
, где В процессе статических испытаний в некоторых экспериментах, когда деформация в образцах уже выходила за предел упругости, нагрузка, доведенная до некоторого значения P, снималась. В таких случаях линия разгружения на диаграмме P - y получалась параллельной линии нагружения в пределах упругости (см. рис. 17, б). Когда нагрузка прикладывалась повторно, то вначале линия загрузки почти совпадала с линией разгрузки, пока усилие не достигало величины максимальной нагрузки P, предшествующей разгрузке. Затем прибор продолжал вычерчивать линию диаграммы, характеризующую неупругую работу образца. Если нагрузка снималась тогда, когда она уже достигала предела несущей способности 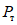 , проекция линии упругой разгрузки получалась максимальной. Эта проекция как раз и представляет собой максимальную упругую деформацию образца
, проекция линии упругой разгрузки получалась максимальной. Эта проекция как раз и представляет собой максимальную упругую деформацию образца 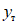 , о котором уже говорилось выше (см. рис. 17, б). Следует отметить, что при повторных загружениях образцов диаграммы зависимости P - y по форме получались еще более близкими к диаграмме Прандтля, чем при первой загрузке. Учитывая достаточно простую форму такой диаграммы, в дальнейшем будет целесообразно использовать ее для практических расчетов.
, о котором уже говорилось выше (см. рис. 17, б). Следует отметить, что при повторных загружениях образцов диаграммы зависимости P - y по форме получались еще более близкими к диаграмме Прандтля, чем при первой загрузке. Учитывая достаточно простую форму такой диаграммы, в дальнейшем будет целесообразно использовать ее для практических расчетов.
По формуле 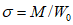 были вычислены условные напряжения, возникающие в ригелях, когда нагрузка достигала предельного значения
были вычислены условные напряжения, возникающие в ригелях, когда нагрузка достигала предельного значения 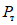 . У образцов типа Б и В они в среднем составляли 41,5 кг/мм2, а у образцов типа А - 43,5 кг/мм2.
. У образцов типа Б и В они в среднем составляли 41,5 кг/мм2, а у образцов типа А - 43,5 кг/мм2.
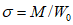 были вычислены условные напряжения, возникающие в ригелях, когда нагрузка достигала предельного значения
были вычислены условные напряжения, возникающие в ригелях, когда нагрузка достигала предельного значения Такая разница в напряжениях у образцов А, с одной стороны, и у образцов Б и В - с другой, объясняется тем, что образцы А ввиду наличия накладок на полках ригелей обладали более высокой жесткостью, чем образцы Б и В. В тех случаях, когда образцы Б и В усиливались элементами жесткости, воспринимаемая ими предельная нагрузка 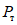 возрастала примерно на 10 - 12%, воспринимаемые ригелями условные напряжения
возрастала примерно на 10 - 12%, воспринимаемые ригелями условные напряжения 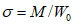 также соответственно повышались примерно до тех же величин, которые имели место в образцах типа А.
также соответственно повышались примерно до тех же величин, которые имели место в образцах типа А.
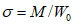 также соответственно повышались примерно до тех же величин, которые имели место в образцах типа А.
также соответственно повышались примерно до тех же величин, которые имели место в образцах типа А.Помимо проведенных испытаний, были также выполнены статические испытания образцов типа К (рис. 18), размеры которых соответствовали размерам ригелей рамных каркасов реальных конструкций. Работа проводилась по заданию ЦНИИПроектстальконструкции сотрудниками Казахского отделения института Г.А. Ажермачевым, Г.М. Остриковым, В.Л. Медниковым и др.
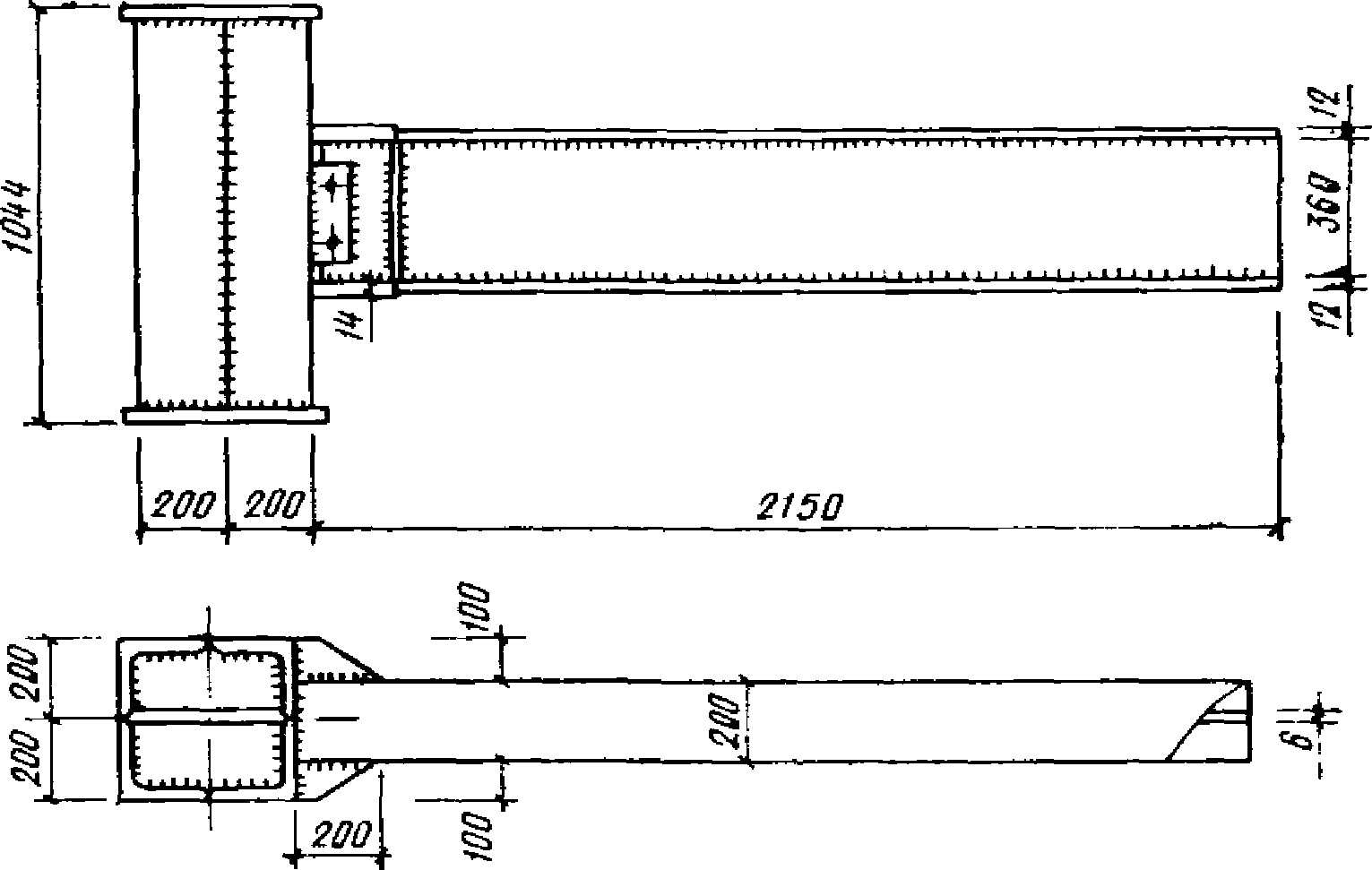
Рис. 18. Образец узла типа К
Ригели образцов представляли собой консоли с развитыми опорными сечениями и имели ребра жесткости в местах перехода от обычного сечения к усиленному (см. рис. 18). При статическом нагружении образцов зона развития пластических деформаций возникала в области изменения сечения ригеля. Максимальные напряжения, вычисленные по формуле 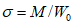 , составили 42 кг/мм2. Диаграммы зависимости усилий от деформаций, как и у образцов типа А, Б, В, по форме были близки к диаграмме Прандтля. Однако величина относительного прогиба получалась сравнительно небольшой - примерно
, составили 42 кг/мм2. Диаграммы зависимости усилий от деформаций, как и у образцов типа А, Б, В, по форме были близки к диаграмме Прандтля. Однако величина относительного прогиба получалась сравнительно небольшой - примерно 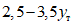 . При этом энергия, поглощенная на развитие пластических деформаций, была равной
. При этом энергия, поглощенная на развитие пластических деформаций, была равной 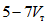 . Такая низкая энергоемкость объясняется тем, что толщины стенок ригелей были сравнительно небольшие, всего лишь 6 мм, в то время как высота ее составляла 360 мм. В результате в стенке ригеля быстро наступала потеря местной устойчивости, которая приводила к снижению несущей способности ригелей.
. Такая низкая энергоемкость объясняется тем, что толщины стенок ригелей были сравнительно небольшие, всего лишь 6 мм, в то время как высота ее составляла 360 мм. В результате в стенке ригеля быстро наступала потеря местной устойчивости, которая приводила к снижению несущей способности ригелей.
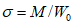 , составили 42 кг/мм2. Диаграммы зависимости усилий от деформаций, как и у образцов типа А, Б, В, по форме были близки к диаграмме Прандтля. Однако величина относительного прогиба получалась сравнительно небольшой - примерно
, составили 42 кг/мм2. Диаграммы зависимости усилий от деформаций, как и у образцов типа А, Б, В, по форме были близки к диаграмме Прандтля. Однако величина относительного прогиба получалась сравнительно небольшой - примерно 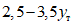 . При этом энергия, поглощенная на развитие пластических деформаций, была равной
. При этом энергия, поглощенная на развитие пластических деформаций, была равной Вопрос о влиянии местной устойчивости стенок на несущую способность ригелей ниже будет рассмотрен более обстоятельно.
Наряду с испытаниями, проведенными с экспериментальными образцами, были также определены характеристики прочности металла, из которых изготовлены образцы. Предел текучести стали образцов типа А, Б, В в среднем составлял  , а предел прочности
, а предел прочности  (табл. 5).
(табл. 5).
 , а предел прочности
, а предел прочности  (табл. 5).
(табл. 5).Таблица 5
N п.п. | Элементы ригеля | Предел текучести | Предел прочности |
1 | А-стенка | 27,7 | 39,2 |
2 | А-полка | 24,8 | 38,8 |
3 | А-накладка | 27,8 | 39,5 |
4 | Б-полка | 27,7 | 38,8 |
5 | Б-стенка | 28,5 | 40,5 |
6 | В-полка | 25,9 | 38,7 |
7 | В-полка | 24,5 | 38,6 |
8 | В-стенка | 26,9 | 39,6 |
У образцов типа К предел текучести стенок ригелей составлял 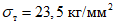 , а предел прочности
, а предел прочности  . Полки ригелей были выполнены из высокопрочной стали, их предел текучести был порядка
. Полки ригелей были выполнены из высокопрочной стали, их предел текучести был порядка 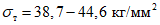 , а предел прочности
, а предел прочности 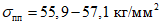 .
.
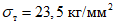 , а предел прочности
, а предел прочности  . Полки ригелей были выполнены из высокопрочной стали, их предел текучести был порядка
. Полки ригелей были выполнены из высокопрочной стали, их предел текучести был порядка 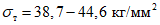 , а предел прочности
, а предел прочности 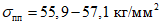 .
.Основной объем экспериментальных исследований приходился на долю динамических испытаний, которые проводились с образцами типа А, Б и В.
Испытания проводились как при однозначных, так и при знакопеременных нагрузках. При этом нагрузка 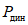 задавалась различной интенсивности по отношению к пределу несущей способности ригелей
задавалась различной интенсивности по отношению к пределу несущей способности ригелей 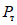 , полученной во время статических испытаний.
, полученной во время статических испытаний.
В результате динамических испытаний у образцов типа А, несмотря на то, что уширенные соединительные накладки обеспечивали некоторое снижение напряжений, разрушения происходили в области сварных стыков (рис. 19). При этом на разрушение образцов затрачивалось гораздо меньшее количество циклов загружений, чем у образцов типа Б и В. У образцов Б и В разрушения ригелей, как и следовало ожидать, происходили в пластических зонах, удаленных от сварных стыков (рис. 20, 21). Причем область сварных стыков оставалась совершенно неповрежденной.
Более надежная работа ригелей типа В по сравнению с типом А наглядно иллюстрируется графиком на рис. 22, где представлены зависимости 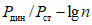 . Обе корреляционные прямые почти параллельны, но прямая, относящаяся к образцам типа В, проходит значительно выше.
. Обе корреляционные прямые почти параллельны, но прямая, относящаяся к образцам типа В, проходит значительно выше.
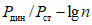 . Обе корреляционные прямые почти параллельны, но прямая, относящаяся к образцам типа В, проходит значительно выше.
. Обе корреляционные прямые почти параллельны, но прямая, относящаяся к образцам типа В, проходит значительно выше.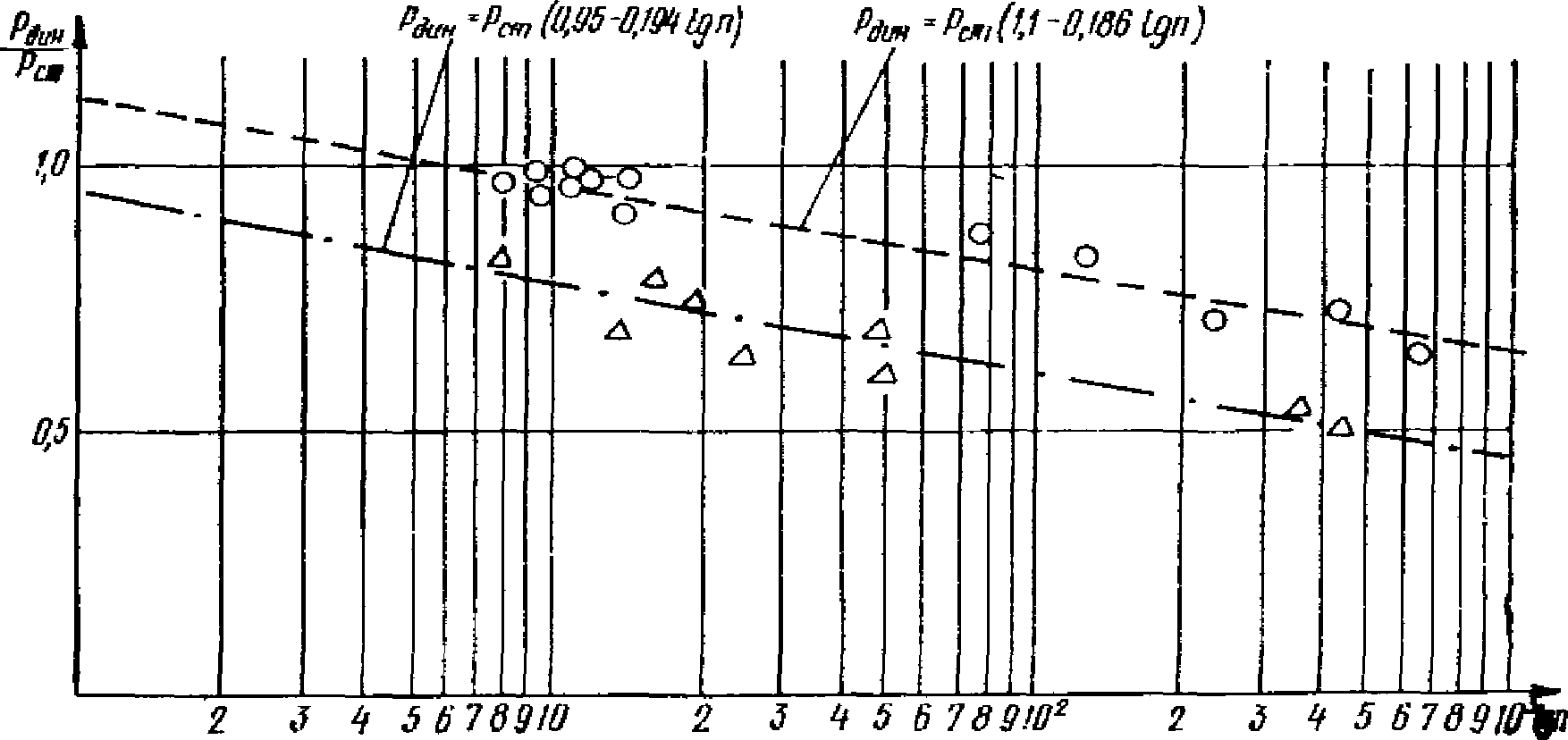
Рис. 22. Графики зависимости 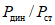 от lg n
от lg n
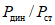 от lg n
от lg nПри динамических испытаниях, как и при испытаниях на статическую нагрузку, строились диаграммы зависимости усилий от прогибов P - y.
При нагружениях образцов повторной однозначной нагрузкой зависимость P - y получалась в виде следующих одна за другой петель (рис. 23, а). Угол наклона линии диаграммы при упругой стадии и предел несущей способности 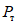 получались примерно такими же, как во время испытаний образцов повторной статической нагрузкой. При этом переход от упругой стадии к пластической у диаграмм получался более резким, чем при статических испытаниях. Таким образом, формы диаграмм были еще более близкими к диаграмме Прандтля, чем диаграммы образцов, испытанных статической нагрузкой.
получались примерно такими же, как во время испытаний образцов повторной статической нагрузкой. При этом переход от упругой стадии к пластической у диаграмм получался более резким, чем при статических испытаниях. Таким образом, формы диаграмм были еще более близкими к диаграмме Прандтля, чем диаграммы образцов, испытанных статической нагрузкой.
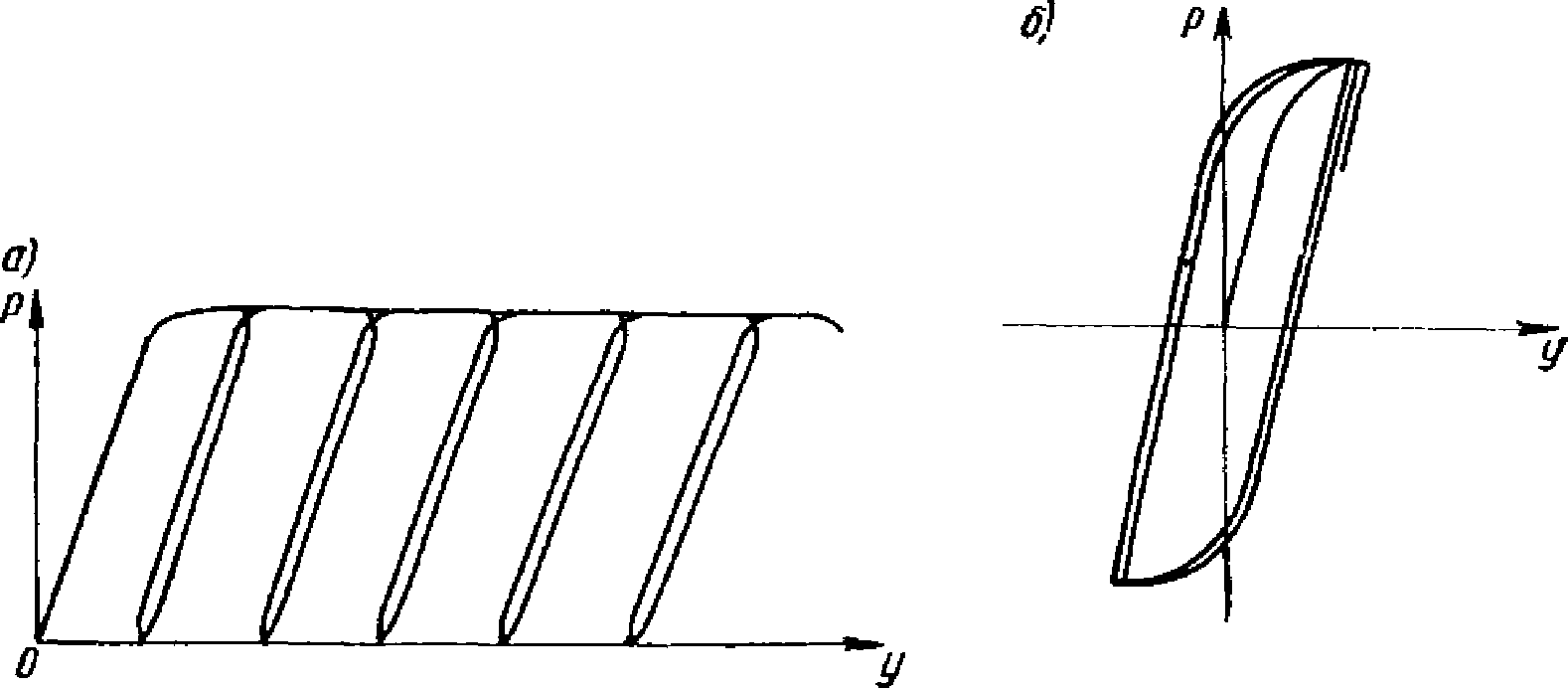
при динамических испытаниях образцов
а - при повторной однозначной нагрузке;
б - при повторной знакопеременной нагрузке
Образцы типа Б и В при динамических испытаниях однозначной нагрузкой не были доведены до разрушения, несмотря на развитие значительных деформаций. Поэтому точно их энергоемкость установить не удалось. Что касается образцов типа А, то они в большинстве своем обычно разрушались, еще не достигнув такого деформированного состояния, как образцы Б и В.
При динамических испытаниях знакопеременной нагрузкой с изменением знака нагрузки менялось и направление деформации ригелей. В результате диаграммы P - y при каждом цикле получались в виде петли гистерезиса, наложенной на аналогичные петли от предшествующих загружений (рис. 23, б).
Знакопеременное нагружение обычно проводилось до тех пор, пока в ригелях не наступало разрушение.
Как видно из графика, приведенного на рис. 24, в тех случаях, когда интенсивность прикладываемой к ригелям образцов Б и В нагрузки достигала предельной величины 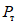 <*>, общая энергоемкость [W] более чем в 200 раз превышала значение максимальной потенциальной энергии
<*>, общая энергоемкость [W] более чем в 200 раз превышала значение максимальной потенциальной энергии 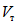 . С уменьшением прикладываемой нагрузки
. С уменьшением прикладываемой нагрузки 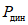 энергоемкость еще более возрастала. Уже при отношении
энергоемкость еще более возрастала. Уже при отношении 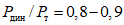 значение [W] было примерно в 1000 раз больше
значение [W] было примерно в 1000 раз больше 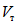 . В некоторых случаях при таком значении
. В некоторых случаях при таком значении 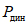 ригели вообще не удалось довести до разрушения. Таким образом,
ригели вообще не удалось довести до разрушения. Таким образом, 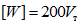 являлось нижней границей энергоемкости, которой обладают ригели данного типа при условии, когда зона пластических деформаций достаточно удалена от сварных стыков. Иначе говоря, указанное значение
являлось нижней границей энергоемкости, которой обладают ригели данного типа при условии, когда зона пластических деформаций достаточно удалена от сварных стыков. Иначе говоря, указанное значение 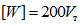 является гарантированным минимумом энергоемкости, полученным при экспериментах.
является гарантированным минимумом энергоемкости, полученным при экспериментах.
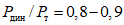 значение [W] было примерно в 1000 раз больше
значение [W] было примерно в 1000 раз больше 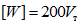 являлось нижней границей энергоемкости, которой обладают ригели данного типа при условии, когда зона пластических деформаций достаточно удалена от сварных стыков. Иначе говоря, указанное значение
являлось нижней границей энергоемкости, которой обладают ригели данного типа при условии, когда зона пластических деформаций достаточно удалена от сварных стыков. Иначе говоря, указанное значение 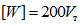 является гарантированным минимумом энергоемкости, полученным при экспериментах.
является гарантированным минимумом энергоемкости, полученным при экспериментах.--------------------------------
<*> Выше нагрузки 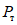 усилия в ригеле развиваться не могут, так как
усилия в ригеле развиваться не могут, так как 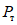 является пределом несущей способности.
является пределом несущей способности.
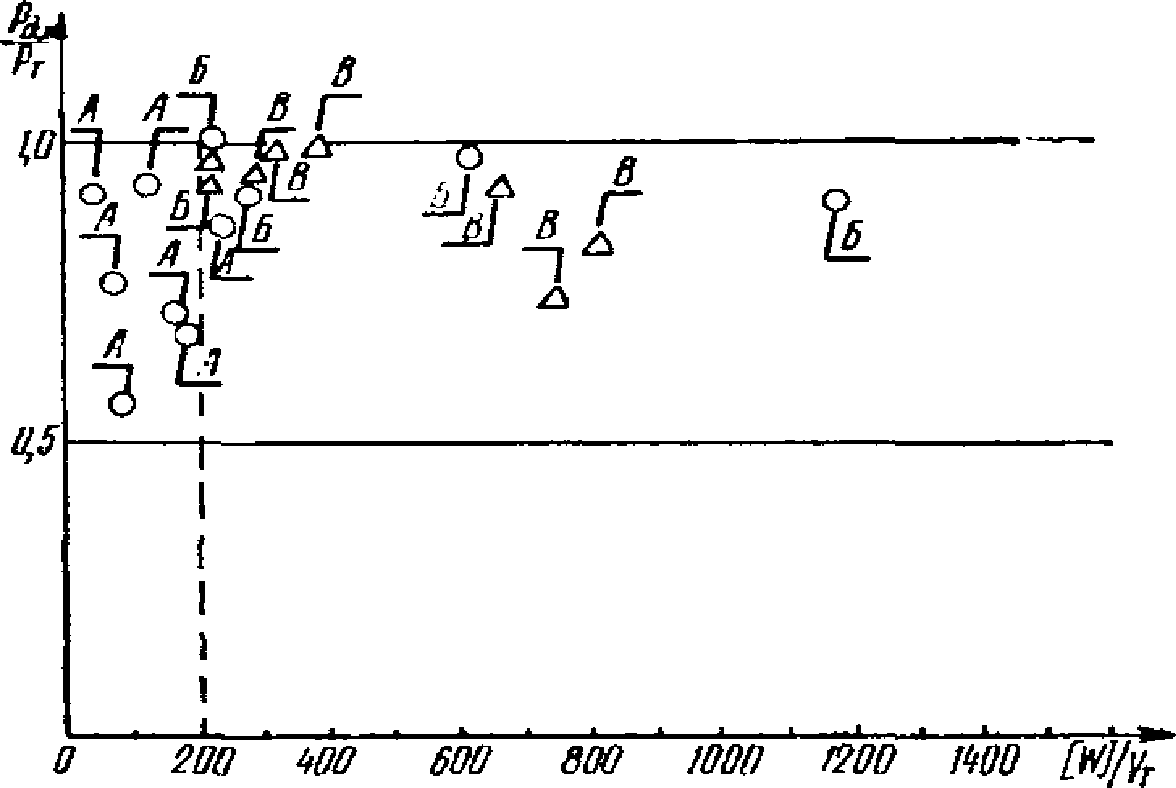
энергоемкости от интенсивности прикладываемой нагрузки
Энергоемкость образцов типа А оказалась значительно ниже, чем у образцов Б и В. Так, например, когда интенсивность динамической нагрузки 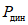 была близка к
была близка к 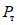 , в одном случае при
, в одном случае при 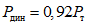 образец разрушился через 6 циклов загружений. При этом поглощенная энергия составляла лишь
образец разрушился через 6 циклов загружений. При этом поглощенная энергия составляла лишь 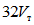 . В другом случае образец разрушился через 10 циклов. Его энергоемкость получалась
. В другом случае образец разрушился через 10 циклов. Его энергоемкость получалась 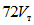 . Лишь в единственном случае при
. Лишь в единственном случае при 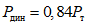 разрушение произошло через 45 циклов, а объем поглощенной энергий составил
разрушение произошло через 45 циклов, а объем поглощенной энергий составил 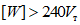 .
.
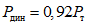 образец разрушился через 6 циклов загружений. При этом поглощенная энергия составляла лишь
образец разрушился через 6 циклов загружений. При этом поглощенная энергия составляла лишь 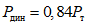 разрушение произошло через 45 циклов, а объем поглощенной энергий составил
разрушение произошло через 45 циклов, а объем поглощенной энергий составил 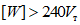 .
.Таким образом, конструкции, у которых пластические зоны благодаря развитым опорным сечениям ригелей достаточно удалены от сварных стыков, способны достаточно долго противостоять действию повторной динамической нагрузки. Напротив, конструкции, у которых зона максимальных напряжений возникает в области сварных стыков, при действии динамической нагрузки быстро разрушаются.
Как показали эксперименты, самым рациональным из испытанных образцов оказался образец типа В. Стенки его ригелей имеют постоянную высоту, а полки имеют развитые опорные сечения. В стенках ригелей таких образцов даже при больших прогибах ригелей 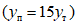 не происходило потери местной устойчивости, а в связи с этим и не понижалась несущая способность. Вместе с тем ригели обладали высокой энергоемкостью
не происходило потери местной устойчивости, а в связи с этим и не понижалась несущая способность. Вместе с тем ригели обладали высокой энергоемкостью 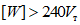 . Поэтому принцип сопряжения ригелей со стойками, который принят в образцах В, можно рекомендовать при проектировании металлических рамных каркасов.
. Поэтому принцип сопряжения ригелей со стойками, который принят в образцах В, можно рекомендовать при проектировании металлических рамных каркасов.
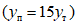 не происходило потери местной устойчивости, а в связи с этим и не понижалась несущая способность. Вместе с тем ригели обладали высокой энергоемкостью
не происходило потери местной устойчивости, а в связи с этим и не понижалась несущая способность. Вместе с тем ригели обладали высокой энергоемкостью 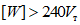 . Поэтому принцип сопряжения ригелей со стойками, который принят в образцах В, можно рекомендовать при проектировании металлических рамных каркасов.
. Поэтому принцип сопряжения ригелей со стойками, который принят в образцах В, можно рекомендовать при проектировании металлических рамных каркасов.Остановимся на одном из возможных конструктивных вариантов (рис. 25) сопряжения ригелей со стойками.
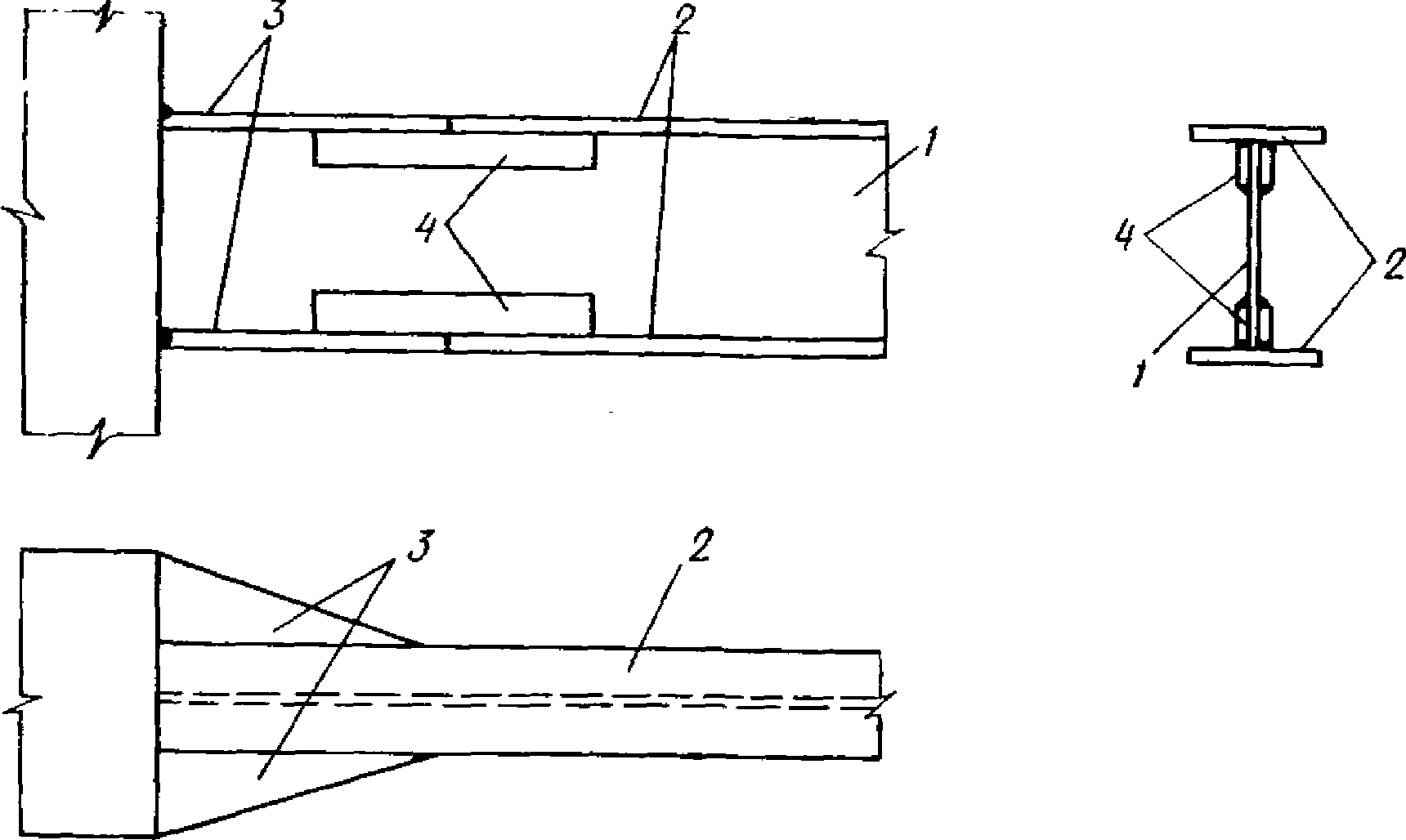
узла сопряжения ригеля со стойкой
1 - стенка ригеля; 2 - полка ригеля;
3 - фасонка; 4 - накладка
По этому варианту стенки ригелей имеют постоянную высоту. Полки ригелей составлены из листового элемента постоянного сечения и приваренных к нему треугольных фасонок. Таким образом, в опорной части полок образуются уширения.
ригелей с учетом пластических шарниров
3.4. Перейдем теперь к вопросу о том, как следует рассчитывать ригели рамных каркасов с учетом образования в них пластических шарниров.
Рассмотрим конкретный пример. Возьмем опорную часть ригеля рамного узла (рис. 26). В сечении 1 - 1, где конструктивно намечен переход от основного поперечного размера ригеля к усиленному опорному сечению 2 - 2, предполагается образование пластического шарнира. Допустим, что изгибающие моменты в раме от действия всех приложенных к ней сил определены. При этом полученные моменты в сечениях 1 - 1 и 2 - 2 соответственно составляют 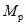 и
и 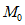 . Для условия образования в сечении 1 - 1 пластического шарнира необходимо размеры сечения подобрать так, чтобы предельный момент
. Для условия образования в сечении 1 - 1 пластического шарнира необходимо размеры сечения подобрать так, чтобы предельный момент 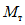 , который способно воспринять сечение, был не больше момента
, который способно воспринять сечение, был не больше момента 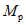 . О приемлемых соотношениях между значениями
. О приемлемых соотношениях между значениями 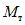 и
и 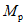 далее будет сказано более подробно. Предположим, что предел текучести стали, из которой выполнен ригель, составляет
далее будет сказано более подробно. Предположим, что предел текучести стали, из которой выполнен ригель, составляет 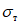 . В таком случае размеры сечения 1 - 1 можно определить, выполняя расчет, ориентируясь на величину
. В таком случае размеры сечения 1 - 1 можно определить, выполняя расчет, ориентируясь на величину 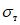 . Что касается сечения 2 - 2, то его размеры следует подбирать из расчета, чтобы возникающие при этом напряжения
. Что касается сечения 2 - 2, то его размеры следует подбирать из расчета, чтобы возникающие при этом напряжения 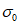 были не выше расчетных сопротивлений.
были не выше расчетных сопротивлений.
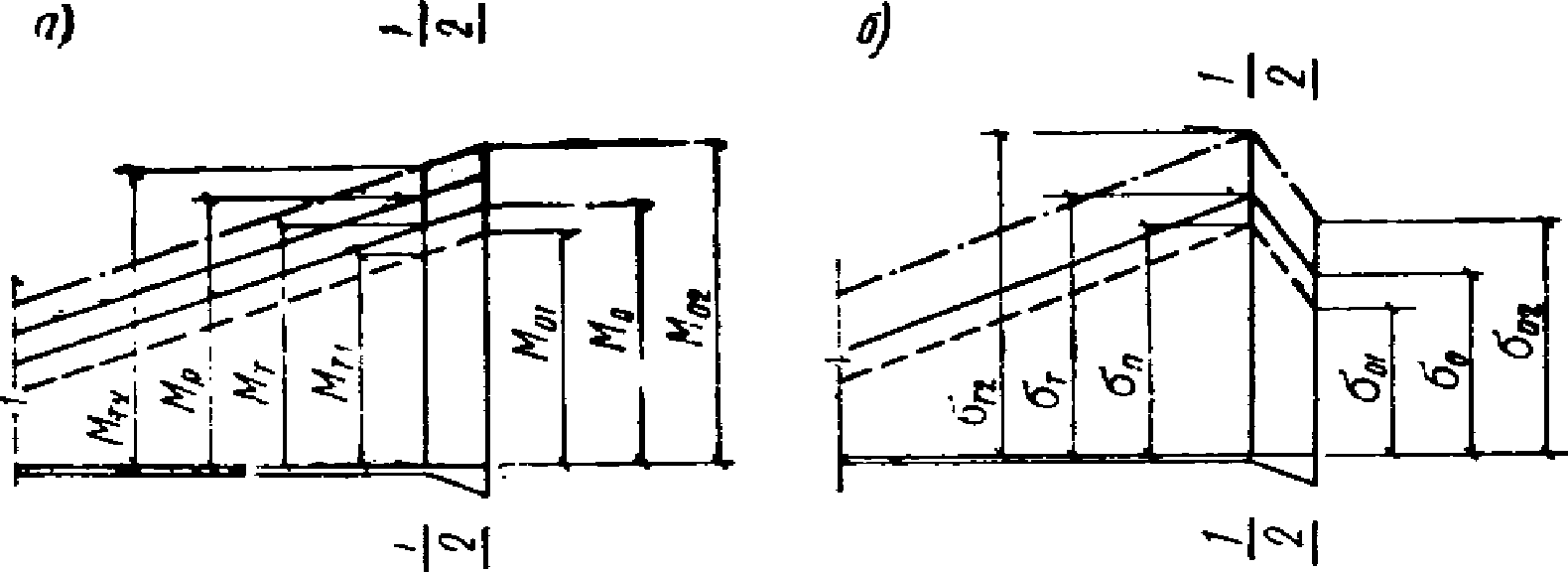
а - эпюра изгибающих моментов; б - эпюра напряжений
Теперь допустим, что фактический предел текучести стали несколько ниже, чем принятый в расчете 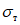 . В таком случае пластический шарнир возникнет в сечении 1 - 1 при моменте
. В таком случае пластический шарнир возникнет в сечении 1 - 1 при моменте 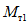 , который ниже момента
, который ниже момента 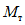 . Тогда момент
. Тогда момент 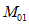 , возникший при этом в опорном сечении, будет также меньше момента
, возникший при этом в опорном сечении, будет также меньше момента 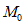 . В связи с этим и напряжения в сечении 2 - 2
. В связи с этим и напряжения в сечении 2 - 2 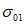 окажутся ниже расчетных
окажутся ниже расчетных 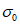 , поэтому они не будут опасны для сварных соединений ригелей со стойкой.
, поэтому они не будут опасны для сварных соединений ригелей со стойкой.
Представим себе теперь обратный случай, когда фактический предел текучести стали 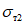 выше принятого в расчете предела текучести
выше принятого в расчете предела текучести 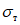 . Тогда в области сечения 1 - 1 будет возникать момент
. Тогда в области сечения 1 - 1 будет возникать момент 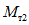 , больший, чем
, больший, чем 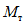 . Соответственно в сечении 2 - 2 будет появляться момент
. Соответственно в сечении 2 - 2 будет появляться момент 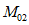 , который больше
, который больше 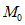 . В результате напряжения
. В результате напряжения 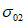 в сечении 2 - 2 могут оказаться выше расчетных
в сечении 2 - 2 могут оказаться выше расчетных 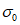 . Такие повышенные напряжения уже представляют реальную опасность для сварных стыков ригелей со стойками. Чтобы этого избежать, при подборе сечения ригеля, в котором планируется образование пластических шарниров, в качестве предела текучести следует принимать такое значение, при котором в подавляющем большинстве случаев гарантируется появление пластических деформаций. С целью выбора такого напряжения рассмотрим характеристику прочности стали марки Ст.3. Если принять во внимание приведенные в работе [13] кривые распределения текучести стали марки Ст.3 (рис. 27), взятые по ряду лет, то по ним нетрудно заметить, что величина расчетного сопротивления 2100 кг/см2 является, по существу, минимально возможным пределом текучести. При таком напряжении более чем в 99% случаев в конструкциях не будет достигаться фактического предела текучести. Поэтому использовать значение
. Такие повышенные напряжения уже представляют реальную опасность для сварных стыков ригелей со стойками. Чтобы этого избежать, при подборе сечения ригеля, в котором планируется образование пластических шарниров, в качестве предела текучести следует принимать такое значение, при котором в подавляющем большинстве случаев гарантируется появление пластических деформаций. С целью выбора такого напряжения рассмотрим характеристику прочности стали марки Ст.3. Если принять во внимание приведенные в работе [13] кривые распределения текучести стали марки Ст.3 (рис. 27), взятые по ряду лет, то по ним нетрудно заметить, что величина расчетного сопротивления 2100 кг/см2 является, по существу, минимально возможным пределом текучести. При таком напряжении более чем в 99% случаев в конструкциях не будет достигаться фактического предела текучести. Поэтому использовать значение 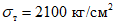 при подборе сечения, в котором планируется образование пластического шарнира, недопустимо.
при подборе сечения, в котором планируется образование пластического шарнира, недопустимо.
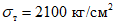 при подборе сечения, в котором планируется образование пластического шарнира, недопустимо.
при подборе сечения, в котором планируется образование пластического шарнира, недопустимо.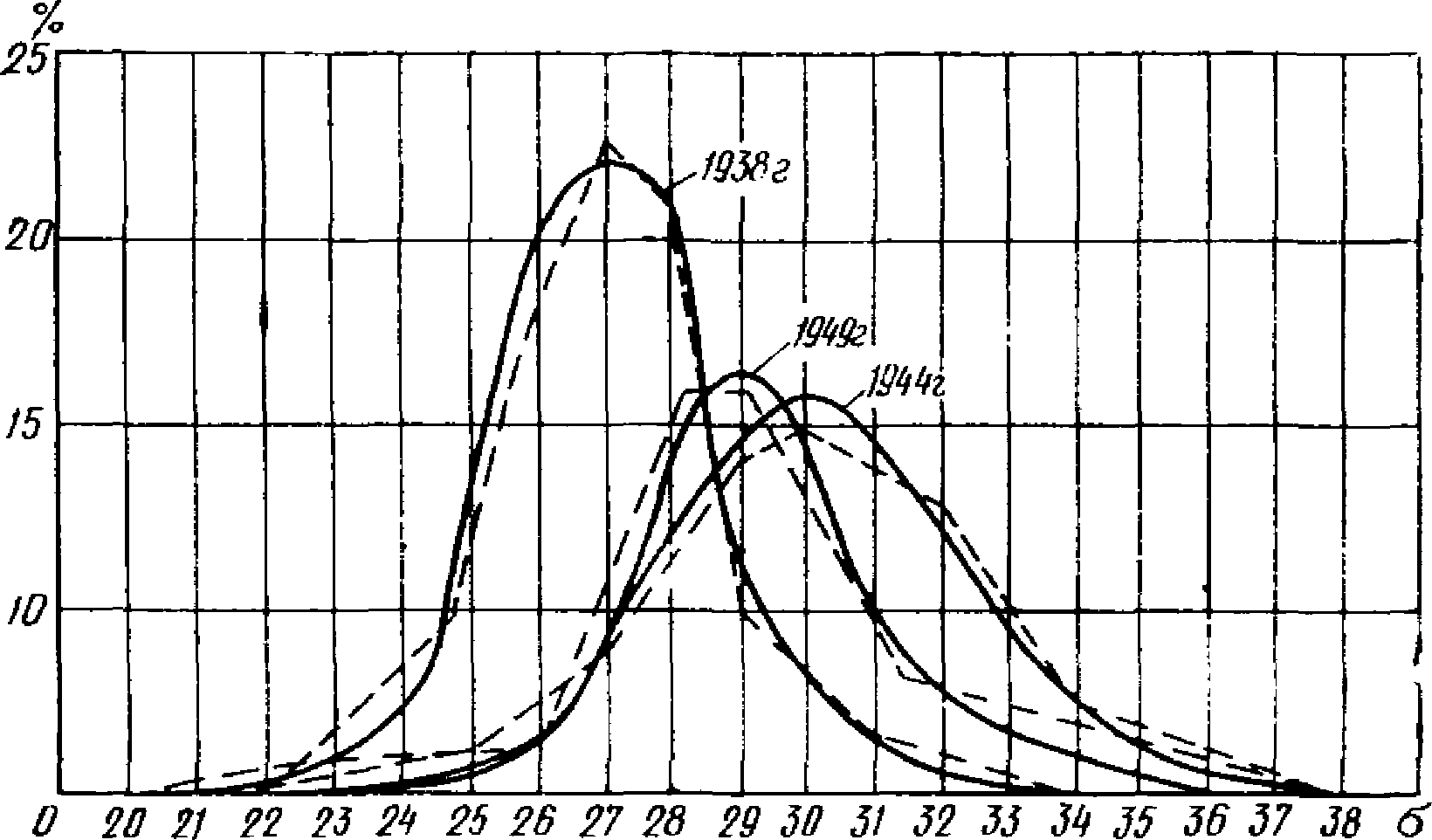
Ст.3 по результатам испытаний разных лет
Наиболее правильным для данных случаев, по-видимому, будет использование фактического значения предела текучести стали, из которой выполнена конструкция. Однако в производственных условиях, когда при строительстве объектов расходуется большое количество металла различных плавок, определение характеристик прочности и использование их при разработке проектов являются крайне затруднительными и практически неосуществимыми.
Учитывая это, представляется целесообразным в качестве расчетного предела текучести использовать напряжение, близкое к максимально возможным пределам текучести, при которых в подавляющем большинстве в металле обеспечивается развитие пластических деформаций. Эти напряжения могут быть определены из приведенных выше кривых распределения пределов текучести (см. рис. 27).
Предварительно условимся для практических расчетов применять не абсолютную величину верхнего предела текучести стали, а отношение этой величины к нижнему пределу текучести, которое обычно используется в качестве расчетного сопротивления.
Обратимся к кривой распределения, полученной по результатам испытаний в 1938 г. Нижний предел текучести по этой кривой 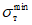 составляет 21 кг/мм2, верхний предел
составляет 21 кг/мм2, верхний предел 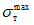 равен 34 кг/мм2. Отношение указанных пределов будет
равен 34 кг/мм2. Отношение указанных пределов будет 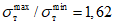 . Верхний предел текучести гарантирует 100%-ную вероятность развития в ригеле пластических деформаций. Однако в практических расчетах, по-видимому, будет достаточным обеспечение развития пластических деформаций в 95% случаев. Этому условию согласно подсчетам, сделанным на основании данных кривой распределения пределов текучести, соответствует напряжение
. Верхний предел текучести гарантирует 100%-ную вероятность развития в ригеле пластических деформаций. Однако в практических расчетах, по-видимому, будет достаточным обеспечение развития пластических деформаций в 95% случаев. Этому условию согласно подсчетам, сделанным на основании данных кривой распределения пределов текучести, соответствует напряжение 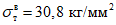 . Его отношение к нижнему пределу текучести составляет 30,8/21 = 1,47.
. Его отношение к нижнему пределу текучести составляет 30,8/21 = 1,47.
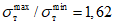 . Верхний предел текучести гарантирует 100%-ную вероятность развития в ригеле пластических деформаций. Однако в практических расчетах, по-видимому, будет достаточным обеспечение развития пластических деформаций в 95% случаев. Этому условию согласно подсчетам, сделанным на основании данных кривой распределения пределов текучести, соответствует напряжение
. Верхний предел текучести гарантирует 100%-ную вероятность развития в ригеле пластических деформаций. Однако в практических расчетах, по-видимому, будет достаточным обеспечение развития пластических деформаций в 95% случаев. Этому условию согласно подсчетам, сделанным на основании данных кривой распределения пределов текучести, соответствует напряжение 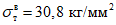 . Его отношение к нижнему пределу текучести составляет 30,8/21 = 1,47.
. Его отношение к нижнему пределу текучести составляет 30,8/21 = 1,47.Таким же образом производится оценка кривых распределения пределов текучести, полученных по результатам испытаний в 1944 и 1949 гг. Сведем полученные оценки, включая и значения по 1938 г., в одну таблицу (табл. 6).
Таблица 6
Год получения результатов | Минимальный предел текучести | Максимальный предел текучести | Напряжения, рекомендуемые для расчета, | 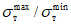 | 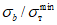 |
1938 | 21 | 34 | 30,8 | 1,62 | 1,47 |
1944 | 23 | 38 | 34 | 1,65 | 1,48 |
1949 | 22 | 36 | 33 | 1,635 | 1,5 |
Полученные во всех трех случаях отношения 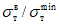 для 95% вероятности достижения пределов текучести близки к 1,5. В связи с этим для Ст.3 в качестве коэффициента
для 95% вероятности достижения пределов текучести близки к 1,5. В связи с этим для Ст.3 в качестве коэффициента 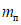 , обусловливающего возможность образования пластических деформаций, по-видимому, следует принимать значение
, обусловливающего возможность образования пластических деформаций, по-видимому, следует принимать значение 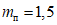 . Причем брать значение
. Причем брать значение 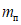 ниже чем 1,5 представляется недопустимым, потому что в соответствии с главой СНиП II-В.12-69 коэффициент условия работ
ниже чем 1,5 представляется недопустимым, потому что в соответствии с главой СНиП II-В.12-69 коэффициент условия работ 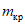 для стальных конструкций уже составляет 1,4.
для стальных конструкций уже составляет 1,4.
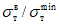 для 95% вероятности достижения пределов текучести близки к 1,5. В связи с этим для Ст.3 в качестве коэффициента
для 95% вероятности достижения пределов текучести близки к 1,5. В связи с этим для Ст.3 в качестве коэффициента 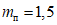 . Причем брать значение
. Причем брать значение Аналогичным образом коэффициент 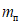 может определяться и для других марок стали.
может определяться и для других марок стали.
В заключение еще раз отметим, что наличие в ригелях пластических шарниров обеспечивает сохранность сварных соединений ригелей со стойками от хрупкого разрушения, что должно повышать надежность сооружений.
Утверждение, что при обеспечении образования пластических шарниров в ригелях рамы работа конструкции в целом становится более надежной, на первый взгляд может показаться странным, ибо работа материала в пластической стадии сопряжена с расходованием последних резервов системы и, казалось бы, преднамеренное расходование их не должно повышать надежности системы. Однако это не так. Поясним на примере.
Предположим, имеются два стержня одинакового диаметра и одинаковой длины, причем один из них изготовлен из высокопрочного, но хрупкого металла (рис. 28, а), а другой - из материала, вдвое менее прочного, но обладающего большой пластичностью и деформирующегося по закону Прандтля (рис. 28, б). Примем, что диаграммы "нагрузка-деформация" для этих стержней соответствуют схемам (см. рис. 28, г, д) и что предельная упругая деформация для первого стержня 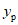 в 2 раза больше, чем упругая деформация второго стержня
в 2 раза больше, чем упругая деформация второго стержня 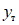 , а предельные пластические деформации второго стержня
, а предельные пластические деформации второго стержня 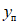 в 20 раз превышают упругие
в 20 раз превышают упругие 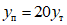 <*>.
<*>.
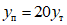 <*>.
<*>.--------------------------------
<*> Это примерно соответствует характеристикам стали Ст.3.
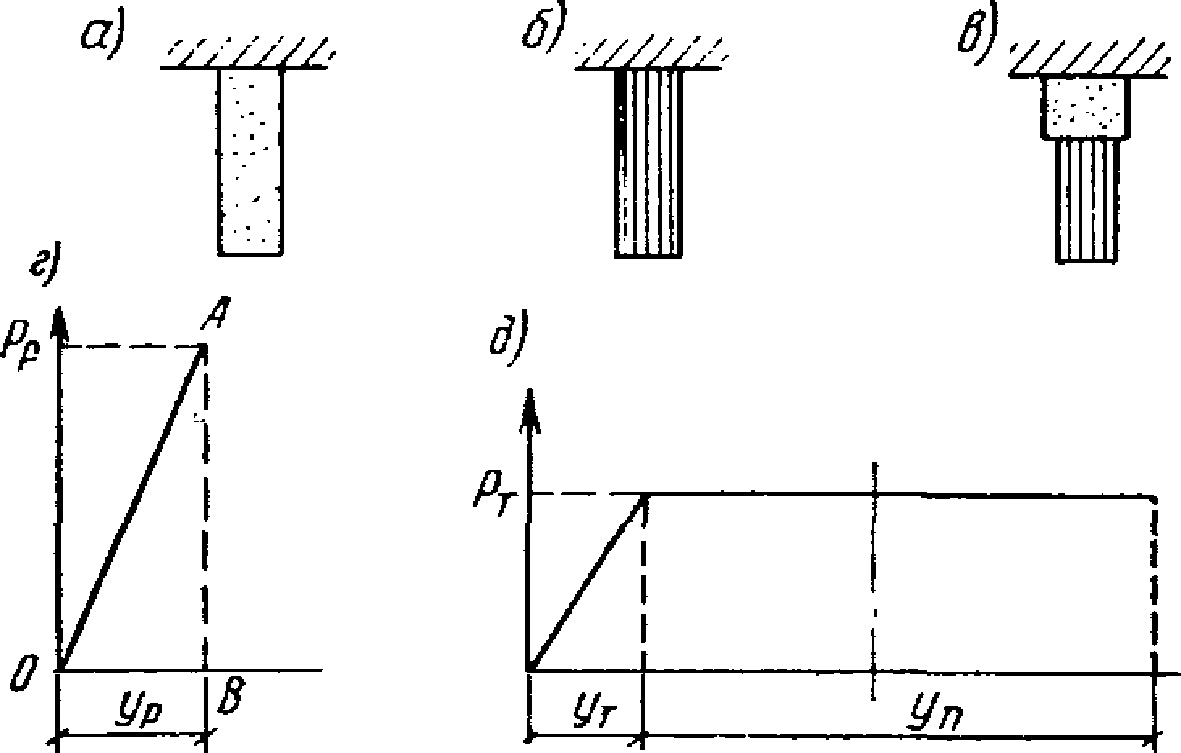
из хрупких и пластичных материалов
а - стержни из высокопрочного, но хрупкого металла;
б - стержни из пластичного металла; в - составной стержень;
г - диаграмма работы стержня из высокопрочного металла;
д - диаграмма работы стержня из пластичного металла
Если эти стержни загрузить статической нагрузкой, то окажется, что первый стержень выдержит нагрузку 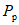 , вдвое превышающую предельную несущую способность второго
, вдвое превышающую предельную несущую способность второго 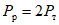 .
.
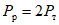 .
.Если же стержни подвергнуть ударным испытаниям, например действию падающего груза, то легко убедиться, что первый стержень разрушится раньше. Действительно, для разрушения первого стержня нужно произвести работу, равную площади треугольника ОАВ, т.е.
а для разрушения второго стержня
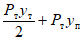 ,
,или в соответствии с принятыми выше значениями 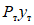 и
и 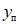 по отношению к величинам
по отношению к величинам 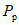 и
и 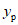 работа будет:
работа будет:
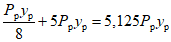 ,
,т.е. для разрушения второго потребуется произвести работу, превышающую ту, которая требовалась для разрушения первого, более чем в 10 раз.
Теперь рассмотрим, что будет, если исследуемый стержень сделать составным: одну его половину выполнить из прочного и хрупкого металла, а другую из пластичного (см. рис. 28, в). В этом случае статическая прочность стержня будет равна прочности второго стержня по той причине, что разрушение произойдет на участке более слабого материала. Вследствие этого напряжения в области более прочного материала никогда не будут превышать вполне безопасной величины, т.е. наличие участка пластического материала предохранит от разрушения часть стержня, выполненную из хрупкого материала. При загружении же стержня динамической нагрузкой, хотя распределение усилий будет такое же, как и при статическом загружении, тем не менее количество энергии, необходимое для разрушения образца, изменится и будет равным:
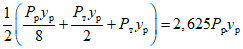 ,
,т.е. примерно вдвое меньше, чем для разрушения второго стержня, но примерно в 5 раз больше, чем для разрушения первого.
Если длину более прочной части уменьшать, а длину менее прочной увеличивать, то динамическая несущая способность стержня будет возрастать и работа, необходимая для его разрушения, постепенно приблизится к пределу 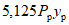 .
.
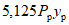 .
.Таким образом, из примеров видно, что путем снижения статической прочности стержня и использования пластических свойств более слабого материала удалось резко повысить динамическую несущую способность элемента, включающего в себя также и хрупкий материал.
То же самое имеет место также и в предлагаемом решении узла рамного каркаса. Путем относительного (по отношению к опорному сечению) ослабления сечения ригеля в месте, где намечено образование пластического шарнира, с одной стороны, устраняется опасность роста напряжений в местах сварки ригеля со стойкой, а с другой - достигается возможность использования пластических свойств металла. В результате повышается динамическая несущая способность всей системы в целом и, следовательно, повышается ее общая надежность.
сечений ригелей рамных каркасов
3.5. В связи с образованием в ригелях пластических шарниров, часть энергии от нагрузки, прикладываемой к конструкции, будет поглощаться при развитии пластических деформаций. В связи с этим при расчете сечений ригелей, в области которых планируется появление пластических шарниров, необходимо соблюдать следующее условие. Энергия, которая затрачивается внешними силами на развитие пластических деформаций в шарнире за n циклов загружений, ожидаемых при землетрясении, не должна превышать энергоемкость рассматриваемого сечения [W]. В данном случае под энергоемкостью [W] понимается количество энергии, которую способен поглотить ригель в месте образования пластического шарнира, не потеряв при этом несущей способности.
Рассмотрим, каким образом следует учитывать энергоемкость при подборе сечения ригеля.
Для этого вначале возьмем простейшую систему в виде консольного стержня (рис. 29, а). К свободному концу стержня прикладывается поперечная нагрузка S. Зависимость усилий от деформаций в стержне S - y выражается диаграммой Прандтля (рис. 29, б). 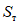 - предельное усилие воспринимается системой;
- предельное усилие воспринимается системой; 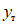 - упругая деформация, соответствующая усилию
- упругая деформация, соответствующая усилию 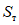 . Допустим, что система упругая и прикладываемая к ней расчетная сейсмическая нагрузка
. Допустим, что система упругая и прикладываемая к ней расчетная сейсмическая нагрузка 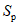 определена. Потенциальная энергия деформированной системы в таком случае будет:
определена. Потенциальная энергия деформированной системы в таком случае будет:
где 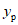 - перемещение системы от приложения нагрузки
- перемещение системы от приложения нагрузки 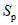 ;
;
c - коэффициент жесткости, представляющий собой реакцию системы от действия силы S = 1.
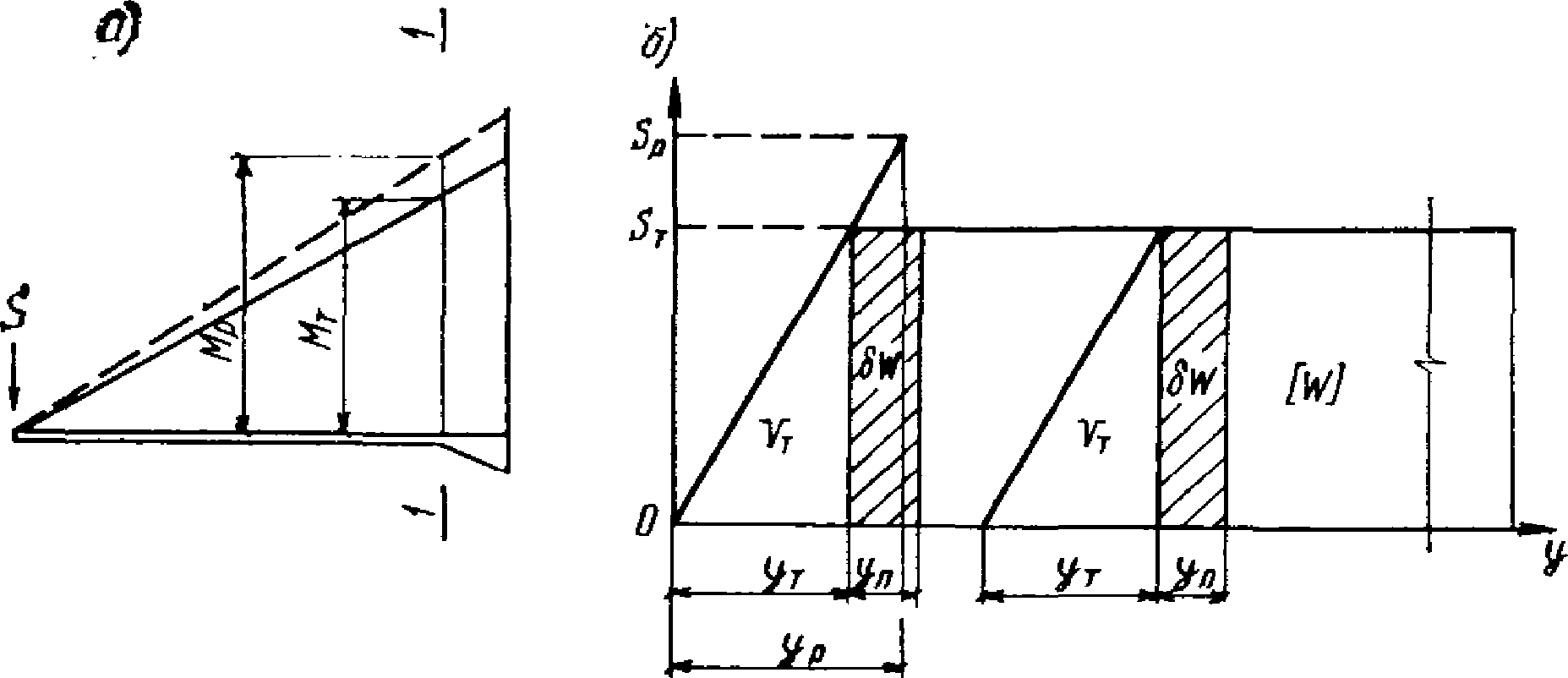
а - ригеля, работающего по упругой и упругопластической
схемам; б - диаграмма зависимости усилий
от деформаций в пластическом шарнире ригеля
Энергия 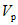 равна кинетической энергии, сообщаемой системе. Поскольку в действительности система упругопластическая, часть энергии
равна кинетической энергии, сообщаемой системе. Поскольку в действительности система упругопластическая, часть энергии 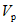 расходуется на деформирование системы в упругой стадии. Она равна:
расходуется на деформирование системы в упругой стадии. Она равна:
Другая часть энергии, составляющая
затрачивается на деформирование системы в пластической стадии. На диаграмме (см. рис. 29, б) энергия 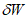 представляет собой прямоугольную площадку с ординатой
представляет собой прямоугольную площадку с ординатой 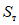 . Эта энергия поглощается системой при одном цикле загружений. За n циклов загружений, ожидаемых при землетрясении, система может поглотить энергию, равную
. Эта энергия поглощается системой при одном цикле загружений. За n циклов загружений, ожидаемых при землетрясении, система может поглотить энергию, равную 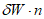 . Данный объем энергии не должен превышать энергоемкость системы [W], т.е. должно соблюдаться условие
. Данный объем энергии не должен превышать энергоемкость системы [W], т.е. должно соблюдаться условие
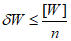 . (16)
. (16)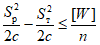 , (17)
, (17)отсюда получим:
При обработке результатов экспериментов энергоемкость образцов [W] выражалась через потенциальную энергию 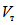 ; обозначим отношение
; обозначим отношение 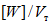 через f, тогда будем иметь:
через f, тогда будем иметь:
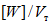 через f, тогда будем иметь:
через f, тогда будем иметь: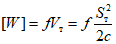 . (19)
. (19)Подставляя значение (19) в выражение (18), получим:
Отметим, что усилие 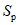 , возникающее в упругой системе, а также предельное усилие
, возникающее в упругой системе, а также предельное усилие 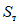 , воспринимаемое упругопластической системой, соответственно пропорциональны моментам
, воспринимаемое упругопластической системой, соответственно пропорциональны моментам 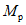 и
и 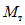 (см. рис. 29, а), возникающим в месте образования пластических шарниров. Условие пропорциональности можно выразить равенством отношений
(см. рис. 29, а), возникающим в месте образования пластических шарниров. Условие пропорциональности можно выразить равенством отношений 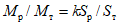 , в котором k - некоторый постоянный коэффициент; в рассматриваемом случае он равен единице. В связи со сказанным значения
, в котором k - некоторый постоянный коэффициент; в рассматриваемом случае он равен единице. В связи со сказанным значения 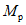 и
и 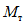 можно подставить в выражение (20) вместо
можно подставить в выражение (20) вместо 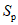 и
и 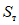 , тогда будем иметь:
, тогда будем иметь:
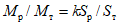 , в котором k - некоторый постоянный коэффициент; в рассматриваемом случае он равен единице. В связи со сказанным значения
, в котором k - некоторый постоянный коэффициент; в рассматриваемом случае он равен единице. В связи со сказанным значения Обратим внимание, что условия работы той части ригеля, которая примыкает к стойке, совершенно аналогичны условиям работы рассмотренного консольного стержня. Поэтому формула (21) может применяться для расчета рамной конструкции.
Использовать выражение (21) можно следующим образом. При предварительном расчете рамы как упругой системы находятся моменты 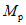 , действующие в сечениях, где предполагается образование пластических шарниров. Возможность появления шарнира в сечении обеспечивается в том случае, если сечение ригеля подобрано таким образом, что воспринимаемый им предельный момент
, действующие в сечениях, где предполагается образование пластических шарниров. Возможность появления шарнира в сечении обеспечивается в том случае, если сечение ригеля подобрано таким образом, что воспринимаемый им предельный момент 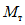 ниже момента
ниже момента 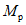 , который в таком случае является по существу фиктивным моментом. Однако разница между
, который в таком случае является по существу фиктивным моментом. Однако разница между 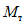 и
и 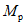 не должна выходить за определенную границу, которая зависит как от энергоемкости [W] в пластической зоне ригеля, так и от числа циклов загружений n, ожидаемых при землетрясении. Эту разницу, или, точнее говоря, допустимое соотношение между
не должна выходить за определенную границу, которая зависит как от энергоемкости [W] в пластической зоне ригеля, так и от числа циклов загружений n, ожидаемых при землетрясении. Эту разницу, или, точнее говоря, допустимое соотношение между 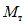 и
и 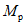 , как раз и можно определить с помощью выражения (21).
, как раз и можно определить с помощью выражения (21).
Назначая величину энергоемкости [W], следует учитывать, что моменты, вызывающие в ригелях пластические деформации, складываются из моментов от статической и сейсмической нагрузок (рис. 30). Знаки моментов от статической нагрузки остаются постоянными. Знаки моментов от сейсмической нагрузки, напротив, в процессе сейсмоколебаний сооружения меняются.
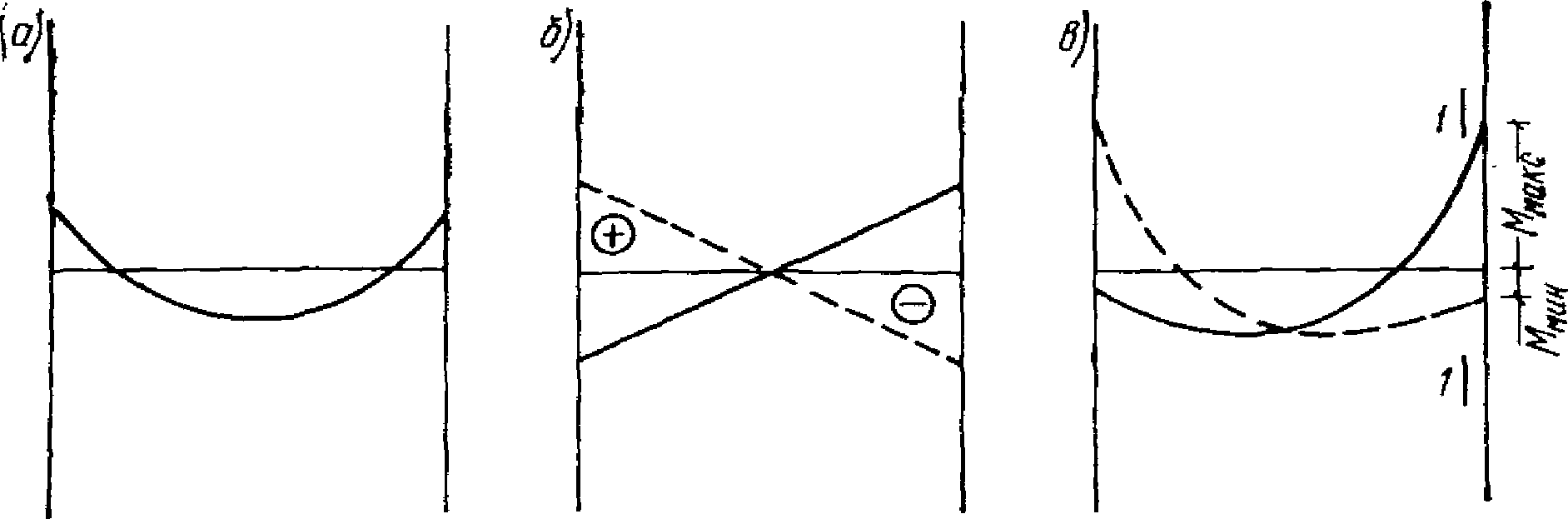
а - от статической нагрузки; б - от сейсмической
нагрузки; в - суммарная эпюра
Таким образом, в тех случаях, когда знаки моментов в сечении, где возникает пластический шарнир, совпадают, усилия в этом сечении максимальные, что собственно и приводит к образованию пластического шарнира. В тех же случаях, когда знаки моментов разные, усилия в сечении будут минимальные и могут вообще не достигнуть предельного момента 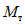 . В связи с этим в зоне образования пластического шарнира наиболее вероятным будет одностороннее развитие остаточных деформаций.
. В связи с этим в зоне образования пластического шарнира наиболее вероятным будет одностороннее развитие остаточных деформаций.
Эксперименты показали, что одностороннее развитие остаточных деформаций приводит к потере местной устойчивости стенки ригеля и снижению его несущей способности. При экспериментах выяснилось, что наибольшая сохранность местной устойчивости оказалась у ригелей образцов типа В, имеющих постоянную высоту стенки и уширенные в области опор пояса. При статических испытаниях остаточная деформация 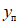 ригелей образцов типа В доводилась до величины, в 15 раз превосходящей максимальную упругую деформацию, т.е.
ригелей образцов типа В доводилась до величины, в 15 раз превосходящей максимальную упругую деформацию, т.е. 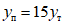 ; добиться большей деформации не позволила возможность испытательной установки. Однако и при такой деформации несущая способность ригелей продолжала сохраняться прежней. Поскольку зависимость усилий от деформаций в ригеле имеет форму, близкую диаграмме Прандтля, поглощенная им энергия в соответствии с остаточной деформацией составляет
; добиться большей деформации не позволила возможность испытательной установки. Однако и при такой деформации несущая способность ригелей продолжала сохраняться прежней. Поскольку зависимость усилий от деформаций в ригеле имеет форму, близкую диаграмме Прандтля, поглощенная им энергия в соответствии с остаточной деформацией составляет 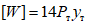 .
.
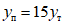 ; добиться большей деформации не позволила возможность испытательной установки. Однако и при такой деформации несущая способность ригелей продолжала сохраняться прежней. Поскольку зависимость усилий от деформаций в ригеле имеет форму, близкую диаграмме Прандтля, поглощенная им энергия в соответствии с остаточной деформацией составляет
; добиться большей деформации не позволила возможность испытательной установки. Однако и при такой деформации несущая способность ригелей продолжала сохраняться прежней. Поскольку зависимость усилий от деформаций в ригеле имеет форму, близкую диаграмме Прандтля, поглощенная им энергия в соответствии с остаточной деформацией составляет 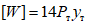 .
.Из выражения (14) следует 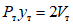 ; подставляя это значение в выражение энергоемкости, будем иметь
; подставляя это значение в выражение энергоемкости, будем иметь 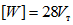 . Отсюда отношение
. Отсюда отношение 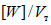 составляет f = 28.
составляет f = 28.
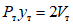 ; подставляя это значение в выражение энергоемкости, будем иметь
; подставляя это значение в выражение энергоемкости, будем иметь 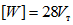 . Отсюда отношение
. Отсюда отношение 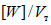 составляет f = 28.
составляет f = 28.При динамических испытаниях значение энергоемкости получалось гораздо больше полученной величины. Таким образом, величину 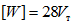 можно назначить как гарантированный минимум энергоемкости для образцов типа В. Поскольку форма и соотношение размеров сечений этих образцов подбирались близкими к соответствующим значениям реальных конструкций, полученное значение энергоемкости представляется возможным для использования при проектировании рамных каркасов.
можно назначить как гарантированный минимум энергоемкости для образцов типа В. Поскольку форма и соотношение размеров сечений этих образцов подбирались близкими к соответствующим значениям реальных конструкций, полученное значение энергоемкости представляется возможным для использования при проектировании рамных каркасов.
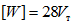 можно назначить как гарантированный минимум энергоемкости для образцов типа В. Поскольку форма и соотношение размеров сечений этих образцов подбирались близкими к соответствующим значениям реальных конструкций, полученное значение энергоемкости представляется возможным для использования при проектировании рамных каркасов.
можно назначить как гарантированный минимум энергоемкости для образцов типа В. Поскольку форма и соотношение размеров сечений этих образцов подбирались близкими к соответствующим значениям реальных конструкций, полученное значение энергоемкости представляется возможным для использования при проектировании рамных каркасов.Что касается числа циклов загружений, ожидаемых при землетрясении, то этот вопрос уже рассматривался в работе [10]. Ее авторы в результате обработки ряда акселерограмм считают возможным принять n = 100.
Будем ориентироваться на принятие приведенных значений f = 28 и n = 100. Подставим их в выражение (21) и получим:
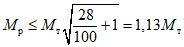 , (22)
, (22)округлим это значение до
Обратим внимание, что принятое округление соответствует случаю, когда энергоемкость деформируемого элемента примерно равна 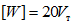 .
.
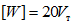 .
.Значение 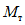 представляет собой момент, по которому следует подбирать сечение ригеля в том месте, где планируется образование пластического шарнира. При этом напряжение, которое воспринимается в пластической зоне, берется равным расчетному сопротивлению
представляет собой момент, по которому следует подбирать сечение ригеля в том месте, где планируется образование пластического шарнира. При этом напряжение, которое воспринимается в пластической зоне, берется равным расчетному сопротивлению 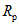 , умноженному на коэффициент
, умноженному на коэффициент 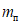 , обусловливающий развитие пластического шарнира.
, обусловливающий развитие пластического шарнира.
3.6. Как указывалось выше, в ряде случаев при загружении образцов как статической, так и динамической нагрузкой стенки ригелей теряли устойчивость, что сопровождалось падением несущей способности ригелей в целом. Так, в образцах типа Б потеря устойчивости стенок ригелей в некоторых случаях наступала уже при прогибе, составляющем 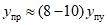 , а в крупных образцах типа К, испытывавшихся в Алма-Ате, при
, а в крупных образцах типа К, испытывавшихся в Алма-Ате, при 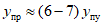 <1>, где
<1>, где 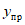 - упругопластический прогиб;
- упругопластический прогиб; 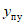 - упругий прогиб.
- упругий прогиб.
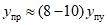 , а в крупных образцах типа К, испытывавшихся в Алма-Ате, при
, а в крупных образцах типа К, испытывавшихся в Алма-Ате, при 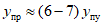 <1>, где
<1>, где --------------------------------
<1> Обратим внимание, что здесь в отличие от величины 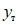 , указанной на рис. 17, используется величина
, указанной на рис. 17, используется величина 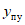 , отвечающая действительному пределу текучести, вследствие чего соотношение между полными прогибами
, отвечающая действительному пределу текучести, вследствие чего соотношение между полными прогибами 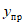 и упругими
и упругими 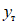 , приведенными в п. 3.3, отличается от приведенных здесь.
, приведенными в п. 3.3, отличается от приведенных здесь.
ИС МЕГАНОРМ: примечание. Взамен СНиП II-В.3-62 Постановлением Госстроя СССР от 29.12.1972 N 222 с 1 июля 1973 года введены в действие СНиП II-В.3-72. Взамен СНиП II-В.3-72 Постановлением Госстроя СССР от 14.08.1981 N 144 с 1 января 1982 года введены в действие СНиП II-23-81. |
В то же время проверка устойчивости стенок этих образцов по формулам, приведенным в главе СНиП II-В.3-62*, п. 6.4*, удовлетворяла требованиям норм. Такое несоответствие требований норм и фактической несущей способности образцов объясняется тем, что формулы, приведенные в нормах, рассматривают лишь упругую работу конструкций, в то время как в наших экспериментах конструкции работали в пластической области. Поскольку преждевременная потеря устойчивости стенки приводит к ранней стадии падения общей несущей способности ригеля, то это ограничивает возможность использования пластических свойств конструкции. В связи с этим возникает необходимость в изыскании путей, позволяющих оценивать критическое состояние стенки при пластической работе материала.
Известно, что задачи, связанные с устойчивостью элементов конструкций, работающих в пластической стадии, относятся к наиболее сложным вопросам, не имевшим до недавнего времени надежного решения. В настоящее время в печати появились работы, в которых рассматриваются вопросы устойчивости пластинок и стенок металлических балок за пределом упругости [3, 11, 12].
В частности, в статьях [11, 12] предлагается сравнительно простой метод расчета на устойчивость за пределом текучести. Не останавливаясь на изложении этого метода, укажем лишь порядок расчета, а также основные допущения, принятые нами в целях дальнейшего упрощения вычислений.
Предполагается, что верхние и нижние грани стенки балки находятся за пределом пропорциональности, и напряжения в них составляют 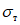 . Тогда характеристика напряженного состояния стенки в соответствии с работой [11] определяется величиной
. Тогда характеристика напряженного состояния стенки в соответствии с работой [11] определяется величиной
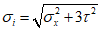 ,
,где 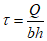 .
.
Q - поперечная сила;
b и h - толщина и высота стенки,
а характеристика относительных удлинений
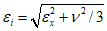 ,
,ИС МЕГАНОРМ: примечание. Обозначение дано в соответствии с официальным текстом документа. |
где 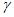 - деформация сдвига.
- деформация сдвига.
Основываясь на принятой ранее предпосылке, что материал работает в соответствии с диаграммой Прандтля, принимаем, что 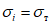 , и тогда краевые нормальные напряжения вычисляются по формуле
, и тогда краевые нормальные напряжения вычисляются по формуле
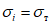 , и тогда краевые нормальные напряжения вычисляются по формуле
, и тогда краевые нормальные напряжения вычисляются по формуле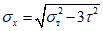 .
.Далее определяются критические нормальные 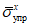 и касательные
и касательные 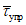 напряжения в стенке в предположении, что материал стенки работает неограниченно упруго. Эти напряжения в статье [12] приведены в относительных величинах по отношению к пределу текучести
напряжения в стенке в предположении, что материал стенки работает неограниченно упруго. Эти напряжения в статье [12] приведены в относительных величинах по отношению к пределу текучести 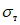 и равняются:
и равняются:
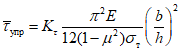 , (25)
, (25)где E и 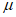 - модуль Юнга
- модуль Юнга 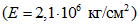 и коэффициент Пуассона
и коэффициент Пуассона 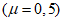 .
.
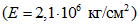 и коэффициент Пуассона
и коэффициент Пуассона 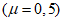 .
.Коэффициенты 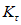 и
и 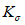 , а также коэффициент C, необходимый для дальнейших расчетов, определяются по табл. 1 и 3 работы [12] в зависимости от величин
, а также коэффициент C, необходимый для дальнейших расчетов, определяются по табл. 1 и 3 работы [12] в зависимости от величин 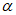 ,
, 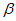 и
и 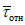 , равного
, равного 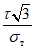 . Для случая, когда относительные удлинения по верху и по низу стенки одинаковы, но различны по знаку, значение
. Для случая, когда относительные удлинения по верху и по низу стенки одинаковы, но различны по знаку, значение 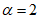 . Значение
. Значение 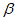 представляет собой отношение сторон отсека стенки. Вычисления показывают, что критические краевые удлинения слабо зависят от изменения отношения сторон
представляет собой отношение сторон отсека стенки. Вычисления показывают, что критические краевые удлинения слабо зависят от изменения отношения сторон 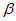 . Поэтому без существенных погрешностей можно пользоваться значениями
. Поэтому без существенных погрешностей можно пользоваться значениями 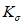 и
и 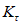 , отвечающими
, отвечающими 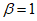 .
.
В работе [12] принимается предпосылка, что отношения нормальных и касательных напряжений в упругой пластинке (стенке) равняются отношению соответствующих напряжений за пределом упругости. Это достигается подбором соответствующих значений коэффициентов 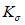 и
и 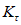 . В этом случае
. В этом случае
Значения коэффициента C определяются по табл. 3 (см. [12]) в соответствии с принятыми параметрами 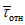 ,
, 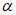 и
и  приведены в табл. 1.
приведены в табл. 1.
Используя выражения (24) и (26), находят критические напряжения для неограниченно упругой стенки:
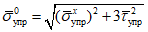 . (27)
. (27)Соответствующее этим напряжениям критическое краевое удлинение стенки определяется выражением
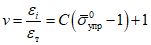 , (28)
, (28)где 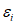 - полное, т.е. упругое и пластическое удлинение;
- полное, т.е. упругое и пластическое удлинение;
Для оценки соответствия экспериментальных данных с изложенной выше методикой были проведены проверочные расчеты. Проверке были подвергнуты образцы типа А, В и К. Ригели образцов типа Б в зоне примыкания к стойке имели развитое по высоте сечение. Это являлось причиной быстрой потери устойчивости ригеля в целом. Поэтому конструктивный вариант ригелей типа Б признан неудачным и проверочный расчет стенок ригелей типа Б не производился.
Результаты расчетов образцов типа А, В и К помещены в табл. 7, где во второй колонке помещены экспериментально полученные величины 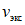 , которые представляют собой отношения
, которые представляют собой отношения 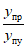 (см. рис. 17).
(см. рис. 17).
Тип образцов | v | |
1 | ||
12,3 | 47 | |
12 | 48,5 | |
14,1 <*> | 46,5 | |
22,1 | 48,5 | |
16,5 | 46,6 | |
30 | 46,6 | |
9,6 | 56 | |
9,6 | 52,3 | |
14,3 | 53,2 | |
19,4 | 53 | |
16,5 | 56,3 | |
20 | 56,5 | |
21,5 | 53,5 | |
21,5 | 53,2 | |
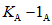 | 6,6 | 6,44 |
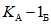 | 6,05 | 6,5 |
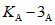 | 5,85 | 6,74 |
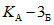 | 7,67 | 6,62 |
6,13 | 6,72 | |
6,37 | 6,7 |
--------------------------------
В третьей колонке помещены данные расчета величины критических краевых деформаций стенок, которые представляют собой отношения упругопластических краевых деформаций стенок к удлинениям упругой части:
Поскольку пластическое краевое удлинение стенки пропорционально пластическому прогибу ригеля, а упругое краевое удлинение 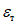 пропорционально упругому прогибу
пропорционально упругому прогибу 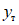 , составляющему по сравнению с пластическим очень малую величину, можно с незначительной погрешностью принять, что
, составляющему по сравнению с пластическим очень малую величину, можно с незначительной погрешностью принять, что
Для стенок ригелей А и В в расчет вводился действительный предел текучести, полученный в результате испытания образцов металла стенок 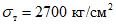 , а для образцов К -
, а для образцов К - 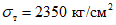 .
.
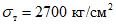 , а для образцов К -
, а для образцов К - 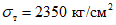 .
.Как видно из табл. 7, у всех образцов типа А и В полученные значения 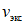 оказались ниже представленных в третьей колонке величин v. Это объясняется тем, что возможности эксперимента не позволяли развивать больших деформаций в ригелях, хотя даже такие прогибы составляли весьма значительные величины, доходящие до
оказались ниже представленных в третьей колонке величин v. Это объясняется тем, что возможности эксперимента не позволяли развивать больших деформаций в ригелях, хотя даже такие прогибы составляли весьма значительные величины, доходящие до 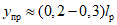 (
(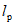 - длина ригеля).
- длина ригеля).
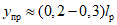 (
(На диаграммах P - y при таких прогибах падение нагрузки не отмечалось, т.е. стенки ригелей не теряли устойчивости и, по-видимому, способны были нести нагрузку и при  деформациях. Расчетные величины v для стенок А и В находятся в пределах от 46 до 56. Результаты сопоставления экспериментальных данных с расчетной методикой более ощутимо проявились при проверке образцов К. Стенки ригелей образцов К более гибкие, поэтому потеря их устойчивости, а вслед за ней и потеря несущей способности происходила уже при
деформациях. Расчетные величины v для стенок А и В находятся в пределах от 46 до 56. Результаты сопоставления экспериментальных данных с расчетной методикой более ощутимо проявились при проверке образцов К. Стенки ригелей образцов К более гибкие, поэтому потеря их устойчивости, а вслед за ней и потеря несущей способности происходила уже при 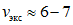 . Расчетные значения v показали такие же величины.
. Расчетные значения v показали такие же величины.
 деформациях. Расчетные величины v для стенок А и В находятся в пределах от 46 до 56. Результаты сопоставления экспериментальных данных с расчетной методикой более ощутимо проявились при проверке образцов К. Стенки ригелей образцов К более гибкие, поэтому потеря их устойчивости, а вслед за ней и потеря несущей способности происходила уже при
деформациях. Расчетные величины v для стенок А и В находятся в пределах от 46 до 56. Результаты сопоставления экспериментальных данных с расчетной методикой более ощутимо проявились при проверке образцов К. Стенки ригелей образцов К более гибкие, поэтому потеря их устойчивости, а вслед за ней и потеря несущей способности происходила уже при 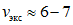 . Расчетные значения v показали такие же величины.
. Расчетные значения v показали такие же величины.Из данных, приведенных в графах 2 и 3 табл. 7, видно, что из двадцати проверочных расчетов в шести случаях экспериментальные и расчетные величины v дают хорошую сходимость, в тринадцати случаях нет противоречий и только в одном случае (образец 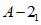 ) результаты сравнения эксперимента с расчетом не сходятся. Таким образом, можно сделать вывод, что методика проверки устойчивости по деформациям дает достаточно близкое совпадение с экспериментами и может быть использована в настоящих рекомендациях.
) результаты сравнения эксперимента с расчетом не сходятся. Таким образом, можно сделать вывод, что методика проверки устойчивости по деформациям дает достаточно близкое совпадение с экспериментами и может быть использована в настоящих рекомендациях.
Следует, однако, напомнить, что в изложенной выше проверке устойчивости использовался предел текучести, полученный при скоростях нагружения, отвечающих обычным статическим испытаниям. При больших скоростях загружения предел текучести стали значительно возрастает. Например, по данным экспериментов Б. Гопкинсона, Дж. Тейлора [9] и др., предел текучести стали при больших скоростях загружения становился более чем в 1,6 раза выше, чем предел текучести, полученный при статических испытаниях. Величина предела текучести 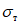 примерно соответствовала временному сопротивлению
примерно соответствовала временному сопротивлению 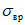 . Сейсмические нагрузки также обладают достаточно высокими скоростями. В связи с этим пределы текучести стали в конструкции при сейсмическом воздействии должны возрастать.
. Сейсмические нагрузки также обладают достаточно высокими скоростями. В связи с этим пределы текучести стали в конструкции при сейсмическом воздействии должны возрастать.
Учитывая сказанное, а также руководствуясь приведенными в п. 3.4. соображениями, примем для расчета стенок ригеля на устойчивость
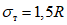 ,
,где R - расчетное сопротивление стали.
Отметим, что величина энергии, которая может быть поглощена ригелем в месте образования пластического шарнира, тесно зависит от предельной деформации в пластическом шарнире 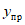 , при которой происходит потеря несущей способности в стенке ригеля. Значение
, при которой происходит потеря несущей способности в стенке ригеля. Значение 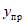 представляет собой сумму упругой и пластической деформации
представляет собой сумму упругой и пластической деформации 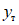 и
и 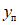 :
:
Та часть энергии, которая поглощается при развитии пластической деформации 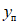 , является энергоемкостью ригеля [W]. Как уже неоднократно ранее отмечалось, зависимость усилий от деформации в ригеле выражается диаграммой Прандтля. В связи с этим энергоемкость определяется произведением
, является энергоемкостью ригеля [W]. Как уже неоднократно ранее отмечалось, зависимость усилий от деформации в ригеле выражается диаграммой Прандтля. В связи с этим энергоемкость определяется произведением
Из отношения (30) с учетом значения (31) получаем:
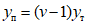 . (33)
. (33)Подставим это значение в (32):
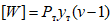 .
.Учитывая, что 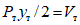 , будем иметь:
, будем иметь:
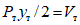 , будем иметь:
, будем иметь: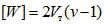 , (34)
, (34)отсюда отношение энергоемкости [W] к максимальной упругой энергии 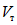 будет равным:
будет равным:
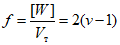 . (35)
. (35)Подставляя полученное значение в (21), будем иметь выражение фиктивного изгибающего момента, который может быть воспринят в месте образования пластического шарнира:
Как показано в выражении (23), значение 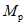 рекомендуется принимать равным
рекомендуется принимать равным 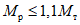 . Может, однако, в результате расчета по формуле (36) оказаться, что
. Может, однако, в результате расчета по формуле (36) оказаться, что 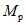 заведомо меньше
заведомо меньше 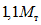 . Это значит, что по условию местной устойчивости в стенке ригеля не допускается развитие значительных пластических деформаций. Тогда соотношения
. Это значит, что по условию местной устойчивости в стенке ригеля не допускается развитие значительных пластических деформаций. Тогда соотношения 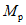 и
и 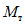 следует принимать согласно расчету по формуле (36), либо необходимо провести конструктивные мероприятия по усилению стенки ригеля. Если же расчет по формуле (36) дает величину
следует принимать согласно расчету по формуле (36), либо необходимо провести конструктивные мероприятия по усилению стенки ригеля. Если же расчет по формуле (36) дает величину 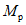 , большую, чем
, большую, чем 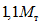 , то данное значение рекомендуется ограничивать величиной
, то данное значение рекомендуется ограничивать величиной 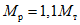 . Такое ограничение необходимо вводить в связи с тем, что при возрастании разности
. Такое ограничение необходимо вводить в связи с тем, что при возрастании разности 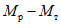 будет происходить чрезмерное возрастание моментов в стойках.
будет происходить чрезмерное возрастание моментов в стойках.
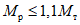 . Может, однако, в результате расчета по формуле (36) оказаться, что
. Может, однако, в результате расчета по формуле (36) оказаться, что 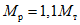 . Такое ограничение необходимо вводить в связи с тем, что при возрастании разности
. Такое ограничение необходимо вводить в связи с тем, что при возрастании разности 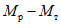 будет происходить чрезмерное возрастание моментов в стойках.
будет происходить чрезмерное возрастание моментов в стойках.В тех случаях, когда по условию обеспечения местной устойчивости в пластической зоне стенку ригеля необходимо усиливать, в качестве элементов жесткости могут использоваться накладки, которые привариваются в местах сопряжения стенок ригелей с полками (см. рис. 25), ограничивая тем самым свободную высоту стенок. Длина накладок должна быть такова, чтобы их концы выходили за пределы пластической зоны.
Теперь остановимся на выборе расчетной нагрузки, которую следует принимать при проверке сечения стенки ригеля на местную устойчивость. Дело в том, что если использовать момент, возникающий в ригеле при действии расчетной сейсмической нагрузки, то это, по-видимому, будет недостаточным.
При землетрясениях неизбежно происходят выбросы ускорений грунта, в 2 - 3 раза превышающие средние значения ускорений, на основе которых определяется нормативная сейсмическая нагрузка. При этих выбросах в сооружении возникают значительные перегрузки, которые представляют наибольшую опасность для устойчивости тонкостенных элементов. Поэтому проверку местной устойчивости как раз и следует выполнять с учетом действия таких перегрузок.
В ЦНИИПроектстальконструкции уже проводились исследования по теме "Предложения по расчету каркасов зданий на сейсмические воздействия с учетом протяженности". Выполненный в работе анализ статистических данных реальных акселерограмм показал, что число выбросов, которые превышают стандарты ускорения в 2 раза, примерно составляет 10% случаев общего количества колебаний грунта при землетрясении. Учитывая такую высокую вероятность, полагаем необходимым проверочный расчет производить при условии, когда ускорения грунта в 2 раза выше стандарта. На основе данных указанной работы можно прийти к выводу, что в сооружениях типа рамных каркасов такие ускорения вызывают перегрузки, которые примерно на 40% выше расчетной сейсмической нагрузки. В связи с этим при проверке стенок ригелей на устойчивость момент от действия сейсмической силы целесообразно увеличивать в 1,4 раза.
при учете влияния пластических деформаций
3.7. Как известно, методы расчета статически неопределимых систем с учетом пластических деформаций в конструкциях на действие статических сил за последнее время получают все более широкое распространение и все более совершенствуются. Этим исследованиям посвящена уже относительно обширная литература, поэтому останавливаться здесь на их рассмотрении нет необходимости. Отметим только, что применение таких методов в практике связано с громоздкими вычислениями.
В связи с этим при решении поставленного вопроса уместно принять во внимание реальную возможность прогнозирования ожидаемой сейсмической нагрузки на сооружение. Здесь мы имеем в виду существующую в настоящее время достоверность назначения величин интенсивности сейсмической активности для того или иного района. Сама классификация интенсивности землетрясений в виде балльности, когда сила воздействия назначается в градациях увеличения ее в 2 раза, говорит сама за себя, показывая, что точность прогнозирования сейчас еще очень невелика. Если же учесть к тому же и неизбежные здесь просчеты, как, например, это имело место с балльностями для районов Ашхабада и Ташкента (где после землетрясений 1948 и 1966 г. балльность была повышена в Ашхабаде с 7 до 9 баллов, а в Ташкенте с 8 до 9 баллов, т.е. в 4 и в 2 раза соответственно <1>), то станет совершенно очевидным, что достоверность прогноза будущего сейсмического воздействия очень невелика и не может быть сопоставлена с достоверностью назначения других эксплуатационных нагрузок на сооружение.
--------------------------------
<1> В Ташкенте это имело место только для центральной части города.
Вместе с тем отметим, что ввиду опасности потерь местной устойчивости в ригелях и возможного перераспределения дополнительных усилий с ригелей на стойки развитие пластических деформаций в ригелях допустимо в ограниченных пределах. При соблюдении такого условия усилия в рамной системе, полученные с учетом пластических шарниров в ригелях, фактически будут мало отличаться от усилий в аналогичной рамной упругой системе. Поэтому при разработке методики расчета конструкций на сейсмические воздействия нет никакого практического смысла стремиться к использованию точных методов расчета, лишь незначительно уточняющих значения усилий, возникающих в том или ином элементе системы. Более рационально будет применить упрощенный приближенный метод расчета и в то же время обеспечить в конструкции возможность использования скрытых резервов пластической энергоемкости.
В поддержку целесообразности использования упрощенного способа расчета уместным будет привести довольно категоричное мнение американского специалиста по сейсмостойкому строительству Дж. Х. Уиггинса (John H. Wiggins) [15] относительно ориентировочного задания расчетной сейсмической нагрузки: "Новые нормы проектирования зданий на сейсмические нагрузки, действующие в настоящее время в Лонг-Биче (штат Калифорния), ... составлены с учетом того, что мы никогда не можем с уверенностью знать, когда или где произойдет землетрясение и какова будет его сила".
Исходя из сказанного, а также учитывая, что вся методика определения сейсмической нагрузки принята на основе рассмотрения упругой работы системы, ниже принята упрощенная постановка вопроса по определению усилий, возникающих в каркасе при появлении в нем пластических шарниров. Задача ставится так. В результате расчета рамного каркаса по упругой схеме на все виды приходящихся на него нагрузок получены эпюры моментов (рис. 31). Выделим из этого каркаса любую стойку, например крайнюю правую (рис. 31, а), и приложим к ней приходящиеся на ее долю горизонтальные усилия, которые передаются через ригели и возникающие в опорных сечениях ригелей моменты (рис. 31, б). Построим эпюру моментов в стойке, возникающих от действия на стойку горизонтальных сил (рис. 31, в). Очертания эпюры получаются в виде ломаной линии.
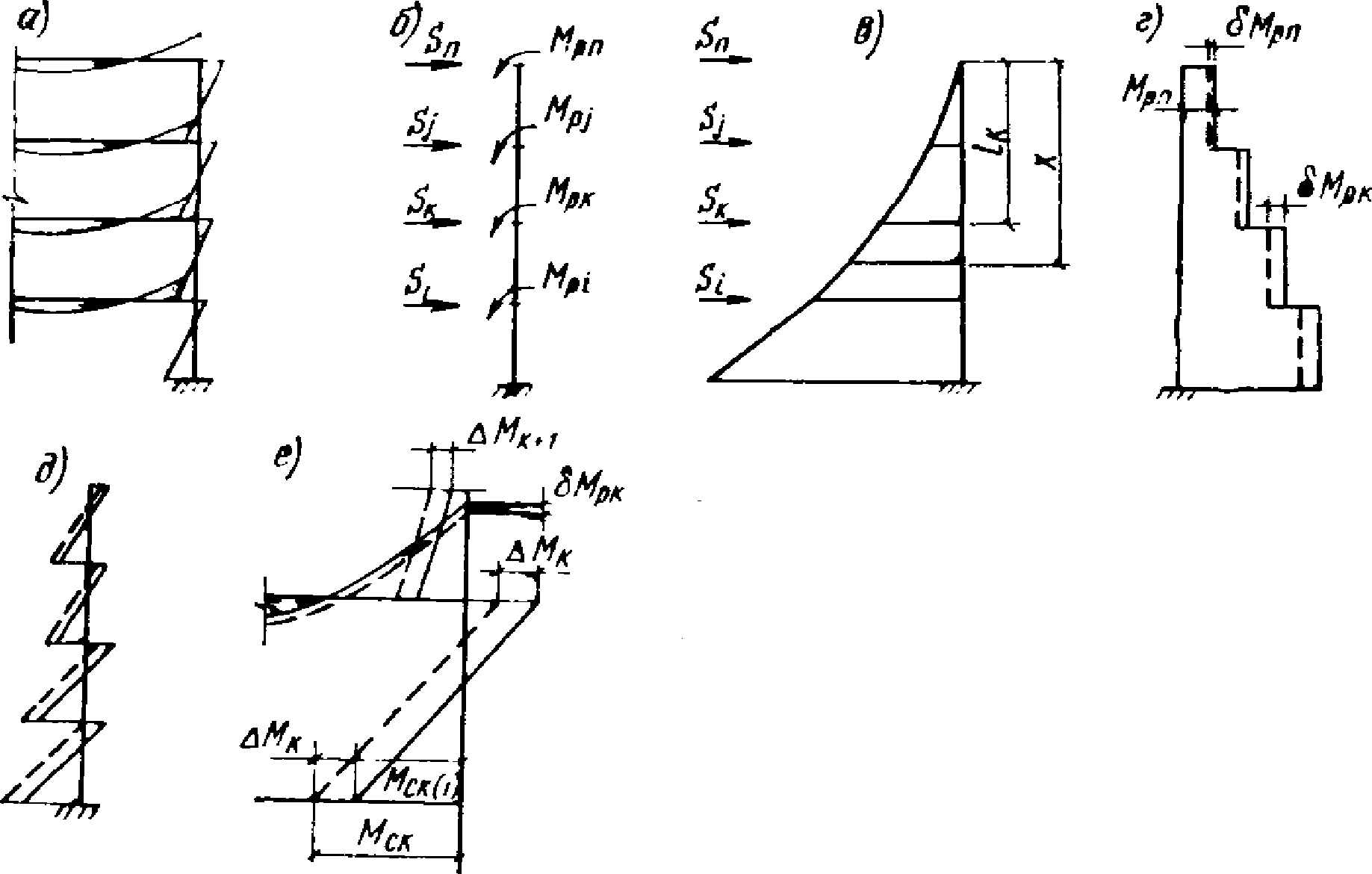
рамы при образовании пластических шарниров
а - эпюры моментов, полученные в результате расчета каркаса
по упругой схеме; б - схема распределения усилий в стойках;
в - эпюра моментов в стойке от действия горизонтальных сил;
г - эпюра моментов в стойке от передачи опорных моментов
ригелей; д - суммарная эпюра от совместного действия
горизонтальных сил и опорных моментов; е - суммарная эпюра,
учитывающая изменение моментов при образовании
в ригелях пластических шарниров
Ее ординаты будут:
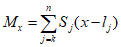 , (37)
, (37)где 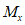 - момент в стойке на расстоянии x от уровня верхнего этажа;
- момент в стойке на расстоянии x от уровня верхнего этажа;
Построим также эпюру, возникающую в стойке от передачи опорных моментов ригелей (рис. 31, г). Полученная эпюра имеет ступенчатую форму. Ее ординаты на каждом этаже складываются из опорных моментов ригелей вышележащих этажей:
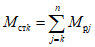 , (38)
, (38)где 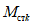 - ордината эпюры моментов на k-м этаже;
- ордината эпюры моментов на k-м этаже;
Сложим обе эпюры (см. рис. 31, в и г). Получим характерную эпюру изгибающих моментов пилообразной формы, которая возникает при учете совместного действия горизонтальных сил и опорных моментов (рис. 31, д).
Посмотрим, какое влияние оказывают на моменты в стойках возникающие в ригелях пластические шарниры.
Поскольку предельные моменты 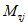 , воспринимаемые в местах образования пластических шарниров, меньше, чем моменты
, воспринимаемые в местах образования пластических шарниров, меньше, чем моменты 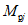 , полученные при расчете рамы по упругой схеме, ординаты эпюры в действительности окажутся смещенными в меньшую сторону на разности моментов
, полученные при расчете рамы по упругой схеме, ординаты эпюры в действительности окажутся смещенными в меньшую сторону на разности моментов 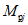 и
и 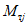 ригелей вышележащих этажей. Так, например, в верхнем этаже момент у стойки изменится на величину
ригелей вышележащих этажей. Так, например, в верхнем этаже момент у стойки изменится на величину
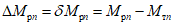 . (39)
. (39)Момент в k-м этаже изменится на суммарную величину изменения моментов в ригелях вышележащих этажей, т.е.
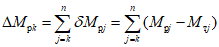 , (40)
, (40)где 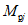 ;
; 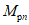 - моменты в опорных сечениях ригелей, полученные при расчете по упругой схеме;
- моменты в опорных сечениях ригелей, полученные при расчете по упругой схеме;
Таким образом, при учете пластических шарниров в ригелях изменится только эпюра, показанная на рис. 31, г, возникающая от опорных моментов ригелей. Сложим эту эпюру, взятую с учетом изменений, с эпюрой, показанной на рис. 31, в. Получим суммарную эпюру, учитывающую изменение моментов и возникающую при образовании в ригелях пластических шарниров. Эта эпюра изображена пунктирной линией на рис. 31, е.
При практических расчетах рамных конструкций уже нет необходимости повторять указанные действия, т.е. разбивать эпюру в каждой стойке на составляющие и т.п. Достаточно с помощью приведенных выше выражений только подсчитать, на какую величину изменяются опорные моменты в ригелях рамы при появлении пластических шарниров, и внести соответствующие поправки в эпюру моментов рамы. Изменение момента в опорном сечении ригеля каждого этажа будет составлять:
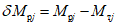 , (41)
, (41)где 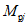 - момент в опорном сечении ригеля, вычисленный при расчете по упругой схеме;
- момент в опорном сечении ригеля, вычисленный при расчете по упругой схеме;
Соответственно изменение момента в стойке k-го этажа складывается из вычисленных поправок вышерасположенных этажей:
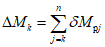 . (42)
. (42)После того как определены значения 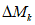 , они вводятся в качестве поправки в эпюру моментов стойки, т.е. значение
, они вводятся в качестве поправки в эпюру моментов стойки, т.е. значение 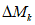 вычитается из момента
вычитается из момента 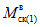 в верхнем сечении стойки k-го этажа, поскольку знаки той и другой величины разные:
в верхнем сечении стойки k-го этажа, поскольку знаки той и другой величины разные:
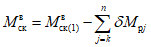 , (43)
, (43)и складывается с моментом 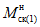 в нижнем сечении стойки k-го этажа, поскольку в этом случае знаки того и другого момента совпадают:
в нижнем сечении стойки k-го этажа, поскольку в этом случае знаки того и другого момента совпадают:
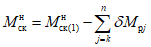 , (44)
, (44)где 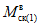 ,
, 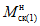 - моменты в верхнем и нижнем сечениях стойки, вычисленные по упругой схеме.
- моменты в верхнем и нижнем сечениях стойки, вычисленные по упругой схеме.
Таким путем можно учитывать перераспределение моментов как в крайних, так и в средних стойках рамы.
Так как эпюра моментов в раме несимметричная (см. рис. 30), пластические шарниры обычно возникают поочередно: то у одной опоры ригеля, то у другой. Поскольку разница между предельным моментом 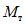 , воспринимаемым в пластическом шарнире, отличается незначительно от момента
, воспринимаемым в пластическом шарнире, отличается незначительно от момента 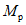 в том же сечении, вычисленного при расчете рамы как упругой системы, можно допустить, что с появлением пластического шарнира момент у противоположной опоры ригеля не меняется. Поэтому будем считать, что на изменение моментов в стойке влияют только моменты тех ригелей, у которых пластические шарниры возникают в непосредственной близости от мест примыкания к данной стойке. При такой предпосылке методика перераспределения моментов в средних стойках ничем не будет отличаться от методики определения моментов в крайних стойках.
в том же сечении, вычисленного при расчете рамы как упругой системы, можно допустить, что с появлением пластического шарнира момент у противоположной опоры ригеля не меняется. Поэтому будем считать, что на изменение моментов в стойке влияют только моменты тех ригелей, у которых пластические шарниры возникают в непосредственной близости от мест примыкания к данной стойке. При такой предпосылке методика перераспределения моментов в средних стойках ничем не будет отличаться от методики определения моментов в крайних стойках.
Таким образом, расчет рамной конструкции делится на два основных этапа. На первом этапе конструкция рассчитывается на действие всех приложенных к ней сил как обычная упругая система в соответствии с существующей методикой. Затем производится корректировка моментов в раме, связанная с учетом образования пластических шарниров в ригелях. Эта часть вычислений, как видно из вышеизложенного, достаточно проста и не может вызывать никаких затруднений при практических расчетах.
Для того чтобы оценить порядок возможных ошибок, связанных с использованием предлагаемого приближенного метода, при условии, что момент в пластическом шарнире 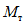 не более чем на 10% отличается от
не более чем на 10% отличается от 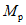 , рассмотрим работу одноэтажной многопролетной (число пролетов =
, рассмотрим работу одноэтажной многопролетной (число пролетов = 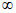 ) рамы под действием горизонтальной нагрузки (рис. 32, а). Выделим промежуточный пролет рамы с приходящейся на него нагрузкой (рис. 32, б). Если система работает в упругой стадии, то точки перегиба ригелей будут находиться в середине их пролетов и для расчета может быть принята схема (рис. 32). Результаты расчета для случая, когда отношения l/H = 2 и
) рамы под действием горизонтальной нагрузки (рис. 32, а). Выделим промежуточный пролет рамы с приходящейся на него нагрузкой (рис. 32, б). Если система работает в упругой стадии, то точки перегиба ригелей будут находиться в середине их пролетов и для расчета может быть принята схема (рис. 32). Результаты расчета для случая, когда отношения l/H = 2 и 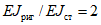 (
(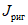 - момент инерции ригеля;
- момент инерции ригеля; 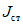 - то же, стойки), представлены на рис. 32, г.
- то же, стойки), представлены на рис. 32, г.
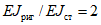 (
(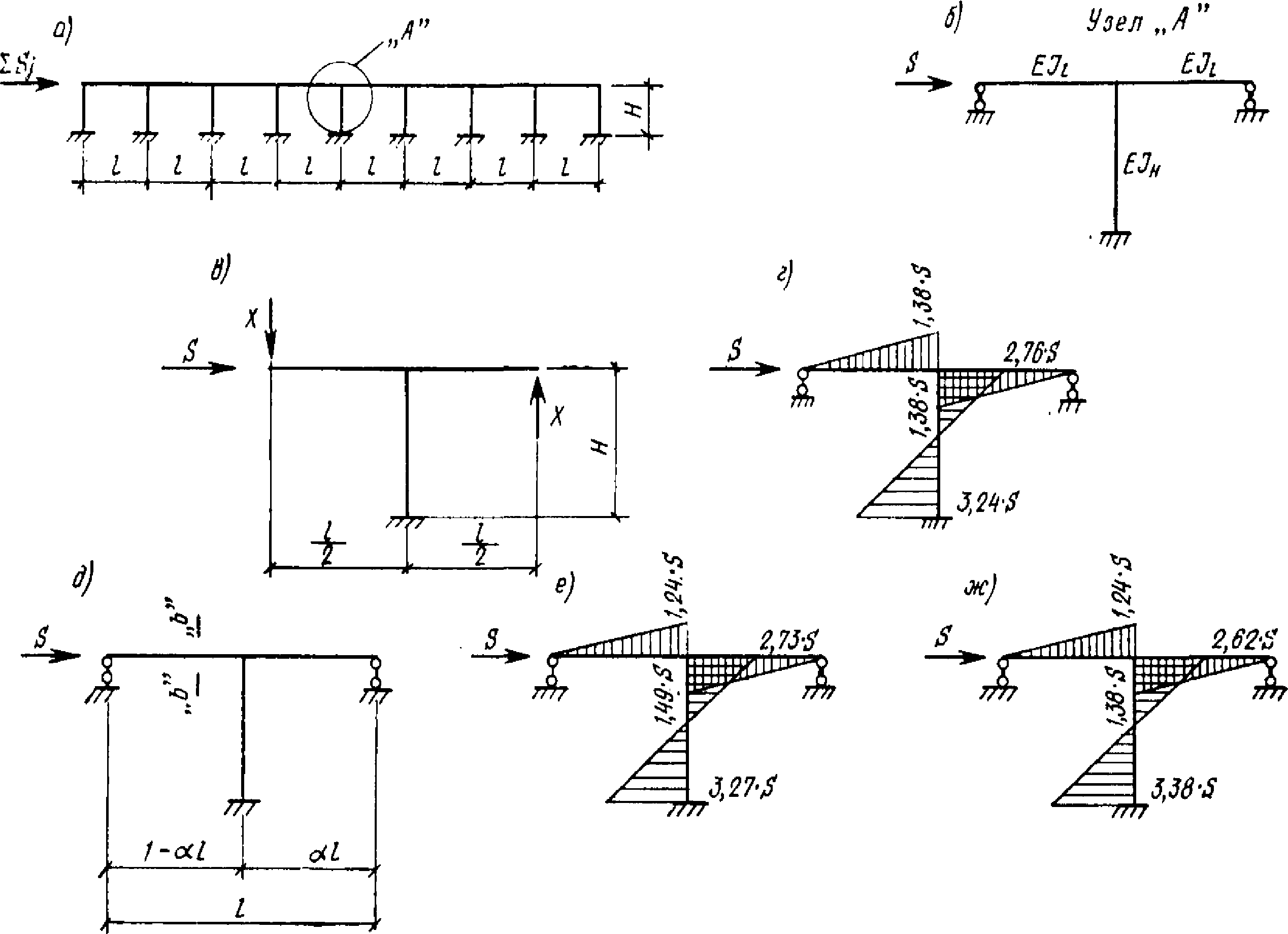
в многопролетной одноэтажной раме
а - схема многопролетной рамы; б - промежуточный элемент
рамы; в - схема усилий в элементе рамы; г - эпюра моментов
в элементе рамы, работающем в упругой стадии; д - схема
элемента рамы сечением b-b, в котором образуется
пластический шарнир; е - эпюра моментов в элементе рамы
при образовании пластического шарнира; ж - эпюра моментов
в элементе рамы при образовании пластического
шарнира по приближенному расчету
В том случае, когда работа рамы перейдет в упругопластическую стадию и в правом ригеле в сечении b образуется пластический шарнир (рис. 32, д), точки перегибов в ригелях переместятся влево, и так как соседние пролеты находятся в таких же условиях, то новая расчетная схема рамы будет отличаться от прежней только тем, что длины консолей станут другими, сохраняя при этом условие
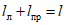
или
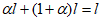 ,
,где 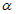 - некоторый коэффициент, меньший единицы.
- некоторый коэффициент, меньший единицы.
Решая эту новую систему и вводя условие, что узловой момент в правом ригеле составляет 0,9 величины момента в том же сечении в первой (т.е. упругой) системе, легко найти значения всех моментов в системе (рис. 32, д).
На рис. 32, е представлены эпюры моментов, отвечающие этой расчетной схеме.
Отметим, что эти эпюры представляют точные значения моментов для упругопластической системы, когда 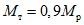 упругой системы.
упругой системы.
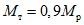 упругой системы.
упругой системы.Наконец, на рис. 32, ж представлены эпюры моментов для такой же системы, определенные по приближенной методике, изложенной выше. Разница в значении моментов, возникающих в наиболее опасном сечении стойки, найденных точным и приближенным методами, составляет:
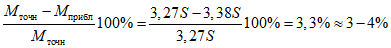 .
.Аналогичный расчет, проведенный для такой же системы, но с другими соотношениями l/H и 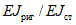 , а именно при l/H = 1 и
, а именно при l/H = 1 и 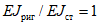 , показал, что ошибка составляет 2,9%, т.е. того же порядка.
, показал, что ошибка составляет 2,9%, т.е. того же порядка.
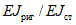 , а именно при l/H = 1 и
, а именно при l/H = 1 и 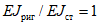 , показал, что ошибка составляет 2,9%, т.е. того же порядка.
, показал, что ошибка составляет 2,9%, т.е. того же порядка.Надо полагать, что с практической точки зрения, учитывая все сказанное выше (см. стр. 49 - 50), такая погрешность является вполне допустимой, и поэтому всякое усложнение расчета с целью его уточнения не имеет смысла.
Переходя теперь к вопросу подбора сечений элементов рамы, напомним, что напряжения в стойках по отмеченным ранее соображениям (см. стр. 20) не должны превышать расчетных сопротивлений. В случае если требуемые сечения стоек получаются слишком большими и это приводит к неэкономичным конструкциям, в ригелях рам следует создать условие, приводящее к меньшей разности моментов 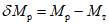 , чтобы тем самым еще больше ограничить передачу усилий на стойки. Это можно осуществить, либо увеличив расстояние от зоны пластического шарнира до стыка ригеля со стойкой, либо путем увеличения основного сечения ригеля. Пользуясь тем и другим способом, целесообразно варьировать жесткостями элементов рамы в целях получения оптимального решения.
, чтобы тем самым еще больше ограничить передачу усилий на стойки. Это можно осуществить, либо увеличив расстояние от зоны пластического шарнира до стыка ригеля со стойкой, либо путем увеличения основного сечения ригеля. Пользуясь тем и другим способом, целесообразно варьировать жесткостями элементов рамы в целях получения оптимального решения.
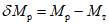 , чтобы тем самым еще больше ограничить передачу усилий на стойки. Это можно осуществить, либо увеличив расстояние от зоны пластического шарнира до стыка ригеля со стойкой, либо путем увеличения основного сечения ригеля. Пользуясь тем и другим способом, целесообразно варьировать жесткостями элементов рамы в целях получения оптимального решения.
, чтобы тем самым еще больше ограничить передачу усилий на стойки. Это можно осуществить, либо увеличив расстояние от зоны пластического шарнира до стыка ригеля со стойкой, либо путем увеличения основного сечения ригеля. Пользуясь тем и другим способом, целесообразно варьировать жесткостями элементов рамы в целях получения оптимального решения.Наряду с подбором основного сечения ригелей определяются также усиленные сечения в местах стыков ригелей со стойками. Размеры усиленных сечений должны быть таковы, чтобы напряжения в области сварных стыков не превышали расчетных сопротивлений. В качестве расчетного момента, в соответствии с которым определяется размер сечения, берется момент, возникающий в заделке в то время, когда в пластической зоне достигается предельный момент 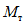 .
.
Согласно приведенным в п. 3.3. данным, следует отметить, что увеличение высоты стенок ригелей у опор приводит к ухудшению местной устойчивости и преждевременному снижению несущей способности ригелей. Поэтому усиление опорных сечений рекомендуется осуществлять за счет развития полок ригелей. Вместе с тем эксперименты показали, что удаление пластических зон в ригелях от стоек целесообразно брать на расстоянии, равном приблизительно утроенной ширине полки, чтобы не допустить развития в сварных стыках деформаций, выходящих за предел упругости.
Жесткости сечений элементов рам, полученные в результате расчетов, могут отличаться от первоначально заданных. При существенном изменении жесткостей расчет конструкций следовало бы производить повторно. Критериями для выяснения необходимости повторного расчета могут служить следующие соображения.
Как известно, квадраты частот пропорциональны жесткости конструкции, в то же время частоты прямо пропорциональны сейсмическим нагрузкам.
В связи с этим изменение жесткостей на 20 - 30% повлечет соответствующее изменение сейсмической нагрузки примерно на 10 - 14%. Поэтому, если рассматривать здания, каркасы которых не имеют заполнений, то при изменении жесткости уже более чем на 20% следовало бы производить повторный расчет.
Однако в действительности на жесткость здания большое влияние оказывают стеновые заполнения, так что даже значительное изменение жесткости самого каркаса не будет оказывать существенного влияния на жесткость здания в целом. Поэтому представляется допустимым при изменении жесткости каркаса менее чем на 30% повторных расчетов не производить.
Для апробации изложенной методики был произведен расчет рамы каркаса здания санаторного типа с учетом пластических деформаций в ригелях (см. пример расчета).
Кроме того, был выполнен расчет для случая, когда сейсмические силы отсутствуют, а также был произведен вариант расчета в соответствии с нормами в целях сопоставления полученных данных с расчетом, выполненным согласно разработанной методике.
При расчете были получены следующие результаты расхода стали:
при расчете рамы, полученном без учета антисейсмических мероприятий, - 10,36 т;
при расчете рамы по главе СНиП II-А.12-69 - 15,65 т;
при расчете по методике, учитывающей пластические деформации, - 14,1 т.
Из этих данных следует, что расход стали на антисейсмические мероприятия при расчете рамы, выполненном по нормам, составляет
15,65 - 10,36 = 5,29 т.
Расход стали на антисейсмические мероприятия при расчете рамы, выполненном по предлагаемой методике, равен:
14,1 - 10,36 = 3,74 т.
Отсюда видно, что учет влияния пластических деформаций в раме дал экономию в расходовании стали на антисейсмические мероприятия
5,29 - 3,74 = 1,55 т,
что составляет:
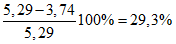 .
.Общая экономия стали в процентах будет:
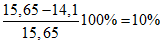 .
.Таким образом, рациональный учет пластических свойств элементов рамной конструкции приводит к некоторой экономии в расходе металла и, самое важное, устраняет опасность хрупких разрушений в узлах, благодаря чему надежность рамных конструкций значительно повышается.
1. Бородин Л.А. Учет энергии неупругих деформаций в расчете конструкций на действие сейсмических сил. - "Строительное проектирование промышленных предприятий", 1969, N 4.
2. Бородин Л.А. Влияние неупругих деформаций на работу сооружений в условиях сейсмических воздействий. - В сб. ЦНИИСК им. В.А. Кучеренко "Сейсмостойкость зданий и инженерных сооружений", вып. 14, 1970.
3. Броуде Б.М. Устойчивость пластинок в элементах стальных конструкций. Изд. министерства строительства предприятий машиностроения. М., 1949.
4. Гвоздев А.А. К расчету конструкций на действие взрывной волны. - "Строительная промышленность", 1943, N 1, 2.
5. Дарбиян С.С. К определению сейсмических сил в сооружениях за пределом упругости. Изд. АН АрмССР, серия техн. наук, т. XIX, 1966, N 6.
6. Карцивадзе Г.Н., Медведев С.В., Напетваридзе Ш.Г. Сейсмостойкое строительство за рубежом. М., Госстройиздат, 1962.
7. Килимник Л.Ш., Лаврентьева Л.Э. Исследование узлов стальных каркасных зданий, строящихся в сейсмических районах. Материалы к Всесоюзному совещанию по сейсмостойкому строительству. Фрунзе, 1971.
8. Корчинский И.Л. Оценка несущей способности конструкций при сейсмическом воздействии с энергетических позиций. - "Бетон и железобетон", 1967, N 2.
9. Корчинский И.Л., Беченева Г.В. Прочность строительных материалов при динамических нагружениях. М., Стройиздат, 1966.
10. Корчинский И.Л., Ржевский В.А., Цепенюк И.Ф. О расчете железобетонных каркасных зданий на сейсмические воздействия с учетом пластических деформаций. - "Бетон и железобетон", 1972, N 1.
11. Моисеев В.И. Устойчивость пластин при внецентренном сжатии и сдвиге за пределом упругости. - "Строительная механика и расчет сооружений", 1971, N 3.
12. Моисеев В.И. Расчет на устойчивость стенок металлических балок и колонн за пределом упругости. - "Строительная механика и расчет сооружений", 1973, N 6.
14. Танабаши Р., Канета К. Экспериментальные исследования пластичности сооружений и коэффициенты пластичности (докл.), Токио, 1966.
15. Уиггинс Дж. (John H. Wiggins), президент фирмы "Д.Х. Уиггинс компани", "Палос-Вердес-Истеэйс" (штат Калифорния). Принцип сбалансированного риска: новый подход к нормам проектирования зданий в сейсмических районах. - "Гражданское строительство инженерных сооружений", август 1972, N 8 (Civil Engineering. The Magasine of Enginured Construction, August 1972, vol. 42, N 8).
16. Хансон Р.Д. Динамическая реакция стальных конструкций в пластической стадии (докл.). Токио, 1966.
17. Хачиян Э.Е. Расчет сооружений на сейсмостойкость с учетом упругопластических деформаций. Изд. АН АрмССР, т. XVII, 1964, N 4
18. Berg G.V., Thomaides S.S. Energy Consuption by Structures in Strong-Moton Earthquakes Proc. SWCEE, v. II.
19. Popov E.P. Performance of Steel Beans and Their Connestions to Columns During Severe Cyclic Lodding Eighth Congress: New Jork, September 9 - 14, 1968.
20. Veletsos A.S., Newmark N.M. Effect of Jnelastic Bahavior on the Response of Simple Systems to Earthquake Proc. SWCEE, v. II.