СПРАВКА
Источник публикации
М.: Стройиздат, 1986
Примечание к документу
Название документа
"Рекомендации по прогнозу устойчивости обвально-оползневых склонов"
"Рекомендации по прогнозу устойчивости обвально-оползневых склонов"
ПО ИНЖЕНЕРНЫМ ИЗЫСКАНИЯМ В СТРОИТЕЛЬСТВЕ
(ПНИИИС) ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО ПРОГНОЗУ УСТОЙЧИВОСТИ ОБВАЛЬНО-ОПОЛЗНЕВЫХ СКЛОНОВ
Рекомендовано к изданию решением секции Научно-технического совета инженерно-геологических исследований ПНИИИС Госстроя СССР.
Обобщены результаты многолетних исследований авторов по вопросам устойчивости оползневых - обвальных склонов и прогнозу изменения устойчивости склонов под воздействием природных и антропогенных факторов. Рассмотрены регионально-геологические и зонально-климатические закономерности (законы), предопределяющие формирование, активизацию и устойчивость оползневых - обвальных склонов, а также рассмотрены методы выполнения ориентировочных и уточненных оценок и прогнозов устойчивости склонов в зависимости от стадии инженерно-геологических изысканий.
Для инженерно-технических работников проектных, строительных, инженерно-изыскательских организаций.
Необходимость разработки Рекомендаций возникла в связи с тем, что оценка устойчивости и прогноз развития оползневых - обвальных склонов слабо освещены в литературе. Уже известные расчетные методы устойчивости оползневых склонов основаны на сильно упрощенных схемах, не учитывают многообразия формирования оползней и обвалов, изменение во времени прочностных свойств зон ослабления массивов пород, влияние антропогенных воздействий на породы склонов.
В Рекомендациях рассмотрены теоретические основы и даны примеры оценок устойчивости прогноза изменения устойчивости оползневых - обвальных склонов различными математическими методами. Рекомендуемые методы хорошо разработаны и апробированы на примере многих построенных и строящихся объектов в нашей стране и за рубежом. Рекомендации - результат 20-летних исследований.
Рекомендации разработаны ПНИИИС Госстроя СССР (канд. геол.-минерал. наук Н.Л. Шешеня при участии доцента ОГУ Ю.Г. Баландина).
ЗАКОНОМЕРНОСТИ (ЗАКОНЫ), ПРЕДОПРЕДЕЛЯЮЩИЕ ФОРМИРОВАНИЕ,
АКТИВИЗАЦИЮ И УСТОЙЧИВОСТЬ ОПОЛЗНЕВЫХ И ОБВАЛЬНЫХ СКЛОНОВ
РЕЧНЫХ ДОЛИН РАВНИННЫХ ОБЛАСТЕЙ
1.1. Условия формирования оползней и обвалов на речных склонах равнинных областей имеют свои отличительные особенности. Они обусловлены значительно меньшей, по сравнению с предгорными областями, интенсивностью новейших и современных тектонических движений структурных блоков данных территорий, весьма низкой их сейсмической активностью, поэтому влиянием сейсмичности на развитие оползней и обвалов на этих склонах можно пренебречь. На устойчивость оползневых и обвальных склонов могут оказывать влияние только антропогенные динамические воздействия типа массовых взрывов, работы механизмов и движения тяжелого транспорта вдоль скоростных магистралей. Склоны рек и оврагов сложены слаболитифицированными породами. Это предопределяет их способность легко размываться под воздействием поверхностных вод; песчаные и супесчаные разности пород часто являются суффозионно неустойчивыми, а глинистые - набухают под влиянием воды с развитием текучепластических деформаций в массиве, разжижения при динамических нагрузках. Характерной особенностью состава дисперсных пород является наличие в них включений известковистых конкреций, кристаллов, друз гипса, пирита, которые при взаимодействии с водой выщелачиваются, способствуя образованию в массивах указанных пород зон ослабления.
1.2. В большинстве случаев поверхности смещения оползней на отмеченных склонах приурочены к слабым глинистым прослоям мягко-, текучепластичной консистенции, к суффозионно неустойчивым прослоям песка или лессовым образованиям, к лигнитизированным прослоям. Перечисленные поверхности смещения имеют горизонтальное или слабонаклонное (в сторону склона) залегание.
1.3. Оползневые склоны речных долин равнинных территорий сформировались в основном в средне-, верхнечетвертичное время. Для него характерна активизация дифференцированных тектонических перемещений земной коры, формирование переуглублений в долинах рек и крупные смещения блоков и пакетов пород со склонов (причем, оползни и обвалы чаще встречаются в пределах подмываемых правобережных склонов). Несмотря на то, что за новейший и современный этап тектонической активизации подвижек земли отмеченные склоны на некоторых участках отступили на несколько десятков километров, они всегда были крутыми и высокими. Урезы рек тогда были на более низких отметках по сравнению с современным врезом. Поэтому на участках, где имели место оползни и обвалы, их накопления в большинстве случаев перекрыты более молодыми современными речными или оползневыми образованиями. В современную эпоху на отмеченных участках склонов резко преобладают повторные смещения пород с захватом древних оползневых накоплений, реже наблюдаются смещения в верхних частях склонов в пределах крутых стенок отрыва древних оползней.
МОРСКИХ ПОБЕРЕЖИЙ РАВНИННЫХ ОБЛАСТЕЙ
1.4. Особенности формирования оползневых - обвальных склонов морских побережий равнинных областей обусловлены их структурно-тектоническими условиями. Данные области располагаются в пределах ровных платообразных приморских низменностей, которые испытывали в новейший и современный этап неравномерные во времени и в пространстве дифференцированные перемещения структурных блоков. Современные скорости опусканий, например, блоков Черноморской впадины, изменяются от 1,0 до 10 мм/год. Опускание приморских участков поверхности земли вызывает активизацию процессов абразии, интенсивность которых больше на участках с большей скоростью опусканий.
1.5. Береговая и донная абразия волнами, течением и льдом (ледовая коррозия) выражается посредством размыва пород берегового склона, морского дна и гряд выдавливания. Средняя скорость донного размыва в пределах, например территории г. Одессы, изменяется от 0,2 до 4,0 см/год. Скорость размыва берега на разных участках, сложенных различными по прочности литолого-генетическими комплексами пород, колеблется от 0,5 до 6,0 м/год. На участках с постоянной интенсивной активизацией современных оползневых смещений скорость абразии больше или равна 0,8 м/год; при периодически повторяющихся подвижках пород на склонах она в среднем равна 0,65 м/год, а на участках со слабыми современными смещениями скорость абразии не превышает 0,5 м/год. Установлена отчетливая эмпирическая зависимость между скоростью смещения со склонов оползней и скоростью размыва пород в их языковой части с корреляционным отношением 0,95.
1.6. Абразия относится к числу основных факторов, вызывающих формирование новых и активизацию ранее образовавшихся, но находящихся в состоянии временной стабилизации, оползней на морских склонах. Процессы абразии способствуют образованию уступов в нижних частях склонов и, как следствие, к перераспределению напряжений в приповерхностных частях массивов пород, больших градиентов напряжений. Их величины, например, в породах склонов Одесского побережья Черного моря, могут достигать значений 10 - 12 МПа. Поэтому при прочности глинистых пород на раздавливание 4 - 5 МПа образуются зоны разрушения пород, их пластические деформации и выдавливание.
1.7. Значительное влияние на устойчивость оползневых - обвальных склонов оказывает донная абразия. Установлено, что при высоте волны 0,5 м смываются пески, при шторме силой 5 баллов - галечники. При волнении оползневые гряды, сложенные плотными глинами, исчезают в течение суток, а при штиле - в течение не скольких суток. В профиле дна моря следы гряд, образовавшихся при единовременных смещениях пород со склонов, уничтожаются за 3 - 4 мес.
1.8. Лиманная абразия оказывает значительно меньшее влияние на формирование оползней-обвалов и устойчивость склонов. Она развита на участках, где урез воды сопрягается с относительно высокими (более 15 м) и крутыми (более 20°) склонами лиманов. Эти процессы активизируются при высоких уровнях воды в лиманах, вызывая усиление склоновых процессов.
1.9. Неравномерные дифференцированные новейшие и современные тектонические перемещения земной коры в приморских равнинных областях происходят по сериям крупных глубинных разломов и разрывов. Эти перемещения создали ступенчатые в плане профили склонов и рельефа с максимальными перепадами высот между отдельными платообразными поверхностями древних пенепленов в пределах разных структурных блоков около 40 - 50 м. При прочих равных условиях максимальное количество оползней и обвалов на склонах данных областей встречены на участках с высотой склонов 40 м и более. На склонах высотой 15 - 35 м современные оползни-обвалы развиты в меньшей степени.
РЕЧНЫХ ДОЛИН ПРЕДГОРНЫХ ОБЛАСТЕЙ
1.10. Территории предгорных областей включают в себя краевые части древних платформ и предгорные прогибы, вовлеченные на новейшем этапе в интенсивные тектонические глыбово-блоковые перемещения со скоростью, например, в Кодрах Молдавской ССР до 10 мм/год. Разнонаправленные движения тектонических блоков вызывают на этих территориях интенсивное развитие процессов эрозии, формирование высоких (до 300 м) и довольно крутых (в среднем 25 - 35°) склонов. Амплитуды максимальных поднятий этих территорий составляют 350 - 400 м, опусканий - 500 м. Участками наиболее сильного проявления оползневых - обвальных процессов являются структурные блоки, имеющие в новейший этап максимальные скорости поднятия. Данные процессы имеют также большое распространение на границе смежных структурно-тектонических блоков, испытывающих либо разнонаправленные, либо однонаправленные, но разной скорости, движения.
1.11. Отмеченные территории характеризуются высокой активностью и силой землетрясений. Так, например, для территории Кодр Молдавской ССР одно 8 - 9-балльное землетрясение происходит в среднем один раз в 17 лет; одно 7-балльное - в 12,5 лет, 6-балльное - в 8 лет, менее шести баллов - 1 - 3 раза в год. Упругие сейсмические волны действуют на породы склонов как силовой фактор. Он может вызвать плывунные или тиксотропные процессы в породах, предрасположенных к их развитию, а также вытекание отмеченных пород со склонов и откосов. Сейсмичность приводит также к резкому снижению прочности структурных связей за счет увеличения трещиноватости массива пород. Супесчано-глинистые или песчано-глинистые элювиальные образования, имеющие на территориях рассматриваемых областей большое развитие и значительные мощности (до 25 - 30 м), обладают малыми величинами акустической жесткости. При землетрясениях такие образования имеют большие скорости колебания частиц, достигающих 100 см/с, что может вызвать оползни в данных грунтах.
1.12. Основными зонами смещения и отчленения в массивах пород предгорных областей являются крупные тектонические трещины, зоны рассланцевания и повышенной трещиноватости разрывов, литогенетические трещины. Оползни и обвалы приурочены к присклоновым зонам выветривания и разгрузки напряжений, суммарная мощность которых на склонах речных долин (Кодры Молдавской ССР) среднечетвертичного вреза достигает в среднем 20 м.
ДОЛИН ГОРНО-СКЛАДЧАТЫХ ОБЛАСТЕЙ
1.13. Склоновые гравитационные процессы в горно-складчатых областях представлены чаще в сложных переходных формах, что обусловлено большой крутизной и высотой речных склонов. При зарождении и проявлении отмеченных процессов практически всегда наблюдается начальное скользящее движение пород на склонах l, затем их обрушение, раскол и скатывание на различные расстояния L. В зависимости от величины соотношения длин скользящего (оползневого) и обвального L движений пород со склонов рекомендуется выделять следующие склоны:
обвального сноса, когда отношение l x 100%/(l + L) <= 10%; возможные обвальные накопления на пологих частях склонов представлены неотсортированным материалом. Для склонов, вскрывающих породы с прочными кристаллизационными структурными связями, эти накопления состоят из глыб различных размеров, перемешанных со щебнем;
оползнеобвального сноса при отношении 10% < l x 100%/(l + L) <= 90%; в оползнеобвальных накоплениях могут присутствовать отдельные пакеты и блоки пород с сохранившейся исходной текстурой;
оползневого сноса, если отношение l x 100%/(l + L) > 90%. Для этих склонов характерны накопления в виде блоков и пакетов пород, более трещиноватых и раздробленных, чем в коренном залегании, с гнездами щебня, дресвы или суглинистого материала.
1.14. Основными зонами ослабления массивов пород являются разрывные тектонические нарушения различных порядков (масштабов), серии экзогенных трещин выветривания, бортового отпора и разгрузки. Объемы склоновых гравитационных процессов во многом определяются порядком разрывных нарушений, вскрытых склонами, их ориентировкой по отношению к простиранию склонов.
1.15. В зонах влияния глубинных разломов I - II порядков, субпараллельных склону (ограничивающих крупные структурно-формационные зоны, протяженностью более 10 км, шириной зоны тектонического изменения пород более 1 км, с суммарной амплитудой неотектонических перемещений более 2 км), оползни, оползни-обвалы и обвалы могут формироваться в пределах присклоновых зон слабой разгрузки и слабого линейного выветривания с глубиной захвата до 250 м. Объемы единовременных смещений здесь достигают нескольких сотен миллионов м3. Смещения приурочены к верхним частям склонов высотой не менее 1000 м, имеющих олигоцен-нижнечетвертичный или среднечетвертичный возраст. В смещение могут быть вовлечены и водораздельные части склонов. Поводом к их образованию служат землетрясения в 8 - 10 баллов, имеющие в зонах глубинных разломов большую повторяемость  . Частость указанных явлений невелика и составляет около 0,5% общего числа зарегистрированных в горных районах обрушений.
. Частость указанных явлений невелика и составляет около 0,5% общего числа зарегистрированных в горных районах обрушений.
 . Частость указанных явлений невелика и составляет около 0,5% общего числа зарегистрированных в горных районах обрушений.
. Частость указанных явлений невелика и составляет около 0,5% общего числа зарегистрированных в горных районах обрушений.1.16. В зонах влияния разрывов III - IV порядков, субпараллельных склону (протяженностью до 10 км, шириной зоны тектонического изменения пород в первые сотни метров и суммарной амплитудой неотектонических перемещений до 2 км), обвально-оползневые процессы развиваются в зонах интенсивной разгрузки напряжений и выветривания пород. Глубина захвата ими пород данных зон достигает в среднем 60 м. Объемы их единовременных обрушений изменяются от нескольких сотен тысяч до первых миллионов м3. Они также приурочены к верхним частям склонов олигоцен-нижнечетвертичного или среднечетвертичного врезов рек. При обрушении блоки, пакеты пород иногда падают на обломочные обвально-осыпные или пролювиальные образования, расположенные на более низких и пологих частях склонов, вызывая осовы объемом в первые миллионы м3.
1.17. Обвально-оползневые процессы, формирующиеся в узлах пересечения тектонических разрывов III - IV или глубинных разломов I - II порядков, приурочены к зонам интенсивной разгрузки напряжений и выветривания пород. Они могут иметь глубину захвата до 60 м и объемы обрушений до первых миллионов м3. В зонах влияния отмеченных выше нарушений, субперпендикулярных склону, а также в зонах влияния пересекающихся между собой разноориентированных разрывов V - VI порядков разной крутизны (протяженностью до 1 км, шириной зоны тектонического изменения пород до нескольких десятков метров и суммарной амплитудой неотектонических перемещений до нескольких сотен метров) смещения и обрушения пород со склонов приурочены к зонам интенсивно выветрелых и полностью разгруженных пород. Мощность захвата ими пород изменяется от 1 - 2 до 20 м. По объему здесь преобладают обрушения в тысячи и десятки тысяч м3.
1.18. Склоны обвального, оползнеобвального и оползневого сноса горно-складчатых областей имеют длительную историю своего формирования. Активизация развития рассматриваемых процессов тесно связана с основными этапами активизации дифференцированных неотектонических перемещений земной коры:
для указанных областей Советского Союза первый этап активизации перемещений тектонических блоков начался в верхнем олигоцене. Это отразилось в интенсивном эрозионном расчленении рельефа горно-складчатых областей с образованием в межгорных впадинах мощных толщ грубообломочных накоплений в плиоцен-нижнечетвертичное время. Средняя величина речного вреза в пределах территорий с максимально поднятыми в современном рельефе структурно-тектоническими блоками составляла 400 м, крутизна склонов - 35 - 40°. Склоны речных долин имели вогнутый в плане профиль с редкими обрывами. Они были относительно устойчивыми;
второй этап активизации тектонических подвижек начался во вторую половину нижнечетвертичного времени. Интенсивность врезов рек в этот этап характеризуется как "средняя", имея глубину вреза для территорий максимально поднятых блоков порядка 350 м. Склоны долин данного вреза имели ступенчато-вогнутый (вогнутость внизу) в плане профиль и среднюю крутизну 40°. Для них характерны небольшие по объему и интенсивности оползни и обвалы;
среднечетвертичное время для горно-складчатых областей характеризуется резкой активизацией дифференцированных тектонических перемещений (с перекосом) земной коры с усиленной и весьма усиленной интенсивностью эрозионного вреза (третий и четвертый этапы активизации). Его глубина за это время достигает 700 м. Склоны речных долин имели выпуклые и ступенчато-выпуклые в плане профили при средней крутизне 65 - 70°. Для данных этапов активизации типичны грандиозные (до несколько сот миллионов м3) единовременные смещения и обрушения пород со склонов при максимальной, для всего неотектонического периода, их интенсивности. Подобные обрушения пород способствовали образованию многочисленных запрудных озер в пределах территорий горных областей;
пятый этап активизации новейших тектонических перемещений земной коры и формирования склоновых гравитационных процессов приходится на верхнечетвертичное время. Интенсивность речных врезов в этот этап оценивается категорией "весьма усиленная", а их величина достигает 150 м. Средняя крутизна склонов рек равна 75°. С пятым этапом связаны грандиозные и крупные (сотни тысяч м3) обрушения, которые на многих участках горных речных долин создали запрудные озера или обусловили смещения речных русел, а также образование в руслах рек переуглублений. Современный (весьма усиленный) врез на многих участках горных рек размывает свое древнее верхнечетвертичное русло, выполненное аллювиальными, обвально-оползневыми и пролювиальными образованиями. Склоны современного вреза (шестой этап) достигают 50 м высоты при крутизне 75 - 80°. Для данного этапа развития рельефа горно-складчатых областей характерно усиление формирования склоновых процессов.
1.19. Разные по величине тектонические перемещения структурных блоков обусловили ступенеобразное их положение в современном рельефе. Поверхности выравнивания данных блоков имеют перекосы с разницей в высотах в пределах одного блока до 300 м. Роль неотектонических движений в образовании оползней, оползнеобвалов и обвалов проявляется в их приуроченности к структурно-тектоническим блокам с разной интенсивностью и величиной поднятий в отмеченные выше этапы активизации тектонических перемещений.
1.20. Горно-складчатые области в пределах осваиваемых территорий Советского Союза относятся к 7 - 10-балльной зоне с высокой сейсмической активностью  и повторяемостью сильных землетрясений. Период землетрясений 14, 15 и даже 16-го энергетических классов равен 80 - 200 лет. Эпицентры землетрясений, произошедших за последние 40 лет, приурочены к активно проявляющимся в новейшее и современное время тектоническим разломам, разрывам и узлам их пересечения. Установлена миграция во времени землетрясений по простиранию указанных нарушений. Участки расположения ниш и поверхностей отрыва грандиозных (сотни миллионов м3) и крупных (первые миллионы и сотни тысяч м3) обвалов, оползнеобвалов, оползней в пространстве увязываются с направлением осей растяжения, которые получены по слабым и сильным землетрясениям. При землетрясениях в горно-складчатых областях возникают резкие внезапные перераспределения напряжений, которые в ослабленных зонах массивов пород нередко превышают по величине прочность самих пород и служат поводом к возникновению крупных и грандиозных обвалов и оползней. При прохождении упругих сейсмических волн через обводненные заполнители широких трещин бортового отпора или разгрузки возможны гидравлические удары (обратный сейсм), развитие плавунных или тиксотропных процессов в глинисто-суглинистом и супесчаном заполнителе.
и повторяемостью сильных землетрясений. Период землетрясений 14, 15 и даже 16-го энергетических классов равен 80 - 200 лет. Эпицентры землетрясений, произошедших за последние 40 лет, приурочены к активно проявляющимся в новейшее и современное время тектоническим разломам, разрывам и узлам их пересечения. Установлена миграция во времени землетрясений по простиранию указанных нарушений. Участки расположения ниш и поверхностей отрыва грандиозных (сотни миллионов м3) и крупных (первые миллионы и сотни тысяч м3) обвалов, оползнеобвалов, оползней в пространстве увязываются с направлением осей растяжения, которые получены по слабым и сильным землетрясениям. При землетрясениях в горно-складчатых областях возникают резкие внезапные перераспределения напряжений, которые в ослабленных зонах массивов пород нередко превышают по величине прочность самих пород и служат поводом к возникновению крупных и грандиозных обвалов и оползней. При прохождении упругих сейсмических волн через обводненные заполнители широких трещин бортового отпора или разгрузки возможны гидравлические удары (обратный сейсм), развитие плавунных или тиксотропных процессов в глинисто-суглинистом и супесчаном заполнителе.
 и повторяемостью сильных землетрясений. Период землетрясений 14, 15 и даже 16-го энергетических классов равен 80 - 200 лет. Эпицентры землетрясений, произошедших за последние 40 лет, приурочены к активно проявляющимся в новейшее и современное время тектоническим разломам, разрывам и узлам их пересечения. Установлена миграция во времени землетрясений по простиранию указанных нарушений. Участки расположения ниш и поверхностей отрыва грандиозных (сотни миллионов м3) и крупных (первые миллионы и сотни тысяч м3) обвалов, оползнеобвалов, оползней в пространстве увязываются с направлением осей растяжения, которые получены по слабым и сильным землетрясениям. При землетрясениях в горно-складчатых областях возникают резкие внезапные перераспределения напряжений, которые в ослабленных зонах массивов пород нередко превышают по величине прочность самих пород и служат поводом к возникновению крупных и грандиозных обвалов и оползней. При прохождении упругих сейсмических волн через обводненные заполнители широких трещин бортового отпора или разгрузки возможны гидравлические удары (обратный сейсм), развитие плавунных или тиксотропных процессов в глинисто-суглинистом и супесчаном заполнителе.
и повторяемостью сильных землетрясений. Период землетрясений 14, 15 и даже 16-го энергетических классов равен 80 - 200 лет. Эпицентры землетрясений, произошедших за последние 40 лет, приурочены к активно проявляющимся в новейшее и современное время тектоническим разломам, разрывам и узлам их пересечения. Установлена миграция во времени землетрясений по простиранию указанных нарушений. Участки расположения ниш и поверхностей отрыва грандиозных (сотни миллионов м3) и крупных (первые миллионы и сотни тысяч м3) обвалов, оползнеобвалов, оползней в пространстве увязываются с направлением осей растяжения, которые получены по слабым и сильным землетрясениям. При землетрясениях в горно-складчатых областях возникают резкие внезапные перераспределения напряжений, которые в ослабленных зонах массивов пород нередко превышают по величине прочность самих пород и служат поводом к возникновению крупных и грандиозных обвалов и оползней. При прохождении упругих сейсмических волн через обводненные заполнители широких трещин бортового отпора или разгрузки возможны гидравлические удары (обратный сейсм), развитие плавунных или тиксотропных процессов в глинисто-суглинистом и супесчаном заполнителе.1.21. При формировании речной долины в горно-складчатых областях особо интенсивно проявляются процессы разгрузки естественных напряжений, выветривания, выщелачивания и суффозии в породах приповерхностных частей массивов. С данными процессами парагенетически связаны оползни, оползни-обвалы и обвалы. Они обусловливают также образование таких четырех присклоновых зон:
весьма интенсивного выветривания и разгрузки естественных напряжений. Породы здесь находятся полностью в разгруженном состоянии;
интенсивного выветривания по трещинам и разгрузки. В породах зоны развиты пониженные (по сравнению с геостатическими) напряжения, в том числе отрицательные касательные напряжения;
слабой разгрузки напряжений и слабого выветривания по трещинам. В породах зоны развиты пониженные напряжения;
слабого линейного выветривания по крупным тектоническим трещинам, разрывам, разломам. В породах зоны обособляются подзоны повышенных и нормально возрастающих напряжений.
1.22. Мощность и степень экзогенного изменения пород в перечисленных зонах разная на склонах разного возраста. Развитие процессов выветривания определяется по следующим основным закономерностям:
интенсивность процесса выветривания зависит от минералогического состава, термодинамических и физико-химических условий образования горных пород, от степени их трещиноватости и обводнения, от климатических условий и воздействия организмов, от продолжительности действия агентов выветривания и условий сноса продуктов выветривания;
скорость процессов выветривания массивов горных пород одинакового минералогического состава и состояния, образованных при одинаковых термодинамических и физико-химических условиях, определяется зонально-климатическими условиями территории;
тип коры выветривания определяется климатическими, тектоническими условиями и вещественным составом пород.
Прослеживается устойчивая связь между приуроченностью оползней, оползней-обвалов, обвалов и мощностью, степенью выветривания пород, характером и величинами распределения естественных напряжений в приповерхностных зонах (см. п. 1.21). Эта связь наиболее отчетливо проявляется в пределах склонов горно-складчатых областей на участках, где склонами вскрыты породы с прочными кристаллизационными структурными связями. Выявленная связь используется для прогнозов образования отмеченных процессов.
ПОБЕРЕЖИЙ ГОРНО-СКЛАДЧАТЫХ ОБЛАСТЕЙ
1.23. Формирование оползневых - обвальных склонов морских побережий в горно-складчатых областях также имеет свои отчетливо выраженные специфические особенности. Здесь особо резко проявляется связь между интенсивностью, режимом разнонаправленных неотектонических дифференцированных перемещений и объемами, интенсивностью оползней, оползнеобвалов и обвалов. Установлено, что активизация оползневых - обвальных смещений и обрушений пород со склонов приурочена к этапам активизации дифференцированных разнонаправленных тектонических перемещений структурных блоков в пределах прибрежных морских территорий.
1.24. В пределах рассматриваемых областей различаются пять этапов активизации неотектонических подвижек:
первый этап приурочен к верхненеогеновому или к среднечетвертичному времени. Амплитуда поднятий приморских структурных блоков Южного берега Крыма составила в этот этап 120 - 400 м. Высокие и крутые склоны в это время осложнялись крупными и выдержанными депрессиями, с которыми связаны оползни большой интенсивности развития и грандиозного объема. Суммарные мощности оползневых - обвальных накоплений в основании Черноморских склонов достигали 120 м;
второй этап активизации развития оползневых - обвальных склонов приходится на первую половину верхнечетвертичного времени, а для территорий, где первый этап начался в верхнем неогене, - на первую половину нижнечетвертичного времени. Амплитуда поднятий прибрежных структурных блоков составила около 60 м, а мощность оползней-обвалов данного возраста в основании склонов порядка 55 м;
третий этап активизации отмечен во второй половине верхнечетвертичного, реже - в первой половине среднечетвертичного времени. Амплитуда поднятий структурных блоков за этап составляла в среднем 50 м, мощность оползневых - обвальных накоплений - 30 м;
четвертый этап развития склонов начинается на большинстве приморских территорий горно-складчатых областей в первую половину голоценового времени;
пятый - повсеместно во вторую половину голоцена.
1.25. Дифференцированные разнонаправленные перемещения прибрежных структурных блоков создали ступенчатый в плане профиль склонов: крутые части (средние уклоны порядка 30°) сменяются пологими (уклоны 3 - 6°). Наибольшая интенсивность оползней и обвалов приурочена к крутым участкам склонов. За счет детрузивного воздействия гравитационных смещений пород с крутых частей начинают формироваться оползни и на пологих участках склонов.
1.26. Оползневые - обвальные склоны морских побережий горно-складчатых областей сформированы в зонах влияния глубинных разломов или разрывов, по которым происходит опускание морских структурных блоков и поднятие прибрежных блоков. Наибольшая интенсивность проявления оползнеобвальных процессов отмечается на участках, где морские склоны вскрывают пересекающиеся между собой разрывные нарушения, субпараллельные и субперпендикулярные по отношению к простиранию склонов.
1.27. Для горно-складчатых областей морских побережий СССР характерна высокая сейсмическая активность. Это, как правило, зоны 7 - 8-балльных землетрясений. Особые грунтовые условия названных территорий (зоны разрывных нарушений, большие мощности разновозрастных и в разной степени обводненных оползнеобвальных накоплений в крупных эрозионных депрессиях) повышают их сейсмичность на отдельных участках на 1 - 2 балла по сравнению с фоновой. Максимальный эффект от сейсмических упругих волн наблюдается при условии совпадения по времени землетрясений силой 6 и более баллов с периодами затяжных или ливневых водообильных дождей и морских штормов более 4 баллов. Причем установлен эффект запаздывания между временем проявления обвалов, оползней и временем действия перечисленных факторов, достигающий двух лет.
1.28. Значительное влияние на развитие обвально-оползневых склонов названных областей оказывает волновой режим моря. В историческом плане донный размыв пород незначительный на участках, где оползни смещались к более низкому уровню моря; здесь преобладает размыв оползневых накоплений в языках оползней, за счет чего образовались клифы высотой от 3 - 16 до 30 - 60 м и крутизной 50 - 70°. Для всех обвально-оползневых склонов морских побережий горно-складчатых областей типичными являются следующие признаки: практически полное отсутствие или же наличие узких (5 - 15 м) пляжей, вдольбереговой перенос пляжевого материала и приглубый берег. Эти особенности природных условий создают благоприятные возможности для размыва пород берегов штормовыми волнами с балльностью 4 и более. Абразия вызывает активизацию развития склоновых процессов только в прибрежной полосе глубиной до 100 м (по нормали от поверхности склона).
1.29. Величина и характер влияния климатических условий на формирование оползней-обвалов данных областей имеет резко выраженную вертикальную зональность. В нижних частях склонов эти условия проявляются в формировании волнового режима моря. Количество осадков, приходящееся на единицу площади, с высотой изменяется (в сторону увеличения) более чем в два раза, а это создает разные условия дополнительного увлажнения пород склонов, пригрузки склонов зимой от больших скоплений снега в понижениях.
ФОРМИРОВАНИЯ ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ
1.30. Несмотря на рассмотренные в пп. 1.1 - 1.29 отличительные особенности образования оползней-обвалов на склонах равнинных, предгорных и горно-складчатых областей, имеется ряд эмпирически установленных регионально-геологических и зонально-климатических закономерностей, которые имеют всеобщий характер. Поэтому такие закономерности с полным основанием могут быть названы законами развития и активизации оползней, обвалов, оползней-обвалов. Соответственно, они регламентируют не только условия формирования данных процессов, но и условия потери склонами устойчивости на участках, где проявляются эти процессы. Поэтому названные законы могут рассматриваться в качестве критериев прогноза устойчивости оползневых - обвальных склонов. Основные из них сформулированы в пп. 1.31 - 1.44.
1.31. Оползни, оползни-обвалы, обвалы парагенетически связаны с определенными литолого-генетическими и петрографическими комплексами пород.
На склонах правого берега р. Днепр в пределах территории г. Киева Демчишиным М.Г. установлено следующее: к верхнечетвертичным лессовым образованиям приурочено около 37% оползней и обвалов, зафиксированных в последние 100 лет; к нижнечетвертичным бурым глинам - 22%; к нижне-, верхненеогеновым пестрым глинам - 13%; к среднечетвертичным моренам и пескам харьковской свиты - по 7%; к нижнечетвертичным пресноводным суглинкам - 5%; к нижненеогеновым отложениям полтавской свиты - 4%; к среднечетвертичным надморенным и подморенным пескам - по 2%; к спондиловым глинам среднего палеогена киевской свиты - около 1%. В нижнекаменноугольных и средне-, верхнедевонских известняках и доломитах, слагающих высокие (до 2000 м) и крутые (в среднем 65°) склоны долины р. Нарын (Киргизская ССР) из 600 изученных оползнеобвальных склонов на долю оползней приходится 26%, оползнеобвалов - 53%, обвалов - 7%. В глинистых метаморфизованных сланцах, ритмично переслаивающихся с туфогенными конгломератобрекчиями и песчаниками каракольской свиты нижнего карбона, резко преобладают оползни в приповерхностной зоне выветривания и разгрузки пород; на их долю приходится около 6%. Обвалы здесь составляют около 2%. В песчаниках и конгломератобрекчиях келематинской свиты верхнего карбона обвалы составляют 2%; оползни-обвалы - 3%, оползни - 1%.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
1.33. Интенсивность проявления и типы оползней по механизму смещения определяются вещественным и минеральным составом пород (и их примесей), слагающих склоны. Закон имеет следствия:
при взаимодействии с водой в глинистых грунтах монтмориллонит-гидрослюдистого состава твердой консистенции (в природных условиях), содержащих более 5% примесей пирита, хорошо разложившегося органического вещества или гипса, развиваются деформации незатухающей ползучести с образованием на склонах и откосах строительных, дорожных и иных выемок оползней скольжения и выдавливания;
глинистые грунты Na-монтмориллонитового состава при взаимодействии с водой способны вытекать со склонов и откосов с образованием оползней течения и выплывания;
при взаимодействии со щелочными или кислыми водами в глинистых грунтах любого минералогического состава, содержащих более 5% примесей гипса, пирита или хорошо разложившегося органического вещества, развиваются деформации незатухающей ползучести с образованием на склонах или откосах оползней выдавливания и скольжения;
в пределах склонов, сложенных водонасыщенными тонко-, мелкозернистыми и пылеватыми песками, содержащими 5% и более глинистых частиц монтмориллонитового состава, формируются оползни внезапного разжижения. Их активизация может быть вызвана незначительными по величине антропогенными статическими и динамическими нагрузками на породы склонов;
лессы и лессовидные образования при взаимодействии с водой легко размокают, размываются, обладают проселочными свойствами с образованием на склонах и откосах просадочных оползней и оползней течения;
интенсивность развития просадочных оползней увеличивается на участках склонов, где лессы содержат горизонты погребенных почв;
в водонасыщенных дисперсных грунтах с защемленными газообразными соединениями образуются на склонах и откосах оползни выплывания и внезапного разжижения;
сыпучие слюдистые разнозернистые пески являются суффозионно-неустойчивыми, легко размываются поверхностными водами с образованием на склонах и откосах суффозионных оползней и оползней течения;
элювиальные глинистые грунты с низкой гидрофильной способностью и малой пластичностью способны переходить из устойчивого твердого состояния в разжиженное текучее при влажности 18 - 22% с образованием оползней потоков;
дисперсные грунты с карбонатными, сульфатными или железистыми соединениями в приконтактных с подземными водами зонах интенсивно выщелачиваются с образованием в приповерхностных частях склонов зон ослабления и, как следствие, оползней скольжения.
1.33. Интенсивность развития оползней, оползней-обвалов, обвалов зависит от интенсивности и знака неотектонических перемещений отдельных участков земной коры (структурных блоков). Неотектонические движения приводят к увеличению общей раздробленности массивов пород при активизации древних (соскладчатых) или образовании новых (постскладчатых) разрывных нарушений, к усилению (или ослаблению) процессов эрозии и абразии. В результате изменяются величины и характер распределения естественных напряжений, прочностные и фильтрационные свойства массивов пород, их обводненность. Эти напряжения в ослабленных зонах могут и часто превышают по величине прочность самих пород. Таким образом создаются условия для формирования или образования оползней, оползней-обвалов, обвалов. Установлено, что в пределах равнинных, предгорных и горно-складчатых областей около 60% рассматриваемых процессов, при прочих равных условиях, приходится на максимально поднятые в современном рельефе (для региона) структурные блоки; только 6% этих явлений зафиксировано в пределах наименее поднятых блоков. Причем, в первом случае объемы оползней-обвалов составляют сотни тысяч и миллионы м3, а во втором - основная масса обвально-оползневых накоплений имеет объемы тысячи, десятки тысяч м3. Структурные блоки во времени и в пространстве испытывают неравномерные, импульсные, дифференцированные перемещения, а их древние платообразные поверхности выравнивания имеют перекосы (см. пп. 1.18, 1.19). Эта особенность неотектонических перемещений отчетливо отражается в интенсивности развития оползней, оползнеобвалов, обвалов в пределах всех изученных регионов Советского Союза и особенно в предгорных и горно-складчатых областях (см. пп. 1.10 - 1.29). Она сформулирована в двух следствиях закона (см. п. 1.33):
периодам резкой активизации восходящих неотектонических перемещений структурных блоков земной коры соответствуют периоды резкой активизации развития оползневых, обвально-оползневых, обвальных процессов;
максимальное количество оползней, оползней-обвалов, обвалов приурочено к участкам склонов, развитых в пределах структурно-тектонических блоков с максимальной скоростью новейших поднятий; на границе двух смежных тектонических блоков, испытывающих либо разнонаправленные, либо однонаправленные, но с разной скоростью движения; на участках перекосов блоков.
1.34. Максимальные объемы и интенсивность гравитационных процессов на склонах, сложенных дисперсными породами и расположенных вне эпицентра землетрясений, приурочены, при прочих равных условиях, к участкам, где подземные воды залегают на глубине менее 10 м, а упругие сейсмические волны подходят к поверхности земли под углом 30 - 60°. Большую роль в проявлении силы сейсмического толчка играют инженерно-геологические условия территории. Обводненные грунты имеют большее приращение балльности (по сравнению с фоновой для региона), чем грунты необводненные. В пределах верхней 10-метровой толщи повышение уровня подземных вод до 4 м от поверхности склона вызывает повышение балльности на 0,5 балла в песчаных, супесчаных и глинистых грунтах; если воды залегают на глубине 1 м - на 1 балл. В районе эпицентра сильных землетрясений (более 6 баллов) при подходе сейсмических волн к поверхности склонов под углом более 60° сила сейсмического воздействия на породы склонов будет так велика, что влияние инженерно-геологических условий на устойчивость склонов может уже не учитываться.
1.35. Объемы и интенсивность обвально-оползневых процессов на склонах, сложенных породами с прочными кристаллизационными связями, при прочих равных условиях, зависят от направления растягивающих напряжений, возникающих в массивах пород при землетрясениях.
Для условий долины р. Нарын (Киргизская ССР) установлено, что во время 8-балльного землетрясения 1946 г. обвал объемом 1,8 млн. м3 произошел на участке, где направление оси растягивающих напряжений нормально к простиранию склона; здесь же образовался осов объемом в 5,2 млн. м3. Обвалы, оползни-обвалы, оползни объемами до 200 тыс. м3 произошли на участках, где указанные оси напряжений составляют со склоном угол 40 - 60°; на участках, где они имеют угол менее 40°, возникли многочисленные малые по объему обрушения пород со склонов.
1.36. Интенсивность, объемы и типы поверхностей отчленения и смещения оползней, оползней-обвалов, обвалов в прочных трещиноватых породах зависят от порядка разрывных нарушений и их ориентировки по отношению к простиранию склонов. Типы поверхностей отчленения и смещения предопределяют характер распределения и величины напряжений на опорной площади обвально-оползневого блока пород, условия его развития и механизм развития начальных деформаций. Трещины (или иные зоны ослабления массивов пород), ограничивающие блоки пород, по их роли в устойчивости этих блоков разделяются на трещины отчленения и смещения. К первым относятся те из них, которые имеют угол падения более 60°, ко вторым - 60° и меньше, а устойчивость оценивается прочностью пород на срез. Поверхности ослабления, у которых угол между их простиранием и направлением склона равен 0 - 30°, называются тыловыми (при углах падения более 60°) или подошвенными (при углах падения 60° и меньше); при больших углах они считаются боковыми отчленяющими. Закон имеет два следствия:
объемы оползней, оползней-обвалов и обвалов, формирующихся в зонах влияния разрывных нарушений, субпараллельных склону, при прочих равных условиях, зависят от среднего расстояния между трещинами - сместителями разрывов;
объемы оползней, оползнеобвалов, обвалов, формирующихся в зонах влияния разрывных нарушений, при прочих равных условиях, зависят от углов падения трещин, отчленяющих блоки пород от основного массива.
1.37. Подавляющее количество оползней, оползней-обвалов, обвалов формируется в приповерхностной зоне весьма интенсивного выветривания и разгрузки пород. Следует подчеркнуть, что около 84% оползней-обвалов (из 1600 изученных в различных регионально-геологических и зонально-климатических условиях) образовались в регламентируемой законом зоне. Прослежены четкие зависимости интенсивности и объемов оползней-обвалов от возраста геоморфологических элементов склонов. Эти региональные и зонально-климатические закономерности сформулированы таким образом:
максимальное количество оползней, оползней-обвалов, обвалов приурочено к склонам, сформировавшимся во второй половине среднечетвертичного времени;
интенсивность проявления оползней, оползней-обвалов, обвалов, сформированных в приповерхностных зонах выветривания пород и разгрузки напряжений, зависит от глубины экзогенного изменения пород (заполнителей) в трещинах отчленения и смещения блоков (и пакетов) пород;
объемы оползней, оползней-обвалов и обвалов, сформированных в приповерхностной зоне весьма интенсивного выветривания пород и разгрузки напряжений (см. п. 1.21) и имеющих одинаковый генетический тип и крутизну падения поверхностей отчленения (и смещения), зависят от высоты и крутизны частей склонов, откуда происходят обрушения пород.
1.38. Поверхности смещения оползней и оползней-обвалов водосодержащих грунтов, при прочих равных условиях, формируются на участках склонов, где подземные воды имеют повышенное, по сравнению с другими участками, содержание сульфатных соединений и свободной углекислоты; низкая минерализация поровых вод грунтов на контакте со слабоминерализованными горизонтами подземных вод является причиной интенсивного выщелачивания пород, резкого снижения их прочности и образования поверхностей смещения оползней или оползней-обвалов; поверхности смещения и отчленения оползней, оползней-обвалов, обвалов в массивах трещиноватых пород формируются по благоприятно ориентированным по отношению к склонам трещинам, сместителям разрывов и разломов, а также частично по межтрещинным целикам. В дополнение к п. 1.36 следует отметить, что так называемая "малая трещиноватость" пород (образованная тонкими литогенетическими, тектоническими, экзогенными и иными первичными трещинами) предопределяет образование на склонах небольших по объему обвалов и осыпания обломков пород.
1.39. Прогрессирующее во времени увеличение скорости роста поверхностей ослабления в массивах пород происходит при определенном, пропорционально изменяющемся во времени, напряженном состоянии массива.
1.40. Карбонатные, сульфатные и железистые соединения в подземных водах на участках их выхода на поверхность склонов, сложенных дисперсными породами, образуют приповерхностные зоны кольматации пород, локальные подпоры вод и являются причиной образования внезапных катастрофических оползней прорыва.
1.41. Интенсивность проявления и объемы приповерхностных оползней типа оплывин, сплывов, потоков, при прочих равных условиях, определяются климатическими условиями территории. Необходимо отметить, что 80% приповерхностных оползней типа сплывов, оплывин, потоков, зафиксированных за последние 100 лет в г. Киеве, связаны с продолжительными водообильными дождями, такими как: в 1764, 1826, 1839, 1844, 1846, 1848, 1849, 1853, 1870, 1871, 1880, 1892, 1906, 1907, 1915, 1932, 1933, 1960, 1961, 1980 гг. Катастрофические оползни течения, образованные в 1915, 1962, 1965 гг. в г. Ульяновске, связаны с периодами оттепелей, снеготаяния и затяжных водообильных дождей, когда выпадало около трех месячных норм осадков. Установлено, что максимальное количество оползней в г. Ульяновске наблюдается на три месяца позже после периодов совпадения по времени водообильных дождей, интенсивного таяния снега и штормов в Куйбышевском водохранилище.
1.42. На участках древних погребенных эрозионных ложбин, осложняющих склоны, могут формироваться оползни. В среднечетвертичных эрозионных ложбинах прибрежных склонов Южного берега Крыма и Кавказа, протягивающихся от древних поверхностей выравнивания до отметок - 20 м ниже современного уровня моря и имеющих глубину от 10 м вверху до 150 м внизу, образуются крупные и грандиозные по объему оползни. Существенная роль в их формировании принадлежит потоку грунтовых вод с уклоном более 0,3, который создает значительные по величине гидродинамические и гидростатические давления воды на породы.
1.43. Оползневые, обвально-оползневые и обвальные процессы характеризуются цикличностью своего развития, инерционностью проявления, кумулятивным эффектом запаздывания во времени воздействия факторов на процессы и их проявлением, эффектом совпадения во времени экстремальных характеристик факторов и их одновременного воздействия на развитие оползней, оползней-обвалов, обвалов. Закон имеет большое методическое значение для прогнозов развития оползней, оползней-обвалов, обвалов, поскольку он устанавливает следующее:
возможность временного прогноза, которая обеспечивается установленной цикличностью развития рассматриваемых процессов. При этом вероятностно-статистический анализ результатов наблюдений за процессами предпочтительнее, чем наблюдения за факторами, вызывающими развитие этих процессов. Прогнозы в этом случаев сводятся к экстраполяции непрерывного ряда значений активности процесса в будущее. При отсутствии рядов процессов можно использовать ряды факторов после установления тесноты корреляционных связей между активностью проявления процессов и факторами, их определяющими;
изменение информативности факторов и их роли в развитии процессов в пространстве и во времени, а также от стадии к стадии и внутри каждой стадии;
режимно-резонансный эффект, означающий совпадение во времени экстремальных значений характеристик факторов, определяющих развитие оползней-обвалов с кумулятивным эффектом запаздывания между временем проявления процесса и временем действия факторов (см. п. 1.42);
парагенетический эффект или эффект одновременного, не сводимого к простой сумме, воздействия всех факторов, определяющих развитие процессов.
1.44. Грунтовые и подземные воды, дренируемые склонами, оказывают существенное влияние на формирование оползней-обвалов. Роль воды, заполняющей трещины в массиве пород, проявляется в гидростатическом и гидродинамическом давлении на их стенки. Оно уменьшает сопротивление трению по стенкам трещин и при крутом падении трещины стремится сместить часть массива пород. Подобные давления возникают не только в закрытых глухих трещинах, но и в сквозных, если их нижнее сечение, через которое вытекает вода, меньше верхнего сечения. Воздействие воды в трещиноватом массиве в целом проявляется в изменении напряженного состояния в породах, уменьшении их прочности.
УСТОЙЧИВОСТИ ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ
2.1. Оценка устойчивости и прогноз развития оползневых - обвальных склонов относятся к числу наиболее сложных и недостаточно хорошо разработанных проблем. Для ее решения необходимо выявить, количественно оценить основные регионально-геологические и зонально-климатические закономерности и законы, предопределяющие образование названных склонов и изложенные в разд. 1. В зависимости от стадии инженерно-геологических изысканий, сложности геологического строения, типов смещений пород со склонов, вида строительства и использования склонов и присклоновых территорий оценка устойчивости и прогноз развития оползней-обвалов могут быть выполнены с разной степенью точности. Поэтому следует различать ориентировочные и уточненные оценки и прогнозы устойчивости склонов.
2.2. Ориентировочные оценки и прогнозы устойчивости оползневых - обвальных склонов выполняются по результатам их инженерно-геологического картирования в масштабах 1:25000 - 1:50000 и отдельных типичных для рассматриваемых процессов участков в масштабе 1:5000 - 1:2000. По продолжительности действия эти прогнозы имеют период упреждения от одного до пяти лет. Следовательно, их результатами можно пользоваться только в течение времени возведения инженерных сооружений. После этого ориентировочные прогнозы должны быть уточнены.
2.3. Уточненные оценки и прогнозы устойчивости оползневых - обвальных склонов выполняются с использованием результатов следующих работ: инженерно-геологического картирования склонов в масштабе 1:1000 - 1:500; разведочных буровых, горных; опытных геотехнических, геофизических, лабораторных; экспериментального моделирования; стационарных инженерно-геологических наблюдений за оползне-обвалоопасными склонами. По продолжительности действия - это долгосрочные прогнозы с периодом упреждения от пяти до пятнадцати лет. Их результаты можно использовать на протяжении всего срока стабилизации осадок инженерных сооружений. При необходимости время действия данных прогнозов увеличивается на срок эксплуатации склонов и инженерных сооружений на них. Поэтому названные прогнозы являются перманентными и уточняются во времени по мере поступления новой прогнозной информации.
2.4. Для оценки и прогноза устойчивости оползневых - обвальных склонов в настоящее время применяются методы, основанные на детерминированных и стохастических моделях. В детерминированных моделях наиболее широко используются методы прямого расчета коэффициента устойчивости склона. Эти традиционно расчетные методы весьма многочисленны, общеизвестны и разнообразны по исходным положениям и содержанию. Они исходят из условий предельного равновесия, а вычисления осуществляются по формулам и графическим приемам классической механики грунтов. Успех применения данных методов зависит от нескольких причин: расчетных схем, наиболее удачно выбранных и соответствующих основным особенностям строения склона, а также отражающих ослабленные зоны, генетический тип оползня или оползня-обвала, механизм их смещения; от учитываемых в расчетах региональных значений показателей сопротивления сдвигу по поверхностям ослабления; характера распределения величин естественных напряжений в породах неустойчивых частей склонов. Подавляющее большинство имеющихся методов расчета коэффициента устойчивости склонов основаны на решении плоской задачи. В ней рассматриваются условия равновесия смещающихся пород по линии разреза по направлению общего уклона рельефа в полосе шириной один метр без учета влияния боковых и тыловых граней и моментов сил. Поэтому названные методы имеют ограниченные пределы применения и низкую точность. Кроме того, они основаны на сильно упрощенных схемах, не учитывающих вышеуказанных требований. Главное, данные расчетные схемы не могут учесть всего многообразия особенностей и закономерностей, предопределяющих формирование оползней-обвалов (см. разд. 1), их изменение во времени. Кроме того, прямые расчетные методы для высоких и крутых горных склонов в большинстве случаев не могут быть использованы из-за невозможности получить параметры прочностных свойств пород зон ослабления.
2.5. На современном уровне развития инженерно-геологических изысканий, их обеспеченности вычислительной техникой, а также с учетом требований проектирования, строительства, охраны и рационального использования земель наиболее перспективными следует считать стохастические методы оценок и прогноза устойчивости склонов, опирающиеся на сравнительно-геологический анализ. Этот анализ сводится к изучению природной обстановки, совокупного взаимодействия между собой и воздействия на устойчивость оползней-обвалов закономерностей (законов) формирования данных процессов у хорошо изученных склонов с известной устойчивостью склонов-аналогов и к распространению полученных результатов на склоны с неизвестной устойчивостью (склоны объекта прогнозирования). В качестве математического обеспечения сравнительно-геологического анализа применяются наиболее простые и хорошо проверенные алгоритмы теории распознавания образов (дискриминантных функций, нахождения информационных весов природных аналогов, голосования по тупиковым тестам), гармонические функции, последовательная множественная регрессия. Совместно с данным анализом рекомендуются к применению также методы обратных расчетов для оценки устойчивости оползней и оползней-обвалов.
2.6. Выбор аналогов на стадии выполнения ориентировочных прогнозов производится только по тем локальным (местным) особенностям, а также регионально-геологическим и зонально-климатическим закономерностям (законам), которые предопределяют формирование и активизацию развития оползней-обвалов на склонах-аналогах и объектах прогнозирования. Эти особенности и закономерности устанавливаются после выполнения картирования склонов, как это предусмотрено п. 2.2 настоящих Рекомендаций. Установленные для склонов-аналогов и объекта прогноза закономерности (законы) являются признаками прогноза и оценки устойчивости склонов. После установления отмеченных признаков прогноза отбор аналогов среди имеющихся в архивах материалах хорошо изученных склонов осуществляется по принципу:
чтобы оползневые - обвальные склоны или их части были подобны друг другу; необходимо и достаточно, чтобы они были качественно одинаковы (подобны), характеризовались одними и теми же признаками прогноза и имели близкие условия однозначности. Этот принцип доказывает достаточность выявленных признаков прогноза для поиска аналога.
2.7. Качественное подобие склонов-аналогов и объекта прогнозирования означает, что они имеют одинаковые признаки прогноза: литолого-генетические или петрографические комплексы пород в одинаковой степени трещиноватых и вторично измененных процессами выветривания, разгрузки и деятельности человека; располагаются в пределах одинаковых элементов складчатых структур (крыло, шарнир, ядро) и частях структурно-тектонических блоков, ограничивающих их разрывных нарушений одного порядка (масштаба); сейсмические условия формирования склонов; обводненность пород, слагающих склоны, условия дренирования подземных вод склонами; количество в водах сульфатных, железистых, карбонатных соединений и свободной углекислоты; имеют одинаковые соотношения зон ослабления в массивах пород с простиранием и крутизной склонов; геоморфологические особенности строения склонов (их профили в плане, высоту, крутизну и возраст отдельных элементов); климатические условия развития склонов (экспозиция; характер распределения, вид, количество атмосферных осадков и продолжительность их выпадения; глубина зоны сезонного промерзания и скорость ее оттаивания; воздействие ветров в приповерхностной зоне на здания и сооружения, построенные на склонах, и их влияние на устойчивость); степень воздействия на породы склонов процессов эрозии, абразии и деятельности человека.
2.8. В состав условий однозначности входят подобие геометрическое, граничных условий, начального состояния пород. Геометрическое подобие предполагает качественное подобие всех возможных поверхностей (зон) ослабления в породах склонов, по которым могут произойти смещения или обрушения пород. Граничные условия включают качественное подобие фильтрационных свойств пород, морфологии трещин и их заполнителей, отчленяющих блоки пород от основного массива. Начальное состояние пород предполагает подобие степени экзогенного изменения пород в пределах оползневых - обвальных частей склонов, возможных величин гидростатического, гидродинамического и взвешивающего давлений воды в трещинах (и других зонах ослабления), отчленяющих породы от основного массива.
2.9. Перечисленные в пп. 2.7 - 2.8 признаки характеризуют вполне определенную устойчивость оползневых - обвальных склонов. Поэтому они достаточны для выбора на стадии ориентировочных прогнозов аналога согласно приведенному в п. 2.6 принципу.
2.10. Выбор аналогов на стадии выполнения уточненных прогнозов и оценок устойчивости склонов осуществляется более строго, чем на стадии ориентировочных прогнозов. Они выбираются с помощью так называемых критериев геологического подобия. Это вычисленные с помощью анализа размерности простые функциональные безразмерные зависимости. Эти зависимости составлены из представляющих количественных размерных показателей местных, регионально-геологических, зонально-климатических закономерностей и законов формирования оползневых - обвальных склонов по методике, изложенной в Прил. 1. Доказательством возможности использования названных критериев является хорошо известное положение о том, что эмпирически установленные закономерности (и законы) представляют собой сложные функциональные зависимости между характеризующими их величинами. Для каждой из закономерностей (законов) можно выбрать такое количество этих величин, чтобы они полностью отражали ее сущность. Эти величины называются представляющими показателями. Система указанных представляющих показателей позволяет выявить простые безразмерные количественно выражаемые связи между отдельными закономерностями в виде прогнозных критериальных уравнений в том случае, если представляющие показатели обладают свойствами полноты, имеют размерность и выражены количественно. Следует подчеркнуть, что в критериальное уравнение входят также такие безразмерные представляющие показатели-симплексы, от которых существенно зависит устойчивость склонов.
первый - у подобных оползневых - обвальных блоков пород или склонов значения главных критериев подобия совпадают или отличаются на величины, пропорционально отражающие изменение устойчивости склонов; второстепенные критерии могут по своим величинам не совпадать и изменяться непропорционально. Разделение критериев на главные и второстепенные производится по величинам их удельного веса в формировании устойчивости склона. Значения удельного веса вычисляются при исследованиях дисперсионных или многофакторных регрессионных моделей по методике, изложенной в Прил. 6. Допустимая величина ошибки в подобии объекта прогнозирования аналогам может быть вызвана несовпадением значений второстепенных критериев геологического подобия и изменчивостью количественных представляющих показателей, по которым составлены критерии. Она зависит также от представительности статистически обработанных критериев подобия, от выбранной математической модели, степени аппроксимации, от разделения критериев на главные и второстепенные. Следовательно, величина этой ошибки может быть задана и определяться задачами проектирования, строительства и ценностью осваиваемых оползневых - обвальных склонов;
второй - уравнения связи между представляющими показателями закономерностей формирования оползневых - обвальных склонов составляются из критериев геологического подобия и называются критериальными уравнениями. Они являются прогнозными в пределах влияния качественно выражаемых (на данной стадии изученности) закономерностей (законов), учет которых может быть осуществлен на основе принципов сравнительно-геологического анализа (см. п. 2.7).
2.12. Сущность статистического подобия, регламентируемая вторым принципом (см. п. 2.11), сводится к характеристике оползней-обвалов такими критериями геологического подобия, которые имитируют взаимодействие случайных закономерностей развития отмеченных процессов посредством их представляющих количественных показателей. По критериальному уравнению можно оценить удельный вес каждого из критериев, вошедших в уравнение, в их общем совокупном воздействии на устойчивость склонов. Полученные значения справедливы при заданных критериями начальных условиях и при случайных численных значениях представляющих их показателей. Следовательно, выбор аналога по указанным критериям означает вероятностное геологическое подобие.
2.13. Правила пп. 2.6, 2.11 сформулированы на основе соответствующих двух теорем физического подобия. Однако эти правила интерпретированы на вероятностном (статистическом) принципе, что вытекает из следующего допущения. Введем в индикаторы подобия реализации случайных величин, тогда они будут не равны единице, как это требуется условиями теории физического подобия, а какому-то заранее неизвестному числу. Более того, по Е.С. Венцелю, вероятность равенства индикатора случайного явления единице равна нулю, то есть имеет место неравенство
 ,
,где k = 1, 2, ..., n,
 (j = 1, 2, 3...).
(j = 1, 2, 3...).При этом условии подобие перестает быть детерминированным и осуществляется с погрешностью не более  . Можно легко найти вероятность выполнения неравенства, а само подобие будет называться "подобие по вероятности" (или статистическое).
. Можно легко найти вероятность выполнения неравенства, а само подобие будет называться "подобие по вероятности" (или статистическое).
2.14. Для быстрого поиска аналогов рекомендуется всю информацию об оползневых - обвальных склонах, их закономерностям (см. разд. 1) и критериям геологического подобия (Прил. 1) заносить на перфокарты с краевой перфорацией ПКП ручной обработки типа К-5. Эта информационно-поисковая система ИПС позволяет накапливать информацию о склонах в виде банка перфокарт БПКП. Он занимает немного места и позволяет в течение нескольких минут найти интересующий нас склон. Поиск аналогов из БПКП производят поочередно по всем тем закономерностям, которые закодированы на внешних полях перфокарты и которые характерны для объекта прогнозирования. Для ориентировочных прогнозов отобранные таким образом перфокарты дадут необходимую информацию о склонах - аналогах объекта прогнозирования (согласно принципу п. 2.6). При уточненных прогнозах среди отобранных ПКП выбираются только те из них, у которых совпадают по величине значения соответствующих критериев геологического подобия (согласно первому принципу п. 2.11). Значения одноименных критериев подобия в пространстве и во времени в пределах качественно одинаковых природных условий имеют, в основном, случайный характер изменения. Поэтому даже при полном совпадении значений этих критериев будет иметь место какая-то ошибка в выборе аналога, дополнительная к той ошибке, которая регламентирована первым принципом п. 2.11. Ее величина в статистическом подобии определяется взвешенными среднеквадратическими  отклонениями каждого из критериев в критериальном уравнении (принцип второй п. 2.11) от своего среднего значения и от прогнозного коэффициента устойчивости (кривой регрессии), статистически связанного со всеми другими критериями:
отклонениями каждого из критериев в критериальном уравнении (принцип второй п. 2.11) от своего среднего значения и от прогнозного коэффициента устойчивости (кривой регрессии), статистически связанного со всеми другими критериями:
 ,
,где  ,
,  , ...,
, ...,  - удельный вес критериев, определяемый при исследованиях критериального уравнения (многофакторная последовательная регрессия, см. Прил. 6);
- удельный вес критериев, определяемый при исследованиях критериального уравнения (многофакторная последовательная регрессия, см. Прил. 6);
Следовательно, полная или допустимая величина ошибки в выборе аналога и соответственно оценке устойчивости будет равна  .
.
 .
.2.15. При значительном объеме БПКП информацию о склонах необходимо заносить в память ЭВМ. Для городских территорий и крупных инженерных сооружений (промышленных комплексов), в пределах которых имеют место развитие и активизация оползней-обвалов, информация БПКП должна входить в подсистему единой автоматизированной системы управления АСУ. Эта АСУ является системой мониторинга геодинамической обстановки города (или комплекса инженерных сооружений). Такой мониторинг позволит обоснованно и с наименьшей затратой средств управлять склоновыми гравитационными процессами. Его конечной и основной задачей должна быть выдача в заданные моменты времени результатов перманентного прогноза изменения устойчивости склонов.
2.16. Мониторинг геодинамической обстановки города аккумулирует в себе всю информацию подсистемы АСУ (см. п. 2.15). В целом в нем должны быть данные, которые характеризуют следующее:
строение, свойства или состояние массивов пород, слагающих склоны, на момент их освоения;
изменения строения, свойств и состояния массивов, вызванные природными факторами - современными тектоническими движениями (включая сейсмичность); глубинной и боковой эрозией или абразией; влиянием процессов выветривания и разгрузки на состояние и свойства массивов пород.
Названные две группы факторов характеризуют медленно изменяющуюся во времени часть информации АСУ. Поэтому для получения перманентных уточненных прогнозов необходимо вовремя получать сведения о тех антропогенных изменениях в строении, свойствах, состоянии пород склонов, которые могут вызвать ущербные для города (или промышленного комплекса) проявления оползней-обвалов и других, парагенетически связанных с ними, процессов. Кроме того, мониторинг должен содержать специально подобранные для решения главной задачи стандартные математические программы по обработке поступающей информации и выдаче прогнозных показателей, характеризующих состояние склоновых гравитационных процессов.
2.17. В случаях когда при выборе аналогов выполнены все требования пп. 2.6 - 2.8, можно считать, что устойчивость склонов объекта прогнозирования примерно соответствует устойчивости склонов-аналогов. Однако полного выполнения требований указанных пунктов добиться очень трудно из-за большого разнообразия геологического строения, истории формирования склонов, взаимовлияния и взаимообусловленности закономерностей и законов развития оползней-обвалов. В таких случаях необходимо прибегать к помощи математических методов, рекомендуемых в п. 2.5.
ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ С ПОМОЩЬЮ
МЕТОДОВ ТЕОРИИ РАСПОЗНАВАНИЯ ОБРАЗОВ
3.1. Прогноз устойчивости оползневых - обвальных склонов с помощью отмеченных методов сводится к распознаванию состояния объекта прогнозирования на момент, соответствующий времени измерения признаков прогноза, к заключению об изменении устойчивости склонов с помощью экстраполяции выявленных местных (локальных) и региональных закономерностей развития склонов и объекта прогнозирования. Методы распознавания образов позволяют оценить устойчивость изучаемых склонов, исходя из совместного рассмотрения даже качественно выражаемых всех тех признаков прогноза, которые удалось установить на стадии ориентировочных прогнозов. Это дает возможность максимально использовать при прогнозах всю имеющуюся информацию о склонах и получать более точные результаты, чем при оценке устойчивости склонов по каждому признаку прогноза в отдельности, в том числе и методами прямого расчета (п. 2.4).
3.2. Применение методов возможно при наличии обучающей выборки. Она должна содержать не менее семи склонов-аналогов разного состояния с коэффициентом устойчивости, изменяющемся, например, от  до
до  . Пределы колебаний
. Пределы колебаний  устанавливаются, исходя из ценности осваиваемых склонов, класса строительных объектов, задач проектирования и охраны геологической среды. Поэтому использование данных методов ограничивается объемом БПКП (п. 2.14), хотя удовлетворительные результаты в ряде случаев можно получить при наличии в обучающей выборке 2 - 3 аналогов.
устанавливаются, исходя из ценности осваиваемых склонов, класса строительных объектов, задач проектирования и охраны геологической среды. Поэтому использование данных методов ограничивается объемом БПКП (п. 2.14), хотя удовлетворительные результаты в ряде случаев можно получить при наличии в обучающей выборке 2 - 3 аналогов.
 до
до 3.3. Основная идея применения методов распознавания образов для локальных прогнозов устойчивости оползневых - обвальных склонов заключается в следующем. Допустим, что имеется несколько склонов-аналогов, прошедших за время T стационарных инженерно-геологических наблюдений проверку и разделенных по результатам этих наблюдений на два класса: устойчивых (с  ) и неустойчивых (с
) и неустойчивых (с  ) в течение времени T. Перед началом наблюдений по каждому аналогу был установлен некоторый набор признаков прогноза (п. 2.6). Приведенная формулировка задачи совпадает с формулировкой задачи теории распознавания образов: имеется обучающая последовательность объектов классов A и B, каждый из которых характеризуется вектором признаков
) в течение времени T. Перед началом наблюдений по каждому аналогу был установлен некоторый набор признаков прогноза (п. 2.6). Приведенная формулировка задачи совпадает с формулировкой задачи теории распознавания образов: имеется обучающая последовательность объектов классов A и B, каждый из которых характеризуется вектором признаков  ,
, 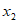 , ...,
, ...,  ; требуется на основании обучающей последовательности построить правило, которое позволит отнести произвольный объект, не входящий в обучающую последовательность (выборку), к классу A или B на основе имеющихся его прогнозных признаков. Подобным образом задача формулируется и для случая, когда имеются склоны-аналоги, разделяющиеся по величине коэффициента устойчивости более чем на два класса; например, классы, находящиеся в промежутках
; требуется на основании обучающей последовательности построить правило, которое позволит отнести произвольный объект, не входящий в обучающую последовательность (выборку), к классу A или B на основе имеющихся его прогнозных признаков. Подобным образом задача формулируется и для случая, когда имеются склоны-аналоги, разделяющиеся по величине коэффициента устойчивости более чем на два класса; например, классы, находящиеся в промежутках  ,
, 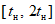 ,
,  и т.д.
и т.д.
 ) и неустойчивых (с
) и неустойчивых (с 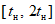 ,
,  и т.д.
и т.д.3.4. Для повышения точности оценки коэффициента устойчивости склонов в число признаков прогноза необходимо включать признаки, замеренные через некоторое время t <= T после разделения склонов-аналогов на классы. В этом случае прогнозирование методами распознавания образов заключается в предсказании изменения состояния склонов объекта прогнозирования на время T по результатам наблюдений за склонами в течение времени t. Минимально допустимое количество склонов-аналогов в каждом классе (для условий, если их больше 2) зависит от применяемых методов математической обработки признаков прогноза, основные из которых изложены в пп. 3.5 - 3.12.
3.5. Метод статистических решений при аппроксимации распределений склонов-аналогов и объектов прогнозирования в классах с нормальными распределениями широко применяется в прогнозировании состояния геологических процессов и состоит в следующем. По данным обучающей выборки склонов-аналогов вычисляются в отдельности для классов устойчивых (класс 1) и неустойчивых (класс 2) склонов (п. 3.3) оценки элементов вектора средних значений и элементов ковариационной матрицы прогнозирующих значений коэффициента устойчивости. Строится функция логарифма отношения плотностей распределения в классах, которая определена в пространстве признаков прогноза  и имеет вид
и имеет вид

где 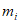 - вектор оценок значений коэффициента устойчивости для i-го класса, i = 1, 2;
- вектор оценок значений коэффициента устойчивости для i-го класса, i = 1, 2;
* - знак транспонирования.
Прогнозирующее правило задается в виде функции L(X) и некоторого порогового значения  , выбор которого определяется задачами исследований. Локальный прогноз устойчивости склонов объекта прогнозирования сводится к выполнению следующих операций:
, выбор которого определяется задачами исследований. Локальный прогноз устойчивости склонов объекта прогнозирования сводится к выполнению следующих операций:
измеряется вектор признаков прогноза X изучаемого склона;
вычисляется функция L(X) и ее значение сравнивается с пороговым значением  ;
;
если значение функции  , склон относится к классу устойчивых, если
, склон относится к классу устойчивых, если  - к неустойчивым.
- к неустойчивым.
 , склон относится к классу устойчивых, если
, склон относится к классу устойчивых, если  - к неустойчивым.
- к неустойчивым.Выбор порога 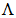 имеет большое значение, поскольку он определяет соотношение ошибок первого и второго рода и надежность прогнозирования. Вероятности ошибок можно уменьшить за счет установления двух порогов
имеет большое значение, поскольку он определяет соотношение ошибок первого и второго рода и надежность прогнозирования. Вероятности ошибок можно уменьшить за счет установления двух порогов  и
и  , причем
, причем  , а решение принимается в соответствии с правилом:
, а решение принимается в соответствии с правилом:
 , а решение принимается в соответствии с правилом:
, а решение принимается в соответствии с правилом: - склон объекта прогнозирования устойчивый;
- склон объекта прогнозирования устойчивый; - необходимо отказаться от прогнозирования по данным склонам-аналогам и признакам прогноза;
- необходимо отказаться от прогнозирования по данным склонам-аналогам и признакам прогноза; - склон объекта прогнозирования неустойчивый.
- склон объекта прогнозирования неустойчивый.3.6. Разделяющие поверхности в пространстве признаков прогноза методом статистических решений (см. п. 3.5) описываются линейными уравнениями второго порядка  . Если
. Если  , то поверхности являются гиперплоскостями. Для применения данного метода на стадии ориентировочных прогнозов не требуется проверки гипотез о нормальном распределении. Он применим во всех случаях, когда обеспечивается требуемая вероятность ошибок прогнозных параметров, оцениваемых на практике по экзаменационной выборке склонов-аналогов. Формальным условием применимости метода является выполнение требований о том, что количество склонов-аналогов каждого класса устойчивости в обучающей выборке было не меньше количества признаков прогноза. Разделение склонов на классы по алгоритму функции L(X) (см. п. 3.5) рекомендуется осуществлять с помощью ЭВМ.
, то поверхности являются гиперплоскостями. Для применения данного метода на стадии ориентировочных прогнозов не требуется проверки гипотез о нормальном распределении. Он применим во всех случаях, когда обеспечивается требуемая вероятность ошибок прогнозных параметров, оцениваемых на практике по экзаменационной выборке склонов-аналогов. Формальным условием применимости метода является выполнение требований о том, что количество склонов-аналогов каждого класса устойчивости в обучающей выборке было не меньше количества признаков прогноза. Разделение склонов на классы по алгоритму функции L(X) (см. п. 3.5) рекомендуется осуществлять с помощью ЭВМ.
 . Если
. Если 3.7. Метод статистических решений на основе локальной оценки отношения правдоподобия применяется в случаях, когда разделяющая поверхность, построенная по методу п. 3.5, плохо аппроксимирует границу между классами. Решение об отнесении склонов к устойчивым или неустойчивым принимается на основании сравнения функции логарифма отношения правдоподобия  с пороговым значением
с пороговым значением  вычисляется из формулы
вычисляется из формулы
 вычисляется из формулы
вычисляется из формулы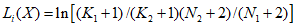 ,
,где 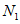 ,
,  - количество склонов первого и второго классов устойчивости в обучающей выборке;
- количество склонов первого и второго классов устойчивости в обучающей выборке;
Окрестность в пространстве признаков прогноза формируется вокруг точки  как центра и расширяется до тех пор, пока количество склонов первого и второго классов в ней не достигнет заданной величины, определяемой условием
как центра и расширяется до тех пор, пока количество склонов первого и второго классов в ней не достигнет заданной величины, определяемой условием
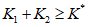 , где
, где  .
.Особенностью метода является возможность его применения, когда количество признаков прогноза больше количества склонов первого и (или) второго классов обучающей выборки.
3.8. Метод обобщенного портрета для целей локальных ориентировочных прогнозов устойчивости склонов состоит в следующем. Исходное пространство признаков прогноза преобразуется в некоторое бинарное пространство B, в котором координаты каждого из векторов могут принимать значения 0 или 1. Диапазон изменения каждого j-го исходного признака прогноза разбивается на  интервалов и
интервалов и  координате вектора, соответствующего рассматриваемому склону в бинарном пространстве B, присваивается значение 1, если значение j-го признака прогноза попадает в l-й интервал
координате вектора, соответствующего рассматриваемому склону в бинарном пространстве B, присваивается значение 1, если значение j-го признака прогноза попадает в l-й интервал 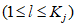 , или 0, если не попадает. При таком преобразовании размерность пространства признаков прогноза возрастает до величины
, или 0, если не попадает. При таком преобразовании размерность пространства признаков прогноза возрастает до величины  , где m - число исходных признаков прогноза. По данным обучающей выборки в пространстве B строится гиперплоскость
, где m - число исходных признаков прогноза. По данным обучающей выборки в пространстве B строится гиперплоскость
 координате вектора, соответствующего рассматриваемому склону в бинарном пространстве B, присваивается значение 1, если значение j-го признака прогноза попадает в l-й интервал
координате вектора, соответствующего рассматриваемому склону в бинарном пространстве B, присваивается значение 1, если значение j-го признака прогноза попадает в l-й интервал 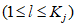 , или 0, если не попадает. При таком преобразовании размерность пространства признаков прогноза возрастает до величины
, или 0, если не попадает. При таком преобразовании размерность пространства признаков прогноза возрастает до величины  ,
,  ,
,где  - так называемый "обобщенный портрет", который представляет собой комбинацию векторов
- так называемый "обобщенный портрет", который представляет собой комбинацию векторов  , соответствующих объектам класса 1, и векторов
, соответствующих объектам класса 1, и векторов  , соответствующих объектам класса 2,
, соответствующих объектам класса 2,
 , соответствующих объектам класса 1, и векторов
, соответствующих объектам класса 1, и векторов 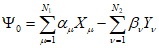 ,
,где 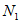 ,
,  - число склонов первого и второго классов в обучающей выборке. Коэффициенты
- число склонов первого и второго классов в обучающей выборке. Коэффициенты  ,
,  определяются путем нахождения максимума функции
определяются путем нахождения максимума функции
 ,
,где 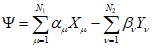 ;
;  в положительном квадрате пространства B. Отсутствие максимума означает, что в данном пространстве классы 1 и 2 (см. п. 3.3) с помощью гиперплоскости неразделимы и необходимо либо изменить пространство признаков прогноза, либо построить разделяющую поверхность более сложного вида.
в положительном квадрате пространства B. Отсутствие максимума означает, что в данном пространстве классы 1 и 2 (см. п. 3.3) с помощью гиперплоскости неразделимы и необходимо либо изменить пространство признаков прогноза, либо построить разделяющую поверхность более сложного вида.
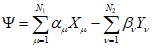 ;
;  в положительном квадрате пространства B. Отсутствие максимума означает, что в данном пространстве классы 1 и 2 (см. п. 3.3) с помощью гиперплоскости неразделимы и необходимо либо изменить пространство признаков прогноза, либо построить разделяющую поверхность более сложного вида.
в положительном квадрате пространства B. Отсутствие максимума означает, что в данном пространстве классы 1 и 2 (см. п. 3.3) с помощью гиперплоскости неразделимы и необходимо либо изменить пространство признаков прогноза, либо построить разделяющую поверхность более сложного вида.3.9. Локальный прогноз устойчивости склонов методом обобщенного портрета (см. п. 3.8) сводится к тому, что по значениям признаков прогноза склону объекта прогнозирования ставится в соответствие вектор X в пространстве B и вычисляется скалярное произведение  . Если
. Если  , то склон относится к классу устойчивых, если
, то склон относится к классу устойчивых, если  , склон относится к неустойчивым.
, склон относится к неустойчивым.
 . Если
. Если  , то склон относится к классу устойчивых, если
, то склон относится к классу устойчивых, если  , склон относится к неустойчивым.
, склон относится к неустойчивым.3.10. Прогноз устойчивости склонов с помощью алгоритма дискриминантных функций рекомендуется применять в случаях, когда признаки прогноза имеют качественное выражение. Общая постановка задачи сводится к следующему. Пусть имеется совокупность оползневых - обвальных склонов M и совокупность признаков прогноза  ,
,  ,
,  , ...,
, ...,  , наличие или отсутствие которых можно рассматривать как реализацию оползневого - обвального процесса. При каждом испытании из совокупности M выбирается один склон. Проведено (n + 1) независимых испытаний и выбрано (n + 1) склонов (простой случайный отбор). Количество испытаний (n + 1) меньше чем
, наличие или отсутствие которых можно рассматривать как реализацию оползневого - обвального процесса. При каждом испытании из совокупности M выбирается один склон. Проведено (n + 1) независимых испытаний и выбрано (n + 1) склонов (простой случайный отбор). Количество испытаний (n + 1) меньше чем  , хотя бы по одному из признаков
, хотя бы по одному из признаков  ,
,  , ...,
, ...,  . Для n выбранных оползневых склонов (обучающая выборка) известны наличие или отсутствие всех (n + 1) признаков, обусловивших смещение и активизацию оползней, а для одного из них
. Для n выбранных оползневых склонов (обучающая выборка) известны наличие или отсутствие всех (n + 1) признаков, обусловивших смещение и активизацию оползней, а для одного из них  - всех признаков прогноза, кроме
- всех признаков прогноза, кроме  , который назовем целевым, остальные
, который назовем целевым, остальные 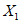 ,
,  , ...,
, ...,  - косвенными признаками. Используя меры связи
- косвенными признаками. Используя меры связи 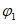 ,
,  , ...,
, ...,  признака
признака  с косвенными признаками и учитывая наличие или отсутствие последних в прогнозируемом оползнеопасном склоне
с косвенными признаками и учитывая наличие или отсутствие последних в прогнозируемом оползнеопасном склоне  , нужно определить наличие или отсутствие признака
, нужно определить наличие или отсутствие признака  в прогнозируемом склоне
в прогнозируемом склоне 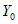 . Причем условие
. Причем условие  существенно, поскольку при его отсутствии решение задачи сводилось бы к оценке условной вероятности присутствия в склоне
существенно, поскольку при его отсутствии решение задачи сводилось бы к оценке условной вероятности присутствия в склоне 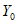 целевого признака при наличии или отсутствии в нем косвенных признаков. Для решения этой задачи применяется идея построения дискриминантной функции, удовлетворяющей таким условиям:
целевого признака при наличии или отсутствии в нем косвенных признаков. Для решения этой задачи применяется идея построения дискриминантной функции, удовлетворяющей таким условиям:
 существенно, поскольку при его отсутствии решение задачи сводилось бы к оценке условной вероятности присутствия в склоне
существенно, поскольку при его отсутствии решение задачи сводилось бы к оценке условной вероятности присутствия в склоне ее аргументами являются качественно выражаемые признаки  ,
,  , ...,
, ...,  , вероятно связанные с целевым признаком
, вероятно связанные с целевым признаком  ;
;
значения функции вычисляются для каждого объекта в зависимости от наличия или отсутствия на данном склоне каждого из признаков  ,
,  , ...,
, ...,  ;
;
константы, входящие в функцию, подбираются такими, чтобы обеспечить наиболее тесную связь между значениями этой функции и целевым признаком.
Рассматриваемая задача интерпретируется в следующую. Для склонов выборки из аналогов известны значения дискриминантной функции и наличие или отсутствие целевого признака. Требуется найти оптимальное по заданному критерию правило отнесения склонов по значению дискриминантной функции к одному из двух классов. При построении дискриминантной функции, удовлетворяющей отмеченным условиям, используется коэффициент согласованности двух качественно выражаемых признаков прогноза, который удовлетворяет следующим требованиям:
если P(A/B) = P(A), то  ;
;
где P(A) - вероятность того, что случайно выбранный из изучаемой совокупности оползневый склон обладает целевым признаком A;
P(A/B) - вероятность того, что он обладает признаком A при наличии признака B;
Указанным требованиям отвечает коэффициент связи Юла
где 1 <= Q <= 1,
a - число склонов, которые обладают признаком A и B;
d - число склонов, не имеющих признаков A и B;
c - число склонов, не обладающих признаком A, но имеющих B;
b - число склонов, которые имеют признак A, но не имеют B;
 - число всех оползневых склонов изучаемой совокупности. Данный коэффициент чувствителен при достаточно больших выборках; когда одна из частот a, b, c, d равна нулю, он не работает. Поэтому рекомендуется коэффициент связи между качественно выражаемыми признаками, который принимает крайние значения -1 и 1 лишь при a + d = 0 или b + c = 0.
- число всех оползневых склонов изучаемой совокупности. Данный коэффициент чувствителен при достаточно больших выборках; когда одна из частот a, b, c, d равна нулю, он не работает. Поэтому рекомендуется коэффициент связи между качественно выражаемыми признаками, который принимает крайние значения -1 и 1 лишь при a + d = 0 или b + c = 0.Такая задача решается тогда, когда косвенное определение целевого признака по соображениям экономичности, удобства и т.п. предпочтительнее прямого определения.
3.11. Можно показать, что в случае, когда признаки A и B независимы, общее число склонов, обладающих этими признаками прогноза или не имеющих их, равно
где n = a + b + c + d.
Введем функцию W(g), удовлетворяющую условиям, если
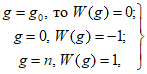 (4)
(4)где g = a + d.
Функцию W(g) будем искать в виде
 (5)
(5)где  ,
,  ,
,  ,
,  - константы, которые выбираются таким образом, чтобы выполнялись условия уравнения (4). Подставив их в уравнения (5), получим
- константы, которые выбираются таким образом, чтобы выполнялись условия уравнения (4). Подставив их в уравнения (5), получим
 , (6)
, (6)где


Функция W(g) называется коэффициентом согласованности двух качественно выражаемых признаков прогноза.
Значение дискриминантной функции
где  - мера связи целевого признака
- мера связи целевого признака  с i-ым косвенным признаком прогноза, удовлетворяющая условиям (1);
с i-ым косвенным признаком прогноза, удовлетворяющая условиям (1);
 , если он не обладает этим признаком;
, если он не обладает этим признаком;  , если о наличии или отсутствии признака
, если о наличии или отсутствии признака В случае когда нужно сопоставить результаты, полученные по двум совокупностям признаков прогноза, различающихся числом их, вместо выражения (7) более удобно выражение
 ,
,  . (8)
. (8)Пусть  ,
,  , ...,
, ...,  - значения функции (7) для склонов-аналогов, вошедших в обучающую выборку и обладающих целевым признаком;
- значения функции (7) для склонов-аналогов, вошедших в обучающую выборку и обладающих целевым признаком;  ,
, 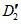 , ...,
, ...,  - то же, но не обладающих целевым признаком;
- то же, но не обладающих целевым признаком; 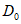 - значение функции (7) для склона объекта прогнозирования
- значение функции (7) для склона объекта прогнозирования  . Тогда распознавание объекта
. Тогда распознавание объекта  сводится к сопоставлению
сводится к сопоставлению  с рядами чисел
с рядами чисел 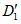 ,
,  , ...,
, ...,  и
и  ,
, 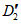 , ...,
, ...,  .
.
3.12. При классификации склонов по степени их устойчивости сопоставляются значения дискриминантной функции для них с критическим (пороговым) значением, граничным между значениями функции для склонов, обладающих и не обладающих целевым признаком прогноза. Используя обучающую выборку из склонов-аналогов известными методами теории статистических решающих функций, можно оценить критическое значение дискриминантной функции  .
.
Пример ориентировочного прогноза устойчивости склонов с помощью алгоритма дискриминантных функций приведен в Прил. 2. Метод не требует применения ЭВМ, так как все расчеты легко и быстро могут быть выполнены с помощью малой вычислительной техники.
3.13. В настоящее время в теории распознавания образов для прогнозов широко применяются три алгоритма: нахождение информационных весов природных аналогов, голосование по тупиковым тестам и выборкам аналогов длины K. Общая постановка задачи в данном случае сводится к следующему. Предположим, что некоторый оползневый - обвальный склон A находится в одном из состояний C, которое описано системой признаков прогноза  ,
, 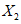 , ...,
, ...,  . Их различные наборы могут характеризовать одно и то же состояние склона по устойчивости. Пусть задана матрица
. Их различные наборы могут характеризовать одно и то же состояние склона по устойчивости. Пусть задана матрица  , строки которой описывают состояние оползневого - обвального склона и являются природными аналогами (
, строки которой описывают состояние оползневого - обвального склона и являются природными аналогами ( - значение j-го признака на i-ом аналоге). Каждый аналог характеризует известную устойчивость оползневого - обвального склона (или его состояние). В соответствии с этим все строки матрицы поделены на C групп: в l-ю группу входят те и только те аналоги, которые описывают l-е состояние склона (1 <= l <= C). Считается, что система признаков прогноза является достаточной, если любые два аналога, характеризующие различные состояния оползневых - обвальных склонов, различны. Требуется следующее:
- значение j-го признака на i-ом аналоге). Каждый аналог характеризует известную устойчивость оползневого - обвального склона (или его состояние). В соответствии с этим все строки матрицы поделены на C групп: в l-ю группу входят те и только те аналоги, которые описывают l-е состояние склона (1 <= l <= C). Считается, что система признаков прогноза является достаточной, если любые два аналога, характеризующие различные состояния оползневых - обвальных склонов, различны. Требуется следующее:
 , строки которой описывают состояние оползневого - обвального склона и являются природными аналогами (
, строки которой описывают состояние оползневого - обвального склона и являются природными аналогами (найти алгоритм, который по любому набору 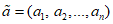 , характеризующему какое-либо состояние оползневого - обвального склона и не обязательно принадлежащему множеству аналогов, позволяет предсказать состояние оползневого - обвального склона;
, характеризующему какое-либо состояние оползневого - обвального склона и не обязательно принадлежащему множеству аналогов, позволяет предсказать состояние оползневого - обвального склона;
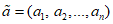 , характеризующему какое-либо состояние оползневого - обвального склона и не обязательно принадлежащему множеству аналогов, позволяет предсказать состояние оползневого - обвального склона;
, характеризующему какое-либо состояние оползневого - обвального склона и не обязательно принадлежащему множеству аналогов, позволяет предсказать состояние оползневого - обвального склона;каждому признаку прогноза 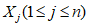 поставить в соответствие число, которое является мерой важности этого признака при прогнозе состояния оползневого - обвального склона.
поставить в соответствие число, которое является мерой важности этого признака при прогнозе состояния оползневого - обвального склона.
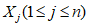 поставить в соответствие число, которое является мерой важности этого признака при прогнозе состояния оползневого - обвального склона.
поставить в соответствие число, которое является мерой важности этого признака при прогнозе состояния оползневого - обвального склона.Тупиковым тестом матрицы  называется тест, любое собственное подмножество столбцов которого не есть тест.
называется тест, любое собственное подмножество столбцов которого не есть тест.
Информационным весом признака прогноза  называется величина
называется величина  , где
, где  - число всех тупиковых тестов матрицы
- число всех тупиковых тестов матрицы 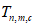 ;
;  - число всех тупиковых тестов, в которые входит признак
- число всех тупиковых тестов, в которые входит признак  ; 1 <= j <= n. Корреляционным весом признаков
; 1 <= j <= n. Корреляционным весом признаков  и
и  называется величина
называется величина  , где
, где  - число тупиковых тестов, в которые одновременно входят признаки
- число тупиковых тестов, в которые одновременно входят признаки  и
и  . При тестовом подходе к решению задачи прогноза возможны два варианта:
. При тестовом подходе к решению задачи прогноза возможны два варианта:
 , где
, где  , где
, где матрица  полностью описывает склон A, то есть не существует описаний состояний склонов, отличных от аналогов. При этом достаточно найти тупиковый тест матрицы, так как значение признаков прогноза, образующих тест, позволяет однозначно предсказать состояние обвально-оползневого склона;
полностью описывает склон A, то есть не существует описаний состояний склонов, отличных от аналогов. При этом достаточно найти тупиковый тест матрицы, так как значение признаков прогноза, образующих тест, позволяет однозначно предсказать состояние обвально-оползневого склона;
матрица  содержит не все возможные описания состояния оползневого - обвального склона. Тестовые алгоритмы в этом случае используют все множество тупиковых тестов. Меру важности признака
содержит не все возможные описания состояния оползневого - обвального склона. Тестовые алгоритмы в этом случае используют все множество тупиковых тестов. Меру важности признака  для определения состояния оползневого - обвального склона в тестовых алгоритмах определяет его информационный вес
для определения состояния оползневого - обвального склона в тестовых алгоритмах определяет его информационный вес 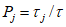 , 1 <= j <= n. Величина
, 1 <= j <= n. Величина  показывает, в какой степени вхождение в тест признака
показывает, в какой степени вхождение в тест признака  влечет вхождение в тест признака
влечет вхождение в тест признака 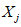 . Она характеризует степень зависимости
. Она характеризует степень зависимости  от
от 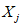 . Примем, что строки матрицы
. Примем, что строки матрицы  упорядочены таким образом, что аналоги, характеризующие одно и то же состояние оползневого склона, следуют друг за другом в естественном порядке. Обозначим через
упорядочены таким образом, что аналоги, характеризующие одно и то же состояние оползневого склона, следуют друг за другом в естественном порядке. Обозначим через  и
и  соответственно минимальный и максимальный порядковые номера аналогов, характеризующих l-е состояние оползневого - обвального склона. Пусть
соответственно минимальный и максимальный порядковые номера аналогов, характеризующих l-е состояние оползневого - обвального склона. Пусть  ,
,  , ...,
, ...,  признаки, образующие тупиковый тест матрицы
признаки, образующие тупиковый тест матрицы  . Рассмотрим систему функций
. Рассмотрим систему функций  , где
, где  - множество всех тупиковых тестов;
- множество всех тупиковых тестов;
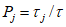 , 1 <= j <= n. Величина
, 1 <= j <= n. Величина  показывает, в какой степени вхождение в тест признака
показывает, в какой степени вхождение в тест признака  , где
, где 
Функция  по существу вычисляет число "голосов", подаваемых наборам
по существу вычисляет число "голосов", подаваемых наборам  за l-е состояние обвально-оползневого склона. Алгоритм голосования по тупиковым тестам заключается в том, что вычисляются функции
за l-е состояние обвально-оползневого склона. Алгоритм голосования по тупиковым тестам заключается в том, что вычисляются функции 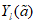 для всех l = 1, 2, ..., c. Вывод о состоянии оползневого - обвального склона делается по следующему правилу:
для всех l = 1, 2, ..., c. Вывод о состоянии оползневого - обвального склона делается по следующему правилу:
 , решение не принимается, если
, решение не принимается, если  ,
, 3.14. Алгоритм нахождения информационных весов природных аналогов объясняется следующим образом:
пусть  ,
, 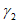 , ...,
, ...,  - некоторые величины, являющиеся дополнительными характеристиками склонов-аналогов
- некоторые величины, являющиеся дополнительными характеристиками склонов-аналогов  ,
,  , ...,
, ...,  матрицы
матрицы  . Обозначим через
. Обозначим через  множество аналогов, у которых значение признака
множество аналогов, у которых значение признака  равно
равно  .
.
 .
.Разделяющим весом признака 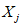 будем называть величину:
будем называть величину:
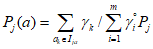 , j = 1, 2, ..., n,
, j = 1, 2, ..., n,где  - информационный вес признака
- информационный вес признака  .
.
Информационным весом набора аналогов a назовем величину  , найденную одним из двух способов: первый -
, найденную одним из двух способов: первый -  , где
, где  - информационный вес признака
- информационный вес признака  ; второй -
; второй -  , где
, где  - разделяющий вес признака
- разделяющий вес признака  .
.
 , где
, где  , где
, где Находим все тупиковые тесты матрицы  и вычисляем информационные веса склонов-аналогов одним из двух способов. Определим ряд чисел (порогов)
и вычисляем информационные веса склонов-аналогов одним из двух способов. Определим ряд чисел (порогов)  ,
,  , ...,
, ..., 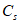 так, чтобы для максимального числа аналогов матрицы выполнялось следующее условие: если признак
так, чтобы для максимального числа аналогов матрицы выполнялось следующее условие: если признак  характеризует l-е состояние (устойчивость) склона, то
характеризует l-е состояние (устойчивость) склона, то  . Вывод о состоянии (устойчивости) склона объекта прогнозирования делается по правилу: признак
. Вывод о состоянии (устойчивости) склона объекта прогнозирования делается по правилу: признак 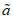 характеризует l-е состояние склона объекта прогнозирования, если
характеризует l-е состояние склона объекта прогнозирования, если 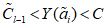 ; решение не принимается, если
; решение не принимается, если  , l = 1, 2, ..., s.
, l = 1, 2, ..., s.
 . Вывод о состоянии (устойчивости) склона объекта прогнозирования делается по правилу: признак
. Вывод о состоянии (устойчивости) склона объекта прогнозирования делается по правилу: признак 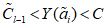 ; решение не принимается, если
; решение не принимается, если  , l = 1, 2, ..., s.
, l = 1, 2, ..., s.предположим, что строки матрицы  упорядочены так, что склоны-аналоги, имеющие одно и то же состояние (устойчивость), следуют друг за другом в естественном порядке. Обозначим через
упорядочены так, что склоны-аналоги, имеющие одно и то же состояние (устойчивость), следуют друг за другом в естественном порядке. Обозначим через  и
и  соответственно минимальный и максимальный порядковые номера аналогов, характеризующих l-е состояние (устойчивость) склонов объекта прогнозирования;
соответственно минимальный и максимальный порядковые номера аналогов, характеризующих l-е состояние (устойчивость) склонов объекта прогнозирования;
пусть  ,
, 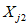 , ...,
, ...,  - признаки прогноза, образующие тупиковый тест матрицы
- признаки прогноза, образующие тупиковый тест матрицы  ;
;
рассмотрим систему функций:  , l = 1, 2, ..., s, где
, l = 1, 2, ..., s, где 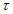 - множество всех тупиковых тестов;
- множество всех тупиковых тестов;
 , l = 1, 2, ..., s, где
, l = 1, 2, ..., s, где 
Функция  вычисляет число "голосов", подаваемых набором склонов-аналогов
вычисляет число "голосов", подаваемых набором склонов-аналогов  за l-е состояние склона объекта прогнозирования;
за l-е состояние склона объекта прогнозирования;
вычислим функции  для всех l = 1, 2, ..., s. Вывод о состоянии склона объекта прогнозирования (его устойчивости) делается по правилу:
для всех l = 1, 2, ..., s. Вывод о состоянии склона объекта прогнозирования (его устойчивости) делается по правилу:  характеризует l-е состояние (устойчивость) склона, если
характеризует l-е состояние (устойчивость) склона, если 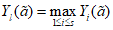 ; решение не принимается, если
; решение не принимается, если  ,
,  .
.
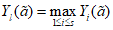 ; решение не принимается, если
; решение не принимается, если  ,
, за систему опорных множеств Q выбирается множество равномощных подмножеств множества признаков прогноза устойчивости оползневых - обвальных склонов. Мощность каждого подмножества определяется параметром K;
пусть  есть часть набора
есть часть набора  , высекаемая из набора фиксированным опорным множеством
, высекаемая из набора фиксированным опорным множеством  ;
;
 ;
;пусть  - произвольный двоичный набор длины n. Обозначим через
- произвольный двоичный набор длины n. Обозначим через  число совпадающих разрядов
число совпадающих разрядов 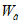 и
и  . Функцию "близости"
. Функцию "близости"  и
и  определим из выражения
определим из выражения
 число совпадающих разрядов
число совпадающих разрядов 
где 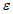 - некоторое число, также являющееся параметром алгоритма; оценка "голосов", поданных набором признаков прогноза за 1-е состояние склона объекта прогнозирования, вычисляется по формуле
- некоторое число, также являющееся параметром алгоритма; оценка "голосов", поданных набором признаков прогноза за 1-е состояние склона объекта прогнозирования, вычисляется по формуле
 ,
,где m(l) - мощность множества склонов аналогов матрицы  , характеризующих l-е состояние (устойчивость) склона объекта прогнозирования;
, характеризующих l-е состояние (устойчивость) склона объекта прогнозирования;
 - расстояние Хеминга между двумя наборами склонов-аналогов a, определяемое из выражения:
- расстояние Хеминга между двумя наборами склонов-аналогов a, определяемое из выражения: .
.При абсолютном подобии склонов-аналогов и склонов объекта прогнозирования  , а при принципиальном их различии
, а при принципиальном их различии  ;
;  - признак прогноза i-го склона; решающее правило о состоянии склона в данном алгоритме аналогично алгоритму п. 3.15. Для выбора параметров K и
- признак прогноза i-го склона; решающее правило о состоянии склона в данном алгоритме аналогично алгоритму п. 3.15. Для выбора параметров K и  проводится такая процедура: для каждого склона-аналога
проводится такая процедура: для каждого склона-аналога  матрицы
матрицы  и для всевозможных пар целых чисел (K,
и для всевозможных пар целых чисел (K,  ), для которых
), для которых
 , а при принципиальном их различии
, а при принципиальном их различии  ;
;  ,
,  ,
,решается задача распознавания с помощью рассмотренного алгоритма (причем аналог  из матрицы
из матрицы  удаляется). После этого K и
удаляется). После этого K и  выбираются такими, при которых правильно распозналось наибольшее число склонов-аналогов экзаменационной матрицы
выбираются такими, при которых правильно распозналось наибольшее число склонов-аналогов экзаменационной матрицы  .
.
3.17. Пример ориентировочного прогноза устойчивости склонов с помощью приведенных в пп. 3.13 - 3.16 алгоритмов дан в Прил. 3. Эти алгоритмы рекомендуется использовать с помощью ЭВМ. Их описание изложено в работах ВСЕГИНГЕО.
3.18. Вероятности ошибок ориентировочного прогноза с помощью алгоритмов теории распознавания образов (пп. 3.1 - 3.16) рекомендуется оценивать с помощью трех методов: экзамен по независимой выборке, экзамен по обучающей выборке, скользящий экзамен.
3.19. Экзамен по независимой выборке склонов-аналогов, отобранных согласно правилу пп. 2.6 - 2.8, сводится к следующему. Склоны-аналоги обрабатываются по выбранному алгоритму из пп. 3.1 - 3.16 и классифицируются по степени их устойчивости на устойчивые и неустойчивые (см. пп. 3.2 - 3.3). Эти склоны-аналоги составляют так называемую "обучающую выборку" (см. п. 3.2). Далее выборка склонов-аналогов проверяется по другой выборке аналогов, не вошедших в обучающую выборку и являющуюся "экзаменационной выборкой". По этой экзаменационной выборке устанавливается надежность разделения склонов в обучающей выборке на классы по степени их устойчивости. Состоятельные оценки вероятностей ошибок находятся по формулам
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где  - оценка вероятности отнесения устойчивого склона к неустойчивому;
- оценка вероятности отнесения устойчивого склона к неустойчивому;
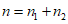 .
.Верхние доверительные границы этих вероятностей определяются из уравнения
 (10)
(10)где 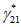 ,
,  - соответствующие доверительные вероятности.
- соответствующие доверительные вероятности.
При достаточно больших  ,
,  для определения доверительных границ рекомендуется использовать приближения данного распределения с помощью
для определения доверительных границ рекомендуется использовать приближения данного распределения с помощью  или нормального распределения.
или нормального распределения.
3.20. Экзамен на обучающей выборке склонов-аналогов сводится к тому, что в качестве экзаменационной выборки используют обучающую выборку. Оценки вероятностей ошибок определяются по формуле (9) п. 3.19, и они являются смещенными. Величина смещения зависит от величины отношения  числа склонов-аналогов в каждом классе обучающей выборки к числу признаков прогноза. Для случая нормальных распределений с равными ковариационными матрицами это смещение становится несущественным при K = 5 - 10. Следовательно, данный метод рекомендуется использовать только при большом количестве склонов-аналогов, когда их число более чем в 5 раз превышает число выбранных признаков прогноза.
числа склонов-аналогов в каждом классе обучающей выборки к числу признаков прогноза. Для случая нормальных распределений с равными ковариационными матрицами это смещение становится несущественным при K = 5 - 10. Следовательно, данный метод рекомендуется использовать только при большом количестве склонов-аналогов, когда их число более чем в 5 раз превышает число выбранных признаков прогноза.
3.21. Скользящий экзамен состоит в том, что из обучающей выборки поочередно исключается один или несколько склонов-аналогов. Оставшиеся аналоги составят обучающую выборку, а исключенные - экзаменационную. Оценки вероятностей ошибок определяются как отношение числа неправильно классифицируемых склонов за все циклы экзамена к общему числу предъявленных для экзамена склонов заданного класса устойчивости.
ИНТЕНСИВНОСТИ ОБРАЗОВАНИЯ ПРИПОВЕРХНОСТНЫХ
ОПОЛЗНЕВЫХ СМЕЩЕНИЙ С ПОМОЩЬЮ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
4.1. Для прогноза интенсивности приповерхностных оползней-потоков, сплывов, оплывин, в образовании которых большую роль играют зонально-климатические особенности территории, рекомендуется использовать гармонический анализ.
4.2. Гармонический анализ целесообразно применять для периодически повторяющихся процессов, которые можно представить бесконечным рядом синусоидных и косинусоидных функций. Нахождение конечной суммы членов с косинусами и синусами называется гармоническим анализом. Каждый член суммы представляет собой гармонику с определенным периодом. Первая гармоника имеет период, равный длине исследуемого периода, вторая - имеет период, равный половине основного, третья - одной трети основного и т.д. В целом, если есть K наблюдений, то число гармоник не будет превышать K/2. Если функция имеет не синусоидальный характер, то требуется большее количество определяющих ее гармоник.
4.3. При записи величины изучаемого показателя в виде части длины окружности, равной  ,
,  , ...,
, ...,  , ...,
, ..., 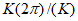 (где K - число значений изучаемого показателя или величина периода), зависимость соответствующих им значений показателя запишется суммой
(где K - число значений изучаемого показателя или величина периода), зависимость соответствующих им значений показателя запишется суммой
 ,
,  , ...,
, ...,  , ...,
, ..., 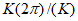 (где K - число значений изучаемого показателя или величина периода), зависимость соответствующих им значений показателя запишется суммой
(где K - число значений изучаемого показателя или величина периода), зависимость соответствующих им значений показателя запишется суммой (11)
(11)или
 , (12)
, (12)где K - полный период;
i - номер гармоники;
 - переменная;
- переменная;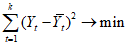 . (13)
. (13)Получение формул для коэффициентов  ,
,  облегчается благодаря свойству ортогональности
облегчается благодаря свойству ортогональности
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 . (14)
. (14)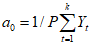 , (15)
, (15)Отсюда видно, что  - есть среднее значение показателя за период. По формулам (15), (16), (17) необходимо рассчитывать коэффициенты для (K/2 = 1) гармоник. Для последней гармоники всегда A-0,
- есть среднее значение показателя за период. По формулам (15), (16), (17) необходимо рассчитывать коэффициенты для (K/2 = 1) гармоник. Для последней гармоники всегда A-0,
 .
.4.5. Пример прогноза интенсивности оплывин с помощью гармонического анализа показан в текстовом Прил. 4. При этом считается, что такой прогноз можно выполнять при допущении сохранения в будущем периодичности развития отмеченных оползней, которая была установлена в процессе выполнения инженерно-геологических изысканий или стационарных наблюдений за оползнями и которая была заложена в анализ гармонических функций.
4.6. Расчет значений прогнозной функции вида (16) или (17) следует осуществлять с учетом значений предполагаемого тренда прогнозного показателя, а не от его среднего уровня (см. Прил. 4).
В общем виде прогнозное уравнение имеет вид:
 , (18)
, (18)f(x) - тренд;
t - номер наблюдения (t = 1, 2, 3, ..., K);
i - номер гармоники;
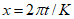 .
.4.7. Предлагаемая методика ориентировочного прогноза интенсивности развития оползней является наиболее эффективной для кратко-, среднесрочных прогнозов. Более строгое выделение гармоник различного порядка рекомендуется осуществлять на основе анализа спектральных функций, а для большого ряда наблюдений - периодограмм. Для анализа временных рядов целесообразно использовать стандартные программы типа "Диск" на ЭВМ, разработанные во ВСЕГИНГЕО.
4.8. <*> Прогноз ритмичности оползневого процесса с помощью аналогово-аналитического гелиогеофизического метода выполняется на базе теории о связях между ритмами оползней T на склонах и воздействием на энергетическое состояние пород оползней солнечной активности и лунно-солнечного притяжения. Воздействия проявляются через климатогидрологические, неотектонические, геомагнитные параметры и геоэлектрические поля, смену напряжений в массивах пород склонов при вариациях ротационных сил. Их воздействие на приповерхностные блоки пород имеет резонансно-избирательный характер. При расчете ритма оползней T используются солнечный (S = 11, 18 лет) и чандлеровский (Z = 1,24222 года) ритмы, которые находятся в простых соотношениях с главным членом нутации земли N, равным 18,6 лет.
--------------------------------
4.9. Для геологически подобных регионов параметры их ритмов T, протяженности участков между эрозионными врезами L, высоты водораздела над базисом эрозии H оползня связаны между собой соотношениями
 ; (19)
; (19) , (20)
, (20)где  равны отношению природных давлений P у сопоставляемых склонов, т.е. сил, определяющих напряженно-деформируемое состояние;
равны отношению природных давлений P у сопоставляемых склонов, т.е. сил, определяющих напряженно-деформируемое состояние;
 равны отношению природных давлений P у сопоставляемых склонов, т.е. сил, определяющих напряженно-деформируемое состояние;
равны отношению природных давлений P у сопоставляемых склонов, т.е. сил, определяющих напряженно-деформируемое состояние;K - отношение (в целых числах) скоростей изменения за ритмы  и
и  напряжений в элементах i и j пород склонов.
напряжений в элементах i и j пород склонов.
4.10. Подобие объекта прогноза и его аналогов определяется совпадением критериев геологического подобия, как это рекомендовано в пп. 3.6 - 3.11 настоящих Рекомендаций. У генетически подобных процессов и явлений должно быть одинаковым либо сходным их математическое описание или, например, статистически подобные ансамбли, изофункционализм моделей, интегральное подобие критериальных условий. Рекомендуется считать, что склоны морских и речных побережий, для которых экспериментально установлен ритм проявления обвалов-оползней T более 100 лет, находятся в устойчивом состоянии; при T < 50 - 100, 25 - 50, 10 - 25 лет целесообразно считать их как потенциально устойчивые, относительно устойчивые и находящиеся в предельном состоянии. Период T < 10 лет определяет неустойчивые склоны.
4.11. В качестве определяющих у склонов-аналогов рекомендуется рассматривать параметры, учитывающие кинематическую и динамическую обстановку и геометрические характеристики склонов. К ним относятся параметры H, L (см. п. 4.1) и мощность смещаемых пород l; сопротивления сдвигу G или модули деформации E пород зон ослабления; массы смещаемых пород M, ускорение свободного падения g, плотность 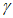 или объемная масса
или объемная масса  пород оползневого участка; интенсивность воздействия внешних сил F на равновесное состояние пород склонов во времени T - FT; скорость протекания процесса изменения состояния пород в оползне-обвалоопасном склоне U. Существование природной системы, характеризуемой перечисленными параметрами, определяется энергетическим балансом взаимодействующих в ней сил. Используя
пород оползневого участка; интенсивность воздействия внешних сил F на равновесное состояние пород склонов во времени T - FT; скорость протекания процесса изменения состояния пород в оползне-обвалоопасном склоне U. Существование природной системы, характеризуемой перечисленными параметрами, определяется энергетическим балансом взаимодействующих в ней сил. Используя  - теорему подобия и метод Релея анализа размерностей, взаимосвязь между показателями этой системы можно записать в виде степенного многочлена
- теорему подобия и метод Релея анализа размерностей, взаимосвязь между показателями этой системы можно записать в виде степенного многочлена
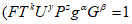 , где
, где  ,
,  ,
,несложное решение которого приводит к уравнению, состоявшему из четырех безразмерных комплексных параметров:
 .
.Отсюда:
 | 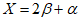 |
 |  |
 | 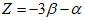 , , |
что приводит к критериальному уравнению
 ,
,либо, в окончательном виде
где  - критерий подобия Фруда;
- критерий подобия Фруда;
 - критерий подобия Фруда;
- критерий подобия Фруда; - критерий механического подобия Ньютона;
- критерий механического подобия Ньютона; - критерий гомохронности Струхаля, характеризующий однородность протекания процесса (однородность явления) во времени;
- критерий гомохронности Струхаля, характеризующий однородность протекания процесса (однородность явления) во времени; - число устойчивости Д. Тейлора или критерий геодинамического подобия по Е.П. Емельяновой и Л.Б. Розовскому.
- число устойчивости Д. Тейлора или критерий геодинамического подобия по Е.П. Емельяновой и Л.Б. Розовскому.4.12. Для условий плоской задачи для двух прибрежных склонов, сложенных одинаковыми породами и испытывающих сходные внешние воздействия, условия (19) можно записать в виде
 ; (21)
; (21) . (22)
. (22)Далее, из (21) и (22) с учетом условия (20) получим
и  . (24)
. (24)
 . (24)
. (24)Нетрудно видеть, что при 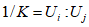 выражение (24) представляет собой левую часть зависимости (19). В то же время, из (23) следует, что
выражение (24) представляет собой левую часть зависимости (19). В то же время, из (23) следует, что
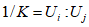 выражение (24) представляет собой левую часть зависимости (19). В то же время, из (23) следует, что
выражение (24) представляет собой левую часть зависимости (19). В то же время, из (23) следует, что ,
,где  - кинетическая энергия процесса изменения состояния системы.
- кинетическая энергия процесса изменения состояния системы.
 - кинетическая энергия процесса изменения состояния системы.
- кинетическая энергия процесса изменения состояния системы.В связи с тем, что энергетический баланс равновесной системы возможен лишь при равенстве ее кинетической энергии потенциальной (работе сил тяготения), равенство (23) преобразуется к виду
 . (25)
. (25)4.12. При условии равенства величин  в уравнении (25), т.е. приближенного равенства линейных параметров, изменяющихся под действием сил тяжести при сохранении квазистационарности состояния системы (например, равенство величин ползучести пород сравниваемых склонов), получим окончательное выражение
в уравнении (25), т.е. приближенного равенства линейных параметров, изменяющихся под действием сил тяжести при сохранении квазистационарности состояния системы (например, равенство величин ползучести пород сравниваемых склонов), получим окончательное выражение
где P - природное давление межбалочного блока пород на уровне базиса эрозии, а само выражение (26) справедливо при соблюдении литологического подобия и подобия сил внешних воздействий; причем модуль подобия для симплекса времени  равен отношению скоростей протекания процессов изменения состояния сравниваемых процессов.
равен отношению скоростей протекания процессов изменения состояния сравниваемых процессов.
4.13. Воздействие S, Z и N во времени на параметры элементарных полей напряжений в породах склонов обусловливает ритмичную активизацию разгрузки склонов от напряжений путем гравитационного смещения грунтов. Имеет значение также то обстоятельство, что предельное значение чандлерова цикла (Z = 1,242) является производным из солнечного цикла S и представляет собой сумму бесконечно убывающей прогрессии
 .
.Поэтому проявление указанных разгрузок напряжений более вероятно в девяти сериях комбинаторных ситуаций (R, лет) воздействия цикла S в сочетании с его же главными производными (N и Z), на поля напряжений пород в береговых склонах: 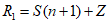 ;
;  ;
; 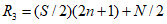 ;
;  ;
;  ;
;  ;
;  , где
, где  . Числовые ряды всех девяти серий объединяются прогрессией
. Числовые ряды всех девяти серий объединяются прогрессией
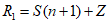 ;
;  ;
; 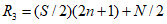 ;
;  ;
;  ;
;  ;
;  , где
, где  . Числовые ряды всех девяти серий объединяются прогрессией
. Числовые ряды всех девяти серий объединяются прогрессией , (27)
, (27)где m - ряд натуральных чисел, имеющих вид
m = 9 n + (номер серии от 1 до 9).
Выражение (27) используется в таком логическом оправданном допущении: для объемов циклов (T) активизации обвально-оползневой эрозии, различающихся не более чем на порядок, все возможные наиболее вероятные отношения  определяются средним из серий комбинаторных ситуаций
определяются средним из серий комбинаторных ситуаций  в масштабе 10 лет, т.е.
в масштабе 10 лет, т.е.
 .
.Отсюда для соответствий значений K = m получим
 , (28)
, (28)т.е., выражение (20).
Операции расчета цикла  по (26) - (28) рекомендуются для береговых склонов, сложенных породами, способными к развитию деформаций вязкопластичного течения.
по (26) - (28) рекомендуются для береговых склонов, сложенных породами, способными к развитию деформаций вязкопластичного течения.
4.14. В современном понимании развития цикла оползневого процесса объем временного интервала T включает стадии затухания его активизации, перехода в новую систему равновесия, относительной стабилизации и новой активизации оползневого процесса. Интерпретация зависимости (26) позволяет утверждать о реальности в природе закономерности о том, что одинаковые периоды T оползневого процесса могут иметь склоны с различными показателями H, L, l (см. п. 4.2), но в сочетаниях (HLl) = const, соответствующих примерному равенству масс пород береговых блоков и их интегральных гравитационных воздействий на породы, которые расположены выше уровня базиса эрозии. Период квазистационарного режима в 100 лет теоретически имеет место для серии береговых блоков в сочетании L км - H м, равным 1 - 30, 2 - 15, 3 - 10. Для 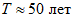 рассчитан ряд L - H: 1,5 - 62; 2 - 47; 3 - 31; 4 - 23; 5 - 19; склоны с
рассчитан ряд L - H: 1,5 - 62; 2 - 47; 3 - 31; 4 - 23; 5 - 19; склоны с  имеют сочетания: L:Н: 2 - 140; 3 - 93; 4 - 70; 5 - 56; 7,5 - 37; 10 - 28; цикл T порядка 10 лет теоретически соответствует значениям L - H: 5 - 270; 6 - 220; 8 - 166; 10 - 133; 12 - 110; 15 - 90. Произведение LH каждой серии постоянно и аппроксимируется гиперболой. Ветви гипербол с T - 50 лет практически сливаются для склонов-аналогов в области L = 0,5 км - H = 200 м и H = 10 м - L = 10 км.
имеют сочетания: L:Н: 2 - 140; 3 - 93; 4 - 70; 5 - 56; 7,5 - 37; 10 - 28; цикл T порядка 10 лет теоретически соответствует значениям L - H: 5 - 270; 6 - 220; 8 - 166; 10 - 133; 12 - 110; 15 - 90. Произведение LH каждой серии постоянно и аппроксимируется гиперболой. Ветви гипербол с T - 50 лет практически сливаются для склонов-аналогов в области L = 0,5 км - H = 200 м и H = 10 м - L = 10 км.
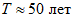 рассчитан ряд L - H: 1,5 - 62; 2 - 47; 3 - 31; 4 - 23; 5 - 19; склоны с
рассчитан ряд L - H: 1,5 - 62; 2 - 47; 3 - 31; 4 - 23; 5 - 19; склоны с  имеют сочетания: L:Н: 2 - 140; 3 - 93; 4 - 70; 5 - 56; 7,5 - 37; 10 - 28; цикл T порядка 10 лет теоретически соответствует значениям L - H: 5 - 270; 6 - 220; 8 - 166; 10 - 133; 12 - 110; 15 - 90. Произведение LH каждой серии постоянно и аппроксимируется гиперболой. Ветви гипербол с T - 50 лет практически сливаются для склонов-аналогов в области L = 0,5 км - H = 200 м и H = 10 м - L = 10 км.
имеют сочетания: L:Н: 2 - 140; 3 - 93; 4 - 70; 5 - 56; 7,5 - 37; 10 - 28; цикл T порядка 10 лет теоретически соответствует значениям L - H: 5 - 270; 6 - 220; 8 - 166; 10 - 133; 12 - 110; 15 - 90. Произведение LH каждой серии постоянно и аппроксимируется гиперболой. Ветви гипербол с T - 50 лет практически сливаются для склонов-аналогов в области L = 0,5 км - H = 200 м и H = 10 м - L = 10 км.ОПОЛЗНЕВЫХ СКЛОНОВ МЕТОДАМИ "ОБРАТНЫХ РАСЧЕТОВ"
5.1. Одним из объективных методов количественной оценки устойчивости оползневых склонов, сложенных прочными трещиноватыми и выветрелыми породами, являются "обратные расчеты". По сравнению с другими расчетными методами, их основное преимущество заключается в том, что необходимые для оценки устойчивости параметры сдвига определяются по всей площади поверхности смещения у оползней-аналогов для склона - объекта прогнозирования. Поэтому в расчетах используются данные по откартированным в пределах типичных участков единовременно произошедшим оползням. Для этих участков должна быть проведена инженерно-геологическая съемка в масштабе 1:1000 - 1:5000. Для выбранных оползней должны быть также сохранены либо поверхности отрыва и смещения блоков и пакетов пород, либо сами накопления на склоне, разделенные по возрастным генерациям, либо поверхности и накопления.
5.2. Теоретической основой метода "обратных расчетов" является решение уравнений теории предельного равновесия. Предполагается, что в момент начала движения оползневого блока пород величины минимальных сопротивлений сдвигу по поверхностям смещения уравновешиваются сдвигающими усилиями.
5.3. Инженерно-геологическое картирование ниш отрыва и смещения оползней, расположенных на высоких и труднодоступных склонах, выполняется на базе полевого дешифрирования аэро-, фототеодолитных снимков с последующей их обработкой на стереоавтографе. При картировании оползней склонов нужно выполнить следующее:
выявить общие регионально-геологические (законы) и местные закономерности развития оползневых деформаций на склонах (см. пп. 1.30 - 1.43) и описать состояние пород в приповерхностных зонах разгрузки, выветривания на участках развития оползней, а также установить типы возможных ниш отрыва и смещения;
охарактеризовать и типизировать ослабленные зоны массивов пород и трещины, отчленяющие блоки пород от основного массива и служащие поверхностями смещения оползней; описать трещины, обусловливающие общую раздробленность пород оползневого блока;
получить (по возможности) данные о пьезометрических уровнях и напорах подземных вод и о характере сезонной обводненности пород и склона; установить микрогеоморфологические особенности и формирование склона, возраст его отдельных частей, особенно, где возможны оползни;
определить возможные направления смещения, возраст и объемы произошедших оползней.
5.4. Законы и закономерности, определяющие устойчивость оползневых склонов, рекомендуется объединить в две группы:
закономерности, характеризующие среду формирования оползневых склонов (назовем их как факторы среды). К ним относятся литолого-генетические комплексы пород, степень тектонической и иной трещиноватости пород, обводненность пород и пространственное соотношение основных систем трещин (и других поверхностей ослабления) с направлением действия сил на склоны и развития оползневых деформаций пород на склонах, степень экзогенного изменения пород и заполнителя трещин, предельные высоты и крутизна склона, морфология поверхностей смещения пород и направление пути смещения оползневых масс, зонально-климатические особенности формирования склонов;
закономерности, изменяющие состояние и свойства пород, а также величины и распределение напряжений в массиве (факторы, изменяющие среду). К их числу относятся современные тектонические движения, включая сейсмичность; изменение степени экзогенного изменения пород и их обводненности; изменение высоты и крутизны склонов под влиянием различных видов хозяйственной деятельности человека или после оползневых смещений; энергичная глубинная и боковая эрозия или абразия склонов; искусственные факторы.
5.5. Замеры геометрических параметров и объемов произошедших и оползнеопасных блоков пород рекомендуется производить непосредственно по фототеодолитным или аэроснимкам в масштабе изображения 1:5000 - 1:2000 (или крупнее). Для подсчета объемов оползней восстанавливается поверхность склона до смещения с него блока пород. Для этого склон с оползневой нишей сопоставляется с аналогичными по возрасту, составу пород и их состоянию, по морфологии и истории развития элювиально-делювиальными склонами.
5.6. Число и тип уравнений равновесия зависит от количества поверхностей ослабления, ограничивающих блоки пород от основного массива, и природной обстановки, в которой произошли смещения. Оползневые ниши отрыва, по которым составляются уравнения равновесия, должны характеризовать однотипные явления, у которых факторы среды (см. п. 5.4) качественно одинаковы. Перенос показателей сдвига с аналога на поверхности ослабления, по которым еще не произошли смещения и которые отчленяют блоки пород, следует выполнять с учетом также и факторов, изменяющих состояние среды (см. п. 5.4). Такой учет может быть чисто качественным. Кроме того, на возможных поверхностях смещения должны быть равны средние нормальные напряжения, создаваемые весом оползневого блока пород (см. текст Прил. 5).
5.7. Поверхности отрыва и смещения оползней по их роли в развитии деформаций целесообразно разделить на поверхности отчленения и смещения. Поверхностями отчленения будут те из них, которые имеют угол падения 70° и больше; они практически не оказывают сопротивления смещению пород оползня. Соответственно, поверхности с меньшими углами рекомендуется считать поверхностями смещения и по ним происходит скольжение или срез блоков пород. Показатели сдвига определяются только для поверхностей смещения.
5.8. Типы расчетных схем зависят от соотношения в массиве пород поверхностей смещения и их числа. Для склонов, сложенных прочными трещиноватыми и выветрелыми породами, рекомендуются следующие четыре типа расчетных схем: типичны и наиболее распространены, а также соответствующие им уравнения равновесия для определения показателей сдвига и нормальных напряжений:
первый тип - имеется одна подвешенная (1) поверхность смещения и три (две боковые и одна тыловая) субперпендикулярные поверхности отчленения
 ;
;  ,
,второй тип - две боковые (2) поверхности смещения падают навстречу друг другу, третья тыловая (3) - субвертикальная
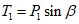 ;
;  ;
;  ;
;  ;
; ;
;  ;
; 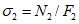 ,
,третий тип - подошвенная и две боковые, падающие навстречу друг другу, поверхности смещения; тыловая поверхность отчленения субвертикальная  ;
;  ;
; 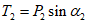 ;
;  ;
;  ;
;  ;
; 
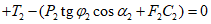 ;
;  ;
;  ;
; 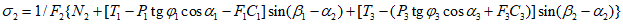 ;
;
 ;
;  ;
; 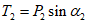 ;
;  ;
;  ;
;  ;
; 
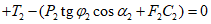 ;
;  ;
;  ;
; 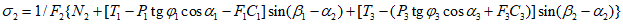 ;
;четвертый тип - подошвенная и две боковые, падающие навстречу друг другу, и тыловая поверхности смещения; одна или обе боковые поверхности могут быть субвертикальными  ;
; 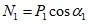 ;
;  ;
;  ;
;  ;
;  ;
;  .
.
 ;
; 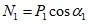 ;
;  ;
;  ;
;  ;
;  ;
;  .
.5.9. Пример оценки устойчивости оползневых склонов с помощью методов "обратных расчетов" показан в Прил. 5. Для расчетов взяты правобережные склоны долины р. Ангары на участке строящегося Богучанского гидроузла. Здесь была выполнена специализированная инженерно-геологическая съемка в масштабе 1:2000, откартированы разновозрастные оползневые смещения пород со склонов и в разной степени отчлененные от основного массива блоки пород. Необходимо оценить устойчивость данных блоков пород и оползневых накоплений на склонах.
5.10. Предлагаемая методика может быть рекомендована для склонов, сложенных любыми литолого-генетическими или петрографическими комплексами пород при условии, если на склонах сохранилось достаточное для составления уравнения равновесия количество ниш отрыва оползней, их накопления и удается восстановить исходный профиль склонов (до смещения из них пород). Выбор аналогов рекомендуется осуществлять по ИПС, согласно методике, изложенной в пп. 2.14 - 2.15.
ОБВАЛЬНЫХ СКЛОНОВ И ПРОГНОЗ ЕЕ ИЗМЕНЕНИЯ
С ПОМОЩЬЮ ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИХ МЕТОДОВ
6.1. Рекомендуются следующие вероятностно-статистические методы оценки и прогноза устойчивости оползневых - обвальных склонов:
основанные на предположении о случайном распределении моментов образования оползней во времени. Метод позволяет предсказать вероятность того или иного числа оползней в заданный промежуток времени на заданной территории;
основанные на предположении наличия ритмов в распределении оползней-обвалов во времени или стадий в развитии оползней;
основанные на установленных корреляционных зависимостях (линейных уравнений связи) между отдельными показателями оползневого - обвального процесса и закономерностями, его определяющими, а также на последовательном регрессионном анализе (исследования многофакторных моделей развития оползней-обвалов).
6.2. Методы, основанные на предположении о случайном распределении моментов образования оползней во времени, рекомендуется применять в разработке ВСЕГИНГЕО. Прогноз развития оползней в данной разработке выражается в виде карт районирования 1:1000000 (для крупных регионов) и 1:200000 (для отдельных опорных участков). Он выполняется по стадиям:
построение карты распространения оползней (или обвалов) по их типам;
разделение закономерностей, определяющих формирование оползней-обвалов, на классы. Из набора m закономерностей для каждой из них (если есть данные) строится гистограмма распределения каждой закономерности, установленной в пределах исследуемой территории. Число классов определяется с учетом полученных экстремумов на гистограмме распределения оползней-обвалов. Если кривая на гистограмме плавная с одним максимумом, то число классов условно принимается равным 3 - 6;
построение аналитических карт распределения классов отдельных закономерностей с таблицей площадей, приходящихся на каждый класс;
расчет удельного оползне-, обвалопроявления в пределах выделенных классов закономерностей.
6.3. В результате построения карт закономерностей каждая из закономерностей из множества 1, 2, ..., j, ..., m имеет S классов (1, 2, ..., i, ..., s). В пределах площади  распространения i-го класса j-й закономерности подсчитывается количество проявлений исследуемого типа оползня-обвала
распространения i-го класса j-й закономерности подсчитывается количество проявлений исследуемого типа оползня-обвала 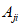 . В соответствии с теорией вероятностей, под
. В соответствии с теорией вероятностей, под  рекомендуется понимать количество элементарных площадок, в каждой из которых оползень (или обвал)
рекомендуется понимать количество элементарных площадок, в каждой из которых оползень (или обвал)  может произойти или не произойти
может произойти или не произойти  .
.
 .
.6.4. Следующей стадией прогноза является определение вероятности проявления оползней или обвалов. При построении карт крупных и средних масштабов, когда можно измерить площади, пораженные оползнями или обвалами, вероятность  образования или активизации оползней или обвалов в пределах площади i-го класса закономерности
образования или активизации оползней или обвалов в пределах площади i-го класса закономерности  определяется как отношение площади оползней в пределах класса
определяется как отношение площади оползней в пределах класса 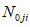 к площади всего класса
к площади всего класса
 .
.6.5. Определив вероятность  , выполняется оценка влияния отдельных закономерностей на развитие оползней или обвалов. В качестве оценки степени влияния закономерностей на развитие оползней-обвалов рекомендуется использовать весовой коэффициент
, выполняется оценка влияния отдельных закономерностей на развитие оползней или обвалов. В качестве оценки степени влияния закономерностей на развитие оползней-обвалов рекомендуется использовать весовой коэффициент 
 ,
,где  - информационный коэффициент, предложенный А.Б. Вистелиусом;
- информационный коэффициент, предложенный А.Б. Вистелиусом;
 - определяется по значениям энтропии.
- определяется по значениям энтропии.Нормированная вероятность - это среднеарифметическая вероятность, приходящаяся на S классов j-ой закономерности:  и характеризующая степень влияния на оползневый - обвальный процесс классов закономерностей. Весовые коэффициенты
и характеризующая степень влияния на оползневый - обвальный процесс классов закономерностей. Весовые коэффициенты 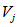 позволяют ранжировать закономерности по степени их влияния на оползневый - обвальный процесс, выделяя те из них, которые содержат основную информацию о процессе и которые принимаются в качестве прогнозных.
позволяют ранжировать закономерности по степени их влияния на оползневый - обвальный процесс, выделяя те из них, которые содержат основную информацию о процессе и которые принимаются в качестве прогнозных.
 и характеризующая степень влияния на оползневый - обвальный процесс классов закономерностей. Весовые коэффициенты
и характеризующая степень влияния на оползневый - обвальный процесс классов закономерностей. Весовые коэффициенты 6.6. Следующей стадией прогноза по рекомендуемой п. 6.2 методике является расчет оползневого или обвального потенциала. Для этого последовательным совмещением всех карт закономерностей, названных выше, устанавливаются участки пересечения площадей различных классов рассматриваемых m закономерностей. Число таких результирующих участков на специализированной карте, получаемой после совмещения карт закономерностей, близко к числу сочетаний 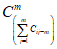 . Соответствующая результирующая вероятность может быть названа оползневым (обвальным) потенциалом
. Соответствующая результирующая вероятность может быть названа оползневым (обвальным) потенциалом 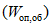 . Она определяется как вероятность суммы конечного числа событий с допущением независимости закономерностей
. Она определяется как вероятность суммы конечного числа событий с допущением независимости закономерностей
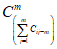 . Соответствующая результирующая вероятность может быть названа оползневым (обвальным) потенциалом
. Соответствующая результирующая вероятность может быть названа оползневым (обвальным) потенциалом 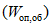 . Она определяется как вероятность суммы конечного числа событий с допущением независимости закономерностей
. Она определяется как вероятность суммы конечного числа событий с допущением независимости закономерностей ,
,где П - знак произведения;
6.7. Конечным этапом прогнозирования является построение карты районирования территории по значениям оползневых (или обвальных) потенциалов. Для построения названных карт рекомендуется использовать разработанную во ВСЕГИНГЕО стандартную программу "Ботос" для ЭВМ. Она позволяет составлять карту районирования по значениям оценочной функции автоматически. При этом можно исключить операцию по составлению специальных карт закономерностей. В качестве исходной информации непосредственно используются материалы точечного изучения данных процессов.
6.8. Методы прогноза, основанные на выявленных в ходе стационарных инженерно-геологических наблюдений периодах (ритмах) активизации оползневых (или обвальных) процессов, исходят из того, что развитие названных процессов представляет собой последовательную смену их состояний в пространстве и во времени. При переходе из одного состояния в другое меняются значения некоторых параметров процесса (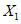 ,
, 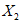 , ...,
, ...,  ), которые являются прогнозными и зависят от времени и пространственной координаты. Обобщенная оценка состояний процесса в таких случаях выражается формулой
), которые являются прогнозными и зависят от времени и пространственной координаты. Обобщенная оценка состояний процесса в таких случаях выражается формулой
 ,
,где  ,
,  , ... - зависимые переменные процесса;
, ... - зависимые переменные процесса;
 , ... - зависимые переменные процесса;
, ... - зависимые переменные процесса;6.9. Сущность вероятностно-статистического прогноза стадии развития рассматриваемого процесса заключается в том, что на вход динамической системы (оползневого или обвального склона) поступают воздействующие закономерности в виде установленных при изысканиях их реализаций 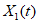 ,
,  , ...,
, ...,  , а на выходе, после соответствующего преобразования, получается изменяющееся во времени значение прогнозной величины Y(t). В качестве такой величины может быть рекомендована, например, скорость смещения оползней. Связь между выходом и входом излагаемой динамической системы можно выразить интегралом Дюамеля
, а на выходе, после соответствующего преобразования, получается изменяющееся во времени значение прогнозной величины Y(t). В качестве такой величины может быть рекомендована, например, скорость смещения оползней. Связь между выходом и входом излагаемой динамической системы можно выразить интегралом Дюамеля
 ,
,где  ,
, 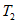 , ...,
, ...,  - время, в течение которого соответствующие прогнозные закономерности после их воздействия на склоны оказывают существенное влияние на значение выходной величины Z(t) в момент времени t;
- время, в течение которого соответствующие прогнозные закономерности после их воздействия на склоны оказывают существенное влияние на значение выходной величины Z(t) в момент времени t;
6.10. Величина вклада каждой из рассматриваемых закономерностей в значение выходной функции динамической системы (см. п. 6.9) в момент времени t устанавливается только после выявления предыстории воздействия закономерностей во времени от  до t. Весовые функции находятся из условия минимума функционала
до t. Весовые функции находятся из условия минимума функционала
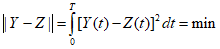 ,
,определяющего, что рассогласование между расчетными значениями и фактически наблюдаемыми величинами выхода системы Y(t) должно быть мало на всем интервале наблюдения T.
6.11. Для более точного установления момента предкатастрофической фазы оползневых (обвальных) смещений пород со склонов рекомендуется метод оперативного статистического контроля за развитием оползневых (обвальных) деформаций. По результатам стационарных наблюдений за оползнями (обвалами), выполняемых в пределах типичных участков-аналогов, строится распределение  пород со склонов в стадию подготовки оползня (обвала).
пород со склонов в стадию подготовки оползня (обвала).
 пород со склонов в стадию подготовки оползня (обвала).
пород со склонов в стадию подготовки оползня (обвала).ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 3.22 отсутствует. |
6.12. Стадии оползневого процесса рекомендуется устанавливать по индексам Е.П. Емельяновой, характеризующим геометрические параметры оползневых склонов и используемых в методике, разработанной во ВСЕГИНГЕО. Решается следующая задача: пусть на изучаемых оползневых склонах в момент времени  измеряется n прогнозных признаков. Рассматривается n-мерное пространство R, в котором каждой координате соответствует один из признаков прогноза. Каждому i-ому набору значений n в пространстве
измеряется n прогнозных признаков. Рассматривается n-мерное пространство R, в котором каждой координате соответствует один из признаков прогноза. Каждому i-ому набору значений n в пространстве  соответствует точка
соответствует точка  , а каждый вектор признаков
, а каждый вектор признаков  имеет информацию о прогнозируемом признаке
имеет информацию о прогнозируемом признаке  . Эта задача может быть сведена к задаче разделения множества точек
. Эта задача может быть сведена к задаче разделения множества точек  на классы по набору признаков (
на классы по набору признаков ( ,
,  , ...,
, ...,  ) (задачи теории распознавания образов, см. пп. 3.3 - 3.22). Построенные классы
) (задачи теории распознавания образов, см. пп. 3.3 - 3.22). Построенные классы  отвечают различным стадиям оползневого процесса.
отвечают различным стадиям оползневого процесса.
 имеет информацию о прогнозируемом признаке
имеет информацию о прогнозируемом признаке  . Эта задача может быть сведена к задаче разделения множества точек
. Эта задача может быть сведена к задаче разделения множества точек 6.13. Принцип построения алгоритма для решения задачи разделения состоит в восстановлении в пространстве признаков прогноза 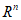 координатной оси, которой соответствует прогнозируемый параметр
координатной оси, которой соответствует прогнозируемый параметр  . Восстанавливаемая ось строится между нулевым классом
. Восстанавливаемая ось строится между нулевым классом  , который характеризует начальную стадию развития оползневого процесса, и классом
, который характеризует начальную стадию развития оползневого процесса, и классом  , характеризующим стадию, предшествующую периоду основного смещения. Положение промежуточных стадий определяется проекциями их точек на восстановленную координатную ось. Структура математической модели для оценочной функции описывается выражением
, характеризующим стадию, предшествующую периоду основного смещения. Положение промежуточных стадий определяется проекциями их точек на восстановленную координатную ось. Структура математической модели для оценочной функции описывается выражением
 ,
,где  - относительное значение прогнозируемого признака
- относительное значение прогнозируемого признака  для p-го класса;
для p-го класса;
6.14. Деятельность человека и вносимые им изменения в формирование оползневых - обвальных склонов можно рассматривать как управляемую пространственную систему. Развитие названных процессов в этой системе протекает при взаимодействии двух различных неоднородных групп закономерностей (см. п. 5.4), характеризующих среду (условия) развития процессов и ее изменения - естественные и антропогенные. При этом необходимо помнить, что антропогенным изменениям часто подвергается не весь процесс, а отдельные элементы его. Например, при подрезках или пригрузках оползневых склонов, находящихся до этого в устойчивом состоянии, поверхность смещения пород со склонов вначале формируется на участках, где естественные напряжения в присклоновой части массива будут больше прочности пород на срез, разрыв или раздавливание (что определяется механизмом развития деформаций). Неоднородность прочностных свойств массивов пород, их изменение в пространстве и во времени под влиянием отмеченных двух групп закономерностей требуют от инженеров-геологов сформулировать задачу управления пространственной системой обвально-оползневый склон таким образом, чтобы появилась возможность дать прогноз антропогенным изменениям системы с целью исключения нежелательных ее изменений в динамическом равновесии геологической среды.
6.15. Отмеченную в п. 6.14 задачу в терминах теории графов рекомендуется формулировать следующим образом:
для каждого изучаемого оползне-, обвалоопасного склона строится граф G(X) возможных состояний системы (оползень или обвал - вид антропогенного воздействия). Под вершинами графа (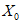 ,
,  ,
, 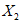 , ...,
, ...,  ) подразумевается пространственное положение элементов системы X(t) в момент времени t, при котором реализуется развитие обвально-оползневого процесса в соответствии с поставленной целью функционирования системы. Тогда
) подразумевается пространственное положение элементов системы X(t) в момент времени t, при котором реализуется развитие обвально-оползневого процесса в соответствии с поставленной целью функционирования системы. Тогда  (i = 0, 1, 2, ..., n) - есть ситуация, которая означает, что система X в момент времени t находится в состоянии
(i = 0, 1, 2, ..., n) - есть ситуация, которая означает, что система X в момент времени t находится в состоянии  . Вероятность этого события запишется
. Вероятность этого события запишется  ; (i = 0, 1, 2, ..., n). Для любого момента времени сумма вероятностей всех возможных состояний системы
; (i = 0, 1, 2, ..., n). Для любого момента времени сумма вероятностей всех возможных состояний системы 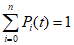 . Необходимо определить вероятности
. Необходимо определить вероятности  изменения структуры системы в пределах описанного графа G(X), вершины которого составляют совокупность возможных состояний системы
изменения структуры системы в пределах описанного графа G(X), вершины которого составляют совокупность возможных состояний системы  .
.
 (i = 0, 1, 2, ..., n) - есть ситуация, которая означает, что система X в момент времени t находится в состоянии
(i = 0, 1, 2, ..., n) - есть ситуация, которая означает, что система X в момент времени t находится в состоянии  ; (i = 0, 1, 2, ..., n). Для любого момента времени сумма вероятностей всех возможных состояний системы
; (i = 0, 1, 2, ..., n). Для любого момента времени сумма вероятностей всех возможных состояний системы 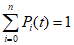 . Необходимо определить вероятности
. Необходимо определить вероятности  .
.6.16. Допустим, что изучаемый район возможной активизации оползней-обвалов подвержен влиянию i-го вида хозяйственной деятельности человека. Тогда элементарная последовательность пространственной локализации данного антропогенного воздействия в каждый момент времени t будет описываться следующими состояниями:
антропогенные воздействия не вызывают нежелательных изменений в установившемся динамическом равновесии оползневого - обвального процесса;
антропогенные воздействия вызывают нежелательные изменения факторов среды (условий) формирования обвалов-оползней;
антропогенные воздействия вызывают нежелательные изменения факторов изменения среды, которые обусловливают развитие или активизацию обвалов-оползней;
антропогенные воздействия вызывают развитие нового или активизацию старого природного процесса. Обозначив каждое из указанных состояний номерами 1, 2, 3, ..., K, запишем вероятность K-го состояния в виде  . Показатель интенсивности перехода процесса из одного состояния в другое обозначим как
. Показатель интенсивности перехода процесса из одного состояния в другое обозначим как 
 , подразумевая под этим, что с периодичностью
, подразумевая под этим, что с периодичностью  антропогенное воздействие i-го вида вызывает переход процесса из состояния K в состояние l. В общем виде интенсивность перехода
антропогенное воздействие i-го вида вызывает переход процесса из состояния K в состояние l. В общем виде интенсивность перехода
 ,
,где  - среднее время антропогенного влияния i-го вида k-го состояния оползня-обвала.
- среднее время антропогенного влияния i-го вида k-го состояния оползня-обвала.
6.17. Можно считать, что переход рассматриваемых процессов из одного состояния в другое подчиняется закону распределения Пуассона. В этом случае правомерно допущение, что за произвольно взятый бесконечно малый промежуток времени t система, находящаяся в состоянии K, может совершить переход в состояние l с вероятностью 
 . Вероятность перехода системы в этот момент времени в какое-либо еще состояние очень мала и имеет иной порядок (вторая или третья производная), если интервал времени dt выбран достаточно малым. Вероятность состояния системы в момент времени (t + dt) связывается с вероятностями состояний системы в момент времени t посредством соответствующих уравнений. Аналитически рекомендуются два пути, по которым природный обвально-оползневый процесс рассматриваемой системы может находиться в состоянии K:
. Вероятность перехода системы в этот момент времени в какое-либо еще состояние очень мала и имеет иной порядок (вторая или третья производная), если интервал времени dt выбран достаточно малым. Вероятность состояния системы в момент времени (t + dt) связывается с вероятностями состояний системы в момент времени t посредством соответствующих уравнений. Аналитически рекомендуются два пути, по которым природный обвально-оползневый процесс рассматриваемой системы может находиться в состоянии K:
первый - в момент времени t природный процесс уже находится в состоянии K и в течение промежутка времени dt не меняет своего состояния. Это выразится вероятностями  и
и  соответственно;
соответственно;
 соответственно;
соответственно;второй - в момент времени t природный процесс может находиться в каком-либо другом состоянии l  и за время dt перейти из него в состояние K. Вероятность этих событий
и за время dt перейти из него в состояние K. Вероятность этих событий  и
и  соответственно. В таком случае
соответственно. В таком случае
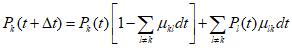
или
 .
.Переходя к пределу  , имеем
, имеем
 .
.6.18. Описанные в п. 6.16 четыре состояния системы представляют собой замкнутую в пространстве цепь. Поэтому состояние рассматриваемой системы рекомендуется записать в виде системы дифференциальных уравнений

Уравнения даны в неявном виде. Для их решения необходимо составить матрицу интенсивностей 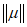 и матрицу-столбец начальных условий
и матрицу-столбец начальных условий  . Поскольку переход системы из одного состояния в другое подчиняется закону распределения Пуассона
. Поскольку переход системы из одного состояния в другое подчиняется закону распределения Пуассона
 ,
,где n - число возможных состояний,
6.19. Для марковских процессов с вероятностями  ,
,  , ...,
, ...,  можно составить систему линейных дифференциальных уравнений. При этом удобно пользоваться графом состояний системы, на котором против каждой стрелки, ведущей из состояния в состояние, поставлена интенсивность перехода. В левой части каждого уравнения стоит производная
можно составить систему линейных дифференциальных уравнений. При этом удобно пользоваться графом состояний системы, на котором против каждой стрелки, ведущей из состояния в состояние, поставлена интенсивность перехода. В левой части каждого уравнения стоит производная  , а в правой части - столько членов, сколько стрелок связано непосредственно с данным состоянием (+, если в данное состояние, -, если из него):
, а в правой части - столько членов, сколько стрелок связано непосредственно с данным состоянием (+, если в данное состояние, -, если из него):
 , а в правой части - столько членов, сколько стрелок связано непосредственно с данным состоянием (+, если в данное состояние, -, если из него):
, а в правой части - столько членов, сколько стрелок связано непосредственно с данным состоянием (+, если в данное состояние, -, если из него):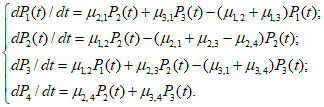
Начальные условия для интегрирования такой системы дифференциальных уравнений отражают состояние системы в начальный момент времени (если при t = 0 было состояние K, то  ;
;  при
при  ).
).
 ;
;  при
при 6.20. Предложенная в пп. 6.14 - 6.19 модель прогноза пространственного развития оползней-обвалов должна быть реализована на ЭВМ.
6.21. Методы прогнозов устойчивости оползневых - обвальных склонов, основанные на исследовании линейных уравнений связи (см. п. 6.1), имеют математическое обоснование:
обозначим через X ту наблюдаемую переменную величину, которая может быть легко измерена без погрешностей (или с допустимыми погрешностями) при инженерно-геологическом картировании оползневых - обвальных склонов (см. п. 2.2); является представляющим (количественным или качественным) показателем закономерностей и законов формирования (и активизации) оползней-обвалов (см. разд. 1); через Y - случайную, обычно трудноопределимую, прогнозную величину (в данном случае коэффициент устойчивости -  ). Математическое ожидание
). Математическое ожидание  (или среднее) величины Y при заданных
(или среднее) величины Y при заданных  (в первом приближении) находится в линейной зависимости от X. Математическая модель для названных величин имеет вид
(в первом приближении) находится в линейной зависимости от X. Математическая модель для названных величин имеет вид
 (в первом приближении) находится в линейной зависимости от X. Математическая модель для названных величин имеет вид
(в первом приближении) находится в линейной зависимости от X. Математическая модель для названных величин имеет вид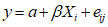 , (29)
, (29)где a,  - неизвестные параметры уравнения;
- неизвестные параметры уравнения;
обозначим через  сумму квадратических отклонений
сумму квадратических отклонений  значения от среднего
значения от среднего  :
:  , аналогично SSXY - сумма из произведений отклонений
, аналогично SSXY - сумма из произведений отклонений 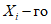 и
и  значений от своих средних:
значений от своих средних: 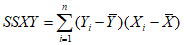 ;
;  - сумма квадратических отклонений
- сумма квадратических отклонений  значения от своего среднего:
значения от своего среднего:  . Перечисленные оценки параметров определяются из формул:
. Перечисленные оценки параметров определяются из формул:  ;
;  ;
;  (при заданном значении
(при заданном значении  );
);  . После оценки параметров искомое прогнозное уравнение имеет вид
. После оценки параметров искомое прогнозное уравнение имеет вид
 значения от среднего
значения от среднего  , аналогично SSXY - сумма из произведений отклонений
, аналогично SSXY - сумма из произведений отклонений 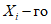 и
и 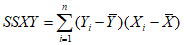 ;
;  . Перечисленные оценки параметров определяются из формул:
. Перечисленные оценки параметров определяются из формул:  ;
;  ;
;  (при заданном значении
(при заданном значении  );
);  . После оценки параметров искомое прогнозное уравнение имеет вид
. После оценки параметров искомое прогнозное уравнение имеет вид . (30)
. (30)Доверительные интервалы колебания названных параметров для заданного уровня надежности  определяются
определяются
для параметров a:  ;
;
 ;
;для параметра  :
:  ;
;
 ;
;для параметра  :
:  ;
;
 ;
;для  в точке
в точке  :
:  ,
,
 :
:  ,
,где  - значение случайной величины, распределенной по закону Стьюдента с (n - 2) степенями свободы;
- значение случайной величины, распределенной по закону Стьюдента с (n - 2) степенями свободы;
n - число измерений;
Для проверки гипотезы о том, что параметр a равен заданной константе  при заданном уровне надежности
при заданном уровне надежности  , определяется величина критерия
, определяется величина критерия  . Гипотеза
. Гипотеза  отклоняется, если
отклоняется, если  или
или  ; во всех остальных случаях она принимается. Аналогично, для проверки гипотезы
; во всех остальных случаях она принимается. Аналогично, для проверки гипотезы  :
:  при заданном уровне надежности
при заданном уровне надежности 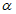 необходимо определить критерий
необходимо определить критерий 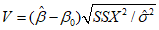 ; если
; если  или если
или если 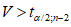 - гипотеза отклоняется, в других случаях она верна. Проверка этих гипотез является одной из важнейших процедур при исследовании простой линейной модели. Принятие той или иной гипотезы означает, что выбранные для прогноза функции фактора
- гипотеза отклоняется, в других случаях она верна. Проверка этих гипотез является одной из важнейших процедур при исследовании простой линейной модели. Принятие той или иной гипотезы означает, что выбранные для прогноза функции фактора  непригодны. Статистической мерой пригодности величины
непригодны. Статистической мерой пригодности величины  для прогноза значения Y служит оценка коэффициента корреляции
для прогноза значения Y служит оценка коэффициента корреляции
 при заданном уровне надежности
при заданном уровне надежности  . Гипотеза
. Гипотеза  или
или  ; во всех остальных случаях она принимается. Аналогично, для проверки гипотезы
; во всех остальных случаях она принимается. Аналогично, для проверки гипотезы 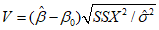 ; если
; если  или если
или если 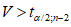 - гипотеза отклоняется, в других случаях она верна. Проверка этих гипотез является одной из важнейших процедур при исследовании простой линейной модели. Принятие той или иной гипотезы означает, что выбранные для прогноза функции фактора
- гипотеза отклоняется, в других случаях она верна. Проверка этих гипотез является одной из важнейших процедур при исследовании простой линейной модели. Принятие той или иной гипотезы означает, что выбранные для прогноза функции фактора  ,
,которая характеризует меру надежности искомой величины (Y) по измерениям  ;
;
применение одной переменной X для предсказания величины Y в большинстве случаев не дает хороших результатов из-за того, что на изменение Y оказывает влияние не одна переменная (представляющий показатель), а, например, две. В этом случае рекомендуется исследовать уравнение с двумя переменными величинами  и
и 
где  - значения прогнозного показателя (функции);
- значения прогнозного показателя (функции);
Чтобы определить параметры  ,
,  ,
,  , также подсчитываются сумма квадратических отклонений i-го значения
, также подсчитываются сумма квадратических отклонений i-го значения  ,
,  , Y от своих средних (
, Y от своих средних ( ,
, 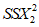 ,
,  ) и сумма из произведений отклонений
) и сумма из произведений отклонений  ,
, 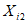 и
и  от своих средних (
от своих средних ( ,
,  ,
, 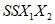 ). Указанные суммы запишем в виде матрицы S* и вектора-столбца g
). Указанные суммы запишем в виде матрицы S* и вектора-столбца g
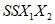 ). Указанные суммы запишем в виде матрицы S* и вектора-столбца g
). Указанные суммы запишем в виде матрицы S* и вектора-столбца g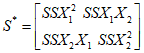 ;
;  ,
,оценки параметров 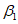 и
и  находятся из уравнения
находятся из уравнения
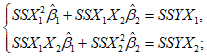 (32)
(32)оценку  находят по формуле
находят по формуле  .
.
 .
.Для решения системы уравнений (31) применяется метод Дуллитла, изложенный в Прил. 7. Характеристикой пригодности случайных величин  ,
,  для предсказания величины Y служит множественный коэффициент корреляции R. Оценку для R можно определить по методу наименьших квадратов из выражения
для предсказания величины Y служит множественный коэффициент корреляции R. Оценку для R можно определить по методу наименьших квадратов из выражения
 ,
,ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 18 в Приложении 7 отсутствует. Возможно, имеется в виду таблица 16 Приложения 7. |
где  - сумма произведений соответствующих строк столбца g в табл. 18 Прил. 7.
- сумма произведений соответствующих строк столбца g в табл. 18 Прил. 7.
Линейные модели типа (30 и 31) - частные случаи общей линейности модели. Однако число переменных величин  в ней равно K, поэтому
в ней равно K, поэтому
где i = 1, 2, ..., K;
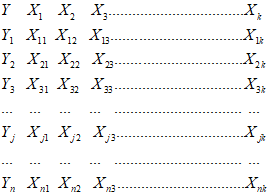
При исследовании линейных уравнений может оказаться, что более хорошие результаты дает не линейная связь между функцией Y и аргументами  , а, например, квадратичная. Тогда, естественно, изучается модель
, а, например, квадратичная. Тогда, естественно, изучается модель
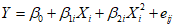 . (34)
. (34)В общем случае модель (34) запишется в виде выражения
 . (35)
. (35)Модель (35) называется полиномиальной k-ой степени. Легко показать, что это частный случай общей линейной модели. Для этого нужно заменить  в уравнении (35) на
в уравнении (35) на  и получим линейную модель вида (33).
и получим линейную модель вида (33).
6.22. Изложенная в п. 6.21 методика исследования линейных уравнений связи основана на методе наименьших квадратов. Этот метод исходит из предпосылки о независимости друг от друга результатов отдельных наблюдений по одной и той же переменной  . В наблюдениях за оползневыми - обвальными склонами такие наблюдения могут зависеть друг от друга, т.е. между данными наблюдениями существует автокорреляция. В подобных случаях оценки коэффициентов регрессии
. В наблюдениях за оползневыми - обвальными склонами такие наблюдения могут зависеть друг от друга, т.е. между данными наблюдениями существует автокорреляция. В подобных случаях оценки коэффициентов регрессии  ,
,  не имеют оптимальных статистических свойств.
не имеют оптимальных статистических свойств.
6.23. Для выявления наличия между разновременными измерениями автокорреляции в отклонениях от тренда или от кривой регрессии рекомендуется использовать критерий Дурбина-Уитсона d вида
 ,
,где  - случайные отклонения результатов наблюдений
- случайные отклонения результатов наблюдений  от тренда или кривой регрессии; при этом, если
от тренда или кривой регрессии; при этом, если  (табличное значение, рекомендуется брать из работ по статистике), то гипотеза об отсутствии автокорреляции принимается; если
(табличное значение, рекомендуется брать из работ по статистике), то гипотеза об отсутствии автокорреляции принимается; если  , то необходимы дальнейшие исследования, например, по большему числу наблюдений. Для исключения автокорреляции рекомендуется применять прием включения параметра времени в качестве аргумента в общее линейное уравнение.
, то необходимы дальнейшие исследования, например, по большему числу наблюдений. Для исключения автокорреляции рекомендуется применять прием включения параметра времени в качестве аргумента в общее линейное уравнение.
 , то необходимы дальнейшие исследования, например, по большему числу наблюдений. Для исключения автокорреляции рекомендуется применять прием включения параметра времени в качестве аргумента в общее линейное уравнение.
, то необходимы дальнейшие исследования, например, по большему числу наблюдений. Для исключения автокорреляции рекомендуется применять прием включения параметра времени в качестве аргумента в общее линейное уравнение.6.24. При построении многофакторных линейных уравнений по результатам разновременных наблюдений за склонами может возникнуть проблема мультиколлинеарности (наличие сильной корреляции между переменными, которая может существовать вне всякой зависимости между функцией и аргументами). Она возникает также, когда в качестве независимых представляющих показателей (переменных) берутся некоторые синтетические показатели. Мультиколлинеарность является признаком скудного экспериментального материала. В связи с изложенным, значительно усложняется процесс выделения из переменных  наиболее существенных признаков прогноза. В подобных случаях не работает правило, по которому степень влияния аргументов на функцию однозначно определяется абсолютной величиной коэффициентов
наиболее существенных признаков прогноза. В подобных случаях не работает правило, по которому степень влияния аргументов на функцию однозначно определяется абсолютной величиной коэффициентов  . Оно справедливо только при условии взаимной некоррелированности или достаточно слабой коррелируемости представляющих показателей. По вышеизложенной причине искажается смысл коэффициентов регрессии.
. Оно справедливо только при условии взаимной некоррелированности или достаточно слабой коррелируемости представляющих показателей. По вышеизложенной причине искажается смысл коэффициентов регрессии.
6.25. Проверку наличия мультиколлинеарности рекомендуется осуществлять посредством показателя Ферраря-Глобера
 ,
,где n - число наблюдений;
p - число представленных в уравнении показателей;
X - матрица изучаемых аргументов;
X* - матрица, транспортированная к матрице X. Причем этот показатель приближенно имеет распределение  с 1/2P (P - 1) степенями свободы. Устранить или существенно уменьшить мультиколлинеарность можно несколькими способами:
с 1/2P (P - 1) степенями свободы. Устранить или существенно уменьшить мультиколлинеарность можно несколькими способами:
построением уравнений регрессии по отклонениям от тренда или по конечным разностям;
привлечением в уравнения регрессии дополнительной информации;
преобразованием множества независимых переменных в несколько ортогональных множеств, используя для этой цели методы многомерного статистического анализа и метода главных компонент;
исключением из рассмотрения одного или нескольких линейно-связанных аргументов, основываясь на грамотном сравнительно-геологическом анализе и накопившемся опыте изучения оползневых - обвальных склонов.
6.26. Задачу построения динамической модели, учитывающей требования пп. 6.22 - 6.25, рекомендуется осуществлять согласно следующим положениям:
пусть имеется (m + 1) временных рядов результатов наблюдений за устойчивостью оползневых - обвальных склонов и представляющих показателей закономерностей, от которых зависит эта устойчивость за T лет (T = 1, 2, ..., n). Построенная по этим данным многофакторная регрессионная математическая модель (с учетом исключения эффектов автокорреляции и мультиколлинеарности)
 <*> (36)
<*> (36)характеризует среднее влияние представляющих показателей-аргументов на устойчивость склонов за учитываемый в модели промежуток времени. Естественно, величина этого влияния будет изменяться во времени. Чтобы учесть это изменение, разобьем период времени T на S интервалов, в пределах которых коэффициенты регрессии останутся постоянными или будут изменяться незначительно. Каждый коэффициент регрессии  новых S уравнений будет иметь S оценок, т.е. получим временной ряд для каждого коэффициента регрессии. По этим рядам строятся прогнозы для коэффициентов устойчивости склонов на момент времени (T + l), используя для этого методы прогнозирования по одному временному ряду.
новых S уравнений будет иметь S оценок, т.е. получим временной ряд для каждого коэффициента регрессии. По этим рядам строятся прогнозы для коэффициентов устойчивости склонов на момент времени (T + l), используя для этого методы прогнозирования по одному временному ряду.
--------------------------------
Предположим, что имеются данные, характеризующие обвалы-оползни за каждый год T-го периода по всем изучаемым (прогнозируемым) склонам. Обозначим число объектов в t-ом году через  . Для каждого года строится статическая пространственная математическая модель
. Для каждого года строится статическая пространственная математическая модель
 , где t = 1, 2, ..., n. (37)
, где t = 1, 2, ..., n. (37)Если для наблюдаемых оползневых - обвальных склонов установлены закономерности с эффектом запаздывания (см. п. 1.43) на коэффициент устойчивости склонов, то модель (37) получит вид
 . (38)
. (38)Таким образом строятся n уравнений типа (38), в которых изменяются не только значения переменных, но и коэффициентов регрессии. Вычисленные коэффициенты регрессии (коэффициенты устойчивости склонов) рассматриваются как временные ряды 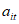 (t = 1, 2, ..., n) с трендом
(t = 1, 2, ..., n) с трендом  .
.
Используя полученные временные ряды  коэффициентов регрессии, строится динамическая модель оползневого - обвального склона
коэффициентов регрессии, строится динамическая модель оползневого - обвального склона
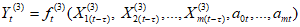 . (39)
. (39)Расчеты по модели (39) рекомендуется выполнять согласно следующей методике:
пусть имеются данные по показателям  ,
,  , ...,
, ...,  для N объектов (j = 1, 2, ..., N) за t лет (t = 1, 2, ..., n).
для N объектов (j = 1, 2, ..., N) за t лет (t = 1, 2, ..., n).
Построим уравнения регрессии, характеризующие зависимость устойчивости оползневых - обвальных склонов Y от представляющих показателей  ,
,  , ...,
, ...,  для моментов времени t = 1, t = 2, t = 3, ..., t = n
для моментов времени t = 1, t = 2, t = 3, ..., t = n
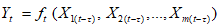 . (40)
. (40)Для каждого аргумента  получили n коэффициентов регрессии, которые являются временными рядами
получили n коэффициентов регрессии, которые являются временными рядами  . Линейная модель прогноза устойчивости обвально-оползневого склона на момент времени
. Линейная модель прогноза устойчивости обвально-оползневого склона на момент времени  будет иметь вид
будет иметь вид
 . (41)
. (41)Эта модель (41) удовлетворяет следующим условиям:
развитие оползней-обвалов подчиняется закону, изложенному в п. 1.43;
период времени t (t = 1, 2, ..., n) достаточен для того, чтобы установить существующие закономерности развития и активизации оползней-обвалов;
правильно выбрана математическая модель прогноза коэффициентов регрессии и метод оценки параметров этой модели.
Прогноз коэффициента устойчивости по модели типа (41) может быть выполнен только после определения значений аргументов  ,
,  , ...,
, ...,  на прогнозируемый момент времени.
на прогнозируемый момент времени.
6.27. Пример ориентировочной оценки устойчивости и прогноза развития оползневых - обвальных склонов с помощью исследования многофакторных регрессионных моделей показан в Прил. 6.
РАЗВИТИЯ ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ С ПОМОЩЬЮ
ПРАВИЛ ВЕРОЯТНОСТНОГО ГЕОЛОГИЧЕСКОГО ПОДОБИЯ
7.1. Уточненные оценки и прогнозы устойчивости оползневых - обвальных склонов выполняются для локальных участков расположения особо ответственных сооружений. Для их производства необходимо иметь следующие данные:
детальные инженерно-геологические разрезы в масштабе 1:500 - 1:1000. Каждый из оцениваемых оползневых - обвальных склонов или их частей должен быть охарактеризован не менее чем двумя разрезами, которые проводятся по направлению возможных смещений пород и перпендикулярно ему;
характеристики трещин или иных контактов, отчленяющих блоки пород от основного массива, а также трещин, обусловливающих общую раздробленность пород;
пространственные соотношения трещин (поверхностей ослабления оползней-обвалов), отчленяющих блоки пород, выделив определенные типы возможных ниш отрыва и смещения (как это показано, например, на рис. 1);
распространение, пьезометрические уровни, химический состав и напоры подземных вод, а также характер сезонной обводненности пород и склона;
характеристики приповерхностных зон разгрузки, выветривания пород, полученных по данным съемки, их разведки горными выработками и геофизическими методами;
сопротивление пород сдвигу по типичным контактам, заполнителям при разном увлажнении, а также показатели плотности пород оползневых - обвальных накоплений и оползне-, обвалоопасных блоков, одноосного сжатия и динамического модуля упругости пород зон возможных смещений блоков пород;
величины, характер распределения естественных напряжений в массиве и дополнительные нагрузки от инженерных сооружений на склонах;
закономерности (регионально-геологические и зонально-климатические), формирование и антропогенная активизация оползней, которые должны быть отражены на графиках коррелятивных зависимостей с количественной характеристикой их роли в формировании устойчивости склона;
опыт строительства на склонах инженерных сооружений и эффективности проведенных укрепительных мероприятий.
7.2. Результаты уточненных оценок и прогнозов рекомендуется сопоставлять с данными о региональных закономерностях развития склонов, оползней и обвалов на них, отраженных в ориентировочных прогнозах. Следует помнить, что получение достоверных результатов по вышеперечисленным вопросам не всегда возможно из-за сложности геологического строения оползневого склона и его недоступности для проведения разведочных работ. В таких случаях допускается применение приближенных характеристик. Например, для получения данных о расположении зон концентрации и величинах естественных напряжений в породах на участках, где напряжения превышают прочность пород, рекомендуются такие исследования:
на физических моделях (оптических, эквивалентных материалах, тензосетки) воспроизводят детальный инженерно-геологический разрез склона по направлению предполагаемого смещения и определяют величины и распределение напряжений. На моделях учитываются возможные воздействия на породы склона инженерных сооружений (пригрузки, подрезки и т.п.);
на породах из выявленных очагов "дефицита прочности", особенно если это зоны ослабления, определяются показатели физико-механических свойств (сопротивления сдвигу, временного сопротивления сжатию, объемного веса и влажности) лабораторными и полевыми методами. При распространении этих свойств на массив (или зону ослабления) используют модели дисперсионного анализа, в которые дополнительно вводят скорости упругих сейсмоакустических волн. С помощью этих моделей выявляется степень качественного подобия или отличия зон ослабления, как это показано на примере в табл. 16 Прил. 7;
на основе полученных данных составляется наиболее приемлемая для данного склона расчетная схема и определяется его устойчивость;
моделированием на эквивалентных материалах и методом тензосетки проверяют возможные деформации по выявленным зонам ослабления;
результаты моделирования и расчетов рекомендуется сопоставлять и подтверждать данными прогнозов по соответствующим математическим инженерно-геологическим моделям, составленным по аналогам изучаемого склона, и анализом инженерно-геологической обстановки района исследований.
7.3. Наиболее часто встречаемые виды антропогенных воздействий на склоны при уточненных прогнозах рекомендуется свести в соответствующие критерии геологического подобия, как это показано в табл. 1. Они являются дополнением к критериям, характеризующим природные условия формирования склонов (см. Прил. 1).
Вид критерия | Критерии подобия | Обозначения |
 | Подрезки склонов в нижних частях | F - площадь подрезки; |
 | Крутизны подрезанных склонов | |
 | Пригрузки обводненных верхних частей склонов, вызванные искусственным обводнением массива пород, а также возможного проявления гидростатического, гидродинамического давлений воды | |
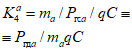 | ||
 | ||
 | Влияния динамических воздействий от взрывов, работающих механизмов и т.п., а также совместного влияния динамических воздействий и химического растворения (цементации) пород в ослабленных зонах промышленными стоками | |
 | ||
Дноуглубительных работ у основания склона | ||
Выпуска плывунов и сыпунов в откосах карьеров, выемок и т.п. |
7.4. Оценку устойчивости оползневых - обвальных склонов и уточненный прогноз их развития рекомендуется осуществлять в следующей последовательности:
среди всех изученных склонов с произошедшими оползнями-обвалами отбираются качественно подобные склоны, у которых одинаковы: литолого-генетические и петрографические комплексы пород, слагающие сравниваемые склоны; структурные условия развития районов формирования оползневых - обвальных склонов; текстурные особенности пород, слагающих оползневые - обвальные склоны; приуроченность оползней-обвалов к склонам одного возраста; степень и характер экзогенного изменения пород; характер тектонической нарушенности и трещиноватости пород; типы поверхностей ослабления и типы возможных ниш отрыва и смещения; расположение в пределах структурного блока одной интенсивности новейших и современных тектонических движений;
отобранные качественно подобные природные аналоги сравнивают по критериям геологического подобия и условиям однозначности, добиваясь выполнения второго принципа вероятностного геологического подобия (см. п. 2.6). При выполнении этого правила оцениваемый склон будет подобен аналогу, а его устойчивость близка к предельной и равна  , здесь
, здесь  - величина ошибки, вызванная изменчивостью показателей прогноза, вошедших в критерии подобия, и отсутствием в критериях второстепенных признаков прогноза. Она обусловливает некоторый запас прочности массива пород при условии, если для оцениваемого склона указанные признаки учитываются при анализе как качественно выражаемые факторы.
- величина ошибки, вызванная изменчивостью показателей прогноза, вошедших в критерии подобия, и отсутствием в критериях второстепенных признаков прогноза. Она обусловливает некоторый запас прочности массива пород при условии, если для оцениваемого склона указанные признаки учитываются при анализе как качественно выражаемые факторы.
 , здесь
, здесь 7.5. При невыполнении каких-либо требований третьего правила подобия для выбора аналога и оценки устойчивости изучаемого оползневого - обвального склона применяется первый принцип (см. п. 2.11). Для этого необходимо критерии геологического подобия разделить на главные и второстепенные, применительно к конкретным условиям и требованиям хозяйственного освоения изучаемых склонов.
7.6. Разделение критериев геологического подобия на данной стадии рекомендуется осуществлять по величине их вклада в формирование устойчивости склона. Эта величина определяется из исследований общих линейных уравнений по методике, изложенной в пп. 6.21 - 6.27 и в текстовом Прил. 8. В качестве функции (прогнозного критерия) в линейном уравнении связи рекомендуется брать критерий, характеризующий изменение скалывающих или нормальных напряжений по поверхностям возможного смещения пород со склонов (критерий  в Прил. 1), при котором происходят их катастрофические подвижки. Следовательно, исследуется общее линейное уравнение
в Прил. 1), при котором происходят их катастрофические подвижки. Следовательно, исследуется общее линейное уравнение
7.7. Согласно правилу вероятностного геологического подобия пункта 2.11, при сопоставлении оцениваемого (прогнозного) оползневого - обвального склона и его аналогов возможны два случая:
абсолютные значения главных критериев геологического подобия совпадают. В этом случае оцениваемый склон находится в состоянии предельного равновесия, а его устойчивость равна  . Величина ошибки
. Величина ошибки  определяется по формулам (2) и (3) п. 2.15;
определяется по формулам (2) и (3) п. 2.15;
 . Величина ошибки
. Величина ошибки ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 19 в Приложении 8 отсутствует. |
один или несколько критериев геологического подобия оцениваемого оползневого - обвального склона и его аналогов не совпадают. Величина отклонения коэффициента устойчивости от единицы в данном случае определяется из общего уравнения связи (42) согласно второму принципу вероятностного геологического подобия (см. п. 2.11). Она может быть также определена по величине отклонения критериев подобия объекта прогноза и аналога, исходя из величины относительной роли несовпадающих критериев в формировании устойчивости, как это показано в табл. 19 Прил. 8.
1. В качестве примера взяты оползневые - обвальные склоны долины р. Нарын (Киргизская ССР). В ходе выполнения инженерно-геологической съемки склонов в масштабе 1:25000 и детального картирования отдельных типичных (в отношении развития на склонах древних, старых и современных оползней-обвалов) участков в масштабах 1:5000 - 1:1000 были установлены местные и регионально-геологические закономерности и их представляющие показатели (см. табл. 2).
Таблица 2
Закономерности | Представляющие количественные показатели | Размерность | Обозначение | ||||
Пространственное соотношение крупных тектонических трещин с простиранием и крутизной склонов (см. п. 1.36) | Угол падения подошвенной поверхности отчленения известняков от основного массива | б/р | |||||
Длина подошвенной трещины склонов отчленения | L | ||||||
Морфология поверхности смещения, оцениваемая отношением веса оползня к линейному размеру неровности | G | ||||||
Сейсмические условия формирования склонов (см. п. 1.35) | Ускорение горизонтальной составляющей растягивающих напряжений при землетрясениях в сухих | ||||||
Ускорение силы тяжести | g | ||||||
Возраст оползнево-обвалоопасных частей склонов (см. п. 1.37) | Глубина захвата пород склона оползнем-обвалом в пределах зоны весьма интенсивного выветривания и разгрузки | L | |||||
Глубина значительного экзогенного изменения заполнителя по тыловым трещинам отчленения | L | ||||||
| |||||||
Инженерно-геологические свойства пород в присклоновых зонах и трещинах | Величины среднего сопротивления сдвигу по породам |  | |||||
Временное сопротивление сжатию пород зон смещения и обрушения | R | ||||||
Плотность пород |  | ||||||
Динамический модуль упругости |  | E | |||||
Гидрогеологические условия пород склонов (см. п. 1.44) | Гидростатическое давление воды в трещинах отчленения |  | |||||
Гидродинамическое давление воды | |||||||
Распределение и величины нормальных напряжений в массиве | Среднее нормальное напряжение - |  | |||||
Геоморфологические особенности строения склонов | Высота оползневых - обвальных частей склонов | L | H | ||||
Крутизна оползневых - обвальных частей склонов | б/р | ||||||
Климатические условия формирования склонов (см. п. 1.41) | Продолжительность единовременно выпадающих дождей | T | |||||
Объем выпадаемых осадков и инфильтрующихся в породы | Q | ||||||
2. За функцию степенного комплекса (42), составленного из представляющих количественных показателей, взят коэффициент устойчивости 
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
 , (42)
, (42)где c - коэффициент пропорциональности;
А, В, Д, Г, ..., П - представляющие показатели;
X, Y, Z, P, ..., 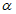 - неизвестные степени.
- неизвестные степени.
Заменив индексы А, В, Д, Г, ..., П соответствующими обозначениями (см. табл. 3) представляющих показателей, получим
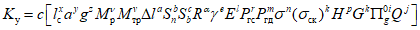 . (43)
. (43)В уравнение (43) вместо обозначений представляющих показателей подставим их размерности
 (44)
(44)В уравнении (44) неизвестны показатели степени, но известны размерности их членов. Приравняем показатели степени при одинаковых единицах размерности и решим это уравнение относительно любых трех неизвестных. Тогда получим 13 выражений функций, которые являются критериями геологического подобия. По своему физическому содержанию они объединяются в три группы:
критерии геологического подобия, характеризующие среду, в которой формируются оползни-обвалы. В эту группу включены критерии, отражающие подобие сопротивления сдвигу пород зон интенсивного выветривания и разгрузки  , заполнителей крупных тектонических трещин:
, заполнителей крупных тектонических трещин:  сухом или обводненном состоянии; неоднородности строения массива пород склона
сухом или обводненном состоянии; неоднородности строения массива пород склона  в сухом и обводненном состоянии; геометрических параметров оползней-обвалов
в сухом и обводненном состоянии; геометрических параметров оползней-обвалов  и
и  ; степени экзогенного изменения заполнителя трещин отчленения
; степени экзогенного изменения заполнителя трещин отчленения  в приповерхностной зоне весьма интенсивного выветривания и разгрузки пород и вне зон по крупным тектоническим трещинам; углов наклона возможных подошвенных поверхностей смещения оползней-обвалов (критерий-симплекс
в приповерхностной зоне весьма интенсивного выветривания и разгрузки пород и вне зон по крупным тектоническим трещинам; углов наклона возможных подошвенных поверхностей смещения оползней-обвалов (критерий-симплекс  ) и равенства склонов по крутизне (критерий-симплекс
) и равенства склонов по крутизне (критерий-симплекс  ); поверхностей смещения по их морфологии
); поверхностей смещения по их морфологии 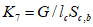 ;
;
 , заполнителей крупных тектонических трещин:
, заполнителей крупных тектонических трещин:  сухом или обводненном состоянии; неоднородности строения массива пород склона
сухом или обводненном состоянии; неоднородности строения массива пород склона  в сухом и обводненном состоянии; геометрических параметров оползней-обвалов
в сухом и обводненном состоянии; геометрических параметров оползней-обвалов  и
и  ; степени экзогенного изменения заполнителя трещин отчленения
; степени экзогенного изменения заполнителя трещин отчленения  в приповерхностной зоне весьма интенсивного выветривания и разгрузки пород и вне зон по крупным тектоническим трещинам; углов наклона возможных подошвенных поверхностей смещения оползней-обвалов (критерий-симплекс
в приповерхностной зоне весьма интенсивного выветривания и разгрузки пород и вне зон по крупным тектоническим трещинам; углов наклона возможных подошвенных поверхностей смещения оползней-обвалов (критерий-симплекс  ) и равенства склонов по крутизне (критерий-симплекс
) и равенства склонов по крутизне (критерий-симплекс  ); поверхностей смещения по их морфологии
); поверхностей смещения по их морфологии 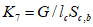 ;
;критерии подобия, характеризующие изменения состояния и свойств пород оползней-обвалов. В эту группу включены критерии, отражающие подобие прочности пород зон ослабления на раздавливание при начавшихся деформациях смещения под влиянием собственного веса пород  ; изменений скалывающих или нормальных напряжений в зоне возможного смещения, создаваемых весом оползня-обвала
; изменений скалывающих или нормальных напряжений в зоне возможного смещения, создаваемых весом оползня-обвала  ,
,  ; условий влияния сейсмичности на величину сопротивления смещения пород в сухом или обводненном состоянии
; условий влияния сейсмичности на величину сопротивления смещения пород в сухом или обводненном состоянии  ; влияния на устойчивость склона гидростатического
; влияния на устойчивость склона гидростатического  или гидродинамического
или гидродинамического  давлений воды; обводнения пород во время затяжных или дневных дождей и их влияния на устойчивость склонов
давлений воды; обводнения пород во время затяжных или дневных дождей и их влияния на устойчивость склонов  ;
;
 ; изменений скалывающих или нормальных напряжений в зоне возможного смещения, создаваемых весом оползня-обвала
; изменений скалывающих или нормальных напряжений в зоне возможного смещения, создаваемых весом оползня-обвала  ,
,  ; условий влияния сейсмичности на величину сопротивления смещения пород в сухом или обводненном состоянии
; условий влияния сейсмичности на величину сопротивления смещения пород в сухом или обводненном состоянии  ; влияния на устойчивость склона гидростатического
; влияния на устойчивость склона гидростатического  или гидродинамического
или гидродинамического  давлений воды; обводнения пород во время затяжных или дневных дождей и их влияния на устойчивость склонов
давлений воды; обводнения пород во время затяжных или дневных дождей и их влияния на устойчивость склонов  ;
;критерии геологического подобия, характеризующие условия изменения характера и величин естественных напряжений и создающие зоны сниженных и повышенных напряжений. К ним следует отнести все критерии второй группы, а также критерии  и
и  первой группы для случаев, когда происходит увеличение высоты
первой группы для случаев, когда происходит увеличение высоты 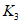 или крутизны
или крутизны  склонов. Критерии
склонов. Критерии  ,
,  ,
,  могут отражать те числовые значения, при которых происходит внезапное резкое изменение напряжений в породах.
могут отражать те числовые значения, при которых происходит внезапное резкое изменение напряжений в породах.
ЗАДАЧИ С АЛГОРИТМОМ ДИСКРИМИНАНТНЫХ ФУНКЦИЙ
ДЛЯ ОРИЕНТИРОВОЧНОЙ ОЦЕНКИ УСТОЙЧИВОСТИ
ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ
1. Решению задачи предшествует выбор для объекта прогноза его аналогов, которые изучены в ходе детальных разведочных работ. Для целей ориентировочных прогнозов с помощью выбранного алгоритма оползневые - обвальные склоны аналогов достаточно разделить по степени их устойчивости на две категории: неустойчивые и относительно устойчивые.
2. К неустойчивым оползне-, обвалоопасным склонам, например долины р. Нарын, сложенных прочными трещиноватыми породами, отнесены склоны, в пределах которых имеются образования:
обвальные, осыпные и другие гравитационные накопления на склонах средней крутизной 30° и более, незакрепленные, находящиеся в состоянии медленного смещения;
элювиальные образования, которые обводнены или периодически увлажняются поверхностными водами;
подготовленные к смещению блоки и пакеты пород, практически полностью отчлененные от основного массива широкими трещинами бортового отпора и разгрузки.
Коэффициент устойчивости названных склонов  , т.е. это склоны, находящиеся в состоянии предельного равновесия.
, т.е. это склоны, находящиеся в состоянии предельного равновесия.
 , т.е. это склоны, находящиеся в состоянии предельного равновесия.
, т.е. это склоны, находящиеся в состоянии предельного равновесия.3. К относительно устойчивым склонам относятся следующие:
участки современных склонов, а также поверхности отрыва современных и исторических оползней, в пределах которых породы слабо разгружены и выветрелые;
старые и древние оползневые, обвальные, осыпные и другие гравитационные накопления на склонах крутизной менее 30°, закрепленные травянисто-кустарниковой и древесной растительностью, без следов медленных смещений;
блоки пород, частично отчлененные от основного массива тектоническими трещинами без следов выветривания и разгрузки.
Коэффициент устойчивости отмеченных склонов  .
.
 .
.4. На стадии ориентировочных прогнозов устойчивость оползневых - обвальных склонов по перечисленным в пп. 2.2, 2.3 качественным признакам или с помощью традиционных расчетных классических методов часто оценить невозможно из-за отсутствия достоверных геологических данных о рассматриваемых склонах, породах, их слагающих, оползнях-обвалах. Для разделения оползневых - обвальных склонов в подобных случаях можно рекомендовать алгоритмы теории распознавания образов, к числу которых относятся дискриминантные функции.
5. Разделение склонов на две категории по степени их устойчивости с помощью отмеченного алгоритма осуществляется посредством сопоставления значений дискриминантных функций, построенных для объекта прогноза с пороговым значением функций, построенных для склонов-аналогов.
 , (45)
, (45)где Д' - средневзвешенное значение дискриминантной функции для выборки оползневых - обвальных склонов, обладающих так называемым целевым признаком  . Этот признак выбирается из группы регионально-геологических закономерностей формирования оползней-обвалов, установленных в ходе детального инженерно-геологического картирования склонов;
. Этот признак выбирается из группы регионально-геологических закономерностей формирования оползней-обвалов, установленных в ходе детального инженерно-геологического картирования склонов;
Д" - то же, но без целевого признака.
7. Применительно к условиям долины р. Нарын (Киргизская ССР) в пределах участка створа плотины Токтогульской ГЭС при детальном инженерно-геологическом картировании оползневых - обвальных склонов в пределах типичных (по условиям развития названных процессов) участков было установлено, что интенсивность, объемы, типы смещений пород со склонов зависят от особенностей строения и состояния склонов (являющихся регионально-геологическими и местными закономерностями формирования оползней-обвалов и признаками прогноза устойчивости склонов):
возраста склонов, в пределах которых развиты оползни-обвалы (см. п. 1.37). Было установлено, что объемы и интенсивность проявления на склонах оползней-обвалов разные в пределах склонов верхнечетвертичного, первой и второй половины среднечетвертичного и второй половины нижнечетвертичного времени. Обозначим их соответственно через  ,
,  ,
,  ,
,  ;
;
типа поверхностей смещения и отчленения оползней-обвалов, среди которых встречены литогенетический контактный (обозначим его посредством переменной  ), тектонический контактный
), тектонический контактный  , тектонический с зоной дробления
, тектонический с зоной дробления  и литогенетический слоевой
и литогенетический слоевой 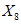 типы поверхностей ослабления массива известняков;
типы поверхностей ослабления массива известняков;
характеристики формы склона в плане. Для условий долины р. Нарын было установлено, что большинство склонов, с которых произошли оползневые - обвальные смещения пород, имели выпуклый профиль. На склонах с вогнутым профилем данные смещения пород на отмечены. Склоны сложного профиля в плане (выпукло-вогнутые, вогнутость внизу; вогнуто-выпуклые, вогнутость вверху; ступенчатые; ступенчато-выпуклые и т.п.) занимают промежуточное положение в отношении развития на них оползней-обвалов. Поэтому, применительно к местным условиям, данный признак прогноза рекомендуется принять в качестве целевого признака  (см. п. 2.6). Обоснованием для этого может служить сильная корреляционная зависимость между формой склонов в плане и интенсивностью оползней-обвалов (при прочих равных условиях) с коэффициентом корреляции
(см. п. 2.6). Обоснованием для этого может служить сильная корреляционная зависимость между формой склонов в плане и интенсивностью оползней-обвалов (при прочих равных условиях) с коэффициентом корреляции  ;
;
 ;
;типов заполнителей в зонах смещения и отчленения оползней-обвалов, среди которых встречены супесчаный карбонатный материал мягкопластичной консистенции 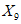 и супесчано-дресвяный рыхлого сложения, влажный
и супесчано-дресвяный рыхлого сложения, влажный  ;
;
углов между простираниями продольных (по отношению к склону), перечисленных выше поверхностей ослабления массивов карбонатных пород и отчленяющих блоки пород от основного массива, и направлением склонов. Среди этих углов рекомендуется выделять три интервала их изменений: от 0 до 10°, от 11 до 20°, от 21 до 30°; обозначим их  ,
,  ,
,  соответственно;
соответственно;
углов падения поверхностей смещения (оползней) или отчленения (обвалов), среди которых целесообразно выделять пять интервалов их изменений: 10 - 20°  , 21 - 30°
, 21 - 30° 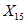 , 31 - 40°
, 31 - 40°  , 41 - 50°
, 41 - 50°  , 51 - 60°
, 51 - 60°  .
.
8. Перечисленные в п. 7 признаки прогноза составят дискриминантную функцию
причем  , если для каждого из рассматриваемых оползневых (или обвальных) склонов установлен признак прогноза i;
, если для каждого из рассматриваемых оползневых (или обвальных) склонов установлен признак прогноза i;  , если такой признак не характерен для данных склонов.
, если такой признак не характерен для данных склонов.
 , если такой признак не характерен для данных склонов.
, если такой признак не характерен для данных склонов.9. Допустим, что имеется 136 качественно подобных природных аналогов, отобранных согласно пункту 6. Их устойчивость известна и они составляют обучающую выборку. Анализ этой обучающей выборки показал, что 13 оползней-обвалов на склонах-аналогах располагаются в пределах верхнечетвертичных склонов (обозначенных в п. 7  ) с выпуклым в плане профилем
) с выпуклым в плане профилем 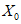 ; это допущение удобно записать в виде такого выражения
; это допущение удобно записать в виде такого выражения  ; в пяти случаях (из 26 аналогов) оползни-обвалы произошли на склонах с выпуклым профилем, но иного возраста, что соответственно можно записать
; в пяти случаях (из 26 аналогов) оползни-обвалы произошли на склонах с выпуклым профилем, но иного возраста, что соответственно можно записать  . В пяти случаях прогнозируемые
. В пяти случаях прогнозируемые  (см. п. 10) оползни-обвалы встречены на верхнечетвертичных склонах с невыпуклым профилем, т.е.
(см. п. 10) оползни-обвалы встречены на верхнечетвертичных склонах с невыпуклым профилем, т.е.  ; в трех случаях из имеющихся 26 прогнозируемые оползни-обвалы располагаются на склонах другого возраста, не имеющих выпуклого профиля, т.е.
; в трех случаях из имеющихся 26 прогнозируемые оползни-обвалы располагаются на склонах другого возраста, не имеющих выпуклого профиля, т.е.  . Подставив значения a = 13, b = 5, c = 5, d = 3 в формулы (47), (48) (см. пп. 10 - 11), вычислим коэффициент согласованности W(g) верхнечетвертичных склонов
. Подставив значения a = 13, b = 5, c = 5, d = 3 в формулы (47), (48) (см. пп. 10 - 11), вычислим коэффициент согласованности W(g) верхнечетвертичных склонов  со склонами, имеющими выпуклый в плане профиль
со склонами, имеющими выпуклый в плане профиль  (или косвенных признаков прогноза с целевым признаком прогноза, см. п. 10),
(или косвенных признаков прогноза с целевым признаком прогноза, см. п. 10),  . Аналогично определяются остальные коэффициенты согласованности, значения которых для рассматриваемого примера приведены ниже:
. Аналогично определяются остальные коэффициенты согласованности, значения которых для рассматриваемого примера приведены ниже:
 ; в пяти случаях (из 26 аналогов) оползни-обвалы произошли на склонах с выпуклым профилем, но иного возраста, что соответственно можно записать
; в пяти случаях (из 26 аналогов) оползни-обвалы произошли на склонах с выпуклым профилем, но иного возраста, что соответственно можно записать  . В пяти случаях прогнозируемые
. В пяти случаях прогнозируемые  ; в трех случаях из имеющихся 26 прогнозируемые оползни-обвалы располагаются на склонах другого возраста, не имеющих выпуклого профиля, т.е.
; в трех случаях из имеющихся 26 прогнозируемые оползни-обвалы располагаются на склонах другого возраста, не имеющих выпуклого профиля, т.е.  . Подставив значения a = 13, b = 5, c = 5, d = 3 в формулы (47), (48) (см. пп. 10 - 11), вычислим коэффициент согласованности W(g) верхнечетвертичных склонов
. Подставив значения a = 13, b = 5, c = 5, d = 3 в формулы (47), (48) (см. пп. 10 - 11), вычислим коэффициент согласованности W(g) верхнечетвертичных склонов  . Аналогично определяются остальные коэффициенты согласованности, значения которых для рассматриваемого примера приведены ниже:
. Аналогично определяются остальные коэффициенты согласованности, значения которых для рассматриваемого примера приведены ниже: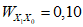 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 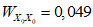 ;
; 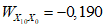 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.10. Подставим значения коэффициентов согласованности в формулу (46) (см. п. 8) и получим выражение дискриминантной функции
В формулу (47) для всех  подставляется 1 или -1 и определяется средневзвешенное значение дискриминантной функции для двух совокупностей оползней-обвалов:
подставляется 1 или -1 и определяется средневзвешенное значение дискриминантной функции для двух совокупностей оползней-обвалов:
содержащих целевой признак 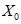 , то есть для оползней, расположенных на склонах с выпуклым профилем
, то есть для оползней, расположенных на склонах с выпуклым профилем

совокупность оползней без  , т.е. расположенных на склонах с невыпуклым профилем
, т.е. расположенных на склонах с невыпуклым профилем

Критические значения линейной дискриминантной функции (46) после подстановки значений для выборки оползневых - обвальных склонов с целевым признаком (Д') и без него (Д")
Д* = (0,0257 + 0,0678)/2 = 0,0467.
При этом предполагается, что стандартные отклонения  дискриминантных функций равны между собой.
дискриминантных функций равны между собой.
11. Оползневые склоны, значения дискриминантной функции, у которых окажутся больше ее критического значения, т.е.  , следует считать относительно устойчивым. Напротив, если
, следует считать относительно устойчивым. Напротив, если  , эти склоны являются неустойчивыми.
, эти склоны являются неустойчивыми.
 , следует считать относительно устойчивым. Напротив, если
, следует считать относительно устойчивым. Напротив, если  , эти склоны являются неустойчивыми.
, эти склоны являются неустойчивыми.12. Оценка величины ошибки прогноза выполняется по экзаменационной выборке согласно п. 3.21, поскольку число склонов-аналогов для рассматриваемого примера более чем в 5 раз превышает число признаков прогноза и равно 136 против 90 допустимых предлагаемой методикой. Вероятности ошибок следующие:
отнесения устойчивого склона к неустойчивому
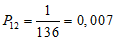 ;
;отнесения неустойчивого склона к устойчивому
 .
.13. Применяемый подход к построению дискриминантной функции можно обосновать таким образом. Признаки прогноза, положительно связанные с целевым признаком  в объектах, обладающих им, в среднем будут встречаться чаще, чем в объектах, не обладающих этим признаком, и тем чаще, чем сильнее их связи. Наоборот, признаки, отрицательно связанные с признаком
в объектах, обладающих им, в среднем будут встречаться чаще, чем в объектах, не обладающих этим признаком, и тем чаще, чем сильнее их связи. Наоборот, признаки, отрицательно связанные с признаком 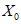 , в объектах, обладающих им, будут обнаруживаться реже, чем в объектах, не обладающих им, и тем реже, чем сильнее их связи. Поэтому если просуммировать оценки мер связи в соответствии с отсутствием или присутствием признаков
, в объектах, обладающих им, будут обнаруживаться реже, чем в объектах, не обладающих им, и тем реже, чем сильнее их связи. Поэтому если просуммировать оценки мер связи в соответствии с отсутствием или присутствием признаков  ,
,  , ...,
, ...,  в данном объекте
в данном объекте  , то сумма будет, вероятно, зависеть от того, обладает ли этот объект целевым признаком или нет.
, то сумма будет, вероятно, зависеть от того, обладает ли этот объект целевым признаком или нет.
14. Область работы данных ориентировочных прогнозов распространяется на склоны с признаками прогноза, вошедшими в обучающую выборку. При необходимости расширить эту область за счет, например, ввода новых признаков прогноза, характеризующих тот или иной вид строительной деятельности человека, необходимо определить коэффициенты согласованности целевого признака с интересующими антропогенными признаками прогноза и оценить новые значения дискриминантной функции.
ПО ТУПИКОВЫМ ТЕСТАМ ДЛЯ ОРИЕНТИРОВОЧНОЙ ОЦЕНКИ
УСТОЙЧИВОСТИ ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ
1. Предположим, что в ходе инженерно-геологических изысканий для обоснования проектного задания строительства промышленных сооружений в пределах долины горной реки были выявлены большие по объему и интенсивности оползни и обвалы. Склоны долины реки сложены толщей моноклинально залегающих нижнекаменноугольных известняков. По отдельным опорным участкам установлены закономерности, характеризующие развитие оползневых склонов. Эти закономерности имеют качественное выражение, согласно перечню могут быть рекомендованы в качестве признаков ориентировочного прогноза.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
1. Склоны среднечетвертичного вреза средней высотой над уровнем реки 900 м и крутизной 40°.
2. Разрывы, субпараллельные склону, и шириной зоны интенсивного дробления и трещиноватости пород до 200 м; трещины - сместители разрыва секут склон через 20 м.
3. Направление осей растяжения, установленных по слабым (до 5 баллов) и сильным (более 6 баллов) землетрясениям, перпендикулярно склону.
4. То же, что и выше, но косые к склону и составляют угол 40 - 50°.
5. Зоны весьма интенсивной разгрузки и выветривания пород.
6. Зоны интенсивного выветривания пород по трещинам и разгрузки напряжений.
7. Зоны слабой разгрузки пород и выветривания по крупным трещинам.
8. Литогенетический контактный тип поверхностей ослабления пород.
9. Тектонический контактный тип поверхностей смещения пород со склонов.
10. Тектонический с зоной дробления тип поверхностей смещения пород.
11. Литогенетический слоевой (неустойчивые пластичные, суффозионные и иные слабые прослои).
12. Блоки пород, полностью отчлененные от основного массива трещинами бортового отпора и разгрузки.
13. Блоки пород, частично отчлененные от основного массива трещинами бортового отпора и выветривания.
14. Блоки пород, полностью отчлененные от основного массива тектоническими трещинами без следов выветривания и разгрузки напряжений.
15. Блоки пород, частично отчлененные от основного массива тектоническими трещинами без следов выветривания и разгрузки напряжений.
16. Суглинисто-глинистый заполнитель трещин, отчленяющих блоки пород от основного массива, мягко-, текучепластичной консистенции, монтмориллонитового состава.
17. То же, но твердой консистенции с примесью гипса и хорошо разложившейся органики.
18. Супесчано-дресвяный заполнитель рыхлого сложения в трещинах, отчленяющих блоки пород от основного массива.
19. Дресвяно-щебенчатый заполнитель трещин.
20. Заполнитель трещин отсутствует.
21. Прямолинейный в плане профиль склонов.
22. Выпуклый профиль склонов в плане.
23. Выпукло-вогнутый (выпуклость вверху) профиль склона в плане.
24. Ступенчатый профиль склона в плане.
25. Ожидаются подрезки склона внизу, за счет чего угол склона увеличивается до 50°.
26. Ожидаются эпизодические обводнения склона за счет сброса бытовых вод, обогащенных ионами  ,
,  ,
, 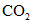 агрессивной и свободной.
агрессивной и свободной.
27. Эпизодические массовые взрывы, имитирующие землетрясения силой до 5 баллов.
28. Возможны максимальные пригрузки склонов вверху до 2 МПа.
Основываясь на определенных их сочетаниях в пределах хорошо изученных опорных участков (природных аналогов), требуется дать ориентировочный прогноз устойчивости оползневых - обвальных склонов на неизученных участках. Причем названные в перечне признаки прогноза при решении задачи с алгоритмом голосования по тупиковым тестам могут принимать одно из двух значений: 1, если тот или иной признак характеризует развитие или активизацию оползней-обвалов, и 0, если он не характерен для рассматриваемых оползневых - обвальных склонов. Все оползневые - обвальные склоны по степени устойчивости разделены на две категории: неустойчивые и относительно устойчивые.
2. Установлено, что для рассматриваемого примера развитие и активизацию оползней-обвалов предопределяют 28 основных качественно выражаемых признаков прогноза (см. перечень). В табл. 3 дан пример описания восьми природных аналогов обучающей матрицы и десяти аналогов экзаменационной матрицы. Для относительно устойчивых и неустойчивых склонов характерны определенные сочетания приведенных в перечне признаков прогноза (табл. 3). В табл. 4 приведены алгоритм, по которому выполнен прогноз; значения параметров, характеризующих размеры обучающей  и экзаменационной
и экзаменационной  матрицы; время решения задачи на ЭВМ; результат прогноза.
матрицы; время решения задачи на ЭВМ; результат прогноза.
Матрицы | N аналога | Номера признаков прогноза | Количество | ||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | единиц | нулей | ||
Обучающая матрица | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 13 | 15 |
2 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 14 | 14 | |
3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 13 | 15 | |
4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 14 | 14 | |
Неустойчивые склоны | |||||||||||||||||||||||||||||||
Относительно устойчивые склоны | 5 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 7 | 21 |
6 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 8 | 20 | |
7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | 22 | |
8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | 22 | |
Экзаменационная матрица | 9 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 14 | 14 |
10 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 15 | 13 | |
11 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 12 | 16 | |
12 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 11 | 17 | |
13 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 12 | 16 | |
14 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 14 | 14 | |
15 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 14 | 14 | |
16 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 16 | 12 | |
17 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 16 | 12 | |
18 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 13 | 15 | |
Алгоритм | Количество признаков прогноза | Количество аналогов | Продолжительность поиска на ЭВМ, с | Тупиковые тесты | |
обучающей | экзаменацион. | ||||
матрицы | |||||
Голосование по тупиковым тестам | 28 | 8 | 10 | 78 | 1844 |
3. Для рассматриваемых оползневых склонов количество тупиковых тестов  ; все 10 экзаменационных аналогов оползневых - обвальных склонов были правильно отнесены к своей категории устойчивости. Правильность выполненных прогнозов позже была подтверждена в процессе строительства и эксплуатации отмеченных промышленных объектов.
; все 10 экзаменационных аналогов оползневых - обвальных склонов были правильно отнесены к своей категории устойчивости. Правильность выполненных прогнозов позже была подтверждена в процессе строительства и эксплуатации отмеченных промышленных объектов.
 ; все 10 экзаменационных аналогов оползневых - обвальных склонов были правильно отнесены к своей категории устойчивости. Правильность выполненных прогнозов позже была подтверждена в процессе строительства и эксплуатации отмеченных промышленных объектов.
; все 10 экзаменационных аналогов оползневых - обвальных склонов были правильно отнесены к своей категории устойчивости. Правильность выполненных прогнозов позже была подтверждена в процессе строительства и эксплуатации отмеченных промышленных объектов.4. Оценку устойчивости и прогноза развития оползневых - обвальных склонов с помощью алгоритма голосования по тупиковым тестам также рекомендуется применять на ранних стадиях изысканий при наличии у исполнителей возможности использовать ЭВМ. В противном случае применяются дискриминантные функции.
ОПЛЫВИН С ПОМОЩЬЮ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
1. В элювиальных глинистых грунтах натрий-монтмориллонитового состава в периоды весеннего протаивания грунтов ежегодно формируются оплывины с объемами в первые тысячи м3. Было установлено, что применительно к рассматриваемым условиям наиболее представительным для ориентировочных прогнозов является период с двенадцатью наблюдениями за интенсивностью проявления оплывин, выполняемые в течение трех лет зимой, весной, летом и осенью. Более длительные наблюдения для данного района оказались неоправданными, потому что рекомендуемая методика анализа гармонических функций основана на исследовании колебаний показателя интенсивности оплывин вокруг какого-то ее среднего уровня.
2. Тенденция ряда наблюдений при гармоническом анализе не учитывается. Использование среднего уровня интенсивности оплывин за 3 года дает меньшие ошибки по сравнению с заменой этой тенденции каким-то средним уровнем за более длительный промежуток времени стационарных режимных наблюдений.
3. В анализ взят ряд наблюдений за оплывинами, образованными за период с 1965 по 1967 г. Наибольшее число гармоник, которое можно рассчитать для этого ряда, равно 6. В качестве примера определим вид прогнозных функций с четырьмя и шестью гармониками. Периодическая функция с четырьмя гармониками
где  ; K = 12;
; K = 12;
 ; K = 12;
; K = 12; ;
;Таблица 5
t | sinX | sin2X | sin3X | sin4X | sin5X | cosX | cos2X | cos3X | cos4X | cos5X | cos6X |
1 | 0,500 | 0,866 | 1 | 0,866 | 0,500 | 0,866 | 0,5 | 0 | -0,5 | -0,866 | -1 |
2 | 0,866 | 0,866 | 0 | -0,866 | -0,866 | 0,500 | -0,5 | 1 | -0,5 | 0,500 | 1 |
3 | 1,000 | 0,000 | -1 | 0,000 | 1,000 | 0,000 | -1,0 | 0 | 1,0 | 0,000 | -1 |
4 | 0,866 | -0,866 | 0 | 0,866 | -0,866 | -0,500 | -0,5 | 1 | -0,5 | -0,500 | 1 |
5 | 0,500 | -0,866 | 1 | -0,866 | 0,500 | -0,866 | 0,5 | 0 | -0,5 | 0,866 | -1 |
6 | 0,000 | 0,000 | 0 | 0,000 | 0,000 | -1,000 | 1,0 | -1 | 1,0 | -1,000 | 1 |
7 | -0,500 | 0,866 | -1 | 0,866 | -0,500 | -0,866 | 0,5 | 0 | -0,5 | 0,866 | -1 |
8 | -0,866 | 0,866 | 0 | -0,866 | 0,866 | -0,500 | -0,5 | 1 | -0,5 | -0,500 | 1 |
9 | -1,000 | 0,000 | 1 | 0,000 | -1,000 | 0,000 | -1,0 | 0 | 1,0 | 0,000 | -1 |
10 | -0,866 | -0,866 | 0 | 0,866 | 0,866 | 0,500 | -0,5 | -1 | -0,5 | 0,500 | 1 |
11 | -0,500 | -0,866 | -1 | -0,866 | -0,500 | 0,866 | 0,5 | 0 | -0,5 | -0,866 | -1 |
12 | 0,000 | 0,000 | 0 | 0,000 | 0,000 | 1,000 | 1,0 | 1 | 1,0 | 1,000 | 1 |
t | X | sinX | cosX | Суммарное за сезон количество оплывин | 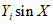 |  | Значения коэффициентов | |
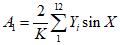 |  | |||||||
1 | П/6 | 0,500 | 0,866 | 12 | 6,0 | 10,4 |  |  |
2 | П/3 | 0,866 | 0,500 | 14 | 12,1 | 7,0 | ||
3 | П/2 | 1,000 | 0,000 | 6 | 6,0 | 0,0 | ||
4 | 2П/3 | 0,866 | -0,500 | 12 | 10,4 | -6,0 | ||
5 | 5П/3 | 0,500 | -0,866 | 12 | 6,0 | -10,4 | ||
6 | П | 0,000 | -1,000 | 14 | 0,0 | -14,0 | ||
7 | 7П/6 | -0,500 | -0,866 | 7 | -3,5 | -6,1 | ||
8 | 4П/3 | -0,866 | -0,500 | 12 | -10,4 | -6,0 | ||
9 | 3П/2 | -1,000 | 0,000 | 13 | -13,0 | 0,0 | ||
10 | 5П/3 | -0,866 | 0,500 | 15 | -13,0 | 7,5 | ||
11 | 11П/6 | -0,500 | 0,866 | 8 | -4,0 | 6,9 | ||
12 | 0 | 0 | 1,000 | 15 | 0,0 | 15,0 | ||
Итого | - | - | - | 140 | -3,4 | 4,3 | ||
Аналогично подсчитываются коэффициенты для второй, третьей, четвертой, пятой и шестой гармоник. После их расчета получены значения:  ;
; 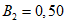 ;
; 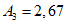 ;
;  ;
;  ;
;  ;
; 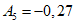 ;
;  ;
;  .
.
 ;
; 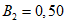 ;
; 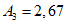 ;
;  ;
;  ;
;  ;
; 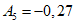 ;
;  ;
;  .
.4. Гармонические функции с четырьмя и шестью гармониками после подстановки в уравнение типа (48) значений коэффициентов  и
и 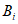 имеют вид
имеют вид
+ 0,58cosX + 0,5cos2X - 0,67cos3X - 0,33cos4X; (49)
- 0,27sin5X + 0,58cosX + 0,5cos2X - 0,67cos3X + 0,33cos4X +
+ 0,45cos5X + 4cos6X. (50)
5. В табл. 7 приведены расчетные (прогнозные) значения интенсивности оплывин по полученным уравнениям (49) и (50), фактически наблюдаемые значения интенсивности оплывин, а также отклонения прогнозных значений от фактических данных по сезонам года.
6. Согласно данным табл. 7 средняя ошибка прогноза интенсивности образования оплывин в элювиальных глинистых грунтах по сезонам года составляет около 17%, что равно двум оплывинам на сезон.
Таблица 7
Виды наблюдений | Результаты по годам, шт. | |||||||||||
1965 | 1966 | 1967 | ||||||||||
I | II | III | IV | I | II | III | IV | I | II | III | IV | |
Фактически наблюдаемое количество оплывин | 12 | 14 | 6 | 12 | 12 | 14 | 7 | 12 | 13 | 15 | 8 | 15 |
Прогнозное количество оплывин, рассчитанное по уравнению (49) | 9 | 12 | 8 | 10 | 14 | 13 | 9 | 10 | 15 | 13 | 10 | 13 |
Отклонение | -3 | 2 | -2 | 2 | -2 | 1 | -2 | 2 | -2 | 2 | -2 | 2 |
Прогнозное количество оплывин, рассчитанное по уравнению (50) | 10 | 16 | 4 | 14 | 10 | 16 | 5 | 13 | 11 | 17 | 6 | 16 |
Отклонение | 2 | -2 | 2 | -2 | 2 | -2 | 2 | -1 | 2 | -2 | 2 | -1 |
7. Для прогноза интенсивности оплывин элювиальных глинистых грунтов со склонов рассматриваемого района на период с 1968 по 1971 г. прогнозная функция с шестью гармониками будет иметь вид
Y = (7,7 + 0,161t) - 0,45sinX - 0,12sin2X + 2,67sin3X +
+ 0,017sin4X - 0,27sin5X + 0,58cosX + 0,5cos2X - 0,67cos3X +
+ 0,33cos4X + 0,45cos5X + 4cos6X.
8. Средняя ошибка аппроксимации для уравнений типа (49) и (50) может быть также оценена по общей дисперсии, которая учитывается четырьмя или шестью гармониками. Дисперсия, учитываемая одной гармоникой
 ,
,где  ; для последней гармоники
; для последней гармоники 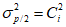 . Часть дисперсии, которая предопределена определенной гармоникой, представляется в виде отношения величины
. Часть дисперсии, которая предопределена определенной гармоникой, представляется в виде отношения величины  (или
(или  ) к общей дисперсии
) к общей дисперсии  . Поскольку никакие две гармоники не коррелируются между собой, то они не будут учитывать одну и ту же часть общей дисперсии, т.е. дисперсии, которые входят в различные гармоники, складываются. Доля общей дисперсии, учитываемая гармониками, согласно данным вычислений табл. 8, составляет: первой - 4,7%, второй - 1,7%, третьей - 40,7%, четвертой - 0,6%, пятой - 5,5%, шестой - 11,6%. Следовательно, общая доля дисперсии, учитываемая всеми четырьмя гармониками, равна 47,7%, а всеми шестью гармониками - 64,8%. Это означает, что периодическая функция, состоящая из шести гармоник, довольно хорошо учитывает колебания в интенсивности проявления оплывин во временном трехлетнем ряду наблюдений (см. табл. 8).
. Поскольку никакие две гармоники не коррелируются между собой, то они не будут учитывать одну и ту же часть общей дисперсии, т.е. дисперсии, которые входят в различные гармоники, складываются. Доля общей дисперсии, учитываемая гармониками, согласно данным вычислений табл. 8, составляет: первой - 4,7%, второй - 1,7%, третьей - 40,7%, четвертой - 0,6%, пятой - 5,5%, шестой - 11,6%. Следовательно, общая доля дисперсии, учитываемая всеми четырьмя гармониками, равна 47,7%, а всеми шестью гармониками - 64,8%. Это означает, что периодическая функция, состоящая из шести гармоник, довольно хорошо учитывает колебания в интенсивности проявления оплывин во временном трехлетнем ряду наблюдений (см. табл. 8).
 ; для последней гармоники
; для последней гармоники 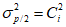 . Часть дисперсии, которая предопределена определенной гармоникой, представляется в виде отношения величины
. Часть дисперсии, которая предопределена определенной гармоникой, представляется в виде отношения величины Таблица 8
N гармоник | Часть  | Доля дисперсии  , % , %  , % , % | ||
1 | 0,829 | 0,414 | 0,198 | 4,7 |
2 | 0,264 | 0,132 | 0,063 | 1,5 |
3 | 7,129 | 3,564 | 1,710 | 40,7 |
4 | 0,109 | 0,054 | 0,026 | 0,6 |
Итого по четырем гармоникам | 47,5 | |||
5 | 0,275 | 0,138 | 0,68 | 5,5 |
6 | 16,00 | 8,00 | 1,32 | 10,8 |
Итого по шести гармоникам | 64,8 | |||
СКЛОНОВ С ПОМОЩЬЮ МЕТОДОВ "ОБРАТНЫХ РАСЧЕТОВ"
1. При детальном специализированном инженерно-геологическом картировании оползней в пределах опорных участков было установлено, что имеющиеся на склоне современные оползневые накопления можно разделить на две разновозрастные генерации (см. рис. 1). Первая генерация  представляет собой смещенные блоки и пакеты пород объемом единовременного смещения
представляет собой смещенные блоки и пакеты пород объемом единовременного смещения 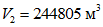 ; их базисом смещения был уровень высокой поймы реки. Вторая генерация
; их базисом смещения был уровень высокой поймы реки. Вторая генерация 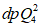 - в смещение были вовлечены верхние части пакетов пород из произошедшего оползня первой генерации; базисом смещения был современный врез реки, объем
- в смещение были вовлечены верхние части пакетов пород из произошедшего оползня первой генерации; базисом смещения был современный врез реки, объем  . Оба оползня отчетливо фиксируются в рельефе двумя тыловыми рвами. Анализ факторов среды формирования этих двух оползней показал их качественное подобие. Поэтому они могут быть взяты в качестве исходных для оценки параметров сдвига по их поверхностям смещения. Оползни могут быть рассчитаны по плоской схеме, так как тыловые поверхности отчленения у них субвертикальные (раскрытые процессами бортового отпора и частично выполнены вмытым супесчаным заполнителем рыхлого сложения); поэтому параметры сдвига по ним
. Оба оползня отчетливо фиксируются в рельефе двумя тыловыми рвами. Анализ факторов среды формирования этих двух оползней показал их качественное подобие. Поэтому они могут быть взяты в качестве исходных для оценки параметров сдвига по их поверхностям смещения. Оползни могут быть рассчитаны по плоской схеме, так как тыловые поверхности отчленения у них субвертикальные (раскрытые процессами бортового отпора и частично выполнены вмытым супесчаным заполнителем рыхлого сложения); поэтому параметры сдвига по ним  ;
;  . Следовательно, для получения искомых показателей в этом случае необходимо принять первую расчетную схему.
. Следовательно, для получения искомых показателей в этом случае необходимо принять первую расчетную схему.
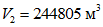 ; их базисом смещения был уровень высокой поймы реки. Вторая генерация
; их базисом смещения был уровень высокой поймы реки. Вторая генерация  . Оба оползня отчетливо фиксируются в рельефе двумя тыловыми рвами. Анализ факторов среды формирования этих двух оползней показал их качественное подобие. Поэтому они могут быть взяты в качестве исходных для оценки параметров сдвига по их поверхностям смещения. Оползни могут быть рассчитаны по плоской схеме, так как тыловые поверхности отчленения у них субвертикальные (раскрытые процессами бортового отпора и частично выполнены вмытым супесчаным заполнителем рыхлого сложения); поэтому параметры сдвига по ним
. Оба оползня отчетливо фиксируются в рельефе двумя тыловыми рвами. Анализ факторов среды формирования этих двух оползней показал их качественное подобие. Поэтому они могут быть взяты в качестве исходных для оценки параметров сдвига по их поверхностям смещения. Оползни могут быть рассчитаны по плоской схеме, так как тыловые поверхности отчленения у них субвертикальные (раскрытые процессами бортового отпора и частично выполнены вмытым супесчаным заполнителем рыхлого сложения); поэтому параметры сдвига по ним  ;
;  . Следовательно, для получения искомых показателей в этом случае необходимо принять первую расчетную схему.
. Следовательно, для получения искомых показателей в этом случае необходимо принять первую расчетную схему.
(правый берег р. Ангары, район Богучанского гидроузла)
Поверхности смещения оползней: 1 - древних; 2 - старых;
3 - молодых; 4 - современных. Крупные тектонические
трещины, расширенные процессами разгрузки и выветривания:
5 - подсекающие блоки и пакеты пород снизу и являющиеся
подошвенными поверхностями смещения пород со склонов;
6 - отчленяющие блоки пород с боков; 7 - крупные широкие
трещины разгрузки и бортового отпора; 8 - оползневые
накопления на склоне двух разновозрастных генераций;
9 - номер оползневых или оползнеопасных блоков пород;
10 - нижнеордовикские отложения нижнеустькутской свиты;
11 - разведочные шурфы и их номер; 12 - разведочные
скважины и их номер; 13 - линия разреза;
14 - погребенные границы; 15 - крупные трещины
разгрузки и бортового отпора, превращенные в рвы
2. Смещение рассматриваемых блоков пород (см. рис. 1) происходило по ослабленному прослою аргиллитов с углом падения в сторону склона  . Расчетные значения плотности оползневых накоплений равны
. Расчетные значения плотности оползневых накоплений равны  . Подставив соответствующие расчетные показатели в уравнение равновесия для первой схемы (см. п. 5.8), получим, что тангенс угла внутреннего трения пород (в зоне смещения площадью от 13225 м2 до 20066 м2)
. Подставив соответствующие расчетные показатели в уравнение равновесия для первой схемы (см. п. 5.8), получим, что тангенс угла внутреннего трения пород (в зоне смещения площадью от 13225 м2 до 20066 м2)  , а сцепление C = 0,16 МПа (см. рис. 1).
, а сцепление C = 0,16 МПа (см. рис. 1).
 . Расчетные значения плотности оползневых накоплений равны
. Расчетные значения плотности оползневых накоплений равны  . Подставив соответствующие расчетные показатели в уравнение равновесия для первой схемы (см. п. 5.8), получим, что тангенс угла внутреннего трения пород (в зоне смещения площадью от 13225 м2 до 20066 м2)
. Подставив соответствующие расчетные показатели в уравнение равновесия для первой схемы (см. п. 5.8), получим, что тангенс угла внутреннего трения пород (в зоне смещения площадью от 13225 м2 до 20066 м2)  , а сцепление C = 0,16 МПа (см. рис. 1).
, а сцепление C = 0,16 МПа (см. рис. 1).3. Откартированные оползни (см. рис. 1) при сравнительно-геологическом анализе оказались аналогами для трех оползнеопасных (по геологическим соображениям) блоков пород, устойчивость которых необходимо оценить в естественных условиях, а также дать прогноз изменения этой устойчивости после затопления блоков пород будущим водохранилищем (см. рис. 2).

выделенных по геологическим соображениям
Второй, третий и четвертый оползнеопасные блоки (см. рис. 2) отчленены от основного массива сформированными трещинами бортового отпора крутизной 80°, которые представляют собою рвы шириной до 10 м, глубиной зияющей части до 1,0 м. На глубине 8 м ширина трещин составляет 0,5 м и они выполнены вмытым суглинистым заполнителем рыхлого сложения. С восточной и западной части (с боков) оползневые блоки отчленены тектоническими трещинами с углом падения 60°, падающими навстречу друг другу [ (см. рис. 1)]. Эти трещины расширены процессами разгрузки до 0,3 м и выполнены вмытым суглинистым заполнителем рыхлого сложения, качественно подобным заполнителю оползневых блоков аналога 13 (см. рис. 1), а также заполнителю подошвенной трещины, подсекающей блоки пород снизу и имеющий угол падения:
(см. рис. 1)]. Эти трещины расширены процессами разгрузки до 0,3 м и выполнены вмытым суглинистым заполнителем рыхлого сложения, качественно подобным заполнителю оползневых блоков аналога 13 (см. рис. 1), а также заполнителю подошвенной трещины, подсекающей блоки пород снизу и имеющий угол падения:  (см. рис. 2).
(см. рис. 2).
 (см. рис. 1)]. Эти трещины расширены процессами разгрузки до 0,3 м и выполнены вмытым суглинистым заполнителем рыхлого сложения, качественно подобным заполнителю оползневых блоков аналога 13 (см. рис. 1), а также заполнителю подошвенной трещины, подсекающей блоки пород снизу и имеющий угол падения:
(см. рис. 1)]. Эти трещины расширены процессами разгрузки до 0,3 м и выполнены вмытым суглинистым заполнителем рыхлого сложения, качественно подобным заполнителю оползневых блоков аналога 13 (см. рис. 1), а также заполнителю подошвенной трещины, подсекающей блоки пород снизу и имеющий угол падения:  (см. рис. 2).
(см. рис. 2).4. Второй, третий и четвертый оползнеопасные блоки по соотношению у них поверхностей ослабления следует отнести к третьей расчетной схеме (см. п. 5.8).
ОПОЛЗНЕВЫХ СКЛОНОВ С ПОМОЩЬЮ ПОСЛЕДОВАТЕЛЬНОГО
МНОГОФАКТОРНОГО РЕГРЕССИОННОГО АНАЛИЗА
1. В качестве примера взяты оползневые - обвальные склоны долины р. Нарын на участке Токтогульского гидроузла. Долина реки здесь имеет каньонообразную форму, высоту склонов до 1500 м при средней крутизне 65°. Склоны сложены сильно метаморфизованными нижнекаменноугольными известняками. В ходе крупномасштабного инженерно-геологического картирования склонов в пределах участка створа плотины были откартированы полуотчлененные и полностью отчлененные от основного массива широкими трещинами блоки пород, которые по геологическим соображениям считались как потенциально неустойчивые и неустойчивые соответственно. Суммарный объем этих оползне-, обвалоопасных блоков составляет 9,2 млн. м3. Объемы единовременных смещений пород со склонов оценивались в несколько сот тысяч м3. Район исследований относится к 8 - 10-балльной зоне с большой повторяемостью сильных землетрясений.
2. Результатами картирования склонов было установлено, что оползни и обвалы формируются под влиянием многочисленных взаимосвязанных и взаимообусловленных признаков. Их исследование в общих уравнениях связи проводится после предварительного отбора и разделения признаков на главные и второстепенные, который осуществляется по величинам парных коэффициентов корреляции (или корреляционным отношениям) при обязательном сравнительно-геологическом анализе рассматриваемых признаков. Парная связь устанавливалась между объемами оползней-обвалов и выявленными признаками (закономерностями, их определяющими) по методике, показанной в табл. 9. Полученные значения коэффициентов корреляции приведены в табл. 10, 11.
Средние расстояния между трещинами, м | Частость встречаемости в классах объемов, | |||||||||
0 - 50 | 50 - 100 | 100 - 150 | 150 - 200 | 200 - 250 | 250 - 300 | 300 - 350 | 350 - 400 | 400 - 450 | 450 - 500 | |
2,5 | 22 | 2 | - | - | - | - | - | - | - | - |
7,5 | 30 | 17 | 5 | 4 | 2 | 1 | 3 | 1 | 1 | - |
12,5 | 15 | 11 | 2 | 4 | 4 | 1 | 5 | 4 | 5 | 6 |
17,5 | 65 | 23 | 8 | 4 | 2 | 3 | 3 | 2 | 4 | 4 |
-19,5 | -18,5 | -17,5 | -16,5 | -15,5 | -14,5 | -13,5 | -12,5 | -11,5 | -10,5 | |
-2574 | -980 | -262,5 | -198 | -124 | -72,5 | -148,5 | -87,5 | -172,5 | -105 | |
50193 | 18139 | 4594 | 3267 | 1922 | 1051,2 | 2004,8 | 1093,8 | 1083,7 | 1102,5 | |
57 | 28,5 | 10,5 | 6,0 | 4,0 | 4,5 | 10,5 | 9,0 | -1,5 | 9,0 | |
-1111,5 | -527 | -184 | -99 | -62 | -65,2 | -74,3 | -56,2 | -120,8 | -94,5 | |
132 | 53 | 15 | 12 | 8 | 5 | 11 | 7 | 10 | 10 | |
-14,90 | ||||||||||
301,90 | ||||||||||
8,90 | ||||||||||
-7,50 | ||||||||||
500 - 550 | 550 - 600 | 600 - 650 | 650 - 700 | 700 - 750 | 750 - 800 | 800 - 850 | 850 - 900 | 900 - 1000 | > 1000 | |
- | - | - | - | - | - | - | - | - | - | |
1 | 3 | - | - | - | - | - | - | - | - | |
1 | - | 2 | 2 | - | 3 | - | - | - | 19 | |
1 | - | - | - | - | - | - | - | - | - | |
-9,5 | -8,5 | -7,5 | -6,5 | -5,5 | -4,5 | -3,5 | -2,5 | -1,5 | 19,5 | |
-28,5 | -25,5 | -15,0 | -13,0 | 0,0 | -13,5 | 0,0 | -1,0 | 0,0 | 234,0 | |
270,8 | 216,8 | 112,5 | 84,5 | 0,0 | 60,8 | 0,0 | 0,0 | 0,0 | 4563,0 | |
1,5 | -1,5 | 1,0 | 1,0 | 0,0 | 1,5 | 0,0 | 0,0 | 0,0 | 6,0 | |
14,2 | 12,8 | -7,5 | -6,5 | 0,0 | -6,7 | 0,0 | 0,0 | 0,0 | 117,0 | |
3 | 3 | 2 | 2 | - | 3 | - | - | - | 19 | |
Интервалы повторяемости трещин-сместителей | Статистические характеристики | Корреляционное отношение  | |||||||||
1 | 24 | -1,5 | -36 | 54,0 | -466,0 | 699,0 | Распределение объемов оползней-обвалов имеет нормальное распределение.  соответствует вероятность соответствует вероятность  | ||||
2 | 68 | -0,5 | -34 | 17,0 | -1198,0 | 599,0 | |||||
3 | 92 | 0,5 | 46 | 23,0 | -712,0 | -360,5 | 0,50 | 1,19 | 0,97 | -7,50 | |
4 | 119 | 1,5 | 178,6 | 267,8 | -2136,5 | -3204,7 | |||||
5 | - | 151,5 | 361,8 | -4521,5 | -2267,2 | ||||||
Представляющие показатели | Коэффициенты корреляции (корреляционные отношения) r | Среднеквадратические отклонения | Объем выборки n, шт. |
Зоны разрывных нарушений III - IV порядков, вскрытых склонами | 0,68 | 8,9 | 295 |
Типы ниш отрыва и смещения оползней-обвалов | 0,56 | 322,6 | 56 |
Угол между простиранием разрывов III - IV порядков и направлением склонов | 0,42 | 266,7 | 50 |
Угол падения подошвенных поверхностей смещения | 0,79 | 1,00 | 250 |
Длина подошвенных поверхностей смещения | 0,64 | 1,80 | 116 |
Высота оцениваемых склонов | 0,38 | 237,9 | 600 |
Крутизна оцениваемых склонов до смещения из них оползней-обвалов | 0,76 | 12,6 | 94 |
Блочность пород, слагающих оцениваемые склоны | 0,76 | 1,74 | 100 |
Мощность зон разгрузки и выветривания | 0,86 | 8,3 | 484 |
Глубина экзогенного изменения заполнителей тыловых трещин отчленения пород | 0,87 | 6,2 | 600 |
Высота склона, где происходят оползни-обвалы | 0,84 | 8,7 | 350 |
3. В табл. 9 обрабатывались только качественно однородные результаты наблюдений за оползнями-обвалами. В каждой однородной выборке определялись следующие характеристики: частость W; накопленная  и теоретическая
и теоретическая  частота; накопленный и теоретический начальный момент первого
частота; накопленный и теоретический начальный момент первого  и второго
и второго  порядка; условные накопления
порядка; условные накопления 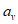 и теоретические
и теоретические 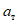 варианты; средние квадратические отклонения
варианты; средние квадратические отклонения  - накопленные,
- накопленные,  - теоретические; суммы квадратов отклонений
- теоретические; суммы квадратов отклонений  - накопленная,
- накопленная,  - теоретическая; проверка гипотезы о нормальном распределении каждого из обрабатываемых показателей посредством критерия согласия
- теоретическая; проверка гипотезы о нормальном распределении каждого из обрабатываемых показателей посредством критерия согласия  А.Н. Колмогорова.
А.Н. Колмогорова.
Частость W - это отношение частоты (количества наблюдений) класса (интервала измерения) определенной группы оползней-обвалов Z к общему объему всей наблюдаемой выборки из совокупности вариант n, выраженное в процентах (или долях единицы)
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
 .
.Накопленной частотой  для данной группы (или типов) оползней-обвалов, а также обрабатываемых признаков (закономерностей), называется сумма частот всех классов, подсчитанная, начиная с первого класса, включая данный.
для данной группы (или типов) оползней-обвалов, а также обрабатываемых признаков (закономерностей), называется сумма частот всех классов, подсчитанная, начиная с первого класса, включая данный.
Начальный момент первого порядка  есть среднее значение вариант (или среднеарифметическое) из всех n вариант
есть среднее значение вариант (или среднеарифметическое) из всех n вариант
 ,
,где M - среднее арифметическое значение признака  ;
;
Z - частота варианты.
Начальный момент второго порядка
 .
.Условные варианты равны отношению разности между серединами классов 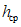 и серединой класса, занимающего в статистическом ряду центральное положение
и серединой класса, занимающего в статистическом ряду центральное положение 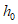 к классовому промежутку
к классовому промежутку 
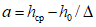 .
.Среднее квадратическое отклонение равно корню квадратному из дисперсии
 .
.Критерий согласия 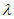 А.Н. Колмогорова определяется из формулы
А.Н. Колмогорова определяется из формулы
 ,
,где D - максимальная разность между эмпирическими (наблюдаемыми) и теоретическими частотами;
n - объем выборки, для которого рассчитывается теоретическое распределение. Если полученному значению 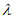 соответствует вероятность
соответствует вероятность  , то теоретическое распределение считается достаточно близким к эмпирическому, а распределение довольно точно описывается нормальным законом. Расчет частот теоретической кривой нормального распределения проводится по двум характеристикам M и
, то теоретическое распределение считается достаточно близким к эмпирическому, а распределение довольно точно описывается нормальным законом. Расчет частот теоретической кривой нормального распределения проводится по двум характеристикам M и  . Функция нормального распределения строится по формуле
. Функция нормального распределения строится по формуле
 , то теоретическое распределение считается достаточно близким к эмпирическому, а распределение довольно точно описывается нормальным законом. Расчет частот теоретической кривой нормального распределения проводится по двум характеристикам M и
, то теоретическое распределение считается достаточно близким к эмпирическому, а распределение довольно точно описывается нормальным законом. Расчет частот теоретической кривой нормального распределения проводится по двум характеристикам M и  .
.Корреляционное отношение определяется из выражения
 .
.4. Представляющие показатели (признаки), парные коэффициенты корреляции (корреляционные отношения) у которых меньше 0,3, исключались из дальнейшего их исследования в общих многофакторных уравнениях связи при регрессионном анализе. К главным признакам отнесены те показатели, которые имеют парные корреляционные отношения, равные или более 0,5, а к дополнительным соответственно 0,3 - 0,5. При этом возможны ситуации, когда для некоторых иных типов оползней-обвалов, откартированных в иных регионально-геологических и зонально-климатических условиях, дополнительные признаки могут быть главными, а главные - дополнительными. Кроме того, рекомендуется учитывать, что не все признаки на стадии ориентировочных прогнозов могут быть замерены с одинаковой точностью или же некоторая часть из них выражена только качественно. Отнесение последних к главным или дополнительным производится, опираясь на опыт инженерно-геологических исследований в других районах или на частость встречаемости определенного типа оползня-обвала в пределах такой качественно выражаемой закономерности.
5. Разделение представляющих показателей, выявленных в ходе картирования закономерностей развития и активизации оползней-обвалов на склонах р. Нарын (Киргизская ССР), на главные и второстепенные показано в табл. 1. Оценивая устойчивость оползне-, обвалоопасных блоков пород с использованием сравнительно-геологического анализа, соблюдались условия:
сопоставление состояния прогнозируемых склонов с неизвестной устойчивостью и отобранных аналогов с известной устойчивостью по набору главных и дополнительных признаков прогноза (см. табл. 12) выполнялось при условии, что оползни-обвалы сформированы в одном петрографическом комплексе пород;
на склонах или их частях одного возраста; в одинаковых структурных условиях, обусловливающих типы гравитационных явлений, типы ниш отрыва и поверхностей ослабления;
другие признаки, как, например, степень экзогенного изменения пород и трещин, отчленяющих оползне-, обвалоопасные блоки от основного массива, обводненность пород данных блоков и заполнителей трещин отчленения и смещения, их свойства и т.п., могут быть различными и по ним проводятся сопоставления и дается прогноз оползне-, обвалоопасности.
Перечень закономерностей | Закономерности, выражаемые на стадии ориентировочных прогнозов | Обозначение | Роль для прогноза | |
количественно | качественно | |||
Природные | ||||
Литолого-генетические комплексы пород | Мощность слоев слабых прослоев | Типы пород; структурные и текстурные особенности | Главные | |
Мощность смещаемых блоков | Учет при геологическом анализе | |||
Крупные тектонические нарушения | Угол между направлением склона и простиранием нарушений | Расположение нарушений в пределах структурного блока | Главный | |
Главный | ||||
Повторяемость трещин-сместителей в зоне влияния нарушений | Расположение оползней по отношению к нарушениям | Учет при геологическом анализе | ||
Пространственное соотношение нарушений со склоном | Угол падения трещин смещения (подсекающих блоки пород снизу) | Типы ниш отрыва и смещения блоков пород | Главный | |
Главный | ||||
Отношение площади поверхности смещения к поверхности, отчленяющей блоки пород от массива | Типы поверхности отчленения и смещения | Учет при геологическом анализе | ||
Новейшие и современные тектонические движения | Амплитуда поднятия | Расположение участка изысканий в пределах складчатых и разрывных структур, сейсмоактивных в новейший этап тектонической жизни района | Второстепенный | |
Крутизна и высота склонов | Главный | |||
Главный | ||||
Магнитуда землетрясений | Учет при геологическом анализе | |||
Общая интенсивность трещиноватости пород | Коэффициенты трещинной пустотности | - | Второстепенный | |
Главный | ||||
Блочность пород | ||||
Геологическая история формирования склона и его возраст | Мощность зон разгрузки и выветривания пород | Приуроченность оползней к определенным геоморфологическим элементам склонов | Главный | |
Главный | ||||
Учет при геологическом анализе | ||||
Глубина значительного изменения заполнителя в трещинах отчленения | ||||
Инженерно-геологические свойства пород | Величина среднего сопротивления сдвигу по поверхности смещения | Главный | ||
Прочность пород на раздавливание | - | Второстепенный | ||
Объемный вес | Второстепенный | |||
Динамический модуль упругости | Второстепенный | |||
Гидрогеологические условия | Гидростатическое | - | Второстепенный | |
Распределение и величины напряжения в массиве | Среднее нормальное напряжение на поверхности смещения, обусловленное весом оползневого блока пород | - | Главный | |
Высота оцениваемой части склона | - | - | Главный | |
Морфология поверхности смещения | - | Типы поверхностей смещения по их морфологии | Учет при геологическом анализе | |
Типы и состояние заполнителя | - | Типы заполнителей трещин, отчленяющих блоки пород от основного массива | Учет при геологическом анализе | |
Зонально-климатические условия | - | Климатические зоны | Второстепенный | |
Антропогенные | ||||
Подрезка склонов в нижней части | Высота подрезанного склона | Главный | ||
Крутизна подрезанного склона | Главный | |||
Площадь срезки | Главный | |||
Мощность срезанных пород | - | Главный | ||
Искусственное обводнение пород зон ослабления за счет утечек из водопроводной сети | Влажность пород зон ослабления (отчленения) | Главный | ||
Гидростатическое давление воды в трещинах отчленения | Второстепенный | |||
Гидродинамическое давление | Главный | |||
Динамические воздействия от взрывов и работающих механизмов | Скорости упругих волн | Второстепенный | ||
Расстояние от источника возбуждения | - | Второстепенный | ||
Обратный "сейсм" за счет гидродинамического удара | Главный | |||
Дноуглубительные работы в основании склона | Глубина врезки | Главный | ||
Угол врезки | Главный | |||
Площадь врезки | Главный | |||
6. Для упрощения сопоставления прогнозируемого склона с его аналогами все признаки прогноза (см. табл. 12) были разделены на две группы, характеризующие среду формирования склонов (признаки среды) и состояние склонов на момент их сопоставления (признаки начальных условий).
7. К признакам среды отнесены следующие: мощность слоев слабых прослоев; типы пород и их структурно-текстурные особенности; угол между простиранием разломов, разрывов и направлением склона; повторяемость трещин-сместителей в разрыве (разломе); расположение оползня-обвала по отношению к разрывным нарушениям; типы ниш отрыва и возможного смещения; типы поверхностей отчленения и смещения; угол падения подошвенной поверхности смещения; отношение площади подошвенной поверхности отчленения к тыловой; расположение оползня-обвала в пределах структурного блока и магнитуда землетрясений; мощность присклоновой зоны разгрузки и выветривания пород, к которой приурочен оползень-обвал.
8. К признакам начальных условий отнесены: крутизна склонов, где формируются оползни, обвалы; блочность пород в пределах оползневых - обвальных блоков; глубина значительного изменения заполнителя в тыловых трещинах отчленения; средняя величина нормального напряжения в зоне смещения и сопротивления сдвигу по поверхности смещения, определенная методом "обратных расчетов" по методике Прил. 5; высота оцениваемой части склона; тип и состояние заполнителя.
9. Дальнейшая процедура прогноза сводилась к следующему. Среди 600 изученных ниш отрыва-смещения оползней-обвалов, закодированных на ПКП, отбирались такие, у которых признаки среды их формирования (см. п. 7) подобны с аналогичными признаками в оползне-, обвалоопасном прогнозируемом блоке пород. При отборе перфокарт по всем критериям среды отмечались два случая.
10. В первом случае отобранных аналогов недостаточно для статистической обработки в общих линейных уравнениях связи. В этом случае у объекта прогноза и его аналога сопоставлялись признаки начальных условий. Вначале сравнивались значения признака глубины значительного экзогенного изменения заполнителя в тыловых и подошвенных трещинах отчленения  (см. табл. 12). Поскольку у несмещенного блока пород это изменение трудно проследить без проходки горных выработок, то сопоставлялась ширина раскрытия отмеченных трещин и глубина зияющей части, а также тип и состояние заполнителя в приповерхностной части склона. Если у прогнозного склона названный признак (или заменяющие его показатели) равны или больше, чем у склонов-аналогов, а также одинаковы тип и состояние заполнителей, то в последующем рекомендуется поступать, основываясь на типе поверхности смещения. При тектоническом контактном типе наряду с равенством численных значений высоты оползневого - обвального блока
(см. табл. 12). Поскольку у несмещенного блока пород это изменение трудно проследить без проходки горных выработок, то сопоставлялась ширина раскрытия отмеченных трещин и глубина зияющей части, а также тип и состояние заполнителя в приповерхностной части склона. Если у прогнозного склона названный признак (или заменяющие его показатели) равны или больше, чем у склонов-аналогов, а также одинаковы тип и состояние заполнителей, то в последующем рекомендуется поступать, основываясь на типе поверхности смещения. При тектоническом контактном типе наряду с равенством численных значений высоты оползневого - обвального блока  и среднего нормального напряжения в зонах смещения необходимо совпадение крутизны склонов; при тектоническом с зоной дробления типе поверхности - угол падения склонов может не совпадать по абсолютным величинам; так как блочность пород
и среднего нормального напряжения в зонах смещения необходимо совпадение крутизны склонов; при тектоническом с зоной дробления типе поверхности - угол падения склонов может не совпадать по абсолютным величинам; так как блочность пород  (см. табл. 12) на устойчивость оползня-обвала не влияет, то она учитывалась только при оценке объемов возможных вывалов глыб пород со склонов. При равенстве перечисленных признаков у аналога и объекта прогноза оцениваемый склон считался весьма неустойчивым.
(см. табл. 12) на устойчивость оползня-обвала не влияет, то она учитывалась только при оценке объемов возможных вывалов глыб пород со склонов. При равенстве перечисленных признаков у аналога и объекта прогноза оцениваемый склон считался весьма неустойчивым.
11. На склонах долины р. Нарын и ее притоков, сложенных прочными трещиноватыми известняками, к весьма неустойчивым отнесены отчлененные (широкими зияющими или с рыхлым заполнителем трещинами бортового отпора и разгрузки) от основного массива блоки пород; как правило, они располагаются на склонах крутизной более 50°. При несовпадении какого-либо из названных в п. 8 признаков начальных условий рекомендуются три степени оценки устойчивости горных склонов:
неустойчивые оползне-, обвалоопасные блоки пород. К ним относятся полностью отчлененные (широкими трещинами бортового отпора с рыхлым заполнителем) блоки пород, расположенные на склонах с крутизной 50° и менее. Причем, у оползне-, обвалоопасных блоков с тектоническим контактным или литогенетическим контактным типами поверхностей смещения допустимо некоторое несовпадение признаков (угол падения склонов может быть меньше, чем у аналога на 10° и более; высоты оцениваемых частей склонов; у оползне-, обвалоопасных блоков с тектоническим с зоной дробления типом поверхности смещения могут быть меньше по величине или признак глубины экзогенного изменения заполнителя в тыловых трещинах отчленения или величина нормального напряжения на поверхности смещения);
потенциально неустойчивые - это полуотчлененные тектоническими и трещинами бортового отпора (реже разгрузки) блоки пород, расположенные на склонах крутизной 30 - 60°. К этому типу устойчивости относятся оползне-, обвалоопасные блоки, у которых значительно меньше, чем у аналога, значения признаков глубины экзогенного изменения заполнителя в трещинах отчленения, среднего нормального напряжения на поверхностях смещения;
относительно стабильные оползневые - обвальные блоки пород. К ним отнесены полуотчлененные тектоническими трещинами блоки пород, а также современные части склонов со слабо выветренными и трещиноватыми породами. У объекта прогноза признаки начальных условий значительно отличаются по своему значению от признаков его аналогов на величины, повышающие устойчивость склонов.
12. В горно-складчатых областях с активной неотектоникой, энергичной эрозией и высокой активностью землетрясений не рекомендуется выделять полностью устойчивые склоны. В некоторых случаях среди весьма неустойчивых оползне-, обвалоопасных склонов целесообразно обособлять две категории склонов, у которых неизбежны обвалы, оползни и необходимы самые срочные меры по удалению со склона опасных блоков пород или перенос инженерных сооружений из зоны влияния вероятностного схода оползневых - обвальных масс; быстро осуществленные укрепительные мероприятия могут оказаться эффективными, но требуются наблюдения за их состоянием.
13. Во втором случае (см. п. 9) отобранных аналогов достаточно для их статистической обработки в общих линейных уравнениях. Такое исследование для условий рассматриваемого примера выполнялось только для склонов, у которых не совпадали по величинам один (или более) главных признаков прогноза. В общие уравнения связи включались только склоны-аналоги с подобными качественно выражаемыми признаками среды (см. п. 7).
14. При решении общих линейных уравнений определялись коэффициенты регрессии, средние арифметические значения прогнозной функции, среднеквадратические отклонения прогнозной функции от исследуемой кривой регрессии, коэффициенты множественной корреляции, частные коэффициенты корреляции и частные коэффициенты детерминации. Для исследования использовалась стандартная программа В.П. Игнатова по определению статистических характеристик "Покос". Частные коэффициенты детерминации D поочередно измеряют долю в общей вариации зависимой переменной Y (прогнозной функции) переменных  (признаков прогноза). Они определяются по формуле
(признаков прогноза). Они определяются по формуле
 .
.15. Для выявления количественных связей между главными признаками прогноза (см. табл. 13) и для определения удельного веса каждого из признаков в общем балансе их взаимодействия на устойчивость склонов решены две задачи с двумя вариантами каждая.
Первая задача | Вторая задача | ||||
Виды связи | Коэффициенты | Виды связи | Коэффициенты | ||
корреляции | детерминации | корреляции | детерминации | ||
 - параболическая третьей степени | 0,40 | (150,4/194,4) x x (16,0/16,2) |  - параболическая пятой степени | 0,46 | (769,8/766,1) x x (53,6/52,6) |
 - параболическая третьей степени | 0,38 | (0,4/1,3) x x (0,03/0,04) |  - параболическая третьей степени | 0,29 | (7,134/7,21) x x (0,31/0,005) |
 - параболическая третьей степени | 0,53 | (258,1/306,8) x x (25,2/28,0) |  - параболическая второй степени | 0,32 | (389,12/456,32) x x (27,2/33,4) |
 - параболическая третьей степени | 0,60 | (53,4/112,8) x x (4,2/11,8) |  - параболическая второй степени | 0,49 | (109,76/106,38) x x (7,6/7,1) |
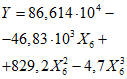 - параболическая третьей степени | 0,43 | (184,9/257,5) x x (15,2/28,0) |  - параболическая второй степени | 0,13 | (16,6/17,8) x x (1,18/1,25) |
 - параболическая второй степени | 0,79 | (52,90/96,06) x x (4,5/10,03) |  - параболическая пятой степени | 0,35 | (68,25/-) x (4,9/-) |
 - параболическая второй степени | 0,59 | (0,016/0,023) x x (0,01/0,01) |  - параболическая второй степени | 0,13 | (0,0003/0,00045) x x (0,01/0,005) |
 - параболическая третьей степени | 0,59 | 395,3 (33,2) |  - линейная | 0,49 | (74,48/-) x 5,2 |
 - параболическая третьей степени | 0,54 | 0,297 (0,32) |  - параболическая третьей степени | 0,04 | 0,006 x 0,33 |
 - линейная | 0,11 | 19,8 (1,66) |  - параболическая третьей степени | 0,34 | 75,58 x 5,18 |
 - параболическая третьей степени | 0,39 | 52,6 (5,6) | |||
Примечание. Коэффициенты детерминации приведены для первого (верхнее значение) и второго (нижнее значение) вариантов задач; в скобках даны относительные значения коэффициентов детерминации в %.
16. В первом варианте первой задачи в число переменных 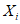 вошли признаки: угол падения подошвенных трещин смещения
вошли признаки: угол падения подошвенных трещин смещения  ; высота склона, измеряемая от уреза реки и до выхода в склон трещин смещения
; высота склона, измеряемая от уреза реки и до выхода в склон трещин смещения  ; мощность смещаемых блоков пород
; мощность смещаемых блоков пород 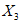 ; длина подошвенной трещины
; длина подошвенной трещины  ; высота оцениваемой части склона
; высота оцениваемой части склона  ; угол падения склона до смещения пород со склонов
; угол падения склона до смещения пород со склонов  ; объем сместившихся пород
; объем сместившихся пород 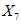 ; глубина значительного экзогенного изменения заполнителя в тыловых трещинах отчленения
; глубина значительного экзогенного изменения заполнителя в тыловых трещинах отчленения  ; угол между направлением склона и простиранием подошвенной трещины изменялся от 0 до 30°
; угол между направлением склона и простиранием подошвенной трещины изменялся от 0 до 30°  . Число наблюдений каждой из
. Число наблюдений каждой из  равнялось 141. После решения системы линейных уравнений получено прогнозное уравнение регрессии (переменные в нем написаны по мере убывания абсолютного значения коэффициентов регрессии)
равнялось 141. После решения системы линейных уравнений получено прогнозное уравнение регрессии (переменные в нем написаны по мере убывания абсолютного значения коэффициентов регрессии)  .
.
 .
.Коэффициент множественной корреляции R = 0,74 при среднеквадратической ошибке в его определении +/- 0,08. Следует отметить, что знак плюс или минус перед коэффициентами регрессии  не несет физической нагрузки коэффициента устойчивости, что определено сущностью используемого для исследования уравнений метода наименьших квадратов.
не несет физической нагрузки коэффициента устойчивости, что определено сущностью используемого для исследования уравнений метода наименьших квадратов.
17. Во втором варианте первой задачи переменные признаки  и
и  являются постоянными (см. п. 16), а вместо них в уравнение связи были введены значения гидростатического
являются постоянными (см. п. 16), а вместо них в уравнение связи были введены значения гидростатического  и гидродинамического
и гидродинамического  давлений воды в тыловых трещинах отчленения. Число наблюдений каждой из переменной
давлений воды в тыловых трещинах отчленения. Число наблюдений каждой из переменной 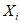 равно 141. После решения систем линейных уравнений получено следующее уравнение регрессии
равно 141. После решения систем линейных уравнений получено следующее уравнение регрессии

Коэффициент множественной корреляции r = 0,76.
Виды частных уравнений связи, значения частных коэффициентов корреляции r и детерминации D для рассмотренных вариантов задачи приведены в табл. 13. В таблице даны абсолютные значения коэффициентов детерминации и их относительные значения в %, что облегчает определение величин удельных весов переменных  . Так, например, роль глубины значительного экзогенного изменения заполнителя по тыловым трещинам отчленения
. Так, например, роль глубины значительного экзогенного изменения заполнителя по тыловым трещинам отчленения  в общем совокупном взаимодействии девяти показателей составляет 33,2% (см. табл. 13). Это означает, что если под действием процессов разгрузки, выветривания, выщелачивания заполнитель тыловой трещины отчленения с сцементированного превратится в рыхлый на глубину 1 п.м, то устойчивость обвально-оползневого блока уменьшится в среднем на 1,21% (применительно к рассматриваемым условиям).
в общем совокупном взаимодействии девяти показателей составляет 33,2% (см. табл. 13). Это означает, что если под действием процессов разгрузки, выветривания, выщелачивания заполнитель тыловой трещины отчленения с сцементированного превратится в рыхлый на глубину 1 п.м, то устойчивость обвально-оползневого блока уменьшится в среднем на 1,21% (применительно к рассматриваемым условиям).
18. Согласно результатам исследований (см. п. 16) линейных уравнений по первому варианту первой задачи, для оползней-обвалов, формирующихся в присклоновых зонах весьма интенсивно разгруженных и выветрелых пород и имеющих тектонический контактный тип поверхностей ослабления, наибольшее значение для устойчивости смещаемых блоков пород имеют глубина экзогенного изменения и мощность смещаемых блоков пород. Роль угла падения подошвенной трещины и крутизны склонов до обрушения из них пород примерно одинакова. Малая роль объема оползней-обвалов объясняется тем, что его роль в исследуемом выражается через мощность смещаемых блоков пород, длину подошвенной трещины смещения и ее угол падения. Вследствие малой роли в устойчивости оползней-обвалов таких признаков, как угол между направлением склона и простиранием подошвенной трещины, высоты склона, измеряемой от уреза реки до выхода в склон подошвенной трещины, объема оползня-обвала, их можно исключить из общего уравнения регрессии. Тогда в окончательном виде
 .
.19. Для второго варианта первой задачи, в которой исследовались оползни-обвалы с постоянной (одинаковой) глубиной экзогенного изменения заполнителя в трещинах отчленения, также сформированные в присклоновых зонах весьма интенсивной разгрузки и выветривания, основная роль в формировании устойчивости оползней-обвалов принадлежит крутизне склонов до обрушения из них пород и мощности смещаемых блоков пород. Роль угла падения подошвенных трещин такая же, как и для данных первого варианта. Напротив, здесь значительно повышается роль высоты оцениваемых частей склонов и длины подошвенной трещины. Незначительное влияние на устойчивость блоков оказывают те же показатели, что в первом варианте задачи. Поэтому общее уравнение для второго варианта
 .
.20. Поскольку на устойчивость склонов наибольшее влияние оказывают четыре признака 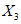 ,
, 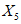 ,
,  ,
, 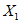 , то для примера второго варианта первой задачи решалась задача нахождения минимально возможного среднеквадратического отклонения функции Y от исследуемой кривой регрессии. Исследовались уравнения до третьей степени включительно с тремя признаками
, то для примера второго варианта первой задачи решалась задача нахождения минимально возможного среднеквадратического отклонения функции Y от исследуемой кривой регрессии. Исследовались уравнения до третьей степени включительно с тремя признаками  ,
, 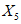 ,
,  для выборки из 60 аналогов, у которых угол падения подошвенной поверхности смещения постоянный. Получено уравнение связи
для выборки из 60 аналогов, у которых угол падения подошвенной поверхности смещения постоянный. Получено уравнение связи

Множественный коэффициент корреляции этого уравнения значительно выше, чем в уравнении первой степени, и равен 0,84. Следовательно, на долю не учтенных (в уравнении параболы третьей степени) признаков прогноза приходится около 16%, что вполне приемлемо для производства ориентировочных прогнозов.
21. Во вторую задачу включались аналоги оползней-обвалов, сформированных в присклоновых зонах интенсивной разгрузки и выветривания с тектоническим с зоной дробления типом поверхностей ослабления; угол между направлением склона и простиранием подошвенных трещин отчленения у них равен 0 - 10°.
22. В первом варианте второй задачи в число переменных (признаков прогноза) вошли показатели: угол падения подошвенной трещины  ; высота склона, измеряемая от уреза и до выхода в склон подошвенной трещины
; высота склона, измеряемая от уреза и до выхода в склон подошвенной трещины  ; мощность смещаемого блока пород
; мощность смещаемого блока пород  ; длина подошвенных трещин
; длина подошвенных трещин  ; высота оцениваемой части склона
; высота оцениваемой части склона 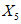 ; угол падения склона до обрушения блоков пород
; угол падения склона до обрушения блоков пород  ; объем оползня-обвала
; объем оползня-обвала  ; глубина значительного экзогенного изменения заполнителя в тыловых трещинах отчленения
; глубина значительного экзогенного изменения заполнителя в тыловых трещинах отчленения 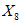 . Число аналогов равно 133. Получено уравнение вида
. Число аналогов равно 133. Получено уравнение вида

Коэффициент множественной корреляции равен 0,66.
23. Во втором варианте второй задачи рассматривались оползни-обвалы, у которых глубина экзогенного изменения заполнителя по тыловым трещинам отчленения одинаковая. В задачу включались данные по оползням-обвалам, расположенным на склонах одной крутизны. Вместо этих показателей были включены значения гидростатического  и гидродинамического
и гидродинамического  давлений воды в трещинах отчленения. После исследования получено уравнение
давлений воды в трещинах отчленения. После исследования получено уравнение

Коэффициент множественной корреляции равен 0,69.
24. Согласно данным табл. 14, основная роль в устойчивости оползней-обвалов, включенным в первый вариант второй задачи, принадлежит углу падения их подошвенной трещины смещения и мощности смещаемого блока. Незначительная, в отличие от оползней-обвалов первой задачи, роль глубины экзогенного изменения заполнителя в тыловых трещинах отчленения и угла падения склона до смещения из него пород объясняется следующим образом. Оползневые - обвальные блоки пород, включенные во вторую задачу, приурочены к зонам разрывов III - IV порядков (см. пп. 1.15 - 1.17) и имеют значительно большие по величине тыловые трещины отчленения по сравнению с подошвенными. Поскольку степень экзогенного изменения заполнителя в трещинах отчленения в произошедших оползнях-обвалах данной выборки значительно меньше, чем в оползнях-обвалах выборок первой задачи, то на первое место выходят такие показатели, как угол падения подошвенной трещины отчленения и мощность оползней-обвалов. Исключив из уравнения п. 22 значения переменных  ,
,  ,
,  (в связи с их малой ролью в формировании устойчивости), получим более простое уравнение
(в связи с их малой ролью в формировании устойчивости), получим более простое уравнение
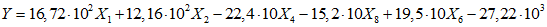 .
.Признаки прогноза | Изучаемый объект | Природный аналог | Ориентировочное изменение | |
Качественно выражаемые | ||||
Литолого-генетические комплексы пород | Мелкокристаллические однородные метаморфизованные известняки с азимутом падения 320° < 65° | Мелкокристаллические однородные метаморфизованные известняки с азимутом падения 30° < 65° | Качественно однородные породы, изменений | |
Крупные тектонические нарушения | В зоне влияния разрыва III порядка, перпендикулярного склону | В зоне влияния разрыва III порядка, перпендикулярного склону | То же | |
Пространственное соотношение тектонических нарушений: | ||||
типы ниш отрыва | Первый тип | Первый тип | " | |
типы поверхностей ослабления | Тектоническая с зоной дробления | Тектоническая с зоной дробления | " | |
Новейшие и современные тектонические движения, включая сейсмичность | В южном крыле структурного блока III порядка; северное крыло антиклинали. Зона выхода сейсмических упругих волн под углом 40° | В южном крыле структурного блока III порядка; северное крыло антиклинали. Зона выхода сейсмических упругих волн под углом 40° | " | |
Количественно выражаемые | ||||
Глубина экзогенного изменения заполнителя по трещинам, отчленяющим блоки пород от основного массива | 0,0 | 20,0 | 1,21 x 20 = 24,2 = +0,24 | |
Мощность оползня | 13 | 30 | +0,22 | |
Угол падения подошвенных трещин смещения | 35 | 30 | -0,13 | |
Высота оцениваемой части склона | 45 | 50 | +0,03 | |
Отношение площадей отчленения и смещения | 0,84 | 0,95 | -0,08 | |
Подрезка склона при строительстве, обусловившая изменение крутизны склона | 45 | 30 | -0,39 |  |
С учетом  | ||||
Примечание. Плюс означает увеличение устойчивости склона при несовпадении признаков прогноза, минус - ее уменьшение. Коэффициент устойчивости оцениваемого природного склона больше предельного состояния его аналога на  , где 0,1 - ошибка вычислений; строительные подрезки оползневого склона приведут к изменению его устойчивости и она будет меньше предельного состояния, что вызовет смещение оползня
, где 0,1 - ошибка вычислений; строительные подрезки оползневого склона приведут к изменению его устойчивости и она будет меньше предельного состояния, что вызовет смещение оползня  , т.е. это неустойчивый склон.
, т.е. это неустойчивый склон.
 , где 0,1 - ошибка вычислений; строительные подрезки оползневого склона приведут к изменению его устойчивости и она будет меньше предельного состояния, что вызовет смещение оползня
, где 0,1 - ошибка вычислений; строительные подрезки оползневого склона приведут к изменению его устойчивости и она будет меньше предельного состояния, что вызовет смещение оползня Аналогично, вследствие малой роли в устойчивости склонов, вошедших во второй вариант второй задачи, таких показателей, как высота оцениваемой части склона, гидростатическое давление воды, объем оползней-обвалов, высота склона от уреза реки до выхода в склон подошвенной трещины 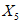 ,
,  ,
,  ,
,  (см. табл. 14), в уравнении п. 23 их можно исключить, получив его в упрощенном виде:
(см. табл. 14), в уравнении п. 23 их можно исключить, получив его в упрощенном виде:
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
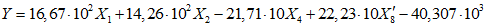 .
.25. В приведенных уравнениях не рассмотрена роль сейсмичности в формировании оползней-обвалов. Ее недоучет в исследуемых уравнениях связи между показателями второй задачи является одной из причин сравнительно низкой коррелируемости функции Y с переменными  . Влияние сейсмичности на устойчивость оползней-обвалов для данных первой задачи проявлялось в постепенном снижении прочности пород, что отразилось в большей коррелируемости функции Y с
. Влияние сейсмичности на устойчивость оползней-обвалов для данных первой задачи проявлялось в постепенном снижении прочности пород, что отразилось в большей коррелируемости функции Y с  (см. п. 20). Во вторую задачу включались данные по оползням-обвалам, поводом к возникновению которых служат сильные землетрясения, что и отразилось на тесноте связи между Y и
(см. п. 20). Во вторую задачу включались данные по оползням-обвалам, поводом к возникновению которых служат сильные землетрясения, что и отразилось на тесноте связи между Y и  .
.
26. Исследования общих уравнений связи показали, что при ориентировочных прогнозах устойчивости оползневых - обвальных склонов долины р. Нарын роль основных признаков (закономерностей) разная для оползней-обвалов с тектоническим контактным типом поверхностей смещения и сформированных в присклоновых зонах весьма интенсивной разгрузки и выветривания; для оползней-обвалов с тектоническим с зоной дробления типом поверхности смещения и сформированных в присклоновой зоне интенсивной и слабой разгрузки и выветривания. Среди включенных в исследование девяти показателей  (количественно выражаемых) для дальнейшего анализа рекомендуется только четыре признака для первой и пять признаков для второй задачи. Сравнение относительных значений этих признаков при сопоставлении объекта прогноза с его аналогами необходимо считать обязательным условием, а сами признаки прогноза в последующем удобно называть обязательными признаками прогноза.
(количественно выражаемых) для дальнейшего анализа рекомендуется только четыре признака для первой и пять признаков для второй задачи. Сравнение относительных значений этих признаков при сопоставлении объекта прогноза с его аналогами необходимо считать обязательным условием, а сами признаки прогноза в последующем удобно называть обязательными признаками прогноза.
27. Для условий первой задачи суммарное воздействие отмеченных четырех признаков прогноза в изменении коэффициента устойчивости оползневых - обвальных склонов составляет 90% общего совокупного взаимодействия всех представляющих показателей (признаков прогноза). С учетом пересчета их значений на единицу измерения (на один метр, один градус) получим для первой задачи - глубина значительного экзогенного изменения заполнителя в тыловых трещинах отчленения  ; мощность смещаемых блоков пород
; мощность смещаемых блоков пород  ; угол падения подошвенных трещин смещения
; угол падения подошвенных трещин смещения  ; угол падения оцениваемой части склона до смещения из него пород
; угол падения оцениваемой части склона до смещения из него пород  ; для второй задачи - угол падения подошвенной трещины отчленения
; для второй задачи - угол падения подошвенной трещины отчленения  ; мощность смещаемых блоков пород
; мощность смещаемых блоков пород 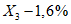 ; длина подошвенных трещин отчленения
; длина подошвенных трещин отчленения  ; гидродинамическое давление воды в трещинах отчленения
; гидродинамическое давление воды в трещинах отчленения  ; глубина экзогенного изменения заполнителей в тыловых трещинах отчленения
; глубина экзогенного изменения заполнителей в тыловых трещинах отчленения  .
.
 ; мощность смещаемых блоков пород
; мощность смещаемых блоков пород  ; угол падения подошвенных трещин смещения
; угол падения подошвенных трещин смещения  ; угол падения оцениваемой части склона до смещения из него пород
; угол падения оцениваемой части склона до смещения из него пород  ; для второй задачи - угол падения подошвенной трещины отчленения
; для второй задачи - угол падения подошвенной трещины отчленения  ; мощность смещаемых блоков пород
; мощность смещаемых блоков пород 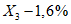 ; длина подошвенных трещин отчленения
; длина подошвенных трещин отчленения  ; гидродинамическое давление воды в трещинах отчленения
; гидродинамическое давление воды в трещинах отчленения  ; глубина экзогенного изменения заполнителей в тыловых трещинах отчленения
; глубина экзогенного изменения заполнителей в тыловых трещинах отчленения  .
.28. В случаях несовпадения перечисленных в п. 27 обязательных признаков для условий р. Нарын рекомендованы следующие категории устойчивости оползневых - обвальных склонов:
для первой задачи - неустойчивые оползне-, обвалоопасные склоны. Обязательные признаки прогноза у прогнозируемых склонов совпадают по величине с аналогичными признаками, полученными по склонам-аналогам, или изменяются на величины, пропорционально увеличивающие устойчивость склона. Признаки  ,
,  (см. п. 27) (один или в сумме) у объекта прогноза могут быть меньше, чем у аналогов, на 20°. Такое несовпадение вызывает повышение устойчивости склона на
(см. п. 27) (один или в сумме) у объекта прогноза могут быть меньше, чем у аналогов, на 20°. Такое несовпадение вызывает повышение устойчивости склона на  ; +/- 0,10 - возможные ошибки за счет среднеквадратических отклонений функции от средних значений кривой регрессии; потенциально неустойчивые склоны. Здесь могут не совпадать признаки
; +/- 0,10 - возможные ошибки за счет среднеквадратических отклонений функции от средних значений кривой регрессии; потенциально неустойчивые склоны. Здесь могут не совпадать признаки  ,
,  (п. 27); причем у объекта прогноза они меньше, чем у аналога, на 10 м (один или в сумме), а признаки
(п. 27); причем у объекта прогноза они меньше, чем у аналога, на 10 м (один или в сумме), а признаки  и
и  - на 10° или на другие величины, но чтобы
- на 10° или на другие величины, но чтобы 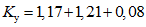 ; относительно стабильные склоны. Заполнитель трещин отчленения у таких блоков не изменен экзогенными процессами, т.е.
; относительно стабильные склоны. Заполнитель трещин отчленения у таких блоков не изменен экзогенными процессами, т.е. 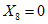 ; остальные признаки меньше на величины, пропорционально повышающие в сумме устойчивость до
; остальные признаки меньше на величины, пропорционально повышающие в сумме устойчивость до  ;
;
 ; +/- 0,10 - возможные ошибки за счет среднеквадратических отклонений функции от средних значений кривой регрессии; потенциально неустойчивые склоны. Здесь могут не совпадать признаки
; +/- 0,10 - возможные ошибки за счет среднеквадратических отклонений функции от средних значений кривой регрессии; потенциально неустойчивые склоны. Здесь могут не совпадать признаки 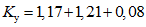 ; относительно стабильные склоны. Заполнитель трещин отчленения у таких блоков не изменен экзогенными процессами, т.е.
; относительно стабильные склоны. Заполнитель трещин отчленения у таких блоков не изменен экзогенными процессами, т.е.  ;
;для второй задачи - неустойчивые оползне-, обвалоопасные склоны, если у объекта прогноза величины признака  (см. п. 27) меньше, чем у аналогов, не менее чем на 100 м, признака
(см. п. 27) меньше, чем у аналогов, не менее чем на 100 м, признака  - на 25 м, признака
- на 25 м, признака  - на 0,1 МПа или на другие величины, суммарное воздействие которых увеличит устойчивость до
- на 0,1 МПа или на другие величины, суммарное воздействие которых увеличит устойчивость до  ;
;
 ;
;потенциально неустойчивые склоны. Признак  меньше, чем у аналога, на 10° или при равенстве этого признака меньше на 15 м признак
меньше, чем у аналога, на 10° или при равенстве этого признака меньше на 15 м признак 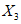 (см. п. 27). Другие признаки (один или вместе) могут отличаться на величины, увеличивающие в сумме устойчивость до
(см. п. 27). Другие признаки (один или вместе) могут отличаться на величины, увеличивающие в сумме устойчивость до  ;
;
 ;
;относительно стабильные склоны. Признак  у объекта прогноза меньше, чем у аналогов, на 15°
у объекта прогноза меньше, чем у аналогов, на 15°  , а признак
, а признак  - на 10 м,
- на 10 м,  - на 100 м,
- на 100 м,  - на 50 м, тогда
- на 50 м, тогда  . При ином неравенстве признаков прогноза их суммарное воздействие на устойчивость должно составлять
. При ином неравенстве признаков прогноза их суммарное воздействие на устойчивость должно составлять  .
.
 , а признак
, а признак  . При ином неравенстве признаков прогноза их суммарное воздействие на устойчивость должно составлять
. При ином неравенстве признаков прогноза их суммарное воздействие на устойчивость должно составлять  .
.29. В табл. 14 приведен пример сопоставления качественно и количественно (определяющих признаков прогноза) выражаемых признаков прогноза (см. табл. 14) по величинам их относительной роли в формировании устойчивости склонов.
ПРЕДСТАВЛЯЮЩИХ ПОКАЗАТЕЛЕЙ У ОБЪЕКТА
ПРОГНОЗА И ЕГО АНАЛОГОВ
1. Для анализа взяты результаты определения естественной влажности  , влажности верхнего предела пластичности
, влажности верхнего предела пластичности 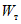 , плотности грунта
, плотности грунта  , коэффициента сжимаемости a лессовидных суглинков
, коэффициента сжимаемости a лессовидных суглинков  , которые характеризуют объект прогноза (составляют выборку A) и его 81 аналогов (выборка B). Аналоги представляют собой участки, где пройдены опорные скважины (в пределах зоны подтопления промышленной площадки) и где наблюдались просадочные оползни течения. Из скважин отобраны монолиты, по которым определялись вышеперечисленные показатели свойств. Скважины пройдены и отобраны монолиты до и после подтопления. Чтобы оценить, насколько существенно или несущественно изменение названных свойств грунтов в зоне подтопления с целью учета подтопления при прогнозах изменения устойчивости откосов промплощадки, рекомендуется применять дисперсионные модели со случайным эффектом. Исходные данные и методика их обработки приведены в табл. 15.
, которые характеризуют объект прогноза (составляют выборку A) и его 81 аналогов (выборка B). Аналоги представляют собой участки, где пройдены опорные скважины (в пределах зоны подтопления промышленной площадки) и где наблюдались просадочные оползни течения. Из скважин отобраны монолиты, по которым определялись вышеперечисленные показатели свойств. Скважины пройдены и отобраны монолиты до и после подтопления. Чтобы оценить, насколько существенно или несущественно изменение названных свойств грунтов в зоне подтопления с целью учета подтопления при прогнозах изменения устойчивости откосов промплощадки, рекомендуется применять дисперсионные модели со случайным эффектом. Исходные данные и методика их обработки приведены в табл. 15.
Выборки чисел (результаты определений свойств до подтопления - выборка А и после - выборка Б) | ||||||||||||||||
Естественная влажность, % | Влажность верхнего предела пластичности, % | Плотность грунта, г/см3 | Коэффициент сжимаемости при 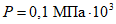 | |||||||||||||
Выборка А | Выборка Б | Выборка А | Выборка Б | Выборка А | Выборка Б | Выборка А | Выборка Б | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||||
23, 24, 20, 22, 22, 21, 19, 23, 22, 25, 20, 25, 20, 19, 24, 23, 21, 22, 23, 22, 22, 21, 23, 18, 20, 24, 19, 18, 22, 20, 16, 18, 18, 20, 20 | 27, 28, 29, 26, 23, 24, 24, 25, 26, 27, 26, 28, 25, 27, 26, 24, 28, 28, 26, 25, 26, 25, 26, 27, 28, 29, 27, 28, 25, 28, 28, 29, 26 | 35, 35, 36 38, 35, 36, 35, 33, 34, 36, 35, 33, 33, 37, 38, 38, 35, 32, 36, 39, 42, 36, 32, 38, 36, 36 | 33, 32, 32, 29, 30, 32, 33, 29, 30, 31, 30, 32, 31, 31, 32, 32, 32, 32, 28, 31, 32, 31, 32, 32, 30, 31, 30, 29, 25, 30, 30, 30, 31, 30 | 1,87; 1,64; 1,86; 1,61; 1,67; 1,81; 1,88; 1,89; 1,80; 1,93; 1,87; 1,97; 1,82; 1,80; 1,89; 1,75; 1.89; 1,65; 1,65; 1,77; 1,85; 1,65 | 1,95; 1,92; 2,04; 1,81; 1,80; 1,97; 2,02; 1,99; 1,91; 2.00; 1,89; 1,95; 1,91; 2,00; 1,93; 1,99; 2,05; 1,98; 1,98; 1,84; 1,97; 1,99; 1,95; 2,02; 1,95; 2,04; 1,98; 1,94; 1,94; 1,92; 1,98; 1,97; 2,04; 2,02; 1,94; 1,94; 1,88; 1,97; 1,84; 1,89 | 1; 2,7; 2,6; 2,6; 3; 4; 3,5; 4; 1,4; 3,6; 3,4; 2,6; 2,8; 2,2; 3,2; 1,0; 1,8; 2,2; 2,6 | 6; 4,2; 4; 5,2; 12; 4,8; 6,0; 6,2; 4,4; 8,8; 5,2; 4,4 | |||||||||
Число определений | ||||||||||||||||
J = 35 | j = 33 | J = 26 | j = 34 | J = 22 | j = 40 | J = 19 | j = 12 | |||||||||
Обобщенные результаты | ||||||||||||||||
Выборки | Выборочное среднее | Сумма квадратов | Оценка дисперсии | Выборочное среднее | Сумма квадратов | Оценка дисперсии | Выборочное среднее | Сумма квадратов | Оценка дисперсии | Выборочное среднее | Сумма квадратов | Оценка дисперсии | ||||
A | 21 | 166 | 4,88 | 36 | 131 | 5,24 | 1,80 | 0,2333 | 0,011 | 0,025 | 0,001486 | 0,000083 | ||||
B | 27 | 91 | 2,84 | 31 | 85 | 2,58 | 1,95 | 0,1477 | 0,0038 | 0,059 | 0,373871 | 0,03399 | ||||
A и B | 24 | 743 | 11,09 | 33 | 266 | 4,51 | 1,88 | 0,7593 | 0,0124 | 0,042 | 1,033262 | 0,03444 | ||||
2. Установим геологически значимые различия между средними значениями перечисленных показателей свойств грунтов у объекта прогноза и его аналогов до и после подтопления. Для этого рассмотрим следующие суммы квадратов:
общая сумма квадратов отклонений равна 743; 266; 0,7593; 1,033262;
сумма квадратов отклонений внутри выборок 257; 216; 0,3810; 0,375357;
разность квадратов отклонений между выборками 486; 50; 0,3783; 0,65791.
Числа степеней свободы для данных выборок соответственно равны 67; 59; 61; 30. Разности между общей суммой и суммой квадратов внутри совокупностей будет соответствовать одна степень свободы, а сумме квадратов внутри совокупностей - 66, 58, 60, 29 степеней свободы. Тогда средние значения квадратов равны внутри совокупностей 257/66 = 3,89; 216/58 = 3,72; 0,381/60 = 0,0064; 0,375357/29 = 0,0129 (обозначим квадраты через 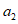 );
);
между совокупностями 486/1 = 486; 50; 0,3783; 0,65791 (обозначим квадраты через 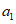 ); здесь квадраты
); здесь квадраты  являются мерой изменчивости между средними значениями рассматриваемых свойств грунтов до и после замачивания, тогда как квадраты
являются мерой изменчивости между средними значениями рассматриваемых свойств грунтов до и после замачивания, тогда как квадраты 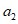 характеризуют изменчивость отдельных измерений внутри совокупности. Если
характеризуют изменчивость отдельных измерений внутри совокупности. Если  , различия между сравниваемым свойством совокупностей считаются существенными. Для данного примера различия в естественной влажности, влажности в пределе текучести, плотности грунта, коэффициенте сжимаемости лессовидных суглинков до и после подтопления являются существенными. Следовательно, подтопление территории обусловливает значительные изменения отмеченных свойств грунтов. Они должны учитываться при строительстве на этих грунтах инженерных сооружений.
, различия между сравниваемым свойством совокупностей считаются существенными. Для данного примера различия в естественной влажности, влажности в пределе текучести, плотности грунта, коэффициенте сжимаемости лессовидных суглинков до и после подтопления являются существенными. Следовательно, подтопление территории обусловливает значительные изменения отмеченных свойств грунтов. Они должны учитываться при строительстве на этих грунтах инженерных сооружений.
3. Для оценки роли в общей изменчивости величин названных свойств лессовидных суглинков процессов подтопления и суммарно показателей (факторов), характеризующих состав и строение грунтов, рекомендуются двухфакторные дисперсионные модели. Дополнительно к вычислениям табл. 15 определяются следующие суммы квадратов отклонений:
факториальные суммы квадратов отклонений средних по выборкам A и B для каждого свойства от их общей средней (для выборок A и B), взвешенных соответствующим числом повторностей 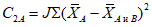 ;
; 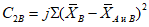 . Подставив числовые значения, получим для влажности
. Подставив числовые значения, получим для влажности 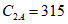 ; для влажности верхнего предела пластичности
; для влажности верхнего предела пластичности  ; для объемного веса
; для объемного веса  ; для коэффициента уплотнения
; для коэффициента уплотнения  . Аналогично
. Аналогично  ; 136; 0,196; 0,003468 соответственно;
; 136; 0,196; 0,003468 соответственно;
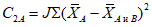 ;
; 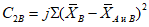 . Подставив числовые значения, получим для влажности
. Подставив числовые значения, получим для влажности 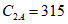 ; для влажности верхнего предела пластичности
; для влажности верхнего предела пластичности  ; для объемного веса
; для объемного веса  ; для коэффициента уплотнения
; для коэффициента уплотнения  . Аналогично
. Аналогично  ; 136; 0,196; 0,003468 соответственно;
; 136; 0,196; 0,003468 соответственно;случайная сумма квадратов отклонений единичных определений от своих средних для первой и второй совокупностей  . Для данных табл. 15 она равна 263; 216; 0,3937 и 0,005742 соответственно.
. Для данных табл. 15 она равна 263; 216; 0,3937 и 0,005742 соответственно.
 . Для данных табл. 15 она равна 263; 216; 0,3937 и 0,005742 соответственно.
. Для данных табл. 15 она равна 263; 216; 0,3937 и 0,005742 соответственно.4. Дисперсии для сумм квадратов в данных типах моделей определяются из выражений
 ,
,n - число совокупностей для каждого свойства, n = 2; 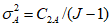 ;
;  ;
;  ; после подстановки соответствующих значений получим:
; после подстановки соответствующих значений получим:
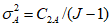 ;
;  ;
;  ; после подстановки соответствующих значений получим:
; после подстановки соответствующих значений получим:для показателей естественной влажности  ;
;  ;
;  ;
;  при числах степеней свободы 2309; 34; 32; 1088;
при числах степеней свободы 2309; 34; 32; 1088;
 ;
;  ;
;  ;
;  при числах степеней свободы 2309; 34; 32; 1088;
при числах степеней свободы 2309; 34; 32; 1088;для влажности верхнего предела пластичности  ;
;  ;
;  ;
;  при числах степеней свободы 1767; 25; 33; 825;
при числах степеней свободы 1767; 25; 33; 825;
 ;
;  ;
;  ;
;  при числах степеней свободы 1767; 25; 33; 825;
при числах степеней свободы 1767; 25; 33; 825;для плотности грунта  ;
;  ;
;  ;
;  при числах степеней свободы 1759; 21; 39; 819;
при числах степеней свободы 1759; 21; 39; 819;
 ;
;  ;
;  ;
;  при числах степеней свободы 1759; 21; 39; 819;
при числах степеней свободы 1759; 21; 39; 819;для коэффициента сжимаемости 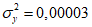 ;
;  ;
;  ;
; 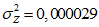 при числах степеней свободы 455; 18; 11; 198.
при числах степеней свободы 455; 18; 11; 198.
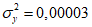 ;
;  ;
;  ;
; 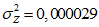 при числах степеней свободы 455; 18; 11; 198.
при числах степеней свободы 455; 18; 11; 198.ИС МЕГАНОРМ: примечание. Формулы даны в соответствии с официальным текстом документа. |
Обозначим влияние фактора подтопления грунтов через  , а суммарное влияние факторов состава и строения через
, а суммарное влияние факторов состава и строения через  . Значимость факторов
. Значимость факторов  и
и  определяется для данных табл. 15 по формулам для фиксированных моделей, т.е.
определяется для данных табл. 15 по формулам для фиксированных моделей, т.е.  ;
;  . Допустимые значения критерия
. Допустимые значения критерия  для 95% уровня надежности и заданных чисел степеней свободы (
для 95% уровня надежности и заданных чисел степеней свободы ( ,
,  ;
;  ,
,  ;
; 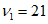 ,
,  ;
;  ,
,  ) находятся из таблиц приложений учебников по статистике. Подставив соответствующие числа в формулы для
) находятся из таблиц приложений учебников по статистике. Подставив соответствующие числа в формулы для  ,
,  и выписав допустимые значения, получим:
и выписав допустимые значения, получим:
 ;
;  . Допустимые значения критерия
. Допустимые значения критерия  ;
;  ;
;  ;
;  ) находятся из таблиц приложений учебников по статистике. Подставив соответствующие числа в формулы для
) находятся из таблиц приложений учебников по статистике. Подставив соответствующие числа в формулы для для естественной влажности -  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;для влажности верхнего предела пластичности - 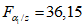 ;
;  ;
;  ;
;
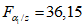 ;
;  ;
;  ;
;для плотности грунта -  ;
; 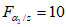 ;
;  ;
;
 ;
; 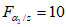 ;
;  ;
;для коэффициента сжимаемости -  ;
;  ;
;  .
.
 ;
;  ;
;  .
.5. Поскольку для всех показателей свойств величины  ,
,  больше допустимого (табулированного) значения, то влияние фактора подтопления и суммарного воздействия состава и строения грунтов на изменчивость свойств является существенным. Количественная величина факторов
больше допустимого (табулированного) значения, то влияние фактора подтопления и суммарного воздействия состава и строения грунтов на изменчивость свойств является существенным. Количественная величина факторов  и
и  находится из выражений:
находится из выражений:  (для фактора
(для фактора  ) и
) и  (для факторов
(для факторов  ), т.е.
), т.е.  ;
;
 (для фактора
(для фактора  (для факторов
(для факторов  ;
;для изменения естественной влажности грунтов в зоне подтопления  ;
; 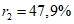 . Следовательно, на долю подъема уровня грунтовых вод в величине общей изменчивости естественной влажности данных типов грунтов для условий Крыма приходится около 52,1%; оставшиеся 47,9% изменчивости влажности лессов обусловлены их составом и строением;
. Следовательно, на долю подъема уровня грунтовых вод в величине общей изменчивости естественной влажности данных типов грунтов для условий Крыма приходится около 52,1%; оставшиеся 47,9% изменчивости влажности лессов обусловлены их составом и строением;
 ;
; 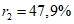 . Следовательно, на долю подъема уровня грунтовых вод в величине общей изменчивости естественной влажности данных типов грунтов для условий Крыма приходится около 52,1%; оставшиеся 47,9% изменчивости влажности лессов обусловлены их составом и строением;
. Следовательно, на долю подъема уровня грунтовых вод в величине общей изменчивости естественной влажности данных типов грунтов для условий Крыма приходится около 52,1%; оставшиеся 47,9% изменчивости влажности лессов обусловлены их составом и строением;для изменения влажности верхнего предела пластичности  ;
;  . Для данного показателя свойств на долю суммарного воздействия факторов
. Для данного показателя свойств на долю суммарного воздействия факторов  и
и  приходится около 87,8%. Оставшиеся 12,2% приходятся на долю не учтенных в модели факторов, например таких, как изменение дисперсности грунтов в зоне затопления, что подтверждается результатами гранулометрического состава;
приходится около 87,8%. Оставшиеся 12,2% приходятся на долю не учтенных в модели факторов, например таких, как изменение дисперсности грунтов в зоне затопления, что подтверждается результатами гранулометрического состава;
 ;
;  . Для данного показателя свойств на долю суммарного воздействия факторов
. Для данного показателя свойств на долю суммарного воздействия факторов для изменения показателей плотности грунта 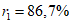 ;
;  , т.е. изменчивость данного показателя в наибольшей степени предопределена повышением уровня грунтовых вод;
, т.е. изменчивость данного показателя в наибольшей степени предопределена повышением уровня грунтовых вод;
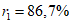 ;
;  , т.е. изменчивость данного показателя в наибольшей степени предопределена повышением уровня грунтовых вод;
, т.е. изменчивость данного показателя в наибольшей степени предопределена повышением уровня грунтовых вод;для изменения величины коэффициента сжимаемости лессовидных суглинков при нагрузках 0,1 МПа  ,
,  .
.
 ,
,  .
.6. Следовательно, согласно п. 5 изменение коэффициента сжимаемости лессовидных суглинков в большей мере (примерно на 42,9%) обусловлено их составом и особенностями строения (факторы  ) и в несколько меньшей степени (примерно 32,1%) - подъемом уровня грунтовых вод (фактор
) и в несколько меньшей степени (примерно 32,1%) - подъемом уровня грунтовых вод (фактор  ). Около 15% изменчивости данного показателя вызвано влиянием не учитываемых в модели факторов. Как и для показателей влажности верхнего предела пластичности, к числу таких факторов следует отнести изменение в зоне подтопления гранулометрического состава грунтов.
). Около 15% изменчивости данного показателя вызвано влиянием не учитываемых в модели факторов. Как и для показателей влажности верхнего предела пластичности, к числу таких факторов следует отнести изменение в зоне подтопления гранулометрического состава грунтов.
7. Выполненный в пп. 1 - 6 дисперсионный анализ показывает, что на долю факторов  и
и  падает подавляющая величина изменения основных свойств грунтов. Поэтому по количественным показателям данных факторов можно предсказать величину возможного изменения свойств грунтов в зоне подтопления, причем в первую очередь механических свойств, определение которых на современном этапе развития методов инженерно-геологических изысканий трудоемко и дорого. Задача сводится к тому, чтобы по показателям, легко определяемым по существующей методике изысканий, построить такое прогнозное уравнение связи, по которому с заданным уровнем надежности и с достаточной точностью можно было бы рассчитывать механические свойства грунтов. Для условий рассматриваемого примера данные показатели должны в полной мере характеризовать факторы
падает подавляющая величина изменения основных свойств грунтов. Поэтому по количественным показателям данных факторов можно предсказать величину возможного изменения свойств грунтов в зоне подтопления, причем в первую очередь механических свойств, определение которых на современном этапе развития методов инженерно-геологических изысканий трудоемко и дорого. Задача сводится к тому, чтобы по показателям, легко определяемым по существующей методике изысканий, построить такое прогнозное уравнение связи, по которому с заданным уровнем надежности и с достаточной точностью можно было бы рассчитывать механические свойства грунтов. Для условий рассматриваемого примера данные показатели должны в полной мере характеризовать факторы 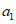 и
и 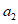 , т.е. быть представляющими этих факторов и входить в число стандартных определений, предусмотренных СНиПами.
, т.е. быть представляющими этих факторов и входить в число стандартных определений, предусмотренных СНиПами.
8. В качестве прогнозного показателя взят угол внутреннего трения лессовидных суглинков в зоне подтопления. Влияние подтопления (фактора  ) выразим посредством показателей естественной влажности и объемного веса, определенные для грунтов в зоне подтопления. Названные показатели наиболее существенно реагируют на затопление пород. Особенности состава и строения грунтов (факторы
) выразим посредством показателей естественной влажности и объемного веса, определенные для грунтов в зоне подтопления. Названные показатели наиболее существенно реагируют на затопление пород. Особенности состава и строения грунтов (факторы  ) выразим показателями влажности нижнего и верхнего пределов пластичности, а также содержанием пылеватых и глинистых частиц в грунте до подтопления. Таким образом, располагая лабораторными определениями шести показателей физических свойств лессовидных суглинков, являющихся качественно однородными по геоморфологическому положению, генезису, условиям образования и изменения, необходимо установить следующее: а) возможно ли предсказать величину угла внутреннего трения данных грунтов по прогнозному уравнению связи между показателями их физических свойств; б) если возможно это сделать, то с какой точностью (надежностью).
) выразим показателями влажности нижнего и верхнего пределов пластичности, а также содержанием пылеватых и глинистых частиц в грунте до подтопления. Таким образом, располагая лабораторными определениями шести показателей физических свойств лессовидных суглинков, являющихся качественно однородными по геоморфологическому положению, генезису, условиям образования и изменения, необходимо установить следующее: а) возможно ли предсказать величину угла внутреннего трения данных грунтов по прогнозному уравнению связи между показателями их физических свойств; б) если возможно это сделать, то с какой точностью (надежностью).
9. Для построения прогнозного уравнения связи используем метод Дуллитла, как это показано в табл. 16.
Переменные | Отклонения единичных значений от средних | ||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
0,509 | 1,77 | 40,6 | 29,7 | 44,1 | 93,2 | 4,3 | 0,051 | -0,18 | 14,0 | 8,0 | 11,6 | 28,3 | -8,2 |
0,488 | 1,77 | 40,6 | 29,7 | 44,1 | 93,2 | 4,3 | 0,030 | -0,18 | 14,0 | 8,0 | 11,6 | 28,3 | -8,2 |
0,532 | 2,03 | 27,0 | 21,0 | 30,4 | 84,5 | 9,2 | 0,074 | 0,07 | 0,5 | -0,7 | -2,1 | 19,6 | -3,5 |
0,577 | 1,93 | 25,0 | 19,6 | 27,2 | 85,8 | 4,4 | 0,119 | -0,04 | -1,5 | -2,1 | -5,2 | 20,9 | -8,1 |
0,510 | 1,95 | 27,0 | 20,4 | 30,2 | 42,3 | 10,7 | 0,052 | -0,01 | 0,5 | -1,3 | -2,3 | -22,6 | -2,0 |
0,532 | 1,82 | 36,0 | 29,0 | 39,5 | 90,7 | 1,4 | 0,074 | -0,12 | 9,4 | 7,3 | 7,0 | 25,8 | -11,1 |
0,510 | 1,96 | 27,0 | 20,7 | 30,1 | 69,4 | 8,0 | 0,052 | 0 | 0,5 | -0,7 | -2,4 | 4,5 | -4,7 |
0,532 | 1,99 | 26,0 | 20,2 | 29,0 | 58,0 | 14,4 | 0,074 | 0,03 | -0,5 | -1,5 | -3,5 | -6,9 | 1,7 |
0,510 | 2,00 | 30,0 | 22,6 | 34,2 | 53,0 | 2,7 | 0,052 | 0,04 | 3,4 | 0,9 | 1,7 | -11,9 | -10,0 |
0,555 | 1,93 | 26,0 | 20,8 | 29,3 | 90,9 | 2,7 | 0,097 | -0,03 | -0,5 | -0,9 | -3,2 | 26,0 | -10,0 |
Продолжение табл. 16
Среднеквадратические отклонения | ||||||
 |  |  | 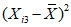 |  |  |  |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
0,002601 | 0,0324 | 196,00 | 64,00 | 134,56 | 800,89 | 67,24 |
0,000900 | 0,0324 | 196,00 | 64,00 | 134,56 | 800,89 | 67,24 |
0,005476 | 0,0049 | 0,25 | 0,49 | 4,41 | 384,16 | 12,25 |
0,014161 | 0,0016 | 2,25 | 4,41 | 27,04 | 432,64 | 65,61 |
0,002704 | 0,0001 | 0,25 | 1,69 | 5,29 | 510,76 | 4,00 |
0,005476 | 0,0144 | 88,36 | 53,29 | 49,00 | 665,64 | 123,21 |
0,002704 | 0,0000 | 0,25 | 0,49 | 5,76 | 20,25 | 22,09 |
0,005476 | 0,0009 | 0,25 | 2,25 | 12,25 | 47,61 | 2,89 |
0,002704 | 0,0016 | 11,56 | 0,81 | 2,89 | 141,61 | 100,00 |
0,009409 | 0,0009 | 0,25 | 0,81 | 10,24 | 676,00 | 100,00 |
Продолжение табл. 16
Переменные | Отклонения единичных значений от средних | ||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
0,532 | 1,92 | 29,0 | 21,0 | 32,4 | 77,0 | 16,7 | 0,074 | -0,04 | 2,3 | -0,7 | -0,1 | 12,1 | 4,0 |
0,489 | 1,86 | 34,8 | 23,1 | 38,3 | 80,3 | 17,4 | 0,031 | -0,10 | 8,1 | 1,4 | 5,8 | 15,4 | 4,7 |
0,296 | 2,10 | 17,5 | 23,6 | 36,7 | 45,1 | 20,5 | -0,162 | 0,14 | -9,0 | 1,9 | 4,2 | -19,8 | 7,8 |
0,562 | 2,20 | 14,0 | 19,0 | 29,2 | 68,2 | 16,1 | 0,104 | 0,24 | -12,5 | -2,7 | -3,3 | 3,3 | 3,4 |
0,288 | 2,17 | 14,0 | 14,7 | 23,7 | 42,8 | 29,8 | -0,170 | 0,21 | -12,5 | -7,0 | -8,6 | -22,1 | 17,1 |
0,193 | 2,30 | 18,1 | 16,6 | 25,6 | 11,9 | 28,1 | -0,265 | 0,34 | -8,4 | -5,1 | -6,7 | -53,0 | 15,4 |
0,248 | 1,74 | 13,0 | 16,0 | 24,6 | 21,4 | 15,0 | -0,210 | -0,18 | -13,5 | -5,7 | -7,7 | -43,5 | 2,3 |
0,211 | 2,17 | 14,0 | 16,7 | 26,4 | 45,9 | 26,2 | -0,240 | 0,21 | -12,5 | -5,0 | -6,1 | -19,0 | 13,5 |
0,510 | 1,97 | 27,1 | 20,3 | 30,2 | 42,0 | 10,2 | 0,052 | 0,01 | 0,6 | -1,4 | -2,3 | -22,9 | -2,5 |
0,532 | 1,92 | 29,0 | 21,0 | 32,4 | 77,0 | 16,7 | 0,074 | -0,05 | 2,4 | -0,7 | -0,1 | 12,1 | 4,0 |
0,509 | 1,77 | 40,6 | 29,7 | 44,1 | 90,5 | 7,0 | 0,051 | -0,18 | 13,0 | 8,0 | 11,6 | 25,5 | -5,6 |
 | 41,27 | 556,3 | 455,4 | 681,7 | 1363,1 | 265,8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Среднее П = 0,458 |  |  |  |  | 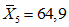 |  | - | - | - | - | - | - | - |
Продолжение табл. 16
Среднеквадратические отклонения | ||||||
15 | 16 | 17 | 18 | 19 | 20 | 21 |
0,005476 | 0,0016 | 5,29 | 0,49 | 0,01 | 146,41 | 16,00 |
0,000961 | 0,0100 | 65,61 | 1,96 | 33,64 | 237,16 | 22,09 |
0,026244 | 0,0196 | 81,00 | 3,61 | 17,64 | 392,04 | 60,84 |
0,010816 | 0,0576 | 156,25 | 7,29 | 10,89 | 10,89 | 11,56 |
0,028900 | 0,0441 | 156,25 | 49,00 | 73,96 | 488,41 | 292,41 |
0,070225 | 0,1156 | 70,56 | 26,01 | 44,89 | 2809,00 | 237,16 |
0,044100 | 0,0324 | 182,25 | 32,49 | 59,29 | 1892,25 | 5,29 |
0,057600 | 0,0441 | 156,25 | 25,00 | 37,21 | 361,00 | 182,25 |
0,002704 | 0,0001 | 0,36 | 1,96 | 5,29 | 524,41 | 6,25 |
0,005476 | 0,0025 | 5,76 | 0,49 | 0,01 | 146,41 | 16,00 |
0,002601 | 0,0324 | 169,00 | 64,00 | 134,56 | 650,25 | 31,36 |
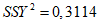 |  |  |  |  |  | 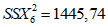 |
- | - | - | - | - | - | - |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
 |  | 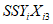 |  |  |  |  |  |  |  |  |  |  |  |
-0,1767 | 13,3263 | 5,2559 | 5,8899 | 46,0042 | -15,7200 | -18,1000 | -8,8310 | -11,7380 | -42,2300 | 17,6430 | 700,3300 | 947,4900 | 3136, 9800 |
Исследуются уравнения вида  | |||||||||||||
Матричный анализ | |||||||||||||
Симметричная матрица из сумм |  | ||||||||||||
Продолжение табл. 16
 |  | 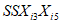 |  |  |  |  | |||||||||
-1029,7800 | 553,3500 | 1545,3100 | -502,9600 | 1987,0700 | -555,0500 | -2726,5100 | |||||||||
Матричный анализ | |||||||||||||||
Вектор-столбец g | 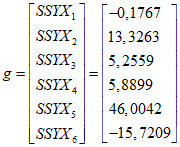 | ||||||||||||||
Решение матриц методом Дуллитла | |||||||||||||||
Пояснения | Строка | ||||||||||||||
Коэффициенты при | 0,4492 | -18,1000 | -8,8310 | -11,7380 | -42,2300 | 17,6430 | |||||||||
-18,1000 | 1544,0000 | 700,3300 | 947,4900 | 3136,9800 | -1029,7800 | ||||||||||
-8,8310 | 700,3300 | 404,5400 | 553,3500 | 1545,3100 | -502,9600 | ||||||||||
-11,7380 | 947,4900 | 553,3500 | 803,3900 | 1987,0700 | -555,0500 | ||||||||||
-42,2300 | 3136,9800 | 154,53100 | 1987,0700 | 12138,6800 | -2726,5100 | ||||||||||
17,6430 | -1029,7800 | -502,9600 | -555,0500 | -2726,5100 | 1445,7400 | ||||||||||
Переписана 1-я строка   | 0,4492 | -18,1000 | -8,8310 | -11,7380 | -42,2300 | 17,6430 | |||||||||
1 | -40,2938 | -19,6594 | -26,1309 | -94,0116 | 39,2765 | ||||||||||
- | 814,6822 | 344,4949 | 474,5207 | 1435,3790 | -318,8754 | ||||||||||
Продолжение табл. 16
g | Сумма C | ||||||
-0,1767 | 1 | 0 | 0 | 0 | 0 | 0 | -61,9835 |
13,3263 | 0 | 1 | 0 | 0 | 0 | 0 | 5295,2463 |
5,2559 | 0 | 0 | 1 | 0 | 0 | 0 | 2697,9949 |
5,8899 | 0 | 0 | 0 | 1 | 0 | 0 | 3731,4019 |
46,0042 | 0 | 0 | 0 | 0 | 1 | 0 | 16086,3032 |
-15,7200 | 0 | 0 | 0 | 0 | 0 | 1 | -3365,6370 |
-0,1767 | 1 | 0 | 0 | 0 | 0 | 0 | -61,9835 |
-0,3934 | 2,2262 | 0 | 0 | 0 | 0 | 0 | -137,9864 |
6,2058 | 40,2942 | 1 | 0 | 0 | 0 | 0 | 2797,7014 |
 | - | 1 | 0,4228 | 0,5825 | 1,7619 | -0,3914 | |
 | - | - | 85,2754 | 121,9197 | 108,1280 | -21,2739 | |
 | - | - | 1 | 1,4297 | 1,2679 | -0,2495 | |
 | - | - | - | 45,9486 | -107,0782 | 122,1240 | |
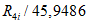 | - | - | - | 1 | -2,3304 | 2,6578 | |
 | - | - | - | - | 5252,9454 | -194,4857 | |
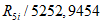 | - | - | - | - | 1 | -0,0370 | |
 | - | - | - | - | 290,8919 | ||
 | - | - | - | - | - | 1 | |
0,0076 | 0,0495 | 0,0012 | 0 | 0 | 0 | 0 | 3,4341 |
-0,8364 | 2,6071 | -0,4134 | 1 | 0 | 0 | 0 | 296,4065 |
0,0098 | 0,0306 | -0,0048 | 0,0117 | 0 | 0 | 0 | 3,4759 |
-1,1394 | -1,0884 | 0,0158 | -1,4265 | 1 | 0 | 0 | 58,3559 |
-0,0248 | -0,0237 | 0,0003 | -0,0310 | 0,0218 | 0 | 0 | 1,2700 |
16,8861 | 17,1147 | -1,1713 | -4,5845 | 2,3343 | 1 | 0 | 5090,0497 |
0,0032 | 0,0033 | -0,0002 | -0,0009 | 0,004 | 0,0002 | 0 | 0,9690 |
-2,9133 | -19,3054 | 0,2050 | 6,0619 | -2,5845 | 0,0389 | 1 | 273,3945 |
-0,0100 | -0,0664 | 0,0007 | 0,0208 | -0,0089 | 0,0001 | 0,0034 | 0,9398 |
Сумма из произведений элементов 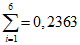 | |||||||
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 16, а не таблица 15. |

Необходимо решить систему уравнений
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
 (43)
(43)Из системы уравнений (43) находим оценки коэффициентов  :
:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.Уравнение для предсказания угла внутреннего трения лессовидных суглинков по результатам определения их физических свойств имеет вид
11. Оценка дисперсии равна:
 ,
,где n - число измерений.
Дисперсия характеризует "внутреннюю" изменчивость угла внутреннего трения грунтов. Судя по величине этой изменчивости, данный показатель имеет относительно небольшую величину изменчивости и может быть оценен по измерениям введенных в уравнение (51) показателей физических свойств грунтов. Допустим, что по случайным определениям введенных в уравнение (51) переменных 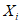 были получены их точечные значения:
были получены их точечные значения:  ;
;  ;
;  ;
;  ;
;  ;
;  . Определим по этим значениям величину угла внутреннего трения, подставив их в уравнение (51),
. Определим по этим значениям величину угла внутреннего трения, подставив их в уравнение (51),  .
.
 ;
;  ;
;  ;
;  ;
;  ;
;  . Определим по этим значениям величину угла внутреннего трения, подставив их в уравнение (51),
. Определим по этим значениям величину угла внутреннего трения, подставив их в уравнение (51),  .
.12. Построим доверительный интервал для среднего значения прогнозной функции Y при 95%-ном уровне надежности. Доверительный интервал для  при заданных точечных оценках
при заданных точечных оценках 
 ,
,где  ; так как в данном случае
; так как в данном случае  ;
;  (заданные точечные значения
(заданные точечные значения 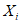 ,
, 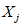 равны их средним значениям - для простоты вычислений), то
равны их средним значениям - для простоты вычислений), то
 ; так как в данном случае
; так как в данном случае  ;
;  (заданные точечные значения
(заданные точечные значения  ;
;отсюда 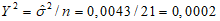 или
или  ;
;
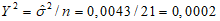 или
или  ;
; - критерий Стьюдента;
- критерий Стьюдента;  ; подставив значения V и t в формулу доверительного интервала, получим
; подставив значения V и t в формулу доверительного интервала, получим .
.Таким образом, в 95 случаях из 100 среднее значение угла внутреннего трения  лессовидных суглинков в зоне подтопления может быть оценено по названным показателям свойств и не превышает указанных пределов. Оно отклоняется на величину +/- 0,03:
лессовидных суглинков в зоне подтопления может быть оценено по названным показателям свойств и не превышает указанных пределов. Оно отклоняется на величину +/- 0,03:  .
.
 .
.13. Надежность оценки прогнозной величины угла внутреннего трения грунтов по значениям рассматриваемых шести показателей их физических свойств  . Это означает, что на долю совместного влияния показателей, характеризующих лессовидные суглинки в зоне подтопления (естественная влажность затопленных грунтов и их плотность), и показателей, характеризующих состав и особенности их строения до подтопления (влажности нижнего и верхнего пределов пластичности, содержание пылеватых и глинистых частиц), приходится около 76% общей изменчивости среднего значения угла внутреннего трения. На долю не учитываемых в уравнении факторов приходится около 24%. К их числу для данных условий относится количество растворимых солей в грунтах.
. Это означает, что на долю совместного влияния показателей, характеризующих лессовидные суглинки в зоне подтопления (естественная влажность затопленных грунтов и их плотность), и показателей, характеризующих состав и особенности их строения до подтопления (влажности нижнего и верхнего пределов пластичности, содержание пылеватых и глинистых частиц), приходится около 76% общей изменчивости среднего значения угла внутреннего трения. На долю не учитываемых в уравнении факторов приходится около 24%. К их числу для данных условий относится количество растворимых солей в грунтах.
 . Это означает, что на долю совместного влияния показателей, характеризующих лессовидные суглинки в зоне подтопления (естественная влажность затопленных грунтов и их плотность), и показателей, характеризующих состав и особенности их строения до подтопления (влажности нижнего и верхнего пределов пластичности, содержание пылеватых и глинистых частиц), приходится около 76% общей изменчивости среднего значения угла внутреннего трения. На долю не учитываемых в уравнении факторов приходится около 24%. К их числу для данных условий относится количество растворимых солей в грунтах.
. Это означает, что на долю совместного влияния показателей, характеризующих лессовидные суглинки в зоне подтопления (естественная влажность затопленных грунтов и их плотность), и показателей, характеризующих состав и особенности их строения до подтопления (влажности нижнего и верхнего пределов пластичности, содержание пылеватых и глинистых частиц), приходится около 76% общей изменчивости среднего значения угла внутреннего трения. На долю не учитываемых в уравнении факторов приходится около 24%. К их числу для данных условий относится количество растворимых солей в грунтах.14. Оценка устойчивости склонов, сложенных лессовыми грунтами, выполняется посредством сопоставления параметров прочности пород у объекта прогноза и его аналогов.
РАЗВИТИЯ ОПОЛЗНЕВЫХ - ОБВАЛЬНЫХ СКЛОНОВ
1. В качестве примера рассматриваются данные по оползням-обвалам, вошедшие во второй вариант второй задачи (см. Прил. 6). Оползни-обвалы по этому варианту имеют тектонический с зоной дробления тип поверхностей ослабления, сформированы в пределах присклоновых зон интенсивно разгруженных и выветрелых известняков, а критерии  ,
,  ,
,  (см. Прил. 1) равны по абсолютной величине или изменяются пропорционально, не нарушая в сумме устойчивости склонов. Примем обозначения: критерий
(см. Прил. 1) равны по абсолютной величине или изменяются пропорционально, не нарушая в сумме устойчивости склонов. Примем обозначения: критерий 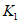 обозначим через
обозначим через  ,
, 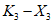 ,
,  ,
, 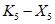 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 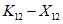 . Виды частных уравнений связи, значения коэффициентов взаимной корреляции, детерминации, общее критериальное уравнение связи показаны в табл. 17.
. Виды частных уравнений связи, значения коэффициентов взаимной корреляции, детерминации, общее критериальное уравнение связи показаны в табл. 17.
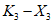 ,
,  ,
, 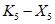 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 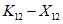 . Виды частных уравнений связи, значения коэффициентов взаимной корреляции, детерминации, общее критериальное уравнение связи показаны в табл. 17.
. Виды частных уравнений связи, значения коэффициентов взаимной корреляции, детерминации, общее критериальное уравнение связи показаны в табл. 17.Таблица 17
Вид связи  | Виды полиномиальных уравнений связи | Коэффициенты | Относительная роль | Главные критерии подобия и их роль в формировании | |
взаимной корреляции | детерминации | ||||
 |  | 0,16 | 0,0072 | 10,03 |  |
 |  | 0,28 | 0,0005 | 0,65 |  |
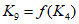 |  | 0,34 | 0,0102 | 14,65 |  |
 | 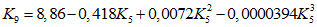 | 0,30 | 0,0021 | 61,80 | 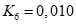 |
 |  | 0,94 | 0,043 | 3,20 |  |
 |  | 0,31 | 0,0007 | 0,95 |  |
 |  | 0,31 | 0,0002 | 0,24 | |
 |  | 0,29 | 0,00038 | 0,54 | |
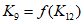 |  | 0,40 | 0,00003 | 5,46 | |
 |  | 0,54 | 0,00173 | 2,48 | |
 | |||||
Коэффициент множественной корреляции равен: 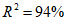 . Ошибка в определении
. Ошибка в определении  .
.
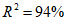 . Ошибка в определении
. Ошибка в определении  .
.2. В зависимости от величины несовпадения главных критериев геологического подобия рекомендуются три категории склонов по степени их устойчивости:
неустойчивые оползне-, обвалоопасные блоки пород. Возможные несовпадения критерия  у объекта прогноза меньше, чем у его аналогов, на 3 единицы; критерия-симплекса
у объекта прогноза меньше, чем у его аналогов, на 3 единицы; критерия-симплекса  меньше на 20°; критерия
меньше на 20°; критерия  - на 10 единиц; другие критерии могут не совпадать на величины, повышающие устойчивость до величины
- на 10 единиц; другие критерии могут не совпадать на величины, повышающие устойчивость до величины 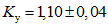 ;
;
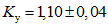 ;
;потенциально неустойчивые оползне-, обвалоопасные блоки пород, когда у объекта прогноза значения главных критериев подобия меньше, чем у аналогов, на следующие величины:  - на 5 единиц,
- на 5 единиц, 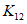 - на 15 единиц, критерия-симплекса
- на 15 единиц, критерия-симплекса  - на 30°; при равенстве названных критериев критерий-симплекс
- на 30°; при равенстве названных критериев критерий-симплекс 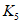 может быть меньше на 6 - 7°. При любых других различиях необходимо, чтобы
может быть меньше на 6 - 7°. При любых других различиях необходимо, чтобы  ;
;
 ;
;относительно стабильные склоны. Критерий  у объекта прогноза близок к нулю и меньше, чем у аналогов, 6 единиц; критерий-симплекс
у объекта прогноза близок к нулю и меньше, чем у аналогов, 6 единиц; критерий-симплекс  меньше на 5°. Возможны несовпадения величин других критериев на величины, суммарно повышающие устойчивость до
меньше на 5°. Возможны несовпадения величин других критериев на величины, суммарно повышающие устойчивость до  .
.
 .
.ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 6 в Приложении 8 отсутствует. |
3. В табл. 18 приведен пример сопоставления значений критериев геологического подобия в оползнеопасном блоке с неизвестной устойчивостью и в его аналоге с известной устойчивостью. Сопоставляя данные таблицы по объекту прогноза и его аналогу, видим, что склоны качественно подобны друг другу. Согласно правилу вероятностного геологического подобия (см. п. 6), рассматриваемые склоны можно считать подобными и по их состоянию с ошибкой в величине коэффициента устойчивости  . Эта ошибка вызвана за счет неучета указанным правилом количественно выражаемых критериев подобия. При сопоставлении у объекта прогноза и его аналога критериев геологического подобия оказалось, что критерий
. Эта ошибка вызвана за счет неучета указанным правилом количественно выражаемых критериев подобия. При сопоставлении у объекта прогноза и его аналога критериев геологического подобия оказалось, что критерий  у аналога больше, чем у объекта, за счет чего устойчивость прогнозируемого склона повысится на 0,2; критерий-симплекс
у аналога больше, чем у объекта, за счет чего устойчивость прогнозируемого склона повысится на 0,2; критерий-симплекс  не совпадает на 5° и это вызывает повышение устойчивости еще на 0,05; критерий
не совпадает на 5° и это вызывает повышение устойчивости еще на 0,05; критерий  у аналога меньше, чем у объекта, на 0,07 единиц, что вызывает понижение устойчивости на 0,06. В целом объект прогноза в природных условиях имеет устойчивость
у аналога меньше, чем у объекта, на 0,07 единиц, что вызывает понижение устойчивости на 0,06. В целом объект прогноза в природных условиях имеет устойчивость  , т.е. оползнеопасный блок относится к категории потенциально неустойчивых. Намечаемое строительство гидроузла на рассматриваемом участке должно привести к увеличению у прогнозного склона критериев
, т.е. оползнеопасный блок относится к категории потенциально неустойчивых. Намечаемое строительство гидроузла на рассматриваемом участке должно привести к увеличению у прогнозного склона критериев  на 15°,
на 15°,  на 0,05 единиц, что должно отразиться на изменении коэффициента устойчивости в сторону его уменьшения на суммарную величину 0,25, т.е.
на 0,05 единиц, что должно отразиться на изменении коэффициента устойчивости в сторону его уменьшения на суммарную величину 0,25, т.е.  . Данный прогноз в последующем подтвердился результатами наблюдений за склонами. После проведения строительных работ и антропогенных изменений величин перечисленных критериев (
. Данный прогноз в последующем подтвердился результатами наблюдений за склонами. После проведения строительных работ и антропогенных изменений величин перечисленных критериев ( ,
,  ,
,  ), в потенциально неустойчивом блоке начали проявляться деформации смещения блока пород со склона, его растрескивание. После выполнения защитных мероприятий данный блок стабилизировался.
), в потенциально неустойчивом блоке начали проявляться деформации смещения блока пород со склона, его растрескивание. После выполнения защитных мероприятий данный блок стабилизировался.
 . Эта ошибка вызвана за счет неучета указанным правилом количественно выражаемых критериев подобия. При сопоставлении у объекта прогноза и его аналога критериев геологического подобия оказалось, что критерий
. Эта ошибка вызвана за счет неучета указанным правилом количественно выражаемых критериев подобия. При сопоставлении у объекта прогноза и его аналога критериев геологического подобия оказалось, что критерий  , т.е. оползнеопасный блок относится к категории потенциально неустойчивых. Намечаемое строительство гидроузла на рассматриваемом участке должно привести к увеличению у прогнозного склона критериев
, т.е. оползнеопасный блок относится к категории потенциально неустойчивых. Намечаемое строительство гидроузла на рассматриваемом участке должно привести к увеличению у прогнозного склона критериев  . Данный прогноз в последующем подтвердился результатами наблюдений за склонами. После проведения строительных работ и антропогенных изменений величин перечисленных критериев (
. Данный прогноз в последующем подтвердился результатами наблюдений за склонами. После проведения строительных работ и антропогенных изменений величин перечисленных критериев (Последовательность прогноза | Изучаемый оползнеопасный склон | Аналог | Изменение коэффициента устойчивости за счет несовпадения | ||||
| |||||||
Литолого-генетические комплексы пород, слагающих склоны | Качественно подобные, изменений | ||||||
Качественное подобие и выполнение условий однозначности согласно второму принципу подобия | Верхнепермские песчаники с прослоями аргиллитов с падением в сторону склона под углом 12° | Верхнепермские песчаники с прослоями аргиллитов с падением в сторону склона под углом 12° | |||||
Типы поверхностей отчленения и типы ниш отрыва и смещения | То же | ||||||
Тектонический с зоной дробления, четвертый (см. п. 40) | Тектонический с зоной дробления, четвертый | ||||||
Приуроченность склонов к тектоническим разрывам и трещинам | " | ||||||
В зоне влияния разрыва IV порядка, секущего склон под углом 60° | В зоне влияния разрыва IV порядка, секущего склон под углом 60° | ||||||
Типы и состояние заполнителей трещин отчленения и смещения | Качественно подобные. Изменений | ||||||
Суглинистый; глинистая составляющая - монтмориллонит; мягкопластичной консистенции | Суглинистый; глинистая составляющая - монтмориллонит; мягкопластичной консистенции | ||||||
Новейшие и современные тектонические движения, включая сейсмичность | |||||||
В центральной части структурного блока IV порядка. Северное крыло антиклинали. Зона 8-балльного землетрясения и выхода упругих сейсмических волн на поверхность под углом 20° | В центральной части структурного блока IV порядка. Северное крыло антиклинали. Зона 8-балльного землетрясения и выхода упругих сейсмических волн на поверхность под углом 20° | То же | |||||
Критерий подобия сопротивления сдвигу пород зон смещения | |||||||
0,09 | 0,09 | 0,0 | |||||
Выполнение оценки устойчивости согласно первому принципу подобия | Критерий подобия экзогенного изменения заполнителя трещин смещения оползневых блоков | Увеличение | |||||
1,2 | 1,3 | ||||||
Критерий подобия углов падения возможных поверхностей смещения | |||||||
35° | 35° | 0,0 | |||||
Критерий подобия углов падения склонов | Увеличение | ||||||
60 | 65 | ||||||
Критерий подобия возможного гидродинамического давления воды в трещинах отчленения | |||||||
1,3 МПа | 1,3 МПа | 0,0 | |||||
Критерий подобия морфологии поверхности смещений (макрорельефа) | Уменьшение -0,06 | ||||||
5,07 | 5,00 | ||||||
Следовательно, коэффициент устойчивости оползнеопасного склона больше предельного состояния его аналога на 0,19 и равен 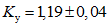 ; 0,4 - ошибка вычислений ; 0,4 - ошибка вычислений |  | ||||||
Прогноз антропогенного изменения устойчивости склона | Изменение критерия подобия крутизны склона при строительстве | Уменьшение -0,15 | |||||
80 | 65 | ||||||
Изменение критерия степени экзогенного изменения пород зон отчленения и смещения | Уменьшение -0,10 | ||||||
1,35 | 1,3 | ||||||
Строительство обусловит изменение устойчивости ниже предельного состояния аналога, что приведет к катастрофическому обрушению блока пород |  | ||||||
4. Следует отметить, что по критериальному уравнению связи рекомендуется определять меру надежности в оценках относительной роли критериев геологического подобия в формировании устойчивости склонов. Прогноз устойчивости склонов и ее изменение рекомендуется выполнять путем сопоставления абсолютных значений критериев геологического подобия. Это сравнение необходимо осуществлять согласно принципам, изложенным в пп. 2.6 и 2.11.
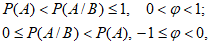




 , (9)
, (9)



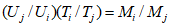

 ;
;  (обозначения здесь и в остальных случаях даны на
(обозначения здесь и в остальных случаях даны на