СПРАВКА
Источник публикации
М.: ЦНИИЭП им. Б.С. Мезенцева, 1989
Примечание к документу
Название документа
"Рекомендации по проектированию деревянных клееных куполов для покрытий залов общественных зданий"
"Рекомендации по проектированию деревянных клееных куполов для покрытий залов общественных зданий"
Содержание
ПО ПРОЕКТИРОВАНИЮ ДЕРЕВЯННЫХ КЛЕЕНЫХ КУПОЛОВ
ДЛЯ ПОКРЫТИЙ ЗАЛОВ ОБЩЕСТВЕННЫХ ЗДАНИЙ
Рекомендации освещают вопросы проектирования полносборных ребристых куполов при многоугольном или круглом плане с несущими конструкциями из клееной древесины. Приводятся технические решения куполов и их монтажных узлов, правила и примеры расчета и конструирования, указания по области применения, примеры расчета некоторых вариантов куполов, а также ориентировочные данные по расходу древесины и стали при разных диаметрах и конструкциях.
Для инженерно-технических работников проектных организаций и студентов строительных ВУЗов.
Рекомендованы к изданию решением научно-технического совета ЦНИИЭП им. Б.С. Мезенцева.
Рекомендации разработали и составили:
д.т.н., проф. В.И. Травуш, к.т.н., ст. научн. сотр. О.М. Жак и С.М. Строганова; научн. сотр. М.В. Корес; при участии научн. сотр. Е.М. Тимонина и инж. Л.А. Карпушиной.
Внедрение пространственных конструкций из клееной древесины в строительство общественных зданий расширит область применения этого эффективного материала. Первым шагом на пути освоения пространственных КДК может стать широкое применение наиболее простых несущих систем - ребристых куполов. Целесообразность применения куполов в покрытиях зальных помещений общественных зданий определяется рядом их преимуществ по сравнению с традиционными решениями:
- высокие архитектурно-художественные и функционально-технологические качества сооружений;
- снижение эксплуатационных расходов за счет оптимального соотношения площадей ограждения и внутреннего объема здания;
- простота в изготовлении, технологичность конструкции ребристых куполов.
Использование полносборных куполов позволит повысить индустриальность возводимых сооружений и сократить сроки их монтажа.
"Рекомендации", посвященные вопросам проектирования полносборных ребристых куполов с несущими элементами из клееной древесины, могут содействовать их распространению. Принципы проектирования несущих и ограждающих конструкций высокой заводской готовности выработаны на основе научно-исследовательских и проектных разработок, проводившихся в ЦНИИЭП им. Б.С. Мезенцева. Предлагаемые конструктивные решения отвечают технологическим требованиям и возможностям существующих предприятий по изготовлению клееных деревянных конструкций.
1.1. Деревянные клееные купола предназначены для покрытий залов общественных зданий - спортивных, зрелищных, универсальных, торговых, выставочных.
1.2. В "Рекомендациях" рассмотрены конструктивные типы ребристых куполов на многоугольных и круглых планах. Они могут применяться в зданиях со стенами из кирпича или каркасных с заполнением эффективными видами каменной кладки, а также навесными или самонесущими панелями.
1.3. Выбор варианта конструкции купола определяется технологическими и архитектурными соображениями, а также возможностями производственной базы.
Технико-экономические показатели различных типов куполов при одинаковых диаметрах отличаются незначительно и не служат решающим критерием при выборе варианта конструкции.
1.4. Все приведенные в "Рекомендациях" типы куполов допускают устройство в вершине купола вентиляционной или осветительной шахты. В шатровых и арочно-вспарушенных куполах возможно освещение через витражи по периметру купола.
1.5. Степень огнестойкости куполов должна соответствовать нормам проектирования различных залов общественных зданий.
1.6. Проектирование деревянных конструкций куполов должно выполняться на основе действующих норм по проектированию деревянных конструкций [1], [2], а также руководящих материалов по изготовлению, отделке, транспортированию и складированию клееных конструкций. Степень огнестойкости куполов должна обеспечиваться в соответствии с нормами [3].
1.7. Проектирование стальных элементов куполов выполняется в соответствии с нормами по проектированию стальных конструкций [4].
2.1. Ребристые купола состоят из прямолинейных или криволинейных ребер, соединенных в вершине непосредственно или через коньковое опорное кольцо, и опирающихся на опорный контур, расположенный на стенах, или фундаменты.
Ребра образуют систему перекрестных арок (или рам), несущих нагрузку от панелей кровли, прогонов или второстепенных арок.
Распор арок передается на опорный контур или непосредственно на фундаменты, а также на коньковое опорное кольцо или на соединение ребер в вершине купола.
Во всех куполах прогоны и второстепенные арки присоединяются к ребрам куполов с помощью стальных карманов разного типа (см. ниже раздел 5). Карманы для присоединения второстепенных арок, располагаемых по оси стен шатровых и арочно-вспарушенных куполов, могут совмещаться с опорными башмаками ребер куполов.
2.2. Конструктивные варианты куполов с прямолинейными ребрами.
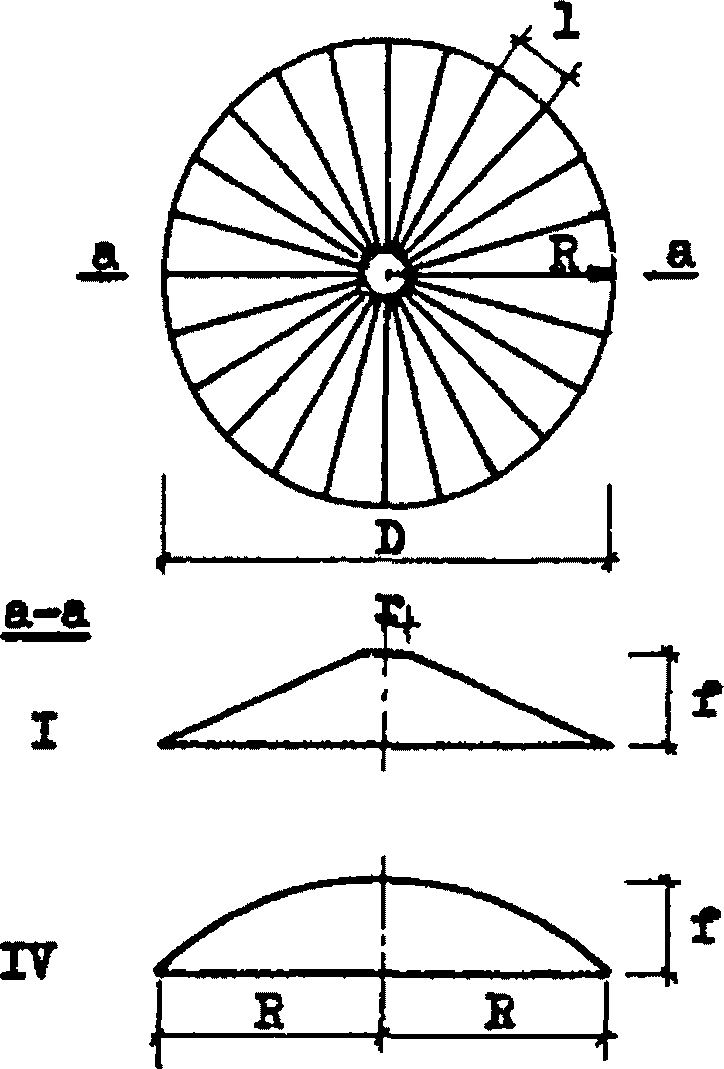
2.2.1. Конический купол (тип I табл. 1 и 2) на круглом (или многоугольном) плане. Утепленные трапециевидные панели покрытия укладываются по радиально расположенным ребрам купола. Опорный контур рекомендуется многоугольным (по числу ребер) для исключения местного изгиба при передаче распоров ребер. Рекомендуемые диаметры - до 60 м при стреле подъема  . Возможны подъемы
. Возможны подъемы  .
.
 . Возможны подъемы
. Возможны подъемы  .
.2.2.2. Пирамидальный купол (тип II табл. 1 и 2) на шестиугольном или восьмиугольном плане образуется шестью или восемью ребрами, к которым присоединяются прогоны, несущие панели покрытия; длина панелей определяет шаг прогонов (обычно - 3 м по скату кровли). Рекомендуемые пролеты (по диагоналям купола) - до 45 м. Рекомендуемая стрела подъема  . Пирамидальный купол может быть образован системой перекрестных гнутоклееных рам.
. Пирамидальный купол может быть образован системой перекрестных гнутоклееных рам.
 . Пирамидальный купол может быть образован системой перекрестных гнутоклееных рам.
. Пирамидальный купол может быть образован системой перекрестных гнутоклееных рам.Таблица 1
I - Конический,  | IV - Сферический,  |
II - Пирамидальный,  | V - Сомкнутый,  |
III - Шатровый,  | VI - Арочно-вспарушенный  |
1 - ребра купола, 2 - прогоны, 3 - опорное коньковое кольцо, 4 - опорный контур, 5 - коньковый прогон, - для варианта III-б, 6 - второстепенные арки | |
Таблица 2
ТИПЫ КУПОЛОВ | ||
 |  |  |
2.2.3. Шатровый купол (тип III табл. 1 и 2). Складчатая форма покрытия допускает два конструктивных варианта:
IIIа - трехшарнирные второстепенные арки устанавливаются на диагональные; по второстепенным аркам укладываются ограждающие панели;
IIIб - вдоль осей стен устанавливаются торцевые трехшарнирные арки, на них и на опорное кольцо укладывается коньковый прогон, а второстепенные трехшарнирные арки заменяются прогонами, несущими панели ограждения.
Рекомендуемые диаметры: при шестиугольном плане - до 45 м, при восьмиугольном - до 60 м.
2.3. Конструктивные варианты куполов с криволинейными ребрами.
2.3.1. Сферический купол (тип IV табл. 1 и 2) отличается от конического (см. п. 2.2.1) тем, что вместо прямолинейных применяются ребра из круговых арок при тех же плане и высоте купола.
2.3.2. Сомкнутый купол на шестиугольном и восьмиугольном плане (тип V табл. 1 и 2) отличается от пирамидального так же, как сферический от конического, т.е. заменой прямолинейных ребер арочными. Наибольший диаметр при восьмиугольном плане - 60 м.
2.3.3. Арочно-вспарушенный купол (тип VI табл. 1 и 2) на шестиугольном и восьмиугольном плане образуется шестью или восемью криволинейными ребрами, на которые опираются двухшарнирные второстепенные круговые арки, несущие панели покрытия. Высота подъема первой второстепенной арки, устанавливаемой по оси стен, назначается примерно равной высоте подъема ребер купола.
Второстепенные арки по верхней грани описаны одним радиусом и образуют горизонтальные цилиндрические поверхности, пересекающиеся на ребрах купола эллиптического очертания.
Шестиугольные купола этого типа предпочтительнее восьмиугольных из-за простоты сопряжений. Купола на восьмиугольном плане рекомендуются при диаметрах более 45 м.
2.4. Типы куполов II, III, V, VI могут применяться и на квадратном плане. При этом арочно-вспарушенный купол превращается в крестовый свод. Примером шатрового купола на квадратном плане может служить конструкция покрытия рынка в Ржеве [5].
3.1. Постоянные нагрузки - вес несущих и ограждающих конструкций купола, а также вес стационарного подвесного оборудования, определяемый техническим заданием на проектирование. Коэффициенты надежности и коэффициенты перегрузки принимаются в соответствии с [6].
3.2. Временные нагрузки - снеговая, для которой рассматриваются два случая расположения:
- равномерно распределенная по всей площади покрытия;
- односторонняя, распределенная на половине поверхности покрытия.
3.3. Нормативный вес снегового покрова S0 принимается по [6].
Равномерно распределенная снеговая нагрузка на площади покрытия сферических, конических, пирамидальных и сомкнутых куполов согласно [7] определяется умножением расчетной снеговой нагрузки на коэффициент  , равный для D <= 60 м
, равный для D <= 60 м
 (3.1)
(3.1)где v - средняя многолетняя скорость ветра за зимний период [6]. Для I и II снегового районов v = 0.
При диаметрах перечисленных куполов D >= 100 м, а также для любых диаметров шатровых и арочно-вспарушенных типов куполов  . При промежуточных значениях диаметров
. При промежуточных значениях диаметров  определяется по интерполяции.
определяется по интерполяции.
Расчетная снеговая равномерно распределенная нагрузка на площади покрытия купола
 (3.2)
(3.2)где 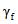 - коэффициент надежности, определяемый по [6].
- коэффициент надежности, определяемый по [6].
3.4. Для сферических, конических, пирамидальных и сомкнутых куполов интенсивность односторонней снеговой нагрузки, рассматриваемой на одной из половин покрытия, определяется, согласно [7], введением коэффициента
 (3.3)
(3.3)где  - характеристика коэффициента перехода в точке полукруга с максимальным значением снеговой нагрузки, определяемая по графику на рис. 1;
- характеристика коэффициента перехода в точке полукруга с максимальным значением снеговой нагрузки, определяемая по графику на рис. 1;
m = 1 - для конических и пирамидальных куполов;
m = 2 - для сферических и сомкнутых куполов.
Для шатрового и арочно-вспарушенного куполов односторонняя снеговая нагрузка принимается равномерно-распределенной с коэффициентом  .
.
3.5. Расчетная односторонняя снеговая нагрузка
 (3.4)
(3.4)
1 - для сферического и сомкнутого куполов
(в зависимости от f/D)
2 - для конического и пирамидального куполов
(в зависимости от угла крутизны - 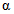 )
)
3.6. Схемы загружения ребер рассматриваемых типов куполов постоянной и снеговой нагрузками показаны на рисунках 2 - 6.
При загружении конических и сферических куполов постоянной и равномерно распределенной снеговой нагрузками соответствующие расчетные погонные нагрузки на ребра (рис. 2) описываются зависимостями
где q и qсн - расчетные постоянная и снеговая равномерно-распределенные на площади купола нагрузки;
l - шаг ребер.
При расчете ребер на одностороннюю снеговую нагрузку:
при этом принимается

 и
иn = 2 для конического купола и
n = 3 для сферического.
Собственный вес ребер учитывается погонной нагрузкой gсв, а постоянная нагрузка от вентиляционных шахт - сосредоточенными силами Pш.
3.7. Расчетные нагрузки на ребра пирамидальных или сомкнутых куполов могут приниматься либо по формулам (3.5) и (3.6) (рис. 2), либо в виде сосредоточенных усилий от прогонов, приложенных в местах примыкания прогонов к ребрам (рис. 3). Давление прогона можно определить по приближенной формуле
 (3.7)
(3.7)
и сферического куполов

и сомкнутого куполов

(конструкция с коньковым прогоном)

(конструкция с второстепенными арками)

Варианты 

здесь:  - для постоянной нагрузки;
- для постоянной нагрузки;
 - для полной снеговой нагрузки;
- для полной снеговой нагрузки; - односторонней снеговой нагрузки.
- односторонней снеговой нагрузки.Для постоянной и полной снеговой нагрузок n = 1, для односторонней нагрузки на пирамидальном куполе n = 2, на сомкнутом n = 3.
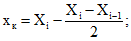 (3.8)
(3.8) (3.9)
(3.9)Xi, Xi-1, Xi+1 - абсциссы места примыкания рассматриваемого прогона, предыдущего и следующего соответственно.
Учитывая большой шаг ребер в пирамидальном и сомкнутом вариантах куполов, при расчете их на одностороннюю нагрузку следует заменить величину  в формуле (3.6) на усредненные коэффициенты 0,85 - для восьмиугольного плана, и 0,75 - для шестиугольного.
в формуле (3.6) на усредненные коэффициенты 0,85 - для восьмиугольного плана, и 0,75 - для шестиугольного.
3.8. Ребра шатровых или арочно-вспарушенных куполов рассчитывают на вертикальные силы и распоры, передаваемые на них треугольными или круговыми арками от действия постоянной и снеговых нагрузок (рис. 5 и 6).
3.9. Ветровая нагрузка при расчете несущих конструкций рассматриваемых типов куполов обычно не учитывается. Ее следует учитывать при расчете витражей, конструкций вентиляционных или осветительных шахт, расположенных в вершинах куполов.
Если шатровый купол образуется с помощью конькового прогона, то давление от него учитывается силами Pп и Pсн,п (см. схему на рис. 4).
4.1. Каждая пара перекрестных ребер может рассматриваться как трех- или двухшарнирная арка, передающая распор на опорный контур и опорное коньковое кольцо. Двухшарнирные арки со стрелой подъема  допускается рассчитывать как трехшарнирные.
допускается рассчитывать как трехшарнирные.
4.2. Опорный контур купола рассчитывается на растяжение от максимальных распоров арок, загруженных постоянной и полной снеговой нагрузкой. Усилия в круглом опорном контуре
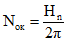 (4.1)
(4.1)где H - распоры арок от постоянной и полной снеговой нагрузок;
n - число ребер купола.
Усилие в многоугольном опорном контуре:
 (4.2)
(4.2)4.3. При одностороннем загружении куполов в жестком опорном контуре возникают изгибающие моменты и нормальные силы, приведенные в таблице 3. Исключение - шатровый и арочно-вспарушенный типы куполов, в опорном контуре которых односторонняя снеговая нагрузка вызывает только нормальные силы.
Эти изгибающие моменты, как правило, не могут быть восприняты сечением опорного контура, рассчитываемого обычно только на растяжение от максимальных распоров. Кроме того, разнозначные изгибающие моменты вызывают значительные горизонтальные деформации, которые не могут быть допущены. Поэтому опорный контур целесообразно рассматривать как шарнирный многоугольник с подвижными опорами под пятой каждого ребра, допускающими перемещения по направлению радиуса и не допускающими тангенциальных перемещений. Число шарниров соответствует числу углов контура. Нагрузка от распоров, возникающая при одностороннем загружении купола снегом, приложенная к каждому шарниру, раскладывается по направлению примыкающих участков контура; эти усилия, действующие вдоль участков стен, должны быть на них переданы и учтены при их расчете и конструировании [8].
4.4. Опорное коньковое кольцо должно быть жестким, круглым, шестиугольным или восьмиугольным в плане. Возможно применение взамен шестиугольного или восьмиугольного кольца - крестовин.
4.5. При шарнирном опирании ребер купола на коньковое опорное кольцо для обеспечения неизменяемости купола устраиваются крестовые связи жесткости в плоскости покрытия, что трудоемко [9]. Возможно присоединение полуарок к коньковому опорному кольцу жестко, на сварке, при помощи накладок (см. ниже п. 5.5 и рис. 11) [14]. При этом арки превращаются в двухшарнирные, ребра которых в ключе соединены стальным кольцом, воспринимающим поперечные силы и изгибающие моменты от кососимметричной составляющей односторонней снеговой нагрузки.
4.6. Изгибающие и крутящие моменты, действующие в соответствии с 4.5 перпендикулярно плоскости конькового кольца, для разных в плане куполов приведены в таблице 4.
4.7. Изгибающие моменты от распоров при односторонней снеговой нагрузке, действующие в плоскости конькового кольца, определяются по формулам таблицы 3, в которых вместо R принимается радиус кольца rк, для круглого кольца T0 заменяется распором ребер, отнесенным к 1 м периметра кольца.
4.8. Кольцо должно быть рассчитано на совместное действие указанных выше моментов и нормальной силы от постоянной и односторонней снеговой нагрузок.
4.9. Элементы крестовин, заменяющих кольцо, рассчитываются как продолжение ребер купола; в месте сопряжения их с ребрами действует изгибающий момент от кососимметричной составляющей односторонней снеговой нагрузки; кроме того они воспринимают максимальный распор арки от постоянной и полной снеговой нагрузки.
Тип купола | Схема загружения | Эпюра изгибающих моментов | Изгибающие моменты, Mиз Нормальные силы, N | ||
сферический, конический |  |  | - |  | |
(n = 2) | Mиз = -0,149T0R2 | - | Mиз = 0,137T0R2 | ||
(n = 3) | N = 0,785T0R | N = 0,5T0R | |||
Пирамидальный, сомкнутый |  |  |  |  | |
Mиз = -0,289HR | Mиз = 0,145HR | Mиз = 0,145HR | |||
N = 0,75H | N = 0,5H | ||||
шатровый, арочно-вспарушенный |  | - |  |  | |
Mиз = 0 | Mиз = 0 | Mиз = 0 | |||
N = H | N = H | N = H | |||
пирамидальный, сомкнутый |  |  |  |  | |
Mиз = -0,275HR | Mиз = 0,025HR | Mиз = 0,225HR | |||
N = 0,924H | N = 0,653H | ||||
шатровый, арочно-вспарушенный |  | - |  |  | |
Mиз = 0 | Mиз = 0 | Mиз = 0 | |||
N = 1,3H | N = 1,3H | N = 1,3H | |||
Тип купола | Схема загружения | Эпюра расчетных моментов | Изгибающие моменты Mи | Крутящие моменты Mкр |
сферический, конический |  |  |  |  |
 |  | |||
 |  | |||
пирамидальный, сомкнутый |  |  |  | |
 |  | |||
 | ||||
шатровый, арочно-вспарушенный |  |  |  |  |
 |  | |||
 | ||||
пирамидальный, сомкнутый |  |  |  |  |
 |  | |||
 | ||||
e = 1,2 | ||||
шатровый, арочно-вспарушенный |  |  |  |  |
 |  | |||
 |  | |||
 | ||||
 |

1кр - момент инерции при кручении
1х - момент инерции при изгибе
5.1. Ребра купола рассчитывают в соответствии с [1, 2] на сжатие с изгибом; принимается, что верхняя кромка ребер раскреплена прогонами или второстепенными арками и панелями покрытия. Сечения ребер принимаются прямоугольными; исходя из технологии действующих заводов клееных деревянных конструкций, высоту сечения следует назначать не более 1,65 м, а ширину - не более 0,20 м. В случае необходимости большей ширины, сечение устраивается из двух ветвей, соединенных болтами, с учетом п. 4.6 норм [1].
5.2. При проектировании опорного контура следует учитывать его упругие деформации от растягивающих усилий
 (5.1)
(5.1)где  - растягивающие напряжения в арматуре железобетонного контура или в стальном опорном контуре;
- растягивающие напряжения в арматуре железобетонного контура или в стальном опорном контуре;
l0 - сторона многоугольного контура или радиус круглого контура;
Ea - модуль упругости металла контура.
Опорный контур купола может быть из железобетона с непосредственным опиранием на него башмаков ребер купола (рис. 7).
Чтобы не передавать деформации опорного контура на стены, его выполняют из предварительно-напряженного железобетона или устраивают опирание ребер купола с помощью подвижных опор (рис. 9 и 10). В этом случае применяется металлический опорный контур.
5.3.1. Опирание ребер купола на железобетонный опорный контур (рис. 7).
Распор и вертикальная составляющая опорной реакции ребер передаются на опорный контур через стальной башмак, присоединяемый к нему анкерными болтами.

1 - ребро купола
2 - опорный башмак
3 - опорный контур
4 - анкерные болты

1 - торцевая пластина
2 - боковая пластина
3 - опорная пластина
Башмак ( на рис. 7) состоит из торцевого (
на рис. 7) состоит из торцевого ( на рис. 8) и двух боковых вертикальных листов (
на рис. 8) и двух боковых вертикальных листов ( на рис. 8), приваренных к горизонтальному листу (
на рис. 8), приваренных к горизонтальному листу ( на рис. 8).
на рис. 8).
Размеры башмака назначаются такими, чтобы напряжения сжатия в опорных плоскостях ребра не превышали соответствующих расчетных величин:
 (5.2)
(5.2) (5.3)
(5.3)где:  и
и  - напряжения в древесине под торцевой
- напряжения в древесине под торцевой  и под опорной горизонтальной
и под опорной горизонтальной  пластинами башмака;
пластинами башмака;
H, A - максимальные значения опорных реакций;
b - ширина сечения ребра;
Полученные значения уточняются исходя из конструктивных соображений: высота башмака не должна быть слишком малой, чтобы вертикальная пластина не была толще 20 - 25 мм, и в то же время не слишком большой, чтобы опрокидывающий момент от распора не потребовал применения очень мощных анкерных болтов.
Расчет вертикальной торцевой пластины "1".
Пластина рассчитывается как опертая по трем сторонам 10 на воздействие контактных напряжений  . Толщина пластины определяется с учетом развития в ней пластических деформаций по формуле
. Толщина пластины определяется с учетом развития в ней пластических деформаций по формуле
где Mпл - расчетный момент в пластине "1";
Rу - расчетное сопротивление стали по [4].
Расчет боковых пластин  и их присоединения к опорной пластине
и их присоединения к опорной пластине  .
.
Распор вызывает в пластинах  (см. рис. 8) сдвиг и изгибающий момент
(см. рис. 8) сдвиг и изгибающий момент
 (5.5)
(5.5)Напряжения в пластинах  :
:
 (5.6)
(5.6) (5.7)
(5.7)здесь:
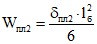 и
и  (5.8)
(5.8)- момент сопротивления и площадь каждой пластины;
В данном случае необходима проверка приведенных напряжений:
 (5.9)
(5.9)На те же воздействия проверяется сварной шов, присоединяющий боковую пластину к горизонтальной.
Расчет анкерных болтов и опорной пластины башмака.
Нормальные напряжения в бетоне опорного контура под опорной пластиной башмака не должны превышать расчетного сопротивления смятию:
 (5.10)
(5.10)где  - опрокидывающий момент;
- опрокидывающий момент;
 - опрокидывающий момент;
- опрокидывающий момент;A - вертикальная опорная реакция арки;
 - момент сопротивления и площадь пластины
- момент сопротивления и площадь пластины
Bпл3 - ширина пластины  ;
;
для рассматриваемых случаев  .
.
 .
.Схема расчетных напряжений и усилий приведена на рис. 8. В соответствии с [12] усилие, действующее в анкерных болтах:
 (5.11)
(5.11)где y - расстояние от оси анкерных болтов до центра тяжести эпюры сжимающих напряжений в бетоне.
 - расстояние от линии действия реакции A до той же точки.
- расстояние от линии действия реакции A до той же точки.На эту силу должны быть подобраны растянутые анкеры крайнего ряда, рассчитываемые по ослабленному нарезкой сечению. Требуемая площадь сечения анкеров определяется по расчету на срез силой H (площадь сечения растянутых анкеров крайнего ряда входит в общую площадь среза).
Нижний лист башмака должен быть рассчитан на изгиб от воздействия силы Z на участке l-l0, принимая условно равномерное распределение напряжения по ширине сечения. На остальных участках внешней части листа, закрепленных анкерными болтами, а также под пятой ребра, проверка напряжений не требуется.

1 - ребро купола
2 - башмак
3 - катки
4 - опорный контур
5 - обвязка
6 - подкладочный лист

1 - ребро купола
2 - опорный башмак
3 - катки
4 - опорный контур
5 - железобетонная обвязка стены
6 - сварной шов
Подвижное опирание ребер купола устраивается с помощью катков, помещаемых под горизонтальную пластину башмака. Катки передают опорную реакцию на стены. Распор купола воспринимается стальным растянутым опорным контуром, приваренным к башмакам. Возможно устройство подвижной опоры без катков, в которой скольжение обеспечивается графитово-вазелиновой смазкой.
Расчет башмака:
- вертикальная торцевая пластина и боковые вертикальные пластины рассчитываются так же, как в первом варианте, на воздействие распора H;
- горизонтальная пластина рассчитывается на совместное действие изгибающего момента от вертикального давления ребра и растяжения усилием в опорном контуре купола Nок;
- подбирается количество, шаг и сечение катков исходя из их работы на сжатие; рекомендуется применение двух катков; расстояние между катками lк (рис. 9 и 10) определяется из расчета узла на опрокидывание:
 (5.12)
(5.12)- следует подобрать сечение опорного контура и рассчитать на изгиб пластину, через которую передается давление катков на стену (или каркас).
5.4. В случаях, когда конец ребра не в состоянии воспринять поперечную силу на опоре арки (что иногда наблюдается в ребрах эллиптических арок большого пролета), конец ребра заключается в стальную обойму, высота которой доводится до сечения, в котором древесина воспринимает поперечную силу. Схема такого башмака показана на рис. 10.
Для арочно-вспарушенных куполов при опирании ребер на катки нижний лист башмака работает только на растяжение усилием в опорном контуре.
5.5. При шарнирном присоединении ребер купола к кольцу устраивается система связей в виде ферм, располагаемых в плоскостях скатов  . При жестком присоединении ребер купола к кольцу (п. 4.5) одним из конструктивных вариантов может служить устройство на концах ребер стального замкнутого оголовника, который жестко присоединяется к кольцу с помощью горизонтальной накладки
. При жестком присоединении ребер купола к кольцу (п. 4.5) одним из конструктивных вариантов может служить устройство на концах ребер стального замкнутого оголовника, который жестко присоединяется к кольцу с помощью горизонтальной накладки 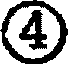 и двух вертикальных косынок
и двух вертикальных косынок  . Косынки позволяют учесть возможные пики напряжений в горизонтальных швах, присоединяющих накладки к оголовнику, и обеспечивают передачу поперечной силы примерно по вертикальной оси сечения кольца.
. Косынки позволяют учесть возможные пики напряжений в горизонтальных швах, присоединяющих накладки к оголовнику, и обеспечивают передачу поперечной силы примерно по вертикальной оси сечения кольца.
Расчет деталей  ,
,  .
.
Соединение оголовника и кольца должно воспринимать поперечную силу от односторонней снеговой нагрузки Qa, вызываемый ею изгибающий момент Ma, распор от постоянной и односторонней снеговой нагрузки  (рис. 11).
(рис. 11).
 (5.13)
(5.13)где rк - радиус кольца;
Суммарные горизонтальные усилия в месте присоединения накладок
 (5.14)
(5.14)где hк - высота сечения кольца;
На эти усилия должны быть рассчитаны сварные швы, присоединяющие оголовник к опорному коньковому кольцу, и сам оголовник.
Сварные швы 1, на рис. 11, присоединяющие горизонтальные накладки к кольцу, рассчитываются на полную силу N1.

1 - ребро купола, 2 - оголовник, 3 - коньковое кольцо,
4 - горизонтальная накладка, 5 - вертикальная косынка
с ребром купола
Сварные швы 2, присоединяющие горизонтальные накладки к оголовнику - на 70% N1, горизонтальные швы 3, присоединяющие косынки к горизонтальным накладкам - на 30% силы N1 (срез) и на силу Qa (сжатие или отрыв), вертикальные швы 4, присоединяющие косынки к оголовнику - на 30% силы N1 (сжатие или отрыв) и силу Qa (срез).
Расчет оголовника.
Если 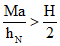 , оголовник рассчитывается как условная балка с одним защемленным и одним шарнирно опертым концом, имеющая сечение в виде швеллера из торцевой и двух боковых пластин. Расчетная схема приведена на рис. 12.
, оголовник рассчитывается как условная балка с одним защемленным и одним шарнирно опертым концом, имеющая сечение в виде швеллера из торцевой и двух боковых пластин. Расчетная схема приведена на рис. 12.
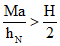 , оголовник рассчитывается как условная балка с одним защемленным и одним шарнирно опертым концом, имеющая сечение в виде швеллера из торцевой и двух боковых пластин. Расчетная схема приведена на рис. 12.
, оголовник рассчитывается как условная балка с одним защемленным и одним шарнирно опертым концом, имеющая сечение в виде швеллера из торцевой и двух боковых пластин. Расчетная схема приведена на рис. 12.
Рис. 12. Расчетная схема оголовника
Опорные реакции и момент в заделке для такой балки:
 (5.15)
(5.15) (5.16)
(5.16) (5.17)
(5.17)где 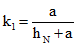 ;
; 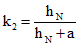 .
.
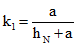 ;
; 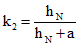 .
.Крепление оголовника к ребру должно быть рассчитано на действие реакции условной балки Б. В зависимости от знака и величины этой реакции оголовник крепится к ребру шурупами (если отрыва не возникает, их ставят конструктивно) или на вклеенных штырях, если Б велико и для размещения необходимого количества шурупов требуется увеличение размеров оголовника. Крепление на вклеенных штырях обеспечит не только требуемую несущую способность, но и значительно снизит податливость соединения оголовника с ребром купола.
Торцевая пластина оголовника рассчитывается на воздействие наибольшего из сжимающих напряжений в древесине ребра под оголовником:
 или
или  (5.18)
(5.18)здесь Fр = b x h; Wр = bh2/6
h, b - высота и ширина ребра под оголовником
H - распор арки от постоянной и полной снеговой нагрузок на купол
5.6. Опорное коньковое кольцо при шестиугольном, восьмиугольном и круглом плане, которое работает на косой изгиб со сжатием (см. 4.8), рекомендуется выполнять прямоугольного сечения, полым, сваренным из полосовой или листовой стали.
5.7. Прогоны применяются дощато-клееные прямоугольного сечения разной высоты в пределах одного купола (в зависимости от пролета) шириной 14 - 16,5 см. Они располагаются вертикально и имеют верхнюю грань горизонтальную в шатровых куполах, скошенную по скату в пирамидальных и двускатную с разными скосами в сомкнутых. Прогоны рассчитываются на нагрузку от панелей покрытия, собственный вес которых определяется с учетом их фактических наклонов на вес подвесного оборудования, а также на снеговую нагрузку.
5.8. Прогоны присоединяются к ребрам купола с помощью стальных карманов (рис. 13).

Прогоны укладываются на пластины  , приваренные к пластинам
, приваренные к пластинам  и
и  ; через последние опорные реакции прогонов передаются на пластины
; через последние опорные реакции прогонов передаются на пластины  , уложенные по верху ребер купола.
, уложенные по верху ребер купола.
Пластина 1. Минимальная площадь пластины определяется исходя из работы на смятие поперек волокон опирающихся на них прогонов:
 (5.19)
(5.19)где Ai - опорная реакция одного прогона <*>.
--------------------------------
<*> Для прогонов шатрового купола пластина  по форме и расчету аналогична пластине
по форме и расчету аналогична пластине  кармана для второстепенных арок (см. ниже рис. 15).
кармана для второстепенных арок (см. ниже рис. 15).
Пластина опирается по трем сторонам, она имеет в плане вид параллелограмма, который заменяется прямоугольником со сторонами lк и bп. Ширина прогона, обычно, задана, поэтому длина lк = Fпл1/bп. Распределение давления от прогона принимаем равномерным
 (5.20)
(5.20)Изгибающие моменты определяются как для плит, опертых по трем сторонам и со свободной четвертой.

1 - коньковый прогон, 2 - главная арка,
3 - опорное коньковое кольцо, 4 - второстепенная
торцовая арка, 5 - оси прогонов, 6 - стенка
вентиляционной шахты
При определении толщины пластины учитывается развитие пластических деформаций - см. формулу (5.4).
Сечения пластин  и
и  назначаются конструктивно.
назначаются конструктивно.
Пластина 4. Минимальные размеры пластины в плане назначаются исходя из работы древесины на смятие поперек волокон под влиянием составляющей опорной реакции прогона, нормальной к поверхности ребра купола (рис. 13).
 (5.21)
(5.21)где  - угол наклона касательной к верхней грани ребра
- угол наклона касательной к верхней грани ребра
a - размер пластины вдоль ребра
b - ширина сечения ребра
Распределение напряжений под пластиной принимается в виде двух треугольников (рис. 13) с ординатой Pсм <= 1,5Rсм 90.
Рассчитывается пластина как простая балка (т.к. пластины  не могут обеспечить защемление пластины
не могут обеспечить защемление пластины  ). Изгибающий момент в такой балке
). Изгибающий момент в такой балке
 (5.22)
(5.22)Толщина пластина определяется с учетом развития пластических деформаций.
Все пластины соединяются сварными швами, воспринимающими на срез опорную реакцию А.
Шурупы 5 - с потайной головкой ставятся конструктивно.
Шурупы 6 - воспринимают скатную составляющую опорной реакции прогона, которая равна 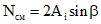 .
.
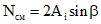 .
.После расстановки шурупов уточняется длина пластины "а" и ее толщина.
В тех случаях, когда скатная составляющая велика и по расчету требуется такое число шурупов  , что это влечет за собой увеличение размеров пластины
, что это влечет за собой увеличение размеров пластины  , возможно применение вместо шурупов вклеенных стержней.
, возможно применение вместо шурупов вклеенных стержней.
5.9. Коньковый прогон шатрового купола типа IIIб одним концом опирается на специальную балку "в", параллельную стороне конькового опорного кольца, а другим - на второстепенную торцевую арку, расположенную по оси стены (рис. 14). Балка "в" опирается на стальные карманы, приваренные к оголовнику ребер купола.
Сопряжение конькового прогона и торцевой арки (узел А рис. 14) осуществляется с помощью специальной детали M-I, показанной на том же рисунке.
5.10. Второстепенные арки арочно-вспарушенных куполов двухшарнирные, шириной 14 - 16,5 см, рассчитываются как трехшарнирные арки на вертикальные нагрузки, и как двухшарнирные - на неуравновешенные распоры при односторонней снеговой нагрузке, распределенные поровну между всеми арками.
5.11. Второстепенные арки арочно-вспарушенных и шатровых типа IIIа куполов опираются на диагональные ребра с помощью стальных "карманов", показанных на рис. 15.

На карманы действуют вертикальные опорные реакции второстепенных арок Aвi и горизонтальные составляющие их распоров, действующие в плоскости ребер
 (5.23)
(5.23)где Hвi - распор i-той второстепенной арки при загружении ее снеговой нагрузкой на всем пролете
n - число ребер купола.
Вертикальная опорная реакция А приложена к пластине  . Усилия
. Усилия  должны быть переданы на шурупы, присоединяющие к ребру купола пластину
должны быть переданы на шурупы, присоединяющие к ребру купола пластину  . Нагрузка на нее передается через пластину
. Нагрузка на нее передается через пластину  , на которую действует усилие
, на которую действует усилие  (рис. 15).
(рис. 15).
 (рис. 15).
(рис. 15).Трапециевидная форма пластины  приводится к прямоугольной со сторонами
приводится к прямоугольной со сторонами  и bп, нагруженной равномерно-распределенной нагрузкой.
и bп, нагруженной равномерно-распределенной нагрузкой.
Пластина  работает как консоль переменной высоты, приваренная к пластине
работает как консоль переменной высоты, приваренная к пластине  . Определение толщины пластины
. Определение толщины пластины  производится без учета развития пластических деформаций. Ее боковой вид имеет треугольное очертание.
производится без учета развития пластических деформаций. Ее боковой вид имеет треугольное очертание.
Пластина  рассчитывается так же, как в кармане для опирания прогонов. Шурупы
рассчитывается так же, как в кармане для опирания прогонов. Шурупы  рассчитываются на усилие
рассчитываются на усилие  . Шурупы
. Шурупы  рассчитываются так же, как в кармане для прогонов.
рассчитываются так же, как в кармане для прогонов.
6.1. Панели покрытия рассматриваемых куполов должны иметь каркасную конструкцию с жесткими ребрами из древесины. Во всех куполах могут быть применены известные конструкции вентилируемых панелей. Когда почему-нибудь невозможно обеспечить надежное вентилирование покрытия, допускается применение невентилируемых панелей.
6.2. Конструкция невентилируемых панелей.
ИС МЕГАНОРМ: примечание. Взамен ГОСТ 10354-73 Постановлением Госстандарта СССР от 02.06.1982 N 2253 с 1 июля 1983 года введен в действие ГОСТ 10354-82. |
Панели состоят из антисептированных продольных и поперечных ребер, поверх которых на шурупах с потайной головкой укреплена асбестоцементная обшивка толщиной 10 мм. По контуру обшивки укрепляется антисептированная рамка из досок высотой, равной толщине утеплителя. Рамка и обшивка оклеиваются пароизоляцией из лавсановой пленки ПЭТФ толщиной 50 мк на битумно-кукерсольной мастике (ГОСТ 10354-73).
Пространство между рамками заполняется минераловатными плитами повышенной жесткости (или другим эффективным утеплителем), которые закрепляются упаковочной лентой и оклеиваются на заводе одним слоем рубероида.
Для зданий, требующих акустического благоустройства, по низу ребер может быть устроена акустическая подшивка. Панели без акустической подшивки могут быть с декоративной подшивкой или с открытыми ребрами (на рис. 16 показана конструкция панели с вариантами подшивки).

1 - 1 слой рубероида
2 - минераловатные плиты повышенной жесткости
3 - пароизоляция
4 - асбестоцементный лист, 

5 - минераловатные маты,
6 - перфорированная плитка ДВП, 

7 - декоративная подшивка
8 - антисептированный каркас
9 - антисептированная рамка
а) - торец панели для опирания на криволинейную арку
б) - торец панели для опирания на прогон
невентилируемой панели покрытия:
I - с акустической подшивкой,
II - с декоративной подшивкой, III - без подшивки
По панелям можно устраивать кровлю рулонную или из листовых материалов (алюминия, стали); в последнем случае обрешетка прибивается к рамкам, обрамляющим утеплитель.
6.3. Принцип раскладки панелей в конических куполах (тип I табл. 1 и 2) показан на рис. 17. Панели, как правило, принимаются с номинальной шириной 1,5 м, трапециевидные в плане с параллельными продольными ребрами переменной длины. Покрытие разбивается на зоны, в пределах которых высота ребер принимается одинаковой; в зависимости от нагрузки и пролета ребра могут быть из целых досок (при высоте ребра до 17 см) или клееные из брусков.

I - конический купол, IV - сферический купол.
Раскладка панелей при 24-угольном плане,
п-1 - пn - марки панелей; число зон показано условно
В местах сопряжения панелей с разной высотой ребер необходимо сохранять кровлю без уступов, образуя последние на потолке путем подрезки на опоре крайних ребер более высоких панелей (рис. 18).

Каркас панели и сечения по покрытию
6.4. Принцип устройства покрытия в сферических куполах (тип IV табл. 1 и 2) такой же, как и в конических, но для определения длины ребер панелей необходимо построить развертки граней сферического купола по верху ребер в соответствии с приведенными ниже правилами (см. ниже п. 6.8).
6.5. Покрытие по прогонам или второстепенным аркам, располагаемым с шагом по скату, равным номинальной длине панелей, выполняется из следующих панелей:
а) прямоугольные рядовые с номинальной шириной, как правило, не более 1,50 м (наибольшее количество в покрытии);
б) то же - карнизные;
в) трапециевидные (правые и левые) такой же длины, что и прямоугольные, располагаемые в местах примыкания покрытия к ребрам купола;
г) то же - карнизные (рис. 19).

lп - длина панели, bп - ширина панели,
bпк - ширина карнизной трапециевидной панели

(а - рядовая, б - карнизная, в - трапециевидная,
г - карнизная трапециевидная, д - трапециевидная
для арочно-вспарушенного купола)
Желательно, чтобы ширина трапециевидных панелей не превышала 3 м; при большей ширине они должны выполняться из двух частей (см. ниже рис. 27).
Номинальную ширину панели удобно назначить равной половине разности длин соседних прогонов, или по формуле
где  - угол между ребрами, определяемый на развертке.
- угол между ребрами, определяемый на развертке.
Покрытие собирается из одного типоразмера прямоугольных панелей, одного типоразмера трапециевидных панелей (правых и левых), а также (при необходимости) индивидуальных трапециевидных панелей у опорного конькового кольца (правых и левых) - длиной, зависящей от диаметра кольца.
При устройстве стен из легких панелей, покрытие дополняется карнизными панелями, т.е. удлинением панелей первого ряда на величину вылета карниза.
Развертка покрытия и раскладка панелей восьмиугольного купола показана на рис. 20.

1 - панель рядовая, 2п/л - панель трапециевидная,
3п/л - панель коньковая
при восьмиугольном плане
Если необходимо, чтобы ширина прямоугольной панели купола на шестиугольном плане не превышала 1,5 м, ее ширина назначается равной одной трети разности длин соседних прогонов. Тогда ряды с четным и нечетным количеством прямоугольных панелей чередуются, т.е. через ряд смещаются продольные стыки панелей на половину их ширины.
6.7. Сомкнутый купол (тип V табл. 1 и 2). Ширина прямоугольных панелей определяется так же, как в пирамидальном куполе. Но так как в рассматриваемом куполе разница длин соседних прогонов - величина не постоянная (см. ниже п. 6.8), ширина трапециевидных панелей в каждом ряду не одинакова, а в формуле (6.1) желательно применять значение угла вблизи вершины купола.
Развертка поверхности купола производится между вертикальными гранями ребер (рис. 21). Из развертки поверхности определяются места примыкания прогонов к ребрам купола, их длина, а также углы наклона скосов верхних двускатных граней прогонов (см. ниже рис. 29 и 30).

1 - панель рядовая, 2л/п - 7л/п - панели трапециевидные,
8л/п - панель коньковая (число трапециевидных панелей
показано условно)
при восьмиугольном плане
Варианты примыкания невентилируемых панелей к ребрам пирамидального и сомкнутого куполов даны на рис. 22 сеч. 1-1, где видно, что панели выступают над верхней гранью ребер. Это позволяет перекрыть возможные неточности изготовления и монтажа, облегчает устройство кровли по ребрам пирамидальной поверхности купола. Здесь также показана заделка продольного шва между панелями (для всех типов куполов), а также вариант устройства карниза при кирпичных стенах (сеч. 2-2).

Сечения по покрытию
Для построения разверток сферических и сомкнутых куполов, определения габаритных размеров панелей, а для сомкнутых куполов также и длин прогонов, задаемся следующими исходными данными (рис. 23 а):
D - осевой диаметр купола в плане, м;
f - стрела подъема ребер купола, м;
n - число ребер купола;
t - ширина панели или шаг прогонов, м;
b - ширина ребра купола, м;
h - высота ребра купола, м;
r - радиус вентиляционной шахты, м; обычно совпадает с радиусом кольца;
k - целочисленный параметр, превышающий требуемое количество панелей или прогонов сектора купола (рис. 23 б).
Радиус кривизны оси ребер купола
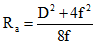 (6.2)
(6.2)Переход от осевых размеров к конструктивным:

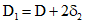
 (6.3)
(6.3)Для сферического купола  , поэтому f1, D1, R1 являются стрелой подъема, диаметром в плане и радиусом кривизны поверхности, описывающей верхние грани ребер.
, поэтому f1, D1, R1 являются стрелой подъема, диаметром в плане и радиусом кривизны поверхности, описывающей верхние грани ребер.
 , поэтому f1, D1, R1 являются стрелой подъема, диаметром в плане и радиусом кривизны поверхности, описывающей верхние грани ребер.
, поэтому f1, D1, R1 являются стрелой подъема, диаметром в плане и радиусом кривизны поверхности, описывающей верхние грани ребер.Рассмотрим сектор купола, образованный внутренними гранями смежных ребер (рис. 23 б) и его план (рис. 23 в). Начало координат поместим в точку пересечения оси верхней грани прогона с вертикальной плоскостью боковой грани ребра, а для сферического купола - в точку пересечения плоскости ребра купола с ребром первой панели.

и сомкнутого куполов
Длины прогонов или ребер панелей определяются по формуле:
где: i = 1, 2, ..., m, ..., k
m - требуемое количество прогонов или панелей, которое определяется в ходе расчета;
 - угол между смежными ребрами в плане;
- угол между смежными ребрами в плане;где:  ;
;  ;
;  .
.
 ;
;  ;
;  .
.Определив для i-ой панели искомый угол  , подставляем его в выражение (6.4), с учетом (6.5), после чего переходим к следующей панели.
, подставляем его в выражение (6.4), с учетом (6.5), после чего переходим к следующей панели.
Запишем условие, при котором определяется требуемое количество прогонов или панелей m и вычисления можно прекратить:
Для последней панели:

 (6.8)
(6.8)Если вентиляционной или осветительной шахты нет, т.е. r = 0, то lm = 0.
Разработан алгоритм и составлена программа на языке Бейсик, позволяющая получить все геометрические размеры, необходимые для проектирования. Исходный текст программы, ее логическая схема, а также пример построения развертки сектора сферического купола приведены в Приложении 1.
6.9. Шатровый купол (тип III табл. 1 и 2). Номинально ширину прямоугольных панелей удобно принимать равной разности длины соседних прогонов. Развертка покрытия и раскладка панелей в шестиугольном куполе показаны на рис. 24.

1 - панель рядовая
2л/п - панель трапециевидная
3л/п - панель трапециевидная карнизная
4л/п - панель коньковая
5 - панель карнизная
Рис. 24. Шатровый купол. Раскладка панелей
при шестиугольном плане
На рис. 25 доказаны детали примыкания панелей покрытия к ребрам купола (сеч. 2-2), где видно, как устраивается ендова кровли; примыкание к коньковому прогону ясно из сеч. 1-1, а опирание карнизных панелей на торцовую второстепенную арку - из сеч. 3-3.

6.10. Арочно-вспарушенный купол (тип VI табл. 1 и 2). Развертка покрытия (рис. 26 и 27) строится исходя из длины верхних граней второстепенных арок, которые (по оси) совмещаются с верхом ребра купола. Примыкание трапециевидных панелей к ребрам купола показано на рис. 28. Из него видно, что продольные ребра панелей, параллельные ребрам купола, нависают над их верхней гранью; при высоте ребер панелей 150 мм ширина ребра купола должна быть около 300 мм. При меньшей расчетной ширине ребер, по их верху сбоку пришиваются бруски нужной ширины (рис. 28). Трапециевидные панели укладываются у ребер купола с зазором, достаточным, чтобы при наклоне панелей они не упирались в выпуклость арочного ребра. Номинальная ширина прямоугольных панелей принимается равной 150 см; ширина трапециевидных панелей, различная в каждом ряду, назначается с учетом указанного выше зазора.

1 - панель рядовая
2 - панель карнизная
3л/п - панель трапециевидная
4л/п - панель трапециевидная карнизная
5л/п - панель коньковая
при шестиугольном плане

1 - панель рядовая
2 - панель карнизная
3л/п - панель трапециевидная
4л/п - панель трапециевидная карнизная
5л/п - панель коньковая
Раскладка панелей при восьмиугольном плане
Примыкание панелей к ребрам купола и устройство ендов показано на рис. 28. Принята ширина ендов по всему скату - 400 мм.
Трапециевидные панели при устройстве ендов по рис. 28, т.е. одинаковой ширины по низу, требуют смещения рамки, ограничивающей утеплитель со стороны ребер купола на разную величину в каждом узле примыкания второстепенных арок; поэтому крайняя продольная рамка устанавливается не параллельно крайнему продольному ребру панели, прилегающему к ребру купола (см. рис. 19).

ИС МЕГАНОРМ: примечание. При публикации в издании М.: ЦНИИЭП им. Б.С. Мезенцева, 1989 допущен типографский брак. Текст, не пропечатанный в официальном тексте документа, в электронной версии данного документа выделен треугольными скобками. |
1 - ребра купола, 2 - панель покрытия, 3 - антисептированный
настил из досок <...>, 4 - антисептированная доска, 
на ребро, шаг 750, 5 - пароизоляция, 6 - минераловатные
плиты, 7 - нащельник
6.11. Опирание панелей на ребра куполов, прогоны или второстепенные арки предусматривается двух типов:
а - двумя крайними продольными ребрами (тип "а" рис. 16); крепление панелей выполняется с помощью шурупов (винтов) через стальные соединительные детали;
б - опорной горизонтальной доской (тип "б" рис. 16), прибиваемой гвоздями.
Первый вариант - универсален, но более целесообразен при опирании на криволинейные ребра купола или на второстепенные арки. Второй вариант предназначен для опирания на прямолинейные прогоны.
6.12. Рекомендуемые способы сопряжения панелей покрытия между собой с прогонами или второстепенными арками приведены на рис. 18, 22, 29 и 30.
6.13. В конических и сферических куполах крепление панелей рассчитывается на скатную составляющую опорной реакции панелей от постоянной и снеговой нагрузки. Рекомендуется определять диаметр и количество шурупов или гвоздей для каждой зоны покрытия (см. рис. 17).
Примечание: в конических куполах большого диаметра при разной высоте ребер панелей и образовании уступа на потолке применяются панели первого типа "а".

1 - прогон, 2 - панель покрытия, 3 - жесткие минераловатные
плиты, 4 - пароизоляция, 5 - антисептированная доска,
6 - нащельник, 7 - второстепенная арка
и второстепенные арки:
а - в шатровом куполе, б - в арочно-вспарушенном куполе,
в - в пирамидальном куполе, г - в сомкнутом куполе
6.14. В пирамидальных и сомкнутых куполах панели крепятся к прогонам шурупами или гвоздями, рассчитанными также на скатную составляющую опорной реакции панелей от постоянной и снеговой нагрузок (см. п. 6.13).
6.15. В шатровых куполах (вариант II) крепление карнизных панелей к торцовым аркам рассчитывается на совместное действие скатной составляющей опорной реакции панелей и давления ветра на витраж (или глухой торец), располагаемый в пределах торцевой арки.
ИС МЕГАНОРМ: примечание. Обозначения рисунков даны в соответствии с официальным текстом документа. |

1 - прогон, 2 - панель покрытия, 3 - жесткие минераловатные
плиты, 4 - пароизоляция, 5 - антисептированная доска,
6 - 1 слой рубероида, наклеенный по месту, 7 - минеральная
вата, 8 - крепежная пластина, 9 - нащельник
а - в шатровом куполе, б - в пирамидальном куполе,
г - в сомкнутом куполе, д - опирание карнизной панели
6.16. В арочно-вспарушенных куполах, так же как и в шатровых, крепление панелей рассчитывается на совместное действие скатной составляющей опорной реакции панели и ветровой нагрузки на витраж (или глухой торец). Следует отдельно рассмотреть карнизные трапециевидные панели, имеющие наибольший наклон, и остальные (рядовые) карнизные панели, с учетом изменения угла наклона касательной к оси торцевой арки.
6.17. Вентиляционные (или осветительные) шахты в вершине купола рекомендуются шестиугольные или восьмиугольные в плане (в том числе и при круглом куполе), сборные из асбестоцементных панелей, соединенных в углах нащельниками. Как правило, шахта опирается на опорное коньковое кольцо.
Покрытие шахты рекомендуется выполнять в виде целой панели, собираемой заранее и устанавливаемой на стены шахты как единая деталь. На месте устраивается только кровля (рулонная или из листовых материалов).
Иногда в конических, сферических, пирамидальных и сомкнутых куполах осветительные шахты при больших диаметрах могут располагаться вне конькового кольца, опираясь на ребра или прогоны. В этом случае должны быть уточнены расчетные схемы куполов; в частности следует учитывать одностороннюю снеговую нагрузку от шахты.
Шахта рассчитывается на воздействие постоянной и полной снеговой нагрузки, а крепление - на ветровую нагрузку.
Для перекрытия двадцатичетырехугольного в плане зала с диаметром описанного круга в осях 60 м принят сферический купол со стрелой подъема  . Конструкция купола состоит из 24 ребер кругового очертания, опирающихся в вершине купола на круглое коньковое кольцо диаметром 4 м (рис. 31). По ребрам купола укладываются утепленные панели кровли, а на коньковое кольцо опирается восьмиугольная вентиляционная шахта.
. Конструкция купола состоит из 24 ребер кругового очертания, опирающихся в вершине купола на круглое коньковое кольцо диаметром 4 м (рис. 31). По ребрам купола укладываются утепленные панели кровли, а на коньковое кольцо опирается восьмиугольная вентиляционная шахта.
 . Конструкция купола состоит из 24 ребер кругового очертания, опирающихся в вершине купола на круглое коньковое кольцо диаметром 4 м (рис. 31). По ребрам купола укладываются утепленные панели кровли, а на коньковое кольцо опирается восьмиугольная вентиляционная шахта.
. Конструкция купола состоит из 24 ребер кругового очертания, опирающихся в вершине купола на круглое коньковое кольцо диаметром 4 м (рис. 31). По ребрам купола укладываются утепленные панели кровли, а на коньковое кольцо опирается восьмиугольная вентиляционная шахта.

7.1. Расчетные нагрузки на покрытие
Нормативную нагрузку от собственного веса ребер купола принимаем, задаваясь сечением b x h = 0,2 x 1,65 м с учетом кривизны их оси.
 (7.1)
(7.1)что соответствует qсва = 450 Па.
Здесь: h, b - высота и ширина сечения арки,
cф - коэффициент, учитывающий кривизну оси арки.
Нормативная постоянная нагрузка
- от собственного веса панелей покрытия и кровли 900 Па,
- от веса подвесного технологического оборудования
180 Па
__________________________________________________
Итого нормативная постоянная нагрузка qн - 1530 Па
Расчетная постоянная нагрузка
- от собственного веса панели покрытия и веса подвесного оборудования q = 1080·1,1 = 1200 Па
- от собственного веса арок gсва = 1,76·1,1 = 1,94 кН/м
Нагрузка от вентиляционной шахты Pш = 1,7 кН.
Покрытие рассчитано исходя из нормативного веса снегового покрова S0 = 1500 Па (IV снеговой район).
Определяем соотношение

Согласно [6]  .
.
 .
.Расчетная равномерно распределенная снеговая нагрузка на площадь покрытия купола
 (7.2)
(7.2)При одностороннем расположении снега на куполе определяем по графику на рис. 1 коэффициент 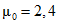 , тогда односторонняя снеговая нагрузка
, тогда односторонняя снеговая нагрузка
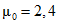 , тогда односторонняя снеговая нагрузка
, тогда односторонняя снеговая нагрузка (7.3)
(7.3)Расчетные нагрузки на ребра определяем по п. 3.6
шаг ребер

- Постоянная погонная нагрузка:
 (7.4)
(7.4)- Снеговая погонная нагрузка на ребро при равномерном снеге на всей поверхности купола
 (7.5)
(7.5)- Снеговая погонная нагрузка на ребро при одностороннем снеге на куполе
 (7.6)
(7.6)Расчетные схемы загружения приведены на рис. 32.
Рассчитываем ребра купола как трехшарнирные арки.
7.2. Определение усилий в ребрах купола
7.2.1. Постоянная нагрузка
Опорные реакции арки
 (7.7)
(7.7)Распор
 (7.8)
(7.8)Изгибающие моменты от постоянной нагрузки в пределах от опоры до стены шахты вычисляются по уравнению:
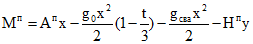 (7.9)
(7.9)y - ордината оси арки, образуемой ребрами, определяется по формуле:
 (7.10)
(7.10)где Ra - радиус кривизны ребра при принятой стрелке подъема f, определяется по формуле (6.1), при f/D = 1/6:
 (7.11)
(7.11)7.2.2. Снеговая нагрузка на всем пролете
Опорные реакции
 (7.12)
(7.12)Распор
 (7.13)
(7.13)Изгибающие моменты
 (7.14)
(7.14)7.2.3. Односторонняя снеговая нагрузка
Опорные реакции
 (7.15)
(7.15) (7.16)
(7.16) (7.17)
(7.17)Координаты сечения | Значения изгибающих моментов M | ||||||||
x м | y м | t | X м | Fx кН | Mп кНм | Mс кНм | кНм | Mп + Mс кНм |  кНм |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
3 | 2,093 | 0,1 | 1,421 | 102,14 | 65,60 | 131,7 | 455,0 | 197,3 | 520,6 |
6 | 3,863 | 0,2 | 2,67 | 175,35 | 112,0 | 213,6 | 675,7 | 325,6 | 787,7 |
9 | 5,376 | 0,3 | 3,725 | 255,69 | 131,5 | 250,7 | 736,2 | 382,2 | 867,7 |
12 | 6,647 | 0,4 | 4,57 | 258,51 | 132,6 | 250,5 | 694,6 | 383,1 | 827,2 |
15 | 7,697 | 0,5 | 5,2 | 278,43 | 116,7 | 221,1 | 595,1 | 337,8 | 711,8 |
18 | 8,539 | 0,6 | 5,62 | 289,4 | 90,1 | 172,4 | 467,8 | 262,5 | 557,9 |
21 | 9,183 | 0,7 | 5,863 | 294,59 | 58,8 | 114,9 | 335,9 | 173,7 | 394,7 |
24 | 9,639 | 0,8 | 5,97 | 296,52 | 26,8 | 59,0 | 210,1 | 85,8 | 236,9 |
27 | 9,91 | 0,9 | 5,998 | 296,97 | 4,8 | 16,8 | 97,2 | 21,6 | 102 |
30 | 10 | 1,0 | 6,0 | 297 | 0 | 0 | 0 | 0 | 0 |
33 | 9,91 | 4,8 | 16,8 | -81,1 | 21,6 | -76,3 | |||
36 | 9,639 | 26,8 | 59,0 | -146,0 | 85,8 | -119,2 | |||
39 | 9,183 | 58,8 | 114,9 | -194,5 | 173,7 | -135,7 | |||
42 | 8,539 | 90,1 | 172,4 | -226,2 | 262,5 | -136,1 | |||
45 | 7,697 | 116,7 | 221,1 | -240,3 | 337,8 | -123,6 | |||
48 | 6,647 | 132,6 | 250,5 | -235,8 | 383,1 | -103,2 | |||
51 | 5,376 | 131,5 | 250,7 | -211,7 | 382,2 | -80,2 | |||
54 | 3,863 | 112,0 | 213,6 | -166,0 | 325,6 | -54,0 | |||
57 | 2,083 | 65,5 | 131,7 | -96,5 | 197,3 | -31,0 | |||
60 | 0 | 0 | 0 | 0 | 0 | 0 | |||
Уравнения изгибающих моментов
 (0 <= x <= R) (7.18)
(0 <= x <= R) (7.18) (R <= x <= 2R) (7.19)
(R <= x <= 2R) (7.19)Здесь Fx и xс - равнодействующая и координата центра тяжести части нагрузки слева от x:
 (7.20)
(7.20)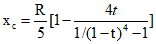 (7.21)
(7.21)Значения координат оси арки, некоторых вспомогательных величин и изгибающих моментов в арке приведены в табл. 5.
Сочетания постоянной и полной снеговой нагрузок дают максимальные значения вертикальных реакций, распоров и усилий в опорном контуре, а расчетными будут изгибающие моменты от сочетания постоянной и односторонней снеговой нагрузок.
Наибольший положительный изгибающий момент возникает в сечении x = 9 м и равен 868 кН/м, а отрицательный в сечении x = 18 м и равен 136 кН/м.
Опорные реакции при сочетании нагрузок 1 и 3:
 (7.22)
(7.22)Из уравнения для синуса угла наклона касательной к оси арки  найдем, что при x = 9 м,
найдем, что при x = 9 м,  , а при x = 18 м
, а при x = 18 м  .
.
 найдем, что при x = 9 м,
найдем, что при x = 9 м,  , а при x = 18 м
, а при x = 18 м  .
.Балочная поперечная сила в сечении x = 9 м
ИС МЕГАНОРМ: примечание. Уравнение дано в соответствии с официальным текстом документа. |


Продольная сила в арке при x = 9 м
 (7.23)
(7.23)Балочная поперечная сила в сечении x = 18 м
 (7.24)
(7.24)Нормальная сила в сечении x = 18 м
 (7.25)
(7.25)7.2.4. Подбор сечения арки
Принимаем высоту и ширину сечения арки h = 1,65 м, b = 0,2 м из досок второго сорта толщиной 20 мм.
Площадь сечения и момент сопротивления сечения
Fбр = b·h = 0,2·1,65 = 0,33 м2 (7.26)
 (7.27)
(7.27)Отношение минимального радиуса гнутья доски к ее толщине

Rс = R·mб·mгн·mсл = 15·0,8·1·1,08 = 13 МПа (7.28)
По верху арка раскреплена панелями покрытия с шагом 1,5 м, что меньше величины

Следовательно имеет место сплошное раскрепление верхней кромки: при положительном моменте в арке - сжатой, а при отрицательном - растянутой.
Арка рассчитывается как сжато-изогнутая в соответствии с п.п. 4.17, 6.25 и 6.26 СНиПа [1] при действии в сечении x = 9 м
M = 868 кНм и N = 353 кН
Расчетная длина:
Lр = 0,58D·1,07 = 0,58·60·1,07 = 37,2 м (7.29)
Гибкость:
 (7.30)
(7.30)Коэффициент продольного изгиба:
 (7.31)
(7.31) (7.32)
(7.32) (7.33)
(7.33)Наибольшие напряжения в арке определяются по формуле:
 (7.34)
(7.34)7.2.5. Устойчивость плоской формы деформирования
Устойчивость плоской формы деформирования проверяется в сечении с максимальным отрицательным моментом по формуле 33 [1]:
 (7.35)
(7.35)На рассматриваемом участке ребро купола имеет раскрепление кровельными панелями со стороны растянутой кромки, поэтому n = 1, а к значениям  и
и  вводятся поправочные коэффициенты кпN и кпM.
вводятся поправочные коэффициенты кпN и кпM.
При расчетной длине от опоры до конькового опорного кольца
 (7.36)
(7.36)Гибкость:
 (7.37)
(7.37) (7.39)
(7.39)Коэффициенты кпN и кпM при m >= 4 определяются по формулам:
 (7.40)
(7.40) (7.41)
(7.41)Здесь Lр = Lу
 (7.42)
(7.42)Используя прежнее значение  , определим
, определим
 , определим
, определим (7.43)
(7.43)Подставив все значения в (7.38), получаем
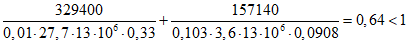 (7.44)
(7.44)Следовательно, устойчивость обеспечена.
7.2.6. Расчет опорного узла опирания ребра купола
Рассматриваем два варианта узлов:
- опирание ребра купола непосредственно на железобетонный опорный контур (рис. 7);
Угол наклона касательной к оси арки в опорном сечении  .
.
 .
.Опорные реакции, а также нормальные и поперечные силы в опорном сечении при загружении купола постоянной нагрузкой и двумя видами снеговой нагрузки приведены в табл. 6.
Таблица 6
Сочетание нагрузок | Усилие | ||||
опорные реакции | поперечная сила на опоре | ||||
A кН | H кН | кН | кН | Qоп кН | |
Постоянная плюс снег на всем куполе | 410 | 440 | - | - | 61,4 |
Постоянная плюс снег на половине поверхности купола | - | - | 467 | 319 | 182,2 |
Минимальная высота сечения арки на опоре определяется из условий скалывания
 (7.45)
(7.45)1 вариант узла (рис. 7).
На вертикальную торцевую пластину металлического башмака передается распор, а на горизонтальную пластину - опорная реакция. Принимаем высоту башмака hб = 0,36 м, а длину его подошвы Lб = 0,65 м.
Расчетное сопротивление древесины смятию в местах контакта с башмаком
 (7.46)
(7.46) (7.47)
(7.47)Напряжения сжатия в местах контакта древесины с торцевой и горизонтальной пластинами башмака
 (7.48)
(7.48) (7.49)
(7.49)Пластина 1 (рис. 8) оперта по трем сторонам, т.к.

момент в ней определим как в шарнирно-опертой балке
 (7.50)
(7.50)Требуемая толщина пластины (п. 5.3)
 (7.51)
(7.51)Принимаем толщину пластины 25 мм.
Расчетная длина швов, присоединяющих торцевую пластину к боковым листам и горизонтальной пластине
Iш = 2·36 + 20 - 2 = 90 см.
Принимаем высоту швов kf =6 мм, Rwf = 180 МПа.
Напряжения в швах
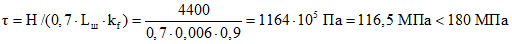 (7.52)
(7.52)Принимаем толщину боковых пластин  . На каждую из них передается изгибающий момент
. На каждую из них передается изгибающий момент
 . На каждую из них передается изгибающий момент
. На каждую из них передается изгибающий момент (7.53)
(7.53)и растягивающая сила
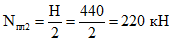 (7.54)
(7.54)Напряжения в пластине
 (7.55)
(7.55) (7.56)
(7.56) (7.57)
(7.57)В сварных швах, присоединяющих пластины 2 к горизонтальному листу башмака, проверим напряжения по формуле 126 п. 11.5 СНиПа [4]:
 (7.58)
(7.58)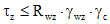 (7.59)
(7.59)где Rwf, Rwz - расчетные сопротивления стали и материала шва соответственно.
В рассматриваемом случае  ,
,  ,
,  .
.
 (7.60)
(7.60) (7.61)
(7.61)здесь: 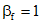 ;
;  ; kf - высота катета углового шва;
; kf - высота катета углового шва;
 ; kf - высота катета углового шва;
; kf - высота катета углового шва;kf = 0,008 м; Lш = 0,64 м - расчетная длина шва.
Принимаем высоту шва kf = 8 мм, расчетная длина шва 64 см.


Ширина и толщина горизонтальной пластины 3 bпл3 = 0,4 м,  , ее площадь и момент сопротивления
, ее площадь и момент сопротивления
 , ее площадь и момент сопротивления
, ее площадь и момент сопротивленияFпл3 = bпл3·Lб = 0,4·0,65 = 0,26 м2 (7.62)
 (7.63)
(7.63)Опрокидывающий момент
 (7.64)
(7.64)Напряжения под горизонтальным листом башмака
 (7.65)
(7.65)где  - расчетные напряжения сжатия в бетоне;
- расчетные напряжения сжатия в бетоне;
 .
. (7.66)
(7.66) (7.67)
(7.67)Таким образом, наибольшие напряжения сжатия
 (7.68)
(7.68)могут быть восприняты бетоном практически любой марки.
Растягивающие напряжения
 (7.69)
(7.69)воспринимаются анкерными болтами.
Согласно п. 5.3
 (7.70)
(7.70) (7.71)
(7.71) (7.72)
(7.72)Расчетные растягивающие усилия в анкерных болтах
 (7.73)
(7.73)Требуемое сечение болтов по условиям среза
 (7.74)
(7.74)Принимаем  .
.
 .
.Площадь двух крайних растянутых болтов по ослабленному нарезкой сечению
 (7.75)
(7.75)Напряжение растяжения в болте
 (7.76)
(7.76)не превышает расчетного сопротивления фундаментных болтов
Rba = 145 МПа
На участке Lб - L0 нижняя пластина проверяется на действие изгибающего момента

Здесь C = (40 - 20 - 2·1)/2 = 9 см (см. рис. 8)
Напряжение:
 (7.77)
(7.77)Следовательно, требуется увеличить толщину пластины. Примем 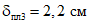 . Соответствующее напряжение -
. Соответствующее напряжение -
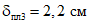 . Соответствующее напряжение -
. Соответствующее напряжение -= 206 МПа < 215 МПа
Башмак ребра купола передает давление на стену через два цилиндрических шарнира (катка). Расчетное сопротивление катков сжатию Rcd = 8 МПа. Длина катков 25 см, следовательно, требуемый диаметр катка
 (7.78)
(7.78)Расстояние между катками определяем исходя из необходимости обеспечения устойчивости башмака на опрокидывание наибольшим распором при соответствующей ему опорной реакции (см. п. 5.3).
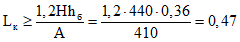 (7.79)
(7.79)Вертикальная торцевая пластина башмака такая же, как и в первом варианте, т.е. высотой 36 см и толщиной 2,5 см.
Нижняя плита внутри башмака растягивается усилием, действующим в опорном контуре
 (7.80)
(7.80)и изгибается контактными напряжениями
 (7.81)
(7.81)Изгибающий момент в пластине
 (7.82)
(7.82)При толщине листа пластины  напряжения в ней
напряжения в ней
 напряжения в ней
напряжения в ней (7.83)
(7.83)Опорный контур принят из полосовой стали марки 14Г2 сечением 20 x 3 см2 F = 0,20·0,03 = 0,006 м2.
 (7.84)
(7.84)Присоединение к нижнему листу башмака выполняем угловыми швами высотой kf = 18 мм электродами Э 50А. При длине шва Lш = 65 см
 (7.85)
(7.85)На металлический лист размерами 0,65 x 0,3 м2, укладываемый на стены под катками, действует отпор
 (7.86)
(7.86)вызывающий в пластине изгибающие моменты:
на опоре  (7.87)
(7.87)
 (7.87)
(7.87)в пролете  (7.88)
(7.88)
 (7.88)
(7.88)Требуемая толщина листа
 (7.89)
(7.89)7.2.7. Закрепление опорного контура купола на стенах
Согласно п. 4.3 металлический опорный контур необходимо закрепить на стене так, чтобы обеспечить передачу усилий от него вдоль стены и не препятствовать смещению контура, вызываемому полной снеговой нагрузкой на купол поперек стены.
Вариант такого крепления показан на рис. 33. Элементы "а" привариваются к опорному контуру до его установки на место.
Между элементами "а" и "б" должен предусматриваться зазор в 1 мм, а плоскости соприкасания обрабатываются графитовой смазкой. При таком закреплении сдвигающая сила, действующая на упор, равна распору от односторонней снеговой нагрузки  .
.
 .
.Определяем напряжения в швах, прикрепляющих упоры "а" к опорному контуру.

Принимаем высоту шва kf = 6 мм, длина шва Lш = 19 см.
Напряжения в швах от среза
 (7.90)
(7.90)Напряжения в швах от изгиба
 (7.91)
(7.91)Суммарные напряжения
 (7.92)
(7.92)Упор для опорного контура таврового сечения заанкерен болтами в железобетонный пояс. На упор передается сила  и момент
и момент
 (7.93)
(7.93)На эти усилия должны быть рассчитаны анкерные болты и швы, прикрепляющие косынки "б" к горизонтальному листу упора.
Длина швов Lш = (8 - 1) = 7 см, высота kf = 6 мм.
Напряжения в швах:
 (7.94)
(7.94)Здесь:

Усилия в анкерных болтах
 (7.95)
(7.95)Принимаем 4 болта d = 20 мм, F = 0,000314 м2.
Нормальные напряжения в болтах по нарезке:
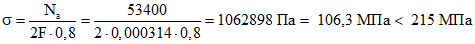 (7.96)
(7.96)Напряжения среза
 (7.97)
(7.97)7.2.8. Расчет конькового опорного кольца
Согласно п. 4.5 предусмотрено жесткое присоединение ребер к опорному коньковому кольцу. На кольцо передается распор, поперечная сила и вызываемый ею крутящий момент от односторонней снеговой нагрузки, распределенной по закону кубической параболы.
 ,
,  (7.98)
(7.98)Ребра примыкают к коньковому кольцу с шагом Lк = 0,523 м, поэтому на 1 п.м кольца
 ,
,  ,
,  (7.99)
(7.99)Эти воздействия вызывают в кольце продольную силу, изгибающий и крутящий моменты (см. таблицы 3 и 4), максимальные значения которых
 (7.100)
(7.100) (7.101)
(7.101) (7.102)
(7.102) (7.103)
(7.103)Кроме того, следует учесть также нормальную силу от постоянной нагрузки
 (7.104)
(7.104)Нормальная сила в кольце
 (7.105)
(7.105)Задаемся сечением кольца 50 x 25 см при 
 ,
,  - толщина стенки и полки соответственно.
- толщина стенки и полки соответственно.

Площадь сечения
 (7.106)
(7.106)Моменты инерции и моменты сопротивления
ИС МЕГАНОРМ: примечание. Единицы измерения даны в соответствии с официальным текстом документа. |
 (7.107)
(7.107) (7.108)
(7.108) (7.109)
(7.109) (7.110)
(7.110)Момент инерции и момент сопротивления при кручении
 (7.111)
(7.111) (7.112)
(7.112)Здесь
 (7.113)
(7.113)При вычислении изгибающих и крутящих моментов в кольце использован параметр
 (7.114)
(7.114)Суммарные нормальные напряжения в кольце
 (7.115)
(7.115)Касательные напряжения от кручения
 (7.116)
(7.116)Металлические оголовники ребра присоединяются к коньковому кольцу при помощи горизонтальных накладок и вертикальных косынок, на которые действуют распор от постоянной и односторонней снеговой нагрузки  , поперечная сила
, поперечная сила  и вызываемый ею момент
и вызываемый ею момент
 , поперечная сила
, поперечная сила  и вызываемый ею момент
и вызываемый ею момент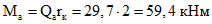 (7.117)
(7.117)Усилия, действующие на сопряжение
 (7.118)
(7.118) (7.119)
(7.119)- сжимающие. Поэтому шурупы, присоединяющие оголовник к ребру, ставим конструктивно.
При действии распора, вызываемого постоянной и полной снеговой нагрузками H = 440 кН, в торце ребра возникают сжимающие напряжения
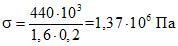 (7.120)
(7.120)Эти напряжения вызывают в торцевой пластине оголовника изгибающий момент
 (7.121)
(7.121)Требуемая толщина пластины
 (7.122)
(7.122)Принимаем пластину толщиной  .
.
 .
.АРОЧНО-ВСПАРУШЕННОГО КУПОЛА
Рассмотрим особенности расчета и конструирования арочных вспарушенных куполов на примере купола на шестиугольном плане диаметром 45 м и отношения f/D = 1/6 (рис. 35).
8.1. Нагрузки на купол
Постоянная нагрузка | Нормативная нагрузка, Па | Расчетная нагрузка, Па | |
Кровельные панели и кровля | 870 | 1000 | |
Технологическая нагрузка | 180 | 200 | |
Собственный вес второстепенных арок | 180 | 200 | |
Итого: | qк = 12,30 | q = 1400 | |
Собственный вес главных арок |  | qсвА = 200 | |
Итого: |  | q1 = 1000 | |
Нормативный вес снегового покрова:
S0 = 1500 Па

8.2. Предварительный расчет главных ребер (без учета распоров второстепенных арок)
Конструктивная особенность данной системы состоит в том, что очертания их осей зависят от принятого сечения.
Поэтому необходим предварительный приближенный расчет и подбор сечения главных арок.
Предварительные размеры сечений главных арок определяются при равномерно распределенных постоянной и снеговой односторонней нагрузках. На этом этапе удобно и собственный вес главных арок включить в постоянную нагрузку, как равномерно распределенную.

Рис. 34. Монтажный план и разрез арочно-вспарушенного купола


Тогда погонные нагрузки на диагональные арки будут распределены по линейному закону:
g(x) = g0(R - x)/R
p(x) = p0(R - x)/R
g0 = q1L
p0 = qснL (8.1)
где  , L, D и n - сторона, диаметр описанной окружности и число сторон многоугольного плана соответственно.
, L, D и n - сторона, диаметр описанной окружности и число сторон многоугольного плана соответственно.
 , L, D и n - сторона, диаметр описанной окружности и число сторон многоугольного плана соответственно.
, L, D и n - сторона, диаметр описанной окружности и число сторон многоугольного плана соответственно.Схема загружения главных арок постоянной и односторонней снеговой нагрузкой приведена на рис. 35.
От этих нагрузок максимальный изгибающий момент возникает в полуарке, свободной от снеговой нагрузки.
Если представить часть распределенной нагрузки в виде двух сосредоточенных сил, приложенных на опоре и в месте примыкания первой второстепенной арки - как показано на рис. 35, максимальный изгибающий момент и координаты сечения, в котором он возникает, определяются по формулам:
 (8.2)
(8.2)здесь: 



d - шаг второстепенных арок в плане;
где 

 (8.5)
(8.5)--------------------------------
<*> Выражения (8.3) и (8.5), данные для оси арки, содержат радиус цилиндрической поверхности, которой принадлежат лишь верхние грани арок. Это допустимо только для первого приближения.
В данном примере D = 45 м; f = 7,5 м, n = 6, d = 3 м; тогда

g0 = 1600·22,5 = 36000 Н = 36 кН
p0 = 2100·22,5 = 47250 Н = 47,25 кН
 ;
;





Mmax = 437,86·3,272 - 676,6·2,79 = -455 кН м
продольная сила в расчетном сечении:
 (8.6)
(8.6)здесь:
 (8.7)
(8.7)Примем в качестве исходного сечение главных арок:
h x b = 190·1500 мм
h, b - высота и ширина сечения главной арки соответственно.
Эллиптическая ось полуарки полога, поэтому приближенно расчетную длину полуарки можно определить, как для части окружности:
S0 = 1,07·0,58D = 1,07·0,58·45 = 27,93 м
тогда
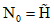 ; F = h x b = 1,5·1,9 = 0,285 м2
; F = h x b = 1,5·1,9 = 0,285 м2

Напряжение в расчетном сечении
где W = bh2/6 = 0,19·1,52/6 = 0,07125 м3.
После предварительного определения сечения главных арок становится возможным получить их точные геометрические очертания, а также параметры второстепенных арок.
8.3. Расчет второстепенных арок
Наружные грани второстепенных арок образуют цилиндрическую поверхность с радиусом, определяемым по формуле (8.4). Назначим сечения второстепенных арок из условия:
 (8.10)
(8.10)i - номер второстепенной арки;
hвi - высота сечения i-той второстепенной арки;
Li - ее пролет, определяемый по формуле:
 (8.11)
(8.11)при b = 0 получим пролеты второстепенных арок в осях  . Тогда:
. Тогда:
 (8.12)
(8.12) (8.13)
(8.13)Rоi, fi - радиусы и подъемы второстепенных арок соответственно.
Для конструирования узлов потребуются также углы наклона касательных к оси и к верхней грани второстепенных арок в местах их примыкания к главным:
 (8.14)
(8.14) (8.15)
(8.15)Необходимо определить также длины осей и верхних граней второстепенных арок:
 (8.16)
(8.16) (8.17)
(8.17)В таблице 7 приведены основные геометрические характеристики второстепенных арок для рассматриваемого примера.
Далее следует проверить напряжения, возникающие во второстепенных арках от постоянной и снеговой нагрузки.
Возможные схемы загружения второстепенных арок представлены на рис. 36. Постоянная нагрузка на второстепенные арки распределена по закону:
 (8.18)
(8.18)Такую нагрузку можно приближенно заменить суммой постоянной равномерно распределенной нагрузки и нагрузки, описываемой квадратной параболой с максимальным значением на опоре
 (8.19)
(8.19)где ci - является коэффициентом увеличения нагрузки.

Величины ci для нашего примера приведены в таблице 7.
N арки | А-1 торц. | А-2 | А-3 | А-4 | А-5 | А-6 | Кольцо коньковое |
Сечения, мм | 560 x 140 | 460 x 140 | 330 x 140 | 330 x 140 | 330 x 140 | 330 x 140 | 330 x 140 |
Радиусы осевые, м | 11,92 | 11,970 | 12,035 | 12,035 | 12,035 | 12,035 | 12,035 |
Пролеты в осях | 22,5 | 19,036 | 15,572 | 12,108 | 8,644 | 5,18 | 1,716 |
Li, м | 22,281 | 18,817 | 15,353 | 11,889 | 8,425 | 4,961 | 1,45 |
fi, м | 7,679 | 4,567 | 2,766 | 1,517 | 0,761 | 0,258 | - |
fi/Li | 1/3 | 1/4 | 1/6 | 1/8 | 1/11 | 1/19 | - |
69,162° | 51,782° | 39,63° | 29,6° | 20,49° | 11,892° | - | |
65,943° | 50,46° | 39,0° | 29,16° | 20,2° | 11,73° | - | |
28,78 | 21,645 | 16,65 | 12,434 | 8,61 | 4,996 | - | |
28,08 | 21,49 | 16,6 | 12,42 | 8,6 | 5,0 | - | |
ci | 1,81 | 0,616 | 0,3 | 0,15 | 0,0675 | 0,022 | - |
Тогда реакции второстепенных арок от постоянной нагрузки будут следующими:
 (8.20)
(8.20) (8.21)
(8.21)где: gВ - постоянная погонная нагрузка на второстепенную арку.
Второстепенные арки двухшарнирные, кроме торцевой, однако опорные реакции в них определяются как в трехшарнирных.
Результаты предварительных расчетов показывают, что максимальные моменты во второстепенных арках, для которых отношение fi/Li > 1/6, возникают обычно от постоянной и равномерно распределенной на половине пролета снеговой нагрузок (см. рис. 36).
Например, для арки А-2:
i = 2;
погонные нагрузки:
постоянная - gВ = 1400·3,0 = 4,2 кН/пм
снеговая - pВ = 2200·3,0 = 6,6 кН/пм.
Опорные реакции:
 (8.22)
(8.22) (8.23)
(8.23) (8.24)
(8.24)Максимальный момент в арке А-2 возникает в свободной от снеговой нагрузки половине арки при загружении ее постоянной и равномерно распределенной снеговой нагрузкой на половине пролета. Усилия в рассматриваемой половине арки:
изгибающие моменты -
 (8.25)
(8.25)(см. [10], табл. 8.3.2).
нормальные силы -
 (8.26)
(8.26)здесь:  ;
;  ;
; 
 ;
;  ;
; 
Максимальный момент возникает в сечении x = 0,2L2, для которого:


ИС МЕГАНОРМ: примечание. Уравнение дано в соответствии с официальным текстом документа. |

Нормальная сила:

Расчетная длина арки А-2:
Lо2 = 0,58Sо2 = 0,58·21,645 = 12,55 м
В соответствии с [1] формулой 30 п. 4.17:

где: F = 0,14·0,46 = 0,0644 м2;
 N0 = H2В
N0 = H2В ;
;
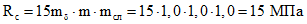
и окончательно:


В более пологих арках, при  преобладающими становятся моменты от неуравновешенных распоров при одностороннем загружении купола снеговой нагрузкой, передающихся на все второстепенные арки. Кроме того, при расчете этих арок можно не учитывать неравномерность распределения постоянной нагрузки, т.к. ci становятся малыми (см. табл. 7).
преобладающими становятся моменты от неуравновешенных распоров при одностороннем загружении купола снеговой нагрузкой, передающихся на все второстепенные арки. Кроме того, при расчете этих арок можно не учитывать неравномерность распределения постоянной нагрузки, т.к. ci становятся малыми (см. табл. 7).
 преобладающими становятся моменты от неуравновешенных распоров при одностороннем загружении купола снеговой нагрузкой, передающихся на все второстепенные арки. Кроме того, при расчете этих арок можно не учитывать неравномерность распределения постоянной нагрузки, т.к. ci становятся малыми (см. табл. 7).
преобладающими становятся моменты от неуравновешенных распоров при одностороннем загружении купола снеговой нагрузкой, передающихся на все второстепенные арки. Кроме того, при расчете этих арок можно не учитывать неравномерность распределения постоянной нагрузки, т.к. ci становятся малыми (см. табл. 7).Моменты от неуравновешенных распоров имеют максимальные значения в коньке второстепенных арок:
Все второстепенные арки должны иметь провозные габариты, с этой целью некоторые из них, например рассматриваемая арка А-2, должны иметь монтажный стык в коньке. Расчетными усилиями для стыков будут моменты от неуравновешенных распоров, определяемые по формуле 8.27.
Далее необходимо определить действительные очертания осей диагональных арок.

арочно-вспарушенного купола


8.4. Геометрия диагональных арок
Верхняя грань диагональной арки является эллипсом, построенным из условия пересечения цилиндрической поверхности с вертикальной плоскостью боковой грани главной арки.
Дальнейшие вычисления удобнее вести в системе координат, приведенной на рис. 37. Тогда уравнение, описывающее верхнюю грань диагональной арки:
 (8.28)
(8.28)Ось последней не является эллипсом, она строится как траектория точки на нормали к эллипсу, отстоящей от него на расстояние h/2 (рис. 38).
Чтобы определить координаты точек оси главной арки, необходимо для каждого xi решить трансцендентное уравнение относительно синуса угла наклона касательной к оси арки:
Решив это уравнение одним из известных способов, определим координаты точек оси арки:
здесь:

Таким же путем могут быть получены ординаты точек нижней грани арок, если в выражениях 8.29 - 8.30 заменить  на ha.
на ha.
Для конструирования купола и дальнейшего его расчета могут понадобиться следующие величины: ординаты точек оси и верхней грани главного ребра в местах примыкания к ним второстепенных арок, на опорах и в коньке, а также углы наклона касательных к обеим кривым в этих точках.
В качестве примера приводится вычисление вышеперечисленных величин в месте примыкания одной из второстепенных арок при известных уже исходных данных: D = 45 м, n = 6; Rц = 12,2 м; h = 1,50 м; d = 3,0 м; b = 0,19 м.
Координаты пересечений второстепенных арок с боковыми плоскостями главных ребер (см. рис. 37):
 (8.31)
(8.31)здесь:
Li - пролеты второстепенных арок;
i - номер второстепенной арки; для торцевой i = 1.
Например, для второстепенной арки А-2: i = 2,
L2 = 18,817 м

ордината верхней грани главной арки в рассматриваемом месте примыкания определяется по формуле 8.30.

угол наклона касательной в этой точке:

уравнение относительно синуса угла наклона касательной к оси главной арки в рассматриваемом сечении по формуле 8.29:

Решив это уравнение методом половинного деления (например, так, как это сделано в Приложении 1), получим  и
и  , а затем, подставляя это значение в формулу 8.30, получим:
, а затем, подставляя это значение в формулу 8.30, получим:
 и
и  , а затем, подставляя это значение в формулу 8.30, получим:
, а затем, подставляя это значение в формулу 8.30, получим:

Таким же образом вычисляются аналогичные величины для остальных мест примыкания второстепенных арок, а также в коньковом сечении, координата которого
 (8.32)
(8.32)b - ширина сечения главной арки.
Точки пересечения осей главных арок с диагоналями многоугольного плана имеют абсциссы:
 (8.33)
(8.33)Они будут считаться точками опирания главных арок (на рис. 37 это точки 0).
Остальные величины для этого сечения и другие, необходимые для расчета и конструирования главных арок, приведены в табл. 8.
Подъемом главных арок впредь будет считаться разность:
f = yк - y0 (8.34)
Ординаты точек приложения распоров второстепенных арок (см. рис. 38):
 (8.35)
(8.35)N точки | x м | y | yв | ||
1 | 2 | 3 | 4 | 5 | |
0 | 22,336 | 0,8127 | 0,9487 | 3,676 | 4,88 |
1 | 22,281 | 0,8064 | 0,9381 | 3,752 | 4,943 |
2 | 18,817 | 0,5397 | 0,5701 | 6,863 | 7,747 |
3 | 15,353 | 0,3859 | 0,3962 | 8,655 | 9,466 |
4 | 11,889 | 0,2747 | 0,2783 | 9,860 | 10,640 |
5 | 8,425 | 0,1843 | 0,1854 | 10,673 | 11,436 |
6 | 4,961 | 0,1050 | 0,1052 | 11,178 | 11,932 |
7 | 1,585 | 0,0331 | 0,0331 | 11,411 | 12,162 |
К | 0 | 0 | 0 | 11,411 | 12,2 |
Подъем диагональных арок:
f = yк - y0 = 11,411 - 3,676 = 7,74 м (8.36)
8.5. Расчет диагональных арок
Определив координаты точек приложения распоров второстепенных арок и очертание осей диагональных ребер, можно уточнить значения возникающих расчетных усилий.
Нагрузки на диагональные арки
Интенсивность постоянной равномерно распределенной нагрузки от собственного веса арки:
gсва = h·b·rд·n·S/D = 1,5·0,19·5·1,1·1,07 = 1,68 кН/пм (8.37)
где: rд - удельный вес древесины;
n - коэффициент перегрузки;
S/D = 1,07 - приближенное значение отношения длины оси диагональной арки к ее пролету.
Сосредоточенные нагрузки - опорные реакции второстепенных арок, приложенные в местах их присоединения к диагональным:
- от постоянной нагрузки:
 (8.38)
(8.38)- от снеговой нагрузки:
 (8.39)
(8.39)Для дальнейших вычислений удобно поместить начало координат в точку 0 (см. рис. 37). Соответствующие координаты осей диагональных арок, а также значения расчетных сосредоточенных нагрузок приведены в таблице 9.
Собственный вес диагональных арок вызывает реакции:
 (8.40)
(8.40) (8.41)
(8.41)Реакции от постоянной вертикальной нагрузки:
 (8.42)
(8.42) (8.43)
(8.43)Реакции от полной снеговой нагрузки:
 (8.44)
(8.44) (8.45)
(8.45)Реакции от односторонней снеговой нагрузки:
 (8.46)
(8.46) (8.47)
(8.47)N точки | xi м | yi м | кН | кН | кН | кН | yкi м |
0 | 0 | 0 | - | - | - | - | - |
1 | 0,055 | 0,076 | 150,46 | 147,05 | 44,17 | 53,23 | 0,543 |
2 | 3,519 | 3,187 | 95,34 | 124,19 | 44,83 | 63,86 | 3,712 |
3 | 6,983 | 4,979 | 70,93 | 101,33 | 46,96 | 70,13 | 5,564 |
4 | 10,447 | 6,184 | 52,43 | 78,46 | 48,44 | 74,27 | 6,791 |
5 | 13,911 | 6,997 | 36,18 | 55,60 | 49,51 | 76,94 | 7,600 |
6 | 17,375 | 7,502 | 20,98 | 32,74 | 50,20 | 78,60 | 8,103 |
7 | 20,75 | 7,735 | 20 | - | - | - | |
8 | 22,5 | 7,74 | - | - | - | - | |
9 | 24,161 | 7,735 | 20 | - | - | - | |
10 | 27,625 | 7,502 | 20,98 | 32,74 | 50,20 | 78,60 | 8,103 |
11 | 31,009 | 6,997 | 36,18 | 55,6 | 49,51 | 76,94 | 7,600 |
12 | 34,553 | 6,184 | 52,43 | 78,46 | 48,44 | 74,27 | 6,791 |
13 | 38,017 | 4,979 | 70,93 | 101,33 | 46,86 | 70,13 | 5,564 |
14 | 41,481 | 3,187 | 95,34 | 124,19 | 44,83 | 63,86 | 3,712 |
15 | 44,945 | 0,076 | 150,46 | 147,05 | 44,17 | 53,23 | 0,543 |
16 | 0 | 0 | - | - | - | - | - |
Расчетная схема диагональной арки приведена на рис. 39.
 (8.48)
(8.48)Реакции от воздействия распоров второстепенных арок:
- постоянная нагрузка
 (8.49)
(8.49) (8.50)
(8.50)- полная снеговая нагрузка
 (8.51)
(8.51) (8.52)
(8.52)- односторонняя снеговая нагрузка
 (8.54)
(8.54)Суммарные реакции
- от постоянной и полной снеговой нагрузок
А = Асв + Ап + Ас + Апр + Аср =
= 37,8 + 446,31 + 539,37 + 0 + 0 = 1023,48 т (8.56)
Б = А (8.57)
Н = Нсв + Нп + Нс + Нпр + Нср =
= 54,98 + 345,1 + 428,51 + 81,93 + 109,06 = 1019,6 т (8.58)
- от постоянной и односторонней снеговой нагрузок
 (8.59)
(8.59) (8.60)
(8.60)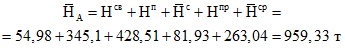 (8.61)
(8.61) (8.62)
(8.62)Изгибающие моменты
- от постоянной и полной снеговой нагрузки:
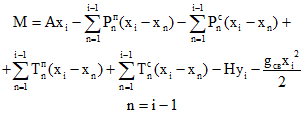 (8.63)
(8.63)- от постоянной и односторонней снеговой нагрузки:
 (8.64)
(8.64) (8.65)
(8.65)Нормальные силы
- от постоянной и полной снеговой нагрузок
 (8.66)
(8.66)Таблица 10
N сеч. | x м | y м | постоянная и полная снеговая нагрузка | постоянная и односторонняя снеговая нагрузка | ||
M кНм | N кН | кНм | кН | |||
1 | 0,055 | 0,076 | -21,0 | -1428,2 | -17,57 | -1375,85 |
2 | 3,519 | 3,187 | -431,62 | -1165,0 | -312,43 | -1103,05 |
3 | 6,983 | 4,979 | -222,56 | -941,41 | -67,15 | -877,81 |
4 | 10,447 | 6,184 | -23,39 | -756,7 | 132,88 | -693,05 |
5 | 13,911 | 6,997 | 68,77 | -597,1 | 202,28 | -534,08 |
6 | 17,375 | 7,502 | 62,02 | -454 | 154,17 | -391,41 |
7 | 20,75 | 7,735 | -2,57 | -432 | 33,7 | -303,2 |
8 | 22,5 | 7,74 | 0 | |||
9 | 24,25 | 7,735 | -2,57 | -432 | -38,8 | -303,2 |
10 | 27,625 | 7,502 | 62,02 | -454 | -105,42 | -314,17 |
11 | 31,009 | 6,997 | 68,77 | -597,1 | -173,53 | -372,57 |
12 | 34,553 | 6,184 | -23,39 | -756,7 | -252,08 | -437,66 |
13 | 38,017 | 4,979 | -222,56 | -941,41 | -335,8 | -513,63 |
14 | 41,481 | 3,187 | -431,62 | -1165 | -366,78 | -607,42 |
15 | 44,945 | 0,076 | -21,0 | -1428,2 | -13,33 | -727,71 |
- от постоянной и односторонней снеговой нагрузки
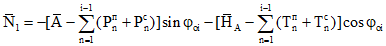 (8.67)
(8.67) (8.68)
(8.68)Значения расчетных усилий приведены в таблице 10.
Максимальный расчетный момент Mmax = -431,62 кН·м возникает в сечении x = 3,519 м. Ему соответствует нормальная сила N = -1165 кН.
Проверим напряжение в расчетном сечении (см. раздел 8.2, формулы 8.8, 8.9): значения S0, L0,  ,
, 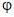 , F, W, Rс не изменяются. N0 = 432 кН, тогда:
, F, W, Rс не изменяются. N0 = 432 кН, тогда:
 (8.69)
(8.69)
Напряжение в расчетном сечении:
 (8.70)
(8.70)Устойчивость плоской формы изгиба обеспечивается раскреплением главных ребер от поворота сжатыми второстепенными арками. Это одна из особенностей пространственной работы рассматриваемой конструкции.
8.6. Расчет опорного узла
Сечение ребра на опоре следует проверить на скалывание по клеевому шву по формуле:
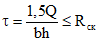 (8.71)
(8.71)где Rск - расчетное сопротивление древесины скалыванию;
b, h - ширина и высота сечения ребра на опоре.
Наибольшее значение поперечная сила имеет в сечении x1 = 0,055 м при воздействии постоянной и полной снеговой нагрузки:
 (8.72)
(8.72)Напряжение в этом сечении:

Опорное сечение не способно воспринять поперечную силу, поэтому применяем вариант узла, показанный на рис. 40. Считаем, что поперечная сила на опорном конце ребра воспринимается стальной обоймой. Высота обоймы назначается такой, чтобы скалывающие напряжения могли быть восприняты сечением ребра.
Абсцисса этого сечения определяется из соотношения:
 (8.73)
(8.73)здесь:
 (8.74)
(8.74) (8.75)
(8.75)
1 - ребро арки, 2 - опорный башмак, 3 - винты  16 мм,
16 мм,
4 - шурупы  20 мм, 5 - карман для опирания второстепенной
20 мм, 5 - карман для опирания второстепенной
арки, 6 - катки, d = 220, l = 300, 7 - нижний лист,  ,
,
8 - опорный контур

Ордината сечения определяется по формуле (8.30).
Высота обоймы должна удовлетворять соотношению:
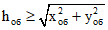 (8.76)
(8.76)Расчетная схема обоймы приведена на рис. 41.
На обойму действуют:
поперечная сила Qоп, вызываемый ею момент
 (8.77)
(8.77)и нормальная сила
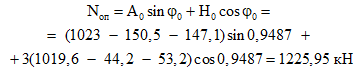 (8.78)
(8.78)Считаем, что сила Qоп передается на одну пластину, сминающую ребро.
Нижняя, пластина имеет размеры 0,75 x 0,19 м. Площадь F = 0,19 x 0,75 = 0,1425 м2.
Момент сопротивления

Напряжения в торце ребра от нормальной силы
 (8.79)
(8.79)Напряжения от момента
 (8.80)
(8.80) (8.81)
(8.81) (8.82)
(8.82)Давление на боковую пластину от составляющей Qоп, нормальной к пластине
 (8.83)
(8.83)Смятие древесины происходит под углом 72°. Допускаемое напряжение

Нижняя пластина работает на давление 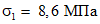 . Отношение длины пластины к ее ширине > 2, поэтому плита рассчитывается как балка на двух опорах.
. Отношение длины пластины к ее ширине > 2, поэтому плита рассчитывается как балка на двух опорах.
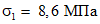 . Отношение длины пластины к ее ширине > 2, поэтому плита рассчитывается как балка на двух опорах.
. Отношение длины пластины к ее ширине > 2, поэтому плита рассчитывается как балка на двух опорах.
 принимаем толщину пластины: = 2,8 мм.
принимаем толщину пластины: = 2,8 мм.Пластина приварена по контуру к вертикальным и боковым листам угловыми швами (и вертикальным - снизу). Максимальное давление на шов:

Требуется высота шва

принимаем Kf = 8 мм.
Боковую пластину рассчитываем также на давление
 (8.84)
(8.84)
Требуемая толщина пластины  , принимаем
, принимаем  .
.
 , принимаем
, принимаем  .
.Давление на 1 п.м шва

Шов конструктивный Kf = 6.
Определяем расстояние между катками.
На обойму действует опрокидывающий момент от распора (рис. 41)
Mоп = H·0,22 + (H - H0)(0,4 + 0,22) - (A - A0)·0,055 =
= 1019,6·0,2 + 974·(0,4 + 0,22) - 297,6·0,055 =
= 224,31 + 60,39 - 16,37 = 268,3 кНм (8.85)
и удерживающий момент
 (8.86)
(8.86)Принимая отношение Mуд/Mоп = 1,2, определим
 , принимаем = 60 см. (8.87)
, принимаем = 60 см. (8.87)Ввиду того, что опорная реакция передается на катки за счет работы обоймы на изгиб в вертикальной плоскости, верхняя кромка ее должна быть присоединена к ребру.
Боковые наклонные пластины конструктивно присоединяются к ребру шурупами.
Опорный контур.
Усилие в опорном контуре

Применяем сталь 14Г2 с Rу = 310 МПа
Требуемая площадь сечения
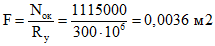
Принимаем сечение опорного контура
hок·bок = 0,14·0,03 м
Fок = 0,14·0,03 = 0,0042 м3
Напряжение, возникающее в опорном контуре

Закрепление контура на стене для передачи на нее сдвигающих усилий (см. п. 4.8), равных максимальному распору от односторонней снеговой нагрузки, располагаем посередине длины контура между башмаками и совмещаем с его стыком (рис. 10, сеч. а-а).
Толщина горизонтального листа башмака определяется из условий растяжения силой Nок.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 8.8 отсутствует. Возможно, имеется в виду рисунок 8. |
Длина листа (рис. 8.8)  .
.
 .
.Требуемая его толщина:
 (8.88)
(8.88)Принимаем  .
.
 .
.Принимаем высоту швов, присоединяющих опорный контур к башмаку: кf = 14 мм.
Требуется длина швов:
 (8.89)
(8.89)Принимаем Lш = 60 см - по 30 см с каждой стороны контура. Удлинение опорного контура между смежными узлами
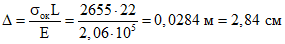 (8.90)
(8.90)Нормативная нагрузка составляет от расчетной:
 и
и 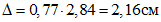
Составляющая перемещения, нормальная плоскости стены:

Дополнительные напряжения контура от этого смещения
 (8.91)
(8.91)Удлинение  от температурных деформаций при условной разности температур 30°
от температурных деформаций при условной разности температур 30°
 (8.92)
(8.92)Дополнительные напряжения
 (8.93)
(8.93)Суммарное напряжение в опорном контуре
 (8.94)
(8.94)Остальные элементы узла рассчитываются так же, как в примере сферического купола.
8.7. Опорное коньковое кольцо (рис. 42)
В соответствии с п. 4.8 кольцо должно быть рассчитано на косой изгиб и сжатие нормальной силой от постоянной и односторонней снеговой нагрузки.
а) изгибающие моменты, действующие перпендикулярно к плоскости кольца, определяются в соответствии с п. 4.6 от поперечных сил и моментов, возникающих в месте присоединения ребра к кольцу при односторонней снеговой нагрузке.
В нашем случае Qа и Mа определяются от вертикальных опорных реакций второстепенных арок, а также от их распоров  , действующих вдоль оси ребер, при загружении купола односторонней снеговой нагрузкой.
, действующих вдоль оси ребер, при загружении купола односторонней снеговой нагрузкой.
Поперечные силы от кососимметричной составляющей вертикальных воздействий определяются по формуле:
 (8.95)
(8.95)где:  - угол наклона касательной к оси арки;
- угол наклона касательной к оси арки;
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 8.3 отсутствует. |
 (8.96)
(8.96)В нашем случае:
Aк = 1/45[147,05(22,5 - 0,055) + 124,19(22,5 - 3,519) +
+ 101,33(22,5 - 6,983) + 78,46(22,5 - 10,447) +
+ 55,6(22,5 - 13,911) + 32,74(22,5 - 17,375)] = 196,03 кН



Поперечные силы от односторонне приложенных распоров второстепенных арок, нагруженных полной снеговой нагрузкой:
 - для свободной от нагрузки половины арки (8.97)
- для свободной от нагрузки половины арки (8.97) - для загруженной половины (8.98)
- для загруженной половины (8.98)В данном случае:
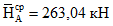 ;
; 
Воздействие распоров второстепенных арок уменьшает поперечные силы Qа и отвечающие им моменты Mа, полученные от вертикальных воздействий.
Расчетная величина  .
.
 .
.Mа = Qаrк = 20,71·1,75 = 36,25 кНм (8.99)
В соответствии с табл. 4 максимальный изгибающий момент в кольце
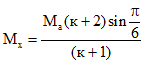 (8.100)
(8.100)Задаемся сечением кольца (рис. 42):
hк = 0,26 м
bк = 0,20 м
 .
. 





F = 2(0,26 + 0,18)·0,01 = 0,0088 м2


Тогда:
 .
.б) Изгибающий момент, действующий в плоскости кольца по табл. 3, равен:
 (8.101)
(8.101)где  - распор, приложенный к кольцу от односторонней снеговой нагрузки:
- распор, приложенный к кольцу от односторонней снеговой нагрузки:
 (8.102)
(8.102)Mу = 0,145·90,89·1,75 = 22,98 кНм
Распор от постоянной и односторонней снеговой нагрузки

Напряжения в кольце:
 (8.103)
(8.103)Итого  (8.104)
(8.104)
 (8.104)
(8.104)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 4.2 отсутствует. |
Проверка на кручение (см. табл. 4.2)
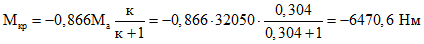 (8.105)
(8.105)Момент сопротивления кручению
 (8.106)
(8.106) (8.107)
(8.107)Соединение вертикальных и горизонтальных элементов между собой выполняется встык с подваркой корня или с прокладкой по ГОСТ 5264-80.
Минимальная допустимая толщина стенки определяется по табл. 28 п. 7.15 норм проектирования стальных конструкций [4].
Радиус инерции 

Радиус инерции 

Расчетная длина Lр = 1,75 м
Гибкость 


ИС МЕГАНОРМ: примечание. Уравнение дано в соответствии с официальным текстом документа. |
Приведенная гибкость 

Приведенный эксцентриситет 


и 

 ;
; 



ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 15 приводится в пункте 5.11, а не в пункте 5.9. |
8.8. Расчет кармана (п. 5.9, рис. 15)
Выполняем для второстепенной арки А-3, пролетом L3 = 15,6 м со стрелой подъема f3 = 2,75 м. Сеч. арки 32 x 14 см.
Опорная реакция Aв3 = 85 кН
Распор Hв3 = 120 кН
Угол наклона касательной к оси этой арки в точке примыкания к ребру купола




Рис. 43. Расчетная схема узла примыкания
второстепенной арки к главной
Угол между направлением волокон арки к опорной реакции 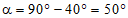 .
.
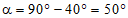 .
.ИС МЕГАНОРМ: примечание. Уравнение дано в соответствии с официальным текстом документа. |

Пластина 1.
Требуемая площадь по условиям смятия торца арки
 (8.108)
(8.108)При ширине арки 14 см средняя длина пластинки

Угол между осями ребра и второстепенной арки  (см. рис. 15 - внизу), тогда длинная сторона пластины
(см. рис. 15 - внизу), тогда длинная сторона пластины
 (см. рис. 15 - внизу), тогда длинная сторона пластины
(см. рис. 15 - внизу), тогда длинная сторона пластины
Принимаем L'к = 16 см (ширина пластины 2 по низу).
Пластину 1 рассчитываем, как прямоугольную с размерами = 12 x 14 см, опертую по трем сторонам и свободной четвертой.
Fп = 0,12·0,14 = 0,0168 м2
 ;
; 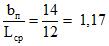 .
.Для этого соотношения в соответствии с  максимальный изгибающий момент
максимальный изгибающий момент

Требуемая толщина
 , принимаем
, принимаем 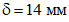
Толщина пластины 3 назначается конструктивно:

Шурупы 5 воспринимают усилие 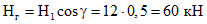 .
.
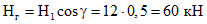 .
.Угол наклона касательной к ребру арки  . Допускаемое усилие на шуруп Tн = 2,50d2; принимаем d = 2 см.
. Допускаемое усилие на шуруп Tн = 2,50d2; принимаем d = 2 см.
 . Допускаемое усилие на шуруп Tн = 2,50d2; принимаем d = 2 см.
. Допускаемое усилие на шуруп Tн = 2,50d2; принимаем d = 2 см.Tн = 2,50·0,022 = 10,000 Н.
Требуется  .
.
 .
.Пластина 4
Опорная реакция от двух арок 2 x Aв3 = 2·87 = 174 кН
Нагрузка нормальная к пластине
 (8.109)
(8.109)В соответствии с рекомендациями п. 5.7, напряжение смятия в древесине под пластиной:

и длина пластины

Скатная составляющая
 (8.110)
(8.110)Ставим шурупы  , требуемое число их
, требуемое число их
 (8.111)
(8.111)Ставим 8 шурупов в два ряда, длина пластины равна 60 см. Среднее напряжение смятия

Изгибающий момент в пластине
 (8.112)
(8.112)Требуемая толщина

Принимаем  .
.
 .
.Сварные швы, присоединяющие пластину 3 к пластине 4, должны воспринять опорную реакцию A = 87 кН.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: возможно, имеется в виду приложение 1. |
ДЛЯ ПОСТРОЕНИЯ РАЗВЕРТОК СФЕРИЧЕСКИХ И СОМКНУТЫХ КУПОЛОВ
На основании расчета п. 6.8 составлена программа "KUPOL" на языке Бейсик, выходные данные которой позволяют строить развертки секторов сферических и сомкнутых куполов различной геометрии, с произвольным числом ребер и с учетом вентиляционной или осветительной шахты. Логическая схема программы приведена на рис. 44.
Программа состоит из двух модулей - главного и подпрограммы. В главном модуле осуществляется открытие выходного файла на диске, интерактивный ввод исходных данных и их вывод на дисплей, вычисление геометрических параметров Rа, R1, D1, f1, l0,  , а также с помощью цикла - массивов выходных величин
, а также с помощью цикла - массивов выходных величин  , li, gi (i = 1, ..., m). На каждом шаге цикла выполняется обращение к подпрограмме, реализующей решение трансцендентного уравнения (6.6) относительно
, li, gi (i = 1, ..., m). На каждом шаге цикла выполняется обращение к подпрограмме, реализующей решение трансцендентного уравнения (6.6) относительно  методом половинного деления. Предварительно задаются границы интервала
методом половинного деления. Предварительно задаются границы интервала  и
и  для
для  и точность решения
и точность решения  . Поскольку значения углов наклона панелей
. Поскольку значения углов наклона панелей 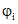 монотонно уменьшаются (рис. 23 б), правая граница интервала
монотонно уменьшаются (рис. 23 б), правая граница интервала  на каждом шаге цикла понижается до предыдущей величины
на каждом шаге цикла понижается до предыдущей величины  .
.
Условием выхода из цикла является выражение (6.7). Если конечное значение индекса К меньше требуемого числа панелей m, то на дисплей выводится сообщение: "Необходимо увеличить К I", и программа ждет ввода нового значения К, которое должно быть больше предыдущего. Затем выполнение расчета продолжается.
В зависимости от величины радиуса вентиляционной или осветительной шахты вычисляются параметры последней панели lm, gm, tm.
После окончания расчета на диске формируется файл результатов "KUP. DAT", который состоит из исходных данных D, f, n, t, b, h,  ,
,  , r, k и массивов выходных величин
, r, k и массивов выходных величин  , li-1, li, gi (i = 1, ..., m), представленных в табличной форме.
, li-1, li, gi (i = 1, ..., m), представленных в табличной форме.
Текст программы на языке Бейсик приводится ниже (стр. 120).
Для удобства пользования программой представим описание некоторых ее идентификаторов (см. табл. 11).
Программа "KUPOL" реализована на микро ЭВМ ДВК-2М.
В качестве примера, выполним построение развертки сектора сферического купола, рассмотренного в разделе 7, содержащем пример расчета такого купола.
ИСХОДНЫЕ ДАННЫЕ:
D = 60 | F = 10 | N = 24 | T = 1,5 | B = 0 |
H = 0 | E1 = 0 | E2 = 0 | R3 = 2 | К =30 |
РЕЗУЛЬТАТЫ СЧЕТА:
N/N | F1 | L(I - 1) | L(I) | G(I) |
П - 1 | 36,2384 | 7,83157 | 7,51301 | 0,159279 |
П - 2 | 34,5088 | 7,51301 | 7,18755 | 0,16273 |
П - 3 | 32,769 | 7,18755 | 6,85545 | 0,166052 |
П - 4 | 31,037 | 6,85545 | 6,51703 | 0,169207 |
П - 5 | 29,298 | 6,51703 | 6,1726 | 0,172219 |
П - 6 | 27,5563 | 6,1726 | 5,82244 | 0,175076 |
П - 7 | 25,8172 | 5,82244 | 5,46691 | 0,177769 |
П - 8 | 24,0807 | 5,46691 | 5,10632 | 0,180293 |
П - 9 | 22,3375 | 5,10632 | 4,741 | 0,18266 |
П - 10 | 20,5979 | 4,741 | 4,37129 | 0,184854 |
П - 11 | 18,8428 | 4,37129 | 3,9975 | 0,186895 |
П - 12 | 17,1085 | 3,9975 | 5,62002 | 0,18874 |
П - 13 | 15,3584 | 3,62002 | 3,23917 | 0,190426 |
П - 14 | 13,6148 | 3,23917 | 2,85531 | 0,19193 |
П - 15 | 11,8698 | 2,85531 | 2,4688 | 0,193256 |
П - 16 | 10,1224 | 2,4688 | 2,07999 | 0,194405 |
П - 17 | 8,36774 | 2,07999 | 1,68924 | 0,195376 |
П - 18 | 6,63127 | 1,68924 | 1,29692 | 0,196158 |
П - 19 | 4,87308 | 1,29692 | 0,903391 | 0,196785 |
П - 20 | 3,12658 | 0,903391 | 0,522105 | 0,190643 |
T(M) = 1,44808 | ||||
На рис. 45 изображена развертка, построенная на основе полученных результатов.




Идентификатор | Переменная |
D | D |
F | f |
N | n |
T | t |
B | b |
E1 | |
E2 | |
R3 | г |
K | k |
R1 | R1 |
D1 | D1 |
F1 | f1 |
A | |
Y0 | y |
K1 | |
K2 | |
E | |
X1 | |
Y1 | |
X | |
Y | |
F7(I) | |
L(I) | |
G(I) | gi |
T4 | tm |

ТЕХНИКО-ЭКОНОМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
СБОРНЫХ РЕБРИСТЫХ КЛЕЕНЫХ КУПОЛОВ
Технико-экономические характеристики куполов зависят от расхода древесины и стали, формы элементов, а также формы поверхности купола, влияющей на расход термоизоляционных и кровельных материалов.
Сопоставление экономичности вариантов выполняют по приведенным затратам, которые учитывают, помимо сметной стоимости конструкций, капиталовложения в производство материалов и изделий, стоимость монтажа и затраты на эксплуатацию.
Расход древесины и стали на несущие и ограждающие конструкции вариантов куполов при разных диаметрах (20 - 65 м) приведен в табл. 12. В ней помимо общего расхода древесины показан удельный расход ее на несущие конструкции, прогоны или второстепенные арки и панели покрытия.
Расходы древесины на различные варианты куполов при исходных диаметрах различаются незначительно (за исключением арочно-вспарушенного купола, требующего наименьшего расхода древесины при увеличенном расходе стали).
Следует отметить, что расход древесины на 1 м2 плана зала большинства куполов при диаметрах 40 - 45 м - очень близки к расходам на прямоугольные залы пролетом 24 м, перекрытые типовыми балками или гнутоклееными рамами (12,5 - 14,5 см/м2), а для арочно-вспарушенного купола диаметром 45 м - при шестиугольном плане - 10 см/м2, меньше, чем для залов, перекрытых типовыми эллиптическими арками пролетом 24 м (11,5 см/м2).
Из данных таблицы следует, что, как правило, в куполах с ребрами из криволинейных элементов расход древесины несколько меньше. Однако, следует иметь в виду, что стоимость криволинейных клееных элементов на 30% выше, чем прямолинейных (а неклееная древесина, например в панелях покрытия, - в 5 - 6 раз дешевле клееной). Поэтому при выборе варианта расход древесины (так же, как и стали) не является решающим. Выбор варианта, в основном, определяется архитектурно-планировочными соображениями и возможностями производственной базы.
В таблице 13 на примере нескольких вариантов куполов диаметром 45 - 65 м показано распределение расхода стали между отдельными частями купола. Они очень устойчивы в процентах к общему расходу при разных вариантах куполов, а также конструкции опорного контура и опорных узлов ребер.
В среднем около 35% стали расходуется на опорный контур, 16% - на опорные башмаки, 7% - на опорное коньковое кольцо, 8% - на оголовники ребер и стыковые накладки, 17% - на карманы и около 18% - на панели покрытия.
Данные табл. 12 позволяют также сделать вывод об относительной экономичности ДК при увеличении диаметра купола, так как расход древесины возрастает, примерно, пропорционально увеличению диаметра, а площадь зала вырастает пропорционально квадрату диаметра.
Таблица 12
(для IV снегового района)
Тип | Д м | Древесина см/% | Сталь кг | ||||
V1 | V2 | V3 | V | ||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Шестиугольник  | II | 45 | 7,7 ----- 55 | 3,8 ----- 27 | 2,5 ----- 18 | 14,0 ------ 100 | 8,0 |
30 | 3,5 ----- 35 | 3,2 ----- 32 | 3,3 ----- 33 | 10 ------ 100 | 7,0 | ||
20 | 2,5 ----- 33 | 1,6 ----- 22 | 3,4 ----- 45 | 7,5 ------ 100 | 7,0 | ||
V | 45 | 6,7 ----- 48 | 3,8 ----- 29 | 3,0 ----- 23 | 13 ----- 100 | 8,5 | |
30 | 3,5 ----- 35 | 3,0 ----- 30 | 3,5 ----- 35 | 10 ------ 100 | 7,5 | ||
20 | 2,5 ----- 32 | 1,6 ----- 21 | 3,6 ----- 47 | 7,7 ------ 100 | 7,5 | ||
 | III | 45 | 4,0 ----- 28 | 7,0 <*> ----- 40 | 3,5 ------ 37 | 14,5 ------ 100 | 9,6 |
30 | 2,8 ------ 23 | 4,8 <*> ----- 40 | 4,4 ------ 37 | 12,0 ------ 100 | 9,0 | ||
VI | 45 | 4,0 ----- 40 | 2,5 ------ 25 | 3,5 ------ 35 | 10,0 ------ 100 | 10,6 | |
30 | 4 ----- 33 | 3,6 ------ 30 | 4,4 ------ 37 | 12,0 ------ 100 | 10,0 | ||
Восьмиугольник  | II | 40 | 7,70 ----- 59 | 2,8 ----- 22 | 2,5 ----- 19 | 13 ----- 100 | 8,5 |
25 | 3,2 ----- 38 | 1,8 ----- 21 | 3,5 ----- 41 | 8,5 ----- 100 | 7,5 | ||
20 | 2,0 ----- 29 | 1,5 ----- 21 | 3,5 ----- 50 | 7,0 ----- 100 | 7,0 | ||
V | 60 | 7,8 ----- 52 | 4,7 ----- 31 | 2,5 ----- 17 | 15,0 ----- 100 | - | |
40 | 5,0 ----- 45 | 2,5 ----- 23 | 3,5 ----- 32 | 11,0 ----- 100 | 8,5 | ||
25 | 2,8 ----- 35 | 1,6 ----- 20 | 3,6 ----- 45 | 8,0 ----- 100 | 7,5 | ||
20 | 2,5 ----- 33 | 1,4 ----- 19 | 3,6 ----- 48 | 7,5 ----- 100 | 7,5 | ||
 | III | 60 | 6,4 ----- 38 | 7,6 <*> ----- 45 | 2,8 ----- 17 | 16,8 ------ 100 | - |
40 | 4,0 ----- 30 | 6,0 <*> ----- 44 | 3,5 ----- 26 | 13,5 ----- 100 | - | ||
25 | 4,0 ----- 38 | 3,2 <*> ----- 31 | 3,2 ----- 31 | 10,4 ----- 100 | - | ||
VI | 65 | 7,0 ----- 51 | 3,2 ----- 23 | 3,5 ----- 26 | 13,7 ----- 100 | 11,2 | |
Круг  | I | 60 | 10,2 ----- 65 | - | 5,6 ----- 35 | 15,8 ----- 100 | - |
40 | 7,0 ----- 64 | - | 4,0 ----- 36 | 11,0 ----- 100 | 8,0 | ||
IV | 60 | 8,4 ----- 60 | - | 5,6 ----- 40 | 14,0 ------ 100 | 9,5 | |
40 | 6,0 ----- 60 | - | 4,0 ----- 40 | 10,0 ------ 100 | 8,0 | ||
Примечания: V1 - расход на ребра; V2 - расход на прогоны или второстепенные арки; V3 - расход на панели. -------------------------------- | |||||||
Таблица 13
ИС МЕГАНОРМ: примечание. Сноски даны в соответствии с официальным текстом документа. |
Часть конструкции | |||||||
II Д - 45 м 6-угольн. | III Д - 45 м 6-угольн. | IV Д - 60 м круг | V Д - 45 м 6-угольн. | IV | Средний % | ||
Д - 45 м 6-угольн. | Д - 65 м 8-угольн. | ||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Опорный контур | 2,75 ------ 34 | 3,5 ------ 36 | 3,45 <*> ------ 36 | 2,75 ------ 34 | 4,0 ------ 38 | 3,7 <*> ----- 33 | 35 |
Опорные башмаки | 1,25 ------ 16 | 1,3 ------ 13,5 | 1,7 ------ 18 | 1,25 ------ 16 | 1,5 ------ 14 | 2,3 ------ 20 | 16 |
Опорное коньковое кольцо | 0,6 ------ 7,5 | 0,7 ----- 7 | 0,6 ------ 6,5 | 0,6 ------ 7,5 | 0,6 ------ 5,5 | 0,8 ------ 7,25 | 7 |
Оголовники и накладки полуарок | 0,65 ------ 8 | 0,65 ------ 7 | 1,10 ------ 11,5 | 0,65 ------ 8 | 0,6 ------ 5,5 | 0,8 ------ 7,25 | 8 |
Карманы | 1,45 ------ 18 | 1,65 ------ 17 | - | 1,45 ------ 18 | 1,9 ------ 18 | 1,6 ------ 14,5 | 17 |
Всего | 6,7 ------ 81 | 7,8 ------ 81 | 6,8 ------ 72 | 6,7 ------ 84 | 8,6 ------ 81 | 9,2 ------ 82 | 82 |
Панели покрытия | 1,3 ------ 16 | 1,8 ------ 19 | 2,6 ------ 28 | 1,3 ------ 16 | 2,0 ------ 19 | 2,0 ------ 18 | 18 |
ИТОГО | 8,0 ------ 100 | 9,6 ------ 100 | 9,5 ------ 100 | 8,0 ------ 100 | 10,6 ------ 100 | 11,2 ------ 100 | 9,48 |
Примечания: 1. В куполах типов II, III, V и VI диаметром 45 м опорный контур железобетонный с растянутой арматурой из стали А-III: опирание опорных башмаков - непосредственно на опорный контур.
2. В куполе IV при Д - 60 м и VI при Д - 65 м опорный контур из полосовой стали марки 14Г2. приваривается к нижнему листу опорного башмака ребер, передающего опорную реакцию на ж.б. обвязку стен через стальные катки.
1. Деревянные конструкции. Нормы проектирования: СНиП II-25-80. - М.: Стройиздат, 1982. - 64 с.
2. Пособие по проектированию деревянных конструкций/ЦНИИСК им. Кучеренко. - М.: Стройиздат, 1986. - 216 с.
3. Противопожарные нормы. СНиП 2.01.02-85/Госстрой СССР. - М.: ЦИТП Госстроя СССР, 1986. - 16 с.
4. Стальные конструкции. Нормы проектирования: СНиП II-23-81*/Госстрой СССР. - М.: ЦИТП Госстроя СССР, 1988. - 96 с.
5. Иллюстрированный каталог проектов общественных зданий с покрытиями из клееных деревянных конструкций/Госгражданстрой. - М.: ЦНТИ по гражданскому строительству и архитектуре, 1985. - 73 с.
6. Нагрузки и воздействия. Нормы проектирования: СНиП 2.01.07-85/Госстрой СССР. - М.: ЦИТП Госстроя СССР, 1986. - 36 с.
7. Рекомендации по определению снеговой нагрузки для некоторых типов покрытий/ЦНИИСК им. В.А. Кучеренко. - М.: 1984. - 22 с.
9. Липницкий М.Е., Горенштейн Б.В., Виноградов Г.Г. Железобетонные пространственные покрытия зданий. - Л-М.: Издательство литературы по строительству, 1965. - 474 с.
11. Бетонные и железобетонные конструкции. Нормы проектирования: СНиП 2.03.01-84/Госстрой СССР. - М.: ЦИТП Госстроя СССР, 1985. - 79 с.
12. Металлические конструкции. Учебник для ВУЗов. Под общей ред. Е.И. Беленя. - М., Стройиздат, 1976. - 600 с.
13. Беляев И.М. Сопротивление материалов. - М.: Изд. "Наука", 1976. - 608 с.
14. Жак С.М., Травуш В.И., Тимонин Е.М., Корес М.В. Авторское свидетельство N 1106880, кл. Е 04 В 1/32; Е 04 В 7/08, 1984.
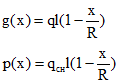








 ,
,  см,
см, 








 (см.
(см. 