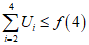СПРАВКА
Источник публикации
М.: Стройиздат, 1976
Примечание к документу
Название документа
"Пособие по расчетам опробования грунтов при инженерных изысканиях для строительства"
"Пособие по расчетам опробования грунтов при инженерных изысканиях для строительства"
Содержание
ПО РАСЧЕТАМ ОПРОБОВАНИЯ ГРУНТОВ
ПРИ ИНЖЕНЕРНЫХ ИЗЫСКАНИЯХ ДЛЯ СТРОИТЕЛЬСТВА
Настоящее Пособие содержит решения нескольких задач, относящихся к выбору наилучшего плана инженерно-геологического опробования грунтов: выбор метода исследования, оптимальное размещение точек опробования в слоистой толще и их концентрация в выработках, определение необходимого числа проб. Рекомендации, вытекающие из этих решений, рассчитаны на практическое применение инженерами-геологами на участках изысканий.
Табл. 5. Рис. 2.
В настоящем Пособии освещаются вопросы инженерно-геологического опробования методами математической статистики. Пособие содержит алгоритмы принятия решений инженером-геологом в простейших задачах оптимизации опробования и оценки необходимого числа наблюдений. Оно адресовано изыскателям-практикам; изложенный материал не требует от читателя специальной математической подготовки, рекомендуемые процедуры изложены подробно, алгоритмы расчетов расписаны по пунктам и сопровождаются примерами расчетов.
Изложение материала построено так, чтобы последовательно отвечать на вопросы, которые приходится разрешать инженеру-геологу в практике изысканий. Вначале рассмотрены задачи о выборе из ряда методов исследования, отличающихся по точности и стоимости, наиболее подходящего, затем об оптимальном соотношении числа технических выработок и отбираемых из них проб и о распределении точек опробования по разрезу слоистой толщи. Последний раздел посвящен процедурам определения необходимого числа наблюдений для достижения заданной точности и надежности оценки нормативного значения варьирующего показателя.
Работа составлена канд. техн. наук М.Т. Ойзерманом и мл. науч. сотрудником Б.Г. Слепцовым под руководством д-ра геол.-минер. наук М.В. Раца на основании теоретических разработок, выполненных лабораторией математических методов ПНИИИС.
1.1. В настоящем Пособии изложены математические приемы, позволяющие принимать научно обоснованные оптимальные решения при планировании опробования массивов грунтов. Рекомендуемые алгоритмы моделируют соображения, которыми руководствуется на практике опытный инженер-геолог, принимая те или иные методические решения.
1.2. Решение изыскательских задач, которым посвящено данное пособие, требует точных сведений об инженерных задачах, решаемых обычно проектировщиками по результатам изысканий. В Пособии рассматриваются только интегральные инженерные задачи, т.е. такие, в ходе решения которых производится осреднение нерегулярно меняющихся в пространстве свойств горных пород. Примерами таких задач являются расчет фильтрационного расхода, определение осадки сооружений и т.д. Не рассматриваются задачи, решение которых определяется экстремальными свойствами пород в "слабом звене".
1.3 Алгоритмические решения, рекомендуемые настоящим Пособием, требуют количественной характеристики изучаемых грунтов. Эти сведения всегда имеются в распоряжении инженера-геолога и их количество зависит от этапа изысканий и степени изученности района исследований. В силу этого настоящее Пособие может быть использовано как при составлении программы работ, так и на всех этапах проведения изысканий. Эффективность использования изложенных в Пособии математических методов находится в прямой зависимости от гибкости методики изысканий, объема и качества инженерно-геологической информации, которая может быть привлечена для планирования опробования на очередном этапе изысканий.
1.4. Общие принципы, которыми обычно руководствуется инженер-геолог в ходе работы, основываются на опыте инженерно-геологических изысканий и включают принципы: обратной связи; максимума информации; адаптации.
Эти принципы не связаны с математическими моделями геологических объектов, и не накладывают специальных ограничений на методику или результаты изысканий.
1.5. Принцип обратной связи применительно к инженерной геологии требует строить решение геологической задачи на основе результатов решения соответствующей инженерной задачи. В противном случае возникает разрыв между геологами и проектировщиками, препятствующий эффективному использованию результатов опробования при проектировании сооружений. Учет влияния результатов решения инженерной задачи позволяет математически ставить и решать конкретные задачи инженерно-геологических изысканий.
1.6. Необходимость разумной экономии средств при изысканиях находит выражение в виде принципа максимума информации, который выражается в двух формально эквивалентных формулировках:
1) минимизация затрат для получения заданного количества информации или заданной точности результатов при составлении программы изысканий и согласовании ее с Заказчиком;
2) получение максимума информации или максимальной точности результатов при фиксированных затратах, что больше подходит к периоду проведения изысканий, когда требуется наилучшим образом израсходовать выделенные на изыскания средства.
1.7. Принцип адаптации заключается в многошаговой коррекции плана инженерно-геологических изысканий в ходе их выполнения по мере поступления информации о структуре изучаемого объекта. Необходимость адаптации обусловлена тем фактом, что теоретические решения задач статистического характера содержат в качестве параметров неизвестные характеристики исследуемых объектов (например, характеристики степени неоднородности грунтов - дисперсии - в разных слоях). Планы опробования на последовательных этапах изысканий являются как бы последовательными приближениями к теоретически оптимальному плану, что позволяет на заключительных этапах сделать план опробования близким к теоретическому.
1.8. Подход к конкретным задачам статистической теории опробования, по результатам решения которых строятся формальные процедуры управления инженерно-геологическими изысканиями, разбивается на следующие этапы:
1) принятие той или иной модели пространственного распределения свойств грунтов, определяющих решение инженерной задачи;
2) формулировка инженерной задачи в терминах принятой модели;
3) выбор параметров оптимизации, т.е. тех величин, максимизация или минимизация которых является задачей исследования;
4) выбор параметров управления, значение которых меняет величину параметров оптимизации и процедуру опробования.
1.9. В качестве модели для результатов экспериментальных определений показателей физико-механических свойств грунтов используется модель независимых случайных величин, позволяющая получать состоятельные в научном отношении данные, необходимые для проектных расчетов.
1.10. Результат решения инженерной задачи (величины осадки, фильтрационного расхода, давления и т.п.) является в силу принятой модели функцией случайных аргументов (показателей свойств грунтов) и, поэтому может принимать различные значения. Таким образом, результат решения инженерной задачи тоже оказывается случайной величиной и характеризуется своим собственным распределением, средним значением и дисперсией.
1.11. Задачи расчета сооружений на естественных основаниях, как правило, строятся на замене реальных оснований сооружений фиктивной однородной средой, характеризуемой определенными значениями показателей свойств грунтов. В большинстве случаев расчетная схема или имеет вид линейной функции, или поддается линеаризации. В этом случае рассматривается среднее решение инженерной задачи, являющееся линейной функцией средних значений показателей свойств грунтов. Критерием точности (или количества информации) будет дисперсия этого среднего значения, которая и является основным параметром оптимизации. Параметрами управления являются различные характеристики сети опробования: количество проб и скважин, их стоимость, способ размещения точек опробования по слоям, концентрация проб в выработках.
1.12. В ходе инженерно-геологических изысканий неизбежно возникает задача определения необходимого числа наблюдений для оценки среднего значения показателя свойств грунтов с заранее заданной точностью и надежностью.
Рекомендуемые методы, распространяются лишь на те случаи оценки необходимого числа определений физико-механических или фильтрационных свойств грунтов, когда в ходе инженерно-геологических изысканий выполняются следующие условия:
1) цель работы формулируется как задача оценки неизвестного математического ожидания показателя свойств грунтов;
2) результаты определений свойств грунтов рассматриваются как случайные независимые величины, подчиняющиеся нормальному закону распределения;
3) известна необходимая точность и надежность оценки среднего значения показателя по результатам исследования.
1.13. Настоящую методику следует использовать, когда выполнена инженерно-геологическая съемка и проведено предварительное выделение инженерно-геологических элементов. Расчетная схема инженерной задачи носит детерминированный характер, в нее входят нормативные или расчетные значения показателей свойств грунтов. Оценка последних и представляет собой оценку неизвестного математического ожидания показателя.
1.14. На практике результаты определений свойств грунтов можно считать независимыми при достаточно редкой сети опробования.
Гипотезе о нормальном распределении в большинстве случаев не противоречат результаты определения физико-механических свойств грунтов в пределах инженерно-геологических элементов.
1.15. В настоящее время не существует формальной процедуры обоснованного назначения надежности исследования. В большинстве случаев проектировщики удовлетворяются 95%-ной надежностью. Точность оценки среднего значения показателя должна устанавливаться на основе соображений конструктивного характера по первым значениям результатов определений исследуемого показателя (подробнее об этом см. ниже).
1.16. Необходимое число определений зависит от степени неоднородности изучаемого грунта и в большинстве случаев оно не может быть установлено заранее. Как правило, прекращение процесса опробования (или определения свойств грунтов в лаборатории) может быть обосновано лишь в процессе проведения изысканий, на основе обработки поступающей информации о свойствах пород основания проектируемого сооружения. Момент прекращения опробования формально должен быть связан с достижением требуемой точности результатов исследования: либо среднего значения изучаемого показателя, либо среднего значения результата решения инженерной задачи, в которой данный показатель используется.
1.17. Основное преимущество такого подхода состоит в максимальном использовании непрерывно поступающей в ходе опробования информации. Основной недостаток - в противоречии с существующей практикой организации и планирования изысканий, когда объемы работ лимитируются заранее составленными программами и сметами. Так как избежать этого недостатка, очевидно, невозможно, в настоящем Пособии рассматриваются два подхода к задаче оценки необходимого числа определений, основанные: первый - на непрерывном (точнее многошаговом) и второй - на двухшаговом планировании исследований свойств грунтов. В зависимости от конкретной обстановки надлежит использовать тот или иной из этих путей. Оба они, и в особенности первый, наиболее эффективны при планировании и проведении дорогостоящих испытаний.
2.1. Выбор тех или иных методов изучения свойств грунтов определяется целевым назначением работ, особенностями объекта изысканий и реальными возможностями изыскательской организации. Обоснование выбора методов в процессе разработки программы инженерно-геологических изысканий основывается на соответствующих указаниях нормативно-методических документов в сочетании с предварительными соображениями об инженерно-геологических условиях площадки. В соответствии с этим устанавливаются методы и объемы опробования и определяется стоимость работ.
2.2. При производстве изысканий используют широкие комплексы методов исследования, что связано со сложностью изучаемого объекта. В процессе изысканий, после оценки систематических ошибок и установления различных корреляционных связей, возникает некоторая свобода выбора, в частности между точными и грубыми, прямыми и косвенными методами изучения свойств грунтов. С развитием экспресс-методов, полевых и геофизических методов вопрос о выборе между точными и дорогими методами, с одной стороны, и грубыми и дешевыми, с другой, становится все более актуальным.
2.3. Из предусмотренных программой методов определения свойств грунтов <*> следует выбирать тот, который характеризуется максимумом величины:
--------------------------------
<*> Имеются в виду методы, не имеющие систематических ошибок.
где 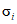 - среднеквадратичное отклонение результатов экспериментов, выполняемых i-м методом (способ его расчета см. в приложении);
- среднеквадратичное отклонение результатов экспериментов, выполняемых i-м методом (способ его расчета см. в приложении);
ci - стоимость единичного эксперимента, выполняемого i-м методом.
Величина  получила наименование эффективности i-го метода, а само правило - критерия максимума эффективности (КМЭ).
получила наименование эффективности i-го метода, а само правило - критерия максимума эффективности (КМЭ).
2.4. Выбор метода по КМЭ обеспечивает в рассматриваемых условиях максимальную точность оценки среднего значения показателя при фиксированных затратах на исследования или минимизирует затраты для достижения заранее заданной точности.
2.5. В соответствии с КМЭ решение вопроса о выборе одного из двух конкурирующих методов, отличающихся по точности, сводится к исследованию выражения:
 . (2)
. (2)При выполнении условия < предпочтение отдается первому методу, в противном случае - второму.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
2.7. Имеется прямой и дорогостоящий метод определения показателя Lп со стоимостью единичных определений cп. Известно также, что между показателем Lп и некоторым другим простейшим показателем Lк имеется линейная корреляционная зависимость с коэффициентом корреляции r (способ расчета коэффициента корреляции и уравнения регрессии приведен в приложении). Тогда целесообразно использовать уравнение корреляционной связи Lп = f(Lк) для замены дорогостоящих прямых определений дешевыми определениями Lк с последующим вычислением значений Lп по этому уравнению.
При этом следует решить вопрос, достаточно ли тесна корреляционная зависимость, чтобы подобная процедура была оправдана. Если задачей является оценка среднего значения показателя  , ответ дается следующим правилом: применение косвенного метода оценки
, ответ дается следующим правилом: применение косвенного метода оценки 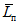 пересчетом через уравнение регрессии целесообразно при условии выполнения неравенства
пересчетом через уравнение регрессии целесообразно при условии выполнения неравенства
где  - абсолютная величина истинного коэффициента корреляции. Неравенство (3) является модификацией КМЭ (1).
- абсолютная величина истинного коэффициента корреляции. Неравенство (3) является модификацией КМЭ (1).
2.8. На практике мы располагаем лишь статистическими оценками  - выборочными значениями коэффициента корреляции r. Чтобы избежать ошибок при решении вопроса о выборе того или иного метода, надлежит поступать нижеследующим образом.
- выборочными значениями коэффициента корреляции r. Чтобы избежать ошибок при решении вопроса о выборе того или иного метода, надлежит поступать нижеследующим образом.
2.9. В тех случаях, когда выборочное значение  , следует в (3) использовать нижнюю доверительную границу коэффициента корреляции
, следует в (3) использовать нижнюю доверительную границу коэффициента корреляции  , где
, где  - уровень значимости; если
- уровень значимости; если 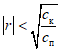 - верхнюю границу
- верхнюю границу  . Если при этой замене знак исходного неравенства не изменился, то выбор осуществляется в соответствии с КМЭ. При перемене знака на противоположный КМЭ не дает ответа на вопрос о выборе метода. В этом случае необходимо либо увеличить объем параллельных определений для более точной оценки величины
. Если при этой замене знак исходного неравенства не изменился, то выбор осуществляется в соответствии с КМЭ. При перемене знака на противоположный КМЭ не дает ответа на вопрос о выборе метода. В этом случае необходимо либо увеличить объем параллельных определений для более точной оценки величины  , либо воспользоваться для выбора метода какими-то другими соображениями (например, соображениями удобства, быстроты проведения работ и т.п.). Для того чтобы упростить пользование критерием (3), составлены номограммы для 95 и 99% доверительных вероятностей (рис. 1) <*>.
, либо воспользоваться для выбора метода какими-то другими соображениями (например, соображениями удобства, быстроты проведения работ и т.п.). Для того чтобы упростить пользование критерием (3), составлены номограммы для 95 и 99% доверительных вероятностей (рис. 1) <*>.
 , следует в (3) использовать нижнюю доверительную границу коэффициента корреляции
, следует в (3) использовать нижнюю доверительную границу коэффициента корреляции 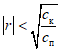 - верхнюю границу
- верхнюю границу --------------------------------
<*> Техника использования номограммы будет рассмотрена ниже на конкретном примере.
2.10. Решение вопроса на основе КМЭ, как и в п. 2.4, обеспечивает достижение максимальной точности оценки при фиксированных затратах или минимизацию затрат для достижения заданной точности.

при 10 <= Nпк <= 100 при уровнях значимости 0,05 и 0,01
Пример 1. При изучении суглинков на территории строящегося в Рязанской области филиала з-да ЗИЛ наряду с дорогостоящими штамповыми определениями деформируемости суглинков производились более дешевые компрессионные испытания. Уравнение регрессии и коэффициент корреляции между результатами штамповых и компрессионных испытаний (способ расчета в приложении) таковы:
Eшт = 7,18Eкомпр - 35,5;
r = 0,94 при Nпк = 13 пар. параллельных определений.
При решении вопроса о выборе метода будем исходить из представления, что штамповые испытания дают истинные значения модуля деформации, компрессионные же - лишь некую косвенную характеристику, ценность которой состоит в возможности перехода к значениям Eшт с помощью уравнения регрессии. Определяем стоимости прямого и косвенного определений.
Стоимость единичного испытания грунта штампом площадью 5000 см2 в шурфе нагрузкой до 5 кгс - 440 руб. <*> Проходка шурфа глубиной до 5 м - 267 руб. |
Итого cп = 707 руб. |
Стоимость компрессионного испытания - 29 руб. Отбор монолита - 7 руб. Проходка шурфа - 267 руб. |
Итого - cк = 303 руб. |
--------------------------------
<*> Сборник цен на проектные и изыскательские работы для строительства, ч. 1. М., Стройиздат, 1967, табл. 187, § 5; табл. 220, § 7а; табл. 186, § 1.
Таким образом,
 .
.Так как r = 0,94, то по неравенству (3)
 .
.Нижняя граница выборочного коэффициента корреляции r95% = 0,76 (см. приложение):
 .
.Знак неравенства не изменился и, следовательно, предпочтительнее метод компрессионных испытаний с оценкой истинного модуля деформации (штампового) через приведенное выше уравнение регрессии.
Пример 2. Рассмотрим вопрос о выборе метода исследования для оценки модуля деформации лессов Дунай-Днестровского массива. Здесь выполнено 48 параллельных определений штампами и в компрессионных приборах. По Nпк = 48 параллельным определениям r = 0,33 и неравенство (3) не выполняется. Используя верхнюю границу доверительного интервала r95% = 0,56, получаем
r95% = 0,56 < 0,65.
Так как неравенство (3) не выполняется, то следует отдать предпочтение прямому (штамповому) методу изучения деформируемости.
С другой стороны, для лессов выявлена тесная связь модуля деформации с показателем динамической пенетрации (H - приведенное число ударов)
Eшт = 43,4H + 10,9; r = 0,87; Nпк = 26.
Проверим целесообразно ли продолжать штамповые испытания или можно ограничиться динамической пенетрацией (стоимость единичного определения - 21 руб). Отношение стоимостей
 .
.Обращаясь к неравенству (3), делаем вывод, что и при существенно меньшей величине коэффициента корреляции при исследовании лессов Дунай-Днестровского массива орошения в дальнейшем предпочтительно использовать пенетрацию.
Пример 3. Использование номограммы.
Чтобы избежать несложных, но часто повторяющихся вычислений доверительных границ коэффициентов корреляции при использовании КМЭ, на рис. 1 приведены специальные номограммы для уровней значимости 0,05 и 0,01. Номограммы позволяют принять решение о выборе метода по критерию  при 10 <= Nпк <= 100.
при 10 <= Nпк <= 100.
 при 10 <= Nпк <= 100.
при 10 <= Nпк <= 100.Пусть, например, по результатам 30 параллельных определений требуется принять решение о выборе метода при  и
и  . Пусть
. Пусть  . В точке Nпк = 30 оси абсцисс номограммы восстанавливаем перпендикуляр до пересечения с кривыми 0,8. Получаем верхнюю и нижнюю доверительную границы для
. В точке Nпк = 30 оси абсцисс номограммы восстанавливаем перпендикуляр до пересечения с кривыми 0,8. Получаем верхнюю и нижнюю доверительную границы для  (равные соответственно 0,90 и 0,62). Нижняя доверительная граница находится выше горизонтальной линии с ординатой
(равные соответственно 0,90 и 0,62). Нижняя доверительная граница находится выше горизонтальной линии с ординатой  .
.
 и
и  . Пусть
. Пусть  . В точке Nпк = 30 оси абсцисс номограммы восстанавливаем перпендикуляр до пересечения с кривыми 0,8. Получаем верхнюю и нижнюю доверительную границы для
. В точке Nпк = 30 оси абсцисс номограммы восстанавливаем перпендикуляр до пересечения с кривыми 0,8. Получаем верхнюю и нижнюю доверительную границы для  .
.Следовательно, косвенный метод предпочтительнее.
Если верхняя доверительная граница лежит ниже горизонтальной линии с ординатой  , то предпочтительнее прямой метод оценки показателя. В тех случаях, когда
, то предпочтительнее прямой метод оценки показателя. В тех случаях, когда  попадает в интервал между значениями верхней и нижней границ доверительного интервала для коэффициента корреляции, выбор метода исследования определяется факторами, не учтенными в КМЭ.
попадает в интервал между значениями верхней и нижней границ доверительного интервала для коэффициента корреляции, выбор метода исследования определяется факторами, не учтенными в КМЭ.
и его дисперсии по разноточным наблюдениям
(включая комплекс прямых и косвенных признаков)
2.11. Во всех случаях использования разноточных (в том числе прямых и косвенных) методов исследования физико-механических свойств грунтов на завершающем этапе исследования необходимо использовать всю накопленную информацию для максимально точной оценки нормативных и расчетных значений показателей. При этом надлежит использовать все независимые (т.е. выполненные в разных точках массива) определения исследуемого свойства. Из числа параллельных определений (выполненных в одних и тех же точках прямым и косвенным методами для установления корреляционной связи) используются только прямые; косвенные не дают в этом случае никакой дополнительной информации.
2.12. Одновременный учет результатов прямых Lп и косвенных Lк определений осуществляется по формуле
ИС МЕГАНОРМ: примечание. Формула дана в соответствии с официальным текстом документа. |
где 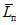 - оценка среднего значения показателя по результатам прямых определений;
- оценка среднего значения показателя по результатам прямых определений;
Nп - число определений показателя Lп прямым методом;
rj - коэффициенты корреляции, характеризующие тесноту используемых линейных корреляционных связей между прямым и косвенным показателями.
n - общее число (j = 1, 2, ..., n) используемых косвенных признаков.
2.13. Оценку  по формуле (4) следует использовать взамен обычно употребляющегося среднего арифметического, вычисляемого только по прямым или только по косвенным определениям.
по формуле (4) следует использовать взамен обычно употребляющегося среднего арифметического, вычисляемого только по прямым или только по косвенным определениям.
2.14. Дисперсия этой комплексной оценки  рассчитывается по формуле
рассчитывается по формуле
где  - дисперсия прямых определении, рассчитанная обычным способом (см. приложение).
- дисперсия прямых определении, рассчитанная обычным способом (см. приложение).
2.15. Доверительный интервал для неизвестного истинного значения ML при использовании оценок (4) - (4') заметно сужается (см. примеры). Оценка дисперсии (4') является приближенной. При практических расчетах целесообразно ширину доверительного интервала рассчитывать по прямым определениям, помещая его центр в точке L, рассчитанной по (4). Оценка (4') служит для ориентировочного суждения о величине получаемого выигрыша в точности.
2.16. При использовании разноточных прямых определений одного и того же показателя (при отсутствии систематических расхождений) среднее значение результата надлежит вычислять по формуле
 , (5)
, (5)где  - средние, вычисляемые по Ni определениям признака i-м методом (i = 1, 2, ..., n) с дисперсией
- средние, вычисляемые по Ni определениям признака i-м методом (i = 1, 2, ..., n) с дисперсией 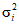 .
.
Дисперсия этой оценки
 (6)
(6)должна быть использована при построении доверительного интервала для выбора расчетных значений показателя L.
пород по комплексу прямых и косвенных определений
Воспользуемся приведенным ранее материалом по Рязани. Рассмотрим, какой эффект может быть получен за счет использования косвенных характеристик грунтов при вычислении максимально эффективной оценки такого важного показателя, как модуль деформации, при ограниченном числе его прямых определений посредством полевых испытаний штампом Eшт.
Для суглинков Рязанской области рассчитаны уравнения регрессии и коэффициенты корреляции между значениями модуля деформации по штамповым испытаниям, с одной стороны, и значениями коэффициента пористости и результатами компрессионных испытаний, с другой:
ИС МЕГАНОРМ: примечание. При публикации в издании М.: Стройиздат, 1976 допущен типографский брак. Текст, не пропечатанный в официальном тексте документа, в электронной версии данного документа выделен треугольными скобками. |
Eшт = 1702,20 - 1825,9<...>; r = 0,62 (Nпк = 17);
Eшт = 7,180Eкомпр - 35,50; r = 0,94 (Nпк = 13);
Eшт по 17 определениям равно 380·105 Па +/- 70·105 Па. С учетом 35 дополнительных определений коэффициента пористости рассчитываем 35 косвенных значений Eшт по уравнению регрессии. Оценка доверительного интервала с учетом косвенных определений по (4):
Eшт = 330·105 Па +/- 50·105 Па.
Если помимо штамповых наблюдений учесть 55 испытаний на компрессионном приборе, то доверительный интервал
Eшт = 380·105 Па +/- 40·105 Па.
Совместный учет компрессионных испытаний и пористости приводит к доверительному интервалу
Eшт = 370·105 Па +/- 30·105 Па.
Так как в расчете использованы выборочные оценки коэффициента корреляции, то полученный интервал несколько заужен. При практических расчетах надежности следует использовать оценку среднеквадратичного отклонения по прямым наблюдениям (70·105 Па), а среднее значение  по (4), т.е.
по (4), т.е.
Eшт = 370·105 Па +/- 70·105 Па.
И ЧИСЛА ТЕХНИЧЕСКИХ СКВАЖИН <*>
--------------------------------
<*> Эта и следующая задачи являются важнейшими частными случаями более общей задачи об исследовании слоистого основания. В настоящем Пособии общая задача и ее решение не рассматриваются ввиду их сложности. Интересующимся рекомендуются работы по статистической теории опробования Лаборатории математических методов ПНИИИС.
3.1. При инженерно-геологических исследованиях часто возникает задача оценки среднего значения показателя свойств грунтов:
 . (7)
. (7)При обычном способе расчета дисперсии этой оценки (см. приложение) предполагается, что значения показателей распределены в массиве грунтов совершенно беспорядочно. В реальных же массивах всегда существуют элементы неоднородности разных масштабов: более мелкие, обусловливающие вариацию показателя на небольших расстояниях, и более крупные, связанные с изменениями средних значений показателя от одной части массива к другой. При опробовании горных выработок эти разномасштабные элементы неоднородности проявляются в возникновении двух составляющих разброса данных: межскважинной и внутрискважинной.
3.2. В этом случае дисперсия среднего значения показателя свойств грунтов рассчитывается с учетом межскважинной и внутрискважинной составляющих дисперсии. Межскважинная составляющая дисперсии определяется флуктуацией средних по скважинам значений показателя; внутрискважинная - флуктуацией индивидуальных значений показателя в пределах скважин:
 , (8)
, (8)где J - число скважин, пробуренных на рассматриваемом участке;
n - число проб, отбираемых и анализируемых из каждой скважины;
3.3. При указанном в п. 3.1. строении грунтового массива точность оценки нормативных и расчетных значений показателей зависит от соотношения числа технических выработок J и числа проб n. Максимальная точность достигается при определенном (оптимальном) соотношении J и n. Это же соотношение позволяет достигнуть заданной точности при минимальных затратах на бурение и опробование.
Фиксируя  и минимизируя затраты на бурение технических скважин и опробование, определяем оптимальное число проб в скважине
и минимизируя затраты на бурение технических скважин и опробование, определяем оптимальное число проб в скважине
где cск и cпр - соответственно стоимость проходки скважины и стоимость отбора и анализа одной пробы.
3.4. Число технических скважин рассчитывается по формуле
где  - величина дисперсии среднего значения оцениваемого показателя (т.е. точность), которая должна быть достигнута в результате опробования.
- величина дисперсии среднего значения оцениваемого показателя (т.е. точность), которая должна быть достигнута в результате опробования.
3.5. Если же (как это нередко бывает на практике) фиксирована суммарная стоимость c опробования и бурения технических скважин, то число последних с учетом оптимальной детальности их опробования оценивается из выражения
 . (11)
. (11)3.6. Свойства полученного решения (9) таковы, что нет необходимости отбирать из каждой технической скважины в точности n* проб. Иногда это технически невыполнимо. Доказано, что небольшие отклонения от n* в отдельных скважинах при сохранении общего числа проб незначительно сказываются на точности оценки исследуемых показателей.
3.7. Теоретические решения содержат дисперсии исследуемых показателей свойств грунтов основания. Эти показатели могут быть рассчитаны по результатам инженерно-геологической съемки, по фондовым данным или результатам инженерно-геологических исследований на сходных в геологическом отношении участках. Такой подход позволяет планировать проводящиеся изыскания в виде двухэтапной процедуры, эффективность которой доказана теоретически.
Пример определения оптимального соотношения между
числом технических скважин и проб с целью оценки
среднего значения показателей свойств грунтов
Требуется спланировать бурение и опробование Первомайского месторождения пильных известняков в Дербентском районе Дагестана. Подробно рассмотрим порядок действий.
1. По результатам инженерно-геологических исследований на сопредельных или сходных в геологическом отношении участках, а также по фондовым материалам рассчитывается среднее значение изучаемого показателя и оцениваются компоненты общей дисперсии методом однофакторного дисперсионного анализа. Для этой цели в данном случае можно воспользоваться результатами ранее проведенных работ на расположенном поблизости и в сходных геологических условиях Дербентском месторождении. По этим данным вычислены (приложение, п. 2) оценки внутрискважинной и межскважинной составляющих дисперсии предела прочности 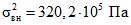 ,
,  (предел прочности является той основной характеристикой, которая используется при назначении марки известняка, как строительного камня).
(предел прочности является той основной характеристикой, которая используется при назначении марки известняка, как строительного камня).
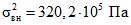 ,
,  (предел прочности является той основной характеристикой, которая используется при назначении марки известняка, как строительного камня).
(предел прочности является той основной характеристикой, которая используется при назначении марки известняка, как строительного камня).2. По данным о геологическом строении площадки (например, результатам инженерно-геологической съемки) и в зависимости от поставленной задачи определяется средняя глубина проходки скважин; в зависимости от категории грунтов по буримости устанавливается стоимость проходки 1 м скважины и средняя стоимость проходки одной скважины. Одновременно устанавливается стоимость монолита и анализа одной пробы.
Подошва продуктивной толщи на Первомайском месторождении находится на глубине 12 м, породы относятся ко II категории по буримости, чем и определяется глубина и стоимость проходки разведочных скважин (cск = 264 руб). Стоимость отбора одного монолита и единичное определение предела прочности при раздавливании cпр = 11,2 руб.
3. Далее задача может ставиться одним из двух способов. Если уточняется план опробования тогда, когда программа изысканий уже составлена, ставится задача наилучшего использования средств (т.е. при фиксированных затратах требуется максимальная точность оценки среднего значения показателя).
Если составляется программа изысканий, имеется возможность обоснованно оценить объемы опробования и число технических скважин, а следовательно, и объем работ в денежном выражении.
Назначаем точность  - величину допустимого среднеквадратичного отклонения среднего предела прочности. Другими словами, нам необходимо, чтобы истинное значение предела прочности MRсж с вероятностью
- величину допустимого среднеквадратичного отклонения среднего предела прочности. Другими словами, нам необходимо, чтобы истинное значение предела прочности MRсж с вероятностью  попало в интервал
попало в интервал
 - величину допустимого среднеквадратичного отклонения среднего предела прочности. Другими словами, нам необходимо, чтобы истинное значение предела прочности MRсж с вероятностью
- величину допустимого среднеквадратичного отклонения среднего предела прочности. Другими словами, нам необходимо, чтобы истинное значение предела прочности MRсж с вероятностью  попало в интервал
попало в интервал .
.При  этот интервал будет
этот интервал будет
 этот интервал будет
этот интервал будет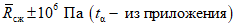 .
.По формулам (9) и (10) рассчитываем характеристики сети опробования:
 ;
;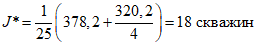 .
.Следовательно, для достижения заданной точности оценки среднего значения предела прочности известняков  на Первомайском месторождении необходимо пробурить 18 скважин и из каждой отобрать по 4 пробы.
на Первомайском месторождении необходимо пробурить 18 скважин и из каждой отобрать по 4 пробы.
 на Первомайском месторождении необходимо пробурить 18 скважин и из каждой отобрать по 4 пробы.
на Первомайском месторождении необходимо пробурить 18 скважин и из каждой отобрать по 4 пробы.После обработки результатов разведки Первомайского месторождения по схеме приложения рассчитаем следующие характеристики:
 ;
; .
.Фактически полученная точность оценки среднего значения предела прочности очень близка к требуемой. Используя эти данные, по формулам (9) и (10) получаем:
n* = 5 проб; J* = 18 скважин.
Таким образом, заложенный в программу первичный план опробования оказался близок к оптимальному.
Для достижения меньшей точности следует по (10) сократить число технических скважин.
Хорошая сходимость результатов в данном примере объясняется большим сходством в геологическом строении рассматриваемых месторождений и высокой детальностью опробования Дербентского месторождения. Для надежной оценки  и
и 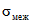 необходимо иметь не менее чем по 3 определения в трех или более скважинах. Если изыскания многолетние или имеется возможность их поэтапного планирования, то первичные рекомендации целесообразно распространять не на весь объем изысканий, а на некоторую его часть с последующим их уточнением.
необходимо иметь не менее чем по 3 определения в трех или более скважинах. Если изыскания многолетние или имеется возможность их поэтапного планирования, то первичные рекомендации целесообразно распространять не на весь объем изысканий, а на некоторую его часть с последующим их уточнением.
ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКОГО ОПРОБОВАНИЯ МЕЖДУ СЛОЯМИ ОСНОВАНИЯ
ПРИ ЛИНЕЙНОЙ РАСЧЕТНОЙ СХЕМЕ ИНЖЕНЕРНОЙ ЗАДАЧИ <*>
--------------------------------
<*> Линейной схемой называется такая схема решения инженерной задачи, в которую показатели свойств грунтов входят линейно, т.е. в первой степени. К числу таких схем относятся расчеты осадки, суммарной просадочности слоистой толщи, фильтрации вдоль слоистости и др.
4.1. От соотношения детальности опробования разных слоев зависит точность решения инженерной задачи и стоимость бурения и опробования. Поэтому возникает задача оптимального размещения точек опробования между слоями основания сооружения. Оптимальное соотношение числа проб обеспечивает максимальную точность решения при фиксированных затратах или минимизирует затраты на опробование для получения заданной точности.
4.2. При линейной расчетной схеме оценки параметров среднего решения инженерной задачи  следует рассчитывать по формулам:
следует рассчитывать по формулам:
 (12)
(12)где ai - весовые коэффициенты, зависящие от физического смысла инженерной задачи;
Li - среднее значение исследуемого показателя в i-м слое;
D(Li) - дисперсия среднего значения показателя в i-м слое;
 - дисперсия среднего решения инженерной задачи.
- дисперсия среднего решения инженерной задачи.4.3. Заданное значение дисперсии среднего решения инженерной задачи при минимальном общем числе проб N достигается при условии
где  - оптимальное число проб в слое с номером i;
- оптимальное число проб в слое с номером i;
В соответствии с формулой (13) и следует распределять точки опробования между слоями. Эта формула позволяет также при фиксированном общем числе проб достигать максимальной точности среднего решения инженерной задачи.
4.4. Для двухслойного основания выражение (13) приобретает вид:

или, что то же самое:
Последнее выражение не зависит от общего объема опробования и дает оптимальное соотношение между объемами опробования в двухслойном основании. Оно называется коэффициентом контрастности k.
4.5. В том случае, когда необходимо достигнуть заданной точности  - оценки среднего решения инженерной задачи, объемы опробования следует рассчитывать из выражений:
- оценки среднего решения инженерной задачи, объемы опробования следует рассчитывать из выражений:
4.6. При планировании общих объемов опробования и способа их размещения между слоями величины  и
и  должны оцениваться по данным ранее проведенных изысканий, по аналогии или на основании фондовых материалов.
должны оцениваться по данным ранее проведенных изысканий, по аналогии или на основании фондовых материалов.
4.7. Величина точности  устанавливается на основе соображений конструктивного характера в зависимости от этапа изысканий, класса и капитальности сооружения.
устанавливается на основе соображений конструктивного характера в зависимости от этапа изысканий, класса и капитальности сооружения.
Пример оптимального размещения точек
инженерно-геологического опробования между слоями
основания при линейной расчетной схеме инженерной задачи
Оптимальное размещение точек опробования при послойном опробовании может быть проиллюстрировано на примере исследования лессов и лессовидных суглинков Дунай-Днестровского массива орошения. Суммарная просадка двухслойной лессовой толщи  может быть представлена как линейная функция средних значений относительной просадочности по выделенным слоям:
может быть представлена как линейная функция средних значений относительной просадочности по выделенным слоям:
 может быть представлена как линейная функция средних значений относительной просадочности по выделенным слоям:
может быть представлена как линейная функция средних значений относительной просадочности по выделенным слоям: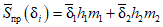 ,
,где  - средняя относительная просадочность i-го слоя;
- средняя относительная просадочность i-го слоя;
hi - мощность i-го слоя;
mi - коэффициент условий работы слоя.
Для нахождения оптимального способа распределения точек опробования воспользуемся формулами (14).
Для двух горизонтов лессов по каталогу скважин были получены средние мощности слоев: h1 = 2,9 м; h2 = 2,8 м. Роль весовых коэффициентов в этой задаче играет произведение мощности слоя на коэффициент условий его работы.
По результатам компрессионных испытаний для каждого горизонта были выписаны коэффициенты относительной просадочности при нагрузке 3 кгс/см2 (25 определений по верхнему горизонту и 28 определений - по нижнему). Оценки параметров относительной просадочности, рассчитанные по данным опробования согласно приложению 1, равны, соответственно:  ; S1 = 0,0032;
; S1 = 0,0032;  ; S2 = 0,0033. Коэффициент условий работы верхнего слоя m1 = 2, а для нижнего слоя m2 = 1. Фактически отобранные пробы лучше было разместить так:
; S2 = 0,0033. Коэффициент условий работы верхнего слоя m1 = 2, а для нижнего слоя m2 = 1. Фактически отобранные пробы лучше было разместить так:
 ; S1 = 0,0032;
; S1 = 0,0032;  ; S2 = 0,0033. Коэффициент условий работы верхнего слоя m1 = 2, а для нижнего слоя m2 = 1. Фактически отобранные пробы лучше было разместить так:
; S2 = 0,0033. Коэффициент условий работы верхнего слоя m1 = 2, а для нижнего слоя m2 = 1. Фактически отобранные пробы лучше было разместить так: ;
; .
.Коэффициент контрастности для рассматриваемого случая k = 2. Величина среднего значения суммарной просадки двухслойного основания  . Среднеквадратичное отклонение, по данным фактического опробования,
. Среднеквадратичное отклонение, по данным фактического опробования,  . Таким образом по результатам проведенного опробования с доверительной вероятностью 95% истинное среднее значение суммарной просадочности лежит в интервале 8 см +/- 0,85 см. Однако по формулам (15) легко показать, что полученная точность могла быть достигнута при оптимальном опробовании с меньшими затратами:
. Таким образом по результатам проведенного опробования с доверительной вероятностью 95% истинное среднее значение суммарной просадочности лежит в интервале 8 см +/- 0,85 см. Однако по формулам (15) легко показать, что полученная точность могла быть достигнута при оптимальном опробовании с меньшими затратами:
 . Среднеквадратичное отклонение, по данным фактического опробования,
. Среднеквадратичное отклонение, по данным фактического опробования,  . Таким образом по результатам проведенного опробования с доверительной вероятностью 95% истинное среднее значение суммарной просадочности лежит в интервале 8 см +/- 0,85 см. Однако по формулам (15) легко показать, что полученная точность могла быть достигнута при оптимальном опробовании с меньшими затратами:
. Таким образом по результатам проведенного опробования с доверительной вероятностью 95% истинное среднее значение суммарной просадочности лежит в интервале 8 см +/- 0,85 см. Однако по формулам (15) легко показать, что полученная точность могла быть достигнута при оптимальном опробовании с меньшими затратами: ;
; .
.Таким образом, 44 пробы, отобранные в соответствии в оптимальными рекомендациями, позволили бы получить такую же точность при снижении объема опробования примерно на 20%.
ПРИ ОЦЕНКЕ СРЕДНЕГО ЗНАЧЕНИЯ ПОКАЗАТЕЛЯ
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: п. 1.18 отсутствует. |
5.1. Процедуру оценки необходимого числа проб, изложенную в настоящем разделе, следует использовать при выполнении пп. 1.13 - 1.18.
5.2. Задача оценки необходимого числа наблюдений сводится к проверке выполнения неравенства
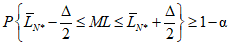 . (16)
. (16)Необходимо установить число экспериментальных определений (момент остановки исследования), когда неизвестное значение математического ожидания исследуемого показателя ML принадлежит интервалу  с вероятностью, не меньшей
с вероятностью, не меньшей  . Дисперсия показателя
. Дисперсия показателя  предполагается неизвестной и оценивается в ходе исследования, как это и бывает на практике. Величина
предполагается неизвестной и оценивается в ходе исследования, как это и бывает на практике. Величина  характеризует необходимую точность оценки среднего значения показателя.
характеризует необходимую точность оценки среднего значения показателя.
5.3. По мере поступления экспериментальных данных последовательно рассчитываем для числа выполненных определений показателя i = 2, 3, 4,..., N вспомогательные величины
5.4. В качестве решения N* выбираем минимальное целое значение N, удовлетворяющее неравенству
где N - общее число выполненных определений показателя;
5.5. Для оценки величины  надлежит использовать ориентировочные сведения о значении исследуемого показателя, результаты косвенных определений (в том числе и результаты экспресс-методов) или первые результаты прямых планируемых определений. Уровень надежности устанавливается исходя из характера исследуемого свойства, типа и класса капитальности сооружения и стадии проектирования, но из-за неразработанности соответствующих методов он обычно принимается
надлежит использовать ориентировочные сведения о значении исследуемого показателя, результаты косвенных определений (в том числе и результаты экспресс-методов) или первые результаты прямых планируемых определений. Уровень надежности устанавливается исходя из характера исследуемого свойства, типа и класса капитальности сооружения и стадии проектирования, но из-за неразработанности соответствующих методов он обычно принимается 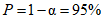 . По этим данным составляется таблица значений функции
. По этим данным составляется таблица значений функции
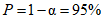 . По этим данным составляется таблица значений функции
. По этим данным составляется таблица значений функции . (19)
. (19)Первоначально следует ограничиться N <= 10 - 20 в зависимости от изменчивости исследуемого свойства пород и величины выбранного интервала  .
.
5.6. Приступая к оцениванию, пользуясь формулой (17), рассчитываем значения U2, U3 и U4 по первым четырем значениям показателя: L1, L2, L3, L4.
5.7. Вычисляем величину  и сравниваем ее со значением f(4), рассчитанным в п. 5.5. Если выполняется условие
и сравниваем ее со значением f(4), рассчитанным в п. 5.5. Если выполняется условие
то исследование следует прекратить, принять N* = 4, а в качестве оценки среднего значения показателя использовать величину
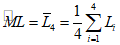 . (21)
. (21)5.8. Если условие (20) не выполняется, то исследование следует продолжать, причем каждый шаг (поступление очередной пробы) сводится к ряду нижеследующих стандартных расчетных операций.
5.9. Берем очередное (5-е и т.д.) значение исследуемого свойства и вычисляем величину Ui по (17).
Рассчитываем сумму  , для чего прибавляем величину к ранее полученному значению суммы.
, для чего прибавляем величину к ранее полученному значению суммы.
5.10. Проверяем неравенство
Если условие (20') выполняется, то исследование прекращаем, полагаем N* = N и в качестве оценки используем величину
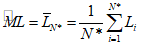 . (21')
. (21')5.11. При несоблюдении условия (20') расчетная процедура полностью повторяется, начиная с п. 5.9, причем при каждом обращении к п. 5.9 значение i увеличивается на единицу.
5.12. В тех случаях, когда характер изысканий не позволяет проводить опробование в несколько этапов, с помощью настоящей методики следует планировать число лабораторных экспериментов. В особо важных случаях, учитывая соотношение стоимости отбора монолита и лабораторного исследования, целесообразно отбирать заведомо большее число монолитов, а количество лабораторных экспериментов оценивать с помощью последовательной процедуры.
Рассмотрим результаты определения модуля деформации аллювиальных суглинков обских террас, полученные при изысканиях под строительство нефтепроводов и дорог на одном из участков долины р. Оби. Уже по первым нескольким значениям модуля деформации можно предположить, что среднее значение его будет более 100 кгс/см2. Необходимая точность исследования зависит от целого ряда причин, однако важнейшими из них являются требования проектировщиков и величина среднего значения модуля. В данном случае можно предположить, что точность +/- 25·105 Па достаточна для проектировщиков, и возможные при такой точности колебания среднего значения не потребуют изменения конструктивного решения. Необходимо установить количество определений модуля деформации, при котором с надежностью P = 95% истинное значение модуля попадает в интервал  .
.
 .
.Таблица 1
суглинков обских террас ( ;
;  )
)
 ;
;  )
)i | Li | (i - 1)Li |  |  | i(i - 1) | Ui | f(i) | Вывод | ||
1 | 149 | - | - | - | - | - | - | - | - | - |
2 | 160 | 160 | 149 | 11 | 121 | 2 | 61 | 61 | - | - |
3 | 174 | 348 | 309 | 39 | 1 521 | 6 | 254 | 315 | - | - |
4 | 90 | 270 | 483 | 213 | 45 369 | 12 | 3781 | 4096 | 648 | Опробование продолжать |
5 | 123 | 492 | 573 | 81 | 6 561 | 20 | 328 | 4424 | 1 620 | То же |
6 | 149 | 745 | 696 | 49 | 2 401 | 30 | 80 | 4504 | 2 920 | " |
7 | 96 | 576 | 845 | 269 | 72 361 | 42 | 1723 | 6227 | 4 540 | " |
8 | 172 | 1204 | 941 | 263 | 69 169 | 56 | 1238 | 7465 | 6 480 | " |
9 | 98 | 784 | 1113 | 329 | 108 241 | 72 | 1503 | 8968 | 8 745 | " |
10 | 108 | 972 | 1211 | 239 | 57 121 | 90 | 635 | 9603 | 11 335 | Опробование прекратить, N* = 10 |
ME = 132·105 Па +/- 25·105 Па (с вероятностью 95%) | ||||||||||
Назначив точность 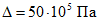 и надежность
и надежность 
 , рассчитаем значения функции f(i) по формуле (18). Заполняем табл. 1, вычисляя величины Ui по (17) и
, рассчитаем значения функции f(i) по формуле (18). Заполняем табл. 1, вычисляя величины Ui по (17) и  по поступлении каждого очередного значения Ei. На каждом этапе последовательно проверяем выполнение неравенства (20'). В нашем примере оно выполняется при i = 10. Необходимое число определений N* = 10. Среднее значение модуля деформации при этом
по поступлении каждого очередного значения Ei. На каждом этапе последовательно проверяем выполнение неравенства (20'). В нашем примере оно выполняется при i = 10. Необходимое число определений N* = 10. Среднее значение модуля деформации при этом 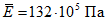 .
.
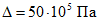 и надежность
и надежность 
 , рассчитаем значения функции f(i) по формуле (18). Заполняем табл. 1, вычисляя величины Ui по (17) и
, рассчитаем значения функции f(i) по формуле (18). Заполняем табл. 1, вычисляя величины Ui по (17) и 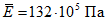 .
.
деформации методом последовательного оценивания
Следовательно, десяти определений модуля деформации аллювиальных суглинков обских террас достаточно для того, чтобы утверждать, что истинное значение модуля деформации с 95%-ной надежностью попадает в интервал 132·105 +/- 25·105 Па.
Устойчивость рекомендаций, получаемых в результате последовательного оценивания, была подтверждена также методом статистических испытаний (Монте-Карло) на ЭВМ, что свидетельствует об эффективности предложенной процедуры.
При практических расчетах рекомендуется представление результатов в виде специального графика (рис. 2). Точка пересечения графика f(i) с ломаной  указывает на выполнение неравенства (20').
указывает на выполнение неравенства (20').
5.13. В тех случаях, когда находящихся в распоряжении инженера геолога результатов прямых определений исследуемого показателя недостаточно для оценки среднего значения показателя с заданной точностью и надежностью, рекомендуется применять двухэтапную процедуру последовательного оценивания. При этом на основе имеющейся информации производится оценка "второго шага", т.е. определяется число проб, которое необходимо дополнительно отобрать для решения поставленной задачи.
5.14. При двухэтапной процедуре на первом этапе отбирается и анализируется n проб. Затем на основе этой информации вычисляется количество m проб, которое необходимо отобрать на втором этапе исследования, чтобы сделать вывод: математическое ожидание исследуемого свойства ML с вероятностью  принадлежит интервалу фиксированной длины
принадлежит интервалу фиксированной длины  .
.
5.15. На основании полученных на первом этапе исследования (или имеющихся в фондах) данных о свойствах пород основания рассчитываем величину
 , (22)
, (22)являющуюся несмещенной оценкой неизвестной генеральной дисперсии показателя  , где Li и Ln - соответственно индивидуальные и среднее значения показателя исследуемого, свойства пород.
, где Li и Ln - соответственно индивидуальные и среднее значения показателя исследуемого, свойства пород.
5.16. По таблицам распределения Стьюдента с f = n - 1 степенями свободы (см. приложение) находим такое значение,
что
 ,
,где  - случайная величина, имеющая распределения Стьюдента с f = n - 1 степенями свободы.
- случайная величина, имеющая распределения Стьюдента с f = n - 1 степенями свободы.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
5.11. Проверяем выполнение условия
Если условие (23) выполняется, то решением задачи будет N = n. В этом случае исследование следует прекратить и в качестве оценки неизвестного среднего принять
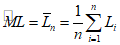 . (24)
. (24)5.18. Если условие (23) не выполняется, то необходимо провести второй этап исследования, объем которого оценивается нижеследующим образом. Полагаем N* наименьшим целым положительным числом, удовлетворяющим неравенству
 . (25)
. (25)5.19. Дополнительный объем опробования, который следует отобрать на втором этапе исследования, равен
m = N* - n,
а в качестве оценки ML надлежит использовать величину
 . (26)
. (26)Предположим, что в нашем распоряжении имеется пять (n = 5) экспериментальных определений модуля деформации суглинков из предыдущего примера (табл. 1). Среднее значение модуля по этим наблюдениям:
 ,
,а дисперсия  . Зададимся точностью
. Зададимся точностью 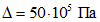 и надежностью
и надежностью  . При этом величина
. При этом величина  (см. приложение). Необходимо выяснить, какое число определений модуля деформации следует выполнить с тем, чтобы истинное значение среднего попадало в интервал
(см. приложение). Необходимо выяснить, какое число определений модуля деформации следует выполнить с тем, чтобы истинное значение среднего попадало в интервал  с надежностью 95%.
с надежностью 95%.
 . Зададимся точностью
. Зададимся точностью 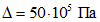 и надежностью
и надежностью  . При этом величина
. При этом величина  (см. приложение). Необходимо выяснить, какое число определений модуля деформации следует выполнить с тем, чтобы истинное значение среднего попадало в интервал
(см. приложение). Необходимо выяснить, какое число определений модуля деформации следует выполнить с тем, чтобы истинное значение среднего попадало в интервал  с надежностью 95%.
с надежностью 95%.Подставив заданные значения в (23), увидим, что это условие не выполняется, так как n < 15. При этом N* = 15. Таким образом, число проб, которое надлежит отобрать дополнительно m = N* - n = 15 - 5 = 10. Это значит, что на основании первых пяти наблюдений общее число проб существенно завышено.
Однако если в качестве первого этапа отобрать 10 проб, а не 5, то  ;
; 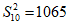 и условие (23) выполняется, т.е. опробование следует закончить. Таким образом, получается совпадение с последовательной процедурой.
и условие (23) выполняется, т.е. опробование следует закончить. Таким образом, получается совпадение с последовательной процедурой.
 ;
; 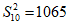 и условие (23) выполняется, т.е. опробование следует закончить. Таким образом, получается совпадение с последовательной процедурой.
и условие (23) выполняется, т.е. опробование следует закончить. Таким образом, получается совпадение с последовательной процедурой.Из этого примера видно, что точность двухэтапной процедуры существенно зависит от объема имеющейся на первом этапе информации. В качестве первого этапа следует использовать материалы предыдущих изысканий, а также данные по сходным в геологическом отношении участкам.
5.20. Эффективность двухэтапной процедуры, как видно из примера, существенно зависит от объема и количества информации, имеющейся в распоряжении инженера-геолога на стадии составления программы исследования, а также на ранних этапах изысканий.
5.21. Так как в теории отсутствуют какие-либо указания относительно выбора оптимального объема опробования на первом этапе, методом статистического моделирования (Монте-Карло) составлена табл. 2, в которой приведены данные, характеризующие возможный разброс N* в зависимости от объема первого шага n и коэффициента вариации VL, %.
5.22. В распоряжении геологов часто нет прямых определений показателя, который необходимо исследовать. В этом случае ориентировочные данные о характере распределения этого показателя могут быть получены по результатам исследования сходных в инженерно-геологическом отношении объектов или же по значениям косвенных показателей, определенных на исследуемом участке. На основе этих данных устанавливаются приближенные значения  ,
,  и VL. После этого назначается точность
и VL. После этого назначается точность  и надежность
и надежность  . Располагая этими данными, с помощью табл. 2 назначается объем опробования на первом этапе исследования.
. Располагая этими данными, с помощью табл. 2 назначается объем опробования на первом этапе исследования.
Таблица 2
( ;
; 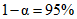 )
)
 ;
; 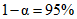 )
)n проб | ||||||
5 | 10 | 15 | 20 | 25 | 30 | |
V = 10% | 2 - 9 | 3 - 7 | 2 - 6 | 3 - 5 | 3 - 5 | 3 - 5 |
V = 15% | 7 - 25 | 6 - 26 | 6 - 14 | 6 - 12 | 6 - 12 | 7 - 11 |
V = 20% | 18 - 38 | 8 - 28 | 11 - 23 | 12 - 22 | 11 - 21 | 12 - 20 |
V = 30% | 17 - 73 | 20 - 62 | 26 - 52 | 28 - 50 | 26 - 46 | 27 - 45 |
5.23. В качестве оптимального объема опробования на первом этапе следует выбирать нижнюю границу разброса, приведенную в табл. 2. Под величиной n проб в данном случае следует понимать тот объем исходной информации, на основе которого производилась оценка VL.
5.24. В ходе лабораторного исследования отобранных проб полезно осуществлять вторичный контроль необходимого объема экспериментов, используя последовательную методику. В силу ориентировочного задания VL может оказаться, что часть отобранных проб анализировать не следует. Это позволяет избежать лишних объемов лабораторных работ.
5.25. При проведении изысканий изучение различных свойств грунтов проводится с различной точностью и надежностью. В этом случае не всегда можно непосредственно пользоваться данными табл. 2. Необходимо ее пересчитать для требуемых значений t и  . При назначении нового
. При назначении нового  (в % от среднего значения показателя) следует рассчитать величину
(в % от среднего значения показателя) следует рассчитать величину  и все табличные значения разделить на эту величину. Если изменяется t, то, пользуясь новым значением tн, вычисляют величину
и все табличные значения разделить на эту величину. Если изменяется t, то, пользуясь новым значением tн, вычисляют величину  и табличные значения умножают на нее.
и табличные значения умножают на нее.
 и все табличные значения разделить на эту величину. Если изменяется t, то, пользуясь новым значением tн, вычисляют величину
и все табличные значения разделить на эту величину. Если изменяется t, то, пользуясь новым значением tн, вычисляют величину  и табличные значения умножают на нее.
и табличные значения умножают на нее.необходимого числа наблюдений
Допустим, что необходимо исследовать сжимаемость суглинков компрессионным методом на некотором участке. По фондовым материалам устанавливаем, что VE ~= 30%. Точность оценки Eкомпр +/- 10% заведомо достаточна для проектировщиков (в действительности столь высокая точность практически никогда и не требуется). Величина VE оценивалась по 20 определениям Eкомпр. Возможный разброс N в этом случае 28 - 50 определений. Объем опробования на первом этапе должен составить 28 определений. Однако если фондовые материалы были подобраны по достаточно близким по свойствам участкам, то они могут быть учтены в расчетах. Тогда следует отобрать лишь 8 проб и затем совместно обработать результаты полевых и фондовых данных, определить недостающий объем опробования. Объем первого шага n = 28 в данном случае оптимален. Действительно, при n < 28 ухудшается качество оценки дополнительного объема m = N* - n, а при n > 28 может оказаться, что уже на первом этапе допущен перебор и n > N*. Проверка достигнутой точности и необходимости дополнительного опробования осуществляется далее по алгоритму двухэтапной процедуры.
1. Среднее значение исследуемого показателя рассчитывается по формуле
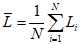 ,
,где N - число экспериментальных определений значений свойств грунтов;
Li - частное значение показателя.
Дисперсия показателя рассчитывается по формуле
 .
.Среднеквадратичное отклонение
 .
.Оценка точности определения среднего значения показателя (среднеквадратичное отклонение среднего значения показателя)
 .
.2. Вычисление компонент дисперсии - межскважинной и внутрискважинной - по стандартной схеме однофакторного дисперсионного анализа производится следующим образом. Число скважин J (j = 1, 2, ..., J), число проб в скважине n (i = 1, 2, ..., n), частное значение показателя Lij. Обозначим сумму значений показателя L по j-й скважине:
 .
.Рассчитываем три суммы:
 ,
,где N - общее число проб.
Если в скважинах отобрано различное число проб, то

Внутрискважинная составляющая дисперсии рассчитывается по формуле
 .
.Межскважинная составляющая может быть оценена следующим образом:
 ,
,где  рассчитывается по формуле
рассчитывается по формуле
 .
.Вычисление всех названных характеристик рассмотрим на результатах исследования прочности сарматских известняков Дербентского района (табл. 3).
Таблица 3
Скв. 14 | Скв. 33 | Скв. 36 | Скв. 38 | Скв. 44 | Скв. 40 | Скв. 54 |
43 | 125 | 41 | 66,2 | 85,5 | 95 | 60,5 |
64,4 | 93 | 61,6 | 74,8 | 98,2 | 111,1 | 86 |
88 | 135,2 | 86,2 | 81,5 | 107 | 136,1 | 76,8 |
79 | 93 | 51,2 | 93 | 100 | 94,3 | 104 |
55,2 | 118 | 44,1 | 49,5 | 63 | 100 | 52,6 |
 | ||||||
329,6 | 564,2 | 284,1 | 365 | 453,7 | 536,5 | 379,9 |
 ;
;
 ;
; ;
; .
.Теперь рассчитаем межскважинную и внутрискважинную составляющие дисперсии:
 ;
; ;
;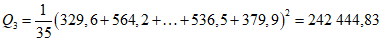 ;
; ;
;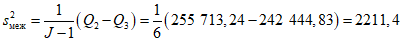 .
.Отсюда
 .
.3. Расчет коэффициента корреляции и уравнения регрессии. Имеется 15 параллельных определений природной влажности и модуля деформации Eкомпр, представленных в табл. 4.
Таблица 4
Wпр | E | Wпр | E | Wпр | E |
36 | 44,7 | 26 | 58,3 | 24 | 57,5 |
36 | 46,4 | 35 | 46,2 | 46 | 28,7 |
46 | 39,7 | 33 | 48,1 | 51 | 34,2 |
36 | 43,3 | 43 | 36,1 | 42 | 51,3 |
50 | 31 | 34 | 50,5 | 38 | 46,4 |
 ;
; ;
; ;
; .
.Отсюда величина коэффициента корреляции
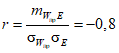 .
.Отыскивается линейная регрессия вида:
 ,
,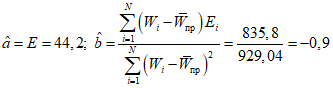 ;
;E = 44,2 - 0,9(Wпр - 38) = 78,4 - 0,9Wпр.
4. Значения P % пределов для t - распределения Стьюдента в зависимости от числа f степеней свободы представлены в табл. 5.
Таблица 5
f = n - 1 | Значения | ||||
10 | 5 | 2,5 | 2 | 1,5 | |
1 | 6,314 | 12,706 | 25,452 | 31,821 | 63,657 |
2 | 2,920 | 4,308 | 6,205 | 6,965 | 9,925 |
3 | 3,353 | 3,182 | 4,177 | 4,541 | 5,841 |
4 | 2,132 | 2,776 | 3,495 | 3,747 | 4,604 |
5 | 2,015 | 2,571 | 3,163 | 3,365 | 4,032 |
6 | 1,943 | 2,447 | 2,969 | 3,143 | 3,707 |
7 | 1,895 | 2,365 | 2,841 | 2,998 | 3,499 |
8 | 1,860 | 2,306 | 2,852 | 2,896 | 3,355 |
9 | 1,833 | 2,262 | 2,685 | 2,821 | 3,250 |
10 | 1,812 | 2,228 | 2,634 | 2,764 | 3,169 |
12 | 1,782 | 2,179 | 2,560 | 2,681 | 3,055 |
14 | 1,761 | 2,245 | 2,510 | 2,624 | 2,977 |
16 | 1,746 | 2,120 | 2,473 | 2,583 | 2,921 |
18 | 1,734 | 2,101 | 2,445 | 2,552 | 2,878 |
20 | 1,725 | 2,086 | 2,423 | 2,528 | 2,845 |
22 | 1,717 | 2,074 | 2,405 | 2,508 | 2,819 |
24 | 1,711 | 2,064 | 2,391 | 2,492 | 2,797 |
26 | 1,706 | 2,056 | 2,379 | 2,479 | 2,779 |
28 | 1,701 | 2,048 | 2,369 | 2,467 | 2,763 |
30 | 1,697 | 2,042 | 2,360 | 2,457 | 2,750 |
1,645 | 1,960 | 2,241 | 2,326 | 2,576 | |
При  значения P % пределов t - распределения Стьюдента совпадает со значением P % пределов нормального распределения.
значения P % пределов t - распределения Стьюдента совпадает со значением P % пределов нормального распределения.
УДК 624.131.3 |