"Пособие по гидравлическим расчетам малых водопропускных сооружений"

В пособии изложены рекомендации для выполнения гидравлических расчетов малых водопропускных сооружений на железных и автомобильных дорогах: водопропускных труб, малых мостов, фильтрующих и переливных насыпей, водоотводных и сопрягающих сооружений (быстротоков, перепадов, водобойных колодцев и стенок, консольных сбросов, рассеивающих трамплинов, виражей и др.). Даны указания по выбору рациональных типов и отверстий сооружений, приведена методика расчета размывов и назначения укрепления за ними.

Рассчитано на инженерно-технических работников, занятых проектированием железных и автомобильных дорог.

Выпущено по заказу Всесоюзного научно-исследовательского института транспортного строительства.

ПРЕДИСЛОВИЕ

Пособие разработано в развитие СНиП 2.05.03-84 применительно к гидравлическим расчетам малых водопропускных сооружений.

По сравнению с Руководством по гидравлическим расчетам малых искусственных сооружений, вышедшим в 1974 г., в настоящем документе существенно переработан ряд глав, посвященных гидравлическим расчетам основных типов малых искусственных сооружений: водопропускных труб, малых мостов, их нижних бьефов, сопрягающих сооружений.

Разработанные в Пособии методы позволяют вычислить детальные гидравлические характеристики в любой точке водопропускного тракта сооружений, установить деформации в их нижних бьефах и на основе этого определить рациональные размеры сооружений и их элементов.

В Пособии приведены как упрощенные зависимости, номограммы и графики, ускоряющие расчеты, так и детальные алгоритмы, на основе которых разработаны программы, позволяющие вести гидравлические расчеты малых водопропускных сооружений с учетом всего многообразия реальных условий их работы.

Учитывая исключительную важность защиты окружающей среды, в Пособии излагаются экологические аспекты гидравлики малых водопропускных сооружений.

Пособие рассмотрено и одобрено научно-техническими советами Минтрансстроя и МПС и рекомендовано Главным управлением проектирования и капитального строительства Минтрансстроя для использования при выполнении гидравлических расчетов в процессе проектирования малых водопропускных сооружений на железных и автомобильных дорогах страны.

В составлении Пособия приняли участие сотрудники лаборатории гидравлики, гидрологии и ледовых воздействий ЦНИИСа, учебных и проектных институтов: гл. 1 - Г.Я. Волченков (ЦНИИС); гл. 2 - В.В. Беликов, В.С. Муромов, П.Г. Петров (ЦНИИС), К.В. Матвеев (МИИТ); гл. 3 - Г.Я. Волченков и В.Ф. Залесский (ЦНИИС), Б.Ф. Перевозников (Союздорпроект); гл. 4 - Н.М. Константинов (МАДИ), Л.И. Высоцкий (Саратовский политехнический институт), В.В. Беликов, В.С. Муромов (ЦНИИС), М.Л. Шаталов (МИСИ); гл. 5 - Г.Я. Волченков, В.В. Беликов, А.Н. Милитеев (ЦНИИС), Г.С. Пичугов (Гипродорнии), В.И. Алтунин (МАДИ); гл. 6 - Г.С. Пичугов (Гипродорнии), В.А. Большаков (КАДИ), В.Ш. Цыпин (ЦНИИС); гл. 7 - Г.Я. Волченков, В.В. Беликов, В.Ш. Цыпин (ЦНИИС), Н.М. Константинов (МАДИ), Н.М. Букраба, И.Д. Денисенко (КАДИ); гл. 8 - Н.М. Константинов, Н.А. Петров, В.А. Ширченко (МАДИ), Б.Ф. Перевозников (Союздорпроект); гл. 9 - В.А. Александров (МАДИ); гл. 10 - Г.Я. Волченков, Л.Г. Бегам, В.Ш. Цыпин (ЦНИИС); гл. 11 - Н.А. Петров, Н.И. Павлова (МАДИ); гл. 12 - Н.М. Константинов, Н.А. Петров (МАДИ).

УСЛОВНЫЕ ОБОЗНАЧЕНИЯ

b - отверстие водопропускного сооружения; ширина водослива, м;

b_к - средняя ширина потока в сечении с критической глубиной, м;

b_дн - ширина сечения по дну, м;

B - ширина потока поверху в нестесненном состоянии, м;

B_к - то же, при критической глубине, м;

B_разл и B_раст - соответственно ширина разлива и растекания, м;

C - коэффициент Шези, м^0,5/с;

C_р - сцепление связных грунтов, МПа;

D - диаметр круглой трубы в свету, м;

d, d_н - соответственно диаметр частиц грунта и каменной наброски, мм;

F - площадь водосбора, км²;

- число Фруда (параметр кинетичности);

g - ускорение силы тяжести, равное 9,8 м/с²;

H - подпертая глубина относительно нижней точки входного сечения трубы или моста, м;

H₀ - напор перед сооружением с учетом скорости подхода потока, м;

H_нас - высота насыпи, м;

h, h_нб, h_с, h_к и h₀ - глубины воды соответственно в произвольном сечении, нижнем бьефе, в сжатом сечении, критическая и нормальная, м;

h_вх, h_вых и h_вых(ог) - соответственно глубины воды на входе, выходе из трубы и на выходе из оголовка трубы или конусов моста, м;

- глубины размыва соответственно в произвольной точке, предельная, максимальная за данный период времени при отсутствии каменной наброски, то же, при ее наличии, м;

h_w, h_м и h_дл - потери напора соответственно полные, местные и по длине сооружения, м;

h_т - высота трубы, м;

i, i_f, i_т, i_л - уклоны соответственно гидравлический (или уклон дна), трения, сооружения и лога;

I_л, I_с - соответственно уклоны лога и склонов бассейна;

- то же, на участке перед сооружением;

K и K₀ - соответственно расходная характеристика русла в общем случае и при нормальной глубине, м³/с;

K - коэффициент формы воронки размыва;

K_ф - коэффициент фильтрации, м/с;

L - полная длина сооружения вдоль потока; длина укрепления, м;

l - частная длина вдоль потока; расстояние между сечениями, м;

m - коэффициент расхода при безнапорном режиме;

m_от - коэффициент заложения откоса;

n - число; коэффициент шероховатости;

P - коэффициент размыва;

p - давление, МПа;

p_m - эмпирическая вероятность;

p_ст - высота водобойной стенки или стенки падений, м;

p_i - процентное содержание в грунте частиц данной фракции;

Q - расход, м³/с;

Q_пр - предельный расход, допускаемый для данного укрепления из каменной наброски, м³/с;

Q_k - эталонный расход, м³/с;

Q_р и Q_max - соответственно расчетный и наибольший расход притока, м³/с;

Q_соор(р) и Q_{соор(max)} - те же расходы в сооружении с учетом аккумуляции, м³/с;

q - удельный расход, м²/с;

R - гидравлический радиус, м;

r - радиус, м; коэффициент;

S - дальность падения струй в гасителе ЦНИИС, м; показатель степени;

S₀ - глубина водобойного колодца, м;

t - продолжительность паводка, с;

t_в - время водоотдачи;

t₀ - эталонное время размыва, с;

v - средняя скорость потока в сечении; средние скорости на вертикали (в точке), м/с;

v₀, v_доп - соответственно неразмывающие скорости для грунтов и допускаемые скорости для укреплений, м/с;

u - осредненная во времени скорость в точке, м/с;

W - объем; объем стока за время паводка, м³;

- удельный объем камня в наброске, м³/м;

x, y, z - продольная, поперечная и высотная координаты;

- разность отметок, м; подпор;

Э - удельная энергия сечения, м;

П_Q - параметр расхода;

- коэффициент кинетической энергии (Кориолиса); для мостов и труб принят

;

- угол раструбности оголовка (угол между осью трубы и стенкой оголовка);

- удельный вес воды, Н/м³;

- приращение, доля величины; высота элементов высокой шероховатости, м;

- толщина стенки, м;

- коэффициент сжатия в сечениях:

- в сжатом,

- в определяющем;

- относительное подтопление;

- коэффициент гидравлических сопротивлений;

- то же, на входе в сооружение;

- то же, по длине сооружения;

- относительный размыв;

- коэффициент гидравлического трения (Дарси);

- коэффициент расхода для труб;

- то же, при полунапорном режиме;

- то же, при напорном режиме;

- коэффициент скорости;

- смоченный периметр, м;

- угол падения струй; коэффициент, учитывающий тип концевой части укрепления при размыве;

- площадь поперечного сечения сооружения или потока, м².

1. ДОРОЖНЫЕ ВОДОПРОПУСКНЫЕ СООРУЖЕНИЯ И ПРИНЦИПЫ

ИХ ПРОЕКТИРОВАНИЯ

ТИПЫ СООРУЖЕНИЙ И СФЕРЫ ИХ ПРИМЕНЕНИЯ

1.1. Для пропуска воды на пересечениях водотоков с полотном дорог устраивают водопропускные сооружения, которые в зависимости от местных условий (топографических, гидравлических и геологических) могут быть различных типов. К ним относятся трубы, мосты, лотки, дюкеры, фильтрующие и переливные насыпи. На автомобильных дорогах низших категорий допускают перелив воды через полотно дороги по специальным лоткам, являющимся одновременно и проезжей частью дороги.

Для отвода воды от земляного полотна к ближайшему водопропускному сооружению, а также перехвата воды на склоне косогора у дороги устраивают специальные водоотводные канавы.

На автомобильных дорогах используют также комплекс устройств, уводящих воду с проезжей части дороги и разделительных полос.

Водопропускные сооружения делят на малые, средние и большие. В настоящем Пособии рассматриваются малые сооружения: трубы, малые мосты полной длиной до 25 м, лотки, дюкеры, переливные и фильтрующие насыпи, а также водоотводные устройства и канавы.

1.2. Водопропускные трубы подразделяют по материалу - бетонные, железобетонные, металлические (обычно из тонкого гофрированного металла), по форме сечения - круглые, прямоугольные, овоидальные.

В настоящее время в основном применяют круглые (отверстия от 0,75 до 2,0 м) и прямоугольные (отверстия от 1,0 до 6,0 м) бетонные и железобетонные трубы, а также круглые металлические гофрированные трубы (отверстия 1,5; 2,0 и 3,0 м).

Особое место занимают трубы для северной климатической зоны, для которых нормы устанавливают более жесткие требования, в том числе и для гидравлической работы.

Трубы обычно имеют входные и выходные оголовки, обеспечивающие более благоприятные гидравлические условия. Однако благодаря простоте устройства и монтажа гофрированные металлические трубы в большинстве случаев применяют без оголовков.

При малых расходах воды рационально применение всех типов труб без оголовков. Подробно расчеты водопропускных труб изложены в гл. 5.

1.3. Малые мосты различают в зависимости от материала (каменные и железобетонные), а также от конструкции пролетных строений (балочные, арочные, рамные) и опор (с массивными опорами, стоечные). Они могут иметь укрепленные и неукрепленные русла (в большинстве случаев укрепленные). Современные малые мосты обычно бывают эстакадного типа с пролетами 3, 6, 9, 12 и 15 м.

Ввиду высокой грузонапряженности современных дорог малые мосты и трубы достаточно часто могут располагаться под острым углом к оси дороги, т.е. могут быть так называемыми "косыми" сооружениями.

1.4. Лотки - закрытые и открытые прямоугольные водоотводы - устраивают на железных дорогах между шпалами для пропуска малых расходов воды при высоте насыпи, недостаточной для укладки круглых труб, а также продольного водоотвода. Лотки выполняют из бетона и железобетона отверстиями 0,50 - 0,75 м. На автомобильных дорогах открытые лотковые сооружения устраивают на переливаемых насыпях для пропуска воды непосредственно через полотно дороги (см. гл. 8).

1.5. В ряде случаев, особенно при малых расходах и отсутствии в воде взвешенных и влекомых наносов, на дорогах используют фильтрующие насыпи, имеющие фильтрующую прослойку из крупных камней в теле земляного полотна, или комбинированные сооружения, состоящие из трубы и фильтрующей насыпи.

1.6. Для пропуска небольших расходов воды при зарегулированном стоке (преимущественно на мелкой мелиоративной сети) под низкими насыпями или мелкими выемками устраивают дюкеры. Дюкер состоит из двух колодцев, расположенных по обеим сторонам дороги, соединенных трубой под полотном.

При пропуске селевых потоков устраивают специальные сооружения: селедуки, селеспуски, принципы расчета которых в настоящем Пособии не излагаются, они приводятся в соответствующей литературе [36].

Для защиты сооружений от карчехода применяют улавливающие устройства (решетки, свайные ряды и т.п.).

1.7. Наиболее распространенный тип водопропускных сооружений - трубы. Они не нарушают целостности земляного полотна, могут применяться на любых сочетаниях плана и профиля дороги, индустриальны, удобны для применения механизации при их сооружении и достаточно экономичны. Широкое распространение в последнее время получили гофрированные трубы, отличающиеся высокой экономичностью и обеспечивающие условия быстрого возведения сооружений. Применение водопропускных труб обычно ограничивается недостаточной высотой насыпи. По конструктивным соображениям устройство труб возможно при высоте насыпи более 1,5 м. Другой причиной, ограничивающей возможность применения труб, является высокая мутность потока, угрожающая заилением сооружения.

Железобетонные мосты также применимы при любых сочетаниях плана и профиля дороги. Преимущество мостов по сравнению с трубами - возможность их использования при меньшей высоте насыпи. Малые мосты экономически целесообразны при малых высотах насыпей и относительно больших расходах воды через их отверстия. Открытые лотковые сооружения и переливные насыпи обычно бывают рациональны на автомобильных дорогах низших категорий. Их применение для указанных условий обычно обеспечивает экономический эффект без снижения надежности работы.

ТРЕБОВАНИЯ К ПРОЕКТИРОВАНИЮ МАЛЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

1.8. Основными нормативными документами при проектировании малых водопропускных сооружений являются:

1) Строительные нормы и правила. Железные дороги колеи 1520 мм. Нормы проектирования (СНиП II-39-76);

2) Строительные нормы и правила. Автомобильные дороги (СНиП 2.05.02-85);

3) Строительные нормы и правила. Мосты и трубы (СНиП 2.05.03-84);

4) Строительные нормы и правила. Определение гидрологических характеристик (СНиП 2.01.14-83);

5) Инструкция по расчету стока с малых бассейнов (ВСН 63-76).

1.9. Малые водопропускные сооружения на воздействие водного потока на железных дорогах общей сети и подъездных, не связанных с технологическими перевозками, согласно СНиП 2.05.03-84 рассчитывают на два паводка (расчетный и наибольший) и соответствующие им уровни.

Расходы на пике паводков также носят название "расчетный" и "наибольший".

Малые водопропускные сооружения на остальных путях промышленных предприятий, на автомобильных дорогах, а также все водоотводные каналы рассчитывают только на расчетные расходы и соответствующие им уровни, имеющие согласно СНиП 2.05.03-84 вероятности превышения, указанные в табл. 1.1, с соблюдением требований СНиП 2.05.03-84 о допустимом возвышении низа конструкции пролетных строений и бровки земляного полотна над соответствующим уровнем воды, а для железнодорожных сооружений также требований о предельно допустимом заполнении труб при пропуске расчетных расходов.

Таблица 1.1

Железные дороги				Автомобильные, городские улицы и дороги
Сооружения	Категория дорог	Вероятность превышения максимальных расходов паводков, %		Сооружения	Категория дорог <1>	Вероятность превышения максимальных расходов расчетных паводков, %
		расчетных	наибольших
Мосты и трубы	I и II (общей сети)	1	0,33	Малые мосты и трубы	I	1 <***>
То же	III и IV (общей сети)	2	1 <*>	То же	II, III, III-п и городские улицы и дороги	2 <***>
"	IV и V (подъездные пути)	2 <**>	-
"	Внутренние пути промышленных предприятий	2	-	"	IV, IV-п, V и внутрихозяйственные дороги	3 <***>

--------------------------------

<1> Кроме римских цифр в обозначении категорий автомобильных дорог применяют индекс "п" - промышленные дороги.

<*> При расчетах бровок земляного полотна, незатопляемых регуляционных сооружений и оградительных дамб русел блуждающих рек для железных дорог II категории вероятность превышения максимального расхода при наибольшем паводке следует принимать 0,33%.

<**> Если по технологическим причинам предприятий перерыв в движении не допускается, вероятность превышения следует принимать равной 1%.

<***> В районах с малоразвитой сетью автомобильных дорог для сооружений, имеющих особо важное народнохозяйственное значение, при технико-экономическом обосновании вероятность превышения допускается принимать 0,33% вместо 1% и 1% - вместо 2%. В районах с развитой сетью автомобильных дорог для автодорожных малых мостов и труб при технико-экономическом обосновании вероятность превышения допускается принимать 2% вместо 1%, 3% - вместо 2%, 5% - вместо 3%.

При определении расходов воды в сооружениях [39] допускается учитывать аккумуляцию воды перед сооружениями для ливневого стока и лишь в виде исключения для снегового (при отсутствии снежных заносов перед сооружением, т.е. на юге страны).

Особые требования предъявляются к защите сооружений от подмыва.

Водопропускная способность искусственных сооружений на автомобильных дорогах, проектируемых в непосредственной близости от железнодорожных линий, должна обеспечивать нормальную работу последних в соответствии с действующими нормативными документами.

1.10. В результате гидравлических расчетов должны быть установлены следующие параметры, определяющие размеры сооружений:

1) наибольшие глубины перед сооружениями (при спокойном потоке - равнинные условия - подпертые глубины H, при бурном - косогорные условия - высота наибольших всплесков потока), определяющие высоту насыпи;

2) глубины воды на входе в сооружение или наибольшие глубины воды в сооружениях, по которым устанавливают заполнение и режим протекания воды в трубах и возвышение низа пролетных строений мостов;

3) глубины воды и скорости на выходе из сооружений, по которым определяют размеры и тип укреплений на выходе;

4) максимальные глубины размыва в конце укреплений, по величине которых определяют ширину укреплений в конце его и глубины заделки их концевых частей.

Глубины размыва на выходах из малых водопропускных сооружений на железных дорогах определяют по двум расходам, причем расчетный расход увеличивают на 30% для учета возможных ошибок с целью обеспечения нормальных условий эксплуатации, что соответствует увеличению глубины размыва на 20%.

При назначении отверстий малых водопропускных сооружений должны учитываться требования охраны окружающей среды.

НАЗНАЧЕНИЕ ОТВЕРСТИЙ И ВЫБОР ТИПОВ СООРУЖЕНИЙ

1.11. Требуемым гидравлическим и конструктивным условиям могут удовлетворить различные варианты сооружений, отличающихся лишь стоимостью. Наиболее рациональный вариант сооружения может быть установлен лишь в результате технико-экономического сравнения.

При выборе типов сооружений надо учитывать особенности индустриального изготовления конструкций и производственные возможности строительных организаций. В проект дороги следует включать возможно меньшее число типов сооружений.

Круглые и прямоугольные трубы сооружают в соответствии с типовыми проектами (приложение 1.1), основные гидравлические характеристики которых приведены в приложении 1.2. Указанные характеристики являются ориентировочными и могут быть использованы лишь при составлении вариантов сооружений.

Для проектирования косогорных труб используют типовой проект инв. N 538 (см. приложение 1.1).

Перечень типовых решений опор малых мостов, т.е. элементов сооружений, взаимодействующих с потоком, приведен в приложении 1.1, а гидравлические характеристики этих сооружений - в приложении 1.3.

Следует отметить, что в последнее время меняется взгляд на типовое проектирование. Вместо типового проектирования и принятия в проекте полностью типовых решений с привязкой их к местности имеется тенденция к элементному типовому проектированию. В этом случае сооружение проектируют из типовых элементов, т.е., например, для труб используют типовые звенья, оголовки, гасители, элементы укреплений и сочетают их применительно к конкретным условиям (топографии, грунтам лога, гидрологическим условиям и т.п.), что обеспечивает значительный экономический эффект. Минимальную высоту насыпи для размещения труб определяют по формулам:

а) для железных дорог

(1.1)

где h_т - высота трубы в свету (без учета повышенных звеньев);

- толщина свода трубы;

- толщина засыпки над сводом трубы от ее верха до подошвы рельса, принимаемая согласно п. 1.8 СНиП 2.05.03-84 и приведенная в табл. 1.2;

h_б - толщина балласта под шпалами;

h_ш - высота шпалы;

0,15 - высота сливной призмы;

б) для автомобильных дорог

(1.2)

Таблица 1.2

Тип дорог	Толщина засыпки <*>, м, над
Тип дорог	железобетонными трубами	металлическими гофрированными трубами	сводами мостов
Железные:
общей сети и подъездные пути предприятий	1,0	1,2	0,7
внутренние пути предприятий	0,4	1,0	0,7
Автомобильные общего пользования, дороги и улицы в городах, поселках и сельских населенных пунктах, а также автодороги промышленных предприятий	0,5	0,5 <**>	0,2
Внутрихозяйственные автомобильные в колхозах, совхозах и других сельскохозяйственных предприятиях и организациях	0,2 <***>	-	-

--------------------------------

<*> Считая от верха звена (плиты перекрытия) трубы или от верхней точки свода до подошвы рельса на железных дорогах или до низа дорожной одежды - на автомобильных дорогах.

<**> Но не менее 0,8 м от верха звена трубы до поверхности дорожного покрытия.

<***> Но не менее 0,5 м до уровня бровки земляного полотна.

Примечание. Толщину засыпки над железобетонными трубами и пешеходными тоннелями, расположенными в пределах железнодорожных станций, допускается принимать менее 1,0 м.

Для железных дорог данные для расчета минимальной высоты насыпи из конструктивных соображений для типовых труб могут быть получены из соответствующих нормативных документов (высоты h_б и h_ш) и из приложения 1.2 (h_т и

Для автомобильных дорог эти данные приведены в приложении 1.2.

Данные для мостов принимают по типовым проектам. Исходными данными для назначения вариантов малых водопропускных сооружений являются результаты гидрологических и гидравлических расчетов.

По величине расходов (для сооружений на железных дорогах по расчетному и наибольшему и сооружений на автомобильных дорогах - по расчетному) подбирают сооружения, отвечающие требованиям СНиП 2.05.03-84. Подбор выполняют для труб по таблицам гидравлических характеристик, приведенных в приложении 1.2, а для мостов - либо задавшись вариантами удельных расходов воды под мостами 1, 2 и 3 м³/с, либо типом укреплений на выходе из них.

Затем для принятых сооружений определяют глубины размыва на выходе, а по ним - тип и размер выходных русел. После этого определяют стоимость сооружения. При варьировании проектной линии учитывают стоимость подходов. Рассматривают также варианты пропуска воды с нескольких бассейнов в одно сооружение путем устройства продольного водоотвода или сброса расхода из одного сооружения в другое.

Рассматриваются также варианты излома профиля сооружения, применения гасителей на выходе из сооружений, устройства рациональных типов выходных русел и т.п.

В итоге на основе технико-экономического сравнения вариантов выбирают тип сооружения.

Для учета большого многообразия условий гидравлической работы сооружения и ускорения расчета Мосгипротрансом с участием ЦНИИСа разработаны технологические линии проектирования водопропускных труб, включая косогорные, и малых мостов.

2. ОСНОВЫ ГИДРАВЛИЧЕСКИХ РАСЧЕТОВ

МАЛЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

СХЕМЫ ГИДРАВЛИЧЕСКОЙ РАБОТЫ СООРУЖЕНИЯ

И ОБЩИЕ ПРИНЦИПЫ РАСЧЕТА

2.1. С точки зрения характера протекания потока водопропускной тракт малых сооружений можно представить в виде схемы на рис. 2.1, причем на практике встречаются различные комбинации вариантов гидравлической работы его элементов.

Рис. 2.1. Классификация малых водопропускных сооружений

по условиям их гидравлической работы

2.2. При расчете водопропускного сооружения каждый из приведенных на рис. 2.1 основных пяти элементов водопропускного тракта должен быть исследован отдельно или в совокупности с прилегающими элементами (при выборе оптимального проектного решения может производиться многократный пересчет). В результате должны быть получены те глубины и скорости течения, которые могут лимитировать использование конкретного элемента конструкции (например, максимальная скорость больше допустимой для материала конструкции, максимальная глубина превосходит допустимую и т.д.), а также необходимые данные для гидравлического расчета прилегающих элементов (например, глубины и скорости на выходе из трубы для расчета нижнего бьефа и т.п.).

В зависимости от характера течения, определяемого расходами воды, уклонами местности, видами конструкций, а также исходя из требований точности возможно применение различных методов расчета. Эти методы можно подразделить на два основных класса:

1) теоретические методы, основанные на уравнениях движения жидкости и наносов (при расчете размывов) в той или иной идеализации (уравнение Бернулли, уравнения равномерного и неравномерного движения, полные одномерные нестационарные уравнения гидравлики, двухмерные уравнения мелкой воды и т.д.);

2) эмпирические методы, основанные на опытном и натурном материале.

Применение теоретических методов (возможно, с использованием эмпирических зависимостей для ряда входящих в уравнения параметров) является более желательным, так как обычно дает более точные результаты в широком диапазоне изменения исходных данных. Однако не все вопросы гидравлики малых водопропускных сооружений в настоящее время поддаются теоретическому исследованию, что приводит к необходимости зачастую применять эмпирические зависимости (например, для максимальных высот всплеска в сужающихся быстротоках, глубины воронки размыва за трубами и т.п.). Ниже в настоящей главе будут рассмотрены основные уравнения и математические модели, используемые при расчетах элементов водопропускного тракта, а также приведены зависимости для параметров этих уравнений и других часто встречающихся в расчетах величин. В последующих главах будут даны конкретные методы расчета всех элементов водопропускного тракта.

УРАВНЕНИЕ БЕРНУЛЛИ

2.3. Большинство практических расчетов водопропускных сооружений выполняют на основе уравнения Д. Бернулли (рис. 2.2), которое характеризует удельную энергию в двух сравниваемых сечениях (Э₁, Э₂). В общем случае уравнение Д. Бернулли имеет вид

(2.1)

где z₁ и z₂ - высота положения двух точек в сечениях 1 и 2 потока над общей горизонтальной плоскостью отсчета;

p₁ и p₂ - гидродинамическое давление в тех же точках;

v₁ и v₂ - средняя скорость потока соответственно в сечениях 1 и 2, в общем случае не равная скорости в точке;

- коэффициенты кинетической энергии в тех же сечениях (коэффициенты Кориолиса);

- вес единицы объема жидкости (удельный вес);

h_w - потеря напора на участке между рассматриваемыми сечениями.

Рис. 2.2. Схема к пояснению уравнения Д. Бернулли

Величины, входящие в уравнение Бернулли, имеют названия и физический смысл, приведенные в табл. 2.1.

Таблица 2.1

Величина	Гидравлическое название	Физический смысл
z	Высота положения точки или геометрический напор	Удельная энергия положения
	Приведенная высота давления	Удельная энергия давления
	Скоростной напор	Удельная кинетическая энергия
	Пьезометрический напор	Удельная потенциальная энергия
	Гидравлический или гидродинамический напор	Удельная энергия

Если скорости во всех точках сечения потока одинаковы, то коэффициент Кориолиса

. Фактически скорости в отдельных точках сечения различны, и

. Обычно при расчетах сооружений и открытых русел принимают

. При небольших скоростях (примерно до 1 м/с) допустимо принимать

Для постоянных водотоков коэффициент Кориолиса [14] допускается определять по формуле

(2.2)

где Fr - число Фруда, характеризующее кинетичность потока;

i - гидравлический уклон (см. ниже).

2.4. Там, где крайние линии тока образуют между собой сравнительно небольшой угол и имеют малую кривизну, движение считается плавно изменяющимся. В сечениях с плавно изменяющимся движением пьезометрический напор во всех точках одинаков. Поэтому для точек на поверхности потока, где избыточное давление равно нулю, уравнение Бернулли получает вид

(2.3)

Если дно потока в продольном профиле прямолинейно, то падение его на длине l будет

, где i₀ - уклон дна. Отношение потерь напора на участке потока к его длине h_w/l = i_ср называется средним гидравлическим уклоном на участке. Если длину участка уменьшать, то получаемая в пределе величина i = dh_w/dl называется гидравлическим уклоном в данном сечении потока.

Гидравлический уклон следует отличать от уклона дна русла и от уклона поверхности потока.

2.5. Входящий в правую часть уравнения Бернулли член h_w (потери напора) вычисляют обычно по формуле

(2.4)

где

- коэффициент сопротивления;

- средняя скорость потока в рассматриваемом устройстве или перед ним;

Q - расход жидкости;

- площадь поперечного сечения потока (живого сечения).

Различают два типа потерь напора: местное - h_м и путевые (или по длине) - h_дл.

Об определении путевых потерь сказано ниже.

РАВНОМЕРНОЕ ДВИЖЕНИЕ

2.6. Равномерным называется движение жидкости, при котором гидравлические элементы потока не изменяются. При этом размеры и форма поперечного сечения потока и распределение скоростей одинаковы во всех сечениях потока. Когда некоторые из этих условий не соблюдены, движение считается неравномерным, даже если средняя скорость остается постоянной. При равномерном движении гидравлические элементы потока связаны между собой формулой Шези:

(2.5)

где Q - расход жидкости, м³/с;

- площадь поперечного сечения потока, м²;

v - скорость потока, м/с;

C - коэффициент Шези, м^0,5/с;

- гидравлический радиус сечения, м;

- смоченный периметр, м;

i - гидравлический уклон, который при равномерном движении потока со свободной поверхностью равен уклону дна и свободной поверхности.

2.7. Коэффициент Шези определяют по формуле Н.Н. Павловского:

(2.6)

где n - коэффициент шероховатости;

y - показатель степени.

В свою очередь

Значения коэффициента шероховатости принимают по табл. 2.2.

Таблица 2.2

Характеристика поверхности	Значения коэффициента шероховатости n при состоянии поверхности
Характеристика поверхности	хорошем	среднем	плохом
Трубы
Поверхность из цементного раствора	0,011	0,013	0,015
Бетонная необработанная поверхность, выполненная в опалубке:
стальной	0,012	0,013	0,014
гладкой деревянной	0,012	0,014	0,016
негладкой деревянной	0,015	0,017	0,020
Кирпичная кладка, покрытая цементным раствором	0,012	0,015	0,017
Бутовая кладка на цементном растворе	0,018	0,025	0,030
Открытые искусственные русла
Стальная неокрашенная поверхность	0,011	0,012	0,014
" рифленая "	0,021	0,025	0,030
Бетонная затертая "	0,011	0,013	0,015
Бетонная поверхность, отделанная мастерком	0,013	0,015	0,016
То же, с гравием на дне	0,015	0,017	0,020
Бетонная неотделанная поверхность	0,014	0,017	0,020
Поверхность из торкрет-бетона:
хорошо уложенного	0,016	0,019	0,023
имеющего волнистую поверхность	0,018	0,022	0,025
Мощение:
из булыжного камня	0,020	0,022	0,027
из рваного камня	0,022	0,027	0,030
с "изюмом"	-	0,040	0,045
Земляные канавы правильной формы в плотном лессе или мелком гравии с илистым слоем	0,017	0,018	-
То же, в лессе или гравии с илистой пленкой	0,017	0,020	0,025
Габионная кладка	0,025	0,027	0,029
Канавы в галечнике	0,025	0,030	0,033
Земляные канавы неправильной формы (с отвалами) заросшие, каменная наброска	0,027	0,030	0,035
Канавы с земляным дном и одернованными или сложенными сухой кладкой откосами	0,028	0,033	0,035
Канавы с одернованными откосами и мощеным дном или грубо высеченные в скале (неправильной формы)	0,025	0,035	0,040
Естественные водотоки шириной до 30 м
Русла чистые прямые, без перекатов и омутов	0,025	0,030	0,033
То же, но при наличии больших камней и растительности	0,030	0,035	0,040
Русла чистые, извилистые, с заводями и омутами	0,033	0,040	0,045
То же, но при наличии камней и растительности	0,035	0,045	0,050
То же, при большом количестве камней	0,045	0,050	0,060
То же, при низких уровнях воды, незначительных уклонах и малых живых сечениях	0,040	0,048	0,055
Русла при наличии участков с медленным течением, зарослей и глубоких омутов	0,050	0,070	0,080
Русла с весьма заросшими участками, глубокими омутами или при наличии кустарника и завалов деревьями	0,075	0,100	0,150

Для расчета коэффициента Шези C по формуле (2.6) в справочниках приводятся таблицы и номограммы. Коэффициент Шези можно вычислять также по формуле работы [14]:

(2.7)

Для облегчения расчетов по формуле (2.7) рекомендуется пользоваться табл. 2.3.

Таблица 2.3

R, м	Значения коэффициента Шези C при n, равном
R, м	0,010	0,015	0,020	0,025	0,030	0,040	0,050	0,080	0,10	0,20
0,1	80,7	49,3	34,5	26,0	20,5	14,1	10,5	5,47	3,92	1,01
0,2	86,3	54,3	38,7	29,7	23,8	16,8	12,7	7,00	5,20	1,79
0,3	89,7	57,3	41,1	32,1	26,0	18,6	14,3	8,09	6,13	2,37
0,4	92,1	59,5	43,4	33,9	27,6	20,0	15,5	8,98	6,89	2,86
0,5	94,0	61,2	44,9	35,3	28,9	21,1	16,5	9,73	7,54	3,29
0,6	95,0	62,6	46,2	36,5	30,0	22,7	17,4	10,4	8,12	3,68
0,7	96,9	63,8	47,4	37,6	31,0	22,9	18,1	11,0	8,65	4,04
0,8	98,0	64,9	48,3	38,4	31,3	23,7	18,8	11,5	9,13	4,38
0,9	99,1	65,8	49,2	39,3	32,6	24,4	19,4	12,0	9,58	4,69
1,0	100,0	66,7	50,0	40,0	33,3	25,0	20,0	12,5	10,0	5,00
1,2	101,6	68,2	51,4	41,3	34,5	26,1	21,0	13,3	10,8	5,56
1,4	103,0	69,4	52,6	42,4	35,6	27,1	21,9	14,1	11,4	6,07
1,6	104,1	70,5	53,6	43,4	36,5	27,9	22,7	14,8	12,1	6,55
1,8	105,2	71,5	54,5	44,2	37,4	28,7	23,4	15,4	22,6	7,00
2,0	106,1	72,4	55,4	45,1	38,1	29,4	24,1	16,0	13,2	7,43
2,5	108,1	74,3	57,1	46,8	39,8	31,0	25,6	17,2	14,4	8,41
3,0	109,7	75,8	58,6	48,2	41,1	23,2	26,8	18,3	15,4	9,28
3,5	111,1	77,1	59,9	49,4	42,3	33,3	27,8	19,3	16,3	10,1
4,0	112,3	78,3	61,0	50,5	43,3	34,3	28,8	20,2	17,1	10,8
4,5	113,4	79,3	61,9	51,4	44,2	35,2	29,6	20,9	19,9	21,5
5,0	114,3	80,2	62,8	52,2	45,1	36,0	30,4	21,6	18,6	12,1
5,5	115,2	81,0	63,6	53,0	45,8	36,7	31,1	22,3	19,2	12,7
6,0	116,0	81,8	64,4	53,7	46,5	37,4	31,7	22,9	19,8	73,2
6,5	116,7	82,5	65,0	54,4	47,2	38,0	32,3	23,5	20,4	13,8
7,0	117,4	83,1	65,6	55,0	47,8	38,6	32,9	24,0	21,0	14,2
7,5	118,0	83,7	66,2	55,6	48,3	39,1	33,4	24,5	21,4	14,7
8,0	118,6	84,3	66,8	56,1	48,8	39,6	23,9	25,0	21,9	15,2
8,5	119,2	84,8	67,3	56,6	49,4	40,1	34,4	25,4	22,3	15,6

Весьма удобен для расчетов график скоростной характеристики

(рис. 2.3), построенный по формуле Н.Н. Павловского. В этом случае среднюю скорость течения определяют как

, а расход

Рис. 2.3. График для определения скоростной характеристики

потока

при коэффициенте Шези C, вычисленном

по формуле Н.Н. Павловского

Формула Шези и табл. 2.2 предусматривают размерность всех величин в метрах.

2.8. Глубина h₀, при которой заданный расход Q протекает в условиях равномерного движения, называется нормальной.

В общем случае нормальную глубину определяют подбором по формуле Шези. Для этого вычисляют расходную характеристику русла при заданном расходе

. Затем пробуют ряд значений глубины h и определяют соответствующие им значения расходной характеристики

. Обычно считают задачу решенной, если значение расходной характеристики отличается от истинного (K₀) не более чем на 1%.

Удобно также строить кривую K = f(h), по которой искомое значение нормальной глубины находят графически.

Для ускорения гидравлических расчетов русел геометрически определенных форм существуют графики (см. приложения 2.1 - 2.3).

НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ

2.9. Неравномерным называется движение жидкости, при котором гидравлические элементы потока изменяются от сечения к сечению вдоль русла. Неравномерное течение может быть установившимся (все параметры течения не зависят от времени) и неустановившимся. Ниже в настоящем параграфе рассматриваются только установившиеся течения.

Неравномерное установившееся движение может быть плавно изменяющимся и резко изменяющимся (внезапное расширение или сужение, гидравлический прыжок). На участках плавно изменяющегося движения свободная поверхность может рассчитываться с помощью уравнения Бернулли, дополненного потерями энергии на трение по дну; для расчета резко изменяющегося движения в уравнения Бернулли должны быть добавлены потери энергии, вызванные внезапным изменением потока.

Русло, образованное цилиндрической поверхностью произвольного поперечного сечения, называется призматическим или цилиндрическим. Наиболее часто встречаются призматические русла прямоугольного, трапецеидального, параболического и кругового очертания.

В призматических руслах для описания изменения глубины потока h на длине l используется следующее дифференциальное уравнение:

(2.8)

при этом

где i - уклон дна;

- число Фруда (параметр кинетичности);

B - ширина потока поверху (по урезу воды).

В свою очередь

. (2.9)

2.10. Продольный профиль поверхности потока воды называется кривой свободной поверхности. Увеличение глубины воды в сторону течения называется подпором, а свободная поверхность потока при этом - кривой подпора. При убывании глубины свободная поверхность образует кривую спада.

Для анализа формы кривой свободной поверхности необходимо знать нормальную глубину h₀ и критическую глубину h_к.

Критическая глубина определяется из уравнения

(2.10)

где

и B_к - значения

и B при критической глубине h_к.

Для прямоугольного русла

(2.11)

где q = Q/b - удельный расход.

Для определения критической глубины в руслах различных поперечных сечений имеются вспомогательные таблицы (см. приложения 2.4 и 2.5) и графики.

Потоки с Fr > 1 (h_к > 1) называются бурными, с Fr < 1 (h_к < 1) - спокойными. Чем больше число Фруда, тем резче проявляется бурное состояние.

Уклон i_к для открытого призматического русла, при котором нормальная глубина является критической, называется критическим и вычисляется по формуле:

(2.12)

При i > i_к равномерный поток будет в бурном состоянии, при i < i_к - в спокойном.

Полученные из уравнения (2.8) типы кривых свободной поверхности представлены на рис. 2.4. Принято обозначать кривые свободной поверхности следующим образом:

I. Если h₀ > h_к (уклон дна i < i_к):

h₀ < h - кривая типа a_I;

h_к < h < h₀ - кривая типа b_I;

h < h_к - кривая типа c_I.

II. Если h₀ < h_к (уклон дна i > i_к):

h₀ < h - кривая типа a_II;

h₀ < h < h_к - кривая типа b_II;

h < h_к - кривая типа c_II.

III. Если h₀ = h_к (уклон дна i = i_к):

h₀ < h - кривая типа a_III;

h₀ > h - кривая типа c_III.

Рис. 2.4. Кривые свободной поверхности потока

в призматическом русле:

а - при i < i_к; б - при i > i_к; в - при i = i_к

В зонах a_I, a_II, a_III, c_I, c_II, c_III возможны только кривые подпора (глубина возрастает по течению), в зонах b_I, b_II - только кривые спада (глубина убывает по течению).

Линия нормальных глубин N-N при i > i_к и i < i_к является асимптотой и глубины приближаются к нормальной асимптотически, поэтому рассчитывать кривую свободной поверхности следует, не доходя до нормальной ближе, чем 0,02h₀. Не следует также приближаться к критической глубине ближе, чем 0,02h_к, поскольку точность расчетов в другом диапазоне будет недостаточная.

2.11. Расчет кривых свободной поверхности сводится к интегрированию уравнения (2.8), однако использование стандартных программ решения дифференциальных уравнений в данном случае нежелательно, поскольку функция f при

имеет особенность.

Для определения расстояния l между глубинами h₁ и h₂ (глубины h₁ и h₂ обязательно должны быть на кривой одного типа) можно использовать способ Н.Н. Павловского:

(2.13)

В этом уравнении

индекс "нуль" означает, что данная величина вычислена при нормальной глубине h₀:

(2.14) <*>

(2.15)

--------------------------------

<*> В расчетах в качестве j берут его значение, вычисленное при среднем значении глубины на рассматриваемом участке.

Значения

берут по табл. 2.4.

Таблица 2.4


0	0	0,77	1,020	0,980	2,297	1,20	1,199	1,49	0,813
0,05	0,05	0,78	1,045	0,985	2,442	1,21	1,117	1,50	0,805
0,10	0,10	0,79	1,071	0,990	2,646	1,22	1,156	1,55	0,767
0,15	0,151	0,80	1,098	0,995	3,000	1,23	1,136	1,60	0,733
0,20	0,202	0,81	1,127	1,000		1,24	1,117	1,65	0,703
0,25	0,225	0,82	1,156	1,005	2,997	1,25	1,098	1,70	0,675
0,30	0,309	0,83	1,188	1,010	2,652	1,26	1,081	1,75	0,650
0,35	0,365	0,84	1,221	1,015	2,450	1,27	1,065	1,80	0,626
0,40	0,423	0,85	1,256	1,020	2,307	1,28	1,049	1,85	0,605
0,45	0,484	0,86	1,293	1,025	2,197	1,29	1,033	1,90	0,585
0,50	0,549	0,87	1,333	1,040	2,107	1,30	1,018	1,95	0,507
0,55	0,619	0,88	1,375	1,035	2,031	1,31	1,004	2,00	0,550
0,60	0,693	0,89	1,421	1,040	1,966	1,32	0,990	2,10	0,518
0,61	0,709	0,90	1,472	1,045	1,908	1,33	0,977	2,20	0,490
0,62	0,725	0,905	1,499	1,050	1,857	1,34	0,964	2,30	0,466
0,63	0,741	0,910	1,527	1,06	1,768	1,35	0,952	2,40	0,444
0,64	0,758	0,915	1,557	1,07	1,693	1,36	0,940	2,50	0,424
0,65	0,775	0,920	1,589	1,08	1,629	1,37	0,928	2,60	0,405
0,66	0,792	0,925	1,622	1,09	1,573	1,38	0,917	2,70	0,389
0,67	0,810	0,930	1,658	1,10	1,522	1,39	0,906	2,80	0,374
0,68	0,829	0,935	1,696	1,11	1,477	1,40	0,896	2,90	0,360
0,69	0,848	0,940	1,738	1,12	1,436	1,41	0,886	3,00	0,346
0,70	0,867	0,945	1,782	1,13	1,398	1,42	0,876	3,50	0,294
0,71	0,887	0,950	1,831	1,14	1,368	1,43	0,866	4,00	0,255
0,72	0,907	0,955	1,885	1,15	1,331	1,44	0,856	4,50	0,226
0,73	0,928	0,960	1,945	1,16	1,301	1,45	0,847	5,00	0,203
0,74	0,950	0,965	2,013	1,17	1,273	1,46	0,838	6,00	0,168
0,75	0,972	0,970	2,092	1,18	1,247	1,47	0,829	8,00	0,126
0,76	0,996	0,975	2,184	1,19	1,122	1,48	0,821	10,00	0,100

Величину

можно принимать постоянной для данного русла, вычислив ее для крайних значений глубины h.

Можно также пользоваться другим способом:

(2.16)

где f(h) - значение f при

В свою очередь

(2.17)

Для увеличения точности расчетов в обоих способах можно участок между глубинами h₁ и h₂ разбить на несколько интервалов, потом для каждого из интервалов определить расстояние между крайними глубинами и все расстояния сложить.

Пример. В трапецеидальном канале с уклоном i = 0,0002 ширина по дну b = 12 м, коэффициент шероховатости n = 0,025, коэффициент откоса m = 1,5, расход Q = 47,66 м³/с. Требуется определить расстояние между глубинами h₁ = 3,1 м и h₂ = 4 м.

Решение. Из уравнения (2.5) определяем нормальную глубину h₀ = 3,01 м (h₁ > h₀; h₂ > h₀). Затем из уравнения (2.10) находим критическую глубину h_к = 1,11 м (h₁ > h_к; h₂ > h_к). Следовательно, обе глубины принадлежат одному типу кривой свободной поверхности a_I и рассчитывать между ними расстояние можно.

Вычисляем l с помощью формулы (2.16). Для этого:

а) определим

, м, по формуле (2.17):

б) определим площадь, м²:

в) определим смоченный периметр, м:

г) определим гидравлический радиус, м:

д) определим коэффициент Шези

, м^0,5/с, по формуле Маннинга:

е) определим

, м³/с:

ж) определим ширину поверху, м:

з) определим число Фруда

при

и) определим K₀, м³/с:

к) наконец, находим l, м, по формуле (2.16):

Для привязки кривой свободной поверхности к каналу необходимо в одном из сечений знать глубину. Как правило, она известна перед сооружением (плотина, водослив, щит и т.д.) или за ним, в начале или в конце канала.

2.12. Если русло не призматическое, то расстояние между сечениями с глубинами h₁ и h₂ определяют по формуле

(2.18)

где i_f = (Q/K_ср)² - средний уклон трения между сечениями.

Этот прием расчета называют методом В.И. Чарномского. Он удобен для построения всей кривой и применим при любой форме поперечного профиля русла.

2.13. Для расчета кривой свободной поверхности в русле с изменением уклона необходимо перед расчетом проанализировать свободную поверхность исходя из требований, что в зонах a_I, a_II, c_I, c_II возможны только кривые подпора, а в зонах b_I и b_II - только кривые спада; кроме того, глубина должна быть непрерывной функцией, за исключением гидравлических прыжков.

На рис. 2.5, 2.6 приведены некоторые частные случаи течения. Благодаря анализу удается установить глубину в переломном сечении, необходимую для расчета кривой свободной поверхности. Гидравлический прыжок происходит в сечении, где глубины до прыжка и за прыжком являются сопряженными. Для определения места прыжка необходимо построить линии сопряженных глубин, и там, где они пересекают свободную поверхность, произойдет прыжок. Для построения линии сопряженных глубин в зоне возможного прыжка необходимо в нескольких сечениях по глубинам в бурном потоке определить вторую сопряженную глубину и нанести полученные значения в масштабе на схему, а затем соединить линией. При наличии двойного перелома дна вид решения может быть неоднозначным (см. рис. 2.6). Одна из двух ветвей решения в этих случаях определяется конкретными значениями длин элементов и их уклонов.

Рис. 2.5. Кривые свободной поверхности потока

в призматическом русле, состоящем из двух элементов

разного уклона

Рис. 2.6. Кривые свободной поверхности потока

в призматическом русле, состоящем из трех элементов

разного уклона

ГИДРАВЛИЧЕСКИЙ ПРЫЖОК

2.14. Резкое увеличение глубины потока при переходе его из бурного состояния в спокойное называется гидравлическим прыжком. Глубины бурного потока перед прыжком h' и спокойного за прыжком h" носят название сопряженных глубин (рис. 2.7). Если бурный поток перед прыжком характеризуется числом Фруда Fr >= 3, то в нестесненном русле получается совершенный прыжок, характерный наличием поверхностного вальца. При Fr < 3 получается прыжок-волна без поверхностного вальца. Другой критерий совершенного прыжка - h"/h' >= 2. В призматическом русле любой формы сопряженные глубины связаны уравнением прыжковой функции:

(2.19)

где

- глубины погружения центра тяжести соответственно первого и второго сечений;

- площади этих сечений.

Рис. 2.7. Схема гидравлического прыжка:

1 - бурный поток; 2 - спокойный поток; 3 - валец

Если глубина первого сечения h' известна, то вычисляют левую часть и подбирают для правой части такое значение глубины h", при котором уравнение (2.19) обращается в тождество; это и будет вторая сопряженная глубина.

2.15. Для русла прямоугольного сечения

(2.20)

где Fr₁ - число Фруда при глубине h'.

Величины h' и h" в уравнении (2.20) можно поменять местами, но тогда вместо Fr₁ под корнем пишут Fr₂, т.е. число Фруда при большей сопряженной глубине h". Для ускорения расчетов используют графики, приведенные в приложениях 2.6, 2.7. Длину совершенного прыжка определяют по формуле Н.Н. Павловского:

l_пр = 2,5(1,9h" - h') (2.21)

или М.Д. Чертоусова:

(2.22)

Для решения задач по формуле М.Д. Чертоусова разработан график (см. приложение 2.8). При Fr₁ < 2 получается прыжок-волна (без вальца). Сопряженные глубины прыжка-волны связаны формулой

h" = h'Fr₁. (2.23)

Длина прыжка-волны

l_в = 10,6h'(Fr₁ - 1). (2.24)

Сопряженные глубины подпертого прыжка, т.е. прыжка, образующегося перед преградой, определяют так же, как совершенного. Длина же его меньше и приближенно может быть принята по формуле

l_пп = 3h". (2.25)

ВОДОСЛИВЫ

2.16. Водосливом называется преграда на пути открытого потока, через которую жидкость переливается, имея свободную поверхность. В зависимости от формы преграды различают водосливы с тонкой стенкой, с широким порогом и практических профилей.

Водосливами с тонкой стенкой называют такие водосливы, при переливе через которые активная струя омывает кромки отверстия с напорной стороны. Это будет в случае скошенных кромок (с расширением в низовую сторону) или при малой толщине стенки.

Водослив с широким порогом (рис. 2.8) имеет порог в виде горизонтальной площадки, причем поверхность потока на пороге в средней части становится почти параллельной поверхности порога.

Рис. 2.8. Схемы потока на водосливе с широким порогом

при его длине l:

а -

; б -

; в -

;

г - l > 20H₀

Водосливы практических профилей (криволинейные и полигональные) применяют в гидротехнике в качестве водосбросов. В дорожном деле к ним могут относиться некоторые переливные сооружения.

Расход через прямоугольный водослив с широким порогом

(2.26)

где

- коэффициент затопления, учитывающий положение уровня воды в отводящем русле;

m - коэффициент расхода, числовое значение которого зависит от геометрии водослива;

b - ширина водослива;

g - ускорение силы тяжести;

- полный напор истечения;

H - геометрический напор истечения, т.е. возвышение уровня воды перед водосливом над порогом;

v₀ - скорость подхода к водосливу там, где спад поверхности незначителен (примерно на расстоянии 2H от порога).

2.17. Для водослива с тонкой стенкой расход

(2.27)

где m₀ - коэффициент расхода с учетом скорости подхода;

H - геометрический напор истечения.

Для прямоугольного водослива в вертикальной тонкой стенке при прямоугольной форме подводящего лотка коэффициент расхода

(2.28)

где p - высота водосливной стенки с напорной (верховой) стороны, м;

B - ширина подводящего русла, м.

Числовые значения m₀ заключаются в пределах приблизительно от 0,41 до 0,50.

Водослив с отводящим руслом, имеющим ширину, равную ширине водослива, считается затопленным, если глубина воды в нижнем бьефе превышает высоту водосливной стенки со стороны нижнего бьефа p₁, а также если выполнено условие

(2.29)

где z - разность отметок свободной поверхности в верхнем и нижнем бьефах;

p₁ - высота водосливной стенки со стороны нижнего бьефа.

Критическое значение относительного перепада (z/p₁)_к определяют по графикам, представленным на рис. 2.9, в зависимости от коэффициента расхода m и отношения H/p₁. Если водослив не затоплен, то в формуле расхода (2.26) принимают

Рис. 2.9. График для определения критического значения

относительного перепада (z/p₁)_к = f(H/p₁) при m = 0,42;

0,45; 0,48 - для водосливов с тонкой стенкой и практических

профилей; при m = 0,35 и 0,385 - для водослива

с широким порогом

Для затопленных водосливов коэффициент затопления вычисляют по формуле

(2.30)

где h_н - возвышение свободной поверхности воды в нижнем бьефе над гребнем водослива.

2.18. Расход через водослив с широким порогом в общем виде

(2.31)

где

- площадь живого сечения потока на пороге при глубине h;

- коэффициент скорости;

h - глубина воды на пороге водослива.

Глубину на пороге незатопленного водослива выражают в виде доли полного напора:

h = kH₀,

где k - коэффициент вертикального сжатия потока.

Тогда для прямоугольного водослива применяют формулу (2.26). Значения коэффициентов m,

, k для водослива без бокового сжатия при p >= 4H приведены в табл. 2.5.

Таблица 2.5

Тип входа на водослив	m		k
Напорная грань - вертикальная, ребро - незакругленное	0,32	0,85	0,59
Напорная грань - вертикальная, ребро - закругленное	0,35	0,92	0,63
Напорная грань - наклонная	0,38	0,97	0,66

При p < 4H коэффициенты

, k и m возрастают. По А.Р. Березинскому для острого ребра

(2.32)

для закругленного ребра

(2.33)

Если глубина нижнего бьефа h_нб > p₁ + h_н, водослив считается затопленным.

Расход через затопленный водослив находят или по формуле (2.31), где h = h_нб - p₁, а

- площадь сечения потока на водосливе при глубине h, или по формуле (2.26) с учетом коэффициента затопления

. Коэффициенты затопления водослива с широким порогом (по А.Р. Березинскому) приведены в табл. 2.6.

Таблица 2.6

h_н/H₀		h_н/H₀
0,80	1,0	0,94	0,70
0,84	0,97	0,95	0,65
0,88	0,90	0,96	0,59
0,90	0,84	0,97	0,50
0,92	0,72	0,98	0,40

ОДНОМЕРНЫЕ УРАВНЕНИЯ ГИДРАВЛИКИ

2.19. Для расчета неравномерных (с переменным сечением и уклоном дна) и нестационарных (с переменным расходом) течений через водопропускные сооружения во многих случаях могут быть использованы одномерные уравнения гидравлики (уравнения Сен-Венана):

(2.34)

(2.35)

где t - время;

x - координата вдоль потока;

y_л(x, t), y_п(x, t) - координаты урезов на левом и правом берегах соответственно;

- глубина потока;

- отметка свободной поверхности воды;

z_д(x, y) - отметка дна;

- наклон оси ox к горизонту;

- коэффициент гидравлического трения;

F - удельная сила (на единицу длины), отнесенная к плотности, обусловленная непризматичностью русла.

Согласно [3.20] F можно представить в следующем виде:

(2.36)

если предположить, что z_д = z_д(x, y) является однозначной функцией y.

Рассмотрение уравнений (2.34), (2.35) можно найти, например, в работе [20]. С помощью этих уравнений на ЭВМ по специальным алгоритмам могут быть рассчитаны быстротоки произвольного поперечного сечения с переменным уклоном дна, водопропускные трубы (в безнапорном режиме), канавы, малые мосты и т.п., в том числе с образованием гидравлических прыжков. В лаборатории гидравлики ЦНИИС разработан универсальный комплекс программ "Водоток" для решения уравнений (2.34), (2.35) при достаточно общих граничных и начальных условиях, а также с учетом размыва дна и берегов.

ДВУХМЕРНЫЕ (ПЛАНОВЫЕ) УРАВНЕНИЯ ГИДРАВЛИКИ

2.20. Двухмерные (в плане) уравнения гидравлики, называемые также уравнениями мелкой воды, могут применяться для исследования существенно неравномерных сужающихся или расширяющихся потоков и потоков со значительными изменениями глубины в поперечных сечениях при условии, что характерный горизонтальный масштаб течения много больше характерной глубины. В гидравлике малых водопропускных сооружений такими объектами могут являться малые мосты и нижние бьефы труб. В некоторых случаях удовлетворительные результаты дает и применение этих уравнений к расчету сужений на входе в косогорные трубы (см. гл. 4) с образованием косых прыжков, если исключить из рассмотрения образование локальных всплесков (брызг), не оказывающих влияния на пропускную способность трубы.

Двухмерные уравнения мелкой воды в интегральной форме имеют следующий вид:

(2.37)

(2.38)

где

- вектор осредненной по глубине скорости потока, лежащий в горизонтальной плоскости;

G - произвольная область в горизонтальной плоскости, полностью или частично занятая жидкостью;

dG - элемент площади;

- граница G;

- векторный элемент

;

- внешняя нормаль к

;

- элемент кривой.

Уравнения (2.37), (2.38) допускают разрывные решения типа гидравлических прыжков. При соответствующих начальных и граничных условиях они решаются численно, причем для стационарных (не зависящих от времени) задач используется метод установления. Некоторые универсальные и надежные алгоритмы решения двухмерных уравнений мелкой воды описаны в [3, 21]. В лаборатории гидравлики ЦНИИСа разработан пакет программ "Каскад", включающий в себя три комплекса программ "Поток", "Бор", "Мост", каждый из которых предназначен для решения двухмерных уравнений мелкой воды в широком диапазоне ситуационных условий и чисел Фруда. Программы апробированы на многочисленных тестовых и реальных задачах и широко используются в расчетах по заданиям проектных организаций. В частности, с помощью комплекса "Бор" исследовались течения в сужающихся быстротоках (см. главу 4) и на выходах из равнинных и косогорных труб ([2], глава 7) в реальных условиях для существующих и проектируемых железнодорожных линий. Число задач, решаемых с помощью одно- и двухмерных уравнений гидравлики, неуклонно растет в связи с развитием ЭВМ и численных методов.

ДОПУСКАЕМЫЕ СКОРОСТИ ТЕЧЕНИЯ

2.21. При расчете водопропускных сооружений (канав, труб, отводных русел и т.п.) проверяют скорость

, которая должна быть не более допускаемой.

Утвержденные МПС Временные нормы допускаемых (неразмывающих) средних скоростей течения воды для несвязных грунтов приведены в табл. 2.7, для связных грунтов - в табл. 2.8 и для искусственных укреплений - в табл. 2.9.

Таблица 2.7

Грунты	Размеры частиц грунтов, мм	Средние скорости течения, м/с, при средней глубине потока, м
Грунты	Размеры частиц грунтов, мм	0,4	1,0	2,0	3,0	5,0	10 и более
Пыль и ил с мелким песком; растительная земля	0,005 - 0,05	0,15 - 0,20	0,20 - 0,30	0,25 - 0,40	0,30 - 0,45	0,40 - 0,55	0,45 - 0,65
Песок:
мелкий с примесью среднего	0,05 - 0,25	0,20 - 0,35	0,30 - 0,45	0,40 - 0,55	0,45-0,60	0,55 - 0,70	0,65 - 0,80
мелкий с глиной; средний с примесью крупного	0,25 - 1,00	0,35 - 0,50	0,45 - 0,60	0,55 - 0,70	0,60 - 0,75	0,70 - 0,85	0,80 - 0,95
крупный с примесью гравия; среднезернистый с глиной	1,00 - 2,50	0,50 - 0,65	0,60 - 0,75	0,70 - 0,80	0,75 - 0,90	0,85 - 1,00	0,95 - 1,20
Гравий:
мелкий с примесью среднего	2,50 - 5,00	0,65 - 0,80	0,75 - 0,85	0,80 - 1,00	0,90 - 1,10	1,00 - 1,20	1,20 - 1,50
крупный с песком и мелким гравием	5,00 - 10,0	0,80 - 0,90	0,85 - 1,05	1,00 - 1,15	1,10 - 1,30	1,20 - 1,45	1,50 - 1,75
Галька:
мелкая с песком и гравием	10,0 - 15,0	0,90 - 1,10	1,05 - 1,20	1,15 - 1,35	1,30 - 1,50	1,45 - 1,65	1,75 - 2,00
средняя с песком и гравием	15,0 - 25,0	1,10 - 1,25	1,20 - 1,45	1,35 - 1,65	1,50 - 1,85	1,65 - 2,00	2,00 - 2,30
крупная с примесью гравия	25,0 - 40,0	1,25 - 1,50	1,45 - 1,85	1,65 - 2,10	1,85 - 2,30	2,00 - 2,45	2,30 - 2,70
Булыжник:
мелкий с гравием	40,0 - 75,0	1,50 - 2,00	1,85 - 2,40	2,10 - 2,75	2,30 - 3,10	2,45 - 3,30	2,70 - 3,60
средний с галькой	75,0 - 100	2,00 - 2,45	2,40 - 2,80	2,75 - 3,20	3,10 - 3,50	3,30 - 3,80	3,60 - 4,20
средний с примесью крупного; крупный с мелкими примесями	100 - 150	2,45 - 3,00	2,80 - 3,35	3,20 - 3,75	3,50 - 4,10	3,80 - 4,40	4,20 - 4,50
крупный с примесью мелких валунов и гальки	150 - 200	3,00 - 3,50	3,35 - 3,80	3,75 - 4,30	4,10 - 4,65	4,40 - 5,00	4,50 - 5,40
Валуны:
мелкие с примесью гальки	200 - 300	3,50 - 3,85	3,80 - 4,35	4,30 - 4,70	4,65 - 4,90	5,00 - 5,50	5,40 - 5,90
средние с примесью булыжника	300 - 400	-	4,35 - 4,75	4,70 - 4,95	4,90 - 5,30	5,50 - 5,60	5,90 - 6,00
особо крупные	400 - 500 и более	-	-	4,95 - 5,35	5,30 - 5,50	5,60 - 6,00	6,00 - 6,20

Примечания. 1. Нижние пределы скорости течения соответствуют нижним пределам размеров частиц грунта, а верхние - верхним.

2. Значения скоростей не следует интерполировать. При промежуточных размерах частиц и глубинах водотока скорости принимаются по ближайшим табличным значениям размеров частиц и глубины водотока.

Таблица 2.8

Грунты	Содержание частиц, %, размером		Средние скорости потока, м/с, при средней глубине потока, м
	Содержание частиц, %, размером		0,4	1,0	2,0	3,0	0,4	1,0	2,0	3,0	0,4	1,0	2,0	3,0	0,4	1,0	2,0	3,0
	менее 0,005 мм	0,005 - 0,05 мм	для грунтов
	менее 0,005 мм	0,005 - 0,05 мм	малоплотных				среднеплотных				плотных				очень плотных
Глины	30 - 50	70 - 50	0,35	0,40	0,45	0,50	0,70	0,85	0,95	1,10	1,00	1,20	1,40	1,50	1,40	1,70	1,90	2,10
Суглинки:
тяжелые	20 - 30	80 - 70	0,35	0,40	0,45	0,50	0,65	0,80	0,90	1,00	0,95	1,20	1,40	1,50	1,40	1,70	1,90	2,10
тощие	10 - 20	90 - 80	0,35	0,40	0,45	0,50	0,65	0,80	0,90	1,00	0,95	1,20	1,40	1,50	1,40	1,70	1,90	2,10
Лессовые грунты в условиях закончившихся просадок	-	-	-	-	-	-	0,60	0,70	0,60	0,85	0,80	1,00	1,20	1,30	1,10	1,30	1,50	1,70
Супеси	5 - 10	20 - 40	По табл. 2.7 в зависимости от крупности песчаных фракций

Примечания. 1. Грунты малоплотные имеют приведенную порозность 1,2 - 1,9 и объемный вес грунтового скелета до 1,20 т/м³; среднеплотные - соответственно 0,9 - 0,6 и 1,20 - 1,20 - 1,66 т/м³; плотные - 0,6 - 0,3 и 1,66 - 2,09 т/м³; очень плотные - 0,3 - 0,2 и 2,04 - 2,14 т/м³.

2. Значения скоростей не следует интерполировать. При промежуточных глубинах водотока скорости принимаются по глубинам, ближайшим к натурным.

3. Значения допускаемых скоростей течения при глубинах водотока, больших 3 м (в случае отсутствия специальных исследований и расчетов) принимаются по их значениям для глубины 3 м.

4. При проектировании поверхностных водоотводов в подверженных выветриванию плотных и очень плотных грунтах допускаемые скорости ограничиваются теми же значениями, что и для грунтов средней плотности.

Таблица 2.9

Тип укреплений	Скорости течений, м/с, при средней глубине потока, м
Тип укреплений	0,4	1,0	2,0	3,0
Одерновка:
плашмя (на плотном основании)	0,9	1,2	1,3	1,4
в стенку	1,5	1,8	2,0	2,2
Каменная наброска:
из булыжного или рваного камня в зависимости от его крупности	По табл. 2.7 с коэффициентом 0,90
в два слоя в плетнях в зависимости от крупности камня	По табл. 2.7 с коэффициентом 1,10
Одиночное мощение на мху (слой не менее 5 см):
из булыжника размером 15 см	2,0	2,5	3,0	3,5
то же 20 см	2,5	3,0	3,5	4,0
" 25 см	3,0	3,5	4,0	4,5
Одиночное мощение на щебне (слой не менее 10 см):
из рваного камня размером 15 см	2,5	3,0	3,5	4,0
то же 20 см	3,0	3,5	4,0	4,5
" 25 см	3,5	4,0	4,5	5,0
Одиночное мощение с подбором лица и грубым приколом на щебне (слой не менее 10 см):
из камней размером 20 см	3,5	4,5	5,0	5,5
то же 25 см	4,0	4,5	5,5	5,5
" 30 см	4,0	5,0	6,0	6,0
Одиночное мощение на цементном растворе (тип раствора в соответствии с [39]):
из рваного камня размером 15 см	3,1	3,7	4,4	5,0
то же 20 см	3,7	4,4	5,0	5,5
" 25 см	4,4	5,0	5,6	6,2
Двойное мощение из рваного камня на щебне (слой не менее 10 см): нижний слой - из камней 15 см, верхний - из камней 20 см	3,5	4,5	5,0	5,5
Хворостяная выстилка и хворостяные покрывала на плотном основании (для временных укреплений):
при толщине выстилки 20 - 25 см	-	2,0	2,5	-
при других толщинах выстилки	То же, с коэффициентом
Фашинные тюфяки:
при толщине 50 см	2,5	3,0	3,5	-
при других толщинах	То же, с коэффициентом
Габионы (размерами не менее 0,5 x 0,5 x 1,0 м)	До 4,0	До 5,0	До 5,5	До 6,0
Бутовая кладка из камня:
известняковых пород	3,0	3,5	4,0	4,5
крепких пород	6,5	8,0	10,0	12,0
Укрепление бетонными плитами	3,0	3,5	4,0	4,5
Бетон как одежда для креплений (класс бетона по прочности и марки по морозостойкости и водонепроницаемости принимается в соответствии с действующими нормативными документами [39])	6,0	7,0	8,0	9,0
Бетонные лотки с гладкой поверхностью (класс бетона по прочности и марки по морозостойкости и водонепроницаемости принимаются в соответствии с действующими нормативными документами [39])	12	14	16	18
Деревянные лотки гладкие при надежном основании и течении вдоль водотоков	8	10	12	14

Примечания. 1. Значения скоростей не следует интерполировать. При промежуточных глубинах скорости принимаются по глубинам, ближайшим к натурным.

2. Значения допускаемых скоростей течения при глубинах водотока, больших 3 м (в случае отсутствия специальных исследований и расчетов), принимаются по их значениям для глубины 3 м.

При определении допускаемых скоростей для грунтов можно применять также формулы, рекомендуемые ВНИИ ВОДГЕО (для несвязных грунтов):

при h/d <= 600 (формула Б.И. Студеничникова) [2.10]

(2.39)

при h/d > 600 (формула А.М. Латышенкова)

v₀ = 5d^0,3h^0,2 м/с, (2.40)

где d - средний диаметр частиц грунта, м;

h - глубина воды, м.

Для быстрого расчета по этим формулам используют номограммы, приведенные в приложении 2.9.

Допускается расчет по формулам Ц.Е. Мирцхулавы для связных и несвязных грунтов [22].

Кроме того, существуют обоснованные специальными исследованиями рекомендации по допускаемым скоростям для определенного вида сооружений.

ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ ПРИ ПОВЫШЕННОЙ

И НЕОДНОРОДНОЙ ШЕРОХОВАТОСТИ РУСЕЛ

2.22. Естественные русла с каменным дном, а также искусственные лотки и трубы, в которых для уменьшения скоростей течения на смоченной поверхности устраивают специальные выступы или ступени, называются руслами высокой шероховатости; течение воды в них и гидравлические расчеты имеют следующие особенности.

При уклоне меньше критического течение происходит при спокойном режиме (рис. 2.10, а). При уклоне дна больше критического, но на сравнительно малой глубине в канале с поперечными донными ребрами получается перепадный режим и вода переливается через ребра, как через водосливы (рис. 2.10, б). При этом режиме сопротивление русла оказывается наибольшим. При увеличении расхода перепадный режим сменяется переходным (рис. 2.10, в), он характерен волнистой поверхностью потока, причем гребни волн находятся над ребрами, а между ними транзитный поток опускается до гладкого дна. При еще большем расходе устанавливается быстроточный режим (рис. 2.10, г), характерный тем, что поверхность потока становится почти прямой, параллельной дну, а пространство между ребрами заполняется вихрями, по которым скользит транзитная струя.

Рис. 2.10. Схемы течения воды в канале

высокой шероховатости при режимах:

а - спокойном; б - перепадном; в - переходном;

г - быстроточном

Описанные режимы осуществляются при числах Фруда

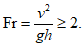
При Fr от 0,75 до 2,0 имеют место особые прикритические режимы. При шероховатости иного типа режимы течения остаются в главных чертах теми же. Каждому режиму присущ определенный закон сопротивления.

2.23. Коэффициент Шези C прямоугольных русел высокой шероховатости определяют по формуле П.И. Гордиенко:

(2.41)

где n₀ - особый коэффициент шероховатости;

- относительная глубина;

m - показатель, зависящий от вида шероховатости и режима течения;

- высота выступа шероховатости.

При быстроточном режиме m = 0 и

Быстроточный режим осуществляется при

Эмпирические значения коэффициентов n₀, m,

и C для расчета труб и русел высокой шероховатости приведены в табл. 2.10 (l и

- длина и высота шероховатости соответственно). Для условий, не охваченных в табл. 2.10, принимают:

а) для поперечных квадратных ребер при

при спокойном и быстроточном режимах

(2.42)

(только для спокойного режима); (2.43)

(2.44)

б) для шашек-кубов в шахматном порядке при

(2.45)

(2.46)

в) для ступеней по течению при

для быстроточного режима:

(2.47)

(2.48)

Таблица 2.10

Вид шероховатости		Спокойный и напорный режимы		Быстроточный режим
Вид шероховатости		n₀	m		C
Ребра поперечные квадратные	10	0,0540	0,31	3,3	18,5
Ребра поперечные квадратные	5	0,0476	0,34	2,5	21,1
Ребра прямоугольные	7,7	0,0590	0,23	-	17,0
Ребра прямоугольные	3,7	0,0248	0,23	2,4	40,3
Ступени по потоку прямоугольные	4	0,0435	-	1,1	23,0
Ступени по потоку прямоугольные	6	0,0440	-	1,2	22,7
Шашки-кубы в шахматном порядке	4,5	0,0338	-	3,8	29,6
	1,5	0,0413	0,012	3,0	24,2
	1,0	0,0325	0,115	1,2	30,8
Пирамиды с квадратным основанием в шахматном порядке	1,0	0,0508	0,37	2,7	19,7
Полушария в шахматном порядке	1	0,0383	0,18	1,9	26,1
Рассредоточенные гранулированные частицы	1,4	0,020	-	-	50
Шарообразные выступы	1,4	0,020	-	3,0	50
Рваный камень, укладка	-	0,0434	0,25	2,4	23,0
Окатанный камень, укладка	-	0,0466	0,35	2,4	21,4
Песчаная шероховатость	-	0,044	0,204	2,4	22,7
Торкрет	-	0,031	0,11	2,4	32,2
Бетонная поверхность в средних условиях	-	0,025	0,10	2,4	40,0
Хорошая бетонировка	-	0,020	0,08	2,4	50
Сталь окрашенная	-	0,0161	-	-	62

2.24. Коэффициент Шези прямоугольных лотков и труб при ступенчатой укладке и при условии

(l,

- длина и высота ступени соответственно) определяют по формуле

(2.49)

где i - средний уклон дна.

При горизонтальных звеньях

, откуда

(2.50)

2.25. Коэффициент Шези круглых труб при ступенчатой укладке звеньев (рис. 2.11, а) определяют в следующем порядке.

1. Находят безразмерный модуль расхода при заполнении трубы наполовину:

(2.51)

В свою очередь

(2.52)

где D - диаметр трубы, м;

- безразмерный модуль расхода трубы без повышенной шероховатости, заполненной наполовину;

C' - коэффициент Шези в этих условиях.

2. Вычисляют коэффициент шероховатости n:

а) при h >= 0,225D

(2.53)

б) при h < 0,225D

(2.54)

где h - глубина потока в трубе;

n_0,5 - коэффициент, определяемый по формуле (2.53).

3. Определяют коэффициент Шези по формуле

(2.55)

где l - длина ступени трубы;

R - гидравлический радиус живого сечения при данной глубине воды.

Рис. 2.11. Круглые трубы высокой шероховатости:

а - ступенчатая; б - с поперечными ребрами

2.26. Коэффициент Шези круглых труб с повышенной шероховатостью в виде поперечных ребер прямоугольного сечения (рис. 2.11, б) определяют в следующем порядке.

1. Вычисляют безразмерный модуль расхода при заполнении трубы наполовину:

(2.56)

где

- безразмерный модуль расхода трубы из того же материала диаметром D₀ без повышенной шероховатости при заполнении на половину высоты, определяемый по формуле (2.52);

i - уклон трубы;

- высоты ребер шероховатости;

D₀ - полный диаметр трубы.

2. При

находят максимальный для данных ребер коэффициент шероховатости

(2.57)

и вычисляют соответствующий коэффициент Шези

(2.58)

где R - гидравлический радиус живого сечения потока в створе ребра, т.е. в месте, где диаметр в свету

В случае заполнения трубы h < 0,225D вместо формулы (2.57) пользуются формулой

(2.59)

3. Если

менее 0,8 или более 1,2, то вычисляют величину

(2.60)

где e = 2,718 - основание натуральных логарифмов.

Находят коэффициент шероховатости n по формуле

(2.61)

где n₀ - коэффициент шероховатости трубы диаметром

из того же материала, но без повышенной шероховатости;

n₂ - коэффициент шероховатости, вычисленный по формуле (2.57) или (2.59).

Значение n₀ определяют по формуле

(2.62)

где

- коэффициент Шези, вычисленный по Маннингу для тех же условий;

n_м - коэффициент шероховатости материала трубы, определяемый по табл. 2.2.

Вычисляют коэффициент Шези

(2.63)

Допускать наполнение ступенчатых круглых труб более чем до половины не рекомендуется, так как тогда поток будет ударяться в поперечные стенки верхней половины, вследствие чего возникает опасность перехода к напорному режиму при значительно более высоком сопротивлении трубы и, как следствие, к резкому повышению уровня перед трубой.

2.27. Встречаются случаи, когда шероховатость отдельных частей смоченной поверхности русла различна, например при укладке звеньев прямоугольных труб с уступами. Тогда общий коэффициент трапецеидального русла

(2.64)

где C - коэффициент Шези, вычисленный в предположении, что гидравлический радиус равен глубине воды;

C₁ и K₃C₁ = C₂ - коэффициенты Шези зон потока, подверженных преимущественному влиянию дна (индекс 1) и стенок (индекс 2); соответственно K₃ = C₂/C₁;

K₁ и K₂ - отношение средних скоростей этих зон v₁ и v₂ к общей средней скорости v;

b₁ - расчетная ширина канала по дну на уровне выступов шероховатости;

h - расчетная глубина потока;

m_от - котангенс угла наклона бортов (коэффициент откосов).

Для прямоугольных лотков и труб m_от = 0 и

(2.65)

В прямоугольном канале с донной повышенной шероховатостью при b₁/h >= 3 и

поток считается как в широком русле, т.е. принимают R = h.

Трапецеидальные быстротоки с технически гладкими бортами

и дном повышенной шероховатости можно рассчитывать как широкое русло при той же глубине потока, если при коэффициенте заложения откосов от 0,5 до 1,5 отношение ширины быстротока по дну к глубине потока не менее 4,5 - 20 (соответственно).

Если изложенные выше условия не выполнены, то из точек сопряжения дна со стенками проводят вертикали и рассчитывают отдельно среднюю и боковые зоны. При этом для средней зоны берут R = h, а для боковых

(2.66)

АЭРАЦИЯ ПОТОКА

2.28. При высоких скоростях течения в быстротоках и безнапорных трубах поток захватывает воздух и в результате этого образуется водно-воздушная смесь. Это явление называют аэрацией. Глубина потока вследствие аэрации увеличивается.

Верхняя зона аэрированного потока состоит из разобщенных водных брызг, средняя зона - из воды, насыщенной воздухом; количество воздуха в средней зоне уменьшается сверху вниз. У самого дна движется слой чистой воды. Чем больше скорость, тем больше насыщение воды воздухом, и в зависимости от условий верхних либо нижних зон может не быть.

Аэрация возникает при тем более высоком числе Фруда, чем меньше шероховатость русла. Отношение объема воздуха V_а к объему воды V_в в аэрированном потоке определяют по формуле

(2.67)

где

- высота выступов шероховатости;

Fr - число Фруда, вычисленное в предположении, что аэрации нет.

Для технически гладких русел

(2.68)

Если

, аэрации нет.

Рассчитывают аэрированный поток в следующем порядке. Строят кривую свободной поверхности, считая, что аэрации не происходит, и вычисляют значения числа Фруда

для ряда сечений. По формуле (2.67) или (2.68) определяют

. Находят площади поперечного сечения аэрированного потока

и по ним соответствующие глубины h_а. Затем по глубинам аэрированного потока h_а строят уточненную кривую свободной поверхности.

3. ПРИНЦИПЫ РАСЧЕТА СТОКА И АККУМУЛЯЦИИ

ОБЩИЕ ПОЛОЖЕНИЯ

3.1. Основными факторами, определяющими тип и размер малых водопропускных сооружений, являются рельеф местности и расходы воды, притекающей к ним. Величину и характер распределения расходов во времени, характеризуемые гидрографами паводков, определяют в результате гидрологических расчетов.

Вода, притекающая к малому водопропускному сооружению, в общем случае при отсутствии специальных подводящих сооружений, например быстротоков, частично поступает в его отверстие, а частично растекается в обе стороны от него. Происходит так называемая аккумуляция (накопление) воды перед сооружением. При этом время истечения притекающей с бассейна воды через отверстие увеличивается, а максимальный расход в сооружении уменьшается, т.е. происходит растягивание во времени гидрографа паводка в сооружении по сравнению с гидрографом притока и снижение его пикового расхода.

При этом следует иметь в виду, что гидрологические расчеты предшествуют гидравлическим и являются независимыми от гидравлики сооружений, а учет аккумуляции возможен лишь совместно с гидравлическими расчетами, так как при этом необходимо знать конкретный тип и отверстие сооружения, обладающего определенной пропускной способностью.

Учитывая важность определения расходов притока с бассейна и особенностей формирования расходов в сооружении, являющихся как бы "гидравлической нагрузкой" его, ниже кратко рассмотрены общие принципы расчета стока и применяемые методы определения аккумуляции воды перед сооружением. Кроме того, в данной главе изложены приближенные методы расчета стока и аккумуляции, позволяющие быстро и просто с точностью, достаточно близкой к нормам, определить величину расходов и аккумуляции. Эти данные могут быть использованы в полевых условиях для предварительного назначения отверстий сооружений, а также на стадии ТЭО.

ПРИНЦИПЫ РАСЧЕТА СТОКА

3.2. Основной документ, по которому производятся гидрологические расчеты в нашей стране, - СНиП 2.01.14-83. Однако, учитывая сложность, а в большинстве случаев невозможность выполнения требований [41] о подборе аналогов малых, особенно периодических, водотоков, применительно к ливневому стоку последний для малых водопропускных сооружений с одобрения МПС и Минтрансстроя допускается рассчитывать по ВСН 63-76, учитывающим специфику малых водосборов, примыкающих к дорогам. Согласно [15] выполняют расчеты максимальных расходов ливневого стока с бассейнов площадью до 100 км². Наряду с этим используется метод Союздорпроекта, изложенный в работе [26].

Максимальные расходы снегового стока рассчитывают по работе [41].

3.3. Основным принципом установления расчетного расхода заданной вероятности превышения, используемым в работе [41], при наличии гидрометрических наблюдений является применение теории вероятностей и математической статистики для обработки собранных натурных гидрометрических данных.

Для этого используются данные гидрометеорологических наблюдений, опубликованные в официальных документах, а также данные, собранные в результате изысканий. Считается, что сток - случайное явление, а ряд расходов - одна из его реализаций.

3.4. Согласно [41] при определении расчетных гидрологических характеристик необходимо применять следующие приемы расчетов:

а) при наличии данных гидрометрических наблюдений - непосредственно по этим данным;

б) при недостаточности данных гидрометрических наблюдений - приведением их к многолетнему периоду по данным рек-аналогов с более длительными рядами наблюдений;

в) при отсутствии данных гидрометрических наблюдений - по формулам с применением данных о реках-аналогах и картам, а также по линейно-региональным нормам, основанным на совокупности данных наблюдений всей сети гидрометрических станций и постов данного района или более обширной территории, включая материалы инженерно-гидрометеорологических изысканий.

3.5. Малые водопропускные сооружения рассчитывают на воздействие паводков, вероятность превышения которых определяется согласно СНиП 2.05.03-84, причем для железных дорог расчет ведется на два паводка: расчетный и наибольший, для автомобильных дорог - только на расчетный.

3.6. Расчет расходов и уровней расчетной вероятности превышения производят, учитывая следующие требования:

а) обрабатываемый ряд должен содержать выдающиеся значения расходов (уровней) воды. При отсутствии такого значения ряд является ограниченно пригодным для статической обработки. Под выдающимся расходом понимается расход, превышающий следующий за ним (т.е. второй расход в ранжированном ряду) на 25% и более;

б) как правило, используются генетически однородные расходы и уровни (снеговые, дождевые, от таяния ледников). В случае когда паводки разного происхождения накладываются одни на другие (горные районы) и разделение их не представляется возможным как статистически, так и генетически, составляется ряд паводков смешанного происхождения;

в) если период наблюдений уровней воды H больше периода наблюдений расходов Q, то по имеющимся данным строят кривую Q = f(H), экстраполируют ее согласно существующим правилам и затем снимают с нее требуемые значения расходов;

г) необходимо исключить влияние подпорных или сгонно-нагонных явлений, так как в этом случае связь Q = f(H) нарушается;

д) если на реке построены гидротехнические сооружения, изменившие паводковый режим, то уровни и расходы приводят к однородным условиям.

3.7. Эмпирическая вероятность каждого члена ряда определяется по формуле

(3.1)

где m - порядковый номер членов ряда;

n - число членов в ряду наблюдений.

Вероятность выдающегося члена

(3.2)

где N - число лет непревышения выдающегося расхода, часто определяемое с привлечением архивов, летописей и других достоверных источников.

Тогда m в формуле (3.1) принимает значения m = 2, ..., n.

3.8. Статистическую обработку рядов с выдающимся расходом рекомендуется выполнять графоаналитическим методом. Подробное изложение методов статистической обработки рядов и определение расходов заданной вероятности превышения изложено в СНиП 2.01.14-83 и в Пособии [29] к нему. Там же приведены комплекты карт и таблиц, позволяющих вести расчеты стока.

Однако для малых бассейнов, как отмечено выше, расчеты встречают затруднения, основным и наиболее распространенным из которых является случай отсутствия данных в сочетании с отсутствием реки-аналога. Особенные сложности в поисках аналога возникают при расчете ливневого стока. Поэтому для расчета ливневого стока используют ВСН 63-76, составленные Н.Н. Чегодаевым на основе разработанной им теории ливневого стока с малых бассейнов, и методические указания Союздорпроекта, разработанные Б.Ф. Перевозниковым.

3.9. Максимальный расход ливневого стока Q, м³/с, притекающий с бассейна к водопропускному сооружению, определяется согласно [15] по формуле

(3.3)

где a₁ - расчетная интенсивность водоотдачи, соответствующая заданной вероятности превышения расхода и ливневому подрайону, мм/мин;

- коэффициент полноты стока;

F - площадь бассейна, км²;

- коэффициент, учитывающий неравномерность распределения осадков по площади;

- коэффициент озерности и заболоченности.

Объем воды, м³, притекающей и проходящей через водопропускное сооружение при ливневом стоке,

(3.4)

где t_в - расчетное время водоотдачи, мин.

В работе [15] подробно изложен метод определения всех указанных величин, приведены номограммы, графики и таблицы.

Расчеты можно вести по всей территории СССР, которая разбита на 15 ливневых районов, учитывая деление районов на подрайоны. Таких различных в смысле стока подрайонов всего 69.

3.10. Не все особенности формирования ливневого стока по стране могут быть учтены указанной разбивкой на ливневые районы и подрайоны. Поэтому при необходимости рекомендуется использовать данные метеорологических станций, расположенных в районе строящейся дороги. Для этого составляется схема их расположения на плане.

Интенсивности ливневых осадков a, мм/мин, вычисляются для дождей продолжительностью 5, 10, 20, 40, ..., 300 мин. Для этого слой осадков, выпавших за время дождя продолжительностью 5, 10, 20 мин и т.д., делится на его продолжительность и оценивается эмпирическая вероятность превышения каждой интенсивности по формуле (3.1).

Все ряды наносятся на спрямляющую клетчатку для коротких ливней [24]. Затем строится в логарифмических шкалах график зависимости интенсивности осадков a, мм/мин, от продолжительности ливней для различных повторяемостей. Общий вид указанных зависимостей в виде примера приведен на рис. 3.1 и 3.2.

Рис. 3.1. График зависимости интенсивности ливневых

осадков a от их повторяемости T_э для интервалов времени

t = 5, 10, 20, 40, 60, 90, 150, 300 мин (точки и значки

на рисунке - данные наблюдений)

Рис. 3.2. График зависимости интенсивности осадков a

от времени t для повторяемостей T_э = 300, 100, 50 и 25 лет

Применительно к категории почв в данном районе согласно указаниям [15] определяют интенсивности впитывания, а затем, вычитая из интенсивностей ливней интенсивности впитывания, получают таблицы зависимости интенсивности водоотдачи a₁ от продолжительности ливней и вероятности превышения, аналогичные таблицам, приведенным в [15], используя которые, выполняют расчет стока в данном неизученном районе согласно методике, изложенной в [15].

3.11. Для уточнения расчетных расходов могут быть использованы данные о расходах воды малых водотоков в районах расположения дороги. Их используют для получения эмпирических зависимостей модулей стока от площади бассейна. Для этого по данным наблюдений на водпостах определяют для каждого водотока расходы заданной повторяемости превышения Q_p_% и по ним вычисляют модули стока

(3.5)

где F_i и

- соответственно площадь бассейна и коэффициенты заболоченности и озерности для данного водотока.

Далее строя в логарифмических координатах зависимость M_p_% = f(F), которая обычно имеет вид прямой и выражается уравнением M_p_% = A_p%/Fⁿ, где n - угол наклона прямой к оси абсцисс. В таком случае расход для конкретного водотока

Пример определения таких зависимостей для модулей стока M_1% = f(F) и M_0,3% = f(F) приведен на рис. 3.3. Полученные зависимости имеют вид:

Рис. 3.3. Графики зависимостей модулей стока

M_1% (а) и M_0,33% (б) от площади бассейна

(точки на рисунке - данные наблюдений)

УЧЕТ АККУМУЛЯЦИИ И ЕЕ ХАРАКТЕРНЫЕ СЛУЧАИ

Аккумуляция воды перед сооружениями

3.12. В Руководстве [34], составленном в развитие [15], изложена методика расчета отверстий малых водопропускных сооружений с учетом аккумуляции. Там отмечено, что аккумуляцию следует учитывать лишь при ливневом стоке. Уменьшение расходов в сооружениях за счет аккумуляции допускается не более чем на ²/₃. (Это соответствует требованиям [39].)

В обоснованных случаях при наличии значительных аккумулирующих пространств перед водопропускными сооружениями, особенно при проверке долго существующих и нормально работающих сооружений, допускается и более значительное снижение расходов.

Наибольший эффект от аккумуляции достигается в равнинной и слабопересеченной местности. В косогорных условиях она мала и учитывать ее не рекомендуется.

3.13. Расчет аккумуляции в большинстве случаев допускается вести упрощенным способом. При этом расходы, пропускаемые сооружением (расходы в сооружении Q_соор), находят графически как точку пересечения графика пропускной способности сооружения с кривой зависимости наибольшего возможного расхода в сооружении Q_{соор(возм)} от глубины подпертой воды H перед ним. По полученным значениям Q_соор и H для ряда вариантов сооружений на основе технико-экономического сравнения выбирают тип и размеры отверстия сооружения.

3.14. Кривые зависимости Q_{соор(возм)} = f(H) для наиболее распространенной треугольной формы гидрографа ливневого паводка строят исходя из формулы Д.И. Кочерина методом А.А. Александрова. Этот метод подробно изложен в Руководстве [3]. Там же приводится реконструированная Союздорнии формула Д.И. Кочерина, рекомендованная для построения зависимости Q_соор = f(H) для автомобильных дорог.

В связи с широким использованием метода А.А. Александрова и удобством его применениям, а также тесной связью гидравлических расчетов малых водопропускных сооружений с аккумуляцией воды перед ними ниже приводится указанный метод расчета аккумуляции (расчет аккумуляции допускается производить и по рекомендациям Союздорпроекта [26]).

Расчетная зависимость (формула Д.И. Кочерина) наибольшего возможного расхода в сооружении от подпертой глубины перед ним

(3.6)

где Q_пр и W - соответственно расход принятой вероятности превышения, м³/с, на пике паводка и объем стока для гидрографа с наибольшим расходом, тыс. м³;

- соответственно уклоны лога и склонов перед сооружением, %;

k₀ - коэффициент, зависящий от планового очертания пруда перед сооружением, а также продольного и поперечного профиля по логу [15] (табл. 3.1).

Таблица 3.1

Очертание зеркала воды пруда в плане	Значения коэффициента k₀ в зависимости от профиля лога
	Продольный профиль лога перед сооружением	Поперечный профиль лога (берегов)
	Продольный профиль лога перед сооружением	выпуклый	прямолинейный	вогнутый
С вогнутыми линиями урезов	Выпуклый	190	230	270
	Прямоугольный	230	280	320
	Вогнутый	270	320	380
С прямолинейными линиями урезов	Выпуклый	230	280	320
	Прямолинейный	280	330	370
	Вогнутый	320	370	450
С выпуклыми линиями урезов	Выпуклый	270	320	380
	Прямолинейный	320	370	450
	Вогнутый	380	450	530

Расчет по уравнению (3.6) выполняют графически в системе координат Q, H³, в которой эта зависимость изобразится прямой линией. Причем величина H³ располагается на оси ординат, а Q - на оси абсцисс. Кроме того, на оси ординат дается совмещенная с H³ шкала H. Рассмотрим последовательность расчета.

1. Определяют координаты точек пересечения прямых с осями координат:

при H³ = 0 Q_соор = Q_пр;

при Q_{соор(возм)} = 0

По этим двум точкам проводят на графике Q = f(H³) прямую, соответствующую указанной зависимости.

2. Строят зависимости Q_соор = f(H³) для принятых сооружений согласно рекомендациям гл. 6 и 7.

3. Находят точку пересечения Q_{соор(возм)} = f(H³) и Q_соор = f(H³). Абсцисса этой точки соответствует расходу в сооружении с учетом аккумуляции воды перед ним, а ордината - H³. По совмещенной с H³ шкале H находят подпертую глубину перед сооружением.

Учет перелива воды из бассейна в бассейн

3.15. В ряде случаев при достаточно низких водоразделах, особенно при значительной аккумуляции воды перед сооружениями, возможен перелив вод из бассейна в бассейн или из сооружения в сооружение при наличии низких водоразделов непосредственно у насыпи дороги. При этом возможны различные случаи:

а) простой перелив из одного сооружения в сооружение;

б) перелив из двух соседних сооружений в сооружение, расположенное между ними;

в) цепочка перелива из сооружения в сооружение.

Особенно часто переливы встречаются на эксплуатируемых линиях. Расчет перелива удобно вести графоаналитическим методом. Схемы такого расчета приведены на рис. 3.4, 3.5 и 3.6, где все зависимости, участвующие в графическом решении, обозначены цифрами, приведенными в подрисуночных подписях.

Рис. 3.4. Схемы для определения расходов воды в сооружениях

Q_соор и соответствующих им подпертых глубин H

при однократном переливе:

а - в верховом сооружении (N 1); б - в низовом (N 2):

1 - Q_соор(1) = f(H); 2 - Q_сб(1) = f(H);

3 - Q_{соор(возм)1} = f(H³); 4 - (Q_сб(1) + Q_соор(1)) = f(H);

5 - (Q_соор(1) + Q_сб(1)) = f(H³); 6 - Q_пр(1) = f(t);

7 - (Q_соор(1) + Q_сб(1)) = f(t); 8 - Q_пр(2) = f(t);

9 - Q_сб(1) = f(t); 10 - (Q_пр(2) + Q_сб(1)) = f(t);

11 - Q_соор(2) = f(H); 12 - Q_соор(2) = f(H³);

13 - Q_{соор(возм)2} = f(H³)

Рис. 3.5. Схемы для определения расходов воды в сооружениях

Q_соор и соответствующих им подпертых глубин H

при цепочке перелива:

а - в верховом сооружении (N 1); б - в промежуточном

сооружении (N 2); в - в низовом сооружении (N 3):

1 - Q_соор(1) = f(H); 2 - Q_сб(1) = f(H);

3 - Q_{соор(возм)1} = f(H³); 4 - (Q_соор(1) + Q_сб(1)) = f(H);

5 - (Q_соор(1) + Q_сб(1)) = f(H³); 6 - Q_пр(1) = f(t);

7 - (Q_соор(1) + Q_сб(1)) = f(t); 8 - Q_пр(2) = f(t);

9 - Q_сб(1) = f(t); 10 - (Q_пр(2) + Q_сб(1)) = f(t);

11 - Q_сб(2) = f(H); 12 - Q_соор(2) = f(H);

13 - (Q_соор(2) + Q_сб(2)) = f(H);

14 - (Q_соор(2) + Q_сб(2)) = f(H³); 15 - Q_{соор(возм)2} = f(H³);

16 - (Q_соор(2) + Q_сб(2)) = f(t); 17 - Q_пр(3) = f(t);

18 - Q_сб(2) = f(t); 19 - (Q_пр(3) + Q_сб(2)) = f(t);

20 - Q_соор(3) = f(H); 21 - Q_соор(3) = f(H³);

22 - Q_{соор(возм)3} = f(H³)

Рис. 3.6. Схемы для определения расходов в сооружениях Q_соор

и соответствующих им подпертых уровней H при переливе

воды из двух соседних сооружений в одно, расположенное

между ними:

а - в верховом сооружении (N 1); б - в верховом

сооружении (N 3); в - в низовом сооружении (N 2):

1 - Q_соор(1) = f(H); 2 - (Q_соор(1) + Q_сб(1)) = f(H);

3 - (Q_соор(1) + Q_сб(1)) = f(H³); 4 - Q_{соор(возм)1} = f(H³);

5 - Q_пр(1) = f(t); 6 - (Q_соор(1) + Q_сб(1)) = f(H);

7 - Q_соор(3) = f(H); 8 - (Q_соор(3) + Q_сб(3)) = f(H);

9 - (Q_соор(3) + Q_сб(3)) = f(H³);

10 - Q_{соор(возм)3} = f(H³); 11 - Q_пр(3) = f(t);

12 - (Q_соор(3) + Q_сб(3)) = f(t); 13 - Q_сб(1) = f(t);

14 - Q_сб(3) = f(t); 15 - Q_пр(2) = f(t);

16 - (Q_пр(2) + Q_сб(1) + Q_сб(3)) = f(t);

17 - Q_соор(2) = f(H); 18 - Q_соор(2) = f(H³);

19 - Q_{соор(возм)2} = f(H³)

3.16. Последовательность расчетов при однократном переливе следующая.

1. Выполняют для верхового и низового сооружений расчеты стока и определяют расчетные и наибольшие (для железных дорог) расходы притока воды Q_р и Q_max и соответствующие им объемы стока W_р и W_max, а также время от начала паводка до его пика. Этому времени соответствует время водоотдачи для ливневого стока t_в и время подъема паводка t_под для снегового.

2. Определяют продолжительность паводка для сооружений исходя из наиболее распространенной треугольной формы гидрографа паводка:

(3.7)

где W_пр - объем притока с бассейна, м³;

Q_пр - расход притока на пике паводка, м³/с;

k_пав - коэффициент; для ливневого паводка k_пав = 1; для снегового k_пав = 0,7.

3. Строят для верхового сооружения зависимости Q_соор(1) = f(H) согласно рекомендациям гл. 5 и 6 и Q_{соор(возм)1} = f(H³) по уравнению Д.И. Кочерина [формула (3.6)]. Расходы откладывают по оси ординат, подпертые глубины H и H³ - по оси абсцисс. Причем указанные зависимости располагают с левой стороны чертежа (с левой стороны от оси ординат - см. рис. 3.4, а).

4. Устанавливают по продольному профилю дороги или по планам местности на участке, примыкающем к дороге, место перелива и форму поперечного сечения в нем - форму определяющего, т.е. формирующего сбросный расход сечения.

5. Определяют подпертую глубину перед сооружением в начале перелива

H_{нач.пер} = z_п - z_л, (3.8)

где z_п - отметка подпертого уровня перед сооружением;

z_л - отметка лотка у сооружения на входе в него.

6. Строят зависимость расхода сброса из верхового сооружения Q_сб от глубины воды в определяющем сечении Q_сб = f(H') по приведенным ниже формулам (3.9) или (3.10), предварительно задавшись глубинами в определяющем сечении H' = H - H_{нач.пер}, где H - подпертая глубина перед сооружением.

При этом сбросный расход вычисляют исходя из установления в определяющем сечении критической глубины по формулам:

при прямоугольной форме определяющего сечения

(3.9)

при треугольной его форме

(3.10)

где b - ширина потока при прямоугольном определяющем сечении;

m_от(1) и m_от(2) - заложение откосов треугольного сечения.

При иных формах сечений последние приводят к прямоугольным или треугольным.

Зависимость Q_сб = f(H) строят в координатах Q и H, принимая за начало отсчета подпертую глубину, соответствующую отметке начала перелива.

7. Строят зависимость Q_соор(1) + Q_сб(1) = f(H) путем сложения графиков Q_соор(1) = f(H) и Q_сб(1) = f(H).

8. Строят зависимость Q_соор(1) + Q_сб(1) = f(H³).

9. Находят точку пересечения зависимости Q_{соор(возм)1} = f(H³), построенной по уравнению (3.6), и зависимости Q_соор(1) + Q_сб(1) = f(H³) для данного сооружения. Ордината ее соответствует максимальному значению Q_соор(1) + Q_сб(1). Затем проводят через найденную точку линию, параллельную оси абсцисс, до пересечения ее с зависимостью Q_соор(1) + Q_сб(1) = f(H). Абсцисса этой точки соответствует искомому значению подпертой глубины H.

10. По значению H, используя зависимость Q_соор(1) = f(H) для данного сооружения, находят искомое значение Q_соор(1).

11. С правой стороны графика строят гидрограф притока к верховому сооружению Q_пр(1) = f(t), принимая его форму треугольной. Основание треугольника соответствует продолжительности паводка t_пав1, определяемого по формуле (3.7), а вершина, соответствующая максимальному расходу притока Q_пр(1), располагается в точке на оси абсцисс, соответствующей времени водоотдачи t_в1 для ливневого стока и примерно ¹/₃ t_пав1 для снегового. Значение t_в1 также определяется в процессе расчета стока.

12. Строят гидрограф суммы расходов: расхода в верховом сооружении Q_соор(1) и расхода сброса Q_сб(1).

Для этого определяют предварительно продолжительность прохождения паводка в верховом сооружении по формуле (3.7):

Затем проводят через ординату, соответствующую расходу Q_соор(1) + Q_сб(1), линию, параллельную оси абсцисс, и находят точку пересечения ее с ветвью спада гидрографа притока Q_пр(1) = f(t). Соединив эту точку с началом координат и точкой на оси абсцисс, имеющей координату t = t_{пав(соор)1}, получают гидрограф расходов Q_соор(1) + Q_сб(1) = f(t).

13. Находят время начала t_н(пер)1 и конца t_к(пер)1, сброса, а также время установления пика паводка в сооружении t_(max _Q_)пер1.

Для нахождения t_н(пер)1 и t_к(пер)1 пересекают гидрограф расхода Q_соор(1) + Q_сб(1) = f(t) прямой, параллельной оси абсцисс на ординате, соответствующей расходу, определяемому подпертой глубиной перед сооружением, при которой начинается перелив. Время t_(max _Q_)пер1 соответствует пику паводка в сооружении.

Все указанные построения относятся к верховому сооружению и приведены на рис. 3.4, а).

Для получения расхода и соответствующей ему подпертой глубины в низовом сооружении выполняют следующие расчеты и построения (последние выполняют с правой стороны графика - см. рис. 3.4, б).

1. Строят гидрограф паводка притока к низовому сооружению N 2 Q_пр(2) = f(t) аналогично тому, как было указано выше для верхового.

2. По значению сбросного расхода Q_сб(1), определяемого для верхового сооружения, и временам начала t_н(пер)1 и конца t_к(пер)1 перелива и времени t_(max _Q_)пер1, соответствующего наибольшему значению расхода Q_соор(1) + Q_сб(1), строят гидрограф сбросного расхода Q_сб(1) = f(t), принимая его треугольной формы (на рис. 3.4, б он изображен штриховой линией). Затем складывают геометрически гидрограф расходов притока с собственного бассейна сооружения N 2 Q_пр(2) = f(t) и гидрограф расхода сброса из сооружения N 1 Q_сб(1) = f(t) и получают суммарный максимальный расход притока к низовому сооружению Q_пр(2) + Q_сб(1) и соответствующий ему суммарный гидрограф притока Q_пр(2) + Q_сб(1) = f(t).

3. Аналогично верховому сооружению с левой стороны графика строят зависимости Q_соор(2) = f(H), Q_соор(2) = f(H³) и Q_{соор(возм)2} = f(H³). Но при вычислении Q_{соор(возм)2} = f(H³) по уравнению Д.И. Кочерина вводят следующие коррективы:

а) объем притока увеличивают на величину объема стока через сбросный водовод, т.е. полный объем стока определяют как сумму объемов стока с собственного бассейна W_пр(2) и объема сброса из верхового сооружения W_сб(1)

W_полн(2) = W_пр(2) + W_сб(1). (3.11)

Значение W_сб(1), м³, определяют по формуле

(3.12)

где t_сб1 - продолжительность сброса, мин.

В свою очередь t_сб(1) = t_к(пер)1 - t_н(пер)1;

б) точку прямой Q_{соор(возм)2} = f(H³) с координатами Q = Q_пр(max)2 и H₂ = 0 находят графически в месте пересечения прямой, проведенной с правой стороны графика через высшую точку гидрографа паводка Q_пр(2) + Q_сб(1) = f(t) параллельно оси абсцисс, с осью ординат (см. рис. 3.4, б);

в) вторая точка, необходимая для построения прямой Q_{соор(возм)2} с координатами Q_соор = 0 и H_max, определяется обычным путем с учетом отмеченной выше корректировки объема стока.

4. Находят (аналогично верховому сооружению) в точке пересечения зависимостей Q_{соор(возм)2} = f(H³) и Q_соор(2) = f(H³) для данного сооружения Q_соор(2) и соответствующую ему подпертую глубину H₂ (см. рис. 3.4, б).

3.17. При цепочке перелива из сооружения в сооружение (см. рис. 3.5) расчет верхового сооружения такой же, как и для однократного перелива. Расчет последующих сооружений, кроме последнего, имеет отличия, излагаемые ниже.

Расчет сооружения N 2 полностью включает расчеты, выполняемые для второго сооружения при однократном переливе, но должен быть в этом случае дополнен следующими расчетами и построениями.

1. Строят гидрограф суммы расходов: расхода во втором сооружении Q_соор(2) и расхода сброса из него Q_сб(2).

Предварительно определяют продолжительность прохождения паводка во втором сооружении по формуле (3.7):

(3.13)

2. Проводят через ординату, соответствующую расходу Q_соор(2) + Q_сб(2), линию, параллельную оси абсцисс, и находят точку пересечения ее с ветвью спада гидрографа притока Q_пр(2) + Q_сб(1) = f(t). Соединив эту точку с началом координат и точкой на оси абсцисс, имеющей координату t = t_{пав соор(2)}, получают гидрограф расходов Q_соор(2) + Q_сб(2) = f(t). Далее, проводя линию, параллельную оси абсцисс на ординате, соответствующей расходу начала перелива и определяемой по подпертой глубине начала (конца) перелива, находят в точках пересечения этой линии со сторонами треугольного гидрографа Q_соор(2) + Q_сб(2) = f(t) время t_н(пер)2 и t_к(пер)2. Абсцисса, соответствующая пику гидрографа, определит время t_(max _Q₎₂.

Построения для последнего сооружения цепочки перелива аналогичны построениям для низового сооружения при однократном переливе.

3.18. На рис. 3.6 приведены графические расчеты для случая перелива из двух соседних сооружений в сооружение между ними.

Как и в ранее рассмотренном случае, расчеты для верхового сооружения N 1 не имеют особенностей. Верховое сооружение N 3 решается так же как сооружение N 1. Отличается расчет лишь для сооружения N 2, в которое происходит сброс расходов из сооружений N 1 и 3. Для этого сооружения аналогично расчетам для низового сооружения в двух ранее рассмотренных случаях (см. рис. 3.4, б и 3.5, в) определяют расход в сооружении (см. левую сторону графика рис. 3.6, в) с коррективом объема стока, вычисленным следующим образом.

По полученным для сооружений N 2 и 3 данным строят с правой стороны графика гидрографы Q_сб(1) = f(t) и Q_сб(3) = f(t) (на рис. 3.6, в они показаны штриховой линией) и гидрограф расхода с собственного бассейна Q_пр(2) = f(t). Сложив эти графики, получают гидрограф расхода притока к сооружению N 3 Q_пр(3) + Q_сб(1) + Q_сб(3) = f(t). Вычислив площадь

, ограниченную указанной зависимостью и осью абсцисс, определяют объем стока, м³,

. Это значение используют при расчете Q_соор по уравнению Д.И. Кочерина.

Остальные расчеты аналогичны изложенным выше для низового сооружения при однократном переливе. Примеры расчета однократного перелива из сооружения в сооружение приведены в приложении 3.1.

ПРИБЛИЖЕННЫЕ РАСЧЕТЫ СТОКА И АККУМУЛЯЦИИ

Снеговой сток

3.19. Приведенные ниже приближенные расчеты стока и аккумуляции основаны на использовании методики, разработанной в Союздорпроекте Б.Ф. Перевозниковым [26].

Максимальный расход снегового стока 1%-ной вероятности превышения (p = 1%) определяют по номограмме на рис. 3.7 в функции площади бассейна F, модуля снегового стока C_1%, заболоченности и озерности. Модули снегового стока, или, как их еще называют, модули стока весеннего половодья, определяют по карте на рис. 3.8 <*>.

--------------------------------

<*> Снеговой сток считают для районов, расположенных севернее штриховой линии. Южнее указанной линии считают только ливневый сток.

Рис. 3.7. Номограмма для определения расходов от снеготаяния

вероятностью превышения p = 1%

Рис. 3.8. Карта изолиний элементарного модуля

снегового стока (стока весеннего половодья) C_1%

вероятностью превышения 1%

Расход иных вероятностей превышения p рассчитывают по формуле

Q = Q_номk_с, (3.14)

где Q_ном - расход по номограмме;

k_с - поправочный коэффициент, равный 1,37 при p = 0,3% и 0,87 при p = 2%.

Озерность и заболоченность устанавливают по планам бассейнов или картам как выраженное в процентах отношение площади озер и болот к общей площади бассейна. При отсутствии заболоченности расчет по номограмме условно ведут для заболоченности 1%.

При степени озерности более 20% влияние заболоченности не учитывают и расчет по номограмме выполняют для озерности 20% и заболоченности 1%.

При предварительных расчетах влияние карста и искусственной аккумуляции стока не учитывают.

Пример. Требуется определить максимальный расход снегового стока вероятностью превышения p = 0,3% для расположенного в районе г. Архангельска бассейна площадью F = 1,5 км², характеризующегося озерностью 20% и заболоченностью 3,5%.

Решение. На карте (см. рис. 3.8) для района Архангельска принимаем модуль элементарного снегового стока C_1% = 2,5.

На шкале F номограммы (см. рис. 3.7) находим точку, соответствующую F = 1,5 км², и проводим вертикальную прямую до пересечения с линией, соответствующей элементарному модулю снегового стока C_1% = 2,5. От точки пересечения проводим горизонтальную линию до пересечения с вертикальной шкалой x.

На шкале "заболоченность" находим точку, соответствующую 3,5%, проводим через нее вертикальную линию до пересечения с линией 20% озерности. Через точку пересечения проводим горизонтальную линию до пересечения со шкалой y.

Полученные точки на шкалах x и y соединяем прямой линией и в месте ее пересечения со шкалой Q находим расход Q_1% = 1,6 м³/с.

Для определения Q_0,3% принимаем поправочный коэффициент k_с = 1,37.

Искомый расход Q_0,3% = Q_0,3%k_с = 1,6·1,37 = 2,19 м³/с.

Ливневый сток

3.20. Максимальный расход ливневого стока 1%-ной вероятности превышения для бассейнов с песчаными и супесчаными почвами определяют по номограмме, приведенной на рис. 3.9.

Рис. 3.9. Номограмма для определения ливневых расходов

вероятностью превышения 1% для песчаных и супесчаных почв

[римские и арабские цифры обозначают соответственно группы

и номера климатических и ливневых районов (см. табл. 3.2)]

Таблица 3.2

Группа климатических районов	Номера районов дождевых паводков (ливневых районов)
I	10
II	7, 8, 9
III	5, 6
IV	3а и 4
V	1, 2, 3

Расход находят в функции площади F и уклона главного лога I бассейна для каждого из ливневых районов или, как их еще называют, районов дождевых паводков, по карте-схеме на рис. 3.10 и групп климатических районов, устанавливаемых по табл. 3.2.

Рис. 3.10. Карта-схема районов дождевых паводков

(ливневых районов) в СССР

Для определения расходов Q иных вероятностей превышения и в случае почв бассейна отличных от песчаных в результаты, полученные по номограмме, вводят по табл. 3.3 поправочные коэффициенты k_л.

При этом расход

Q = Q_номk_л. (3.15)

Таблица 3.3

Вероятность превышения паводка p, %	Значения коэффициентов k_л при грунтах бассейна			Вероятность превышения паводка p, %	Значения коэффициентов k_л при грунтах бассейна
Вероятность превышения паводка p, %	глинистых и суглинистых	песчаных и супесчаных	рыхлых (осыпях)	Вероятность превышения паводка p, %	глинистых и суглинистых	песчаных и супесчаных	рыхлых (осыпях)
0,3	1,46	1,39	1,32	3,0	0,80	0,76	0,73
1,0	1,05	1,00	0,96	5,0	0,71	0,67	0,64
2,0	0,88	0,84	0,80	10,0	0,60	0,57	0,54

Пример. Требуется определить максимальный ливневый расход 1%-ной вероятности превышения для расположенного в Московской области бассейна площадью F = 5 км², имеющего уклон лога

; грунты бассейна - суглинки.

Решение. По карте-схеме на рис. 3.10 устанавливаем номер ливневого района, а по табл. 3.2 - номер группы климатических районов. Московской области соответствует ливневый район N 5 и группа климатических районов III.

На шкале I номограммы (см. рис. 3.9) находим точку, соответствующую уклону главного лога

. Через эту точку проводим вертикаль до пересечения с линией, соответствующей номеру группы климатических районов III. Через полученную точку проводим горизонтальную прямую до пересечения со шкалой x (в примере длина горизонтальной линии равна нулю).

На шкале F находим точку, соответствующую площади бассейна F = 5 км², и через нее проводим вертикальную прямую до пересечения с линией, соответствующей ливневому району N 5. Через полученную точку проводим горизонтальную прямую до пересечения со шкалой y.

Соединяем прямой полученные точки на шкалах x и y и в месте ее пересечения со шкалой Q находим Q_ном = 24,8 м³/с. Этот расход имеет вероятность превышения p = 1% и соответствует песчаным и супесчаным почвам.

Для суглинистых грунтов при p = 1% находим по табл. 3.3 поправочный коэффициент k_л = 1,05.

Искомый расход Q = Q_номk_л = 24,8·1,05 = 26,0 м³/с.

РАСЧЕТ РАСХОДОВ В СООРУЖЕНИИ С УЧЕТОМ АККУМУЛЯЦИИ

3.21. Для определения расходов в сооружении Q_соор с учетом аккумуляции решают совместно два уравнения:

1) уравнение возможного поступления воды в сооружение при данном напоре H

(3.16)

где Q - расход притока с бассейна, определяемый согласно указаниям, изложенным выше;

- расход, идущий на увеличение уровня перед сооружением, определяемый по номограмме, проведенной на рис. 3.11;

2) уравнение пропускной способности заданного сооружения

Q_соор = f(H) <*>. (3.17)

--------------------------------

<*> Методика решения этого уравнения изложена в гл. 5.

Рис. 3.11. Номограмма для определения расхода аккумуляции

при живом сечении лога треугольной формы

Уравнение (3.16) решают графическим методом. Для этого задаются рядом значений подпертых глубин перед сооружением H и по продольному профилю дороги находят соответствующие этим глубинам ширины разлива B_разл в створе перехода. При этом если форма живого сечения пруда в створе перехода отличается от треугольной или прямоугольной, то B_разл определяют по одной из условных форм, приведенных на рис. 3.12. Затем по номограмме на рис. 3.11 определяют расход

для каждого из значений H и B_разл при известной площади бассейна F, уклоне лога у сооружения i_л (при отсутствии данных принимают его равным уклону лотка сооружения) и уклоне главного лога бассейна I. Порядок расчета следующий.

Рис. 3.12. Схемы к определению размеров B и H

при схематизации живого сечения лога по треугольнику

и прямоугольнику (сплошная линия - фактическое сечение;

штриховая - схематизированное сечение)

На шкале H находят точку, соответствующую заданной глубине воды перед сооружением, и через нее проводят вертикаль до пересечения с линией заданного уклона лога у сооружения и через полученную точку проводят горизонтальную прямую до пересечения со шкалой F. В правой части номограммы на шкале B_разл находят точку, соответствующую ширине разлива в створе перехода при заданной глубине H, и проводят через нее вертикаль до пересечения с линией заданного уклона главного лога бассейна, через полученную точку проводят горизонталь до пересечения со шкалой y. Соединяют полученные на шкалах F и y точки прямой линией и находят ее пересечение со шкалой x. Наконец, на шкале F находят точку, соответствующую площади бассейна, и соединяют ее прямой с точкой на шкале x; продолжение полученной прямой до шкалы

дает на ней расход воды, идущей на увеличение уровня перед сооружением.

Номограмма (см. рис. 3.11) соответствует треугольной форме живого сечения пруда в створе перехода и климатическим условиям, отличным от муссонных.

Для прямоугольной формы живого сечения в створе перехода и муссонных условий в расход, полученный по номограмме, вводят поправочный коэффициент k_ак из табл. 3.4.

Таблица 3.4

Форма живого сечения пруда в створе перехода	Значения коэффициентов k_ак для условий
Форма живого сечения пруда в створе перехода	всех, кроме муссонных	муссонных
Треугольная	1,0	0,58
Прямоугольная	2,0	1,16

Расход в этом случае

(3.18)

Завершают расчет построением кривых Q_{соор(возм)} = f(H) и Q_соор = f(H), точка пересечения которых соответствует искомому расходу в сооружении и подпертой глубине перед ним.

Пример. Требуется определить Q_соор и соответствующую ему подпертую глубину H для прямоугольной трубы 2,0 x 2,0 м с раструбными оголовками

. Площадь бассейна F = 5 км². Расход с бассейна Q_1% = 26,0 м³/с. Уклоны главного лога I = 1%, лога у сооружения i_л = 5%. Район - Московская область.

Поперечное сечение пруда у сооружения (по продольному профилю) приведено к треугольному.

Решение. Расход в сооружении Q_соор определяют, решая совместно уравнение (3.16) и уравнение пропускной способности для трубы Q_соор = f(H) (см. гл. 5).

Для определения расхода

задаются рядом подпертых глубин перед сооружением H и для каждой из них по продольному профилю дороги находят соответствующие ширины разлива B_разл.

Предположим, что при значениях H получены B_разл, приведенные в табл. 3.5. Затем по известным I, i_л и площади бассейна F находят по номограмме (см. рис. 3.11) расход

, а по уравнению (3.16) - расход в сооружении Q_соор. Результаты заносят в расчетную табл. 3.5.

Таблица 3.5

Номер точек	H, м	B_разл, м	, м³/с (по номограмме на рис. 3.11)	, м/с		Q_соор, м³/с (по номограмме на рис. 5.16)
1	1,0	60	0,4	25,6	0,5	3,0
2	1,5	90	1,4	24,6	0,75	5,5
3	2,0	120	3,0	23,0	1,0	8,7
4	2,5	150	6,1	19,9	1,25	11,0
5	3,0	180	11,0	15,0	1,50	13,5
6	3,5	216	19,0	7,0	1,75	16,0

После этого по номограмме, приведенной в гл. 5 на рис. 5.16, определяют расходы, пропускаемые трубой при подпертых глубинах, соответствующих заданным значениям H (см. последнюю графу таблицы расчета).

Расчет по номограмме, приведенной на рис. 5.16, рекомендуется вести следующим образом.

По шкале h откладывают высоту трубы, т.е. h_т = 2,0 м, а по шкале b - отверстие трубы b = 2,0 м; соединив эти точки прямой, находят точку пересечения ее с безымянной шкалой.

Затем на шкале H/h_т, соответствующей трубе с раструбными оголовками

, откладывают заданные значения H/h_т, т.е. подпертую глубину, деленную на высоту трубы (в нашем случае h_т = 2 м). Каждую из полученных на шкале H/h_т точек соединяют с найденной ранее точкой на безымянной шкале и на шкале Q находят расход, пропускаемый трубой при заданном H (при H/h_т <= 1,1 результат получают на шкале Q для безнапорного режима, в противном случае - на шкале Q при полунапорном режиме).

Результаты определения Q_соор = f(H) также заносят в расчетную табл. 3.5. По данным, сведенным в таблицу, строят кривые (рис. 3.13) Q_{соор(возм)} = f(H) и Q_соор = f(H), где Q_соор - расход, пропускаемый трубой.

Рис. 3.13. График для определения расхода воды в сооружении

с учетом аккумуляции

Искомый расход Q_соор и подпертая глубина H, соответствующие точке пересечения указанных кривых, будут соответственно равны 14,0 м³/с и 3,10 м.

4. СОПРЯГАЮЩИЕ СООРУЖЕНИЯ

ТИПЫ СОПРЯГАЮЩИХ СООРУЖЕНИЙ

4.1. Поток может быть введен в сооружение как в спокойном, так и в бурном состоянии. В последнем случае может быть обеспечено существенное повышение пропускной способности сооружений.

Для надежного ввода бурного потока в основное сооружение применяют специальные типы сооружений, называемые сопрягающими. Их обычно устраивают на участках водопропускного тракта с большим перепадом отметок. На сопрягающих сооружениях поток, как правило, развивает высокие скорости, поэтому необходимо предупредить образование высокой кинетической энергии потока или погасить ее. Для изменения скоростей потока по длине сопрягающих сооружений применяют повышенную шероховатость, а для гашения энергии используют водобойные стенки и колодцы.

4.2. Ввод спокойного потока в сооружение не требует применения специальных устройств, как при вводе бурного потока. Однако с целью обеспечения более плавного сопряжения потока с элементами сооружений применяют специальные устройства (оголовки труб, направляющие стенки и конуса мостов), обеспечивающие повышение пропускной способности сооружений.

Подробно эти устройства и их гидравлические характеристики приводятся в соответствующих главах настоящего Пособия применительно к конкретным типам сооружений.

В конце настоящей главы излагается гидравлический расчет входных участков сооружений равнинного типа, являющийся общим для всех сооружений данного типа.

4.3. Простейшее сопрягающее сооружение - одноступенчатый перепад. Ниже перепада обычно требуется установка одного из видов водобойных сооружений. Большое падение отметок на участке сопряжения часто приводит к использованию многоступенчатых перепадов, на которых поток тормозится за счет трения.

На крутых косогорных участках применяют многоступенчатые перепады колодезного и полунапорного типа. Для гашения энергии потока на последних используют затопленный гидравлический прыжок.

При пересечении дорогой глубокого лога, в частности при отводе воды с нагорной стороны на крутых участках местности, используют консольные перепады, а иногда устройства типа шахтного водосброса. Консольные перепады позволяют устроить быстроток над полотном дороги, а опасность размыва дорожных сооружений предотвратить отбросом падающей струи струенаправляющим носком на большое расстояние.

В качестве разновидностей струенаправляющего носка могут быть использованы рассеивающие трамплины, уменьшающие глубину размывов.

При больших уклонах местности для перехвата воды с верховой стороны косогора и ввода его в сооружение устраивают быстротоки, представляющие собой призматические бетонные или железобетонные лотки, уложенные с уклонами, большими критических. Ширину быстротоков обычно назначают большей отверстия сооружения, что вызывается необходимостью снижения в нем скоростей.

С этой же целью устраивают в быстротоках повышенную шероховатость в виде ребер, шашек и т.п. (см. гл. 2).

Для сопряжения призматических быстротоков с сооружением устраивают сужающиеся быстротоки, характер течения в которых весьма сложен.

В некоторых случаях для гашения скоростей на входе в сооружение используются водоприемные колодцы, в которых гашение энергии осуществляется за счет перевода бурного потока в спокойный путем затопления гидравлического прыжка.

Ниже подробно излагаются гидравлические расчеты основных типов сопрягающих сооружений.

ОДНОСТУПЕНЧАТЫЕ ПЕРЕПАДЫ

4.4. Одноступенчатые перепады применяют для сопряжения участков каналов в различных уровнях. Высоту одноступенчатых перепадов обычно принимают не более 2,5 - 3 м, поскольку при большей высоте трудно погасить энергию потока после падения.

Одноступенчатый перепад (рис. 4.1) состоит из входной части, вертикальной, наклонной или криволинейной стенки падения и закрепленного начального участка нижнего бьефа - водобоя.

Рис. 4.1. Схема одноступенчатого перепада:

1 - входная часть; 2 - стенка падения; 3 - водобой

4.5. Расчет одноступенчатого перепада заключается в определении глубин на входном участке и на водобое, а также длины последнего. По известным глубинам определяют скорости воды и назначают типы одежды [3].

4.6. При расчете водобоя в первую очередь определяют глубину в сжатом сечении h_с подбором из уравнения

(4.1)

где T₀ - удельная энергия потока для сечения A-A;

- коэффициент Кориолиса; можно принять

;

- коэффициент бокового сжатия, равный 0,90 - 0,95, если ширина подводящего русла больше ширины перепада;

- коэффициент скорости.

Значения коэффициента скорости

в зависимости от отношения

приведены ниже.

...... 0,15 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90

....... 0,75 0,80 0,85 0,87 0,89 0,91 0,92 0,93 0,94

Удельная энергия потока для сечения A-A

(4.2)

где h и v_h - глубина и скорость потока в сечении A-A. В зависимости от типа входного участка и продольного уклона подводящего русла может быть: h = h_к при спокойном состоянии потока в призматическом русле;

- нормальной глубине - при бурном состоянии и равномерном движении в подводящем русле; при неравномерном движении h определяется по уравнению неравномерного движения (см. гл. 2);

p - высота стенки падения потока.

Если поперечное сечение русла до стенки падения имеет другую форму или большей ширины, то перед стенкой падения образуется подпор, высоту которого вычисляют по формулам водослива соответствующей формы; при этом

- гидродинамическому напору перед водосливом.

Глубину h", сопряженную с глубиной h_с, определяют по приложению 2.6.

4.7. Для упрощения расчетов при вычислении сжатых глубин в случаях прямоугольной и трапецеидальной форм русла можно использовать графические приемы, изложенные ниже.

При определении h_с в прямоугольных руслах можно воспользоваться приведенным в приложении 2.7 графиком. Расчет начинают с нахождения на оси абсцисс точки, соответствующей значению

, и из нее проводят вертикаль до пересечения с кривой, соответствующей заданному коэффициенту

. Из точки пересечения проводят горизонталь, которая пересекает кривую

и ось ординат. Абсцисса точки пересечения равна искомому значению

, по которому находят

. На оси ординат указанная горизонтальная прямая дает значение

и, следовательно,

При трапецеидальной форме русла для определения сжатой глубины можно использовать график, приведенный в приложении 2.6 (рис. 1).

В этом случае, предварительно вычислив параметры

, отыскивают прямую, соответствующую значению A, и кривую, отвечающую параметру B. Абсцисса их пересечения дает искомое значение

. Глубина в сжатом сечении

. Глубину

, сопряженную с h_с, определяют по приложению 2.6 (рис. 2).

4.8. При бурном состоянии потока в отводящем русле участок за сжатым сечением рассчитывают по уравнениям неравномерного движения. При спокойном состоянии за сжатым сечением образуется гидравлический прыжок: при

- отогнанный, при

- надвинутый и при

- затопленный.

Отогнанный и надвинутый прыжки нежелательны. В этих случаях обычно добиваются образования затопленного прыжка устройством водобойных сооружений.

4.9. Длину водобоя принимают

L = l₁ + l₂ + l_п + l_пп, (4.3)

где l₁ - дальность полета струи;

l₂ - длина отгона прыжка;

l_п - длина гидравлического прыжка;

l_пп - зона успокоения потока за прыжком (послепрыжковый участок).

Формулу (4.3) можно рассматривать как общую для любого вида сопряжения бьефов. В случае надвинутого прыжка в формуле (4.3) следует принять длину отгона прыжка равной нулю.

Дальность полета струи, т.е. расстояние от стенки падения до сжатого сечения C-C, обычно определяют по уравнению

(4.4)

где h' и v' - глубина и скорость потока над стенкой падения в сечении A'-A' непосредственно при выходе со стенки падения, определяемые при расчете входной части перепада (см. выше).

Если в сечении A-A глубина h = h_к, то длину l₁ можно определять по формуле

l₁ = p + h_к. (4.5)

Когда входной участок перепада прямоугольного сечения заканчивается водосливом, дальность полета струи

(4.6)

где H₀ - гидродинамический напор перед водосливом;

m и n - коэффициенты; m = 1,25 и n = 0,45 - для водослива с тонкой стенкой; m = 1,33 и n = 0,30 - для водослива практического профиля; m = 1,64 и n = 0,24 - для водослива с широким порогом.

Расстояние l₁ включает не только дальность полета струи, но и некоторый участок за местом ее падения, на котором глубина падает до h_с. Более точно

(4.7)

Длину отгона прыжка l₂ определяют по уравнениям неравномерного движения. При затопленном и надвинутом прыжке l₂ = 0.

Длина гидравлического прыжка в русле прямоугольного сечения

l_п = 2,5(1,9h" - h). (4.8)

В руслах трапецеидального сечения длина прыжка

(4.9)

При отогнанном прыжке (см. рис. 4.1) в качестве h' принимают глубину h₂ в конце кривой подпора перед прыжком (сечение B-B). При надвинутом и затопленном прыжках считают, что h' = h_с, а B₁ и B₂ - ширина потока поверху при глубинах h' и h". Длину послепрыжкового участка принимают равной удвоенной глубине h_нб за прыжком:

l_пп = 2h_нб. (4.10)

4.10. По установленным глубинам в характерных сечениях перепада устанавливают скорости потока из уравнения неразрывности:

(4.11)

Затем подбирают типы укреплений.

МНОГОСТУПЕНЧАТЫЕ ПЕРЕПАДЫ

4.11. Многоступенчатые перепады (рис. 4.2) используют для сопряжения участков каналов и в качестве сборных участков из сооружений при больших перепадах отметок для предотвращения высокой кинетичности потока.

Рис. 4.2. Схема многоступенчатого перепада

Для сокращения земляных работ многоступенчатый перепад (см. рис. 4.2) вписывают в профиль поверхности земли, т.е. отношение высоты перепада p к длине ступени L должно примерно равняться среднему уклону местности. Для этого при больших уклонах местности ступени делают по возможности короткими, горизонтальными, а иногда даже с обратным уклоном. В дорожном строительстве обычно применяют многоступенчатые перепады, у которых продольные уклоны ступеней прямые (i₀ > 0).

4.12. Длину ступени определяют, как правило, из условия, чтобы в конце каждой ступени кинетическая энергия была одна и та же и равна кинетической энергии в конце входного участка перепада. Для этого необходимо, чтобы на ступени в конце участка с плавно изменяющимся движением (сечение A-A) глубина была равна критической.

4.13. Глубины в конце входного участка и в сжатом сечении C-C, а также расстояния l₁ и l₂ определяют так же, как и при расчете одноступенчатых перепадов. Длину участка с плавно изменяющимся движением l₂ между сечениями с глубинами h_с и h_к определяют по уравнениям неравномерного движения. При горизонтальных ступенях расстояние может быть определено по упрощенной формуле

(4.12)

Полная длина ступени равна сумме трех участков

L = l₁ + l₂ + l₃, (4.13)

где l₃ - длина третьего участка, определяемая по формуле

При более коротких ступенях глубина в конце ступени будет меньше критической, а скорость соответственно повысится. В пределе при малой высоте ступени сооружение можно рассматривать как русло высокой шероховатости и рассчитывать по методике, указанной в гл. 2. При этом не должно нарушаться условие p <= h_к/2.

4.14. Если же длину ступени увеличивать против формулы (4.12), то на ступени перепада возникает гидравлический прыжок (рис. 4.3). Удлинением ступени можно добиться затопления гидравлического прыжка в сжатом сечении, обеспечив превышение глубины спокойного потока в начале ступени над глубиной

, сопряженной со сжатой; на ступенях с прямым уклоном это возможно, если

. Общая длина ступени в этом случае

L = l₁ + l₂ + l_п + l₀ + l₃, (4.14)

где l₀ - длина кривой спада между сечениями с глубинами h" и h_к.

Рис. 4.3. Схема перепада с образованием

гидравлического прыжка на ступенях

4.15. Создавая на ступенях повышенную шероховатость, длину ступеней можно уменьшить до

(4.15)

где l₂ - длина кривой при обычной шероховатости;

i_к и i_к,ш - соответственно критический уклон при обычной и усиленной шероховатости.

4.16. Если уклон местности позволяет, то следует ступеням придавать положительный уклон, чтобы на них не задерживалась вода.

При обратном уклоне для этой цели вдоль ступени устраивают прорезь.

ВОДОБОЙНЫЕ КОЛОДЦЫ

4.17. Водобойный колодец (рис. 4.4) глубиной S₀ для затопления гидравлического прыжка должен обеспечить в месте его образования глубину спокойного потока выше второй сопряженной глубины

Рис. 4.4. Схема водобойного колодца

С учетом коэффициента затопления прыжка

(4.16)

Устройство колодца увеличивает первоначальную высоту стенки падения p, поэтому глубину колодца определяют методом последовательного приближения.

Первоначально глубину h_с и

определяют так же, как и в перепадах. Пренебрегая в первом приближении значением

и полагая

, находят по формуле (4.16) глубину колодца S₀₁.

Во втором приближении расчет проводят аналогично, но глубины h_с1 и

определяют с учетом увеличения высоты падения T₀ на глубину S₀₁, т.е. принимают

T₀₁ = T₀ + S₀₁. (4.17)

Обычно второе приближение можно принять за окончательное. Поэтому в формуле (4.16) используют

в случае пренебрежения перепадом на выходе из колодца

. Если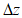

учитывают, то принимают

. Выход из колодца работает как подтопленный водослив с широким порогом, и перепады отметок на выходе

(4.18)

где

- коэффициент скорости;

При устройстве водоотвода от полотна дороги поперечное сечение перепада с водобойными колодцами часто устраивают трапецеидальной формы. В этом случае для расчета сопряжения бьефов и определения глубины водобойного колодца используют график, приведенный на рис. 4.5.

Рис. 4.5. График к расчету водобойных колодцев

Расчет сводится к следующему:

1) определяют удельную энергию T₀ для сечения A-A относительно дна отводящего русла. Тогда перепад z₀ = T₀ - h_нб;

2) определяют

, где

;

3) по графику на рис. 4.5 находят

Если

, то прыжок затопленный, если

, то прыжок отогнанный. В первом случае расчет на этом заканчивается - колодец не нужен.

Во втором случае для затопления прыжка необходим водобойный колодец, глубину которого, пренебрегая

, определяют по формуле (4.16), принимая

Длину водобойного колодца принимают равной дальности полета струи и длине подпертого гидравлического прыжка:

(4.19)

Изложенные выше способы определения глубины водобойного колодца используют связь между сопряженными глубинами совершенного гидравлического прыжка. В действительности в водобойных устройствах образуется подпертый прыжок. На рис. 4.6 помещен график для определения глубины водобойного колодца с учетом подпертого прыжка. Расчет с использованием этого графика сводится к следующему:

1) определяют значения

, где T₀ - запас удельной энергии потока в верхнем бьефе сооружения относительно дна отводящего русла без колодца;

2) через точку a, соответствующую заданным значениям

(правая ось ординат) и коэффициента скорости

, проводим линию, параллельную двум соседним, до пересечения в точке b с абсциссой

. Линия ab соответствует относительной глубине сжатого сечения

при заданных условиях;

3) ордината точки b на левой оси - это относительная глубина колодца

Рис. 4.6. График для определения глубины колодца

с учетом подпертого прыжка

Использование графика исключает метод подбора при определении глубины колодца. Найденная таким образом глубина колодца

является окончательной и соответствует степени затопленного подпертого гидравлического прыжка

. График, представленный на рис. 4.6, справедлив для русел прямоугольной формы с вертикальной выходной стенкой водобойного колодца в диапазоне

Длина колодца в этом случае

(4.20)

В формуле (4.20) относительную глубину сжатого сечения

находят относительно дна колодца, т.е. по запасу энергии T = T₀ + S₀. Для ускорения расчетов значение

можно принимать из графика на рис. 4.6 при

и соответствующем значении коэффициента скорости

ВОДОБОЙНЫЕ СТЕНКИ И КОМБИНИРОВАННЫЕ ВОДОБОЙНЫЕ СООРУЖЕНИЯ

4.18. Водобойные стенки (рис. 4.7) рассчитывают исходя из тех же принципов, что и при расчете водобойных колодцев. Разница лишь в том, что перед водобойной стенкой, работающей как водослив, образуется подпор, и приходится проверять сопряжение бьефов ниже стенки. Высота водобойной стенки

(4.21)

где

- степень затопления прыжка;

H - напор перед стенкой относительно ее гребня.

Рис. 4.7. Схема водобойной стенки

Напор перед стенкой определяют в первом приближении из условия работы водобойной стенки как незатопленного водослива; при этом принимают коэффициент расхода

Полный напор перед стенкой

(4.22)

Затем последовательными приближениями находят статический напор

(4.23)

Расстояние от стенки падения до водобойной стенки определяют так же, как и длину водобойного колодца.

При расчете водобойных стенок обязательно проверяют тип сопряжения потока ниже водобойной стенки. Если оказывается возможным надвинутый или отогнанный прыжок, то требуется установка второй стенки меньшей высоты.

Методика расчета второй (а в некоторых случаях и третьей) водобойной стенки та же, что и первой. Запас удельной энергии над гребнем водобойной стенки

T₀ = H₀ + p_ст. (4.24)

В случае затопленного гидравлического прыжка ниже водобойной стенки и одновременного превышения бытовой глубины над стенкой последняя работает как подтопленный водослив. При этом высоту водобойной стенки можно уменьшить.

Уточнение выполняют по формулам (4.21) и (4.23), определяя коэффициент подтопления

по табл. 4.1 как функцию

, где h_п = h_нб - p_ст - глубина подтопления.

Таблица 4.1

h_п/H		h_п/H		h_п/H
0,10	0,997	0,60	0,906	0,950	0,470
0,15	0,995	0,70	0,856	0,975	0,319
0,20	0,985	0,80	0,776	0,990	0,170
0,30	0,972	0,850	0,710	0,995	0,100
0,40	0,957	0,900	0,621	1,000	0
0,50	0,935	0,925	0,555

4.19. Если колодец получается слишком глубоким, а водобойная стенка настолько высокой, что трудно обеспечить затопление прыжка за нею, то проектируют комбинированное сооружение (рис. 4.8), которое образуют углублением водобоя и установкой водобойной стенки.

Рис. 4.8. Схема комбинированного водобойного устройства

При расчете комбинированных сооружений высоту водобойной стенки подбирают из условия, чтобы за ней сопряжение бьефов осуществлялось по типу затопленного прыжка без дополнительных мер. Для этого находят глубину в сжатом сечении прямоугольного русла ниже стенки при коэффициенте затопления прыжка

по формуле

(4.25)

По известной глубине в сжатом сечении вычисляют запас энергии перед водобойной стенкой:

(4.26)

Высота водобойной стенки

p_ст = T_вк - H₀. (4.27)

Напор H₀ перед водобойной стенкой находят из формулы (4.22). Значения коэффициента скорости устанавливают, как в расчете одноступенчатых перепадов. Глубину в сжатом сечении перед водобойной стенкой h_с и сопряженную с ней глубину

определяют, как при всех расчетах сопряжения бьефов за перепадом. В первом приближении принимают глубину водобойного колодца

(4.28)

Определяют глубину h_с1 в сжатом сечении на дне колодца из формулы

(4.29)

Находят глубину

(см. приложение 2.6), сопряженную с глубиной h_с1, а затем, подбором, гидродинамический напор перед водобойной стенкой из формулы

(4.30)

Глубина воды перед водобойной стенкой

h_ст = H + p_ст + S₀₁. (4.31)

Если

, то глубина водобойного колодца определена правильно. Если же

, то находят глубину водобойного колодца во втором приближении

(4.32)

и проверяют ее аналогично предыдущей проверке. Длину водобойного колодца определяют аналогично соответствующему расчету для обычного колодца.

ПЕРЕПАДЫ КОЛОДЕЗНОГО ТИПА

4.20. Максимального сокращения длины ступеней перепада можно достичь устройством на каждой ступени водобойной стенки высотой p_ст. Перепад такого типа называют многоступенчатым колодезным перепадом (рис. 4.9).

Рис. 4.9. Схема многоступенчатого колодезного перепада

Число ступеней назначают исходя из условия, чтобы разность отметок верха смежных водобойных стенок p не превышала 0,8 - 1,5 м. При более высоких ступенях резко снижается гашение энергии. Число ступеней перепада n = P/p, где P - общее падение местности.

Входную и выходную части колодезного многоступенчатого перепада рассчитывают так же, как и одноступенчатого. Высоты водобойных стенок промежуточных ступеней подбирают из условия затопления гидравлического прыжка, т.е.

(4.33)

где

- коэффициент затопления прыжка;

- глубина, сопряженная с глубиной в сжатом сечении на дне i-го колодца.

Статический напор H перед водобойной стенкой определяют по формулам водослива (4.22) и (4.23), а длину каждой ступени - по зависимости (4.19).

Для максимального сокращения длины ступеней допускают уменьшение длины подпертого гидравлического прыжка на перепадах по сравнению с длиной свободного гидравлического прыжка при тех же исходных условиях.

Многоколодезные перепады прямоугольного поперечного сечения рассчитывают следующим образом.

1. Назначив число ступеней n исходя из общего перепада отметок местности, определяют коэффициент скорости для сжатого сечения

(4.34)

Находят высоту водобойных стенок:

а) при

для всех ступеней

(4.35)

б) при

для первой ступени - по формуле (4.35), а для всех последующих

p_ст = 0,23p + 0,39h_к. (4.36)

2. Принимают длину всех ступеней

(4.37)

где

- толщина порога водобойной стенки.

Значение

определяют по уравнению (2.20) или по графику (см. приложение 2.6).

3. Сопряжение бьефов за многоколодезным перепадом рассчитывают исходя из запаса энергии в последнем сжатом сечении

(4.38)

здесь

где H₀ - гидродинамический напор перед входом в перепад.

Изложенный способ рекомендуется при

Многоколодезные перепады трапецеидального поперечного сечения рассчитывают в такой последовательности.

1. Назначают высоту ступеней (без учета высоты водобойных стенок p_ст) исходя из общей высоты падения P и числа ступеней n:

(4.39)

2. Определяют параметры потока и сооружения на первой ступени в предположении образования свободного гидравлического прыжка:

а) вычисляют запас энергии в подводящем русле относительно дна сжатого сечения

T₀₁ = p₁ + H₀, (4.40)

где H₀ - гидродинамический напор в подводящем русле относительно его дна;

б) пользуясь приложением 2.6, определяют вторую сопряженную глубину свободного гидравлического прыжка

;

в) находят высоту первой водобойной стенки

(4.41)

При этом гидростатический напор H₁ находят подбором из уравнения расхода для трапецеидального водослива:

(4.42)

где m - коэффициент расхода водослива;

m_от - коэффициент откоса.

3. Предварительно определяют высоту первой водобойной стенки при надвинутом прыжке

(4.43)

4. Определяют размеры колодца первой ступени при затопленном прыжке:

а) высота стенки

(4.44)

вторая сопряженная глубина подпертого гидравлического прыжка

(4.45)

где

- степень подпора прыжка; обычно

;

глубина над водобойной стенкой

(4.46)

Здесь

(4.47)

(4.48)

б) длина первого колодца

l_к1 = l_пад1 + l_п1, (4.49)

где l_пад1 - дальность полета струи при свободном падении [см. ниже формулу (4.58)];

l_п1 - длина подпертого гидравлического прыжка.

В свою очередь

(4.50)

K = 4,4 + 2,6m_от. (4.51)

5. Определяют размеры колодца на каждой следующей ступени:

а) находят запас энергии

T₀_i = p_i + p_п(_i_-1) + H₀ (4.52)

и безразмерный параметр

(4.53)

где p_п(_i_-1) - высота водобойной стенки на предыдущей ступени;

б) по кривым, приведенным на рис. 4.10, при

находят безразмерные параметры

по кривой 1

(4.54)

здесь

;

по кривой 2

(4.55)

по кривой 3

(4.56)

в) высота водобойной стенки при надвинутом прыжке

(4.57)

Рис. 4.10. График для расчета многоколодезных перепадов

6. Определяют размеры колодца при затопленном прыжке.

Расчет высоты стенки на второй и последующих ступенях аналогичен соответствующим расчетам для первой ступени и выполняют его по формулам (4.44) - (4.48).

Дальность отлета струй

(4.58)

Длина подпертого гидравлического прыжка

(4.59)

Длина колодца

l_к_i = l_пад + l_пi. (4.60)

Размеры сооружений на второй и всех последующих ступенях принимают одинаковыми.

7. Глубина водобойного колодца в отводящем русле при надвинутом прыжке

(4.61)

Глубина колодца при затопленном прыжке

(4.62)

Глубину колодца уточняют во втором приближении по тем же формулам с учетом роста высоты падения. За счет глубины колодца новая высота падения струи

Длину колодца в отводящем русле определяют так же, как и на любой промежуточной ступени (кроме первой), т.е. по формуле (4.60). На всех ступенях принимают

Способ определения второй сопряженной глубины и длины гидравлического прыжка на первой ступени применим и к случаю одноступенчатого перепада. Если при этом не устраивают водобойного колодца или других водобойных сооружений, то для определения свободного гидравлического прыжка в формуле (4.45) достаточно принять

Этот способ применим при высоте стенок падения p > 1,2h_к(1 + m_от) и

ПЕРЕПАДЫ ПОЛУНАПОРНОГО ТИПА

4.21. В полунапорных перепадах (рис. 4.11), как и в перепадах колодезного типа, используется принцип гашения избыточной энергии потока с помощью затопленного подпертого гидравлического прыжка.

Рис. 4.11. Схема перепада полунапорного типа

Обычные перепады колодезного типа можно вписать в косогоры с уклоном до 0,25 - 0,35, а с укороченной ступенью - до 0,55. Полунапорные перепады позволяют устроить водоотвод на косогорах с уклонами до 0,4 - 0,7. Следовательно, они позволяют обеспечить нормальную эксплуатацию водоотвода в наиболее тяжелых условиях, на склонах, где без специальных сооружений поток в состоянии размывать галечные отложения и даже перемещать камни.

Сокращение длины ступени полунапорных перепадов по сравнению с обычными колодезными достигается влиянием короткой стенки в конце каждой ступени, т.е. такой, нижний край которой не выходит за пределы толщины дна ступеней. При истечении потока через донное отверстие перед этой стенкой несколько сокращается длина отлета струи, сокращается и длина подпертого затопленного гидравлического прыжка за счет более интенсивного гашения энергии при повышенном искривлении струй потока и повышении роли водоворотных зон.

Отверстие в конце ступени может работать в нескольких режимах:

I - неполным сечением, обеспечивая слив со ступени, как в обычных бесколодезных перепадах;

II - как малое отверстие в тонкой стенке при соответственно высоких отношениях;

III - IV режимы - промежуточные между I и II, соответствующие истечению через большое донное горизонтальное отверстие от спокойного потока над ним (III) до гидравлического прыжка (V).

Режим V с гидравлическим прыжком над отверстием наиболее эффективен. Он обеспечивает максимальное гашение энергии при наименьших габаритах каждой ступени, т.е. прохождение косогоров с уклонами порядка 0,6 - 0,7. Этот режим принимается за расчетный. Область его существования:

(4.63)

В ходе расчетов высота ступени должна быть проверена исходя из условия предотвращения перелива потока через короткую поперечную стенку в конце ступеней и подтопления уступа перепада ниже донного отверстия за счет подъема уровня в подструйном пространстве.

Перепады с короткой стенкой просты по устройству, что позволяет осуществить их разрезку на сборные блоки. В частности, по принципу: каждый блок - одна ступень. Такие блоки удобны при изготовлении и монтаже. Они обеспечивают надежное сопряжение стыков между ступенями. Ниже изложена методика гидравлического расчета полунапорных перепадов с короткой поперечной стенкой, предложенная П.И. Штительманом.

Особенности движения потока в подводящем русле к каскаду перепадов делают необходимыми самостоятельный расчет первой ступени. Затем рассчитывается вторая ступень, а все последующие принимаются такими же.

За последней ступенью требуется проверить и обеспечить благоприятное сопряжение бьефов в отводящем русле.

Порядок расчета следующий.

1. Назначается высота ступеней перепада исходя из общей высоты всего каскада

и принятого числа ступеней n:

. При этом высота ступени может быть несколько большей по сравнению с обычными перепадами за счет более эффективного гашения энергии.

2. Рассчитывается первая ступень как обычный одноступенчатый перепад. При этом определяется критическая глубина h_к, запас энергии потока в подводящем русле T₀ относительно дна первой ступени и по ней - глубина в сжатом сечении h_с; вторая сопряженная с нею глубина h_в определяется с помощью графика на рис. 4.12, где

(4.64)

Рис. 4.12. График для определения

второй сопряженной глубины прыжка h_в

При определении h_с из выражения T₀ коэффициент скорости

при режиме V рекомендуется определять по методике Ю.М. Константинова для перепадов колодезного типа с уменьшающим коэффициентом 0,85 за счет дополнительного гашения энергии при взаимодействии потока с короткой поперечной стенкой.

Принимают длину донного отверстия

(4.65)

После этого проверяют по критериям (4.63) обеспеченность наиболее рационального режима V. При необходимости изменяют размер c или высоту ступеней для создания соответствующего числа Фруда в сжатом сечении. Далее находят коэффициент расхода донного отверстия

(4.66)

и проверяют совпадение расхода с заданным. Расход воды через отверстие

(4.67)

При этом возможна корректировка расхода длиной отверстия c.

Проверяется высота ступени для исключения перелива потока через ее стенку и подтопления уступа при подъеме уровня в подструйном пространстве h_пс, что выражается неравенствами:

p > h_в и p > h_пс. (4.68)

Глубина h_пс определяется по формуле

(4.69)

где

- угол падения струи; принимается при режиме V

; для первой ступени

Длина ступени l складывается из дальности отлета струи X_с и длины подпертого прыжка l_пп при режиме V:

(4.70)

(4.71)

l = X_с + l_пп. (4.72)

Уклон косогора, в который может быть вписан перепад полунапорного типа,

(4.73)

Для расчета сопряжения бьефов на второй (т.е. и всех последующих) ступени, а также в отводящем русле запас энергии

T₀ = p + h_с(1 + 5Fr). (4.74)

БЫСТРОТОКИ

4.22. Быстротоки - лотки и каналы с уклонами дна больше критического - применяют при проектировании нагорных канав, в подводящих и отводящих руслах водопропускных сооружений, кюветов.

Поперечное сечение быстротока может отличаться от примыкающих к нему участков канала. В этом случае устраивают переходные участки, пользуясь при их расчетах рекомендациями по расчету сужающихся и расширяющихся бурных потоков (см. соответствующие разделы настоящей главы).

Гидравлический расчет быстротоков, включающий определение глубин и скоростей потока в характерных его сечениях, может быть выполнен по уравнениям одномерной гидравлики на ЭВМ. При расчете вручную по уравнениям неравномерного движения вначале устанавливают формы свободной поверхности потока в пределах быстротока и сопрягающих участков (см. гл. 2). Последующий расчет неравномерного движения на быстротоке при i < 0,1 также не имеет особенностей.

Быстроток - важнейший элемент косогорного водопропускного сооружения; его применяют либо как самостоятельное сооружение, либо как подводящее (отводящее) русло косогорной трубы.

Если ширина и глубина быстротока не ограничены и не определяются конструктивными соображениями, принимают гидравлически наивыгоднейшее сечение. При трапецеидальной форме поперечного сечения гидравлически наивыгоднейшим будет сечение, удовлетворяющее условию

(4.75)

где b - ширина по дну;

h - глубина воды;

m_от - коэффициент откоса, т.е. котангенс угла наклона стенок.

У гидравлически наивыгоднейших сечений

R = 0,5h. (4.76)

Числовые значения коэффициента

в зависимости от m_от приведены ниже:

m_от	0	0,5	0,50	1,0	1,5	2,0	2,5
	2	1,56	1,24	0,82	0,61	0,47	0,385

Размеры гидравлически наивыгоднейшего сечения определяют подбором. При не слишком больших отклонениях ширины дна от гидравлически наивыгоднейшей площадь сечения изменяется мало. После принятия определенной ширины дна выясняют, какая будет соответствующая ей глубина, т.е. решают задачу о нормальной глубине (см. гл. 2).

Скорость течения в быстротоке не должна превышать допускаемой для материала дна и стенок. Если это условие невыполнимо, то можно применять повышенную шероховатость.

При поступлении воды в быстроток из нагорных канав считают, что в начале быстротока устанавливается критическая глубина, а ниже - кривая спада типа b_II.

При резком изменении уклона дна быстротока движение воды становится неравномерным. При этом возможны следующие основные случаи:

1) уклон остается больше критического i₂ > i_к;

ИС МЕГАНОРМ: примечание.

Текст дан в соответствии с официальным текстом документа.

2) уклон становится меньше критического i₂ > i_к.

В случае i₂ > i_к неравномерное движение устанавливается только на нижнем участке. Если уклон убывает, то устанавливается кривая подпора типа c_II (рис. 4.13, а), а если же возрастает, то получается вогнутая кривая спада типа b_II (рис. 4.13, б).

Рис. 4.13. Кривые свободной поверхности потока

в призматическом русле при резком изменении уклона

В случае i₂ < i_к в зависимости от соотношения глубин на верхнем и нижнем участках возможны следующие схемы сопряжения:

если глубина

(рис. 4.13, в), сопряженная с глубиной верхнего участка h₁ в створе изменения уклона i, больше глубины нижнего участка h₂

, то в нижнем участке происходит отгон прыжка; между прыжком и створом изменения уклона размещается вогнутая кривая подпора типа c_I;

если

(рис. 4.13, г), то прыжок располагается вблизи створа изменения уклона; движение на обоих участках остается при этом таким же, как без изменения уклона;

если

(рис. 4.13, д), то прыжок надвигается на верхний участок; между прыжком и створом изменения уклона устанавливается выпуклая кривая подпора типа c_II.

Случай i₂ < i_к возможен, например, при переходе русла с косогора в долину.

Высоту стенок быстротока принимают с некоторым запасом (например, 25 см), чтобы вода не вытекала на прилегающую местность.

Расчет быстротоков как сопрягающих сооружений в косогорных трубах изложен ниже (см. гл. 5), а здесь приводятся лишь некоторые не отмеченные там специфические особенности.

4.23. Когда быстроток используется как самостоятельное сооружение и за ним в отводящем канале возникает прыжок, для сокращения участков крепления в конце быстротока или в начале отводящего канала устраивают водобойные стенки (рис. 4.14).

Рис. 4.14. Схема водобойной стенки за быстротоком

Расчет водобойных колодцев, устраиваемых для гашения энергии в конце быстротоков, имеет некоторые особенности.

Если водобойный колодец устраивают с уступом в конце быстротока, т.е. по обычной схеме, то порядок расчета не отличается от изложенного выше в соответствующем разделе настоящей главы.

Длина таких колодцев

(4.77)

При этом

(4.78)

где h - глубина в конце быстротока.

При больших продольных уклонах быстротоков (порядка 0,25 - 0,40) определяют глубину в конце быстротока h и находят сопряженную с ней глубину h". Тогда глубина водобойного колодца будет:

с учетом перепада

на выходе колодца

(4.79)

без учета перепада

(4.80)

Длину водобойного колодца в этом случае определяют только как длину гидравлического прыжка.

СУЖАЮЩИЕСЯ БЫСТРОТОКИ

4.24. Для сопряжения быстротока с трубой или при изменении ширины быстротока обычно устраивают участок прямолинейного сужения. Сужение может быть симметричным (рис. 4.15, а - в) и несимметричным (рис. 4.15, г, д). Несимметричное сужение может оказаться экономически целесообразным при косом пересечении водотока насыпью дороги.

Рис. 4.15. Схемы протекания воды при симметричном (а - в)

и несимметричном (г, д) сужениях:

а - план симметричного сужения; б - продольный профиль

свободной поверхности потока вдоль оси сооружения;

в - то же, вдоль стенок; г - план несимметричного сужения;

д - продольный профиль свободной поверхности потока вдоль

левой (сплошная линия) и правой (штриховая)

стенок сооружения

При отклонении бурного потока боковыми стенками сужения возникают косые гидравлические прыжки. В месте пересечения косых прыжков на оси потока (для симметричного сужения) образуется местное повышение свободной поверхности (гребень). При отражении потока от оси симметрии возникает второй косой гидравлический прыжок, который взаимодействует со стенками сужения, снова отражается от них и образует второй гребень на оси потока и т.д. (см. рис. 4.15, а). Таким образом, в сужении и за ним в канале или трубе образуется цепочка гребней и впадин убывающей амплитуды как на оси потока (см. рис. 4.15, б), так и на стенках (см. рис. 4.15, в). Кроме того, в сужении и за ним возрастает средняя по сечению глубина потока, а на стенках сужения возникает локальное увеличение глубин, которое в ряде случаев может превышать глубину в первом (максимальном) гребне на оси. Иногда при большой степени сжатия потока и больших углах сужения может произойти затопление косых прыжков и образование прямого гидравлического прыжка. Весьма сложный характер течения в сужении в реальных условиях усложняется еще и наложением условий геометрического сопряжения сооружений (например, трапецеидального быстротока с прямоугольной трубой, прямоугольного быстротока с круглой трубой и т.п.), а также переменным уклоном дна (часто перед трубами для удобства обслуживания делают горизонтальные площадки).

4.25. Расчет сужений необходимо проводить в целях определения высоты стенок сужения из условия недопущения перелива, а также в целях определения скоростей, средних и максимальных глубин в конце сужения для дальнейшего расчета быстротока или трубы.

В настоящее время разработано несколько методов расчета сужений, которые можно использовать независимо и в сочетании исходя из целей расчета:

1) определение средних по сечению глубин и скоростей по одномерным уравнениям гидравлики;

2) определение глубин и скоростей в каждой точке плана потока (в том числе положение косых прыжков) по двухмерным (плановым) уравнениям гидравлики;

3) определение положения косых прыжков и глубин за ними, высоты максимальных гребней на оси потока и на стенках на основе двухмерной теории косых прыжков (для схематизированных условий: прямоугольных быстротоков, сужения и трубы, постоянного уклона дна, нормальной глубины быстротока в начале сужения) - приближенная методика.

Ниже рассмотрим подробнее каждый из этих методов.

4.26. Расчет сужений по одномерным уравнениям гидравлики (2.34 - 2.35) производится на ЭВМ по программе "Водоток" (см. п. 2.19) либо по методике, изложенной в гл. 5 (п. 5.23). При этом задаются реальные профили поперечного сечения сужения в нескольких створах, их отметки, постоянный либо переменный коэффициент шероховатости по длине сужения, глубина и расход потока на входе в сужение. В результате расчета получают средние по сечению уровни свободной поверхности и скорости потока в каждом створе. При этом в зоне косых прыжков будет получаться плавное нарастание средней глубины потока, а если по условиям протекания (резкое сужение) возникает прямой гидравлический прыжок, то он получится в расчетах автоматически. Средняя глубина потока на выходе из сужения является важной характеристикой, так как по ней в первую очередь назначается высота трубы (см. гл. 5).

По одномерным уравнениям можно произвести расчет при любых формах поперечного сечения и переменных уклонах, а также расчет всего водопропускного тракта (быстротока, сужения, трубы) сквозным счетом. Однако из этого расчета нельзя получить глубин максимальных гребней на оси и на стенке, а также положения косых прыжков.

4.27. Более детальную информацию о характере течения в сужении можно получить из расчета по двухмерной математической модели (см. п. 2.20) с использованием алгоритма, описанного в работе [3] и реализованного в комплексе программ "БОР". Расчет производится в следующем порядке.

1. Строится разностная сетка, примерно такая, как показана на рис. 1 приложения 4.1. Для симметричных сужений можно рассматривать половину области течения. В поперечном направлении достаточно брать 10 - 12 узлов сетки, продольные размеры ячеек сетки могут быть в 1,5 - 2 раза больше поперечных. Сетка должна быть такой, чтобы на ней с достаточной точностью аппроксимировался рельеф дна в сужении и за ним (например, для расположенной за участком сужения круглой трубы надо задать на сетке плавный переход от прямоугольного сечения к круглому).

Конечный участок быстротока длиной примерно ¹/₁₀ ширины и участок быстротока или трубы за сужением длиной одна-две ширины также должны быть покрыты разностной сеткой.

2. После того как в узлах сетки заданы реальные отметки дна и коэффициенты шероховатости, на твердых границах (стенках) и оси симметрии ставятся условия непротекания (v_п = 0); на входной границе (в конце быстротока) задаются глубина h₁ и скорость v₁; на выходной границе ставятся условия сноса скорости и глубины потока. Начальные условия во всей области течения: v = v₁, глубина h вычисляется в каждом поперечном сечении из условия постоянства расхода воды

(4.81)

3. Расчет ведется методом установления до тех пор, пока глубины и скорости в каждом узле не перестанут меняться в двух-трех десятичных знаках при переходе на новый слой по времени.

В результате расчетов получаются глубины и скорости потока в каждом узле сетки. Анализируя рельеф свободной поверхности, находят положение косых прыжков, глубину в максимальном гребне на оси и его местоположение, глубину потока вдоль стенок сужения.

Осредняя параметры течения по поперечному направлению в конце сужения (на входе в трубу), вычисляют средние глубину и скорость потока.

Описанный подход дает весьма точную общую картину течения (см. приложение 4.1) для любых сужений (в том числе несимметричных и с переменным уклоном). Исключение составляют размеры гребней (всплесков) на стенке и на оси сужений, которые при больших числах Фруда и больших углах сужения могут превышать глубины из расчета по двухмерной математической модели. Поэтому глубины воды в гребнях рассчитываются также с помощью методики, изложенной ниже в пп. 4.28, 4.29, и после сопоставления к проектированию принимаются наибольшие. Следует отметить, что высота гребней не сказывается на пропускной способности трубы, расположенной за сужением (высота трубы лимитируется средней глубиной), однако должна учитываться при расчете высоты стенок сужения и укрепления откоса насыпи над трубой для предотвращения переливов воды за борта и размыва насыпи.

4.28. Метод расчета, основанный на теории косых прыжков, требует принятия следующих допущений: быстроток и сужение имеют прямоугольное поперечное сечение; уклон дна быстротока и сужения постоянен; коэффициент шероховатости постоянен; глубина в конце быстротока (начале сужения) близка к нормальной; сужение симметричное.

Еще ряд ограничений будет приведен при изложении метода. Чем больше отклонение от указанных условий, тем больше погрешность расчета. Трапецеидальные быстротоки приводят к прямоугольным, принимая их ширину равной средней линии живого сечения.

Для расчета сужения необходимо иметь следующие данные:

ширину в начале сужения B, равную ширине подходящего быстротока;

ширину в конце сужения b, равную ширине трубы или отводящего быстротока;

угол сужения

;

глубину воды h₁ на входе в сужение;

Q - расход воды;

n - коэффициент шероховатости.

Уклон сужения в расчетах не учитывается, так как его влияние практически уравновешивается трением. Это справедливо при отмеченном выше допущении о том, что глубина воды в конце быстротока близка к нормальной при равных уклонах быстротока и сужения. Скорость потока в сужении можно практически считать постоянной и равной скорости в конце подходного быстротока.

4.29. В результате расчета должны быть определены размеры и местоположение максимальных глубин как по оси потока, так и у стенок сужения.

Расчет производят в такой последовательности.

1. Вычисляют число Фруда в начале сужения

(4.82)

2. Находят степень сжатия бурного потока на участке сужения

(4.83)

3. Проверяют отсутствие прямого гидравлического прыжка в сужении. Если

(4.84)

то согласно [13] возникает прямой гидравлический прыжок. В этом случае следующую за сужением трубу либо рассчитывают по условиям равнинного входа (см. гл. 5), либо увеличивают ее диаметр и переходят к п. 2.

4. Находят длину участка сужения

(4.85)

5. Определяют параметры первого косого прыжка на участке сужения (

, Fr₂ и h₂) по номограммам на рис. 4.16 и 4.17 либо из решения уравнений:

(4.86)

(4.87)

где

- угол наклона фронта первого косого прыжка (рис. 4.18);

h₂ - глубина за прыжком (вторая сопряженная);

Fr₂ - число Фруда за прыжком.

Рис. 4.16. Номограмма для определения угла косых прыжков

и относительных глубин прыжка h₂/h₁

Рис. 4.17. Номограмма для определения числа Фруда

за косым прыжком Fr₂

Решения уравнения (4.86) существуют при

; в противном случае косых прыжков не образуется и расчет сужения ведется просто по уравнению неравномерного движения.

Для нахождения

из уравнения (4.86) можно использовать итерационную процедуру:

(4.88)

причем

должно выбираться с избытком (обычно достаточно 3 - 4 итераций, n = 0, 1, 2, 3).

Зная

, из уравнения (4.86) находят h₂.

6. Определяют параметры

, h₃ и Fr₃ второго (отраженного) косого прыжка (см. рис. 4.18) по формулам (4.86) - (4.88) либо по номограммам (см. рис. 4.16 и 4.17), заменяя Fr₁ на Fr₂ и h₁ на h₂. Значение h₃ принимают за среднюю глубину на выходе из сужения.

7. Определяют максимальную глубину потока на оси сооружения h_ось(max), возникающую в результате взаимодействия косых прыжков (см. рис. 4.18):

(4.89)

Рис. 4.18. Расчетные схемы формирования глубин в сужении:

а - глубина по оси потока; б - то же, у стенок сужения;

в - план сужения; 1 - быстроток; 2 - сужение; 3 - труба

При h_ось(max) < h₃ к расчету принимают глубину h₃.

Для сужающихся быстротоков на входе в трубу высота трубы должна быть не менее h_ось(max).

8. Определяют глубины вдоль стенки сужения в такой последовательности.

Находят максимально возможную глубину у стенки сужения h_ст(max) и расстояние до нее от начала сужения l_max:

(4.90)

(4.91)

Устанавливают глубины у стенки h_ст в характерных местах:

а) при l_max < l_суж в трех точках:

в начале стенки h_ст = h₂;

при l = l_max максимальную из глубин h_ст = max(h₂, h_ст(max));

при l = l_суж максимальную из глубин h_ст = max (h₃, h_ст(max));

б) при l_max >= l_суж в двух точках:

в начале стенки h_ст = h₂;

при l = l_суж максимальную из глубин h_ст = max (h₃, h_ст(max)).

Между характерными точками глубины у стенки сужения определяют линейной интерполяцией.

4.30. При расчете несимметричных сужений (см. рис. 4.15, г, д) наилучший результат получается при использовании двухмерной программы расчета (см. п. 4.27) в сочетании с методикой для определения максимальной глубины гребня на стенке (пп. 4.28, 4.29).

В случае когда сужение имеет такую форму, что первый косой прыжок попадает в угловую точку сужения на противоположной стенке (наиболее благополучном с точки зрения работы сооружения), можно пользоваться формулами (4.87) - (4.89) для нахождения параметров косого прыжка и принимать глубину h₃ за среднюю глубину на выходе из сужения.

ВОДОПРИЕМНЫЕ КОЛОДЦЫ

4.31. Водоприемные колодцы на входе в косогорные трубы устраивают при значительных уклонах местности с целью гашения энергии на входе в трубу.

В колодце происходят два процесса (рис. 4.19): сброс потока из подходных быстротоков и истечение воды из него через трубу. При этом уровень воды в колодце при пропуске расходов, равных и больших расчетного, как правило, определяется подпертым уровнем воды перед трубой.

Рис. 4.19. Схема протекания воды в водоприемном колодце:

1 - подходной быстроток; 2 - колодец; 3 - труба;

4 - канава продольного водоотвода; 5 - насыпь;

6 - свободная поверхность в колодце прн H < h";

7 - то же, при H = h"; 8 - то же, при H > h";

9 - гидравлический прыжок

Размеры водоприемных колодцев определяют исходя из условия обеспечения в них перехода потока из бурного состояния в спокойное, т.е. затопления гидравлического прыжка. Для этого подпертая глубина перед трубой H должна быть больше второй сопряженной глубины

для сжатой глубины h_с в месте падения струи на дно колодца.

Расчет выполняют в изложенной ниже последовательности.

1. Определяют подпертую глубину перед трубой H по формулам для равнинных труб (см. гл. 5).

2. Определяют подбором сжатую глубину потока h_с в колодце из уравнения (предварительно задавшись высотой стенки падения колодца p):

(4.92)

где h_под и v_под - соответственно глубина и скорость потока в подводящем русле;

b_б - ширина быстротока (подводящего русла).

При быстротоке большей ширины, чем отверстие трубы b, что, как правило, имеет место в практике проектирования, полученную глубину h_с корректируют в связи с имеющим место в этом случае сужением потока, определяя ее по формуле

(4.93)

3. Определяют вторую сопряженную глубину

сжатой глубины:

(4.94)

где

- число Фруда при h_с(испр).

4. Сравнивают

с H и устанавливают, затапливается ли гидравлический прыжок, для чего должно соблюдаться условие

(4.95)

При несоблюдении условия (4.95) принимают меры по обеспечению затопления прыжка (изменяют высоту колодца, изменяют ширину или уклон быстротока и т.п.).

5. Определяют длину колодца

l_кол = l_под + 0,5, (4.96)

где l_под - дальность падения струи, т.е. горизонтальное расстояние от уступа до места падения струи на дно колодца, м.

Значение l_под определяют из уравнения

(4.97)

где

- угол наклона подводящего русла к горизонту.

6. Назначают ширину колодца. При подводе воды с торца колодца ширина его должна быть не меньше ширины быстротока и не меньше удвоенного отверстия трубы. При боковом поступлении воды размер колодца вдоль оси трубы определяется шириной подводящих канав, а поперек оси трубы - значением l_под.

КОНСОЛЬНЫЕ СБРОСЫ

4.32. Консольным сбросом называют лоток большого уклона, приподнятый на опорах над земной поверхностью (рис. 4.20), в конце которого имеется струенаправляющий носок с обратным или равным нулю уклоном. Свободно падая с носка, струи отбрасываются за пределы сооружения. Такие сооружения устраивают при сбросе воды через полотно дороги на весьма крутых косогорах, при сбросе воды в овраги и т.п.

Рис. 4.20. Схема консольного сброса

Обратный уклон струенаправляющего носка консоли принимают i_н <= 0,25, а длину носка

У места падения струи образуется воронка размыва, размер которой в начальный период работы консольного перепада быстро растет, а затем стабилизируется. Эта воронка играет роль гасителя энергии ниспадающего потока.

Гидравлический расчет консольного перепада заключается в определении: 1) глубины h в конце быстротока; 2) дальности падения l_пад струи; 3) размеров воронки размыва в нижнем бьефе. Глубина в конце быстротока определяется изложенным ранее методом.

Дальность падения струи без учета ее аэрации и сопротивления воздуха определяют по приближенной формуле

(4.98)

при этом

где v - скорость потока в конечном сечении струенаправляющего носка.

Если носок горизонтальный, т.е. i_н = 0, то

(4.99)

Фактическая дальность полета струи оказывается на 10 - 20% меньше, чем по формулам свободного падения.

Снос струи нормальной плотности боковым ветром определяют для перепадов параболического поперечного сечения по формуле

(4.100)

где v_в - скорость ветра, м/с;

Q - расход сброса, м³/с;

p - высота падения струи, м.

Учет сноса струи ветром особо важен, если за перепадом устраивают специальные водобойные сооружения.

Глубину размыва за консольными перепадами определяют по формуле, например, Б.И. Студеничникова [44]:

(4.101)

где

- относительный скоростной напор в месте падения струи;

- высота падения струи с учетом скоростного напора;

- коэффициент скорости;

a = 0,8 - коэффициент, учитывающий аэрацию потока;

h_п - высота падения;

- критическая глубина потока в месте падения;

- коэффициент расширения струи в месте падения; для консольных сбросов принимают

;

b - ширина быстротока или трубы на выходе;

l_сл - ширина следа струи в месте падения; для консольных сбросов принимают

;

d - средний диаметр частиц грунта;

h_нб - глубина воды в нижнем бьефе;

- удельный расход в конце выходного быстротока или трубы.

РАССЕИВАЮЩИЕ ТРАМПЛИНЫ

4.33. Рассеивающие трамплины (рис. 4.21) предназначены для отбрасывания потока от сооружения на безопасное расстояние и уменьшения удельного расхода в месте падения потока путем его расширения.

Рис. 4.21. Рассеивающий трамплин:

а - общий вид трамплина; б - продольный и поперечный

профили; в - очертание планов поверхностных линий токов

при введении параметра

Дно расширяющего трамплина представляет собой криволинейную поверхность двоякой кривизны: выпуклую в поперечном направлении и вогнутую в продольном. В плане трамплин расширяется к выходу.

Конфигурацию поверхности трамплина по методу Л.И. Высоцкого отыскивают путем решения интегродифференциального уравнения свободной поверхности и приближенного уравнения неразрывности. В общем случае это уравнение может быть решено при помощи ЭЦВМ [10].

Для некоторых случаев расчета в приложении 4.2 приведены рассчитанные на ЭВМ таблицы безразмерных координат поверхности рассеивающих трамплинов для прямоугольных труб или быстротоков. Таблицы соответствуют степени расширения потока в плане в пределах рассеивающего трамплина

(где B - ширина трамплина на выходе; b - ширина быстротока при угле расширения потока в плане

, угле отброса потока к горизонту

, уклоне быстротока

i_н - 0,15; 0,30 и 0,50; наполнении лотка (отношении толщины потока t к его ширине b) t/b = 0,1; 0,2 и 0,3; числах Фруда

Безразмерные координаты поверхности трамплина x, y и z в указанных таблицах выражены в функции безразмерной длины плана граничной поверхностной линии тока s_к и параметра

, где

- угол поворота струйки с параметром n (приложение 4.2).

Для определения истинных координат полученные из таблиц значения умножают на длину крайней линии потока в плане, определяемую по формуле

(4.102)

где b - ширина выхода из быстротока (или трубы) перед трамплином.

Границы трамплина в плане описываются зависимостью

(4.103)

где p = const - показатель степени (p = 5).

Глубину размыва за трамплином и его положение рассчитывают следующим путем.

1. Определяют дальность отброса потока от трамплина

(4.104)

где v_п - скорость в конце выходного быстротока или трубы;

h_п - высота падения.

2. Находят длину следа струи в месте падения

(4.105)

3. Определяют удельный расход в месте падения

(4.106)

где

- коэффициент запаса.

4. Вычисляют глубину размыва по формуле (4.101).

Пример расчета рассеивающего трамплина приведен в приложении 4.3.

УСТРОЙСТВА, ПРИМЕНЯЕМЫЕ ДЛЯ ГАШЕНИЯ ЭНЕРГИИ ПОТОКА

НА ВЫХОДАХ ИЗ ТРУБ

4.34. Для гашения энергии потока на выходах из дорожных водопропускных труб в действующих типовых проектах применяют следующие типы гасителей энергии:

ребро в конце укрепления (см. рис. 7.2, тип 3; 3к);

стенка в раструбном оголовке в сочетании с ребром в конце укрепления (см. рис. 7.3);

гаситель системы ЦНИИСа (рис. 4.22, а) в виде раструба с двумя водобойными стенками (порогами);

гаситель в виде расширяющегося раструба со стенкой падения в конце его (4.22, б) и без стенки (рис. 4.22, в).

Рис. 4.22. Гасители энергии:

а - гаситель системы ЦНИИСа; б - расширяющийся водобойный

колодец со стенкой падения; в - то же, без стенки падения;

1 - труба; 2 - первая водобойная стенка; 3 - вторая

водобойная стенка; 4 - стенка падения; 5 - водобойная

стенка; 6 - стенка раструба

Первые два типа гасителей энергии применяют, как правило, в трубах, уложенных со сравнительно малыми уклонами, т.е. для равнинных труб (см. приложение 1.1), два других - для косогорных сооружений, имеющих значительные уклоны, и поток на выходе из которых обладает высокой кинетичностью и имеет большие скорости (см. приложение 1.1, типовой проект N 538).

Гасители в виде ребра и стенки в раструбном оголовке в основном влияют на режим протекания потока (см. гл. 7) в нижнем бьефе и приводят лишь к уменьшению размыва за сооружением, практически не снижая скоростей. Отсюда скорости и глубины на выходе из этих сооружений могут быть с некоторым запасом приняты такими же, как и для труб без гасителей. Поэтому гидравлический расчет их здесь не приводится.

Ниже излагается гидравлический расчет остальных двух типов гасителей, применяемых в типовых проектах косогорных труб.

Расчет гасителей согласно рекомендациям норм [39] производят для железных дорог при прохождении двух паводков - расчетного и наибольшего, характеризующихся расходами на пике их (соответственно называемых расчетным Q_р и наибольшим Q_max) и объемами стока W_р и W_max; для автомобильных дорог - при прохождении расчетного паводка.

Мы рассмотрим более общий случай, соответствующий расчету на два расхода. Для сооружений на автомобильных дорогах используют лишь рекомендации для расчета по Q_р. В приведенном ниже алгоритме расчет этот больше не оговаривается.

4.35. Расчет заключается в определении следующих величин:

размеров элементов гасителей (высота и местоположения водобойных стенок, длины, угла и высоты стенок раструба);

отметок поверхности потока в раструбе и на выходе из трубы с учетом влияния водобойных стенок, расположенных в раструбе;

скоростей на выходе из гасителя;

деформаций дна русла за гасителем, назначения типов выходных русел и размеров укреплений.

При расчете по двум расходам приняты следующие принципы:

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: пункт 1.24 в СНиП [39] отсутствует.

а) заполнение на выходе из труб (т.е. отношение глубины воды к высоте трубы

с учетом подтопления от стенок гасителя определяют по двум расходам, при этом для расчетного расхода должны быть выполнены требования п. 1.24 СНиП [39]; для наибольшего расхода заполнение не должно превышать единицы, т.е. глубина воды в этом сечении не должна превышать высоты трубы h_т;

б) уровни в гасителе определяют при двух расходах, причем при определении высоты стенок гасителя при пропуске Q_р вводится запас 0,25 м, при Q_max запас отсутствует; высоту водобойных стенок определяют при пропуске Q_р; длину раструба гасителя назначают большей из дальностей полета струй при пропуске Q_р и Q_max;

в) тип и размеры укреплений выбирают исходя из расчета по двум расходам, при этом при пропуске Q_max и назначении материала укреплений допускаемые скорости увеличиваются на 35%, а глубина заделки концевой части укреплений при пропуске расчетного расхода (для учета запаса) увеличивается на 20%.

Необходимые исходные данные: форма сечения трубы, отверстие прямоугольной трубы b, диаметр круглой D, расходы воды Q_р и Q_max, глубины и скорости на выходе из трубы h_вых и v_вых уклон трубы i_т, уклон дна гасителя i_г, тип гасителя, грунт выходного лога, тип выходного русла.

4.36. Расчет гасителя ЦНИИСа (см. рис. 4.22, а) ведется в следующем порядке.

1. Принимают предварительно глубину на входе в раструб равной глубины на выходе из трубы h_вых.

Для круглых труб заменяют сегментное живое сечение потока равновеликим по площади прямоугольником с эквивалентной шириной:

для труб диаметром D <= 1,5 м

b_эк = D - 0,25 м; (4.107)

для труб диаметром D = 2,0 м

b_эк = D - 0,5 м. (4.108)

Глубина потока в эквивалентном прямоугольном сечении

(4.109)

где

- площадь живого сечения круглой трубы на выходе из нее, соответствующая значению h_вых.

2. Вычисляют критическую глубину в трубе, считая ее прямоугольной, по формуле (2.11):

(4.110)

Причем для круглых труб вместо b подставляют b_эк, вычисленное по формулам (4.107) и (4.109).

3. Назначают высоту первой водобойной стенки

p₁ = (1,2 - 1,5)h_вых. (4.111)

Обычно принимают p₁ = 1,3h_вых; для круглых труб во всех формулах при расчете гасителей вместо h_вых подставляют h_вых(эк).

4. Определяют глубину потока h_р в начале раструба с учетом подтопления от порога:

при p₁/h_вых <= 1,4

(4.112)

при 1,4 <= p₁/h_вых <= 2,6

(4.113)

5. Проверяют заполнение трубы на выходе при пропуске расчетного Q_р и наибольшего Q_max расходов:

(4.114)

где

при пропуске Q_р согласно СНиП [39] равна 0,75 для круглых труб и

- для прямоугольных; при пропуске Q_max значение

При выполнении условия (4.114) расчет прекращают и приступают к п. 12, при невыполнении - устанавливают повышенное звено h_т(пов) и вновь проверяют выполнение условия (4.114). При его выполнении расчет прекращают и приступают к п. 12, при невыполнении - отказываются от повышенного звена и приступают к следующему пункту.

6. Определяют число Фруда Fr_вых на выходе из трубы по формуле (2.10):

7. Определяют глубину

, сопряженную с глубиной h_вых, по формуле (2.20):

8. Строят кривую свободной поверхности на концевом участке трубы перед раструбом.

Для этого сравнивают h_р с

. При

в конце трубы возникает несовершенный гидравлический прыжок. Расчет этого случая изложен в данном пункте. При

см. п. 10. Свободную поверхность в случае

строят вверх по течению по величине обратного уклона. Построение ведется с глубины h_р (начало раструба) участками по

Расчет выполняют в следующем порядке:

а) вычисляют обратный уклон поверхности воды на первом участке по формуле

(4.115)

где

;

б) определяют глубину воды в конце первого участка на расстоянии

перед раструбом (нумерация участков ведется от конца раструба вверх по течению):

(4.116)

в) проверяют выполнение условия (4.114), подставляя в него h_р1 вместо h_р. При соблюдении условия расчет прекращают и переходят к п. 9, при несоблюдении - приступают к построению кривой свободной поверхности воды на следующем участке, т.е. переходят к следующему пункту;

г) устанавливают уклон поверхности воды вышележащего участка:

(4.117)

д) определяют глубину воды в конце второго участка:

(4.118)

Вновь проверяют выполнение условия (4.114), подставляя в него вместо h_р глубину h_р2 и расчет повторяют до того сечения, где будет выполнено условие (4.114).

9. Определяют длину l_вст и высоту h_ст(вст) вставки между трубой и раструбом гасителя, имеющей параллельные стенки и ширину по дну, равную отверстию трубы:

(4.119)

h_ст(вст) = h_р + 0,25 м, (4.120)

где

- сумма расстояний от начала раструба до створа, где выполняется условие (4.114).

Далее приступают к расчету элементов гасителя, начиная с п. 12.

10. В случае если

, гидравлический прыжок возникает не непосредственно перед стенкой гасителя, а смещается внутрь трубы, при этом между прыжком и стенкой устанавливается кривая подпора. Построение свободной поверхности в этом случае выполняют в следующем порядке:

а) строят в трубе вверх по течению, начиная от глубины, h_р, кривую свободной поверхности спокойного потока по уравнению неравномерного течения (см. гл. 2) участками по

и в каждом из них определяют по приведенной ниже формуле глубины бурного потока

, для которых вычисленные глубины спокойного потока являются сопряженными:

где

и h_р_x - соответственно глубины бурного и спокойного потоков, сопряженные между собой, в сечениях, расположенных на расстоянии x от конца трубы;

Fr_р(_x₎ - число Фруда для спокойного потока в тех же сечениях, определяемое по формуле (2.10):

б) сопоставляют глубины

с глубинами, вычисленными при гидравлическом расчете трубы (без гасителя) в каждом из рассмотренных створов, и устанавливают координату створа начала прыжка исходя из условия

(4.121)

в) выше указанного створа располагается гидравлический прыжок. Строят свободную поверхность воды на участке гидравлического прыжка аналогично случаю

в соответствии с п. 8, но за исходную глубину в конце прыжка принимают глубину h_р(_x₎ в створе с координатой x_н(пр), в котором соблюдается условие (4.121).

11. Задавшись глубиной

, соответствующей створу с расчетным заполнением трубы, находят координату его

, используя уравнение неравномерного движения.

12. Назначают длину l_вст и высоту стенок h_ст(вст) вставки, расположенной между трубой и раструбом и имеющей параллельные стенки и ширину по дну, равную отверстию трубы, по формулам (4.119) и (4.120), заменив

на

Далее выполняют расчет элементов гасителя.

13. Определяют расстояние от начала раструба до первого водобойного порога

(4.122)

Обычно принимают

l = 0,63b. (4.122')

Для круглых труб вместо b подставляют b₀.

14. Принимают высоту второго водобойного порога

(4.123)

при этом должно быть соблюдено условие

p₂ >= 0,1 м.

Обычно принимают

p₂ = 0,27h_вых. (4.123')

15. Устанавливают глубину потока в плоскости напорной грани первого водобойного порога:

при

(4.124)

при

(4.125)

16. Находят наибольшую высоту подъема струй потока в раструбе

(4.126)

17. Определяют дальность падения струй по горизонтали s_x, считая от напорной грани первого водобойного колодца, и расстояние до второго водобойного порога l₂ по формулам:

а) при i_г <= 0,05

(4.127)

l₂ = l₁ + s_x, (4.128)

где Fr_вых - число Фруда на выходе из трубы, определяемое по формуле (2.10);

s - дальность падения струй по длине гасителя;

б) при 0,05 < i_г <= 0,20

(4.129)

(4.130)

18. Ширина раструба гасителя в створе конца второй водобойной стенки

b_рг = b + 2L_гtg30^o = b + 1,15L_г, (4.131)

где L_г - длина раструба гасителя.

Здесь

(4.132)

где

- толщина стенки второго порога.

19. Находят горизонтальное расстояние от напорной грани первого водобойного порога (стенки) до наибольшего подъема струй. Здесь возможны два случая:

а) при

(4.133)

Здесь

(4.134)

б) при

принимают x_max = 0, что соответствует условию h_max = h_ст(1).

20. Строят кривую свободной поверхности в вертикальной плоскости по оси потока:

а) при

используют уравнение

h_x = Ax² + Ex + h_ст(1), (4.135)

где h_x - глубина воды на расстоянии x от напорной грани первой водобойной стенки;

A и E - коэффициенты, определяемые по формулам:

(4.136)

(4.137)

Здесь x, как и во всех остальных формулах, - горизонтальное расстояние по оси сооружения от нижней точки напорной грани первого водобойного колодца;

б) при

используют уравнение

(4.138)

При невозможности разместить в пределах ширины лога гаситель ЦНИИСа с углом раструбности

принимают меньший угол между боковыми стенками (в пределах 30 - 60°). Боковые стенки делают в плане прямолинейными, а высоту и положение водобойных порогов определяют так же, как и при нормальном угле раструбности

. Траектория крайних струй в проекции на плоскость симметрии

(4.139)

здесь

(4.140)

21. Назначают очертания боковых стенок раструба и участка между трубой и раструбом (если он необходим) по касательным к поверхностям потока, выбирая невыгодный случай при пропуске Q_р и Q_max.

22. Определяют скорость потока на выходе из гасителя при пропуске Q_р и Q_max:

v_вых(г) = 0,45v_вых. (4.141)

4.37. Расширяющиеся водобойные колодцы могут быть двух видов: со стенкой падения и без нее. Ниже рассмотрен расчет расширяющегося колодца со стенкой падения (см. рис. 4.22, б). Расчет колодца без стенки падения (см. рис. 4.22, в) выполняется практически аналогично и отличается лишь тем, что вычисления начинают с совместного решения зависимостей (4.149), (4.150) и (4.151), т.е. с пункта 3 приведенного далее алгоритма расчета.

Расчет расширяющегося водобойного колодца со стенкой падения ведется в следующем порядке (см. рис. 4.22, б).

1. Определяют дальность полета струи со стенки падения l₁, решая квадратное уравнение

(4.142)

Коэффициенты A, B и C здесь соответственно равны:

(4.143)

(4.144)

(4.145)

где

- угол наклона выходного участка трубы к горизонту; при i_г <= 0,1

;

Y - высота оси потока над дном колодца.

2. Определяют подбором глубину потока в сжатом сечении из уравнения Бернулли, записанного для сечений над уступом и в месте падения струи:

(4.146)

где p₁ - высота стенки падения на входе в колодец;

h_вых, v_вых - соответственно глубина и скорость на выходе из трубы; для круглого сечения предварительно вычисляют h_вых(эк) [см. формулу (4.109)];

- площадь сжатого сечения;

- соответственно коррективы количества движения на выходе из трубы и в сжатом сечении; приближенно принимают

Если стенки раструба вертикальные, то предварительно вычисляют ширину раструба в сечении со сжатой глубиной

(4.147)

где b - отверстие трубы;

- угол раструбности колодца, считая от оси в одну сторону (обычно принимают

Затем из уравнения Бернулли, записанного для тех же сечений при прямоугольной форме, находят подбором h_с:

(4.148)

3. Определяют длину подпертого гидравлического прыжка l₂, глубину, сопряженную со сжатой,

, ширину стенки b_ст, решая совместно следующие зависимости:

(4.149)

(4.150)

(4.151)

где

- глубина, сопряженная с глубиной сжатого сечения;

;

b_с - ширина раструба в сечении со сжатой глубиной;

b_ст и

- соответственно ширина и площадь живого сечения потока в створе напорной грани стенки p₂.

4. Определяют полный напор перед стенкой p₂:

(4.152)

где m = 0,42 - коэффициент расхода.

5. Определяют геометрический напор H над верхом стенки p₂:

(4.153)

6. Определяют высоту стенки гасителя:

(4.154)

7. Определяют скорости потока в колодце перед стенкой p₂:

(4.155)

8. Вычисляют дальность падения струи, переливающейся через стенку:

(4.156)

9. Находят длину колодца:

l_кол = l₁ + l₂ + l_зап, (4.157)

где l_зап - запас в длине раструба, принимаемый равным 1,0 м.

10. Находят ширину раструба в месте падения струи:

(4.158)

Определяют ширину раструба в конце его (с учетом запаса):

(4.159)

11. Определяют глубину на выходе из гасителя (сжатую за стенкой p₂) подбором из выражения

(4.160)

12. Определяют скорость потока на выходе из гасителя:

(4.161)

13. Подбирают материал дна и боковых стенок гасителя путем сравнения v_вых(г) с допускаемой по материалу v_доп исходя из условия

v_вых(г) <= v_доп. (4.162)

14. Определяют высоту стенок раструба, м, исходя из выражения

c_ст(р) = p₂ + H + 0,25. (4.163)

Примеры расчета гасителей на выходах из косогорных труб приведены в приложении 4.4.

МЕТОДИКА ГИДРАВЛИЧЕСКОГО РАСЧЕТА ВХОДНЫХ УЧАСТКОВ

СООРУЖЕНИЙ РАВНИННОГО ТИПА

Основной гидравлической характеристикой, определяющей тип и размеры укреплений на подходе к равнинным сооружениям при уклонах подходного лога i_Л <= 0,05, является скорость потока, которая меняется в широком диапазоне. В то же время уровень свободной поверхности в условиях подпора от сооружения изменяется мало. Поэтому глубина потока определяется подпертой глубиной и уклоном дна.

Определение скоростей и глубин потока с учетом многообразия реальных условий работы сооружений (уклонов, формы сечения и шероховатости лога, типов сооружений и их оголовков, расходов и наполнения труб и т.п.) выполняют по программе "БОР", основанной на численном решении двухмерных (плановых) уравнений гидравлики. Программа "БОР" разработана и эксплуатируется в лаборатории гидравлики, гидрологии и ледовых воздействий ЦНИИСа (см. гл. 7).

На основе математического и физического моделирования установлена следующая кинематика потока в верхнем бьефе малых водопропускных сооружений (рис. 4.23) <*>.

--------------------------------

<*> На рис. 4.23 эпюры скоростей повернуты на 180°.

Рис. 4.23. Расчетная схематизация распределения скоростей

потока на входном участке сооружения

Наибольшие скорости v = v_ось наблюдаются на оси потока, причем с удалением от входа в сооружение в верховую сторону они уменьшаются. В поперечном направлении на участке от оси трубы до координаты y, соответствующей половине ширины входного сечения в сооружение b_р/2, скорости уменьшаются по параболическому закону от v_ось до v_*. Далее к бортам лога они изменяются по линейному закону. Причем на этом участке скорости сравнительно невелики.

При затопленном входе (что имеет место лишь в трубах) в непосредственной близости от него, как правило, возникают вихревые воронки и существенно изменяются эпюры скоростей на вертикалях. Скорости у дна становятся больше средних, а на участке, расположенном выше высоты трубы, они весьма малы.

На основе анализа результатов математического и физического моделирования для наиболее характерных условий работы сооружений были получены приведенные ниже зависимости, позволяющие определять скорости на подходном участке без обращения к расчету на машине.

При расчете возможны два случая: вход в сооружение не затоплен; вход в сооружение затоплен.

Расчеты в этих случаях отличаются в способе определения скорости на оси сооружения (лога). Поэтому ниже в начале излагается методика определения скоростей при незатопленном входе, а затем даются коррективы на учет затопления.

Скорости по оси потока

(4.164)

где v_л - скорость по оси потока в рассматриваемом створе, соответствующая равномерному течению;

v_р - средняя скорость потока в расчетном створе;

b_р - ширина расчетного сечения;

x - расстояние от расчетного сечения до рассматриваемого створа.

В свою очередь

(4.165)

(4.166)

где Q - расход воды в сооружении;

- средняя ширина лога в рассматриваемом створе;

H_л - глубина потока по оси сооружения при отметке подпертого уровня в рассматриваемом створе;

H_р - глубина потока в расчетном сечении;

m_от - коэффициент заложения откоса;

H_л = H - (i_лx + i_рl_р); (4.167)

(4.168)

H - подпертая глубина (см. гл. 5 и 6);

i_л и i_р - соответственно уклоны лога и оголовка;

l_р - длина оголовка;

- площадь сечения потока в рассматриваемом створе при глубине H_л.

Положение расчетного сечения и значения b_р и H_р определяют применительно к конкретным типам сооружений следующим образом:

1) для труб без оголовков расчетное сечение принимают на входе в сооружение. При этом H_р = h_вх, где h_вх - глубина на входе в трубу. Ширину расчетного сечения принимают равной:

для прямоугольных труб - отверстию сооружения b_р = b;

для непрямоугольных сечений

(4.169)

где

- площадь потока в расчетном сечении при глубине H_р;

2) для труб с оголовками и мостов с раструбными стенками расчетное сечение принимают на входе в оголовок (раструб), при этом H_р = H - i_рb_р, а b_р равно ширине оголовка;

3) для мостов с конусами расчетное сечение располагается на расстоянии 0,5m_от(кон)H_нас от подошвы насыпи в низовую сторону (m_от(кон) - заложение откоса конуса; H_нас - высота насыпи); H_р = 0,9H; b_р = b + H_нас. Скорости в точке рассматриваемого створа, расположенной на расстоянии y от оси сооружения, определяют по формулам:

при y <= 0,5b_р

(4.170)

при

(4.171)

при

(4.172)

где B_л и b_дн - соответственно ширина лога по урезам и по дну;

v_ст и v_* - скорости потока соответственно при y = b_дн/2 (для прямоугольного лога это скорости у бортов лога) и y = b_р/2.

Значения v_* и v_ст определяют по формулам:

при

(4.173)

v_ст = v_*; (4.174)

при

(4.175)

(4.176)

здесь

(4.177)

(4.178)

(4.179)

вычисляют по формуле (4.173) при

В случае затопленного входа в сооружение принимают H_р = H при отсутствии оголовков и H_р = H - i_рl_р при их наличии.

Затем выполняют расчет скоростей на оси потока по формуле (4.164) и производят их корректировку на участке 0 <= x <= 2(H - h_т) исходя из зависимости

(4.180)

Далее расчет выполняют аналогично случаю незатопленного входа.

Тип и размеры укрепления на входе в сооружение назначают в зависимости от скоростей, вычисленных на основе приведенного выше расчета, при этом скорости на откосе насыпи с некоторым запасом принимают равными скоростям у подошвы откоса.

Размеры укрепления с некоторым запасом можно установить следующим образом.

Находится координата створа, в котором скорость на оси потока равна допускаемой v_доп для рассматриваемого типа укрепления:

(4.181)

Ширину укрепления в этом створе принимают равной b_р, при этом укрепление располагают симметрично относительно оси сооружения (по b_р/2 в каждую сторону). По подошве насыпи по формуле (4.170) также находят скорости, равные допускаемым, и соответствующие им координаты y. Для обеспечения запаса откладывают от полученных точек примерно по 1 м в каждую сторону. Полученные четыре точки ограничат размер укрепления, имеющего трапецеидальную форму.

Размеры укрепления на откосе насыпи привязывают к ширине трубы или оголовка с запасом в 1,0 м.

5. РАСЧЕТ ВОДОПРОПУСКНЫХ ТРУБ

ТИПЫ ТРУБ И ЭЛЕМЕНТЫ ИХ ВОДОПРОПУСКНОГО ТРАКТА

5.1. На дорогах страны эксплуатируются десятки тысяч водопропускных труб, отличающихся материалом изготовления, размером отверстия и формой сечения, типом оголовков, уклоном укладки и другими конструктивными особенностями, в той или иной мере влияющими на их гидравлическую работу (рис. 5.1).

Рис. 5.1. Формы и типы оголовков водопропускных труб

(а - г - фасад и план; д, е - фасад и продольный разрез):

а - круглой с портальным оголовком; б - с вертикальными

стенками и коридорным оголовком; в - прямоугольной

с раструбным оголовком с обратными стенками; г - круглой

с коническим звеном и раструбным оголовком; д - круглой

безоголовочной; е - овоидальной с воротниковым оголовком

С конца 20-х годов нашего века трубы строятся по типовым проектам, а до этого - лишь по индивидуальным.

Около 90% труб имеет отверстие не более 2,5 м, 50% - менее 1,2 м. Средняя величина отверстия 1,4 м. Менее 10% труб расположено под насыпями высотой более 10 м, а 50% труб - под насыпями высотой менее 4,0 м. Средняя высота насыпи у труб 5,4 м. Около 50% труб, главным образом круглых малых диаметров, имеют оголовки портального типа, представляющие собой вертикальную стенку, обсыпанную с обеих сторон от отверстия конусами, сопрягающимися с откосами насыпи (рис. 5.1, а).

Значительное распространение получили раструбные оголовки, представляющие собой обычно вертикальные стенки, срезанные параллельно откосу насыпи (рис. 5.1, в, г). Угол сходимости стенок варьирует от 4 до 22°. Наименьшую длину имеют оголовки с коротким высоким раструбом, построенные по проектам 1946 - 1952 гг. (см. рис. 5.1, в), а наибольшую - до подошвы насыпи - оголовки без обратных стенок, построенные по типовым проектам 1961 и последующих годов (см. рис. 5.1, г).

В некоторых проектах до 1928 г. встречаются оголовки с раструбными стенками, несколько отодвинутыми от отверстия, что создает менее плавный вход потока и ухудшает гидравлические характеристики.

Коридорные оголовки (рис. 5.1, б) применялись в проектах до 1946 г. для размещения кривой спада в пределах оголовка и понижения глубины на входе в трубу, что обеспечивало возможность применения для тех же гидравлических условий труб меньшей высоты. Однако последующие исследования показали ухудшение гидравлических условий труб с данным типом оголовков по сравнению с раструбными, а также значительный перерасход материала на их сооружение, т.е. их неэкономичность. В связи с этим коридорные оголовки в настоящее время не применяются. Однако на сети дорог продолжает эксплуатироваться значительное число труб с коридорными оголовками, отличающихся длиной, шириной обратных стенок и степенью закругленности входной части оголовка.

Некоторое, хотя и небольшое распространение получили трубы с воротниковыми оголовками, представляющими собой срез круглой трубы параллельно откосу насыпи, окаймленный по контуру выступающей из насыпи частью - "воротником" (рис. 5.1, е).

Сравнительно небольшое распространение среди бетонных и железобетонных труб получили так называемые безоголовочные, обычно круглые трубы (рис. 5.1, д), которые характеризуются вертикальным срезом трубы у подошвы насыпи. Но этот тип оголовка нашел самое широкое распространение и, можно сказать, явился основным для металлических гофрированных труб, о которых будет сказано ниже.

Применение с 1955 г. в круглых трубах конических звеньев на входе в трубу обеспечило снижение гидравлического сопротивления на входе и зарядку труб, т.е. работу их полным сечением.

В действующем типовом проекте конические звенья сочетаются с раструбными открылками. Этот тип оголовка относится к обтекаемым и обладает наибольшей пропускной способностью из всех применяемых в настоящее время. Из существующих типов необтекаемых оголовков наилучшие гидравлические характеристики имеют раструбные без обратных крыльев с углом раструбности

, которые в основном и применяются в типовых проектах круглых и прямоугольных труб. Портальные оголовки применяются на автомобильных дорогах для круглых труб малых диаметров (0,5 и 0,75 м). Эти оголовки дешевле раструбных, но их применение ограничивается возможностью размыва конусов.

В прямоугольных трубах распространение получили повышенные звенья на входе в трубу, расширяющие диапазон работы труб в безнапорном режиме и уменьшающие степень заполнения трубы при безнапорном режиме, регламентируемую нормами [39]. Это позволяет в ряде случаев получить снижение стоимости за счет уменьшения высоты основной части трубы. Широкое распространение в последнее десятилетие получили металлические гофрированные трубы. Ленгипротрансмостом разработаны типовые проекты указанных типовых сооружений диаметрами 1,5 - 3,0 м. Предусмотрены следующие типы гофрированных труб: без оголовков (вертикальный срез); со срезом параллельно откосу насыпи; с раструбным оголовком с

Гофрированные трубы весьма удобны в строительстве благодаря своей малой массе, а следовательно, транспортабельности, быстроте монтажа и вводе в эксплуатацию.

5.2. Элементы водопропускного тракта труб рассмотрим с помощью рис. 5.2, на котором представлены наиболее характерные в гидравлическом отношении типы водопропускных труб и их элементы.

Рис. 5.2. Типы водопропускных труб и их элементы:

а - труба равнинного типа; б - косогорная труба

с быстротоком, сужением на входе и гасителем на выходе;

в - входная часть трубы с быстротоком и водоприемным

колодцем; г - труба с быстротоком и шахтным сбросом;

1 - собственно труба; 2 - оголовки трубы; 3 - укрепления;

4 - предохранительный откос; 5 - каменная наброска;

6 - насыпь; 7 - нагорная канава; 8 - быстроток;

9 - сужение; 10 - гаситель; 11 - колодец-шахта

На рис. 5.2, а изображен наиболее распространенный и в конструктивном отношении наиболее простой тип водопропускной трубы, используемый для равнинных условий. Его основные элементы собственно труба 1 и оголовки 2. Для защиты от размыва на входе и выходе сооружения устраивают укрепления 3, завершаемые предохранительным откосом 4, на который обычно укладывается каменная наброска 5. Указанный тип труб применяют в равнинных условиях, т.е. при малых уклонах местности i_л < 0,02. Таких сооружений на сети дорог имеется более 60 - 85%, причем подавляющее число сооружений имеют уклоны, близкие к критическим для технически гладких труб, т.е.

Перед равнинной трубой в расчетных условиях обычно формируется пруд, откуда происходит истечение спокойного потока в трубу. Он обычно находится в критическом состоянии, т.е. при числах Фруда

(где v и h - соответственно скорость и глубина потока в трубе; g - ускорение силы тяжести), либо в бурном, но при малой кинетичности (число Фруда 1 < Fr < 3).

При значительных уклонах местности устраивают так называемые косогорные трубы. На рис. 5.2, б приведена косогорная труба наиболее распространенного типа. Характер протекания воды по ее элементам следующий. Поток с косогора попадает в нагорную канаву 7, а оттуда через быстроток 8 и сужение 9 - в трубу 1. Поток, выходящий из трубы, попадает в гаситель 10, в виде расширяющегося колодца с водобойной стеной и далее на укрепление.

Обычно в такое сооружение поток попадает в бурном состоянии. Обладая высокой кинетичностью (числа Фруда достигают 30 - 50), в трубе он проходит с высокими скоростями (10 - 12 м/с). Для снижения скоростей в подобных трубах применяют либо ступенчатую укладку звеньев (наиболее рационален этот способ для прямоугольных труб), либо повышенную шероховатость в виде ребер в прямоугольных трубах или диафрагм - в круглых. В ряде случаев вместо гасителей в трубе устраивают гасители на выходе из нее, как это имеет место в трубе, приведенной на рис. 5.2, б.

В практике проектирования применяют также способы гашения энергии, обеспечивающие перевод бурного потока, подходящего с косогора к сооружению по быстротоку, в спокойный посредством затопления гидравлического прыжка. Для этого на входе в трубу устраивают водоприемный колодец (рис. 5.2, в). Из колодца поток изливается в трубу, как в равнинных условиях, что обеспечивает существенное снижение скоростей.

В ряде случаев при соответствующей конфигурации местности снижение скоростей в трубе обеспечивают посредством устройства шахтного сброса (рис. 5.2, г). Вода здесь попадает сначала в колодец-шахту, а оттуда в трубу, уложенную с малым уклоном и работающую полным сечением. При этом скорости в ней существенно ниже, чем в быстротоке.

Элементы сопряжений подходных устройств (быстротоков и сужений) в косогорных условиях (при значительных уклонах местности) представлены на рис. 5.3 и 5.4.

Рис. 5.3. Сопряжения прямоугольных быстротоков

шириной b_б с круглыми трубами диаметром D при:

а - b_б = 2D и трубе без конического звена на входе;

б - b_б = 2D и трубе с коническим звеном, в - b_б = D;

1 - быстроток; 2 - сужение; 3 - труба; 4 - примазка;

5 - коническое звено

Рис. 5.4. Сопряжения трапецеидальных быстротоков шириной

по дну b_б(дн) с круглыми трубами диаметром D при:

а - b_б(дн) = 2D и трубе без конического звена;

б - b_б(дн) = 2D и трубе с коническим звеном; в - b_б(дн) = D;

г - b_б(дн) = 0,42D; 1 - быстроток; 2 - сужение; 3 - труба;

4 - примазки; 5 - коническое звено

В косогорных условиях применяют также металлические гофрированные трубы. Однако по условиям прочности укладку их допускают с уклонами не более 0,03. При больших уклонах лога их укладывают на подсыпке со сбросом потока на укрепленные откосы насыпи, в лотки или с отбрасыванием струи от подошвы насыпи с помощью консольных сбросов.

Консольный сброс применяют не только в гофрированных трубах, но и в других типах косогорных труб. В ряде случаев он сочетается с рассеивающими трамплинами, позволяющими существенно расширить бурный поток и тем самым снизить удельные расходы его.

СОПРЯЖЕНИЯ ПОДХОДНЫХ УСТРОЙСТВ С ТРУБАМИ

5.3. Важнейшим фактором, определяющим пропускную способность труб и режимы протекания воды в них, является характер сопряжения их с подходными устройствами, в значительной степени зависящий от рельефа местности.

Известно два основных типа сопряжения: ввод в сооружение спокойного потока и ввод в него потока в бурном состоянии. Первый случай сопряжения носит название равнинного, так как он в основном характерен для равнинных сооружений, уложенных с малыми уклонами, что обычно соответствует малым уклонам бытового лога i_л <= 0,02. Примером таких сооружений может служить труба, представленная на рис. 5.2, а.

Второй случай обычно имеет место в пересеченной местности при значительных уклонах бытового лога i_л > 0,02 (в ряде случаев

и более). При этом для сохранения бурного состояния потока на входе в трубу устраивают специальные устройства, обычно быстротоки. При ширине быстротока, большей отверстия трубы (наиболее частый случай), между быстротоком и трубой устраивают сужения. Пример такого сооружения, называемого косогорным, представлен на рис. 5.2, б. Гидравлические расчеты быстротоков и сужений изложены в гл. 4.

Топографические условия, характерные для нашей страны, определили и распространенность указанных видов сооружений. Наибольшее распространение (80 - 85%) имеют равнинные трубы. Обычно их укладывают с уклонами, близкими к критическим i_к, или с уклоном, соответствующим сжатым глубинам i_с (см. приложение 1.2). Характер сопряжения сказывается и на пропускной способности сооружения: большей пропускной способностью обладают сооружения, в которые поток вводится в бурном состоянии. Поэтому ввод спокойного потока в косогорную трубу нежелателен, так как это приводит к снижению ее пропускной способности.

Для косогорных труб характерны высокие скорости как в трубе, так на выходе из нее, которые ограничивают полное использование пропускной способности, в связи с чем применяют и иные входные условия косогорных труб: использование водоприемных колодцев на входе (см. рис. 5.2, в), шахтные сбросы (см. рис. 5.2, г) и т.п. Гидравлические расчеты подходных устройств приводятся в гл. 4.

Пропускная способность труб зависит также от режимов протекания.

Существует три основных режима протекания:

1) безнапорный, когда входное сечение не затоплено и на всем протяжении трубы поток имеет свободную поверхность (рис. 5.5);

2) полунапорный, когда входное сечение затоплено, т.е. на входе труба работает полным сечением, а на остальном протяжении поток имеет свободную поверхность (рис. 5.6, а);

3) напорный, когда входное сечение трубы затоплено и на большей своей части труба работает полным сечением (рис. 5.6, б).

Рис. 5.5. Схема протекания воды в трубе

при безнапорном режиме

Рис. 5.6. Схемы протекания воды в трубе

при полунапорном (а) и напорном (б) режимах

Кроме того, возможны промежуточные режимы, например частично напорный, когда труба работает полным сечением лишь на части своей длины. Возникновение тех или иных режимов зависит от вида подходных устройств, входных оголовков и уклонов труб, их шероховатости, расходов воды в трубах и т.п.

Учитывая сравнительно узкий диапазон условий гидравлической работы равнинных труб и значительное внимание, которое уделили ему исследователи как в экспериментальном, так и в теоретическом плане, этот класс сооружений изучен достаточно полно, в том числе в отношении режимов протекания.

Гидравлические расчеты этих сооружений изложены ниже в отдельной рубрике.

Несмотря на то, что в косогорных трубах возможны те же режимы протекания, их следует рассмотреть особо из-за многообразия условий, влияющих на их возникновение.

Обычно к входному отверстию трубы поток подходит в бурном состоянии. Режимы протекания воды в трубе зависят от условий сопряжения подходных устройств с трубой;

наличия быстротока, соотношения его ширины и отверстия трубы;

наличия сужений, водоприемных колодцев, а также уклонов и шероховатости трубы быстротока и сужения.

Рассмотрим вначале случаи безнапорного режима протекания в трубах.

При ширине подходного быстротока, равной отверстию трубы, в круглой трубе должны быть устроены специальные направляющие (примазки). Поток входит в трубу и протекает в ней в бурном состоянии. При этом глубина воды на всем протяжении водопропускного тракта меньше высоты трубы.

При ширине подходного быстротока большей, чем отверстие трубы и наличия сужения на входе в нее поток может поступать в трубу как в бурном состоянии - в этом случае перед трубой возникает всплеск (рис. 5.7, а), так и в спокойном - в случае возникновения перед трубой гидравлического прыжка (рис. 5.7, б).

Рис. 5.7. Схемы протекания воды в косогорных трубах

В последнем случае втекание воды в трубу происходит, как в равнинных трубах. Такой характер втекания воды в трубу возможен также при:

а) малых уклонах подходного лога;

б) при неявно выраженном логе и отсутствии подходных быстротоков;

в) наличии водоприемных колодцев.

Некоторые модификации кривой свободной поверхности возникают при вводе бурного потока в трубу, но при наличии перелома на входе в нее (разные уклоны быстротока и трубы) или, что эквивалентно указанному случаю, при повышенной шероховатости в трубе (рис. 5.7, в). При этом за всплеском происходит снижение глубин, а далее возникает кривая подпора, а на выходе кривая слива.

Похожая картина имеет место при наличии перелома в трубе (рис. 5.7, г).

Во всех рассмотренных выше случаях (см. рис. 5.7, а - г) глубина на входе в трубу h_вх и нормальная глубина в трубе были меньше высоты трубы, что обеспечивает безнапорный режим протекания. В случае затопления входа в трубу, что возможно при h_вх > h_т (для бурного потока средняя глубина его на входе с учетом всплесков должна быть больше высоты трубы) и нормальной глубине, меньшей высоты трубы, в трубе возникает полунапорный режим протекания (рис. 5.7, д). Он полностью аналогичен подобному режиму в равнинных трубах.

В случае затопленного входа и нормальной глубины больше высоты трубы (h₀ > h_т) сразу за сжатым сечением возникает кривая подпора. При этом при сравнительно "короткой" трубе свободная поверхность не достигает верха трубы и в конце завершается кривой слива (рис. 5.7, е). В трубе возникает полунапорный режим.

При значительных уклонах трубы сжатая глубина не образуется, и на всей длине трубы устанавливается кривая спада (рис. 5.7, ж).

При значительной длине трубы кривая подпора достигает шелыги трубы, и в трубе возникает напорный режим (рис. 5.7, з). Случаи, аналогичные изображенным на рис. 5.7, д - з, могут возникнуть и при переломе профиля трубы.

РАВНИННЫЕ ВОДОПРОПУСКНЫЕ ТРУБЫ

Режимы протекания

5.4. Гидравлические расчеты равнинных труб выполняют в зависимости от режимов их работы.

Безнапорный режим протекания сохраняется вплоть до затопления входного сечения трубы. При его затоплении происходит переход от безнапорного режима к полунапорному или напорному. Затопление входного отверстия трубы устанавливают по значениям параметра расхода П_Q, приведенным в табл. 5.1. Значения П_Q определяют по номограммам (рис. 5.8 и 5.9). Приближенно можно принимать, что затопление происходит при H/h_т = 1,1 для всех типов оголовков, кроме воротниковых и коридорных. Затопление входа с воротниковым оголовком происходит при H/h_т = 1,2, а с коридорным - при H/h_т = 1,3. Точнее момент затопления для труб с коридорными оголовками устанавливают по глубине на входе в трубу (h_вх, _нз), соответствующей затоплению входного отверстия трубы h_вх, _нз = h_т, определяя h_вх, _нз по формуле (5.16).

Таблица 5.1

Форма поперечного сечения трубы	Формула параметра расхода П_Q	Заполнение входного сечения	Значение параметра расхода труб при типах входных оголовков
			без оголовков	портальных с конусами	коридорных	воротниковых с	раструбных
			без оголовков	портальных с конусами	коридорных	воротниковых с
Прямоугольная		0,833	-	0,420	-	0,565	0,570	0,580	0,525
Прямоугольная		1,0	-	0,560	-	0,588	0,620	0,665	0,645
Круглая		0,75	0,275	0,275	-	0,400	0,300	0,305 (0,390)	0,300
Круглая		1,0	0,415	0,440	-	0,460	0,475	0,495 (0,600)	0,475
Овоидальная		0,75	-	0,325	0,545	-	-	0,350	-
Овоидальная		1,0	-	0,455	0,605	-	-	0,485	-

Примечания. 1. Для каждого типа труб приведены параметры расхода для расчетного (первая строка) и полного (вторая строка) заполнения.

2. В скобках приведены значения П_Q для труб с коническим звеном на входе.

3. При вычислении П_Q для прямоугольных труб с повышенными звеньями на входе вместо высоты трубы h_т следует подставлять высоту повышенного звена на входе в сооружение h_т(вх).


Рис. 5.8	Рис. 5.9

Рис. 5.8. Номограмма для определения безразмерного параметра

расхода для круглых труб

Рис. 5.9. Номограмма для определения безразмерных параметров

расхода

(для входа) и

(для выхода) для прямоугольных труб

При наличии на входе в круглую трубу обтекаемого оголовка или конического звена при затоплении входного сечения в трубе образуется напорный режим.

Трубы с необтекаемыми оголовками при затоплении входного сечения трубы обычно работают в полунапорном режиме, хотя в некоторых случаях могут работать в напорном режиме. В практических расчетах трубы с необтекаемыми оголовками с затопленным входным сечением можно рассчитывать по полунапорному режиму; при фактической зарядке трубы результат будет получен с некоторым запасом.

Для уточнения возможности зарядки труб рекомендуется использовать следующую методику.

1. При i_т < i_к и h_к < h_т определяют h_с (в предположении полунапорного режима) и длину кривой подпора l₀ (см. гл. 2) между глубинами h_с и h_к. Если длина трубы l_т < l₀ + l_вх + l_сл, то в трубе возникает устойчивый полунапорный режим; если же l_т > l₀ + l_вх + l_сл, то будет напорный режим с местным отделением струй от потолка трубы в ее конце.

Можно принимать l_вх ~= 1,4h_т и

, а h_с определять из выражения

(5.1)

где

- коэффициент расхода при полунапорном режиме (см. табл. 5.2).

Таблица 5.2

Форма поперечного сечения трубы	Расчетные коэффициенты	Гидравлические характеристики труб при типах входных оголовков
		без оголовков	портальных с конусами	коридорных	воротниковых	раструбных с
		без оголовков	портальных с конусами	коридорных	воротниковых
Прямоугольная	m	0,310	0,325	0,340	0,315	0,36	0,36	0,35
		0,86	0,74	0,83	0,74	0,76	0,78	0,81
		0,63	0,62	0,61	9,58	0,61	0,64	0,68
Круглая	m	0,31	0,31	0,32	0,31	0,33	0,33 (0,35)	0,33
		0,66	0,79	0,79	0,75	0,79	0,79	0,79
		0,56	0,65	0,58	0,62	0,66	0,69	0,70
Овоидальная		-	0,63	0,69	-	-	0,63	-
Овоидальная		-	0,60	0,58	-	-	0,61	-

Примечания. 1. В скобках дано значение m для труб с коническим звеном на входе.

2. Значения m для прямоугольных труб с раструбными оголовками соответствуют условиям

при

. В остальных случаях m следует определять по формулам: при

и при

Напор H определяют в предположении полунапорного режима. Выражение (5.1) получено для прямоугольных труб; для круглых и овоидальных вместо

принимают

2. При i_т < i_к и h_к >= h_т <*> определяют длину кривой подпора l₀ как расстояние между глубинами h_с и h_т. При l_т < l_вх + l₀ + l_сл будет полунапорный режим, а при l_т > l_вх + l₀ + l_сл - напорный (без местного отделения струй от потолка трубы).

--------------------------------

<*> Для круглых и овоидальных труб этот случай невозможен.

3. При i_т > i_к <*> вычисляют длину кривой подпора l₀ между глубинами h_с и h_т. Приближенно принимают

; h_с - из выражения (5.1).

--------------------------------

<*> Для круглых и овоидальных труб при i_т < i_к теоретически напорная работа невозможна, но из-за резкой деформации потока, особенно при больших H/h_т, такие трубы могут заряжаться.

При выборе режима работы трубы следует учитывать, что наиболее безопасен безнапорный режим с обеспечением возвышения высшей точки внутренней поверхности трубы над поверхностью воды согласно п. 1.24 СНиП 2.05.03-84, при котором возможно проплывание через трубу некрупных предметов. При затоплении входного сечения через трубу проходит больший расход, но при этом возникают дополнительные трудности в эксплуатации сооружений. Наиболее опасен переход от полунапорного к напорному режиму и неустойчивый напорный режим, при которых в трубе возникает переменное давление как большее, так и меньшее атмосферного. В этом случае возможно просачивание воды через швы и трещины с последующим проникновением грунта насыпи внутрь трубы. При работе трубы с затопленным входом должны быть обеспечены водонепроницаемость стыков звеньев и блоков, отсутствие сквозных трещин, а также устойчивость насыпи против воздействия подпора воды и ее фильтрации через тело насыпи.

5.5. При безнапорном и полунапорном режимах протекания (по условиям работы дорожных водопропускных труб) основным является случай, когда сжатое сечение не затоплено и пропускная способность зависит только от условий входного участка трубы (до сечения, в котором спокойный поток переходит в бурный).

Когда сжатое сечение затоплено, пропускная способность трубы снижается. Затопление сжатого сечения может быть вызвано влиянием сопротивления по длине трубы при относительно большой ее длине и малом уклоне (рис. 5.10), повышенной шероховатостью или затоплением с нижнего бьефа (рис. 5.11).

Рис. 5.10. Схема протекания воды в "длинной" трубе

Рис. 5.11. Схема протекания воды по трубе,

затопленной с нижнего бьефа

В зависимости от влияния длины трубы на пропускную способность различают "короткие" и "длинные" трубы. У "коротких" труб сжатое сечение не затоплено, и общая длина их не оказывает влияния на пропускную способность. В "длинных" трубах сжатое сечение затоплено, и на протяжении всей длины трубы сохраняется спокойный поток, вследствие чего сопротивления по длине трубы влияют на пропускную способность.

Предельная длина "коротких" труб l_пр при

для бетонных труб с обычной (не повышенной) шероховатостью может быть определена по эмпирическим зависимостям:

(5.2)

(5.3)

где H₀ - напор перед трубой с учетом скоростного напора; обычно при расчете дорожных водопропускных сооружений скоростным напором пренебрегают и принимают H₀ = H;

m - коэффициент расхода, определяемый по табл. 5.2;

h_к - критическая глубина в трубе.

При уклонах трубы, близких к критическому, значения l_пр, найденные по формулам (5.2) и (5.3), увеличивают на 30%.

При i_т > i_к трубы любой длины являются "короткими".

Для определения

можно пользоваться графиком, приведенным на рис. 5.12.

Рис. 5.12. График зависимости

В общем случае предельная длина "короткой" трубы (см. рис. 5.5)

l_пр = l_вх + l₀ + l_сл. (5.4)

Длину входного участка l_вх и участка слива l_сл можно определить по эмпирическим формулам [31].

Для всех оголовков, кроме воротникового,

(5.5)

или

(5.6)

Для воротникового оголовка

(5.7)

или

(5.8)

где

- угол наклона откоса насыпи к горизонту.

Значения

определяют по формулам (5.5) и (5.6);

(5.9)

Длину среднего участка l₀ определяют как длину кривой подпора между глубинами h_с и h_к (см. гл. 2).

Глубину в сжатом сечении h_с при

можно определять по графику, представленному на рис. 5.20, или по формуле

(5.10)

При i_т > 0

(5.11)

Приближенно для круглых труб можно принимать при плавных (раструбных) входных оголовках

, при неплавных -

По влиянию глубины воды в нижнем бьефе трубы делят на "затопленные" с нижнего бьефа и "незатопленные".

Затопленными с нижнего бьефа считают трубы (см. рис. 5.11), работающие в условиях, при которых уровень нижнего бьефа влияет на пропускную способность трубы вследствие затопления сжатого сечения; в противном случае трубы считаются незатопленными с нижнего бьефа (рис. 5.13). Затопленными будут такие трубы, на всех участках которых - участке входа I, среднем участке II и участке сопряжения с нижним бьефом III (см. рис. 5.11) - будет спокойный режим, т.е. критерий затопления трубы соответствует такому горизонту воды в нижнем бьефе, при котором происходит смена бурного режима в трубе спокойным.

Рис. 5.13. Схема протекания воды по трубе, подтопленной

с нижнего бьефа, с незатопленным сжатым сечением

Для труб с обычной (не повышенной) шероховатостью с уклонами i_т <= i_к и для труб с уклонами i_т > i_к при небольших относительных их длинах порядка

можно приближенно пользоваться следующими критериями затопления, полученными на основании экспериментов [31]:

или

(5.12)

где h_нб - глубина воды в нижнем бьефе над нижней точкой дна трубы в выходном сечении.

В общем случае рассматривают два случая.

1. При "коротких" (без подтопления) трубах, а также трубах с уклоном i_т > i_к затопление трубы начинается тогда, когда глубина в сжатом сечении h_сз больше глубины

, сопряженной с h_с. При этом "затопляющую" глубину нижнего бьефа h_п определяют в следующем порядке: находят для данных условий входа сжатую глубину h_с (см. приложение 2.7); для разных h_п определяют на участке III глубины (см. рис. 5.11) по уравнению неравномерного движения (см. гл. 2); затем также строят кривую свободной поверхности на среднем участке II и определяют глубины h_сз. Значение h_п, при котором

, является критерием ее затопления.

2. Если при отсутствии подтопления труба работает как "длинная", то для затопления такой трубы необходимо, чтобы на участке слива в конце трубы поток находился в спокойном состоянии. В этом случае в соответствующей зависимости (5.20), связывающей для участка III величины Q, h₁ и h_п, принимают h₁ = h_к.

При больших значениях h_п, чем полученные из этого уравнения, труба будет затопленной.

Безнапорные "короткие" незатопленные трубы

5.6. Гидравлические расчеты труб заключаются в определении по известному расходу подпертой глубины воды перед трубой, по которой проверяют возвышение бровки земляного полотна, или расхода по известной подпертой глубине степени затопления трубы при безнапорном режиме протекания потока и скорости на выходе из труб для назначения укрепления.

Расход воды, пропускаемый безнапорной "короткой" неподтопленной трубой,

(5.13)

где m - коэффициент расхода при совершенном сжатии потока на входе, принимаемый по табл. 5.2 <*>;

- средняя ширина потока в сечении с критической глубиной; для прямоугольных труб b_к = b; для круглых и овоидальных b_к определяют по графику, приведенному на рис. 5.14.

--------------------------------

<*> Для овоидальных труб значение коэффициента расхода принимают, как для прямоугольных труб, с уменьшением на 3%; для труб с портальными оголовками без конусов коэффициент расхода уменьшают на 2%.

Рис. 5.14. График для определения средней ширины

потока в сечении с критической глубиной в трубах

непрямоугольного сечения

В табл. 5.2 приведены значения m для уклона трубы i_т = 0,01. При уклоне, отличном от 0,01, для более точного расчета значения m следует увеличивать при i_т > 0,01 или уменьшать при i_т < 0,01 на 2% на каждую 0,01 уклона.

Для упрощения расчетов пропускной способности круглых, прямоугольных и овоидальных незатопленных коротких труб с оголовками основных типов при безнапорном и полунапорном режимах рекомендуется пользоваться номограммами на рис. 5.14, 5.15, 5.16, построенными по формулам (5.15) - (5.17), и значениям расчетных коэффициентов, приведенным в табл. 5.2.

Рис. 5.15. Номограмма для определения

пропускной способности круглых труб

Рис. 5.16. Номограмма для определения

пропускной способности прямоугольных труб

Номограмма для определения пропускной способности труб с овоидальным поперечным сечением (рис. 5.17), так же как и график на рис. 5.14, построена для труб, у которых поперечное сечение очерчено по эллипсу, причем площадь поперечного сечения

. При определении пропускной способности по номограммам, если режим протекания потока в трубе заранее не известен, отсчет сначала берут по шкале Q для безнапорного режима.

Рис. 5.17. Номограмма для определения

пропускной способности овоидальных труб

Если для всех типов оголовков, кроме воротникового и коридорного, получается значение

, а для воротниковых оголовков

и для коридорных оголовков

, то режим безнапорный. Если получается, что

больше этих граничных значений, то выполняют расчет по шкале Q для полунапорного режима.

В том случае, если ширина разлива при подпертом расчетном уровне высоких вод менее шести отверстий трубы, имеет место несовершенное сжатие потока при входе в трубу, и коэффициент расхода

(5.14)

где m_табл - значение коэффициента расхода по табл. 5.2;

- площадь поперечного сечения потока в трубе при подпертой глубине;

- площадь поперечного сечения потока в подводящем русле.

Для определения m при несовершенном сжатии можно пользоваться графиком на рис. 5.18.

Рис. 5.18. График зависимости

При определении глубин воды в характерных сечениях трубы необходимо иметь в виду следующее.

При безнапорном режиме перед трубой и в пределах входной части трубы наблюдается кривая спада от подпертой глубины до сжатого сечения. Сжатое сечение в зависимости от типа входного оголовка, поперечного сечения и уклона находится на расстоянии

от входа в трубу, а глубина в сжатом сечении колеблется в пределах

Далее устанавливают форму свободной поверхности в зависимости от уклона трубы:

1) при i_т > i_с,

где

(5.15)

от сжатой глубины h_с до глубины на выходе из трубы h_вых расположена пологая кривая спада, при i_т = i_с за сжатым сечением устанавливается глубина h_с;

2) при 0 < i_т < i_с за сжатым сечением глубина увеличивается (см. рис. 5.5), а при i_т = i_к за сжатым сечением в трубе устанавливается критическая глубина h_к.

Обычно для труб без повышенных звеньев на входе лимитирующим по заполнению является их входное сечение. При уклонах, близких к нулю, возможен случай, при котором лимитирующим по заполнению может быть сечение за сжатым сечением, глубину в котором определяют построением кривой свободной поверхности в трубе (см. гл. 2).

Глубину воды на входе в трубу h_вх определяют по графикам на рис. 5.19, находя параметр расхода по номограммам на рис. 5.8 или 5.9.

Рис. 5.19. Графики для определения глубины воды на входе

в прямоугольные (а), круглые (б) и овоидальные (в) трубы

при типах оголовков:

1 - портальном; 2 - раструбном с

;

3 - раструбном с

; 4 - раструбном с

;

5 - воротниковом с

; 6 - без оголовка;

7 - раструбном с коническим звеном; 8 - коридорном

(штриховая линия характеризует расчетное заполнение

трубы при h_т <= 3,0 м)

Графики на рис. 5.19 построены для уклона i_т = 0,01. В диапазоне равнинных труб (i_т <= 0,020) при i_т >= i_к глубина на входе h_вх практически не зависит от уклона, а при

при тех же параметрах расхода h_вх больше на величину, примерно равную 5% высоты трубы.

В прямоугольных трубах с повышенными звеньями лимитирующим может быть сечение на входе в нормальное звено. Среднюю глубину в этом сечении при условии, что оно находится между входом в трубу и сжатым сечением, определяют по эмпирической зависимости

(5.16)

где h_с - глубина воды в сжатом сечении, расположенном на расстоянии

от входа в трубу, определяемая по графику на рис. 5.20 или по формуле (5.11);

l_пз - длина повышенного звена трубы.

Рис. 5.20. График зависимости

При определении степени заполнения трубы за сжатым сечением глубину обычно принимают равной критической глубине h_к, как, например, в действующих типовых проектах. В тех случаях, когда уклон трубы i_т больше критического уклона, глубина за сжатым сечением будет меньше h_к, а при уклоне, равном i_с [см. формулу (5.15)], глубина равна h_с. Если на входе в трубу сделать достаточно высокие и длинные повышенные звенья, чтобы входное сечение не лимитировало по заполнению, то можно уменьшить высоту остальной части трубы, определяя при уклоне i_т > i_к степень заполнения трубы по глубине h < h_к, а при i_т = i_с - по глубине h_с.

Безнапорные "длинные" и затопленные трубы

5.7. Напор перед круглыми "длинными" трубами H_дл с обычной (не повышенной) шероховатостью при уклонах, близких к нулю, определяют по формуле

(5.17)

где H - напор перед аналогичной "короткой" трубой.

В первом приближении эту формулу можно применять и для труб с другими формами поперечного сечения. Более точно "длинные" трубы, а также трубы, подтопленные с нижнего бьефа, рассчитывают следующим образом [31].

Для предварительного назначения отверстия при заданном расходе трубу приближенно рассчитывают как "короткую", а затем отверстия несколько увеличивают и уже как для "длинной" трубы определяют глубину h_сз в конце участка входа. Для этого строят кривую свободной поверхности на среднем участке трубы длиной l_сз = l_т - l_вх - l_сл, принимая l_сл = h_к. При этом длину участка входа l_вх приближенно определяют по формулам (5.5), (5.6), (5.7) или (5.8), а участка слива - по формуле

(5.18)

Если в трубе устанавливается равномерный режим, то l_сл не зависит от длины трубы. При большой относительной длине трубы и уклонах 0 < i_т < i_к без большой погрешности можно принимать h_сз = h₀, где h₀ - глубина равномерного движения в трубе.

Пропуская способность

(5.19)

где

- коэффициент подтопления, определяемый для прямоугольных труб по графику, приведенному на рис. 5.21.

Рис. 5.21. График зависимости

Так как

зависит от

, а H₀ неизвестно, то задачу решают последовательными приближениями. При заданном H₀ задачу также решают последовательными приближениями. В этом случае при известном Q, задаваясь

, по формуле (5.19) определяют b_к, а затем поперечное сечение потока в трубе. После этого строят кривую спада, определяют h_сз и проверяют, соответствует ли коэффициент по графику на рис. 5.21 (при полученном

) принятому в первоначальном расчете. При несовпадении этих значений сечение трубы изменяют и расчет повторяют.

Подтопление трубы следует рассчитывать, рассматривая совместно участки I, II и III трубы (см. рис. 5.11). Для участков I и II сохраняют приведенные выше зависимости и указания, но кривую свободной поверхности на среднем участке II строят между глубинами h₁ и h₂ = h_сл > h_к.

Для труб прямоугольного сечения и прямоугольного поперечного сечения нижнего бьефа для участка III пользуются графиками для определения перепада восстановления, приведенными на рис. 5.22. Перепад восстановления z по этим графикам определяют для трех случаев сопряжения с нижним бьефом: внезапного (сопряжение плоскостью с уклоном не положе 1:2 или криволинейной поверхностью со средним уклоном не положе 1:1,5), относительно плавного расширения (соответственно уклоны 1:4 - 1:5 и 1:3) и весьма плавного (уклоны порядка 1:6 - 1:7).

Рис. 5.22. График для определения перепада восстановления

при переходе от трубы или водослива к каналу:

а - при резком переходе; б - при плавном сопряжении;

в - при весьма плавном сопряжении;

Для труб непрямоугольных поперечных сечений для приближенного расчета z и h₂ = h_сл используют метод расчета прямоугольных труб. В первом приближении ширину эквивалентной прямоугольной трубы b принимают равной наибольшей ширине непрямоугольной трубы; потом полученные значения z и h₂ уточняют, подсчитывая

, и по значению

находят глубину наполнения h, а затем во втором приближении ширину эквивалентной прямоугольной трубы

; после этого при значении b' определяют z и h₂ и так далее до совпадения h ~= h₂ с необходимой точностью.

Подтопленную трубу рассчитывают от нижнего бьефа к верхнему. Размерами трубы предварительно задаются.

Если при заданном расходе надо определить подпертый уровень перед трубой, то сначала по графикам на рис. 5.22 определяют h_сл = h_п - z, затем строят кривую способной поверхности на длине l₀ (см. рис. 5.11) и определяют глубину h₁. При малых l₀/H влиянием потерь по длине l₀ можно пренебречь, т.е. принять h_сл = h₁.

После этого подбором по формуле (5.19) находят H. Если задан напор H, а расход Q неизвестен, то, вычисляя ряд значений Q, строят кривую Q = f(H) и по ней определяют искомое Q, соответствующее заданному H.

Полунапорные трубы

5.8. Расход полунапорных труб

(5.20)

где

- коэффициент расхода, принимаемый по табл. 5.2;

- коэффициент, определяемый по табл. 5.2.

Для прямоугольных труб с повышенным звеном вместо h_т подставляют высоту этого звена на входе в сооружение h_т(вх).

В диапазоне уклонов "равнинных" труб влияние уклона трубы на пропускную способность незначительно; при увеличении уклона от 0 до 0,02 коэффициент расхода возрастает до 3%. Малое влияние на пропускную способность оказывает и отношение высоты h_т к ширине b прямоугольных труб; при изменении h_т/b от 1 до 2 увеличение коэффициента расхода

не превышает 3%. В табл. 5.2 значения

приведены для уклона трубы i_т = 0,01 и h_т/b = 1,5.

Напорные трубы

5.9. Пропускную способность труб при незатопленном со стороны нижнего бьефа выходе (h_п < h_т) рассчитывают по формуле

(5.21)

где

- коэффициент расхода, в общем случае определяемый по формуле (5.22), а для круглых бетонных труб с коническим звеном на входе - по графику на рис. 5.23;

- коэффициент, учитывающий характер распределения давления в выходном сечении трубы, принимаемый равным 0,85.

Рис. 5.23. График для определения

круглых

бетонных труб с коническим звеном на входе

Коэффициент расхода

(5.22)

где

- коэффициент сопротивления на входе в сооружение для труб без оголовка

; для раструбных оголовков с

; для раструбных с коническим звеном

;

- коэффициент сопротивления на трение по длине; определяется по формуле (5.23) или (5.24).

Для труб с любым поперечным сечением

(5.23)

где n - коэффициент шероховатости, принимаемый по табл. 2.2; для обычных бетонных труб без повышенной шероховатости n = 0,015;

R - гидравлический радиус;

- длина входного участка трубы, потери на котором учитываются коэффициентом

Для круглых труб

(5.24)

при

;

(5.25)

Формула (5.24) при l_вх = 3,6h_т для обычных круглых труб без повышенной шероховатости (n = 0,015) дает

(5.26)

Для круглых труб с обтекаемыми оголовками или коническими звеньями на входе, принятыми в типовых проектах

(5.27)

По формуле (5.27) построен график на рис. 5.23. При затопленном со стороны нижнего бьефа выходном сечении трубы (h_нб > h_т) пропускную способность рассчитывают по формуле

(5.28)

где h_нб - глубина в нижнем бьефе над нижней точкой дна трубы в выходном сечении.

ШАХТНЫЕ ВОДОСБРОСЫ

5.10. Для создания перед дорогой прудов и водохранилищ, а также сброса воды на косогорах в качестве водопропускных сооружений используют шахтные водосбросы (рис. 5.24).

Рис. 5.24. Схема шахтного водосброса

Напор перед шахтным водосбросом определяют из условия

(5.29)

где p - высота шахты;

- возвышение бровки полотна над подпертым уровнем; согласно СНиП 2.05.03-84

Гидравлический расчет шахтного водосброса заключается в определении диаметра шахты и диаметра трубы, проложенной в насыпи.

Расчет выполняют в следующем порядке.

1. Назначают высоту шахты p в зависимости от требований к объему и глубине пруда и местных условий. Обычно принимают p до 4,5 м, с тем чтобы глубина пруда перед полотном дороги не превышала 5 м.

2. Определяют диаметр шахты из уравнения расхода шахтного водосброса:

(5.30)

где m - коэффициент расхода, определяемый по графику на рис. 5.25.

Рис. 5.25. График для определения коэффициента

расхода шахтного водосброса

При расчетах стремятся к D_ш/H_ш > 4. Для этого вначале задаются m = 0,38 (что соответствует D_ш/H_ш = 4) и определяют D_ш. По полученному значению D_ш определяют D_ш/H_ш и, если нужно, уточняют значение D_ш.

3. Определяют площадь живого сечения трубы

(5.31)

где v_т - скорость в трубе, которую обычно принимают (по условиям протекания в нижнем бьефе) не более 5 - 6 м/с.

4. Определяют число очков трубы и размеры поперечного сечения каждого очка. Для круглых труб диаметр одного очка

(5.32)

где N - число очков трубы, принимаемое в зависимости от местных условий и по конструктивным соображениям.

Полученные значения D округляют до ближайшего стандартного значения и проверяют скорость в трубе, состоящей из N очков:

(5.33)

где

- суммарная площадь сечения всех труб.

5. При незатопленном выходе подпор перед трубой

(5.34)

Коэффициент расхода трубы

(5.35)

где

- коэффициент сопротивления входа;

- коэффициент трения по длине, который можно принимать равным 0,025;

- коэффициент сопротивления поворота.

В свою очередь

(5.36)

где

- коэффициент сопротивления входа в шахту, равный 0,59;

- площадь живого сечения шахты.

Незатопленное истечение в отводящее русло будет иметь место в том случае, если глубина воды в отводящем русле h_нб < h_т.

Глубину воды в шахте сравнивают с высотой шахты p. Должно быть выдержано условие H < p. Если получается H > p, то либо увеличивают диаметр трубы, либо принимают большее число очков.

При затопленном выходном сечении напор перед трубой

(5.37)

Если входное отверстие шахты затоплено, шахтный водосброс рассчитывают как дюкер (см. ниже) с одним поворотом. Для этого в формуле (5.39) вместо

следует подставлять

ДЮКЕРЫ

5.11. Дюкеры (рис. 5.26) - трубы в выемках, как правило, устраивают на зарегулированных водотоках (например, оросительных каналах), и поэтому их расчет сводится к подбору отверстия трубы по одному заданному расходу.

Рис. 5.26. Схема дюкера

Труба дюкера всегда работает полным сечением, и, как правило, ее устраивают круглой. В отдельных случаях, когда дюкер, помимо нормального, периодически пропускает паводковые расходы, его проектируют из двух труб с ярусным расположением, с тем чтобы верхняя труба работала только при повышенных (паводковых) расходах. В этом случае верхняя труба должна иметь затвор. Для возможности осмотра колодцев их диаметр должен быть не менее 1 м.

При одновременном проектировании дюкера и оросительного канала может быть рассмотрен вариант дополнительного понижения выхода из дюкера с соответствующим увеличением глубины канала за дюкером (для возможности увеличения

Исходные данные для расчета дюкера:

1) расход водотока Q, м³/с; 2) разность в отметках дна канала у входного и выходного колодцев дюкера

; 3) длина дюкера между колодцами L, м.

Дюкер рассчитывают, исходя из следующих положений:

Q_дюк = Q_канала;

при заданном

скорость воды в дюкере

(5.38)

здесь

(5.39)

В расчетах можно принимать: для входа с острым ребром

;

(при повороте на 90°).

Если окажется, что v_дюк >= v_канала, диаметр дюкера

(5.40)

Для сохранения условия v_дюк >= v_канала округляют D в меньшую сторону, но определяют при этом новое значение

(5.41)

Если v_дюк < v_канала, то диаметр трубы уменьшают, и расчет повторяют.

ГОФРИРОВАННЫЕ ТРУБЫ

Общие положения

5.12. Гофрированные трубы отличаются от технически гладких существенно большей шероховатостью, что связано с наличием на внутренней их поверхности гофров. В нашей стране приняты следующие типоразмеры гофров: l_гофрa_гофр = 130 x 32 мм или 150 x 50 мм, где l_гофр и a_гофр - соответственно длина и высота гофра.

Гофрированные трубы обычно имеют гладкие бетонные лотки, располагаемые на ¹/₄ или ¹/₃ периметра их сечения. Коэффициент шероховатости в этом случае n_гофр = 0,025, при отсутствии гладких лотков n_гофр = 0,030. Эта особенность приводит к существенно большим критическим уклонам гофрированных труб по сравнению с технически гладкими, значение которых в гофрированных трубах при безнапорном режиме достигает 0,02 - 0,03. Поэтому для предотвращения снижения водопропускной способности уклоны гофрированных труб должны быть не меньше указанных значений и, в крайнем случае, не меньше 0,01.

В каждом конкретном случае предварительно устанавливается критический уклон сооружения i_к, учитывая который, а также уклон местности, назначают уклон трубы из условия

i_т >= i_к. (5.42)

В случае несоблюдения условия (5.42) пропускная способность трубы понижается, причем при i_т >= 0,01 этим можно пренебречь; при i_т < 0,01 реальная пропускная способность сооружения должна устанавливаться в соответствии с рекомендациями пп. 5.5 и 5.7.

5.13. Общие принципы гидравлического расчета гофрированных труб существенно не отличаются от принципов, положенных в основу расчета технически гладких труб; отличия заключаются лишь в определении конкретных гидравлических характеристик, методика расчета которых излагается в настоящей рубрике.

5.14. В связи с тем что гофрированные трубы по условиям прочности укладываются с уклонами i_т <= 0,03, что практически соответствует равнинным условиям, в настоящей рубрике излагаются лишь расчеты равнинных гофрированных труб. При необходимости расчета косогорных труб следует пользоваться рекомендациями пп. 5.20 - 5.22 с учетом специфики расчета отдельных величин применительно к гофрированным трубам, излагаемым ниже.

5.15. В настоящем пункте приводятся расчеты "коротких" в гидравлическом отношении гофрированных труб, под которыми понимают сооружения, для которых соблюдается условие (5.42). Критический уклон наиболее распространенных отверстий труб с гладкими лотками диаметром 1,5 и 2,0 м находят по графику на рис. 5.27 в функции параметра расхода, определяемого по номограмме на рис. 5.8. Для остальных отверстий и при иных коэффициентах шероховатости критический уклон

(5.43)

где i_к(граф) и D_граф - соответственно критический уклон и диаметр трубы, представленный на графике (см. рис. 5.27), это может быть D = 1,5 и 2,0 м;

n_гофр - фактический коэффициент шероховатости гофрированной трубы.

Рис. 5.27. График для определения критического

уклона i_к для круглых гофрированных труб

с гладкими лотками (n_гв = 0,025):

1 - при D = 1,5 м; 2 - при D = 2,0 м

При i_т < i_к допустимо с некоторым приближением считать "короткими" трубы при соблюдении критерия l_т/D <= 20.

Глубины на входе h_вх(дл) и подпертые глубины H_дл перед "длинными" трубами можно определять по формулам, полученным из аналогичных зависимостей для технически гладких труб, с введением в них корректива для учета повышенной шероховатости гофрированных труб:

ИС МЕГАНОРМ: примечание.

Нумерация формул дана в соответствии с официальным текстом документа.

(5.54)

(5.45)

где

- соответственно относительная глубина на входе в трубу и относительная подпертая глубина для "коротких" труб, определяемые согласно рекомендациям настоящей главы, изложенным в рубрике "Равнинные водопропускные трубы" (пп. 5.4 - 5.9);

n = 0,015 и n_гофр - коэффициенты шероховатости соответственно для технически гладких и гофрированных труб.

Режимы протекания

5.16. В гофрированных трубах возможны те же режимы протекания, что и в технически гладких трубах. В то же время они отличаются характерной особенностью - способностью сравнительно легко "заряжаться", т.е. переходить к напорному режиму. Причем в отличие от технически гладких гофрированные трубы не требуют для "зарядки" специальных оголовков.

При прочих равных условиях пропускная способность напорных труб больше, чем полунапорных. Однако наличие гофров приводит к значительному повышению шероховатости труб, и следовательно, к увеличению гидравлических сопротивлений по длине, существенно снижающих пропускную способность при напорном режиме. (При безнапорном и полунапорном режимах сопротивление по длине оказывает весьма малое влияние на пропускную способность, так как оно проявляется лишь на сравнительно коротком входном участке до определяющего сечения.) Поэтому в зависимости от местных условий гофрированные трубы могут иметь пропускную способность как большую, так и меньшую, чем аналогичные гладкие, работающие в полунапорном режиме.

Гофрированные трубы рациональны без оголовков со срезом вертикальным, параллельно откосу насыпи и типа "капюшон", а также с раструбным оголовком с углом раструбности

(рис. 5.28). Следует отметить, что оголовок типа "капюшон", обеспечивающий "зарядку" гофрированных труб при сравнительно малых подпертых глубинах, в нашей практике не применяется. Он широко распространен в США. Его недостаток - неустойчивый напорный режим при относительных подпертых глубинах (H/h_т), близких к единице.

Рис. 5.28. Типы гофрированных труб:

а - без оголовка со срезом перпендикулярно оси трубы;

б - со срезом параллельно откосу; в - с оголовком

типа "капюшон"; г - с раструбным оголовком

5.17. Безнапорный режим протекания в гофрированных трубах, так же как и в технически гладких, сохраняется до полного затопления входного сечения, что характеризуется условием

, где D - диаметр входного сечения, считая по впадинам гофра (наименьший диаметр).

Возможность существования безнапорного режима и заполнение "коротких" труб на входе определяют по графику на рис. 5.29, на котором приведена зависимость относительной глубины на входе в трубу

от параметра расхода

, определяемого по графику на рис. 5.8. График на рис. 5.29 позволяет также по заданному заполнению установить соответствующий ему расход.

Рис. 5.29. График для определения глубины потока

на входе в гофрированную трубу:

1 - с оголовком типа "капюшон"; 2 - без оголовка

с вертикальным срезом; 3 - с раструбным оголовком

; 4 - со срезом параллельно откосу насыпи

При

и П_Q >= 1,35 в гофрированной трубе возникает устойчивый напорный режим.

При

и П_Q < 1,35 в гофрированной трубе со всеми типами оголовков возможен полунапорный или частично напорный режим. В этом случае режим протекания определяют в такой последовательности.

1. Вычисляют подпертую глубину перед трубой H при полунапорном режиме (см. п. 5.8).

2. Находят относительную граничную подпертую глубину потока

, соответствующую верхней границе полунапорного режима (началу возникновения частично напорного режима), по формуле

(5.46)

где

- относительная граничная подпертая глубина для труб без гладких лотков, определяемая по графику на рис. 5.30 в зависимости от относительной длины трубы

и ее уклона;

- коэффициент увеличения относительной граничной подпертой глубины в трубах с гладкими лотками.

Рис. 5.30. График для определения относительной граничной

подпертой глубины

для гофрированной трубы

без гладкого лотка при разных ее уклонах

В свою очередь

(5.47)

где

- доля, занимаемая гофрированной поверхностью в поперечном сечении трубы (вся поверхность за вычетом части ее, занимаемой гладким лотком, отнесенная ко всей поверхности);

m - показатель степени; при 0,01 <= i_т <= 0,05

; коэффициент

можно также определить по графику на рис. 5.31.

Рис. 5.31. График для определения коэффициента

3. Сравнивают относительную подпертую глубину

с относительной подпертой граничной глубиной

и устанавливают режимы протекания:

при

- полунапорный; при

- частично напорный.

В трубах с оголовками типа "капюшон" при

и П_Q < 0,645 возникает полунапорный режим, а при

и П_Q >= 0,645 - частично напорный режим.

Определение пропускной способности гофрированных труб

5.18. Подпертые глубины перед безнапорными и полунапорными гофрированными трубами определяют по тем же зависимостям, что и для равнинных технически гладких труб (см. пп. 5.7 и 5.8) с расчетными коэффициентами, приведенными в табл. 5.3.

Таблица 5.3

Тип оголовка	Расчетные коэффициенты
Тип оголовка	m
Без оголовка	0,33	0,56	0,63	0,70
Срезанный параллельно откосу насыпи	0,33	0,52	0,59	1,10
"Капюшон"	0,33	0,53	0,64	1,10
Раструбный	0,365	0,65	0,64	0,35

Подпертые глубины перед гофрированными трубами при напорном режиме определяют по зависимостям, используемым для равнинных труб (см. п. 5.9), с внесением в них ряда корректив.

В формуле (5.21) коэффициент

принимают равным 0,5.

Коэффициент расхода при напорном режиме

(5.48)

где

- коэффициент гидравлических сопротивлений по длине (см. гл. 2).

В свою очередь

где

- гидравлический радиус при полном заполнении трубы.

Коэффициент шероховатости n_гофр для труб с принятым в нашей стране гофром при отсутствии в трубе покрытия (гладкого лотка) составляет около 0,03; при наличии лотка, покрывающего ¹/₄ - ¹/₃ внутренней поверхности трубы, - 0,025.

В общем случае при гладком лотке, покрывающем любую часть поперечного сечения трубы, коэффициент шероховатости

(5.49)

где

- части поперечного сечения трубы, покрытые соответственно гладким лотком и гофрированной поверхностью;

n и n_гофр - коэффициенты шероховатости соответственно для гладкого лотка (n = 0,015) и гофрированной поверхности (n_гофр = 0,03).

При распространенном в практике типа поперечного сечения гофрированной трубы с гладким лотком на ¹/₃ части периметра сечения коэффициент расхода

можно определить по графику на рис. 5.32.

Рис. 5.32. График для определения коэффициента

расхода

гофрированных труб с гладким лотком

на 1/3 периметра поперечного сечения трубы

При затоплении выхода вместо

в формулу (5.21) подставляют глубину воды в нижнем бьефе.

Подпертую глубину перед трубами при частично напорном режиме определяют по формуле (5.21), принимая

по графику на рис. 5.33 в зависимости от параметра расхода. При этом в качестве расчетной длины трубы принимают

(5.50)

где l₀ - расстояние от конца трубы до створа, где труба работает полным сечением; l₀ определяют по параметру расхода

с помощью графика на рис. 5.34.

Рис. 5.33. График зависимости

Рис. 5.34. График для определения l₀

Затем проверяют возможность сохранения частично напорного режима. В трубах с оголовками всех типов, кроме типа "капюшон", частично напорный режим сохраняется при соблюдении условия H >= 1,4D. В противном случае труба "разряжается", и в ней возникает полунапорный режим. При этом подпертую глубину определяют по формуле (5.20).

В трубах с оголовками типа "капюшон" возможен переход частично напорного режима в его особую форму. Для установления возможности сохранения частично напорного режима в этом случае подпертую глубину H сравнивают с глубиной H', вычисляемой по формуле

(5.51)

При H > H' частично напорный режим сохраняется и дальнейшего пересчета подпертой глубины H, определяемой по формуле (5.20), не требуется.

При H < H' наблюдается особая форма частично напорного режима, и в качестве искомой подпертой глубины принимают H'.

Для определения расчетной подпертой глубины перед трубами с оголовками всех типов, кроме типа "капюшон", сравнивают подпертую глубину H с граничной H_г, определяемой по формуле (5.46). При H > H_г в качестве расчетной глубины принимают H, при H < H_г - глубину H_г. Для труб с оголовками типа "капюшон" сравнивают подпертую глубину, принятую выше в п. 5.18 для дальнейших расчетов, с подпертой глубиной H", определяемой по формуле (5.51) при

. При H > H" в качестве расчетной глубины принимают H, при H < H" - глубину H".

Для безоголовочных труб с гладкими лотками, расположенными на ¹/₃ или ¹/₄ параметра поперечного сечения сооружения, в целях упрощения вычислений рекомендуется пользоваться графиками, приведенными на рис. 5.35 и 5.36. На графиках зависимости H = f(Q) при частично напорном и напорном режимах соответствуют уклону i_т = 0,01. При иных уклонах в значении H для указанных режимов вводится поправка

Подпертая глубина в этом случае

(5.52)

где H_граф - подпертая глубина, определяемая по графикам на рис. 5.35 и 5.36.

Рис. 5.35. Зависимости H = f(Q) для трубы

диаметром D = 1,5 м при i_т = 0,01

Рис. 5.36. Зависимости H = f(Q) для трубы

диаметром D = 2,0 м при i_т = 0,01

Зависимости H = f(Q) даны на графиках для разных длин и отверстий труб. Они пересечены кривыми, соответствующими различным уклонам труб. Точки пересечения их соответствуют минимальным расходам и подпертой глубине H, при которых труба, уложенная с данным уклоном, работает в частично напорном режиме. При меньших значениях Q и H в трубе имеет место безнапорный или полунапорный режим протекания, при которых пропускная способность труб не зависит от их уклона.

На указанных графиках зависимости H = f(Q) для полунапорного режима выше кривой i_т = 0,01 изображены штриховой линией.

Порядок пользования графиком следующий. На графике, соответствующем принятому отверстию трубы, находят кривую H = f(Q) для заданной длины трубы l_т. На этой кривой по значению расхода находят подпертую глубину H. Интерполируя кривые, пересекающие зависимости H = f(Q), находят уклон для кривой, проходящей через точку, соответствующую заданному расходу (подпертой глубине H). Сравнивая фактический уклон трубы с уклоном указанной кривой i_т, устанавливают возможность возникновения частично напорного (или напорного) режима в трубе.

При i_т < i_г в трубе возникает частично напорный (напорный) режим, при l_т > i_т - полунапорный.

При частично напорном (напорном) режиме в полученное по графику значение H_граф вводят поправку

согласно формуле (5.52).

Сравнивая установленное значение H с 1,4D, определяют возможность существования частично напорного режима. При H >= 1,4D частично напорный режим сохраняется, и полученное значение H принимается к дальнейшему расчету. При H < 1,4D возникает полунапорный режим, и H определяют по зависимости H = f(Q) для данного режима трубы заданной длины.

В качестве расчетной подпертой глубины перед трубами, работающими в частично напорном режиме, принимают большее из значений H и H_г.

H_г на графиках (см. рис. 5.35 и 5.36) определяют следующим образом:

находят точку пересечения зависимости H = f(Q) для трубы заданной длины с линией заданного уклона (при отсутствии на графике линии соответствующего уклона ее положение определяют интерполяцией);

через полученную точку проводят линию, параллельную оси ординат, и доводят ее до пересечения со штриховой линией для трубы заданной длины; ордината этой точки и будет искомой граничной глубиной H_г.

При полунапорном режиме подпертую глубину определяют непосредственно по зависимости H = f(Q) для данного режима (на графиках она изображена штриховой линией).

Многоочковые и многоярусные гофрированные трубы

5.19. Пропускную способность гофрированных многоочковых и многоярусных труб при условии из раздвижки на величину не менее 0,25D определяют как сумму отдельно работающих одноочковых труб.

Расчет многоочковых труб аналогичен расчету одноочковых, при этом расход каждой трубы принимают

, где n_т - число труб.

Многоярусные трубы (рис. 5.37) целесообразно устраивать без оголовка. Расчет многоярусных труб начинают с определения подпертой глубины перед трубой в предположении, что весь расход проходит через трубы нижнего яруса. Для этого весь расход делят на число труб нижнего яруса и производят расчет отдельной трубы согласно рекомендациям для одноочковых труб, изложенным выше. Установив подпертую глубину перед трубой, ее сравнивают с расстоянием между лотками труб первого и второго ярусов. Если она меньше указанного расстояния, второй ярус не работает, и расчет на этом заканчивают, принимая в качестве искомой полученную подпертую глубину.

Рис. 5.37. Схема многоярусной трубы (размеры S₁, S₂,

)

определяются по СНиП 2.05.03-84

В противном случае расчет продолжают, для чего строят зависимости H = f(Q) в такой последовательности.

1. Задают ряд расходов в трубах верхнего яруса и для каждого из них определяют подпертые глубины, пользуясь рекомендациями для одноочковых труб. При этом расход отдельной трубы определяют путем деления общего расхода на число труб n_т.

2. Устанавливают подпертые уровни перед многоярусной трубой при пропуске каждого из заданных расходов путем прибавления к отметке лотка труб верхнего яруса соответствующих подпертых глубин.

3. Определяют подпертые глубины перед трубами всех нижерасположенных ярусов, вычитая из отметок подпертых уровней для каждого из заданных расходов, пропускаемых трубами верхнего яруса, отметки их лотков.

4. Устанавливают режимы протекания в трубах каждого из ярусов, определяя относительные подпертые глубины перед ними

при пропуске заданных расходов в трубах верхнего яруса и сравнивая их с относительными граничными напорами, которые вычисляются согласно рекомендациям для одноочковых труб.

При

в трубах данного яруса возникает полунапорный режим, при

- частично напорный или напорный.

5. Для полунапорного режима

определяют расходы, пропускаемые трубой соответствующего яруса, по формуле (5.20).

При

определяют расходы труб каждого яруса по формуле (5.21) при

и находят параметры расходов по формуле

, где n_т - число труб в данном ярусе.

При

режим напорный и расход должен быть пересчитан по формуле (5.21) при

При

по графику на рис. 5.33 определяют

и вновь вычисляют расход по формуле (5.21) с полученным значением

. Если он отличается от исходного не более чем на 3%, расчет заканчивают; в противном случае расчет продолжают до указанной точности.

6. Проверяют возможность сохранения частично напорного режима согласно рекомендациям п. 5.18.

7. Определяют расчетные подпертые глубины перед трубами в соответствии с рекомендациями п. 5.18.

8. Определяют расходы всех труб данного яруса исходя из выражения

Q_яр = Q_nn_т,

где Q_n - расход отдельной трубы данного яруса.

9. Для каждого из расходов, пропускаемых верхним ярусом, определяют полный расход всех ярусов при соответствующем подпертом уровне. По указанным данным строятся зависимости H = f(Q) для труб данного яруса.

10. По зависимости H = f(Q) для многоярусной трубы находят по известному расходу подпертую глубину перед трубой, а затем скорости на выходе из труб. К расчету принимают скорости на выходе из труб нижнего яруса.

Примеры назначения отверстий и определения пропускной способности круглых гофрированных труб приведены в приложении 5.1.

КОСОГОРНЫЕ ТРУБЫ

5.20. К косогорным относятся трубы, имеющие средний уклон водопропускного тракта 0,02 и более. В косогорных сооружениях, как правило, поток приобретает бурное состояние. При встрече донных или боковых препятствий в бурном потоке возникают местные подъемы уровня (всплески), поверхность воды в поперечном сечении становится сильно криволинейной. На выходах из косогорных сооружений поток обладает высокой размывающей способностью.

К косогорным трубам относятся все требования СНиП 2.05.03-84 по пропуску расчетного и наибольшего расходов, за исключением допущения напорного режима.

Косогорная труба может пропускать расход больше расчетного для равнинных труб с обеспечением регламентируемого СНиП 2.05.03-84 зазора между высшей точкой внутренней поверхности трубы и уровнем воды. Не допускается расчет косогорных труб с учетом аккумуляции.

При выборе схемы косогорной трубы следует избегать устройств, способствующих отложению наносов. Поэтому нежелательно предусматривать уменьшение продольного уклона вдоль трубы. Ослабить этот эффект можно применением на крутом участке повышенной шероховатости.

Также следует избегать устройств, в которых возможен застой воды и ее замерзание. Для этого при устройстве водобойных стенок, поперечных ребер шероховатости и т.п. в них предусматривают для стока воды отверстия, расширяющиеся в низовую сторону во избежание их засорения.

В местах перехода от одного элемента сооружения к другому нельзя допускать поперечных выступов и резких сужений.

В необходимых случаях форму сечения рекомендуется изменять по экспериментально проверенным схемам. Не следует применять повышенную шероховатость в сооружениях на водотоках, несущих крупные гравийно-галечные наносы. Повышенную шероховатость в виде поперечных ребер применяют в каналах и трубах отверстием не менее 1,25 м в случаях, не требующих больших затрат труда по очистке сооружения от льда и наносов в процессе эксплуатации. Боковые стенки открытых лотков (быстротоков) принимают на 25 - 30 см выше расчетного уровня воды с учетом аэрации. Если поток несет бурелом, карчи, камни и т.п., то принимают специальные меры против засорения входа в трубу.

При укладке звеньев со ступенями на стыках высоту ступеней прямоугольных труб допускают до 0,5 м, а круглых - не более ²/₃ толщины звена. Длину секции между ступенями принимают 1 - 3 м.

Для уменьшения длины трубы ее иногда выносят из тальвега на склон лога. При этом перед насыпью образуется бессточный водоем и насыпь должна быть рассчитана на продолжительную фильтрацию.

Трубы чаще всего составляют из звеньев, которые укладывают горизонтально со ступенями либо наклонно (при малом уклоне). Возможна укладка звеньев без ступеней с уклоном меньше уклона лога; в этом случае на входе устраивают гаситель энергии.

Когда естественный лог подвержен интенсивному разрушению потоком, воду подводят к трубе по искусственным подходным руслам. Непосредственно перед входом в трубу предусматривают приемные устройства.

При слабо выраженном поперечном профиле лога для перехвата воды применяют поперечные канавы, по которым подводят воду в продольную канаву или быстроток.

При хорошо выраженном поперечном профиле лога и сравнительно крутых склонах, когда поток концентрируется на небольшой ширине, подачу воды в трубу осуществляют раструбным оголовком. Размеры его зависят от ширины и глубины потока перед трубой.

Когда лог особенно широк, имеет почти плоское дно и неустойчивый в плане тальвег, вместо поперечных канав может быть целесообразно устройство поперечной стенки (преградительной плотины); стенка должна надежно врезаться в склоны лога и не допускать перелива при небольшом расходе воды.

Ниже будут даны методы расчета собственно труб. Расчеты подводящих быстротоков, сопрягающих устройств и выходных русел приводятся в соответствующих главах Пособия.

5.21. По условиям гидравлической работы можно выделить три типа косогорных труб:

1) трубы с условиями равнинного входа;

2) трубы с условиями косогорного входа;

3) трубы особых конструкций.

К первому типу относятся трубы, уложенные на местности с уклонами i_л > 0,02 и либо не имеющие подводящего быстротока (пруд равнинного типа перед трубой), либо имеющие за быстротоком перед трубой водоприемный колодец (см. гл. 4). В обоих случаях перед входом в трубу поток находится в спокойном состоянии, и ее пропускная способность определяется, как для равнинных труб.

Если труба технически гладкая, то в силу большого уклона при удалении от входа с равнинными условиями втекания глубина потока будет уменьшаться, а скорость увеличиваться. При этом единственным критерием применимости конструкции является допускаемая скорость в трубе и на выходе из трубы. Если труба достаточно длинная, проверка может производиться по нормальной глубине или, более точно, с использованием уравнения неравномерного движения либо по одномерным уравнениям гидравлики (см. гл. 2). Если труба с повышенной шероховатостью (ступени, ребра) либо с переломом уклона, причем часть трубы уложена с очень малым уклоном, то может происходить и нарастание глубины по длине трубы. В этом случае выбирается максимальная из нормальных глубин для разнородных участков трубы, проверяется требование СНиП 2.05.03-84 по заполнению, и если оно не выполнено, изменяют конструкцию, либо увеличивают высоту трубы. Возможно уточнение расчета с использованием уравнений неравномерного движения или одномерных уравнений гидравлики. При расчете на максимальный расход зазор между верхом трубы и поверхностью воды можно не обеспечивать, однако образование напорного режима нежелательно.

Следует отметить, что расчет труб с повышенной шероховатостью ведется совершенно аналогично расчету обычных гидравлически гладких труб, только коэффициент Шези принимается по специальным формулам, учитывающим параметры повышенной шероховатости (см. гл. 2). При этом в качестве глубины потока получаем ее значение над ребром или концом ступени, т.е. в самом узком по высоте месте продольного сечения трубы.

К третьему типу труб относятся трубы с шахтным колодцем на входе и консольные сбросы.

Шахтные колодцы устраивают при размещении труб в узких оврагах при большом уклоне, когда необходимо сбросить воду с большой высоты. В зависимости от продольного профиля лога и геологических условий их размещают с верховой или низовой стороны. Консольные сбросы могут применяться как самостоятельные сооружения или как устройства для сопряжения с выходным руслом на крутых логах или косогорах.

Методы расчета этих сооружений описаны в гл. 4.

5.22. Наиболее типичны для косогорных условий трубы с условиями косогорного входа, т.е. с подводящим быстротоком и бурным потоком на входе в трубу. Быстроток может быть равной или большей ширины, чем труба. Во втором случае для сопряжения быстротока устраивают сужение, примазки и т.п. (см. п. 5.3).

Особенностью труб с условиями косогорного входа является их гораздо большая пропускная способность, чем у труб с равнинным входом. Теоретически она может быть больше в десятки раз (при ширине быстротока равной ширине трубы), и только ограничения на допускаемые для материалов быстротока и трубы скорости не позволяют в полной мере реализовать такую возможность на практике.

Расчеты пропускной способности таких труб выполняют при пропуске расчетных Q_р и наибольших Q_max (только для железных дорог) расходов применительно к рассмотренным в п. 5.4 режимах протекания.

При вводе потока в трубу в бурном состоянии глубины определяют следующим образом. При ширине подходного быстротока, равной отверстию трубы, и одинаковой форме сечений быстротока и трубы - путем построения кривой свободной поверхности потока в быстротоке и в трубе по методике, изложенной при расчете быстротоков (см. гл. 4), и установления по ней глубины на входе в трубу и максимальной глубины в трубе.

При этом возможны два случая:

1) глубина воды в конце быстротока меньше высоты трубы: h_б(вых) > h_т;

2) глубина воды в конце быстротока больше либо равна высоте трубы h_б(вых).

В каждом из этих случаев возможны варианты.

В первом случае, т.е. при h_б(вых) < h_т, возможны следующие варианты:

а) нормальная глубина в трубе меньше высоты трубы, т.е. в трубе всегда сохраняется безнапорный режим. При этом в зависимости от соотношения уклонов трубы i_т и быстротока i_б возможно различное положение створа с максимальной глубиной в трубе h:

при i_т < i_б глубина в трубе будет возрастать, приближаясь к нормальной; для приближенных расчетов, особенно при наличии в трубе повышенной шероховатости, можно принять h_max = h₀;

при i_т > i_б глубина в трубе убывает и h_max = h_вх = h_б(вых);

б) нормальная глубина в трубе больше высоты трубы h₀ > h_т и i_т < i₀ - глубина воды в трубе возрастает, причем при "короткой" трубе она может не достигнуть высоты h_т и в трубе сохраняется безнапорный режим протекания при h_max < h₀; при "длинной" трубе глубина в трубе может достигнуть h_т - в трубе возникает напорный режим (рис. 5.7, з). В этом случае расчет пропускной способности трубы выполняют, как для равнинных труб при напорном режиме (при условии непротиворечия СНиП [39].

Во втором случае, т.е. при h_б(вых) >= h_т, возможны следующие варианты:

а) при h₀ < h_т - в трубе возникает полунапорный режим; расчет ведется, как для равнинных условий;

б) при h_б > h_т возможны два подварианта:

при i_б > i_т глубина в трубе возрастает и при "короткой" трубе может достигнуть высоты трубы - режим полунапорный, а при "длинной" достигает h_т - режим напорный;

при i_б < i_т глубина в трубе убывает - режим полунапорный.

При ширине подходного быстротока более отверстия трубы и наличии на входе в трубу сужения расчет отличается от рассмотренного выше тем, что исходная средняя глубина на входе в трубу получается в результате расчета сужения (см. гл. 4). Для расчетного расхода зазор в трубе должен быть не меньше регламентируемого СНиП [39]. Кроме того, высота максимального гребня на оси потока h_гр не должна превышать высоты трубы, а стенки сужения должны быть запроектированы с учетом глубины воды в гребне у стенки h_гс и запасом 0,25 м.

Если прямоугольный или трапецеидальный быстроток сопрягается с круглой трубой (с помощью примазок), то глубины h_б(вых) и h_гр должны быть пересчитаны (увеличены) из условия

Тогда

где

- живые сечения в конце быстротока и в начале трубы в функции средних глубин потока;

- новые значения средней и максимальной глубин на входе в круглую трубу, принимаемые к расчету.

АЛГОРИТМЫ ВЫБОРА РАЦИОНАЛЬНОГО ТИПА

ВОДОПРОПУСКНОГО ТРАКТА ТРУБ

5.23. В основе алгоритма лежит методика расчета водопропускного тракта, изложенная в главах 2, 4, 5, 7 настоящей книги. В алгоритме предполагается, что продольный профиль всего водопропускного тракта и его отдельных элементов задан.

5.24. Основные элементы алгоритма <1>:

1) расчет размеров подходных быстротоков и гидравлических характеристик потока в них, в том числе с учетом переломов (изменения уклонов поверхности дна) и аэрации потока;

2) расчет сопряжений быстротока с трубой (сужений и водоприемных колодцев);

3) расчет глубин и скоростей на всей длине трубы, включая входной и выходной участки, с учетом условий сопряжения с быстротоком, ступенчатой укладки звеньев и аэрации (см. гл. 2);

4) расчет глубин и скоростей потока на укреплении, в том числе с учетом гасителей;

5) расчет глубин размыва за укреплением нижнего бьефа с учетом гидрографа паводка различных типов гасителей, каменной наброски и возможности образования промоины (канавы) в выходном логе;

6) определение размеров укреплений нижнего бьефа;

7) выбор вариантов конструкций водопропускного тракта, удовлетворяющих всем требуемым ограничениям (по допускаемым скоростям, зазорам в трубе, глубинам воронок размыва в выходном логе и т.п.).

--------------------------------

<1> В ряде случаев могут отсутствовать отдельные элементы водопропускного тракта, например для равнинных труб расчеты подходных быстротоков, сужений, гасителей энергии. В этих случаях расчет начинают с последующих элементов.

Определение наилучшего из допускаемых вариантов должно осуществляться на основе технико-экономического сравнения. Возможно также изменение (перепроектирование) продольного профиля водопропускного тракта с последующим повторением расчетов.

5.25. Расчет водопропускного тракта ведется: для автомобильных дорог - на расчетный расход Q_р, для железных дорог - на наибольший расход Q_max (соответствующие объемы стока W_р и W_max). При наличии снегового и ливневого стока Q_р и Q_max выбирают как максимальные из соответствующих расходов. Аккумуляция при расчете косогорных труб не учитывается.

5.26. Расчет ведется в такой последовательности:

1. Назначают тип трубы (круглая или прямоугольная) с учетом характера шероховатости (гладкая, ступенчатая, с ребрами); а также начальное отверстие трубы (обычно b = 1 м).

2. Рассчитывают быстроток (см. гл. 4). Длину быстротока принимают от выхода из нагорной канавы до входа в трубу.

Начинают с быстротока шириной по дну b_б = b и трапецеидальной формы с наиболее слабым типом укреплений (обычно из бетонных плит 49 x 49 см). Последовательно увеличивают ширину b_б с шагом 0,25 м до выполнения двух условий:

а) h_к < h_нг, где h_к - критическая глубина на входе в быстроток; h_нг - глубина воды в нагорной канаве в месте ее сопряжения с быстротоком (приближенно ее можно принимать равной глубине канавы);

б) v_б(max) < v_доп, где v_б(max) - максимальная скорость воды в быстротоке; v_доп - допускаемая скорость для материала и конструкции быстротока.

Потом определяют стоимость быстротока и переходят к расчету быстротока с более мощным типом укрепления (трапецеидального из монолитного бетона, прямоугольного, бетонного или железобетонного и т.п.). Если допустимо устройство ребер (повышенной шероховатости), то производят расчет и для этого случая по формулам гл. 2. Затем на основе технико-экономического сравнения вариантов выбирают более дешевый.

3. Рассчитывают сужение (см. гл. 4). Начинают с максимального угла сужения

. Задаваясь характером сопряжения сужающейся части быстротока с трубой и степенью сужения

, определяют глубины и скорости на входе в трубу. Если при пропуске расчетного расхода Q_р зазор между верхом трубы и средней по сечению отметкой свободной поверхности на начальном участке трубы меньше допускаемого СНиП 2.05.03-84, либо если высота максимального всплеска на стенке сужения h_гс больше высоты трубы (h_гс > h_т), либо если глубина в гребне на оси трубы больше высоты трубы h_гр > h_т, то уменьшают угол сужения на 5° и повторяют расчет сужения.

При этом необходимо учитывать, что при уменьшении угла сужения уменьшается длина быстротока, поэтому на входе в сужение при изменении

будут меняться скорости и глубины потока, устанавливаемые при расчете быстротока.

При пропуске Q_max средний уровень воды на входе в трубу должен быть меньше отметки верха трубы, а максимальный всплеск на стенке сужения h_гс < h_т.

Если при каком-либо угле

указанные выше ограничения выполнены, то расчет сужения заканчивают. В противном случае назначают типовое повышенное звено на входе в трубу и расчет повторяется (переход на начало п. 3 алгоритма). Если и при этом не выполняются ограничения на величину зазора в трубе, то назначают следующее отверстие трубы и переходят к п. 2 алгоритма.

4. Если по каким-либо причинам подходной быстроток и сужение отсутствуют, то расчет отверстия трубы производится, как для равнинных условий. При этом для Q_max допускаются все режимы протекания при выполнении требований СНиП 2.05.03-84 о возвышении бровки полотна, а для Q_р - только безнапорный и только при выполнении требования о величине зазора в трубе согласно СНиП.

5. Рассчитывают среднюю часть трубы (см. пп. 4.1, 4.2) исходя из глубин и скоростей на входном участке трубы по уравнению неравномерного движения. Аналогично расчету быстротоков строят кривую свободной поверхности и проверяют условие, чтобы при расчетном расходе Q_р оставался регламентируемый СНиП 2.05.03-84 зазор между поверхностью воды и верхом трубы. При невыполнении этого условия переходят к следующему отверстию трубы и, если оно больше ширины быстротока b_б, возвращаются к п. 2 алгоритма, принимая b_б равной новому отверстию трубы, а если меньше - то к п. 3 алгоритма. Для приближенных расчетов допускается вместо построения кривой свободной поверхности рассчитывать нормальную глубину в трубе (для труб с переломами - нормальную глубину для участка с максимальным уклоном). При пропуске максимального расхода Q_max и наличии подходного быстротока к большему отверстию трубы переходят при ее полном заполнении (без учета зазора).

6. Рассчитывают глубины и скорости на выходе из трубы [см. следующую рубрику настоящей главы (пп. 5.27 - 5.31)].

7. Назначают начальный тип укрепления выходного русла (каменная наброска, плиты, монолитный бетон, сборные блоки и т.п.). Если v_вых > v_доп, то меняют тип укрепления на более мощный, и так до тех пор, пока не будет удовлетворено условие v_вых <= v_доп либо не будут исчерпаны все возможные типы укреплений. В последнем случае:

а) если по условиям проектирования допускается устройство гасителей в нижнем бьефе, то последовательно производят расчет гасителей типов 5 или 6 (см. гл. 7) и проверяют выполнение условия v_гас < v_доп, каждый раз начиная перебор с наиболее слабого типа укрепления. Если при каком-либо сочетании типа гасителя и типа укрепления получено v_гас <= v_доп, то переходят к п. 8 алгоритма;

б) если устройство гасителя не предусматривается, то увеличивают отверстие трубы и при b < b_б переходят к п. 3 алгоритма, а если b > b_б - то к п. 2.

8. Назначают начальный тип выходного русла из числа 1 - 6 (см. гл. 7), если он еще не избран в п. 7.

9. Рассчитывают глубины размыва в выходном русле (см. гл. 7) заданного типа. Если максимальная глубина размыва (с учетом образования канала) больше 2,5 м, то переходят на следующий, более мощный тип выходного русла (в порядке возрастания номеров и индексов) и расчет повторяют. Если никакой из типов выходных русел не обеспечивает глубины размыва меньше допустимой, то увеличивают отверстие трубы и переходят к п. 2.

10. Рассчитывают скорости и глубины потока на укреплении (см. гл. 7).

11. Рассчитывают ширину укрепления и глубину заделки его концевой части (см. гл. 7) с учетом растекания потока на укреплении и глубины воронки размыва.

12. Если в результате расчетов осуществлен перебор всех допустимых отверстий труб и при этом не найден вариант, удовлетворяющий всем необходимым ограничениям, то водопропускной тракт необходимо перепроектировать. При этом возможны следующие варианты:

а) устроить повышенную шероховатость в трубе;

б) допустить возможность использования гасителей, если она не была предусмотрена;

в) изменить уклоны отдельных частей водопропускного тракта;

г) предусмотреть устройство водоприемного колодца с изменением уклонов быстротока и трубы.

В последнем случае производят расчет размеров колодца (гл. 4), расчет быстротока длиной от нагорной канавы до входа в колодец, расчет глубин и скоростей на входе в трубу, определение отверстия трубы исходя из требований СНиП 2.05.03-84. Если на входе в трубу получается бурный поток, то можно изменить высоту колодца и произвести пересчет. Если и это не помогает, то устройство колодца неэффективно.

После введения соответствующих корректив для пп. 12, а - в повторяют расчеты начиная с п. 1 алгоритма, а при устройстве колодца - с п. 5 алгоритма. Если расчеты по перепроектированному варианту опять не удовлетворяют ограничениям, снова производят перепроектировку и т.д.

ГЛУБИНЫ И СКОРОСТИ ПОТОКА НА ВЫХОДЕ ИЗ ТРУБ

5.27. Глубины потока h_вых на выходе из дорожных технических гладких (негофрированных) водопропускных труб различных поперечных сечений при безнапорном и полунапорном режимах протекания и параметрах расхода П_Q, меньших или равных граничным значениям П_Q_(гр), определяют из выражения

(5.53)

где h_к - критическая глубина в трубе, определяемая согласно рекомендациям гл. 2 или по графикам приложений 2.4, 2.5.

Функцию уклона f(i_т) находят по формуле

(5.54)

а коэффициент A_к и граничные значения параметра расхода для разных типов труб - по табл. 5.4.

Таблица 5.4

Тип трубы	Граничные значения параметра расхода П_Q_(гр)	Коэффициент A_к
Круглая	1,2	0,93
Овоидальная	1,2	0,79
Прямоугольная	0,8	0,88

При параметрах расхода П_Q > П_Q_(гр) глубины на выходе из труб определяют через относительные глубины потока по формуле

(5.55)

Значения коэффициентов A_т, показателей степени s_т и диапазон возможного изменения параметров расходов в зависимости от типа труб и режимов протекания приведены в табл. 5.5.

Таблица 5.5

Тип трубы	Режим протекания	Параметр расхода П_Q	Коэффициент A_т	Показатель степени s_т
Круглая	Любой, кроме напорного	П_Q <= 0,8	0,98	0,50
Круглая	Любой, кроме напорного	0,8 < П_Q <= 1,8	0,88	0,25
Овоидальная	То же	П_Q <= 0,8	0,80	0,55
Овоидальная	То же	0,8 < П_Q <= 1,6	0,75	0,25
Прямоугольная	Любой, кроме напорного	П_Q <= 0,8	0,88	0,667
	Безнапорный	0,8 < П_Q <= 1,6	0,88	0,667
	Полунапорный	0,8 < П_Q <= 1,6	0,83	0,25

При напорном режиме глубины на выходе из технически гладких труб принимают равными

(5.56)

5.28. Глубины на выходе из гофрированных труб с коэффициентом шероховатости

определяют по формулам:

при П_Q <= 0,8

(5.57)

при 0,8 < П_Q < 1,35

(5.58)

при П_Q >= 1,35 принимают

h_вых = D. (5.59)

При параметрах расхода П_Q <= 0,8 глубины на выходе из гофрированных труб можно также определять по формулам для круглых труб.

Для упрощения и ускорения расчетов глубин на выходе рекомендуется пользоваться графиками, приведенными в приложении 5.2.

5.29. При уклонах технически гладких труб i_т >= 0,1 и труб с повышенной шероховатостью, создаваемой за счет ступенчатой укладки звеньев, при средних их уклонах i_т > 0,04 глубины на выходе допустимо принимать равными нормальным; вычисляют их либо по рекомендациям, приведенным в гл. 2, либо по графикам приложений 2.1 - 2.3.

Для круглых труб пользуются графиком приложения 2.3 (рис. 1), где по оси абсцисс отложен параметр

. Приведенную повышенную шероховатость n_пов(пр) определяют по графику на рис. 3, а (где

- высота ступеней) того же приложения, причем при h_вых/D < 0,225 она корректируется путем умножения на коэффициент k_h, который находится по графику рис. 3, б (см. там же). Для прямоугольных труб пользуются графиком на рис. 2 приложения 2.2, где по оси абсцисс отложен параметр

(l - длина ступеней).

5.30. Скорости на выходе из труб

(5.60)

где

- площадь живого сечения потока на выходе из трубы.

Для прямоугольных труб

(5.61)

для круглых и овоидальных труб относительную площадь живого сечения потока определяют по табл. 5.6.

Таблица 5.6

Относительная глубина потока h/D_э	Относительная площадь живого сечения потока
	Сотые доли h/D_э
	0	2	4	6	8
Для круглых труб
0,0	0,000	0,004	0,010	0,019	0,029
0,1	0,041	0,053	0,067	0,081	0,098
0,2	0,112	0,128	0,145	0,162	0,170
0,3	0,198	0,217	0,235	0,255	0,274
0,4	0,293	0,313	0,333	0,352	0,373
0,5	0,393	0,413	0,433	0,453	0,472
0,6	0,492	0,512	0,531	0,550	0,569
0,7	0,587	0,605	0,623	0,640	0,657
0,8	0,674	0,689	0,704	0,719	0,732
0,9	0,745	0,756	0,766	0,775	0,782
Для овоидальных труб
0,0	0,00	0,002	0,012	0,022	0,037
0,1	0,052	0,07	0,085	0,102	0,132
0,2	0,137	0,157	0,180	0,200	0,220
0,3	0,240	0,262	0,280	0,302	0,322
0,4	0,340	0,362	0,282	0,400	0,422
0,5	0,437	0,457	0,477	0,492	0,510
0,6	0,527	0,542	0,562	0,580	0,595
0,7	0,612	0,625	0,640	0,655	0,670
0,8	0,680	0,692	0,707	0,722	0,735
0,9	0,745	0,757	0,767	0,777	0,782

С целью упрощения расчетов в приложении 5.3 приводятся графики для определения скоростей на выходах из круглых труб.

5.31. Глубины на выходе из раструбных оголовков труб определяют из зависимости

(5.62)

где b - отверстие трубы;

b_р - ширина оголовка в конце его.

6. РАСЧЕТ МАЛЫХ МОСТОВ

ТИПЫ МОСТОВ И РЕЖИМЫ ИХ ГИДРАВЛИЧЕСКОЙ РАБОТЫ

6.1. По геометрическим формам, влияющим на гидравлические условия работы, различают следующие типы малых мостов: с обратными стенками и конусами (рис. 6.1, а), с откосными крыльями (рис. 6.1, б), эстакадные с конусами (рис. 6.1, в), с заборными стенками (рис. 6.1, г).

Рис. 6.1. Типы малых мостов

Как правило, малые мосты имеют укрепленные русла. Особенности гидравлических расчетов мостов с неукрепленными руслами см. в п. 6.15.

Значения коэффициента расхода m и коэффициента k_вх для мостов различных типов указаны в табл. 6.1.

Таблица 6.1

Типы мостов	m	k_вх
С обратными стенками и конусами	>= 0,32 <*>	0,83
С откосными крыльями	0,35	0,80
С заборными стенками	0,32	0,70
Эстакадные с конусами	>= 0,33 <*>	0,85

--------------------------------

<*> Конкретные значения m в этих случаях находят по формулам (6.1), (6.3) и (6.4).

При относительно небольшом затоплении конусов, когда

(где h_кон - высота конуса), увеличение пропускной способности учитывают формулой:

(6.1)

где m_табл - коэффициент расхода по табл. 6.1.

При несовершенном сжатии потока на входе под мост увеличение значения m учитывают по формуле (5.14).

6.2. Подмостовое русло не подтоплено (рис. 6.2, а, б) и уровень воды в нижнем бьефе не влияет на пропускную способность сооружения при соблюдении условия

(6.2)

где h_нб - бытовая глубина в нижнем бьефе;

H₀ - напор воды перед мостом;

N - критерий подтопления [45], принимаемый по табл. 6.2.

Таблица 6.2

m	N	k_с		m	N	k_с
0,32	0,84	0,45	0,76	0,35	0,80	0,52	0,83
0,33	0,83	0,47	0,78	0,36	0,78	0,54	0,84
0,34	0,81	0,49	0,81	0,37	0,76	0,56	0,86
				0,38	0,74	0,58	0,88

Рис. 6.2. Схемы протекания потока под мостом:

а - незатопленное подмостовое русло при двухперепадном

протекании потока; б - незатопленное подмостовое

русло при одноперепадном протекании потока;

в - затопленное подмостовое русло

Если условие (6.2) не соблюдается, подмостовое русло подтоплено (рис. 6.2, в) и уровень воды влияет на пропускную способность сооружения.

6.3. В зависимости от относительной длины моста с неподтопленным подмостовым руслом устанавливается двухперепадное протекание потока (см. рис. 6.2, а) или одноперепадное (см. рис. 6.2, б).

При двухперепадном протекании (

, где L_м - длина моста вдоль потока) пропускная способность практически не зависит от длины моста.

При одноперепадном протекании

пропускная способность увеличивается с уменьшением отношения

; при этом

(6.3)

6.4. В зависимости от относительной ширины сооружения

мосты делятся на узкосливные (при

) и широкосливные (при

). У широкосливных мостов с увеличением отношения

пропускная способность увеличивается, что можно учесть [4] по формуле

(6.4)

ОДНОПРОЛЕТНЫЕ МОСТЫ

6.5. Гидравлический расчет малых мостов заключается в определении отверстия моста, подпертой глубины перед мостом, определяющей минимальное возвышение бровки земляного полотна, максимальной глубины под мостом, по которой проверяется возвышение низа пролетного строения, и максимальной скорости потока под мостом, определяющей тип подмостового укрепления.

6.6. Пропускная способность малых мостов

ИС МЕГАНОРМ: примечание.

Формула дана в соответствии с официальным текстом документа.

(6.5)

где

- коэффициент подтопления [45], определяемый по табл. 6.3;

b_к - средняя ширина потока под мостом при критической глубине; при прямоугольном подмостовом сечении b_к равно отверстию моста.

Таблица 6.3

	Параметры для расчета малых мостов по затопленной схеме
		k_п					k_п					k_п
	m = 0,32					m = 0,33					m = 0,34
0,81	-	-	-	-	-	-	-	-	-	-	1,00	0,61	1,00	1,23	7,30
0,82	-	-	-	-	-	-	-	-	-	-	0,98	0,63	1,10	1,20	6,30
0,83	-	-	-	-	-	1,00	0,60	1,10	1,20	7,10	0,96	0,65	1,20	1,17	5,50
0,84	1,00	0,59	1,00	1,19	6,90	0,98	0,62	1,25	1,17	6,10	0,94	0,67	1,31	1,14	4,73
0,86	0,96	0,64	1,26	1,13	4,80	0,93	0,67	1,50	1,11	4,30	0,90	0,71	1,56	1,08	3,60
0,88	0,90	0,69	1,57	1,07	3,40	0,88	0,72	1,80	1,05	3,00	0,85	0,75	1,88	1,02	2,60
0,90	0,84	0,74	2,04	1,00	2,25	0,82	0,76	2,08	0,97	2,10	0,79	0,80	2,35	0,95	1,95
0,92	0,76	0,80	2,65	0,92	1,40	0,75	0,81	2,68	0,90	1,35	0,72	0,84	2,90	0,88	1,15
0,94	0,67	0,85	3,52	0,82	0,80	0,66	0,86	3,57	0,81	0,80	0,64	0,88	3,70	0,78	0,70
0,96	0,56	0,90	5,00	0,71	0,40	0,55	0,91	5,20	0,70	0,35	0,53	0,92	5,30	0,68	0,35
0,98	0,40	0,95	8,60	0,55	0,10	0,39	0,95	8,65	0,54	0,10	0,38	0,96	8,65	0,53	0,10
0,99	0,28	0,97	15,00	0,43	0,05	0,28	0,98	15,00	0,43	0,05	0,27	0,98	15,00	0,42	0,05

Продолжение табл. 6.3

	Параметры для расчета малых мостов по затопленной схеме
		k_п					k_п
	m = 0,35					m = 0,36
0,78	-	-	-	-	-	1,0	0,64	1,0	1,28	8,05
0,80	1,0	0,63	1,0	1,25	7,75	0,97	0,67	1,14	1,23	6,50
0,82	0,97	0,67	1,18	1,19	6,00	0,94	0,71	1,34	1,17	5,10
0,84	0,93	0,70	1,36	1,13	4,60	0,91	0,74	1,54	1,11	4,05
0,86	0,89	0,74	1,61	1,07	3,60	0,86	0,77	1,77	1,05	3,05
0,88	0,84	0,78	1,94	1,01	2,55	0,81	0,81	2,11	0,99	2,25
0,90	0,78	0,82	2,36	0,94	1,80	0,75	0,84	2,53	0,92	1,55
0,92	0,71	0,85	2,90	0,86	1,15	0,69	0,87	3,05	0,85	1,05
0,94	0,62	0,89	3,80	0,77	0,65	0,60	0,90	3,90	0,76	0,60
0,96	0,52	0,93	5,20	0,67	0,35	0,51	0,93	5,20	0,67	0,35
0,98	0,37	0,96	8,65	0,53	0,10	0,36	0,97	8,70	0,52	0,10
0,99	0,27	0,98	15,00	0,42	0,05	0,26	0,98	15,00	0,41	0,05

Окончание табл. 6.3

	Параметры для расчета малых мостов по затопленной схеме
		k_п					k_п
	m = 0,37					m = 0,38
0,74	-	-	-	-	-	1,00	0,68	1,0	1,35	8,95
0,76	1,0	0,66	1,0	1,33	8,70	0,97	0,70	1,15	1,30	7,10
0,78	0,97	0,69	1,15	1,27	6,95	0,95	0,73	1,30	1,25	5,90
0,80	0,95	0,72	1,28	1,21	5,80	0,93	0,75	1,42	1,19	5,05
0,82	0,92	0,74	1,50	1,15	4,50	0,90	0,78	1,65	1,13	3,90
0,84	0,89	0,77	1,70	1,09	3,66	0,87	0,80	1,85	1,07	3,25
0,86	0,84	0,80	1,92	1,03	2,85	0,85	0,83	2,09	1,01	2,45
0,88	0,79	0,83	2,20	0,97	2,15	0,78	0,85	2,35	0,95	1,95
0,90	0,73	0,85	2,65	0,90	1,47	0,72	0,87	2,80	0,88	1,37
0,92	0,67	0,88	3,15	0,84	0,95	0,66	0,90	3,30	0,83	0,85
0,94	0,59	0,81	4,05	0,75	0,55	0,58	0,92	4,15	0,74	0,50
0,96	0,50	0,94	5,25	0,66	0,35	0,49	0,95	5,30	0,66	0,35
0,98	0,35	0,97	8,70	0,52	0,10	0,34	0,98	8,70	0,51	0,10
0,99	0,26	0,98	15,00	0,40	0,05	0,25	0,99	15,09	0,40	0,05

Критическая глубина для трапецеидальных подмостовых русел

(6.6)

где h_к(п) - критическая глубина для прямоугольного русла (см. гл. 2);

- параметр, определяемый по графику на рис. 6.3.

Рис. 6.3. График для определения коэффициента

В свою очередь

где m_от - коэффициент заложения откоса под мостом;

b_дн - ширина подмостового русла по дну.

6.7. Максимальная глубина воды устанавливается на входе потока под мост - h_вх. По этой величине принимают минимальное возвышение низа пролетного строения. Для малых мостов

h_вх = k_вхH₀, (6.7)

где k_вх - коэффициент, учитывающий снижение кривой подпора, определяемый по табл. 6.1.

6.8. Максимальная скорость под мостом при двухперепадном протекании потока находится в сжатом сечении, эту скорость принимают за расчетную и определяют по формуле

(6.8)

где b_с - отверстие моста; для трапецеидальных русел - это средняя ширина потока при глубине в сжатом сечении h_с.

В свою очередь

h_с = k_сH₀, (6.8')

где k_с - коэффициент, определяемый по табл. 6.2.

При одноперепадном протекании потока под мостом максимальная расчетная скорость устанавливается на выходе из-под моста при глубине потока, равной бытовой глубине воды в нижнем бьефе:

(6.9)

где b_нб - отверстие моста; для трапецеидальных русел - это средняя ширина потока при глубине h_нб.

При подтопленном подмостовом русле за максимальную расчетную принимают скорость под мостом с учетом перепада восстановления:

(6.10)

где b_п - отверстие моста; для трапецеидальных русел - это средняя ширина потока при глубине h_п = k_пH₀;

k_п - коэффициент, принимаемый по табл. 6.3.

Расчетная максимальная скорость под мостом должна быть меньше допускаемой скорости для принятого типа укрепления: v_р < v_доп, где v_доп принимают по табл. 2.9. Если это условие не выполняется, переходят на более мощное укрепление или увеличивают отверстие моста для уменьшения v_р.

6.9. Обычно при известном расходе воды Q по высоте насыпи назначают напор перед мостом H₀ и определяют отверстие моста b_к.

Первоначально по формуле (6.2) проверяют возможность подтопления подмостового русла. Если подмостовое русло не подтоплено (

), то, решая уравнение (6.5), определяют отверстие моста. Полученное по расчету отверстие моста b_к округляют до ближайшего большего стандартного размера

. Затем определяют новое значение напора:

(6.11)

По значению

снова проверяют условие подтопления. Если подмостовое русло не подтоплено, по формуле (6.7) проверяют достаточность возвышения низа пролетного строения и в зависимости от характера протекания потока по формуле (6.8) или (6.9) - достаточность принятого типа укрепления.

Если подмостовое русло подтоплено

, по табл. 6.3 в зависимости от значения m, соответствующего принятому типу моста, и

находят

и, решая уравнение (6.5), определяют отверстие моста b_к. Затем округляют b_к до ближайшего большего стандартного значения

и определяют вспомогательный параметр

(6.12)

Далее по табл. 6.3 по принятому значению m и полученному

находят

и новое значение напора

(6.13)

а также новое значение отношения

Если

, вновь уточняют

и расчет повторяют до получения достаточной сходимости результатов.

Затем проверяют достаточность возвышения низа пролетного строения по формуле (6.7) и принятого типа укрепления по формуле (6.10).

6.10. В том случае, когда напор перед мостом не является лимитирующим фактором, расчет ведут исходя из допускаемой скорости v_доп для принятого типа укрепления подмостового русла. При этом по коэффициенту расхода m, соответствующему принятому типу моста, по табл. 6.2 определяют параметры

и N.

Сначала при

определяют напор перед мостом:

(6.14)

Потом проверяют возможность подтопления подмостового русла; если условие (6.2) соблюдается и подтопление отсутствует, то, решая уравнение (6.5), определяют отверстие моста. Далее расчет выполняют, как в случае, рассмотренном в п. 6.9 при отсутствии подтопления.

Если подмостовое русло подтоплено

, определяют наибольшую возможную скорость течения под мостом

(6.15)

Устанавливают расчетную скорость v_р:

v_р = v_max при v_доп > v_max и v_р = v_доп при v_доп < v_max.

Затем определяют вспомогательный параметр

(6.16)

и по табл. 6.3 находят параметры

Определяют напор

и по полученным значениям

находят необходимое отверстие моста b_к.

Далее расчет выполняют, как в случае, рассмотренном в п. 6.9 при подтоплении подмостового русла.

При известном отверстии моста, что соответствует расчету сооружений при реконструкции дорог или строительстве вторых путей на железных дорогах, либо в случае назначения отверстия моста по удельному расходу

(где b_дн - ширина отверстия моста по дну; обычно принимают

), вначале определяют подпертую глубину H₀ по формуле (6.5), предполагая незатопленное подмостовое русло, т.е. принимая

. Дальнейшие расчеты выполняют с использованием номограммы А.А. Александрова, приведенной в приложении 6.1.

Расчет начинают с определения по номограмме истинной подпертой глубины

по значениям H₀, h_нб и m, для чего находят точки пересечения кривых, соответствующих значениям H₀ и h_нб при известном коэффициенте расхода m. Следует отметить, что на номограмме даны два вида зависимостей

: при m = 0,38 (сплошные линии) и m = 0,34 (штриховые), причем для промежуточных значений m указанные кривые интерполируются. Ордината указанной точки дает значение истинной подпертой глубины, абсцисса - значение

При

к расчету принимают

. Далее по формуле (6.7) определяют h_вх и по формуле (6.8) - v_р, определив предварительно h_с по формуле (6.8'), где k_с берется по табл. 6.2.

При

по табл. 6.3 при известном коэффициенте расхода m и полученном значении

находят коэффициент k_п, а затем по формуле (6.10) - скорость v_р. Глубину на входе потока под мост h_вх определяют по той же зависимости, что и при

, т.е. по формуле (6.7).

Примеры расчета малых мостов приводятся в приложении 6.2.

МНОГОПРОЛЕТНЫЕ МОСТЫ

6.11. Пропускная способность многопролетных мостов с массивными опорами

(6.17)

где k_ср - средний коэффициент, учитывающий плавность входного сечения моста;

n - число пролетов моста.

В свою очередь

(6.18)

где k_пр и k_кр - коэффициенты, учитывающие плавность входа потока соответственно для промежуточных и крайних пролетов.

Коэффициенты k_пр и k_кр могут быть приняты равными для закругленных устоев и быков 0,91, для прямоугольных устоев и пролетов - 0,83. Влиянием пазов в быках пренебрегают. При наличии быков характер водной поверхности под мостом практически такой же, как и без них, но от верховой грани быков появляются дополнительные косые волны.

Для относительно коротких мостов (L_м < 2,5H₀) несовершенство сжатия потока при входе и увеличение пропускной способности при относительно малом затоплении конусов учитывают так же, как и для однопролетных мостов.

6.12. Многопролетные эстакадные неподтопленные мосты на свайных опорах рассчитывают по формуле

(6.19)

где

- коэффициент, учитывающий потери на входе от стоек, определяемый по графику на рис. 6.4 в зависимости от k_ст.

Рис. 6.4. График для определения

1 - при стойках с округленными углами;

2 - при прямоугольных стойках

В свою очередь

где b_к - средняя ширина потока при критической глубине; b_к = m_отh_к + b_дн.

Входящая в формулу (6.19) величина

представляет собой среднюю ширину потока при критической глубине за вычетом ширины стоек

Критерий подтопления подмостового сечения для мостов такого типа следует рассматривать с учетом влияния стоек. Можно считать, что мост с промежуточными стойками будет затоплен, если глубина под мостом h, вычисленная по глубине нижнего бьефа, удовлетворяет условию

или

(6.20)

где

и соответственно

Приближенно критерий заполнения многопролетных мостов можно определять так же, как и для однопролетных.

При расчете многопролетных затопленных мостов в расчетные формулы (6.17) и (6.19), как для однопролетных мостов, добавляют множитель

, определяемый по табл. 6.3.

МОСТЫ НА ЗАЛИВАХ ВОДОХРАНИЛИЩ

6.13. Под сооружением, отделяющим залив водохранилища, пойменного озера, ильменя или лимана от его основной части, поток периодически меняет направление в связи с колебаниями уровня реки или основной части водоема.

При равенстве уровней в бьефах перелива потока через сооружение нет. При изменении уровня речного бьефа возникает перелив. При понижении уровня речного бьефа отсеченная часть опорожняется (рис. 6.5, а), а при повышении наполняется через отверстие сооружения (рис. 6.5, б).

Рис. 6.5. Схемы работы мостов на заливах водохранилищ

при их опорожнении (а) и наполнении (б)

Если перепад в уровнях увеличивается, то скорость потока растет до тех пор, пока скорость изменения уровня воды в отсеченной части не станет равна скорости изменения уровня речного бьефа, что соответствует максимуму скорости потока в отверстии моста.

Скорость изменения уровня в отсеченной части может и не достигнуть скорости изменения уровня речного бьефа до конца периода изменения уровней в интервале от H₀ до H₁. В этом случае максимум перепада установится при достижении уровнем речного бьефа своего крайнего положения (H₁ - при наполнении и H₀ - при опорожнении).

Движение воды под отсекающим сооружением рассчитывают по номограммам для опорожнения (рис. 6.6) и наполнения (рис. 6.7). При пользовании номограммами сначала по исходным данным F₁, F₀, H₁, H₀ и a вычисляют характеристики

(6.21)

где F₁, F₀ - площади отсеченной части водохранилища соответственно при нижнем и верхнем уровнях речного бьефа;

a - расчетная скорость изменения уровня речного бьефа, м/сут.

Рис. 6.6. Номограммы для расчета мостов

при опорожнении водоемов

Рис. 6.7. Номограммы для расчета мостов

при наполнении водоемов

Нужно иметь в виду, что чем больше a, тем при прочих равных условиях требуется большее отверстие моста для сохранения допустимой скорости.

При вычислении вспомогательных характеристик выражают F в квадратных километрах (км²) и H в метрах (м).

При заданной допускаемой скорости определяют значение максимально допустимого относительного перепада

(6.22)

где

- коэффициент скорости, принимаемый по табл. 2.5.

По относительному перепаду

и вычисленным K и L для соответствующих n по номограмме определяют относительное отверстие

и отверстие

Номограммы составлены для K >= 1. Если характеристика K получается менее единицы, то принимают

K = 1 и

(6.23)

Расчетную скорость изменения уровня речного бьефа можно принимать средней (рис. 6.8, а):

(6.24)

где T - продолжительность изменения уровней от H₀ до H₁.

Рис. 6.8. Графики для определения a_ср (а)

и поправок к F₀ и F₁ (б)

Расчетные значения F₀ и F₁, определенные по кривой F = f(H) на участке от H₀ до H₁ (рис. 6.8, б), существенно отличающейся от прямой, для большей точности расчета принимают с поправками, пользуясь следующим методом.

Между точками кривой F = f(H), соответствующими H₀ и H₁, проводят хорду и параллельную ей секущую на расстоянии ²/₃ высоты сегмента f. В этом случае площадь треугольника ABE близка к площади фигуры KCLN. На пересечении секущей с абсциссами H₀ и H₁ получают точки расчетных значений

Если при наполнении водоема скорость подъема уровня a значительно больше, чем при опорожнении, то за расчетный случай принимают наполнение. При значениях a, близких как для наполнения, так и для опорожнения, рассчитывают отверстие моста для обоих случаев и принимают большее.

Номограммы не учитывают поступления или утечки воды из отсеченной части водоема помимо рассчитываемого сооружения (испарение, расходы на орошение, постоянный приток в отсеченную часть и т.п.). Влияние этих дополнительных расходов учитывают, вводя в расчет среднюю постоянную поправку к скорости изменения уровня отсеченной части

(6.25)

здесь

С учетом дополнительного расхода отверстие

(6.26)

где b - отверстие, определяемое по номограмме без учета дополнительного расхода.

Невыгодными расчетными случаями, когда P принимают со знаком "плюс", являются:

при опорожнении - приток дополнительного расхода в отсеченную часть;

при наполнении - забор воды из отсеченной части.

В приложении 6.3 приводятся примеры определения требуемых отверстий мостов при наполнении и опорожнении. Номограммы позволяют рассчитывать отверстия моста без подбора, а также пригодны для расчета отверстий трапецеидальных мостов. В этом случае вычисленная ширина моста принимается как средняя между глубинами H и H₀.

Ширина моста по дну

b_дн = b - m_от(H₁ - H₀). (6.27)

МОСТЫ-ВОДОСПУСКИ

6.14. Мосты-водоспуски с затворами для перекрытия отверстия предназначаются для работы только при определенном уровне воды в верхнем бьефе.

Если приспособление для перекрытия устроено в виде шандорного затвора, то отверстие моста работает по схеме водослива с острым порогом (рис. 6.9). Если приспособление для перекрытия устроено в виде подъемного щита, то отверстие моста работает по схеме истечения из-под щита (рис. 6.10).

Рис. 6.9. Схема работы моста-водоспуска

с шандорным затвором

Рис. 6.10. Схема работы моста-водоспуска

с подъемным щитом

Мосты-водоспуски рассчитывают на строго зарегулированный расход, определяемый уровнем верхнего бьефа и степенью открытия затвора. Они работают по схеме незатопленного водослива, так как включаются в работу только при условии понижения уровня в нижнем бьефе ниже уровня затвора.

Первый тип мостов-водоспусков (шандорные мосты) рассчитывают по формуле водослива с тонкой стенкой. Значение H в шандорных мостах невелико и определяется высотой одного или пары шандоров; практически эта высота колеблется от 0,14 до 0,70 м.

Для шандорного моста приходится решать следующие задачи (см. рис. 6.9):

а) по заданному времени опорожнения верхнего бьефа и высоте подпора H определить потребное отверстие моста b;

б) по принятому отверстию моста b и высоте подпора H определить расход моста и время, потребное для опорожнения верхнего бьефа.

За порогом шандорного затвора образуется перепад, для которого должно быть рассчитано сопряжение с нижним бьефом. Расчету подвергается случай снятия самого верхнего шандора, когда струя, сливающаяся с затвора, имеет самую большую высоту падения.

Длину падения струи, сливающейся с гребня затвора, определяют по упрощенной формуле

L₁ = H_п + h_к, (6.28)

где H_п - высота порога (шандора);

h_к - критическая глубина, ее определяют (по расходу на пороге Q) по формуле (2.11).

Длина прыжка

L₃ = 2h_к. (6.29)

Длина отгона прыжка

(6.30)

где i_к определяют по формуле (2.12).

Глубина в сжатом сечении

h_с = 0,9h_к.

Таким образом, полная длина укрепления за шандорным затвором

L = L₁ + L₂ + L₃. (6.31)

Далее (за прыжком) поток приобретает бытовую глубину, и русло не нуждается в укреплении.

За расчетную следует принимать скорость в сжатом сечении

(6.32)

Зона русла возможного падения струи, т.е. на протяжении L₁, должна быть усиленно укреплена.

В мостах-водоспусках мер по гашению энергии потока не предусматривают, так как на пропуск расчетных расходов они работают редко и кратковременно.

Второй тип мостов-водоспусков - щитовые мосты (см. рис. 6.10) - рассчитывают по формуле истечения воды из-под щита в незатопленный нижний бьеф:

(6.33)

где

при вертикальном расположении плоского щита;

a - высота отверстия под щитом;

z - возвышение уровня верхнего бьефа над свободной поверхностью потока в сжатом сечении.

Глубина в сжатом сечении

(6.34)

где

- коэффициент вертикального сжатия.

Далее определяют скорость в сжатом сечении по формуле (6.32) и по ней принимают соответствующий тип крепления нижнего бьефа.

Уравнение (6.33) решается для первоначального положения уровня в верхнем бьефе, как для наиболее ответственного. По мере вытекания из-под щита уровень в верхнем бьефе снижается и условия в нижнем бьефе облегчаются. Это позволяет постепенно поднимать щит и, таким образом, поддерживать постоянный расход Q.

ОСОБЕННОСТИ РАСЧЕТА МОСТОВ С НЕУКРЕПЛЕННЫМИ РУСЛАМИ

6.15. При пересечении водотоков, дно которых подстилается крупным галечным или плотным связным грунтом <1>, может оказаться экономичным устройство малого моста с неукрепленным руслом.

--------------------------------

<1> Характеристики грунтов см. в п. 7.29.

К условиям, благоприятствующим такому решению, относится нормальное (некосое) пересечение водотока однопролетным мостом.

Устройство малого моста с неукрепленным руслом на пойме и особенно при косом пересечении подходной насыпью речной долины связано, как правило, со значительным увеличением расхода воды в размываемом подмостовом сечении по сравнению с бытовыми условиями, которое, в свою очередь, приводит к увеличению размывов в отверстии.

6.16. Гидравлический расчет малых мостов с неукрепленным руслом производится теми же методами, что и большие мосты [24]. Расчет включает определение подпора воды перед насыпью и размывов под мостом при заданном отверстии. В качестве искомого принимают отверстие, при котором обеспечивается устойчивость конусов моста, подпор не приводит к излишнему увеличению строительной стоимости мостового перехода в целом (включая насыпь подходов), а также возможно использование имеющихся или запланированных (по условиям однотипности, доставки и т.п.) конструктивных элементов.

При выборе отверстия следует иметь в виду, что требования нормативных документов [39] в части русловых деформаций ориентированы на большие мосты. Для малых мостов с небольшой глубиной потока определяющим является не коэффициент общего размыва, а наибольшая глубина общего размыва под мостом, которая для обеспечения устойчивости конусов (или устоев) не должна превышать 2 - 2,5 м.

При гидравлическом расчете малых мостов с размываемым руслом возможны три основных случая:

а) мост перекрывает водоток, несущий в паводок донные наносы; степень стеснения потока, т.е. отношение расхода воды под мостом Q к расходу, проходящему в бытовых условиях на ширине отверстия Q_м.б

;

б) по какой-либо причине наблюдается дефицит донных наносов на пересекаемом водотоке (например, на суходоле дно подстилается связным материалом и т.д.) или степень стеснения потока

;

в) мост расположен на пойме и является элементом мостового перехода с отверстием через главное русло.

6.17. В случае, предусмотренном в п. 6.16, а, наибольшую глубину размыва в однородных несвязных грунтах с учетом времени прохождения паводка определяют по формуле

(6.35)

где q_max - удельный расход потока в отверстии моста на вертикали с наибольшей глубиной H_max (до размыва);

;

- средний удельный расход воды в отверстии моста размером L_м (здесь, как и в больших мостах, отверстие - это расстояние между урезами воды под мостом в расчетный паводок);

Q - расход воды в отверстии;

H - средняя глубина потока под мостом до размыва;

d - средний диаметр частиц грунта, подстилающего русло;

- безразмерный коэффициент Лиштвана, зависящий от вероятности превышения расхода p на пике паводка.

Значения коэффициента

в зависимости от вероятности превышения расхода p, %, приведены ниже:

p, %	0,33	1	2	4	10	20
	1,07	1,0	0,97	0,92	0,86	0,81

В формуле (6.35) коэффициент

, учитывающий время воздействия паводка при расчете общего размыва, может быть определен в первом приближении по табл. 6.4 в зависимости от продолжительности паводка T (строго говоря - от продолжительности затопления поймы) и степени стеснения потока

Таблица 6.4

Степень стеснения потока	Значения коэффициента при продолжительности паводка T
Степень стеснения потока	0,0835 сут (2 ч)	0,125 сут (3 ч)	0,25 сут (6 ч)	0,5 сут (12 ч)	1 сут (24 ч)	3 сут	10 сут	15 сут	30 сут	>= 60 сут
1,2	0,86	0,87	0,79	0,90	0,91	0,93	0,95	0,96	0,98	1,0
1,5	0,72	0,74	0,76	0,78	0,81	0,85	0,90	0,93	0,97	1,0
1,8	0,59	0,61	0,64	0,68	0,72	0,79	0,87	0,90	0,96	1,0
2,1	0,49	0,51	0,56	0,60	0,66	0,74	0,84	0,88	0,95	1,0
2,5	0,45	0,47	0,52	0,56	0,62	0,71	0,82	0,87	0,94	1,0
3,0	0,38	0,41	0,46	0,49	0,55	0,65	0,79	0,84	0,92	0,99
5,0	0,23	0,27	0,32	0,35	0,42	0,52	0,71	0,77	0,88	0,97

6.18. В случае, предусмотренном п. 6.16, б, наибольшую глубину общего размыва под мостом с учетом времени прохождения паводка определяют по формуле:

(6.36)

где

- средняя глубина общего размыва под мостом с учетом времени прохождения паводка.

В свою очередь

определяют по зависимостям:

для несвязных однородных грунтов

(6.37)

для связных грунтов

(6.38)

где X₀ - расстояние от моста до вертикали, где образуется предмостовой подпор (см. п. 6.22), м;

T - время затопления поймы, сут.

При определении общего размыва с учетом фактора времени требования СНиП 2.05.03-84 о выполнении условия прохода расчетного паводка "после серии натурных наблюденных паводков одного из многоводных периодов" могут быть заменены расчетом на воздействие двух расчетных паводков. Тогда в формулах (6.37) и (6.38) время воздействия потока следует принимать 2T.

В приведенных формулах H и v - средние глубина и скорость потока под мостом до размыва (соответственно в м и м/с).

Глубины размыва, рассчитанные по формулам (6.37) и (6.38), не должны быть больше предельной глубины, при которой на рассматриваемом участке (или вертикали) устанавливается размывающая скорость. Предельную глубину размыва определяют по формулам:

для несвязных грунтов

(6.39)

для связных грунтов

(6.40)

где

- коэффициент, принимаемый равным единице, когда по руслу не влекутся песчаные наносы, и

при их влечении;

C_р - расчетное сцепление, МПа.

6.19. В случаях, предусмотренных пп. 6.16, а и 6.16, б, предельную глубину потока после общего размыва в неоднородных несвязных грунтах определяют без учета фактора времени по формуле

(6.41)

где D и p - средний диаметр отмащивающих частиц и их содержание по массе в перерабатываемом материале.

Значения D и p определяют с учетом гранулометрического состава грунта подбором из уравнения

(6.42)

здесь

Полученная глубина размыва не должна быть больше той, при которой наступает стабилизация размыва в подмостовом сечении из-за динамического равновесия донных наносов или невозможности по гидравлическим условиям выноса из подмостового сечения мелких частиц грунта.

Глубину потока в указанных случаях определяют соответственно по формулам (6.35) и (6.36), в которых вместо среднего диаметра частиц грунта d принимают средний диаметр частиц донных наносов или мелких частиц грунта

6.20. В случае, предусмотренном п. 6.16, в, наибольшую глубину общего размыва под мостом с учетом времени прохождения паводка определяют по формуле (6.36), в которой

принимают:

для несвязных однородных и неоднородных грунтов (кроме грунтов, содержащих крупные включения)

(6.43)

для связных грунтов

(6.44)

В формулах (6.43) и (6.44) принимают наибольшую скорость потока под мостом на пике паводка

(6.45)

где

- коэффициент скорости, принимаемый равным 0,75;

- перепад уровней в верхнем и нижнем бьефах моста (см. п. 6.21).

Расчет размыва в несвязных грунтах, содержащих в перерабатываемом материале p крупных включений со средним диаметром D, производят по формуле (6.41). Для всех случаев, предусмотренных в п. 6.16, коэффициент общего размыва для малых мостов с неукрепленным руслом определяют как

или

6.21. Подпор воды у насыпи в случаях, предусмотренных пп. 6.16, а и 6.16, б, определяют по формуле

(6.46)

где коэффициент

принимают по графику на рис. 6.11 или по формуле

(6.47)

Рис. 6.11. График для определения коэффициента

характеризующего максимальный подпор перед насыпью

В свою очередь

(6.48)

где n_р, H_р - коэффициент шероховатости и средняя глубина потока в русле;

L_разл - ширина разлива.

При

принимают

Среднюю скорость под мостом v_м следует определять с учетом размыва на момент наибольшего подпора воды по приближенной формуле

(6.49)

где

- площадь живого сечения под мостом до размыва;

j - доля от полной величины размыва, принимаемая равной 0,25 при времени затопления поймы до 10 сут и 0,5 - при T > 10 сут;

H_max, H_maxпр - наибольшие глубины потока соответственно до и после размыва.

6.22. В случаях, предусмотренных п. 6.16, в, перепад уровней воды у насыпи

(6.50)

где УВВ_п - уровень воды на пике расчетного паводка у насыпи перед проектируемым мостом с учетом подпора, вызванного стеснением потока подходными насыпями подходов к мосту через главное русло;

УВВ_б - уровень воды на пике расчетного паводка в створе моста в бытовых условиях.

Расстояние, где расположена вертикаль с предмостовым подпором,

(6.51)

В свою очередь

ИС МЕГАНОРМ: примечание.

Формула дана в соответствии с официальным текстом документа.

(6.52)

где v_б - средняя скорость по всему живому сечению нестесненного потока;

- степень стеснения потока (см. п. 6.16);

i_б - уклон водной поверхности нестесненного потока.

Формула (6.52) справедлива при 0,4 <= a <= 0,25. Если рассчитанное значение выходит за указанные пределы, то коэффициент a принимают равным соответственному граничному значению.

6.23. В случае, предусмотренном п. 6.16, в, ширина разлива у сооружения

(6.53)

где B_р - ширина русла водотока;

B_г - ширина поймы между рассматриваемым водотоком на пойме и главным руслом;

n_р, n_п - коэффициенты шероховатости соответственно в русле и на пойме, примыкающей к водотоку с противоположной стороны от главного русла;

Q_р, Q_гр - расходы воды, проходящие под мостами соответственно на пойме и через главное русло;

y - показатель степени; y = 2n_гр/n_пг;

n_гр, n_пг - коэффициенты шероховатости соответственно главного русла и поймы между главным руслом и водотоком.

6.24. Глубину размыва у конусов моста, считая от отметки после общего размыва, определяют по формуле [1]

(6.54)

где v_г - скорость потока у конуса в месте его сопряжения с насыпью (см. п. 6.25);

v₀ - неразмывающая скорость для грунтов, в которых происходит размыв, при глубине потока H_н у насыпи перед мостом при уровне воды, соответствующем максимальному подпору

;

K_m - коэффициент, учитывающий влияние на размыв крутизны откосов конуса:

при m = 1,5 K_m = 0,8; при m = 2,0 K_m = 0,77;

при m = 2,5 K_m = 0,72.

Суммарную глубину общего и местного размыва у подошвы конусов в первом приближении можно определять также по формуле

(6.55)

где v_мдр, v_бм - скорость потока под мостом до размыва и на ширине отверстия моста в бытовых условиях.

6.25. Скорость потока у конуса

(6.56)

где C - коэффициент Шези, который может быть определен по Маннингу с коэффициентом шероховатости n ~= 0,03

- коэффициент стеснения потока подходами;

i_м - уклон свободной поверхности потока перед мостом.

В свою очередь

(6.57)

6.26. Глубину размыва у устоя, боковая грань которого не обсыпана конусом, определяют по формулам:

при b/H_max >= 1

(6.58)

при b/H_max < 1

(6.59)

где b - расчетная ширина сооружения, в качестве которой принимают среднюю ширину под водой (после общего размыва) боковой грани опоры, перпендикулярной направлению потока и выступающей из конуса (рис. 6.12).

Рис. 6.12. Схема к определению

расчетной ширины береговой опоры

7. РАСЧЕТЫ НИЖНИХ БЬЕФОВ СООРУЖЕНИЙ

КЛАССИФИКАЦИЯ ВЫХОДНЫХ РУСЕЛ И ПРИНЦИПЫ ИХ РАСЧЕТА

7.1. Под расчетами нижнего бьефа дорожных водопропускных сооружений понимают расчет комплекса устройств, находящихся за выходными оголовками труб, конусами мостов и на участке выхода потока из других водопропускных сооружений (лотков, фильтрующих и переливных насыпей и т.п.). Эти устройства будем в дальнейшем называть выходными руслами в отличие от естественного выходного лога. Выходные русла включают укрепления с концевыми частями, гасители и каменную наброску.

При расчете нижних бьефов могут встретиться два основных случая:

1) выходное русло размываемое, т.е. сопряжение его с бытовым логом происходит с образованием воронки размыва в конце сравнительно короткого укрепления;

2) выходное русло неразмываемое на всем протяжении потока до створа с бытовыми характеристиками. В этом случае за выходным сечением сооружения устраивают укрепленный канал.

Наиболее распространенным в практике проектирования является размываемое выходное русло.

В некоторых случаях, например в населенных пунктах, возникает необходимость применения неразмываемых выходных русел. Особенности их расчета излагаются в одной из рубрик настоящей главы (пп. 7.54 - 7.62). В основном же в данной главе излагаются общие принципы и методика расчета размываемых выходных русел.

7.2. Наиболее распространенные типы малых водопропускных сооружений на дорогах - водопропускные трубы и малые мосты. Поэтому наибольшее внимание в настоящей главе уделяется расчетом нижних бьефов этих сооружений и в первую очередь наиболее часто встречаемым в практике случаям расчета. Некоторые специфические случаи расчета выходных русел рассматриваются в отдельных рубриках настоящей главы, например сброс потока из сооружений на укрепленные откосы насыпи или лотки, уложенные на них, что характерно для металлических гофрированных труб, укладка которых с уклонами более 0,03 не допустима по условиям прочности; расчеты выходных русел с укреплениями из каменной наброски, а также расчеты выходных русел с укреплениями из синтетических материалов.

Расчет выходных русел некоторых сооружений рассматривается непосредственно в главах, посвященных гидравлическим расчетам указанных типов сооружений. Сюда относятся фильтрующие или переливные насыпи, лотковые сооружения, канавы, а из сопрягающих сооружений - консольные сбросы и рассеивающие трамплины.

7.3. Выходные русла, которые используются или могут быть использованы в малых дорожных водопропускных сооружениях, по характеру связи между элементами делят на две основные группы (рис. 7.1):

1) с укреплениями из связанных между собой элементов;

2) с укреплениями из не связанных между собой элементов.

Рис. 7.1. Классификация выходных русел

В свою очередь по возможности деформаций под воздействием потока выходные русла первой группы подразделяются на следующие:

выходные русла с жесткими (недеформируемыми) укреплениями;

выходные русла с гибкими (деформируемыми) укреплениями.

Каждое из этих подразделений выходных русел по сплошности укреплений делится на два вида:

со сплошными укреплениями;

со сквозными укреплениями.

В качестве примеров выходных русел из связанных между собой элементов с жесткими недеформируемыми укреплениями можно привести выходные русла из монолитного бетона, омоноличенных бетонных или железобетонных плит, блоков и мощения. Примером выходных русел той же группы, но со сквозными укреплениями могут служить бетонные ящики с заполнением камнем.

Выходные русла с укреплениями из связанных гибких элементов подразделяются на следующие виды:

выходные русла с укреплениями из тяжелых элементов - асфальтобетонные и бетонные тюфяки и т.п.);

выходные русла с укреплениями из легких элементов - укрепления из легких синтетических материалов;

то же, с укреплениями, сочетающими легкий синтетический каркас с различным тяжелым заполнением (песком, камнем и т.п.) как по всей поверхности (замкнутая оболочка с заполнением), так и на ее части (пригрузки по всей поверхности или в специальных карманах);

выходные русла со сквозными укреплениями, включающими бетонные гибкие элементы, заполненные камнем.

Выходные русла из не связанных между собой элементов в основном имеют укрепления из каменной наброски, состоящей как из однородных, так и неоднородных элементов. Можно также использовать и специально изготовленные не связанные между собой элементы из достаточно прочных морозостойких материалов. Сюда же относятся выходные русла без укреплений.

Эта группа делится на три вида:

неразмываемые, т.е. с устойчивыми к размыву укреплениями;

размываемые (самоотмостки);

без укреплений.

Выходные русла с неразмываемыми укреплениями в свою очередь делятся на два вида:

недеформируемые (т.е. с недеформируемыми укреплениями); сюда относятся выходные русла с укреплениями из однородной каменной наброски, не допускающие выноса грунта лога из-под них (поэтому их элементы сохраняют под воздействием потока свое первоначальное положение в пространстве);

деформируемые, допускающие вынос потоком частиц грунта из-под них. Это приводит к деформации укрепления без перемещения потоком его частиц (к вертикальному перемещению элементов наброски). При этом устойчивость укреплений обеспечивается и они сохраняют свои защитные свойства.

Выходные русла с размываемыми укреплениями допускают размыв и вынос элементов укрепления. Их устойчивость обеспечивается за счет отмостки поверхности крупными частицами, накапливающимися по мере выноса мелких частиц. Выходные русла с подобным типом укреплений, изготавливаемых из неоднородной наброски, носят название самоотмостки.

Наиболее распространенными в нижних бьефах малых дорожных водопропускных сооружений до 50-х годов нашего века были выходные русла с укреплениями в виде мощения, уложенного поверх каменной наброски. В дальнейшем использовались выходные русла с мощением без наброски и широко стали применяться выходные русла с укреплениями из бетона: монолитные и плитные.

Современные типы выходных русел водопропускных труб и малых мостов имеют укрепления из бетонных элементов (плит и блоков), омоноличенных раствором. При этом при больших скоростях (чаще в косогорных трубах, но в ряде случаев и в равнинных) применяются гасители энергии, а также в качестве дополнительной защиты от размыва - каменная наброска в конце укрепления. Все эти выходные русла относятся к группе выходных русел из связанных между собой элементов с жесткими (недеформируемыми) укреплениями.

Выходные русла, состоящие из связанных между собой элементов с гибкими укреплениями всех видов, для защиты от размыва малых водопропускных сооружений в нашей стране практически не применяются. Известно лишь несколько случаев использования выходных русел с укреплениями из синтетических материалов. Не используются также выходные русла с укреплениями из тюфяков. Между тем в зарубежной практике указанные виды выходных русел находят применение.

Выходные русла из несвязанных между собой элементов с укреплениями из каменной наброски начинают достаточно широко применяться у нас для защиты нижних бьефов малых водопропускных сооружений. Они включены и в действующие типовые проекты укреплений (см. приложение 1.1).

7.4. Для расчета все выходные русла, приведенные в классификации (см. рис. 7.1), должны быть отнесены к определенному типу, позволяющему конкретизировать расчетную схему, устанавливать гидравлические характеристики (глубины и скорости) и определить возможность деформаций укрепления и глубину размыва за ним.

Для защиты нижних бьефов от размыва при применении выходных русел из связанных между собой элементов с жесткими укреплениями рекомендуется использовать следующие шесть основных типов выходных русел (рис. 7.2). Они в основном и используются в практике дорожного строительства.

Рис. 7.2. Типы выходных русел

Тип 1 представляет собой укрепление с концевой частью в виде предохранительного откоса, тип 2 - то же, с вертикальной стенкой. Тип 3 отличается от типа 1 наличием ребра в конце укрепления, тип 4 - сочетанием стенки в раструбном оголовке с ребром в конце укрепления. Основные размеры ребра и гасителя в виде стенки в раструбном оголовке и их взаимное расположение представлены на рис. 7.3. Следует отметить, что этот тип гасителя разработан в ЦНИИСе. В результате исследований было установлено, что ребро 2 в конце укрепления обеспечивает благоприятный с точки зрения размыва поверхностный режим. Сочетание же ребра со стенкой 1 в раструбе приводит к малому росту размыва при возрастании расхода в сооружении, а при достижении определенной величины расхода возрастание размыва прекращается. Причина - с ростом расхода возрастает роль гасителя в гашении энергии. Указанное свойство данного выходного русла приводит к равнопрочности его при прохождении реальных паводков.

Рис. 7.3. Выходное русло с ребром и гасителем

(слева - продольный разрез; справа - план)

Тип 5 представляет собой расширяющийся водобойный колодец с одной стенкой, а тип 6 - с двумя стенками (гаситель ЦНИИСа). Типы 5а и 6а отличаются от типов 5 и 6 наличием вертикальной стенки вместо предохранительного откоса. Во всех типах выходных русел эффективно применение каменной наброски в концевых частях. Соответствующие номера типов выходных русел помечены индексом "к".

Для расчета выходных русел с укреплениями, состоящими из не связанных между собой элементов, рекомендуются три типа выходных русел (рис. 7.4). Эти типы отличаются между собой наличием или отсутствием за укреплением (в качестве дополнительной меры защиты от размыва) каменной наброски более мелкой, чем камень укрепления. (В типе I наброска отсутствует, в типах II и III - имеется). При этом выходные русла типов I и II применяют при глубинах размыва, меньших толщины укрепления, а типа III - при глубинах размыва, больших толщины укрепления.

Рис. 7.4. Типы выходных русел из каменной наброски:

а - тип I; б - тип II; в - тип III; 1 - укрепление

из наброски; 2 - щебеночная подготовка; 3 - обратная засыпка

грунта; 4 - рисберма;

- толщина наброски; h_ук - глубина

заложения укрепления; h_рисб - высота рисбермы; b_р - ширина

укрепления у оголовка, B₁, B₂ и B_ук - ширина соответственно

в начале, в конце и у концевой части укрепления

7.5. При назначении типов выходных русел целесообразно основываться на следующих принципах:

1) проводить технико-экономическое сравнение вариантов. Этот принцип является общим принципом выбора типа выходного русла;

2) при назначении вариантов выходных русел, изображенных на рис. 7.2, следует иметь в виду, что защитные свойства русел возрастают вместе с увеличением номера типа, но одновременно, как правило, растет их стоимость;

3) наименьшими защитными свойствами обладает выходное русло типа 1, несколько большими - типа 2. Причина - концевая часть в виде вертикальной стенки по сравнению с предохранительным откосом обеспечивает снижение глубины размыва более чем на 60%. Типы 1 и 2 рекомендуется использовать при глубинах размыва не более 1,5 м.

Существенно повышает защитные свойства выходных русел наличие каменной наброски за концевой частью укрепления. Напоминаем, что типы 1к и 2к представляют собой выходные русла 1 и 2, усиленные каменной наброской. Обычно эти выходные русла, как, впрочем и более мощные, используют при глубине размыва не более 2,5 м. Типы 3 (3к), 4 (4к) представляют собой выходные русла с гасителями, обычно используемые в равнинных сооружениях или в косогорных с малыми уклонами.

Эффективность применения этих типов существенно возрастает с увеличением заполнения труб. Типы 5 (5а, 5к, 5ак) и 6 (6а, 6к, 6ак) наиболее мощны. Они обеспечивают как существенное снижение скоростей на укреплении, так и значительное уменьшение размыва. Обычно их используют для косогорных сооружений.

Выходные русла с укреплениями из не связанных между собой элементов используются в районах, где возможна высокая деформативность укреплений (северная климатическая зона, особенно при наличии вечной мерзлоты), а также в тех местах, где стоимость каменных материалов сравнительно невелика. Обычно эта группа выходных русел используется при скоростях течения на выходе из труб

Последовательность применения выходных русел, представленных на рис. 7.4, также соответствует нумерации I, II и III. При этом тип I используют, если глубина размыва не превышает толщины укрепления (толщины слоя наброски). В противном случае уменьшают глубину размыва размещением за укреплением каменной наброски из более мелкого материала, чем камень укрепления, т.е. применяют тип II. При этом вновь добиваются условия, чтобы глубина размыва не превышала толщины укрепления. Если и в этом случае указанное условие не выдержано, то применяют тип III выходных русел.

7.6. Исходными данными для расчетов нижних бьефов дорожных водопропускных сооружений являются:

а) характеристики водопропускного сооружения (форма поперечного сечения, отверстие, тип выходного оголовка, уклон лотка);

б) регламентируемые СНиП [39] расходы в сооружении;

в) гидравлические характеристики на выходе из сооружений (глубины и скорости потока), определяемые на основе рекомендаций соответствующих глав настоящего Пособия;

г) характеристика бытового лога - форма сечения, уклон, грунты (связные или несвязные); для связных приводится величина сцепления, для несвязных - гранулометрический состав; пробы грунтов должны обеспечить получение указанных выше грунтовых характеристик по всей глубине, но не менее 2 м;

д) характеристика каменного материала (для выходных русел, представленных на рис. 7.4) - название, крепость, трещиноватость породы и ее вероятный гранулометрический состав;

е) наличие нижерасположенных сооружений на соседних дорогах или на других объектах, влияющих на гидравлическую работу рассчитываемых сооружений;

ж) другие данные, оказывающие влияние на гидравлический расчет сооружений.

7.7. Расчеты нижних бьефов малых водопропускных сооружений для принятого типа выходных русел включают следующие вопросы:

а) определение гидравлических характеристик потока в выходных руслах и за ними - глубин, скоростей и характера растекания потока на укреплении; расчет может выполняться в двух вариантах: на основе математической модели и по эмпирическим зависимостям;

б) оценку устойчивости укреплений и величину их деформаций (для выходных русел из несвязанных между собой элементов);

в) определение глубин размыва за укреплениями;

г) определение размеров укреплений и глубин заложения их концевых частей.

КИНЕМАТИКА ПОТОКА ПРИ РАЗМЫВАЕМЫХ ВЫХОДНЫХ РУСЛАХ

7.8. Гидравлические характеристики потока на укреплениях в размываемых выходных руслах, а также размеры и характер деформаций за ними в значительной мере определяются кинематикой потока в нижних бьефах сооружений и условиями взаимодействия его с размываемым руслом. Отсюда следует важность правильной оценки кинематики потока для выработки методики расчета и выбора зависимостей для конкретных случаев гидравлического расчета выходных русел малых водопропускных сооружений.

Кинематика потока в нижнем бьефе определяется условиями растекания его, на которые влияют скорость и кинетичность потока на выходе из сооружения, уклоны дна, глубины и поперечные сечения выходного лога, а также характер размыва. Весьма важную роль среди этих факторов играют уклоны выходного лога (укреплений).

Возможны два основных случая растекания потока: свободное, при котором глубина его в выходном логе (в бытовых условиях) не оказывает существенного влияния на течение потока на укреплении (рис. 7.5, 7.6), и не свободное, где она оказывает это влияние (рис. 7.7).

Рис. 7.5. Кинематическая схема потока в нижнем бьефе

при свободном растекании и донном режиме:

1 - пространственный гидравлический прыжок;

2 - транзитный поток; 3 - водоворотные зоны

Рис. 7.6. Кинематическая схема потока в нижнем бьефе

при свободном растекании и поверхностном режиме:

1 - донный валец; 2 - транзитный поток;

3 - слабые водоворотные зоны; 4 - волнистая поверхность

при сходе с укрепления

Рис. 7.7. Кинематические схемы потока при различных

степенях подтопления нижнего бьефа:

а - свободное растекание

;

б - несвободное растекание

;

в - сбойные течения (

; штриховой линией

показано возможное перемещение транзитного потока)

При этом свободное растекание по характеру взаимодействия с потоком в нижнем бьефе может быть затопленным и незатопленным, а несвободное растекание - всегда только затопленным. Затопленное растекание отличается истечением в нижний бьеф, в котором имеется определенный уровень воды; при этом наблюдаются течения с водоворотными массами, которые сужают ("поджимают") транзитную струю (см. рис. 7.5, 7.6). При незатопленном растекании истечение из трубы происходит в так называемое "сухое" русло, а водоворотные зоны отсутствуют (рис. 7.8).

Рис. 7.8. Кинематическая схема потока в нижнем бьефе

при свободном незатопленном растекании

Можно считать, что свободное затопленное растекание возможно при уклонах лога укреплений i_л <= 0,02. При больших уклонах растекание незатопленное.

7.9. Наличие свободного и несвободного растекания определяют по отношению бытовой глубины к так называемой предельной глубине h_п, при которой наступает затопление гидравлического прыжка в створе наибольшего растекания потока. При h_нб <= 0,85h_п возникает свободное растекание, при h_нб > 0,85h_п - несвободное растекание и сбойные течения. Здесь 0,85 - коэффициент запаса.

Отношение предельной глубины отводящего русла к критической

определяют по табл. 7.1 в функции степени расширения русла

(здесь B_л - ширина лога по поверхности потока при бытовой глубине h_нб) и числа Фруда на выходе из сооружения

где v_вых, h_вых - соответственно скорость и глубина на выходе из сооружения (см. гл. 5 и 6).

Таблица 7.1

	Значения при , равном
	1	2	4	6	8	10	12	14
1,3	1,2	1,55	1,9	2,1	2,2	2,2	2,1	1,8
1,5	1,3	1,6	2,0	2,2	2,3	2,3	2,1	1,8
1,75	1,4	1,75	2,15	2,3	2,4	2,35	2,15	1,8
2,0	1,55	1,9	2,3	2,5	2,55	2,45	2,2	1,8
2,5	1,7	2,05	2,55	2,7	2,65	2,55	2,35	1,8
3,0	1,9	2,25	2,75	2,85	2,8	2,65	2,3	1,8
4,0	2,15	2,55	3,05	3,25	3,2	2,9	2,45	1,8
5,0	2,35	2,75	3,2	3,9	3,85	3,1	2,55	1,8

Отношение

характеризует степень подтопления выхода из сооружения (здесь h_нб - глубина в нижнем бьефе). При

принимают 0,85h_п ~= 1,5h_к.

Краткая характеристика различных видов растекания потока в размываемых выходных руслах дается ниже.

7.10. При свободном затопленном растекании (наиболее частый случай) в выходных руслах с предохранительным откосом без гасителей энергии поток, попадая с укрепления на размываемую часть русла, образует пространственный гидравлический прыжок 1 (см. рис. 7.5). Транзитная часть 2 потока проходит под вальцом прыжка вдоль предохранительного откоса; с обеих сторон ее образуются мощные водоворотные зоны 3. Этот режим протекания называют донным, а сопряжение бьефов - сопряжением по схеме донного режима. При этом наибольшие скорости наблюдаются вблизи дна и при отсутствии надлежащего укрепления получается глубокий размыв.

При условиях, зависящих от глубины потока на сходе с укрепления, его кинетичности (числа Фруда), крутизны предохранительного откоса, размеров и глубины воронки размыва, а при наличии гасителя и от его типа, донный режим сменяется поверхностным (см. рис. 7.6). В этом случае на предохранительном откосе за сходом с укрепления образуется донный валец 1 с донными струями, идущими к сооружению, и транзитным потоком 2, проходящим над ним. В эпюре скоростей транзитного потока наибольшие скорости расположены вблизи поверхности. Донные течения, направленные к сооружению, интенсивно замывают яму, пока ее максимальная глубина не уменьшится до определенной величины, зависящей, в свою очередь, от характеристик подходного потока. После этого вновь возникает донный режим, и явление повторяется. Поэтому в выходных руслах с предохранительным откосом без гасителей глубина размыва в зависимости от режима пульсирует, увеличиваясь при донном режиме. Расчет рекомендуется вести на донный режим, наиболее опасный по размыву.

Воронка размыва формируется транзитным потоком и водоворотными зонами и имеет в плане форму эллипса, размеры полуосей которого зависят от максимальной глубины размыва и типа укрепления.

При применении в конце укрепления вертикального уступа или гасителя в виде ребра обеспечивается устойчивый поверхностный режим. В этих случаях допускается рассчитывать размыв на поверхностный режим сопряжения бьефов.

7.11. При свободном незатопленном растекании (см. рис. 7.8), что происходит обычно при уклонах выходного лога (укрепления) i_л > 0,02, водоворотные зоны отсутствуют, и поток существенно расширяется (при тех же гидравлических условиях). Это может привести к увеличению ширины укрепления. Однако в дальнейшем с увеличением уклона ширина растекания уменьшается.

7.12. При несвободном растекании (при подтоплении нижнего бьефа какими-либо сооружениями) гидравлический прыжок надвигается на сооружение. При этом нижний бьеф гасит энергию водоворотных зон, играющих большую роль в размыве за сооружениями.

Чем больше степень подтопления нижнего бьефа, тем больше стеснение потока и слабее водоворотные зоны (см. рис. 7.7, а и б). При

возникает сбойное течение (см. рис. 7.7, в).

При сбойном течении происходит увеличение удельного расхода потока на части ширины русла. Однако в условиях дорожных водопропускных сооружений блуждание сбойной струи приводит и к уменьшению расчетных глубин размыва, соответствующих данной продолжительности паводка.

При несвободном растекании (подтоплении со стороны нижнего бьефа) воронка размыва сужается и удлиняется.

7.13. На характер растекания потока также оказывает влияние ширина выходного лога B_л, оцениваемая путем сопоставления ее с эквивалентным диаметром D_э, представляющим собой диаметр круга, равновеликого по площади поперечному сечению водопропускного сооружения

При очень малой ширине лога B_л <= 2D_э и неразмываемых берегах "лист" растекания формируется целиком на укреплении, и на сходе с него возникает устойчивый поверхностный режим (рис. 7.9, а). При большей ширине лога возможен донный режим, но с водоворотными зонами меньшей ширины (рис. 7.9, б). Лишь при

возможен донный режим, соответствующий условиям свободного растекания (рис. 7.9, в).

Рис. 7.9. Кинематические схемы растекания потока

при различной ширине лога B_л:

а - B_л <= 2D_э - поверхностный режим;

б - 2D_э < B_л < 10D_э - донный режим с суженными водоворотными

зонами; в - B_л > 10D_э - режим свободного растекания

При весьма значительной ширине лога

водоворотные зоны начинают вновь сокращаться при одновременном уменьшении глубин и скоростей в них. Для этого случая с некоторым приближением можно пользоваться зависимостями, приводимыми в настоящей главе для определения гидравлических характеристик и размыва при B_л <= 10D_э. Более точно этот расчет можно выполнить на основе двухмерной математической модели.

7.14. В ряде случаев при уклонах лога i_л > 0,02 за воронкой размыва ниже по течению возможно образование промоины (канавы), которое приводит к увеличению глубины воронки размыва на величину, равную глубине канавы на ее входе, а также повышает вероятность оврагообразования. На рис. 7.10 дано сопоставление характера размыва для случая отсутствия канавы (рис. 7.10, а) и ее наличия (рис. 7.10, б). В зависимости от гидравлических характеристик потока, уклона и грунтов лога промоина может иметь ограниченный характер либо развиваться на всем протяжении лога. В последнем случае необходимы специальные меры защиты, так как это угрожает сохранности водопропускного сооружения.

Рис. 7.10. Схемы деформаций в нижних бьефах труб

при отсутствии (а) и наличии (б) промоины (канавы):

1 - воронка размыва; 2 - промоина (канава);

3 - граница растекания

КИНЕМАТИКА ПОТОКА ПРИ НЕРАЗМЫВАЕМЫХ ВЫХОДНЫХ РУСЛАХ

7.15. Кинематика потока в нижних бьефах сооружений при неразмываемых выходных руслах существенно отличается от рассмотренной выше, что сказывается и на методике расчета.

Несмотря на наличие тех же режимов пространственного сопряжения бьефов, что и при размываемых выходных руслах, т.е. свободного растекания и сбойных течений, каждый из этих режимов в данных условиях имеет свои особенности.

Свободное растекание бурного потока (рис. 7.11, а) характерно интенсивным расширением транзитной струи, сопровождающимся уменьшением глубин и ростом скоростей. На участке AB и CD бурный поток граничит с водоворотными областями ABF и CDG, а на участке BHEKD сопрягается с бурным потоком в отводящем русле. При спокойном состоянии потока в отводящем русле в пределах клина BHEKD образуется гидравлический прыжок HK. Предельное положение последнего соответствует сечению BD. В том и другом случае распределение скоростей по ширине отводящего русла за фронтом прыжка очень неравномерное.

Рис. 7.11. Кинематические схемы режимов течения

потока в нижних бьефах сооружений:

а - свободное растекание; б - сбойные течения;

1 - косые прыжки; 2 - гидравлический прыжок

С продвижением фронта гидравлического прыжка выше сечения BD заполняется до уровня воды в отводящем русле одна из боковых водоворотных областей ABF или CDG. Поперечное равновесие потока нарушается, и транзитная струя отклоняется к противоположному берегу. Устанавливается режим сбойного течения (рис. 7.11, б). Предельная глубина в отводящем русле h_п, соответствующая положению гидравлического прыжка в сечении BD, определяющая режим сопряжения бьефов, находится так же, как и для размываемых русел, по табл. 7.1: при h_нб <= 0,85h_п возникает свободное растекание потока, при h_нб > 0,85h_п возникают сбойные течения.

Сбойное течение, как и свободное растекание, имеет несколько форм движения потока в нижнем бьефе, начиная от сбойного течения бурного потока и кончая сбойным течением спокойного потока. Наиболее опасно сбойное течение бурного потока из-за наличия высоких скоростей, часто направленных под большим углом к берегу отводящего русла. Сбойное течение, как и свободное растекание, обычно приводит к увеличению скоростей за выходом из сооружения.

ОПРЕДЕЛЕНИЕ ГИДРАВЛИЧЕСКИХ ХАРАКТЕРИСТИК

ПОТОКА НА УКРЕПЛЕНИИ

Расчеты на основе математической модели

7.16. Все описанные выше режимы течения в нижнем бьефе (затопленное и незатопленное, свободное и несвободное растекание в размываемых руслах) могут быть рассчитаны на основе двухмерной математической модели.

Математическая модель, описывающая течения потока в нижних бьефах водопропускных труб при фиксированной (неизменной во времени) поверхности дна, состоит из системы уравнений двухмерной (плановой) гидравлики (уравнений мелкой воды с трением) и граничных условий, соответствующих реальным условиям протекания.

Уравнения в форме интегральных законов сохранения приведены в п. 2.20. Граничные условия для наиболее характерного для нижних бьефов труб случая, когда число Фруда на выходе из трубы больше единицы (Fr_вых > 1), имеют следующий вид:

h = h_вых на

; v_n = 0 на

, (7.1)

где

- часть границы области течения, соответствующая выходному отверстию трубы;

- то же, соответствующая твердым (непроницаемым) стенкам (берегам лога);

v_n - нормальная составляющая к границе компонента скорости течения.

Система уравнений (2.37), (2.38) с граничными условиями (7.1) решается численно методом конечных разностей на регулярных и нерегулярных четырехугольных и треугольных сетках. Применяются схемы сквозного счета первого и второго порядков точности, основанные на использовании аналитического решения задачи о распаде гидродинамического разрыва [3].

По указанным алгоритмам в лаборатории гидравлики ЦНИИСа разработан и эксплуатируется комплекс программ "БОР" на языке Фортран для ЭВМ серии ЕС. Программа позволяет рассчитывать гидравлические характеристики потока в каждой точке укрепления при различных уклонах трубы и лога, различных коэффициентах шероховатости n и параметрах расхода П_Q с учетом влияния формы воронки размыва и условий протекания в выходном логе, в том числе при подтоплении со стороны нижнего бьефа. Примеры расчета нижнего бьефа по программе приведены в работе [2], примеры расчета других гидравлических задач - в [3]. Общая последовательность расчетов такова:

а) на плане нижнего бьефа водопропускной трубы строится разностная сетка, учитывающая реальные очертания выходного лога, расположение и диаметр трубы, длину и ширину укрепленной части, размеры воронки размыва (рассчитанной по эмпирическим формулам);

б) в узлах сетки задаются реальные отметки дна на укреплении и в выходном логе (с учетом ямы размыва), а также коэффициенты шероховатости и начальные значения скорости и глубины потока в нижнем бьефе (обычно они принимаются бытовыми);

в) на сторонах элементов сетки, прилегающих к графикам, задаются граничные условия (7.1);

г) производится расчет по программе до нахождения стационарного решения, когда поля скоростей и глубин на укреплении на нескольких последовательных шагах по времени практически совпадают. При определенных условиях стационарное решение может не существовать (сбойность течения). Тогда необходимо анализировать результаты расчета на различные моменты времени.

Примеры разностных сеток и результатов расчета по программе приведены в справочном приложении 7.1.

Расчеты на основе эмпирических зависимостей

7.17. При уклонах лога i_л <= 0,02 гидравлические характеристики потока на укреплении определяют по следующим зависимостям.

Принимают максимальную скорость на укреплении

v_max = 1,2v_вых. (7.2)

Средние глубины потока в конце укрепления длиной

вычисляют по формуле

h_укр(к) = 0,2П_QD_э. (7.3)

Ширину растекания потока на укреплении в створе, расположенном на расстоянии x от конца оголовка, находят по зависимости

(7.4)

b_р - ширина оголовка его в конце.

Показатель степени

(7.5)

где K - коэффициент формы воронки размыва, определяемый по графику на рис. 7.12;

- максимальная глубина размыва на данное время (см. ниже);

- эталонный расход.

Рис. 7.12. График для определения

коэффициента формы воронки размыва K

Приближенно в средних условиях показатель степени можно определять по формуле

(7.6)

полученной из формулы (7.5) при K = 0,8 и

7.18. Гидравлические характеристики потока на укреплении при уклонах лога i_л > 0,02 определяют по приводимым ниже формулам, лишь при коэффициенте шероховатости укрепления

. В остальных случаях расчет следует проводить по программе, основанной на математической модели протекания потока.

Принимают максимальную скорость на укреплении

v_max = v_вых. (7.7)

Скорости v на укреплении определяют из уравнения

(7.8)

где v_ось - скорость на оси потока на расстоянии x от конца оголовка;

y - расстояние от оси потока (середины укрепления) до данной точки;

- половина ширины растекания.

Осевая скорость задается соотношением

(7.9)

Формулами (7.8), (7.9) можно пользоваться в диапазоне

0 <= x/D_э <= 20.

Глубины на укреплении при 0,5 <= x/D_э <= 20 определяют из формул:

(7.10)

(7.11)

Ширина растекания потока на укреплении

B_раст = MN + b_р. (7.12)

Здесь параметры M и N определяются соотношениями:

(7.13)

(7.14)

где C_укр - коэффициент Шези на укреплении.

В свою очередь

(7.15)

где h_укр - средняя глубина потока в конце укрепления, принимаемая по формуле (7.3).

Для упрощения расчетов значения B_раст, v (x, y), h (x, y) можно определять по графикам приложения 7.2.

7.19. В выходных руслах с гасителями глубины, скорости и границы растекания потока определяют следующим образом:

а) при применении гасителей в виде ребра и стенки в раструбном оголовке (типы выходных русел 3 и 4) с некоторым приближением можно пользоваться рекомендациями для выходных русел без гасителей;

б) при применении гасителей в виде раструбов с водобойными стенками характеристики на выходах из сооружений определяют в соответствии с методикой, изложенной в гл. 4 (пп. 4.26 - 4.30). Ширину растекания на укреплении определяют по формулам:

при гасителе в виде расширяющегося колодца с водобойной стенкой (тип 5)

(7.16)

при гасителе с двумя водобойными стенками (гаситель ЦНИИСа, тип 6)

(7.17)

где b_рг - ширина выхода из гасителя;

i_г - уклон дна гасителя.

Особенности определения гидравлических характеристик

потока на укреплении в неразмываемых выходных руслах

7.20. При свободном растекании возникает три характерных участка нижнего бьефа (рис. 7.13):

1) участок (зона) растекания длиной l_раст;

2) переходной участок длиной l_пер, на котором поток обладает повышенной турбулентностью и более высокими скоростями по сравнению с бытовыми условиями;

3) бытовой поток.

Рис. 7.13. Характерные зоны при свободном растекании потока:

1 - зона растекания; 2 - переходной участок;

3 - бытовой поток

Расчетом устанавливается протяженность зоны растекания и переходного участка, а также максимальные скорости и глубины на них. Наиболее универсальные и точные результаты получаются при расчете неразмываемых выходных русел на основе двухмерной (плановой) математической модели (см. пп. 7.16 и 2.20). При уклонах лога i_л < 0,02 этот способ оказывается практически единственным для получения реальной картины течения. При i_л > 0,02 (т.е. при отсутствии водоворотных зон) можно пользоваться также приближенным способом, изложенным ниже.

Для определения границы участка растекания потока выполняют следующие расчеты.

1. Находят ширину растекания потока B_раст в различных створах укрепления по формуле (7.12).

2. Находят точку пересечения граничной струи с берегами лога (в случае непрямоугольного поперечного сечения приводят его к прямоугольному) и устанавливают в этой точке глубину потока h₁, скорость v₁ и число Фруда

. Координата этой точки x₁ (см. рис. 7.11).

3. Находят графически угол

отклонения растекающегося потока от продольной оси x в месте встречи с берегами (см. рис. 7.11).

4. По значениям

находят на левой части графика, представленного на рис. 7.14, угол отклонения

, возникающего в точке встречи потока с берегом фронта косого гидравлического прыжка от направления вектора скорости. На рис. 7.14 верхняя часть графиков (выше штриховой линии) соответствует спокойному состоянию потока за косыми прыжками с Fr" < 1, а ниже пунктира - бурному с Fr" > 1.

Рис. 7.14. Графики для определения границы зоны

растекания и режимов потока на переходном участке

5. Определяют расстояние x₂ (см. рис. 7.11) от выхода из сооружения до точки пересечения косых гидравлических прыжков (точка E):

x₂ = x₁ + x₃; (7.18)

здесь

6. Находят в точке E, имеющей координаты x = x₂ и y = 0, глубину h₂, скорость v₂ и число Фруда Fr₂, пользуясь эмпирическими зависимостями (7.9) и (7.11).

7. Определяют, пользуясь графиком, приведенным на рис. 7.14, глубину отводящего русла в сечении с координатой x = x₂, предполагая спокойное состояние потока за точкой пересечения косых прыжков (точкой E). Для этого по значениям

в этой точке находят на левой части графика выше штриховой линии угол

и затем на правой части графика - отношение h"/h' (h', h" - сопряженные глубины гидравлического прыжка, причем h' = h₂). Умножая это отношение на h' = h₂, получают большую сопряженную глубину прыжка h", сопоставляя которую с бытовой глубиной в канаве или логе h_нб, устанавливают состояние потока на переходном участке:

при h" > h_нб поток на переходном участке, располагающемся ниже точки E, будет в бурном состоянии. Глубина за прыжком h₃ при этом определяется аналогично предыдущему расчету при тех же параметрах

по левой части графика на рис. 7.14, но на участке ниже штриховой линии. Длина участка растекания в этом случае l_раст = x₂;

при h" < h_нб - прыжок занимает промежуточное положение между точкой E и сечением BD (сечение HK на рис. 7.11) - поток на переходном участке, располагающемся за линией прыжков (HK), будет находиться в спокойном состоянии.

Расстояние x от выхода из сооружения до фронта прыжка, определяющее длину участка растекания в этом случае, можно найти по формуле

где h_п - предельная глубина (см. п. 7.9).

Теперь перейдем к рассмотрению переходного участка. Если поток в отводящем русле находится в бурном состоянии, то максимум скоростей образуется на оси отводящего русла и расчетная скорость с учетом пульсации

v_пер(max) ~= 1,6v_пер, (7.19)

где v_пер - средняя скорость в отводящем русле в заданном сечении.

При спокойном состоянии потока в отводящем русле максимум скоростей образуется у берегов и отношения расчетных максимальных скоростей с учетом пульсации v_пер(max) к бытовым v_нб определяют по графику, представленному на рис. 7.15 в функции отношения бытовой глубины h_нб в логе к критической h_к(нб) и степени расширения русла

(см. табл. 7.1).

Рис. 7.15. График для определения максимальных скоростей

на переходном участке при спокойном состоянии потока

Длину переходного участка l_пер, на котором происходит выравнивание скоростей примерно до бытовых (превышение не более 15%), определяют по формуле (при

)

где h_к(нб) - критическая глубина в канаве.

Считают, что на переходном участке скорости от v_пер(max) до бытовых изменяются по линейному закону.

Укрепления в начале переходного участка подбирают по большей из скоростей: v_пер(max) и максимальной скорости в конце участка растекания (см. выше). На остальной части переходного участка укрепления назначают по соответствующим скоростям в заданных сечениях, определяемых путем линейной интерполяции между v_пер(max) и v_нб в функции отношения

, где l_пер(_i₎ - расстояние от начала переходного участка до заданного сечения.

7.21. Расчет сбойного течения сводится к следующему.

1. Определяют скорость на выходе из сооружения. Для этого по графику, приведенному на рис. 7.16, находят отношение скорости на выходе из сооружения и критической скорости в нем

в функции отношения бытовой глубины h_нб к критической в нижнем бьефе (канаве) h_к(нб). Причем расчет выполняют для заданного отношения

, где a (см. рис. 7.11, б) - расстояние от продольной оси сооружения до ближайшего уреза воды; при симметричном расположении канавы относительно сооружения

Рис. 7.16. График для определения скорости

на выходе из сооружения v_вых при сбойном

течении потока

По значению отношения

и критической скорости находят v_вых.

2. Определяют длину участка расширения транзитного потока до бытовых условий, что соответствует длине большого водоворота

где f(m) - функция, определяемая по графику, представленному на рис. 7.17, в зависимости от отношения

Рис. 7.17. График зависимости

3. По графику, приведенному на рис. 7.18, определяют отношение максимальных скоростей вдоль отводящего русла v_max(сб) к скоростям на выходе из сооружения v_вых в функции отношения расстояния x от подошвы насыпи на выходе из сооружения до рассматриваемого сечения к длине большого водоворота L_б.в.

Рис. 7.18. График для определения максимальных скоростей

при сбойном течении v_max(сб)

При недопущении размыва в конце канавы

используется кривая графика, соответствующая отношению

, при допущении размыва - кривые, соответствующие различной величине размыва с отношениями

; 0,7; 1,0; 1,5; 1,75; 2,0.

Расчетная глубина размыва

определяется в соответствии с рекомендациями настоящей главы для размываемых выходных русел. Допущение размыва в конце канавы позволяет при

сократить длину укрепления.

РАСЧЕТЫ РАЗМЫВА

Общие положения

7.22. Основной величиной при расчете размываемых выходных русел является максимальная глубина размыва

, формируемая потоком в бытовом логе за время прохождения паводка. Она в значительной мере определяет как плановые размеры укреплений, так и глубины заложения их концевых частей.

Расчеты максимальных глубин размыва ведут по методике, разработанной в ЦНИИСе. В качестве одного из основных параметров для расчета размыва используют так называемую предельную глубину размыва

, соответствующую неограниченному во времени прохождению заданных расходов.

7.23. Учет времени прохождения паводков выполняют в двух вариантах:

по эквивалентному времени, соответствующему условному (эквивалентному) паводку с гидрографом прямоугольной формы и расходом, равным расходу на пике паводка, при прохождении которого глубина размыва будет равна размыву при прохождении реального паводка;

по реальному гидрографу паводка, заменяя его гидрографом ступенчатой формы.

7.24. Различают размыв в однородных (связных и несвязных) и неоднородных грунтах, причем для каждого из этих грунтов возможны случаи свободного (затопленного и незатопленного) и несвободного растекания и узкого лога, т.е. лога, ширина которого недостаточна для формирования воронки размыва.

Кроме того, существенными особенностями отличается картина размыва в выходных руслах с каменной наброской, расположенной в виде рисбермы в конце укрепления.

Размыв в однородных грунтах

7.25. Однородными считаются все связные грунты и несвязные при соблюдении условия

d_max/d <= 2, (7.20)

где d_max - средний диаметр крупных частиц, которые составляют 5% массы грунта, или диаметр самой крупной фракции, если она составляет не менее 5% массы грунта;

d - расчетный диаметр частиц однородного несвязного грунта (см. п. 7.29).

7.26. Максимальные глубины размыва в условиях свободного затопленного растекания, соответствующего уклонам лога i_л <= 0,02, определяют по формуле

(7.21)

где

- соответственно предельная и максимальная глубины размыва в заданном выходном русле при отсутствии каменной наброски (

см. в п. 7.28);

- коэффициент, учитывающий время прохождения паводка (см. п. 7.20).

7.27. Максимальные глубины размыва в условиях свободного незатопленного растекания, соответствующего уклонам лога i_л > 0,02, определяют по формуле

(7.22)

где

- глубина размыва выходного лога за счет возможного образования канавы (см. п. 7.31).

7.28. Предельные глубины размыва, соответствующие свободному затопленному растеканию (i_л < 0,02), определяют по формуле

(7.23)

где r, s - коэффициент и показатель степени, значения которых для различных типов выходных русел приведены в табл. 7.2;

s₁ - показатель степени; s₁ = 1 для типов, приведенных в табл. 7.2; s₁ для каменной наброски см. в п. 7.64;

- масштабный коэффициент;

здесь D₀ = 1 м; для ускорения расчетов в табл. 7.3 приведены значения

для принятых в практике значений D_э;

- коэффициент, учитывающий тип концевой части выходных русел; при наличии предохранительного откоса

, при его отсутствии или наличии вертикальной стенки

, для выходных русел с ребром

независимо от наличия стенки;

- эквивалентный диаметр (эквивалентное отверстие), представляющий собой диаметр круга, равновеликого по площади поперечному сечению сооружения

; для мостов при определении

принимают высоту отверстия

; здесь v_m = 3 м/с - условная скорость под мостом; для многоочковых труб эквивалентный диаметр определяют по суммарной площади очков;

Q - максимальный расход регламентируемого нормами паводка (расчетного или наибольшего);

L - длина укрепления, м;

b - отверстие сооружения, принимаемое равным: для прямоугольных труб - их ширине; для мостов с вертикальными стенками - расстоянию между устоями или средней ширине потока под мостом для непрямоугольных подмостовых сечений; для круглых труб - их диаметру; для овоидальных - максимальной ширине поперечного сечения; для многоочковых труб - сумме отверстий очков;

b_р - ширина сечения: для труб - в конце оголовка; при портальных оголовках - в конце конусов; для мостов b_р = b + H_нас, здесь H_нас - высота насыпи у моста.

Таблица 7.2

Тип выходного русла	Коэффициент r	Показатель степени s	Относительный граничный расход (Q/Q_к)_гр
1, 1к	0,9	0,6	Без ограничений
2, 2к	0,9	0,6	То же
3, 3к	0,6	0,4	1,0
4, 4к, 5, 5к, 5а, 5ак	1,0	1,0	0,5
6, 6к, 6а, 6ак	1,0	1,0	0,3

Таблица 7.3

D_э, м		Q_min, м³/с, при		D_э, м		Q_min, м³/с, при
D_э, м				D_э, м
0,5	0,89	0,25	0,6	3,0	0,79	0,8	1,8
0,75	0,87	0,3	0,75	4,0	0,77	0,9	2,1
1,0	0,85	0,4	0,9	5,0	0,76	1,0	2,5
1,25	0,83	0,45	1,1	6,0	0,75	1,2	2,75
1,50	0,82	0,5	1,25	10,0	0,73	1,6	3,7
2,0	0,81	0,6	1,5	15,0	0,70	2,1	4,9

В последнем столбце табл. 7.2 выписаны граничные значения (Q/Q_к)_гр, при превышении которых в формулу (7.23) вместо Q/Q_к должны подставляться эти значения.

7.29. При расчете размывов грунты в логе подразделяются на связные и несвязные. К несвязным грунтам относятся крупнообломочные и песчаные грунты, не обладающие свойством пластичности (раскатывания). К связным относятся глинистые, суглинистые и супесчаные грунты с числом пластичности более 0,01, а также глинистые и песчаные грунты при степени заторфованности (содержании растительных остатков) более 10%.

Расчетный диаметр частиц однородного несвязного грунта

(7.24)

где p_i - содержание по массе в процентах i-й фракции со средним диаметром частиц d_i.

Расчетный (эквивалентный) диаметр пылеватого грунта, содержащего пылеватые частицы, доля которых в грунте p_п > 0,1 - d_э, мм, определяют по формуле

Расчетный (эквивалентный) диаметр связного грунта, мм,

d_э = 7,5(0,1 + 100C_р), (7.25)

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: СНиП отсутствует в [43]. Видимо, имеется в виду пункт [42].

где C_р - расчетное сцепление, МПа, которое определяют на основании стандартных методов испытаний образцов с учетом возможного (вероятного) отклонения значения сцепления от нормативного; для предварительных расчетов значение C_р для глинистых грунтов можно принимать по данным СНиП [43], а для торфов - по табл. 7.4.

Таблица 7.4

Характристика заторфованного грунта		Расчетное сцепление C_р, МПа
Содержание растительных остатков в грунте, %	Вид торфа	Расчетное сцепление C_р, МПа
> 60	Древесный	0,0005
> 60	Хвощевый	0,0025
60 - 40	Осоковогипновый	0,0025
60 - 40	Сфагновый	0,004
40 - 25	Осоковогипновый	0,0075
40 - 25	Сфагновый	0,01

При наличии в логе засоленных и мерзлых связных грунтов расчетный их диаметр определяют по формуле (7.25) с введением в нее коэффициента

Коэффициент

принимают по табл. 7.5 в зависимости от состава породы и содержания льда, которые определяют криогенную текстуру, т.е. совокупность признаков сложения мерзлого грунта, обусловленную ориентировкой, относительным расположением и распределением различных по форме и размерам ледяных включений и льда-цемента.

Таблица 7.5

Криогенная структура	Содержание льда, %	Коэффициент
Атакситовая	> 50	0 - 0,12
Сетчатая	50 - 30	0,12 - 0,25
Слоистая	40 - 25	0,25 - 1
Массивная и корковая	< 25	1

При содержании легкорастворимых солей до 3% коэффициент

принимают по табл. 7.6. При большем содержании солей в грунте коэффициент

устанавливается на основании специальных исследований.

Таблица 7.6

Расчетное сцепление C_р, МПа	<= 0,0005	0,001	0,002	0,003	0,004	0,005	0,0075	>= 0,01
Коэффициент	0,85	0,80	0,64	0,56	0,52	0,45	0,40	0,35

Для несвязных грунтов температурный режим не оказывает влияния на их размываемость, и поэтому следует принимать

. При содержании в несвязных грунтах легкорастворимых солей средний диаметр частиц определяют по формуле (7.24) с коэффициентом 0,85.

7.30. Коэффициент

в формуле (7.21) при пропуске постоянного расхода Q в течение времени t рассчитывают по формуле

(7.26)

В свою очередь

(7.27)

причем в случае наличия гасителей граничные значения Q/Q_к определяют по табл. 7.2. В формуле (7.27) величина C_р дана в мегапаскалях (МПа).

Для реальных гидрографов (показательного, треугольного, трапециевидного), форма которых регламентирована [41], расчетное время определяется зависимостью

(7.28)

где W - объем стока за время паводка.

Для более точного учета фактора времени, особенно при гидрографах сложной формы (многопиковых и т.п.), рекомендуется пользоваться методикой расчета, изложенной в приложении 7.3.

Для определения значения

наряду с формулой (7.26) можно пользоваться графиком на рис. 7.19. Для приближенных расчетов можно принимать: для несвязных грунтов

; для связных -

Рис. 7.19. График для определения

относительной глубины размыва

7.31. Глубину промоины определяют в такой последовательности (см. рис. 7.10).

1. Вычисляют ширину потока B_нр, при которой скорость в логе равна неразмывающей:

ИС МЕГАНОРМ: примечание.

Формула дана в соответствии с официальным текстом документа.

(7.29)

Здесь для одернованных логов принимают v_н = 1,5 м/с, а во всех остальных случаях

(7.30)

где d_э - эквивалентный диаметр грунта лога (см. п. 7.29).

ИС МЕГАНОРМ: примечание.

Нумерация пунктов дана в соответствии с официальным текстом документа.

22. Сравнивают ширину потока B_нр с шириной лога (для явно выраженного лога) либо с предельной шириной растекания потока на наклонной плоскости:

B_{раст(пр)} = M + b_р, (7.31)

где M находят по формуле (7.13) или по зависимостям приложения 7.2 (с заменой i_укр и C_укр на i_л и C_л).

Если B_нр > B_л либо B_нр > B_{раст(пр)}, то размыв дна лога может происходить на большой длине и сопровождаться значительным понижением отметок, в том числе и у концевой части укрепления. В этом случае необходимо принимать специальные меры защиты: устраивать перепады, укреплять лог до его подошвы или на значительном протяжении.

В противном случае определяют положение створа x = X_нр, в котором прекращается размыв, и глубину потока в нем по формулам:

(7.32)

(7.33)

где значение N определяют из формулы (7.12), приняв B_раст = B_нр.

(7.34)

Вместо формулы (7.34) можно использовать график на рис. 2 приложения 7.2.

3. Производят расчет параметров (ширины и глубины потока) на входе в канаву. Вначале определяют максимальную глубину размыва

для случая отсутствия промоины (канавы) по формуле (7.21). Затем находят (в первом приближении) расстояние от выхода из трубы до входа в канаву (см. рис. 7.10):

(7.35)

где m_от - коэффициент заложения откоса укрепления.

Если X_кан > X_нр, то полагают

Вычисляют ширину растекания B_{раст(кан)} в створе начала канавы B_{раст(кан)} = B_раст(x_кан) по формулам (7.11) - (7.13).

Находят ширину b_кан и глубину h_кан потока на выходе в канаву при стабилизации размыва:

(7.36)

(7.37)

Если B_{раст(кан)} < b_кан, то принимают b_кан = B_{раст(кан)}, а h_кан вычисляют по формуле (7.37); в противном случае к расчету принимают b_кан и h_кан, вычисленные по формулам (7.36) и (7.37).

4. Определяют среднюю глубину потока в канаве

(7.38)

5. Определяют глубину размыва канавы

(7.39)

где коэффициент Шези определяют при h = h_кан(ср) по формуле

(7.40)

6. Определяют уточненное расстояние от выхода из трубы до входа в канаву

(7.41)

Если

, то заменяют X_кан на

и производят повторный расчет канавы.

Если

, то либо увеличивают отверстие сооружения, либо принимают специальные меры защиты (устраивают перепады, консольные сбросы и т.п.).

7.32. Максимальная глубина размыва при несвободном растекании

(7.42)

где

- максимальная глубина размыва при свободном растекании, определяемая при любых уклонах лога i_л по формуле (7.21), так как канава (промоина) в условиях подтопления не образуется;

- показатель степени, учитывающий замедление процесса размыва в условиях несвободного растекания.

В свою очередь

(7.43)

где

- степень подтопления нижнего бьефа (см. п. 7.8).

"Узкими" считают лога, ширина которых B_л < 10D_э, а берега слабо размываемы. В узких логах шириной B_л > 2D_э максимальную глубину размыва при i_л <= 0,02 определяют по формуле

(7.44)

где

- находится по формуле (7.21);

- коэффициент ширины лога (если K_л < 1, то принимают K_л = 1);

K - коэффициент формы воронки размыва при свободном растекании (см. рис. 7.12);

- показатель степени, учитывающий замедление процесса размыва в "узких" логах.

В свою очередь

(7.45)

В случаях когда i_л > 0,02, максимальную глубину размыва находят с учетом возможного образования канавы по формуле

(7.46)

в которой

вычисляется по методике п. 7.31 с соответствующей заменой

на

по формуле (7.44).

7.33. Максимальную глубину размыва в "узких" логах при B_л <= 2D_э и i_л <= 0,02 дополнительно корректируют по формуле

(7.47)

причем в правую часть подставляют

из формулы (7.44). При больших уклонах лога (i_л > 0,02) расчет ведут по формуле (7.46) с заменой

на

, найденное по формуле (7.47).

При

принимают

7.34. В случае сочетания подтопления и "узкого" лога расчет размыва ведут только на один фактор: при

не учитывают ширину лога, принимая K_л = 1 и

, а при

- как в "узком" логе при отсутствии подтопления, принимая

Размыв в неоднородных несвязных грунтах

7.35. При расчете размывов за укреплениями в неоднородных грунтах (без каменной наброски) следует учитывать возможность образования в отводящем русле естественной отмостки.

Неоднородными грунтами при расчете размывов за малыми равнинными водопропускными сооружениями считают грунты, содержащие крупные включения или удовлетворяющие неравенству d_от/d > 2, где d_от - средний диаметр частиц, образующих отмостку на дне воронки размыва. Размер d_от зависит от гранулометрического состава грунта, гидравлических характеристик потока и геометрических характеристик сооружения; определяют его подбором из уравнения

(7.48)

где p_от - весовая доля отмащивающих частиц в размываемом грунте;

- предельная глубина размыва в грунте со средним диаметром частиц d.

Глубина

определяется:

а) при несвободном и свободном затопленном растекании (i_л <= 0,02) - по формуле (7.23), т.е.

;

б) при свободном незатопленном растекании (i_л > 0,02) - по формуле

(7.49)

где

см. в п. 7.31;

в) в узком логе при 2D_э < B_л < 10D_э - по формуле

(7.50)

г) в узком логе при

- по формуле

(7.51)

Под крупными включениями понимают крупные фракции грунта в количестве не менее 0,5%, для которых соблюдается неравенство

d_max/d_м > 15,

где d_м - средний диаметр частиц крупных включений, весовая доля которых в размываемом грунте выражается числом p_max; при наличии крупных включений d_max и p_max принимают в качестве характеристик отмостки; примером крупных включений является галька (или гравий) в песке;

ИС МЕГАНОРМ: примечание.

Обозначения даны в соответствии с официальным текстом документа.

d_м - средний диаметр частиц мелких фракций, не вошедших в слой отмостки.

В свою очередь

(7.52)

Для определения d_от из уравнения (7.48) вначале находят величину

. Затем, принимая некоторое значение весовой доли p_от крупных (отмащивающих) частиц в размываемом грунте, подсчитывают для него средний диаметр частиц

где

Если отношение

, повторяют те же действия до тех пор, пока подберут (с точностью +/- 5%) значения p_от и d_от, удовлетворяющие уравнению (7.48).

Для ускорения расчетов по формуле (7.48) рекомендуется пользоваться графиком, приведенным на рис. 7.20, и находить по нему

, а затем вычислять N = p_отN₀, подставляя p_от в долях единицы.

Рис. 7.20. График для определения

Если расчетом получено значение p_от менее 0,5%, глубину размыва определяют по формулам для однородного несвязного грунта. Если же самая крупная фракция со средним диаметром составляет не менее 0,5% и удовлетворяет неравенству

, в расчете размывов принимают средний диаметр и весовое содержание этой фракции.

Предельную глубину воронки размыва за водопропускными трубами и мостами в неоднородных несвязных грунтах определяют по формуле

(7.53)

где

- коэффициент, характеризующий увеличение размываемости крупных частиц d_от при воздействии на них мелких фракций d_м: при d_от/d_м <= 15

, а при d_от/d_м > 15

;

- коэффициент неоднородности частиц в слое отмостки, характеризующий отношение площадей проекций частиц, подсчитанных с учетом гранулометрического состава и по среднему диаметру на поверхность выстилки;

;

p_i, d_i - весовые (в долях) содержания фракций, отмащивающих воронку, и средние диаметры их частиц.

Когда грунт содержит крупные включения, первый член формулы (7.53) определяют при d = d_м.

При содержании крупных включений в материале русла рассчитанная по формуле (7.53) глубина воронки может оказаться больше той, при которой уже не выносятся мелкие частицы грунта со средним диаметром d_м. Поэтому при наличии крупных включений за расчетную глубину воронки принимают меньшую из глубин, полученных по формуле (7.53), и для однородного грунта со средним диаметром частиц d_м - по соответствующим формулам (7.21), (7.22), (7.42) и (7.47).

Размыв в выходных руслах с каменной наброской

7.36. Для уменьшения размыва за водопропускными сооружениями применяют каменную наброску. Камень укладывают в конце укрепления в виде рисбермы треугольного или трапецеидального сечения (см. рис. 7.2, типы с индексами "к").

Размеры рисбермы из каменной наброски назначают расчетом из условия обеспечения устойчивости сооружения от подмыва и характера работы камня. В зависимости от гидравлических характеристик потока на выходе из сооружения, а также крупности и количества камня возможны следующие случаи взаимодействия рисбермы с грунтом русла:

размыв происходит только в каменной наброске (рис. 7.21, а);

камень и грунт нижнего бьефа работают совместно (рис. 7.21, б);

каменная наброска работает как гибкая конструкция (например, тюфяк): по мере размыва камень сползает в образующуюся воронку размыва, защищая укрепление (рис. 7.21, в).

Рис. 7.21. Схемы расположения камня в воронке размыва:

а - размыв происходит только в каменной наброске;

б - совместная работа камня и грунта лога;

в - рисберма работает как гибкая конструкция

Ниже приведены расчеты размывов в нижних бьефах сооружений в соответствии с ролью наброски в конструкции укрепления.

7.37. Размыв в наброске из камня рассчитывают для камня как для грунта, слагающего русло. Применительно к равнинным водопропускным сооружениям (трубам и малым мостам с закрепленным руслом) предельную глубину размыва

определяют по формулам (7.23), (7.49), (7.50) или (7.51) в зависимости от условия растекания потока. При этом в качестве среднего диаметра частиц грунта d принимают среднюю крупность камня d_н.

Для обеспечения работы укрепления из каменной наброски по такому типу задают следующие размеры каменной рисбермы:

ширину рисбермы в направлении, перпендикулярном оси сооружения - более 12 - 15 эквивалентных диаметров сооружения

или равной ширине размываемого русла при B_н <= 12D_э и неразмываемых откосах лога;

ширину рисбермы l_н (направление вдоль потока) - больше размера воронки в этом направлении при глубине размыва

в грунте лога

где m_от, m_н - коэффициенты заложения предохранительного и низового откосов; обычно предохранительные откосы устраивают с m_от = 1,5; при свободном растекании можно принять m_н = 2, а несвободном - крутизну низового откоса определяют в зависимости от степени подтопления

по табл. 10.1.

Глубину укладки камня

назначают из условия, что ниже отметки дна воронки размыва располагается не менее трех слоев камня:

Расчет правомерен, если силовое воздействие потока на сходе с жесткой части укрепления достаточно для выноса камня из рисбермы. Это условие соблюдается, если расход в сооружении больше указанного в табл. 7.3. В иных случаях расчет следует вести на грунты лога с учетом удлинения укрепления на ширину каменной рисбермы поверху. Конструкции такого типа неэкономичны, так как требуют много камня.

В отличие от этого случая работы камня существуют, как отмечено выше, выходные русла с укреплениями из каменной наброски. Их размеры существенно меньше, чем в данном типе, и они находят в практике дорожного строительства достаточно широкое применение. Расчет этих типов выходных русел приведен ниже в отдельной рубрике данной главы (пп. 7.50 - 7.64).

7.38. Случай взаимодействия наброски с грунтом лога, при котором обеспечивается совместная работа камня и грунта русла нижнего бьефа сооружения, наиболее часто применяют в выходных руслах равнинных водопропускных труб и малых мостов с закрепленным руслом. Он соответствует условиям свободного растекания. При этом расходы в сооружении должны превышать Q_min (см. табл. 7.3).

Ширину рисбермы B_н назначают равной ширине укрепления. Остальные размеры рисбермы назначают по расчету из условия устойчивости сооружения от подмыва, но меньшими, чем соответствующие размеры рисбермы в рассмотренном выше случае.

При совместной работе камня и грунта лога глубину размыва определяют, рассматривая каменную наброску как крупные включения, отмащивающие откосы воронки.

Максимальная глубина размыва при свободном затопленном растекании (i_л <= 0,02)

(7.54)

где

- соответственно предельная и максимальная глубины размыва в заданном выходном русле при установленном характере растекания потока и отсутствии каменной наброски, рассчитанные по среднему диаметру частиц грунта (при расчете

неоднородность несвязных грунтов не учитывают); при свободном незатопленном и несвободном растекании, а также в узких логах под

понимают глубины, вычисляемые по формулам (7.21) - (7.23) и (7.39) - (7.51);

d - расчетный диаметр частиц грунта (см. п. 7.29);

A - коэффициент, принимаемый в выходных руслах с вертикальной стенкой или предохранительным откосом в конце укрепления, равным 0,13, в выходных руслах без них - 0,5 (последний тип выходных русел использовался в эксплуатируемых сооружениях старой постройки);

- объем каменной наброски на единицу ширины укрепления, м³/м.

Для эффективной работы камня в наброске объем его следует задавать в пределах

, а крупность - не менее полученной из выражения

(7.55)

Минимальный

и максимальный

удельные объемы камня определяют по формулам:

(7.56)

(7.57)

При

расчет размыва следует производить без учета наброски. При

глубина размыва

(7.58)

Максимальная глубина размыва при свободном незатопленном растекании (при уклонах лога i_л > 0,02)

(7.59)

где

- глубины размыва выходного лога за счет возможного образования промоины (канавы) в ее начале (см. п. 7.31).

При i_л > 0,02 минимальный объем камня в рисберме определяют по формуле (7.56), а поправку на избыток камня не вводят.

7.39. Случай применения каменной наброски в виде гибкой конструкции характерен в условиях несвободного растекания и узких логов, когда размыв происходит при поверхностном режиме с максимальными скоростями у поверхности, а также для незагруженных сооружений, когда поток не способен перемещать камень в рисберме и размыв начинается за камнем в грунте.

Здесь незагруженными сооружениями названы такие, у которых при свободном растекании силовое воздействие потока на сходе с жесткой части укрепления недостаточно для выноса камня из рисбермы, т.е.

, где

- размыв, определяемый по формуле (7.23), в которой в качестве среднего диаметра частиц грунта принят d_н. Это условие соблюдается, когда расход в сооружении Q < Q_min, где Q_min определяется по табл. 7.3. При несвободном растекании и узких логах фактор незагруженности сооружений не учитывают. В образовавшуюся воронку сваливается камень, отчего рисберма разрушается. При окончательном разрушении рисбермы дальнейший размыв в нижнем бьефе связан с совместным действием двух факторов: размывом за камнем и вымыванием частиц грунта из-под камня. Размыв частиц грунта из-под каменной наброски прекращается только после стабилизации размыва за камнем, так как вследствие значительной подвижности последний не образует слоя, предохраняющего от размыва грунт на верховом откосе воронки.

Крутизну верхового откоса воронки из каменной наброски при стабилизации размыва за камнем принимают равной 1:2. Под воздействием поступающего в воронку камня наибольшие глубины за ним удаляются от сооружения, что приводит к некоторому замедлению размыва. Предельную же глубину размыва за камнем

, не зависящую от наличия и размера камня в рисберме, рассчитывают по формулам (7.23), (7.49) - (7.51), как для грунта лога при отсутствии камня в аналогичных гидравлических и прочих условиях.

Максимальную глубину размыва за камнем

определяют по одной из формул (7.21), (7.22), (7.42), (7.44) и (7.47) для соответствующих условий.

При значительном объеме камня рисберма может разрушаться не полностью и, следовательно, не весь камень будет участвовать в процессе размыва. Камень в неразрушенной рисберме обладает малой подвижностью по сравнению с камнем, участвующим в образовании верхового откоса воронки. Рисберма разрушается при соблюдении условия, что удельный объем камня в ней

не превышает критериального удельного объема

, который определяют по формулам:

при несвободном растекании и незагруженных сооружениях

(7.60)

для узких логов

(7.61)

При разрушении рисбермы

максимальную глубину размыва в камне определяют по формулам:

при несвободном растекании потока

(7.62)

для узких логов

(7.63)

для незагруженных сооружений

(7.64)

где

- максимальная глубина размыва в камне, определяемая по формуле (7.54);

j - коэффициент, учитывающий степень подтопления нижнего бьефа.

В свою очередь

(7.65)

здесь

Для определения j можно пользоваться графиком, представленным на рис. 7.22. Рассчитывать максимальную глубину размыва в камне по формулам (7.62) и (7.63) можно при достаточном объеме камня в рисберме. Условие достаточности камня проверяют по неравенству (7.56).

Рис. 7.22. График для определения коэффициента j

при расчете размыва в каменной наброске

При значительном объеме камня в рисберме

максимальная глубина размыва в камне

(7.66)

где

вычисляют по формуле (7.60) или (7.61).

При сочетании подтопления и узкого лога размыв в камне рассчитывают по одному из факторов, как и при расчете размыва без камня (см. п. 7.34).

7.40. При выходных руслах с каменной наброской оптимальную по стоимости глубину заложения предохранительного откоса или "зуба" в конце укрепления назначают из условия, чтобы максимальная глубина размыва в камне была

(7.67)

где r_н - коэффициент, принимаемый для укреплений с предохранительным откосом с крутизной 1:1,5 равным 0,27 и для укреплений с вертикальным зубом в конце - 0,36;

c₁, c₂, c₃ - стоимость соответственно 1 м³ камня, 1 м² предохранительного откоса и 1 м³ бетона вертикального зуба;

- толщина зуба вертикального.

7.41. Обычно при проектировании выходных русел глубину заложения концевой части укрепления назначают по конструктивным соображениям и расчет выходных русел с каменной наброской сводится к определению объема и размера камня для заданной из условия устойчивости укрепления от подмыва глубины размыва в камне

Необходимый удельный объем камня

для заданной максимальной глубины размыва

при

определяют по формуле

(7.68)

Если необходимый удельный объем камня

, вычисленный по формуле (7.63), окажется больше критериального

, то

определяют подбором, пользуясь выражением

(7.69)

В формулах (7.67), (7.68), (7.69) при свободном растекании потока и широких логах принимают j = 1 и K_л = 1; при учете только подтопления - K_л = 1; для узких логов j = 1.

Оптимальный размер камня d_н, при котором его требуется наименьшее количество для заданной глубины размыва

, определяют из уравнения

ИС МЕГАНОРМ: примечание.

Формула дана в соответствии с официальным текстом документа.

(7.70)

где

- предельная или максимальная глубины размыва соответственно в каменной рисберме и в грунте лога;

K - коэффициент, учитывающий размеры воронки в плане и принимаемый по графику на рис. 7.12.

В эксплуатируемых сооружениях обычно уложен крупный камень размером

, хотя наиболее рациональным может оказаться более мелкий материал размером

Все приведенные выше формулы глубин размыва в камне справедливы при d_н/d > 15. При несоблюдении неравенства расчеты глубин размыва по указанным формулам дают некоторые запасы.

7.42. Переход к типам выходных русел с каменной наброской, как правило, диктуется конструктивными соображениями, а именно сложностью устройства заглубления концевой части укрепления более 1,5 - 2,0 м.

При сопоставлении по стоимости типов выходных русел с каменной наброской и без нее критерием рациональности применения камня служит неравенство

(7.71)

где r₀ - коэффициент, принимаемый для укрепления с предохранительным откосом с крутизной 1:1,5 равным 2,16; для укреплений с вертикальным зубом в конце - 1,2;

- глубины размыва соответственно в грунте лога и в камне.

Назначение основных размеров выходных русел

7.43. Исходными данными для назначения основных размеров выходных русел являются гидравлические характеристики потока в нижнем бьефе (глубины, скорости и границы растекания) и глубины размыва. В результате расчетов определяют длину и ширину укрепления на выходе из трубы, глубину заложения концевой части, мероприятия по уменьшению размывов за укреплением (устройство гасителей, назначение размеров каменной рисбермы и т.д.).

7.44. Расчет основных размеров выходных русел выполняют в такой последовательности.

1. Предварительно назначают тип выходного русла из числа рекомендованных (см. рис. 7.2) исходя из следующих соображений:

для полностью загруженных труб (т.е. работающих при расчетных заполнениях) рекомендуются типы 1к и 2к, причем при значительных уклонах сооружений i_т > 0,04 применяют ступенчатую укладку звеньев труб;

для недогруженных труб применяют тип 1 или 2;

в качестве вариантов для труб при расчетном заполнении и особенно при больших уклонах труб и лога (i_т и i_л, больших 0,05) применяют типы 3 (3к) - 4 (4к) и 5 (5а, 5к, 5ак), 6 (6а, 6к, 6ак), рассматривая при этом случай укладки труб без ступеней.

2. Определяют глубины и скорости потока на выходе из труб и на укреплении согласно рекомендациям гл. 5 и пп. 7.16 - 7.21.

3. Назначают тип и длину укреплений, принимая ее (из конструктивных соображений)

4. Определяют глубину размыва на выходе из труб. При глубине размыва

переходят на другой тип выходного русла, обеспечивающий снижение размыва, и расчет повторяют. При

увеличивают отверстие сооружения либо принимают специальные меры защиты.

5. Определяют глубины заделки концевой части.

6. Определяют ширину растекания потока.

7. Определяют ширину укреплений и устанавливают их окончательные размеры.

8. При использовании выходных русел типов 5 (5а) и 6 (6а) определяют размеры гасителей согласно рекомендациям гл. 4 пп. 4.26 - 4.30.

7.45. Тип и материал укреплений устанавливают по максимальной скорости на укреплении, сравнивая ее с допускаемыми скоростями для укреплений, приведенными в табл. 2.9.

7.46. Глубина заложения концевой части укрепления

(7.72)

где

- максимальная глубина размыва в заданном выходном русле без учета размыва канавы применительно к конкретным гидравлическим условиям (характеру растекания, наличию каменной наброски, влиянию ширины лога), определяемая по формулам настоящей главы, приведенным выше;

m_от - коэффициент заложения откоса (для вертикальной стенки m_от = 0).

В качестве искомой выбирают максимальную из двух глубин

при наибольшем расходе и при расчетном, причем последнее из этих двух значений умножают (для обеспечения необходимого запаса) на коэффициент 1,2; при

изменяют тип выходных русел.

7.47. Ширину растекания потока при свободном растекании и уклонах лога i_л <= 0,02 определяют по формуле (7.4), при i_л > 0,02 - по формуле (7.12), либо по графикам, приведенным в приложении 7.2, либо по программе "БОР" (см. гл. 2); при наличии гасителей ширину растекания определяют по формулам (7.16) и (7.17).

7.48. Ширину укрепления при свободном растекании на всей длине, за исключением концевой части (длину ее принимают равной 1 м), устанавливают по ширине растекания потока с запасом в 1 м в каждую сторону.

Допускается уменьшить ширину укрепления из жестких бетонных элементов, ограничив ее либо изолиниями скоростей на укреплении, равных допускаемым скоростям для грунтов выходного лога, либо заменив часть укрепления наброской из щебня или камня определенной крупности на участке, где скорости потока не превышают допускаемых для указанного материала. Такое сокращение ширины укрепления допускается на всей его длине, за исключением концевой части.

В качестве расчетной ширины укрепления в концевой его части принимают большую из двух величин: ширину растекания B_раст в конце укрепления, определяемую по формуле (7.4) или (7.19), и B_min.

Минимальная ширина укрепления, соответствующая ширине воронки размыва в створе конца укрепления,

(7.73)

ИС МЕГАНОРМ: примечание.

Обозначения даны в соответствии с официальным текстом документа.

где Q - коэффициент;

при предохранительном откосе и

при концевой части в виде вертикальной стенки;

K - коэффициент формы воронки размыва (см. рис. 7.12); при L/D_э > 10 принимают L/D_э = 10;

- глубина размыва в грунте лога (т.е. в выходных руслах без каменной наброски) применительно к конкретным гидравлическим условиям.

При несвободном растекании ширина укрепления на всей длине

(7.74)

При степени подтопления

принимают

В узких логах B_min принимают равной ширине лога.

7.49. При применении ребра и гасителя в виде стенки в раструбном оголовке (см. рис. 7.3) следует учесть следующие положения.

Ребро устанавливают в конце укрепления как у труб, так и мостов. Длина его l_р ~= 4,6D_э, сечение равно

, причем большее число относится к сооружениям больших отверстий. Гаситель размещают в раструбном оголовке труб так, чтобы передняя его грань находилась на расстоянии 0,5D_э от выхода из раструба.

Длина стенки гасителя l составляет от 0,85 до 0,90 ширины раструба в створе передней грани l_с. Высота стенки в середине - 0,25D_э, в крайних четвертях - 0,15D_э.

Расчет гасителей в виде расширяющегося раструба и гасителя ЦНИИСа приведен в гл. 4.

Камень укладывают по всей ширине укрепления в приготовленный котлован так, чтобы верх находился не менее чем на 0,5 м ниже поверхности земли.

Рациональные типы и размеры выходных русел выбираются на основе технико-экономического сравнения вариантов. Примеры расчета выходных русел с укреплениями из связанных между собой элементов приведены в приложении 7.4.

ОСОБЕННОСТИ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ВЫХОДНЫХ РУСЕЛ

С УКРЕПЛЕНИЯМИ ИЗ КАМЕННОЙ НАБРОСКИ

Общие принципы

7.50. Гидравлические расчеты выходных русел с укреплениями из каменной наброски включают:

а) оценку однородности каменного материала;

б) определение минимальной крупности однородного камня или проверку устойчивости неоднородной наброски по ее гранулометрическому составу;

в) определение толщины наброски - для недеформируемых выходных русел;

г) определение деформаций укреплений и установление на их основе минимальных плановых размеров укреплений для деформируемых выходных русел.

Дальнейшие расчеты выходных русел с укреплениями из каменной наброски (определение глубин размыва за укреплениями глубин заложения их концевых частей, а также окончательное определение ширины укрепления) являются общими для всех типов выходных русел и излагались выше в рубрике "Расчеты размыва" (пп. 7.22 - 7.49). Однако в связи с некоторой спецификой указанных расчетов для выходных русел из каменной наброски они рассматриваются и в настоящей рубрике с акцентированием на особенности расчета и ссылкой на общие формулы.

7.51. Гранулометрический состав несортированного камня, получаемого взрывным способом, зависит от прочности и трещиноватости пород, а также вида и метода взрывных работ. Согласно СНиП [42] скальные породы подразделяются на сильно-, средне- и слаботрещиноватые и практически монолитные. Вероятный гранулометрический состав каменного материала устанавливается при разработке проекта буровзрывных работ применительно к заданным карьерам с учетом потребной крупности камня.

Для предварительных расчетов можно допустить, что из скальных прочных малотрещиноватых пород взрывным способом получается однородный камень заданной крупности. При взрыве средне- и сильнотрещиноватых скальных пород можно ориентироваться на гранулометрический состав, приведенный в табл. 7.7.

Таблица 7.7

Крупность камней, см	Содержание фракций данной крупности, %
Более 40	15 - 30
40 - 20	50 - 70
20 - 5	10 - 20
Менее 5	5 - 10

7.52. Рекомендуемые типы выходных русел с укреплениями из каменной наброски рассмотрены выше и изображены на рис. 7.4.

7.53. Гидравлические расчеты указанных выходных русел, общие для всех типов, выполняют в изложенной ниже последовательности. Специфические особенности каждого из типов излагаются в соответствующих пунктах.

1. Устанавливают, является ли наброска однородной в отношении размыва из условия

(7.75)

где d_н(max) - средний диаметр крупных частиц, которые составляют не менее 5% массы наброски;

d_н - средний диаметр частиц наброски.

При несоблюдении условия (7.75) каменная наброска неоднородна.

2. Для однородной наброски определяют минимальный диаметр ее частиц, м, при котором укрепление будет устойчивым от размыва:

(7.76)

где v_вых - скорость на выходе из сооружений, определяемая согласно рекомендациям гл. 5 и 6;

K_ог(_v₎ - коэффициент, учитывающий влияние оголовка на размывающую скорость для частиц наброски; для безоголовочной трубы K_ог(_v₎ = 1, для труб с портальными и раструбными оголовками и малых мостов K_ог(_v₎ = 0,8.

Формулу (7.76) можно представить в следующих видах:

для безоголовочной трубы

(7.76')

для труб с раструбными или портальными оголовками и малых мостов

(7.76")

3. Для неоднородной наброски, заданной своим гранулометрическим составом, устанавливают, будут ли устойчивы ее частицы под воздействием потока исходя из любого из двух приведенных ниже условий:

(7.77)

(7.78)

где Q - расход в сооружении, м³/с;

Q_пр, v_пр - соответственно предельный расход, м³/с, и предельная скорость, м/с, при которой наброска сохраняет устойчивость против размыва;

K_ог(_Q₎ - коэффициент, учитывающий влияние оголовка на величину предельного расхода, при котором сохраняется устойчивость наброски; K_ог(_Q₎ определяют по табл. 7.8 в зависимости от типа труб и режима протекания потока в трубе; для мостов K_ог(_Q₎ определяют как для прямоугольных труб при безнапорном режиме;

K_нр - коэффициент неоднородности грунта, учитывающий влияние гранулометрического состава наброски на ее устойчивость;

- показатель степени, определяемый по табл. 7.9.

Таблица 7.8

Типы труб	Режим протекания	K_ог(_Q₎
Круглые	Безнапорный	1,95
	Полунапорный	1,40
	Напорный	1,35
Прямоугольные	Безнапорный	2,95
Прямоугольные	Полунапорный	1,35

Таблица 7.9

Типы труб и мостов	Режим протекания
Круглые трубы	Безнапорный	1/3
	Полунапорный	2/3
	Напорный	3/4
Прямоугольные трубы	Безнапорный	1/4
Прямоугольные трубы	Полунапорный	3/4
Малые мосты	Безнапорный	1/4

В свою очередь

(7.79)

где d_н - средний диаметр частиц наброски, м.

В формулах (7.78) и (7.79) d_н(м) и p_н(м) - это соответственно диаметр частиц, м, и весовое содержание самой мелкой фракции, которой в наброске содержится не менее 10%, т.е. p_н(м) >= 0,1. В случае если ее содержание составляет менее 10%, под d_н(м) понимают средний диаметр частиц смеси, состоящей из самой мелкой фракции и последующих фракций, дополняющих ее до 10%, т.е.

;

(7.80)

где p_н(_i₎, d_н(_i₎ - соответственно весовая доля и средний диаметр, м, фракций, дополняющих мелкую фракцию до 10%.

Если по формуле (7.79) получают K_нр < 1, то принимают K_нр = 1.

Режим протекания потока в трубах можно определить путем сравнения параметра расхода П_Q с П_Q_(гр), где П_Q_(гр) - граничный параметр расхода, соответствующий переходу к полунапорному режиму для всех типов технически гладких труб, кроме круглых с коническими звеньями, и к напорному для круглых труб с коническими звеньями, т.е. удовлетворяющий условию h_вх/h_т = 1 (см. табл. 5.1); для гофрированных труб возможны граничные параметры расхода, соответствующие как переходу к полунапорному режиму (П_Q_(гр)пн), так и к напорному (П_Q_(гр)н) (см. п. 5.17).

При использовании формулы (7.78) расчет начинают, предполагая безнапорный режим протекания. Затем, вычислив v_пр, определяют соответствующий ей параметр расхода П_Q. При этом расчет зависит от типа труб.

Для круглых труб вычисляют относительную скорость

и по ее значению находят по графику приложения 5.3 (рис. 1 - технически гладкие трубы, рис. 2 - гофрированные) искомое значение П_Q. Для прямоугольных труб предварительно вычисляют по формуле (5.60) глубину на выходе из трубы h_вых(_пр), соответствующую v_пр, т.е.

, и далее по номограмме приложения 5.2 (рис. 2) находят параметр расхода на выходе из трубы

, а затем вычисляют искомый параметр расхода на входе в трубу

, определяющий режим протекания (для круглых труб

. Для этого значения

надо умножить на величину

, т.е.

Сравнивая

с П_Q_(гр), приведенными в гл. 5 (табл. 5.1 и п. 5.17), устанавливают режимы протекания.

При

- режим безнапорный, следовательно, v_пр вычислена правильно. Далее расчет продолжают, устанавливая устойчивость наброски из условия (7.78).

При

- режим полунапорный или напорный. В этом случае для установленного режима протекания определяют показатель степени

по табл. 7.9 и пересчитывают v_пр. После этого, используя условие (7.78), устанавливают устойчивость наброски.

При соблюдении условий (7.77) и (7.78) укрепление из неоднородной наброски будет устойчивым и неразмываемым. В противном случае укрепление будет размываемым, и для определения его устойчивости выполняют дополнительные расчеты.

4. Определяют минимально допустимый диаметр частиц наброски d_н(доп) по формулам (7.76') и (7.76"), считая ее однородной.

5. Сравнивают полученный диаметр частиц наброски d_н(доп) со средним диаметром частиц наиболее крупной фракции d_н(max), содержащейся в ней.

При d_н(max) > d_н(доп) укрепление может работать как самоотмостка, а возможность применения его для заданного сооружения может быть определена специальным расчетом для данного типа укреплений (см. ниже).

При d_н(max) < d_н(доп) наброска неустойчива и не может быть использована для защиты выходных русел сооружения от размыва. Ее требуется заменить наброской с частицами большей крупности или другим типом выходных русел.

Неразмываемые недеформируемые выходные русла

7.54. Толщину слоя наброски

, при которой укрепление будет недеформируемым, определяют по формулам:

а) для наброски, состоящей из нескольких фракций,

ИС МЕГАНОРМ: примечание.

Формула дана в соответствии с официальным текстом документа.

(7.81)

где

- коэффициент, учитывающий влияние оголовка на глубину деформации наброски; для безоголовочной трубы

; для раструбных и портальных оголовков

При p_н(м) >= 0,95 наброску считают однородной со средним диаметром частиц d_н(м), для чего в формуле (7.81) условно принимают p_н(м) = 0;

б) для наброски, состоящей из одной фракции,

(7.82)

Для несвязных грунтов средний диаметр частиц отдельной фракции, мм,

(7.83)

где p_i - весовая доля фракции, %.

Для связных грунтов расчетный диаметр d, мм, определяют по формуле (7.25).

Для наброски, состоящей из нескольких слоев различного гранулометрического состава (например, при наличии щебеночной подготовки) вместо d_н подставляют эквивалентный диаметр

(7.84)

где d_н(1) и

, d_н(2) и

, ..., d_н(_n₎ и

- соответственно средний диаметр и толщина первого, второго, третьего и n-го слоя наброски, м.

Полная толщина всех слоев наброски, м,

По этой же формуле (7.84) вычисляют для каждого слоя средний диаметр мелкой фракции d_нм(э), м.

7.55. Определяют размеры укрепления:

1) назначают длину укрепления согласно рекомендациям п. 7.44.

;

2) определяют ширину растекания потока B_раст по формуле (7.4) или (7.19);

3) назначают размеры укрепления в плане, м, с учетом принятой длины укрепления:

в створе на выходе из оголовка

B₁ = b_p + 2;

в конце укрепления

B₂ = B_раст + 1,

где 2 и 1 м - запас в ширине укрепления, назначаемый соответственно по 1 и 0,5 м с каждой стороны укрепления.

Далее определяют глубину размыва, глубину заложения концевой части и назначают ширину укрепления в этом месте согласно рекомендациям, изложенным ниже в п. 7.64.

Неразмываемые деформируемые выходные русла

7.56. Предельную глубину деформации укрепления

за счет выноса грунта из-под него определяют по формулам:

а) для наброски, состоящей из нескольких фракций,

(7.85)

При p_н(м) >= 0,95 считают наброску однородной со средним диаметром частиц d_н(м), для чего в формуле (7.85) условно принимают p_н(м) = 0;

б) для однородной наброски

При наличии в наброске слоев разного гранулометрического состава в формулу (7.85) вместо d_н и d_н(м) подставляют d_н(э) и d_нм(э), определяемые по формуле (7.84).

Толщиной слоя наброски

задаются, принимая ее равной не менее 2d_н.

7.57. Глубины потока на выходе из сооружений определяют согласно рекомендациям гл. 5 и 6.

7.58. Глубины на выходе из оголовков труб

h_вых(ог) = h_выхK_ог(_h₎, (7.86)

где K_ог(_h₎ - коэффициент, учитывающий влияние оголовков на глубину потока на выходе из сооружения.

В свою очередь

K_ог(_h₎ = (b/b_р)^4/3. (7.87)

7.59. Расстояние, м, от выхода из трубы или моста до месторасположения предельной глубины деформации укрепления

(7.88)

7.60. Устанавливают предельную глубину деформации укрепления у выходного сечения сооружения

(7.89)

При

либо изменяют параметры укрепления из каменной наброски (толщину слоя, крупность камня и т.п.), либо применяют иной тип укрепления.

7.61. Определяют минимальные размеры укрепления в плане исходя из размеров воронки деформаций:

(7.90)

где L и B - соответственно длина и ширина укрепления.

Длину укрепления L, вычисленную по формуле (7.90), принимают для дальнейшего расчета.

7.62. Назначают ширину укрепления, м:

а) в конце оголовка труб или на выходе из малого моста

B₁ = b_p + 2; (7.91)

б) в конце укрепления при

принимают B₂ по большему из значений B₁ и B, определяемой по формуле (7.90); при

принимают B₂ по большему из значений B и B_раст, вычисляемой по формуле (7.4) или (7.19), но не менее B₁.

Выходные русла-самоотмостки

7.63. Расчеты этого типа выходных русел основаны на методике определения размыва в неоднородных грунтах, изложенной в п. 7.35.

Последовательность расчетов следующая.

1. Определяют долю p_от и средний диаметр d_от фракций отмостки. Для этого:

а) вычисляют параметр

(7.92)

здесь

(7.93)

где

;

б) по гранулометрическому составу наброски вычисляют сначала средний диаметр первой (самой крупной) фракции (причем ее должно быть больше 5%, т.е. p_от > 0,05), принимая его за d_от;

в) сравнивают

с N_расч.

Если

, то в расчет включают следующую фракцию (или ее часть) и так продолжают до тех пор, пока не будет соблюдено условие

с точностью до 5%.

Если

будет меньше N_расч для всех фракций, то отмостка не образуется и предельные глубины деформации определяют как для однородного грунта по формулам (7.23), (7.49) - (7.51), принимая

, а максимальные глубины - по формулам (7.21), (7.22), (7.42) - (7.44), (7.47).

Если для частиц самой крупной фракции, которых в наброске более 5%,

, то эти частицы определяют отмостку.

2. Определяют максимальную глубину размыва в неоднородной наброске:

(7.94)

где

- максимальная глубина размыва в наброске со средним диаметром частиц d_от, определяемая по одной из формул (7.42) - (7.44) или (7.47) при

; здесь

- предельная глубина размыва в наброске со средним диаметром частиц d_от, м, определяемая по формулам (7.23), (7.49) - (7.51) при

3. Принимают толщину слоя наброски в укреплении

Дальнейший расчет ведут согласно пп. 7.59 - 7.61 деформируемых выходных русел, подставляя вместо

глубину

, вычисленную по формуле (7.94).

При значительных глубинах размыва в выходном сечении сооружения

[см. формулу (7.89)] целесообразно выходные русла-самоотмостки заменять на иные типы выходных русел.

Размыв за укреплениями, определение их размеров

и глубины заделки концевых частей в выходных руслах

из каменной наброски

7.64. Расчеты выполняют в такой последовательности.

1. Определяют предельную глубину размыва в грунте лога за укреплением по формулам (7.23), (7.49) - (7.51). При этом в формуле (7.23) член L/D_э + 1 заменяется выражением

, где s₁ - показатель степени, равный 5/2 для недеформируемых русел и 10/3 для деформируемых и самоотмосток; коэффициент

принимают равным 0,6.

2. Определяют максимальную глубину размыва

по формулам (7.21), (7.22), (7.42) - (7.44) или (7.47).

3. Сравнивают толщину наброски

с максимальной глубиной размыва

При

назначают выходное русло типа I (см. рис. 7.4), для которого принимается глубина заложения концевой части

, и дальнейший расчет ведут, начиная с п. 8.

При

за укреплением назначают рисберму из камня крупностью

(выходное русло типа II) и продолжают расчет.

4. Определяют максимальную глубину размыва за укреплением при наличии там рисбермы из каменной наброски по формулам (7.58), (7.59). При этом принимают удельный объем камня в рисберме

(исходя из крутизны откосов рисбермы: верхового 1:1, низового 1:1,5 и глубины

5. Сравнивают

При

выходное русло типа II принято правильно, и глубина заложения концевой части укрепления равна

При

указанный тип выходного русла будет неустойчив, и его заменяют выходным руслом типа III.

6. Для случая

(выходное русло типа II) пересчитывают глубину рисбермы h_рисб при глубине ее заложения

по формуле

(7.95)

Дальнейший расчет для этого типа русел ведут начиная с п. 8.

7. Для случая

(выходное русло типа III) глубину заложения концевой части укрепления h_ук = h_рисб в выходных руслах типа III находят из уравнения

(7.96)

где коэффициенты M и N определяют по формулам:

(7.97)

(7.98)

8. Определяют ширину воронки размыва B_min в конце укрепления для всех типов выходных русел по формуле (7.73) при

9. Сравнивают ширину воронки размыва B_min с шириной в конце укрепления B₁ (см. п. 7.62) и в качестве расчетной ширины укрепления в концевой его части B_ук принимают большее из этих значений.

Протяженность концевой части укрепления по длине (участок, имеющий ширину B_ук) принимают равной 1 м.

При длине оставшейся части укрепления (без концевой части) менее 1 м назначают укрепление трапецеидальной формы в плане шириной на выходе из трубы B₁ и в конце укрепления - B_ук.

Примеры расчета выходных русел с укреплениями из каменной наброски приведены в приложении 7.4.

ВЫХОДНЫЕ РУСЛА ГОФРИРОВАННЫХ ТРУБ, РАСПОЛОЖЕННЫХ НА ПОДСЫПКЕ

7.65. Поток, выходящий из гофрированных труб, расположенных на подсыпке, сбрасывается либо на низовой откос насыпи, либо отбрасывается за подошву ее путем устройства консольного сброса (или, как вариант, рассеивающего трамплина), либо, наконец, сбрасывается в нижний бьеф путем устройства шахтного сброса.

Расчет консольных сбросов и рассеивающих трамплинов приведен в гл. 4, а определение гидравлических характеристик потока в нижних бьефах шахтных сбросов может выполняться по тем же зависимостям, что и для укреплений за трубами, изложенным выше в настоящей главе.

Особенности определения гидравлических характеристик потока при сбросе воды на низовой откос насыпи излагаются ниже.

7.66. Возможны следующие варианты сброса потока на низовой откос насыпи:

а) сброс потока непосредственно на укрепленный монолитным бетоном или омоноличенными плитами откос насыпи (рис. 7.23, а);

б) сброс потока на отсыпку из камня, расположенную в низовой части насыпи (рис. 7.23, б);

в) сброс потока по лоткам, уложенным на откосе (для этой цели могут быть использованы элементы гофрированных труб) (рис. 7.23, в).

Рис. 7.23. Схемы укладки гофрированных косогорных труб

на насыпной грунт в теле насыпи:

1 - укрепленный откос; 2 - рисберма;

3 - каменная отсыпка; 4 - лоток

При сбросе потока на укрепленный откос насыпи или на отсыпку из камня для снижения динамического воздействия потока устраивают берму.

7.67. При сбросе потока на укрепленные откосы насыпи расчеты выполняют в такой последовательности.

1. Определяют минимальный размер бермы вдоль потока по формуле, полученной из уравнения свободного падения тела:

(7.99)

где 1,2 - коэффициент запаса.

2. Определяют ширину растекания потока на берме (эта ширина сохраняется на откосе насыпи):

(7.100)

где B_раст(б) - ширина растекания потока на берме в створе, проекция расстояния которого от выхода из трубы равна x;

D - диаметр трубы;

L_б - длина бермы вдоль потока;

- эталонный расход, т.е. расход, при прохождении которого критическая глубина в сооружении равна 0,75D.

Ширину растекания потока на берме можно также определить на основе математической модели или по зависимости (7.12), соответствующей уклону лога i_л > 0,02, так как на берме, за которой следует откос насыпи, водоотводные зоны, сжимающие поток, не образуются и кинематика потока соответствует указанному случаю.

По ширине растекания назначают ширину укрепления бермы.

3. Определяют скорости и глубины потока на сходе его с бермы по зависимости (7.8) - (7.10) или на основе математической модели и назначают по этим характеристикам тип укрепления (см. табл. 2.9).

4. Определяют глубины и скорости потока у подошвы откоса h_пд либо на основе математической модели, либо с некоторым приближением находят среднюю глубину потока по уравнению неравномерного движения (см. гл. 2), считая ширину потока на откосе равной ширине растекания на сходе с бермы B_раст(б). Можно также (в запас) принять среднюю глубину потока у подошвы откоса равной нормальной глубине, считая сечение потока прямоугольным:

(7.101)

где m_от и n - соответственно заложение и коэффициент шероховатости укрепленного откоса.

В случае расчета средних глубин у подошвы откоса по уравнению неравномерного или равномерного движения скорости у подошвы откоса определяют по формуле

(7.102)

5. По скоростям и глубинам у подошвы откоса назначают тип укрепления откоса (см. табл. 2.9).

7.68. При сбросе потока в лотки, уложенные на откосе насыпи, гидравлические характеристики определяют в такой последовательности.

1. По глубине на выходе из трубы h_вых определяют высоту стенок лотка

a = h_вых + 0,25, (7.103)

где 0,25 - возвышение стенки лотка над уровнем воды в нем, м.

2. Определяют проекцию расстояния от выхода из трубы до сечения падения струй в лотке:

(7.104)

Разность отметок лотка в сечениях падения струй и выхода из трубы z_x = x/m_от.

3. Определяют полную энергию потока в сечении падения струй по формуле (4.2), принимая ее равной полной энергии на выходе из трубы:

(7.105)

где

4. Находят подбором из уравнения (4.1) глубину потока в сечении падения струй, принимая ее равной сжатой глубине h_с, а

(7.106)

где

- площадь потока в сжатом сечении;

- коэффициент скорости, определяемый в функции h_к/z_x (см. п. 4.6).

Для этого задаются относительной сжатой глубиной h_с/D и по ней определяют площадь живого сечения потока в лотке кругового очертания по табл. 5.6 или по формуле, справедливой при 0,05 <= h/D <= 0,75,

(7.107)

Подставляя значения h_с,

в формулу (7.106), добиваются равенства значения T₀ в этой формуле значению T₀, полученному по формуле (7.105).

5. Устанавливают глубину потока в конце лотка у подошвы откоса h_пд из уравнения неравномерного движения (см. гл. 2), определяя коэффициент Шези для быстроточного режима по формуле (2.41); при этом для гофрированных элементов трубы с гладким лотком принимают n = 0,025.

Приближенно при 0,05 <= h/D <= 0,050 можно принять глубину потока в лотке у подошвы откоса равной нормальной глубине и определять ее при лотках кругового сечения либо по трафику приложения 2.3, либо по формуле

(7.108)

где n - коэффициент шероховатости лотка;

m_от - крутизна откоса, на котором лежит лоток;

D - диаметр лотка.

6. Вычисляют относительную глубину потока в лотке у подошвы откоса h_пд/D и по ее значению находят площадь поперечного сечения потока в конце лотка

по формуле (7.107) или по табл. 5.6.

7. Вычисляют скорость потока на выходе из лотка (у подошвы откоса)

(7.109)

8. Подбирают по скорости v_пд тип укрепления у подошвы откоса. Для этого находят тип укрепления по табл. 2.9, для которого соблюдается условие v_пд <= v_доп, где v_доп - допускаемая скорость.

7.69. При отводе воды на берму и откос насыпи, отсыпанной из камня, гидравлические характеристики потока определяют, рассматривая подсыпку как фильтрующую насыпь, через которую сбрасывается поток в нижний бьеф (рис. 7.24). Расчет ведут в следующем порядке:

1. Определяют скорости на выходе из трубы v_вых согласно рекомендациям гл. 5.

2. Устанавливают, является ли наброска однородной или нет, и определяют ее устойчивость от размыва согласно рекомендациям п. 7.53 [формулы (7.75) - (7.80)].

3. Определяют минимальный размер бермы вдоль потока, при котором поток, вытекающий из трубы, не попадает непосредственно на откос, по формуле (7.99).

4. Вычисляют ширину растекания потока на берме B_раст(б) по формуле (7.100) с введением в нее понижающего коэффициента 0,6, учитывающего особенности работы каменной наброски по сравнению с бетонным укреплением. На откосе эта ширина сохраняется. Можно также определить ширину растекания потока на основе двухмерной математической модели или по формуле (7.101).

5. Назначают протяженность участка насыпи, отсыпанного из камня, - ширину фильтрующей части подсыпки b_ф. В первом приближении принимают b_ф = B_раст(б).

Рис. 7.24. Расчетная схема нижнего бьефа гофрированной

трубы, уложенной на подсыпке, при сбросе потока

непосредственно на каменную наброску:

1 - фильтрующий поток; 2 - поверхность воды для случая,

когда весь расход фильтруется через подсыпку; 3 - то же,

когда часть расхода сливается по откосу отсыпки;

4 - обратный фильтр; 5 - рисберма; 6 - экран

Далее каменная наброска рассматривается как фильтрующая насыпь (переливаемая или непереливаемая). Расчет ее, выполняемый согласно рекомендациям гл. 8 (пп. 8.1 - 8.15), излагается ниже.

6. Определяют нормальную глубину фильтрационного потока, принимая его сечение прямоугольным и предполагая, что весь расход профильтруется через подсыпку, по формуле (8.12), заменяя в ней

на

, где m_от(кос) - коэффициент заложения откоса косогора:

(7.110)

Для однородной наброски коэффициент фильтрации K_ф определяют по табл. 8.1, для неоднородной [35] - по формуле

(7.111)

где K_ф(одн) - коэффициент фильтрации для однородной наброски, имеющей диаметр частиц d_н, равный среднему диаметру частиц неоднородной наброски;

n_одн, n_неодн - пористость соответственно однородной и неоднородной наброски.

Средний диаметр частиц наброски

где d_н(i) - средний диаметр частиц отдельной фракции;

P_i - весовая доля фракции.

Пористость неоднородной наброски определяют опытным путем, заливая поры водой. Толщина исследуемого слоя должна быть не менее 5d_max, где d_max - диаметр наиболее крупных частиц, которых в наброске не менее 5%. Для грубых приближений можно считать, что в неоднородной наброске, имеющей небольшой процент мелких частиц (5 - 7%), коэффициент фильтрации по сравнению с однородной наброской уменьшается на 25 - 30%.

7. Определяют глубину фильтрационного потока H в створе конца трубы (см. рис. 7.24) из уравнения (8.10):

(7.112)

где l_п - проекция расстояния от конца трубы до точки пересечения откосов отсыпки и косогора в случае отсутствия подтопления со стороны нижнего бьефа или до створа, проходящего через урез воды в нижнем бьефе, при подтоплении;

- функции относительных глубин соответственно в створе конца трубы

и конца подсыпки

, определяемые при прямоугольном сечении наброски по табл. 8.4; иные формы сечений приводят к прямоугольным.

При отсутствии подтопления со стороны нижнего бьефа (h_нб = 0) уравнение (7.112) имеет вид

(7.113)

8. Определяют устойчивость низового откоса подсыпки из условия

z < z_пр, (7.114)

где z - разность отметок уровней в створах конца трубы и конца подсыпки;

z_пр - предельная разность, при превышении которой нарушается устойчивость откоса подсыпки.

В свою очередь

(7.115)

(7.116)

где

- угол естественного откоса каменной наброски, равный 35 - 36°;

;

- угол наклона низового откоса к горизонту.

При соблюдении условия (7.114) расчет заканчивают, в противном случае уполаживают откос, вновь производят проверку условия (7.114) и так продолжают до его удовлетворения.

ИС МЕГАНОРМ: примечание.

Нумерация пунктов дана в соответствии с официальным текстом документа.

8. Проверяют устойчивость основания насыпи от размыва при ламинарной фильтрации. Для этого сравнивают глубину H с предельной глубиной H_пр, обеспечивающей устойчивость против ламинарной фильтрации:

(7.117)

где

- коэффициент, определяемый по табл. 8.2.

При H < H_пр устойчивость против ламинарной фильтрации обеспечена, в противном случае или увеличивают ширину фильтрующей прослойки b_ф и повторяют расчет, или устраивают в основании обратный фильтр.

10. Сравнивают глубину потока H с толщиной подсыпки в сечении, проходящем через конец лотка трубы на выходе

. При

весь поток профильтрует внутрь подсыпки, при

часть расхода попадет на откос подсыпки.

11. Для случая

устанавливают, не выходит ли поток на откос подсыпки. Для этого делят расстояние l_п на 4 - 5 равных частей и в конце каждой из них (считая от конца подсыпки) определяют глубину потока h₀ по уравнению (7.112) или (7.113), подставляя вместо l_п расстояния l_i от конца подсыпки [уравнение (7.113)] и от уреза воды в нижнем бьефе [уравнение (7.112)] до рассматриваемых створов. Затем в каждом из сечений устанавливают толщину подсыпки

. При однообразном уклоне косогора для этой цели можно воспользоваться формулой

(7.118)

При этом возможны два случая:

- весь поток фильтрует через подсыпку (безнапорная фильтрующая подсыпка);

- часть потока выходит на поверхность откоса (напорная фильтрующая подсыпка).

Рассмотрим случай 1

12. Находят расчетную глубину фильтрационного потока, определяющую максимальные скорости турбулентной фильтрации:

а) при отсутствии подтопления со стороны нижнего бьефа по формуле (8.15):

(7.119)

где

- коэффициент кинетической энергии;

;

p - пористость наброски;

- коэффициент, учитывающий образование в порах каменной наброски застоя воды;

;

б) при наличии подтопления

h_р = h_нб,

где h_нб - глубина в нижнем бьефе в конце подсыпки.

13. Определяют максимальную скорость турбулентной фильтрации по формуле (8.4), подставив в нее значение средней скорости по формуле (8.5):

(7.120)

14. Сравнивают v_м с допускаемыми скоростями для грунтов основания насыпи v_доп.

При v_м <= v_доп устойчивость основания от турбулентной фильтрации обеспечивается, в противном случае - нет. Для достижения устойчивости делают вырезку грунта и заменяют его грунтом с v_доп >= v_м. Толщина вырезки должна обеспечить возможность укладки не менее трех слоев частиц грунта общей толщиной не менее 8 - 10 см.

15. Устраивают обратный фильтр у подошвы подсыпки высотой не менее h_р.

Рассмотрим случай 2

16. Устанавливают расстояние от конца подсыпки до места выклинивания потока на откос:

(7.121)

17. Определяют толщину фильтрующей подсыпки, равную глубине фильтрации потока h_р1, в месте выклинивания потока на откос:

(7.122)

18. Делят расстояние l_гр на 3 - 4 равные части и в конце каждого сечения подсыпки (считая от ее конца) определяют фильтрационный расход:

(7.123)

где

- толщина подсыпки в рассматриваемом створе;

Q - полный расход сооружения.

19. Определяют средние скорости турбулентной фильтрации

(7.124)

20. Определяют максимальную скорость турбулентной фильтрации

(7.125)

21. Сравнивают v_м с допускаемыми скоростями для грунтов основания подсыпки.

При v_м <= v_доп устойчивость основания подсыпки от турбулентной фильтрации обеспечивается, в противном случае - нет.

Для обеспечения устойчивости требуется произвести вырезку грунта и заменить его грунтом с v_доп > v_м. Толщина вырезки должна быть не менее трех слоев частиц грунта общей толщиной не менее 8 - 10 см.

22. Устанавливают расход потока Q₂₍_i₎, протекающего на откосе подсыпки в различных сечениях на участке от места выклинивания потока до конца подсыпки:

Q₂₍_i₎ = Q - Q₁₍_i₎. (7.126)

23. Определяют глубину потока на откосе подсыпки из уравнения Шези при C = 1/n (как для быстроточного режима):

(7.127)

где m_от(под) - коэффициент заложения низового откоса подсыпки;

n - коэффициент шероховатости откоса.

При n = 0,05 (для камня)

(7.128)

24. Вычисляют скорость потока на откосе

(7.129)

25. Определяют допускаемые скорости для камней наброски на откосе подсыпки по формулам п. 7.53:

а) при однородной наброске [см. формулы (7.76') и (7.76")]:

для труб без оголовка

(7.130)

для труб с портальными и раструбными оголовками

(7.131)

б) при неоднородной наброске [см. формулу (7.78)]

(7.132)

где k_от - коэффициент, учитывающий снижение устойчивости камней на откосе.

Коэффициент

(7.133)

где m_от - коэффициент заложения откоса;

m₀ - коэффициент естественного заложения откоса; для камня m₀ ~= 1,10 +/- 1,3, причем меньшее значение относится к грубооколотым камням, большее - к окатанным.

Значения K_ог(_v₎, K_нр,

приведены в п. 7.53.

26. Определяют устойчивость каменной наброски на откосе подсыпки

v_отн(_i₎ <= v_{доп(отк)}. (7.134)

При несоблюдении условия (7.134) крупность камня на поверхности откоса увеличивается, причем укладывают не менее трех слоев требуемой крупности.

27. Назначают конструктивно обратный фильтр у подошвы откоса высотой 0,5 м и шириной понизу 1 м.

Последующий расчет одинаков для случаев а и б.

28. Назначают у подошвы откоса укрепление из каменной наброски, размеры которого определяют в соответствии с рекомендациями, изложенными в пп. 7.50 - 7.64. При этом вычисляют глубины размыва, принимая длину укрепления равной сумме длин откоса подсыпки, укрепления у ее подошвы и ширины бермы.

Примеры расчета нижних бьефов гофрированных труб, уложенных на подсыпке, приведены в приложении 7.4.

ВЫХОДНЫЕ РУСЛА С УКРЕПЛЕНИЯМИ ИЗ СИНТЕТИЧЕСКИХ МАТЕРИАЛОВ

7.70. Наряду с традиционными типами выходных русел укреплений дорожных водопропускных труб может быть использована дешевая, легкая и технологичная мягкая конструкция [17, 35], позволяющая на 20 - 40% уменьшить глубину размыва по сравнению с типовым бетонным укреплением (рис. 7.25) и представляющая собой полотнище синтетического материала, уложенное на предварительно спланированный естественный грунт и прикрепленное только к торцу плиты выходного оголовка с помощью специального кассетного устройства (рис. 7.26).

Рис. 7.25. Рельеф дна после размыва в выходных руслах

с укреплениями из синтетических материалов (а)

и с типовыми жесткими бетонными укреплениями (б),

уложенными за круглой трубой D = 1 м при пропуске расчетного

расхода Q_р = 1 м³/с (координаты даны в метрах, отметки

на горизонталях - в сантиметрах; отметки на плане -

со знаком "+" означают намыв)

Рис. 7.26. Выходное русло с укреплением из синтетических

материалов (слева - вид сбоку, справа - план)

Кассетное устройство состоит из омоноличенной в торце бетонного зуба 1 металлической трубы 5 диаметром 5 - 7 см с прорезью по всей длине, в которую вставляется металлический стержень 2 с закрепленным на нем полотнищем мягкого материала 3, причем диаметр стержня с материалом должен быть больше ширины прорези. Торцы металлической трубы 5 закрываются деревянными пробками 4. Предложенная конструкция отличается простотой, позволяет в течение 10 - 15 мин производить монтаж и демонтаж укрепления, сводит к минимуму затраты на его строительство, ремонт и эксплуатацию.

Эффект уменьшения глубины размыва за мягким укреплением достигается за счет его способности при различных расходах формировать оптимальные условия для гашения энергии потока и в значительно большей степени, чем типовые бетонные конструкции, распределять транзитную струю, а также средние на вертикалях скорости и глубины на выходе в размываемое русло.

Работа мягких укреплений в натурных условиях подтвердила их экономическую целесообразность, производственную и эксплуатационную пригодность [7]. Опытные образцы мягкого укрепления выполнены из нетканого вязально-прошивного материала ВПР-10 (разновидность стеклоткани).

К применяемым для мягких укреплений синтетическим текстильным материалам предъявляются следующие требования [18]: устойчивость к атмосферным воздействиям; эластичность, достаточная прочность, износоустойчивость и долговечность; водопроницаемость; отсутствие компонентов, являющихся питательной средой для микроорганизмов, плесневых грибков и животных; отсутствие вредного воздействия на окружающую среду и людей; наличие широкой сырьевой базы и небольшая стоимость, позволяющая конкурировать с укреплениями из традиционных строительных материалов.

Этим требованиям в наибольшей степени соответствуют материалы на основе полиамидного (капрон), акрилонитрильного (нитрон), полиэфирного (лавсан) и поливинилспиртового (куралон) волокон.

Для указанного типа выходных русел в качестве расчетной принимают скорость на выходе из трубы, глубины размыва для труб диаметром от 1,0 до 1,5 м не рассчитывают и размеры укреплений назначают конструктивно.

8. РАСЧЕТ ФИЛЬТРУЮЩИХ И ПЕРЕЛИВНЫХ НАСЫПЕЙ,

ЛОТКОВЫХ СООРУЖЕНИЙ

ФИЛЬТРУЮЩИЕ НАСЫПИ

8.1. Фильтрующие насыпи, имеющие в своем теле прослойку из камня, допускается применять на железных и автомобильных дорогах III категории и ниже при малых расходах воды (обычно менее 3 - 4 м³/с), незначительном количестве взвешенных частиц грунта в воде и достаточном технико-экономическом обосновании.

8.2. При узких логах и больших расходах воды применяют комбинированные сооружения, состоящие из фильтрующей насыпи и трубы.

8.3. Фильтрующие насыпи рассчитывают без учета аккумуляции. Камень фильтрующей прослойки должен быть крепких кристаллических пород и по возможности одних размеров: мелкие фракции в отсыпку не допускаются.

В ряде случаев перед входом в фильтрующую насыпь устраивают заграждения в виде плетней или вала камней для задержания возможных наносов и плывущих предметов.

8.4. Фильтрующие насыпи бывают двух типов:

напорные (рис. 8.1, а), когда горизонт верхнего бьефа выше верха входного отверстия и насыпь работает полным сечением, а движение потока в наброске равномерное. Обеспечить надежную изоляцию крупнообломочного фильтрующего слоя и плотное сопряжение его с грунтом насыпи трудно, поэтому напорные насыпи применяют лишь в отдельных случаях при достаточном обосновании;

безнапорные (рис. 8.1, б), когда горизонт верхнего бьефа ниже верха каменной наброски; при этом фильтрующая прослойка пропускает поток со свободной поверхностью.

Рис. 8.1. Фильтрующие насыпи:

а - напорная; б - безнапорная; 1 - земляная часть;

2 - изоляция (слой мха, соломы и пр.) толщиной 5 - 10 см;

3 - фильтрующая часть; 4 - укрепление основания;

5 - свободная поверхность (кривая депрессии)

8.5. В поперечном сечении фильтрующую прослойку в напорных насыпях устраивают постоянной высоты. В безнапорных насыпях каменную прослойку укладывают ступенями. Высоту каждой ступени назначают на 15 - 20% больше глубины фильтрационного потока.

В направлении, перпендикулярном оси насыпи, форма поперечного сечения фильтрующей прослойки может быть прямоугольной, трапецеидальной, параболической или треугольной. Прямоугольную и трапецеидальную формы применяют в широких логах, причем в очень распластанных логах нижнее основание трапеции больше верхнего, а в узких наоборот.

Приближенно все поперечные сечения можно свести к прямоугольному и треугольному, и в дальнейшем расчетные зависимости приводятся применительно к этим поперечным сечениям.

8.6. Глубину воды перед напорной фильтрующей насыпью H [37] определяют по формулам:

а) при h_нб <= h_цт

H = h_цт + l_ф(i - i₀); (8.1)

б) при h_нб > h_цт

H = h_нб + l_ф(i - i₀), (8.2)

где h_нб - бытовая глубина потока в нижнем бьефе;

h_цт - расстояние от подошвы насыпи до центра тяжести поперечного сечения фильтрующей прослойки в ее конце;

l_ф - длина фильтрующей прослойки, обычно соответствующая ширине насыпи понизу (вдоль потока);

i - гидравлический уклон;

i₀ - уклон дна фильтрующей прослойки, обычно равный продольному уклону лога.

8.7. Для области квадратичного сопротивления турбулентной фильтрации (для рекомендуемых расходов в фильтрующих насыпях она соответствует крупности камней прослойки d_н > 5 см)

(8.3)

где

- площадь поперечного сечения фильтрующей прослойки;

K_ф - коэффициент турбулентной фильтрации каменной наброски, определяемый по табл. 8.1 в зависимости от среднего диаметра камней d_н и их пористости p.

Таблица 8.1

Средний диаметр камней, приведенный к шару d_н, см	Значение коэффициента K_ф, м/с, для наброски из камней			Средний диаметр камней, приведенный к шару d_н, см	Значение коэффициента K_ф, м/с, для наброски из камней
Средний диаметр камней, приведенный к шару d_н, см	круглых (p = 0,40)	промежуточных (p = 0,45)	остроугольных (p = 0,50)	Средний диаметр камней, приведенный к шару d_н, см	круглых (p = 0,40)	промежуточных (p = 0,45)	остроугольных (p = 0,50)
5	0,15	0,17	0,19	30	0,43	0,48	0,53
10	0,23	0,26	0,29	35	0,46	0,52	0,58
15	0,30	0,33	0,37	40	0,50	0,56	0,62
20	0,35	0,39	0,43	45	0,53	0,60	0,66
25	0,39	0,44	0,49	50	0,56	0,63	0,70

8.8. Если глубина воды перед насыпью задана, то из формул (8.1) или (8.2) и (8.3) находят

, а затем размеры фильтрующей прослойки.

Ширину фильтрующей прослойки (перпендикулярно потоку) при известной площади сечения назначают из условия, чтобы удельные расходы в сооружении были от 0,25 до 1,0 м²/с.

8.9. Глубину H, вычисленную по формуле (8.1) или (8.2), сравнивают с предельной глубиной H_пр, обеспечивающей устойчивость (невымываемость) основания под влиянием ламинарной фильтрации [5].

Значения H_пр находят по отношению

из табл. 8.2.

Таблица 8.2

Грунты основания	для оснований		Грунты основания	для оснований
Грунты основания	не защищенных обратным фильтром	защищенных обратным фильтром	Грунты основания	не защищенных обратным фильтром	защищенных обратным фильтром
Илистые	12	8	Гравелистые	7	4 - 3,5
Мелкопесчаные	9 - 10	6	Суглинистые	7 - 6	3,5 - 3
Средне- и крупнопесчаные	8	5 - 4	Галечниковые	6	3
Средне- и крупнопесчаные			Торф	7 - 12	8 - 5
Лессовидные	8 - 7	4 - 3,5

8.10. Дополнительно проверяют устойчивость сооружения под воздействием турбулентной фильтрации. Для этого определяют расчетную местную скорость в придонном слое

v_м = 1,7v, (8.4)

где v - средняя скорость.

Средняя скорость

(8.5)

где

- расчетная площадь поперечного сечения потока, принимаемая для напорных насыпей равной поперечному сечению фильтрующей прослойки;

p - пористость каменной наброски (см. табл. 8.1);

- коэффициент, учитывающий образование в порах каменной наброски застоя воды;

Расчетную скорость v_м сравнивают с допускаемой скоростью для грунтов основания (см. табл. 2.7 и 2.8) и при необходимости либо заменяют грунт основания гравием или галькой, подбирая диаметр частиц исходя из допускаемых скоростей (см. табл. 2.7 и 2.8), либо назначают тип укрепления по табл. 2.9.

Определив H, проверяют, будет ли насыпь напорной, т.е. будет ли H > h_ф, где h_ф - высота фильтрующей прослойки.

При H < h_ф фильтрующая насыпь будет безнапорной, и ее нужно либо рассчитать по формулам для безнапорной насыпи, либо уменьшить площадь поперечного сечения прослойки.

8.11. Глубину воды перед безнапорной фильтрующей насыпью [5, 30] при уклоне дна фильтрационного потока i₀ <= i_пр (i_пр - предельный продольный уклон, при котором влиянием уклона при расчете можно пренебречь; значения i_пр приведены в табл. 8.3) определяют по формулам:

а) для прямоугольного поперечного сечения фильтрующей прослойки

(8.6)

где b_ф - ширина фильтрующей прослойки (размер, перпендикулярный потоку).

При

бытовой глубиной пренебрегают; тогда

(8.7)

б) для треугольного поперечного сечения фильтрующей прослойки

(8.8)

где m_от - среднее арифметическое значение коэффициентов заложения откосов каменной наброски в плоскости поперечного сечения.

Таблица 8.3

Грунты основания	Значения i_пр при поперечном сечении фильтрующей прослойки		Грунты основания	Значения i_пр при поперечном сечении фильтрующей прослойки
Грунты основания	прямоугольном	треугольном	Грунты основания	прямоугольном	треугольном
Илистые	0,00213	0,00139	Лессовидные	0,00365	0,00238
Пески средней крупности и крупные	0,00320	0,00208	Гравелистые	0,00370	0,00240
			Суглинистые	0,00427	0,00276
			Галечниковые	0,00430	0,00280
Пески мелкие	0,00284	0,00185	Торф	0,00370	0,00240

При

бытовой глубиной пренебрегают; тогда

(8.9)

8.12. Глубину перед безнапорной насыпью при i₀ > i_пр определяют по уравнению (принимая h_вых = h_нб)

(8.10)

либо при

(что допустимо принимать, если нет подтопления от каких-либо сооружений с низовой стороны) по уравнению

(8.11)

В этих уравнениях h₀ - нормальная глубина, определяемая по формулам:

а) для прямоугольного поперечного сечения

(8.12)

б) для треугольного поперечного сечения

(8.13)

В уравнениях (8.10), (8.11)

- функции относительных глубин, соответственно перед фильтрующей насыпью

и за ней

, которые находят по табл. 8.4 для прямоугольных и табл. 8.5 для треугольных поперечных сечений фильтрующей прослойки.

Таблица 8.4


0,00	0,0000	0,69	0,1579	0,900	0,5722
0,05	0,0000	0,70	0,1673	0,905	0,5942
0,10	0,0000	0,71	0,1772	0,910	0,6175
0,15	0,0011	0,72	0,1876	0,915	0,6442
0,20	0,0027	0,73	0,1988	0,920	0,6690
0,25	0,0051	0,74	0,2105	0,925	0,6976
0,30	0,0095	0,75	0,2230	0,930	0,7284
0,35	0,0151	0,76	0,2362	0,935	0,7617
0,40	0,0236	0,77	0,2503	0,940	0,7980
0,45	0,0347	0,78	0,2654	0,945	0,8378
0,50	0,0493	0,79	0,2814	0,950	0,8818
0,55	0,0684	0,80	0,2986	0,955	0,9307
0,60	0,0931	0,81	0,3170	0,960	0,9859
0,61	0,0989	0,82	0,3368	0,965	1,0489
0,62	0,1050	0,83	0,3581	0,970	1,1223
0,63	0,1114	0,84	0,3812	0,975	1,2097
0,64	0,1182	0,85	0,4062	0,980	1,3176
0,65	0,1253	0,86	0,4333	0,985	1,4573
0,66	0,1323	0,87	0,4631	0,990	1,6566
0,67	0,1407	0,88	0,4958	0,995	1,9995
0,68	0,1491	0,89	0,5319	1,000

Таблица 8.5


0,00	0,0000	0,69	0,0360	0,900	0,2024
0,05	0,0000	0,70	0,0390	0,905	0,2123
0,10	0,0000	0,71	0,0423	0,910	0,2229
0,15	0,0000	0,72	0,0458	0,915	0,2340
0,20	0,0001	0,73	0,0496	0,920	0,2461
0,25	0,0002	0,74	0,0538	0,925	0,2591
0,30	0,0005	0,75	0,0582	0,930	0,2731
0,35	0,0011	0,76	0,0630	0,935	0,2883
0,40	0,0021	0,77	0,0682	0,940	0,3048
0,45	0,0038	0,78	0,0739	0,945	0,3228
0,50	0,0062	0,79	0,0800	0,950	0,3426
0,55	0,0106	0,80	0,0867	0,955	0,3658
0,60	0,0168	0,81	0,0939	0,960	0,3930
0,61	0,0183	0,82	0,1018	0,965	0,4216
0,62	0,0200	0,83	0,1104	0,970	0,4538
0,63	0,0218	0,84	0,1199	0,975	0,4915
0,64	0,0237	0,85	0,1303	0,980	0,5347
0,65	0,0258	0,86	0,1418	0,985	0,5853
0,66	0,0281	0,87	0,1545	0,990	0,6450
0,67	0,0305	0,88	0,1687	0,995	0,7164
0,68	0,0331	0,89	0,1846	1,000

При определении глубины H перед насыпью при i₀ > i_пр и h_нб > 0 придерживаются следующего порядка:

приводят поперечное сечение фильтрующей прослойки к прямоугольному или треугольному;

вычисляют нормальную глубину по формуле (8.12) или (8.13); определяют

;

по полученному значению

по табл. 8.4 или 8.5 находят

; определяют функцию

из уравнения (8.10):

по значению

по табл. 8.4 и 8.5 находят значение

и определяют глубину перед насыпью

При определении глубины H перед насыпью при h_пб = 0 расчет ведут в такой последовательности:

приводят поперечное сечение прослойки к прямоугольному или треугольному;

вычисляют по формулам (8.12) и (8.13) нормальную глубину;

определяют

по уравнению (8.11);

по значению

находят значение

из табл. 8.4 или 8.5;

определяют глубину перед насыпью

(8.14)

8.13. Для безнапорных насыпей, так же, как и для напорных, проверяют устойчивость основания насыпи под воздействием ламинарной фильтрации по табл. 8.2 и турбулентной фильтрации по формулам (8.4) и (8.5). При этом площадь сечения потока в формуле (8.5) берут при расчетной глубине h_р = 0,8h_к:

а) для прямоугольного сечения

(8.15)

б) для треугольного сечения

(8.16)

где

- коэффициент кинетической энергии;

;

- коэффициент, учитывающий образование в порах каменной наброски застоя воды;

8.14. Для безнапорных насыпей проверяют также устойчивость низового откоса из условия

z < z_пр,

где z - разность уровней бьефов; обычно при отсутствии подтопления со стороны сооружений z = H + i₀l_ф;

z_пр - предельная разность уровней бьефов, при превышении которой нарушается устойчивость низового откоса.

Значение z_пр определяется из формулы

(8.17)

где

- угол естественного откоса наброски, равный 35 - 36°;

- угол наклона низового откоса;

d_н - расчетный диаметр камня.

8.15. Если фильтрующая прослойка удовлетворяет указанным выше требованиям, определяют размеры ее вдоль потока (поперек насыпи). Для этого строят кривую депрессии, используя уравнения (8.10) и (8.11), заменяя в них значение l_ф текущей координатой x, отсчитываемой от подошвы низового откоса насыпи. Для расчета длину фильтрующей прослойки делят на равные интервалы и определяют глубину потока в конце каждого интервала.

Высоту прослойки в конце интервала принимают на 15 - 20% больше глубины потока, т.е.

, где h_i - глубина потока (ордината кривой депрессии) в конце каждого интервала.

Фильтрующая прослойка вдоль потока (поперек насыпи) имеет ступенчатый вид, следуя с некоторым запасом за кривой депрессии.

Примеры расчета фильтрующих насыпей приведены в приложении 8.1.

ПЕРЕЛИВНЫЕ НАСЫПИ

8.16. Насыпи автомобильных дорог, допускающие перелив паводковых вод через полотно дороги без его повреждений, называют переливными. Переливные насыпи применяют на автомобильных дорогах III категории и ниже. Целесообразность устройства переливной насыпи и выбор ее параметров обосновывают технико-экономическим сравнением вариантов. При их оценке необходимо учитывать не только изменение стоимостных показателей сооружений, но и ущерб от перерыва или ограничения движения транспорта на время перелива.

Если по дороге допускается движение транспорта во время перелива, то для предотвращения возможного съезда с насыпи необходимо предусматривать ограждения-ориентиры.

8.17. Задачами гидравлического расчета переливных насыпей являются:

установление отметок уровней воды в верхнем и нижнем бьефах;

определение значений удельного расхода, длины участка перелива напора над осью или верховой бровкой дороги и отметок их высотного положения;

определение глубин и скоростей в характерных точках поперечного сечения полотна дороги;

расчет сопряжения бьефов.

8.18. Переливную насыпь рассчитывают в следующем порядке [30].

1. Задавшись подпертым уровнем воды в верхнем бьефе (ПУВВ), устанавливают в результате гидравлического расчета водопропускного сооружения расход, пропускаемый им (Q_соор) на участке дороги с переливаемой насыпью, ПУВВ и бытовую отметку воды в нижнем бьефе z_нб (при отсутствии подтопления со стороны нижерасположенных сооружений эта отметка соответствует бытовой глубине h_нб, определяемой для заданного лога по формуле Шези).

2. Определяют приближенно расход, пропускаемый через насыпь, как разность между расходом притока с бассейна Q и расходом, пропускаемым водопропускным сооружением:

Q_пер = Q - Q_соор. (8.18)

Несколько уточнить расчет возможно, используя указания п. 8.29 [формула (8.45)]. Пример такого расчета приведен в приложении 8.2 (пример 1). Более точно см. [30].

3. Задаются либо длиной участка перелива l_пер, либо удельным расходом на нем, и из выражения

Q_пер = l_перq_пер (8.19)

находят искомое значение q_пер или l_пер.

4. Вычисляют критическую глубину переливающегося потока

(8.20)

где

5. Устанавливают формы перелива потока через насыпь:

при h_нб < H_нас + h_к насыпь не затоплена со стороны нижнего бьефа (рис. 8.2, а);

б) при h_нб > H_нас + h_к насыпь затоплена со стороны нижнего бьефа (рис. 8.2, б).

Здесь H_нас - высота насыпи по оси дороги, а h_нб - бытовая глубина в нижнем бьефе.

Рис. 8.2. Виды переливных насыпей:

а - незатопленная; б - затопленная;

K-K - линия критических глубин

6. В случае незатопленной насыпи по ее оси устанавливается критическая глубина h_к. Расчет ведут в следующем порядке:

а) определяют напор над осью дороги

(8.21)

где m - коэффициент расхода; m = 0,37;

б) находят напор над верховой бровкой

(8.22)

где i_п - поперечный уклон проезжей части; i_п = 0,02;

h_нас - ширина земляного полотна поверху, зависящая от категории дороги;

в) по известной отметке уровня воды в верхнем бьефе ПУВВ, определенной гидравлическим расчетом сооружения, и напору

или

находят отметку оси дороги или верхней бровки:

(8.23)

(8.24)

Если задана отметка оси или бровки насыпи, то в зависимости от уровня в верхнем бьефе и напора находят удельный расход q_пер, а затем длину участка перелива l_пер.

7. В случае затопленной засыпи соблюдают такой порядок расчета:

а) при заданных отметках уровня воды в верхнем бьефе (ПУВВ) и оси дороги (z_оси) определяют напор по оси дороги:

(8.25)

б) определяют глубину подтопления переливной насыпи

(8.26)

При h_п >= 1,44h_к насыпь работает как подтопленный водослив (см. рис. 8.2, б), при 0 < h_п < 1,44h_к участок CD работает как быстроток (см. рис. 8.2, а), на низовой бровке (у точки D) возникает гидравлический прыжок, при этом максимум скоростей определяется по глубине на низовой бровке;

в) находят коэффициент подтопления

в функции относительной глубины подтопления

по табл. 8.6;

г) определяют удельный расход, пропускаемой затопленной насыпью,

(8.27)

д) находят длину участка перелива

Таблица 8.6


0,80 и менее	1,0	0,94	0,70
0,84	0,97	0,95	0,65
0,88	0,90	0,96	0,59
0,90	0,84	0,97	0,40
0,95	0,72	1,0	0

Если задан удельный расход q_пер и отметки горизонтов в верхнем и нижнем бьефах и требуется определить отметку оси дороги, то ее рассчитывают по формулам (8.25) - (8.27) методом последовательного приближения, причем в первом приближении принимают

8. Определяют глубину и скорости в характерных точках поперечного сечения насыпи.

Для незатопленной насыпи расчет производят в следующей очередности:

а) находят критическую глубину по формуле (8.20) и нормальные глубины на участках насыпи CD и DF (см. рис. 8.2, а):

(8.28)

где n - коэффициент шероховатости;

i - уклон участка;

б) определяют глубину на низовой бровке дороги h_бр(н) (точка D) по уравнению неравномерного движения (см. гл. 2), составляя его для участка CD и принимая глубину по оси дороги h_оси = h_к;

в) по найденной глубине на бровке h_бр(н) и длине участка DF, а также по уравнению неравномерного движения определяют глубину h_пд у подошвы насыпи в точке F.

Эта глубина, а при расчете глубин в других точках и эти глубины должны быть увеличены с учетом аэрации потока умножением на коэффициент 1,09 при откосе 1:4, на 1,14 при откосе 1:2 и на 1,2 при откосе 1:1,5;

г) находят по уравнению неравномерного движения глубину на верховой бровке (точка B), рассматривая участок BC как русло с обратным уклоном дна; для этого находят фиктивную нормальную глубину на этом участке

(8.29)

где [i_п] - абсолютный поперечный уклон проезжей части дороги;

д) по известным глубинам h в точках B, C, D и F находят скорости потока

(8.30)

е) определяют скорости у подошвы верхового откоса

(8.31)

Коэффициенты шероховатости принимают: для проезжей части и обочины n₁ = 0,013; для низового откоса n₂ = 0,017.

Для затопленной насыпи, так же как и незатопленной, скорости рассчитывают по формуле (8.30) при глубинах:

на оси дороги h = h_п;

верховой бровки

;

низовой бровки

В расчетах крепления низового откоса можно воспользоваться табл. 8.7, где для условий выше одиночной ломаной линии можно применять следующее крепление: булыжник, валун диаметром до 30 см, мощение на мху, соломе, в плетневых клетках, фашины, посадки кустарника и др.; над двойной линией - габионы; грунт, обработанный органическим вяжущим; литой асфальт; асфальтобетонные плиты; в остальных случаях - бетон, железо-, буто-, асфальтобетон, деревянный настил. Данные табл. 8.7 соответствуют переливу потока через насыпь высотой до 4 м с откосом 1:2.

Таблица 8.7

Глубина воды, м		Напор над осью , м	Удельный расход q_пер, м²/с	Скорость течения, м/с, на расстоянии от низовой бровки вдоль по откосу
по оси	на низовой бровке
по оси	на низовой бровке			0 м	1 м	2 м	4 м	6 м	8 м
0,2	0,15	0,3	0,3	1,9	2,3	2,8	3,3	3,5	3,8
0,4	0,3	0,6	0,8	2,6	3,4	4,2	4,8	5,5	5,7
0,6	0,4	0,9	1,4	5,1	4,0	4,7	5,6	6,3	6,7
0,8	0,6	1,2	2,1	3,7	4,5	5,1	6,2	6,9	7,5
1,0	0,7	1,6	3,0	4,1	4,9	5,6	6,7	7,4	8,0
1,2	0,9	1,9	4,0	4,6	5,4	5,9	7,0	7,8	8,4
1,5	1,1	2,4	5,5	5,0	5,8	6,3	7,3	8,2	8,8
2,0	1,5	3,1	8,4	5,8	6,3	6,8	7,8	8,7	9,4

9. Рассчитывают сопряжение бьефов.

Возможны два режима сопряжения бьефов за насыпью автомобильных дорог: поверхностный и донный.

Для поверхностного режима (см. рис. 8.2, б) характерен гидравлический прыжок с донным вальцом.

Донный же режим сопровождается образованием за насыпью отогнанного, надвинутого или затопленного совершенного гидравлического прыжка с поверхностным вальцом (см. рис. 8.2, а). В этом случае на низовом откосе и в отводящем русле поток имеет значительные скорости, что требует затрат на крепление и устройство водобойных сооружений.

Поверхностный режим получить нельзя, если за насыпью образуется отогнанный прыжок, т.е. если глубина

, сопряженная с глубиной у подошвы низового откоса (точка F на рис. 8.2, а), h_пд больше бытовой глубины в нижнем бьефе:

(8.32)

Без специальных конструктивных мер поверхностный режим за насыпью (см. рис. 8.2, а) возникает при соблюдении условия

(8.33)

где T₀ - полная удельная энергия потока перед насыпью, относительно подошвы насыпи.

В свою очередь

(8.34)

При донном режиме сопряжения бьефов определяют глубину h", сопряженную с глубиной у подошвы насыпи, по уравнению совершенного гидравлического прыжка (см. гл. 2) и, сравнивая ее с глубиной нижнего бьефа, устанавливают тип сопряжения и потребность в водобойных сооружениях.

Если обеспечивается надежное затопление гидравлического прыжка, т.е.

h_нб >= 1,1h", (8.35)

то водобойных сооружений не требуется. Во всех остальных случаях необходимо запроектировать водобойные сооружения. По условиям эксплуатации за переливной насыпью наиболее удобна водобойная стенка с небольшими отверстиями (15 x 15 см) у основания.

Расчет водобойной стенки изложен в гл. 4.

В случае отгона прыжка за стенкой дополнительно отсыпают каменную призму над предохранительным откосом, высоту которой определяют аналогично высоте водобойной стенки.

Возможность размыва неукрепленного русла в нижнем бьефе определяется сопоставлением скоростей потока v с допустимыми скоростями v_доп для грунта русла. Размыв будет происходить при

v < v_доп. (8.36)

Глубина размыва

(8.37)

ЛОТКОВЫЕ СООРУЖЕНИЯ

8.19. Открытые искусственные сооружения на автомобильных дорогах, предназначенные для пропуска паводковых вод в местах пересечения водотоков и пониженных мест, называют лотковыми [25]. Лотковые сооружения могут применяться в сочетании с устраиваемыми под ними трубами.

8.20. Водопропускные сооружения лоткового типа представляют собой либо укрепленные пониженные участки насыпи различной конфигурации в зависимости от расхода воды и параметров вертикальных кривых рельефа местности (рис. 8.3), либо сочетание таких участков с отверстиями под ними в виде труб прямоугольного или круглого сечения (рис. 8.4). В последнем случае меженный расход, а иногда и часть паводка проходит через отверстия, а перелив происходит лишь в наиболее высокие паводки.

Рис. 8.3. Примерный профиль лотка вдоль дороги

Рис. 8.4. Переливные лотки с отверстиями:

а - прямоугольного сечения; б - круглого сечения

Водопропускные сооружения лоткового типа применяют на автомобильных дорогах низших категорий с периодическим дождевым стоком.

8.21. Лотки без отверстий применяют на периодических водотоках без твердого стока в распластанных логах, где иначе потребовалось бы несколько сооружений, работающих при одном уровне, при отсутствии или неопределенности водоразделов между смежными водосборами, а также в местах ожидаемого увеличения расхода в результате перераспределения расчетных расходов между отдельными водотоками.

Лотки с отверстиями применяют на водотоках с постоянной меженью или при наличии твердого стока на распластанных водотоках с хорошо выраженным руслом, используемым в качестве водоисточника поливочных земель или для сброса воды с них.

8.22. Лотковые сооружения содержат следующие элементы: подводящие и отводящие русла; регуляционные сооружения; укрепления на входе и выходе из сооружения; собственно лоток; противофильтрационные сооружения.

8.23. Для относительно ровной местности применяют переливную насыпь (см. рис. 8.3) общей длиной L с минимальной длиной горизонтального участка l_г, для холмистой местности - без горизонтального участка.

8.24. Максимальную глубину воды на верховой бровке лотка в самой низкой точке h_в (рис. 8.5) назначают либо из условия беспрепятственного прохода автомобиля во время паводка, либо с учетом перерывов движения. Для обеспечения беспрепятственного движения максимальную глубину принимают не более 0,4 м при продольных уклонах водотоков до 0,01 и 0,25 - 0,35 м при больших уклонах.

Рис. 8.5. Схема гидравлической работы лотка с отверстиями

Пропускную способность лотка без отверстий определяют исходя из задаваемых глубин воды на верховой бровке.

8.25. Для лотка на рис. 8.5 пропускная способность, м³/с,

(8.38)

где Q_г - пропускная способность лотка на горизонтальном участке;

- суммарная пропускная способность лотка на участках вогнутых кривых, определяемая по табл. 8.7 в зависимости от заданных длины l_к и радиуса R_к вертикальной кривой и максимальной глубины перелива h_в.

В свою очередь

Q_г = v_гh_вl_г, (8.39)

где v_г - расчетная скорость воды, м/с;

l_г - длина горизонтальной вставки, м.

Расчетная скорость, м/с,

(8.40)

8.26. При отсутствии горизонтального участка пропускную способность лотка, м³/с, определяют по табл. 8.8 для заданных h_в, длины вертикальной кривой l_к и радиуса R_к. При недостаточности данных табл. 8.8 используют формулу

(8.41)

где v - средняя скорость перелива при параболическом очертании живого сечения потока, м/с.

Средняя скорость перелива потока, м/с,

(8.42)

Площадь живого сечения потока при переливе

(8.43)

Таблица 8.8

Радиус вертикальной вогнутой кривой R_к, м	Значения пропускной способности лотка, м³/с, и длин вогнутых кривых, м
	Q	l_к	Q	l_к	Q	l_к	Q	l_к	Q	l_к	Q	l_к	Q	l_к
	при максимальной глубине перелива h_в, м
	0,10		0,15		0,20		0,25		0,30		0,35		0,40
1000	1,5	28	3,5	35	6,1	40	9,6	45	14	50	19	53	24	56
1500	1,8	34	4,2	42	7,5	49	12	55	17	60	23	65	30	69
2000	2,2	40	4,9	49	8,6	56	14	63	19	69	27	75	34	80
2500	2,4	46	5,4	54	8,8	64	15	71	22	78	30	84	39	90
3000	2,7	49	6,0	60	11	70	17	78	24	85	33	92	43	98
4000	3,1	57	7,0	70	12	80	19	90	27	98	38	106	49	113
5000	3,4	62	7,8	78	14	90	21	100	31	110	42	118	54	126
6000	3,8	69	8,4	84	15	98	23	110	34	120	46	130	60	138
8000	4,3	79	10	98	17	113	27	126	39	138	53	150	69	160
10 000	4,9	90	11	109	19	126	30	141	44	155	60	168	77	178
12 500	5,4	100	12	123	22	141	34	158	49	173	67	187	86	200
15 000	6,0	110	13	132	24	156	37	172	53	188	72	204	95	220
20 000	6,8	126	16	156	28	180	43	200	62	220	84	236	109	252
25 000	7,7	142	18	176	31	200	48	224	68	244	94	264	122	284
30 000	8,5	156	19	188	34	220	52	244	76	268	102	288	133	308

8.27. Глубины и скорости потока на всех участках лотка рассчитывают в соответствии с рекомендациями рубрики "Переливные насыпи" (пп. 8.16 - 8.18) настоящей главы. Расчеты нижнего бьефа выполняют по методике, изложенной в гл. 7.

8.28. Поперечный уклон обочин и проезжей части принимают одинаковым и равным бытовому уклону водотока.

На лотках с отверстиями уклоны проезжей части и обочин сохраняются такими же, как и на всей дороге.

На виражах с поперечным уклоном, не совпадающим по знаку с уклоном водотока, устройство лотков не допускается.

8.29. Превышение ПУВВ над верховой бровкой лотка

в пониженной точке продольного профиля определяют из гидравлических условий протекания воды через водослив с широким порогом как

, где v - определяют по формуле (8.40) для лотка с горизонтальной вставкой и по формуле (8.42) для лотка без нее.

Подпертую глубину перед переливными лотками с отверстиями при наличии перелива по лотку определяют по формуле

(8.44)

а при отсутствии перелива - в соответствии с рекомендациями гл. 5. В формуле (8.44) h_нк - расстояние от верха отверстия до проезжей части.

Возможны следующие схемы пропуска воды через лоток с отверстиями.

При H < 1,1h_т (где h_т - высоты отверстия) под лотком пропускают весь расход при безнапорном режиме (кривая 3 на рис. 8.5).

При H > 1,1h_т режим протекания через отверстия полунапорный и возможны два случая:

H < h_т + h_нк - перелива нет (кривая 2 на рис. 8.5);

H > h_т + h_нк - часть расхода переливается по лотку (кривая 1 на рис. 8.5).

При отсутствии перелива по лотку отверстия рассчитывают по рекомендациям гл. 5.

Минимальную отметку насыпи на подходах к лотку принимают на 0,5 м выше ПУВВ.

Отверстие лотка с учетом перелива

Q_п = Q_с + Q_пер, (8.45)

где Q_с - суммарная пропускная способность отверстий, определяемая по рекомендациям гл. 5;

Q_пер - расход, переливающийся через лоток, определяемый согласно методике, изложенной выше [см. формулы (8.38) - (8.41)].

Уравнение (8.45) решают подбором, добиваясь того, чтобы отметка ПУВВ для лотка и для отверстий была одна и та же.

Укрепление и конструкция верховой обочины и откоса лотка представлены на рис. 8.6.

Рис. 8.6. Типы укрепления верховой части лотка:

а - с заделкой концевой части; б - без заделки

Размер горизонтального участка вдоль потока на выходе принимают не менее 0,8L, где L - длина лотка (рис. 8.7), и с обязательным устройством зуба укрепления или рисбермы из камня глубиной заложения h_укр, определяемой согласно рекомендациям гл. 7.

Рис. 8.7. Профили лотков без отверстий (вдоль потока)

Лотки типа 1 применяют при неразмываемых и трудноразмываемых грунтах, типа 2 - при глубинах размыва не более 1,0 м, типа 3 - при глубинах размыва более 1,0 м, необходимости отгона струи и удаления воронки размыва от низовой бровки, а также в случаях возможного развития эрозионного вреза, типа 4 - в нулевых отметках.

Следует отметить, что при проектировании лотковых сооружений и выполнении их гидравлических расчетов может быть использован типовой проект этих сооружений на лесохозяйственных автомобильных дорогах [19], а также монография Б.Ф. Перевозникова [25].

9. РАСЧЕТЫ КАНАВ

КАНАВЫ НЕБОЛЬШОЙ ДЛИНЫ С ПОСТОЯННЫМ УКЛОНОМ ДНА

9.1. Прямолинейные длиной до 200 м канавы с постоянным уклоном дна рассчитывают по формуле Шези (2.5):

Скоростную характеристику

находят по графику (на рис. 2.3), причем коэффициент шероховатости n, зависящий от грунта канавы (для неукрепляемых канав) или от вида укрепления смоченной поверхности канавы, определяют по табл. 2.2. Для канав с неоднородной шероховатостью дна и откосов вычисляют приведенный коэффициент шероховатости по приближенной формуле

(9.1)

где

- части смоченного периметра канавы с коэффициентами шероховатости соответственно n₁ и n₂.

Площадь поперечного сечения потока для канав трапецеидального поперечного сечения (рис. 9.1)

(9.2)

где b_дн - ширина канавы по дну;

h - глубина потока в канаве при равномерном движении, заданном расходе и характеристиках сечения;

- относительная ширина по дну;

- коэффициент откоса (см. рис. 9.1).

Рис. 9.1. Поперечное сечение канавы

Гидравлический радиус канавы

(9.3)

где

Для канав треугольного поперечного сечения

(9.4)

(9.5)

Для канав прямоугольного поперечного сечения

(9.6)

(9.7)

9.2. По формулам (9.11), (9.2) решаются следующие задачи.

1. Определение расхода. По известным поперечному профилю канавы, его размерам (h, b_дн, m_от), шероховатости стенок и дна, а также уклону i определяют расход воды, протекающий при равномерном движении, непосредственным вычислением по формуле Шези.

2. Определение уклона. Когда известны b_дн, h, m_от, n, Q, а требуется определить уклон дна i, при котором движение будет равномерным, то формулу Шези приводят к следующему виду:

и находят искомый уклон, подставляя в формулу значения соответствующих величин, которые вычисляют по формулам (9.2) - (9.7).

3. Определение глубины воды. По заданным характеристикам поперечного профиля канавы b_дн, m_от, n и уклону i, а также расходу воды Q определяют h, т.е. нормальную глубину. Эту задачу решают подбором такого значения h, при котором удовлетворяется формула Шези.

4. Расчет поперечного профиля. По заданным расходу воды Q, уклону i и шероховатости стенок и дна n определяют ширину дна b_дн, коэффициент откоса m_от и глубину воды h. Эта задача однозначно не решается, так как входящие в формулу Шези значения

, R и C зависят от двух переменных - b_дн и h. Коэффициент откоса определяют в зависимости от грунта и конструкции укрепления. Если ширину по дну принимают без расчета по конструктивным соображениям, то задача сводится к предыдущему типу.

Если известно отношение

, то вычисляют

, задаются значением h, а затем определяют

, R, W и

Вычисленную расходную характеристику K сравнивают с K₀ и повторяют подбор до совпадения K и K₀ с точностью порядка 1 - 2%. Окончательно принимают округленное в большую сторону значение и уточняют глубину.

Когда ни b_дн, ни h не ограничены, иногда бывает возможно придать канаве гидравлически наивыгоднейшее сечение. Входящая в формулы (9.2) и (9.3) относительная ширина потока по дну

может быть подобрана так, что при заданной шероховатости пропускная способность поперечного сечения канавы будет максимальная. Такое сечение называется гидравлически наивыгоднейшим. Для него

(9.8)

Если коэффициент откоса назначен, то задача о расчете поперечного сечения становится определенной; подбором находят такое b_дн и

, при котором удовлетворяется формула Шези.

При этом учитывают, что гидравлически наивыгоднейшие сечения канав с коэффициентом откосов m_от = 1,5 имеют большие глубины при малой ширине по дну, что в большинстве случаев нежелательно, так как при этом увеличивается стоимость земляных работ. Кроме того, уменьшение сопротивления приводит к увеличению скорости течения и размывающей способности потока. Поэтому гидравлически наивыгоднейшее сечение часто оказывается нецелесообразным. При увеличении относительной ширины дна в 1,5 - 2 раза против гидравлически наивыгоднейшей площадь сечения потока увеличивается незначительно.

5. Проверка на неразмываемость и незаиляемость. Средняя скорость течения в канаве должна быть не менее той, при которой начинается осаждение наносов и заиление канавы. Нижний предел скорости, определяемый условием незаиления канавы, называется незаиляющей скоростью. Незаиляющая скорость, м/с,

(9.9)

где

- гидравлическая крупность частиц (скорость осаждения частиц диаметром d в неподвижной воде), см/с, принимаемая по табл. 9.1;

d - средний диаметр взвешенных частиц, мм;

p - процент (по массе) взвешенных наносов с крупностью d >= 0,25 мм.

Таблица 9.1

d, мм	, см/с	d, мм	, см/с	d, мм	, см/с	d, мм	, см/с	d, мм	, см/с	d, мм	, см/с
0,01	0,007	0,25	2,70	1,5	12,6	7	29,7	50	76,9	180	145
0,03	0,062	0,30	3,24	2,0	15,3	10	35,2	60	84,2	200	152
0,05	0,178	0,40	4,32	2,5	17,7	15	43,0	80	96,9	250	170
0,08	0,443	0,50	5,40	3,0	19,3	20	49,2	100	108	300	186
0,10	0,692	0,60	6,48	3,5	20,9	25	54,8	120	119	350	201
0,15	1,557	0,80	8,07	4,0	22,3	30	60,0	140	128	400	215
0,20	2,160	1,00	9,44	5,0	24,9	40	68,9	160	137	500	240

Для практических расчетов, когда насыщенность потока наносами крупнее 0,25 мм не превышает 0,01% по массе при R = 1 м, незаиляющая скорость может быть определена по табл. 9.2; для канав с

значения и v_нез умножают на

Таблица 9.2

d, мм	v_нез, м/с	d, мм	v_нез, м/с	d, мм	v_нез, м/с
0,1	0,22	0,6	0,82	1,5	1,03
0,2	0,45	0,8	0,90	2,0	1,10
0,4	0,67	1,0	0,95	3,0	1,11

Верхний предел средней скорости потока в канаве, определяемый из условия отсутствия размыва потоком грунта канавы или укрепления, называют допускаемой (неразмывающей) скоростью v_доп. Допускаемая скорость потока зависит от характеристик грунта канавы или укрепления ее поверхности, от глубины потока, формы его поперечного сечения и характеристик турбулентности потока.

Значения v_доп определяют по табл. 2.7 - 2.9 или (для равномерного потока) по формуле

(9.10)

где K_р - коэффициент, принимаемый по графикам, представленным на рис. 9.2, в зависимости от участка поперечного сечения канавы (дно или откос) и отношений

и b_дн/h (здесь

- высота выступов шероховатости, определяемая по табл. 1 приложения 9.1);

- допускаемая местная пристеночная скорость (на высоте выступов шероховатости), определяемая по табл. 1 приложения 9.1 (для связных грунтов - по табл. 1 и 2).

Пример. Требуется определить допускаемую скорость для дна и стенок канавы трапецеидального поперечного сечения, проложенной в несвязном грунте с крупностью частиц d = 0,25 мм и коэффициентом естественного откоса m₀ = 1,5. Коэффициент откосов канавы m_от = 1,75, ширина канавы по дну b_дн = 0,5 м; глубина потока h = 1,0 м.

Решение. В соответствии с данными табл. 1 приложения 9.1 определяем допускаемую пристеночную скорость для дна канавы

(согласно примечанию 4 к табл. 1 член

равен нулю) и для откосов по формуле

Вычисляем отношения

; далее по графику на рис. 9.2 определяем значения коэффициента K_р: для откосов канавы K_р(отк) = 3,53, для дна K_р(дн) = 3,30.

Рис. 9.2. График для определения коэффициента K_р

для канав трапецеидального сечения:

штриховая линия - дно; сплошные линии - откосы.

При промежуточных сечениях b_дн/h и m коэффициент K_р

определяют интерполяцией

По формуле (9.10) определяем средние по сечению потока допускаемые скорости:

для откосов

для дна

9.3. При оценке необходимости укрепления канавы и подборе типа одежды следует иметь в виду, что значения скорости потока на концевом участке канавы зависят от условий выхода потока из канавы. Если поток из канавы поступает в водоем, резерв или водоток, отметка уровня свободной поверхности воды в которых при расчетном расходе Z_в незначительно отклоняется от расчетного уровня свободной поверхности в концевом сечении канавы Z_к_N, подбор одежды следует производить по изложенной выше методике. Если же Z_в > Z_к_N более чем на 15% расчетной глубины потока в канаве, то следует проанализировать соотношение нормальной и критической глубин потока в канаве.

Критическую глубину определяют в соответствии с указаниями гл. 2. При h₀ < h_к поток находится в бурном состоянии и на концевом участке канавы сохраняется нормальная глубина; в этом случае концевой участок укрепляют так же, как и основную часть канавы. Если же h₀ > h_к, на концевом участке возникает спад с постепенным уменьшением глубин до глубины, соответствующей положению уровня воды в нижнем бьефе канавы Z_в при Z_к_N > Z_в > Z_кк, где Z_кк - отметка горизонта свободной поверхности потока в концевом сечении канавы при h = h_к (рис. 9.3, а), или до глубины, практически равной критической глубине потока при Z_в < Z_кк (рис. 9.3, б). В последнем случае скорость потока и его размывающая способность увеличиваются. В этих случаях для концевого участка канавы длиной

, где h₀ - нормальная глубина потока в канаве при заданном расходе, защитную одежду подбирают по сечению с критической глубиной.

Рис. 9.3. Поток на концевом участке канавы:

а - при Z_в выше Z_к; б - при Z_в ниже Z_к

9.4. Для ускорения расчетов, сопряженных с подбором ширины или глубины потока, полезен следующий графоаналитический прием. Строят кривую зависимости расхода или расходной характеристики от искомой величины, например

, и при заданном значении K (или Q) снимают с графика значение искомой величины, удовлетворяющее условию

или уравнению Шези. При этом удобно пользоваться графиком скоростной характеристики (см. рис. 9.6).

9.5. В гидравлических справочниках и в виде отдельных изданий существуют специальные таблицы и графики, позволяющие быстро решать частные задачи о равномерном движении воды в канавах, в том числе и те, которые иначе требуют подбора.

Пользуясь номограммой В.А. Александрова (рис. 9.4), можно решать все основные задачи по расчету канав (рис. 9.5), включая оценку размываемости и подбор одежды, при заданных характеристиках грунта или укрепления канавы. Коэффициент шероховатости n (при хорошем состоянии поверхности) оценивают по табл. 3 приложения 9.1. Пристеночные допускаемые скорости потока

и высоту выступов шероховатости

определяют по табл. 1 или 4 приложения 9.1, где характеристики грунтов и укреплений сгруппированы по близким (приведенным в номограммах) значениям

Рис. 9.4. Номограмма В.А. Александрова для расчета канав

трапецеидального сечения с m_от = 1,5

Для несвязных грунтов (в особенности мелких и среднезернистых) на откосах канав допускаемые скорости более точно определяют по табл. 1 приложения 9.1 и графику, представленному на рис. 9.2.

9.6. Задачу, представленную на рис. 9.5, а, так же, как и на всех остальных рис. 9.5, начинают решать с определения по табл. 1, 3 и 4 приложения 9.1 значений n,

для заданного грунта и укрепления. Затем вычисляют

и от точки, соответствующей этому значению на оси

, проводят горизонтальную прямую 1 до пересечения с линией заданного значения b_дн, а от точки пересечения - вертикальную прямую 2 до оси

, определяя таким образом значение

канавы. Далее проводят прямую 3, являющуюся продолжением 2 до линии заданного значения b_дн (см. выше), и от точки пересечения - горизонтальную прямую 4 до линии n, соответствующей типу укрепления или грунта канавы. Затем проводят вертикальную прямую 5 до линии заданного уклона i и от нее - горизонтальную прямую 6 до соответствующей линии

. От точки пересечения проводят горизонтальную прямую 7 до оси v и вертикальную 8 до оси Q, определяя тем самым искомые значения v и Q.

Рис. 9.5. Определение параметров для расчета канав

по номограмме В.А. Александрова:

а - Q, v и v_доп (для дна и откосов) по известным b_дн, h и i;

б -

, h, b_дн и v_доп (для дна) по Q, v и i;

в - v, h, b_дн, v_доп (для дна) по Q,

, i;

г - h, v, v_доп (для дна) по Q, i и b_дн;

д - допустимых v, Q, i при отсутствии размыва по h и b_дн;

е - v, v_доп (для дна) и i по Q, b_дн и h;

ж - Q, h и v_доп (для дна) по i, v и b_дн;

з - v_доп, Q по b_дн и i

Проводят горизонтальную линию 9 вправо от оси

до соответствующей линии

(причем для дна канавы линии сплошные, для откосов - штриховые; для остальных рассмотренных на рис. 9.5 случаев показано определение v_доп лишь для дна канавы) и от точки пересечения вертикальную прямую для заданного значения

. Проведя горизонтальную прямую (10 или 11) до оси v_доп, находят искомое значение v_доп отдельно для дна и откосов канавы.

9.7. Задачу, представленную на рис. 9.5, б, решают следующим образом.

Через точки с заданными значениями Q и v на соответствующих осях номограммы проводят прямые 1 и 2. Точка их пересечения определяет искомое значение

. Затем проводят прямую 3, являющуюся продолжением 2, до пересечения с линией заданного уклона i, а от точки пересечения - прямую 4 до линии заданного значения n и далее горизонтальную прямую 5. Пересечение ее с вертикальной прямой 6, проведенной через найденное ранее значение

на соответствующей оси графика, определяет значение b_дн.

Прямую 6 продолжают вертикально вниз до линии заданного значения b_дн (прямая 7), а из точки пересечения проводят горизонтальную прямую 8 до оси

, на которой определяют значение

, и по нему находят h.

Дальнейшие вычисления аналогичны случаю, представленному на рис. 9.5, а.

9.8. Для решения задачи, приведенной на рис. 9.5, в, через точку с заданным значением Q на соответствующей оси номограммы проводят вертикальную прямую 1 до пересечения с линией заданного значения

. Проведенная из точки пересечения горизонтальная прямая 2 определяет искомое значение v. Прямую 3, являющуюся продолжением вправо прямой 2, проводят до пересечения с линией заданного значения i; прямую 4 - до пересечения с линией определенного по табл. 3 приложения 9.1 значения n. Из точки пересечения проводят горизонтальную прямую 5, а из точки с заданным значением

на соответствующей оси номограммы - вертикальную прямую 6. Пересечение прямых 5 и 6 определяет искомое значение b_дн. Прямую 7, являющуюся продолжением 6, проводят до пересечения с линией определенного выше значения b_дн.

Прямую 8 проводят до оси

. По определенному таким образом значению

вычисляют h, затем с учетом

, определенного по табл. 1 приложения 9.1, отношение

. Прямую 9, являющуюся продолжением прямой 8, проводят до пересечения с линией вычисленного значения

, а прямую 10 - до пересечения с линией определенного по табл. 4 приложения 9.1 значения

. Прямую 11 определяет искомое значение v_доп.

9.9. Задачу, приведенную на рис. 9.5, г, решают методом последовательного приближения. Задаются произвольным значением

и откладывают на соответствующей оси номограммы. Начиная с этой точки, проводят цепочку прямых: прямую 1 до пересечения с линией заданного значения b_дн, 2 - до линии заданного значения n, 3 - до линии заданного значения i, 4 - до линии принятого выше значения

и затем 5 - до пересечения с осью Q. Определенное таким образом значение Q_выч сравнивают с заданным значением Q. При несовпадении этих значений задаются новым значением

и построение повторяют вновь в том же порядке. Совпадение значений Q и Q_выч (с точностью до 3 - 5%) означает, что принятое значение

соответствует его действительному значению.

Продолжением решения задачи является продление прямой 4 до пересечения с осью v номограммы (прямая 6) и определение тем самым v канавы. Далее из точки оси

номограммы, соответствующей определенному выше значению

, проводят прямую 7 до пересечения с линией заданного значения b_дн и затем прямую 8 - до пересечения с осью

номограммы. Полученная точка пересечения позволяет по формуле

определить искомое значение h. Далее вычисляют отношение

. После этого проводят прямую 9 до пересечения с линией соответствующего значения

и прямую 10 - до пересечения с линией определенного по табл. 4 приложения 9.1 значения

, затем прямую 11 - до пересечения с осью v_доп, что дает искомое значение v_доп.

9.10. Ход решения задачи, представленной на рис. 9.5, д, следующий.

По формуле

вычисляют значение

, затем с учетом величины

, определенной по табл. 1 приложения 9.1, - отношение

. Построение начинают с проведения прямой 1 от полученного значения

на соответствующей оси номограммы до пересечения с линией определенного выше значения

, затем проводят прямую 2 - до пересечения с линией определенного по табл. 4 приложения 9.1 значения

и прямую 3 - до пересечения с осью v_доп, что и дает искомое значение v_доп.

Проводят прямую 4 от определенного выше значения

на оси

до пересечения с линией заданного значения b_дн и затем вертикальную прямую 5 до пересечения с осью

номограммы. Точка пересечения определяет искомое значение

. Прямую 6, являющуюся продолжением прямой 5, проводят до пересечения с линией заданного значения b_дн. Из точки пересечения прямой 6 с линией b_дн проводят прямую 7 до пересечения с линией определенного по табл. 3 приложения 9.1 значения n, затем вертикально вниз прямую 8. Из точки на оси v номограммы со значением v = v_доп проводят горизонтальную прямую 9. Пересечение прямых 8 и 9 определяет искомое значение i. Из точки пересечения прямой 9 с линией определенного выше значения

проводят вертикально вниз прямую 10, пересечение которой с осью Q номограммы определяет искомое значение Q канавы.

9.11. Задачу, приведенную на рис. 9.5, е, решают следующим образом.

Определяют

, значение которого откладывают по соответствующей оси номограммы. Из этой точки проводят прямую 1 до пересечения с линией заданного значения b_дн, затем проводят вертикальную прямую 2 до пересечения с осью

, где и получают искомое значение площади поперечного сечения канавы. Прямую 3, являющуюся продолжением прямой 2, проводят до пересечения с линией заданного значения b_дн. Далее проводят прямую 4 до пересечения с линией определенного по табл. 3 приложения 9.1 значения n, после чего вертикально вниз - прямую 5. Из точки на оси Q номограммы, соответствующей заданному значению расхода, вертикально вверх проводят прямую 6 до пересечения с линией определенного выше значения

. Пересечение проведенной из этой точки горизонтальной прямой 7 и прямой 5 определяет искомое значение i. Пересечение проведенной из этой точки в другую сторону прямой 8 с осью v номограммы дает искомое значение v.

Для определения v_доп из полученной ранее точки на оси

проводят вправо прямую 9 до пересечения с линией вычисляемого по заданной величине h и определенной по табл. 1 приложения 9.1 величине

отношения

. Из точки пересечения проводят прямую 10 до линии определяемого по табл. 4 приложения 9.1 значения

, затем прямую 11 до пересечения с осью v_доп, что и дает искомое значение v_доп.

9.12. Задачу, представленную на рис. 9.5, ж, решают в следующем порядке.

По оси v откладывают заданное значение v. Из этой точки проводят горизонтальную прямую 1 до пересечения с линией заданного значения i. Отсюда ведут прямую 2 до пересечения с линией определяемого по табл. 3 приложения 9.1 значения n, затем прямую 3 до пересечения с линией заданного значения b_дн и прямую 4 до пересечения с осью

, что определяет искомое значение

Далее находят точку пересечения прямой 1 с линией определенного выше значения

, из которой проводят вертикально вниз прямую 5 до пересечения с осью Q, что дает искомое значение Q.

Прямую 6, являющуюся продолжением прямой 4, ведут до пересечения с линией заданного значения b_дн, а затем из этой точки - прямую 7 до пересечения с осью

. Определяемое при этом значение

позволяет вычислить искомую величину h. Далее определяют по табл. 1 приложения 9.1 значение

, после чего вычисляют отношение

. Прямую 8, являющуюся продолжением прямой 7, проводят до пересечения с линией вычисленного значения

, после чего проводят вертикальную прямую 9 до пересечения с линией определяемого по табл. 4 приложения 9.1 значения

, а затем горизонтальную прямую 10 до пересечения с осью v_доп, что и определяет искомое значение v_доп.

9.13. Задачу, представленную на рис. 9.5, з, решают методом последовательного приближения. Задаются произвольным значением

и откладывают его на соответствующей оси номограммы. Затем проводят цепочку прямых: из полученной точки - прямую 1 до пересечения с линией заданного значения b_дн, прямую 2 до пересечения с линией определяемого по табл. 3 приложения 9.1 значения n, прямую 3 до линии заданного значения i и 4 - до пересечения с линией принятого ранее значения

. Из полученной точки проводят горизонтальную прямую 5 и вертикальную 6, которые на соответствующих осях номограммы определяют значения v и Q. Далее проводят прямую 7 (продолжение прямой 1 в противоположном направлении) до линии заданного значения b_дн и прямую 8 до пересечения с осью

. Определенное таким образом значение

позволяет вычислить значение

, после чего вычисляют отношение

. Прямую 9, являющуюся продолжением прямой 8, проводят до линии вычисленного значения отношения

, после чего прямую 10 ведут до линии определенного по табл. 4 приложения 9.1 значения

, а затем прямую 11 проводят до оси v_доп, что и определяет значение v_доп.

Задача является решенной при совпадении значений v и v_доп или незначительном (5 - 10%) превышении значения v_доп над значением v. В противном случае задаются новым значением

и построение повторяют в изложенном выше порядке.

9.14. Пример. Канава трапецеидального сечения с коэффициентом откосов m_от = 1,5 проложена в несвязном грунте со средним размером частиц d = 5 мм. Ширина канавы по дну b_дн = 0,6 м; глубина воды в канаве h = 0,4 м; уклон канавы i = 0,005. Требуется определить расход, скорость воды и допускаемую скорость для грунта на дне канавы.

Решение. По табл. 3 приложения 9.1 определяем n = 0,0175, а по табл. 1 и 4 этого же приложения

Вычисляем

;

В соответствии со схемой на рис. 9.5, а по номограмме, представленной на рис. 9.4, определяем v = 1,55 м/с, Q = 0,75 м³/с, v_доп = 0,9 м/с. Отсюда следует, что дно канавы нуждается в укреплении.

КАНАВЫ БОЛЬШОЙ ПРОТЯЖЕННОСТИ

9.15. Канавы большой протяженности рассчитывают последовательно, по отдельным участкам. Границы расчетных участков назначают в соответствии с точками перегиба продольного профиля канавы. При наличии участков постоянного уклона с длиной, превышающей 200 м, канаву разделяют на отдельные участки длиной 100 - 200 м.

Расчетный расход каждого участка

(9.11)

где Q_n и Q_n_-1 - расчетные расходы соответственно рассматриваемого и предыдущего участков канавы;

- приток воды с водосборного бассейна непосредственно к рассматриваемому участку.

Расчет последующих участков, как правило, сводится к определению расчетной глубины потока при новом значении расхода Q и значениях b_дн, m_от, n, i, одинаковых с предыдущим участком. Для последнего участка анализируют условия выхода потока из канавы и проверяют неразмываемость концевой части участка (см. выше).

9.16. При числе расчетных участков n > 2 глубины потока в канаве целесообразно определять с использованием построенного для этой цели графика зависимости расходной характеристики канавы от глубины потока.

Пример. Канава длиной 500 м имеет одинаковый уклон дна i = 0,001. Форма поперечного сечения канавы трапецеидальная, ширина по дну b = 0,1, крутизна откосов и шероховатость характеризуются коэффициентами m_от = 1,5 и n = 0,0275. Поступающий с водосборной территории расход Q = 0,1 м³/с равномерно распределен по длине канавы.

Требуется определить глубину потока (без учета влияния концевого участка канавы) в сечениях 1, 2, 3 и 4, расположенных на расстояниях от начала канавы, соответственно 125 м, 250 м, 375 м и в конце канавы.

Решение. Для ряда произвольно выбранных значений глубин потока по формуле

определяем соответствующие значения расходных характеристик (табл. 9.3); затем строим график K = f(h) (рис. 9.6).

Таблица 9.3

h, м	, м²	R, м	C, м^0,5/с	K, м³/с
0,1	0,025	0,044	21,65	0,113
0,2	0,08	0,079	23,86	0,537
0,3	0,165	0,109	25,17	1,37
0,4	0,28	0,142	26,29	2,774
0,5	0,425	0,174	27,2	4,822

Рис. 9.6. График к примеру определения глубин потока

на участке постоянного уклона

Считая, что расход потока в концевом сечении канавы Q₄ равен полному расходу, поступающему с примыкающей к канаве водосборной территории, а в сечениях 1, 2 и 3 - соответственно Q₁ = 0,25Q₄, Q₂ = 0,5Q и Q₃ = 0,75Q₄, определяем расходные характеристики в каждом из рассмотренных сечений по формуле

Тогда получим

; K₁ = 0,83 м³/с; K₂ = 1,67 м³/с и K₃ = 2,5 м³/с.

По графику на рис. 9.6 находим значения глубин потока h₁ = 0,25 м; h₂ = 0,33 м; h₃ = 0,38 м и h₄ = 0,42 м, соответствующие полученным выше значениям K.

9.17. При различных уклонах дна канавы расчет ведут в следующем порядке:

1. Определяют расчетные расходы участков по формуле (9.11).

2. Для каждого участка находят нормальные и критические глубины, а также критические уклоны потока.

3. Строят и анализируют схематический продольный профиль канавы с линиями нормальных и критических глубин и примерным очертанием кривой свободной поверхности потока.

Возможный вариант кривой свободной поверхности представлен на рис. 9.7.

Рис. 9.7. Кривая свободной поверхности потока

в канаве с переменным уклоном дна

(i₀₂ < i₀₁ < i_к; i₀₃ > i_к)

4. Определяют расчетную глубину потока на рассматриваемом участке исходя из максимальной глубины потока в пределах рассматриваемого участка и требуемого возвышения бровки канавы над уровнем воды.

5. Вычисляют допускаемую скорость потока по характеристикам сечения с минимальной глубиной.

На участках с уклоном дна, меньшим критического, расположенных непосредственно за участками с уклоном, большим критического, происходит переход потока из бурного состояния в спокойное с образованием гидравлического прыжка (рис. 9.8). Одежду для начальной части таких участков следует назначать по сечению, разделяющему указанные участки, считая, что глубина здесь нормальная для участка с бурным течением. Длину участка подобранного таким образом укрепления вниз от раздельного сечения принимают приближенно:

(9.12)

Рис. 9.8. Поток на сопряжении участков канавы

с уменьшением уклона (i₀₁ > i_к; i₀₂ < i_к)

Первый член правой части уравнения (9.12), отражающий длину отгона прыжка l_отг, учитывают лишь при положительном значении этого члена.

6. Определяют незаиливающую скорость для первого участка, а также для участков со скоростями меньшими, чем на первом участке.

КРИВОЛИНЕЙНЫЕ КАНАВЫ

9.18. Закругления канав располагают на участках со спокойным движением потока, т.е. при уклоне дна участков меньше критического. В этом случае глубину потока на участке закругления можно определить по формуле Шези.

Допускаемая скорость на криволинейном участке

(9.13)

где K_з - коэффициент, определяемый по номограмме, представленной на рис. 9.9, в зависимости от отношений r_min/B,

, b/B и

;

r_min - расстояние от центра закругления до ближайшей линии уреза воды в канаве;

- угол поворота.

Рис. 9.9. Номограмма для определения коэффициента K_з

для канав на закруглении

При определении коэффициента K_з для грунтов и укреплений на откосах канавы принимают

9.19. Пример. Требуется определить коэффициент K_з для участка канавы шириной по дну b_дн = 60 см, глубиной h = 40 см и коэффициентом откосов m_от = 1,5. Угол поворота участка канавы

при радиусе поворота R = 12 м. Канава проложена в песчаном грунте со средним диаметром частиц d = 2,0 мм.

Решение. Находим коэффициент K_з для дна канавы. Для этого определяем

(по табл. 1 приложения 9.1);

B = b_дн + 2m_отh = 0,6 + 2·1,5·0,4 = 1,7 м;

b_дн/B = 0,6/0,8 = 0,333;

r_min/B = 11,1/1,8 = 6,2.

По графику на рис. 9.9 находим K_з(дн) = 2,34. Вычислив значения

а также используя известное отношение r_min/B = 6,2, по графику на рис. 9.9 определяем для откосов канавы K_з(отк) = 2,05.

10. РАСЧЕТЫ МАЛЫХ ИСКУССТВЕННЫХ СООРУЖЕНИЙ

ПРИ ПРОЕКТИРОВАНИИ ВТОРЫХ ПУТЕЙ, РЕКОНСТРУКЦИИ ДОРОГ

И ОЦЕНКЕ ВОДОПРОПУСКНОЙ СПОСОБНОСТИ СООРУЖЕНИЙ

ОБЩИЕ СВЕДЕНИЯ

10.1. При реконструкции дорог и строительстве вторых путей необходимо оценить водопропускную способность эксплуатируемых сооружений и учесть специфические особенности, вызываемые переустройством дороги. В этих условиях иногда бывает возможно уточнить гидрологические и гидравлические расчеты, используя данные о работе сооружений в прошлом. Данные наблюдений о работе нижних бьефов сооружений и размывах за укреплениями позволяют более обоснованно назначать тип выходного русла. Ряд условий работы сооружений (отложение наносов, оврагообразование и т.п.) дают возможность обоснованно назначить мероприятия для предотвращения нарушений работы сооружений. Расчет сооружений на вторых путях требует учета специфики их работы (взаимная работа сооружений, удлинение труб и т.п.).

10.2. Для оценки водопропускной способности существующих сооружений при проектировании вторых путей, реконструкции железнодорожных линий и классификации сооружений по водопропускной способности необходимы следующие исходные данные, получаемые из архивных и проектных материалов [33]:

тип и отверстие сооружения;

тип входных и выходных оголовков труб;

год постройки, инвентарный номер проекта (если есть);

продольный профиль дороги на ширине разлива при подпертом уровне высоких вод (ПУВВ) при пропуске наибольшего расхода;

отметка и уклон лотка сооружения;

отметка низа конструкции пролетного строения;

тип выходного укрепления и его концевой части с указанием, имеется ли каменная наброска (рисберма) и ее объем; при отсутствии данных о размерах укреплений и каменной наброски можно воспользоваться данными применительно к конструкциям, которые использовались в период постройки сооружений;

площадь бассейна и уклон лога;

род почв на бассейне (глинистые, песчаные и рыхлые); если нет данных о грунтах, то в расчет принимают глинистые почвы;

архивные и проектные данные о работе сооружений (переливы через насыпь, размывы, заиление и т.п.).

10.3. При необходимости переустройства существующих сооружений, а также при реконструкции дороги и строительстве вторых путей дополнительно собирают на месте следующие материалы:

состояние конусов мостов и род их укреплений; состояние оголовков, укрепления входных и выходных русел; схематический план выходного лога с указанием воронки размыва и границы сохранившегося укрепления, а также расположения вынесенных потоком отдельных элементов укрепления и их размеров;

дата и состав производившихся ремонтных работ, а также их причины; эскизы измененных частей конструкции, влияющих на гидравлические условия работы сооружения; данные об удлинении сооружения в связи с постройкой второго пути и изменении его сечения, переустройстве оголовков, конусов, укреплений, установке гасителей энергии потока, восстановлении сооружения в связи с выносом его после паводка или частичном разрушении и т.п.;

чертежи сооружения, включая фундаменты и укрепления, с указанием глубины заложения фундаментов и концевой части укрепления (для мостов - продольный разрез по оси сооружения, план и фасад; для труб - дополнительно фасады входных и выходных оголовков);

профиль и схематический план лога с указанием резервов, расположенных вблизи сооружения, влияющих на его работу и способствующих образованию оврагов;

схематический план района расположения искусственного сооружения;

живые сечения по логу;

план пересечения оси дороги с осью трубы с указанием угла пересечения;

данные о грунтах лога на выходе из сооружения с указанием гранулометрического состава для несвязных грунтов и сцепления - для связных;

данные о работе сооружений: отметки ПУВВ на трубе или мосту или других сооружениях с указанием года и месяца наблюдения; переливы через насыпь и ее разрушения с указанием года, месяца и расхода (уровня) прошедшего паводка; размывы на выходе с указанием времени их возникновения и вызвавших их расходов (план размыва или при его отсутствии - максимальная глубина размыва и ее положение); уровни воды на выходе из сооружения; глубины потока на укреплении и в выходном логе; данные о протекании потока через трубу; заиление сооружений (сведения о связи толщины слоя наносов над лотком трубы с уровнем паводка по годам); наличие, положение и активность оврагов в районе перехода (данные о перемещении верховой оконечности оврагов по годам);

данные о работе сооружений на расположенных вблизи обследуемой дороги шоссейных и железных дорогах (размеры сооружений, отметки ПУВВ с указанием года наблюдений и месторасположения).

ОСОБЕННОСТИ ГИДРАВЛИЧЕСКИХ РАСЧЕТОВ СУЩЕСТВУЮЩИХ СООРУЖЕНИЙ.

РАСЧЕТЫ СООРУЖЕНИЙ НА ВТОРЫХ ПУТЯХ

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: СНиП 2.01.14-83 указан в пункте [40].

10.4. Основными документами для определения расходов заданной вероятности превышения в сооружениях на эксплуатируемых дорогах, так же, как и для вновь проектируемых, являются: для снегового стока СНиП 2.01.14-83 [41], для ливневого ВСН 63-76 [15]. В этих документах приведены рекомендации по особенностям гидрологических расчетов существующих сооружений в зависимости от объема имеющихся данных. (Для предварительного отбора сооружений с достаточной пропускной способностью расход можно определить в соответствии с рекомендациями гл. 3.)

10.5. Гидравлические расчеты существующих сооружений выполняют в зависимости от принятых методов гидрологических расчетов.

При определении расчетных расходов путем обработки их рядов гидравлические расчеты предшествуют гидрологическим (установление расходов по наблюденным уровням), являясь вспомогательными.

При определении расходов, включаемых в ряд по наблюденным уровням, необходимо иметь в виду следующее.

Уровни, отмеченные на предметах, расположенных выше сооружения (на откосах насыпи, линиях электропередачи и т.п.), соответствуют подпертым уровням, непосредственно используемым при расчете расходов по формулам, приведенным в гл. 5 и 6. Уровни, отмеченные на оголовках трубы или входной ее части, соответствуют глубине на входе в трубу h_вх. В этом случае по графикам для h_вх = f(П_Q) (см. гл. 5) находят соответствующий этой глубине расход трубы.

После определения расчетного Q_р.соор и наибольшего Q_{max соор} расходов по нормам стока [15, 41] подпертые глубины перед сооружениями при прохождении этих расходов получают построением натурных кривых связи расходов и уровней, экстраполируя их до Q_р.соор и Q_{max соор}. Возможен и обычный способ определения подпертых глубин по расходу, приведенный в гл. 5 и 6.

Скорости на выходе из сооружений определяют по тем же зависимостям, что и при расчете новых сооружений (см. гл. 5 и 6).

10.6. Сооружение второго пути в ряде случаев приводит к следующим особенностям в гидравлической работе труб как на существующем пути, так и на вновь сооружаемых.

При устройстве второго пути на едином с существующим земляном полотне новое сооружение является продолжением старого, и длина сооружений (вдоль потока) увеличивается. При удлинении труба может стать в гидравлическом отношении "длинной", т.е. ее длина начнет влиять на условия гидравлической работы (см. гл. 5).

Пристройка моста на втором пути к существующему мосту изменяет схему его гидравлической работы, делая его двухперепадным, аналогично трубе (см. гл. 6).

Иногда существующие мосты удлиняют трубами. При этом возникает комбинированное сооружение мост-труба (рис. 10.1).

Рис. 10.1. Комбинированное сооружение мост-труба:

а - продольный разрез; б - план (насыпь не показана);

в - фасад; 1 - мост; 2 - труба

При пристройке трубы с низовой стороны гидравлические расчеты ведут, как для трубы с портальными оголовками и конусами (см. гл. 5), причем мост играет роль повышенного звена. Режим течения определяют в сечении на входе в трубу с одновременной проверкой возвышения низа пролетного строения.

При пристройке трубы с верховой стороны подпертую глубину перед сооружением определяют, как для трубы, размыв же на выходе из сооружения рассчитывают с учетом формы и размеров конусов у моста.

10.7. При укладке путей на раздельном полотне верховое сооружение работает в условиях подтопления снизу (рис. 10.2), что учитывают как при расчете пропускной способности труб, так и при расчете размыва. Размыв за верховой трубой рассчитывают с учетом того, что он происходит в условиях несвободного растекания, вызванного подтоплением со стороны низового сооружения (см. гл. 5).

Рис. 10.2. Схема гидравлической работы сооружений

при раздельном земляном полотне

Продукты размыва у верхового сооружения могут отлагаться перед низовым сооружением и затруднять его работу. Поэтому минимальное расстояние между концом укрепления верхового сооружения и началом низового

(10.1)

где

- максимальная глубина размыва на выходе из верхового сооружения (см. гл. 7);

m_от - крутизна предохранительного откоса верхового сооружения; при вертикальном "зубе" m_от = 0;

m_вн - крутизна низового откоса воронки размыва верхового сооружения, определяемая по табл. 10.1 в зависимости от степени подтопления сооружения

h_п - предельная глубина потока в нижнем бьефе верхового сооружения, до которой имеет место свободное растекание потока (см. гл. 7);

h_нб - глубина потока в нижнем бьефе верхового сооружения.

Таблица 10.1

	m_вн		m_вн		m_вн		m_вн
1	2,0	3	5,5	6	3,5	10	2,7
2	5,5	4	4,5	8	3,0	>= 15	2,0

В узких логах (K_л > 1 и

, см. гл. 7) l_min определяют из условия обеспечения укрепления на входе в низовое сооружение от обрушения воронкой размыва верхового сооружения по формуле

(10.2)

где D_э - эквивалентный диаметр отверстия верхового сооружения (см. гл. 7).

10.8. Расчет водопропускных сооружений при проектировании вторых путей ведут в следующем порядке.

1. Определяют пропускную способность существующих сооружений без влияния второго пути. Если водопропускная способность существующих сооружений недостаточна, то назначают меры ее увеличения (см. пп. 10.10 - 10.14).

2. Рассчитывают сооружения с учетом постройки второго пути, т.е. учитывают удлинение труб, пристройку к мосту трубы (комбинированные сооружения) и т.п.

3. Определяют отверстие проектируемого водопропускного сооружения. При расположении второго пути на раздельном полотне рассматривают следующие случаи:

а) второй путь с низовой стороны. В этом случае отверстие проектируемого сооружения подбирают так, чтобы были соблюдены следующие условия:

при пропуске расчетного расхода Q_р:

для труб

H_р.н <= sh_т.в + il; (10.3)

для мостов

(10.4)

при пропуске наибольшего расхода Q_max:

для мостов

(10.5)

для мостов и труб

(10.6)

ИС МЕГАНОРМ: примечание.

Обозначения даны в соответствии с официальным текстом документа.

где H_р.н и H_{max н} - соответственно подпоры перед низовым сооружением на втором пути при пропуске расчетного и наибольшего расходов;

H_{max в} - подпор перед верховым сооружением при пропуске наибольшего расхода;

h_т.в - высота верховой трубы;

s = h/h_т.в - регламентируемое СНиП 2.05.03-84 предельное заполнение трубы (здесь h - глубина воды в трубе);

h_нк.в - расстояние от лотка верхового моста до низа пролетного строения;

- регламентируемые возвышения низа конструкций пролетных строений верхового моста над уровнем воды соответственно при пропуске расчетного и наибольшего расходов;

- возвышение бровки полотна верхового сооружения над подпертым уровнем воды;

;

H_нас.в - высота насыпи у верхового сооружения на первом пути;

l, i - соответственно расстояние и уклон между сооружениями.

Проверку по формуле (10.6) выполняют только при h_нб = H_max(н) - il > h_т.в для труб или h_нб > 1,25h_к - для мостов. В этом случае подпертую глубину определяют: для труб - при напорном режиме; для мостов - при несвободном режиме протекания;

б) второй путь с верховой стороны. В этом случае отверстие сооружения вначале назначают равным отверстию существующего сооружения и расчет производят так же, как и в случае расположения второго пути с низовой стороны.

Если хотя бы одно из условий (10.3) - (10.6) применительно к виду сооружения (мост или труба) не удовлетворяется, то отверстие проектируемого сооружения увеличивают и определяют для него новые расходы в сооружении с учетом аккумуляции. После этого проверяют отверстие существующего низового сооружения по заполнению и высоте насыпи. Если оно достаточно, проверяют отверстие проектируемого верхового сооружения согласно условиям (10.3) - (10.6), считая, что вверху как бы находится построенное сооружение.

После выполнения гидравлических расчетов определяют размывы с учетом совместной работы сооружений и при необходимости намечают меры по усилению нижнего бьефа существующего сооружения.

КЛАССИФИКАЦИЯ СООРУЖЕНИЯ ПО ВОДОПРОПУСКНОЙ СПОСОБНОСТИ

10.9. Для предупреждения разрушения сооружений, не обеспечивающих пропуск расчетных паводков, МПС проводит классификацию сооружений по водопропускной способности. В результате классификации выявляют сооружения, требующие усиления.

Работы по классификации выполняют в таком порядке:

1) обследуют сооружение, причем собирают данные о размерах сооружений, их конструкции и работе по пропуску паводков;

2) производят расчет стока и гидравлические расчеты для установления запасов в сооружениях по элементам, ограничивающим водопропускную способность. К этим элементам относятся: гидравлический режим работы трубы и ее заполнение; возвышение низа пролетных строений мостов над уровнем воды; возвышение бровки полотна подходов к малым мостам и трубам над подпертым уровнем; возвышение подходного быстотока к косогорным мостам и трубам; размывы на выходе из труб и мостов; оврагообразование в отводящем русле моста или трубы;

3) по результатам расчетов относят сооружение к той или иной категории водопропускной способности.

При этом относят: к I категории сооружения, запасы по водопропускной способности которых отвечают требованиям норм (СНиП 2.05.03-84); к II категории сооружения, у которых повреждаются только второстепенные элементы при проходе паводков нормированной вероятности превышения; к III категории сооружения, устойчивость которых не обеспечивается при пропуске паводков нормированной вероятности превышения.

На основании результатов классификации устанавливают перечень сооружений, по которым должны быть разработаны проекты усиления; в перечень включают сооружения, относящиеся к III категории. На сооружениях, относящихся к II категории, ведут наблюдения и решения по ним принимают по результатам наблюдений. Сооружения, относящиеся к I категории, из дальнейшего рассмотрения исключают.

Работы по классификации сооружений по водопропускной способности выполняют в два этапа:

I этап - приближенные упрощенные расчеты [33] для выявления сооружений, относящихся к I категории;

II этап - детальные расчеты [33] для отнесения оставшихся сооружений к II и III категориям.

Подробно вопросы классификации малых водопропускных сооружений по водопропускной способности излагаются в Руководстве [33] и Дополнениях к нему [12], разработанных ЦНИИСом Минтрансстроя.

УВЕЛИЧЕНИЕ ВОДОПРОПУСКНОЙ СПОСОБНОСТИ

ЭКСПЛУАТИРУЕМЫХ СООРУЖЕНИЙ

10.10. Увеличение водопропускной способности эксплуатируемых сооружений обосновывают результатами классификации сооружений (см. выше) или гидрологическими и гидравлическими расчетами.

10.11. Различают два вида мероприятий по усилению сооружений:

мероприятия по усилению сооружений на входе, связанные с необходимостью обеспечения требований Технических условий о возвышении бровки полотна и низа конструкции пролетных строений над соответствующими уровнями воды, а также заполнения на входе в трубу на железных дорогах при пропуске расчетного расхода;

мероприятия по усилению сооружений на выходе, направленные на обеспечение устойчивости сооружения от подмыва с низовой стороны.

10.12. Если у эксплуатируемой железнодорожной трубы не соблюдаются условия по заполнению на входе (СНиП 2.05.03-84), то по графикам h_вх = f(П_Q) (см. гл. 5) подбирают в зависимости от расчетного расхода, отверстия и формы поперечного сечения сооружения тип оголовков, обеспечивающий требуемое заполнение.

Если эта мера окажется недостаточной, то в прямоугольных трубах устраивают повышенные, а в круглых - конические звенья. Для этого по тем же графикам в зависимости от типа оголовка находят по расчетному расходу глубину воды на входе в трубу и по ней подбирают высоту повышенного звена с обеспечением регламентируемого заполнения на входе в него.

Для круглых труб найденную таким образом высоту повышенного звена h_пз сопоставляют с входным диаметром типового конического звена для заданного отверстия D_вх. Если h_пз < D_вх, то применяют коническое звено типовой круглой трубы; в противном случае эта мера усиления для круглой трубы не применима.

Для прямоугольных труб, кроме того, из выражения (5.16) определяют длину повышенного звена, обеспечивающую требуемое заполнение на входе в нормальное звено трубы. Для этого в выражение (5.16) подставляют найденную глубину h_вх, глубину на входе в нормальное звено h_нз, принимаемую равной

, и сжатую глубину h_с.

Если все эти меры не обеспечивают выполнения требований СНиП 2.05.03-84 по заполнению, то либо переустраивают сооружение (увеличивают отверстие), либо по согласованию с утверждающей инстанцией сохраняют существующие отверстия и назначают меры по обеспечению сооружения от заноса посторонними предметами (ограничения на входе, решетки).

Для мостов, если не обеспечиваются требования о возвышении низа пролетных строений над подпертым уровнем, можно либо установить новые пролетные строения с более низкой строительной высотой, либо увеличить отверстие сооружения.

10.13. Согласно СНиП 2.05.03-84 бровка земляного полотна на подходах к малым мостам и трубам должна возвышаться над уровнем подпертой воды не менее чем на 0,5 м. Если это требование для переходов с трубами не выдерживается, то его можно в некоторых случаях обеспечить созданием в трубах, имеющих необтекаемые оголовки и не подтопленных снизу, напорного режима. (Для труб с обтекаемыми входными оголовками или подтопленных с нижнего бьефа снижение подпертого уровня указанными способами невозможно.)

В качестве таких способов рекомендуется устройство на входе в трубу обтекаемых открылков (рис. 10.3) с обеспечением зарядки труб при напоре H > 1,2h_т или горизонтальных козырьков зарядкой при H > 1,35h_т. Открылок очерчен по дуге круга радиусом R = 1,7D и опирается на портальную стенку оголовка и две стойки.

Рис. 10.3. Обтекаемые открылки для круглых труб:

а - диаметром 1 м с портальным оголовком;

б - диаметром 1,5 м с раструбным оголовком

При портальном оголовке стойки опираются на грунт. В случае недостаточной несущей способности грунта под стойки укладывают опорные подушки. При раструбных оголовках стойки устанавливают на крылья оголовка. Подпертую глубину перед трубой с обтекаемыми открылками определяют по графикам, приведенным на рис. 10.4.

Рис. 10.4. График пропускной способности круглых труб

с обтекаемыми открылками

Конструкция трубы с горизонтальным козырьком, нижняя поверхность которого расположена в плоскости верха отверстия трубы, представлена на рис. 10.5.

Рис. 10.5. Труба с горизонтальным козырьком

(для прямоугольной трубы длина козырька l_к = 0,3h_т;

для круглой трубы l_к = 0,25D)

Подпертую глубину перед трубами с горизонтальным козырьком на входе определяют по формуле (5.21) с коэффициентами:

для круглых труб
для прямоугольных труб

Если обеспечение напорного режима в трубах не приводит к выполнению требования действующих норм о возвышении бровки полотна над подпертым уровнем, а также для переходов с мостами, в которых указанное требование нарушено, мерой повышения водопропускной способности может быть только увеличение отверстия.

10.14. Выходные русла сооружений подлежат усилению, если глубина размыва

или

при пропуске наибольшего паводка превышает глубину заложения концевой части укреплений h_ук, а при пропуске расчетного паводка превышает h_ук/1,2.

В качестве мер усиления возможны: каменная наброска, постановка гасителей, увеличение заглубления концевой части укрепления.

Усиление каменной наброски производят при

(10.7)

где j и K_л - соответственно коэффициенты, учитывающие подтопление и ширину лога, определяемые согласно рекомендациям гл. 7;

- коэффициент, равный 1,2 при расчетном и 1,0 при наибольшем расходе.

Необходимый удельный объем камня в наброске, м³/м,

(10.8)

где

- при пропуске Q_max и

при пропуске Q_р; остальные обозначения см. в гл. 7.

К расчету принимают наибольшее количество камня, определенное по Q_max и Q_р (на два расхода рассчитывают только для железных дорог).

В случае свободного растекания или при

(см. гл. 7) принимают

В остальных случаях уравнение (10.8) решают подбором.

При невозможности усиления выходного русла каменной наброской, т.е. несоблюдении неравенства (10.7), используют средства активной защиты от размыва: гасители и растекатели (ребро в конце укрепления или сочетание его со стенкой в оголовке). Размыв при наличии гасителей рассчитывают согласно рекомендациям гл. 7. При этом сначала проверяют возможность применения гасителей без каменной наброски, а если устойчивость концевой части не обеспечивается, то применяют наброску, рассчитывая ее количество по формуле (10.8).

11. РАСЧЕТ ПОВЕРХНОСТНОГО ВОДООТВОДА С ПОКРЫТИЙ

ТРАНСПОРТНЫХ СООРУЖЕНИЙ

НАЗНАЧЕНИЕ И СХЕМЫ ОРГАНИЗАЦИИ ПОВЕРХНОСТНОГО ВОДООТВОДА

11.1. Обеспечение отвода поверхностных вод с искусственных покрытий, неукрепленных площадок, газонов в настоящее время приобретает все большее значение и остроту в разных отраслях народного хозяйства, в том числе и в транспортном строительстве, в связи с широкой программой развития сети автомобильных дорог, городов и сельских населенных мест, повышением уровня благоустройства, интенсивным строительством сельскохозяйственных и промышленных предприятий, а также в связи с возросшими требованиями к надежности и долговечности покрытий, повышением безопасности движения.

11.2. Неудовлетворительная работа сооружений систем поверхностного водоотвода приводит к разнообразным неблагоприятным последствиям. Наиболее распространенным среди них является преждевременное разрушение покрытий вследствие насыщения поверхностными водами как конструкций покрытий, так и их оснований. Свободная вода в порах конструктивных слоев и в неплотностях между слоями под действием нагрузок от проходящего транспорта оказывает импульсное динамическое воздействие и может привести к расслаиванию, разрушению слоев покрытия. В сочетании с периодическим воздействием отрицательных температур интенсивность разрушения увеличивается. Насыщение водой основания ведет к резкому повышению порового давления при прогибах плит покрытия под нагрузкой, разжижению материала основания, выносу мелких фракций через щели и швы между плитами, снижению несущей способности основания, потере сплошности опирания плит, их сдвигу. Анализ причин разрушений дорожных одежд и аэродромных покрытий в США показал, что скорость разрушения покрытия при наличии свободной воды, образовавшейся в результате неудовлетворительного водоотвода, в десятки, сотни и тысячи раз больше по сравнению со скоростью разрушения аналогичного покрытия, не содержащего свободной воды. Преждевременный износ покрытий ведет к сокращению межремонтных сроков, что, в свою очередь, приводит к непроизводительному расходованию сырьевых ресурсов, сокращению их запасов, значительным убыткам.

11.3. Другим проявлением плохого водоотвода является затопление пониженных участков дорог общей сети и городских дорог, что сопровождается ощутимыми материальными и моральными издержками. Они связаны с нарушениями работы и простоями транспорта, неудобствами для пешеходов, затоплениями подвальных этажей зданий, магазинов, складов и т.п. поверхностными водами. Застой поверхностных вод на покрытиях проездов животноводческих комплексов при значительном содержании органических веществ ухудшает санитарное состояние и вызывает химическое разрушение конструкций дорожных одежд.

Важным следствием неудовлетворительного водоотвода с покрытий является значительное снижение безопасности движения транспорта на улицах и дорогах.

11.4. Отвод поверхностных вод осуществляется по системе различных по типу и назначению сооружений. Системы сооружений поверхностного водоотвода подразделяются на системы закрытого типа, в состав которых входят подземные трубопроводы, и открытого типа, когда для отвода поверхностных вод используются открытые каналы. Такое деление достаточно условно, поскольку первым звеном в системе сооружений водоотвода закрытого типа являются открытые водоотводные лотки.

Системы водоотвода закрытого типа имеют наиболее широкое применение. Они используются для отвода поверхностных вод с покрытий городских дорог и улиц, мостов, проездов животноводческих комплексов (рис. 11.1), разделительных полос и прикромочных лотков автомобильных дорог общей сети (рис. 11.2), с покрытий взлетно-посадочных полос и рулежных дорожек аэродромов (рис. 11.3).

Рис. 11.1. Схема водоотвода закрытого типа с улиц, мостов,

проездов, животноводческих комплексов:

1 - прикромочный водоотводный лоток; 2 - дождеприемники

с дождеприемными колодцами; 3 - водосточные ветки;

4 - смотровые и перепадные колодцы; 5 - коллекторы

Рис. 11.2. Схемы водоотвода закрытого типа на автодорогах:

а - с разделительных полос; б - из продольных прикромочных

лотков; 1 - разделительная полоса; 2 - проезжая часть;

3 - прикромочный лоток; 4 - водосточная ветка;

5 - дождеприемник с дождеприемным колодцем

Рис. 11.3. Схема водоотвода закрытого типа с аэродромов:

1 - прикромочный водоотводной лоток; 2 - дождеприемники

с дождеприемными колодцами; 3 - перепуски; 4 - смотровые

и перепадные колодцы; 5 - коллекторы

Системы открытого водоотвода широко применяются на автомобильных дорогах общей сети.

ДВИЖЕНИЕ ПОВЕРХНОСТНЫХ ВОД НА ПОЛОСЕ СКЛОНА ПОКРЫТИЯ

И В ВОДООТВОДНЫХ ЛОТКАХ

11.5. Одна из задач проектирования и расчета поверхностного водоотвода - определение параметров потока и прежде всего расхода в водоотводных лотках. При этом неустановившееся с изменяющимся вдоль пути расходом движение поверхностных вод, существующее в реальных условиях, схематизируется. Наиболее распространены расчетные схемы равномерного движения воды в лотках. Применительно к лоткам треугольного сечения задача решается в одномерной или в двухмерной постановке.

11.6. В одномерной постановке значение расхода в треугольном несимметричном лотке (рис. 11.4, а) при продольном i₀ и поперечном i_п уклонах лотка, ширине B потока по свободной поверхности определяется по формулам Шези

(11.1)

и Маннинга

(11.2)

где

- площадь живого сечения потока;

C - коэффициент Шези;

n - коэффициент шероховатости;

- гидравлический радиус.

Рис. 11.4. Схемы сечения лотков

Если для треугольного лотка (см. рис. 11.4, а) принять смоченный периметр

примерно равным ширине потока по свободной поверхности, т.е.

, то формулы (11.1) и (11.2) приводятся к выражению:

(11.3)

Треугольные симметричные лотки (рис. 11.4, б) рассчитывают методом фрагментов (см. п. 11.40).

11.7. В двухмерной постановке вопроса поток в лотке водоотвода делится по ширине на элементарные струйки шириной каждая в dB и глубиной h. Принимая для каждой струйки при малых значениях поперечного уклона

, вычисляя средние по глубине скорости v_h с использованием формул (11.1) и (11.2) и суммируя расходы струек v_h hdB по ширине потока B, получают формулу для определения расхода в лотке.

Имеются и другие предложения по расчетным зависимостям для определения расходов воды в водоотводных лотках на дорогах (Полякова А.В., Студеничникова Б.М. [44], Голова А.П.). Они отличаются от формулы (11.3) числовыми коэффициентами. Но наибольшее распространение все же нашла формула (11.3).

КЛАССИФИКАЦИЯ ДОЖДЕПРИЕМНИКОВ ВОДООТВОДА ЗАКРЫТОГО ТИПА

И ОСОБЕННОСТИ ФОРМИРОВАНИЯ РАСХОДОВ ПЕРЕД НИМИ

11.8. Поверхностные воды из лотков отводятся в подземную водосточную сеть через дождеприемники, которые подразделяются на три типа:

с отверстием (горизонтальным) в плоскости лотка, перекрытым решеткой (рис. 11.5, а), с отверстием (вертикальным) в плоскости бордюрного камня (рис. 11.5, б), комбинированные с отверстиями как горизонтальными, так и вертикальными (рис. 11.5, в). В системах водоотвода на автомобильных дорогах общей сети и аэродромах используются дождеприемники первого типа. На городских дорогах и улицах находят применение дождеприемники всех трех типов, причем они отличаются большим разнообразием форм, габаритных размеров, ширины стержней и прозоров между ними, их ориентацией по отношению к направлению движения потока в лотке.

Рис. 11.5. Типы дождеприемников

11.9. В зависимости от схемы расположения в водоотводном лотке в связи с принципиальными отличиями в условиях работы и, следовательно, методике расчета пропускной способности дождеприемники следует классифицировать на расположенные в лотках с продольным уклоном (при этом возможен проскок части расхода мимо дождеприемника) и расположенные в пониженных местах (в том случае каждый дождеприемник принимает весь объем стока поверхностных вод, который к нему поступает).

11.10. При расположении дождеприемников в лотках с продольным уклоном могут быть выделены два характерных режима их работы. Первый, когда весь идущий по лотку расход Q₀ поступает в дождеприемник (рис. 11.6, а), и второй, когда в дождеприемник поступает лишь часть общего расхода Q_дожд < Q₀, а другая его часть - расход проскока Q_пр - проходит мимо дождеприемника (рис. 11.6, в). Граничным является положение, когда по лотку движется предельный расход, полностью принимаемый дождеприемником - Q₀ = Q_* = Q_дожд (рис. 11.6, б). Величина Q_* является, таким образом, критерием, определяющим режим работы дождеприемника. Как показали исследования в лаборатории и в натуре, дождеприемники в основном работают во втором режиме. В наиболее часто встречающихся условиях поток в лотке является бурным. Он обладает значительной кинетической энергией. Поэтому при Q₀ > Q_* часть потока (при интенсивных дождях - большая по величине) обтекает дождеприемник и движется по лотку далее. К каждому из расположенных ниже дождеприемников притекает все больший расход. В наиболее трудных условиях оказываются дождеприемники, установленные в пониженных местах - в конце участков спусков. Это и является причиной затоплений пониженных мест.

Рис. 11.6. Схемы приема воды из лотков решеткой

11.11. В каждой из схем расположения дождеприемники следует подразделить на две категории в зависимости от условий формирования расхода в лотке Q₀. Таким образом могут быть выделены следующие четыре расчетных случая.

1. Дождеприемники в лотках с уклоном, установленные первыми от водораздела (рис. 11.7, а). Расход в лотке перед дождеприемником равен расчетному расходу дождевых вод с площади водосброса дождеприемника:

Q₀ = Q_расч. (11.4)

Рис. 11.7. Схемы расположения дождеприемников

Расход дождеприемника при Q₀ > Q_дожд составляет некоторую долю расхода в лотке:

Q_дожд = kQ₀, (11.5)

где коэффициент k <= 1 зависит от характеристик лотка, параметров дождеприемника и значения Q₀.

Расход проскока мимо дождеприемника определяется как разность расходов Q₀ и Q_дожд:

Q_пр = Q₀ - Q_дожд = (1 - k)Q₀. (11.6)

2. Дождеприемники, установленные в лотке с уклоном, начиная со второго от водораздела (на рис. 11.7, а - это дождеприемники 2 - n). Расход в лотке перед каждым i-м дождеприемником находится с учетом расхода проскока мимо предыдущего (i - 1-го) дождеприемника:

Q₀_i = Q_расч(_i₎ + Q_пр(_i_-1). (11.7)

Расход i-го дождеприемника находится по формуле (11.5) и расход проскока мимо него - по формуле (11.6).

3. Дождеприемники, установленные в пониженных местах в конце затяжных участков спусков (на рис. 11.7, а - дождеприемник K). Расход, притекающий по лотку к дождеприемнику, в этом случае определяется как сумма расчетного расхода дождевых вод с площади водосбора, относящегося к дождеприемнику, и расходов проскока мимо последних дождеприемников на участках спусков (на рис. 11.7, а - дождеприемники n, n') по зависимости, аналогичной (10.7). Расход дождеприемника

Q_дожд = Q₀. (11.8)

4. Дождеприемники, установленные в пониженных местах лотков с пилообразным продольным профилем (рис. 11.7, б). Расход в лотке перед каждым из таких дождеприемников равен расчетному расходу дождевых вод с площади водосбора и целиком принимается дождеприемником, т.е. для них справедливы равенства (11.4), (11.8).

11.12. Гидравлический расчет дождеприемников сводится к определению их пропускной способности с учетом влияния действующих факторов и особенностей работы в зависимости от схемы расположения в лотке в соответствии с принятой классификацией.

МЕТОДИКА РАСЧЕТА ПРОПУСКНОЙ СПОСОБНОСТИ ДОЖДЕПРИЕМНИКОВ

ВОДООТВОДА ЗАКРЫТОГО ТИПА В ЛОТКАХ С ПРОДОЛЬНЫМ УКЛОНОМ

Выбор типа дождеприемников

11.13. Основными факторами, определяющими расход, принимаемый дождеприемником Q_дожд в треугольном несимметричном лотке на участке улицы с продольным уклоном одного знака в случае, когда Q₀ > Q_* (см. рис. 11.6, в), являются: расход в лотке Q₀, значения продольного i₀ и поперечного i_п уклонов лотка, тип дождеприемника и габаритные размеры его отверстия, сквозность (отношение площади отверстий между стержнями решетки дождеприемника к общей площади дождеприемника), характер расположения и форма стержней решеток, перекрывающих отверстия дождеприемников.

11.14. Дождеприемники разных типов (см. рис. 11.5) в лотках с продольным уклоном одного знака при одних и тех же условиях характеризуются различной пропускной способностью. В результате выполненных на кафедре гидравлики МАДИ исследований установлено, что при одних и тех же условиях (уклонах лотка и длине дождеприемника) пропускная способность дождеприемников с вертикальным отверстием в бордюрном камне в 5 - 6 раз ниже, чем решетки. Еще хуже работает бордюрное отверстие дождеприемника комбинированного типа. Таким образом, для применения в лотках с уклоном могут быть рекомендованы только дождеприемники с горизонтальным отверстием, перекрытым решеткой. При этом возникают вопросы об эффективности использования отверстий решеток, о выборе оптимальных размеров решеток, влиянии их сквозности и параметров лотка на пропускную способность.

11.15. Эффективность использования 18 отверстий "московской" дождеприемной решетки характеризуется результатами измерений распределения принимаемого ею расхода Q_дожд в литрах и процентах на рис. 11.8. Отверстия первого ряда наиболее нагружены. Принимаемый ими расход составляет 70% общего расхода решетки. Во втором и третьем рядах работают практически только крайние отверстия, в которые расход поступает с боковой стороны. Остальные 10 отверстий (по пяти отверстий во втором и третьем рядах) практически не работают. При общей площади этих отверстий, равной примерно 55% площади всех отверстий решетки, проходящий через них суммарный расход составляет всего лишь около 5% общего расхода, принимаемого решеткой. Эти данные показывают, что в целях более рационального использования металла и увеличения пропускной способности решеток, устанавливаемых в лотках с продольным уклоном, наиболее рациональной мерой является увеличение их ширины. Это нашло отражение при разработке ГОСТ 26008-83 на дождеприемные решетки, которым для применения на улицах и дорогах с продольным уклоном i₀ >= 0,005 и в пониженных местах в конце затяжных участков спусков рекомендуется решетка (рис. 11.9) шириной b = 80 см и длиной l₀ = 40 см, обладающая примерно в 1,5 раза более высокой пропускной способностью по сравнению с "московской".

Q_I = 18,6 - 73,5%; Q_II = 3,2 - 12,7%; Q_III = 3,5 - 13,8%;

Q_дожд = 25,3 л/с

Рис. 11.8. Схема распределения расхода по отверстиям

"московской" дождеприемной решетки

Рис. 11.9. Дождеприемная решетка ДБ по ГОСТ 26008-83

11.16. Влияние поперечного уклона лотка i_п вполне определенно по своему характеру - с увеличением i_п увеличивается концентрация расхода у бордюрного камня и возрастает расход Q_дожд. Увеличение поперечного уклона лотка - достаточно эффективная мера повышения производительности решеток.

Пропускная способность дождеприемников

11.17. Пропускная способность решеток, установленных в лотках с продольным уклоном, определяется для каждого расчетного случая с учетом влияния их габаритных размеров, сквозности и уклонов лотка в зависимости от расхода в лотке Q₀ [27].

11.18. Расчеты выполняют в такой последовательности:

а) определяют предельный расход, принимаемый дождеприемником, применительно к лоткам несимметричного треугольного сечения с вертикальной стенкой по формуле

(11.9)

где B_* - ширина потока в лотке перед решеткой при пропуске расхода Q_*.

Ширина потока

(11.10)

где

- величина отклонения линии уреза воды от внешней грани решетки в предельном случае, когда крайняя линия тока выходит на внешний нижний по течению угол решетки (см. рис. 11.6, б).

В свою очередь

(11.11)

где K - эмпирический коэффициент, учитывающий взаимодействие между струйками и сопротивления движению в окрестности решетки;

v_* - скорость струйки на краю решетки при глубине h_*, соответствующей Q_*.

Эмпирический коэффициент

K = K_iK_b, (11.12)

где K_i и K_b - соответственно коэффициенты, учитывающие влияние уклонов лотка и габаритных размеров решетки, определяемые по графику на рис. 11.10.

Рис. 11.10. График для определения коэффициента K_i

по отношению i_п/i₀ (кривая 1) и коэффициента K_b

по отношению l_р/b (кривая 2)

Скорость струйки

(11.13)

Значение

вычисляется путем совместного решения уравнений (11.11) и (11.13).

Для упрощения расчетов значение Q_* можно установить по таблицам приложений 11.1 и 11.2;

б) определяют расходы воды, принимаемые дождеприемной решеткой, Q_дожд и проскока Q_пр при Q₀ <= Q_* по формуле (11.4), при Q₀ > Q_* - по формулам (11.5) и (11.6). При этом значение коэффициента k <= 1 находят по графику на рис. 11.11 в зависимости от сквозности решетки

(d - ширина отверстий решетки между стержнями;

- ширина стержней) и отношения расходов Q_*/Q₀.

Рис. 11.11. График для определения коэффициента k

11.19. Изложенная методика разработана для решеток в лотках несимметричного треугольного сечения с вертикальной стенкой (см. рис. 11.4, а) и, следовательно, может быть непосредственно применена при расчете водоотвода с городских дорог и улиц, мостов, проездов животноводческих комплексов и т.п. Расчет дождеприемных решеток в треугольных лотках с обоими наклонными откосами на разделительных полосах и в прикромочных лотках автомобильных дорог, на аэродромах, промплощадках выполняется методом фрагментов. Лоток делится вертикальной плоскостью по линии тальвега на два фрагмента (рис. 11.12). Фрагменты рассчитываются по тем же зависимостям. Для симметричного водоотводного лотка расчет выполняется для фрагмента, представляющего собой половину лотка с расходом Q₀ при ширине решетки b. Фактические значения расходов для всего лотка при общем расходе в нем 2Q₀ и ширине решетки 2b находятся как удвоенные значения, т.е. 2Q_*, 2Q_р, 2Q_пр. Способ фрагментов позволяет рассчитывать по предложенной методике пропускную способность решеток в несимметричных лотках при разных значениях ширин и длин решеток, поперечных уклонах и коэффициентах шероховатости в левой и правой частях лотка.

Рис. 11.12. Схема деления лотка по методу фрагментов

ПРОПУСКНАЯ СПОСОБНОСТЬ ДОЖДЕПРИЕМНИКОВ ВОДООТВОДА

ЗАКРЫТОГО ТИПА В ПОНИЖЕННЫХ МЕСТАХ

11.20. При расположении дождеприемников в пониженных местах выделяются два режима их работы: по схеме истечения через водослив с широким порогом и по схеме истечения через отверстие. В качестве расчетных формул предполагается модификация известных формул расхода водослива и отверстия.

11.21. Пропускная способность горизонтальных дождеприемных решеток (см. рис. 11.5, а), установленных в пониженных местах лотков улиц, согласно исследованиям ВНИИГа им. Б.Е. Веденеева при

, когда решетка работает по схеме водослива с широким порогом, определяется по зависимости

(11.14)

и при

, когда решетка работает по схеме истечения через отверстие, - по зависимости

(11.15)

где m и

- коэффициенты расхода; m = 0,350;

;

L - длина той части периметра решетки, через которую поступает вода;

- площадь отверстий решетки;

H₀ - гидродинамический напор перед решеткой.

В свою очередь

где h - глубина потока в лотке перед решеткой;

- коэффициент Кориолиса;

;

v - скорость потока на подходе к решетке.

11.22. Пропускная способность дождеприемников с вертикальным отверстием в бордюрном камне (см. рис. 11.5, б) в лотках улиц при H₀ < 1,9h_отв, что соответствует работе по схеме водослива с широким порогом, согласно исследованиям МАДИ может быть определена по формуле

(11.16)

и при H₀ >= 1,9h_отв, т.е. при работе по схеме истечения через отверстие, - по формуле

(11.17)

где h_отв - высота отверстия в бордюрном камне;

m и

- коэффициенты расхода; m = 0,334;

;

l_отв - длина отверстия;

- площадь отверстия.

11.23. Пропускная способность комбинированного дождеприемника (см. рис. 11.5, в) определяется по приведенным выше формулам в зависимости от глубины потока. При

, когда поток в дождеприемник поступает только через горизонтальную решетку и вертикальное отверстие не работает, пропускная способность определяется по формуле (11.14).

При

часть расхода начинает поступать в дождеприемник через отверстие в бордюрном камне. Решетка в этом случае работает по схеме истечения через отверстие, а отверстие в бордюрном камне - по схеме истечения через водослив, и пропускная способность дождеприемника определяется как сумма расходов решетки по формуле (11.15) и бордюрного отверстия по формуле (11.16). При H₀ >= 1,9h_отв и

отверстие в бордюрном камне затапливается и начинает работать по схеме истечения через отверстие, тогда расход дождеприемника определяется по формулам (11.15) и (11.17).

РЕЖИМЫ РАБОТЫ КОЛЛЕКТОРОВ И ДРУГИХ ТРУБЧАТЫХ СООРУЖЕНИЙ

ВОДООТВОДА ЗАКРЫТОГО ТИПА

11.24. Коллекторы, трубопроводы водосточных веток (на аэродромах - перепуски) в системах поверхностного водоотвода закрытого типа устраивают обычно из железобетонных труб круглого поперечного сечения. В районах старой городской застройки можно встретить коллекторы лоткового сечения. В особых случаях при заключении, например, речки или ручья в коллектор он может быть прямоугольного (квадратного) сечения. Коллекторы - распространенные и ответственные сооружения водоотвода. Нарушения работы коллекторов и водосточных веток (перепусков) могут привести к затоплениям территорий, создать угрозу безопасности движения транспорта. Ремонт трубопроводов водостоков связан со вскрышными работами. Помимо прямых затрат это приводит к частичному или полному прекращению движения транспорта. Одной из причин аварий коллекторов является их работа в режиме, не соответствующем расчетному.

11.25. Расчет размеров сечений (диаметров) коллекторов и трубопроводов водосточных веток, обычно выполняемый по формуле Шези (11.1) с использованием значений K_n и W_n (табл. 11.1) из условия пропуска расчетного расхода при полном (h/D = a = 1) или при частичных наполнениях

основан на предположении, что эти сооружения работают в режиме равномерного движения. В реальных же условиях расходы, пропускаемые коллекторами и трубопроводами водостоков, существенно отличаются от расчетного, изменяясь в широком диапазоне от Q = 0 до значений, превышающих в некоторых случаях расчетный расход. При этом в трубопроводах неизбежны переходы от частичного наполнения к полному и наоборот.

Таблица 11.1

Диаметр трубы D, мм	Бетонные и железобетонные трубы (коэффициент шероховатости (n = 0,014)		Керамические и чугунные трубы (n = 0,013)		Асбоцементные и полиэтиленовые трубы (n = 0,012)
Диаметр трубы D, мм	K_n	W_n	K_n	W_n	K_n	W_n
200	-	-	0,33	10,50	0,35	11,14
300	-	-	0,96	13,58	1,05	14,85
400	1,93	15,35	2,08	16,55	2,25	17,90
500	-	-	3,77	19,20	4,09	20,84
600	5,78	20,16	6,13	21,68	6,64	23,49
700	-	-	9,25	24,04	-	-
800	12,27	24,41	13,21	26,28	-	-
900	-	-	18,09	28,43	-	-
1000	22,25	28,33	23,96	30,51	-	-
1200	36,17	31,98	-	-	-	-
1400	54,58	35,46	-	-	-	-
1500	65,60	37,13	-	-	-	-
1600	77,90	38,74	-	-	-	-
2000	141,30	44,97	-	-	-	-
2400	228,93	50,61	-	-	-	-
3000	416,53	59,01	-	-	-	-
3400	557,58	61,41	-	-	-	-
4000	897,16	71,37	-	-	-	-

11.26. В связи с тем, что резервуарами верхнего бьефа трубопроводов водосточных веток (перепусков) и участков коллекторов являются соответственно дождеприемные и смотровые или перепадные колодцы, имеющие ограниченную емкость, определяющую особый характер их гидравлической работы, эти сооружения выделяются в отдельную категорию трубчатых водопропускных сооружений с емкостью верхнего бьефа ограниченных размеров.

11.27. Особенности этих сооружений:

безнапорный режим сохраняется в них при уровнях, существенно меньших высоты коллектора;

при увеличении расхода безнапорное движение в коллекторе сменяется резко нестационарным, цикличным "пробковым" режимом работы, за которым следует напорный режим.

11.28. При нестационарном "пробковом" режиме работы в коллекторе периодически возникают и перемещаются вниз по течению сосредоточенные массы жидкости, заполняющие все сечение коллектора - "пробки", чередующиеся с замкнутыми воздушными включениями у шелыги. При этом циклично образуется и срывается вакуум, возникает пульсация скоростей и расхода, происходит изменение (раскачка) уровней в колодцах с верховой и низовой стороны участка коллектора.

Нестационарный "пробковый" режим в коллекторах имеет определенную последовательность. В сменяющих друг друга циклах можно выделить характерные фазы процесса: подъем уровня в верховом колодце и образование волн на начальном участке коллектора (рис. 11.13, а), заполнение жидкостью всего сечения коллектора на участке входа при понижении давления - возникновении вакуума (рис. 11.13, б), образование "пробки", медленно перемещающейся вниз по течению (рис. 11.13, в, г). На участке коллектора между входом и "пробкой" поток движется со свободной поверхностью, над которой давление p ниже атмосферного p_а, т.е. вакуум. Между "пробкой" и концевым сечением коллектора поток также движется со свободной поверхностью, но давление над ней равно атмосферному p_а. При выходе "пробки" из коллектора в область над поверхностью потока с низовой стороны в достаточном количестве проникает воздух и над поверхностью потока по всему коллектору устанавливается давление, равное атмосферному. Происходит срыв вакуума. Пропускная способность коллектора при этом уменьшается и в верховом колодце вновь повышается уровень (см. рис. 11.13, а) до тех пор, пока увеличение глубины потока в колодце не приведет к образованию новой "пробки", после чего цикл повторяется.

Рис. 11.13. Фазы пробкового режима

11.29. Периодическое возникновение и срыв вакуума в коллекторе при резко нестационарном "пробковом" режиме работы сопровождается чередующимся проникновением через неплотности в стыках, трещины и свищи в стенках коллектора воды в грунт обсыпки, его разжижением и выносом в коллектор. Вокруг коллектора при этом возникают пустоты, которые могут вызвать просадку грунта под коллектором, его разрушение. Образование пустот вокруг коллекторов (труб перепусков) под покрытиями улиц, дорог, аэродромов может создать опасную аварийную ситуацию для транспорта.

Поскольку значения наполнений (и расходов), при которых происходит возникновение нестационарного "пробкового" режима, значительно менее расчетных, коллекторы в этом режиме работают чаще, чем появляются расчетные расходы.

11.30. Для определения параметров потока в круглом бетонном или железобетонном коллекторе (трубопроводе) при частичном наполнении используют номограмму, приведенную на рис. 11.14. Линия h_к/D позволяет судить об энергетическом состоянии потока. Область выше и левее соответствует спокойному состоянию потока, ниже и правее - бурному. Линия h_пр/D определяет возникновение в коллекторе резко нестационарного "пробкового" режима. Область ниже этой линии соответствует безнапорному движению, для которого по формуле Шези построена номограмма; в области выше этой линии безнапорного равномерного движения не существует, и поэтому рассчитанные по формуле Шези линии относительных наполнений h/D и скоростей v/D^0,5 даны штриховой линией.

Рис. 11.14. Номограмма для определения параметров потока

в круглом бетонном или железобетонном коллекторе

По номограмме на рис. 11.14 может решаться как прямая, так и обратная задача. В первом случае по известному диаметру и уклону при заданном наполнении коллектора определяют пропускаемый через него расход, скорость и энергетическое состояние потока, а также режим работы коллектора. Обратная задача заключается в определении по известному расходу и уклону коллектора и принятому значению наполнения диаметра коллектора, скорости течения, энергетического состояния потока и режима работы. При решении обратной задачи может возникнуть необходимость в повторном выполнении решения, если найденный диаметр трубы не соответствует стандартному (см. табл. 11.1). В этом случае его значение округляют до ближайшего стандартного и уточняют величину наполнения трубопровода, скорость потока и режим работы. Расход и скорость потока при использовании для расчетов номограммы на рис. 11.14, в случае если диаметр коллектора

, определяются умножением относительного расхода Q/D^2,5 и скорости v/D^0,5 соответственно на D^2,5 и D^0,5.

11.31. При проектировании коллекторов водостоков их работу в резко нестационарном "пробковом" режиме, учитывая неблагоприятные последствия, допускать не следует. Согласно номограмме на рис. 11.14 при уклонах i < 0,01 это обеспечивается, если наполнения коллектора при расчетном расходе ограничить в соответствии с кривой h_пр/D = f(i) значениями

. При больших значениях уклонов коллектора

необходимость указанного требования приводит к резкому уменьшению значений допустимых наполнений до

, что влечет значительное увеличение размеров сечения коллекторов, т.е. увеличение строительных затрат.

В этом случае следует предусматривать меры, исключающие возникновение "пробкового" режима работы коллектора. Одной из таких мер является устройство на входных участках патрубков диаметром d_воз ~ 0,1D, обеспечивающих подвод в достаточном количестве воздуха в область сжатого сечения, как показано на рис. 11.15, 11.17.

Рис. 11.15. Колодец перепадный водосливной

ПЕРЕПАДНЫЕ КОЛОДЦЫ НА КОЛЛЕКТОРАХ ВОДОСТОКОВ

11.32. Перепадные колодцы на коллекторах водостоков делятся на два типа. При высоте перепада

устраивают колодцы водосливного типа (см. рис. 11.15), а при большей высоте - водобойного типа (рис. 11.16) с одной (при

) или двумя (при

) водобойными решетками.

Рис. 11.16. Колодцы водобойные

11.33. Длину перепадного колодца следует назначать из условия, чтобы поступающий в колодец по подводящему коллектору поток не оказывал гидродинамического воздействия на противоположную (от подводящего коллектора) стенку колодца.

Длина перепадного колодца водосливного типа l_к, м, при высоте перепада p, м, может быть принята равной дальности полета струи под действием силы тяжести с начальной скоростью v, м/с, вектор которой ориентирован горизонтально:

(11.18)

11.34. Скорость потока, поступающего в колодец, может быть найдена по номограмме на рис. 11.14. Сопряжение отметок лотков подводящего и отводящего коллекторов в перепадном колодце водосливного типа рекомендуется осуществлять лотком плавного очертания.

11.35. Длина перепадного колодца водобойного типа назначается с учетом диаметра люка D_л, м, в перекрытии колодца и характера расположения стержней водобойной решетки (при двух решетках - от расположения стержней верхней решетки). При горизонтальной решетке (рис. 11.16, а) длина колодца

(11.18')

где коэффициент k₁ = 0,45, как и в формуле (11.18). При наклонной решетке длина колодца сокращается в зависимости от величины возвышения балок водобойной решетки над лотком подводящего коллектора. Если балки возвышаются на D/3 (рис. 11.6, б), то в формуле (11.18') k₁ = 0,37, а если балки возвышаются на D/2 (рис. 11.6, в), то в формуле (11.18') k₁ = 0,32. Применение наклонных решеток позволяет получить сокращение длины перепадного колодца водобойного типа примерно на 10%.

11.36. В типовых проектных решениях "Камеры и колодцы ливневой канализации" Гипрокоммундортранс для перепадных колодцев водобойного типа были применены наклонные решетки, возвышающиеся на D/2 над лотком подводящего коллектора, из балок шириной 100 мм и высотой 400 мм. Оказалось, что при натекании на эти балки, установленные с равным шагом по высоте, поток фонтанирует. Во избежание этого были изменены форма и схема расположения балок в решетке (рис. 11.17).

Рис. 11.17. Колодцы перепадные с решетками-гасителями

из прямоугольных стержней (а) и сегментов труб (б)

Балки второй решетки (при высотах перепада

) прямоугольного сечения располагаются под отверстиями между балками верхней решетки, т.е. в шахматном порядке.

СООРУЖЕНИЯ ВОДООТВОДА ОТКРЫТОГО ТИПА

С ПОЛОТНА АВТОМОБИЛЬНЫХ ДОРОГ

11.37. Сооружения системы открытого водоотвода с покрытия автомобильных дорог I - III категорий включают прикромочные водоотводные лотки, дождеприемные (переходные, сопрягающие) лотки, поперечные водосбросные (откосные) лотки, водобойные устройства на выходе из откосных лотков (рис. 11.18).

Рис. 11.18. Сооружения системы водоотвода открытого типа

с полотна дороги:

а - несимметричного очертания в плане; б - симметричного

очертания в плане; 1 - прикромочный водоотводной лоток;

2 - дождеприемный лоток; 3 - водосбросный (откосный) лоток;

4 - водобойные устройства на выходе из откосных лотков

11.38. Водоотводные прикромочные лотки располагаются вдоль кромки проезжей части или остановочной полосы дороги. Они обычно выполняются из сборных блоков и имеют треугольную форму сечения шириной 75 (50) см и глубиной 7 - 9 см (рис. 11.19).

Рис. 11.19. Блоки прикромочных лотков

Гидравлический расчет прикромочных лотков выполняют по уравнению равномерного движения (11.3).

11.39. Дождеприемные (переходные, сопрягающие) лотки водоотвода открытого типа на участках спусков имеют несимметричное в плане очертание (см. рис. 11.18, а), а в пониженных местах продольного профиля дороги - симметричное (см. рис. 11.18, б).

При проектировании и расчете дождеприемных лотков на участках спусков дороги следует учитывать, что в зависимости от расхода в лотке Q₀ они могут работать в двух режимах. При Q₀ <= Q_* дождеприемным лотком принимается весь расход Q₀. При Q₀ > Q_* из водоотводного лотка принимается лишь часть расхода Q_дожд < Q₀. Другая часть образует расход проскока Q_пр. Второй режим работы дождеприемных лотков наиболее распространен, причем доля расходов проскока может быть существенной (рис. 11.20).

Рис. 11.20. Пример распределения расхода прикромочного лотка

дороги по дождеприемным лоткам

11.40. Гидравлический расчет дождеприемных лотков с учетом проскока части расхода выполняется методом фрагментов аналогично тому, как указано в п. 11.19. Водоотводный прикромочный лоток делится перед дождеприемным лотком по линии наибольшей глубины на два фрагмента (рис. 11.21). Для каждого фрагмента определяются расходы в лотке Q₀₁, Q₀₂. Принимается, что расход во внешнем фрагменте 1 прикромочного лотка целиком поступает в дождеприемный лоток и отводится с дороги, т.е. Q_дожд1 - Q₀₁ и Q_пр1 = 0. Внутренний фрагмент 2 рассчитывается по методике, изложенной в п. 11.19, т.е. для него определяют Q_*2, Q_дожд2, Q_пр2. Значение предельного расхода Q_*, целиком принимаемого внутренним фрагментом дождеприемного лотка, находится по приложениям 11.1 и 11.2. Ширина дождеприемника внутреннего фрагмента 2 принимается равной нулю и длина l_дожд - равной ширине входного отверстия дождеприемного лотка. Общий расход, поступающий из прикромочного лотка, определяется как суммарный для обоих фрагментов, т.е. Q_дожд = Q_дожд1 + Q_дожд2, и расход проскока Q_пр = Q_пр2.

Рис. 11.21. Схема к расчету дождеприемных лотков

методом фрагментов

11.41. Водосбросные поперечные (откосные) лотки обычно выполняют из сборных элементов телескопическими. Поскольку уклоны лотков на откосах насыпи превышают критический (i₀ > i_к), на входе в телескопический лоток устанавливается глубина h_к и в пределах лотка кривая спада. Глубины потока в конце телескопического лотка h определены Б.Ф. Перевозниковым по формулам неравномерного движения

при расходе Q = 41 л/с, вычисленном по уравнению критического состояния потока

(11.19)

Скорости v при выходе из телескопического лотка равны 1,5 - 1,8 м/с.

11.42. В качестве водобойного сооружения за телескопическими лотками целесообразно применять малые трапецеидальные колодцы, конструкция которых разработана в Союздорпроекте.

11.43. Расстояния между типовыми телескопическими лотками на автомобильных дорогах следует определять по табл. 11.2 с использованием рис. 11.22, разработанных Б.Ф. Перевозниковым.

Таблица 11.2

Ливневый район (рис. 11.22)	Категория дороги	Расстояния для сброса с проезжей части телескопическими лотками, м, при продольном уклоне дороги, %
Ливневый район (рис. 11.22)	Категория дороги	0,3	0,5	1	2	3	4	5	6
I	I	60 ---- 70	70 ---- 90	60 ---- 80	50 ---- 70	40 ---- 60	30 ---- 50	25 ---- 40	25 ---- 30
	II	115 ---- 65	130 ---- 80	120 ---- 70	105 ---- 60	85 ---- 50	75 ---- 40	50 ---- 35	55 ---- 30
	III	120 ---- 65	140 ---- 80	130 ---- 70	110 ---- 55	90 ---- 45	75 ---- 35	65 ---- 30	60 ---- 25
II	I	75 ---- 110	90 ---- 125	80 ---- 110	60 ---- 95	50 ---- 75	40 ---- 65	30 ---- 55	25 ---- 45
	II	145 ---- 90	160 ---- 110	150 ---- 100	125 ---- 75	110 ---- 60	90 ---- 45	80 ---- 40	70 ---- 35
	III	145 ---- 100	160 ---- 110	150 ---- 100	125 ---- 70	110 ---- 55	90 ---- 45	80 ---- 40	70 ---- 35
III	I	45 ---- 65	60 ---- 80	45 ---- 70	35 ---- 60	30 ---- 50	25 ---- 40	25 ---- 35	20 ---- 30
	II	115 ---- 65	130 ---- 80	120 ---- 70	105 ---- 60	85 ---- 50	75 ---- 40	60 ---- 35	55 ---- 30
	III	115 ---- 60	130 ---- 70	120 ---- 60	105 ---- 60	85 ---- 40	74 ---- 60	60 ---- 25	35 ---- 25
IV	I	110 ---- 135	125 ---- 150	110 ---- 140	95 ---- 115	75 ---- 100	65 ---- 85	55 ---- 75	45 ---- 65
	II	215 ---- 120	235 ---- 140	220 ---- 130	190 ---- 110	165 ---- 90	145 ---- 75	125 ---- 65	110 ---- 60
	III	215 ---- 120	235 ---- 140	220 ---- 130	190 ---- 110	165 ---- 90	145 ---- 75	125 ---- 65	110 ---- 60

Примечание. Для I категории в числителе представлены данные для дорог с укрепленной обочиной, в знаменателе - с неукрепленной; для II и III категорий в числителе - для дорог без виража, в знаменателе - с виражом.

Рис. 11.22. Карта-схема ливневых районов для расчета

поверхностного водоотвода

12. ЭКОЛОГИЧЕСКИЕ АСПЕКТЫ ГИДРАВЛИКИ

МАЛЫХ ДОРОЖНЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

ОСОБЕННОСТИ ВЗАИМОДЕЙСТВИЯ МАЛЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

С ОКРУЖАЮЩЕЙ СРЕДОЙ

12.1. В нашей стране охрана природы стала всенародной задачей. Она закреплена в Конституции СССР. Приняты важнейшие законодательные акты природоохранного содержания.

Строительство и последующая эксплуатация дорог оказывает многофакторное влияние на прилегающую к ним территорию как с нагорной стороны, так и ниже трассы дороги. Особенно это относится к верхнему и нижнему бьефам дорожных водопропускных сооружений, к косогорным участкам с сопрягающими сооружениями. Это воздействие может приводить к ряду экологических изменений негативного характера на указанной территории. В то же время большинство этих изменений в значительной мере определяют условия нормальной эксплуатации дорог. Следовательно, экологические аспекты строительства и эксплуатации дорог тесно связаны с нормальным их функционированием.

12.2. При строительстве дороги в полосе отвода, а часто и вне ее, нарушается естественный рельеф местности, меняется состав и состояние верхнего слоя почвы, разрушается растительный покров, существенно меняются условия формирования и характеристики поверхностного стока, водный режим территории.

Размыв почвы и подстилающих пород, образование оврагов представляют угрозу как земельному фонду, так и устойчивости дорожных сооружений и их элементов. Насыщение водных потоков твердыми частицами при размыве и перенос последних создают предпосылки противоположного процесса - заиления.

Подъем уровня воды перед водопропускными сооружениями приводит к затоплению верхнего бьефа - части территории выше труб и мостов, к подпору на постоянных водотоках на значительном удалении от трассы дороги. Аккумуляция стока перед водопропускными дорожными сооружениями вызывает снижение скоростей течения в верхнем бьефе и его заиление. Часто заиление распространяется и на саму дорожную трубу или подмостовое русло. Заиление водопропускного тракта уменьшает площадь его поперечного сечения и пропускную способность. Это приводит к дальнейшему росту уровня и заилению перед сооружением при пропуске даже относительно малых расходов воды, а в период паводков - вплоть до катастрофических последствий в виде перелива через насыпь дороги и ее разрушения. Повышение уровня воды перед дорожными водопропускными сооружениями обусловливает не только затопление за счет образования пруда аккумуляции стока в верхнем бьефе, но и подъем уровня грунтовых вод на прилегающей территории, обводнение. Изменение водного режима может вызвать переувлажнение таких территорий, изменение состава растительности, заболачивание местности, а в ряде регионов и засоление. Изменения водного режима, вызванные строительством дороги и водопропускных сооружений, в ряде случаев способны опасно активизировать карстовые явления, оползневые и просадочные процессы. В северных районах они нарушают естественный режим вечной мерзлоты, часто вызывают усиление наледеобразования у дорожных труб и мостов.

В нижнем бьефе дорожных водопропускных сооружений наиболее массовым процессом является размыв и оврагообразование. Этот процесс может распространяться на значительные расстояния от дороги вплоть до нескольких километров. Первопричина отмеченного негативного явления - концентрация стока, перевод его из склонового в русловый. Для сопрягающих сооружений характерны переливы, особенно на сочленениях водоотводных систем и резких их поворотах, что также приводит к крупномасштабным размывам, появлению оврагов.

Различные виды нефтепродуктов, часть теряемых при транспортировании материалов, особенно сыпучих, продукты сгорания топлива в двигателях - все это вызывает загрязнение полосы дороги и прилегающей территории. Этим объясняются причины интенсивного химического, биологического и других видов загрязнения ливневого стока и талых вод с участков дорог. Максимум загрязнения стока падает на городские улицы, подъезды к крупным промышленным объектам, магистрали с интенсивным движением. Перечисленные обстоятельства требуют очистки стока поверхностных вод с дорог. Наиболее жесткие требования в этом смысле предъявляются к дорогам у водоохранных зон, биологических заповедников и т.д.

Возможность проявления перечисленных выше процессов, их интенсивность и масштабы конечных последствий зависят, как уже было отмечено выше, от совокупности природных характеристик региона и степени их нарушения возведением дорожных сооружений, а также под действием других видов деятельности человека.

12.3. Предупреждение и борьба с водной эрозией - это не только одна из важных общегосударственных задач, но и глобальная экологическая проблема.

Водная эрозия при строительстве дорог имеет ряд специфических особенностей. Но в то же время она, как и при других случаях вторжения человека в природу, подчиняется общим законам. Поэтому условия образования и механизм водной эрозии при строительстве дорог, возможность прогноза, учета и сведения к минимуму интенсивности этого процесса требуют знания общих закономерностей.

Водная эрозия почвы (эрозия в переводе с латинского означает "разъедание") вызывается движением воды по поверхности земли. В естественных условиях возникает нормальная, геологическая эрозия - смыв поверхностных слоев при образовании стока талых, ливневых и смешанных вод.

Ускоренная эрозия возникает как результат хозяйственной деятельности человека без учета особенностей естественного процесса эрозии. Как показывают многочисленные примеры, строительство дорог - одно из основных направлений производственного воздействия человека на природу, инициирующее ускоренную эрозию.

Естественно, что характеристики поверхностного стока являются определяющим фактором нормальной и ускоренной водной эрозии. Исходные ливневые характеристики, такие, как интенсивность и продолжительность выпадения дождя, практически мало зависят от дорожного строительства. Однако расход и объем ливневого стока в отдельных створах могут претерпеть заметные изменения под влиянием преобразования рельефа местности, переброски части стока или полностью из одного водосборного бассейна в другой как итог целенаправленных мероприятий или общих планировочных работ.

Самые негативные последствия имеет концентрация поверхностного стока системами водоотвода и особенно дорожными водопропускными сооружениями. Распределенный обычно по ширине в сотни метров склоновый сток переводится этими сооружениями в сосредоточенные потоки, удельный расход которых обычно на порядок превышает естественный на склоне. Это вызывает аналогичное увеличение скорости течения, далеко превышающее допускаемые. Поэтому размывы и образование оврагов за дорожными сооружениями носят массовый характер.

Обследование тысяч дорожных труб и малых мостов в самых разных регионах от Прибалтики до Дальнего Востока показывает, что порядка 80% отводящих русел имеют размыв. Подсчитанный ущерб от оврагов за каждым из водопропускных сооружений на одной из автомобильных дорог составил 0,6 га.

Толщина снежного покрова на отдельных участках дорог и прилегающей территории и интенсивность таяния могут заметно меняться по сравнению с естественными их величинами в результате нарушения природного рельефа местности. Способы определения гидрометеорологических характеристик расчета поверхностного стока в дорожной практике общеизвестны. Существуют способы учета влияния на толщину снежного покрова таких факторов, как высота насыпей и древесно-кустарниковых полос, их ориентации к направлению господствующих ветров. Можно оценить влияние на сток талых вод и экспозиции склона. Однако следует подчеркнуть, что точность определения гидрометеорологических характеристик применительно к расчету эрозии в дорожном строительстве может оказаться резко пониженной из-за малости водосборных бассейнов. В расчетах эрозии почвы площадь водосборных бассейнов может быть ограничена сотнями и даже десятками квадратных метров.

12.4. В зависимости от климатических и ряда других особенностей в ряде регионов страны эрозию почв в основном определяют сток ливневых вод, в других регионах - сток талых вод. К первым относятся часть европейской территории от Прибалтики до Закавказья, республики Средней Азии, Дальний Восток. Значительную долю эрозии в некоторых областях Украины, Белоруссии, Прибалтики, Центрально-черноземной зоны и Поволжья дает сток талых вод, превышая по объему в 2 - 3 раза ливневый сток. Активная эрозия от стока талых вод характерна для лесостепных районов Зауралья и Восточной Сибири, для значительных пространств Западной Сибири.

12.5. Поверхность территории в полосе дорожного строительства в отличие от гидрометеорологических характеристик меняется полностью. Уничтожается естественный растительный покров, разрыхляется и меняется состав поверхностного слоя, преобразуется рельеф. Совместное действие первых двух факторов, а при изменении рельефа в сторону увеличения уклонов - и последнего, создает предпосылки для качественного скачка, многократного роста интенсивности эрозии.

12.6. Влияние рельефа на процессы эрозии почв определяется в основном уклонами, а при определенных условиях - и расчлененностью территории гидрографической сетью.

На суглинках эрозия склонов начинает проявляться при уклонах порядка 0,5 - 1,0°, на супесях - при 1 - 2°. С ростом уклонов, особенно при повреждении естественных склонов, интенсивность резко возрастает. На склонах с углом 25 - 35° водная эрозия усугубляется гравитационным осыпанием поддерненного слоя. Влияние уклона на интенсивность эрозии приближенно можно оценить по следующим данным: при уклоне 5° масса смытой почвы может быть порядка 10 т/га в год, при 10° - 25 т/га, при 30° - 40 т/га.

Большую роль в процессе эрозии почв играет микрорельеф. Требования агротехники проводить вспашку только поперек склона обеспечивают создание системы микрозапруд бороздами и гребнями. При этом резко повышается впитывание, что снижает объем поверхностного стока. Одновременно такой микрорельеф поверхности уменьшает скорости течения и размыв за счет высоких гидравлических сопротивлений. Изменение дорожным строительством естественной гидрографической сети водосборных бассейнов, увеличение расходов на отдельных ее участках - одна из важных причин ускоренной эрозии. Как уже отмечалось выше, результатом интенсивно действующей в настоящее время ускоренной эрозии являются промоины и овраги - узкие углубления с крутыми незадернованными склонами. Они возникают как результат местного нарушения рельефа, покрова местности, концентрации стока: от борозды и колеи, устройства насыпей и выемок, от увеличения расхода в естественных логах ниже дорожных сооружений. Роль уничтожения растительности, разрыхления поверхностного слоя и подстилающих пород при дорожном строительстве можно оценить при помощи близкого аналога из сельского хозяйства. Эрозия при распашке возникает уже при уклонах порядка 1°, а на пастбищах, даже перегруженных, - только при 15 - 20°. Следовательно, незащищенные откосы дорожных выемок и насыпей при их заложении 1:1,5 - объекты самой интенсивной эрозии, что подтверждают натурные наблюдения. Промоины на откосах насыпей можно обнаружить практически на каждой дороге, особенно на участках понижений продольного профиля. На многих дорогах этот процесс вызывает необходимость периодического ремонта насыпей. Иначе промоины быстро прогрессируют, захватывая обочины и само полотно дороги.

12.7. Растительность очень существенно влияет на эрозию, резко снижая ее интенсивность. Это определяет защиту склонов растительным покровом как одно из самых эффективных направлений по борьбе с эрозией при минимальных затратах средств. Корневая система растений связывает поверхностный слой, повышая его устойчивость к размыву. Наземная часть увеличивает гидравлическое сопротивление, как правило, во много раз, снижая скорость течения и вынос частиц грунта. Чем гуще травостой - тем выше эффект. Поэтому максимальный эффект достигается в борьбе с эрозией от ливневого стока в период расцвета растений, в борьбе с эрозией от стока талых вод он ниже.

Роль древесно-кустарниковой растительности защитных полос проявляется в основном в повышении водопоглощения и снижении поверхностного стока как ливневых, так и талых вод. В условиях Центрально-черноземной зоны полоса шириной 50 м даже после суровых зим поглощает ²/₃ талой воды, более чем втрое снижает коэффициент стока (0,75 - на поле; 0,22 - в полосе). В теплые зимы полосы перехватывают весь сток талых вод. В полосах накапливается больше снега, меньше глубина промерзания и сроки оттаивания. На полевых площадках сток талых вод при уклоне 0,03 идет со скоростью 0,08 - 0,14 м/с, а в снежном шлейфе у полос она падает в десятки раз, составляя только 0,0016 - 0,004 м/с. Поэтому здесь задерживается до 80 - 90% смытых выше по склону частиц. На поле резкие максимумы суточного гидрографа талых вод возникают в середине дня, в шлейфе у полос гидрограф несравненно равномернее, сток идет в основном ночью. Водопроницаемость под полосами с кустарниками в 2 - 2,6 раза выше, чем в полевых условиях.

Состояние поверхностного слоя и подстилающих пород в ряде случаев может иметь ключевое значение. При стоке талых вод определяющими факторами могут быть общая глубина промерзания и глубина оттаявшего слоя на момент появления стока. Для условий обширных районов Сибири характерны вечная мерзлота, глубокое промерзание при излишнем увлажнении поверхностных слоев. При быстром оттаивании эти слои становятся перенасыщенными влагой и могут оплывать по промерзшим нижним слоям. Кроме того, наличие льдистости в вечномерзлых грунтах приводит к снижению сопротивления их размыву при оттаивании, степень которого зависит от структуры грунтов (см. п. 7.29).

МЕРЫ ЗАЩИТЫ ОКРУЖАЮЩЕЙ СРЕДЫ В ЗОНЕ ВЛИЯНИЯ

МАЛЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

12.8. Сопоставление факторов, способствующих эрозии, и хотя бы основных особенностей вторжения дороги в естественные условия говорит об опасности экологически негативных последствий. Многолетние данные натурных наблюдений большого числа организаций подтверждают не только реальность серьезных потерь, но и возможность профилактики или хотя бы уменьшения их масштабов.

12.9. На всех этапах от проектирования и изысканий до эксплуатации водопропускных сооружений необходимо принятие соответствующих мер по защите окружающей среды. В первую очередь следует предусмотреть предотвращение или уменьшение наиболее массовых последствий от строительства дорожных сооружений: размывов за ними и оврагообразования, заиления, затопления и заболачивания. Естественно, что эти меры могут дать эффект только при комплексном подходе, при взаимодействии с другими организациями и с учетом их деятельности. Это в первую очередь сельскохозяйственные, мелиоративные, лесозаготовительные, а также строительные и другие организации.

12.10. Трассу новых дорог на эрозионно опасной территории, особенно на косогорах, в предгорных и горных районах, желательно не удалять значительно от подошвы склонов. За водопропускными сооружениями необходимо укрепление отводящих русел до подошвы склона и устройство водобойных сооружений в конце крепления с обеспечением расширения потока. Наилучший эффект при этом дают рассеивающие трамплины. При большом удалении трассы от подошвы склона крепление отводящего русла, обычно в виде бетонного лотка, может вызвать значительные затраты, а его отсутствие - появление размыва за трубой и развитие оврага. Прогноз обязательно должен учитывать концентрацию и перераспределение стока дорожными сооружениями.

12.11. На прилегающей к трассе дороги территории, особенно ниже ее, необходимо проведение защитных мероприятий на участках интенсивных эрозионных процессов посевом трав, древесно-кустарниковыми посадками, устройством специальных противоэрозионных сооружений. Обследование водоотводных систем на косогорах выявляет высокий процент их повреждения и размыва близлежащих участков.

Причина этих явлений - плохая организация входных участков, выплескивание бурного потока из лотков на виражах и в местах сочленения. Поэтому плавные очертания конструкций входных участков перед косогором должны гарантировать перехват стока со всей вышележащей территории. Виражи и сочленения лотков на косогорах должны проектироваться с местным, часто значительным увеличением высоты бортов на основе современных расчетов бурных потоков. Повышение бортов особо обязательно на вогнутой стороне виражей и несколько ниже них, а на магистральных лотках - против ввода боковых сбросов и ниже сочленения. Из-за аналогичного неучета особенностей бурных потоков часты размывы насыпей с последующим заилением систем водоотвода, водопропускных сооружений и прилегающей местности. Действующий на затяжных спусках насыпей водоотвод не выполняет своих функций из-за проскока бурным потоком входов во встроенные лотки, что ведет к многократному превышению расчетных расходов в понижениях и отмеченным выше негативным последствиям. Входные участки к сбросным лоткам должны иметь плавные очертания конструкции с верховой стороны и обеспечивать перехват потока, идущего вдоль насыпи. Отмеченная ситуация резко ухудшается в реальных условиях нарушением поперечного профиля сооружений, колеями на обочинах, отсыпкой грунта на них в период ремонта и образованием при этом на насыпи корытообразного поперечного сечения.

12.12. Возведение насыпей и создание крутых откосов других сооружений не должно иметь разрывов во времени между отсыпкой грунта, уплотнением и закреплением откосов хотя бы посевом трав. Известен случай интенсивного размыва свежеотсыпанной высокой насыпи только за один летне-осенний сезон, что, кроме ремонта насыпи сразу после ее возведения, привело к заилению сопутствующих систем водоотвода, всех дорожных труб до трети их сечения, заилению и заболачиванию пониженных участков местности вдоль дороги.

Поврежденная местность вдоль дороги при строительстве, реконструкции и ремонте подлежит планировке, рекультивации, а при необходимости - и закреплению посевом трав во избежание размывов. Это особенно относится к временным подъездам и колеям на них. При малых продольных уклонах планировка прилегающей к дороге полосы местности должна обеспечить отвод воды к дорожным сооружениям для предотвращения затопления и заболачивания.

12.13. В борьбе с заилением следует в первую очередь установить причины появления твердого стока. Чаще всего - это нарушение агротехнических требований о поперечной распашке склонов, распашка прилегающих непосредственно к дороге участков без оставления защитных полос с многолетними травами и кустарниками, вырубка леса, строительные работы без противоэрозионной защиты, поступление наносов из развивающихся оврагов и др. Перечисленное говорит о необходимости согласованных усилий заинтересованных организаций в решении этого вопроса. В то же время действующий закон об охране земельного фонда и постоянно ужесточающиеся требования, в том числе юридические, по экологии не исключают соответствующие экономические и другие санкции как взаимного характера, так и со стороны государственных органов. Меры по уменьшению размывов и последующего заиления при возведении и эксплуатации собственно дорожных сооружений были уже отмечены выше.

12.14. Необходимо использовать все возможные меры по предотвращению или хотя бы уменьшению эрозии на той территории, откуда поступают продукты размыва. Если остановить эрозию не удается, то в зависимости от конкретных местных условий возможны два варианта решения: перехватить и остановить наносы выше трассы дороги или пропустить их, обеспечив транзит. Возможен и одновременный комплекс мер как по задержанию наносов, так и транзит их через водопропускные трубы. Для задержания наносов осуществляются меры, обеспечивающие снижение скорости течения сверх допускаемых на заиление. Транзит наносов требует поддержания высоких скоростей. Наименьшие скорости обычно характерны в пруду аккумуляции стока перед водопропускными сооружениями. Поэтому при опасности заиления объем пруда аккумуляции должен быть сведен к минимуму, в частности за счет назначения повышенных сечений водопропускных труб и мостов. Аналогичные решения следует принимать для уменьшения площади затопления. Перехвату наносов выше дороги способствуют защитные полосы с густым травостоем, нарезка поперечных борозд для создания микрозапруд, террасирование и устройство других специальных сооружений. Транзиту наносов способствует укладка труб по тальвегу, профилирование и поддержание чистого сосредоточенного русла на подходах к водопропускным трубам и малым мостам с достаточным для транспорта наносов уклоном, в том числе в пределах водопропускного тракта, а часто и ниже его.

Комплексное использование обоих направлений предполагает перехват наносов на дальних подступах к дорожным сооружениям, особенно на участках малых уклонов, и транзит в непосредственной близости от дороги и под ней.

Выше затронуты только основные экологические аспекты гидравлики дорожных сооружений в самых типичных условиях. При решении конкретных задач экологии дорожного строительства в том или ином районе необходим учет всего комплекса региональных особенностей. Тем более это касается специфических вопросов экологии в условиях вечной мерзлоты, карста и т.д. Специального рассмотрения требует вопрос предотвращения загрязнения поверхностного стока и его очистки, излагаемый ниже.

ЗАГРЯЗНЕННОСТЬ И ОЧИСТКА ВОД ПОВЕРХНОСТНОГО СТОКА

Загрязненность поверхностных вод

12.15. Во всех видах поверхностных вод содержатся различные по характеру загрязнения в количествах, существенно превышающих предельно допустимые концентрации (ПДК). Поверхностный сток является одним из основных источников загрязнения водоемов.

Загрязнение поверхностных вод в значительной мере связано с выбросами загрязнений в атмосферу промышленными предприятиями различного профиля, а также автомобильным транспортом. Вследствие резкого увеличения парка автомобилей вызываемое ими загрязнение воздуха в последнее десятилетие возросло примерно вдвое, т.е. автомобильный транспорт превратился в один из основных источников загрязнения воздушного бассейна. Часть загрязнений в сухую погоду оседает на покрытиях в виде пыли, сажи и копоти, а также выпадает вместе с осадками. Имеются данные, что, например, в Токио в среднем за год на 1 км² площади выпадает до 400 т загрязнений.

При производстве строительных работ поверхностные воды в значительной степени насыщаются минеральными взвешенными веществами. Так, по данным наблюдений в штате Вирджиния (США) объем взвешенных веществ в поверхностных водах с 1 га территории, на которой велось дорожное, коммунальное и промышленное строительство, составил 60 т в год, что в 10 раз больше, чем с сельскохозяйственных угодий, и в 2000 раз больше, чем с облесенных участков.

12.16. Основные виды загрязнений поверхностных вод - взвешенные вещества и нефтепродукты. Именно с их выносом связано загрязнение водоемов. Однако в поверхностных водах в количествах, превышающих ПДК, содержатся также и такие виды загрязнений, как органические вещества, хлориды, сульфаты, азотистые соединения, соединения металлов: серебра, цинка, свинца, меди, ртути, олова и др.

Содержание взвешенных веществ в дождевых водах достигает 80 - 90% общего количества загрязнений. По данным многолетних наблюдений для разных по характеру застройки и интенсивности движения районов крупного города оно составляет 44 - 13 900 мг/л, что существенно превышает ПДК. Талые воды содержат взвешенных веществ в несколько раз больше. Отличительной особенностью взвешенных веществ в водах поверхностного стока является очень широкий диапазон крупности частиц от гравелистых (2 - 5 мм) до чрезвычайно мелких - глинистых.

Нефтепродукты и другие эфирорастворимые вещества, как показывают исследования, составляют по разным районам города 6 - 350 мг/л. Нефтепродукты эмульгируются и сорбируются частицами взвешенных веществ. При этом их удельный вес изменяется и становится близким к единице. В таком виде содержание нефтепродуктов в поверхностных водах достигает 50 - 90%.

На территориях предприятий характер и степень загрязнения вод поверхностного стока связаны с технологией производства. На предприятиях строительных конструкций поверхностный сток в основном загрязнен минеральными взвешенными веществами. На автотранспортных предприятиях, таких, как автостоянки, автопарки, гаражи, автодормехбазы, авторемонтные заводы, наряду со взвешенными веществами наблюдаются высокие концентрации нефтепродуктов. На территориях аэропортов воды поверхностного стока загрязнены взвешенными веществами, горюче-смазочными материалами, препаратами обработки покрытий при гололеде и машин против обледенения, моющими жидкостями.

Поверхностные стоки в связи с повышенным по сравнению с ПДК содержанием загрязнений подлежат очистке перед их сбросом в водоемы.

Отстойники для очистки вод поверхностного стока

12.17. Для очистки поверхностных вод от взвешенных веществ, нефтепродуктов, плавающего мусора применяются в основном отстойники камерного типа (закрытые подземные сооружения) и пруды-отстойники (открытые сооружения). Работа этих сооружений основана на так называемом методе механической очистки - на принципе сепарации частиц загрязнений в зависимости от их удельного веса: выпадании в осадок тяжелых частиц, например минеральных взвешенных веществ, и всплывании на поверхность легких, например эмульгированных частиц нефтепродуктов. Характерной особенностью этих сооружений является наличие обгонного коллектора.

Отстойники камерного типа в зависимости от площади водосборного бассейна имеют одну или несколько камер (рис. 12.1). Они широко используются для очистки поверхностных вод в городах, с территорией автохозяйств, бензозаправочных станций, мест стоянки автомашин, на мостовых переходах, аэродромах и т.п.

Рис. 12.1. Типы камерных отстойников:

а - однокамерный отстойник; б - многокамерный отстойник;

1 - подводящий трубопровод; 2 - участок входа;

3 - мусороулавливающая решетка; 4 - отстойная часть;

5 - фильтры доочистки; 6 - отводящий трубопровод;

7 - маслонефтесборники; 8 - обгонный коллектор

Пруды-отстойники обычно состоят из нескольких секций и работают по схеме одноступенчатой очистки стоков при параллельном расположении камер или по схеме двухступенчатой очистки при последовательном расположении камер (рис. 12.2). Для задержания мусора и сбора нефтепродуктов пруды-отстойники оборудуются решетками и маслонефтесборниками. Чаще пруды-отстойники возводятся из сборных железобетонных элементов и их емкости (камеры) выполняются призматическими. Однако в ряде случаев они выполняют декоративную функцию, и тогда в плане им придается произвольная форма и емкости выполняются непризматическими (рис. 12.3).

Рис. 12.2. Схемы очистки стоков:

а - одноступенчатая; б - двухступенчатая;

1, 2, 3 - номера секций

Рис. 12.3. Пруд-отстойник произвольной формы:

1 - подводящий коллектор; 2 - вход в первую секцию;

3 - первая секция; 4 - водосброс; 5 - вторая секция;

6 - выход из второй секции; 7 - отводящий коллектор;

8 - вход во вторую секцию; 9 - обгонный коллектор;

10 - маслонефтесборники

В отстойниках могут быть выделены: входная часть, в пределах которой поток поступает в камеру, очищается от мусора на грубых решетках и должен равномерно перераспределяться по живому сечению; камера отстаивания, где происходит выпадание твердых частиц и всплытие нефтепродуктов; выходная часть, где на фильтрах осуществляется доочистка воды, производится сбор и удаление нефтепродуктов.

Расчет отстойников поверхностного стока

12.18. Для расчета отстойников поверхностного стока принята [9] норма интенсивности стока дождевых вод q = 4,5 л/(с·га) при расчетной продолжительности дождя T = 20 мин. При этой норме период превышения расчетной интенсивности T будет зависеть от климатических характеристик района расположения отстойника. Пиковые расходы дождей большей интенсивности сбрасываются в водоемы без очистки по обгонным коллекторам, минуя очистные сооружения. Для района Москвы, например, из выпадающих за лето в среднем 70 дождей около 50, что составляет примерно 70%, поступает на очистные сооружения полностью, а остальные - частично.

12.19. Расчет отстойников сводится к определению размеров их проточной части. Суммарная ширина сечения проточной части вычисляется по уравнению расхода:

(12.1)

где Q_р - расчетный расход, подлежащий очистке;

v - средняя скорость потока в проточной части отстойника, принимаемая равной не более 0,01 м/с;

h - глубина потока в отстойнике.

Ширина камер прудов-отстойников принимается не более 40 м, а камер очистных сооружений закрытого типа - не более 4 м.

Длина проточной части l определяется регламентируемыми значениями скорости в отстойнике v <= 0,01 м/с и продолжительностью времени пребывания очищаемой жидкости в отстойнике T_отст, которая принимается равной не менее 2 ч для прудов-отстойников и 1 ч - для камерных отстойников:

l = vT_отст·3600. (12.2)

Наряду с этим длина проточной части отстойника должна быть уточнена расчетом на осаждение взвешенных частиц и всплытие на поверхность нефтепродуктов.

Взвешенная частица, находящаяся в начале координат на поверхности жидкости во входном сечении отстойника (рис. 12.4), опускаясь на дно отстойника, за отрезок времени dt, проходит путь dy со скоростью, равной гидравлической крупности w, т.е.

. Одновременно вместе с потоком частица движется вдоль камеры отстойника с расчетной скоростью v и проходит за тот же отрезок времени путь dx, т.е.

. Приравнивая эти выражения, получаем при y = h длину проточной части

(12.3)

Рис. 12.4. Расчетная схема определения размеров

горизонтального отстойника

Очевидно, что крупные частицы с гидравлической крупностью w_с выпадают на дно отстойника в точке C, а частицы с малой гидравлической крупностью w_а, двигаясь по траектории m - a, не выпадут в осадок. В конце камеры отстойника на дно будут выпадать по траектории m - b наиболее мелкие (расчетные) частицы с гидравлической крупностью w_b. При расчете отстойников поверхностного стока размер наименьших взвешенных частиц, которые должны выпадать в осадок, принимается по СН 496-77 равным 0,05 мм с гидравлической крупностью w = 1,73 мм/с.

При турбулентном режиме движения потока в отстойнике осаждение частиц тормозится вертикальными составляющими скорости пульсации

. Влияние вертикальной пульсационной составляющей скорости на процесс осаждения взвешенных частиц и, следовательно, размеры отстойника учитывается введением в формулу (12.3) коэффициента

, т.е.

(12.3')

По рекомендациям разных авторов

Аналогичным образом определяется длина проточной части отстойника, необходимая для всплытия нефтяных частиц:

(12.4)

Наименьшие размеры частиц нефтепродуктов (расчетные), всплытие которых должно быть обеспечено, приняты для прудов-отстойников равными 0,08 - 0,1 мм и для камерных отстойников 0,10 - 0,12 мм. Скорости всплытия частиц нефтепродуктов в зависимости от их размера приведены ниже:

Размер частиц нефтепродуктов, мм	0,12	0,1	0,08
Скорость всплытия w_в, мм/с	1,02	0,71	0,465

Коэффициент

при расчете прудов-отстойников принимается равным 1,75 при v/w = 20 и 1,65 при v/w = 15. При расчете камерных отстойников

. Окончательно длина проточной части отстойника принимается равной наибольшему из значений, полученных по формулам (12.2) - (12.4). Общая длина отстойника

(12.5)

12.20. Схемой расчета отстойников предусматривается очистка вод поверхностного стока лишь от частиц взвешенных веществ с размерами не менее 0,05 мм и нефтепродуктов с размерами частиц не менее 0,08 - 0,12 мм и тем самым допускается остаточное загрязнение поверхностных вод на выходе из отстойников меньшими по размерам частицами этих видов загрязнений. Для оценки степени остаточного загрязнения поверхностных вод, допускаемой расчетами, необходимы данные о весовом содержании мелких частиц. Имеющиеся данные по дисперсному составу взвешенных веществ показывают, что, например, в поверхностных водах с территорий промышленных площадок содержание частиц с размерами менее 0,05 мм достигает 94,4%, составляя в среднем 61%. По-видимому, это обстоятельство является причиной того, что эффект очистки вод поверхностного стока с территорий промплощадок получен равным лишь 5 - 16,5%. Эффективность очистки поверхностных вод с городских территорий составляет 20 - 40%.

Расчет отстойников ведется на среднюю скорость потока в проточной части v <= 0,01 м/с. В реальных условиях это не выполняется. Распределение скоростей в проточной части отстойников характеризуется значительной неравномерностью, особенно резко проявляющейся при несимметричном и боковом подводе потока в камеру. В плане и в вертикальной плоскости образуются мощные вихревые зоны с обратными скоростями. Это приводит к многократному, до 25 раз, увеличению по сравнению с принятой в расчете средней скоростью, значений скоростей потока на тех частях живых сечений, где сохраняется прямое направление движения, повышению турбулизации, транспортирующей способности потока и, как следствие, к снижению эффективности очистки поверхностных вод от взвешенных веществ и нефтепродуктов. Существенное влияние на формирование кинетической структуры потока в проточной части оказывают конструктивные решения участка входа. Разработка и подбор конструкций этого участка является одной из мер обеспечения равномерного распределения скоростей и повышения эффективности работы отстойников. В результате конструктивных изменений участков входа удавалось снижать неравномерность скоростей в камере отстойника с 25 до 3 - 4 раз.

12.21. При проектировании отстойников следует иметь в виду, что в процессе эксплуатации происходит заиление камеры. Рельеф отложений и распределение их по фракциям в проточной части зависят от кинематики потока и в то же время вызывают перераспределение поля скоростей. В связи с этим следует предусматривать удаление осадка при заилении проточной части отстойников на 30 - 40%. Опыт эксплуатации показывает, что накопление такого слоя осадка происходит в течение нескольких месяцев.

12.22. Горизонтальные отстойники по типу камерных и прудов-отстойников могут быть использованы и как сооружения первичной, грубой очистки при разработке более совершенных схем очистки поверхностных вод.

В последнее время для механической очистки вод поверхностного стока находят применение тонкослойные отстойники.

Приложение 1.1

ПЕРЕЧЕНЬ ДЕЙСТВУЮЩЕЙ ТИПОВОЙ ПРОЕКТНОЙ ДОКУМЕНТАЦИИ

МАЛЫХ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

Серия 3.501.1-144 (инв. N 1313). Трубы водопропускные круглые железобетонные сборные для железных и автомобильных дорог:

Вып. 0-0.

Материалы для проектирования.

Вып. 0-1.

Трубы водопропускные железобетонные круглые с плоским опиранием для железных дорог в обычных климатических условиях.

Вып. 0-2.

Трубы водопропускные железобетонные круглые с плоским опиранием для автомобильных дорог в обычных климатических условиях.

Вып. 0-3.

Трубы водопропускные железобетонные круглые с плоским опиранием северного исполнения для железных и автомобильных дорог.

Вып. 0-4.

Трубы водопропускные железобетонные круглые для автомобильных дорог в обычных климатических условиях.

Серия 3.501.3-133. Трубы водопропускные круглые отверстием 1,5 - 3,0 м из гофрированного металла для железных и автомобильных дорог:

Вып. 0.

Материалы для проектирования.

Серия 3.501-65 (инв. N 1016). Водопропускные трубы для железных и автомобильных дорог при расчетной температуре минус 40 °C и ниже, глубоком сезонном промерзании и наледях:

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: возможно, имеется в виду выпуск 1, а не выпуск 111.

Вып. 111.

Прямоугольные бетонные трубы.

Серия 3.501-104 (инв. N 1072). Сборные железобетонные прямоугольные водопропускные трубы для железных и автомобильных дорог.

Часть 1.

Трубы под автомобильную дорогу.

Часть 2.

Трубы под железную дорогу.

Часть 3.

Блоки заводского изготовления.

Серия 3.501.1-107 (инв. N 1130). Прямоугольные сборные бетонные водопропускные трубы для железных и автомобильных дорог.

Часть 1.

Конструкция труб. Материалы для проектирования.

Часть 2.

Блоки заводского изготовления.

Серия 3.501-126 (инв. N 1245). Трубы водопропускные сборные железобетонные прямоугольные для железных и автомобильных дорог Северной строительно-климатической зоны:

Вып. 0.

Конструкция труб. Материалы для проектирования.

Вып. 1.

Индустриальные строительные изделия.

Серия 501-96 (инв. N 538). Унифицированные косогорные трубы для железных и автомобильных дорог.

Серия 3.501.1-121 (инв. N 1222). Опоры железнодорожных мостов пролетами до 15 м, сооружаемые с использованием местных материалов.

Серия 3.501.1-150. Опоры унифицированных железнодорожных мостов для обычных северных условий с применением изделий заводского изготовления:

Вып. 0-3.

Опоры столбчатые. Материалы для проектирования.

Серия 3.501.1-156. Укрепления русел конусов и откосов насыпи у малых и средних мостов и водопропускных труб:

Вып. 0.

Конструкции укреплений. Материалы для проектирования.

Вып. 1.

Блоки укреплений. Технические условия. Рабочие чертежи.

Приложение 1.2

ХАРАКТЕРИСТИКИ ТИПОВЫХ ДОРОЖНЫХ ВОДОПРОПУСКНЫХ ТРУБ

ИС МЕГАНОРМ: примечание.

Сноски даны в соответствии с официальным текстом документа.

Отверстие b, м	Высота трубы h_т, м	Толщина свода трубы , м	Тип оголовка	Размеры повышенных звеньев, м		Ширина выходного оголовка в его конце b_р, м	Гидравлические характеристики сооружений
				Размеры повышенных звеньев, м			Характерные расходы Q, м³/с	Подпертая глубина H, м	Режим протекания <1>	Относительное заполнение на входе h_вх/h_т	Критическая глубина h_к, м	Критический уклон i_к	Сжатая глубина h_с, м	Уклон при сжатой глубине i_с	Скорость на выходе v_вых, м/с	Минимальная высота насыпи дорог по конструктивным соображениям H_нас(min), м
				высота h_пз	длина l_пз		Характерные расходы Q, м³/с	Подпертая глубина H, м	Режим протекания <1>	Относительное заполнение на входе h_вх/h_т	Критическая глубина h_к, м	Критический уклон i_к	Сжатая глубина h_с, м	Уклон при сжатой глубине i_с	Скорость на выходе v_вых, м/с
Круглые железобетонные трубы под железную дорогу <2>. Серия 3.501.1-144 (инв. N 1313)
1,0	1,0	0,10	Раструбный с и коническим входным звеном	1,20	1,70	2,50	1,40	1,03	Б	0,75	0,68	0,007	0,62	0,009	2,7	2,10
							2,20	1,39	Б	1,00	0,85	0,011	0,77	0,013	3,4
							3,50	2,02	Н	-	-	-	-	-	5,0
1,25	1,25	0,12	То же	1,50	1,70	3,20	2,50	1,29	Б	0,75	0,88	0,007	0,80	0,009	3,0	2,37
							3,90	1,74	Б	1,00	1,06	0,01	0,96	0,012	3,8
							6,00	2,45	Н	-	-	-	-	-	5,4
1,50	1,50	0,14	"	1,80	1,70	3,88	3,90	1,54	Б	0,75	1,04	0,006	0,95	0,008	3,3	2,64
							6,00	2,08	Б	1,00	1,27	0,009	1,16	0,010	4,1
							8,50	2,58	Н	-	-	-	-	-	5,3
2,00	2,00	0,16	"	2,40	1,70	5,32	8,00	2,14	Б	0,75	1,37	0,005	1,25	0,007	3,9	-
							12,50	2,78	Б	1,00	1,70	0,008	1,55	0,011	4,8
							16,50	3,22	Н	-	-	-	-	-	5,8
Круглые железобетонные трубы под автомобильную дорогу. Серия 3.501.1-144 (инв. N 1313)
1,0	1,0	1,0	Раструбный с и цилиндрическим входным звеном	-	-	2,08	1,70	1,27	Б	1,00	0,75	0,008	0,68	0,011	2,7	2,10
			Раструбный с и цилиндрическим входным звеном				2,80	2,54	П	-	-	-	-	-	6,0
			То же, с коническим входным звеном	1,20	1,70	2,50	2,20	1,39	Б	1,00	0,85	0,011	0,77	0,013	3,4
			То же, с коническим входным звеном				3,50	2,02	Н	-	-	-	-	-	5,0
1,25	1,25	0,12	Раструбный с и цилиндрическим входным звеном	-	-	2,50	3,00	1,60	Б	1,0	0,94	0,008	0,85	0,010	3,3	2,37
			Раструбный с и цилиндрическим входным звеном				4,40	2,73	П	-	-	-	-	-	6,0	2,37
			То же, с коническим входным звеном	1,50	1,70	3,20	3,90	1,74	Б	1,0	1,06	0,010	0,96	0,012	3,8	2,37
			То же, с коническим входным звеном				6,00	2,45	Н	-	-	-	-	-	5,4	2,37
1,50	1,50	0,14	Раструбный с и цилиндрическим входным звеном	-	-	3,20	4,70	1,91	Б	1,0	1,13	0,007	1,03	0,009	3,7	2,64
			Раструбный с и цилиндрическим входным звеном				6,36	2,85	П	-	-	-	-	-	6,0	2,64
			То же, с коническим входным звеном	1,8	1,70	3,88	6,00	2,08	Б	1,0	1,27	0,009	1,16	0,010	4,1	2,64
			То же, с коническим входным звеном				8,50	2,54	Н	-	-	-	-	-	5,3	2,64
2,0	2,0	0,16	Раструбный с и коническим звеном	2,40	1,70	5,32	12,50	2,78	Б	1,0	1,70	0,008	1,55	0,01	4,8	3,16
2,0	2,0	0,16	Раструбный с и коническим звеном				16,50	3,22	Н	-	-	-	-	-	5,8	3,16
Круглые трубы из гофрированного металла. Серия 3.501.3-133
1,5	1,5	0,05	Без оголовка с вертикально срезанным торцом трубы	-	-	1,5	2,4	1,24	Б	0,75	0,77	0,017	0,69	0,017	3,24	2,75
							3,1	1,51	Б	0,9	0,9	0,018	0,81	0,025	3,53
							3,6	1,57	Б	1,0	0,98	0,019	0,88	0,025	3,71
							7,4	3,85	П	-	-	-	-	-	5,99
			Раструбный с	-	-	3,88	2,6	1,23	Б	0,75	0,81	0,017	0,73	0,026	3,33	2,75
							4,3	1,67	Б	0,9	1,09	0,022	0,98	0,024	3,93
							7,4	3,06	П <*>	-	-	-	-	-	5,99
2,0	2,0	0,05	Без оголовка с вертикально срезанным торцом трубы	-	-	2,0	4,9	1,65	Б	0,75	1,03	0,015	0,93	0,024	3,73	3,25
							6,4	2,02	Б	0,9	1,20	0,017	1,08	0,023	4,08
							7,3 <*>	2,09	Б	1,0	1,29	0,017	1,16	0,023	4,26
							12,2	3,78	П <*>	-	-	-	-	-	5,98
			Без оголовка с торцом трубы, срезанным по откосу насыпи	-	-	2,0	6,2	1,89	Б	0,75	1,18	0,016	1,06	0,023	4,04	3,25
							7,8	2,16	Б	1,9	1,35	0,017	1,22	0,022	4,36
							8,0 <*>	2,20	Б	1,0	1,37	0,018	1,23	0,022	4,39
							12,2	3,50	П <*>	-	-	-	-	-	5,98
			Раструбный с	-	-	5,18	5,4	1,65	Б	0,75	1,08	0,015	0,97	0,025	3,85	3,25
							8,0	2,08	Б	0,90	1,37	0,017	1,23	0,022	4,39
							8,8 <*>	2,21	Б	1,0	1,45	0,028	1,31	0,021	4,54
							12,2	3,21	П <*>	-	-	-	-	-	5,98
3,0	3,0	0,05	Без оголовка с торцом трубы, срезанным по откосу насыпи	-	-	3,0	17,1	2,84	Б	0,75	1,76	0,016	1,53	0,021	4,95	4,25
							20,1	3,13	Б	0,90	1,92	0,017	1,73	0,020	5,22
							22,0	3,31	Б	1,0	1,98	0,18	1,78	0,022	5,38
							24,9	3,90	П <*>	-	-	-	-	-	6,0
Прямоугольные железобетонные трубы. Серия 3.501-104 (инв. N 1072)
1,00	1,5	0,11	Раструбный с	2,0	3,0	2,66	4,60	2,0	Б	0,835	1,31	0,010	1,11	0,018	4,1	3,11
							5,00	2,12	Б	1,0	1,41	0,011	1,19	0,020	4,2
							8,00	3,34	П	-	-	-	-	-	8,4
1,25	1,5	0,13	То же	2,0	3,0	2,93	5,75	2,0	Б	0,835	1,31	0,008	1,11	0,014	4,1	3,13
							6,25	2,12	Б	1,0	1,41	0,009	1,19	0,015	4,2
							10,00	3,26	П	-	-	-	-	-	8,4
1,50	2,00	0,15	"	2,50	3,0	3,72	9,45	2,49	Б	0,835	1,64	0,008	1,36	0,014	4,7	3,65
							11,25	2,77	Б	1,0	1,85	0,008	1,56	0,014	4,8
							15,80	3,99	П	-	-	-	-	-	8,3
2,00	2,00	0,17	"	2,50	3,0	4,24	12,60	2,49	Б	0,835	1,64	0,006	1,36	0,011	4,6	3,67
							15,50	2,77	Б	1,0	1,85	0,007	1,56	0,013	4,8
							21,00	3,97	П	-	-	-	-	-	8,3
2,50	2,00	0,20	"	2,50	3,0	4,74	15,75	2,49	Б	0,835	1,64	0,005	1,36	0,009	4,4	3,70
							18,75	2,77	Б	1,0	1,85	0,005	1,56	0,009	4,6
							26,50	4,00	П	-	-	-	-	-	8,3
3,00	2,50	0,29	"	-	-	5,90	18,90	2,49	Б	0,835	1,64	0,005	1,36	0,009	4,6	3,79
							22,50	2,77	Б	1,0	1,85	0,005	1,56	0,009	4,8
							31,50	3,97	П	-	-	-	-	-	6,6
4,00	2,50	0,30	"	-	-	6,94	25,20	2,49	Б	0,835	1,64	0,004	1,36	0,007	4,7	3,80
							30,00	2,77	Б	1,0	1,85	0,004	1,56	0,007	4,8
							42,00	3,97	П	-	-	-	-	-	6,6
Прямоугольные бетонные трубы. Серия 3.501-107 (инв. N 1130)
1,5	2,0	0,20	Раструбный с и нормальным входным звеном	-	-	3,12	6,75	1,97	Б	0,835	1,31	0,007	1,11	0,011	4,1	3,70
							7,5	2,12	Б	1,0	1,41	0,007	1,19	0,010	4,2
							13,5	3,99	П	-	-	-	-	-	7,1
			То же, с повышенным входным звеном	2,50	3,08	3,68	9,45	2,49	Б	0,835	1,64	0,008	1,36	0,009	4,6
							11,25	2,77	Б	1,0	1,85	0,008	1,56	0,013	4,8
							15,8	3,99	П	-	-	-	-	-	8,3
2,0	2,0	0,23	Раструбный с и нормальным входным звеном	-	-	3,62	9,0	1,97	Б	0,835	1,31	0,006	1,11	0,009	4,1	3,75
							10,0	2,12	Б	1,00	1,41	0,006	1,19	0,009	4,2
							18,0	3,99	П	-	-	-	-	-	7,1
			То же, с повышенным входным звеном	2,50	3,50	4,18	12,6	3,49	Б	0,835	1,64	0,006	1,36	0,010	4,6
							15,0	2,77	Б	1,0	1,85	0,007	1,56	0,010	4,8
							21,0	3,47	П	-	-	-	-	-	8,3
3,0	2,0	0,32	Раструбный с и нормальным входным звеном	-	-	4,62	13,5	1,97	Б	0,835	1,31	0,004	1,11	0,007	4,1	4,73
							15,0	2,12	Б	1,0	1,41	0,004	1,19	0,007	4,2
							27,0	3,99	П	-	-	-	-	-	7,1
			То же, с повышенным входным звеном	2,50	3,00	5,18	18,9	2,49	Б	0,835	1,64	0,004	1,36	0,008	4,6
							22,5	2,77	Б	1,0	1,85	0,004	1,56	0,006	4,8
							31,6	3,99	П	-	-	-	-	-	8,3
2,0	3,0	0,23	Раструбный с и нормальным входным звеном	-	-	4,7	17,0	3,01	Б	0,835	2,01	0,007	1,7	0,010	5,0	3,75
							19,0	3,27	Б	1,0	2,17	0,007	1,82	0,011	5,2
							23,6	3,99	П	-	-	-	-	-	6,2
	3,5	-	То же, с повышенным входным звеном	3,50	3,0	5,24	21,0	3,47	Б	0,835	2.31	0,007	1,95	0,011	5,4
							23,0	3,71	Б	1,0	2,46	0,007	2,08	0,012	5,5
							25,6	4,07	П	-	-	-	-	-	5,7
3,0	3,0	0,32	Раструбный с и нормальным входным звеном	-	-	5,7	25,5	3,01	Б	0,835	2,01	0,005	1,7	0,008	5,0	4,73
							28,5	3,27	Б	1,0	2,17	0,005	1,82	0,008	5,2
							35,4	3,99	П	-	-	-	-	-	6,2
			То же, с повышенным входным звеном	3,50	3,0	6,24	31,5	3,47	Б	0,835	2,31	0,005	1,95	0,008	5,4
							35,4	3,71	Б	1,00	2,46	0,006	2,08	0,009	5,5
							38,04	4,03	П	-	-	-	-	-	6,7
4,0	3,0	0,38	Раструбный с и нормальным входным звеном	-	-	6,7	34,0	3,01	Б	0,835	2,01	0,004	1,7	0,006	5,0	4,88
							38,0	3,27	Б	1,0	2,17	0,004	1,82	0,007	5,2
							47,2	3,99	П	-	-	-	-	-	6,2
			То же, с повышенным входным звеном	3,50	2,50	7,24	42,0	3,47	Б	0,835	2,31	0,004	1,95	0,007	5,4
							46,0	3,71	Б	1,0	2,46	0,004	2,08	0,007	5,5
							51,2	4,03	П	-	-	-	-	-	6,7
5,0	3,0	0,46	Раструбный с и нормальным входным звеном	-	-	7,7	42,5	3,01	Б	0,835	2,01	0,004	1,7	0,006	5,0	4,96
							48,0	3,27	Б	1,0	2,17	0,004	1,82	0,006	5,2
							59,0	3,99	П	-	-	-	-	-	6,2
			То же, с повышенным входным звеном	3,50	2,00	8,24	52,5	3,47	Б	0,835	2,31	0,004	1,95	0,007	5,4
							57,5	3,71	Б	1,0	2,46	0,004	2,08	0,06	5,5
							64,0	4,03	П	-	-	-	-	-	6,7
6,0	3,0	0,53	Раструбный с и нормальным входным звеном	-	-	8,7	51,0	3,01	Б	0,835	2,01	0,003	1,7	0,005	5,0	5,03
							57,0	3,27	Б	1,0	2,17	0,003	1,82	0,006	5,2
							70,8	3,99	П	-	-	-	-	-	6,2
			То же, с повышенным входным звеном	3,50	2,00	9,24	63,0	3,47	Б	0,835	2,31	0,003	1,95	0,005	5,4
							69,0	3,71	Б	1,0	2,46	0,003	2,08	0,005	5,5
							76,8	4,03	П	-	-	-	-	-	6,7
Прямоугольные железобетонные трубы для Северной климатической зоны. Серия 3.501.1-126 (инв. N 1245)
1,5	2,0	0,15	Раструбный с параллельными стенками и нормальным входным звеном	-	-	1,5	7,0	2,24	Б	0,835	1,31	0,007	1,11	0,010	4,5	3,70
							7,4	2,33	Б	1,0	1,41	0,007	1,20	0,011	4,6
			То же, с повышенным входным звеном	2,5	3,0	1,5	9,6	2,76	Б	0,835	1,64	0,008	1,39	0,009	5,0
			То же, с повышенным входным звеном				10,0	2,86	Б	1,00	1,68	0,008	1,42	0,010	5,1
2,0	2,0	0,17	Раструбный с и нормальным входным звеном	-	-	2,0	10,0	2,34	Б	0,835	1,31	0,006	1,20	0,009	4,6	3,75
			Раструбный с и нормальным входным звеном				10,5	2,42	Б	1,00	1,46	0,006	1,24	0,009	4,7
			То же, с повышенным входным звеном	2,5	3,0	2,0	13,4	2,85	Б	0,835	1,72	0,006	1,46	0,010	5,0
			То же, с повышенным входным звеном				14,2	2,96	Б	1,00	1,78	0,007	1,51	0,010	5,7
2,5	2,0	0,20	Раструбный с и нормальным входным звеном	-	-	2,5	12,9	2,39	Б	0,835	1,45	0,005	1,23	0,008	4,5	3,78
			Раструбный с и нормальным входным звеном				13,9	2,49	Б	1,00	1,52	0,005	1,29	0,008	4,6
			То же, с повышенным входным звеном	2,5	3,0	2,5	17,4	2,92	Б	0,835	1,78	0,005	1,50	0,009	5,1
			То же, с повышенным входным звеном				18,3	3,02	Б	1,00	1,82	0,006	1,55	0,009	5,2
3,0	2,5	0,29	Раструбный с и нормальным входным звеном	-	-	3,0	21,4	2,97	Б	0,835	1,78	0,004	1,51	0,009	5,1	3,83
3,0	2,5	0,29	Раструбный с и нормальным входным звеном				22,5	3,08	Б	1,00	1,85	0,004	1,57	0,009	5,2	3,83
4,0	2,5	0,30	То же	-	-	4,0	30,0	3,07	Б	0,835	1,85	0,004	1,57	0,007	5,2	3,85
4,0	2,5	0,30	То же				31,5	3,17	Б	1,00	1,91	0,004	1,63	0,007	5,3	3,85
Прямоугольные бетонные трубы для районов с расчетной температурой -40 °C и ниже, глубоким сезонным промерзанием и наледями. Серия 3.501-65 (инв. N 1016)
1,5	2,0	0,16	Раструбный с параллельными стенками с нормальным входным звеном	-	-	1,5	7,0	2,15	Б	0,835	1,30	0,007	1,11	0,011	4,4	3,70
							7,4	2,28	Б	1,00	1,41	0,007	1,20	0,010	4,5
			То же, с повышенным входным звеном	2,5	3,0	1,5	9,5	2,68	Б	0,835	1,64	0,008	1,39	0,009	4,6
			То же, с повышенным входным звеном				10,0	2,78	Б	1,0	1,68	0,008	1,42	0,010	4,6
2,0	2,0	0,17	Раструбный с и нормальным входным звеном	-	-	2,0	10,0	2,35	Б	0,835	1,41	0,006	1,20	0,009	4,5	3,75
			Раструбный с и нормальным входным звеном				10,5	2,43	Б	1,0	1,46	0,006	1,24	0,009	4,6
			То же, с повышенным входным звеном	2,5	3,0	2,0	13,0	2,81	Б	0,835	1,45	0,006	1,23	0,010	4,6
			То же, с повышенным входным звеном				14,0	2,94	Б	1,0	1,52	0,007	1,29	0,010	4,7
2,0	3,0	0,20	Раструбный с и нормальным входным звеном	-	-	2,0	16,9	3,34	Б	0,835	2,00	0,007	1,70	0,010	5,4	3,82
			Раструбный с и нормальным входным звеном				17,8	3,45	Б	1,0	1,91	0,007	1,63	0,011	5,5
			То же, с повышенным входным звеном	3,5	3,0	2,0	20,8	3,82	Б	0,835	2,30	0,007	1,96	0,007	5,5
			То же, с повышенным входным звеном				22,0	3,98	Б	1,0	2,39	0,007	2,03	0,006	5,6
3,0	2,0	0,29	Раструбный с и нормальным входным звеном	-	-	3,0	15,9	2,44	Б	0,835	1,92	0,004	1,63	0,007	4,6	4,73
			Раструбный с и нормальным входным звеном				16,8	2,53	Б	1,0	1,99	0,004	1,69	0,007	4,7
			То же, с повышенным входным звеном	2,5	3,0	3,0	21,4	2,98	Б	0,835	1,78	0,004	1,51	0,006	5,1
			То же, с повышенным входным звеном				22,6	3,11	Б	1,0	1,85	0,004	1,57	0,006	5,2
3,0	3,0	0,32	Раструбный с и нормальным входным звеном	-	-	3,0	27,2	3,49	Б	0,835	2,10	0,004	1,78	0,008	5,5	4,73
			Раструбный с и нормальным входным звеном				28,7	3,82	Б	1,0	2,17	0,004	1,84	0,008	5,6
			То же, с повышенным входным звеном	3,5	3,0	3,0	33,6	4,02	Б	0,835	2,41	0,004	2,05	0,009	6,0
4,0	3,0	0,38	Раструбный с и нормальным входным звеном	-	-	4,0	38,1	3,57	Б	0,835	2,11	0,004	1,84	0,007	5,6	4,88
			Раструбный с и нормальным входным звеном				40,2	3,74	Б	1,0	2,25	0,004	1,91	0,007	5,7
			То же, с повышенным входным звеном	3,5	3,0	4,0	40,0	3,73	Б	0,70	2,24	0,004	1,91	0,007	6,0
5,0	3,0	0,46	Раструбный с и нормальным входным звеном	-	-	5,0	49,7	3,74	Б	0,835	2,23	0,004	1,90	0,006	5,6	4,96
			Раструбный с и нормальным входным звеном				52,5	3,85	Б	1,0	2,31	0,004	1,96	0,006	5,8
			То же, с повышенным входным звеном	3,5	3,0	5,0	53,0	3,87	Б	0,70	2,33	0,004	1,98	0,007	5,6
			То же, с повышенным входным звеном				56,0	4,00	Б	0,72	2,41	0,004	2,05	0,006	5,8
6,0	3,0	0,53	Раструбный с и нормальным входным звеном	-	-	6,0	61,2	3,78	Б	0,835	2,27	0,003	1,93	0,005	5,7	5,03
			Раструбный с и нормальным входным звеном				64,5	3,91	Б	1,0	2,35	0,003	2,00	0,005	5,8
			То же, с повышенным входным звеном	3,5	3,0	6,0	60,0	3,73	Б	0,60	2,24	0,003	1,91	0,005	5,6
			То же, с повышенным входным звеном				67,0	4,00	Б	0,70	2,41	0,003	2,05	0,005	5,9

--------------------------------

Б - безнапорный; Н - напорный; П - полунапорный.

Для труб под железную дорогу в первой строке для каждого отверстия приведены расчетные расходы при заполнении, регламентированном СНиП 2.05.03-84, во второй - то же, при полном заполнении, в третьей - максимально возможные расходы по скоростям на выходе и подпорам.

<*> Для гофрированных труб под автомобильную дорогу.

Примечание. Критические уклоны и уклоны, соответствующие сжатой глубине, для технически гладких труб вычислялись при коэффициенте шероховатости n = 0,015, для гофрированных - при n = 0,025, причем последняя цифра соответствует гофрированным трубам с гладкими лотками. При иной шероховатости указанные уклоны следует умножать на отношения: для технически гладких труб (n/0,015)², гофрированных (n/0,025)², где n - фактический коэффициент шероховатости.

Приложение 1.3

ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ

ТИПОВЫХ МАЛЫХ ОДНОПРОЛЕТНЫХ МОСТОВ

Длина пролетного строения l_п, м	Длина пролета в свету l₀, м	Высота насыпи H_нас, м	, ^M (см. рисунок)	Ширина отверстия по дну b_дн, м	Предельные расходы Q_пр, м³/с, допускаемые скорости под мостом v_доп(м), м/с, и соответствующие им глубины H и h_м, м, при типах укрепления
					каменная наброска				монолитным бетоном				плиты 50 x 50, толщиной				гибкие плитные покрытия
					каменная наброска				монолитным бетоном				плиты 50 x 50, толщиной
					Q_пр	v_доп(м)	H	h_м	Q_пр	v_доп(м)	H	h_м	Q_пр	v_доп(м)	H	h_м	Q_пр	v_доп(м)	H	h_м	Q_пр	v_доп(м)	H	h_м
Схема 1. Мост с массивными опорами
6,00	4,60	2,5	0,40	3,20	1,6	2,08	0,44	0,20	15,5	4,43	2,00	0,87	2,8	2,50	0,64	0,29	2,2	2,29	0,54	0,25	6,6	3,33	1,13	0,51
6,00	4,60	6,0	0,85	2,90	1,2				21,7	5,42	3,00	1,33	2,1				1,7				5,0
9,30	7,90	3,0	0,30	7,30	3,10				41,6	4,95	2,50	1,09	5,4				4,2				12,6
9,30	7,90	8,0	1,10	5,70	2,40				42,6	5,42	3,00	1,33	4,2				3,3				9,9
11,50	10,00	3,5	0,45	9,10	3,8				68,1	5,42	3,00	1,33	6,7				5,2				15,7
11,50	10,00	8,0	1,20	7,60	3,2				56,9	5,42	3,00	1,33	5,6				4,3				13,1
13,50	12,00	5,0	0,80	10,40	4,4				77,8	5,42	3,00	1,33	7,7				5,9				18,0
13,50	12,00	8,0	1,20	9,60	4,0				71,8	5,42	3,00	1,33	7,1				5,5				16,6
16,50	15,00	5,0	0,80	13,40	5,6				100,3	5,42	3,00	1,33	9,9				7,7				23,2
16,50	15,00	8,0	1,20	12,60	5,3				94,3	5,42	3,00	1,33	9,3				7,2				21,5
Схема 2. Мост с обсыпными устоями
9,30	-	3,00	-	5,32	2,4	2,08	0,44	0,20	38,4	4,86	2,41	1,13	4,3	2,50	0,64	0,30	3,3	2,29	0,54	0,25	10,7	3,33	1,13	0,53
9,30	-	4,00	-	2,32	1,1				34,2	5,42	3,00	1,41	2,1				1,6				5,5
11,50	-	3,0	-	7,52	3,3				46,1	4,74	2,29	1,07	5,9				4,5				14,5
11,50	-	4,0	-	4,52	2,0				50,6	5,42	3,00	1,41	3,7				2,8				9,3
13,50	-	3,0	-	9,52	4,1				51,7	4,62	2,18	1,01	7,4				5,7				17,9
13,50	-	5,0	-	3,52	1,6				43,2	5,42	3,00	1,41	2,9				2,2				7,6
16,50	-	3,0	-	12,52	5,4				54,4	4,36	1,94	0,90	9,6				7,4				23,1
16,50	-	5,0	-	6,52	2,9				65,6	5,42	3,00	1,41	5,2				4,0				12,7

Примечание. Схемы мостов приведены ниже на рисунке.

Схемы малых однопролетных мостов

(размер в скобках действителен при H_нас > 6 м)

Приложение 2.1

ОПРЕДЕЛЕНИЕ НОРМАЛЬНОЙ ГЛУБИНЫ В ТРАПЕЦЕИДАЛЬНОМ РУСЛЕ

ПО ГРАФИКУ

Пример. Коэффициент шероховатости n = 0,0225; b_дн = 1,2 м; m_от = 1; i = 0,005; Q = 2,0 м³/с.

Требуется определить нормальную глубину h₀.

Решение. 1. Определяют расходную характеристику при нормальной глубине

2. Находят

3. Вычисляют

4. Откладывают это значение на оси абсцисс в верхней части графика

и проводят ординату до пересечения с кривой m_от = 1.

5. Находят ординату, соответствующую точке пересечения.

6. Определяют

h₀ = 0,535·1,2 = 0,64 м.

График для определения нормальной глубины

в трапецеидальных руслах

Рис. 1. График для определения нормальных глубин

в прямоугольных трубах

Рис. 2. График для определения глубин h₀

в прямоугольных трубах при ступенчатой укладке звеньев

Приложение 2.2

ОПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ ГЛУБИН В ПРЯМОУГОЛЬНЫХ РУСЛАХ

ПО ГРАФИКАМ

Для технически гладких русел и труб пользуются графиком на рис. 1 (см. 307).

Пример. Коэффициент шероховатости n = 0,015; b = 2,0 м; Q = 12,6 м³/с; i_т = 0,10. Требуется определить нормальную глубину h₀.

Расчет.

; b^2,67 = 2^2,67 = 6,36;

и по нижней левой части графика находим

и h₀ = 0,29·2 = 0,58 м.

Для русел и труб со ступенями пользуются графиком на рис. 2 (см. с. 307), где по оси абсцисс отложен параметр

. Здесь

Приложение 2.3

ОПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ ГЛУБИН В КРУГЛЫХ ТРУБАХ ПО ГРАФИКАМ

Для технически гладких труб пользуются графиком на рис. 1. Он составлен при коэффициенте шероховатости n = 0,015. При

параметр П_Q заменяют на

Пример. Коэффициент шероховатости n = 0,013; D = 1 м; Q = 1,4 м³/с; i_т = 0,16. Требуется определить нормальную глубину h₀.

Рис. 1. График для определения нормальных глубин h₀

и соответствующих им скоростей v₀ в круглых трубах

Расчет.

По графику находим:

; h₀ = 0,26·1,0 = 0,26 м и

;

Для круглых труб с повышенной шероховатостью из-за ступенчатой укладки звеньев пользуются графиком на рис. 2, где по оси абсцисс отложен параметр

Рис. 2. График для определения нормальных глубин h₀

в круглых трубах при ступенчатой их укладке

Приведенную повышенную шероховатость n_пов(пр) определяют непосредственно по графику на рис. 3, а (где

- высота ступеней), а при h/D < 0,225 она корректируется путем умножения на коэффициент K_h, который находится по графику на рис. 3, б.

а)

б)

Рис. 3. Графики для определения коэффициента

повышенной шероховатости n_пов(пр) круглых труб

при ступенчатой их укладке

Следовательно, при h/D >= 0,225 n_пов(пр) = h_{пов(пр)(граф)}, а при h/D < 0,225 n_пов(пр) = n_{пов(пр)(граф)}K_h, где n_{пов(пр)(граф)} - значение n_пов(пр), полученное по графику на рис. 3, а.

Приложение 2.4

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ГЛУБИН В ПРЯМОУГОЛЬНЫХ

И ТРАПЕЦЕИДАЛЬНЫХ РУСЛАХ ПО ГРАФИКАМ

Пример. Ширина дна русла b_дн = 3 м; m_от = 2; Q = 12 м³/с.

Требуется определить критическую глубину h_к.

Решение. 1. Вычисляют параметр

2. Пользуясь первым графиком, при

и m_от = 2 находим

и h_к = 0,31·3 = 0,93 м.

Графики для определения критических глубин в прямоугольных

и трапецеидальных руслах

Приложение 2.5

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ ГЛУБИНЫ

В КРУГЛЫХ И ОВОИДАЛЬНЫХ ТРУБАХ ПО ГРАФИКУ

График для определения критической глубины в круглых

(линия 1) и овоидальных (линия 2) трубах

Приложение 2.6

ОПРЕДЕЛЕНИЕ ГЛУБИНЫ ПОТОКА В СЖАТОМ СЕЧЕНИИ

И СОПРЯЖЕННЫХ ГЛУБИН В ТРАПЕЦЕИДАЛЬНОМ РУСЛЕ

Пример 1. Расход Q = 1,5 м³/с. Удельная энергия в сечении на сходе со стенки падения одноступенчатого перепада T₀ = 3,5 м, ширина трапецеидального русла по дну b_дн = 1,5 м; m_от = 1,5;

;

. Требуется определить сжатую глубину h_с, используя график, приведенный на рис. 1.

Рис. 1. График для определения глубины сжатого сечения

в трапецеидальном русле

Решение. Вычисляем параметры:

Затем на графике отыскиваем прямую, соответствующую значению A = 0,169, и кривую, отвечающую параметру B = 3,5. Абсцисса их пересечения дает значение

. Искомая глубина

Пример 2. Критическая глубина h_к = 0,8 м; m_от = 3; h = 0,16 м.

Требуется определить сопряженную глубину h" по графику на рис. 2.

Рис. 2. График для определения сопряженных глубин

в трапецеидальном русле

Решение. Имеем

; находим

. Тогда по графику определяем

. Следовательно,

График для определения глубины сжатого сечения

и сопряженных глубин в прямоугольном русле

Приложение 2.7

ОПРЕДЕЛЕНИЕ ГЛУБИНЫ СЖАТОГО СЕЧЕНИЯ И СОПРЯЖЕННЫХ ГЛУБИН

В ПРЯМОУГОЛЬНОМ РУСЛЕ ПО ГРАФИКУ

Пример. Критическая глубина h_к = 1,37 м; T₀ = 3,55 м;

Требуется определить сжатую глубину на водобое h_с и вторую сопряженную глубину

(см. рисунок на с. 314).

Решение. 1. Определяют

2. Откладывают это значение на оси

3. Восстанавливают перпендикуляр до пересечения с кривой

при

и от точки пересечения проводят горизонтальную прямую до оси

(ось ординат), на которой находят значение

4. В месте пересечения горизонтальной прямой с кривой

опускают перпендикуляр до оси

(ось абсцисс) и находят

5. Вычисляют

;

Приложение 2.8

ОПРЕДЕЛЕНИЕ ДЛИНЫ ГИДРАВЛИЧЕСКОГО ПРЫЖКА ПО ФОРМУЛЕ

М.Д. ЧЕРТОУСОВА С ПОМОЩЬЮ НОМОГРАММЫ

Пример. Скорость потока перед прыжком v₁ = 3 м/с; первая сопряженная глубина h' = 0,20 м.

Требуется определить длину гидравлического прыжка по формуле М.Д. Чертоусова (2.22).

Решение. 1. Вычисляют число Фруда перед прыжком

2. Находят по номограмме при Fr₁ = 4,6 функцию f = 11,5.

Номограмма для определения длины гидравлического прыжка

по формуле М.Д. Чертоусова

3. Вычисляют длину прыжка l_п = fh' = 11,5·0,2 = 2,1 м.

Приложение 2.9

ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ СКОРОСТЕЙ ПОТОКА

ДЛЯ НЕСВЯЗНЫХ ГРУНТОВ С ПОМОЩЬЮ НОМОГРАММЫ

Пример. Глубина потока h = 1,50 м; d = 11 мм.

Требуется определить неразмывающую скорость потока по формулам (2.39) и (2.40).

Номограмма для определения допускаемых скоростей

для несвязных грунтов по формулам (2.39) и (2.40)

Решение. Проводим прямую, соединяющую точку h = 1,5 м на шкале h и точку d = 11 мм на шкале d. Пересечение этой прямой со шкалами v, построенными по формулам (2.39) и (2.40), определяют соответственно скорости v₁ = 1,3 м/с и v₂ = 1,39 м/с.

Приложение 3.1

ПРИМЕР РАСЧЕТА ОДНОКРАТНОГО ПЕРЕЛИВА ВОДЫ ИЗ СООРУЖЕНИЯ

В СООРУЖЕНИЕ

Верховое сооружение (N 1). Железобетонный мост отверстием 3,2 м расположен на железной дороге; отметка подпертого уровня у сооружения в начале перелива составляет 117,99 м; отметка дна в определяющем сечении z_дн(опр) = z_{н(нач.пер)}. Определяющее сечение приводится к треугольной форме (равнобедренный треугольник с m_от(1) = m_от(2) = 200). Отметка лотка на входе под мост z_л = 116,11 м; продольный уклон лога перед сооружением

, средний уклон склонов лога у сооружения

; расчетный расход Q_р = 15,5 м³/с, наибольший Q_max = 24 м³/с (расчет ведем для наибольшего расхода); время водоотдачи t_в = 28 мин; объем притока с бассейна при Q_max W_пр(max) = 174 тыс. м³.

Решение. Вычисление ведем согласно указаниям п. 3.16.

1. Основные гидрологические данные были получены в результате расчета стока и приведены в исходных данных.

2. Определяем продолжительность паводка для верхового сооружения (N 1) по формуле (3.7):

3. Строим для верхового сооружения (N 1) зависимости Q_{соор(возм)1} = f(H³) по формуле Д.И. Кочерина (3.6) и зависимости Q_соор(1) = f(H) и Q_соор(1) = f(H³) по рекомендациям гл. 6. Для построения зависимости (прямой) Q_{соор(возм)1} = f(H³) определяем две точки:

при Q_соор = Q_max = 24,0 м³/с H³ = 0 (H = 0);

при Q_соор = 0

Значение k₀ = 320 было определено по табл. 3.1 для очертания зеркала воды пруда перед сооружением в плане с выпуклыми линиями урезов и прямолинейным поперечным профилем лога.

Вычисляем данные для построения зависимости Q_соор(1) = f(H) и Q_соор(1) = f(H³) согласно указаниям гл. 6. Эти данные приведены в таблице.

H, м	H³	Q_соор(1), м³/с	H, м	H³	Q_соор(1), м³/с
0,5	0,125	1,83	2,5	15,8	20,0
1,0	1,0	5,08	2,7	19,9	22,5
1,5	3,4	9,35	3,0	27,0	26,4
2,0	8,0	14,30	3,0	27,0	26,4

Далее выполняем построение.

Посередине листа проводим ось ординат Q (рис. 1) и делим лист на левую и правую части. Проводим перпендикулярно ей ось абсцисс.

Рис. 1. График для определения расходов в верховом

сооружении (N 1), расходов сброса и соответствующих

им подпертых глубин при наличии перелива воды

С левой стороны графика по оси абсцисс откладываем H и H³, с правой - время t.

По двум точкам, координаты которых вычислены выше, строим зависимость Q_{соор(возм)} = f(H³), а по данным, приведенным в таблице, - зависимости Q_соор(1) = f(H) и Q_соор(1) = f(H³).

4. Устанавливаем место перелива и форму определяющего сечения. В нашем случае оно задано и имеет треугольную форму с m_от(1) = m_от(2) = 200.

5. Определяем подпертую глубину в начале перелива по формуле (3.8):

H_{нач.пер} = z_{п(нач.пер)} - z_л = 117,99 - 116,11 = 1,88 м.

6. Строим зависимость расхода верхового сооружения от глубины воды в определяющем сечении Q_сб(1) = f(H').

Сначала вычисляем данные для построения зависимости Q_сб(1) = f(H') для треугольной формы определяющего поперечного сечения по формуле (3.10), задаваясь подпертой глубиной и вычисляя глубину в определяющем сечении H' = H - H_{нач.пер} = H - 1,88 м,

Результаты расчета приведены ниже:

H, м	0,1	0,2	0,3	0,4
Q_сб(1), м³/с	1,3	7,5	20,6	42,1

Зависимость Q_сб(1) = f(H') строим в координатах Q и H, принимая за начало отсчета подпертую глубину, соответствующую началу перелива (см. рис. 1).

7. Строим зависимость Q_соор(1) + Q_сб(1) = f(H). Для этого складываем графически графики Q_соор(1) = f(H) и Q_сб(1) = f(H) (см. рис. 1, левая сторона графика).

8. Строим зависимость Q_соор(1) + Q_сб(1) = f(H³), пользуясь совмещенной с H шкалой H³ на оси абсцисс.

9. Находим точку пересечения зависимостей Q_{соор(возм)1} = f(H³) и Q_соор(1) + Q_сб(1) = f(H³) для моста (верхового сооружения), ордината которой определит максимальный расход Q_соор(1) + Q_сб(1) = 21,9 м³/с.

Проведя в точке пересечения вертикальную линию до пересечения с зависимостью Q_соор(1) = f(H³), находим искомый расход в сооружении Q_соор(1) = 15,2 м³/с и расход сброса Q_сб(1) = 6,7 м³/с как разность (Q_соор(1) + Q_сб(1)) - Q_сб(1). Расход сброса необходим для гидравлического расчета низового сооружения. Зная расход в сооружении, находим по зависимости Q_соор(1) = f(H) искомую подпертую глубину H_max(1) = 2,08 м.

10. В месте пересечения прямой, проведенной на ординате Q_соор(1) + Q_сб(1) параллельно оси абсцисс, с низовой ветвью гидрографа притока находим положение пика гидрографа расхода в сооружении. Зная этот расход, находим продолжительность паводка в сооружении

Соединив точку пика паводка в сооружении (с учетом сброса) с началом координат и точкой, имеющей абсциссу t_{пав(соор)1} = 264 мин, получают гидрограф расходов в сооружении с учетом сброса Q_соор(1) + Q_сб(1) = f(t). Затем проводим через точку, соответствующую расходу в начале перелива Q_пер(1) = 13 м³/с (этот расход определен по подпертой глубине в начале перелива H = 1,88 м), линию параллельно оси абсцисс и в месте пересечения ее с ветвями гидрографа расхода Q_соор(1) + Q_сб(1) = f(t) находим (считая от начала паводка) время начала перелива t_н(пер) = 28 мин, время установления пика расхода сброса t_max(_Q₎ = 47 мин и время конца перелива t_к(пер) = 135 мин. Эти значения необходимы для гидравлического расчета низового сооружения (N 2).

Низовое сооружение (N 2). Тип сооружения - металлический мост отверстием 6,4 м; отметка лотка на входе - 114,2 м. В результате расчетов стока получено Q_пр(р)2 = 11,5 м³/с и Q_пр(max)2 = 19,3 м³/с. Объем стока W_пр(2) = 161 000 м³; время водоотдачи t_в(2) = 28 мин.

Решение. 1. Определяем продолжительность паводка

2. Вычисляем данные для построения зависимости Q_соор(2) = f(H³) по формуле (3.6). Для этого предварительно уточняем объем притока за счет объема сброса по формуле (3.12):

W_{пр(полн)2} = W_пр(2) + W_сб(1),

где объем сброса, м³,

. Причем t_{пав(сб)1} - t_к(пер)1.

В нашем случае имеем (по данным расчета верхового сооружения):

t_{пав(сб)1} = 135 - 28 = 107 мин;

W_{пр(полн)2} = 161 000 + 21 600 = 182 600 м³.

Затем путем графического суммирования гидрографов расходов притока Q_пр(2) = f(t) и сброса из сооружения N 1 строим гидрограф Q_пр(2) + Q_сб(1) = f(t) и находим максимальный расход притока Q_пр(2) + Q_сб(1) = 24,5 м³/с (рис. 2).

Рис. 2. График для определения расхода в низовом сооружении

(N 2) и соответствующей ему подпертой глубины

при наличии перелива

Далее определяем данные для построения прямой Q_{соор(возм)2} = f(H³):

при Q_соор(2) = Q_пр(2) + Q_сб(1) = 24,5 м³/с H³ = 0;

при Q_соор(2) = 0

3. Вычисляем данные для построения зависимостей Q_соор(2) = f(H) и Q_соор(2) = f(H³):

H, м	0,5	0,75	1,0	1,2	1,5	2,0	2,5
H³, м³	0,125	0,43	1,0	1,74	3,4	8,0	15,7
Q, м³/с	3,5	6,2	9,6	12,6	17,6	28,0	38,0

Графическое решение. В правой части графика на рис. 2 геометрически с учетом времени t_н(пер)1, t_max(_Q₎ и t_к(пер)1 складываем графики притока с бассейна Q_пр(2) = f(t) и Q_сб(1) = f(t).

В левой части графика аналогичным путем, как и для верхового сооружения (но без учета сброса), определяем Q_соор(2) = 23,0 м³/с и H₂ = 1,80 м.

Приложение 4.1

РАСЧЕТ СУЖАЮЩИХСЯ БЫСТРОТОКОВ ПО УРАВНЕНИЯМ ГИДРАВЛИКИ

На рис. 1 изображены (для половины области течения) вариант расчетной сетки размером 7 x 26 ячеек (рис. 1, а), фрагмент сетки размером 28 x 104 ячейки (рис. 1, б) и изолинии рассчитанных на ЭВМ глубин (в миллиметрах) на этих сетках. Угол сужения

; число Фруда на входе Fr₁ = 9; глубина на входе - 100 мм; уклон дна и трение отсутствуют. Длина сужения подобрана так, чтобы аналитическое решение по теории косых прыжков (фронт его изображен штриховой линией) давало отраженный (второй) косой прыжок, попадающий точно в конец сужающейся части. Видно, что при сгущении сетки численное решение приближается к точному (аналитические значения глубин на "пиках" за первым и вторым косыми прыжками соответственно равны 161 и 236 мм).

а)

б)

Рис. 1. Результаты расчета течения в сужающемся быстротоке

по программе "БОР":

а - на редкой сетке размером 7 x 26 ячеек;

б - на густой сетке размером 28 x 104 ячейки

На рис. 2 представлены рассчитанные на ЭВМ изолинии глубин в сужении с углом

на наклонном дне с трением (рис. 2, а) и на горизонтальном дне без трения (рис. 2, б). Картины течения в целом похожи, но максимальный всплеск на оси потока при наклонном дне (230 мм) меньше, а понижение глубин за концом сужения у стенки (151 мм) больше, чем на горизонтальном дне (соответственно 265 и 212 мм). На рис. 2, б виден также второй гребень на стенке быстотока (уже за сужением).

а)

б)

Рис. 2. Графическое изображение результатов расчета течения

в сужающемся быстротоке по программе "БОР" при различных

уклонах и шероховатостях:

а - при n = 0,016 и i_л = 0,05; б - при n = 0 и i_л = 0

На рис. 3 приведено сравнение эпюр расчета сужения (сплошные линии) по двухмерной численной модели (программа "БОР") с экспериментом (крестики). В сужении и за ним наглядно видна перестройка глубин в поперечных сечениях при движении вдоль русла.

Рис. 3. Эпюры глубин течения в сужающемся быстротоке

при следующих гидравлических условиях:

скорость v₁ = 1,3 м/с; глубина h₁ = 30 мм; число Фруда

на входе

; уклон i_л = 0,1; шероховатость n = 0,014;

масштаб глубин: 1 см - 20 мм

Приложение 4.2

БЕЗРАЗМЕРНЫЕ ОТМЕТКИ ДНА РАССЕИВАЮЩИХ ТРАМПЛИНОВ

И БЕЗРАЗМЕРНЫЕ КООРДИНАТЫ ПОВЕРХНОСТНЫХ ЛИНИЙ ТОКА

Таблица 1

Безразмерные отметки дна рассеивающих трамплинов

s_к	Безразмерные отметки дна z_дн при n
s_к	1,0	0,8	0,6	0,4	0,2	0,0
i_н = 0,15; t/b = 0,1; Fr_н = 10
0,0	0,0286	0,0286	0,0286	0,0286	0,0286	0,0286
0,1	0,0414	0,0416	0,0418	0,0419	0,0421	0,0422
0,2	0,0545	0,0546	0,0548	0,0550	0,0551	0,0553
0,3	0,0667	0,0666	0,0665	0,0665	0,0666	0,0667
0,4	0,0769	0,0760	0,0754	0,0749	0,0747	0,0748
0,5	0,0831	0,0810	0,0794	0,0783	0,0777	0,0777
0,6	0,0830	0,0794	0,0765	0,0745	0,0733	0,0730
0,7	0,0739	0,0685	0,0642	0,0611	0,0592	0,0587
0,8	0,0529	0,0462	0,0406	0,0363	0,0336	0,0327
0,9	0,0177	0,0115	0,0052	0,0008	-0,0034	-0,0048
1,0	-0,0260	-0,0290	-0,0352	-0,0414	-0,0460	-0,0483
i_н = 0,15; t/b = 0,1; Fr_н = 20
0,0	0,0286	0,0286	0,0286	0,0286	0,0286	0,0286
0,1	0,0424	0,0425	0,0426	0,0427	0,0427	0,0428
0,2	0,0572	0,0560	0,0560	0,0560	0,0560	0,0561
0,3	0,0689	0,0682	0,0677	0,0674	0,0672	0,0672
0,4	0,0794	0,0776	0,0762	0,0752	0,0746	0,0745
0,5	0,0857	0,0822	0,0795	0,0775	0,0764	0,0761
0,6	0,0855	0,0799	0,0754	0,0722	0,0702	0,0696
0,7	0,0761	0,0679	0,0614	0,0566	0,0537	0,0527
0,8	0,0545	0,0436	0,0349	0,0284	0,0244	0,0230
0,9	0,0177	0,0046	-0,0064	-0,0145	-0,0198	-0,0217
1,0	-0,0353	-0,0475	-0,0602	-0,0701	-0,0765	-0,0791
i_н = 0,15; t/b = 0,1; Fr_н = 50
0,0	0,0286	0,0286	0,0286	0,0286	0,0286	0,0286
0,1	0,0431	0,0431	0,0430	0,0430	0,0430	0,0430
0,2	0,0574	0,0569	0,0564	0,0562	0,0560	0,0559
0,3	0,0706	0,0688	0,0675	0,0665	0,0660	0,0658
0,4	0,0813	0,0776	0,0748	0,0727	0,0714	0,0710
0,5	0,0878	0,0816	0,0767	0,0733	0,0712	0,0705
0,6	0,0875	0,0783	0,0710	0,0657	0,0625	0,0615
0,7	0,0778	0,0659	0,0549	0,0473	0,0425	0,0409
0,8	0,0556	0,0385	0,0256	0,0162	0,0101	0,0080
0,9	0,0177	-0,0048	-0,0210	-0,0320	-0,0386	-0,0409
1,0	-0,0384	-0,0665	-0,0866	-0,0993	-0,1062	-0,1086
i_н = 0,15; t/b = 0,1; Fr_н = 100
0,0	0,0286	0,0286	0,0286	0,0286	0,0286	0,0286
0,1	0,0433	0,0432	0,0430	0,0427	0,0423	0,0421
0,2	0,0578	0,0568	0,0561	0,0555	0,0549	0,0547
0,3	0,0712	0,0683	0,0663	0,0647	0,0637	0,0633
0,4	0,0821	0,0766	0,0723	0,0690	0,0666	0,0658
0,5	0,0886	0,0800	0,0733	0,0685	0,0655	0,0644
0,6	0,0883	0,0763	0,0670	0,0603	0,0565	0,0554
0,7	0,0785	0,0626	0,0504	0,0401	0,0336	0,0314
0,8	0,0560	0,0353	0,0200	0,0081	-0,0008	-0,0047
0,9	0,0177	-0,0098	-0,0281	-0,0399	-0,0474	-0,0505
i_н = 0,15; t/b = 0,2; Fr_н = 10
0,0	0,0572	0,0572	0,0572	0,0572	0,0572	0,0572
0,1	0,0699	0,0701	0,0703	0,0705	0,0706	0,0707
0,2	0,0827	0,0829	0,0831	0,0832	0,0834	0,0836
0,3	0,0947	0,0944	0,0942	0,0942	0,0941	0,0943
0,4	0,1045	0,1032	0,1021	0,1014	0,1011	0,1012
0,5	0,1101	0,1072	0,1050	0,1034	0,1025	0,1024
0,6	0,1091	0,1042	0,1003	0,0974	0,0958	0,0954
0,7	0,0989	0,0915	0,0855	0,0812	0,0785	0,0777
0,8	0,0767	0,0665	0,0584	0,0523	0,0485	0,0472
0,9	0,0402	0,0275	0,0170	0,0091	0,0040	0,0021
1,0	-0,0092	-0,0225	-0,0352	-0,0450	-0,0515	-0,0544
i_н = 0,15; t/b = 0,2; Fr_н = 20
0,0	0,0572	0,0572	0,0572	0,0572	0,0572	0,0572
0,1	0,0847	0,0845	0,0844	0,0842	0,0842	0,0842
0,2	0,0847	0,0845	0,0844	0,0842	0,0842	0,0842
0,3	0,0974	0,0963	0,0954	0,0947	0,0943	0,0943
0,4	0,1076	0,1049	0,1027	0,1011	0,1002	0,0999
0,5	0,1135	0,1086	0,1046	0,1018	0,1002	0,0997
0,6	0,1125	0,1048	0,0987	0,0942	0,0916	0,0907
0,7	0,1019	0,0909	0,0821	0,0756	0,0756	0,0701
0,8	0,0787	0,0638	0,0524	0,0439	0,0385	0,0366
0,9	0,0404	0,0208	0,0616	-0,0041	-0,0104	-0,0127
1,0	-0,0135	-0,0377	-0,0560	-0,0682	-0,0760	-0,0781
i_н = 0,15; t/b = 0,2; Fr_н = 50
0,0	0,0572	0,0572	0,0572	0,0572	0,0572	0,0572
0,1	0,0717	0,0717	0,0713	0,0704	0,0692	0,0687
0,2	0,0860	0,0852	0,0844	0,0834	0,0822	0,0818
0,3	0,0993	0,0966	0,0944	0,0925	0,0909	0,0903
0,4	0,1099	0,1046	0,1002	0,0964	0,0934	0,0922
0,5	0,1160	0,1077	0,1010	0,0958	0,0921	0,0907
0,6	0,1150	0,1033	0,0939	0,0871	0,0830	0,0816
0,7	0,1040	0,0884	0,0758	0,0656	0,0586	0,0563
0,8	0,0800	0,0599	0,0446	0,0321	0,0223	0,0180
0,9	0,0405	0,0139	-0,0042	-0,0167	-0,0255	-0,0294
1,0	0,0157	0,0507	-0,0730	-0,0857	-0,0904	-0,0906
i_н = 0,15; t/b = 0,3; Fr_н = 10
0,0	0,0857	0,0857	0,0857	0,0857	0,0857	0,0857
0,1	0,0985	0,0988	0,0990	0,0992	0,0993	0,0994
0,2	0,1114	0,1116	0,1118	0,1119	0,1121	0,1123
0,3	0,1234	0,1230	0,1226	0,1224	0,1224	0,1225
0,4	0,1331	0,1314	0,1301	0,1291	0,1287	0,1287
0,5	0,1384	0,1349	0,1322	0,1302	0,1291	0,1290
0,6	0,1368	0,1309	0,1263	0,1229	0,1210	0,1205
0,7	0,1255	0,1167	0,1097	0,1045	0,1013	0,1003
0,8	0,1017	0,0896	0,0801	0,0730	0,0685	0,0669
0,9	0,0636	0,0475	0,0350	0,0260	0,0203	0,0181
1,0	0,0126	-0,0072	-0,0230	-0,03342	-0,0412	-0,0442
i_н = 0,15; t/b = 0,3; Fr_н = 20
0,0	0,0857	0,0857	0,0857	0,0857	0,0857	0,0857
0,1	0,0997	0,0999	0,0999	0,0996	0,0993	0,0991
0,2	0,1135	0,1133	0,1130	0,1127	0,1124	0,1123
0,3	0,1263	0,1248	0,1236	0,1226	0,1219	0,1217
0,4	0,1367	0,1332	0,1303	0,1281	0,1265	0,1260
0,5	0,1424	0,1363	0,1316	0,1281	0,1259	0,1252
0,6	0,1408	0,1317	0,1245	0,1193	0,1162	0,1152
0,7	0,1289	0,1164	0,1062	0,0983	0,0930	0,0912
0,8	0,1041	0,0875	0,0746	0,0645	0,0576	0,0550
0,9	0,0641	0,0418	0,0259	0,0148	0,0076	0,0048
1,0	0,0093	-0,0197	-0,0396	-0,0522	-0,0591	-0,0616
i_н = 0,3; t/b = 0,1; Fr_н = 10
0,0	0,0294	0,0294	0,0294	0,0294	0,0294	0,0294
0,1	0,0555	0,0558	0,0561	0,0563	0,0566	0,0568
0,2	0,0285	0,0826	0,0830	0,0833	0,0836	0,0839
0,3	0,1089	0,1087	0,1086	0,1086	0,1088	0,1091
0,4	0,1329	0,1316	0,1308	0,1302	0,1300	0,1302
0,5	0,1522	0,1493	0,1472	0,1458	0,1450	0,1451
0,6	0,1641	0,1591	0,1552	0,1526	0,1511	0,1509
0,7	0,1653	0,1578	0,1520	0,1479	0,1456	0,1450
0,8	0,1521	0,1421	0,1343	0,1288	0,1255	0,1246
0,9	0,1206	0,1089	0,0994	0,0926	0,0885	0,0873
1,0	0,0678	0,0588	0,0487	0,0412	0,0365	0,0350
i_н = 0,3; t/b = 0,1; Fr_н = 20
0,0	0,0294	0,0294	0,0294	0,0294	0,0294	0,0294
0,1	0,0572	0,0574	0,0576	0,0577	0,0578	0,0579
0,2	0,0851	0,0851	0,0852	0,0852	0,0853	0,0855
0,3	0,1120	0,1113	0,1108	0,1105	0,1104	0,1105
0,4	0,1363	0,1343	0,1327	0,1327	0,1311	0,1311
0,5	0,1557	0,1517	0,1487	0,1465	0,1453	0,1451
0,6	0,1675	0,1610	0,1560	0,1525	0,1504	0,1499
0,7	0,1685	0,1591	0,1519	0,1467	0,1436	0,1427
0,8	0,1550	0,1426	0,1330	0,1261	0,1220	0,1208
0,9	0,1232	0,1077	0,0956	0,0872	0,0821	0,0806
1,0	0,0698	0,0537	0,0398	0,0300	0,0242	0,0222
i_н = 0,3; t/b = 0,1; Fr_н = 50
0,0	0,0295	0,0295	0,0295	0,0295	0,0295	0,0295
0,1	0,0583	0,0584	0,0584	0,0584	0,0584	0,0584
0,2	0,0869	0,0866	0,0863	0,0861	0,0860	0,0861
0,3	0,1143	0,1129	0,1118	0,1110	0,1106	0,1105
0,4	0,1389	0,1356	0,1331	0,1313	0,1303	0,1300
0,5	0,1584	0,1528	0,1484	0,1453	0,1435	0,1430
0,6	0,1702	0,1617	0,1551	0,1503	0,1475	0,1467
0,7	0,1710	0,1594	0,1502	0,1435	0,1394	0,1381
0,8	0,1573	0,1420	0,1303	0,1220	0,1169	0,1152
0,9	0,1251	0,1054	0,0909	0,0810	0,0752	0,0734
1,0	0,0710	0,0477	0,0302	0,0188	0,0124	0,0103
i_н = 0,3; t/b = 0,1; Fr_н = 100
0,0	0,0295	0,0295	0,0295	0,0295	0,0295	0,0295
0,1	0,0590	0,0589	0,0587	0,0585	0,0583	0,0582
0,2	0,0881	0,0872	0,0864	0,0859	0,0855	0,0854
0,3	0,1160	0,1131	0,1110	0,1095	0,1086	0,1083
0,4	0,1409	0,1355	0,1312	0,1280	0,1260	0,1253
0,5	0,1607	0,1524	0,1459	0,1411	0,1382	0,1373
0,6	0,1725	0,1612	0,1522	0,1458	0,1420	0,1409
0,7	0,1732	0,1585	0,1489	0,1383	0,1327	0,1308
0,8	0,1502	0,1404	0,1266	0,1164	0,1098	0,1075
0,9	0,1266	0,1023	0,0856	0,0747	0,0684	0,0663
1,0	0,0719	0,0413	0,0208	0,0087	0,0028	0,0011
i_н = 0,3; t/b = 0,2; Fr_н = 10
0,0	0,0588	0,0588	0,0588	0,0588	0,0588	0,0588
0,1	0,0844	0,0848	0,0852	0,0855	0,0858	0,0860
0,2	0,1107	0,1111	0,1114	0,1118	0,1121	0,1125
0,3	0,1362	0,1360	0,1359	0,1359	0,1361	0,1365
0,4	0,1592	0,1577	0,1567	0,1561	0,1559	0,1562
0,5	0,1774	0,1740	0,1715	0,1699	0,1691	0,1693
0,6	0,1879	0,1822	0,1778	0,1747	0,1731	0,1730
0,7	0,1876	0,1790	0,1724	0,1677	0,1651	0,1645
0,8	0,1730	0,1614	0,1524	0,1461	0,1424	0,1414
0,9	0,1409	0,1300	0,1146	0,1066	0,1019	0,1005
1,0	0,0895	0,0733	0,0597	0,0503	0,0447	0,0428
i_н = 0,3; t/b = 0,2; Fr_н = 20
0,0	0,0589	0,0589	0,0589	0,0589	0,0589	0,0589
0,1	0,0866	0,0869	0,0869	0,0870	0,0871	0,0872
0,2	0,1142	0,1141	0,1141	0,1140	0,1141	0,1143
0,3	0,1407	0,1396	0,1388	0,1382	0,1380	0,1381
0,4	0,1644	0,1615	0,1594	0,1578	0,1570	0,1570
0,5	0,1829	0,1777	0,1738	0,1710	0,1695	0,1692
0,6	0,1935	0,1856	0,1794	0,1750	0,1725	0,1719
0,7	0,1929	0,1818	0,1732	0,1669	0,1630	0,1619
0,8	0,1778	0,1631	0,1520	0,1441	0,1392	0,1377
0,9	0,1448	0,1258	0,1118	0,1023	0,0967	0,0949
1,0	0,0922	0,0691	0,0521	0,0409	0,0346	0,0326
i_н = 0,3; t/b = 0,2; Fr_н = 50
0,0	0,0589	0,0589	0,0589	0,0589	0,0589	0,0589
0,1	0,0880	0,0880	0,0878	0,0873	0,0867	0,0864
0,2	0,1168	0,1159	0,1152	0,1145	0,1139	0,1137
0,3	0,1442	0,1414	0,1393	0,1377	0,1366	0,1362
0,4	0,1685	0,1633	0,1590	0,1557	0,1533	0,1525
0,5	0,1875	0,1794	0,1730	0,1682	0,1651	0,1642
0,6	0,1982	0,1872	0,1784	0,1720	0,1681	0,1669
0,7	0,1974	0,1831	0,1717	0,1629	0,1572	0,1553
0,8	0,1818	0,1635	0,1499	0,1396	0,1327	0,1302
0,9	0,1480	0,1244	0,1079	0,0970	0,0904	0,0881
1,0	0,0941	0,0640	0,0439	0,0317	0,0256	0,0238
i_н = 0,3; t/b = 0,3; Fr_н = 10
0,0	0,0885	0,0885	0,0885	0,0885	0,0885	0,0885
0,1	0,1157	0,1156	0,1155	0,1155	0,1154	0,1154
0,2	0,1397	0,1420	0,1420	0,1418	0,1416	0,1415
0,3	0,1647	0,1669	0,1661	0,1652	0,1647	0,1645
0,4	0,1874	0,1882	0,1861	0,1843	0,1831	0,1827
0,5	0,2048	0,2038	0,1999	0,1969	0,1950	0,1945
0,6	0,2142	0,2106	0,2046	0,2000	0,1972	0,1963
0,7	0,2125	0,2057	0,1972	0,1907	0,1867	0,1854
0,8	0,1964	0,1858	0,1749	0,1668	0,1818	0,1602
0,9	0,1630	0,1475	0,1339	0,1245	0,1189	0,1172
1,0	0,1120	0,0914	0,0745	0,0638	0,0579	0,0561
i_н = 0,3; t/b = 0,3; Fr_н = 20
0,0	0,0885	0,0885	0,0885	0,0885	0,0885	0,0885
0,1	0,1160	0,1169	0,1168	0,1163	0,1160	0,1158
0,2	0,1437	0,1445	0,1440	0,1434	0,1430	0,1428
0,3	0,1702	0,1698	0,1680	0,1665	0,1656	0,1652
0,4	0,1936	0,1914	0,1877	0,1846	0,1828	0,1821
0,5	0,2116	0,2070	0,2013	0,1969	0,1943	0,1934
0,6	0,2213	0,2139	0,2058	0,1998	0,1962	0,1950
0,7	0,2193	0,2086	0,1979	0,1895	0,1841	0,1823
0,8	0,2025	0,1879	0,1749	0,1647	0,1585	0,1562
0,9	0,1680	0,1479	0,1323	0,1218	0,1154	0,1132
1,0	0,1152	0,0885	0,0692	0,0575	0,0515	0,0497
i_н = 0,5; t/b = 0,1; Fr_н = 10
0,0	0,0313	0,0313	0,0313	0,0313	0,0313	0,0313
0,1	0,0752	0,0757	0,0761	0,0765	0,0768	0,0771
0,2	0,1216	0,1220	0,1223	0,1223	0,1227	0,1231
0,3	0,1669	0,1665	0,1664	0,1664	0,1665	0,1669
0,4	0,2097	0,2078	0,2067	0,2059	0,2057	0,2059
0,5	0,2469	0,2430	0,2402	0,2383	0,2373	0,2373
0,6	0,2751	0,2686	0,2637	0,2604	0,2586	0,2583
0,7	0,2904	0,2811	0,2740	0,2690	0,2662	0,2655
0,8	0,2884	0,2754	0,2671	0,2606	0,2569	0,2559
0,9	0,2642	0,2497	0,2385	0,2307	0,2262	0,2249
1,0	0,2126	0,1989	0,1869	0,1785	0,1736	0,1722
i_н = 0,5; t/b = 0,1; Fr_н = 20
0,0	0,0314	0,0314	0,0314	0,0314	0,0314	0,0314
0,1	0,0778	0,0781	0,0783	0,0786	0,0788	0,0790
0,2	0,1248	0,1249	0,1250	0,1251	0,1253	0,1256
0,3	0,1707	0,1700	0,1694	0,1691	0,1691	0,1693
0,4	0,2136	0,2112	0,2094	0,2083	0,2077	0,2078
0,5	0,2507	0,2460	0,2425	0,2401	0,2388	0,2386
0,6	0,2787	0,2713	0,2656	0,2617	0,2594	0,2589
0,7	0,2937	0,2834	0,2755	0,2698	0,2665	0,2655
0,8	0,2914	0,2788	0,2681	0,2609	0,2567	0,2555
0,9	0,2670	0,2508	0,2385	0,2301	0,2251	0,2237
1,0	0,2155	0,1987	0,1850	0,1756	0,1703	0,1687
i_н = 0,5; t/b = 0,1; Fr_н = 50
0,0	0,0315	0,0315	0,0315	0,0315	0,0315	0,0315
0,1	0,0799	0,0799	0,0800	0,0800	0,0801	0,0802
0,2	0,1280	0,1275	0,1272	0,1270	0,1269	0,1270
0,3	0,1746	0,1729	0,1715	0,1706	0,1701	0,1701
0,4	0,2179	0,2140	0,2110	0,2089	0,2075	0,2075
0,5	0,2551	0,2486	0,2436	0,2400	0,2380	0,2375
0,6	0,2830	0,2737	0,2664	0,2612	0,2581	0,2572
0,7	0,2978	0,2855	0,2760	0,2691	0,2648	0,2636
0,8	0,2951	0,2798	0,2682	0,2599	0,2550	0,2534
0,9	0,2703	0,2514	0,2375	0,2280	0,2226	0,2209
1,0	0,2188	0,1972	0,1811	0,1705	0,1647	0,1629
i_н = 0,5; t/b = 0,1; Fr_н = 100
0,0	0,0316	0,0316	0,0316	0,0316	0,0316	0,0316
0,1	0,0802	0,0802	0,0802	0,0802	0,0802	0,0803
0,2	0,1286	0,1280	0,1275	0,1272	0,1270	0,1270
0,3	0,1754	0,1733	0,1716	0,1705	0,1699	0,1698
0,4	0,2188	0,2144	0,2109	0,2085	0,2071	0,2068
0,5	0,2561	0,2490	0,2434	0,2395	0,2372	0,2365
0,6	0,2840	0,2741	0,2663	0,2607	0,2573	0,2563
0,7	0,2987	0,2859	0,2759	0,2686	0,2641	0,2627
0,8	0,2959	0,2800	0,2680	0,2595	0,2543	0,2527
0,9	0,2711	0,2514	0,2370	0,2274	0,2219	0,2201
1,0	0,2195	0,1967	0,1890	0,1692	0,1633	0,1614
i_н = 0,5; t/b = 0,2; Fr_н = 10
0,0	0,0632	0,0632	0,0632	0,0632	0,0632	0,0632
0,1	0,1055	0,1061	0,1066	0,1071	0,1076	0,1080
0,2	0,1500	0,1506	0,1511	0,1516	0,1522	0,1528
0,3	0,1940	0,1937	0,1937	0,1939	0,1942	0,1948
0,4	0,2351	0,2333	0,2320	0,2314	0,1213	0,2318
0,5	0,2705	0,2664	0,2635	0,2616	0,2608	0,2610
0,6	0,2967	0,2900	0,2849	0,2815	0,2798	0,2797
0,7	0,3101	0,3005	0,2931	0,2880	0,2851	0,2847
0,8	0,3064	0,2938	0,2843	0,2776	0,2738	0,2730
0,9	0,2813	0,2657	0,2539	0,2459	0,2414	0,2403
1,0	0,2312	0,2145	0,2011	0,1921	0,1870	0,1857
i_н = 0,5; t/b = 0,2; Fr_н = 20
0,0	0,0632	0,0632	0,0632	0,0632	0,0632	0,0632
0,1	0,1089	0,1095	0,1097	0,1095	0,1100	0,1102
0,2	0,1552	0,1552	0,1553	0,1554	0,1556	0,1559
0,3	0,2002	0,1991	0,1983	0,1978	0,1977	0,1980
0,4	0,2419	0,2389	0,2366	0,2351	0,2344	0,2345
0,5	0,2775	0,2720	0,2678	0,2650	0,2635	0,2633
0,6	0,3036	0,2954	0,2890	0,2845	0,2820	0,2815
0,7	0,3166	0,3054	0,2968	0,2906	0,2869	0,2860
0,8	0,3223	0,2981	0,2874	0,2798	0,2753	0,2741
0,9	0,2867	0,2690	0,2559	0,2470	0,2420	0,2406
1,0	0,2365	0,2162	0,2008	0,1908	0,1852	0,1837
i_н = 0,5; t/b = 0,2; Fr_н = 50
0,0	0,0632	0,0632	0,0632	0,0632	0,0632	0,0632
0,1	0,1114	0,1114	0,1113	0,1111	0,1108	0,1108
0,2	0,1593	0,1584	0,1577	0,1572	0,1569	0,1569
0,3	0,2056	0,2028	0,2006	0,1991	0,1982	0,1981
0,4	0,2481	0,2428	0,2385	0,2354	0,2335	0,2329
0,5	0,2842	0,2762	0,2699	0,2652	0,2624	0,2616
0,6	0,3104	0,2997	0,2913	0,2852	0,2816	0,2806
0,7	0,3231	0,3097	0,2991	0,2913	0,2865	0,2850
0,8	0,3183	0,3018	0,2804	0,2804	0,2749	0,2731
0,9	0,2921	0,2716	0,2568	0,2470	0,2413	0,2395
1,0	0,2413	0,2168	0,1993	0,1883	0,1824	0,1807
i_н = 0,5; t/b = 0,3; Fr_н = 10
0,0	0,0948	0,0948	0,0948	0,0948	0,0948	0,0948
0,1	0,1273	0,1279	0,1285	0,1290	0,1294	0,1298
0,2	0,1716	0,1722	0,1727	0,1732	0,1738	0,1744
0,3	0,2152	0,2148	0,2146	0,2147	0,2150	0,2157
0,4	0,2556	0,2535	0,2520	0,2512	0,2510	0,2516
0,5	0,2900	0,2856	0,2823	0,2803	0,2794	0,2797
0,6	0,3150	0,3079	0,3025	0,2987	0,2970	0,2970
0,7	0,3270	0,3170	0,3093	0,3039	0,3009	0,3005
0,8	0,3219	0,3089	0,2991	0,2922	0,2883	0,2875
0,9	0,2959	0,2795	0,2673	0,2592	0,2546	0,2535
1,0	0,2465	0,2278	0,2135	0,2041	0,1989	0,1976
i_н = 0,5; t/b = 0,3; Fr_н = 20
0,0	0,0948	0,0948	0,0948	0,0948	0,0948	0,0948
0,1	0,1307	0,1311	0,1313	0,1315	0,1316	0,1318
0,2	0,1772	0,1770	0,1769	0,1769	0,1770	0,1773
0,3	0,2221	0,2205	0,2193	0,2185	0,2183	0,2185
0,4	0,2634	0,2596	0,2568	0,2548	0,2538	0,2538
0,5	0,2983	0,2920	0,2871	0,2838	0,2820	0,2818
0,6	0,3234	0,3144	0,3073	0,3023	0,2995	0,2990
0,7	0,3450	0,3232	0,3140	0,3072	0,3032	0,3022
0,8	0,3293	0,3145	0,3033	0,2953	0,2905	0,2892
0,9	0,3026	0,2839	0,2704	0,2613	0,2562	0,2548
1,0	0,2526	0,2304	0,2142	0,2038	0,1982	0,1967
i_н = 1,0; t/b = 0,1; Fr_н = 10
0,0	0,0384	0,0385	0,0387	0,0388	0,0389	0,0389
0,1	0,1273	0,1280	0,1287	0,1293	0,1299	0,1305
0,2	0,2216	0,2220	0,2224	0,2229	0,2234	0,2240
0,3	0,3155	0,3147	0,3143	0,3142	0,3143	0,3148
0,4	0,4055	0,4026	0,4004	0,3991	0,3986	0,3988
0,5	0,4876	0,4816	0,4772	0,4742	0,4727	0,4725
0,6	0,5568	0,5477	0,5406	0,5357	0,5330	0,5324
0,7	0,6078	0,5958	0,5865	0,5798	0,5759	0,5749
0,8	0,6340	0,6203	0,6094	0,6016	0,5970	0,5956
0,9	0,6285	0,6142	0,6027	0,5944	0,5895	0,5881
1,0	0,5834	0,5725	0,5624	0,5547	0,5502	0,5489
i_н = 1,00; t/b = 0,1; Fr_н = 20
0,0	0,0391	0,0392	0,0393	0,0393	0,0394	0,0394
0,1	0,1318	0,1323	0,1328	0,1332	0,1337	0,1341
0,2	0,2267	0,2269	0,2271	0,2274	0,2278	0,2283
0,3	0,3206	0,3195	0,3188	0,3184	0,3184	0,3188
0,4	0,4103	0,4069	0,4044	0,4028	0,4021	0,4022
0,5	0,4919	0,4855	0,4806	0,4773	0,4755	0,4753
0,6	0,5607	0,5510	0,5436	0,5384	0,5355	0,5348
0,7	0,6110	0,5988	0,5891	0,5922	0,5782	0,5771
0,8	0,6368	0,6228	0,6117	0,6037	0,5990	0,5977
0,9	0,6310	0,6164	0,6046	0,5962	0,5913	0,5898
1,0	0,5861	0,5746	0,5640	0,5562	0,5515	0,5502
i_н = 1,00; t/b = 0,1; Fr_н = 50
0,0	0,0396	0,0397	0,0397	0,0397	0,0397	0,0398
0,1	0,1359	0,1361	0,1363	0,1365	0,1367	0,1369
0,2	0,2323	0,2319	0,2316	0,2315	0,2316	0,2318
0,3	0,3268	0,3247	0,3232	0,3222	0,3218	0,3210
0,4	0,4166	0,4119	0,4083	0,4059	0,4046	0,4045
0,5	0,4980	0,4902	0,4841	0,4799	0,4775	0,4770
0,6	0,5661	0,5554	0,5470	0,5410	0,5344	0,5365
0,7	0,6157	0,6027	0,5924	0,5849	0,5804	0,5792
0,8	0,6408	0,6262	0,6146	0,6063	0,6013	0,5999
0,9	0,6347	0,6194	0,6071	0,5983	0,5932	0,5917
1,0	0,5901	0,5772	0,5660	0,5577	0,5528	0,5513
i_н = 1,00; t/b = 0,1; Fr_н = 100
0,0	0,0398	0,0398	0,0398	0,0399	0,0399	0,0400
0,1	0,1377	0,1377	0,1377	0,1377	0,1377	0,1378
0,2	0,2352	0,2341	0,2333	0,2329	0,2326	0,2327
0,3	0,3303	0,3271	0,3246	0,3230	0,3221	0,3220
0,4	0,4205	0,4243	0,4094	0,4060	0,4040	0,4036
0,5	0,5018	0,4926	0,4854	0,4801	0,4770	0,4761
0,6	0,5698	0,5580	0,5486	0,5418	0,5378	0,5366
0,7	0,6190	0,6051	0,5941	0,5862	0,5814	0,5799
0,8	0,6437	0,6284	0,6163	0,6075	0,6024	0,6007
0,9	0,6373	0,6213	0,6085	0,5994	0,5941	0,5924
1,0	0,5928	0,5788	0,5670	0,5584	0,5533	0,5518
i_н = 1,00; t/b = 0,2; Fr_н = 10
0,0	0,0767	0,0770	0,0772	0,0774	0,0776	0,0778
0,1	0,1630	0,1642	0,1652	0,1661	0,1670	0,1678
0,2	0,2538	0,2547	0,2556	0,2565	0,2575	0,2585
0,3	0,3446	0,3442	0,3441	0,3443	0,3449	0,3459
0,4	0,4316	0,4288	0,4269	0,4259	0,4257	0,4264
0,5	0,5106	0,5047	0,5004	0,4976	0,4964	0,4968
0,6	0,5767	0,5676	0,5607	0,5560	0,5536	0,5535
0,7	0,6245	0,6127	0,6036	0,5972	0,5936	0,5930
0,8	0,6482	0,6436	0,6239	0,6164	0,6121	0,6112
0,9	0,6414	0,6270	0,6155	0,6074	0,6028	0,6018
1,0	0,5975	0,5857	0,5753	0,5675	0,5631	0,5621
i_н = 1,00; t/b = 0,2; Fr_н = 20
0,0	0,0782	0,0784	0,0785	0,0786	0,0788	0,0789
0,1	0,2698	0,1705	0,1711	0,1717	0,1722	0,1727
0,2	0,2626	0,2629	0,2633	0,2637	0,2642	0,2649
0,3	0,3542	0,3529	0,3521	0,3518	0,3519	0,3525
0,4	0,4413	0,4374	0,4346	0,4329	0,4322	0,4327
0,5	0,5198	0,5129	0,5077	0,5042	0,5025	0,5025
0,6	0,5850	0,5752	0,5675	0,5622	0,5593	0,5589
0,7	0,6318	0,6195	0,6099	0,6030	0,5991	0,5983
0,8	0,6545	0,6405	0,6295	0,6217	0,6172	0,6162
0,9	0,6472	0,6323	0,6204	0,6120	0,6073	0,6061
1,0	0,6037	0,5908	0,5797	0,5716	0,5669	0,5658
i_н = 1,00; t/b = 0,2; Fr_н = 50
0,0	0,0792	0,0792	0,0792	0,0792	0,0792	0,0792
0,1	0,1752	0,1754	0,1755	0,1755	0,1756	0,1758
0,2	0,2709	0,2699	0,2693	0,2689	0,2689	0,2691
0,3	0,3641	0,3609	0,3585	0,3570	0,3563	0,3563
0,4	0,4519	0,4458	0,4411	0,4378	0,4359	0,4357
0,5	0,5304	0,5215	0,5144	0,5093	0,5064	0,5058
0,6	0,5951	0,5836	0,5745	0,5680	0,5643	0,5634
0,7	0,6409	0,6274	0,6167	0,6090	0,6045	0,6033
0,8	0,6626	0,6476	0,6358	0,6273	0,6223	0,6210
0,9	0,6456	0,6386	0,6260	0,6170	0,6118	0,6104
1,0	0,6112	0,5967	0,5846	0,5758	0,5708	0,5695
i_н = 1,00; t/b = 0,2; Fr_н = 100
0,0	0,0796	0,0796	0,0796	0,0796	0,0796	0,0796
0,1	0,1775	0,1772	0,1771	0,1767	0,1759	0,1756
0,2	0,2745	0,2724	0,2711	0,2702	0,2696	0,2696
0,3	0,3688	0,3638	0,3599	0,3571	0,3552	0,3547
0,4	0,4573	0,4493	0,4428	0,4355	0,4338	0,4323
0,5	0,5361	0,5356	0,5172	0,5110	0,5072	0,5061
0,6	0,6006	0,5880	0,5779	0,5707	0,5664	0,5652
0,7	0,6461	0,6316	0,6202	0,6116	0,6063	0,6046
0,8	0,6673	0,6515	0,6391	0,6300	0,6242	0,6224
0,9	0,6589	0,6421	0,6290	0,6197	0,6142	0,6126
1,0	0,6154	0,5998	0,5870	0,5778	0,5725	0,5709
i_н = 1,00; t/b = 0,3; Fr_н = 10
0,0	0,1150	0,1150	0,1150	0,1150	0,1150	0,1150
0,1	0,2002	0,2016	0,2029	0,2040	0,2051	0,2061
0,2	0,2889	0,2900	0,2912	0,2934	0,2936	0,2948
0,3	0,3773	0,3769	0,3770	0,3775	0,3784	0,3797
0,4	0,4616	0,4588	0,4570	0,4561	0,4563	0,4574
0,5	0,5376	0,5317	0,5275	0,5249	0,5240	0,5247
0,6	0,6004	0,5915	0,5848	0,5803	0,5781	0,5784
0,7	0,6449	0,6335	0,6247	0,6185	0,6153	0,6151
0,8	0,6659	0,6526	0,6423	0,6351	0,6311	0,6306
0,9	0,6576	0,6432	0,6319	0,6241	0,6198	0,6191
1,0	0,6148	0,6022	0,5914	0,5836	0,5794	0,5787
i_н = 1,00; t/b = 0,3; Fr_н = 20
0,0	0,1153	0,1153	0,1153	0,1153	0,1153	0,1153
0,1	0,2084	0,2092	0,2099	0,2105	0,2111	0,2116
0,2	0,3003	0,3004	0,3006	0,3011	0,3016	0,3024
0,3	0,3903	0,3885	0,3874	0,3870	0,3871	0,3878
0,4	0,4752	0,4708	0,4676	0,4656	0,4648	0,4654
0,5	0,5510	0,5436	0,5380	0,5343	0,5325	0,5327
0,6	0,6129	0,6029	0,5951	0,5897	0,5868	0,5866
0,7	0,6563	0,6440	0,6344	0,6276	0,6238	0,6233
0,8	0,6761	0,6621	0,6512	0,6435	0,6392	0,6386
0,9	0,6669	0,6518	0,6399	0,6316	0,6270	0,6261
1,0	0,6241	0,6103	0,5986	0,5903	0,5857	0,5848
i_н = 1,00; t/b = 0,3; Fr_н = 50
0,0	0,1159	0,1159	0,1159	0,1159	0,1159	0,1159
0,1	0,2148	0,2148	0,2148	0,2147	0,2145	0,2146
0,2	0,3100	0,3083	0,3073	0,3068	0,3066	0,3068
0,3	0,4024	0,3980	0,3947	0,3925	0,3912	0,3912
0,4	0,4886	0,4814	0,4756	0,4712	0,4685	0,4679
0,5	0,5648	0,5550	0,5473	0,5416	0,5383	0,5376
0,6	0,6265	0,6145	0,6050	0,5983	0,5945	0,5937
0,7	0,6690	0,6552	0,6442	0,6363	0,6316	0,6304
0,8	0,6878	0,6725	0,6605	0,6518	0,6466	0,6452
0,9	0,6776	0,6611	0,6483	0,6393	0,6342	0,6328
1,0	0,6345	0,6188	0,6060	0,5970	0,5920	0,5908

Таблица 2

Безразмерные координаты x и y поверхностных линий тока

s_к	x	y при n
s_к	x	1,0	0,8	0,6	0,4	0,2	0,0
0,0	0,0000	0,1414	0,1131	0,0848	0,0566	0,0283	0,0
0,1	0,1000	0,1414	0,1131	0,0848	0,0566	0,0283	0,0
0,2	0,2000	0,1415	0,1132	0,0849	0,0566	0,0283	0,0
0,3	0,3000	0,1418	0,1134	0,0851	0,0567	0,0284	0,0
0,4	0,4000	0,1429	0,1143	0,0857	0,0572	0,0286	0,0
0,5	0,4999	0,1458	0,1167	0,0875	0,0583	0,0292	0,0
0,6	0,5997	0,1524	0,1219	0,0914	0,0610	0,0305	0,0
0,7	0,6982	0,1652	0,1321	0,0991	0,0660	0,0330	0,0
0,8	0,7962	0,1878	0,1501	0,1125	0,0749	0,0445	0,0
0,9	0,8882	0,2249	0,1792	0,1340	0,0891	0,0445	0,0
1,0	0,9698	0,2828	0,2228	0,1653	0,1094	0,0545	0,0

Приложение 4.3

ПРИМЕР РАСЧЕТА РАССЕИВАЮЩЕГО ТРАМПЛИНА

Исходные данные. Имеется прямоугольный быстроток шириной b = 2 м с уклоном i_н = 0,3; расход воды Q = 9,35 м³/с; толщина потока в конце быстротока t = 0,4 м; высота падения потока h_п = 3 м; глубина воды в нижнем бьефе h_нб = 0,5 м; средний диаметр частиц грунта d = 0,5 см.

Требуется найти конфигурацию рассеивающего трамплина, отбрасывающего поток в широкий нижний бьеф при значении угла расширения потока в плане

под углом

к горизонту.

Решение. 1. Определяем параметры, характеризующие трамплин:

отношение

;

скорость в начале трамплина

;

число Фруда

2. Приняв p = 5,

, вычисляем по формуле (4.102)

3. Проинтерполировав данные таблиц приложения 4.2 между Fr_н = 20 и 50, получаем безразмерные координаты дна рассеивающего трамплина (табл. 1).

Таблица 1

s_к	Безразмерные отметки дна - z_дн при n
s_к	1,0	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0,0
0,0	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0,1	0,0290	0,0289	0,0288	0,0287	0,0286	0,0286	0,0286	0,0285	0,0285	0,0284	0,0284
0,2	0,0575	0,0570	0,0566	0,0561	0,0558	0,0556	0,0554	0,0552	0,0551	0,0550	0,0550
0,3	0,0848	0,0832	0,0819	0,0808	0,0799	0,0792	0,0786	0,0782	0,0778	0,0776	0,0766
0,4	0,1088	0,1060	0,1035	0,1014	0,0996	0,0981	0,0968	0,0958	0,0952	0,0947	0,0946
0,5	0,1274	0,1232	0,1194	0,1162	0,1134	0,1110	0,1092	0,1076	0,1067	0,1061	0,1060
0,6	0,1376	0,1318	0,1267	0,1218	0,1184	0,1152	0,1126	0,1106	0,1092	0,1085	0,1082
0,7	0,1365	0,1289	0,1222	0,1165	0,1115	0,1072	0,1036	0,1008	0,0988	0,0976	0,0972
0,8	0,1208	0,1110	0,1027	0,0956	0,0894	0,0843	0,0800	0,0766	0,0742	0,0725	0,0721
0,9	0,0874	0,0748	0,0641	0,0554	0,0482	0,0424	0,0378	0,0342	0,0316	0,0301	0,0296
1,0	0,0347	0,0181	0,0054	-0,0053	-0,0138	-0,0203	-0,0252	-0,0286	-0,0308	-0,0320	-0,0324

4. Умножив безразмерные координаты дна z_дн на характерную длину L₀ = 7,07 м, получаем отметки дна, м (табл. 2).

Таблица 2

s_к	Отметки дна - z_дн L_0, м, при n
s_к	1,0	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0,0
0,0	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00
0,1	0,20	0,20	0,20	0,20	0,20	0,20	0,20	0,20	0,20	0,20	0,20
0,2	0,41	0,40	0,40	0,40	0,40	0,39	0,39	0,39	0,39	0,39	0,39
0,3	0,60	0,59	0,58	0,57	0,56	0,56	0,56	0,55	0,55	0,55	0,54
0,4	0,77	0,75	0,73	0,72	0,70	0,70	0,68	0,67	0,67	0,67	0,67
0,5	0,90	0,87	0,84	0,82	0,80	0,79	0,77	0,76	0,75	0,75	0,75
0,6	0,97	0,93	0,89	0,86	0,84	0,81	0,79	0,78	0,77	0,77	0,77
0,7	0,97	0,91	0,86	0,82	0,79	0,76	0,71	0,70	0,69	0,69	0,69
0,8	0,85	0,69	0,72	0,68	0,63	0,50	0,57	0,54	0,52	0,51	0,51
0,9	0,62	0,53	0,45	0,39	0,34	0,30	0,27	0,24	0,22	0,21	0,21
1,0	0,25	0,13	0,04	-0,04	-0,10	-0,14	-0,18	-0,20	-0,22	-0,23	-0,23

5. Умножив безразмерные координаты x и y на характерную длину L₀ = 7,07 м, получаем координаты точек поверхности дна трамплина, имеющих отметки, вычисленные в предыдущем пункте (табл. 3).

Таблица 3

s_к	x, м	y, м, при n
s_к	x, м	1,0	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0,00
0,0	0,00	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
0,1	0,71	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
0,2	1,41	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
0,3	2,12	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
0,4	2,83	1,01	0,91	0,81	0,71	0,61	0,50	0,40	0,30	0,20	0,10	0,00
0,5	3,53	1,03	0,93	0,82	0,72	0,62	0,52	0,41	0,31	0,21	0,10	0,00
0,6	4,24	1,08	0,97	0,86	0,75	0,65	0,54	0,43	0,32	0,22	0,11	0,00
0,7	4,93	1,17	1,05	0,93	0,82	0,70	0,58	0,47	0,35	0,23	0,12	0,00
0,8	5,63	1,33	1,19	1,06	0,93	0,79	0,66	0,53	0,40	0,26	0,13	0,00
0,9	6,28	1,59	1,43	1,27	1,11	0,95	0,79	0,63	0,47	0,31	0,16	0,00
1,0	6,85	2,00	1,79	1,57	1,37	1,17	0,97	0,77	0,58	0,39	0,19	0,00

6. Вычисляем по формуле (4.104) дальность отброса потока

7. По формуле (4.105) находим ширину следа струи в месте ее падения при

--------------------------------

<*> Делим на 57,3 для перевода градусов в радианы.

8. Определяем по формуле (4.106) расчетный удельный расход в месте падения с учетом запаса в 10%:

9. Вычисляем глубину размыва по формуле (4.101). В данном случае:

Принимаем

; a = 0,8.

Тогда

10. Выполняем расчет для случая устройства при тех же условиях обычной горизонтальной консоли:

по формуле (4.101) глубина размыва

При этом дальность отброса потока l_пад была равна лишь 9 м.

Сопоставляя характеристики размывов, можно судить об эффективности рассеивающего трамплина.

Приложение 4.4

ПРИМЕРЫ РАСЧЕТА ГАСИТЕЛЕЙ НА ВЫХОДАХ ИЗ КОСОГОРНЫХ ТРУБ

Пример 1. Прямоугольная ступенчатая труба размерами b x h_т = 1,5 x 2,0 м уложена с уклоном l_т = 0,3 на железной дороге. Расходы на пике паводков и объемы стока составляют: расчетный Q_р = 9,5 м³/с; W_р = 51·10³ м³; наибольший Q_max = 12,0 м³/с; W_max = 126·10³ м³. Глубины и скорости на выходе из трубы: при пропуске расчетного расхода h_вых(р) = 0,87 м, v_вых(р) = 7,27 м/с; при пропуске наибольшего расхода h_вых(max) = 1,05 м, v_вых(max) = 7,69 м/с. Уклон и грунт лога: i_л = 0,02, песок d = 0,5 мм.

Требуется запроектировать для гашения скоростей на выходе из трубы гаситель ЦНИИСа с уклоном i_г = i_л = 0,02.

Решение. Сначала расчет ведем при пропуске Q_р.

1. Принимаем предварительно глубину на входе в раструб равной глубине на выходе из трубы h_вых(р) = 0,87 м.

2. Вычисляем критическую глубину в трубе по формуле (2.11):

3. Назначаем высоту первой водобойной стенки по формуле (4.111)

p₁ = 1,3h_вых = 1,3·0,87 = 1,13 м.

4. Определяем глубину потока h_р в начале раструба с учетом подтопления от порога при p₁/h_вых <= 1,4 по формуле (4.112):

h_р = 1,18h_к(p₁/h_вых) = 1,18·1,60·1,3 = 2,45 м.

5. Проверяем выполнение условия (4.114)

;

- условие не выполнено - устанавливаем на выходе из трубы повышенное звено h_т(пов) = 2,50 м и вновь проверяем выполнение условия (4.114):

- условие не выдержано - приступаем к следующему пункту.

6. Определяем число Фруда Fr на выходе из трубы по формуле (2.10):

7. Определяем глубину

, сопряженную с глубиной h_вых, по формуле (2.20):

8. Строим кривую свободной поверхности потока на концевом участке трубы перед раструбом. Для этого сравниваем h_р с

. В нашем случае

, т.е. в конце трубы возникает гидравлический прыжок.

Строим свободную поверхность потока вверх по течению по значению обратного уклона, начиная с глубины h_р (начало раструба) участками по

Расчет выполняем в следующем порядке:

а) вычисляем обратный уклон поверхности воды на первом участке по формуле (4.115):

б) определяем глубину воды в конце первого участка (сечение А-А на рис. 4.22, а) по формуле (4.116):

в) проверяем выполнение условия заполнения трубы по формуле (4.114), заменив h_р на h_р1:

- условие не выдержано, расчет продолжаем;

г) устанавливаем уклон поверхности воды следующего вышележащего (второго) участка по формуле (4.117):

д) определяем глубину воды в конце второго участка по формуле (4.118), т.е. в сечении Б-Б:

е) проверяем выполнение условия (4.114):

- условие не выдержано, расчет продолжаем;

ж) устанавливаем уклон поверхности воды следующего (третьего) участка по формуле (4.117):

з) определяем глубину воды в конце третьего участка по формуле (4.118), т.е. в сечении В-В:

и) проверяем выполнение условия (4.114):

- условие выдержано.

9. Определяем длину l_вст и высоту стенок h_ст(вст) между трубой и раструбом гасителя по формулам (4.119) и (4.120):

;

h_ст(вст) = h_р + 0,25 м = 2,45 + 0,25 = 2,70 м.

Далее приступаем к расчету элементов гасителя, начиная с п. 12.

ИС МЕГАНОРМ: примечание.

Нумерация пунктов дана в соответствии с официальным текстом документа.

12. Определяем расстояние от начала раструба до первого водобойного порога (первой стенки) по формуле (4.122'):

l₁ = 0,63b = 0,63·1,5 = 0,95 м.

(Высота первой стенки p₁ была определена выше в п. 3, она оказалась равной 1,13 м.)

13. Определяем высоту второй водобойной стенки по формуле (4.123'):

p₂ = 0,27h_вых = 0,27·0,87 = 0,23 м > 0,1 м.

14. Устанавливаем глубину потока в плоскости напорной грани первого водобойного порога (стенки) при p₁/h_вых <= 1,4 по формуле (4.124):

15. Находим наибольшую высоту подъема струй потока в раструбе по формуле (4.126):

16. Определяем дальность падения струй s, считая от напорной грани первого водобойного порога (стенки), по формуле (4.127) и расстояние от начала раструба до второго водобойного порога по формуле (4.128):

l₂ = l₁ + s = 0,95 + 6,05 = 7,00 м.

17. Определяем ширину раструба в створе конца водобойной стенки b_рг по формуле (4.131), предварительно вычислив L_г по формуле (4.132):

здесь

;

b_рг = b + 1,15L_г = 1,5 + 1,15·7,50 = 10,1 м.

18. Находим горизонтальное расстояние от напорной грани первого водобойного порога (стенки) до места наибольшего подъема струй.

Предварительно определяем отношение

- принимаем x_max = 0 - максимальная глубина располагается у напорной грани первой водобойной стенки.

19. Строим кривую свободной поверхности потока в вертикальной плоскости по оси потока по уравнению (4.138):

Расчеты выполняем в табличной форме (табл. 1).

Таблица 1

x	x²		h_x	x	x²		h_x
0	0	0	2,56	4,0	16,0	-1,12	1,44
2,5	6,25	-6,43	2,13	4,5	20,25	- 1,41	1,15
3,0	9,0	-0,61	1,95	6,0	25,10	-1,74	0,82
3,5	12,25	-0,84	1,72	6,05	36,60	-2,56	0

Далее выполняем проверку размеров элементов гасителя по наибольшему расходу, при этом сохраняем нумерацию позиций расчета, принятую при пропуске расчетного расхода, но добавляем к ним индекс "а".

2а. Вычисляем критическую глубину в трубе по формуле (2.11), принимая

3а. Размеры стенок в раструбе сохраняем те же, что и при пропуске Q_р, т.е. p₁ = 1,3h_вых(р) = 1,3·0,87 = 1,13 м.

4а. Определяем глубину потока h_р в начале раструба с учетом подтопления от порога при p₁/h_вых <= 1,4 по формуле (4.112):

5а. Проверяем выполнение условия по заполнению на выходе из трубы по формуле (4.114):

- условие не выдержано.

6а. Определяем число Фруда Fr на выходе из трубы по формуле (2.10) (повышенное звено не используется, так как оно не прошло при пропуске Q_р):

7а. Определяем глубину

, сопряженную с глубиной h_вых, по формуле (2.20):

8а. Строим кривую свободной поверхности потока на концевом участке трубы перед раструбом. Для этого сравниваем h_р с

. В нашем случае

, т.е. в конце трубы возникает гидравлический прыжок. Строим свободную поверхность потока вверх по течению по значению обратного уклона, начиная с глубины h_р (начало раструба), участками по

Расчет выполняем в такой последовательности:

а) вычисляем обратный уклон поверхности воды на первом участке по формуле (4.115):

б) определяем глубину воды в конце первого участка по формуле (4.116):

в) проверяем выполнение условия заполнения трубы по формуле (4.114), заменив h_р на h_р1:

- условие выдержано.

Следовательно, по условиям пропуска наибольшего расхода требуется вставка между гасителем и трубой.

9а. Определяем длину l_вст и высоту стенок h_ст(вст) между трубой и раструбом гасителя по формулам (4.119) и (4.120):

h_{ст(вст)max} = h_р + 0,25 м = 2,37 + 0,25 = 2,62 м.

При пропуске Q_р (см. п. 9) длина вставки l_вст(р) = 3,0 м > l_вст(max) = 1,0 м и высота ее h_{ст(вст)р} = 2,70 м > h_{ст(вст)max} = 2,62 м. Поэтому к расчету принимаем l_вст = 3,0 м и h_вст = 2,70 м.

Далее расчет продолжаем с п. 14, а не с п. 12, как при пропуске Q_р, так как высота стенок сохраняется.

14а. Устанавливаем глубину потока в плоскости напорной грани первого водобойного порога (стенки) при p₁/h_вых <= 1,4 по формуле (4.124):

15а. Находим наибольшую высоту подъема струй потока в раструбе по формуле (4.126):

16а. Определяем дальность падения струй, считая от напорной грани первого водобойного порога (стенки) s, по формуле (4.127) и расстояние до второго водобойного порога l₂ по формуле (4.128):

l₂ = l₁ + s = 0,95 + 6,70 = 7,65 м.

17а. Определяем ширину раструба в створе конца водобойной второй стенки по формуле (4.131), предварительно вычислив L_г по формуле (4.132):

b_рг(max) = b + 1,15L_г(max) = 1,5 + 1,15·8,15 = 10,87 м.

18а. Находим горизонтальное расстояние от напорной грани первого водобойного порога до места наибольшего подъема струй. Предварительно определяем отношение

Расчет ведем по формулам (4.133) и (4.134):

19а. Строим кривую свободной поверхности в вертикальной плоскости по оси потока по уравнению (4.135), предварительно вычислив коэффициенты его по формулам (4.136) и (4.137):

h_x = Ax² + Ex + h_ст(1) = 0,122x² + 0,43x + 2,58.

Расчет по уравнению (4.135) ведем в табличной форме (табл. 2).

Таблица 2

x	x²	Ax²	Ex	h_x
0	0	0	0	2,58
2,5	6,25	-0,76	1,08	2,90
3,0	9,0	-1,10	1,29	2,77
3,5	12,25	-1,49	1,51	2,60
4,0	16,0	- 1,95	1,72	2,35
4,5	20,25	-2,47	1,94	2,11
5,0	25,0	-3,05	2,15	1,68
6,0	36,0	-4,39	2,58	0,77
6,70	44,89	-5,47	2,88	~ 0

Следующие пункты являются общими для расчета по Q_р и Q_max.

20. Назначаем очертание боковых стенок раструба и участка между трубой и раструбом по касательным к свободной поверхности потока по значениям x и h_x, приведенным в табл. 2, при Q_р и Q_max (при Q_р вводим запас 0,25 м).

21. Назначаем длину L_г и ширину b_рг раструба гасителя в его конце, принимая наибольшие их значения, полученные по расчету при пропуске Q_р и Q_max (см. пп. 17, 17а):

при Q_р L_г(р) = 7,50 м, b_рг = 10,1 м;

при Q_max L_г(_max) = 8,15 м, b_рг = 10,87 м.

Принимаем к расчету L_г = 8,15 м и b_рг = 10,87 м.

22. Определяем скорость на выходе из гасителя по формуле (4.141) при пропуске Q_р и Q_max:

v_вых(г)р = 0,45v_вых(р) = 0,45·7,27 = 3,27 м/с;

v_{вых(г)max} = 0,45·7,69 = 3,46 м/с.

Далее ведем расчет нижнего бьефа сооружения.

23. Назначаем длину укрепления L = 1,5D_э:

L = 1,5·1,96 = 3,0 м.

Устанавливаем материал укрепления по значениям скоростей на выходе из гасителя при пропуске Q_р и Q_max с учетом повышения допускаемых скоростей при Q_max на 35%. Для этого определяем отношение

; к расчету принимаем v_вых(г)р = 3,27 м/с.

По значению этой скорости назначаем укрепление из плит 50 x 50 см толщиной 8 - 10 см.

24. Определяем расчетную ширину растекания потока в конце укрепления (x = 3,0 м) за гасителем при принятой ширине раструба по формуле (7.17):

25. Определяем деформации за укреплением и ширину воронки размыва B_min согласно рекомендациям по расчету размыва по двум расходам в такой последовательности:

а) вычисляем предельную глубину размыва

по формуле (7.23):

Предварительно вычисляем:

Для выходного русла с гасителем ЦНИИСа r = 1,0, s = 1,0,

(см. табл. 7.3).

Отсюда имеем:

при Q_р

при Q_max

б) определяем продолжительность паводка по формуле (7.28):

при Q_р

при Q_max

в) определяем эталонное время размыва при C_р = 0 (несвязные грунты) по формуле (7.27):

г) определяем долю предельной глубины размыва, осуществляемую за время прохождения паводка, по формуле (7.26):

д) определяем максимальную глубину размыва по формуле (7.21):

е) находим ширину воронки размыва по формуле (7.73), предварительно определив K по графику на рис. 7.12 при L/D_э = 3,00/1,96 = 1,5:

при Q_р

и K = 0,50;

при Q_max

и K = 0,51.

Ширина воронки размыва

при Q_р

при Q_max

ж) назначаем расчетную ширину укрепления, м, B_укр = B + 2,0. Под B понимается большее из значений B_min и B_раст(г). В нашем случае B_раст(г) = 20,4 м, откуда B_укр = 20,4 + 2,0 = 22,4 м;

з) для сокращения глубины размыва заменяем тип выходного русла 6 на 6к, т.е. используем каменную наброску за гасителем. Глубину размыва определяем по формуле (7.54), предварительно определив минимальный удельный объем наброски по формуле (7.56), принимая крупность камня d_н = 0,15 м:

При Q_р

;

при Q_max

;

принимаем

- практически минимально допустимое количество камня.

Глубина размыва

При Q_р

;

при Q_max

;

и) находим глубину заделки концевой части укрепления h_укр:

при Q_р h_укр(р) = 1,2·0,39 = 0,47 м;

при Q_max h_укр(max) = 0,40 м.

К расчету принимаем h_укр = 0,50 м.

Результаты расчета сведем в таблицу (табл. 3).

Таблица 3

Показатели	При пропуске		Принято
Показатели	Q_р	Q_max	Принято
Длина укрепления L	3,0	3,0	3,0
Длина гасителя L_г	7,50	8,15	8,15
Ширина раструба гасителя в его конце b_рг	10,10	10,87	10,9
Скорость на выходе из гасителя v_вых(г)	3,27	3,46	3,27
Ширина растекания B_раст	20,4	20,4	20,4
Ширина воронки размыва B_min	8,5	8,5	8,5
Глубина размыва	1,42	1,45	-
То же с камнем	0,39	0,40	-
Ширина укрепления	-	-	22,4
Глубина заделки	0,47	0,40	0,50

Примечание. Тип выходного русла 6к; гаситель ЦНИИСа, на выходе каменная наброска.

Пример 2. Для условий примера 1 требуется запроектировать расширяющийся водобойный колодец без стенки падения; угол раструба к оси сооружения

Решение. 1. Определяем длину подпертого гидравлического прыжка l₂, глубину, сопряженную с глубиной на выходе из трубы, h_вых и ширину стенки b_ст (см. рис. 4.23, б), решая совместно зависимости (4.149), (4.150) и (4.151):

а) при Q_р:

примем

. Тогда имеем:

l₂ = 3,2·1,70 = 5,44 м;

b_ст = 1,5 + 2·5,44·0,268 = 4,41 м;

В итоге получаем

Следовательно,

, l₂ = 5,44 м и b_ст = 4,41 м подобраны правильно;

б) при Q_max:

примем

. Тогда имеем:

l₂ = 3,2·1,90 = 6,08 м;

b_ст = 1,5 + 2·6,08·0,268 = 4,76 м;

В итоге получаем

Следовательно,

, l₂ = 6,08 м и b_ст = 4,76 м подобраны правильно.

Таким образом лимитирует Q_max. Окончательно принимаем:

, l₂ = 6,08 м, b_ст = 4,76 м.

2. Определяем полный напор перед стенкой p₂ по формуле (4.152) при m = 0,42 при пропуске Q_max:

3. Определяем геометрический напор над верхом стенки p₂ по формуле (4.153) при пропуске Q_max:

4. Определяем высоту стенки гасителя p₂ по формуле (4.154) при Q_max:

5. Определяем скорость потока в колодце перед стенкой высотой p₂ по формуле (4.155) при Q_max:

6. Вычисляем дальность падения струи, переливающейся через стенку, по формуле (4.156):

7. Находим длину колодца по формуле (4.157) при l₁ = 0 (стенка падения отсутствует):

l_кол = l₂ + l₃ + l_зап = 6,08 + 0,50 + 1,0 = 7,58 м.

8. Находим ширину раструба в месте падения струи, переливающейся через стенку высотой p₂, по формуле (4.158) и ширину раструба в его конце по формуле (4.159):

9. Определяем глубину на выходе из гасителя (сжатую глубину за стенкой высотой p₂) подбором из выражения (4.160):

Примем h_{с(вых.г)} = 0,43 м. Тогда

В итоге получаем

Следовательно, h_{с(вых.г)} = 0,43 м определена правильно.

10. Определяем скорость потока на выходе из гасителя по формуле (4.161):

11. Подбираем материал дна и боковых стенок гасителя путем сравнения скорости на выходе из гасителя v_вых(г) с допускаемой по материалу v_доп исходя из условия (4.162):

v_вых(г) <= v_доп.

Для v_вых(г) = 5,54 м/с принимаем укрепление из монолитного бетона.

12. Определяем высоту стенок раструба исходя из выражения (4.163):

c_ст(р) = p₂ + H + 0,25 = 0,83 + 1,16 + 0,25 = 2,24 м.

13. Назначаем длину укрепления за гасителем, конструктивно принимая ее равной

, где

14. Определяем ширину растекания потока на укреплении по формуле (7.16):

15. Определяем деформации за укреплением:

а) вычисляем предельную глубину размыва

по формуле (7.23):

Сначала определим

Примем выходное русло типа 5к.

Для выходного русла типа 5к

; r = 1,0; s = 1,0;

Отсюда при Q_р = 9,5 м³/с > 0,5Q_к = 4,3 м³/с и Q_max = 12,0 м³/с > 0,5Q_к имеем (в расчет вводим Q/Q_к = 0,5)

б) определяем продолжительность паводка по формуле (7.28):

При Q_р

;

при Q_max

;

в) определяем эталонное время размыва по формуле (7.27) при C_р = 0 (несвязные грунты):

При Q_р

при Q_max

г) определяем долю предельной глубины размыва, осуществляемую за время прохождения паводка, по формуле (7.26):

При Q_р

при Q_max

д) определяем максимальную глубину размыва по формуле (7.21):

При Q_р

при Q_max

е) определяем глубину размыва в русле с каменной наброской по формуле (7.54):

Предварительно определяем минимальный объем каменной наброски по формуле (7.56), принимая крупность камня d_н = 0,15 м:

При Q_р

;

при Q_max

Принимаем

При Q_р

;

при Q_max

;

ж) назначаем глубину заложения концевой части укрепления h_укр:

при Q_р

;

при Q_max

К расчету принимаем h_укр = 1,04 м;

з) определяем ширину воронки размыва по формуле (7.73), предварительно определив по графику на рис. 7.12 коэффициент K:

при Q_р

и K = 0,75;

при Q_max

и K = 0,77.

Ширина воронки размыва

При Q_р

при Q_max

и) назначаем расчетную ширину укрепления B по большему из двух значений B_раст(г) и B_min с запасом в

B = B_раст(г) + 2,0 = 10,0 + 2,0 = 12,0 м.

Приложение 4.5

ПРИМЕР РАСЧЕТА СУЖЕНИЯ ПО ПРИБЛИЖЕННОЙ МЕТОДИКЕ

Исходные данные. К прямоугольной железобетонной трубе отверстием b x h_т = 1,5 x 2,0 м подходит с косогора расход Q = 13 м³/с. Для обеспечения ввода бурного потока в трубу на подходе к ней устраивается прямоугольный быстроток шириной b_б = B = 5,0 м, укладываемый с уклоном i = 0,1, и сужение с углом сужения

. Глубина воды на входе в сужение h₁ = 0,34 м.

Требуется выполнить гидравлический расчет сужения по двухмерной теории косых прыжков (пп. 4.28, 4.29), проверить требования СНиП 2.05.03-84 по заполнению на входе в трубу и назначить высоту стенок сужения.

Решение. 1. Вычисляем число Фруда в начале сужения по формуле (4.82):

2. Находим степень сжатия бурного потока на участке сужения по формуле (4.83):

3. Проверяем отсутствие прямого гидравлического прыжка в сужении из условия (4.84):

- прямой гидравлический прыжок отсутствует.

4. Находим длину участка сужения по формуле (4.85):

5. Определяем параметры первого косого прыжка на участке сужения

и h₂ по номограмме на рис. 4.16 и Fr₂ по номограмме на рис. 4.17:

при

и Fr₁ = 17,5 имеем:

;

; Fr₂ = 8,4 и h₂ = h₁·1,85 = 0,34·1,85 = 0,63 м.

6. Определяем параметры

, h₂ и Fr₃ второго косого прыжка по номограмме на рис. 4.16 и 4.17, заменяя значения Fr₁ на Fr₂ и h₁ на h₂:

при

, Fr₂ = 8,4 и h₂ = 0,63 м имеем:

;

; Fr₃ = 4,5 и h₃ = 1,6h₂ = 1,01 м.

Считаем, что средняя глубина на входе в трубу h_вх = h₃. В этом случае заполнение на входе в трубу

- требование СНиП 2.05.03-84 удовлетворено.

Скорость на входе в трубу

, что вполне допустимо по материалу трубы и сужения.

7. Определяем максимальную глубину на оси сооружения h_ось(max) по формуле (4.89):

Сравниваем h₃ с h_т:

h₃ = 1,01 м < h_т = 2,00 м - высота трубы достаточна.

8. Определяем глубины вдоль стенки сужения.

Находим максимально возможную глубину у стенки сужения h_ст(max) и расстояние до нее от начала сужения l_max по формулам соответственно (4.90) и (4.91):

Устанавливаем глубины у стенки h_ст в характерных местах. Так как в нашем случае l_max = 1,85 м < l_суж = 10 м, то глубины устанавливаем в трех точках:

в начале стенки h_ст = h₂ = 0,63 м;

при l = l_max принимаем максимальную из глубин h_ст = max(h₂; h_ст(max)); h_ст(max) = 9,63 м = h₂ = 0,63 м; к расчету принимаем h₂ = 0,63 м;

при l = l_суж выбираем максимальную из глубин h_ст = max(h₃; h_ст(max)); h₃ = 1,01 м > h_ст(max) = 0,63 м; к расчету принимаем h₃ = 1,01 м.

Соединяем полученные точки прямыми линиями.

9. Определяем высоту стенок, приняв возвышение их над уровнем воды в каждой точке на

. Результаты расчета приведены на рисунке.

а)

б)

в)

Сужение:

а - продольный профиль по оси потока;

б - то же вдоль стенки; в - план сужения; 1 - стенка

сужения; 2 - труба; 3 - сужение; 4 - быстроток

Приложение 5.1

ПРИМЕРЫ НАЗНАЧЕНИЯ ОТВЕРСТИЙ И ОПРЕДЕЛЕНИЯ

ПРОПУСКНОЙ СПОСОБНОСТИ КРУГЛЫХ ГОФРИРОВАННЫХ ТРУБ

Пример 1. Гофрированная труба без оголовков (с вертикальным срезом) расположена на железной дороге. Высота насыпи H_нас = 3,5 м, ширина поверху b_нас = 6,5 м, крутизна откосов 1:1,5. Уклон лотка трубы соответствует уклону лога i_т = 0,03. Гладкий лоток расположен на ¹/₃ периметра поперечного сечения трубы.

Расходы притока с бассейна Q_р = 2,4 м³/с, Q_max = 4,0 м³/с. Сток снеговой - аккумуляция не учитывается.

Требуется подобрать отверстие трубы и определить подпертые глубины, а также глубины и скорости на выходе из нее.

Решение. 1. Определяем длину трубы l_т = 6,5 + 3,5·2·1,5 = 17 м.

2. Находим отверстие трубы.

Согласно Инструкции по проектированию и строительству металлических гофрированных водопропускных труб (ВСН 176-78) гофрированные трубы на железных дорогах должны пропускать расчетные и наибольшие расходы при безнапорном режиме и иметь при этом заполнение на входе при пропуске расчетного расхода

, при пропуске наибольшего расхода

По графику на рис. 5.19, б находим для трубы без оголовка с вертикальным срезом (кривая 6) параметры расхода, соответствующие указанным выше заполнениям:

при

Зная параметры расхода, находим по ним минимальные диаметры трубы по формуле

при Q_р = 2,4 м³/с

;

при Q_max = 4,0 м³/с

Принимаем к расчету ближайшее большее типовое отверстие D = 2,0 м.

3. Устанавливаем, будет ли труба "длинной" или "короткой" в гидравлическом отношении.

Сравниваем уклон трубы i_т с критическим i_к. Находим i_к по графику на рис. 5.27 для трубы D = 2,0 м:

при Q_р

, i_к = 0,015 < i_т = 0,03;

при Q_max

, i_к = 0,016 < i_т = 0,03.

Следовательно, труба "короткая". Проверка по критерию относительной длины трубы не требуется.

4. Определяем подпертые глубины перед трубой из формулы (5.13) для безнапорного режима:

Предварительно находим коэффициент расхода для трубы без оголовка по табл. 5.3 (m = 0,33) и b_к по графику на рис. 5.14.

Для расчетного расхода Q_р = 2,4 м³/с:

b_к(р) = 1,40 м;

Для наибольшего расхода Q_max = 4,0 м³/с:

b_к(max) = 1,56 м;

5. Находим возвышение бровки полотна над подпертым уровнем

при высоте насыпи H_нас = 3,5 м:

Требования технических условий выдержаны.

6. Определяем глубины и скорости на выходе из трубы соответственно по приложениям 5.2 (рис. 4) и 5.3 (рис. 2):

при Q_р = 2,4 м³/с

;

h_вых(р) = 0,21·2 = 0,42 м;

при Q_(max) = 4,0 м³/с

;

; h_вых(max) = 0,335·2 = 0,67;

Пример 2. Гофрированная труба без оголовка (с вертикальным срезом) расположена на автомобильной дороге. Гладкий лоток расположен на ¹/₃ периметра поперечного сечения трубы. Высота насыпи H_нас = 4,0 м, ширина поверху b_нас = 12 м, крутизна откосов 1:1,5, уклон лотка трубы i_т = 0,02. Расчетный расход притока с бассейна Q_р = 8,0 м³/с; сток снеговой - аккумуляция не учитывается.

Решение. 1. Определяем длину трубы l_т = 12 + 3·4 = 24 м.

2. Задаемся минимально принятым в практике проектирования отверстием гофрированной трубы D = 1,5 м.

3. Устанавливаем, будет ли труба "длинной" или "короткой" в гидравлическом отношении:

а) сравниваем уклон трубы i_т с критическим i_к.

Предварительно определяем параметр расхода по номограмме на рис. 5.8. При Q_р = 8,0 м³/с П_Q = 0,94.

По графику на рис. 5.27 для D = 1,5 м и П_Q = 0,94 находим i_к = 0,0475. Таким образом, i_т = 0,02 < i_к = 0,0475;

б) производим проверку по критерию относительной длины:

. Следовательно, труба "короткая".

4. Определяем подпертые глубины перед трубой:

а) устанавливаем режим протекания потока. Для этого определяем вначале относительную глубину на входе в трубу

по графику на рис. 5.29. Для трубы без оголовка (кривая 2) при П_Q = 0,94 < 1,35 находим

. Следовательно, в трубе возможен полунапорный или частично напорный режим.

Для установления режима протекания в этом случае определяем подпертую глубину перед трубой H при полунапорном режиме из формулы (5.20) для "коротких" труб:

Предварительно находим коэффициент расхода

и коэффициент сжатия

в определяющем сечении при полунапорном режиме по табл. 5.3:

Расчетная подпертая глубина

Следовательно, относительная подпертая глубина

Затем находим относительную граничную подпертую глубину потока

по формуле (5.46):

Для этого определяем коэффициент

по графику на рис. 5.31 при

Далее находим относительную граничную подпертую глубину для труб без гладких лотков по графику на рис. 5.30 в зависимости от относительной длины трубы

и ее уклона i_т = 0,02:

откуда

Сравнивая относительную подпертую глубину

, устанавливаем режим протекания

. Режим частично напорный, но не напорный, так как П_Q = 0,94 < 1,35;

б) находим подпертую глубину при частично напорном режиме из формулы (5.21). Для этого определяем корректив к расчетной длине трубы l₀ по графику на рис. 5.34:

при П_Q = 0,94 l₀/D = 0,65 и

Затем по формуле (5.50) находим

. Далее по графику на рис. 5.32 определяем

и по графику на рис. 5.33 при П_Q = 0,94 устанавливаем

Подпертая глубина

5. Определяем возвышение бровки полотна над подпертым уровнем:

при высоте насыпи H_нас = 4,0 м

. Требования Технических условий не выдерживаются. Увеличиваем отверстие трубы до D = 2,0 м и повторяем расчеты, начиная с п. 3.

6. Устанавливаем, будет ли труба "длинной" или "короткой" в гидравлическом отношении:

сравниваем уклон трубы i_т с критическим i_к.

Предварительно определяем параметр расхода по номограмме на рис. 5.8: при Q = 8,0 м³/с имеем П_Q = 0,45.

По графику на рис. 5.27 для D = 2,0 м и П_Q = 0,45 находим i_к = 0,0175.

Таким образом, i_т = 0,02 > i_к = 0,0175 - труба "короткая".

Проверка по критерию относительной длины не требуется.

7. Определяем подпертые глубины перед трубой. Устанавливаем режим протекания потока.

Для этого определяем вначале относительную глубину на входе в трубу

по графику на рис. 5.29. Для трубы без оголовка (кривая 2) при П_Q = 0,45 < 1,35 находим

- в трубе возможен полунапорный или частично напорный режим.

Для установления режима протекания определяем подпертую глубину перед трубой H при полунапорном режиме из формулы (5.20) при тех же коэффициентах

, что и при расчете трубы D = 1,5 м:

Следовательно, относительная подпертая глубина

Затем находим относительную граничную подпертую глубину потока по формуле (5.46) при

и K = 1,29.

Для этого сначала находим относительную граничную подпертую глубину для труб без гладких лотков по графику на рис. 5.30 в зависимости от относительной длины трубы

и ее уклона i_т = 0,02 (2%):

откуда

Сравнивая относительную подпертую глубину

со значением

, устанавливаем режим протекания:

- режим полунапорный.

Принимаем к расчету H = 2,31 м.

8. Определяем возвышение бровки над подпертым уровнем. При высоте насыпи H_нас = 4,0 м

. Следовательно, требования технических условий выдержаны.

9. Определяем глубины и скорости на выходе из трубы соответственно по приложениям 5.2 (рис. 4) и 5.3 (рис. 2).

При Q_р = 8,0 м³/с П_Q = 0,45;

;

h_вых = 0,49·2 = 0,98 м;

;

Пример 3. Двухъярусная гофрированная труба без оголовков с гладкими лотками на ¹/₃ ширины поперечного сечения расположена на железной дороге.

Первый ярус состоит из трех труб D = 2,0 м, второй - из двух труб D = 1,5 м. Сток снеговой. Расходы притока с бассейна: Q_р = 40 м³/с; Q_max = 55,0 м³/с. Высота насыпи 10 м, ширина поверху b_нас = 6,5 м. Уклоны труб i_т = 0,01. Остальные данные приведены на рис. 1.

Рис. 1. Схема многоярусной трубы

Требуется определить подпертый уровень перед двухъярусной трубой, скорости на выходе и подобрать тип укрепления.

Решение. Так как сток снеговой, то аккумуляцию воды перед сооружением не учитываем и принимаем расходы притока в качестве расходов в сооружении. Расчет ведем согласно рекомендациям п. 5.19.

Предварительно определяем длину труб обоих ярусов: длина труб первого яруса l_т(1) = 6,5 + 3·10 = 36,5 м; второго яруса - l_т(2) = 6,5 + 3·7,5 = 29 м.

Далее устанавливаем, работают ли трубы второго яруса. Для этого определяем расход, пропускаемый трубами первого яруса при уровне, соответствующем отметке лотка на входе в трубы второго яруса. Согласно данным, приведенным на рис. 1, подпертая глубина перед трубами первого яруса в этом случае будет равна разности отметок лотков второго яруса (z_л(2)) и первого ярусов (z_л(1)):

H₁ = z_л(2) - z_л(1) = 101,73 - 99,23 = 2,5 м.

Определяем расход, пропускаемый трубами первого яруса при H₁ = 2,5 м, предполагая полунапорный режим протекания.

По формуле (5.20) находим

где n_т - число труб в ярусе, в первом ярусе n_т = 3.

Коэффициенты

берем по табл. 5.3 для трубы без оголовка с вертикальным срезом:

Тогда

Полученный расход меньше расчетного и наибольшего расходов трубы. Следовательно, работают трубы обоих ярусов.

Дальнейший расчет выполняем в табличной форме (табл. 1). Сущность расчета заключается в следующем. Задаемся расходами второго яруса и по ним находим расходы первого яруса и всей трубы. Затем строим зависимость H = f(Q) и по заданным Q_р и Q_max находим соответствующие им H_р и H_max.

Таблица 1

N п/п	Элементы расчета	Расходы каждой трубы второго яруса Q₂, м³/с
N п/п	Элементы расчета	1,0	3,0	5,0
Второй ярус
1	Диаметр труб D₂, м	1,5	1,5	1,5
2	Параметр расхода	0,115	0,345	0,578
3	Уклон трубы i_т	0,01	0,01	0,01
4	Критический уклон i_к, определяемый по графику на рис. 5.27	0,016	0,018	0,024
5	Длина трубы l_т, м	29	29	29
6	Относительная длина трубы l_т(2)/D₂	19,3	19,3	19,3
7	Труба "короткая" или "длинная"	"Короткая", так как	"Короткая"
8	Относительная глубина на входе в трубу h_вх(2)/D₂ (см. рис. 5.19, б)	0,43	0,87	1
9	Режим протекания	Безнапорный	Безнапорный	Полунапорный или частично напорный
10	Подпертая глубина H_2(б), м, при безнапорном режиме [формула (5.13)]	0,76	1,42	-
11	Подпертая глубина H_2(п), м, при полунапорном режиме [формула (5.20)]	-	-	2,23
12	Относительная подпертая глубина при полунапорном режиме	-	-	1,56
13	Граничная подпертая глубина для гофрированных труб без гладкого лотка (см. рис. 5.30)	-	-	1,26
14	Коэффициент , учитывающий влияние гладких лотков (см. рис. 5.31)	-	-	1,20
15	Граничная подпертая глубина для труб с гладкими лотками [формула (5.46)]	-	-	1,48
16	Уточненный режим протекания	Безнапорный	Безнапорный	H_2(п)/D₂ = 1,56 > H_г/D₂ = 1,48 - частично напорный
17	Длина концевого участка трубы, на котором имеется отрыв потока от верха трубы l₀, м (см. рис. 5.34)	-	-	6
18	Расчетная длина трубы , м	-	-	23
19	Коэффициент расхода при напорном или частично напорном режиме (см. рис. 5.32)	-	-	0,60
20	i_тl_т	-	-	0,23
21	Коэффициент (см. рис. 5.33)	-	-	0,97
22	Подпертая глубина при частично напорном режиме H_2(чн), м [формула (5.21)]	-	-	2,36
	Относительная подпертая глубина	-	-	1,57 > H_г/D₂ = 1,48 > 1,4 - подпертая глубина сохраняется
23	Отметка лотка на входе в трубу, м	101,73	101,73	101,73
24	Отметка подпертого уровня ПУВВ z₂, м	102,49	103,15	104,09
Первый ярус
25	Отметка лотка на входе в трубу z_1(л), м	99,23	99,23	99,23
26	Подпертая глубина H = z₂ - z_1(л), м	3,26	3,92	4,86
27	Относительная подпертая глубина	1,63	1,96	2,43
28	Длина трубы l_т(1), м	36,5	36,5	36,5
29	Относительная длина трубы	18,25	18,25	18,25
30	Граничная подпертая глубина (см. рис. 5.30) для труб без гладких лотков	1,26	1,26	1,26
31	Коэффициент (см. рис. 5.31)	1,2	1,2	1,2
32	Граничная подпертая глубина	1,51	1,51	1,51
33	Режим протекания	1,63 > 1,51 - частично напорный	1,96 > 1,51 частично напорный	2,43 > 1,51 - частично напорный
34	Коэффициент (см. рис. 5.32)	0,59	0,59	0,59
35	i_тl_т	0,36	0,36	0,36
36	Расход Q₁₍₁₎ - формула (5.21) при	12,0	13,7	15,5
37	Параметр расхода	0,68	0,78	0,88
38	Длина l₀₍₁₎ (см. рис. 5.34) при , м	4,2	2,5	1,2
39	Расчетная длина трубы , м	32,3	34,0	35,3
40	Коэффициент (см. рис. 5.32) в функции l_т(1)	0,60	0,60	0,59
41	Коэффициент (см. рис. 5.33)	0,92	0,85	0,79
42	i_тl_т	0,32	0,34	0,35
43	Расход Q₁₍₂₎ [формула (5.21)] при и	11,0	13,2	15,3
44	Погрешность	8,3 > 3	1,5 < 3	1,3 < 3
45	Параметр расхода	0,62	-	-
46	Длина l₀₍₂₎ (см. рис. 5.34) при	6,5	-	-
47	Расчетная длина трубы , м	30	-	-
48	Коэффициент (см. рис. 5.32)	0,61	-	-
49	Коэффициент (см. рис. 5.33)	0,97	-	-
50		0,30	-	-
51	Расход Q₁₍₃₎, м³/с [формула (5.21)] при и	10,8	-	-
52	Погрешность	1,8 < 3	-	-
53	Принятые расходы каждой трубы первого яруса, м³/с	11,0	13,7	15,5
54	Расход всех труб первого яруса , м³/с	33,0	41,1	46,5
55	Расход всех труб второго яруса , м³/с	2,0	6,0	10,0
56	Расход многоярусной трубы Q, м³/с	35,0	47,1	56,5

Для существенного ускорения расчета многоярусных гофрированных труб D = 1,5 м и D = 2,0 м можно пользоваться графиками на рис. 5.35 и 5.36.

Порядок расчета следующий.

Определяют по графикам на рис. 5.35 и 5.36 расход многоярусной трубы при подпертой глубине, соответствующей отметке лотка труб второго яруса.

При H = 2,5 м находим по графику на рис. 5.36 для D₁ = 2,0 м Q₁ = 8,7 м³/с и

. Этот расход меньше Q_р = 40 м/с и Q_max = 55 м³/с. Следовательно, трубы второго яруса работают.

Далее расчет аналогичен приведенному выше и отличается от него тем, что выполняется полностью по графикам. Расчет выполняют в табличной форме (табл. 2).

Таблица 2

N п/п	Элементы расчета	Расходы каждой трубы второго яруса Q₂, м³/с
N п/п	Элементы расчета	1,0	3,0	5,0
Второй ярус
1	Диаметр трубы D₂, м	1,5	1,5	1,5
2	Длина трубы l_т(2), м	29,0	29,0	29,0
3	Подпертая глубина H₂, м (см. рис. 5.35)	0,76	1,42	2,33
4	Отметка лотка на входе в трубы второго яруса z_2(л)	101,73	101,73	101,73
5	Отметка подпертого уровня ПУВВ = z_2(л) + H₂, м	102,49	103,15	104,06
Первый ярус
6	Отметка лотка на входе в трубу, м	99,23	99,23	99,23
7	Подпертая глубина H₁ = ПУВВ - z_1(л), м	3,26	3,92	4,83
8	Расход Q₁, м³/с (см. рис. 5.35)	11,1	13,3	15,7
9	Расход всех труб первого яруса , м³/с	33,3	39,9	47,1
10	Расход всех труб второго яруса , м³/с	2,0	6,0	10,0
11	Расход двухъярусной трубы , м³/с	35,3	45,9	57,1
12	Разница в расходах при расчете по графикам по сравнению с расчетом по формулам	0,8	2,6	1,0

Разница в расходах, определяемых по графикам и формулам, получается небольшая (не более 3%).

Искомые подпертые глубины (уровни) определяем путем построения зависимости Q = f(H) для многоярусной трубы (рис. 2). На рис. 2 для Q_р = 40,0 м/с находим H_р = 3,54 м и ПУВВ_р = 99,23 + 3,54 = 102,77 м.

Рис. 2. График для определения пропускной способности

многоярусной трубы:

1 -

- для труб первого яруса;

2 -

- то же для всей трубы

Для Q_max = 55,0 м/с H_max = 4,64 м и ПУВВ_max = 99,23 + 4,64 = 103,87 м.

Определяем скорости потока на выходе из труб первого яруса, по которым устанавливаем тип укрепления на выходе.

Предварительно находим по графику на рис. 2 расходы труб первого яруса при установленных подпертых глубинах:

Затем по приложению 5.2 (рис. 2) определяем:

при

и i_т = 0,01

при

и i_т = 0,01

Допускаемые скорости при пропуске Q_max увеличиваем на 35% или фактические скорости уменьшаем на эту же величину.

Поэтому v_вых(max) = 5,71:1,35 = 4,22 м/с < v_вых(р) = 5,32 м/с.

Принимаем к расчету v_вых(р) = 5,32 м/с.

По скорости v_вых = 5,32 м/с подбираем по табл. 2.9 тип укрепления: монолитное укрепление из бетона.

Приложение 5.2

ОПРЕДЕЛЕНИЕ ГЛУБИН ПОТОКА НА ВЫХОДЕ ИЗ ТРУБ ПО ГРАФИКАМ

Рис. 1. График для определения глубин потока на выходе

из круглых труб

Рис. 2. График для определения глубин потока на выходе

из прямоугольных труб, работающих при П_Q > 0,8

при полунапорном режиме

Рис. 3. График для определения глубин потока на выходе

из овоидальных труб

Рис. 4. График для определения глубин потока на выходе

из гофрированных труб с учетом их возможной зарядки

Приложение 5.3

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПОТОКА НА ВЫХОДЕ ИЗ ТРУБ ПО ГРАФИКАМ

Рис. 1. График для определения скоростей потока на выходе

из круглых технически гладких труб

Рис. 2. График для определения скоростей потока на выходе

из гофрированных труб с учетом их возможной зарядки

Приложение 6.1

ОПРЕДЕЛЕНИЕ ПОДПЕРТЫХ ГЛУБИН И ГЛУБИН ПОД МОСТАМИ

ПРИ ЗАТОПЛЕННОМ ПОДМОСТОВОМ РУСЛЕ ПО НОМОГРАММЕ

Номограмма для определения подпертых глубин H₃ и глубин

под мостами при затопленном подмостовом русле (сплошные

линии - глубины в нижнем бьефе, h_нб, соответствующие

коэффициенту расхода m = 0,38, штриховые

линии - то же при m = 0,34)

Приложение 6.2

ПРИМЕРЫ РАСЧЕТА МАЛЫХ МОСТОВ

Пример 1. Требуется рассчитать отверстие малого моста с откосными крыльями и подобрать тип укрепления подмостового русла для расчетного расхода Q = 30 м³/с. Бытовая глубина воды в логе h_нб = 0,53 м; напор воды перед мостом H₀ = 1,7 м.

Решение. По табл. 6.1 мосту с откосными крыльями соответствует коэффициент расхода m = 0,35, тогда по табл. 6.2 критерий подтопления N = 0,8.

1. Проверяем условие подтопления. Так как h_нб < NH₀ (0,53 < 0,8·1,7), то подмостовое русло неподтоплено и поэтому коэффициент подтопления

2. Определяем размер отверстия моста из формулы (6.5):

Принимаем ближайшее стандартное значение b_н = 10 м.

3. Новое (уточненное) значение напора перед мостом

4. Условие

не изменилось: 0,53 < 0,8·1,55.

5. По табл. 6.2 устанавливаем, что k_с = 0,52, следовательно, глубина в расчетном сечении

и скорость

6. По данным, приведенным в табл. 2.9, устанавливаем, что при v_р = 3,7 м/с и h_с = 0,81 подмостовое русло необходимо укрепить мощением из камня размером 25 см на слое щебня 10 см или бетонными плитами размером 50 x 50 или 100 x 100 см.

Пример 2. Требуется определить размер отверстия малого моста и подобрать тип укрепления подмостового русла при следующих расчетных данных: Q = 19,8 м³/с; устои моста с откосными крыльями; напор воды перед мостом не должен превышать 1,8 м; h_нб = 1,65 м.

Решение. 1. По табл. 6.2 устанавливаем, что при m = 0,35 N = 0,8. Тогда NH₀ = 0,8·1,8 = 1,44. Так как h_нб > NH₀ (1,65 > 1,44), то подмостовое русло подтоплено.

2. Определяем степень подтопления:

По табл. 6.3 устанавливаем, что при

и m = 0,35 коэффициент подтопления

3. Размер отверстия моста

Округляем это число до стандартного значения

4. Для определения нового значения напора

подсчитаем вспомогательную функцию:

По табл. 6.3 при m = 0,35 и

устанавливаем, что

. Так как стандартное отверстие моста незначительно отличается от расчетного, то значения

не изменились, т.е. практически не изменился напор воды перед мостом, и можно принять

При иных значениях

новое значение напора следует подсчитывать по правилам, изложенным в примере настоящего приложения.

5. Определим глубину и скорость потока в расчетном сечении, предварительно установив, что k_п = 0,85 по табл. 6.3:

при m = 0,35 и

k_п = k_пH₀ = 0,85·1,8 = 1,53 м;

6. По данным расчета может быть принята одерновка плашмя или любой другой тип укрепления подмостового русла по типовому проекту.

Пример 3. Требуется рассчитать отверстие малого моста с откосными крыльями и определить напор воды перед ним при Q = 26 м³/с и бытовой глубине воды в логе h_нб = 0,5 м. Подмостовое русло предполагается укрепить мощением из камня размером 25 см на слое щебня 10 см.

Решение. 1. В соответствии с заданным типом укрепления русла устанавливаем (см. табл. 2.9), что v_доп = 4 м/с.

2. Коэффициент расхода для принятого типа устоев моста m = 0,35. По табл. 6.2

; N = 0,8; k_с = 0,52.

3. Принимая, что подмостовое русло неподтоплено, т.е.

, вычисляем напор:

Так как условие h_нб < NH₀ (0,50 < 0,8·1,8) выполнено, то подмостовое русло действительно неподтоплено, и поэтому полученное значение напора может быть использовано для дальнейших расчетов.

4. Определяем размер отверстия моста:

Принимаем ближайший стандартный размер отверстия

5. Уточненное значение напора

Так как напор изменился незначительно, то и критерий подтопления практически остался таким же (0,5 < 0,8·1,75) и подмостовое русло остается неподтопленным.

6. Вычисляем глубину потока в расчетном сечении

h_с = k_сH₀ = 0,52·1,75 = 0,91 м

и скорость протекания потока в подмостовом русле

что меньше допускаемой (v_р < v_доп), поэтому условие расчета выполнено.

Пример 4. Требуется определить размер отверстия моста и напор воды перед мостом при следующих расчетных данных: Q = 16 м³/с; v_доп = 4 м/с; устои моста с заборными стенками; h_нб = 1,6 м.

Решение. 1. По табл. 6.2 устанавливаем, что при m = 0,32 N = 0,84 и

2. Принимая в первом приближении

, определяем

Тогда NH₀ = 0,84·1,6 = 1,34 м и h_нб > NH₀ (1,6 > 1,34), т.е. подмостовое русло подтоплено и напор должен быть пересчитан.

3. Определим наибольшую возможную скорость в подмостовом русле по зависимости (6.15):

Так как v_max < v_доп (3,3 < 4), то в расчет принимаем скорость v_max = 3,3 м/с (если окажется, что v_max > v_доп, то в расчет надо принимать v_доп).

4. Для вычисления действительного напора определим сначала вспомогательную функцию:

Затем по табл. 6.3 для m = 0,32 устанавливаем, что при

Тогда напор в первом приближении

а размер отверстия моста

Округляем этот размер до стандартного значения

5. Для установления напора во втором приближении вычислим вспомогательную функцию:

По табл. 6.3 при m = 0,32 и

находим, что

, тогда

Так как

, то принимаем

и тогда

, а напор

В связи с тем, что значения

близки, дальнейшего уточнения не требуется и окончательно принимаем H₀ = 1,78 м.

Условие подтопления выдержано:

h_нб = 1,6 м > NH₀ = 0,84·1,78 = 1,5 м.

6. Глубина потока в расчетном сечении при k_п = 0,74 (см. табл. 6.3),

и m = 0,32

h_п = k_пH₀ = 0,74·1,78 = 1,31 м.

Скорость потока в расчетном сечении

Таким образом, условие v_р < v_доп выполнено.

Приложение 6.3

ПРИМЕРЫ РАСЧЕТА МОСТА НА ЗАЛИВЕ ВОДОХРАНИЛИЩА

Пример 1. Скорость повышения уровня речного бьефа a = 0,2 м/сут (наполнение); допускаемая скорость v_доп = 2,5 м/с; H₁ = 3 м; H₀ = 1 м; F₀ = 6 км²; F₁ = 12 км²;

;

Решение. Находим следующие характеристики:

По номограмме на рис. 6.7 находим

, откуда искомое b_ном = 1,6H₁ = 4,8 м;

Применительно к типовым размерам принимаем b = 6 м.

Пример 2. Средняя скорость понижения уровня в речном бьефе a = 0,25 м/сут; H₁ = 2 м; H₀ = 1 м; F₁ = 15 км²; F₀ = 5 км;

; n = 0,5.

Решение. Находим:

Принимаем K = 1, тогда

По номограмме для опорожнения (см. рис. 6.6) находим, что

, откуда b_ном = 10,2 м. Тогда

Установлено, что в расчетный период испарение с зеркала отсеченной части P составляет 5 см/сут.

Тогда расчетное отверстие

Принимаем b_доп = 8 м.

Приложение 7.1

СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТОВ

С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

Рис. 1. Вариант неравномерной разностной сетки для расчета

растекания потока в логе с прямолинейными боковыми стенками

(в силу симметрии области течения относительно оси трубы

сетка построена для половины области)

Рис. 2. Эпюры скоростей и глубин потока при истечении его

в лог шириной 1,8 м с плоским бетонным наклонным дном

(i_л = 0,05, n_л = 0,014) из круглой трубы диаметром

D = 0,1 м; скорость и глубина на выходе v_вых = 1,78 м/с,

h_вых = 0,035 м, приведенная ширина выхода b_вых = 0,064 м:

сплошные линии - результаты расчета; точки - данные

эксперимента; штриховые линии - границы растекания

в эксперименте

Рис. 3. Эпюры глубин и скоростей потока при истечении

его в лог с уклоном дна i_л = 0,001 (остальные параметры

те же, что и на рис. 2): сплошная линия на эпюрах

скоростей - линия нулевых скоростей; стрелки обозначают

векторы скорости, а цифры - их абсолютные значения, см/с

Приложение 7.2

ОПРЕДЕЛЕНИЕ ШИРИНЫ РАСТЕКАНИЯ, ГЛУБИН И СКОРОСТЕЙ ПОТОКА

НА УКРЕПЛЕНИИ ПО ГРАФИКАМ ПРИ УКЛОНЕ ВЫХОДНОГО

ЛОГА i_л > 0,02

Ширину растекания потока находят по формуле (7.12):

где

, N и K_м - параметры, определяемые соответственно по рис. 1, 2 и таблице данного приложения;

n_ш - коэффициент шероховатости дна;

0,015 - принятый в графике коэффициент шероховатости.

Рис. 1. График для определения параметра

Рис. 2. График для определения параметра N

D_э, м	Поправочный коэффициент K_м при П_Q, равном						D_э, м	Поправочный коэффициент K_м при П_Q, равном
D_э, м	0,1	0,2	0,4	0,8	1,2	1,6	D_э, м	0,1	0,2	0,4	0,8	1,2	1,6
1,0	0,91	0,93	0,96	0,99	1,01	1,02	3,00	2,49	2,55	2,63	2,71	2,77	2,79
1,25	1,12	1,14	1,18	1,22	1,24	1,25	3,50	2,87	2,93	3,02	3,12	3,18	3,21
1,50	1,32	1,34	1,39	1,44	1,46	1,48	4,00	3,24	3,32	3,42	3,52	3,60	3,63
2,00	1,72	1,75	1,81	1,87	1,91	1,93	4,50	3,61	3,69	3,81	3,93	4,01	4,05
2,50	2,11	2,16	2,23	2,30	2,34	2,37	5,00	3,98	4,06	4,20	4,33	4,41	4,46

Графики для определения глубины потока h и глубин по оси потока h_ось на укреплении даны на рис. 3 и 4, скоростей потока v - на рис. 5.

Рис. 3. График для определения глубины потока

h на укреплении

Рис. 4. График для определения глубин по оси потока h_ось

на укреплении

Рис. 5. График для определения скоростей потока v

на укреплении

Приложение 7.3

РАСЧЕТ МАКСИМАЛЬНОЙ ГЛУБИНЫ РАЗМЫВА С УЧЕТОМ ГИДРОГРАФА

ПАВОДКА ПРОИЗВОЛЬНОЙ ФОРМЫ

При формах гидрографа паводка, не поддающихся введенной в п. 3.9 схематизации (например, многопиковой), расчет

непосредственно по формулам (7.21), (7.23), (7.26) - (7.28) может привести к заметным погрешностям. В этом случае применяется следующий алгоритм расчета.

1. Гидрограф заменяют ступенчатым, т.е. представляют в виде последовательности пар чисел (Q_j, T_j), j = 1, ..., N, где Q_j, T_j - соответственно расход на j-й ступени и ее продолжительность; N - число ступеней, выбираемое из условия обеспечения необходимой точности расчетов (обычно N >= 10).

2. Задают начальную глубину размыва

(обычно

) и считают j = 0.

3. Увеличивают j на 1 (j = j + 1); если j > N - расчет завершен.

4. Рассчитывают

по формуле (7.23) при Q = Q_j. Если

, полагают

и переходят к п. 3 алгоритма.

5. Уравнение (7.21) с учетом (7.26), (7.27) и значения

разрешают относительно t при

и находят t_j - время, за которое постоянный расход Q_j размоет дно на глубину

(т.е. на начало j-й ступени):

6. Полагают t = t_j + T_j и по формулам (7.21), (7.23), (7.26), (7.27) при Q = Q_j вычисляют глубину

на конец j-й ступени:

после чего переходят к п. 3 алгоритма.

По описанному алгоритму в ЦНИИСе разработана и эксплуатируется программа для расчета

при пропуске гидрографов типовой или произвольной формы при любых рекомендуемых типах выходных русел.

Приложение 7.4

ПРИМЕРЫ РАСЧЕТА НИЖНЕГО БЬЕФА ТРУБ

I. Расчеты выходных русел с укреплениями

из связанных между собой элементов (бетонных)

Пример 1. Уклон лога i_л <= 0,02. Круглая железобетонная труба D = 1,5 м без конических звеньев с раструбным оголовком b_р = 3,2 м расположена на автомобильной дороге; уклон трубы i_т = 0,05, уклон лога i_л = 0,01; расчетный расход в сооружении Q_р = 4 м³/с; объем стока W_р = 21·10³ м³; лог широкий в виде наклонной плоскости; грунты лога - пески со средним диаметром частиц d = 1 мм. Требуется назначить тип выходного русла и определить размеры укреплений на выходе из трубы.

Решение. 1. Назначаем тип выходного русла. Труба практически полностью загружена, так как согласно табл. 1.2 расход в указанной трубе при расчетном заполнении Q_р = 4,7 м³/с, что близко к Q_р = 4 м³/с; согласно указаниям п. 7.4 назначаем выходное русло типа 1к.

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: приложение 5.4 отсутствует.

2. Определяем скорости на выходе из трубы v_вых. Для этого находим параметр расхода по номограмме на рис. 5.8 или по формуле

и по графику на рис. 1 приложения 5.4 находим

, откуда

. Максимальные скорости на укреплении v_укр(max) при i_т > 0,02 согласно п. 7.18 принимаем равными v_вых = 5,4 м/с.

3. Назначаем тип укрепления. По табл. 2.9 при v_укр(max) = 5,4 м/с принимаем бетонное монолитное укрепление длиной L = 2D = 2·1,5 = 3 м (см. п. 7.44).

4. Определяем глубину размыва в принятом выходном русле в такой последовательности:

а) вычисляем предельную глубину размыва по формуле (7.23), для чего предварительно вычисляем Q_к и

[см. пояснения соответственно к формулам (7.17) и (7.23)]:

Для принятого выходного русла типа 1к

и для него по табл. 7.2 находим r = 0,9 и s = 0,6. Тогда имеем

б) определяем продолжительность паводка по формуле (7.28):

в) определяем эталонное время размыва по формуле (7.27) при C_р = 0 (несвязные грунты):

г) определяем долю предельной глубины размыва, осуществляемую за время прохождения паводка по формуле (7.26):

д) определяем максимальную глубину размыва по формуле (7.21):

е) назначаем расчетное значение удельного объема камня в рисберме исходя из условия

, для чего находим значения W_к(min) и

соответственно по формулам (7.56) и (7.57). В первом приближении крупность камня при этом принимаем d_н = 0,1 м:

Принимаем

;

ж) уточняем принятую крупность камня в рисберме исходя из формулы (7.55):

Следовательно, крупность камня d_н = 0,1 м принята правильно;

з) определяем глубину размыва в принятом выходном русле по формуле (7.58):

т.е. тип выходного русла 1к назначен правильно.

5. Назначаем глубину заделки концевой части укрепления для типа 1к - глубину заложения предохранительного откоса. Согласно указаниям п. 7.46 принимаем глубину заложения концевой части укрепления

6. Определяем ширину растекания потока. При i_л <= 0,02 расчет выполняем по формуле (7.4), предварительно вычислив показатель степени z по формуле (7.5) и коэффициент K по графику на рис. 7.12.

При

K = 0,73;

Результаты расчета приведены ниже:

x, м ...........................................	0	1,0	2,0	3,0
x/D ...........................................	0	0,67	1,33	2,0
B_раст, м .....................................	3,2	3,7	4,11	4,5

7. Определяем ширину укрепления. Расчет выполняем в такой последовательности:

а) назначаем ширину укрепления на всей ее длине, кроме концевой части, по ширине растекания с запасом, равным по 1 м с каждой стороны укрепления, т.е. B = B_раст + 2,0 м;

б) находим ширину укрепления в его конце по формуле (7.74) при

в) принимаем окончательные размеры укрепления в плане исходя из кратности их 0,5 м (рис. 1).

Рис. 1. Конструкция и размеры укреплений, полученные

в результате расчета нижнего бьефа трубы при i_л <= 0,02:

1 - граница растекания; 2 - контур воронки размыва

Пример 2. Уклон лога i_л > 0,02. Прямоугольная типовая железобетонная труба отверстием b x h_т = 1,5 x 2,0 м с раструбным оголовком b_р = 3,7 м расположена на железной дороге в средней полосе страны; уклон трубы i_т = 0,15. Труба запроектирована со ступенчатой укладкой звеньев, со ступенями высотой

и длиной l = 2,0 м. Уклон и коэффициент шероховатости лога соответственно равны: i_л = 0,05, n_л = 0,045; расчетный расход в сооружении Q_р = 9,0 м³/с, наибольший расход Q_max = 11,5 м³/с. В результате гидравлического расчета установлено, что расчетный и наибольший расходы проходят при безнапорном режиме. Объем стока: при расчетном паводке W_р = 116 x 10³ м³, при наибольшем паводке W_max = 155·10³ м³. Лог широкий в виде наклонной плоскости, грунт лога - глины с расчетным сцеплением C_р = 0,068 МПа.

Требуется назначить тип выходного русла и определить размеры укреплений на выходе из трубы.

Решение. 1. Назначаем тип выходного русла. Труба практически полностью загружена и имеет большой уклон. Согласно рекомендациям п. 7.4 назначаем выходное русло типа 1к.

2. Определяем глубины и скорости потока на выходе из трубы при ступенчатой укладке звеньев и на укреплении в следующем порядке:

а) вычисляем параметр

(см. п. 5.29):

при Q_р

;

при Q_max

;

б) по графику на рис. 2 приложения 2.2 находим:

при Q_р

и h_вых(р) = 0,61·1,5 = 0,92 м;

при Q_max

и h_вых(max) = 0,74·1,5 = 1,11 м;

в) находим скорости на выходе из трубы по формулам (5.60) и (5.61):

при Q_р

;

при Q_max

;

г) максимальные скорости на укреплении v_укр(max) по формуле (7.7) равны v_вых.

Следовательно

при Q_р v_{укр(max)р} = v_вых(р) = 6,5 м/с;

при Q_max v_{укр(max)max} = v_вых(max) = 6,9 м/с.

Так как

, а допускаемые скорости при прохождении наибольшего расхода можно повышать на 35%, то к расчету принимаем максимальную скорость при расчетном расходе v_{укр(max)р} = 6,5 м/с.

3. Назначаем тип укрепления по табл. 2.9: при v_max = 6,5 м/с принимаем бетонное монолитное укрепление. Предварительно определим эквивалентный диаметр сооружения по формуле (см. пояснение к п. 7.28)

Согласно п. 7.43 длина укрепления L = 1,5D_э = 1,5·1,96 = 3 м.

4. Определяем глубину размыва в принятом выходном русле в такой последовательности:

а) вычисляем предельную глубину размыва по формуле (7.23). Для этого предварительно вычисляем Q_к и

[см. пояснение соответственно к формулам (7.17) и (7.23)] и расчетный диаметр грунтов по формуле (7.25):

Расчетный диаметр грунтов при C_р = 0,068 МПа

d = 7,5(0,1 + 100C_р) = 7,5(0,1 + 100·0,068) = 51 мм.

Для принятого выходного русла типа 1к имеем

, а значения r = 0,9 и s = 0,6 находим по табл. 7.2.

Тогда получим:

при Q_р

при Q_max

;

б) определяем продолжительность паводка по формуле (7.28):

при Q_р

;

при Q_max

;

в) определяем эталонное время размыва по формуле (7.27):

при Q_р

при Q_max

;

г) определяем долю предельной глубины размыва за время прохождения паводка по формуле (7.26):

при Q_р

;

при Q_max

;

д) определяем максимальную глубину размыва по формуле (7.21):

при Q_р

;

при Q_max

Так как глубины размыва как при Q_р, так и при Q_max оказались менее 2,0 м, то корректируем тип выходного русла и принимаем в качестве расчетного выходное русло типа 1, т.е. отказываемся от каменной наброски.

В связи с тем что выходной лог имеет уклон i_л = 0,05 > 0,02, определяем основные размеры промоины. При неявно выраженном логе расчет промоины ведем в такой последовательности.

1. Вычисляем по формуле (7.29) ширину потока B_нр, при которой скорость в логе равна неразмывающей скорости, предварительно вычисленной по формуле (7.30):

Тогда имеем:

при Q_р

при Q_max

2. Определяем ширину створа предельного растекания по формуле (7.3) при N = 1, предварительно установив параметры расхода (см. табл. 5.1) и параметры

и K_м соответственно по рис. 1 и таблице приложения 7.2 и M по формуле, приведенной в том же приложении.

При i_л = 0,05 и

по графику на рис. 1 приложения 7.2 для Q_р и

находим

; по таблице приложения 7.2 при D_э = 1,96 и П_Q = 0,68 находим коэффициент K_м = 1,88 и по формуле находим

Тогда B_{раст(пр)} = 60,2 + 3,7 = 63,9 м.

При Q_max и

; K_м = 1,88;

. B_{раст(пр)} = 60,8 + 3,7 = 64,5 м.

3. Сравниваем B_нр с B_{раст(пр)}:

при Q_р B_нр = 36,6 м < B_{раст(пр)} = 63,7 м;

при Q_max B_нр = 46,7 м < B_{раст(пр)} = 64,5 м.

Следовательно, промоина имеет ограниченное протяжение.

4. Определяем положение створа, в котором прекращается размыв, по формуле (7.32), предварительно вычислив N по формуле (7.34):

при Q_р

;

при Q_max

;

5. Определяем глубину потока в створе прекращения размыва по формуле (7.33):

при Q_р

6. Определяем ширину растекания потока в створе на входе в канаву B_{раст(кан)} по формуле (7.12) при x = X_кан, предварительно вычислив X_кан по формуле (7.35) и определив параметр N по графику на рис. 2 приложения 7.2 (параметры M вычислены ранее):

при Q_р

и по значениям

и П_Q = 0,68 находим N = 0,32, а затем B_{раст(кан)} = MN + b_р = 60,2·0,32 + 3,7 = 23 м.

При Q_max

. По

и П_Q = 0,87 находим N = 0,36, а затем B_{раст(кан)} = 60,8·0,36 + 3,7 = 25,6 м.

7. Находим b_кан и глубину потока h_кан на входе в канаву при стабилизации размыва по формулам (7.36) и (7.37):

при Q_р

и к расчету принимаем b_кан = 9,44 м;

при Q_max

и к расчету принимаем b_кан = 10,75 м;

8. Определяем среднюю глубину потока в канаве по формуле (7.38):

при Q_р

;

при Q_max

9. Определяем глубины размыва канавы по формуле (7.39), предварительно определив C_кан по формуле (7.40):

при Q_р

;

при Q_max

;

10. Уточняем расстояние до входа в канаву по формуле (7.41) при m_от = 1,5:

при Q_р

;

- корректировка X_кан не требуется;

при Q_max

;

- корректировка X_кан не требуется.

Вычисленные значения X_кан принимаются к расчету.

11. Определяем глубину заложения концевой части укрепления по формуле (7.72), причем при Q_р

увеличиваем на 20%:

при Q_р

при Q_max

;

для расчета принимаем

12. Определяем ширину растекания потока на укреплении при n = 0,015. При i_л > 0,02 расчет выполняем по формуле (7.12) при x = 1, 2 и 3 м, предварительно вычислив параметр

по графику на рис. 1

и формуле приложения 7.2 и параметр N по графику на рис. 2 того же приложения. Расчет ведем в табличной форме (табл. 1).

Таблица 1

x, м	x/D_э	Расчетные параметры и ширина растекания при пропуске расхода
		расчетного (П_Q = 0,68)				наибольшего (П_Q = 0,87)
		K_м	N		B_раст	K_м	N		B_раст
1,0	0,5	1,86	0,80	2,8	6,5	1,88	0,105	3,7	7,4
2,0	1,0	1,86	0,155	5,4	9,1	1,88	0,170	6,0	9,7
3,0	1,5	1,86	0,210	7,3	11,0	1,88	0,230	8,1	11,8

Для расчета принимаем величину растекания при наибольшем расходе.

13. Определяем ширину укрепления. Расчет выполняем в такой последовательности:

а) назначаем ширину укрепления на всей его длине, кроме концевой части длиной 1 м, по ширине растекания с запасом по 1 м с каждой стороны укрепления: B = B_раст + 2,0 м.

Результаты расчета приведены ниже:

x, м ...........................................	0	1,0	2,0
B, м ...........................................	5,7	9,4	11,7

б) находим ширину воронки размыва в конце укрепления B_min по формуле (7.73) при

(концевая часть с предохранительным откосом), определив коэффициент формы воронки размыва по графику на рис. 7.12 при L/D_э = 1,5:

при Q_р

; K = 0,62;

при Q_max

; K = 0,80;

Следовательно, ширина укрепления на всем его протяжении определяется шириной растекания, которая оказалась весьма значительной. Для сокращения ширины укрепления ограничим его изолиниями, соответствующими неразмывающей скорости потока v_н для грунтов лога, определенной выше и равной 1,49 м/с. Для этого воспользуемся графиком на рис. 5 приложения 7.2, предварительно заменив скорость v на v_н:

при Q_р

;

при Q_max

По графику на рис. 5 приложения 7.2 находим значение относительной граничной ширины растекания

в каждом створе, ограничивающей область, за пределами которой скорости потока на укреплении не будут превосходить неразмывающих, и определим размеры укрепления, соответствующие этой ширине B_гр, с запасом по 1 м в каждую сторону. Результаты расчета приведены в табличной форме (табл. 2).

Таблица 2

x, м	x/D_э	Относительная и абсолютная граничная ширина растекания и ширина укрепления при пропуске расхода
		расчетного			наибольшего
			B_гр, м	B, м		B_гр, м	B, м
0	0	0,55	3,7	5,7	0,56	3,7	5,7
1,0	0,5	0,56	3,7	5,7	0,57	4,2	6,2
2,0	1,0	0,57	5,2	7,2	0,575	5,6	7,6
3,0	1,5	0,575	6,3	8,3	0,58	6,8	8,8

Ширину укрепления в его конце, необходимую при пропуске наибольшего расхода B_укр = 8,8 м, сравниваем с B_min: B_укр = 8,8 м < B_min = 10,65 м - для расчета принимаем B_укр = 10,65 и корректируем размеры укрепления из конструктивных соображений, принимая их кратными 0,5. Результаты расчета приведены на рис. 2.

Рис. 2. Конструкция и размеры укреплений, полученные

в результате расчета нижнего бьефа трубы при уклоне

выходного лога i_л > 0,02

II. Расчеты выходных русел с укреплениями

из каменной наброски

Пример 3. Расчет недеформируемых выходных русел. Круглая железобетонная труба D = 1 м без конических звеньев с раструбным оголовком b_р = 2,1 м расположена на автомобильной дороге; сток снеговой - аккумуляция не учитывается; расчетный расход в сооружении Q_р = 1,5 м³/с; грунты лога - пески со средним диаметром частиц d = 1 мм; уклон лога трубы i_т = 0,01.

Требуется определить размеры неразмываемого недеформируемого выходного русла, изготавливаемого из однородного камня на щебеночной подготовке.

Решение. 1. Определение лимитирующего расхода

Для обеспечения запаса устойчивости укрепления увеличиваем расчетный расход на 30%:

и принимаем этот расход для дальнейших расчетов.

II. Определение размеров укреплений

1. Определяем скорости на выходе из трубы по графику на рис. 1 приложения 5.3.

Предварительно по номограмме на рис. 5.8 определяем параметр расхода

. При D = 1 м и Q = 2,0 м³/с П_Q = 0,63. Зная П_Q и i_т = 0,01, находим по графику на рис. 1 приложения 5.3

2. Определяем минимальный диаметр частиц наброски, при котором укрепление будет устойчивым от размыва. Для трубы с раструбным оголовком воспользуемся формулой (7.76"):

Принимаем средний диаметр камней наброски d_н = 0,25 м.

3. Определяем по формуле (7.82) толщину слоя наброски, при котором укрепление будет недеформируемым (расчет вначале ведем без учета подсыпки):

В нашем случае D_э = D = 1 м; d_н = 0,25 м; d = 0,001 м; v_вых = 3,95 м/с;

Подставим эти значения в формулу, получим

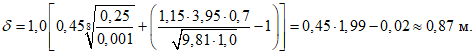
Примем, что 20% этой глубины составит подготовка из щебня со средней крупностью частиц d_н(щ) = 0,05 м, и повторим расчет по той же формуле, подставив в нее вместо d_н значение d_(н)э, определяемое по формуле (7.84):

Тогда имеем

Принимаем укрепление состоящим из каменной наброски толщиной

и щебеночной подготовки

4. Принимаем длину укрепления L = 1,5D_э = 1,5·1,0 = 1,5 м.

5. Определяем ширину растекания потока в конце укрепления (x = L = 1,5 м) по формуле (7.4):

Предварительно вычисляем эталонный расход Q_к и показатель степени z по формуле (7.5):

Остальные входящие в формулу (7.4) значения равны: b = D = 1,0 м; b_р = 2,1 м.

Отсюда имеем

6. Назначаем ширину укрепления:

в створе на выходе из оголовка:

B₁ = h_р + 2,0 = 2,1 + 2,0 = 4,1 м;

в створе конца укрепления

B₂ = B_раст + 1,0 = 3,1 + 1,0 = 4,1 м = B₁.

III. Расчеты размыва за укреплениями и определение размеров их концевых частей

I. Определяем глубину размыва в грунте лога за укреплениями по формуле (7.23), заменяя согласно указаниям п. 7.64 выражение

выражением

Находим величины, входящие в формулу.

Масштабный коэффициент

для трубы D = 1 м находим по табл. 7.3:

По табл. 7.2 s = 0,6 и r = 0,9.

Согласно п. 7.64 показатель степени для недеформируемых укреплений s₁ = 2,5 и коэффициент

Остальные значения определены выше.

Подставив все значения в формулу, получим

2. Определяем максимальную глубину размыва за время паводка по формуле (7.21):

Применяем выходное русло типа 1. Концевая часть этого укрепления представляет собой часть наброски, уложенную за укреплением с откосом 1:1 и глубиной

. Рисберма за укреплением в этом типе выходных русел не устраивается.

3. Определяем ширину воронки размыва в конце укрепления по формуле (7.73):

Предварительно определяем коэффициент K по графику на рис. 7.12:

при

K = 0,57,

откуда

Ввиду относительно малой длины укрепления L = 1,5 м не устраиваем на концевом участке его полосу длиной 1 м и шириной B_ук, а назначаем укрепление прямоугольной формы шириной B_ук = 4,5 м и длиной L = 1,5 м.

Конструкция укрепления представлена на рис. 3.

Рис. 3. Основные размеры укреплений из каменной наброски

в примерах расчета недеформируемых выходных русел:

1 - каменная наброска; 2 - щебеночная подготовка

Объем камня в укреплении (без щебеночной подготовки)

Объем щебеночной подготовки

Общий объем

W = W_к + W_щ = 6,0 м³.

Пример 4. Расчет деформируемых выходных русел. Круглая металлическая гофрированная труба D = 1,5 м без оголовков расположена на железной дороге; сток снеговой, аккумуляция не учитывается; расчетный расход Q_р = 2,3 м³/с, наибольший расход Q_max = 3,0 м³/с; объемы стыка W_т = W_max = 8,1·10³ м³; грунты лога - суглинки с расчетным сцеплением C_р = 0,01 МПа; уклон лотка трубы i_т = 0,01.

Требуется определить размеры неразмываемого деформируемого выходного русла, изготавливаемого из однородного камня на щебеночной подготовке толщиной слоя

со средним диаметром частиц 5 см.

Решение. I. Определение лимитирующего расхода

Расчет начинаем с определения лимитирующего расхода. Для этого увеличиваем расчетный расход на 30% (для учета запаса) и сравниваем его с наибольшим расходом:

Для дальнейшего расчета принимаем расход Q_р = Q_max = 3,0 м³/с.

II. Определение размеров укреплений

1. Определяем скорости на выходе из трубы по графику на рис. 2 приложения 5.3.

Предварительно по номограмме на рис. 5.8 определяем параметр расхода

По значениям П_Q = 0,33 и i_т = 0,01 находим по рис. 2 приложения 5.3:

2. Определяем минимальный диаметр частиц наброски, при котором укрепление будет устойчивым от размыва.

Для трубы без оголовка воспользуемся формулой (7.76'):

Принимаем средний диаметр частиц наброски d_н = 35 см.

3. Определяем предельную глубину деформации укрепления за счет выноса грунта из-под него по формуле (7.85):

Предварительно задавшись толщиной слоя наброски

и зная толщину слоя щебеночной подготовки

, а также полную толщину укрепления

, находим по формуле (7.84) эквивалентный диаметр частиц наброски:

Затем по формуле (7.25) при C_р = 0,01 МПа определяем эквивалентный диаметр частиц грунта:

d_э = 7,5(0,1 + 100C_р) = 7,5(0,1 + 100·0,01) = 8,2 мм,

откуда

4. Определяем глубины потока на выходе из трубы по формуле (5.55):

Предварительно находим по табл. 5.5 для случая П_Q = 0,33 < 0,8 A_т = 0,98 и s_т = 0,5 и вычисляем f(i_т) по формуле (5.54):

Тогда имеем

h_вых = 0,98·1,5·0,833·0,33^0,5 = 0,70 м.

Находим расстояние от выхода из трубы до места расположения предельной глубины деформации укрепления по формуле (7.88):

5. Устанавливаем предельную глубину деформации укрепления сечения на выходе из трубы по формуле (7.80):

- лоток трубы не будет подмыт.

6. Определяем минимальные размеры укрепления в плане по формуле (7.90):

7. Назначаем длину укрепления L = 3,5 м.

8. Находим ширину укрепления.

Предварительно определяем отношение

Ширина укрепления в конце оголовка

B₁ = b_р + 2,0 = 1,50 + 2,0 = 3,50 > B = 3,4 м.

Принимаем B₁ = 3,5 м.

Ширина укрепления в конце его B₂ принимается по большему из значений B₁ и B; в расчете принимаем B₂ = B₁ = 3,5 м.

III. Расчеты размыва за укреплениями и определение размеров их концевых частей

1. Определяем глубину размыва в грунте лога за укреплениями по формуле (7.23):

Предварительно находим величины, входящие в эту формулу: масштабный коэффициент

для трубы D = 1,5 м находим по табл. 7.3

; коэффициенты

; r = 0,9 и показатель степени s = 0,6 находим по табл. 7.2.

Показатель степени s₁ для деформируемых выходных русел равен

. Величины b = b_р = D = 1,5 м; D_э = D = 1,5 м. Эталонный расход Q_к находим по формуле

Подставив значения всех величин в формулу (7.23), получим

2. Определяем максимальную глубину размыва за время паводка

по формуле (7.21).

Предварительно вычисляем эталонное время t₀ по формуле (7.27) и время паводка t по формуле (7.28):

По величине отношения

находим по графику на рис. 7.19

. Тогда

Применяем выходное русло типа 1. Концевая часть этого укрепления представляет собой часть наброски, уложенной за укреплением с откосом 1:1 и глубиной заложения

Рисберма за укреплением в этом типе выходных русел не делается.

3. Определяем ширину воронки размыва в конце укрепления по формуле (7.73).

Предварительно определяем коэффициент K по графику на рис. 7.12 при

. Получаем K = 0,25, откуда

Принимаем ширину укрепления на концевом участке длиной 1 м равной B_ук = B_в = 7,0 м.

Конструкция укрепления приведена на рис. 4.

Рис. 4. Основные размеры укреплений из каменной наброски

в примерах расчета деформируемых русел:

1 - каменная наброска; 2 - щебеночная подготовка

Объем камня в укреплении (без щебеночной подготовки)

Объем щебеночной подготовки

W_щ = 3,5·2,4 + 6,9(1,0 + 0,78)0,15 = 3,1 м³.

Итого объем наброски W_н = 12,4 + 3,1 = 15,5 м³.

Для сравнения при заданных условиях определим размеры укреплений недеформируемого выходного русла. Расчет продолжаем с п. 3.

3. Определяем по формуле (7.81) толщину слоя наброски, при которой укрепление будет недеформируемым, приняв d_н = 0,25 м.

Расчет вначале ведем без учета подсыпки:

Примем, что 20% этой глубины составляет щебеночная подготовка крупностью d_н(щ) = 0,05 м, и повторим расчет по той же формуле, подставив в нее вместо d_н значение d_н(э), определяемое по формуле (7.84), а также

, откуда

Тогда имеем

Эффективность учета слоя щебеночной подготовки, составляющей 20% толщины слоя наброски, мала, поэтому при определении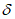

ее можно не учитывать.

Принимаем укрепление состоящим из каменной наброски, уложенной слоем толщиной

, и щебеночной подготовки слоем

4. Назначаем длину укрепления L равной 1,5·1,5 = 2,25 м, или с округлением до 0,5 м L = 2,5 м.

5. Определяем ширину растекания потока в конце укрепления (x = L = 2,5 м) по формуле (7.4), определив предварительно значение z по формуле (7.5):

B_раст = 1,5[(1,5 + 1)^0,84 - 1] + 1,5 = 3,25 м.

6. Назначаем ширину укрепления:

в створе на выходе из трубы

B₁ = B_р + 2,0 = 1,5 + 2,0 = 3,5 м;

в створе конца укрепления

Выполняем расчеты размыва за укреплениями для определения размеров их концевых частей.

1. Определяем глубину размыва в грунте лога за укреплениями по формуле (7.23):

2. Определяем максимальную глубину размыва за время паводка по формуле (7.21):

Применяем выходное русло типа 1.

3. Определяем ширину воронки размыва в конце укрепления по формуле (7.73).

Предварительно находим коэффициент K по графику на рис. 7.12 при

, т.е. K = 0,35; тогда

Назначаем ширину концевой части укреплений B_ук на участке длиной 1 м равной 6,9 м.

Объем камня в укреплении (без щебеночной подготовки)

Объем щебеночной подготовки

Итого объем наброски

При деформируемом укреплении объем наброски W_н был равен 15,3 м³. Таким образом, допущение деформаций укрепления обеспечивает снижение объема наброски, т.е. экономический эффект.

Пример 5. Расчет выходных русел-самоотмосток. Исходные данные те же, что и в примере 1 (расчеты недеформируемых выходных русел), за исключением состава наброски, гранулометрический состав которой задан и приведен ниже (средний диаметр частиц наброски d_н = 122,5 мм):

Средние диаметры частиц наброски по фракциям d_н(1), мм ......................	400 - 200	200 - 100	100 - 50	менее 50
Весовое содержание фракций, % ....	5	50	40	5

Требуется определить размеры выходных русел-самоотмосток и рассчитать глубины размыва за ними.

Определение размеров выходных русел-самоотмосток

Решение. 1. Устанавливаем, будет ли наброска однородной в отношении размыва из условия (7.75):

- наброска неоднородная.

2. Используем гидравлические характеристики, полученные в примере 1, и приведенные там исходные данные: D = 1,0 м; Q = 2,0 м³/с; v_вых = 3,95 м/с; Q_к = 1,6 м³/с; П_Q = 0,63; i_т = 0,01.

3. Устанавливаем, будут ли устойчивы частицы наброски под воздействием потока, исходя из условия (7.78):

Предварительно определяем величины, входящие в формулу. Согласно п. 7.53 необходимо, чтобы содержание самой мелкой фракции было больше 10%, т.е. p_н(м) >= 0,1. В нашем случае самая мелкая фракция (менее 50 мм) имеет содержание 5%. Поэтому дополняем ее последующей фракцией до 10% и находим средний диаметр частиц смеси по формуле (7.80):

Теперь p_н(м) = 0,1.

Затем вычисляем коэффициент неоднородности:

Показатель степени

находим из табл. 7.9 для заданного типа труб, предполагая безнапорный режим протекания потока. Для круглой трубы с раструбными оголовками без конических звеньев при безнапорном режиме

Тогда

Относительная скорость

По графику на рис. 1 приложения 5.3 находим при

П_Q = 0,4. Сравнивая П_Q = 0,4 со значением

, соответствующим заполнению на входе

(см. табл. 5.1), устанавливаем, что режим протекания (безнапорный) установлен правильно.

Затем из условия (7.18) определяем устойчивость наброски против размыва: v_вых = 3,95 м/с > v_пр = 3,25 м/с - наброска размывается.

Проверяем возможность работы укреплений как самоотмосток из условия (7.76"), подставляя d_н(max) вместо d_н. При этом фракция d_н(max) должна содержаться в количестве p_н(max) >= 5%.

В нашем случае фракция

имеет содержание p_н(max) = 5%, следовательно, ее принимаем в расчет.

Проверяем выполнение условия (7.76"). Для этого вычисляем правую его часть:

Укрепление может работать как самоотмостка.

4. Определяем глубину потока на выходе из цилиндрической части трубы по графику на рис. 1 приложения 5.3 при П_Q = 0,63 и на выходе из оголовка по формуле (7.86):

h_вых = 0,61;

h_вых(ог) = h_выхK_ог(h) = 0,61·0,40 = 0,24 м.

5. Определяем долю p_от и средний диаметр d_от фракций отмостки в такой последовательности:

а) вычисляем по формуле (7.92) параметр

Предварительно по формуле (7.93) находим Ф:

Тогда

;

б) по гранулометрическому составу наброски вычисляем

и сравниваем с N_расч. Расчет начинаем с наиболее крупной фракции. Предварительно определяем средний диаметр ее частиц:

Затем находим

. Следовательно, необходимо включить в расчет следующую фракцию.

Находим средний диаметр частиц первых двух фракций:

Следовательно, необходимо к первой фракции добавить лишь часть второй.

Добавляем к первой фракции 30% второй:

но отклонение менее 5%.

Следовательно, обеспечивающие самоотмостку фракции будут иметь p_от = 0,30 и d_от = 0,17 м.

6. Определяем предельную глубину размыва в неоднородной наброске по формуле (7.94):

Предварительно определяем

по формулам (7.23) и (7.21), принимая d_н = d_от при L = 0:

При D_э = D = 1,0 м; b_р = 2D = 2,0 м; r = 0,9;

;

; s = 0,6; Q = 2,0 м³/с; Q_к = 1,6 м³/с (см. пример 1).

Тогда имеем:

Отсюда

Укладываем наброску слоем

без щебеночной подготовки.

7. Находим расстояние от выхода трубы до места расположения максимальной глубины размыва по формуле (7.88), подставляя

вместо

8. Устанавливаем максимальную глубину размыва укрепления у выходного сечения трубы по формуле (7.89), заменяя

соответственно на

Лоток трубы на выходе и подошва насыпи подмыты не будут.

9. Определяем размеры укрепления в плане по формуле (7.90), подставляя в нее

вместо

10. Назначаем длину укрепления L = 3,0 м.

11. Назначаем ширину укрепления.

Предварительно вычисляем

. В этом случае согласно п. 7.62 ширину укрепления определяем по большему из значений B₁ и B. Для этого находим:

ширину укрепления в конце оголовка по формуле (7.91):

B₁ = b_р + 2,0 = 2,1 + 2,0 = 4,1 м > B = 2,8 м;

ширину укрепления в конце его:

B₂ = 4,1 = B₁.

II. Расчеты размыва грунта за укреплениями и определение размеров их концевых частей

1. Определяем предельную глубину размыва в грунте лога за укреплениями по формуле (7.23) с учетом рекомендаций п. 7.64:

2. Определяем максимальную глубину размыва за время паводка по формуле (7.21):

Назначаем выходное русло типа 1.

3. Определяем ширину воронки размыва в конце укрепления по формуле (7.73).

Предварительно находим коэффициент K по графику на рис. 7.12 при

. Получаем K = 0,31, откуда

Принимаем ширину укрепления B_ук в концевой его части на длине в 1 м, равной 5,1 м.

Конструкция укрепления приведена на рис. 5. Объем камня в укреплении W_к = 4,1·1,8·0,70 + 5,1(1,0 + 0,70·1/2)0,70 = 10,0 м³.

Рис. 5. Основные размеры укреплений из каменной наброски

в примерах расчета выходных русел-самоотмосток

III. Расчеты нижних бьефов гофрированных труб, расположенных на подсыпке

Пример 6. Гофрированная косогорная труба расположена на железной дороге; отверстие трубы D = 1,5 м; уклон лога i_л = 0,25 (соответствует заложению откосов косогора m_от(кос) = 4); высота насыпи по оси труб H_нас = 5,0 м; ширина насыпи поверху 6,5 м; верховой откос имеет крутизну 1:1,5; расходы в сооружении Q_р = 2,3 м³/с, Q_max = 3,0 м³/с; подтопление со стороны нижнего бьефа отсутствует. В основании насыпи залегают среднезернистые пески со средним диаметром частиц d = 0,5 мм.

Требуется назначить тип выходных русел указанной косогорной трубы и произвести соответствующие гидравлические расчеты.

Решение. Так как труба расположена на крутом косогоре, то укладываем ее в теле насыпи на подсыпке (рис. 6). Уклон трубы i_т назначаем равным 0,01. Откосы и берму насыпи отсыпаем из однородного камня. Низовой откос насыпи назначаем m_от(под) = 2 (на рис. 6 этот откос показан штриховой линией).

Рис. 6. Нижний бьеф косогорной гофрированной трубы

при сбросе потока на каменную подсыпку:

1 - экран; 2 - фильтрующий поток; 3 - обратный фильтр

высотой

; 4 - укрепление из каменной наброски;

5 - рисберма

Расчет выполняем в соответствии с рекомендациями п. 7.69 применительно к рассматриваемому случаю.

Предварительно увеличиваем расчетный расход на 30% для учета возможной ошибки и обеспечения необходимого запаса:

1,3Q_р = 1,3·2,3 = 3,0 м³/с = Q_max = 3,0 м³/с.

Расчет ведем на расход Q_max = 3,0 м³/с.

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: рисунок 4 отсутствует в Приложении 5.3.

ИС МЕГАНОРМ: примечание.

В официальном тексте документа, видимо, допущена опечатка: приложение 5.4 отсутствует.

1. Определяем глубины и скорости на выходе из трубы по графикам приложений 5.3 (рис. 4) и 5.4 (рис. 2).

Предварительно находим параметр расхода

Далее по П_Q и i_т = 0,01 находим:

и h_вых = 0,48·1,5 = 0,72 м;

2. Устанавливаем по формуле (7.76') средний диаметр наброски, считая ее однородной:

Принимаем d_н = 35 см.

Отсыпаем на берме и откосе три слоя камня крупностью d_н = 35 см, остальную часть - из горной массы (средний диаметр частиц d_н = 25 см) с содержанием мелких частиц 5 - 7%.

3. Определяем по формуле (7.99) минимальный размер бермы вдоль потока, при которой поток, вытекающий из трубы, не попадает непосредственно на откос:

Принимаем с запасом L_б = 3,0 м.

4. Определяем ширину растекания потока на берме по формуле (7.100) с введением в нее понижающего коэффициента 0,6, учитывающего особенности каменной наброски по сравнению с бетонным укреплением (см. п. 7.69):

где x = L_б = 3,0 м, а

Отсюда

5. Назначаем длину участка насыпи, отсыпанной из камня, т.е. ширину фильтрующей насыпи прослойки b_ф. Принимаем

Далее ведем расчет фильтрующей подсыпки как фильтрующей насыпи.

6. Определяем по формуле (7.110) нормальную глубину фильтрационного потока, предполагая, что весь расход профильтрует через подсыпку.

Предварительно находим коэффициент фильтрации для горной массы K_ф(г) со средней крупностью камней d_н = 25 см. Расчет можно произвести по формуле (7.111), но из-за отсутствия данных о пористости горной массы приближенно находим по табл. 8.1 коэффициент фильтрации для однородной наброски и уменьшаем его на 25%:

Тогда

7. Определяем глубину фильтрационного потока H в створе, проходящем через конец трубы, из уравнения (7.113). Подтопление снизу отсутствует. Предварительно находим проекцию расстояния от конца трубы до точки пересечения откосов отсыпки и косогора (см. рис. 6) - l_п = 23,4 м.

Затем вычисляем

Согласно табл. 8.4 по

находим

и H = h₀ = 1,50 м.

8. Определяем устойчивость низового откоса подсыпки из условия (7.114).

Предварительно определяем разность отметок бьефов по формуле (7.115).

Вычисляем z_пр по формуле (7.116) при крутизне откосов подсыпки 1:2

, d_н = 0,35 м и

Следовательно, откос неустойчив и требуется сделать его положе.

Принимаем

и по рис. 6 находим

(откос 1:2,25 изображен сплошной линией).

Тогда имеем

При этом

Следовательно, устойчивость низового откоса обеспечена.

9. Проверяем устойчивость основания насыпи от ламинарной фильтрации. Для этого определяем H_пр по формуле (7.117), причем входящий в нее коэффициент

находим по табл. 8.2. Для зернистых песков, не защищенных обратным фильтром,

. Отсюда

; H = 1,50 м < H_пр = 3,72 м. Следовательно, устойчивость основания насыпи против ламинарной фильтрации обеспечена.

10. Сравниваем глубину потока H с толщиной подсыпки

в сечении, проходящем через конец лотка трубы на выходе. На рис. 6 настоящего приложения

, т.е. весь поток, выходящий из трубы, профильтровывает через подсыпку.

11. Устанавливаем, не выходит ли поток в каком-либо из сечений подсыпки на поверхность. Для этого делим расстояние

на пять равных частей

и в конце каждой из них (считая от конца подсыпки) определяем глубину потока h_i из уравнения (7.113). Затем в каждом из сечений устанавливаем толщину подсыпки

, для чего можно воспользоваться формулой (7.118).

Сравниваем h_i с

и устанавливаем, выйдет ли поток на откос. Это случится при

Расчет выполняем в табличной форме (табл. 3).

Таблица 3

Номер участка	Проекция расстояния от конца подсыпки до данного створа l, м		(по табл. 8.4)	, м			Вид потока
1	5,80	1,0	0,96	1,43	1,13	< 0	Поверхностный
2	11,60	2,0	1,00	1,48	2,25	> 0	Фильтрационный
3	17,40	3,0	1,00	1,50	3,38	> 0	То же
4	23,10	3,98	1,00	1,50	4,48	> 0	"
5	28,90	4,98	1,00	1,50	4,20	> 0	"

Анализ результатов расчета показывает, что фильтрационный поток на части откоса выходит на поверхность.

Нанеся глубины фильтрационного потока на чертеж, устанавливаем, что поток выклинивается на откос на втором участке.

Устанавливаем расстояние от конца подсыпки до места выклинивания потока по формуле (7.121):

12. Определяем толщину подсыпки в этом сечении, равную глубине потока, по формуле (7.118):

Выше этого сечения имеется лишь фильтрационный поток (безнапорная фильтрующая подсыпка), ниже его часть потока выходит на откос (напорная фильтрующая подсыпка).

13. Определяем фильтрационные расходы в различных створах напорной фильтрующей подсыпки. Для этого делим расстояние от конца подсыпки до сечения, где поток выклинивается на поверхность откоса, на три участка длиной

каждый и в конечном сечении каждого участка подсыпки (считая от ее конца) определяем фильтрационный расход по формуле (7.123) при глубине потока

. Эту глубину можно вычислить по формуле (7.118).

Расчет производим в табличной форме (табл. 4).

Таблица 4

Номер участка	Расстояние от конца подсыпки до заданного сечения l, м	, м, по формуле (7.118)	Фильтрационный расход
Подошва откоса	0	0	0
1	2,37	0,46	1,0
2	4,74	0,92	2,0
3	7,1	1,37	3,0

14. Определяем средние скорости турбулентной фильтрации по формуле (7.124):

15. Находим максимальную скорость турбулентной фильтрации по формуле (7.125):

Пористость каменной наброски p = 0,40 либо принимаем по табл. 8.1 для камня той же крупности, что и однородный камень, но для круглых частиц, либо уменьшаем K_ф(доп) = 0,49 на 25%.

16. Сравниваем v_м с допускаемыми скоростями для среднезернистых песков. Для этого по табл. 2.7 находим v_доп = 0,35 м/с; v_м = 1,04 м/с > v_доп = 0,35 м/с. Следовательно, устойчивость основания подсыпки от турбулентной фильтрации не обеспечена.

Вырезаем грунт основания и заменяем его материалом, допускаемая скорость для которого больше или равна v_м. По табл. 2.7 находим, что этому условию удовлетворяет галька (или щебень) с частицами крупностью 1,5 - 2,0 см. Укладываем ее не менее трех слоев, поэтому вырезку надо делать на глубину 8 - 10 см.

17. Определяем расходы потока, протекающего по откосу подсыпки в каждом из створов, по формуле (7.126): Q₂ = Q - Q₁, а также глубины и скорости течения на откосе по формулам (7.127) и (7.129).

Затем сравниваем полученные скорости с допускаемыми для камня по формуле (7.130) и устанавливаем его устойчивость. Расчет ведем в табличной форме (табл. 5) для тех же сечений, что и в п. 13, принимая установленную ранее крупность камня на откосе d_н = 0,35 м.

Таблица 5

Номер участка	Расстояние от конца подсыпки, м	Q₂ = Q - Q₁, м³/с	h_отн, м, по формуле (7.127)	, м³	v_отк, м/с, по формуле (7.129)	v_{доп(отк)}, м/с, по формуле (7.130)
Подошва откоса	0	3,0	0,083	0,83	3,61	3,65
1	2,37	2,0	0,063	0,63	3,17	3,65
2	4,74	1,0	0,040	0,40	2,5	3,66
3	7,1	0	0	0	0	3,65

Анализ результатов расчета показывает, что устойчивость камня d_н = 0,35 м на откосе обеспечена.

18. Устраиваем конструктивно обратный фильтр подошвы откоса высотой 0,5 м и шириной понизу 1 м.

19. Назначаем у подошвы отсыпки недеформируемое выходное русло из каменной наброски, размеры которого определяем в соответствии с рекомендациями, изложенными в пп. 7.43, 7.44, с учетом специфических особенностей указанных типов выходных русел, изложенных в пп. 7.54, 7.55 и 7.64. Расчет ведем в такой последовательности:

1) определяем толщину слоя однородной наброски, при которой укрепление будет недеформируемым, по формуле (7.81):

2) определяем размеры укрепления:

а) назначаем длину укрепления за подошвой откоса согласно рекомендациям п. 7.44:

. Принимаем

;

б) определяем расчетную длину укрепления (см. п. 7.65), которая складывается из ширины бермы L_б = 3,0 м, длины откоса подсыпки

и длины укрепления у подошвы косогора L' = 2,25 м:

Далее расчет выполняем согласно рекомендациям п. 7.64;

в) определяем предельную глубину размыва в грунте лога по формуле (7.23) с введением в нее коррективов согласно указаниям п. 7.64.

Предварительно вычисляем величины, входящие в эту формулу: по табл. 7.3 находим при D_э = D = 1,50 м

, по табл. 7.2 для выходного русла без гасителей (1 или 1к) находим r = 0,9 и s = 0,6 и согласно п. 7.28 находим

. Отверстие b = b_р = 1,5 м. Средний диаметр грунта d = 0,0005 м, эталонный расход Q_к = 1,6D^5/2 = 1,6·1,5^5/2 = 4,42 м³/с.

Согласно п. 7.64 показатель степени s₁ для недеформируемых выходных русел из каменной наброски равен 5/2 = 2,5.

Таким образом имеем

г) определяем максимальную глубину размыва по формуле (7.21).

Учитывая, что данные об объеме стока W отсутствуют, расчет ведем приближенно, принимая

(как для несвязных грунтов). Отсюда

д) сравниваем толщину наброски

с максимальной глубиной размыва:

, следовательно, возможно назначить выходное русло типа 1, для которого глубину заложения концевой части укрепления h_ук принимаем равной

;

е) определяем ширину воронки размыва B_min в конце укрепления по формуле (7.73) при

Так как

, то принимаем

Тогда при

;

ж) сравниваем ширину воронки размыва B_min с шириной растекания B_раст: B_min = 10,8 > B_раст = 9,4 м и к расчету принимаем ширину укрепления B = 10,8 м.

Результаты расчета нижнего бьефа гофрированной трубы с полученными размерами укреплений на подсыпке приведены на рис. 6.

Приложение 8.1

ПРИМЕРЫ РАСЧЕТА ФИЛЬТРУЮЩИХ НАСЫПЕЙ

Пример 1. Железная дорога III категории пересекает лог треугольного поперечного сечения с откосами, имеющими среднее заложение m_от = 3; высота насыпи H = 3,0 м; длина фильтрующей прослойки l_ф = 15 м; расход притока с бассейна Q_max = 2,0 м³/с (аккумуляцию не учитываем); уклон лога i₀ = 0,005; бытовая глубина h_нб = 0. Грунты лога и в основании насыпи - среднезернистые пески; основание насыпи не защищено обратным фильтром; средний диаметр камней, приведенный к шару, d_н = 20 см; форма камней - остроугольная.

Требуется определить размеры поперечного сечения каменной прослойки напорной фильтрующей насыпи для обеспечения требуемого техническими условиями возвышения бровки полотна над подпертым уровнем (0,5 м) и для обеспечения устойчивости основания.

Решение. Задаем высоту фильтрующей прослойки h_ф = 2 м и определяем площадь ее поперечного сечения, считая его треугольным:

По табл. 8.1 при d_н = 20 см и остроугольной форме камней находим коэффициент турбулентной фильтрации K_ф = 0,43 м/с.

Определяем гидравлический уклон по формуле (8.3):

Вычисляем расстояние от подошвы насыпи до центра тяжести поперечного сечения фильтрующей прослойки:

Определяем глубину воды перед насыпью по формуле (8.1):

H = h_цт + l_ф(i - i₀) = 0,67 + 15(0,15 - 0,005) =

= 2,85 м > h_ф = 2,0 м.

Так как H > H_ф, значит насыпь напорная, т.е. расчет выполнен правильно.

Проверяем устойчивость основания насыпи от ламинарной фильтрации. Для этого находим отношение

по табл. 8.2. При основании из среднезернистых песков, не защищенных обратным фильтром,

В нашем случае H = 2,85 м > H_пр = 1,87 м, т.е. устойчивость основания от ламинарной фильтрации не обеспечена.

Устраиваем обратный фильтр. Тогда из табл. 8.2 находим

. Теперь H = 2,85 м < H_пр = 3,0 м, т.е. устойчивость обеспечена.

Проверяем устойчивость сооружения под воздействием турбулентной фильтрации. Для этого предварительно по формуле (8.5) вычисляем среднюю скорость:

причем пористость p = 0,5 определяем по табл. 8.1.

Вычисляем по формуле (8.4) местную скорость в придонном слое:

v_м = 1,7v = 1,7·0,37 = 0,63 м/с,

что больше, чем допускаемые скорости (см. табл. 2.7) для грунта лога

(при

скорость определяем по графе табл. 2.7 при глубине 0,4 м).

Следовательно, естественный грунт в основании насыпи следует заменить мелким гравием с примесью крупного, для которого

; толщина слоя гравия 15 - 20 см.

Пример 2. Железная дорога III категории пересекает лог прямоугольного поперечного сечения шириной b_ф = 10 м; высота насыпи 3,5 м; коэффициенты заложения откосов m_от = 1,5; длина фильтрующей прослойки (ширина насыпи понизу) l_ф = 16,5 м; расход притока с бассейна Q_max = Q_{max(соор)} = 1,5 м³/с; уклон лога i₀ = 0,003; бытовая глубина

; грунты лога и в основании насыпи - мелкий песок со средним диаметром частиц d = 0,25 мм; средний диаметр камней наброски d_н = 25 см; форма камней - остроугольная.

Требуется определить размеры поперечного сечения каменной прослойки безнапорной фильтрующей насыпи.

Решение. Определяем предварительно по табл. 8.3 предельный уклон лога i_пр = 0,00284 < i₀ = 0,003.

Затем по формуле (8.12) при коэффициенте K_ф = 0,49 (см. табл. 8.1 для d_н = 25 см и остроугольной формы камней) определяем нормальную глубину живого сечения:

По уравнению (8.11) вычисляем

В табл. 8.4 по значению

находим для прямоугольного поперечного сечения значение

Определяем глубину перед насыпью

При этой глубине требование Технических условий о величине возвышения бровки полотна над уровнем воды обеспечивается:

H_нас - H = 3,50 - 1,62 = 1,88 м > 0,50 м.

Проверяем устойчивость основания насыпи против ламинарной фильтрации. Для этого по табл. 8.2 при мелкопесчаных грунтах находим для оснований, не защищенных обратными фильтрами,

При этом H = 1,62 м < H_пр = 1,83 м, следовательно, устойчивость основания обеспечивается.

Проверяем устойчивость сооружения под воздействием турбулентной фильтрации. Для этого:

по формуле (8.15) вычисляем расчетную глубину

где для остроугольных камней p = 0,50 (см. табл. 8.1);

находим площадь поперечного сечения фильтрационного потока

по формуле (8.5) определяем среднюю скорость фильтрации

по формуле (8.4) определяем местную скорость фильтрации

v_м = 1,7v = 1,7·1,38 = 2,34 м/с.

Эта скорость больше допускаемой для мелкопесчаных грунтов v_доп = 0,35 м/с (см. табл. 2.7).

Назначаем укрепление основания фильтрующей насыпи одиночным мощением на щебне из камня средним диаметром d_н = 15 см (см. табл. 2.9), для которого v_доп = 2,5 м/с > v_м = 2,34 м/с.

По уравнению (8.17) проверяем устойчивость низового откоса. Для этого находим

. Угол

соответствует коэффициенту заложения низового откоса насыпи m_от = 1,5;

Разность уровней бьефов z = H - h_б + i₀l_ф = 1,62 - 0 + 0,003·16,5 = 1,67 м. Отсюда z = 1,67 м > z_пр = 0,78 м, т.е. устойчивость откоса не обеспечивается.

Принимаем заложение низового откоса m_от = 1,75, т.е.

. Тогда

и z = 1,67 м < z_пр = 2,32 м, т.е. устойчивость откоса при m_от = 1,75 обеспечивается.

При этом длина фильтрующей прослойки l_ф = 1,5·3,5 + 6,0 + 1,75·3,5 = 17,35 м.

Определяем размеры фильтрующей прослойки вдоль потока (поперек насыпи). Расчет ведем по уравнению (8.11), заменив в нем l_ф на x. Длину прослойки l_ф = 17,35 м разбиваем на пять равных интервалов длиной по

; для сечения в конце каждого интервала вычисляем функцию

и по табл. 8.4 находим

, а затем и глубину потока

Результаты вычислений сведены в таблицу и по ним построен продольный профиль фильтрующей насыпи, приведенный на рисунке.

Номер участка	x, м		(по табл. 8.4)		Принятая высота прослойки h_ср = 1,2h_i
1	3,45	0,00192	0,17	0,92	1,11
2	6,90	0,00382	0,22	1,13	1,35
3	10,35	0,00575	0,25	1,35	1,62
4	13,8	0,00767	0,27	1,46	1,72
5	17,35	0,00962	0,295	1,62	Участок откоса насыпи

Схема к расчету фильтрующей насыпи (пример 2)

Приложение 8.2

ПРИМЕРЫ РАСЧЕТА ПЕРЕЛИВНЫХ НАСЫПЕЙ

Пример 1. Переливная насыпь с отметкой по оси z_оси = 76,0 м находится на автомобильной дороге III категории; длина участка перелива l_пер = 25 м. На данном участке запроектирована прямоугольная труба отверстием b x h_т = 1,0 x 1,5 м, имеющая раструбные оголовки с

; отметка лотка трубы на входе в нее z_л(вх) = 73,0 м; расчетный расход притока с бассейна Q_р = 10 м³/с; сток снеговой, аккумуляция не допускается. Глубиной в нижнем бьефе можно пренебречь.

Требуется определить расход перелива Q_пер, напор относительно оси дороги

, расход в сооружении Q_соор и отметку подпертого уровня ПУВВ.

Решение. Предполагаем, что прямоугольная труба будет работать с полным заполнением входа, т.е. при полунапорном режиме.

Расчет ведем в следующем порядке.

1. Выразим в общем виде применительно к заданным условиям зависимость для определения подпертой глубины перед трубой, работающей в полунапорном режиме, используя формулу (5.20):

Для прямоугольной трубы с раструбными оголовками с

по табл. 5.2 находим

. Площадь поперечного сечения сооружения

Таким образом, выражение для H_соор будет иметь следующий вид:

или

(1)

2. Аналогично H_соор выразим напор над осью дороги по формуле (8.21):

(2)

3. Записываем выражения для ПУВВ для сооружения и переливной насыпи и приравниваем их друг другу (работать они должны при едином ПУВВ); получаем зависимость, из которой подбором находим Q_пер:

или

Заменяя H_соор и

установленными выше выражениями (1) и (2), получаем зависимость (3), из которой подбором находим значение Q_пер, а затем Q_соор, отметку ПУВВ, H_соор и

(3)

В результате расчета получены следующие значения:

Q_пер = 3,9 м³/с; Q_соор = Q = Q_пер = 10,0 - 3,9 = 6,1 м³/с;

H_соор = ПУВВ - z_л(вх) = 76,21 - 73,00 = 3,21 м.

Пример 2. На пересечении водотока автомобильной дорогой III категории запроектирована водопропускная труба в сочетании с переливной насыпью; ширина насыпи поверху b_нас = 12 м, высота H_нас = 3,12 м; поперечный уклон проезжей части i_н = 0,02; заложение низового откоса m_от = 1,5; расход притока с бассейна Q = 76 м³/с; расход, пропускаемый трубой, Q_соор = 34 м³/с; отметка уровня верхнего бьефа ПУВВ = 3,44 м; бытовая глубина в нижнем бьефе h_нб = 2,5 м; длина участка перелива l_пер = 150 м.

Требуется рассчитать переливную насыпь.

Решение. Расход, пропускаемый поверху насыпи, находим по формуле (8.19):

Q_пер = Q - Q_соор = 76 - 34 = 42 м³/с.

Удельный расход на участке перелива

Критическая глубина по формуле (8.20)

Напор относительно оси дороги определяем по формуле (8.21) в предположении, что насыпь не затоплена со стороны нижнего бьефа, и принимая коэффициент расхода m = 0,37:

Напор над верховой бровкой по формуле (8.22)

Отметка оси дороги и верховой бровки по зависимостям (8.23) и (8.24): z_осн = 3,44 - 0,32 = 3,12 м; z_бр = 3,44 - 0,44 = 3,0 м.

Проверяем справедливость принятого предположения о том, что насыпь не затоплена со стороны нижнего бьефа. При высоте насыпи H_нас = 3,12 м (от подошвы до отметки оси проезжей части) H_нас + h_к = 3,12 + 0,20 = 3,32 > h_нб = 2,5 м, т.е. насыпь действительно не затоплена со стороны нижнего бьефа.

При глубинах на оси h = h_к < 0,5 м скорости на верховой бровке не представляют опасности для размыва откоса и обочины у бровки. Поэтому определяем глубины и скорости потока на низовой бровке и у подошвы низового откоса (точки D и F на рис. 8.2, а).

По зависимости (8.28) находим нормальные глубины на участках насыпи CD и DF. При заложении низового откоса m_от = 1,5 уклон его

. Принимаем для проезжей части коэффициент шероховатости n = 0,013, для обочины n = 0,023 и в среднем для участка CD n = 0,018. Для низового откоса с учетом растительности примем n = 0,04.

Нормальные глубины:

По уравнению неравномерного движения (см. гл. 2) находим глубины потока на низовой бровке (точка D) и у подошвы (точка F): h_D = 0,14 м; h_F = 0,08 м, а с учетом аэрации (см. п. 8.18) при m_от = 1,5 h_D = 0,14·1,2 = 0,168 м и h_F = 0,08·1,2 = 0,096 м.

Вычисляем по формуле (8.30) скорости потока на оси дороги, низовой бровки и у подошвы низового откоса:

Определяем характер сопряжения в нижнем бьефе насыпи. Для этого по формуле (2.20) находим глубину, сопряженную с глубиной у подошвы насыпи:

где

[см. формулу (2.10)].

Поскольку

, сопряжение за насыпью происходит с затопленным гидравлическим прыжком, и устройство водобойных сооружений не требуется.

Приложение 9.1

ТАБЛИЦЫ ОСНОВНЫХ РАСЧЕТНЫХ ХАРАКТЕРИСТИК КАНАВ

Таблица 1

Допускаемые скорости потока

Наименование грунта или укрепления	Характеристика грунта или укрепления	Высота выступов шероховатости , мм, ее формула	Значение , м/с, или ее формула
Несвязный грунт - песок мелко- и среднезернистый	d = 0,05 мм	0,035
	d = 0,25 мм	0,175
	d = 1,0 мм	0,7
Несвязный грунт - песок крупнозернистый, гравий и галька	d = 1,0 мм	0,7
Связный (глинистый) грунт	Структура грунта нарушена; грунт максимально водонасыщен; инородных включений в грунте и растительности на его поверхности нет	3,0	0,17 + 25C_р
Конгломерат, мергель, сланцы	-	50	1,5
Пористый известняк, плотный конгломерат, слоистый известняк, известковый песчаник	Грубая поверхность породы	50	2,2
	Гладкая поверхность породы	20	2,5
Доломитовый песчаник, плотный, неслоистый известняк, мрамор	Грубая поверхность породы	50	3,1
Доломитовый песчаник, плотный, неслоистый известняк, мрамор	Гладкая поверхность породы	20	3,5
Граниты, диабазы, базальты, андезиты, кварциты	-	50	12,0
Одерновка плашмя	-	50	0,67
Хворостяные выстилки	Толщина не менее 20 см	100	1,65
Фашинные тюфяки	Толщина не менее 50 см	100	2,30
Габионы	Не менее 0,5 x 0,5 x 1,0 м	50	3,15
Каменная наброска	-
Мощение камнем	-
Бутовая кладка	Предел прочности на сжатие:
	10 МПа = 100 кгс/см²	50	2,4
	30 МПа = 300 кгс/см²	50	5,3
Бетон как одежда для крепления <1>	-	5	3,10
Бетонные водоводы с гладкой поверхностью <1>	-	2	5,50
Сборные покрытия из бетонных блоков <1>	Блоки сочленены по всей поверхности защищаемого объекта	25	3,10

--------------------------------

<1> Класс бетона по прочности и марки морозостойкости и водонепроницаемости принимают в соответствии с действующими нормативными документами [39].

Примечания. 1. В приведенных формулах приняты обозначения; m_от - коэффициент откоса боковой стенки канала; m₀ - коэффициент естественного откоса грунта для несвязных грунтов, приближенно можно принимать m₀ = 1,5; g - ускорение силы тяжести;

- удельный вес соответственно грунта и воды; C_р - сцепление грунта, МПа, определяемое по табл. 2 настоящего приложения; d - средний размер камней наброски мощения; d_max - среднее значение наибольших размеров камней.

2. В формуле для определения

при мощении камнем в зависимости от конструкции принимают: для одиночной мостовой, нормально уложенной и расклиненной щебнем

; для двойного мощения, а также для одиночного, но при наличии бордюрных рядков из крупного камня и поперечных поясков через 5 - 10 м по длине покрытия

; для одиночного мощения в клетках размером не более 2,5 x 2,5 м из крупного камня или ивового плетня

3. В той же формуле в зависимости от характера основания, на которое укладывается мощение, принимают: для галечниковых и гравийных грунтов, а также при наличии подготовки в виде обратного фильтра

; при плотных суглинистых грунтах

; при слабых суглинистых грунтах

4. В формулах для несвязных грунтов член

учитывают лишь в случаях определения v_доп для участков поверхности на откосах каналов при условии обеспечения их общей устойчивости.

5. При наличии трещиноватости или выветрелости каменных пород значения размывающих скоростей надо уменьшать. Для очень выветрелых пород (разборных) размывающие скорости следует определять как для несвязного грунта соответствующей крупности.

6. Качество материалов конструкций укрепления, а также технология их укладки должны отвечать требованиям соответствующих технических условий и норм.

7. Конструкции укреплений не должны допускать вымывания частиц грунта основания через промежутки между элементами укреплений.

Таблица 2

Расчетные коэффициенты сцепления глинистых грунтов

Влажность на границе раскатывания, %	Значения коэффициента сцепления C_р, МПа, при коэффициенте пористости
Влажность на границе раскатывания, %	0,41 - 0,5	0,51 - 0,6	0,61 - 0,7	0,71 - 0,8	0,81 - 0,95	0,96 - 1,1
< 9,4	0,002	0,001	0,001	-	-	-
9,5 - 12,4	0,003	0,001	0,001	-	-	-
12,5 - 15,4	0,014	0,007	0,004	0,002	-	-
15,5 - 18,4	-	0,019	0,011	0,008	0,004	0,002
18,5 - 22,4	-	-	0,028	0,019	0,010	0,006
22,5 - 26,4	-	-	-	0,036	0,025	0,012
26,5 - 30,4	-	-	-	-	-	0,022

Таблица 3

Коэффициенты шероховатости n поверхности канавы

N п/п	Характер поверхности русла канавы	n
1	Мелкозернистые несвязные грунты с частицами d <= 4 мм Бетонные водоводы с гладкой поверхностью	0,015
2	Несвязные грунты с частицами 4 < d <= 9 мм Связные грунты Бетон как одежда для укреплений	0,0175
3	Несвязные грунты с частицами 9 < d <= 18 мм	0,02
4	Несвязные грунты с частицами 18 < d <= 36 мм Скальные грунты - известняки, известковый песчаник, плотный конгломерат, мрамор с тщательно обработанной поверхностью Сборные покрытия из бетонных блоков	0,0225
5	Несвязные грунты с частицами 36 < d <= 64 мм Мощение с наибольшими размерами камней 12,5 < d_max <= 22 см	0,025
6	Несвязные грунты 65 < d <= 150 мм Скальные грунты, перечисленные в п. 4, с грубо обработанной поверхностью, а также граниты, диабазы, базальты, андезиты, кварциты, порфиры Одерновка плашмя Бутовая кладка Мощение с наибольшими размерами камней d_max > 22 см	0,0275

Таблица 4

Допускаемые пристеночные скорости

, сгруппированные

по сопротивляемости дна и стенок каналов воздействию

водного потока

, м/с	Характеристика грунта или укрепления	Средний диаметр частиц d, мм	Коэффициент сцепления C_р, МПа
0,11	Несвязные грунты	0,05	-
0,16	То же	0,25	-
0,20	"	1,0	-
0,35	"	3,0	-
0,35	Связные грунты	-	0,007
0,45	Несвязные грунты	5,0	-
0,45	Связные грунты	-	0,011
0,64	Несвязные грунты	10,0	-
0,64	Связные грунты	-	0,019
0,64	Одерновка плашмя	-	-
1,0	Несвязные грунты	25,0	-
1,0	Связные грунты	-	0,034
1,5	Несвязные грунты	50,0	-
1,5	Связные грунты	-	0,053
1,5	Конгломерат, мергель, сланцы	-	-
1,5	Каменная наброска	75,0	-
2,0	Несвязные грунты	100,0	-
2,0	Каменная наброска	150,0	-
2,0	Мощение камнем	100,0	-
2,2	Пористый известняк, плотный конгломерат, слоистый известняк, известковый песчаник с грубой поверхностью породы	-	-
2,4	Мощение камнем	150,0	-
2,4	Бутовая кладка с пределом прочности на сжатие 10 МПа	-	-
2,5	Несвязный грунт	150,0	-
2,5	Пористый известняк, плотный конгломерат, слоистый известняк, известковый песчаник с гладкой поверхностью породы	-	-
2,5	Каменная наброска	225,0	-
2,65	Мощение камнем	175,0	-
2,8	То же	200,0	-
3,0	Доломитовый песчаник, плотный, неслоистый известняк, мрамор с грубой поверхностью породы; бетон как одежда для крепления и сборные бетонные покрытия из бетонных блоков <1>	-	-
3,5	Доломитовый песчаник, плотный, неслоистый известняк, мрамор с гладкой поверхностью	-	-
5,3	Бутовая кладка с пределом прочности на сжатие 30 МПа	-	-
6,0	Бетонные водоводы с гладкой поверхностью <1>	-	-
12,0	Граниты, диабазы, базальты, андезиты, кварциты, порфиры	-	-

--------------------------------

<1> Класс бетона по прочности и марки морозостойкости и водонепроницаемости определяют в соответствии с действующими нормативными документами [39].

Примечание. Значения

для мощения камнем определены для одиночной нормально уложенной мостовой, расклиненной щебнем при наличии подготовки в виде обратного фильтра или уложенной на галечниковое или гравийное основание. Удельный вес камней мощения, наброски и частиц несвязного грунта

принят равным 26,5 кН/м³.

Приложение 11.1

ЗНАЧЕНИЯ РАСХОДА Q_*·10³ ДЛЯ ЛОТКА ТРЕУГОЛЬНОЙ ФОРМЫ СЕЧЕНИЯ

С ВЕРТИКАЛЬНОЙ ГРАНЬЮ

Габаритные размеры дождеприемника		Значения расхода Q_*·10³, м³/с, при продольном уклоне лотка i₀
Ширина b, м	Длина l, м	0,003	0,005	0,01	0,02	0,03	0,04	0,05	0,06	0,07
Поперечный уклон i_п = 0,01
0,4	0,4	-	0,9	1,1	1,4	1,4	1,6	1,7	1,7	-
	0,8	-	1,7	1,9	2,2	2,4	2,6	2,7	2,9	-
	1,2	-	2,5	2,8	3,2	3,5	3,7	3,9	4,0	-
	1,6	-	3,4	3,8	4,3	4,6	4,9	5,1	5,3	-
	2,4	-	5,7	6,3	7,0	7,5	7,8	8,1	8,4	-
0,6	0,3	-	1,5	1,8	2,2	2,5	2,7	2,9	3,1	-
	0,4	-	1,8	2,2	2,7	3,0	3,3	3,5	3,7	-
	0,6	-	2,5	2,9	3,5	3,9	4,3	4,5	4,6	-
	0,8	-	3,7	3,7	4,4	4,9	5,2	5,5	5,8	-
	1,6	-	5,9	6,7	7,8	8,5	9,1	9,5	9,9	-
	2,4	-	9,1	10,2	11,6	12,6	13,3	13,9	14,4	-
0,8	0,4	-	3,0	3,7	4,5	5,1	5,6	6,0	6,4	-
	0,8	-	5,1	6,0	7,2	8,1	8,8	9,3	9,8	-
	1,6	-	9,1	10,6	12,4	13,6	14,6	15,4	16,1	-
1,2	0,4	-	6,3	7,8	9,8	11,2	12,4	13,4	14,3	-
1,2	0,8	-	10,1	12,2	15,0	20,0	18,5	19,9	21,0	-
1,6	0,4	-	10,8	13,6	17,3	29,3	22,5	24,0	25,6	-
1,6	0,8	-	16,8	10,7	25,7	46,1	32,2	34,9	36,7	-
2,4	0,4	-	23,9	30,6	39,6	64,7	51,5	56,1	60,2	-
2,4	0,8	-	35,5	44,4	56,2	76,0	71,6	77,5	82,7	-
3,2	0,4	-	42,9	55,6	72,7	85,3	95,6	104,5	112,4	-
3,2	0,8	-	61,5	78,0	99,9	115,9	128,9	139,9	149,8	-
Поперечный уклон i_п = 0,02
0,2	0,8	1,4	1,5	1,6	1,8	1,6	1,4	1,3	1,1	1,0
0,3	0,3	0,9	1,0	1,2	1,5	1,5	1,4	1,3	1,2	-
0,4	0,4	2,0	2,1	2,4	2,9	3,1	2,9	2,7	2,6	2,5
	0,8	-	3,7	4,2	4,9	5,5	5,9	6,3	6,6	-
	1,2	-	5,5	6,1	7,1	7,8	8,4	8,8	9,3	-
	1,6	-	7,5	8,2	9,5	10,4	11,0	11,6	12,2	-
	2,4	-	12,5	13,5	15,3	16,6	17,7	18,5	19,2	-
0,6	0,3	-	3,4	4,1	5,1	5,8	6,4	7,0	7,4	-
	0,4	-	4,1	4,9	6,1	6,9	7,6	8,2	8,7	-
	0,6	-	5,5	6,5	7,9	9,0	9,8	10,5	11,2	-
	0,8	-	7,0	8,1	9,8	11,0	12,0	12,8	13,5	-
	1,6	-	13,0	14,7	17,2	19,1	20,5	21,8	22,8	-
	2,4	-	20,0	22,1	25,6	28,1	30,0	31,7	33,1	-
0,8	0,4	-	6,9	8,3	10,5	12,0	13,3	14,4	15,3	-
	0,8	-	11,3	13,3	16,3	18,4	20,2	21,6	22,9	-
	1,6	-	20,1	23,0	27,4	30,5	33,1	35,2	37,1	-
1,2	0,4	-	14,7	18,2	23,2	26,9	30,0	32,6	34,9	-
1,2	0,8	-	22,8	27,6	34,4	39,3	43,4	46,8	49,9	-
1,6	0,4	-	25,7	32,4	41,8	48,8	54,6	59,5	64,0	-
1,6	0,8	-	38,6	47,3	59,7	68,9	76,3	82,7	88,4	-
2,4	0,4	-	58,8	75,4	99,0	116,4	130,8	143,3	154,4	-
2,4	0,8	-	83,6	104,6	134,4	156,5	174,5	190,0	203,8	-
3,2	0,4	-	108,0	140,3	185,8	219,8	247,9	272,3	194,1	-
3,2	0,8	-	148,2	188,0	244,3	286,1	320,4	350,1	376,5	-
Поперечный уклон i_п = 0,03
0,2	0,8	2,2	2,3	2,4	2,7	2,9	3,1	2,7	2,5	2,3
0,3	0,3	1,6	1,7	1,9	2,3	2,6	2,8	2,7	2,7	2,6
0,4	0,4	3,3	3,4	3,8	4,7	5,4	5,7	5,4	5,3	5,2
	0,8	-	6,0	6,6	7,8	8,7	9,4	10,0	10,6	-
	1,2	-	8,8	9,5	10,7	12,2	13,2	14,0	14,7	-
	1,6	-	12,0	12,7	14,6	16,1	17,3	18,3	19,2	-
	2,4	-	20,0	20,8	23,5	25,7	27,4	28,8	30,1	-
0,6	0,3	-	5,6	6,6	8,3	9,6	10,6	11,5	12,3	-
	0,4	-	6,8	7,9	9,8	11,3	12,5	13,5	14,4	-
	0,6	-	9,1	10,4	12,7	14,5	15,9	17,1	18,2	-
	0,8	-	11,4	12,9	15,5	17,5	19,2	20,6	21,8	-
	1,6	-	21,0	22,9	26,9	29,9	32,4	34,5	36,2	-
	2,4	-	32,1	34,2	39,5	43,6	46,9	49,7	52,2	-
0,8	0,4	-	11,4	13,6	17,2	19,8	22,0	23,9	25,5	-
	0,8	-	18,4	21,3	26,1	29,7	32,6	35,2	37,4	-
	1,6	-	32,4	36,0	43,0	48,2	52,5	56,2	59,3	-
1,2	0,4	-	24,8	30,4	38,9	45,3	50,6	55,2	59,3	-
1,2	0,8	-	37,8	44,8	56,0	64,4	71,4	77,3	82,6	-
1,6	0,4	-	44,1	54,8	71,1	83,3	93,4	102,2	110,0	-
1,6	0,8	-	64,6	77,9	98,7	114,3	127,2	138,3	148,2	-
2,4	0,4	-	102,4	130,3	171,4	202,5	128,3	250,7	270,7	-
2,4	0,8	-	142,3	175,8	226,5	264,9	296,5	323,9	348,2	-
3,2	0,4	-	190,7	245,8	326,6	387,7	438,5	474,4	522,4	-
3,2	0,8	-	255,3	320,5	417,8	491,3	552,2	556,1	652,0	-
Поперечный уклон i_п = 0,04
0,2	0,8	3,1	3,2	3,4	3,7	4,1	4,3	4,6	4,3	4,0
0,3	0,3	2,3	2,4	2,7	3,2	3,7	4,0	4,3	4,1	4,1
0,4	0,4	4,8	4,9	5,4	6,5	7,4	8,1	8,8	8,7	8,6
	0,8	-	8,6	9,1	10,7	12,0	13,0	13,9	14,7	-
	1,2	-	12,6	13,1	15,1	16,7	18,1	19,2	20,3	-
	1,6	-	17,3	17,5	19,9	21,9	23,6	25,0	26,3	-
	2,4	-	28,6	28,3	31,6	34,6	37,0	39,0	40,8	-
0,6	0,3	-	8,2	9,5	11,9	13,7	15,2	16,6	17,7	-
	0,4	-	9,9	11,3	13,9	16,0	17,7	19,2	20,5	-
	0,6	-	13,2	14,6	17,8	20,3	22,4	24,1	25,7	-
	0,8	-	16,4	18,8	21,6	24,6	26,8	28,9	30,7	-
	1,6	-	30,1	31,6	36,8	41,1	44,6	47,6	50,2	-
	2,4	-	45,9	46,9	53,7	59,3	64,0	68,0	71,5	-
0,8	0,4	-	16,8	19,6	24,6	28,4	31,6	34,4	36,8	-
	0,8	-	26,8	30,0	36,6	41,8	46,0	49,7	53,0	-
	1,6	-	46,6	50,0	59,3	68,7	72,0	78,0	82,6	-
1,2	0,4	-	36,8	44,2	56,5	66,0	73,9	80,7	86,8	-
1,2	0,8	-	55,3	63,9	79,7	91,9	102,0	110,8	118,5	-
1,6	0,4	-	65,8	80,6	104,3	121,6	137,5	151,0	162,7	-
1,6	0,8	-	95,1	112,2	141,9	164,8	183,8	200,2	214,8	-
2,4	0,4	-	154,7	194,1	255,2	302,1	341,2	375,3	405,9	-
2,4	0,8	-	211,7	256,9	330,7	387,5	434,7	475,7	512,3	-
3,2	0,4	-	290,0	368,7	491,0	584,1	661,7	729,4	790,2	-
3,2	0,8	-	382,8	473,2	616,3	726,3	817,9	897,5	968,7	-
Поперечный уклон i_п = 0,1 (фрагмент лотка разделительной полосы дорог I - III категорий)
0,2	0,8	17,5	13,0	9,9	10,0	10,7	11,5	12,2	12,9	13,5
0,3	0,3	11,2	9,5	8,6	9,7	10,9	11,9	12,9	13,9	14,7
0,4	0,4	22,6	19,4	17,6	19,9	22,5	24,8	26,7	28,6	30,4
Поперечный уклон i_п = 0,125 (фрагмент лотка разделительной полосы дорог I - III категорий)
0,2	0,8	23,9	19,5	13,6	13,0	13,8	14,7	15,6	16,4	17,2
0,3	0,3	15,5	14,1	12,0	13,0	14,5	15,9	17,2	18,4	19,5
0,4	0,4	31,3	28,6	24,5	26,7	29,9	32,7	35,6	38,1	40,3
Поперечный уклон i_п = 0,270 (внешний фрагмент прикромочного лотка дорог I - III категорий при использовании блоков Б-1)
0,2	0,8	74,3	61,0	49,5	37,9	36,8	37,7	39,3	40,9	42,5
0,3	0,3	49,1	45,7	43,0	40,6	42,8	45,9	49,2	52,2	55,2
0,4	0,4	96,5	92,5	88,9	84,0	89,2	27,7	102,1	109,5	115,2
Поперечный уклон i_п = 0,450 (внешний фрагмент прикромочного лотка дорог I - III категорий при использовании блоков Б-1)
0,2	0,8	145,4	122,8	99,9	83,9	75,2	73,3	74,2	76,1	78,2
0,3	0,3	101,1	93,8	90,4	89,9	90,3	94,5	99,4	104,6	110,2
0,4	0,4	202,9	192,0	184,6	186,1	187,6	207,9	207,9	219,2	230,1

Приложение 11.2

ЗНАЧЕНИЯ РАСХОДА Q_*·10³ ДЛЯ ВНУТРЕННЕГО ФРАГМЕНТА

ПРИКРОМОЧНОГО ЛОТКА ДОРОГ I - III КАТЕГОРИЙ

Поперечный уклон прикромочного лотка i_п	Габаритные размеры дождеприемного лотка		Значения Q_*·10³, м³/с, при продольном уклоне прикромочного лотка i₀
Поперечный уклон прикромочного лотка i_п	Ширина b, м	Длина l, м	0,003	0,005	0,01	0,02	0,03	0,04	0,05	0,06	0,07
0,02	0,00	1,0	0,8	0,8	0,7	0,7	0,6	0,5	0,4	0,3	0,2
		1,25	1,4	1,3	1,2	1,2	1,1	0,8	0,6	0,5	0,4
		1,50	2,1	1,9	1,8	1,8	1,7	1,3	0,9	0,8	0,7
		1,75	3,0	2,8	2,7	2,6	2,5	1,8	1,4	1,1	0,9
		2,0	4,1	3,9	3,8	3,6	3,4	2,4	1,9	1,5	1,3
0,03	0,00	1,0	1,4	1,2	1,1	1,1	1,0	1,0	0,9	0,7	0,6
		1,25	2,4	2,1	2,0	1,9	1,8	1,7	1,5	1,4	1,1
		1,50	3,6	3,4	3,1	3,0	2,8	2,7	2,3	1,9	1,6
		1,75	5,2	4,4	4,3	4,2	4,1	4,0	3,4	2,8	2,4
		2,0	7,0	6,3	6,2	6,1	6,0	5,8	4,6	3,8	3,3
0,04	0,00	1,0	2,3	1,8	1,7	1,6	1,5	1,5	1,3	1,2	1,1
		1,25	3,6	3,1	3,0	2,9	2,8	2,8	2,7	2,3	1,9
		1,50	5,5	4,7	4,3	4,2	4,1	4,0	3,7	3,4	3,0
		1,75	7,9	7,0	6,6	6,2	5,9	5,7	5,5	5,0	4,3
		2,0	10,9	9,5	8,8	8,3	8,1	7,8	7,5	6,8	5,8

СПИСОК ЛИТЕРАТУРЫ

1. Бегам Л.Г., Цыпин В.Ш. Надежность мостовых переходов через водотоки. М.: Транспорт, 1984. 254 с.

2. Беликов В.В., Залесский В.Ф. Исследование течений в нижних бьефах водопропускных труб численными методами//Тр. ВНИИТрансстрой. Пути повышения качества и надежности проектирования и строительства транспортных сооружений. М.: ЦНИИС, 1988. С. 131 - 134.

3. Беликов В.В., Семенов А.Ю. Явный численный метод распада разрывов для решения уравнений мелкой воды//Предпринт, N 42. М.; ИОФ АН СССР, 1988. 46 с.

4. Богданов Г.Г. Гидравлический расчет беспороговых водосливов в укрепляемых руслах//Тр. БелИИЖТ. Вып. 50. Минск; Вышейшая школа, 1968. 140 с.

5. Большаков В.А. Гидравлические сооружения на автомобильных дорогах. М.; Транспорт, 1985. 319 с.

6. Большаков В.А., Галецкий В.И. Мягкие укрепления отводящих русел водопропускных труб//Автомобильные дороги. 1984. N 1. С. 14 - 15.

7. Букраба Н.М., Денисенко И.Д. Оценка работы бетонных и мягких укреплений за дорожными трубами//Трансп. стр-во. 1985. N 9. С. 12 - 13.

8. Волченков Г.Я. Расчет размыва у конусов моста//Трансп. стр-во. 1981. N 4. С. 46.

9. Временная инструкция по проектированию сооружений для очистки поверхностных вод (СН 496-77), М.: Стройиздат, 1978. 40 с.

10. Высоцкий Л.И. Управление бурными потоками на водосбросах. М.: Энергия, 1977. 280 с.

11. Гидравлические расчеты конструкций, управляющих бурными потоками. Л.: Энергия, 1974. С. 110.

12. Дополнения к "Руководству по классификации переходов через малые водотоки по водопропускной способности". М.: МПС, 1983. 21 с.

13. Емцев Б.Т. Двухмерные бурные потоки. М.: Энергия, 1967. 212 с.

14. Железняков Г.В. Гидравлика и гидрология. М.: Транспорт, 1989. 376 с.

15. Инструкция по расчету ливневого стока воды с малых бассейнов (ВСН 63-76). М.: Оргтрансстрой, 1976. 104 с.

16. Константинов Н.М., Шаталов М.Л. Бурный поток на участке прямолинейного сужения водосборного сооружения//Сб. "Методы исследований и гидравлических расчетов водосборных гидротехнических сооружений". Л.: Энергоатомиздат, 1985. С. 96 - 99.

17. Круцак М.Д., Большаков В.А., Букраба И.И. Защита выходных участков водопропускных труб//Автомобильные дороги. 1979. N 6. С. 18.

18. Круцак М.Д., Максименко С.Ф. Эксплуатация горных автомобильных дорог и защита окружающей среды. Киев: Будiвельник, 1981. 191 с.

19. Лотковые сооружения на лесохозяйственных автомобильных дорогах. Типовые материалы для проектирования (508-0-50.87). М.: Стройиздат, 1987. 43 с.

20. Лятхер В.М., Милитеев А.Н. Гидравлические исследования численными методами//Водные ресурсы. 1981. N 3. С. 51 - 69.

21. Милитеев А.Н., Сладкевич М.С. Разностная схема для решения плановых уравнений мелкой воды//Деп. Информэнерго. N 1234, ЭНД-831. М., 1983. 4 с.

22. Мирцхулава Ц.Е. Размыв русел и методика оценки их устойчивости. М.: Колос, 1967. 179 с.

23. Муромов В.С., Лившиц М.Х. Косогорные водопропускные трубы. М., Стройиздат, 1975. 144 с.

24. Наставление по изысканиям и проектированию железнодорожных и автодорожных мостовых переходов через водотоки (НИМП-72). М.: Транспорт, 1972. 280 с.

25. Перевозников Б.Ф. Водопропускные сооружения лоткового типа. М.: Транспорт, 1978. 170 с.

26. Перевозников Б.Ф. Расчеты максимального стока при проектировании дорожных сооружений. М.: Транспорт, 1975. 296 с.

27. Петров Н.А., Уйма. Особенности работы и методика расчета дождеприемников поверхностного водоотвода//Тр. МАДИ. Течения жидкости при различной степени нестационарное и их практическое применение на транспорте и в строительстве, 1976. 37 с.

28. Подсистема автоматизированного проектирования водопропускных труб на железнодорожных линиях//Мосгипротранс Минтрансстроя СССР, 1989. 57 с.

29. Пособие по определению расчетных гидрологических характеристик. Л.: Гидрометиздат, 1984. 448 с.

30. Примеры гидравлических расчетов. М.: Транспорт, 1988. 439 с.

31. Розанов Н.П. Гидравлические расчеты водопропускных труб. М.: ВНИИГиМ, 1979. 69 с.

32. Ротенбург И.С., Вольнов В.С., Поляков М.П. Мостовые переходы. М.: Высшая школа, 1977. 328 с.

33. Руководство по классификации переходов через малые водотоки по водопропускной способности (временное). М.: ЦНИИС, 1975. 100 с.

34. Руководство по расчету ливневого стока воды с малых бассейнов: М.: ЦНИИС, 1978. 44 с.

35. Руководство по расчету турбулентной фильтрации в каменнонабросных сооружениях. М.: Энергия, 1975. 51 с.

36. Сели в СССР и меры борьбы с ними/Г.В. Лопатин, В.Е. Иогансон, М.С. Гагошидзе и др. М.: Наука, 1964. 280 с.

37. Срибный М.Ф. Теория и практика фильтрующих сооружений. М.: Трансжелдориздат, 1934. 208 с.

38. СНиП 2.05.02-85. Автомобильные дороги. М.: ЦИТП Госстроя СССР, 1985. 152 с.

39. СНиП II-39-76. Часть II. Нормы проектирования. Гл. 39. Железные дороги колеи 1520 мм. М.: Стройиздат, 1977. 70 с.

40. СНиП 2.01.14-83. Определение гидрологических характеристик. М.: Стройиздат, 1985. 36 с.

41. СНиП IV-13-71. Сметные нормы. Гл. 8. Буровзрывные работы. М.: Стройиздат, 1982. 132 с.

42. СНиП 2.02.01-83. Основания зданий и сооружений. М.: Стройиздат, 1985. 41 с.

43. Студеничников Б.И. Размывающая способность потока и методы русловых расчетов. М.: Стройиздат, 1964. 184 с.

44. Хомяк Я.В. Гидравлiчнi разрахунки малих мостiв i дорожних труб. Киiв: Вiдавництво Киiвського унiверситету, 1961. 91 с.

45. Шаталов М.Л. Параметры косых прыжков на участке сужения при наклонном дне//Сб. "Гидравлика водопропускных сооружений". Саратов, 1985. С. 87 - 90.