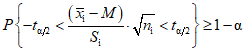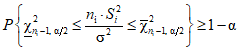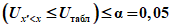СПРАВКА
Источник публикации
М.: Издательство стандартов, 1985
Примечание к документу
Название документа
"МИ 656-84. Методические указания. Оценка достоверности численных данных о свойствах нефти и нефтепродуктов"
(утв. и введены в действие Протоколом НТС ВНИЦ ПВ от 11.12.1984 N 13)
"МИ 656-84. Методические указания. Оценка достоверности численных данных о свойствах нефти и нефтепродуктов"
(утв. и введены в действие Протоколом НТС ВНИЦ ПВ от 11.12.1984 N 13)
Содержание
Протоколом
научно-технического совета ВНИЦ ПВ
от 11 декабря 1984 г. N 13
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ОЦЕНКА ДОСТОВЕРНОСТИ ЧИСЛЕННЫХ ДАННЫХ
О СВОЙСТВАХ НЕФТИ И НЕФТЕПРОДУКТОВ
МИ 656-84
РАЗРАБОТАНЫ Казанским филиалом Всесоюзного ордена Трудового Красного Знамени научно-исследовательского института физико-технических и радиотехнических измерений (ВНИИФТРИ); Всесоюзным научно-исследовательским центром по изучению свойств поверхности и вакуума (ВНИЦ ПВ)
ИСПОЛНИТЕЛИ:
В.Г. Гизатуллина, канд. техн. наук А.Д. Козлов (руководитель темы)
ВНЕСЕНЫ Казанским филиалом ВНИИФТРИ
Директор Н.М. Хусаинов
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ научно-техническим советом ВНИЦ ПВ от 11 декабря 1984 г. (протокол N 13)
Настоящие методические указания устанавливают единые принципы оценки достоверности данных о физико-химических и эксплуатационных свойствах нефти и нефтепродуктов.
1.1. Оценку данных о свойствах нефти и нефтепродуктов проводят с целью определения степени достоверности этих данных, установления числового интервала их погрешности и отбора наиболее надежных данных для обеспечения потребности народного хозяйства достоверной информацией о свойствах нефти и нефтепродуктов, необходимой при оценке их качества.
1.2. Под оценкой достоверности численных данных понимают:
выбор и обоснование методов отбора и анализа исходных данных;
нахождение оптимальных требований к методам и средствам измерений, применяемых при исследовании показателя или свойства;
выбор и обоснование методов анализа и обобщения данных для конкретной области их применения;
определение алгоритмов обработки данных.
ИС МЕГАНОРМ: примечание. Взамен ГОСТ 8.326-78 Постановлением Госстандарта СССР от 15.12.1989 N 3554 с 01.01.1991 введен в действие ГОСТ 8.326-89. Взамен ГОСТ 8.326-89, утратившего силу на территории Российской Федерации с 01.12.2001, введены ПР 50.2.009-94 "ГСИ. Порядок проведения испытаний и утверждения типа средств измерений" (Постановление Госстандарта России от 27.09.2001 N 394-ст). |
1.3. При оценке достоверности численных данных о свойствах нефти и нефтепродуктов необходимо руководствоваться ГОСТ 8.344-79, ГОСТ 22013-76, ГОСТ 8.326-78, МУ 38.101003-81, РД 50-262-81, РД 50-326-82.
2.1. При отборе численных данных о свойствах нефти и нефтепродуктов необходимо учитывать следующие характеристики продуктов и их свойств:
марку продукта и его назначение;
технологию получения продукта;
условия транспортировки и хранения;
исходное сырье;
метод определения продукта и его свойств.
2.2. Исходной информацией при отборе численных данных о свойствах нефти и нефтепродуктов являются результаты испытаний, полученные: стандартизованными методами; методами, включенными в комплексы квалификационной оценки; нестандартизованными методами, прошедшими метрологическую аттестацию в соответствии с МУ 38.101003-81; на специальных установках, прошедших метрологическую аттестацию в соответствии с ГОСТ 8.326-78.
2.3. При отборе данных предпочтительно использовать результаты, полученные по аттестованным методикам (РД 50-326-82).
3.1. Настоящие методические указания рекомендуют оценивать данные двумя величинами: математическим ожиданием M и дисперсией 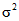 при заданном уровне значимости
при заданном уровне значимости 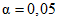 . В основу определения этих величин положено следующее предположение: результаты испытаний x1, x2, ..., xn являются независимыми в совокупности величинами и распределены по нормальному закону.
. В основу определения этих величин положено следующее предположение: результаты испытаний x1, x2, ..., xn являются независимыми в совокупности величинами и распределены по нормальному закону.
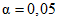 . В основу определения этих величин положено следующее предположение: результаты испытаний x1, x2, ..., xn являются независимыми в совокупности величинами и распределены по нормальному закону.
. В основу определения этих величин положено следующее предположение: результаты испытаний x1, x2, ..., xn являются независимыми в совокупности величинами и распределены по нормальному закону.3.2. Качественное заключение о нормальности распределения получают графическим путем, используя метод гистограмм (рекомендуется для случая, когда n > 50). Если объем имеющихся численных данных недостаточен (n < 50), то гистограмму строят по совокупности малых выборок. Однако строить гистограмму в этом случае возможно, если выборки малого объема проверены попарно на однородность.
3.3. Однородность выборок проверяют по критерию Вилкоксона и его модификации - критерию Манна - Уитни. Пусть x1, ..., 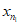 , x'2, ...,
, x'2, ..., 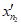 - данные двух выборок. Обозначим через Ux'<x число пар (xi; x'j), где x'j < xi. Приведенная статистика Манна-Уитни (Ux'<x) линейно связана со статистикой Вилкоксона (Tx; Tx') соотношением
- данные двух выборок. Обозначим через Ux'<x число пар (xi; x'j), где x'j < xi. Приведенная статистика Манна-Уитни (Ux'<x) линейно связана со статистикой Вилкоксона (Tx; Tx') соотношением
Ux'<x = n1·n2 + n1(n1 + 1)/2 - Tx' =
= Tx - n2(n2 + 1)/2, (1)
где n1, n2 - число данных в каждой выборке.
Для нахождения статистики Tx и Tx' из двух выборок составляется общий вариационный ряд 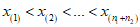 , в котором для одного значения xi определяют номер места <*> ri - ранг. Аналогично определяют ранги aj для одного значения x'j.
, в котором для одного значения xi определяют номер места <*> ri - ранг. Аналогично определяют ранги aj для одного значения x'j.
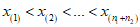 , в котором для одного значения xi определяют номер места <*> ri - ранг. Аналогично определяют ранги aj для одного значения x'j.
, в котором для одного значения xi определяют номер места <*> ri - ранг. Аналогично определяют ранги aj для одного значения x'j.--------------------------------
<*> Если два или более значения совпадают, то им приписывают один и тот же ранг, равный среднему арифметическому рангов, несовпавших значений.
Вычисляют значения Tx и Tx
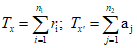 (2)
(2)Однородность выборок не отвергается, если эмпирическое значение Ux'<x превосходит табличное значение Uтабл (при уровне значимости 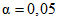 ).
).
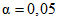 ).
).Значения Uтабл представлены в табл. 1 приложения 1 при условии
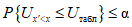 .
.Критерий Вилкоксона применим для любого вида распределения и не требует большого числа данных в каждой выборке (n >= 5).
Однородность выборок по критерию Вилкоксона и Манна - Уитни выявляется как по форме распределения, так и по средним.
3.4. Если гипотеза об однородности выборок не противоречит данным общей выборки, то выполняют проверку крайних значений по ГОСТ 11.002-73 при уровне значимости, равном 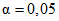 , и строят гистограмму.
, и строят гистограмму.
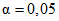 , и строят гистограмму.
, и строят гистограмму.3.5. Проверку нормальности закона распределения выполняют с помощью коэффициентов асимметрии и эксцесса, согласно приложению I ГОСТ 22013-76.
3.6. Рассчитывают параметры распределения: среднее арифметическое 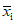 и среднее квадратическое отклонение Si для каждой i-й выборки общей выборки.
и среднее квадратическое отклонение Si для каждой i-й выборки общей выборки.
4.1. Проверку согласованности данных выполняют по сумме минимального отклонения оценок дисперсий каждой i-й выборки общей выборки (n >= 5). Наилучшей оценкой в этом случае является среднее взвешенное 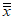 :
:
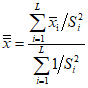 , (3)
, (3)где S2i - дисперсия каждой i-й выборки; L - число всех выборок.
Согласованность данных не отвергается, если сохраняется условие
A2min ~= F, (4)
где F - число степеней свободы (F = N - L) при уровне значимости 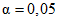 ; N - число всех данных; A2min - вычисленное значение, равное
; N - число всех данных; A2min - вычисленное значение, равное
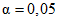 ; N - число всех данных; A2min - вычисленное значение, равное
; N - число всех данных; A2min - вычисленное значение, равное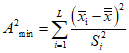 . (5)
. (5)4.2. Если вычисленное значение A2min превышает ожидаемое значение F, то рекомендуется выполнить анализ накопленных данных и выявить факторы, влияющие на их разброс.
4.3. Для приведения численных данных к согласию в ряде случаев (для фундаментальных констант) рекомендуется использовать расчетный коэффициент Берджа. Согласование численных данных по коэффициенту Берджа выполняют в соответствии с рекомендованным приложением 2.
КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ
5.1. Анализ точности данных чаще основан на подсчете точечных оценок. Однако ошибки, допускаемые в процессе испытаний, приводят к большому разбросу данных, который не позволяет объективно оценить исследуемое свойство. Поэтому наряду с вычислением точечных оценок рекомендуется использовать интервальные. Интервальное оценивание в данном случае основано на построении доверительных интервалов для выборочной средней 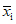 и для выборочной дисперсии S2i при доверительной вероятности P = 0,95.
и для выборочной дисперсии S2i при доверительной вероятности P = 0,95.
В табл. 1 приложения 4 дан пример вычисления точечных и интервальных оценок.
5.1.1. При построении доверительного интервала для выборочной средней 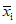 используют распределение Стьюдента. Из таблиц распределения Стьюдента с ni - 1 степенями свободы находят величину
используют распределение Стьюдента. Из таблиц распределения Стьюдента с ni - 1 степенями свободы находят величину 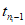 , для которой справедливо равенство
, для которой справедливо равенство
Преобразуя выражение (6), строят двусторонний доверительный интервал для каждой i-й выборки:
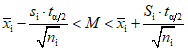 , (7)
, (7)где 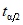 - квантили уровня
- квантили уровня 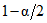 ,
, 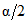 ; ni - число данных в i-й выборке.
; ni - число данных в i-й выборке.
5.1.2. Доверительный интервал для выборочной дисперсии S2i строят на основании того, что случайная величина 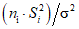 имеет распределение
имеет распределение 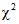 с ni - 1 степенями свободы, т.е.
с ni - 1 степенями свободы, т.е. 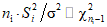 , где
, где 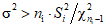 .
.
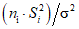 имеет распределение
имеет распределение 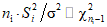 , где
, где 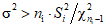 .
.Доверительный интервал для выборочной дисперсии строят из условия
Преобразуя выражение (8) в 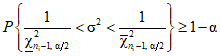 , строят двусторонний доверительный интервал
, строят двусторонний доверительный интервал
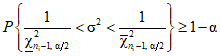 , строят двусторонний доверительный интервал
, строят двусторонний доверительный интервал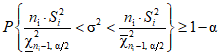 , (9)
, (9)где 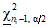 ;
; 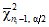 - квантили, которые определяются по
- квантили, которые определяются по 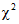 с ni - 1 степенями свободы при уровне значимости
с ni - 1 степенями свободы при уровне значимости 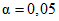 .
.
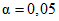 .
.Значения 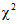 представлены в табл. 1 приложения 3.
представлены в табл. 1 приложения 3.
5.2. Чем больше взят объем выборки, тем выше надежность оценки, т.е. тем более узкий доверительный интервал может быть принят при оценке данных.
Обязательное
n2 | n1 | |||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
1 | - | |||||||||||||||||||
2 | - | - | ||||||||||||||||||
3 | - | - | - | |||||||||||||||||
4 | - | - | - | - | ||||||||||||||||
5 | - | - | - | - | 0 | |||||||||||||||
6 | - | - | - | 0 | 1 | 2 | ||||||||||||||
7 | - | - | - | 0 | 1 | 3 | 4 | |||||||||||||
8 | - | - | - | 1 | 2 | 4 | 6 | 7 | ||||||||||||
9 | - | - | 0 | 1 | 3 | 5 | 7 | 9 | 11 | |||||||||||
10 | - | - | 0 | 2 | 4 | 6 | 9 | 11 | 13 | 16 | ||||||||||
11 | - | - | 0 | 2 | 5 | 7 | 10 | 13 | 16 | 18 | 21 | |||||||||
12 | - | - | 1 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | ||||||||
13 | - | - | 1 | 3 | 7 | 10 | 13 | 17 | 20 | 24 | 27 | 31 | 34 | |||||||
14 | - | - | 1 | 4 | 7 | 11 | 15 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | ||||||
15 | - | - | 2 | 5 | 8 | 12 | 16 | 20 | 24 | 29 | 33 | 37 | 42 | 46 | 51 | |||||
16 | - | - | 2 | 5 | 9 | 13 | 18 | 22 | 27 | 31 | 36 | 41 | 45 | 50 | 55 | 60 | ||||
17 | - | - | 2 | 6 | 10 | 15 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 60 | 65 | 70 | |||
18 | - | - | 2 | 6 | 11 | 16 | 21 | 26 | 31 | 37 | 42 | 47 | 53 | 58 | 64 | 70 | 75 | 81 | ||
19 | - | 0 | 3 | 7 | 12 | 17 | 22 | 28 | 33 | 39 | 45 | 51 | 57 | 63 | 69 | 74 | 81 | 87 | 93 | |
20 | - | 0 | 3 | 8 | 13 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 67 | 73 | 79 | 86 | 92 | 99 | 105 |
Рекомендуемое
1. Согласование данных нарушается, если вычисленное значение A2min превышает ожидаемое значение F согласно п. 4.1.
Для устранения несогласованности данных рекомендуется использовать расчетный коэффициент Берджа
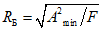 . (1)
. (1)В этих случаях вычисленное по п. 3.6 значение среднего квадратического отклонения Si каждой i-й выборки общей выборки изменяют на RБ число, равное коэффициенту Берджа, и находят измененные значения среднего квадратического отклонения S'i каждой i-й выборки:
S'i = Si·RБ, (2)
с помощью которых, аналогично величине A2min, вновь вычисляют величину 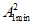 согласно п. 4.1.
согласно п. 4.1.
Если вычисленное значение 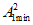 не превышает ожидаемое F (при
не превышает ожидаемое F (при 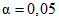 ), то согласованность данных принимается.
), то согласованность данных принимается.
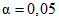 ), то согласованность данных принимается.
), то согласованность данных принимается.2. В случае, если необходимо вычислить коэффициент Берджа Ri для каждой i-й выборки, используют следующую формулу:
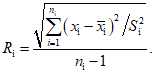 (3)
(3)Затем находят измененные оценки дисперсий (S"i)2 каждой i-й выборки
(S"i)2 = S2iRi (4)
и вычисляют величину 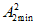
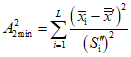 , (5)
, (5)где 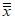 - среднее взвешенное, вычисленное с помощью измененных оценок (S"i)2, согласно п. 4.1.
- среднее взвешенное, вычисленное с помощью измененных оценок (S"i)2, согласно п. 4.1.
Согласованность данных принимается, если сумма квадратов относительных изменений оценок дисперсий (S"i)2 минимальна:
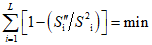
Обязательное
свободы с (ni - 1) 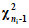 - распределение
- распределение 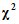
K | Вероятность P | ||||||||||||
0,005 | 0,010 | 0,025 | 0,05 | 0,10 | 0,20 | 0,80 | 0,90 | 0,95 | 0,975 | 0,990 | 0,995 | 0,999 | |
1 | 0,0393 | 0,0157 | 0,0982 | 0,0393 | 0,0158 | 0,0642 | 1,64 | 2,71 | 3,84 | 5,02 | 6,63 | 7,88 | 10,8 |
2 | 0,0100 | 0,0201 | 0,0506 | 0,103 | 0,211 | 0,446 | 3,22 | 4,61 | 5,99 | 7,38 | 9,21 | 10,6 | 13,8 |
3 | 0,0717 | 0,115 | 0,216 | 0,352 | 0,584 | 1,00 | 4,64 | 6,25 | 7,81 | 9,35 | 11,3 | 12,8 | 16,3 |
4 | 0,207 | 0,297 | 0,484 | 0,711 | 1,06 | 1,65 | 5,99 | 7,78 | 9,49 | 11,1 | 13,3 | 14,9 | 18,5 |
5 | 0,412 | 0,554 | 0,831 | 1,15 | 1,61 | 2,34 | 7,29 | 9,24 | 11,1 | 12,8 | 15,1 | 16,7 | 20,5 |
6 | 0,676 | 0,872 | 1,24 | 1,64 | 2,20 | 3,07 | 8,56 | 10,6 | 12,6 | 14,4 | 16,8 | 18,5 | 22,5 |
7 | 0,989 | 1,24 | 1,69 | 2,17 | 2,83 | 3,82 | 9,80 | 12,0 | 14,1 | 16,0 | 18,5 | 20,3 | 24,3 |
8 | 1,34 | 1,65 | 2,18 | 2,73 | 3,49 | 4,59 | 11,0 | 13,4 | 15,5 | 17,5 | 20,1 | 22,0 | 26,1 |
9 | 1,73 | 2,09 | 2,70 | 3,33 | 4,17 | 5,38 | 12,2 | 14,7 | 16,9 | 19,0 | 21,7 | 23,6 | 27,9 |
10 | 2,16 | 2,56 | 3,25 | 3,94 | 4,87 | 6,18 | 13,4 | 16,0 | 18,3 | 20,5 | 23,2 | 25,2 | 29,6 |
11 | 2,60 | 3,05 | 3,82 | 4,57 | 5,58 | 6,99 | 14,6 | 17,3 | 19,7 | 21.9 | 24,7 | 26,8 | 31,3 |
12 | 3,07 | 3,57 | 4,40 | 5,23 | 6,30 | 7,81 | 15,8 | 18,5 | 21,0 | 23,3 | 26,2 | 28,3 | 32,9 |
13 | 3,57 | 4,11 | 5,01 | 5,89 | 7,04 | 8,63 | 17,0 | 19,8 | 22,4 | 24,7 | 27,7 | 29,8 | 34,5 |
14 | 4,07 | 4,66 | 5,63 | 6,57 | 7,79 | 9,47 | 18,2 | 21,1 | 23,7 | 26,1 | 29,1 | 31,3 | 36,1 |
15 | 4,60 | 5,23 | 6,26 | 7,26 | 8,55 | 10,3 | 19,3 | 22,3 | 25,0 | 27,5 | 30,6 | 32,8 | 37,7 |
16 | 5,14 | 5,81 | 6,91 | 7,96 | 9,31 | 11,2 | 20,5 | 23,5 | 26,3 | 28,8 | 32,0 | 34,3 | 39,3 |
17 | 5,70 | 6,41 | 7,56 | 8,67 | 10,1 | 12,0 | 21,6 | 24,8 | 27,6 | 30,2 | 33,4 | 35,7 | 40,8 |
18 | 6,26 | 7,01 | 8,23 | 9,39 | 10,9 | 12,9 | 22,8 | 26,0 | 28,9 | 31,5 | 34,8 | 37,2 | 42,3 |
19 | 6,84 | 7,63 | 8,91 | 10,1 | 11,7 | 13,7 | 23,9 | 27,2 | 30,1 | 32,9 | 36,2 | 38,6 | 43,8 |
20 | 7,43 | 8,26 | 9,59 | 10,9 | 12,4 | 14,6 | 25,0 | 28,4 | 31,4 | 34,2 | 37,6 | 40,0 | 45,3 |
Справочное
ИС МЕГАНОРМ: примечание. Взамен ГОСТ 3900-47 Постановлением Госстандарта СССР от 20.12.1985 N 4544 с 01.01.1987 введен в действие ГОСТ 3900-85. |
топлива ТС-1 по ГОСТ 3900-47
Номер выборки | Результаты определения плотности при 20 °C | Среднее арифметическое результатов испытаний | Дисперсия | Среднее взвешенное | Вычисленное значение | Коэффициент Берджа RБ | Пределы значения плотности при 20 °C | Требования по ГОСТ 3900-47 |
1. | 778,0; 778,0; 778,0; 778,0, 779,0; 780,0; 779,7; 778,0; 779,0, 779,0, 779,0, 780,0 | 778,18 | 0,64 | 779,79 | 2,46 | 0,33 | 778,4 - 779,9 | Не менее 775,0 |
2. | 779,5; 779,8; 779,6; 781,0, 781,0, 781,0, 781,0, 781,0, 780,0, 780,0, 781,0, 780,0 | 780,41 | 0,40 | 780,1 - 780,7 |
УДК 665.6 : 53.081.7 |