СПРАВКА
Источник публикации
М., 2016
Примечание к документу
Документ рекомендован к применению с 9 ноября 2016 года Распоряжением Росавтодора от 09.11.2016 N 2326-р.
Взамен ОДН 218.0.032-2003.
Название документа
"ОДМ 218.4.027-2016. Отраслевой дорожный методический документ. Рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Металлические и сталежелезобетонные конструкции"
(издан на основании Распоряжения Росавтодора от 09.11.2016 N 2326-р)
"ОДМ 218.4.027-2016. Отраслевой дорожный методический документ. Рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Металлические и сталежелезобетонные конструкции"
(издан на основании Распоряжения Росавтодора от 09.11.2016 N 2326-р)
Содержание
Распоряжения Федерального
дорожного агентства
от 9 ноября 2016 г. N 2326-р
ОТРАСЛЕВОЙ ДОРОЖНЫЙ МЕТОДИЧЕСКИЙ ДОКУМЕНТ
РЕКОМЕНДАЦИИ
ПО ОПРЕДЕЛЕНИЮ ГРУЗОПОДЪЕМНОСТИ ЭКСПЛУАТИРУЕМЫХ МОСТОВЫХ
СООРУЖЕНИЙ НА АВТОМОБИЛЬНЫХ ДОРОГАХ ОБЩЕГО ПОЛЬЗОВАНИЯ.
МЕТАЛЛИЧЕСКИЕ И СТАЛЕЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ
ОДМ 218.4.027-2016
1. РАЗРАБОТАН Федеральным государственным бюджетным образовательным учреждением высшего профессионального образования "Сибирский государственный университет путей сообщения".
2. ВНЕСЕН Управлением строительства и эксплуатации автомобильных дорог Федерального дорожного агентства.
3. ИЗДАН на основании распоряжения Федерального дорожного агентства от 09.11.2016 N 2326-р.
4. ИМЕЕТ рекомендательный характер.
5. ВВЕДЕН взамен ОДН 218.0.032-2003 Временное руководство по определению грузоподъемности мостовых сооружений на автомобильных дорогах.
Настоящий отраслевой дорожный методический документ (далее - методический документ, Рекомендации) является актом рекомендательного характера в дорожном хозяйстве, содержащим методику определения грузоподъемности мостовых сооружений с учетом технического состояния элементов их конструкций.
Настоящий методический документ рекомендуется для применения при определении грузоподъемности мостовых сооружений, эксплуатируемых на федеральных автомобильных дорогах Российской Федерации. В остальных случаях методический документ может использоваться по решению органов управления автомобильных дорог субъектов РФ.
Положения настоящего методического документа предназначены для применения проектными и специализированными организациями, выполняющими работы по диагностике, обследованию, испытаниям и оценке технического состояния мостовых сооружений, а также мостовыми подразделениями органов управления автомобильными дорогами при организации и приемке обследовательских работ в соответствии с правилами применения документов технического регулирования в сфере дорожного хозяйства [1].
Настоящий методический документ включает следующие тома (книги):
ОДМ 218.4.025-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Общая часть.
ОДМ 218.4.026-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Бетонные и железобетонные конструкции.
ОДМ 218.4.027-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Металлические и сталежелезобетонные конструкции.
ОДМ 218.4.028-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Опорные части, опоры и фундаменты.
ОДМ 218.4.029-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Определение грузоподъемности конструкций деревянных мостов.
При определении грузоподъемности допускается использование иных от приведенных в настоящем методическом документе алгоритмов и программ. Обоснованность применения таких алгоритмов и программ должна быть подтверждена сертификатом их соответствия действующим нормам проектирования мостовых сооружений, выданным уполномоченным органом, либо предыдущим успешным опытом применения при проведении технических экспертиз соответствующей направленности по заданиям Федерального дорожного агентства.
В настоящем методическом документе использованы нормативные ссылки на следующие документы:
СП 16.13330.2011. Свод правил. Стальные конструкции. Актуализированная редакция СНиП II-23-81*;
СП 35.13330.2011. Свод правил. Мосты и трубы. Актуализированная редакция СНиП 2.05.03-84*;
ОДМ 218.1.001-2010 Рекомендации по разработке и применению документов технического регулирования в сфере в дорожного хозяйства;
ОДМ 218.4.025-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Общая часть;
ОДМ 218.4.026-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Бетонные и железобетонные конструкции;
ОДМ 218.4.003-2009 Рекомендации по объединению металлических балок с монолитной железобетонной плитой посредством непрерывных гребенчатых упоров в сталежелезобетонных пролетных строениях мостов;
ОДМ 218.2.044-2014 Рекомендации по выполнению приборных и инструментальных измерений при оценке технического состояния мостовых сооружений на автомобильных дорогах.
В настоящем методическом документе применены следующие термины с соответствующими определениями:
временная вертикальная нагрузка: Произвольное транспортное средство (средства), расположенное в пределах ездового полотна мостового сооружения.
воздействие от нагрузки: Усилия, напряжения, деформации, перемещения в конструкции (элементе конструкции), возникающие от действия внешних нагрузок (постоянных, временных, температурных и пр.).
грузоподъемность: Характеристика (показатель) технического состояния мостового сооружения, соответствующая максимальному воздействию временной вертикальной нагрузки, при котором не наступает предельное состояние первой группы ни в одной из основных несущих конструкций сооружения.
Примечание. Грузоподъемность сооружения в целом определяется грузоподъемностью наиболее слабой из основных несущих конструкций.
дефект в мостовом сооружении (дефект): Каждое отдельное несоответствие в мостовом сооружении установленным требованиям нормативно-технической и (или) конструкторской (проектной) документации.
допустимый класс нагрузки: Мера экстремально допустимого воздействия временной вертикальной нагрузки определенной структуры, которое не вызывает наступление предельного состояния первой группы в несущих конструкциях при нормальной эксплуатации сооружения.
Примечания
1. Для эталонных нагрузок по схемам АК и НК допустимые классы нагрузки выражаются безразмерными величинами KАК и KНК как отношение величины экстремального воздействия от эталонной нагрузки к воздействию от аналогичной единичной эталонной нагрузки класса K = 1.
2. Для нагрузок от колонн автомобилей допустимый класс нагрузки соответствует допустимой массе отдельного автомобиля из состава колонны.
класс грузоподъемности: Мера грузоподъемности сооружения (конструкции, элемента конструкции), выраженная значением допустимого класса или массы рассматриваемой временной вертикальной нагрузки.
конструкция: Часть мостового сооружения, состоящая из конструктивно объединенных элементов, выполняющая определенные функции (несущие, ограждающие, защитные и (или) другие).
Примечания
1. В мостовом сооружении конструкции делят на основные, обеспечивающие основные функциональные свойства мостового сооружения, и неосновные (вспомогательные), обеспечивающие, например, защиту и безопасность только в экстремальных ситуациях, удобство содержания в период эксплуатации и другие вспомогательные функциональные свойства.
2. Из множества основных конструкций выделяют несущие конструкции, основной функцией которых является восприятие воздействий от постоянных и временных нагрузок.
контролируемый режим движения: Режим движения, при котором пропуск транспортных средств по сооружению осуществляется по специальному разрешению в сопровождении представителей службы эксплуатации и/или ГИБДД и, как правило, в одиночном порядке.
мостовое сооружение: Искусственное сооружение, состоящее из одного или нескольких пролетных строений и опор, предназначенное для пропуска различных видов транспорта и пешеходов, а также водотоков, селей, скота, коммуникаций различного назначения, порознь или в различных комбинациях над естественными или искусственными препятствиями.
Примечание. К искусственным препятствиям относятся искусственные водоемы, водные каналы, автомобильные и железные дороги, другие инженерные сооружения, а также территории предприятий, городские территории, через которые проходит автомобильная дорога.
неконтролируемый режим движения: Режим движения, при котором регулирование пропуска транспортных средств осуществляется техническими средствами организации дорожного движения.
основная несущая конструкция: Конструкция сооружения, предназначенная для восприятия воздействий от постоянных и временных нагрузок, наступление предельного состояния первой группы в которой приводит к утрате работоспособного состояния (жесткости и устойчивости) сооружения в целом.
опора моста: Несущая конструкция мостового сооружения, поддерживающая пролетные строения и передающая нагрузки от них на основание.
опорная часть: Несущая конструкция мостового сооружения, передающая нагрузку от пролетного строения на опоры и обеспечивающая угловые и линейные, либо только угловые перемещения пролетного строения.
основание опоры: Массив грунта, в котором размещены собственно строительные конструкции фундамента опоры.
пролетное строение: Несущая конструкция мостового сооружения, перекрывающая все пространство или часть его между двумя или несколькими опорами, воспринимающая нагрузку от элементов мостового полотна, транспортных средств и пешеходов, и передающая ее на опоры.
сталежелезобетонная конструкция: Единая несущая конструкция со стальными и железобетонными элементами, совместно воспринимающими воздействия от нагрузки.
Примечание. Применительно к сталежелезобетонным пролетным строениям автодорожных мостов конструктивным железобетонным элементом является железобетонная плита проезжей части, объединенная с металлическими несущими элементами главных балок (ферм).
условная несущая способность: Величина максимального воздействия на элемент от временных проектных нагрузок, определяемая в соответствии с указаниями тех норм проектирования, по которым конструкция была запроектирована.
ширина проезда: Расстояние в свету между ограждениями безопасности ездового полотна мостового сооружения.
элемент конструкции: Составная часть сложного технического объекта, рассматриваемая как единое целое, не подлежащее дальнейшему разукрупнению, имеющая самостоятельные характеристики, используемые при расчетах, и выполняющая определенную частную функцию в интересах сложного объекта, который по отношению к элементу представляет собой систему.
Примечание. Элементами могут быть балка, плита, диафрагма, ригель и т.д.
эталонные автомобильные нагрузки: Временные вертикальные нагрузки заданной структуры.
4.1.1 Общие положения расчета грузоподъемности изложены в разделах 4 и 5 [2].
4.1.2 Расчет несущей способности элементов металлических пролетных строений производят с учетом их фактического состояния по данным обследования сооружения. Расчетные характеристики материалов принимают согласно указаниям нормам на проектирование мостовых сооружений [3] с учетом положений пп. 4.1.8 - 4.1.14.
4.1.3 Значения используемых в расчетах коэффициентов  ,
,  ,
, 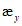 ,
,  ,
,  ,
,  ,
,  ,
,  допускается определять при невыгодном загружении конструкции фактическими постоянными и схемами тех временных нагрузок, под которые данная конструкция была запроектирована. При этом правила расстановки временной нагрузки и значения расчетных коэффициентов принимают в соответствии с [2].
допускается определять при невыгодном загружении конструкции фактическими постоянными и схемами тех временных нагрузок, под которые данная конструкция была запроектирована. При этом правила расстановки временной нагрузки и значения расчетных коэффициентов принимают в соответствии с [2].
4.1.4 Коэффициенты условий работы m при определении несущей способности элементов конструкций принимают согласно нормам проектирования мостовых сооружений (п. 8.19 [3]).
4.1.5 При одновременном действии в сечении нескольких силовых факторов F1, F2, ..., Fn, невыгодное положение временной нагрузки на сооружении определяется в соответствии с рекомендациями п. 5.4.3 [2].
4.1.6 Грузоподъемность элементов металлических конструкций определяют:
При расчете изгибаемых элементов (сплошные главные балки и балки проезжей части пролетных строений):
- по условию обеспечения прочности по нормальным напряжениям: в сечениях в середине пролетов, в надопорных зонах для консольных и неразрезных конструкций, в местах изменения сечения балок, в стыках элементов балок, в местах наибольших ослаблений сечений дефектами, в других необходимых случаях;
- по условию обеспечения прочности по касательным напряжениям: по нейтральной оси балок в опорных сечениях, в местах наибольших ослаблений сечений дефектами, в других необходимых случаях;
- по условию обеспечения прочности поясных заклепок (болтов) или сварных швов объединения поясов со стенкой балки: на приопорных участках, а также в начале участков с увеличенным шагом заклепок или с уменьшенным сечением сварных швов, в других необходимых случаях;
- по условию обеспечения общей устойчивости сжатого пояса: в сечениях в середине свободной длины сжатого пояса в местах приближенных к середине пролетов, а также над опорами - для консольных и неразрезных конструкций, а также в местах изменения сечения балок и свободной длины сжатого пояса, и в других необходимых случаях;
- по условию обеспечения местной устойчивости стенки балки или отсека стенки балки, ограниченного вертикальными, горизонтальным ребрами жесткости и поясами: при отсутствии ребер жесткости для стенок балок при  , при наличии ребер жесткости, расставленных на расстоянии более 2h или 2 м, а также во всех случаях при
, при наличии ребер жесткости, расставленных на расстоянии более 2h или 2 м, а также во всех случаях при 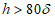 - для стенок из углеродистой стали и
- для стенок из углеродистой стали и  - для стенок из низколегированной стали (здесь h - расчетная высота стенки, принимается для сварной балки равной полной высоте стенки, а для клепаной балки - расстоянию между ближайшими к оси балки рисками поясных заклепок,
- для стенок из низколегированной стали (здесь h - расчетная высота стенки, принимается для сварной балки равной полной высоте стенки, а для клепаной балки - расстоянию между ближайшими к оси балки рисками поясных заклепок,  - толщина стенки балки);
- толщина стенки балки);
 , при наличии ребер жесткости, расставленных на расстоянии более 2h или 2 м, а также во всех случаях при
, при наличии ребер жесткости, расставленных на расстоянии более 2h или 2 м, а также во всех случаях при 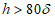 - для стенок из углеродистой стали и
- для стенок из углеродистой стали и  - для стенок из низколегированной стали (здесь h - расчетная высота стенки, принимается для сварной балки равной полной высоте стенки, а для клепаной балки - расстоянию между ближайшими к оси балки рисками поясных заклепок,
- для стенок из низколегированной стали (здесь h - расчетная высота стенки, принимается для сварной балки равной полной высоте стенки, а для клепаной балки - расстоянию между ближайшими к оси балки рисками поясных заклепок, - по условию обеспечения прочности прикрепления балок проезжей части, по прочности сечения и прикрепления "рыбок" (при их наличии).
При расчете элементов сквозных ферм:
- по условию обеспечения прочности сечений и прикреплений элементов решетки фермы;
- по условию обеспечения устойчивости работающих на сжатие элементов решетки фермы.
При расчете элементов ортотропных плит необходимо выполнить проверки, предусмотренные п. 4.4.
При расчете элементов пролетных строений рамных и прочих сложных систем положение расчетных (наиболее нагруженных) сечений с учетом их ослабления дефектами может быть определено по огибающим эпюрам соответствующих усилий.
4.1.7 Для элементов, ослабленных отверстиями под обычные болты, при определении несущей способности по прочности принимают сечения нетто, по устойчивости - сечения брутто. Геометрические характеристики сечения нетто элементов конструкций принимают в местах с наибольшими ослаблениями.
Несущую способность элементов с фрикционными соединениями на высокопрочных болтах при расчете на устойчивость принимают по сечению брутто, а при расчете по прочности - по сечению нетто с учетом того, что половина усилия, воспринимаемая болтами в рассматриваемом сечении, уже передана силами трения на накладки (фасонки).
4.1.8 При известной марке стали расчетные сопротивления проката для различных видов напряженных состояний принимают по нормам проектирования мостовых сооружений (п. 8.8 [3]). Характеристики стали Ст.3, М16С, литого железа допускается принимать как для стали марки 16Д. Для сталей, сведения о марках которых отсутствуют в действующих нормах проектирования мостовых сооружений, нормативные значения предела текучести Ryn и временного сопротивления Run принимают:
- для сталей, у которых приведенные в сертификатах или полученные при испытаниях значения предела текучести и временного сопротивления соответствуют требованиям действовавших на момент строительства моста государственных стандартов или технических условий на сталь - по минимальному значению, указанному в этих документах;
- для сталей, у которых приведенные в сертификатах или полученные при испытаниях значения предела текучести и временного сопротивления ниже предусмотренных государственными стандартами или техническими условиями на сталь, действовавшими на момент строительства моста - по минимальному значению предела текучести из приведенных в сертификатах или полученных при испытаниях.
Если типовым проектом допускалось изготовление несущих конструкций из различных марок стали, но документальные сведения о конкретно примененной марке отсутствуют, в предварительных расчетах следует использовать меньшие из соответствующих возможных значений расчетных сопротивлений. Если определенная таким образом грузоподъемность конструкции окажется недостаточной, следует установить фактическую марку стали проведением испытаний, и, при необходимости, произвести перерасчет.
4.1.9 При определении характеристик и механических свойств сталей неизвестных марок следует руководствоваться Приложением В.
4.1.10 В случае определения расчетного сопротивления стали по результатам испытаний коэффициенты надежности по материалу принимают:
- для конструкций, запроектированных по нормам СНиП 2.05.03-84* и более поздним - по нормам проектирования мостовых сооружений [3];
- для конструкций, запроектированных по более ранним нормам - элементов из углеродистой стали по ГОСТ 6713-91  , из низколегированной стали 15ХСНД по ГОСТ 6713-91
, из низколегированной стали 15ХСНД по ГОСТ 6713-91  , из низколегированной стали 10ХСНД по ГОСТ 6713-91
, из низколегированной стали 10ХСНД по ГОСТ 6713-91  , из низколегированной стали с пределом текучести до 39 кгс/см2 по ГОСТ 19281-89
, из низколегированной стали с пределом текучести до 39 кгс/см2 по ГОСТ 19281-89  , свыше 39 кгс/см2 -
, свыше 39 кгс/см2 -  .
.
 , из низколегированной стали 15ХСНД по ГОСТ 6713-91
, из низколегированной стали 15ХСНД по ГОСТ 6713-91  , из низколегированной стали 10ХСНД по ГОСТ 6713-91
, из низколегированной стали 10ХСНД по ГОСТ 6713-91  , из низколегированной стали с пределом текучести до 39 кгс/см2 по ГОСТ 19281-89
, из низколегированной стали с пределом текучести до 39 кгс/см2 по ГОСТ 19281-89  , свыше 39 кгс/см2 -
, свыше 39 кгс/см2 -  .
.4.1.11 Расчетные сопротивления сварных соединений, болтовых стыков и соединений, работающих на срез, смятие и растяжение, принимают в соответствии с нормами проектирования мостовых сооружений (таблицы 8.8, 8.9 и 8.10 [3]).
4.1.12 Значения коэффициента трения  по контактным поверхностям элементов во фрикционных соединениях и соответствующих коэффициентов надежности
по контактным поверхностям элементов во фрикционных соединениях и соответствующих коэффициентов надежности  принимают в соответствии с нормами проектирования мостовых сооружений (таблица 8.12 [3]). Способ обработки контактных поверхностей принимают по технической документации, а при ее отсутствии - как наиболее вероятный в момент строительства или (в запас прочности) дающий наихудшие значения несущей способности соединения.
принимают в соответствии с нормами проектирования мостовых сооружений (таблица 8.12 [3]). Способ обработки контактных поверхностей принимают по технической документации, а при ее отсутствии - как наиболее вероятный в момент строительства или (в запас прочности) дающий наихудшие значения несущей способности соединения.
4.1.13 Расчетные сопротивления заклепочных соединений при расчете на срез и смятие определяют по расчетному сопротивлению металла соединяемой конструкции Ry с использованием коэффициентов перехода (таблица 4.1.1). Расчетное сопротивление заклепочных соединений при расчете на отрыв головок принимают с переходным коэффициентом 0,6 к расчетному сопротивлению металла заклепки.
Таблица 4.1.1
Тип соединения | Характер работы | Коэффициенты перехода к сопротивлениям заклепочных соединений по отношению к сопротивлению металла конструкции Ry, для марок стали | ||
заклепок | ||||
Ст.2 (Ст.3) | 09Г2 | |||
конструкции | ||||
углеродистой | низколегированной | |||
Заводское | Срез | 0,80 | 0,55 | 0,80 <*> |
Смятие | 2,00 | 2,00 | 2,00 | |
Монтажное | Срез | 0,70 | 0,50 | 0,70 <*> |
Смятие | 1,75 | 1,75 | 1,75 | |
4.1.14 Модуль упругости E и модуль сдвига G прокатной стали, стального литья, пучков и канатов принимают в соответствии с нормами проектирования мостовых сооружений (таблицы 8.13, 8.14 [3]). Модули упругости канатов, сведения о которых отсутствуют в нормах проектирования мостовых сооружений [3], определяют по технической документации или, при возможности, по испытаниям.
4.1.15 Расчет грузоподъемности изгибаемых элементов и элементов, подверженных действию осевой силы и изгибу, как правило, следует выполнять с учетом ограниченных пластических деформаций, учитываемых коэффициентом  согласно указаниям норм проектирования мостовых сооружений (п. 8.26 [3]). Допускается принимать
согласно указаниям норм проектирования мостовых сооружений (п. 8.26 [3]). Допускается принимать 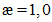 в случаях, когда это приводит к запасу прочности. Если определенная таким образом грузоподъемность конструкции окажется недостаточной, следует установить фактическое значение
в случаях, когда это приводит к запасу прочности. Если определенная таким образом грузоподъемность конструкции окажется недостаточной, следует установить фактическое значение  и произвести перерасчет. При определении значения коэффициента
и произвести перерасчет. При определении значения коэффициента  допускается учитывать рекомендации п. 4.1.3.
допускается учитывать рекомендации п. 4.1.3.
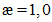 в случаях, когда это приводит к запасу прочности. Если определенная таким образом грузоподъемность конструкции окажется недостаточной, следует установить фактическое значение
в случаях, когда это приводит к запасу прочности. Если определенная таким образом грузоподъемность конструкции окажется недостаточной, следует установить фактическое значение Примечание. Если суммарные касательные напряжения от постоянных и временной нагрузок в рассматриваемом сечении не превышают 0,25Rs, где Rs = 0,58Ry - предел прочности стали на сдвиг, то коэффициент 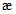 зависит только от состава сечения элемента. Как правило, это бывает справедливым для сечений изгибаемых элементов в середине пролета при загружении подвижными нагрузками по схеме АК.
зависит только от состава сечения элемента. Как правило, это бывает справедливым для сечений изгибаемых элементов в середине пролета при загружении подвижными нагрузками по схеме АК.
При величине касательных напряжений больше 0,25Rs (например, для сечений в четвертях пролетов, над опорами неразрезных балок, в серединах пролетов при загружении нагрузками по схеме НК) коэффициент  зависит от уровня нагрузок и может оказаться понижающим (меньше 1,0). В этом случае неучет ограниченных пластических деформаций может привести к необоснованному завышению классов элементов по грузоподъемности.
зависит от уровня нагрузок и может оказаться понижающим (меньше 1,0). В этом случае неучет ограниченных пластических деформаций может привести к необоснованному завышению классов элементов по грузоподъемности.
4.1.16 Расчет на прочность без учета ограниченных пластических деформаций может быть допущен для элементов, воспринимающих усилия разных знаков (при  ) при соблюдении условия
) при соблюдении условия
 ) при соблюдении условия
) при соблюдении условия (4.1.1)
(4.1.1)где  ,
,  - соответственно расчетные максимальные и минимальные (со своими знаками) нормальные напряжения в проверяемой точке от суммарных постоянных и временной нагрузки, вычисленные в предположении упругой работы материала;
- соответственно расчетные максимальные и минимальные (со своими знаками) нормальные напряжения в проверяемой точке от суммарных постоянных и временной нагрузки, вычисленные в предположении упругой работы материала;  ,
,  - касательные напряжения в проверяемой точке (с учетом их знаков), вычисленные соответственно от тех же нагрузок, что и
- касательные напряжения в проверяемой точке (с учетом их знаков), вычисленные соответственно от тех же нагрузок, что и 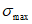 и
и  .
.
4.1.17 Расчетная схема конструкции должна отражать действительные условия ее работы, при этом строительный подъем и деформации под нагрузкой допускается не учитывать (кроме пилонов вантовых мостов).
При определении усилий в элементах конструкций соединения элементов следует рассматривать как неподатливые. Жесткие соединения в узлах решетчатых схем допускается принимать шарнирными, если при этом конструкция сохраняет свою неизменяемость, а отношение высоты сечения элементов к их длине не превышает 1:15.
При определении положения центра тяжести сечения его ослабление болтовыми или заклепочными отверстиями допускается не учитывать. При смещении нейтральной оси элемента относительно линии, соединяющей центры узлов геометрической схемы ферменной конструкции, эксцентриситет учитывают в расчете, если он превосходит: для П-образных, коробчатых, двухшвеллерных и двутавровых элементов - 1,5% высоты сечения; для тавровых и Н-образных элементов - 0,7% высоты сечения.
4.1.18 При численном моделировании методом конечных элементов, как правило, следует использовать пространственные расчетные схемы. При создании расчетной модели рекомендуется использовать стержневые балочные конечные элементы общего вида. В случае необходимости построения поверхностей влияния для компонент напряженно-деформированного состояния плоских конструктивов (например, листа настила ортотропной плиты) возможно применение плитных (пластинчатых) конечных элементов. Геометрические характеристики сечений элементов рассчитываемой конструкции при определении усилий и перемещений следует принимать без учета ослаблений болтовыми (заклепочными) отверстиями и перфорациями.
4.1.19 Расчетную длину lef элементов решетки ферм принимают по таблице 4.1.2.
Таблица 4.1.2
Направление продольного изгиба | Расчетная длина lef | |
поясов, опорных раскосов и опорных стоек | прочих элементов решетки | |
В плоскости фермы | l | 0,8l |
В направлении, перпендикулярном плоскости фермы (из плоскости фермы) | l1 | l1 |
Примечание. l - геометрическая длина элемента (расстояние между центрами узлов) в плоскости фермы; l1 - расстояние между узлами, закрепленными от смещения из плоскости фермы.
4.1.20 Расчетную длину сжатого пояса главной балки или фермы в пролетном строении "открытого" типа (не имеющему продольных связей в уровне сжатого пояса) из плоскости фермы определяют по формуле
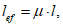 (4.1.2)
(4.1.2)где l - длина пояса, равная расчетному пролету для балок и ферм с параллельными поясами, полной длине пояса для балок с криволинейным верхним поясом и ферм с полигональным верхним поясом;  - коэффициент расчетной длины (таблица 4.1.3), зависящий от параметра
- коэффициент расчетной длины (таблица 4.1.3), зависящий от параметра 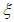
 (4.1.3)
(4.1.3)где d - расстояние между рамами, закрепляющими пояс от поперечных горизонтальных перемещений (длина панели фермы); Im - момент инерции сжатого пояса балки или фермы относительно вертикальной оси (среднее значение по длине пролета); 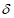 - наибольшее горизонтальное поперечное перемещение верхнего узла неопорной наиболее нагруженной гибкой полурамы от силы F = 1,0 кН, приложенной в этом узле.
- наибольшее горизонтальное поперечное перемещение верхнего узла неопорной наиболее нагруженной гибкой полурамы от силы F = 1,0 кН, приложенной в этом узле.
Таблица 4.1.3
0 | 1 | 5 | 10 | 15 | 30 | 60 | |
0,696 | 0,662 | 0,524 | 0,433 | 0,396 | 0,353 | 0,321 | |
100 | 150 | 200 | 300 | 500 | 1000 и более | ||
0,290 | 0,268 | 0,246 | 0,225 | 0,204 |  | ||
Примечание. При промежуточных значениях 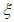 коэффициент
коэффициент 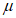 определяют по линейной интерполяции.
определяют по линейной интерполяции.
Величину  определяют из пространственного расчета фермы (балки). Для конструкций с двумя главными фермами (балками) значение
определяют из пространственного расчета фермы (балки). Для конструкций с двумя главными фермами (балками) значение  допускается определять по формуле
допускается определять по формуле
 (4.1.4)
(4.1.4)где hr - высота стойки фермы (или ребра жесткости балки), равная расстоянию от центра тяжести сечения сжатого пояса до верха поперечной балки; Ir - момент инерции сечения стойки фермы (ребра жесткости балки), соответствующий изгибу из плоскости фермы (среднее значение по высоте); B - расстояние между осями главных ферм (балок); Is - момент инерции сечения поперечной балки.
4.1.21 Расчетные длины lef элементов арок сплошного постоянного сечения в плоскости арок определяют по п. 8.53 [3].
4.1.22 В сплошностенчатых балках расчетную длину lef опорных стоек, состоящих из одного или нескольких опорных ребер жесткости и примыкающих к ним участков стенки, определяют по п. 8.55 [3].
4.2.1 Несущую способность по прочности элементов, подверженных центральному растяжению или сжатию, определяют по формуле
где An - площадь нетто поперечного сечения элемента; m - коэффициент условий работы.
4.2.2 Несущую способность по прочности элементов, изгибаемых в одной из главных плоскостей, определяют по формуле
где  - коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении и определяемый согласно п. 4.1.15; Wn - минимальный момент сопротивления сечения нетто, определяемый с учетом эффективной ширины пояса bef; m - коэффициент условий работы, принимаемый по п. 4.1.4.
- коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении и определяемый согласно п. 4.1.15; Wn - минимальный момент сопротивления сечения нетто, определяемый с учетом эффективной ширины пояса bef; m - коэффициент условий работы, принимаемый по п. 4.1.4.
Эффективную ширину пояса bef принимают согласно указаниям норм на проектирование мостовых сооружений (п. 8.26 [3]).
4.2.3 Определение грузоподъемности элементов, изгибаемых в двух главных плоскостях, по прочности выполняют исходя из соблюдения условий
с двутавровыми и коробчатыми сечениями с двумя осями симметрии
 (4.2.3)
(4.2.3)с сечениями других типов
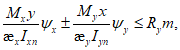 (4.2.4)
(4.2.4)где  ,
,  - коэффициенты, определяемые по п. 4.1.15 как независимые величины для случаев изгиба относительно осей x и y;
- коэффициенты, определяемые по п. 4.1.15 как независимые величины для случаев изгиба относительно осей x и y;  ,
, 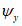 - коэффициенты, определяемые по п. 8.27 [3]; Mx, My - расчетные значения изгибающих моментов, действующих в главных плоскостях относительно осей x и y, и вычисленных от суммарных постоянных и временных нагрузок; Ixn, Iyn - моменты инерции сечения нетто относительно главных осей x и y; x, y - расстояние от главных осей y и x соответственно до наиболее удаленной фибры сечения.
- коэффициенты, определяемые по п. 8.27 [3]; Mx, My - расчетные значения изгибающих моментов, действующих в главных плоскостях относительно осей x и y, и вычисленных от суммарных постоянных и временных нагрузок; Ixn, Iyn - моменты инерции сечения нетто относительно главных осей x и y; x, y - расстояние от главных осей y и x соответственно до наиболее удаленной фибры сечения.
Расчет выполняют итерационным путем согласно рекомендациям п. 4.1.5 и п. Б.3.2 [2] с использованием поверхностей влияния двух усилий Mx и My или фибровых напряжений.
4.2.4 Определение грузоподъемности по прочности внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов при изгибе в одной из главных плоскостей выполняют итерационным путем согласно рекомендациям п. Б.3.2 [2] с использованием поверхностей влияния двух усилий N и M или фибровых напряжений как указано в п. 5.4.3 [2].
Расчет выполняют исходя из соблюдения условия
 (4.2.5)
(4.2.5)где N - суммарная продольная сила от постоянных и временной нагрузок, действующая в проверяемом сечении со своим знаком ("плюс" - растяжение); M - приведенный изгибающий момент в сечении;  - коэффициент, определяемый по формулам п. 8.28 [3];
- коэффициент, определяемый по формулам п. 8.28 [3];  - коэффициент, определяемый п. 4.1.15. При определении коэффициентов
- коэффициент, определяемый п. 4.1.15. При определении коэффициентов  ,
,  допускается руководствоваться указаниями п. 4.1.3.
допускается руководствоваться указаниями п. 4.1.3.
Приведенный изгибающий момент M при гибкости элементов 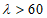 следует вычислять для сечений, находящихся в пределах двух средних четвертей длины шарнирно-опертого стержня или в пределах всей длины стержня, защемленного по концам, по формуле
следует вычислять для сечений, находящихся в пределах двух средних четвертей длины шарнирно-опертого стержня или в пределах всей длины стержня, защемленного по концам, по формуле
 (4.2.6)
(4.2.6)где M1 - суммарный момент от постоянных и временной нагрузок, действующий в проверяемом сечении; 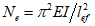 - Эйлерова критическая сила в плоскости действия момента, вычисленная для соответствующих закреплений стержня; lef - расчетная длина элемента конструкции, принимаемая в соответствии с таблицей 4.1.2; при
- Эйлерова критическая сила в плоскости действия момента, вычисленная для соответствующих закреплений стержня; lef - расчетная длина элемента конструкции, принимаемая в соответствии с таблицей 4.1.2; при  допускается принимать M = M1.
допускается принимать M = M1.
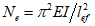 - Эйлерова критическая сила в плоскости действия момента, вычисленная для соответствующих закреплений стержня; lef - расчетная длина элемента конструкции, принимаемая в соответствии с таблицей 4.1.2; при
- Эйлерова критическая сила в плоскости действия момента, вычисленная для соответствующих закреплений стержня; lef - расчетная длина элемента конструкции, принимаемая в соответствии с таблицей 4.1.2; при 4.2.5 Допускается в запас прочности для всех типов сечений и всех случаев закрепления стержней определять грузоподъемность элементов, исходя из условия не превышения фибровыми напряжениями, определенными в предположении упругой работы, расчетных сопротивлений, принимаемых с учетом коэффициентов условий работы:
- при изгибе в одной плоскости
- при изгибе в двух плоскостях
В последнем случае для расчетов используют поверхности влияния усилий N, Mx, My и последовательно рассматривают варианты загружений как указано в 4.1.5.
Расчет по формулам (4.2.7) и (4.2.8) выполняют итерационным путем согласно рекомендациям п. Б.3.2 [2].
4.2.6 Несущая способность сечений изгибаемых, внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов по поперечной силе в местах, где изгибающий момент равен нулю, определяют по формуле
где t - толщина стенки с учетом ослаблений; I, S - момент инерции сечения (брутто) и статический момент отсеченной части сечения в точке проверки;
 (4.2.10)
(4.2.10)Smin, Smax - наименьший и наибольший статические моменты в стенке сечения (для двутавровых сечений и приведенных к ним Smin = Sпояса, Smax = Sполусечения).
4.2.7 Определение грузоподъемности изгибаемых, внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов по приведенным напряжениям в стенках сечений выполняют, исходя из соблюдения условий

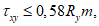 (4.2.11)
(4.2.11)где  - параллельные оси элемента нормальные (положительные при сжатии) напряжения от суммарного действия постоянных и временной нагрузок в проверяемой точке срединной плоскости стенки;
- параллельные оси элемента нормальные (положительные при сжатии) напряжения от суммарного действия постоянных и временной нагрузок в проверяемой точке срединной плоскости стенки; 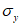 - такие же напряжения, перпендикулярные оси элемента;
- такие же напряжения, перпендикулярные оси элемента; 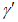 - коэффициент, равный 1,15 при
- коэффициент, равный 1,15 при  и 1,10 при
и 1,10 при  ;
;  - касательное напряжение в проверяемой точке стенки элемента.
- касательное напряжение в проверяемой точке стенки элемента.
Напряжение 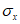 может быть вычислено по формуле
может быть вычислено по формуле
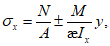 (4.2.12)
(4.2.12)где y - расстояние от нейтральной оси до проверяемой точки (с учетом знака);  - коэффициент, определяемый по п. 4.1.15.
- коэффициент, определяемый по п. 4.1.15.
Поперечное нормальное напряжение 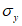 (положительное при сжатии) от временной нагрузки может быть определено по формуле
(положительное при сжатии) от временной нагрузки может быть определено по формуле
 (4.2.13)
(4.2.13)где P - распределенное давление по кромке стенки; t - толщина стенки.
Расчет выполняют итерационным путем согласно рекомендациям п. Б.3.2 [2], при этом рассматривают варианты загружения согласно п. 4.1.5.
4.3.1 Несущую способность по условию недопущения плоской формы потери устойчивости сплошностенчатых элементов замкнутого и открытого сечений (как правило - главных элементов сквозных конструкций, а также элементов связей), подверженных центральному сжатию, сжатию с изгибом и внецентренному сжатию при изгибе в плоскости наибольшей гибкости, определяют по формуле
где  - коэффициент продольного изгиба, определяемый в соответствии с нормами проектирования мостовых сооружений (приложение Ф [3]) в зависимости от гибкости элемента, приведенного относительного эксцентриситета и класса прочности (марки) стали.
- коэффициент продольного изгиба, определяемый в соответствии с нормами проектирования мостовых сооружений (приложение Ф [3]) в зависимости от гибкости элемента, приведенного относительного эксцентриситета и класса прочности (марки) стали.
4.3.2 Для определения коэффициента  для рассчитываемого элемента в общем случае вычисляют:
для рассчитываемого элемента в общем случае вычисляют:
- расчетную длину lef (см. п. 4.1);
- площадь брутто A сечения;
- момент инерции брутто I сечения относительно оси, перпендикулярной к плоскости изгиба;
- момент сопротивления Wc для наиболее сжатой фибры сечения;
- радиус инерции сечения относительно оси, перпендикулярной плоскости наибольшей гибкости (плоскости изгиба)
- гибкость
- условную гибкость, учитывающую ограниченную упругость материала
 (4.3.4)
(4.3.4)- ядровое расстояние по направлению эксцентриситета
 (4.3.5)
(4.3.5)- расчетный эксцентриситет продольной силы
e = M/N, (4.3.6)
где N - продольная сила в сечении элемента от суммарных постоянных и временной нагрузок; M - изгибающий момент, сопутствующий силе N (определяют для рассчитываемого элемента с учетом положений п. 4.3.3);
- относительный эксцентриситет в плоскости изгиба
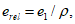 (4.3.7)
(4.3.7)где e1 - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет при сжатии с изгибом (e);
- приведенный относительный эксцентриситет 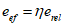 , где
, где  - коэффициент формы сечения, определяемый по приложению Д [4], как функцию от
- коэффициент формы сечения, определяемый по приложению Д [4], как функцию от  и erel.
и erel.
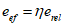 , где
, где 4.3.3 Расчетное сечение для определения изгибающего момента M назначают с учетом положения экстремумов огибающих эпюр. При этом назначенное сечение должно быть расположено:
- для элементов с одним защемленным, а другим свободным концом - на участке, отстоящем от заделки на треть длины элемента;
- для сжатых поясов ферм, воспринимающих внеузловую нагрузку - в пределах средней трети длины панели пояса.
4.3.4. Гибкость 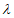 сквозных элементов замкнутого сечения, ветви которых соединены соединительной решеткой, планками или перфорированными листами определяют:
сквозных элементов замкнутого сечения, ветви которых соединены соединительной решеткой, планками или перфорированными листами определяют:
- в случае изгиба из плоскости соединительной решетки, планок или перфорированных листов - по формуле (4.3.3);
- в случае изгиба в плоскости соединительных решеток, планок или перфорированных листов, гибкость  равна приведенной гибкости
равна приведенной гибкости  , которая определяется по формуле
, которая определяется по формуле
где  - гибкость элемента в плоскости соединительной решетки, планок или перфорированных листов, вычисленная как для сплошного сечения по формуле (4.3.3);
- гибкость элемента в плоскости соединительной решетки, планок или перфорированных листов, вычисленная как для сплошного сечения по формуле (4.3.3);  - гибкость ветви, вычисленная по формуле (4.3.3), где за расчетную длину lef принимают длину панели соединительной решетки, расстояние между крайними заклепками соединительных планок, расстояние в свету между приваренными планками или 80% длины отверстия в перфорированном листе. За радиус инерции i принимают радиус инерции сечения ветви относительно собственной оси, перпендикулярной плоскости соединительной решетки, планок или перфорированных листов.
- гибкость ветви, вычисленная по формуле (4.3.3), где за расчетную длину lef принимают длину панели соединительной решетки, расстояние между крайними заклепками соединительных планок, расстояние в свету между приваренными планками или 80% длины отверстия в перфорированном листе. За радиус инерции i принимают радиус инерции сечения ветви относительно собственной оси, перпендикулярной плоскости соединительной решетки, планок или перфорированных листов.
В случае соединения ветвей элемента соединительной решеткой и при изгибе в плоскости этой решетки значение гибкости  принимают по формуле (4.3.8), но не менее
принимают по формуле (4.3.8), но не менее
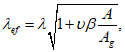 (4.3.9)
(4.3.9)где  - коэффициент, принимаемый равным
- коэффициент, принимаемый равным 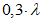 при
при  и равным
и равным  при
при  ;
;  - коэффициент, отражающий влияние жесткости диагоналей соединительной решетки: для диагоналей из уголков, а также диагоналей из уголков и полос (крестовая решетка)
- коэффициент, отражающий влияние жесткости диагоналей соединительной решетки: для диагоналей из уголков, а также диагоналей из уголков и полос (крестовая решетка) 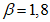 ; для диагоналей из полос
; для диагоналей из полос 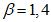 ; A - площадь брутто поперечного сечения всего элемента; Ag - площадь брутто поперечного сечения всех диагоналей, попадающих в один поперечный разрез элемента.
; A - площадь брутто поперечного сечения всего элемента; Ag - площадь брутто поперечного сечения всех диагоналей, попадающих в один поперечный разрез элемента.
 и равным
и равным  при
при  ;
; 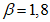 ; для диагоналей из полос
; для диагоналей из полос 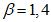 ; A - площадь брутто поперечного сечения всего элемента; Ag - площадь брутто поперечного сечения всех диагоналей, попадающих в один поперечный разрез элемента.
; A - площадь брутто поперечного сечения всего элемента; Ag - площадь брутто поперечного сечения всех диагоналей, попадающих в один поперечный разрез элемента.Гибкость элемента определяют с учетом наличия по его длине перфораций или соединительных планок. Например, при подсчете площади и момента инерции элемента при наличии соединительных планок толщиной t в расчет допускается вводить приведенную толщину листа tef, вычисленную по формуле
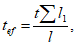 (4.3.10)
(4.3.10)где  - суммарная длина планок по длине элемента; l - длина элемента.
- суммарная длина планок по длине элемента; l - длина элемента.
4.3.5 Практическое развитие изгибно-крутильной формы потери устойчивости элементов для широко применяемых мостовых конструкций возможно: в пролетных строениях со сплошностенчатыми главными балками и ездой понизу; в неразрезных пролетных строениях со сплошностенчатыми главными балками и ездой поверху в зоне действия отрицательных моментов в приопорных зонах у промежуточных опор, в балках проезжей части с неподкрепленным плитой верхним поясом. Проверка общей устойчивости сжатой зоны пояса балки не производится в случае, если сжатый пояс объединен с железобетонной или металлической плитой проезжей части.
Другие виды сплошностенчатых конструктивных элементов, в которых возможна изгибно-крутильная форма потери устойчивости при центральном и внецентренном сжатии с изгибом, изгибе в двух плоскостях, для мостовых конструкций массового применения на этапе эксплуатации являются нехарактерными. К таким элементам следует относить конструкции пролетных строений и опор рамных мостов, арки, а также пилоны висячих и вантовых мостов. Грузоподъемность этих элементов следует определять с учетом положений пп. 4.3.7 - 4.3.10.
4.3.6 Несущую способность при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в одной плоскости, определяют по формуле
где Wс - момент сопротивления сечения балки для крайней фибры сжатого пояса;  - коэффициент продольного изгиба. Коэффициенты
- коэффициент продольного изгиба. Коэффициенты  и
и 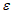 определяют в соответствии с п. 8.41 [3], при этом значение коэффициента
определяют в соответствии с п. 8.41 [3], при этом значение коэффициента 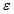 допускается принимать равным 1,0 (в запас прочности) или рассчитывать с учетом рекомендаций п. 4.1.3.
допускается принимать равным 1,0 (в запас прочности) или рассчитывать с учетом рекомендаций п. 4.1.3.
За расчетное сечение принимают сечение посередине рассматриваемой расчетной длины сжатого пояса балки.
Изгибно-крутильную оценку общей устойчивости изгибаемых балок допускается (в запас прочности) заменять на проверку ее сжатого пояса как сжатого стержня, а коэффициент  вычислять по приложению Ф [3] в зависимости от приведенной гибкости
вычислять по приложению Ф [3] в зависимости от приведенной гибкости  , при eef = 0,0, здесь lef - расчетная длина сжатого пояса балки. При вычислении радиуса инерции i по формуле (4.3.2) в расчет принимают характеристики I и A для сжатого пояса балки.
, при eef = 0,0, здесь lef - расчетная длина сжатого пояса балки. При вычислении радиуса инерции i по формуле (4.3.2) в расчет принимают характеристики I и A для сжатого пояса балки.
 , при eef = 0,0, здесь lef - расчетная длина сжатого пояса балки. При вычислении радиуса инерции i по формуле (4.3.2) в расчет принимают характеристики I и A для сжатого пояса балки.
, при eef = 0,0, здесь lef - расчетная длина сжатого пояса балки. При вычислении радиуса инерции i по формуле (4.3.2) в расчет принимают характеристики I и A для сжатого пояса балки.Для определения коэффициента  расчетную длину сжатого пояса балки lef принимают равной:
расчетную длину сжатого пояса балки lef принимают равной:
- при наличии продольных связей в зоне сжатых поясов и поперечных связей в опорных сечениях - расстоянию между узлами продольных связей;
- при наличии продольных связей только в зоне растянутых поясов и поперечных связей в пролете и в опорных сечениях - расстоянию между поперечными связями;
- если в пролете нет связей - пролету балки lp.
Для поперечных балок за расчетную длину сжатого пояса принимают  из двух величин: расстояние между продольными балками или расстояние от оси главной фермы (балки) до ближайшей продольной балки.
из двух величин: расстояние между продольными балками или расстояние от оси главной фермы (балки) до ближайшей продольной балки.
 из двух величин: расстояние между продольными балками или расстояние от оси главной фермы (балки) до ближайшей продольной балки.
из двух величин: расстояние между продольными балками или расстояние от оси главной фермы (балки) до ближайшей продольной балки.Для пролетных строений "открытого" типа расчетную длину сжатого пояса определяют по указаниям п. 4.1.20.
В сечение сжатого пояса включаются: для клепаных балок - поясные листы и уголки, а также часть стенки балки, расположенная в пределах высоты поясных уголков; для сварных балок - горизонтальные поясные листы и часть стенки в пределах величины hcw, вычисленной по формуле
 (4.3.12)
(4.3.12)где tw - толщина стенки.
4.3.7 Несущую способность при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в двух плоскостях, определяют по формуле (4.3.11), при этом коэффициент 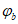 определяют с учетом указаний п. 8.42 [3], а значение erel допускается вычислять при действии постоянных и проектных временных нагрузок.
определяют с учетом указаний п. 8.42 [3], а значение erel допускается вычислять при действии постоянных и проектных временных нагрузок.
4.3.8 Несущую способность центрально сжатых сплошностенчатых элементов с сечениями открытого профиля, при возможности возникновения в них местной формы потери устойчивости наравне с общей формой, определяют меньшим из значений, вычисленных по формуле (4.3.1) и по формуле
 (4.3.13)
(4.3.13)где  - коэффициент продольного изгиба, определяемый по таблицам приложения Ф [3] при eef = 0,0. При этом гибкость следует определять по формуле
- коэффициент продольного изгиба, определяемый по таблицам приложения Ф [3] при eef = 0,0. При этом гибкость следует определять по формуле
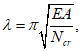 (4.3.14)
(4.3.14)где Ncr - критическая сила, определяемая по теории тонкостенных упругих стержней для заданных условий закрепления и нагружения, при этом рекомендуется применение конечно-элементных расчетных комплексов.
4.3.9 Определение грузоподъемности по изгибно-крутильной форме потери устойчивости сплошностенчатых элементов, подверженных сжатию с изгибом и внецентренному сжатию в плоскости наименьшей гибкости, выполняют итерационным путем, исходя из соблюдения условия
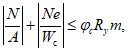 (4.3.15)
(4.3.15)где e - действительный эксцентриситет силы N при внецентренном сжатии или расчетный эксцентриситет e = M/N при сжатии с изгибом; Wс - момент сопротивления сечения брутто, вычисляемый для наиболее сжатой фибры;  - коэффициент продольного изгиба, определяемый в соответствии с п. 8.39 [3].
- коэффициент продольного изгиба, определяемый в соответствии с п. 8.39 [3].
4.3.10 Определение грузоподъемности по изгибно-крутильной форме потери устойчивости сплошностенчатых элементов, подверженных сжатию с изгибом и внецентренному сжатию в двух плоскостях, выполняют итерационным путем, исходя из соблюдения условия
 (4.3.16)
(4.3.16)где ey, ex - действительные эксцентриситеты по направлению осей y и x при внецентренном сжатии или расчетные эксцентриситеты при сжатии с изгибом; yc, xc - координаты наиболее сжатой точки сечения от совместного действия Mx, My и N; Ix, Iy - моменты инерции сечения брутто относительно главных осей x и y;  - коэффициент продольного изгиба, определяемый в соответствии с п. 8.40 [3].
- коэффициент продольного изгиба, определяемый в соответствии с п. 8.40 [3].
Кроме того, должен быть выполнен расчет грузоподъемности элемента при плоской форме потери устойчивости, при вычислении его несущей способности по формуле (4.3.1). При этом в плоскости оси y эксцентриситет 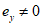 , а ex = 0, и в плоскости оси x эксцентриситет
, а ex = 0, и в плоскости оси x эксцентриситет 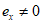 , а ey = 0.
, а ey = 0.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
4.3.10 Несущую способность по устойчивости полок и стенок элементов, не подкрепленных ребрами жесткости, при среднем касательном напряжении, не превышающем  , определяют по формулам таблицы 4.3.1.
, определяют по формулам таблицы 4.3.1.
Таблица 4.3.1
Предельные значения продольных напряжений 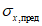 , МПа
, МПа
Класс прочности (марка) стали | Значение | Формулы для определения предельных значений продольных напряжений |
С235 (16Д, Ст.3) | До 176 |  |
Свыше 176 до 205 |  | |
Св. 205 |  | |
С235 - С345 (15ХСНД) | До 186 |  |
Свыше 186 до 284 | 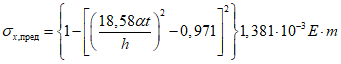 | |
Свыше 284 |  | |
С390 (10ХСНД, 390-14Г2АФД39, 390-15Г2АФДпс) | До 206 |  |
Свыше 206 до 343 | 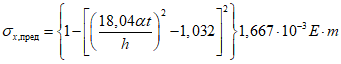 | |
Свыше 343 | 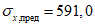 |
Примечание. Здесь значение  определяют по формуле
определяют по формуле

где h - высота стенки или ширина полки элемента; t - толщина стенки или полки элемента;  - коэффициент (п. 4.3.11); E - модуль упругости стали; m - коэффициент условий работы (п. 4.1.4).
- коэффициент (п. 4.3.11); E - модуль упругости стали; m - коэффициент условий работы (п. 4.1.4).
- для пластин, опертых по одной стороне (для полосовых ребер, свесов сжатых элементов и т.д.):
- для пластин, опертых по двум сторонам (для листа настила ортотропной плиты, стенок не полосовых и не тавровых ребер и т.д.):
ИС МЕГАНОРМ: примечание. Текст дан в соответствии с официальным текстом документа. |
В формулах (4.3.17) и (4.3.18) обозначено:  - коэффициент защемления пластинки, зависящий от ее геометрических размеров и формы поперечного сечения, см. табл. 8.22 [3], в запас прочности допускается принимать
- коэффициент защемления пластинки, зависящий от ее геометрических размеров и формы поперечного сечения, см. табл. 8.22 [3], в запас прочности допускается принимать  ;
; 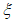 - коэффициент
- коэффициент
 ;
; 4.3.12 Коэффициент перекоса эпюры напряжений  , зависящий от соотношения максимальных и минимальных продольных нормальных напряжений по границам пластинки, определяют по формуле
, зависящий от соотношения максимальных и минимальных продольных нормальных напряжений по границам пластинки, определяют по формуле
где  ,
, 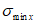 - максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые с учетом указаний п. 4.1.3 при невыгодном для устойчивости пластинки загружении. Коэффициенты
- максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые с учетом указаний п. 4.1.3 при невыгодном для устойчивости пластинки загружении. Коэффициенты  ,
,  ,
,  ,
, 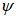 ,
,  ,
, 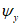 при определении
при определении  и
и  в формуле (4.3.19) принимают равными 1,0.
в формуле (4.3.19) принимают равными 1,0.
Напряжения  ,
,  допускается определять по формуле
допускается определять по формуле
где N - среднее значение продольной силы в пределах рассчитываемого отсека; M - среднее значение изгибающего момента в пределах рассчитываемого отсека, если длина отсека a менее его расчетной ширины (высоты) hef. При a > hef среднее значение изгибающего момента следует принимать на более напряженной части длины отсека (часть отсека с наибольшими значениями изгибающего момента), равной hef. Если в пределах отсека момент меняет знак, то M следует вычислять на участке отсека с моментом одного знака.
Величина ymax/min в формуле (4.3.20) принимает значения ymax, ymin - наибольшее и наименьшее расстояние от нейтральной оси до границ отсека (с учетом правила знаков - большему сжатию соответствует ymax, а меньшему сжатию или растяжению - ymin).
При действии в сечении только изгибающего момента, коэффициент 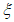 допускается принимать равным
допускается принимать равным  .
.
 .
.Равномерному сжатию соответствует значение 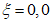 .
.
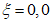 .
.4.3.13 Определение грузоподъемности по устойчивости стенок (полок), подкрепленных ребрами жесткости, проводят итерационным путем в соответствии с рекомендациями п. Б.3.2 [2], добиваясь выполнения условий по формулам (4.3.21), (4.3.25), (4.3.27), (4.3.31), приведенных в таблицах 4.3.3 - 4.3.11 в зависимости от расчетного случая. Выбор расчетного случая осуществляют по критериям, приведенным в таблице 4.3.2.
Таблица 4.3.2
Расчетные случаи для проверки устойчивости стенок
N расчетного случая | Критерии отнесения к расчетному случаю | |||
Напряженное состояние стенки | Число продольных ребер | Положение отсека по высоте стенки | Напряженное состояние отсека | |
1 | Сжато-растянутая | Отсутствуют | Крайний | Сжато-растянутый |
2 | Одно | Крайний | Наибольшее растяжение | |
3 | Крайний | Наибольшее сжатие | ||
4 | Два и более | Крайний | Растянутый | |
5 | Промежуточный | Растянутый | ||
6 | Промежуточный | Сжато-растянутый | ||
7 | Промежуточный | Сжатый | ||
8 | Крайний | Сжатый | ||
9 | Сжатая | - | - | - |
Таблица 4.3.3
Формулы условий и вычисления промежуточных значений | N формул |
1 | 2 |
 | |
где 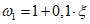 ; ;  , вводимый при , вводимый при  . . | |
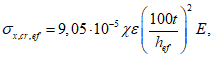 | |
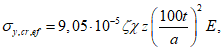 | |
z - по таблице Х.8 [3]. | |
 | |
Таблица 4.3.4
Расчетный случай N 2
Формулы условий и вычисления промежуточных значений | N формул |
Условие для проверки - формула (4.3.21) при 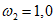 . . | - |
- | |
- | |
- |
Таблица 4.3.5
Расчетный случай N 3
Формулы условий и вычисления промежуточных значений | N формул |
 | |
где  . . | |
Значение  - для элементов с болтовыми или заклепочными соединениями, - для элементов с болтовыми или заклепочными соединениями,  - для всех элементов при объединении с железобетонной плитой, - для всех элементов при объединении с железобетонной плитой, | - |
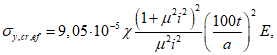 | |
где i = 1,0 при 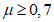 и i = 2,0 - в иных случаях; и i = 2,0 - в иных случаях; | |
- |
Таблица 4.3.6
Расчетный случай N 4
Формулы условий и вычисления промежуточных значений | N формул |
 | |
 | |
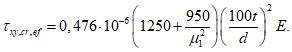 | (4.3.29) |
Таблица 4.3.7
Расчетный случай N 5
Формулы условий и вычисления промежуточных значений | N формул |
Условие для проверки - формула (4.3.27). | - |
Значение | - |
 | (4.3.30) |
Таблица 4.3.8
Расчетный случай N 6
Формулы условий и вычисления промежуточных значений | N формул |
- | |
- | |
- | |
- |
Таблица 4.3.9
Расчетный случай N 7
Формулы условий и вычисления промежуточных значений | N формул |
Условие для проверки - формула (4.3.25). | - |
- | |
- | |
- |
Таблица 4.3.10
Расчетный случай N 8
Формулы условий и вычисления промежуточных значений | N формул |
Условие для проверки - формула (4.3.25). | - |
- | |
Значение | - |
Значение | - |
Таблица 4.3.11
Формулы условий и вычисления промежуточных значений | N формул |
 | |
где  . . | |
Значение | - |
Значение | - |
Значение | - |
Примечания к таблицам 4.3.3 - 4.3.11.
1. В таблицах обозначено: E - модуль упругости стали; 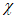 - коэффициент упругого защемления стенки; hw - полная высота стенки; t - толщина проверяемой стенки; a - длина стенки, равная расстоянию между осями смежных поперечных ребер (рисками уголков) жесткости; d - меньшая сторона стенки (a или hef);
- коэффициент упругого защемления стенки; hw - полная высота стенки; t - толщина проверяемой стенки; a - длина стенки, равная расстоянию между осями смежных поперечных ребер (рисками уголков) жесткости; d - меньшая сторона стенки (a или hef);  ,
,  - при a >= hef и
- при a >= hef и  - при a < hef; hef - расчетная высота стенки, равная: для прокатных или сварных элементов - расстоянию между осями поясов или осями продольных ребер (при их наличии); для составных элементов с болтовыми или заклепочными соединениями - расстоянию между ближайшими рисками поясных уголков или осями продольных ребер (при их наличии); lef - условная длина распределения сосредоточенной нагрузки, действующей на стенку.
- при a < hef; hef - расчетная высота стенки, равная: для прокатных или сварных элементов - расстоянию между осями поясов или осями продольных ребер (при их наличии); для составных элементов с болтовыми или заклепочными соединениями - расстоянию между ближайшими рисками поясных уголков или осями продольных ребер (при их наличии); lef - условная длина распределения сосредоточенной нагрузки, действующей на стенку.
 ,
,  - при a >= hef и
- при a >= hef и  - при a < hef; hef - расчетная высота стенки, равная: для прокатных или сварных элементов - расстоянию между осями поясов или осями продольных ребер (при их наличии); для составных элементов с болтовыми или заклепочными соединениями - расстоянию между ближайшими рисками поясных уголков или осями продольных ребер (при их наличии); lef - условная длина распределения сосредоточенной нагрузки, действующей на стенку.
- при a < hef; hef - расчетная высота стенки, равная: для прокатных или сварных элементов - расстоянию между осями поясов или осями продольных ребер (при их наличии); для составных элементов с болтовыми или заклепочными соединениями - расстоянию между ближайшими рисками поясных уголков или осями продольных ребер (при их наличии); lef - условная длина распределения сосредоточенной нагрузки, действующей на стенку.2. Коэффициент 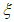 допускается определять по формуле (4.3.19).
допускается определять по формуле (4.3.19).
4.3.14 Значения критических напряжений 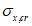 и
и 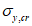 в формулах (4.3.21), (4.3.25), (4.3.27), (4.3.31) определяют по графику рисунка 4.3.1 в зависимости от напряжений
в формулах (4.3.21), (4.3.25), (4.3.27), (4.3.31) определяют по графику рисунка 4.3.1 в зависимости от напряжений 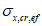 ,
,  соответственно. Напряжения
соответственно. Напряжения 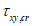 вычисляются по формуле
вычисляются по формуле
 (4.3.32)
(4.3.32)где напряжения  определяются по графику рисунка 4.3.1 в зависимости от напряжений
определяются по графику рисунка 4.3.1 в зависимости от напряжений  .
.
 .
.
Примечание. Значение напряжений  ,
,  или
или 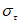 , определяемое по графикам рисунка, необходимо умножить на коэффициент условий работы m.
, определяемое по графикам рисунка, необходимо умножить на коэффициент условий работы m.
4.3.15 Силовыми факторами для расчета устойчивости являются продольное усилие N, средний по отсеку изгибающий момент M и средняя в пределах отсека поперечная сила Q.
ортотропной плиты
4.4.1 Расчет элементов ортотропной плиты должен учитывать совместную работу листа настила, подкрепляющих его ребер и главных балок, на которые опирается ортотропная плита. Ортотропную плиту допускается условно разделять на отдельные системы - продольные и поперечные ребра с соответствующими участками листа настила (рисунок 4.4.1).

а) - продольный разрез; б) - план; в) - поперечный разрез;
г) - ребро нижней плиты; 1, 2, 3, ..., i - номер
поперечного ребра верхней плиты; I, II, III - номер
расчетных сечений; A, B, C, D*, A1, B1, D1 - точки проверки
Примечание. Проверка поперечного ребра в точке D* не является обязательной.
4.4.2 Грузоподъемность элементов ортотропной плиты (листа настила, продольных и поперечных ребер) определяют из условия обеспечения их прочности, местной и общей устойчивости через определение напряжений от постоянной и временной нагрузок в точках A, B, C, D*, A1, B1, D1 сечений I, II, III (см. рис. 4.4.1).
Расчет выполняют итерационным путем согласно рекомендациям п. 4.1.5 и п. Б.3.2 [2], исходя из соблюдения условий, указанных ниже или в приложении Ш [3].
4.4.3 Определение грузоподъемности продольного ребра по прочности выполняют:
1) во всех случаях - в точке B в зоне действия положительных моментов в главной балке (рисунок 4.4.2, а, в);
2) для неразрезных конструкций главных балок - дополнительно в зоне действия отрицательных моментов в точке A (см. рисунок 4.4.2, а, б).

Расчет грузоподъемности в точке B выполняют исходя из соблюдения условия:
расчет грузоподъемности в точке A выполняют исходя из соблюдения условий:
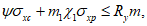 (4.4.2)
(4.4.2)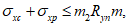 (4.4.3)
(4.4.3)где Ry, Ryn - расчетное и нормативное сопротивления металла продольного ребра;  ,
,  - коэффициенты, определяемые по пп. 8.28 и 8.26 [3] с учетом рекомендаций п. 4.1.3;
- коэффициенты, определяемые по пп. 8.28 и 8.26 [3] с учетом рекомендаций п. 4.1.3;  - коэффициент влияния собственных остаточных напряжений, принимаемый
- коэффициент влияния собственных остаточных напряжений, принимаемый  - для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и
- для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и  - для ребра в виде сварного тавра;
- для ребра в виде сварного тавра;  - коэффициент влияния собственных остаточных напряжений, принимаемый
- коэффициент влияния собственных остаточных напряжений, принимаемый 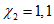 - для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и
- для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и  - для ребра в виде сварного тавра; m - коэффициент условий работы, равный 0,85 при расчете моста, расположенного в северном районе Б, или равный 1,0 в остальных случаях; m1, m2 - коэффициенты условий работы, принимаемые в зависимости от соотношения напряжений
- для ребра в виде сварного тавра; m - коэффициент условий работы, равный 0,85 при расчете моста, расположенного в северном районе Б, или равный 1,0 в остальных случаях; m1, m2 - коэффициенты условий работы, принимаемые в зависимости от соотношения напряжений  по таблице Ш.2 [3].
по таблице Ш.2 [3].
 - для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и
- для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и  - для ребра в виде сварного тавра;
- для ребра в виде сварного тавра; 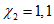 - для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и
- для крайней нижней фибры ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и  - для ребра в виде сварного тавра; m - коэффициент условий работы, равный 0,85 при расчете моста, расположенного в северном районе Б, или равный 1,0 в остальных случаях; m1, m2 - коэффициенты условий работы, принимаемые в зависимости от соотношения напряжений
- для ребра в виде сварного тавра; m - коэффициент условий работы, равный 0,85 при расчете моста, расположенного в северном районе Б, или равный 1,0 в остальных случаях; m1, m2 - коэффициенты условий работы, принимаемые в зависимости от соотношения напряжений  по таблице Ш.2 [3].
по таблице Ш.2 [3].4.4.4 Определение грузоподъемности поперечного ребра по прочности выполняют посередине его пролета для крайней нижней фибры сечения в точке C (см. рис. 4.4.1, а, в; рис. 4.4.2, г), исходя из соблюдения условия
4.4.5 Определение грузоподъемности листа настила по прочности выполняют в точках A1, B1, D1 (см. рис. 4.4.1, рис. 4.4.2), исходя из соблюдения условий:
где  ;
; 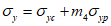 ;
; 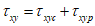 ; m3 - коэффициент, равный 1,15 при
; m3 - коэффициент, равный 1,15 при  или 1,10 при
или 1,10 при  ; m4 - коэффициент условий работы, принимаемый равным 1,05 - при проверке прочности листа настила в точке A1 или 1,0 - во всех остальных случаях.
; m4 - коэффициент условий работы, принимаемый равным 1,05 - при проверке прочности листа настила в точке A1 или 1,0 - во всех остальных случаях.
 ;
; 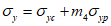 ;
; 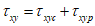 ; m3 - коэффициент, равный 1,15 при
; m3 - коэффициент, равный 1,15 при При выполнении данной проверки допускается принимать в качестве расчетных те загружения, при которых достигает максимального значения одно из действующих в данной точке ортотропной плиты напряжений -  ,
,  или
или 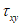 .
.
4.4.6 Грузоподъемность по местной устойчивости листа настила между продольными ребрами, продольных полосовых ребер, свесов поясов тавровых продольных и поперечных ребер определяют, руководствуясь п. 4.3.10.
4.4.7 Грузоподъемность по местной устойчивости стенок тавровых ребер определяют, руководствуясь п. 4.3.14.
4.4.8 Грузоподъемность по общей устойчивости определяют, исходя из соблюдения условия:
где  - наибольшие сжимающие напряжения в сечении ортотропной плиты (положительные при сжатии) при ее совместной работе с главными балками; m - коэффициент условий работы;
- наибольшие сжимающие напряжения в сечении ортотропной плиты (положительные при сжатии) при ее совместной работе с главными балками; m - коэффициент условий работы;  - коэффициент продольного изгиба, зависящий от гибкости ортотропной плиты
- коэффициент продольного изгиба, зависящий от гибкости ортотропной плиты  , таблица Ш.3 [3].
, таблица Ш.3 [3].
4.4.9 Грузоподъемность по прочности на смятие элементов металлических пролетных строений определяют из условия
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: таблица 8.3 отсутствует. |
где Aсм - площадь поверхности смятия; Wсм - момент сопротивления поверхности смятия; h - расстояние от подошвы подушки тангенциальной опорной части или от центра шарнира (для опорных частей с шарнирами) до подошвы нижнего или верхнего балансиров; N, H - соответственно, допускаемые расчетные вертикальное и горизонтальное усилия, приходящиеся на опорную часть (глава 7 [10]); m = 1 - коэффициент условий работы; Rp - расчетное сопротивление стали смятию торцевой поверхности (таблица 8.3 [9]).
За поверхность смятия принимается площадь опирания вертикальной стенки и опорных ребер жесткости. В фермах давление передается фасонками опорных узлов.
Из условия (4.4.8) можно непосредственно выразить величины допускаемых классов K нагрузок АК и НК и давлений на ось P эталонных транспортных средств по условию смятия или найти их же итерационным путем.
4.5.1 Несущую способность соединений на цилиндрических и на конических болтах, работающих на срез, смятие и на растяжение, определяют по формуле
где n - число болтов в соединении; mb, m - коэффициенты условий работы, принимаемые соответственно по таблицам 8.36 и 8.15 [3]; Nb,min - меньшее из значений расчетного усилия Nb для одного болта, вычисленных по формулам:
на срез болта
Nb = RbsAbsns; (4.5.2)
на смятие
 (4.5.3)
(4.5.3)на растяжение
Nb = RbtAbn, (4.5.4)
где Rbs, Rbp, Rbt - расчетные сопротивления металла болтов на срез, смятие и растяжение; d - диаметр рабочего тела болта (или отверстия); Abs - площадь рабочего сечения тела болта; Abn - площадь сечения болта нетто по резьбе;  - наименьшая суммарная толщина элементов, сминаемых в одном направлении; ns - число расчетных срезов одного болта.
- наименьшая суммарная толщина элементов, сминаемых в одном направлении; ns - число расчетных срезов одного болта.
4.5.2 Несущую способность болтового поля в соединении стыкуемой конструкции при действии в его плоскости изгибающего момента определяют по формуле:
где 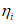 - расстояние от нейтральной оси стыкуемой конструкции до оси i-го болта. Для болтов, ориентированных собственной осью перпендикулярно плоскости изгибающего момента, принимается до оси болта, а для болтов, ориентированных собственной осью параллельно плоскости изгибающего момента - до соответствующей плоскости среза;
- расстояние от нейтральной оси стыкуемой конструкции до оси i-го болта. Для болтов, ориентированных собственной осью перпендикулярно плоскости изгибающего момента, принимается до оси болта, а для болтов, ориентированных собственной осью параллельно плоскости изгибающего момента - до соответствующей плоскости среза;
ymax - максимальное расстояние от нейтральной оси до наиболее удаленной фибры рабочей части соединения.
4.5.3 Болты, работающие на срез от одновременного действия продольной силы и изгибающего момента, проверяют на усилие, определяемое как равнодействующее усилий, найденных отдельно от продольной силы и момента.
4.5.4 Грузоподъемность болтовых соединений, работающих одновременно на срез и растяжение, допускается проверять отдельно из расчетов на срез и на растяжение.
4.5.5 Несущую способность болтовых соединений стенки с поясами составных балок, определяют по формулам:
при отсутствии непосредственной передачи давления от подвижной вертикальной нагрузки (местного давления) на пояс балки
при непосредственной передаче на пояс балки местного давления q
где Nb,min - меньшее из значений расчетного усилия для одного болта, определяемых по п. 4.5.1; I - момент инерции сечения брутто балки относительно горизонтальной оси, проходящей через центр тяжести сечения; a - шаг поясных болтов; S' - статический момент площади поперечного сечения брутто пояса балки (поясных уголков, горизонтальных листов и части вертикального листа, заключенного между поясными уголками) относительно горизонтальной оси, проходящей через центр тяжести сечения; q - давление от подвижной вертикальной расчетной нагрузки, вычисляемое по формуле
где a1 - длина распределения нагрузки от колеса вышележащими конструкциями, см. формулу (4.2.1) [5]; P - давление от колеса временной нагрузки. Допускается принимать давление P для той нагрузки, под которую конструкция была запроектирована (при двух и более проектных нагрузках - от действия которой величина q приобретает более невыгодное значение).
4.5.6 Несущую способность фрикционных соединений на высокопрочных болтах при действии продольной силы N, проходящей через центр тяжести соединения, определяют по формуле
Nпред = n·m·Qbh·ns, (4.5.9)
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: формула (4.9.8) отсутствует. Возможно, имеется в виду формула (4.5.8). |
где n - число болтов в соединении; Qbh - расчетное усилие на один болтоконтакт, определяемое по формуле (4.9.8); ns - число контактов в соединении.
4.5.7 Расчетное усилие Qbh, которое может быть воспринято каждой контактной поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом (одним болтоконтактом), определяют по формуле
где P - фактическое усилие натяжения высокопрочного болта, принимаемое по технической документации;  ,
, 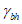 - коэффициент трения и коэффициент надежности, принимаемые по п. 4.1.10.
- коэффициент трения и коэффициент надежности, принимаемые по п. 4.1.10.
4.5.8 При действии в плоскости соединения изгибающего момента или продольной силы с изгибающим моментом усилие, приходящееся на рассматриваемый высокопрочный болт, определяют согласно указаниям пп. 4.5.2 и 4.5.3.
4.5.9 Несущую способность фрикционных соединений на высокопрочных болтах стенки с поясами составных балок определяют по формулам:
при отсутствии непосредственной передачи давления от подвижной вертикальной нагрузки (местного давления) на пояс балки
 (4.5.11)
(4.5.11)при непосредственной передаче на пояс балки местного давления q
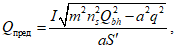 (4.5.12)
(4.5.12)где ns - число контактов в соединении; Qbh - расчетное усилие, воспринимаемое одним болтоконтактом и определяемое по формуле (4.5.10). Остальные обозначения приведены в п. 4.5.5.
4.5.10 Расчет по прочности сварных стыковых соединений выполняют:
- при сварке материалами, для которых расчетное сопротивление сварного шва Rwy менее расчетного сопротивления металла стыкуемых деталей Ry;
- при сварке деталей, для которых lw < b или tw,min < t или Aw < A, где lw - полная длина стыкового шва; tw,min - наименьшая толщина сечения стыкового шва; b, t - ширина и толщина стыкуемых деталей; Aw - площадь сечения стыковых швов; A - площадь сечения стыкуемых деталей.
4.5.11 Несущую способность сварных стыковых соединений в случае центрального растяжения или сжатия определяют по формуле
Nпред = m·Rwytwlw, (4.5.13)
где Rwy - расчетное сопротивление сварного соединения (п. 4.1.11); tw - расчетная высота сечения шва, принимаемая в соответствии с п. 8.83 [3]; lw - полная длина шва.
Расчет по прочности сварных стыковых соединений в случае изгиба в одной или двух главных плоскостях, а также действия осевой силы с изгибом в одной или двух главных плоскостях выполняют по формулам п. 4.2, в которых геометрические параметры и коэффициенты 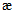 ,
,  ,
,  ,
,  ,
,  ,
,  вычисляют для сечения стыкового соединения, принимаемого согласно п. 8.84 [3], а в правой части вместо Ry подставляют величину Rwy.
вычисляют для сечения стыкового соединения, принимаемого согласно п. 8.84 [3], а в правой части вместо Ry подставляют величину Rwy.
4.5.12 Несущую способность на срез (условный) сварных соединений с угловыми швами при действии продольных или поперечных сил определяют для двух сечений (рисунок 4.5.1):
по металлу шва (сечение 0-1)
Nпред = mRwftflw; (4.5.14)
по металлу границы сплавления (сечение 0-2)
Nпред = mRwztzlw, (4.5.15)
где Rwf, Rwz - расчетные сопротивления сварного соединения (п. 4.1.11); tf, tz - расчетная высота сечения шва, принимаемая в соответствии с п. 8.83 [3]; lw - полная длина шва.

углового шва при расчете на срез
4.5.13 Несущую способность сварных соединений с угловыми швами при действии момента в плоскости, перпендикулярной плоскости расположения швов, определяют для двух сечений (рисунок 4.5.2 а, б) по формулам:
по металлу шва
Mпред = mRwfWf; (4.5.16)
по металлу границы сплавления
Mпред = mRwzWz, (4.5.17)
где Wf - момент сопротивления расчетного сечения по металлу шва; Wz - то же, по металлу границы сплавления.

а - перпендикулярной; б - параллельной
с угловыми швами при действии момента в плоскости
4.5.14 Несущую способность сварных соединений с угловыми швами при действии момента в плоскости расположения этих швов определяют для двух сечений (рисунок 4.5.2 а, б) по формулам:
по металлу шва
 (4.5.18)
(4.5.18)по металлу границы сплавления
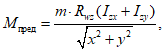 (4.5.19)
(4.5.19)где Ifx, Ify - моменты инерции расчетного сечения по металлу шва относительно его главных осей; Izx, Izy - то же, по металлу границы сплавления; x, y - координаты точки шва, наиболее удаленной от центра тяжести расчетного сечения швов, относительно главных осей этого сечения.
4.5.15 Грузоподъемность по прочности сварных стыковых соединений при одновременном действии в одном сечении нормальных и касательных напряжений определяют итерационным путем, исходя из соблюдения условий п. 8.31 [3], где принимают:  и
и  - нормальные напряжения в сварном соединении по двум взаимно перпендикулярным направлениям;
- нормальные напряжения в сварном соединении по двум взаимно перпендикулярным направлениям;  - касательное напряжение в сварном соединении; Ry = Rwy.
- касательное напряжение в сварном соединении; Ry = Rwy.
 и
и  - нормальные напряжения в сварном соединении по двум взаимно перпендикулярным направлениям;
- нормальные напряжения в сварном соединении по двум взаимно перпендикулярным направлениям;  - касательное напряжение в сварном соединении; Ry = Rwy.
- касательное напряжение в сварном соединении; Ry = Rwy.4.5.16 Несущую способность сварных соединений с угловыми швами прикрепления листов составного пояса между собой и к стенке изгибаемых балок определяют по формулам:
при отсутствии непосредственной передачи давления от подвижной вертикальной нагрузки (местного давления) на пояс балки:
по металлу шва
 (4.5.20)
(4.5.20)по металлу границы сплавления
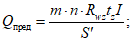 (4.5.21)
(4.5.21)при непосредственной передаче на пояс балки местного давления q:
по металлу шва
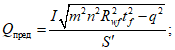 (4.5.22)
(4.5.22)по металлу границы сплавления
 (4.5.23)
(4.5.23)где n - число угловых швов. Остальные обозначения те же, что и в п. 4.5.5.
4.5.17 При прикреплении к узлам главных ферм составных сплошностенчатых элементов, отдельные части сечения которых непосредственно не прикрепляются к узловым фасонкам, грузоподъемность по прочности сварных швов присоединения неприкрепляемой части сечения к прикрепляемой рассчитывают с учетом указаний п. 8.93 [3].
4.5.18 Несущую способность заклепочных соединений при действии продольной силы N, проходящей через центр тяжести соединения, следует определять по формуле
Nпред = nmbmNr,min, (4.5.24)
где n - число заклепок в соединении; mb, m - см. формулу (4.5.1); Nr,min - меньшее из значений расчетного усилия Nr для одной заклепки, вычисленных по формулам:
на срез заклепки
на смятие
где Rbs, Rbp - расчетные сопротивления металла заклепки на срез и смятие, принимаемые по расчетному сопротивлению основного металла с учетом коэффициентов перехода по таблице 4.1.1; d - диаметр заклепки (или отверстия); Abs - площадь рабочего сечения тела заклепки, 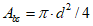 ;
;  - наименьшая суммарная толщина элементов, сминаемых в одном направлении; ns - число расчетных срезов одной заклепки.
- наименьшая суммарная толщина элементов, сминаемых в одном направлении; ns - число расчетных срезов одной заклепки.
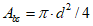 ;
; ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: формулы (4.5.28) и (4.5.29) отсутствуют. |
4.5.19 Несущую способность заклепочного соединения при действии в его плоскости изгибающего момента определяют по формуле (4.5.5) с подстановкой в нее значения Nb = Nr, вычисляемого по (4.5.28) и (4.5.29).
4.5.20 Заклепки, работающие на срез от одновременного действия продольной силы и изгибающего момента, определяют на усилие, определяемое как равнодействующее усилий, найденных отдельно от продольной силы и момента.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: формулы (4.9.25) и (4.9.26) отсутствуют. Возможно, имеются в виду формулы (4.5.25) и (4.5.26) |
4.5.21 Заклепки, соединяющие стенки и пояса составных балок, рассчитывают по формулам (4.5.6), (4.5.7) с подстановкой в них значения Nb,min = Nr, вычисляемого по (4.9.25) и (4.9.26).
пролетных строений
5.1.1 К сталежелезобетонным относят пролетные строения, в которых воздействие от внешних нагрузок воспринимается стальными несущими конструкциями главных балок совместно с железобетонной плитой проезжей части. Рекомендации раздела могут быть использованы для расчета грузоподъемности поясов главных ферм и балок проезжей части, включенных в совместную работу с железобетонной плитой.
5.1.2 Расчет грузоподъемности главных балок сталежелезобетонных пролетных строений производят с использованием основных положений главы 9 [8] и настоящих Рекомендаций. При этом необходимо учитывать ряд особенностей работы конструкций, к которым относятся:
- совместная статическая работа элементов конструкций, выполненных из различных материалов (стали и железобетона), которая зависит как от состояния этих элементов, так и от эффективности работы объединительных деталей (упоров и др.);
- многостадийный характер статической работы с последовательным включением различных элементов при возведении;
- регулирование усилий при монтаже.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт Б.3.2 отсутствует. |
5.1.3 Определение грузоподъемности объединенных балок рекомендуется производить методом последовательных приближений с использованием методологии норм проектирования [8] путем подбора величины класса рассматриваемой нагрузки, которой соответствуют предельные усилия с учетом имеющихся дефектов. Примерный порядок расчета приведен в п. Б.3.2 [6].
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
5.1.6 Расчеты целесообразно выполнять в пространственной постановке, используя программные комплексы, основанные, в том числе, на методе конечных элементов и обязательно имеющие применение в практике проектирования. В этом случае можно получать линии влияния воздействий, непосредственно учитывающие пространственный характер работы конструкций, или, что предпочтительнее для автоматизированных расчетов - поверхности влияния. Рекомендации по составлению конечно-элементных моделей пролетного строения и построению поверхностей влияния приведены в приложении А.
5.1.4 Расчеты допускается выполнять с использованием аппарата "плоских" линий влияния. При этом пространственную работу конструкции следует учитывать с помощью коэффициентов поперечной установки, принимая поперечное распределение усилий по методу "рычага" (при двух главных балках и отсутствии нижних продольных горизонтальных связей), по методу внецентренного сжатия или по методу упруго проседающих опор.
5.1.5 При наличии двух главных балок, связанных между собой поперечными связями, железобетонной плитой проезда и нижними продольными связями, следует учитывать крутильную жесткость пространственной конструкции.
5.1.7 Расчетные сопротивления и модули упругости бетона и арматуры плиты принимают согласно рекомендациям по пп. 4.1.3 - 4.3.7 [5]. Расчетные сопротивления, коэффициенты условий работы и модули упругости прокатного металла принимают в соответствии пп. 4.1.8 - 4.1.14.
nb = Es/Eb, nr = Es/Er, (5.1.1)
где Es - модуль упругости стали, МПа (принимается Es = 2,06·105 МПа); Eb - модуль упругости бетона, МПа (принимается по п. 4.1.17 [5]); Er - модуль упругости арматуры, МПа (для стержневой арматуры принимается Er = Es).
5.1.9 Для расчета геометрических характеристик сложное составное сечение целесообразно разбивать на элементы, имеющие простые геометрические формы - прямоугольники и треугольники (рисунок 5.1.1), приводя криволинейные участки (например, вуты плиты) к указанным фигурам.
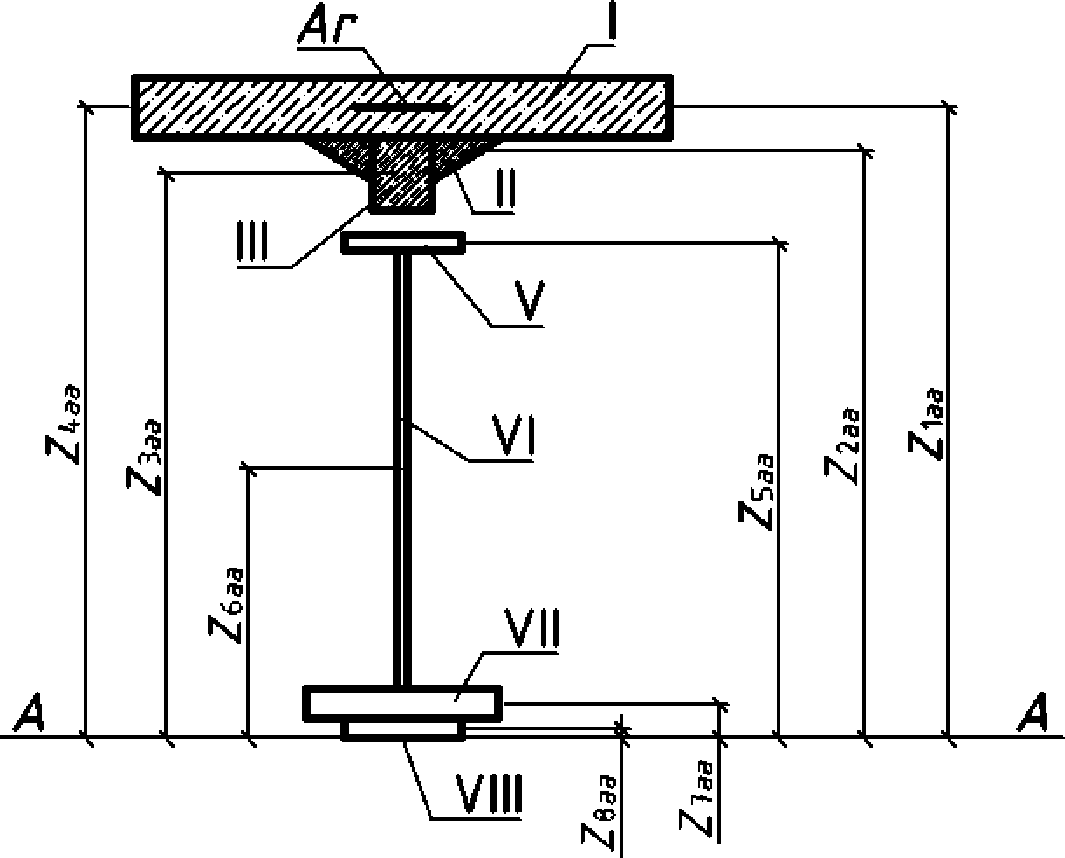
Рисунок 5.1.1 - Пример представления сложных сечений
набором простейших фигур:
I - III - элементы железобетонной плиты проезжей части;
V - VIII - элементы стальной балки;
Ar - стальная арматура, задаваемая своей площадью
При этом следует различать элементы стальной балки и железобетонной плиты. При незначительных размерах ребер и вутов плиты можно плиту представить только одним элементом I, площадь и положение центра тяжести которого равны площади и положению центра тяжести исходной конструкции.
Для каждого (бетонного и стального) элемента сечения вычисляют площадь элемента (Abi, Ar - приведенные к стальной части балки, Asi); статический момент относительно оси A-A (Sb,aa.i, Ss,aa.i); момент инерции относительно оси A-A (Ib,aa.i, Is,aa.i), момент инерции относительно собственных центров тяжести (Ib,co,i, Is,co,i), принимая n = nb - для бетонных элементов, n = nr - для арматуры, n = 1 - для стальных элементов. Величину Icoi для арматурных элементов не вычисляют.
Для элементов плиты (бетонных частей и арматуры) вычисляют суммы
ИС МЕГАНОРМ: примечание. Формулы и расшифровки к формулам даны в соответствии с официальным текстом документа. |
 ;
;  ;
;  ;
; 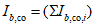 , (5.1.2)
, (5.1.2)где Ab - площадь плиты и арматуры, приведенные к площади стали главной балки; Sb,aa - статический момент бетонной части сечения с арматурой относительно оси A-A; Ib,aa - момент инерции плиты относительно оси A-A; Ib,co - момент инерции плиты относительно ее центра тяжести.
Для элементов стальной балки вычисляют суммы
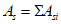 ;
;  ;
; 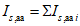 ;
;  , (5.1.3)
, (5.1.3)где As - площадь стальной части балки; Ss,aa - статический момент стального сечения относительно его нижней фибры (оси A-A); Is,aa - момент инерции стального сечения относительно его нижней фибры (оси A-A); Is,co - момент инерции стального сечения относительно его центра тяжести.
Для всего сечения
Astb = Ab + As; Sstb,aa = Sb,aa + Ss,aa;
Istb,aa = Ib,aa + Is,aa; Istb,co = Ib,co + Is,co, (5.1.4)
где Sstb,aa - статический момент объединенного сечения относительно фибры s1; Istb,aa - момент инерции объединенного сечения относительно его нижней фибры s1; Istb,co - момент инерции объединенного сечения относительно его центра тяжести.
Формулы для определения характеристик сечения
- положение центра тяжести стального сечения Cs
Zs1,s = Ss,aa/As; (5.1.5)
- расстояние от центра тяжести стального сечения до верхней фибры стальной балки
Zs2,s = hs - Zs1,s, (5.1.6)
где hs - высота стальной части балки;
- положение центра тяжести железобетонной плиты Cbr
Zbr = Sb,aa/Ab; (5.1.7)
- положение центра тяжести объединенного сечения Cstb
Zstb = Sstb,aa/Astb. (5.1.8)
Если Zstb > Zb1 (расстояния от оси A-A до низа железобетонной плиты), то из состава сечения следует исключать растянутый бетон;
- расстояние между центрами тяжести объединенного сечения и плиты
Zb,stb = Zbr - Zstb; (5.1.9)
- расстояние между центрами тяжести стального сечения и плиты
Zbs = Zbr - Zs1,s; (5.1.10)
- момент инерции стальной части сечения
Is = Is,aa + Is,co - Zs1,sSs,aa; (5.1.11)
- момент инерции объединенного сечения
Istb = Istb,aa + Istb,co - ZstbSstb,aa; (5.1.12)
- моменты сопротивления
Wb,stb = Istb/Zb,stb; Ws1,s = Is/Zs1,s; Ws2,s = Is/Zs2,s;
Wbs = Is/Zbs. (5.1.13)
Проверяют применимости гипотезы "тонкой плиты"
Если условие (5.1.14) не выполняется, то дополнительно вычисляют:
- положение центра тяжести плиты относительно нижней фибры плиты Cbr
Zb1,b = Sb1,b/Ab, (5.1.15)
где Sb1,b - статический момент плиты относительно ее нижней фибры b1;
- расстояние от центра тяжести объединенного сечения до верхней фибры железобетонной плиты
- расстояние от центра тяжести железобетонной плиты до верхней фибры железобетонной плиты
где hstb - высота расчетного сечения объединенной балки;
- расстояние от центра тяжести стального сечения до верхней фибры железобетонной плиты
Zbf,st = hstb - Zs1,s; (5.1.18)
- моменты сопротивления
Wbf,stb = Istb/Zbf,stb; Wb2,b = Ib/(hstb - Zbr);
Wbf3,stb = Istb/(Zbf,stb - h2), (5.1.19)
где h2 - высота верхней полки железобетонной плиты.
Возможны и другие способы определения указанных характеристик сечения.
5.1.10 Постоянные нагрузки и воздействия принимают в соответствии с [3], а коэффициенты надежности к ним - согласно п. 5.1.1 [2]. Постоянные нагрузки вводят в расчет с учетом последовательности монтажа, регулирования усилий и ремонтов.
5.1.11 Для рассчитываемого сечения, как правило, рассматривают две стадии приложения постоянных нагрузок:
1 стадия - собственный вес стальных балок и железобетонной плиты и другие нагрузки, воспринимаемые на этапе монтажа пролетного строения только стальной частью сечения;
2 стадия - вес покрытия проезжей части, конструкций мостового полотна и другие нагрузки, воспринимаемые объединенным сечением.
В большинстве случаев дополнительные нагрузки (например, от регулирования усилий) при большем количестве стадий монтажа (например, для неразрезного пролетного строения) могут быть приведены к указанным двум стадиям.
Последовательность монтажа и порядок приложения нагрузок следует устанавливать по данным проектной и исполнительной документации. При отсутствии таких данных допускается принимать наиболее вероятную последовательность монтажа на основе известного опыта строительства.
5.1.12 Воздействия ползучести и усадки бетона, а также неравномерные температурные воздействия учитывают совместно с воздействиями от постоянных и временных нагрузок в двух сочетаниях (п. 5.4 [2]):
1 сочетание - основное сочетание нагрузок (постоянные и временные вертикальные нагрузки), ползучесть и усадка бетона;
2 сочетание - дополнительное сочетание нагрузок 3 (постоянные и временные вертикальные нагрузки и разность температур), ползучесть и усадка бетона.
Воздействия ползучести и усадки бетона, а также неравномерные температурные воздействия не учитывают при расчете грузоподъемности главных балок на участках с полным расстройством объединения с железобетонной плитой.
5.1.13 Временные вертикальные и горизонтальные нагрузки, и нагрузку от пешеходов учитывают согласно пп. 5.2 и 5.3 [2].
5.1.14 При расчете главных балок следует учитывать неисправности, влияющие на грузоподъемность - уменьшение площади сечения элементов, пониженную прочность (и, соответственно, - модуль упругости) бетона плиты, расстройство объединения плиты и стальных балок.
5.2.1 Необходимость учета ползучести бетона и обжатия швов определяется условием
где 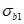 - напряжение на уровне центра тяжести бетонной плиты; M2g - изгибающий момент от расчетных постоянных нагрузок второй стадии работы сечения, МН·м (тс·м).
- напряжение на уровне центра тяжести бетонной плиты; M2g - изгибающий момент от расчетных постоянных нагрузок второй стадии работы сечения, МН·м (тс·м).
Если условие (5.2.1) выполняется, то учет ползучести не требуется. Однако, если при этом условие применимости метода "тонкой плиты" (5.1.14) не выполняется, то необходимо дополнительно проверить условие
где 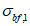 - напряжение на уровне крайней фибры бетонной плиты.
- напряжение на уровне крайней фибры бетонной плиты.
в статически определимых конструкциях
5.2.2 Если условия (5.2.1) и/или (5.2.2) не выполняются, то учет ползучести необходим, и следует вычислить напряжения от ползучести бетона на уровне центра тяжести и крайней фибры бетонной плиты, определив следующие величины:
- положение центра тяжести стального сечения, включая арматуру
Zs1,st = (Ss,aa + Sr,aa)/Ast; (5.2.3)
- расстояние от центра тяжести стального сечения до центра тяжести плиты
Zb,st = Zbr - Zs1,st; (5.2.4)
- коэффициент
 (5.2.5)
(5.2.5)где Ist - момент инерции стального сечения (включая арматуру); Ast = As + Ar - площадь стального сечения (включая арматуру); Ab - приведенная к стали площадь бетона;
- предельную характеристику ползучести бетона
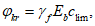 (5.2.6)
(5.2.6)где  - коэффициент надежности;
- коэффициент надежности;  - предельная деформация ползучести бетона, определяемая по п. 7.32 [3], с учетом указаний по приложениям Р и Т [3]; cn - нормативное значение деформации ползучести бетона;
- предельная деформация ползучести бетона, определяемая по п. 7.32 [3], с учетом указаний по приложениям Р и Т [3]; cn - нормативное значение деформации ползучести бетона;  ,
,  ,
, 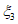 ,
,  - коэффициенты, зависящие соответственно от передаточной прочности бетона на сжатие в долях от проектного класса бетона; возраста бетона в момент загружения; модуля удельной поверхности элемента (отношения открытой поверхности элемента к его объему); относительной влажности воздуха.
- коэффициенты, зависящие соответственно от передаточной прочности бетона на сжатие в долях от проектного класса бетона; возраста бетона в момент загружения; модуля удельной поверхности элемента (отношения открытой поверхности элемента к его объему); относительной влажности воздуха.
 - коэффициент надежности;
- коэффициент надежности;  - предельная деформация ползучести бетона, определяемая по п. 7.32 [3], с учетом указаний по приложениям Р и Т [3]; cn - нормативное значение деформации ползучести бетона;
- предельная деформация ползучести бетона, определяемая по п. 7.32 [3], с учетом указаний по приложениям Р и Т [3]; cn - нормативное значение деформации ползучести бетона; При определении величины  при отсутствии данных исполнительной и проектной документации допускается принимать: передаточную прочность бетона на сжатие в долях проектного класса бетона равной 1,0
при отсутствии данных исполнительной и проектной документации допускается принимать: передаточную прочность бетона на сжатие в долях проектного класса бетона равной 1,0  ; возраст бетона в момент загружения 28 сут.
; возраст бетона в момент загружения 28 сут. 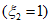 ; относительную влажность воздуха 60%
; относительную влажность воздуха 60%  .
.
 ; возраст бетона в момент загружения 28 сут.
; возраст бетона в момент загружения 28 сут. 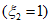 ; относительную влажность воздуха 60%
; относительную влажность воздуха 60%  .
.Для монолитной плиты, а также для сборной плиты, в которой конструктивно исключены деформации обжатия поперечных швов (например, в случае объединения продольной арматуры в стыках блоков сборной плиты) принимают
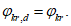 (5.2.7)
(5.2.7)Для сборной плиты, где возможны деформации обжатия поперечных швов, принимают
 (5.2.8)
(5.2.8)где L - длина плиты, сжатой постоянными нагрузками (для разрезной балки - равна длине пролета); Sd - суммарная деформация обжатия поперечных швов, расположенных на длине L.
Величину Sd, м, допускается вычислять как
 (5.2.9)
(5.2.9)где bd - ширина шва, см (зазор между торцами сборных плит).
Напряжения от ползучести на уровне центра тяжести железобетонной плиты, МПа (тс/м2)
где  - сжимающие напряжения, принимаемые по формуле (5.2.1) со знаком "плюс";
- сжимающие напряжения, принимаемые по формуле (5.2.1) со знаком "плюс"; 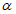 - коэффициент, определяемый по формуле
- коэффициент, определяемый по формуле
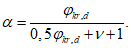 (5.2.11)
(5.2.11)Если центр тяжести арматуры совпадает (+/- 5%) с центром тяжести плиты, то напряжения от ползучести в арматуре определяют
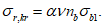 (5.2.12)
(5.2.12)Если условия (5.1.14) и (5.2.2) не выполняются, то дополнительно определяют напряжения от ползучести в крайней фибре бетона
где  ; Zbf,st - расстояние от центра тяжести стального сечения до центра тяжести плиты (при Zbf,st = Zb,st формула (5.2.13) переходит в формулу (5.2.10));
; Zbf,st - расстояние от центра тяжести стального сечения до центра тяжести плиты (при Zbf,st = Zb,st формула (5.2.13) переходит в формулу (5.2.10));  - сжимающие напряжения на уровне крайней фибры бетона, принимаемые по формуле (5.2.2) со знаком "плюс".
- сжимающие напряжения на уровне крайней фибры бетона, принимаемые по формуле (5.2.2) со знаком "плюс".
 ; Zbf,st - расстояние от центра тяжести стального сечения до центра тяжести плиты (при Zbf,st = Zb,st формула (5.2.13) переходит в формулу (5.2.10));
; Zbf,st - расстояние от центра тяжести стального сечения до центра тяжести плиты (при Zbf,st = Zb,st формула (5.2.13) переходит в формулу (5.2.10)); неопределимых конструкциях
5.2.4 При учете ползучести бетона в статически неопределимых конструкциях внутренние напряжения и внешние силовые факторы (опорные реакции, изгибающие моменты и пр.) допускается вычислять методом последовательных приближений, принимая усилия 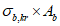 в центре тяжести бетонной части сечения за нагрузки.
в центре тяжести бетонной части сечения за нагрузки.
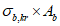 в центре тяжести бетонной части сечения за нагрузки.
в центре тяжести бетонной части сечения за нагрузки.Расчеты могут выполняться методом сил, методом замены деформаций ползучести эквивалентными деформациями от температуры или другими методами на базе уточненных моделей, учитывающих перераспределение внутренних усилий от ползучести бетона.
5.2.5 Расчет методом сил ведут в следующей последовательности.
1) Задаются статически определимой основной системой, например, как показано на рисунке 5.2.2.

системы для расчета ползучести в статически
неопределимой системе
2) Выполняют расчет статически неопределимой системы на постоянные нагрузки второй стадии работы, предварительного напряжения и регулирования усилий в предположении упругой работы без учета ползучести бетона: строят эпюру суммарного момента от указанных нагрузок M2g и по формуле (5.2.1) находят напряжения первого приближения  в центрах тяжести бетона в расчетных сечениях.
в центрах тяжести бетона в расчетных сечениях.
3) Принимают  .
.
 .
.4) Определяют по формулам п. 5.2.2 напряжения от ползучести бетона  в тех же сечениях (первое приближение) и определяют усилия, вызванные этими напряжениями.
в тех же сечениях (первое приближение) и определяют усилия, вызванные этими напряжениями.
 ,
,  , (5.2.14)
, (5.2.14)где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения; Zbs - расстояние между центрами тяжести стального сечения и плиты (п. 5.1.8).
5) Определяют грузовые перемещения по направлениям лишних неизвестных Xk от напряжений 
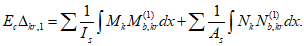 (5.2.15)
(5.2.15)6) Находят моменты инерции  и площади
и площади  сталежелезобетонных сечений по формулам пп. 5.1.8 и 5.1.9, принимая модуль упругости бетона
сталежелезобетонных сечений по формулам пп. 5.1.8 и 5.1.9, принимая модуль упругости бетона
7) Определяют основные и побочные перемещения
 (5.2.17)
(5.2.17)8) Из решения системы канонических уравнений (5.2.17) находят лишние неизвестные  и определяют изгибающие моменты
и определяют изгибающие моменты  и осевые усилия от этих неизвестных.
и осевые усилия от этих неизвестных.
 и осевые усилия от этих неизвестных.
и осевые усилия от этих неизвестных.9) Определяют напряжения  в центре тяжести бетона от моментов
в центре тяжести бетона от моментов  , вызванных ползучестью
, вызванных ползучестью
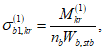 (5.2.18)
(5.2.18)где nb, Wb,stb вычислены при начальном модуле упругости бетона Eb.
10) Вычисляют напряжения второго приближения в центре тяжести бетона
 (5.2.19)
(5.2.19)11) В соответствии с п. Щ.2 [3] расчет повторяют еще дважды, начиная с п. 4, принимая последовательно 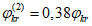 при второй итерации и
при второй итерации и 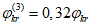 при третьей итерации (Щ.2 [3]). Вычисляют суммарные напряжения
при третьей итерации (Щ.2 [3]). Вычисляют суммарные напряжения  (и аналогичные им
(и аналогичные им 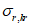 ) и подставляют в дальнейшем в формулы (5.4.2) и (5.4.3).
) и подставляют в дальнейшем в формулы (5.4.2) и (5.4.3).
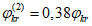 при второй итерации и
при второй итерации и 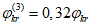 при третьей итерации (Щ.2 [3]). Вычисляют суммарные напряжения
при третьей итерации (Щ.2 [3]). Вычисляют суммарные напряжения  (и аналогичные им
(и аналогичные им Пример. Для балки, показанной на рисунке 5.2.2, система уравнений будет иметь вид
- грузовые перемещения
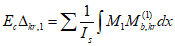 ;
;  ;
;- основные и побочные перемещения
 ;
;  ;
; 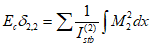 ;
;- система канонических уравнений

- изгибающий момент от ползучести

5.2.6 Расчет на базе метода конечных элементов с использованием для моделирования стержневых изгибаемых конечных элементов рекомендуется выполнять в следующем порядке.
1) Составляют расчетную схему из стержневых изгибаемых конечных элементов, в которой стержни стальной балки и стержни плиты объединены между собой жесткими вставками и находятся на расстоянии Zbs друг от друга (рисунок 5.2.3).

Рисунок 5.2.3 - Фрагмент схемы неразрезной балки
2) Загружают расчетную схему нагрузками, вызывающими ползучесть, и определяют осевые усилия Nb (при сжатии принимают положительными) и напряжения в бетоне элементов плиты 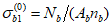 , где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
, где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
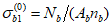 , где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
, где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.3) В соответствии с п. 5.2.2 для каждого типа сечения расчетной схемы определяют коэффициенты  ,
, 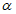 и характеристику ползучести
и характеристику ползучести 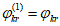 .
.
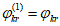 .
.5) Для следующего шага расчета в расчетной схеме для каждого конечного элемента плиты в виде начальных условий могут быть заданы:
- либо относительные удлинения стержней плиты  (Nb - усилия в конечных элементах стержней плиты на предыдущем шаге расчета, см. пример расчета в п. Б.4);
(Nb - усилия в конечных элементах стержней плиты на предыдущем шаге расчета, см. пример расчета в п. Б.4);
 (Nb - усилия в конечных элементах стержней плиты на предыдущем шаге расчета, см. пример расчета в п. Б.4);
(Nb - усилия в конечных элементах стержней плиты на предыдущем шаге расчета, см. пример расчета в п. Б.4);- либо условный перепад температур 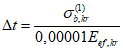 , вызывающего в бетоне такую же деформацию, что и ползучесть бетона (если программа позволяет выполнять расчеты на изменение температур).
, вызывающего в бетоне такую же деформацию, что и ползучесть бетона (если программа позволяет выполнять расчеты на изменение температур).
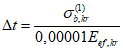 , вызывающего в бетоне такую же деформацию, что и ползучесть бетона (если программа позволяет выполнять расчеты на изменение температур).
, вызывающего в бетоне такую же деформацию, что и ползучесть бетона (если программа позволяет выполнять расчеты на изменение температур).Возможны и другие способы задания деформаций (усилий) ползучести, по физическому смыслу эквивалентные описанным.
6) Назначают  (
(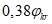 при втором и
при втором и  при третьем) и определяют величины
при третьем) и определяют величины  и
и  .
.
 (
(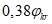 при втором и
при втором и  при третьем) и определяют величины
при третьем) и определяют величины 7) Изменяют жесткости элементов плиты на  , выполняют расчет с начальными условиями, сформированными на предыдущем шаге, и получают дополнительные усилия
, выполняют расчет с начальными условиями, сформированными на предыдущем шаге, и получают дополнительные усилия  .
.
 , выполняют расчет с начальными условиями, сформированными на предыдущем шаге, и получают дополнительные усилия
, выполняют расчет с начальными условиями, сформированными на предыдущем шаге, и получают дополнительные усилия 8) Определяют дополнительные напряжения  , где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
, где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
 , где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.
, где Ab - приведенная к стали площадь сечения плиты; nb - коэффициент приведения.9) Вычисляют напряжения второго приближения в центре тяжести бетона
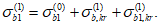
10) Дважды повторяют расчет с п. 5, последовательно назначая 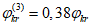 и
и  . Вычисляют суммарные напряжения
. Вычисляют суммарные напряжения  (и аналогичные им
(и аналогичные им  ) и подставляют в дальнейшем в формулы (5.4.2) и (5.4.3).
) и подставляют в дальнейшем в формулы (5.4.2) и (5.4.3).
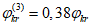 и
и  . Вычисляют суммарные напряжения
. Вычисляют суммарные напряжения  (и аналогичные им
(и аналогичные им ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 11 в Библиографии отсутствует. |
4.2.7 Расчеты с учетом ползучести и усадки бетона в неразрезных системах могут быть также выполнены на основании рекомендаций [11]. Как правило, такие расчеты выполняют совместно с расчетами на последовательность монтажа и регулирование усилий. Результатом расчетов должны быть напряжения 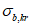 и
и  на уровне центра тяжести плиты от указанных факторов для последующего учета их в формулах (5.4.2) и (5.4.3).
на уровне центра тяжести плиты от указанных факторов для последующего учета их в формулах (5.4.2) и (5.4.3).
5.3.1 Для расчета усадки пересчитывают характеристики сечения по формулам п. 5.1.9, заменяя nb на 2nb, и вычисляют дополнительные величины:
- положение центра тяжести стального сечения Cst
Zs1,st = (Ss,aa + Sr,aa)/Ast; (5.3.1)
- положение центра тяжести объединенного сечения Cstb
Zstb,shr = Sstb,aa/Astb; (5.3.2)
- расстояние между центрами тяжести объединенного сечения и плиты
Z = -Zbr + Zstb,shr; (5.3.3)
- расстояние между центрами тяжести стального сечения и плиты
Zst,stb = Zstb,shr - Zs1,st; (5.3.4)
- момент инерции объединенного сечения
Istb,shr = Istb,aa + Istb,co - Zstb,shrSstb,aa; (5.3.5)
- статический момент объединенного сечения
Sshr = AstZst,stb, (5.3.6)
где Ast = As + Ar.
5.3.2 Напряжения от усадки на уровне центра тяжести бетонной части плиты и арматуры плиты вычисляют по формулам
в бетоне  (5.3.7)
(5.3.7)
 (5.3.7)
(5.3.7)в арматуре  (5.3.8)
(5.3.8)
 (5.3.8)
(5.3.8)где  - если плита сборная;
- если плита сборная; 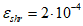 - если плита монолитная.
- если плита монолитная.
 - если плита сборная;
- если плита сборная; 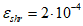 - если плита монолитная.
- если плита монолитная.Примечание. Z - расстояние от центра тяжести Astb,shr до фибры, где определяется  (положительное направление оси Z принято вниз).
(положительное направление оси Z принято вниз).
At = 0,8Awt + 0,3As1,t;
Zb1,stb = tf1 + hw - Zstb; (5.3.9)
St = (0,4hw - 0,8Zb1,stb)Awt + 0,3As1,tZs1,stb,
где Awt - площадь вертикальных элементов стальной балки (стенка, полки уголков и т.д.); As1,t - площадь стальных горизонтальных элементов нижнего пояса балки; tf1 - толщина листов нижнего пояса; hw - высота вертикального листа.
Напряжения от разности температур определяют
в бетоне 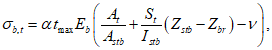 (5.3.10)
(5.3.10)
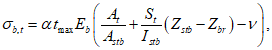 (5.3.10)
(5.3.10)в арматуре  (5.3.11)
(5.3.11)
 (5.3.11)
(5.3.11)где  - коэффициент линейного расширения стали и бетона; tmax - максимальная разность температур, принимается согласно п. 9.1 [3] (для одной из крайних балок со сплошной стенкой и ездой поверху +30 °C и -15 °C, для средней балки со сплошной стенкой и ездой поверху +/- 15 °C), с учетом коэффициента надежности 1,2;
- коэффициент линейного расширения стали и бетона; tmax - максимальная разность температур, принимается согласно п. 9.1 [3] (для одной из крайних балок со сплошной стенкой и ездой поверху +30 °C и -15 °C, для средней балки со сплошной стенкой и ездой поверху +/- 15 °C), с учетом коэффициента надежности 1,2;  - при наличии покрытия железобетонной плиты.
- при наличии покрытия железобетонной плиты.
 - коэффициент линейного расширения стали и бетона; tmax - максимальная разность температур, принимается согласно п. 9.1 [3] (для одной из крайних балок со сплошной стенкой и ездой поверху +30 °C и -15 °C, для средней балки со сплошной стенкой и ездой поверху +/- 15 °C), с учетом коэффициента надежности 1,2;
- коэффициент линейного расширения стали и бетона; tmax - максимальная разность температур, принимается согласно п. 9.1 [3] (для одной из крайних балок со сплошной стенкой и ездой поверху +30 °C и -15 °C, для средней балки со сплошной стенкой и ездой поверху +/- 15 °C), с учетом коэффициента надежности 1,2; Примечания. 1. Если покрытие железобетонной плиты отсутствует, то величину  определяют согласно п. 9.10 [3], принимают tmax = +20 °C и вычисляют
определяют согласно п. 9.10 [3], принимают tmax = +20 °C и вычисляют
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
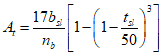 ;
; 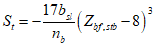 , (5.3.11)
, (5.3.11)где bsl и tsl - расчетные ширина и толщина плиты; Zbf,stb - расстояние от центра тяжести объединенного сечения Cstb до крайней фибры плиты.
2. Величины  ,
,  ,
,  ,
,  ,
, 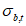 ,
, 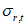 допускается определять иными обоснованными методами, используемыми в практике проектирования, в том числе и с применением численных методов расчета.
допускается определять иными обоснованными методами, используемыми в практике проектирования, в том числе и с применением численных методов расчета.
5.3.4 В статически неопределимых конструкциях усадка бетона и разность температур вызывают изменение внешних усилий. При определении внешних усилий геометрические характеристики принимают как при расчете статически определимых конструкций. Напряжения от разности температур могут быть приняты как сумма напряжений, полученных как для статически определимой системы, и напряжений от изменения внешних усилий.
5.4.1 В первом сочетании нагрузок учитывают кроме постоянных и временных нагрузок только ползучесть бетона и обжатие швов.
Вычисляют изгибающие моменты:
где M1 - изгибающий момент от нагрузок первой стадии работы сечения; M2g - изгибающий момент от постоянных нагрузок второй стадии работы сечения; Mv - изгибающий момент от временных нагрузок.
Далее порядок расчета зависит от возможности использовать метод "тонкой плиты".

Рисунок 5.4.1 - Схемы к расчету сталежелезобетонных сечений:
а - расчетное сечение; б - эпюра деформаций; в - д - эпюры
напряжений соответственно для расчетных случаев А, Б,
В [3]; 1 - центр тяжести стальной балки; 2 - центр
тяжести железобетонной плиты; 3 - центр тяжести
сталежелезобетонной балки
5.4.2 Если условие (5.1.14) выполняется (т.е. метод "тонкой плиты" применим), то расчет ведут в следующей последовательности.
Вычисляют напряжения на уровне центра тяжести плиты
Если 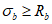 , то принимают
, то принимают  , если
, если  , то принимают
, то принимают  .
.
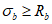 , то принимают
, то принимают  , если
, если  , то принимают
, то принимают  .
.5.4.3 Вычисляют величину разгружающей силы
где Ab - площадь бетона плиты без приведения ее к стали, м2; Ar - площадь арматуры, м2.
 ,
, 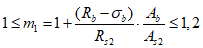 ,
, 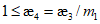 ,
,где 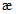 - коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении, определяемый согласно п. 8.26 [3],
- коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении, определяемый согласно п. 8.26 [3],  - коэффициент, принимаемый по таблице 5.4.1.
- коэффициент, принимаемый по таблице 5.4.1.
Примечания. 1. Принятие  допускает только упругую работу металла, что упрощает расчеты и идет в "запас прочности", но не всегда (см. п. 4.1.15).
допускает только упругую работу металла, что упрощает расчеты и идет в "запас прочности", но не всегда (см. п. 4.1.15).
2. Если  и
и  , то для балочных пролетных строений, не имеющих дефектов, снижающих грузоподъемность и при проектных значениях постоянных нагрузок, допускается принимать m1 = 1,2,
, то для балочных пролетных строений, не имеющих дефектов, снижающих грузоподъемность и при проектных значениях постоянных нагрузок, допускается принимать m1 = 1,2,  .
.
 и
и  , то для балочных пролетных строений, не имеющих дефектов, снижающих грузоподъемность и при проектных значениях постоянных нагрузок, допускается принимать m1 = 1,2,
, то для балочных пролетных строений, не имеющих дефектов, снижающих грузоподъемность и при проектных значениях постоянных нагрузок, допускается принимать m1 = 1,2, Таблица 5.4.1
As2/As1 | Значения коэффициента | ||||||||||||||
0 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | 0,55 | 0,60 | 0,65 | 0,70 | |
0 | 1,0 ---- 1,0 | 1,0 ----- 0,98 | 1,0 ----- 0,94 | 1,0 ----- 0,90 | 1,0 ----- 0,87 | 1,0 ----- 0,81 | 1,0 ----- 0,75 | 0,98 ----- 0,67 | 0,96 ----- 0,58 | 0,95 ----- 0,45 | 0,92 ----- 0,28 | 0,88 ----- 0,52 | 0,83 ----- 0,68 | 0,75 ----- 0,76 | 0,63 ----- 0,82 |
0,2 | 1,0 ---- 1,0 | 1,0 ----- 0,97 | 1,0 ----- 0,92 | 1,02 ----- 0,87 | 1,03 ----- 0,80 | 1,04 ----- 0,70 | 1,05 ----- 0,57 | 1,06 ----- 0,38 | 1,07 ----- 0,49 | 1,06 ----- 0,61 | 1,05 ----- 0,72 | 1,02 ----- 0,82 | 0,99 ----- 0,91 | 0,90 ----- 0,99 | 0,75 ----- 1,05 |
0,4 | 1,0 ---- 1,0 | 1,04 ----- 0,90 | 1,08 ----- 0,80 | 1,12 ----- 0,67 | 1,14 ----- 0,52 | 1,16 ----- 0,34 | 1,19 ----- 0,53 | 1,20 ----- 0,68 | 1,21 ----- 0,84 | 1,20 ----- 0,98 | 1,18 ----- 1,12 | 1,16 ----- 1,22 | 1,13 ----- 1,30 | 1,09 ----- 1,38 | 1,04 ----- 1,42 |
0,6 | 1,0 ---- 1,0 | 1,10 ----- 0,84 | 1,19 ----- 0,64 | 1,28 ----- 0,40 | 1,35 ----- 0,56 | 1,40 ----- 0,75 | 1,44 ----- 0,95 | 1,46 ----- 1,13 | 1,47 ----- 1,30 | 1,46 ----- 1,45 | 1,45 ----- 1,58 | 1,42 ----- 1,69 | 1,39 ----- 1,76 | 1,35 ----- 1,84 | 1,30 ----- 1,90 |
0,8 | 1,0 ---- 1,0 | 1,20 ----- 0,61 | 1,39 ----- 0,51 | 1,55 ----- 0,84 | 1,70 ----- 1,12 | 1,83 ----- 1,36 | 1,93 ----- 1,60 | 1,98 ----- 1,86 | 2,00 ----- 2,08 | 2,02 ----- 2,29 | 2,01 ----- 2,47 | 1,99 ----- 2,52 | 1,97 ----- 2,50 | 1,91 ----- 2,46 | 1,84 ----- 2,38 |
1,0 | 1,0 ---- 1,0 | 1,29 ----- 1,29 | 1,63 ----- 1,63 | 2,04 ----- 2,04 | 2,47 ----- 2,47 | 2,86 ----- 2,86 | 3,20 ----- 3,20 | 3,38 ----- 3,38 | 3,49 ----- 3,49 | 3,56 ----- 3,56 | 3,57 ----- 3,57 | 3,53 ----- 3,53 | 3,43 ----- 3,43 | 3,29 ----- 3,29 | 3,05 ----- 3,05 |
Примечания: 1. As1 - больший по площади пояс стальной балки (для одноплитной конструкции, как правило, - нижний пояс); As2 - меньший по площади пояс стальной балки (для одноплитной конструкции, как правило, - верхний пояс);
2. Значения  принимаются над чертой, если напряжения от момента и разгружающей силы суммируются в меньшем по площади поясе балки, под чертой, если напряжения от момента и разгружающей силы суммируются в большем по площади поясе балки.
принимаются над чертой, если напряжения от момента и разгружающей силы суммируются в меньшем по площади поясе балки, под чертой, если напряжения от момента и разгружающей силы суммируются в большем по площади поясе балки.
3. При положительном моменте напряжения складываются в нижнем поясе. При отрицательном - в верхнем. Поэтому, для одноплитной конструкции в середине пролета следует брать числа под чертой, над опорой - над чертой.
прочность верхнего пояса
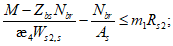 (5.4.5)
(5.4.5)прочность нижнего пояса
 (5.4.6)
(5.4.6)Если 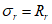 , то дополнительно проверяют условие:
, то дополнительно проверяют условие:
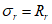 , то дополнительно проверяют условие:
, то дополнительно проверяют условие: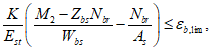 (5.4.7)
(5.4.7)где  - предельная деформация бетона на сжатие;
- предельная деформация бетона на сжатие;
 - предельная деформация бетона на сжатие;
- предельная деформация бетона на сжатие;
 ;
; 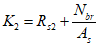 ;
;Rs1 - расчетное сопротивление стали нижнего пояса; Rs2 - расчетное сопротивление стали верхнего пояса; Rr - расчетное сопротивление арматуры плиты; Rb - расчетное сопротивление бетона (все величины - в МПа).
Примечание. Отсутствие разделения проверок на три случая А, Б и В (как это предусмотрено [3]) позволяет унифицировать расчеты, которые будут выполняться "в запас прочности" для случая Б.
5.4.6 Если условие (5.1.14) не выполняется (т.е. метод "тонкой плиты" не применим), но напряжения на уровне центра тяжести плиты  , то расчет выполняют согласно пп. 5.4.2 - 5.4.5.
, то расчет выполняют согласно пп. 5.4.2 - 5.4.5.
 , то расчет выполняют согласно пп. 5.4.2 - 5.4.5.
, то расчет выполняют согласно пп. 5.4.2 - 5.4.5.5.4.7 Если условие (5.1.14) не выполняется, и напряжения на уровне центра тяжести плиты 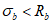 , то дополнительно вычисляют напряжения в крайней фибре бетона от всех нагрузок второй стадии работы и величину изгибающего момента в плите
, то дополнительно вычисляют напряжения в крайней фибре бетона от всех нагрузок второй стадии работы и величину изгибающего момента в плите
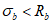 , то дополнительно вычисляют напряжения в крайней фибре бетона от всех нагрузок второй стадии работы и величину изгибающего момента в плите
, то дополнительно вычисляют напряжения в крайней фибре бетона от всех нагрузок второй стадии работы и величину изгибающего момента в плите (5.4.8)
(5.4.8) (5.4.9)
(5.4.9)где Wb2,b - момент сопротивления сечения плиты для фибры b2.

Рисунок 5.4.2 - Схема к расчету составной балки
без использования метода "тонкой плиты"
5.4.8 Если  , то переходят к проверке условий прочности (п. 5.4.9). Если
, то переходят к проверке условий прочности (п. 5.4.9). Если  , то следует определить величины уменьшения сжимающего усилия в бетоне за счет развития в нем пластических деформаций.
, то следует определить величины уменьшения сжимающего усилия в бетоне за счет развития в нем пластических деформаций.
 , то переходят к проверке условий прочности (п. 5.4.9). Если
, то переходят к проверке условий прочности (п. 5.4.9). Если  , то следует определить величины уменьшения сжимающего усилия в бетоне за счет развития в нем пластических деформаций.
, то следует определить величины уменьшения сжимающего усилия в бетоне за счет развития в нем пластических деформаций.Расстояние от верхней фибры плиты до точки с напряжением в бетоне Rb равно
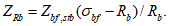 (5.4.10)
(5.4.10)Если Zbf,b <= ZRb, то принимают  и переходят к проверке условий прочности (п. 5.4.9). Величины Zbf,stb, Zbf,b определяют по формулам (5.1.16) и (5.1.17).
и переходят к проверке условий прочности (п. 5.4.9). Величины Zbf,stb, Zbf,b определяют по формулам (5.1.16) и (5.1.17).
 и переходят к проверке условий прочности (п. 5.4.9). Величины Zbf,stb, Zbf,b определяют по формулам (5.1.16) и (5.1.17).
и переходят к проверке условий прочности (п. 5.4.9). Величины Zbf,stb, Zbf,b определяют по формулам (5.1.16) и (5.1.17).Если ZRb < h2 (т.е. при расположении фибры с Rb в пределах полки) величины уменьшения сжимающего усилия в бетоне определяют как
 ; Nd2 = 0. (5.4.11)
; Nd2 = 0. (5.4.11)Плечо приложения силы Nd1
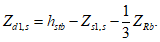 (5.4.12)
(5.4.12)Если ZRb >= h2 (т.е. при расположении фибры с Rb в пределах ребра), то следует вычислить напряжение на уровне фибры b3 (с учетом ползучести при необходимости):
- напряжение на уровне фибры 3 от постоянных нагрузок
 (5.4.13)
(5.4.13)где M2g - положительный изгибающий момент от постоянных нагрузок второй стадии работы;
- если 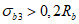 , то вычислить напряжение на уровне фибры 3 от ползучести
, то вычислить напряжение на уровне фибры 3 от ползучести
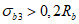 , то вычислить напряжение на уровне фибры 3 от ползучести
, то вычислить напряжение на уровне фибры 3 от ползучести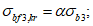 (5.4.14)
(5.4.14)- напряжение на уровне фибры 3 от нагрузок второй стадии
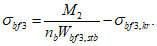 (5.4.15)
(5.4.15)Величины уменьшения сжимающего усилия в бетоне
 ;
;  . (5.4.16)
. (5.4.16)Плечи приложения сил Nd1 и Nd2
 ;
; 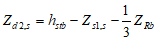 . (5.4.17)
. (5.4.17)Момент от сил Nd1 и Nd2 относительно центра тяжести стального сечения
Md = Nd1 x Zd1,s + Nd2 x Zd2,s. (5.4.18)
Вычислить силу
N = Nbr - (Nd1 + Nd2). (5.4.19)
5.4.9 Вычислить коэффициенты для учета пластических деформаций в стальных поясах по п. 5.4.4 и таблице 5.4.1, принимая силу N по формуле (5.4.19).
Проверить выполнение условий:
прочность верхнего пояса
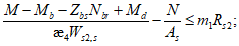 (5.4.20)
(5.4.20)прочность нижнего пояса
 (5.4.21)
(5.4.21)Если  , то дополнительно проверяют условие:
, то дополнительно проверяют условие:
 , то дополнительно проверяют условие:
, то дополнительно проверяют условие: (5.4.22)
(5.4.22)где
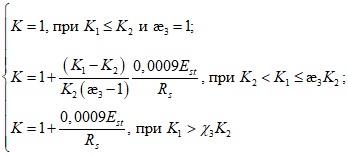
 ;
;  .
.5.4.10 Расчет на второе сочетание нагрузок выполняют с учетом ползучести, усадки бетона и разности температур стальной и бетонной частей сечения. Вычисляют:
- изгибающие моменты:
- напряжения на уровне центра тяжести плиты
- для расчета на первое сочетание нагрузок - по формулам (5.4.1);
- для расчета на второе сочетание нагрузок - по формулам (5.4.23).
При этом отрицательные моменты принимают со знаком плюс, а положительные - со знаком минус.
5.5.2 Вычисляют напряжения на уровне центра тяжести плиты:
- для расчета на первое сочетание нагрузок по формулам (5.4.2) и (5.4.3);
- для расчета на второе сочетание нагрузок - по формулам (5.4.24) и (5.4.25).
5.5.3 Если  , то расчет выполняют на оба сочетания нагрузок.
, то расчет выполняют на оба сочетания нагрузок.
 , то расчет выполняют на оба сочетания нагрузок.
, то расчет выполняют на оба сочетания нагрузок.Коэффициенты для учета пластических деформаций в стальных поясах вычисляют с учетом п. 5.4.4 и таблицы 5.4.1, принимая силу N по формуле (5.4.4):
 ;
;  ;
; 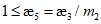 .
.Грузоподъемность находят из соблюдения условий:
для верхнего пояса
 (5.5.1)
(5.5.1)для нижнего пояса
 (5.5.2)
(5.5.2) ;
;  ;
; 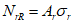 , (5.5.3)
, (5.5.3) (5.5.4)
(5.5.4)где 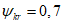 при гладкой арматуре и
при гладкой арматуре и  - при арматуре периодического профиля;
- при арматуре периодического профиля; 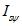 - момент инерции стального сечения с арматурой площадью
- момент инерции стального сечения с арматурой площадью 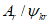 ;
;  - расстояние между центрами тяжести стального сечения с арматурой площадью
- расстояние между центрами тяжести стального сечения с арматурой площадью 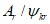 и арматуры плиты.
и арматуры плиты.
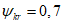 при гладкой арматуре и
при гладкой арматуре и  - при арматуре периодического профиля;
- при арматуре периодического профиля; 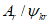 ;
;  - расстояние между центрами тяжести стального сечения с арматурой площадью
- расстояние между центрами тяжести стального сечения с арматурой площадью 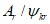 и арматуры плиты.
и арматуры плиты.Грузоподъемность находят из соблюдения условий
для верхнего пояса
 (5.5.5)
(5.5.5)для нижнего пояса
 (5.5.6)
(5.5.6)где Zrs - расстояние между центрами тяжести стальной балки и арматуры плиты.
5.5.5 В запас прочности расчет на отрицательный момент сталежелезобетонных сечений допускается производить в предположении полного выключения железобетонной плиты из работы по формулам главы 4. Однако если в этом случае класс конструкций окажется недостаточным, то следует выполнить уточненный расчет согласно рекомендациям пп. 5.5.1 - 5.5.4.
со стальной конструкцией
5.6.1 Определение грузоподъемности по прочности конструкций объединения плиты и стальных балок ведут по общим формулам, указанным в гл. 4 [2], на сдвиг по длине объединения и на отрыв концевых участков железобетонной плиты, в том числе с учетом температурных воздействий и усадки бетона.
5.6.2 Пролетное строение делят на расчетные участки таким образом, чтобы границы участков располагались над промежуточными опорами (и над концевой опорой, если сталежелезобетонный элемент имеет существенную консольную часть), а места сосредоточенного заанкеривания предварительно напрягаемой арматуры, центры узлов примыкания вант, раскосов, подпруг, места изменений поперечного сечения элементов и приложения местного сосредоточенного давления располагались по середине соответствующих участков (рисунок 5.6.2).

Рисунок 5.6.2 - Схема размещения участков сбора нагрузок
на анкера и эпюры погонных сдвигающих усилий s
(SN - дополнительное продольное усилие от сосредоточенного
заанкеривания предварительно напрягаемой арматуры,
примыкания вант, раскосов, подпруг и т.д.)
При этом длины участков определяют по формулам
Зона I (приопорные участки) - | aI = 0,18(H + bsl); |
Зона II (участки приложения местного сосредоточенного давления) - | aII = 0,36(H + bsl); |
Зона III (участки в крайних четвертях пролета) - | aIII <= 0,8(H + bsl); |
Зона IV (участки в средних четвертях пролета) - | aIV <= 1,6(H + bsl). |
Здесь H - расчетная высота сталежелезобетонной балки; bsl - расчетная ширина плиты (по п. 8.15 [3]). Зона II может оказаться в пределах любой из указанных зон.
5.6.3 Сдвигающее усилие по шву объединения железобетонной плиты и стальной конструкции на i-том участке отдельно от постоянных (с учетом ползучести бетона), пешеходных, прочих нагрузок (а для второго сочетания нагрузок - в том числе, от разности температур и от усадки бетона) и от временных нагрузок от транспортных средств определяют по общей формуле
где  ,
,  - напряжения в центре тяжести поперечного сечения бетона соответственно в сечении, ближнем к середине пролета, и в сечении, ближнем к опоре, расчетного участка плиты длиной ai от соответствующих нагрузок;
- напряжения в центре тяжести поперечного сечения бетона соответственно в сечении, ближнем к середине пролета, и в сечении, ближнем к опоре, расчетного участка плиты длиной ai от соответствующих нагрузок; 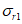 ,
,  - напряжения в продольной арматуре соответственно в тех же сечениях; Ab, Ar - площади бетона и арматуры без приведения их к металлу балок.
- напряжения в продольной арматуре соответственно в тех же сечениях; Ab, Ar - площади бетона и арматуры без приведения их к металлу балок.
Напряжения  и
и 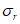 определяют согласно указаниям п. 5.4.2 путем загружения линий (поверхностей) влияния изгибающих моментов в начале и конце рассматриваемого участка. При этом рассматривают загружение на максимум момента M1 и сопутствующее значение момента M2, и загружение на максимум момента M2 и сопутствующее значение момента M1.
определяют согласно указаниям п. 5.4.2 путем загружения линий (поверхностей) влияния изгибающих моментов в начале и конце рассматриваемого участка. При этом рассматривают загружение на максимум момента M1 и сопутствующее значение момента M2, и загружение на максимум момента M2 и сопутствующее значение момента M1.
Допускается выполнять построение и загружение поверхности влияния разности моментов M1 и M2. Тогда в формуле (5.6.1) остается только одно слагаемое.
5.6.4 В запас прочности допускается сдвигающие усилия (включая построение поверхностей влияния) на участках растяжения плиты определять в предположении наличия в плите трещин и вычислять напряжения в арматуре 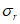 при жесткостных характеристиках, вычисленных при Ab = 0 и
при жесткостных характеристиках, вычисленных при Ab = 0 и 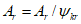 . Однако если при этом класс по грузоподъемности окажется недостаточным, то расчет следует выполнять с учетом появления трещин только при превышении растягивающими напряжениями в железобетонной плите величины 0,4Rbt,ser.
. Однако если при этом класс по грузоподъемности окажется недостаточным, то расчет следует выполнять с учетом появления трещин только при превышении растягивающими напряжениями в железобетонной плите величины 0,4Rbt,ser.
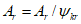 . Однако если при этом класс по грузоподъемности окажется недостаточным, то расчет следует выполнять с учетом появления трещин только при превышении растягивающими напряжениями в железобетонной плите величины 0,4Rbt,ser.
. Однако если при этом класс по грузоподъемности окажется недостаточным, то расчет следует выполнять с учетом появления трещин только при превышении растягивающими напряжениями в железобетонной плите величины 0,4Rbt,ser.ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
5.6.6 В зоне I у концевой опоры погонные сдвигающие усилия si определяют как
ИС МЕГАНОРМ: примечание. Нумерация формул дана в соответствии с официальным текстом документа. |
 (5.6.4)
(5.6.4)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: формула (4.6.1) отсутствует. Возможно, имеется в виду формула (5.6.1). |
где SeN - принимают по формуле (4.6.1), в которой 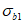 и
и 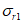 определяют в сечении ae от конца плиты,
определяют в сечении ae от конца плиты,  ; Qi - поперечная сила в сечении aI от оси опирания; ae = 0,36(H + bsl) - длина концевого расчетного участка.
; Qi - поперечная сила в сечении aI от оси опирания; ae = 0,36(H + bsl) - длина концевого расчетного участка.
 ; Qi - поперечная сила в сечении aI от оси опирания; ae = 0,36(H + bsl) - длина концевого расчетного участка.
; Qi - поперечная сила в сечении aI от оси опирания; ae = 0,36(H + bsl) - длина концевого расчетного участка.5.6.7 Для участков III - IV погонные сдвигающие усилия от постоянных, временных, пешеходных и прочих нагрузок допускается определять как
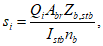 (5.6.5)
(5.6.5)где Qi - поперечная сила в середине сечения ai.
5.6.8 Для участков II (в местах заанкеривания предварительно напрягаемой арматуры, узлов примыкания вант, раскосов, подпруг) определяют дополнительные продольные усилия в плите ScN от указанных воздействий, которые учитывают при определении напряжений 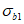 ,
, 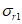 ,
,  ,
, 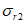 на границах участка длиной 0,72·(H + bsl).
на границах участка длиной 0,72·(H + bsl).
5.6.9 Концевые усилия Sab, отрывающие железобетонную плиту от стальной конструкции, определяют по формуле
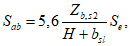 (5.6.6)
(5.6.6)где Zb,s2 - расстояние от центра тяжести поперечного сечения бетона до верхней фибры стальной конструкции; Se - полное концевое сдвигающее усилие, включающее усилия от температуры и усадки (с учетом коэффициентов сочетания).
Отрывающее усилие Sab принимают приложенным на расстоянии 0,024·(H + bsl) от конца плиты.
5.6.10 Силу, действующую на анкер, расположенный на рассматриваемом участке, определяют на основе полученных погонных сдвиговых усилий как
S = si/a, (5.6.7)
где a - шаг анкеров на рассматриваемом участке.
5.6.11 Несущую способность конструкций объединения стальной части с железобетонной плитой при жестких упорах определяют:
Sh = 1,6RbAb,drmbl, (5.6.8)
где Ab,dr - площадь поверхности смятия бетона уголковым упором; при цилиндрических и дугообразных упорах - площадь их диаметрального сечения; mbl - коэффициент условий работы, принимаемый: mbl = 1, если плита не имеет ребер или вутов; mbl = 0,9 при 1,5 bdr >= brib > 1,3bdr, mbl = 0,7 при brib <= 1,3bdr; bdr - ширина площади смятия бетона упором; brib - ширина ребра или вута на уровне центра тяжести расчетной площади смятия бетона упором.
Примечания. 1. В запас прочности при наличии ребер и вутов в плите допускается принимать mbl = 0,7.
2. При расположении упоров в окнах расчетное сопротивление Rb принимают по классу бетона блоков, а при расположении упоров в продольных швах плиты расчетные сопротивления принимают по классу бетона замоноличивания швов.
3. При расположении упоров в окнах толщину подливки не включают в площадь смятия. При расположении упоров в продольных швах плиты площадь смятия учитывают полностью.
ИС МЕГАНОРМ: примечание. Нумерация пунктов дана в соответствии с официальным текстом документа. |
5.6.11 Несущую способность конструкций объединения стальной части с железобетонной плитой при других видах упоров определяют
а) при вертикальных гибких упорах и наклонных анкерах - согласно приложению Я [3];
б) при закладных деталях плиты, объединенных со стальными поясами высокопрочными болтами, - согласно пп. 8.100 и 8.101 [3];
в) при объединительных швах на высокопрочных болтах, обжимающих железобетон, - согласно приложению 1 [3];
г) при болтоклеевых объединительных швах - в соответствии с подпунктом "б" или "в", но с учетом сил сцепления от склеивания;
д) при гребенчатых упорах на действие расчетных сдвигающих и отрывающих усилий с учетом равномерного распределения усилий по длине пролета в соответствии с [7].
5.6.12 При одновременном использовании в конструкции объединения жестких упоров и наклонных анкеров допускается учитывать их совместную работу, полагая полное сопротивление объединительного шва равным сумме сопротивлений упоров и анкеров.
5.6.13 При отсутствии данных об анкерах грузоподъемность объединения железобетонной плиты и стальных балок определяют по сопоставлению сдвигающих усилий, определенных от проектных нагрузок года проектирования конструкции, и усилий от нагрузок АК, НК и ЭН3.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: пункт 4.7 отсутствует. |
5.7.1 Величины K и P, полученные при определении грузоподъемности согласно п. 5.4, используют при проверках расчетных сечений балки на действие касательных напряжений, совместное действие нормальных и касательных напряжений, при проверках общей устойчивости металлических балок (на участках действия сжимающих напряжений в нижних поясах), местной устойчивости вертикальных стенок и свесов сжатых полок поясов балок согласно п. 4.7.
С использованием тех же величин K и P производится проверка прочности среднего прогона (при его наличии), прочности и устойчивости элементов поперечных и продольных связей, а также их прикреплений.
При проверке прочности прогона расчетная ширина плиты должна иметь величину, при которой центр тяжести объединенного сечения располагается в уровне нижней фибры плиты. Грузоподъемность прогона определяют согласно рекомендациям настоящей книги.
1. ОДМ 218.1.001-2010 Рекомендации по разработке и применению документов технического регулирования в сфере в дорожного хозяйства.
2. ОДМ 218.4.025-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Общая часть.
3. СП 35.13330.2011 Мосты и трубы. Актуализированная редакция СНиП 2.05.03-84*.
4. СП 16.13330.2011 Стальные конструкции. Актуализированная редакция СНиП II-23-81.
5. ОДМ 218.4.026-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Бетонные и железобетонные конструкции.
6. Рекомендации по учету ползучести и усадки бетона при расчете бетонных и железобетонных конструкций/НИИЖБ Госстроя СССР. - М.: Стройиздат, 1988. - 120 с.
7. ОДМ 218.4.003-2009 Рекомендации по объединению металлических балок с монолитной железобетонной плитой посредством непрерывных гребенчатых упоров в сталежелезобетонных пролетных строениях мостов. М.: ФДА - 2009. - 21 с.
8. СТО 002494680-0032-2004 Сталежелезобетонные пролетные строения автодорожных мостов. Реконструкция и ремонт/ЦНИИПСК им. Мельникова. - М., 2004.
9. ОДМ 218.2.044-2014 Рекомендации по выполнению приборных и инструментальных измерений при оценке технического состояния мостовых сооружений на автомобильных дорогах. М.: ФДА - 2014. - 160 с.
10. ОДМ 218.4.028-2016 Методические рекомендации по определению грузоподъемности эксплуатируемых мостовых сооружений на автомобильных дорогах общего пользования. Опорные части, опоры и фундаменты.
МЕТАЛЛИЧЕСКИХ И СТАЛЕЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ МОСТОВ
Составление конечно-элементных моделей выполняют согласно общим рекомендациям приложения Б [2] с учетом настоящего раздела.
балочных пролетных строений
В целом моделирование таких балок не отличается от моделирования железобетонных балок (см. приложение Б.1 [2]). Однако существенное влияние на распределение усилий между главными балками оказывают нижние продольные связи. Поперечными связями можно пренебречь.
В стержневой постановке нижние продольные связи прикрепляются на значительном удалении от центров тяжести главных балок, что требует введения соответствующих дополнительных узлов, которые следует объединить с узлами на главных балках с помощью жестких вставок или двухузловых упругих связей (пружин) с характеристиками жестких вставок (что предпочтительнее).
Пример расчетной модели пролетного строения по типовому проекту серии 3.503.3-56 показан на рисунке А.1.2.
ИС МЕГАНОРМ: примечание. Нумерация рисунков дана в соответствии с официальным текстом документа. |

по типовому проекту 3.503.3-56: а) схема в геометрических
осях с закреплениями и упругими связями; б) схема "в теле"
Расчет выполняют с использованием двух расчетных моделей:
Модель N I. Ортотропная плита при совместной работе с главными балками. На основании этой модели определяют напряжения в элементах ортотропной плиты  ,
, 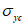 и
и  .
.
Модель N II. Ортотропная плита при работе на местную нагрузку. На основании этой модели определяют напряжения в элементах ортотропной плиты  ,
,  и
и  .
.
В результате расчета по указанным моделям получают поверхности влияния:
а) нормальных напряжений в листе настила, продольных и поперечных ребрах;
б) касательных напряжений в листе настила.
при совместной работе с главными балками
Модель N I должна позволять вычислять напряжения  в точках проверки A, B, A1, B1, D1 (см. рисунки 4.4.1 и 4.4.2) и исключать появление напряжений от местных нагрузок в этих точках (которые будут учтены в модели N II). Рекомендуется воспользоваться балочной условно-пространственной или балочной пространственной расчетной моделью. При этом напряжения
в точках проверки A, B, A1, B1, D1 (см. рисунки 4.4.1 и 4.4.2) и исключать появление напряжений от местных нагрузок в этих точках (которые будут учтены в модели N II). Рекомендуется воспользоваться балочной условно-пространственной или балочной пространственной расчетной моделью. При этом напряжения  и
и  в формулах (4.4.5) и (4.4.6) допускается принимать равными нулю.
в формулах (4.4.5) и (4.4.6) допускается принимать равными нулю.
Рекомендации по подготовке модели N I соответствуют рекомендациям для балочных пролетных строений мостов (Приложение Б.1.1 [2]). Поверхность влияния напряжений допускается строить из поверхности влияния изгибающих моментов по формуле
где My - ордината поверхности влияния изгибающего момента в поперечном сечении балки (сечение I-I или II-II на рисунке 4.4.1); yн.о. - расстояние от точки проверки до нейтральной оси балки; Iz - момент инерции поперечного сечения балки, принимают с учетом расчетной эффективной ширины пояса bef (п. 8.26 [3]). Значение bef определяют по формуле (8.9) [3], при этом максимальные и минимальные напряжения по участкам пояса допускается определять от проектной нагрузки.
При расчете по условно-пространственной модели поверхность влияния изгибающих моментов получают путем перемножения ординат линии влияния изгибающих моментов на ординаты линии КПУ.
при работе плиты на местную нагрузку
Модель N II (рисунки А.2.1, А.2.2) должна позволять вычислять напряжения 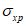 в точках проверки A и B, напряжения
в точках проверки A и B, напряжения  в точках C и D*, напряжения
в точках C и D*, напряжения  ,
,  и
и  в точках A1, B1, D1 (см. рисунки 4.4.1 и 4.4.2), а также и исключать появление напряжений от общей работы пролетного строения. Для вычисления трех компонент напряженно-деформированного состояния
в точках A1, B1, D1 (см. рисунки 4.4.1 и 4.4.2), а также и исключать появление напряжений от общей работы пролетного строения. Для вычисления трех компонент напряженно-деформированного состояния 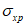 ,
,  и
и  в листе настила модель должна содержать элемент плиты или пластины.
в листе настила модель должна содержать элемент плиты или пластины.
Рекомендуется моделировать пять-шесть пролетов ортотропной плиты l (где l - расстояние между поперечными ребрами, см. рисунок 4.4.1).
Моделирование рекомендуется осуществлять двумя типами конечных элементов. Для моделирования продольных и поперечных ребер следует использовать стержневой изгибаемый элемент общего вида типа "балка" ("beam"), для моделирования листа настила - плоский изгибаемый элемент типа "плита" ("plate"). Следует использовать четырехузловые прямоугольные элементы с соотношением длины большей стороны к длине меньшей не более 4,0.
Целесообразно направление глобальной оси "Y" следует совмещать с направлением продольной оси моста, глобальную ось "Z" направлять вверх, перпендикулярно листу настила.
Продольные ребра следует по возможности разбивать на четное число стержней.
В модель следует вводить фактические значения толщины листа настила и размеров ребер, располагая их в соответствии с реальной конструкцией.
Граничные условия. При расчете методом перемещений (методом конечных элементов), следует ограничивать только те направления перемещений, которые вызывают общую деформацию модели и не препятствуют местным деформациям. Рекомендуется использовать следующие типы закреплений.
1. Вертикальные перемещения. Устанавливают в каждом узле пересечения главных балок с поперечными ребрами. Запрещают общий вертикальный изгиб модели и не препятствуют всем прочим деформациям.
2. Горизонтальные перемещения поперек пролетного строения. Устанавливают в каждом узле пересечения первой главной балки (крайней левой) с поперечными ребрами. Запрещают общий горизонтальный изгиб модели.
3. Горизонтальные перемещения вдоль пролетного строения. Устанавливают на пересечении первого поперечного ребра с главными балками. Запрещают общее продольное смещение модели.
4. Углы поворота вокруг продольной оси. Устанавливают на пересечении первого поперечного ребра с главными балками. Запрещают деформации общего кручения.
5. Углы поворота вокруг поперечной оси. Устанавливают в одном из узлов, где запрещен угол поворота вокруг продольной оси или вовсе не устанавливать.
6. Углы поворота вокруг вертикальной оси. Устанавливают в крайних опорных узлах для исключения общего горизонтального изгиба.
Загружение модели должно позволять определять искомые напряжения при произвольном положении единичной нагрузки на листе настила, что фактически позволяет строить поверхность влияния. Сетка установки единичной нагрузки не должна быть слишком грубой (снижение точности расчета) или слишком мелкой (увеличение времени расчета). Оптимальный шаг сетки для ортотропных плит мостов составляет 30 - 80 см. Рекомендуется осуществлять загружение по узлам плоских элементов, моделирующих настил. В этом случае оптимальные размеры конечных элементов должны быть выбраны заранее, на этапе создания топологии модели.
За искомые напряжения принимают напряжения в узлах, которые соответствуют проверяемым точкам (см. рисунки 4.4.1 и 4.4.2).

с прорисовкой "в осях"
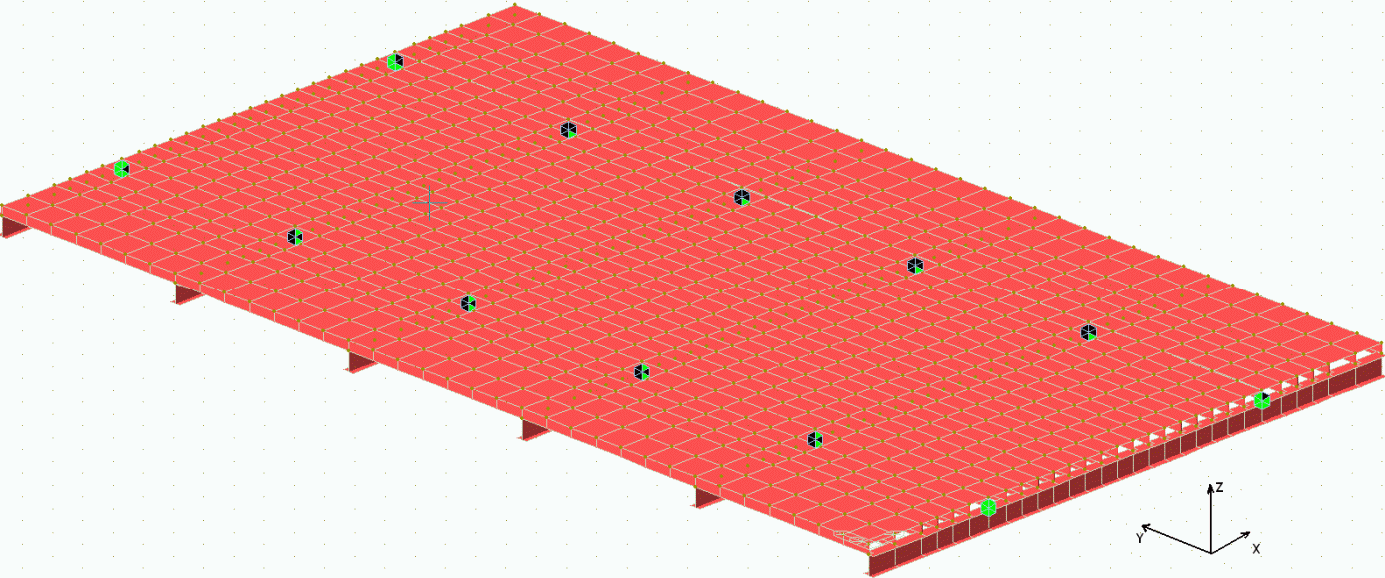
(с прорисовкой "в теле")
Обозначения закреплений опор приведены на рисунке А.2.3.

Рисунок А.2.3 - Пример обозначений закреплений
в конечно-элементном расчетном комплексе
ПРИМЕРЫ РАСЧЕТОВ ГРУЗОПОДЪЕМНОСТИ
В примерах разделов Б.1 и Б.2 использована система единиц измерения "СИ".
металлического пролетного строения
со сквозными фермами
Металлическое балочное разрезное пролетное строение полной длиной 21,9 м состоит из трех главных ферм, расставленных с шагом 2,3 м. Фермы с треугольной решеткой расчетным пролетом 21,6 м и высотой 2,07 м объединены системой продольных и поперечных связей, а также железобетонной плитой проезжей части, которая включена в совместную работу с элементами верхнего пояса через упоры. Пролетное строение запроектировано под нагрузки Н-13, НГ-60 и изготовлено в 1950-х годах.
Мостовое полотно включает проезд шириной 8 м и два тротуара шириной по 0,8 м. Одежда ездового полотна на мосту состоит из выравнивающего слоя (3 см), гидроизоляции (1 см), защитного слоя (4 см) и асфальтобетонного покрытия (8 см). Покрытие на тротуарах выполнено из слоя асфальтобетона толщиной 4 см.
Определение механических характеристик стали показало, что временное сопротивление элементов поясов ферм соответствует стали 15ХСНД, а всех прочих элементов решетки - стали Ст.3. Бетон плиты по прочности соответствует классу B15. Расчетные сопротивления стали приняты для поясов R = 340 МПа (сталь 15ХСНД), для остальных элементов ферм R = 210 МПа (сталь Ст.3). Заклепки выполнены из стали Ст.2 и посажены в отверстия  . Конструкция пролетного строения приведена на рисунках Б.1.1 - Б.1.3.
. Конструкция пролетного строения приведена на рисунках Б.1.1 - Б.1.3.
 . Конструкция пролетного строения приведена на рисунках Б.1.1 - Б.1.3.
. Конструкция пролетного строения приведена на рисунках Б.1.1 - Б.1.3.

Рисунок Б.1.2 - Расположение и конструкция связей ферм
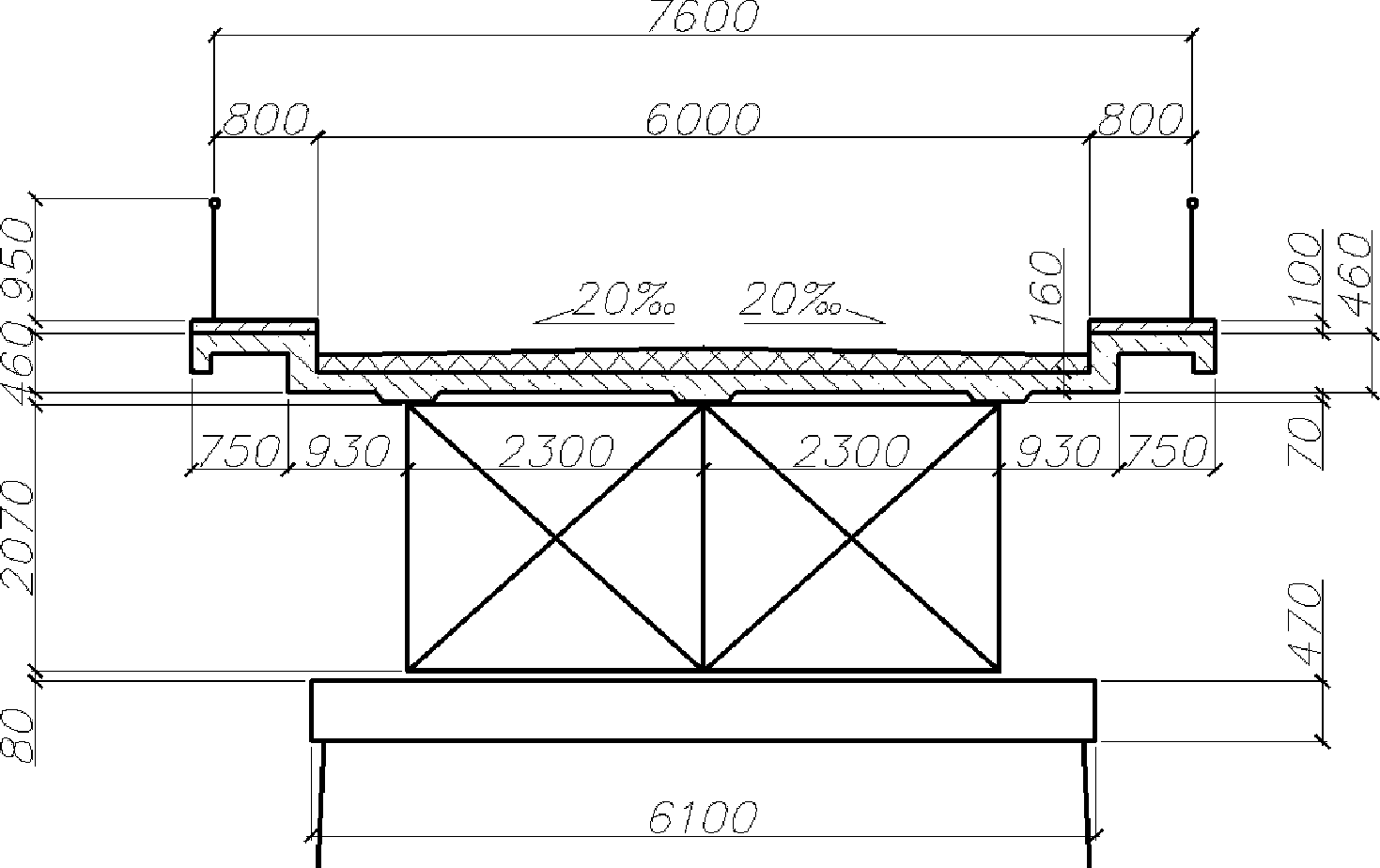
Расчетная интенсивность постоянной нагрузки определена по формуле:
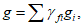 (Б.1.1)
(Б.1.1)где gi,  - нормативная интенсивность и коэффициент надежности к соответствующим нагрузкам.
- нормативная интенсивность и коэффициент надежности к соответствующим нагрузкам.
Нормативная нагрузка от веса металла ферм g1 определена по формуле:
g1 = Pф/lp, (Б.1.2)
где Pф - вес металла ферм, с учетом заклепок, фасонок и т.д., кН; lp - расчетный пролет фермы, м.
g1 = 131,4/21,6 = 6,083 кН/м.
Нагрузка от веса плиты g2 определена по формуле:
 (Б.1.3)
(Б.1.3)где Aплиты - площадь поперечного сечения железобетонной плиты с учетом тротуаров, м2; 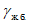 - удельный вес железобетона, кН/м3.
- удельный вес железобетона, кН/м3.
g2 = 1,25·24,5 = 30,63 кН/м.
Интенсивность нагрузок от веса слоев одежд ездового полотна определена по формуле:
 (Б.1.4)
(Б.1.4)где  ,
, 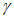 , B - толщина, удельный вес и ширина соответствующего слоя одежды ездового полотна.
, B - толщина, удельный вес и ширина соответствующего слоя одежды ездового полотна.
Нормативная нагрузка от веса перильного ограждения g8 = 0,14 кН/м.
Таблица Б.1.1
Интенсивности постоянных нагрузок
Вид нагрузки | Нормативная нагрузка, кН/м | Коэффициент надежности | Расчетная нагрузка, кН/м |
Металл ферм (g1) | 6,083 | 1,05 | 6,388 |
Железобетонная плита (g2) | 30,63 | 1,05 | 32,16 |
Выравнивающий слой (g3) | 0,03·24,5·6,0 = 4,41 | 1,15 | 5,072 |
Гидроизоляция (g4) | 0,01·15·6,0 = 0,90 | 1,15 | 1,035 |
Защитный слой (g5)  | 0,04·24,5·6,0 = 5,88 | 1,15 | 6,762 |
Асфальтобетонное покрытие проезжей части (g6) | 0,08·23,0·6,0 = 11,04 | 1,2 | 13,25 |
Асфальтобетонное покрытие тротуаров (g7) | 0,04·23,0·1,6 = 1,472 | 1,2 | 1,766 |
Перильное ограждение (g8) | 0,14 | 1,05 | 0,147 |
Итого: | 66,58 | ||
Для определения усилий от действия постоянных и пешеходных нагрузок (мост расположен в населенном пункте), а также для построения поверхностей влияния в элементах ферм использована пространственная расчетная модель пролетного строения (рисунок Б.1.4), реализованная в конечно-элементном расчетном комплексе. Геометрические и жесткостные характеристики элементов главных ферм и плиты проезжей части соответствуют фактическому исполнению конструкций. Узлы ферм приняты шарнирными.
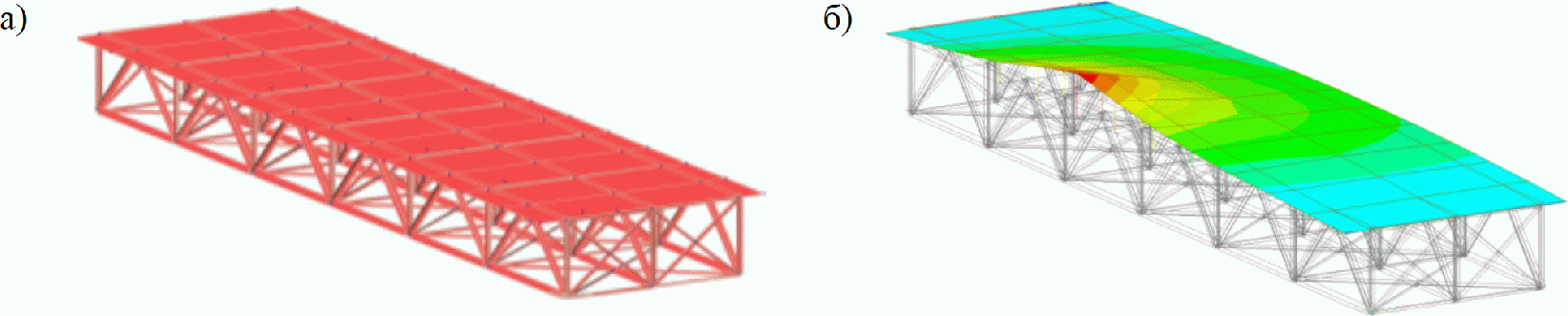
Рисунок Б.1.4 - Расчетная модель в конечно-элементном
расчетном комплексе (а) и поверхность влияния
продольного усилия N в элементе H5-H7 (б)
Сечения и прикрепления одноименных элементов крайних и средней ферм одинаковы, поэтому поверхности влияния продольных сил получены для всех элементов только крайней фермы, заведомо испытывающей большее воздействие, чем средняя ферма. Расчетные площади нетто и брутто поперечных сечений и площади прикреплений приведены в таблицах Б.1.2 - Б.1.4. Предельные значения усилий в таблице Б.1.5 определены по формулам (4.2.1) и (4.3.1). Поскольку верхний пояс ферм, анкеруясь с железобетонной плитой проезда, потерять общую устойчивость не может ни при каких обстоятельствах, его сечение рассчитано только по прочности. Величины предельных усилий Nr для заклепок вычислены по формулам (4.5.25) и (4.5.26). Классы элементов приведены в таблице Б.1.6.
Таблица Б.1.2
элементов главных ферм
Обозначение элемента | Схема сечения | Состав сечения, мм | A, см2 | Ослабление заклепками | An, см2 | |||
d, см | n, шт. | |||||||
H1-5 H9-13 |  | T N 17x18 | 46,46 | - | - | 0 | 0,0 | |
Итого: | 46,46 | 0,0 | 46,46 | |||||
H5-9 |  | ГЛ 200x8 | 16,00 | 2,0 | 0,8 | 2 | 3,20 | |
T N 17x18 | 46,46 | 2,0 | 1,6 | 4 | 12,80 | |||
Итого: | 62,46 | 16,00 | 46,46 | |||||
Верхний пояс |  | T N 17x18 | 46,46 | - | - | 0 | 0,0 | |
Итого: | 46,46 | 0,0 | 46,46 | |||||
P1-2 P12-13 |  | 2L 150x100x10 | 48,60 | 2,0 | 1,0 | 2 | 4,0 | |
Итого: | 48,60 | 4,0 | 44,60 | |||||
P2-3 P11-12 |  | 2L 130x90x10 | 42,30 | 2,0 | 1,0 | 2 | 4,0 | |
Итого: | 42,30 | 4,0 | 38,30 | |||||
P3-4 P10'-11 |  | 2L 130x90x8 | 34,40 | 2,0 | 0,8 | 2 | 3,2 | |
Итого: | 34,40 | 3,2 | 31,2 | |||||
P4-5 P5-6 P6-7 P7-8 P8-9 P9-10 |  | 2L120x120x10 | 46,36 | 2,0 | 1,0 | 2 | 4,0 | |
Итого: | 46,36 | 4,0 | 42,36 | |||||
Стойки |  | 2L 75x75x8 | 22,94 | 2,0 | 0,8 | 2 | 3,2 | |
Итого: | 22,94 | 3,2 | 19,74 | |||||
Примечания. d - диаметр заклепки; n - количество заклепок в сечении; A - площадь сечения брутто;  - толщина элемента в месте ослабления; n - число ослаблений элемента;
- толщина элемента в месте ослабления; n - число ослаблений элемента;  - площадь ослабления элемента; An - площадь сечения нетто.
- площадь ослабления элемента; An - площадь сечения нетто.
Таблица Б.1.3
Расчетные площади несимметричных поперечных сечений
сжатых элементов главных ферм
Обозначение элемента | Схема сечения | Состав сечения, мм | A, см2 | Sбр, см3 | Z0, см | Ix, см4 | Iy, см4 | ix, см | iy, см | lef,x, см | lef,y, см | ||||
P1-2 |  | 2L 150x100x10 | 48,60 | 233,8 | |||||||||||
48,60 | 233,8 | 4,8 | 1 114,0 | 824,9 | 4,8 | 4,1 | 233 | 205 | 48,7 | 49,8 | 0,82 | 39,89 | |||
P2-3 |  | 2L 130x90x10 | 42,30 | 175,5 | |||||||||||
42,30 | 175,5 | 4,1 | 716,8 | 608,7 | 4,1 | 3,8 | 233 | 205 | 56,6 | 54,0 | 0,79 | 33,57 | |||
P3-4 |  | 2L 130x90x8 | 34,40 | 140,4 | |||||||||||
34,40 | 140,4 | 4,1 | 594,0 | 488,6 | 4,2 | 3,8 | 233 | 205 | 56,1 | 54,4 | 0,80 | 27,37 | |||
P4-5 P5-6 P6-7 |  | 2L 120x120x10 | 46,36 | 153,5 | |||||||||||
46,36 | 153,5 | 3,3 | 627,0 | 1 335,8 | 3,7 | 5,4 | 233 | 205 | 63,4 | 38,2 | 0,77 | 35,54 | |||
Стойки |  | 2L 75x75x8 | 22,94 | 48,9 | |||||||||||
22,94 | 48,9 | 2,1 | 117,8 | 288,8 | 2,3 | 3,5 | 182 | 166 | 80,3 | 46,8 | 0,69 | 15,79 |
Примечания. d - диаметр заклепки; n - количество заклепок в сечении; A - площадь сечения брутто;  - толщина элемента в месте ослабления; n - число ослаблений элемента;
- толщина элемента в месте ослабления; n - число ослаблений элемента;  - площадь ослабления элемента; An - площадь сечения нетто.
- площадь ослабления элемента; An - площадь сечения нетто.
Таблица Б.1.4
Обозначение элемента | Состав расчетного сечения стыка или прикрепления, мм | Расчетная площадь нетто частей, входящих в сечение разрушения, Ant, см2 | Характеристики стыка или прикрепления | Несущая способность стыка или прикрепления Nпред, кН | ||||||
Число заклепок в соединении n | Площадь сечения заклепок Abs, см2 | Расчетные усилия заклепок Nr, кН | Ant·Ry, кН | |||||||
односрезных ns = 1 | двухсрезных ns = 2 | на срез | на смятие | |||||||
Стык в нижнем поясе H3-5 | ГЛ 210x26 | 44,20 | 10 | - | 2,6 | 31,42 | 534,1 | 3094 | 1503 | 534,1 |
2ВЛ 140x12 | 24,00 | - | 4 | 1,2 | 12,57 | 427,4 | 571,2 | 816,0 | 427,4 | |
ГЛ 200x8 | 12,80 | - | - | - | - | - | - | 435,2 | 435,2 | |
Итого: | 1397 | |||||||||
Раскос 1-2 | 2L 150x100x10 | 46,60 | - | 7 | 1,2 | 21,99 | 646,5 | 617,4 | 978,6 | 617,4 |
Итого: | 617,4 | |||||||||
Раскос 2-3 | 2L 130x90x10 | 40,30 | - | 6 | 1,2 | 18,85 | 554,2 | 529,2 | 846,3 | 529,2 |
Итого: | 529,2 | |||||||||
Раскос 3-4 | 2L 130x90x8 | 32,80 | - | 5 | 1,2 | 15,71 | 461,9 | 441,0 | 688,8 | 441,0 |
Итого: | 441,0 | |||||||||
Раскосы 4-7 | 2L 120x120x10 | 44,36 | - | 4 | 1,2 | 12,57 | 369,6 | 352,8 | 931,6 | 352,8 |
Итого: | 352,8 | |||||||||
Стойки | 2L 75x75x8 | 21,34 | - | 3 | 1,2 | 9,426 | 277,1 | 264,6 | 448,1 | 264,6 |
Итого: | 264,6 | |||||||||
Примечание. d = 2,0 см; Abs = 3,142 см2; Rbs = 340·0,5 = 170 МПа (пояса); Rbs = 210·0,7 = 147 МПа (раскосы и стойки); Rbp = 340·1,75 = 595 МПа (пояса); Rbp = 210·1,75 = 367,5 МПа (раскосы и стойки); mb = 1,0; m = 1,0.
Таблица Б.1.5
Обозначение элемента | Ry, МПа | An, см2 | Nпрпред, кН | Nустпред, кН | Nсппред, кН | Nпред, кН | Nпост, кН | Nдоп, кН | |
H1-3 | 340 | 46,46 | - | 1580 | - | - | 1580 | 226,8 | 1353 |
H3-5 | 340 | 46,46 | - | 1580 | - | 1397 | 1397 | 556,9 | 840,1 |
H5-7 | 340 | 46,46 | - | 1580 | - | - | 1580 | 721,8 | 858,2 |
B2-3 | 340 | 46,46 | 26,49 | 1580 | - | - | -1580 | -412,5 | -1168 |
B4-5 | 340 | 46,46 | 26,49 | 1580 | - | - | -1580 | -659,9 | -920,1 |
B6-7 | 340 | 46,46 | 26,49 | 1580 | - | - | -1580 | -742,5 | -837,5 |
P1-2 | 210 | 44,60 | 39,89 | 936,6 | 837,7 | 617,4 | -617,4 | -344,8 | -272,6 |
P2-3 | 210 | 38,30 | 33,57 | 804,3 | 705,0 | 573,0 | 573,0 | 282,9 | 290,1 |
P3-4 | 210 | 31,20 | 27,57 | 655,2 | 579,0 | 477,0 | -477,0 | -221,5 | -255,5 |
P4-5 | 210 | 42,36 | 35,54 | 890,0 | 746,3 | 382,0 | 382,0 | 160,8 | 221,2 |
P5-6 | 210 | 42,36 | 35,54 | 890,0 | 746,3 | 382,0 | -382,0 | -100,7 | -281,3 |
P6-7 | 210 | 42,36 | 35,54 | 890,0 | 746,3 | 382,0 | 382,0 | 41,2 | 340,8 |
C1-1 | 210 | 19,74 | 15,79 | 414,5 | 331,6 | 287,0 | -287,0 | -23,9 | -263,1 |
C3-3 | 210 | 19,74 | 15,79 | 414,5 | 331,6 | 287,0 | -287,0 | -47,9 | -239,1 |
Примечание. Nпрпред, Nустпред, Nсппред - предельные продольные силы, вычисленные соответственно для расчетов по прочности сечения, устойчивости элемента и по прочности прикрепления; Nпред - предельная продольная сила для элемента, принята со знаком "-" для элементов, преимущественно работающих на сжатие; Nпост - усилие в элементе от постоянных нагрузок; Nдоп = Nпред - Nпост - допускаемое усилие в элементе для восприятия временных нагрузок.
Таблица Б.1.6
Обозначение элемента | Nпеш, кН | Nврем, кН от расчетного воздействия нагрузки | Классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | ||
H1-3 | 29,0 | 275,1 | 261,3 | 280,4 | 52,9 | 55,7 | 141,7 |
H3-5 | 71,30 | 622,6 | 599,7 | 601,0 | 13,6 | 14,1 | 38,4 |
H5-7 | 92,40 | 784,4 | 749,0 | 754,9 | 10,7 | 11,2 | 30,4 |
B2-3 | -52,80 | -61,10 | -61,31 | -54,73 | 201 | 200 | 611 |
B4-5 | -84,50 | -88,90 | -89,25 | -82,89 | 103 | 103 | 302 |
B6-7 | -95,0 | -92,93 | -92,24 | -87,95 | 87,9 | 88,5 | 253 |
P1-2 | -44,10 | -443,4 | -454,6 | -417,7 | 5,67 | 5,53 | 16,4 |
P2-3 | 36,90 | 367,4 | 381,4 | 365,8 | 9,79 | 9,43 | 26,8 |
P3-4 | -30,20 | -329,3 | -350,3 | -284,5 | 7,53 | 7,08 | 23,8 |
P4-5 | 24,10 | 287,2 | 302,5 | 292,2 | 7,55 | 7,17 | 20,2 |
P5-6 | -18,70 | -231,7 | -251,1 | -175,9 | 12,5 | 11,5 | 44,8 |
P6-7 | 13,90 | 190,7 | 201,7 | 195,1 | 18,9 | 17,8 | 50,3 |
C1-1 | -3,40 | -168,4 | -140,0 | -174,7 | 17,0 | 20,4 | 44,6 |
C3-3 | -6,70 | -146,1 | -144,3 | -144,0 | 17,5 | 17,7 | 48,4 |
Примечание. Nпеш - продольное усилие в элементе от пешеходной нагрузки.
со сплошными балками
Металлическое балочное разрезное пролетное строение полной длиной 14,64 м изготовлено предположительно из старогодних сплошностенчатых клепаных балок, использованных ранее в пролетных строениях под железнодорожную нагрузку. В поперечном сечении применено четыре главные балки высотой 1,18 м, расставленные с шагом 2,5 м и объединенные системой продольных и поперечных связей. Мост расположен в населенном пункте. Сведения о проектных нагрузках отсутствуют.
Деревянное мостовое полотно включает проезд шириной 8 м и два тротуара шириной по 0,8 м. По верхним поясам балок уложены деревянные поперечины из бруса сечением 25 x 22 см, на которые сплошным настилом опираются деревянные продольные брусья сечением 10 x 10 см. На брусьях уложен поперечный деревянный настил толщиной 5 см и колейный настил износа, так же толщиной 5 см. Элементы мостового полотна выполнены из сосны с удельным весом 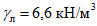 .
.
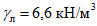 .
.ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок Б.1.6 отсутствует. |
Определение механических характеристик стали показало, что временное сопротивление металла соответствует стали Ст.3. Заклепки 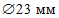 выполнены из стали Ст.2. Конструкция пролетного строения приведена на рисунках Б.1.5 и Б.1.6.
выполнены из стали Ст.2. Конструкция пролетного строения приведена на рисунках Б.1.5 и Б.1.6.
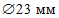 выполнены из стали Ст.2. Конструкция пролетного строения приведена на рисунках Б.1.5 и Б.1.6.
выполнены из стали Ст.2. Конструкция пролетного строения приведена на рисунках Б.1.5 и Б.1.6.
Расчетная интенсивность постоянной нагрузки.
Таблица Б.1.7
Интенсивности постоянных нагрузок
Вид нагрузки | Нормативная нагрузка, кН/м | Коэффициент надежности | Расчетная нагрузка, кН/м |
Металл балок (g1) | 9,50 | 1,05 | 9,975 |
Поперечины (g2) | 32 шт.·6,6 кН/м3·0,22 м·0,25 м·10,6 м/14,0 м = 8,795 кН/м | 1,05 | 9,235 |
Продольный брус (g3) | 6,6 кН/м3·10,6 м·0,1 м = = 6,996 кН/м | 1,05 | 7,346 |
Настил (g4) | 6,6 кН/м3·10,6 м·0,05 м = = 3,498 кН/м | 1,2 | 4,198 |
Колейный настил износа (g5) | 6,6 кН/м3·4 м·0,05 м = = 1,32 кН/м | 1,2 | 1,584 |
Колесоотбойный брус (g6) | 2 шт.·6,6 кН/м3·(0,2 м·0,35 м) = 0,924 кН/м | 1,05 | 0,9702 |
Перильное ограждение (g7) | 0,5 кН/м | 1,05 | 0,525 |
Итого: | 33,83 | ||
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок Б.1.6 отсутствует. |
Для определения усилий от действия постоянных и пешеходных нагрузок, а также для построения поверхностей влияния усилий и напряжений использована пространственная расчетная модель пролетного строения (рисунок Б.1.6), реализованная в конечно-элементном расчетном комплексе. Геометрические и жесткостные характеристики элементов главных балок и связей соответствуют фактическому исполнению конструкций. Геометрические характеристики главной балки приведены в таблице Б.1.8.
Таблица Б.1.8
Геометрические характеристики главных балок
Балка, сечение | Схема сечения | Состав сечения | A, см2 | An, см2 | Ix, см4 | Ix,n, см4 | W, см3 | Wn, см3 | S, см3 |
Б1 - Б4, 1-1 | 2L 120x120x10 (-4 отв. 10x23) | 46,6 | 37,4 | 172170 | |||||
ВЛ 1280x10 (-11 отв. 10x23) | 128,0 | 105,0 | 174760 | ||||||
2L 120x120x10 (-4 отв. 10x23) | 46,6 | 37,4 | 172170 | ||||||
221,2 | 207,4 | 519 100 | 416 600 | 8111 | 6509 | 4875 |
Конструкции пролетного строения и мостового полотна симметричны относительно продольной оси, поэтому грузоподъемность рассчитана для двух главных балок. Для каждой из них предусмотрено по 11 проверок.
1) Расчет грузоподъемности балок на прочность по нормальным напряжениям
Несущая способность вычислена по формуле (4.2.2).
Таблица Б.1.9
Классы балок на прочность по нормальным напряжениям
 ; m = 1,0; Ry = 210,0 МПа
; m = 1,0; Ry = 210,0 МПаБалка, N сечения | Wn, см3 | Mпред, кН·м | Mпост, кН·м | Mврем от расчетного воздействия эталонной нагрузки, кН·м | Допустимые классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | ||||
Б1, 1-1 | 6509 | 1367 | 113,8 | 411,9 | 202,8 | 406,6 | 31,2 | 68,0 | 92,5 |
Б2, 1-1 | 6509 | 1367 | 132,9 | 436,6 | 422,1 | 422,8 | 31,1 | 32,2 | 87,6 |
2) Расчет грузоподъемности балок на прочность по касательным напряжениям
Несущая способность вычислена по формуле (4.2.9).
Таблица Б.1.10
Классы балок на прочность по касательным напряжениям
m = 1,0; Ry = 210,0 МПа
Балка, N сечения | Ix, см4 | t, см | Smax/Smin, см3 | Qпред, кН | Qпост, кН | Qврем от расчетного воздействия эталонной нагрузки, кН | Допустимые классы нагрузок | |||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | |||||||
Б1, 2-2 | 519 100 | 1,0 | 4875/1588 | 1,169 | 1516 | 47,87 | 160,2 | 40,3 | 168,6 | 100 | 401 | 261 |
Б2, 2-2 | 519 100 | 1,0 | 4875/1588 | 1,169 | 1516 | 70,54 | 293,5 | 268,9 | 306,9 | 54,2 | 59,13 | 141 |
3) Расчет балок на прочность поясных заклепок
Несущая способность вычислена по формуле (4.5.7) с учетом указаний п. 4.5.21. Расчетная нагрузка для определения значения q соответствует H-10.
Таблица Б.1.11
Вычисление несущей способности балок
m = 1,0; Rbs = 147,0 МПа; Rbp = 367,5 МПа; ns = 2;
d = 2,3 см; Abs = 4,153 см2
N сечения | Состав сечения | S', см3 | I, см4 | a, см | P, кН | a1, см | q, кН/м | Nr, кН | Nr,min, кН | Qпред, кН | |
срез | смятие | ||||||||||
2-2 | 2L 120x120x10 ВЛ 1280x10 | 2828 696,0 | 519 100 | 10 | 46,6 | 104 | 44,81 | 122,1 | 84,53 | 84,53 | 1243 |
3524 | |||||||||||
Таблица Б.1.12
Классы балок на прочность поясных заклепок
Балка, N сечения | Qпред, кН | Qпост, кН | Qврем от расчетного воздействия эталонной нагрузки, кН | Допустимые классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | |||
Б1, 2-2 | 1243 | 47,87 | 160,2 | 40,3 | 168,6 | 82,1 | 326,2 | 213 |
Б2, 2-2 | 1243 | 70,54 | 293,5 | 268,9 | 306,9 | 43,9 | 48,0 | 115 |
4) Расчет балок на общую устойчивость сжатого пояса
Несущая способность вычислена по формуле (4.3.11).
Таблица Б.1.13
Вычисление несущей способности балок
m = 1,0; Ry = 210,0 МПа; 
N сечения | Состав сечения пояса | A, см2 | Ix, см4 | lef, см | i, см | Wc, см3 | Mпред, кН·м | ||
3-3 | 2L 120x120x10 ВЛ 120x10 | 46,6 12,0 | 844,0 | 175,0 | 3,8 | 46,05 | 0,85 | 8111 | 1448 |
58,6 |
Таблица Б.1.14
Классы балок на общую устойчивость сжатого пояса
Балка, N сечения | Mпред, кН·м | Mпост, кН·м | Mврем от расчетного воздействия эталонной нагрузки, кН·м | Допустимые классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | |||
Б1, 3-3 | 1448 | 108,9 | 350,0 | 190,4 | 346,3 | 42,1 | 77,4 | 116 |
Б2, 3-3 | 1448 | 126,2 | 342,1 | 333,1 | 337,2 | 42,5 | 43,6 | 117 |
5) Расчет балок на местную устойчивость стенки
Значения критических напряжений вычислены по формулам таблицы 4.3.3 для расчетного случая N 1.
Таблица Б.1.15
Вычисление критических напряжений для отсеков балок
m = 1,0; E = 2,1·105 МПа; t = 1,0 см; hef = 117 см;
hw = 126 см;  ;
;  ;
;  ;
; 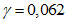 ;
;
 ;
;  ;
;  ;
; 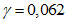 ;
; ;
;  ; t1 = 1,0 см;
; t1 = 1,0 см;  ; b1 = 24 см; c = 4,5;
; b1 = 24 см; c = 4,5;I = 844,0 см4; lef = 42,53 см; 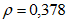
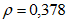
N отсека | a, см | d, см | z | ||||||||||
1 | 60 | 60 | 0,513 | 0,513 | 25,41 | 1,612 | 5,153 | 426,9 | 530,6 | 1313 | 211 | 214 | 136 |
2 | 80 | 80 | 0,684 | 0,684 | 25,34 | 1,749 | 5,555 | 425,7 | 349,1 | 499,8 | 210 | 205 | 135 |
3 | 90 | 90 | 0,769 | 0,769 | 24,21 | 1,801 | 5,735 | 406,7 | 293,2 | 344,2 | 208 | 200 | 128 |
4 | 110 | 110 | 0,940 | 0,940 | 25,00 | 1,886 | 6,122 | 420,0 | 219,4 | 187,9 | 209 | 185 | 123 |
5 | 120 | 117 | 1,026 | 0,975 | 24,10 | 1,910 | 6,339 | 404,9 | 193,4 | 152,8 | 208 | 170 | 114 |
6 | 110 | 110 | 0,940 | 0,940 | 25,00 | 1,886 | 6,122 | 420,0 | 219,4 | 187,9 | 209 | 185 | 123 |
Таблица Б.1.16
Напряжения в отсеках от расчетного воздействия нагрузки, МПа
Балка, N отсека | Постоянные нагрузки | А11 | Н11 | ЭН3 | ||||||||
Б1, 1 | -0,2 | 0,6 | 4,3 | 9,0 | 13,5 | 14,3 | 4,7 | 23,5 | 3,6 | 9,2 | 13,3 | 15,0 |
Б1, 2 | 3,3 | 0,6 | 3,8 | 8,6 | 13,5 | 12,8 | 4,2 | 23,5 | 3,2 | 8,7 | 13,3 | 13,5 |
Б1, 3 | 7,5 | 0,6 | 3,3 | 22,3 | 13,5 | 11,0 | 3,6 | 23,5 | 2,8 | 22,6 | 13,3 | 11,5 |
Б1, 4 | 7,9 | 0,6 | 2,6 | 24,3 | 13,5 | 8,8 | 2,9 | 23,5 | 2,2 | 24,9 | 13,3 | 9,3 |
Б1, 5 | 12,3 | 0,6 | 1,1 | 42,1 | 13,5 | 3,7 | 1,2 | 23,5 | 0,9 | 42,3 | 13,3 | 3,9 |
Б1, 6 | 13,4 | 0,6 | 0,4 | 46,1 | 13,5 | 1,3 | 0,4 | 23,5 | 0,3 | 45,9 | 13,3 | 1,3 |
Б2, 1 | -1,3 | 0,6 | 6,3 | 0,7 | 13,5 | 26,2 | 31,5 | 23,5 | 24,0 | 0,3 | 13,3 | 27,4 |
Б2, 2 | 3,6 | 0,6 | 5,6 | 9,9 | 13,5 | 23,4 | 28,2 | 23,5 | 21,5 | 9,9 | 13,3 | 24,5 |
Б2, 3 | 9,7 | 0,6 | 4,8 | 31,5 | 13,5 | 20,1 | 24,2 | 23,5 | 18,4 | 31,9 | 13,3 | 21,0 |
Б2, 4 | 8,6 | 0,6 | 3,9 | 28,0 | 13,5 | 16,1 | 19,4 | 23,5 | 14,8 | 28,2 | 13,3 | 16,9 |
Б2, 5 | 13,9 | 0,6 | 1,6 | 42,2 | 13,5 | 6,9 | 8,2 | 23,5 | 6,3 | 41,6 | 13,3 | 7,2 |
Б2, 6 | 15,6 | 0,6 | 0,6 | 45,5 | 13,5 | 2,3 | 2,8 | 23,5 | 2,1 | 45,4 | 13,3 | 2,4 |
ИС МЕГАНОРМ: примечание. Нумерация таблиц дана в соответствии с официальным текстом документа. |
Таблица Б.1.16
Классы балок на местную устойчивость стенки
Балка, N отсека | Левая часть условия (4.3.21) | Допустимые классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | |
Б1, 1 | 0,153 | 0,139 | 0,157 | 81 | 83 | 216 |
Б1, 2 | 0,156 | 0,154 | 0,158 | 83 | 81 | 223 |
Б1, 3 | 0,212 | 0,170 | 0,214 | 61 | 79 | 165 |
Б1, 4 | 0,219 | 0,177 | 0,222 | 58 | 76 | 158 |
Б1, 5 | 0,303 | 0,196 | 0,303 | 42 | 72 | 114 |
Б1, 6 | 0,314 | 0,186 | 0,312 | 40 | 80 | 111 |
Б2, 1 | 0,211 | 0,299 | 0,218 | 60 | 39 | 159 |
Б2, 2 | 0,219 | 0,297 | 0,224 | 58 | 40 | 155 |
Б2, 3 | 0,287 | 0,298 | 0,291 | 44 | 42 | 119 |
Б2, 4 | 0,261 | 0,274 | 0,264 | 49 | 46 | 131 |
Б2, 5 | 0,314 | 0,238 | 0,311 | 41 | 58 | 112 |
Б2, 6 | 0,320 | 0,204 | 0,319 | 40 | 74 | 110 |
6) Расчет балок на прочность стыка
Несущая способность болтового поля вычислена по формуле (4.5.5) с учетом указаний п. 4.5.19.
Таблица Б.1.17
Вычисление несущей способности стыка
m = 1,0; mb = 1,0; Ry = 210,0 МПа; Rbs = 147,0 МПа;
Rbp = 367,5 МПа; ns = 2; d = 2,3 см; Abs = 4,153 см2;
ymax = 64,0 см
N сечения | Состав стыка | S', см3 | Ix, см4 | Ix,n, см4 | Nr, кН | Nr,min, кН | Mпред, кН | ||
срез | смятие | ||||||||
4-4 | 2L 120x120x10 2BH 1020x10 | 2828 | 344 300 | 276 400 | - | - | - | - | 907,0 |
2601 | 176 900 | 150 400 | 16 500 | 122,1 | 84,53 | 84,53 | 218,0 | ||
5429 | 521 200 | 426 800 | 1125 | ||||||
Таблица Б.1.18
Классы балок на прочность стыка
Балка, N сечения | Mпред, кН·м | Mпост, кН·м | Mврем от расчетного воздействия эталонной нагрузки, кН·м | Допустимые классы нагрузок | ||||
А11 | Н11 | ЭН3 | АК | НК | ЭН3 | |||
Б1, 4-4 | 1125 | 93,57 | 310,4 | 154,2 | 308,2 | 36,6 | 73,6 | 100 |
Б2, 4-4 | 1125 | 111,1 | 335,6 | 331,1 | 331,0 | 33,2 | 33,7 | 91,9 |
Пролетное строение расчетным пролетом 42,0 м запроектировано под нагрузки А11, Н11. В поперечном сечении две балки высотой 2,48 м, расставленных на 5,4 м. Шаг поперечных ребер равен панели продольных и поперечных связей и составляет 3,5 м. Основные несущие элементы пролетного строения изготовлены из стали 10ХСНД. Конструкция пролетного строения изображена на рисунке Б.2.1.
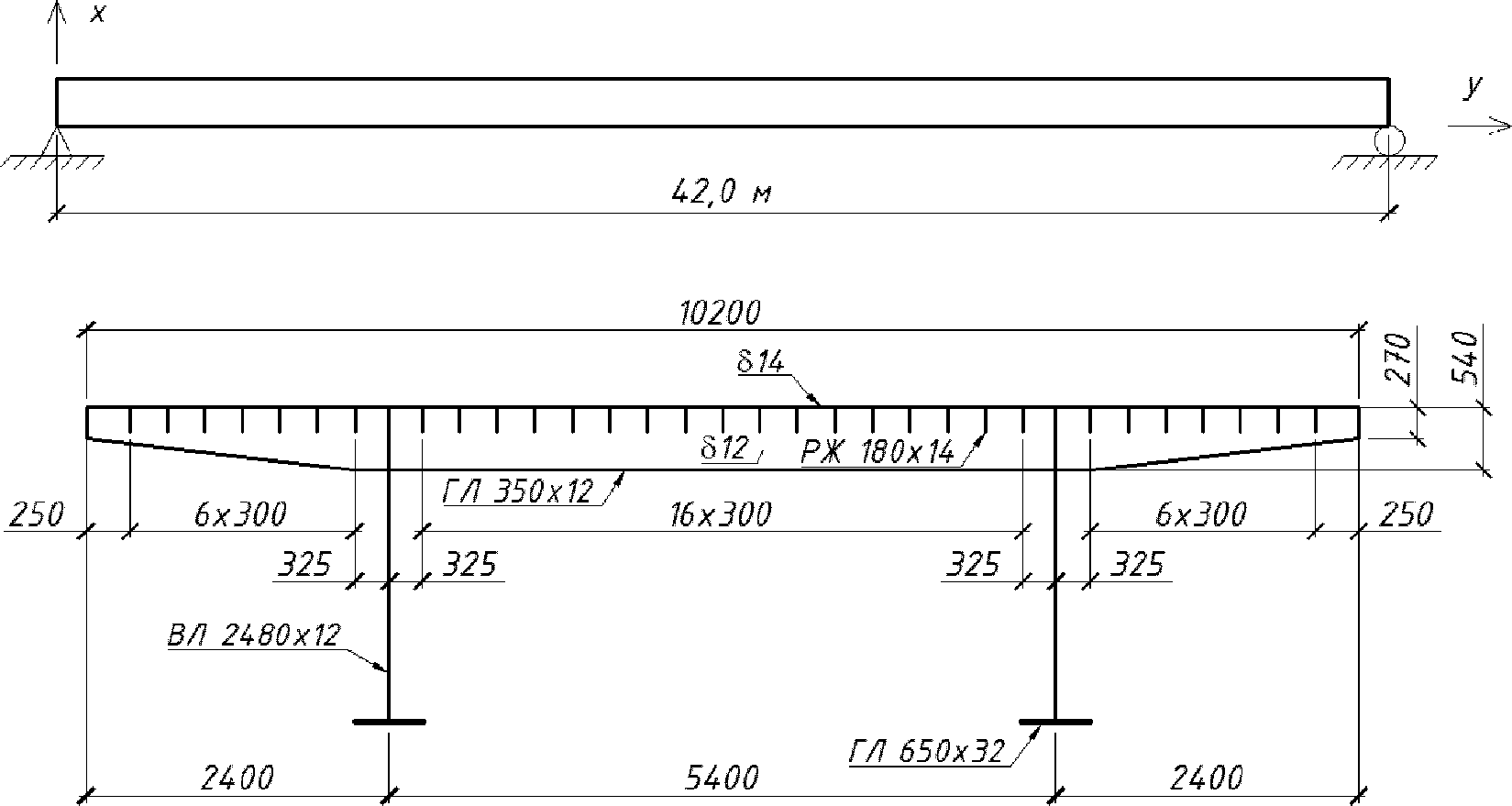
Рисунок Б.2.1 - Поперечное сечение пролетного строения
(связи не показаны)
Модель N I (см. п. А.2.1). Использована плоская балочная расчетная схема. Напряжения вычислены по формуле А.2.1 при наиболее невыгодном положении нагрузки.
Модель N II (см. п. А.2.2). Для составления расчетной модели применен конечно-элементный расчетный комплекс. Использовано два типа конечных элементов - для моделирования продольных и поперечных ребер стержневой изгибаемый элемент "балка" ("beam"), для моделирования листа настила - плоский изгибаемый четырехузловой элемент "плита" ("plate"). Из конструкции средней части пролетного строения выделено пять пролетов ортотропной плиты, длина каждого пролета l = 3,5 м.
Продольные ребра в каждом пролете разбиты на 7 частей длиной по 0,5 м. Разбивка поперечных ребер соответствует шагу продольных ребер в поперечном направлении, и составляет от 0,3 до 0,325 м. Сетка плитных элементов настила образуется пересечением прямых, проходящих через узлы продольных и поперечных ребер. Размер плитных элементов составляет от 0,5 x 0,3 м до 0,5 x 0,325 м, это дает отношение большей стороны к меньшей 1,43 - 1,54, что удовлетворяет условию соотношения сторон. Типы закреплений в модели приняты в соответствии с рекомендациями приложения А.2. Вид модели N II приведен на рисунке Б.2.2.

Рисунок Б.2.2 - Модель ортотропной плиты N II
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: рисунок 4.8.1 отсутствует. |
Расчетные сечения I - III (см. рисунок 4.8.1) располагаются в среднем пролете продольных ребер. Далее найдены номера конечных элементов, близлежащих к точкам A - D1 (см. рисунки А.2.1, А.2.2). Напряжения, возникающие в этих элементах, определены по направлениям глобальных осей. В загружениях временной нагрузкой принята наиболее невыгодная схема ее установки.
Для вычисления коэффициента  определены: а) величина поперечной силы в соответствующем сечении главной балки при действии расчетных постоянных и проектных временных нагрузок - из модели N I; б) величина касательных напряжений
определены: а) величина поперечной силы в соответствующем сечении главной балки при действии расчетных постоянных и проектных временных нагрузок - из модели N I; б) величина касательных напряжений  , возникающих близ точки B в максимально загруженном (рассчитываемом) продольном ребре от действия этих же нагрузок - из модели N II.
, возникающих близ точки B в максимально загруженном (рассчитываемом) продольном ребре от действия этих же нагрузок - из модели N II.

Рисунок Б.2.3 - Расчетная схема (модель N I)
и ее загружение
Для вычисления коэффициента из моделей N I и N II определены значения максимальных и минимальных продольных напряжений,  и
и 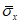 , возникающих по продольным границам максимально загруженного (рассчитываемого) продольного ребра, при действии проектных нагрузок.
, возникающих по продольным границам максимально загруженного (рассчитываемого) продольного ребра, при действии проектных нагрузок.
Для вычисления коэффициента  для расчета общей устойчивости ортотропной плиты определено значение максимального прогиба продольного ребра между поперечными балками от временной нагрузки А11 и Н11.
для расчета общей устойчивости ортотропной плиты определено значение максимального прогиба продольного ребра между поперечными балками от временной нагрузки А11 и Н11.
Коэффициент  для расчета продольного ребра на прочность
для расчета продольного ребра на прочность
Коэффициент  , учитывающий ограниченное развитие пластических деформаций, для расчета продольного ребра
, учитывающий ограниченное развитие пластических деформаций, для расчета продольного ребра
Среднее касательное напряжение в продольном ребре:
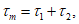 (Б.2.1)
(Б.2.1)где  - касательные напряжения в продольном ребре от работы в составе главной балки;
- касательные напряжения в продольном ребре от работы в составе главной балки;  - касательные напряжения в продольном ребре от местной нагрузки.
- касательные напряжения в продольном ребре от местной нагрузки.
 (Б.2.2)
(Б.2.2)где Q - поперечная сила в главной балке от постоянных и временных нагрузок; S - статический момент части сечения, отсеченного по низу ребра, относительно нейтральной оси, S = 0,122 м3; I - момент инерции сечения, I = 0,2773 м4; b - суммарная толщина продольных ребер работающих в составе главной балки.
Таблица Б.2.1
Интенсивность постоянных нагрузок
Наименование нагрузки | Коэффициент надежности, | Нормативная интенсивность, кН/м | Расчетная интенсивность, кН/м | |
Для загружения отрицательного участка линии влияния, g- | Для загружения положительного участка линии влияния, g+ | |||
Гидроизоляция | 1,15 (0,95) | 0,1 | 0,095 | 0,115 |
Асфальтобетон | 1,20 (0,90) | 3,45 | 3,105 | 4,140 |
Металл пролетного строения | 1,05 (0,90) | 16,6 | 14,94 | 17,43 |
Перила | 1,05 (0,90) | 0,55 | 0,495 | 0,5775 |
Барьерное ограждение | 1,05 (0,90) | 1,1 | 0,990 | 1,155 |
Итого: | 19,63 | 23,42 | ||
Поперечная сила от действия расчетных постоянных нагрузок:
Qпост = 21/2·0,5·(23,42 - 19,63) = 19,9 кН.
Поперечная сила при загружении нагрузкой А11:
Qвр = 1,5·1,4·110·(0,5 + 0,5/21·19,5)·(1,15 + 0,78)/2 +
+ 1,1·11·21·0,5/2·(1,15 + 0,78)/2 = 276,3 кН.
Суммарная поперечная сила Q = 276,3 + 19,9 = 296,2 кН.
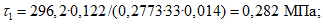


При 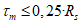 коэффициент
коэффициент  следует определять по формуле 8.6 [3]. При
следует определять по формуле 8.6 [3]. При 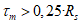 коэффициент
коэффициент 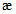 следует определять по формуле 8.7 [3].
следует определять по формуле 8.7 [3].
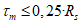 коэффициент
коэффициент 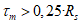 коэффициент
коэффициент Rs = 0,58·Ry, (Б.2.3)
где Ry - расчетное сопротивление металла, Ry = 350 МПа.
Rs = 0,58·350 = 203 МПа.
0,25·Rs = 0,25·203 = 50,75 МПа.
Условие 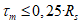 выполняется: 1,207 МПа < 50,75 МПа.
выполняется: 1,207 МПа < 50,75 МПа.
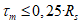 выполняется: 1,207 МПа < 50,75 МПа.
выполняется: 1,207 МПа < 50,75 МПа.Коэффициент 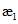 для таврового расчетного сечения продольного ребра определен по таблице 8.16 [3]. При площади меньшего пояса Af,min = 0, площади вертикального листа Aw = 0,00252 м2, площади расчетного поперечного сечения A = 0,00672 м2,
для таврового расчетного сечения продольного ребра определен по таблице 8.16 [3]. При площади меньшего пояса Af,min = 0, площади вертикального листа Aw = 0,00252 м2, площади расчетного поперечного сечения A = 0,00672 м2, 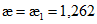 .
.
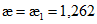 .
.Коэффициент 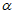 для расчета устойчивости продольного ребра
для расчета устойчивости продольного ребра
При определении коэффициента  следует руководствоваться п. 4.3.11 настоящих рекомендаций. При определении коэффициента
следует руководствоваться п. 4.3.11 настоящих рекомендаций. При определении коэффициента  использована формула (4.3.17) для пластины, опертой по одной стороне.
использована формула (4.3.17) для пластины, опертой по одной стороне.
Для сечения расположенного в пролете:
t = 0,014 м, th = 0,014 м, bh = 0,15 м, h = 0,18 м.
 ;
; 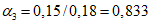 ;
;  .
.Изгибающий момент от постоянных нагрузок:
Mп = 23,42·220,5 = 5164 кН·м.
Изгибающий момент от временных нагрузок:
MА11 = 1,5·1,4·110·(10,5 + 9,89)·(1,15 + 0,78)/2 +
+ 1,1·11·(1,15 + 0,78)/2·(42·10,5/2) = 7120 кН·м.
MН11 = 1,1·11·18·(0,79 + 0,28)/2·(10,5 + 10,5/21·19,8 +
+ 10,5/21·18,6 + 10,5/21·17,4) = 4474 кН·м.
Суммарные напряжения (положительные при сжатии):
для нагрузки А11:  ;
;
 ;
;для нагрузки Н11:  .
.
 .
.Напряжения от местной нагрузки получены из модели N II (положительные при сжатии):
для нагрузки А11: 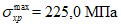 ,
,  ;
;
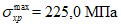 ,
,  ;
;для нагрузки Н11: 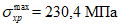 ,
,  .
.
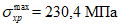 ,
,  .
.Суммарные максимальные и минимальные продольные напряжения по продольным границам продольного ребра:
для нагрузки А11:  ,
, 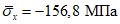 ;
;
 ,
, 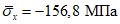 ;
;для нагрузки Н11: 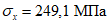 ,
,  .
.
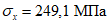 ,
,  .
.Коэффициент  :
:
для нагрузки А11:  ;
;
 ;
;для нагрузки Н11: 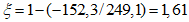 .
.
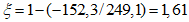 .
.Коэффициент  для расчета устойчивости продольного ребра ортотропной плиты вычислен по формуле (4.3.17):
для расчета устойчивости продольного ребра ортотропной плиты вычислен по формуле (4.3.17):
для нагрузки А11: 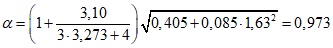 ;
;
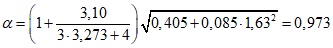 ;
;для нагрузки Н11: 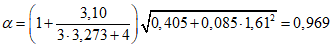 .
.
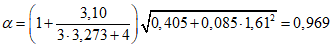 .
.Коэффициент  для расчета общей устойчивости ортотропной плиты
для расчета общей устойчивости ортотропной плиты
При определении коэффициента  следует руководствоваться п. Ш.12 [3] и таблицей Ш.4 [3] в зависимости от класса прочности стали и гибкости ортотропной плиты
следует руководствоваться п. Ш.12 [3] и таблицей Ш.4 [3] в зависимости от класса прочности стали и гибкости ортотропной плиты  (формула Ш.14 [3]).
(формула Ш.14 [3]).
Исходные данные:
Толщина листа настила: th = 0,014 м; расстояние между главными балками: L = 5,4 м; шаг поперечных балок: l = 3,5 м; шаг продольных ребер: a = 0,3 м; число продольных ребер на рассчитываемом участке ортотропной плиты k = 17 шт. Коэффициент  . Площадь расчетного сечения продольного ребра: A = 0,3·0,014 + 0,18·0,014 = 6,72·10-3 м2. Момент инерции расчетного сечения продольного ребра относительно горизонтальной оси: Isl = 2,169·10-5 м4. Момент инерции полного сечения поперечной балки с прилегающим участком настила шириной 0,2·L = 0,2·5,4 = 1,08 м: Is = 1,282·10-3 м4. Максимальный прогиб продольного ребра между поперечными балками получен от расчетной временной нагрузки А11: f = 3,0·10-3 м. Радиус инерции расчетного сечения продольного ребра: i = 5,681·10-2 м.
. Площадь расчетного сечения продольного ребра: A = 0,3·0,014 + 0,18·0,014 = 6,72·10-3 м2. Момент инерции расчетного сечения продольного ребра относительно горизонтальной оси: Isl = 2,169·10-5 м4. Момент инерции полного сечения поперечной балки с прилегающим участком настила шириной 0,2·L = 0,2·5,4 = 1,08 м: Is = 1,282·10-3 м4. Максимальный прогиб продольного ребра между поперечными балками получен от расчетной временной нагрузки А11: f = 3,0·10-3 м. Радиус инерции расчетного сечения продольного ребра: i = 5,681·10-2 м.
 . Площадь расчетного сечения продольного ребра: A = 0,3·0,014 + 0,18·0,014 = 6,72·10-3 м2. Момент инерции расчетного сечения продольного ребра относительно горизонтальной оси: Isl = 2,169·10-5 м4. Момент инерции полного сечения поперечной балки с прилегающим участком настила шириной 0,2·L = 0,2·5,4 = 1,08 м: Is = 1,282·10-3 м4. Максимальный прогиб продольного ребра между поперечными балками получен от расчетной временной нагрузки А11: f = 3,0·10-3 м. Радиус инерции расчетного сечения продольного ребра: i = 5,681·10-2 м.
. Площадь расчетного сечения продольного ребра: A = 0,3·0,014 + 0,18·0,014 = 6,72·10-3 м2. Момент инерции расчетного сечения продольного ребра относительно горизонтальной оси: Isl = 2,169·10-5 м4. Момент инерции полного сечения поперечной балки с прилегающим участком настила шириной 0,2·L = 0,2·5,4 = 1,08 м: Is = 1,282·10-3 м4. Максимальный прогиб продольного ребра между поперечными балками получен от расчетной временной нагрузки А11: f = 3,0·10-3 м. Радиус инерции расчетного сечения продольного ребра: i = 5,681·10-2 м.Соответственно при f/i = 0,0528 коэффициент  .
.
 .
.Момент инерции кручения расчетного сечения продольного ребра может быть вычислен по формуле
 (Б.2.4)
(Б.2.4)где bi и ti - соответственно длина и толщина горизонтального листа и пластинки ребра, входящих в расчетное сечение продольного ребра.
It = 1,08/3·(0,3·0,0143 + 0,18·0,0143) = 4,742·10-7 м4.
Коэффициент 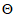 :
:
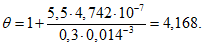
Расчетная (свободная) длина продольных ребер lef = 3,5 м.

Сталь 10ХСНД относится к классу прочности С390. Согласно таблице Ш.4 [3], коэффициент продольного изгиба ортотропной плиты: 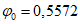 .
.
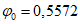 .
.Напряжения от действия постоянных нагрузок при совместной работе с главными балками определены загружением расчетной модели N I. Напряжения от действия постоянных нагрузок при работе на местную нагрузку определены загружением пространственной модели N II. Загружение моделей временной нагрузкой осуществлено по наиболее невыгодным схемам ее установки. При загружении временной нагрузкой модели N II учтено распределение сосредоточенных осевых сил по площади (a1 x b1), см. формулу (4.2.1) [5]. Суммарная толщина одежд ездового полотна 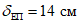 .
.
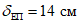 .
.Расчеты элементов ортотропной плиты сведены в таблицы Б.2.2 - Б.2.6. Классы нагрузок определены из соответствующих уравнений предельного состояния (номера уравнений указаны в таблицах) путем последовательного подбора величины класса.
Таблица Б.2.2
Расчет на прочность продольного ребра (в зоне
положительных моментов, близ точки B,
см. рисунок 4.4.1)
N п/п | Наименование | Значение | |
Модель N I | Модель N II | ||
1. | Расчетные нормальные напряжения от временной нагрузки А11/Н11, МПа | 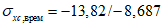 | 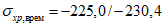 |
2. | Расчетные напряжения от постоянных нагрузок, МПа |  | 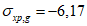 |
3. | Расчетные напряжения от пешеходной нагрузки, МПа |  |  |
4. | Коэффициент |  | - |
5. | Коэффициент влияния собственных остаточных напряжений | - | 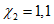 |
6. | Коэффициент, учитывающий ограниченное развитие пластических деформаций | - |  |
7. | Расчетное сопротивление стали, МПа | Ry = 350,0 | |
8. | Коэффициент условий работы | m = 1,0 | |
9. | Классы КАК/КНК | 17,55/17,63 | |
Таблица Б.2.3
Расчет на прочность поперечной балки близ точки C,
см. рисунок 4.4.1
N п/п | Наименование | Значение (модель N II) | ||||
1. | Расчетные нормальные напряжения от временной нагрузки А11/Н11, МПа |  | ||||
2. | Расчетные нормальные напряжения от постоянных нагрузок, МПа |  | ||||
3. | Расчетные нормальные напряжения от пешеходной нагрузки, МПа |  | ||||
| ||||||
3. | Коэффициент, учитывающий ограниченное развитие пластических деформаций | = 1,0 | ||||
4. | Расчетное сопротивление стали, МПа | Ry = 350,0 | ||||
5. | Коэффициент условий работы | m = 1,0 | ||||
6. | Классы КАК/КНК (4.4.4) | 27,76/27,80 | ||||
Примечание. В формуле (4.4.4) напряжения  .
.
 .
.Таблица Б.2.4
Расчет на прочность листа настила близ точки A1,
см. рисунок 4.4.1
N п/п | Наименование | Значение | |
Модель N I | Модель N II | ||
1. | Расчетные нормальные продольные напряжения от временной нагрузки А11/Н11, МПа |  |  |
2. | Расчетные нормальные поперечные напряжения от временной нагрузки А11/Н11, МПа |  | 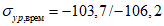 |
3. | Расчетные касательные напряжения от временной нагрузки А11/Н11, МПа |  |  |
4. | Расчетные нормальные продольные напряжения от постоянных нагрузок, МПа |  |  |
5. | Расчетные нормальные поперечные напряжения от постоянных нагрузок, МПа |  |  |
6. | Расчетные касательные напряжения от постоянных нагрузок, МПа | 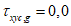 |  |
7. | Расчетные продольные напряжения от пешеходной нагрузки, МПа | 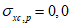 | 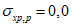 |
8. | Расчетные поперечные напряжения от пешеходной нагрузки, МПа |  |  |
9. | Расчетные касательные напряжения от пешеходной нагрузки, МПа |  | 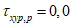 |
10. | Коэффициент условий работы | - | m4 = 1,05 |
11. | Расчетное сопротивление стали, МПа | Ry = 350,0 | |
12. | Расчетное сопротивление стали сдвигу, МПа | Rs = 203,0 | |
13. | Коэффициент условий работы | m = 1,0 | |
14. | Коэффициент | m3 = 1,1 | |
15. | Классы КАК/КНК | 41,56/41,67 | |
Примечание. В формулах (4.4.5) и (4.4.6):
 ,
,  ,
, ,
, 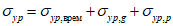 ,
, ,
, 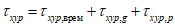 .
.Таблица Б.2.5
Расчет устойчивости продольного ребра близ точки B,
см. рисунок 4.4.1
N п/п | Наименование | Значение | |
Модель N I | Модель N II | ||
1. | Расчетные нормальные напряжения от временной нагрузки А11/Н11, МПа | 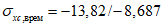 | 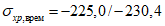 |
2. | Расчетные нормальные напряжения от постоянных нагрузок, МПа |  |  |
3. | Расчетные нормальные напряжения от пешеходной нагрузки, МПа | 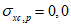 |  |
5. | Класс прочности стали | С390 | |
6. | Высота проверяемой пластинки | h = 0,180 | |
7. | Толщина проверяемой пластинки | t = 0,014 | |
8. | Коэффициент  | 0,973/0,969 | |
9. | Коэффициент условий работы | m = 1,0 | |
10. | Значение напряжений  , МПа , МПа | 1088/1079 | |
11. | Предельное значение напряжений | 591,0 | |
12. | Классы КАК/КНК (4.2.3) [2]  | 26,5/26,5 | |
Примечание. Значения  ,
,  ,
, 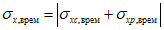 .
.
 ,
,  ,
, 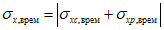 .
.Таблица Б.2.6
N п/п | Наименование | Значение (модель N I) |
1. | Расчетные нормальные напряжения от временной нагрузки А11/Н11, МПа | 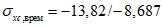 |
2. | Расчетные нормальные напряжения от постоянных нагрузок, МПа |  |
3. | Расчетные нормальные напряжения от пешеходной нагрузки, МПа |  |
4. | Коэффициент продольного изгиба | 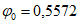 |
5. | Расчетное сопротивление стали, МПа | Ry = 350,0 |
6. | Коэффициент условий работы | m = 1,0 |
7. | Классы КАК/КНК | 147,6/234,9 |
Примечание. В формуле (4.4.7) напряжения  .
.
 .
.сталежелезобетонного пролетного строения
Исходные данные
Пролетное строение - разрезное, выполнено применительно к типовому проекту серии 3.503, инв. N 608/1. Расчетный пролет 41,4 м. Проектные нагрузки Н-30, НК-80. Пролетное строение выполнено из стали марки 15ХСНД и бетона класса B35. При ремонте сооружения были увеличены консольные свесы плиты и габарит проезда (рисунок Б.3.1). Расчетное сечение показано на рисунке Б.3.2.

Рисунок Б.3.1 - Конструкция пролетного строения

Таблица Б.3.1
Параметры расчетного сечения, мм
Расположение | Bc | hc | Hh | ВП | ВЛ | НП |
Середина пролета | 5370 | 160 | 200 | 420 x 16 | 2480 x 12 | 750 x 32 |
Площадь продольной арматуры, учитываемой в расчете, Ar = 0,00338 м2.
Таблица Б.3.2
Модуль упругости стали, МПа | 206000 |
Модуль упругости арматуры, МПа | 206000 |
Модуль упругости бетона, МПа | 34500 |
Предельная деформация бетона на сжатие | 0,0016 |
Расчетное сопротивление стали верхнего пояса, МПа | 295 |
Расчетное сопротивление стали нижнего пояса, МПа | 295 |
Расчетное сопротивление арматуры плиты, МПа | 210 |
Расчетное сопротивление бетона, МПа | 17,5 |
Максимальная разность температур, C | 36 |
Коэффициенты приведения nb = 5,97, nr = 1.
Постоянные нагрузки
Расчетная интенсивность постоянной нагрузки определена по формуле:
 (Б.3.1)
(Б.3.1)где: gПС - нормативный погонный вес пролетного строения, тс/м; gпокр - то же от веса асфальтобетонного покрытия проезжей части, тс/м; gсл. - то же от веса выравнивающего и защитного слоев, тс/м; gГИ - то же от веса гидроизоляционного слоя, тс/м; gОБ - то же от веса ограждений безопасности, тс/м; gперил - то же от веса перил, тс/м.
Равномерно распределенная нагрузка от веса металла пролетного строения принята по данным типового проекта серии 3.503-15 вып. 608/1 - 0,73 тс/м. Нагрузка от плиты проезжей части принята по фактическим размерам.
Нормативные и расчетные интенсивности от всех постоянных нагрузок для балок пролетного строения приведены в таблице Б.3.2.
Площадь линии влияния момента в середине балки расчетным пролетом 41,4 м

Усилия от постоянных нагрузок составили
для первой стадии Mпост1 = 3,02 214,25 = 647,04 тс·м = 6,47 МН·м;
для второй стадии Mпост2 = 3,642 214,25 = 780,3 тс·м = 7,80 МН·м.
Таблица Б.3.3
Интенсивности постоянных нагрузок
Наименование нагрузки | Ширина, м | Толщина, м | Площадь, м2 | Объемный вес, тс/м3 | Норм. интенсивность, тс/м | Коэфф. надежности, | Расчетная интенсивность, тс/м |
Металл пролетного строения | - | - | - | 7,85 | 0,73 | 1,05 | 0,77 |
Вес железобетонной плиты | 5,37 | 0,16 | 0,8592 | 2,5 | 2,15 | 1,05 | 2,26 |
Итого по стадии I | 2,88 | 3,02 | |||||
Перила | - | - | - | 0,036 | 1,10 | 0,040 | |
Ограждение безопасности | - | - | - | 0,071 | 1,10 | 0,078 | |
Выравнивающий слой | 4 | 0,08 | 0,32 | 2,5 | 0,800 | 1,15 | 0,920 |
Гидроизоляция | 5,26 | 0,005 | 0,0263 | 1,0 | 0,026 | 1,15 | 0,030 |
Защитный слой | 5,26 | 0,06 | 0,3156 | 2,5 | 0,789 | 1,15 | 0,907 |
Покрытие (асфальтобетон) | 5,26 | 0,11 | 0,5786 | 2,4 | 1,389 | 1,2 | 1,666 |
Итого по стадии II | 0,255 | 3,111 | 3,642 |
Пешеходные нагрузки
Нагрузка от пешеходов принята согласно [2] - 2,0 кПа. При ширине тротуаров 0,83 м нормативная нагрузка составила p = 0,83·0,204 тс/м = 0,166 тс/м. Коэффициент надежности по нагрузке 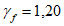 . Итоговая расчетная интенсивность 0,20 тс/м (1,99 кН/м).
. Итоговая расчетная интенсивность 0,20 тс/м (1,99 кН/м).
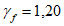 . Итоговая расчетная интенсивность 0,20 тс/м (1,99 кН/м).
. Итоговая расчетная интенсивность 0,20 тс/м (1,99 кН/м).Расчетный изгибающий момент в среднем сечении разрезной балки от пешеходной нагрузки определен загружением соответствующей поверхности влияния:
M0.5пеш = 51,6 тсм = 0,516 МН·м.
Определение грузоподъемности
Определение класса по грузоподъемности произведено итерациями согласно рекомендациям п. Б.3 [2] с заданием начального значения класса нагрузки АК равным 11 и сравнением значений напряжений в поясах стальной балки со значением расчетного сопротивления металла. Критерием завершения расчета является минимальный запас прочности, составляющий не более 2%.
Расчеты выполнены на два сочетания нагрузок согласно п. 5.4.
Определение внутренних усилий от временной нагрузки А11 выполнено путем загружения соответствующих поверхностей влияния с учетом пространственного характера работы пролетных строений. Расчетная схема составлена согласно общим рекомендациям пп. Б.1 [2] и п. А.1 и представляет собой балочный ростверк, состоящий из стержневых элементов общего вида, работающих на продольную силу, на кручение и изгиб в двух плоскостях. Главные балки представлены продольными стержневыми элементами. Продольные элементы жестко объединены поперечными стержневыми элементами, жесткостные характеристики которых соответствуют сечению плиты между главными балками.
Шаг разбивки конечно-элементной сетки в продольном направлении принят равным 1/32 длины расчетного пролета. В поперечном направлении сечение разбито на 12 участков - по два на консолях и восемь между главными балками.
Расчет на первое сочетание нагрузок
На начальном шаге итерационного расчета при К = 11 запасы по напряжениям в поясах главной балки составили: в верхнем поясе 41%, в нижнем поясе - 9%, по деформациям в плите 87%. Последовательными приближениями получена допустимая величина класса К = 14,5 (далее приведены только окончательные значения, соответствующие этому классу).
Изгибающие моменты
от постоянных нагрузок первой стадии | M1 = | 6,47 | МН·м |
от постоянных нагрузок второй стадии | M2g = | 7,80 | МН·м |
от пешеходных нагрузок | Mпеш = | 0,516 | МН·м |
от временных нагрузок АК (при К = 14,5) | Mv = | 10,137 | МН·м |
полный момент на второй стадии | M2 = | 18,453 | МН·м |
полный изгибающий момент | M = | 24,923 | МН·м |
Геометрические характеристики сечения
Геометрические характеристики сечения приведены в таблице Б.3.4. По данным этой таблицы рассчитаны величины, указанные в п. 5.1.8:
положение центра тяжести стального сечения Cs, м

расстояние от центра тяжести стального сечения Cs до верхней фибры стальной балки, м

положение центра тяжести железобетонной плиты Cbr, м

положение центра тяжести объединенного сечения Cstb, м

расстояние между Cstb и Cbr, м
Zb,stb = Zbr - Zstb = 2,808 - 2,256 = 0,552;
расстояние между Cs и Cbr, м
Zbs = Zbr - Zs1,s = 2,808 - 0,912 = 1,896;
момент инерции стальной части сечения, м4
Is = Is,aa + Is,со - Zs1,sSs,aa = 0,090832036 +
+ 0,015255183 - 0,912·0,05517312 = 0,055755322;
момент инерции объединенного сечения, м4
Istb = Istb,aa + Istb,со - ZstbSstb,aa = 1,252499072 +
+ 0,015562331 - 2,256·0,468905859 = 0,210130405;
моменты сопротивления, м3

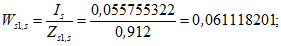


Таблица Б.3.4
Приведенная к стали площадь сечения плиты, м2 | |
без учета арматуры | Ab,aa = 0,143976 |
с учетом арматуры | Ab,aa = 0,147353 |
Приведенный к стали статический момент сечения плиты, включая статический момент арматуры, м3 | Sb,aa = 0,404283299 |
Приведенный к стали момент инерции сечения плиты, включая момент инерции арматуры, м4 | Ib,aa = 1,135227505 |
Приведенный к стали момент инерции сечения плиты относительно собственного центра тяжести, исключая собственный момент инерции арматуры, м4 | Ib,со = 0,000307 |
Площадь сечения стальной балки, м2 | As,aa = 0,060480 |
Статический момент сечения стальной балки, м3 | Ss,aa = 0,05517312 |
Момент инерции сечения стальной балки, м4 | Is,aa = 0,090832036 |
Момент инерции сечения стальной балки относительно собственного центра тяжести, м4 | Is,со = 0,015255183 |
Высота стальной балки, м | hs = 2,528 |
Площадь сечения сталежелезобетонной балки, м2 | Astb,aa = 0,207833 |
Статический момент сечения сталежелезобетонной балки, м3 | Sstb,aa = 0,468905859 |
Момент инерции сечения сталежелезобетонной балки, м4 | Istb,aa = 1,252499072 |
Момент инерции сечения сталежелезобетонной балки относительно собственного центра тяжести, м4 | Istb,со = 0,015562331 |
Применимость метода тонкой плиты
EbIb = 34500·(5,37·0,163)/12 = 63,24 < 0,2EsIs =
= 0,2·206000·0,006852407 = 2262,86.
Условие (5.1.14) выполняется, метод применим.
Проверка необходимости учета ползучести бетона

Учет ползучести бетона не требуется.
Напряжения на уровне центра тяжести плиты
Напряжения в бетоне, МПа

Напряжения в арматуре, МПа

Разгружающая сила, МН

Поправочные коэффициенты
Коэффициент  (см. таблицу 5.4.1)
(см. таблицу 5.4.1)
As2/As1 = 0,28; N/(As·m·Ry) = 0,40;  .
.
 .
.Коэффициент ограниченных пластических деформаций
Af,min/Aw = 0,226; (Af,min + Aw)/As = 0,111;
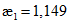 (п. 8.26 [8]).
(п. 8.26 [8]).Коэффициент 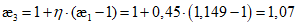 .
.
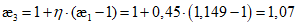 .
.Коэффициент 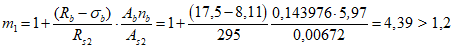 , принимаем 1,2;
, принимаем 1,2;
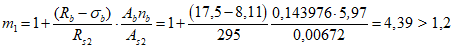 , принимаем 1,2;
, принимаем 1,2;Коэффициент  , принимаем 1,0.
, принимаем 1,0.
 , принимаем 1,0.
, принимаем 1,0.Проверки стальной балки
Прочность верхнего пояса

Прочность нижнего пояса

Деформации бетона плиты при К = 14,5 не являются лимитирующими, поэтому их расчет здесь не приводится.
Условие прочности нижнего стального пояса выполняется с запасом менее 2%, значит, величина допускаемого класса нагрузки АК принята правильно.
Расчет на второе сочетание нагрузок
На начальном шаге итерационного расчета при К = 11 запасы по напряжениям в поясах главной балки составили: в верхнем поясе 34%, в нижнем поясе - 13%, по деформациям в плите 80%. Последовательными приближениями получена допустимая величина класса К = 15,7 (далее приведены только окончательные значения, соответствующие этому классу). Для временных нагрузок применен коэффициент сочетания 0,8.
Изгибающие моменты
от постоянных нагрузок первой стадии | M1 = | 6,47 | МН·м |
от постоянных нагрузок второй стадии | M2g = | 7,80 | МН·м |
от пешеходных нагрузок | Mпеш = | 0,516 | МН·м |
от временных нагрузок АК (при К = 15,7) | Mv = | 9,19 | МН·м |
полный момент на второй стадии | M2 = | 16,994 | МН·м |
полный изгибающий момент | M = | 23,464 | МН·м |
Геометрические характеристики для расчета на усадку
Модуль упругости бетона для расчета усадки Eb,shr = 34500*0,5 = 17250 МПа.
Коэффициент приведения nb = 11,94.
положение центра тяжести стального сечения Cs, м

расстояние от центра тяжести стального сечения Cs до верхней фибры стальной балки, м
Zs2,s = hs - Zs1,s = 2,528 - 0,912 = 1,616;
положение центра тяжести железобетонной плиты Cbr, м

положение центра тяжести объединенного сечения Cstb, м

расстояние между Cstb и Cbr, м
Zb,stb = Zbr - Zstb = 2,808 - 1,964 = 0,844;
расстояние между Cs и Cbr, м
Zbs = Zbr - Zs1,s = 2,808 - 0,912 = 1,895;
положение центра тяжести стального сечения с арматурой, м
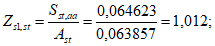
момент инерции объединенного сечения, м4
Istb,shr = Istb,aa + Istb,со - Zstb,shrSstb,aa =
= 0,684885320 + 0,015408757 - 1,964·0,266764209 =
= 0,176438549;
моменты сопротивления, м3


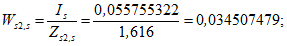
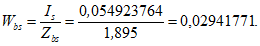
Таблица Б.3.5
Приведенная к стали площадь сечения плиты, м2 | |
без учета арматуры | Ab,aa = 0,071988 |
с учетом арматуры | Ab,aa = 0,075365 |
Приведенный к стали статический момент сечения плиты, включая статический момент арматуры, м3 | Sb,aa = 0,211591089 |
Приведенный к стали момент инерции сечения плиты, включая момент инерции арматуры, м4 | Ib,aa = 0,594053284 |
Приведенный к стали момент инерции сечения плиты относительно собственного центра тяжести, исключая собственный момент инерции арматуры, м4 | Ib,со = 0,000153574 |
Площадь сечения стальной балки, м2 | As,aa = 0,060480 |
Статический момент сечения стальной балки, м3 | Ss,aa = 0,05517312 |
Момент инерции сечения стальной балки, м4 | Is,aa = 0,090832036 |
Момент инерции сечения стальной балки относительно собственного центра тяжести, м4 | Is,со = 0,015255183 |
Высота стальной балки, м | hs = 2,528 |
Площадь сечения стальной балки с арматурой, м2 | Ast,aa = 0,063857 |
Статический момент сечения стальной балки с арматурой, м3 | Sst,aa = 0,064623 |
Площадь сечения сталежелезобетонной балки, м2 | Astb,aa = 0,135845 |
Статический момент сечения сталежелезобетонной балки, м3 | Sstb,aa = 0,266764209 |
Момент инерции сечения сталежелезобетонной балки, м4 | Istb,aa = 0,684885320 |
Момент инерции сечения сталежелезобетонной балки относительно собственного центра тяжести, м4 | Istb,со = 0,015408757 |
Проверка необходимости учета ползучести бетона
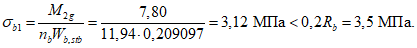
Учет ползучести не требуется.
Напряжения от усадки бетона
Предельная относительная деформация усадки бетона для сборной плиты
Дополнительные характеристики сечения для расчета на усадку приведены в таблице Б.3.6.
Таблица Б.3.6
Дополнительные характеристики сечения при расчете на усадку
Расстояние между центрами тяжести объединенного сечения и плиты, м | Z = -(Zbr - Zstb,shr) = -(2,808 - 1,964) = -0,844 |
Расстояние между центрами тяжести стального сечения и плиты, м | Zst,stb = Zstb,shr - Zs1,st = 1,964 - 1,012 = 0,952 |
Статический момент объединенного сечения, м3 | Sshr = AstZst,stb = 0,063857·0,952 = 0,049362107 |
Напряжения (МПа) от усадки на уровне центра тяжести
бетонной части плиты

арматуры

Напряжения от разности температур бетонной плиты
и стальной балки (п. 5.3.3)
Площадь вертикального листа Awt = 0,02976 м2; площадь горизонтального листа нижнего пояса балки As1,t = 0,024 м2;
At = 0,8Awt + 0,3As1,t = 0,8·0,02976 + 0,3·0,024 =
= 0,031008, м2;
Zb1,stb = tf1 + hw - Zstb = 0,032 + 2,48 - 1,964 =
= 0,548, м;
St = (0,4hw - 0,8Zb1,stb)Awt + 0,3As1,tZs1,stb =
= (0,4·2,48 - 0,8·0,548)·0,02976 + 0,3·0,024·1,012 =
= 0,023755238 м3.
Напряжения от разности температур, МПа
в бетоне

в арматуре

где tmax - максимальная разность температур с учетом коэффициента надежности 1,2 (принимаем согласно п. 9.1 [3] для крайней балки +30 °C).
Напряжения на уровне центра тяжести плиты
Напряжения в бетоне, МПа
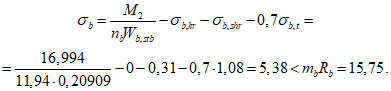
Напряжения в арматуре, МПа

Разгружающая сила, МН

Поправочные коэффициенты
Коэффициент 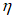 (см. таблицу 5.4.1)
(см. таблицу 5.4.1)
As2/As1 = 0,28; N/(As·m·Ry) = 0,273;  .
.
 .
.Коэффициент ограниченных пластических деформаций
Af,min/Aw = 0,226; (Af,min + Aw)/As = 0,111;
 (п. 8.26 [8]).
(п. 8.26 [8]).Коэффициент 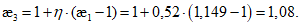
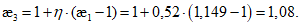
Коэффициент  , принимаем 1,2.
, принимаем 1,2.
 , принимаем 1,2.
, принимаем 1,2.Коэффициент 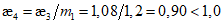 , принимаем 1,0.
, принимаем 1,0.
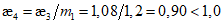 , принимаем 1,0.
, принимаем 1,0.Проверки стальной балки
Прочность верхнего пояса
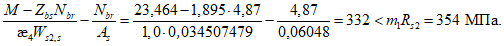
Прочность нижнего пояса
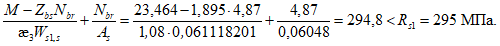
Деформации бетона плиты при К = 15,7 не являются лимитирующими, поэтому их расчет здесь не приводится.
Условие прочности нижнего стального пояса выполняется с запасом менее 2%, значит, величина допускаемого класса нагрузки АК принята правильно.
сталежелезобетонного пролетного строения
Пролетное строение неразрезное с пролетами 63 + 84 + 63 м. Используем плоскую расчетную схему стальной балки с вынесенными на жестких консолях железобетонными плитами.
Расчет ведем по программе, выполняющей расчеты стержневых систем по МКЭ. Поперечные сечения балки пролетного строения принимаем по типовому проекту 1180/5, серия 3.503-50 Ленгипротрансмоста.
Марка стали главных балок - 15ХСНД, связей, домкратных балок - 16Д, смотровых ходов и ограждений - ВСТ.3. Проектная марка бетона сборной железобетонной плиты проезда - М400.
Проектная схема пролетного строения представляет собой две главные балки, объединенные в пространственную конструкцию включенной в совместную работу с балками железобетонной плитой проезжей части, нижними продольными связями крестовой системы и поперечными связями с треугольной решеткой. Расчетная схема главных балок 63 + 84 + 63 м, сечение стенки 3160 x 12 мм (над промежуточными опорами толщина стенки увеличена до 14 мм), расстояние по осям стенок 7600 мм. Нижние пояса имеют переменное сечение (от 560 x 32 мм до 1050 x 32 + 950 x 32 + 850 x 32 мм). Верхние пояса также имеют переменное сечение (от 420 x 20 мм до 1050 x 32 + 950 x 32 + 850 x 32 мм). Посередине ширины пролетного строения расположен центральный прогон плиты проезжей части двутаврового сечения (вгл300x16 + вл440x12 + нгл300x16 мм), опирающийся на поперечные связи. В опорных сечениях установлены поперечные связи, являющиеся решетчатой домкратной балкой. Сечения промежуточных распорок нижних продольных связей - 2 уголка 125 x 125 x 12 мм, диагоналей - 2 швеллера N 14. Сечения крайних раскосов промежуточных поперечных связей - 2 уголка 90 x 90 x 9 мм, средних раскосов - 2 уголка 100 x 100 x 12 мм. Домкратные балки на крайних опорах включают поперечную балку двутаврового сечения (вгл420x20 + вл300x16 + нгл420x20 мм), два раскоса, поддерживающие центральный прогон домкратной балки, из 2 уголков 100 x 100 x 10 мм, и две верхних распорки сечением из двух уголков 90 x 90 x 9 мм. Сечение домкратных балок на промежуточных опорах - двутавровое вгл420x25 + вл2514x20 + нгл420x25.
Разбивку главных балок пролетного строения по длине на стержни постоянной жесткости выполняем в соответствии с листами 48 и 49 типового проекта инв. N 1180/5. Узлы расчетной схемы располагаем в местах изменения состава сечений балки. Площадь поперечного сечения плиты проезжей части, учитываемую в совместной работе с главными балками, принимаем по данным проектного расчета 1,2648 м2, площадь продольной арматуры плиты на участках с типами сечений с I по V принимаем 47 см2, на участках с типами сечений с VI по XIV - 94 см2, коэффициент приведения бетона к стали - 1/6. Данные по сечениям приведены в таблице Б.4.1.
Таблица Б.4.1
стальной главной балки
N сеч. | Состав сечения | A, м2 | Yc, м | I, м4 | Wн, м3 | Wв, м3 |
1 | ВГЛ420x20 + ВЛ3160x12 + НГЛ560x32 | 0,0642 | 1,837 | 0,095 | 51,61 | 68,98 |
2 | ВГЛ420x20 + ВЛ3160x12 + НГЛ750x32 | 0,0703 | 1,955 | 0,105 | 53,75 | 83,58 |
3 | ВГЛ560x25 + ВЛ3160x12 + НГЛ(750x32 + 560x25) | 0,0899 | 2,036 | 0,148 | 72,91 | 123,08 |
4 | ВГЛ560x25 + ВЛ3160x12 + НГЛ750x32 | 0,0759 | 1,816 | 0,125 | 68,74 | 89,08 |
5 | ВГЛ560x25 + ВЛ3160x12 + НГЛ(850x32 + 560x32) | 0,0970 | 2,123 | 0,158 | 74,31 | 140,15 |
6 | ВГЛ750x25 + ВЛ3160x12 + НГЛ750x32 | 0,0859 | 1,612 | 0,154 | 95,42 | 95,42 |
7 | ВГЛ560x25 + ВЛ3160x12 + НГЛ850x32 | 0,0791 | 1,872 | 0,131 | 69,83 | 97,17 |
8 | ВГЛ560x32 + ВЛ3160x12 + НГЛ850x32 | 0,0830 | 1,790 | 0,144 | 80,35 | 100,34 |
9 | ВГЛ(950x32 + 1050x32) + ВЛ3160x12 + НГЛ(1050x32 + 950x32) | 0,1659 | 1,644 | 0,364 | 221,34 | 221,34 |
10 | ВГЛ(750x32 + 950x32 + 1050x32) + ВЛ3160x12 + НГЛ(1050x32 + 950x32 + 750x32) | 0,2139 | 1,676 | 0,496 | 296,03 | 296,03 |
11 | ВГЛ(560x32 + 750x32) + ВЛ3160x12 + НГЛ(750x32 + 560x32) | 0,1218 | 1,644 | 0,249 | 151,35 | 151,35 |
12 | ВГЛ(750x32 + 950x32 + 1050x32) + ВЛ3160x14 + НГЛ(1050x32 + 950x32 + 750x32) | 0,2202 | 1,676 | 0,501 | 299,17 | 299,17 |
13 | ВГЛ(850x32 + 950x32 + 1050x32) + ВЛ3160x14 + НГЛ(1050x32 + 950x32 + 850x32) | 0,2266 | 1,676 | 0,519 | 309,70 | 309,70 |
14 | ВГЛ(560x32 + 850x32) + ВЛ3160x12 + НГЛ(850x32 + 560x32) | 0,1282 | 1,644 | 0,265 | 161,27 | 161,27 |
В таблице Б.4.1 положение центра тяжести Yc, м, дано относительно верха стенки. Моменты сопротивления приведены для нижней и верхней фибр сечений.
Типы сечений участков балки от опоры 1 до середины пролета 2 приведены в таблице Б.4.2.
Таблица Б.4.2
Типы сечений участков балки
N участка | Длина участка | Тип сечения |
1 | 5,25 | 1 |
2 | 6,70 | 2 |
3 | 6,20 | 3 |
4 | 6,20 | 3 |
5 | 6,20 | 3 |
6 | 6,20 | 3 |
7 | 3,80 | 4 |
8 | 6,70 | 6 |
9 | 5,70 | 11 |
10 | 4,80 | 9 |
11 | 1,45 | 10 |
12 | 2,30 | 12 |
13 | 1,50 | 13 |
14 | 1,50 | 13 |
15 | 2,30 | 12 |
16 | 1,45 | 10 |
17 | 4,80 | 9 |
18 | 5,70 | 14 |
19 | 3,80 | 8 |
20 | 6,70 | 7 |
21 | 7,875 | 5 |
22 | 7,875 | 5 |
Площадь бетона плиты проезжей части в расчете на одну балку принималась Ab = 1,17 м2.
Расстояния от центра тяжести балки до центра тяжести плиты до центра тяжести стальной балки вычислялись по формуле Zb c = Yc + 0,39 - 0,0867 (м).
Интенсивность второй части расчетных постоянных нагрузок по проекту составляет 3,875 тс/м. Также учитываем регулирование усилий в балке после укладки плиты и набора прочности бетона путем поднятия ее на крайних опорах на 0,47 м. Такое регулирование предусмотрено проектом с целью более эффективного использования плиты в работе пролетного строения. При этом по данным проекта возникают дополнительные реакции на крайних опорах примерно 20 тс и снижается отрицательный момент над промежуточными моментами примерно на 1260 тс·м. В наших расчетах соответствующие усилия регулирования составили 21 тс и 1323 тс·м. Перед укладкой плиты выполняется опускание концов балки на крайних опорах на те же 0,47 м.
Нормативную деформацию ползучести для бетона класса B30 принимаем по п. 7.35 [3] cn = 8,4·10-6 МПа-1 = 8,6·10-6 кгс-1/см2. Определяем коэффициенты, необходимые для вычисления предельного значения удельной деформации ползучести, по таблице 7.13 [3].
Коэффициент 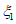 принимаем для передаточной площади 0,8 равным 1,25.
принимаем для передаточной площади 0,8 равным 1,25.
Коэффициент  принимаем для возраста бетона в момент загружения 40 суток равным 0,925.
принимаем для возраста бетона в момент загружения 40 суток равным 0,925.
Коэффициент 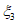 принимаем для приведенной характеристики поперечного сечения 11170/1450 = 7,7 равным 0,757.
принимаем для приведенной характеристики поперечного сечения 11170/1450 = 7,7 равным 0,757.
Коэффициент  принимаем при влажности 60% равным 1.
принимаем при влажности 60% равным 1.
Предельное значение удельной деформации ползучести
clim = 1,25·0,925·0,757·1·8,6·10-6 = 7,53·10-6 кгс-1/см2.
Предельное значение характеристики ползучести составляет

Расчеты на ползучесть выполняем методом последовательных приближений с использованием коэффициентов, которые вводятся к предельным характеристикам ползучести согласно таблице Щ.1 [3].
1. Составляем стержневую расчетную схему, включающие стержни стальную балку, разбитую на участки с постоянной жесткостью и бетонную плиту, вынесенную на жесткие консоли. Положение бетонной плиты по высоте принимаем Zb = 0. Положение участка балки по высоте Zst = -Zbc. Фрагмент расчетной схемы показан на рисунке Б.4.1.

Рисунок Б.4.1 - Фрагмент расчетной схемы
2. Модуль упругости бетона принимаем Eb = 3,32·105 кгс/см2. Вычисляем усилия и перемещения в железобетонной плите проезжей части от второй части постоянных нагрузок и усилий регулирования. Сохраняем полученные усилия и перемещения в файле.
3. Выполняем первое приближение расчета на ползучесть. Вычисляем условный модуль упругости бетона 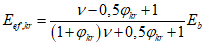 . Он зависит от геометрических характеристик сечения и поэтому вычисляется для каждого типа сечения. Предельная характеристика ползучести
. Он зависит от геометрических характеристик сечения и поэтому вычисляется для каждого типа сечения. Предельная характеристика ползучести  при определении условного модуля уменьшается вдвое по сравнению с коэффициентом
при определении условного модуля уменьшается вдвое по сравнению с коэффициентом 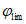 , т.е.
, т.е.  . Вычисляем жесткости сечений стержней железобетонных плит Eef,kr·Ab. Жесткости стержней стальной балки не меняются. Вычисляем элементы массива "Начальные состояния". В нем надо задать для каждого стержня железобетонной плиты начальное состояние в виде относительного удлинения на величину
. Вычисляем жесткости сечений стержней железобетонных плит Eef,kr·Ab. Жесткости стержней стальной балки не меняются. Вычисляем элементы массива "Начальные состояния". В нем надо задать для каждого стержня железобетонной плиты начальное состояние в виде относительного удлинения на величину  . Здесь величина
. Здесь величина 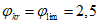 . Усилия Nпл берутся из файла, сохраненного в п. 2. В результате расчета получим напряжения и перемещения в балке и плите от ползучести первого порядка малости. Сохраним полученные результаты в файле.
. Усилия Nпл берутся из файла, сохраненного в п. 2. В результате расчета получим напряжения и перемещения в балке и плите от ползучести первого порядка малости. Сохраним полученные результаты в файле.
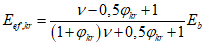 . Он зависит от геометрических характеристик сечения и поэтому вычисляется для каждого типа сечения. Предельная характеристика ползучести
. Он зависит от геометрических характеристик сечения и поэтому вычисляется для каждого типа сечения. Предельная характеристика ползучести  . Вычисляем жесткости сечений стержней железобетонных плит Eef,kr·Ab. Жесткости стержней стальной балки не меняются. Вычисляем элементы массива "Начальные состояния". В нем надо задать для каждого стержня железобетонной плиты начальное состояние в виде относительного удлинения на величину
. Вычисляем жесткости сечений стержней железобетонных плит Eef,kr·Ab. Жесткости стержней стальной балки не меняются. Вычисляем элементы массива "Начальные состояния". В нем надо задать для каждого стержня железобетонной плиты начальное состояние в виде относительного удлинения на величину  . Здесь величина
. Здесь величина 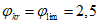 . Усилия Nпл берутся из файла, сохраненного в п. 2. В результате расчета получим напряжения и перемещения в балке и плите от ползучести первого порядка малости. Сохраним полученные результаты в файле.
. Усилия Nпл берутся из файла, сохраненного в п. 2. В результате расчета получим напряжения и перемещения в балке и плите от ползучести первого порядка малости. Сохраним полученные результаты в файле.4. Выполняем второе приближение расчета на ползучесть. Заново вычисляем условные модули упругости бетона, принимая  и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для второго приближения. Относительное удлинение стержней плиты
и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для второго приближения. Относительное удлинение стержней плиты  вычисляем при
вычисляем при 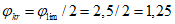 . Усилия Nпл берутся из файла, сохраненного в п. 3. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести второго порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести первого порядка малости). Сохраним полученные результаты в файле.
. Усилия Nпл берутся из файла, сохраненного в п. 3. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести второго порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести первого порядка малости). Сохраним полученные результаты в файле.
 и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для второго приближения. Относительное удлинение стержней плиты
и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для второго приближения. Относительное удлинение стержней плиты  вычисляем при
вычисляем при 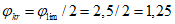 . Усилия Nпл берутся из файла, сохраненного в п. 3. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести второго порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести первого порядка малости). Сохраним полученные результаты в файле.
. Усилия Nпл берутся из файла, сохраненного в п. 3. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести второго порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести первого порядка малости). Сохраним полученные результаты в файле.5. Выполняем третье приближение расчета на ползучесть. Заново вычисляем условные модули упругости бетона, принимая  и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для третьего приближения. Относительное удлинение стержней плиты
и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для третьего приближения. Относительное удлинение стержней плиты  вычисляем при
вычисляем при  . Усилия Nпл берутся из файла, сохраненного в п. 4. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести третьего порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести второго порядка малости). Сохраним полученные результаты в файле. Выполняем не более трех приближений.
. Усилия Nпл берутся из файла, сохраненного в п. 4. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести третьего порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести второго порядка малости). Сохраним полученные результаты в файле. Выполняем не более трех приближений.
 и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для третьего приближения. Относительное удлинение стержней плиты
и соответствующие жесткости стержней плиты. Вычисляем элементы массива "Начальные состояния" для третьего приближения. Относительное удлинение стержней плиты  вычисляем при
вычисляем при  . Усилия Nпл берутся из файла, сохраненного в п. 4. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести третьего порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести второго порядка малости). Сохраним полученные результаты в файле. Выполняем не более трех приближений.
. Усилия Nпл берутся из файла, сохраненного в п. 4. В результате расчета получим добавку к напряжениям и перемещениям в балке и плите от ползучести третьего порядка малости (ползучесть, возникающая от изменения усилий за счет протекания ползучести второго порядка малости). Сохраним полученные результаты в файле. Выполняем не более трех приближений.6. Просуммируем усилия и перемещения, сохраненные в файлах по пп. 2, 3, 4 и 5. В результате получим усилия и перемещения от второй части постоянных нагрузок с учетом регулирования усилий и ползучести бетона.
В таблице Б.4.3 приведены данные по условным модулям упругости бетона стержней плиты для расчетов по пп. 2, 3, 4 и 5.
Таблица Б.4.3
Данные по условным модулям упругости плиты
Тип сеч. плиты |  | 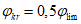 | 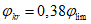 | |
Eb | Eef,kr1 | Eef,kr2 | Eef,kr3 | |
18 | 332·104 | 1626484 | 1861433 | 2004063 |
19 | 332·104 | 1625924 | 1861018 | 2003725 |
20 | 332·104 | 1616158 | 1853782 | 1997838 |
21 | 332·104 | 1617084 | 1854467 | 1998396 |
22 | 332·104 | 1615863 | 1853563 | 1997660 |
23 | 332·104 | 1602014 | 1843318 | 1989336 |
24 | 332·104 | 1616839 | 1854285 | 1998247 |
25 | 332·104 | 1610771 | 1849793 | 1994596 |
26 | 332·104 | 1546699 | 1802635 | 1956390 |
27 | 332·104 | 1518518 | 1782049 | 1939788 |
28 | 332·104 | 1575284 | 1823614 | 1973357 |
29 | 332·104 | 1516630 | 1780674 | 1938680 |
30 | 332·104 | 1513178 | 1778159 | 1936656 |
31 | 332·104 | 1570967 | 1820438 | 1970786 |
В таблице Б.4.4 приведены усилия в стержнях плиты от опоры 1 до середины пролета балки, взятые из файлов для пп. 2 - 5, а также суммарные усилия в стержнях плиты.
Таблица Б.4.4
Усилия в стержнях плиты проезжей части
пролетного строения, тс
N стержня | Xн, м | Xк, м | Ng2+рег | Nполз1 | Nполз2 | Nполз3 | Ng2+рег+ролз |
4 | 0 | 5,25 | -82,73 | 20,77 | -3,78 | 0,76 | -64,97 |
8 | 5,25 | 11,95 | -237,80 | 62,30 | -11,76 | 2,41 | -184,85 |
12 | 11,95 | 18,15 | -339,64 | 107,42 | -22,01 | 4,49 | -249,73 |
15 | 18,15 | 24,35 | -406,03 | 135,72 | -29,30 | 6,19 | -293,41 |
18 | 24,35 | 30,55 | -428,41 | 154,47 | -35,52 | 7,80 | -301,66 |
21 | 30,55 | 36,75 | -406,77 | 163,66 | -40,70 | 9,32 | -274,49 |
25 | 36,75 | 40,55 | -380,16 | 172,44 | -46,10 | 10,95 | -242,86 |
29 | 40,55 | 47,25 | -281,24 | 175,59 | -54,50 | 13,68 | -146,47 |
32 | 47,25 | 52,95 | -124,46 | 140,25 | -56,07 | 16,05 | -24,23 |
35 | 52,95 | 57,75 | 12,25 | 81,95 | -47,28 | 16,28 | 63,20 |
38 | 57,75 | 59,2 | 87,23 | 31,99 | -33,96 | 14,32 | 99,58 |
41 | 59,2 | 61,5 | 138,91 | 6,04 | -27,24 | 13,06 | 130,78 |
44 | 61,5 | 63 | 190,94 | -22,57 | -19,13 | 11,37 | 160,60 |
48 | 63 | 64,5 | 186,83 | -19,33 | -20,41 | 11,75 | 158,83 |
51 | 64,5 | 66,8 | 124,21 | 17,52 | -31,70 | 14,38 | 124,41 |
54 | 66,8 | 68,25 | 62,15 | 51,49 | -41,51 | 16,55 | 88,68 |
57 | 68,25 | 73,05 | -34,77 | 115,77 | -59,35 | 19,60 | 41,26 |
60 | 73,05 | 78,75 | -209,16 | 196,04 | -75,10 | 21,15 | -67,06 |
63 | 78,75 | 82,55 | -190,88 | 275,42 | -165,04 | 70,63 | -9,87 |
67 | 82,55 | 89,25 | -527,07 | 259,74 | -72,31 | 17,47 | -322,16 |
71 | 89,25 | 97,125 | -622,95 | 274,55 | -72,07 | 16,94 | -403,52 |
74 | 97,125 | 105 | -692,74 | 289,79 | -73,76 | 17,08 | -459,63 |
Нормативные значения предела текучести Ryn или временного сопротивления Run обычно назначают в соответствии с марками стали обследуемых конструкций.
При отсутствии достоверных данных расчетные сопротивления сталей неизвестных марок в общем случае назначают по значениям Ryn и Run, определенным в результате статистической обработки данных соответствующих испытаний. Практикуются как разрушающие, так и неразрушающие методы определения прочности [9].
Вычисление предела текучести Ryn или временного сопротивления Run по результатам статистической обработки производится по формуле
 (В.1)
(В.1)где  - среднее арифметическое значение предела текучести или временного сопротивления, полученных по результатам испытаний;
- среднее арифметическое значение предела текучести или временного сопротивления, полученных по результатам испытаний;  - коэффициент, учитывающий объем выборки;
- коэффициент, учитывающий объем выборки; 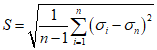 - среднеквадратическое отклонение результатов испытаний;
- среднеквадратическое отклонение результатов испытаний;  - предел текучести или временное сопротивление i-го испытания (образца); n - число испытаний (испытанных образцов).
- предел текучести или временное сопротивление i-го испытания (образца); n - число испытаний (испытанных образцов).
 - среднее арифметическое значение предела текучести или временного сопротивления, полученных по результатам испытаний;
- среднее арифметическое значение предела текучести или временного сопротивления, полученных по результатам испытаний;  - коэффициент, учитывающий объем выборки;
- коэффициент, учитывающий объем выборки; 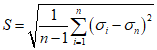 - среднеквадратическое отклонение результатов испытаний;
- среднеквадратическое отклонение результатов испытаний; Если  , использовать результаты испытаний не допускается.
, использовать результаты испытаний не допускается.
 , использовать результаты испытаний не допускается.
, использовать результаты испытаний не допускается.Тип (марка) материала металлоконструкций старых мостов проектировки до 30-х годов XX в., изготавливаемых из сварочного и литого железа, может быть определена по виду излома с изъятой из конструкции стружки или мелкого фрагмента металла. Если металл в изломе светлый мелкозернистой структуры, то это литое железо, если слоистой структуры темно-серого цвета - сварочное железо. Изымать образцы рекомендуется из различных элементов несущих конструкций (поясов, раскосов, стоек, продольных и поперечных балок проезжей части), поскольку практиковалось использование различных материалов для изготовления различных элементов. Если пролетное строение подвергалось усилению, восстановлению, или заменяли его отдельные элементы (например, проезжей части), то прочностные характеристики металла усиления также должны быть установлены.
и способы их изъятия
Отбор образцов для лабораторных исследований следует производить в местах, где ослабление сечений не повлияет на снижение грузоподъемности конструкции в целом. Если места вырезки заготовок все же ослабляют конструкцию, то они должны быть соответствующим способом перекрыты, чтобы компенсировать ослабление. Входящие углы вырезки образцов в месте изъятия перед перекрытием следует предварительно засверливать сверлом диаметром 14 - 20 мм.
Рациональному выбору мест вырезки заготовок для образцов может способствовать предварительное определение твердости металла различных элементов конструкции.
Заготовки для образцов следует выпиливать или высверливать (допускается также газовая резка), но не вырубать. В некоторых случаях можно заготовки не вырезать, а снять какую-либо часть (например, элемент соединительной решетки, диафрагмы, уголок жесткости), если предварительное определение твердости металла подтверждает, что снимаемый элемент выполнен из того же металла, что и основные несущие элементы конструкции.
Места вырезки заготовок, произведенной высверливанием или газовой резкой, должны быть обработаны механической зачисткой для уничтожения резких концентратов напряжений.
Вырезанные заготовки следует промаркировать для последующей лабораторной идентификации с местом изъятия и ориентации реза по отношению к направлению оси моста.
Если нужно определить материал заклепок, то удаляют отдельные заклепки, вместо которых немедленно ставят высокопрочные болты.
Для определения по каждому сорту металла предела прочности, предела текучести относительного удлинения, относительного сужения и ударной вязкости требуется испытать по три стандартных образца согласно ГОСТ 1497-84 (рисунок В.1.1). Испытание на разрыв может быть выполнено на цилиндрических или плоских образцах с размером в поперечном сечении не менее 3 мм.
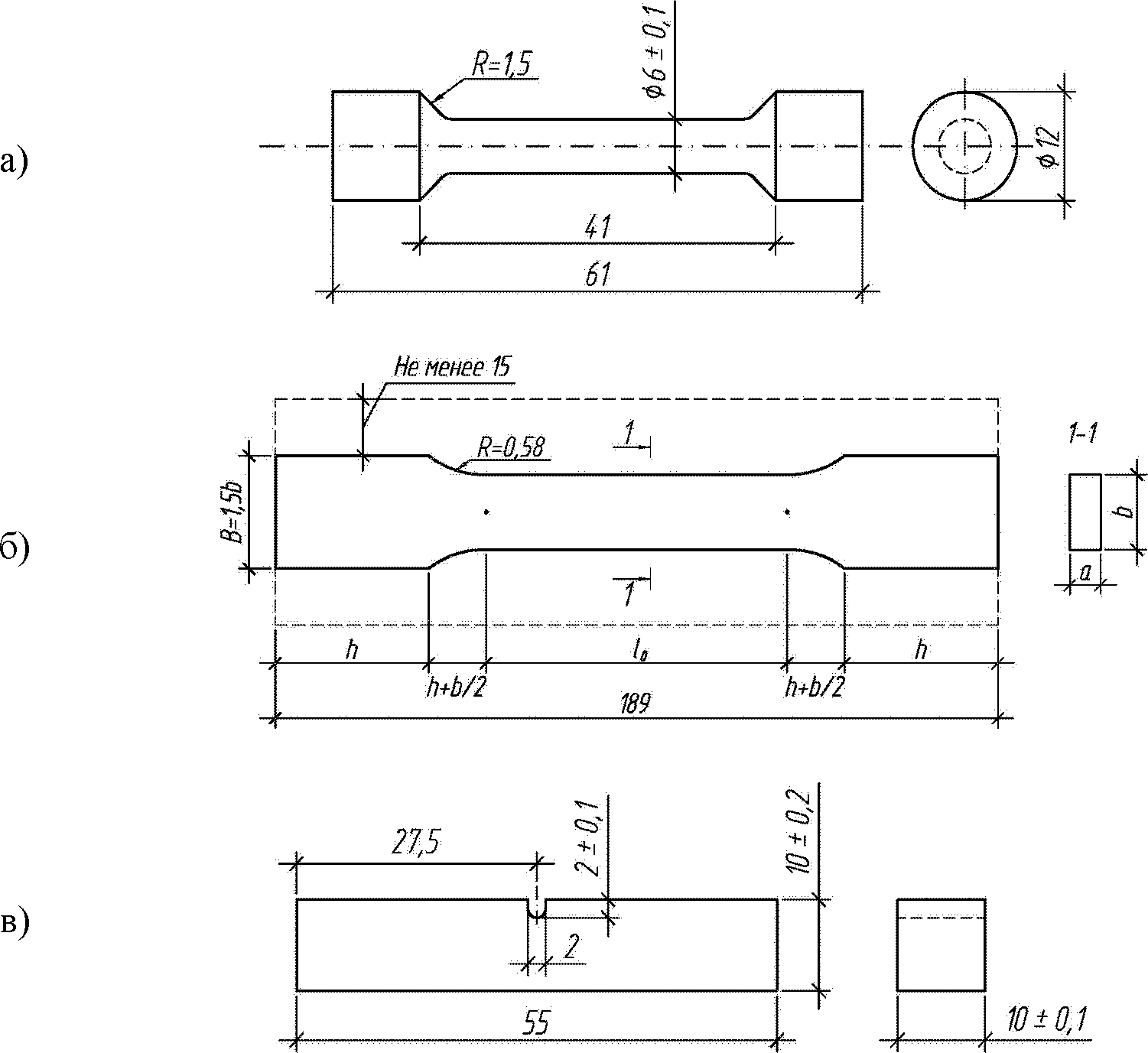
Рисунок В.1.1 - Стандартные образцы для испытаний:
а - пятикратный цилиндрический; б - нормальный плоский,
где b = 20 - 30 мм;  ; L = l0 + 5b + 10; h >= 2b;
; L = l0 + 5b + 10; h >= 2b;
 ; L = l0 + 5b + 10; h >= 2b;
; L = l0 + 5b + 10; h >= 2b;в - с надрезом для испытания на ударную вязкость
Размеры вырезаемых заготовок для образцов устанавливаются из указанной потребности в количестве образцов и нижеследующих размеров металла на один образец (с припуском на его обработку): на цилиндрический образец 15 x 65 мм, на плоский образец 45 x 200 мм, на ударную пробу 15 x 60 мм; толщина при этом берется равной толщине металла в элементе конструкции (желательно не менее 10 мм).
ПРИМЕР ОПРЕДЕЛЕНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ
В СЕЧЕНИЯХ НЕРАЗРЕЗНОГО СТАЛЕЖЕЛЕЗОБЕТОННОГО
ПРОЛЕТНОГО СТРОЕНИЯ С УЧЕТОМ РЕГУЛИРОВАНИЯ УСИЛИЙ
Общие данные
Пролетное строение выполнено по индивидуальному проекту применительно к типовому проекту серии 3.503-50, инв. N 1180/3, северное исполнение, с увеличением длины центрального пролета до 64 м. Продольная схема пролетного строения, в расчетных длинах пролетов составляет 42 + 64 + 42 м. Проектные нагрузки - Н-30 и НК-80 (по СН 200-62).
Для определения грузоподъемности по прочности сечений находят изгибающие моменты M в балках пролетного строения для крайних пролетов на расстоянии 1/3l от крайних опор, для промежуточного пролета - в 1/2l, где l - соответствующий расчетный пролет. Для определения грузоподъемности по устойчивости сжатого нижнего пояса опорных сечений находят изгибающие моменты в сечениях над промежуточными опорами.
Геометрические параметры поперечного сечения
и материалы пролетного строения
Геометрические параметры рассчитываемого поперечного сечения, материалы пролетного строения, приняты по данным натурных измерений:
- материал главных балок - низколегированная сталь марок 15ХСНД;
- материал плиты проезжей части - конструкционный тяжелый бетон класса прочности на сжатие B30;
- материал продольного армирования плиты проезжей части - арматурная сталь класса А-I.
В поперечном сечении пролетного строения установлено две главных балки (рисунок Г.1.1), параметры которых в расчетных сечениях приведены в таблице Г.1.1.
Таблица Г.1.1
Параметры главных балок пролетного строения
в расчетных сечениях
Расчетное сечение | Верхний горизонтальный лист, мм | Нижний горизонтальный лист, мм | Стенка балки, мм |
1/3 расчетной длины крайних пролетов | 420 x 20 | 560 x 25 | 2480 x 12 |
1/2 расчетной длины среднего пролета | 420 x 20 | 850 x 32 | 2480 x 12 |
Опорное сечение на промежуточной и концевой опорах | пакет листов 1050 x 32 и 950 x 32 | пакет листов 1050 x 32 и 950 x 32 | 2480 x 14 |

пролетного строения
Расстояние по осям главных балок - 7,6 м.
Плита проезжей части железобетонная, толщиной 160 мм. Размер свеса консоли плиты (во внешнюю сторону) составляет 4,05 м. Армирование плиты выполнено в 2 горизонтальных ряда, арматурой диаметром 10 мм, расположенной в сечении с шагом 200 мм.
Параметры плиты, включаемой в расчет, определены в соответствии с требованиями п. 9.15 [3] и составляют (расчетное сечение балки показано на рисунке Г.1.2):
- свес в сторону соседнего стального элемента - 3,8 м;
- свес в сторону консоли - 4,05 м.
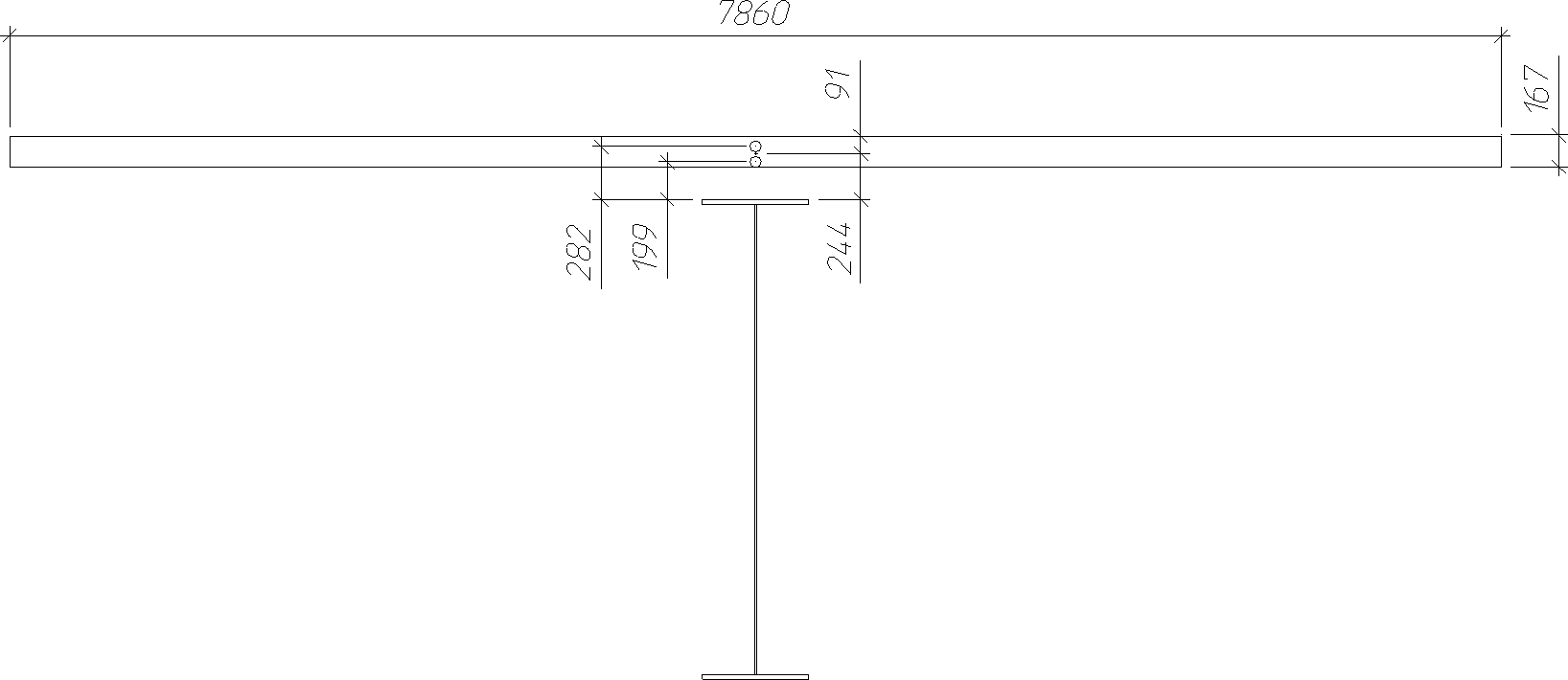
Рисунок Г.1.2 - Расчетное сечение сталежелезобетонной балки
При расчете к характеристикам материалов, введены следующие коэффициенты условий работы:
- к стальной части конструкции m = 1,0;
- к железобетонной конструкции плиты проезжей части m = 1,0.
Расчетные воздействия от постоянных нагрузок
Расчетные воздействия от постоянных нагрузок определены из условия равномерного распределения постоянных нагрузок между балками.
Нормативные и расчетные интенсивности от нагрузок первой и второй стадии для балки пролетного строения приведены в таблице Г.1.2.
Таблица Г.1.2
Нормативные и расчетные интенсивности постоянных нагрузок
Наименование нагрузки | Толщина, м | Удельный вес, тс/м3 | Норм. интенсивность, тс/м | Коэфф. надежности, | Расчетная интенсивность, тс/м |
Нагрузки первой стадии | |||||
Собственный вес металлической балки | 1,23 | 1,1 | 1,35 | ||
Собственный вес железобетонной плиты | 3,59 | 1,1 | 3,95 | ||
Итого нагрузки первой стадии | 4,82 | 5,30 | |||
Нагрузки второй стадии | |||||
Перила | 0,14 | 1,1 | 0,15 | ||
Ограждение безопасности | 0,055 | 1,1 | 0,06 | ||
Подготовительный слой | 0,03 | 2,2 | 0,52 | 1,15 | 0,60 |
Гидроизоляция | 0,006 | 1,0 | 0,05 | 1,15 | 0,05 |
Защитный слой | 0,04 | 2,4 | 0,75 | 1,15 | 0,87 |
Асфальтобетон | 0,07 | 2,3 | 1,26 | 1,15 | 1,45 |
Итого нагрузки второй стадии | 2,78 | 3,18 | |||
Учет последовательности возведения
Статический расчет конструкции на действие постоянных нагрузок первой и второй стадии выполнен методом конечных элементов с использованием сертифицированного программного комплекса, реализующего расчет с учетом последовательности монтажа.
Итоговая пространственная модель пролетного строения представлена стержневыми конечными элементами общего вида, жестко объединенными между собой. Граничные условия заданы в узлах расчетной схемы в соответствии с местом их фактической установки. Геометрические характеристики сечений главных балок приняты соответствующими типовому проекту серии 3.503-50, инв. N 1180/3, приведенным к металлу. Продольные стержневые конечные элементы главных балок жестко объединены между собой поперечными стержневыми конечными элементами, жесткостные характеристики которых определены сечением железобетонной плиты между главными балками, а также стержневыми элементами, по своему размещению и жесткостным характеристикам соответствующим нижним продольным связям. Объединение узлов элементов, имитирующих нижние продольные связи, с узлами стержней главных балок выполнено через двухузловые упругие связи с характеристиками жестких вставок, длина которых соответствует реальному расстоянию от центра тяжести главных балок до уровня размещения продольных связей.
Шаг разбивки в продольном направлении принят переменным, исходя из необходимости размещения в расчетной модели узлов нижних продольных связей и разбиения плиты проезжей части, но не более 1/10 пролета.
В расчете учтена стадийность монтажа, а также изменение геометрических характеристик сечений балки (на первых стадиях монтажа металлическое сечение, после монтажа железобетонной плиты - включение ее в работу сталежелезобетонного сечения). Последовательность возведения конструкции принята по типовому проекту серии 3.503-50, выпуск 3.
Деформированный вид конструкции в процессе расчета показан на рисунках Г.1.3 - Г.1.7. Эпюры изгибающих моментов на различных этапах расчета приведены на рисунках Г.1.8 - Г.1.12.

Рисунок Г.1.3 - Первая стадия работы конструкции.
Стальные балки воспринимают собственный вес интенсивностью
q = 1,35 тс/м

Рисунок Г.1.4 - Первая стадия работы конструкции.
Стальные балки воспринимают собственный вес интенсивностью
q = 1,35 тс/м, производится регулирование усилий,
путем опускания домкратами главных балок
на крайних опорах на 450 мм

Рисунок Г.1.5 - Первая стадия работы конструкции.
Стальные балки воспринимают собственный вес интенсивностью
q = 1,35 тс/м, а также вес железобетонной плиты
q = 3,95 тс/м
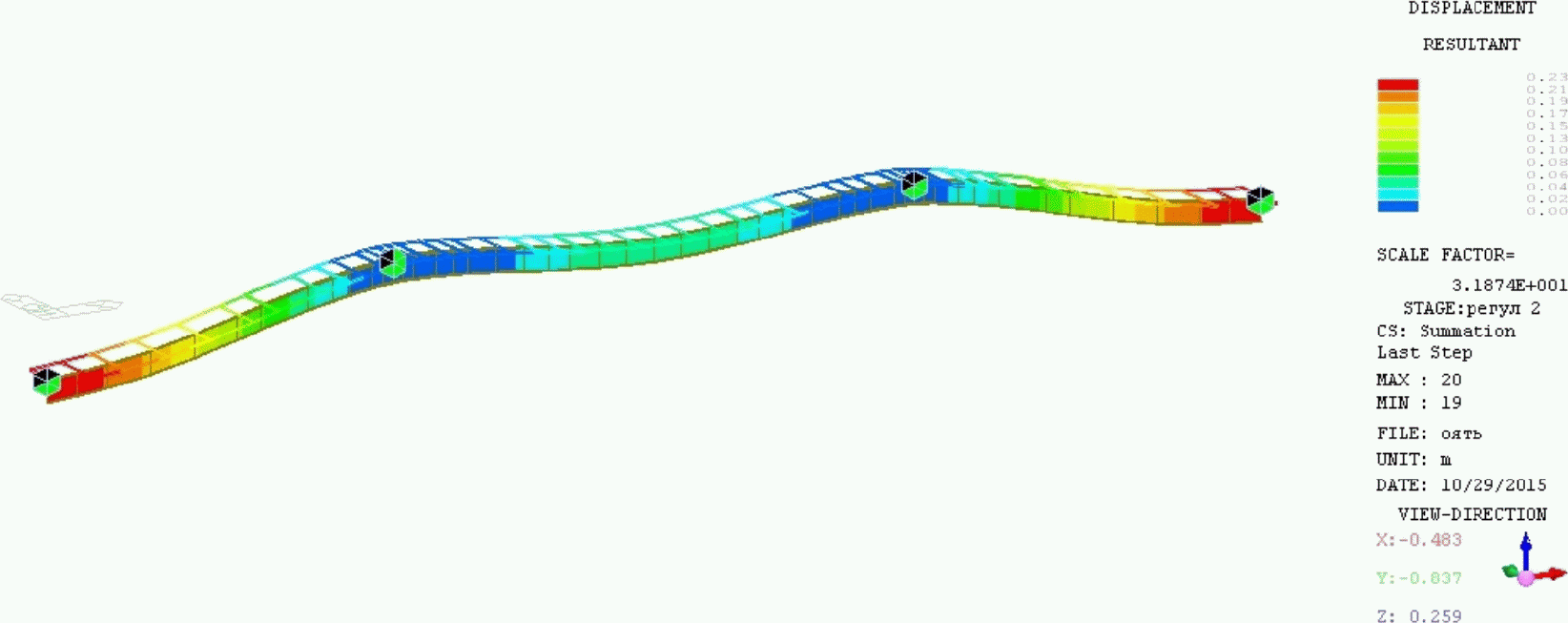
Рисунок Г.1.6 - Вторая стадия работы конструкции.
Стальные балки, объединенные с железобетонной плитой,
воспринимают собственный вес интенсивностью q = 1,35 тс/м,
вес железобетонной плиты q = 3,95 тс/м, производится
регулирование усилий, путем подъема домкратами
главных балок на крайних опорах на 220 мм

Стальные балки, объединенные с железобетонной плитой,
воспринимают собственный вес интенсивностью q = 1,35 тс/м,
вес железобетонной плиты q = 3,95 тс/м, и нагрузки
2-ой стадии интенсивностью 3,18 тс/м
Усилия в элементах главных балок
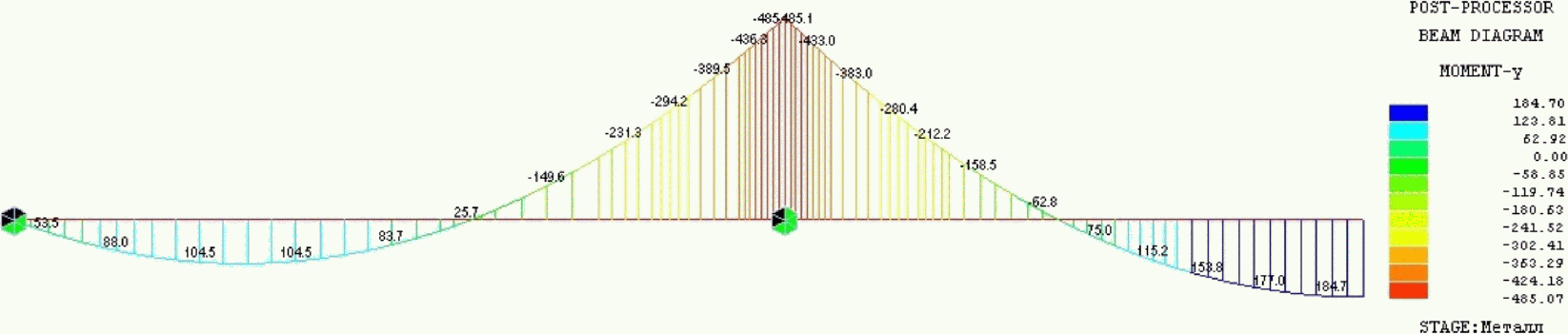
Изгибающий момент от собственного веса металлоконструкций

Рисунок Г.1.9 - Первая стадия работы конструкции.
Изгибающий момент от собственного веса металлоконструкций
и регулирования усилий

Рисунок Г.1.10 - Первая стадия работы конструкции.
Изгибающий момент от собственного веса металлоконструкций,
регулирования усилий и веса железобетонной плиты

Рисунок Г.1.11 - Вторая стадия работы конструкции.
Изгибающий момент от собственного веса металлоконструкций,
регулирования усилий, веса железобетонной плиты
и обратного регулирования

Изгибающий момент от собственного веса металлоконструкций,
регулирования усилий, веса железобетонной плиты, обратного
регулирования и второй части постоянной нагрузки
Полученные значения накопленных усилий приведены в таблице Г.1.3.
Таблица Г.1.3
Накопленные изгибающие моменты в расчетных сечениях
от постоянных нагрузок первой и второй стадии (тс·м)
N п/п | l/2 (средний пролет) | опорное сечение | l/3 (крайний пролет) |
1 | 184,7 | -485,1 | 104,5 |
2 | -247,7 | -909,8 | 16,5 |
3 | 300,4 | -2329,1 | 298,8 |
4 | 1024 | -1605,4 | 503,6 |
5 | 1539,9 | -2667,3 | 772,7 |
I стадия | 300,4 | -2329,1 | 298,8 |
II стадия (5-3) | 1239,5 | -338,2 | 473,9 |
Прочие параметры
Нагрузка от пешеходов учтена согласно п. 5.2 [2].
При ширине тротуара 1,5 м нормативная интенсивность пешеходной нагрузки на один тротуар составляет
p = 200·1,5 = 300 кгс/м = 0,3 тс/м.
Коэффициент надежности по нагрузке (п. 5.2.1 [2]) 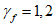 .
.
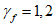 .
.Итоговая расчетная интенсивность - 0,36 тс/м.
Расчетные изгибающие моменты в рассматриваемых сечениях от действия пешеходной нагрузки приведены в таблице Г.1.4.
Таблица Г.1.4
Изгибающие моменты от пешеходной нагрузки (тс·м)
Нагрузка | l/2 (средний пролет) | опорное сечение | l/3 (крайний пролет) |
Пешеходная | 125,3 | 191,2 | 81,9 |
Ширина полос безопасности принята равной 2,0 м.
При построении поверхностей влияния учтены также зоны раскрытия трещин в плите путем назначения жесткости железобетонной плиты, входящей в сечение главных балок в указанных зонах, согласно п. 9.12 [3].
Руководитель
организации-разработчика
СГУПС
Проректор по научной работе
С.А.БОКАРЕВ
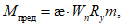












 - в иных случаях;
- в иных случаях; - в иных случаях;
- в иных случаях;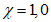 - в иных случаях.
- в иных случаях. .
. ;
;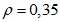 ) - для lef < 0,5·a, и
) - для lef < 0,5·a, и 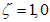 - в иных случаях.
- в иных случаях. .
. .
. и
и 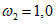 .
.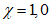 .
. ;
; ) - для lef < 0,5·a, и
) - для lef < 0,5·a, и  - в иных случаях.
- в иных случаях. .
.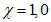 .
.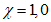 .
.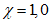 .
.
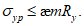
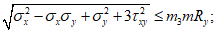



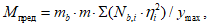
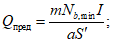

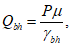
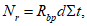

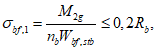






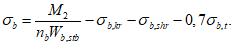

 , то расчет выполняют только на первое сочетание нагрузок.
, то расчет выполняют только на первое сочетание нагрузок.

 .
. .
.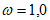 .
.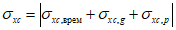 ,
, 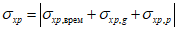 .
.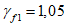 ;
;  ;
;  ;
;  ;
;  ;
;  .
. (по
(по