СПРАВКА
Источник публикации
Киев: НИИСК Госстроя СССР, 1983
Примечание к документу
Название документа
"Методические рекомендации по учету влияния ползучести бетонов при расчете сборно-монолитных стержневых конструкций"
(одобрены Протоколом Госстроя СССР от 18.08.1982 N 10)
"Методические рекомендации по учету влияния ползучести бетонов при расчете сборно-монолитных стержневых конструкций"
(одобрены Протоколом Госстроя СССР от 18.08.1982 N 10)
Содержание
Протоколом секции N 1
Научно-технического совета
НИИСК Госстроя СССР
от 18 августа 1982 г. N 10
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО УЧЕТУ ВЛИЯНИЯ ПОЛЗУЧЕСТИ БЕТОНОВ
ПРИ РАСЧЕТЕ СБОРНО-МОНОЛИТНЫХ СТЕРЖНЕВЫХ КОНСТРУКЦИЙ
Изложены инженерные методы оценки влияния ползучести бетонов, вызванной длительным действием нагрузок (собственный вес сборных элементов и монолитного бетона, внешние нагрузки, силы предварительного обжатия) и деформаций (мгновенное смещение опор, усадка бетонов) на напряженно-деформированное состояние статически определимых и статически неопределимых сборно-монолитных конструкций; приведены формулы для определения напряжений в сечениях, нормальных к продольной оси конструкции, и усилий в многопролетных неразрезных балках, а также формулы для расчета по образованию трещин, нормальных к продольной оси конструкции, ширине раскрытия и закрытию таких трещин; даны рекомендации по определению параметров усадки и ползучести бетонов.
Задачи решаются для области линейной ползучести. В основу решений положен технический вариант феноменологической теории ползучести - модернизированная теория старения.
В качестве иллюстрации приведены числовые примеры.
Рекомендации распространяются на конструкции из тяжелых бетонов и легких бетонов плотной структуры.
Рассчитаны на инженерно-технических работников проектных и научно-исследовательских организаций, а также на студентов и аспирантов вузов и факультетов строительного профиля.
Разработаны Курским ПИ (канд. техн. наук В.П. Полищук, инж. И.Г. Чернушиц), НИИСК (докт. техн. наук А.Б. Голышев, канд. техн. наук В.Ф. Усманов) и ЦНИИС Минтрансстроя СССР (канд. техн. наук Е.Н. Щербаков - раздел 8).
Отзывы и замечания направлять по адресу: 252180 Киев-180, ул. И. Клименко, 5/2, НИИСК Госстроя СССР, лаборатория теории расчета железобетонных конструкций.
1.1. В методических рекомендациях рассматриваются с.о.к. и с.н.к. <x>, состоящие из заранее изготовленных предварительно напряженных сборных элементов, рассчитанных на восприятие нагрузок, возникающих в период строительства, и монолитного (дополнительно уложенного) бетона (рис. 1).
--------------------------------
<x> См. с. 50.
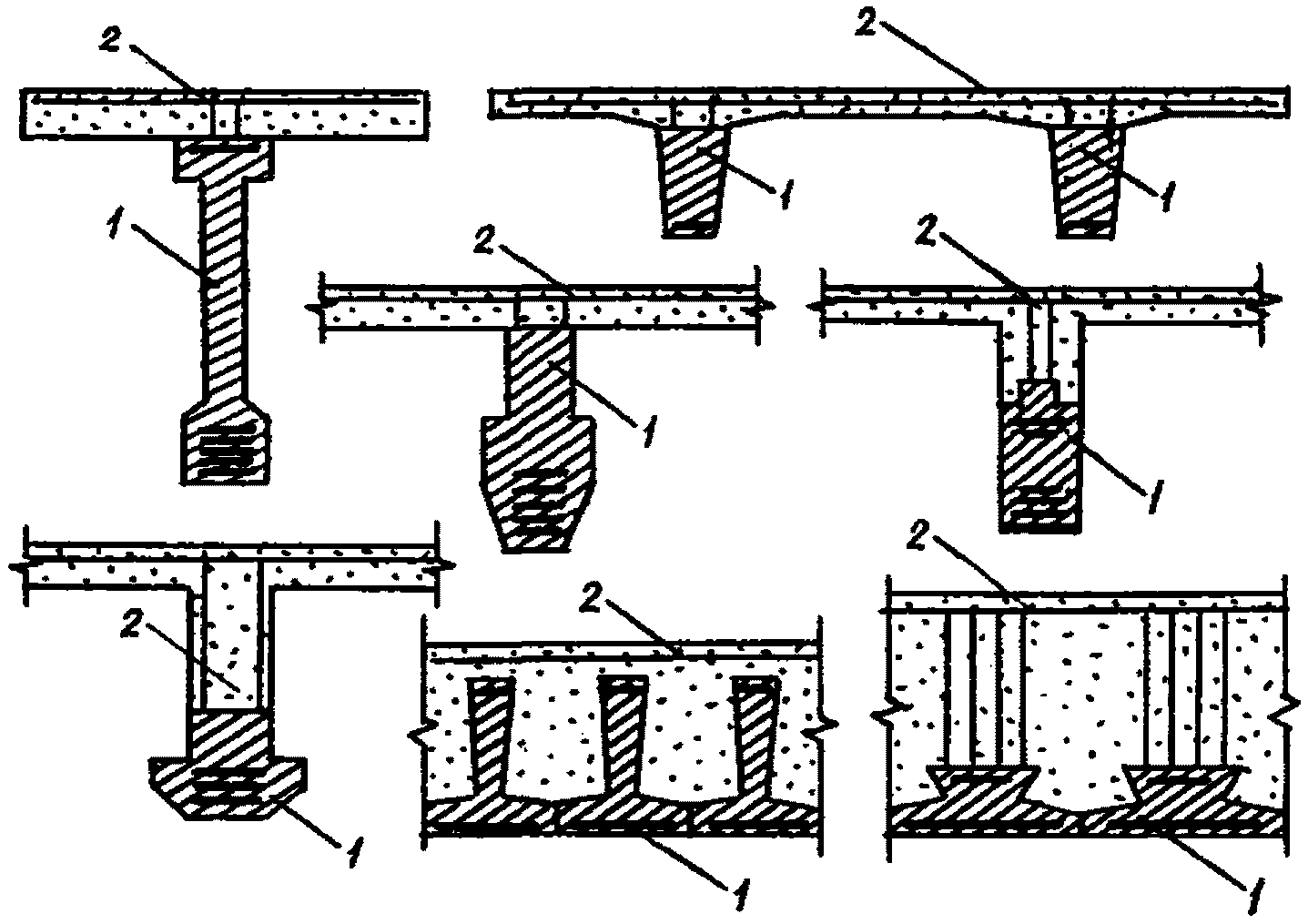
1 - предварительно напряженные сборные элементы;
2 - монолитный бетон
На надопорных участках с.н.к. (ограничиваемых в ту и другую сторону от рассматриваемой опоры нулевыми точками на эпюре изгибающих моментов) монолитный бетон выходит на растянутую грань конструкции. В качестве растянутой рабочей арматуры надопорных участков используются напрягаемые или ненапрягаемые стальные стержни (рис. 2).
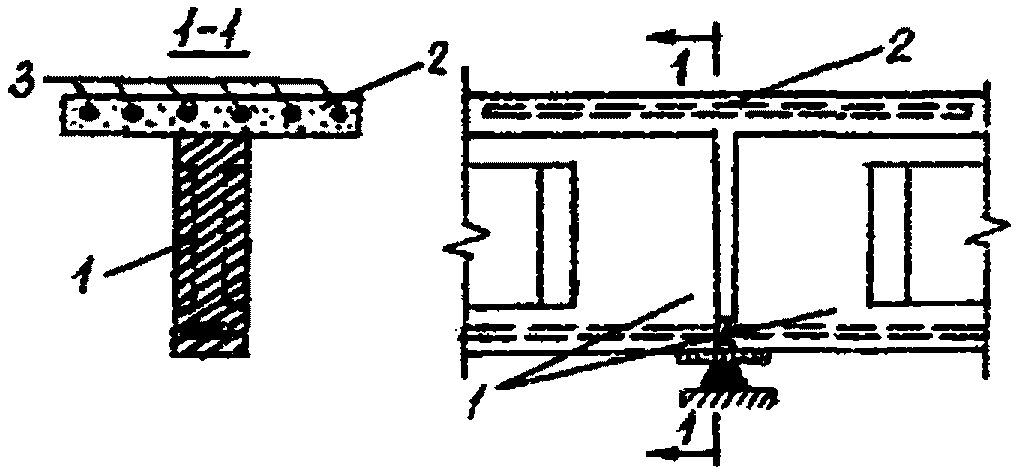
Рис. 2. Надопорные участки с.н.к.
1 - предварительно напряженные сборные элементы;
2 - монолитный бетон; 3 - надопорная напрягаемая
или ненапрягаемая арматура
1.2. Расчет на ползучесть производится для двух стадий работы конструкции:
до приобретения монолитным бетоном заданной прочности (учет влияния ползучести, вызванной действием нагрузок и деформаций, возникающих в период строительства);
после приобретения монолитным бетоном заданной прочности (учет влияния ползучести, вызванной действием нагрузок и деформаций, возникающих в период строительства и в процессе эксплуатации сооружения).
Оценка влияния ползучести на напряженно-деформированное состояние до приобретения монолитным бетоном заданной прочности выполняется в соответствии с рекомендациями работы [3], после приобретения монолитным бетоном заданной прочности - в соответствии с настоящими методическими рекомендациями.
Примечание. Применительно к с.н.к. под "приобретением монолитным бетоном заданной прочности" подразумевается замыкание системы, т.е. создание неразрезности конструкции.
2.1. На участках, где не образуются нормальные трещины, напряжения от усадки бетонов определяются по формулам:
в арматуре
в монолитном бетоне
в бетоне сборных элементов
В этих формулах:
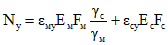 ; (2.4)
; (2.4)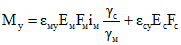 ; (2.5)
; (2.5)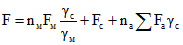 ; (2.6)
; (2.6)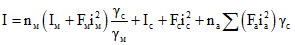 ; (2.7)
; (2.7)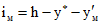 ; (2.8)
; (2.8)iс = y* - yс; (2.9)
iа = y* - yа; (2.10)
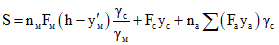 ; (2.12)
; (2.12)Fа и 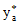 - площадь поперечного сечения арматуры на уровне рассматриваемого ряда и расстояние от точки 0* до центра тяжести сечения указанной арматуры;
- площадь поперечного сечения арматуры на уровне рассматриваемого ряда и расстояние от точки 0* до центра тяжести сечения указанной арматуры;
yа - расстояние от нижней грани сечения конструкции до ц.т. сечения арматуры рассматриваемого ряда;
Верхние знаки в формулах (2.1) - (2.3) принимаются, если рассматриваемый ряд арматуры или рассматриваемые волокна бетона расположены выше точки 0* (см. рис. 3), нижние - если ниже. Положение точки 0* определяется по формуле (2.11).
Здесь и везде в дальнейшем сжимающим напряжениям присваивается знак плюс, растягивающим - минус.

а - поперечное сечение; б - эпюры напряжений в бетонах;
1 - сборный элемент; 2 - монолитный бетон
2.2. На участках, где не образуются нормальные трещины, напряжения от нагрузок, приложенных до приобретения монолитным бетоном заданной прочности, определяются по формулам:
а) от предварительного обжатия сборных элементов (рис. 4)
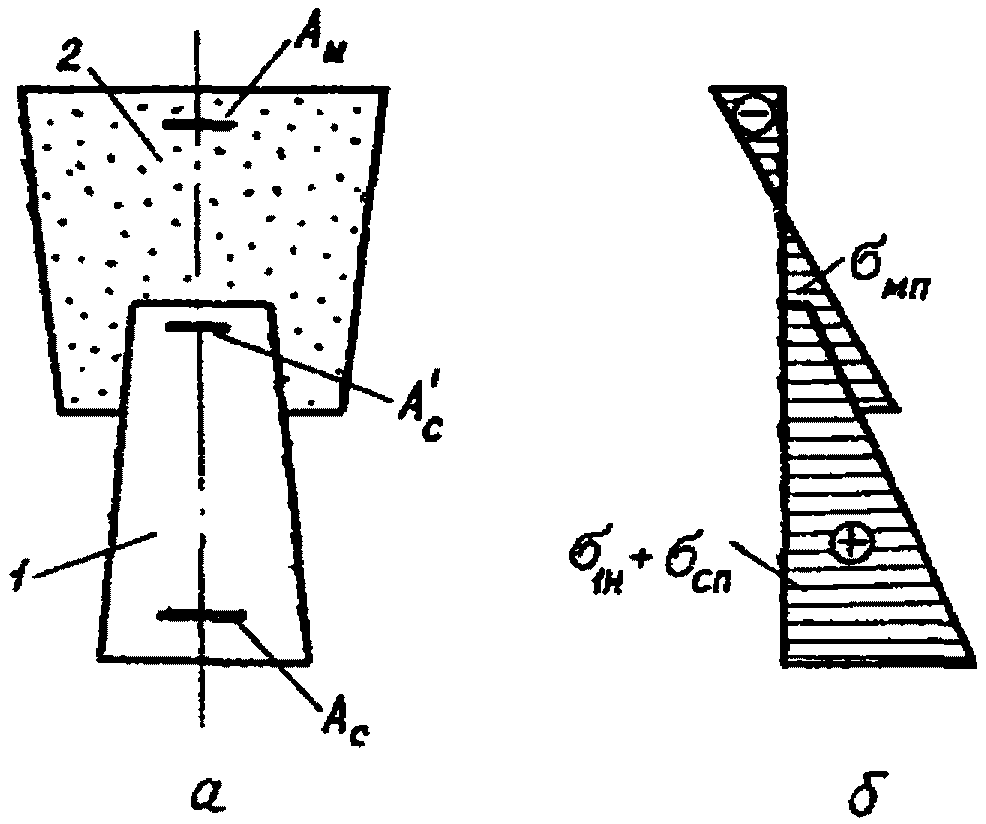
Рис. 4. Напряженное состояние сечений с.о.к.
и пролетных участков с.н.к. от предварительного обжатия
сборного элемента
а - поперечное сечение; б - эпюры напряжений в бетонах;
1 - сборный элемент; 2 - монолитный бетон
в арматуре
в монолитном бетоне
в бетоне сборных элементов
б) от собственного веса бетонов и от внешних нагрузок (рис. 5)
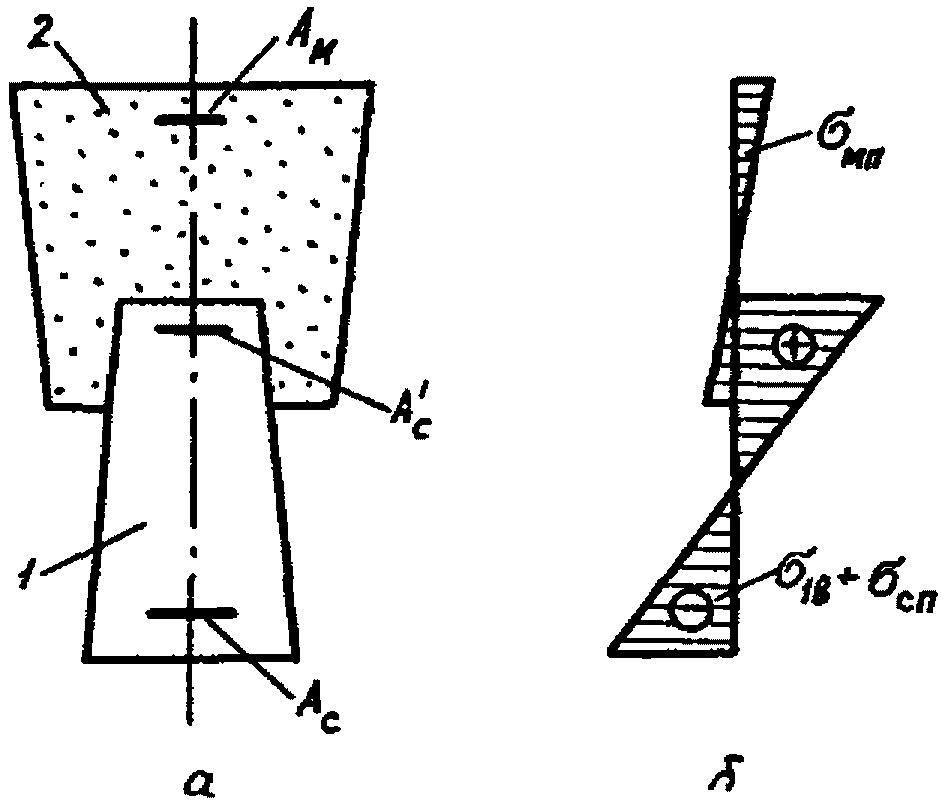
Рис. 5. Напряженное состояние сечений с.о.к.
и пролетных участков с.н.к. от собственного веса
и внешних нагрузок, приложенных до приобретения
монолитным бетоном заданной прочности
а - поперечное сечение; б - эпюры напряжений в бетонах;
1 - сборный элемент; 2 - монолитный бетон
в арматуре
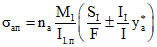 ; (2.16)
; (2.16)в монолитном бетоне
в бетоне сборных элементов
В этих формулах: 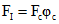 ;
;  ;
; 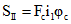 ;
;  ;
;
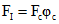 ;
;  ;
; 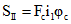 ;
;  ;
;Верхние знаки в формулах (2.13) - (2.18) принимаются, если рассматриваемый ряд арматуры или рассматриваемые волокна бетона расположены выше точки 0* (см. рис. 3), нижние - если ниже.
2.3. На участках, где не образуются нормальные трещины, полные напряжения <x> от нагрузок, приложенных после приобретения монолитным бетоном заданной прочности, определяются по формулам:
--------------------------------
<x> Под полными имеются в виду напряжения, равные алгебраической сумме начальных напряжений, возникающих в момент нагружения, и дополнительных, вызванных ползучестью бетона
а) от предварительного обжатия надопорных участков с.н.к. (рис. 6)
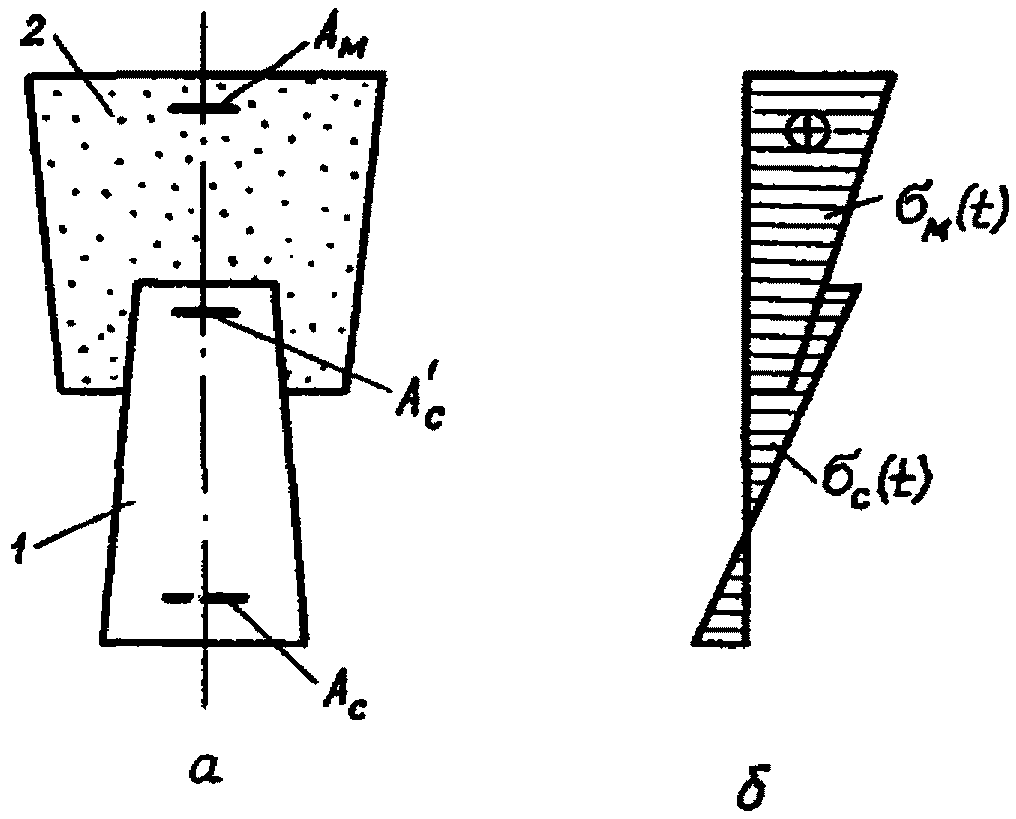
Рис. 6. Напряженное состояние сечений надопорных участков
с.н.к. от предварительного обжатия указанных участков
а - поперечное сечение; б - эпюры напряжений в бетонах;
1 - сборный элемент; 2 - монолитный бетон
в арматуре
в монолитном бетоне
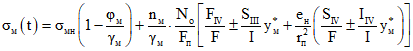 ; (2.20)
; (2.20)в бетоне сборных элементов
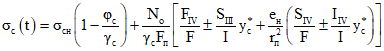 ; (2.21)
; (2.21)б) от внешних нагрузок (рис. 7)
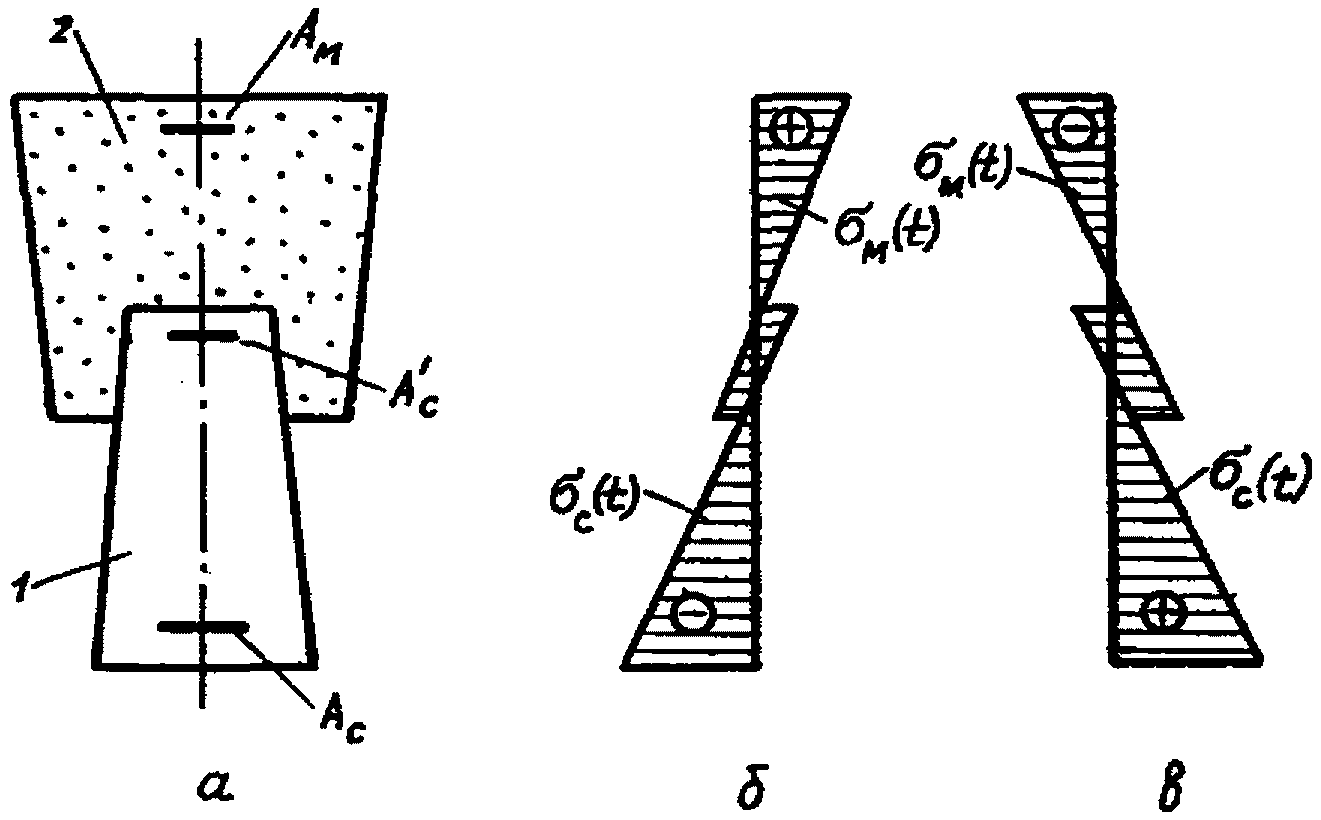
Рис. 7. Напряженное состояние сечений от внешних нагрузок,
приложенных после приобретения монолитным бетоном
заданной прочности
а - поперечное сечение; б - эпюры напряжений в бетонах
с.о.к. и на пролетных участках с.н.к.; в - то же,
на надопорных участках с.н.к.; 1 - сборный элемент;
2 - монолитный бетон
в арматуре
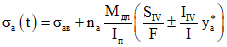 ; (2.22)
; (2.22)в монолитном бетоне
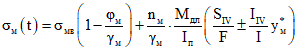 ; (2.23)
; (2.23)в бетоне сборных элементов
В этих формулах:
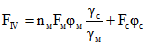 ; (2.25)
; (2.25)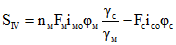 ; (2.26)
; (2.26)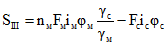 ; (2.27)
; (2.27)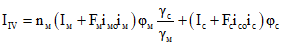 . (2.28)
. (2.28)Верхние знаки в формулах (2.19) - (2.24) принимаются, если рассматриваемый ряд арматуры или рассматриваемые волокна бетона расположены выше точки 0* (см. рис. 3), нижние - если ниже.
2.4. Численные значения параметров 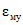 ,
, 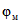 ,
, 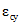 ,
, 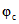 определяются в соответствии с настоящими методическими рекомендациями (раздел 8).
определяются в соответствии с настоящими методическими рекомендациями (раздел 8).
За начало отсчета времени при определении 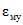 ,
, 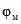 ,
, 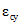 ,
, 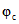 в п. 2.1 и
в п. 2.1 и 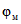 ,
, 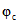 в п. 2.2 принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении
в п. 2.2 принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении  и
и 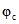 в п. 2.3 - момент нагружения после приобретения монолитным бетоном заданной прочности.
в п. 2.3 - момент нагружения после приобретения монолитным бетоном заданной прочности.
Численные значения коэффициентов 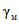 и
и 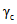 в зависимости, соответственно, от
в зависимости, соответственно, от 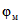 и
и 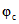 и в зависимости от возраста бетона к началу отсчета времени
и в зависимости от возраста бетона к началу отсчета времени 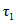 принимаются по табл. 1.
принимаются по табл. 1.
Возраст бетона к началу отсчета времени | |||||||||
3 | 7 | 14 | 28 | 45 | 60 | 90 | 180 | 365 и более | |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
0,5 | 1,45 | 1,47 | 1,48 | 1,52 | 1,55 | 1,58 | 1,62 | 1,68 | 1,73 |
1,0 | 1,92 | 1,96 | 1,99 | 2,05 | 2,13 | 2,18 | 2,26 | 2,38 | 2,47 |
1,5 | 2,41 | 2,46 | 2,52 | 2,60 | 2,71 | 2,78 | 2,91 | 3,08 | 3,22 |
2,0 | 2,90 | 2,98 | 3,05 | 3,17 | 3,30 | 3,40 | 3,56 | 3,79 | 3,97 |
2,5 | 3,41 | 3,51 | 3,58 | 3,73 | 3,90 | 4,01 | 4,22 | 4,50 | 4,72 |
3,0 | 3,92 | 4,03 | 4,12 | 4,29 | 4,49 | 4,63 | 4,88 | 5,21 | 5,47 |
Примечание. Промежуточные значения | |||||||||
3.1. На участках, где не образуются нормальные трещины, кривизна от усадки бетонов определяется по формуле
Значения Mу и I расшифрованы в п. 2.1 настоящих методических рекомендаций.
3.2. На участках, где не образуются нормальные трещины, кривизна от нагрузок, приложенных до приобретения монолитным бетоном заданной прочности, определяется по формулам:
от предварительного обжатия сборных элементов
где 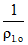 - начальная (упруго-мгновенная) кривизна сборных элементов до приобретения монолитным бетоном заданной прочности [6], [3];
- начальная (упруго-мгновенная) кривизна сборных элементов до приобретения монолитным бетоном заданной прочности [6], [3];
от собственного веса бетонов и от длительно действующей части внешних нагрузок
где 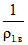 - начальная (упруго-мгновенная) кривизна сборных элементов до приобретения монолитным бетоном заданной прочности [6], [3];
- начальная (упруго-мгновенная) кривизна сборных элементов до приобретения монолитным бетоном заданной прочности [6], [3];
3.3. На участках, где не образуются нормальные трещины, полная кривизна <x> от нагрузок, приложенных после приобретения монолитным бетоном заданной прочности, определяется по формулам:
--------------------------------
<x> Под полной имеется в виду кривизна, равная сумме начальной кривизны, возникающей в момент нагружения, и дополнительной, вызванной ползучестью бетонов.
от предварительного обжатия надопорных участков с.н.к.
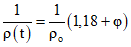 , (3.6)
, (3.6)где
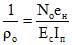 ; (3.7)
; (3.7)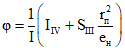 ; (3.8)
; (3.8)от внешних нагрузок
где
 ; (3.10)
; (3.10)с.о.к., пролетные участки с.н.к. - трещины образуются от нагрузок, приложенных до приобретения монолитным бетоном заданной прочности;
с.о.к., пролетные участки с.н.к. - трещины образуются от нагрузок, приложенных после приобретения монолитным бетоном заданной прочности;
надопорные участки с.н.к. - трещины образуются от нагрузок, приложенных после приобретения монолитным бетоном заданной прочности.
3.5. Для первого случая на участках, где образуются нормальные трещины, полная кривизна определяется по формуле
где
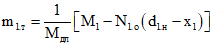 ; (3.18)
; (3.18)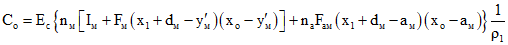 ; (3.19)
; (3.19)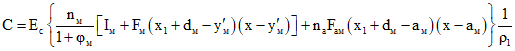 ; (3.20)
; (3.20)e1.о и e1 - расстояния от точки приложения силы N1.о до н.о. соответственно в начальный момент времени и в рассматриваемый момент времени t (см. п. 3.8);
Iо.т.с и Iт.с - моменты инерции площади сечения сжатой зоны бетона сборных элементов относительно н.о. соответственно в начальный момент времени и в рассматриваемый момент времени t (см. п. 3.8);
Iо.т.м и Iт.м - то же, сжатой зоны монолитного бетона;
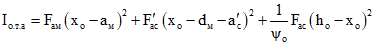 ; (3.23)
; (3.23)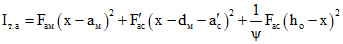 ; (3.24)
; (3.24)d1.н - расстояние от точки приложения силы N1.о до верхней грани сборного элемента;
I1.о.т - момент инерции площади приведенного сечения сборных элементов с трещинами относительно н.о. при высоте сжатой зоны x1 [3];
x1 - высота сжатой зоны сечения сборных элементов от нагрузок, приложенных до приобретения монолитным бетоном заданной прочности [6, 3];
Высота сжатой зоны xо и x отыскивается из уравнений:
и
где
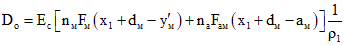 ; (3.27)
; (3.27) ; (3.28)
; (3.28)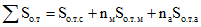 ; (3.29)
; (3.29)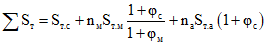 ; (3.30)
; (3.30)Sо.т.с и Sт.с - статические моменты площади сечения сжатой зоны бетона сборных элементов относительно н.о. соответственно в начальный момент времени и в рассматриваемый момент времени t (см. п. 3.8);
Sо.т.м и Sт.м - то же, сжатой зоны монолитного бетона;
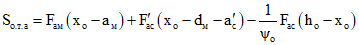 ; (3.31)
; (3.31)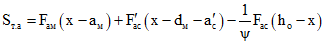 ; (3.32)
; (3.32)Численные значения 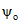 и
и 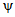 определяются по формулам
определяются по формулам
и
где
F1 - площадь поперечного сечения сборных элементов высотой h1.о без учета арматуры и свесов сжатой полки;
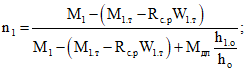 (3.35)
(3.35)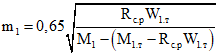 ; (3.36)
; (3.36)M1.т - момент образования нормальных трещин в сборных элементах до приобретения монолитным бетоном заданной прочности [6, 3];
b1 и h1.о - ширина и рабочая высота поперечного сечения сборных элементов.
При отсутствии нагрузок, приложенных после приобретения монолитным бетоном заданной прочности (Mдл = 0), кривизна определяется по формуле
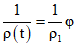 , (3.37)
, (3.37)где
Высота сжатой зоны x отыскивается из уравнения (3.26) при Mдл = 0, коэффициент 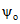 - по формуле (3.33) при n1 = 1.
- по формуле (3.33) при n1 = 1.
3.6. Для второго случая на участках, где образуются трещины, полная кривизна определяется по формулам (3.12) и (3.13), где
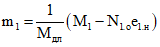 . (3.41)
. (3.41)Численные значения mо.т и mт определяются по формулам (3.16) и (3.17), высота сжатой зоны xо и x - из уравнений (3.25) и (3.26), где
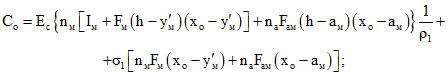 (3.42)
(3.42)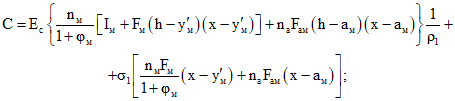 (3.43)
(3.43)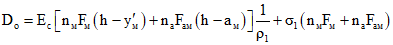 ; (3.44)
; (3.44) ; (3.45)
; (3.45) ; (3.46)
; (3.46)Численное значение 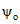 определяется по формуле
определяется по формуле
где F - площадь поперечного сечения конструкции высотой hо, приведенного к бетону сборных элементов, без учета арматуры и свесов сжатой полки;
Fа = Fас;
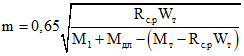 ; (3.48)
; (3.48)Mт - момент образования нормальных трещин, определяемый по формуле (4.1).
3.7. Для третьего случая на участках, где образуются трещины, полная кривизна определяется по формуле (3.12), где
 ; (3.49)
; (3.49)высота сжатой зоны xо и x - из уравнений
и
Здесь:
eо и e - расстояния от точки приложения силы Nо до н.о. соответственно в начальный момент времени и в рассматриваемый момент времени t (см. п. 3.8).
Численное значение 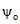 определяется по формуле (3.47), где
определяется по формуле (3.47), где
Fа = Fам;
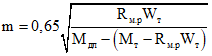 ; (3.54)
; (3.54)Mт - момент образования нормальных трещин, определяемый по формуле (4.4);
3.8. Численные значения параметров 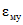 ,
, 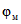 ,
, 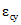 и
и 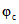 определяются в соответствии с разделом 8 настоящих методических рекомендаций.
определяются в соответствии с разделом 8 настоящих методических рекомендаций.
За начало отсчета времени при определении 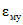 ,
, 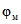 ,
, 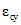 ,
, 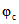 в п. 3.1 и
в п. 3.1 и  ,
, 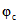 в п. 3.2 принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении
в п. 3.2 принимается момент приобретения монолитным бетоном заданной прочности, за начало отсчета времени при определении 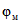 и
и 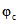 в пп. 3.3 и 3.5 - 3.7 - момент нагружения после приобретения монолитным бетоном заданной прочности.
в пп. 3.3 и 3.5 - 3.7 - момент нагружения после приобретения монолитным бетоном заданной прочности.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 1, а не таблица 2.1. |
Численные значения коэффициентов 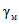 и
и 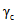 в зависимости, соответственно, от
в зависимости, соответственно, от 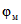 и
и 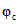 в зависимости от возраста бетона к началу отсчета времени
в зависимости от возраста бетона к началу отсчета времени 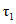 принимаются по табл. 2.1.
принимаются по табл. 2.1.
с.о.к. и пролетные участки с.н.к. - трещины образуются в предварительно напряженных сборных элементах;
надопорные участки с.н.к. - трещины образуются в монолитном бетоне.
где
k1 и k - коэффициенты, учитывающие возможность развития неупругих деформаций в сжатых бетонах.
Если сборные элементы попадают в сжатую зону конструкции и выполняется условие
где 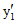 и
и  - расстояния, соответственно, от ц.т. приведенных сечений сборных элементов и конструкции до сжатого края сечения элементов, величина k1 принимается равной 0,8; если сборные элементы не попадают в сжатую зону конструкции или попадают, но условие (4.2) не выполняется, величина k1 принимается равной единице.
- расстояния, соответственно, от ц.т. приведенных сечений сборных элементов и конструкции до сжатого края сечения элементов, величина k1 принимается равной 0,8; если сборные элементы не попадают в сжатую зону конструкции или попадают, но условие (4.2) не выполняется, величина k1 принимается равной единице.
Если выполняется условие
где  - расстояние от ц.т. приведенного сечения конструкции до сжатого края указанного сечения, величина k принимается равной 0,8; если условие (4.3) не выполняется, величина k принимается равной единице.
- расстояние от ц.т. приведенного сечения конструкции до сжатого края указанного сечения, величина k принимается равной 0,8; если условие (4.3) не выполняется, величина k принимается равной единице.
где
Если выполняется условие
где y1 и yс - расстояния, соответственно, от ц.т. приведенных сечений сборных элементов и конструкции до сжатого края надопорного сечения элементов, величина k принимается равной 0,8; если условие (4.5) не выполняется, величина k принимается равной единице.
5.1. Ширина раскрытия нормальных трещин определяется на уровне ц.т. сечения арматуры наиболее растянутого ряда.
5.2. При определении ширины раскрытия нормальных трещин следует предусматривать три случая - см. п. 3.4.
--------------------------------
<x> Под полной имеется в виду ширина раскрытия трещин, равная сумме начальной величины раскрытия, соответствующей моменту нагружения, и дополнительной, вызванной ползучестью бетонов.
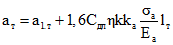 , (5.1)
, (5.1)где
a1.т - максимальная ширина, раскрытия трещин в сборных элементах от нагрузок, приложенных до приобретения монолитным бетоном заданной прочности; определяется по формуле (138) [6] или по формуле (4) [4];
Cдл - коэффициент, учитывающий влияние ползучести бетонов на ширину раскрытия трещин после приобретения монолитным бетоном заданной прочности:
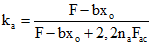 ; (5.4)
; (5.4)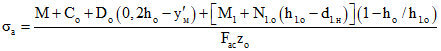 (5.5)
(5.5)lт - расстояние между трещинами:
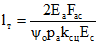 ; (5.6)
; (5.6)pа - периметр поперечного сечения арматуры Aс;
kсц - коэффициент, определяемый по табл. 2 в зависимости от вида бетона сборных элементов, его марки и степени обжатия;
для тавровых и двутавровых сечений
Вид бетона | Уровень предварительного обжатия | Проектная марка бетона | ||||||
M100 | M150 | M200 | M300 | M400 | M600 | M800 | ||
Тяжелый | 0 | - | 0,56 | 0,51 | 0,45 | 0,42 | 0,39 | 0,37 |
0,2 | - | - | 0,5 | 0,44 | 0,41 | 0,38 | 0,36 | |
0,4 | - | - | 0,44 | 0,38 | 0,35 | 0,32 | 0,3 | |
0,6 | - | - | 0,35 | 0,29 | 0,27 | 0,24 | 0,22 | |
0,8 | - | - | 0,2 | 0,18 | 0,16 | 0,13 | 0,11 | |
Легкий плотной структуры | 0 | 0,8 | 0,7 | 0,65 | 0,55 | 0,49 | - | - |
0,2 | - | - | 0,64 | 0,53 | 0,48 | - | - | |
0,4 | - | - | 0,57 | 0,46 | 0,43 | - | - | |
0,6 | - | - | 0,44 | 0,35 | 0,33 | - | - | |
0,8 | - | - | 0,23 | 0,18 | 0,16 | - | - | |
В табл. 2:
Rо - передаточная прочность бетона сборных элементов.
5.4. Для второго случая полная максимальная ширина раскрытия трещин определяется по формуле
 , (5.8)
, (5.8)где
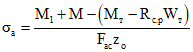 . (5.9)
. (5.9)Значения Cдл, 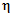 , k, kа, pа, kсц и zо расшифрованы в п. 5.3; xо, x,
, k, kа, pа, kсц и zо расшифрованы в п. 5.3; xо, x, 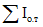 и
и 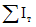 - в п. 3.5 настоящих методических рекомендаций.
- в п. 3.5 настоящих методических рекомендаций.
Момент образования трещин Mт определяется по формуле (4.1).
5.5. Для третьего случая полная максимальная ширина раскрытия трещин определяется по формуле
где
pа - периметр поперечного сечения арматуры Aм;
kсц - коэффициент, определяемый по табл. 2 в зависимости от вида монолитного бетона, его марки и степени обжатия.
Коэффициент k определяется по формуле (5.3), где 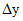 - расстояние от ц.т. сечения арматуры Aм до ц.т. сечения арматуры наиболее растянутого ряда, коэффициент kа - по формуле
- расстояние от ц.т. сечения арматуры Aм до ц.т. сечения арматуры наиболее растянутого ряда, коэффициент kа - по формуле
Момент образования трещин Mт определяется по формуле (4.2).
В табл. 2:
Rо - передаточная прочность монолитного бетона.
5.6. Численные значения параметра 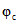 определяются в соответствии с настоящими методическими рекомендациями (раздел 8).
определяются в соответствии с настоящими методическими рекомендациями (раздел 8).
За начало отсчета времени при определении 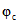 принимается момент нагружения после приобретения монолитным бетоном заданной прочности.
принимается момент нагружения после приобретения монолитным бетоном заданной прочности.
6.1. При расчете по закрытию нормальных трещин следует предусматривать два случая (см. п. 4.1).
6.2. Для первого случая расчет по закрытию трещин производится из условий:
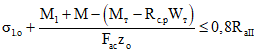 , (6.1)
, (6.1)где
и
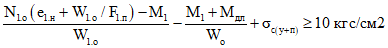 . (6.2)
. (6.2)Первое условие обеспечивает от возникновения необратимых деформаций в предварительно напряженной пролетной арматуре от действий постоянных, длительных и кратковременных нагрузок, второе - надежное зажатие трещин при действии постоянных и длительных нагрузок.
6.3. Для второго случая расчет по закрытию трещин производится из условий:
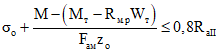 , (6.3)
, (6.3)где
и
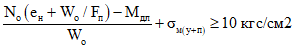 . (6.4)
. (6.4)Первое условие обеспечивает от возникновения необратимых деформаций в предварительно напряженной надопорной арматуре от действия постоянных, длительных и кратковременных нагрузок, второе - надежное зажатие трещин от действия постоянных и длительных нагрузок.
7.1. Определение усилий от усадки бетонов и нагрузок, приложенных до замыкания системы, в конструкциях, на пролетных и надопорных участках которых от действия указанных нагрузок трещины не образуются, производится путем решения системы трехчленных уравнений вида (рис. 8,а)
 , (7.1)
, (7.1)где
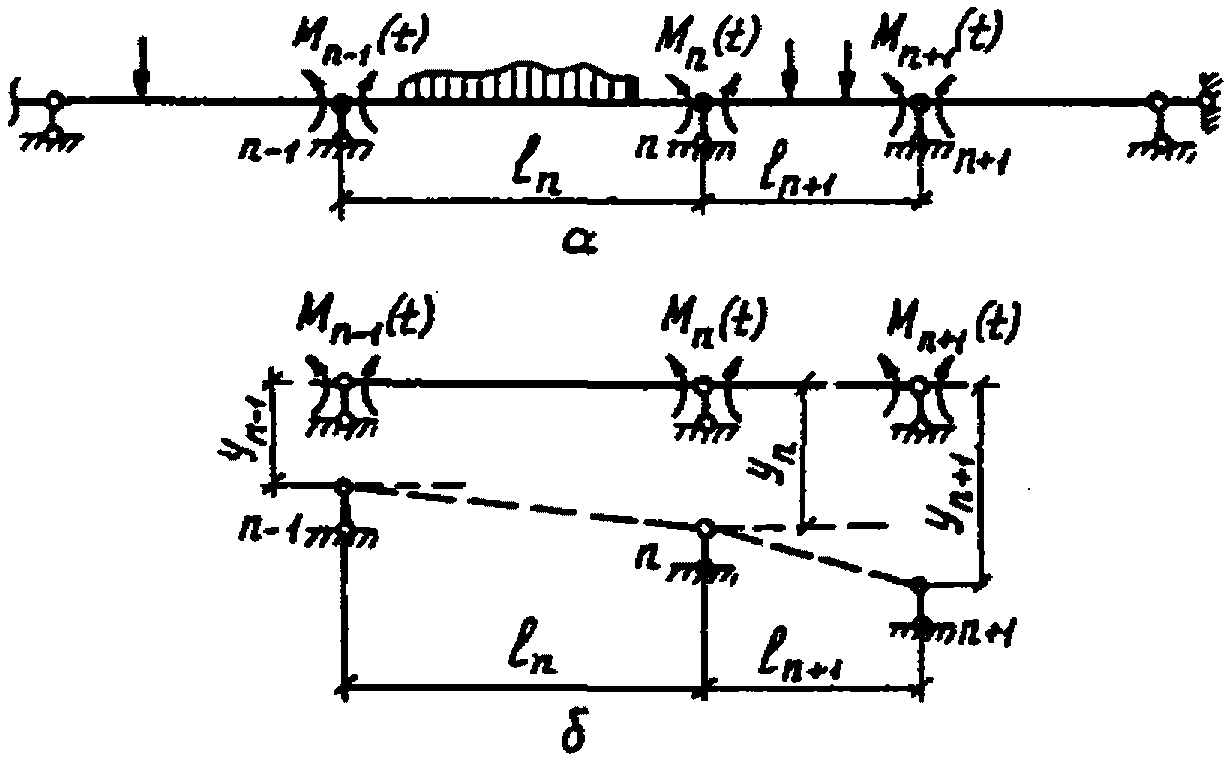
а - на действие внешних нагрузок; б - на смещение опор
Численные значения  определяются по формуле (3.11).
определяются по формуле (3.11).
При расчете на усадку бетонов
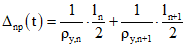 , (7.2)
, (7.2)где
При расчете на действие сил предварительного обжатия
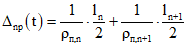 , (7.3)
, (7.3)где
При расчете на действие собственного веса бетонов и длительно действующей части внешних нагрузок
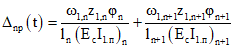 , (7.4)
, (7.4)где
z1 - расстояние от ц.т. указанной эпюры до оси соответствующей опоры.
Численные значения 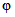 определяются по формуле (3.5).
определяются по формуле (3.5).
7.2. Определение полных усилий <x> от мгновенного смещения опор и нагрузок, приложенных после замыкания системы, в конструкциях, на пролетных и надопорных участках которых от действия указанных нагрузок трещины не образуются, производится путем решения системы трехчленных уравнений вида
--------------------------------
<x> Под полными имеются в виду усилия, равные алгебраической сумме начальных усилий, возникающих в момент нагружения, и дополнительных, вызванных ползучестью бетонов.
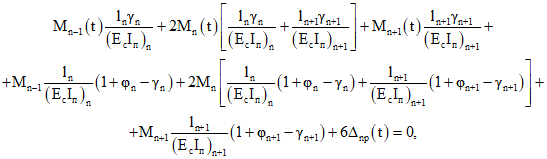 (7.5)
(7.5)где
Mn-1, Mn и Mn+1 - начальные значения усилий, полученные в результате расчета балки как упругой системы.
При расчете на мгновенное смещение опор (рис. 8,б)
При расчете на действие внешних нагрузок
 , (7.7)
, (7.7)где
z - расстояние от ц.т. указанной эпюры до оси соответствующей опоры.
7.3. Определение полных усилий от мгновенного смещения опор и нагрузок, приложенных до и после замыкания системы, в конструкциях, на пролетных и надопорных участках которых образуются трещины, производится методом последовательных приближений. В качестве первого приближения принимаются усилия, полученные в результате расчета балки как упругой системы. Затем каждый пролет балки разбивается на m одинаковых по длине участков (m >= 10). На каждом участке жесткость принимается постоянной, соответствующей изгибающему моменту в первом приближении в середине данного участка. Определение усилий во втором приближении производится путем решения системы трехчленных уравнений вида
При расчете на мгновенное смещение опор:
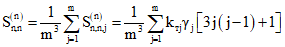 ; (7.10)
; (7.10)Численные значения  определяются по формуле (7.6).
определяются по формуле (7.6).
При расчете на действие нагрузок, приложенных до и после замыкания системы или только после замыкания системы, численные Sn,n-1; 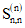 ;
;  и Sn,n+1 определяются по формулам (7.9) - (7.11),
и Sn,n+1 определяются по формулам (7.9) - (7.11),  - по формуле
- по формуле
где
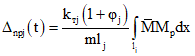 ; (7.13)
; (7.13)lj - длина j-го участка;
Mр - то же, от заданных нагрузок в основной системе.
Для участков без трещин коэффициенты kтj принимаются равными единице.
Для участков с трещинами (см. п. 3.4 настоящих методических рекомендаций) для первого случая коэффициенты kтj определяются по формуле (3.15), для второго случая - по формуле (3.40), для третьего - по формуле (3.51).
Для участков без трещин численные значения 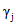 определяются по табл. 1 в зависимости от величины
определяются по табл. 1 в зависимости от величины 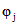 , определяемой по формуле (3.11).
, определяемой по формуле (3.11).
Для участков с трещинами (см. п. 3.4) численные значения  определяются по формуле
определяются по формуле
где численные значения 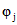 для первого случая определяются по формуле (3.14), для второго случая - по формуле (3.39), для третьего - по формуле (3.50).
для первого случая определяются по формуле (3.14), для второго случая - по формуле (3.39), для третьего - по формуле (3.50).
При расчете на действие нагрузок, приложенных только до замыкания системы
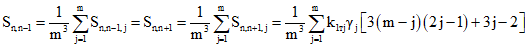 ; (7.15)
; (7.15)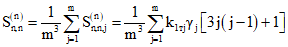 ; (7.16)
; (7.16)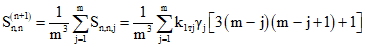 . (7.17)
. (7.17)Численные значения 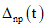 определяются по формуле (7.12), где
определяются по формуле (7.12), где
 ; (7.18)
; (7.18)M1р - изгибающий момент от заданных нагрузок в основной системе.
Для участков без трещин
 . (7.19)
. (7.19)Численные значения 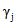 определяются по табл. 1 в зависимости от величин
определяются по табл. 1 в зависимости от величин 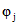 , определяемых по формуле (3.5).
, определяемых по формуле (3.5).
Для участков с трещинами
 . (7.20)
. (7.20)По вычисленным во втором приближении усилиям определяются новые значения kтj, 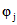 и
и 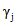 и производится расчет усилий в третьем приближении. Процесс итераций повторяется до тех пор, пока в дальнейшем уточнении расчета не будет необходимости.
и производится расчет усилий в третьем приближении. Процесс итераций повторяется до тех пор, пока в дальнейшем уточнении расчета не будет необходимости.
При медленно сходящемся или расходящемся процессе итераций необходимо увеличить количество участков и повторить расчет.
7.4. После определения опорных моментов по формулам строительной механики вычисляются пролетные моменты и опорные реакции. При этом каждый пролет рассматривается как однопролетная свободно лежащая балка, нагруженная опорными моментами и заданной нагрузкой.
Полученные таким образом усилия используются в качестве внешних при определении напряжений в нормальных сечениях, при расчете по образованию, раскрытию и закрытию трещин, а также при вычислении кривизн конструкций, а по ним - прогибов и углов поворота.
8.1. Предельные значения числовых параметров ползучести 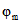 и усадки
и усадки 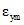 , соответствующих фактическим условиям эксплуатации конструкции, определяются по формулам:
, соответствующих фактическим условиям эксплуатации конструкции, определяются по формулам:
где
Cн и  - нормативные значения меры ползучести и деформаций усадки; определяются в соответствии с пп. 8.3 и 8.4;
- нормативные значения меры ползучести и деформаций усадки; определяются в соответствии с пп. 8.3 и 8.4;
8.2. Определение промежуточных значений параметров 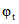 и
и  , соответствующих заданному времени t, производится по данным табл. 3.
, соответствующих заданному времени t, производится по данным табл. 3.
Вид деформации | Величины 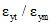 к моменту времени t, сут. к моменту времени t, сут. | ||||||||
3 | 7 | 28 | 60 | 90 | 180 | 360 | 720 | 2000 | |
Ползучесть | |||||||||
Усадка | |||||||||
Примечания: 1. В числителе приведены значения для стержневых элементов с величиной открытой удельной поверхности 0,4 см-1 и более, в знаменателе - для элементов, у которых эта величина составляет 0,1 см-1 и менее (для промежуточных значений открытой удельной поверхности следует пользоваться линейной интерполяцией). 2. Открытую удельную поверхность стержневых элементов вычисляют как отношение открытого для влагопотерь периметра поперечного сечения к его площади.
8.3. Нормативные значения меры ползучести Cн (см2/кгс) и деформаций усадки 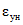 определяются по формулам:
определяются по формулам:
где
B - удельное (по объему) суммарное количество воды затворения и вовлеченного воздуха в литрах на 1000 л уплотненной бетонной смеси;
kп и kу - безразмерные коэффициенты, зависящие от вида заполнителя бетона.
Значения коэффициентов в зависимости от вида заполнителя для бетона:
kп·106 | kу·106 | |
Щебень или гравий из плотных изверженных пород (гранит, базальт, кварц, др.) ................................ | 20 | 0,14 |
Щебень из плотных осадочных пород (известняк) ....... | 17 | 0,14 |
Кварцевый песок (без крупного заполнителя) ............... | 18 | 0,14 |
Керамзитовый гравий (с кварцевым песком) ................. | 21 | 0,19 |
Примечание. При расчете по формулам (8.3) и (8.4) количество вовлеченного воздуха рекомендуется учитывать только при применении воздухововлекающих (газообразующих) добавок. Для бетонов, изготовленных с пластифицирующими добавками или без них, влияние вовлеченного воздуха в бетонной смеси можно не учитывать.
8.4. При отсутствии данных о дозировке составляющих бетонной смеси нормативные значения Cн (см2/кгс) и 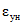 рекомендуется ориентировочно назначать по табл. 4 для тяжелых бетонов (в числителе) и для легких бетонов плотной структуры (в знаменателе).
рекомендуется ориентировочно назначать по табл. 4 для тяжелых бетонов (в числителе) и для легких бетонов плотной структуры (в знаменателе).
Подвижность (удобоукладываемость) бетонной смеси | Значения Cн·106, см2/кгс, для бетона с кубиковой прочностью | Значения 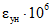 для бетона проектной марки для бетона проектной марки | |||||||||
150 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | ||||
осадка конуса, см | жесткость, с | ||||||||||
150 - 200 | 300 и более | ||||||||||
- | 80 - 60 | - | - | - | |||||||
- | 35 - 30 | - | |||||||||
1 - 2 | - | - | |||||||||
5 - 6 | - | - | - | ||||||||
9 - 10 | - | - | - | - | |||||||
Примечания: 1. Для бетонов, подвергнутых тепловлажностной обработке, нормативные значения Cн и 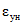 по табл. 4 или формулам (8.3) и (8.4) следует уменьшить на 10%. 2. Нормативные значения Cн по формуле (8.3) или по табл. 4 следует, кроме того: а) для бетонов, изготовленных на пуццолановом портландцементе - увеличить на 35%; б) для бетонов, изготовленных на шлаковом портландцементе - увеличить на 25%, если элемент нагружен в условиях атмосферной влажности, или уменьшить на 35% при его нагружении во влагонасыщенной среде.
по табл. 4 или формулам (8.3) и (8.4) следует уменьшить на 10%. 2. Нормативные значения Cн по формуле (8.3) или по табл. 4 следует, кроме того: а) для бетонов, изготовленных на пуццолановом портландцементе - увеличить на 35%; б) для бетонов, изготовленных на шлаковом портландцементе - увеличить на 25%, если элемент нагружен в условиях атмосферной влажности, или уменьшить на 35% при его нагружении во влагонасыщенной среде.
8.5. Числовые значения поправочных коэффициентов  и
и 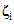 в формулах (8.1) и (8.2) принимаются для тяжелого и легкого бетона по табл. 5 в зависимости от возраста бетона в момент нагружения
в формулах (8.1) и (8.2) принимаются для тяжелого и легкого бетона по табл. 5 в зависимости от возраста бетона в момент нагружения 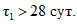 (для ползучести) или начала высыхания
(для ползучести) или начала высыхания 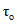 (для усадки), а также от размеров поперечного сечения элемента и влажности окружающей среды.
(для усадки), а также от размеров поперечного сечения элемента и влажности окружающей среды.
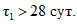 (для ползучести) или начала высыхания
(для ползучести) или начала высыхания 8.6. Если силовые воздействия от внешней нагрузки или вынужденных деформаций прикладываются к элементу конструкции последовательно в разном возрасте, то числовые параметры 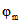 и
и 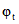 определяются с учетом возраста бетона к моменту приложения каждого из этих воздействий (согласно табл. 5).
определяются с учетом возраста бетона к моменту приложения каждого из этих воздействий (согласно табл. 5).
8.7. Если воздействие усадки на напряженно-деформированное состояние элемента начинается по истечении некоторого периода времени после начала его высыхания, то числовые параметры  и
и 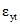 следует уменьшить на величину деформации, проявившуюся за этот период (согласно табл. 3).
следует уменьшить на величину деформации, проявившуюся за этот период (согласно табл. 3).
Возраст бетона в момент нагружения, сут. | 28 и менее | 45 | 60 | 90 | 180 | 360 | 720 и более |
1 | 0,87 | 0,80 | 0,70 | 0,60 | 0,54 | 0,50 | |
Возраст бетона к началу высыхания, сут. | 1 | 7 | 28 | 90 и более | - | - | - |
1,05 | 1 | 0,95 | 0,90 | - | - | - | |
Открытая удельная поверхность элемента, см-1 | 0 | 0,05 | 0,1 | 0,2 | 0,4 | 0,8 | 1 и более |
0,46 | 0,59 | 0,68 | 0,83 | 1 | 1,15 | 1,20 | |
0,20 | 0,59 | 0,75 | 0,90 | 1 | 1,05 | 1,10 | |
Относительная влажность среды, % | 40 и менее | 50 | 60 | 70 | 80 | 90 | 100 |
1,45 | 1,31 | 1,15 | 1 | 0,85 | 0,70 | 0,54 | |
1,45 | 1,31 | 1,15 | 1 | 0,85 | 0,64 | 0 |
Примечания: 1. При нагружении элемента в возрасте, большем чем 28 сут., прочность бетона 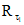 принимается равной его марочной прочности R. 2. Относительная влажность среды для эксплуатации конструкций на открытом воздухе принимается в зависимости от климатического района расположения сооружения согласно СНиП II-А.6-72 как средняя относительная влажность воздуха наиболее жаркого месяца. При отсутствии данных о районе расположения сооружения, а также для элементов типовых конструкций допускается принимать
принимается равной его марочной прочности R. 2. Относительная влажность среды для эксплуатации конструкций на открытом воздухе принимается в зависимости от климатического района расположения сооружения согласно СНиП II-А.6-72 как средняя относительная влажность воздуха наиболее жаркого месяца. При отсутствии данных о районе расположения сооружения, а также для элементов типовых конструкций допускается принимать 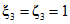 . 3. Для районов, относящихся по СНиП II-А.6-72 к IV климатической зоне (районы с сухим жарким климатом), относительную влажность воздуха рекомендуется устанавливать как среднемесячную влажность, соответствующую времени нагружения (начала высыхания) элемента конструкции. 4. Для массивных элементов с открытой удельной поверхностью 0,05 см-1 и менее, а также элементов, полностью гидроизолированных до начала нагружения (высыхания), независимо от влажности воздуха следует принимать
. 3. Для районов, относящихся по СНиП II-А.6-72 к IV климатической зоне (районы с сухим жарким климатом), относительную влажность воздуха рекомендуется устанавливать как среднемесячную влажность, соответствующую времени нагружения (начала высыхания) элемента конструкции. 4. Для массивных элементов с открытой удельной поверхностью 0,05 см-1 и менее, а также элементов, полностью гидроизолированных до начала нагружения (высыхания), независимо от влажности воздуха следует принимать 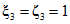 . 5. Для элементов, находящихся в воде или насыщенной влагой среде, независимо от размеров поперечного сечения следует принимать
. 5. Для элементов, находящихся в воде или насыщенной влагой среде, независимо от размеров поперечного сечения следует принимать  .
.
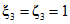 . 3. Для районов, относящихся по СНиП II-А.6-72 к IV климатической зоне (районы с сухим жарким климатом), относительную влажность воздуха рекомендуется устанавливать как среднемесячную влажность, соответствующую времени нагружения (начала высыхания) элемента конструкции. 4. Для массивных элементов с открытой удельной поверхностью 0,05 см-1 и менее, а также элементов, полностью гидроизолированных до начала нагружения (высыхания), независимо от влажности воздуха следует принимать
. 3. Для районов, относящихся по СНиП II-А.6-72 к IV климатической зоне (районы с сухим жарким климатом), относительную влажность воздуха рекомендуется устанавливать как среднемесячную влажность, соответствующую времени нагружения (начала высыхания) элемента конструкции. 4. Для массивных элементов с открытой удельной поверхностью 0,05 см-1 и менее, а также элементов, полностью гидроизолированных до начала нагружения (высыхания), независимо от влажности воздуха следует принимать 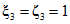 . 5. Для элементов, находящихся в воде или насыщенной влагой среде, независимо от размеров поперечного сечения следует принимать
. 5. Для элементов, находящихся в воде или насыщенной влагой среде, независимо от размеров поперечного сечения следует принимать  .
.Пример 1. Определить изгибающие моменты в четырехпролетном неразрезном ригеле перекрытия и проверить трещиностойкость его сечений. Длина каждого пролета 7,5 м, шаг ригелей - 6 м. Ригель состоит из сборных предварительно напряженных элементов, монолитного бетона и дополнительно укладываемых сборных ненапряженных железобетонных плит (см. рисунок).
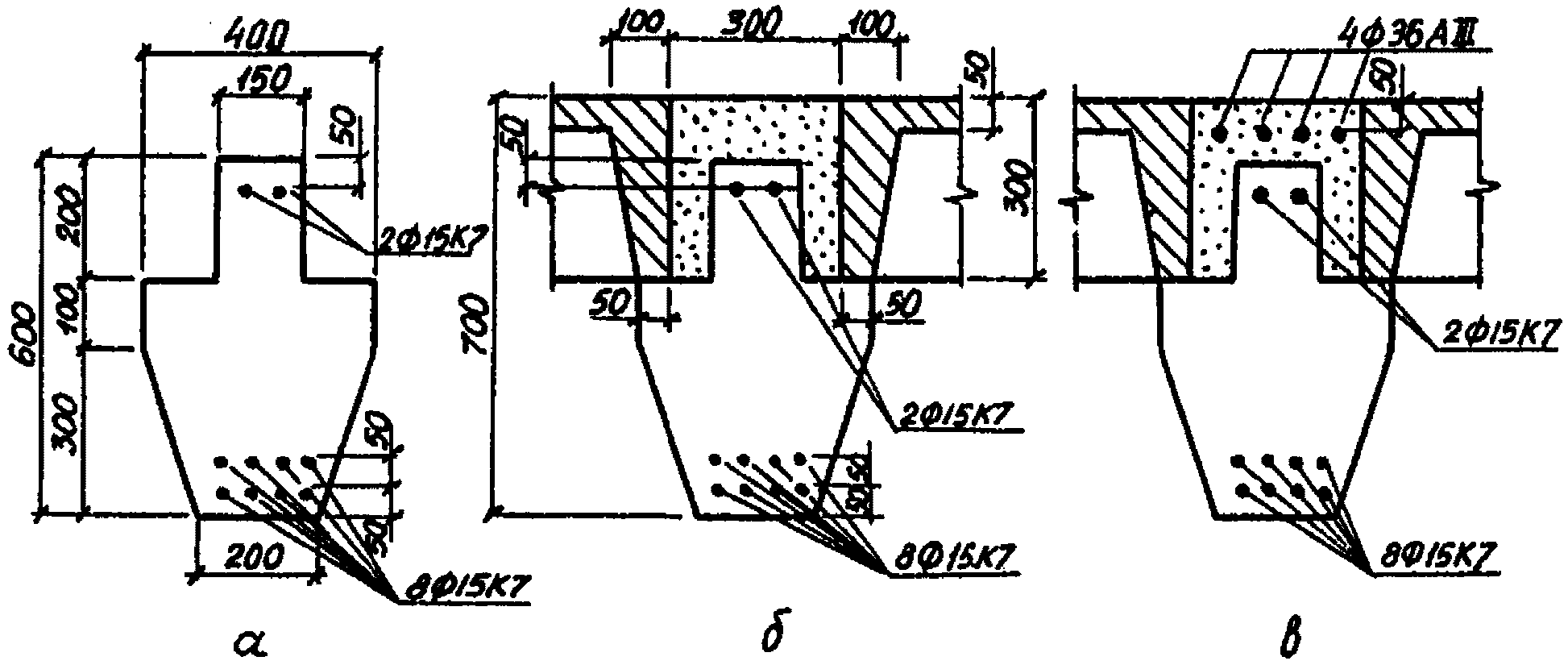
а - сечение сборного преднапряженного элемента;
б - пролетное сечение ригеля; в - опорное сечение перекрытия
Данные для расчета.
Сборные элементы: бетон M500 пропаренный Fс = 1600 см2, yс = 27,5 см; 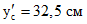 ; hс = 60 см; dм = 10 см; Iс = 358300 см4; Eс = 3,25·105 кгс/см2; RпрII = 280 кгс/см2; RрII = 20 кгс/см2: напрягаемая арматура класса К-7, Fас = 11,33 см2;
; hс = 60 см; dм = 10 см; Iс = 358300 см4; Eс = 3,25·105 кгс/см2; RпрII = 280 кгс/см2; RрII = 20 кгс/см2: напрягаемая арматура класса К-7, Fас = 11,33 см2; 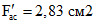 ; Eа = 1,8·106 кгс/см2; RаII = 13200 кгс/см2; nа = 5,54; aс = 7,5 см;
; Eа = 1,8·106 кгс/см2; RаII = 13200 кгс/см2; nа = 5,54; aс = 7,5 см; 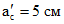 .
.
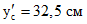 ; hс = 60 см; dм = 10 см; Iс = 358300 см4; Eс = 3,25·105 кгс/см2; RпрII = 280 кгс/см2; RрII = 20 кгс/см2: напрягаемая арматура класса К-7, Fас = 11,33 см2;
; hс = 60 см; dм = 10 см; Iс = 358300 см4; Eс = 3,25·105 кгс/см2; RпрII = 280 кгс/см2; RрII = 20 кгс/см2: напрягаемая арматура класса К-7, Fас = 11,33 см2; 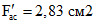 ; Eа = 1,8·106 кгс/см2; RаII = 13200 кгс/см2; nа = 5,54; aс = 7,5 см;
; Eа = 1,8·106 кгс/см2; RаII = 13200 кгс/см2; nа = 5,54; aс = 7,5 см; 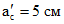 .
.Монолитный бетон M200 естественного твердения: Fм2 = 600 см2; yм2 = 17,5 см;  ; hм2 = 30 см; Iм2 = 46250 см4; Eм2 = 2,4·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм2 = 0,738.
; hм2 = 30 см; Iм2 = 46250 см4; Eм2 = 2,4·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм2 = 0,738.
 ; hм2 = 30 см; Iм2 = 46250 см4; Eм2 = 2,4·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм2 = 0,738.
; hм2 = 30 см; Iм2 = 46250 см4; Eм2 = 2,4·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм2 = 0,738.Сборные плиты: бетон M200 пропаренный, Fм1 = 3225 см2; yм1 = 25,92 см; 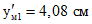 ; hм1 = 30 см; Iм1 = 86130 см4; Eм1 = 2,15·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм1 = 0,662.
; hм1 = 30 см; Iм1 = 86130 см4; Eм1 = 2,15·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм1 = 0,662.
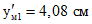 ; hм1 = 30 см; Iм1 = 86130 см4; Eм1 = 2,15·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм1 = 0,662.
; hм1 = 30 см; Iм1 = 86130 см4; Eм1 = 2,15·105 кгс/см2; RпрII = 115 кгс/см2; RрII = 11,5 кгс/см2; nм1 = 0,662.Надопорная арматура класса А-III; Fам = 40,72 см2; Eа = 2·106 кгс/см2; nа = 6,15; aм = 6 см.
Обжатие сборных элементов произведено в возрасте бетона 3 сут. при передаточной прочности 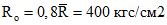 . Укладка монолитного бетона осуществлена при возрасте бетона сборных элементов 45 сут, плит перекрытия - 30 сут. Временная нагрузка на перекрытие приложена в возрасте бетона сборных элементов 60 сут., плит перекрытия - 45 сут. и монолитного бетона - 15 сут.
. Укладка монолитного бетона осуществлена при возрасте бетона сборных элементов 45 сут, плит перекрытия - 30 сут. Временная нагрузка на перекрытие приложена в возрасте бетона сборных элементов 60 сут., плит перекрытия - 45 сут. и монолитного бетона - 15 сут.
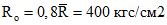 . Укладка монолитного бетона осуществлена при возрасте бетона сборных элементов 45 сут, плит перекрытия - 30 сут. Временная нагрузка на перекрытие приложена в возрасте бетона сборных элементов 60 сут., плит перекрытия - 45 сут. и монолитного бетона - 15 сут.
. Укладка монолитного бетона осуществлена при возрасте бетона сборных элементов 45 сут, плит перекрытия - 30 сут. Временная нагрузка на перекрытие приложена в возрасте бетона сборных элементов 60 сут., плит перекрытия - 45 сут. и монолитного бетона - 15 сут.Нагрузки равномерно распределенные: постоянная q1 = 1,8 тс/м; временная 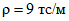 ; в т.ч. длительно действующая pдл = 6 тс/м. Постоянную нагрузку воспринимают сборные элементы ригеля, временную - вся конструкция.
; в т.ч. длительно действующая pдл = 6 тс/м. Постоянную нагрузку воспринимают сборные элементы ригеля, временную - вся конструкция.
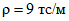 ; в т.ч. длительно действующая pдл = 6 тс/м. Постоянную нагрузку воспринимают сборные элементы ригеля, временную - вся конструкция.
; в т.ч. длительно действующая pдл = 6 тс/м. Постоянную нагрузку воспринимают сборные элементы ригеля, временную - вся конструкция.Геометрические характеристики: приведенного сечения сборного элемента - F1.п = 1678 см2; y1.с = 27 см; i1 = 0,5 см; I1.п = 394920 см4; W1.о = 14630 см3;  ; приведенного сечения конструкции в пролете - Fп = 4255 см2; yк = 49,7 см; Iп = 1939240 см4; Wо = 39020 см3; Wт = 77250 см3; приведенного сечения конструкции у промежуточных опор - Fп = 4505 см2; yк = 19,5 см; Iп = 1987600 см4; Wо = 101876 см3; Wт = 160953 см3.
; приведенного сечения конструкции в пролете - Fп = 4255 см2; yк = 49,7 см; Iп = 1939240 см4; Wо = 39020 см3; Wт = 77250 см3; приведенного сечения конструкции у промежуточных опор - Fп = 4505 см2; yк = 19,5 см; Iп = 1987600 см4; Wо = 101876 см3; Wт = 160953 см3.
 ; приведенного сечения конструкции в пролете - Fп = 4255 см2; yк = 49,7 см; Iп = 1939240 см4; Wо = 39020 см3; Wт = 77250 см3; приведенного сечения конструкции у промежуточных опор - Fп = 4505 см2; yк = 19,5 см; Iп = 1987600 см4; Wо = 101876 см3; Wт = 160953 см3.
; приведенного сечения конструкции в пролете - Fп = 4255 см2; yк = 49,7 см; Iп = 1939240 см4; Wо = 39020 см3; Wт = 77250 см3; приведенного сечения конструкции у промежуточных опор - Fп = 4505 см2; yк = 19,5 см; Iп = 1987600 см4; Wо = 101876 см3; Wт = 160953 см3.Характеристики усадки и ползучести бетонов находим по настоящим методическим рекомендациям (раздел 8):
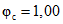 ;
; 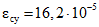 ;
; 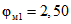 ;
; 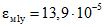 ;
; 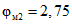 ;
; 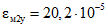 .
.По табл. 1 определяем:
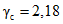 ;
; 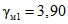 ;
;  .
.По формулам раздела 2 находим вспомогательные геометрические параметры сечения конструкции в пролете:
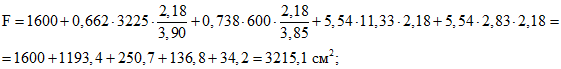
S = 1600·27,5 + 1193,4(70 - 4,08) + 250,7(70 - 12,5) + 136,8·7,5 + 34,2·55 = 139991 см3;
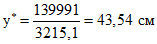 ;
;iс = 43,54 - 27,5 = 16,04 см;
iм1 = 70 - 43,54 - 4,08 = 22,38 см;
iм2 = 70 - 43,54 - 12,5 = 13,96 см;
iас = 43,54 - 7,5 = 36,04 см;
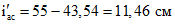 ;
;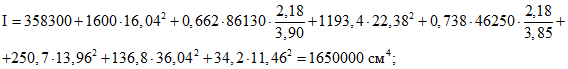
FI = 1600·1 = 1600 см2;
FIV = 1193,4·2,5 + 250,7·2,75 + 1600·1 = 2983,5 + 689,4 + 1600 = 5272,9 см2;
SI = 1600·16,04·1 = 25664 см3;
SII = 1600·0,5·1 = 800 см3;
SIII = 2983,5·22,38 + 689,4·13,96 - 1600·16,04 = 50731 см3;
SIV = 2983,5·16,22 + 689,4·7,8 - 1600·22,2 = 18250 см3;
II = (358300 - 1600·0,5·16,04)·1 = 345500 см4;

Численное значение 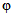 определяем по формуле (3.11):
определяем по формуле (3.11):
 .
.Усилие предварительного обжатия сборных элементов (при коэффициенте точности натяжения арматуры, равном 1) к моменту замыкания системы N1.о = 150000 кгс; эксцентриситет указанного усилия e1.н = 9,65 см. Максимальный изгибающий момент в сборных элементах от постоянных нагрузок M1 = 12,66 тс·м. Моменты образования трещин при замыкании системы:
в пролетных сечениях Mт = 67,84 тс·м;
в опорных сечениях Mт = 18,50 тс·м.
Определяем усилия в неразрезном ригеле как упругой системе. При действии длительно действующей части временной нагрузки опорные моменты равны:
на первых промежуточных опорах
 ;
;на средней опоре
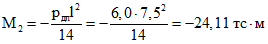 .
.Так как на всех трех опорах M > Mт, в зоне действия отрицательных моментов в ригеле возникают трещины. Для определения усилий в ригеле с учетом влияния ползучести бетонов используем метод последовательных приближений. Результаты расчета по упругой стадии принимаем в качестве первого приближения. Каждый пролет ригеля разбиваем на 30 участков lj = 0,25 м. В табл. 1 настоящего приложения приведены вспомогательные величины, необходимые для расчета ригеля методом последовательных приближений. В табл. 2 приведены параметры деформативности ригеля в зоне действия отрицательных моментов, вычисленные в соответствии с указаниями п. 3.7 настоящих методических рекомендаций. Последовательность определения этих параметров покажем для изгибающего момента M = -20 тс·м.
Таблица 1
методом последовательных приближений
Номер участка | Mр,j-1, тс·м | Mр,ср, тс·м | Mр,j, тс·м | 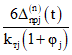 , тс·м , тс·м | 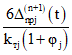 , тс·м , тс·м | ||||
1 | 0,0 | 2,7656 | 5,4375 | 2611 | 88 | 1 | 0,0122 | 0,5378 | 0,83 |
2 | 5,4375 | 8,0156 | 10,50 | 2437 | 256 | 7 | 0,0828 | 1,5172 | 2,40 |
3 | 10,50 | 12,8906 | 15,1875 | 2269 | 412 | 19 | 0,2172 | 2,3578 | 3,87 |
4 | 15,1875 | 17,3906 | 19,50 | 2107 | 556 | 37 | 0,4078 | 3,0672 | 5,22 |
5 | 19,50 | 21,5156 | 23,4375 | 1951 | 688 | 61 | 0,6472 | 3,6528 | 6,45 |
6 | 23,4375 | 25,2656 | 27,00 | 1801 | 808 | 91 | 0,9278 | 4,1222 | 7,58 |
7 | 27,00 | 28,6406 | 30,1875 | 1657 | 916 | 127 | 1,2422 | 4,4828 | 8,59 |
8 | 30,1875 | 31,6406 | 33,00 | 1519 | 1012 | 169 | 1,5828 | 4,7422 | 9,49 |
9 | 33,00 | 34,2656 | 35,4375 | 1387 | 1096 | 217 | 1,9422 | 4,9078 | 10,28 |
10 | 35,4375 | 36,5156 | 37,50 | 1261 | 1168 | 271 | 2,3128 | 4,9872 | 10,95 |
11 | 37,50 | 38,3906 | 39,1875 | 1141 | 1228 | 331 | 2,6872 | 4,9878 | 11,52 |
12 | 39,1875 | 39,8906 | 40,50 | 1027 | 1276 | 397 | 3,0578 | 4,9172 | 11,97 |
13 | 40,50 | 41,0156 | 41,4375 | 919 | 1312 | 469 | 3,4172 | 4,7828 | 12,30 |
14 | 41,4375 | 41,7656 | 42,00 | 817 | 1336 | 547 | 3,7578 | 4,5922 | 12,53 |
15 | 42,00 | 42,1406 | 42,1875 | 721 | 1348 | 631 | 4,0722 | 4,3528 | 12,64 |
16 | 42,1875 | 42,1406 | 42,00 | 631 | 1348 | 721 | 4,3528 | 4,0722 | 12,64 |
17 | 42,00 | 41,7656 | 41,4375 | 547 | 1336 | 817 | 4,5922 | 3,7578 | 12,53 |
18 | 41,4375 | 41,0156 | 40,50 | 469 | 1312 | 919 | 4,7828 | 3,4172 | 12,30 |
19 | 40,50 | 39,8906 | 39,1875 | 397 | 1276 | 1027 | 4,9172 | 3,0578 | 11,97 |
20 | 39,1875 | 38,3906 | 37,50 | 331 | 1228 | 1141 | 4,9878 | 2,6872 | 11,52 |
21 | 37,50 | 36,5156 | 35,4375 | 271 | 1168 | 1261 | 4,9872 | 2,3128 | 10,95 |
22 | 35,4375 | 34,2656 | 33,00 | 217 | 1096 | 1387 | 4,9078 | 1,9422 | 10,28 |
23 | 33,00 | 31,6406 | 30,1875 | 169 | 1012 | 1519 | 4,7422 | 1,5828 | 9,49 |
24 | 30,1875 | 28,6406 | 27,00 | 127 | 916 | 1657 | 4,4828 | 1,2422 | 8,59 |
25 | 27,00 | 25,2656 | 23,4375 | 91 | 808 | 1801 | 4,1222 | 0,9278 | 7,58 |
26 | 23,4375 | 21,5156 | 19,50 | 61 | 688 | 1951 | 3,6528 | 0,6472 | 6,45 |
27 | 19,50 | 17,3906 | 15,1875 | 37 | 556 | 2107 | 3,0672 | 0,4078 | 5,22 |
28 | 15,1875 | 12,8906 | 10,50 | 19 | 412 | 2269 | 2,3578 | 0,2172 | 3,87 |
29 | 10,50 | 8,0156 | 5,4375 | 7 | 256 | 2437 | 1,5172 | 0,0828 | 2,40 |
30 | 5,4375 | 2,7656 | 0,0 | 1 | 88 | 2611 | 0,5378 | 0,0122 | 0,83 |
Таблица 2
в приопорных сечениях
Изгибающий момент M, тс·м | до 18,5 | 18,5 | 19,0 | 20,0 | 21,0 | 23,0 | 25,0 | 30,0 | 40,0 | 50,0 |
xо, см | - | 28,40 | 28,33 | 28,27 | 28,24 | 28,14 | 28,05 | 27,85 | 27,56 | 27,36 |
x, см | - | 32,16 | 32,16 | 32,15 | 32,13 | 32,12 | 32,11 | 32,09 | 32,07 | 32,05 |
- | 636600 | 635400 | 633000 | 630600 | 626500 | 622900 | 615100 | 603800 | 595950 | |
- | 895400 | 895300 | 895000 | 894700 | 894200 | 893800 | 892900 | 891700 | 890760 | |
kт | 1,0 | 3,121 | 3,127 | 3,139 | 3,151 | 3,172 | 3,190 | 3,230 | 3,291 | 3,334 |
1,345 | 0,422 | 0,419 | 0,414 | 0,410 | 0,401 | 0,394 | 0,378 | 0,354 | 0,338 | |
2,53 | 1,422 | 1,419 | 1,414 | 1,410 | 1,401 | 1,394 | 1,378 | 1,354 | 1,338 |
Расчет начинаем с определения 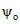 . Высоту сжатой зоны xо, входящую в формулу (3.47) настоящих методических рекомендаций, отыскиваем из уравнения (3.52) при
. Высоту сжатой зоны xо, входящую в формулу (3.47) настоящих методических рекомендаций, отыскиваем из уравнения (3.52) при 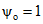 . Предположим сначала, что н.о. пересекает сборный элемент ригеля в пределах переменной ширины его сечения. Тогда:
. Предположим сначала, что н.о. пересекает сборный элемент ригеля в пределах переменной ширины его сечения. Тогда:
 ;
;nаSо.т.а = 5,54·11,33(xо - 7,5) - 5,54·2,83(55 - xо) - 6,15·40,72(64 - xо) = 329xо - 17320.
С учетом этого уравнение (3.52) примет вид:
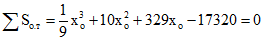 ,
,откуда xо = 26,05 см < 30 см.
Значения F и m определяем по формулам:
F = 1600 + 0,662·7,5(64 - 40)·2 + 0,738(15·20 + 30·4) = 2029 см2;
 ;
;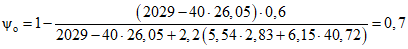 ;
;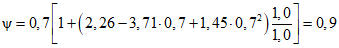 .
.Определяем положение н.о. при вычисленных значениях 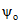 и
и 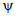 . При этом будем полагать, что xо < 30 см и 30 см < x < 40 см (см. рисунок). Тогда:
. При этом будем полагать, что xо < 30 см и 30 см < x < 40 см (см. рисунок). Тогда:
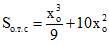 ;
;Sт.с = 20·30(x - 15) + 2·0,5·10·30(x - 20) + 0,5·40(x - 30)2 = 20x2 - 300x + 3000;
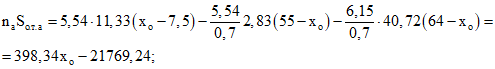

Уравнения (3.52) и (3.53) примут вид:
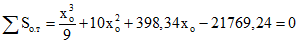
и
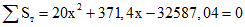 ,
,откуда xо = 28,27 см и x = 32,15 см.
По формулам (3.21) и (3.22) настоящих методических рекомендаций вычисляем:
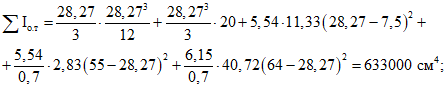
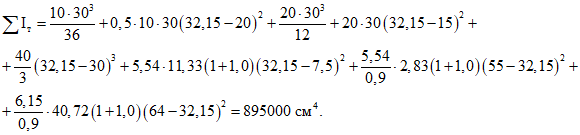
По формулам (3.51) и (3.50) находим:
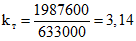 ;
;  .
.Так как ригель полностью симметричен относительно средней опоры, при расчете будем рассматривать только левую половину ригеля, т.е. два левых пролета.
Значения изгибающих моментов в середине каждого участка в первом приближении (упругий расчет) приведены во втором столбце табл. 3. Из этих данных следует, что на участках 28 - 30 первого по пролета и 1, 2, 3, 30 второго пролета изгибающие моменты превышают моменты трещинообразования; на остальных участках трещины отсутствуют. Используя данные табл. 2 настоящего приложения, определяем (по интерполяции) параметры деформативности участков с трещинами - kтj, 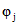 и
и 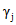 . Затем, используя данные табл. 1, определяем элементы перемещений для каждого участка. Так, для участка 2 второго пролета по формулам (7.9) - (7.11) настоящих методических рекомендаций имеем:
. Затем, используя данные табл. 1, определяем элементы перемещений для каждого участка. Так, для участка 2 второго пролета по формулам (7.9) - (7.11) настоящих методических рекомендаций имеем:
S11j = 3,210·1,386·2437 = 10842,36;
S12j = S21j = 3,210·1,386·256 = 1138,96;
S22j = 3,210·1,386·7 = 31,14;
 ;
;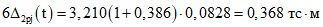 .
.Вычисленные аналогичным образом элементы перемещений для всех остальных участков приведены в табл. 3.
Таблица 3
методом последовательных приближений
Номер участка, j | Mj(t), тс·м, в первом приближении | kтj | S11j | S12j = S21j | S22j | 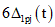 , тс·м , тс·м |  , тс·м , тс·м | Mj(t), тс·м, во втором приближении | Mj(t), тс·м, в третьем приближении | ||
1 | 3 | 4 | 5 | 11 | |||||||
Первый пролет | |||||||||||
1 | 2,17 | 1,0 | 1,345 | 2,53 | 2,53 | - | - | 0,029 | - | 2,28 | 2,27 |
2 | 6,21 | 1,0 | 1,345 | 2,53 | 17,71 | - | - | 0,194 | - | 6,56 | 6,52 |
3 | 9,88 | 1,0 | 1,345 | 2,53 | 48,07 | - | - | 0,509 | - | 10,46 | 10,39 |
4 | 13,17 | 1,0 | 1,345 | 2,53 | 93,61 | - | - | 0,956 | - | 13,99 | 13,89 |
5 | 16,10 | 1,0 | 1,345 | 2,53 | 154,33 | - | - | 1,518 | - | 17,15 | 17,02 |
6 | 18,64 | 1,0 | 1,345 | 2,53 | 230,23 | - | - | 2,176 | - | 19,93 | 19,77 |
7 | 20,81 | 1,0 | 1,345 | 2,53 | 321,31 | - | - | 2,913 | - | 22,33 | 22,14 |
8 | 22,60 | 1,0 | 1,345 | 2,53 | 427,57 | - | - | 3,712 | - | 24,36 | 24,14 |
9 | 24,02 | 1,0 | 1,345 | 2,53 | 549,01 | - | - | 4,554 | - | 26,02 | 25,77 |
10 | 25,07 | 1,0 | 1,345 | 2,53 | 685,63 | - | - | 5,424 | - | 27,30 | 27,02 |
11 | 25,73 | 1,0 | 1,345 | 2,53 | 837,43 | - | - | 6,301 | - | 28,20 | 27,89 |
12 | 26,03 | 1,0 | 1,345 | 2,53 | 1004,41 | - | - | 7,171 | - | 28,73 | 28,39 |
13 | 25,95 | 1,0 | 1,345 | 2,53 | 1186,57 | - | - | 8,013 | - | 28,89 | 28,52 |
14 | 25,50 | 1,0 | 1,345 | 2,53 | 1383,91 | - | - | 8,812 | - | 28,67 | 28,27 |
15 | 24,66 | 1,0 | 1,345 | 2,53 | 1596,43 | - | - | 9,549 | - | 28,07 | 27,64 |
16 | 23,46 | 1,0 | 1,345 | 2,53 | 1824,13 | - | - | 10,207 | - | 27,10 | 26,64 |
17 | 21,88 | 1,0 | 1,345 | 2,53 | 2067,01 | - | - | 10,769 | - | 25,76 | 25,27 |
18 | 19,93 | 1,0 | 1,345 | 2,53 | 2325,07 | - | - | 11,216 | - | 24,04 | 23,52 |
19 | 17,59 | 1,0 | 1,345 | 2,53 | 2598,31 | - | - | 11,531 | - | 21,94 | 21,39 |
20 | 14,89 | 1,0 | 1,345 | 2,53 | 2886,73 | - | - | 11,696 | - | 19,47 | 18,89 |
21 | 11,81 | 1,0 | 1,345 | 2,53 | 3190,33 | - | - | 11,695 | - | 16,63 | 16,02 |
22 | 8,35 | 1,0 | 1,345 | 2,53 | 3509,11 | - | - | 11,509 | - | 13,41 | 12,77 |
23 | 4,52 | 1,0 | 1,345 | 2,53 | 3843,07 | - | - | 11,120 | - | 9,81 | 9,14 |
24 | 0,31 | 1,0 | 1,345 | 2,53 | 4192,21 | - | - | 10,512 | - | 5,84 | 5,14 |
25 | -4,26 | 1,0 | 1,345 | 2,53 | 4556,53 | - | - | 9,667 | - | 1,50 | 0,77 |
26 | -9,22 | 1,0 | 1,345 | 2,53 | 4936,03 | - | - | 8,566 | - | -3,22 | -3,98 |
27 | -14,55 | 1,0 | 1,345 | 2,53 | 5330,71 | - | - | 7,193 | - | -8,32 | -9,11 |
28 | -20,26 | 3,142 | 0,413 | 1,413 | 10073,56 | - | - | 10,468 | - | -13,79 | -14,61 |
29 | -26,33 | 3,201 | 0,390 | 1,390 | 10843,16 | - | - | 6,751 | - | -19,63 | -20,48 |
30 | -32,79 | 3,247 | 0,371 | 1,371 | 11623,22 | - | - | 2,394 | - | -25,85 | -26,73 |
Второй пролет | |||||||||||
1 | -33,19 | 3,250 | 0,370 | 1,370 | 11625,48 | 391,82 | 4,45 | 2,395 | 0,054 | -26,23 | -27,10 |
2 | -27,54 | 3,210 | 0,386 | 1,386 | 10842,36 | 1138,96 | 31,14 | 6,750 | 0,368 | -20,77 | -21,60 |
3 | -22,27 | 3,164 | 0,404 | 1,404 | 10079,48 | 1830,21 | 84,40 | 10,474 | 0,965 | -15,70 | -16,48 |
4 | -17,36 | 1,0 | 1,345 | 2,53 | 5330,71 | 1406,68 | 93,61 | 7,193 | 0,956 | -10,99 | -11,73 |
5 | -12,84 | 1,0 | 1,345 | 2,53 | 4936,03 | 1740,64 | 154,33 | 8,566 | 1,518 | -6,65 | -7,35 |
6 | -8,63 | 1,0 | 1,345 | 2,53 | 4556,53 | 2044,24 | 230,23 | 9,667 | 2,176 | -2,69 | -3,35 |
7 | -4,91 | 1,0 | 1,345 | 2,53 | 4192,21 | 2317,48 | 321,31 | 10,512 | 2,913 | 0,89 | 0,27 |
8 | -1,51 | 1,0 | 1,345 | 2,53 | 3843,07 | 2560,36 | 427,57 | 11,120 | 3,712 | 4,09 | 3,52 |
9 | 1,52 | 1,0 | 1,345 | 2,53 | 3509,11 | 2772,88 | 549,01 | 11,509 | 4,554 | 6,93 | 6,40 |
10 | 4,18 | 1,0 | 1,345 | 2,53 | 3190,33 | 2955,04 | 685,63 | 11,695 | 5,424 | 9,39 | 8,90 |
11 | 6,45 | 1,0 | 1,345 | 2,53 | 2886,73 | 3106,84 | 837,43 | 11,696 | 6,301 | 11,47 | 11,02 |
12 | 8,35 | 1,0 | 1,345 | 2,53 | 2598,31 | 3228,28 | 1004,41 | 11,531 | 7,171 | 13,17 | 12,77 |
13 | 9,89 | 1,0 | 1,345 | 2,53 | 2325,07 | 3319,36 | 1186,57 | 11,216 | 8,013 | 14,51 | 14,15 |
14 | 11,03 | 1,0 | 1,345 | 2,53 | 2067,01 | 3380,08 | 1383,91 | 10,769 | 8,812 | 15,47 | 15,15 |
15 | 11,81 | 1,0 | 1,345 | 2,53 | 1824,13 | 3410,44 | 1596,43 | 10,207 | 9,549 | 16,05 | 15,77 |
16 | 12,20 | 1,0 | 1,345 | 2,53 | 1596,43 | 3410,44 | 1824,13 | 9,549 | 10,207 | 16,26 | 16,02 |
17 | 12,24 | 1,0 | 1,345 | 2,53 | 1383,91 | 3380,08 | 2067,01 | 8,812 | 10,769 | 16,09 | 15,90 |
18 | 11,89 | 1,0 | 1,345 | 2,53 | 1186,57 | 3319,36 | 2325,07 | 8,013 | 11,216 | 15,55 | 15,40 |
19 | 11,16 | 1,0 | 1,345 | 2,53 | 1004,41 | 3228,28 | 2598,31 | 7,171 | 11,531 | 14,63 | 14,52 |
20 | 10,06 | 1,0 | 1,345 | 2,53 | 837,43 | 3106,84 | 2886,73 | 6,301 | 11,696 | 13,34 | 13,27 |
21 | 8,60 | 1,0 | 1,345 | 2,53 | 685,63 | 2955,04 | 3190,33 | 5,424 | 11,695 | 11,67 | 11,65 |
22 | 6,74 | 1,0 | 1,345 | 2,53 | 549,01 | 2772,88 | 3509,11 | 4,554 | 11,509 | 9,63 | 9,65 |
23 | 4,52 | 1,0 | 1,345 | 2,53 | 427,57 | 2560,36 | 3843,07 | 3,712 | 11,120 | 7,21 | 7,27 |
24 | 1,93 | 1,0 | 1,345 | 2,53 | 321,31 | 2317,48 | 4192,21 | 2,913 | 10,512 | 4,42 | 4,53 |
25 | -1,05 | 1,0 | 1,345 | 2,53 | 230,23 | 2044,24 | 4556,53 | 2,176 | 9,667 | 1,26 | 1,41 |
26 | -4,39 | 1,0 | 1,345 | 2,53 | 154,33 | 1740,64 | 4936,03 | 1,518 | 8,566 | -2,29 | -2,09 |
27 | -8,12 | 1,0 | 1,345 | 2,53 | 93,61 | 1406,68 | 5330,71 | 0,956 | 7,193 | -6,21 | -5,97 |
28 | -12,22 | 1,0 | 1,345 | 2,53 | 48,07 | 1042,36 | 5740,57 | 0,509 | 5,529 | -10,50 | -10,22 |
29 | -16,69 | 1,0 | 1,345 | 2,53 | 17,71 | 647,68 | 6165,61 | 0,194 | 3,558 | -15,16 | -14,84 |
30 | -21,54 | 3,157 | 0,408 | 1,408 | 4,45 | 391,16 | 11606,04 | 0,054 | 2,391 | -20,20 | -19,84 |
Примечания. 1. Сумма по всем участкам первого пролета в графах 6 - 82337,93 9 - 207,124. 2. Сумма по всем участкам второго пролета в графах 6 - 82347,23; 7 - 69926,83; 8 - 73361,89; 9 - 207,157; 10 - 199,645.
Коэффициенты суммирования:
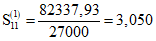 ;
; 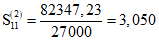 ;
;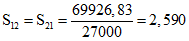 ;
; 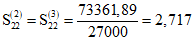 ;
;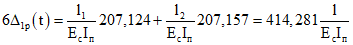 ;
;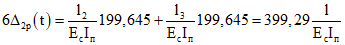 .
.Учитывая, что для всех пролетов ригеля величины l и EсIп одинаковы, составляем систему трехчленных уравнений вида (7.8):
2M1(t)(3,050 + 3,050) + M2(t)2,590 + 414,281 = 0;
M1(t)2,590 + 2M2(t)(2,717 + 2,717) + M3(t)2,590 + 399,29 = 0;
M2(t)2,590 + 2M3(t)(3,050 + 3,050) + 414,281 = 0,
откуда во втором приближении
M1(t) = M3(t) = -29,11 тс·м; M2(t) = -22,87 тс·м.
Затем в той же последовательности находим величины лишних неизвестных в третьем приближении:
M1(t) = M3(t) = -30,00 тс·м; M2(t) = -22,49 тс·м.
Так как в четвертом приближении получены практически такие же величины опорных моментов, в качестве окончательных принимаем значения, полученные в третьем приближении.
В последней колонке табл. 3 приведены величины изгибающих моментов по участкам после перераспределения усилий. Из этой таблицы видно, что наибольший положительный момент возникает в первом пролете на участке 13 (M = 28,52 тс·м). Величина момента MI на этом же участке от нагрузок, приложенных до замыкания ригеля, равна 12,30 тс·м (см. последний столбец табл. 1 настоящего приложения).
Для этого участка производим окончательный расчет по образованию трещин.
По формулам раздела 2 настоящих методических рекомендаций определяем напряжения, вызванные усадкой и ползучестью бетонов.
Усилия и напряжения в бетоне сборных элементов на уровне растянутого края сечения конструкции от усадки бетонов:
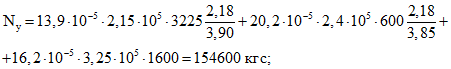
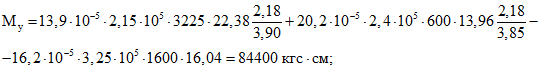
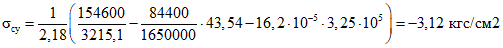 .
.Напряжения в бетоне сборных элементов на уровне растянутого края сечения конструкции к моменту приобретения монолитным бетоном заданной прочности от предварительного обжатия сборных элементов:
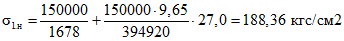 ;
;то же, после приобретения монолитным бетоном заданной прочности - см. формулу (2.15) настоящих методических рекомендаций
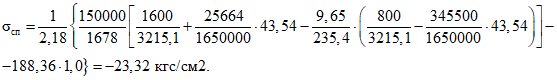
Напряжения в бетоне сборных элементов на уровне растянутого края сечения конструкции к моменту приобретения монолитным бетоном заданной прочности от постоянных нагрузок:
 ;
;то же, после приобретения монолитным бетоном заданной прочности - см. формулу (2.18) настоящих методических рекомендаций
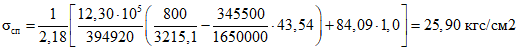 .
.Начальные и полные значения напряжений в бетоне сборных элементов на уровне растянутого края сечения конструкции от внешних нагрузок, приложенных после замыкания конструкции:
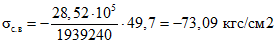 ;
;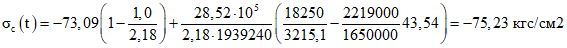 .
.Напряжения в бетоне сборных элементов на уровне растянутого края сечения конструкции, вызванные усадкой и ползучестью бетонов (см. п. 4.2 настоящих методических рекомендаций):
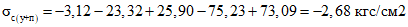 .
.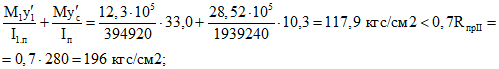
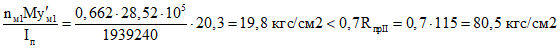 .
.Так как оба условия не выполняются, принимаем k1 = k = 1. В результате
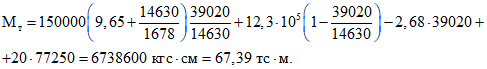
Изгибающие моменты в сечениях ригеля при действии различных видов нагрузок приведены в табл. 4.
Таблица 4
Сечение ригеля | Изгибающие моменты, тс·м, при действии нагрузки | |||
постоянной | временной | общей | ||
длительной | кратковременной | |||
В крайнем пролете (участок 13) | 12,30 | 28,52 | 12,98 | 53,80 |
На первой промежуточной опоре | 0,0 | -30,00 | -18,08 | -48,08 |
Во втором от края пролете (участок 16) | 12,64 | 16,02 | 6,10 | 34,76 |
На средней опоре | 0,0 | -22,49 | -12,05 | -34,54 |
Из этих данных видно, что во всех пролетных сечениях выполняется условие
M + M1 < Mт.
Для опорных сечений ригеля ширину раскрытия трещин определяем по наибольшему значению опорного момента - на первой промежуточной опоре. Полная ширина раскрытия трещин равна [6]
aт = aт1 - aт2 + aт3,
где
aт1 - ширина раскрытия трещин от кратковременного действия всей нагрузки;
aт2 - то же, от кратковременного действия постоянной и длительной нагрузок;
aт3 - ширина раскрытия трещин от длительного действия постоянной и длительной нагрузок.
Все величины aтi вычисляем по формуле (5.10) настоящих методических рекомендаций.
При кратковременном действии всей нагрузки имеем:
F = 2029 см2; Fам = 40,72 см2; pа = 45,24 см; hо = 64 см.
По формуле (5.12) находим
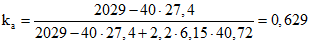 .
.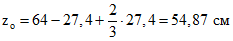 ;
;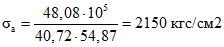 .
.ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 2, а не таблица 5.1. |
При 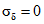 по табл. 5.1 имеем kсц = 0,51. Тогда
по табл. 5.1 имеем kсц = 0,51. Тогда
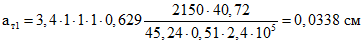 .
.Аналогичным образом определяем величину aт2:
xо = 27,85 см; kа = 0,624; zо = 54,72 см; 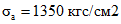 ;
;
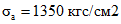 ;
;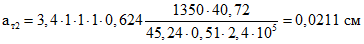 .
.При длительном действии нагрузки xо = 27,85 см;
По формуле (5.2) вычисляем:
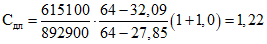 ;
;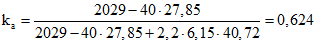 ;
;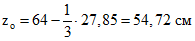 ;
;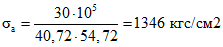 ;
;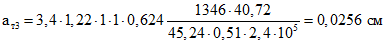 .
.Полная ширина раскрытия трещин:
aт = 0,0338 - 0,0211 + 0,0256 = 0,0383 см.
Пример 2. Определить прогиб в середине пролета сборно-монолитной конструкции, сечение которой показано на рисунке настоящего приложения.
Данные для расчета. Конструкция представляет собой свободнолежащую на двух опорах балку пролетом l = 10 м. К балке приложена равномерно распределенная нагрузка как до, так и после приобретения монолитным бетоном заданной прочности. Сборный элемент воспринимает нагрузку q1 = 1 тс/м; нагрузка на конструкцию qдл = 4 тс/м. Сборный элемент преднапряжен, N1.о = 150 тс, e1.н = 9,65 см. Остальные данные - по примеру 1 настоящего приложения.
Максимальные изгибающие моменты в середине пролета:
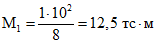 ;
;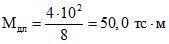 ;
;M1 + Mдл = 62,5 тс·м.
Момент образования трещин равен 67,39 тс·м (см. пример 1), поэтому нормальные трещины в конструкции отсутствуют.
Кривизну от усадки бетонов определяем по формуле (3.1) настоящих методических рекомендаций:
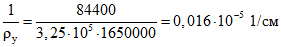 .
.Кривизну от длительного действия усилий предварительного обжатия сборных элементов находим по формулам (3.2) и (3.3):
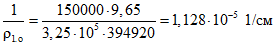 ;
; ;
;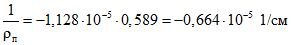 .
.Кривизну от длительного действия нагрузки q1 вычисляем по формулам (3.4) и (3.5):
 ;
;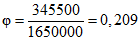 ;
;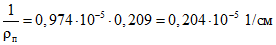 .
.Кривизну сечений от длительного действия нагрузок, приложенных после приобретения монолитным бетоном заданной прочности, определяем по формулам (3.9) - (3.11):
 ;
;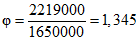 ;
;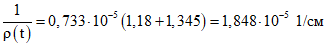 .
.Полный прогиб конструкции в середине пролета
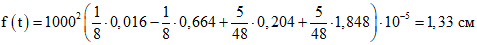 .
.M1 | - | изгибающий момент от собственного веса сборных элементов и монолитного бетона и от внешних нагрузок, действующих к моменту приобретения монолитным бетоном заданной прочности. |
M и Mдл | - | изгибающий момент от внешних нагрузок, приложенных после приобретения монолитным бетоном заданной прочности, и длительно действующая часть указанного момента. |
N1.о | - | равнодействующая сил предварительного обжатия сборных элементов с учетом потерь, проявившихся до приобретения монолитным бетоном заданной прочности. |
Nо | - | равнодействующая сил предварительного обжатия надопорных участков с.н.к. с учетом первых потерь. |
Eа | - | модуль упругости арматурной стали. |
Eс и Eм | - | модули упругости, соответственно, бетона сборных элементов и монолитного бетона. 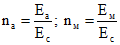 . . |
- | относительные деформации усадки бетона сборных элементов и монолитного бетона к рассматриваемому моменту времени t. | |
- | характеристики ползучести бетона сборных элементов и монолитного бетона к рассматриваемому моменту времени t. | |
Rс.пр и Rм.пр | - | сопротивления бетона сборных элементов и монолитного бетона осевому сжатию. |
Rс.р и Rм.р | - | то же, осевому растяжению. |
Rа | - | сопротивление арматуры растяжению. |
Fам, Fас и | - | площади поперечных сечений арматуры, соответственно Aм, Aс и |
Fс и Iс | - | площадь бетона в поперечном сечении сборных элементов и собственный момент инерции указанной площади. |
Fм и Iм | - | площадь поперечного сечения монолитного бетона и собственный момент инерции указанной площади. |
F1.п и I1.п | - | площадь приведенного сечения сборных элементов и собственный момент инерции указанного сечения. |
Fп и Iп | - | то же, сечения конструкции, приведенного к бетону сборных элементов. 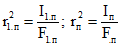 . . |
e1.н и eн | - | эксцентриситеты сил N1.о и Nо относительно ц.т., соответственно, приведенного сечения сборных элементов и сечения конструкции, приведенного к бетону сборных элементов. |
W1.о и W1.т | - | моменты сопротивления приведенного сечения сборных элементов относительно крайних растянутых волокон, определяемые, соответственно, как для упругого материала и с учетом неупругих деформаций растянутого бетона. |
Wо и Wт | - | то же, сечения конструкции, приведенного к бетону сборных элементов. |
b, | - | ширина ребра и ширина сжатой и растянутой полок сечения конструкции, приведенного к бетону сборных элементов. |
hо, | - | рабочая высота поперечного сечения конструкции и высота сжатой и растянутой полок указанного сечения. |
i1 | - | расстояние от ц.т. приведенного сечения сборных элементов до ц.т. площади бетона в указанном сечении. |
iмо и iсо | - | расстояния от ц.т. сечения конструкции, приведенного к бетону сборных элементов, до ц.т., соответственно, площади монолитного бетона и площади бетона в сечении сборных элементов. |
Принятые сокращения: | ц.т. - центр тяжести; н.о. - нейтральная ось; с.о.к. - статически определимые конструкции; с.н.к. - статически неопределимые конструкции. |
1. Бондаренко В.М. Некоторые вопросы нелинейной теории железобетона. - Харьков: изд-во Харьковского университета, 1968, 323 с.
2. Инструкция по проектированию бетонных и железобетонных конструкций из плотного силикатного бетона. СН 165-76. - М.: Стройиздат, 1977, 48 с.
3. Методические рекомендации по учету влияния ползучести бетона при расчете железобетонных стержней и стержневых систем/НИИСК Госстроя СССР. - Киев, 1981, 73 с.
4. Методические рекомендации по определению ширины раскрытия трещин в железобетонных элементах/НИИСК Госстроя СССР. - Киев, 1982, 32 с.
5. Проектирование и изготовление сборно-монолитных конструкций. - Киев: БудIвельник, 1982, 152 с.
6. Строительные нормы и правила, ч. II, гл. 21. "Бетонные и железобетонные конструкции. Нормы проектирования" (СНиП II-21-75). - М.: Стройиздат, 1976; 89 с.
7. Улицкий И.И., Чжан Чжун-яо, Голышев А.Б. Расчет железобетонных конструкций с учетом длительных процессов. - Киев: Госстройиздат УССР, 1960, 495 с.
УДК 624.044:539.376 |
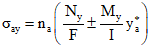
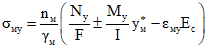
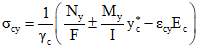
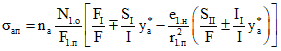
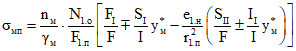

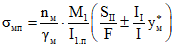
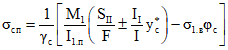
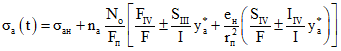
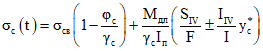

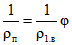
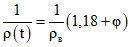
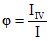
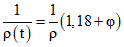
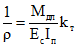

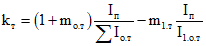
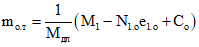
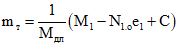
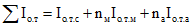
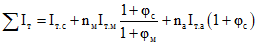
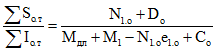
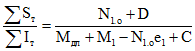
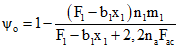
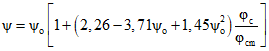
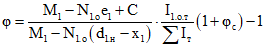
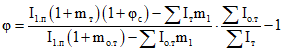

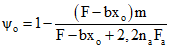
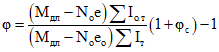
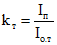
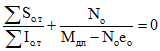

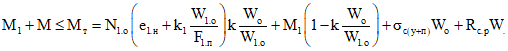
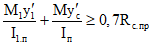
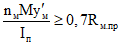
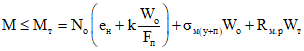
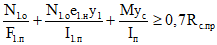
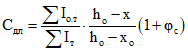
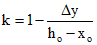
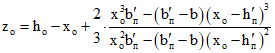

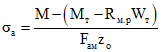
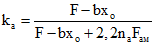
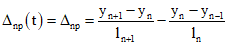
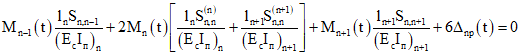
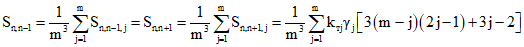
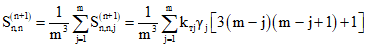
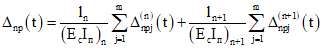
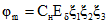
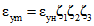
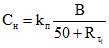

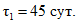 и
и 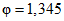 имеем
имеем 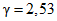 .
.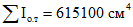 ;
; 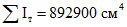 (см.
(см.