СПРАВКА
Источник публикации
Документ опубликован не был
Примечание к документу
Документ утратил силу с 13.03.2024 в связи с введением в действие ОФС.1.1.0013, утв. Приказом Минздрава России от 13.03.2024 N 120.
Текст документа приведен в соответствии с публикацией на сайте https://minzdrav.gov.ru/ по состоянию на 15.08.2023.
В соответствии с Приказом Минздрава России от 20.07.2023 N 377 данный документ введен в действие с 01.09.2023.
Взамен ОФС.1.1.0013.15.
Название документа
"ОФС.1.1.0013. Общая фармакопейная статья. Статистическая обработка результатов физических, физико-химических и химических испытаний"
(утв. и введена в действие Приказом Минздрава России от 20.07.2023 N 377)
("Государственная фармакопея Российской Федерации. XV издание")
"ОФС.1.1.0013. Общая фармакопейная статья. Статистическая обработка результатов физических, физико-химических и химических испытаний"
(утв. и введена в действие Приказом Минздрава России от 20.07.2023 N 377)
("Государственная фармакопея Российской Федерации. XV издание")
Содержание
МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОБЩАЯ ФАРМАКОПЕЙНАЯ СТАТЬЯ
Статистическая обработка результатов физических, физико-химических и химических испытаний | ОФС.1.1.0013 |
Взамен ОФС.1.1.0013.15 |
Настоящая общая фармакопейная статья содержит сведения об основных статистических подходах к обработке и оценке данных, полученных при проведении испытаний лекарственных средств физическими, физико-химическими и химическими методами анализа.
Задача статистической обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится истинное значение. Статистические методы обработки результатов измерений используют для описания полученных данных, наиболее близких к истинному значению, для оценки систематических и случайных погрешностей измерений - результатов испытаний.
Статистическая обработка результатов физических, физико-химических и химических испытаний, которые могут быть изменчивыми, позволяет научно обосновывать и корректно интерпретировать полученные аналитические данные, а затем на их основе решать ряд прикладных задач, связанных с определением статистической достоверности результатов испытаний лекарственных средств. Правильное применение статистических принципов к аналитическим данным испытаний лекарственных средств возможно при условии, что такие данные собраны, зарегистрированы прослеживаемым образом и не содержат систематических ошибок. Получение таких данных необходимо осуществлять в соответствии с требованиями ОФС "Отбор проб", ОФС "Стандартные образцы", ОФС "Валидация аналитических методик". В настоящей общей фармакопейной статье используются некоторые термины, определение которых приведено в ОФС "Отбор проб" и ОФС "Валидация аналитических методик".
Представленные в настоящей общей фармакопейной статье данные носят информационный характер и не являются исчерпывающими.
A - измеряемая величина;
a - свободный член линейной зависимости;
b - угловой коэффициент линейной зависимости;
F - критерий Фишера;
f - число степеней свободы; функция плотности вероятности нормального распределения;
i - порядковый номер варианты;
L - фактор, используемый при оценке сходимости результатов параллельных определений;
m, n - объемы выборки;
P - доверительная вероятность без конкретизации постановки задачи;
(P2), (P1) - доверительная вероятность соответственно при двух- и односторонней постановке задачи;
Q1, Qn - контрольные критерии для идентификации грубых погрешностей;
R - размах варьирования;
Rc - общий индекс корреляции (линейной);
r - (линейный) коэффициент корреляции;
 - относительное стандартное отклонение среднего значения, %;
- относительное стандартное отклонение среднего значения, %;s - стандартное отклонение;
sr - относительное (по отношению к среднему результату) стандартное отклонение;
s2 - дисперсия;
slg - логарифмическое стандартное отклонение;
t - критерий Стьюдента;
U - коэффициент для расчета границ среднего результата гарантии качества испытуемого продукта;
x, y - текущие координаты в уравнении линейной зависимости;
Xi, Yi - вычисленные, исходя из уравнения линейной зависимости, значения переменных x и y;
xi, yi - i-тая варианта (i-тая пара экспериментальных значений x и y);
d или  - разность некоторых величин;
- разность некоторых величин;
p - уровень значимости, степень надежности;
однородной выборки
При статистической обработке результатов физических, физико-химических и химических испытаний используют термин "выборка" для обозначения совокупности реально полученных, статистически эквивалентных результатов испытаний (вариант). В качестве такой совокупности можно, например, рассматривать ряд результатов, полученных при параллельных определениях содержания какого-либо вещества (величины x) в однородной по составу пробе. Количество полученных результатов представляет собой число наблюдений n, образующих выборку, называемых "объемом выборки" Отдельные значения вариант выборки объема n обозначают через xi (1 <= i <= n). Упорядоченная в порядке возрастания вариант выборка может быть представлена в виде:
При статистической обработке результатов физических, физико-химических и химических испытаний различают выборку малого (n <= 10) и большого объема (n > 10). В других случаях статистической обработки результатов выборка "малого объема" может быть определена, как не превышающая 30 (n <= 30).
В большинстве случаев среднее значение выборки  является наилучшей оценкой истинного значения измеряемой величины
является наилучшей оценкой истинного значения измеряемой величины  , если его вычисляют как среднее арифметическое всех вариант:
, если его вычисляют как среднее арифметическое всех вариант:
При этом разброс вариант xi вокруг среднего значения  характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:
характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:
 (1.3)
(1.3)Стандартное отклонение среднего  результата рассчитывают по уравнению:
результата рассчитывают по уравнению:
При обработке результатов испытаний лекарственных средств во многих случаях целесообразно использовать относительные (по отношению к  ) величины, например, относительное стандартное отклонение sr, относительную дисперсию
) величины, например, относительное стандартное отклонение sr, относительную дисперсию  . Их рассчитывают по формулам:
. Их рассчитывают по формулам:
 (1.5а)
(1.5а)Указанные относительные величины в зависимости от решаемой задачи могут выражаться в процентах относительно  . В этом случае их часто обозначают RSD:
. В этом случае их часто обозначают RSD:
 (1.6б)
(1.6б)Относительное стандартное отклонение среднего результата, выраженное в процентах  называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.
называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.
 называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.
называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.Если при измерениях получают логарифмы искомых вариант, среднее значение выборки вычисляют как среднее геометрическое, используя логарифм вариант:
где:
Значения s2, s и  в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s, slg,
в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s, slg,  .
.
Пример вычисления среднего значения и дисперсии приведен в разделе 7.1.
Результаты, полученные при статистической обработке выборки, будут достоверными лишь в том случае, если эта выборка однородна, т.е. если варианты, составляющие выборку, не отягощены грубыми погрешностями, допущенными при измерении или расчете. Для принятия решения об исключении таких выпадающих значений вариант, перед окончательным вычислением статистических характеристик проводят проверку однородности выборки, используя различные подходы в зависимости от объема выборки.
Вместе с тем, следует учитывать, что могут быть такие испытания лекарственных препаратов, которые предусматривают проверку данных каждой из вариант выборки без предварительной оценки ее однородности и исключения вариант, например, при определении показателя "Однородность дозированных" в соответствии с ОФС "Однородность дозирования", когда должны быть учтены и проанализированы все полученные результаты (значения вариант).
Для проверки однородности выборки и исключения резко выделяющихся, выпадающих, отягощенных грубыми погрешностями значений вариант используют различные подходы в зависимости от объема выборки. Для проверки однородности выборок малого и большого объема наиболее часто используют следующие подходы.
Подход 1. Проверку однородности выборок малого объема (n <= 10) осуществляют без предварительного вычисления статистических характеристик. С этой целью все значения выборки представляют в виде (1.1) и предполагают, что крайние, граничные значения вариант выборки, то есть, x1 и xn, являются выпадающими, отягощенными грубыми погрешностями. Для этих крайних значений выборки рассчитывают значения контрольного критерия для идентификации грубых погрешностей Q, исходя из величины размаха варьирования (размаха вариации) R, то есть разности значений между x1 и xn.
R = |x1 - xn| | для n = 3 - 7 | (1.10а) |
для n = 8 - 10 | (1.10б) | |
 | (1.11а) | |
 | (1.11б) |
Выборка признается неоднородной, если хотя бы одно из вычисленных значений Q превышает критическое значение контрольного критерия Q(P, n), найденное для доверительной вероятности P (таблица 8.1 Приложения). Варианты x1 или xn, которым соответствует значение Q > Q(P, n), отбрасывают и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.10) и (1.11) с целью проверки ее однородности.
Если в исходной выборке следующие значения вариант: |x1 - x2| < |x2 - x3| и |xn - xn-1| < |xn-1 - xn-2|, то уравнения (1.11а) и (1.11б) принимают вид:
 (1.12а)
(1.12а) (1.12б)
(1.12б)Полученная в конечном счете однородная выборка используется для вычисления  , s2, s и
, s2, s и  .
.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду раздел 7.2, а не раздел 6.2. |
Пример проверки однородности выборки малого объема приведен в разделе 6.2.
Подход 2. Для проверки однородности выборки большого объема (n > 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности согласно уравнению (1.13).
Вычисляют статистические характеристики  , s2, s и
, s2, s и  для выборки большого объема и проверяют ее однородность. Выборка признается однородной, если для всех вариант выполняется условие:
для выборки большого объема и проверяют ее однородность. Выборка признается однородной, если для всех вариант выполняется условие:
Если выборка признана неоднородной, то варианты, для которых |di| > З·s, отбрасывают как отягощенные грубыми погрешностями с доверительной вероятностью P > 99,0%. В этом случае для полученной выборки сокращенного объема повторяют цикл вычислений статистических характеристик по уравнениям (1.2) - (1.7) и снова проводят проверку однородности. Вычисление статистических характеристик считают законченным, когда выборка сокращенного объема оказывается однородной.
1.4.1. Объединенная дисперсия и объединенное среднее значение
Если имеется g выборок из одной и той же генеральной совокупности с порядковыми номерами k (1 <= k <= g), расчет объединенной дисперсии 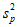 проводят по формуле:
проводят по формуле:
или для объединенных относительных величин:
При этом объединенное число степеней свободы fp равно:
где nk - число вариант в k-той выборке;
fk - число степеней свободы в k-той выборке;
dik - отклонение i-той варианты в k-той выборке.
Если g выборок из одной и той же генеральной совокупности с порядковыми номерами k (1 <= k <= g) характеризуются выборочными средними значениями  , полученными из nk вариант, объединенное среднее значение
, полученными из nk вариант, объединенное среднее значение  по всем выборкам рассчитывают по формуле:
по всем выборкам рассчитывают по формуле:
 (1.16)
(1.16)Необходимым условием совместной статистической обработки нескольких однородных выборок является отсутствие статистически значимой разницы между отдельными значениями  в уравнении (1.14),
в уравнении (1.14),  в уравнении (1.14а) или
в уравнении (1.14а) или  в уравнении (1.14б), т.е. справедливость гипотезы равенства дисперсий. В простейшем случае можно ограничиться сравнением крайних значений
в уравнении (1.14б), т.е. справедливость гипотезы равенства дисперсий. В простейшем случае можно ограничиться сравнением крайних значений  с использованием критерия Фишера F. В более общем случае можно использовать критерии Бартлетта и Кохрена.
с использованием критерия Фишера F. В более общем случае можно использовать критерии Бартлетта и Кохрена.
1.4.2. Критерий Бартлетта
Для проверки гипотезы, что все  принадлежат к одной генеральной совокупности, используют выражение, приближенно распределенное как
принадлежат к одной генеральной совокупности, используют выражение, приближенно распределенное как  :
:
При этом величины s2 и fp рассчитывают по уравнениям (1.14) и (1.15). Найденную таким образом величину  сравнивают с процентной точкой хи-квадрат распределения
сравнивают с процентной точкой хи-квадрат распределения  (таблица 8.5 Приложения). Если имеется g выборок, то число степеней свободы для
(таблица 8.5 Приложения). Если имеется g выборок, то число степеней свободы для  берут равным
берут равным  . Проверяемую гипотезу принимают при условии
. Проверяемую гипотезу принимают при условии  . В противном случае вычисленное значение
. В противном случае вычисленное значение  корректируют по формуле:
корректируют по формуле:
 (таблица 8.5 Приложения). Если имеется g выборок, то число степеней свободы для
(таблица 8.5 Приложения). Если имеется g выборок, то число степеней свободы для  берут равным
берут равным  . Проверяемую гипотезу принимают при условии
. Проверяемую гипотезу принимают при условии  . В противном случае вычисленное значение
. В противном случае вычисленное значение  (1.18)
(1.18)где:
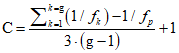 , (1.19)
, (1.19)и снова сравнивают с процентной точкой хи-квадрат распределения  . Если
. Если  , то между некоторыми стандартными отклонениями имеются значимые различия. В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях.
, то между некоторыми стандартными отклонениями имеются значимые различия. В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях.
 . Если
. Если  , то между некоторыми стандартными отклонениями имеются значимые различия. В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях.
, то между некоторыми стандартными отклонениями имеются значимые различия. В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях.Описанный критерий Бартлетта применим только при условии, что число степеней свободы у всех объединяемых дисперсий больше 3, т.е. все fk > 3.
1.4.3. Критерий Кохрена
В том случае, когда все объединяемые дисперсии имеют одинаковое число степеней свободы (т.е. f1 = f2 = ...= fg = f) для проверки гипотезы равенства дисперсий (однородности дисперсий) можно применять значительно более простой критерий Кохрена со статистикой:
где 

В формулах (1.17) и (1.20) вместо абсолютных величин  могут быть использованы относительные величины
могут быть использованы относительные величины  и RSDk.
и RSDk.
Критические значения критерия Кохрена приведены в таблице 8.6. Приложения. Для подтверждения гипотезы об однородности дисперсий рассчитанное значение G на выбранном уровне значимости (95% или 99%) не должно превосходить критическое значение (Gрассчитанное <= Gкритическое). В противном случае гипотеза равенства дисперсий не может быть принята: формулы (1.15) - (1.17) объединения выборок не являются корректными, наибольшую дисперсию в исследуемом наборе дисперсий считают выбросом.
Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины A, имеющей истинное значение  , то среднее этой выборки
, то среднее этой выборки 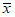 следует рассматривать лишь как приближенную оценку величины A. Достоверность этой оценки характеризуется величиной доверительного интервала
следует рассматривать лишь как приближенную оценку величины A. Достоверность этой оценки характеризуется величиной доверительного интервала  , для которой с заданной доверительной вероятностью P выполняется условие:
, для которой с заданной доверительной вероятностью P выполняется условие:
Данный доверительный интервал не характеризует погрешность определения величины  , поскольку найденная величина
, поскольку найденная величина  может быть в действительности очень близка к истинному значению
может быть в действительности очень близка к истинному значению  , которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности истинного значения
, которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности истинного значения  величины A по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о "неопределенности результатов анализа", которая характеризуется доверительным интервалом, вместо выражения "погрешность результатов анализа", которое нередко не совсем корректно используется.
величины A по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о "неопределенности результатов анализа", которая характеризуется доверительным интервалом, вместо выражения "погрешность результатов анализа", которое нередко не совсем корректно используется.
Расчет граничных значений доверительного интервала при известном значении стандартного отклонения s или для выборок большого объема проводят по уравнению:
 , (1.22а)
, (1.22а)предполагая, что варианты, входящие в выборку, распределены нормально. Здесь U(P) - табличное значение функции нормального распределения.
Для выборок небольшого объема расчет граничных значений доверительного интервала проводят с использованием критерия Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально:
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 8.2, а не таблица 7.2. |
Здесь t(P, f) - табличное значение критерия Стьюдента (таблица 7.2 Приложения).
Распределение по критерию Стьюдента t(P, f) является обобщением нормального распределения U(P) и переходит в него при достаточно большом числе степеней свободы f, т.е.  . С учетом этого далее для единообразия везде используется более часто употребляемое соотношение (1.22б), даже в случае выборок достаточно большого объема.
. С учетом этого далее для единообразия везде используется более часто употребляемое соотношение (1.22б), даже в случае выборок достаточно большого объема.
 . С учетом этого далее для единообразия везде используется более часто употребляемое соотношение (1.22б), даже в случае выборок достаточно большого объема.
. С учетом этого далее для единообразия везде используется более часто употребляемое соотношение (1.22б), даже в случае выборок достаточно большого объема.Если при измерении одной и той же методикой двух близких значений A были получены две случайные однородные выборки с объемами n и m, то при m < n для выборки объема m справедливо уравнение:
где индекс указывает принадлежность величин к выборке объема m или n.
Уравнение (1.23) позволяет оценить величину доверительного интервала среднего  , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего
, найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего  для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14) - (1.15).
для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14) - (1.15).
Аналогично уравнениям (1.21) - (1.22) определяют доверительный интервал результата отдельного определения. Подставляя n = 1 в уравнение (1.22б) или m = 1 в уравнение (1.23), получают:
или с использованием относительных величин:
 (1.24а)
(1.24а)Этот интервал является доверительным интервалом результата отдельного определения. Для него с доверительной вероятностью P выполняются взаимосвязанные условия:
 (1.25)
(1.25) (1.26)
(1.26)Значения  и
и  из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты
из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты  и среднего результата
и среднего результата  , выражая эти величины в процентах:
, выражая эти величины в процентах:
Пример расчета доверительных интервалов в процентах и относительных неопределенностей приведен в разделе 7.3.
Если при измерениях получают логарифмы исходных вариант, то уравнения (1.22б) и (1.24) принимают вид:
Потенцирование выражений (1.29) и (1.30) приводит к несимметричным доверительным интервалам для значений  и xi.
и xi.
где:
 ; (1.33)
; (1.33)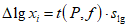 (1.34)
(1.34)При этом для нижних и верхних границ доверительных интервалов  и x относительные неопределенности составляют:
и x относительные неопределенности составляют:
 (1.35б)
(1.35б)1.5.1. Односторонние и двусторонние доверительные интервалы
Выражения (1.21) - (1.35) характеризуют так называемые "двусторонние" доверительные интервалы. Они основаны на двустороннем t-распределении и широко применяются при оценке правильности и прецизионности методик и представлении результатов. Вместе с тем, при решении некоторых задач, например, при контроле готовой продукции, в частности, при контроле качества лекарственных средств, нередко возникает необходимость использования так называемых "односторонних" доверительных интервалов. Например, для какого-нибудь лекарственного препарата допуски количественного содержания действующего вещества установлены от 90% до 110% от номинального. В процессе анализа получено среднее значение содержания  от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90 - 110%). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90%), но не верхнего (110%) одновременно. Вопрос о возможности выхода истинной величины
от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90 - 110%). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90%), но не верхнего (110%) одновременно. Вопрос о возможности выхода истинной величины  за пределы верхнего допуска не рассматривают, в связи с его крайне низкой вероятностью. Таким образом, истинное значение
за пределы верхнего допуска не рассматривают, в связи с его крайне низкой вероятностью. Таким образом, истинное значение  находится в интервале:
находится в интервале:
 от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90 - 110%). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90%), но не верхнего (110%) одновременно. Вопрос о возможности выхода истинной величины
от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90 - 110%). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90%), но не верхнего (110%) одновременно. Вопрос о возможности выхода истинной величины Аналогичное выражение можно записать для случая, когда  превышает 100% (например, 105%):
превышает 100% (например, 105%):
Выражения (1.36а) и (1.36б) характеризуют односторонние доверительные интервалы, поскольку величина  ими ограничивается только с одной стороны. Это отличает их от выражения (1.21), где величина
ими ограничивается только с одной стороны. Это отличает их от выражения (1.21), где величина  ограничивается с обеих сторон.
ограничивается с обеих сторон.
Существует следующее соотношение между двусторонним (P2) и односторонним (P1) критериями Стьюдента:
t[P2, f] = t[(2P1 - 1)f] (1.37)
В частности, односторонний критерий Стьюдента для вероятности 0,95 (т.е. 95%) совпадает с двусторонним критерием Стьюдента для вероятности 0,90 (т.е. 90%).
Таким образом, P2 - это вероятность того, что математическое ожидание (или истинное значение) оцениваемой величины находится в двусторонне ограниченных пределах (1.21) - (1.35), а P1 - это вероятность того, что оно находится в односторонне ограниченных пределах (1.36) - (1.35). Также могут использоваться величины, обозначаемые (1 - P2) и (1 - P1), которые характеризуют вероятность того, что математическое ожидание (или истинное значение) оцениваемой величины выходит за вышеуказанные пределы. Во многих случаях такие величины являются более удобными.
Для решения вопроса о наличии или отсутствии статистически значимой погрешности для выборки объема m, если величина  , используют критерий Стьюдента, обозначаемый t и рассчитываемый по формуле:
, используют критерий Стьюдента, обозначаемый t и рассчитываемый по формуле:
 , используют критерий Стьюдента, обозначаемый t и рассчитываемый по формуле:
, используют критерий Стьюдента, обозначаемый t и рассчитываемый по формуле:или для относительных величин:
 (1.38а)
(1.38а)Если, например, при P = 95% и f = m - 1, реализуется неравенство:
то полученные данной методикой результаты отягощены систематической погрешностью, относительная величина которой  может быть вычислена по формуле:
может быть вычислена по формуле:
 (1.40)
(1.40)Статистически значимая систематическая погрешность может быть приемлема для решения поставленной аналитической задачи, если она критически не влияет на принятие решения по результатам анализа.
На статистическую значимость систематической погрешности влияет прецизионность. Вследствие высокой прецизионности систематическая погрешность может оказаться статистически значимой, и наоборот, низкая прецизионность может привести к статистической незначимости систематической погрешности (эффект маскировки).
Предположим, что для методики 1 систематическая погрешность  и стандартное отклонение s1 = 1,20%, а для методики 2 данные величины имеют значения
и стандартное отклонение s1 = 1,20%, а для методики 2 данные величины имеют значения  и s2 = 0,33%. За счет худшей прецизионности систематическая погрешность методики 1 оказывается статистически незначимой. Лучшая прецизионность методики 2 приводит к статистической значимости систематической погрешности, несмотря на то, что ее значение меньше в 2 раза, чем у методики 1. Поэтому создается ложное представление о невозможности использования методики 2 для конкретной аналитической задачи, например, количественного определения действующего вещества в лекарственном препарате. В действительности, для данной цели целесообразно использовать именно методику 2.
и s2 = 0,33%. За счет худшей прецизионности систематическая погрешность методики 1 оказывается статистически незначимой. Лучшая прецизионность методики 2 приводит к статистической значимости систематической погрешности, несмотря на то, что ее значение меньше в 2 раза, чем у методики 1. Поэтому создается ложное представление о невозможности использования методики 2 для конкретной аналитической задачи, например, количественного определения действующего вещества в лекарственном препарате. В действительности, для данной цели целесообразно использовать именно методику 2.
 и стандартное отклонение s1 = 1,20%, а для методики 2 данные величины имеют значения
и стандартное отклонение s1 = 1,20%, а для методики 2 данные величины имеют значения  и s2 = 0,33%. За счет худшей прецизионности систематическая погрешность методики 1 оказывается статистически незначимой. Лучшая прецизионность методики 2 приводит к статистической значимости систематической погрешности, несмотря на то, что ее значение меньше в 2 раза, чем у методики 1. Поэтому создается ложное представление о невозможности использования методики 2 для конкретной аналитической задачи, например, количественного определения действующего вещества в лекарственном препарате. В действительности, для данной цели целесообразно использовать именно методику 2.
и s2 = 0,33%. За счет худшей прецизионности систематическая погрешность методики 1 оказывается статистически незначимой. Лучшая прецизионность методики 2 приводит к статистической значимости систематической погрешности, несмотря на то, что ее значение меньше в 2 раза, чем у методики 1. Поэтому создается ложное представление о невозможности использования методики 2 для конкретной аналитической задачи, например, количественного определения действующего вещества в лекарственном препарате. В действительности, для данной цели целесообразно использовать именно методику 2.Таким образом, статистически значимая систематическая погрешность, может быть приемлемой и неприемлемой для решения поставленной аналитической задачи. В связи с этим статистически значимые систематические погрешности, т.е. погрешности, для которых выполняется неравенство (1.39), в дальнейшем оценивают на их практическую значимость.
Сравнение двух методик анализа по прецизионности проводят путем выяснения значимости различия выборочных дисперсий анализа этих двух методик. В более общем случае данный подход применяют для оценки значимости различия двух выборочных дисперсий, например, с целью выяснения, можно ли их считать выборочными оценками одной и той же дисперсии генеральной совокупности.
При сравнении прецизионности двух методик анализа с оценками дисперсий  и
и 
 вычисляют критерий Фишера F.
вычисляют критерий Фишера F.
 вычисляют критерий Фишера F.
вычисляют критерий Фишера F.Критерий F характеризует при  достоверность различия между
достоверность различия между  и
и  .
.
Вычисленное значение F сравнивают с табличным значением F(P, f1, f2), найденным при P1 = 99% (таблица 8.3 Приложения).
Если для вычисленного значения F выполняется неравенство:
то различие дисперсий  и
и  признается статистически значимым с вероятностью P1, что позволяет сделать заключение о более высокой прецизионности второй методики.
признается статистически значимым с вероятностью P1, что позволяет сделать заключение о более высокой прецизионности второй методики.
Если выполняется неравенство:
то различие значений  и
и  не может быть признано значимым и заключение о различии прецизионности (сходимости) методов сделать нельзя ввиду недостаточного объема информации.
не может быть признано значимым и заключение о различии прецизионности (сходимости) методов сделать нельзя ввиду недостаточного объема информации.
Если:
F(P1 = 0,95, f1, f2) < F < F(P1 = 0,99, f1, f2) (2.4)
то целесообразно провести дальнейшие экспериментальные исследования для методики с лучшей прецизионностью (сходимостью).
При сравнении двух методик анализа результаты статистической обработки могут быть представлены в виде табл. 2.1.
Таблица 2.1
двух методик анализа по прецизионности
Методика N п/п | f | s | P | t(P, f) (табл.) | tвыч | F(P1, f1, f2) (табл.) при P = 99% | Fвыч | Примечания | |||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | ||
1 | |||||||||||||
2 |
Сравнение методик анализа желательно проводить при  , f1 > 10 и f2 > 10. Если точные значения
, f1 > 10 и f2 > 10. Если точные значения  и
и  неизвестны, величины
неизвестны, величины  и tвыч не определяют.
и tвыч не определяют.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (2.1), а не уравнение (3.1). |
Если при измерениях получают логарифмы исходных вариант, то вместо величин  ,
,  и s в табл. 2.1. приводят величины
и s в табл. 2.1. приводят величины  ,
,  и slg. При этом в графу 8 вносят величину
и slg. При этом в графу 8 вносят величину  , а в графу 9 - максимальное по абсолютной величине значение
, а в графу 9 - максимальное по абсолютной величине значение 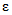 . Аналогичные замены проводят при вычислении t по уравнению (1.38) и F - по уравнению (3.1).
. Аналогичные замены проводят при вычислении t по уравнению (1.38) и F - по уравнению (3.1).
Пример сравнения двух методик анализа по прецизионности приведен в разделе 7.4.
Если с помощью данной методики анализа определяют значение некоторой величины A, то для экспериментально полученной однородной выборки объема m рассчитывают значения величин, приведенных в таблице 3.1. Если же для данной методики уже имеются данные для статистической обработки (например, полученные при сравнении методик по прецизионности (табл. 2.1)), то в целях значительного сужения границ доверительного интервала за счет большего числа степеней свободы (уравнение 1.23) возможно их использование при заполнении граф 2, 4, 5, 7, 8 и 9 таблицы 3.1.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (1.14), а не уравнение (1.21). |
Таблица 3.1
m | f | s | P | t(P, f) | |||||
1 | 6 |
Во многих случаях проще использовать относительные (по отношению к  ) величины. В этом случае целесообразно использовать данные табл. 3.2.
) величины. В этом случае целесообразно использовать данные табл. 3.2.
Таблица 3.2
Данные для сравнения средних результатов
выборок с использованием относительных величин
m | f | s | sr | P | t(P, f) | ||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Таким образом, на основании уравнения (1.21) для измеряемой величины A при незначительной систематической погрешности с вероятностью P выполняется условие:
 , (3.1)
, (3.1)т.е., величина A при незначительной систематической погрешности лежит в пределах:
 (3.2)
(3.2)или с использованием относительных величин:
 (3.2а)
(3.2а)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (1.35а), а не уравнение (1.33а). |
Если при измерениях получают логарифмы исходных вариант, в графе 9 таблицы 3.1 приводят величину  , а каждую из граф 3, 9 и 10 разбивают на две (а, б). В графе 3а приводят значение
, а каждую из граф 3, 9 и 10 разбивают на две (а, б). В графе 3а приводят значение  , в графе 3б - значение
, в графе 3б - значение  , в графах 9а и 9б - соответственно значения нижней и верхней границ доверительного интервала для
, в графах 9а и 9б - соответственно значения нижней и верхней границ доверительного интервала для  (уравнения (1.31) и (1.32)). Наконец, в графе 10 приводят максимальное по абсолютной величине значение
(уравнения (1.31) и (1.32)). Наконец, в графе 10 приводят максимальное по абсолютной величине значение  (уравнение (1.33а)).
(уравнение (1.33а)).
Если в результате измерений одной и той же величины A получены две выборки объема n1 и n2, причем  , может возникнуть необходимость проверки статистической достоверности гипотезы:
, может возникнуть необходимость проверки статистической достоверности гипотезы:
т.е. значимости величины разности  .
.
 .
.Такая проверка необходима, например, если величина A определялась двумя разными методиками с целью их сравнения, или, если величина A определялась одной и той же методикой для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы (3.3) следует установить, существует ли статистически значимое различие между дисперсиями  и
и  . Эта проверка проводится так же, как при сравнении двух методик анализа по воспроизводимости согласно уравнениям (2.1) - (2.3).
. Эта проверка проводится так же, как при сравнении двух методик анализа по воспроизводимости согласно уравнениям (2.1) - (2.3).
Рассматривают три случая.
Различие дисперсий  и
и  статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию
статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию 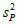 разности
разности  - по уравнению:
- по уравнению:
 - по уравнению:
- по уравнению: . (3.4а)
. (3.4а)Далее вычисляют критерий Стьюдента:
при f = n1 + n2 - 2. (3.5а)
Если при выбранном значении P2 (например, при P2 = 95%):
t > t(P2, f), (3.6)
то результат проверки положителен: разность  является значимой и гипотезу
является значимой и гипотезу  отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.
отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.
 является значимой и гипотезу
является значимой и гипотезу Различие дисперсий  и
и  статистически значимо, когда справедливо неравенство (2.2). Если
статистически значимо, когда справедливо неравенство (2.2). Если  , дисперсию
, дисперсию 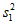 разности
разности  находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8):
находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8):
 находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8):
находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8): , (3.7)
, (3.7)Следовательно, в данном случае:
Вычисленное по уравнению (3.9) значение t сравнивают с табличным значением t(P2, f'), как это описано выше для первого случая.
Приведенные выше расчеты упрощаются, когда  и
и  . Тогда в отсутствие систематической погрешности среднее
. Тогда в отсутствие систематической погрешности среднее 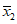 выборки объема n2 принимают за достаточно точную оценку величины A, т.е. принимают
выборки объема n2 принимают за достаточно точную оценку величины A, т.е. принимают  . Справедливость гипотезы
. Справедливость гипотезы  , эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1 = n1 - 1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39).
, эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1 = n1 - 1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39).
 . Тогда в отсутствие систематической погрешности среднее
. Тогда в отсутствие систематической погрешности среднее Известно точное значение величины A. Если  , проверяют две гипотезы:
, проверяют две гипотезы:  и
и  . Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена.
. Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена.
Если при измерениях получают логарифмы исходных вариант, при сравнении средних используют величины 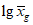 ,
, 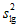 и slg. В тех случаях, когда разность
и slg. В тех случаях, когда разность  оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних
оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних  :
:
 оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних
оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних  :
:Пример сравнения средних результатов двух выборок приведен в разделе 7.5.
Оценка сходимости результатов параллельных определений. При рядовых исследованиях аналитик обычно проводит 2 - 3, реже 4 параллельных определения. Варианты полученной при этом упорядоченной выборки объема m, как правило, довольно значительно отличаются друг от друга. Если метод анализа метрологически аттестован, то максимальная разность результатов двух параллельных определений должна удовлетворять неравенству:
где L(P, m) - фактор, вычисленный по Пирсону при P = 95%.
Таблица 4.1
Фактор, вычисленный по Пирсону
m | 2 | 3 | 4 |
L(95%, m) | 2,77 | 3,31 | 3,65 |
Если неравенство (4.1) не выполняется, необходимо провести дополнительное определение и снова проверить, удовлетворяет ли величина |x1 - xn| неравенству (4.1).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду неравенство (4.1), а не неравенство (5.1). |
Если для результатов 4 параллельных определений неравенство (4.1) не выполняется, одна из вариант (x1 или xn) должна быть отброшена и заменена новой. При невозможности добиться выполнения неравенства (5.1) следует считать, что конкретные условия анализа привели к снижению воспроизводимости метода и принятая оценка величины s применительно к данному случаю является заниженной. В этом случае поступают, как указано в разделе 1.
Определение необходимого числа параллельных определений. Если необходимо получить средний результат 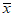 с относительной погрешностью
с относительной погрешностью  с
с  , причем метод анализа метрологически аттестован, необходимое число параллельных определений m находят учетом с уравнений (1.23) и (1.24):
, причем метод анализа метрологически аттестован, необходимое число параллельных определений m находят учетом с уравнений (1.23) и (1.24):
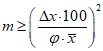 (4.2)
(4.2)Гарантия качества продукции. Предположим, что качество продукции регламентируется предельными значениями amin и amax величины A, которую определяют на основании результатов анализа. Примем, что вероятность соответствия качества продукта условию:
должна составлять 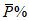 .
.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду условие (4.3), а не условие (5.3). |
Пусть величину A находят экспериментально, как среднее выборки объема m, а метод ее определения метрологически аттестован. Тогда условие (5.3) будет выполняться с вероятностью  , если значение
, если значение  будет лежать в пределах:
будет лежать в пределах:
 , (4.4)
, (4.4)где:
Значения коэффициента U для вероятности  и
и  соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины A на практике следует ограничить значениями:
соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины A на практике следует ограничить значениями:
 и
и  соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины A на практике следует ограничить значениями:
соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины A на практике следует ограничить значениями:Наоборот, если заданы значения Amin и Amax, значения amin и amax, входящие в неравенство (4.3), могут быть найдены путем решения уравнений (4.6) и (4.7). Наконец, если заданы пары значений Amin, amin и Amax, amax, то уравнения (4.6) и (4.7) могут быть решены относительно m. Это может быть использовано для оценки необходимого числа параллельных определений величины A.
Примечание 4.1. В уравнениях (4.5), (4.6) и (4.7) величина коэффициента  должна быть заменена величиной
должна быть заменена величиной  , если значение f, определенное по уравнениям (1.4) или (1.14), меньше 15.
, если значение f, определенное по уравнениям (1.4) или (1.14), меньше 15.
 , если значение f, определенное по уравнениям (1.4) или (1.14), меньше 15.
, если значение f, определенное по уравнениям (1.4) или (1.14), меньше 15.Примечание 4.2. Для случая, предусмотренного примечанием 5.1, описанные в разделе 5 вычисления проводят с использованием величин  ,
,  , slg и т.п.
, slg и т.п.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду таблица 7.4, а не таблица 3. |
Пример 4.1. Рассмотрим данные табл. 3, относящиеся к выборке 1, как метрологическую характеристику используемого метода анализа.
а) Пусть amin = 98%, amax = 100,50%. Тогда для испытуемого образца продукта средний результат анализа  при проведении трех параллельных определений (m = 3) должен находиться в пределах:
при проведении трех параллельных определений (m = 3) должен находиться в пределах:
 .
.При 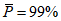 :
:
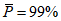 :
: ;
;98,62 < A < 99,88.
При  :
:
 :
: ;
;98,44 < A < 100,06.
б) Реальный средний результат анализа образца испытуемого продукта A = 99% (при m = 3). Тогда определение пределов amin и amax, гарантированно характеризующих качество данного образца с заданной доверительной вероятностью  , проводим, исходя из уравнения (4.6) или (4.7), полагая
, проводим, исходя из уравнения (4.6) или (4.7), полагая
Amin = Amax = A,
 ,
,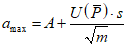 .
.При  :
:
 :
: ;
; .
.При  :
:
 :
: ;
;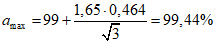 .
.Полученные оценки amin и amax близки к границам доверительного интервала  , что соответствует примечанию 4.1.
, что соответствует примечанию 4.1.
 , что соответствует примечанию 4.1.
, что соответствует примечанию 4.1.линейной зависимости
При использовании физических, физико-химических и химических методов анализа для количественного определения веществ непосредственному измерению подвергается некоторая величина y (аналитический сигнал), которая является, как правило, линейной функцией искомой концентрации (количества) x определяемого вещества или элемента. Иными словами, в основе таких методов анализа лежит экспериментально подтвержденная линейная зависимость:
где y - измеряемая величина (измеряемое значение аналитического сигнала);
x - концентрация (количество) определяемого вещества или элемента;
b - угловой коэффициент линейной зависимости;
a - свободный член линейной зависимости.
(Здесь b и a рассматривают как коэффициенты (параметры) линейной регрессии y на x).
Для использования зависимости (5.1) в аналитических целях, т.е. для определения конкретной величины x по измеренному значению y, необходимо заранее найти числовые значения констант b и a, т.е. провести калибровку. Иногда константы зависимости (5.1) имеют тот или иной физический смысл, и их значения должны оцениваться с учетом соответствующего доверительного интервала. Если калибровка проведена и значения констант a и b определены, величину xi находят по измеренному значению yi:
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду зависимость (5.1), а не зависимость (7.1). |
При калибровке величину x рассматривают как аргумент, а величину y - как функцию. Наличие линейной зависимости между x и y не всегда является очевидным, ее наличие целесообразно подтверждать расчетным путем. Для этого по экспериментальным данным, полученным при калибровке, оценивают достоверность линейной связи между x и y с использованием корреляционного анализа и лишь затем рассчитывают значения констант a и b зависимости (7.1) и их доверительные интервалы. В первом приближении судить о достоверности линейной связи между переменными x и y можно по величине линейного коэффициента корреляции (или просто коэффициента корреляции) r, который вычисляют по формуле, исходя из экспериментальных данных:
Линейный коэффициент корреляции r изменяется в пределах от -1 до +1. Положительные значения r указывают на рост, а негативные - на уменьшение y с ростом x.
Линейный коэффициент корреляции r является частным случаем общего индекса корреляции Rc, который применим также и для нелинейных зависимостей между величинами y и x:
где so - остаточное стандартное отклонение (стандартное отклонение линейной зависимости) (уравнение 5.7);
sy - стандартное отклонение величин у относительно среднего значения  (5.15); рассчитывают с использованием уравнения (1.5).
(5.15); рассчитывают с использованием уравнения (1.5).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (5.3), а не уравнение (4.3). |
Уравнение (5.3а) в силу своей простоты и наглядности нередко используют вместо уравнения (4.3) в том случае, когда знак коэффициента корреляции не имеет значения.
Чем ближе абсолютная величина |r| к единице, тем менее случайна наблюдаемая линейная зависимость между переменными x и y. Коэффициент корреляции r используют обычно для выявления стохастической взаимосвязи между величинами, функциональная зависимость между которыми может и отсутствовать. Коэффициент корреляции является значимым, если его величина для данной вероятности P и числа степеней свободы f превышает значения, приведенные табл. 8.4. Приложения. В противном случае нельзя говорить о существовании значимых зависимостей (5.1) - (5.2).
Значимость коэффициента корреляции является обязательным, но не достаточным условием использования уравнений (5.1) - (5.2) для аналитических целей. При статистической обработке результатов физического, физико-химического или химического методов анализа лекарственных средств могут быть использованы линейные зависимости с коэффициентом корреляции |r| >= 0,98 (при соответствии требованиям табл. 8.4. Приложения), а при анализе следовых количеств определяемых веществ рассматривают линейные зависимости с коэффициентом корреляции |r| >= 0,90. При столь близких значениях величины |r| к единице формальное подтверждение наличия линейной связи между переменными x и y проводить не следует. Вместе с тем необходимо учитывать, что для различных методов анализа лекарственных средств, требования к линейности метода, могут быть различными.
Коэффициенты a и b и другие характеристики линейной зависимости (5.1) рассчитывают с использованием регрессионного анализа, т.е. методом наименьших квадратов по экспериментально измеренным значениям переменной y для заданных значений аргумента x. Пусть в результате эксперимента найдены представленные в таблице 5.1 пары значений аргумента x и функции y.
Таблица 5.1
i | xi | yi |
1 | x1 | y1 |
2 | x2 | y2 |
... | ... | ... |
m | xm | ym |
Тогда, если величины y1 имеют одинаковую неопределенность (а такое допущение обычно выполняется для достаточно узкого диапазона варьирования величин y1), то
 (5.4)
(5.4) (5.5)
(5.5)f = m - 2 (5.6)
Если полученные значения коэффициентов a и b использовать для вычисления значений y по заданным в таблице 5.1 значениям аргумента x согласно зависимости (5.1), то вычисленные значения y обозначают через Y1, Y2, ..., Yi, ... Yn. Разброс значений yi относительно значений Yi характеризует величина остаточной дисперсии  (дисперсии линейной зависимости), которую вычисляют по формуле:
(дисперсии линейной зависимости), которую вычисляют по формуле:
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеются в виду уравнения (5.1) - (5.2), а не уравнения (4.1) - (4.2). |
Для того, чтобы уравнения (4.1) - (4.2) адекватно описывали экспериментальные данные, необходимо, чтобы остаточная дисперсия  не отличалась значимо по критерию Фишера (уравнения (2.1) и (2.2)) от дисперсии прецизионности величин y1. Последняя может быть найдена или спрогнозирована из паспортных данных оборудования.
не отличалась значимо по критерию Фишера (уравнения (2.1) и (2.2)) от дисперсии прецизионности величин y1. Последняя может быть найдена или спрогнозирована из паспортных данных оборудования.
В свою очередь, дисперсии констант b и a находят по уравнениям:
 (5.8)
(5.8) (5.9)
(5.9)Стандартные отклонения sb и sa и величины  и
и  , необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям:
, необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям:
 (5.10)
(5.10) (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13)Коэффициенты a и b должны значимо отличаться от нуля, т.е. превышать, соответственно, величины  и
и  .
.
Уравнению (5.1) с константами a и b обязательно удовлетворяет точка с координатами  и
и 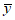 , называемая центром калибровочного графика:
, называемая центром калибровочного графика:
 (5.14)
(5.14)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеются в виду уравнения (5.1) и (5.2), а не уравнения (4.1) и (4.2). |
Наименьшие отклонения значений yi от значений Yi наблюдаются в окрестностях центра графика. Стандартные отклонения sy и sx величин y и x, рассчитанных соответственно по уравнениям (4.1) и (4.2), исходя соответственно из известных значений x и y, определяют с учетом удаления последних от центра графика:
где  - среднее значение;
- среднее значение;
nj - число вариант y, использованных при определении  .
.
 (5.16а)
(5.16а) (5.17а)
(5.17а)С учетом значений sy и sx могут быть найдены значения величин  и
и 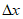 .
.
 (5.18)
(5.18) (5.19)
(5.19)Значения sx и  , найденные при nj = 1, являются характеристиками прецизионности аналитической методики, если x - концентрация (количество), а y - функция x.
, найденные при nj = 1, являются характеристиками прецизионности аналитической методики, если x - концентрация (количество), а y - функция x.
Обычно результаты статистической обработки по методу наименьших квадратов сводят в таблицу (табл. 5.2).
Таблица 5.2
Результаты статистической обработки экспериментальных
данных, полученных при изучении линейной зависимости
y = bx + a
f | b | a | t(P2; f) при P2 = 95% | r | sx при nj = 1, |  % % | ||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
1. Если целью экспериментальной работы являлось определение констант b и a, графы 11, 12 и 13 таблицы не заполняют
2. Если y = b·lg x + a, вычисления, описанные в настоящем разделе, выполняют с использованием уравнений (1.8), (1.9), (1.29) - (1.32).
3. Сравнение дисперсий  , полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 2.
, полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 2.
случайных переменных
Описанные в разделах 1 - 4 настоящей общей фармакопейной статьи расчеты доверительных интервалов результатов методик анализа применимы лишь в том случае, если измеряемая величина (концентрация, содержание и т.д.) является функцией только одной случайной переменной. Однако большинство методик количественного определения при испытании лекарственных средств методами физического, физико-химического и химического анализа являются косвенными, то есть используют стандартные образцы. Следовательно, измеряемая величина является функцией, как минимум, двух случайных переменных - аналитических сигналов (оптическая плотность или поглощение, высота или площадь пика и т.д.) испытуемого и стандартного образцов. Кроме того, нередко возникает проблема прогнозирования неопределенности аналитической методики, состоящей из нескольких стадий (взвешивание, разведение, конечная аналитическая операция), каждая из которых является по отношению к другой случайной величиной.
Таким образом, возникает общая проблема оценки неопределенности косвенно измеряемой величины, зависящей от нескольких измеряемых величин, в частности, как рассчитывать неопределенность всей аналитической методики, если известны неопределенности отдельных ее составляющих (стадий).
Если измеряемая на опыте величина y является функцией п независимых случайных величин xi, то есть:
y = f(x1, x2,.... xn) (6.1)
и число степеней свободы величин xi одинаково или достаточно велико (> 30, чтобы можно было применять статистику Гаусса, а не Стьюдента), то дисперсия величины y связана с дисперсиями величин xi соотношением (правило распространения неопределенностей):
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (6.2), а не уравнение (5.2). |
Однако на практике степени свободы величин xt обычно невелики и не равны друг другу. Кроме того, обычно интерес представляют не сами дисперсии (стандартные отклонения), а доверительные интервалы, рассчитать которые, используя уравнение (5.2), при небольших и неодинаковых степенях свободы невозможно. Поэтому для расчета неопределенности величины y  предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча-Сатертуэйта.
предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча-Сатертуэйта.
Если случайные переменные xi статистически независимы, то доверительный интервал функции  связан с доверительными интервалами переменных
связан с доверительными интервалами переменных  соотношением (доверительные интервалы берутся для одной и той же вероятности):
соотношением (доверительные интервалы берутся для одной и той же вероятности):
 . (6.3)
. (6.3)Данное выражение является обобщением соотношения (6.2).
При испытании лекарственных средств методами физического, физико-химического и химического анализа, измеряемая величина y представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разведений, поглощений или площадей пиков и т.д.), т.е. (K - некая константа):
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду соотношение (6.2), а не соотношение (4.2). |
В этом случае соотношение (4.2) принимает вид:
где использованы относительные доверительные интервалы.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду соотношение (6.4), а не соотношение (5.4). |
Соотношение (5.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин xi. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду выражение (6.5), а не выражение (5.5). |
При проведении испытаний лекарственных средств в суммарной неопределенности  анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки
анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки  , неопределенность конечной аналитической операции
, неопределенность конечной аналитической операции  и неопределенность аттестации стандартного образца
и неопределенность аттестации стандартного образца  . Величина
. Величина  обычно мала, поэтому в приведенном выражении она не использована. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс "smp") и для раствора сравнения (индекс "st"), выражение (5.5) можно представить в виде:
обычно мала, поэтому в приведенном выражении она не использована. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс "smp") и для раствора сравнения (индекс "st"), выражение (5.5) можно представить в виде:
 и неопределенность аттестации стандартного образца
и неопределенность аттестации стандартного образца ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (6.5), а не уравнение (5.5). |
При этом каждое из слагаемых рассчитывают из входящих в него компонентов по уравнению (5.5).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду выражение (6.5), а не выражение (5.5). |
Если число степеней свободы величин xi одинаково или достаточно велико (> 30), выражение (5.5) дает:
Это же соотношение получают при тех же условиях и из выражения (6.2).
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду соотношение (6.2), а не соотношение (5.2). |
В этом подходе дисперсию величины y (s2y) рассчитывают по соотношению (5.2), не обращая внимания на различие в степенях свободы (vi) величин xi Для полученной дисперсии s2y рассчитывают некое "эффективное" число степеней свободы veff (которое обычно является дробным), на основе которого затем по таблицам для заданной вероятности находят интерполяцией значения критерия Стьюдента. На основе его далее рассчитывают обычным путем доверительный интервал величины y  :
:
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеются в виду выражение (6.7) и соотношение (6.8), а не выражение (5.7) и соотношение (5.8). |
Для определения величины y обычно выполняется уравнение (6.4). В этом случае в подходе Уэлча-Сатертуэйта соотношение (6.2) переходит в выражение (5.7), и соотношение (5.8) принимает более простой вид:
 (6.9)
(6.9)ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду соотношение (6.7), а не соотношение (5.7). |
Здесь величину sy,r4 рассчитывают из соотношения (5.7).
Подход Уэлча-Сатертуэйта обычно дает более узкие доверительные интервалы, чем линейная модель. Однако он гораздо сложнее в применении и не позволяет выделить так просто неопределенности разных этапов (с последующими рекомендациями по их минимизации), как линейная модель в форме выражения (6.6).
При прогнозе неопределенности анализа используют генеральные величины (с бесконечным числом степеней свободы). В этом случае подход Уэлча-Сатертуэйта совпадает с линейной моделью.
Пример расчета неопределенности функции нескольких переменных приведен в разделе 7.6.
При количественном определении действующего вещества в образце лекарственного препарата, были получены данные, указанные в табл. 7.1.
Таблица 7.1
Содержание действующего вещества в образце | Порядковый номер варианты i | ||||
1 | 2 | 3 | 4 | 5 | |
xi, % | 9,52 | 9,55 | 9,83 | 10,12 | 10,33 |
n = 5; f = n - 1 = 5 - 1 = 4.
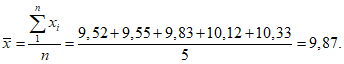
 ,
,т.е.
di=1 = |9,52 - 9,87| = 0,35 и т.д. до i = 5.

 ;
; ;
;RSD = sr·100% = 3,59%;
 ;
; ;
; .
.При количественном определении действующего вещества в каждой из девяти (n = 9) выборок лекарственного препарата были получены данные, указанные в табл. 7.2 (в порядке возрастания).
Таблица 7.2
Содержание действующего вещества | Порядковый номер варианты i | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
xi, % | 0,62 | 0,81 | 0,83 | 0,86 | 0,87 | 0,90 | 0,94 | 0,98 | 0,99 |
По уравнениям (1.10б) и (1.11а) находим:
R = |x1 - xn-1| = |0,62 - 0,98| = 0,36;
 .
.По табл. 8.1. Приложения находим:
Q(9; 95%) = 0,46 < Q1 = 0,53;
Q(9; 99%) = 0,55 > Q1 = 0,53.
Следовательно, гипотеза о том, что значение x1 = 0,62 должно быть исключено из рассматриваемой совокупности результатов измерений как отягощенное грубой погрешностью, может быть принята с доверительной вероятностью 95%, но должна быть отвергнута, если выбранное значение доверительной вероятности равно 99%.
При определении количественного содержания действующего вещества в образце активной фармацевтической субстанции были получены данные (n = 10), указанные в таблице 7.3.
Таблица 7.3
Содержание действующего вещества | Порядковый номер варианты i | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
xi, % | 49,80 | 49,83 | 49,87 | 49,87 | 49,92 | 50,01 | 50,05 | 50,06 | 50,10 | 50,11 |
 .
.Доверительные интервалы результата отдельного определения и среднего результата при P2 = 90% получаются согласно (1.24) и (1.22):

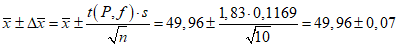 .
. ;
; .
.Обозначая истинное содержание действующего вещества в фармацевтической субстанции через  , можно считать, что с 90% доверительной вероятностью справедливы неравенства:
, можно считать, что с 90% доверительной вероятностью справедливы неравенства:
 ;
; ;
; .
.Пусть для двух выборок аналитических данных (1 и 2), характеризующих, например, различные методики анализа, получены данные для статистической обработки, приведенные в графах 1 - 10 табл. 7.4.
Номер выборки | f | s | P2, % | t(P2, f) (табл.) | tвыч | F(P1, f1, f2) (табл.) при P = 99% | Fвыч | |||||
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
1 | 100 | 20 | 100,13 | 0,464 | 95 | 2,09 | 0,97 | 0,97 | 1,28 | 3,36 | 17,92 | - |
2 | 100 | 15 | 98,01 | 0,110 | 95 | 2,13 | 0,23 | 0,24 | 72,36 | 3,36 | 17,92 | 1,99 |
Для заполнения графы 10 вычисляем значения tвыч(1) и tвыч(2):
 ;
; .
.Поскольку tвыч(1) = 1,28 < t1 (95%, 20) = 2,09, гипотеза  может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки.
может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки.
 может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки.
может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки.Напротив, поскольку tвыч(2) = 72,36 >> t2 (95%, 15) = 2,13, гипотезу  приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение
приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение 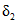 :
:
 приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение
приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение  .
.F(99%; 20; 15) = 3,36;
 ;
;F = 17,92 >> F(99%; 20; 15) = 3,36.
Следовательно, при P1 = 99% гипотезу о различии дисперсий 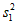 и
и  следует признать статистически достоверной.
следует признать статистически достоверной.
Выводы:
- результаты, полученные при использовании первой методики, являются правильными, т.е. они не отягощены систематической погрешностью;
- результаты, полученные при использовании второй методики, отягощены систематической погрешностью;
- по прецизионности вторая методика существенно превосходит первую методику.
При определении содержания действующего вещества в двух образцах лекарственного препарата, произведенных по разной технологии, получены данные для статистической обработки средних результатов, приведенные в таблице 7.5. Требуется определить, является ли первый образец по данному показателю лучшим в сравнении со вторым образцом.
Таблица 7.5
N образца | n | f | s | P2, % | t(P2, f) | |||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1 | 8 | 7 | 99,10 | 0,50 | 0,18 | 95 | 2,36 | 1,18 | 0,42 | 0,42 |
2 | 6 | 5 | 98,33 | 0,56 | 0,23 | 95 | 2,57 | 1,44 | 0,59 | 0,60 |
Поскольку  ,
,
 ,
, ;
; .
. ;
; .
.f = n1 + n2 - 2 = 8 + 6 - 2 = 12.
 .
.t = 2,72 > t(95%; 12) = 2,18.
t = 2,72 < t(99%; 12) = 3,08.
Следовательно, с доверительной вероятностью P2 = 95% гипотеза 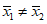 может быть принята (т.е. первый образец лучше второго по содержанию действующего вещества). Однако с доверительной вероятностью P2 = 99% принять эту гипотезу нельзя из-за недостатка информации.
может быть принята (т.е. первый образец лучше второго по содержанию действующего вещества). Однако с доверительной вероятностью P2 = 99% принять эту гипотезу нельзя из-за недостатка информации.
Если гипотеза  принята, то определяют доверительный интервал разности генеральных средних
принята, то определяют доверительный интервал разности генеральных средних  и
и  (уравнение (3.10)):
(уравнение (3.10)):

(P2 = 95%; f = 12);
 ,
, .
.7.6. Расчет неопределенности результатов анализа лекарственных препаратов методом высокоэффективной жидкостной хроматографии
В таблетке со средней массой 0,50 г содержание вещества А составляет 0,050 г. Для количественного определения вещества А методом высокоэффективной жидкостной хроматографии готовили испытуемый раствор: навеску m = 0,5052 г порошка растертых таблеток поместили в мерную колбу вместимостью 50 мл и довели объем раствора растворителем до метки. Параллельно готовили раствор сравнения: 0,0508 г стандартного образца поместили в мерную колбу на 50 мл и довели объем раствора растворителем до метки. Попеременно хроматографировали испытуемый раствор и раствор сравнения, получая по 5 хроматограмм. Площади полученных пиков представлены в таблице 7.6.
Таблица 7.6
Наименование раствора | Площади пиков (S и Sst) для хроматограммы N | ||||
1 | 2 | 3 | 4 | 5 | |
Испытуемый раствор | 13957605 | 13806804 | 13924245 | 13715195 | 14059478 |
Раствор сравнения | 14240777 | 14102192 | 14316388 | 14205217 | 14409585 |
7.6.1. Конечная аналитическая операция
Рассчитывают средние значения, содержание вещества А в одной таблетке и относительные стандартные отклонения площадей пиков для испытуемого раствора и раствора сравнения в конечной аналитической операции.
Средние значения площадей пиков:
- испытуемый раствор:
(13957605 + 13806804 + 13924245 + 13715195 + 14059478)/5 = 13892665.
- раствор сравнения:
(14240777 + 14102192 + 14316388 + 14205217 + 14409585)/5 = 14254832.
Содержание анализируемого вещества А в граммах в пересчете на среднюю массу таблетки:
 .
.Относительные стандартные отклонения площадей пиков:
- испытуемый раствор:

- аналогично для раствора сравнения: RSDst = 0,81%
7.6.2. Суммарная неопределенность пробоподготовки 
Неопределенности:
- неопределенность для мерной колбы вместимостью 50 мл - не более 0,17%;
- неопределенность взвешивания на аналитических весах - не более 0,2 мг (0,0002 г), что составляет:
 для испытуемого образца;
для испытуемого образца; для стандартного образца.
для стандартного образца.Данные неопределенности можно считать доверительными интервалами для вероятности 95%.
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду формула (6.5), а не формула (5.5). |
Суммарную неопределенность пробоподготовки рассчитывают по формуле (5.5):  .
.
 .
.Приведенный расчет является корректным для обоих подходов - линейной модели и подхода Уэлча-Сатертуэйта, поскольку число степеней свободы для каждого члена здесь бесконечно, то используется статистика Гаусса.
7.6.3. Расчет суммарной неопределенности анализа 
Данный расчет различен для линейной модели и подхода Уэлча-Сатертуэйта.
7.6.3.1 Линейная модель
Общий случай. Рассчитывают неопределенности конечной аналитической операции  для испытуемого раствора и раствора сравнения. При расчете доверительных интервалов используют односторонний коэффициент Стьюдента для вероятности 95% (равен 90% для двустороннего распределения), который для числа степени свободы (5 - 1 = 4) равен 2,13. Доверительные интервалы рассчитывают для среднего из 5 результатов, поэтому в знаменателе ставим
для испытуемого раствора и раствора сравнения. При расчете доверительных интервалов используют односторонний коэффициент Стьюдента для вероятности 95% (равен 90% для двустороннего распределения), который для числа степени свободы (5 - 1 = 4) равен 2,13. Доверительные интервалы рассчитывают для среднего из 5 результатов, поэтому в знаменателе ставим  :
:
- для испытуемого:

- для стандартного:

Суммарная неопределенность конечной аналитической операции:

ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (6.7), а не уравнение (5.7). |
Используя уравнение (5.7), рассчитывают суммарную неопределенность анализа  :
:

Использование объединенного стандартного отклонения.
Суммарную неопределенность анализа можно уменьшить за счет использования объединенного стандартного отклонения для конечной аналитической операции. Для этого нужно учесть, что RSD и RSDst являются выборочными величинами одной и той же генеральной совокупности. Проверяют вначале по Фишеру гипотезу о равенстве дисперсий:

Как видно, расчетное значение отношения дисперсий гораздо ниже табличного значения F-критерия на 95% уровне значимости. Поэтому можно принять гипотезу о равенстве дисперсий и принять формулы подраздела 1.4. настоящей общей фармакопейной статьи для объединения выборок.
Рассчитывают объединенное стандартное отклонение по уравнению:

RSDtot имеет число степеней свободы 2·(5 - 1) = 8. Коэффициент Стьюдента для данного числа степеней свободы и односторонней вероятности 0,95 равен 1,86. Тогда доверительные интервалы результатов конечной аналитической операции для испытуемого и стандартного растворов будут равны:

Суммарная неопределенность конечной аналитической операции равна:  .
.
 .
.ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду уравнение (6.7), а не уравнение (5.7). |
Как видно, данная величина меньше величины, полученной для обычного случая (1,29%).
7.6.3.2 Подход Уэлча-Сатертуэйта
Находят стандартное отклонение пробоподготовки из доверительного интервала  , используя коэффициент Гаусса 1,65 для односторонней вероятности 0,95 (поскольку число степеней свободы бесконечно, как для генеральной совокупности):
, используя коэффициент Гаусса 1,65 для односторонней вероятности 0,95 (поскольку число степеней свободы бесконечно, как для генеральной совокупности):
 , используя коэффициент Гаусса 1,65 для односторонней вероятности 0,95 (поскольку число степеней свободы бесконечно, как для генеральной совокупности):
, используя коэффициент Гаусса 1,65 для односторонней вероятности 0,95 (поскольку число степеней свободы бесконечно, как для генеральной совокупности):
ИС МЕГАНОРМ: примечание. В официальном тексте документа, видимо, допущена опечатка: имеется в виду соотношение (6.5), а не соотношение (5.5). |
Из соотношения (5.5) найденное стандартное отклонение всей аналитической методики RSD2 и (RSDst)2 делят на 5, как для дисперсий среднего результата:

Находят эффективное число степеней свободы veff. При этом для RSD и RSDst число степеней свободы равно 5 - 1 = 4, а для SSP,r - бесконечность.

Находят коэффициент Стьюдента для числа степеней свободы 10,5 и односторонней вероятности 0,95 методом интерполяции - это 1,81. Тогда доверительный интервал всей аналитической методики будет:
 .
.Таким образом, рассчитанный доверительный интервал по подходу Уэлча-Сатертуэйта (1,10%) получается меньше, чем для обычного случая и для линейной модели (1,29% и 1,15% соответственно).
Таблица 8.1
n | Q | ||
P = 90% | P = 95% | P = 99% | |
3 | 0,89 | 0,94 | 0,99 |
4 | 0,68 | 0,77 | 0,89 |
5 | 0,56 | 0,64 | 0,76 |
6 | 0,48 | 0,56 | 0,70 |
7 | 0,43 | 0,51 | 0,64 |
8 | 0,40 | 0,48 | 0,58 |
9 | 0,38 | 0,46 | 0,55 |
Таблица 8.2
f | Доверительная вероятность | f | Доверительная вероятность | ||||
P = 95% | P = 99% | P = 99,9% | P = 95% | P = 99% | P = 99,9% | ||
1 | 12,71 | 63,60 | 21 | 2,08 | 2,83 | 3,82 | |
2 | 4,30 | 9,93 | 31,60 | 22 | 2,07 | 2,82 | 3,79 |
3 | 3,18 | 5,84 | 12,94 | 23 | 2,07 | 2,81 | 3,77 |
4 | 2,78 | 4,60 | 8,61 | 24 | 2,06 | 2,80 | 3,75 |
5 | 2,57 | 4,03 | 6,86 | 25 | 2,06 | 2,79 | 3,73 |
6 | 2,45 | 3,71 | 5,96 | 26 | 2,06 | 2,78 | 3,71 |
7 | 2,37 | 3,50 | 5,41 | 27 | 2,05 | 2,77 | 3,69 |
8 | 2,31 | 3,36 | 5,04 | 28 | 2,05 | 2,76 | 3,67 |
9 | 2,26 | 3,25 | 4,78 | 29 | 2,04 | 2,76 | 3,66 |
10 | 2,23 | 3,17 | 4,59 | 30 | 2,04 | 2,75 | 3,65 |
11 | 2,20 | 3,11 | 4,44 | 40 | 2,02 | 2,70 | 3,55 |
12 | 2,18 | 3,06 | 4,32 | 50 | 2,01 | 2,68 | 3,50 |
13 | 2,16 | 3,01 | 4,22 | 60 | 2,00 | 2,66 | 3,46 |
14 | 2,15 | 2,98 | 4,14 | 80 | 1,99 | 2,64 | 3,42 |
15 | 2,13 | 2,95 | 4,07 | 100 | 1,98 | 2,63 | 3,39 |
16 | 2,12 | 2,92 | 4,02 | 120 | 1,98 | 2,62 | 3,37 |
17 | 2,11 | 2,90 | 3,97 | 200 | 1,97 | 2,60 | 3,34 |
18 | 2,10 | 2,88 | 3,92 | 500 | 1,96 | 2,59 | 3,31 |
19 | 2,09 | 2,86 | 3,88 | 1,96 | 2,58 | 3,29 | |
20 | 2,09 | 2,85 | 3,85 | ||||
f | p = 0,05 | p = 0,01 | p = 0,001 | f | p = 0,05 | p = 0,01 | p = 0,001 |
Уровень значимости | Уровень значимости | ||||||
Таблица 8.3
f2 - число степеней свободы для меньшей дисперсии | f1 - число степеней свободы для большей дисперсии | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 20 | ||
3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,66 | 8,53 |
34,12 | 30,81 | 29,46 | 28,71 | 28,24 | 27,91 | 27,67 | 27,49 | 26,69 | 26,12 | |
6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 3,87 | 3,67 |
13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,26 | 8,10 | 7,39 | 6,88 | |
9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,87 | 3,29 | 3,23 | 2,93 | 2,71 |
10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,62 | 5,47 | 4,80 | 4,31 | |
12 | 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,54 | 2,30 |
9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,64 | 4,50 | 3,86 | 3,36 | |
15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,33 | 2,07 |
8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,14 | 4,00 | 3,37 | 2,87 | |
20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,12 | 1,84 |
8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,70 | 3,56 | 2,94 | 2,42 | |
30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 1,93 | 1,62 |
7,56 | 5,39 | 4,51 | 4,02 | 3,70 | 3,47 | 3,30 | 3,17 | 2,55 | 2,01 | |
60 | 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 1,75 | 1,39 |
7,08 | 4,98 | 4,13 | 3,65 | 3,34 | 3,12 | 2,95 | 2,82 | 2,20 | 1,60 | |
3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 2,01 | 1,94 | 1,57 | 1,00 | |
6,63 | 4,61 | 3,78 | 3,32 | 3,02 | 2,80 | 2,64 | 2,51 | 1,88 | 1,00 | |
f для P = 95% напечатаны жирным шрифтом, а f для P = 99% - обычным.
Таблица 8.4
Вероятность P1 или P2 | ||||||
95% | 97,5% | 99% | 99,5% | 99,75% | 99,95% | |
90% | 95% | 98% | 99% | 99,5% | 99,9% | |
Число степеней свободы | Значения R (P, f) | |||||
1 | 0,9877 | 0,99692 | 0,999507 | 0,999877 | 0,999969 | 0,999999 |
2 | 0,900 | 0,950 | 0,980 | 0,990 | 0,9950 | 0,999000 |
3 | 0,805 | 0,878 | 0,9343 | 0,9587 | 0,9740 | 0,99114 |
4 | 0,729 | 0,811 | 0,882 | 0,9172 | 0,9417 | 0,9741 |
5 | 0,669 | 0,754 | 0,833 | 0,875 | 0,9056 | 0,9509 |
6 | 0,621 | 0,707 | 0,789 | 0,834 | 0,870 | 0,9249 |
7 | 0,582 | 0,666 | 0,750 | 0,798 | 0,836 | 0,898 |
8 | 0,549 | 0,632 | 0,715 | 0,765 | 0,805 | 0,872 |
9 | 0,521 | 0,602 | 0,685 | 0,735 | 0,776 | 0,847 |
10 | 0,497 | 0,576 | 0,658 | 0,708 | 0,750 | 0,823 |
11 | 0,476 | 0,553 | 0,634 | 0,684 | 0,726 | 0,801 |
12 | 0,457 | 0,532 | 0,612 | 0,661 | 0,703 | 0,780 |
13 | 0,441 | 0,514 | 0,592 | 0,641 | 0,683 | 0,760 |
14 | 0,426 | 0,497 | 0,574 | 0,623 | 0,664 | 0,742 |
15 | 0,412 | 0,482 | 0,558 | 0,606 | 0,647 | 0,725 |
16 | 0,400 | 0,468 | 0,543 | 0,590 | 0,631 | 0,708 |
17 | 0,389 | 0,456 | 0,529 | 0,575 | 0,616 | 0,693 |
18 | 0,378 | 0,444 | 0,516 | 0,561 | 0,602 | 0,679 |
19 | 0,369 | 0,433 | 0,503 | 0,549 | 0,589 | 0,665 |
20 | 0,360 | 0,423 | 0,492 | 0,537 | 0,576 | 0,652 |
25 | 0,323 | 0,381 | 0,445 | 0,487 | 0,524 | 0,597 |
30 | 0,296 | 0,349 | 0,409 | 0,449 | 0,484 | 0,554 |
35 | 0,275 | 0,325 | 0,381 | 0,428 | 0,452 | 0,519 |
40 | 0,257 | 0,304 | 0,358 | 0,393 | 0,425 | 0,490 |
45 | 0,243 | 0,288 | 0,338 | 0,372 | 0,403 | 0,465 |
50 | 0,231 | 0,273 | 0,322 | 0,354 | 0,380 | 0,443 |
60 | 0,211 | 0,250 | 0,295 | 0,325 | 0,352 | 0,408 |
70 | 0,195 | 0,232 | 0,274 | 0,302 | 0,327 | 0,380 |
80 | 0,183 | 0,217 | 0,257 | 0,283 | 0,307 | 0,357 |
90 | 0,173 | 0,205 | 0,242 | 0,267 | 0,290 | 0,338 |
100 | 0,164 | 0,195 | 0,230 | 0,254 | 0,276 | 0,321 |
P1 - вероятность того, что r < R или R < r (односторонний критерий); P2 - вероятность того, что коэффициент корреляции r находится в интервале R < r < R (двусторонний критерий); Выборочный коэффициент корреляции r значимо (с надежностью P1 или P2) отличается от нуля, если его абсолютная величина |r| превышает табличное значение R (P, f). | ||||||
Таблица 8.5
f | P1 = 95% | P1 = 99% |
1 | 3,841 | 6,635 |
2 | 5,991 | 9,210 |
3 | 7,815 | 11,345 |
4 | 9,488 | 13,277 |
5 | 11,070 | 15,086 |
6 | 12,592 | 16,812 |
7 | 14,067 | 18,475 |
8 | 15,507 | 20,090 |
9 | 16,919 | 21,666 |
10 | 18,307 | 23,209 |
11 | 19,675 | 24,725 |
12 | 21,026 | 26,217 |
13 | 22,362 | 27,688 |
14 | 23,685 | 29,141 |
15 | 24,996 | 30,578 |
16 | 26,296 | 32,000 |
17 | 27,587 | 33,409 |
18 | 28,869 | 34,805 |
19 | 30,144 | 36,191 |
20 | 31,410 | 37,566 |
21 | 32,671 | 38,932 |
22 | 33,924 | 40,289 |
23 | 35,172 | 41,638 |
24 | 36,415 | 42,980 |
25 | 37,652 | 44,314 |
26 | 38,885 | 45,642 |
27 | 40,113 | 46,963 |
28 | 41,337 | 48,278 |
29 | 42,557 | 49,588 |
30 | 43,773 | 50,892 |
40 | 55,758 | 63,691 |
50 | 67,505 | 76,154 |
P1 - вероятность того, что оцениваемое значение | ||
Таблица 8.6
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 36 | ||
G(P = 95%) | |||||||||||||
2 | 0,9985 | 0,9750 | 0,9392 | 0,9057 | 0,8772 | 0,8534 | 0,8332 | 0,8159 | 0,8010 | 0,7880 | 0,7341 | 0,6602 | 0,5000 |
3 | 0,9669 | 0,8709 | 0,7977 | 0,7457 | 0,7071 | 0,6771 | 0,6530 | 0,6333 | 0,6167 | 0,6025 | 0,5466 | 0,4748 | 0,3333 |
4 | 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0,5365 | 0,5175 | 0,5017 | 0,4884 | 0,4366 | 0,3720 | 0,2500 |
5 | 0,8412 | 0,6838 | 0,5981 | 0,5440 | 0,5063 | 0,4783 | 0,4564 | 0,4387 | 0,4241 | 0,4118 | 0,3645 | 0,3066 | 0,2000 |
6 | 0,7808 | 0,6161 | 0,5321 | 0,4803 | 0,4447 | 0,4184 | 0,3980 | 0,3817 | 0,3682 | 0,3568 | 0,3135 | 0,2612 | 0,1667 |
7 | 0,7271 | 0,5612 | 0,4800 | 0,4307 | 0,3974 | 0,3726 | 0,3535 | 0,3384 | 0,3259 | 0,3154 | 0,2756 | 0,2278 | 0,1429 |
8 | 0,6798 | 0,5157 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0,3185 | 0,3043 | 0,2926 | 0,2829 | 0,2462 | 0,2022 | 0,1250 |
9 | 0,6385 | 0,4775 | 0,4027 | 0,3584 | 0,3286 | 0,3067 | 0,2901 | 0,2768 | 0,2659 | 0,2568 | 0,2226 | 0,1820 | 0,1111 |
10 | 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0,2666 | 0,2541 | 0,2439 | 0,2353 | 0,2032 | 0,1655 | 0,1000 |
12 | 0,5410 | 0,3924 | 0,3264 | 0,2880 | 0,2624 | 0,2439 | 0,2299 | 0,2187 | 0,2098 | 0,2020 | 0,1737 | 0,1403 | 0,0833 |
15 | 0,4709 | 0,3346 | 0,2758 | 0,2419 | 0,2195 | 0,2034 | 0,1911 | 0,1815 | 0,1736 | 0,1671 | 0,1429 | 0,1144 | 0,0667 |
20 | 0,3894 | 0,2705 | 0,2205 | 0,1921 | 0,1735 | 0,1602 | 0,1501 | 0,1422 | 0,1357 | 0,1303 | 0,1108 | 0,0879 | 0,0500 |
24 | 0,3434 | 0,2354 | 0,1907 | 0,1656 | 0,1493 | 0,1374 | 0,1286 | 0,1216 | 0,1160 | 0,1113 | 0,0912 | 0,0743 | 0,0417 |
30 | 0,2929 | 0,1980 | 0,1593 | 0,1377 | 0,1237 | 0,1137 | 0,1061 | 0,1002 | 0,0958 | 0,0921 | 0,0771 | 0,0604 | 0,0333 |
40 | 0,2370 | 0,1576 | 0,1259 | 0,1082 | 0,0968 | 0,0887 | 0,0827 | 0,0780 | 0,0745 | 0,0713 | 0,0595 | 0,0462 | 0,0250 |
60 | 0,1737 | 0,1131 | 0,0895 | 0,0765 | 0,0682 | 0,0623 | 0,0583 | 0,0552 | 0,0520 | 0,0497 | 0,0411 | 0,0316 | 0,0167 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 36 | ||
G(P = 99%) | |||||||||||||
2 | 0,9999 | 0,9950 | 0,9794 | 0,9586 | 0,9373 | 0,9172 | 0,8988 | 0,8823 | 0,8674 | 0,8539 | 0,7949 | 0,7067 | 0,5000 |
3 | 0,9933 | 0,9423 | 0,8831 | 0,8335 | 0,7933 | 0,7606 | 0,7335 | 0,7107 | 0,6912 | 0,6743 | 0,6059 | 0,5153 | 0,3333 |
4 | 0,9676 | 0,8643 | 0,7814 | 0,7212 | 0,6761 | 0,6410 | 0,6129 | 0,5897 | 0,5702 | 0,5536 | 0,4884 | 0,4057 | 0,2500 |
5 | 0,9279 | 0,7885 | 0,6957 | 0,6329 | 0,5875 | 0,5531 | 0,5259 | 0,5037 | 0,4854 | 0,4697 | 0,4094 | 0,3351 | 0,2000 |
6 | 0,8828 | 0,7218 | 0,6258 | 0,5635 | 0,5195 | 0,4866 | 0,4608 | 0,4401 | 0,4229 | 0,4081 | 0,3529 | 0,2858 | 0,1667 |
7 | 0,8376 | 0,6644 | 0,5685 | 0,5080 | 0,4659 | 0,4347 | 0,4105 | 0,3911 | 0,3751 | 0,3616 | 0,3105 | 0,2494 | 0,1429 |
8 | 0,7945 | 0,6152 | 0,5209 | 0,4627 | 0,4226 | 0,3932 | 0,3704 | 0,3522 | 0,3373 | 0,3248 | 0,2779 | 0,2214 | 0,1250 |
9 | 0,7544 | 0,5727 | 0,4810 | 0,4251 | 0,3870 | 0,3592 | 0,3378 | 0,3207 | 0,3067 | 0,2950 | 0,2514 | 0,1992 | 0,1111 |
10 | 0,7175 | 0,5358 | 0,4469 | 0,3934 | 0,3572 | 0,3308 | 0,3106 | 0,2945 | 0,2813 | 0,2704 | 0,2297 | 0,1811 | 0,1000 |
12 | 0,6528 | 0,4751 | 0,3919 | 0,3428 | 0,3099 | 0,2861 | 0,2680 | 0,2535 | 0,2419 | 0,2320 | 0,1961 | 0,1535 | 0,0833 |
15 | 0,5747 | 0,4069 | 0,3317 | 0,2882 | 0,2593 | 0,2386 | 0,2228 | 0,2104 | 0,2002 | 0,1918 | 0,1612 | 0,1251 | 0,0667 |
20 | 0,4799 | 0,3297 | 0,2654 | 0,2288 | 0,2048 | 0,1877 | 0,1748 | 0,1646 | 0,1567 | 0,1501 | 0,1248 | 0,0960 | 0,0500 |
24 | 0,4247 | 0,2871 | 0,2295 | 0,1970 | 0,1759 | 0,1608 | 0,1495 | 0,1406 | 0,1338 | 0,1283 | 0,1060 | 0,0810 | 0,0417 |
30 | 0,3632 | 0,2412 | 0,1913 | 0,1635 | 0,1454 | 0,1327 | 0,1232 | 0,1157 | 0,1100 | 0,1054 | 0,0867 | 0,0658 | 0,0333 |
40 | 0,2940 | 0,1915 | 0,1508 | 0,1281 | 0,1135 | 0,1033 | 0,0957 | 0,0898 | 0,0853 | 0,0816 | 0,0668 | 0,0503 | 0,0250 |
60 | 0,2151 | 0,1371 | 0,1069 | 0,0902 | 0,0796 | 0,0721 | 0,0668 | 0,0625 | 0,0594 | 0,0567 | 0,0461 | 0,0344 | 0,0167 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |















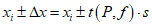
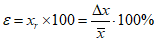


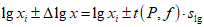

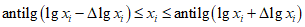




 , величины s и f целесообразно вычислять по
, величины s и f целесообразно вычислять по 






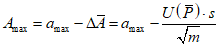













 .
.