ГОСТ Р ИСО 5725-6-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ
(ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ)
МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 6
Использование значений точности на практике
|
|
Москва Стандартинформ 2009 |
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России
ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 23 апреля 2002 г. № 161-ст
3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-6:1994 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике»
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Март 2009 г.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ К ГОСУДАРСТВЕННЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 ПОД ОБЩИМ ЗАГОЛОВКОМ «ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»
Целью разработки Государственных стандартов Российской Федерации ГОСТ Р ИСО 5725-1-2002, ГОСТ Р ИСО 5725-2-2002, ГОСТ Р ИСО 5725-3-2002, ГОСТ Р ИСО 5725-4-2002, ГОСТ Р ИСО 5725-5-2002, ГОСТ Р ИСО 5725-6-2002, далее - ГОСТ Р ИСО 5725, является прямое применение в Российской Федерации шести частей основополагающего международного стандарта ИСО 5725 под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений» в практической деятельности по метрологии (разработке, аттестации и применению методик выполнения измерений), стандартизации методов контроля (испытаний, измерений, анализа), испытаниям продукции, в том числе для целей подтверждения соответствия, оценке компетентности испытательных лабораторий согласно требованиям ГОСТ Р ИСО/МЭК 17025-2000*.
_____________
* С 1 июля 2007 г. введен в действие ГОСТ Р ИСО/МЭК 17025-2006.
ГОСТ Р ИСО 5725 представляют собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».
Каждая часть содержит аутентичный перевод предисловия и введения к международному стандарту ИСО 5725, а также предисловие к государственным стандартам Российской Федерации ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 и издается самостоятельно.
Пользование частями 2 - 6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.
В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Стандарты ИСО 5725 могут применяться для оценки точности выполнения измерений различных физических величин, характеризующих измеряемые свойства того или иного объекта, в соответствии со стандартизованной процедурой. При этом в пункте 1.2 ИСО 5725-1 особо отмечено, что стандарт может применяться для оценки точности выполнения измерений состава и свойств очень широкой номенклатуры материалов, включая жидкости, порошкообразные и твердые материалы - продукты материального производства или существующие в природе, при условии, что учитывают любую неоднородность материала.
Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».
В ИСО 5725:1994-1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).
Более того, в оригинале ИСО 5725 очень часто употребляется в качестве понятия «метод измерений» и английский термин «test method», перевод которого на русский язык - «метод испытаний» (см. примечание 1 к пункту 3.2 ИСО 5725-1) и который по смыслу совпадает с термином 6.2 ИСО 5725-1 «standard measurement method» (стандартизованный метод измерений). Соответственно в качестве термина «результат измерений» в оригинале стандарта чаще используется английский термин «test result» (см. пункт 3.2 ИСО 5725-1), причем в контексте как с термином «test method» (см. пункт 3.2), так и с термином «measurement method» (см. в оригинале, например, пункты 1.2 или 7.2.1 ИСО 5725-1).
При этом следует иметь в виду, что область применения ИСО 5725 - точность стандартизованных методов измерений, в том числе предназначенных для целей испытаний продукции, позволяющих количественно оценить характеристики свойств (показателей качества и безопасности) объекта испытаний (продукции). Именно поэтому во всех частях стандарта результаты измерений характеристик образцов, взятых в качестве выборки из партии изделий (или проб, отобранных из партии материала), являются основой для получения результатов испытаний всей партии (объекта испытаний). Когда объектом испытаний является конкретный образец (test speciment, sample), результаты измерений и испытаний могут совпадать. Такой подход имеет место в примерах по определению показателей точности стандартного (стандартизованного) метода измерений, содержащихся в ИСО 5725.
Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).
В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.
Термины «правильность» (trueness) и «прецизионность» (precision) в отечественных нормативных документах по метрологии до настоящего времени не использовались. При этом «правильность» - степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в случае отсутствия эталона измеряемой величины - степень близости среднего значения, полученного на основании большой серии результатов измерений (или результатов испытаний) к принятому опорному значению. Показателем правильности обычно является значение систематической погрешности (см. пункт 3.7 ГОСТ Р ИСО 5725-1).
В свою очередь «прецизионность» - степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Эта характеристика зависит только от случайных факторов и не связана с истинным или условно истинным значением измеряемой величины (см. пункт 3.12 ГОСТ Р ИСО 5725-1). Мера прецизионности обычно вычисляется как стандартное (среднеквадратическое) отклонение результатов измерений, выполненных в определенных условиях. Количественные значения мер прецизионности существенно зависят от заданных условий. Экстремальные показатели прецизионности - повторяемость, сходимость (repeatability) и воспроизводимость (reproducibility) регламентируют и в отечественных нормативных документах, в том числе в большинстве государственных стандартов на методы контроля (испытаний, измерений, анализа) (см. пункты 3.12 - 3.20 ГОСТ Р ИСО 5725-1).
В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:
а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);
б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);
в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);
г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);
д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;
е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).
Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.
Алгоритмы проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.
Использование приведенных в приложениях А к каждому стандарту условных обозначений в качестве обязательных рекомендуется только для тех показателей точности, которые до настоящего времени в отечественной метрологической практике не использовались (например, для показателей по пунктам 3.9 - 3.12 ГОСТ Р ИСО 5725-1). Для остальных показателей и критериев используемые в ГОСТ Р ИСО 5725 условные обозначения, как правило, могут применяться наряду с условными обозначениями этих показателей и критериев, принятых в действующих отечественных документах (например, предел повторяемости (сходимости) с условным обозначением r по пункту 3.16 ГОСТ Р ИСО 5725-1 наряду с условным обозначением d, принятым для этого показателя в ряде рекомендаций по метрологии, а также в государственных стандартах на методы испытаний продукции).
ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
Международная организация по стандартизации (ИСО) является Всемирной федерацией национальных организаций по стандартизации (комитетов - членов ИСО). Разработка международных стандартов обычно осуществляется техническими комитетами ИСО. Каждый член ИСО, заинтересованный в деятельности соответствующего технического комитета, имеет право быть представленным в этом комитете. Правительственные и неправительственные международные организации, сотрудничающие с ИСО, также принимают участие в этой работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов, принятые техническими комитетами, направляются техническим комитетам - членам ИСО на голосование перед их утверждением Советом ИСО в качестве международных стандартов. Стандарты утверждаются в качестве международных в соответствии с установленными в ИСО требованиями: в случае их одобрения по меньшей мере 75 % комитетов - членов ИСО, принимавших участие в голосовании.
Международный стандарт ИСО 5725-6 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».
ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
ИСО 5725 (части 1 - 6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).
Приложение А является обязательным для настоящей части стандарта ИСО 5725, приложение В - справочное.
ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
0.1 В ИСО 5725 для описания точности метода измерений используются два термина: «правильность» и «прецизионность». Термин «правильность» характеризует степень близости среднего арифметического значения большого числа результатов измерений к истинному или принятому опорному значению, термин «прецизионность» - степень близости результатов измерений друг к другу.
0.2 Необходимость рассмотрения «прецизионности» возникает из-за того, что измерения, выполняемые на предположительно идентичных материалах при предположительно идентичных обстоятельствах, не дают, как правило, идентичных результатов. Это объясняется неизбежными случайными погрешностями, присущими каждой измерительной процедуре; факторы, оказывающие влияние на результат измерения, не поддаются полному контролю. При практической интерпретации данных измерений эта изменчивость должна учитываться. Например, нельзя установить фактическое отклонение полученного результата измерений от некоторого определенного значения измеряемой величины, если он лежит в области неизбежных случайных погрешностей измерительной процедуры. Аналогичным образом, сопоставление результатов измерений измеряемых характеристик двух партий материала не выявит какого-либо существенного различия в качестве, если расхождение между результатами лежит в вышеупомянутой области.
0.3 В частях 1 - 5 ИСО 5725 обсуждаются подходы и приводятся методы оценки прецизионности (выраженной через стандартные отклонения повторяемости и воспроизводимости) и правильности (выраженной через различные составляющие систематической погрешности) измерений, выполняемых стандартным методом. Такая оценка, однако, была бы бесцельной, если бы ее результаты нельзя было использовать на практике.
0.4 Исходя из того, что точность методы измерений установлена, в настоящей части ИСО 5725 даны области применения значений точности на практике, например в области продвижения коммерческих сделок или контроля показателей работы лабораторий и признания их технической компетентности.
ГОСТ Р ИСО 5725-6-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ
И ПРЕЦИЗИОННОСТЬ)
МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 6
Использование значений точности на практике
Accuracy (trueness and precision) of
measurement methods and results.
Part 6. Use in practice of
accuracy values
Дата введения 2002-11-01
1 Область применения
1.1 Цель настоящего стандарта - дать общее представление о некоторых способах использования данных о точности в различных практических ситуациях, а именно:
a) представить стандартный метод расчета пределов повторяемости (сходимости), воспроизводимости и других пределов, используемых при рассмотрении результатов измерений, полученных при реализации стандартного метода измерений;
b) обеспечить способы проверки приемлемости результатов измерений, полученных в условиях повторяемости или воспроизводимости;
c) описать способ оценки стабильности результатов, получаемых в пределах одной лаборатории за определенный период времени, и таким образом внедрить метод «контроля качества» операций в пределах этой лаборатории;
d) описать подходы к оценке способности данной лаборатории правильно применять (реализовывать) данной стандартный метод измерений;
e) описать способы сопоставления альтернативных методов измерений.
1.2 Настоящий стандарт относится исключительно к методам измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающим в качестве результата измерений единственное значение. При этом единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
1.3 Предполагается, что оценки правильности и прецизионности были получены в соответствии с ГОСТ Р ИСО 5725-1 - ГОСТ Р ИСО 5725-5.
1.4 Дополнительная информация, относящаяся к сфере применения значений точности на практике, будет представляться в начале каждого раздела.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ 8.315-97 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ГОСТ Р 50779.42-99 (ИСО 8258-91) Статистические методы. Контрольные карты Шухарта
3 Определения
В настоящем стандарте применяют термины с определениями, представленные в ИСО 3534-1 [1] и ГОСТ Р ИСО 5725-1.
Условные обозначения, используемые в ГОСТ Р ИСО 5725, приведены в приложении А.
4 Нахождение пределов
4.1 Пределы повторяемости и воспроизводимости
4.1.1 В ГОСТ Р ИСО 5725-2 основное внимание было сосредоточено на оценке стандартных отклонений при работе в условиях повторяемости или воспроизводимости. Однако в обычной лабораторной практике требуется рассмотрение различий между двумя или большим числом результатов измерений, и для этого требуется некая мера, близкая скорее к критическому различию, чем к стандартному отклонению.
4.1.2 Мера, основывающаяся на суммах или
разностях из п независимых случайных величин, каждая из которых
характеризуется стандартным отклонением s, будет иметь
стандартное отклонение ![]() Предел воспроизводимости (R)
или предел повторяемости (r)
- расхождения между двумя результатами
измерений; для них стандартное отклонение составит
Предел воспроизводимости (R)
или предел повторяемости (r)
- расхождения между двумя результатами
измерений; для них стандартное отклонение составит ![]()
Обычно в статистике для рассмотрения
различия между этими двумя случайными величинами используют множитель f
перед стандартным отклонением, то есть ![]() Величина f
(называемая коэффициентом критического диапазона) зависит от доверительного
уровня вероятности и закона распределения случайной величины. Для пределов
воспроизводимости и повторяемости доверительный уровень вероятности составляет
95 %, и в ГОСТ Р ИСО 5725 делается допущение, что лежащее в основе
распределение является приближенно нормальным. Для нормального распределения на
уровне вероятности 95 % коэффициент f равен
1,96, и
Величина f
(называемая коэффициентом критического диапазона) зависит от доверительного
уровня вероятности и закона распределения случайной величины. Для пределов
воспроизводимости и повторяемости доверительный уровень вероятности составляет
95 %, и в ГОСТ Р ИСО 5725 делается допущение, что лежащее в основе
распределение является приближенно нормальным. Для нормального распределения на
уровне вероятности 95 % коэффициент f равен
1,96, и ![]() тогда
равен 2,77.
тогда
равен 2,77.
Поскольку цель настоящего стандарта -
дать несколько простых правил для применения не статистиками при рассмотрении
результатов измерений, представляется целесообразным использовать округленное
значение 2,8 вместо ![]()
4.1.3 Процедура оценки прецизионности основывается на оценке истинных стандартных отклонений, в то время как сами истинные стандартные отклонения остаются неизвестными. Следовательно, в статической практике они должны быть обозначены скорее через s, чем через s. Однако, если при этом предусматривается использование процедур, данных в ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2, то эти оценки будут основываться на существенном количестве результатов измерений и дадут наилучшую информацию, которую можно иметь об истинных значениях стандартных отклонений. В других рассматриваемых ниже случаях для оценок стандартных отклонений, основанных на более ограниченных данных, используют символ s (оценка стандартного отклонения). Таким образом, лучше использовать символ s для обозначения значений, полученных из полного эксперимента по оценке прецизионности, и воспринимать его как истинное стандартное отклонение, с которым будут сопоставляться другие оценки (s).
4.1.4 Исходя из 4.1.1 - 4.1.3, сопоставление разностей двух результатов измерений, полученных в условиях повторяемости или воспроизводимости должно осуществляться с пределом повторяемости r = 2,8sr или с пределом воспроизводимости R = 2,8sR.
4.2 Сопоставления на основании произвольного количества значений (более двух)
4.2.1 Две группы измерений в одной лаборатории
Если в одной лаборатории в условиях
повторяемости выполнено две группы измерений: первая группа, давшая n1 результатов измерений со средним арифметическим
значением ![]() и
вторая группа, давшая п2 результатов измерений со средним
арифметическим значением
и
вторая группа, давшая п2 результатов измерений со средним
арифметическим значением ![]() - то стандартное отклонение разности
- то стандартное отклонение разности ![]() составит
составит

и критическая разность для ![]() будет выглядеть
следующим образом
будет выглядеть
следующим образом

на уровне вероятности 95 %.
Примечание 1 - Если n1 и n2 равны единице, то, как и должно быть, получим r = 2,8sr.
4.2.2 Две группы измерений в двух лабораториях
Если первая из лабораторий получает n1 результатов измерений со средним арифметическим
значением ![]() а
вторая - п2 результатов измерений со средним арифметическим
значением
а
вторая - п2 результатов измерений со средним арифметическим
значением ![]() причем
в каждом случае - в условиях повторяемости, то стандартное отклонение разности
причем
в каждом случае - в условиях повторяемости, то стандартное отклонение разности ![]() составит:
составит:

и критическая разность для ![]() будут выглядеть
следующим образом:
будут выглядеть
следующим образом:

на уровне вероятности 95 %.
Примечание 2 - Если n1 и n2 равны единице, то как и должно быть, получим R = 2,8sR.
4.2.3 Сопоставление с опорным значением для одной лаборатории
Если в пределах одной лаборатории в
условиях повторяемости получено п результатов измерений со средним
арифметическим значением ![]() затем выполнено сопоставление с данным
опорным значением m0, то в отсутствие конкретных данных по лабораторной
составляющей систематической погрешности стандартное отклонение интересующей
нас разности
затем выполнено сопоставление с данным
опорным значением m0, то в отсутствие конкретных данных по лабораторной
составляющей систематической погрешности стандартное отклонение интересующей
нас разности ![]() (где m0 -
принятое опорное значение) равно
(где m0 -
принятое опорное значение) равно
![]()
и критическая разность для ![]() составит
составит
![]()
4.2.4 Сопоставление с опорным значением более чем для одной лаборатории
Если р лабораториями было получено
ni результатов
измерений со средними арифметическими значениями ![]() (в каждом случае - в условиях
повторяемости), общее среднее значение
(в каждом случае - в условиях
повторяемости), общее среднее значение ![]() , рассчитывают по формуле
, рассчитывают по формуле
![]()
и это общее среднее сравнивают с опорным значением m0; в таком
случае стандартное отклонение для ![]() составит:
составит:
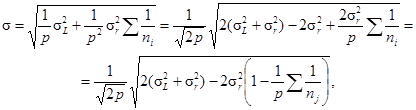
и критическая разность для ![]() будет выглядеть следующим образом
будет выглядеть следующим образом

на уровне вероятности 95 %.
4.2.5 Трактовка результатов сопоставления
Если абсолютное расхождение превышает соответствующий предел, приведенный в предыдущих пунктах, то разность должна рассматриваться в качестве подозрительной, и, следовательно, все измерения, которые в результате дали эту разность, должны считаться подозрительными и подлежать дополнительному изучению.
5 Методы проверки приемлемости результатов измерений (испытаний) и установления окончательного результата
5.1 Общие положения
5.1.1 Методы проверки, описанные в настоящем разделе, должны применяться только в том случае, когда измерение выполняют в точном соответствии со стандартным методом измерений, стандартные отклонения которого sr и sR известны. При этом, когда диапазон N результатов измерений превышает соответствующий предел, заданный в раздел 4, считают, что один, два или все N результатов измерений являются отклонениями. Рекомендуется, чтобы причина возникновения отклонений была изучена с технической точки зрения. Тем не менее по соображениям коммерческого характера может оказаться необходимым получение некоторого приемлемого значения и в этих случаях, и когда с результатами измерений необходимо обращаться в соответствии с положениями настоящего раздела.
5.1.2 Настоящий раздел был подготовлен в предположении, что результаты измерений были получены в условиях повторяемости и воспроизводимости, и что доверительный уровень вероятности составляет 95 %. Если результаты измерений были получены в промежуточных условиях (см. ГОСТ Р ИСО 5725-3), то sr необходимо заменить соответствующей промежуточной мерой.
5.1.3 В некоторых случаях, там, где процедуры, описываемые в 5.2, приводят к медиане как к конечному результату, более предпочтительным мог бы оказаться отказ от таких данных.
5.2 Методы проверки приемлемости результатов измерений, полученных в условиях повторяемости
Примечание 3 - Ссылки в 5.2.2.1 и 5.2.2.2 относятся к измерениям, являющимся или не являющимся дорогостоящими, и должны истолковываться не только с финансовой точки зрения, но и исходя из того, является ли измерение сложным, затруднительным или трудоемким (требующим много времени на выполнение).
5.2.1 Единичный результат измерений
Получение только одного результата измерений не является общепринятым в производственной практике. В этом случае невозможно провести прямую статистическую проверку приемлемости такого результата измерений относительно заданного показателя повторяемости. Если результат измерений может оказаться некорректным, должен быть получен второй результат. Наличие двух результатов измерений является основанием для более распространенной практики, которая будет описана ниже.
5.2.2 Два результата измерений
Два результата измерений должны быть получены в условиях повторяемости. Абсолютное расхождение между ними должно в таком случае сравниваться с пределом повторяемости r = 2,8sr.
5.2.2.1 Случай, когда получение результатов измерений не является дорогостоящим
Если абсолютное расхождение между результатами двух измерений не превышает r, оба результата признают приемлемыми, и в качестве окончательного результата должно указываться среднее арифметическое значение результатов двух измерений. Если абсолютное расхождение превышает r, лаборатория должна получить еще два результата измерений.
Если при этом диапазон (хmax - xmin) результатов четырех измерений равен или меньше по значению критического диапазона для уровня вероятности 95 % для п = 4, CR0,95(4), то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Коэффициенты критического диапазона f(n) для интервала от п = 2 до п = 40 и для выбранных значений от п = 45 до п = 100 представлены в таблице 1 и предназначены для использования в расчетах критического диапазона согласно равенству
CR0,95(n) = f(n)sr.
Если диапазон результатов четырех измерений больше критического диапазона для п = 4, то в качестве окончательного результата должна фиксироваться медиана результатов четырех измерений. Данная процедура резюмируется в блок-схеме, представленной на рисунке 1.
5.2.2.2 Случай, когда получение результатов измерений является дорогостоящим
Если абсолютное расхождение между результатами двух измерений не превышает r, оба результата признают приемлемыми, и в качестве окончательного результата должно указываться среднее арифметическое значение результатов этих двух измерений. Если абсолютное расхождение превышает r, лаборатория должна получить еще один результат измерений.
где x(2) - второй наименьший результат; x(3) - третий наименьший результат
Рисунок 1 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при первоначальном получении результатов двух измерений и условии, что получение результатов измерений не является дорогостоящим (случай 5.2.2.1)
где x(2) - второй наименьший результат
Рисунок 2 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при первоначальном получении двух результатов измерений и условии, что получение результатов измерений является дорогостоящим (случай 5.2.2.2 а)
Если при этом диапазон (xmax - xmin) результатов трех измерений равен или меньше критического диапазона для п = 3, CR0,95(3), то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов трех измерений.
Если диапазон результатов трех измерений больше критического диапазона для п = 3, решение принимают в соответствии с нижеследующей альтернативой.
a) Случай, когда невозможно получить четвертый результат измерений
Лаборатория должна использовать в качестве окончательного результата медиану результатов трех измерений.
Данная процедура резюмируется в блок-схеме, представленной на рисунке 2.
b) Случай, когда возможно получить четвертый результат измерений
Лаборатория должна получить четвертый результат измерений. Если при этом диапазон (xmax - xmin) результатов четырех измерений равен или меньше критического диапазона для п = 4, CR0,95(4), то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Если диапазон результатов четырех измерений больше критического диапазона для п = 4, то в качестве окончательного результата лаборатория должна использовать медиану результатов четырех измерений.
Данная процедура резюмируется в блок-схеме, представленной на рисунке 3.
где x(2) - второй наименьший результат; х(3) - третий наименьший результат
Рисунок 3 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при первоначальном получении результатов двух измерений и условии, что получение результатов измерений является дорогостоящим (случай 5.2.2.2b)
Таблица 1 - Коэффициенты критического диапазона f(n)
|
f(n) |
n |
f(n) |
|
|
2 |
2,8 |
25 |
5,2 |
|
3 |
3,3 |
26 |
5,2 |
|
4 |
3,6 |
27 |
5,2 |
|
5 |
3,9 |
28 |
5,3 |
|
6 |
4,0 |
29 |
5,3 |
|
7 |
4,2 |
30 |
5,3 |
|
8 |
4,3 |
31 |
5,3 |
|
9 |
4,4 |
32 |
5,3 |
|
10 |
4,5 |
33 |
5,4 |
|
11 |
4,6 |
34 |
5,4 |
|
12 |
4,6 |
35 |
5,4 |
|
13 |
4,7 |
36 |
5,4 |
|
14 |
4,7 |
37 |
5,4 |
|
15 |
4,8 |
38 |
5,5 |
|
16 |
4,8 |
39 |
5,5 |
|
17 |
4,9 |
40 |
5,5 |
|
18 |
4,9 |
45 |
5,6 |
|
19 |
5,0 |
50 |
5,6 |
|
20 |
5,0 |
60 |
5,8 |
|
21 |
5,0 |
70 |
5,9 |
|
22 |
5,1 |
80 |
5,9 |
|
23 |
5,1 |
90 |
6,0 |
|
24 |
5,1 |
100 |
6,1 |
|
Примечание - Коэффициент критического диапазона f(n) представляет собой 95 %-ный квантиль распределения (xmax - хmin)/s, где xmax и xmin - экстремальные значения в выборке и из нормального распределения со стандартным отклонением σ. |
|||
5.2.3 Более двух первоначальных результатов измерений
На практике иногда оказывается более двух первоначальных результатов измерений. Метод получения окончательно приводимого результата в условиях повторяемости для случаев, где п > 2, подобен методу для п = 2.
Диапазон (xmax - xmin) результатов измерений сопоставляют с критическим диапазоном CR0,95(n), рассчитанным по данным таблицы 1 для соответствующего значения п. Если диапазон результатов не превышает критический, то среднее арифметическое значение результатов всех п измерений используют в качестве окончательного результата.
Если диапазон результатов превышает критический диапазон CR0,95(n), то для получения окончательного результата должно быть принято решение в соответствии с одним из вариантов А, В или С, представленных на рисунках 4 - 6.
Варианты А и В соответствуют ситуациям, когда получение результатов измерений не является и является дорогостоящим соответственно. Вариант С является альтернативным; рекомендуется в случае, когда первоначальное количество результатов измерений равно пяти или больше и когда получение результата каждого измерения не является дорогостоящим, или в случае, когда первоначальное количество результатов измерений равно четырем или больше и когда получение результата каждого измерения является дорогостоящим.
Для недорогостоящих измерений различие между вариантами А и С состоит в том, что вариант А требует п последующих измерений, в то время как в варианте С требуется менее половины этого количества. Решение будет зависеть от величины п и от легкости выполнения измерений.
Для дорогостоящих измерений различие между вариантами В и С состоит в том, что вариант С требует последующих измерений, тогда как в варианте В никаких последующих измерений не проводят. Вариант В должен рассматриваться только при таких обстоятельствах, когда выполнение последующих измерений является настолько дорогостоящим, что его можно считать недоступным.
Рисунок 4 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при первоначальном получении и результатов измерений и условии, что получение n результатов измерений не является дорогостоящим (вариант А)
Рисунок 5 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при первоначальном получении n результатов измерений и условии, что получение результатов измерений является дорогостоящим (вариант В)
_____________
1) т должно быть выбрано в качестве целого числа, удовлетворяющего условию n/3 £ т £ n/2.
Рисунок 6 - Метод проверки приемлемости результатов измерений, полученных в условиях повторяемости, при n ³ 5 и условии, что получение результатов измерений не является дорогостоящим, или при n ³ 4 и при условии, что получение результатов измерений является дорогостоящим (вариант С)
5.2.4 Пример варианта В. Дорогостоящий химический анализ
Дорогостоящие случаи часто встречаются в химических анализах, которые состоят из сложных и трудоемких процедур, требующих двух, трех или более суток для выполнения одного анализа, при этом затруднительно и дорого выполнить повторный анализ, если при первом анализе обнаруживаются подозрительные данные или выброс. Следовательно, обычно получают три или четыре первоначальных результата измерений в условиях повторяемости, и процесс измерений соответствует случаю В (см. рисунок 5).
Например, при определении содержания золота и серебра в рудах посредством пробирной плавки существующие методы требуют дорогостоящего специального оборудования, высококвалифицированных операторов и много времени, обычно около 2 сут и даже больше, если руда содержит металлы платиновой группы или другие специфические сопутствующие элементы.
Нижеследующие результаты четырех измерений для определения содержания золота были получены на медном концентрате в условиях повторяемости:
|
Au (г/т): |
11,0 |
11,0 |
10,8 |
10,5 |
Эти результаты измерений были обработаны по методу В.
Метод определения содержания золота и серебра не был оформлен в качестве международного стандарта, тем не менее, если установлено значение sr = 0,12 г/т для определения золота, то критический диапазон CR0,95(4) = 3,6´0,12 = 0,43 г/т в соответствии с таблицей 1, где f(4) = 3,6.
Поскольку диапазон вышеприведенных результатов четырех измерений составляет 11,0 - 10,5 = 0,5 г/т, что больше, чем CR0,95(4), окончательным приводимым результатом измерений является медиана результатов четырех измерений, то есть
(11,0 + 10,8)/2 = 10,9 г/т.
5.2.5 Примечание, касающееся эксперимента по оценке прецизионности
Если процедуры, представленные в 5.2.2 или 5.2.3, в результате часто приводят к значениям, превышающим критические, то необходимо обратить внимание на прецизионность метода измерений для данной лаборатории и/или на соблюдение процедуры проведения эксперимента.
5.2.6 Представление окончательного результата
При представлении окончательно приводимого результата измерений необходимо указать:
- количество результатов измерений, использованных для расчета окончательного результата;
- способ определения окончательного результата: среднее арифметическое значение или медиана результатов измерений.
5.3 Методы проверки приемлемости результатов измерений, полученных в условиях как повторяемости, так и воспроизводимости
5.3.1 Общие положения
Эти методы распространяются на случай получения результатов измерений двумя лабораториями, когда существует определенное различие в самих результатах или в их средних арифметических значениях. При этом статистическая проверка основывается на стандартном отклонении не только повторяемости, но и воспроизводимости.
Во всех случаях должно быть предусмотрено достаточное количество материала с целью получения результатов измерений плюс резерв, который может быть использован при необходимости каких-либо повторных испытаний. Величина необходимого резерва зависит от метода измерений и его сложности. В любом случае избыточный (резервный) материал должен храниться защищенным от повреждений или нежелательных изменений.
Пробы (образцы) для выполнения измерений должны быть идентичными, другими словами лабораториями должны использоваться пробы, прошедшие полностью все стадии подготовки.
5.3.2 Статистическая проверка совместимости результатов измерений для двух лабораторий
5.3.2.1 Случай получения только одного результата измерений в каждой лаборатории
Когда каждая лаборатория получила только один результат измерений, абсолютное расхождение между двумя результатами измерений должно проверяться по отношению к пределу воспроизводимости R = 2,8sR. Если абсолютное расхождение между результатами двух измерений не превышает R, эти результаты измерений считают согласующимися, и в качестве окончательного результата может использоваться их среднее арифметическое значение.
Если предел воспроизводимости R превышен, необходимо выяснить, обусловлено ли расхождение в результатах низкой прецизионностью метода измерений и/или различием в испытуемых пробах (образцах). Для проверки прецизионности в условиях повторяемости каждая из лабораторий должна следовать процедурам, описанным в 5.2.2.
5.3.2.2 Случай, когда в двух лабораториях получают более одного результата измерений
Предполагается, что каждая лаборатория должна будет выполнять процедуры, описанные в 5.2, и получит свой окончательный результат. Таким образом, необходимо лишь рассмотреть приемлемость этих двух окончательных результатов. Чтобы проверить, совместимы ли окончательные результаты этих лабораторий, необходимо сравнить абсолютное расхождение между двумя окончательными результатами с критической разностью CD0,95, как это представлено ниже.
a) Критическая разность CD0,95 для двух средних арифметических значений п1 и п2 результатов измерений равна

Если в этом выражении п1 = п2 = 1, оно сводится к R, что соответствует 5.3.2.1.
Если n1 = п2 = 2, выражение упрощается до
![]()
b) Критическая разность CD0,95 для среднего арифметического значения n1 и медианы п2 результатов измерений равна

где с(n) - отношение стандартного отклонения медианы к стандартному отклонению среднего арифметического значения. Его значения приведены в таблице 2.
с) Критическая разность CD0,95 для двух медиан п1 и п2 результатов измерений равна

Если критическая разность не превышается, то приемлемы оба результата измерений, приводимых двумя лабораториями, и в качестве окончательного может использоваться их общее среднее значение. Если критическая разность превышена, то нужно выполнить процедуры, изложенные в общих чертах в 5.3.3.
Таблица 2 - Значения с(n)
|
с(п) |
Число результатов измерений п |
с(п) |
|
|
1 |
1,000 |
11 |
1,228 |
|
2 |
1,000 |
12 |
1,187 |
|
3 |
1,160 |
13 |
1,232 |
|
4 |
1,092 |
14 |
1,196 |
|
5 |
1,197 |
15 |
1,235 |
|
6 |
1,135 |
16 |
1,202 |
|
7 |
1,214 |
17 |
1,237 |
|
8 |
1,160 |
18 |
1,207 |
|
9 |
1,223 |
19 |
1,239 |
|
10 |
1,176 |
20 |
1,212 |
5.3.3 Разрешение противоречий между результатами двух лабораторий
Наличие противоречий между результатами измерений или окончательно приводимыми результатами двух лабораторий может быть объяснено:
- систематическими расхождениями между двумя лабораториями,
- разницей в испытуемых пробах (образцах),
- погрешностями при определении sr и/или sR.
Если имеется возможность поменять испытуемые пробы и/или стандартные образцы между лабораториями, то каждая из них должна получить результаты измерений, пользуясь другой испытуемой пробой, - с целью определения наличия и значения систематической ошибки. Если обмен испытуемыми пробами невозможен, то каждая лаборатория должна получить результаты измерений на одной обычной пробе (предпочтительно на материале с известной измеряемой характеристикой). Использование материала с известной измеряемой характеристикой обладает тем преимуществом, что в итоге становится ясным, на счет какой (или обеих) лаборатории может быть отнесена систематическая ошибка. В случаях, когда использование материала с известной измеряемой характеристикой невозможно, чтобы приписать систематическую ошибку лабораториям, между двумя лабораториями по этому вопросу должно быть достигнуто согласие прибегнуть к помощи референтной лаборатории.
Если расхождение обусловлено различиями между испытуемыми пробами (образцами), обе лаборатории должны объединиться, чтобы совместно отобрать и подготовить пробы (образцы), либо для отбора и подготовки проб должна быть приглашена третья сторона.
5.3.4 Арбитраж
Две стороны контракта могут согласовать процедуру арбитража при заключении контракта или в случае возникновения спорной ситуации.
6 Методы контроля стабильности результатов измерений в пределах лаборатории
6.1 Основные положения
6.1.1 Первым шагом в контроле качества является получение количественных показателей качества (квантификация) посредством химического анализа, физического теста, сенсорной проверки и т.д. Наблюдаемые величины, получаемые при помощи методов квалификации, всегда сопровождаются некоторыми погрешностями, которые можно разделить на погрешности, обусловленные
- отбором проб (образцов),
- подготовкой проб (образцов),
- измерениями и т.д.
Данный раздел будет посвящен только погрешностям, обусловленным измерениями; это погрешность измерения, включающая как неотъемлемую часть неидентичность (вариацию) испытуемых порций или испытуемых проб (образцов).
6.1.2 Считают, что погрешность измерений далее может быть разделена на:
- погрешность, вызываемую случайными причинами (прецизионность), и
- погрешность, вызываемую систематическими причинами (правильность).
6.1.3 От метода измерений естественно ожидать, чтобы его прецизионность и правильность были удовлетворительными. Однако нельзя гарантировать, что метод измерений удовлетворяет требованиям по значению правильности, даже если он удовлетворителен с точки зрения прецизионности. Поэтому при оценке стабильности результатов измерений в пределах лаборатории необходимо проверять как их прецизионность, так и правильность, и поддерживать оба этих показателя на требуемых уровнях в течение длительного периода времени.
6.1.4 Однако может оказаться, что для измеряемой данным методом характеристики не существует истинного значения, или, если даже условно истинное значение существует, то отсутствует возможность проверки правильности результатов измерений из-за того, что нет необходимого стандартного образца. Такие примеры приведены в таблице 3.
Трудно проверить правильность результата измерений, если нет стандартного образца. Тем не менее на практике вместо аттестованного значения измеряемой характеристики во многих случаях в качестве опорного значения может быть использован результат измерений, полученный квалифицированным оператором в хорошо оборудованной лаборатории, строго, безукоризненно и тщательно придерживающейся стандартного метода измерений.
6.1.5 Для контроля стабильности результатов измерений в пределах лаборатории в настоящей части ГОСТ Р ИСО 5725 используют контрольные карты Шухарта (см. ГОСТ Р 50779.42) и контрольные карты кумулятивных сумм.
Если прецизионность или правильность изменяются со временем постепенно, карты кумулятивных сумм более эффективны по сравнению с контрольными картами Шухарта, тогда как при внезапных изменениях применение карт кумулятивных сумм вместо карт Шухарта не дает никаких преимуществ.
Поскольку медленные изменения наиболее характерны и важны применительно к правильности, а внезапные изменения - применительно к прецизионности, для контроля правильности рекомендуются контрольные карты кумулятивных сумм, а для контроля прецизионности - контрольные карты Шухарта.
Однако может оказаться полезным параллельное использование карт обоих типов для контроля как прецизионности, так и правильности.
6.1.6 Поскольку процедуры контроля охватывают довольно длительный период времени и, по всей вероятности, предусматривают смену оператора и замену оборудования, условия повторяемости в этих случаях не применимы. Поэтому при контроле необходимо использовать промежуточные показатели прецизионности, описанные в ГОСТ Р ИСО 5725-3.
6.2 Методы контроля стабильности
6.2.1 Общие положения
a) для результатов рутинных измерений, применяемых для производственного контроля и
b) для результатов измерений, используемых при назначении цены сырья и изготовленных изделий (продукции, товаров).
6.2.1.2 В варианте 6.2.1.1а в принципе необходимо в течение длительного времени контролировать стандартные отклонения промежуточной прецизионности с одним, двумя или тремя изменяющимися факторами, получаемые на основании результатов измерений, чтобы убедиться, что эти показатели поддерживаются на требуемом уровне (см. пример 2 и 6.2.3). Однако обычно достаточен контроль всего лишь одного показателя прецизионности, так как даже в случае, когда результаты измерений имеют смещения, существует возможность обнаружить соответствующие изменения производственного процесса, если отклонения результатов измерений достаточно малы по сравнению с этими смещениями.
В то же время надо иметь в виду, что если для этой цели использовать стандартное отклонение повторяемости, возможно перерегулирование процесса из-за чрезмерной чувствительности; поэтому лучше использовать для этих целей подходящее стандартное отклонение промежуточной прецизионности.
Таблица 3 - Классификация характеристик испытуемых материалов по способам получения истинных значений этих характеристик и параметрам, существенным для контроля точности (правильности и прецизионности) их оценок
|
Примеры |
|||
|
Характеристики |
Наличие стандартного образца (СО)2) |
Параметры, существенные для контроля точности3) |
|
|
Теоретическое значение, опирающееся на научные принципы, может быть установлено в качестве истинного значения. |
Содержание химического компонента бензойной кислоты |
Есть4) |
D и sW |
|
Несмотря на то, что истинное значение теоретически существует, на практике его установить, пользуясь имеющейся техникой, невозможно; таким образом, согласованное значение, основанное на совместной экспериментальной работе при содействии научной или инженерной группы, принимают в качестве условного истинного значения. |
а) Содержание железа в руде, в процентах по массе |
Есть |
D и sW |
|
b) Содержание серы в пирите, в процентах по массе |
Нет5) |
sW и sL |
|
|
Приписанное значение, основанное на методе измерений, установленном в международном, национальном стандарте или частной организацией, принимают в качестве условного истинного значения. |
а) Октановое число бензина |
Есть |
D и sW |
|
b) Прочность кокса |
Нет6) |
sM/sW, sL и sW |
|
|
с) Текучесть расплава термопластов |
Нет7) |
sW и sL |
|
|
1) См. ИСО 3534-1 [1]. 2) См. ИСО Руководство 35 [2] и ГОСТ 8.315. 3) D-систематическая
погрешность результата лаборатории при реализации стандартного метода
измерений; sW
- внутрилабораторное стандартное отклонение; sL - межлабораторное стандартное отклонение; 4) Испытуемый материал сам по себе может быть использован в качестве СО, если он чист и стабилен. 5) СО не может быть утвержден, поскольку материал является нестабильным. 6) СО не может быть утвержден по причине большой массы, состоящей из твердых, хрупких частиц, различающихся размером, формой и составом, которая необходима для каждого испытания, являющегося разрушающим. 7) Опорное значение определяется самим методом измерений. |
|||
6.2.1.3 В варианте 6.2.1.2b контролю необходимо подвергать как правильность (см. пример 3 в 6.2.4), так и прецизионность, чтобы убедиться, что соответствующие показатели выдерживаются на требуемом уровне; таким образом, в данном случае требуется знать опорное значение измеряемой (испытуемой) характеристики.
6.2.1.4 Далее представлены следующие четыре примера:
- примеры 1 и 2 показывают, как с помощью карт Шухарта контролировать стабильность повторяемости или показателя промежуточной прецизионности;
- примеры 3 и 4 показывают как контролировать правильность, используя либо карты Шухарта, либо метод кумулятивных сумм.
6.2.2 Пример 1. Контроль стабильности стандартного отклонения повторяемости рутинного анализа
6.2.2.1 Основные положения
а) Метод измерений
Определение содержания никеля методом, регламентированным в ИСО 6352:1985 [3].
b) Источник
Отчет лаборатории ферроникелевого плавильного завода от сентября 1985 г.
с) Описание
В производственной лаборатории ферроникелевого плавильного завода каждый день выполняется химический анализ с целью определения химического состава ферроникелевых сплавов совместно с контролем стабильности определения содержания никеля, используя собственный стандартный образец, приготовленный лабораторией (далее - стандартный образец лаборатории).
Для контроля стабильности результатов определения содержания никеля анализу ежедневно подвергают две порции стандартного образца лаборатории в условиях повторяемости, то есть одним и тем же оператором, использующим одно и то же оборудование, в одно и то же время.
Химический состав стандартного образца лаборатории таков:
|
Ni ... 47,21 % |
Со ... 1,223 % |
Si ... 3,50 % |
|
Mn ... 0,015 % |
Р ... 0,003 % |
S ... 0,001 % |
|
Cr ... 0,03 % |
Cu ... 0,038 % |
6.2.2.2 Исходные данные
Результаты рутинного анализа содержания никеля в стандартном образце лаборатории, полученные в условиях повторяемости, представлены в таблице 5 как х1 и х2, выраженные в процентах по массе.
6.2.2.3 Проверка стабильности с применением контрольных карт Шухарта
Применяя метод контрольных карт Шухарта (R-диаграмм) (см. ГОСТ Р 50779.42) к результатам измерений, представленным в таблице 5, проверяют стабильность этих результатов измерений и оценивают стандартное отклонение повторяемости. При расчете средней линии и контрольных пределов (UCL и LCL) используют коэффициенты, приведенные в таблице 4.
Примечание 4 - Во избежание путаницы с символом R, используемым в настоящем стандарте применительно к воспроизводимости, R-карта из ГОСТ Р 50779.42 далее будет упоминаться как карта пределов (a range chart).
Таблица 4 - Коэффициенты для расчета параметров карты пределов
|
Коэффициенты для расчета средней линии и пределов действия1) |
Коэффициенты для расчета пределов предупреждения2) |
||||
|
Число наблюдений в подгруппе |
Коэффициент для средней линии |
Коэффициент для предела действия |
Коэффициенты для пределов предупреждения |
||
|
d2 |
D2 |
d3 |
D1(2) |
D2(2) |
|
|
2 |
1,128 |
3,686 |
0,853 |
- |
2,834 |
|
3 |
1,693 |
4,358 |
0,888 |
- |
3,469 |
|
4 |
2,059 |
4,698 |
0,880 |
0,299 |
3,819 |
|
5 |
2,326 |
4,918 |
0,864 |
0,598 |
4,054 |
|
1) Данные взяты из таблицы 2 ГОСТ Р 50779.42. 2) Коэффициенты, применяемые для расчета пределов предупреждения, вычисляют по формулам: D1(2) = d2 - 2d3; D2(2) = d2 + 2d3. |
|||||
Таблица 5 - Данные контрольной карты для примера 1 (6.2.2)
|
2 Единица измерения: 3 Метод анализа: 4 Период: 5 Лаборатория: |
содержание никеля в стандартном образце лаборатории. % (по массе). по ИСО 6352:1985 [3]. с 1 по 30 сентября 1985 г. производственная лаборатория «А» ферроникелевого плавильного завода. |
||||
|
Дата проведения анализа (номер подгруппы) |
Данные наблюдений |
Расхождение |
Примечание |
||
|
x1 |
x2 |
w |
|||
|
1 |
47,379 |
47,333 |
0,046 |
||
|
2 |
47,261 |
47,148 |
0,113 |
Сверх предела предупреждения |
|
|
3 |
47,270 |
47,195 |
0,075 |
||
|
4 |
47,370 |
47,287 |
0,083 |
||
|
5 |
47,288 |
47,284 |
0,004 |
||
|
6 |
47,254 |
47,247 |
0,007 |
||
|
7 |
47,239 |
47,160 |
0,079 |
||
|
8 |
47,239 |
47,193 |
0,046 |
||
|
9 |
47,378 |
47,354 |
0,024 |
||
|
10 |
47,331 |
47,267 |
0,064 |
||
|
11 |
47,255 |
47,278 |
0,023 |
||
|
12 |
47,313 |
47,255 |
0,058 |
||
|
13 |
47,274 |
47,167 |
0,107 |
Сверх предела предупреждения |
|
|
14 |
47,313 |
47,205 |
0,108 |
Сверх предела предупреждения |
|
|
15 |
47,296 |
47,231 |
0,065 |
||
|
16 |
47,264 |
47,247 |
0,017 |
||
|
17 |
47,238 |
47,253 |
0,015 |
||
|
18 |
47,181 |
47,255 |
0,074 |
||
|
19 |
47,327 |
47,240 |
0,087 |
||
|
20 |
47,358 |
47,308 |
0,050 |
||
|
21 |
47,295 |
47,133 |
0,162 |
Сверх предела действия |
|
|
22 |
47,310 |
47,244 |
0,066 |
||
|
23 |
47,366 |
47,293 |
0,073 |
||
|
24 |
47,209 |
47,185 |
0,024 |
||
|
25 |
47,279 |
47,268 |
0,011 |
||
|
26 |
47,178 |
47,200 |
0,030 |
||
|
27 |
47,211 |
47,193 |
0,018 |
||
|
28 |
47,195 |
47,216 |
0,021 |
||
|
29 |
47,274 |
47,252 |
0,022 |
||
|
30 |
47,300 |
47,212 |
0,088 |
||
|
Всего |
1,660 |
||||
|
Среднее значение |
0,0553 |
|
|||
|
Пояснения sr = 0,0375. а) Средняя линия d2sr = 1,128´0,0375 = 0,0423. б) Пределы действия: UCL @ D2sr = 3,686´0,0375 = 0,1382; LCL - отсутствует, в) Пределы предупреждения: UCL @ D2(2)sr = 2,834´0,0375 = 0,1062; LCL - отсутствует. |
|||||
Поскольку в данном примере заранее задано стандартное отклонение повторяемости (sr), полученное на основании результатов измерений в предыдущем квартале, параметры контрольной карты пределов рассчитывают следующим образом.
a) Средняя линия - d2sr = 1,128´0,0375 = 0,0423.
b) Пределы действия:
UCL = D2sr = 3,686´0,0375 = 0,1382;
UCL - отсутствует
c) Пределы предупреждения:
UCL = D2(2)sr = 2,834´0,0375 = 0,1062;
LCL - отсутствует.
Рисунок 7 - Карта пределов для содержания никеля (%) в стандартном образце лаборатории, полученных в условиях повторяемости
Оценку стандартного отклонения повторяемости (sr) получают из следующих уравнений:
![]()
![]()
Расхождения рассчитаны для 30 подгрупп, каждая из которых содержит две пробы. Таблица 5 - пример рабочей карты для выполнения данного расчета, а рисунок 7 - пример представления данных карты с нанесенными контрольными пределами.
Карта, приведенная на рисунке 7, свидетельствует, что результаты измерений не являются стабильными, так как имеется одна точка выше предела действия и пара последовательных точек выше предела предупреждения.
6.2.3.1 Основные положения
a) Метод измерений
Определение содержания серы в доменном коксе в процентах по массе методом, регламентированным в ИСО 351:1:1984 [4].
b) Источник
Отчет лаборатории сталеплавильного завода от августа 1985 г.
c) Описание
Пробы доменного кокса отбирают из коксовой батареи в плановом порядке от каждой производственной партии, в каждую рабочую смену при трехсменном производственном режиме, ежедневно. После отбора испытуемую пробу от каждой партии подготавливают в лаборатории для химического анализа с целью определения содержания серы (% по массе).
6.2.3.2 Исходные данные
Результаты контрольного анализа содержания серы в пробах кокса из батареи № 1 (август 1985 г.) представлены в таблице 6. Одна проба кокса, выбранная наугад из проб, подвергавшихся анализу во время смены (х1), анализировалась повторно другим оператором в другую смену на следующий день (х2), и результаты испытаний ежедневно сравнивались.
6.2.3.3 Проверка стабильности методом контрольных карт Шухарта
Применяя метод контрольных карт Шухарта (карт пределов, см. ГОСТ Р 50779.42) к данным таблицы 6, проверяют стабильность этих результатов измерений и оценивают стандартное отклонение промежуточной прецизионности с изменяющимися факторами «время» и «оператор».
Что касается коэффициентов для расчета средней линии, а также пределов действия и предупреждения (UCL и LCL), см. пример 1 в 6.2.2. Поскольку в данном примере также заранее задано стандартное отклонение промежуточной прецизионности с изменяющимися факторами «время» и «оператор» sI(TO), полученное на основании результатов измерений в предыдущем квартале, параметры контрольной карты пределов рассчитывают следующим образом.
a) Средняя линия - d2sr = 1,128´0,0133 = 0,0150.
b) Пределы действия:
UCL = D2sI(TO) = 3,686´0,0133 = 0,0490;
LCL отсутствует.
c) Пределы предупреждения:
UCL = D2(2)sI(TO) = 2,834´0,0133 = 0,0378;
LCL отсутствует.
Оценку стандартного отклонения промежуточной прецизионности с изменяющимися факторами «время» и «оператор» sI(TO) получают из следующих уравнений:
![]()
![]()
Расхождения рассчитаны для 31 подгруппы, каждая из которых содержит две пробы, как в таблице 6, и приведены на рисунке 8 с найденными выше контрольными пределами.
Карта, изображенная на рисунке 8, не дает никаких оснований считать эти результаты измерений нестабильными.
Рисунок 8 - Карта пределов для содержания серы (%) в доменном коксе, полученных в условиях промежуточной прецизионности с изменяющимися факторами «время» и «оператор»
Таблица 6 - Данные контрольной карты для примера 2 (6.2.3)
|
2 Единица измерения: 3 Метод анализа: 4 Период: 5 Лаборатория: |
содержание серы в доменном коксе. % (по массе). по ИСО 351:1:1984 [4]. с 1 по 31 августа 1985 г. производственная лаборатория «В» сталеплавильного завода. |
||||
|
Дата проведения анализа (номер подгруппы) |
Данные наблюдений |
Расхождение |
Примечание |
||
|
x1 |
x2 |
w |
|||
|
1 |
0,56 |
0,56 |
0,00 |
||
|
2 |
0,48 |
0,50 |
0,02 |
||
|
3 |
0,57 |
0,58 |
0,01 |
||
|
4 |
0,60 |
0,58 |
0,02 |
||
|
5 |
0,58 |
0,58 |
0,00 |
||
|
6 |
0,50 |
0,49 |
0,01 |
||
|
7 |
0,56 |
0,58 |
0,02 |
||
|
8 |
0,56 |
0,56 |
0,00 |
||
|
9 |
0,48 |
0,46 |
0,02 |
||
|
10 |
0,54 |
0,53 |
0,01 |
||
|
11 |
0,55 |
0,57 |
0,02 |
||
|
12 |
0,46 |
0,45 |
0,01 |
||
|
13 |
0,58 |
0,58 |
0,00 |
||
|
14 |
0,54 |
0,56 |
0,02 |
||
|
15 |
0,56 |
0,56 |
0,00 |
||
|
16 |
0,57 |
0,58 |
0,01 |
||
|
17 |
0,46 |
0,45 |
0,01 |
||
|
18 |
0,56 |
0,56 |
0,00 |
||
|
19 |
0,56 |
0,57 |
0,01 |
||
|
20 |
0,57 |
0,55 |
0,02 |
||
|
21 |
0,44 |
0,45 |
0,01 |
||
|
22 |
0,59 |
0,55 |
0,04 |
Выше предела предупреждения1) |
|
|
23 |
0,55 |
0,57 |
0,02 |
||
|
24 |
0,58 |
0,56 |
0,02 |
||
|
25 |
0,46 |
0,45 |
0,01 |
||
|
26 |
0,60 |
0,58 |
0,02 |
||
|
27 |
0,59 |
0,56 |
0,03 |
||
|
28 |
0,54 |
0,56 |
0,02 |
||
|
29 |
0,47 |
0,49 |
0,02 |
||
|
30 |
0,59 |
0,58 |
0,01 |
||
|
31 |
0,49 |
0,52 |
0,03 |
||
|
Всего |
16,84 |
16,72 |
0,44 |
||
|
Среднее значение |
0,0142 |
|
|||
|
Пояснения sI(TO) = 0,0133. x1 - первый рутинный анализ. х2 - второй анализ на следующий день, выполняемый другим оператором. а) Средняя линия d2sI(TO) = 1,128´0,0133 = 0,0150. б) Пределы действия: UCL = D2sI(TO) = 3,686´0,0133 = 0,0490; LCL - отсутствует. в) Пределы предупреждения: UCL = D2(2)sr(TO) = 2,834´0,0133 = 0,0378; LCL - отсутствует. 1) Фактическая температура нагрева для получения х2 была ниже заданной. |
|||||
6.2.4 Пример 3. Контроль стабильности показателей правильности рутинного анализа
6.2.4.1 Основные положения
a) Метод измерений
Определение зольности угля (в процентах по массе) методом, регламентированным в ИСО 1171:1981 [5].
b) Источник
Отчет лаборатории сталеплавильного завода от июня 1985 г.
с) Описание
На сталеплавильный завод поступают угольные фракции для производства доменного кокса при трехсменном режиме работы коксовой батареи.
Чтобы контролировать качество коксового производства, в каждую смену анализируют зольность углей методом, регламентированным в ИСО 1171. Контроль стабильности стандартного отклонения промежуточной прецизионности рутинного анализа с изменяющимися факторами «время» и «оператор» проводят так же, как в примере 2 (6.2.3).
В данном примере показан метод контроля стабильности показателя правильности рутинного анализа с использованием собственного стандартного образца (содержание золы 10,29 %).
6.2.4.2 Исходные данные
Ежедневно собственный стандартный образец (стандартный образец лаборатории) анализирует оператор, которого назначают наугад из числа всех операторов трех смен. Результаты анализа представлены, как в таблице 7.
6.2.4.3 Проверка стабильности методом контрольных карт Шухарта
Применяя метод контрольных карт шухарта к данным таблицы 7, проверяют стабильность показателя правильности результатов рутинного анализа и оценивают его систематическую погрешность.
Поскольку в данной лаборатории рутинный анализ выполняют в условиях промежуточной прецизионности с изменяющимися факторами «время» и «оператор», стандартное отклонение повторяемости sr не представляет фактической прецизионности результатов анализа, получаемых в лаборатории, и не может быть использовано для контроля систематической погрешности. Вместо проведения эксперимента с целью получения стандартного отклонения промежуточной прецизионности с изменяющимися факторами «время» и «оператор» si(TO), в качестве более простого способа предпочитают карты текущих расхождений.
Контрольную карту готовят, используя формулы, приведенные в пояснениях к таблице 7, и предварительно установленные значения m и sI(TO). На картах, приведенных на рисунке 9, показаны периоды, когда систематическая погрешность и расхождения невелики, и другие периоды, когда результаты анализа отличаются повышенной нестабильностью, подтверждая необходимость изучения причин этих отклонений.
6.2.4.4 Проверка стабильности методом контрольных карт кумулятивных сумм
Значения (Н; К)
на контрольной карте кумулятивных сумм для оценки ![]() систематической погрешности при
(h = 4,79 k
= 0,5) рассчитывают следующим образом
(см. рисунок 10).
систематической погрешности при
(h = 4,79 k
= 0,5) рассчитывают следующим образом
(см. рисунок 10).
|
Нижняя сторона |
|
|
Н = hsI(ТO) = 4,79´0,06645 = 0,318. |
-Н = -0,138. |
|
K1 = m + ksI(TO) = 10,29 + 0,5´0,06645 = 10,323. |
K2 = m - ksI(ТO) = 10,29 - 0,5´0,06645 = 10,257. |
Таблица 7 - Данные контрольной карты для примера 3 (6.2.4)
|
1 Характеристика качества: 2 Единица измерения: 3 Метод анализа: 4 Период: 5 Лаборатория: |
зольность собственного стандартного образца. % (по массе). ИСО 1171:1981 [5]. С 01 по 30 июня 1985 г. производственная лаборатория «С» сталеплавильного завода. |
||||
|
Дата проведения анализа (номер подгруппы) |
Результат анализа у |
Оценка
систематической погрешности |
Текущее расхождение w |
Примечание |
|
|
1 |
10,30 |
0,01 |
0,01 |
||
|
2 |
10,29 |
0,00 |
0,01 |
||
|
3 |
10,28 |
-0,01 |
0,02 |
||
|
4 |
10,30 |
0,01 |
0,01 |
||
|
5 |
10,29 |
0,00 |
0,00 |
||
|
6 |
10,29 |
0,00 |
0,09 |
||
|
7 |
10,20 |
-0,09 |
0,08 |
||
|
8 |
10,28 |
-0,01 |
0,01 |
||
|
9 |
10,29 |
0,00 |
0,00 |
||
|
10 |
10,29 |
0,00 |
0,10 |
||
|
11 |
10,19 |
- 0,10 |
0,10 |
||
|
12 |
10,29 |
0,00 |
0,00 |
||
|
13 |
10,29 |
0,00 |
0,00 |
||
|
14 |
10,29 |
0,00 |
0,01 |
||
|
15 |
10,28 |
-0,01 |
0,02 |
||
|
16 |
10,30 |
0,01 |
0,01 |
||
|
17 |
10,29 |
0,00 |
0,00 |
||
|
18 |
10,29 |
0,00 |
0,01 |
||
|
19 |
10,28 |
-0,01 |
0,00 |
||
|
20 |
10,28 |
-0,01 |
0,00 |
||
|
21 |
10,28 |
-0,01 |
0,03 |
||
|
22 |
10,31 |
0,02 |
0,12 |
||
|
23 |
10,19 |
-0,10 |
0,10 |
||
|
24 |
10,29 |
0,00 |
0,07 |
||
|
25 |
10,36 |
0,07 |
0,00 |
||
|
26 |
10,36 |
0,07 |
0,07 |
||
|
27 |
10,29 |
0,00 |
0,01 |
||
|
28 |
10,30 |
0,01 |
0,02 |
||
|
29 |
10,28 |
-0,01 |
0,09 |
||
|
30 |
10,19 |
-0,10 |
|||
|
Всего |
308,44 |
-0,26 |
0,99 |
||
|
Среднее значение |
-0,0866 |
0,0341 |
|
||
|
Пояснения Зольность собственного стандартного образца m = 10,29. Стандартное отклонение, полученное на основании результатов испытаний за предыдущий квартал, sI(TO) = 0,06645. Оценка систематической погрешности Текущее расхождение х-карта: Средняя линия - нулевая или равна нулю Пределы действия: UCL = +3sI(TO) = 0,1994, LCL = -3sI(TO) = -0,1994; Пределы предупреждения UCL = +2sI(TO) = 0,1329, LCL = -2sI(TO) = -0,1329. Карта текущих расхождений: Средняя линия d2sI(TO) = 1,128´0,06645 = 0,07496; Пределы действия: UCL = D2sI(TO) = 3,396´0,06645 = 0,245, LCL - отсутствует; Пределы предупреждения: UCL = D2(2)sI(TO) = 2,834´0,06645 = 0,1883, LCL - отсутствует. |
|||||
Рисунок 9 - Контрольная карта
Шухарта для оценки ![]() - систематической погрешности определения
зольности, % (по массе) собственного стандартного образца
- систематической погрешности определения
зольности, % (по массе) собственного стандартного образца
Рисунок 10 - Контрольная карта
кумулятивных сумм для оценки ![]() - систематической погрешности определения
зольности, % (массе) собственного стандартного образца
- систематической погрешности определения
зольности, % (массе) собственного стандартного образца
6.2.5 Пример А Другой способ контроля стабильности показателя
6.2.5.1 Основные положения
а) Метод измерений
Определение содержания мышьяка в оксиде
b) Источник
Новости стандартизации ASTM [6].
6.2.5.2 Исходные данные
См. таблицу 8.
6.2.5.3 Проверка стабильности метода контрольных карт Шухарта
Контрольную карту Шухарта для ![]() (рисунок 11) готовят, используя формулы,
приведенные в пояснениях к таблице 8,
и предварительно установленные значения μ и σr.
(рисунок 11) готовят, используя формулы,
приведенные в пояснениях к таблице 8,
и предварительно установленные значения μ и σr.
Карта показывает нестабильность результатов измерений, поскольку на ней одна выше предела действия и две серии измерений из семи или более результатов находятся ниже средней линии.
6.2.5.4. Контроль стабильности методом контрольных куммулятивных сумм
Расчет на контрольной карте куммулятивных сумм для средних значений k производят следующим образом (см. рисунок 12).
Таблица 8 - Данные ![]() - карты для примера 4 (6.2.5)
- карты для примера 4 (6.2.5)
|
2 Единица измерения: 3 Метод анализа: |
содержание As в собственном стандартном образце. млн-1 (по массе). выделение диэтилдитиокарбамат-арсенида серебра колориметрированием. |
||||
|
Номер группы |
Данные наблюдений |
|
Примечание |
||
|
x1 |
x2 |
||||
|
1 |
3,70 |
3,80 |
3,75 |
||
|
2 |
3,76 |
3,86 |
3,81 |
||
|
3 |
3,64 |
3,38 |
3,51 |
||
|
4 |
4,01 |
3,62 |
3,82 |
||
|
5 |
3,40 |
3,52 |
3,46 |
||
|
6 |
3,65 |
3,53 |
3,59 |
||
|
7 |
3,20 |
3,58 |
3,39 |
||
|
8 |
4,19 |
4,65 |
4,42 |
Выше предела действия |
|
|
9 |
3,97 |
3,77 |
3,87 |
||
|
10 |
2,95 |
3,69 |
3,32 |
||
|
11 |
3,43 |
3,55 |
3,49 |
||
|
12 |
3,85 |
3,53 |
3,69 |
||
|
13 |
3,77 |
3,17 |
3,47 |
||
|
14 |
3,19 |
3,60 |
3,40 |
||
|
15 |
3,75 |
3,45 |
3,60 |
||
|
16 |
3,55 |
3,25 |
3,40 |
||
|
17 |
3,98 |
3,76 |
3,87 |
||
|
18 |
3,56 |
3,78 |
3,67 |
||
|
19 |
3,54 |
4,02 |
3,78 |
||
|
20 |
3,35 |
3,55 |
3,45 |
||
|
21 |
3,37 |
3,25 |
3,31 |
||
|
22 |
3,42 |
3,42 |
3,42 |
||
|
23 |
3,71 |
3,87 |
3,79 |
||
|
24 |
3,77 |
3,62 |
3,70 |
||
|
25 |
3,82 |
3,58 |
3,70 |
||
|
26 |
3,73 |
3,02 |
3,38 |
||
|
27 |
3,48 |
3,28 |
3,38 |
||
|
28 |
4,01 |
4,19 |
4,10 |
||
|
29 |
3,63 |
3,11 |
3,37 |
||
|
30 |
3,51 |
3,23 |
3,37 |
||
|
Всего |
108,28 |
||||
|
Среднее значение |
3,609 |
||||
|
Пояснения Содержание мышьяка в собственном стандартном образце m = 3,80. Стандартное отклонение по данным предыдущих анализов sr = 0,236.
Средняя линия равна 3,80 (см. рисунок 11); Пределы действия:
|
|||||
Рисунок 11 - Контрольная карта
Шухарта для средних значений ![]() содержания мышьяка в оксиде цинка
содержания мышьяка в оксиде цинка
Рисунок 12 - Контрольная карта
кумулятивных сумм для средних значений ![]() содержания мышьяка в оксиде цинка
содержания мышьяка в оксиде цинка
7 Использование стандартных отклонений повторяемости и воспроизводимости при оценке деятельности лабораторий
7.1 Метод оценки
7.1.1 Основные положения
Настоящий раздел посвящен оценке деятельности лабораторий в отношении только одного метода измерений, который стандартизован и используется в различных лабораториях. Поэтому возможно оценить прецизионность метода в форме стандартных отклонений повторяемости (сходимости) и воспроизводимости. Предполагается, что значения этих стандартных отклонений были определены ранее в эксперименте по оценке прецизионности.
Существуют оценки трех типов, зависящие от наличия стандартных образцов для метода или опорной лаборатории. Если стандартные образцы существуют для необходимого числа уровней, оценка может быть выполнена при участии лишь одной испытуемой лаборатории. Относительно метода измерений, для которого стандартных образцов нет, такой простой способ оценки невозможен. Такая лаборатория должна сопоставляться с лабораторией, обеспечивающей высокое качество испытаний и широко признанной как лаборатория высокого рейтинга. При постоянной оценке деятельности лабораторий часто несколько лабораторий должно подвергаться оценке одновременно. В этом случае целесообразен совместный оценочный эксперимент как оценка третьего типа.
Целью проведения совместного оценочного эксперимента является сопоставление результатов каждой лаборатории с той из числа других лабораторий, которая является примером совершенного исполнения своих функций.
7.1.2 Возможности совместного оценочного эксперимента
Стандартное отклонение повторяемости метода измерений является мерой неопределенности результатов измерений, получаемых при постоянных условиях в пределах лаборатории. В этом случае оно является выражением внутрилабораторной прецизионности в условиях повторяемости, определения которым даны в ГОСТ Р ИСО 5725-1.
Систематическая погрешность результатов лаборатории при реализации конкретного метода измерений (см. 3.9 ГОСТ Р ИСО 5725-1) может быть определена непосредственно при условии, что существует и известно истинное значение измеряемой характеристики, как в случае со стандартными образцами. Когда истинное значение неизвестно, систематическая погрешность должна определяться косвенным путем. Одним из способов является сопоставление результатов лаборатории с другой «референтной» лабораторией, систематическая погрешность результатов которой при реализации данного метода измерений известна. Целесообразность данного решения, однако, в очень сильной степени зависит от прецизионности и систематической погрешности при реализации этого метода измерений в «референтной» лаборатории.
В случае совместного оценочного эксперимента мерой согласованности результатов, полученных в различных лабораториях, является воспроизводимость, которая также может быть использована для оценки систематической погрешности результатов каждой лаборатории. Результат лаборатории, которая обнаруживает большое систематическое отклонение, будет являться выбросом при определении воспроизводимости в ходе оценочного межлабораторного эксперимента.
В настоящем разделе предполагается, что
прецизионность метода измерений определена заранее. Это означает, что дисперсия
повторяемости ![]() , межлабораторная дисперсия
, межлабораторная дисперсия ![]() и дисперсия
воспроизводимости
и дисперсия
воспроизводимости ![]() известны.
известны.
Методы, изложенные в разделе 7, главным образом предназначены для контроля систематической погрешности результатов лаборатории (при реализации конкретного метода измерений). Методы, представленные в разделе 6, более эффективны при контроле повторяемости результатов лаборатории или ее промежуточной прецизионности (при реализации конкретного метода измерений).
7.2 Оценка качества применения метода измерений лабораторией, не проходившей прежде процедуру оценки ее деятельности
7.2.1 Оценка деятельности лаборатории
Общие критерии оценки деятельности лаборатории приведены в руководстве 25 ИСО/МЭК* (ГОСТ Р ИСО/МЭК 17025-2000). Лаборатория должна работать на достойном уровне и осуществлять удовлетворительный внутренний контроль качества. Методы внутреннего контроля качества были описаны в разделе 6. Эта часть контроля базируется только на инспектировании каждой лаборатории в ее обычной рабочей обстановке. Это может быть выполнено немедленно без использования специального испытуемого материала и без привлечения других лабораторий.
_____________
* С 1999 г. в ИСО/МЭК 17025:1999.
Для количественной оценки выполняемого лабораторией метода измерений необходимо провести контрольный эксперимент. Это может быть сделано в пределах лаборатории, используя стандартные образцы (см. 7.2.3), либо посредством сопоставления с лабораторией высокого рейтинга (см. 7.2.4).
7.2.2 Общие соображения по контрольным экспериментам
При планировании контрольного эксперимента должны быть рассмотрены следующие вопросы:
a) На каком количестве уровней (q) должен проводиться эксперимент? Этот вопрос изложен в подразделе 6.3 ГОСТ Р ИСО 5725-1.
b) Сколько повторных измерений (n) должно быть выполнено на каждом уровне?
c) Сколько лабораторий (р) примет участие в случае совместного оценочного эксперимента?
При планировании эксперимента необходимо также принять во внимание подраздел 6.1 ГОСТ Р ИСО 5725-1 и разделы 5 и 6 ГОСТ Р ИСО 5725-2.
Испытуемый материал должен быть отправлен в лабораторию анонимно, то есть таким образом, чтобы быть уверенным в том, что с ним будут обращаться как в обычной практике в данной лаборатории, не уделяя ему особого внимания.
7.2.3 Метод измерений, для которого имеются стандартные образцы
7.2.3.1 Общие положения
7.2.3.1.1 Когда имеются стандартные образцы, оценка может производиться в одной лаборатории. Поскольку прецизионность метода установлена, известное значение стандартного отклонения повторяемости используют при оценке внутренней прецизионности, тогда как систематическую погрешность определяют путем сопоставления результатов измерений с опорным значением.
Иногда бывает уместным ввести поддающуюся обнаружению систематическую погрешность лаборатории Dm в качестве минимального значения лабораторной систематической погрешности реализуемого метода измерений (см. 3.11 ГОСТ Р ИСО 5725-1), которую экспериментатор стремится выявить с высокой вероятностью на основании результатов эксперимента.
7.2.3.1.2 Для оценки внутренней прецизионности необходимо в пределах лаборатории выполнить повторяющиеся измерения. После рассмотрения вопросов, упомянутых в 7.2.2, испытуемый материал распределяют по q уровням и на каждом уровне выполняют п повторных измерений. Обрабатывая результаты, используют метод, приведенный в разделе 7 ГОСТ Р ИСО 5725-2. При оценке внутренней прецизионности внутриэлементное стандартное отклонение sr сопоставляют с известным стандартным отклонением повторяемости sr. Критерий приемлемости (критерий приемлемого значения прецизионности) определяют по соотношению
![]() (1)
(1)
где ![]() - это (1 - a)-квантиль c2-распределения
с v = n - 1 степенями свободы. При отсутствии других
установок уровень значимости a предполагается равным 0,05.
- это (1 - a)-квантиль c2-распределения
с v = n - 1 степенями свободы. При отсутствии других
установок уровень значимости a предполагается равным 0,05.
Приведенное выше неравенство должно быть справедливым для 95 % из q уровней. Как правило, q скорее всего невелико; это значит, что критерий (1) для лаборатории должен выполняться на всех q уровнях.
7.2.3.1.3 При оценке систематической
погрешности среднее значение ![]() для каждого уровня сопоставляется с
соответствующим опорным значением m. Поскольку
для каждого уровня сопоставляется с
соответствующим опорным значением m. Поскольку
![]() (2)
(2)
критерий приемлемости значения систематической погрешности определяется неравенством
![]() (3)
(3)
которое должно выполняться на каждом из q уровней.
При n = 2 критерий (3) приводится к виду
Если имеется поддающаяся обнаружению систематическая погрешность, вводят еще один критерий приемлемости в виде
![]() (5)
(5)
7.2.3.2 Пример. Определение содержания цемента в бетоне
7.2.3.2.1 Основные положения
Содержание цемента является важным показателем, так как он оказывает влияние на прочность бетона, и часто в технических условиях на бетон устанавливают минимальное значение содержания цемента. Содержание цемента может определяться на основании измерений содержания кальция в пробах цемента и в образцах бетона. Для оценки деятельности лаборатории можно приготовить конкретные образцы бетона с известным содержанием цемента.
Для оценки шести лабораторий были приготовлены стандартные образцы с содержанием цемента 425 кг/м3. В каждой лаборатории выполнялись два параллельных определения.
7.2.3.2.2 Исходные данные
См. таблицу 9. Значения стандартных отклонений повторяемости и воспроизводимости составляют: sr = 16;
sR = 25.
Таблица 9 - Содержание цемента в бетоне, кг/м3
|
Данные наблюдений |
||
|
yi1 |
yi2 |
|
|
1 |
406 |
431 |
|
2 |
443 |
455 |
|
3 |
387 |
431 |
|
4 |
502 |
486 |
|
5 |
434 |
456 |
|
6 |
352 |
399 |
7.2.3.2.3 Расчет средних значений и расхождений в базовых элементах
См. таблицу 10.
Таблица 10 - Средние значения и расхождения в базовых элементах, кг/м3
|
Среднее значение |
Расхождение |
|
|
1 |
418,5 |
25 |
|
2 |
449 |
12 |
|
3 |
409 |
44 |
|
4 |
494 |
16 |
|
5 |
445 |
22 |
|
6 |
375,5 |
47 |
7.2.3.2.4 Оценка внутрилабораторной прецизионности
Расхождения, приведенные в таблице 10, сопоставляются со стандартным отклонением повторяемости (сходимости) в соответствии с неравенством
![]()
в котором при a = 0,05 и v
= 1 значение ![]()
В лаборатории № 6 было обнаружено отклонение:
(y6; 1 - у6; 2)2 = 2209; так что значение в левой части формулы равно 4,31.
7.2.3.2.5 Оценка систематической погрешности
Формула (4) для критерия приемлемости систематической погрешности дает в результате
![]()
Для лаборатории № 4 полученное значение в левой части составляет
![]()
Для лаборатории № 6 полученное значение в левой части составляет
![]()
Отсюда следует, что обе лаборатории имеют неудовлетворительную систематическую погрешность при измерении содержания цемента в бетоне.
7.2.4 Метод измерений, для которого нет стандартных образцов
7.2.4.1 Когда не существует стандартных образцов, оценка деятельности лаборатории должна производиться посредством сопоставления с лабораторией высокого рейтинга. Чтобы сделать обоснованный вывод относительно новой лаборатории, необходимо найти лабораторию, работающую с хорошей прецизионностью и малой систематической погрешностью при реализации конкретного метода измерений.
Как и в случае со стандартными образцами, иногда бывает уместным ввести поддающуюся обнаружению разность l между систематическими погрешностями результатов двух лабораторий при реализации одного и того же метода измерений. Она определяется как минимальное значение разности между ожидаемыми значениями результатов, полученными двумя лабораториями, которое экспериментатор стремится выявить с высокой вероятностью.
7.2.4.2 Испытуемые материалы направляют в обе лаборатории, как описано в 7.2.3.1.2, и подобным же образом в каждой лаборатории оценивают внутрилабораторную прецизионность. Предпочтительно, чтобы эти лаборатории выполнили одинаковое количество (n) измерений на каждом уровне.
7.2.4.3 При оценке систематической погрешности метода измерений d, средние арифметические значения на каждом уровне по двум лабораториям сравнивают друг с другом. Пусть п1 - число результатов измерений от первой лаборатории и n2 - число результатов измерений от второй лаборатории.
Поскольку
 (6)
(6)
критерий приемлемости значения систематической погрешности имеет следующий вид
Критерий приемлемости (7) должен действовать на каждом из q уровней.
При n1 = п2 = 2 критерий (7) принимает вид
![]() (8)
(8)
7.3 Текущая оценка ранее признанных компетентными лабораторий
7.3.1 Общие соображения о постоянных контрольных экспериментах
Чтобы гарантировать, что признанная компетентной лаборатория продолжает функционировать удовлетворительно, необходима постоянная оценка, и она должна осуществляться либо путем инспекционных посещений лаборатории, либо путем участия ее в оценочных экспериментах. Не существует никакого жесткого и твердого правила для того, чтобы сказать, насколько часто должна осуществляться такая оценка, так как различные факторы оказывают влияние на такое решение, например технические, экономические и факторы безопасности. Решение должно приниматься ответственной инстанцией в зависимости от обстоятельств.
Постоянная оценка часто становится причиной возникновения ситуации, при которой большое количество лабораторий должно оцениваться одновременно. В данной ситуации сопоставление с лабораторией высокого рейтинга не рекомендуется, так как даже наилучшая лаборатория должна быть подвергнута проверке. В этом случае необходимо проводить совместный оценочный эксперимент.
7.3.2 Оценка практической деятельности лабораторий
Практическая деятельность лабораторий оценивается путем инспекционных посещений, как описано в 7.2.1.
7.3.3 Метод измерений с использованием стандартных образцов
Метод, описанный в ГОСТ Р ИСО 5725-4, при постоянной оценке деятельности лаборатории может быть соответствующим образом использован.
7.3.4 Метод измерений, для которого нет стандартных образцов
7.3.4.1 Общие положения
7.3.4.1.1 В случае отсутствия стандартных образцов оценка каждой лаборатории основывается на совместном оценочном эксперименте при участии нескольких лабораторий.
Планирование оценочного эксперимента очень сходно с планированием эксперимента по оценке прецизионности; поэтому здесь применимы многие соображения, изложенные в частях 1 и 2 ГОСТ Р ИСО 5725. Целью является оценка каждой лаборатории, поэтому выбор количества повторяющихся измерений на каждом уровне подобен ситуации с одной лабораторией, описанной в 7.2.2.
Поскольку целью является оценочный эксперимент, участвовать может меньшее количество лабораторий, чем в эксперименте по оценке прецизионности. Например, этот эксперимент может выполняться только для национальных участников (лабораторий стран-организаторов). Особенно важно, что снижение количества не уменьшает систематического отклонения между лабораториями. При таком уменьшении повысился бы риск невозможности обнаружить выпадающую лабораторию.
7.3.4.1.2 После рассмотрения вопросов, упомянутых в 7.2.2, испытуемый материал рассылают p лабораториям с q уровнями, и на каждом уровне осуществляют по п измерений. При оценке результатов следует пользоваться методами, представленными в разделе 7 ГОСТ Р ИСО 5725-2. Так как возможно отсутствие или получение дополнительных результатов измерений, в базовых элементах может оказаться их различное количество.
Внутреннюю прецизионность оценивают для каждой лаборатории, как изложено в разделе 6 настоящего стандарта.
7.3.4.1.3 С целью суммарной оценки систематических погрешностей на каждом уровне рассчитывают дисперсию воспроизводимости (см. 7.5 ГОСТ Р ИСО 5725-2)
![]() (9)
(9)
где
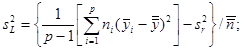 10)
10)
и
![]() (11)
(11)
Межлабораторную дисперсию ![]() сравнивают с
известной межлабораторной дисперсией
сравнивают с
известной межлабораторной дисперсией ![]() с точки зрения соответствия критерию,
описываемому неравенством
с точки зрения соответствия критерию,
описываемому неравенством
в котором ![]() -
это (1 - a)-квантиль c2-распределения с v
= р - 1 степенями свободы. При отсутствии других указаний
уровень значимости a предполагается равным 0,05.
-
это (1 - a)-квантиль c2-распределения с v
= р - 1 степенями свободы. При отсутствии других указаний
уровень значимости a предполагается равным 0,05.
Если неравенство (12) выполняется,
то межлабораторная дисперсия ![]() является приемлемой, и можно сделать
вывод, что всеми лабораториями на рассматриваемом уровне были получены
достаточно точные результаты.
является приемлемой, и можно сделать
вывод, что всеми лабораториями на рассматриваемом уровне были получены
достаточно точные результаты.
Если неравенство (12) не выполняется, то путем вычисления значений статистики Граббса находят наиболее отклоняющееся наблюдение (выброс), после чего результаты соответствующей лаборатории исключают и дисперсии оценивают снова для оставшихся (р - 1) лабораторий. Если при этом скорректированная дисперсия удовлетворяет критерию (12), то (р - 1) лабораторий признают прошедшими проверку удачно или снова рассчитывают значения статистик Граббса, и процедуру повторяют, в случае необходимости, несколько раз. Как было упомянуто в ГОСТ Р ИСО 5725-2, критерий Граббса неудобен для повторных применений, так как большое количество выбросов может привести к инспектированию всех данных на всех уровнях. Если одни и те же лаборатории характеризуются отклонениями на нескольких уровнях, то можно сделать вывод, что данные лаборатории работают с систематической погрешностью, которая чересчур высока. Если отклонения отмечены только на одном уровне, это является достаточным основанием для того, чтобы исследовать испытуемый материал на предмет его неоднородности. Если отклонения имеют место на различных уровнях в различных лабораториях, то отклонения, возможно, являются следствием несовершенства самого оценочного эксперимента. В таком случае необходимо критически проверить каждую отдельную часть оценочного эксперимента, чтобы по возможности найти объяснения.
Лаборатория, которая оказалась источником выбросов (независимо от того, идет ли речь о внутренней прецизионности или систематической погрешности), должна быть проинформирована о результатах экспериментов, и с целью улучшения практической деятельности лаборатории необходимо рассмотреть методологию ее работы.
7.3.4.1.4 В последовательных оценочных экспериментах должны использоваться различные испытуемые материалы с тем, чтобы лаборатории при работе с одним специфическим материалом не впадали в искушение демонстрировать чрезвычайно высокую прецизионность. Более того, как указано в 7.2.2, материал должен отправляться анонимно, чтобы гарантировать, что измерения выполняют в лаборатории как обычно.
Если оценочный эксперимент дает результаты, существенно отличающиеся от результатов более ранних экспериментов, то чтобы найти возможные объяснения данным непредвиденным наблюдениям, необходимо подвергнуть анализу всю доступную информацию.
7.3.4.2 Пример. Анализ щелочности воды
7.3.4.2.1 Основные положения
При контроле качества воды химические анализы выполняют во многих лабораториях. Чтобы быть признанными, деятельность таких лабораторий должна быть неоднократно проверена. В настоящем примере рассматривают определение общей щелочности воды методом потенциометрического титрования. Для этой задачи не существует стандартных образцов, поэтому оценка была проведена с применением оценочного эксперимента.
В проведенном эксперименте принимали участие 18 лабораторий, при этом рассматривалось два уровня, и по два параллельных определения выполнялось на каждом уровне в каждой лаборатории.
7.3.4.2.2 Исходные данные
См. таблицу 11.
Таблица 11 - Щелочность воды
|
Уровень |
Номер лаборатории |
Уровень |
|||
|
1 |
2 |
1 |
2 |
||
|
1 |
2,040 |
5,250 |
10 |
2,170 |
5,520 |
|
2,040 |
5,300 |
2,200 |
5,330 |
||
|
2 |
2,100 |
5,460 |
11 |
1,980 |
4,990 |
|
2,110 |
5,460 |
1,940 |
5,020 |
||
|
3 |
2,070 |
5,240 |
12 |
2,120 |
5,340 |
|
2,070 |
5,200 |
2,110 |
5,330 |
||
|
4 |
2,070 |
5,308 |
13 |
2,160 |
5,330 |
|
2,090 |
5,292 |
2,150 |
5,420 |
||
|
5 |
2,740 |
5,850 |
14 |
2,050 |
5,330 |
|
2,610 |
5,850 |
2,070 |
5,330 |
||
|
6 |
2,086 |
5,305 |
15 |
2,070 |
5,387 |
|
2,182 |
5,325 |
2,056 |
5,335 |
||
|
7 |
2,128 |
5,296 |
16 |
2,010 |
5,210 |
|
2,076 |
5,346 |
2,030 |
5,330 |
||
|
8 |
2,060 |
5,340 |
17 |
2,066 |
5,300 |
|
2,080 |
5,340 |
2,070 |
5,280 |
||
|
9 |
2,060 |
5,310 |
18 |
2,060 |
5,300 |
|
2,080 |
5,300 |
2,070 |
5,280 |
||
7.3.4.2.3 Расчет средних значений и расхождений в базовых элементах
Средние значения в базовых элементах представлены в таблице 12, а расхождения - в таблице 13.
Таблица 12 - Средние значения в базовых элементах по данным таблицы 11
|
Уровень |
Номер лаборатории |
Уровень |
|||
|
1 |
2 |
1 |
2 |
||
|
1 |
2,040 |
5,275 |
10 |
2,185 |
5,425 |
|
2 |
2,105 |
5,460 |
11 |
1,960 |
5,005 |
|
3 |
2,070 |
5,220 |
12 |
2,115 |
5,335 |
|
4 |
2,080 |
5,300 |
13 |
2,155 |
5,375 |
|
5 |
2,675 |
5,850 |
14 |
2,060 |
5,330 |
|
6 |
2,134 |
5,315 |
15 |
2,063 |
5,361 |
|
7 |
2,102 |
5,321 |
16 |
2,020 |
5,270 |
|
8 |
2,070 |
5,340 |
17 |
2,068 |
5,290 |
|
9 |
2,070 |
5,305 |
18 |
2,065 |
5,290 |
Таблица 13 - Расхождения в базовых элементах по данным таблицы 11
|
Уровень |
Лаборатории |
Уровень |
|||
|
1 |
2 |
1 |
2 |
||
|
1 |
0,000 |
0,050 |
10 |
0,030 |
0,190 |
|
2 |
0,010 |
0,000 |
11 |
0,040 |
0,030 |
|
3 |
0,000 |
0,040 |
12 |
0,010 |
0,010 |
|
4 |
0,020 |
0,016 |
13 |
0,010 |
0,090 |
|
5 |
0,130 |
0,000 |
14 |
0,020 |
0,000 |
|
6 |
0,096 |
0,020 |
15 |
0,014 |
0,052 |
|
7 |
0,052 |
0,050 |
16 |
0,020 |
0,120 |
|
8 |
0,020 |
0,000 |
17 |
0,004 |
0,020 |
|
9 |
0,020 |
0,010 |
18 |
0,010 |
0,020 |
Предварительно установленные значения стандартных отклонений повторяемости (сходимости) и воспроизводимости на двух уровнях составляют:
sr1 = 0,023, sr2 = 0,027,
sR1 = 0,045, sR2 = 0,052.
7.3.4.2.4 Оценка внутренней прецизионности
Расхождения wij, приведенные в таблице 13, сравнивают со стандартным отклонением повторяемости с использованием формулы
![]()
При a = 0,05 и v
= 1 значение ![]()
Для уровня 1 отклонения обнаружены в следующих лабораториях:
- лаборатория № 5: w2 = 0,0169, полученное значение равно 15,974 (левая часть неравенства);
- лаборатория № 6: w2 = 0,009216, полученное значение равно 8,711.
Для уровня 2 отклонения обнаружены в следующих лабораториях:
- лаборатория № 10: w2 = 0,0361, полученное значение равно 24,76;
- лаборатория № 13: w2 = 0,0081, полученное значение равно 5,55;
- лаборатория № 16: w2 = 0,0144, полученное значение равно 9,88.
7.3.4.2.5 Оценка систематической погрешности
В соответствии с 7.3.4.1.3 сначала для проверки выполнения неравенства (12) на основании данных таблицы 12 рассчитывают оценку межлабораторной дисперсии по формуле

Для уровня 1 s2 составляет 0,04436, а значение
![]()
так что значение в левой части неравенства (12) равно 12,60.
В то же время при a = 0,05 и v = 17 значение ![]() то есть неравенство не выполняется.
то есть неравенство не выполняется.
Наиболее резко отклоняющееся среднее значение в таблице 12 относится к лаборатории № 5.
Значение статистики Граббса для лаборатории № 5 составляет
G = (2,675 - 2,1132)/0,1489 = 3,77
и превышает оба критических значения, приведенные в разделе 9 ГОСТ Р ИСО 5725-2 (для p = 18, это значение равно 2,651), являясь, таким образом, выбросом.
После изъятия результатов лаборатории № 5 расчеты дают следующие результаты:
s2 = 0,005357,
сравниваемое значение равно 1,521.
При a = 0,05 и v
= 16 значение ![]() так что неравенство (12)
теперь удовлетворяется.
так что неравенство (12)
теперь удовлетворяется.
Приведенные выше данные свидетельствуют о том, что всеми лабораториями, кроме лаборатории № 5, на уровне 1 были получены достаточно точные результаты.
Для уровня 2 найдены следующие результаты:
![]()
s2 = 0,05034,
сравниваемое значение, равное 10,758.
При a = 0,05 и v
= 17 значение ![]()
Наиболее отклоняющееся среднее значение снова обнаружено для лаборатории № 5.
Значение статистики Граббса для лаборатории № 5 составляет:
G = (5,85 - 5,3370)/0,1586 = 3,235
и превышает критические значения (2,651) для p = 18.
После изъятия результатов лаборатории № 5 расчеты дают следующие результаты:
s2 = 0,01867,
сравниваемое значение равно 3,990.
При a = 0,05 и v
= 16 значение ![]()
Наиболее отклоняющееся среднее значение (теперь минимальное) обнаружено для лаборатории № 11.
Значение статистики Граббса для лаборатории № 11 составляет
G = (5,005 - 5,3069)/0,09661 = -3,125.
Критические значения на уровнях значимости 1 % и 5 % для р = 17 составляют соответственно 2,894 и 2,620.
После изъятия результатов лаборатории № 11 расчеты дают следующие результаты:
s2 = 0,00700,
сравниваемое значение равно 1,496.
При a = 0,05 и v
= 15 значение ![]() т.е. неравенство (12) выполняется.
т.е. неравенство (12) выполняется.
Это означает, что всеми лабораториями, кроме лабораторий № 5 и № 11, на уровне 2 были получены достаточно точные результаты.
7.3.4.2.6 Выводы
Оценочный эксперимент показал, что несколько лабораторий работают с неудовлетворительной внутренней прецизионностью. Это лаборатории № 5, № 6, № 10, № 13 и № 16. Кроме того, две лаборатории (№ 5 и № 11) показали существенную систематическую погрешность на одном или обоих уровнях.
Все лаборатории, в которых выявлены отклонения, должны быть проинформированы о результате.
8 Сопоставление альтернативных методов измерений
8.1 Источники причин появления альтернативных методов измерений
Принятый на международном уровне стандартный метод представляет собой метод измерений, который был стандартизован с целью удовлетворения разнообразных требований. Среди этих требований существенны следующие.
a) Метод должен быть применим к широкому диапазону уровней измеряемых характеристик с тем, чтобы охватить большинство материалов, являющихся предметом международной торговли. Например, метод определения общего содержания железа в железных рудах должен быть применим к возможно большему спектру железных руд, находящихся в международном товарообороте
b) Оборудование, реагенты и персонал должны иметь международный уровень.
c) Стоимость выполнения измерений должна быть приемлемой.
d) Прецизионность и правильность метода измерений должны быть приемлемыми для пользователей его результатами.
Стандартные методы, как правило, это компромиссы, которые иногда могут быть чрезмерными для применения в повседневной работе. Отдельная лаборатория может принять решение, что для ее собственных нужд достаточен более простой метод. Например, если большинство материалов, подлежащих измерениям в лаборатории, поступает из одного и того же источника, а различия в их характеристиках относительно невелики, достаточным может оказаться более простой и менее дорогостоящий метод.
Некоторым методам измерений может быть отдано предпочтение в определенных регионах по историческим причинам. В данном случае подходящим может оказаться альтернативный международный стандартный метод.
Сопоставление, описываемое в настоящем разделе, основывается на результатах, полученных от одной испытуемой пробы (образца). При этом настоятельно рекомендуется, чтобы для сравнения прецизионности и правильности двух методов измерений использовалось более одной пробы. Количество требуемых проб для испытаний зависит от различных факторов, таких как диапазон измеряемой характеристики, определяющий необходимое число уровней, чувствительность методов измерений к изменениям в составе проб и т.д.
8.2 Цель сопоставления методов измерений
8.2.1 В разделе 8 описывается процедура сопоставления прецизионности и правильности двух методов измерений, когда один из них (метод А) является либо международным стандартным методом, либо первым кандидатом на принятие в качестве международного стандартного метода. Процедура обеспечивает доказательство, имеют или нет два метода различную прецизионность и/или правильность, не давая рекомендаций по выбору того или иного метода для конкретного применения. Решение по данному вопросу должно приниматься в сочетании с другими факторами, например стоимостью, наличием оборудования и т.д.
8.2.2 Подраздел 8.2 в первую очередь предполагает следующие применения:
a) При разработке международного стандартного метода технический комитет иногда сталкивается с проблемой выбора из методов-кандидатов наиболее подходящего для принятия в качестве международного стандарта. Среди критериев, обосновывающих этот выбор, фигурируют прецизионность и правильность.
b) Иногда разработка альтернативного стандартного метода оказывается необходимой. Кандидат в такие методы должен быть таким же точным, как и первый метод. Описываемая процедура поможет определить, удовлетворяет ли метод-кандидат предъявляемым требованиям.
c) Для некоторых лабораторий большинство проб, подлежащих измерениям, поступают из одного и того же источника. Данные пробы имеют, как правило, почти одинаковый состав. В такой ситуации повседневное применение международного стандартного метода может быть излишне дорогостоящим. Для лаборатории может оказаться желательным принятие более простого метода для повседневного применения (для выполнения рутинных анализов). Этот метод должен обеспечивать получение результатов измерений, правильность и прецизионность которых должны соответствовать существующему международному стандартному методу.
8.3 Метод В, предлагаемый в качестве альтернативного стандартному методу измерений
Методы А и В должны сопоставляться на основании результатов экспериментов по оценке прецизионности. Если метод А является хорошо обоснованным стандартным методом, то его прецизионность может быть использована как основа для сравнения. Если метод А сам по себе все еще находится в стадии разработки в качестве стандартного метода, то он тоже должен быть подвергнут эксперименту по оценке прецизионности. Оба эксперимента по оценке прецизионности должны проводиться в соответствии с ГОСТ Р ИСО 5725-2.
Задачами эксперимента являются следующие:
a) Определить, является ли прецизионность метода В такой же, как метода А. Результаты эксперимента должны позволить обнаружить, превышает или нет заданное значение отношение показателей прецизионности методов В и А.
b) Определить, является ли правильность метода В такой же, как и метода А. Результаты эксперимента должны показать, что в статистическом отношении незначима:
- либо разница между общими средними значениями результатов экспериментов по оценке прецизионности при использовании идентичных образцов (проб) для обоих методов,
- либо разница между аттестованным значением стандартного образца и общим средним значением результатов измерений стандартного образца, полученных для метода В в эксперименте по оценке прецизионности, используя аттестованный стандартный образец в качестве испытуемой пробы.
Кроме того, должна существовать возможность определить, превышает ли заданную величину разность либо между ожидаемыми значениями результатов двух методов, либо между ожидаемыми значениями результатов каждого метода и аттестованным значением.
8.4 Эксперимент по оценке точности
8.4.1 Основные требования
Эксперимент по оценке точности должен проводиться в соответствии с общими правилами, изложенными в ГОСТ Р ИСО 5725-1.
Процедуры выполнения измерений для обоих методов должны быть документально оформлены в существенных деталях, чтобы избежать неправильного их толкования лабораториями-участниками. В ходе выполнения эксперимента не допускаются какие-либо видоизменения его процедуры.
Участвующие в эксперименте лаборатории должны образовывать представительную выборку из числа потенциальных пользователей метода.
8.4.2 Пробы для испытаний
На прецизионность многих методов измерений оказывает влияние матрица образцов для испытаний, равно как и уровень измеряемой характеристики. Для таких методов сопоставление прецизионности лучше всего проводить на идентичных испытуемых пробах. Более того, сопоставление правильности методов можно осуществлять только при использовании идентичных проб. По этой причине связь между рабочими группами, проводящими эксперименты по оценке точности каждого метода, должна достигаться путем назначения общего ответственного исполнителя.
Основное требование к пробе для испытаний заключается в том, что она должна быть гомогенной, то есть каждая лаборатория должна использовать идентичные образцы для испытаний. Если имеются предположения, что образец может быть внутри неоднородным, в документ должны быть включены четкие указания по отбору и подготовке проб для испытаний. Определенные преимущества дает использование стандартных образцов (СО) в качестве нескольких проб для испытаний. Гомогенность СО гарантируется, и результаты измерений этим методом могут исследоваться на предмет установления систематической погрешности по отношению к аттестованному значению СО. Недостатком, как правило, является высокая стоимость СО. Во многих случаях это можно преодолеть путем перераспределения экземпляров СО. Что касается методики использования СО в качестве проб для испытаний - см. ИСО Руководство 33 [7].
8.4.3 Количество проб для испытаний
Количество испытуемых проб определяется диапазоном измеряемой характеристики, а также обусловлено зависимостью точности измерений от уровня. Во многих случаях количество испытуемых проб ограничивается предусмотренным объемом работы и наличием пробы для испытаний на требуемом уровне.
8.4.4 Количество лабораторий и количество измерений
8.4.4.1 Общие сведения
Количество лабораторий и количество измерений из расчета на лабораторию, необходимые для выполнения программы межлабораторного эксперимента применительно к обоим методам, зависят от:
a) прецизионности двух методов;
b) поддающегося обнаружению соотношения r или j между показателями прецизионности двух методов; это минимальное отношение показателей прецизионности, которое экспериментатор должен стремиться выявлять с высокой вероятностью на основании результатов экспериментов с использованием двух методов; прецизионность может быть представлена либо в виде стандартного отклонения повторяемости (и тогда соотношение выражается через r), либо в виде квадратного корня из средних квадратов показателей межлабораторной воспроизводимости (и тогда соотношение выражается через j);
c) поддающийся обнаружению разности l между систематическими погрешностями двух методов (это минимальное значение разности между ожидаемыми значениями результатов, получаемых двумя методами на идентичных образцах).
Рекомендуется, чтобы для сравнения оценок прецизионности использовался уровень значимости, равный a = 0,05, и чтобы вероятность необнаружения выбранного минимального соотношения стандартных отклонений, или минимальной разности l между систематическими погрешностями методов была равна b = 0,05.
При данных значениях a и b для определения разности l может быть использована следующая формула
где А и В - подстрочные индексы, относящиеся к методам А и В соответственно;
![]() - межлабораторная дисперсия, учитывающая различия
между операторами и оборудованием;
- межлабораторная дисперсия, учитывающая различия
между операторами и оборудованием;
![]() - дисперсия повторяемости (оценивается средним
арифметическим значением внутрилабораторных дисперсий);
- дисперсия повторяемости (оценивается средним
арифметическим значением внутрилабораторных дисперсий);
п - количество результатов измерений, полученных в одной лаборатории на одном уровне;
р - количество лабораторий, участвующих в межлабораторном эксперименте.
В большинстве случаев прецизионность методов В неизвестна. Тогда в качестве заменяющей величины следует использовать прецизионность метода А, что даст
Экспериментатор должен подставлять в уравнения (13) или (14) значения пА, пB, рА и рB до тех пор, пока не будут найдены значения, которые достаточны для подтверждения необходимого значения l. Следует принять во внимание значения этих параметров при постановке адекватного эксперимента с целью сравнения оценок прецизионности.
В таблице 14 представлены минимальные отношения стандартных отклонений для заданных выше значений a и b в зависимости от числа степеней свободы vА и vB.
Для стандартных отклонений повторяемости
vA = pA(пA - 1) и vB = pB(nB - 1).
Для межлабораторных средних квадратов
vA = pA - 1 и vB = рB - 1.
Если прецизионность одного из методов хорошо обоснована, следует считать, что число степеней свободы в таблице 14 равно 200.
8.4.4.2 Пример. Определение содержания железа в железных рудах
8.4.4.2.1 Общие положения
Рассматривают два аналитических метода определения суммарного содержания железа в железных рудах. Предполагается, что они характеризуются одинаковой прецизионностью:
srA = srB = 0,1 % Fe
sLA = sLB = 0,2 % Fe.
8.4.4.2.2 Требования
l = 0,4 % Fe
r = j = 4.
Минимальное количество лабораторий, необходимых для каждой программы межлабораторного эксперимента, рассчитывают в предположении, что число лабораторий и параллельных определений одинаково
рА = рB и пА = пB = 2.
a) Исходя из требований к правильности при l = 0,4 % Fe и n = 2 формула (14) имеет вид
![]()
Отсюда
pA = pB = 9.
b) Исходя из требований к соотношению показателей прецизионности двух методов следует, что при r = 4 или j = 4 из таблицы 14 получается
vA = vB = 9.
Для сравнения стандартных отклонений повторяемости
vA = pA и vB = pB, поэтому рА = рB = 9.
Для сравнения межлабораторных средних квадратов
vA = pA - 1 и vB = pB - 1, поэтому рА = рB = 10.
8.4.4.2.3 Выводы
Минимальное количество лабораторий-участниц, необходимое для выполнения каждого межлабораторного эксперимента, равно 10.
8.4.5 Распределение проб для испытаний
Ответственный исполнитель по межлабораторной программе испытаний должен взять на себя функцию организации получения, приготовления и распределения проб (образцов) для испытаний. Необходимо обеспечить получение проб лабораториями-участницами в хорошем состоянии и четко идентифицированными. Лаборатории-участницы должны быть проинструктированы относительно того, что анализ проб должен выполняться на одной и той же (например, на сухой) основе (например, проба высушивается перед взвешиванием при температуре 105 °С в течение х часов).
8.4.6 Лаборатория, принимающая участие в эксперименте
Лаборатория, принимающая участие в эксперименте, должна назначить из своего состава сотрудника, ответственного за соблюдением указаний координатора. Сотрудник должен быть квалифицированным аналитиком. Чтобы предотвратить получение неправдоподобно низкой оценки стандартного отклонения метода, необходимо избегать назначения в качестве ответственного наиболее квалифицированных сотрудников (например, исследовательского персонала или «лучшего» оператора). Назначенный сотрудник должен выполнить требуемое количество измерений в условиях повторяемости. Лаборатория несет ответственность за сообщение результатов измерений координатору в течение установленного периода времени.
Таблица 14 - Значения r(vA, vB, a, b) или j (vA, vB, a, b) для a = 0,05 и b = 0,05
|
vB |
||||||||||||||||||
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
25 |
50 |
200 |
|
|
6 |
5,82 |
5,40 |
5,10 |
4,88 |
4,72 |
4,58 |
4,47 |
4,38 |
4,31 |
4,24 |
4,19 |
4,14 |
4,09 |
4,06 |
4,02 |
3,89 |
3,65 |
3,47 |
|
7 |
5,40 |
4,99 |
4,71 |
4,50 |
4,34 |
4,21 |
4,10 |
4,01 |
3,94 |
3,88 |
3,82 |
3,78 |
3,74 |
3,70 |
3,67 |
3,54 |
3,30 |
3,13 |
|
8 |
5,10 |
4,71 |
4,43 |
4,23 |
4,07 |
3,94 |
3,84 |
3,76 |
3,68 |
3,62 |
3,57 |
3,52 |
3,48 |
3,45 |
3,41 |
3,29 |
3,06 |
2,89 |
|
9 |
4,88 |
4,50 |
4,23 |
4,03 |
3,87 |
3,75 |
3,65 |
3,56 |
3,49 |
3,43 |
3,38 |
3,33 |
3,29 |
3,26 |
3,23 |
3,11 |
2,88 |
2,71 |
|
10 |
4,72 |
4,34 |
4,07 |
3,87 |
3,72 |
3,59 |
3,50 |
3,41 |
3,34 |
3,28 |
3,23 |
3,19 |
3,15 |
3,11 |
3,08 |
2,96 |
2,73 |
2,57 |
|
11 |
4,58 |
4,21 |
3,94 |
3,75 |
3,59 |
3,47 |
3,38 |
3,29 |
3,22 |
3,16 |
3,11 |
3,07 |
3,03 |
2,99 |
2,96 |
2,85 |
2,62 |
2,45 |
|
12 |
4,47 |
4,10 |
3,84 |
3,65 |
3,50 |
3,38 |
3,28 |
3,20 |
3,13 |
3,07 |
3,02 |
2,97 |
2,93 |
2,90 |
2,87 |
2,75 |
2,52 |
2,36 |
|
13 |
4,38 |
4,01 |
3,76 |
3,56 |
3,41 |
3,29 |
3,20 |
3,12 |
3,05 |
2,99 |
2,94 |
2,89 |
2,85 |
2,82 |
2,79 |
2,67 |
2,44 |
2,28 |
|
14 |
4,31 |
3,94 |
3,68 |
3,49 |
3,34 |
3,22 |
3,13 |
3,05 |
2,98 |
2,92 |
2,87 |
2,83 |
2,79 |
2,75 |
2,72 |
2,60 |
2,38 |
2,21 |
|
15 |
4,24 |
3,88 |
3,62 |
3,43 |
3,28 |
3,16 |
3,07 |
2,99 |
2,92 |
2,86 |
2,81 |
2,77 |
2,73 |
2,69 |
2,66 |
2,55 |
2,32 |
2,15 |
|
16 |
4,19 |
3,82 |
3,57 |
3,38 |
3,23 |
3,11 |
3,02 |
2,94 |
2,87 |
2,81 |
2,76 |
2,72 |
2,68 |
2,64 |
2,61 |
2,50 |
2,27 |
2,10 |
|
17 |
4,14 |
3,78 |
3,52 |
3,33 |
3,19 |
3,07 |
2,97 |
2,89 |
2,83 |
2,77 |
2,72 |
2,67 |
2,63 |
2,60 |
2,57 |
2,45 |
2,22 |
2,05 |
|
18 |
4,09 |
3,74 |
3,48 |
3,29 |
3,15 |
3,03 |
2,93 |
2,85 |
2,79 |
2,73 |
2,68 |
2,63 |
2,60 |
2,56 |
2,53 |
2,41 |
2,18 |
2,01 |
|
19 |
4,06 |
3,70 |
3,45 |
3,26 |
3,11 |
2,99 |
2,90 |
2,82 |
2,75 |
2,69 |
2,64 |
2,60 |
2,56 |
2,53 |
2,50 |
2,38 |
2,15 |
1,98 |
|
20 |
4,02 |
3,67 |
3,41 |
3,23 |
3,08 |
2,96 |
2,87 |
2,79 |
2,72 |
2,66 |
2,61 |
2,57 |
2,53 |
2,50 |
2,46 |
2,35 |
2,12 |
1,95 |
|
25 |
3,89 |
3,54 |
3,29 |
3,11 |
2,96 |
2,85 |
2,75 |
2,67 |
2,60 |
2,55 |
2,50 |
2,45 |
2,41 |
2,38 |
2,35 |
2,23 |
2,00 |
1,82 |
|
50 |
3,65 |
3,30 |
3,06 |
2,88 |
2,73 |
2,62 |
2,52 |
2,44 |
2,38 |
2,32 |
2,27 |
2,22 |
2,18 |
2,15 |
2,12 |
2,00 |
1,75 |
1,56 |
|
200 |
3,47 |
3,13 |
2,89 |
2,71 |
2,57 |
2,45 |
2,36 |
2,28 |
2,21 |
2,15 |
2,10 |
2,05 |
2,01 |
1,98 |
1,95 |
1,82 |
1,56 |
1,32 |
|
Примечания 1 2 |
||||||||||||||||||
8.4.7 Сбор результатов измерений
Координатор программы выполнения измерений по каждому из методов организует сбор всех результатов в пределах приемлемого периода времени.
В обязанности координатора входит тщательное и критическое изучение результатов на предмет физических отклонений. Речь идет о результатах, которые вследствие объяснимых физических причин не принадлежат к тому же множеству, что и другие результаты измерений.
8.4.8 Оценка результатов измерений
Результаты измерений должны быть оценены квалифицированным специалистом по статистике, пользующимся процедурами, регламентированными в ГОСТ Р ИСО 5725-2.
Для каждой испытуемой пробы должны быть рассчитаны следующие величины:
srA - оценка стандартного отклонения повторяемости для метода А;
srB - оценка стандартного отклонения повторяемости для метода В;
sRA - оценка стандартного отклонения воспроизводимости для метода А;
sRB - оценка стандартного отклонения воспроизводимости для метода В;
![]() - общее среднее значение для метода А;
- общее среднее значение для метода А;
![]() -
общее среднее значение для метода В.
-
общее среднее значение для метода В.
8.4.9 Сравнение результатов для метода А и метода В
Результаты выполнения межлабораторных программ выполнения измерений сравнивают для каждого из уровней. Вполне возможно, что метод В будет иметь лучшую прецизионность и/или большую систематическую погрешность на более низких уровнях значений измеряемой характеристики, но худшую прецизионность и/или меньшую систематическую погрешность на более высоких уровнях (или наоборот).
8.4.9.1 Графическое представление необработанных данных эксперимента
Для каждого уровня желательно иметь графическое представление необработанных данных. Иногда расхождение между результатами двух методов, выраженными через прецизионность и/или систематическую погрешность, настолько очевидно, что дальнейшая статистическая оценка становится ненужной.
Желательно также иметь графическое представление прецизионности и общих средних значений для всех уровней.
8.4.9.2 Сравнение прецизионности
8.4.9.2.1 Метод А является установленным стандартным методом.
Прецизионность метода А установлена надежно.
a) Внутрилабораторная прецизионность
Если
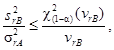
то нет оснований считать, что внутрилабораторная прецизионность метода В хуже, чем метода А.
Если
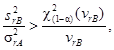
имеется основание считать, что внутрилабораторная прецизионность метода В уступает прецизионности метода А.
Здесь ![]() представляет собой (1 - a)-квантиль c2-распределения
с vrB степенями
свободы и
представляет собой (1 - a)-квантиль c2-распределения
с vrB степенями
свободы и
vrB = pB(пB - 1).
b) Полная прецизионность
Если
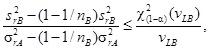
то нет оснований считать, что среднеквадратичное отклонение межлабораторной воспроизводимости для метода В хуже (больше), чем для метода А.
Если

имеется основание считать, что среднеквадратичное отклонение воспроизводимости для метода В хуже, чем для метода А.
Здесь ![]() представляет собой (1 - a)-квантиль c2-распределения
с vLB степенями
свободы и
представляет собой (1 - a)-квантиль c2-распределения
с vLB степенями
свободы и
vLB = pB - 1.
8.4.9.2.2 Оба метода претендуют (являются кандидатами) быть новыми стандартными методами.
a) Внутрилабораторная прецизионность
![]()
Если
Fa/2(vrA, vrB) ≤ Fr ≤ F(1 - a/2)(vrA, vrB),
то нет оснований считать, что методы имеют различные значения внутрилабораторной прецизионности.
Если
Fr < Fa/2(vrA, vrB),
то имеется основание считать, что метод В имеет лучшую внутрилабораторную прецизионность, чем метод А.
Если
Fr > F(1 - a/2)(vrB, vrA),
имеется основание считать, что метод В имеет худшую внутрилабораторную прецизионность, чем метод А.
Здесь Fa/2(vrA, vrB) и F(1 - a/2)(vrB, vrA) представляют собой a/2- и (1 - a/2)-квантили F-распределения со степенями свободы числителя vRA и знаменателя vRB, причем
vrA = pA(nA - 1),
vrB = pB(nB - 1).
b) Полная прецизионность
![]()
Если
Fa/2(vRB, vRA) ≤ FR ≤ F(1 - a/2)(vRB, vRA),
то нет оснований считать, что методы имеют различные значения межлабораторной прецизионности.
Если
FR < Fa/2(vRB, vRA),
то имеется основание считать, что метод В имеет лучшую полную прецизионность, чем метод А.
Если
FR > F(1 - a/2)(vRB, vRA),
то имеется основание считать, что метод В имеет худшую полную прецизионность, чем метод А.
Fa/2(vRB, vRA) и F(1 - a/2)(vRB, vRA) представляют собой a/2- и (1 - a/2)-квантили F-распределения со степенями свободы числителя vRB и знаменателя vRA, при этом
vLA = pA - 1,
vLB = pB - 1.
Примечание 5 - Во многих таблицах приводятся лишь (1 - a/2)-квантили F-распределения. В данном случае для нахождения a/2-квантилей могут быть использованы следующие зависимости:
Fa/2(vrB, vrA) = 1/F(1 - a/2)(vrA, vrB),
Fa/2(vRB, vRA) = 1/F(1 - a/2)(vRA, vRB),
8.4.9.3 Сравнение правильности
8.4.9.3.1 Сравнение среднего значения с аттестованным значением стандартного образца
Общее среднее значение результатов измерений, полученное каждым методом, может быть сравнено с аттестованным значением стандартного образца, используемого в качестве одной из испытуемых проб. При этом можно использовать следующую проверку:
а) если
![]()
то разность между общим средним значением результатов, полученных данным методом, и аттестованным значением не является статистически значимой;
b) если
![]()
то разность между общим средним значением результатов, полученных данным методом, и аттестованным значением не является статистически значимой. При этом существуют две возможности:
1) если
![]()
то нет оснований считать, что метод измерений имеет неприемлемую систематическую погрешность;
2) если
![]()
то имеется основание считать, что метод измерений имеет неприемлемую систематическую погрешность.
Здесь dm представляет собой минимальную разность между ожидаемым значением результатов, полученных данным методом, и аттестованным значением стандартного образца, которую экспериментатор стремится выявить с высокой вероятностью на основании результатов эксперимента.
8.4.9.3.2 Сравнение средних значений для методов А и В
a) Если
![]()
то разность между средними значениями для методов А и В не является статистически значимой.
b) Если
![]()
то разность между средними значениями для методов А и В является статистически значимой.
Здесь
![]()
![]()
![]()
При этом существуют две возможности:
1) если
![]()
то нет оснований считать, что разность между систематическими погрешностями двух методов является неприемлемой;
2) если
![]()
имеется основание считать, что разность между систематическими погрешностями двух методов является неприемлемой.
Здесь l представляет собой поддающуюся обнаружению разность между систематическими погрешностями методов.
8.5 Метод В как кандидат в повседневно используемые (рутинные) методы
8.5.1 Параметры
Важными параметрами для повседневно используемого (рутинного) лабораторного метода являются стабильное в течение длительного времени среднее значение mt измеряемой характеристики, прецизионность в условиях повторяемости, выраженная через стандартное отклонение повторяемости sr, и промежуточная прецизионность, выраженная через стандартное отклонение промежуточной прецизионности с изменяющимся фактором времени sI(Т).
Чтобы оценить данные параметры, лаборатория должна проводить квазимежлабораторную программу выполнения измерений, заменяя лаборатории, участвующие в эксперименте, «временем» (см. ГОСТ Р ИСО 5725-3). Математическая модель, используемая для представления данной квазимежлабораторной программы выполнения измерений, представляет собой ту же модель, которая используется для межлабораторной программы, только при условии замены подстрочного индекса L на Т («лаборатории» на «время»). В данном случае вариация, обусловленная собственно изменяющимся фактором времени, включает в себя вариацию, обусловленную разнообразными изменениями, которые обычно имеют место в лаборатории, такими как калибровка оборудования, различие реагентов, участие в измерениях разных аналитиков, изменения условий окружающей среды и т.д. Таким образом, квазимежлабораторная программа, как правило, должна распространяться на период времени, охватывающий эти изменения. Процедуры сравнения прецизионности - те же, что в 8.4.9.2.
Систематическая погрешность может быть определена посредством применения в каждом методе аттестованного стандартного образца, где m - принятое опорное значение аттестованной измеряемой характеристики стандартного образца.
8.5.2 Проверка стабильности систематической погрешности в течение длительного времени
Среднее арифметическое значение результатов измерений одной и той же измеряемой характеристики, полученных в течение длительного периода времени, рассчитывают по формуле
![]()
где i и j - индексы, относящиеся соответственно к долгосрочным (в условиях промежуточной прецизионности) и краткосрочным (в условиях повторяемости) измерениям соответственно.
a) Если

то разность между средним значением ![]() результатов
измерений одного и того же образца за длительный период времени и принятым
опорным значением mt не является
статистически значимой.
результатов
измерений одного и того же образца за длительный период времени и принятым
опорным значением mt не является
статистически значимой.
b) Если
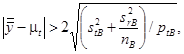
то разность между средним значением ![]() результатов
измерений одного и того же образца за длительный период времени и принятым
опорным значением mt не является
статистически значимой.
результатов
измерений одного и того же образца за длительный период времени и принятым
опорным значением mt не является
статистически значимой.
При этом существуют две возможности:
1) если
![]()
то нет оснований полагать, что стабильность значения систематической погрешности метода является неприемлемой;
2) если
![]()
то есть основания полагать, что стабильность значения систематической погрешности метода является неприемлемой.
Здесь dm представляет собой стабильную в течение длительного периода времени, поддающуюся обнаружению разность, заданную экспериментатором.
ПРИЛОЖЕНИЕ А
(обязательное)
Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725
|
а |
Отсекаемый на оси ординат отрезок в соотношении s = а + bт |
|
А |
Показатель, используемый для расчета неопределенности оценки |
|
b |
Угловой коэффициент прямой в соотношении s = а + bт |
|
В |
Лабораторная составляющая систематической погрешности измерений при реализации конкретного метода - разность между систематической погрешностью лаборатории при реализации конкретного метода измерений (конкретной МВИ) и систематической погрешностью метода измерений |
|
B0 |
Составляющая величины В, представляющая все факторы, которые не изменяются в условиях промежуточной прецизионности |
|
B(1), B(2) и т.д. |
Составляющие величины В, представляющие факторы, которые изменяются в условиях промежуточной прецизионности |
|
с |
Отсекаемый на оси ординат отрезок в соотношении lgs = с + dlgm |
|
С, С¢, С² |
Тестовые статистики |
|
Сcrit, С¢crit, C²crit |
Критические значения для статистик |
|
CDP |
Критическая разность для вероятности Р |
|
CRP |
Критический диапазон для вероятности Р |
|
d |
Угловой коэффициент прямой в соотношении lgs = с + dlgm |
|
е |
Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений |
|
f |
Коэффициент критического диапазона |
|
Fp(v1, v2) |
p-квантиль F-распределения с v1 и v2 степенями свободы |
|
G |
Статистика Граббса |
|
h |
Статистика Манделя для межлабораторной совместимости |
|
k |
Статистика Манделя для внутрилабораторной совместимости |
|
LCL |
Нижний предел контроля (действия либо предупреждения) |
|
т |
Общее среднее значение измеряемой характеристики; уровень |
|
М |
Количество факторов, рассматриваемых в условиях промежуточной прецизионности |
|
N |
Количество повторений (итераций) |
|
n |
Количество результатов измерений, полученных в одной лаборатории на одном уровне (т.е. в пределах ячейки - базового элемента) |
|
р |
Количество лабораторий, участвующих в межлабораторном эксперименте |
|
Р |
Вероятность |
|
q |
Количество уровней измеряемой характеристики в межлабораторном эксперименте |
|
r |
Предел повторяемости (сходимости) |
|
R |
Предел воспроизводимости |
|
RM |
Стандартный образец |
|
s |
Оценка стандартного (среднеквадратического) отклонения |
|
|
Прогнозируемое стандартное (среднеквадратическое) отклонение |
|
Т |
Итог или сумма какого-либо выражения |
|
t |
Количество объектов испытаний или групп объектов |
|
UCL |
Верхний предел контроля (действия либо предупреждения) |
|
W |
Весовой коэффициент, используемый при расчете взвешенной регрессии |
|
w |
Диапазон изменения выборки результатов измерений |
|
х |
Заданная величина, используемая для критерия Граббса |
|
у |
Результат измерений (или результат испытаний) |
|
|
Среднее арифметическое значение результатов измерений (или результат испытаний) |
|
|
Общее среднее значение результатов измерений (или результат испытаний) |
|
a |
Уровень значимости |
|
b |
Вероятность ошибки второго рода |
|
g |
Отношение стандартного отклонения воспроизводимости к стандартному отклонению повторяемости (сходимости) (sR/sr) |
|
D |
Систематическая погрешность лаборатории при реализации конкретного стандартного метода измерений (конкретной МВИ) |
|
|
Оценка D |
|
d |
Систематическая погрешность метода измерений |
|
|
Оценка d |
|
l |
Поддающаяся обнаружению разность между систематическими погрешностями двух лабораторий при реализации одного и того же метода измерений или систематическими погрешностями двух методов измерений (МВИ) одного и того же назначения на идентичных образцах |
|
m |
Истинное или принятое опорное значение измеряемой величины (характеристики) |
|
v |
Число степеней свободы |
|
r |
Поддающееся обнаружению соотношение между стандартными отклонениями повторяемости (сходимости) для методов В и А |
|
s |
Истинное (действительное) значение стандартного отклонения |
|
t |
Составляющая результата измерений, представляющая изменение, обусловленное временем, прошедшим с момента последней калибровки |
|
j |
Поддающееся обнаружению соотношение между квадратными корнями из межлабораторных средних квадратов для методов В и А |
|
|
p-квантиль c2-распределения с v степенями свободы |
Символы, используемые в качестве подстрочных индексов
|
С |
Различие, определяемое калибровкой |
|
Е |
Различие, определяемое оборудованием |
|
i |
Идентификатор для конкретной лаборатории |
|
I() |
Идентификатор для промежуточных мер прецизионности; в скобках - идентификация типа промежуточной ситуации |
|
j |
Идентификатор для уровня (ГОСТ Р ИСО 5725-2) |
|
Идентификатор для группы испытаний или для фактора (ГОСТ Р ИСО 5725-3) |
|
|
k |
Идентификатор для конкретного результата испытаний в лаборатории i на уровне j |
|
L |
Межлабораторный |
|
m |
Идентификатор для поддающейся обнаружению систематической погрешности |
|
М |
Различие, обусловленное неидентичностью проб (образцов) |
|
О |
Различие, определяемое сменой оператора |
|
Р |
Вероятность |
|
r |
Повторяемость |
|
R |
Воспроизводимость |
|
Т |
Различие, обусловленное периодом (временем), в течение которого проводят измерения или оценочный эксперимент |
|
W |
Внутрилабораторный |
|
1, 2, 3 ... |
Для результатов измерений, нумеруемых в порядке их получения |
|
(1), (2), (3) ... |
Для результатов измерений (испытаний), нумеруемых в порядке возрастания измеряемой величины |
ПРИЛОЖЕНИЕ В
(справочное)
[2] ISO Guide 35:1989 Certification of reference materials - General and statistical principles
[5] ISO 1171:1981 Solid mineral fuels - Determination of ash
[7] ISO Guide 33:1989. Use of certified reference materials
Ключевые слова: измерение, испытания, метод измерений, стандартизация метода измерений, результаты измерений, результаты испытаний, точность, правильность, прецизионность, систематическая погрешность, повторяемость, воспроизводимость, методы проверки приемлемости результатов измерений и установления окончательного результата, методы контроля точности результатов измерений, контрольные карты Шухарта, методы оценки деятельности лаборатории

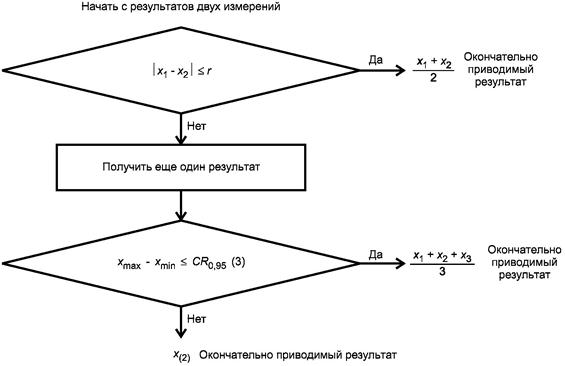
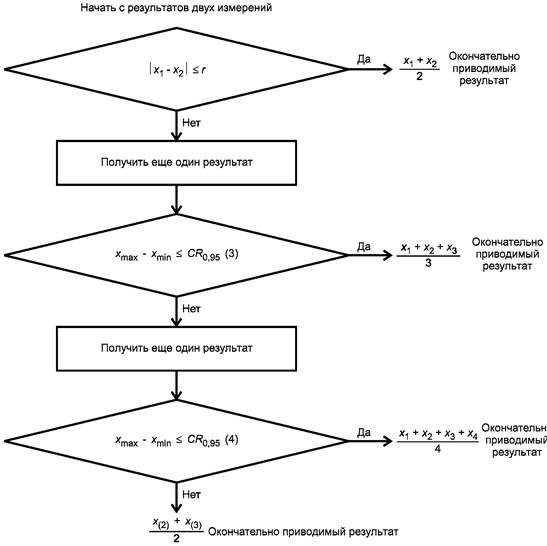

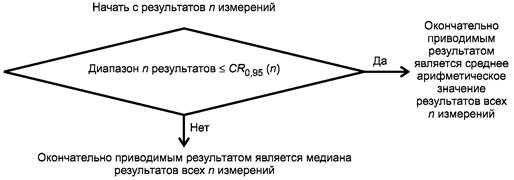
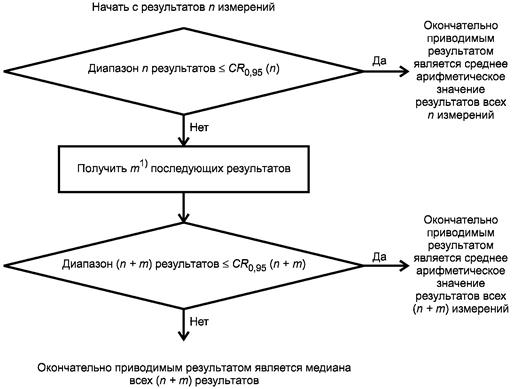
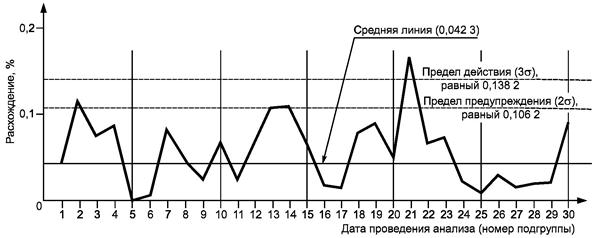
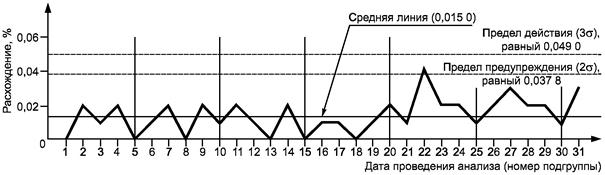
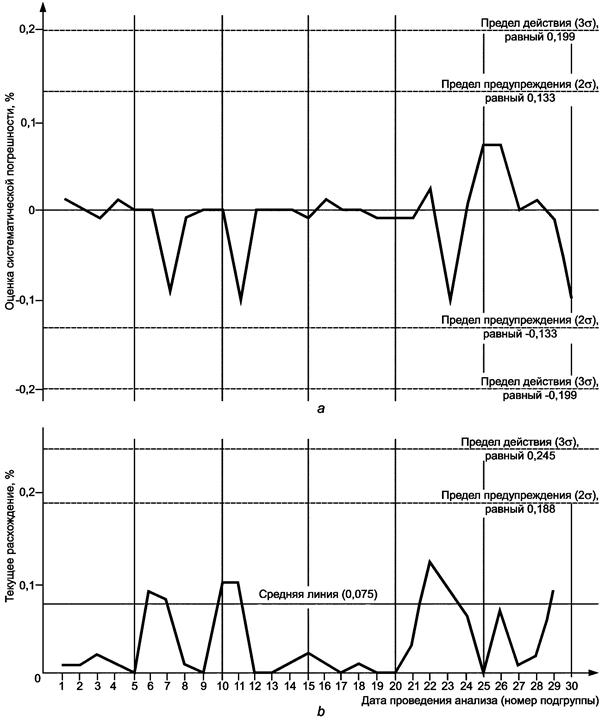
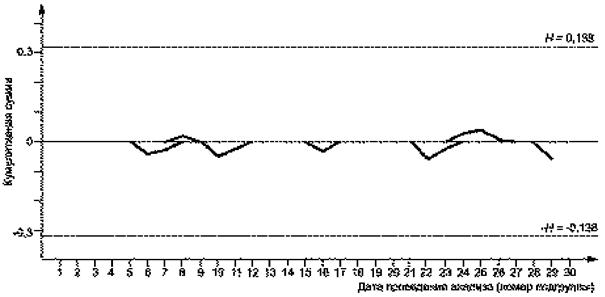
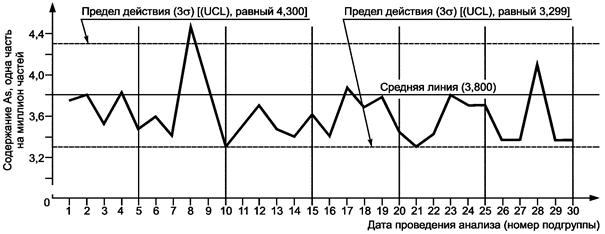
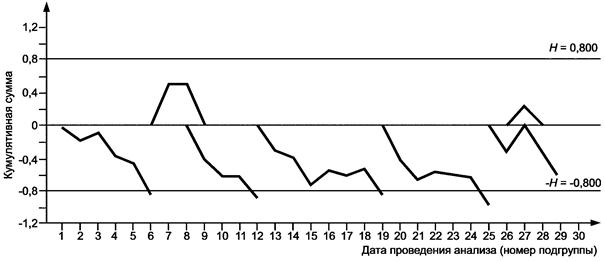

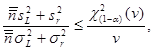
 vA = pA - 1;
vB = pB - 1.
vA = pA - 1;
vB = pB - 1.